Kế hoạch bài dạy Toán 11 Chân Trời Sáng Tạo

GV soạn: Nguyễn Thị Kim Ngân– THPT số 4 TP Lào Cai.
GV phản biện:...................- THPT số 1 Bảo Yên
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: GÓC LƯỢNG GIÁC
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (01 tiết) I. MỤC TIÊU:
1. Về kiến thức, kỹ năng:
- Nhận biết các khái niệm góc lượng giác, hệ thức Chasles (Sa-lơ), đường tròn lượng giác
- Hiểu được đơn vị đo radian
- Hiểu công thức chuyển đổi số đo góc từ đơn vị đo góc sang radian và ngược lại
- Biết cách chuyển đổi số đo góc sang radian và ngược lại
- Biết biểu diễn các góc lượng giác trên đường tròn lượng giác
- Vận dụng giải quyết các vấn đề thực tiễn gắn với góc lượng giác 2. Về năng lực
- Năng lực tư duy và lập luận Toán học: nhận biết và thể hiện được các khái niệm cơ bản của góc
lượng giác, sử dụng hệ thức Chales, biểu diễn các góc lượng giác.
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay. 3. Về phẩm chất
- Có ý thức học tập, ý thức tìm tòi, khám phá và sáng tạo, có ý thức làm việc nhóm, tôn trọng ý kiến
các thành viên khi hợp tác.
- Chăm chỉ tích cực xây dựng bài, có trách nhiệm, chủ động chiếm lĩnh kiến thức theo sự hướng dẫn của GV.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu, …..
III. TIẾN TRÌNH DẠY HỌC
1. Hoạt động 1: Khởi động a) Mục tiêu:
- Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học.
- Dựa vào hình ảnh trực quan về một chuyển động quay của bánh lái tàu để giúp HS có được hình
dung ban đầu về nhu cầu sử dụng góc lượng giác để mô tả chuyển động quay.
b) Nội dung: HS đọc tình huống mở đầu, suy nghĩ trả lời câu hỏi.
Mỗi hình dưới đây thể hiện chuyển động quay của một điểm trên bánh lái tàu từ vị trí A đến vị trí B.
Các chuyển động này có điểm nào giống nhau, điểm nào khác nhau?
c) Sản phẩm: câu trả lời của học sinh.
d) Tổ chức thực hiện:
Chuyển giao
- GV trình chiếu hình ảnh; yêu cầu học sinh đọc tình huống mở đầu
Thực hiện
- HS quan sát và tìm câu trả lời
- HS làm việc cặp đôi theo bàn.
Báo cáo thảo luận - Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
Đánh giá, nhận xét, - GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt HS vào bài học mới.
tổng hợp
2. Hoạt động 2: Hình thành kiến thức mới
Hoạt động 2.1: Góc lượng giác a) Mục tiêu:
- HS nhận biết và thể hiện được khái niệm góc lượng giác, số đo góc lượng giác.
- HS hiểu, phát biểu và vận dụng được hệ thức Chasles. b) Nội dung:
- HĐ1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và
Hình 2, lúc đầu thanh OM ở vị trí OA.
a)Khi quay bánh lái ngược chiều kim đồng hồ (Hình 1), cứ mỗi giây, bánh lái
quay một góc 60 . Bảng dưới đây cho ta góc quay α của thanh OM sau t giây
kể từ lúc bắt đầu quay.
Thay dấu ? bằng số đo thich hợp.
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim
đồng hồ (Hình 2 ) với cùng tốc độ như trên, người ta ghi 60
−  để chỉ góc mà thanh
OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay α của thanh OM
sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp. Lời giải: a) Thời gian 𝑡𝑡 (giây) 1 2 3 4 5 6 Góc quay 𝛼𝛼 60∘ 120∘ 180∘ 240∘ 300∘ 360∘ b) Thời gian 𝑡𝑡 (giây) 1 2 3 4 5 6 Góc quay 𝛼𝛼
−60∘ −120∘ −180∘ −240∘ −300∘ −360∘
- Kiến thức trọng tâm: Cho hai tia Oa, Ob.
+ Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia 𝑂𝑂𝑂𝑂 và dừng
ở vị trí tia 𝑂𝑂𝑂𝑂 thì ta nói tia 𝑂𝑂𝑂𝑂 quét một góc lượng giác có tia đầu 𝑂𝑂𝑂𝑂, tia cuối 𝑂𝑂𝑂𝑂, kí hiệu (𝑂𝑂𝑂𝑂, 𝑂𝑂𝑂𝑂).
+ Khi tia 𝑂𝑂𝑂𝑂 quay một góc 𝛼𝛼, ta nói số đo của góc lượng giác (𝑂𝑂𝑂𝑂, 𝑂𝑂𝑂𝑂) bằng 𝛼𝛼, kí hiệu
𝑠𝑠đ(𝑂𝑂𝑂𝑂, 𝑂𝑂𝑂𝑂) = 𝛼𝛼.
Chú ý: Với hai tia Oa và Ob cho trước:
+ Có vô số góc lượng giác có tia đầu là Oa và tia cuối Ob. + Kí hiệu: (Oa,Ob).
- Ví dụ 1. Xác định số đo của các góc lượng giác (Oa,Ob) trong Hình 5. - Nhận xét: SGK
- Thực hành 1: Cho 
MON = 60 . Xác định số đo của các góc lượng giác được biểu diễn trong Hình
6 và viết công thức tổng quát của số đo góc lượng giác (OM ,ON ).
- Vận dụng 1: Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng
giác là bao nhiêu độ?
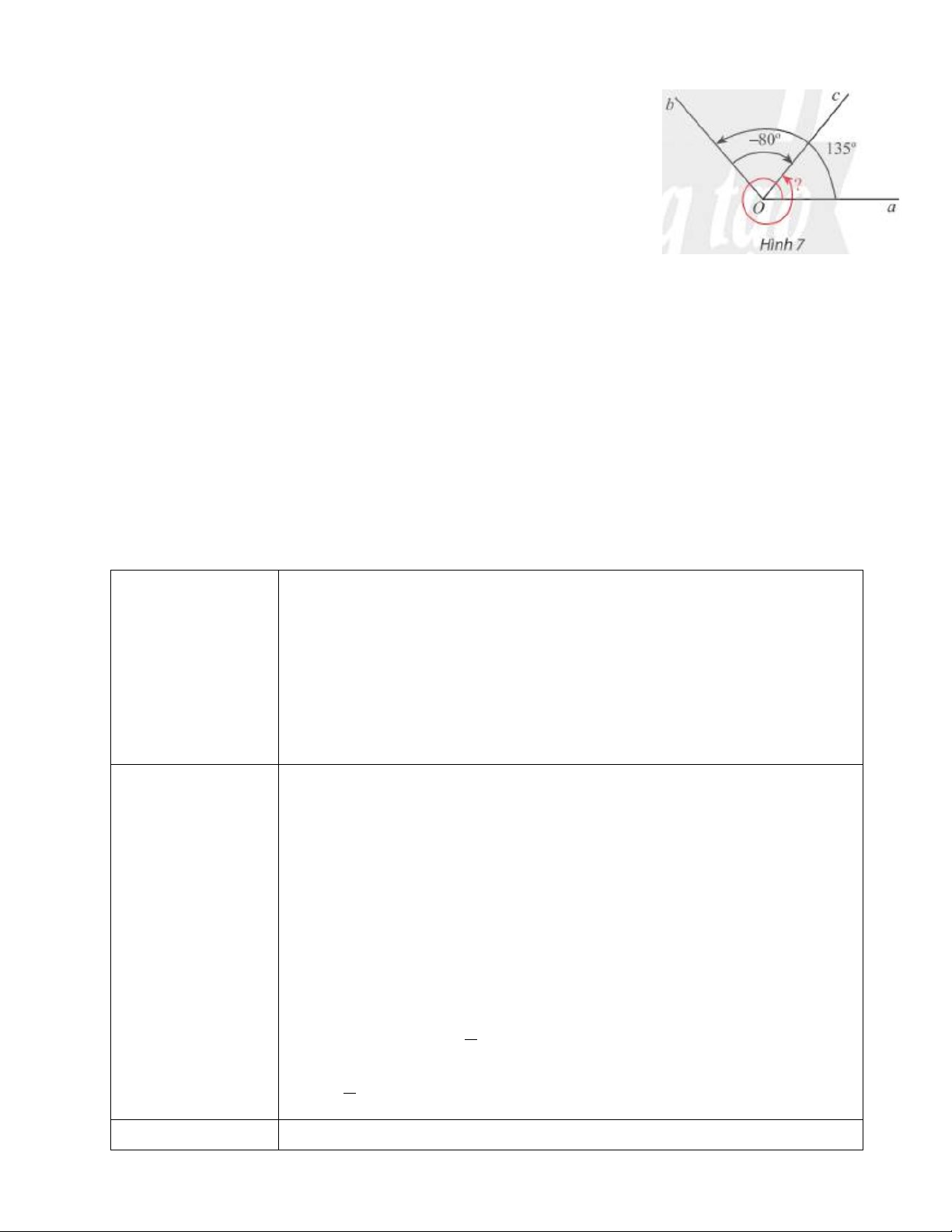
- HĐ2: Hệ thức Chasles (Sa-lơ) Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob),(Ob,Oc) và (Oa,Oc) .
b) Nhận xét về mối liên hệ giữa ba số đo góc này. Lời giải:
a) Số đo góc lượng giác(Oa,Ob) trong hình là 0 135
Số đo góc lượng giác (Ob,Oc) trong hình là 0 80 Dựa vào hình, ta có  0 0 0 aOc =135 −80 = 55
Trong hình, góc lượng giác (Oa,Oc) tương ứng với chuyển động quay theo chiều dương từ Oa đến
Oc sau đó quay thêm 1 vòng. Do đó số đo góc lượng giác (Oa,Oc) trong hình là 0 0 0 55 + 360 = 415
b) Như vậy đối với ba góc trong hình, ta có tổng số đo góc lượng giác (Oa,Ob),(Ob,Oc)chênh
lệch với số đo góc lượng giác (Oa,Oc) là một số nguyên lần 360∘. Kết luận
- Hệ thức Chasles: Với ba tia Oa, ,
Ob Oc bất kì, ta có
sđ (Oa,Ob) + sđ (Ob,Oc) =sđ (Oa,Oc) + 0 k360 (k ∈)
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của HS cho các câu hỏi.
d) Tổ chức thực hiện: - GV tổ chức hoạt động trao đổi thảo luận của các nhóm làm HĐ1
- Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa kiến thức, từ đó
nêu khái niệm góc lượng giác và chú ý
- HS đọc ví dụ 1 sgk trang 8 trả lời câu hỏi
Chuyển giao
- Từ câu trả lời ở ví dụ 1 của HS, GV đưa ra nhận xét
- GV yêu cầu HS làm TH1 và VD1 sgk trang 9
- GV tổ chức hoạt động trao đổi thảo luận của các nhóm làm HĐ2
- Từ câu trả lời của Hs, GV chuẩn hoá kiến thức, từ đó đưa ra khái niệm về hệ thức Chasles
- HS hoạt động nhóm (cặp đôi theo bàn) thực hiện HĐ1
- HS ghi nhớ khái niệm về góc lượng giác và chú ý
- Đọc, hiểu ví dụ 1 sgk và trả lời câu hỏi
- Ghi nhớ nội dung nhận xét sgk - Thực hiện TH1 và VD1
- HS thực hiện HĐ2 và ghi nhớ khái niệm hệ thức Chasles Mong đợi: TH1:
Thực hiện a) 0 60 b) 0 0 0 60 + 2.360 = 780 c) 0 300 − 1
VD1: Kim phút quay 2 vòng theo chiều âm nên số đo góc lượng giác là: 4 1 0 0 α = 2 − .360 = 810 − 4
Báo cáo thảo luận - Đại diện nhóm báo cáo TH1,VD1 các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.2: Đơn vị radian a) Mục tiêu:
- HS nhận biết đơn vị radian.
- HS chuyển đổi số đo góc lượng giác từ đơn vị radian sang đơn vị độ và ngược lại. b) Nội dung:
- HĐ3: Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung 
AB có độ dài đúng bằng R (Hình 9). Đo và cho biết 
AOB có số đo bằng bao nhiêu độ. Giải: Số đo 
AOB không phụ thuộc vào đường tròn được vẽ và bằng khoảng 0 57 - Kết luận:
+ Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là
một góc có số đo 1 radian (đọc là 1 ra – đi – an, viết tắt là 1rad ).
+ Do đó ta có công thức chuyển đổi số đo góc từ đơn vị radian sang độ và ngược lại như sau: ° * π a  α a° = rad . * 180 α rad  = . 180  π    - Ví dụ 2:
Đổi các số đo góc sau đây từ radian sang độ hoặc ngược lại: π a) 60 − ° . b) 2 rad . c) 3 rad . 5
- TH2 : Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
Số đo theo 0° ? 45° 60° ? 120° ? 150° 180° độ Số đo theo ? π π π π rad rad ? ? rad ? 3 rad ? rad 6 2 4 Chú ý.
a) Khi ghi số đo của một góc theo đơn vị radian, người ta thường bỏ đi chữ rad sau số đo. Ví dụ, π π
rad được viết là , 2 rad được viết là 2. 2 2
b) Với đơn vị radian, công thức số đo tổng quát của góc lượng giác (Oa,Ob) là
(Oa,Ob) =α + k2π (k ∈) ,
trong đó α là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối
Ob . Lưu ý không được viết α + k360° hay a° + k2π (vì không cùng đơn vị đo).
c) Sản phẩm: HS hình thành được kiến thức bài học, lời giải cho các bài tập
d) Tổ chức thực hiện: - GV tổ chức hoạt động trao đổi thảo luận của các nhóm làm HĐ3
- Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa kiến thức, từ đó
nêu đưa ra khái niệm đơn vị radian và công thức chuyển đổi số đo góc từ đơn
vị radian sang độ hoặc ngược lại.
Chuyển giao
- HS đọc ví dụ 2 sgk trang 10
- Từ ví dụ 2 GV yêu cầu HS vận dụng làm TH2 sgk trang 10 (HĐ cặp đôi theo bàn) - GV đưa ra chú ý - Hs ghi nhớ chú ý
- HS hoạt động nhóm (cặp đôi theo bàn) thực hiện HĐ2
- HS ghi nhớ khái niệm đơn vị radian và công thức chuyển đổi số đo góc từ
Thực hiện
đơn vị radian sang độ hoặc ngược lại.
- Đọc, hiểu ví dụ 2 sgk trang 10 - Thực hiện TH2 - Ghi nhớ chú ý
- Đại diện 1 HS lên trình bày lời giải của TH2
Báo cáo thảo luận - Các HS khác quan sát bài làm của HS trên bảng, đối chiếu vở bài làm của
mình và nêu nhận xét phản hồi
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.3: Đường tròn lượng giác a) Mục tiêu:
- HS nhận biết và thể hiện được khái niệm đường tròn lượng giác.
- HS biểu diễn góc lượng giác với số đo cho trước trên đường tròn lượng giác. b) Nội dung:
- HĐ4: Trong mặt phẳng tọa độ Oxy , vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1;0) .
a) Cho điểm B(0 )
;1 . Số đo góc lượng giác (OA,OB) bằng bao nhiêu radian ?
b) Xác định các điểm A′ và B′ trên đường tròn sao cho các góc lượng giác (OA,OA′) , (OA,OB′)
có số đo lần lượt là π và π − . 2 π
Lời giải : a) (OA,OB) = + k2π (k ∈) 2 b) A’(-1;0) và B’(0;-1)
- Kết luận: Trong mặt phẳng tọa độ Oxy , cho đường tròn tâm O bán kính bằng 1. Trên đường tròn
này, chọn điểm A(1;0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là
chiều cùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.
- Ví dụ 3 : Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là: a) 865 π ° ; b) 7 − . 3
- TH3 : Biểu điễn trên đường tròn lượng giác các góc lượng giác có số đo là: a) π 1485 − ° ; b) 19 . 4 a) Ta có 0 0 0 1485 − = 45 − − 4.360
Vậy điểm biễu diễn góc lượng giác có số đo 1485 −
° là điểm D trên phần đường tròn lượng giác
thuộc góc phần tư thứ IV sao cho  0 AOD = 45 19π 3π b) Ta có = + 4π 4 4 19π
Vậy điểm biểu diễn góc lượng giác có số đo là điểm 4
𝐸𝐸 trên phần đường tròn lượng giác thuộc π
góc phần tư thứ II sao cho  3 AOE = 4
c) Sản phẩm: HS hình thành được kiến thức bài học, lời giải cho các bài tập
d) Tổ chức thực hiện: - GV tổ chức hoạt động trao đổi thảo luận của các nhóm làm HĐ4
- Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa kiến thức, từ đó
Chuyển giao
nêu đưa ra khái niệm đường tròn lượng giác.
- HS đọc ví dụ 3 sgk trang 11
- Từ ví dụ 3 GV yêu cầu HS vận dụng làm TH3 sgk trang 12 (HĐ cặp đôi theo bàn)
- HS hoạt động nhóm (cặp đôi theo bàn) thực hiện HĐ3
Thực hiện
- HS ghi nhớ khái niệm đường tròn lượng giác
- Đọc, hiểu ví dụ 3 sgk trang 11 - Thực hiện TH3
- Đại diện 2 HS lên trình bày lời giải của TH3: HS1: ý a; HS2: ý b
Báo cáo thảo luận - Các HS khác quan sát bài làm của HS trên bảng, đối chiếu vở bài làm của
mình và nêu nhận xét phản hồi
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và
Đánh giá, nhận xét, tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tổng hợp
tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
3. Hoạt động 3: luyện tập
a) Mục tiêu: Học sinh củng cố lại kiến thức đã học.
b) Nội dung: HS vận dụng các kiến thức của bài học làm bài tập Bài 1, 2, 3, 4, 5, 7 (SGK -tr12+13) Bài 1. π π 0  3  1 a) 0 19 38 = (rad) ; b) 0 23 115 − = − (rad) c) =   (rad) 90 36  π  60 Bài 2. π 0  900  13π a) 0 (rad) =15 b) 0 5 − = ≈   286,479 c) 0 = 260 12  π  9 Bài 3. 17π π a) Ta có: − = − 3.2π 3 3 17π
Vậy điểm biểu diễn góc lượng giác có số đo − là điểm 3
𝑀𝑀 trên phần đường tròn lượng giác π
thuộc góc phần tư thứ I sao cho  AOM = 3 13π 3π 13π b) Ta có = −
+ 2.2π . Vậy điễm biểu diễn góc lượng giác có số đo là điểm 4 4 4 𝑁𝑁 trên phần π
đường tròn lượng giác thuộc góc phần tư thứ III sao cho  3 AON = 4 c) Ta có 0 0 0 765 − = 45 − − 2.360
Vậy điểm biểu diễn góc lượng giác có số đo 0 765 −
là điểm 𝑃𝑃 trên phần đường tròn lượng giác thuộc
góc phần tư thứ IV sao cho  0 AOP = 45 Bài 4. 31π 3π 31π 10π 31π 25 − π Ta có : = + 4π; = + 3π; = + 8π 7 7 7 7 7 7
Do đó 31π có cùng điểm biểu diễn với 3π và 25 − π 7 7 7 Bài 5. 0 0 0 0 ( ,
OA OM ) =120 + k360 (k ∈);( , OA ON) = 75 −
+ k360 (k ∈); Bài 7. a) b)
c) Sản phẩm học tập: Câu trả lời của HS.
d) Tổ chức thực hiện:
Chuyển giao nhiệm vụ - GV yêu cầu HS trao đổi theo bàn về nội dung bài làm đã được giao về nhà
của HS (Bài 1 đến 5 và bài 7 ): (6’)
- GV gọi HS lên bảng trình bày lời giải
- Yêu cầu HS hoàn thiện vào vở nếu BTVN làm còn sai sót
Thực hiện nhiệm vụ
- HS thảo luận BTVN từ 1 đến 5 và bài 7 GV gợi ý:
Bài 4: Biểu diễn góc 31π thành tổng của các góc đề bài cho với một bội của 7
π từ đó chỉ ra được góc 31π có cùng điểm biểu diễn với góc nào. 7
- Chỉnh sửa vào vở nếu sai sót
- Lên bảng trình bày theo yêu cầu của GV
Báo cáo, thảo luận
- HS lên bảng trình bày lời giải
Lượt 1: HS1: Bài 1 – HS2: Bài 2
Lượt 2: HS1: Bài 3 ý a,b – HS2: Bài 3 ý c
Lượt 3: HS1: Bài 4– HS2: Bài 5- HS3: Bài 7
Đánh giá, nhận xét, tổng - GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và hợp
tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại
tích cực, cố gắng hơn trong các hoạt động học tiếp theo
- Chốt kiến thức .
4. Hoạt động 4: Vận dụng a) Mục tiêu:
- Học sinh thực hiện làm bài tập vận dụng để nắm vững kiến thức.
b) Nội dung: Bài 6, 8,9 sgk trang 12,13 Bài 6. 0
(Ox,ON) = (Ox,OM ) + (OM ,ON) + k360 (k ∈) 0 2 0 0
= 45 − .360 + k360 (k ∈) 5 0 0 = 99 −
+ k360 (k ∈) Bài 8. π 2π π π + k (k ∈ 2 ) và − + k (k ∈) 2 3 6 3 Bài 9. Ta có 1 π π α = . = (rad) 60 180 10800
Vì mỗi radian chắn một cung bằng bán kính trái đất R ≈ 6371km nên α chắn cung có độ dài π .6371≈1,85(km) 10800
Vậy một hải lí dài khoảng 1,85km.
c) Sản phẩm học tập: Bài làm của HS
d) Tổ chức thực hiện:
Chuyển giao nhiệm vụ
- GV yêu cầu HS hoạt động nhóm hoàn thành bài tập 6, 8,9 (SGK - tr.12,13).
Thực hiện nhiệm vụ
- HS suy nghĩ, trao đổi, thảo luận thực hiện nhiệm vụ.
- GV điều hành, quan sát, hỗ trợ.
Báo cáo, thảo luận
- Bài tập: đại diện HS trình bày kết quả, các HS khác theo dõi, đưa ý kiến.
Đánh giá, nhận xét, tổng - GV nhận xét, đánh giá, đưa ra đáp án đúng, chú ý các lỗi sai của học sinh hợp hay mắc phải.
* HƯỚNG DẪN VỀ NHÀ
• Ghi nhớ kiến thức trong bài.
• Hoàn thành các bài tập trong SBT
• Chuẩn bị bài mới: “Bài 2. Giá trị lượng giác của một góc lượng giác”.
Họ và tên giáo viên: Phạm Thị Hải Chiến
Trường THPT số 4 TP Lào Cai Phản biện:
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (01 tiết) I. Mục tiêu 1. Về kiến thức:
-Nhận biết khái niệm giá trị lượng giác của một góc lượng giác.
-Mô tả bảng giá trị lượng giác của một số góc lượng giác thường gặp; hệ thức cơ bản giữa
các giá trị lượng giác của một góc lượng giác; quan hệ giữa các giá trị lượng giác của các góc
lượng giác có liên quan đặc biệt: bù nhau, phụ nhau, đối nhau, hơn kém nhau 𝜋𝜋.
-Tính giá trị lượng giác bằng MTCT 2. Về năng lực:
- Năng lực tư duy và lập luận Toán học: Trong chứng minh các công thức.
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay. 3. Về phẩm chất:
- Chăm chỉ, hoàn thành các nhiệm vụ được giao.
- Trách nhiệm, cố gắng chiếm lĩnh kiến thức mới, cố gắng làm đúng các bài tập.
- Có thế giới quan khoa học
II. Thiết bị dạy học và học liệu
- Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu, phần mềm GSP…
III. Tiến trình dạy học
1. Hoạt động 1: Khởi động
a) Mục tiêu: Tạo hứng thú, thu hút HS tìm hiểu nội dung bài học. Thông qua bài toán thực
tế và tích hợp Toán học với Vật lí để dẫn đến việc mở rộng khái iệm giá trị lượng giác cho góc lượng giác.
b) Nội dung: Đọc tình huống mở đầu, quan sát hình vẽ và trả lời câu hỏi:
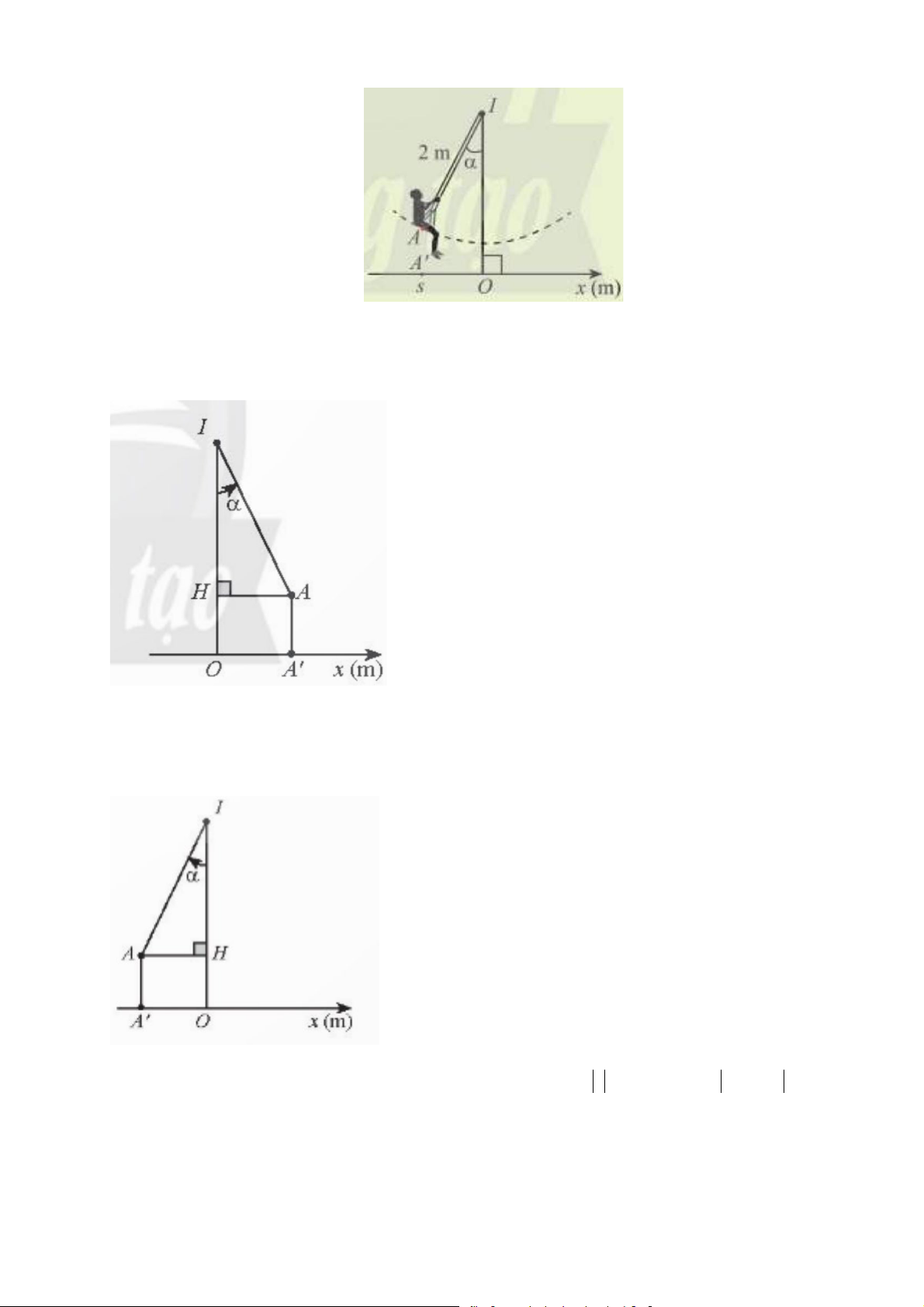
Câu hỏi: Làm cách nào để tính li độ dựa vào li độ góc? 2
GV hướng dẫn HS tìm hiểu với góc 𝛼𝛼 sao cho 90o − ≤ ≤ 90o α
+ Khi 0o ≤ ≤ 90o α
ta có thể biểu diễn góc α như sau
Tọa độ s mang dấu gì? Có độ lớn bằng độ dài đoạn nào? s > 0,
s = OA' = AH = IAsinα + Khi 90o − ≤ ≤ 90o α
ta có thể biểu diễn góc α như sau
Tọa độ s mang dấu gì? Có độ lớn bằng độ dài đoạn nào? s < 0, s = OA' = AH = IA.sinα
→ Ở đây không thể sử dung công thức của trường hợp trên để tính vì chưa có khái niệm sin của
góc âm. Có thể mở rộng khái niệm giá trị lượng giác cho góc lượng giác bất kì để thống nhất công thức tính. 3
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện:
Chuyển giao
* Giáo viên trình chiếu hình ảnh - HS quan sát.
- HS tìm câu trả lời, tuy nhiên sẽ khó để giải quyết câu hỏi .
Thực hiện
- Mong đợi: Kích thích sự tò mò của HS :
+ Huy động các kiến thức đã học để xác định được hình chiếu của một
điểm, góc giữa hai đường thẳng.
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
Đánh giá, nhận xét, lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo
tổng hợp
-Bài học hôm nay chúng ta cùng đi tìm hiểu mối quan hệ giữa góc lượng
giác và tọa độ của điểm biểu diễn góc lượng giác đó và các tính chất liên quan
2. Hoạt động 2: Hình thành kiến thức mới
Hoạt động 2.1.Giá trị lượng giác của góc lượng giác a) Mục tiêu:
- HS nhận biết khái niệm giá trị lượng giác của một góc lượng giác, b) Nội dung:
Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo α . Khi đó:
 Tung độ y của M gọi là sin của α , kí hiệu sinα . M
 Hoành độ x của M gọi là côsin của α , kí hiệu cosα . M α
 Nếu x ≠ thì ti số yM sin =
gọi là tang của α , kí hiệu tanα . M 0 x α M cos α
 Nếu y ≠ thì tỉ sô xM cos =
gọi là côtang của α , kí hiệu cotα . M 0 y α M sin
Các giá trị sinα,cosα, tanα và cotα được gọi là các giá trị luợng giác cuia góc lương giác α . Chú ý:
a) Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.
Trục As có gốc ở điểm A(1;0) và song song với trục sin (Hình 3a) gọi là trục tang.
Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan α .
Trục Bt có gốc ở điểm B(0; )
1 và song song với trục côsin (Hình 3b ) gọi là trục côtang.
Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cotα . 4 a) b) Hinh 3
b) sinα và cosα xác định với mọi α ∈ ;
tanα chỉ xác định với các góc π
α ≠ + kπ (k ∈) ; 2
cotα chi xác định với các góc α ≠ kπ (k ∈).
c) Với mọi góc lượng giác α và số nguyên k , ta có
sin (α + k2π ) = sinα;
tan (α + kπ ) = tanα;
cos(α + k2π ) = cosα ;
cot (α + kπ ) = cotα .
d) Ta đã biết bảng giá trị lượng giác của một số góc α đặc biệt với π
0 ≤ α ≤ (hay 0 ≤ α ≤ 90 2 ) như sau: α π π π π 0 6 4 3 2 Giá trị
(30) (45) (60) (90) lượng giác 1 sinα 0 2 2 3 1 2 2 cosα 1 1 3 2 0 2 2 2 1 tanα 0 1 3 3  1 cotα  3 1 0 3 5 Hinh 4
Sử dụng bảng trên và Hình 4 , ta có thể xác định được giá trị lượng giác của một số góc đặc biệt khác.
Ví dụ 1. Tính các giá trị lượng giác của các góc: a) 13π ; b) 45 −  . 3 Giải π π π π a) Vi 13π π = + 4π nên: 13 3 13 1 sin = sin = ; cos = cos = ; 3 3 3 3 2 3 3 2 13π 13 sin cos π 13π 3 13π 3 3 tan = = 3; cot = = . 3 13π 3 13π 3 cos sin 3 3
b) Vì điểm biểu diễn của góc 45
−  và góc 45 trên đường tròn lượng giác đối xứng nhau qua
trục hoành (Hình 4), nên chúng có cùng hoành độ và tung độ đối nhau. Do đó ta có: (− ) −  2 = − = (− )  2 sin 45 sin45 ; cos 45 = cos45 = ; 2 2   (− ) sin( 45 − ) cos 45 − tan 45 =  (− ) = 1 − ; cot ( 45 − ) ( ) = (− ) = 1. − cos 45 sin 45 Hs làm luyện tập 1  π Tính 2 sin  −  và tan495 . 3    Giải  2π   2π  3 sin − =  si − n = −  3  3      2 tan495 = tan ( 4
− 5o 3.180o ) tan( 45o ) tan (45o + = − = − ) = 1 − 6
c) Sản phẩm: HS hình thành được kiến thức bài học, câu trả lời của học sinh cho các câu hỏi, hs
nhận biết và thể hiện được giá trị lượng giác.
d) Tổ chức thực hiện: Học sinh thực hiện thảo luận cặp đôi. π
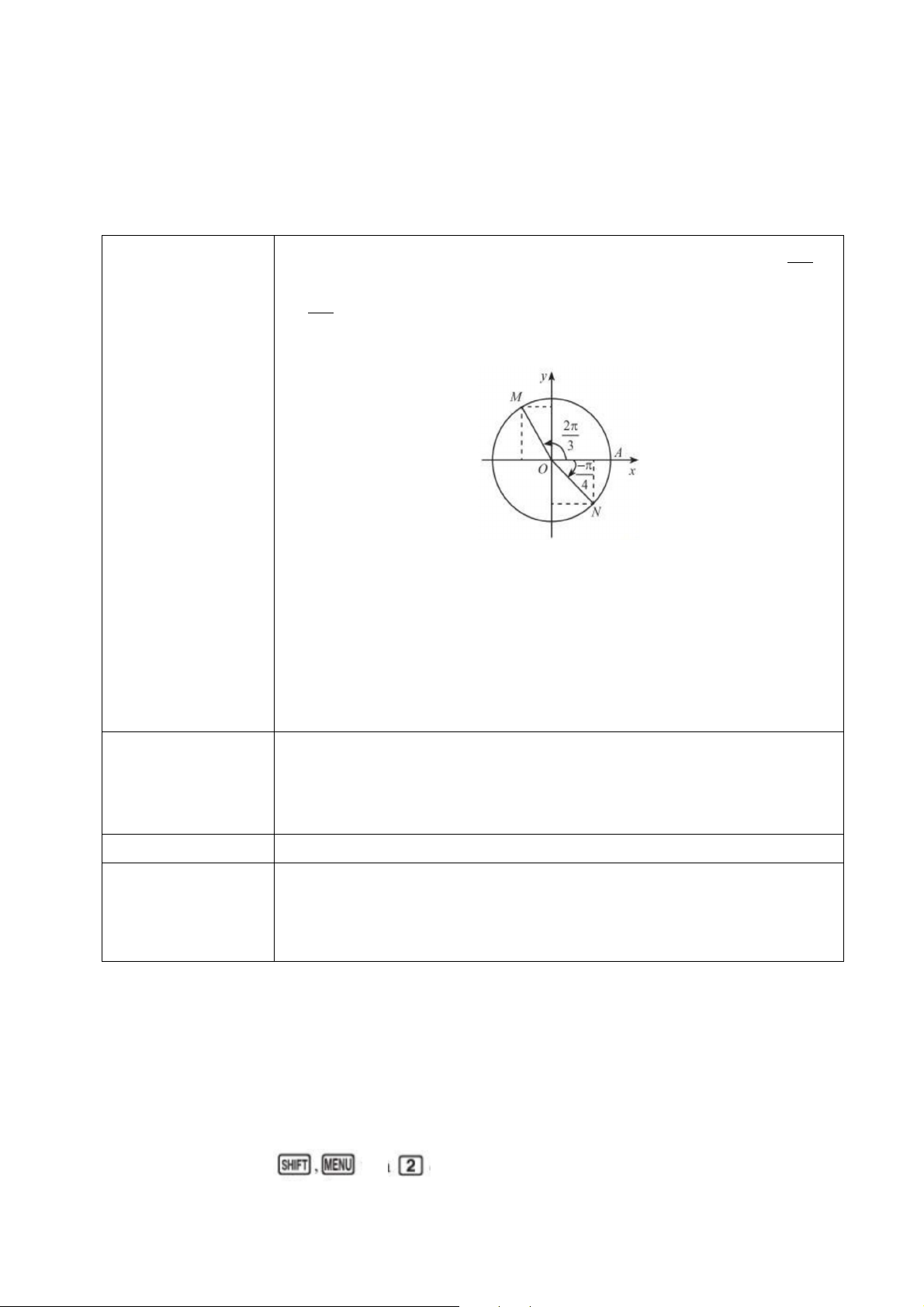
-Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác 2 3 π
và − trên đường tròn lượng giác. Xác định tọa độ của M và N trong 4
hệ trục toạ độ Oxy .
Chuyển giao Hinh 1
CH1: Nhắc lại tỷ số lượng giác trong tam giác vuông? CH2: 𝐴𝐴𝐴𝐴𝐴𝐴 � =? Suy ra xM = ? Tương tự với điểm N
-Quan sát hình vẽ rút ra nhận xét -Đọc VD và làm LT1 - Tìm câu trả lời
Thực hiện
- HS làm việc cặp đôi theo bàn.
Báo cáo thảo luận * Đại diện nhóm báo cáo, các nhóm còn lại theo dõi thảo luận.
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay.
a) Mục tiêu: tính giá trị lượng giác của một góc lượng giác bất kì bằng máy tính cầm tay b) Nội dung:
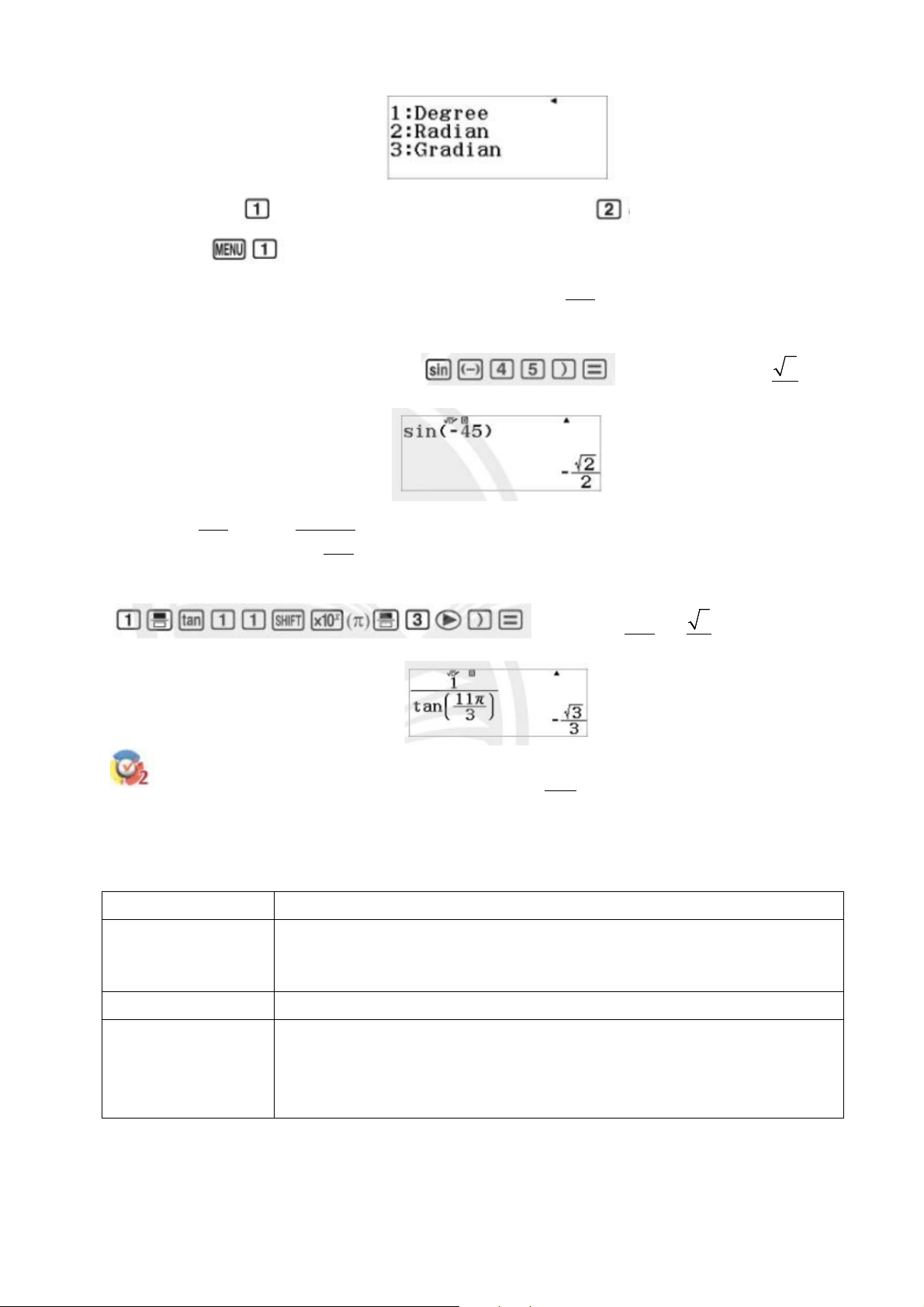
Lưu ý trước khi tính, cần chọn đơn vị góc như sau: Lần lượt ấn các phím và
để màn hình hiện lên bảng lựa chọn đơn vị góc 7 Tiếp tục ấn phím
để chọn đơn vị độ ( Degrree ) hoặc phím
để chọn đơn vị radian. Ấn các phím
để vào chế độ tính toán . π
Ví dụ 2: Sử dụng máy tính cầm tay để tính ( 0 sin 45 − )và 11 cot . 3 Giải
Chọn đơn vị góc là độ . Ấn tiếp các phím ta được ( 0 − ) 2 sin 45 = 2 π Để tính 11 cot , ta tính 1 3 11 tan π như sau: 3
Chọn đơn vị góc là radian . Ấn tiếp các phím π ta được 11 3 cot = − . 3 3  π
Sử dụng máy tính cầm tay để tính 0 cos75 và 19 tan  −  . 6   
c) Sản phẩm: Kết quả bấm máy của học sinh d) Tổ chức thực hiện:
Chuyển giao
-HS đọc sgk tìm ra quy trình bấm máy
* Học sinh đọc sách VD2 SGK
Thực hiện
Tự thực hành bấm máy thực hành 2
Báo cáo thảo luận * HS đọc kết quả
- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận
Đánh giá, nhận xét, và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn
tổng hợp
lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt kiến thức
Hoạt động 2.3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
a) Mục tiêu: HS phát biểu được các hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác. 8
- HS vận dụng được các hệ thức cơ bản. b) Nội dung: 2 2 sin α + cos α =1 2 1 π 1+ tan α =
(α ≠ + kπ ,k ∈ Z) 2 cos α 2 2 1 1+ cot α =
(α ≠ kπ ,k ∈ Z) 2 sin α π
tanα.cotα =1 (α ≠ k ,k ∈ Z) 2 Ví dụ 3 (SGK ) Thực hành 3 2 1 2  2  13 = 1+ tan α =1+ = 2 cos α  3    9 π 3 13
π < α < 3 ⇒ cosα = − 2 13 2  3 13  2 13 sinα = cosα.tanα = −  = − 3  13  13  
c) Sản phẩm: Công thức liên hệ về giá trị lượng giác của hai góc bù và bảng giá trị lượng giác
của các góc đặc biệt.
d) Tổ chức thực hiện: Học sinh thảo luận cặp đôi; hoạt động nhóm lớn;
- GV yêu cầu HS thảo luận nhóm đôi, hoàn thành HĐKP 2.
Chuyển giao
- Từ đó GV giới thiệu một số công thức lượng giác cơ bản.