









Preview text:
lOMoAR cPSD| 58540065
KẾ HOẠCH DẠY HỌC
Mạch kiến thức: Khái niệm xác suất – Quy tắc tính xác suất Tổng số tiết:
Tiết theo phân phối chương trình: Lớp: 10 A. MỤC TIÊU
1. Kiến thức {Phát biểu dựa trên Yêu cầu cần đạt của chương trình, rõ ràng và có thể đánh giá được}
Sau khi học xong bài này, học sinh sẽ
- Hiểu được các khái niệm không gian mẫu, biến cố sơ cấp, biến cố, biến cố đặc biệt (biến cố giao, hợp, đối, độc lập)
- Hiểu được khái niệm xác suất theo nghĩa tổng quát, nghĩa cổ điển, nghĩa tần suất.
- Hiểu được nguyên lí xác suất nhỏ qua ví dụ đơn giản
- Hiểu công thức tính xác suất các biến cố đặc biệt trong tình huống cân bằng xác suất.
2. Năng lực cụ thể {Phát biểu dựa trên Yêu cầu cần đạt của chương trình, rõ ràng và có thể đánh giá được}
- Mô tả không gian mẫu và biến cố theo ngôn ngữ tập hợp
- Tính xác suất dựa vào định nghĩa tổng quát
- Tính xác suất bằng cách dùng công thức trong một tình huống cân bằng xác suất
- Sử dụng sơ đồ (Hình cây, bảng hai chiều, Venn) để hỗ trợ tính xác suất
- Vận dụng mối liên hệ giữa xác suất và tần suất để lựa chọn mô hình xác suất phù hợp -
Vận dụng tổng hợp xác
suất vào giải quyết vấn đề thực tế và liên môn.
3. Năng lực chung {Góp phần hình thành các năng lực toán học nào}
- Giao tiếp toán học, sử dụng công cụ và phương tiện toán học, tư duy và lập luận, giải quyết vấn đề, mô hình hoá.
4. Phẩm chất {Góp phần hình thành các phẩm chất, thái độ chung nào}
- Có thế giới quan khoa học, hiểu ứng dụng rộng rãi của toán học
- Hứng thú và niềm tin trong học toán - Linh hoạt, sáng tạo, tự học. lOMoAR cPSD| 58540065 B. CHUẨN BỊ
1. Giáo viên: máy tính, máy chiếu 2. Học sinh:
C. TIẾN TRÌNH DẠY HỌC {Gồm một hoặc nhiều tiết học}
Pha (Bước): KHỞI ĐỘNG
Hoạt động 1. Nhận ra xác suất và ngôn ngữ xác suất
Mục tiêu: Nhớ lại khái niệm xác suất và ngôn ngữ xác suất qua các bài tập trắc nghiệm khách quan đơn giản {đã học ở lớp 9} Chuẩn
bị: Máy tính và máy chiếu để chiếu đề bài. Thời
Vai trò của GV (câu hỏi, chỉ
Nhiệm vụ của HS (công gian Tiến trình nội dung dẫn)
việc và thể thức thực hiện) lOMoAR cPSD| 58540065
Bài tập 1. Đối với mỗi câu sau, hãy tìm câu trả lời đúng.
GV có thể soạn trước Bài tập 1 Tìm câu trả lời cho các câu
1) Một xác suất có thể bằng (xấp xỉ):
và Bài tập 2 trên powerpoint để hỏi của Bài tập 1.
A. Một tần suất B. Một tần số trình chiếu đề bài. C. Số 2,3 D. Một số âm HS làm việc cá nhân
Hướng dẫn: chọn A.
GV: Để nhắc lại một số khái
2) Một hộp chứa 4 bi xanh, 5 bi đỏ, 3 bi vàng. Rút ngẫu nhiên một bi. Xác niệm liên quan đến xác suất, các
suất lấy được bi vàng là
em sẽ trả lời nhanh các câu hỏi A. 3 B. 12
của hai bài tập nhỏ sau. C.1/3. D.1/4.
Hướng dẫn: chọn D.
GV gọi HS trả lời các câu hỏi
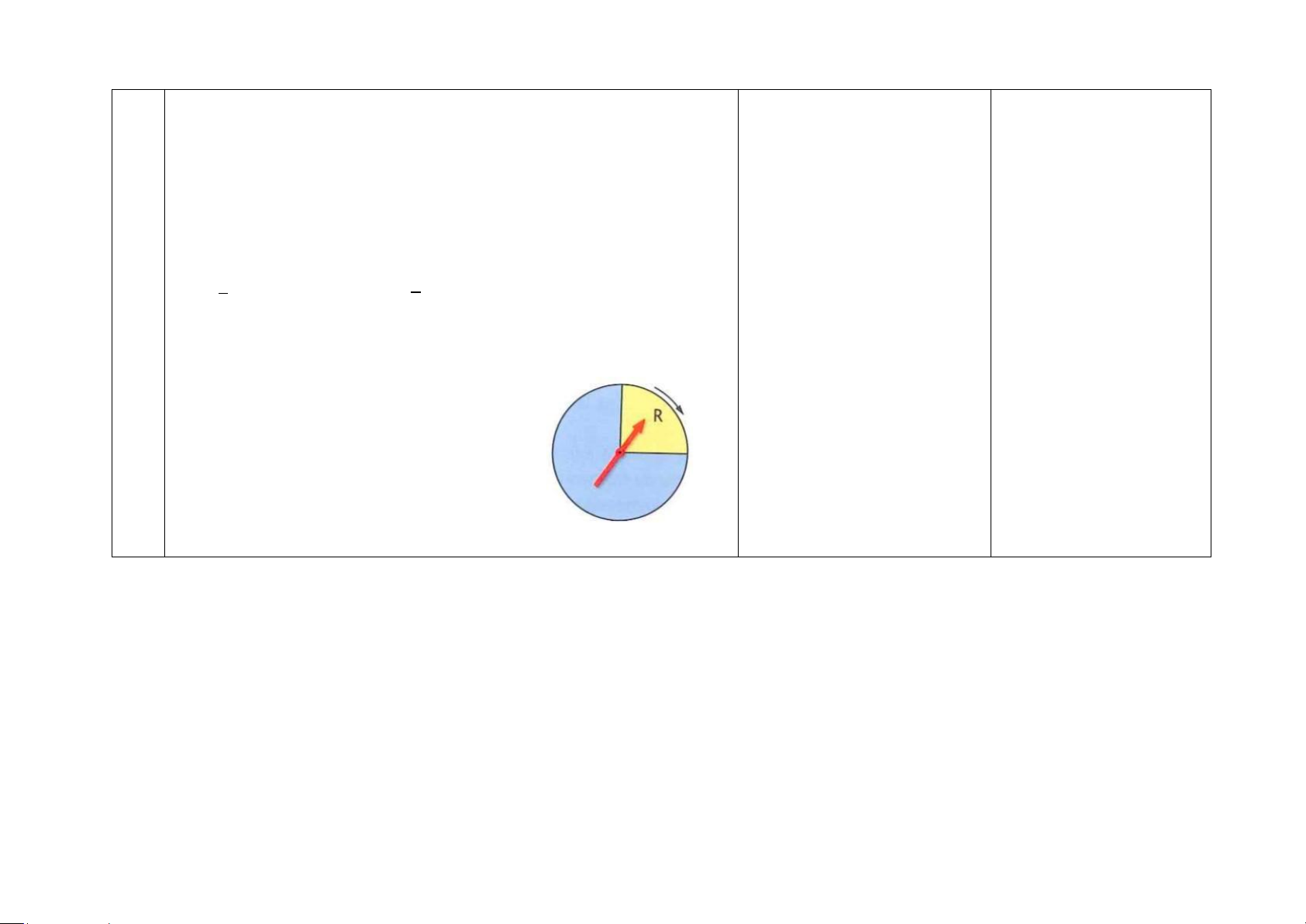
3) Khi ta quay bánh xe lôtô cân bằng như dưới đây, xác suất mà mũi tên GV nhắc lại: chỉ vào vùng R là
o Xác suất có thể lấy (xấp xỉ) A. 0. B. 90
bằng giá trị tần suất trong thực C.1/4. D. 0,5
tế. o Xác suất có thể hiểu theo tỷ số diện tích.
Hướng dẫn: chọn C. lOMoAR cPSD| 58540065
Bài tập 2. Tìm câu trả lời đúng
1) Tung đồng thời hai con xúc xắc sáu mặt cân đối, đồng chất, một con GV: Với giả thiết cân bằng và HS tìm câu trả lời cho Bài
màu xanh và một con màu đỏ. Biến cố “xuất hiện mặt 3 trên con xúc xắc đồng chất, thì khả năng xuất tập 2.
màu xanh và mặt 6 trên con xúc xắc màu đỏ” và biến cố “xuất hiện mặt hiện mặt 3 và mặt 6 khi tung con
6 trên con xúc xắc màu xanh và mặt 3 trên con xúc xắc màu đỏ” là những xúc xắc như thế nào? HS làm việc cá nhân biến cố:
GV: Thế nào là một sự kiện hay
biến cố chắc chắn xảy ra, không thể xảy ra?
GV nhấn mạnh các thuật ngữ A. Không thể B. có khả năng
xảy ra như nhau C. chắc chắn Hướng dẫn: chọn B.
liên quan đến xác suất: chắc
2) Tung đồng thời hai con xúc sắc sáu mặt cân bằng và đồng chất. Xét biến chắn, không thể, khả năng, cơ
cố “Xuất hiện cùng một số trên cả hai mặt của hai con xúc xắc”. Ta có hội…
thể nói rằng đây là biến cố: A. không thể
B. ít có khả năng xảy ra
C. có cơ hội xảy ra là một trên hai D. chắc chắn.
Hướng dẫn: chọn B.
Pha: HÌNH THÀNH KIẾN T HỨC MỚI
Hoạt động 1.
Mục iêu: Tìm hiểu tính chất của tần suất để tiếp cận khái niệm xác suất t Thời Tiến trình nội dung
Vai trò của GV (câu hỏi, chỉ
Nhiệm vụ của HS (công gian dẫn)
việc và thể thức thực hiện) lOMoAR cPSD| 58540065
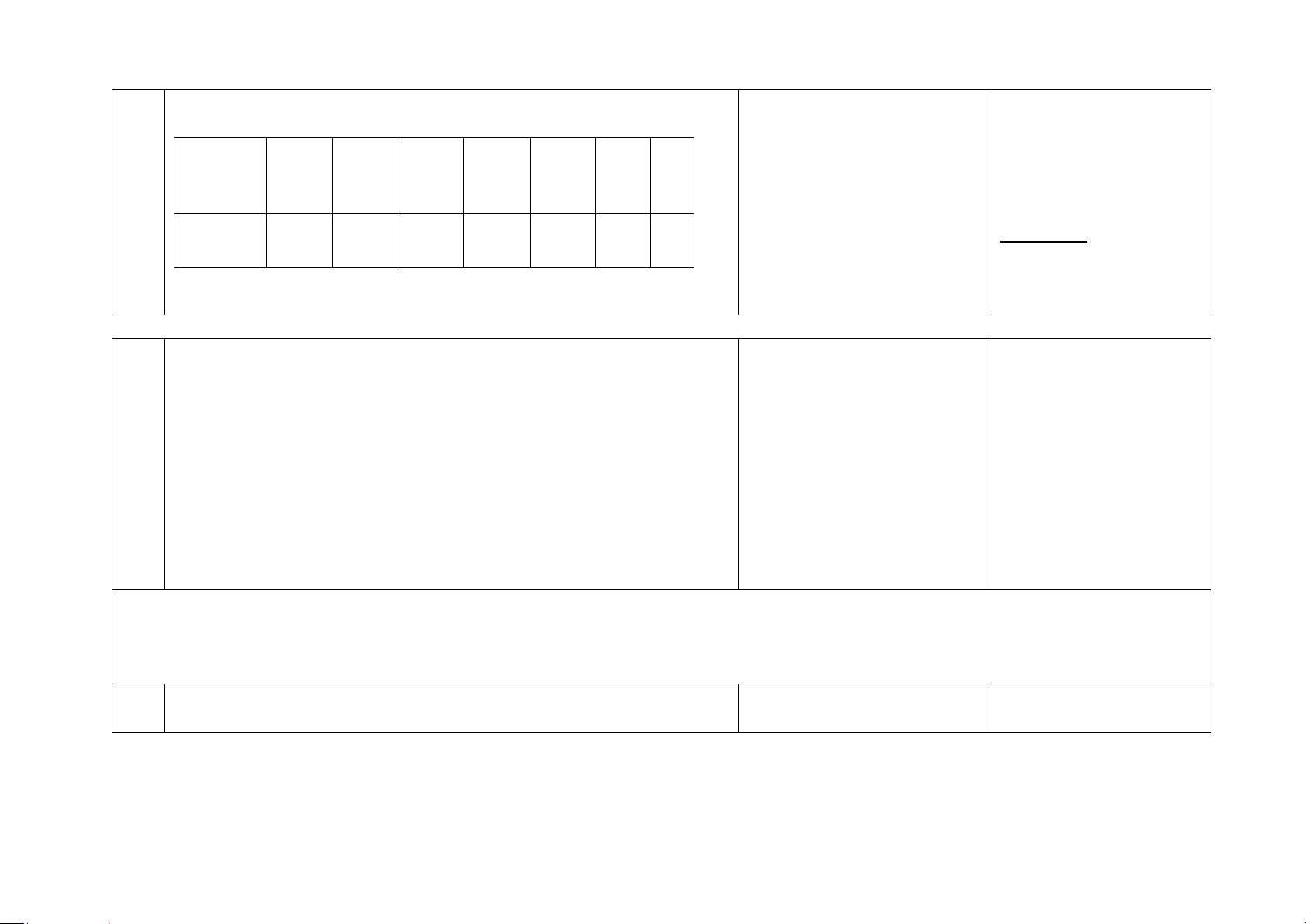
Bài tập 3. Một cuộc điều tra trên số lượng 10 000 cặp vợ chồng về số lượng GV giới thiệu Bài tập 3
HS có thể làm việc theo cặp
con dưới 22 tuổi của họ cho kết quả như sau:
(2 HS) để giải Bài tập 3. Số con
GV: Em nào có thể nhắc lại dưới 22 0 1 2 3 4 5 6
cách tính tần suất trong một HS trả lời các câu hỏi của tuổi thực nghiệm? Bài tập 3.
Số cặp vợ 4 200 2 400 2 200 900 150 100 50 GV nhắc lại:
Mong đợi: HS tính được chồng
o Tần suất của một kết quả các tần suất và phát hiện ra
quan sát bằng tỷ số giữa tần tính chất: tổng tất cả các
tần suất bằng 1.
1) Tính tần suất tương ứng với mỗi kết quả. Tổng của bảy tần suất có được
số (số lần xuất hiện) và độ là bao nhiêu? lớn của mẫu.
2) Tính tần suất của các cặp vợ chồng có bốn con trở lên. Tổng quát, làm
o Tổng tất cả các tần suất của
thế nào để tính tần suất của một nhóm nhiều kết quả có thể có?
các kết quả có thể có bằng 1.
3) Làm thế nào để tính tần suất của các cặp vợ chồng có ít nhất một con?
Hướng dẫn: 1) Tổng của tất cả các tần suất bằng 1. 2)
Tổng quát, để tính tần suất của một nhóm nhiều kết quả có thể có, ta
lấy tổng tần suất của từng kết quả. 3)
Lấy 1 trừ đi tần suất của các cặp vợ chồng có 0 con dưới 22 tuổi. Hoạt động 2.
Mục tiêu: Trải nghiệm và khám phá mối quan hệ giữa tần suất và xác suất thông qua mô hình hoá phép thử ngẫu nhiên với công cụ công nghệ
Chuẩn bị: Máy tính với phần mềm Excel Thời
Vai trò của GV (câu hỏi, chỉ
Nhiệm vụ của HS (công Tiến trình nội dung gian dẫn)
việc và thể thức thực hiện) lOMoAR cPSD| 58540065 Bài tập 4.
GV giới thiệu Bài tập 4 và phát HS làm việc theo nhóm
1) Trong Excel, hàm RAND() sẽ cho ra một số thực ngẫu nhiên trong
Phiếu học tập cho các nhóm. khoảng (0;
1). Sử dụng hàm này để thực hiện 20 lần mô phỏng Các nhóm làm việc với
Nếu HS mỗi nhóm không có
việc chọn một số ngẫu nhiên trong khoảng máy tính và hoàn thành (0; 1). Đếm số lượng
máy tính để thực hiện mô phỏng
những con số lớn hơn 0,5 có được. Đây có phải là kết quả “có thể dự
Phiếu học tập (chứa nội
trên Excel thì GV gọi đại diện
kiến trước” hay không? dung Bài tập 4).
từng nhóm lên thực hiện trên
2) Mô phỏng phép thử tung con xúc xắc sáu mặt.
máy tính của GV, trình chiếu Đại diện các nhóm trình
a. Hàm INT(x) trong Excel cho ra phần nguyên của số thực dương x, cho toàn thể lớp xem.
bày kết quả và trả lời các
tức là số nguyên lớn nhất không vượt quá x. Sử dụng Excel để tìm câu hỏi.
INT(3,56) và INT(0,15).
GV: Số lượng các con số lớn
hơn 0,5 xuất hiện trong tổng số Mong đợi:
b. Giải thích tại sao để mô phỏng việc tung con xúc xắc cân bằng sáu 20 lần mô phỏng tung xúc xắc
mặt trong Excel, ta có thể sử dụng hàm RANDBETWEEN(1,6).
là có thể dự kiến trước không? HS phát hiện kết quả của
c. Thực hiện 100 lần mô phỏng việc tung con xúc xắc sáu mặt trong
hàm RAND() là “không thể
Excel. Các kết quả ghi vào các ô từ B1 đến B100. dự kiến trước”. lOMoAR cPSD| 58540065
d. Sử dụng hàm COUNTIF(B1:B100.”1”) để đếm số lần các giá trị 1 GV đến từng nhóm và hỗ trợ học Thực hiện được mô phỏng
xuất hiện trong các ô từ B1 đến B100. Sao chép công thức để đếm sinh mô phỏng với Excel. con xúc xắc 6 mặt với
lần lượt số lần xuất hiện của các giá trị 2, 3, 4, 5 và 6. Excel với 100 lần mô
e. Tính tần suất xuất hiện số 6 và so sánh với xác suất xuất hiện mặt 6 GV: Em có nhận xét gì về tần phỏng.
chấm khi tung một con xúc xắc cân bằng, đồng chất.
suất xuất hiện số 6?
HS phát hiện ra được kết
Hướng dẫn: 1) Viết công thức =RAND() vào một ô của Excel. Sau đó sao GV cho các nhóm trình bày kết quả thực nghiệm: khi số
chép công thức bằng cách kéo xuống cho đến dòng thứ 20. Số lượng những quả và nhận xét.
lượng phép thử mô phỏng
con số lớn hơn 0,5 là ngẫu nhiên, không thể dự kiến trước.
càng lớn, tần suất xuất hiện
2) a) INT(3,56) = 3 và INT(0,15) = 0.
số 6 dần đến giá trị 1/6 b)
Công thức =RANDBETWEEN(1,6) chính
sẽ cho ra một số nguyên ngẫu
nhiên trong tập hợp {1,2,3,4,5,6}, tức mô phỏng được phép thử tung con xúc xắc 6 mặt.
là xác suất xuất hiện mặt 6
chấm khi tung con xúc xắc c)
Sử dụng công thức =𝐼𝑁𝑇 𝑅𝐴𝑁𝐷()) +
1, sau đó sao GV đưa ra chú ý: Ta chấp nhận cân đối, đồng chất.
chép bằng cách kéo xuống từ ô B1 đến ô B100.
rằng, khi số lượng phép mô
phỏng tăng lên, tần suất xuất
e) Tính tần suất dựa trên tần số có được. Xác suất xuất hiện mặt 6 khi tung hiện số 6 có xu hướng gần với
con xúc xắc cân bằng, đồng chất là 1/6 .
giá trị 1/6, đúng bằng với xác suất xuất hiện mặt 6.
Chú ý: khi số lần phép mô phỏng tăng lên, tần suất xuất hiện số 6 có xu
hướng gần với giá trị 1/6 đúng bằng với xác suất xuất hiện mặt 6. Thời Tiến trình nội dung Vai trò của GV Nhiệm vụ của HS gian lOMoAR cPSD| 58540065
1. Không gian mẫu, biến cố {Trình bày khái niệm, định lý mới … của bài học}
GV trình bày bài học mới HS chú ý lắng nghe
Định nghĩa: Một kết quả có thể có của một phép thử ngẫu nhiên gọi là một biến cố sơ cấp.
Tập hợp tất cả các biến cố sơ cấp của một phép thử ngẫu nhiên gọi là không
gian mẫu của phép thử này. Ta thường ký hiệu không gian mẫu là Ω.
Một biến cố A là một tập hợp con của không gian mẫu Ω. Ta nói rằng một
kết quả thuận lợi cho biến cố A nếu kết quả này là một bộ phận của A. lOMoAR cPSD| 58540065
Biến cố đặc biệt:
- Biến cố không thể là tập hợp rỗng
∅: không có kết quả nào của phép thử
thuận lợi cho biến cố không thể cả.
- Biến cố chắc chắn là toàn bộ không gian mẫu Ω: mọi kết quả của phép thử
đều thuận lợi cho biến cố này.
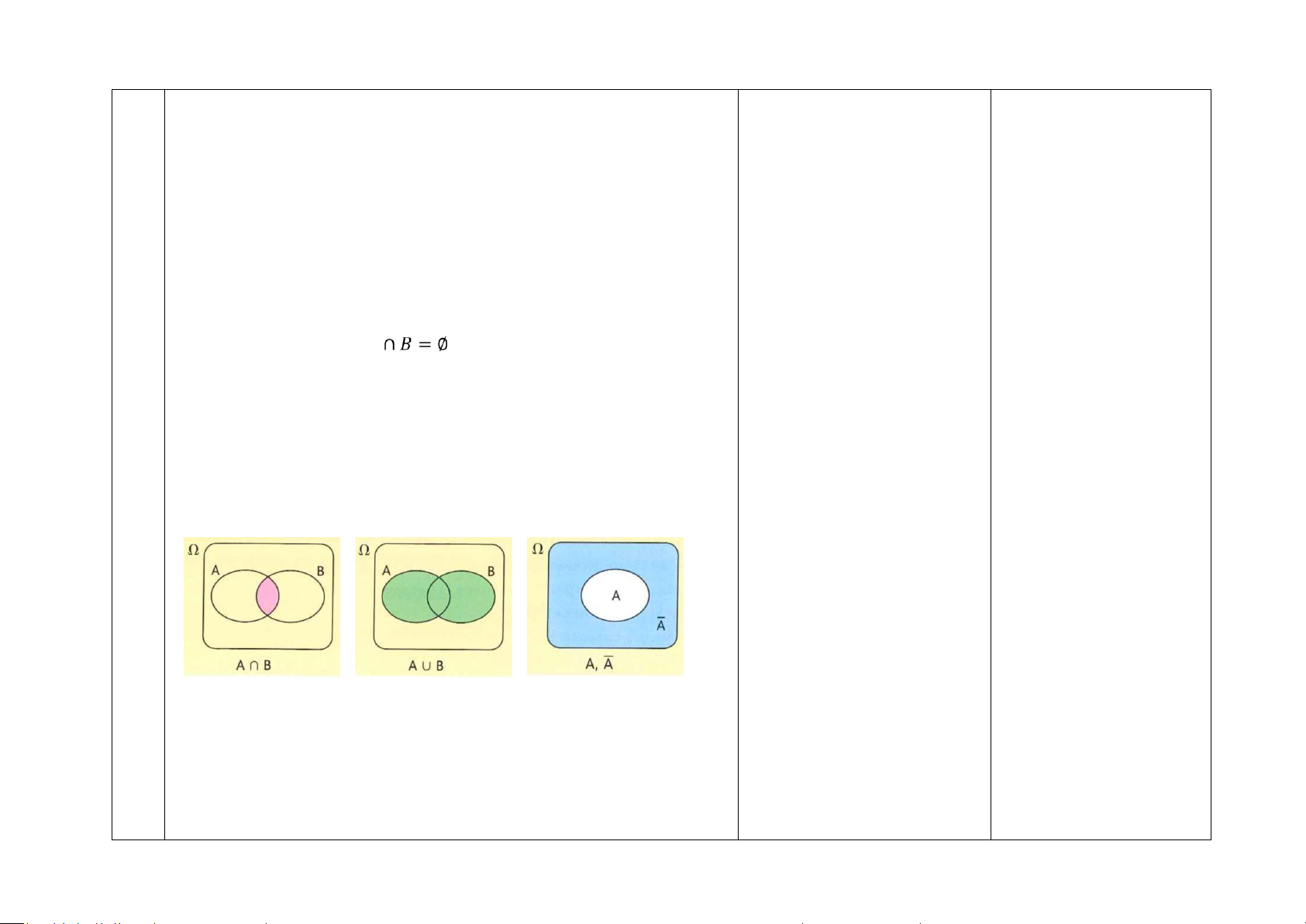
2. Giao, hợp các biến cố
Định nghĩa: Cho A và B là hai biến cố.
Giao của hai biến cố A và B, ký hiệu là 𝐴 ∩ 𝐵 hay AB, là biến
cố tạo thành từ các kết quả thuận lợi cho đồng thời cả A và B. Nếu 𝐴
thì ta nói A và B là hai biến cố xung khắc.
Hợp của hai biến cố A và B, ký hiệu là 𝐴 ∪ 𝐵 hay “A hoặc B”
là biến cố tạo thành từ các kết quả thuận lợi cho A hoặc B.
Biến cố đối của biến cố A, ký hiệu là 𝐴 , là biến cố được tạo thành từ các kết
quả không thuận lợi cho A.
A và B là hai biến cố độc lập nếu việc xảy ra hay không xảy ra biến cố này
không ảnh hưởng đến xác suất xảy ra của biến cố kia.
GV minh họa trực quan biến cố
giao, biến cố hợp, biến cố đối.
Ví dụ 1. {Năng lực mô tả các biến cố theo ngôn ngữ tập hợp}
GV giới thiệu Ví dụ 1 và hướng
Một thùng chứa hai bi đỏ, ký hiệu Đ1 và Đ2 và hai bi vàng ký hiệu là V2
HS chú ý nghe hướng dẫn
dẫn học sinh tìm lời giải.
và tham gia tìm lời giải của
và V3. Rút ngẫu nhiên một bi trong thùng, không bỏ lại vào thùng, rồi rút Ví dụ 1.
ngẫu nhiên bi thứ hai. Ta ghi lại màu và số của bi sau mỗi lần rút.
GV: Để xác định một kết quả có
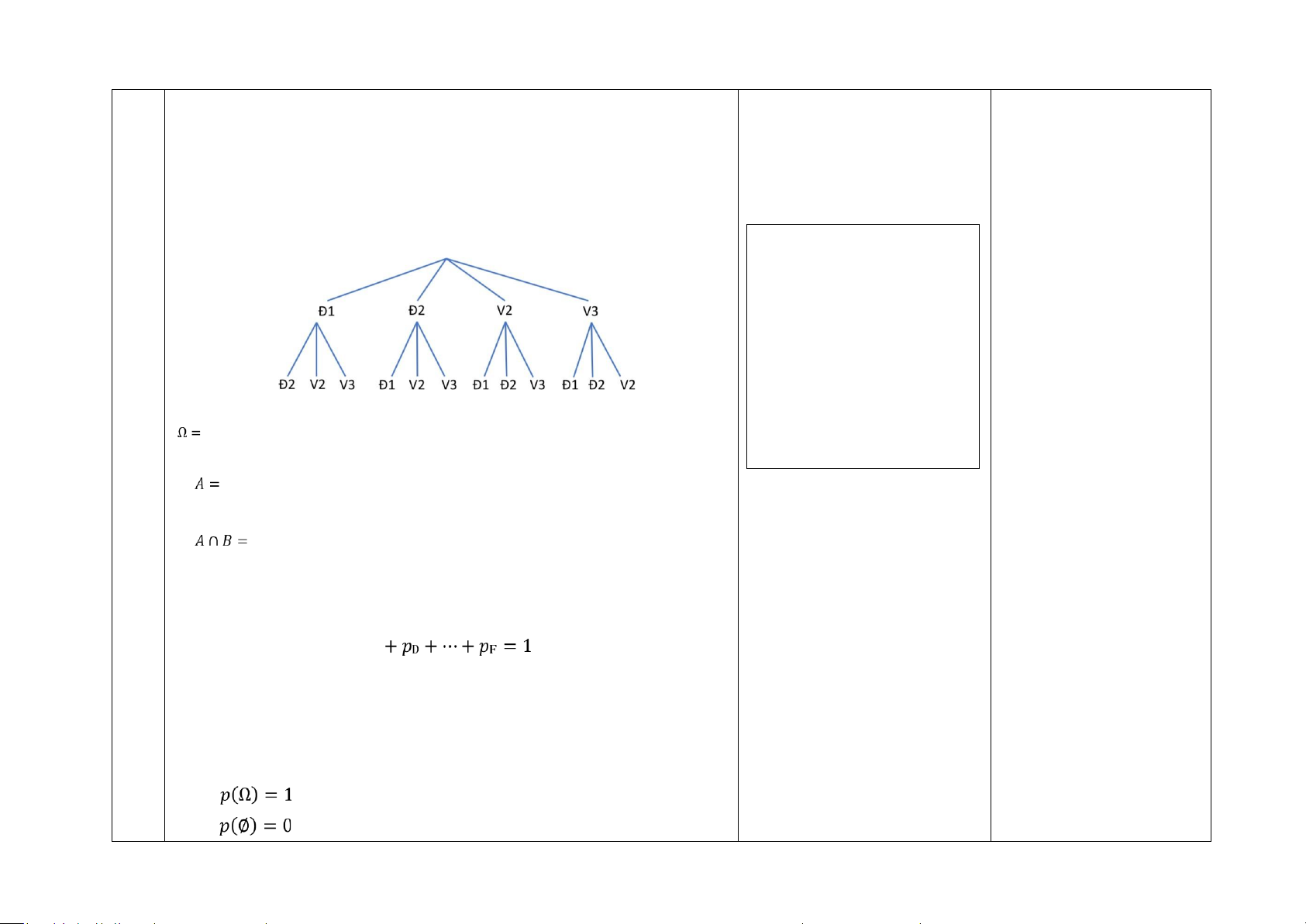
1) Sử dụng một sơ đồ hình cây, hãy mô tả không gian mẫu dưới dạng tập thể có của phép thử dựa vào sơ hợp. lOMoAR cPSD| 58540065 lOMoAR cPSD| 58540065
2) Viết dưới dạng tập hợp các biến cố sau:
đồ hình cây, ta phải làm thế
A: “Đạt được hai bi cùng màu hoặc cùng số” nào?
B: “Đạt hai bi với các số có độ chênh lệch 1”.
3) Xác định biến cố “Đạt được A và B”.
GV nhấn mạnh phương pháp giải tương ứng: Hướng dẫn: Phương pháp
- Để xác định tất cả các kết
quả có thể xảy ra của một
phép thử ngẫu nhiên, ta có
thể sử dụng sơ đồ hình cây, bảng…
- Để xác định các kết quả 1) Không gian mẫu
thuận lợi cho một biến cố, ta {Đ1Đ2, Đ1𝑉2, Đ1𝑉3, Đ2Đ1, Đ2𝑉2, Đ2𝑉3, 𝑉2Đ1, 𝑉2Đ2, 𝑉2𝑉3,
đi theo các đường đi thoả 𝑉3Đ1, 𝑉3Đ2, 𝑉3𝑉2}
điều kiện xác định biến cố 2)
{Đ1Đ2, Đ2Đ1, 𝑉2𝑉3, 𝑉3𝑉2, Đ2𝑉2, 𝑉2Đ2} 𝐵 =
{Đ1Đ2, Đ1𝑉2, Đ2Đ1, Đ2𝑉3, 𝑉2Đ1, 𝑉2𝑉3, 𝑉3Đ2, 𝑉3𝑉2} 3)
GV trình bày định nghĩa khái
{Đ1Đ2, Đ2Đ1, 𝑉2𝑉3, 𝑉3𝑉2}
niệm xác suất tổng quát.
3. Định nghĩa xác suất: Cho một phép thử ngẫu nhiên có không gian mẫu hữu hạn Ω = {𝑒!, 𝑒D, … ,
𝑒F}. Xác suất của mỗi HS chú ý nghe giảng.
biến cố sơ cấp {𝑒G} là một số thực không âm 𝑝G sao cho 𝑝! . Ký hiệu 𝑝G = 𝑝({𝑒G}).
Xác suất của một biến cố A, ký hiệu 𝑝(𝐴), là tổng của tất cả các xác suất của
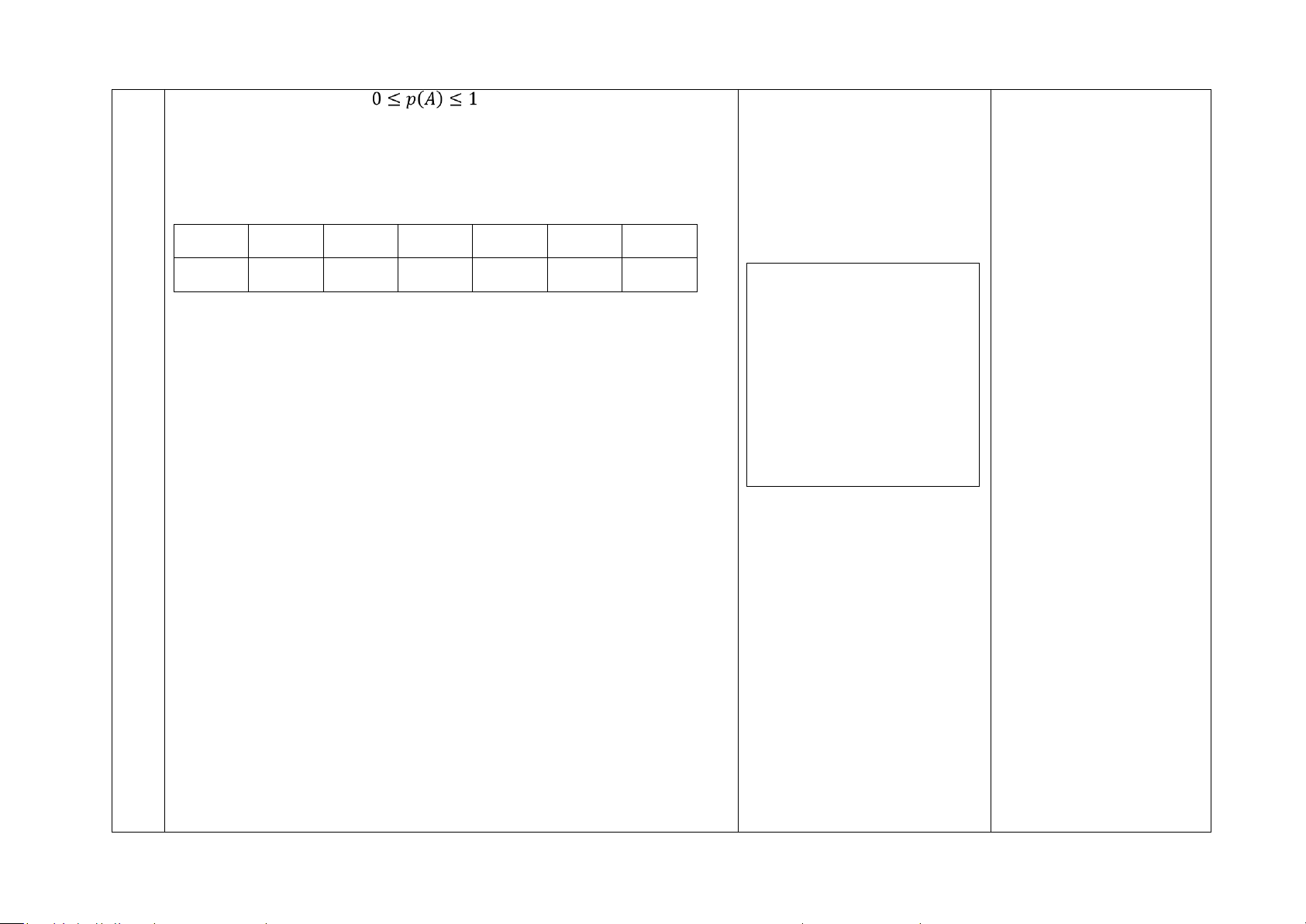
các biến cố sơ cấp thuận lợi cho biến cố A. Tính chất: - - lOMoAR cPSD| 58540065 lOMoAR cPSD| 58540065 - Với mọi biến cố A, .
Ví dụ 2. {Năng lực tính xác suất dựa vào định nghĩa tổng quát}
Tung một con xúc sắc sáu mặt không cân bằng. Ký hiệu 𝑝 GV trình bày Ví dụ 2
HS chú ý nghe hướng dẫn G là xác
suất xuất hiện mặt thứ i. Bảng sau cho thấy mô hình dự đoán xác suất của và cùng tham gia tìm lời phép thử này, trong đó giải của Ví dụ 2. 𝑝
GV nhấn mạnh phương pháp K chưa biết: i 1 2 3 4 5 6 giải tương ứng: 𝑝G 0,3 0,1 0,1 0,15 𝑝K 0,07 Phương pháp
- Trong một không gian 1) Tính 𝑝
mẫu, tổng tất cả các xác K
suất của các biến cố sơ cấp
2) Ký hiệu A là biến cố “số chấm xuất hiện là một số chẵn”. Tính p(A). bằng 1. Hướng dẫn:
- Để tính xác suất một biến 1) Ta có 0,3 + 0,1 + 0,1 + 0,15 + 𝑝 K
cố, ta tính tổng tất cả xác + 0,07 = 1. Từ đó 𝑝K = 0,28. 2) Ta có 𝐴
suất của các biến cố sơ cấp
thuận lợi cho biến cố đó. =
{2,4,6}. Vì vậy, 𝑝(𝐴) = 𝑝 2 + 𝑝4 + 𝑝6 = 0,32.
GV trình bày mối liên hệ giữa HS chú ý lắng nghe
4. Liên hệ với xác suất theo nghĩa cổ điển
xác suất theo nghĩa tổng quát
với xác suất theo nghĩa cổ điển.
Khi mà tất cả các biến cố sơ cấp của không gian mẫu Ω đều có cùng xác
suất, ta nói rằng ta có một tình huống cân bằng xác suất.
GV nhấn mạnh đến các thuật
Trong một tình huống cân bằng xác suất trên không gian mẫu Ω có
n ngữ thường để chỉ một tình
phần tử, mỗi biến cố sơ cấp sẽ có xác suất là (1/n).
huống cân bằng xác suất như
“con xúc xắc cân bằng và đồng
chất”, “rút ngẫu nhiên”, “các
Quy ước: Các thuật ngữ như “con xúc xắc cân bằng và đồng chất”, “rút đồng xu không phân biệt được
ngẫu nhiên”, “các đồng xu không phân biệt được khi chạm vào”… dùng khi chạm vào”
để chỉ các tình huống cân bằng xác suất.
Tính chất: Trong một tình huống cân bằng xác suất trên không gian mẫu Ω
có tất cả n kết quả có thể có, xác suất của một biến cố A là: lOMoAR cPSD| 58540065 𝑛(𝐴) 𝑝(𝐴) = 𝑛 trong đó 𝑛(𝐴)
là số kết quả thuận lợi cho biến cố A. lOMoAR cPSD| 58540065 lOMoAR cPSD| 58540065
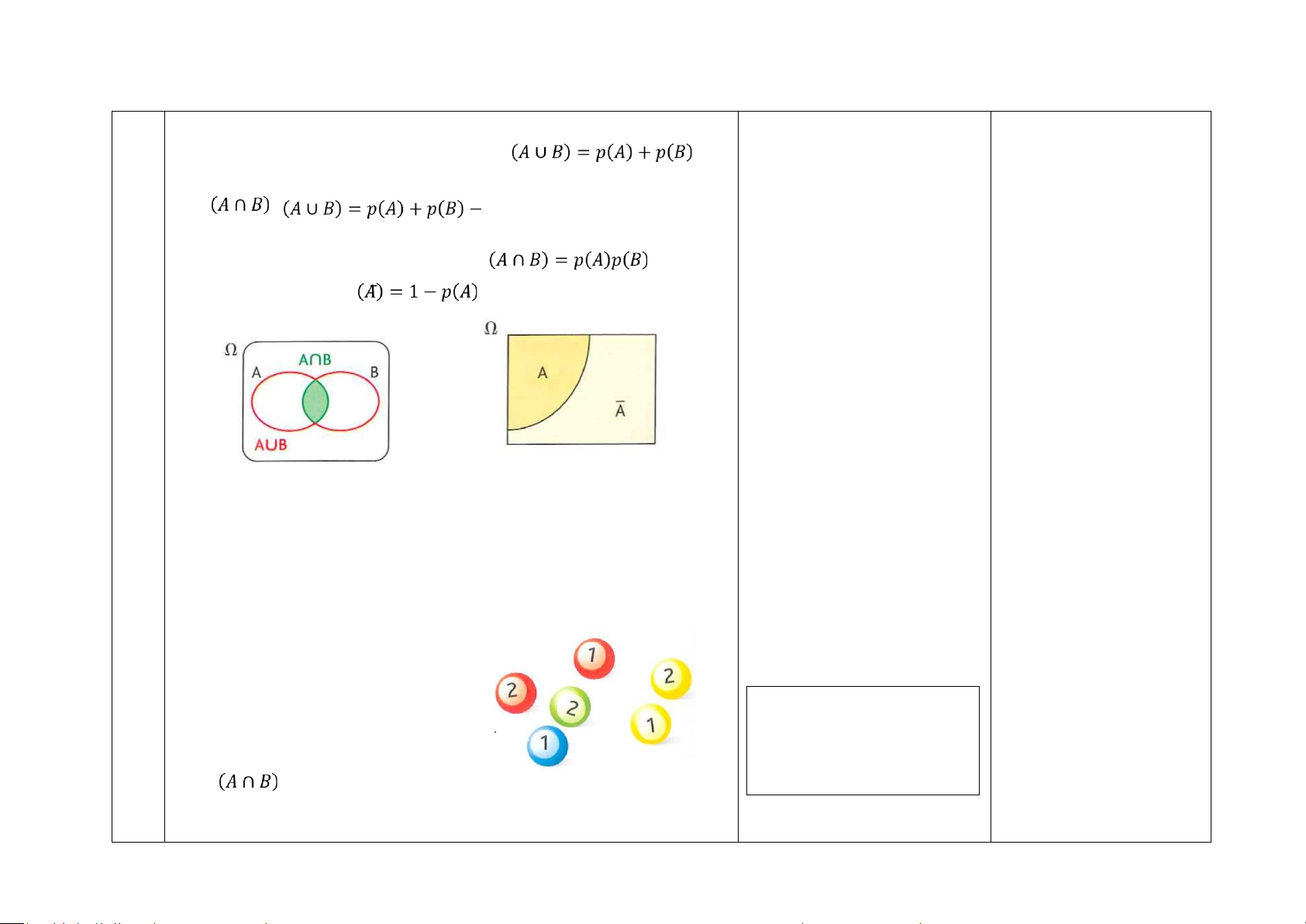
Xác suất của biến cố hợp, biến cố giao và biến cố đối:
- Nếu A và B là hai biến cố xung khắc thì 𝑝 . -
Nếu A và B là hai biến cố bất kỳ thì 𝑝
GV minh họa trực quan các biến 𝑝 .
cố giao, hợp, đối để học sinh
hiểu công thức tính xác suất của
- Nếu A và B là hai biến cố độc lập thì 𝑝 . các biến cố này.
- Với mọi biến cố A, 𝑝 .
Ví dụ 3. {Năng lực tính xác suất bằng cách dùng công thức trong một tình GV trình bày nội dung Ví dụ 3
huống cân bằng xác suất} HS lắng nghe và tham gia
và hướng dẫn học sinh tìm lời tìm lời giải theo hướng dẫn
Một thùng chứa 100 viên bi không thể phân biệt được khi chạm vào, trong giải. của GV
đó gồm 25 bi đỏ được đánh số 1; 15 bi đỏ được đánh số 2; 20 bi xanh lá cây
được đánh số 2; 20 bi xanh nước biển được đánh số 1; 10 bi vàng được đánh GV: Đây có phải là tình huống
số 1; 10 bi vàng được đánh số 2. Ta rút ngẫu nhiên một bi từ trong thùng. cân bằng xác suất không? Tại sao?
Gọi A và B là các biến cố.
GV nhấn mạnh phương pháp
A: “bi rút ra có màu đỏ” giải tương ứng:
B: “bi rút ra được đánh số 2”. Phương pháp
- Nhận ra tình huống đề cập
1) Tính các xác suất p(A) và p(B).
đến là một tình huống cân 2) Mô tả bằng lời biến bằng xác suất. cố 𝐴 ∩ 𝐵 và tính 𝑝 . lOMoAR cPSD| 58540065
3) Từ đó hãy suy ra các xác suất 𝑝(𝐴 ) và 𝑝 .
Hướng dẫn: 1) Đây là tình huống cân bằng xác suất. Vì vậy, lOMoAR cPSD| 58540065 𝑝(𝐴) = 0,4 và 𝑝(𝐵)
= - Sử dụng công thức tính xác 0,45
suất đối với tình huống cân bằng xác suất. lOMoAR cPSD| 58540065 2) 𝐵 là biến cố:
“Bi rút ra có màu đỏ và được đánh số 2”. 𝑝 100
GV giới thiệu nội dung Ví dụ
HS làm việc theo cặp (2 HS 3) 4
gần nhau) để tìm lời giải cho Ví dụ 4. 𝑝
GV: Mỗi cặp phải vẽ một sơ đồ
Ví dụ 4. {Năng lực sử dụng sơ đồ (Venn, hình cây, bảng hai chiều) để tính
Venn biểu diễn dữ liệu bài toán xác suất}
trước. Mỗi môn thể thao được
Một lớp có 25 học sinh, trong đó có 12 học sinh thích môn bóng chuyền, minh hoạ bởi một sơ đồ dạng
20 học sinh thích môn bóng đá, và 12 học sinh thích môn bóng rổ. Có 10 tập hợp.
học sinh thích cả hai môn bóng chuyền và bóng đá, và trong số này có 1
học sinh thích chơi môn bóng rổ nữa. Không có học sinh nào thích bóng GV: Chúng ta bắt đầu điền số
chuyền và bóng rổ mà không thích bóng đá. Có 3 học sinh chỉ thích duy HS vào các phần giao nhau nhất môn bóng rổ.
trước. Có bao nhiêu HS thích cả i
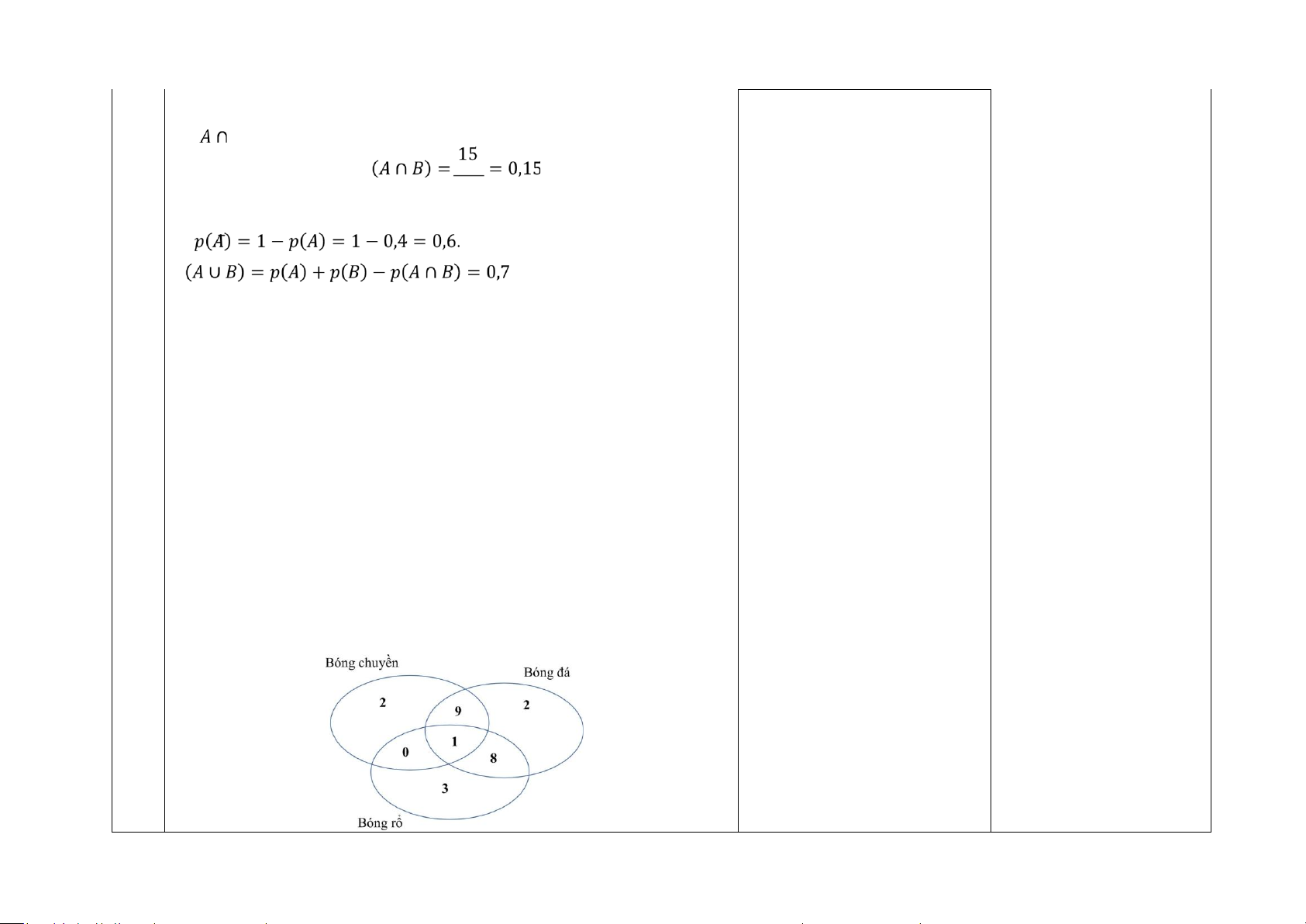
1) Biểu diễn dữ liệu bài toán dưới dạng một sơ đồ Venn ba môn thể thao?
GV: Có bao nhiêu HS thích
2) Gặp ngẫu nhiên một học sinh trong lớp, tính xác suất để em học sinh bóng chuyền và bóng rổ mà đó:
không thích bóng đá? a. Thích môn bóng chuyền
GV: Đây có phải là tình huống b.
Thích đúng hai môn thể thao. Hướng dẫn: 1)
cân bằng xác suất không? Tạ sao? lOMoAR cPSD| 58540065




