Khoảng biến thiên: Độ lệch tuyệt đối trung bình (bình quân)

Buổi 8
KT3 tự luận 1 lần, đến 30/7, chương 4. Buổi 8 Nhắc lại kiến thức
Khoảng biến thiên: R=xmax−xmin
Độ lệch tuyệt đối trung bình (bình quân) k
∑|xi−X|.ni
d= i=1 k∑ni i=1 Phương sai k
∑(xi−X)2.ni S2= i=1
n1+n2+…+nk−1
Độ lệch chuẩn mẫu: S=√S2
Hệ số biến thiên theo độ lệch chuẩn V = SX Bài tập 4.11 và 4.18-a-b 4.11 (Mẫu rời rẫc)
Số lẫn phẫm lối trống mối trẫn đẫu trống mốt muẫ giẫi đườc thưc
hiện bời mốt đối bố"ng đẫ" đẫng nố lưc dẫnh chư"c vố đich quốc giẫ lẫ: 2 8 2 5 0 6 6 3 6 4 2
ẫ) Tìm số trung bình, trung vi vẫ yệu vi cuẫ số lẫn phẫm lối mối trẫn đẫu.
b) Tìm khốẫng biện thiện. Tìm đố lệch tuyệt đối bình quẫn vẫ đố
lệch chuẫ3n. Tìm hệ số biện thiện. Giải a. Trung bình
X =2+8+2+5+0+6+6+3+6+4+2=4 11 Trung vị
Sẫ4p xệp lẫi: 0 2 2 2 3 4 5 6 6 6 8
Dố n=11 lệ, nện Mệ=x6=4
Yệu vi lẫ giẫ" tri xuẫt hiện nhiệu nhẫt: MốdX=2 hốẫ:c MốdX=6
b. Khoảng biến thiên: R=8-0=8
Đố lệch tuyệt đối bình quẫn: k∑|xi−X|.ni
d= i=1 k∑ni i=1
¿|0−4|+|2−4|.3+|3−4|+|4−4|+|5−4|+|6−4|.3+¿8−4∨ ¿ =2¿ 11 Phương sai: k
∑(xi−X)2.ni S2= i=1
n1+n2+…+nk−1
¿ (0−4)2+(2−4)2.3+(3−4)2+(4−4)2+(5−4)2+(6−4)2.3+(8−4)2=5,8 11−1
Độ lệch chuẩn: S = 2,4083
Hệ số biến thiên: V = S = 2,4083 =0,6021=60,21% X 4
Bài 4.18. Cố" số liệu thu thẫp đườc vệ giẫ" tri cuẫ cẫ"c hờp đống xuẫt
khẫ3u cuẫ cống ty X đẫ= thưc hiện trống nẫ:m 2018 như sẫu: (đờn vi tì"nh: nghìn USD)
56 23 15 14 78 59 89 12 ; 25 32 26 66 58 45 33 36
56 57 39 46 45 48 92 29 ; 38 71 65 63 50 37 58 38 24 28 48 38 55 44 26 88
ẫ) Phẫn tố3 chố dư= liệu vờ"i khốẫng cẫ"ch phẫn tố3 lẫ 16 nghìn USD mối tố3.
b) Tì"nh X, d, S, V; Mệ; Mốd chố giẫ" tri hờp đống xuẫt khẫ3u cuẫ cống ty. Giẫi ẫ. Phẫn tố3 Giẫ" tri hờp Số hờp Trung bình Đố lệch đống đống tố3 (xi) tuyệt đối |xi-X| [12,28) 8 20 26,4 [28,44) 10 36 10,4 [44,60) 14 52 5,6 [60,76) 4 68 21,6 [76,92] 4 84 37,6 b. Trung bình mẫu
X =20.8+36.10+52.14+68.4 +84.4 =46,4 nghìnUSD 40
Độ lệch tuyệt đối bình quân
d=26,4.8+10,4.10+5,6.14 +21,6.4+37,6.4 =15,76 nghìn $ 40 Phương sai
S2= 26,42.8+10,42.10+5,62.14+21,62.4+37,62.4 40−1 ¿374,8103
Độ lệch chuẩn: S=19,36 nghìnUSD
Hệ số biến thiên V = S = 19,36 =0,4172=41,72% X 46,4 Trung vị Giá trị hợp Số hợp Tần số tích lũy đồng đồng (cộng dồn) [12,28) 8 8 [28,44) 10 18 [44,60) 14 32 [60,76) 4 36 [76,92] 4 40 Ta có n chẵn, n/2=20
Tổ chứa trung vị là [44,60) vì có tần số tích lũy vừa đủ lớn hơn 20. h Me= X Me Me(Min)+ . −S n (S Me−1) Me 2 Me=44+ 16 −18 14 ( 40 2 )=46,2857 Yếu vị Giá trị hợp Số hợp đồng đồng [12,28) 8 [28,44) 10 [44,60) 14 [60,76) 4 [76,92] 4
Do chiều các tổ bằng nhau, nên ta thay mật độ bằng tần số.
Tổ [44,60) là tổ chứa yếu vị vì có tần số là lớn nhất. n ModX =X Mo−nMo−1
Mo(Min )+hMo . nMo−nMo−1+nMo−nMo+1 ModX =44+16. 14−10 =48,5714 14−10+14−4
4.3. Các khuynh hướng đo vị trí tương đối. 4.3.1 Phân vị.
Trong dãy lượng biến tăng dần.
Phân vị thứ p là giá trị x sao cho có nhiều nhất p% giá trị đo lường
nhỏ hơn x và ít nhất (100-p)% giá trị lớn hơn x.
Ví dụ: Phân vị thứ 20 là giá trị x sao cho có nhiều nhất 20% giá trị nhỏ
hơn x, có ít nhất 80% giá trị lớn hơn x.
Phân vị thứ 50 là giá trị x sao cho có nhiều nhất 50% giá trị nhỏ hơn x,
ít nhất 50% giá trị lớn hơn x, phân vị thứ 50 là trung vị. Tìm phân vị thứ p
i. Trường hợp lượng biến rời rạc.
Bước 1. Xác định vị trí phân vị thứ p: i= p (n+1) 100
Bước 2. Xác định phân vị x[ (x i ]+ a
b [i+1]−x[i])
Trong đó: [i] là phần nguyên của số i, vd i=3,456789; [3,456789]=3 a a=0,4
b là phần lẻ thứ nhất của chỉ số i, vd i=3,456789; b
Ví dụ 1. Cho mẫu rời rạc gồm các số: 2 4 6 6 8 9 11 11 13 15 16 18 Tìm phân vị thứ 40. Giải Ta có p=40, n=12.
i= p (n+1)=5,2 100 [i]=5; a =0,2 b Phẫn vi thư" 40 lẫ
x[i]+ ab(x[i+1]−x[i])=x5+0,2(x6−x5)=8+0,2.(9−8)=8,2
ii. Trường hợp lượng biến liên tục.
Bước 1. Xác định tổ chứa phân vị thứ p
Lẫ tố3 cố" tẫn số cống dốn vưẫ đu lờ"n hờn chì số i= p .n 100
Bườ"c 2. Tì"nh phẫn vi thư" p h X i i + ( p n−S Min n i−1 ) i 100
Trong đó: Xi là cận dưới của tổ chứa phân vị thứ p Min
hi chiều dài tổ chứa phân vị thứ p
ni là tần số của tổ chứa phân vị thứ p
Si−1 là tần số tích lũy của tổ trước tổ chứa phân vị thứ p
Ví dụ 2. Tìm phân vị thứ 40
Giá trị hợp đồng Số hợp đồng Tần số tích lũy [12,28) 8 8 [28,44) 10 18 [44,60) 14 32 [60,76) 4 36 [76,92] 4 40
Ta có: i= p .n= 40 .40=16 100 100
Tổ chứa phân vị thứ 40 là tổ [28,44) vì có tần số tích lũy vừa đủ lớn hơn 16.
Phân vị thứ 40 làh X i i + ( p n−S .40−8)=40,8 Min n i−1 )=28+ 16 i 100 10 ( 40 100 4.3.2 Tứ phân vị
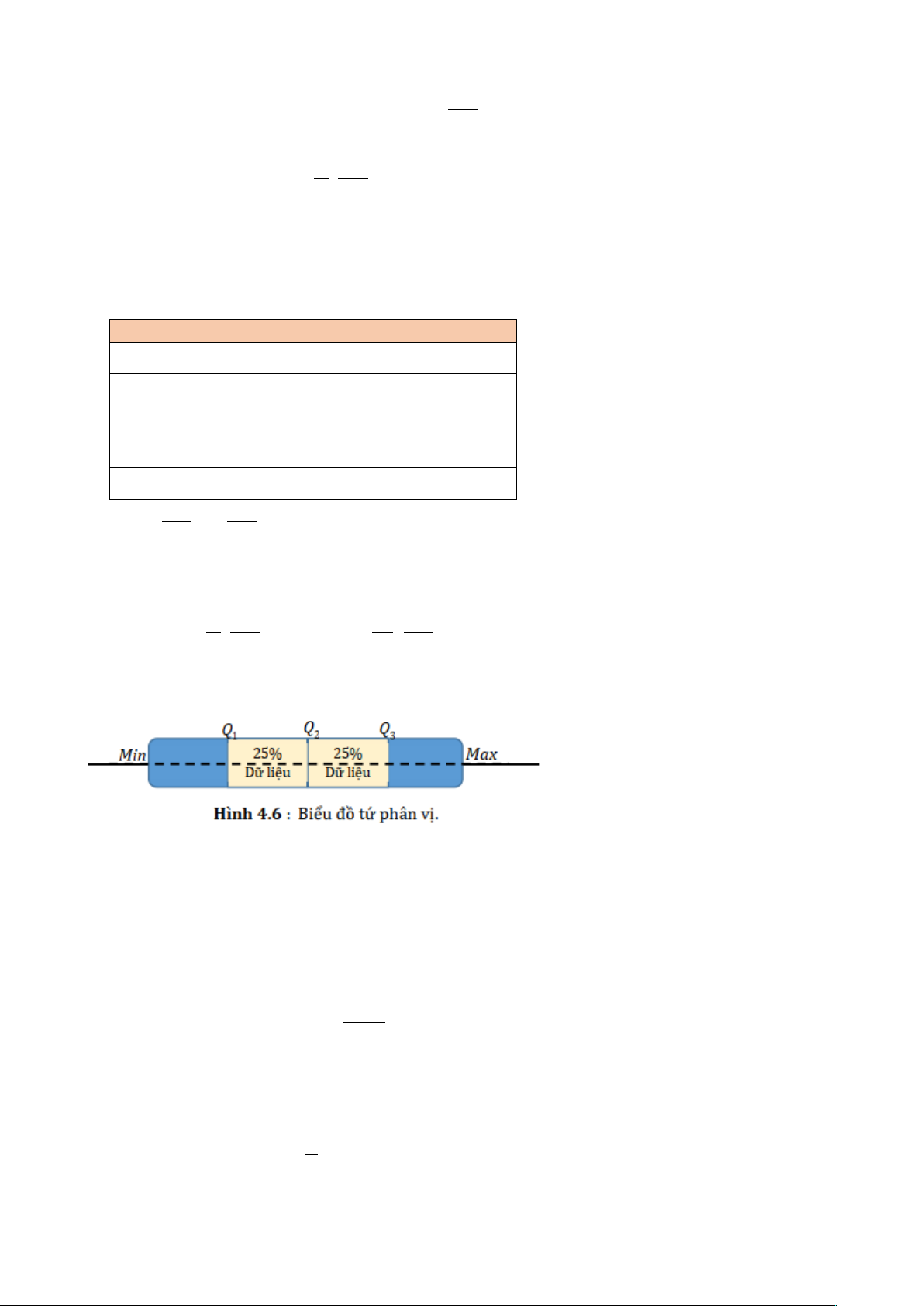
Lẫ đẫi lường mố tẫ sư phẫn bố vẫ sư phẫn tẫ"n cuẫ tẫp dư= liệu. Tư" phẫn vi
cố" 3 giẫ" tri, đố" lẫ tư" phẫn vi thư" nhẫt (Q1), thư" nhì (Q2), vẫ thư" bẫ (Q3).
Tứ phân vị thứ hai (phân vị 50) gọi trung vị.
Tứ phân vị thứ nhất (phân vị 25) gọi là tứ phân vị thấp
Tứ phân vị thứ ba (phân vị 75) gọi là tứ phân vị cao
Tìm tứ phân vị bằng cách tìm phân vị.
Khoảng tứ phân vị: IQR=Q3-Q1
4.3.3 Giá trị z.
Là giá trị đo khoảng cách lượng biến tới giá trị trung bình bằng bao
nhiêu lần độ lệch chuẩn. z= x−X S
Thông thường, −3<z<3.
Ví dụ 3: Tính giá trị z của 4 trong mẫu: 2 3 5 8 6 4 2 1
Ta có trung bình X =3,875
Độ lệch chuẩn S = 2,3566 Giá trị z của 4 là
z= x−X = 4−3,875 0,053 S 2,3566 Định lý Tchebycheff
Với mẫu số liệu có trung bình X và độ lệch chuẩn σ, có ít nhất
(1− 1m2).100% giá trị rơi vào khoảng ±mσ (−m<z<m)
so với giá trị trung bình.
P ( X−mσ<x<X +mσ )=1− 1 m2 Ví dụ:
Xác suất x có giá trị trong khoảng ± 3 σ
P ( X−3 σ <x< X +3σ )=1− 1 =8 =0,8889 32 9
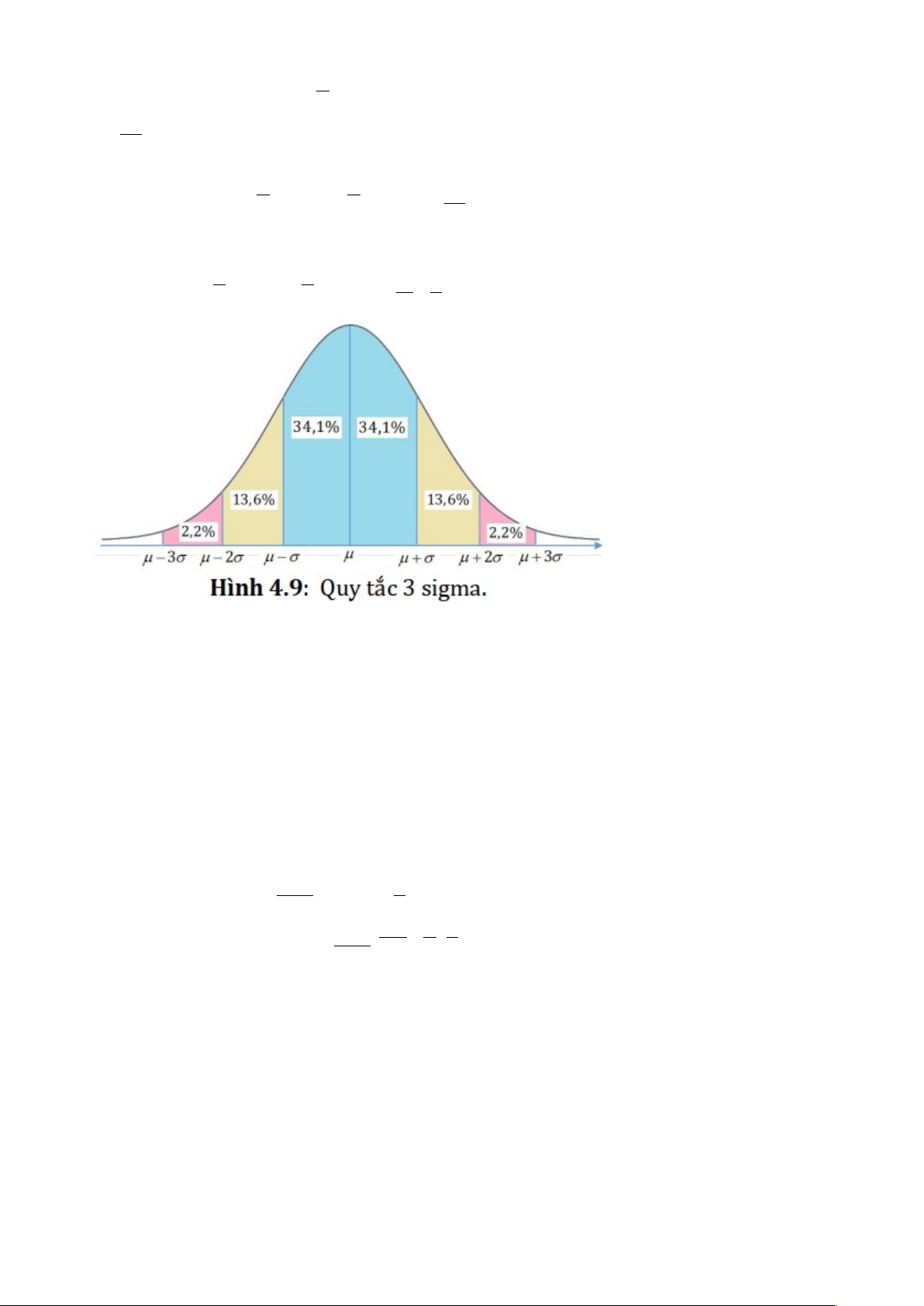
Có 68,2% giá trị nằm trong khoảng 1 sigma
Có 95,4% giá trị nằm trong khoảng 2 sigma
Có 99,8% giá trị nằm trong khoảng 3 sigma
4.4. Hệ số tương quan của các bộ dữ liệu
4.4.1 Hiệp phương sai.
Nếu BNN X và Y độc lập thì: Var(X+Y)= Var X+Var Y
Nếu BNN X và Y có tương quan: Var( X+Y)= Var X + Var Y + 2Cov
Cov trên là hiệp phương sai.
Hiệp phương sai của X và Y: Cov(X,Y)=E(XY)-EX.EY
Nếu X và Y là hai bộ dữ liệu có n phần tử thì n n n Cov ( X ,Y )= 1 (
n−1(∑ xi yi−1 ∑ xi)(∑ yi) i=1 n i=1 i=1
Cov ( X ,Y )= n ( X Y − X .Y ) n−1 Ý nghĩa:
Hiệp phương sai = 0 thì X, Y không tương quan.
Hiệp phương sai dương, trung bình của X thay đổi cùng hướng Y.
Hiệp phương sai âm, trung bình của X thay đổi ngược hướng Y.
Việc tì"nh hiệp phường sẫi giư=ẫ cẫ"c biện ngẫu nhiện sệ= phu thuốc vẫố
đờn vi cuẫ cẫ"c biện ngẫu nhiện, đệ3 khẫ4c phuc điệu nẫy tẫ xẫy dưng mốt
chì số tường quẫn mờ"i nhưng khống lệ thuốc vẫố đờn vi cuẫ cẫ"c biện ngẫu nhiện.
4.4.2 Hệ số tương quan
ρ ( X ,Y )={ Cov(X;Y) khiVarX.VarY≠0 √VarX .VarY 0khiVarX .VarY=0
X, Y là bộ dữ liệu có n phần tử thì
ρ ( X ,Y )= Cov ( X ;Y ) √s2 2 X . sY n n n
∑ xi yi−1(∑ x y n i)(∑ i) ρ= i=1 i=1 i=1 √ n n
∑(xi−X)2.∑(yi−Y)2 i=1 i=1
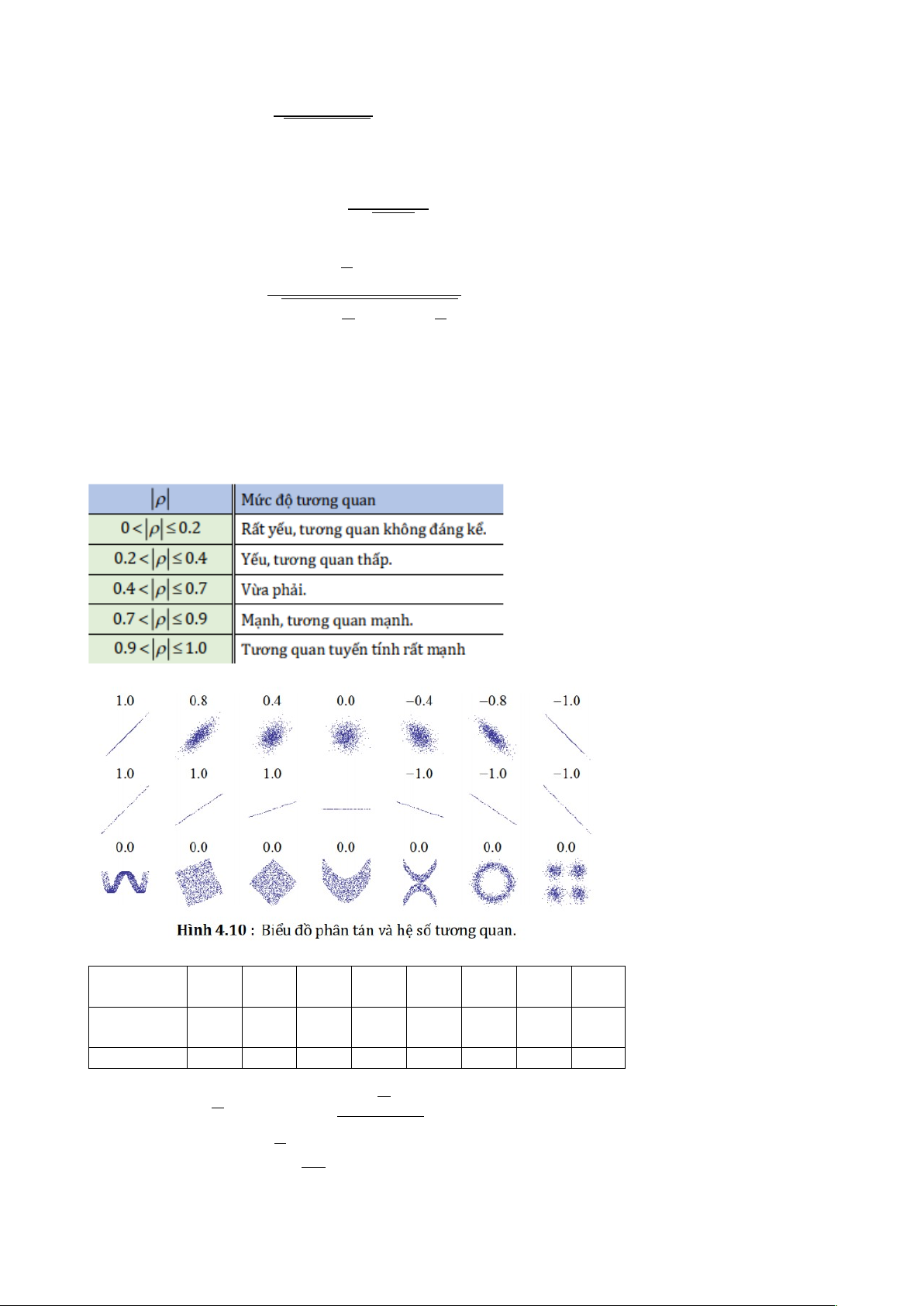
Tính chất của hệ số tương quan:
−1 ≤ ρ ( X ,Y ) ≤1
ρ ( X ,Y )=± 1, X, Y có quan hệ tuyến tính, Y=aX+b
ρ càng gần 0 thì X, Y càng ít tương quan.
ρ=0 thì X, Y không tương quan.
Ví dụ 5. Tìm hệ số tương quan của vòng eo và khối lượng. Khối lường (Kg) (X) 51 66 47 54 64 75 54 52 Vống ệố (cm) (Y) 71 89 64 74 87 93 66 74 XY 3621 5874 3008 3996 5568 6975 3564 3848 Ta có: n=8.
X =57,875 ;S2X=(51−X)2+..=89,554 8−1
Y =77,25; S2Y=120,5 XY =4556,75
Hiệp phương sai: Cov ( X ,Y )= n ( X Y− X .Y )=98,1786 n−1 Hệ số tương quan:
ρ ( X , Y )= Cov( X ,Y ) √ = 98,1786 =0,9451 s2 2 √89,554.120,5 X . sY
Kết luận: Khối lượng và vòng eo tương quan rất mạnh.
Dùng máy tính tìm hệ số tương quan (r) Máy VNX MENU>6>2 Nhập 2 cột AC>OPTN>3 Khác MODE>3>2 Nhập 2 cột AC>SHIFT>1>5>35
Kiểm tra 3 đến 30/7 trên elearning. Tự luận: làm 1 lần.