Kĩ năng tìm biểu thức liên hợp hoặc nhân tử của phương trình vô tỉ – Vũ Hồng Phong

Tài liệu gồm 206 trang hướng dẫn kỹ năng tìm biểu thức liên hợp hoặc nhân tử của phương trình vô tỉ để giải các phương trình vô tỉ, tài liệu được biên soạn bởi thầy Vũ Hồng Phong.

Chuyên đề 1. Phương trình vô tỉ không dùng Casio hỗ trợ
Chuyên đề này gồm các phương trình có nghiệm đẹp ta hoàn toàn nhẩm được. Dù vất vả trong việc nhẩm và tính toán nhưng giúp chúng ta tiến bộ khi học môn toán.
I. Các phương trình tìm biểu thức liên hợp không dùng Casio


Một số ví dụ ngoài cách nhân liên hợp có thể làm theo hướng đưa về tích hoặc tìm tổng và hiệu các căn rồi tìm từng căn theo x.
II. Các phương trình tìm nhân tử không dùng Casio

 

86 43 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

206 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
1
PHƢƠNG TRÌNH VÔ TỈ ĐƢA VỀ DẠNG TÍCH
KĨ NĂNG TÌM BIỂU THỨC LIÊN HỢP HOẶC NHÂN TỬ
CỦA PHƢƠNG TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh
BẢN CHÍNH THỨC
Lƣu ý trƣớc khi sử dụng tài liệu
+Bài viết gồm 5 chuyên đề: Chuyên đề 1 là các phƣơng trình không dùng Casio .Chuyên đề 2 và 3 là các thí dụ dùng máy
tính Casio có hƣớng dẫn sơ lƣợc, chuyên đề 4 và 5 là lí thuyết hƣớng dẫn chi tiết cách dùng máy tính Caiso tìm biểu thức
liên hợp hoặc tìm nhân tử cần xuất hiện trong phƣơng trình của chuyên đề 2 và 3. Trong đó có chuyên đề phụ một cách
tạo ra một phƣơng trình tích từ các biểu thức phù hợp
+Do có nhiều phƣơng trình mới lạ và phức tạp nên bài viết không là tài liệu để ôn tập cho các kì thi
+Các PT trong bài viết có nghiệm là nghiệm của PT bậc 3,bậc 4 nên nó phức tạp hơn các dạng PT khác
+Các phƣơng trình chƣa đƣợc sắp xếp thành hệ thống hợp lí và có thể có sai sót
+Tài liệu cung cấp một số ý tƣởng để tạo ra các phƣơng trình vô tỷ đƣa về dạng tích
Chuyên đề 1. PHƢƠNG TRÌNH VÔ TỈ KHÔNG DÙNG CASIO HỖ TRỢ
Chuyên đề này gồm các PT có nghiệm đẹp ta hoàn toàn nhẩm được. Dù vất vả trong việc nhẩm và tính
toán nhưng giúp chúng ta tiến bộ khi học môn Toán.
A.Các Phƣơng trình tìm biểu thức liên hợp không dùng Casio
Một số ví dụ ngoài cách nhân liên hợp có thể làm theo hướng đưa về tích hoặc tìm tổng và hiệu các căn
rồi tìm từng căn theo x.
Thí dụ 1 Giải phƣơng trình
322122126
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
2
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
PTcó 3 nghiệm
3;1;0 xxx
Nâng cấp: Giải phƣơng trình
23
32
122
1
126
1
)
2
xx
x
xxxxxx
a
23
75
122
3
126
2
)
2
xx
x
xxxxxx
b
PTcó 2 nghiệm
;0x
1x
(lƣu ý coi
3 xt
là nghiệm ngoại lai)
25
286
126)
2
2334
2
xx
xxxxx
xxc
Hƣớng dẫn.
0)1261)(126126(
2222
xxxxxxxxpt
PTcó 4 nghiệm
3
1
;3;1;0
xxxx
9122126)
3
22
3
22
xxxxxxxxd
PTcó 3 nghiệm
3;1;0 xxx
1332122126)
23
3
22
3
22
xxxxxxxxxxe
PTcó 3 nghiệm
3;1;0 xxx
2
12
122
1
2
22
)
2
2
2
xx
xx
x
xx
x
f
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
3
Hƣớng dẫn.
2
)1(2
12
122
1
2
2
2
2
xx
x
xx
xx
xPT
2
1
122
1221
2
2
2
2
xx
x
xx
xxx
0)1(1222)2(11221
222222
xxxxxxxxxxx
Nhân liên hợp suy ra PTcó 3 nghiệm
3;1;0 xxx
Chú ý: biểu thức liên hợp cần tìm là
1222
22
xxxx
biểu thức liên hợp nữa cần tìm là
12211
22
xxxx
2
12
422
2
2
)
2
234
2
xx
xxx
xx
x
h
Hƣớng dẫn.
2
2
122
422
2
2
2
234
xx
x
xx
xxx
PT
Biến đổi tƣơng tự bài trƣớc và nhân liên hợp suy ra PTcó 3 nghiệm
3;1;0 xxx
3
1
62
126
)
2
2
2
xx
xx
xx
k
Hƣớng dẫn.
0)1(62311263
2222
xxxxxxxxPT
nhân liên hợp suy ra PTcó 2 nghiệm
3;1 xx
4
4
126
13102
)
22
2
xx
x
xx
xx
p
Hƣớng dẫn. Nhận thấy
4x
0)4(621413102)4(
2222
xxxxxxxxxxPT
nhân liên hợp suy ra PTcó 2 nghiệm
3;1 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
4
433
28
12126)
2
2
22
xx
xx
xxxxq
Hƣớng dẫn.
433
)12126)(12126(2
12126
2
2222
22
xx
xxxxxxxx
xxxxPT
(*)4331221262
012126
222
22
xxxxxx
xxxx
PT
Giải (*):Biểu thức liên hợp cần tìm là
1261
22
xxxx
biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
PT đã cho có 4 nghiệm
4
1
;3;1;0 xxxx
(*)3212623122)
22
xxxxxxxs
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1;0
Giả sử biểu thức liên hợp cần tìm là
)(23122
2
baxxxx
Do
1;0
là nghiệm PT nên ta có hệ
3
2
ba
b
2
1
b
a
Biểu thức liên hợp cần tìm là
)2(23122
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)1(126
2
xxxx
Do
0(*) VT
suy ra
2
3
x
Xét
2
3
1
x
có:
xxx 126
2
xxxx 1224
22
124
2
xxxxx
suy ra
1(*) VT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
5
Do
2
3
1
x
suy ra
132(*) xVP
Vì vậy PT(*) có nghiệm
1x
Khi đó
0)1(126
2
xxxx
0)2(23122
2
xxxx
0
2
)1(126
1
)2(122
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
1;0 xx
1077
10212
1231262)
2
2
22
xx
xx
xxxxt
Hƣớng dẫn.
1077
)1231262)(1231262(2
1231262
2
2222
22
xx
xxxxxxxx
xxxxPT
(*)10771261264
01231262
222
22
xxxxxx
xxxx
PT
Giải (*):Biểu thức liên hợp cần tìm là
1261
22
xxxx
biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
PT đã cho có 4 nghiệm
6
5
;3;1;0 xxxx
*Một cách tạo ra phƣơng trình từ 2 biểu thức liên hợp
Dạng PT:
B
a
b
A
hay
B
b
a
A
Cách giải.
0)()( bBaaAB
B
b
a
A
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
6
Nhân liên hợp ta sẽ giải quyết đƣợc PT đã cho
Thí dụ minh họa Giải phƣơng trình
122
1
2
126
2
2
2
2
xx
xx
xx
xx
Hƣớng dẫn.
0)2(112622122126
222222
xxxxxxxxxxxxPT
Nhân liên hợp PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 2 Giải phƣơng trình
5441221263
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
01222]1261[3
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 3 Giải phƣơng trình
53
1262
122
124
2
2
2
2
xx
xxx
xx
xx
Hƣớng dẫn.
Ta có
xxxxxxxx 224)1(4126
22222
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
7
nên đkxđ:
Rx
53
1262
)2(126
124
2
2
2
2
2
2
xx
xxx
xxx
xxpt
533124126
222
xxxxxx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
0]1222[21261
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 4 Giải phƣơng trình
24
1261
15
122
2
2
2
2
xx
xxx
x
xx
Hƣớng dẫn.
24
1261
)1(126
.3122
2
2
2
2
2
2
xx
xxx
xxx
xxpt
5441221263
222
xxxxxx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
8
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
01222]1261[3
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 5 Giải phƣơng trình
794
126
125
12
666
2
2
2
2
2
xx
xxx
xx
xxx
xx
Hƣớng dẫn.
794
126
)(126
2122
)2(122
.3
2
2
2
2
2
2
2
2
2
xx
xxx
xxx
xxx
xxx
pt
5441221263
222
xxxxxx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
01222]1261[3
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
9
Thí dụ 6 Giải phƣơng trình
76391274852
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
0912732)48522(2
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Nâng cấp: Giải phƣơng trình
23
52
29127
1
2485
1
)
2
xx
x
xxxxxx
a
23
73
29127
2
2485
1
)
2
xx
x
xxxxxx
b
PTcó 3 nghiệm
;0x
9;1 xx
c)
9127
32
22
485
2
2
2
2
xx
xx
xx
xx
Hƣớng dẫn.
0)22(329127224859127
222222
xxxxxxxxxxxxPT
Nhân liên hợp PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
10
763
72013
91274852)
2
2
22
xx
xx
xxxxd
Hƣớng dẫn.
763
)91279852)(91279852(
91274852
2
2222
22
xx
xxxxxxxx
xxxxPT
091274852
091274852
22
22
xxxx
xxxx
PT
PT đã cho có 4 nghiệm
13
7
;3;1;0 xxxx
(*)3216912714485)
22
xxxxxxxe
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
)(14485
2
baxxxx
Do
3;1;0
là nghiệm PT nên ta có hệ
43
1
1
ba
ba
b
2
1
b
a
Biểu thức liên hợp cần tìm là
)1(14485
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)2(169127
2
xxxx
ĐKXĐ:
)1(014485
2
xxx
và
)2(0169127
2
xxx
Có:
11
3
)1(
x
29
94212
)2(
x
suy ra
11
3
x
Khi đó
0)1(14485
2
xxxx
0)2(169127
2
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
11
0
2
)32(9127
1
)22(885
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
3;1;0 xxx
Thí dụ 7 Giải phƣơng trình
3
6104
912732
8
485
2
2
2
2
xx
xxx
xx
xx
Hƣớng dẫn.
3
6104
)912732(3
)329127)(329127(
485
2
2
22
2
xx
xxx
xxxxxx
xxpt
3
6104
3
329127
485
22
2
xxxxx
xx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
0912732)48522(3
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 8 Giải phƣơng trình
3
944
912732
8
12485
312
2
2
2
2
2
xx
xxx
xx
xxx
xx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
12
3
944
)912732(3
)329127)(329127(
12485
)12485)(12485(
2
2
22
2
22
xx
xxx
xxxxxx
xxx
xxxxxx
pt
3
944
3
329127
12485
22
2
xxxxx
xxx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
0912732)48522(3
2222
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 9 Giải phƣơng trình
622810184614
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
13
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
081018446142
2222
xxxxxxxxPT
PTcó 4 nghiệm
4;1;2 xxx
Nâng cấp:
81018
4
2
4614
2
2
2
2
xx
xx
xx
xx
0)2(4810182461481018
222222
xxxxxxxxxxxxPT
PTcó 4 nghiệm
4;1;2 xxx
Thí dụ 10 Giải phƣơng trình
773
8101814
7182
46142
2
2
2
2
xx
xxx
xx
xx
Hƣớng dẫn.
773
8101814
)1481018)(1481018(
46142
2
2
22
2
xx
xxx
xxxxxx
xxPT
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
0810184]46142[2
2222
xxxxxxxxPT
PTcó 4 nghiệm
3;2;1 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
14
Thí dụ 11 Giải phƣơng trình
10448101846143
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
0810184]46142[3
2222
xxxxxxxxPT
PTcó 4 nghiệm
4;1;2 xxx
Thí dụ 12 Giải phƣơng trình
723
1481018
1444
461413
5125
2
2
2
2
2
xx
xxx
xx
xxx
xx
Hƣớng dẫn.
723
1481018
)1481018)(1481018(
.2
461413
)134614)(134614(
2
2
22
2
22
xx
xxx
xxxxxx
xxx
xxxxxx
PT
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
15
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
0]810184[246142
2222
xxxxxxxxPT
PTcó 4 nghiệm
3;2;1 xxx
Thí dụ 13 Giải phƣơng trình
742283213212811
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;2;1
Giả sử biểu thức liên hợp cần tìm là
212811
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
1124
324
2
caa
cba
cba
3
2
1
c
b
a
Biểu thức liên hợp cần tìm là
21281132
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
28321342
22
xxxx
02832134221281132
2222
xxxxxxxxPT
PTcó 4 nghiệm
3;2;1 xxx
Nâng cấp: Giải phƣơng trình
127
72
2283213
1
2212811
1
)
2
xx
x
xxxxxx
a
127
103
29127
2
2485
1
)
2
xx
x
xxxxxx
a
PTcó 3 nghiệm
;1x
9;4 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
16
Thí dụ 14 Giải phƣơng trình
5221314102322
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức liên hợp cần tìm là
23222
22
xxxx
và
1314103
22
xxxx
PTcó 3 nghiệm
2;1 xx
Thí dụ 15 Giải phƣơng trình
114413141032322
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức liên hợp cần tìm là
23222
22
xxxx
và
1314103
22
xxxx
PTcó 3 nghiệm
2;1 xx
Thí dụ 16 Giải phƣơng trình
7331314102324
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức liên hợp cần tìm là
23222
22
xxxx
và
1314104
22
xxxx
PTcó 3 nghiệm
2;1 xx
Thí dụ 17 Giải phƣơng trình
x
xx
xxxx
225
889664
2
22
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
17
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2
1
;1
Biểu thức liên hợp cần tìm là
66412
22
xxxxx
và
88913
22
xxxxx
PTcó 3 nghiệm
2
1
;1 xx
Thí dụ 18 Giải phƣơng trình
x
xx
xxxx
449
8896643
2
22
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2
1
;1
Biểu thức liên hợp cần tìm là
66412
22
xxxxx
và
88913
22
xxxxx
PTcó 3 nghiệm
2
1
;1 xx
Thí dụ 19 Giải phƣơng trình
x
xx
xxxx
337
8896642
2
22
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2
1
;1
Biểu thức liên hợp cần tìm là
66412
22
xxxxx
và
88913
22
xxxxx
PTcó 3 nghiệm
2
1
;1 xx
Thí dụ 20 Giải phƣơng trình
2
2
5889664
22
x
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
18
Hƣớng dẫn.
x
xx
xxxxPT
225
889664
2
22
Do
0225
2
xx
nên
0x
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là
2
1
;1
Biểu thức cần tìm là
2342
66412 xxxxx
và
2342
889123 xxxxx
PTcó 2 nghiệm
;1x
2
1
x
Thí dụ 21 Giải phƣơng trình
3
3
78896642
22
x
xxxxx
Hƣớng dẫn.
x
xx
xxxxPT
337
889664
2
22
Do
0337
2
xx
nên
0x
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là
2
1
;1
Biểu thức cần tìm là
2342
66412 xxxxx
và
2342
889123 xxxxx
PTcó 2 nghiệm
;1x
2
1
x
225889664
2234234
xxxxxxxxPT
3378896642
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
19
Thí dụ 22 Giải phƣơng trình
x
xx
xxxx
423
631054
2
22
Hƣớng dẫn.
Do
0423
2
xx
nên
0x
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là
2;1
Biểu thức cần tìm là
2342
105422 xxxxx
và
2342
632 xxxxx
PTcó 2 nghiệm
1x
2; x
Thí dụ 23 Giải phƣơng trình
x
xx
xxxx
845
6331054
2
22
Hƣớng dẫn.
Do
0423
2
xx
nên
0x
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là
2;1
Biểu thức cần tìm là
2342
105422 xxxxx
và
2342
632 xxxxx
PTcó 2 nghiệm
1x
2; x
Thí dụ 24 Giải phƣơng trình
132110241242
223434
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2
1
;0;2
423631054
2234234
xxxxxxxxPT
8456331054
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
20
Biểu thức liên hợp cần tìm là
12412
342
xxxx
và
1102412
2342
xxxxx
PTcó 3 nghiệm
2
1
;0;2
xxx
Thí dụ 25 Giải phƣơng trình
62516491669
22424
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức liên hợp cần tìm là
xxxxx 692
242
và
xxxxx 16491644
242
PTcó 3 nghiệm
2;1 xx
Thí dụ 26 Giải phƣơng trình
12543216224214
22424
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1;2
Biểu thức liên hợp cần tìm là
xxxxx 2421442
242
và
xxxxx 32162842
242
PTcó 3 nghiệm
1;2 xx
Thí dụ 27 Giải phƣơng trình
432)25(2)8134(
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1;2
Biểu thức liên hợp cần tìm là
)8134(2
22
xxxxx
và
)25(222
22
xxxxx
PTcó 4 nghiệm
1;2 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
21
Thí dụ 28 Giải phƣơng trình
31454
22334
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;1;0
Biểu thức liên hợp cần tìm là
42
342
xxxx
và
1451
23
xxx
PTcó 3 nghiệm
4;1;0 xxx
Thí dụ 29 Giải phƣơng trình
2)15(44
2334
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;1;0
Biểu thức liên hợp cần tìm là
42
342
xxxx
và
xxx 45
3
PTcó 3 nghiệm
4;1;0 xxx
Thí dụ 30 Giải phƣơng trình
52)15(5144
2334
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;1;0
Với
1x
thì
0105141514
3
xx
.
Do đó nghiệm PT phải thỏa mãn
011 xx
Biểu thức liên hợp cần tìm là
42
342
xxxx
và
514)1(5
3
xxx
PTcó 3 nghiệm
4;1;0 xxx
Thí dụ 31 Giải phƣơng trình
1)1)(42(1
2224
xxxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
22
1)1)(42(1)(
2224
xxxxxxxfPT
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1,0
12
4242
143
1
2
)('
23
2
24
3
x
xxx
xx
xx
xx
xf
Ta có
0)1(' f
nên PT có nghiệm bội
1x
(tính
0)1('' f
Pt có nghiệm kép
1x
)
Các ví dụ kiểm tra chính xác là nghiệm kép xin dành cho bạn đọc)
Giả sử biểu thức liên hợp cần tìm là
1
242
xxcbxax
Lấy đạo hàm đƣợc biêu thức
1
2
2)(
24
3
xx
xx
baxxP
Do
0;1
là nghiệm PT nên ta có hệ
(*)
1
1
c
cba
3
2
1
c
b
a
Do PT có nghiệm kép
1x
nên nó là nghiệm của P(x)
suy ra
(**)012 ba
Từ (*) và (**) suy ra
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
11
242
xxxx
Tƣơng tự
1)1)(42(
2
xx
PTcó 2 nghiệm
1;0 xx
Thí dụ 32 Giải phƣơng trình
34216244)1(
232
xxxxxxx
Hƣớng dẫn.
Nếu
1x
thì
07162162
3
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
23
Suy ra
011 xx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1,0 xx
và dùng đạo hàm thấy
1x
là nghiệm
kép
Biểu thức cần tìm là
44)1(222
22
xxxxx
và
16212
3
xxx
PTcó 2 nghiệm
1;0 xx
Thí dụ 33 Giải phƣơng trình
221621)1(
232
xxxxxxx
Hƣớng dẫn.
Nếu
1x
thì
07162162
3
xx
Suy ra
011 xx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1,0 xx
và dùng đạo hàm thấy
1x
là nghiệm kép
Biểu thức cần tìm là
1)1(1
22
xxxxx
và
16212
3
xxx
PTcó 2 nghiệm
1;0 xx
Thí dụ 34 Giải phƣơng trình
23122131
222
xxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
1,0 xx
và đều là nghiệm kép
Biểu thức cần tìm là
13112
22
xxxx
và
1221
22
xxxx
PTcó 2 nghiệm
1;0 xx
Thí dụ 35 Giải phƣơng trình
462369
2232
xxxxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
24
ĐK :
3
2
x
.Ta nhẩm đƣợc các nghiệm đẹp của PT là
3
2
;2,1 xxx
Chú ý:Ta phải tinh ý khi thấy xuất hiện các biểu thức
46;23;69
23
xxxx
để nhẩm
nghiệm khó là
3
2
x
Biểu thức cần tìm là
6923
22
xxxxx
và
23
323 xxx
PTcó 3 nghiệm
3
2
;2,1 xxx
Thí dụ 36 Giải phƣơng trình
53292871212
2
3
24
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
1;2,1 xxx
Biểu thức cần tìm là
121222
42
xxxx
và
3
2
292873 xxx
Chú ý
3
2
29287;3 xxx
không đồng thời bằng 0.
PTcó 3 nghiệm
1;2,1 xxx
Thí dụ 37 Giải phƣơng trình
23221212
2
3
24
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
1;2,1 xxx
Biểu thức cần tìm là
121222
42
xxxx
và
3
2
22 xxx
Chú ý
3
2
22; xxx
không đồng thời bằng 0.
PTcó 3 nghiệm
1;2,1 xxx
Thí dụ 38 Giải phƣơng trình
xxxxxx 361381212
2
3
24
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
25
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
1;2,1 xxx
Biểu thức cần tìm là
121222
42
xxxx
và
3
2
61382 xxx
Chú ý
3
2
6138;2 xxx
không đồng thời bằng 0.
PTcó 3 nghiệm
1;2,1 xxx
PT có 3 nghiệm là
1;2,1 xxx
Thí dụ 39 Giải phƣơng trình
333101236
2
3
24
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
4,1 xx
Với
1x
là nghiệm bội(bài này nghiệm kép)
Biểu thức cần tìm là
123622
42
xxxx
và
3
2
3101 xxx
PTcó 2 nghiệm
4,1 xx
Thí dụ 40 Giải phƣơng trình
323741054
2
3
22
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
2;2,1 xxx
Biểu thức cần tìm là
105422
22
xxxxx
và
3
2
3741 xxx
Chú ý
3
2
374;1 xxx
không đồng thời bằng 0.
Nghiệm của PT là
2;2,1 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
26
PHẦN BỔ XUNG CÁCH TÌM NGHIỆM NGOẠI LAI KIỂU MỚI
Thí dụ 41 Giải phƣơng trình
231826485
22
xxxxxxx
Hƣớng dẫn. Điều kiện
3
1
x
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
3,1 xx
Để tìm thêm nghiệm ngoại lai khi nay ta để ý
1826 xxx
có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời
01826 xxx
thấy thỏa mãn
Các biểu thức cần tìm là
48522
22
xxxx
và
26
2
xxxx
và
1`82
2
xxxx
Lƣu ý:Chỉ cần tìm
261 xx
và
1`82 xx
có 2 nghiệm
3,1 xx
Nghiệm của PT là
3,1 xx
Thí dụ 42 Giải phƣơng trình
2428326485
222
xxxxxxx
Hƣớng dẫn. Điều kiện
3
1
x
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
3,1 xx
Để tìm thêm nghiệm ngoại lai khi này ta để ý
28326
2
xxxx
có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời
01826 xxx
thấy thỏa mãn
Các biểu thức cần tìm là
48522
22
xxxx
và
26
2
xxxx
và
2832
22
xxxxx
Nghiệm của PT là
3,1 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
27
Thí dụ 43 Giải phƣơng trình
xxxxxxx 23221)2(228125
222
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
1,1 xx
Để tìm thêm nghiệm ngoại lai khi này ta để ý
xxxx 23221)2(
22
có nhân tử là
2x
Thay x=2 vào PT với qui ƣớc tạm thời
023221)2(
22
xxxx
thấy thỏa mãn
0228125
2
xxx
Các biểu thức cần tìm là
812522
22
xxxx
và
xxx 2322
2
Nghiệm của PT là
1,1 xx
Thí dụ 44 Giải phƣơng trình
222)2(8125
222
xxxxx
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
1,1 xx
Để tìm thêm nghiệm ngoại lai khi này ta để ý
22
2)2( xx
có nhân tử là
2x
Thay x=2 vào PT với qui ƣớc tạm thời
22
2)2( xx
thấy thỏa mãn
228125
2
xxx
Các biểu thức cần tìm là
812522
22
xxxx
và
xxx 2322
2
Nghiệm của PT là
1,1 xx
Thí dụ 45 Giải phƣơng trình
22421826485
2322
xxxxxxxx
Hƣớng dẫn. Điều kiện
3
1
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
28
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
3,1 xx
Để tìm thêm nghiệm ngoại lai khi nay ta để ý
1826 xxx
có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời
01826 xxx
thấy thỏa mãn
Các biểu thức cần tìm là
48522
22
xxxx
và
261 xx
và
1`82 xx
Nghiệm của PT là
3,1 xx
Thí dụ 46 Giải phƣơng trình
23891017485
2
3
2
3
22
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
3,1;0 xxx
Các biểu thức cần tìm là
48522
22
xxxx
và
3
2
171 xx
và
3
2
89102 xxx
Nghiệm của PT là
3,1;0 xxx
Thí dụ 47 Giải phƣơng trình
1438158273011126
2
3
2
3
22
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
1;3,0 xxx
Các biểu thức cần tìm là
1261
22
xxxx
(và
3
2
2730113 xxx
và
3
2
81582 xxx
tìm với 2 nghiệm
1;3 xx
)
Nghiệm của PT là
1;3,0 xxx
Thí dụ 48 Giải phƣơng trình
4431826)1(247
22
xxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
29
Hƣớng dẫn. Điều kiện
3
1
x
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
3,1 xx
Để tìm thêm nghiệm ngoại lai khi nay ta để ý
1826)1( xxx
có nhân tử là x+1
Thay x=-1 vào PT với qui ƣớc tạm thời
01826)1( xxx
thấy thỏa mãn
Các biểu thức cần tìm là
2471
22
xxxx
và
26)1(12
2
xxxx
và
1`8)1(23
2
xxxx
Lƣu ý:Có thể chỉ cần tìm
261 xx
và
1`82 xx
có 2 nghiệm
3,1 xx
Nghiệm của PT là
3,1 xx
Thí dụ 49 Giải phƣơng trình
34428326)1(247
222
xxxxxxxx
Hƣớng dẫn. Điều kiện
3
1
x
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
3,1 xx
Để tìm thêm nghiệm ngoại lai khi nay ta để ý
28326)1(
2
xxxx
có nhân tử là x+1
Thay x=-1 vào PT với qui ƣớc tạm thời
01826)1( xxx
thấy thỏa mãn
Các biểu thức cần tìm là
2471
22
xxxx
và
26)1(12
2
xxxx
và
283)1(132
22
xxxxx
Lƣu ý:Chỉ cần tìm
261 xx
và
1`812 xx
có 2 nghiệm
3,1 xx
Nghiệm của PT là
3,1 xx
Thí dụ 50 Giải phƣơng trình
77110742)2(
2222
xxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
30
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
2,0 xx
Các biểu thức cần tìm là
422
2
xx
và
11071
22
xxxx
Nghiệm của PT là
2,0 xx
Thí dụ 51 Giải phƣơng trình
3426212225
22222
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
3;1,0 xxx
Các biểu thức cần tìm là
623
222
xxxx
và
3423
222
xxxx
1222
22
xxxx
Nghiệm của PT là
3;1,0 xxx
Thí dụ 52 Giải phƣơng trình
)3421(3212222
22
3
4522
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
3;1,0 xxx
Các biểu thức cần tìm là
3
2
3
452
3232 xxxxxxx
và
3423
222
xxxx
và
1222
22
xxxx
Lƣu ý: xét x=0 và
0x
Nghiệm của PT là
3;1,0 xxx
Thí dụ 53 Giải phƣơng trình
242892.485
2
3
22
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
3;1,0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
31
Các biểu thức cần tìm là
3
22
892.2 xxxxx
và
48522
22
xxxx
Nghiệm của PT là
3;1,0 xxx
Thí dụ 54 Giải phƣơng trình
228158.122
2
3
22
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
3;1,0 xxx
Các biểu thức cần tìm là
3
22
8158.2 xxxxx
và
1222
22
xxxx
Nghiệm của PT là
3;1,0 xxx
Thí dụ 55 Giải phƣơng trình
2226138)2(8125
2
3
22
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
2;1,1 xxx
Các biểu thức cần tìm là
3
2
61382 xxx
và
812522
22
xxxx
Nghiệm của PT là
2;1,1 xxx
Thí dụ 56 Giải phƣơng trình
2785)1(453
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
4;1 xx
Các biểu thức cần tìm là
xxxx 453432
22
nhận nghiệm là
4;1 xx
và
852
2
xx
nhận nghiệm là
4;1 xx
Nghiệm của PT là
4;1 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
32
Thí dụ 57 Giải phƣơng trình
19135)1(453
2222
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
4;1 xx
Các biểu thức cần tìm là
xxxx 453432
22
nhận nghiệm là
4;1 xx
và
1353
2
xx
nhận nghiệm là
4;1 xx
Nghiệm của PT là
4;1 xx
Thí dụ 58 Giải phƣơng trình
3555)1(453
2222
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
4;1 xx
Các biểu thức cần tìm là
xxxx 453432
22
nhận nghiệm là
4;1 xx
và
851
2
xx
nhận nghiệm là
4;1 xx
Nghiệm của PT là
4;1 xx
Thí dụ 59 Giải phƣơng trình
121221126
22
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
33
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Suy ra
126
2
xxx
tƣơng ứng với
1)1(1
22
xxxxx
1221
2
xxx
tƣơng ứng với
1)1(21
22
xxxxx
0112211126
22
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 60 Giải phƣơng trình
151281145126173
2222
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Suy ra
126173
22
xxxx
tƣơng ứng với
12 x
1281145
22
xxxx
tƣơng ứng với
13 x
013128114512126173
2222
xxxxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
34
Thí dụ 61 Giải phƣơng trình
3211221126458
22
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Suy ra
126458
2
xxx
tƣơng ứng với
32)32(44458
22
xxxxx
1221
2
xxx
tƣơng ứng với
1)1(21
22
xxxxx
01122132126458
22
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 62 Giải phƣơng trình
32312818126152133
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
35
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Suy ra
126152133
22
xxxx
tƣơng ứng với
322 x
12818
2
xxx
tƣơng ứng với
32 x
3212818322126152133
222
xxxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
01429127262485
3
22
3
22
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 63 Giải phƣơng trình
112261628
3
22
3
22
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
36
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
02122631628
3
22
3
22
xxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 64 Giải phƣơng trình
31223165
2222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
0112232165
2222
xxxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 65 Giải phƣơng trình
512211165
2222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
37
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
03122112165
2222
xxxxxxxxPt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 66 Giải phƣơng trình
71221016
3
22
3
22
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
0812210116
3
22
3
22
xxxxxxxxPt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 67 Giải phƣơng trình
86411261263
22222
xxxxxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
38
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
0)532(1126)332(163
2
2
222
2
22
xxxxxxxxxxPt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 68 Giải phƣơng trình
171142912734853
22222
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
0)1162(291273)652(4853
2
2
222
2
22
xxxxxxxxxxxPt
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
39
Thí dụ 69 Giải phƣơng trình
93381018146143
2222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
0)4(81018)532(146143
2
2
22
2
22
xxxxxxxxxPt
PTcó 4 nghiệm
3;2;1 xxx
Thí dụ 70 Giải phƣơng trình
2112212632
3
22
3
23
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
40
011122112632
3
22
3
23
xxxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 71 Giải phƣơng trình
1212212632
3
232
3
23
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
02122112632
3
232
3
23
xxxxxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 72 Giải phƣơng trình
1242.126
2
3
222
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
2242
3
2
xx
0)2242()1(126
3
2222
xxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
41
Thí dụ 73 Giải phƣơng trình
132624.126
23
3
322
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Biểu thức liên hợp cần tìm là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
2242
3
2
xxx
0)2242()1(126
3
2222
xxxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 74 Giải phƣơng trình
5
2
3126
3
421262
2
2
2
2
x
xxx
x
xxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
0
2
)2122(3
3
)1126(2
2
22
2
22
x
xxxx
x
xxxx
pt
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
42
Thí dụ 75 Giải phƣơng trình
4
2
281018
1
3346143
2
2
2
2
x
xxx
x
xxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
01
2
281018
3
1
3346143
2
2
2
2
x
xxx
x
xxx
pt
PTcó 4 nghiệm
3;2;1 xxx
Thí dụ 76 Giải phƣơng trình
2222
)3(11222126 xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
43
2
222222
31122)3(11221126 xxxxxxxxxxxxPT
02122)3(11221126
222222
xxxxxxxxxxxx
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 77 Giải phƣơng trình
2222
)5(18101834614 xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
4;2;1
Giả sử biểu thức liên hợp cần tìm là
4614
22
xxcbxax
Do
2;1
là nghiệm PT nên ta có hệ
824
4
2
caa
cba
cba
2
1
1
c
b
a
Biểu thức liên hợp cần tìm là
46142
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
810184
22
xxxx
0481018)5(18101824614
222222
xxxxxxxxxxxxpt
PTcó 4 nghiệm
3;2;1 xxx
Thí dụ 78 Giải phƣơng trình
222222
)32(11222126 xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
44
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
02122)32(11221126
2222222
xxxxxxxxxxxxxPT
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 79 Giải phƣơng trình
122
124
4
3
2
2
2
2
2
xx
xx
x
xx
x
xx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
01222)
124
4
1(
22
2
2
2
xxxx
xx
x
xx
x
Pt
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 80 Giải phƣơng trình
126
2
104
432
2
2
2
xx
x
x
xx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1261
22
xxxx
01261
2
104
52
22
2
2
xxxx
x
x
xxpt
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
45
0
1261
32
2
32
22
224
2
234
xxxx
xxx
x
xxx
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 81 Giải phƣơng trình
126
2
104
432
2
2
2
xx
x
x
xx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1261
22
xxxx
01261
2
104
52
22
2
2
xxxx
x
x
xxpt
0
1261
32
2
32
22
224
2
234
xxxx
xxx
x
xxx
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 82 Giải phƣơng trình
11221261412
2222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
biểu thức liên hợp nữa cần tìm là
1412|122|
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1261
22
xxxx
014121221261
2222
xxxxxxxxpt
PTcó 3 nghiệm
3;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
46
Thí dụ 83 Giải phƣơng trình
2
2
2
2
2
2
2
2
2
2
2
12)1(2
2
2
122
126
)1)(1(
2
126
1
x
xx
xxx
xx
xx
x
xx
xxx
xx
xx
Hay
12)1(22
122422
126)1)(1(
12621
2234
22
222
22
xxxxxx
xxxx
xxxxxx
xxxx
Hƣớng dẫn.
Giải phƣơng trình đã cho ta không cần nhẩm nghiệm, mà biến đổi về PT tích rồi nhân liên
hợp.
Các bạn đọc phần ghép 2 phƣơng trình thành 1 phƣơng trình viết ở phần tìm biểu thức
liên hợp dùng Casio sẽ biết hƣớng làm cụ thể.
Dạng PT thí dụ này nhƣ sau :
npmq
d
c
b
a
qp
b
a
nm
d
c
qp
d
c
nm
b
a
))(())((
Ý tƣởng :PT ở thí dụ 73 đƣợc tạo ra từ
Thí dụ 1 Giải phƣơng trình
322122126
222
xxxxxx
Biểu thức liên hợp là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa là
1222
22
xxxx
Và chọn
2
;1;2;1 xqxpnm
PTcó 5 nghiệm
(đã kiểm tra)
31;3;1;0 xxxx
Thí dụ 84 Giải phƣơng trình
x
xx
xxx
x
xx
xxx
xx
xx
xx
xx
131410
)3)(1(
2
232)1(2
9
131410
3
9
2
2322
2
2
2
2
2
2
2
2
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
47
Hay
131410)3)(1(
232)1(22
13141093
23221899
22
223
22
22
xxxxxx
xxxxxx
xxxx
xxxx
Hƣớng dẫn.
PT thí dụ 74 được tạo ra từ PT:
5221314102322
222
xxxxxx
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức liên hợp cần tìm là
23222
22
xxxx
và
1314103
22
xxxx
Chọn
xqxpnm ;1;9;1
PTcó 4 nghiệm(đã kiểm tra)
8
9
;2;1
xxx
Thí dụ 85 Giải phƣơng trình
5
122
2
5
1
126
2
122
2
2
1
126
2
345
2
23
2
2
2
2
xx
xxx
xx
xxx
xx
xx
xx
xx
Hay
12102
126.555
1242
126222
2345
232
22
22
xxxxx
xxxxx
xxxx
xxxx
Hƣớng dẫn.
Giải phƣơng trình đã cho nhìn phức tạp ta không cần nhẩm nghiệm, mà cần biết nó có
dạng
npmq
d
c
b
a
qp
b
a
nm
d
c
qp
d
c
nm
b
a
))(())((
Nhƣ vậy ta cần biến đổi về PT tích rồi nhân liên hợp (nếu cần) bằng cách
00110
d
cd
b
ba
d
c
b
a
d
c
b
a
Từ PT
322122126
222
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
48
ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Do
3;1;0
là nghiệm PT nên ta có hệ
739
3
1
caa
cba
c
1
1
1
c
b
a
Biểu thức liên hợp cần tìm là
161
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1222
22
xxxx
PT đã cho có 4 nghiệm(đã kiểm tra)
3
2
5
;3;1;0 xxxx
Thí dụ 86 Giải phƣơng trình
122633
1242
1263
126222
22
22
223
22
xxxxx
xxxx
xxxxx
xxxx
Hƣớng dẫn.
Từ Thí dụ 1 Giải phƣơng trình
322122126
222
xxxxxx
Biểu thức liên hợp là
1261
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa là
1222
22
xxxx
Và chọn
xqpnm ;3;2;1
PTcó 4 nghiệm(đã kiểm tra)
6;3;1;0 xxxx
Thí dụ 87 Giải phƣơng trình
22
21
)2()2(
8125
2
22
2
x
x
xx
xx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
49
22)13()2(8125
222
xxxxxPT
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là
2;1,1 xxx
Các biểu thức cần tìm là
812522
22
xxxx
ứng với nghiệm của PT là
2;1,1 xxx
và
xxx 2322
2
ứng với nghiệm của PT là
1,1 xx
Nghiệm của PT đã cho là
1,1 xx
Thí dụ 88 Giải phƣơng trình
x
xx
xx
xxx
xx 846
633
1054
1053
2
2
2
2
Hƣớng dẫn.
x
xx
xx
xxx
xxxxxx
pt
846
633
1054
)654)(1054(
2
2
2
22
Ta nhẩm đƣợc các nghiệm đẹp của PT(*) là
2;1
Biểu thức cần tìm là
2342
105422 xxxxx
và
2342
632 xxxxx
PTcó 3 nghiệm
1x
2; x
Thí dụ 89 Giải phƣơng trình
x
xx
xx
xxx
xx 846
633
1054
1053
2
2
2
2
Hƣớng dẫn.
Do
010531054
222
xxxxxxxxx
Nên
0VT
mà
0846
2
xx
nên
0x
(*)8456331054
222
xxxxxxxx
8456331054
2234234
xxxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
50
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm ) của PT là
2;1
Biểu thức cần tìm là
2342
105422 xxxxx
và
2342
632 xxxxx
PTcó 2 nghiệm
1x
2; x
Thí dụ 90 Giải phƣơng trình
x
xx
xx
xxx
xx 637
14792
318916
1897
2
2
2
2
Hƣớng dẫn.
x
xx
xx
xxx
xxxxxx
pt
637
14792
318916
)318916)(318916(
2
2
2
22
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức cần tìm là
2342
1891624 xxxxx
và
2342
147923 xxxxx
PTcó 3 nghiệm
1x
2; x
Thí dụ 91 Giải phƣơng trình
x
xx
xx
xxx
xx 637
14792
318916
1897
2
2
2
2
Hƣớng dẫn.
x
xx
xx
xxx
xxxxxx
pt
637
14792
318916
)318916)(318916(
2
2
2
22
8456331054
2234234
xxxxxxxxPT
63101479218916
2234234
xxxxxxxx
63101479218916
2234234
xxxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
51
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức cần tìm là
2342
1891624 xxxxx
và
2342
147923 xxxxx
PTcó 3 nghiệm
1x
2; x
Thí dụ 92 Giải phƣơng trình
x
xx
xx
xxx
xx 637
14792
318916
1897
2
2
2
2
Hƣớng dẫn.
Tƣơng tự các ví dụ trên ta thấy
0x
x
xx
xx
xxx
xxxxxx
pt
637
14792
318916
)318916)(318916(
2
2
2
22
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức cần tìm là
2342
1891624 xxxxx
và
2342
147923 xxxxx
PTcó 3 nghiệm
1x
2; x
Thí dụ 93 Giải phƣơng trình
76346329105
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;0
Biểu thức liên hợp cần tìm là
910532
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
46322
22
xxxx
0)]22(463[2)32(9105
2222
xxxxxxxx
63101479218916
2234234
xxxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
52
PTcó 3 nghiệm
2;1;0 xxx
Nâng cấp:
a )Giải phƣơng trình
4434632
329105
2
22
2
2
xxxx
xxx
xx
4434632
329105
329105329105
22
2
22
xxxx
xxx
xxxxxx
pt
PTcó 3 nghiệm
2;1;0 xxx
b )Giải phƣơng trình
65
52
2463
1
29105
1
2
xx
x
xxxxxx
PTcó 3 nghiệm
4;1;0 xxx
c)Giải phƣơng trình
463
22
32
9105
2
2
2
2
xx
xx
xx
xx
0)3(22463329105463
222222
xxxxxxxxxxxxPT
PTcó 3 nghiệm
2;1;0 xxx
763
)1(7
91054632)
2
2
22
xx
x
xxxxd
Hƣớng dẫn.
763
)91054632)(41054632(
91054632
2
2222
22
xx
xxxxxxxx
xxxxPT
(*)76391054632
091054632
222
22
xxxxxx
xxxx
PT
Giải (*):Biểu thức liên hợp cần tìm là
910532
22
xxxx
biểu thức liên hợp nữa cần tìm là
46322
22
xxxx
PT đã cho có 3 nghiệm
2;1;0 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
53
Thí dụ 94 Giải phƣơng trình
863316728125
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;1
Biểu thức liên hợp cần tìm là
812522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1316732
22
xxxx
PT đã cho có 3 nghiệm
2;1;1 xxx
Nâng cấp: Giải phƣơng trình
(*)12321316718125
22
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1 xx
Biểu thức liên hợp cần tìm là
)1(18125
2
xxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)1(2413167
2
xxxx
Do
0(*) VT
suy ra
2
1
012(*) xxVP
Xét
1
2
1
x
có:
2431167
2
xxx
24131634
22
xxxx
24)133)(1(4
2
xxxx
12
2
1
.626244
2
xxx
suy ra
1(*) VT
Do
1
2
1
x
suy ra
112(*) xVP
Vì vậy PT(*) có nghiệm
1x
Khi đó
0)1(18125
2
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
54
0)1(2413167
2
xxxx
0
2
)32(1387
1
)22(8125
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
2;1 xx
Thí dụ 95 Giải phƣơng trình
9449884663
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;1;0
Biểu thức liên hợp cần tìm là
4662
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
9883
22
xxxx
PT đã cho có 4 nghiệm
0;2;1;1 xxxx
Nâng cấp: Giải phƣơng trình
(*)8413988323466
22
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
0;2;1 xxx
Biểu thức liên hợp cần tìm là
)2(23466
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)2(13988
2
xxxx
Do
0(*) VT
suy ra
2084(*) xxVP
Khi đó
0)2(23466
2
xxxx
0)2(23466
2
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
55
0
2
)3(488
.3
1
)2(466
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 4 nghiệm
0;2;1 xxx
Thí dụ 96 Giải phƣơng trình(Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn)
1
7126
1
22
3422
2
2
2
xx
xx
xx
Hƣớng dẫn.
Biểu thức cần tìm là
712622
22
xxxx
và
342232
22
xxxx
Ta có:
1
7126
1
22
3422
2
2
2
xx
xx
xx
222234227126
2222
xxxxxxxx
0)22(71263234227126
22222
xxxxxxxxxx
Nhân liên hợp PT đã cho có 3 nghiệm
3;1 xx
Thí dụ 97 Giải phƣơng trình
463
442
19105
2
2
2
2
xx
xx
xxx
Hƣớng dẫn.
Biểu thức cần tìm là
46322
22
xxxx
và
910532
22
xxxx
Ta có:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
56
463
442
19105
2
2
2
2
xx
xx
xxx
442129105463
2222
xxxxxxxx
0)227126(2329105463
22222
xxxxxxxxxx
Nhân liên hợp suy ra PT đã cho có 3 nghiệm
2;1;0 xxx
Thí dụ 98 Giải phƣơng trình(Vũ Hồng Phong )
1
232
1
2
5432
2
2
2
xx
xx
xx
Hƣớng dẫn.
Biểu thức cần tìm là
23222
22
xxxx
và
54324
22
xxxx
Ta có:
1
232
1
2
5432
2
2
2
xx
xx
xx
225432232
2222
xxxxxxxx
0)2(532245432232
22222
xxxxxxxxxx
Nhân liên hợp PT suy ra PT đã cho có 3 nghiệm
1;2 xx
Thí dụ 99 Giải phƣơng trình
1107
)1(
391411
2
22
2
xx
xxx
xxx
Hƣớng dẫn.
Biểu thức cần tìm là
914113
22
xxxx
và
11071
22
xxxx
Ta có:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
57
1107
)1(
391411
2
22
2
xx
xxx
xxx
)1(3914111107
2222
xxxxxxxx
0)]1(1107[3914111107
222222
xxxxxxxxxxx
Nhân liên hợp suy ra PT đã cho có 3 nghiệm
2;2;0 xxx
Thí dụ 100 Giải phƣơng trình
2
22
1
1
910171
1
4813
1
x
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
481322
22
xxxx
và
9101732
22
xxxx
Ta có:
2
22
1
1
910171
1
4813
1
x
xxxxxx
0
22
1
910171
1
22
1
4813
1
2
2
2
2
x
xxx
x
xxx
Nhân liên hợp 2 lần ở từng phân thức suy ra PT đã cho có 3 nghiệm
1;1;0 xxx
Chú ý:Biểu thức
04813
2
xxx
và
0910171
2
xxx
Thí dụ 101 Giải phƣơng trình
222
3
51062
1
12322
1
2
22
xx
xxxx
Hƣớng dẫn.
Biểu thức cần tìm là
23222
22
xxxx
và
51061
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
58
Ta có:
222
3
51062
1
12322
1
2
22
xx
xxxx
0
222
1
51062
1
1
1
12322
1
2
2
2
2
xx
xx
xx
xx
Nhân liên hợp 2 lần ở từng phân thức suy ra PT đã cho có 3 nghiệm
2;2;0 xxx
Chú ý:Biểu thức
012322
2
xx
và
05106
2
xx
Thí dụ 102 Giải phƣơng trình
62294)1(91611
2222
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
9161132
22
xxxx
và
943
2
xx
Ta có:
62294)1(91611
2222
xxxxxxx
0)394)(1()32(91611
2222
xxxxxxx
Nhân liên hợp suy ra PT đã cho có 4 nghiệm
4;1;1;0 xxxx
Nâng cấp
a) Giải phƣơng trình
32
1162013
91611
32
2
2
2
2
xx
xx
xx
xx
Hƣớng dẫn.
32
1162013
91611
32
2
2
2
2
xx
xx
xx
xx
0
32
1162013
11
91611
32
2
2
2
2
xx
xx
xx
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
59
0
32
16201342
91611
9161132
2
22
2
22
xx
xxxx
xx
xxxx
Nhân liên hợp suy ra PT đã cho có 3 nghiệm
4;1;1;0 xxxx
b) Giải phƣơng trình
2222
)3(12162013291611 xxxxxxx
Hƣớng dẫn.
3
12162013
291611
3
2
2
2
2
x
xxx
xxx
x
pt
0
3
12162013
11
291611
3
2
2
2
2
x
xxx
xxx
x
0
3
16201342
291611
9161132
2
22
2
22
x
xxxx
xxx
xxxx
Nhân liên hợp suy ra PT đã cho có 4 nghiệm
4;1;1;0 xxxx
Chú ý:
xxxx ,0291611
2
xxxx ,012162013
2
Nên ta có thể đƣa về giải bất phƣơng trình chẳng hạn
Giải bất phƣơng trình
2222
)3(12162013291611 xxxxxxx
Thí dụ 103 Giải phƣơng trình
2
2
191411
1
11107
1
2
22
xx
xxxx
Hƣớng dẫn.
Biểu thức cần tìm là
914113
22
xxxx
và
11071
22
xxxx
Ta có:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
60
2
2
191411
1
11107
1
2
22
xx
xxxx
0
2
1
191411
1
2
1
11107
1
2
2
2
2
xx
xx
xx
xx
Nhân liên hợp suy ra PT đã cho có 3 nghiệm
2;2;0 xxx
Chú ý:Biểu thức
0191411
2
xx
Nâng cấp Giải phƣơng trình
1
1107
91411
3
2
2
2
2
xx
xx
xx
xx
Hƣớng dẫn.
0
1
1107
11
91411
3
2
2
2
2
xx
xx
xx
xx
pt
0
1
11071
91411
914113
2
22
2
22
xx
xxxx
xx
xxxx
Nhân liên hợp suy ra PT đã cho có 3 nghiệm
2;2;0 xxx
B.Các Phƣơng trình tìm nhân tử không dùng Casio
Thí dụ 1 Giải phƣơng trình
54414121226
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
3;1 xx
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau
(*)54414121226
222
xxxxxx
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là
0x
Giả sử biểu thức liên hợp cần tìm là
122
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
61
Do
3;1 xx
là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm
ta có hệ
539
1
cba
cba
Do cách đổi dấu tìm nghiệm ngoại lai x=0 nên x=0 là nghiệm biểu thức
122
22
xxcbxax
suy ra
1c
Từ đó ta có
1;1;1 cba
Biểu thức cần tìm là
1221
22
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
1412122
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0114121222
22
xxxx
suy ra nhân tử cần xuất hiện là:
114121222
22
xxxx
Đặt
0122
2
axx
01412;
2
bxx
Tacó
(*)3444
222
xxba
Thay vào PT đƣợc
0)22)(12( baba
(**)0114121222
22
xxxx
Cách 1. Từ (*) và (**) suy ra
1122
22
xxxx
và
1221412
22
xxxx
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm
3;1 xx
!!*Giải phƣơng trình(nâng cấp thí dụ 1) Tác giả: Vũ Hồng Phong
1412)2(32122)1(2
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
3;1;0 xxx
Nếu coi cả 3 nghiệm là nghiệm của biểu thức thì
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
62
Biểu thức cần tìm là
1221
3
1
3
1
22
xxxx
biểu thức nữa cần tìm là
14121
3
2
3
4
22
xxxx
Đến đây có lẽ ta không phát hiện đƣợc mối liên nào đặc biệt !
Có vẻ cần coi ít nhất một nghiệm nào đó trong 3 nghiệm là nghiệm ngoại lai của biểu thức
cần tìm. Do ở thí dụ 1 ta đã biết x=0 là nghiệm ngoại lai của biểu thức cần tìm thì sẽ có mối
liên hệ đặc biệt!!
Nhƣ vậy biểu thức cần tìm là
1221
22
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
1412122
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0114121222
22
xxxx
suy ra nhân tử cần xuất hiện là:
114121222
22
xxxx
Đặt
0122
2
axx
01412;
2
bxx
Tacó
(*)3444
222
xxba
Thay vào PT đƣợc
0)322)(12( xbaba
+Với
012 ba
(**)0114121222
22
xxxx
Từ (*) và (**) suy ra
1122
22
xxxx
và
1221412
22
xxxx
PTcó 2 nghiệm
3;1 xx
+Với
0232 xba
xxxxx 2314121222
22
Giải tƣơng tự PTcó thêm nghiệm
0x
và
1x
Nghiệm của PT đã cho là
3;1;0 xxx
Thí dụ 2 Giải phƣơng trình
184183142
22
xxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
63
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
1;0 xx
Đặc biệt dùng đạo hàm thấy
0x
là nghiệm kép
(lƣu ý có thể tìm nghiệm ngoại lai
3x
)
Giả sử biểu thức liên hợp cần tìm là
14
22
xxcbxax
Lấy đạo hàm đƣợc
14
2
2
2
xx
x
bax
Do
1;0 xx
là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm
ta có hệ
2
1
cba
c
Do x=0 là nghiệm kép của biểu thức
14
22
xxcbxax
suy ra
20.2 ba
Từ đó ta có
1;2;1 cba
Biểu thức cần tìm là
1412
22
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
181142
2
xxx
Cho 2 biểu thức bằng 0 suy ra
0118142
2
xxx
suy ra nhân tử cần xuất hiện là:
118142
2
xxx
Đặt
014
2
axx
018; bx
Tacó
(*)3844
222
xxba
Thay vào PT đƣợc
0)22)(12( baba
(**)0118142
2
xxx
Cách 1. Từ (*) và (**) suy ra
1214
22
xxxx
và
14218
2
xxx
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm
1;0 xx
Thí dụ 3 Giải phƣơng trình(nâng cấp của thí dụ 3)
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
64
18518)3(14)22(
2222
xxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
1;0 xx
Đặc biệt dùng đạo hàm thấy
0x
là nghiệm kép(hoặc nghiệm ngoại lai
3x
)
Biểu thức cần tìm là
1412
22
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
181142
2
xxx
Cho 2 biểu thức bằng 0 suy ra
0118142
2
xxx
suy ra nhân tử cần xuất hiện là:
118142
2
xxx
Đặt
014
2
axx
018; bx
Tacó
(*)3844
222
xxba
Thay vào PT đƣợc
0)22)(12(
2
xbaba
(**)0118142
2
xxx
Cách 1. Từ (*) và (**) suy ra
1214
22
xxxx
và
14218
2
xxx
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm
1;0 xx
Thí dụ 4 Giải phƣơng trình
1167816317)1(
23342
xxxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
1;0 xx
Đặc biệt dùng đạo hàm thấy
1x
là nghiệm kép(bội)
Biểu thức cần tìm là
17)1(14
22
xxxxx
Tƣơng tự,biểu thức nữa cần tìm là
xxxxx 8164
342
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
65
Cho 2 biểu thức bằng 0 suy ra
0181617)1(
342
xxxxxx
suy ra nhân tử cần xuất hiện là:
181617)1(
342
xxxxxx
Đặt
017)1(
2
axxx
0816;
34
bxxx
Tacó
(*)1167
2322
xxxba
Thay vào PT đƣợc
0)2)(1( baba
(**)0181617)1(
342
xxxxxx
Từ (*) và (**) suy ra
1214
22
xxxx
và
14218
2
xxx
PTcó 2 nghiệm
1;0 xx
Thí dụ 5 Giải phƣơng trình
034248539127
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
3;1;0 xxx
Giả sử biểu thức liên hợp cần tìm là
9127
22
xxcbxax
Do
3;1;0 xxx
là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm
ta có hệ
639
2
3
cba
cba
c
Từ đó ta có
3;2;1 cba
Biểu thức cần tìm là
912732
22
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
48522
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
014859127
22
xxxx
suy ra nhân tử cần xuất hiện là:
014859127
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
66
Đặt
09127
2
axx
0485;
2
bxx
Tacó
(*)342
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
(**)014859127
22
xxxx
Cách 1. Từ (*) và (**) suy ra
329127
22
xxxx
và
22485
22
xxxx
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 6 Giải phƣơng trình
1841241614)1(2
223
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
1;0 xx
Đặc biệt dùng đạo hàm thấy
1x
là nghiệm kép(bội). Hƣớng khác:
( tìm nghiệm ngoại lai x=2 là nghiệm PT:
1841241614)1(2
223
xxxxxx
)
Biểu thức cần tìm là
14)1(12
2
xxxx
Tƣơng tự,biểu thức nữa cần tìm là
12416142
232
xxxx
Cho 2 biểu thức bằng 0 suy ra
031241614)1(2
23
xxxx
suy ra nhân tử cần xuất hiện là:
31241614)1(2
23
xxxx
Đặt
014)1( axx
012416;
23
bxx
Tacó
(*)324124
222
xxba
Thay vào PT đƣợc
0)2)(32( baba
Với
032 ba
(**)031241614)1(2
23
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
67
Từ (*) và (**) suy ra
1214)1(
2
xxxx
và
14212416
223
xxxx
PT(**) có 2 nghiệm
1;0 xx
Với
02 ba
2
32
1241614)1(2
23
xxxxx
PT đã cho có 3 là
1;0 xx
2
32
;
x
Thí dụ 7 Giải phƣơng trình
344252041262
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
1;0 xx
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau
(*)344252041262
222
xxxxxx
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là
3x
Giả sử biểu thức liên hợp cần tìm là
126
22
xxcbxax
Vì cách đổi dấu trƣớc căn nên
3;1;0 xxx
là nghiệm PT của biểu thức cần tìm
ta có hệ
1
1
1
739
3
1
c
b
a
cba
cba
c
Biểu thức cần tìm là
1261
22
xxxx
(1)
Xét
25204
22
xxcbxax
Do cách đổi dấu tìm nghiệm ngoại lai x=3 nên x=3 là
nghiệm biểu thức
25204
22
xxcbxax
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
68
Từ đó ta có
5
2
2
739
1
5
c
b
a
cba
cba
c
biểu thức nữa cần tìm là
25204522
22
xxxx
(2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra
07252041262
22
xxxx
suy ra nhân tử cần xuất hiện là:
7252041262
22
xxxx
Đặt
0126
2
axx
025204;
2
bxx
Tacó
2128284
222
xxba
Thay vào PT đƣợc
0)2)(72( baba
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm
2
3
;
2
1
;1;0
xxxx
Thí dụ 8 Giải phƣơng trình
38481781252
22
xxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
2;1 xx
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau
(*)38481781252
22
xxxxx
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là
1x
Giả sử biểu thức liên hợp cần tìm là
8125
22
xxcbxax
Vì cách đổi dấu trƣớc căn nên
1;2;1 xxx
là nghiệm PT của biểu thức cần tìm
ta có hệ
2
2
1
5
224
1
c
b
a
cba
cba
cba
Biểu thức cần tìm là
812522
22
xxxx
(1)
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
69
Xét
xcbxax 817
2
Do cách đổi dấu tìm nghiệm ngoại lai x=-1 nên x=-1 là
nghiệm biểu thức
xcbxax 817
2
Từ đó ta có biểu thức nữa cần tìm là
xxx 817142
2
(2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra
0581781252
2
xxx
suy ra nhân tử cần xuất hiện là:
581781252
2
xxx
Đặt
08125
2
axx
0817; bx
Tacó
1540204
222
xxba
Thay vào PT đƣợc
0)2)(52( baba
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm
2
3
;
2
1
;2;1 xxxx
Thí dụ 9 Giải phƣơng trình
14258125
222
xxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là
2;1 xx
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau
14258125
222
xxxxx
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là
1x
Giả sử biểu thức liên hợp cần tìm là
8125
22
xxcbxax
Vì cách đổi dấu trƣớc căn nên
1;2;1 xxx
là nghiệm PT của biểu thức cần tìm
ta có hệ
2
2
1
5
224
1
c
b
a
cba
cba
cba
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
70
Biểu thức cần tìm là
812522
22
xxxx
(1)
Xét
22
5 xcbxax
Do cách đổi dấu tìm nghiệm ngoại lai x=-1 nên x=-1 là
nghiệm biểu thức
22
5 xcbxax
Từ đó ta có biểu thức nữa cần tìm là
22
512 xxx
(2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra
0358125
22
xxx
suy ra nhân tử cần xuất hiện là:
0358125
22
xxx
Đặt
08125
2
axx
0817; bx
Tacó
3126
222
xxba
Thay vào PT đƣợc
0))(3( baba
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm
2
1
1;
2
1
1;2;1 xxxx
Thí dụ 10 Giải phƣơng trình
101281224373453
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là
4;1 xx
Các biểu thức cần tìm là
xxxx 453432
22
và
122437232
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
02122437453
22
xxxx
suy ra nhân tử cần xuất hiện là:
2122437453
22
xxxx
Đặt
0453
2
axx
0122437;
2
bxx
Tacó
(*)10128
222
xxba
Thay vào PT đƣợc
0)1)(2( baba
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
71
suy ra
(**)02122437453
22
xxxx
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
Nghiệm của PT là
4;1 xx
Thí dụ 11 Giải phƣơng trình
2441642126
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Các biểu thức cần tìm là
)1(126
22
xxxx
và
)133(1642
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0216421263
22
xxxx
suy ra nhân tử cần xuất hiện là:
216421263
22
xxxx
Đặt
0126
2
axx
01642;
2
bxx
Tacó
(*)812129
222
xxba
)244(329
222
xxba
Thay vào PT đƣợc
0)13)(23( baba
suy ra
(**)0216421263
22
xxxx
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
Nghiệm của PT là
1;3;0 xxx
Thí dụ 12 Giải phƣơng trình
3331736202322
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1
Biểu thức cần tìm là
23222
22
xxxx
và
173620122
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
72
Cho 2 biểu thức bằng 0 suy ra
031736202324
22
xxxx
suy ra nhân tử cần xuất hiện là:
31736202324
22
xxxx
Đặt
02322
2
axx
0173620;
2
bxx
Tacó
(*)1512124
222
xxba
12121234
222
xxba
Thay vào PT đƣợc
0)12)(32( baba
suy ra
(**)031736202324
22
xxxx
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
PTcó 3 nghiệm
2;1 xx
Thí dụ 13 Giải phƣơng trình
3844956244852
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Biểu thức cần tìm là
48522
22
xxxx
và
495624742
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0114956244852
22
xxxx
suy ra nhân tử cần xuất hiện là:
114956244852
22
xxxx
Đặt
0485
2
axx
0495624;
2
bxx
Tacó
)(*)384(114
222
xxba
Thay vào PT đƣợc
0)2)(112( baba
PTcó 5 nghiệm
2
7
1;3;1;0 xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
73
Thí dụ 14 Giải phƣơng trình
7842540244856
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Biểu thức cần tìm là
48522
22
xxxx
và
254024442
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
012540244852
22
xxxx
suy ra nhân tử cần xuất hiện là:
012540244852
22
xxxx
Đặt
0485
2
axx
0254024;
2
bxx
Tacó
)(*)984(4
222
xxba
Thay vào PT đƣợc
0)22)(12( baba
PTcó 3 nghiệm
3;1;0 xxx
Thí dụ 15 Giải phƣơng trình
9127)22(4852622
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
3;1;0
Giả sử biểu thức liên hợp cần tìm là
485
22
xxcbxax
Do
2;1;0
là nghiệm PT nên ta có hệ
539
1
2
caa
cba
c
2
2
1
c
b
a
Biểu thức liên hợp cần tìm là
48522
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
912732
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
74
Cho 2 biểu thức bằng 0 suy ra
014859127
22
xxxx
suy ra nhân tử cần xuất hiện là:
14859127
22
xxxx
Đặt
09127
2
axx
0485;
2
bxx
Tacó
(*)542
222
xxba
Thay vào PT đƣợc
0)12)(1( xbaba
TH1:
014859127
22
xxxx
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm
3;1;0 xxx
TH2:
124859127
22
xxxxx
ta có 2 nghiệm
38
7351
;1
xx
PT đã cho có 4 nghiệm
3;1;0 xxx
38
7351
;
x
Thí dụ 16 Giải phƣơng trình(Tác giả Vũ Hồng Phong Bất Lự,Hoàn Sơn, Tiên Du,Bắc Ninh)
0463)34(9105)63(1072
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;0
Biểu thức liên hợp cần tìm là
910532
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
46322
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
014639105
22
xxxx
suy ra nhân tử cần xuất hiện là:
14639105
22
xxxx
Đặt
09105
2
axx
0463;
2
bxx
Tacó
(*)542
222
xxba
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
75
Thay vào PT đƣợc
0)53)(1( xbaba
TH1:
014639105
22
xxxx
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm
2;1;0 xxx
TH2:
xxxxx 354639105
22
ta có 2 nghiệm
59
21747
;0
xx
PT đã cho có 4 nghiệm
2;1;0 xxx
59
21747
;
x
Thí dụ 17 Giải phƣơng trình
11684632)32)(12(
22
xxxxxx
Hƣớng dẫn.
11684632
1168463211684632
5
1
22
2222
xxxx
xxxxxxxxPt
PT đã cho có 5 nghiệm
2;1;0 xxx
2
3
;
2
1
; xx
Thí dụ 18 Giải phƣơng trình(PT này phức tạp chỉ để tham khảo)
01168)2(443)162()694(5
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;0
Biểu thức liên hợp cần tìm là
46322
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
1168142
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0511684632
22
xxxx
suy ra nhân tử cần xuất hiện là:
511684632
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
76
Đặt
0463
2
axx
01168;
2
bxx
Tacó
(*)1540204
222
xxba
Thay vào PT đƣợc
0)32)(52( xbaba
TH1:
0511684632
22
xxxx
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm
2;1;0 xxx
TH2:
0311684632
22
xxxxx
ta có 2 nghiệm
3
3
6655016033
6655016033
71
86
131
2
;0 xx
PT đã cho có 4 nghiệm
2;1;0 xxx
3
3
6655016033
6655016033
71
86
131
2
;x
Thí dụ 19 Giải phƣơng trình
529824)3(125)2(2
222
xxxxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;0
Biểu thức liên hợp cần tìm là
1251
22
xxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
982432
22
xxx
Cho 2 biểu thức bằng 0 suy ra
0198241252
22
xxxx
suy ra nhân tử cần xuất hiện là:
198241252
22
xxxx
Đặt
0125
2
axx
09824;
2
bxx
Tacó
(*)544
222
xba
Thay vào PT đƣợc
0)522)(12( xbaba
TH1:
0198241252
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
77
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm
2;1;0 xxx
TH2:
xxxxx 2598241252
22
ta có 2 nghiệm
10
41313
;0
xx
PT đã cho có 4 nghiệm
2;1;0 xxx
10
41313
;
x
Thí dụ 20 Giải phƣơng trình
53351062324
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;2 xxx
Biểu thức cần tìm là
23222
22
xxxx
và
51061
22
xxxx
PTcó 3 nghiệm
2;1;2 xxx
Nâng cấp
1) Giải phƣơng trình
0510632322122
222
xxxxxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;2 xxx
Biểu thức cần tìm là
23222
22
xxxx
và
51061
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0151062322
22
xxxx
suy ra nhân tử cần xuất hiện là:
151062322
22
xxxx
Đặt
02322
2
axx
05106;
2
bxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
78
Tacó
322
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
PTcó 3 nghiệm
2;1;2 xxx
2) Giải phƣơng trình
0
6
1616
4232
2
2
xx
x
xxx
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;2 xxx
Biểu thức cần tìm là
23222
22
xxxx
Biểu thức nữa cần tìm(nếu dùng Casio với 2 nghiệm xấu) là
2322
2
xxx
0
6
1616
4232
2
2
xx
x
xxx
6
865
232
2
23
2
xx
xxx
xx
865232)6(
2322
xxxxxxx
02232)2(2322
222
xxxxxxx
PTcó 5 nghiệm
2
577
;2;1;2
xxxx
Muốn PT nhìn phức tạp ta nhân liên hợp và qui đồng đƣợc :
Giải phƣơng trình
0
6
1616
4324
1411
2
2
2
xx
x
xxx
xx
PTcó 5 nghiệm
2
577
;2;1;2
xxxx
3) Giải phƣơng trình
0
2
612
65106
2
2
x
x
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
79
Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là
2;1;2 xxx
Biểu thức cần tìm là
51061
22
xxxx
0
2
612
65106
2
2
x
x
xxx
2
6106
5106
2
23
2
x
xxx
xx
61065106)2(
2322
xxxxxx
510615106)11(
2322
xxxxxxxx
01232)1(5106
222
xxxxxxx
PTcó 4 nghiệm
5
2
;2;1;2 xxxx
Muốn PT nhìn phức tạp ta nhân liên hợp và qui đồng đƣợc:
Giải phƣơng trình
0
2
612
51066
31225
2
2
2
x
x
xxx
xx
PTcó 4 nghiệm
5
2
;2;1;2 xxxx
PHƢƠNG TRÌNH DÙNG CASIO HỖ TRỢ
Chuyên đề 2 TÌM BIỂU THỨC LIÊN HỢP
Chuyên đề này xin đƣợc giới thiệu các phƣơng trình dùng máy tính cầm tay tìm biểu thức
liên hợp có dạng
k
xPcbxax )(
2
,với a,b,c là các số nguyên. Khi a=0 là trƣờng hợp
quen thuộc!
Sau đây là các thí dụ đơn giản của dạng này
Thí dụ 1 Giải phƣơng trình
4
2
546622
22
x
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
80
Hƣớng dẫn.
Do
0245
2
xx
nên
0x
Biểu thức cần tìm là
2342
22122 xxxxx
và
2342
466123 xxxxx
PTcó 2 nghiệm
;1x
3
421
21
1
33
3
x
Thí dụ 2 Giải phƣơng trình
6
3
7466222
22
x
xxxxx
Hƣớng dẫn.
Do
0367
2
xx
nên
0x
Biểu thức cần tìm là
2342
22122 xxxxx
và
2342
466123 xxxxx
PTcó 2 nghiệm
;1x
3
421
21
1
33
3
x
Nâng cấp: Giải phƣơng trình
6
3
6
466
465
222
2
2
2
x
x
xxx
xx
xx
PTcó 2 nghiệm
;1x
3
421
21
1
33
3
x
(*)
245
46622
2
22
x
xx
xxxxPT
24546622(*)
2234234
xxxxxxxxPT
(*)
367
466222
2
22
x
xx
xxxxPT
367466222(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
81
Thí dụ 3 Giải phƣơng trình
8
8
624181228
2
x
xxxx
Hƣớng dẫn.
Do
0886
2
xx
nên
0x
Biểu thức cần tìm là
322
28442 xxxx
và
2342
241812444 xxxxx
PTcó 2 nghiệm
;2x
2
931
33
x
Thí dụ 4 Giải phƣơng trình
12
12
8241812282
2
x
xxxx
Hƣớng dẫn.
Do
0886
2
xx
nên
0x
Biểu thức cần tìm là
322
28442 xxxx
và
2342
241812444 xxxxx
PTcó 2 nghiệm
;2x
2
931
33
x
Nâng cấp: Giải phƣơng trình
12
12
5
2418123
24183
282
2
2
x
x
xxx
xx
x
(*)
886
24181228
2
2
x
xx
xxxPT
88624181228(*)
223432
xxxxxxxPT
(*)
12128
241812282
2
2
x
xx
xxxPT
1212824181228(*)
223432
xxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
82
PTcó 2 nghiệm
;2x
2
931
33
x
Thí dụ 5 Giải phƣơng trình
2
1
42351
22
x
xxxxx
Hƣớng dẫn.
Do
0124
2
xx
nên
0x
Biểu thức cần tìm là
2342
2123 xxxxx
và
2342
2352125 xxxxx
PTcó 2 nghiệm
;1x
5
1641
3
3
x
Thí dụ 6 Giải phƣơng trình
4
2
723513
22
x
xxxxx
Hƣớng dẫn.
Do
04814
2
xx
nên
0x
Biểu thức cần tìm là
2342
2123 xxxxx
và
2342
2352125 xxxxx
PTcó 2 nghiệm
;1x
5
1641
3
3
x
(*)
124
2351
2
22
x
xx
xxxxPT
24823522(*)
2234234
xxxxxxxxPT
(*)
4814
235216
2
22
x
xx
xxxxPT
24823526(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
83
Nâng cấp: Giải phƣơng trình
4
2
8
235
234
13
2
2
2
x
x
xxx
xx
xx
PTcó 2 nghiệm
;1x
5
1641
3
3
x
Thí dụ 7 Giải phƣơng trình
4
6
342322
2
x
xxxx
Hƣớng dẫn.
Do
0643
2
xx
nên
0x
Biểu thức cần tìm là
232
2232 xxxx
và
2342
423322 xxxxx
PTcó 2 nghiệm
;3x
3
21x
Thí dụ 8 Giải phƣơng trình
10
15
74232223
2
x
xxxx
Hƣớng dẫn.
Do
015107
2
xx
nên
0x
Biểu thức cần tìm là
232
2232 xxxx
và
2342
423322 xxxxx
PTcó 2 nghiệm
;3x
3
21x
(*)
643
42322
2
2
x
xx
xxxPT
64342322(*)
223423
xxxxxxxPT
(*)
15107
4232223
2
2
x
xx
xxxPT
151074232223(*)
223423
xxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
84
Nâng cấp: Giải phƣơng trình
010
15
4232
842
22
663
2
22
x
xxx
xx
xx
xx
PTcó 2 nghiệm
;3x
3
21x
Thí dụ 9 Giải phƣơng trình
4
6
54231068
22
x
xxxxx
Hƣớng dẫn.
Do
0645
2
xx
nên
0x
Biểu thức cần tìm là
2342
1068323 xxxxx
và
2342
423322 xxxxx
PTcó 2 nghiệm
;3x
3
21x
Thí dụ 10 Giải phƣơng trình
6
9
742321068
22
x
xxxxx
Hƣớng dẫn.
Do
0967
2
xx
nên
0x
Biểu thức cần tìm là
2342
1068323 xxxxx
và
2342
423322 xxxxx
PTcó 2 nghiệm
;3x
3
21x
(*)
645
4231068
2
22
x
xx
xxxxPT
6454231068(*)
2234234
xxxxxxxxPT
(*)
967
42321068
2
22
x
xx
xxxxPT
96742321068(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
85
Nâng cấp: Giải phƣơng trình
6
9
6
10683
106
423
844
2
2
2
2
x
x
xxx
xx
xxx
xx
PTcó 2 nghiệm
;3x
3
21x
Thí dụ 11 Giải phƣơng trình
4
8
5135853
22
x
xxxxx
Hƣớng dẫn.
Do
0845
2
xx
nên
0x
Biểu thức cần tìm là
2342
1358422 xxxxx
và
2342
1358423 xxxxx
PTcó 2 nghiệm
;4x
3
31x
Thí dụ 12 Giải phƣơng trình
6
12
71358532
22
x
xxxxx
Hƣớng dẫn.
Do
0845
2
xx
nên
0x
Biểu thức cần tìm là
2342
1358422 xxxxx
và
2342
1358423 xxxxx
PTcó 2 nghiệm
;4x
3
31x
(*)
845
135853
2
22
x
xx
xxxxPT
845135853(*)
2234234
xxxxxxxxPT
(*)
1267
1358532
2
22
x
xx
xxxxPT
12671358532(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
86
Thí dụ 13 Giải phƣơng trình
6
4
5)73)(3(17102
2
x
xxxxx
Hƣớng dẫn.
Do
0465
2
xx
nên
0x
Biểu thức cần tìm là
2342
17102232 xxxxx
và
)73)(3(233
22
xxxxx
PTcó 2 nghiệm
;
3
1
x
3
2x
Thí dụ 14 Giải phƣơng trình
12
8
9)73)(3(171023
2
x
xxxxx
Hƣớng dẫn.
Do
08129
2
xx
nên
0x
Biểu thức cần tìm là
2342
17102232 xxxxx
và
)73)(3(233
22
xxxxx
PTcó 2 nghiệm
;
3
1
x
3
2x
Thí dụ 15 Giải phƣơng trình
4
2
58129684
22
x
xxxxx
Hƣớng dẫn.
(*)
465
)73)(3(17102
2
2
x
xx
xxxxPT
465)73)(3(17102(*)
22234
xxxxxxxxPT
(*)
8129
)73)(3(17102
2
2
x
xx
xxxxPT
8129)73)(3(171023(*)
22234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
87
Do
0245
2
xx
nên
0x
Biểu thức cần tìm là
2342
684122 xxxxx
và
2342
8129123 xxxxx
PTcó 2 nghiệm
2
1
1x
Thí dụ 16 Giải phƣơng trình
6
3
781296842
22
x
xxxxx
Hƣớng dẫn.
Do
0367
2
xx
nên
0x
Biểu thức cần tìm là
2342
684122 xxxxx
và
2342
8129123 xxxxx
PTcó 2 nghiệm
2
1
1x
Thí dụ 17 Giải phƣơng trình
2
4
514691044
22
x
xxxxx
Hƣớng dẫn.
Do
0425
2
xx
nên
0x
(*)
245
8129684
2
22
x
xx
xxxxPT
2458129684(*)
2234234
xxxxxxxxPT
(*)
425
14691044
2
22
x
xx
xxxxPT
(*)
367
81296842
2
22
x
xx
xxxxPT
36781296842(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
88
Cần tìm thêm nghiệm ngoại lai từ đó có
Biểu thức cần tìm là
2342
68422 xxxxx
và
2342
146923 xxxxx
PTcó nghiệm duy nhất
222x
Thí dụ 18 Giải phƣơng trình
4
8
9146910443
22
x
xxxxx
Hƣớng dẫn.
Do
0849
2
xx
nên
0x
Cần tìm thêm nghiệm ngoại lai từ đó có
Biểu thức cần tìm là
2342
68422 xxxxx
và
2342
146923 xxxxx
PTcó nghiệm duy nhất
222 x
Thí dụ 19 Giải phƣơng trình
3222533
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
331
22
xxx
và
xxxx 252
22
PTcó 2 nghiệm
;2x
3
2x
Nâng cấp:
a)Giải phƣơng trình
xx
xx
xx
x
25
2
1
33
2
2
2
2
42514691044(*)
2234234
xxxxxxxxPT
(*)
849
146910443
2
22
x
xx
xxxxPT
849146910443(*)
2234234
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
89
0)1(22513325
222222
xxxxxxxxxxxPT
PTcó 2 nghiệm
;2x
3
2x
b)Giải phƣơng trình
6275258533
22
xxxxxx
0)3(7525)3(8533
22
xxxxxxxPT
0
2
)2(25
1
)1(33
2222
MS
xxxx
MS
xxx
PTcó 2 nghiệm
;2x
3
2x
Thí dụ 20 Giải phƣơng trình
755252333
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
331
22
xxx
và
xxxx 252
22
PTcó 2 nghiệm
;2x
3
2x
Thí dụ 21 Giải phƣơng trình
553
1225
12
332
2
2
2
2
xx
xxx
xx
x
Hƣớng dẫn.
553
1225
)1225)(1225(
332
2
2
22
2
xx
xxx
xxxxxx
xpt
Biểu thức cần tìm là
331
22
xxx
và
xxxx 252
22
PTcó 2 nghiệm
;2x
3
2x
Thí dụ 22 Giải phƣơng trình
32422915
222
xxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
90
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
PTcó 2 nghiệm
;1x
3
2
1
x
Nâng cấp
1)Giải phƣơng trình
229
22
12
15
2
2
2
2
xx
xx
xx
x
0)22(12152222915
222222
xxxxxxxxxxPT
PTcó 2 nghiệm
;1x
3
2
1
x
2)Giải phƣơng trình
2
22
4)12)(1(
229
2
3
2
xx
xx
xx
Hƣớng dẫn.
2
22
4)12)(1(
229
2
22
4)12)(1(
229
2
3
22
3
2
xx
xx
xxxx
xx
xx
04)12)(1(222294)12)(1(4229
32232
xxxxxxxxxx
Nhân liên hợp PTcó 2 nghiệm
;1x
3
2
1
x
Thí dụ 23 Giải phƣơng trình
85102293152
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
PTcó 2 nghiệm
;1x
3
2
1
x
Nâng cấp Giải phƣơng trình
436
6211
229152
2
2
22
xx
xx
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
91
Hƣớng dẫn.
436
229152229152
229152
2
2222
22
xx
xxxxxx
xxxpt
(*)436229152
0229152
222
22
xxxxx
xxx
Giải (*) có biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
PT đã cho có 4 nghiệm
;1x
11
671
;
2
1
3
xx
Thí dụ 24 Giải phƣơng trình
46
2229
225
152
2
2
2
2
xx
xxx
xx
x
Hƣớng dẫn.
46
2229
22292229
152
2
2
22
2
xx
xxx
xxxxxx
xpt
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
PTcó 2 nghiệm
;1x
3
2
1
x
Thí dụ 25 Giải phƣơng trình
5421212
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
PTcó 2 nghiệm
;1x
3
41x
Nâng cấp:Giải phƣơng trình
12
32
22
12
2
2
2
2
xx
xx
xx
x
0)32(2212321212
222222
xxxxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
92
PTcó 2 nghiệm
;1x
3
41x
Thí dụ 26 Giải phƣơng trình
98412123
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
PTcó 2 nghiệm
;1x
3
41x
Nâng cấp Giải phƣơng trình
984
13414
12123
2
2
22
xx
xx
xxx
Hƣớng dẫn.
984
1212312123
12123
2
2222
22
xx
xxxxxx
xxxpt
(*)98412123
012123
222
22
xxxxx
xxx
Giải (*) có biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
PT đã cho có 4 nghiệm
;1x
14
1862
;41
3
xx
Thí dụ 27 Giải phƣơng trình
794
1212
38
112
663
2
22
2
xx
xxx
x
xx
xx
Hƣớng dẫn.
794
1212
)1212)(1212(
112
)112)(112(
.3
2
2
22
2
22
xx
xxx
xxxxxx
xx
xxxx
Pt
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
93
PTcó 2 nghiệm
;1x
3
41x
Thí dụ 28 Giải phƣơng trình
762166593
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
9333
22
xxx
và
163543
22
xxxx
PTcó 2 nghiệm
;0x
3
102x
2)Giải phƣơng trình
2
22
4)12)(1(
229
2
3
2
xx
xx
xx
Hƣớng dẫn.
2
22
4)12)(1(
229
2
22
4)12)(1(
229
2
3
22
3
2
xx
xx
xxxx
xx
xx
04)12)(1(222294)12)(1(4229
32232
xxxxxxxxxx
Nhân liên hợp PTcó 2 nghiệm
;1x
3
2
1
x
Thí dụ 29 Giải phƣơng trình
10931665932
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
9333
22
xxx
và
166543
22
xxxx
PTcó 2 nghiệm
;0x
3
102x
Thí dụ 30 Giải phƣơng trình
14144
121665
152
933
2
2
2
2
xx
xxx
xx
x
Hƣớng dẫn.
Biểu thức cần tìm là
9333
22
xxx
và
166543
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
94
PTcó 2 nghiệm
;0x
3
102x
Thí dụ 31 Giải phƣơng trình
762973165
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
16543
22
xxxx
và
97333
22
xxxx
PTcó 2 nghiệm
;0x
3
172x
Nâng cấp: Giải phƣơng trình
127
72
9733
1
1653
1
2
xx
x
xxxxxx
PTcó 2 nghiệm
;0x
2
3
)172( x
Thí dụ 32 Giải phƣơng trình
1715597331652
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
16543
22
xxxx
và
97333
22
xxxx
PTcó 2 nghiệm
;0x
3
172x
Nâng cấp Giải phƣơng trình
1093
20277
1659732
2
2
22
xx
xx
xxxx
Hƣớng dẫn.
1093
16597321659732
1659732
2
2222
22
xx
xxxxxxxx
xxxxpt
(*)10931659732
01659732
222
22
xxxxxx
xxxx
Giải (*) có biểu thức cần tìm là
97333
22
xxxx
và
16543
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
95
PT đã cho có 4 nghiệm
;1x
0;
7
20
;172
3
xxx
Thí dụ 33 Giải phƣơng trình
7629331695
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
169543
22
xxxx
và
93333
22
xxxx
PTcó 2 nghiệm
;0x
3
72 x
Thí dụ 34 Giải phƣơng trình
119393316952
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
169543
22
xxxx
và
93333
22
xxxx
PTcó 2 nghiệm
;0x
3
72x
Thí dụ 35 Giải phƣơng trình
763
224
6641222
2
2
22
xx
xx
xxxx
Hƣớng dẫn.
763
66412226641222
6641222
2
2222
22
xx
xxxxxxxx
xxxxpt
(*)7636641222
06641222
222
22
xxxxxx
xxxx
Giải (*) có biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PT đã cho có 3 nghiệm
;1x
2
1
;21
3
xx
Thí dụ 36 Giải phƣơng trình
542664122
222
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
96
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PTcó 2 nghiệm
;1x
3
21x
Nâng cấp:
a)Giải phƣơng trình
65
52
6642
1
1222
1
2
xx
x
xxxxxx
PTcó 2 nghiệm
;1x
2
3
)21( x
b)Giải phƣơng trình
(*)122466422122
22
xxxxxxx
Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là
25992105,2;1 xx
biểu thức liên hợp cần tìm là
xxxx 22122
2
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)1(24664
2
xxxx
ĐKXĐ:
)1(022122
2
xxx
và
)2(024664
2
xxx
Có:
2
33
)1(
x
6
1
)2(
x
suy ra
2
33
x
Khi đó
022122
2
xxxx
0)1(24664
2
xxxx
0
2
)32(464
1
)22(122
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
;1x
3
21x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
97
Thí dụ 37 Giải phƣơng trình
11846643122
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PTcó 2 nghiệm
;1x
3
21x
Nâng cấp: Giải phƣơng trình
65
125
6642
3
1222
2
2
xx
x
xxxxxx
PTcó 2 nghiệm
;1x
2
3
)21( x
Thí dụ 38 Giải phƣơng trình
683
664
12126
2122
322
2
2
2
2
2
xx
xxx
xx
xx
xx
Hƣớng dẫn.
683
664
)664)(664(
.2
2122
)2122)(2122(
2
2
22
2
22
xx
xxx
xxxxxx
xx
xxxx
PT
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PTcó 2 nghiệm
;1x
3
21x
Thí dụ 39 Giải phƣơng trình
101472241223
22
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
2212
2
xxx
Chú ý :x=1 thì
02212
2
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
98
PTcó 2 nghiệm
;1x
3
21x
Nâng cấp
a)Giải phƣơng trình:
7
9434
1221562
2
22
x
x
xxxx
Hƣớng dẫn.
0)122522)(12222(
2222
xxxxxxxxpt
PTcó 4 nghiệm
2
71
;21;1
3
xxx
b)Giải phƣơng trình
(*)12122214122
2
xxxxxx
Hƣớng dẫn.ĐK:
1x
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là
25992105,2;1 xx
biểu thức liên hợp cần tìm là
xxx 1222
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)1(14122
2
xxxx
Khi đó
01222 xxx
0)1(14122
2
xxxx
0
2
)12(22
1
)22(122
(*)
222
MS
xxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
;1x
3
21x
Thí dụ 40 Giải phƣơng trình
32253835
222
xxxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
99
Biểu thức cần tìm là
8352
22
xxxx
và
531
22
xxxx
PTcó 2 nghiệm
;1x
3
31x
Thí dụ 41 Giải phƣơng trình
7555338352
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
8352
22
xxxx
và
531
22
xxxx
PTcó 2 nghiệm
;1x
3
31x
Thí dụ 42 Giải phƣơng trình
673
153
824
2835
83
2
2
2
2
2
xx
xxx
xx
xxx
xx
Hƣớng dẫn.
673
153
)153)(153(
.2
2835
)2835)(2835(
2
2
22
2
22
xx
xxx
xxxxxx
xxx
xxxxxx
Pt
Biểu thức cần tìm là
8352
22
xxxx
và
531
22
xxxx
PTcó 2 nghiệm
;1x
3
31x
Thí dụ 43 Giải phƣơng trình
11823423423152
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
2315254
22
xxxx
và
3423464
22
xxxx
PTcó 2 nghiệm
;2x
27
3
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
100
Thí dụ 44 Giải phƣơng trình
1612334234231522
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
2315254
22
xxxx
và
3423464
22
xxxx
PTcó 2 nghiệm
;2x
27
3
x
Thí dụ 45 Giải phƣơng trình
4334461242
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1241
22
xxxx
và
4462
22
xxxx
PTcó 3 nghiệm
;0x
21x
Nâng cấp Giải phƣơng trình
433
410
4461242
2
2
22
xx
xx
xxxx
Hƣớng dẫn.
433
44612424461242
4461242
2
2222
22
xx
xxxxxxxx
xxxxpt
(*)4334461242
04461242
222
22
xxxxxx
xxxx
Giải (*) có biểu thức cần tìm là
1241
22
xxxx
và
4462
22
xxxx
PT đã cho có 4 nghiệm
21;
5
2
;0 xxx
Thí dụ 46 Giải phƣơng trình
85544631242
222
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
101
Hƣớng dẫn.
Biểu thức cần tìm là
1231
22
xxxx
và
4452
22
xxxx
PTcó 3 nghiệm
;0x
21x
Thí dụ 47 Giải phƣơng trình
762166997
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
9733
22
xxx
và
1669433
22
xxxx
PTcó 2 nghiệm
;0x
33
9
636981
9
636981
2
x
Thí dụ 48 Giải phƣơng trình
5241864134
22
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
13422
2
xxx
và
186432
22
xxxx
PTcó 2 nghiệm
;1x
2
369369
33
x
Thí dụ 49 Giải phƣơng trình
3241744142
22
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
14212
2
xxx
và
174422
22
xxxx
PTcó 2 nghiệm
;1x
6
181782418178244
33
x
Thí dụ 50 Giải phƣơng trình
54297243
22
xxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
102
Biểu thức cần tìm là
4322
2
xxx
và
97232
22
xxxx
PTcó 2 nghiệm
;0x
1x
Thí dụ 51 Giải phƣơng trình
534122127105
232
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
7105232
22
xxxx
và
1221232
32
xxx
PTcó 2 nghiệm
2
31
x
Thí dụ 52 Giải phƣơng trình
224738773
2232
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
773122
22
xxxx
và
72812
232
xxxx
PTcó 2 nghiệm
4
171
x
Thí dụ 53 Giải phƣơng trình
2362316645518
222
xxxxxx
Biểu thức cần tìm là
551812
22
xxxx
và
231664124
22
xxxx
PTcó 4 nghiệm
;
4
171
x
4
333
x
Thí dụ 54 Giải phƣơng trình
34823166455182
222
xxxxxx
Biểu thức cần tìm là
551812
22
xxxx
và
231664124
22
xxxx
PTcó 4 nghiệm
;
4
171
x
4
333
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
103
Thí dụ 55 Giải phƣơng trình
3369323261114
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
6111422
22
xxxx
và
93232124
22
xxxx
PTcó 4 nghiệm
;
4
171
x
2
1
;1
xx
Thí dụ 56 Giải phƣơng trình
2361736245108
222
xxxxxx
Biểu thức cần tìm là
510812
22
xxxx
và
173624124
22
xxxx
PTcó 2 nghiệm
4
171
x
Thí dụ 57 Giải phƣơng trình
246)17218)(1(5108
222
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
510812
22
xxxx
và
)17218)(1(134
22
xxxxx
PTcó 2 nghiệm
4
171
x
Thí dụ 58 Giải phƣơng trình
34620443785108
2232
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
510812
22
xxxx
và
2044378234
232
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
104
PTcó 2 nghiệm
4
171
x
Thí dụ 59 Giải phƣơng trình
425442912
22344
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1222
42
xxx
và
442923
2342
xxxxx
PTcó 3 nghiệm
1x
8
179
;
x
Thí dụ 60 Giải phƣơng trình
Hƣớng dẫn.
Biểu thức cần tìm là
12)1(2
2
xxxx
và
122232
22
xxxx
PT đã cho có 2 nghiệm:
1x
;
3
691210869121083
33
x
Thí dụ 61 Giải phƣơng trình
Hƣớng dẫn.
Biểu thức cần tìm là
12)1(2
2
xxxx
và
4231
22
xxxx
PT đã cho có 2 nghiệm:
1x
;
3
691210869121083
33
x
Thí dụ 62 Giải phƣơng trình
1
14
2621412)13(
2
23
xx
xxxxx
1
532
122212)1(
2
2
xx
xxxx
4231
32
12
2
2
xxx
x
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
105
Hƣớng dẫn.
Biểu thức cần tìm là
12)13(12
2
xxxx
và
262142
232
xxxx
PT đã cho có 2 nghiệm:
1x
;
6
781235978123595
33
x
Thí dụ 63 Giải phƣơng trình
1
22
432422
2
232
xx
xxxx
Hƣớng dẫn.
Biểu thức cần tìm là
4221
22
xxx
và
4321
232
xxxx
PT đã cho có 2 nghiệm:
1x
;
3
37179371791
33
x
Thí dụ 64 Giải phƣơng trình
1
32
2513)1(
2
23
x
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
13)1(2
2
xxxx
và
251
232
xxxxx
PT đã cho có 2 nghiệm:
1x
;
3
2
633381
2
633381
33
x
Thí dụ 65 Giải phƣơng trình
1
32
2413)1(
2
23
xx
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
106
Hƣớng dẫn.
Biểu thức cần tìm là
13)1(2
2
xxxx
và
241
232
xxxx
PT đã cho có 2 nghiệm:
1x
;
3
33
18
6332763327
x
Thí dụ 66 Giải phƣơng trình
1
44
410413)2(
2
23
xx
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
13)2(32
2
xxxx
và
410412
232
xxxx
PT đã cho có 2 nghiệm:
1x
;
12
)24918281(5)24918281(55
33
x
Thí dụ 67 Giải hệ phƣơng trình
22232
222
98824343)2(
42
yxxxxxx
xyyx
Hƣớng dẫn.
Phƣơng trình thứ nhất của hệ tƣơng đƣơng với
2x
hoặc
22
2
yx
Với x=2 các bạn tự xử lí trƣờng hợp dễ này
Với
22
2
yx
thay vào PT thứ 2 của hệ ta đƣợc
(*)298824343)2(
2232
xxxxxxx
Biểu thức cần tìm là
43)2(23
22
xxxx
và
88242
232
xxxx
PT(*) có 2 nghiệm:
2x
;
3
4
311833
4
311833
1
33
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
107
Đến đây các bạn tự giải tiếp
Thí dụ 68 Giải hệ phƣơng trình
53341162133
0
22
2
1
22222
24
2
2
yxxxxy
yy
y
x
x
Hƣớng dẫn.
Sử dụng Hàm đặc trƣng có
Phƣơng trình thứ nhất của hệ tƣơng đƣơng
22
2
yx
Với
22
2
yx
thay vào PT thứ 2 của hệ ta đƣợc
(*)113341162133)2(
222
xxxxxx
Biểu thức cần tìm là
133)2(632
22
xxxx
và
411625
22
xxx
PT(*) có 2 nghiệm:
2x
;
3
15732157322
33
x
Đến đây các bạn tự giải tiếp
Thí dụ 69 Giải hệ phƣơng trình
153367104133
02
2222
222
xxxxxy
yxxyx
Hƣớng dẫn.
Phƣơng trình thứ nhất của hệ tƣơng đƣơng với
1x
hoặc
22
2
yx
Với x=1 các bạn tự xử lí trƣờng hợp dễ này
Với
22
2
yx
thay vào PT thứ 2 của hệ ta đƣợc
(*)153367104133)2(
222
xxxxxx
Biểu thức cần tìm là
133)2(732
22
xxxx
và
671048
22
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
108
PT(*) có 2 nghiệm:
1x
;
3
6819176819171
33
x
Đến đây các bạn tự giải tiếp
Thí dụ 70 Giải phƣơng trình
3
12
4691213
2
232
x
xxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1313
22
xxx
và
4691223
232
xxxxx
PT đã cho có 2 nghiệm:
0x
;
9
41953419532
33
x
Thí dụ 71 Giải phƣơng trình
xxxxx 4627543
2423
Hƣớng dẫn.
Biểu thức cần tìm là
75412
232
xxxx
PT đã cho có 2 nghiệm:
1x
;
3
4
67579
4
67579
1
33
x
Thí dụ 72 Giải phƣơng trình
132527333
222
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
331
22
xxx
và
xxxx 252
22
PTcó 2 nghiệm
;2x
3
2x
01225273133
222
xxxxxxxxPT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
109
Thí dụ 73 Giải phƣơng trình
12122291321552
2222
xxxxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
012229132121552
2222
xxxxxxxxxPt
PTcó 2 nghiệm
;1x
3
2
1
x
Thí dụ 74 Giải phƣơng trình
11211212)1(
3
22
3
22
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
0212112112)1(
3
22
3
22
xxxxxxPT
PTcó 2 nghiệm
;1x
3
41x
Thí dụ 75 Giải phƣơng trình
416351339343
22
3
22
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
9333
22
xxx
và
163543
22
xxxx
03163513319353
22
3
22
xxxxxxxpt
PTcó 2 nghiệm
;0x
3
102x
Thí dụ 76 Giải phƣơng trình
54612292152
22222
xxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
110
Hƣớng dẫn.
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
0)323(12292)223(152
2
2
222
2
22
xxxxxxxxxpt
PTcó 2 nghiệm
;1x
3
2
1
x
Thí dụ 77 Giải phƣơng trình
2
222
5266421223 xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PTcó 2 nghiệm
;1x
3
21x
Thí dụ 78 Giải phƣơng trình
824
4
2
322
22
1
53
2
2
2
2
xx
xxx
xx
xx
Hƣớng dẫn.
Biểu thức cần tìm là
531
22
xxxx
0)
2
1
824
4
22
1
(153
22
22
xx
x
xx
xxxxpt
PTcó 2 nghiệm
;1x
3
31x
Thí dụ 79 Giải phƣơng trình
2232664122
22
4
2
4
2
xxxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
111
PTcó 2 nghiệm
;1x
3
21x
Thí dụ 80 Giải phƣơng trình
122493)1(53
2
3
22
xxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
531
22
xxxx
và
3
2
4932 xxx
PTcó 2 nghiệm
;1x
3
31x
Thí dụ 81 Giải phƣơng trình
2
3
32
)2(6)1()1(122 xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
3
3
6)1(2 x
PTcó 2 nghiệm
;1x
3
21x
Chuyên đề phụ:
Ý tƣởng ghép 2 phƣơng trình thành 1 phƣơng trình
Hay một cách tạo ra phƣơng trình Tích từ các biểu thức tùy ý
(chọn hợp lí )
Tác giả của ý tưởng:Vũ Hồng Phong Thôn Bất Lự,Hoàn Sơn,Tiên Du,Bắc Ninh
Từ hai phƣơng trình sau:
Giải phƣơng trình:
3222533
222
xxxxx
(1)
Hƣớng dẫn.
Biểu thức cần tìm là
331
22
xxx
và
xxxx 252
22
PTcó 2 nghiệm
;2x
3
2x
Giải phƣơng trình:
5421212
222
xxxxx
(2)
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
112
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
Hƣớng dẫn.
Từ (1) và (2) ta có thể ghép lại thành PT sau:
Thí dụ 82 Giải phƣơng trình(đây là PT chỉ để minh họa ý tƣởng`)
12
25
)32)(2(
)22(
1
1233
2
2
22
2
2
22
xx
xx
xxxx
xx
xx
xx
12
1
33)32(
)22(
25
12)2(
2
2
22
2
2
22
xx
xx
xxx
xx
xx
xxx
12
25
)32)(2(
1233
1
32
22
25
12
)2(
22)12)(33(
2
2
22
22
2
2
2
2
2
2
222
xx
xx
xxxx
xxx
xx
xx
xx
xx
x
xx
xxxx
HD.
Với (a;b),(c;d) là bộ biểu thức liên hợp của PT thứ nhất
(m;n),(p;q) là bộ biểu thức liên hợp của PT thứ hai
Ta có PT:
0)(
npmq
d
c
b
a
qp
b
a
nm
d
c
qp
d
c
nm
b
a
Suy ra PT ở thí dụ 82 đã cho tƣơng đƣơng với PT
0)32)(22(1.122
25
2
1
33
2222
2
2
2
2
xxxxxxx
xx
xx
xx
x
TH1:
0
25
2
1
33
2
2
2
2
xx
xx
xx
x
0
25
2
11
1
33
2
2
2
2
xx
xx
xx
x
0
25
)2(25
1
)1(33
2
22
2
22
xx
xxxx
xx
xxx
PTcó 2 nghiệm
;2x
3
2x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
113
TH2: làm tương tự
0)32)(22(1.122
2222
xxxxxxx
12
32
22
12
2
2
2
2
xx
xx
xx
x
PTcó 2 nghiệm
;1x
3
41x
PT đã cho có 4 nghiệm
;2x
3
2x
;1; x
3
41x
Các PT trên chỉ là minh họa cho ý tƣởng ghép 2 phƣơng trình thành một phƣơng trình.
Mở rộng:Dùng kĩ thuật ghép này cho 2 phƣơng trình liên hợp dạng bậc nhất hoặc hằng số có khả năng sẽ tạo
ra đƣợc Pt đỡ phức tạp
Dạng PT này
npmq
d
c
b
a
qp
b
a
nm
d
c
qp
d
c
nm
b
a
))(())((
có thể mở rộng về dấu
cộng hay trừ và thêm các hằng số trong dấu ngoặc.
npmq
d
c
b
a
qp
b
a
nm
d
c
qp
d
c
nm
b
a
))(())((
Hoặc
npmqbcadbqapdncmdqcpbnam ))(())((
Hoặc
npmqbcadbqapdncmdqcpbnam ))(())((
Nếu ai không thích ghép 2 phƣơng trình thì chỉ cần lấy 1 phƣơng trình tƣơng ứng gồm 2 cặp biểu thức liên
hơp,các biểu thức còn lại chọn tùy ý chứa ẩn hoặc hằng số hay mở rộng ta chọn a,b,c,d,m,n,p,q bất kì!!!
A.Các cách tạo ra phƣơng trình dạng này
Giải phƣơng trình
161;24 xxxx
cùng 1 phƣơng trình nhân liên hợp
6113;192 xxxx
cùng 1 phƣơng trình nhân liên hợp
Sau đây là hƣớng tạo ra một PT dạng này từ các biểu thức trên:
Giải phƣơng trình
3
16
611
)1(1924
2
1 x
x
x
xxx
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
114
3
12244
19
16
23
22
x
x
xx
x
x
xx
Hay
3
16
611
)1(
3
12244
19
16
23
1924
2
1
2
2
x
x
x
x
x
x
xx
x
x
xx
xx
x
Hay
3
16
611
)1(
312244
19
16
23
19242
22
2
x
x
x
x
xxxx
x
x
xx
xxxx
Hay
16)3(611)1(
312244
135423
19242
22
22
xxxx
xxxx
xxxx
xxxx
PT đã cho có 4 nghiệm
22 x
2
135
;
x
B. Vận Dụng
Ta có thể tạo ra các PT đơn giản hơn dƣới đây
(nhìn chỉ hơi khó nhƣng biến đổi nhẹ nhàng gồm kĩ năng đƣa về phƣơng trình Tích và
nhân Liên hợp nếu cần +Casio bậc nhất)
Thí dụ 1,Giải phƣơng trình
4
1
16
4
24
3
1
162
3
24
2
2
x
xx
x
x
x
x
x
x
hay
4416
244
33162
2432
2
xxx
xx
xx
xx
(nhìn tạm ổn)
PT đã cho có 3 nghiệm(đã kiểm tra)
22 x
3
8
; x
Thí dụ 2,Giải phƣơng trình
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
115
2
2
1
163
24
3
2
1
16
2
24
x
x
x
x
x
x
x
x
x
x
hay
23
2
163
243
2216
242
xxx
xxx
xx
xx
(nhìn tạm ổn)
PT đã cho có 3 nghiệm
22 x
6; x
Thí dụ 3,Giải phƣơng trình
2
2
1
163
24
3
2
1
16
2
24
x
x
x
x
x
x
x
x
x
x
hay
23
2
163
243
2216
242
xxx
xxx
xx
xx
(nhìn tạm ổn)
PT đã cho có 3 nghiệm(đã kiểm tra)
22 x
6; x
Thí dụ 4,Giải phƣơng trình
3
3
611
62
2
192
3
611
3
3
2
19
x
x
x
x
x
x
x
x
x
x
hay
61162
2192
61133
6319
3
34
xxx
xxx
xx
xx
(nhìn tạm ổn)
PT đã cho có 3 nghiệm(đã kiểm tra)
2
135
x
3
6; x
Thí dụ 5,Giải phƣơng trình
3
22
22
3
2
2)1(
)1(24
231
3324
xxxx
xxx
xx
xx
Hƣớng dẫn.
Chọn
3
2
2;1;1;24 xxdcxbxa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
116
Chọn
1;;3;1
2
xqxpnm
PT đã cho có 4 nghiệm
(đã kiểm tra)
6
131
x
21; x
Thí dụ 6,Giải phƣơng trình
3
22
2
3
2
44
8438
42
2382
xxx
xxx
xx
xx
Hƣớng dẫn.
Chọn
3
2
4;1;2;38 xxdcxbxa
Chọn
4;;1;2
2
qxpnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
22x
32; x
Chú ý tìm đƣợc 4 nghiệm thì
22x
loại do đkxđ
Thí dụ 7,Giải phƣơng trình
3
2
3
2
2
7256
151013203
722
321320
xx
xx
xxx
xxx
Hƣớng dẫn.
Chọn
3
2
72;2;32;1320 xxdcxbxa
Chọn
5;3;;1 qpxnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
3
5
x
21; x
Thí dụ 8,Giải phƣơng trình
128296
32128.
28342
228
334
xx
xxx
xx
xxx
Hƣớng dẫn.
Chọn
128;22;2;28 xdxcxbxa
Chọn
2;3;;1
3
qpxnm
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
117
PT đã cho có 3 nghiệm
(đã kiểm tra)
3
3
2
x
22; x
Thí dụ 9,Giải phƣơng trình
183324
18312
3242
24
2
22
xxx
xxxx
xx
xx
Hƣớng dẫn.
Chọn
183;12;;24
2
xxdxcxbxa
Chọn
3;2;;1 qpxnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
2
3
x
22; x
Thí dụ 10,Giải phƣơng trình
x
xxxx
x
xxx
255
25)1(22
13
1)1(
22
Hƣớng dẫn.
Chọn
1;252;1;1 dxcbxa
Chọn
3;1;;1
2
qpxnxm
PT đã cho có 2 nghiệm
(đã kiểm tra)
9
1348
x
2
213
;
x
Thí dụ 11,Giải phƣơng trình
12
52
4223.
23.
2
345
22
224
xx
xxx
xxxx
xxxx
Hƣớng dẫn.
Chọn
2;3;5;2
222
xxdxxcbxxa
Chọn
1;;2;1
3
qxpnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
3
2
1
x
2
313
;
x
2
373
;
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
118
Thí dụ 12,Giải phƣơng trình
3
3
12
127
3122
12
xx
x
x
xx
Hƣớng dẫn.
Chọn
1;12;1;12
3
dxcbxa
Chọn
3;2;;1 qpxnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
2
3
x
16
171161
;
x
Thí dụ 13. Cách tạo ra nhƣ sau:
Từ phƣơng trình dùng Casio bậc nhất:
13372016)1(
2
xxxxxx
)163)(1(1720 xxxxx
Chọn
1;1720;1;163 xdxxcbxxa
2;1;1;
3
qpnxm
ta có thể ngụy trang thành phương trình sau
Thí dụ 13,Giải phƣơng trình
12720
1720
2163
1163
3434
xxx
xxxx
xx
xxx
PT đã cho có 3 nghiệm
(đã kiểm tra)
3
3
1
x
22; x
Thí dụ 14,Giải phƣơng trình
3
2
3
3
35
2
3
35
172
1743
3
143
xxx
xxxx
x
xxxx
Hƣớng dẫn.
Chọn
1;2;1;43
2
3
35
dxxcbxxxa
Chọn
3
17;1;1;1 xqpxnm
Sau đó ta phải các giải pt sau:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
119
243
2
3
35
xxxxx
2
1
)0(1
2
3
4
3
2
2
x
x
khix
x
x
x
x
4
1
0
117
3
x
x
x
xx
PT đã cho có 4 nghiệm
(đã kiểm tra)
4;2;1;0 xxxx
Thí dụ 15. Cách tạo ra nhƣ sau:
Từ phƣơng trình dùng Casio :
2
3
2
)2(3)2(37)1( xxxxxx
)32)(2(37)1(
3
2
xxxxxx
Chọn
1;32;2;37
3
2
xdxxxcxbxa
1;2;1;
2
qpnxm
ta có thể ngụy trang thành phương trình sau
Thí dụ 15,Giải phƣơng trình
3
2
3
22232
3253
3.12
3722
37.2
xxx
xxxxxx
xx
xxx
PT đã cho có 3 nghiệm
(đã kiểm tra)
2x
2
53
;
x
Thí dụ 16,Giải phƣơng trình
122422
12212
12621
126.1
22
2234
22
222
xxxx
xxxxx
xxxx
xxxxx
PT đã cho có 5 nghiệm
(đã kiểm tra)
2x
3;1;0; xxx
Thí dụ 17,Giải phƣơng trình
233
231
581
12458
22
xx
xxxx
x
xxxx
Hƣớng dẫn.
Chọn
1;231;1;3458 dxxcxbxxa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
120
Chọn
1;;4;1 qxpnm
Giải PT bằng liên hợp bậc nhất:
245823)1(
2
xxxxx
PT đã cho có 2 nghiệm
(đã kiểm tra)
4
1
x
2
51
;
x
Thí dụ 18,Giải phƣơng trình
141
11212
12
11
222
2
x
xx
xx
xxx
Hƣớng dẫn.
Chọn
1;12;1;11
2
dxcbxxa
Chọn
1;2;;1
2
qpxnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
0x
2
1
; x
Thí dụ 19,Giải phƣơng trình
432
21
222
1
2
3
36
2
3
36
xx
xx
xx
xxx
Hƣớng dẫn.
Chọn
1;232;1;1
2
3
36
dxxcbxxa
Chọn
2;1;;1 qpxnm
Giải PT
3)
1
(21
1
2321
3
3
32
3
36
x
x
x
xxxxx
14
453022
7
2
15
14
11
;1
xx
PT đã cho có 4 nghiệm
(đã kiểm tra)
2;1 xx
14
453022
7
2
15
14
11
;
x
Thí dụ 20,Giải phƣơng trình
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
121
3233
323
4252
1425
2
22
2
22
xx
xxx
xx
xxx
Hƣớng dẫn.
Chọn
1;323;1;1425
222
dxxcbxxxa
Chọn
3;1;;1
2
qpxnm
PT đã cho có 3 nghiệm
(đã kiểm tra)
51x
3; x
Thí dụ 21,Giải phƣơng trình
2222
222)1(
)12(
12
242
2422
2
22
xxxx
xxxx
xx
xxx
Hƣớng dẫn.
Chọn
22;1;1;
2422
xxdxcxbxa
Chọn
xqpnxm ;2;1;2
2
Đƣa về PT tích ta phải giải các PT:
2
51
1
22
1
1
2
24
2
2
xxx
xx
x
x
x
(dùng hàm đặc trƣng)
15
4)2(
0
22
22
2
x
xx
x
xx
PT đã cho có 3 nghiệm
(đã kiểm tra)
2
51
x
15; x
Thí dụ 22,Giải phƣơng trình
2221
22
12
1
242
2424
2
23
xxx
xxxx
xx
xx
Hƣớng dẫn.
Chọn
22;1;1;
2422
xxdxcxbxa
Chọn
2;1;1;
2
qpnxm
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
122
Đƣa về PT tích ta phải giải các PT:
2
51
1
22
1
1
2
24
2
2
xxx
xx
x
x
x
(dùng hàm đặc trƣng)
2
1
12
2
xx
PT đã cho có 3 nghiệm
(đã kiểm tra)
2
51
x
2
1
; x
Thí dụ 23,Giải phƣơng trình
2
2
2
2
.22332
.22
2213
.21
xx
xxx
x
xx
Hƣớng dẫn.
Chọn
1;222;2;1
22
dxcbxa
Chọn
2;3;;1 qpxnm
Đƣa về PT tích ta phải giải các PT:
(*)22
1
1
1
2
)22(21
2
2
2
22
x
x
x
x
xxx
Sử dụng a,b không âm có Bất đẳng thức:
)(2
22
baba
đẳng thức xảy ra
ba
Áp dụng :
(*)22
1
1
1
2
22)
1
1
1
2
(2(*)
2
2
2
2
22
2
2
VP
x
x
x
x
x
x
x
x
VT
đẳng thức xảy ra
12 x
3
2
1.23 xx
PT đã cho có 2 nghiệm
(đã kiểm tra)
3
2
x
12; x
Thí dụ 24,Giải phƣơng trình(Vũ Hồng Phong THPT Tiên Du 1)
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
123
2
2
4
32
3
3183
1
8323
x
xx
x
xxx
Hƣớng dẫn.
Chọn
222
1;1;8;323 xdxcxbxxa
Chọn
2;1;;1
2
qpxnm
Đƣa về PT tích:
2
2
4
32
3
3183
1
8323
x
xx
x
xxx
0)2)](1(8)1(323[
2222
xxxxxx
ta phải giải PT:
)1(8)1(323
222
xxxxx
(*)
1
1
.
1
2
4
1
1
.3
1
2
2
2
22
2
2
x
x
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
Pt(*) trở thành
tttt 2cos2sin42cos32sin
ttt 4sin22cos32sin
)(
39
6
)
3
2sin(4sin Zk
k
t
kt
tt
Suy ra
6
t
9
;
t
9
4
;
t
9
2
;
t
Pt(*) có 4 nghiệm
3
1
x
9
tan;
x
9
4
tan;
x
9
2
tan;
x
Pt(*) có 6 nghiệm
3
1
;2 xx
9
tan;
x
9
4
tan;
x
9
2
tan;
x
Thí dụ 25,Giải phƣơng trình(Vũ Hồng Phong Bất Lự, Hoàn Sơn,Tiên Du )
2
2
432
42
3
3183
1
8323
x
xx
xxx
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
124
Hƣớng dẫn.
Chọn
222
1;1;8;323 xdxcxbxxa
Chọn
2;1;;1
3
qpxnm
Đƣa về PT tích:
2
2
432
42
3
3183
1
8323
x
xx
xxx
xxx
0)2)](1(8)1(323[
3222
xxxxxx
ta phải giải PT:
)1(8)1(323
222
xxxxx
(*)
1
1
.
1
2
4
1
1
.3
1
2
2
2
22
2
2
x
x
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
Pt(*) trở thành
tttt 2cos2sin42cos32sin
ttt 4sin22cos32sin
)(
39
2
6
)
3
2sin(4sin Zk
k
t
kt
tt
Suy ra
6
t
9
2
;
t
9
;
t
9
4
;
t
Pt(*) có 4 nghiệm
3
1
x
9
2
tan;
x
9
tan;
x
9
4
tan;
x
Pt(*) có 5 nghiệm
3
1
;2
3
xx
9
2
tan;
x
9
tan;
x
9
4
tan;
x
Thí dụ 26,Giải phƣơng trình(Vũ Hồng PhongToán K35B ĐHSP TN)
2
322
2
22
3
)1(1
)3216(1
18321
x
xx
xx
xxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
125
Chọn
222
1;1;8;321 xdxcxbxxa
Chọn
2;1;1;1
2
qpxnm
Đƣa về PT tích
2
322
2
22
3
)1(1
)3216(1
18321
x
xx
xx
xxxx
0)21)](1(8)1(321[
2222
xxxxxx
ta phải giải các PT:
0)1(8)1(321
222
xxxxx
(*)
1
1
.
1
2
4
1
1
1
32
2
2
22
2
2
x
x
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
Pt(*) trở thành
tttt 2cos2sin42cos2sin3
ttt 4sin22cos2sin3
)(
336
5
12
)
6
2sin(4sin Zk
k
t
kt
tt
Suy ra
12
t
36
5
;
t
36
17
;
t
36
7
;
t
Pt(*) có 4 nghiệm
32
12
tan
x
36
5
tan;
x
36
17
tan;
x
36
7
tan;
x
Pt(*) có 6 nghiệm
;3x
32
12
tan
x
36
5
tan;
x
36
17
tan;
x
36
7
tan;
x
Thí dụ 27,Giải phƣơng trình
2
322
2
22
3
)1(1
)3216(1
18321
x
xx
xx
xxxx
Hƣớng dẫn.
Chọn
222
1;1;8;321 xdxcxbxxa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
126
Chọn
2;1;1;1
2
qpxnm
Đƣa về PT tích
2
322
2
22
3
)1(1
)3216(1
18321
x
xx
xx
xxxx
0)21)](1(8)1(321[
2222
xxxxxx
ta phải giải các PT:
0)1(8)1(321
222
xxxxx
(*)
1
1
.
1
2
4
1
1
1
32
2
2
22
2
2
x
x
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
Pt(*) trở thành
tttt 2cos2sin42cos2sin3
ttt 4sin22cos2sin3
)(
12
7
336
)4sin()
6
2sin( Zk
kt
k
t
tt
Suy ra
36
t
36
11
;
36
13
;
tt
12
5
;
t
Pt(*) có 4 nghiệm
32
12
5
tan
x
36
tan;
x
36
13
tan;
x
36
11
tan;
x
Pt(*) có 6 nghiệm
;3x
32
12
5
tan
x
36
tan;
x
36
13
tan;
x
36
11
tan;
x
Thí dụ 28,Giải phƣơng trình
2
2
4
32
3
)282(1
1
2421
x
xx
x
xxx
Hƣớng dẫn.
Chọn
222
1;1;24;21 xdxcxbxxa
Chọn
2;1;;1
2
qpxnm
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
127
Đƣa về PT tích:
2
2
4
32
3
)282(1
1
2421
x
xx
x
xxx
0)2)](1(24)1(21[
2222
xxxxxx
ta phải giải PT:
)1(24)1(21
222
xxxxx
(*)
1
1
.
1
2
22
1
1
1
2
2
2
22
2
2
x
x
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
Pt(*) trở thành
tttt 2cos2sin222cos2sin
ttt 4sin22cos2sin
)(
38
8
)
4
2sin(4sin Zk
k
t
kt
tt
Suy ra
8
t
24
11
;
t
24
5
;
t
Pt(*) có 3 nghiệm
12
8
tan
x
26922
24
11
tan;
x
26922
24
5
tan;
x
Pt có 5 nghiệm
;2x
12
8
tan
x
26922
24
11
tan;
x
26922
24
5
tan;
x
Thí dụ 29 Giải phƣơng trình
3112
sin1)sin6(
2344
sin2321
4
24
2
2
xx
xxxx
xx
xxx
Hƣớng dẫn.
Chọn
2242
1;16,2;321 xdxxcbxxa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
128
1;2;sin;1 qpxnm
Ta giải các PT
2
1
sin x
(*)1
1
1
22
1
1
1
32
2
2
2
2
2
2
x
x
x
x
x
x
Đặt
tx tan
với
2
;
2
t
PT(*) trở thành
)12cos2(22cos2sin3
2
ttt
ttt 4cos22cos2sin3
318
2
6
4cos)
3
2cos(
k
t
kt
tt
Suy ra
18
5
;
18
7
;
18
;
6
tttt
PT(*) có 4 nghiệm
)
18
5
tan(;
18
7
tan;
18
tan;
3
1
ttxx
Pt đã cho có nghiệm
)(2
6
5
;2
6
);
18
5
tan(;
18
7
tan;
18
tan;
3
1
Zkkxkxxxxx
Chú ý: Có thể tạo ra nhiều PT giải bằng phương pháp lượng giác hóa như sau
(*)1
1
1
22
1
1
1
32
2
2
2
2
2
2
x
x
x
x
x
x
Từ PT(*) ta có thể tạo ra các PT tương tự:
1
1
1
22
1
1
1
32
2
2
2
2
2
2
x
x
x
x
x
x
1
1
1
22
1
1
1
32
2
2
2
2
2
2
x
x
x
x
x
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
129
2
2
2
2
2
2
1
1
212
1
1
1
32
x
x
x
x
x
x
2
2
2
2
2
2
1
1
212
1
1
1
32
x
x
x
x
x
x
1
1
1
22
1
33
1
2
2
2
2
2
2
2
x
x
x
x
x
x
1
1
1
22
1
33
1
2
2
2
2
2
2
2
x
x
x
x
x
x
1
1
1
22
1
33
1
2
2
2
2
2
2
2
x
x
x
x
x
x
1
1
1
22
1
33
1
2
2
2
2
2
2
2
x
x
x
x
x
x
Các thí dụ trước đều có thể tạo ra các PT (giải bằng lượng giác hóa )theo hướng này
Thêm một số dạng PT lƣợng giác hóa:
tx
x
x
x
x
x
t
x
xx
t
x
xx
t tan;
1
1
2cos;
1
2
2sin;
)1(
16
4cos;
)1(
)1(4
4sin
2
2
222
24
22
2
2
;
2
;
2
2cos1
cos;
1
sin
1
2
2cos1
sin
22
t
t
t
x
x
t
x
x
t
t
Chú ý: Do
2
;
2
t
nên
2
sin;sin
t
t
và x cùng dấu với nhau
22
2
2
2
2
1222
12
11
2
cos1
2
sin;
12
11
2
cos1
2
cos
xx
x
x
xtt
x
xtt
22
1222
2
sin
xx
xt
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
130
222
24
22
2
1
4
)1(
16
3
)1(
)1(4
)
x
x
x
xx
x
xx
a
x
x
xx
x
xx
4
1
16
3
1
)1(4
2
24
2
2
)1(4)16(3)1(4
2242
xxxxxx
2
2
22
24
22
2
1
22
)1(
16
3
)1(
)1(4
)
x
x
x
xx
x
xx
b
222
24
22
2
1
4
)1(
16
)1(
)1(34
)
x
x
x
xx
x
xx
c
2
2
22
24
22
2
1
22
)1(
16
)1(
)1(34
)
x
x
x
xx
x
xx
d
222
24
22
2
1
24
)1(
16
)1(
)1(4
)
x
x
x
xx
x
xx
e
2
2
22
24
22
2
1
22
)1(
16
)1(
)1(4
)
x
x
x
xx
x
xx
f
;....22;
8
sin
2
1
22;3;2;1
)1(
16
3
)1(
)1(4
)
22
24
22
2
x
xx
x
xx
m
2
2
2
2
1
2
1
1
3
1
2
)
x
x
x
x
x
x
n
2
2
2
2
1
1
2
1
1
3
1
2
)
x
x
x
x
x
x
n
2
2
2
2
1
2
1
1
1
32
)
x
x
x
x
x
x
p
2
2
2
2
1
1
2
1
1
1
32
)
x
x
x
x
x
x
p
2
2
2
2
1
2
1
1
3
1
2
)
x
x
x
x
x
q
2
2
2
2
1
2
1
1
1
32
)
x
x
x
x
x
k
2
2
2
2
1
2
1
1
1
2
)
x
x
x
x
x
l
2
2
2
2
1
2
1
1
1
2
)
x
x
x
x
x
x
h
2
2
2
2
1
1
2
1
1
1
2
)
x
x
x
x
x
x
h
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
131
2
22
24
22
2
1
2
)1(
)16(3
)1(
)1(4
)
x
x
x
xx
x
xx
i
2
22
24
22
2
1
1
2
)1(
)16(3
)1(
)1(4
)
x
x
x
xx
x
xx
i
2
22
24
22
2
1
2
)1(
16
)1(
)1(34
)
x
x
x
xx
x
xx
j
2
22
24
22
2
1
1
2
)1(
16
)1(
)1(34
)
x
x
x
xx
x
xx
j
2
22
24
22
2
1
2
)1(
)16(3
)1(
)1(4
)
x
x
xx
x
xx
u
2
22
24
22
2
1
2
)1(
16
)1(
)1(34
)
x
x
xx
x
xx
v
2
22
24
22
2
1
2
)1(
16
)1(
)1(4
)
x
x
xx
x
xx
r
2
22
24
22
2
1
2
)1(
16
)1(
)1(4
)
x
x
x
xx
x
xx
t
2
22
24
22
2
1
1
2
)1(
16
)1(
)1(4
)
x
x
x
xx
x
xx
t
22
2
22
)1(
)1(8
1
3
1
)1
x
xx
xx
x
w
22
24
22
)1(
)16(2
1
1
1
3
)2
x
xx
xx
x
w
22
2
22
)1(
)1(24
1
1
1
)3
x
xx
xx
x
w
22
24
22
)1(
)16(2
1
1
1
)4
x
xx
xx
x
w
2
2
2
2
12
1
2
sin;
12
11
2
cos
x
xx
t
x
xt
Với
22
2
2
2
2
1222
12
11
2
cos1
2
sin;
12
11
2
cos
xx
x
x
xtt
x
xt
22
1222
2
sin
xx
xt
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
132
Xin dành để các bạn có thể tự tạo ra các PT khác(giải bằng lượng giác hóa )theo hướng trên.
Như vậy ta có khá nhiều PT giải bằng lượng giác hóa (Vũ Hồng Phong THPT Tiên Du 1)
Nguồn gốc từ các PT lƣợng giác kiểu nhƣ sau:
ttt 4sin22cos2sin3
ttt 4cos22cos2sin3
ttt 4sin22cos32sin
ttt 4cos22cos32sin
ttt 2sin24cos4sin3
ttt 2cos24cos4sin3
ttt 2sin24cos34sin
ttt 2cos24cos34sin
ttt 2sin24cos4sin
ttt 2cos24cos4sin
ttt 2sin22cos2sin
ttt 2cos22cos2sin
;....}
2
3
;
2
2
;
2
1
{;24cos4sin mmtt
;....}
2
3
;
2
2
;
2
1
{;24cos34sin mmtt
;....}
2
3
;
2
2
;
2
1
{;24cos4sin3 mmtt
ttt sin22cos32sin
ttt sin22cos2sin3
ttt cos22cos32sin
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
133
ttt cos22cos2sin3
ttt sin24cos34sin
ttt sin24cos4sin3
ttt cos24cos34sin
ttt cos24cos4sin3
ttt cos22cos2sin
ttt sin22cos2sin
ttt cos24cos4sin
ttt sin24cos4sin
2
sin24cos4sin
t
tt
2
cos24cos4sin
t
tt
2
sin22cos32sin
t
tt
2
cos22cos32sin
t
tt
…………………….(các bạn tự tìm các dạng khác )
Thí dụ 30 Giải phƣơng trình
x
xx
xxx
xxxx
222
221
122)122(21
122)122(
22
23
Hƣớng dẫn.
Chọn
1;22;122)122(;1
22
dxcxxbxa
2;1;1; qpnxm
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
134
Ta phải giải PT
122122)122(
22
xxxx
)1(24)1)(12(
222
xxxxx
2
2
22
2
2
1
1
1
2
22
1
1
1
2
x
x
x
x
x
x
x
x
Đặt
tx tan
rồi ta giải PT
ttt 4sin22cos2sin
PTđã cho có 4 nghiệm:
;21)
8
tan(
x
(nghiệm kép)
;26922
24
5
tan
x
26922
24
11
tan
x
2
1
; x
Đến đây tác giả tin rằng mọi người sẽ dễ dàng tự tạo ra rất nhiều phương trình Tích dù là dạng
đơn giản hay phức tạp tùy theo ý mình.
Tác giả của ý tưởng :Vũ Hồng Phong THPT Tiên Du1,Tiên Du,Bắc Ninh
Tiếp tục Casio bậc 2
Thí dụ 83 Giải phƣơng trình
3
2
2
3
2
2
2
2
2
2
229
636
12
153
2
229
22
2
12
15
x
xx
xx
x
xx
x
xx
xx
xx
x
Hƣớng dẫn.
Phƣơng trình đƣợc tạo ra từ PT
32422915
222
xxxxx
Biểu thức cần tìm là
1512
22
xxx
và
22922
22
xxxx
PTcó 2 nghiệm
;1x
3
2
1
x
Chọn
3
;3;2;1 xqpnm
PT đã cho có 3 nghiệm
;1x
3
3
6;
2
1
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
135
Thí dụ 84 Giải phƣơng trình
2
2
2
2
2
2
2
2
2
2
1
532
835
422
3
1
53
3
835
2
x
xx
xx
x
xx
xx
xx
xx
xx
xx
Hƣớng dẫn.
Từ PT:
32253835
222
xxxxxx
Biểu thức cần tìm là
8352
22
xxxx
và
531
22
xxxx
PTcó 2 nghiệm
;1x
3
31x
Chọn
2
;2;3;1 xqpnm
PTcó 4 nghiệm
;1x
6;31
3
xx
Thí dụ 85 Giải phƣơng trình
x
xx
xx
x
xx
xx
xx
xx
xx
xx
32
6643
122
663
2
32
664
2
122
22
2
2
2
2
2
2
2
2
Hƣớng dẫn.
Từ PT:
542664122
222
xxxxxx
Biểu thức cần tìm là
12222
22
xxxx
và
66432
22
xxxx
PTcó 2 nghiệm
;1x
6;21
3
xx
Chọn
xqpnm ;3;2;1
PT đã cho có 3 nghiệm
;1x
3
21x
Thí dụ 86 Giải phƣơng trình
2
22
5
52376044
4
271410
3
x
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
136
Hƣớng dẫn.
Biểu thức cần tìm là
714102
22
xxxx
và
376044522
22
xxxx
0
1
52376044
43
271410
3
2
2
2
2
x
xxx
x
xxx
PT đã cho có 4 nghiệm
2
131
;
2
53
xx
Thí dụ 87 Giải phƣơng trình
2
22
2
3
281613
1
32256048
1
x
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
256048322
22
xxxx
và
816132
22
xxxx
0
1
281613
1
2
1
32256048
1
2
2
2
2
x
xxx
x
xxx
pt
PT đã cho có 4 nghiệm
31;22 xx
Thí dụ 88 Giải phƣơng trình
672
53
81613
1
2256048
1
24
2
22
xx
x
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
256048322
22
xxxx
và
816132
22
xxxx
0
2
1
81613
1
32
1
2256048
1
2
2
2
2
x
xxx
x
xxx
PT đã cho có 4 nghiệm
31;22 xx
Thí dụ 89 Giải phƣơng trình
xxxxxxx 3281613642560482
22
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
137
Hƣớng dẫn.
Biểu thức cần tìm là
256048322
22
xxxx
và
816132
22
xxxx
02816132642560482
22
xxxxxxxx
PT đã cho có 4 nghiệm
31;22 xx
Thí dụ 90 Giải phƣơng trình
xxxxxxx 32714101043760442
22
Hƣớng dẫn.
Biểu thức cần tìm là
714102
22
xxxx
và
376044522
22
xxxx
027141021043760442
22
xxxxxxxx
PT đã cho có 4 nghiệm
2
131
;
2
53
xx
Thí dụ 91 Giải phƣơng trình
32
3
2
3
2
)2(9111812125 xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
2512
22
xxxx
và
11812124
22
xxxx
0)2(8111812)2(125
32
3
232
3
2
xxxxxxxxpt
PTcó 2 nghiệm
;1x
3
4
3
x
Thí dụ 92 Giải phƣơng trình(tác giả Vũ Hồng Phong THPT Tiên Du 1)
4
4
2424
7262468 xxxxx
Hƣớng dẫn.
Đặt
0
2
ax
PT đã cho trở thành
2
4
22
7262468 aaaaa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
138
Điều kiện:
1
6
431
0
0726
0468
2
2
a
a
aa
aa
Biểu thức cần tìm là
46822
22
aaaa
và
4
2
7261 aaa
(*)0)]1(726[2)22(468
4
222
aaaaaaapt
PT(*)có 2 nghiệm
3
2;4 aa
PT đã cho có 4 nghiệm
6
2;2 ax
Thí dụ 93 Giải phƣơng trình
17263468
24
4
2424
xxxxxx
Hƣớng dẫn.
Đặt
0
2
ax
PT đã cho trở thành
17262468
2
4
22
aaaaaa
Điều kiện:
1
6
431
0
0726
0468
2
2
a
a
aa
aa
Biểu thức cần tìm là
46822
22
aaaa
và
4
2
7261 aaa
(*)0)]1(726[3)22(468
4
222
aaaaaaapt
PT(*)có 2 nghiệm
3
2;4 aa
PT đã cho có 4 nghiệm
6
2;2 ax
Thí dụ 94 Giải phƣơng trình(tác giả Vũ Hồng Phong )
24
4
2424
11633910 xxxxxx
Hƣớng dẫn.
Đặt
0
2
ax
PT đã cho trở thành
aaaaaa
2
4
22
11633910
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
139
Điều kiện:
1
10
1592
0
0116
03910
2
2
a
a
aa
aa
Biểu thức cần tìm là
391032
22
aaaa
và
4
2
1161 aaa
(*)0)]1(16[3)32(3910
4
222
aaaaaaapt
PT(*)có 2 nghiệm
3
3;4 aa
PT đã cho có 4 nghiệm
6
3;2 ax
Thí dụ 95 Giải phƣơng trình
733414711252
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
11252
22
xxxx
và
41473
22
xxxx
PTcó 2 nghiệm
;1x
16
3
x
Nâng cấp:
Giải phƣơng trình
(*)25341473111252
22
xxxxxxx
Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là
817120592,0;1 xx
biểu thức liên hợp cần tìm là
)1(11125
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
xxxx 34147
2
ĐKXĐ:
)1(011125
2
xxx
và
)2(034147
2
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
140
Có:
4
577
4
577
)1(
x
x
6
464
6
464
)2(
x
x
Do
5
2
025(*)0(*)
xxVPVT
suy ra
6
464
x
Khi đó
0)1(11125
2
xxxx
034147
2
xxxx
0
2
)3(4147
.3
1
)2(1125
.2(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
;1x
16
3
x
Thí dụ 96 Giải phƣơng trình
83351372)115(
22
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
)115(2
2
xxxx
và
51373
22
xxxx
PTcó 2 nghiệm
;1x
3
51x
Nâng cấp:
Giải phƣơng trình
(*)4215513725115
22
xxxxxxx
Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là
709975946,0;1 xx
biểu thức liên hợp cần tìm là
)2(25115
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)2(155137
2
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
141
ĐKXĐ:
)1(025115
2
xxx
và
)2(0155137
2
xxx
Có:
0
40
64131
5
11
)1(
x
x
14
2913
14
2913
36
81723
)2(
x
x
Do
5
2
025(*)0(*)
xxVPVT
suy ra
6
464
x
Khi đó
0)2(25115
2
xxxx
0)2(155137
2
xxxx
0
2
)3(5137
1
)2(115
(*)
2222
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
;1x
3
51x
Thí dụ 97 Giải phƣơng trình
76323382)15)(72(
22
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
)15)(72(22
2
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
233832
22
xxxx
PT đã cho có 2 nghiệm
3
92;2 xx
Nâng cấp: Giải phƣơng trình
(*)441233832)15)(72(
2
xxxxx
Hƣớng dẫn.
Ta dùng casio tìm đƣợc các nghiệm đẹp của PT là
0080083823,0;2 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
142
Biểu thức liên hợp cần tìm là
)1(2)15)(72( xxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
)1(12338
2
xxx
Do
0(*) VT
suy ra
1044(*) xxVP
Khi đó
)1(2)15)(72( xxx
)1(12338
2
xxx
0
2
)22(2338
.3
1
)32()15)(72(
(*)
22
2
MS
xxxx
MS
xxxx
PT
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm
3
92;2 xx
Thí dụ 98 Giải phƣơng trình(Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn)
1
562
1
22
10104
2
2
2
xx
xx
xx
Hƣớng dẫn.
Biểu thức cần tìm là
56222
22
xxxx
và
1010432
22
xxxx
Ta có:
1
562
1
22
10104
2
2
2
xx
xx
xx
222210104562
2222
xxxxxxxx
0)22(5623210104562
22222
xxxxxxxxxx
Nhân liên hợp PT đã cho có 2 nghiệm
3
21;1 xx
Thí dụ 99 Giải phƣơng trình
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
143
12
3
28513
2
1339
1
2
22
xx
xxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
33922
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
8513232
22
xxxx
0
12
2
28513
2
12
1
1339
1
2
2
2
2
xx
xx
xx
xx
PT
Nhân liên hợp 2 lần ở từng phân thức suy ra PTcó 2 nghiệm
3
4
1
;1 xx
Thí dụ 100 Giải phƣơng trình
222
3
3412824
1
1865
1
2
22
xx
xxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
8652
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
412824522
22
xxxx
0
222
1
3412824
1
1
1
1865
1
2
2
2
2
xx
xx
xx
xx
PT
Nhân liên hợp 2 lần ở từng phân thức suy ra PTcó 2 nghiệm
3
2;2 xx
Chú ý:
01865
2
xx
03412824;
2
xx
Thí dụ 101 Giải phƣơng trình
122233)2(753
2
3
22
xxxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
7531
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
3
2
2331 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
144
0]1233)[2()1(753
3
222
xxxxxxxxPT
Nhân liên hợp suy ra PTcó 2 nghiệm
3
3;2 xx
Thí dụ 102 Giải phƣơng trình
2
22
2
3
1241248
1
11173
1
x
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
11731
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
41248122
22
xxxx
2
22
2
3
1241248
1
11173
1
x
xxxxxx
0]
2
1
1241248
1
[]
1
11173
1
[
2
2
2
2
x
xxx
x
xxx
Quy đồng rồi Nhân liên hợp suy ra PTcó 2 nghiệm
3
5;2 xx
Chú ý:
xxxx ;011173
2
xxxx ;01241248;
2
Tƣơng tự: Giải phƣơng trình
xxxxxxx 32441248211173
22
Hƣớng dẫn.
xxxxxxx 32441248211173
22
022441248211173
22
xxxxxxxx
Nhân liên hợp 2 lần suy ra PTcó 2 nghiệm
3
5;2 xx
Thí dụ 103 Giải phƣơng trình
42
2
1113510
1
26318
1
2
22
xx
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
145
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
631822
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
11351032
22
xxxx
0]
42
1
1113510
1
[]
42
1
26318
1
[
2
2
2
2
xx
xx
xx
xx
pt
Quy đồng rồi Nhân liên hợp suy ra PTcó 2 nghiệm
3
72;2 xx
Nâng cấp Giải phƣơng trình
32
1113510
16318
42
2
2
2
2
xx
xx
xx
xx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
631822
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
11351032
22
xxxx
32
1113510
16318
42
2
2
2
2
xx
xx
xx
xx
42
1113510
16318
32
2
2
2
2
xx
xx
xx
xx
0
42
1113510
11
16318
32
2
2
2
2
xx
xx
xx
xx
0
42
11351032
16318
631822
2
22
2
22
xx
xxxx
xx
xxxx
Nhân liên hợp suy ra PTcó 2 nghiệm
3
72;2 xx
Thí dụ 104 Giải phƣơng trình
12
559
235
22
2
2
2
2
x
xxx
xxx
x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
146
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
23512
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
55922
22
xxxx
12
559
235
22
2
2
2
2
x
xxx
xxx
x
22
559
235
12
2
2
2
2
x
xxx
xxx
x
0
22
559
11
235
12
2
2
2
2
x
xxx
xxx
x
0
22
55922
235
23512
2
22
2
22
x
xxxx
xxx
xxxx
Nhân liên hợp suy ra PTcó 2 nghiệm
3
4
1
;1 xx
Chuyên đề 3 TÌM NHÂN TỬ CỦA PHƢƠNG TRÌNH DÙNG CASIO
Thí dụ 1 Giải phƣơng trình
3874362
2342
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
3622
22
xxxx
Chú ý: ta có
3664)362()2(
23422
xxxxxxxx
PT đã cho có 1 nghiệm:
3
21x
Chú ý:
Bấm máy tính ta tìm đƣợc 1 nghiệm.Ta tìm thêm
1x
là nghiệm ngoại lai nó là nghiệm PT:
3874362
2342
xxxxxx
*Giải phƣơng trình sau (không dùng CASIO)
14222362
22
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
147
Đặt
ax 22
bxx 362;
2
suy ra
142
142
222
2
xxba
xxba
Tìm a,b theo x rồi suy ra
3
21x
Thí dụ 2 Giải phƣơng trình
142223623
22
xxxxx
Hƣớng dẫn. Bấm máy tính ta tìm đƣợc 1 nghiệm.
Tìm đƣợc nghiệm ngoại lai đẹp x=1bằng cách đổi dấu trƣớc căn
Đƣợc PT sau:
142223623
22
xxxxx
Biểu thức cần tìm là
3622
22
xxxx
và
2212
2
xxx
Cho 2 biểu thức bằng 0 suy ra
0122362
2
xxx
suy ra nhân tử cần xuất hiện là:
122362
2
xxx
Dùng casio giúp ta định hƣớng đƣợc PT đã cho có thể đƣa về PT tích. Cụ thể nhƣ sau
Đặt
axx 362
2
bx 22;
Tacó
142
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
Giải PT
0122362
2
xxx
bằng cách chuyển vế,bình phƣơng
Hoặc tìm a,b theo x ta Suy ra PT có 1 nghiệm
3
21x
Thí dụ 3 Giải phƣơng trình
0135263
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
xxxx 6323
22
và
513
22
xxx
Cho 2 biểu thức bằng 0 suy ra
01563
22
xxx
suy ra nhân tử cần xuất hiện là:
1563
22
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
148
Đặt
063
2
axx
05;
2
bx
Tacó
562
222
xxba
Thay vào PT đƣợc
0)3)(1( baba
Giải PT
01563
22
xxx
bằng cách chuyển vế,bình phƣơng
Hoặc tìm a,b theo x ta Suy ra
PT có 2 nghiệm
3
21x
3; x
Thí dụ 4 Giải phƣơng trình
02168494342512
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
42512142
22
xxxx
và
494142
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0249442512
22
xxxx
suy ra nhân tử cần xuất hiện là:
249442512
22
xxxx
Đặt
063
2
axx
05;
2
bx
Tacó
xxba 168
222
Thay vào PT đƣợc
0)3)(1( baba
PT có 2 nghiệm
3
4
1
1x
1; x
Thí dụ 5 Giải phƣơng trình
07426925533
22
xxxxx
Hƣớng dẫn. Bấm máy tính ta tìm đƣợc 1 nghiệm.
Tìm thêm nghiệm ngoại lai là nghiệm PT:
07426925533
22
xxxxx
Biểu thức cần tìm là
xxx 5312
2
và
69222
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0169253
2
xxx
suy ra nhân tử cần xuất hiện là:
169253
2
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
149
Đặt
053 ax
0692;
2
bxx
Tacó
342
222
xxba
Thay vào PT đƣợc
0)4)(1( baba
PT có 1 nghiệm
2
173
x
Thí dụ 6 Giải phƣơng trình
0266323164
222
xxxxx
Hƣớng dẫn.
Tìm thêm nghiệm ngoại lai là nghiệm PT:
0266323164
222
xxxxx
Biểu thức cần tìm là
22
23132 xxx
và
26632
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0126623
22
xxx
suy ra nhân tử cần xuất hiện là:
126623
22
xxx
Đặt
023
2
ax
0266;
2
bxx
Tacó
164
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
PT có 1 nghiệm
2
21
x
Thí dụ 7 Giải phƣơng trình
07483332344
222
xxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
332322
22
xxx
và
748222
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
01748332
22
xxx
suy ra nhân tử cần xuất hiện là:
01748332
22
xxx
Đặt
0332
2
ax
0748;
2
bxx
Tacó
544
222
xxba
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
150
Thay vào PT đƣợc
0)2)(1( baba
PT có 2 nghiệm
2
3
1x
Thí dụ 8 Giải phƣơng trình
076122121225132
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
121225332
22
xxxx
và
7612232
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
017612121225
22
xxxx
suy ra nhân tử cần xuất hiện là:
17612121225
22
xxxx
Đặt
0121225
2
axx
07612;
2
bxx
Tacó
564
222
xxba
Thay vào PT đƣợc
0)3)(1( baba
PT có 2 nghiệm
2
153
x
Thí dụ 9 Giải phƣơng trình
03121032432342
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
243232
22
xxxx
và
3121022
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
01312102432
22
xxxx
suy ra nhân tử cần xuất hiện là:
1312102432
22
xxxx
Đặt
02432
2
axx
031210;
2
bxx
Tacó
542
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
PT có 4 nghiệm
1x
52; x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
151
Nâng cấp: Giải phƣơng trình(tác giả Vũ Hồng Phong)
31210)1(243)3(2732
222
xxxxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
243232
22
xxxx
và
3121022
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
01312102432
22
xxxx
suy ra nhân tử cần xuất hiện là:
1312102432
22
xxxx
Đặt
02432
2
axx
031210;
2
bxx
Tacó
542
222
xxba
Thay vào PT đƣợc
0)2)(1( xbaba
+PT :
01312102432
22
xxxx
có 4 nghiệm
1x
52; x
+PT :
xxxxx 2312102432
22
có 2 nghiệm
1x
3
1
;
x
PT đã cho có 5 nghiệm
1x
3
1
;52;
xx
Thí dụ 10 Giải phƣơng trình
022083726102362
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
7261023
22
xxxx
và
220833
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
01220872610
22
xxxx
suy ra nhân tử cần xuất hiện là:
01220872610
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
152
Đặt
072610
2
axx
02208;
2
bxx
Tacó
562
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
PT có 4 nghiệm
21x
62; x
Thí dụ 11 Giải phƣơng trình
082433231216144
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
31216122
22
xxxx
và
82433133
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
01824332312163
22
xxxx
suy ra nhân tử cần xuất hiện là:
01824332312163
22
xxxx
Đặt
031216
2
axx
082433;
2
bxx
Ta dựa vào hệ số bất định giả sử
222
44 pbnamxx
Suy ra
3
5
;
3
4
;3
mpn
nên có
222
3
4
3
3
5
44 baxx
Thay vào PT đƣợc
0)223)(123( baba
PT có 4 nghiệm
1x
21; x
Thí dụ 12 Giải phƣơng trình
031210675644384
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
75644342
22
xxxx
và
3121012
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0131210275644
22
xxxx
suy ra nhân tử cần xuất hiện là:
0131210275644
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
153
Đặt
075644
2
axx
031210;
2
bxx
Ta dựa vào hệ số bất định giả sử
222
84 pbnamxx
Suy ra
5;4;1 mpn
nên có
222
4584 baxx
Thay vào PT đƣợc
0)22)(12( baba
PT có 4 nghiệm
2x
62; x
Thí dụ 13 Giải phƣơng trình
0112428323382584
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
233822
22
xxxx
và
112428342
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0111242823382
22
xxxx
suy ra nhân tử cần xuất hiện là:
111242823382
22
xxxx
Đặt
02338
2
axx
0112428;
2
bxx
Ta dựa vào hệ số bất định giả sử
222
84 pbnamxx
Suy ra
5;1;4 mpn
nên có
222
4584 baxx
Thay vào PT đƣợc
0)22)(12( baba
PT có 2 nghiệm
2x
3
92; x
Thí dụ 14 Giải phƣơng trình
7841316121226
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
12222
22
xxxx
và
131612542
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
011316121222
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
154
suy ra nhân tử cần xuất hiện là:
011316121222
22
xxxx
Đặt
02338
2
axx
0112428;
2
bxx
Thay vào PT đƣợc
0)22)(12( baba
PT có 2 nghiệm
1x
3
21; x
Thí dụ 15 Giải phƣơng trình
204520141893516
222
xxxxxxx
Hƣớng dẫn. (dùng máy tính dùng tính chất
2
AA
)
Biểu thức cần tìm là
512
22
xxxx
và
14189133
22
xxxxx
Cho 2 biểu thức bằng 0 suy ra
0514189513
22
xxxxx
suy ra nhân tử cần xuất hiện là:
514189513
22
xxxxx
Đặt
051
2
axx
014189;
2
bxxx
Chú ý:
459049
222
xxba
Thay vào PT đƣợc
0)13)(53( baba
PT có 2 nghiệm
223x
Thí dụ 16 Giải phƣơng trình
358030263216610418
222
xxxxxxx
Hƣớng dẫn. (dùng máy tính dùng tính chất
2
AA
để mất dấu ||)
Biểu thức cần tìm là
1041322
22
xxxx
và
263216144
22
xxxxx
Cho 2 biểu thức bằng 0 suy ra
0526321610412
22
xxxxx
suy ra nhân tử cần xuất hiện là:
0526321610412
22
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
155
Đặt
01041
2
axx
0263216;
2
bxxx
Chú ý:
4080304
222
xxba
Thay vào PT đƣợc
0)12)(52( baba
PT có 2 nghiệm
2
234
x
Thí dụ 17 Giải phƣơng trình
052036336102544
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
36101
22
xxxx
và
52036322
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
015203636102
22
xxxx
suy ra nhân tử cần xuất hiện là:
015203636102
22
xxxx
Đặt
03610
2
axx
052036;
2
bxx
Tacó
7444
222
xxba
Thay vào PT đƣợc
0)22)(12( baba
PT có 4 nghiệm
2
51
x
2
133
;
x
Thí dụ 18 Giải phƣơng trình
0118123252148
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
2512
22
xxxx
và
11812124
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0111812252
22
xxxx
suy ra nhân tử cần xuất hiện là:
111812252
22
xxxx
Dùng casio giúp ta định hƣớng đƣợc PT đã cho có thể đƣa về PT tích. Cụ thể nhƣ sau
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
156
Đặt
axx 25
2
bxx 11812;
2
Tacó
1484
222
xxba
Thay vào PT đƣợc
0)22)(12( baba
Giải PT
0111812252
22
xxxx
bằng cách chuyển vế,bình phƣơng
Hoặc tìm a,b theo x ta Suy ra PT có 2 nghiệm
;1x
3
4
3
x
Thí dụ 19 Giải phƣơng trình
3333853208
222
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
3852
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
3208122
22
xxxx
Đặt
0385
2
axx
03208;
2
bxx
Suy ra
1512124
222
xxba
Pt đã cho có dạng
0)12)(32( baba
PT đã cho có 2 nghiệm
3
21;1 xx
Thí dụ 20 Giải phƣơng trình (bài khó chỉ để tham khảo)
1)1124(
1123
59
25
22
2
2
2
xxx
x
x
xx
Hƣớng dẫn.
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
1)1124(
)1123(2
)1123)(1123(
25
22
2
22
2
xxx
x
xx
xxpt
1)1124(21231410
2222
xxxxxx
Tìm nghiệm đẹp x=-1 và x=-2,587401052
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
157
Biểu thức cần tìm là
1222
22
xxx
và
1232
22
xxxx
Suy ra
11212
22
xxx
là nhân tử cần xuất hiện
0]12312][11212[
2222
xxxxxxpt
PTcó 4 nghiệm
;1x
14
1862
;41
3
xx
Lƣu ý: +dùng hệ số bất định có
22222
)12(3)12(1410 xxxxx
+dùng Casio nếu tìm đƣợc nghiệm là nghiệm pt bậc 2 vd X=1,117012978 dùng casio ta tinh ý thì
biết đƣợc điều sau
012312
22
xxx
Thí dụ 21 Giải phƣơng trình
163114)12(
2422
xxxxxx
Hƣớng dẫn.
Dùng Casio nếu các bạn tìm đƣợc 2 nghiệm là nghiệm của PT bậc 2 có tổng,tích đẹp thì nó
là pt:
012
2
xx
0)12)(12(3114)12(
2222
xxxxxxxxpt
PT đã cho có 3 nghiệm
3
31;21 xx
Chú ý:
Nếu tìm 1nghiệm không là nghiệm bậc 2 thì cần tìm thêm nghiệm ngoại lai là 1
Thí dụ 22 Giải phƣơng trình
456222
422
xxxxx
Hƣớng dẫn.
Dùng Casio biểu thức cần tìm là
)22(562
22
xxxx
0)22)(22(562)22(
2222
xxxxxxxxpt
PT đã cho có 2 nghiệm
3
21;1 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
158
Thí dụ 23 Giải phƣơng trình
463129622338
222
xxxxxx
Hƣớng dẫn.
Biểu thức cần tìm là
233822
22
xxxx
và
129612
22
xxxx
PTcó 2 nghiệm
3
92;2 xx
Nâng cấp
1) Giải phƣơng trình
0129632338242
222
xxxxxx
Hƣớng dẫn.
Ta dùng Casio tìm đƣợc các nghiệmcủa PT là
0080083823,0;2 xx
Biểu thức cần tìm là
233822
22
xxxx
và
129612
22
xxxx
Cho 2 biểu thức bằng 0 suy ra
0112962338
22
xxxx
suy ra nhân tử cần xuất hiện là:
0112962338
22
xxxx
Đặt
02338
2
axx
01296;
2
bxx
Tacó
342
222
xxba
Thay vào PT đƣợc
0)2)(1( baba
PTcó 2 nghiệm
3
92;2 xx
2) Giải phƣơng trình
32912963
2
22
xxxx
x
x
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
159
Biểu thức cần tìm là
129612
22
xxxx
Biểu thức nữa cần tìm là
12961
2
xxx
32912963
2
22
xxxx
x
x
xxxxxxx 329129623
2322
1299)1(1296112
2322
xxxxxxxx
011296)12(1296
222
xxxxxxx
PTcó 3 nghiệm
10
76927
;29;2
3
xxx
Thí dụ 24 Giải phƣơng trình
433
3167
385632
2
2
22
xx
xx
xxxx
Hƣớng dẫn.
433
3167
385632
2
2
22
xx
xx
xxxx
433
385632385632
385632
2
2222
22
xx
xxxxxxxx
xxxx
0385632
22
xxxx
hoặc
433385632
222
xxxxxx
Biểu thức cần tìm là
xxxx 631
22
và
3852
22
xxxx
PTcó 4 nghiệm
7
858
;21;1
3
xxx
Nâng cấp Giải phƣơng trình
2
58
363
2
2
x
x
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
160
Hƣớng dẫn. ĐKXĐ…
2
58
363
2
2
x
x
xxx
2
163
63
2
23
2
x
xxx
xx
)1)(1(6363)11(
2222
xxxxxxxxxx
0163163
222
xxxxxxx
PTcó 4 nghiệm
2
234
;21;1
3
xxx
Pt trên để nhìn phức tạp hơn ta chuyển thành
Giải phƣơng trình:
2
58
363
9122
2
2
2
x
x
xxx
xx
Hay Giải phƣơng trình:
9122
58
363
2
2
2
2
xx
x
xxx
x
PTcó 4 nghiệm
2
234
;21;1
3
xxx
Thí dụ 25 Giải phƣơng trình
)32)(12(134162832
22
xxxxxx
Hƣớng dẫn. ĐKXĐ……
)32)(12(134162832
22
xxxxxx
7
134162832134162832
134162832
2222
22
xxxxxxxx
xxxx
0134162832
22
xxxx
hoặc
(*)7134162832
22
xxxx
Biểu thức cần tìm là
2831
22
xxxx
và
13416522
22
xxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
161
Có
)(**)32)(12(7)13416()2832(
2222
xxxxxx
Để giải (*) ta kết hợp với (**) suy ra
2831
22
xxxx
và
13416522
22
xxxx
PT đã cho có 3 nghiệm
2
1
;41;1
3
xxx
Thí dụ 26 Giải phƣơng trình
063183113510342
222
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
11351022
22
xxxx
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
11351032
22
xxxx
0]26318113510][16318113510[
2222
xxxxxxxxPT
PT có 2 nghiệm
27;2
3
xx
Hƣớng dẫn một số cách hay dùng để tạo ra phƣơng
trình Tích(Vũ Hồng Phong THPT Tiên Du 1)
Muốn có nghiệm
3
3;2 xx
cần có pt:
632)3)(2(
343
xxxxx
Biểu thức liên hợp cần tìm là
Amxx
2
Nếu cần biểu thức
Axx 1
2
thì
753)3)(2()1(
2322
xxxxxxA
Nếu cần biểu thức
Bxx 2
2
thì
1075)3)(2()2(
2322
xxxxxxB
Nếu cần biểu thức
Cxx 122
2
thì
25168)3)(2(4)122(
2322
xxxxxxC
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
162
Nếu cần biểu thức
Dxx 133
2
thì
553315)3)(2(9)133(
2322
xxxxxxD
Nếu cần biểu thức
Exx 4
2
thì
2257)3)(2()4(
2322
xxxxxxE
Khi này dựa vào các biểu thức tạo ở trên các bạn thích tạo ra PT nhân liên hợp hay đƣa về
PT tích là tùy ý thích
Chẳng hạn
Pt giải bằng nhân liên hợp
43310757532
222
xxxxxx
355251682753
222
xxxxxx
3555533157532
222
xxxxxx
Để tạo ra PT tích ta có thể làm theo hướng sau:
Ta nhận thấy từ cách tạo:
017531075
22
xxxx
01753225168
22
xxxx
057532257
22
xxxx
Ta tạo ra PT tích nhƣ sau
0]27531075][17531075)[
2222
xxxxxxxxa
075331075122
222
xxxxxx
PT có 2 nghiệm
3
3;2 xx
0]2753225168][1753225168)[
2222
xxxxxxxxb
222
)12(7532251683 xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
163
PT có 2 nghiệm
3
3;2 xx
0]7532257][57532257)[
2222
xxxxxxxxc
3227532257
222
xxxxxx
PT có 4 nghiệm
2
71
;3;2
3
xxx
(nhƣ vậy ai cũng đều có khả năng tự tạo ra đƣợc các phƣơng trình tƣơng tự các PT trong
bài viết này)
Một số phƣơng trình khác
Pt nhiều nhân tử,Pt liên hợp có bậc 1,bậc 2,….
1.Giải phƣơng trình
864)1)(3()2(3
2342
xxxxxxxx
Nhân tử cần tìm là
)1)(3(1
22
xxxx
864)1)(3()2(3
2342
xxxxxxxx
0)53)(1()1)(3()1)(3()153(
222222
xxxxxxxxxxxx
0]53)1)(3()][1()1)(3([
2222
xxxxxxxxx
0)]3(21)1)(3()][1()1)(3([
2222
xxxxxxxxxx
0]321][31)][1()1)(3([
2222
xxxxxxxxxx
Pt có 4 nghiệm
31;2;1
3
xxx
2.Giải phƣơng trình
xxxxxx
2322
364)1(27
HD:đkxđ
02
2
3
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
164
xxxxxx
2322
364)1(27
0]264)[1(]227[
222
xxxxx
Nhân liên hợp suy ra Pt có 4 nghiệm
2;1 xx
2.Giải phƣơng trình
xxxxxx
2322
364)1(27
HD:đkxđ
02
2
3
xx
xxxxxx
2322
364)1(27
0]264)[1(]227[
222
xxxxx
Nhân liên hợp suy ra Pt có 4 nghiệm
2;1 xx
Thí dụ 3 Giải phƣơng trình
12374)2(311
2322
xxxxxx
Hƣớng dẫn.
12374)2(311
2322
xxxxxx
)
4
7
:(0]274)[2(]3311[
222
xđkxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
3;2 xx
Thí dụ 4 Giải phƣơng trình
xxxxxx 25233)1(2619
2322
Hƣớng dẫn.
xxxxxx 25233)1(2619
2322
)1:(0]32332)[1(]32619[
222
xđkxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
165
Nhân liên hợp suy ra PT có 4 nghiệm
2
3
;1 xx
Thí dụ 5 Giải phƣơng trình
4364)1(65
2322
xxxxxx
Hƣớng dẫn. đk:
021 xx
4364)1(65
2322
xxxxxx
0)264)(1(]265[
222
xxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
2x
Chú ý:Tìm biểu thức liên hợp
264 xx
từ đó suy đoán biểu thức liên hợp
265
22
xx
Thí dụ 6 Giải phƣơng trình
544258)2(33
2322
xxxxxx
Hƣớng dẫn. đk:
0111 xx
544258)2(33
2322
xxxxxx
0)158)(2(]1233[
222
xxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
2
1
x
Thí dụ 7 Giải phƣơng trình
345)2(3332
2223
xxxxxx
Hƣớng dẫn. đk:
0211 xx
345)2(3332
2223
xxxxxx
0]3452)[2(]1233[
2222
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
166
Nhân liên hợp suy ra PT có 2 nghiệm
2
1
x
Thí dụ 8 Giải phƣơng trình
54354)4(511
2322
xxxxxx
Hƣớng dẫn. đk:
02
4
5
xx
54354)4(511
2322
xxxxxx
0]254)[4(]3511[
222
xxxxx
Nhân liên hợp suy ra PT có 3 nghiệm
2;1 xx
Thí dụ 9 Giải phƣơng trình
14136)1(1213
2322
xxxxxx
Hƣớng dẫn. đk:
03
6
13
xx
14136)1(1213
2322
xxxxxx
0]3136)[1(]41213[
222
xxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2;1 xx
Thí dụ 10 Giải phƣơng trình
2554)2(466
2322
xxxxxxxx
Hƣớng dẫn.
đk:
02
4
5
xx
2554)2(466
2322
xxxxxxxx
0]254)(2(]2466[
222
xxxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2;0;1 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
167
Thí dụ 11 Giải phƣơng trình
156610)2(188
2322
xxxxxxxx
Hƣớng dẫn. đk:
03
3
5
xx
156610)2(188
2322
xxxxxxxx
0]3610)[2(]1188[
222
xxxxxxxx
Nhân liên hợp suy ra PT có 3 nghiệm
3;1;0 xxx
Thí dụ 12 Giải phƣơng trình
442133)2(25
2
3
22
xxxxxxx
Hƣớng dẫn.
442133)2(25
2
3
22
xxxxxxx
0]1133)[2(]225[
3
222
xxxxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
3
2;2 xx
Thí dụ 13 Giải phƣơng trình
421)2(25
2
3
32
xxxxxx
Hƣớng dẫn.
421)2(25
2
3
32
xxxxxx
0]11)[2(]225[
3
322
xxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
3
2;2 xx
Thí dụ 14 Giải phƣơng trình
2
3
32
3)2(25 xxxxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
168
2
3
32
3)2(25 xxxxx
0]31)[2(225
3
322
xxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
3
2;2 xx
Thí dụ 15 Giải phƣơng trình
210)2(25
2
3
32
xxxxxx
Hƣớng dẫn.
210)2(25
2
3
32
xxxxxx
0]210)[2(]225[
3
322
xxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
3
2;2 xx
Thí dụ 16 Giải phƣơng trình
636)2(25
2
3
32
xxxxxx
Hƣớng dẫn.
636)2(25
2
3
32
xxxxxx
0]62)[2(]225[
3
322
xxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
3
2;2 xx
Thí dụ 17 Giải phƣơng trình
12297.1107
2
3
22
xxxxxxx
Hƣớng dẫn.
12297.1107
2
3
22
xxxxxxx
0]197[]11107[
3
222
xxxxxxxx
Nhân liên hợp suy ra PT có 2 nghiệm
0;2;2 xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
169
Thí dụ 18 Giải phƣơng trình
12411012)1(4611
2
3
22
xxxxxxx
Hƣớng dẫn.
12411012)1(4611
2
3
22
xxxxxxx
0]1211012)[1(]224611[
3
222
xxxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2
1
;1;0 xxx
.
Thí dụ 19 Giải phƣơng trình
32212)1(4611
2
3
32
xxxxxxx
Hƣớng dẫn.
32212)1(4611
2
3
32
xxxxxxx
0]121)[1(]224611[
3
322
xxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2
1
;1;0 xxx
.
Thí dụ 20 Giải phƣơng trình
1212)1(4611
2
3
32
xxxxxx
Hƣớng dẫn.
1212)1(4611
2
3
32
xxxxxx
0]121)[1(]224611[
3
322
xxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2
1
;1;0 xxx
.
Thí dụ 21 Giải phƣơng trình
1
72
342)3(74)1(610
2
2222
xx
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
170
Hƣớng dẫn.
1
72
342)3(74)1(610
2
2222
xx
xxxxxx
03342)3(27413610
22222
xxxxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
3;1 xx
.
Thí dụ 22 Giải phƣơng trình
122153)2(165
2
3
22
xxxxxxx
Hƣớng dẫn.
122153)2(165
2
3
22
xxxxxxx
0]1153)[2(]1165[
3
222
xxxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2;2;0 xxx
.
Thí dụ 23 Giải phƣơng trình
12255.165
2
3
22
xxxxxxx
Hƣớng dẫn.
12255.165
2
3
22
xxxxxxx
0]155.[1165
3
222
xxxxxxxx
Nhân liên hợp suy ra PT có 4 nghiệm
2;2;0 xxx
.
Thí dụ 24 Giải phƣơng trình
12355.165
2
3
22
xxxxxx
Hƣớng dẫn.
12355.165
2
3
22
xxxxxx
0]1355[]1165[
3
222
xxxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
171
Nhân liên hợp suy ra PT có 4 nghiệm
2;2;0 xxx
.
Thí dụ 25 Giải phƣơng trình
1)2(3165
232
xxxxx
Hƣớng dẫn.
1)2(3165
232
xxxxx
0]11)[2(1165
2322
xxxxxxxx
Nhân liên hợp và kiểm tra đkxđ suy ra PT có 3 nghiệm
2;2;0 xxx
.
Thí dụ 26 Giải phƣơng trình
42)2(1655
232
xxxxxxx
Hƣớng dẫn.
42)2(1655
232
xxxxxxx
0]242)[2(]1165[
2322
xxxxxxxxx
Nhân liên hợp và kiểm tra đkxđ suy ra PT có 4 nghiệm
2;2;0 xxx
.
Thí dụ 27 Giải phƣơng trình
3
641
)3)(4(
1121
4
2
2
2
2
x
x
xx
x
x
Hƣớng dẫn.
3
641
)3)(4(
1121
4
2
2
2
2
x
x
xx
x
x
0)4(
641
)3)(4(
1
1121
4
2
2
2
2
x
x
xx
x
x
0
641
)642)(4(
1121
1123
2
2
22
x
xxx
x
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
172
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 3 nghiệm
2;2,2 xxx
.
Thí dụ 28 Giải phƣơng trình
2
23
2
2
641
33
27
2
x
x
xxx
xx
xx
Hƣớng dẫn.
2
23
2
2
641
33
27
2
x
x
xxx
xx
xx
2
2
2
2
641
)3)(1(
27
2
x
x
xx
xx
xx
0)1(
641
)3)(1(
1
27
2
2
2
2
2
x
x
xx
xx
xx
0
641
)642)(1(
27
272
2
2
22
x
xxx
xx
xx
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm
2,1 xx
.
Thí dụ 29 Giải phƣơng trình
3
1061
)4)(4(
2988
1
2
2
2
2
x
x
xx
xxx
x
Hƣớng dẫn.
3
1061
)4)(4(
2988
1
2
2
2
2
x
x
xx
xxx
x
0)4(
1061
)4)(4(
1
2988
1
2
2
2
2
x
x
xx
xxx
x
0
1061
)1063)(4(
9882
9883
2
2
22
x
xxx
xxx
xxx
Nhân liên hợp và đối chiếu ĐKXĐ
suy ra PT có 3 nghiệm
2,1 xx
.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
173
Thí dụ 30 Giải phƣơng trình
2
2
2
2
)1(
541
)3)(2(
466
2
x
x
xxx
xxx
x
Hƣớng dẫn.
2
2
2
2
)1(
541
)3)(2(
466
2
x
x
xxx
xxx
x
0)2(
541
)3)(2(
1
466
2
2
2
2
2
xx
x
xxx
xxx
x
0
541
)542)(2(
466
4661
2
2
22
x
xxxx
xxx
xxxx
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm
2;0,1 xxx
.
Thí dụ 31 Giải phƣơng trình
2
22
2
271
3
2
2
2
2
2
x
x
x
x
x
Hƣớng dẫn.
2
22
2
271
3
2
2
2
2
2
x
x
x
x
x
2
22
11
271
3
2
2
2
2
2
x
x
x
x
x
0
2
22
)1(
271
272
2
2
2
2
22
x
x
x
x
xx
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm
2,1 xx
.
Thí dụ 32 Giải phƣơng trình(Vũ Hồng Phong THPT Tiên Du 1)
2
14
12
2172
2
2
2
2
2
2
x
x
x
x
x
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
174
2
14
12
2172
2
2
2
2
2
2
x
x
x
x
x
0
2
14
2
14
2
1
2172
2
2
22
2
2
x
xx
x
x
0
22
)22)(14(
)2172(2
21722
2
22
2
22
x
xx
x
xx
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm
2,
2
1
xx
.
Thí dụ 33 Giải phƣơng trình
15
3
178
6
2
2
x
xx
x
x
Hƣớng dẫn.
15
3
178
6
2
2
x
xx
x
x
0)2)(1(15)21(15
2222
xxxxxx
0)]2(15)][1(15[
222
xxxx
PT đã cho có 6 nghiệm
2
61
;2;1
xxx
Để PT đã cho nhìn phức tạp hơn ta chuyển vế ,nhân liên hợp để đƣa về các PT sau:
152
)1(5
3
178
4
2
2
2
x
x
xx
x
x
0
152
15)4(1325
3
178
2
22
2
x
xxxx
xx
x
Thí dụ 34 Giải phƣơng trình
15
212
12)1(6
2
2
22
x
xx
xxx
Hƣớng dẫn.
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
175
15
212
12)1(6
2
2
22
x
xx
xxx
152121216
2222
xxxxxx
0)11215)(115(
222
xxxx
.
PT đã cho có 4 nghiệm
2;1 xx
Thí dụ 35 Giải phƣơng trình
3
5412
127
1
3
2
2
2
2
x
xx
x
x
x
Hƣớng dẫn. ĐK:
4
5
x
3
5412
127
1
3
2
2
2
2
x
xx
x
x
x
3
5412
21
127
1
2
2
2
2
x
xx
x
x
x
0
3
5422
127
272
2
2
22
x
xxx
x
xx
Nhân liên hợp và đối chiếu điều kiện suy ra PT có 3 nghiệm
2;1 xx
.
Thí dụ 36 Giải phƣơng trình
1522
2722
151
272
22
22
22
23
xx
xx
xxx
xxx
Hƣớng dẫn.
Xem phần tạo ra PT Tích từ các biểu thức
15;1;2;27
2222
xdxcxbxa
1;2;;1 qpxnm
1522
2722
151
272
22
22
22
23
xx
xx
xxx
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
176
0
27
2
1
15
2
2
2
2
x
x
x
x
hoặc
2
1
2
x
0
27
2
11
1
15
2
2
2
2
x
x
x
x
hoặc
2
1
x
Nhân liên hợp suy ra PT đã cho có 5 nghiệm:
2
1
;2;1 xxx
Thí dụ 37 Giải phƣơng trình
15312716)3(27)62(
222
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
272
22
xx
và
71612
22
xx
15312716)3(27)62(
222
xxxxxx
0)716272)(3716272(
2222
xxxxx
PTcó 4 nghiệm
2;1 xx
Chú ý:
072272
22
xxxxxx
Thí dụ 38 Giải phƣơng trình
0153121120)3(18)62(
222
xxxxxx
Hƣớng dẫn.
Biểu thức liên hợp cần tìm là
182
22
xx
và
112012
22
xx
0153121120)3(18)62(
222
xxxxxx
0)1120182)(31120182(
2222
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
177
PTcó 4 nghiệm
3;1 xx
Chú ý:
082182
22
xxxxxx
Thí dụ 39 Giải phƣơng trình
5431
543)2(543
12
2
8653
2
22
2
2
2
xx
xxxxx
x
xx
xx
Hƣớng dẫn.
5431
543)2(543
12
2
8653
2
22
2
2
2
xx
xxxxx
x
xx
xx
5431
5432543
25432543
2
8653
2
22
22
2
2
xx
xxxxx
xxxxxx
xx
xx
5431
543
2543
2
8653
2
2
2
2
2
xx
xx
xxx
xx
xx
5431
543
2
1
2
8653
2
2
2
2
xx
xx
x
xx
xx
543
543
2
2
8653
2
2
2
2
xx
xx
x
xx
xx
543
)1(3
2
8653
2
2
2
2
xx
xx
xx
xx
543
1
2
865
2
2
2
2
xx
xx
xx
xx
0
543
1
11
2
865
2
2
2
2
xx
xx
xx
xx
0
543
)1(543
2
)2(865
2
22
2
22
xx
xxxx
xx
xxxx
Nhân liên hợp suy ra PT có 2 nghiệm là
3
3;2 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
178
Nhận xét:Thí dụ 39 Xuất phát là Giải phƣơng trình
543
1
2
865
2
2
2
2
xx
xx
xx
xx
Thí dụ 40
Xuất phát từ
phƣơng trình
0)2543)(1543(
222
xxxxxxx
522543)1`(
2322
xxxxxxx
1
522
543
2
23
2
xx
xxx
xx
(*)
1
36
12543
2
2
xx
x
xxx
Để ngụy trang tiếp PT(*) ta có một số hƣớng sau:
hƣớng 1
1
36
1)2(543(*)
2
2
xx
x
xxxx
1
36
1
5432
12
2
2
2
xx
x
x
xxx
x
(ở đây ta đã nhân liên hợp để ngụy trang)
hƣớng 2
0
1
36
54312(*)
2
2
xx
x
xxx
0
1
36
54312
4
2
2
2
xx
x
xxx
x
(ở đây ta đã nhân liên hợp để ngụy trang)
1
3
54312
2
2
2
xx
xxx
x
(ở đây ta bỏ bớt 1 nhân tử có chứa nghiệm PT ban đầu)
Thí dụ 40 Giải phƣơng trình
1
36
1
5432
12
)
2
2
2
xx
x
x
xxx
x
a
PT có 3 nghiệm là
1;2;2
3
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
179
1
3
54312
2
)
2
2
xx
xxx
x
b
PT có 2 nghiệm là
1;2
3
xx
Thí dụ 41
Xuất phát từ
phƣơng trình
0)115)(115(
2222
xxxxx
xxxxxxx
322223
5)1(15)1`(
xxxxxx
32222
5)1(15)1`)(1(
1
5
115)1(
2
3
22
x
xx
xxx
Giải phƣơng trình
1
5
115)1(
2
3
22
x
xx
xxx
Chú ý: giải phƣơng trình
0115
22
xxx
1
)1()15(
0
115
2222
22
x
xxx
x
xxx
PT có 4 nghiệm là
2;1 xx
Thí dụ 42
Xuất phát từ
phƣơng trình
0)215)(115(
2222
xxxxx
)2)(1(515)2`(
223223
xxxxxxxx
)2)(1(51515)1`)(1(
223222
xxxxxxxx
1
155
215)1(
2
23
22
x
xxx
xxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
180
phƣơng trình
0)215)(115(
2222
xxxxx
23515)2`(
234223
xxxxxxxx
154
2
672
2
23
2
xx
xxx
xx
Thí dụ 42 Giải phƣơng trình(Vũ Hồng Phong)
154
2
672
)
2
23
2
xx
xxx
xx
a
PT có 5 nghiệm là
8
895
;2;1
xxx
1
155
215)1)(
2
23
22
x
xxx
xxxb
PT có 5 nghiệm là
8
895
;2;1
xxx
Chú ý: giải phƣơng trình
0215
22
xxx
8
895
)2()15(
0
215
2222
22
x
xxx
x
xxx
Thí dụ 43
Xuất phát từ
phƣơng trình
0)15)(115(
222
xxxx
1515)1`(
2322
xxxxxx
xx
xx
x
15
1
14
2
2
2
Thí dụ 43 giải phƣơng trình
xx
xx
x
15
1
14
2
2
2
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
181
PT có 5 nghiệm là
2
1
;2;1 xxx
Nhƣ vậy việc tạo ra đƣợc một phƣơng trình TÍCH là không quá khó khăn và có nhiều cách
để tạo ra. Xin giới thiệu tiếp cách tạo ra PT Tích dạng phức tạp hơn
Thí dụ 44
Xuất phát từ
phƣơng trình
0)31815)(115(
2222
xxxxx
13531815115)1`3(
2322222
xxxxxxxxx
PT có 5 nghiệm là
2
1
;2;1 xxx
Giải phƣơng trình
031815
22
xxx
Ngoài cách chuyển -3x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau
031815
22
xxx
0331515
222
xxxx
đặt ẩn phụ
xbax ;15
2
Thí dụ 45
Xuất phát từ
phƣơng trình
0)18153)(115(
2222
xxxxx
3151815115)3`3(
2322222
xxxxxxxxx
Ta có Giải phƣơng trình
3151815115)3`3(
2322222
xxxxxxxxx
PT có 6 nghiệm là
79
4
;
2
1
;2;1
xxxx
Giải phƣơng trình
018153
22
xxx
Ngoài cách chuyển -x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
182
018153
22
xxx
0315153
222
xxxx
đặt ẩn phụ
xbax ;15
2
Thí dụ 46
Xuất phát từ
phƣơng trình
0)19153)(115(
2222
xxxxx
3151815115)3`3(
2322222
xxxxxxxxx
Ta có Giải phƣơng trình
3151915115)3`3(
2322222
xxxxxxxxx
PT có 6 nghiệm là
1189
)333139(2
;2;1
xxx
Giải phƣơng trình
018153
22
xxx
Ngoài cách chuyển -x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau
019153
22
xxx
0)15(2153
222
xxxx
đặt ẩn phụ
xbax ;15
2
Thí dụ 47
Xuất phát từ PT
xx 0)2)(2(
3
Tạo ra biểu thức
Axx 1
2
và biểu thức
Bxx 2
2
Nhƣ sau:
543)2)(2()1(
2322
xxxxxxA
865)2)(2()2(
2322
xxxxxxB
Suy ra có PT mà
1543
1
2
xxx
ứng với
2
1
x
vế bên kia PT
2865
1
2
xxx
ứng với
2
1
x
vế bên kia PT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
183
có thể tạo ra PT
2
22
2
2865
1
1543
1
x
xxxxxx
nhân liên hợp ta đƣợc PT cần tạo ra nhƣ sau:
22
2
2
2
2
424
2865
422
1543
xxx
xxx
xx
xxx
Ta có Giải phƣơng trình
22
2
2
2
4
22
2865
2
1543
xxx
xxx
xx
xxx
PT có 2 nghiệm
3
2;2 xx
có thể tạo ra PT
2
22
3
2865
2
1543
1
x
xxxxxx
Tƣơng tự ta có Giải phƣơng trình
22
2
2
2
3
22
2865
422
1543
xxx
xxx
xx
xxx
PT có 2 nghiệm
3
2;2 xx
Thí dụ 48
Xuất phát từ PT
xx 0)2)(2(
3
1
1
322
2
2
3
x
x
xx
Biểu thức liên hợp đã biết
5431
22
xxxx
Ta có thể tạo ra PT
11
1
322
543
22
2
3
2
xxx
x
xx
xx
1
1
322
1543
22
2
3
2
xx
x
xx
xxx
1
1
322
1543
422
22
2
3
2
2
xx
x
xx
xxx
xx
Ta có Giải phƣơng trình
1
1
322
1543
422
22
2
3
2
2
xx
x
xx
xxx
xx
PT có 2 nghiệm
3
2;2 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
184
Thí dụ 49
Xuất phát từ PT
xx 0)2)(2(
3
Tạo ra biểu thức
Axx 1
2
và biểu thức
Nhƣ sau:
Nếu muốn kết hợp Nhị thức NiuTơn suy ra
)510(2)1()1(
2455
xxxxx
Ta có Giải phƣơng trình
x
xx
xxxxxx
2
510
54328651
24
22
5
22
Hƣớng dẫn giải:
x
xx
xxxxxx
2
510
54328651
24
22
5
22
Bấm máy tính tìm đƣợc
25992105,1;2 XX
Các biểu thức cần xuất hiện
5431
22
xxxx
8652;
22
xxxx
Suy ra
18651
22
xxxx
15432;
22
xxxx
)510(2)5432()8651(
24522522
xxxxxxxxxPT
55522522
)1()1()5432()8651( xxxxxxxx
0)1()5432()1()8651(
55225522
xxxxxxxx
Sử dụng hằng đẳng thức rồi nhân liên hợp suy ra PT đã cho có 2 nghiệm
Thí dụ 50
Xuất phát từ PT
Tạo ra biểu thức và biểu thức
Nhƣ sau:
Bxx 2
2
543)2)(2()1(
2322
xxxxxxA
865)2)(2()2(
2322
xxxxxxB
3
2;2 xx
xx 0)2)(2(
3
Axx 1
2
Bxx 2
2
543)2)(2()1(
2322
xxxxxxA
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
185
Các biểu thức cần xuất hiện
8652;
22
xxxx
Để PT có căn trong căn thì từ trên ta Suy ra
15432
22
xxxx
Ta có Giải phƣơng trình
2
1
865
5432
22
22
xxxx
xxxx
Hƣớng dẫn giải:
2
1
865
5432
22
22
xxxx
xxxx
2
865
5432
2
2
22
xx
xx
xxxx
1
2
865
15432
2
2
22
xx
xx
xxxx
0
2
8652
]15432[
2
22
22
xx
xxxx
xxxx
Nhân liên hợp 2 lần ở biểu thức đầu,1 lân ở phân thức sau suy ra
PT có 2 nghiệm
Để PT có dấu giá trị tuyệt đối cũng không khó khăn gì. Ta có
54322
22
xxxx
1)1(22
22
xxxxx
Giải phƣơng trình
2
1
865
54322
22
22
xx
x
xx
xxxx
Hƣớng dẫn giải:
2
1
865
54322
22
22
xx
x
xx
xxxx
)1(
2
865
1
54322
2
222
xétx
xx
xx
x
xxxx
865)2)(2()2(
2322
xxxxxxB
5431
22
xxxx
3
2;2 xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
186
)1(1
2
865
1
1
54322
2
222
xétx
xx
xx
x
xxxx
)1(0
2
8652
1
154322
2
22
22
xétx
xx
xxxx
x
xxxxx
Nhân liên hợp 2 lần ở biểu thức đầu,1 lân ở phân thức sau suy ra
Phƣơng trình có 2 nghiệm
3
2,2 xx
Thí dụ 51 Để kết hợp với Đạo hàm
Từ Phƣơng trình
0)7213(3132
222
xxxx
1
)213)(3(
131422322313
22
232
xxx
xxxx
Giải phƣơng trình
1
)213)(3(
131422322313
22
232
xxx
xxxx
Phƣơng trình có 3 nghiệm
22;5;1 xxx
Phƣơng trình
07213
2
xx
có vế trái là hàm đồng biến nên có nghiệm
22x
là nghiệm duy nhất
Thí dụ 52 Để kết hợp với Đạo hàm
Từ Phƣơng trình
0)11233(133
222
xxxxx
1
)1233)(1(
33363624
22
2232
xxxx
xxxxxx
Giải phƣơng trình
1
)1233)(1(
33363624
22
2232
xxxx
xxxxxx
Phƣơng trình có 3 nghiệm
3
2;2;1 xxx
Phƣơng trình
011233
2
xx
có vế trái là hàm đồng biến có nghiệm
1x
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
187
Làm thế nào khi sáng tác ngoài cách mò nghiệm đẹp bằng nhẩm thì còn cách mò bằng máy
tính Casio nhƣ sau: Bấm MODE 7 nhập
33)(
2
XXF
Máy hỏi Start bấm -9, End bấm 9
Quan sát bảng ta thấy F(X) giá trị nguyên khi X là -7,-2;-1;1;2;7
ở ví dụ TRÊN TÁC GiẢ chọn x=1, Bây giờ xin thử thêm với x=-2
Từ Phƣơng trình
0)2333(133
222
xxxxx
333
1
33)32(125
2
2
22
xx
xx
xxxx
Khi này giải PT
02333
2
xx
bằng cách đặt
tx 3
suy ra PTcó 2 nghiệm
6
1295
;2
xx
Giải phƣơng trình
333
1
33)32(125
2
2
22
xx
xx
xxxx
suy ra PTcó 4 nghiệm
6
1295
;2;2;2
3
xxxx
Thử thêm với x=7
Từ Phƣơng trình
0)14
5
13
33(133
222
x
xxxx
Với PT
014
5
13
33
2
x
x
có vế trái là hàm đồng biến nên có nghiệm x=7
là nghiệm duy nhất . các bạn tự tạo ra PT trong trƣờng hợp này
Thí dụ 52 Dùng máy tính Casio trợ giúp sáng tác PT
Làm thế nào khi sáng tác ngoài cách mò nghiệm đẹp mò bằng máy tính Casio nhƣ sau:
Bấm MODE 7 chăng hạn nhập
543)(
2
XXXF
Máy hỏi Start bấm -9, End bấm 9
Quan sát bảng ta thấy F(X) giá trị nguyên khi X là -5,-2;1;2;7
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
188
Nhƣ vậy có khá nhiều lựa chọn nghiệm đẹp chẳng hạn tác giả chọn x=-2
Để tạo ra PT dùng tính đơn điệu để giải ta tạo ra PT:
(*)0841543
2
xxx
Chỉ cần biết tính đơn điệu của hàm số
543
2
xxy
thì sẽ biết tại sao tác giả chọn
x41
Có Vế trái PT(*) là hàm nghịch biến trên khoảng trên khoảng xác định
]
4
1
;(
nên có
nghiệm duy nhất x=-2
Khi này ta có PT tích dạng nhƣ sau:
0)1543)(841543(
222
xxxxxxx
)54341)(1(543)841(131211
2222
xxxxxxxxxx
1
)54341)(1(
543)841(131211
22
22
xxxxx
xxxxx
PT có 2 nghiệm
3
2;2 xx
Khi này khi giải PT nếu bạn nào thử dùng Casio tìm nhân tử thì ta tìm nghiệm đẹp ngoại
lai (kiểu ngoại lai này tác giả đã nói đến ở phần trƣớc)bằng cách coi
041 x
ta giải PT
sau:
)(**)543)(1(5438131211
2222
xxxxxxxx
ta tìm nghiệm đẹp ngoại lai x=2.Khi này một nhân tử cần tìm là:
01543
22
xxxx
Từ (**) ta còn thu về đƣợc một PT sau:
9
131211
543
2
2
2
xx
xx
xx
9
86
11543
2
2
xx
x
xxx
x
xx
x
xx 11
9
86
543
2
2
Cách giải
0)1543)(8543(
222
xxxxxxpT
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
189
PT có 4 nghiệm
3
1812
;2;2
3
xxx
Nếu các bạn thích tạo ra một PT Tích có thêm cách đặt ẩn phụ ở một nhân tử thì có thể làm nhƣ
sau:
Tác giả xin chọn x=1;x=2;…..
Và tạo ra một số PT:
0312543
2
xxx
nghiệm
1x
03543
2
xxx
nghiệm
1x
0112543
2
xxx
nghiệm
3
133
2
133
2
.21;1
33
xx
043543
2
xxx
nghiệm
6
17713
;1
xx
032543
2
xxx
nghiệm
2;1 xx
012543
2
xxx
nghiệm
3
11372
3
11372
1;1
3
3
xx
0123543
2
xxx
nghiệm
2;1 xx
0123543
2
xxx
nghiệm
2;1 xx
032543
2
xxx
nghiệm
2;2 xx
bạn nào không thích nghiệm đẹp thì có thể tạo ra PT kiểu sau:
0232543
2
xxx
có 2 nghiệm
3
645
;
3
645
xx
Việc ghép lại thành phƣơng trình hoàn thiện xin dành cho bạn đọc. chẳng hạn:
0)1543)(43543(
222
xxxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
190
1
)5433)(1(
543)43(987
22
22
xxxxx
xxxxx
PT có 4 nghiệm:
3
2;2;
2
1773
;1
xxxx
Sử dụng lí thuyết của 2 chuyên đề dƣới đây có thể tìm ra các biểu
thức cần xuất hiện ở 2 chuyên đề 2 và 3
KĨ THUẬT “ĐÁNH CẢ CỤM” KHI DÙNG CASIO GIẢI PHƢƠNG TRÌNH VÔ TỈ
Chuyên đề 4
PHƢƠNG PHÁP THẾ TRONG THỦ THUẬT SỬ DỤNG MÁY TÍNH ĐỂ TÌM NHÂN
TỬ CHUNG HOẶC TÌM BIỂU THỨC TRONG NHÂN LIÊN HỢP KHI GIẢI PHƢƠNG
TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh
Một kĩ năng rất hữu ích có thể giúp ta giải đƣợc một phƣơng trình vô tỉ là kĩ năng tìm
nhân tử chung hoặc tìm biểu thức trong nhân liên hợp. Đôi khi việc tìm ra các biểu thức đó
là rất khó khăn nếu ta không có máy tính cầm tay trợ giúp. Bài viết này xin đƣợc giới thiệu
kĩ thuật dùng máy tính cầm tay tìm nhân tử chung hoặc biểu thức để ta xử lí nhân liên hợp
có dạng
k
xPcbxax )(
2
,với a,b,c là các số nguyên. Sau đây là các thí dụ
Thí dụ 1 Giải phƣơng trình
2
63214
10633
22
346
xxx
xxxx
Lời giải
Phƣơng trình(PT) đã cho tƣơng đƣơng với PT:
)1(0634126833
22346
xxxxxxx
Ta tìm nghiệm của PT(1) bằng máy tính CASIO fx-570VN PLUS nhƣ sau:
Nhập biểu thức vế trái(VT) của PT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm X=2
Ấn nút sang trái để quay lại PT(1)
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
191
Sửa biểu thức thành VT(1):( X-2) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm
10
=, máy cho ta nghiệm
546818277,2X
Bấm SHIFT STO A (lƣu nghiệm vừa tìm vào A)
Giả sử nhân tử của PT(1) có dạng
63
22
xxcbxax
chứa 2 nghiệm vừa tìm.
Nghiệm X=2 suy ra
0224 cba
224 bac
Nhân tử của PT(1) trở thành:
63224
22
xxbabxax
632)2()2)(2(
2
xxxbxxa
Xét
0632)2()2)(2(
2
xxxbxxa
suy ra
)2(
2
263
2
xa
x
xx
b
(2)
Vì A là nghiệm của PT(2) nên
ta tìm a,b là số nguyên bằng cách bấm máy tính như sau:
MODE 7 máy hiện f(X)= ,ta nhập
XA
A
AA
)2(
2
263
2
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=1=a thì F(X)=0=b là số nguyên
Nhƣ vậy a=1,b=0,c=
2
Nên nhân tử cần tìm là
632
22
xxx
Suy ra PT xuất hiện
)632(4
22
xxx
Biểu thức còn lại là
461233
2346
xxxxx
Biểu thức này chứa nhân tử cần tìm nên nó chứa nhân tử sau:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
192
235)63()2(
24222
xxxxxx
Thật vậy,sử dụng kĩ năng chia đa thức ta đƣợc
461233
2346
xxxxx
)2)(235(
224
xxxx
Do đó
0)632(4)2)(235()1(
22224
xxxxxxxPT
0)632(4)2)(632)(632(
2222222
xxxxxxxxxx
063)2()632(
22422
xxxxxxx
)4(063)2(
)3(263
224
22
xxxx
xxx
Dễ thấy PT(4) vô nghiệm
4463
02
)3(
242
2
xxxx
x
PT
0)12)(2(
02
23
2
xxxx
x
Giải tiếp ta được nghiệm
2x
và
3
2
29961
2
29961
2
33
x
Vậy PT đã cho có 2 nghiệm:
2x
;
3
2
29961
2
29961
2
33
x
Thí dụ 2 Giải phƣơng trình
1
398)2(3
622
232
234
xxx
xxxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(0398)2(3622
232234
xxxxxxx
Nhập biểu thức vế trái của PT(1) rồi bấm SHIFT SOLVE
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
193
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm
25992105,2X
Bấm SHIFT STO A
Nhập biểu thức
4
)(:)1( AXVT
rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 0 =
, chờ gần 6 phút máy hiện Can’t Solve
Khi này ta sẽ chuyển sang hướng tìm nghiệm ngoại lai (nếu có)của PT bằng cách đổi dấu trước căn PT đã
cho.Dẫn tới tìm nghiệm của PT sau:
)2(0398)2(3622
232234
xxxxxxx
Ta tìm nghiệm “đẹp” (nếu có) của PT(2) như sau:
Bấm MODE 7 máy hiện f(X)=
Ta nhập biểu thức vế trái PT(2) bấm =
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Khi này xem bảng ta thấy
1`X
thì F(X)=0
Vậy nghiệm ngoại lai cần tìm là x= -1
Giả sử nhân tử của PT(1) có dạng
398
232
xxcbxax
Vì x= -1 nghiệm ngoại lai nên nó là nghiệm PT:
0398
232
xxcbxax
suy ra
02 cba
2 bac
Nhân tử của PT(*) trở thành:
3982
232
xxbabxax
3982)1()1)(1(
23
xxxbxxa
Xét
03982)1()1)(1(
23
xxxbxxa
suy ra
Zxa
x
xx
b
)1(
1
2398
23
Ta tìm a,b bằng cách bấm máy tính như sau:
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
194
MODE 7 máy hiện f(X)= ,ta nhập
XA
A
AA
)1(
1
2398
23
bấm =
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=1 thì F(X)=3 là số nguyên
Nhƣ vậy a=1,b=3,c=0.Ta được nhân tử là
3983
232
xxxx
Mà
32)398()3(
342322
xxxxxx
PT(1) trở thành:
0)6983)(2(32
232234
xxxxxxx
0)398232)(6983(
232232
xxxxxxxx
)4(063
8
7
)
4
3
(2
)3(3398
22
223
xxx
xxxx
Dễ thấy PT(4) vô nghiệm
02)1()1(
03
)3(
3
2
xx
xx
PT
3
21 x
.
Vậy PT đã cho có nghiệm duy nhất
3
21x
Thí dụ 3 Giải phƣơng trình
1
41744361
2352
234
2
xxxx
xxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(0141744362352
2342
xxxxxxx
Ta tìm nghiệm “đẹp” (nếu có) của PT(1) như sau:
Bấm MODE 7 máy hiện f(X)=
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
195
Ta nhập biểu thức vế trái PT(1) bấm =
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Khi này ta thấy X=1 thì F(X)=0
Nhập biểu thức VT(1):( X-1) rồi bấm SHIFT SOLVE
Máy hỏi X=? ta bấm
0
=, máy cho ta nghiệm
629960524,0X
Làm tương tự các thí dụ trên ta được:
)1(
1
2235
2
xa
x
xx
b
và
)1(
1
24174436
234
xa
x
xxxx
b
Nên
)12(235
22
xxxx
và
4174436134
2342
xxxxxx
là các biểu thức cần xuất hiện trong phƣơng trình
PT(1) trở thành:
0)4174436134()12235(2
234222
xxxxxxxxxx
0
4174436134
4174436134
12235
12235
2
2342
234
2
2
22
2
22
xxxxxx
xxxxxx
xxxx
xxxx
0]
4174436134
5
12235
2
[144
234222
34
xxxxxxxxxx
xxx
0144
34
xxx
0)14)(1(
3
xx
3
4
1
1
x
x
Kiểm tra điều kiện xác định thấy các nghiệm thỏa mãn.
Vậy PT đã cho có 2 nghiệm
1x
;
3
4
1
x
Thí dụ 4 Giải phƣơng trình
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
196
1
111216685
3274142
2342
2334
xxxxxx
xxxxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(065211121663274
23423423
xxxxxxxxxxx
Bấm máy tính như các thí dụ trên để tìm nghiệm nguyên ta thấy không có
Tìm và lưu các nghiệm ta được ít nhất 3 nghiệm là
732050808,2A
;
414213562,1B
;
732050807,0C
Chú ý: Nếu máy hiện Continue:[=] thì ta bấm = ,đợi một lúc ta đƣợc nghiệm
Giả sử biểu thức thứ nhất có dạng
3274
232
xxxcbxax
Do A,B,C là nghiệm của biểu thức nên ta có
3274
232
AAAcbAaA
3274
232
BBBcbBaB
3274
232
CCCcbCaC
Bấm MODE 5 rồi bấm 2 để giải hệ 3 ẩn a,b,c gồm 3 PT trên.Ta đƣợc a=1;b=1;c=1
Nhƣ vậy biểu thức thứ nhất cần tìm là
32741
232
xxxxx
Tƣơng tự biểu thức thứ hai cần tìm là
111216612
2342
xxxxx
04442111216612
32741)1(
2342342
232
xxxxxxxxx
xxxxxPT
)2(0)()4442(
234
xPxxxx
với
01
111216612
3
32741
1
)(
2342232
xxxxxxxxxx
xP
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
197
Suy ra
04442)2(
234
xxxxPT
0)2)(22(
22
xxx
2
31
x
x
Kiểm tra điều kiện xác định thấy các nghiệm thỏa mãn
Vậy PT đã cho có 4 nghiệm
31x
;
2x
Chú ý: Do
2 CA
;
2AC
nên PT có nhân tử là
22
2
xx
Mở rộng dạng toán: Nếu a,b,c hoặc nghiệm PT là các số hữu tỉ thì ta đƣa về tìm các biểu thức dạng
)()(
2
rqxpxxPn
k
,với p,q,r là số nguyên và n là số nguyên dƣơng ta tìm đƣợc hoặc ta thử
chọn. Vấn đề nữa đặt ra là liệu có phƣơng trình mà ta phải tìm biểu thức dạng phức tạp hơn chẳng
hạn nhƣ
)()(
23
dcxbxaxxP
k
.Hãy làm bài tập dƣới đây các bạn sẽ rõ
Bài tập
Giải phương trình
1
21642
2134
)1
23
24
xxx
xxx
3
33
69337
)2
2
2334
xx
xxxx
1
1434)1(
8532
)3
22
234
xxxx
xxxx
1
23
4234423
)4
2
2234
xx
xxxxx
1
11314732
22324412163
)5
24
234
xxx
xxxxx
1
325121
1412822
)6
24
3
456
xxx
xxxx
1
27342
15323
)7
234
3
56
xxxx
xxxx
1
32262120
3627462
)8
232
2334
xxxxx
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
198
1
61252)2(3
3410642
)9
3
2342
2423
xxxxx
xxxxxx
2
58374
2
5
203092031218
)10
232
232
xxxxx
xxxx
1
6583
734475)2(
)11
2345
23453
xxxxx
xxxxxxx
1
21141126142
5271521387
)12
23424
2343
xxxxxx
xxxxxx
1
6635)112536(14
45443)112928(
)13
22
22
xxxxxx
xxxxxxx
5451219192044
3459131921)14
2345678
23456
xxxxxxxx
xxxxxx
Chuyên đề 5
PHƢƠNG PHÁP CỘNG DÙNG TRONG THỦ THUẬT MÁY TÍNH CẦM TAY TRỢ GIÚP GIẢI
PHƢƠNG TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh
Điều kiện sử dụng phƣơng pháp: Bấm máy tính tìm đƣợc ít nhất 2 nghiệm A,B phân biệt
Nếu PT có chứa
)(xP
thì giả sử biểu thức cần xuất hiện có dạng:
)(
2
xPcbxax
,trong đó
a,b,c là các số nguyên .Do A,B là nghiệm của biểu thức nên
(*)0)(
2
APcbAaA
0)(
2
BPcbBaB
Chú ý: Nếu B là nghiệm ngoại lai ta có
0)(
2
BPcbBaB
(các bạn tự xử lí TH này)
Trừ vế với vế ta đƣợc:
)()()())(( BPAPBAbBABAa
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
199
Suy ra
aBA
BA
BPAP
b )(
)()(
Trƣờng hợp 1:
0 BA
thì
BA
BPAP
b
)()(
Nhập biểu thức
BA
BPAP
)()(
bấm = máy hiện giá trị của b cần tìm
Từ (*) suy ra
bAaAAPc
2
)(
Ta tìm a,c bằng máy tính nhƣ sau:
Bấm MODE 7 máy hiện f(X)= ta nhập
bAXAAP
2
)(
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta chỉ lấy X làm F(X) nhận giá trị nguyên
Suy ra a=X,c=F(X)
Trƣờng hợp 2:
0 BA
Do
aBA
BA
BPAP
b )(
)()(
nên ta tìm a,b bằng máy tính nhƣ sau:
Bấm MODE 7 máy hiện f(X)= ta nhập biểu thức
XBA
BA
BPAP
)(
)()(
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta lấy X làm F(X) nhận giá trị nguyên
Từ đó suy ra a=X,b=F(X)
Từ PT(*) ta tìm
bAaAAPc
2
)(
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
200
Nhập biểu thức
bAaAAP
2
)(
bấm = máy hiện giá trị của c cần tìm
Sau đây là các thí dụ.
Thí dụ 1 Giải phƣơng trình
1
10123
82266
24
23466
xxx
xxxxxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(010123)(
246
xxxxxP
Với
82266)(
2346
xxxxxxP
Nhập biểu thức vế trái(VT) của PT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm
25992105,2X
Bấm nút mũi tên sang trái để quay lại VT(1) ta bấm = để lƣu VT(1)
Bấm ALPHA X SHIFT STO A để lƣu nghiệm vào A
Bấm nút mũi tên đi lên để về VT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm -10 = máy cho ta nghiệm
25992105,2X
Bấm SHIFT STO B
Bấm máy A+B máy hiện 0 suy ra
BA
BPAP
b
)()(
Nhập biểu thức
BA
BPAP
)()(
bấm = máy hiện -1. Vậy b=-1
Do b= -1 nên
AaAAPc )1()(
2
AaAAP
2
)(
Bấm MODE 7 máy hiện f(X)= ta nhập
AXAAP
2
)(
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
201
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=3 thì F(X)=1 nguyên
Suy ra a=3,c=1
Biểu thức cần tìm là:
)13(82266
22346
xxxxxxx
PT(1) trở thành
0993)13()(
2462
xxxxxxP
0993
13)(
)13()(
246
2
22
xxx
xxxP
xxxP
0993
13)(
993
246
2
246
xxx
xxxP
xxx
0)993](1
13)(
1
[
246
2
xxx
xxxP
0993
246
xxx
0)33()3(
2223
xxx
0)333)(333(
2323
xxxxxx
02)1`(2)1(
33
xx
2)1(
2)1(
3
3
x
x
)21(
3
x
Vậy PT đã cho có 2 nghiệm
)21(
3
x
Thí dụ 2 Giải phƣơng trình
1
712102
12574244
23462
23462
xxxxxx
xxxxxxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(43)()(
2
xxxQxP
Với
712102)(
2346
xxxxxxP
125742)(
2346
xxxxxxQ
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
202
Tìm và lưu các nghiệm như thí dụ 1 ta được 2 nghiệm là
793700526,0A
;
25992105,1B
Ta có
04662205239,0 BA
Có
aBA
BA
BPAP
b )(
)()(
nên ta tìm a,b nhƣ sau:
Bấm MODE 7 máy hiện f(X)= ta nhập
XBA
BA
BPAP
)(
)()(
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy F(X)=-2 khi X=1
Suy ra a=1,b= -2. Khi này
AAAPc 2)(
2
Nhập biểu thức
AAAP 2)(
2
bấm = máy hiện số 3
Ta đƣợc c=3
Biểu thức cần tìm là
)32()(
2
xxxP
Tƣơng tự biểu thức nữa cần tìm là
)12()(
2
xxxQ
PT(1) trở thành
0)12()()32()(
22
xxxQxxxP
0
12)(
)12()(
32)(
)32()(
2
22
2
22
xxxQ
xxxQ
xxxP
xxxP
0
12)(
232
32)(
232
2
36
2
36
xxxQ
xx
xxxP
xx
0]
12)(
1
32)(
1
)[12)(2(
22
33
xxxQxxxP
xx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
203
0)12)(2(
33
xx
3
3
2
1
2
x
x
Vậy phƣơng trình có 2 nghiệm
3
2x
;
3
2
1
x
Vấn đề đặt ra là liệu với một biểu thức
)(xP
có khi nào có nhiều lựa chọn biểu thức
dạng
)(
2
xPcbxax
hay không.Ví dụ sau sẽ làm sáng tỏ điều này
Thí dụ 3 Giải phƣơng trình
1
65112642412
322
2323
234
xxxxx
xxxx
Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT:
)1(0)()(322
234
xQxPxxxx
Với
642412)(
23
xxxxP
và
65112)(
23
xxxQ
Tìm và lƣu các nghiệm ta đƣợc 2 nghiệm là
449489743,3A
;
449489743,1B
Bấm máy tính có
02 BA
;
5AB
(Theo Định lí Vi-ét thì PT sẽ có nhân tử là
52
2
xx
)
Có
aBA
BA
BPAP
b )(
)()(
nên ta tìm a,b nhƣ sau:
Bấm MODE 7 máy hiện f(X)= ta nhập biểu thức
XBA
BA
BPAP
)(
)()(
bấm =
Máy hiện Start? Ta bấm
9
=
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy tất cả các giá trị F(X) đều nguyên. Vì thế ta chọn 1 cặp là
X=2;F(X)= 1. Suy ra a=2,b=1
AAAPc
2
2)(
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
204
Nhập biểu thức
AAAP
2
2)(
bấm = máy hiện số 1.Ta đƣợc c=1
Suy ra
)(12
2
xPxx
là biểu thức cần tìm
Tƣơng tự ta chọn đƣợc
)(13
2
xQxx
là biểu thức cần tìm
Phƣơng trình(1) tƣơng đƣơng với PT:
05242)(13)(12
23422
xxxxxQxxxPxx
0)1)(52()(13)(12
2222
xxxxQxxxPxx
01
)(13
19
)(12
14
)52(
2
2
2
2
2
2
x
xQxx
x
xPxx
x
xx
052
2
xx
61 x
Vậy phƣơng trình có 2 nghiệm
61x
Chọn cặp biểu thức khác chẳng hạn
)(63
2
xPxx
;
)(13
2
xQxx
ta cũng giải
đƣợc PT theo cách nhân liên hợp
Chú ý:
+Việc chọn biểu thức trong thí dụ 3 là tùy ý hay cần chọn hợp lí để ta dùng đƣợc cách nhân
liên hợp. Xin dành cho mọi ngƣời tìm hiểu điều này.
+ Một số phƣơng trình ta có thể tìm biểu thức phức tạp hơn chẳng hạn
)()(
23
dcxbxaxxP
và có thể giải quyết theo cách bài viết đã nêu khi điều kiện về
nghiệm của PT ta tìm đƣợc nhiều hơn(kể cả nghiệm ngoại lai hay nghiệm bội)
Bài tập Giải phƣơng trình
1
998
194243
)1
24
233
xxx
xxxx
3
23462
236
3
47129
5599
)2 x
xxxxx
xxx
1
16264103
21241844
)3
2324
233
xxxxx
xxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
205
1
21264916205
69166374
)4
232
2324
xxxxx
xxxxx
1
15211441
5126454
)5
2362
2362
xxxxx
xxxxxx
1
20254
1788334
)6
2462
2462
xxxxx
xxxxxx
1
8232741
14482
)7
2346
246
xxxxx
xxxx
1
52541`
888433
)8
246
2462
xxxx
xxxxxx
3
2346
2456
3884335
282243
)9 x
xxxxx
xxxxx
1
1525441
16124633
)10
2458
24582
xxxxx
xxxxxxx
3
23457
3457
2
15231874
1641862
)11 x
xxxxxx
xxxxx
1
821422196
111918156
)12
234568
24567
xxxxxxx
xxxxxx
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
206
Vũ Hồng Phong Thôn Bất Lự,Hoàn Sơn,Tiên Du,Bắc Ninh
ToánBK35 ĐHSP Thái Nguyên
| 1/206
| | Tải xuống

Có thể bạn quan tâm:

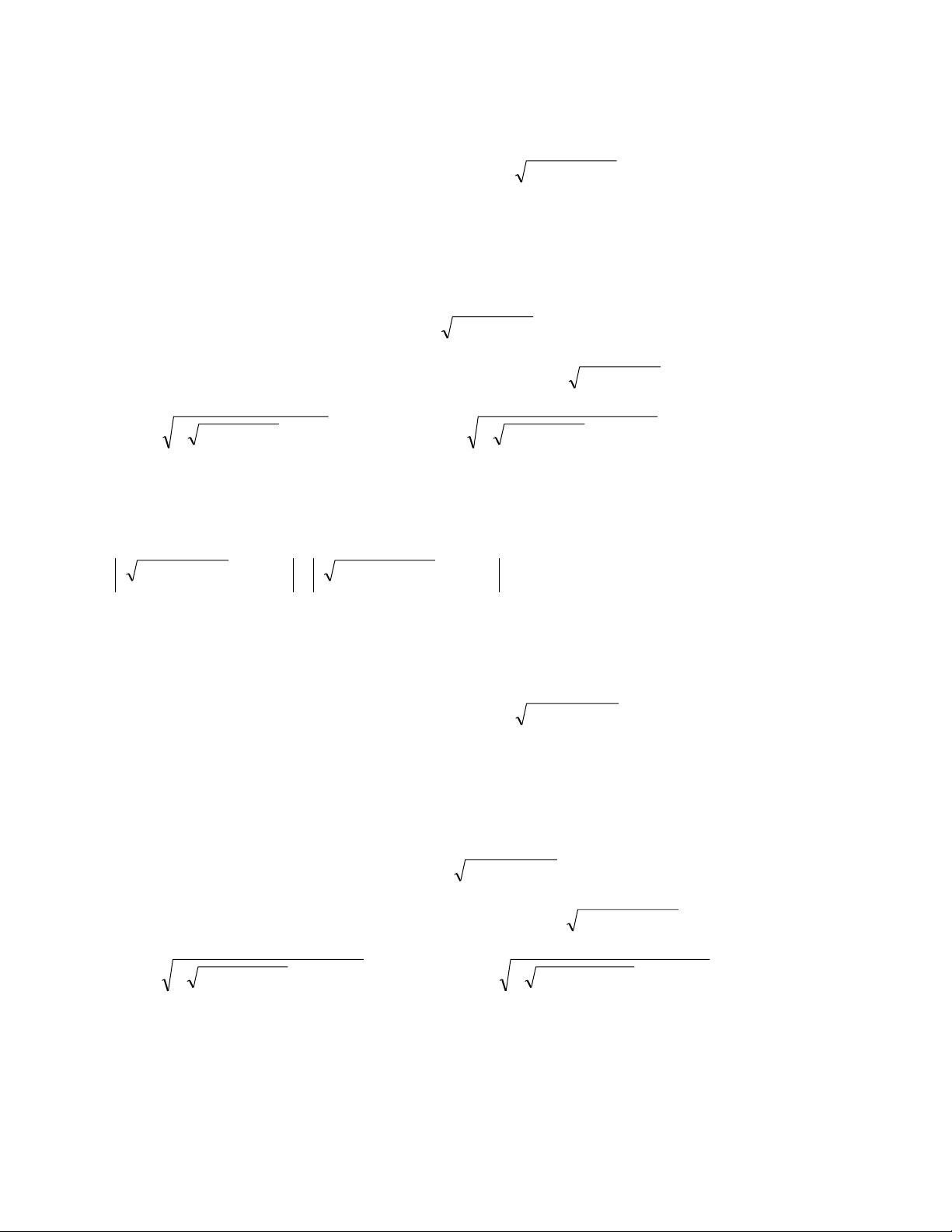
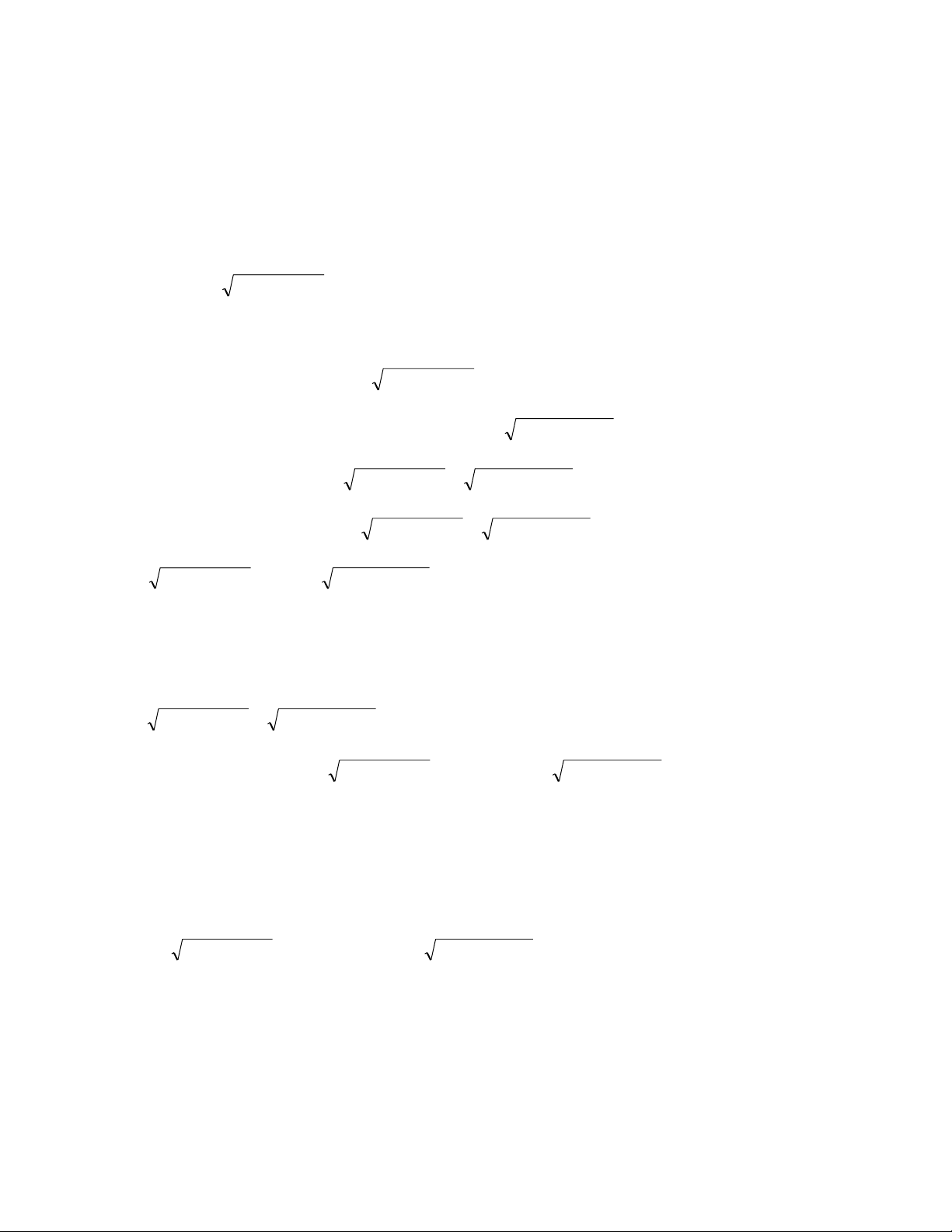
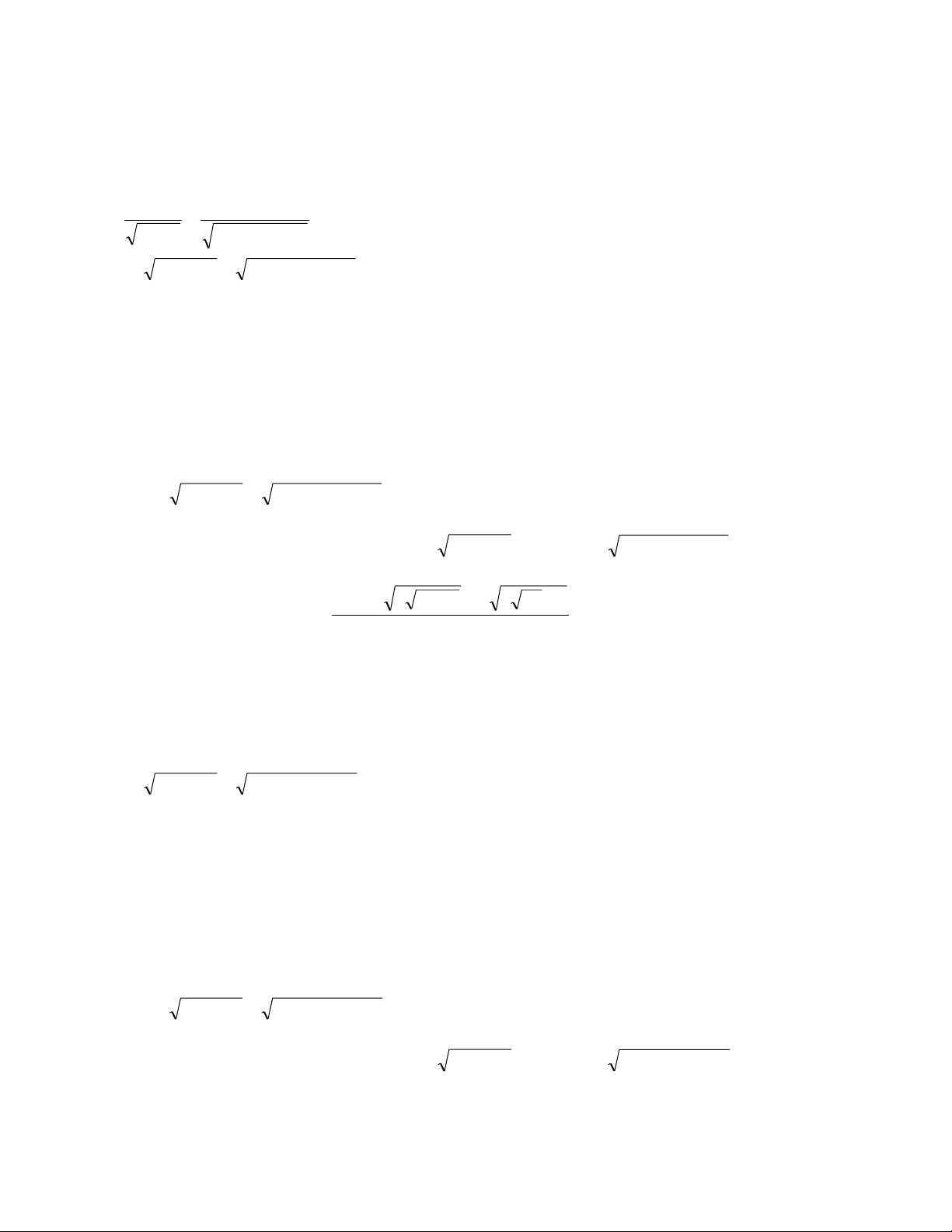
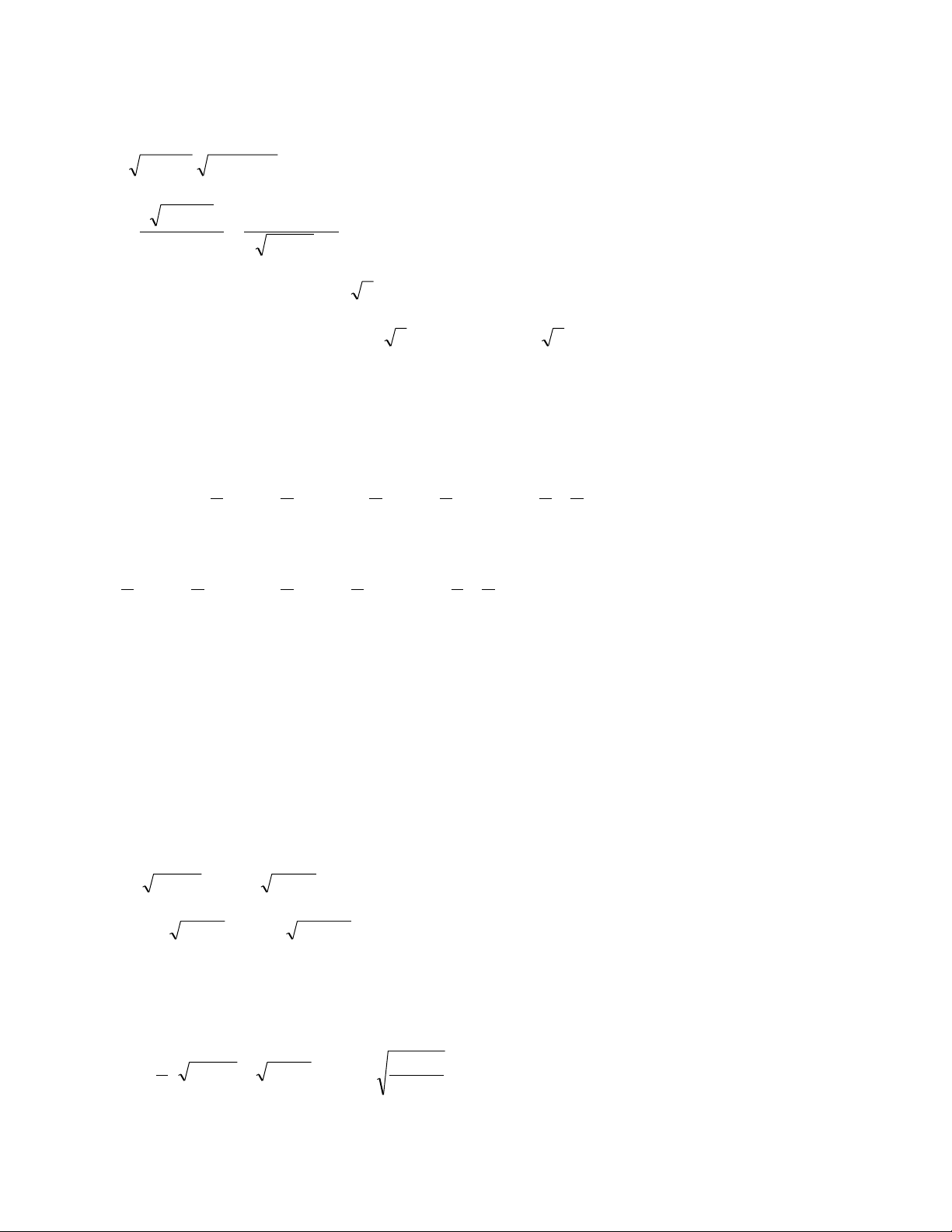
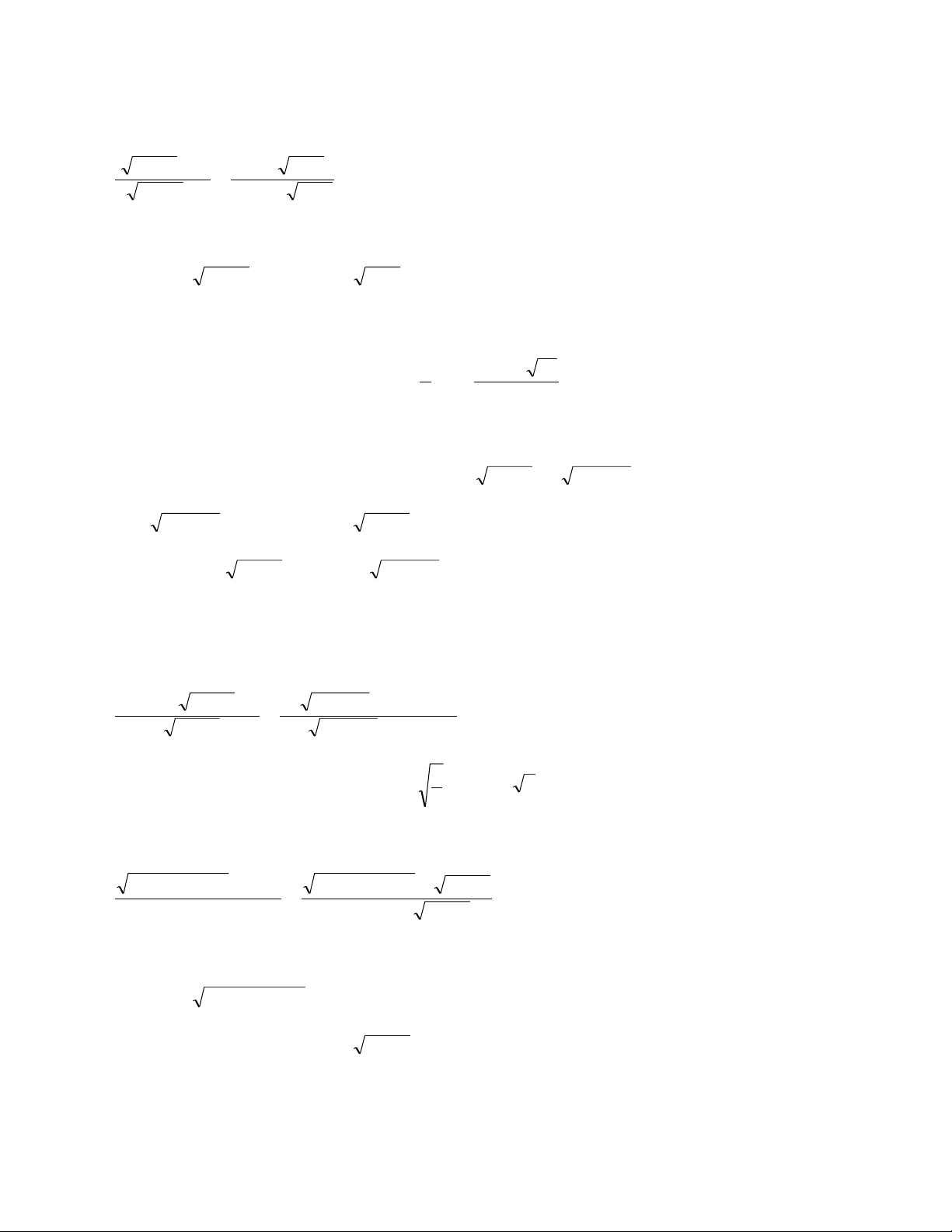
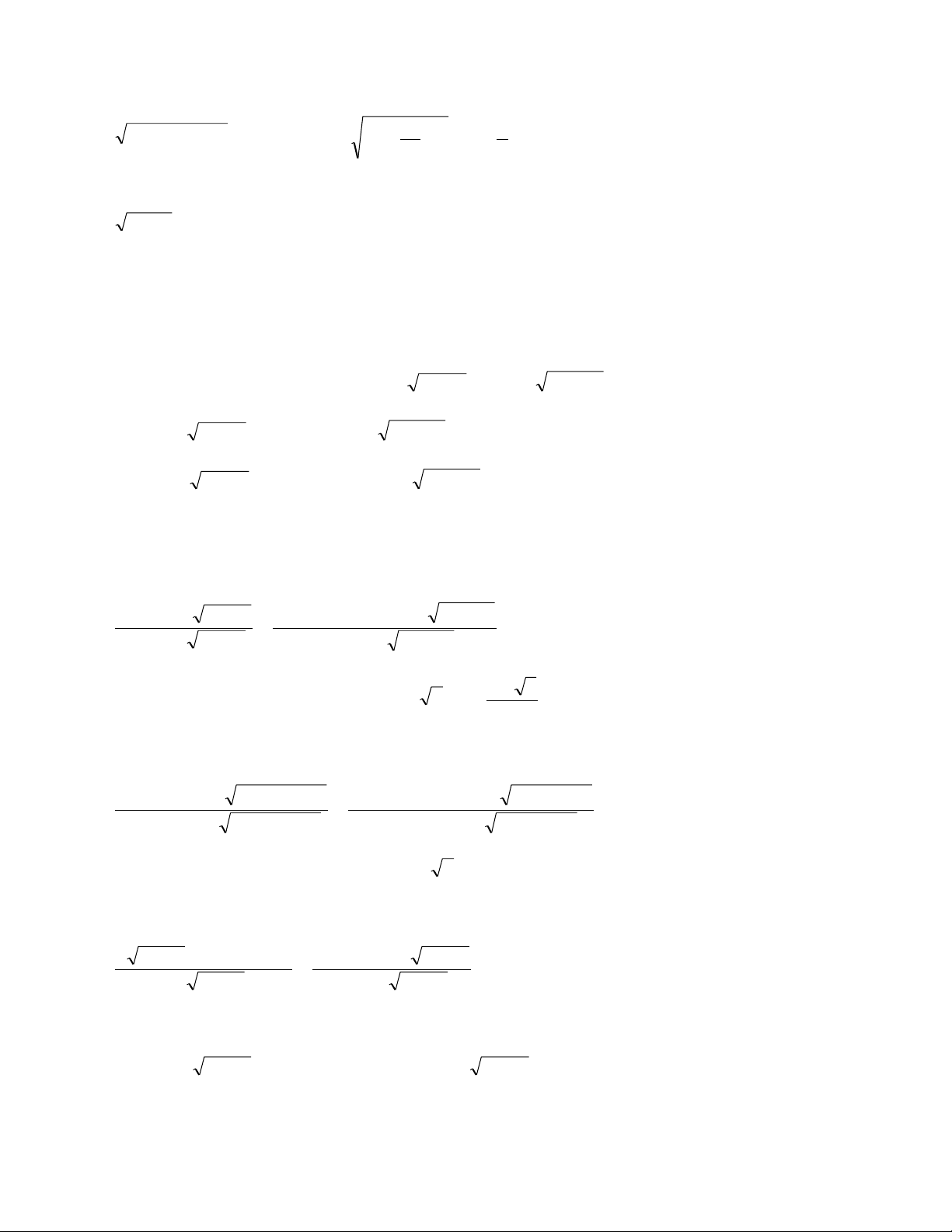
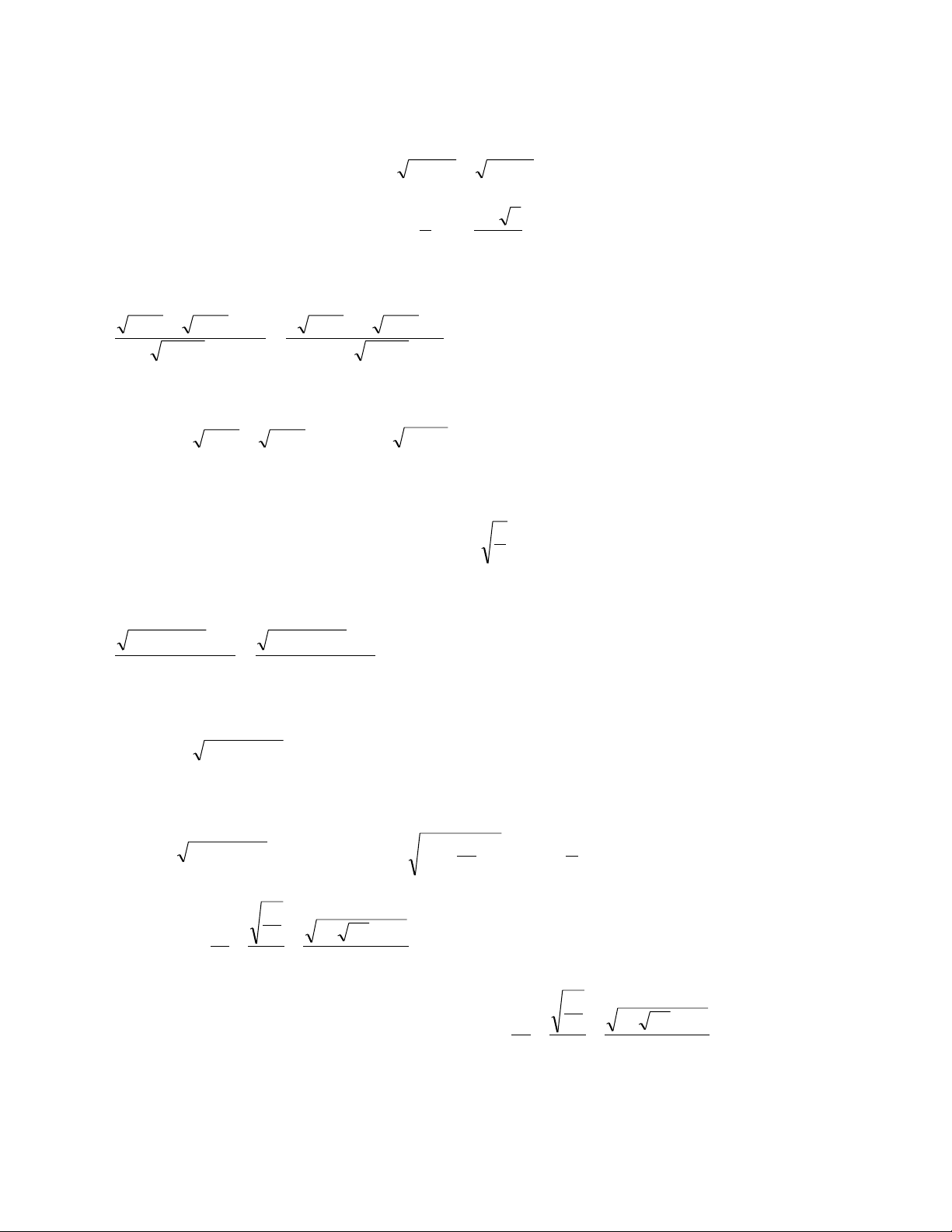
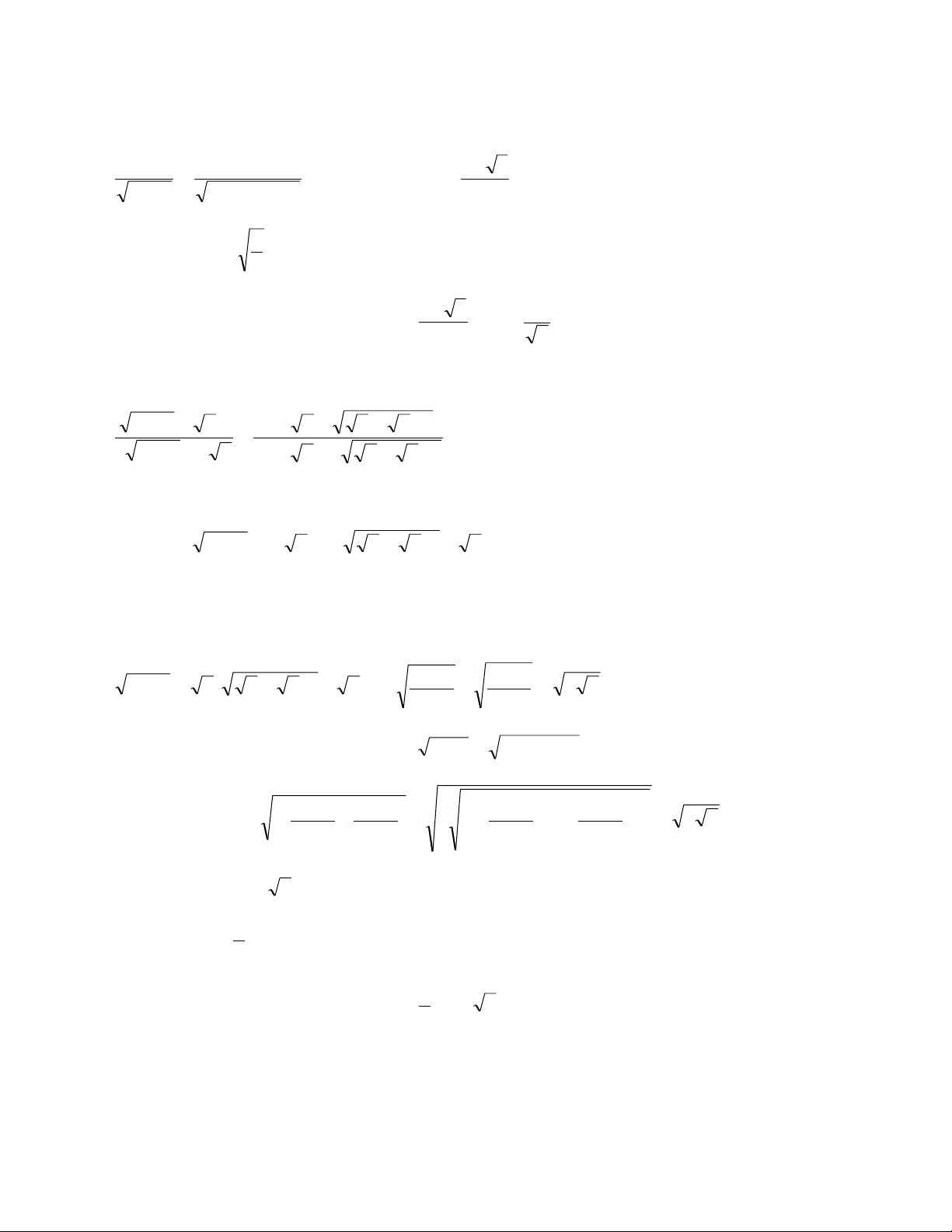
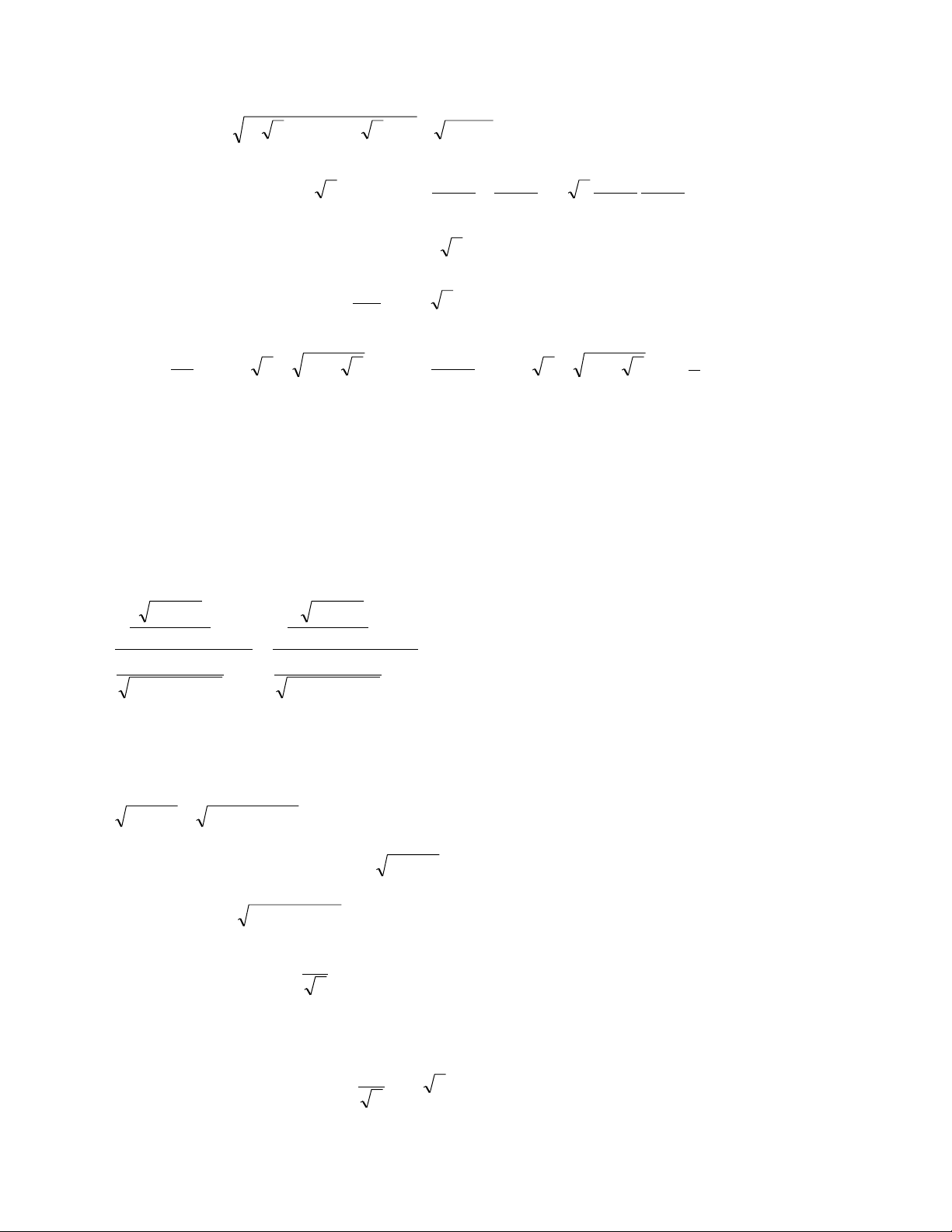
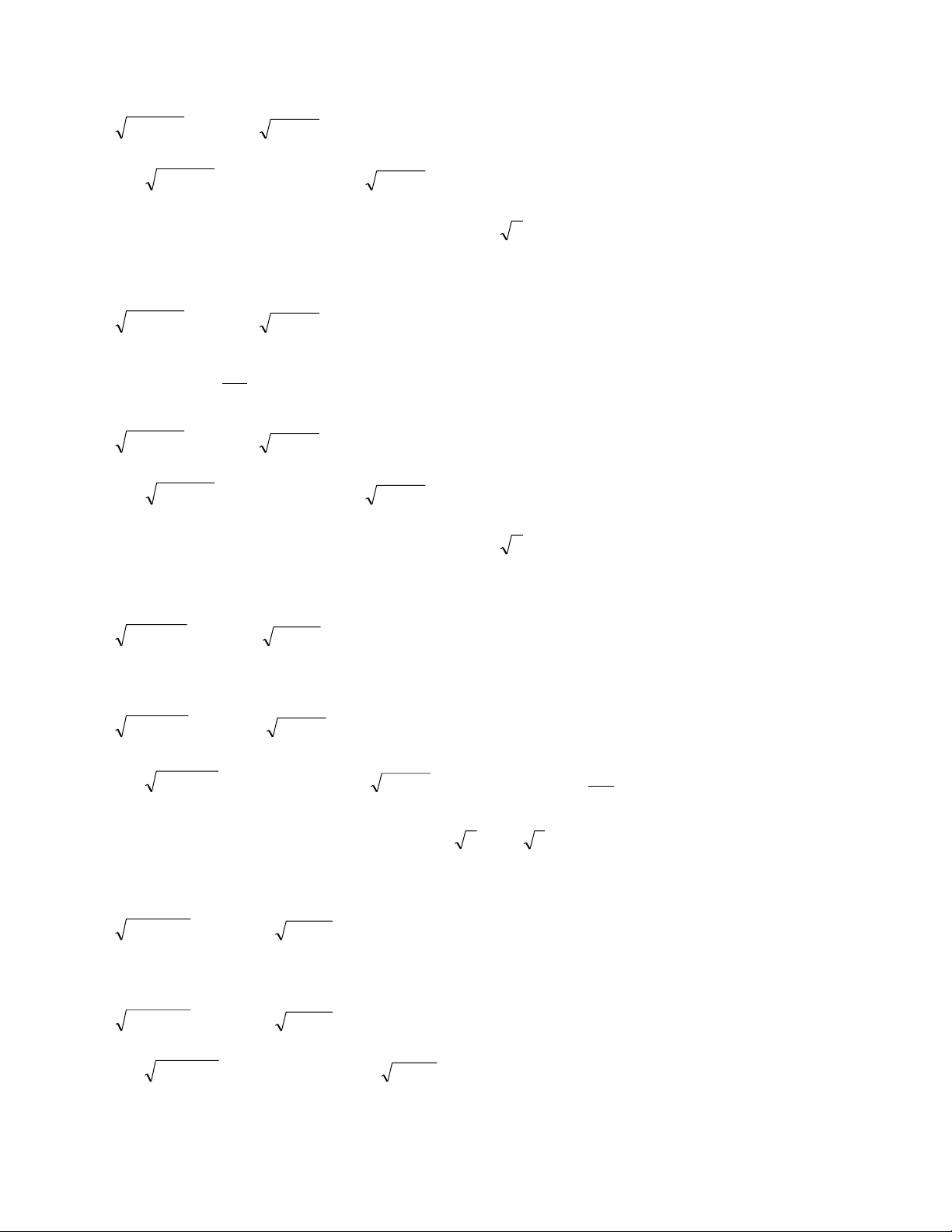
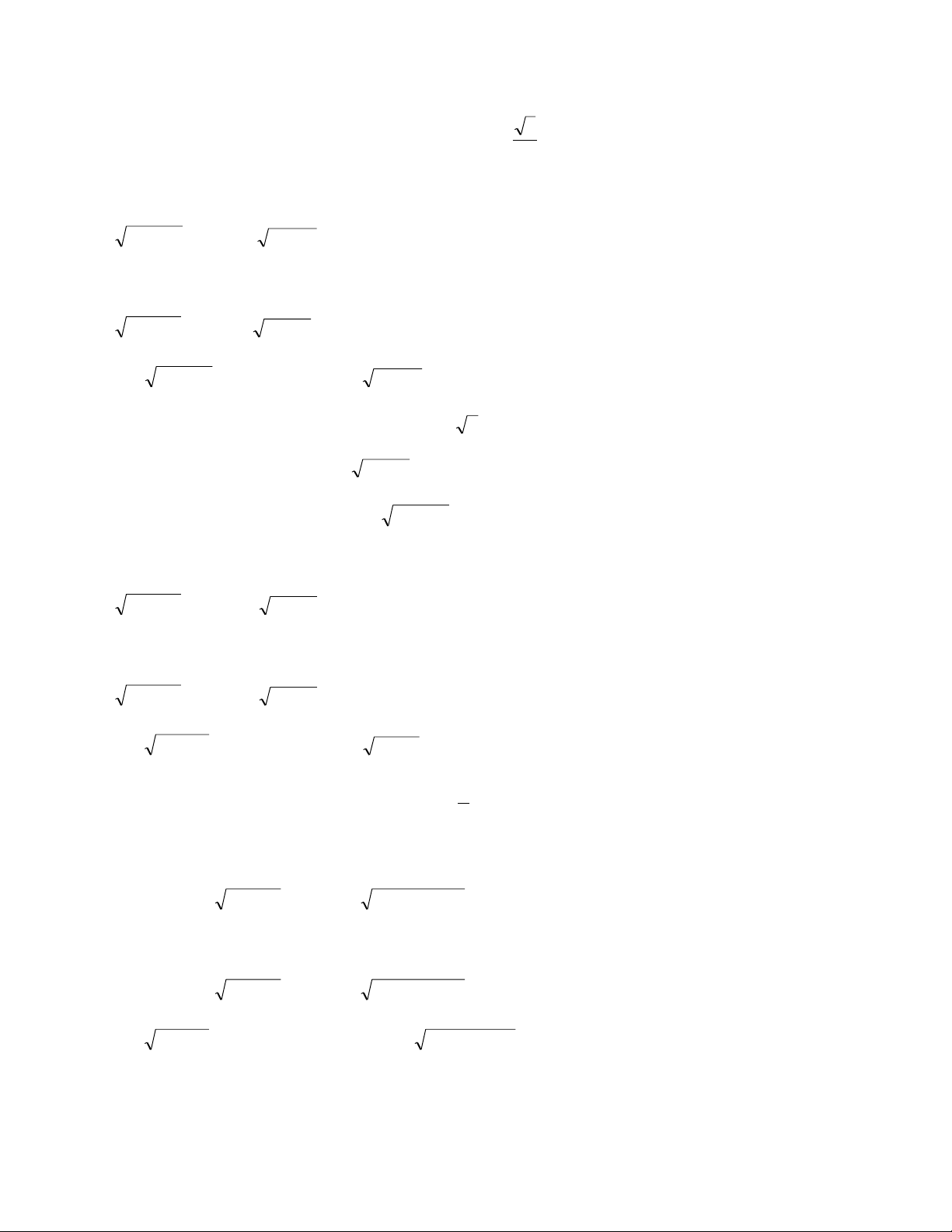
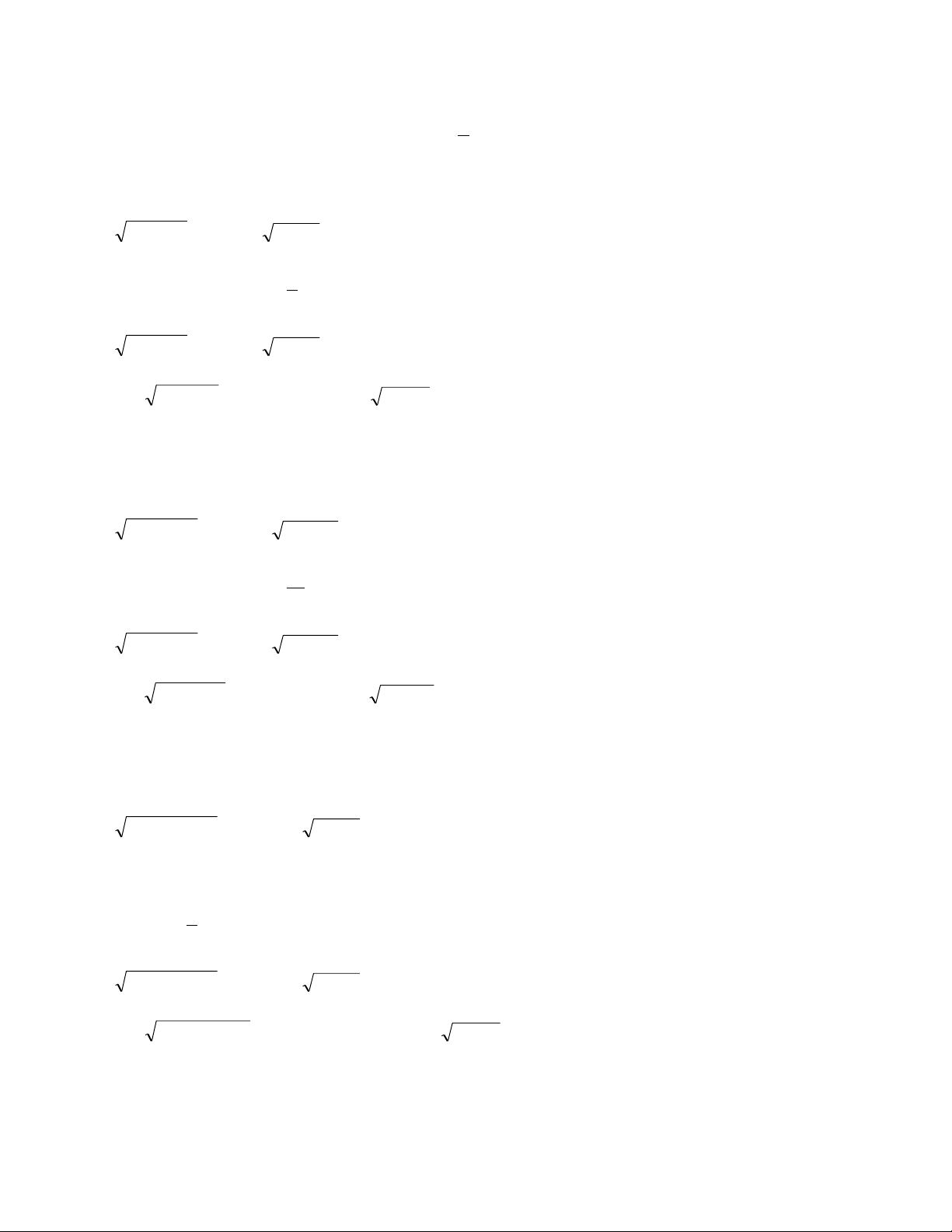
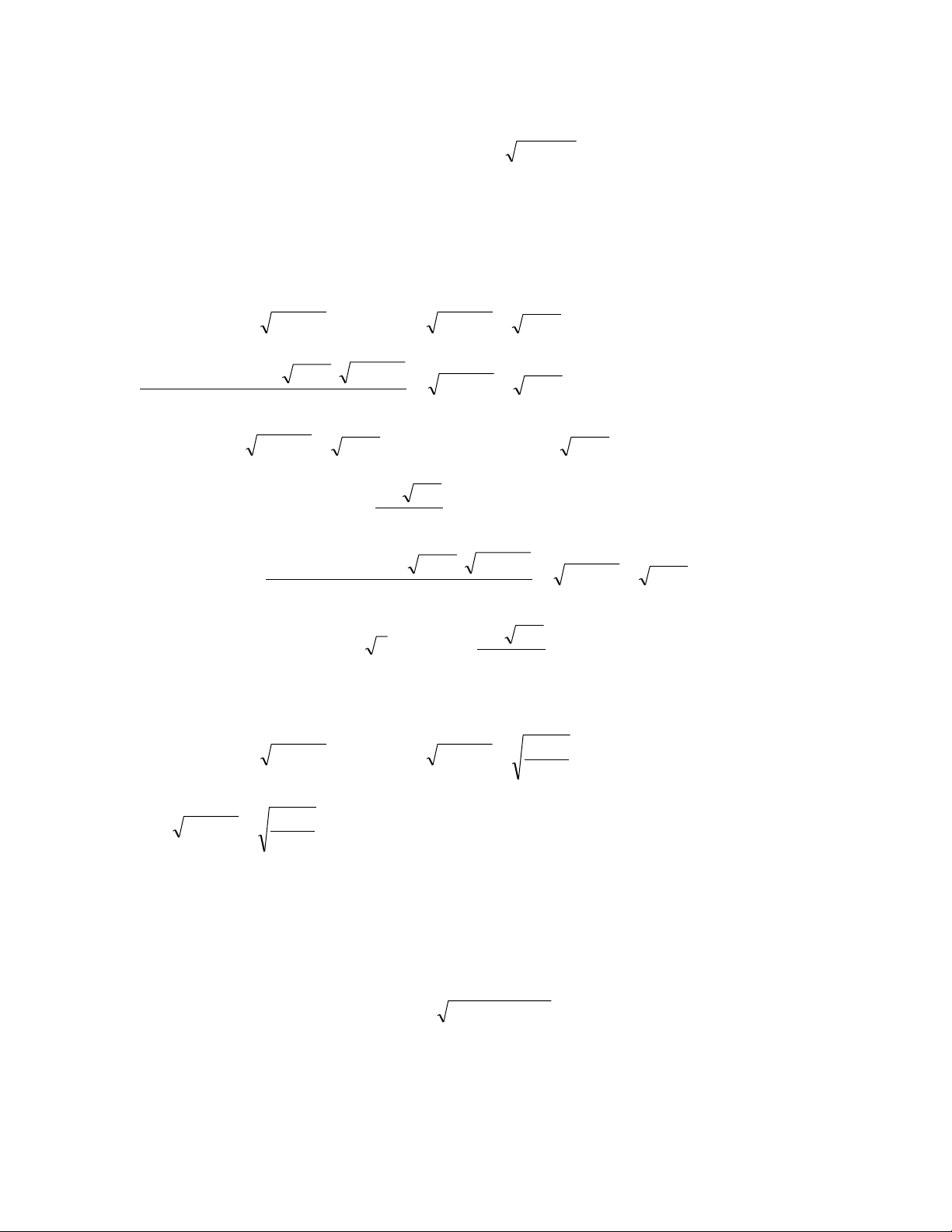
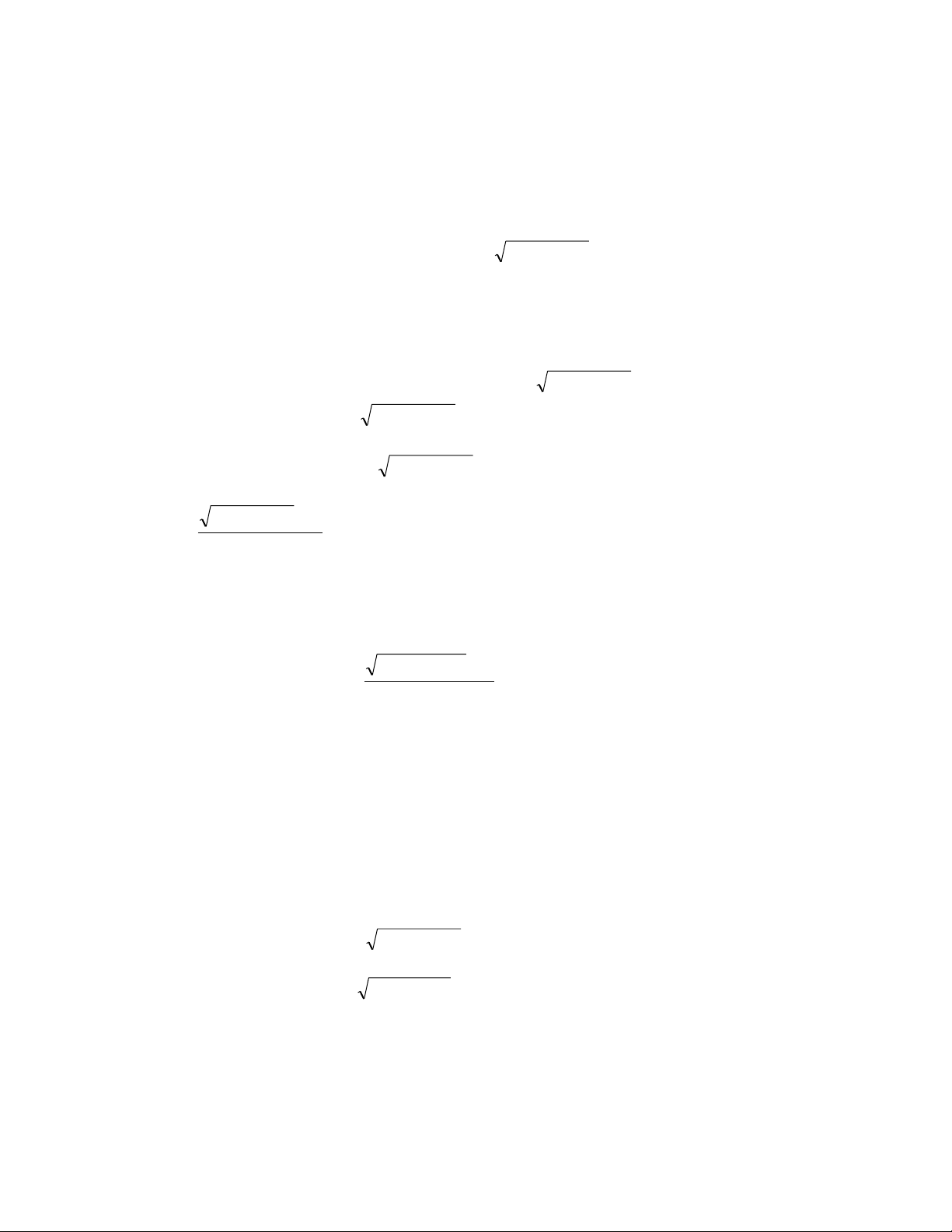
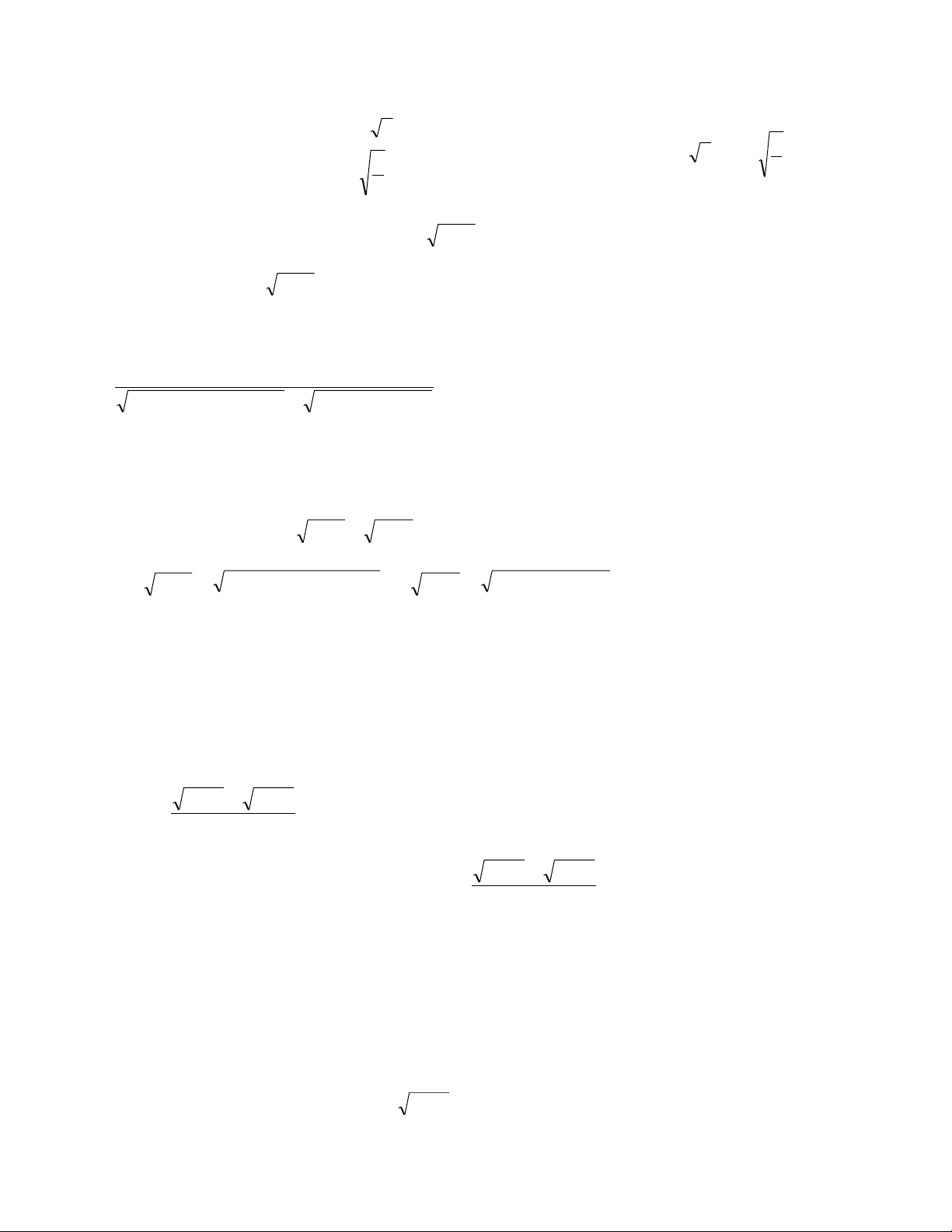
Preview text:

Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PHƢƠNG TRÌNH VÔ TỈ ĐƢA VỀ DẠNG TÍCH
KĨ NĂNG TÌM BIỂU THỨC LIÊN HỢP HOẶC NHÂN TỬ
CỦA PHƢƠNG TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh BẢN CHÍNH THỨC
Lƣu ý trƣớc khi sử dụng tài liệu
+Bài viết gồm 5 chuyên đề: Chuyên đề 1 là các phƣơng trình không dùng Casio .Chuyên đề 2 và 3 là các thí dụ dùng máy
tính Casio có hƣớng dẫn sơ lƣợc, chuyên đề 4 và 5 là lí thuyết hƣớng dẫn chi tiết cách dùng máy tính Caiso tìm biểu thức
liên hợp hoặc tìm nhân tử cần xuất hiện trong phƣơng trình của chuyên đề 2 và 3. Trong đó có chuyên đề phụ một cách
tạo ra một phƣơng trình tích từ các biểu thức phù hợp
+Do có nhiều phƣơng trình mới lạ và phức tạp nên bài viết không là tài liệu để ôn tập cho các kì thi
+Các PT trong bài viết có nghiệm là nghiệm của PT bậc 3,bậc 4 nên nó phức tạp hơn các dạng PT khác
+Các phƣơng trình chƣa đƣợc sắp xếp thành hệ thống hợp lí và có thể có sai sót
+Tài liệu cung cấp một số ý tƣởng để tạo ra các phƣơng trình vô tỷ đƣa về dạng tích
Chuyên đề 1. PHƢƠNG TRÌNH VÔ TỈ KHÔNG DÙNG CASIO HỖ TRỢ
Chuyên đề này gồm các PT có nghiệm đẹp ta hoàn toàn nhẩm được. Dù vất vả trong việc nhẩm và tính
toán nhưng giúp chúng ta tiến bộ khi học môn Toán.
A.Các Phƣơng trình tìm biểu thức liên hợp không dùng Casio
Một số ví dụ ngoài cách nhân liên hợp có thể làm theo hướng đưa về tích hoặc tìm tổng và hiệu các căn
rồi tìm từng căn theo x.
Thí dụ 1 Giải phƣơng trình 6 2
x  2x  1  2 2 2
x x  1  2 2 x  2x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2 x  2x 1 1
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 2
PT x x 1 6 2 x  2x 1 2
x x  2  2 2 2
x x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Nâng cấp: Giải phƣơng trình 1 1 2x  3 a)   2 x  3x  2
6x  2 x  1  x 2 2x x  1  x 2 3 5x  7 b)   2 x  3x  2
6x  2 x 1  x 2 2x x 1  x
PTcó 2 nghiệm x  ;
0 x  1 (lƣu ý coi t x  3
là nghiệm ngoại lai) 6 4
x x x x x  2 8 3 3 2 2
c) 6x  2x  1  5 2 x x  2 Hƣớng dẫn. pt  6 ( 2
x  2x 1 6 2 x  2x  )( 1 2
x x 1 6 2 x  2x  ) 1  0 1
PTcó 4 nghiệm x  ; 0 x  ; 1 x   ; 3 x  3 3 3 d) 6 2 x  2x 1 2
x x  2 2 2 x x 1 2
x x  9
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  3 3 ) e  6 2 x  2x 1 2  x   2 2 2 x x 1 2
x x  2 3 x  3 2 x  3x 1
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  2x  2 2 2 x  2x  1 f )  x 1  2 2 x x  2 2 2 x x  1 2
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. 2 2 2 x  2x  1 ( 2 2 x  ) 1
x  1 2x  2x  1 2 x  1 PT x  1    2 2 x x  1 2 x x  2 2 2 x x x x  2 2 2 1  x 1 2 2 x  2x 1 2  x   1 ( 2 x x  ) 2   2
x x  2  2 2 2
x x 1( 2 x  ) 1  0
Nhân liên hợp suy ra PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Chú ý: biểu thức liên hợp cần tìm là 2
x x  2  2 2 2 x x 1
biểu thức liên hợp nữa cần tìm là 2
x 1 x 1 2 2
x  2x 1 2x 2 4 x  2 3 2 x x  4 ) h   2 2 x x  2 2 2 x x  1 Hƣớng dẫn. 2 4 x  2 3 2 x x  4 2 x  2 PT   2 2 x x x x  2 2 2 1
Biến đổi tƣơng tự bài trƣớc và nhân liên hợp suy ra PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  6 2 x  2x  1 2 x x  1 k)  2 x  2x  6 3 Hƣớng dẫn. PT   3 6 2 x  2x 1 2
x x   1  3 2
x  2x  6( 2 x x  ) 1  0
nhân liên hợp suy ra PTcó 2 nghiệm x  ; 1 x  3  2 2 x  10x  13 x  4 p)  6 2 x  2x  1 2 x x  4
Hƣớng dẫn. Nhận thấy x  4  PT  ( 2 x x  ) 4  2 2
x 10x 13  x  4  2 x x 1 2
x  2x  6(x  ) 4  0
nhân liên hợp suy ra PTcó 2 nghiệm x  ; 1 x  3  3
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x x 2 8 2 2 2
q) 6x  2x  1  2x x  1  3 2 x  3x  4 Hƣớng dẫn. x x   x x x x   x x  2 ( 2 6 2 2 2 1 2 2 )( 1 6 2 2 1 2 2 ) 1 PT
6x  2x 1  2x x 1  3 2 x  3x  4  6 2
x  2x  1  2 2
x x  1  PT   0 2 6 2
x  2x  1  2 2 2
x x  1  3 2 x  3x  ( 4 *)
Giải (*):Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1
PT đã cho có 4 nghiệ 1 m x  ; 0 x  ; 1 x   ; 3 x   4 s) 2 2 2
x x 1  3x  2  6 2
x  2x 1  x  2x  ( 3 *) Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2 2 2
x x 1  3x  2  (ax  ) b b  2 a 1 Do 1 ;
0 là nghiệm PT nên ta có hệ    a b  3 b  2
Biểu thức liên hợp cần tìm là 2 2 2
x x 1  3x  2  (x  ) 2
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 6 2
x  2x 1  x  (x  ) 1  3
Do VT (*)  0 suy ra x  2  3
Xét 1  x có:
6x2  2x 1  x
4x2  2x2  2x 1  x 2  4 2 x x  2 x x x  1
suy ra VT (*)  1 4
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)  3 Do   x VPx   1 suy ra (*) 2 3 1 2
Vì vậy PT(*) có nghiệm x  1  Khi đó 6 2
x  2x 1  x  (x  ) 1  0 2 2 2
x x 1  3x  2  (x  ) 2  0 2 2 2
x x 1  ( 2 x x  ) 2 6 2
x  2x 1  ( 2 x x  ) 1 PT (*)    0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 0 x  1 x x  2 12 2 2 2 10
t)2 6x  2x  1  3 2x x 1  7 2 x  7x  10 Hƣớng dẫn. PT  2 6 2
x  2x  1  3 2 2 x x  1 ( 2 2 6 2
x  2x  1  3 2 2 x x  )( 1 2 6 2
x  2x  1  3 2 2 x x  ) 1  7 2 x  7x  10 2 6 2
x  2x  1  3 2 2
x x  1  PT   0 4 6 2
x  2x  1  6 2 2
x x  1  7 2 x  7x  ( 10 *)
Giải (*):Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1
PT đã cho có 4 nghiệ 5 m x  ; 0 x  ; 1 x   ; 3 x   6
*Một cách tạo ra phƣơng trình từ 2 biểu thức liên hợp A a A b Dạng PT: hayb B a B Cách giải.
A b B( A a)  a( B b)  0 a B 5
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nhân liên hợp ta sẽ giải quyết đƣợc PT đã cho
Thí dụ minh họa Giải phƣơng trình 6 2 x  2x  1 2 x x  1  2 x x  2 2 2 2 x x  1 Hƣớng dẫn. PT  6 2 x  2x   1 2 2 2 x x 1 2
x  2x  2  6 2 x  2x 1 2
x x   1 ( 2 x x  ) 2  0
Nhân liên hợp PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 2 Giải phƣơng trình 3 6 2
x  2x 1  2 2 2
x x 1  4 2 x  4x  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 PT  [ 3 2
x x 1 6 2 x  2x  ] 1 2
x x  2  2 2 2
x x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 3 Giải phƣơng trình 2 2 x x  2 2 1
4 2x x  1   3 2 x x  5 2x  6 2 x  2x  1 Hƣớng dẫn.
Ta có 6x2  2x 1 
4x2  x2  (x  ) 1 2 
4x2  2 x  2  x 6
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
nên đkxđ: x R  2 6 2 x x   x 2 2 1 (2 )2
pt  4 2x x  1   3 2
x x  5 2x  6 2 x  2x  1  6 2
x  2x 1  4 2 2
x x 1  3 2 x  3x  5
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 2
PT x x 1 6 2
x  2x 1  [ 2 2
x x  2  2 2 2 x x  ] 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 4 Giải phƣơng trình x 2 15 2
2 2x x 1   4 2 x x  2 x  1  6 2 x  2x 1 Hƣớng dẫn.  2 6 2 x x   x  2 2 1 ( ) 1 2
pt  2 2x x  1  . 3  4 2 x x  2 x  1  6 2 x  2x  1  3 6 2
x  2x 1  2 2 2
x x 1  4 2 x  4x  5
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 7
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 PT  [ 3 2
x x 1 6 2 x  2x  ] 1 2
x x  2  2 2 2
x x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 5 Giải phƣơng trình 6 2 x  6x  6 5 2 x  2x 1   4 2 x  9x  7 2 2
x x  1  x 6 2
x  2x  1  x Hƣớng dẫn.  2 2 2 2 2
x x  1  (2x)2
 6 2x 2x1 (x)2 pt  . 3   4 2 x  9x  7 2 2 2
x x  1  2x x  6 2 x  2x  1  3 6 2
x  2x 1  2 2 2
x x 1  4 2 x  4x  5
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 PT  [ 3 2
x x 1 6 2 x  2x  ] 1 2
x x  2  2 2 2
x x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  8
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 6 Giải phƣơng trình 2 5 2
x  8x  4  7 2
x 12x  9  3 2 x  6x  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 PT  ( 2 2
x  2x  2  5 2 x  8x  4) 2
x  2x  3  7 2
x 12x  9  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Nâng cấp: Giải phƣơng trình 1 1 2x  5 a)   2 x  3x  2
5x  8 x  4  2 x
7x 12 x  9  2 x 1 2 3x  7 b)   2 x  3x  2
5x  8 x  4  2 x
7x 12 x  9  2 x
PTcó 3 nghiệm x  ; 0 x  ; 1 x  9 5 2 x  8x  4 2 x  2x  3  c) 2 2 x x  2 2 7x 12x  9 Hƣớng dẫn. PT  7 2
x 12x  9 5 2 x  8x  4 2
x  2x  2  7 2 x 12x  9 2
x  2x   3 ( 2 x  2x  ) 2  0
Nhân liên hợp PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 9
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x x  2 13 2 2 20 7
d )2 5x  8x  4  7x 12x  9  3 2 x  6x  7 Hƣớng dẫn. PT  2 5 2
x  8x  4  7 2 x 12x  9 (2 5 2
x  8x  9  7 2
x 12x  9)(2 5 2
x  8x  9  7 2 x 12x  9)  3 2 x  6x  7 2 5 2
x  8x  4  7 2
x 12x  9  PT   0 2 5 2
x  8x  4  7 2
x 12x  9  0
PT đã cho có 4 nghiệ 7 m x  ; 0 x  ; 1 x  ; 3 x 13 ) e 5 2
x  8x  4  4x 1  7 2
x 12x  9  6x 1  2x  ( 3 *) Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 5 2
x  8x  4  4x 1  (ax  ) b b  1  a 1 Do 3 ; 1 ; 0
là nghiệm PT nên ta có hệ a b  1    b  2
3a b  4
Biểu thức liên hợp cần tìm là 5 2
x  8x  4  4x 1  (x  ) 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 7 2
x 12x  9  6x 1  (x  ) 2 ĐKXĐ: x x   x   x x   x   5 2 8 4 4 1 ) 1 ( 0 và 7 2 12 9 6 1 ( 0 ) 2  3 12  2 94  3 Có: ) 1 (  x ( ) 2  x suy ra x  11 29 11 Khi đó 5 2
x  8x  4  4x 1  (x  ) 1  0 7 2
x 12x  9  6x 1  (x  ) 2  0 10
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 5 2
x  8x  8  ( 2 x  2x  ) 2 7 2
x 12x  9  ( 2 x  2x  ) 3 PT (*)    0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 7 Giải phƣơng trình 2 x x x   2 8 4 2 10 6 5x x 8x  4   2 x   x x  3 2 3 7 12 9 Hƣớng dẫn. ( 7 2 x x   x x x   x x   2 12 9 2 )( 3 7 2 12 9 2 ) 3 4 2 10 6 pt x
5x  8x  4   2 x   x x  3 ( 3 2 3 7 12 9) 7 2 x x   x x   2 12 9 2 3 4 2 10 6  x
5x  8x  4   3 3
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 PT  ( 3 2
x  2x  2  5 2 x  8x  4) 2
x  2x  3  7 2
x 12x  9  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 8 Giải phƣơng trình 2 x 12x  3 2 x  8x 4 2 x  4x  9   2 2 x x   x x   x x  3 5 8 4 2 1 2 3 7 12 9 Hƣớng dẫn. 11
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) ( 5 2
x  8x  4  2x  )( 1 5 2
x  8x  4  2x  ) 1 pt  5 2
x  8x  4  2x 1 ( 7 2
x 12x  9  2x  )( 3 7 2
x 12x  9  2x  ) 3 4 2 x  4x  9   2 x   x x  3 ( 3 2 3 7 12 9) 7 2 x x   x x   2 12 9 2 3 4 2 4 9  x
5x  8x  4  2x 1   3 3
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 PT  ( 3 2
x  2x  2  5 2 x  8x  4) 2
x  2x  3  7 2
x 12x  9  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 9 Giải phƣơng trình 14 2
x  6x  4  18 2
x 10x  8  2 2 x  2x  6 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4 12
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 2
PT x x  2  14 2 x  6x  4 2
x x  4  18 2
x 10x  8  0
PTcó 4 nghiệm x   ; 2 x   ; 1 x  4 14 2 x  6x  4 2 x x  4 Nâng cấp: 2 x x  2 2 x x  18 10 8 PT  18 2
x 10x  8 14 2 x  6x  4 2
x x  2  18 2 x 10x  8 2
x x  4( 2 x x  ) 2  0
PTcó 4 nghiệm x   ; 2 x   ; 1 x  4
Thí dụ 10 Giải phƣơng trình 2 2 x x  2 18 7
2 14x  6x  4   3 2 x  7x  7 4x 1  18 2 x 10x  8 Hƣớng dẫn. ( 18 2 x x   x x x   x  2 10 8 4 )( 1 18 2 10 8 4 ) 1
PT  2 14x  6x  4   3 2 x  7x  7 4x 1  18 2 x 10x  8
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 PT  [ 2 2
x x  2  14 2 x  6x  4] 2
x x  4  18 2
x 10x  8  0
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3 13
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 11 Giải phƣơng trình 3 14 2
x  6x  4  18 2
x 10x  8  4 2 x  4x 10 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 PT  [ 3 2
x x  2  14 2 x  6x  4] 2
x x  4  18 2
x 10x  8  0
PTcó 4 nghiệm x   ; 2 x   ; 1 x  4
Thí dụ 12 Giải phƣơng trình 5 2 x 12x  5 4 2 x  4x 14   3 2 x  2x  7 3x 1  14 2 x  6x  4 18 2
x 10x  8  4x  1 Hƣớng dẫn. ( 14 2
x  6x  4  3x  )( 1 14 2
x  6x  4  3x  ) 1 PT  3x  1  14 2 x  6x  4 ( 18 2
x 10x  8  4x  )( 1 18 2
x 10x  8  4x  ) 1  . 2  3 2 x  2x  7 18 2
x 10x  8  4x  1
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2 14
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 2
PT x x  2  14 2
x  6x  4  [ 2 2
x x  4  18 2
x 10x  8]  0
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3
Thí dụ 13 Giải phƣơng trình 11 2
x  28x  21  13 2
x  32x  28  2 2 x  4x  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1  3 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  11 2
x  28x  21
a b c  2 a  1   Do ; 1 2
là nghiệm PT nên ta có hệ 4a  2b c  3  b  2  
4a  2a c  11 c  3
Biểu thức liên hợp cần tìm là 2
x  2x  3  11 2
x  28x  21
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  4  13 2
x  32x  28 2
PT x  2x  3  11 2 x  28x  21 2
x  2x  4  13 2
x  32x  28  0
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3
Nâng cấp: Giải phƣơng trình 1 1 2x  7 a)   2 x  7x  12
11x  28 x  21  2 x
13x  32 x  28  2 x 1 2 3x  10 a)   2 x  7x  12
5x  8 x  4  2 x
7x 12 x  9  2 x
PTcó 3 nghiệm x  ; 1 x  ; 4 x  9 15
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 14 Giải phƣơng trình 2 2 2
x  3x  2  10 2
x 14x 13  2 2 x  2x  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2 
Biểu thức liên hợp cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2
x x  3  10 2 x 14x 13
PTcó 3 nghiệm x   ; 1 x  2 
Thí dụ 15 Giải phƣơng trình 2 2 2
x  3x  2  3 10 2
x 14x 13  4 2 x  4x 11 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2 
Biểu thức liên hợp cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2
x x  3  10 2 x 14x 13
PTcó 3 nghiệm x   ; 1 x  2 
Thí dụ 16 Giải phƣơng trình 4 2 2
x  3x  2  10 2
x 14x 13  3 2 x  3x  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2 
Biểu thức liên hợp cần tìm là 2
x x  2  2 2 2
x  3x  2 và 2
x x  4  10 2 x 14x 13
PTcó 3 nghiệm x   ; 1 x  2 
Thí dụ 17 Giải phƣơng trình   2 5x2 2 2x 2
4x  6x  6  9x  8x  8  x 16
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. 1
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2
Biểu thức liên hợp cần tìm là 2 2
x x 1 x 4 2
x  6x  6 và 3 2
x x 1 x 9 2 x  8x  8 1
PTcó 3 nghiệm x   ; 1 x  2
Thí dụ 18 Giải phƣơng trình   2 9x2 2 4x 4
3 4x  6x  6  9x  8x  8  x Hƣớng dẫn. 1
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2
Biểu thức liên hợp cần tìm là 2 2
x x 1 x 4 2
x  6x  6 và 3 2
x x 1 x 9 2 x  8x  8 1
PTcó 3 nghiệm x   ; 1 x  2
Thí dụ 19 Giải phƣơng trình   2 7x2 2 3x 3
2 4x  6x  6  9x  8x  8  x Hƣớng dẫn. 1
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2
Biểu thức liên hợp cần tìm là 2 2
x x 1 x 4 2
x  6x  6 và 3 2
x x 1 x 9 2 x  8x  8 1
PTcó 3 nghiệm x   ; 1 x  2
Thí dụ 20 Giải phƣơng trình 2 2 2
4x  6x  6  9x  8x  8  5x   2 x 17
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.   2 5x2 2 2x 2 PT
4x  6x  6  9x  8x  8  x Do 5 2
x  2x  2  0 nên x  0 PT  4 4 x  6 3 x  6 2 x  9 4 x  8 3 x  8 2 x  5 2 x  2x  2 1
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là  ; 1 2
Biểu thức cần tìm là 2 4 3 2
2x x 1 4x  6x  6x và 2 4 3 2
3x  2x 1 9x  8x  8x 1
PTcó 2 nghiệm x  ; 1 x  2
Thí dụ 21 Giải phƣơng trình 2 2 3
2 4x  6x  6  9x  8x  8  7x   3 x Hƣớng dẫn.   2 7x2 2 3x 3 PT
4x  6x  6  9x  8x  8  x Do 7 2
x  3x  3  0 nên x  0 PT  2 4 4 x  6 3 x  6 2 x  9 4 x  8 3 x  8 2 x  7 2 x  3x  3 1
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là  ; 1 2
Biểu thức cần tìm là 2 4 3 2
2x x 1 4x  6x  6x và 2 4 3 2
3x  2x 1 9x  8x  8x 1
PTcó 2 nghiệm x  ; 1 x  2 18
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 22 Giải phƣơng trình   2 3x2 2 2x 4
4x  5x  10 
x  3x  6  x Hƣớng dẫn. Do 3 2
x  2x  4  0 nên x  0 PT  4 4 x  5 3 x 10 2 4 x x  3 3 x  6 2 x  3 2 x  2x  4
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  5x 10x và 2 4 3 2
x x  2 
x  3x  6x
PTcó 2 nghiệm x  1 ; x  2
Thí dụ 23 Giải phƣơng trình   2 5x2 2 4x 8
4x  5x  10  3 x  3x  6  x Hƣớng dẫn. Do 3 2
x  2x  4  0 nên x  0 PT  4 4 x  5 3 x 10 2 x  3 4 x  3 3 x  6 2 x  5 2 x  4x  8
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm) của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  5x 10x và 2 4 3 2
x x  2  x  3x  6x
PTcó 2 nghiệm x  1 ; x  2
Thí dụ 24 Giải phƣơng trình 2 4 4 x  2 3 x 1  4 4 x  2 3 x 10 2 x 1  2 2 x  3x 1 Hƣớng dẫn. 1
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 0 ; 2 2 19
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức liên hợp cần tìm là 2 2
x x 1 4 4 x  2 3 x 1 và 2 2
x x 1 4 4 x  2 3 x 10 2 x 1 1
PTcó 3 nghiệm x   ; 2 x  ; 0 x  2
Thí dụ 25 Giải phƣơng trình 4 x  9 2
x  6x  16 4 x  49 2 x 16x  5 2 x  2x  6 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  2 ; 1
Biểu thức liên hợp cần tìm là x2  x  2 
x4  9x2  6x và 4x2  x  4  16x4  49x2 16x
PTcó 3 nghiệm x   ; 1 x  2
Thí dụ 26 Giải phƣơng trình 4 4 x  21 2 x  24x  2 4 x 16 2
x  32x  4 2 x  5x 12 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  1 ; 2
Biểu thức liên hợp cần tìm là 2x2  x  4  4x4  x
21 2  24x và
2x2  4x  8  2 x4 16x2  32x
PTcó 3 nghiệm x   ; 2 x  1
Thí dụ 27 Giải phƣơng trình x(4 2 x 13x  ) 8  2x( 2 x  5x  ) 2  2 2 x  3x  4 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 2 1 
Biểu thức liên hợp cần tìm là 2
x x  2  x(4 2 x 13x  ) 8 và 2
x  2x  2  2x( 2 x  5x  ) 2
PTcó 4 nghiệm x   ; 2 x  1  20
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 28 Giải phƣơng trình 4 3 x x  4 3  x  5 2 x  4x 1 2
x x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 4 ; 1 ; 0
Biểu thức liên hợp cần tìm là 2 x x  2 4 3
x x  4 và 1 3  x  5 2 x  4x 1
PTcó 3 nghiệm x  ; 0 x  ; 1 x  4
Thí dụ 29 Giải phƣơng trình 4 3 x x  4 3  x  4 2
x x  ( 5  ) 1 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 4 ; 1 ; 0
Biểu thức liên hợp cần tìm là 2 x x  2 4 3
x x  4 và 5x x3  4x
PTcó 3 nghiệm x  ; 0 x  ; 1 x  4
Thí dụ 30 Giải phƣơng trình 4 3 x x  4 3
x 14x  5 2  x  ( 5  ) 1 x  2  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 4 ; 1 ; 0 Với x  1  thì 3
x 14x  5  1  14  5  10   0 .
Do đó nghiệm PT phải thỏa mãn x  1
  x 1  0
Biểu thức liên hợp cần tìm là 2 x x  2 4 3
x x  4 và 5(x  ) 1 3
x 14x  5
PTcó 3 nghiệm x  ; 0 x  ; 1 x  4
Thí dụ 31 Giải phƣơng trình 4 2
x x 1  (2x  )( 4 2 x  ) 1 2
x x 1 Hƣớng dẫn. 21
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PT f (x) 4 2
x x 1  (2x  )( 4 2 x  ) 1 2
x x 1
Ta nhẩm đƣợc các nghiệm đẹp của PT là , 0 1  2 3 x x 3 2 x  4x  1 f ' (x)    2x 1 4 2 x x  1 2 3 x  4 2 x  2x  4 Ta có f '( )
1  0 nên PT có nghiệm bội x  1
(tính f ''( )
1  0 Pt có nghiệm kép x  1  )
Các ví dụ kiểm tra chính xác là nghiệm kép xin dành cho bạn đọc)
Giả sử biểu thức liên hợp cần tìm là 2 4 2
ax bx c
x x 1 2 3 x x
Lấy đạo hàm đƣợc biêu thức P(x)  2ax b 4 2 x x  1 a  1
a b c  1  Do  0 ;
1 là nghiệm PT nên ta có hệ
(*)  b  2 c  1  c  3
Do PT có nghiệm kép x  1
nên nó là nghiệm của P(x)
suy ra  2a b 1  ( 0 **) a  1 
Từ (*) và (**) suy ra b  1  c  1
Biểu thức liên hợp cần tìm là 2 x x 1 4 2
x x 1
Tƣơng tự (2x  )( 4 2 x  ) 1 1
PTcó 2 nghiệm x  ; 0 x  1 
Thí dụ 32 Giải phƣơng trình (x  ) 1 4 2
x x  4  2 3
x  6x 1  2 2 x  4x  3 Hƣớng dẫn. Nếu x  1  thì 2 3
x  6x 1  2   6 1  7   0 22
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Suy ra x  1
  x 1  0
Ta nhẩm đƣợc các nghiệm đẹp của PT là x  ,
0 x  1và dùng đạo hàm thấy x  1là nghiệm kép
Biểu thức cần tìm là 2 2
x  2x  2  (x  ) 1 4 2
x x  4 và 2x 1 2 3 x  6x 1
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 33 Giải phƣơng trình (x  ) 1 2
x x 1  2 3 x  6x 1 2
x  2x  2 Hƣớng dẫn. Nếu x  1  thì 2 3
x  6x 1  2   6 1  7   0 Suy ra x  1
  x 1  0
Ta nhẩm đƣợc các nghiệm đẹp của PT là x  , 0 x  1
và dùng đạo hàm thấy x  1là nghiệm kép
Biểu thức cần tìm là 2
x x 1 (x  ) 1 2
x x 1 và 2x 1 2 3 x  6x 1
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 34 Giải phƣơng trình x 1 3 2 x 1  2 2
x  2x 1  3 2 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x  ,
0 x  1và đều là nghiệm kép
Biểu thức cần tìm là 2 2
x x 1 x 1 3 2 x 1 và 2
x x 1 2 2 x  2x 1
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 35 Giải phƣơng trình 2
x x  9x  6  3 3 x  2 2 2
x x  6x  4 Hƣớng dẫn. 23
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) ĐK : 2 2 x
.Ta nhẩm đƣợc các nghiệm đẹp của PT là x  , 1 x  ; 2 x 3 3
Chú ý:Ta phải tinh ý khi thấy xuất hiện các biểu thức 9x  3 ; 6 3 x  2 2 x 6
; x  4 để nhẩm 2
nghiệm khó là x 3
Biểu thức cần tìm là 2 x  3x  2 2
x x  9x  6 và 3 2
3x  2  3x x 2
PTcó 3 nghiệm x  , 1 x  ; 2 x  3
Thí dụ 36 Giải phƣơng trình 4 x 12x 12 3  7 2 x  28x  29 2
x  3x  5 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 1 x   ; 2 x  1 
Biểu thức cần tìm là 2 x  2x  2 4
x 12x 12 và 3 2
x  3  7x  28x  29 Chú ý 3 2 x  ; 3
7x  28x  29 không đồng thời bằng 0.
PTcó 3 nghiệm x  , 1 x   ; 2 x  1 
Thí dụ 37 Giải phƣơng trình 4 x 12x 12 3   2 2 x x  2 2
x  3x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 1 x   ; 2 x  1 
Biểu thức cần tìm là 2 x  2x  2 4
x 12x 12 và 3 2
x   2x x  2 Chú ý 3 2 ; x
 2x x  2 không đồng thời bằng 0.
PTcó 3 nghiệm x  , 1 x   ; 2 x  1 
Thí dụ 38 Giải phƣơng trình x4 12x 12 3
  8x2 13x  6  x2  3x 24
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 1 x   ; 2 x  1 
Biểu thức cần tìm là 2 x  2x  2 4
x 12x 12 và 3 2
x  2   8x 13x  6 Chú ý 3 2 x  ; 2
 8x 13x  6 không đồng thời bằng 0.
PTcó 3 nghiệm x  , 1 x   ; 2 x  1 
PT có 3 nghiệm là x  , 1 x   ; 2 x  1 
Thí dụ 39 Giải phƣơng trình 4 x  36x 12 3 2
x 10x  3 2
x  3x  3 Hƣớng dẫn.
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  4 
Với x  1là nghiệm bội(bài này nghiệm kép)
Biểu thức cần tìm là 2 x  2x  2 4
x  36x 12 và 3 2 x 1 x 10x  3
PTcó 2 nghiệm x  , 1 x  4 
Thí dụ 40 Giải phƣơng trình x 4 2 x  5x 10 3  4 2
x  7x  3  2 2 x  3 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 1 x  ; 2 x  2 
Biểu thức cần tìm là 2 2
x x  2  x 4 2
x  5x 10 và 3 2
x 1 4x  7x  3 Chú ý 3 2 x  ; 1
4x  7x  3 không đồng thời bằng 0.
Nghiệm của PT là x  , 1 x  ; 2 x  2  25
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PHẦN BỔ XUNG CÁCH TÌM NGHIỆM NGOẠI LAI KIỂU MỚI
Thí dụ 41 Giải phƣơng trình 5 2
x  8x  4  x 6x  2  8x 1 3 2 x x  2 Hƣớ 1
ng dẫn. Điều kiện x 3
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  3
Để tìm thêm nghiệm ngoại lai khi nay ta để ý x 6x  2  8x 1 có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời x 6x  2  8x 1 0 thấy thỏa mãn
Các biểu thức cần tìm là 2
x  2x  2  5 2
x  8x  4 và 2
x x x 6x  2 và 2
x x x x  2 8 1 `
Lƣu ý:Chỉ cần tìm x   x x   x x  1 6 2 và 2 8 1 ` có 2 nghiệm , 1 x  3
Nghiệm của PT là x  , 1 x  3
Thí dụ 42 Giải phƣơng trình 5 2
x  8x  4  x 6x  2  3 2
x  8x  2  4 2 x  2 Hƣớ 1
ng dẫn. Điều kiện x 3
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  3 Để
x 6x  2  3 2
x  8x  2 
tìm thêm nghiệm ngoại lai khi này ta để ý có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời x 6x  2  8x 1 0 thấy thỏa mãn
Các biểu thức cần tìm là 2
x  2x  2  5 2 x  8x  4 và 2
x x x 6x  2 và 2 2
x x x x x  2 3 8 2
Nghiệm của PT là x  , 1 x  3 26
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 43 Giải phƣơng trình
5x2 12x  8  2x  2  (x  )
2 2 1 x2  2x  2  3  2x
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  1  Để (x  )
2 2 1 x2  2x  2  3  2x
tìm thêm nghiệm ngoại lai khi này ta để ý
có nhân tử là x  2 (x  ) 2 2 1 2
x  2x  2  3  2x
Thay x=2 vào PT với qui ƣớc tạm thời  0 thấy thỏa mãn 5 2
x 12x  8  2x  2  0
Các biểu thức cần tìm là 2
x  2x  2  5 2
x 12x  8 và 2     x 2x 2 3 2x
Nghiệm của PT là x  , 1 x  1 
Thí dụ 44 Giải phƣơng trình 5 2
x 12x  8  (x  ) 2 2 2 2
x  2x  2
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  1 
Để tìm thêm nghiệm ngoại lai khi này ta để ý 2 2 (x  ) 2 2  x
có nhân tử là x  2
Thay x=2 vào PT với qui ƣớc tạm thời 2 2 (x  ) 2 2  x thấy thỏa mãn 5 2
x 12x  8  2x  2
Các biểu thức cần tìm là 2
x  2x  2  5 2
x 12x  8 và 2     x 2x 2 3 2x
Nghiệm của PT là x  , 1 x  1 
Thí dụ 45 Giải phƣơng trình 5 2 x  8x  4 2
x  6x  2  8x 1 2 3 x  4 2 x  2x  2 Hƣớ 1
ng dẫn. Điều kiện x 3 27
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  3
Để tìm thêm nghiệm ngoại lai khi nay ta để ý x 6x  2  8x 1 có nhân tử là x
Thay x=0 vào PT với qui ƣớc tạm thời x 6x  2  8x 1 0 thấy thỏa mãn
Các biểu thức cần tìm là 2
x  2x  2  5 2
x  8x  4 và x 1 6x  2 và x   x  2 8 1 `
Nghiệm của PT là x  , 1 x  3
Thí dụ 46 Giải phƣơng trình 5 2
x  8x  4  x3 7 2 x 1 3  10 2
x  9x  8 3 2 x x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  ; 0 x  , 1 x  3
Các biểu thức cần tìm là 2
x  2x  2  5 2
x  8x  4 và 3 2
x 1 7x 1 và 3 2 x   x x  2 10 9 8
Nghiệm của PT là x  ; 0 x  , 1 x  3
Thí dụ 47 Giải phƣơng trình 6 2
x  2x 1  x3 11 2 x  30x  27 3  8 2
x 15x  8 3 2 x  4x 1 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x  ; 3 x  1 
Các biểu thức cần tìm là 2
x x 1 6 2
x  2x 1 (và 3 2
x  3  11x  30x  27 và 3 2 x   x x x x   2 8 15
8 tìm với 2 nghiệm ; 3 1 )
Nghiệm của PT là x  , 0 x  ; 3 x  1 
Thí dụ 48 Giải phƣơng trình 7 2
x  4x  2  (x   ) 1
6x  2  8x 1 3 2 x  4x  4 28
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớ 1
ng dẫn. Điều kiện x 3
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  3
Để tìm thêm nghiệm ngoại lai khi nay ta để ý (x  )
1  6x  2  8x 1 có nhân tử là x+1
Thay x=-1 vào PT với qui ƣớc tạm thời (x   ) 1
6x  2  8x 1 0 thấy thỏa mãn
Các biểu thức cần tìm là 2
x x 1 7 2
x  4x  2 và 2
x  2x 1 (x  ) 1 6x  2 và 2
x x   x x  3 2 ( ) 1 8 1 `
Lƣu ý:Có thể chỉ cần tìm x   x x   x x  1 6 2 và 2 8 1 ` có 2 nghiệm , 1 x  3
Nghiệm của PT là x  , 1 x  3
Thí dụ 49 Giải phƣơng trình 7 2
x  4x  2  (x  ) 1  6x  2  3 2
x  8x  2  4 2 x  4x  3 Hƣớ 1
ng dẫn. Điều kiện x 3
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x  3 Để (x  ) 1  6x  2  3 2
x  8x  2 
tìm thêm nghiệm ngoại lai khi nay ta để ý có nhân tử là x+1
Thay x=-1 vào PT với qui ƣớc tạm thời (x   ) 1
6x  2  8x 1 0 thấy thỏa mãn
Các biểu thức cần tìm là 2
x x 1 7 2
x  4x  2 và 2
x  2x 1 (x  ) 1 6x  2 và 2 2
x x   x x x  2 3 1 ( ) 1 3 8 2
Lƣu ý:Chỉ cần tìm x   x x   x x  1 6 2 và 2 1 8 1 ` có 2 nghiệm , 1 x  3
Nghiệm của PT là x  , 1 x  3
Thí dụ 50 Giải phƣơng trình (x  ) 2 2 2
x  2x  4  7 2 x 10x 1 2
x  7x  7 29
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x  2 
Các biểu thức cần tìm là 2 2
x  2x  4 và 2
x x 1 7 2
x 10x 1
Nghiệm của PT là x  , 0 x  2 
Thí dụ 51 Giải phƣơng trình 5 2
x x  2  2 2 2 x x 1 2  x  2
x  2x  6  2 2
x  4x  3 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x   ; 1 x  3
Các biểu thức cần tìm là 3 2 2 2 x x
x  2x  6 và 3 2 2 x x 2 2
x  4x  3 2
x x  2  2 2 2
x x 1
Nghiệm của PT là x  , 0 x   ; 1 x  3
Thí dụ 52 Giải phƣơng trình 2 2
x x  2  2 2 2 x x 1 3  2 5 x  3 4 2 x x 1 (  2 2 x  4x  3) Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x   ; 1 x  3 2 3 5 4
x  2x  3x x 3 2
x  2x  3x
Các biểu thức cần tìm là và 3 2 2 x x 2 2
x  4x  3 và 2 2 x x   x x  2 2 2 1
Lƣu ý: xét x=0 và x  0
Nghiệm của PT là x  , 0 x   ; 1 x  3
Thí dụ 53 Giải phƣơng trình 5 2
x  8x  4  .3 x  2 2
x  9x  8  2 2 x  4x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x  ; 1 x  3 30
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Các biểu thức cần tìm là 2 3 2 x  2x  .
x  2x  9x  8 và 2 2 x x   x x  2 2 5 8 4
Nghiệm của PT là x  , 0 x  ; 1 x  3
Thí dụ 54 Giải phƣơng trình 2 2 2
x x 1  .3 x 8 2
x 15x  8  2 2 x x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 0 x   ; 1 x  3
Các biểu thức cần tìm là 2 3 2 x  2x  .
x 8x 15x  8 và 2
x x  2  2 2 2
x x 1
Nghiệm của PT là x  , 0 x   ; 1 x  3
Thí dụ 55 Giải phƣơng trình 5 2
x 12x  8  (x  ) 2 3 8 2
x 13x  6  2 2 x  2x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x  , 1 x   ; 1 x  2
Các biểu thức cần tìm là 3 2
x  2  8x 13x  6 và 2
x  2x  2  5 2
x 12x  8
Nghiệm của PT là x  , 1 x   ; 1 x  2
Thí dụ 56 Giải phƣơng trình 3 5 2
x  4x  (x  ) 1 2 2
x  5x  8  7x  2 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x   ; 1 x  4 
Các biểu thức cần tìm là 2x2  3x  4  3 5x2  4x nhận nghiệm là x   ; 1 x  4  và 2 2
x  5x  8 nhận nghiệm là x   ; 1 x  4 
Nghiệm của PT là x   ; 1 x  4  31
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 57 Giải phƣơng trình 3 5 2
x  4x  (x  ) 1 2 2 x  5x 13 2
 x  9x 1 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x   ; 1 x  4 
Các biểu thức cần tìm là 2x2  3x  4  3 5x2  4x nhận nghiệm là x   ; 1 x  4  và 3 2
x  5x 13 nhận nghiệm là x   ; 1 x  4 
Nghiệm của PT là x   ; 1 x  4 
Thí dụ 58 Giải phƣơng trình 3 5 2
x  4x  (x  ) 1 2 2 x  5x  5 2
x  5x  3 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x   ; 1 x  4 
Các biểu thức cần tìm là 2x2  3x  4  3 5x2  4x nhận nghiệm là x   ; 1 x  4  và 1 2
x  5x  8 nhận nghiệm là x   ; 1 x  4 
Nghiệm của PT là x   ; 1 x  4 
Thí dụ 59 Giải phƣơng trình x  6 2
x  2x 1  x 1 2 2 2
x x 1  2 x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1 32
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 Suy ra x  6 2
x  2x 1 tƣơng ứng với 2
x x x 1  (x  ) 1 2  x 1 x 1  2 2 2
x x 1 tƣơng ứng với x 1 2
x x  2  (x  ) 1 2  x 1 PT x  6 2
x  2x 1  x 1  x 1 2 2 2
x x 1  x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 60 Giải phƣơng trình 3 2
x  7x 1 6 2
x  2x 1  5 2
x 14x 1 8 2 2
x x 1  5 x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 Suy ra 3 2
x  7x 1 6 2
x  2x 1 tƣơng ứng với 2 x 1 5 2
x 14x 1 8 2 2
x x 1 tƣơng ứng với 3 x  1 PT  3 2
x  7x 1 6 2
x  2x 1  2 x 1  5 2
x 14x 1 8 2 2
x x 1  3 x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  33
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 61 Giải phƣơng trình 8x  5  4 6 2
x  2x 1  x 1 2 2 2
x x 1  x 1  2x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1
Suy ra 8x  5  4 6 2
x  2x 1 tƣơng ứng với 8x  5  4 2
x  4x  4  (2x  ) 3 2  2x  3 x 1  2 2 2
x x 1 tƣơng ứng với x 1 2
x x  2  (x  ) 1 2  x 1
PT  8x  5  4 6 2
x  2x 1  2x  3  x 1 2 2 2
x x 1  x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 62 Giải phƣơng trình 2
x  33x  2115 6 2
x  2x 1  8x 1 8 2 2
x x 1  3 2x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1 34
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 Suy ra 2
x  33x  2115 6 2
x  2x 1 tƣơng ứng với 2 2x  3 8x 1  8 2 2
x x 1 tƣơng ứng với 2x  3 2 PT
x  33x  2115 6 2
x  2x 1  2 2x  3  8x 1 8 2 2
x x 1  2x  3
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 3 PT  5 2 x  8x  4 2
x  2x  6  2 3  7 2 x 12x  9 2
x  2x  4 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 63 Giải phƣơng trình 3 2
x x  28  6 2 x x 1 3 2
x x  6  2 2 2
x x 1  1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 35
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 3 2 PT
x x  28  6 2
x x 1  3 3 2
x x  6  2 2 2
x x 1  2  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 64 Giải phƣơng trình 2
x x  5  6 2 x x 1 2
x x  3  2 2 2
x x 1  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 2 pt
x x  5  6 2
x x 1  2 2
x x  3  2 2 2
x x 1 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 65 Giải phƣơng trình 2
x x  5  6 2 x x 1 2
x x 11 2 2 2
x x 1  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3  36
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 2 Pt
x x  5  6 2
x x 1  2 2
x x 11 2 2 2
x x 1  3  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 66 Giải phƣơng trình  3 3 2 x x  6 2
x x 1   2
x x 10  2 2 2
x x 1  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 Pt   3 3 2 x x  6 2
x x 1 1  2
x x 10  2 2 2
x x 1  8  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 67 Giải phƣơng trình 3 6 2 x  2x 1 2  x  6 2 2 x x 1 2  x 1  4 2 x  6x  8 Hƣớng dẫn. 37
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 Pt   2 2 3 6 2 x x 1 2  x   (2 2 x  3x  ) 3  6 2 2 x x 1 2  x   1  (2 2 x  3x  ) 5  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 68 Giải phƣơng trình 3 5 2 x  8x  4 2
x x  3 7 2 x 12x  9 2  x  2  4 2 x 11x 17 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 Pt   2 2 3 5 2 x  8x  4 2
x x (2 2 x  5x  ) 6  3 7 2 x 12x  9 2  x  2 (2 2 x  6x  ) 11  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 38
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 69 Giải phƣơng trình 3 14 2 x  6x  4 2  x 1  18 2
x 10x  8  x  3 2 x  3x  9 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 Pt   2 2 3 14 2 x  6x  4 2  x   1  (2 2 x  3x  ) 5   18 2
x 10x  8  x  ( 2 x  ) 4  0
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3
Thí dụ 70 Giải phƣơng trình 3 3 x  2  3 6 2 x  2x 1 3  2 2 2 x x 1 2
x x 1  x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 39
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 3 3 pt x  2  3 6 2
x  2x 1  x 1 3  2 2 2 x x 1 2
x x 1 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 71 Giải phƣơng trình 3 3 x  2  3 6 2 x  2x 1 3  2 2 2 x x 1 3 2
x x x  2 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 3 3 pt x  2  3 6 2
x  2x 1  x 1 3  2 2 2 x x 1 3 2
x x x  2  x  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 72 Giải phƣơng trình 6 2 x  2x 1 2  x .3 2 2 x  4x  2 2
 x x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 0  3 ; 1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 3 2 2
x  4x  2  2 pt  6 2
x  2x 1  ( 2 x x  ) 1 2  x (3 2 2
x  4x  2  ) 2  0
PTcó 3 nghiệm x  ; 0 x   ; 1 x  3 40
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 73 Giải phƣơng trình 6 2 x  2x 1 2  x .3 3 x  24x  26 3  x  3 2 x x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 0  3 ; 1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 3 2 2
x  4x  2  x  2 pt  6 2
x  2x 1  ( 2 x x  ) 1 2  x (3 2 2
x  4x  2  x  ) 2  0
PTcó 3 nghiệm x  ; 0 x   ; 1 x  3
Thí dụ 74 Giải phƣơng trình 2 6 2
x  2x 1  2x  4 6 2 2
x x 1  3  x  5 2 x  3 2 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 ( 2 6 2 x  2x 1 2
x x  ) 1 ( 3 2 2 2 x x  1 2
x x  ) 2 pt    0 2 x  3 2 x  2
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  41
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 75 Giải phƣơng trình 3 14 2
x  6x  4  3x  3 18 2
x 10x  8  x  2   4 2 x 1 2 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 3 14 2
x  6x  4  3x  3 18 2
x 10x  8  x  2 pt   3  1  0 2 x 1 2 x  2
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3
Thí dụ 76 Giải phƣơng trình  2
6x  2x 1  2 2
2 2x x 1   2 2
1  (x x  ) 3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 42
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT   2 2
6x  2x 1  x x   1  2
2 2x x 1   2
1  (x x  ) 3  2
2 2x x 1  
1  x x  2 2 3   6 2 x  2x 1 2
x x   1 2 2 2
x x 1   1  ( 2 x x  ) 3 2 2 2 x x 1 2
x x  2 0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 77 Giải phƣơng trình  2
14x  6x  4   3  2
18x 10x  8   2 2
1  (x x  ) 5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1  4 ; 2
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  14 2
x  6x  4
a b c  2 a  1   Do  ; 1 2
là nghiệm PT nên ta có hệ a b c  4  b  1  
4a  2a c  8 c  2
Biểu thức liên hợp cần tìm là 2
x x  2  14 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  4  18 2 x 10x  8 pt   14 2 x  6x  4 2
x x  2 18 2
x 10x  8   1  ( 2 x x  ) 5  18 2 x 10x  8 2
x x  4 0
PTcó 4 nghiệm x  ; 1 x   ; 2 x  3
Thí dụ 78 Giải phƣơng trình  2 2
6x  2x 1  x x  2 2 2
2 2x x 1  x x   2 2 1  (2x  ) 3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 43
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 PT   6 2 x  2x 1 2
x x   1 2 2 2 x x 1 2
x x   1  (2 2 x  ) 3 2 2 2 x x 1 2
x x  2 0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 79 Giải phƣơng trình x x 2 4 2
x x  3    2 2 2 x x 1 2 x x  4 2 2 x x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 x  4 2 Pt x 1 (   ) 2
x x  2  2 2 2
x x 1  0 2 x x  4 2 2 x x 1
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 80 Giải phƣơng trình x  2 4 10
2x  3x  4   6 2 x  2x 1 2 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x 1 6 2 x  2x 1 x  2 4 10
pt x  2x  5 2 
x x 1 6 2
x  2x 1  0 2 x  2 44
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 4 x  2 3 x  3 2 4 x x  2 2 x  3 2   x  0 2 x  2 2
x x 1  6 2 x  2x 1
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 81 Giải phƣơng trình x  2 4 10
2x  3x  4   6 2 x  2x 1 2 x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x 1 6 2 x  2x 1 x  2 4 10
pt x  2x  5 2 
x x 1 6 2
x  2x 1  0 2 x  2 4 x  2 3 x  3 2 4 x x  2 2 x  3 2   x  0 2 x  2 2
x x 1  6 2 x  2x 1
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3 
Thí dụ 82 Giải phƣơng trình 12 2
x  4x 1  6 2
x  2x 1  2 2 x  2x 1 2
x x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
biểu thức liên hợp nữa cần tìm là | 2 2
x  2x 1|  12 2 x  4x  1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x 1 6 2 x  2x 1 2
pt x x 1 6 2
x  2x 1  2 2
x  2x 1  12 2
x  4x 1  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3  45
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 83 Giải phƣơng trình 2 2 x x  1 2 2x x  1  2  2 2 2 6x  2x  1 x x  2  2 2 (x  )( 1 x x  ) 1 2 ( 2 x  ) 1 2x x  1 2  xx 2 2 6x  2x  1 x x  2 2
x x  1  2 6 2 x  2x 1 2 2
x  2x  4  2 2 2 x x  1 Hay  (x  )( 1 2 x x  ) 1 2  x 6 2 x  2x 1 4 3 x x  2 2 x  ( 2 x  ) 1 2 2 x x 1 Hƣớng dẫn.
Giải phƣơng trình đã cho ta không cần nhẩm nghiệm, mà biến đổi về PT tích rồi nhân liên hợp.
Các bạn đọc phần ghép 2 phƣơng trình thành 1 phƣơng trình viết ở phần tìm biểu thức
liên hợp dùng Casio sẽ biết hƣớng làm cụ thể.
Dạng PT thí dụ này nhƣ sau : a c c aa c  ( m n)( p q)  ( m n)( p q)   
mq np b d d bb d
Ý tƣởng :PT ở thí dụ 73 đƣợc tạo ra từ
Thí dụ 1 Giải phƣơng trình 6 2
x  2x 1  2 2 2
x x 1  2 2 x  2x  3
Biểu thức liên hợp là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa là 2
x x  2  2 2 2
x x 1 Và chọn 2 m  ; 1 n  ; 2 p x  ; 1 q x
PTcó 5 nghiệm (đã kiểm tra) x  ; 0 x  ; 1 x   ; 3 x  1 3
Thí dụ 84 Giải phƣơng trình
2 2x2  3x  2 ( 2 x  ) 1 2x2  3x   2 9  x x2  x  2 x2  x   2 x2  x  3 (x  )( 1 x2  x   ) 3 9  x
10x2  14x  13
10x2  14x  13 46
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 9 2
x  9x 18  2 2 2 x  3x  2 3 2
x x  2x  ( 2 x  ) 1 2 2 x  3x  2 Hay  2
x x  3  9 10 2 x 14x 13 (x  )( 1 2 x x  ) 3  x 10 2 x 14x 13 Hƣớng dẫn.
PT thí dụ 74 được tạo ra từ PT: 2 2 2
x  3x  2  10 2
x 14x 13  2 2 x  2x  5
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2 
Biểu thức liên hợp cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2
x x  3  10 2 x 14x 13 Chọn m  ; 1 n  ; 9 p x  ; 1 q x  9
PTcó 4 nghiệm(đã kiểm tra) x   ; 1 x   ; 2 x  8
Thí dụ 85 Giải phƣơng trình 6 2 x  2x  1 3 x 6 2 x  2x  1  2  5 2 x x  1 2 x x  1  2 x x  2 5 4 x x  2 3  x 2  5 2 2 2 x x  1 2 2 2 x x  1 2 2
x  2x  2  6 2 x  2x 1 5 2 x  5x  5 3  x . 6 2 x  2x 1 Hay  2
x x  2  4 2 2 x x 1 5 4 x x  2 3 x 10 2 2 x x 1 Hƣớng dẫn.
Giải phƣơng trình đã cho nhìn phức tạp ta không cần nhẩm nghiệm, mà cần biết nó có a c c aa c
dạng ( m n)( p q)  ( m n)( p q)   
mq np b d d bb d
Nhƣ vậy ta cần biến đổi về PT tích rồi nhân liên hợp (nếu cần) bằng cách a c a c a b d    c 0  11  0    0 b d b d b d Từ PT 6 2
x  2x 1  2 2 2
x x 1  2 2 x  2x  3 47
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1 c  1 a  1   Do ; 1 ; 0 3
là nghiệm PT nên ta có hệ a b c  3  b 1  
9a  3a c  7 c  1
Biểu thức liên hợp cần tìm là 2
x x 1 6 2 x x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  2  2 2 2 x x 1 2
PT x x 1 6 2 x  2x 1 2
x x  2  2 2 2
x x 1  0 PT đã cho có 4 5
nghiệm(đã kiểm tra) 3 x  ; 0 x  ; 1 x   ; 3 x  2
Thí dụ 86 Giải phƣơng trình 2 2
x  2x  2  6 2 x  2x 1 2
x x  2  4 2 2 x x  1  3 2
x x x  3 6 2 x  2x 1 3 2
x  3x  6  2x 2 2 x x  1 Hƣớng dẫn.
Từ Thí dụ 1 Giải phƣơng trình 6 2
x  2x 1  2 2 2
x x 1  2 2 x  2x  3
Biểu thức liên hợp là 2
x x 1 6 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa là 2
x x  2  2 2 2
x x 1
Và chọn m  ; 1 n  ; 2 p  ; 3 q x
PTcó 4 nghiệm(đã kiểm tra) x  ; 0 x  ; 1 x   ; 3 x  6
Thí dụ 87 Giải phƣơng trình (x  ) 2 2 x  2 ( 2 ) 2
5x 12x  8   2x  2 1 2  x  2 Hƣớng dẫn. 48
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT  5 2
x 12x  8  (x  ) 2 2 ( 2 x  3  ) 1  2x  2
Ta nhẩm đƣợc 2 nghiệm đẹp của PT là x  , 1 x   ; 1 x  2
Các biểu thức cần tìm là 2
x  2x  2  5 2
x 12x  8 ứng với nghiệm của PT là x  , 1 x   ; 1 x  2 và 2     x x   x 2x 2
3 2x ứng với nghiệm của PT là , 1 1
Nghiệm của PT đã cho là x  , 1 x  1 
Thí dụ 88 Giải phƣơng trình
3x2  5x  10 6x2   2 4x 8
 3 x  3x  6  2    x 4x 5x 10 x Hƣớng dẫn.
( 4x2  5x  10  x )( 4x2  5x  6  x ) 6x2   2 4x 8 pt
 3 x  3x  6  2    x 4x 5x 10 xx 4 2
x  5x 10  3 2 x
x  3x  6  5 2 x  4x  ( 8 *)  4 4 x  5 3 x 10 2 x  3 4 x  3 3 x  6 2 x  5 2 x  4x  8
Ta nhẩm đƣợc các nghiệm đẹp của PT(*) là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  5x 10x và 2 4 3 2
x x  2  x  3x  6x
PTcó 3 nghiệm x  1 ; x  2 
Thí dụ 89 Giải phƣơng trình
3x2  5x  10 6x2   2 4x 8
 3 x  3x  6  2    x 4x 5x 10 x Hƣớng dẫn. Do 4 2 x  5x 10 2
x x  3 2
x  5x 10  x x x  0
Nên VT  0 mà 6 2
x  4x  8  0 nên x  0 49
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT  4 4 x  5 3 x 10 2 x  3 4 x  3 3 x  6 2 x  5 2 x  4x  8
Ta nhẩm đƣợc các nghiệm đẹp (kể cả nghiệm âm ) của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  5x 10x và 2 4 3 2
x x  2  x  3x  6x
PTcó 2 nghiệm x  1 ; x  2
Thí dụ 90 Giải phƣơng trình
7x2  9x  18 7x2   2 3x 6
 2 9x  7x 14  2    x 16x 9x 18 3 x Hƣớng dẫn.
( 16x2  9x  18  3 x )( 16x2  9x  18  3 x ) 7x2   2 3x 6 pt
 2 9x  7x 14  2    x 16x 9x 18 3 x  16 4 x  9 3 x 18 2 x  2 9 4 x  7 3 x 14 2 x  10 2 x  3x  6
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
4x x  2  16x  9x 18x và 2 4 3 2
3x x  2  9x  7x 14x
PTcó 3 nghiệm x  1 ; x  2 
Thí dụ 91 Giải phƣơng trình
7x2  9x  18 7x2   2 3x 6
 2 9x  7x 14  2    x 16x 9x 18 3 x Hƣớng dẫn.
( 16x2  9x  18  3 x )( 16x2  9x  18  3 x ) 7x2   2 3x 6 pt
 2 9x  7x 14  2    x 16x 9x 18 3 x  16 4 x  9 3 x 18 2 x  2 9 4 x  7 3 x 14 2 x  10 2 x  3x  6 50
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
4x x  2  16x  9x 18x và 2 4 3 2
3x x  2  9x  7x 14x
PTcó 3 nghiệm x  1 ; x  2 
Thí dụ 92 Giải phƣơng trình 7x2  9x 18 7x2   2 3x 6
 2 9x  7x 14  2    x 16x 9x 18 3x Hƣớng dẫn.
Tƣơng tự các ví dụ trên ta thấy x  0
( 16x2  9x  18  3x)( 16x2  9x  18  3 x ) 7x2   2 3x 6 pt
 2 9x  7x 14  2    x 16x 9x 18 3x  16 4 x  9 3 x 18 2 x  2 9 4 x  7 3 x 14 2 x  10 2 x  3x  6
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 2 
Biểu thức cần tìm là 2 4 3 2
4x x  2  16x  9x 18x và 2 4 3 2
3x x  2  9x  7x 14x
PTcó 3 nghiệm x  1 ; x  2 
Thí dụ 93 Giải phƣơng trình 5 2
x 10x  9  2 3 2
x  6x  4  3 2 x  6x  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 2 ; 1 ; 0
Biểu thức liên hợp cần tìm là 2
x  2x  3  5 2 x 10x  9
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  2  3 2 x  6x  4 5 2
x 10x  9  ( 2 x  2x  ) 3  [ 2 3 2
x  6x  4  ( 2 x  2x  )] 2  0 51
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 3 nghiệm x  ; 0 x  ; 1 x  2 Nâng cấp: 2 x  2x
a )Giải phƣơng trình  2 3 2
x  6x  4  3 2
x  4x  4 5 2
x 10x  9  2x  3
 5 2x 10x9 2x 3 5 2x 10x9 2x 3 pt   2 3 2
x  6x  4  3 2 x  4x  4 5 2
x 10x  9  2x  3
PTcó 3 nghiệm x  ; 0 x  ; 1 x  2 1 1 2x  5
b )Giải phƣơng trình   2 x  5x  6
5x 10 x  9  2 x
3x  6 x  4  2 x
PTcó 3 nghiệm x  ; 0 x  ; 1 x  4 5 2 x 10x  9 2 x  2x  2
c)Giải phƣơng trình 2 x  2x  3 2 x x  3 6 4 PT  3 2
x  6x  4 5 2 x 10x  9 2
x  2x   3   3 2 x  6x  4 2
x  2x  2( 2 x x  ) 3  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  2 x  2 2 7( ) 1 2
d )2 3x  6x  4  5x  10x  9  3 2 x  6x  7 Hƣớng dẫn. PT  2 3 2
x  6x  4  5 2 x 10x  9 (2 3 2
x  6x  4  5 2
x 10x  4)(2 3 2
x  6x  4  5 2 x 10x  9)  3 2 x  6x  7 2 3 2
x  6x  4  5 2
x 10x  9  PT   0 2 3 2
x  6x  4  5 2
x 10x  9  3 2
x  6x  7(*)
Giải (*):Biểu thức liên hợp cần tìm là 2
x  2x  3  5 2 x 10x  9
biểu thức liên hợp nữa cần tìm là 2
x  2x  2  3 2 x  6x  4
PT đã cho có 3 nghiệm x  ; 0 x  ; 1 x  2 52
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 94 Giải phƣơng trình 5 2
x 12x  8  2 7 2
x 16x  3  3 2 x  6x  8 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  2 ; 1 ; 1
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x 12x  8
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 16x 13
PT đã cho có 3 nghiệm x   ; 1 x  ; 1 x  2
Nâng cấp: Giải phƣơng trình 5 2
x 12x  8 1  7 2
x 16x 13  2x  3  2x  ( 1 *) Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x  ; 1 x  2
Biểu thức liên hợp cần tìm là 5 2
x 12x  8 1  (x  ) 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 7 2
x 16x 13  4x  2  (x  ) 1 1
Do VT (*)  0 suy ra VP(*)  2x 1  0  x  2 1 Xétx  1 có: 7 2 x 16x  3 1  4x  2  4 2 x  3 2
x 16x 13  4x  2 2  1 4 2 x  (x  3 )( 1 x  ) 13  4x  2  4 2
x  4x  2  6x  2  . 6  2  1 2
suy ra VT (*)  1 1 Dox VPx   1suy ra (*) 2 1 1 2
Vì vậy PT(*) có nghiệm x  1 Khi đó 5 2
x 12x  8 1  (x  ) 1  0 53
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 7 2
x 16x 13  4x  2  (x  ) 1  0 5 2
x 12x  8  ( 2 x  2x  ) 2 7 2
x  8x 13  ( 2 x  2x  ) 3 PT (*)    0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 1 x  2
Thí dụ 95 Giải phƣơng trình 3 6 2
x  6x  4  8 2
x  8x  9  4 2 x  4x  9 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 0  ; 1 ; 1 2 
Biểu thức liên hợp cần tìm là 2
x x  2  6 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x x  3  8 2 x  8x  9
PT đã cho có 4 nghiệm x   ; 1 x  ; 1 x   ; 2 x  0
Nâng cấp: Giải phƣơng trình 6 2
x  6x  4  3x  2  3 8 2
x  8x  9  3x 1  4x  ( 8 *) Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x   ; 1 x   ; 2 x  0
Biểu thức liên hợp cần tìm là 6 2
x  6x  4  3x  2  (x  ) 2
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 8 2
x  8x  9  3x 1  (x  ) 2
Do VT (*)  0 suy ra VP(*)  4x  8  0  x  2  Khi đó 6 2
x  6x  4  3x  2  (x  ) 2  0 6 2
x  6x  4  3x  2  (x  ) 2  0 54
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 6 2
x  6x  4  ( 2 x x  ) 2 8 2
x  8x  4  ( 2 x x  ) 3 PT (*)   . 3  0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 4 nghiệm x   ; 1 x   ; 2 x  0
Thí dụ 96 Giải phƣơng trình(Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn) 2 2 2 x  4x  3 1  1 2 x  2x  2 6 2 x 12x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  6 2
x 12x  7 và 2
x  2x  3  2 2 2 x  4x  3 Ta có: 2 2 2 x  4x  3 1   1 2 x  2x  2 6 2 x  12x  7  6 2
x 12x  7 2 2 2 x  4x  3 2
x  2x  2 2
x  2x  2  6 2
x 12x  72 2 2 x  4x  3 2
x  2x   3  6 2
x 12x  7  ( 2 x  2x  ) 2  0
Nhân liên hợp PT đã cho có 3 nghiệm x   ; 1 x  3 
Thí dụ 97 Giải phƣơng trình 2 x x  5 2
x 10x  9  x  2 2 4 4 1  3 2 x  6x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  3 2
x  6x  4 và 2
x  2x  3  5 2 x 10x  9 Ta có: 55
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 x x  5 2
x 10x  9  x  2 2 4 4 1  3 2 x  6x  4  3 2
x  6x  4 5 2 x 10x  9 2
x  2x   1  2 2
x  4x  4  3 2
x  6x  4 5 2 x 10x  9 2
x  2x   3  ( 2 6 2 x 12x  7 2
x  2x  ) 2  0
Nhân liên hợp suy ra PT đã cho có 3 nghiệm x  ; 0 x  ; 1 x  2
Thí dụ 98 Giải phƣơng trình(Vũ Hồng Phong ) 2 3 2 x  4x  5 1  1 2 x x  2 2 2 x  3x  2 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  2 2 2
x  3x  2 và 2
x x  4  2 3 2 x  4x  5 Ta có: 2 3 2 x  4x  5 1   1 2 x x  2 2 2 x  3x  2  2 2
x  3x  22 3 2 x  4x  5 2
x x  2 2
x x  2  2 2
x  3x  22 3 2 x  4x  5 2
x x  4 2 2 2
x  3x  5  ( 2 x x  ) 2  0
Nhân liên hợp PT suy ra PT đã cho có 3 nghiệm x   ; 2 x  1
Thí dụ 99 Giải phƣơng trình 2 x x x  2 ( 2 ) 1
11x 14x  9  x  3  7 2 x 10x 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  3  11 2
x 14x  9 và 2
x x 1 7 2 x 10x 1 Ta có: 56
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 x x x  2 ( 2 ) 1
11x 14x  9  x  3  7 2 x 10x 1  7 2 x 10x   1 11 2
x 14x  9  x   3 2  x ( 2 x x  ) 1  7 2 x 10x   1 11 2 x 14x  9 2
x x   3 2  x [ 7 2
x 10x 1  ( 2 x x  )] 1  0
Nhân liên hợp suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 2 x  2
Thí dụ 100 Giải phƣơng trình 1 1 1   2 2 2        1 x 13x 8x 4 x 1 17x 10 9  x x Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x  2  13 2
x  8x  4 và 2 2
x x  3  17 2 x 10x  9 Ta có: 1 1 1   2 2 2        1 x 13x 8x 4 x 1 17x 10 9  x x 1 1 1 1      0 x x   2  2 2 2 2 x x x   x   2  2 2 13 8 4 1 17 10 9 x x
Nhân liên hợp 2 lần ở từng phân thức suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 1 x  1
Chú ý:Biểu thức x  13 2
x  8x  4  0 và x 1 17 2
x 10x  9  0
Thí dụ 101 Giải phƣơng trình 1 1 3   2 x x   x x  2 2 2 x  2x  2 2 2 3 2 1 2 6 10 5 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  2 2 2
x  3x  2 và 2
x x 1 6 2 x 10x  5 57
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Ta có: 1 1 3   2 x x   x x  2 2 2 x  2x  2 2 2 3 2 1 2 6 10 5 1 1 1 1      0 2 2 x x   x x 1 x x  2 2 2 x  2x  2 2 2 3 2 1 2 6 10 5
Nhân liên hợp 2 lần ở từng phân thức suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 2 x  2
Chú ý:Biểu thức 2 2 2
x  3x  2 1  0 và 6 2
x 10x  5  0
Thí dụ 102 Giải phƣơng trình 11 2
x 16x  9  1 ( 2  x ) 2
x  4x  9  2 2
x  2x  6 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  3  11 2
x 16x  9 và 3 2
x  4x  9 Ta có: 11 2
x 16x  9  1 ( 2  x ) 2
x  4x  9  2 2
x  2x  6  11 2
x 16x  9  ( 2 x  2x  ) 3  1 ( 2  x )( 2
x  4x  9  ) 3  0
Nhân liên hợp suy ra PT đã cho có 4 nghiệm x  ; 0 x   ; 1 x  ; 1 x  4 Nâng cấp
a) Giải phƣơng trình 2 x  2x  3 13 2
x  20x  16 1  2 2 x x x  2x  3 11 16 9 Hƣớng dẫn. 2 x  2x  3 13 2
x  20x  16 1  2 2 x x x  2x  3 11 16 9 2 x  2x  3 13 2
x  20x 16 1  11  0 2 2 x x x  2x  3 11 16 9 58
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2
x  2x  3  11 2 x 16x  9 2
x  2x  4  13 2 x  20x 16    0 2 2 x x x  2x  3 11 16 9
Nhân liên hợp suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 1 x  ; 1 x  4
b) Giải phƣơng trình  2
11x 16x  9  2x 2
13x  20x 16  2x   2 2 1  (x  ) 3 Hƣớng dẫn. 2 x  3 13 2
x  20x 16  2x 1 pt   2 2 x x   x  3 11 16 9 2x 2 x  3 13 2
x  20x 16  2x 1  11  0 2 2 x x   x  3 11 16 9 2x 2
x  2x  3  11 2 x 16x  9 2
x  2x  4  13 2 x  20x 16    0 2 2 x x   x  3 11 16 9 2x
Nhân liên hợp suy ra PT đã cho có 4 nghiệm x  ; 0 x   ; 1 x  ; 1 x  4 Chú ý: 11 2 16  9  2  , 0 
13 2  20 16  2 1  , 0  x x x x x x x x
Nên ta có thể đƣa về giải bất phƣơng trình chẳng hạn
Giải bất phƣơng trình  2
11x 16x  9  2x 2
13x  20x 16  2x   2 2 1  (x  ) 3
Thí dụ 103 Giải phƣơng trình 1 1 2   2 2 2 x x   x x   x x  2 7 10 1 1 11 14 9 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  3  11 2
x 14x  9 và 2
x x 1 7 2 x 10x 1 Ta có: 59
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 1 2   2 2 2 x x   x x   x x  2 7 10 1 1 11 14 9 1 1 1 1 1     0 2 2 x x   x x  2 2 2 x x   x x  2 7 10 1 1 11 14 9 1
Nhân liên hợp suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 2 x  2
Chú ý:Biểu thức 11 2
x 14x  9 1  0
Nâng cấp Giải phƣơng trình 2 x x  3 7 2 x 10x  1  2 2 x x x x  1 11 14 9 Hƣớng dẫn. 2 x x  3 7 2 x 10x  1 pt  11  0 2 2 x x x x  1 11 14 9 2
x x  3  11 2 x 14x  9 2
x x 1  7 2 x 10x 1    0 2 2 x x x x 1 11 14 9
Nhân liên hợp suy ra PT đã cho có 3 nghiệm x  ; 0 x   ; 2 x  2
B.Các Phƣơng trình tìm nhân tử không dùng Casio
Thí dụ 1 Giải phƣơng trình 6 2 2
x  2x 1  12 2
x  4x 1  4 2 x  4x  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 1 x  3 
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau  6 2 2
x  2x 1  12 2
x  4x 1  4 2 x  4x  ( 5 *)
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là x  0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  2 2
x  2x 1 60
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Do x  ; 1 x  3
là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm
a b c  1 ta có hệ
9a  3b c  5
Do cách đổi dấu tìm nghiệm ngoại lai x=0 nên x=0 là nghiệm biểu thức 2
ax bx c  2 2
x  2x 1 suy ra c  1 
Từ đó ta có a  ; 1 b  ; 1 c  1 
Biểu thức cần tìm là 2
x x 1 2 2 x  2x 1
Tƣơng tự,biểu thức nữa cần tìm là 2 2
x  2x 1 12 2 x  4x 1
Cho 2 biểu thức bằng 0 suy ra 2 2 2
x  2x 1  12 2
x  4x 1 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 2 2 1 12 4 1 1 Đặt 2 2
x  2x 1  a  0 ; 12 2
x  4x 1  b  0 Tacó 4 2 2 a b  4 2
x  4x  ( 3 *)
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0  2 2 2
x  2x 1  12 2
x  4x 1 1  ( 0 **)
Cách 1. Từ (*) và (**) suy ra 2 2 x  2x 1 2
x x 1 và 12 2
x  4x 1  2 2
x  2x 1
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm x  ; 1 x  3 
!!*Giải phƣơng trình(nâng cấp thí dụ 1) Tác giả: Vũ Hồng Phong ( 2 x  ) 1 2 2
x  2x 1  2 2
x  3x  (x  ) 2 12 2 x  4x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  ; 1 x  3 
Nếu coi cả 3 nghiệm là nghiệm của biểu thức thì 61
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 2 1
Biểu thức cần tìm là x x 1  2 2 x  2x 1 3 3 4 2 2
biểu thức nữa cần tìm là x x 1  12 2
x  4x 1 3 3
Đến đây có lẽ ta không phát hiện đƣợc mối liên nào đặc biệt !
Có vẻ cần coi ít nhất một nghiệm nào đó trong 3 nghiệm là nghiệm ngoại lai của biểu thức
cần tìm. Do ở thí dụ 1 ta đã biết x=0 là nghiệm ngoại lai của biểu thức cần tìm thì sẽ có mối
liên hệ đặc biệt!!
Nhƣ vậy biểu thức cần tìm là 2
x x 1 2 2 x  2x 1
Tƣơng tự,biểu thức nữa cần tìm là 2 2
x  2x 1 12 2 x  4x 1
Cho 2 biểu thức bằng 0 suy ra 2 2 2
x  2x 1  12 2
x  4x 1 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 2 2 1 12 4 1 1 Đặt 2 2
x  2x 1  a  0 ; 12 2
x  4x 1  b  0 Tacó 4 2 2 a b  4 2
x  4x  ( 3 *)
Thay vào PT đƣợc (2a b  )(
1 2a b  2x  ) 3  0
+Với 2a b 1  0  2 2 2
x  2x 1  12 2
x  4x 1 1  ( 0 **)
Từ (*) và (**) suy ra 2 2 x  2x 1 2
x x 1 và 12 2
x  4x 1  2 2
x  2x 1
PTcó 2 nghiệm x  ; 1 x  3 
+Với 2a b  3  2x  0  2 2x2  2x 1  12x2  4x 1  3  2x
Giải tƣơng tự PTcó thêm nghiệm x  0 và x  1
Nghiệm của PT đã cho là x  ; 0 x  ; 1 x  3 
Thí dụ 2 Giải phƣơng trình 2 2
x  4x 1  3 8x 1  4 2 x  8x 1 Hƣớng dẫn. 62
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  1
Đặc biệt dùng đạo hàm thấy x  0 là nghiệm kép
(lƣu ý có thể tìm nghiệm ngoại lai x  3 )
Giả sử biểu thức liên hợp cần tìm là 2 2
ax bx c   x  4x 1  x  2
Lấy đạo hàm đƣợc 2ax b 2
x  4x 1 Do x  ;
0 x  1là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm c  1 ta có hệ
a b c  2
Do x=0 là nghiệm kép của biểu thức 2 2
ax bx c   x  4x 1 suy ra 2a 0 .  b  2
Từ đó ta có a   ; 1 b  ; 2 c  1
Biểu thức cần tìm là 2
x  2x 1 2
  x  4x 1
Tƣơng tự,biểu thức nữa cần tìm là  2 2
x  4x 11 8x 1
Cho 2 biểu thức bằng 0 suy ra 2 2
x  4x 1  8x 1 1  0
suy ra nhân tử cần xuất hiện là:
x x   x   2 2 4 1 8 1 1 Đặt 2
x  4x 1  a  0 ; 8x 1  b  0 Tacó 4 2 2 a b  4 2
x  8x  ( 3 *)
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0  2 2
x  4x 1  8x 1 1  ( 0 **)
Cách 1. Từ (*) và (**) suy ra 2
x  4x 1 2
 x  2x 1 và 8x 1  2 2
x  4x 1
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 3 Giải phƣơng trình(nâng cấp của thí dụ 3) 63
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) (2 2 x  ) 2 2
x  4x 1  ( 2 x  ) 3 8x 1  5 2 x  8x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  1
Đặc biệt dùng đạo hàm thấy x  0 là nghiệm kép(hoặc nghiệm ngoại lai x  3 )
Biểu thức cần tìm là 2
x  2x 1 2
  x  4x 1
Tƣơng tự,biểu thức nữa cần tìm là  2 2
x  4x 11 8x 1
Cho 2 biểu thức bằng 0 suy ra 2 2
x  4x 1  8x 1 1  0
suy ra nhân tử cần xuất hiện là:
x x   x   2 2 4 1 8 1 1 Đặt 2
x  4x 1  a  0 ; 8x 1  b  0 Tacó 4 2 2 a b  4 2
x  8x  ( 3 *)
Thay vào PT đƣợc (2a b  )( 1 2 2
a b x  ) 2  0  2 2
x  4x 1  8x 1 1  ( 0 **)
Cách 1. Từ (*) và (**) suy ra 2
x  4x 1 2
 x  2x 1 và 8x 1  2 2
x  4x 1
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 4 Giải phƣơng trình (x  ) 1 2
x  7x 1  3 4 x 16 3 x  8x  7 3 x 16 2 x x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  1
Đặc biệt dùng đạo hàm thấy x  1 là nghiệm kép(bội)
Biểu thức cần tìm là 2
x  4x 1 (x  ) 1 2 x  7x 1
Tƣơng tự,biểu thức nữa cần tìm là x2  4x x4 16x3  8x 64
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Cho 2 biểu thức bằng 0 suy ra (x  ) 1 2 x  7x 1 4  x 16 3
x  8x 1  0
suy ra nhân tử cần xuất hiện là: 2 4 3 x
x x   x x x  ( ) 1 7 1 16 8 1 Đặt (x  ) 1 2
x  7x 1  a  0 ; 4 x 16 3
x  8x b  0 Tacó 2 2 a b  7 3  x 16 2 x x  ( 1 *)
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0  (x  ) 1 2 x  7x 1 4  x 16 3
x  8x 1  ( 0 **)
Từ (*) và (**) suy ra 2
x  4x 1 2
 x  2x 1 và 8x 1  2 2
x  4x 1
PTcó 2 nghiệm x  ; 0 x  1
Thí dụ 5 Giải phƣơng trình 7 2
x 12x  9  3 5 2
x  8x  4  2 2
x  4x  3  0 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  ; 1 x  3
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  7 2
x 12x  9 Do x  ; 0 x  ;
1 x  3 là nghiệm PT nên cũng là nghiệm của biểu thức cần tìm c  3 
ta có hệ a b c  2
9a  3b c  6
Từ đó ta có a  ; 1 b   ; 2 c  3
Biểu thức cần tìm là 2
x  2x  3  7 2 x 12x  9
Tƣơng tự,biểu thức nữa cần tìm là 2
x  2x  2  5 2 x  8x  4
Cho 2 biểu thức bằng 0 suy ra 7 2
x 12x  9  5 2
x  8x  4 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    7 12 9 5 8 4 1 0 65
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Đặt 7 2
x 12x  9  a  0 ; 5 2
x  8x  4  b  0 Tacó 2 2 a b  2 2 x  4x  ( 3 *)
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0  7 2
x 12x  9  5 2
x  8x  4 1  ( 0 **)
Cách 1. Từ (*) và (**) suy ra 7 2 x 12x  9 2
x  2x  3 và 5 2 x  8x  4 2
x  2x  2
Cách 2. Chuyển vế và bình phƣơng PT(**)
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 6 Giải phƣơng trình ( 2 x  ) 1 4x 1  16 3 x  24 2 x 1  4 2 x  8x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  1 
Đặc biệt dùng đạo hàm thấy x  1
là nghiệm kép(bội). Hƣớng khác:
( tìm nghiệm ngoại lai x=2 là nghiệm PT: ( 2 x  ) 1 4x 1  16 3 x  24 2 x 1  4 2
x  8x 1)
Biểu thức cần tìm là 2
x  2x 1 (x  ) 1 4x 1
Tƣơng tự,biểu thức nữa cần tìm là  2 2
x  4x 1 16 3 x  24 2 x 1
Cho 2 biểu thức bằng 0 suy ra ( 2 x  ) 1 4x 1  16 3 x  24 2 x 1  3  0
suy ra nhân tử cần xuất hiện là: 3 2 x x   x x   ( 2 ) 1 4 1 16 24 1 3 Đặt (x  ) 1
4x 1  a  0 ; 16 3 x  24 2
x 1  b  0 Tacó 4 2 2 a b  12 2 x  24x  ( 3 *)
Thay vào PT đƣợc (2a b  )( 3 2a  ) b  0
Với 2a b  3  0  ( 2 x  ) 1 4x 1  16 3 x  24 2 x 1  3  ( 0 **) 66
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Từ (*) và (**) suy ra (x  ) 1 4x 1 2
x  2x 1 và 16 3 x  24 2 x 1  2 2
x  4x 1
PT(**) có 2 nghiệm x  ; 0 x  1    3 2 2 3
Với 2a b  0  ( 2 x  ) 1
4x 1  16x  24x 1  x  2  2  3
PT đã cho có 3 là x  ; 0 x  1  ; x 2
Thí dụ 7 Giải phƣơng trình 2 6 2
x  2x 1   4 2
x  20x  25  4 2 x  4x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 0 x  1 
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau 2 6 2
x  2x 1   4 2
x  20x  25  4 2 x  4x  ( 3 *)
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là x  3
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  6 2
x  2x 1
Vì cách đổi dấu trƣớc căn nên x  ; 0 x   ;
1 x  3 là nghiệm PT của biểu thức cần tìm c  1 a  1  
ta có hệ a b c  3  b  1  
9a  3b c  7 c  1
Biểu thức cần tìm là 2
x x 1 6 2
x  2x 1 (1) Xét 2
ax bx c   4 2
x  20x  25
Do cách đổi dấu tìm nghiệm ngoại lai x=3 nên x=3 là nghiệm biểu thức 2
ax bx c   4 2
x  20x  25 67
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) c  5 a  2  
Từ đó ta có a b c  1  b  2  
9a  3b c  7 c  5
biểu thức nữa cần tìm là  2 2
x  2x  5   4 2
x  20x  25 (2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra 2 6 2
x  2x 1   4 2
x  20x  25  7  0
suy ra nhân tử cần xuất hiện là: 2 2
x x    x x   2 6 2 1 4 20 25 7 Đặt 6 2
x  2x 1  a  0 ;  4 2
x  20x  25  b  0 Tacó 4 2 2 a b  28 2
x  28x  21
Thay vào PT đƣợc (2a b  )( 7 2a  ) b  0 1 3
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm x  ; 0 x   ; 1 x  ; x  2 2
Thí dụ 8 Giải phƣơng trình 2 5 2
x 12x  8  17  8x  4 2 x  8x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 1 x  2
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau 2 5 2
x 12x  8  17  8x  4 2 x  8x  ( 3 *)
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là x  1 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x 12x  8
Vì cách đổi dấu trƣớc căn nên x  ; 1 x  ; 2 x  1
là nghiệm PT của biểu thức cần tìm
a b c  1 a  1  
ta có hệ 4a  2b c  2  b  2  
a b c  5 c  2
Biểu thức cần tìm là 2
x  2x  2  5 2
x 12x  8 (1) 68
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Xét ax2  bx c  17  8x
Do cách đổi dấu tìm nghiệm ngoại lai x=-1 nên x=-1 là
nghiệm biểu thức ax2  bx c  17  8x
Từ đó ta có biểu thức nữa cần tìm là  2x2  4x 1 17  8x (2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra 2 5 2
x 12x  8  17  8x  5  0
suy ra nhân tử cần xuất hiện là: 2 x x    x  2 5 12 8 17 8 5 Đặt 5 2
x 12x  8  a  0 ; 17  8x b  0 Tacó 4 2 2 a b  20 2
x  40x 15
Thay vào PT đƣợc (2a b  )( 5 2a  ) b  0 1 3
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm x  ; 1 x  ; 2 x  ; x  2 2
Thí dụ 9 Giải phƣơng trình 5 2
x 12x  8  5 2  x  2 2 x  4x 1 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT đã cho là x  ; 1 x  2
Có vẻ cần tìm thêm nghiệm ngoại lai. Ta xét PT sau 5 2
x 12x  8  5 2  x  2 2 x  4x 1
Ta nhẩm đƣợc nghiệm đẹp của PT(*) là x  1 
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x 12x  8
Vì cách đổi dấu trƣớc căn nên x  ; 1 x  ; 2 x  1
là nghiệm PT của biểu thức cần tìm
a b c  1 a  1  
ta có hệ 4a  2b c  2  b  2  
a b c  5 c  2 69
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x  2x  2  5 2
x 12x  8 (1) Xét 2 2
ax bx c  5  x
Do cách đổi dấu tìm nghiệm ngoại lai x=-1 nên x=-1 là nghiệm biểu thức 2 2
ax bx c  5  x
Từ đó ta có biểu thức nữa cần tìm là 2 2
x  2x 1 5  x (2)
Cho 2 biểu thức (1),(2)bằng 0 suy ra 5 2
x 12x  8  5 2  x  3  0
suy ra nhân tử cần xuất hiện là: 2 2 x x    x   5 12 8 5 3 0 Đặt 5 2
x 12x  8  a  0 ; 17  8x b  0 Tacó 2 2 a b  6 2
x 12x  3
Thay vào PT đƣợc (a b  )( 3 a  ) b  0 1 1
Giải 2 trƣờng hợp suy PT đã cho có 4 nghiệm x  ; 1 x  ; 2 x  1  ; x  1  2 2
Thí dụ 10 Giải phƣơng trình 3 5 2
x  4x  3 37 2
x  24x 12  8 2 x 12x 10 Hƣớng dẫn.
Ta nhẩm đƣợc 3 nghiệm đẹp của PT là x   ; 1 x  4 
Các biểu thức cần tìm là 2x2  3x  4  3 5x2  4x và 2 2
x  3x  2  37 2
x  24x 12
Cho 2 biểu thức bằng 0 suy ra 3 5 2
x  4x  37 2
x  24x 12  2  0
suy ra nhân tử cần xuất hiện là: 2 2 x x x x   3 5 4 37 24 12 2 Đặt 3 5 2
x  4x a  0 ; 37 2
x  24x 12  b  0 Tacó 2 2 a b  8 2 x 12x  ( 10 *)
Thay vào PT đƣợc (a b  )( 2 a b  ) 1  0 70
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) suy ra 3 5 2
x  4x  37 2
x  24x 12  2  ( 0 **)
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
Nghiệm của PT là x   ; 1 x  4 
Thí dụ 11 Giải phƣơng trình 6 2
x  2x 1  42 2
x  6x 1  4 2 x  4x  2 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 1 ; 0 3 
Các biểu thức cần tìm là 6 2
x  2x 1  ( 2 x x  ) 1 và 42 2
x  6x 1  3 ( 2 x  3x  ) 1
Cho 2 biểu thức bằng 0 suy ra 3 6 2
x  2x 1  42 2
x  6x 1  2  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   3 6 2 1 42 6 1 2 Đặt 6 2
x  2x 1  a  0 ; 42 2
x  6x 1  b  0 Tacó 9 2 2 a b  12 2 x 12x  ( 8 *)  9 2 2
a b  2  ( 3 4 2 x  4x  ) 2 Thay vào PT đƣợc 3 ( a b  3 )( 2 a b  ) 1  0 suy ra 3 6 2
x  2x 1  42 2
x  6x 1  2  ( 0 **)
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
Nghiệm của PT là x  ; 0 x   ; 3 x  1
Thí dụ 12 Giải phƣơng trình 2 2 2
x  3x  2  20 2
x  36x 17  3 2 x  3x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là  ; 1 2 
Biểu thức cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2 2
x  2x 1 20 2 x  36x 17 71
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Cho 2 biểu thức bằng 0 suy ra 4 2 2
x  3x  2  20 2
x  36x 17  3  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   4 2 3 2 20 36 17 3 Đặt 2 2 2
x  3x  2  a  0 ; 20 2
x  36x 17  b  0 Tacó 4 2 2 a b  12 2 x 12x  ( 15 *) 4 2 2
a b  3  12 2
x 12x 12
Thay vào PT đƣợc (2a b  )( 3 2a b  ) 1  0 suy ra 4 2 2
x  3x  2  20 2
x  36x 17  3  ( 0 **)
Từ (*),(**) suy ra a,b theo x (chính là kết quả tìm biểu thức ở trên)
PTcó 3 nghiệm x   ; 1 x  2 
Thí dụ 13 Giải phƣơng trình 2 5 2
x  8x  4   24 2
x  56x  49  4 2 x  8x  3 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Biểu thức cần tìm là 2
x  2x  2  5 2 x  8x  4 và  2 2
x  4x  7   24 2
x  56x  49
Cho 2 biểu thức bằng 0 suy ra 2 5 2
x  8x  4   24 2
x  56x  49 11  0
suy ra nhân tử cần xuất hiện là: 2 2 x x    x x   2 5 8 4 24 56 49 11 Đặt 5 2
x  8x  4  a  0 ;  24 2
x  56x  49  b  0 Tacó 4 2 2 a b  ( 11 4 2 x  8x  ) 3 (*)
Thay vào PT đƣợc (2a b  )( 11 2a  ) b  0 7
PTcó 5 nghiệm x  ; 0 x  ; 1 x  ; 3 x  1  2 72
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 14 Giải phƣơng trình 6 5 2
x  8x  4  24 2
x  40x  25  4 2 x  8x  7 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Biểu thức cần tìm là 2
x  2x  2  5 2 x  8x  4 và 2 2
x  4x  4  24 2
x  40x  25
Cho 2 biểu thức bằng 0 suy ra 2 5 2
x  8x  4  24 2
x  40x  25 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    2 5 8 4 24 40 25 1 0 Đặt 5 2
x  8x  4  a  0 ; 24 2
x  40x  25  b  0 Tacó 4 2 2 a b  (  4 2 x  8x  ) 9 (*)
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0
PTcó 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 15 Giải phƣơng trình 2 2
x  2x  6  2x 5 2
x  8x  4  (2x  ) 2 7 2 x 12x  9 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 3 ; 1 ; 0
Giả sử biểu thức liên hợp cần tìm là 2
ax bx c  5 2
x  8x  4 c  2 a  1   Do 2 ; 1 ; 0
là nghiệm PT nên ta có hệ a b c  1
 b  2  
9a  3a c  5 c  2
Biểu thức liên hợp cần tìm là 2
x  2x  2  5 2 x  8x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  7 2 x 12x  9 73
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Cho 2 biểu thức bằng 0 suy ra 7 2
x 12x  9  5 2
x  8x  4 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   7 12 9 5 8 4 1 Đặt 7 2
x 12x  9  a  0 ; 5 2
x  8x  4  b  0 Tacó 2 2 a b  2 2 x  4x  ( 5 *)
Thay vào PT đƣợc (a b  )(
1 a b  2x  ) 1  0 TH1: 7 2
x 12x  9  5 2
x  8x  4 1  0
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm x  ; 0 x  ; 1 x  3 TH2: 7 2
x 12x  9  5 2
x  8x  4  2x 1 1 5 73
ta có 2 nghiệm x  ; 1 x  38 
PT đã cho có 4 nghiệ 1 5 73 m x  ; 0 x  ;
1 x  3 ; x  38
Thí dụ 16 Giải phƣơng trình(Tác giả Vũ Hồng Phong Bất Lự,Hoàn Sơn, Tiên Du,Bắc Ninh) 2 2
x  7x 10  3 ( x  ) 6 5 2
x 10x  9  (4  3x) 3 2
x  6x  4  0 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 2 ; 1 ; 0
Biểu thức liên hợp cần tìm là 2
x  2x  3  5 2 x 10x  9
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  2  3 2 x  6x  4
Cho 2 biểu thức bằng 0 suy ra 5 2
x 10x  9  3 2
x  6x  4 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   5 10 9 3 6 4 1 Đặt 5 2
x 10x  9  a  0 ; 3 2
x  6x  4  b  0 Tacó 2 2 a b  2 2 x  4x  ( 5 *) 74
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thay vào PT đƣợc (a b  )(
1 a b  3x  ) 5  0 TH1: 5 2
x 10x  9  3 2
x  6x  4 1  0
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm x  ; 0 x  ; 1 x  2 TH2:
5x2 10x  9  3x2  6x  4  5  3x 47  7 21
ta có 2 nghiệm x  ; 0 x  59 
PT đã cho có 4 nghiệ 47 7 21 m x  ; 0 x  ;
1 x  2 ; x  59
Thí dụ 17 Giải phƣơng trình (2x  )( 1 2x  ) 3  2 3 2
x  6x  4   8 2 x 16x 1 Hƣớng dẫn. 1 Pt
2 3 2x 6x4  8 2x 16x12 3 2x 6x4  8 2x 16x1 5  2 3 2
x  6x  4   8 2 x  16x  1
PT đã cho có 5 nghiệ 1 3 m x  ; 0 x  ;
1 x  2 ; x  ; x  2 2
Thí dụ 18 Giải phƣơng trình(PT này phức tạp chỉ để tham khảo) ( 5 4 2 x  9x  ) 6  (2x  ) 16 3 2
x  4x  4  (x  ) 2  8 2
x 16x 1  0 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là 2 ; 1 ; 0
Biểu thức liên hợp cần tìm là 2
x  2x  2  3 2 x  6x  4
Tƣơng tự,biểu thức liên hợp nữa cần tìm là  2 2
x  4x 1  8 2 x 16x 1
Cho 2 biểu thức bằng 0 suy ra 2 3 2
x  6x  4   8 2
x 16x 1  5  0
suy ra nhân tử cần xuất hiện là: 2 2 x x
  x x   2 3 6 4 8 16 1 5 75
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Đặt 3 2
x  6x  4  a  0 ;  8 2
x 16x 1  b  0 Tacó 4 2 2 a b  20 2 x  40x  ( 15 *)
Thay vào PT đƣợc (2a b  )(
5 2a b x  ) 3  0 TH1: 2 3 2
x  6x  4   8 2
x 16x 1  5  0
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm x  ; 0 x  ; 1 x  2 TH2: 2 3 2
x  6x  4   8 2
x 16x 1  x  3  0   2  71 3  x  ; 0 x  86   16033  6550 6 ta có 2 nghiệm 131  3  16033  6550 6     2  71 3 
PT đã cho có 4 nghiệ ; x  86   16033  6550 6 m x  ; 0 x  ; 1 x  2 131  3  16033  6550 6  
Thí dụ 19 Giải phƣơng trình ( 2 x  ) 2 5 2
x  2x 1  3 (  x) 24 2
x  8x  9  2 2 x x  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là ; 0  2 ; 1
Biểu thức liên hợp cần tìm là 2 x 1 5 2 x  2x 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2 x  3  24 2 x  8x  9
Cho 2 biểu thức bằng 0 suy ra 2 5 2
x  2x 1  24 2
x  8x  9 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 5 2 1 24 8 9 1 Đặt 5 2
x  2x 1  a  0 ; 24 2
x  8x  9  b  0 Tacó 4 2 2 a b  4 2  x  ( 5 *)
Thay vào PT đƣợc (2a b  2 )( 1
a b  2x  ) 5  0 TH1: 2 5 2
x  2x 1  24 2
x  8x  9 1  0 76
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Kết hợp với PT(*) tìm a,b theo x hoặc bình phƣơng ta có 3 nghiệm x  ; 0 x   ; 1 x  2
TH2: 2 5x2  2x 1  24x2  8x  9  5  2x 13  3 41
ta có 2 nghiệm x  ; 0 x  10 
PT đã cho có 4 nghiệ 13 3 41 m x  ; 0 x   ;
1 x  2 ; x  10
Thí dụ 20 Giải phƣơng trình 4 2 2
x  3x  2  6 2
x 10x  5  3 2 x  3x  5 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x   ; 2 x  ; 1 x  2
Biểu thức cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2
x x 1 6 2 x 10x  5
PTcó 3 nghiệm x   ; 2 x  ; 1 x  2 Nâng cấp
1) Giải phƣơng trình 2 2
x  2x 1 2 2 2
x  3x  2  3 6 2
x 10x  5  0 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x   ; 2 x  ; 1 x  2
Biểu thức cần tìm là 2
x x  2  2 2 2 x  3x  2 và 2
x x 1 6 2 x 10x  5
Cho 2 biểu thức bằng 0 suy ra 2 2 2
x  3x  2  6 2
x 10x  5 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 2 3 2 6 10 5 1 Đặt 2 2 2
x  3x  2  a  0 ; 6 2
x 10x  5  b  0 77
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Tacó 2 2 a b  2 2
x  2x  3
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0
PTcó 3 nghiệm x   ; 2 x  ; 1 x  2
2) Giải phƣơng trình x  2 16 16
2x  3x  2  x  4   0 2 x x  6 Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x   ; 2 x  ; 1 x  2
Biểu thức cần tìm là 2
x x  2  2 2 2 x  3x  2
Biểu thức nữa cần tìm(nếu dùng Casio với 2 nghiệm xấu) là x  2  2 2 x  3x  2 x  3 2
x x x  2 16 16 2 5 6 8
2x  3x  2  x  4 
 0  2x  3x  2  2 x x  6 2 x x  6  ( 2 x x  ) 6 2 2 x  3x  2 3  x  5 2 x  6x  8  2 2 2
x  3x  2  ( 2 x x  ) 2  2 2
x  3x  2  x  2 0 7  57
PTcó 5 nghiệm x   ; 2 x  ; 1 x  ; 2 x  2
Muốn PT nhìn phức tạp ta nhân liên hợp và qui đồng đƣợc :
Giải phƣơng trình 2 x 11x 14 16x  16   0 2 2 x   x x x x  6 4 2 3 4 7  57
PTcó 5 nghiệm x   ; 2 x  ; 1 x  ; 2 x  2
3) Giải phƣơng trình x  2 12 6
6x 10x  5  x  6   0 2 x  2 78
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Ta nhẩm đƣợc các nghiệm đẹp của PT là x   ; 2 x  ; 1 x  2
Biểu thức cần tìm là 2
x x 1 6 2 x 10x  5 x  3 2 x x x  2 12 6 2 6 10 6
6x 10x  5  x  6 
 0  6x 10x  5  2 x  2 2 x  2  ( 2 x  ) 2 6 2 x 10x  5 3  x  6 2 x 10x  6  ( 2
x x 1 x  ) 1 6 2 x 10x  5 3  x 1 6 2 x 10x  5   6 2
x 10x  5  ( 2 x x  ) 1  2 2
x  3x  2  x   1  0 2
PTcó 4 nghiệm x   ; 2 x  ; 1 x  ; 2 x  5
Muốn PT nhìn phức tạp ta nhân liên hợp và qui đồng đƣợc:
Giải phƣơng trình 5 2 x  22x  31 12x  6   0 2 2 x   x x x  2 6 6 10 5 2
PTcó 4 nghiệm x   ; 2 x  ; 1 x  ; 2 x  5
PHƢƠNG TRÌNH DÙNG CASIO HỖ TRỢ
Chuyên đề 2 TÌM BIỂU THỨC LIÊN HỢP
Chuyên đề này xin đƣợc giới thiệu các phƣơng trình dùng máy tính cầm tay tìm biểu thức liên hợp có dạng 2 k
ax bx c
P(x) ,với a,b,c là các số nguyên. Khi a=0 là trƣờng hợp quen thuộc!
Sau đây là các thí dụ đơn giản của dạng này
Thí dụ 1 Giải phƣơng trình 2 2 2
x  2x  2  6x  6x  4  5x   4 x 79
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. 2 x x  2 2 5 4 2 PT
x  2x  2  6x  6x  4  (*) x Do 5 2
x  4x  2  0 nên x  0 PT (*) 4  x  2 3 x  2 2 x  6 4 x  6 3 x  4 2 x  5 2 x  4x  2
Biểu thức cần tìm là 2 4 3 2
2x  2x 1 x  2x  2x và 2 4 3 2
3x  2x 1 6x  6x  4x 1 1 3  2 3  4
PTcó 2 nghiệm x  ; 1 x   1 3  2 3
Thí dụ 2 Giải phƣơng trình 2 2 3
2 x  2x  2  6x  6x  4  7x   6 x Hƣớng dẫn. 2 x x  2 2 7 6 3
PT  2 x  2x  2  6x  6x  4  (*) x Do 7 2
x  6x  3  0 nên x  0 PT (*)  2 4 x  2 3 x  2 2 x  6 4 x  6 3 x  4 2 x  7 2 x  6x  3
Biểu thức cần tìm là 2 4 3 2
2x  2x 1 x  2x  2x và 2 4 3 2
3x  2x 1 6x  6x  4x 1 1 3  2 3  4
PTcó 2 nghiệm x  ; 1 x   1 3  2 3
Nâng cấp: Giải phƣơng trình 5 2 x x  2 6 4 3
2 x  2x  2   6x   6 x  6 2 x  6x  4 x 1 1 3  2 3  4
PTcó 2 nghiệm x  ; 1 x   1 3  2 3 80
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 3 Giải phƣơng trình 2 8
8  2x  12x 18x  24  6x   8 x Hƣớng dẫn. 2 x x  2 6 8 8
PT  8  2x  12x 18x  24  (*) x Do 6 2
x  8x  8  0 nên x  0 PT (*)  8 2 x  2 3 x  12 4 x 18 3 x  24 2 x  6 2 x  8x  8
Biểu thức cần tìm là 2 2 3
2x  4x  4  8x  2x và 2 4 3 2
4x  4x  4  12x 18x  24x 1 3  3 3  9
PTcó 2 nghiệm x  ; 2 x  2
Thí dụ 4 Giải phƣơng trình 2 12
2 8  2x  12x 18x  24  8x  12 x Hƣớng dẫn. 2 x x  2 8 12 12
PT  2 8  2x  12x 18x  24  (*) x Do 6 2
x  8x  8  0 nên x  0 PT (*)  8 2 x  2 3 x  12 4 x 18 3 x  24 2 x  8 2 x 12x 12
Biểu thức cần tìm là 2 2 3
2x  4x  4  8x  2x và 2 4 3 2
4x  4x  4  12x 18x  24x 1 3  3 3  9
PTcó 2 nghiệm x  ; 2 x  2
Nâng cấp: Giải phƣơng trình 3 2 x 18x  24 12 2 8  2x   5x  12 3x  12 2 x 18x  24 x 81
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 3  3 3  9
PTcó 2 nghiệm x  ; 2 x  2
Thí dụ 5 Giải phƣơng trình 2 2 1
x x 1  5x  3x  2  4x   2 x Hƣớng dẫn. 2 x x  2 2 4 2 1 PT
x x 1  5x  3x  2  (*) x Do 4 2
x  2x 1  0 nên x  0 PT (*)  2 4 3 2
x x x  2 5 4 x  3 3 x  2 2 x  8 2 x  4x  2
Biểu thức cần tìm là 2 4 3 2
3x  2x 1 2 x x x và 2 4 3 2
5x  2x 1 2 5x  3x  2x 1 3  4 3  16
PTcó 2 nghiệm x  ; 1 x  5
Thí dụ 6 Giải phƣơng trình 2 2 2
3 x x 1  5x  3x  2  7x   4 x Hƣớng dẫn. 2 x x  2 2 14 8 4
PT  6 x x 1  2 5x  3x  2  (*) x Do 14 2
x  8x  4  0 nên x  0 PT (*)  6 4 3 2
x x x  2 5 4 x  3 3 x  2 2 x  8 2 x  4x  2
Biểu thức cần tìm là 2 4 3 2
3x  2x 1 2 x x x và 2 4 3 2
5x  2x 1 2 5x  3x  2x 1 3  4 3  16
PTcó 2 nghiệm x  ; 1 x  5 82
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nâng cấp: Giải phƣơng trình 4 2 x x  2 3 2 2
3 x x 1   8x   4 5 2
x  3x  2  x x 1 3  4 3  16
PTcó 2 nghiệm x  ; 1 x  5
Thí dụ 7 Giải phƣơng trình 2 6
2x  2  3x  2x  4  3x   4 x Hƣớng dẫn. 2 x x  2 3 4 6 PT
2x  2  3x  2x  4  (*) x Do 3 2
x  4x  6  0 nên x  0 PT (*)  2 3 x  2 2 x  3 4 x  2 3 x  4 2 x  3 2 x  4x  6
Biểu thức cần tìm là 2 3 2
x  2x  3  2x  2x và 2 4 3 2
2x  2x  3  3x  2x  4x
PTcó 2 nghiệm x  ; 3 3 x  1 2
Thí dụ 8 Giải phƣơng trình 2 15
3 2x  2  2 3x  2x  4  7x  10 x Hƣớng dẫn. 2 x x  2 7 10 15
PT  3 2x  2  2 3x  2x  4  (*) x Do 7 2
x 10x 15  0 nên x  0 PT (*)  3 2 3 x  2 2 x  2 3 4 x  2 3 x  4 2 x  7 2 x 10x 15
Biểu thức cần tìm là 2 3 2
x  2x  3  2x  2x và 2 4 3 2
2x  2x  3  3x  2x  4x
PTcó 2 nghiệm x  ; 3 3 x  1 2 83
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nâng cấp: Giải phƣơng trình 3 2 x  6x  6 2 2 x  4x  8 15   10  0 x  2x  2 2x  3 2 x  2  4 x x
PTcó 2 nghiệm x  ; 3 3 x  1 2
Thí dụ 9 Giải phƣơng trình 2 2 6
8x  6x 10  3x  2x  4  5x   4 x Hƣớng dẫn. 2 x x  2 2 5 4 6
PT  8x  6x 10  3x  2x  4  (*) x Do 5 2
x  4x  6  0 nên x  0 PT (*)  8 4 x  6 3 x 10 2 x  3 4 x  2 3 x  4 2 x  5 2 x  4x  6
Biểu thức cần tìm là 2 4 3 2
3x  2x  3  8x  6x 10x và 2 4 3 2
2x  2x  3  3x  2x  4x
PTcó 2 nghiệm x  ; 3 3 x  1 2
Thí dụ 10 Giải phƣơng trình 2 2 9
8x  6x 10  2 3x  2x  4  7x   6 x Hƣớng dẫn. 2 x x  2 2 7 6 9
PT  8x  6x 10  2 3x  2x  4  (*) x Do 7 2
x  6x  9  0 nên x  0 PT (*)  8 4 x  6 3 x 10 2 x  2 3 4 x  2 3 x  4 2 x  7 2 x  6x  9
Biểu thức cần tìm là 2 4 3 2
3x  2x  3  8x  6x 10x và 2 4 3 2
2x  2x  3  3x  2x  4x
PTcó 2 nghiệm x  ; 3 3 x  1 2 84
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nâng cấp: Giải phƣơng trình 4 2 x  4x  8 2 x  6x 10 9   6x   6 3 2
x  2x  4  x 3x  8 2 x  6x  10 x
PTcó 2 nghiệm x  ; 3 3 x  1 2
Thí dụ 11 Giải phƣơng trình 2 2 8
3x x  5  8x  5x 13  5x   4 x Hƣớng dẫn. 2 x x  2 2 5 4 8 PT
3x x  5  8x  5x 13  (*) x Do 5 2
x  4x  8  0 nên x  0 PT (*)  3 4 3 x x  5 2 x  8 4 x  5 3 x 13 2 x  5 2 x  4x  8
Biểu thức cần tìm là 2 4 3 2
2x  2x  4  8x  5x 13x và 2 4 3 2
3x  2x  4  8x  5x 13x
PTcó 2 nghiệm x  ; 4 3 x  1  3
Thí dụ 12 Giải phƣơng trình 2 2 12
2 3x x  5  8x  5x 13  7x   6 x Hƣớng dẫn. 2 x x  2 2 7 6 12
PT  2 3x x  5  8x  5x 13  (*) x Do 5 2
x  4x  8  0 nên x  0 PT (*)  2 3 4 3 x x  5 2 x  8 4 x  5 3 x 13 2 x  7 2 x  6x 12
Biểu thức cần tìm là 2 4 3 2
2x  2x  4  8x  5x 13x và 2 4 3 2
3x  2x  4  8x  5x 13x
PTcó 2 nghiệm x  ; 4 3 x  1  3 85
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 13 Giải phƣơng trình 4  2 2
x 10x 17  (x  3 )( 3 x  ) 7  5x   6 x Hƣớng dẫn. 2 x x  2 5 6 4 PT
 2x 10x 17  (x  3 )( 3 x  7)  (*) x Do 5 2
x  6x  4  0 nên x  0 PT (*)   2 4 x 10 3 x 17 2 2 x x (x  3 )( 3 x  ) 7  5 2 x  6x  4
Biểu thức cần tìm là 2 4 3 2
2x  3x  2   2x 10x 17x và 3 2 x  3x  2 2  x (x  3 )( 3 x  ) 7 1
PTcó 2 nghiệm x  ; 3 x  2 3
Thí dụ 14 Giải phƣơng trình 2 8
3  2x 10x 17  (x  3 )( 3 x  ) 7  9x  12 x Hƣớng dẫn. 2 x x  2 9 12 8 PT
 2x 10x 17  (x  3 )( 3 x  7)  (*) x Do 9 2
x 12x  8  0 nên x  0 PT (*)  3  2 4 x 10 3 x 17 2 2 x x (x  3 )( 3 x  ) 7  9 2 x 12x  8
Biểu thức cần tìm là 2 4 3 2
2x  3x  2   2x 10x 17x và 3 2 x  3x  2 2  x (x  3 )( 3 x  ) 7 1
PTcó 2 nghiệm x  ; 3 x  2 3
Thí dụ 15 Giải phƣơng trình 2 2 2
4x  8x  6  9x 12x  8  5x   4 x Hƣớng dẫn. 86
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 x x  2 2 5 4 2 PT
4x  8x  6  9x 12x  8  (*) x Do 5 2
x  4x  2  0 nên x  0 PT (*)  4 4 x  8 3 x  6 2 x  9 4 x 12 3 x  8 2 x  5 2 x  4x  2
Biểu thức cần tìm là 2 4 3 2
2x  2x 1 4x  8x  6x và 2 4 3 2
3x  2x 1 9x 12x  8x 1
PTcó 2 nghiệm x  1  2
Thí dụ 16 Giải phƣơng trình 2 2 3
2 4x  8x  6  9x 12x  8  7x   6 x Hƣớng dẫn. 2 x x  2 2 7 6 3
PT  2 4x  8x  6  9x 12x  8  (*) x Do 7 2
x  6x  3  0 nên x  0 PT (*)  2 4 4 x  8 3 x  6 2 x  9 4 x 12 3 x  8 2 x  7 2 x  6x  3
Biểu thức cần tìm là 2 4 3 2
2x  2x 1 4x  8x  6x và 2 4 3 2
3x  2x 1 9x 12x  8x 1
PTcó 2 nghiệm x  1  2
Thí dụ 17 Giải phƣơng trình 2 2 4
4x  4x 10  9x  6x 14  5x   2 x Hƣớng dẫn. 2 x x  2 2 5 2 4 PT
4x  4x 10  9x  6x 14  (*) x Do 5 2
x  2x  4  0 nên x  0 87
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT (*)  4 4 x  4 3 x 10 2 x  9 4 x  6 3 x 14 2 x  5 2 x  2x  4
Cần tìm thêm nghiệm ngoại lai từ đó có
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  8x  6x và 2 4 3 2
3x x  2  9x  6x 14x
PTcó nghiệm duy nhất x  2   2 2
Thí dụ 18 Giải phƣơng trình 2 2 8
3 4x  4x 10  9x  6x 14  9x   4 x Hƣớng dẫn. 2 x x  2 2 9 4 8
PT  3 4x  4x 10  9x  6x 14  (*) x Do 9 2
x  4x  8  0 nên x  0 PT (*)  3 4 4 x  4 3 x 10 2 x  9 4 x  6 3 x 14 2 x  9 2 x  4x  8
Cần tìm thêm nghiệm ngoại lai từ đó có
Biểu thức cần tìm là 2 4 3 2
2x x  2  4x  8x  6x và 2 4 3 2
3x x  2  9x  6x 14x
PTcó nghiệm duy nhất x  2   2 2
Thí dụ 19 Giải phƣơng trình 3 2 x  3  5 2 x  2x  2 2 x  2x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x  3 và x2  x  2  5x2  2x
PTcó 2 nghiệm x  ; 2  3 x   2 Nâng cấp: 3x2  3 x2  x  2
a)Giải phƣơng trình x2  x  1 2  5x 2x 88
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT  5 2 x  2x  3 2 x  3 2
x x   1   5 2 x  2 2
x x x  2( 2 x x  ) 1  0
PTcó 2 nghiệm x  ; 2  3 x   2
b)Giải phƣơng trình 3 2
x  3  5x  8  5 2
x  2x  5x  7  2x  6 PT  3 2
x  3  5x  8  (x  ) 3  5 2
x  2x  5x  7  (x  ) 3  0 3 2 x  3  ( 2 x x  ) 1 5 2 x  2x  ( 2 x x  ) 2    0 1 MS MS 2
PTcó 2 nghiệm x  ; 2  3 x   2
Thí dụ 20 Giải phƣơng trình 3 3 2 x  3  2 5 2 x  2x  5 2 x  5x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x  3 và x2  x  2  5x2  2x
PTcó 2 nghiệm x  ; 2  3 x   2
Thí dụ 21 Giải phƣơng trình 2 x x  2 2 1 2 3x  3   3 2 x  5x  5 5 2
x  2x  2x 1 Hƣớng dẫn. ( 5 2
x x x
x x x  2 2 2 )( 1 5 2 2 2 ) 1
pt  2 3x  3   3 2 x  5x  5 5 2
x  2x  2x 1
Biểu thức cần tìm là 2
x x 1 3 2
x  3 và x2  x  2  5x2  2x
PTcó 2 nghiệm x  ; 2  3 x   2
Thí dụ 22 Giải phƣơng trình 5 2 x 1  9 2
x  2x  2  4 2 x  2x  3 Hƣớng dẫn. 89
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 1
PTcó 2 nghiệm x  ; 1 x  3 2 Nâng cấp 5 2 x 1 2 2 x x  2
1)Giải phƣơng trình 2 2 x x  1 2 x x  9 2 2 PT  5 2 x   1 9 2
x  2x  2  2 2
x x  2  5 2 x 1  2 2 x x   1 (2 2 x x  ) 2  0 1
PTcó 2 nghiệm x  ; 1 x  3 2 9 2 x  2x  2 2 2 x x  2
2)Giải phƣơng trình (x  )( 1 2 3 x  ) 1  4 2 Hƣớng dẫn. 9 2 x  2x  2 2 2 x x  2 9 2 x  2x  2 2 2 x x  2    (x  )( 1 2 3 x  ) 1  4 2 3 x x   2 ( )( 1 2 ) 1 4  9 2
x  2x  24  (x  )( 1 2 3 x  ) 1  4   9 2
x  2x  2  2 2
x x  2 (x  )( 1 2 3 x  ) 1  4  0 1
Nhân liên hợp PTcó 2 nghiệm x  ; 1 x  3 2
Thí dụ 23 Giải phƣơng trình 2 5 2 x 1  3 9 2
x  2x  2  10 2 x  5x  8 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 1
PTcó 2 nghiệm x  ; 1 x  3 2
Nâng cấp Giải phƣơng trình x x  2 11 2 2 2 6
2 5x 1  9x  2x  2  6 2 x  3x  4 90
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. x   x x x   x x  2 2 5 2 2 1 9 2 2 22 5 2 1 9 2 2 2 
pt  2 5x 1  9x  2x  2  6 2 x  3x  4 2 5 2 x 1  9 2
x  2x  2    0
2 5 2x 1  9 2x  2x  2  6 2x  3x  ( 4 *)
Giải (*) có biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2  
PT đã cho có 4 nghiệ 1 1 67 m x  ; 1 3 x  ; x  2 11
Thí dụ 24 Giải phƣơng trình 5 2 x x  2 2 2 2 5x 1   6 2 x x  4 9 2
x  2x  2  2x Hƣớng dẫn.
 9 2x x  x x x  x 2 2 2 2  9 2 2 2 2 
pt  2 5x 1   6 2 x x  4 9 2
x  2x  2  2x
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 1
PTcó 2 nghiệm x  ; 1 x  3 2
Thí dụ 25 Giải phƣơng trình 2 2 x 1  2 2
x x 1  2 2 x  4x  5 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1
PTcó 2 nghiệm x  ; 1  3 x  1   4 2 2 x 1 2 x  2x  3
Nâng cấp:Giải phƣơng trình 2 x  2x  2 2 x x  2 1 PT  2 2 x   1 2 2 x x 1 2
x  2x   3   2 2 x 1 2
x  2x  2( 2 x  2x  ) 3  0 91
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 2 nghiệm x  ; 1  3 x  1   4
Thí dụ 26 Giải phƣơng trình 3 2 2 x 1  2 2
x x 1  4 2 x  8x  9 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1
PTcó 2 nghiệm x  ; 1  3 x  1   4
Nâng cấp Giải phƣơng trình x x  2 14 2 2 4 13
3 2x 1  2 x x  1  4 2 x  8x  9 Hƣớng dẫn. x   x x x   x x  2 3 2 2 2 1 2 2 13 2 2 1 2 2 1
pt  3 2x 1  2 x x 1  4 2 x  8x  9 3 2 2 x 1  2 2
x x  1    0  3 2 2 x 1  2 2
x x  1  4 2 x  8x  ( 9 *)
Giải (*) có biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 
PT đã cho có 4 nghiệ 2 186 m x  ; 1  x  1 3   4; x  14
Thí dụ 27 Giải phƣơng trình 3 2 x  6x  6 8x  3   4 2 x  9x  7 2 2
x 1  x 1 2 2
x x 1  2x 1 Hƣớng dẫn. ( 2 2
x 1  x  )( 1 2 2
x 1  x  ) 1 (2 2
x x 1  2x  )( 1 2 2
x x 1  2x  ) 1 Pt  . 3   4 2 x  9x  7 2 2
x 1  x 1 2 2
x x 1  2x 1
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 92
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 2 nghiệm x  ; 1  3 x  1   4
Thí dụ 28 Giải phƣơng trình 3 2 x  9  5 2
x  6x 16  2 2 x  6x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  3  3 2 x  9 và 2
x  3x  4  5 2 x  3x 16
PTcó 2 nghiệm x  ; 0 3 x  2   10 9 2 x  2x  2 2 2 x x  2
2)Giải phƣơng trình (x  )( 1 2 3 x  ) 1  4 2 Hƣớng dẫn. 9 2 x  2x  2 2 2 x x  2 9 2 x  2x  2 2 2 x x  2    (x  )( 1 2 3 x  ) 1  4 2 3 x x   2 ( )( 1 2 ) 1 4  9 2
x  2x  24  (x  )( 1 2 3 x  ) 1  4   9 2
x  2x  2  2 2
x x  2 (x  )( 1 2 3 x  ) 1  4  0 1
Nhân liên hợp PTcó 2 nghiệm x  ; 1 x  3 2
Thí dụ 29 Giải phƣơng trình 2 3 2 x  9  5 2
x  6x 16  3 2 x  9x 10 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  3  3 2 x  9 và 2
x  3x  4  5 2 x  6x 16
PTcó 2 nghiệm x  ; 0 3 x  2   10
Thí dụ 30 Giải phƣơng trình 2 x x  2 2 15 3 3x  9   4 2
x  14x  14 5 2
x  6x  16  2x 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  3  3 2 x  9 và 2
x  3x  4  5 2 x  6x 16 93
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 2 nghiệm x  ; 0 3 x  2   10
Thí dụ 31 Giải phƣơng trình 5 2
x x 16  3 2
x  7x  9  2 2 x  6x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  4  5 2
x x 16 và 2
x  3x  3  3 2 x  7x  9
PTcó 2 nghiệm x  ; 0 3 x  2  17
Nâng cấp: Giải phƣơng trình 1 1 2x  7   2 x  7x 12 3 x  5x x 16
3 x  3x  7 x  9
PTcó 2 nghiệm x  ; 0 3 2 x  (2  17)
Thí dụ 32 Giải phƣơng trình 2 5 2
x x 16  3 3 2
x  7x  9  5 2 x 15x 17 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  4  5 2
x x 16 và 2
x  3x  3  3 2 x  7x  9
PTcó 2 nghiệm x  ; 0 3 x  2  17
Nâng cấp Giải phƣơng trình x x  2 7 2 2 27 20
2 3x  7x  9  5x x  16  3 2 x  9x  10 Hƣớng dẫn. x x   x x x x   x x  2 2 3 2 2 7 9 5 2 16 2 3 2 7 9 5 2 16 
pt  2 3x  7x  9  5x x 16  3 2 x  9x 10 2 3 2
x  7x  9  5 2
x x  16    0  2 3 2
x  7x  9  5 2
x x  16  3 2 x  9x  ( 10 *)
Giải (*) có biểu thức cần tìm là 2
x  3x  3  3 2
x  7x  9 và 2
x  3x  4  5 2 x x 16 94
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PT đã cho có 4 nghiệ 20 m x  ; 1 x  2 3  17; x   ; x  0 7
Thí dụ 33 Giải phƣơng trình 5 2
x  9x 16  3 2
x  3x  9  2 2 x  6x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  4  5 2
x  9x 16 và 2
x  3x  3  3 2 x  3x  9
PTcó 2 nghiệm x  ; 0 3 x  2   7
Thí dụ 34 Giải phƣơng trình 2 5 2
x  9x 16  3 2
x  3x  9  3 2 x  9x 11 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  4  5 2
x  9x 16 và 2
x  3x  3  3 2 x  3x  9
PTcó 2 nghiệm x  ; 0 3 x  2   7
Thí dụ 35 Giải phƣơng trình x x  2 4 2 2 2 2
2 2x  2x 1  4x  6x  6  3 2x 6x  7 Hƣớng dẫn. x x   x x x x   x x  2 2 2 2 2 2 1 4 2 6 6 2 2 2 2 1 4 2 6 6 
pt  2 2x  2x 1  4x  6x  6  3 2 x  6x  7 2 2 2
x  2x  1  4 2
x  6x  6    0  2 2 2
x  2x  1  4 2
x  6x  6  3 2
x  6x  7(*)
Giải (*) có biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6 1
PT đã cho có 3 nghiệm x  ; 1 x  1 3  2; x   2
Thí dụ 36 Giải phƣơng trình 2 2
x  2x 1  4 2
x  6x  6  2 2 x  4x  5 95
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6
PTcó 2 nghiệm x  ; 1 3 x  1 2 Nâng cấp:
a)Giải phƣơng trình 1 1 2x  5   2 x  5x  6 2 x  2x  2 x  1 2 x  4x  6 x  6
PTcó 2 nghiệm x  ; 1 3 2 x  1 (  2)
b)Giải phƣơng trình 2 2
x  2x 1  2x  2  4 2
x  6x  6  4x  2  2x  ( 1 *) Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là x  ; 1 x  25992105 , 2
biểu thức liên hợp cần tìm là
2x2  2x 1  2x  2  x
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 4 2
x  6x  6  4x  2  (x  ) 1 ĐKXĐ:
x x   x   x x   x   2 2 2 1 2 2 ) 1 ( 0 và 4 2 6 6 4 2 ( 0 ) 2 3  3 1 3  3 Có: ) 1 (  x ( ) 2  x suy ra x  2 6 2 Khi đó 2 2
x  2x 1  2x  2  x  0 4 2
x  6x  6  4x  2  (x  ) 1  0 2 2
x  2x 1  ( 2 x  2x  ) 2 4 2
x  6x  4  ( 2 x  2x  ) 3 PT (*)    0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 1 3 x  1 2 96
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 37 Giải phƣơng trình 2 2
x  2x 1  3 4 2
x  6x  6  4 2 x  8x 11 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6
PTcó 2 nghiệm x  ; 1 3 x  1 2
Nâng cấp: Giải phƣơng trình 2 3 5x 12   2 x  5x  6 2 x  2x  2 x  1 2 x  4x  6 x  6
PTcó 2 nghiệm x  ; 1 3 2 x  1 (  2)
Thí dụ 38 Giải phƣơng trình 2 2 x  2x  3 6 2 x 12x  12   3 2 x  8x  6 2 2
x  2x  1  2 4 2
x  6x  6  x Hƣớng dẫn. ( 2 2
x  2x  1  )( 2 2 2
x  2x  1  ) 2 PT  2 2
x  2x  1  2 ( 4 2
x  6x  6  x)( 4 2
x  6x  6  x)  . 2  3 2 x  8x  6 4 2
x  6x  6  x
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6
PTcó 2 nghiệm x  ; 1 3 x  1 2
Thí dụ 39 Giải phƣơng trình 3 2 2
x  2x 1  4 2x  2  7 2 x 14x 10 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x 1 2x  2 Chú ý :x=1 thì 2
x  2x 1  2x  2  0 97
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 2 nghiệm x  ; 1 3 x  1 2 Nâng cấp x  2 2 34 94
a)Giải phƣơng trình: 2x  6x 15  2x  2x 1  2 x  7 Hƣớng dẫn. pt  ( 2
x  2x  2  2 2 x  2x  )( 1 2 2
x  2x  5  2 2 x  2x  ) 1  0  3 1 7
PTcó 4 nghiệm x  ; 1 x  1 2; x  2
b)Giải phƣơng trình 2 2
x  2x 1  4x 1 
2x  2  2x 1  2x  ( 1 *)
Hƣớng dẫn.ĐK: x 1
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là x  ; 1 x  25992105 , 2
biểu thức liên hợp cần tìm là
2x  2  2x 1  x
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x  2x 1  4x 1  (x  ) 1 Khi đó
2x  2  2x 1  x  0 2 2
x  2x 1  4x 1  (x  ) 1  0 2 2
x  2x 1  ( 2 x  2x  ) 2 2x  2  ( 2 x  2x  ) 1 PT (*)    0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 1 3 x  1 2
Thí dụ 40 Giải phƣơng trình 5 2
x  3x  8  3 2
x x  5  2 2 x  2x  3 Hƣớng dẫn. 98
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x x  2  5 2
x  3x  8 và 2
x x 1 3 2 x x  5
PTcó 2 nghiệm x  ; 1 3 x  1   3
Thí dụ 41 Giải phƣơng trình 2 5 2
x  3x  8  3 3 2
x x  5  5 2 x  5x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  5 2
x  3x  8 và 2
x x 1 3 2 x x  5
PTcó 2 nghiệm x  ; 1 3 x  1   3
Thí dụ 42 Giải phƣơng trình 2 x  3x  8 4 2 x  2x  8   3 2 x  7x  6 5 2
x  3x  8  2x 3 2
x x  5  x 1 Hƣớng dẫn. ( 5 2
x  3x  8  2x)( 5 2
x  3x  8  2x) Pt  5 2
x  3x  8  2x ( 3 2
x x  5  x  )( 1 3 2
x x  5  x  ) 1  . 2  3 2 x  7x  6 3 2
x x  5  x 1
Biểu thức cần tìm là 2
x x  2  5 2
x  3x  8 và 2
x x 1 3 2 x x  5
PTcó 2 nghiệm x  ; 1 3 x  1   3
Thí dụ 43 Giải phƣơng trình 2 2
x 15x  23  4 2
x  23x  34  2 2 x  8x 11 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  4x  5  2 2
x 15x  23 và 2
x  4x  6  4 2
x  23x  34
PTcó 2 nghiệm x  ; 2  3 x  7  2 99
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 44 Giải phƣơng trình 2 2 2
x 15x  23  4 2
x  23x  34  3 2 x 12x 16 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  4x  5  2 2
x 15x  23 và 2
x  4x  6  4 2
x  23x  34
PTcó 2 nghiệm x  ; 2  3 x  7  2
Thí dụ 45 Giải phƣơng trình 2 4 2
x  2x 1  6 2
x  4x  4  3 2 x  3x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 4 2
x  2x 1 và 2
x x  2  6 2 x  4x  4
PTcó 3 nghiệm x  ; 0 x  1   2
Nâng cấp Giải phƣơng trình x x 2 10 2 2 4
2 4x  2x  1  6x  4x  4  3 2 x  3x  4 Hƣớng dẫn. x x   x x x x   x x  2 2 4 2 2 2 1 6 2 4 4 2 4 2 2 1 6 2 4 4 
pt  2 4x  2x 1  6x  4x  4  3 2 x  3x  4 2 4 2
x  2x  1  6 2
x  4x  4    0  2 4 2
x  2x  1  6 2
x  4x  4  3 2 x  3x  ( 4 *)
Giải (*) có biểu thức cần tìm là 2
x x 1 4 2
x  2x 1 và 2
x x  2  6 2 x  4x  4
PT đã cho có 4 nghiệ 2 m x  ; 0 x   ; x  1   2 5
Thí dụ 46 Giải phƣơng trình 2 4 2
x  2x 1  3 6 2
x  4x  4  5 2 x  5x  8 100
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x  2x 1 và 2
x x  2  5 2 x  4x  4
PTcó 3 nghiệm x  ; 0 x  1   2
Thí dụ 47 Giải phƣơng trình 7 2 x  9  9 2
x  6x 16  2 2 x  6x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  3  7 2 x  9 và 3 2
x  3x  4  9 2 x  6x 16 81  6369 81  6369
PTcó 2 nghiệm x  ; 0 3 3 x  2    9 9
Thí dụ 48 Giải phƣơng trình 4x 13  4 2
x  6x 18  4 2 x  2x  5 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x  2  4x 13 và 2 2
x x  3  4 2 x  6x 18 3 9  6 3 3  9  6 3
PTcó 2 nghiệm x  ; 1  x  2
Thí dụ 49 Giải phƣơng trình 2x 14  4 2
x  4x 17  4 2 x  2x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 2x 14 và 2 2
x x  2  4 2 x  4x 17  4 3  24 78 181 3  24 78 181
PTcó 2 nghiệm x  ; 1 x  6
Thí dụ 50 Giải phƣơng trình 3x  4  2 2
x  7x  9  2 2 x  4x  5 Hƣớng dẫn. 101
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x  2x  2  3x  4 và 2
x  2x  3  2 2 x  7x  9
PTcó 2 nghiệm x  ; 0 x  1 
Thí dụ 51 Giải phƣơng trình 5 2
x 10x  7  12 3
x  2x 12  4 2 x  3x  5 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  3x  2  5 2
x 10x  7 và 2 2 x  3  12 3 x  2x 12 1 3
PTcó 2 nghiệm x  2
Thí dụ 52 Giải phƣơng trình 3 2
x  7x  7  8 3 2
x x  3x  7  4 2 x  2x  2 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x 1 3 2
x  7x  7 và 2 2 x 1 8 3 2
x x  2x  7 1  17
PTcó 2 nghiệm x  4
Thí dụ 53 Giải phƣơng trình 18 2
x  5x  5  64 2
x 16x  23  6 2 x  3x  2
Biểu thức cần tìm là 2 2
x x 1 18 2
x  5x  5 và 4 2
x  2x 1 64 2 x 16x  23 1  17  3  33
PTcó 4 nghiệm x  ; x  4 4
Thí dụ 54 Giải phƣơng trình 2 18 2
x  5x  5  64 2
x 16x  23  8 2 x  4x  3
Biểu thức cần tìm là 2 2
x x 1 18 2
x  5x  5 và 4 2
x  2x 1 64 2 x 16x  23 1  17  3  33
PTcó 4 nghiệm x  ; x  4 4 102
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 55 Giải phƣơng trình 14 2
x 11x  6  32 2
x  32x  9  6 2 x  3x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x  2  14 2
x 11x  6 và 4 2
x  2x 1 32 2
x  32x  9 1  17 1
PTcó 4 nghiệm x  ; x   ; 1 x  4 2
Thí dụ 56 Giải phƣơng trình 8 2
x 10x  5  24 2
x  36x 17  6 2 x  3x  2
Biểu thức cần tìm là 2 2
x x 1 8 2
x 10x  5 và 4 2
x  2x 1 24 2 x  36x 17 1  17
PTcó 2 nghiệm x 4
Thí dụ 57 Giải phƣơng trình 8 2
x 10x  5  (x  8 )( 1 2 x  21x  ) 17  6 2 x  4x  2 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 8 2
x 10x  5 và 4 2
x  3x 1 (x  8 )( 1 2 x  21x  ) 17 1  17
PTcó 2 nghiệm x  4
Thí dụ 58 Giải phƣơng trình 8 2
x 10x  5  8 3 x  37 2
x  44x  20  6 2 x  4x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 8 2
x 10x  5 và 4 2
x  3x  2  8 3 x  37 2
x  44x  20 103
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1  17
PTcó 2 nghiệm x  4
Thí dụ 59 Giải phƣơng trình 2 4 x 1  9 4 x  2 3 x  4 2 x  4  5 2 x  2x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x  2  2 4 x 1 và 3 2
x x  2  9 4 x  2 3 x  4 2 x  4  9  17
PTcó 3 nghiệm x  1 ; x  8
Thí dụ 60 Giải phƣơng trình (x  ) 1 2x 1  2 2 2 x  2x 1 1 2 2 x  3x  5 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  (x  ) 1 2x 1 và 2
x  2x  3  2 2 2 x  2x 1 3 3  108 12 69 3  108 12 69
PT đã cho có 2 nghiệm: x  1; x  3
Thí dụ 61 Giải phƣơng trình 2 2 x  3 2x 1  x 1 3 2 x  2x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  (x  ) 1 2x 1 và 2
x x 1 3 2 x  2x  4 3 3  108 12 69 3  108 12 69
PT đã cho có 2 nghiệm: x  1; x  3
Thí dụ 62 Giải phƣơng trình 3 ( x  ) 1 2x 1  14 3 x  2 2 x  6x  2 1 4 2 x x 1 104
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 3 ( x  ) 1 2x 1 và 2 2 x  14 3 x  2 2 x  6x  2 5 3  359 12 78 3  359 12 78
PT đã cho có 2 nghiệm: x  1; x  6
Thí dụ 63 Giải phƣơng trình 2 2
x  2x  4  2 3 x  3 2 x  4 1 2 2 x x  2 Hƣớng dẫn.
Biểu thức cần tìm là 2 x 1 2 2
x  2x  4 và 2
x x 1 2 3 x  3 2 x  4 1 3  9 17  37 3  9 17  37
PT đã cho có 2 nghiệm: x  1; x  3
Thí dụ 64 Giải phƣơng trình (x  ) 1 3x 1 3   x  5 2
x x  2 1 2 2 x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  (x  ) 1 3x 1 và 2 x x 1 3   x  5 2 x x  2 81  3 633 81  3 633 3 3  PT đã cho có 2 nghiệ 2 2
m: x  1; x  3
Thí dụ 65 Giải phƣơng trình (x  ) 1 3x 1 3  x  4 2
x x  2 1 2 2 x x  3 105
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  (x  ) 1 3x 1 và 2 x 1 3  x  4 2 x x  2 3 3 27  633  27  633
PT đã cho có 2 nghiệm: x  1; x  3 18
Thí dụ 66 Giải phƣơng trình (x  ) 2 3x 1 3   x  4 2
x 10x  4 1 4 2 x x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x  3  (x  ) 2 3x 1 và 2 2 x 1 3   x  4 2 x 10x  4  5 3  ( 5 281 18 249) 3  ( 5 281 18 249)
PT đã cho có 2 nghiệm: x  1; x  12
Thí dụ 67 Giải hệ phƣơng trình  2 x  2 2 y  2 xy  4  (x  2 ) 2 3x  4  3 3 4x  2
2x  8x  8  2 9x  2 y Hƣớng dẫn.
Phƣơng trình thứ nhất của hệ tƣơng đƣơng với x  2 hoặc 2
x y  2  2 
Với x=2 các bạn tự xử lí trƣờng hợp dễ này Với 2
x y  2  2
thay vào PT thứ 2 của hệ ta đƣợc (x  ) 2 3 2 x  4  3 4 3 x  2 2
x  8x  8  9 2 x x  ( 2 *)
Biểu thức cần tìm là 3 2
x x  2  (x  ) 2 3 2 x  4 và 2 2 x  4 3 x  2 2 x  8x  8 3 183  31 3 183  31 1 3 3   4 4
PT(*) có 2 nghiệm: x  2 ; x  3 106
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Đến đây các bạn tự giải tiếp
Thí dụ 68 Giải hệ phƣơng trình x 2  2 y    0  2 x  1 4 y  2 2 y  2   2 y 3 2 x  13  2 2
x  16x  41  3 2 x  3 2 y  5 Hƣớng dẫn.
Sử dụng Hàm đặc trƣng có
Phƣơng trình thứ nhất của hệ tƣơng đƣơng 2
x y  2  2  Với 2
x y  2  2
thay vào PT thứ 2 của hệ ta đƣợc (x  ) 2 3 2 x 13  2 2
x 16x  41  3 2 x  3x  ( 11 *)
Biểu thức cần tìm là 2 2
x  3x  6  (x  ) 2 3 2 x 13 và 2 x  5  2 2 x 16x  41
 2  23 3 57 1  23 3 57 1
PT(*) có 2 nghiệm: x  2 ; x  3
Đến đây các bạn tự giải tiếp
Thí dụ 69 Giải hệ phƣơng trình  2 x  2 xy x  2 y  2  0   2 y 3 2 x  13  4 2
x  10x  67  3 2 x  3x  15 Hƣớng dẫn.
Phƣơng trình thứ nhất của hệ tƣơng đƣơng với x  1hoặc 2
x y  2  2 
Với x=1 các bạn tự xử lí trƣờng hợp dễ này Với 2
x y  2  2
thay vào PT thứ 2 của hệ ta đƣợc (x  ) 2 3 2 x 13  4 2
x 10x  67  3 2 x  3x  ( 15 *)
Biểu thức cần tìm là 2 2
x  3x  7  (x  ) 2 3 2 x 13 và 2 x  8  4 2 x 10x  67 107
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 3  17  9 681 3  17  9 681
PT(*) có 2 nghiệm: x  1; x  3
Đến đây các bạn tự giải tiếp
Thí dụ 70 Giải phƣơng trình 3 2 x 1  12 3 x  9 2
x  6x  4  3 2 2 x 1 Hƣớng dẫn.
Biểu thức cần tìm là 3 2
x x 1 3 2 x 1 và 3 2
x x  2  12 3 x  9 2 x  6x  4 2 3  53  9 41 3  53  9 41
PT đã cho có 2 nghiệm: x  0 ; x  9
Thí dụ 71 Giải phƣơng trình
3 4x3  5x2  7  2x4  6x2  4x Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 4 3 x  5 2 x  7 9 57  67 9 57  67 1 3 3   PT đã cho có 2 nghiệ 4 4
m: x  1 ; x  3
Thí dụ 72 Giải phƣơng trình x  3 2 x  3  3 2
x  7x  2  5 2
x  2x  3 x 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x  3 và x2  x  2  5x2  2x
PTcó 2 nghiệm x  ; 2  3 x   2 PT x  3 2
x  3  x 1  3 2
x  7x  2  5 2
x  2x  2 x 1  0 108
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 73 Giải phƣơng trình 2 2 x  5x  5 2 x 1  2 2
x  3x 1 9 2
x  2x  2  2x 1  2x 1 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 Pt  2 2 x  5x  5 2
x 1  2x 1  2 2
x  3x 1 9 2
x  2x  2  2x 1  0 1
PTcó 2 nghiệm x  ; 1 x  3 2
Thí dụ 74 Giải phƣơng trình 3 (x  ) 1 2 2 2 x 1 3 2
x  2x 11 2 2
x x 1  1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 3 PT  (x  ) 1 2 2 2 x 1 1 3 2
x  2x 11 2 2
x x 1  2  0
PTcó 2 nghiệm x  ; 1  3 x  1   4
Thí dụ 75 Giải phƣơng trình 3 2
x  3x  4  3 2 x  9 2
x  3x 13  5 2
x  3x 16  4 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  3  3 2 x  9 và 2
x  3x  4  5 2 x  3x 16 3 2 pt
x  3x  5  3 2 x  9 1 2
x  3x 13  5 2
x  3x 16  3  0
PTcó 2 nghiệm x  ; 0 3 x  2   10
Thí dụ 76 Giải phƣơng trình 2 5 2 x 1 2  x  2 9 2 x  2x  2 2  x 1  6 2 x  4x  5 109
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 pt   2 2 2 5 2 x 1 2  x   3 ( 2 x  2x  ) 2  2 9 2 x  2x  2 2  x   1  3 ( 2 x  2x  ) 3  0 1
PTcó 2 nghiệm x  ; 1 x  3 2
Thí dụ 77 Giải phƣơng trình  2
3  2x  2x 1 2
2  4x  6x  6  x  2x  2 2 5 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6
PTcó 2 nghiệm x  ; 1 3 x  1 2
Thí dụ 78 Giải phƣơng trình x x x  2 1 2 2 2 3 4
3x x  5    2 x  2x  2 2 4 2 x  2x  8 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2 x x  5 x  2 2 1 4 1
pt  3x x  5  x x 1  (   )  0 2 x  2x  2 4 2 x  2x  8 2
PTcó 2 nghiệm x  ; 1 3 x  1   3
Thí dụ 79 Giải phƣơng trình 4 2 2 x  2x 1 4  4 2 x  6x  6 2
x  2x  3 2
x  2x  2 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6 110
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 2 nghiệm x  ; 1 3 x  1 2
Thí dụ 80 Giải phƣơng trình 3 2
x x  5  (x  ) 1 3 3 2
x  9x  4  2 2 x  2x 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x x  5 và 3 2
x  2  3x  9x  4
PTcó 2 nghiệm x  ; 1 3 x  1   3
Thí dụ 81 Giải phƣơng trình 2 2 3 3
2x  2x 1  (x  ) 1 (x  ) 1  6  (x  ) 2 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 3 3 2  (x  ) 1  6
PTcó 2 nghiệm x  ; 1 3 x  1 2 Chuyên đề phụ:
Ý tƣởng ghép 2 phƣơng trình thành 1 phƣơng trình
Hay một cách tạo ra phƣơng trình Tích từ các biểu thức tùy ý (chọn hợp lí )
Tác giả của ý tưởng:Vũ Hồng Phong Thôn Bất Lự,Hoàn Sơn,Tiên Du,Bắc Ninh
Từ hai phƣơng trình sau:
Giải phƣơng trình: 3 2 x  3  5 2 x  2x  2 2
x  2x  3 (1) Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 3 2
x  3 và x2  x  2  5x2  2x
PTcó 2 nghiệm x  ; 2  3 x   2
Giải phƣơng trình: 2 2 x 1  2 2
x x 1  2 2
x  4x  5 (2) 111
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 Hƣớng dẫn.
Từ (1) và (2) ta có thể ghép lại thành PT sau:
Thí dụ 82 Giải phƣơng trình(đây là PT chỉ để minh họa ý tƣởng`)  3 2 x  3 2 2 x 1   ( 2 x x x x 2   )( 2 2  2  ) 3    2 
 (x  2x  ) 2 x x 2   2  1 x x   2   1  5x   2x   2 2   2 2 
 (x x  ) 2 2x 1 x x x 2  (  2  ) 3 3   3 2   
 (x  2x  ) 2 x x 2   2    1 2 5x x x    2x   1  2 x 2  x  3 x   x x  2 2 2 3 2 3 2 2 1 3 ( x  )( 3 2x  )
1  x  2x  2 2 x x 1   2 x  ( 2 x x  )( 2 2 x  2x  ) 3 2 2 1 2 x x   x x   2 2 x x 1 ( ) 2 2 2 5 2 x  2x 5 2 x  2x HD.
Với (a;b),(c;d) là bộ biểu thức liên hợp của PT thứ nhất
(m;n),(p;q) là bộ biểu thức liên hợp của PT thứ hai Ta có PT: a   c   c   a   a c   m n  
p q    m n  
p q     (
mq np)  0 b   d   d   b   b d
Suy ra PT ở thí dụ 82 đã cho tƣơng đƣơng với PT  3 2 x  3 2
x x  2     x
x x   x x x x   2
2 2 2 .1 2 1 ( 2 2 )(2 2 2 )3 0  x x  1  5 2 x  2  x  3 2 x  3 2 x x  2 2 2 x x x    3 3 2      TH1: 0 1 1 0 2 x x  1 2 5 2 x  2x x x 1 5 2 x  2x 3 2 x  3  ( 2 x x  ) 1 5 2 x  2x  ( 2 x x  ) 2    0 2 x x  1 5 2 x  2x
PTcó 2 nghiệm x  ; 2  3 x   2 112
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) TH2: làm tương tự
2 2 2x  .1 2x x1( 2x 2x )(2 2x 2x )30 2 2 x 1 2 x  2x  3   2 x  2x  2 2 2 x x  1
PTcó 2 nghiệm x  ; 1  3 x  1   4
PT đã cho có 4 nghiệm x  ; 2  3
x   2 ; x   ; 1 3 x  1   4
Các PT trên chỉ là minh họa cho ý tƣởng ghép 2 phƣơng trình thành một phƣơng trình.
Mở rộng:Dùng kĩ thuật ghép này cho 2 phƣơng trình liên hợp dạng bậc nhất hoặc hằng số có khả năng sẽ tạo
ra đƣợc Pt đỡ phức tạp a c c aa c Dạng PT này ( m n)( p q)  ( m n)( p q)   
mq npcó thể mở rộng về dấu b d d bb d
cộng hay trừ và thêm các hằng số trong dấu ngoặc. a c c aa c  ( m n)( p q)  ( m n)( p q)   
mq np b d d bb d
Hoặc (am bn cp )(  dq)  cm (
dn)(ap bq)  ad bcmq np
Hoặc (am bn cp )(  dq)  cm (
dn)(ap bq)  ad bcmq np
Nếu ai không thích ghép 2 phƣơng trình thì chỉ cần lấy 1 phƣơng trình tƣơng ứng gồm 2 cặp biểu thức liên
hơp,các biểu thức còn lại chọn tùy ý chứa ẩn hoặc hằng số hay mở rộng ta chọn a,b,c,d,m,n,p,q bất kì!!!
A.Các cách tạo ra phƣơng trình dạng này Giải phƣơng trình
x  4x  2; x 1 6x 1 cùng 1 phƣơng trình nhân liên hợp
x  2  9x  ;
1 x  3  11x  6 cùng 1 phƣơng trình nhân liên hợp
Sau đây là hƣớng tạo ra một PT dạng này từ các biểu thức trên: Giải phƣơng trình  2    11x  6 
1  4x  2  9x 1 (x  ) 1  x   3  x    6x 1  113
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)  2  x  3x  2  2 
 44x  2x 12     9x 1   x   3  6x 1   x   2  44 2 x  2x 12 1
   4x  2  9x 1  x  3  x Hay x 2 x  3x  2 11x  6  9x 1 (x  ) 1  x  3 6x 1 6x 1
x  2 4x  2  x 9x 1 44 2 x  2x 12 2  x  3x Hay  2 x  3x  2 11x  6  9x 1 (x  ) 1  x  3 6x 1 6x 1
x  2 4x  2  x 9x 1 44 2 x  2x 12 2  x  3x Hay  2
x  3x  2  54 2 x  3x 1 (x  )
1 11x  6  (x  ) 3 6x 1 
PT đã cho có 4 nghiệ 5 13 m x  2  2 ; x  2 B. Vận Dụng
Ta có thể tạo ra các PT đơn giản hơn dƣới đây
(nhìn chỉ hơi khó nhƣng biến đổi nhẹ nhàng gồm kĩ năng đƣa về phƣơng trình Tích và
nhân Liên hợp nếu cần +Casio bậc nhất)
Thí dụ 1,Giải phƣơng trình 2 2 xx 3  4 4x  2 4x  2  2 6x 1 x 6x 1  3  4 x  1 x  1
2x  3 4x  2 2 x  4 4x  2 hay  (nhìn tạm ổn)
2 6x 1  3x  3
x 6x 1  4x  4 PT đã cho có 8
3 nghiệm(đã kiểm tra) x  2  2 ; x  3
Thí dụ 2,Giải phƣơng trình 114
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x 3x 2  2  x 4x  2 4x  2  6x 1 3 6x 1 2  2  x x  1 x  1 2 x  2 4x  2 3x x 4x  2 hay  (nhìn tạm ổn) 3 2
6x 1  2x  2
3 6x 1  x x
PT đã cho có 3 nghiệm x  2  2 ; x  6
Thí dụ 3,Giải phƣơng trình x 3x 2  2  x 4x  2 4x  2  6x 1 3 6x 1 2  2  x x  1 x  1 2 x  2 4x  2 3x x 4x  2 hay  (nhìn tạm ổn) 3 2
6x 1  2x  2
3 6x 1  x x
PT đã cho có 3 nghiệm(đã kiểm tra) x  2  2 ; x  6
Thí dụ 4,Giải phƣơng trình 9x  1 2 9x 1 3  3  x x  2 x  2  x  3 2x  6 3  3  x 11x  6 11x  6
9x 1  3x  6 2 9x 1 4  x  2 3 x hay  (nhìn tạm ổn)
x  3  3 11x  6 2x  6 3  x 11x  6 PT đã cho có 5  13
3 nghiệm(đã kiểm tra) x  3 ; x  6 2
Thí dụ 5,Giải phƣơng trình 2 2
4x  2  3x  3 x
4x  2  (x  ) 1  3 2 2 3 2 1 3 x  2x x  (x  ) 1 x  2x Hƣớng dẫn. Chọn 3 2 a
4x  2;b x  ; 1 c  ; 1 d
x  2x 115
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Chọn m  ; 1 n  ; 3 2
p x ; q x 1
PT đã cho có 4 nghiệ 1  13
m (đã kiểm tra) x  ; x  1 2 6
Thí dụ 6,Giải phƣơng trình 2
2 8x  3  x  2 x
8x  3  4x  8  3 2 2 3 2
 2  x  4x
x  4 x  4x Hƣớng dẫn. Chọn 3 2 a  8x  ; 3 b x  ; 2 c   ; 1 d
x  4x Chọn m  ; 2 n  ; 1 2
p x ; q  4
PT đã cho có 3 nghiệm (đã kiểm tra) x  2 2 ; x  2  3
Chú ý tìm đƣợc 4 nghiệm thì x  2  2 loại do đkxđ
Thí dụ 7,Giải phƣơng trình 2
20x 13  2x  3x
3 20x 13 10x 15  3 2 3 2
2  x x  2x  7
6  5 x  2x  7 Hƣớng dẫn. Chọn 3 2 a
20x 13;b  2x  ; 3 c  ; 2 d
x  2x  7 Chọn m  ; 1 n  ; x p  ; 3 q  5 PT đã cho có 5
3 nghiệm (đã kiểm tra) x  ; x  1 2 3
Thí dụ 8,Giải phƣơng trình 8x  2 4  x  2 3 3 x
x . 28x 1  2x  3 
2x  4  3 8x  2
6x  9  2 28x 1 Hƣớng dẫn.
Chọn a  8x  2;b x  ; 2 c  2x  ; 2 d  28x 1 Chọn m  ; 1 3
n x ; p  ; 3 q  2 116
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PT đã cho có 3 nghiệ 2 m (đã kiểm tra) 3 x  ; x  2  2 3
Thí dụ 9,Giải phƣơng trình 4x  2 2  x
2x 1  x 3 2 x  8x 1 
2 4x  2  3x 4x  2  3 3 2 x  8x 1 Hƣớng dẫn. Chọn a  4x  2;b  ; x c  2x  ; 1 d  3 2
x  8x 1 Chọn m  ; 1 n  ; x p  ; 2 q  3 PT đã cho có 3 3
nghiệm (đã kiểm tra) x  ; x  2  2 2
Thí dụ 10,Giải phƣơng trình (x  ) 1 x 1  x2
x2  2x  2  (x  ) 1 5  2x  3  x 1 5  5  2x Hƣớng dẫn. Chọn a x  ; 1 b  ;
1 c  2  5  2x; d  1
Chọn m x  ; 1 2
n x ; p  ; 1 q  3 PT đã cho có 2 8  4 13 3 21
nghiệm (đã kiểm tra) x  ; x  9 2
Thí dụ 11,Giải phƣơng trình 4 x . 2 x  3 2
x x  2 5 4 x x  2 3 x  5  2 2 2 x x   x x x x 12 . 3 2 2 4 Hƣớng dẫn. Chọn 2
a x x  ; 2 b  ; 5 2 c x x  ; 3 2
d x x  2 Chọn m  ; 1 n  ; 2 3
p x ; q  1   PT đã cho có 3 1 13 3 73 3
nghiệm (đã kiểm tra) 3 x  ; x  ; x  2 2 2 117
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 12,Giải phƣơng trình 3 2x 1  x 7  2 1  x  3 2 2x 1  3
x  2  1  x Hƣớng dẫn.
Chọn a  2x  ; 1 b  ; 1 c  2 3
 1 x;d 1 Chọn m  ; 1 n  ; x p  ; 2 q  3
PT đã cho có 3 nghiệ 3 61 11 17
m (đã kiểm tra) x  ; x  2 16
Thí dụ 13. Cách tạo ra nhƣ sau:
Từ phƣơng trình dùng Casio bậc nhất: 2 x x   x x
x x ( ) 1 6 1 20 7 3 3 1
x 20x  7 1  (x  3 )( 1 x  6x  ) 1
Chọn a  3x  6x  ; 1 b  ;
1 c x 20x  7  ; 1 d x 1 3
m x ; n  ; 1 p  ;
1 q  2 ta có thể ngụy trang thành phương trình sau
Thí dụ 13,Giải phƣơng trình 3 4 3 x x 6x 1 1 4 x 20x  7 3  x x 1  3x  6x 1  2
x 20x  7  2x 1
PT đã cho có 3 nghiệ 1 m (đã kiểm tra) 3 x  ; x  2  2 3
Thí dụ 14,Giải phƣơng trình 3 5 3 3 5 3 3
x  3x  4x x 1
x  3x  4x  7x 1  2 2 3 x  3
x x  2  7x 1 Hƣớng dẫn. Chọn 3 5 a x  3 3
x  4x;b  ; 1 2
c x x  ; 2 d  1 Chọn 3 m  ; 1 n x  ; 1 p  ; 1 q  7x 1
Sau đó ta phải các giải pt sau: 118
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x 2 4 2   3 1 5 x  3 3 x  4 2
x x x  2  3 x   3  x   ( 1 khix  ) 0  2  x xx  2 x  0 3 
7x 1  x  1  x 1 x  4
PT đã cho có 4 nghiệm (đã kiểm tra) x  ; 0 x  ; 1 x  ; 2 x  4 
Thí dụ 15. Cách tạo ra nhƣ sau:
Từ phƣơng trình dùng Casio : 3 2 2 x x   x
x x x ( ) 1 7 3 ( ) 2 3 ( ) 2  (x  ) 1
7x  3  (x  )( 2 x  2 3 2  x  3x)
Chọn a  7x  ; 3 b x  ; 2 c x  2 3 2
x  3x;d x 1 2
m x ; n  ; 1 p  ;
2 q  1 ta có thể ngụy trang thành phương trình sau
Thí dụ 15,Giải phƣơng trình 2 3 2 2 3 2
x  2  x . 7x  3
x  2x x 1 x . x  3x  3 2
x  2  2 7x  3
3x  5  2 x  3xPT đã cho có 3 3 5
nghiệm (đã kiểm tra) x  2 ; x  2
Thí dụ 16,Giải phƣơng trình 2 x x 1 2  x . 6 2 x  2x 1 4 3 x x  2 2 x 1 2 2 2 x x 1  2
x x 1 2 6 2 x  2x 1 2 2
x  2x  4  2 2 2 x x 1
PT đã cho có 5 nghiệm (đã kiểm tra) x   2 ; x  ; 0 x  ; 1 x  3 
Thí dụ 17,Giải phƣơng trình
x 8x  5  4 2 x  2x 1 2
x x 1 x 3x  2  1 8x  5
x  3  3x  2 Hƣớng dẫn.
Chọn a  8x  5  4x  ; 3 b x  ;
1 c x 1 3x  2; d  1 119
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Chọn m  ; 1 n  ; 4 p  ; x q  1
Giải PT bằng liên hợp bậc nhất:(x  ) 1
3x  2  8x  5 2
x  4x  2
PT đã cho có 2 nghiệ 1 1 5
m (đã kiểm tra) x  ; x  4 2
Thí dụ 18,Giải phƣơng trình 1 x  1 2  x x
2 1 x  2 1 x 1  2 1 2 2  x x 1 4 2 x 1 Hƣớng dẫn.
Chọn a  1 x  1 x;b  ; 1 c  2 1 2
x ;d 1 Chọn m  ; 1 2
n x ; p  ; 2 q  1
PT đã cho có 3 nghiệ 1
m (đã kiểm tra) x  0 ; x   2
Thí dụ 19,Giải phƣơng trình 3 6 3 x x 1 3 6 3  x
x x 1  2  2 2 x  2x  2 2 2 x  3x  4 Hƣớng dẫn. Chọn 3 6 3 a x x  ; 1 b  ; 1 c  2 2 x  3x  ; 2 d  1 Chọn m  ; 1 n  ; x p  ; 1 q  2 3 6 3 2 3 1 1 Giải PT
x x 1  2x  3x  2 3  x  1  ( 2 x  )  3 3 x x 15 11 2 22 30  45  x  ; 1 x    14 7 14 15 
PT đã cho có 4 nghiệ 11 2 22 30 45
m (đã kiểm tra) x  ;
1 x  2 ; x    14 7 14
Thí dụ 20,Giải phƣơng trình 120
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 5 2 x  2x  4 2  x 1 2 x  3x  2 2 x  3  2  5 2 x  2x  4 3x  3  2 2 x  3 Hƣớng dẫn. Chọn a  5 2 x  2x  4 2  x  ; 1 b  ; 1 c  3x  2 2 x  ; 3 d  1 Chọn m  ; 1 2
n x ; p  ; 1 q  3
PT đã cho có 3 nghiệm (đã kiểm tra) x  1 5 ; x   3
Thí dụ 21,Giải phƣơng trình 2 x x  2 2  x 1 ( 2 x  ) 1 2 x  2 4  x  2 2 x  2  x(2 2  x  ) 1 2 2 x  2 4  x x  2 2 x  2 Hƣớng dẫn. Chọn a  ; 2 x b x  ; 1 2 c x  ; 1 4 d x  2 2 x  2 Chọn m
x2  2; n  ; 1 p  ;
2 q x
Đƣa về PT tích ta phải giải các PT: 2 x x 1  2 1 5 
x x 1  x
(dùng hàm đặc trƣng) 2 4 2 x x x  2 1 2 2 x  0 2 x x  2  2    x  5 1 2 x ( 2 x  ) 2  4
PT đã cho có 3 nghiệ 1  5
m (đã kiểm tra) x  ; x  5 1 2
Thí dụ 22,Giải phƣơng trình 3 2 x x 1 4 2 4 x x x  2 2 x  2  x  2 2 x 1 2 x 1  2 4 x  2 2 x  2 Hƣớng dẫn. Chọn a  ; 2 x b x  ; 1 2 c x  ; 1 4 d x  2 2 x  2 Chọn 2
m x ; n  ; 1 p  ; 1 q  2 121
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Đƣa về PT tích ta phải giải các PT: 2 x x 1  2 1 5 
x x 1  x
(dùng hàm đặc trƣng) 2 4 2 x x x  2 1 2 2 1 2 2
x  1  x   2
PT đã cho có 3 nghiệ 1  5 1
m (đã kiểm tra) x  ; x   2 2
Thí dụ 23,Giải phƣơng trình 2 2 1 x  2.x x x  2  2.x  2 2 3 1 x  2 2 2  3 x  3 2  2.x Hƣớng dẫn. Chọn a  1 2
x ;b  2;c  2  2 2 x  2; d  1 Chọn m  ; 1 n  ; x p  ; 3 q  2
Đƣa về PT tích ta phải giải các PT: xx 2 2 2 1 2 1 x  2( 2  2x x )    2 2 (*) 1 2  x 1 2  x
Sử dụng a,b không âm có Bất đẳng thức: 2   
đẳng thức xảy ra a b ( 2 2 a b ) a b 2 2   2x 1 2  x  2x  1 2  x Áp dụng :          VT (*) ( 2 ) 2 2 2 2 VP(*)   1 2  x 1 2  x 1 2  x  1 2  x     
đẳng thức xảy ra x  2 1 2 3x  1 . 2  x 3 PT đã cho có 2 2
nghiệm (đã kiểm tra) x  ; x  2 1 3
Thí dụ 24,Giải phƣơng trình(Vũ Hồng Phong THPT Tiên Du 1) 122
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 3 2
3  2x  3x  8x 3 18x  3x  4 2 1 x 3  x Hƣớng dẫn. Chọn 2 2 2 a
3  2x  3x ;b  8 ;
x c  1 x ; d  1 x Chọn m  ; 1 2
n x ; p  ; 1 q  2 2 3 2      Đƣa về 3 2x 3x 8x 3 18x 3x PT tích:  4 2 1 x 3  x   [ 3  2x  3 2 x 1 ( 2  x ) 8x 1 ( 2  x )]( 2 x  ) 2  0 ta phải giải PT:
 32x 3 2x1( 2  x )  8x 1 ( 2  x ) 2x 1 2  x 2x 1 2  x   . 3  4 . (*) 1 2  x 1 2  x 1 2  x 1 2  x   Đặ  
t x  tant với t   ;   2 2 
Pt(*) trở thành sin t 2  3 cos t 2  4sin t 2 cos t 2  sin t 2  3 cos t 2  2sin t 4   t   k    6
 sin 4t  sin(2t  )   (k Z ) 3  k   t     9 3   4  2 Suy ra t  ;t  ;t  ;t  6 9 9 9 1  4  2
Pt(*) có 4 nghiệm x  ; x  tan ; x  tan ; x  tan 3 9 9 9 1  4  2
Pt(*) có 6 nghiệm x   2; x  ; x  tan ; x  tan ; x  tan 3 9 9 9
Thí dụ 25,Giải phƣơng trình(Vũ Hồng Phong Bất Lự, Hoàn Sơn,Tiên Du ) 2 4 2
 3  2x  3x  8x
 3 18x  3x  2 3 4 2
1 x x x 3  x 123
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. Chọn 2 2 2
a   3  2x  3x ;b  8 ;
x c  1 x ; d  1 x Chọn m  ; 1 3
n x ; p  ; 1 q  2 2 4 2        Đƣa về 3 2x 3x 8x 3 18x 3x PT tích:  2 3 4 2
1 x x x 3  x   [  3  2x  3 2 x 1 ( 2  x ) 8x 1 ( 2  x )]( 3 x  ) 2  0 ta phải giải PT:
 32x 3 2x1( 2  x )  8x 1 ( 2  x ) 2x 1 2  x 2x 1 2  x   . 3  4 . (*) 1 2  x 1 2  x 1 2  x 1 2  x   Đặ  
t x  tant với t   ;   2 2 
Pt(*) trở thành sin t 2  3 cos t 2  4sin t 2 cos t 2  sin t 2  3 cos t 2  2sin t 4   t   k    6
 sin 4t  sin(2t  )   (k Z ) 3 2 k   t     9 3  2    4 Suy ra t   ;t  ;t  ;t  6 9 9 9 1 2    4
Pt(*) có 4 nghiệm x  ; x  tan ; x  tan ; x  tan 3 9 9 9  2    4 3 1
Pt(*) có 5 nghiệm x  2; x  ; x  tan ; x  tan ; x  tan 3 9 9 9
Thí dụ 26,Giải phƣơng trình(Vũ Hồng PhongToán K35B ĐHSP TN) 2 2 2 2 3
1 2 3x x  8x 1 x 1 x  1 (  x )  2 2 1 16 (  2 3)x x 3  x Hƣớng dẫn. 124
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Chọn 2 2 2
a  1 2 3x x ;b  8 ;
x c  1 x ; d  1 x Chọn m  ; 1 n  1 2  x ; p  ; 1 q  2 2 2 2 2 3        Đƣa về 1 2 3x x 8x 1 x 1 x 1 ( x ) PT tích  2 2 1 16 (  2 3)x x 3  x  [1 2 3 2 x x 1 ( 2  x ) 8x 1 ( 2  x )]( 1 2  x  ) 2  0
ta phải giải các PT:  1 2 3 2 x x  1 ( 2  x ) 8x 1 ( 2  x )  0 2 3x 1 2  x 2x 1 2  x    4 . (*) 1 2  x 1 2  x 1 2  x 1 2  x   Đặ  
t x  tant với t   ;   2 2  Pt(*) trở thành 3 sin t 2  cos t 2  4sin t 2 cos t 2  3 sin t 2  cos t 2  2sin t 4   t   k    12
 sin 4t  sin(2t  )   (k Z ) 6 5 k   t    36 3  5 17  7 Suy ra t  ;t  ;t  ;t  12 36 36 36  5 17  7
Pt(*) có 4 nghiệm x  tan  2  3 ; x  tan ; x  tan ; x  tan 12 36 36 36  5 17  7
Pt(*) có 6 nghiệm x   ; 3 x  tan  2  3 ; x  tan ; x  tan ; x  tan 12 36 36 36
Thí dụ 27,Giải phƣơng trình 2 2 2 2 3
1 2 3x x  8x 1 x 1 x  1 (  x )  2 2 1 16 (  2 3)x x 3  x Hƣớng dẫn. Chọn 2 2 2
a  1 2 3x x ;b  8 ;
x c  1 x ; d  1 x 125
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Chọn m  ; 1 n  1 2  x ; p  ; 1 q  2 2 2 2 2 3        Đƣa về 1 2 3x x 8x 1 x 1 x 1 ( x ) PT tích  2 2 1 16 (  2 3)x x 3  x  [1 2 3 2 x x 1 ( 2  x ) 8x 1 ( 2  x )]( 1 2  x  ) 2  0
ta phải giải các PT:  1 2 3 2 x x  1 ( 2  x ) 8x 1 ( 2  x )  0  2 3x 1 2  x 2x 1 2  x    4 . (*) 1 2  x 1 2  x 1 2  x 1 2  x   Đặ  
t x  tant với t   ;   2 2 
Pt(*) trở thành  3 sin t 2  cos t 2  4sin t 2 cos t 2  3 sin t 2  cos t 2  2  sin t 4   kt     36 3
 sin(2t  )  sin( 4  t)   (k Z ) 6  7   t   k  12  13 11 5 Suy ra t  ;t  ;t  ;t  36 36 36 12 5  13 11
Pt(*) có 4 nghiệm x  tan  2  3 ; x  tan ; x  tan ; x  tan 12 36 36 36 5  13 11
Pt(*) có 6 nghiệm x   ; 3 x  tan  2  3 ; x  tan ; x  tan ; x  tan 12 36 36 36
Thí dụ 28,Giải phƣơng trình 2 3 2
1 2x x  4 2x
1 (2  8 2)x x  4 2 1 x 3  x Hƣớng dẫn. Chọn 2 2 2
a  1 2x x ;b  4 2 ;
x c  1 x ; d  1 x Chọn m  ; 1 2
n x ; p  ; 1 q  2 126
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 3 2       Đƣa về 1 2x x 4 2x 1 (2 8 2)x x PT tích:  4 2 1 x 3  x   [ 1 2 2 x x  1 ( 2
x )  4 2x 1 ( 2  x )]( 2 x  ) 2  0 ta phải giải PT: 12 2 x x  1 ( 2
x )  4 2x 1 ( 2  x ) 2x 1 2  x 2x 1 2  x    2 2 . (*) 1 2  x 1 2  x 1 2  x 1 2  x   Đặ  
t x  tant với t   ;   2 2 
Pt(*) trở thành sin t 2  cos t 2  2 2 sin t 2 cos t 2  sin t 2  cos t 2  2 sin t 4   t   k    8
 sin 4t  sin(2t  )   (k Z ) 4  k   t     8 3  11  5 Suy ra t  ;t  ;t  8 24 24  11
Pt(*) có 3 nghiệm x  tan  2 1 ; x  tan  2  2  9  6 2 8 24  5 ; x  tan
 2  2  9  6 2 24  11
Pt có 5 nghiệm x   2; x  tan  2 1 ; x  tan  2  2  9  6 2 8 24  5 ; x  tan
 2  2  9  6 2 24
Thí dụ 29 Giải phƣơng trình 1  2 3 2
x x  2 sin 4 x
x  (6  sin x) 2 x 1  sin  x 4  4 3x  2 2 x 2 4 x 11x  3 Hƣớng dẫn. Chọn 2 4 2 2
a  1 2 3x x ;b  ,
2 c x  6x  ; 1 d  1 x 127
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) m  ; 1 n  sin ; x p  ; 2 q  1 1
Ta giải các PT sin x 2 2   2 3x 1 2  x 1 2   x     2 2 1 (*)   1 2  x 1 2  x  1 2  x       Đặ   
t x  tant với t   ;   2 2 
PT(*) trở thành 3 sin 2t  cos 2t  ( 2 2 cos2 2t  ) 1  3 sin t 2  cos t 2  2 cos t 4    t   k2 
 cos(2t  )  cos t   6 4 3    kt    18 3   7  5 Suy ra t  ;t  ;t  ;t 6 18 18 18 1  7  5
PT(*) có 4 nghiệm x  ; x  tan ;t  tan ;t  tan( ) 3 18 18 18
Pt đã cho có nghiệm 1  7  5  5 x  ; x  tan ; x  tan ; x  tan( ); x   k2; x
k2 (k Z) 3 18 18 18 6 6
Chú ý: Có thể tạo ra nhiều PT giải bằng phương pháp lượng giác hóa như sau 2   2 3x 1 2  x 1 2   x     2 2 1 (*)   1 2  x 1 2  x  1 2  x    
Từ PT(*) ta có thể tạo ra các PT tương tự: 2  2 2  2 3x 1  x  1 x     2 2 1 1  2 x 1  2 x   2   1  x      2  2 2  2 3x 1  x  1 x      2 2 1 1  2 x 1  2 x   2   1  x      128
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2  2 2  2 3x 1  x  1 x     2 1 2 1  2 x 1  2 x   2   1  x      2  2 2  2 3x 1  x  1 x     2 1 2 1  2 x 1  2 x   2   1  x      2  2 2  2x 3  3x  1 x     2 2 1 1  2 x 1  2 x   2   1  x      2  2 2  2x 3  3x  1 x     2 2 1 1  2 x 1  2 x   2   1  x      2  2 2  2x 3  3x  1 x     2 2 1 1  2 x 1  2 x   2   1  x      2  2 2   2x 3  3x  1 x     2 2 1 1  2 x 1  2 x   2   1  x     
Các thí dụ trước đều có thể tạo ra các PT (giải bằng lượng giác hóa )theo hướng này
Thêm một số dạng PT lƣợng giác hóa: 4x 1 (  x2 ) x4  6x2 1 2x 1  x2 sin t 4  ; cos t 4  ;sin t 2  ; cos 2x  ; x  tan t 1 (  x2 )2 1 (  x2 )2 1  x2 1  x2 1  cos 2t x x 1  cos 2t     sin t    sin t  ; cos t  ; t    ;  2 1  2 x 1  2 2 x  2 2      t
Chú ý: Do t    ;
nên sin t;sin và x cùng dấu với nhau  2 2  2 2 2 t 1 cos t 1 1 x t 1 cos t 1 x 1 x cos   ; sin    2 2 2 2  2 2 2 2 2 1 x 2 1 x
2  2x  2 1 x t x  sin  2 2 2
2  2x  2 1  x 129
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 4 2 4x 1 (  x ) x  6x 1 4x 4x 1 (  x2 ) x4  6x2  1 a)   3      3  4  x 2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 1  x2 1  x2  4  x 1 ( 2  x )  3( 4 x  6 2 x  ) 1  4  x 1 ( 2  x ) 2 4 2 2 4x 1 (  x ) x  6x 1 2  2x b)   3   2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 4 3x 1 (  x ) x  6x  1 4x c)     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 2 4 3x 1 (  x ) x  6x 1 2  2x d )     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 4x 1 (  x ) x  6x  1 4 2x ) e     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 2 4x 1 (  x ) x  6x 1 2  2x f )     2 2 2 2 2 1 (  x ) 1 (  x ) 1 x 4x 1 ( 2  x ) 4 x  6 2 x 1 1  ) m   3   ; 1  2; 3; 2  2  sin ; 2  2 ;.... 1 ( 2  x )2 1 ( 2  x )2 2 8 2 2x 1  x 2 x 2 2x 1 x 2x n)   3   n )   3   2 2 1 2 1  x 1  x 2 2 1  x 2 1 x 1 x  1 x 2 2 3x 1  x 2 x 2 2 3x 1 x 2x p)     p )     2 2 1 2 1  x 1  x 2 2 1  x 2 1 x 1 x  1 x 2 2x 1  x 2 q)   3   2 2 2 1  x 1  x 1  x 2 2 3x 1  x 2 k)     2 2 2 1  x 1  x 1  x 2 2x 1  x 2 l)     2 2 2 1  x 1  x 1  x 2 2x 1  x 2 x 2 2x 1  x 2 x h)     h )     2 2 1 2 1  x 1  x 2 2 1  x 2 1  x 1  x  1 x 130
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 4 2 4x 1 (  x ) 3(x  6x  ) 1 2 x 2 4 2 4x 1 (  x ) 3(x  6x  ) 1 2 x i)     i )     2 2 2 2 1 2 1 (  x ) 1 (  x ) 2 2 2 2 1  x 2 1 (  x ) 1 (  x )  1 x 2 4 2 4 3x 1 (  x ) x  6x  1 2 x 2 4 2 4 3x 1 (  x ) x  6x 1 2x j)     j )     2 2 2 2 1 2 1 (  x ) 1 (  x ) 2 2 2 2 1  x 2 1 (  x ) 1 (  x ) 1 x 2 4 2 4x 1 (  x ) 3(x  6x  ) 1 2 u)     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 4 3x 1 (  x ) x  6x  1 2 v)     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 4x 1 (  x ) x  6x  1 2 r)     2 2 2 2 2 1 (  x ) 1 (  x ) 1  x 2 4 2 4x 1 (  x ) x  6x  1 2 x 2 4 2 4x 1 (  x ) x  6x 1 2x t)     t )     2 2 2 2 1 2 1 (  x ) 1 (  x ) 2 2 2 2 1  x 2 1 (  x ) 1 (  x )  1 x 2 x 3 8x 1 (  x ) w ) 1     2 2 2 2 1 x 1 x 1 (  x ) 4 2 3x 1 ( 2 x  6x  ) 1 w ) 2     2 2 2 2 1  x 1  x 1 (  x ) 2 x 1 4 2x 1 (  x ) w ) 3     2 2 2 2 1 x 1 x 1 (  x ) 4 2 x 1 2(x  6x  ) 1 w ) 4     2 2 2 2 1 x 1 x 1 (  x ) 2 2 t 1 1 x t 1 x x cos  ;sin  2 2 2  2 2 1 x 2 1 x 2 2 t 1 1 x t 1 cos t 1 x 1 x Với cos  ; sin    2 2 2  2 2 2 2 2 1 x 2 1 x
2  2x  2 1 x t x  sin  2 2 2
2  2x  2 1  x 131
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Xin dành để các bạn có thể tự tạo ra các PT khác(giải bằng lượng giác hóa )theo hướng trên.
Như vậy ta có khá nhiều PT giải bằng lượng giác hóa (Vũ Hồng Phong THPT Tiên Du 1)
Nguồn gốc từ các PT lƣợng giác kiểu nhƣ sau:  3 sin t 2  cos t 2  2  sin t 4  3 sin t 2  cos t 2  2  cos t 4  sin t 2  3 cos t 2  2  sin t 4  sin t 2  3 cos t 2  2  cos t 4  3 sin t 4  cos t 4  2  sin t 2  3 sin t 4  cos t 4  2  cos t 2  sin t 4  3 cos t 4  2  sin t 2  sin t 4  3 cos t 4  2  cos t 2  sin t 4  cos t 4   2 sin t 2  sin t 4  cos t 4   2 cos t 2  sin t 2  cos t 2   2 sin t 2  sin t 2  cos t 2   2 cos t 2 1 2 3
 sin 4t  cos 4t   2 ; m m { ; ; ;....} 2 2 2 1 2 3
 sin 4t  3 cos 4t  2  ; m m { ; ; ;....} 2 2 2 1 2 3
 3 sin 4t  cos 4t  2  ; m m { ; ; ;....} 2 2 2  sin t 2  3 cos t 2  2  sint  3 sin t 2  cos t 2  2  sin t  sin t 2  3 cos t 2  2  cos t 132
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)  3 sin t 2  cos t 2  2  cos t  sin t 4  3 cos t 4  2  sin t  3 sin t 4  cos t 4  2  sin t  sin t 4  3 cos t 4  2  cos t  3 sin t 4  cos t 4  2  cos t  sin t 2  cos t 2   2 cos t  sin t 2  cos t 2   2 sin t  sin t 4  cos t 4   2 cos t  sin t 4  cos t 4   2 sin t t
 sin 4t  cos 4t   2 sin 2 t
 sin 4t  cos 4t   2 cos 2 t
 sin 2t  3 cos 2t  2  sin 2 t
 sin 2t  3 cos 2t  2  cos 2
…………………….(các bạn tự tìm các dạng khác )
Thí dụ 30 Giải phƣơng trình
x3  x  (2 2  )
1 x2  2 2x  1 1  x 2  2x  2 2      2  2  2x x 1 2 (2 2 ) 1 x 2 2x 1 Hƣớng dẫn. Chọn 2 a x  ; 1 b  (2 2  ) 1 2 x  2 2x  ; 1 c
2  2x; d  1 m  ; x n  ; 1 p  ; 1 q  2 133
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta phải giải PT (2 2  ) 1 2
x  2 2x 1  2  2 2
x x 1 2 2    2x 1 x 2x 1 x (2 2 x x  1 )( 1 2
x )  4 2x 1 ( 2  x )    2 2 2 2 2 2 1  x 1  x 1  x 1  x
Đặt x  tant rồi ta giải PT sin t 2  cos t 2  2 sin t 4  
PTđã cho có 4 nghiệm: x  tan(
)  1  2; (nghiệm kép) 8 5 11 1 x  tan  2
  2  9  6 2 ; x  tan  2
  2  9  6 2 ; x 24 24 2
Đến đây tác giả tin rằng mọi người sẽ dễ dàng tự tạo ra rất nhiều phương trình Tích dù là dạng
đơn giản hay phức tạp tùy theo ý mình.
Tác giả của ý tưởng :Vũ Hồng Phong THPT Tiên Du1,Tiên Du,Bắc Ninh
Tiếp tục Casio bậc 2
Thí dụ 83 Giải phƣơng trình 2 2 5x 1 3 5x 1 3  2  x 2 2 2x x  1 2x x  1  2 2 2x x  2 6x  3x  6 3  2  x 2 2 9x  2x  2 9x  2x  2 Hƣớng dẫn.
Phƣơng trình đƣợc tạo ra từ PT 5 2 x 1  9 2
x  2x  2  4 2 x  2x  3
Biểu thức cần tìm là 2 2
x x 1 5 2 x 1 và 2 2
x x  2  9 2 x  2x  2 1
PTcó 2 nghiệm x  ; 1 x  3 2 Chọn 3 m  ; 1 n  ; 2 p  ; 3 q x PT đ 1
ã cho có 3 nghiệm x  ; 1 3 x  ; x  6 3 2 134
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 84 Giải phƣơng trình 2 2 x x  2 2x  2x  4 2  3  x 2 2 5x  3x  8 5x  3x  8  2 2 3x x  5 2 3x x  5 2  3  x 2 2 x x  1 x x  1 Hƣớng dẫn. Từ PT: 5 2
x  3x  8  3 2
x x  5  2 2 x  2x  3
Biểu thức cần tìm là 2
x x  2  5 2
x  3x  8 và 2
x x 1 3 2 x x  5
PTcó 2 nghiệm x  ; 1 3 x  1   3 Chọn 2 m  ; 1 n   ; 3 p  ;
2 q  x
PTcó 4 nghiệm x  ; 1 x  1 3   ; 3 x   6
Thí dụ 85 Giải phƣơng trình x2  2x  2 3x2  6x   6 2  x 2x2  2x  1 2x2  2x   1 4x2  6x  6 3 4x2  6x   6 2  x x2  2x  3 x2  2x  3 Hƣớng dẫn. Từ PT: 2 2
x  2x 1  4 2
x  6x  6  2 2 x  4x  5
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2
x  2x  3  4 2 x  6x  6
PTcó 2 nghiệm x  ; 1 x  1 3  2; x  6 Chọn m  ; 1 n  ; 2 p  ;
3 q x
PT đã cho có 3 nghiệm x  ; 1 3 x  1 2
Thí dụ 86 Giải phƣơng trình 3 4 5   2 2 2 10x
14x  7  x  2
44x  60x  37  2  5 x x 135
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  10 2
x 14x  7 và 2 2
x  2x  5  44 2
x  60x  37 3 3 4 1     0 2 2 10 2
x 14x  7   2 x x 44 2
x  60x  37  2  5 x x    PT đã cho 3 5 1 13
có 4 nghiệm x  ; x  2 2
Thí dụ 87 Giải phƣơng trình 1 1 3   2 2 2         2 48x 60x 25 2x 3 13x 16x 8 2 x x Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x  3  48 2
x  60x  25 và 2
x x  2  13 2 x 16x  8 1 1 1 1 pt      0 2 x x    2 2 2 48 60 25 2 3 x x 13 2
x 16x  8   2 x x
PT đã cho có 4 nghiệm x  2  2; x  1   3
Thí dụ 88 Giải phƣơng trình 1 1 3 2 x  5   2 2 x x   x x x   2 4 x  7 2 x  6 48 60 25 2 13 16 8 x Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x  3  48 2
x  60x  25 và 2
x x  2  13 2 x 16x  8 1 1 1 1     0 x x   2 2 2 x  3 2 2 x x x   x  2 48 60 25 2 13 16 8 x
PT đã cho có 4 nghiệm x  2  2; x  1   3
Thí dụ 89 Giải phƣơng trình
2 48x2  60x  25  4x  6 
13x2 16x  8  x  2  3 x 136
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x  3  48 2
x  60x  25 và 2
x x  2  13 2 x 16x  8 2 48 2
x  60x  25  4x  6  2 x  13 2
x 16x  8  x  2  x  0
PT đã cho có 4 nghiệm x  2  2; x  1   3
Thí dụ 90 Giải phƣơng trình
2 44x2  60x  37  4x 10 
10x2 14x  7  x  2  3 x Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  10 2
x 14x  7 và 2 2
x  2x  5  44 2
x  60x  37 2 44 2
x  60x  37  4x 10  2 x  10 2
x 14x  7  x  2  x  0  3  5 1 13
PT đã cho có 4 nghiệm x  ; x  2 2
Thí dụ 91 Giải phƣơng trình
 5x x2  3 2
1   12x  8x 11  3 2 2 3 1  ( 9 2x x) Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 5 2
x x  2 và 4 2
x  2x 1 12 2 x  8x 11 pt   3 3 5 2
x x  2   1  (2 2
x x)3   12 2
x  8x 11   1  ( 8 2 2
x x)3  0 3
PTcó 2 nghiệm x  ; 1 3 x  4
Thí dụ 92 Giải phƣơng trình(tác giả Vũ Hồng Phong THPT Tiên Du 1) 4 2 4 4 2 4
8x  6x  4  2 6x  2x  7  x Hƣớng dẫn. Đặt 2
x a  0 PT đã cho trở thành 2 4 2 2
8a  6a  4  2 6a  2a  7  a 137
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 8 2
a  6a  4  0  Điều kiện: 2 1 43
a a    a   6 2 7 0 1 6 a  0 
Biểu thức cần tìm là 2
a  2a  2  8 2
a  6a  4 và 4 2
a 1 6a  2a  7 pt  8 2
a  6a  4  ( 2 a  2a  ) 2  [ 2 4 6 2
a  2a  7  (a  )] 1  ( 0 *) PT(*)có 2 nghiệm 3 a  ; 4 a  2
PT đã cho có 4 nghiệm 6 x   ; 2 a   2
Thí dụ 93 Giải phƣơng trình 8 4 x  6 2 x  4  34 6 4 x  2 2 x  7 4 2
x x 1 Hƣớng dẫn. Đặt 2
x a  0 PT đã cho trở thành 8 2
a  6a  4  24 6 2 a  2a  7 2
a a 1 8 2
a  6a  4  0  Điều kiện: 2 1 43
a a    a   6 2 7 0 1 6 a  0 
Biểu thức cần tìm là 2
a  2a  2  8 2
a  6a  4 và 4 2
a 1 6a  2a  7 pt  8 2
a  6a  4  ( 2 a  2a  ) 2  [ 3 4 6 2
a  2a  7  (a  )] 1  ( 0 *) PT(*)có 2 nghiệm 3 a  ; 4 a  2
PT đã cho có 4 nghiệm 6 x   ; 2 a   2
Thí dụ 94 Giải phƣơng trình(tác giả Vũ Hồng Phong ) 4 2 4 4 2 4 2
10x  9x  3  3 6x x 11  x x Hƣớng dẫn. Đặt 2
x a  0 PT đã cho trở thành a2 10  a 9  3  4 3 a2 6
a 11  a2  a 138
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 10 2
a  9a  3  0  Điều kiện: 2 2 59 1  a a    a   6 11 0 1 10 a  0 
Biểu thức cần tìm là 2
a  2a  3  10 2
a  9a  3 và 4 2
a 1 6a a 11 pt  10 2
a  9a  3  ( 2 a  2a  ) 3  [ 3 4 6 2
a a 1  (a  )] 1  ( 0 *) PT(*)có 2 nghiệm 3 a  ; 4 a  3
PT đã cho có 4 nghiệm 6 x   ; 2 a   3
Thí dụ 95 Giải phƣơng trình 2 5 2
x 12x 1  7 2
x 14x  4  3 2 x  3x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  5 2
x 12x 1 và 2
x x  3  7 2 x 14x  4
PTcó 2 nghiệm x  ; 1 3 x  6 1 Nâng cấp: Giải phƣơng trình 2 5 2
x 12x 1  x 1  3 7 2
x 14x  4  x  3  5x  ( 2 *) Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là x  ; 1 x  817120592 , 0
biểu thức liên hợp cần tìm là 5 2
x 12x 1  x 1  (x  ) 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là
7x2 14x  4  x  3  x ĐKXĐ: x
x   x   x x   x   5 2 12 1 1 ) 1 ( 0 và 7 2 14 4 3 ( 0 ) 2 139
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)   7  57   4  46 x  x Có: 6 ) 1 (   4 ( ) 2     7  57   4  46 x x    4  6  2  4  46
Do VT (*)  0  VP(*)  5x  2  0  x suy ra x  5 6 Khi đó 5 2
x 12x 1  x 1  (x  ) 1  0 7 2
x 14x  4  x  3  x  0 5 2
x 12x 1  ( 2 x x  ) 2 7 2
x 14x  4  ( 2 x x  ) 3 PT (*)  . 2  . 3  0 1 MS MS2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 1 3 x  6 1
Thí dụ 96 Giải phƣơng trình x 5 ( x  ) 11  2 7 2
x 13x  5  3 2 x  3x  8 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x  2  x 5 ( x  ) 11 và 2
x x  3  7 2 x 13x  5
PTcó 2 nghiệm x  ; 1  3 x  1  5 Nâng cấp: Giải phƣơng trình 5 2
x 11x  5x  2  7 2
x 13x  5  5x 1  2x  ( 4 *) Hƣớng dẫn.
Ta dùng Casio tìm đƣợc nghiệm đẹp của PT là x   ; 1 x  709975946 , 0
biểu thức liên hợp cần tìm là 5 2
x 11x  5x  2  (x  ) 2
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 7 2
x 13x  5  5x 1  (x  ) 2 140
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) ĐKXĐ: x x x   x x   x   5 2 11 5 2 ) 1 ( 0 và 7 2 13 5 5 1 ( 0 ) 2  11  23  817 13  29 x    x  5 Có: 36 14 ) 1 (   ( ) 2    31 641  13  29   x  0 x    40  14  2  4  46
Do VT (*)  0  VP(*)  5x  2  0  x suy ra x  5 6 Khi đó 5 2
x 11x  5x  2  (x  ) 2  0 7 2
x 13x  5  5x 1  (x  ) 2  0 5 2 x 11x  ( 2 x x  ) 2 7 2
x 13x  5  ( 2 x x  ) 3 PT (*)    0 1 MS MS 2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm x  ; 1  3 x  1  5
Thí dụ 97 Giải phƣơng trình (2x  5 )( 7 x  ) 1  2 8 2
x  33x  2  3 2 x  6x  7 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x  2x  2  (2x  5 )( 7 x  ) 1
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  8 2 x  33x  2
PT đã cho có 2 nghiệm 3 x   ; 2 x  2  9
Nâng cấp: Giải phƣơng trình (2x  5 )( 7 x  ) 1  2  3 8 2
x  33x  2 1  4  4x(*) Hƣớng dẫn.
Ta dùng casio tìm đƣợc các nghiệm đẹp của PT là x   ; 2 x   0080083823 , 0 141
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức liên hợp cần tìm là (2x  5 )( 7 x  ) 1  2  1 (  x)
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 8 2
x  33x  2 1  1 (  x)
Do VT (*)  0 suy ra VP(*)  4  4x  0  x  1 Khi đó (2x  5 )( 7 x  ) 1  2  1 (  x) 8 2
x  33x  2 1  1 (  x) (2x  7 5 )( x  ) 1  ( 2 x  2x  ) 3 8 2
x  33x  2  ( 2 x  2x  ) 2 PT (*)   . 3  0 1 MS MS 2
Nhân liên hợp lần nữa kết hợp điều kiện ta suy ra
PT đã cho có 2 nghiệm 3 x   ;
2 x  2  9
Thí dụ 98 Giải phƣơng trình(Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn) 4 2 x  10x  10 1   1 2 x  2x  2 2 2 x  6x  5 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2 x  6x  5 và 2
x  2x  3  4 2 x 10x 10 Ta có: 4 2 x  10x  10 1   1 2 x  2x  2 2 2 x  6x  5  2 2
x  6x  5 4 2 x 10x 10 2
x  2x  2 2
x  2x  2  2 2
x  6x  5 4 2 x 10x 10 2
x  2x   3  2 2
x  6x  5  ( 2 x  2x  ) 2  0
Nhân liên hợp PT đã cho có 2 nghiệm 3 x   ; 1 x  1   2
Thí dụ 99 Giải phƣơng trình 142
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 2 3   2 x x   x x   2 2 2 x x 1 9 3 3 1 13 5 8 2 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2 2
x x  2  9 2 x  3x  3
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x x  3  2 13 2 x  5x  8 1 1 2 2 PT      0 x x   2 2 2 x x 1 x x   2 2 2 x x 1 9 3 3 1 13 5 8 2 1
Nhân liên hợp 2 lần ở từng phân thức suy ra PTcó 2 nghiệm x  ; 1 x  3 4
Thí dụ 100 Giải phƣơng trình 1 1 3   2 x x   x x   2 2 2 x  2x  2 5 6 8 1 24 28 41 3 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x x  2  5 2 x  6x  8
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x  2x  5  24 2
x  28x  41 1 1 1 1 PT      0 2 2 x x   x x 1 x x   2 2 2 x  2x  2 5 6 8 1 24 28 41 3
Nhân liên hợp 2 lần ở từng phân thức suy ra PTcó 2 nghiệm 3 x   ; 2 x  2 x x    2 x x    Chú ý: 5 2 6 8 1 0 ; 24 28 41 3 0
Thí dụ 101 Giải phƣơng trình 3 2
x  5x  7  (x  ) 2 3 3 2
x  3x  2  2 2 x  2x 1 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x x 1 3 2 x  5x  7
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 3 2
x 1 3x  3x  2 143
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT  3 2
x  5x  7  ( 2 x x  ) 1  (x  )[ 2 3 3 2
x  3x  2  x  ] 1  0
Nhân liên hợp suy ra PTcó 2 nghiệm 3 x  ; 2 x   3
Thí dụ 102 Giải phƣơng trình 1 1 3   2 2 2         2 3x 7x 11 x 1 8x 24x 41 2 1 x x Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x x 1 3 2 x  7x 11
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x  2x 1 8 2
x  24x  41 1 1 3   2 2 2         2 3x 7x 11 x 1 8x 24x 41 2 1 x x 1 1 1 1  [  ]  [  ]  0 2 2 2 x x    x x x x    2 2 3 7 11 1 8 24 41 2 1 x x
Quy đồng rồi Nhân liên hợp suy ra PTcó 2 nghiệm 3 x   ; 2 x  5
Chú ý: 3x2  7x 11  x 1  ; 0 x
 ; 8x2  24x  41  2x 1  ; 0 x
Tƣơng tự: Giải phƣơng trình
3x2  7x 11  x 1  2 8x2  24x  41  4x  2  3 x Hƣớng dẫn.
3x2  7x 11  x 1  2 8x2  24x  41  4x  2  3 x  3 2
x  7x 11  x 1  x  2 8 2
x  24x  41  4x  2  2 x  0
Nhân liên hợp 2 lần suy ra PTcó 2 nghiệm 3 x   ; 2 x  5
Thí dụ 103 Giải phƣơng trình 1 1 2   2 2 2 x x   x x   x  2x  4 8 31 6 2 10 35 11 1 144
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x  2x  2  8 2 x  31x  6
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  10 2 x  35x 11 1 1 1 1 pt  [  ]  [  ]  0 2 2 x x   x  2x  4 2 2 x x   x  2x  4 8 31 6 2 10 35 11 1
Quy đồng rồi Nhân liên hợp suy ra PTcó 2 nghiệm 3 x   ;
2 x  2  7
Nâng cấp Giải phƣơng trình 2 x  2x  4 10 2
x  35x 11 1  2 2 x x   x  2x  3 8 31 6 1 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x  2x  2  8 2 x  31x  6
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  10 2 x  35x 11 2 x  2x  4 10 2
x  35x 11 1  2 2 x x   x  2x  3 8 31 6 1 2 x  2x  3 10 2
x  35x 11 1   2 2 x x   x  2x  4 8 31 6 1 2 x  2x  3 10 2
x  35x  11 1  11  0 2 2 x x   x  2x  4 8 31 6 1 2
x  2x  2  8 2 x  31x  6 2
x  2x  3  10 2 x  35x 11    0 2 2 x x   x  2x  4 8 31 6 1
Nhân liên hợp suy ra PTcó 2 nghiệm 3 x   ;
2 x  2  7
Thí dụ 104 Giải phƣơng trình 2 2 x  2 9 2
x  5x  5   x 2 x x   2 2 x 1 5 3 2 x 145
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2 2
x x 1 5 2 x  3x  2
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x x  2  9 2 x  5x  5 2 2 x  2 9 2
x  5x  5   x 2 x x   2 2 x 1 5 3 2 x 2 2 x 1 9 2
x  5x  5    x 2 x x   2 2 x  2 5 3 2 x 2 2 x 1 9 2
x  5x  5    x 1 1   0 2 x x   2 2 x  2 5 3 2 x 2 2
x x  1  5 2 x  3x  2 2 2
x x  2  9 2 x  5x  5    0 2 x x   2 2 x  2 5 3 2 x 1
Nhân liên hợp suy ra PTcó 2 nghiệm 3 x  ; 1 x   4
Chuyên đề 3 TÌM NHÂN TỬ CỦA PHƢƠNG TRÌNH DÙNG CASIO
Thí dụ 1 Giải phƣơng trình  2 2 x  6x  3 4  x  4 3 x  7 2 x  8x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x   2 2
x  6x  3 Chú ý: ta có ( 2 x  2 ) x  ( 2 2
x  6x  ) 3 4  x  4 3 x  6 2
x  6x  3 PT đã cho có 1 nghiệm: 3 x  1 2
Chú ý: Bấm máy tính ta tìm đƣợc 1 nghiệm.Ta tìm thêm
x  1 là nghiệm ngoại lai nó là nghiệm PT:   2 2 x  6x  3 4  x  4 3 x  7 2 x  8x  3
*Giải phƣơng trình sau (không dùng CASIO)  2 2
x  6x  3  2x  2  2 2
x  4x 1 146
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
a b  2 2 x  4x Đặ 1
t 2x  2  a ;  2x2  6x  3  b suy ra  2a  2b  2 2x 4x1
Tìm a,b theo x rồi suy ra 3 x  1 2
Thí dụ 2 Giải phƣơng trình 3  2 2
x  6x  3  2x  2  2 2 x  4x 1
Hƣớng dẫn. Bấm máy tính ta tìm đƣợc 1 nghiệm.
Tìm đƣợc nghiệm ngoại lai đẹp x=1bằng cách đổi dấu trƣớc căn Đƣợc PT sau: 2 2 
x x   x   x x  3 2 6 3 2 2 2 4 1
Biểu thức cần tìm là 2
x  2x   2 2
x  6x  3 và 2
x  2x 1 2x  2
Cho 2 biểu thức bằng 0 suy ra  2 2
x  6x  3  2x  2 1  0
suy ra nhân tử cần xuất hiện là:  2 2
x  6x  3  2x  2 1
Dùng casio giúp ta định hƣớng đƣợc PT đã cho có thể đƣa về PT tích. Cụ thể nhƣ sau
Đặt  2x2  6x  3  a ; 2x  2  b Tacó 2 2 a b  2 2
x  4x 1
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0 Giải PT  2 2
x  6x  3  2x  2 1  0 bằng cách chuyển vế,bình phƣơng
Hoặc tìm a,b theo x ta Suy ra PT có 1 nghiệm 3 x  1 2
Thí dụ 3 Giải phƣơng trình 3 2 x  6x  2 2 x  5 2
x  3x 1  0 Hƣớng dẫn.
Biểu thức cần tìm là x2  3x  2  3x2  6x và 2 x  3x 1 2  x  5
Cho 2 biểu thức bằng 0 suy ra 3 2 x  6 2 x x  5 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x x   3 6 5 1 147
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Đặt 3 2
x  6x a  0 ; 2
x  5  b  0 Tacó 2 2 a b  2 2
x  6x  5
Thay vào PT đƣợc (a b  )( 1 a b  ) 3  0 Giải PT 3 2 x  6 2 x
x  5 1  0 bằng cách chuyển vế,bình phƣơng
Hoặc tìm a,b theo x ta Suy ra PT có 2 nghiệm 3
x  1 2 ; x  3
Thí dụ 4 Giải phƣơng trình 12 2
x  25x  4  3  4 2
x  9x  4  8 2
x 16x  2  0 Hƣớng dẫn.
Biểu thức cần tìm là  2 2
x  4x 1 12 2
x  25x  4 và  2 2
x  4x 1  4 2
x  9x  4
Cho 2 biểu thức bằng 0 suy ra 12 2
x  25x  4   4 2
x  9x  4  2  0
suy ra nhân tử cần xuất hiện là: 2 2  x x
  x x   12 25 4 4 9 4 2 Đặt 3 2
x  6x a  0 ; 2
x  5  b  0 Tacó a2  b2  8
x2 16x
Thay vào PT đƣợc (a b  )( 1 a b  ) 3  0 1 PT có 2 nghiệm 3 x  1  ; x  1 4
Thí dụ 5 Giải phƣơng trình
3 3  5x  5  2 2
x  9x  6  2 2
x  4x  7  0
Hƣớng dẫn. Bấm máy tính ta tìm đƣợc 1 nghiệm.
Tìm thêm nghiệm ngoại lai là nghiệm PT: 2 2  x
x x   x x   3 3 5 5 2 9 6 2 4 7 0
Biểu thức cần tìm là x2  2x 1 3  5x và 2
x  2x  2   2 2
x  9x  6
Cho 2 biểu thức bằng 0 suy ra 3  5x   2 2
x  9x  6 1  0
suy ra nhân tử cần xuất hiện là: 2
x   x x   3 5 2 9 6 1 148
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Đặt 3  5x a  0 ;  2 2
x  9x  6  b  0 Tacó 2 2 a b  2 2
x  4x  3
Thay vào PT đƣợc (a b  )( 1 a b  ) 4  0  3  17
PT có 1 nghiệm x  2
Thí dụ 6 Giải phƣơng trình 4 2
x  6x 1 3  2 2 x  3  6 2
x  6x  2  0 Hƣớng dẫn.
Tìm thêm nghiệm ngoại lai là nghiệm PT: 2 2 2 x x    x
x x   4 6 1 3 2 3 6 6 2 0
Biểu thức cần tìm là 2 2
2x  3x 1 3  2x và 2 2
x  3x   6 2
x  6x  2
Cho 2 biểu thức bằng 0 suy ra 3  2 2 x   6 2
x  6x  2 1  0
suy ra nhân tử cần xuất hiện là: 2 2
x   x x   3 2 6 6 2 1 Đặt 3  2 2
x a  0 ;  6 2
x  6x  2  b  0 Tacó 2 2 a b  4 2
x  6x 1
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0 1 2
PT có 1 nghiệm x  2
Thí dụ 7 Giải phƣơng trình 4 2
x  4x  3  2 3 2 x  3  3 8 2
x  4x  7  0 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x  3  2 3 2 x  3 và 2 2
x  2x  2  8 2
x  4x  7
Cho 2 biểu thức bằng 0 suy ra 2 3 2 x  3  8 2
x  4x  7 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x   x x    2 3 3 8 4 7 1 0 Đặt 2 3 2
x  3  a  0 ; 8 2
x  4x  7  b  0 Tacó 2 2 a b  4 2
x  4x  5 149
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0 3
PT có 2 nghiệm x  1  2
Thí dụ 8 Giải phƣơng trình 2 2
x  3x 1 25 2
x 12x 12  2 12 2
x  6x  7  0 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  3x  3  25 2
x 12x 12 và 2 2
x  3x  2  12 2
x  6x  7
Cho 2 biểu thức bằng 0 suy ra 25 2
x 12x 12  12 2
x  6x  7 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   25 12 12 12 6 7 1 Đặt 25 2
x 12x 12  a  0 ; 12 2
x  6x  7  b  0 Tacó 2 2 a b  4 2
x  6x  5
Thay vào PT đƣợc (a b  )( 1 a b  ) 3  0  3  15
PT có 2 nghiệm x 2
Thí dụ 9 Giải phƣơng trình 2 2
x  4x  3  2 3 2
x  4x  2  3 10 2
x 12x  3  0 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  3  2 3 2
x  4x  2 và 2
x  2x  2  10 2
x 12x  3
Cho 2 biểu thức bằng 0 suy ra 2 3 2
x  4x  2  10 2
x 12x  3 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 3 4 2 10 12 3 1 Đặt 2 3 2
x  4x  2  a  0 ; 10 2
x 12x  3  b  0 Tacó 2 2 a b  2 2
x  4x  5
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0
PT có 4 nghiệm x  1  ; x  2   5 150
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nâng cấp: Giải phƣơng trình(tác giả Vũ Hồng Phong) 2 2
x  3x  7  ( 2 x  ) 3 3 2
x  4x  2  (x  ) 1 10 2
x 12x  3 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  3  2 3 2
x  4x  2 và 2
x  2x  2  10 2
x 12x  3
Cho 2 biểu thức bằng 0 suy ra 2 3 2
x  4x  2  10 2
x 12x  3 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 3 4 2 10 12 3 1 Đặt 2 3 2
x  4x  2  a  0 ; 10 2
x 12x  3  b  0 Tacó 2 2 a b  2 2
x  4x  5
Thay vào PT đƣợc (a b  )(
1 a b x  ) 2  0 +PT : 2 3 2
x  4x  2  10 2
x 12x  3 1  0
có 4 nghiệm x  1  ; x  2   5
+PT : 2 3x2  4x  2  10x2 12x  3  2  x 1
có 2 nghiệm x  1  ; x  3 1
PT đã cho có 5 nghiệm x  1  ; x  2   5; x  3
Thí dụ 10 Giải phƣơng trình 2 2
x  6x  3  2 10 2
x  26x  7  3 8 2
x  20x  2  0 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  3x  2  10 2
x  26x  7 và 2
x  3x  3  8 2
x  20x  2
Cho 2 biểu thức bằng 0 suy ra 10 2
x  26x  7  8 2
x  20x  2 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    10 26 7 8 20 2 1 0 151
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Đặt 10 2
x  26x  7  a  0 ; 8 2
x  20x  2  b  0 Tacó 2 2 a b  2 2
x  6x  5
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0
PT có 4 nghiệm x  1   2 ; x  2   6
Thí dụ 11 Giải phƣơng trình 4 2
x  4x 1 16 2
x 12x  3  2 33 2
x  24x  8  0 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  2x 1 16 2
x 12x  3 và 3 2
x  3x 1 33 2
x  24x  8
Cho 2 biểu thức bằng 0 suy ra 3 16 2
x 12x  3  2 33 2
x  24x  8 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    3 16 12 3 2 33 24 8 1 0 Đặt 16 2
x 12x  3  a  0 ; 33 2
x  24x  8  b  0
Ta dựa vào hệ số bất định giả sử 2 2 2
4x  4x m na pb  4 5 5 4 Suy ra n  ; 3 p  ; m nên có 2 2 2 4x  4x
 3a b 3 3 3 3 Thay vào PT đƣợc 3 ( a  2b  3 )( 1 a  2b  ) 2  0
PT có 4 nghiệm x  1  ; x  1   2
Thí dụ 12 Giải phƣơng trình 4 2
x  8x  3  44 2
x  56x  7  6 10 2
x 12x  3  0 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x  4x  3  44 2
x  56x  7 và 2
x  2x 1 10 2
x 12x  3
Cho 2 biểu thức bằng 0 suy ra 44 2
x  56x  7  2 10 2
x 12x  3 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    44 56 7 2 10 12 3 1 0 152
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Đặt 44 2
x  56x  7  a  0 ; 10 2
x 12x  3  b  0
Ta dựa vào hệ số bất định giả sử 2 2 2
4x  8x m na pb Suy ra n  ; 1 p   ;
4 m  5 nên có 2 2 2
4x  8x  5  a  4b
Thay vào PT đƣợc (a  2b  )( 1 a  2b  ) 2  0
PT có 4 nghiệm x   2 ; x  2   6
Thí dụ 13 Giải phƣơng trình 4 2
x  8x  5  2 8 2
x  33x  2  3 28 2
x 124x 1  0 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  8 2
x  33x  2 và 2 2
x  4x  3  28 2
x 124x 1
Cho 2 biểu thức bằng 0 suy ra 2 8 2
x  33x  2  28 2
x 124x 1 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x   2 8 33 2 28 124 1 1 Đặt 8 2
x  33x  2  a  0 ; 28 2
x 124x 1  b  0
Ta dựa vào hệ số bất định giả sử 2 2 2
4x  8x m na pb Suy ra n  ; 4 p   ;
1 m  5 nên có 2 2 2
4x  8x  5  4a b
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0
PT có 2 nghiệm x  2  3 ; x  2  9
Thí dụ 14 Giải phƣơng trình 6 2 2
x  2x 1  12 2
x 16x 13  4 2 x  8x  7 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2
x  2x 1 và 2 2
x  4x  5  12 2
x 16x 13
Cho 2 biểu thức bằng 0 suy ra 2 2 2
x  2x 1  12 2
x 16x 13 1  0 153
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    2 2 2 1 12 16 13 1 0 Đặt 8 2
x  33x  2  a  0 ; 28 2
x 124x 1  b  0
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0
PT có 2 nghiệm x  1  3 ; x  1   2
Thí dụ 15 Giải phƣơng trình 6 x 1 2
x  5  3 x 9 2
x 18x 14  20 2
x  45x  20
Hƣớng dẫn. (dùng máy tính dùng tính chất 2 A A )
Biểu thức cần tìm là 2
x x  2  x 1 2 x  5 và 3 2
x  3x 1 x 9 2
x 18x 14
Cho 2 biểu thức bằng 0 suy ra 3 x 1 2
x  5  x 9 2
x 18x 14  5  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x x   3 1 5 9 18 14 5 Đặt x 1 2
x  5  a  0 ; x 9 2
x 18x 14  b  0 Chú ý: 9 2 2 a b  4 2
x  90x  45 Thay vào PT đƣợc 3 ( a b  3 )( 5 a b  ) 1  0
PT có 2 nghiệm x  3   2 2
Thí dụ 16 Giải phƣơng trình 8 x 1 4 2
x 10  6 x 16 2
x  32x  26  30 2
x  80x  35
Hƣớng dẫn. (dùng máy tính dùng tính chất 2 A
A để mất dấu ||)
Biểu thức cần tìm là 2 2
x  2x  3  x 1 4 2 x 10 và 4 2
x  4x 1 x 16 2
x  32x  26
Cho 2 biểu thức bằng 0 suy ra 2 x 1 4 2
x 10  x 16 2
x  32x  26  5  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x x    2 1 4 10 16 32 26 5 0 154
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Đặt x 1 4 2
x 10  a  0 ; x 16 2
x  32x  26  b  0 Chú ý: 4 2 2 a b  30 2
x  80x  40
Thay vào PT đƣợc (2a b  )( 5 2a b  ) 1  0 4  3 2
PT có 2 nghiệm x  2
Thí dụ 17 Giải phƣơng trình 4 2
x  4x  5  2 10 2
x  6x  3  3 36 2
x  20x  5  0 Hƣớng dẫn.
Biểu thức cần tìm là 2
x x 1 10 2
x  6x  3 và 2 2
x  2x  3  36 2
x  20x  5
Cho 2 biểu thức bằng 0 suy ra 2 10 2
x  6x  3  36 2
x  20x  5 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    2 10 6 3 36 20 5 1 0 Đặt 10 2
x  6x  3  a  0 ; 36 2
x  20x  5  b  0 Tacó 4 2 2 a b  4 2
x  4x  7
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0 1  5  3  13
PT có 4 nghiệm x  ; x  2 2
Thí dụ 18 Giải phƣơng trình 8 2
x  4x 1 2 5 2
x x  2  3 12 2
x  8x 11  0 Hƣớng dẫn.
Biểu thức cần tìm là 2 2
x x 1 5 2
x x  2 và 4 2
x  2x 1 12 2 x  8x 11
Cho 2 biểu thức bằng 0 suy ra 2 5 2
x x  2  12 2
x  8x 11 1  0
suy ra nhân tử cần xuất hiện là: 2 5 2
x x  2  12 2
x  8x 11 1
Dùng casio giúp ta định hƣớng đƣợc PT đã cho có thể đƣa về PT tích. Cụ thể nhƣ sau 155
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Đặt 5x2  x  2  a ; 12x2  8x 11  b Tacó 4 2 2 a b  8 2
x  4x 1
Thay vào PT đƣợc (2a b  )( 1 2a b  ) 2  0 Giải PT 2 5 2
x x  2  12 2
x  8x 11 1  0 bằng cách chuyển vế,bình phƣơng 3
Hoặc tìm a,b theo x ta Suy ra PT có 2 nghiệm x  ; 1 3 x  4
Thí dụ 19 Giải phƣơng trình 8 2
x  20x  3  5 2
x  8x  3  3 2 x  3x  3 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x x  2  5 2 x  8x  3
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2 2
x  2x 1 8 2 x  20x  3 Đặt 5 2
x  8x  3  a  0 ; 8 2
x  20x  3  b  0 Suy ra 4 2 2 a b  12 2
x 12x 15
Pt đã cho có dạng (2a b  2 )( 3 a b  ) 1  0
PT đã cho có 2 nghiệm 3 x  ; 1 x  1   2
Thí dụ 20 Giải phƣơng trình (bài khó chỉ để tham khảo) 9 2 x  2 5 5x  2x   (4 2 2 x 1  ) 1 2 x x  1 3 2 2 x 1 1 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 3 ( 2 2 x   x   2 1 3 )( 1 2 2 1 ) 1
pt  5x  2x   (4 2 2 x 1  ) 1 2 x x  1 3 ( 2 2 2 x 1  ) 1 10 2
x  4x 1 3 2 2 x 1  ( 2 4 2 2 x 1  ) 1 2 x x 1
Tìm nghiệm đẹp x=-1 và x=-2,587401052 156
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x  2x  2  2 2 x 1 và 2
x  2x  3  2 2 x x 1 Suy ra 2 2
x x 1  2 2
x 1 1 là nhân tử cần xuất hiện pt  [2 2
x x 1  2 2 x 1  ][ 1 2 2
x x 1  3 2 2 x  ] 1  0 2  186
PTcó 4 nghiệm x  ; 1  x  1 3   4; x  14
Lƣu ý: +dùng hệ số bất định có 2 2 2 2 2
10x  4x 1  (2 x x  ) 1  ( 3 2x  ) 1
+dùng Casio nếu tìm đƣợc nghiệm là nghiệm pt bậc 2 vd X=1,117012978 dùng casio ta tinh ý thì
biết đƣợc điều sau 2 2
x x 1  3 2 2 x 1  0
Thí dụ 21 Giải phƣơng trình ( 2 x  2x  ) 1  4 2 x 11x  3 4  x  6 2 x 1 Hƣớng dẫn.
Dùng Casio nếu các bạn tìm đƣợc 2 nghiệm là nghiệm của PT bậc 2 có tổng,tích đẹp thì nó là pt: 2
x  2x 1  0 pt  ( 2 x  2x  ) 1  4 2
x 11x  3  ( 2 x  2x  )( 1 2 x  2x  ) 1  0
PT đã cho có 3 nghiệm 3 x  1
  2; x 1 3 Chú ý:
Nếu tìm 1nghiệm không là nghiệm bậc 2 thì cần tìm thêm nghiệm ngoại lai là 1
Thí dụ 22 Giải phƣơng trình
 2x 2x2 2 2x 6x5 4  x  4 Hƣớng dẫn.
Dùng Casio biểu thức cần tìm là 2 2
x  6x  5  ( 2 x  2x  ) 2 pt  ( 2 x  2x  ) 2 2 2
x  6x  5  ( 2 x  2x  )( 2 2 x  2x  ) 2  0
PT đã cho có 2 nghiệm 3 x   ; 1 x  1   2 157
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 23 Giải phƣơng trình 8 2
x  33x  2  2 6 2
x  29x 1  3 2 x  6x  4 Hƣớng dẫn.
Biểu thức cần tìm là 2
x  2x  2  8 2 x  33x  2 và 2
x  2x 1 6 2 x  29x 1 PTcó 2 nghiệm 3 x  ; 2 x  2   9 Nâng cấp
1) Giải phƣơng trình 2 2
x  4x  2  8 2
x  33x  2  3 6 2
x  29x 1  0 Hƣớng dẫn.
Ta dùng Casio tìm đƣợc các nghiệmcủa PT là x  ; 2 x  0080083823 , 0
Biểu thức cần tìm là 2
x  2x  2  8 2 x  33x  2 và 2
x  2x 1 6 2 x  29x 1
Cho 2 biểu thức bằng 0 suy ra 8 2
x  33x  2  6 2
x  29x 1 1  0
suy ra nhân tử cần xuất hiện là: 2 2 x x   x x    8 33 2 6 29 1 1 0 Đặt 8 2
x  33x  2  a  0 ; 6 2
x  29x 1  b  0 Tacó 2 2 a b  2 2
x  4x  3
Thay vào PT đƣợc (a b  )( 1 a b  ) 2  0 PTcó 2 nghiệm 3 x  ; 2 x  2   9
2) Giải phƣơng trình  2   x   3 6 2 x  29x 1 2
x  9x  32  xHƣớng dẫn. 158
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Biểu thức cần tìm là 2
x  2x 1 6 2 x  29x 1
Biểu thức nữa cần tìm là x 1 6 2 x  29x 1  2   x   3 6 2 x  29x 1 2
x  9x  32  x2  3x  2 6x2  29x 1  x3  9x2  32xx    2
x  2x 1 x   1 6 2
x  29x 1  (x  ) 1 3  9 2 x  29x 1   6 2
x  29x 1  ( 2 x  2x  ) 1  6 2
x  29x 1  x   1  0  27  769
PTcó 3 nghiệm x  ; 2 3 x  9  ; 2 x  10
Thí dụ 24 Giải phƣơng trình x x  2 7 2 2 16 3
2 3x  6x  5x  8x  3  3 2x 3x  4 Hƣớng dẫn. x x  2 7 2 2 16 3
2 3x  6x  5x  8x  3  3 2 x  3x  4 x x x x x x x x  2 2 3 2 2 6 5 2 8 32 3 2 6 5 2 8 3
 2 3x  6x  5x  8x  3  3 2 x  3x  4  2 3 2 x  6x  5 2
x  8x  3  0 hoặc 2 3 2 x  6x  5 2
x  8x  3  3 2 x  3x  4
Biểu thức cần tìm là x2  x 1 3x2  6x và 2
x x  2  5 2 x  8x  3  8  85
PTcó 4 nghiệm x  ; 1 x  1 3   2; x  7
Nâng cấp Giải phƣơng trình x  2 8 5
3x  6x x  3  2 x  2 159
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Hƣớng dẫn. ĐKXĐ… x  3
x x x  2 3 2 6 1 2 8 5
3x  6x x  3 
 3x  6x 2 x  2 2 x  2  ( 2
x x 11 x) 3 2 x  6x  3 2 x  6x  1 (  x)( 2 x x  ) 1   3 2 x  6 2
x x x   1  3 2 x 6
x x   1  0   3 4 3 2
PTcó 4 nghiệm x  ; 1 x  1   2; x  2
Pt trên để nhìn phức tạp hơn ta chuyển thành 2 2 x 12x  9 8x  5 Giải phƣơng trình: 2 2
x x x x  2 3 6 3 2 x  2 8x  5
Hay Giải phƣơng trình:
x x x  2 2 2 x  12x  9 3 6 3   3 4 3 2
PTcó 4 nghiệm x  ; 1 x  1   2; x  2
Thí dụ 25 Giải phƣơng trình 2 3 2
x  8x  2  16 2
x  4x 13  (2x  )( 1 2x  ) 3
Hƣớng dẫn. ĐKXĐ…… 2 3 2
x  8x  2  16 2
x  4x 13  (2x  )( 1 2x  ) 3 2 2  x x
  x x  2 3 8 2 16 4 13 2 3 2
x  8x  2  16 2
x  4x  132 3 2
x  8x  2  16 2
x  4x  13  7  2 3 2
x  8x  2  16 2
x  4x 13  0 hoặc 2 3 2
x  8x  2  16 2
x  4x 13  ( 7 *)
Biểu thức cần tìm là 2
x x 1 3 2 x  8x  2 và  2 2
x  2x  5  16 2 x  4x 13 160
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Có (2 3 2
x  8x  2)2  ( 16 2
x  4x 13)2  ( 7 2x  2 )( 1 x  ) 3 (**)
Để giải (*) ta kết hợp với (**) suy ra 2
x x 1  3 2
x  8x  2 và  2 2
x  2x  5  16 2
x  4x 13  3 1
PT đã cho có 3 nghiệm x   ;
1 x  1 4; x  2
Thí dụ 26 Giải phƣơng trình 2 2
x  4x  3  10 2
x  35x 11  3 8 2
x  31x  6  0 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2
x  2x  2  10 2 x  35x 11
Tƣơng tự,biểu thức liên hợp nữa cần tìm là 2
x  2x  3  10 2 x  35x 11 PT  [ 10 2
x  35x 11  8 2
x  31x  6  ][ 1 10 2
x  35x 11  8 2
x  31x  6  ] 2  0
PT có 2 nghiệm x  ; 2 3 x  7  2
Hƣớng dẫn một số cách hay dùng để tạo ra phƣơng
trình Tích(Vũ Hồng Phong THPT Tiên Du 1) Muốn có nghiệm 3 x  ;
2 x  3 cần có pt: (x  )( 2 3 x  ) 3 4  x  2 3
x  3x  6
Biểu thức liên hợp cần tìm là x2  x m A
Nếu cần biểu thức x2  x 1 A thì A  ( 2 x x  ) 1 2  (x  )( 2 3 x  ) 3  3 2 x  5x  7
Nếu cần biểu thức x2  x  2  B thì B  ( 2 x x  ) 2 2  (x  )( 2 3 x  ) 3  5 2 x  7x 10
Nếu cần biểu thức 2x2  2x 1 C thì C  (2 2 x  2x  ) 1 2  ( 4 x  )( 2 3 x  ) 3  8 2 x 16x  25 161
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nếu cần biểu thức 3x2  3x 1 D thì D  3 ( 2 x  3x  ) 1 2  ( 9 x  )( 2 3 x  ) 3  15 2
x  33x  55
Nếu cần biểu thức x2  x  4  E thì E  ( 2 x x  ) 4 2  (x  )( 2 3 x  ) 3  7 2
x  5x  22
Khi này dựa vào các biểu thức tạo ở trên các bạn thích tạo ra PT nhân liên hợp hay đƣa về
PT tích là tùy ý thích Chẳng hạn
Pt giải bằng nhân liên hợp 2 3 2
x  5x  7  5 2
x  7x 10  3 2 x  3x  4 3 2
x  5x  7  2 8 2
x 16x  25  5 2 x  5x  3 2 3 2
x  5x  7  15 2
x  33x  55  5 2 x  5x  3
Để tạo ra PT tích ta có thể làm theo hướng sau:
Ta nhận thấy từ cách tạo: 5 2
x  7x 10  3 2
x  5x  7 1  0 8 2
x 16x  25  2 3 2
x  5x  7 1  0  7 2
x  5x  22  3 2
x  5x  7  5  0
Ta tạo ra PT tích nhƣ sau a)[ 5 2
x  7x  10  3 2
x  5x  7  ][ 1 5 2
x  7x  10  3 2
x  5x  7  ] 2  0  2 2
x  2x 1  5 2
x  7x 10  3 3 2
x  5x  7  0 PT có 2 nghiệm 3 x  ; 2 x   3 )[ b 8 2
x 16x  25  2 3 2
x  5x  7  ][ 1 8 2
x 16x  25  2 3 2
x  5x  7  ] 2  0 2 2 2
 3 8x 16x  25  2 3x  5x  7  (2x  ) 1 162
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) PT có 2 nghiệm 3 x  ; 2 x   3 c)[  7 2
x  5x  22  3 2
x  5x  7  ][ 5  7 2
x  5x  22  3 2
x  5x  7]  0   7 2
x  5x  22  3 2
x  5x  7  2 2
x  2x  3 1  7
PT có 4 nghiệm x  ; 2 3
x   3; x  2
(nhƣ vậy ai cũng đều có khả năng tự tạo ra đƣợc các phƣơng trình tƣơng tự các PT trong bài viết này)
Một số phƣơng trình khác
Pt nhiều nhân tử,Pt liên hợp có bậc 1,bậc 2,….
1.Giải phƣơng trình ( 3 x  ) 2 3 (  x)( 2 x x  ) 1 4  x  4 3 x  6 2
x x  8
Nhân tử cần tìm là 2 x  1  3 (  x)( 2 x x  ) 1 ( 3 x  ) 2 3 (  x)( 2 x x  ) 1 4  x  4 3 x  6 2 x x  8  ( 2 x  3x  5 2  x  ) 1 3 (  x)( 2 x x  ) 1  3 (  x)( 2 x x  ) 1  ( 2 x  )( 1 2 x  3x  ) 5  0  [ 3 (  x)( 2 x x  ) 1  ( 2 x  )][ 1 3 (  x)( 2 x x  ) 1 2
x  3x  ] 5  0  [ 3 (  x)( 2 x x  ) 1  ( 2 x  )][ 1 3 (  x)( 2 x x  ) 1 2
x x 1 3 ( 2  x)]  0  [ 3 (  x)( 2 x x  ) 1  ( 2 x  )][ 1 2
x x  1  3  x][ 2
x x  1  2 3  x]  0
Pt có 4 nghiệm x   ; 1 3 x  2; x  1   3
2.Giải phƣơng trình
7x2  2  (x2  ) 1
4x  6  x3  3x2  x  3
HD:đkxđ x
x  2  0 2 163
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
7x2  2  (x2  ) 1
4x  6  x3  3x2  x  [ 7 2 x  2 2  x  ] 2  ( 2 x  )[ 1
4x  6  x  ] 2  0
Nhân liên hợp suy ra Pt có 4 nghiệm x   ;
1 x   2
2.Giải phƣơng trình
7x2  2  (x2  ) 1
4x  6  x3  3x2  x  3
HD:đkxđ x
x  2  0 2
7x2  2  (x2  ) 1
4x  6  x3  3x2  x  [ 7 2 x  2 2  x  ] 2  ( 2 x  )[ 1
4x  6  x  ] 2  0
Nhân liên hợp suy ra Pt có 4 nghiệm x   ;
1 x   2
Thí dụ 3 Giải phƣơng trình 11 2 x  3  ( 2 x  ) 2 4x  7 3  x  3 2 x  2x 1 Hƣớng dẫn. 11 2 x  3  ( 2 x  ) 2 4x  7 3  x  3 2 x  2x 1  2 2 2 7
 [ 11x  3  x  ] 3  (x  )[ 2
4x  7  x  ] 2  ( 0 đk : x  ) 4
Nhân liên hợp suy ra PT có 4 nghiệm x   2; x   3
Thí dụ 4 Giải phƣơng trình 19x2  6  ( 2 x2  ) 1
3x  3  2x3  5x2  2x Hƣớng dẫn. 19x2  6  ( 2 x2  ) 1
3x  3  2x3  5x2  2x [ 19 2 x  6  2 2 x  ] 3  ( 2 x  )[
1 2 3x  3  2x  ] 3  (
0 đk : x   ) 1 164
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 3
Nhân liên hợp suy ra PT có 4 nghiệm x   ; 1 x   2
Thí dụ 5 Giải phƣơng trình 5 2 x  6  ( 2 x  ) 1 4x  6 3  x  3 2 x x  4
Hƣớng dẫn. đk: x    x   1 2 0 5 2 x  6  ( 2 x  ) 1 4x  6 3  x  3 2 x x  4  [ 5 2 x  6 2  x  ] 2  ( 2 x  )( 1
4x  6  x  ) 2  0
Nhân liên hợp suy ra PT có 2 nghiệm x   2
Chú ý:Tìm biểu thức liên hợp 4x  6  x  2
từ đó suy đoán biểu thức liên hợp 5 2 x  6 2  x  2
Thí dụ 6 Giải phƣơng trình 3  3 2 x  ( 2 x  ) 2 8x  5  2 3 x  4 2 x  4x  5
Hƣớng dẫn. đk:   x   x   1 1 1 0 3  3 2 x  ( 2 x  ) 2 8x  5  2 3 x  4 2 x  4x  5  [ 33 2 x  2 2 x  ] 1  ( 2 x  )( 2
8x  5  x  ) 1  0 1
Nhân liên hợp suy ra PT có 2 nghiệm x   2
Thí dụ 7 Giải phƣơng trình 3
x  2x  3  3  3 2 x  ( 2 x  ) 2 5 2 x  4x  3
Hƣớng dẫn. đk:   x   x   1 1 2 0 3
x  2x  3  3  3 2 x  ( 2 x  ) 2 5 2 x  4x  3  [ 33 2 x  2 2 x  ] 1  ( 2 x  )[ 2 x  2  5 2
x  4x  3]  0 165
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1
Nhân liên hợp suy ra PT có 2 nghiệm x   2
Thí dụ 8 Giải phƣơng trình 11 2 x  5  ( 2 x  ) 4 4x  5 3  x  3 2 x  4x  5 Hƣớ 5
ng dẫn. đk: x    x   2 0 4 11 2 x  5  ( 2 x  ) 4 4x  5 3  x  3 2 x  4x  5  [ 11 2 x  5 2  x  ] 3  ( 2 x  )[ 4
4x  5  x  ] 2  0
Nhân liên hợp suy ra PT có 3 nghiệm x   ; 1 x  2
Thí dụ 9 Giải phƣơng trình 13 2 x  12  ( 2 x  ) 1 6x  13 3  x  4 2 x x  1 Hƣớ 13
ng dẫn. đk: x    x   3 0 6 13 2 x  12  ( 2 x  ) 1 6x  13 3  x  4 2 x x  1  [ 13 2 x 12 2  x  ] 4  ( 2 x  )[ 1
6x 13  x  ] 3  0
Nhân liên hợp suy ra PT có 4 nghiệm x   ; 1 x  2 
Thí dụ 10 Giải phƣơng trình 6 2
x  6x  4  ( 2
x  2x) 4x  5 3 2
x x 5x  2 Hƣớng dẫn. đk: 5 x    x   2 0 4 6 2
x  6x  4  ( 2
x  2x) 4x  5 3 2
x x 5x  2  [ 6 2 x  6x  4 2
x x  ] 2  ( 2
x  2x)( 4x  5  x  ] 2  0
Nhân liên hợp suy ra PT có 4 nghiệm x   ; 1 x  ; 0 x  2 166
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 11 Giải phƣơng trình 8 2
x  8x  1  ( 2
x  2x) 10x  6 3  x  6 2 x  5x  1 Hƣớ 5
ng dẫn. đk: x    x   3 0 3 8 2
x  8x  1  ( 2
x  2x) 10x  6 3  x  6 2 x  5x  1  [ 8 2 x  8x 1 2
x x  ] 1  ( 2
x  2x)[ 10x  6  x  ] 3  0
Nhân liên hợp suy ra PT có 3 nghiệm x  ; 0 x  ; 1 x  3
Thí dụ 12 Giải phƣơng trình 5 2
x  2x  (x  ) 2 3 3 2
x  3x 1  2 2 x  4x  4 Hƣớng dẫn. 5 2
x  2x  (x  ) 2 3 3 2
x  3x 1  2 2 x  4x  4  [ 5 2 x  2 2
x x x  ] 2  (x  )[ 2 3 3 2
x  3x 1  x  ] 1  0
Nhân liên hợp suy ra PT có 2 nghiệm 3 x   ; 2 x   2
Thí dụ 13 Giải phƣơng trình 5 2
x  2x  (x  ) 2 3 3 x  1 2
x  2x  4 Hƣớng dẫn. 5 2
x  2x  (x  ) 2 3 3 x  1 2
x  2x  4  [ 5 2 x  2 2
x x x  ] 2  (x  1 )[ 2 3 3  x  ] 1  0
Nhân liên hợp suy ra PT có 2 nghiệm 3 x   ; 2 x   2
Thí dụ 14 Giải phƣơng trình 2 3 3 2
5x  2x  (x  ) 2 x  3  x Hƣớng dẫn. 167
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 3 3 2
5x  2x  (x  ) 2 x  3  x  5 2 x  2 2
x x x  2  (x  1 )[ 2 3 3  x  3]  0
Nhân liên hợp suy ra PT có 2 nghiệm 3 x   ; 2 x   2
Thí dụ 15 Giải phƣơng trình 5 2
x  2x  (x  ) 2 3 3 x 10 2
x x  2 Hƣớng dẫn. 5 2
x  2x  (x  ) 2 3 3 x 10 2
x x  2  [ 5 2 x  2 2
x x x  ] 2  (x  )[ 2 3 3 x  10  ] 2  0
Nhân liên hợp suy ra PT có 2 nghiệm 3 x   ; 2 x   2
Thí dụ 16 Giải phƣơng trình 5 2
x  2x  (x  ) 2 3 3 x  6 2
x  3x  6 Hƣớng dẫn. 5 2
x  2x  (x  ) 2 3 3 x  6 2
x  3x  6  [ 5 2 x  2 2
x x x  ] 2  (x  )[ 2 2 3 3  x  6]  0
Nhân liên hợp suy ra PT có 2 nghiệm 3 x   ; 2 x   2
Thí dụ 17 Giải phƣơng trình 7 2
x 10x 1  .3 2 x
x  7x  9  2 2 x  2x 1 Hƣớng dẫn. 7 2
x 10x 1  .3 2 x
x  7x  9  2 2 x  2x 1  [ 7 2 x  10x  1 2
x x  ] 1  [3 2 x
x  7x  9  x  ] 1  0
Nhân liên hợp suy ra PT có 2 nghiệm x   ; 2 x  ; 2 x  0 168
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 18 Giải phƣơng trình 11 2
x  6x  4  (x  ) 1 3 12 2
x  10x  1  4 2 x  2x  1 Hƣớng dẫn. 11 2
x  6x  4  (x  ) 1 3 12 2
x  10x  1  4 2
x  2x  1 [ 11 2
x  6x  4  2 2 x x  ] 2  (x  )[ 1 3 12 2
x 10x 1  2x  ] 1  0 1
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 1 x   . 2
Thí dụ 19 Giải phƣơng trình 11 2
x  6x  4  (x  ) 1 3 2 3
x x 1  2 2 x  2x  3 Hƣớng dẫn. 11 2
x  6x  4  (x  ) 1 3 2 3
x x 1  2 2
x  2x  3  [ 11 2
x  6x  4  2 2 x x  ] 2  (x  1 )[ 1 3  2 3 x x  ] 1  0 1
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 1 x   . 2
Thí dụ 20 Giải phƣơng trình 11 2
x  6x  4  (x  ) 1 3 2 3
x x 1  2 2 x  1 Hƣớng dẫn. 11 2
x  6x  4  (x  ) 1 3 2 3
x x 1  2 2 x  1 [ 11 2
x  6x  4  2 2 x x  ] 2  (x  1 )[ 1 3  2 3 x x  ] 1  0 1
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 1 x   . 2
Thí dụ 21 Giải phƣơng trình 10 2 x  6  ( 2 x  ) 1 4x  7  ( 2 x  ) 3 2 2
x  4x  3 1 2 x  2x  7 169
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Hƣớng dẫn. 10 2 x  6  ( 2 x  ) 1 4x  7  ( 2 x  ) 3 2 2
x  4x  3 1 2 x  2x  7  10 2 x  6 2  x 3  2 x  
1  4x  7  x  2 ( 2 x  ) 3  2 2
x  4x  3  x   3  0
Nhân liên hợp suy ra PT có 4 nghiệm x   ; 1 x   3 .
Thí dụ 22 Giải phƣơng trình 5 2
x  6x  1  (x  ) 2 3 3 2
x  5x  1  2 2 x  2x 1 Hƣớng dẫn. 5 2
x  6x  1  (x  ) 2 3 3 2
x  5x  1  2 2
x  2x 1 [ 5 2 x  6x 1 2
x x  ] 1  (x  )[ 2 3 3 2
x  5x 1  x  ] 1  0
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 2 x   2 .
Thí dụ 23 Giải phƣơng trình 5 2
x  6x 1  .3 2
x x  5x  5  2 2 x  2x 1 Hƣớng dẫn. 5 2
x  6x 1  .3 2
x x  5x  5  2 2
x  2x 1  5 2 x  6x  1 2
x x 1 .[3 2 x
x  5x  5  x  ] 1  0
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 2 x   2 .
Thí dụ 24 Giải phƣơng trình 5 2
x  6x  1  .3 x 5 2
x  5x  3  2 2 x  1 Hƣớng dẫn. 5 2
x  6x  1  .3 x 5 2
x  5x  3  2 2 x  1  [ 5 2 x  6x  1 2
x x  ] 1  [3 x 5 2
x  5x  3  x  ] 1  0 170
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nhân liên hợp suy ra PT có 4 nghiệm x  ; 0 x  ; 2 x   2 .
Thí dụ 25 Giải phƣơng trình 5 2
x  6x  1  3  (x  ) 2 3 2 x x  1 Hƣớng dẫn. 5 2
x  6x  1  3  (x  ) 2 3 2
x x  1 5 2 x  6x  1 2
x x 1 (x  )[ 2 3 2
x x  1  x  ] 1  0
Nhân liên hợp và kiểm tra đkxđ suy ra PT có 3 nghiệm x  ; 0 x  ; 2 x  2 .
Thí dụ 26 Giải phƣơng trình x  5  5 2
x  6x  1  (x  ) 2 3 2
x x  2x  4 Hƣớng dẫn. x  5  5 2
x  6x  1  (x  ) 2 3 2
x x  2x  4 [ 5 2 x  6x 1 2
x x  ] 1  (x  )[ 2 3 2
x x  2x  4  x  ] 2  0
Nhân liên hợp và kiểm tra đkxđ suy ra PT có 4 nghiệm x  ; 0 x  ; 2 x   2 .
Thí dụ 27 Giải phƣơng trình 2 x  4 ( 2 x  )( 4 x  ) 3 2   x  3 1 12 2 x 1 1 4x  6 Hƣớng dẫn. 2 x  4 ( 2 x  )( 4 x  ) 3 2   x  3 1 12 2 x 1 1 4x  6 2 x  4 ( 2 x  )( 4 x  ) 3  1  ( 2 x  ) 4  0 1  12 2 x  1 1  4x  6 2 x  3  12 2 x  1 ( 2 x  )( 4 x  2  4x  6)    0 1  12 2 x  1 1  4x  6 171
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 3 nghiệm x  ,
2 x   2; x  2 .
Thí dụ 28 Giải phƣơng trình 2 3 2 x x  2
x  3x x  3 2   x 2 x  7x  2 1  4x  6 Hƣớng dẫn. 2 3 2 x x  2
x  3x x  3 2   x 2 x  7x  2 1  4x  6 2 2 x x  2 (x  )( 1 x  ) 3 2    x 2 x  7x  2 1  4x  6 2 x x  2 ( 2 x  )( 1 x  ) 3  1  ( 2 x  ) 1  0 x  7 2 x  2 1 4x  6 2 x  2  7 2 x  2 ( 2 x  )(
1 x  2  4x  6)    0 x  7 2 x  2 1 4x  6
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm x   , 1 x   2 .
Thí dụ 29 Giải phƣơng trình 2 x 1 ( 2 x  )( 4 x  ) 4 2   x  3 8 2
x  8x  9  x  2 1 6x 10 Hƣớng dẫn. 2 x 1 ( 2 x  )( 4 x  ) 4 2   x  3 8 2
x  8x  9  x  2 1 6x 10 2 x  1 ( 2 x  )( 4 x  ) 4  1  ( 2 x  ) 4  0 8 2
x  8x  9  x  2 1  6x  10 2 x  3  8 2 x  8x  9 ( 2 x  )(
4 x  3  6x  10)    0 x  2  8 2 x  8x  9 1  6x  10
Nhân liên hợp và đối chiếu ĐKXĐ
suy ra PT có 3 nghiệm x   , 1 x  2 . 172
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Thí dụ 30 Giải phƣơng trình 2 2 x  2
(x  2x)(x  ) 3 2   (x  ) 1 2
6x  6x  4  x 1  4x  5 Hƣớng dẫn. 2 2 x  2
(x  2x)(x  ) 3 2   (x  ) 1 2
6x  6x  4  x 1  4x  5 2 x  2 ( 2
x  2x)(x  ) 3  1  ( 2 x  2x)  0 6 2
x  6x  4  x 1  4x  5 2
x x  1  6 2 x  6x  4 ( 2
x  2x)(x  2  4x  5)    0 6 2
x  6x  4  x 1  4x  5
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm x   , 1 x  ; 0 x  2 .
Thí dụ 31 Giải phƣơng trình 2 x  3 2 2 x  2 2  x  2  1 7 2 x  2 2 x  2 Hƣớng dẫn. 2 x  3 2 2 x  2 2  x  2  1 7 2 x  2 2 x  2 2 x  3 2 2 x  2 2  1 x 1 1  7 2 x  2 2 x  2 2 x  2  7 2 x  2 2 x   2 2 2   (x  ) 1  0 1 7 2 x  2 2 x  2
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm x   , 1 x   2 .
Thí dụ 32 Giải phƣơng trình(Vũ Hồng Phong THPT Tiên Du 1) 2 x  2 4 2 x  2 1  2x 1  2  17 2 x  2 2 x  2 Hƣớng dẫn. 173
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 x  2 4 2 x  2 1  2x 1  2  17 2 x  2 2 x  2 2 x  2 1 4 2 x 1 4 2 x 1      0 2  x  2 2 2 17 2 2 x  2 2 2 x  2  17 2 x  2 (4 2 x  )( 1 2 x  2  ) 2    0 ( 2 2  17 2 x  2) 2 2 x  2 1
Nhân liên hợp và đối chiếu ĐKXĐ suy ra PT có 4 nghiệm x   , x   2 . 2
Thí dụ 33 Giải phƣơng trình 8x 17 x  6   5 2 x 1 2 x x  3 Hƣớng dẫn. 8x 17 x  6   5 2 x 1 2 x x  3  5 2 x 1 ( 2
x 1 x  ) 2 5 2 x 1  ( 2 x  )( 1 x  ) 2  0  [ 5 2 x 1  ( 2 x  )][ 1 5 2
x 1  (x  )] 2  0 
PT đã cho có 6 nghiệ 1 6 m x   ;
1 x   2; x 2
Để PT đã cho nhìn phức tạp hơn ta chuyển vế ,nhân liên hợp để đƣa về các PT sau: 8x 17 ( 5 2 x  ) 1 x  4   2 x x  3 2  5 2 x 1 8x  17 5 2
x  2x 13  (x  ) 4 5 2 x  1    0 2 x x  3 2  5 2 x 1
Thí dụ 34 Giải phƣơng trình 6 2 x  ( 2 x  ) 1 2x 1  5 2 x 1 2
x  2x 1  2 Hƣớng dẫn. 174
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 6 2 x  ( 2 x  ) 1 2x 1  5 2 x 1  6 2 x   2 x   1 2x 1   2
x  2x 1  2 5 2 x 1 2
x  2x 1  2  ( 5 2 x 1 2  x  )( 1 5 2
x 1  2x 1  ) 1  0 x   x
. PT đã cho có 4 nghiệm ; 1  2
Thí dụ 35 Giải phƣơng trình 2 x x   x  2 1  2 21 4 5 x  3   2 x   x  3 7 2 1  Hƣớ 5
ng dẫn. ĐK: x 4 2 x x   x  2 1  2 21 4 5 x  3   2 x   x  3 7 2 1 2 x  1
 2x   x  2 21 4 5   1 x  2  2 x   x  3 7 2 1 2 x  2  7 2 x  2
 2x 2x2 4x5    0 2 x   x  3 7 2 1
Nhân liên hợp và đối chiếu điều kiện suy ra PT có 3 nghiệm x   ; 1 x  2 .
Thí dụ 36 Giải phƣơng trình 3 x  2x  7 2 x  2 2 x  2  2 7 2 x  2  2
x  1  x 5 2 x  1 2 2 x  2  5 2 x  1 Hƣớng dẫn.
Xem phần tạo ra PT Tích từ các biểu thức a  7 2 x  2; 2 b x  ; 2 2 c x  ; 1 d  5 2 x 1 m  ; 1 n  ; x p  ; 2 q  1 3 x  2x  7 2 x  2 2 x  2  2 7 2 x  2  2 x 1 x 5 2 x 1 2 2 x  2  5 2 x 1 175
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 5 2 x  1 2 x  2    2 1 0 hoặc x 2 x  1 7 2 x 2 2 5 2 x 1 2 x  2 1  11
 0 hoặc x  2 x 1 7 2 x 2 2 1
Nhân liên hợp suy ra PT đã cho có 5 nghiệm: x   ;
1 x   2; x 2
Thí dụ 37 Giải phƣơng trình (2x  ) 6 7 2 x  2  3 (  x) 16 2 x  7  12 2 x  3x 15 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2 x  2  7 2 x  2 và 2 2 x  1  16 2 x  7 (2x  ) 6 7 2 x  2  3 (  x) 16 2 x  7  12 2 x  3x 15  (2 7 2 x  2  16 2 x  7  )( 3 2 7 2 x  2  16 2
x  7  x)  0
PTcó 4 nghiệm x   ; 1 x   2 Chú ý: 2 7 2
x  2  x  2 7 2
x x x x  0
Thí dụ 38 Giải phƣơng trình (2x  ) 6 8 2
x  1  (x  ) 3 20 2 x 11  12 2
x  3x  15  0 Hƣớng dẫn.
Biểu thức liên hợp cần tìm là 2 x  2  8 2 x  1 và 2 2 x  1  20 2 x 11 (2x  ) 6 8 2
x  1  (x  ) 3 20 2 x 11  12 2
x  3x  15  0  (2 8 2 x 1  20 2 x 11  )( 3 2 8 2 x 1  20 2
x 11  x)  0 176
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
PTcó 4 nghiệm x   ; 1 x   3 Chú ý: 2 8 2
x 1  x  2 8 2
x x x x  0
Thí dụ 39 Giải phƣơng trình 3 5 2 x  6x  8 2 2 x 1  1 3 2 x  4x  5 2 x x  2 3 2
x  4x  5  (x  ) 2 3 2 x  4x  5 Hƣớng dẫn. 3 5 2 x  6x  8 2 2 x 1  1 3 2
x  4x  5 2 x x  2 3 2
x  4x  5  (x  ) 2 3 2 x  4x  5 3 5 2 x  6x  8
 3 2x 4x5  x2 3 2x 4x5 x2 2     x x  2 x x  2 3 2
x  4x  5x  2  3 2
x  4x  5 1 3 4 5 3 5 2 x  6x  8
 3 2x 4x5x2   1 3 2 x  4x  5 2 x x  2 3 2 x  4x  5 3 5 2 x  6x  8 2    x 1   1 3 2 x  4x  5 2 x x  2 3 2 x  4x  5 3 5 2 x  6x  8 2    x  3 2 x  4x  5 2 x x  2 3 2 x  4x  5 3 5 2 x  6x  8 ( 3 2 x x  ) 1   2 x x  2 3 2 x  4x  5 5 2 x  6x  8 2 x x 1   2 x x  2 3 2 x  4x  5 5 2 x  6x  8 2 x x  1  11  0 2 x x  2 3 2 x  4x  5 5 2
x  6x  8  ( 2 x x  ) 2 3 2
x  4x  5  ( 2 x x  ) 1    0 2 x x  2 3 2 x  4x  5
Nhân liên hợp suy ra PT có 2 nghiệm là 3 x  ; 2 x   3 177
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 5 2 x  6x  8 2 x x  1
Nhận xét:Thí dụ 39 Xuất phát là Giải phƣơng trình  2 x x  2 3 2 x  4x  5 Thí dụ 40 Xuất phát từ phƣơng trình ( 3 2 x  4x  5 2
x x  )( 1 3 2
x  4x  5  2x)  0  ( 2 x x  ) 1 ` 3 2
x  4x  5  2 3 2
x x  2x  5
x x x  2 2 3 2 2 5
 3x  4x  5  2 x x 1  x 2 6 3
 3x  4x  5  2x 1 (*) 2 x x  1
Để ngụy trang tiếp PT(*) ta có một số hƣớng sau: hƣớ x 2 6 3
ng 1 (*)  3x  4x  5  (x  ) 2  x 1 2 x x 1 2 2 x 1 6  3    x x 1
(ở đây ta đã nhân liên hợp để ngụy trang) 2 2 x   x x x x 1 2 3 4 5  hƣớ x 2 6 3
ng 2 (*)  2x 1  3x  4x  5   0 2 x x  1 2 x  4 6  3   x
 0 (ở đây ta đã nhân liên hợp để ngụy trang) 2 2 x   x x x x  1 2 1 3 4 5 x  2 3   2 2 x   x x x x 1 2 1 3 4 5
(ở đây ta bỏ bớt 1 nhân tử có chứa nghiệm PT ban đầu)
Thí dụ 40 Giải phƣơng trình 2 2 x  1 6  3x a)  x 1 2 2 x   x x x x  1 2 3 4 5
PT có 3 nghiệm là x  ; 2 3
x   2; x  1 178
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x  2 3 b)  2 2 x   x x x x 1 2 1 3 4 5 PT có 2 nghiệm là 3
x   2; x  1 Thí dụ 41 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  )( 1 x 5 2 x 1 2  x  ) 1  0
 (x3  x x2  ) 1 `
5x2 1  (x2  2 ) 1  5x3  x  (x  )( 1 x2  ) 1 `
5x2 1  (x2  2 ) 1  5x3  x x x 2 2 5 3  (x  ) 1
5x 1  x 1 2 x 1 x x 2 2 5 3
Giải phƣơng trình (x  ) 1
5x  1  x  1  2 x  1
Chú ý: giải phƣơng trình x 5 2 x 1 2  x 1  0 x  0  x 5 2 x 1 2  x 1    x 1 2 x 5 ( 2 x  ) 1  ( 2 x  ) 1 2
PT có 4 nghiệm là x   ; 1 x   2 Thí dụ 42 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  )( 1 x 5 2 x 1 2  x  ) 2  0  ( 3 2
x x x  ) 2 ` 5 2 x 1  5 3 x x  ( 2 x  )( 1 2 x  ) 2  ( 2 x  )( 1 x  ) 1 ` 5 2 x 1  5 2 x 1  5 3 x x  ( 2 x  )( 1 2 x  ) 2 x x x  2 5 3 2 5 2 1  (x  ) 1
5x 1  x  2  2 x 1 179
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) phƣơng trình ( 5 2 x 1 2  x  )( 1 x 5 2 x 1 2  x  ) 2  0  ( 3 2
x x x  ) 2 ` 5 2 x 1 4  x  5 3 x  3 2 x x  2 2 2 x  7x  6   x  4  5 2 x 1 3 2
x x x  2
Thí dụ 42 Giải phƣơng trình(Vũ Hồng Phong) 2 2 x  7x  6 a)  x  4  5 2 x 1 3 2
x x x  2 5  89
PT có 5 nghiệm là x   ;
1 x   2; x  8 x x x  2 5 3 2 5 2 1 b)(x  ) 1
5x 1  x  2  2 x  1 5  89
PT có 5 nghiệm là x   ;
1 x   2; x  8
Chú ý: giải phƣơng trình x 5 2 x 1 2  x  2  0 x  0  2 2 5 89
x 5x 1  x  2    x  2 x 5 ( 2 x  ) 1  ( 2 x  ) 2 2 8 Thí dụ 43 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  )( 1 5 2
x 1  x)  0  ( 2 x x  ) 1 ` 5 2 x 1 3  x  5 2 x x 1 4x2  
1  5x2 1 x x2  x 1 4 2  Thí dụ 43 x 1 giải phƣơng trình
 5x2 1  x x2  x 1 180
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1
PT có 5 nghiệm là x   ;
1 x   2; x  2
Nhƣ vậy việc tạo ra đƣợc một phƣơng trình TÍCH là không quá khó khăn và có nhiều cách
để tạo ra. Xin giới thiệu tiếp cách tạo ra PT Tích dạng phức tạp hơn Thí dụ 44 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  )( 1 5 2 x 1  8 2
x 1  3x)  0  ( 2 x  3x  ) 1 ` 5 2 x 1   2 x 1 5 2 x 1 8 2 x 1  3 3 x  5 2
x  3x 1 1
PT có 5 nghiệm là x   ;
1 x   2; x  2
Giải phƣơng trình 5 2 x 1  8 2
x 1  3x  0
Ngoài cách chuyển -3x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau 5 2 x 1  8 2
x 1  3x  0  5 2 x 1  5 2 x 1  3 2 x  3x  0
đặt ẩn phụ 5x2 1  a;b x Thí dụ 45 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  3 )( 1 5 2 x 1  8 2
x 1  x)  0  3 ( 2 x x  ) 3 ` 5 2 x 1   2 x  1  5 2 x 1 8 2 x 1 3  x 15 2
x x  3
Ta có Giải phƣơng trình 3 ( 2 x x  ) 3 ` 5 2 x 1   2 x 1 5 2 x 1 8 2 x 1 3  x 15 2 x x  3 1  4
PT có 6 nghiệm là x   ;
1 x   2; x  ; x  2 79
Giải phƣơng trình 3 5 2 x 1  8 2
x 1  x  0
Ngoài cách chuyển -x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau 181
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 3 5 2 x 1  8 2
x 1  x  0  3 5 2 x 1  5 2 x 1 3 2 x x  0
đặt ẩn phụ 5x2 1  a;b x Thí dụ 46 Xuất phát từ phƣơng trình ( 5 2 x 1 2  x  3 )( 1 5 2 x 1  9 2
x 1  x)  0  3 ( 2 x x  ) 3 ` 5 2 x 1   2 x  1  5 2 x 1 8 2 x 1 3  x 15 2
x x  3
Ta có Giải phƣơng trình 3 ( 2 x x  ) 3 ` 5 2 x 1   2 x  1  5 2 x 1 9 2 x 1 3  x 15 2 x x  3 139 ( 2  3 33)
PT có 6 nghiệm là x   ;
1 x   2; x   1189
Giải phƣơng trình 3 5 2 x 1  8 2
x 1  x  0
Ngoài cách chuyển -x rồi bình phƣơng thì còn cách đặt ẩn phụ. Cụ thể nhƣ sau 3 5 2 x 1  9 2
x 1  x  0  3 5 2 x 1  5 ( 2 2 x  ) 1 2
x x  0
đặt ẩn phụ 5x2 1  a;b x Thí dụ 47
Xuất phát từ PT (x  )( 2 x3  ) 2  0
Tạo ra biểu thức x2  x  1 
A và biểu thức x2  x  2  B
Nhƣ sau: A  ( 2 x x  ) 1 2  (x  )( 2 3 x  ) 2  3 2
x  4x  5 B  ( 2 x x  ) 2 2  (x  )( 2 3 x  ) 2  5 2 x  6x  8 1 1 Suy ra có PT mà ứng với vế bên kia PT 2 3 2
x  4x  5  x 1 x 1  1 ứng với vế bên kia PT 2 5 2
x  6x  8  x  2 x 182
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 1 1 2 có thể tạo ra PT   2 2 2 3x
4x  5  x 1
5x  6x  8   2 x x
nhân liên hợp ta đƣợc PT cần tạo ra nhƣ sau: 2 2
3x  4x  5  x 1
5x  6x  8  x  2 2   2 2 2 2x  2x  4 4x  2x  4 x 2 2
3x  4x  5  x  1
5x  6x  8  x  2 4
Ta có Giải phƣơng trình   2 2 2 x x  2 2x x  2 x PT có 2 nghiệm 3 x  ; 2 x   2 1 2 3 có thể tạo ra PT   2 2 2 3x
4x  5  x 1
5x  6x  8   2 x x 2 2         Tƣơng tự 3x 4x 5 x 1 5x 6x 8 x 2 3
ta có Giải phƣơng trình   2 2 2 2x  2x  4 2x x  2 x PT có 2 nghiệm 3 x  ; 2 x   2 Thí dụ 48 2 3 x  2x  3
Xuất phát từ PT (x  )( 2 x3  ) 2  0 2   x 1 2 x 1
Biểu thức liên hợp đã biết 2
x x 1 3 2
x  4x  5 2 3 x x  2 2 3
Ta có thể tạo ra PT 3x  4x  5 2   x x 1 2  x 1 2 x 1 2 3 x x  2 2 3
 3x  4x  5  x 1 2 2   x x 1 2 x  1 2 2 x  2x  4 2 3 x  2x  3 2 2  
x x 1 2 2 x x   x x  1 3 4 5 1 2 2 x  2x  4 2 3 x  2x  3
Ta có Giải phƣơng trình 2 2 
x x 1 2 2 x x   x x  1 3 4 5 1 PT có 2 nghiệm 3 x  ; 2 x   2 183
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Thí dụ 49
Xuất phát từ PT (x  )( 2 x3  ) 2  0
Tạo ra biểu thức x2  x  1 
A và biểu thức x2  x  2  B
Nhƣ sau: A  ( 2 x x  ) 1 2  (x  )( 2 3 x  ) 2  3 2
x  4x  5 B  ( 2 x x  ) 2 2  (x  )( 2 3 x  ) 2  5 2
x  6x  8
Nếu muốn kết hợp Nhị thức NiuTơn suy ra (x  ) 1 5  (x  ) 1 5  2x( 4 x 10 2 x  ) 5  5
x2  1  5x2  6x  8  x2  2  3x2  4x  5
Ta có Giải phƣơng trình  2x
x4  10x2  5 Hƣớng dẫn giải:  5
x2  1  5x2  6x  8  x2  2  3x2  4x  5  2x
x4  10x2  5
Bấm máy tính tìm đƣợc X X  ; 2  , 1 25992105
Các biểu thức cần xuất hiện 2
x x  1  3 2
x  4x  5 ; 2
x x  2  5 2
x  6x  8 Suy ra 2 x  1  5 2
x  6x  8  x 1 ; 2 x  2  3 2
x  4x  5  x  1 PT  ( 2 x 1 5 2
x  6x  8)5  ( 2 x  2  3 2
x  4x  5)5  2x( 4 x 10 2 x  ) 5 2 2 5 2 2 5 5 5
 (x 1 5x  6x  8)  (x  2  3x  4x  5)  (x  ) 1  (x  ) 1  ( 2 x 1 5 2
x  6x  8)5  (x  ) 1 5  ( 2 x  2  3 2
x  4x  5)5  (x  ) 1 5  0
Sử dụng hằng đẳng thức rồi nhân liên hợp suy ra PT đã cho có 2 nghiệm 3 x  ; 2 x   2 Thí dụ 50
Xuất phát từ PT (x  )( 2 x3  ) 2  0
Tạo ra biểu thức x2  x  1 
A và biểu thức x2  x  2  B
Nhƣ sau: A  ( 2 x x  ) 1 2  (x  )( 2 3 x  ) 2  3 2
x  4x  5 184
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) B  ( 2 x x  ) 2 2  (x  )( 2 3 x  ) 2  5 2
x  6x  8
Các biểu thức cần xuất hiện 2
x x  1  3 2
x  4x  5 ; 2
x x  2  5 2
x  6x  8
Để PT có căn trong căn thì từ trên ta Suy ra 2
x x  2  3 2
x  4x  5  1 2
x x  2  3 2 x  4x  5 1
Ta có Giải phƣơng trình 5 2 x  6x  8 2 x x  2 Hƣớng dẫn giải: 2
x x  2  3 2 x  4x  5 1  5 2 x  6x  8 2 x x  2 x x  2 5 2 2 6 8
x x  2  3x  4x  5  2 x x  2 x x  2 5 2 2 6 8
x x  2  3x  4x  5 1  1 2 x x  2 2 x x   x x  2 2 2 5 2 6 8
 [ x x  2  3x  4x  5  ] 1   0 2 x x  2
Nhân liên hợp 2 lần ở biểu thức đầu,1 lân ở phân thức sau suy ra PT có 2 nghiệm 3 x  ; 2 x   2
Để PT có dấu giá trị tuyệt đối cũng không khó khăn gì. Ta có 2 2
x x  2  3 2
x  4x  5  2 2
x x  2  ( 2 x x  ) 1  x  1 2 2
x x  2  3 2 x  4x  5 x  1 Giải phƣơng trình  5 2 x  6x  8 2 x x  2 Hƣớng dẫn giải: 2 2
x x  2  3 2 x  4x  5 x  1  5 2 x  6x  8 2 x x  2 2 2
x x  2  3 2 x  4x  5 5 2 x  6x  8   (xétx   ) 1 x  1 2 x x  2 185
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 2
x x  2  3 2 x  4x  5 5 2 x  6x  8  1   ( 1 xétx   ) 1 x  1 2 x x  2 2 2
x x  2  3 2
x  4x  5  x  1 2
x x  2  5 2 x  6x  8    ( 0 xétx   ) 1 x  1 2 x x  2
Nhân liên hợp 2 lần ở biểu thức đầu,1 lân ở phân thức sau suy ra
Phƣơng trình có 2 nghiệm 3 x  , 2 x   2
Thí dụ 51 Để kết hợp với Đạo hàm
Từ Phƣơng trình 2 3 2 x  1 2  x   3 ( 3 2 x  1  2x  ) 7  0 13 2 x  23  2 3 2 3 x  2x  14 3 2 x  1   1 ( 2 x  )( 3 3 2 x  1  2x ) 13 2 x  23  2 3 2 3
x  2x 14 3 2 x 1 Giải phƣơng trình 1 ( 2 x  )( 3 3 2 x 1  2x )
Phƣơng trình có 3 nghiệm x  ; 1 x  5; x  2 2 Phƣơng trình 3 2 x 1 
2x  7  0 có vế trái là hàm đồng biến nên có nghiệm x  2 2
là nghiệm duy nhất
Thí dụ 52 Để kết hợp với Đạo hàm
Từ Phƣơng trình  3 2 x  3 2
x x   1 ( 3 2
x  3  2x 1  ) 1  0 4 2
x x  2  6 3 x  3 2
x  6x  3  3 2 x  3   1 ( 2 x x  )( 1 3 2 x  3  2x  ) 1 4 2
x x  2  6 3 x  3 2
x  6x  3  3 2 x  3 Giải phƣơng trình  1 ( 2 x x  )( 1 3 2 x  3  2x  ) 1
Phƣơng trình có 3 nghiệm 3 x  ; 1 x  ; 2 x  2 Phƣơng trình 3 2 x  3 
2x 1 1  0 có vế trái là hàm đồng biến có nghiệm x  1 186
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Làm thế nào khi sáng tác ngoài cách mò nghiệm đẹp bằng nhẩm thì còn cách mò bằng máy
tính Casio nhƣ sau: Bấm MODE 7 nhập F(X )  3 2 X  3
Máy hỏi Start bấm -9, End bấm 9
Quan sát bảng ta thấy F(X) giá trị nguyên khi X là -7,-2;-1;1;2;7
ở ví dụ TRÊN TÁC GiẢ chọn x=1, Bây giờ xin thử thêm với x=-2
Từ Phƣơng trình  3 2 x  3 2
x x   1 ( 3 2 x  3  x  3  ) 2  0 5 2
x  2x 1  (2  x  3) 3 2 x  3   3 2 x  3  x  3 2 x x  1 Khi này giải PT 3 2 x  3 
x  3  2  0 bằng cách đặt
x  3  t 5  129
suy ra PTcó 2 nghiệm x   ; 2 x 6 5 2
x  2x 1  (2  x  3) 3 2 x  3 Giải phƣơng trình  3 2 x  3  x  3 2 x x  1 5  129
suy ra PTcó 4 nghiệm x  ; 2 3 x  2; x   ; 2 x 6 Thử thêm với x=7  2 2 2 3 1
Từ Phƣơng trình  3x x
3  x x   1 ( 3x  3   ) 14  0 5 3  1 Với PT 3 2  x x 3 
14  0 có vế trái là hàm đồng biến nên có nghiệm x=7 5
là nghiệm duy nhất . các bạn tự tạo ra PT trong trƣờng hợp này
Thí dụ 52 Dùng máy tính Casio trợ giúp sáng tác PT
Làm thế nào khi sáng tác ngoài cách mò nghiệm đẹp mò bằng máy tính Casio nhƣ sau:
Bấm MODE 7 chăng hạn nhập F( X )  3 2
X  4X  5
Máy hỏi Start bấm -9, End bấm 9
Quan sát bảng ta thấy F(X) giá trị nguyên khi X là -5,-2;1;2;7 187
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Nhƣ vậy có khá nhiều lựa chọn nghiệm đẹp chẳng hạn tác giả chọn x=-2
Để tạo ra PT dùng tính đơn điệu để giải ta tạo ra PT: 3 2
x  4x  5  1  4x  8  ( 0 *)
Chỉ cần biết tính đơn điệu của hàm số y  3 2
x  4x  5
thì sẽ biết tại sao tác giả chọn 1 4x 1
Có Vế trái PT(*) là hàm nghịch biến trên khoảng trên khoảng xác định ( ;  ]nên có 4
nghiệm duy nhất x=-2
Khi này ta có PT tích dạng nhƣ sau: ( 3 2
x  4x  5  1  4x  )( 8 3 2 x  4x  5 2
x x  ) 1  0  11 2
x 12x  13  ( 1  4x  ) 8 3 2
x  4x  5  ( 2 x x  )( 1 1  4x  3 2 x  4x  5) 11 2
x  12x  13  ( 1  4x  ) 8 3 2 x  4x  5   1 ( 2 x x  )( 1 1  4x  3 2 x  4x  5) PT có 2 nghiệm 3 x   ; 2 x   2
Khi này khi giải PT nếu bạn nào thử dùng Casio tìm nhân tử thì ta tìm nghiệm đẹp ngoại
lai (kiểu ngoại lai này tác giả đã nói đến ở phần trƣớc)bằng cách coi 1  4x  0 ta giải PT sau: 11 2
x 12x  13  8 3 2
x  4x  5  ( 2 x x  )( 1 3 2
x  4x  5)(**)
ta tìm nghiệm đẹp ngoại lai x=2.Khi này một nhân tử cần tìm là: 3 2 x  4x  5 2
x x 1  0 11 2 x x  2 12 13
Từ (**) ta còn thu về đƣợc một PT sau: x x   3 4 5 2 x x  9 x   2 x 86 2 86
 3x  4x  5  11x
 3x  4x  5   x 11 2 x x  9 x2  x  9
Cách giải pT  ( 3 2
x  4x  5  )( 8 3 2 x  4x  5 2
x x  ) 1  0 188
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2  181
PT có 4 nghiệm x  ; 2 3
x   2; x  3
Nếu các bạn thích tạo ra một PT Tích có thêm cách đặt ẩn phụ ở một nhân tử thì có thể làm nhƣ sau:
Tác giả xin chọn x=1;x=2;…..
Và tạo ra một số PT: 3 2
x  4x  5 
2x 1  3  0 nghiệm x  1 3 2
x  4x  5 
x  3  0 nghiệm x  1 2 2 3  3 3  13 3  13 3 2
x  4x  5  2x 1 1  0 nghiệm x  ; 1 x  1  . 2 3 13  177 3 2
x  4x  5 
x  3  4  0 nghiệm x  ; 1 x 6 3 2
x  4x  5 
2  x  3  0 nghiệm x  ; 1 x  2 3 3 2 37 11  3 2 37 11 3 2
x  4x  5  2  x 1  0 nghiệm x  ; 1 x  1 3 3 2
x  4x  5  3 2  x  1  0 nghiệm x  ; 1 x  2  3 2
x  4x  5  3x  2 1  0 nghiệm x  ; 1 x  2 3 2
x  4x  5  2  x  3  0 nghiệm x  ; 2 x  2 
bạn nào không thích nghiệm đẹp thì có thể tạo ra PT kiểu sau: 5  4 6 5  4 6 3 2
x  4x  5  2 x  3  2  0 có 2 nghiệm x  ; x 3 3
Việc ghép lại thành phƣơng trình hoàn thiện xin dành cho bạn đọc. chẳng hạn: ( 3 2
x  4x  5  x  3  )( 4 3 2 x  4x  5 2
x x  ) 1  0 189
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 7 2
x  8x  9  ( x  3  ) 4 3 2 x  4x  5   1 ( 2 x x  )( 1 x  3  3 2 x  4x  5) 3  177 PT có 4 nghiệm: 3 x  ; 1 x  ; x  ; 2 x   2 2
Sử dụng lí thuyết của 2 chuyên đề dƣới đây có thể tìm ra các biểu
thức cần xuất hiện ở 2 chuyên đề 2 và 3
KĨ THUẬT “ĐÁNH CẢ CỤM” KHI DÙNG CASIO GIẢI PHƢƠNG TRÌNH VÔ TỈ Chuyên đề 4
PHƢƠNG PHÁP THẾ TRONG THỦ THUẬT SỬ DỤNG MÁY TÍNH ĐỂ TÌM NHÂN
TỬ CHUNG HOẶC TÌM BIỂU THỨC TRONG NHÂN LIÊN HỢP KHI GIẢI PHƢƠNG TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh
Một kĩ năng rất hữu ích có thể giúp ta giải đƣợc một phƣơng trình vô tỉ là kĩ năng tìm
nhân tử chung hoặc tìm biểu thức trong nhân liên hợp. Đôi khi việc tìm ra các biểu thức đó
là rất khó khăn nếu ta không có máy tính cầm tay trợ giúp. Bài viết này xin đƣợc giới thiệu
kĩ thuật dùng máy tính cầm tay tìm nhân tử chung hoặc biểu thức để ta xử lí nhân liên hợp có dạng 2 k
ax bx c
P(x) ,với a,b,c là các số nguyên. Sau đây là các thí dụ
Thí dụ 1 Giải phƣơng trình 6 x  3 4 x  3 3
x  6x 10  2 4 2 x  1  2 2 x  3x  6 Lời giải
Phƣơng trình(PT) đã cho tƣơng đƣơng với PT: 6 x  3 4 x  3 3 x  8 2
x  6x 12  4 2
x  3x  6  ) 1 ( 0
Ta tìm nghiệm của PT(1) bằng máy tính CASIO fx-570VN PLUS nhƣ sau:
Nhập biểu thức vế trái(VT) của PT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm X=2
Ấn nút sang trái để quay lại PT(1) 190
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Sửa biểu thức thành VT(1):( X-2) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 10 =, máy cho ta nghiệm X  546818277 , 2 
Bấm SHIFT STO A (lƣu nghiệm vừa tìm vào A)
Giả sử nhân tử của PT(1) có dạng 2 2
ax bx c
x  3x  6
chứa 2 nghiệm vừa tìm.
Nghiệm X=2 suy ra 4a  2b c  2  0  c  4
a  2b  2
Nhân tử của PT(1) trở thành: 2
ax bx  4a  2b  2 2
x  3x  6  a(x  )( 2 x  ) 2  ( b x  ) 2  2 2
x  3x  6
Xét a(x  )( 2 x  ) 2  ( b x  ) 2  2 2
x  3x  6  0 2
x  3x  6  2 suy ra b   a(x  ) 2 (2) x  2
Vì A là nghiệm của PT(2) nên
ta tìm a,b là số nguyên bằng cách bấm máy tính như sau:
A2  3A  6  2
MODE 7 máy hiện f(X)= ,ta nhập  (A  ) 2 X bấm = A  2
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=1=a thì F(X)=0=b là số nguyên
Nhƣ vậy a=1,b=0,c=  2
Nên nhân tử cần tìm là 2 x  2 2
x  3x  6
Suy ra PT xuất hiện ( 4 2 x  2 2
x  3x  6)
Biểu thức còn lại là 6 x  3 4 x  3 3 x 12 2 x  6x  4
Biểu thức này chứa nhân tử cần tìm nên nó chứa nhân tử sau: 191
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) ( 2 x  ) 2 2  ( 2 x  3x  ) 6 4  x  5 2 x  3x  2
Thật vậy,sử dụng kĩ năng chia đa thức ta đƣợc 6 x  3 4 x  3 3 x 12 2
x  6x  4  ( 4 x  5 2 x  3x  )( 2 2 x  ) 2 Do đó PT ) 1 (  ( 4 x  5 2 x  3x  )( 2 2 x  ) 2  ( 4 2 x  2 2
x  3x  6)  0  ( 2 x  2 2
x  3x  6)( 2 x  2 2
x  3x  6)( 2 x  ) 2  ( 4 2 x  2 2
x  3x  6)  0  ( 2 x  2 2
x  3x  6) 4 x  ( 2 x  ) 2 2
x  3x  6  0  2
x  3x  6  2 x    ) 3 ( 2  4 x  ( 2 x  ) 2 2
x  3x  6  ( 0 ) 4
Dễ thấy PT(4) vô nghiệm  2 x  2   2 x  2  0 PT ) 3 (  0     2
x  3x  6  4 x  4 2 x  4 (x  )( 2 3 x  2 2 x x  ) 1  0 61  9 29 61  9 29  2 3 3   2 2
Giải tiếp ta được nghiệm x  2 và x  3 61  9 29 61  9 29  2 3 3   2 2
Vậy PT đã cho có 2 nghiệm: x  2 ; x  3
Thí dụ 2 Giải phƣơng trình 2 4 3 x x  2 2 x  6x  1 3  ( 2 x  ) 2 8 3 x  9 2 x  3 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: 2 4 3 x x  2 2
x  6x  3  ( 2 x  ) 2 8 3 x  9 2 x  3  ) 1 ( 0
Nhập biểu thức vế trái của PT(1) rồi bấm SHIFT SOLVE 192
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm X  , 2 25992105 Bấm SHIFT STO A Nhập biểu thức 4 VT ) 1 ( : ( X  )
A rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 0 = , chờ gần 6 phút máy hiện Can’t Solve
Khi này ta sẽ chuyển sang hướng tìm nghiệm ngoại lai (nếu có)của PT bằng cách đổi dấu trước căn PT đã
cho.Dẫn tới tìm nghiệm của PT sau: 2 4 3 x x  2 2
x  6x  3  ( 2 x  ) 2 8 3 x  9 2 x  3  ( 0 ) 2
Ta tìm nghiệm “đẹp” (nếu có) của PT(2) như sau:
Bấm MODE 7 máy hiện f(X)=
Ta nhập biểu thức vế trái PT(2) bấm =
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Khi này xem bảng ta thấy X  1 `  thì F(X)=0
Vậy nghiệm ngoại lai cần tìm là x= -1
Giả sử nhân tử của PT(1) có dạng 2
ax bx c  8 3 x  9 2 x  3
Vì x= -1 nghiệm ngoại lai nên nó là nghiệm PT: 2
ax bx c  8 3 x  9 2 x  3  0
suy ra a b c  2  0  c  a b  2
Nhân tử của PT(*) trở thành: 2
ax bx a b  2  8 3 x  9 2 x  3  a(x  )( 1 x  ) 1  ( b x  ) 1  2  8 3 x  9 2 x  3
Xét a(x  )( 1 x  ) 1  ( b x  ) 1  2  8 3 x  9 2 x  3  0
8x3  9x2  3  2 suy ra b   a(x  ) 1  Z x  1
Ta tìm a,b bằng cách bấm máy tính như sau: 193
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
8A3  9A2  3  2
MODE 7 máy hiện f(X)= ,ta nhập  (A  ) 1 X bấm = A  1
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=1 thì F(X)=3 là số nguyên
Nhƣ vậy a=1,b=3,c=0.Ta được nhân tử là 2 x  3x  8 3 x  9 2 x  3 Mà ( 2 x  3x)2  8 ( 3 x  9 2 x  ) 3 4  x  2 3 x  3 PT(1) trở thành: 4 x  2 3 x  3  ( 2 x  )( 2 2 x  3x  8 3 x  9 2 x  6)  0  ( 2 x  3x  8 3 x  9 2 x  6)(2 2
x  3x  2  8 3 x  9 2 x  3)  0  8 3 x  9 2 x  3  2 x   3x ) 3 (   3 2 7 2  ( 2 x  ) 
x  3x  6  ( 0 ) 4  4 8
Dễ thấy PT(4) vô nghiệm  2 x  3x PT ) 3 (  0  3  x  1 2 . (x  ) 1 (x  ) 1 3  2  0
Vậy PT đã cho có nghiệm duy nhất 3 x  1 2
Thí dụ 3 Giải phƣơng trình 2 5 2
x  3x  2  x  1 1  36 4 x  44 3 x  17 2 x x  4 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: 2 5 2
x  3x  2  36 4 x  44 3 x 17 2
x x  4  x 1  ) 1 ( 0
Ta tìm nghiệm “đẹp” (nếu có) của PT(1) như sau:
Bấm MODE 7 máy hiện f(X)= 194
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Ta nhập biểu thức vế trái PT(1) bấm =
Máy hiện Start? Ta bấm -9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Khi này ta thấy X=1 thì F(X)=0
Nhập biểu thức VT(1):( X-1) rồi bấm SHIFT SOLVE
Máy hỏi X=? ta bấm 0 =, máy cho ta nghiệm X  629960524 , 0  5 2
x  3x  2  2
Làm tương tự các thí dụ trên ta được: b   a(x  ) 1 và x 1 36 4 x  44 3 x  17 2
x x  4  2 b   a(x  ) 1 x 1 Nên 5 2
x  3x  2  (2 2 x x  ) 1 và 4 2
x  3x 1 36 4 x  44 3 x 17 2 x x  4
là các biểu thức cần xuất hiện trong phƣơng trình PT(1) trở thành: ( 2 5 2
x  3x  2  2 2 x x  ) 1  (4 2
x  3x 1 36 4 x  44 3 x 17 2
x x  4)  0 2 2 5 2
x  3x  2  2 2 x x   1
4 2x 3x  1 36 4x  44 3x 17 2x x  4  2   0 5 2
x  3x  2  2 2 x x  1 4 2
x  3x  1  36 4 x  44 3 x  17 2 x x  4     4 4 x  4 3 x x   2 5 1 [  ]  0 5 2
x  3x  2  2 2 x x  1 4 2
x  3x  1  36 4 x  44 3 x  17 2 x x  4 x  1   4 4 x  4 3
x x 1  0  (x  )( 1 4 3 x  ) 1  0   1 x  3  4
Kiểm tra điều kiện xác định thấy các nghiệm thỏa mãn. 1
Vậy PT đã cho có 2 nghiệm x  1; 3 x   4
Thí dụ 4 Giải phƣơng trình 195
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 4 x  2 3 x  14  4 3 x  7 2 x  2x  3  1 2 x  5x  8 4  x  6 3 x  16 2 x 12x 11 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: 4 3 x  7 2 x  2x  3 4  x  6 3 x 16 2 x 12x 11 4  x  2 3 2
x x  5x  6  ) 1 ( 0
Bấm máy tính như các thí dụ trên để tìm nghiệm nguyên ta thấy không có
Tìm và lưu các nghiệm ta được ít nhất 3 nghiệm là A  732050808 , 2 ; B  , 1 414213562 ; C  732050807 , 0 
Chú ý: Nếu máy hiện Continue:[=] thì ta bấm = ,đợi một lúc ta đƣợc nghiệm
Giả sử biểu thức thứ nhất có dạng 2
ax bx c  4 3 x  7 2
x  2x  3
Do A,B,C là nghiệm của biểu thức nên ta có 2
aA bA c  4 3 A  7 2 A  2A  3 2
aB bB c  4 3 B  7 2 B  2B  3 2
aC bC c  4 3 C  7 2 C  2C  3
Bấm MODE 5 rồi bấm 2 để giải hệ 3 ẩn a,b,c gồm 3 PT trên.Ta đƣợc a=1;b=1;c=1
Nhƣ vậy biểu thức thứ nhất cần tìm là 2
x x 1 4 3 x  7 2 x  2x  3
Tƣơng tự biểu thức thứ hai cần tìm là 2 2 x 1 4  x  6 3 x 16 2 x 12x 11 PT ) 1 ( 2
x x 1 4 3 x  7 2 x  2x  3  2 2 x  1 4  x  6 3 x  16 2 x 12x 11 4  x  2 3 x  4 2
x  4x  4  0  ( 4 x  2 3 x  4 2 x  4x  ) 4 ( P x)  ( 0 ) 2 với 1 3 P(x)   1  0 2
x x  1  4 3 x  7 2 x  2x  3 2 2 x  1 4  x  6 3 x  16 2 x 12x 11 196
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x  1 3 Suy ra PT ( ) 2 4  x  2 3 x  4 2
x  4x  4  0  ( 2 x  2x  )( 2 2 x  ) 2  0   x   2
Kiểm tra điều kiện xác định thấy các nghiệm thỏa mãn
Vậy PT đã cho có 4 nghiệm x  1  3 ; x   2
Chú ý: Do A C  2 ; AC  2
nên PT có nhân tử là 2
x  2x  2
Mở rộng dạng toán: Nếu a,b,c hoặc nghiệm PT là các số hữu tỉ thì ta đƣa về tìm các biểu thức dạng nk ( P x)  ( 2
px qx r) ,với p,q,r là số nguyên và n là số nguyên dƣơng ta tìm đƣợc hoặc ta thử
chọn. Vấn đề nữa đặt ra là liệu có phƣơng trình mà ta phải tìm biểu thức dạng phức tạp hơn chẳng
hạn nhƣ k P(x)  ( 3 2
ax bx cx d) .Hãy làm bài tập dƣới đây các bạn sẽ rõ
Bài tập Giải phương trình 4 4 x 13 2 x  2x ) 1  1 2  4 3 x  16 2 x x  2 4 x  7 3 x  3  3 3 x  9 2 x  6 ) 2  3  2 x  3x  3 2 4 3 x x  3 2 x  5x  8 ) 3  1 ( 2 x x  ) 1 4 2 x  3x  14 3 4 x  2 3 x  4 2 x  4  3 2 x  2x  4 ) 4  1 3 2 x x  2 3 16 4 x 12 3 x  4 2
x  24x  23  2x ) 5  1 2 3 4 x  7 2
x 14x  13  1 2x  2 3  8 6 x 12 5 x  4 4 x  1 ) 6  1 1  12 4 x  5 2 x  2x  3 3  2 3 6 x x  3 5 x  5x 1 7)  1 2  4 4 3 x x  3 2 x  7x  2 4 x  2 3 x  6  4 3 x  27 2 x  6x  3 ) 8  1 20 2
x x  1  2 3 x  26 2 x  2x  3 197
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 2 3 x  4 2 x  6 4 x x  10 2 x  4x  3 ) 9  1 3  ( 2 x  ) 2 3 2 4 x  5 3 x 12 2 x  6x 18 2 x  12  3 20 3 x  9 2 x  30x  20 ) 10  2 2 5 x x  4  7 3 x  3 2 x  8x  5 2 ( 3 x  2x) 5 5 x  7 4 x  4 3 x  4 2 x  3x  7 ) 11  1 3 5 4 3
x x x  8 2 x  5x  6 7 3 x  8x  3 4 x  21 3 x 15 2 x  27x  5 ) 12  1 2 4 x  14 2 x  6  2 4 x  11 3 x  4 2 x  11x  2 (28 2 x  29x  ) 11 x  43 2
x  4x  5  4x x ) 13  1 4x  1  36 ( 2 x  25x  ) 11 x  35 2 x  6x  6 ) 14 21 6 x  19 5 x 13 4 x  9 3 x  5 2
x  4x  3  4 8 x  4 7 x  20 6 x 19 5 x  19 4 x  12 3 x  5 2 x  4x  5 Chuyên đề 5
PHƢƠNG PHÁP CỘNG DÙNG TRONG THỦ THUẬT MÁY TÍNH CẦM TAY TRỢ GIÚP GIẢI
PHƢƠNG TRÌNH VÔ TỈ
Vũ Hồng Phong GV THPT Tiên Du 1, Bắc Ninh
Điều kiện sử dụng phƣơng pháp: Bấm máy tính tìm đƣợc ít nhất 2 nghiệm A,B phân biệt Nếu PT có chứa
P(x) thì giả sử biểu thức cần xuất hiện có dạng: 2
ax bx c
P(x) ,trong đó
a,b,c là các số nguyên .Do A,B là nghiệm của biểu thức nên 2
aA bA c P( ) A  ( 0 *) 2
aB bB c P(B)  0
Chú ý: Nếu B là nghiệm ngoại lai ta có 2
aB bB c
P(B)  0 (các bạn tự xử lí TH này)
Trừ vế với vế ta đƣợc:
a( A B)(A B)  ( b A  ) B P( ) A P(B) 198
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) P( A)  P(B) Suy ra b
 (A B)a A B P( A)  P(B
Trƣờng hợp 1: A B  0 thì b  ) A B P( A)  P(B) Nhập biểu thức
bấm = máy hiện giá trị của b cần tìm A B
Từ (*) suy ra c
P( A aA2 )  bA
Ta tìm a,c bằng máy tính nhƣ sau:
Bấm MODE 7 máy hiện f(X)= ta nhập
P( A XA2 )  bAbấm =
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta chỉ lấy X làm F(X) nhận giá trị nguyên Suy ra a=X,c=F(X)
Trƣờng hợp 2: A B  0 P( A)  P(B) Do b
 (A B)a nên ta tìm a,b bằng máy tính nhƣ sau: A B P( A)  P(B)
Bấm MODE 7 máy hiện f(X)= ta nhập biểu thức
 (A B)X bấm = A B
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta lấy X làm F(X) nhận giá trị nguyên
Từ đó suy ra a=X,b=F(X)
Từ PT(*) ta tìm c
P( A aA2 )  bA 199
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Nhập biểu thức (  2 ) 
bấm = máy hiện giá trị của c cần tìm P A aA bA
Sau đây là các thí dụ.
Thí dụ 1 Giải phƣơng trình 6 6 x x  6 4 x  6 3 x  2 2
x  2x  8 1 3 4 x  12 2 x x  10 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: P(x) 6  x  3 4 x 12 2
x x 10  ) 1 ( 0
Với P(x) 6  x  6 4 x  6 3 x  2 2
x  2x  8
Nhập biểu thức vế trái(VT) của PT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm 10 = máy cho ta nghiệm X  , 2 25992105
Bấm nút mũi tên sang trái để quay lại VT(1) ta bấm = để lƣu VT(1)
Bấm ALPHA X SHIFT STO A để lƣu nghiệm vào A
Bấm nút mũi tên đi lên để về VT(1) rồi bấm SHIFT SOLVE
Máy hỏi Solve for X ta bấm -10 = máy cho ta nghiệm X  , 2  25992105 Bấm SHIFT STO B P( A)  P(B
Bấm máy A+B máy hiện 0 suy ra b  ) A B P( A)  P(B) Nhập biểu thức
bấm = máy hiện -1. Vậy b=-1 A B
Do b= -1 nên c
P( A)  aA2  ( ) 1 A
P( A aA2 )  A
Bấm MODE 7 máy hiện f(X)= ta nhập
P(A A2 )
X A bấm =
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 = 200
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy khi X=3 thì F(X)=1 nguyên Suy ra a=3,c=1
Biểu thức cần tìm là: 6 x  6 4 x  6 3 x  2 2
x  2x  8  3 ( 2 x x  ) 1 PT(1) trở thành P(x)  3 ( 2 x x  ) 1 6  x  3 4 x  9 2 x  9  0 P(x)  3 ( 2 x x  ) 1 2 6   x  3 4 x  9 2 x  9  0 P(x)  3 2 x x  1 6 x  3 4 x  9 2 x  9 6   x  3 4 x  9 2 x  9  0 P(x)  3 2 x x  1 1  [  ]( 1 6 x  3 4 x  9 2 x  ) 9  0 P(x)  3 2 x x  1 6  x  3 4 x  9 2 x  9  0  ( 3 x  3x)2  3 ( 2 x  ) 3 2  0  ( 3 x  3 2 x  3x  )( 3 3 x  3 2 x  3x  ) 3  0 (x  ) 1 3     2 (x  ) 1 3  2(x  ) 1 ` 3  2  0    x   1 ( 3  2)  (x  ) 1 3  2
Vậy PT đã cho có 2 nghiệm x   1 ( 3  2)
Thí dụ 2 Giải phƣơng trình 4 2
x x  4  2 6 x  4 4 x  7 3 x  5 2
x  2x 1 1 2 x  2 6 4 3
x x x  10 2 x 12x  7 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: P(x)  ( Q x)  3 2 x x  ) 1 ( 4
Với P(x)  2 6 4 3
x x x 10 2
x 12x  7 ( Q x)  2 6 x  4 4 x  7 3 x  5 2
x  2x 1 201
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Tìm và lưu các nghiệm như thí dụ 1 ta được 2 nghiệm là A  793700526 , 0 ; B  , 1  25992105
Ta có A B   , 0 4662205239  0 P( A)  P(B) Có b
 (A B)a nên ta tìm a,b nhƣ sau: A B P( A)  P(B)
Bấm MODE 7 máy hiện f(X)= ta nhập
 (A B)X bấm = A B
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy F(X)=-2 khi X=1
Suy ra a=1,b= -2. Khi này c
P( A)  A2  2A Nhập biểu thức
P( A)  A2  2Abấm = máy hiện số 3 Ta đƣợc c=3
Biểu thức cần tìm là P(x)  ( 2 x  2x  ) 3
Tƣơng tự biểu thức nữa cần tìm là ( Q x)  (2 2 x x  ) 1 PT(1) trở thành ( P x)  ( 2 x  2x  ) 3  ( Q x)  (2 2 x x  ) 1  0 P(x)  ( 2 x  2x  ) 3 2 Q(x)  (2 2 x x  ) 1 2    0 P(x) 2
x  2x  3 Q(x)  2 2 x x  1 2 6 x  3 3 x  2 2 6 x  3 3 x  2    0 P(x) 2
x  2x  3 Q(x)  2 2 x x  1 3 3 1 1  (x  )( 2 2x  )[ 1  ]  0 P(x) 2
x  2x  3 Q(x)  2 2 x x  1 202
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) x  3 2   1 ( 3 x  )( 2 2 3 x  ) 1  0   3 x   x
1 Vậy phƣơng trình có 2 nghiệm 2 ; 3 x  3 2  2
Vấn đề đặt ra là liệu với một biểu thức P(x) có khi nào có nhiều lựa chọn biểu thức dạng 2
ax bx c
P(x) hay không.Ví dụ sau sẽ làm sáng tỏ điều này
Thí dụ 3 Giải phƣơng trình 4 x  2 3 2
x x  2x  3  1 12 3 x  24 2
x  4x  6  12 3 x  51 2 x  6 Lời giải
Phƣơng trình đã cho tƣơng đƣơng với PT: 4 x  2 3 2
x x  2x  3  P(x)  ( Q x)  ) 1 ( 0
Với P(x)  12 3 x  24 2
x  4x  6 và ( Q x)  12 3 x  51 2 x  6
Tìm và lƣu các nghiệm ta đƣợc 2 nghiệm là A  , 3 449489743 ; B  , 1  449489743
Bấm máy tính có A B ; AB  2  0 5 
(Theo Định lí Vi-ét thì PT sẽ có nhân tử là 2
x  2x  5 ) P( A)  P(B) Có b
 (A B)a nên ta tìm a,b nhƣ sau: A B P( A)  P(B)
Bấm MODE 7 máy hiện f(X)= ta nhập biểu thức
 (A B)X bấm = A B
Máy hiện Start? Ta bấm  9 =
Máy hiện End? Ta bấm 9 =
Máy hiện Step? Ta bấm 1 =
Quan sát bảng ta thấy tất cả các giá trị F(X) đều nguyên. Vì thế ta chọn 1 cặp là
X=2;F(X)= 1. Suy ra a=2,b=1 c
P( A)  A2 2  A 203
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) Nhập biểu thức ( )  2 2 
bấm = máy hiện số 1.Ta đƣợc c=1 P A A A Suy ra 2 2
x x 1 P(x) là biểu thức cần tìm
Tƣơng tự ta chọn đƣợc 3 2 x x 1  (
Q x) là biểu thức cần tìm
Phƣơng trình(1) tƣơng đƣơng với PT: 2 2 x x 1 ( P x)  3 2 x x 1 ( Q x) 4  x  2 3 x  4 2
x  2x  5  0  2 2 x x 1 P(x)  3 2 x x 1 ( Q x)  ( 2 x  2x  )( 5 2 x  ) 1  0  4 2 x x   2 1 9 2 1
 (x  2x  ) 5 2    x 1  0   2 2
x x  1  P(x) 3 2
x x  1  Q(x)   2
x  2x  5  0  x  1 6
Vậy phƣơng trình có 2 nghiệm x  1  6
Chọn cặp biểu thức khác chẳng hạn 2
x  3x  6  P(x) ; 3 2 x x 1  (
Q x) ta cũng giải
đƣợc PT theo cách nhân liên hợp Chú ý:
+Việc chọn biểu thức trong thí dụ 3 là tùy ý hay cần chọn hợp lí để ta dùng đƣợc cách nhân
liên hợp. Xin dành cho mọi ngƣời tìm hiểu điều này.
+ Một số phƣơng trình ta có thể tìm biểu thức phức tạp hơn chẳng hạn P(x)  ( 3 2
ax bx cx d) và có thể giải quyết theo cách bài viết đã nêu khi điều kiện về
nghiệm của PT ta tìm đƣợc nhiều hơn(kể cả nghiệm ngoại lai hay nghiệm bội)
Bài tập Giải phƣơng trình 3 3 x  24 3 x  4 2 x  9x 1 ) 1  1 4 x  8 2 x  9x  9 6 3 2
9x  9x  5x  5 3 ) 2  3x 2 6 4 3 2
x  9x x  12x  7x  4 4 3
x  4x  18 3 x  4 2 x  12x  2 ) 3  1 3 4 x  10 2 x  4  6 3 x 2 2
x  6x 1 204
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016) 4 4 x  7 2 x  3  6 3 x  16 2 x  9x  6 ) 4  1 2
x  5x  20  16 3 x  49 2 x  26x  21 4 2 x x  5 6  x  4 3 x  6 2 x 12x  5 ) 5  1 2 x  1  4 6 x  4 3 x 11 2
x  2x 15 4 2 x  3x  3 6 4
x x  8 2 x  8x 17 ) 6  1 2 6 x x  4 4 x 5 2
x  2x  20 2 6 x  8 4 x  4 2 x x 14 7)  1  1  4 6 x  7 4 x  2 3 x  3 2 x  2x  8 3 2 x  3x  4 6 4
x x  8 2 x  8x  8 ) 8  1 1 ` 6  x  4 4 x 5 2
x  2x  5 6 5 4 2
x  3x  24x  2x  8x  2 3 ) 9  x 6 4 3 2 5 
x  33x  4x  8x  8x  3 3 2 x  3x  6 8  x  4 5 4 x x  12 2 x  16x ) 10  1 1 8  x  4 5 x 4 4  x  5 2 x  2x 15 7 5 4 3
x  2x  6x  18x  4x 16 3 ) 11  2x 7 5 4 3 2
x  4x  7x  18x  3x  2x 15  6 7 x 15 6 x 18 5 x  9 4 x  11 2 x x  1 ) 12  1 8 6 x x  6 5 x  19 4 x  22 3 x  14 2 x  2x  8 205
Vũ Hồng Phong Thôn Bất Lự, Hoàn Sơn,Tiên Du, Bắc Ninh ( Hoàn thành 28-5-2016)
Vũ Hồng Phong Thôn Bất Lự,Hoàn Sơn,Tiên Du,Bắc Ninh ToánBK35 ĐHSP Thái Nguyên 206