KT Chương 2: Mô Hình Hồi Quy Đơn trong Kinh Tế Lượng

KT Chương 2 Lý thuyết - Lý thuyết chương 2 - Kinh tế lượng
Phương pháp nghiên cfíu khoa học trong kinh tế (Trường Đại học Thăng Long)
CHƯƠNG 2: MÔ HÌNH HỒI QUY ĐƠN
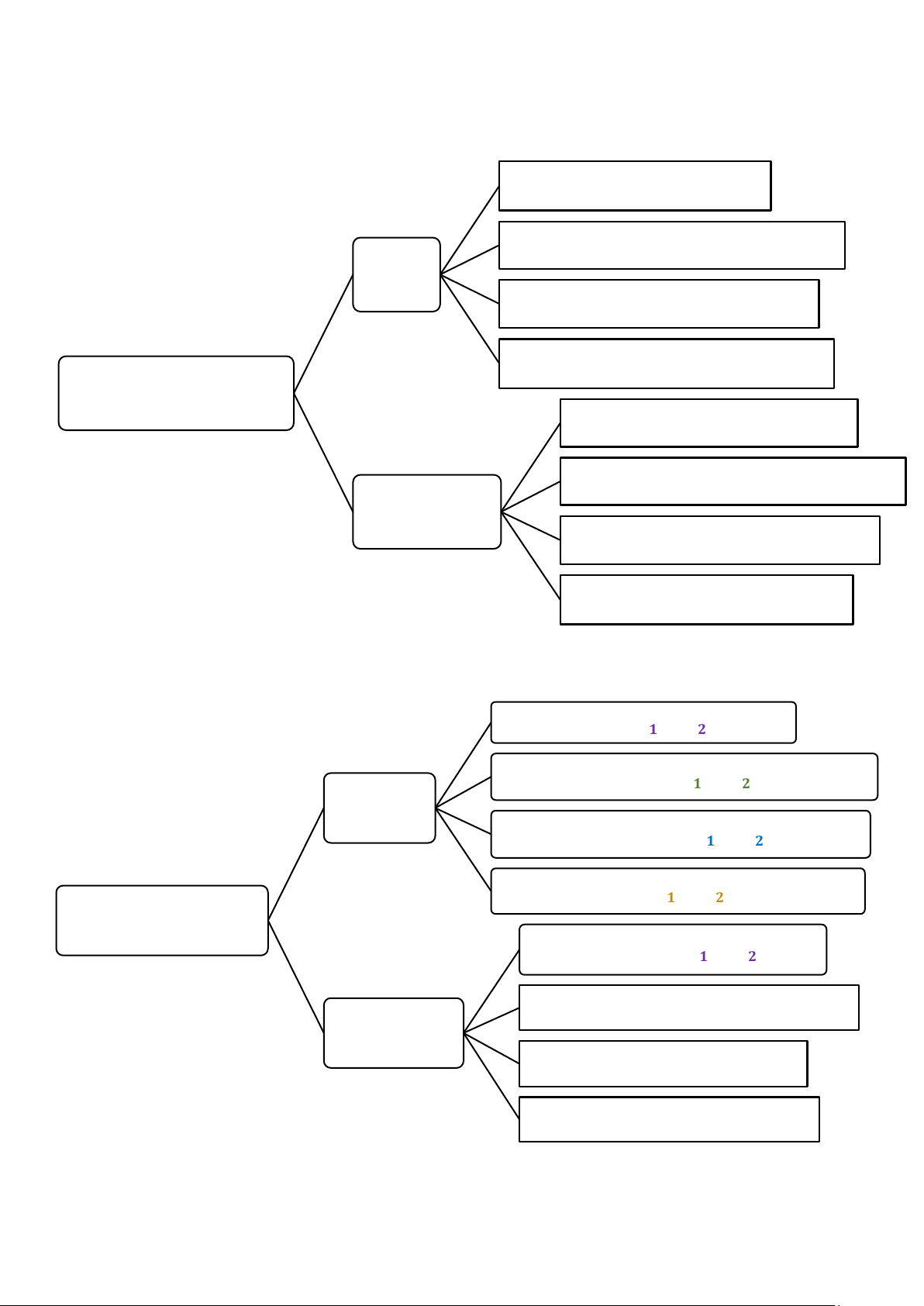
1. Mô hình hồi quy tổng thể và mô hình hồi quy mẫu
Lin - Lin: Yi = 1 + 2*Xi + ui
Log - Log: LogYi = 1 * 2*LogXi + ui Mô hình
Log - Lin: LogYi = 1 + 2*Xi + ui
Lin - Log: Yi = 1 + 2*LogXi + ui
Mô hình hồi quy tổng thể
Lin - Lin: Yi = 1 + 2*Xi
Log - Log: LogYi = 1 + 2*LogXi Phương trình
Log - Lin: LogYi = 1 + 2*Xi
Lin - Log: Yi = 1 + 2*LogXi
Lin - Lin: 𝒀෢𝒊 = ෢ 𝟏 + ෢ 𝟐 ∗ 𝑿𝒊 + 𝒆 𝒊
Log - Log: 𝑳෢𝒐𝒈𝒀𝒊 = ෢ 𝟏
+ ෢ ∗𝟐 𝑳𝒐𝒈𝑿𝒊 + 𝒆 𝒊 Mô hình
Log - Lin: 𝑳෢𝒐𝒈𝒀𝒊 = ෢ 𝟏
+ ෢ ∗𝟐 𝑿𝒊 + 𝒆 𝒊
Lin - Log: 𝒀෢𝒊 = ෢ 𝟏 + ෢ 𝟐
∗ 𝑳𝒐𝒈𝑿𝒊 + 𝒆 𝒊 Mô hình hồi quy mẫu
Lin - Lin: 𝒀෢𝒊 = ෢ 𝟏 + ෢ 𝟐 ∗ 𝑿𝒊
Log - Log: 𝑳෢𝒐𝒈𝒀𝒊 = ෢𝟏 + ෢𝟐 ∗ 𝑳𝒐𝒈𝑿𝒊 Phương trình
Log - Lin: 𝑳෢𝒐𝒈𝒀𝒊 = ෢𝟏 + ෢𝟐 ∗ 𝑿𝒊
Lin - Log: 𝒀෢𝒊 = ෢𝟏 + ෢𝟐 ∗ 𝑳𝒐𝒈𝑿𝒊
2. Phân tích hồi quy
Bài toán: Phân tích tác động của thu nhập hàng tuần của hộ gia đình (income: 1000$/tuần)
đến chi tiêu cho thực phẩm của hộ gia đình hàng tuần (food_exp: $/tuần) theo mô hình hồi quy như sau:
food_expi = 1 + 2*Incomei + ui
(1) Lưu file Log: File => Log => Lưu tên file
(2) Mở file dữ liệu: File => Open => Mở file dữ liệu Note:
− TH1: Mô hình Lin – Lin: food_exp = 1 + 2*income + ui
− TH2: Mô hình Log – Log: Logfood_exp = 1 + 2*Logincome + ui
− TH3: Mô hình Log – Lin: Logfood_exp = 1 + 2*income + ui
− TH4: Mô hình Lin – Log: food_exp = 1 + 2*income + ui
2.1. Phân tích thống kê mô tả dữ liệu
− Giá trị trung bình: sum (biến có trong bài 1) (biến 2) … sum food_exp income
− Giải thích: Bôi đen => Chuột phải => Copy as picture Variable Obs Mean Std. Dev. Min Max food_exp 40 283.5735 112.6752 109.71 587.66 income 40 19.60475 6.847773 3.69 33.4 Phân tích:
+ Số quan sát trong mẫu: 40 hộ gia đình
+ Giá trị trung bình của food_exp là 283.5735$/tuần, độ lệch chuẩn là 112.7652$/tuần, giá trị thấp
nhất là 109.71$/tuần, giá trị cao nhất là 587.66$/tuần.
+ Giá trị trung bình của income là 19,604.75$/tuần, độ lệch chuẩn là 6,847.773$/tuần, giá trị thấp
nhất là 3,690$/tuần, giá trị cao nhất là 33,400$/tuần.
2.2. Ước lượng hồi quy
(a) Mô hình và phương trình hồi quy mẫu Phương trình: Mô hình Lin - Lin: 𝒀෢𝒊 = ෢ 𝟏 + 𝟐 ෢ ∗ 𝑿𝒊
𝒀෢𝒊 = ෢ 𝟏 + ෢ 𝟐 ∗ 𝑿𝒊 + 𝒆 𝒊 Lệnh: reg Y X Phương trình: 𝑳෢𝒐𝒈𝒀𝒊 =  ෢ + 𝟏 𝟐
෢ ∗ 𝑳𝒐𝒈𝑿𝒊 Mô hình Log - Log: Tạo biến Log:
𝑳෢𝒐𝒈𝒀𝒊 = ෢ gen LogX = log(X) 𝟏
+ ෢ ∗𝟐 𝑳𝒐𝒈𝑿𝒊 + 𝒆 𝒊 gen LogY = log(Y) Lệnh: reg LogY LogX Mô hình và phương trình hồi Phương trình: quy mẫu
𝑳෢𝒐𝒈𝒀𝒊 = ෢ + ෢ 𝟏 ∗ 𝑿𝒊 𝟐 Mô hình Log - Lin: Tạo biến Log:
𝑳෢𝒐𝒈𝒀𝒊 = ෢ + ෢ ∗ 𝑿𝒊 + 𝒆 𝟏 𝟐 𝒊 gen LogY = log(Y) Lệnh: reg LogY X Phương trình:
𝒀෢𝒊 = ෢ 𝟏 + ෢ 𝟐 ∗ 𝑳𝒐𝒈𝑿𝒊 Mô hình Lin - Log: Tạo biến Log: 𝒀෢𝒊 = ෢ + 𝟏 ෢ 𝟐
∗ 𝑳𝒐𝒈𝑿𝒊 + 𝒆𝒊 gen LogX = log(X) Lệnh: reg Y LogX
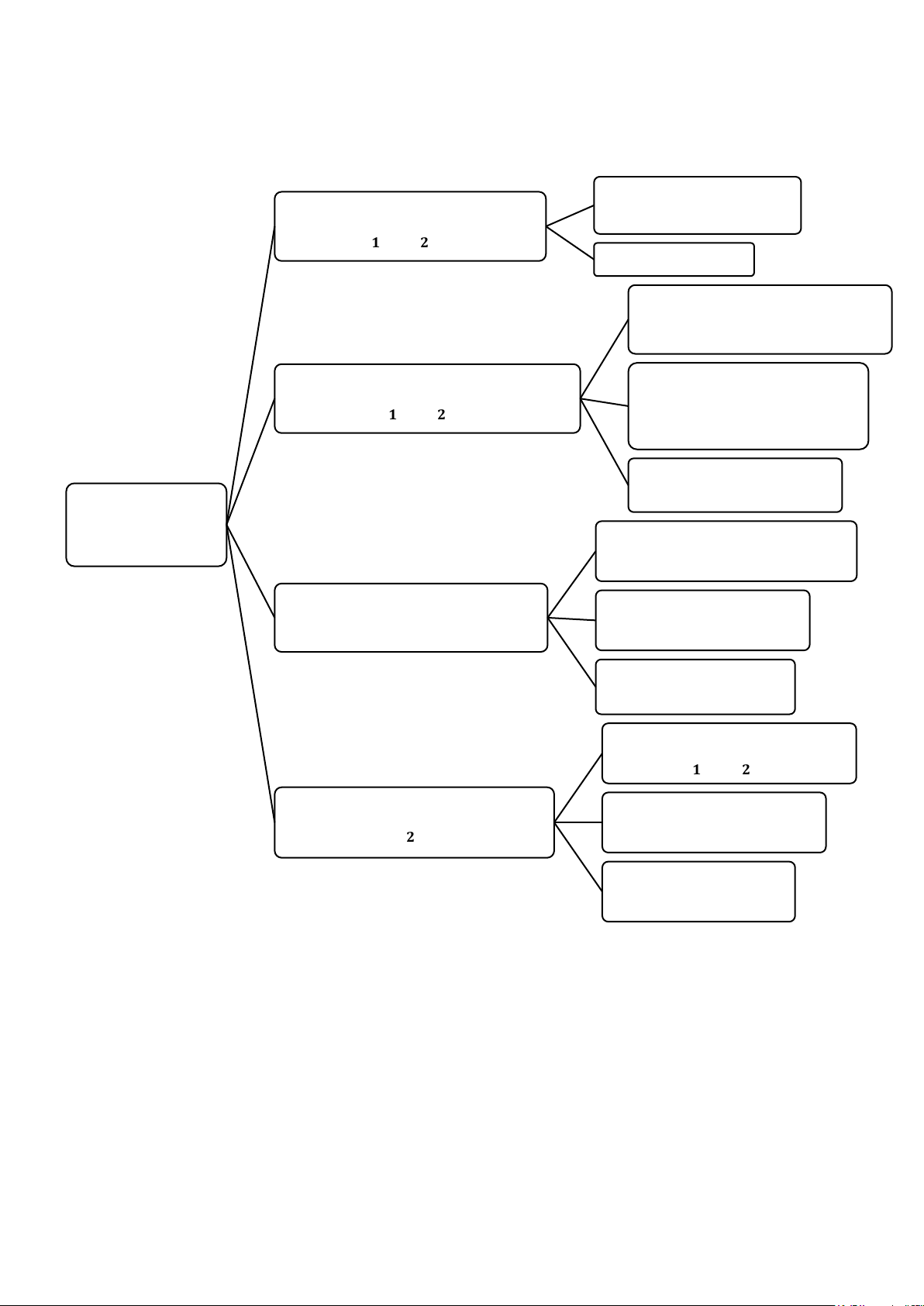
R-square: Mô hình (biến độc lập) giải thích
được (R-square*100%) sự thay đổi của biến M/H - Độ giải phụ thuộc. thích của M/H
(100% - R-square*100%) sự thay đổi của biến
phụ thuộc là do các yếu tố ngẫu nhiên
H0: R-square = 0; H1: R-square # 0 M/H có ý nghĩa thống
Pvalue = Pro>F <= alpha: Bác bỏ kê?
H0, chấp nhận H1 hay mô hình có ý nghĩa thống kê Phân tích hồi quy
Lin - Lin: 𝜷෢ 𝟏: Khi các yếu tố khác không đổi, X = 0
thì giá trị trung bình của Y =𝜷෢ đơn vị; 𝜷෢ : Khi các 𝟏 𝟐
yếu tố khác không đổi, X tăng 1 đơn vị thì giá trị
trung bình của Y tăng/giảm |𝜷෢ 𝟐 | đơn vị Log - Log: 2
β෢ : Khi các yếu tố khác không đổi, X
tăng 1 % thì giá trị trung bình của Y tăng/giảm | 2 β෢ | % Ý nghĩa của các hệ số hồi quy
Log - Lin: Khi các yếu tố khác không đổi, X tăng 1
đơn vị thì giá trị trung bình của Y tăng/giảm |β෢ 2 |*100% Lin - Log: β෢
2 : Khi các yếu tố khác không đổi, X
tăng 1% thì giá trị trung bình của Y tăng/giảm |β෢ 2 |*0.01 đơn vị
Ước lượng hồi quy: reg (biến phụ thuộc) (biến độc lập) reg food_exp income TH1: Mô hình Lin – Lin: Source SS df MS Number of obs = 40 F(1, 38) = 23.79 Model 190626.984 1 190626.984 Prob > F = 0.0000 Residual 304505.176 38 8013.2941 R-squared = 0.3850 Adj R-squared = 0.3688 Total 495132.16 39 12695.6964 Root MSE = 89.517 Biến phụ thuộc Hệ số hồi quy food_exp Coef. Std. Err. t P>|t| [95% Conf. Interval] Se income 10.20964 2.093264 4.88 0.000 5.972052 14.44723 _cons 83.416 43.41016 1.92 0.062 -4.463279 171.2953
(1) Viết mô hình hồi quy mẫu
𝒇𝒐𝒐𝒅෢_ 𝐞𝐱𝐩𝜾 = 𝟖𝟑. 𝟒𝟏𝟔 + 𝟏𝟎. 𝟐𝟎𝟗𝟔𝟒 ∗ 𝑰𝒏𝒄𝒐𝒎𝒆𝒊 + 𝒆𝒊
(2) Viết phương trình hồi quy mẫu
𝒇𝒐𝒐𝒅෢_ 𝐞𝐱𝐩𝜾 = 𝟖𝟑. 𝟒𝟏𝟔 + 𝟏𝟎. 𝟐𝟎𝟗𝟔𝟒 ∗ 𝑰𝒏𝒄𝒐𝒎𝒆𝒊
(3) Giải thích ý nghĩa của các hệ số hồi quy
෢ = 𝟖𝟑. 𝟒𝟏𝟔 => Khi các yếu tố khác không đổi, thu nhập hàng tuần của hộ gia đình (income) bằng 𝟏
0, thì chi tiêu trung bình của hộ gia đình cho thực phẩm là 83.416$/tuần.
෢ = 𝟏𝟎. 𝟐𝟎𝟗𝟔𝟒 => Khi các yếu tố khác không đổi, thu nhập hàng tuần của hộ gia đình tăng 1 đơn 𝟐
vị (1000$/tuần) thì chi tiêu trung bình của hộ gia đình tăng 10.20964 đơn vị ($/tuần)
(4) Mô hình (các biến độc lập) giải thích được bao nhiêu % sự thay đổi của chi tiêu cho thực phẩm
hàng tuần của hộ gia đình?
R-squared = 0.385 => Mô hình giải thích được 38.5% sự thay đổi của chi tiêu cho thực phẩm hàng
tuần của hộ gia đình, còn lại 61.5% sự thay đổi của chi tiêu cho thực phẩm hàng tuần của hộ gia
đình là do các yếu tố ngẫu nhiên.
(5) Mô hình có ý nghĩa thống kê không? (Mô hình có phù hợp sử dụng để giải thích sự thay đổi của
chi tiêu cho thực phẩm hàng tuần)
Kiểm định giả thuyết: - H0: R-square = 0 - H1: R-square # 0
(Với mức ý nghĩa  = 5%)
P-value = Pro > F = 0.000 <  = 5% => Đủ cơ sở để bác bỏ giả thuyết H0 => Chấp nhận giả thuyết
H1 hay R-square # 0 => Mô hình phù hợp
2.3. Kiểm định giả thuyết thống kê Miền bác bỏ (H0) ෢ 𝜷 𝟐 − 𝜷 ∗
𝒕 > 𝒕𝜶 𝒏 − 𝒌 ; (𝒕 = ෢ ) 𝟐 𝑺𝒆 𝜷 𝟐 Kiểm định giá trị tới
B1: Tính t: sca t = (_b[X]-𝜷 ∗)/se[X] hạn
Bước 2: Tính 𝑡𝛼 𝑛 − 𝑘 : 2
sca ttoihan = invttail(e(df_r),alpha/2) H0: 2 = *
Bước 3: In giá trị + Kết luận: sca list t ttoihan H1: 2 # *
Miền bác bỏ: Pvalue <= alpha
B1: Tính t: sca t = (_beta[X]-beta*)/se[X] Kiểm định P-value Bước B2: Tính Pvalue:
sca pvalue = 2*ttail(e(df_r),abs(t))
B3: In giá trị và kết luận: sca list t pvalue Kiểm định giả Miền bác bỏ (H0): thuyết ෢ 𝜷 𝟐 − 𝜷 ∗
𝒕 > 𝒕𝜶 𝒏 − 𝒌 ; (𝒕 = ෢ ) 𝟐 𝑺𝒆 𝜷 𝟐 Kiểm định giá trị tới
B1: Tính t: sca t = (_b[X]-𝜷 ∗)/se[X] hạn
B2: Tính 𝑡𝛼 𝑛 − 𝑘 : 2
sca ttoihan = invttail(e(df_r),alpha) H0: 2 ≤ *
B3: In giá trị + Kết luận: sca list t ttoihan H1: 2 > *
Miền bác bỏ: P-value <= alpha
B1: Tính t: sca t = (_b[X]-𝜷∗)/_se[X]; Kiểm định P-value
B2: Tính pvalue: sca pvalue = ttail(e(df_r),t)
B3: In giá trị và Kết luận: sca list t pvalue Miền bác bỏ (H0):
t < -𝒕 𝒂𝒍𝒑𝒉𝒂 𝒏 − 𝒌 ; (𝒕 = 𝜷෢𝟐−𝜷∗ ) 𝑺𝒆 𝜷෢𝟐
B1: Tính t: sca t=(_b[X]-𝜷∗)/_se[X]; Kiểm định t tới hạn
B2: Tính 𝒕𝒂𝒍𝒑𝒉𝒂 𝒏 − 𝒌 :
sca ttoihan =invttail(e(df_r), 1-alpha);
B3: B3: In giá trị và kết luận: sca list t Kiểm định 𝐻0: 𝛽2 ≥ 𝛽∗ ttoihan giả thuyết 𝐻1: 𝛽2 < 𝛽∗
Miền bác bỏ: Pvalue <= alpha
B1: Tính t: sca t=(_b[X]-𝜷∗)/_se[X]; Kiểm định P-value
B2: Tính pvalue: sca pvalue =1-ttail(e(df_r),t);
B3: In giá trị và KL: sca list t pvalue
Ví dụ: Phân tích tác động của thu nhập hàng tuần của hộ gia đình (income: 1000$/tuần) đến
chi tiêu cho thực phẩm của hộ gia đình hàng tuần (food_exp: $/tuần) với dạng mô hình hồi quy như sau:
TH1: Mô hình Lin- Lin: foodexp_i = β1 + β2*Incomei + ui
(a) Nhà nghiên cứu cho rằng thu nhập có tác động đến chi tiêu. Thiết lập giả thuyết thống kê và
kiểm định với mức ý nghĩa alpha là 5%.
Giả thuyết: H0: Beta2 = 0; H1: Beta 2 # 0
B1: Tính t: sca t1 = (_b[X]-𝜷 ∗)/se[X]
B2: Tính t tới hạn: sca ttoihan1=invttail(e(df_r),0.05/2)
Or B2 (P value): Tính P value: sca pvalue1 = 2*ttail(e(df_r),abs(t_1))
B3: In giá trị và KL: sca list t1 ttoihan1 pvalue1 t1 = 4.8773806 ttoihan1 = 2.0243942 pvalue1 = .00001946
Kết luận: |t| = |t_1| = 4.8773806 > talpha/2(n-k) = ttoihan1 = 2.0243942 hay pvalue = pvalue1 =
.00001946 < alpha = 5% => Đủ cơ sở để bác bỏ H0, chấp nhận H1 => Thu nhập có tác động đến chi tiêu
(b) Khi thu nhập tăng thì chi tiêu tăng, thiết lập giả thuyết thống kê và kiểm định.
Giả thuyết: Ho: Beta 2 <= 0; H1: Beta 2 > 0
Kết luận : t = t_2 = 4.8773806 > talpha(n-k) = ttoihan2 = 1.6859545 hoặc pvalue = pvalue2 =
9.729*10^-6 < alpha = 5% Đủ cơ sở bác bỏ H0, chấp nhận H1 hay khi thu nhập tăng thì chi tiêu tăng.
Note: Thu nhập có tác động cùng chiều hay ngược chiều đến chi tiêu ? H0: Beta 2 <=0 H1: Beta 2 > 0
Kết luận : Pvalue = (P >|t|)/2 = 0.000/2 = 0.0000 < alpha = 5% => Đủ cơ sở bác bỏ H0, chấp nhận
H1 => Thu nhập có tác động cùng chiều đến chi tiêu.
(c) Nhà nghiên cứu cho rằng khi thu nhập giảm 100$/tuần thì chi tiêu cho thực phẩm giảm
110$/tuần. Thiết lập giả thuyết thống kê và kiểm định
|Delta Thu nhập| = 0.1 , Thu nhập giảm => |delta TN| = -delta TN = 0.1 => delta TN = -0.1
|delta chi tiêu| = 110, Chi tiêu giảm => |delta chi tiêu| = - delta chi tiêu = 110 => delta chi tiêu = -110
Delta chi tiêu = beta2* delta TN = beta2 *(-0.1) = -110 => beta2 = 1100
Giả thuyết: H0: Beta2 = 1100; H1: Beta2 # 1100
KL: |t| = |t_3| = |-520.61785| = 520.61785 > talpha/2(n-k) = ttoihan3 = 2.0243942 hay pvalue =
pvalue3 = 7.875*10^-75 < alpha = 5% => Đủ cơ sở bác bỏ H0, chấp nhận H1 hay khi thu nhập
giảm 100$/tuần thì chi tiêu cho thực phẩm giảm khác 110$/tuần
(d) Khi thu nhập tăng 500$/tuần thì chi tiêu cho thực phẩm tăng ít hơn 8$/tuần. Thiết lập giả
thuyết thống kê và kiểm định.
Giả thuyết: H0: beta 2 >= 16; H: beta 2< 16
Kết luận: t = t_4 = -2.7661864 < -t_α (n-k) = ttoihan4 = -1.6859545 hay pvalue = pvalue4 =
.00435429 < alpha = 5% => đủ cơ sở để bác bỏ h0, chấp nhận h1 hay khi thu nhập tăng 500$/tuần
thì chi tiêu tăng ít hơn 8$/tuần.
(e) Khi thu nhập tăng 400$/tuần thì chi tiêu cho thực phẩm tăng nhiều hơn 2$/tuần.
Giả thuyết: H0: Beta 2 <= 5; H1: Beta 2 > 5
Kết luận: t = t_5 = 2.4887659 > t_α (n-k) = ttoihan5 = 1.6859545 hay pvalue = pvalue5 =
.00865818 < alpha = 5% => Đủ cơ sở để bác bỏ H0, chấp nhận H1 hay khi thu nhập tăng 400$/tuần
thì chi tiêu tăng nhiều hơn 2$/tuần.
TH2: Mô hình Log – Log: Logfoodexpi=β1 + β2*LogIncomei + ui
dfoodexp/foodexp = beta2*dincome/income
(a) Khi thu nhập tăng 0.5% thì chi tiêu tăng 2%
|dincome/income| = 0.5/100 , tăng => |dincome/income| = dincome/income = 0.5/100
|dfoodexp/foodexp| = 2/100, tăng => |dfoodexp/foodexp| = dfoodexp/foodexp = 2/100
dfoodexp/foodexp = beta2*dincome/income = beta2*(0.5/100)
beta2*(0.5/100) = 2/100 => Beta2 = 2/0.5 =4
 Giả thuyết: H0: Beta2 =4; H1: Beta 2 # 4
(b) Khi thu nhập giảm 2% thì chi tiêu giảm nhiều hơn 3%
Giả thuyết: H0: Beta2 <= 1.5; H1: Beta2 > 1.5
KL: t = t_2 = -9.3793302 alpha = 5%
=> Không đủ cơ sở để bác bỏ H0 hay khi thu nhập giảm 2% thì chi tiêu giảm nhỏ hơn hoặc bằng 3%.
TH3: Mô hình Log- Lin: Logfoodexpi = β1 + β2*Incomei + ui
(a) Khi thu nhập tăng 500$/tuần thì chi tiêu tăng 5%
|dfoodexp/foodexp| = 5/100, chi tiêu tăng => dfoodexp/foodexp= 5/100
|dincome| = 500/1000, thu nhập tăng => dincome = 0.5
 Giả thuyết: H0: Beta2 = 0.1; H0: Beta2 # 0.1
KL: |t| = |t_1| = 7.8237529 > ttoihan1= 2.0243942, hay pvalue1= 1.944* 10^-9 < alpha=5% => đủ
cơ sở để bác bỏ H0, chấp nhận H1 => Khi thu nhập tăng 500$/tuần thì chi tiêu tăng khác 5%
TH4: Mô hình Lin- Log: foodexpi = β1 + β2*LogIncomei + ui
Khi thu nhập tăng 2% thì chi tiêu tăng 10$/tuần
Khi thu nhập tăng 2% thì chi tiêu tăng nhiều hơn 10$/tuần
Khi thu nhập tăng 2% thì chi tiêu tăng ít hơn 10$/tuần
2.4. Ước lượng khoảng tin cậy cho hệ số hồi quy ෢ 2− 𝑡
⬚ 𝑛 − 𝑘 ∗ 𝑠𝑒 ෢ ≤  ≤ ෢ +
2 𝑡 ⬚ 𝑛 − 𝑘 ∗ 𝑠𝑒 ෢ B1: Tính LB:
sca LB = _b[Biến độc lập] - invttail(e(df_r),alpha/2)*_se[Biến độc lập] Lệnh B2: Tính UB:
sca UB = _b[Biến độc lập] + invttail(e(df_r),alpha/2)*_se[Biến độc lập]
B3: In kết quả và kết luận: sca list LB UB Ước lượng khoảng tin Lệnh reg
reg [Biến phụ thuộc] [Biến độc lập], Level(độ tin cậy) cậy cho hệ số hồi quy Lệnh lincom
lincom [Biến độc lập], level(độ tin cậy)
Mô hình Lin - Lin: Khi các yếu tố các không đổi, X tăng 1
đơn vị thì giá trị trung bình của Y tăng hoặc giảm trong
khoảng từ LB/|UB| đến UB/|LB| đơn vị
Mô hình Log - Log: Khi các yếu tố các không đổi, X
tăng 1% thì giá trị trung bình của Y tăng hoặc giảm Ý nghĩa của
trong khoảng từ LB/|UB| đến UB/|LB|% khoảng tin cậy
Mô hình Log - Lin: Khi các yếu tố các không đổi, X tăng
1 đơn vị thì giá trị trung bình của Y tăng hoặc giảm trong
khoảng từ LB/|UB| đến UB/|LB| %
Mô hình Lin - Log: Khi các yếu tố các không đổi, X
tăng 1% thì giá trị trung bình của Y tăng hoặc giảm
trong khoảng từ LB/|UB| đến UB/|LB| đơn vị
VD: Phân tích tác động của thu nhập hàng tuần của hộ gia đình (income: 1000$/tuần) đến chi tiêu
cho thực phẩm của hộ gia đình hàng tuần (food_exp: $/tuần) với dạng mô hình hồi quy như sau:
Ước lượng khoảng tin cậy cho hệ số hồi quy của 2 với độ tin cậy 99%, nêu ý nghĩa của khoảng tin
cậy này (cho 4 mô hình là 4 trường hợp):
TH1: Mô hình Lin – Lin: Cách 1:
B1: sca LB = _b[ income] - invttail(e(df_r),0.01/2)*_se[ income]
B2: sca UB = _b[ income] + invttail(e(df_r),0.01/2)*_se[ income] B3: sca list LB UB
 Kết quả: LB = 4.5336383; UB = 15.885648
Kết luận: Khoảng tin cậy cho hệ số hồi quy của income là [4.5336383; 15.885648] với độ tin cậy
là 99%. Khi các yếu tố khác không đổi, thu nhập hàng tuần tăng 1 đơn vị (1000$/tuần) thì chi
tiêu cho thực phẩm trung bình tăng từ 4.5336383 đơn vị ($/tuần) đến 15.885648 đơn vị ($/tuần) Cách 2: reg food_exp income food_exp Coef. Std. Err. t P>|t| [99% Conf. Interval] income 10.20964 2.093264 4.88 0.000 4.533638 15.88565 _cons 83.416 43.41016 1.92 0.062 -34.29316 201. 1252 Khoảng tin cậy Cách 3: lincome income, level(99) food_exp Coef. Std. Err. t P>|t| [99% Conf. Interval] (1) 10.20964 2.093264 4.88 0.000 4.533638 15.88565
TH2: Mô hình Log – Log: LogYi = 1 * 2*LogXi + ui
Kết luận: Khoảng tin cậy cho hệ số hồi quy của Logincome là [0.2829372; 0.8288253] với độ tin
cậy là 99%. Khi các yếu tố khác không đổi, thu nhập hàng tuần tăng 1 đơn vị (1000$/tuần) thì chi
tiêu cho thực phẩm trung bình tăng từ 4.5336383 đơn vị ($/tuần) đến 15.885648 đơn vị ($/tuần)
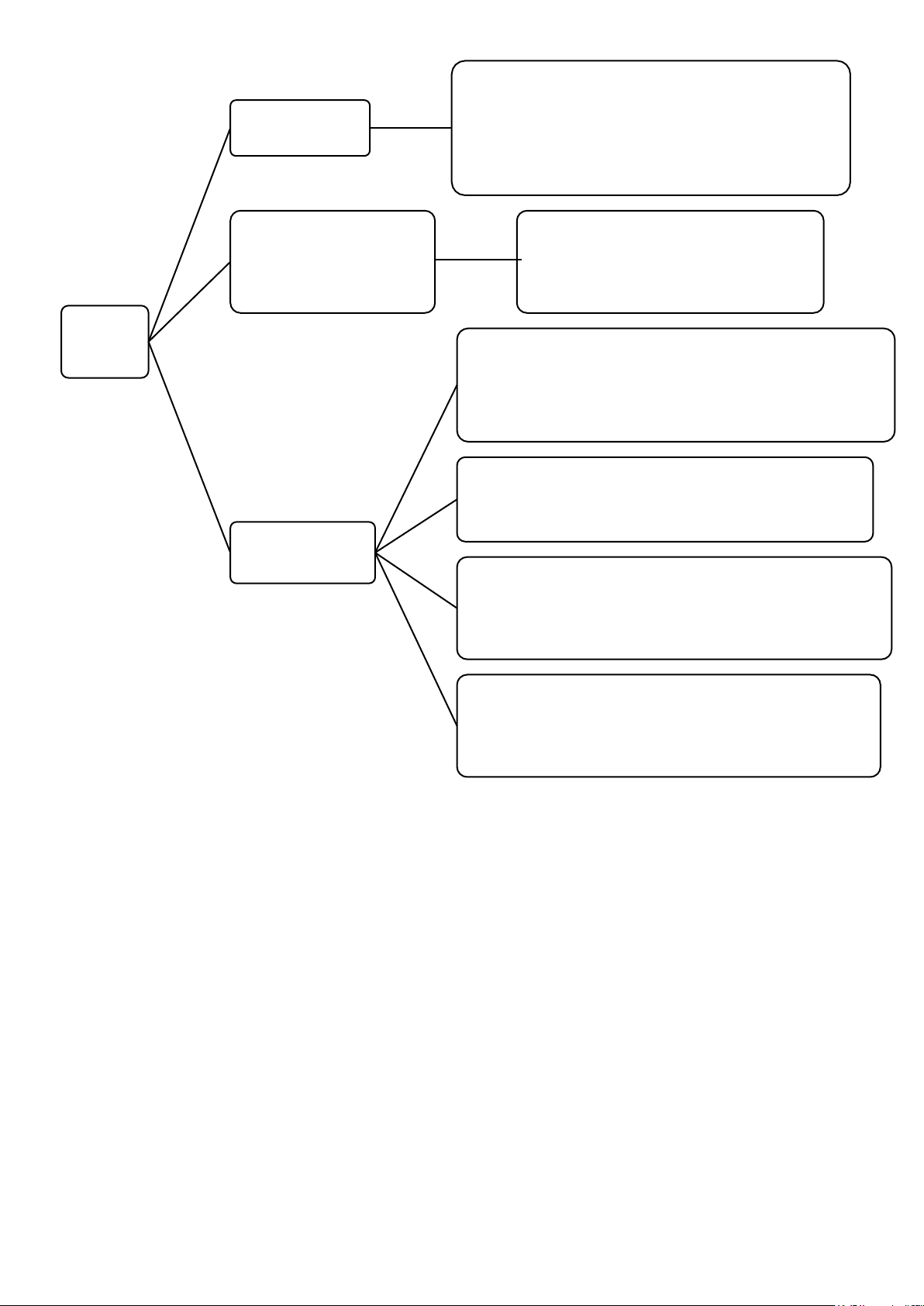
2.5. Dự báo biến phụ thuộc Dự báo
Thay giá trị biến độc lập (bài cho) vào phương trình hồi quy mẫu điểm
=> Tính ra giá trị biến phụ thuộc
B1: Tạo miền giá trị chứa giá trị dự báo:
set obs n+1 (n là số quan sát hiện có) Dự báo
B2: Điền giá trị quan sát n+1 của biến độc lập (đề bài cho)
replace (biến độc lập) = (giá trị bài cho) in n+1
B3: Dự báo biến phụ thuộc: Dự báo
predict (biến phụ thuộc_F) khoảng
B4: Xác định khoảng ước lượng:
Lấy sai số chuẩn: predict SSC, stdf
Tính LB: gen LB = biến phụ thuộc_F - invttail(e(df_r),alpha/2)*SSC
Tính UB: gen UB = biến phụ thuộc_F + invttail(e(df_r),alpha/2)*SSC
B5: In giá trị: list LB biến phụ thuộc_F UB in n+1
VD: Phân tích tác động của thu nhập hàng tuần của hộ gia đình (income: 1000$/tuần) đến chi tiêu
cho thực phẩm của hộ gia đình hàng tuần (food_exp: $/tuần) với dạng mô hình hồi quy như sau:
Dự báo giá trị (ước lượng) của chi tiêu cho thực phẩm của hộ gia đình hàng tuần nếu thu nhập hàng
tuần của hộ gia đình là 2000$/tuần với độ tin cậy 99%.
TH1: Mô hình Lin – Lin:
Note: Hồi quy trước khi làm các bước sau:
B1: Thiết lập giá trị n+1: set obs 41
B2: Thay giá trị income = 2: replace income=2 in 41
B3: Dự báo food_exp: predict food_exp_F
B4: Lấy SSC: predict SSC,stdf B5: Tính LB + UB:
gen LB= food_exp_F - invttail(e(df_r),0.01/2)* SSC
gen UB= food_exp_F + invttail(e(df_r),0.01/2)*SSC
B7: In kết quả: list LB food_exp_F UB in 41
Kết luận: Dự báo điểm cho chi tiêu cho thực phẩm là 103.8353; Dự báo khoảng cho chi tiêu cho
thực phẩm là [-161.4494 ; 369.12]. Khi thu nhập hàng tuần là 2000$/tuần thì chi tiêu cho thực phẩm
trung bình là 103.8353$/tuần. Chi tiêu cho thực phẩm TB bé nhất là 0 và lớn nhất là 369.12$/tuần. TH2: Mô hình Log – Log: B1: set obs 41
B2: replace logincome = log(2) in 41 B3: predict logfoodexp_F B4: predict SSC,stdf B5:
gen LB= logfoodexp_F-invttail(e(df_r), 0.01/2)*SSC
gen UB= logfoodexp_F+invttail(e(df_r), 0.01/2)*SSC B6: list LB logfoodexp_F UB
Document Outline

• Note:
• 2.1. Phân tích thống kê mô tả dữ liệu
• 2.2. Ước lượng hồi quy
• 2.3. Kiểm định giả thuyết thống kê
• sca pvalue = 2*ttail(e(df_r),abs(t))
• sca ttoihan = invttail(e(df_r),alpha)
• Ví dụ: Phân tích tác động của thu nhập hàng tuần của hộ gia đình (income: 1000$/tuần) đến chi tiêu cho thực phẩm của hộ gia đình hàng tuần (food_exp: $/tuần) với dạng mô hình hồi quy như sau:
  • (a) Nhà nghiên cứu cho rằng thu nhập có tác động đến chi tiêu. Thiết lập giả thuyết thống kê và kiểm định với mức ý nghĩa alpha là 5%.
  • (b) Khi thu nhập tăng thì chi tiêu tăng, thiết lập giả thuyết thống kê và kiểm định.
  • Note: Thu nhập có tác động cùng chiều hay ngược chiều đến chi tiêu ?
  • (c) Nhà nghiên cứu cho rằng khi thu nhập giảm 100$/tuần thì chi tiêu cho thực phẩm giảm 110$/tuần. Thiết lập giả thuyết thống kê và kiểm định
  • (d) Khi thu nhập tăng 500$/tuần thì chi tiêu cho thực phẩm tăng ít hơn 8$/tuần. Thiết lập giả thuyết thống kê và kiểm định.
• TH2: Mô hình Log – Log: Logfoodexpi=β1 + β2*LogIncomei + ui
  • (a) Khi thu nhập tăng 0.5% thì chi tiêu tăng 2%
  • (b) Khi thu nhập giảm 2% thì chi tiêu giảm nhiều hơn 3%
• TH3: Mô hình Log- Lin: Logfoodexpi = β1 + β2*Incomei + ui
  • (a) Khi thu nhập tăng 500$/tuần thì chi tiêu tăng 5%
• TH4: Mô hình Lin- Log: foodexpi = β1 + β2*LogIncomei + ui
• 2.4. Ước lượng khoảng tin cậy cho hệ số hồi quy
• TH1: Mô hình Lin – Lin:
• 2.5. Dự báo biến phụ thuộc