Lec5-Graph 1 - cấu trúc dữ liệu và giải thuật môn Kỹ thuật lập trình | Đại học Bách Khoa, Đại học Đà Nẵng
Lec5-Graph 1 - cấu trúc dữ liệu và giải thuật môn Ki thuật lập trình | Đại học Bách Khoa, Đại học Đà Nẵng giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học
Tài liệu liên quan:
Preview text:
Elementary Graph Algorithms
Lecture #5 of Algorithms, Data structures and Complexity November 28, 2015 c JPK&GfH
#5: Elementary Graph Algorithms Plan for today Graphs
• Definitions, terminology, representations • Algorithms
– Breadth-first traversal
– Depth-first traversal
– Finding connected components – Topological sorting
– Critical path analysis c JPK&GfH 1
#5: Elementary Graph Algorithms
The graph as a (mathematical) model
Graphs are used in many (computer science) applications: • Computer networks
• Representation of topological informations (maps, . . .)
• Representation of electronic circuits
• Precedence graphs, workflows, . . .
• Semantic networks (e.g., entity-relationship diagrams)
we concentrate on fundamental graph algorithms c JPK&GfH 2
#5: Elementary Graph Algorithms
Definition – What is a directed graph?
A directed graph (or: digraph) G is a pair (V, E) with • V is a set of vertices
• E ⊆ V × V is a set of ordered pairs of vertices, called (directed) edges
• if E is a set of unordered pairs, G is called undirected Example: • V = { A, . . . , F }
• E = { (A, B), (A, D), (B, E), (C, E), (C, F ), (D, B), (E, D), (F, F ) } A B C D E F c JPK&GfH 3
#5: Elementary Graph Algorithms Terminology
A subgraph of a graph G = (V, E) is a graph G′ = (V ′, E′) with • V ′ ⊆ V and E′ ⊆ E
• as G′ is a graph it follows E′ ⊆ V ′ × V ′
• if V ′ ⊂ V or E′ ⊂ E, G′ is a proper subgraph
Graph G is symmetric if (v, w) ∈ E implies (w, v) ∈ E
• every undirected graph has a corresponding symmetric digraph
Graph G is complete if each pair of vertices is connected via an edge
The transpose of G is GT = (V, E′) with (v, w) ∈ E′ iff (w, v) ∈ E
• the direction of each edge in G is reversed in the transposed graph c JPK&GfH 4
#5: Elementary Graph Algorithms
Terminology – Examples A B C A B D E F D E c JPK&GfH 5
#5: Elementary Graph Algorithms
Definitions – Paths and cycles
A path from vertex v to w is a sequence of edges (vi, vi+1) for
i = 0, . . . , k−1 such that v = v0 and w = vk.
(So v = v0 → v1 → . . . → vk−1 → vk = w )
The length of a path is the number of edges it traverses
Vertex w is reachable from v if there is a path from v to w
A cycle is a non-empty path with the same first and last vertex
• a cycle of the form v v is called a self-cycle (or self-loop)
• a graph is acyclic if it has no cycles
• a cycle of an undirected graph may only visit edges in the same orientation c JPK&GfH 6
#5: Elementary Graph Algorithms
Examples – Paths and cycles A B C D F E
A B E D B and C F F are example paths c JPK&GfH 7
#5: Elementary Graph Algorithms
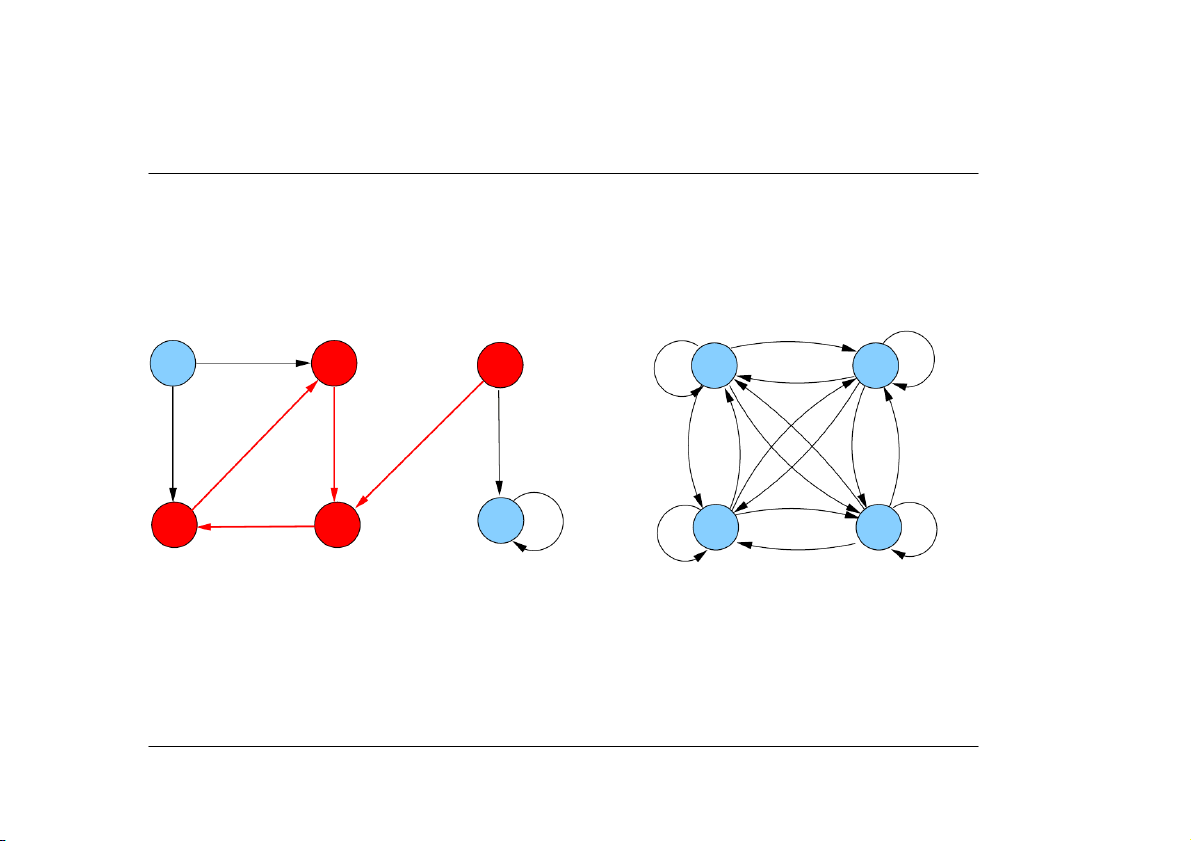
Connected graphs and components
A graph in a collection of graphs is maximal if it is no proper subgraph of any of these graphs Undirected graph G:
• G is connected if each vertex is reachable from any other vertex
• a connected component of G is a maximal connected subgraph of G Directed graph G:
• G is strongly connected if each vertex is reachable from any other vertex
• G is weakly connected if, after making all edges undirected, the resulting undirected graph is connected
• a strongly connected component of G is a maximal strongly connected subgraph of G
A non-connected graph can be uniquely partitioned into separate connected components c JPK&GfH 8
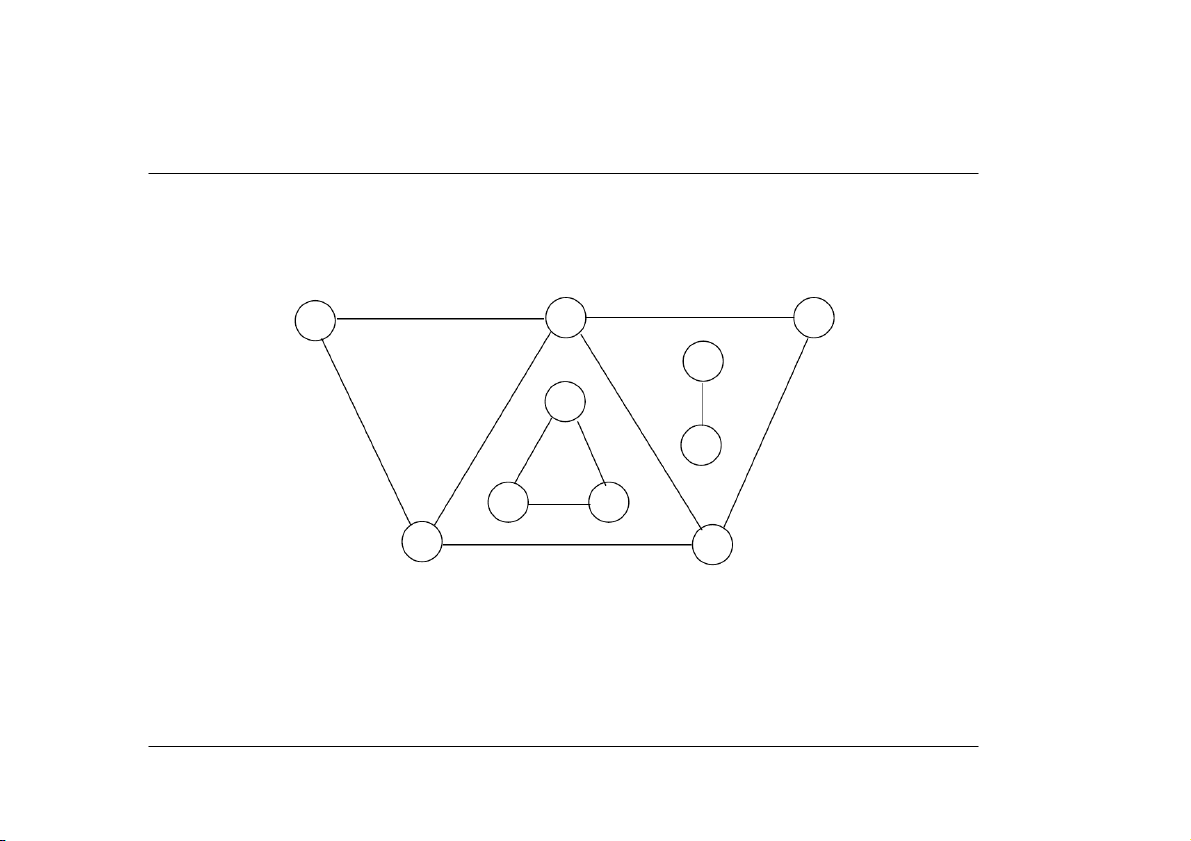
#5: Elementary Graph Algorithms
Connected undirected graphs
an undirected graph; what are its connected components? c JPK&GfH 9