Prepared by Trịnh Ngọc Nhân I) KEY CONCEPT
- Random experiment (phép thử ngẫu nhiên)
- Sample space: không gian mẫu Nguyên t c
ắ của probility (CỰC KÌ QUAN TRỌNG): 0 <= P <= 1
+ Complement Event: phần bù- The complement of an event A i
s denoted A’ and consists of
everything in the sample space e S xcept event A
P(A) + P(A’) = 1
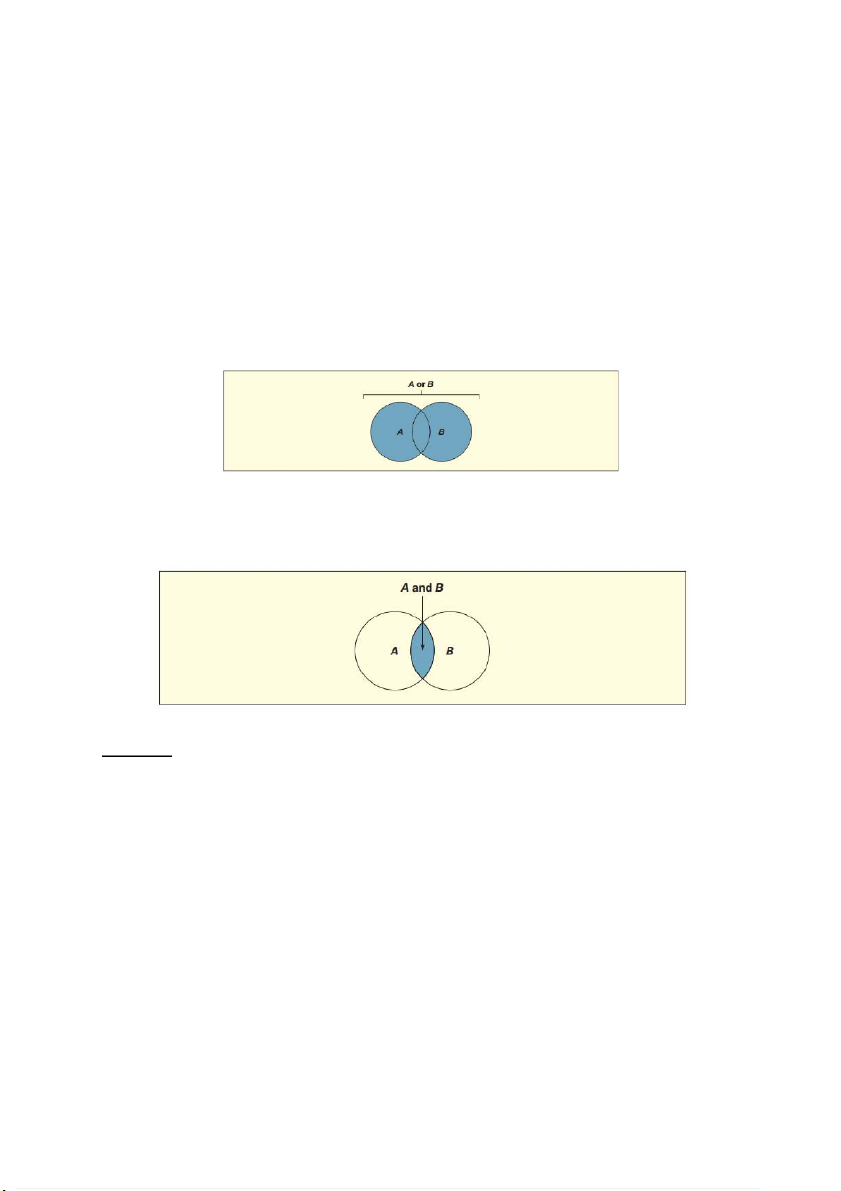
+ Union of two event (hợp c a 2 t ủ p h ậ
ợp): consists of all outcomes in the sample space S that
are contained either in event A or
in event B or in both. Symbol: 𝐀 ∪ 𝐁
+ Intersection of two event (giao c a 2 t ủ p h ậ
ợp): consists of all outcomes in the sample space
S that are contained in both event A a
nd event B. Symbol: 𝐀 ∩ 𝐁
Example: Suppose that A and B are two events. Write expressions involving unions,
intersections, and complements that describe the following:
A) Both events occur 𝐀 ∩ 𝐁
B) At least one occurs (either A or B occur) 𝐀 ∪ 𝐁
C) Neither occurs 𝐀, ∩ 𝐁,
D) Exactly one occurs (𝐀 ∩ 𝐁,) ∪ (𝐁 ∩ 𝐀,)
Prepared by Trịnh Ngọc Nhân
Example: A smoke detector system uses two devices, A and B. If smoke is present, the
probability that it will be detected by device A is 0.9; by device B, 0.85; and by both devices, 0.8.
A) If smoke is present, find the probability that the smoke will be detected by either device A or B or both devices.
B) Find the probability that the smoke will be undetected. Solution:
P(A)= 0.9, P(B)= 0.85, P (𝐴 ∩ 𝐵)= 0.8
=> probability that the smoke will be detected by either device A or B or both devices P (𝐴 ∪ 𝐵 = ) 0.9+0.85-0.8= 0.95.
probability that the smoke will be undetected by either device A or B or both devices: 1-0.95= 0.05
Conditional probability: The probability of A given that B has occured
Example: Suppose 30 percent of video games are purchased as digital content. Of those
games purchased as digital content, 47 percent are acquired from a gaming website. What is
the joint probability that a video game was purchased as digital content through a gaming website?
Independence of the events: A và B là 2 sự kiện c
độ lập với nhau khi và chỉ khi: P(A\B) = P(A)
Nếu như A và B là 2 sự kiện c
độ lập thì P (𝑨 ∩ 𝑩)= P(A) * P(B)
Example: Diseases I and II are prevalent among people in a certain population. It is assumed
that 10% of the population will contract disease I sometime during their lifetime, 15% will
contract disease II eventually, and 3% will contract both diseases.
A) Find the probability that a randomly chosen person from this population will contract at
least one disease. (0.22)
B) Find the conditional probability that a randomly chosen person from this population will
contract both diseases, given that he or she has contracted at least one disease. (3/22)
Prepared by Trịnh Ngọc Nhân
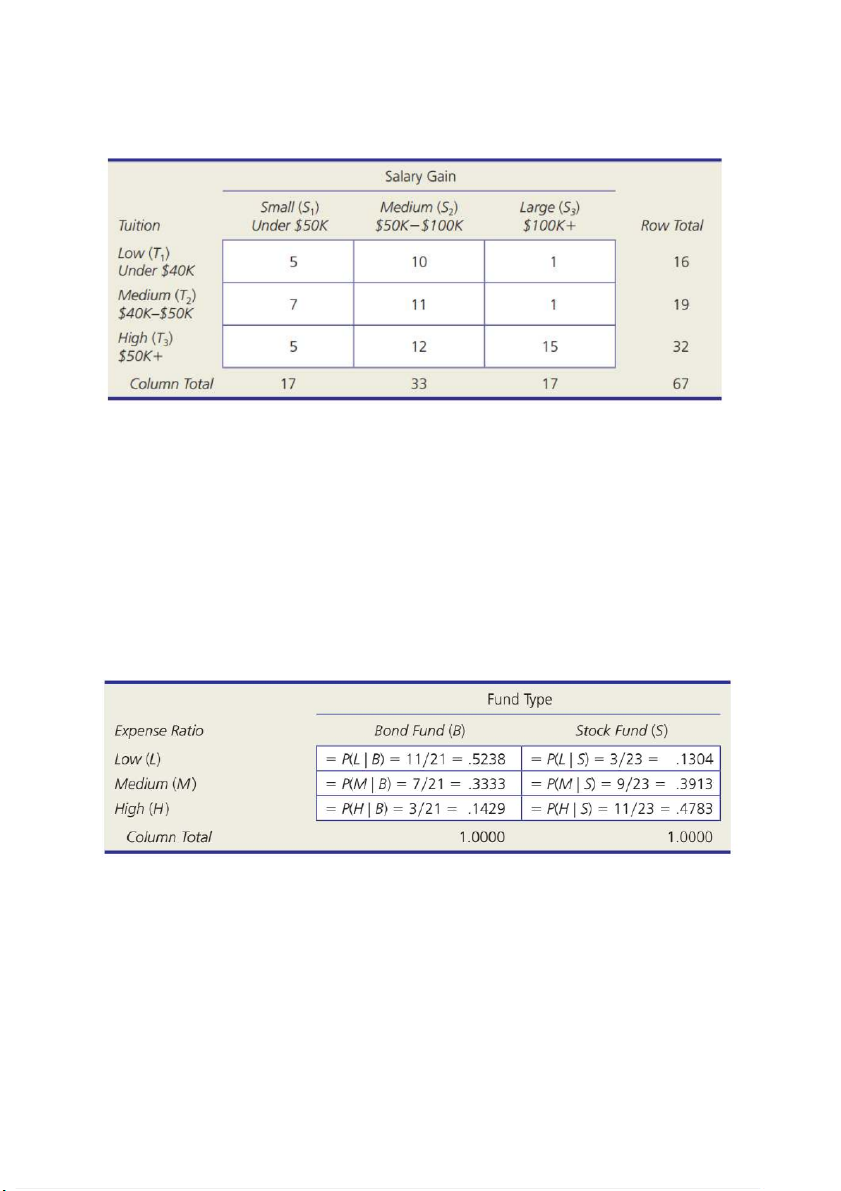
Contingency table is a cross-tabulation of frequencies into rows and columns
Marginal probability: Xác suất c a ủ m t ộ s ki
ự ện “lớn” xảy ra. Vd: P(S1) = 17/67= 0.254
Joint probability: Xác suất mà 2 s ki ự ện ng t đồ
hời xảy ra. Vd: P (S3 ∩ T1) = 1/67
Conditional probability: Xác suất xảy ra c a ủ m t ộ sự kiện khi mình ã đ ch n t ọ rước m t ộ sực kiện khá . V c d: P (S1\T3) = 5/32
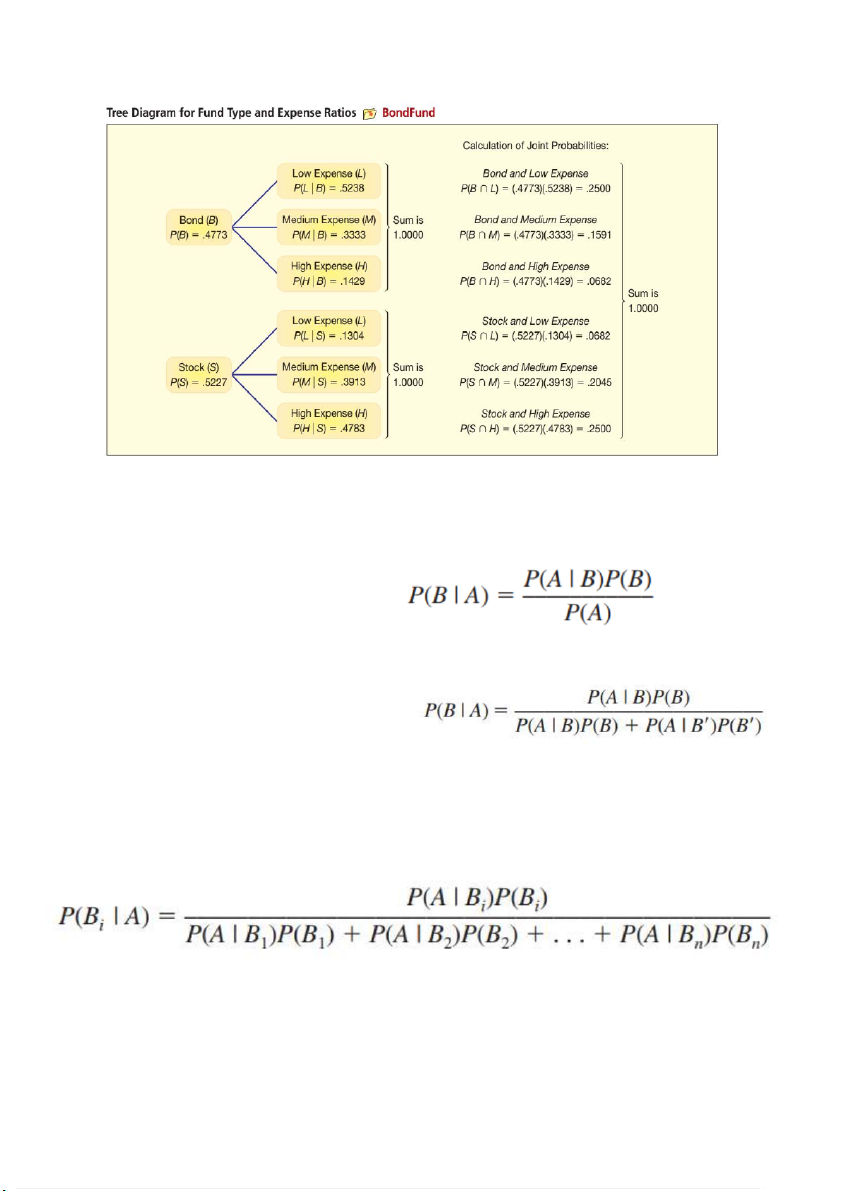
Tree diagram/ decision tree
(Các bạn có thể coi chi tiết hơn trong slide nhé)
Prepared by Trịnh Ngọc Nhân BAYES THEOREM
* Trường hợp cho proba của A
* Trường hợp không cho proba c a ủ A
* Dạng tổng quát (áp dụng nếu cho từ 3 s ki ự ện trở lên)
Prepared by Trịnh Ngọc Nhân Counting rules:
Factorial: giai thừa. n! = n * ( - n 1) * ( - n 2) * … 1
Permutation: phép chỉnh hợp
Combination: phép tổ ợ h p II) EXERCISE
Question 1: The following table gives numbers of claims at a large insurance company by
kind and by geographic region. East South Midwest West Hospitalization 75 128 29 52 Physician’s visit 233 514 104 251 Outpatient treatment 100 326 65 99 Develop the contingency table
a. If a bill is chosen at random, what is the probability that it is from the Midwest? 0.1002
b. What is the probability that a randomly chosen bill is from the East? 0.2065
c. What is the probability that a randomly chosen bill is either from the Midwest or from the
South? What is the relation between these two events? 0.59
d. What is the probability that a randomly chosen bill is for hospitalization? 0.144
e. Given that a bill is for hospitalization, what is the probability that it is from the South? 0.451
f. Given that a bill is from the East, what is the probability that it is for a physician’s visit? 0.571
g. Given that a bill is for outpatient treatment, what is the probability that it is from the West? 0.168
h. What is the probability that a randomly chosen bill is either from the East or for outpatient
treatment (or both)? 0.454
i. What is the probability that a randomly selected bill is either for hospitalization or from the South (or both)? 0.569
Prepared by Trịnh Ngọc Nhân
Question 2: Two cards are drawn from an ordinary deck of 52 cards. Find the probability of
each event, showing your reasoning carefully. a. Two aces. (0.00452)
b. Two red cards. (0.245098)
c. Two red aces. (0.000754)
d. Two honor cards (A, K, Q, J, 10). (0.143288)
Question 3: A drug test for athletes has a 5% false positive rate and a 10% false negative rate.
Of the athletes tested, 4% have actually been using the prohibited drug. If a randomly chosen
athlete tests positive, what is the probability that the prohibited drug has been used? (0.4286)
Question 4: The following table gives the number of products in five types produced by two factories: Type A B C D E Factory X 210 342 186 425 135 Factory Y 320 287 238 266 180
a. A product is randomly selected. What is the probability that it is produced by factory X? (0.5014)
b. What is the probability that a randomly selected product is type B and produced by factory Y? (0.1109)
c. What is the probability that a product, which is not type C, is produced by factory X? (0.5136)
Question 5: A survey showed that 8% of Internet users age 18 and older report keeping a
blog. Referring to the 18 29 age group as young adults, the survey showed that for bloggers –
54% are young adults and for non-bloggers 24% are young adults (Pew Internet & American Life Project, July 19, 2006).
a. Develop a joint probability table for these data with two rows (bloggers vs. non-bloggers)
and two columns (young adults vs. older adults).
b. What is the probability that an Internet user is a young adult? (0.264)
c. What is the probability that an Internet user keeps a blog and is a young adult? (0.0432)
d. Suppose that in a follow-up phone survey we contact someone who is 24 years old. What
is the probability that this person keeps a blog? (0.1636)