

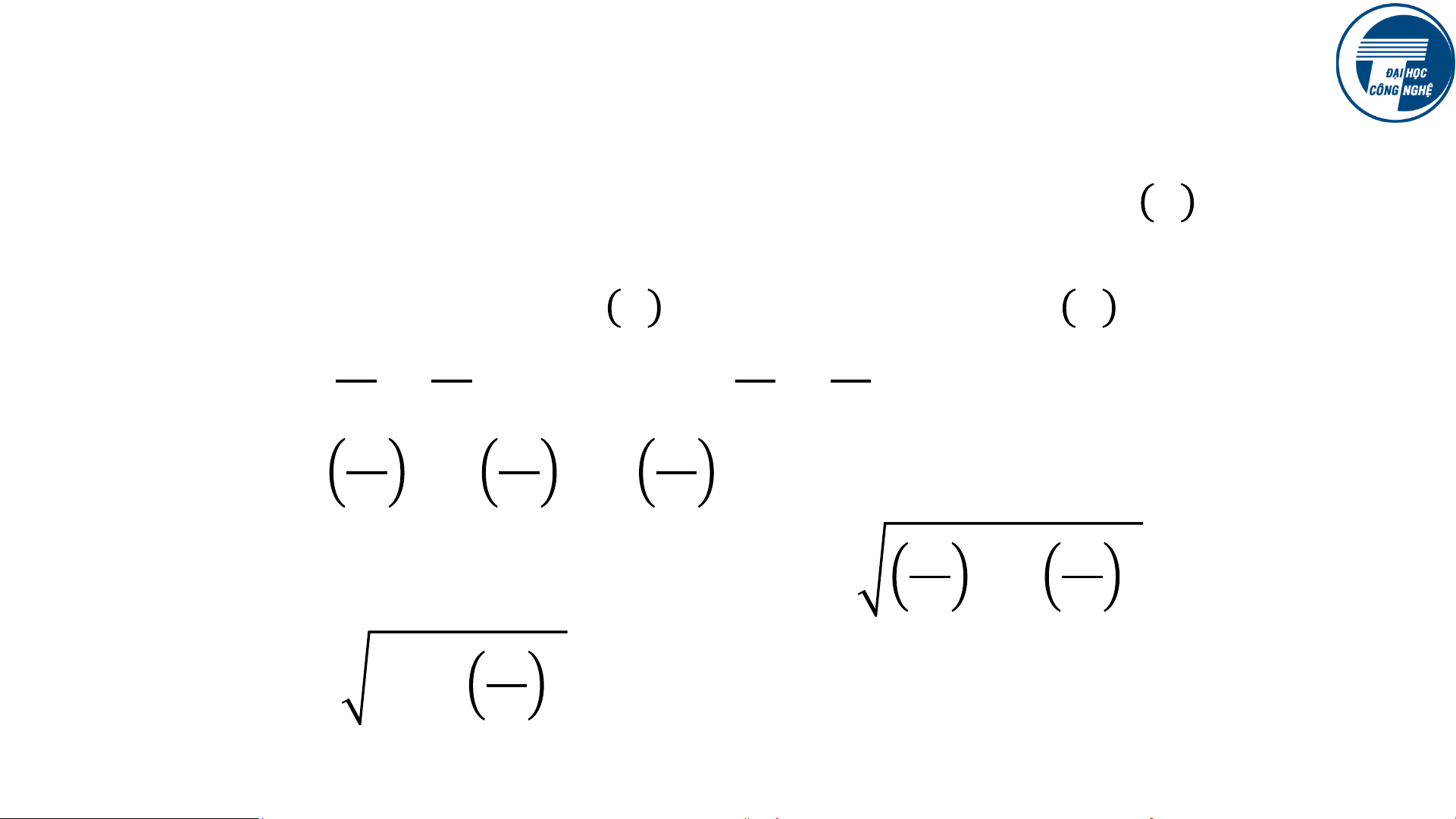

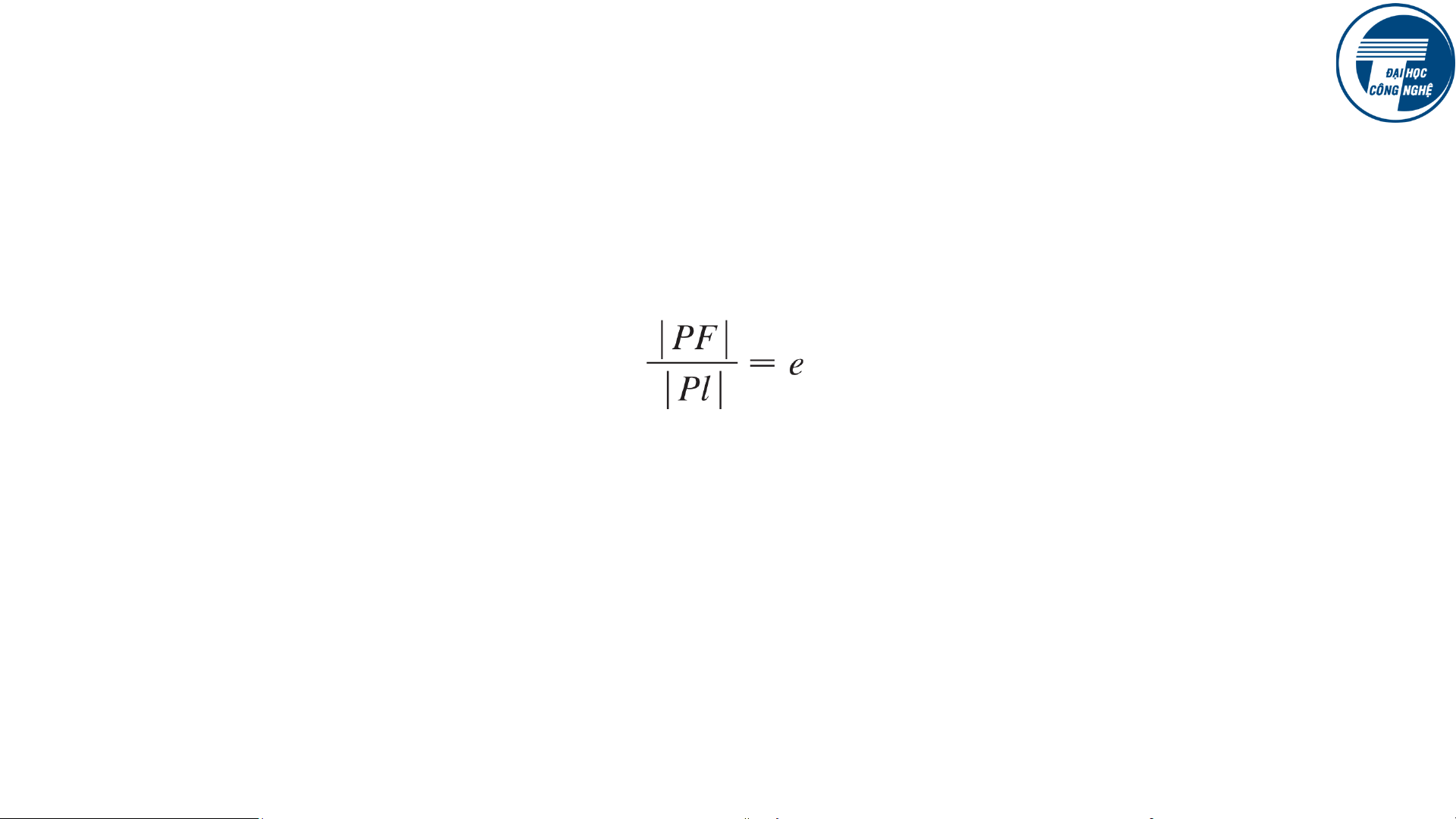
Preview text:
Giải tích 1
Chương 10: Phương trình tham số và tọa độ cực (tiếp theo)
VNU University of Engineering and Technology 1 10.3. Tọa độ cực a, Hệ tọa độ cực
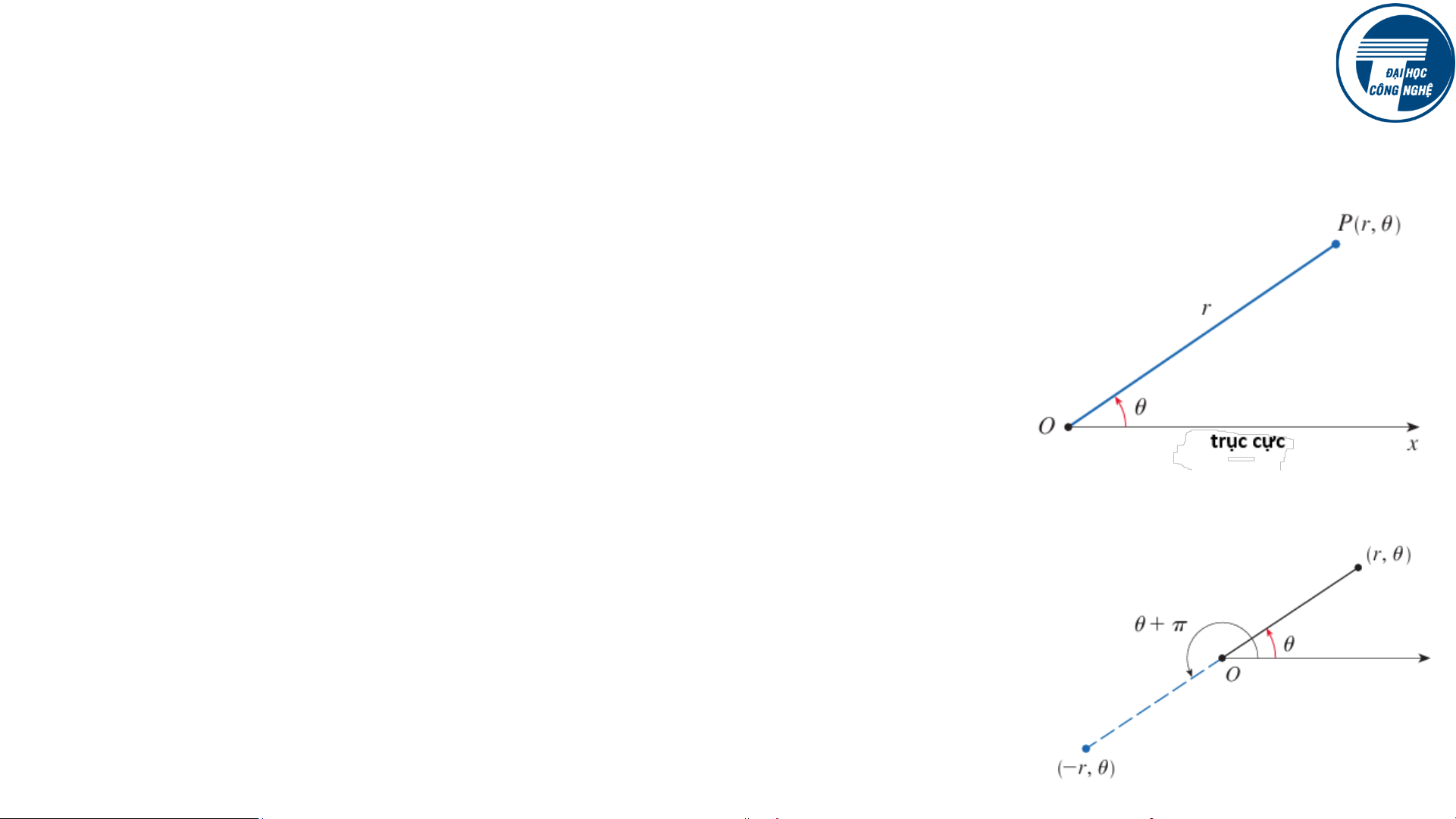
Ta chọn một điểm ký hiệu là O và gọi là cực, và một
tia với gốc là O và gọi là trục cực. Trục này thường
được vẽ ngang, về bên phải tương ứng với chiều
dương của trục x theo tọa độ Cartesian. Với điểm P
• xét r là khoảng cách giữa O và P
• xét 𝜃 là góc giữa trục cực và OP
Quy ước: 𝜃 là dương nếu từ trục cực đến OP là
ngược chiều kim đồng hồ.
Từ đó, điểm P có thể được biểu diễn qua cặp (𝑟, 𝜃),
đây được gọi là tọa độ cực.
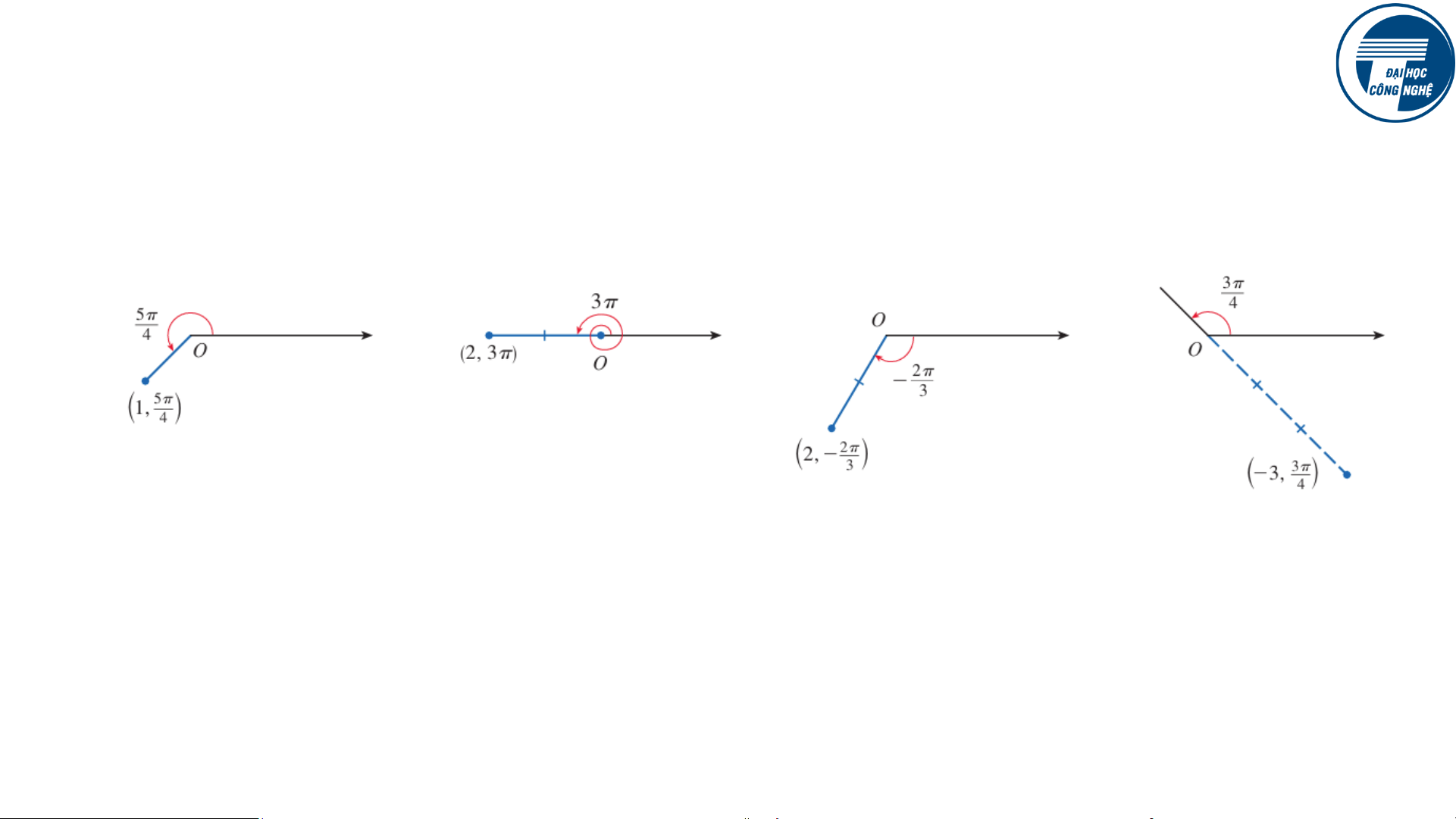
VNU University of Engineering and Technology 2 10.3. Tọa độ cực a, Hệ tọa độ cực Ví dụ:
VNU University of Engineering and Technology 3 10.3. Tọa độ cực
b, Mối liên hệ giữa tọa độ cực và tọa độ Cartesian
Ta có các mối liên hệ sau giữa tọa độ cực (𝑟, 𝜃) và tọa độ Cartesian (𝑥, 𝑦): 𝑥 = 𝑟𝑐𝑜𝑠𝜃,
𝑦 = 𝑟𝑠𝑖𝑛𝜃𝑦 𝑟2 = 𝑥2 + 𝑦2, 𝑡𝑎𝑛𝜃 = 𝑥
VNU University of Engineering and Technology 4 10.3. Tọa độ cực
c, Đường cong tọa độ cực
Đồ thị của phương trình tọa độ cực 𝑟 = 𝑓(𝜃) hoặc 𝐹 𝑟, 𝜃 = 0 được gọi là
đường cong tọa độ cực.
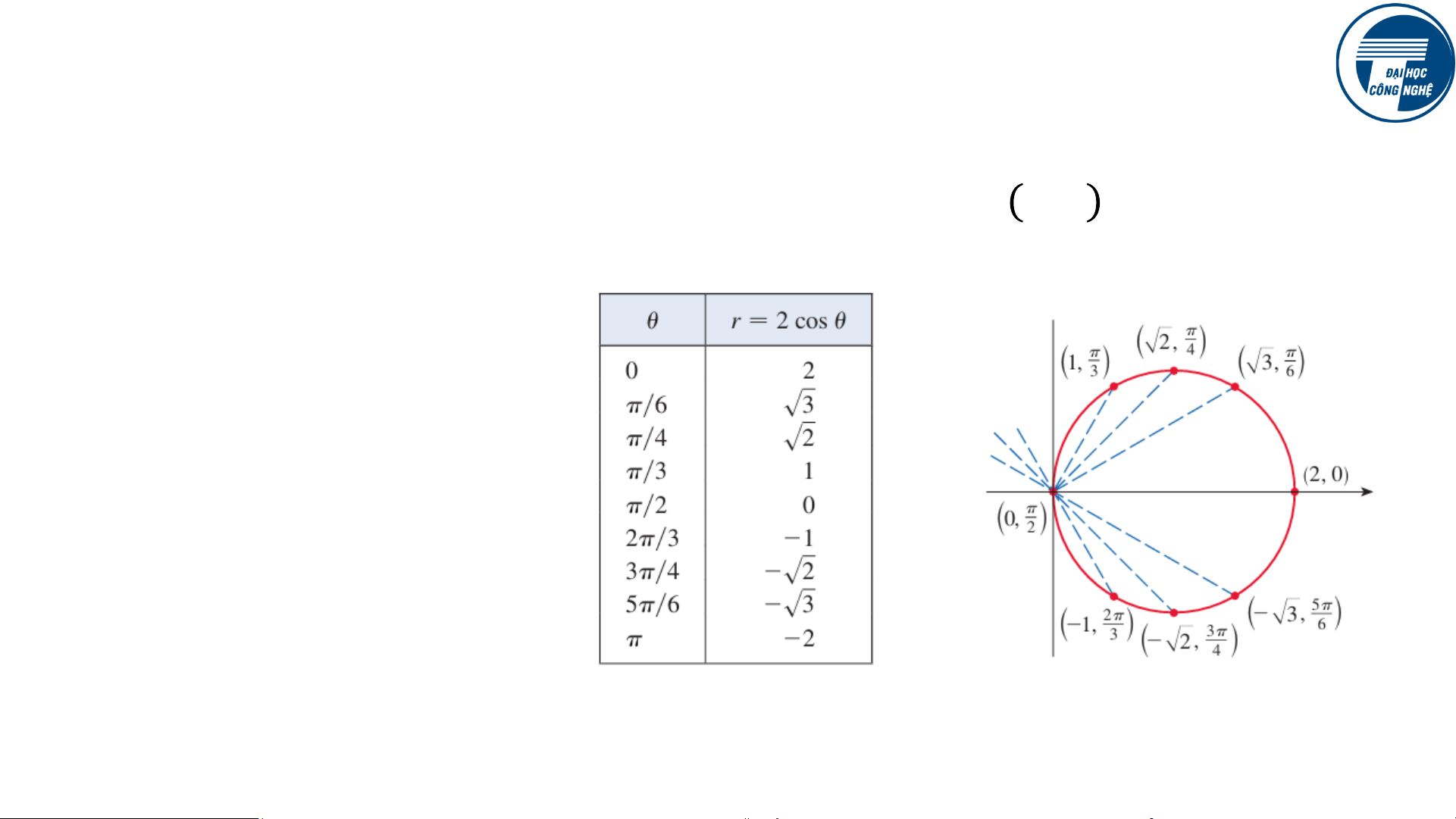
Ví dụ: 𝑟 = 2𝑐𝑜𝑠𝜃
Tìm phương trình trong tọa độ Cartesian?
VNU University of Engineering and Technology 5 10.3. Tọa độ cực
c, Đường cong tọa độ cực
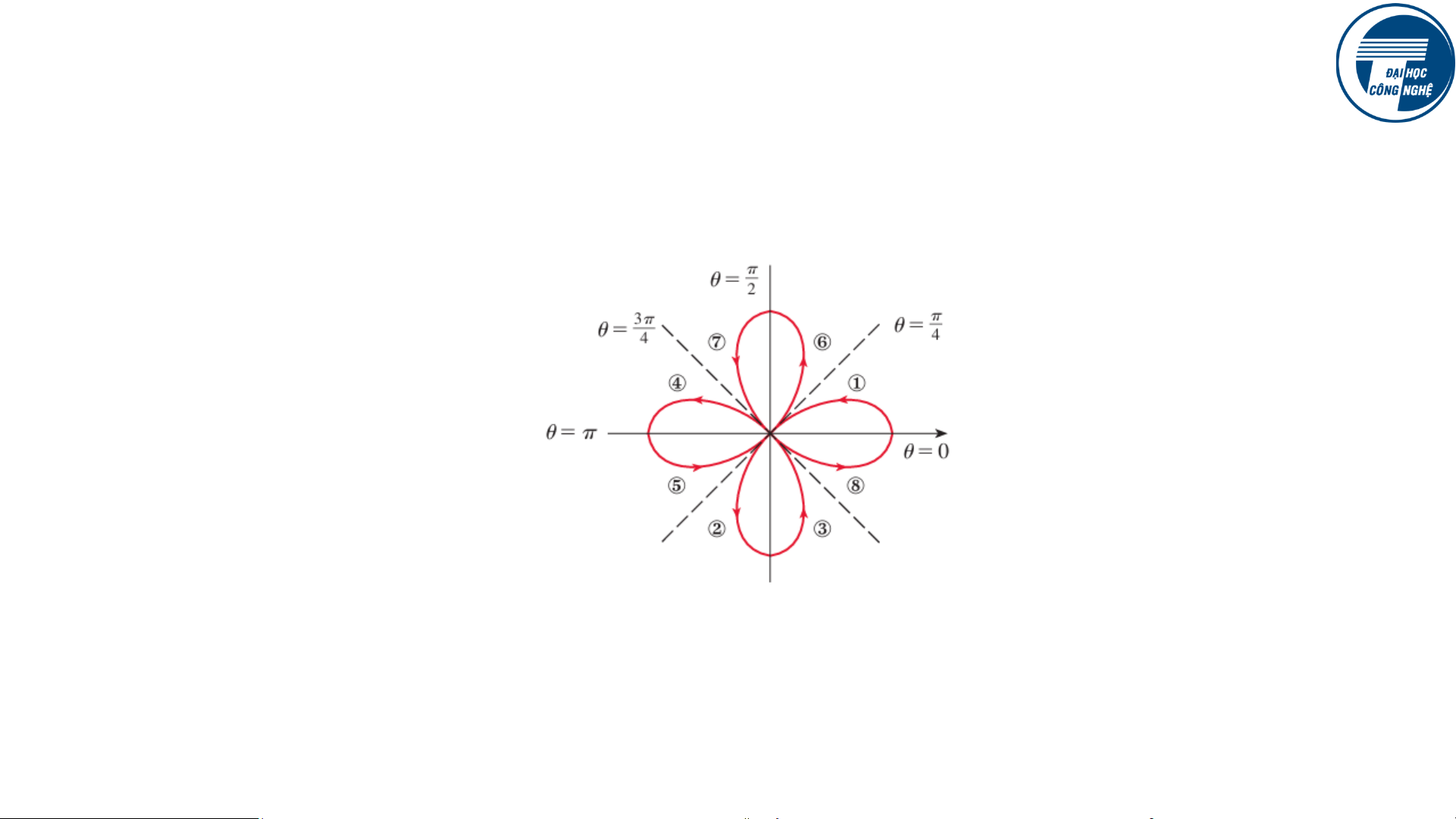
Ví dụ: Cỏ 4 lá 𝑟 = 𝑐𝑜𝑠2𝜃
VNU University of Engineering and Technology 6
10.4. Giải tích trong tọa độ cực a, Diện tích
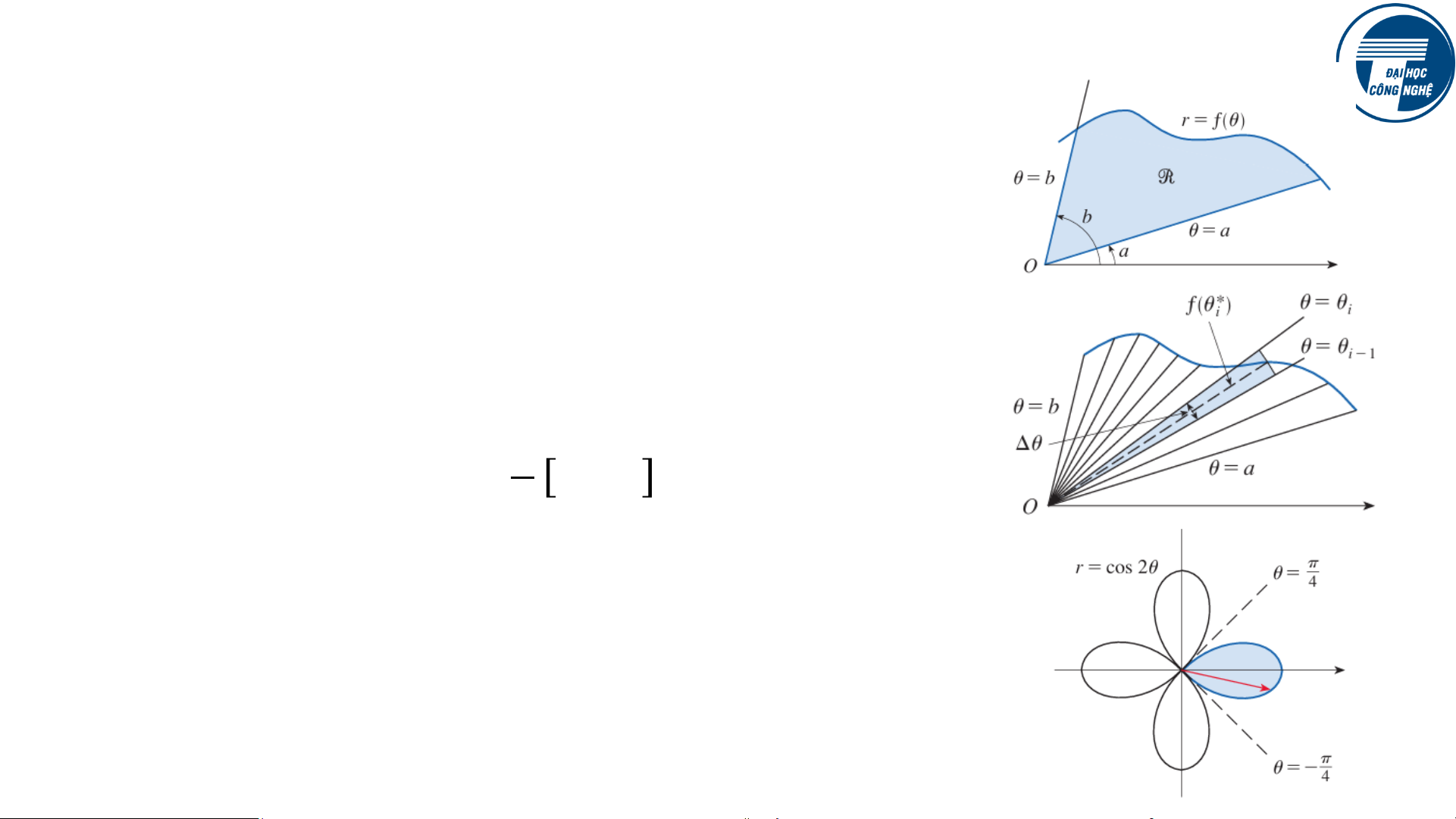
Xét R là miền bị giới hạn bởi đường cong tọa độ
cực 𝑟 = 𝑓(𝜃) và các tia 𝜃 = 𝑎, 𝜃 = 𝑏, với 𝑓 là hàm
liên tục dương và 0 < 𝑏 − 𝑎 ≤ 2𝜋.
Bằng cách chia đủ nhỏ góc và cộng tổng lại, ta có
công thức tính diện tích R là: 𝑏 1 𝐴 = න 𝑓(𝜃) 2𝑑𝜃. 𝑎 2
Ví dụ: tính diện tích một trong bốn phần của cỏ 4 lá 𝑟 = 𝑐𝑜𝑠2𝜃.
VNU University of Engineering and Technology 7
10.4. Giải tích trong tọa độ cực b, Độ dài cung
Ta xét đường cong được tham số hóa trong tọa độ cực 𝑟 = 𝑓 𝜃 với 𝑓′ liên
tục và 𝑎 ≤ 𝜃 ≤ 𝑏. Ta có
𝑥 = 𝑟𝑐𝑜𝑠𝜃 = 𝑓 𝜃 𝑐𝑜𝑠𝜃, 𝑦 = 𝑟𝑠𝑖𝑛𝜃 = 𝑓 𝜃 𝑠𝑖𝑛𝜃 Ta tính được 𝑑𝑥 𝑑𝑟 𝑑𝑦 𝑑𝑟 =
𝑐𝑜𝑠𝜃 − 𝑟𝑠𝑖𝑛𝜃, =
𝑠𝑖𝑛𝜃 + 𝑟𝑐𝑜𝑠𝜃. 𝑑𝜃 𝑑𝜃 𝑑𝜃 𝑑𝜃 2 2 2 Từ đó, ta có 𝑑𝑥 𝑑𝑦 𝑑𝑟 + = + 𝑟2. 𝑑𝜃 𝑑𝜃 𝑑𝜃 2 2
Sử dụng công thức tính độ dài cung 𝑏 𝑑𝑥 𝑑𝑦 𝐿 = + 𝑑𝜃, 𝑎 𝑑𝜃 𝑑𝜃 2 Ta có 𝑏 𝑑𝑟 𝐿 = 𝑟2 + 𝑑𝜃 . 𝑎 𝑑𝜃
VNU University of Engineering and Technology 8
10.4. Giải tích trong tọa độ cực c, Tiếp tuyến
Ta xét đường cong được tham số hóa trong tọa độ cực 𝑟 = 𝑓 𝜃 với 𝑓′ liên
tục và 𝑎 ≤ 𝜃 ≤ 𝑏.
Độ dốc của tiếp tuyến tại điểm (𝑟, 𝜃) là 𝑑𝑦 𝑑𝑟 𝑑𝑦
𝑠𝑖𝑛𝜃+𝑟𝑐𝑜𝑠𝜃 = 𝑑𝜃 = 𝑑𝜃 . 𝑑𝑥 𝑑𝑥
𝑑𝑟𝑐𝑜𝑠𝜃−𝑟𝑠𝑖𝑛𝜃 𝑑𝜃 𝑑𝜃
VNU University of Engineering and Technology 9
10.5. Các đường Conic
Trong phần này, ta đưa ra các
định nghĩa hình học về
parabol, ellipse và hyperbola
và rút ra các phương trình
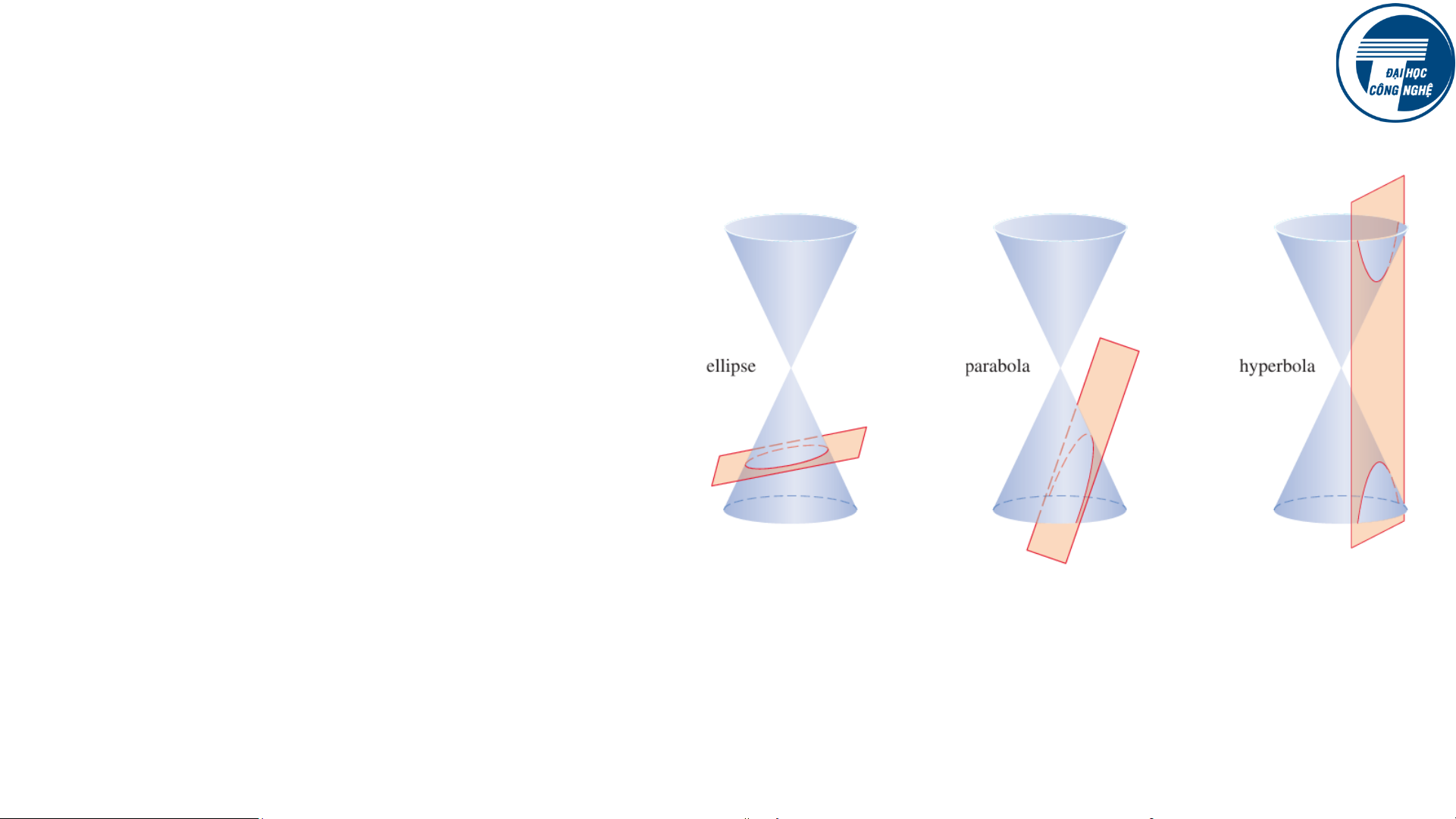
của chúng. Chúng được gọi
là hình côn, hoặc conics, vì
chúng là kết quả của việc cắt
một hình nón bằng một mặt phẳng.
VNU University of Engineering and Technology 10
10.5. Các đường Conic a, Parabol
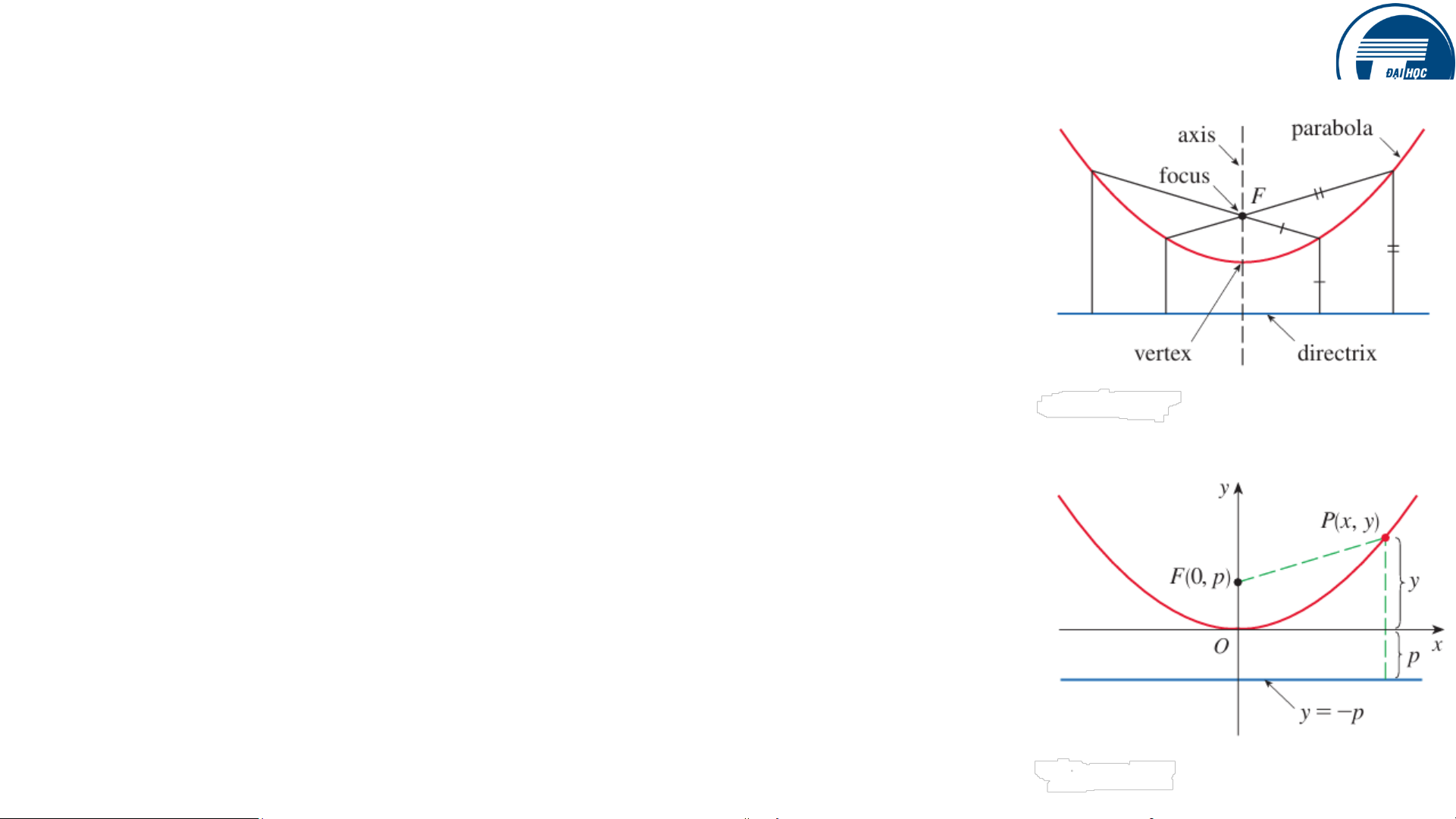
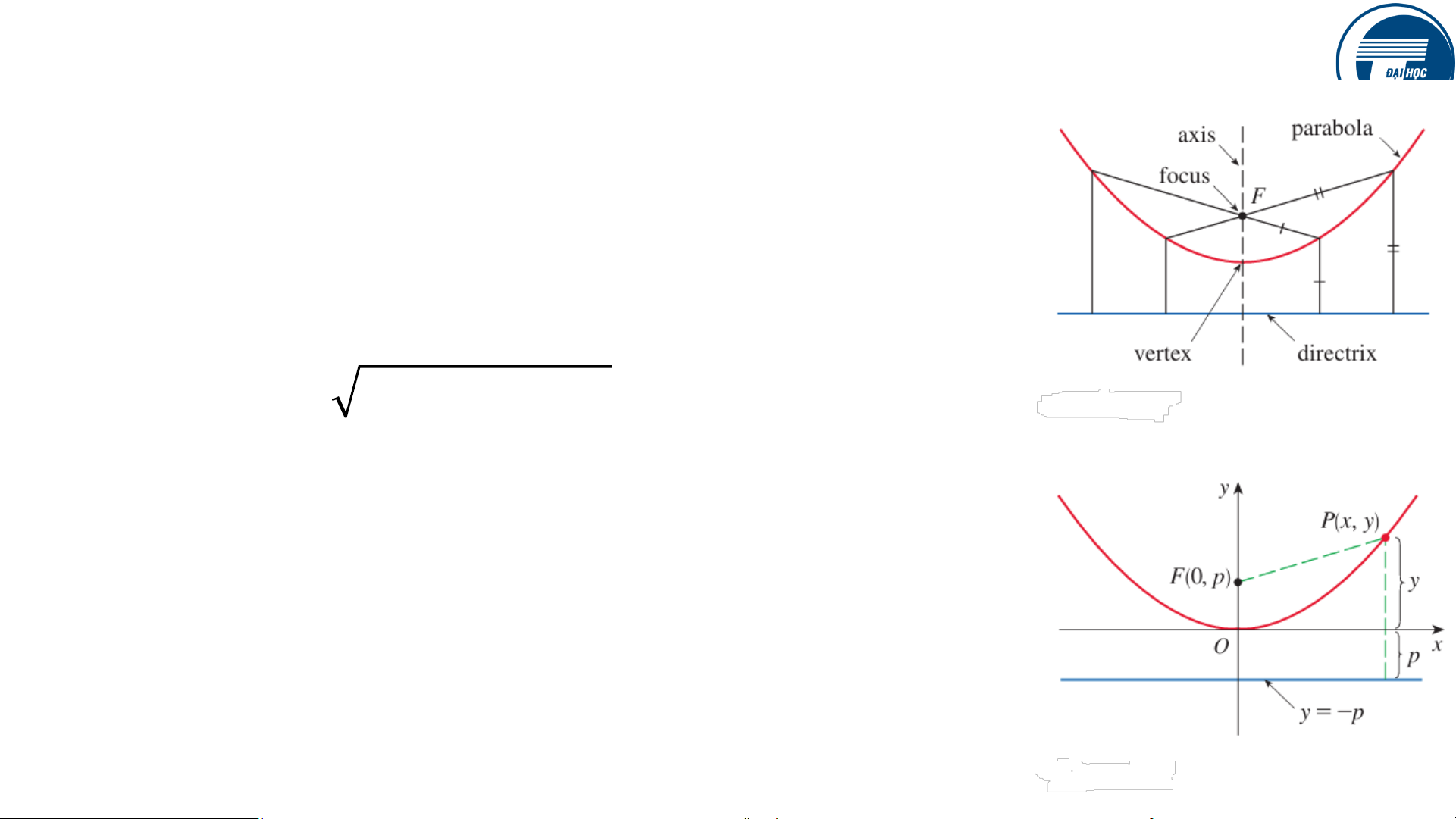
Một parabol là tập hợp các điểm trong mặt phẳng có
khoảng cách bằng nhau từ một điểm cố định F (gọi
là tiêu điểm (focus)) và một đường thẳng cố định
(gọi là đường trực tiếp (directrix)). Lưu ý rằng
trung điểm giữa tiêu điểm và đường trực tiếp nằm
trên parabol; nó được gọi là đỉnh (vertex). Đường
thẳng đi qua tiêu điểm vuông góc với đường trực
tiếp được gọi là trục (axis) của parabol.
VNU University of Engineering and Technology 11
10.5. Các đường Conic a, Parabol
Xét O là tiêu điểm, đường trực tiếp song song với
trục Ox. Xét tiêu điểm có tọa độ (0, 𝑝), đường trực
tiếp có phương trình 𝑦 = −𝑝.
Xét điểm 𝑃(𝑥, 𝑦) nằm trên parabol. Ta có
𝑥2 + (𝑦 − 𝑝)2= |𝑦 + 𝑝| và ta rút ra 𝒙𝟐 = 𝟒𝒑𝒚
VNU University of Engineering and Technology 12
10.5. Các đường Conic a, Parabol
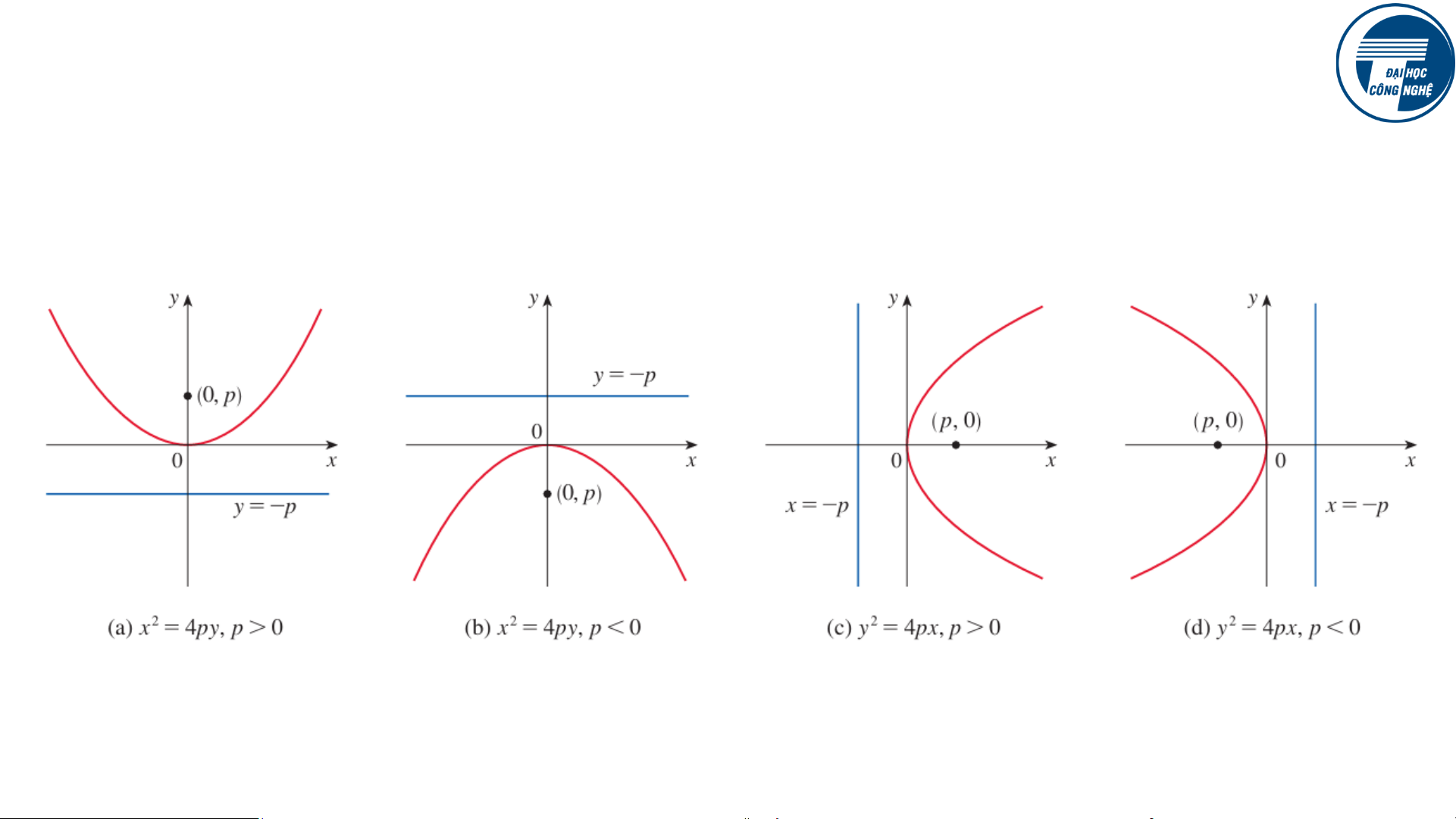
Nếu ta xoay các trục khác, ta có các phương trình khác của parabol
VNU University of Engineering and Technology 13
10.5. Các đường Conic b, Ellipse
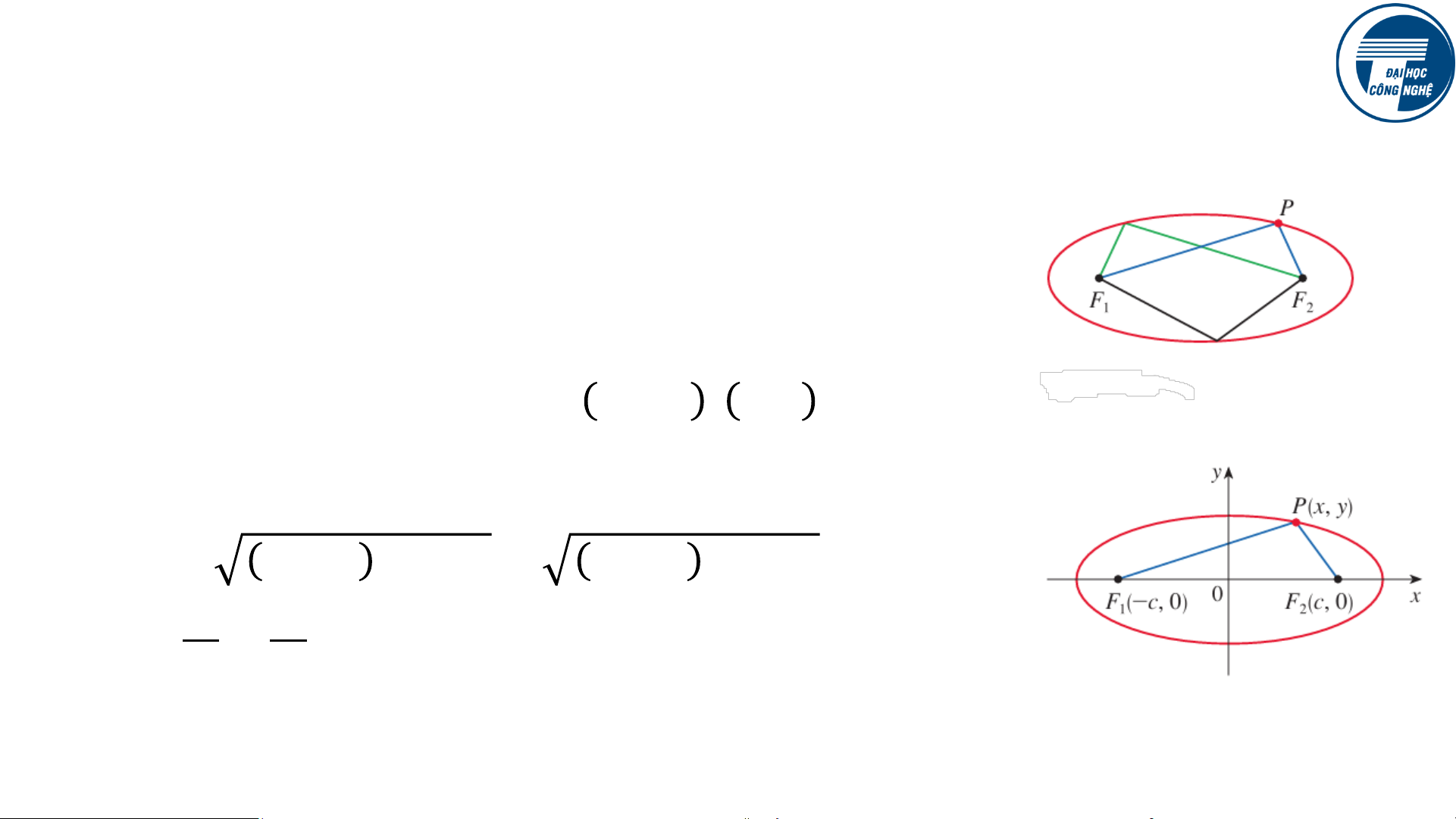
Một ellipse là tập hợp các điểm trong một mặt
phẳng mà tổng khoảng cách từ hai điểm cố định
𝐹1, 𝐹2 là một hằng số. Hai điểm cố định này được
gọi là tiêu điểm (foci - số nhiều của focus).
Xét hai tiêu điểm có tọa độ −𝑐, 0 , 𝑐, 0 , xét điểm
𝑃(𝑥, 𝑦) nằm trên ellipse và giả sử tổng khoảng cách
từ P đến hai tiêu điểm bằng 2𝑎 (𝑎 > 𝑐). Ta có 𝑥 + 𝑐 2 + 𝑦2 +
𝑥 − 𝑐 2 + 𝑦2 = 2𝑎 hay 𝑥2 𝑦2 +
= 1, 𝑣ớ𝑖 𝑏2 = 𝑎2 − 𝑐2. 𝑎2 𝑏2
VNU University of Engineering and Technology 14
10.5. Các đường Conic c, Hyperbol
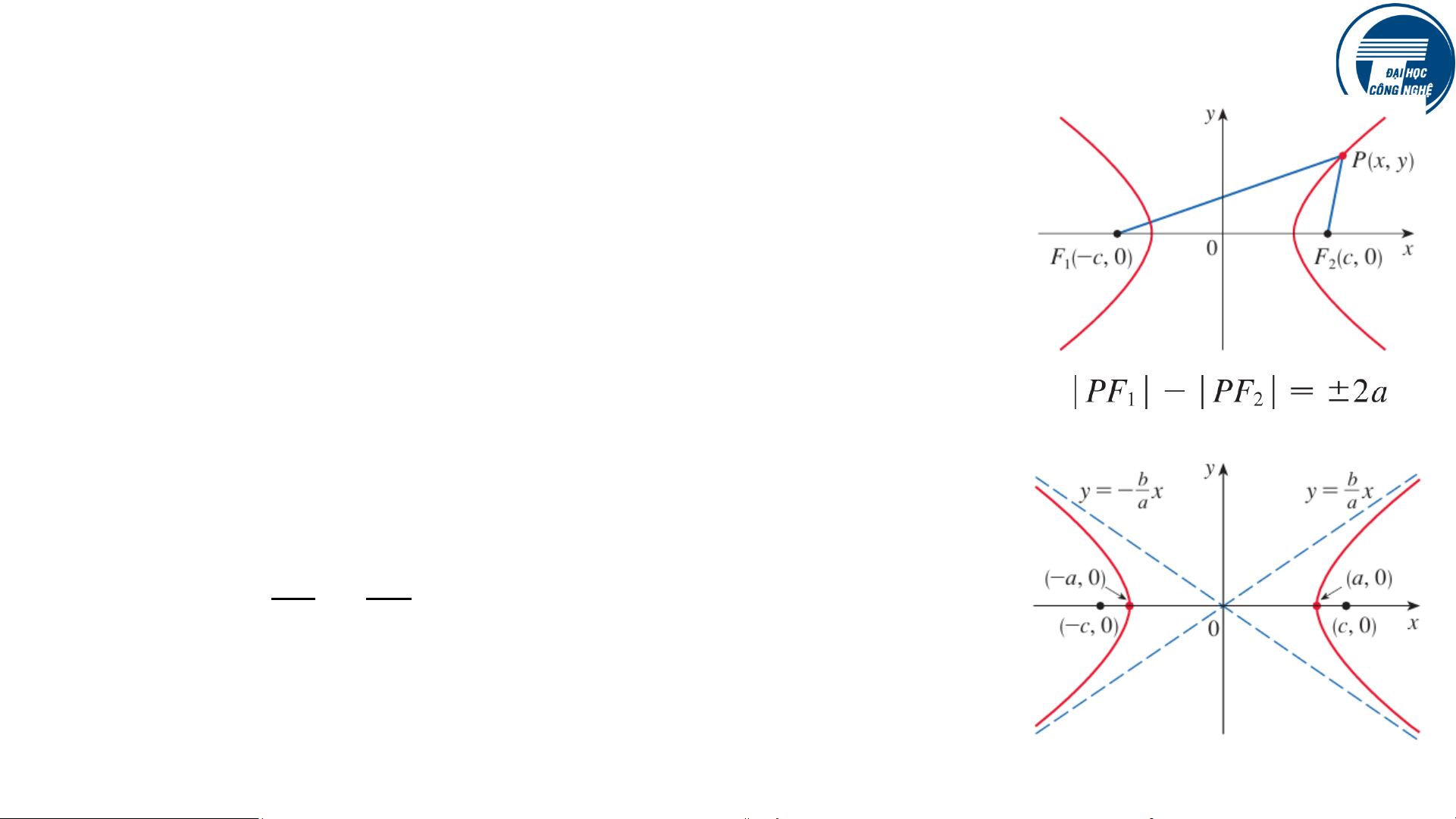
Một hyperbola là tập hợp tất cả các điểm trong một
mặt phẳng mà độ chênh lệch khoảng cách của
chúng từ hai điểm cố định 𝐹1, 𝐹2 (các tiêu điểm
(foci)) là một hằng số. Ta có phương trình: 𝑥2 𝑦2 −
= 1, 𝑣ớ𝑖 𝑏2 = 𝑎2 − 𝑐2. 𝑎2 𝑏2
VNU University of Engineering and Technology 15
10.6. Phương trình các đường Conic trong tọa độ cực
a, Phân loại các đường Conic
Định lý: Xét F là điểm cố định (tiêu điểm) và l là một đường thẳng cố
định (đường trực tiếp). Xét e là một số dương cố định (độ lệch tâm). Tập
các điểm P thỏa mãn
là một đường Conic. Đường conic này là a) Ellipse nếu 𝑒 < 1, b) Parabol nếu 𝑒 = 1, c) Hyperbol nếu 𝑒 > 1.
VNU University of Engineering and Technology 16
10.6. Phương trình các đường Conic trong tọa độ cực
b, Phương trình trong tọa độ cực
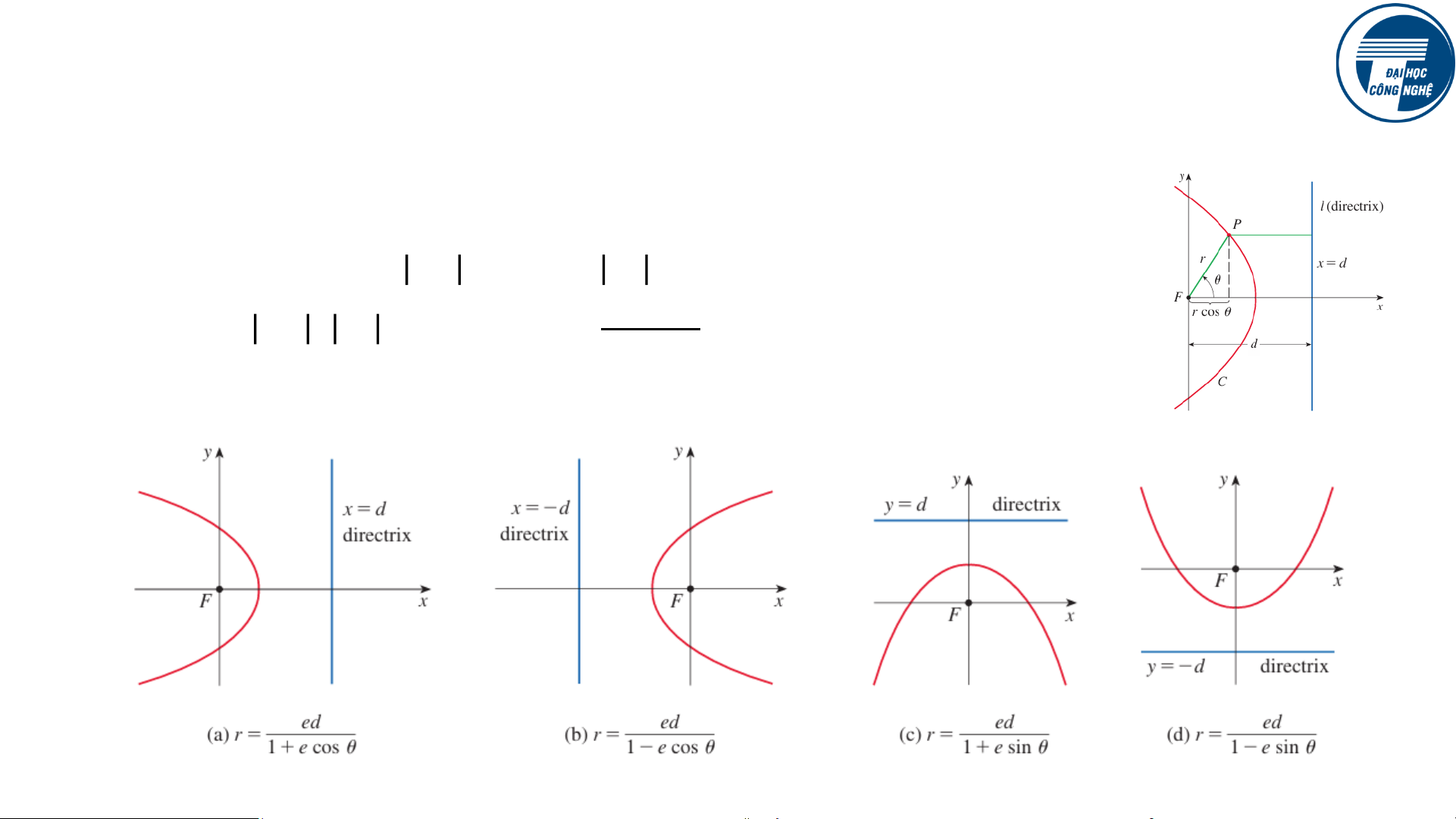
Xét tiêu điểm ở gốc tọa độ, đường trực tiếp có phương trình x=d. Nếu điểm
P có tọa độ cực 𝑃(𝑟, 𝜃), ta có 𝑃𝐹 = 𝑟,
𝑃𝑙 = 𝑑 − 𝑟𝑐𝑜𝑠𝜃. Điều kiện 𝑒𝑑
𝑃𝐹 / 𝑃𝑙 = 𝑒 cho ta 𝑟 = 1+𝑒𝑐𝑜𝑠𝜃
Tương tự, nếu ta chọn đường trực tiếp là x=-d, y=d, y=-d, ta có
VNU University of Engineering and Technology 17
Document Outline
- Slide 1: Giải tích 1
- Slide 2: 10.3. Tọa độ cực a, Hệ tọa độ cực
- Slide 3: 10.3. Tọa độ cực a, Hệ tọa độ cực
- Slide 4: 10.3. Tọa độ cực b, Mối liên hệ giữa tọa độ cực và tọa độ Cartesian
- Slide 5: 10.3. Tọa độ cực c, Đường cong tọa độ cực
- Slide 6: 10.3. Tọa độ cực c, Đường cong tọa độ cực
- Slide 7: 10.4. Giải tích trong tọa độ cực a, Diện tích
- Slide 8: 10.4. Giải tích trong tọa độ cực b, Độ dài cung
- Slide 9: 10.4. Giải tích trong tọa độ cực c, Tiếp tuyến
- Slide 10: 10.5. Các đường Conic
- Slide 11: 10.5. Các đường Conic a, Parabol
- Slide 12: 10.5. Các đường Conic a, Parabol
- Slide 13: 10.5. Các đường Conic a, Parabol
- Slide 14: 10.5. Các đường Conic b, Ellipse
- Slide 15: 10.5. Các đường Conic c, Hyperbol
- Slide 16: 10.6. Phương trình các đường Conic trong tọa độ cực a, Phân loại các đường Conic
- Slide 17: 10.6. Phương trình các đường Conic trong tọa độ cực b, Phương trình trong tọa độ cực



