Dãy và Chuỗi môn Giải tích 1 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Giải tích I Introduction Sequences Definition Convergence Dãy & chuỗi Properties Monotonic Fixed points Series Definition Properties Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 1/37
Dãy & chuỗi GIỚI THIỆU Introduction Sequences Definition • Nội dung: Convergence Properties – Dãy Monotonic – Chuỗi Fixed points – Hội tụ của chuỗi Series Definition Properties Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 2/37 Dãy & chuỗi DÃY Introduction Sequences Định nghĩa Definition Definition Convergence
Một dãy có thể xem như một danh sách các số Properties
được xắp xếp theo thứ tự xác định: Monotonic Fixed points a Series 1, a2,…,an Definition
a1 là số hạng đầu tiên, a2 là số hạng thứ 2,…, an là số Properties hạng thứ n. Divergent Test Examples
Chú ý: Dãy {a1, a2,…,an,…} còn được ký hiệu là {an}. Summary 30/12/2025
Department of Mathematics, National University 3/37 Dãy & chuỗi DÃY Introduction Sequences Definition Definition Ví dụ Convergence Properties
Tìm 6 số hạng đầu tiên của dãy Fibonacci f(n): Monotonic Fixed points  0 n = 0 Series  Definition f (n) =  1 n = 1 Properties  f (n- )
1 + f (n-2 ) n  1 Divergent Test Examples 0, 1, 1, 2, 3, 5, 8, … Summary
Dãy Fibonnaci được phát minh bởi người Ấn Độ
những năm 300 B.C. Nó được ứng dụng trong các
thuật toán máy tính để tạo các số giả ngẫu nhiên. 30/12/2025
Department of Mathematics, National University 4/37 Dãy & chuỗi DÃY Introduction Sequences Definition Definition Ví dụ Convergence Properties
Tìm công thức tổng quát cho số hạng an của dãy: Monotonic Fixed points
{3/5, -4/25, 5/125, -6/625,7/3125,…} Series Definition Properties Giải: Divergent Test Examples a Summary n = (-1)n-1(n+2)/5n 30/12/2025
Department of Mathematics, National University 5/37 Dãy & chuỗi DÃY Introduction Sequences Definition Definition Câu hỏi Convergence Properties
Tìm công thức tổng quát cho số hạng an của dãy: Monotonic Fixed points a) {1, -2/3, 4/9, -8/27,…} Series Definition b) {5, 1, 5, 1, 5, 1, …} Properties Giải: Divergent Test Examples a) a Summary n = (-2/3)n-1 b) an = 3+(-1)n-1.2 30/12/2025
Department of Mathematics, National University 6/37 Dãy & chuỗi DÃY Introduction Sequences Definition Định nghĩa nôm na Conv Convergenc ergence Properties
Dãy {an} có giới hạn L, ký hiệu limn→ a
+∞ n=L, nếu ta có Monotonic
thể tìm được các số hạng an gần L tùy ý bằng cách lấy Fixed points n đủ lớn. Series Definition
Nếu giới hạn L tồn tại và hữu hạn, ta nói {an} hội tụ; Properties
nếu không, nó phân kỳ. Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 7/37 Dãy & chuỗi DÃY Introduction Sequences Definition Định nghĩa chính xác Conv Convergenc ergence Dãy {a Properties
n} có giới hạn L, ký hiệu Monotonic
lim a = L hay a → L khi n →  Fixed points n→ n n Series Definition
Nếu với mọi ε > 0 ta có một số N nguyên tương Properties ứng sao cho: Divergent Test Examples
Khi n > N thì |an – L| < ε Summary 30 30/1 / 2 12/2 / 025 2025
Department of Mathematics, National University 8/37 Dãy & chuỗi DÃY Introduction Sequences Định lý Definition
lim ca = c lim a Convergence n n n→ n→ Properties Properties ( lim a  b ) = ( lim a )  ( lim b ) Monotonic n n n n n→ n→ n→ Fixed points ( lim a b ) = ( lim a ) ( lim b ) Series n n n n n→ n→ n→ Definition ( lim a / b ) = ( lim a ) / ( lim b ) Với lim b  0 Properties n n n n n n→ n→ n→ n→ Divergent Test (
lim f (a )) = f a Với f liên tục n ( ( lim ) n ) Examples n→ n→ Summary 30/12/2025
Department of Mathematics, National University 9/37 Dãy & chuỗi DÃY Introduction Sequences Definition Định lý Convergence Properties Properties
Giả sử rằng f :R→R sao cho lim Monotonic
x→∞f(x) = L. Thì dãy {a Fixed points
n}, an = f(n), cũng hội tụ đến L. Series Definition Properties Divergent Test Examples Summary 30 30/12 /1 / 2 2025 /2025
Department of Mathematics, National University 10/37 Dãy & chuỗi DÃY Introduction Sequences Definition Convergence Ví dụ Properties Properties Monotonic
Dãy {rn} hội tụ hay phân kỳ? Fixed points Series
Ta đã biết limx→∞rx = 0 với 0 < r < 1 Definition
→ khi 0 < r < 1 thì dãy {rn} hội tụ Properties Divergent Test và khi r > 1; lim Examples
x→∞rx là vô cùng. Summary
→ khi 1 < r, thì dãy {rn} phân kỳ.
khi r = 1, thì {rn} = {1,1,…} và limn→∞rn = 1 30 30/1 / 2 12/2 / 025 2025
Department of Mathematics, National University 11/37 Dãy & chuỗi DÃY Introduction Sequences Câu hỏi Definition Convergence
Dãy {rn} hội tụ hay phân kỳ khi r<0? Properties Properties Monotonic Fixed points Series Definition Properties Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 12/37 Dãy & chuỗi DÃY Introduction Sequences Definition Convergence câu hỏi Properties Properties Monotonic
Xét sự hội tụ của dãy: Fixed points Series
a) an = ln(n)/n (gợi ý: sử dụng L’Hosital’s Rule) Definition b) b
gợi ý=(1.2.3..n)/(n.n.n..n)<1/n Properties n = n!/nn Divergent Test Examples Summary ln x ln x 1 a → → lim = lim = 0 n x→ x x x → x 30 30/12 /1 / 2 2025 /2025
Department of Mathematics, National University 13/37 Dãy & chuỗi DÃY Introduction Sequences Định nghĩa Definition Convergence Properties
Một dãy {an} được gọi là tăng nếu an < an+1 với mọi n. Monotonic Dãy {a Monotonic
n} được gọi là giảm nếu an > an+1 với mọi n. Một Fixed points
dãy được gọi là đơn điệu nếu nó chỉ tăng hoặc chỉ Series giảm. Definition Properties Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 14/37 Dãy & chuỗi DÃY Introduction Sequences Định nghĩa Definition Convergence Dãy {a Properties
n} được gọi là bị chặn trên nếu tồn tại một số M Monotonic sao cho a Monotonic
n ≤ M với mọi n. Dãy {an} được gọi là bị chặn Fixed points
dưới nếu tồn tại một số m sao cho an ≥ m với mọi n. Series
Một dãy được gọi là bị chặn nếu nó bị chặn cả trên và Definition dưới. Properties Divergent Test Examples Summary 30/12 / /2025 /
Department of Mathematics, National University 15/37 Dãy & chuỗi DÃY Introduction Sequences Định lý Definition Convergence
Mọi dãy tăng và bị chặn trên thì hội tụ. Properties Monotonic Monotonic
Mọi dãy giảm và bị chặn dưới thì hội tụ. Fixed points Series
Mọi dãy đơn điệu, bị chặn thì hội tụ. Definition Properties Divergent Test Examples Summary 30/12/2025
Department of Mathematics, National University 16/37 Dãy & chuỗi DÃY Introduction Sequences Ví dụ Definition Convergence
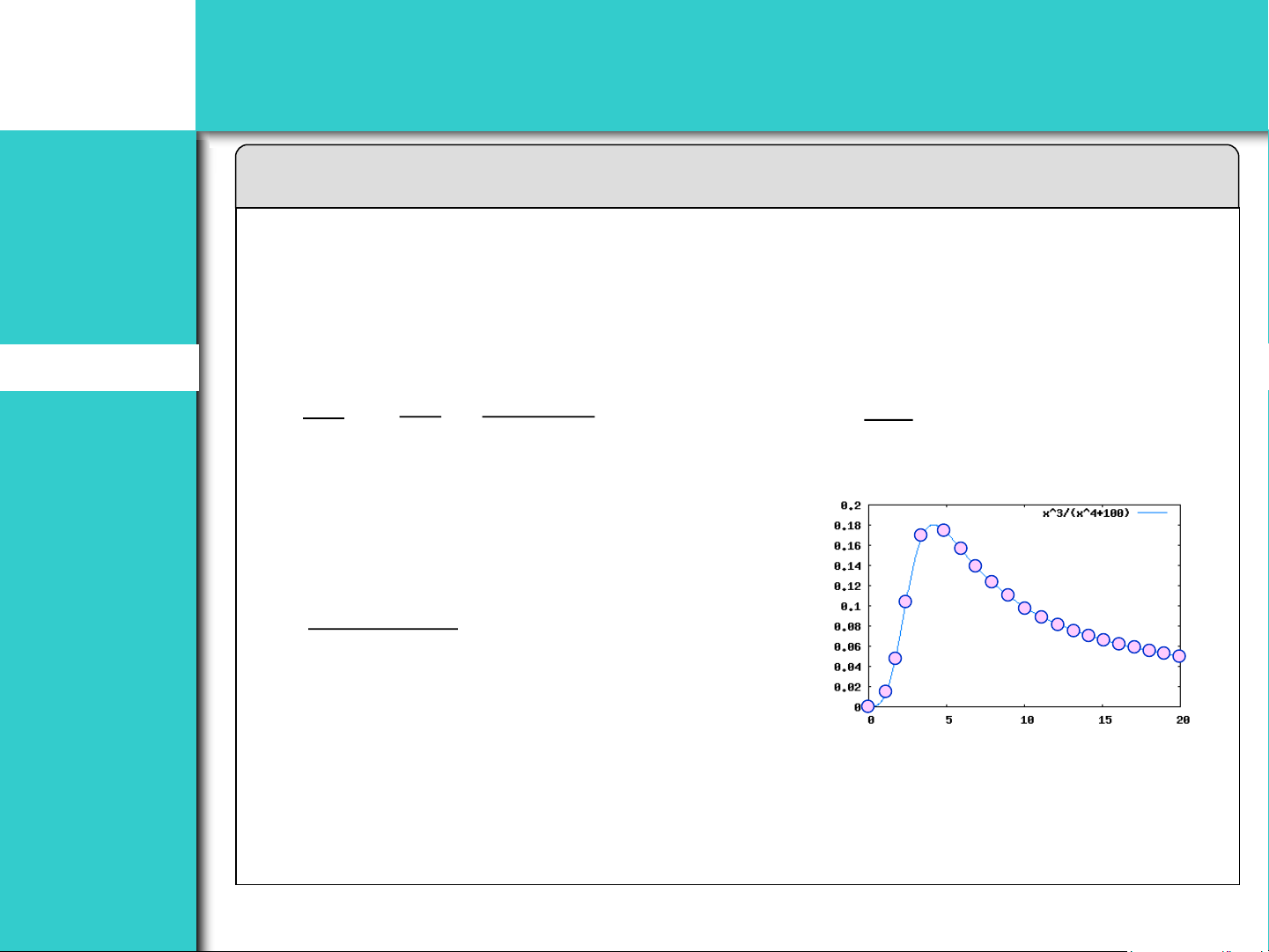
Xét các dãy sau đây. Dãy nào là đơn điệu? Bị chặn? Hội tụ? Properties Monotonic Monotonic Fixed points 1)  2  2 2 2   → giảm; 2   0 2  → bị chặn Series n  2 2 n (n + ) 1 2 n Definition Properties → hội tụ Divergent Test Examples 3 2)  n  Summary 
Đặt f(x)=x3/(x4+100) 4  n + 100 
f ’(x) = −x2(x4−300)/(x4+100)2
→ f ’(x) < 0 khi x ≥ 5
Giảm từ n=5 và bị chặn dưới → hội tụ 30/12/2025
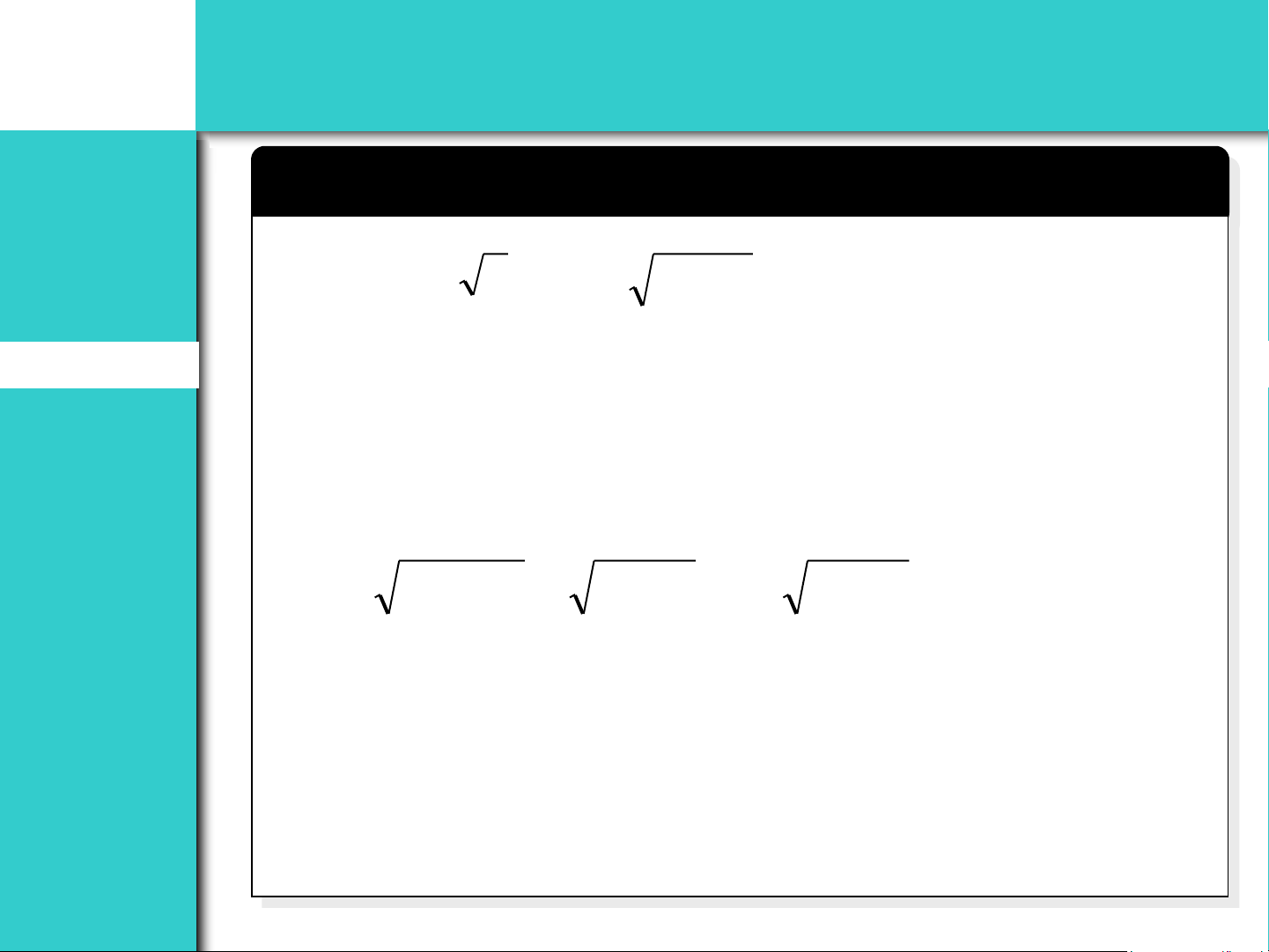
Department of Mathematics, National University 17/37 Dãy & chuỗi DÃY Introduction Sequences Ví dụ Definition Convergence Cho dãy {a a = 2, a = 2 + a Properties n} sao cho 1 n+1 n Monotonic Monotonic a) CMR l im a tồn tại n Fixed points n→ Series b) Tìm lim an → Definition n Properties Divergent Test Examples Summary 30 30/1 / 2 12/2 / 025 2025
Department of Mathematics, National University 18/37 Dãy & chuỗi DÃY Introduction Sequences Ví dụ Definition Convergence Giải: a = 2, a = 2 + a 1 n+1 n Properties Monotonic
a) Ta sẽ chứng minh bằng quy nạp: Giả sử Monotonic Fixed points a a và a n  + n  2 1 n
điều này rõ ràng đúng với n=1. Series Definition
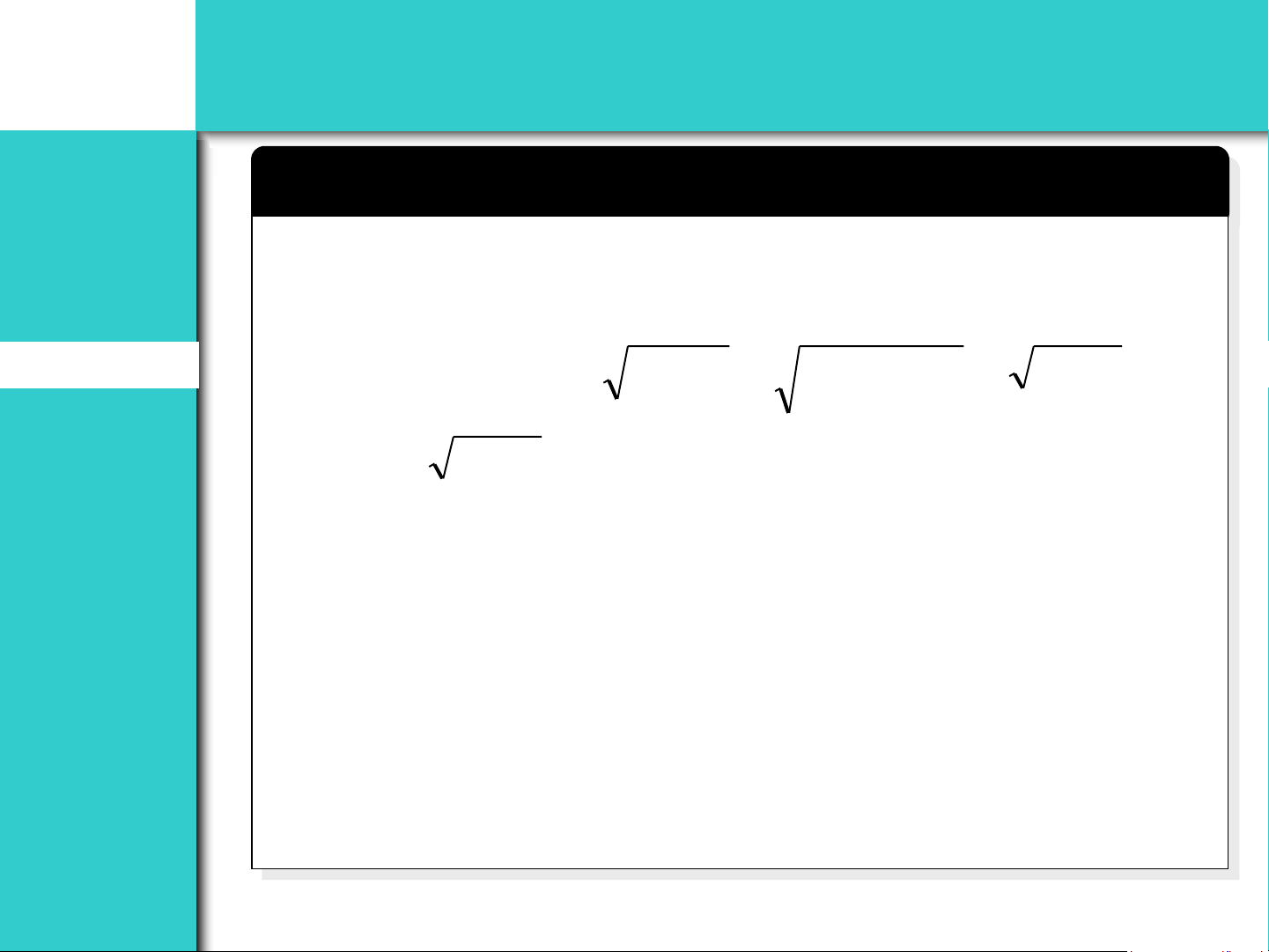
Ta sẽ CMR điều này cũng đúng với n+1, tức là Properties a  a và a  2 n+2 n 1 + n 1 + Divergent Test  + a  + a và + a  Examples 2 2 , 2 2 n 1 + n n Summary
 a  a và a  2 n 1 + n n
Điều này chính là giả thiết ban đầu nên đúng. Do đó
dãy {an} tăng, bị chặn trên nên {an} hội tụ, tức là tồn tại lim an n→ 30 30/1 / 2 12/2 / 025 2025
Department of Mathematics, National University 19/37 Dãy & chuỗi DÃY Introduction Sequences Ví dụ Definition Convergence
b) Đặt li m a = L thì rõ ràng lim a = L do đó n n+1 Properties n→ n→ Monotonic Monotonic L = lim a
= lim 2 + a = 2 + lim a = 2 + L Fixed points n+ n→ 1 → n n → n n Series  L = 2 + L Definition Properties  2
L − L − 2 = 0 Divergent Test Examples −1 Summary  L = 2 Vậy lim a = 2 do L không thể âm. → n n 30/12/2025
Department of Mathematics, National University 20/37