Lý thuyết số trung bình cộng, Số trung vị, Mốt và bài tập

Lý thuyết số trung bình cộng, Số trung vị, Mốt và bài tập
1. Số trung bình cộng
Số trung bình cộng : Kí hiệu:
Trung bình cộng của các số liệu thống kê được tính theo công thức:
Trường hợp Bảng phân bố tần suất và tần số ghép lớp
ci, fi, ni là giá trị đại diện của lớp thứ i.
Ý nghĩa của số trung bình:
Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một
số đặc trưng quan trọng của mẫu số liệu.
Ví dụ 1: Điểm kiểm tra môn Toán của lớp 10A được thống kê trong bảng dưới đây: Số điểm 7 8 9 10 Số học sinh 12 15 8 5
Tính số điểm trung bình của các học sinh trên. Hướng dẫn giải:
Điểm trung bình của các học sinh lớp 10A là:
Ưu điểm của việc sử dụng số trung bình cộng:
- Dễ hiểu và dễ sử dụng: Số trung bình cộng là một chỉ số đơn giản, dễ hiểu và dễ tính toán.
Nó cung cấp một con số duy nhất để đại diện cho toàn bộ tập dữ liệu.
- Đại diện cho dữ liệu: Là một đại lượng thống kê cơ bản, số trung bình cộng giúp đánh giá
mức độ trung bình của các giá trị trong tập dữ liệu, từ đó phản ánh được xu hướng chung của dữ liệu.
- Ứng dụng rộng rãi: Phương pháp này có thể áp dụng trong nhiều lĩnh vực khác nhau như
kinh tế, y tế, giáo dục, và công nghiệp để đánh giá và so sánh dữ liệu.
Nhược điểm của việc sử dụng số trung bình cộng:
- Nhạy cảm với giá trị ngoại lệ: Nếu có giá trị ngoại lệ trong tập dữ liệu, số trung bình cộng
có thể bị chi phối bởi giá trị này, dẫn đến kết quả không chính xác.
- Không phản ánh được sự biến động của dữ liệu: Trong trường hợp dữ liệu có phân bố
không đồng đều, số trung bình cộng không thể phản ánh được sự biến động và đa dạng của các
giá trị trong tập dữ liệu.
- Không phù hợp với dữ liệu phân loại: Số trung bình cộng chỉ phù hợp với dữ liệu số học
và không thể áp dụng cho dữ liệu phân loại như loại sản phẩm, nhóm khách hàng,...
- Yêu cầu số lượng mẫu đủ lớn: Để đảm bảo tính chính xác, số trung bình cộng yêu cầu có
đủ số lượng mẫu đủ lớn. Khi số lượng mẫu quá nhỏ, kết quả có thể không chính xác. 2. Số trung vị Số trung vị:Kí hiệu:
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể
đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không
tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là Me là :
+ Số đứng giữa dãy nếu số phần tử N lẻ:
+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn:
Ví dụ: Cho các mẫu số liệu sau:
a) 8; 6; 1; 6; 10; 3; 8; 2; 11; 15; 12. b) 2; 9; 7; 12; 10; 6; 8; 15.
Tính trung vị và tứ phân vị của các mẫu số liệu trên. Hướng dẫn giải:
a) Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được:
1; 2; 3; 6; 6; 8; 8; 10; 11; 12; 15.
Vì cỡ mẫu là n = 11 nên trung vị của mẫu số liệu trên là số liệu thứ 6. Tức là .
b) Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được: 2; 6; 7; 8; 9; 10; 12; 15
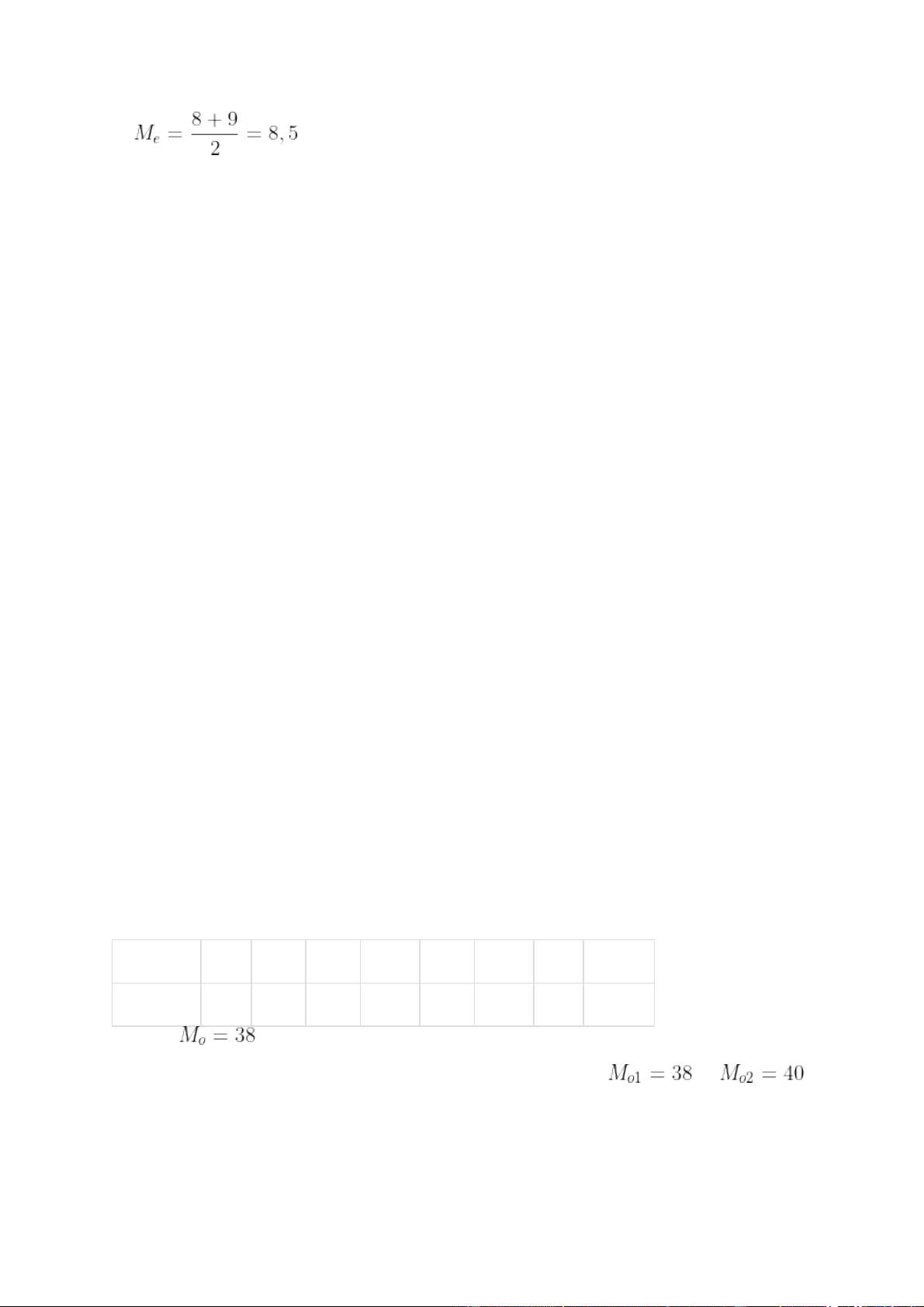
Vì cỡ mẫu là n = 8 nên trung vị của mẫu số liệu trên là trung bình cộng của số liệu thứ 4 và 5. Tức là:
Ưu điểm của việc sử dụng số trung vị:
- Khả năng chống lại ảnh hưởng của giá trị ngoại lệ: Số trung vị là giá trị ở vị trí giữa của
tập dữ liệu khi được sắp xếp theo thứ tự tăng dần. Do đó, nó không bị ảnh hưởng nhiều bởi các
giá trị ngoại lệ (outlier) có giá trị rất cao hoặc thấp.
- Phù hợp với dữ liệu có phân phối lệch: Khi dữ liệu có phân phối lệch (skewed distribution),
số trung vị thường phản ánh chính xác hơn mức trung bình của dữ liệu so với số trung bình cộng.
- Đơn giản và dễ hiểu: Số trung vị là một chỉ số đơn giản và dễ hiểu, không đòi hỏi quá
nhiều tính toán phức tạp như các phương pháp thống kê khác.
Nhược điểm của việc sử dụng số trung vị:
- Không phản ánh được sự biến động của dữ liệu: Số trung vị chỉ cho biết giá trị ở vị trí
trung tâm của dữ liệu mà không phản ánh được mức độ biến động và đa dạng của các giá trị trong tập dữ liệu.
- Khó tính toán khi dữ liệu lớn: Trong một số trường hợp, đặc biệt khi tập dữ liệu lớn, việc
tính toán số trung vị có thể gặp khó khăn hơn so với số trung bình cộng.
- Không phù hợp với dữ liệu phân loại: Số trung vị thường được áp dụng cho dữ liệu số học
và không thể áp dụng cho các biến phân loại 3. Mốt Mốt: Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường
hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
Ví dụ : Cho bảng số liệu: Số áo bán được trong 1 quý của 1 cửa hàng bán áo sơ mi nam. Cỡ áo 36 37 38 39 40 41 42 Tổng Tần số 13 45 126 110 125 40 5 464 Ta có
( giá trị có tần số lớn nhất là 126)
Nếu số áo size 40 bán được cũng là 126 áo thì ta sẽ có 2 mốt là và .
Ưu điểm của việc sử dụng Mốt:
- Phản ánh được xu hướng phổ biến: Mốt là giá trị xuất hiện nhiều nhất trong tập dữ liệu,
cho phép người phân tích nhận biết được sự phân bố và xu hướng của các giá trị.
- Dễ dàng xác định: Sử dụng mốt làm đại diện cho dữ liệu không đòi hỏi tính toán phức tạp
và dễ dàng xác định, đặc biệt với các tập dữ liệu có phân loại rõ ràng.
- Phù hợp với dữ liệu phân loại: Mốt thường được áp dụng hiệu quả cho dữ liệu phân loại,
nơi mà việc xác định giá trị xuất hiện nhiều nhất có ý nghĩa quan trọng.
Nhược điểm của việc sử dụng Mốt:
- Không phản ánh sự biến động của dữ liệu: Mốt chỉ cho biết giá trị xuất hiện nhiều nhất mà
không phản ánh được sự biến động và sự phân bố chi tiết của dữ liệu.
- Không thể áp dụng cho dữ liệu liên tục: Mốt thường không áp dụng được cho dữ liệu liên
tục mà chỉ phù hợp với dữ liệu phân loại.
- Khả năng xuất hiện nhiều giá trị mốt: Trong một số trường hợp, có thể dữ liệu có nhiều
giá trị mốt bằng nhau, dẫn đến việc không thể xác định được giá trị đại diện duy nhất cho tập dữ liệu.
4. So sánh và lựa chọn Đặc Số trung bình cộng Số trung vị Mốt điểm Đại diện Giá trị trung bình của
Giá trị ở vị trí giữa
Giá trị xuất hiện nhiều nhất cho tập dữ liệu của tập dữ liệu trong tập dữ liệu Chống lại ảnh
Phản ánh được xu hướng
Dễ tính toán, ít bị ảnh Ưu điểm
hưởng của giá trị xuất hiện thường xuyên trong
hưởng bởi giá trị ngoại lệ ngoại lệ dữ liệu Được sử dụng nhiều Ứng Phù hợp với dữ liệu
Có thể sử dụng cho dữ liệu trong các nghiên cứu và dụng có phân phối lệch phân loại và số học phân tích Nhược Nhạy cảm với giá trị Không phản ánh sự
Không phù hợp với dữ liệu điểm ngoại lệ
biến động của dữ liệu có nhiều giá trị lặp lại
Khi nào nên sử dụng từng loại số liệu thống kê:
- Sử dụng số trung bình cộng khi:
+ Cần đánh giá giá trị trung bình của toàn bộ tập dữ liệu.
+ Dữ liệu không có quá nhiều giá trị ngoại lệ ảnh hưởng.
+ Muốn đại diện cho mức độ trung bình của dữ liệu một cách đơn giản và nhanh chóng.
Ví dụ: Đánh giá điểm trung bình của học sinh trong một lớp học.
- Sử dụng số trung vị khi:
+ Dữ liệu có phân phối lệch và có nhiều giá trị ngoại lệ.
+ Cần phản ánh giá trị ở vị trí trung tâm của tập dữ liệu mà không bị ảnh hưởng bởi giá trị ngoại lệ.
Ví dụ: Đánh giá thu nhập trung bình của một nhóm người, khi có sự chênh lệch lớn về thu nhập. - Sử dụng mốt khi:
+ Cần phân tích dữ liệu phân loại và biết được giá trị xuất hiện nhiều nhất.
+ Dữ liệu có tính phân bố rõ ràng và có thể thể hiện một xu hướng phổ biến trong tập dữ liệu.
Ví dụ: Xác định loại sản phẩm bán chạy nhất trong một cửa hàng.
Mỗi loại số liệu thống kê có ứng dụng và lợi ích riêng trong việc phân tích và đánh giá dữ
liệu. Việc lựa chọn đúng loại số liệu phù hợp với từng tình huống sẽ giúp cho quá trình phân
tích và đưa ra quyết định hiệu quả hơn.
5. Bài tập áp dụng
Bài 1: Bảng phân bố tần số tuổi thọ của 30 bóng đèn điện. Tuổi thọ Tần số 1150 3 1160 6 1170 12 1180 6 1190 3 Cộng 30 Số trung bình:
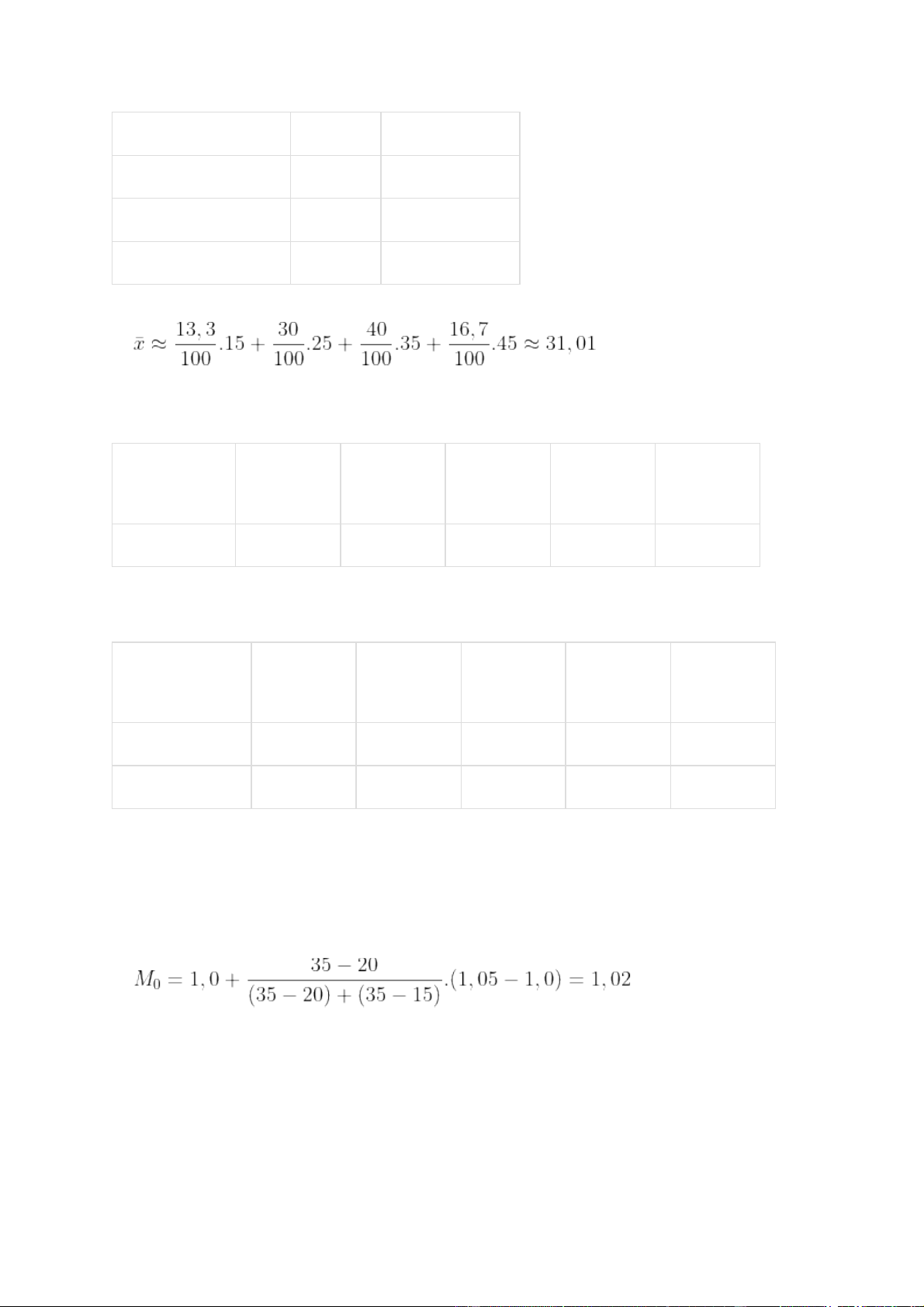
Bài 2: Bảng phân bố tần suất ghép lớp độ dài của 60 lá dương sỉ trưởng thành: Lớp của độ dài (cm) Tần suất Giá trị đại diện [10; 20) 13,3 15 [20; 30) 30,0 25 [30; 40) 40,0 35 [40; 50) 16,7 45 Cộng 100 (%) Số trung bình:
Bài 3: Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau: Điện lượng [0,9; 0,95) [0,95; 1,0) [1,0; 1,05) [1,05; 1,1) [1,1; 1,15) (nghìn mAh) Số viên pin 10 20 35 15 5
Hãy ước lượng số trung bình, mốt của mẫu số liệu ghép nhóm trên. Hướng dẫn giải Điện lượng [0,9; 0,95) [0,95; 1,0) [1,0; 1,05) [1,05; 1,1) [1,1; 1,15) (nghìn mAh) Giá trị đại diện 0,925 0,975 1,025 1,075 1,125 Số viên pin 10 20 35 15 5
Số trung bình của dãy số liệu xấp xỉ bằng:
(0,925.10 + 0,975.20 + 1,025.35 + 1,075.15 + 1,125.5) : 85 = 1,016
Vậy nhóm chứa mốt của dãy số liệu là nhóm [1,0; 1,05).
Mốt của mẫu số liệu trên là: