lOMoARcPSD| 40651217 Lý thuyết trò chơi Trạng Thái
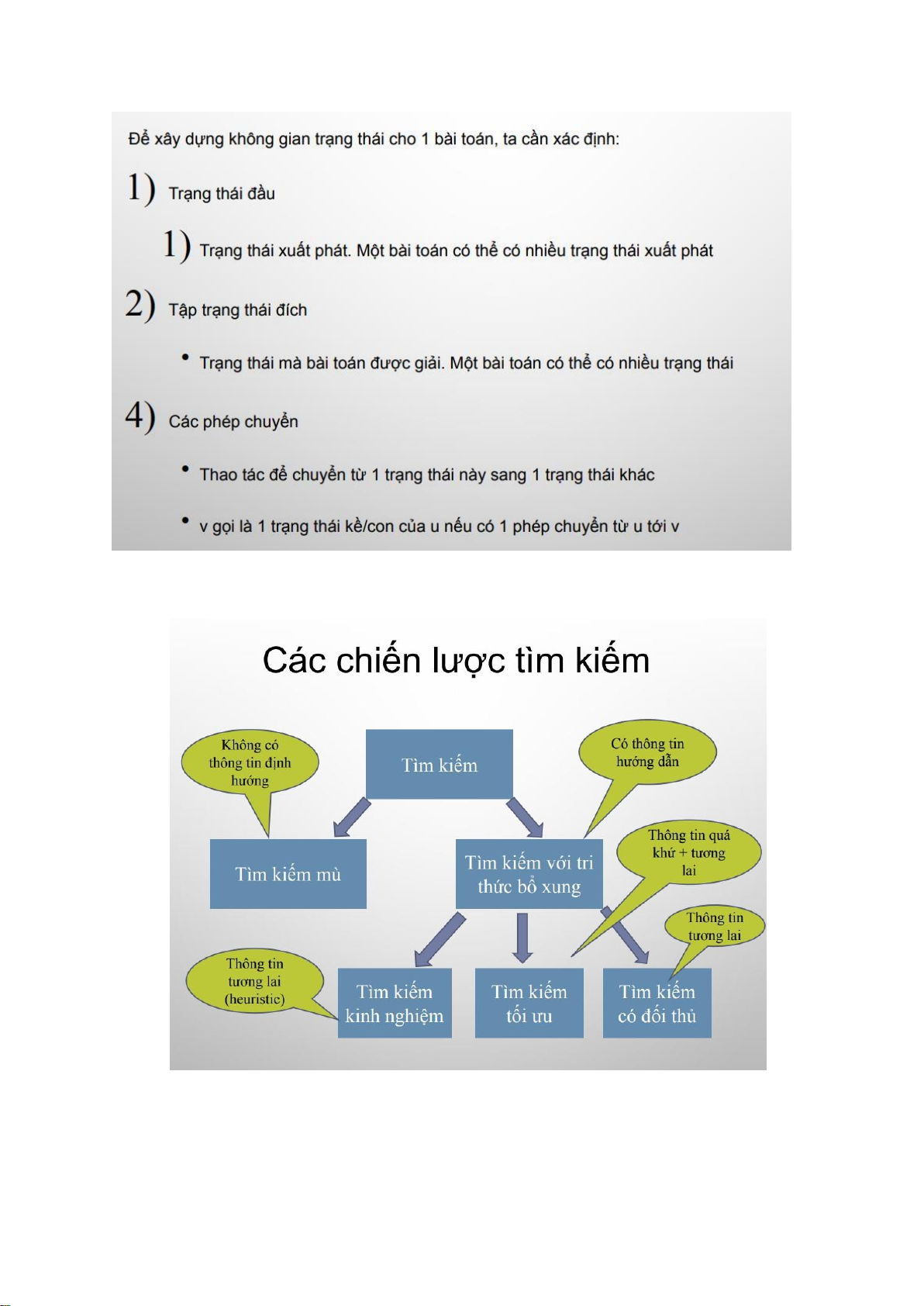
Không gian trạng thái
Là ồ thị có hướng trong ó:
− Mỗi nút là 1 trạng thái
− Mỗi cạnh ứng với 1 phép chuyển ổi trạng thái lOMoARcPSD| 40651217
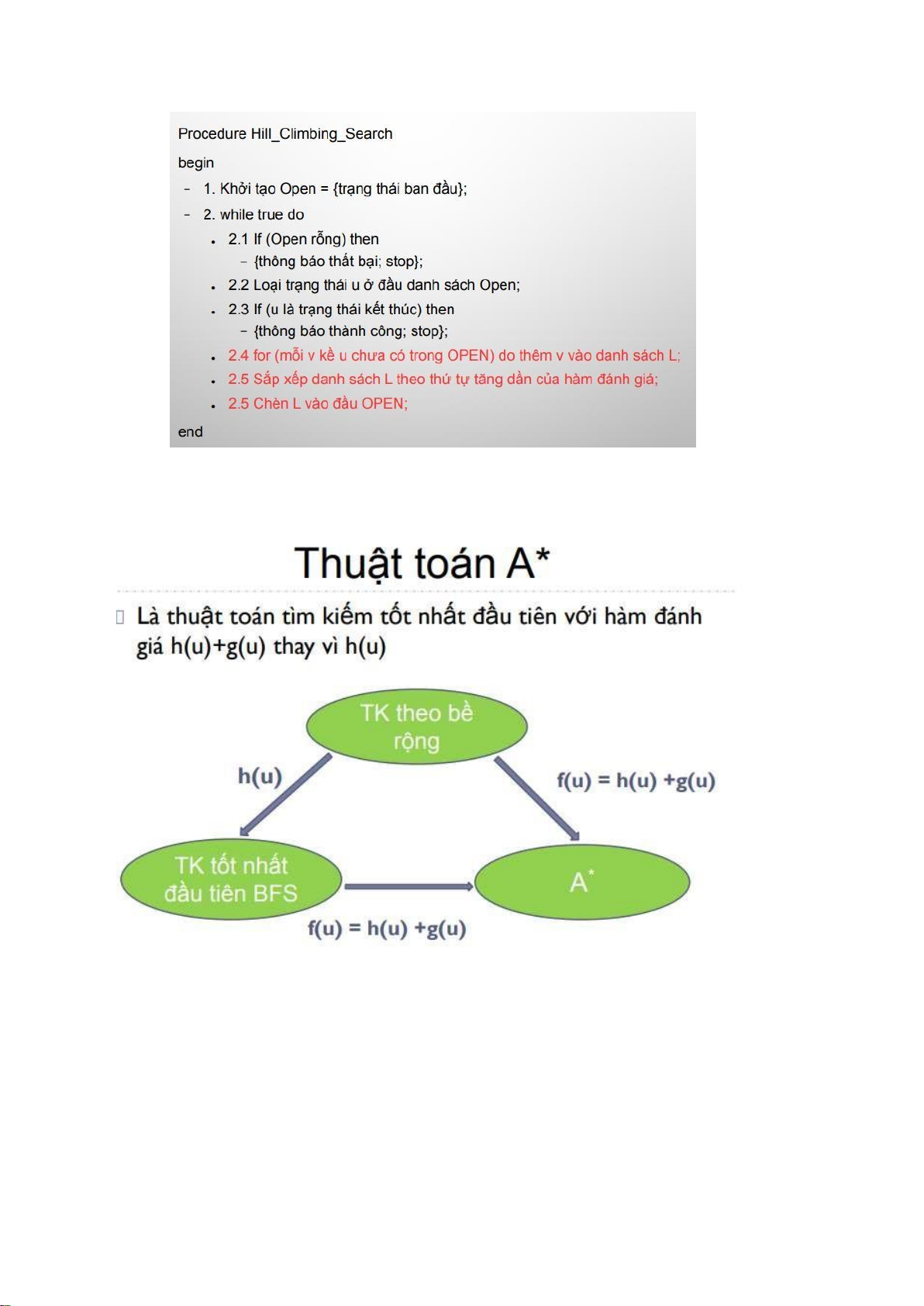
Các chiến lược tìm kiếm lOMoARcPSD| 40651217 Tìm kiếm mù
Tìm kiếm theo chiều rộng Thuật toán lOMoARcPSD| 40651217 Tìm kiếm theo chiều sâu Thuật toán lOMoARcPSD| 40651217 Tìm kiếm sâu lặp
Tìm kiếm với tri thức bổ sung
- Tìm kiếm dựa trên các thông tin ánh giá của các trạng thái - Hiệu quả lOMoARcPSD| 40651217
Tìm kiếm với hàm ánh giá -TQ
TK Tốt nhất ầu tiên(TK kinh nghiệm) lOMoARcPSD| 40651217 Thuật toán Tìm kiếm beam lOMoARcPSD| 40651217 Tìm kiếm leo ồi Thuật toán lOMoARcPSD| 40651217 A* lOMoARcPSD| 40651217 Nhánh cận lOMoARcPSD| 40651217 Tìm kiếm có ối thủ Thuật toán min max lOMoARcPSD| 40651217 Thuật toán lOMoARcPSD| 40651217
Thủ tục cắt nhánh alpha -beta
Cắt bỏ bớt các nhánh không cần thiết cho việc ánh giá giá trị heuristic tại một ỉnh lOMoARcPSD| 40651217
TRI THỨC - SUY DIỄN Biểu diễn tri thức lOMoARcPSD| 40651217 Logic mệnh ề lOMoARcPSD| 40651217
(Luật)Chuẩn hoá về dạng chuẩn hội
Phương pháp Robinson lOMoARcPSD| 40651217 Tổng quát lOMoARcPSD| 40651217
Chứng minh bằng các luật suy diễn
Suy diễn tiến, lùi lOMoARcPSD| 40651217 Suy diễn tiến
Cơ chế max: Nếu có nhiều luật thỏa mãn ta luôn chọn lập luận lớn nhất lOMoARcPSD| 40651217 Logic Vị từ Hạn chế logic mệnh ề Logic Vị từ lOMoARcPSD| 40651217 Thành phần cú pháp lOMoARcPSD| 40651217 Đặc iểm 1. Tính hoán vị: (∀x ∀y) ≡ (∀y ∀x)
2. Đưa các phép lượng tử vào từng vị từ 3. Loại bỏ ∀ ∀x G(x) ≡ G(x) 4. Đặt lại tên biến ∀x G(x) ≡ ∀y G(y) 5. Loại bỏ ¬
¬(∀x G(x)) ≡ ∃x (¬G(x))
¬(∃x G(x)) ≡ ∀x (¬G(x))
6. Hệ quả: mỗi lượng tử (∀,∃) ều có thể biểu diễn bởi lượng tử kia
[∀x friend(An,x)] ≡ [¬∃x ¬friend(An,x)]
An là bạn của mọi người tương ương với không có ai An không là bạn lOMoARcPSD| 40651217
Chứng minh trong logic vị từ lOMoARcPSD| 40651217
So Sánh - Định nghĩa Hàm ánh giá
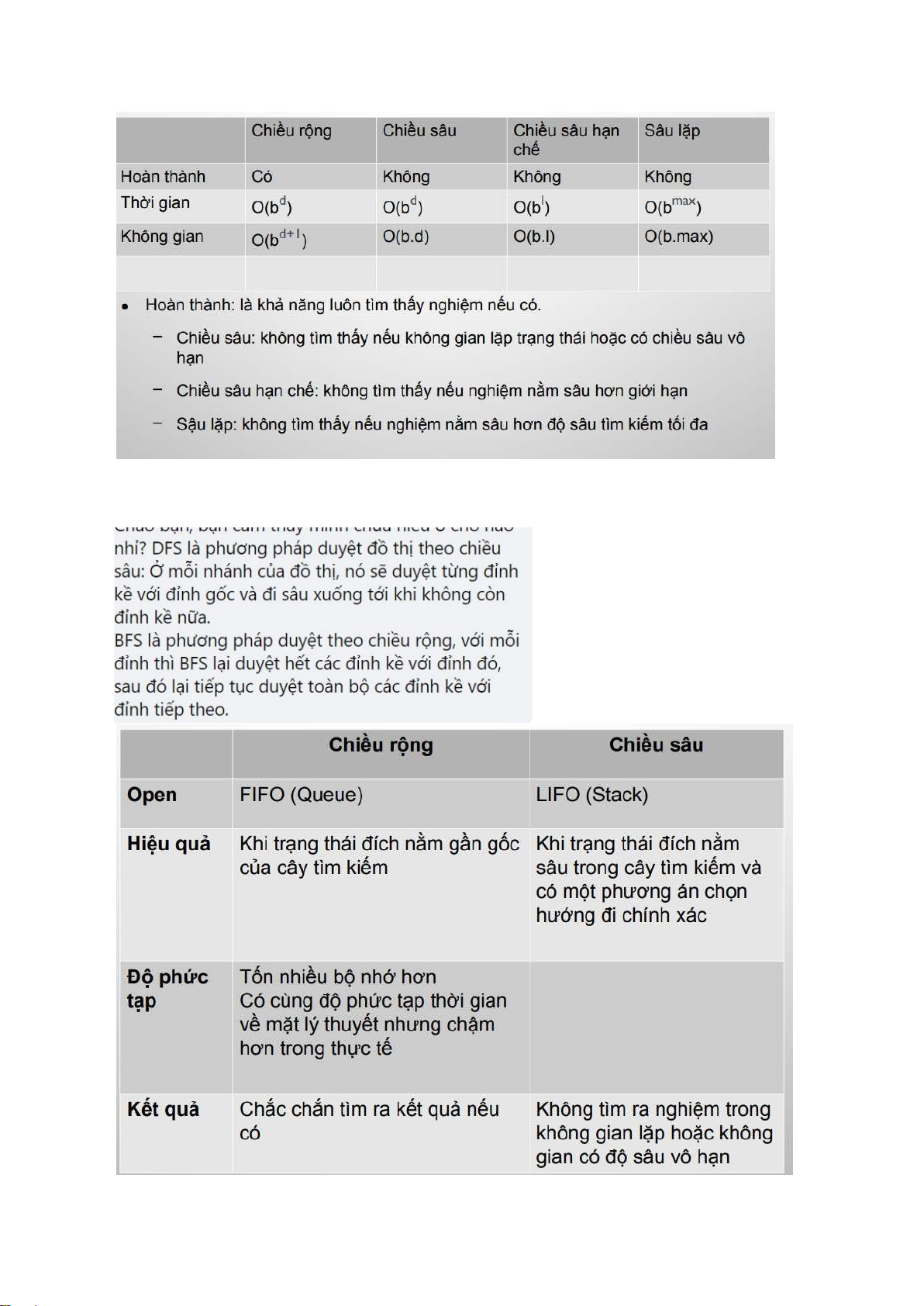
DPT giải thuật tìm kiếm mù lOMoARcPSD| 40651217
Chiều sâu vs Chiều rộng lOMoARcPSD| 40651217
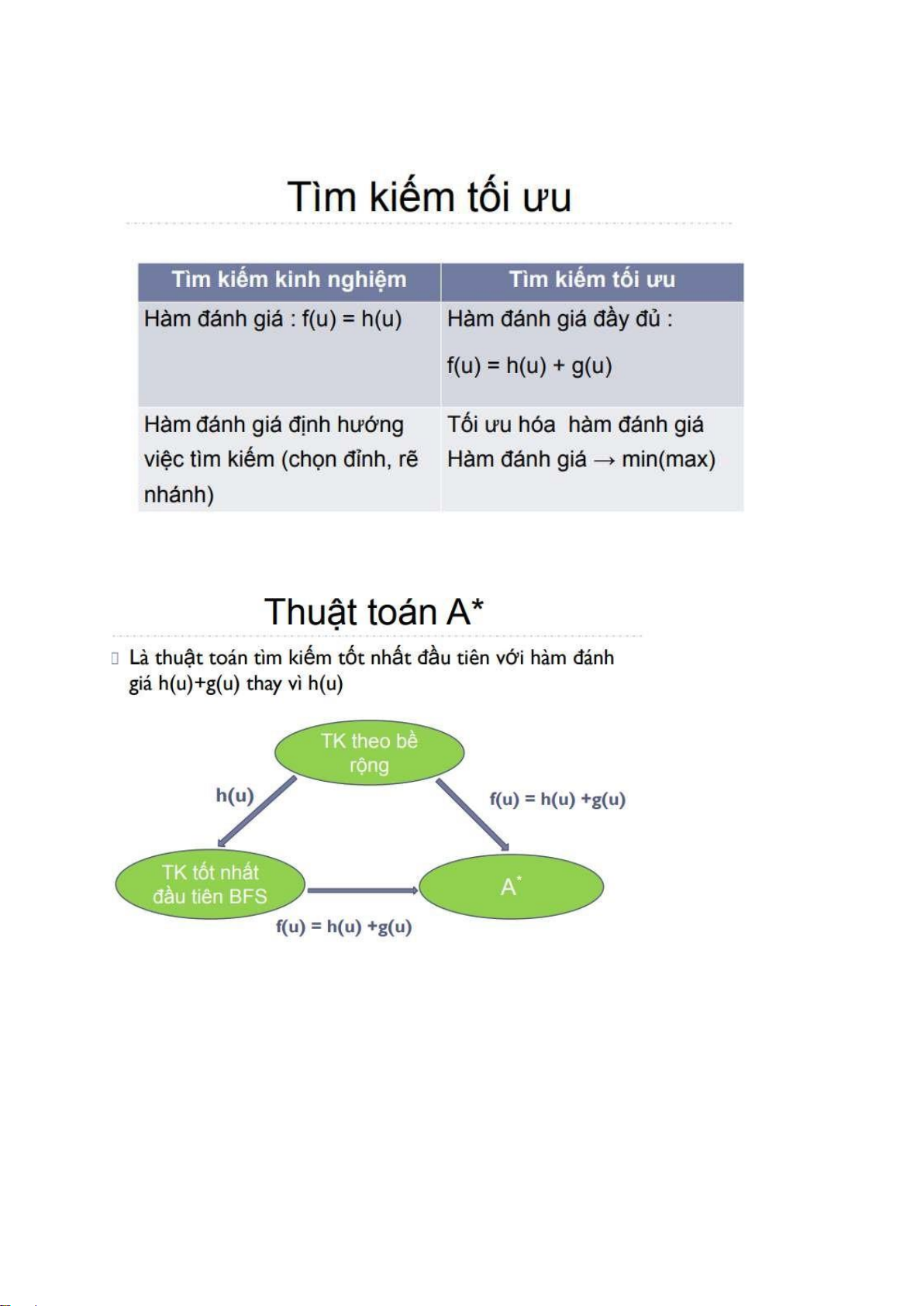
TK kinh nghiệm vs TK tối ưu A* vs BFS Nhánh cận vs A* lOMoARcPSD| 40651217 Nhánh cận vs leo ồi
Tìm kiếm tối ưu và Tìm kiếm Kinh nghiệm lOMoARcPSD| 40651217
Tìm kiếm chiều rộng và tìm kiếm chiều sâu lOMoARcPSD| 40651217 Mạng nơ ron
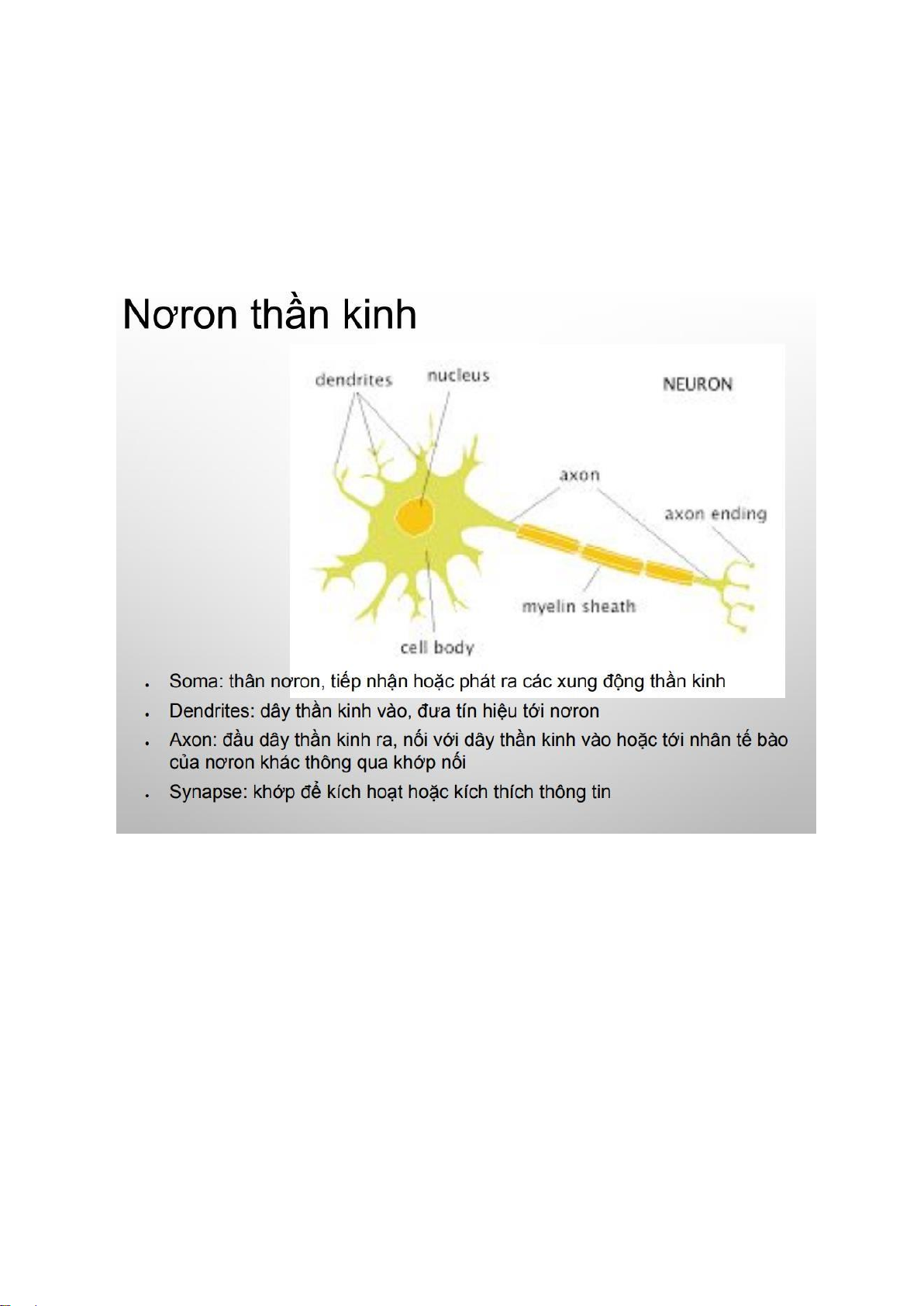
Kĩ thuật tính toán mềm dựa trên mô phỏng hoạt ộng của não bộ (mạng nơron thần kinh) Nơ ron thần kinh Nơron nhân tạo
Tổng thông tin vào của 1 nơron - Net = ∑wi xi Đầu ra -
y = f(Net) = f(∑wi xi ) f ược gọi là hàm truyền
(transfer function) hay kích hoạt (activation function)
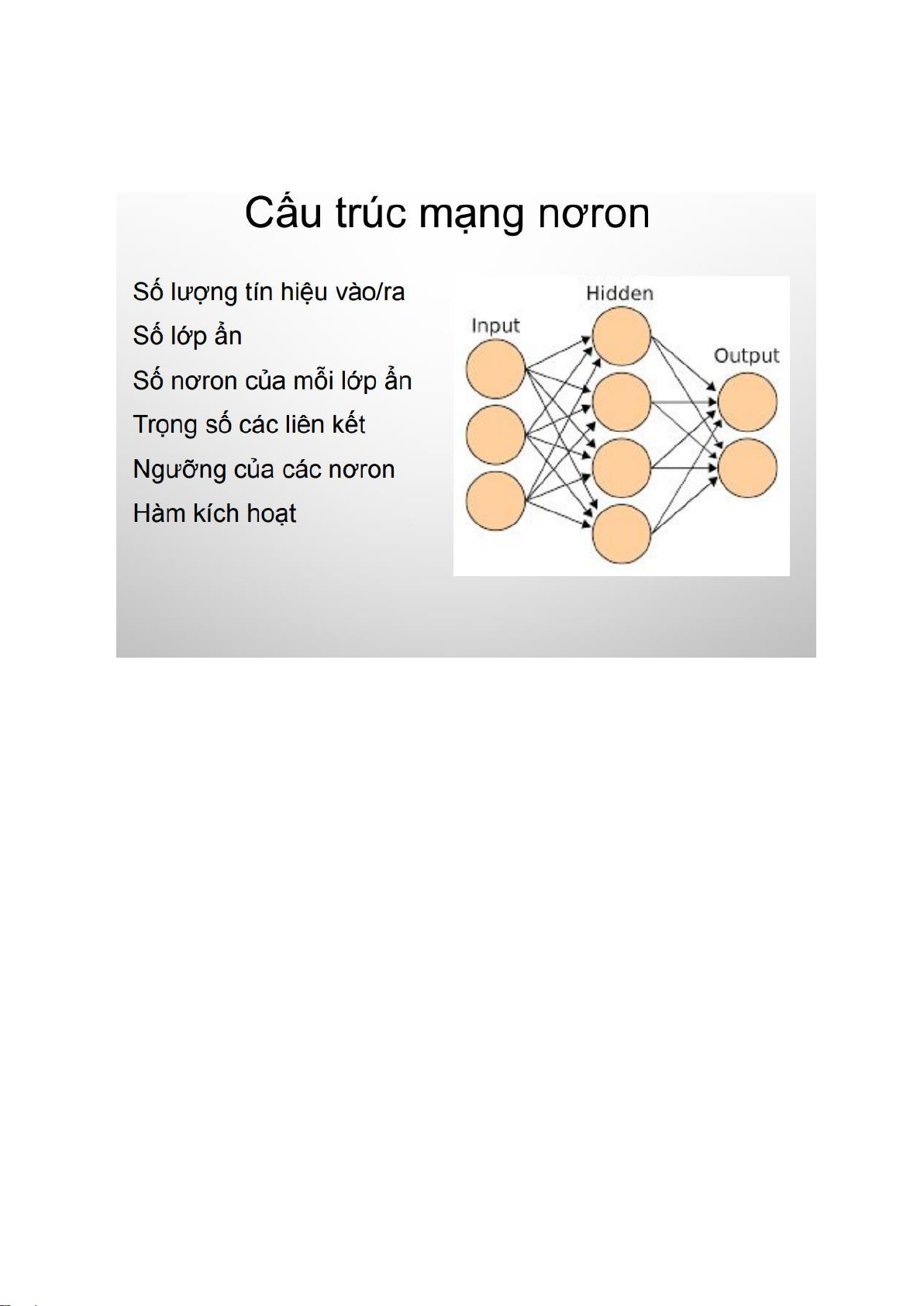
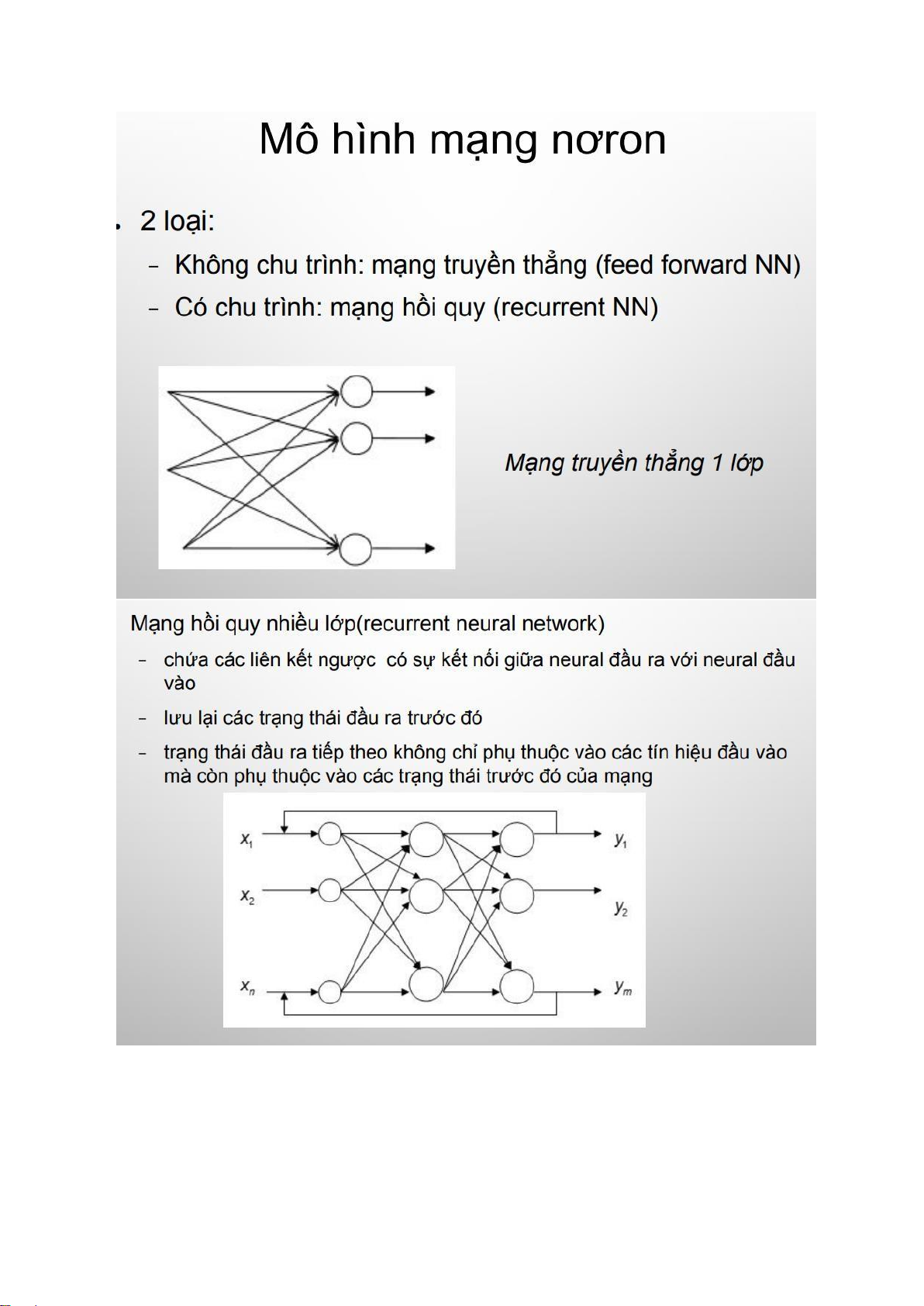
Bản thân mỗi nơron như 1 hàm tính và tính mạnh hơn cổng logic cơ bản lOMoARcPSD| 40651217 Cấu trúc mạng nơ ron Mô hình mạng nơ ron lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 Thiết kế mạng nơ ron Các phương pháp học lOMoARcPSD| 40651217
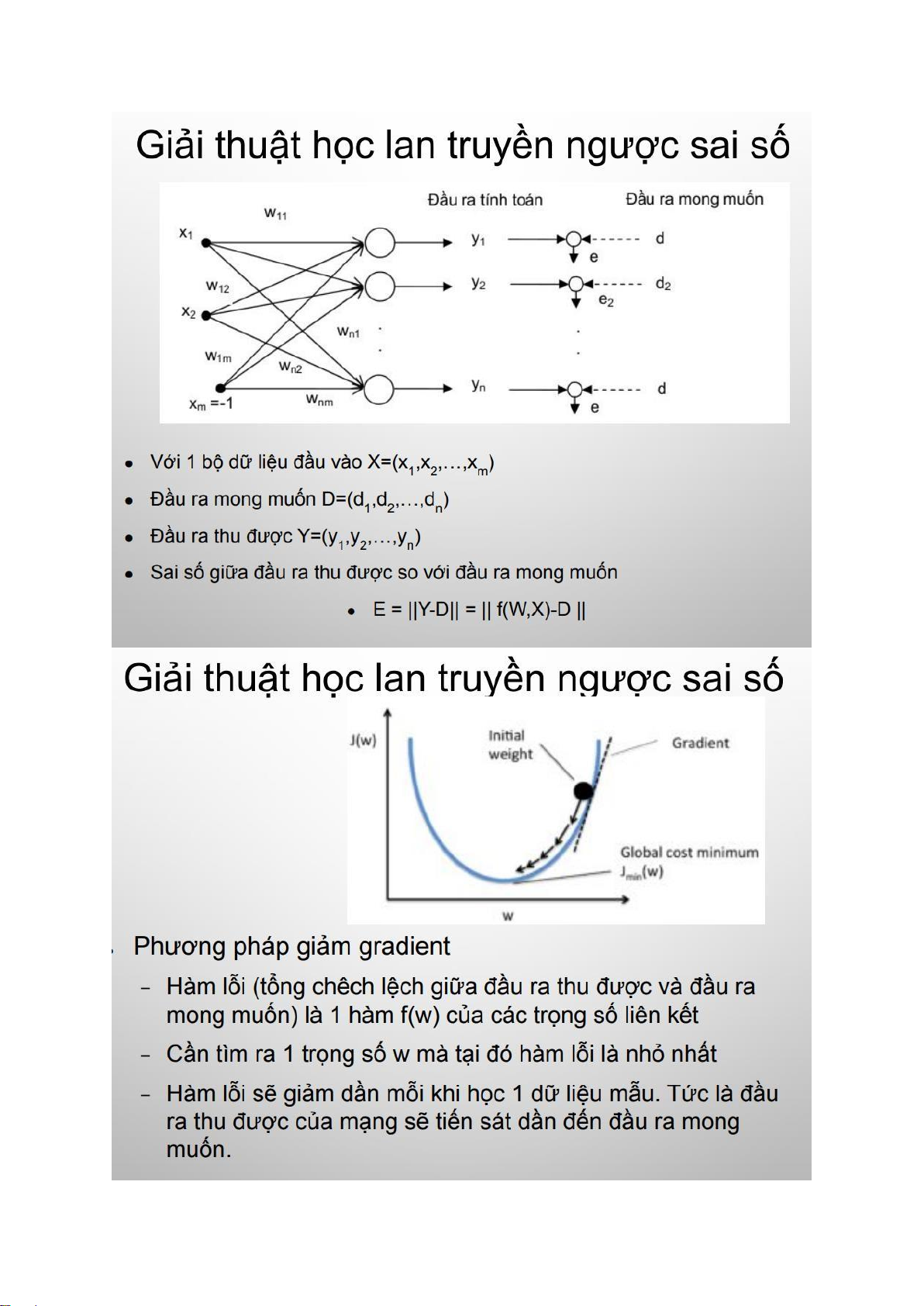
Giải thuật học lan truyền ngược sai số lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 lOMoARcPSD| 40651217 Ứng dụng