lOMoAR cPSD| 47305584 2023/10/10
Toán dành cho tin học
Mathematics for Computing
Giảng viên: TS. Hoàng Anh Khoa CNTT-KD (BIT) Anhh@ueh.edu.vn 1 Nội dung
˗ Giớithiệu(Buổi1)+Tậphợp
˗ LogicvàChứngminh(Buổi2)
˗ LýthuyếtsốvàMãhóa(Buổi3) ˗ Quanhệ(Buổi4)
˗ LMS ( Buổi5_Online )
˗ LýthuyếtĐồthị(Buổi6) ˗ Cây(Buổi7) ˗ ĐạisốBoole(Buổi8) ˗ Xácsuất(Buổi9) 2 1 lOMoAR cPSD| 47305584 2023/10/10
Buổi 1 Giới thiệu Nội dung môn
học Yêu cầu Phương pháp học Đánh
giá kết quả Tài liệu Q&A
Tổ chức lớp học Ôn những
kiến thức cần thiết! 3
WELCOME: Mathematics for Computing
 If you have question? Email me : Anhh@ueh.edu.vn  Họctoánđểlàmgì?
 Nguyênlýhoạtđộngcủamáytính?  Toánrờirạc
 ỨngdụngTOÁN trongchuyênngànhcủabạn? 4
Đánh giá/ How do I pass the module? 2 lOMoAR cPSD| 47305584 2023/10/10 Kế hoạch học tập
Tham gia lớp học: 5% Bài tập (LMS):
15% Thi giữa kỳ (Tự luận): 30% Thi
cuối kỳ (Trắc nghiệm hoặc Tự luận): 50% 5 Who is doing the work? Phươngpháphọc  Bịđộng/ PASSIVE
- Giảngviên: Giảngbài
Gửitàiliệuhọctập Giảibàitập - Sinhviên: Quan sátvàhọc 6 3 lOMoAR cPSD| 47305584 2023/10/10 Who is getting the degree? Chủ động/ ACTIVE
SV đọc/ tìm hiểu trước nội dung buổi học
Chủ động giải quyết vấn đề
SV hỏi/ trao đổi/ thảo luận
SV chủ động làm BT 7 Problems with tutorials?
Q: Bạnsẽlàmgìkhikhônghiểuvấnđề?
A: Bạnnênđọckỹlạitàiliệuhọctập, hỏibạn/ trợgiảng, vàhỏithầy.
Q: Bạnlàmthếnàođểnhậnsựgiúpđỡkhikhôngtựmình giảiquyết?
A:Hỏi/ yêucầusựtrợgiúptừ... 8 4 lOMoAR cPSD| 47305584 2023/10/10 How do I pass the module? Don’t keep quiet if you don’t understand ????? or can’t do the questions. 9 Help is not a question!
 There is a difference in the statements  I’m lost  I’m stuck  I can’t do it  I give up  And the questions
 Could you show me how to…
 I don’t understand how you do….
 Could you give me another similar example to…
 Am I on the right track here…… 10 5 lOMoAR cPSD| 47305584 2023/10/10 Tập hợp/ Sets 11
Các khái niệm về tập hợp
 Địnhnghĩatậphợp làgì?
 Cácphầntử/thànhviêntạonêntậphợpcóthểlà?
 Tậphợpthườngđượckýhiệubằng?
 TậphợpA vàTậphợpB đượcgọilàbằngnhaukhinào?
 Cóthểphânbiệtcácphầntử?
 Phầntửcóđượclặplại?
 Each element only appears once, { a, b, a} = {a, b} - A value
is either a member or not -can’t be in twice or half in.
 Thứtựcácphầntử: { a, b} = {b, a } 12 6 lOMoAR cPSD| 47305584 2023/10/10 Đây có là tập hợp? 13 14 7 lOMoAR cPSD| 47305584 2023/10/10
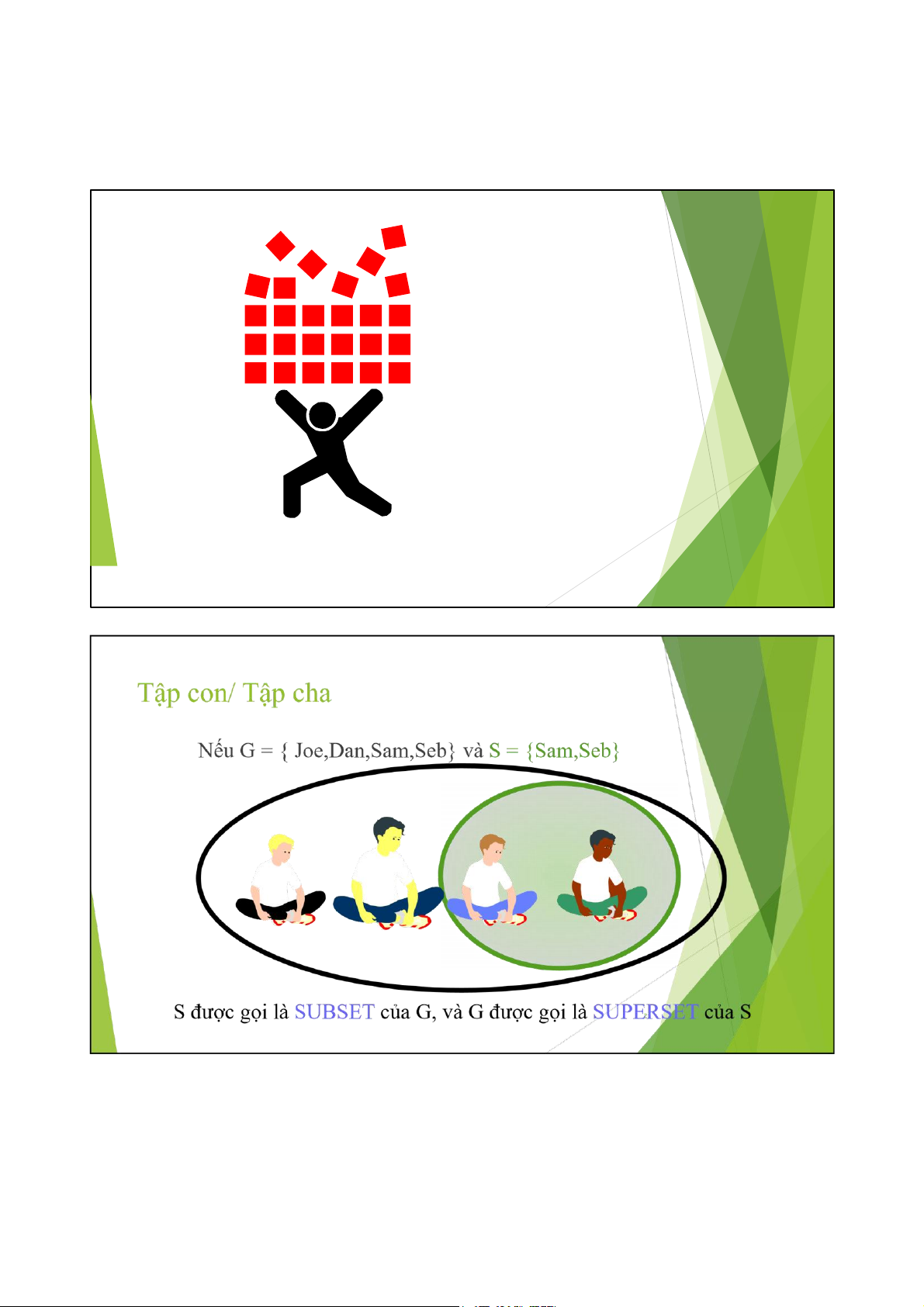
Phần tử thuộc tập hợp? Joe Dan Sam Seb
- Liệt kê: G = { Joe, Dan, Sam, Seb} Joe Î G Cedric Ï G
- Mô tả: G = {boys with 3 letter names} Joe Î G Cedric Cedric Ï G 15 15
Order, duplication and equality each contains the same 3 types My set of glass bottles these two sets are Your set of glass bottles 16 essentially the same 16 8 lOMoAR cPSD| 47305584 2023/10/10
Order, duplication and equality
Tập hợp sử dụng dấu { } liệt kê phần tử và chử in HOA để đặt tên 17 Vídụ: Cáctậphợpsố
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20..
Tậpsốtựnhiên, hoặcsốđếm: kýhiệuN 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20.. Tậpsốlẽ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20..
Tậpsốchẵn, hoặcsốchia hếtcho2 1 2 3 4 5 6 7 8 9 10 11 1 2 13 14 15 16 1 7 18 19 20 .. Tậpcácbộisốcủa5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 … 20 Tậpcácướcsốcủa20 1 2 3 4 5 6 7 8 9 10 1 1 12 13 14 15 16 17 1 8 19 20 .. Tậpsốbìnhphương 18 18 9 lOMoAR cPSD| 47305584 2023/10/10
Số 4 có phải là phần tử của tập hợp? 1. A = {1,2,3,4,5,6,7} 1. 4 Î A 2. B = {x: x ÎN, x>3} 2. B = {4,5,6,7,……} 4 Î B
3. C = {Tập hợp số lẽ} 3. C = {1,3,5,7,..} 4 Ï C
4. E = {Tập số chia hết cho 2} 4. E = {2,4,6,8,…..} 4 Î E 5. F = {x: x2 =16} 5. F = {4,-4} 4 Î F 6. G = {Ước số của 15} 6. G = {1,3,5,15} 4 Ï G
Note {x: is read as ‘the set of x’s such that’ 19 19 ộlớncủa Đ tậphợp
 Tậphợpgiớihạnvàtậphợpkhônggiớihạn  Vídụ:
 N làtậphợpkhônggiớihạncácsốtựnhiên
 T = {ướcsốcủa12} = {1,2,3,4,6,12}
 If a set is finite we call the number of members it contains its order
 So the order of T is 6 this is written |T| = 6 20 20 10 lOMoAR cPSD| 47305584 2023/10/10 Phân rã/Decomposition 
Các vấn đề sẽ được giải
quyết dễ dàng hơn nếu chúng
được chia thành nhiều vấn đề nhỏ  Coding large implementations is often done
by teams each tackling a small section 21 21 22 11 lOMoAR cPSD| 47305584 2023/10/10 Tập con/ Subsets Í Ký hiệu tập con
Ì is a proper subset (equality not allowed )
We had SÌ G (Joe & Dan are in G but not S) If we take some number sets N Z Q R 23 N Ì Z Ì Q Ì R (more later on this) 23 Mởrộng/Extensions
 CácngônngữlậptrìnhHĐT
như C++ hoặc Java ýtưởng G
mởrộngmộtlớp“ extending ” Boys with 3 letter
a class thườngđượcsửdụng names
bằngcáchthêm thuộctính
hoặc phươngthức mới. S Boys with 3 letter G -Generalisation names starting S -Specialisation with S 24 24 12 lOMoAR cPSD| 47305584 2023/10/10 Tập con/Subsets A Í TRUE D Í is a subset D Í FALSE
Ì is a proper subset (equality not allowed ) A
Liệt kê các phần tử cho các tập hợp sau: A Ì TRUE
D = days of the week Thursday Friday Saturday D FALSE
SundayMonday Tuesday Wednesday E Í F = factors of 161,2,4,8,16 E = even numbers less than F 10 2,4,6,8 M TRUE M = multiples of 4 less than Ì F 104,8 Monday Tuesday E TRUE A = days attending for classesThursday Friday É M 25 25 Phát biểu nào đúng?
Tậphợpđặcbiệt/Special Sets
U the Universal set (all elements under consideration)
Æ tậprỗng(contains no members)
A Í U and Æ Í A for all sets A
( all sets are in the universal one and nothing is in all sets ) Vídụ:
If U = natural numbers less than 12 the = {1,2,3,4,5,6,7,8,9, 10,11} universal set con con t t ai ai n n s s a t ll h e F= multiples of 3 the o element nly s tha elements t = {3, 6, 9} you can 26 consi der 26 13 lOMoAR cPSD| 47305584 2023/10/10 Let U = {people in this room} Let S = {Students} Let L = {Lecturers} Let S = {Students}
Let M = {Mature people} (over 21!)
|L| = 1 (U restricted to this room)
L Ì M (I’m definitely over 21)
S ¹Æ (this is not an empty class) 27 27
Phầnbù/Complement and difference
complement of set A -those elements not in a set A written A ¢ or sometimes ! S ¢ = {H. Anh }.
L ¢ = S. M ¢ = {the youngsters }
difference of A and B -elements of A not in B written A\B
S\M = {immature students} L\S = L 28 28 14 lOMoAR cPSD| 47305584 2023/10/10
Phần bù, Hiệu của 2 tập hợp U = {1,2,3…..20}
A = Tập các số lẻ bé hơn 20
A = {1,3,5,7,9,11,13,15,17,19)
B = Tập bội số của 3 bé hơn 20 B = {3,6,9,12,15,18}
Phần bù của tập A – Tập hợp các phần tử không thuộc A
A¢ = {2,4,6,8,10,12,14,16,18,20}
Hiệu của A và B (difference of A and B) – Tập hợp các phần tử của A không thuộc B
A\ B = {1,5,7,11,13,17,19} 29 29 30 15 lOMoAR cPSD| 47305584 2023/10/10 My set of glass bottles Your set of glass bottles Intersection = in both sets Here the intersection is
a new set with two bottles in it 31 31 16 lOMoAR cPSD| 47305584 2023/10/10 Tậpgiao/Intersection Giao của2 tậphợpA vàB A Ç B Vídụ:
A = {1, 2, 3, 4, 5, 6, 7} vàB = {2, 4, 6, 8, 10} Ta có: A Ç B = {2, 4, 6} 32 32 Hợp/Union = altogether 17 lOMoAR cPSD| 47305584 2023/10/10 Here the union is a new set with all the different bottles in it My set of glass bottles Your set of glass bottles 33 33 Hợpcủatậphợp/Union Hợpcủa2 tậphợpA vàB A È B Vídụ
A = {1, 2, 3, 4, 5, 6, 7} vàB = {2, 4, 6, 8, 10}
Ta có: A È B = {1, 2, 3, 4, 5, 6, 7, 8, 10} 34 34 Tìm các tập hợp sau
U = N (we are only considering the Natural Numbers)
P = {1,2,3,4,5,6,7}, Q = {odd numbers }, R = {factors of 15} 18 lOMoAR cPSD| 47305584 2023/10/10 1. P Ç R 1. {1,3,5} 2. P \ Q 2. {2,4,6} 3. P Ç Q Ç R 3. {1,3,5} 4. Q ¢ 4. {even numbers} 5. P È R 5. {1,2,3,4,5,6,7,15} 6. {2,4,6,7} 6. P Ç R ¢ 35 35
Tậphợpcủatậphợp/Sets of Sets
A set can contain sets as members each regarded as a single object in it's own right.
e.g. Vowels == { a, e, i, o, u }
Consonants == { b, c, d, f, ...}
Letters == {Vowels, Consonants}
i.e. Letters == {{ a, e, i, o, u } , { b, c, d, f, ...}} n.b. #Letters = 2
Alphabet = Vowels È Consonants = {a, b, c, d, … z}
Letters = {Vowels} È { Consonants} ¹ Alphabet #Alphabet = 26
N.B. #A == |A|, the order (also called cardinality) of set A.36 36 Powersets: P
PS The set of all subsets of S 19 lOMoAR cPSD| 47305584 2023/10/10
Eg: P{a, b, c} = {{}, {a}, {b}, {c},{a,b}, {a,c}, {b,c}, {a,b,c}} Note:
x Î PA Û x Í A
Cardinality of a Powerset # PA= 2#A The Non-empty powerset P1S The non-empty subsets of S
== {T Î PS | T ¹ Æ } Finite Powerset
FS The set of finite subsets of S 37 37 Vídụ  A = {p, q, r}
 B làtậpcon củaA, B Í A  B?  { }  { p } p q  {q }  { } r r  { } p,q  { } q,r  { p,r }  { p,q,r } 38 38
Intersection = in both sets (like AND) 20