Mô Hình Xếp Hàng và Ứng Dụng trong Lý Thuyết Xác Suất | Môn Hình học và Đại số tuyến tính - Đại học Cần Thơ

lOMoAR cPSD| 58488183
MỘT SỐ MÔ HÌNH XẾP HÀNG VÀ ỨNG DỤNG Mục Lục
MỞ ĐẦU ....................................................................................................... Error! Bookmark not defined.
CHƢƠNG 1 ................................................................................................... Error! Bookmark not defined.
KIẾN THỨC CHUẨN BỊ .............................................................................. Error! Bookmark not defined. 1.1
Phân bố Poisson và phân bố mũ ..................................................... Error! Bookmark not defined.
1.1.1 Phân bố Poisson ............................................................................ Error! Bookmark not defined.
1.1.2 Phân bố mũ: .................................................................................. Error! Bookmark not defined.
1.2. Xích Markov ....................................................................................... Error! Bookmark not defined.
1.2.1. Phân loại trạng thái xích Markov ................................................. Error! Bookmark not defined.
1.3. Quá trình Markov ................................................................................ Error! Bookmark not defined.
1.3.1. Trƣờng hợp không gian trạng thái hữu hạn.................................. Error! Bookmark not defined.
1.3.2. Trƣờng hợp không gian trạng thái vô hạn đếm đƣợc ................... Error! Bookmark not defined.
CHƢƠNG 2: .................................................................................................. Error! Bookmark not defined.
MỘT SỐ MÔ HÌNH XẾP HÀNG ................................................................. Error! Bookmark not defined.
2.1 Khái niệm và phân loại quá trình xếp hàng ......................................... Error! Bookmark not defined.
2.1.1 Khái niệm quá trình xếp hàng ....................................................... Error! Bookmark not defined.
2.1.2 Các yếu tố cơ bản của hàng đợi .................................................... Error! Bookmark not defined.
a. Bố trí vật lí của hệ thống .................................................................... Error! Bookmark not defined.
b. Nguyên tắc phục vụ............................................................................ Error! Bookmark not defined.
c. Các phân phối xác suất của các dòng tín hiệu, dòng phục vụ ............ Error! Bookmark not defined.
2.1.3 Phân tích hàng đợi ......................................................................... Error! Bookmark not defined.
2.1.4 Phân loại Kendall .......................................................................... Error! Bookmark not defined.
2.1.5 Mục tiêu của phân tích hàng đợi ................................................... Error! Bookmark not defined.
2.2 Một số mô hình xếp hàng cơ bản ......................................................... Error! Bookmark not defined.
2.2.1 Mô hình xếp hàng sinh – chết tổng quát ....................................... Error! Bookmark not defined.
2.2.2 Mô hình hàng đợi M/M/1 .............................................................. Error! Bookmark not defined. lOMoAR cPSD| 58488183
a. Phân bố giới hạn ................................................................................. Error! Bookmark not defined.
b. Thời gian khách hàng chờ đợi ............................................................ Error! Bookmark not defined.
c. Thời gian bận rộn ............................................................................... Error! Bookmark not defined.
d. Quá trình dời đi .................................................................................. Error! Bookmark not defined.
e. Bài toán ví dụ ..................................................................................... Error! Bookmark not defined.
2.2.3. Mô hình hàng đợi M/M/s ............................................................. Error! Bookmark not defined.
a. Thời gian chờ đợi ............................................................................... Error! Bookmark not defined.
b. Thời gian bận rộn ............................................................................... Error! Bookmark not defined.
c. Quá trình dời đi .................................................................................. Error! Bookmark not defined.
d. Bài toán ví dụ ..................................................................................... Error! Bookmark not defined.
2.2.4. Mô hình hàng đợi hữu hạn M/M/s/K ........................................... Error! Bookmark not defined.
a. Bài toán ví dụ ..................................................................................... Error! Bookmark not defined.
2.2.5. Mô hình hàng đợi M/G/1 ............................................................. Error! Bookmark not defined.
a. Phân bố giới hạn ................................................................................. Error! Bookmark not defined.
b. Thời gian chờ đợi ............................................................................... Error! Bookmark not defined.
c. Thời gian bận rộn ............................................................................... Error! Bookmark not defined.
d. Bài toán ví dụ ..................................................................................... Error! Bookmark not defined.
2.2.6. Mô hình hàng đợi G/M/1 ............................................................. Error! Bookmark not defined. a.
Phân bố giới hạn ................................................................................. Error! Bookmark not defined. b.
Thời gian chờ đợi ............................................................................... Error! Bookmark not defined. c.
Chu kỳ bận rộn ................................................................................... Error! Bookmark not defined. d.
Bài toán ví dụ ..................................................................................... Error! Bookmark not
defined. CHƢƠNG 3: .................................................................................................. Error! Bookmark not defined.
ỨNG DỤNG .................................................................................................. Error! Bookmark not defined.
3.1 Mô phỏng một số mô hình xếp hàng bằng Matlab............................... Error! Bookmark not defined.
3.1.1 Mô phỏng hàng đợi M/M/1 ........................................................... Error! Bookmark not defined. lOMoAR cPSD| 58488183
3.2 Ứng dụng của mô hình xếp hàng trong bài toán ra quyết định. ........... Error! Bookmark not defined. a)
Xét ba bài toán sau: ............................................................................ Error! Bookmark not defined. b)
Hàm giá: ............................................................................................ Error! Bookmark not
defined. KẾT LUẬN .................................................................................................... Error! Bookmark
not defined. TÀI LIỆU THAM KHẢO ............................................................................. Error! Bookmark not defined. MỞ ĐẦU
Lý thuyết xếp hàng đã đƣợc nghiên cứu và ứng dụng rộng rãi trên thế giới trong
nhiều lĩnh vực ngành nghề khác nhau nhƣ bƣu chính viễn thông, hàng không, đƣờng
sắt, kiểm soát lƣu lƣợng giao thông, đánh giá hiệu năng hệ thống máy tính, y tế và
chăm sóc sức khỏe, không lƣu, bán vé …
Trong nhiều hệ thống phục vụ, các khách hàng (costumer) phải dùng chung tài
nguyên, phải chờ để đƣợc phục vụ và đôi khi bị từ chối phục vụ. Lý thuyết quá trình
xếp hàng (queueing process) xác định và tìm các phƣơng án tối ƣu để hệ thống phục vụ là tốt nhất.
Trong nửa đầu của thế kỷ 20 lý thuyết xếp hàng đã đƣợc ứng dụng để nghiên cứu
thời đợi trong các hệ thống điện thoại. Ngày nay lý thuyết xếp hàng còn có nhiều
ứng dụng trong các lĩnh vực khác nhau nhƣ trong mạng máy tính, trong việc quản
lý xí nghiệp, quản lý giao thông và trong các hệ phục vụ khác … Ngoài ra lý thuyết
xếp hàng cũng còn là cơ sở toán học để nghiên cứu và ứng dụng trong nhiều bài toán
kinh tế nhƣ đầu tƣ, kiểm kê, rủi ro của bảo hiểm, thị trƣờng chứng khoán … Chuỗi
Markov là quá trình xếp hàng với thời gian rời rạc đã đƣợc xem xét trong giáo trình
xác suất thống kê. Quá trình sinh tử cũng là quá trình xếp hàng, trong đó sinh biểu
thị sự đến và tử biểu thị sự rời hàng của hệ thống. lOMoAR cPSD| 58488183
Đối với lý thuyết xếp hàng ta quan tâm đến các số đo hiệu năng, đó là các giá trị
trung bình khi quá trình đạt trạng thái dừng bao gồm: độ dài hàng đợi trung bình của
hàng, độ dài hàng đợi trung bình của hệ thống, thời gian đợi trung bình của hàng (trễ
của hàng) và thời gian đợi trung bình của hệ thống (trễ của hệ thống). Để tính các
đại lƣợng này ta có thể sử dụng phƣơng pháp giải phƣơng trình tích phân dạng
Wiener – Hopf hoặc phƣơng pháp khảo sát chuỗi Markov nhúng. Từ đó suy ra các
công thức tính các phân bố ổn định cho các loại hàng M/M/k, M/M/k/N; Công thức
tổng quát tính các giá trị trung bình này cho các hàng G/G/1 và công thức cụ thể cho
các hàng đặc biệt M/M/1, M/D/1 và M/𝐸𝑘/1 …
Luận văn này tìm hiểu về một số mô hình xếp hàng cơ bản và ứng dụng của nó.
Nội dung của luận văn này gồm ba chƣơng.
Chƣơng 1: Kiến thức chuẩn bị.
Chƣơng này trình bày về một số phân bố xác suất liên quan nhƣ: Phân bố
Poisson, phân bố mũ. Những định nghĩa, định lý về xích Markov, phân loại trạng
thái xích Markov, quá trình Markov gồm trƣờng hợp không gian trạng thái hữu hạn
và không gian trạng thái vô hạn đếm đƣợc.
Chƣơng 2: Một số mô hình xếp hàng.
Trình bày về một số mô hình xếp hàng cơ bản gồm: Mô hình hệ thống xếp hàng
Markov đơn giản gồm mô hình xếp hàng Birth- and – Death tổng quát, trình bày cụ
thể mô hình hàng đợi M/M/1, M/M/s và mô hình hàng đợi hữu hạn M/M/s/K. Mô
hình chuỗi Markov nhúng trình bày tổng quát về chuỗi Markov nhúng cụ thể là mô
hình hàng đợi M/G/1 và G/M/1.
Chƣơng 3: Ứng dụng
Chƣơng này tìm hiểu về một vài ứng dụng đơn giản của mô hình xếp hàng bao
gồm: Mô phỏng một số mô hình bằng Matlab và ứng dụng của mô hình xếp hàng
trong bài toán ra quyết định.
Dù đã có nhiều cố gắng nhƣng do thời gian và khả năng có hạn nên các vấn đề
trong luận văn vẫn chƣa đƣợc trình bày sâu sắc và không thể tránh khỏi những sai
sót. Em rất mong đƣợc sự góp ý xây dựng của thầy cô và các bạn. Em xin chân thành cảm ơn! lOMoAR cPSD| 58488183 CHƢƠNG 1
KIẾN THỨC CHUẨN BỊ
Trong chƣơng này em xin trình bày về một sốphân bốxác suất liên quan là phân
bố Poisson, phân bố mũvà một số định nghĩa, định lý về xích Markov gồm hai trƣờng
hợp là không gian trạng thái hữu hạn và không gian trạng thái vô hạn đếm đƣợc để
chuẩn bị kiến thức cho các chƣơng tiếp theo của khóa luận.
1.1 Phân bố Poisson và phân bố mũ
1.1.1 Phân bố Poisson
Định nghĩa.Biến ngẫu nhiên rời rạc X nhận các giá trị từ 0, 1, 2, … gọi là phân phối
Poisson với tham số λ nếu: .
Ký hiệu: X ~ Poisson(λ) Kỳ vọng: ! Phƣơng sai : D(X) = λ lOMoAR cPSD| 58488183
Do đó, chúng ta có thể viết: X ~ Poisson (µ). Mô hình Poisson:
Giả sử chúng ta quan tâm đến số lần xảy ra của một sự kiện A trong một khoảng
thời gian hoặc không gian liên tục có chiều dài w; với điều kiện là số lần xảy ra trong
những khoảng không giao nhau là độc lập nhau, và xác suất xuất hiện A nhiều hơn
một lần trong khoảng đó là rất bé. Hơn nữa, “cƣờng độ” xuất hiện A là không thay
đổi, tức là số lần xuất hiện trung bình của A trong một khoảng chỉ phụ thuộc vào độ dài của khoảng đó.
Với các điều kiện trên, nếu gọi X là BNN chỉ số lần xuất hiện A trong một khoảng
chiều dài w thì ngƣời ta chứng minh đƣợc rằng X tuân theo luật phân phối Poisson
với tham số λ = mw, trong đó m là một hằng số dƣơng chỉ “cƣờng độ” xuất hiện của A.
Thí dụ, số cuộc điện thoại gọi đến trong một phút tại một trạm nào đó; sốlỗi trên một
trang giấy trong một quyển sách dầy; số đơn đặt hàng gửi tới một cơ sở trong một tháng, …
Biến ngẫu nhiên chỉ số lần xuất hiện nêu trên đã đƣợc nhà toán học Simeon D.
Poisson nghiên cứu và hình thành phân phối Poisson.
Ngoài ra, phân phối Poisson còn đƣợc dùng để tính xấp xỉ phân phối nhịthức B(n;p)
khi n lớn và p khá gần 0 hoặc gần 1. Định lý Poisson.
Giả sử trong một dãy n phép thử độc lập, một biến cố A xuất hiện với xác suất
trong mỗi phép thử. Nếu khi mà → 0 sao cho (λ là một hằng
số dƣơng) thì với mọi , chúng ta có: Hệ quả: Nếu , với và (
thì chúng ta có thể xem như Định lí:
Cho hai biến ngẫu nhiên X và Y độc lập. Nếu và
thì biến ngẫu nhiên . 1.1.2 Phân bố mũ: lOMoAR cPSD| 58488183 Định nghĩa:
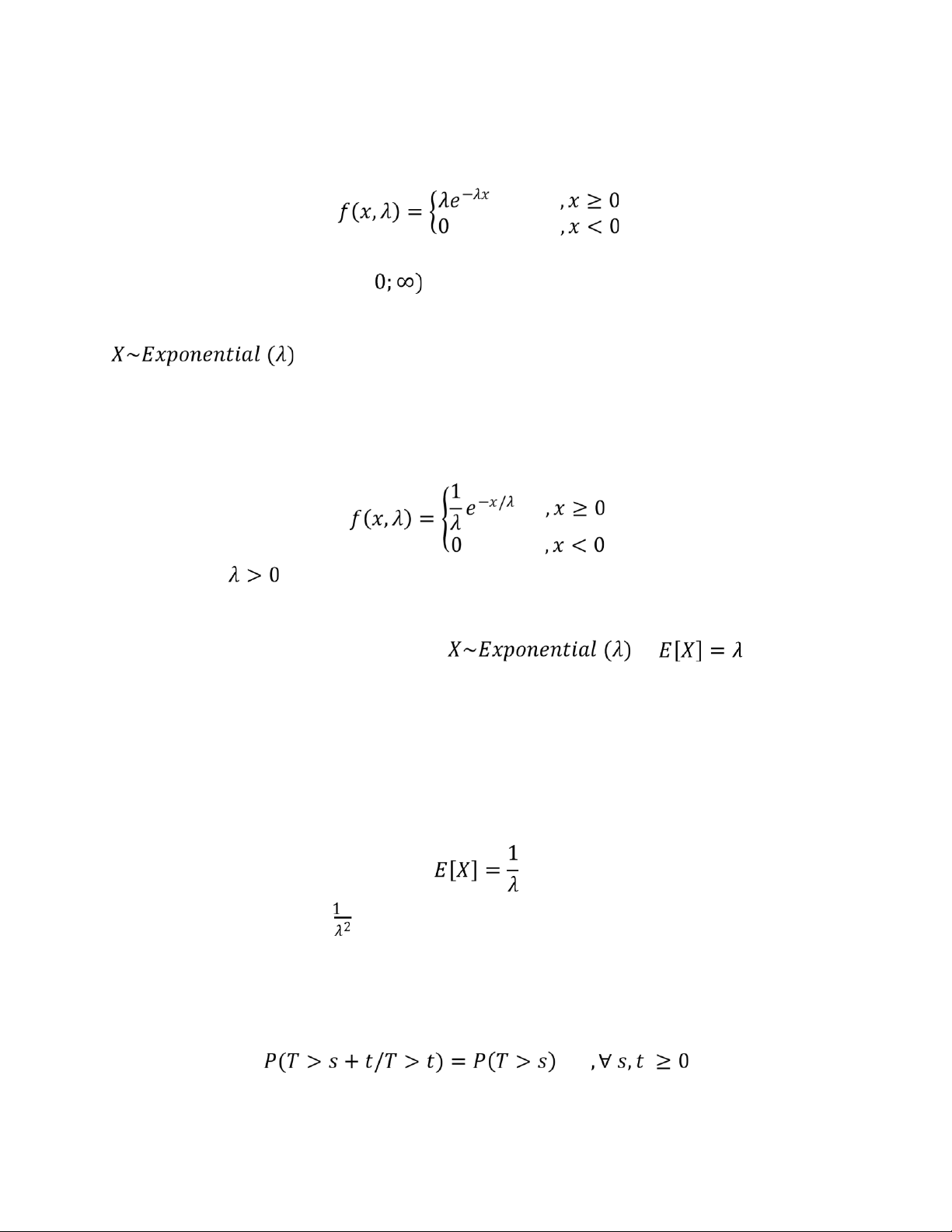
Hàm mật độ xác suất của một phân phối mũ có dạng như sau:
Trong đó λ là tham số của phân bố, thƣờng đƣợc gọi là tham số tỉ lệ. Phân bố
đƣợc hỗ trợ dựa trên khoảng [ .
Nếu một biến ngẫu nhiên X có phân phối này, ta viết: . Đặc tả:
Một cách khác để định nghĩa hàm mật độ xác suất của một phân phối mũ nhƣ sau: Trong đó
là một tham số của phân bố và có thể đƣợc coi là nghịch đảo của
tham số tỉ lệ đƣợc định nghĩa ở trên. Trong đặc tả, λ là một tham số sống sót theo
nghĩa: nếu một biến ngẫu nhiên X là khoảng thời gian mà một hệthống sinh học hoặc
cơ học M cho trƣớc sống sót đƣợc và thì .
Nghĩa là khoảng thời gian sống sót kì vọng của M là λ đơn vị thời gian. Tính chất:
+ Giá trị trung bình và phương sai:
Giá trị trung bình hay giá trị kì vọng của một biến ngẫu nhiên phân phối mũ X với
tham số tỉ lệ λ đƣợc cho bởi công thức: Phƣơng sai của X là: + Tính không nhớ:
Một tính chất quan trọng của phân phối mũ là nó không nhớ. Nghĩa là nếu một
biến ngẫu nhiên T có phân phối mũ xác suất điều kiện của nó phải thỏa mãn: lOMoAR cPSD| 58488183 1.2. Xích Markov
Xét một hệ nào đó đƣợc quan sát tại các thời điểm rời rạc 0,1,2,... Giả sử các quan
sát đó là X0, X1, ..., Xn, ... Khi đó ta có một dãy các đại lƣợng ngẫu nhiên (ĐLNN)
(Xn) trong đó Xn là trạng thái của hệ tại thời điểm n. Giả thiết rằng mỗi Xn, n = 0,1,...
là một ĐLNN rời rạc. Ký hiệu E là tập giá trị của các (Xn). Khi đó E là một tập hữu
hạn hay đếm đƣợc, các phần tử của nó đƣợc ký hiệu là i, j, k... Ta gọi E là không
gian trạng thái của dãy.
Định nghĩa 1.2.1.Ta nói rằng dãy các ĐLNN (Xn) là một xích Markov nếu với mọi
n1< ... < nk< nk+1 và với mọi i1, i2, ..., ik+1 E, ta có: .
Ta coi thời điểm nk+1 là tƣơng lai, nk là hiện tại còn n1, ..., nk -1 là quá khứ. Nhƣ vậy,
xác suất có điều kiện của một sự kiện B nào đó trong tƣơng lai nếu biết hiện tại và
quá khứ của hệ cũng giống nhƣ xác suất có điều kiện của B nếu chỉ biết trạng thái
hiện tại của hệ. Đó chính là tính Markov của hệ. Đôi khi tính Markov của hệ còn
phát biểu dƣới dạng: Nếu biết trạng thái hiện tại của hệ thì quá khứ và tƣơng lai độc lập với nhau. Giả sử
là xác suất để xích tại thời điểm m ở trạng thái i sau n
bƣớc, tại thời điểm m + n chuyển sang trạng thái j. Đây là một con số nói chung phụ
thuộc vào i, j, m, n. Nếu đại lƣợng này không phụ thuộc m ta nói xích là thuần nhất. Ký hiệu: , . Ta gọi (
) là xác suất chuyển sau một bƣớc hay xác suất chuyển còn (
) là xác suất chuyển sau n bƣớc. Chú ý rằng: , .
Phân bố của X0 đƣợc gọi là phân bố ban đầu. Ta ký hiệu .
Định lý 1.2.1.Phân bố đồng thời của (X0, X1, ..., Xn) được hoàn toàn xác định từ
phân bố ban đầu và xác suất chuyển. Cụ thể ta có: . lOMoAR cPSD| 58488183
Nhƣ vậy phân bố đồng thời của
đƣợc xác định bởi phân bố ban đầu và xác suất chuyển.
Định lý 1.2.2.(Phương trình C - K (Chapman-Kolmogorov)): (n + m) = (n) (m).
Trong trƣờng hợp E có d phần tử, ta ký hiệu = ( ), ij(n))là các ma trận vuông cấp
. P đƣợc gọi là ma trận xác suất chuyển, P(n) đƣợc gọi là ma trận
xác suất chuyển sau n bƣớc. Khi đó từ phƣơng trình Chapman - Kolmogorov tƣơng đƣơng với: .
Vì P = P(1) nên bằng quy nạp ta dễ thấy: = . Gọi Ký hiệu vecto là vector hàng d
- chiều mô tả phân bố của , là vector hàng d - chiều
mô tả phân bố ban đầu (Phân bố của ).
Định lý 1.2.3.Ta có: .
Định nghĩa 1.2.2.Phân bố ban đầu
được gọi là phân bố dừng nếu ta có
với mọi n tức là
. Khi đó dãy ( ) có cùng phân bố.
Từ định lý 1.2.3 ta suy ra
là phân bố dừng nếu và chỉ nếu: • 1. và , • 2. .
Định lý 1.2.4.Giả sử ( ) là xích Markov với không gian trạng thái
E = 1,2,... với ma trận xác suất chuyển
và ma trận xác suất chuyển sau n bước là
. Ta nói rằng xích có phân bố giới hạn nếu với mọi i, j E tồn tại giới hạn:
Giới hạn này không phụ thuộc i E. khi đó: • 1. ≤ 1 và πj = . lOMoAR cPSD| 58488183
• 2. Hoặc πj = 0 với mọi j E, hoặc = 1. • 3. Nếu
= 1 thì U = (π1, π2, ...) là phân bố dừng và phân bố dừng là duy nhất.
Nếu πj = 0 với mọi j E thì phân bố dừng không tồn tại.
Ý nghĩa của phân bố giới hạn là nhƣ sau: Gọi ). Ký hiệu vector
là vector hàng d - chiều mô tả phân bố của . Ta có: P(Xn = j) = (X0 = i) (n). Do đó: = = = .
Định nghĩa 1.2.3.Giả sử ( ) là xích Markov với không gian trạng thái
E ={1, 2, ...} với ma trận xác suất chuyển
và ma trận xác suất chuyển sau n bước là
). Ta nói rằng xích có phân bố giới hạn nếu với mọi i, j E
tồn tại giới hạn: (n) = πj .
Giới hạn này không phụ thuộc i E và
= 1. Nói cách khác, vecto giới hạn
lập thành một phân bố xác suất trên E. Vậy phân bố
của hội tụ tới phân bố giới hạn π. Khi n khá lớn ta có .
Theo định lý 1.1.4 nếu phân bố giới hạn tồn tại thì phân bố dừng cũng tồn tại và duy
nhất. Hơn nữa hai phân bố này trùng nhau. Tuy nhiên điều ngƣợc lại không đúng
tức là có những xích Markov có tồn tại phân bố dừng nhƣng không tồn tại phân bố giới hạn.
Định lý 1.2.5.Cho ( ) là xích Markov với không gian trạng thái hữu hạn
E = {1,2,...,d} với ma trận xác suất chuyển sau n bước là ( (n)).Khi đó có
tồn tại phân bố giới hạn π = (π1, ..., πd ) với
khi và chỉ khi xích là
chính quy theo nghĩa: Tồn tại sao cho: . lOMoAR cPSD| 58488183
1.2.1. Phân loại trạng thái xích Markov
Định nghĩa 1.2.4.Ta nói rằng trạng thái i đến được trạng thái j và ký hiệu là nếu tồn tại sao cho . (Ta quy ước nếu(i ≠ j)).
Hai trạng thái i và j được gọi là liên lạc được nếu và . Trong trường hợp đó ta viết .
Định nghĩa 1.2.5.Xích Markov được gọi là tối giản nếu hai trạng thái bất kỳ là liên
lạc được. Có nghĩa là theo cách phân lớp trên thì E không thể phân hoạch thành các lớp con nhỏ hơn.
Định nghĩa 1.1.6.Ký hiệu
là xác suất để hệ xuất phát từ i lần đầu tiên quay lại
i ở thời diểm n. Nghĩa là: (n) = P(Xn = i, i, ..., i|X0 = i) và ký hiệu: .
Định lý 1.2.6.Trạng thái i là hồi quy khi và chỉ khi:
Định lý 1.2.7.Nếu i ↔ j và j hồi quy thì i hồi quy. Chứng minh:
Theo giả thiết tồn tại
sao cho (n) > 0, (m) > 0. Với mỗi số nguyên dƣơng h
từ phƣơng trình C-P suy ra: (n + h + m) ≥ (n) (h) (m). Vậy: Vậy i hồi quy.
Định lý 1.2.8. Ký hiệu là xác suất để hệ xuất phát từ i quay lại i vô số lần, là
xác suất để hệ xuất phát từ i đi qua j vô số lần. Khi đó:
• (i) Nếu i hồi quy thì
, nếu i không hồi quy thì . lOMoAR cPSD| 58488183
• (ii) Nếu i hồi quy thì
. Nói riêng, với xác suất một hệ xuất phát từ i
sau một số hữu hạn bước sẽ đi qua j.
Định lý 1.2.9.Cho ( ) là xích tối giản không hồi quy. Khi đó với mọi i, j: . Nói riêng = 0
và xích không tồn tại phân bố dừng.
Định lý 1.2.10.Cho ( ) là xích tối giản hồi quy không có chu kỳ. Khi đó với mọi i, j ta có: (n) = ở đó:
Định nghĩa 1.2.7.Trạng thái hồi quy i được gọi là trạng thái hồi quy dương nếu
và được gọi là trạng thái hồi quy không nếu .
Định lý 1.2.11.Giả sử
. Nếu i hồi quy dương thì j hồi quy dương. Nếu i hồi quy
không thì j hồi quy không.
Định lý 1.2.12.Giả sử (
là xích tối giản không có chu kỳ với không gian trạng
thái đếm được E. Khi đó sẽ xảy ra một trong ba khả năng sau đây:
• 1)Mọi trạng thái là không hồi quy. Khi đó với mọi i, j ta có: (n) = 0.
Xích không có phân bố dừng.
• 2) Mọi trạng thái là hồi quy không. Khi đó với mọi i, j ta có: = 0.
Xích không có phân bố dừng.
• 3) Mọi trạng thái là hồi quy dương. Khi đó với mọi i, j, ta có: = πj> 0 và
là phân bố giới hạn (và cũng là phân bố dừng) của xích. lOMoAR cPSD| 58488183
Định lý 1.2.13.Giả sử ( ) là xích tối giản không có chu kỳ với không gian trạng
thái hữu hạn E = {1, 2, ..., d}. Khi đó mọi trạng thái đều hồi quy dương và xích có phân bố giới hạn
. Phân bố này cũng là phân bố dừng duy nhất của xích.
Định lý 1.2.14.Giả sử là xích tối giản với không gian trạng thái E đếm được. Khi đó: • 1.Với mỗi : . Nói cách khác dãy
hội tụ theo trung bình Cesaro tới
không phụ thuộc i. • 2.Dãy thoả mãn: a) , b) .
Định lý 1.2.15.Cho ( ) là xích Markov tối giản. Khi đó:
• 1. Nếu E hữu hạn có d phần tử thì
là phân bố dừng duy nhất.
• 2. Chỉ có các khả năng sau:
a) Mọi trạng thái của E là không hồi quy
b) Mọi trạng thái của E là hồi quy không
c) Mọi trạng thái của E là hồi quy dương.
• 3. Nếu E là vô hạn đếm được thì xích có phân bố dừng khi và chỉ khi mọi trạng
thát của E là hồi quy dương. Trong trường hợp này phân bố dừng là duy nhất.
1.3. Quá trình Markov
Xét họ các ĐLNN rời rạc ( ), t ≥ 0 với tập chỉ số t là các số thực không âm . Ký hiệu
là tập giá trị của . Khi đó E là một tập hữu hạn
hay đếm đƣợc, các phần tử của nó đƣợc ký hiệu . Ta gọi ( ) là một quá
trình ngẫu nhiên với không gian trạng thái E .
Định nghĩa 1.3.1. Ta nói rằng ( ) là một quá trình Markov nếu với mọi và với mọi lOMoAR cPSD| 58488183 P{Xt = i| = i1, = i2..., = ik} = P{Xt = i| = ik}.
Nhƣ vậy, xác suất có điều kiện của một sự kiện B nào đó trong tƣơng lai nếu biết
hiện tại và quá khứ của hệ cũng giống nhƣ xác suất có điều kiện của B nếu chỉ biết
trạng thái hiện tại của hệ. Đó chính là tính Markov của hệ. Đôi khi tính Markov của
hệ còn phát biểu dƣới dạng: "Nếu biết trạng thái hiện tại của hệ thì quá khứ , và tƣơng lai ,
là độc lập với nhau." Giả sử: P{ = j|Xs = i}
là xác suất để xích tại thời điểm s ở trạng thái i sau một khoảng thời gian t, tại thời
điểm t + h chuyển sang trạng thái j. Đây là một con số nói chung phụ thuộc vào i, j,
t, s. Nếu đại lƣợng này không phụ thuộc s ta nói xích là thuần nhất. Ký hiệu: (t) = P{ = j|Xs = i}. Ta gọi
là xác suất chuyển của hệ từ trạng thái i sang trạng thái j sau một khoảng
thời gian t . Ký hiệuP(t) = ( (t), i, j → E). P(t) là một ma trận hữu hạn hay vô hạn chiều. Chú ý rằng: • i) (t) ≥ 0. • ii) = 1.
Phân bố của đƣợc gọi là phân bố ban đầu. Ta ký hiệu .
Định lý 1.3.1.Phân bố hữu hạn chiều của quá trình ( ) được hoàn toàn xác định từ
phân bố ban đầu và xác suất chuyển. Cụ thể với phân bố đồng thời của ( , ...,
) được tính theo công thức sau: P( = i1, ..., = in) = = .
Định lý 1.3.2.( Phương trình Chap - Kolmogorov): (t + s) = .
1.3.1. Trƣờng hợp không gian trạng thái hữu hạn lOMoAR cPSD| 58488183
Giả sử E = {1, 2,..., d}. Khi đó từ phƣơng trình C - K P(t), t > 0 là một họ các ma
trận thoả mãn đẳng thức sau: .
Nói cách khác họ (P(t), t > 0) lập thành một nửa nhóm các ma trận. Từ nay về sau ta
sẽ luôn giả thiết thêm rằng: 1. (0) = δij. 2. = δij.
Ở đây là ký hiệu Kronecke:
Định lý 1.3.3.Hàm ma trận P(t) là một hàm liên tục và tồn tại: .
Định lý 1.3.4.Cho quá trình Markov với nửa nhóm P(t), t > 0 các xác suất chuyển.
Gọi A là ma trận cực vi của nửa nhóm. Khi đó ta có: , . (1.3.1) và , . (1.3.2)
với là cƣờng độ chuyển từ trạng thái i sang trạng thái j và là cƣờng độ thoát
khỏi trạng thái i của hệ.
Phƣơng trình (1.3.1) gọi là phƣơng trình thuận và phƣơng trình (1.3.2) gọi là
phƣơng trình ngƣợc Kolmogorov.
Định lý 1.3.5.Cho quá trình Markov tối giản ( ) với không gian trạng thái E = 1,
2,..., d hữu hạn và ma trận xác suất chuyểnP(t) = (t). Khi đó với mỗi tồn
tại giới hạn hữu hạn: lOMoAR cPSD| 58488183
chỉ phụ thuộc j không phụ thuộc i. Thêm vào đó là phân bố
xác suất duy nhất thoả mãn phương trình: .
1.3.2. Trƣờng hợp không gian trạng thái vô hạn đếm đƣợc Định lý 1.3.6.
(1)Với mọi i ≠ j, giới hạn:
luôn tồn tại hữu hạn.
(2)Với mỗi i giới hạn:
tồn tại nhưng có thể bằng vô cùng.
Định lý 1.3.7.Cho quá trình Markov với P(t) = ( (t))là họ các ma trận xác suất
chuyển. Gọi A là ma trận cực vi của quá trình. Khi đó ta có: (t) = P(t)A, ↔ (t) = . (1.3.3) và (t) = AP(t), ↔ (t) = . (1.3.4)
với là cường độ chuyển từ trạng thái i sang trạng thái j và ai là cường độ thoát
khỏi trạng thái i của hệ.
Phương trình (1.3.3) gọi là phương trình thuận và phương trình (1.3.4) gọi là
phương trình ngược Kolmogorov.
Định lý 1.3.8.Cho quá trình Markov tối giản ( ) với không gian trạng thái E = 1,
2,..., đếm được và ma trận xác suất chuyểnP(t) = (t). Khi đó, với mỗi tồn
tại giới hạn hữu hạn: = πj lOMoAR cPSD| 58488183
chỉ phụ thuộc j không phụ thuộc i. Thêm vào đó giới hạn hoặc là
tất cả bằng không:
hoặc là tất cả dương và lập thành một phân bố xác suất. Phân bố đó được gọi là
phân bố giới hạn của quá trình: πj> 0 j E, = 1. lOMoAR cPSD| 58488183 CHƢƠNG 2:
MỘT SỐ MÔ HÌNH XẾP HÀNG
2.1 Khái niệm và phân loại quá trình xếp hàng
Trên thực tế mô hình xếp hàng còn đƣợc ứng dụng trong nhiều lĩnh vực ngành nghề
khác nhau nhƣ bƣu chính viễn thông, hàng không, đƣờng sắt, kiểm soát lƣu lƣợng
giao thông, … Trong lí thuyết xếp hàng ta quan tâm đến số đo hiệu năng, đó là các
giá trị trung bình khi quá trình đạt trạng thái dừng bao gồm: độ dài hàng đợi trung
bình của hàng, độ dài hàng đợi trung bình của hệ thống, thời gian đợi trung bình của
hàng (trễ của hàng) và thời gian đợi trung bình của hệ thống (trễ của hệ thống). Để
tính các đại lƣợng này ta có thể sử dụng phƣơng pháp giải phƣơng trình tích phân
dạng Wiener – Hopf hoặc phƣơng pháp khảo sát chuỗi Markov nhúng. Từ đó suy ra
các công thức tính các phân bố ổn định cho các loại hàng M/M/k, M/M/k/N; Công
thức tổng quát tính các giá trị trung bình này cho các hàng G/G/1 và công thức cụ
thể cho các hàm đặc biệt M/D/1 và M/𝐸𝑘/1 …Mà trong luận văn này em mới đề cập
đến một số dạng tổng quát, các hàng đặc biệt. Em rất mong đƣợc sự góp ý xây dựng
của thầy cô và các bạn.
Em xin chân thành cảm ơn! lOMoAR cPSD| 58488183
TÀI LIỆU THAM KHẢO
[1] Đặng Hùng Thắng, Quá trình ngẫu nhiên và tính toán ngẫu nhiên, Nhà xuất
bản Đại học quốc gia Hà Nội, 2007.
[2] Đặng Hùng Thắng, Mở đầu về lý thuyết xác suất và các ứng dụng, Nhà xuất bản giáo dục, 2005.
[3] U.Narayan Bhat, An Introduction to Queueing Theory - Modeling and 76
Analysis in Applications, Birkhauser Boston, 2008. lOMoAR cPSD| 58488183 77