







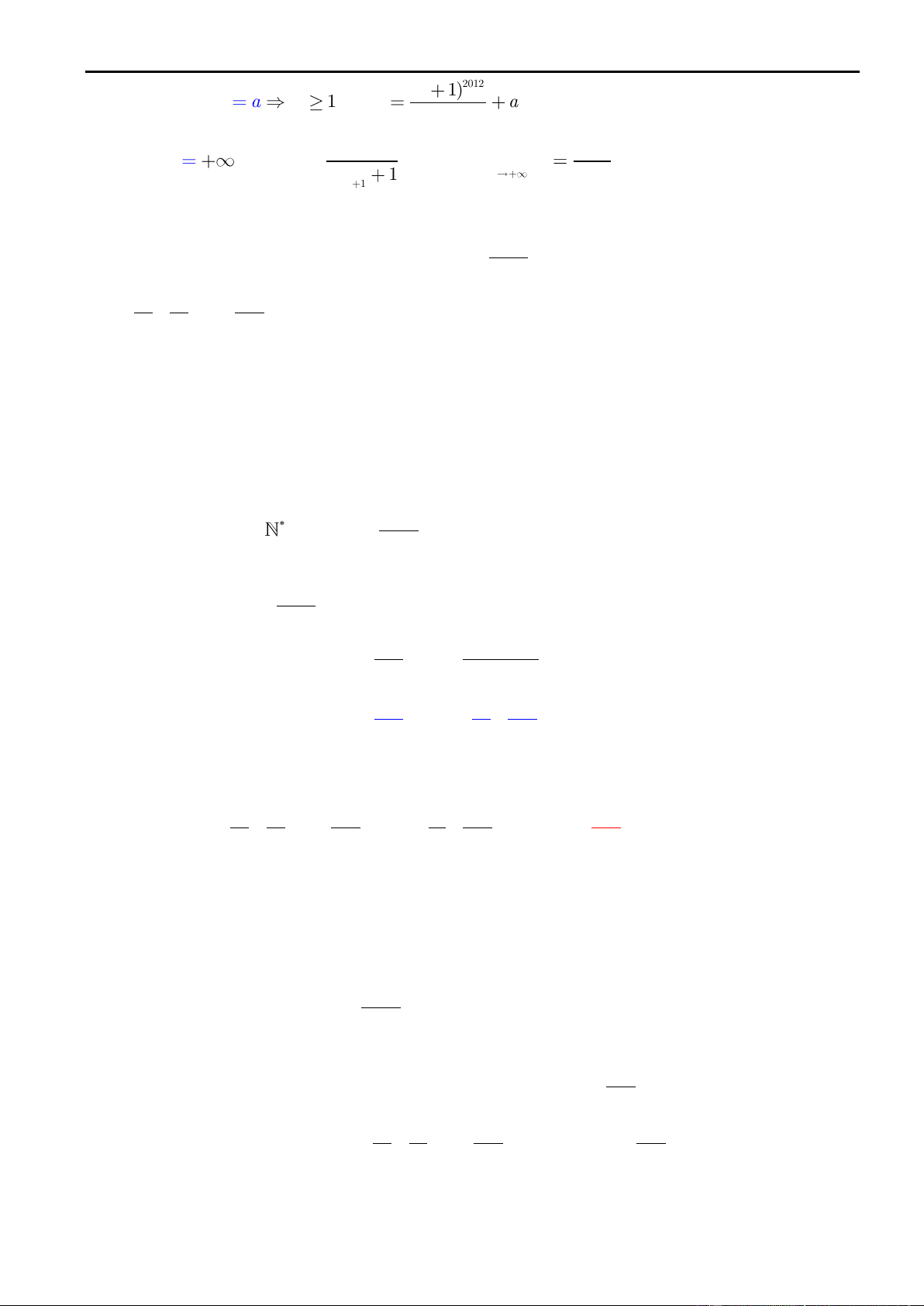

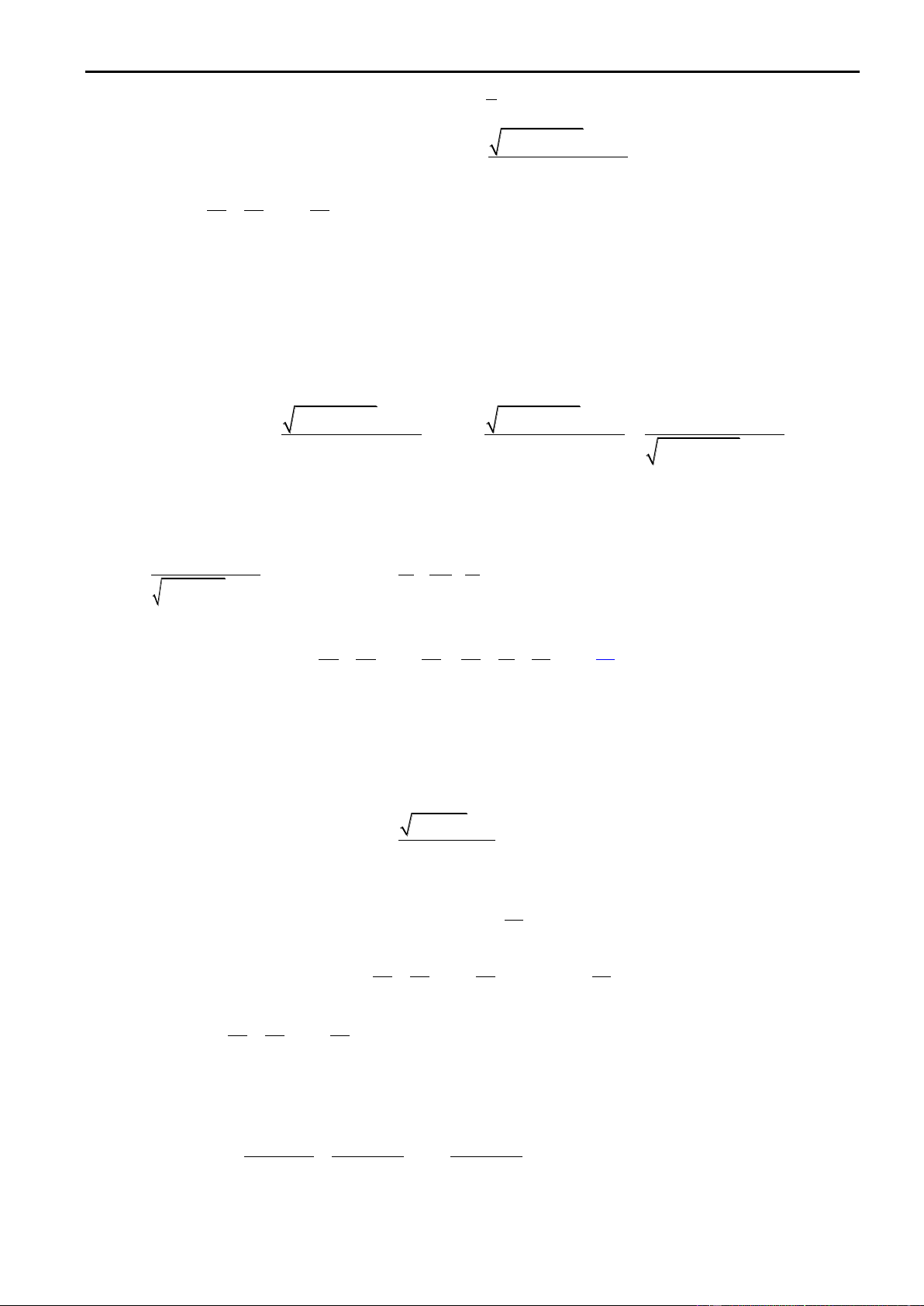







Preview text:
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
MỘT SỐ VẤN ĐỀ CƠ BẢN VỀ GIỚI HẠN CỦA DÃY SỐ
A. TÓM TẮT LÝ THUYẾT 1. Định nghĩa 1
Dãy số u được gọi là dãy số tăng nếu với mọi n ta có u u n n n 1
Dãy số u được gọi là dãy số giảm nếu với mọi n ta có u u n n n 1 2. Định nghĩa 2
Dãy số u được gọi là dãy số bị chặn trên nếu tồn tại một số M sao cho n
u M , n * n
Dãy số u được gọi là dãy số bị chặn dưới nếu tồn tại một số m sao cho n u , m n * n
Dãy số u được gọi là dãy số bị chặn nếu tồn tại một số M và một số m sao cho n
m u M , n * n 3. Định lý 1
a. Mọi dãy tăng và bị chặn trên thì hội tụ.
b. Mọi dãy giảm và bị chặn dưới thì hội tụ. 4. Định lí 2
a. Mọi dãy tăng và không bị chặn trên thì tiến tới .
b. Mọi dãy giảm và không bị chặn dưới thì tiến tới . 5. Định lý 3
a. Nếu một dãy u hội tụ đến a thì mọi dãy con trích từ u cũng hội tụ đến a . n n
b. u hội tụ đến a u và u hội tụ đến a . 2n 1 2n n 6. Định lý 4 1
a. Nếu lim u 0 và u 0, n thì lim n n n n un 1
b. Nếu lim u và u 0, n thì lim 0 n n n n un
7. Định lý 5.(Định lý kẹp giữa về giới hạn). Nếu với mọi n n ta luôn có u x v và 0 n n n
limu lim v a thì lim x a n n n
8. Sử dụng tiêu chuẩn Weierstrass để chứng minh dãy số có giới hạn u a
Bài toán. Chứng minh dãy số 1 u xác định bởi
có giới hạn hữu hạn và n u f u ;n 2 n n 1
tìm giới hạn đó ( f x là hàm số liên tục). Phương pháp giải
a) Dãy x bị chặn. Nếu f x là hàm số tăng trên ;
a b thì dãy x đơn điệu và hội n n
tụ đến L là nghiệm của phương trình f x x .
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 1
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
b) Nếu f x là hàm số nghịch biến thì các dãy con x ; x
của dãy x ngược n 2n 2n 1 chiều biến thiên. Nhận xét: Nếu dãy x
hội tụ đến L , dãy x hội tụ đến K : 2n 1 2n
Với L K thì dãy x không có giới hạn; n
Với L K thì dãy x có giới hạn là L . n II. BÀI TẬP
1. CHỨNG MINH DÃY SỐ CÓ GIỚI HẠN u 3 1
Bài 1. Cho dãy số (u ) xác định bởi công thức 1 3 . Chứng minh n * u 2u ; (n ). n 1 n 2 3 un
dãy số có giới hạn. Tính lim u ? n Lời giải
Theo công thức xác định dãy (u ), ta có * u 0; n . n n
Áp dụng bất đẳng thức Côsi, ta có: 1 3 1 3 3 2 3 * u 2u u u 3 u . 3 ; n . n 1 n 2 n n 2 n 2 3 u 3 u u n n n Do đó: 3 * u 3 ; n . n 3 2 1 1 3 1 3 u Mặt khác: n u u u u u 0 . n 1 n n 2 n 2 n 2 3 u 3 u 3 u n n n
Vậy (u ) là dãy số giảm và bị chặn dưới nên nó có giới hạn. n 2 1 3 Giả sử, limu a .Ta có: 3 a a a a 3 . n 2 2 3 a a Kết luận. 3 limu 3 . n
Bài 2. Chứng minh dãy số có giới hạn và tìm giới hạn đó u 1 0
Bài 3. Chứng minh dãy số 1
có giới hạn và tìm giới hạn đó. u ; n 1, 2, 3... n 3 u n 1 1 3x a) x : x , n x n 1 n 1 6 2x 1 n b) x : x 2;x 2 x n 1 n 1 n n ! c) x : x ;n N n n 2n 1 !! d) x : x 13;x 12 x n 1 n 1 n 1 4 e) x : 2 x ;x x x n 1 n 1 2 3 n n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 2
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 u1 2 f) u n 3u 4 n u , n 1 n 1 2u 1 n x 0;x 1 1 2 g) x 3x 2 n n 1 x ,n 2 n 1 10x 2x 2 n n 1 x 1 1 h) x : 13 n x 20 ,n 1, 2... n 1 xn x 1 1 i) x : 1 2014 n x x ,n 1 n 1 2 n xn x 1 1 j) x : u n n 1 x ,n 2 n 2 u 1 n 1 3 k) x : x ;x 3x 2;n 1 n 1 1 2 n n l) x : x 0;x 6 x ;n 1 n 1 n 1 n 2 2x 1 m) x : x 1; n x ;n 1 n 1 n 1 x 3 n n) x : x 1;x 2;x x x ;n 2 n 1 2 n 1 n n 1 4 4 8 o) x : x ;x 3x ;n 1 n 1 n 1 9 9 9 n 1 3 1 p) x : 2 3 x ;x x x ;n
1 . Hướng dẫn: Xét hàm số. n 1 n 1 2 2 n 2 n 3 1 3 3 f x x x , x 0;1 , f ' x 0; x
0;1 từ đó suy ra f x tăng trên 0;1 . Chứng 2 2 minh u
0;1 bằng quy nạp. Do f x tăng nên f u f u & u u cùng dấu, và do n n n 1 n n 1 3
đó cùng dấu với u u
0 . Từ đó suy ra u là dãy giảm và bị chặn dưới. 2 1 16 n q) x : x 2;x 2 x ;n
1 HD: Xét hàm số f x 2 x ;x 0;2 n 1 n 1 n un x r) x : 2 x 2;x 2 ;n 1 HD: Xét hàm số 2 f x 2 ;x 1;2 n 1 n 1 1 1 s) x : x 1982;x ;n
1 HD: Xét hàm số f x ;x 0;1 . n 1 n 1 4 3x 4 3x n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 3
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 t) x : x 1;x 1 ;n 1 n 1 n 1 xn
MỘT SỐ BÀI TOÁN TÍNH GIỚI HẠN CỦA DÃY SỐ 1 u
Bài 1. Cho dãy số thực u xác định bởi: 1 2 . Tìm giới hạn sau: n 2 u
u u , n 1 (1) n 1 n n 1 1 1 lim ... . n u 1 u 1 u 1 1 2 n 1 Lời giải
Bằng phép quy nạp đơn giản ta thấy rằng: u 1, n 3 n
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n 2 u
u u 0 u tăng. n n 1 n n Tính tổng: 1 1 1 1 2 u u u n 1 n n u u u 1 u u 1 n 1 n n n n 1 1 1 (n 1, 2,...) (*) u 1 u u n n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: 1 1 1 1 ... 2 u 1 u 1 u 1 u 1 2 n 1 n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 0 .Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2
a a a a 0 (vô lý)
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u lim 0 n n 1 n n n un 1 1 1 1 1
Vì thế từ (2) ta suy ra: lim ... lim 2 2 n u 1 u 1 u 1 n u 1 2 n 1 n 1 1 1 1 Vậy lim ... 2 . n u 1 u 1 u 1 1 2 n 1 u 2
Bài 2. Cho dãy số thực u xác định bởi: 1 n 2 u
u u 1, n 1 (1) n 1 n n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 4
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 1 1
Tìm giới hạn sau: lim ... . n u u u 1 1 n Lời giải
Bằng phép quy nạp đơn giản ta chứng minh được rằng: u 2, n 1 n
Xét tính đơn điệu của u Từ hệ thức (1) ta suy ra được n n , u u u , vậy u tăng. n n n 2 1 0 n 1
Tính tổng: Xuất phát từ hệ thức truy hồi (1) ta suy ra được 1 1 1 1 u 1 u u 1 n 1 n n
u 1 u u 1 u 1 u n 1 n n n n 1 1 1 (
n 1, 2,...) u u 1 u 1 n n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: 1 1 1 1 ... 1 u u u u 1 1 1 n n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 2 .Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2 2
a a a 1 a 2a 1 0 a 1 (vô lý)
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u n 1 lim 0 n 1 n n n u 1 n 1 1 1 1 1
Vì thế từ (2) ta suy ra: lim ... lim 1 1 n n u u u u 1 1 1 n n 1 1 1 1 Vậy lim ... 1 . n u u u 1 1 n u 3 1
Bài 3. Cho dãy số u xác định bởi n 1 u u u n n 2 4 , 1; 2;3.... 1 n n 5
a) Chứng minh dãy số u tăng nhưng không bị chặn trên ; n n 1 b) Đặt S
, n 1, 2,3... Tính lim S . n n u k 3 1 k
Bài 4. (Đề kiểm tra đội dự tuyển Nam Định) Cho dãy số x xác định bởi n 2 x 2012; x
x 5x 9 với mọi n nguyên dương. 1 n1 n n
a) Chứng minh x là dãy số tăng; n
b) Chứng minh x không có giới hạn hữu hạn; n n 1
c) Xét dãy y xác định bởi y . Tìm lim y . n n n k 1 x 2 k
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 5
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn Lời giải a) Xét hiệu: 2 2 x
x x 5x 9 x (x 3) 0 n 1 n n n n n
Do x 2012 3 nên x x 0 suy ra dãy đã cho là dãy tăng. 1 n1 n
b) Giả sử dãy (x ) có giới hạn hữu hạn, đặt limx ( a a 2012) . n n Từ công thức truy hồi 2 x
x 5x 9. n1 n n
Lấy giới hạn 2 vế, ta được: 2
a a 5a 9 a 3 (không thỏa mãn).
Do đó dãy đã cho không có giới hạn hữu hạn. 1 1 1 c) Ta có: x 2 x 3 x 3 n n n1 n 1 1 1 1 1
Do đó, ta có: y ... n k 1 x 2 x 3 x 3 2009 x 3 n 1 n1 n1 1
Mà limx nên limy . n n 2009 u 1 n 1
Bài 5. Cho dãy số u 1 ;n 1, 2,... Đặt S . Tìm lim S . n u 1 u u u ...u n u n n n 1 1 2 3 n k 1 k Lời giải Ta có u 1
u u ...u (n 1);u 1
u u ...u ; n 2 , suy ra n 1 1 2 n n 1 2 n 1 u 1 n 1 u , n 2 u 1 u 1 u n n 1 u 1 n n n 1 1 1 1 1 1 1 u 1 u 1 u u 1 u u u 1 u 1 n 1 n n n n n n n 1 1 n 1 1 n 1 1 1 1 1 Sn u u u u u u u u k k 1 1 1 1 2 2 1 k 1 k k 1 1 2 n 1 1
Kết hợp với giả thiết suy ra S 2 n u 1 n 1 Ta có
u 1 u ;u 1 u u 1 u 1 u 1 u 2 1 3 1 2 1 1 1 n
u 1 u u u ....u u n n 1 1 1 1 2 1 Mặt khác u u 1 u u u ...u 1 0 hay u tăng nên n 1 n n 1 2 n 1 n n 1 n 1 u 1 u u ...u u 1 u 2 lim u 1 lim S 2 n 1 1 2 n 1 1 n 1 n n n n 1
Bài 6. Cho dãy số x : x 1,x x x 1 x 2 x 3 1 . Tính lim . n 1 n 1 n n n n n x i 2 1 i
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 6
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn Lời giải Ta có x 5 và x
0 với mọi n 1,2, 2 n 2 2 2 x x (x 1)(x 2)(x 3) 1 x 3x x 3x 2 1 x 3x 1 (1) n 1 n n n n n n n n n n Từ đó suy ra 2 x 1 x 3x 2 x 1 x 2 n 1 n n n n 1 1 1 1 1 1 1 x 1 x 1 x 2 x 1 x 2 x 2 x 1 x 1 n 1 n n n n n n n 1 n 1 n 1 1 1 1 1 1 Do đó y = n x x x x x x i 1 1 1 1 2 1 i 2 1 i 1 i i 1 1 n 1 n 1 Từ (1) 2 k 1 x x 3x 1 3x 3.3 3k k 1 k k k
Ta dễ dàng chứng minh bằng quy nạp 1 x 3n (2) n 1 Nên lim y (vì do (2) x 3n ) n n 2 n 1
Ta có thể chứng minh lim x với cách khác: n
Dễ thấy x là dãy tăng, giả sử lim x a (a 1) n n Nên ta có a ( a a 1)(a 2)(a 3) 1 Suy ra 2 4 3 2 a a a 1 a 2 a 3 1 hay a 6a 10a 6a 1 0
Rõ ràng phương trình này không có nghiệm thỏa mãn a 1. Vậy lim x n 1
Bài 7. Xét dãy số x ; n 1, 2, 3, xác định bởi x 2 và 2 x (x 1)với mọi n 1 n 1 2 n 1 1 1 n 1, 2, 3, . . Đặt S ... . Tìm lim S . n 1 x 1 x 1 x n n 1 2 n Lời giải
Ta có thể tổng quát hóa bài toán như sau: u a 1 Cho dãy u thỏa mãn 2 2 n u (b c)u c n n un 1 b c n 1 1 1 Ta chứng minh S n u b u c u c i 1 i 1 n 1 Thật vậy. 2 2 u (b c)u c 2 u (b c)u bc (u b)(u c) Ta có n n u suy ra n n n n u c n 1 b c n 1 b c b c 1 1 1 1 1 1 Từ đó u c u c u b u b u c u c n 1 n n n n n 1
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 7
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
Khai triển và ước lượng được 1 1 1 u b u c u c 1 1 2 1 1 1 u b u c u c 2 2 3 ……………………. 1 1 1 u b u c u c n n n 1 1 1 Do đó S n u c u c 1 n 1
Từ đó vận dụng vào bài toán trên với b =1, c = - 1 ta có 1 1 1 S 1 n x 1 x 1 x 1 1 n 1 n 1 1 2 Mà x – x x
1 > 0 n N * nên dãy x là dãy tăng. Giả sử lim x a (a n 1 n 2 n n n n > 2). Thì 2 2a a 1 suy ra a = 1. Vô lý. Vậy lim x . Do đó lim S 1 n n n n
Nhận xét. Trong các bài toán tổng quát ta có thể thay các giá trị của a, b, c khác nhau để được các bài
toán mới. Chẳng hạn: 2012 (2x 1)
Bài 8. Cho dãy số x
được xác định bởi: x n x
x . Với n là số nguyên n 1 = 1; n 1 2012 n 2011 2011 2011 2011 (2x 1) (2x 1) (2x 1) (2x 1) dương. Đặt 1 2 3 u ... n . Tìm lim u . n 2x 1 2x 1 2x 1 2x 1 n 2 3 3 n 1 Lời giải 20 2 1 (2x 1) Ta có x – n x , n 1 n 1 n 2012 2011 1 1 2(x x ) (2x 1) Suy ra n 1 n n 2x 1 2x 1 (2x 1)(2x 1) 1006(2x 1) n n 1 n n 1 n 1 n 2011 (2x 1) n 1 1 1 1 i 1006 1006 x x x x x i 2 1 i 2 1 2 1 2 1 2 1 1 1 i 1 i i 1 1 n 1 Mặt khác: x – x 0 nên dãy (x n . Nếu (x n 1 n n) là dãy số tăng 1
n) bị chặn thì limxn tồn tại.
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 8
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 2012 (a 1) Đặt lim x a a 1 và a
a (vô lý). Suy ra x không bị chặn trên n 2012 n 1 1006 hay lim x suy ra lim =0. Suy ra lim u n 2x 1 n n 3 n 1 u 1 1
Bài 9. Cho dãy số thực u xác định bởi: 2 Tìm giới hạn sau: n un u u , n 1 n 1 2012 n u u u 1 2 lim ... n . n u u u 2 3 n 1 Lời giải
Bằng phép quy nạp đơn giản ta thấy rằng: u 1, n 1 n
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n 2 u n , n u u
0, vậy u tăng. n n 1 n 2012
Tính tổng: Xuất phát từ hệ thức truy hồi (1) ta suy ra được 2 un 2 u
u u 2012 u u n 1 n n n 1 n 2012 u u u n n 1 n 2012 u u .u n 1 n n 1 u 1 1 n 2012 n 1,2,... (*) u u u n 1 n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: u u u 1 1 1 1 2 ... n 2012 20121 (2) u u u u u u 2 3 n 1 1 n 1 n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 1.Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2 a a
a a 0 (vô lý) 2012
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u lim 0 n n 1 n n n un 1 u u u 1
Vì thế từ (2) ta suy ra: 1 2 lim ... n lim 20121 2012 n n u u u u 2 3 n 1 n 1
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 9
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn u u u Vậy 1 2 lim ... n 2012 . n u u u 2 3 n 1 u 2 1
Bài 10. Cho dãy số thực u xác định bởi: 2 Tìm giới hạn n u 2011u n n u , n 1 (1) n 1 2012 u u u sau: 1 2 lim ... n n u 1 u 1 u 1 2 3 n 1 Lời giải
Bằng phép quy nạp đơn giản ta thấy rằng: u 2, n 1 n
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n u u n n 1 n , u u
0 , vậy u tăng. n n 1 n 2012
Tính tổng: Từ hệ thức truy hồi (1) ta suy ra được 2 u 2011u n n 2 u
u 2012u 2012u u u 1 2012 u u n 1 n n n 1 n n n 1 n 2012 u
u 1 u 1 u n n 1 n 1 1 2012 n 2012 n 1,2,... (*) u 1 u 1 u 1 u 1 u 1 u 1 n 1
n 1 n n 1 n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: u u u 1 1 2 ... n 20121 (2) u 1 u 1 u 1 u 1 2 3 n 1 n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 2 .Chuyển qua giới hạn hệ thức (1) khi n ta có: n n a(a 1) a
a a(a 1) 0 a 0 a 1 (vô lý) 2012
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u n 1 lim 0 n 1 n n n u 1 n 1 u u u 1
Vì thế từ (2) ta suy ra: 1 2 lim ... n lim 20121 2012 . n u 1 u 1 u 1 n u 1 2 3 n 1 n 1 u u u Vậy 1 2 lim ... n 2012 . n u 1 u 1 u 1 2 3 n 1
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 10
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 u 1 2
Bài 11. Cho dãy số thực u xác định bởi: Tìm giới n 2 u 4u u n 1 n 1 n 1 u , n 2 (1) n 2 1 1 1 hạn sau: lim ... . 2 2 2 n u u u 1 2 n Lời giải
Bằng phép quy nạp đơn giản ta thấy rằng: u 0, n 1 n
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n 2 2 u 4x u u 4x u u n n n n n n 2 1 1 1 1 1 1 n 1 u u u 0 n n 1 n 1 2 2 2 u 4x u n 1 n 1 n 1 Suy ra: u tăng. n Tính tổng: 2u 1 1 1 n 1 2 u u
u u 1 u (n 1,2,...) (*) n n 1 n n n 1 2 2 4 u u u u x u n n 1 1 1 1 n n n n
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: 1 1 1 1 1 1 1 ... 6 ( 2) 2 2 2 2 u u u u u u u 1 2 n 1 1 n n
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 0 .Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2
a 4a a a a 0 (vô lý) 2
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim 0 n n n un 1 1 1 1
Vì thế từ (2) ta suy ra: lim ... lim 6 6 2 2 2 n n u u u u 1 2 n n 1 1 1 Vậy lim ... 6 . 2 2 2 n u u u 1 2 n u 2012
Bài 12. Cho dãy số thực u xác định bởi: 1 Tìm n 2 u
2011u 2013u 1 0, n 1 (1) n n n 1 1 1 1 giới hạn sau: lim ... . n u 2012 u 2012 u 2012 1 2 n Lời giải
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 11
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
Bằng phép quy nạp đơn giản ta thấy rằng: u 2012, n 1 n
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n u n 2 1 u u 0 u tăng. n n 1 n 2010
Tính tổng: Xuất phát từ hệ thức truy hồi (1) ta suy ra được 2 u 2011u 1 2
u 2011u 2013u 1 0 n n u n n n 1 n 1 2013 2 u 2011u 1 u 1 n n 1 n 1 2013 u u n 1 2012 n u 1 n 1 2013 1 1 1 (n=1,2,...) (*) u 2012 u 1 u 1 n n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: 1 1 1 1 1 1 1 ... u 2012 u 2012 u 2012 u 1 u 1 2011 u 1 1 2 n 1 n 1 n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 2012 . Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2
a 2011a 2012a 1 0 a 1 (vô lý)
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u n 1 lim 0 n 1 n n n u 1 n 1 Vì thế từ (2) ta suy ra: 1 1 1 1 1 1 lim ... lim n u 2012 u 2012 u 2012 n 2011 u 1 2011 1 2 n n 1 1 1 1 1 Vậy lim ... . n u 2012 u 2012 u 2012 2011 1 2 n 1 u
Bài 13. Cho dãy số thực u xác định bởi: 1 2012 . Tìm giới hạn n 2 u
2012u u , n 1 (1) n 1 n n u u u sau: 1 2 lim ... n . n u u u 2 3 n 1 Lời giải
Bằng phép quy nạp đơn giản ta thấy rằng: u 0, n 1 n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 12
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
Xét tính đơn điệu của u : Từ hệ thức (1) ta suy ra được n 2 u
u 2012u 0 u tăng. n n 1 n n
Tính tổng: Xuất phát từ hệ thức truy hồi (1) ta suy ra được 2 2012u u u u 1 1 1 2 n n 1 2012 n n u u u ( n=1,2,...) (*) n n 1 n u u u u u 2012 u u n n 1 n n 1 n 1 n n 1
Thay n bởi 1,2,3,...,n vào (*) và cộng vế với vế các đẳng thức ta suy ra được: u u u 1 1 1 1 1 1 1 1 2 ... n ... u u u 2012 u u u u u u 2 3 n 1 1 2 2 3 n n 1 1 1 2012 2012 u n 1
Do u là dãy tăng nên có hai khả năng sau xảy ra: n
1) Dãy u bị chặn trên. Theo tiêu chuẩn Weierstrass, do u tăng và bị chặn trên n n nên nó có giới hạn.
Giả sử lim u a thì a 0 .Chuyển qua giới hạn hệ thức (1) khi n ta có: n n 2
a 2012a a a 0 (vô lý)
2) Dãy u không bị chặn trên, do u tăng và không bị chặn trên nên: n n 1
lim u lim u lim 0 n n 1 n n n un 1 u u u 1 1
Vì thế từ (2) ta suy ra: 1 2 lim ... n lim 2012 1 n n u u u 2012 u 2 3 n 1 n 1 u u u Vậy 1 2 lim ... n 1 . n u u u 2 3 n 1 u 3 1
Bài 14. Cho dãy số thực u xác định bởi: 2 . Tìm giới hạn sau: n u 2009u 2 n n u , n 1 n 1 2012
u 1 u 1 u 1 1 2 lim ... n n u 2 u 2 u 2 2 3 n 1 Lời giải 2
u 2009u 2
(u 1)(u 2) Biến đổi n n u n n u u ( 1) n 1 2012 n 1 n 2012 Vì u = 3 nên 3 = u < u 1 1 2 3 n n
Giả sử dãy {u }bị chặn trên L : limu = L ( L > 3) n n 2
u 2009u 2 2
L 2009L 2 Suy ra limu n n hay L = n 1 = lim 2012 2012
L 2 -3L+2 = 0 L = 1 hoặc L = 2 (vô lý vì L > 3) 1
Do đó {u } không bị chặn trên hay lim u = + hay lim 0 n n n un
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 13
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn
Biến đổi (1) (u -1)(u -2) = 2012(u n n n 1 -un) u 1 1 1 n = 2012 ( - ) (*) u 2 u 2 u 2 n 1 n n 1
Cho n lần lượt nhận các giá trị 1, 2, 3, ….n, sau đó cộng vế theo vế ta được: n u 1 1 S = i = 2012 ( 1- ) n u u 2 i 2 1 i 1 n 1
Vậy lim S = 2012 . n 3 x 2x 4
Bài 15. Cho dãy số (x ) xác định như sau x 3 và n n x n Với n 1 n 1 2 x x với 1, 2,... 6 n n n 1
mỗi số nguyên dương n, đặt y . Tìm lim y . n 2 n x i 4 1 i 2
(x 4)(x 2)
Lời giải. x 2 n n n 1 2 x x (1) 6 n n
Do x 3 nên bằng qui nạp chứng minh được x 2 với mọi * n 1 n 2 (x 2) n x x 0 x là dãy tăng (2). n 1 n 2 x x ( ) 6 n n n Giả sử dãy (x ) bị chặn trên a
3 để lim x a . Khi đó n n 3 a 2a 4 2 a
a 4a 4 0 a (loại) 2 a a 2 6
Do đó: lim x (3) n 1 1 1 1 1 1 Từ (1) suy ra : 2 x
2 x 2 x 4 2 x 4 x 2 x 2 n 1 n n n n n 1 n 1 1 y 1 (4) n 2 x x i 4 2 1 i n 1
Từ (3) và (4) suy ra : lim y 1 n 2017 x 1 2 Bài 16.
Cho dãy số (x ) xác định như sau . Với mỗi số n 9 2 *
x 2x 5x ; n n 1 n n 2 n 1
nguyên dương n, đặt u . Tính limu . n n x k 1 1 k Lời giải 9 9 Xét hàm số 2
f (x) 2x 5x
. Khi đó f (x) x 2 2x 5x x 3 x . 2 2 2 3
Vậy hàm số có một điểm bất động là x . 2 9 3 3 Ta có 2 x
2x 5x x 2 x x 1 n 1 n n n 1 n n 2 2 2 1 1 1 1 1 1 1 1 Từ đó suy ra . 3 2 3 3 x 1 x 1 3 3 x n x x 1 n x x x n 1 n n 2 n n n 1 2 2 2 2
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 14
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn n 1 1 1 1 1 u . n x k 1 3 3 1007 3 1 k x x x 1 n 1 n 1 2 2 2 2017 3
Chứng minh dãy tăng. Do x
nên bằng qui nạp chứng minh được x với mọi 1 2 n 2 * n 1 Xét hiệu x x x * n
(x ) là dãy tăng. n n 2 3 n 2 0 1 2 n
Chứng minh dãy x không bị chặn trên. n 3
Giả sử dãy số (x ) bị chặn trên. Vì dãy tăng và bị chặn nên a
để lim x a . Khi đó n 2 n 9 2 2a 5a a 3 a
(không thỏa mãn). Do đó : lim x 2 2 n 1 Vậy limu . n 1007
Bài 17. (Olympic 30-4-2012) Cho dãy số (x ) xác định bởi: n x 4 1 4 x 9 . n x ; n 1 n 1 3 x x 6 n n n 1
Với mỗi số nguyên dương n, đặt y . Tính lim y . n 3 n x k 3 1 k Lời giải. 4 x 9 4 x 9
+ Xét hàm số f (x) f x x
x x 3. 3
x x . Khi đó ( ) 6 3 x x 6
Vậy hàm số có một điểm bất động là x 3. 4
3x 3 x n x 9 3 n + Ta có n x x 3 n 1 3 x x 6 n 1 3 x x . 6 n n n n
3x 3 x n 3 1 n 1 1 . x 3 x x x x n 3 3 n 3 n 3 n 3 3 1 n 1 1 1 3 x 3 x 3 x . 3 n n n 1 n 1 1 1 1 y 1 . n 3 x x x x k 3 3 3 3 1 k 1 n 1 n 1
+ Chứng minh dãy tăng. Do x 4 nên bằng qui nạp chứng minh được x 3 với mọi * n 1 n x 3 n 2 Xét hiệu x x
0 (x ) là dãy tăng. n 1 n n x 2 x x n 2 2 3 n n
+ Chứng minh dãy (x ) không bị chặn trên. n
Giả sử dãy số (x ) bị chặn trên. Vì dãy tăng và bị chặn nên a
3 để lim x a . Khi đó n n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 15
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 4 a 9
a a 3 (không thỏa mãn). 3 a a 6
Do đó : lim x n Vậy lim y 1. n
Bài 18. (HSG BP 12-13). Cho dãy số (u ) được xác định: n 2 u u u u 1 2013 . Xét dãy số 1 2 n v . Tìm n 2 u (2 9u ) 2u (2 5u ), n 1 1 u 1 u 1 u 1 2 n n n 1 n 1 n lim v . n Lời giải Ta có u 0; n 1. n 2 9u 2 2 4 10 Khi đó 2 n 1 u 2 9u 2u 2 5u 2 5u 9 n n 1 n 1 n 2 n u u 2 u u u n 1 n n 1 n n 2 Đặt x n
1. Khi đó ta có dãy mới x được xác định bởi: n u n n x 2013 1 2 x x 5x 9 n 1 n 1 n n
Chứng minh x là dãy tăng: n 2 Xét hiệu: 2 x x x 5x 9 x x 3 0 n 1 n n n n n Do x 2013 3 nên x x
0 suy ra dãy x là dãy tăng 1 n 1 n n
Chứng minh x không bị chặn hay lim x : n n
Giả sử x bị chặn, do dãy tăng và bị chặn nên tồn tại giới hạn hữu hạn. n
Giả sử dãy x có giới hạn hữu hạn, đặt lim x , a a 2013 . n n Từ công thức truy hồi 2 x x 5x 9 n 1 n n
Lấy giới hạn hai vế, ta được: 2 a a 5a 9 a 3 (không thỏa mãn)
Do đó dãy đã cho không có giới hạn hữu hạn. Ta có: u u 1 1 1 1 1 v ... n 2 ... 2 ... n 1 n 1 u 1 u 2 2 x 2 x 2 1 n 1 2 2 n u u 1 n 1 1 1 Mà x 2 x 3 x 3 n n n 1 1 1 1 1 Do đó, ta có: v 2 2 n x 3 x 3 2013 3 x 3 1 n 1 n 1 1 Mà lim x nên lim v . n n 1005
Bài 19. (Quảng Ngãi) Cho dãy số a thỏa mãn điều kiện: a 2, 4 a 6 a 24 1 n n 1 n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 16
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 1 1 Tính S ... . 2012 a a a 1 2 2012 4a 1 1 2 1
HD giải: Từ công thức truy hồi ta suy ra n 1 a . n 6 a 2 1 a 3a 4 n1 n n 1 3a 4 n1 1 1 3 1 1 3 1 Đặt t
(t ) t t
t (t ) n 1 a 2 n n 1 2 4 n n 1 2 2 2 n 1 3
Đặt u t (u 1) u 3 u
S 2[( )n 1] n n 1 2 n n1 2 n 2 3
Cho n 2012 , ta có 2012 S 2[( ) 1]1006. 2012 2 5 u 1 2 1
Bài 20. Cho dãy số (u ) thỏa mãn: * n
. Tìm limn . n 1 u 2 k k u
u u 2 1 1 n 2 n n u 2 1
Bài 21. Cho dãy số: 2015 u u 1 * (n N ) n n u n 1 2014 u u 3 n n a) Chứng minh * u 1, n
N và (u ) là dãy số tăng. n n n 1 b) Tìm lim . 2014 u i 2 1 i n 1
Bài 22. Cho dãy số u thỏa mãn u 2017;u u
u 1 ; n 1, 2,3... Tính lim 1 n 1 n n 2 n i 1 u 1 i x 2014 2014 2014 x x x
Bài 23. Cho dãy số x : n 1 2014 x 1, 1 x n 1 . Tìm 1 2 lim ... n . n 1 n x n x x x n 2 3 n 1 1 n 1
Bài 24. Cho dãy số x : 2 x 3, x x x 4 n 1 . Tìm lim . n 1 n 1 5 n n n x k 1 k 3
Bài 25. Cho dãy số x
được xác định bởi x 12, x x 1 . Chứng minh rằng n n 1 1 n 1 n n 1 n 1
x là dãy số tăng nhưng không bị chặn trên. Tìm lim . n n x k 3 1 k 1 x
Bài 26. Cho dãy số x
được xác định bởi x , n x . Đặt n 1 n 1 24 1 3 n 2 n 3 xn S x x ...
x . Tính lim S . n 1 2 n n n 1 x
Bài 27. Cho dãy số x
được xác định bởi x : 2 x ;x 2x 1,n 1 . Tìm lim n . n n 1 1 2 n n n n 2 x 1 1
Bài 28. Cho dãy số x : x 1; n x ,n 1 . Tìm lim x . n 1 n 1 x n n n
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 17
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 1 1 1
Bài 29. Cho dãy số x : x : 2 x ;x x x ,n 1 . Tìm lim x . n n 1 n 1 2 2 n n 4n n n x 3 1
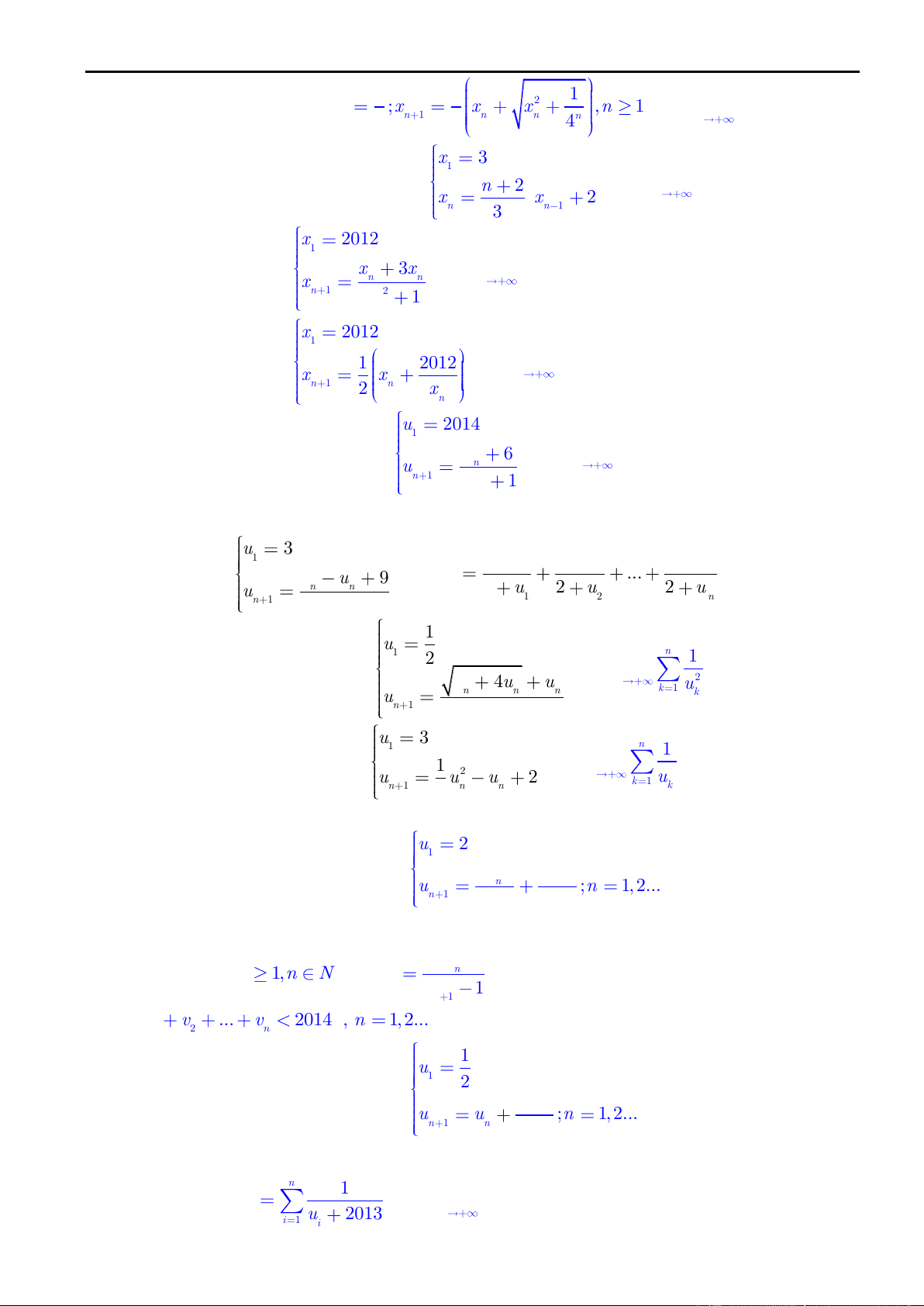
Bài 30. (HSG QG 2012). Cho dãy số x : . Tìm lim x . n n 2 x x 2 n n n n 1 3n x 2012 1
Bài 31. Cho dãy số x : 3 x
3x . Tìm lim x . n n n x n n n 1 2 3x 1 n x 2012 1
Bài 32. Cho dãy số x : 1 2012 . Tìm lim x n x x n n n 1 2 n xn u 2014 1
Bài 33. Cho dãy số u xác định bởi 2 u 6 . Tính lim u n n u n n n 1 2u 1 n
HD: Chứng minh dãy u giảm và bị chặn dưới bởi 2. n u 3 1 1 1 1
Bài 34. Cho u : 2 . Đặt S ...
. Tìm lim S . n u u 9 n n u n 2 u 2 u 2 u n n 1 5 1 2 n 1 u1 2 n 1
Bài 35. Cho dãy số u thỏa mãn . Tìm lim n 2 u 4u u 2 n u n n n u k 1 k n 1 2 u 3 1 n 1
Bài 36. Cho dãy số u thỏa mãn . Tìm lim n 1 2 u u u 2 n u n 1 k 1 2 n n k u 2 1
Bài 37. Cho dãy số x được xác định 2 n u 2013 n u ;n 1, 2... n 1 2014 2014
a) Chứng minh u là dãy số tăng. n u b) Với mỗi n 1,n N , đặt n v . Chứng minh rằng n u 1 n 1 v v ... v 2014 , n 1, 2... 1 2 n 1 u1 2
Bài 38. Cho dãy số u được xác định n 2 n u u ;n 1, 2... n 1 n 2013 a)
Chứng minh rằng dãy số u tăng nhưng không bị chặn trên. n n 1 b) Đặt S . Tính lim S n u n n i 2013 1 i
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 18
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn u 5 1 n 1
Bài 39. Cho dãy số u : 2 . Tính lim n u 2u 16 n n u ;n 1 n u i 2 1 n 1 6 i u 20 1 n 1
Bài 40. Cho dãy số u : 2 . Đặt lim . n u 7u 9 n n u ;n 1, 2... n u i 10 1 n 1 13 i 2014 u1 2013 n 1
Bài 41. Cho dãy số u . Đặt lim . n 2 u 2u n u i 2 n n u ;n 1, 2... 1 i n 1 2 2n x
Bài 42. Cho dãy số x : x 1;x x x ... x ,n 2 . Tính 1 lim n . n 1 n 2 1 2 n 1 n 1 n xn n 1
Bài 43. Cho dãy số u được xác định bởi u 2,u u 1. Tìm lim n 1 n 1 n n u i 1 i HD
Bước 1. Chứng minh lim u n n n 1 n 1 Bước 2. Tính , tính lim . u n u i 1 i i 1 i
Lời giải chi tiết trang 64- Tài liệu 0 x 1 x x x
Bài 44. Cho dãy số x : 1 . Tính 1 2 lim ... n . n 2 x 2014x x n x x x n 1 n n 2 3 n 1
Bài 45. Cho dãy số x : 2 x 3,x x 3x 4 . Tìm n 1 n 1 n n 1 1 1 lim ... . n x 1 x 1 x 1 1 2 n 1 x x x
Bài 46. Cho dãy số x : 2 x a 1,x x . Tìm 1 2 lim ... n . n 1 n 1 n n x 1 x 1 x 1 2 3 n 1 1 x
Bài 47. Cho dãy số x được xác định bởi n 1 1 x 1;x . Đặt n 0 n 2 v 4n 1 u ;w u u ..
. u . Hãy tính limv ; m li w . n n n 1 2 n n n 1 n 1
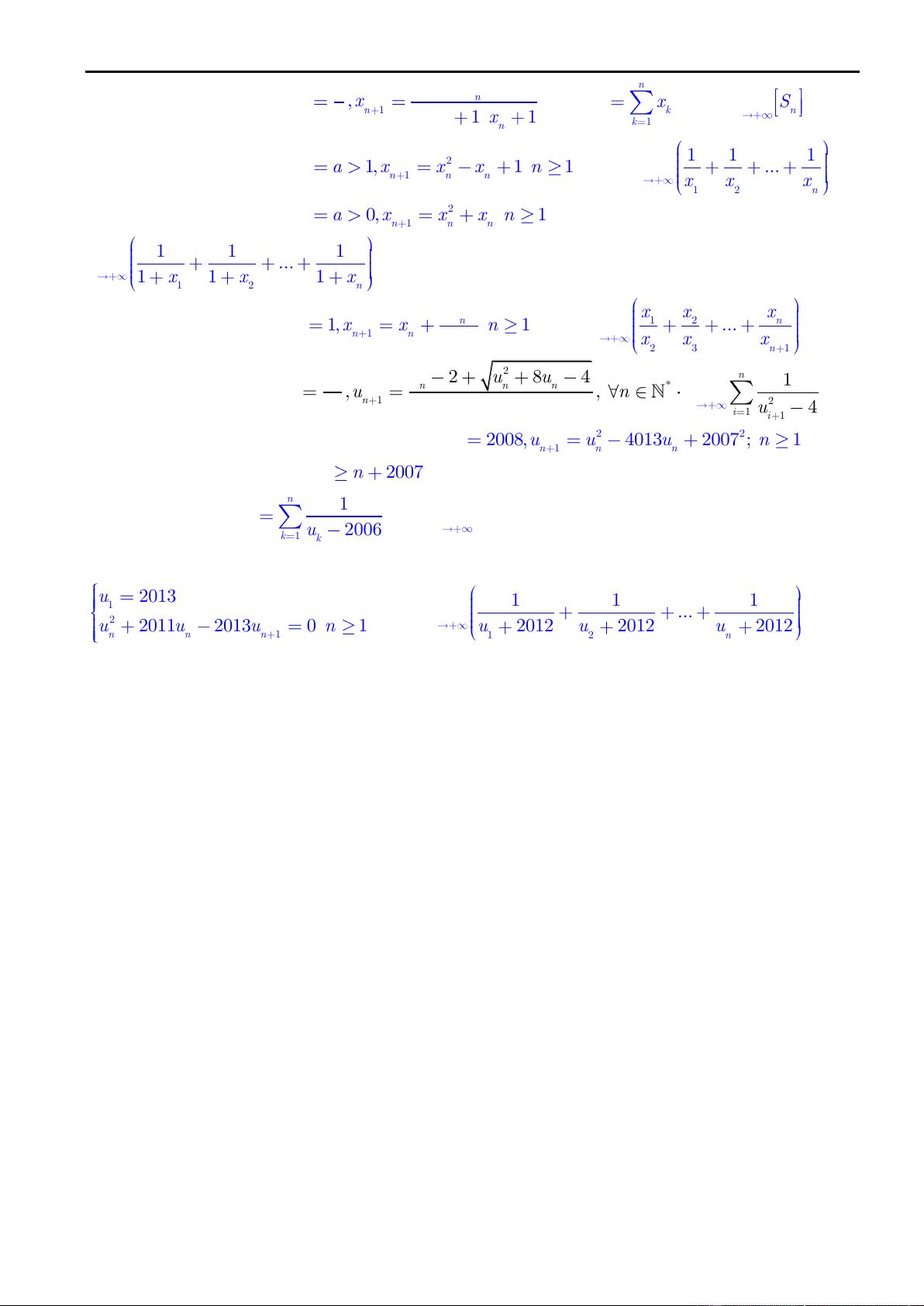
Bài 48. Cho dãy số x : 2 x 8, x x 7x 25 . Tính lim . n 1 n 1 3 n n n x i 2 1 i 2 2009x 1 x 2 n n n 1 x
Bài 49. Cho dãy số x : x 2009, x . Tính lim i . n 1 n 1 2 2009x x 2009 2 n n i 1 x n n 1 i 1 a
Bài 50. Cho dãy số thực a :a 1;a a ;n 1 . Chứng minh rằng lim n 2 . n 1 n 1 n a n n n 1 n 1
Bài 51. Cho dãy số x : 2 x 2, x x 1 . Đặt S
. Tính S ; lim S . n 1 n 1 2 n n x n n n k 1 1 k
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 19
Trường THPT Hùng Vương-Bình Phước
GV. Nguyễn Hữu Hiếu –sưu tầm-biên soạn 2 x n
Bài 52. Cho dãy số x : x , n x . Đặt S
x . Tính lim S . n 1 n 1 3 2 2n 1 x 1 n k n n n k 1 1 1 1
Bài 53. Cho dãy số x : 2 x a 1,x x x 1 n 1 . Tìm lim ... . n 1 n 1 n n n x x x 1 2 n
Bài 54. Cho dãy số x : 2 x a 0,x x x n 1 . Tìm n 1 n 1 n n 1 1 1 lim ... . n 1 x 1 x 1 x 1 2 n 2 x x x x
Bài 55. Cho dãy số x : x 1, n x x n 1 . Tìm 1 2 lim ... n . n 1 n 1 n 2014 n x x x 2 3 n 1 2 21 u 2 u 8u 4 n 1
Bài 56. Cho dãy số (u ) n n n * u ,u , n lim . n 1 n 1 10 2 2 n i 1 u 4 i 1
Bài 57. Cho dãy số u được xác định bởi 2 2 u 2008,u u 4013u 2007 ; n 1 n 1 n 1 n n
a) Chứng minh u n 2007 . n n 1 b) Đặt x ; tính lim x . n u n n k 2006 1 k
Bài 58. (HSG BP 11-12). Cho dãy số u được xác định bởi n u 2013 1 1 1 1 . Tìm lim ... . 2 u 2011u 2013u 0 n 1 n u 2012 u 2012 u 2012 n n n 1 1 2 n Bài 59.
. . . to be continued . . .
Một số vấn đề cơ bản về dãy số và giới hạn của dãy 20




