Nắm trọn chuyên đề khối đa diện và khối tròn xoay

TƯ DUY TOÁN HỌC 4.0 – LUYỆN THI ĐẠI HỌC NĂM 2021

NẮM TRỌN

CHUYÊN ĐỀ

KHỐI ĐA DIỆN

VÀ KHỐI TRÒN XOAY

(Dùng cho học sinh 11,12 và luyện thi Đại học năm 2021)

………………………………………………………………

TÀI LIỆU LƯU HÀNH NỘI BỘ THÁNG 10/2020

LỜI NÓI ĐẦU

Các em học sinh, quý thầy cô và bạn đọc thân mến !

Kỳ thi THPT Quốc Gia là một trong những kỳ thi quan trọng nhất đối với mỗi chúng ta. Để có

thể tham dự và đạt được kết quả cao nhất thì việc trang bị đầy đủ kiến thức và kĩ năng cần thiết là

một điều vô cùng quan trọng. Thấu hiểu được điều đó, chúng tôi đã cúng nhau tiến hành biên soạn

bộ sách “ Nắm trọn các chuyên đề môn Toán 2021 ” giúp các em học sinh ôn luyện và hoàn

thiện những kiến thức trọng tâm phục vụ kỳ thi, làm tài liệu giảng dạy và tham khảo cho quý thầy

cô trước sự thay đổi về phương pháp dạy học và kiểm tra của Bộ Giáo dục và Đào tạo.

Bộ sách chúng tôi biên soạn gồm 4 quyển:

 Quyển 1: Nắm chọn chuyên đề Hàm số

 Quyển 2: Nắm trọn chuyên đề Mũ – Logarit và Tích phân

 Quyển 3: Hình học không gian

 Quyển 4: Hình học Oxyz và Số phức

Trong mỗi cuốn sách, chúng tôi trình bày một cách rõ ràng và khoa học – tạo sự thuận lợi nhất

cho các em học tập và tham khảo. Đầu tiên là tóm tắt toàn bộ lý thuyết và phương pháp giải các

dạng toán. Tiếp theo là hệ thống các ví dụ minh họa đa dạng, tiếp cận xu hướng ra đề của kỳ thi

THPT Quốc Gia các năm gần đây bao gồm 4 mức độ: Nhận biết, Thông hiểu, Vận dụng và Vận

dụng cao. Cuối cùng là phần bài tập rèn luyện từ cơ bản đến nâng cao để các em hoàn thiện kiến

thức, rèn tư duy và rèn luyện tốc độ làm bài. Tất cả các bài tập trong sách chúng tôi đều tiến hành

giải chi tiết 100% để các em tiện lợi cho việc so sánh đáp án và tra cứu thông tin.

Để có thể biên soạn đầy đủ và hoàn thiện bộ sách này, nhóm tác giả có sưu tầm, tham khảo một

số bài toán trích từ đề thi của các Sở, trường Chuyên trên các nước và một số bài toán của các

thầy/cô trên toàn quốc. Chân thành cảm ơn quý thầy cô đã sáng tạo ra các bài toán hay và các

phương pháp giải toán hiệu quả nhất.

Mặc dù nhóm tác giả đã tiến hành biên soạn và phản biện kĩ lưỡng nhất nhưng vẫn không tránh

khỏi sai sót. Chúng tôi rất mong nhận được những ý kiến phản hồi và đóng góp từ quý thầy cô,

các em học sinh và bạn đọc để cuốn sách trở nên hoàn thiện hơn. Mọi ý kiến đóng góp, quý vị vui

lòng gửi về địa chỉ:

 Gmail: Blearningtuduytoanhoc4.0@gmail.com

 Fanpage: 2003 – ÔN THI THPT QUỐC GIA

Cuối cùng, nhóm tác giả xin gửi lời chúc sức khỏe đến quý thầy cô, các em học sinh và quý bạn

đọc. Chúc quý vị có thể khai thác hiệu quả nhất các kiến thức khi cầm trên tay cuốn sách này !

Trân trọng./

NHÓM TÁC GIẢ

MỤC LỤC

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN

Trang

CHỦ ĐỀ: THỂ TÍCH KHỐI ĐA DIỆN……......………………………......…………………..

1

Dạng 1: Mở đầu về khối đa diện…………………………………………………………………...

11

Dạng 2: Thể tích khối lăng trụ……...…………...………………………………………………….

21

Dạng 3: Thể tích khối chóp có cạnh bên vuông góc với đáy………..………………………….

55

Dạng 4: Thể tích khối chóp có mặt bên vuông góc với đáy……...……………………………..

83

Dạng 5: Thể tích khối chóp đều………………..…………………………………………………..

115

Dạng 6: Thể tích khối tứ diện đặc biệt…………...………………………………………...……..

146

Dạng 7: Tỉ số thể tích………………………………..…………………………………………...….

191

Dạng 8: Các bài toán thể tích chọn lọc…………………....……………………………………....

236

Dạng 9: Bài toán về góc – khoảng cách…………………………………………………………...

279

Dạng 10: Cực trị khối đa diện………………...……………………………………………………

321

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU………………...….……

341

CHỦ ĐỀ: KHỐI NÓN, KHỐI TRỤ………………………...………………………………….

341

Dạng 1: Tìm các yếu tố liên quan đến khối nón, khối trụ……………………………………...

346

Dạng 2: Khối tròn xoay nội, ngoại tiếp khối đa diện……...…………………………………….

370

Dạng 3: Cực trị và toán thực tế về khối tròn xoay..……………………………...…………...…..

382

CHỦ ĐỀ: KHỐI CẦU……………………....…….………………………………………………..

409

Dạng 1: Khối cầu ngoại tiếp tứ diện……………………………………………………………….

409

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

1

CHỦ ĐỀ : THỂ TÍCH KHỐI ĐA DIỆN

I. Một số định nghĩa cần nhớ

 Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song

với nhau và các mặt bên đều là các hình bình hành.

 Hình lăng trụ đứng

Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.

Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.

 Hình lăng trụ đều

Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với

mặt đáy.

 Hình hộp là hình lăng trụ có đáy là hình bình hành.

 Hình hộp đứng

Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.

Tính chất. Hình hộp đứng có

2

đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.

 Hình hộp chữ nhật

Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Tính chất. Hình hộp chữ nhật có

6

mặt là

6

hình chữ nhật.

 Hình lập phương

Định nghĩa. Hình lập phương là hình hộp chữ nhật

2

đáy và

4

mặt bên đều là hình vuông

Tính chất. Hình lập phương có

6

mặt đều là hình vuông.

 Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.

II. Thể tích khối đa diện

1. Công thức tính thể tích khối chóp

1

.

3

V S h

Trong đó:

S

là diện tích đáy,

h

là chiều cao khối chóp.

 Chú ý: Nếu khối chóp cần tính thể tích chưa biết chiều cao thì ta phải xác định được vị trí chân

đường cao trên đáy.

LÍ THUYẾT

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

2

 Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.

 Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc

đáy.

 Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.

 Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.

 Chóp có hình chiếu vuông góc của một đỉnh lên xuống mặt đáy thuộc cạnh mặt đáy

đường cao là từ đỉnh tới hình chiếu.

2. Công thức tính thể tích khối lăng trụ

.V B h

Trong đó:

B

là diện tích đáy,

h

là hiều cao khối lăng trụ.

 Thể tích khối hộp chữ nhật:

..V a b c

Trong đó:

, , a b c

là ba kích thước của khối hộp chữ nhật.

 Thể tích khối lập phương:

3

Va

Trong đó

a

là độ dài cạnh của hình lập phương.

III. Tỉ số thể tích

Cho khối chóp

.S ABC

và

,,A B C

  

là các điểm tùy ý lần lượt thuộc

,,SA SB SC

, ta có:

Công thức tỉ số thể tích:

. ' ' '

.

' ' '

..

S A B C

S ABC

V

SA SB SC

V SA SB SC



(hay gọi là công thức Simson)

Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ

dàng hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số

điều kiện sau:

 Hai khối chóp phải cùng chung đỉnh.

 Đáy hai khối chóp phải là tam giác.

 Các điểm tương ứng nằm trên các cạnh tương ứng.

Định lý Menelaus: Cho ba điểm thẳng hàng

. . 1

FA DB EC

FB DC EA



với

DEF

là một đường thẳng

cắt ba đường thẳng

,,BC CA AB

lần lượt tại

,,D E F

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

3

IV. Một số công thức tính nhanh thể tích và tỷ số thế tích khối chóp và khối lăng trụ.

 Công thức 1 : Thể tích tứ diện đều cạnh

a

:

3

.

2

12

S ABC

a

V 

.

 Công thức 2 : Với tứ diện

ABCD

có

,,AB a AC b AD c  

đôi một vuông góc thì thể tích

của nó là

1

6

ABCD

V abc

.

 Công thức 3 : Với tứ diện

ABCD

có

,,AB CD a BC AD b AC BD c     

thì thể tích của

nó là

   

2 2 2 2 2 2 2 2 2

2

12

ABCD

V a b c b c a a c b      

.

 Công thức 4 : Cho khối chóp

.S ABC

có

, , , , ,SA a SB b SC c BSC CSA ASB

  

     

thì

thể tích của nó là

2 2 2

.

1 2cos cos cos cos cos cos

6

S ABC

abc

V

     

    

.

 Công thức 5 : Mặt phẳng cắt các cạnh của khối lăng trụ tam giác

.ABC A B C

  

lần lượt tại

,,M N P

sao cho

,,

AM BN CP

x y z

AA BB CC

  

  

thì ta có

..

3

ABC MNP ABC A B C

x y z

VV

  





.

 Công thức 6 : Mặt phẳng cắt các cạnh của khối hộp

.ABCD A B C D

   

lần lượt tại

, , ,M N P Q

sao cho

, , ,

AM BN CP DQ

x y z t

AA BB CC DD

   

   

thì ta có

..

4

ABCD MNPQ ABCD A B C D

x y z t

VV

   

  



và

x z y t  

.

 Công thức 7 : Mặt phẳng cắt các cạnh của khối chóp tứ giác

.S ABCD

có đáy là hình bình

hành lần lượt tại

, , ,M N P Q

sao cho

, , ,

SM SN SP SQ

x y z t

SA SB SC SD

   

thì ta có công thức sau

đây

..

1 1 1 1

4

S MNPQ S ABCD

xyzt

VV

x y z t



   





và

1 1 1 1

x z y t

   

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

4

Lời giải

Chọn A

Kẻ

SH BC

vì

   

SAC ABC

nên

 

SH ABC

.

Gọi

, IJ

là hình chiếu của

H

trên

AB

và

BC

.

,SJ AB SJ BC  

.

Theo giả thiết

45SIH SJH  

.

Ta có:

SHI SHJ HI HJ    

nên

BH

là đường phân

giác của

ABC

từ đó suy ra

H

là trung điểm của

AC

.

3

1

.

2 3 12

SABC ABC

aa

HI HJ SH V S SH     

.

Lời giải

Chọn D

   

 

,

SAD ABCD AD

SH ABCD

SH AD SH SAD

















Ta có

22

3SH SD DH a  

,

2 2 2 2

15 3 2 3HC SC SH a a a    

.

2 2 2 2

12 11CD HC HD a a a    

.

Ta có

 

BF BC

BF SHC

BF SH













nên

 

, 2 6d B SHC BF a

.

2

11

. .2 3 .2 6 6 2

22

HBC

S BF HC a a a  

Đặt

AB x

nên

1

..

22

AHB

a

S AH AB x

;

2

1 11

.

22

CDH

a

S DH DC

 

1

11

2

ABCD

S CD AB AD a x a   

.

VÍ DỤ MINH HỌA

VÍ DỤ 1: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

, có

BC a

. Mặt phẳng

 

SAC

vuông góc với mặt đáy, các mặt bên còn lại đều tạo với mặt đáy một góc

45

. Tính thể tích khối

chóp

.S ABC

.

A.

3

12

a

B.

3

4

a

. C.

3

6

a

. D.

3

4

a

.

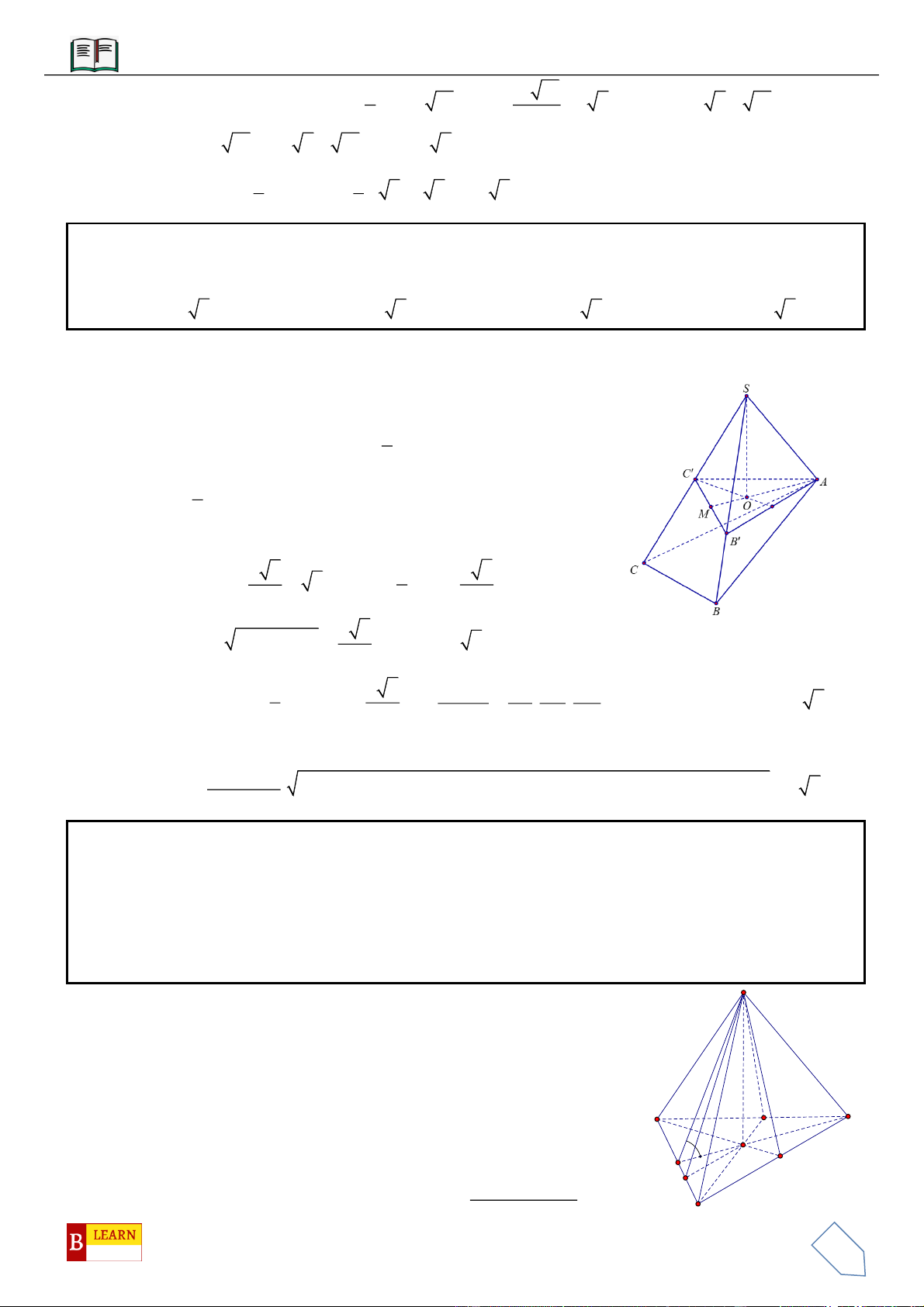
VÍ DỤ 2: Cho hình chóp

.S ABCD

với đáy

ABCD

là hình thang vuông tại

A

và

D

, đáy nhỏ của hình

thang là

CD

, cạnh bên

15SC a

. Tam giác

SAD

là tam giác đều cạnh

2a

và nằm trong mặt phẳng

vuông góc với đáy hình chóp. Gọi

H

là trung điểm cạnh

AD

, khoảng cách từ

B

tới mặt phẳng

 

SHC

bằng

26a

. Tính thể tích

V

của khối chóp

.S ABCD

?

A.

3

24 6Va

. B.

3

86Va

. C.

3

12 6Va

. D.

3

46Va

.

A

B

D

C

S

F

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

5

AHB ABCD CDH BHC

S S S S  

   

2

11

. 11 6 2 12 2 11

22

aa

x a x a a x a       

.

 





2

11 12 2 11 12 2

ABCD

S a a a a   

.

Vậy

23

.

11

. . 3.12 2 4 6

33

S ABCD ABCD

V SH S a a a  

.

Lời giải

Chọn C

Gọi

B



trên

SB

sao cho

2

3

SB SB





và

C



trên

SC

sao cho

1

2

SC SC





.

Khi đó

2SA SB SC



  

.S AB C





là khối tứ diện đều.

Ta có:

23

3

2

AM 

2 2 3

33

AO AM  

Nên

22

26

3

SO SA AO  

và

3

AB C

S





.

Khi đó

.

1 2 2

.

33

S AB C AB C

V S SO

   



mà

.

. S.

S.

. . 3 3 2 2

S ABC

S ABC AB C

AB C

V

SA SB SC

VV

V SA SB SC



    



.

Cách khác: áp dụng công thức 4

2 2 2

.

..

. 1 cos cos cos 2cos .cos. .cos 2 2

6

S ABC

SA SB SC

V ASB BSC CSB ASB BSC CSB     

Lời giải

Chọn B

Vì các mặt phẳng

 

SAB

,

 

SBC

,

 

SCA

đều tạo với đáy một

góc

60

và hình chiếu vuông góc của

S

xuống mặt phẳng

 

ABC

nằm bên trong tam giác

ABC

nên ta có hình chiếu của

S

chính là tâm

I

của đường tròn nội tiếp tam giác

ABC

.

Gọi

p

là nửa chu vi tam giác

ABC

thì

9

2

AB BC CA

p





.

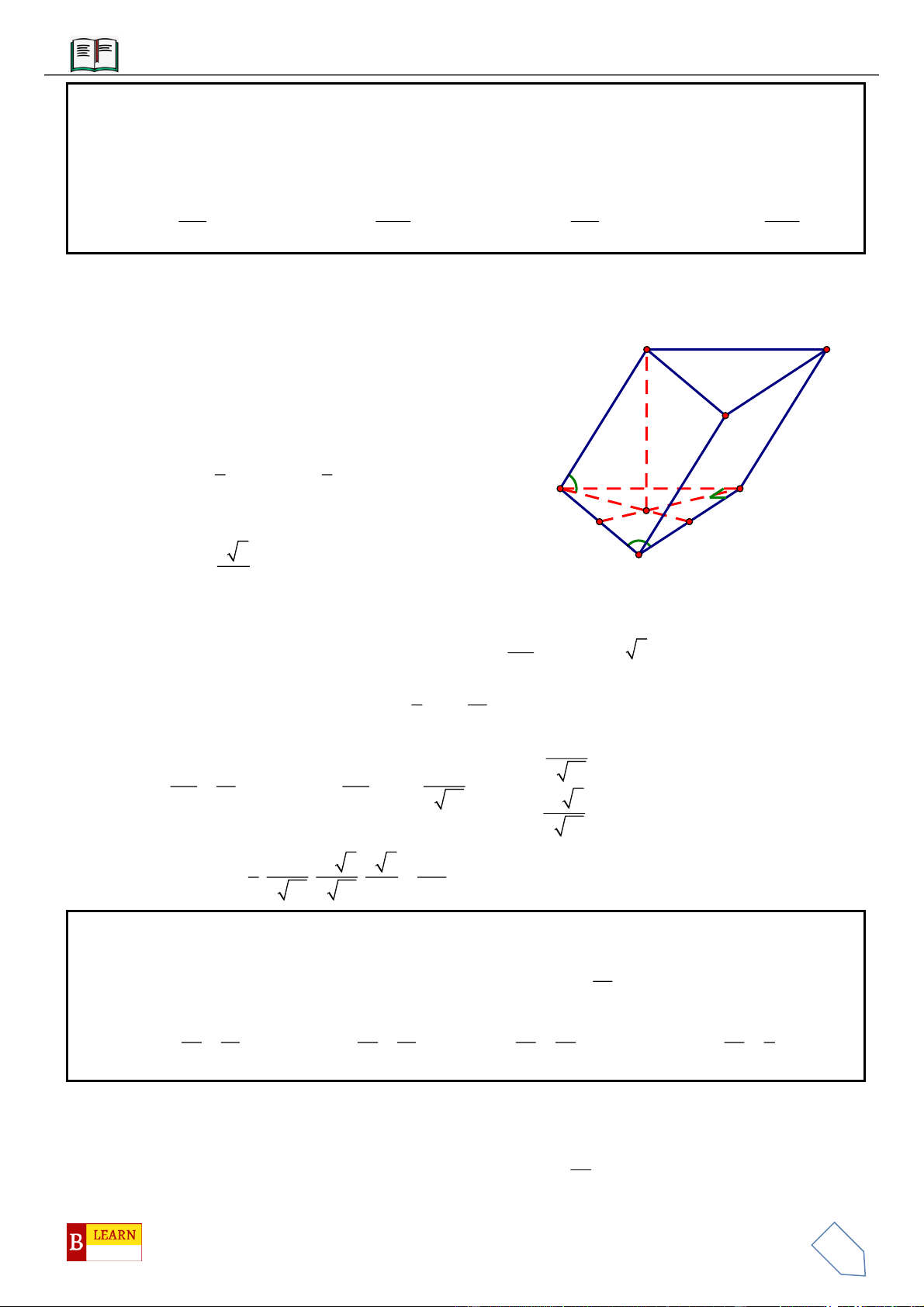
VÍ DỤ 3: Cho khối chóp

.S ABC

có góc

60ASB BSC CSA   

và

2SA 

,

3SB 

,

4SC 

. Thể tích

khối chóp

.S ABC

.

A.

43

. B.

32

. C.

22

. D.

23

.

VÍ DỤ 4: Cho hình chóp

.S ABC

có

5 cmAB 

,

6 cmBC 

,

7 cmCA 

. Hình chiếu vuông góc của

S

xuống mặt phẳng

 

ABC

nằm bên trong tam giác

ABC

. Các mặt phẳng

 

SAB

,

 

SBC

,

 

SCA

đều

tạo với đáy một góc

60

. Gọi

AD

,

BE

,

CF

là các đường phân giác của tam giác

ABC

với

D BC

,

E AC

F AB

. Thể tích

.S DEF

gần với số nào sau đây?

A.

3

3,7 cm

B.

3

3,4 cm

C.

3

2,9 cm

D.

3

4,1 cm

60

°

H

F

E

D

I

C

B

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

6

Ta có :

   

66

ABC

S p p AB p BC p AC    

và

26

3

S

r

p



.

Suy ra chiều cao của hình chóp là :

.tan60 2 2hr  

Vì

BE

là phân giác của góc

B

nên ta có :

EA BA

EC BC



.

Tương tự :

FA CA

FB CB



,

DB AB

DC AC



.

Khi đó :

.

AEF

ABC

S

AE AF

S AC AB



.

AB AC

AB BC AC BC





.

Tương tự :

.

CED

ABC

S

CA CB

S CA AB CB AB





,

.

BFD

ABC

S

BC BA

S BC CA BA CA





.

Do đó,

        

1

DEF ABC

ab bc ac

SS

a c b c b a c a a b c b



   



     



, với

BC a

,

AC b

,

AB c

   

2

.

ABC

abc

S

a b b c c a



  

210 6

143





.

1 210 6

. .2 2

3 143

S DEF

V 

   

33

280 3

cm 3,4 cm

143



Lời giải

Chọn D

.

Gọi

H

là trung điểm của cạnh

 

OC SH ABCD

.

Kẻ

 

HP AB P AB

Ta có

 

AB HP

AB SHP AB SP

AB SH





   







.

Do đó

   

 

0

; 60SAB ABCD SPH

.

0

tan60 3 3

SH

SH HP

HP

    

Trên

 

,ABCD

3 3 3 3 3

//

4 4 4 4

HP AB

HP AH a a

HP BC HP BC SH

BC AB

BC AC





        







.

3

2

1 1 3 3 3

. . . .

3 3 4 4

ABCD

aa

V SH S a   

F

E

D

C

B

A

I

VÍ DỤ 5: Cho hình chóp

.S ABCD

có đáy là hình vuông tâm

O

cạnh bằng

.a

Hình chiếu vuông góc của

đỉnh

S

lên mặt phẳng

 

ABCD

là trung điểm của cạnh

.OC

Góc giữa mặt phẳng

 

SAB

và mặt phẳng

 

ABCD

bằng

60 .

Tính theo

a

thể tích

V

của hình chóp

..S ABCD

A.

3

33

4

a

V 

. B.

3

8

a

V 

. C.

3

33

8

a

V 

. D.

3

4

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

7

Lời giải

Chọn C

Gọi

,MN

là trung điểm của

,AB AC

và

G

là trọng tâm của

ABC

.

 

'B G ABC

 





0

', ' 60BB ABC B BG  

.

'.

11

. . ' . . . '

36

A ABC ABC

V S B G AC BC B G





Xét

'B BG

vuông tại

G

, có

0

' 60B BG 

3

'

2

a

BG

. (nửa tam giác đều)

Đặt

2AB x

. Trong

ABC

vuông tại

C

có

0

60BAC 



tam giác

ABC

là nữa tam giác đều

, 3

2

AB

AC x BC x   

Do

G

là trọng tâm

ABC

33

24

a

BN BG  

. Trong

BNC

vuông tại

C

:

2 2 2

BN NC BC

2 2 2

22

3

9 9 3 2 13

3

16 4 52

33

2 13

a

AC

a x a a

x x x

a

BC







       











Vậy

3

'

1 3 3 3 3 9

. . .

6 2 208

2 13 2 13

A ABC

a a a a

V 

.

Lời giải

Chọn B

TYPS: Hai khối đa diện đồng dạng với tỷ số

k

thì ta có

3

1

2

V

k

V



. Áp dụng vào bài toán sau đây”

VÍ DỤ 6: Cho lăng trụ tam giác

. ' ' 'ABC A B C

có

'BB a

, góc giữa đường thẳng

'BB

và

 

ABC

bằng

60

, tam giác

ABC

vuông tại

C

và góc

60BAC 

. Hình chiếu vuông góc của điểm

'B

lên

 

ABC

trùng với trọng tâm của

ABC

. Thể tích của khối tứ diện

'.A ABC

theo

a

bằng

A.

3

7

106

a

. B.

3

15

108

a

. C.

3

9

208

a

. D.

3

13

108

a

.

60

°

60

°

C'

A'

G

M

N

B

C

A

B'

VÍ DỤ 7: Cho khối tứ diện đều

ABCD

có thể tích

V

. Gọi

,,M N P

lần lượt là trọng tâm các tam giác

,,ABC ACD ADB

và

V



là thể tích khối tứ diện

AMNP

. Tính tỉ số

V



.

A.

8

81

V





. B.

6

81

V





. C.

4

27

V





. D.

4

9

V





.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

8

Ta có mặt phẳng

 

MNP

cắt các mặt của tứ diện theo các đoạn giao tuyến

,EF FH

và

HE

do vậy

thiết diện là tam giác

EFH

. Ta dễ có

   

//MNP BCD

và

 

2

;;

3

d A MNP d A BCD

Ta cũng có

2

1 1 2 1

.

4 4 3 9

MNP EFH BCD BCD

S S S S



  





Do đó

 

1 2 6

; . ; .

3 81 81

AMNP MNP BCD ABCD

V d A MNP S d A BCD S V  

.

Lời giải

Chọn D

Giả sử

.

2020

ABC A B C

VV

  



.

Ta có

 

..

12

;.

3 3 3

C ABC ABC C ABB A

V

V d C ABC S V V

   





   

.

Ta lại có :

 

.

1

. ; .

3

1

. ; .

3

ABC

P ABC

C ABC

ABC

d P ABC S

V

d C ABC S











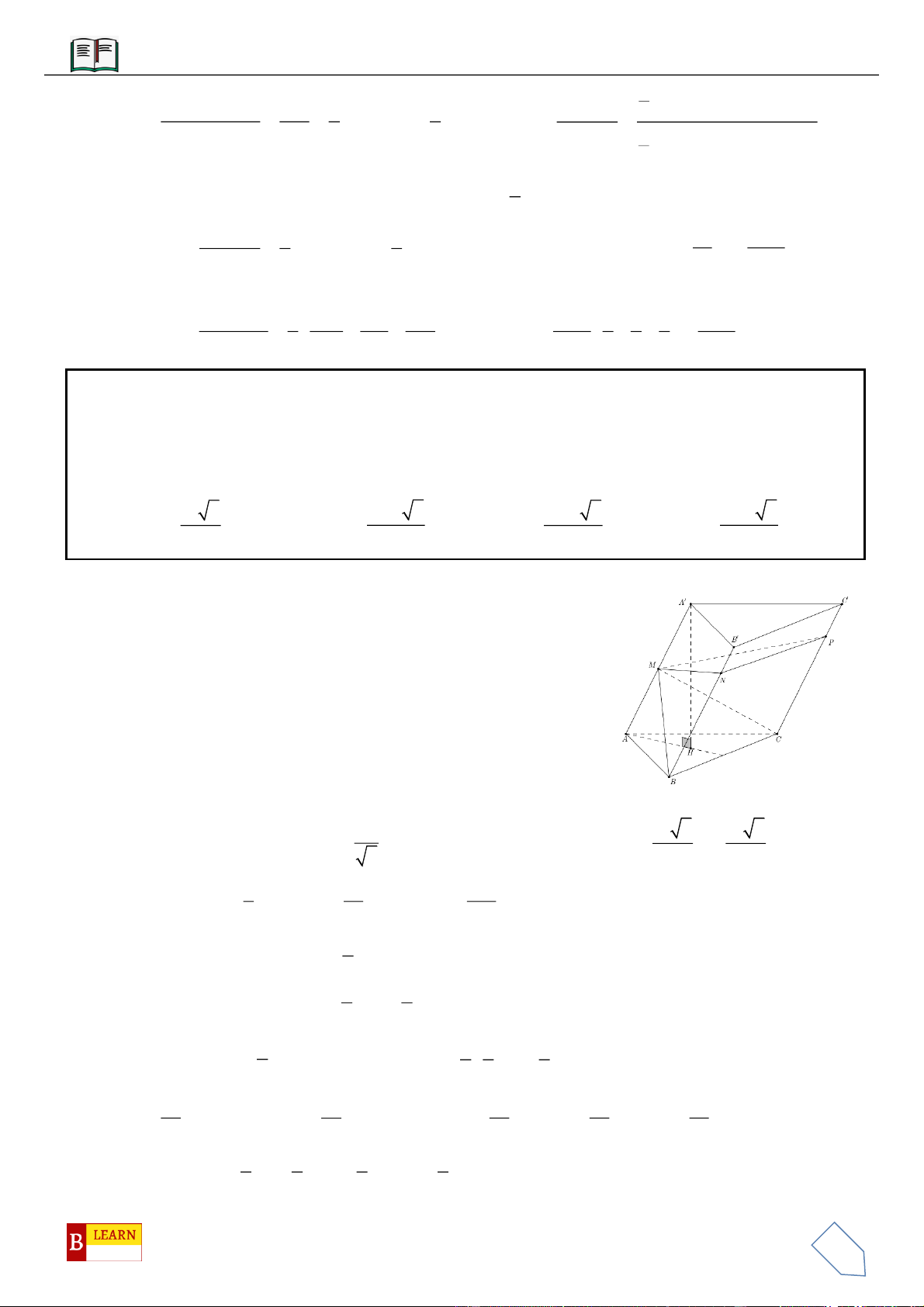
VÍ DỤ 8: Cho khối lăng trụ

.ABC A B C

  

có thể tích bằng 2020. Gọi

,MN

lần lượt là trung điểm của

AA



;

BB



và điểm

P

nằm trên cạnh

CC



sao cho

3PC PC





. Thể tích của khối đa diện lồi có các đỉnh

là các điểm

, , , , ,A B C M N P

bằng

A.

2020

3

. B.

5353

3

. C.

2525

3

. D.

3535

3

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

9

 

.

;

31

44

;

P ABC

d P ABC

PC

VV

CC

d C ABC

    



. Mặt khác:

 

.

1

. ; .

3

1

. ; .

3

ABNM

P ABNM

C ABB A

ABB A

d P ABB A S

V

d C ABB A S

  







.

Mà

 

;;d P ABB A d C ABB A

   



và

1

2

ABNM ABB A

SS





.

Suy ra

.

11

23

P ABNM

C ABB A

V

VV

V

  

  

. Vậy

. . .

7 3535

12 3

ABC MNP P ABNM P ABC

V V V V   

.

Cách 2: Dùng công thức giải nhanh

Ta có:

.

1

3

ABC MNP

ABC A B C

V

AM BN CP

V AA BB CC

  



  



  



.

2020 1 1 3 3535

3 2 2 4 3

ABC MNP

V



    





.

Lời giải

Chọn B

Gọi

V

là thể tích của khối đa diện có các đỉnh là các điểm

, , , , ,A B C M N P

.

1

V

là thể tích của khối lăng trụ

.ABC A B C

  

. Gọi

H

là trọng

tâm của tam giác

ABC

. Vì điểm

A



cách đều các điểm

,,A B C

nên

 

A H ABC





.

Hơn nữa

 

AA ABC A





nên

 

, 60AA ABC A AH







.

Suy ra

.tan60 tan60

3

a

A H AH a





  

. Do đó

23

1

33

..

44

ABC

aa

V S A H a



  

(đvtt)

Mà

11

..

2

1

.

3 3 3

A ABC ABC A BCC B

VV

V S A H V

   



   

.

Từ

4

5

3

33

44

NB BB

NB NB

PC PC

PC CC BB





































Suy ra

   

1

,

2

BCPN

S NB PC d BB CC





 

1 4 3

,

2 5 4

BB BB d BB CC



   







 

31

.,

40

BB d BB CC

  



31

.

40

BCC B

S





. . . 1

31 31 31

40 40 60

M BCPN M BCC B A BCC B

V V V V

    

   

.

Và

. . 1

1 1 1 1

.

3 2 2 6

M ABC ABC A ABC

V S A H V V



  

(vì

M

là trung điểm của

AA



)

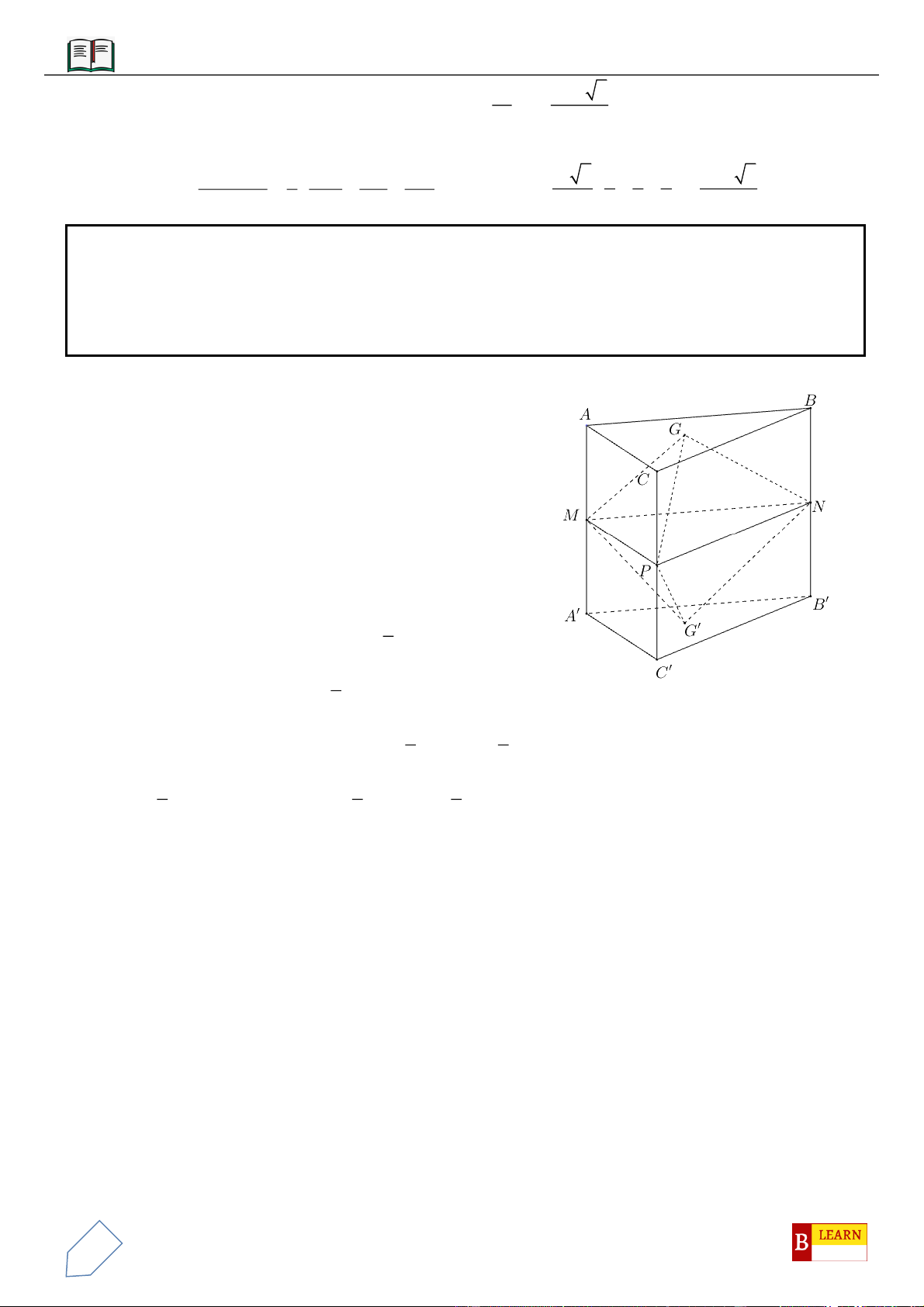
VÍ DỤ 9: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

, góc giữa cạnh bên với mặt

phẳng đáy bằng

60



và

A



cách đều 3 điểm

,,A B C

. Gọi

M

là trung điểm của

AA



;

N BB





thỏa mãn

4NB NB





và

P CC





sao cho

3PC PC





. Thể tích của khối đa diện lồi có các đỉnh là các điểm

, , , , ,A B C M N P

bằng

A.

3

4

a

. B.

3

41 3

240

a

. C.

3

23 3

144

a

. D.

3

19 3

240

a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

10

Vậy thể tích cần tìm là

3

. . 1

41 41 3

60 240

M ABC M BCPN

a

V V V V   

(đvtt)

Cách 2: Dùng công thức giải nhanh

Ta có:

.

1

3

ABC MNP

ABC A B C

V

AM BN CP

V AA BB CC

  



  



  



33

.

3 1 4 3 41 3

12 2 5 4 240

ABC MNP

aa

V



    





.

Lời giải

Chọn C

Ta có:

.

3.5 15

ABC A B C

V

  



(đvtt).

Ta có

. '.GG MNP G MNP G MNP

V V V





.

Do

,,M N P

lần lượt là trung điểm của

,,AA BB CC

  

nên mp

 

MNP

chia khối lăng trụ

.ABC A B C

  

thành hai khối lăng trụ bằng nhau

.ABC MNP

và

.MNP A B C

  

.

Lại có

 

G ABC

nên

..

1

3

G MNP ABC MNP

VV

Tương tự ta có

..

1

3

G MNP A B C MNP

VV

   



Do đó

. '. . .

11

33

GG MNP G MNP G MNP ABC MNP MNP A B C

V V V V V

   

   

 

. . .

1 1 1

.15 5

3 3 3

ABC MNP MNP A B C ABC A B C

V V V

     

    

.

VÍ DỤ 10: Cho lăng trụ

.ABC A B C

  

diện tích đáy bằng 3 và chiều cao bằng 5. Gọi

,,M N P

lần lượt là

trung điểm của

,,AA BB CC

  

.

,GG



lần lượt là trọng tâm của hai đáy

,ABC A B C

  

. Thể tích của khối

đa diện lồi có các đỉnh là các điểm

, , , ,G G M N P



bằng

A.

10

. B.

3

. C.

5

. D.

6

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

11

DẠNG 1 : MỞ ĐẦU KHỐI ĐA DIỆN

Câu 1: Khối tứ diện

ABCD

có thể tích

V

,

AB a

,

CD b

, góc giữa hai đường thẳng

AB

và

CD

là



khoảng cách giữa chúng bằng

c

. Mệnh đề nào dưới đây đúng?

A.

sin

6

abc

V





. B.

sin

2

abc

V





. C.

sin

3

abc

V





D.

sinV abc





.

Câu 2: Khối tứ diện

ABCD

có thể tích

V

,

AB a

góc giữa hai mặt phẳng

 

CAB

và

 

DAB

bằng



.

Các tam giác

CAB

,

DAB

có diện tích lần lượt là

1

S

và

2

S

. Mệnh đề nào dưới đây đúng?

A.

12

2 sinSS

V

a





. B.

12

4 sin

3

SS

V

a





. C.

12

4 sinSS

V

a





D.

12

2 sin

3

SS

V

a





.

Câu 3: Cho hình chóp

.S ABCD

có đáy là một hình vuông cạnh

a

. Cạnh bên

SA

vuông góc với mặt phẳng

đáy, còn cạnh bên

SC

tạo với mặt phẳng

()SAB

một góc

30

. Thể tích của hình chóp đó bằng

A.

3

a

. B.

3

2

4

a

. C.

3

2

a

. D.

3

2

3

a

.

Câu 4: Cho hình chóp

.S ABCD

có đáy là một hình vuông cạnh

a

. Các mặt phẳng

()SAB

và

()SAD

cùng

vuông góc với mặt phẳng đáy, còn cạnh bên

SC

tạo với mặt phẳng đáy một góc

30

. Thể tích

của khối chóp đã cho bằng

A.

3

6

9

a

. B.

3

6

3

a

. C.

3

6

4

a

. D.

3

9

a

.

Câu 5: Cho một hình chóp tứ giác đều có cạnh đáy bằng

a

và diện tích xung quanh gấp đôi diện tích đáy.

Khi đó thể tích của hình chóp bằng

A.

3

6

a

. B.

3

a

. C.

3

2

a

. D.

3

12

a

.

Câu 6: Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên

n

lần thì thể tích của nó tăng lên

A.

2

n

lần. B.

2

2n

lần. C.

3

n

lần. D.

3

2n

lần.

Câu 7: Cho hình lăng trụ

. ' ' 'ABC A B C

có

'2AA 

, khoảng cách từ

A

đến các đường thẳng

',CC'BB

,

lần lượt bằng

1

và

2

; khoảng cách

C

đến đường thẳng

'BB

bằng

5

. Thể tích khối lăng trụ

. ' 'C'ABC A B

bằng

A.

2

. B.

2

3

. C.

4

D.

4

3

.

Câu 8: Cho khối tứ diện

.O ABC

có

,,OA OB OC

đôi một vuông góc thỏa mãn

2 2 2

12OA OB OC  

.

Thể tích lớn nhất của khối tứ diện

.O ABC

bằng

A.

8

. B.

4

3

. C.

4

D.

8

3

.

Câu 9: Thể tích của khối chóp cụt có diện tích hai đáy lần lượt là

12

,SS

có chiều cao bằng

h

là

BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

12

A.

1 2 1 2

()h S S S S

. B.

1 2 1 2

()

3

h S S S S

. C.

1 2 1 2

()

3

h S S S S

D.

1 2 1 2

()h S S S S

.

Câu 10: Cho hình hộp

. ' ' 'D'ABCD A B C

có đáy là hình thoi cạnh

0

, 60a BAD 

và có chiều cao bằng

23a

Gọi

M,N

lần lượt là trung điểm các cạnh

' ', ' 'A B A D

. Tính thể tích khối đa diện

'ABDA MN

A.

3

7

8

a

. B.

3

4

a

. C.

3

5

8

a

D.

3

2

8

a

.

Câu 11: Cho hình hộp đứng

.ABCD A B C D

   

có

,AB AD a

3

2

a

AA





và góc

60

o

BAD 

. Gọi

M

và

N

lần lượt là trung

điểm các cạnh

AD



và

AB



.Thể tích khối chóp

.A BDMN

là:

A.

3

16

a

. B.

3

16

a

.

C.

3

33

16

a

. D.

3

16

a

.

Câu 12: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có tất cả các cạnh bằng

a

. Gọi

,MN

lần lượt là

trung điểm các cạnh

AB

và

BC



. Mặt phẳng

 

A MN



cắt cạnh

BC

tại

P

, Thể tích khối đa diện

.MBP A B N



bằng:

A.

3

24

a

. B.

3

12

a

. C.

3

73

96

a

. D.

3

73

32

a

.

Câu 13: Cho khối tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông góc với nhau và thỏa mãn

6OA OB OC  

. Thể tích lớn nhất của khối tứ diện

OABC

bằng

A.

8

. B.

4

3

. C.

4

. D.

8

3

.

Câu 14: Cho hình hộp

.ABCD A B C D

   

có diện tích đáy bằng

S

, chiều cao bằng

h

. Thể tích khối tứ diện

A ABD



bằng

A.

4

Sh

. B.

6

Sh

. C.

2

Sh

. D.

3

Sh

.

Câu 15: Cho hình lăng trụ đều có độ dài cạnh đáy bằng

.a

Chiều cao của hình lăng trụ bằng

h

, điện tích

một mặt đáy là

S

. Tổng khoảng cách từ một điểm trong hình lăng trụ tới tất cả các mặt của hình

lằng trụ bằng

A.

2S

h

a



. B.

3S

h

a



. C.

2S

a

. D.

3S

a

.

Câu 16: Cho lăng trụ đứng

.'ABC A B C



có đáy là tam giác đều

,2a AA a





. Gọi

,MN

lần lượt là trung

điểm của

,AA BB



và

G

là trọng tâm của tam giác

ABC

. Mặt phẳng

 

MNG

cắt

,CA CB

lần

lượt tại

,EF

. Thể tích khối đa diện có 6 đỉnh là

, , , , ,A B M N E F

bằng

A.

3

9

a

. B.

3

23

9

a

. C.

3

27

a

. D.

3

23

27

a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

13

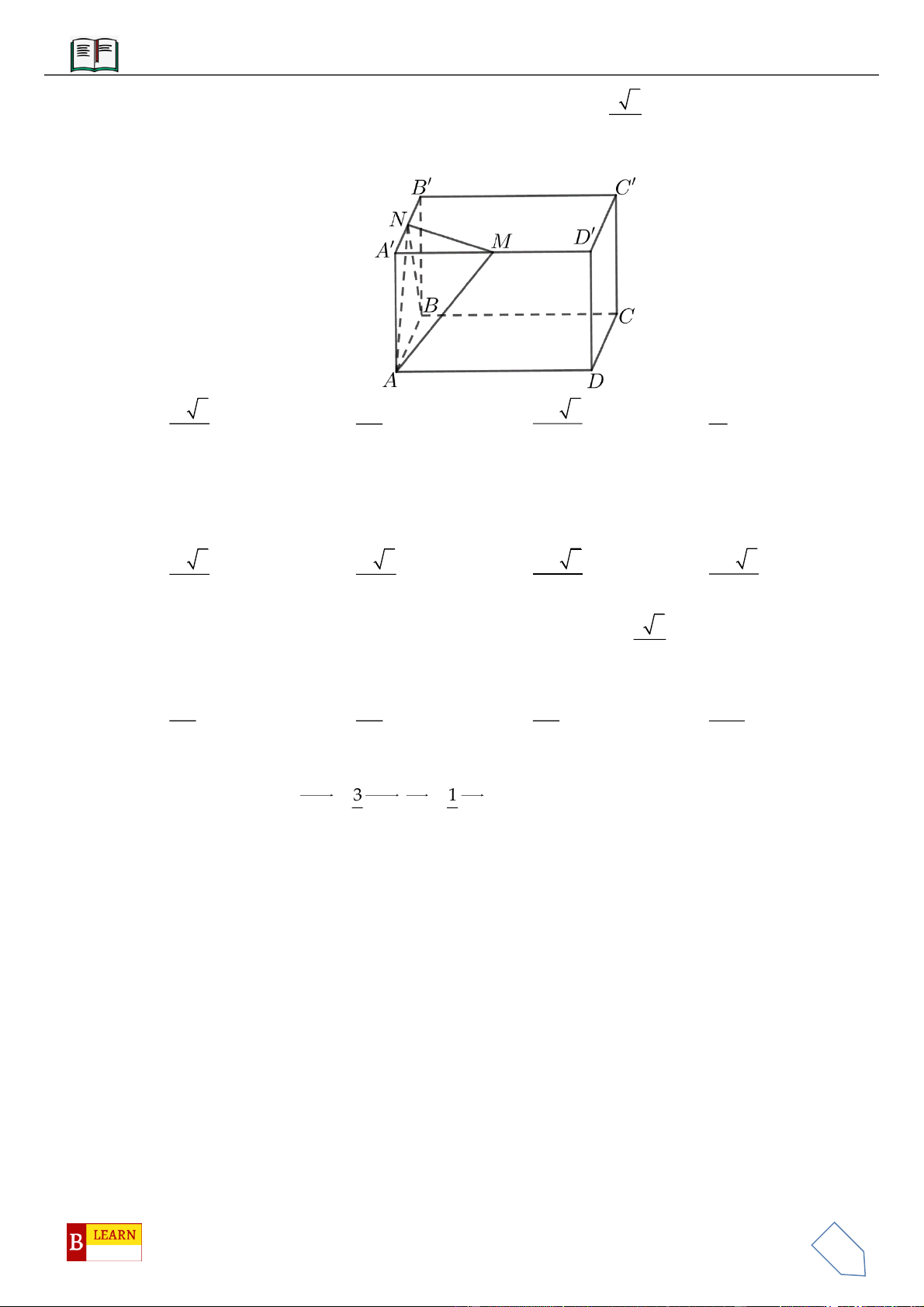
Câu 17: Cho hình hộp đứng

. ' ' ' 'ABCD A B C D

có

AB AD a

,

3

AA'

2

a



và

60

o

BAD 

. Gọi

M

và

N

lần lượt là trung điểm các cạnh

''AD

và

''AB

. Tính thể tích khối chóp

.A BDMN

.

A.

3

16

a

. B.

3

16

a

. C.

3

33

16

a

. D.

3

16

a

.

Câu 18: Cho hình lăng trụ tam giác đều

. ' ' 'ABC A B C

có tất cả các cạnh bằng

a

. Gọi

M

và

N

lần lượt là

trung điểm các cạnh

AB

và

''BC

. Mặt phẳng

 

'A MN

cắt cạnh

BC

tại

P

. Thể tích khối đa diện

. ' 'MBP A B N

bằng

A.

3

24

a

. B.

3

12

a

. C.

3

73

96

a

. D.

3

73

32

a

.

Câu 19: Cho hình hộp đứng

. ’ ’ ’ ’ABCD A B C D

có

3

; AA'

2

a

AB AD a  

và góc

0

60BAD 

. Gọi

;MN

lần lượt là trung điểm của

A'D'; ' 'AB

. Tính thể tích khối đa diện

. ’ ’ ’.BCD MNB C D

A.

3

16

a

. B.

3

7

32

a

. C.

3

9

16

a

. D.

3

17

32

a

.

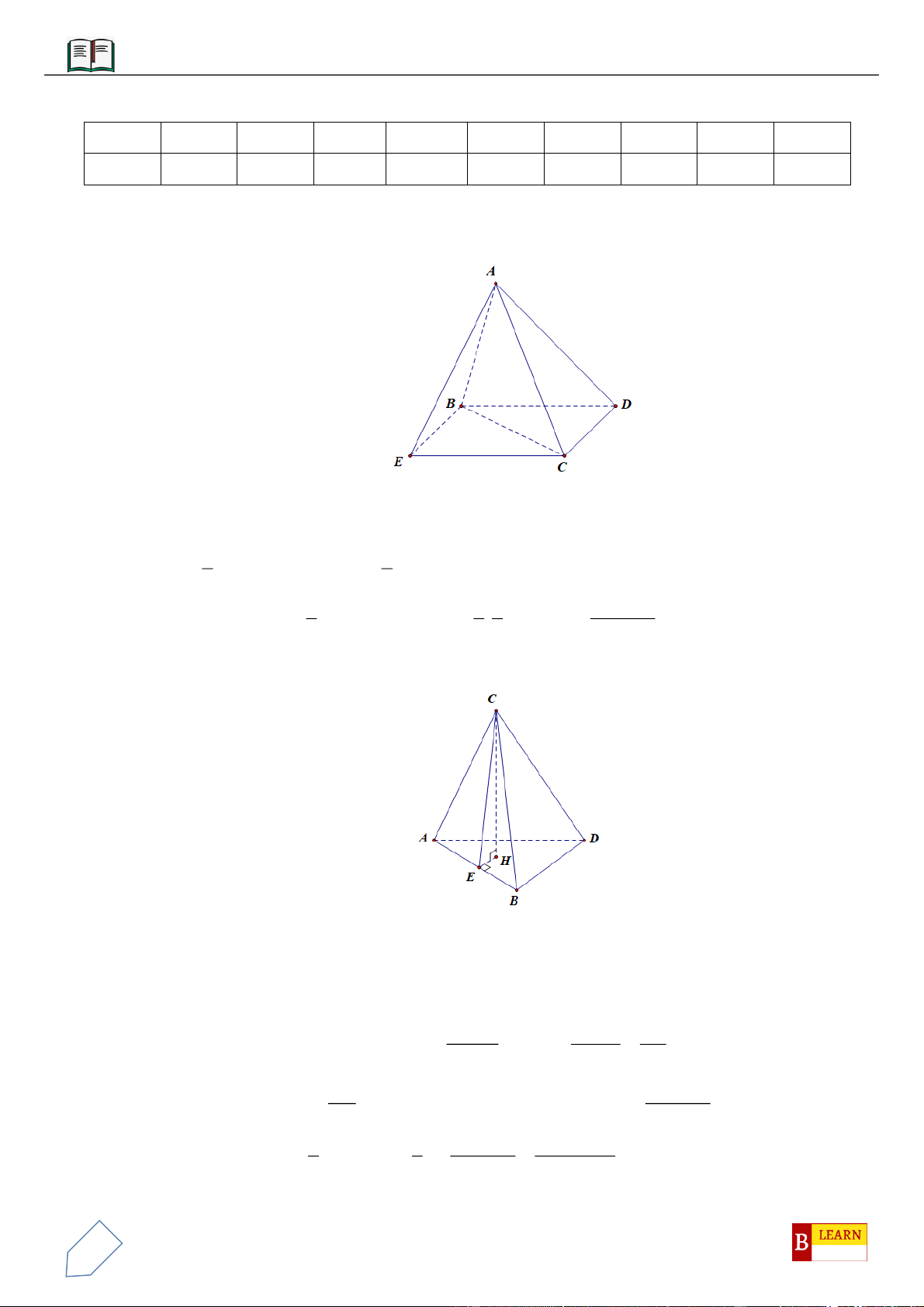
Câu 20: Cho lăng trụ tam giác

. ’ ’ ’ABC A B C

có thể tích bằng 72. Gọi

M

là trung điểm của cạnh

’ ’;AB

các

điểm

,NP

thỏa mãn

31

' ' ';

44

B N B C BP BC

. Đường thẳng

NP

cắt

’BB

tại

E

, đường thẳng

ME

cắt

AB

tại

Q

. tính thể tích khối đa diện

. ’ ’AQPC C A MN

.

A.

55

. B.

59

. C.

52

. D.

56

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

14

BẢNG ĐÁP ÁN

1.A

2.D

3.D

4.A

5.A

6.C

7.A

8.B

9.B

10.A

11.B

12.C

13.B

14.B

15.A

16.A

17.B

18.C

19.D

20.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn A

Dựng điểm

E

sao cho tứ giác

BDCE

là hình bình hành. Khi đó

//CD BE

 

//CD ABE

   

 

,,d AB CD d C ABE c  

;









,,AB CD AB BE





.





11

. .sin , sin

22

ABE

S AB BE AB BE ab







.

Vậy

 

.

1 1 1 sin

. . , . sin .

3 3 2 6

ABCD C ABE ABE

abc

V V S d C ABE ab c





   

.

Câu 2: Chọn D

Gọi

H

là hình chiếu vuông góc của

C

trên

 

ABD

và

E

là hình chiếu vuông góc của

H

trên

AB

. Khi đó

   









,,CAB DAB HE CE CEH



  

.

CH AB

CE AB

HE AB













. Do đó

.

2

ABC

CE AB

S





1

2

ABC

S

CE

AB a



  

.

CEH

vuông tại

H

có

1

2 sin

sin sin .sin

S

CH

CEH CH CE

CE a





    

.

Vậy

1 1 2

.2

2 sin 2 sin

11

. . . .

3 3 3

ABCD C ABD DAB

S S S

V V S CH S

aa





   

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

15

Câu 3: Chọn D

Ta có

 

CB AB

CB SAB

CB SA











.

Suy ra góc giữa

SC

với mặt phẳng

 

SAB

là

30CSB 

.

Do đó,

.cot 30 3SB CB a  

. Suy ra

22

2SA SB AB a  

.

Vì vậy

3

.

12

.

33

S ABCD ABCD

V SA S a

.

Câu 4: Chọn A

Do

   

 

SAB ABCD

SA ABCD

SAD ABCD

















.

Suy ra góc giữa

SC

với mặt phẳng đáy là

30SCA 

.

Suy ra

16

.tan30 2.

3

a

SA AC a   

.

Do đó

3

.

16

.

39

S ABCD ABCD

V SA S a

.

Câu 5: Chọn A

Giả sử hình chóp đều

.S ABCD

có đáy

ABCD

là

hình vuông cạnh

a

tâm

O

. Đặt

SO h

.

Gọi

M

là trung điểm

BC

.

Ta có

2

2 2 2

4

a

SM SO OM h   

.

2

1

4 4. . . 2. .

24

xq SBC

a

S S SM BC h a



   

Có

2

xq day

SS

2

22

3

22

42

aa

h a a h    

.

3

2

.

1 1 3 3

. . .

3 3 2 6

S ABCD ABCD

aa

V SO S a  

.

Câu 6: Chọn C

Ta chỉ xét hai hình chóp đều tam giác, tứ giác

Trường hợp 1: Hình chóp đều tam giác có cạnh đáy bằng

a

và chiều cao

h

.

Thể tích khối chóp tam giác đều ban đầu:

2

1

13

..

34

a

Vh

.

Thể tích khối chóp sau khi tăng chiều cao và cạnh đáy cùng tăng lên

n

lần:

 

2

3

21

3

1

..

34

na

V nh n V

.

M

O

A

B

C

D

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

16

Kết luận: một hình chóp tam giác đều có chiều cao và cạnh đáy cùng tăng lên

n

lần thì thể tích

của nó tăng lên

3

n

lần.

Trường hợp 2: Hình chóp đều tứ giác có cạnh đáy bằng

a

và chiều cao

h

.

Thể tích khối chóp tứ giác đều ban đầu:

2

1

..

3

V a h

.

Thể tích khối chóp tứ giác đều sau khi tăng chiều cao và cạnh đáy cùng tăng lên

n

lần:

 

2

3

21

1

..

3

V na nh n V

.

Kết luận: một hình chóp tứ giác đều có chiều cao và cạnh đáy cùng tăng lên

n

lần thì thể tích của

nó tăng lên

3

n

lần.

Kết luận: Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên

n

lần thì thể tích của

nó tăng lên

3

n

lần.

Nhận xét: Ta có thể dùng một kết quả quen thuộc

Nếu ta tăng các kích thước của đa giác lên

k

lần thì diện tích đa giác sẽ tăng lên

2

k

lần.

Nếu tăng diện tích đáy của khối chóp lên

2

k

lần và chiều cao

k

lần thì thể tích khối chóp sẽ

tăng lên

3

k

lần.

Câu 7: Chọn A

Gọi

,HK

làn lượt là hình chiếu vuông góc của

A

lên

BB',CC'

ta có

( , ') 1, (A,CC') 2AH d A BB AK d   

và

2 2 2

5AH AK HK AHK    

vuông tại

1

.1

2

AHK

A S AH AK  

. Vậy

. ' ' '

. ' 2

ABC A B C AHK

V S AA

.

Câu 8: Chọn B

Ta có

.

1

..

6

O ABC

V OA OB OC

.

Sử dụng bất đẳng thức AM – GM có

3

2 2 2 2 2 2

.

84

12 3 . .OC . . 8

63

O ABC

OA OB OC OA OB OA OB OC V        

Câu 9: Chọn B

Thể tích hình chóp cụt là

1 2 1 2

()

3

h S S S S

Câu 10: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

17

Chú ý:

'ABDA MN

là một hình chóp cụt có hai tam

giác đáy

,'ABD A MN

.

Do đó

1 2 1 2

()

3

h S S S S

V





.

Trong đó,

23ha

và

22

1 2 ' ' ' '

3 1 3

,

4 4 16

ABD A MN A B D

aa

S S S S S    

Vậy

2 2 2 2 2

2 3 3 3 3 3 7

( . )

3 4 16 4 16 8

a a a a a a

V    

.

Câu 11: Chọn B

Ta có:

3

0

.

1 1 1 3

.sin60

3 3 2 2 2 2 32

A A MN A MN

a a a a

V S AA







      





.

Khối chóp cụt

.ABD A MN



có

22

12

3 3 3

,,

2 4 16

ABD A MN

a a a

h S S S S



    

.

Do đó

 

2 2 4 3

. 1 2 1 2

3 3 3 3 7

3 6 4 16 64 32

ABD A MN

h a a a a a

V S S S S







      





Do đó

3 3 3

. . .

73

32 32 16

A BDMN ABD A MN A A MN

a a a

V V V



    

.

Câu 12: Chọn C

Ta có

1

~

2

MP BP BM

MBP A B N

A N B N A B



     

   

theo tỉ số

1

2

Khối đa diện

.MBP A B N



là khối chóp cụt có chiều cao

h BB a





.

Diện tích hai đáy là :

22

12

1 3 1 3

,

2 8 4 32

A B N A B C MBP A B N

aa

S S S S S S

      

     

.

Vậy

 

2 2 2 2 3

1 2 1 2

3 3 3 3 7 3

.

3 3 8 32 8 32 96

MBP A B N

h a a a a a a

V S S S S









      





.

Câu 13: Chọn B

Áp dụng bất đẳng thức Cauchy cho ba số không âm, ta

có:

3

6 3 . .OA OB OC OA OB OC   

. . 8OA OBOC

Ta có

1

..

6

OABC

V OA OB OC

14

.8

63



.

Dấu

""

xảy ra khi

2OA OB OC  

.

Vậy

OABC

V

lớn nhất là

4

3

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

18

Câu 14: Chọn B

Ta có

.

11

22

ABD ABCD A ABD A ABCD

S S V V



  

 

11

. . . ;

2 3 6

ABCD

Sh

S d A ABCD





.

Câu 15: Chọn A

Xét hình lăng trụ đều

 

H

đã cho có đáy là đa giác đều

n

đỉnh. Xét

điểm

I

bất kỳ trong hình lăng trụ đều

 

H

đã cho. Khi đó nối

I

với

các đỉnh của

 

H

ta được

2n

khối chóp có đỉnh là

,I

trong đó có

hai khối chóp có đáy là hai mặt đáy của

 

H

, và

n

khối chóp có đáy

là các mặt bên của

 

H

. Diện tích của mỗi mặt đáy của

 

H

là

,S

diện

tích của mỗi mặt bên của

 

H

bằng

ah

. Gọi

1 2 1 2

, ,..., , ,

n n n

h h h h h



lần

lượt là khoảng cách từ

I

đến các mặt bên và các mặt đáy của

 

H

. Vậy theo công thức tính thể

tích của khối lăng trụ và khối chóp ta có:

 

1 2 1 2 1 1 2

1 1 1 1

... . ... . . .

3 3 3 3

n n n n n n

H

V V V V V V Sh h ah h ah h S h S

   

           

   

1 2 1 2

11

...

33

n n n

h

S

S h h h a h h

h



      

   

1 2 1 2

11

... ...

3 3 3 3

nn

SS

S h h h a h h h a S           

1 2 1 2 1 2

22

... ...

n n n n

SS

h h h h h h h h h

aa



            

.

Câu 16: Chọn D

Ta có

3

2

1.

1 1 3 3

..

3 3 2 6

C ABNM ABNM

aa

V V CH S a   

.

 

   

//

/ / / /

MN GMN

AB ABC

AB MN

GMN ABC EF AB MN















  

.

Suy ra

2

3

CF CG CE

CB CH CA

  

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

19

Suy ra

33

.EFNM

. 1 .EFNM 1

1

33

11

5 4 4 3 2 3

22

33

9 9 9 6 27

4. . .1.1

22

C

BFN AEM C

V

aa

V V V V

V

  

       

Câu 17: Chọn B

Dễ thấy

'.A MN ADB

là hình chóp cụt và hai đáy là hai

tam giác đều đồng dạng theo tỉ số là

1

2

.

Ta có:

2

3

4

ADB

a

S





2

'

13

4 16

A MN ADB

a

SS



  

3

'

1

.

3 32

AA MN A MN

a

V AA S







  

 

3

'.

17

AA .

3 32

A MN ADB A MN ADB A MN ADB

a

V S S S S



   



   

3

. ' . '

3

16

A BDMN A MN ADB AA MN

a

V V V   

.

Câu 18: Chọn C

Ta có

 

//A N ABC



. Gọi

K

là trung điểm của đoạn thẳng

BC

.Suy ra

//AK A N



.

Mặt khác

 

A MN BC P





nên

P

là trung điểm của đoạn

thẳng

BK

.

Dễ thấy

. ' 'MBP A B N

là hình chóp cụt và hai đáy là hai tam

giác đồng dạng theo tỉ số là

1

2

.

Ta có

2

13

. .sin60

28

o

A B N

a

S A B A N





  



2

13

4 32

MBP A B N

a

SS





  

.

Vậy

 

3

. ' ' ' ' ' '

1 7 3

AA .

3 96

MBP A B N MBP A B N MBP A B N

a

V S S S S

   



   

.

Câu 19: Chọn D

Đặt:

1

V

là thể tích của khối hộp đứng

. ’ ’ ’ ’ABCD A B C D

.

2

V

là thể tích của khối chóp cụt

’ . .A MN ABD

V

là thể tích của đa diện

. ’ ’ ’.BCD MNB C D

Ta có:

3

0

1

33

. . .sin60 .

24

aa

V B h a a  

32

' ' ' '

1 3 3

;

4 16 4

A MN A B D ABD

aa

S S S

  

  

 

2 ' '

2 2 2 2 3

.

3

3 3 3 3 3 7

.

6 16 4 16 4 32

A MN ABD A MN ABD

h

V S S S S

a a a a a a

   

   





   





CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

20

Do đó:

3 3 3

12

3 7 17

4 32 32

a a a

V V V    

.

Câu 20: Chọn B

Đặt:

V

là thể tích khối lăng trụ

. ’ ’ ’. V 72ABC A B C 

.

1

V

là thể tích khối đa diện

. ’ ’AQPC C A MN

.

2

V

là thể tích khối chóp cụt

.'BQP B MN

.

Ta có:

11

' ' 3 6

BP BQ BQ

B N B M BA

   

'MN

' ' '

1 1 1 1

.

6 4 24 24

1 3 3 3

.

2 4 8 8

BQP

BQP BAC

BAC

B

B BAC

B A C

S

SS

S

SS

S











    

Suy ra:

 

2 'MN 'MN

.

3

BQP B BQP B

h

V S S S S

   

  

.

1 3 1 3 1 3 1 13

. 13.

3 24 8 24 8 3 24 8 8 72

BAC

BAC BAC BAC BAC

hS

hV

S S S S



   



       





Vậy:

12

72 13 59.V V V    

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

21

DẠNG 2 : THỂ TÍCH KHỐI LĂNG TRỤ ĐỨNG

❖ Thể tích của khối lăng trụ đứng có diện tích đáy

S

, chiều cao (độ dài cạnh bên )

h

là

.V S h=

• Khối lăng trụ đứng là khối lăng trụ có cạnh bên vuông góc với đáy .

• Chiều cao của khối lăng trụ đứng bằng độ dài cạnh bên của khối lăng trụ.

• Khối lăng trụ đa giác đều là khối lăng trụ đứng có đáy là một đa giác đều ( khối lăng trụ tam giác

đều, khối lăng trụ lục giác đều…)

❖ Khai thác các giả thiết góc và khoảng cách cho khối lăng trụ đứng tam giác.

• Kẻ

( ) ( )

,AH BC H BC AK A H K A H



⊥  ⊥ 

ta có

( ) ( )

( )

,A HA A BC ABC





==

và

.tanh AH



=

.

•

( )

AK A H

AK A BC

AK BC





⊥



⊥



⊥



và

( )

,

A

AK d d A A BC



==

có

2 2 2

1 1 1

A

d h AH

=+

❖ Thể tích của một khối lập phương cạnh

a

là

3

Va=

.

Với hình lập phương cạnh

a

ta chú ý:

• Diện tích mỗi mặt của hình lập phương là

2

Sa=

.

• Diện tích toàn phần ( tổng diện tích các mặt) của hình lập phương là

2

6

TP

Sa=

.

• Độ dài đường chéo của hình lập phương là

3da=

.

• Độ dài đường chéo mỗi mặt của hình lập phương là

2a

.

•

( )

3 2 3

, , ,

33

aa

d A A BD d A CB D

  

==

.

•

( ) ( )

2

,,

2

a

d AC CD d AC A B

   

==

.

❖ Thể tích của một khối hộp chữ nhật kích thước

,,a b c

là

..V a b c=

.

• Diện tích toàn phần ( tổng diện tích các mặt ) của hình hộp chữ nhật là

( )

2

TP

S ab bc ca= + +

.

• Độ dài đường chéo của hình hộp chữ nhật là

2 2 2

d a b c= + +

hay

2 2 2

AC AB AD AA



= + +

.

• Kẻ

( )

DH AD H AD



⊥

, ta có

( ) ( )

( )

,DHC ACD ADD A



  

==

.

• Vì

( )

AB BCC B



⊥

nên

( )

,AC B AC BCC B

   

=

.

•

( )

2 2 2 2

,

1 1 1 1

A A BD

d AB AD AA



= + +



LÍ THUYẾT

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

22

Câu 1: Cho hình lập phương

.ABCD A B C D

   

có khoảng cách giữa hai đường thẳng

AC



và

CD



bằng

a

. Tính thể tích

V

của khối lập phương đã cho.

A.

3

8Va=

. B.

3

22Va=

. C.

3

33Va=

. D.

3

27Va=

.

Câu 2: Một khối hộp chữ nhật có diện tích các mặt xuất phát từ cùng một đỉnh lần lượt là

( )

2

10 cm

,

( )

2

20 cm

,

( )

2

80 cm

. Thể tích

V

của khối hộp chữ nhật đó.

A.

( )

3

40V cm=

. B.

( )

3

80V cm=

. C.

( )

3

80 10V cm=

. D.

( )

3

40 10V cm=

.

Câu 3: Khi tăng độ dài mỗi cạnh của một khối hộp chữ nhật lên 2 lần thì thể tích của nó tăng lên bao

nhiêu lân?.

A.

7

lần. B.

2

lần. C.

4

lần. D.

8

lần.

Câu 4: Cho lăng trụ tam đứng

.ABC A B C

  

có đáy

ABC

là tam giác cân với

AB AC a==

,

120BAC =

, mặt phẳng

( )

AB C



tạo với đáy một góc

60

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

8

a

V =

. B.

3

9

8

a

V =

. C.

3

8

a

V =

. D.

3

4

a

V =

.

Câu 5: Cho khối lăng trụ đứng

.ABC A B C

  

có

BB a



=

, đáy

ABC

là tam giác vuông cân tại

B

và

2AC a=

. Tính thể tích

V

của khối lăng trụ đã cho

A.

3

2

a

V =

. B.

3

Va=

. C.

3

6

a

V =

. D.

3

a

V =

.

Câu 6: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

,3AB a AD a==

và mặt phẳng

( ' ' )A D CB

tạo với

đáy một góc

0

60

. Thể tích

V

của khối hộp chữ nhật là

A.

3

Va=

. B.

3

3Va=

. C.

3

3Va=

. D.

3

9Va=

.

Câu 7: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

AB AD a==

và

'AC

tạo với mặt phẳng

( ' ')ABB A

một góc

0

30

. Thể tích

V

của khối hộp chữ nhật là

A.

3

32Va=

. B.

3

2Va=

. C.

3

2Va=

. D.

3

6Va=

.

Câu 8: Cho lăng trụ đứng

.ABC A B C

  

có

AB a=

,

3BC a=

,

2AC a=

và góc giữa

CB



và

( )

ABC

bằng

o

60

. Mặt phẳng

( )

P

qua trọng tâm tứ diện

CA B C

  

, song song với mặt đáy lăng trụ và cắt

các cạnh

AA



,

BB



,

CC



lần lượt tại

E

,

F

,

Q

. Tỉ số thể tích của khối tứ diện

CEFQ

và khối

lăng trụ đã cho gần số nào sau đây nhất?

A.

0,06

. B.

0,25

. C.

0,09

. D.

0,07

.

Câu 9: Cho hình hộp đứng

.ABCD A B C D

   

, đáy là một hình thoi. Biết diện tích của hai mặt chéo

,ACC A BDD B

   

lần lượt là

12

,SS

và góc

o

90BA D



=

. Tính thể tích

V

của khối hộp đã cho.

A.

( )

12

22

4

21

4

SS

V

SS

=

−

. B.

( )

12

22

4

12

2

SS

V

SS

=

−

. C.

( )

12

22

4

21

2

SS

V

SS

=

−

. D.

( )

12

22

4

12

4

SS

V

SS

=

−

BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

23

Câu 10: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông, các tam giác

SAB

và

SAD

là những tam

giác vuông tại

A

. Mặt phẳng

( )

P

qua

A

vuông góc với cạnh bên

SC

cắt

,,SB SC SD

lần lượt

tại các điểm

,,M N P

. Biết

8SC a=

,

0

60ASC =

. Tính thể tích khối cầu ngoại tiếp đa diện

ABCDMNP

?

A.

3

6Va



=

. B.

3

24Va



=

. C.

3

32 3Va



=

. D.

3

18 3Va



=

.

Câu 11: Cho hình lăng trụ đều

.ABC A B C

  

, biết khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



bằng

a

góc giữa hai mặt phẳng

( )

ABC



và

( )

BCC B



bằng



với

1

cos

3



=

(tham khảo hình vẽ bên

dưới).Thể tích khối lăng trụ bằng

A.

3

9 15

20

a

. B

3

3 15

20

a

.

C.

3

3 15

10

a

. D.

3

9 15

10

a

.

Câu 12: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

A

với

22BC a=

.

Biết khoảng cách từ điểm

'C

đến mặt phẳng

( )

'A BC

bằng

4

3

a

. Tính thể tích

V

của khối lăng trụ

. ' ' 'ABC A B C

.

A.

3

4Va=

. B.

3

8

3

a

V =

. C.

3

8Va=

. D.

3

4

3

a

V =

.

Câu 13: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông cân tại

A

, khoảng cách từ

A

đến

mặt phẳng

( )

A BC



bằng

3

. Gọi



là góc giữa hai mặt phẳng

( )

A BC



và

( )

ABC

. Tìm

cos



khi

thể tích của khối lăng trụ

.ABC A B C

  

nhỏ nhất.

A.

2

cos

3



=

. B.

3

cos

3



=

. C.

1

cos

3



=

. D.

2

cos

2



=

.

Câu 14: Cho hình lăng trụ đều

.ABC A B C

  

. Biết khoảng cách từ điểm

C

đến mặt phẳng

( )

ABC



bằng

a

góc giữa hai mặt phẳng

( )

ABC



và

( )

BCC B



bằng



với

1

cos

23



=

(tham khảo hình vẽ bên).

Thể tích khối lăng trụ

.ABC A B C

  

là

A.

3

2

a

. B.

3

32

2

a

. C.

3

32

4

a

. D.

3

32

8

a

Câu 15: Cho lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật với

6AB =

,

3AD =

,

3AC



=

và mặt phẳng

( )

AA C C



vuông góc với mặt đáy. Biết hai mặt phẳng

( )

AA C C



,

( )

AA B B



tạo

với nhau góc



thỏa mãn

3

tan

4



=

. Thể tích khối lăng trụ

.ABCD A B C D

   

bằng?

A.

6V =

. B.

8V =

. C.

12V =

. D.

10V =

.

A

B

C

C'

B'

A'

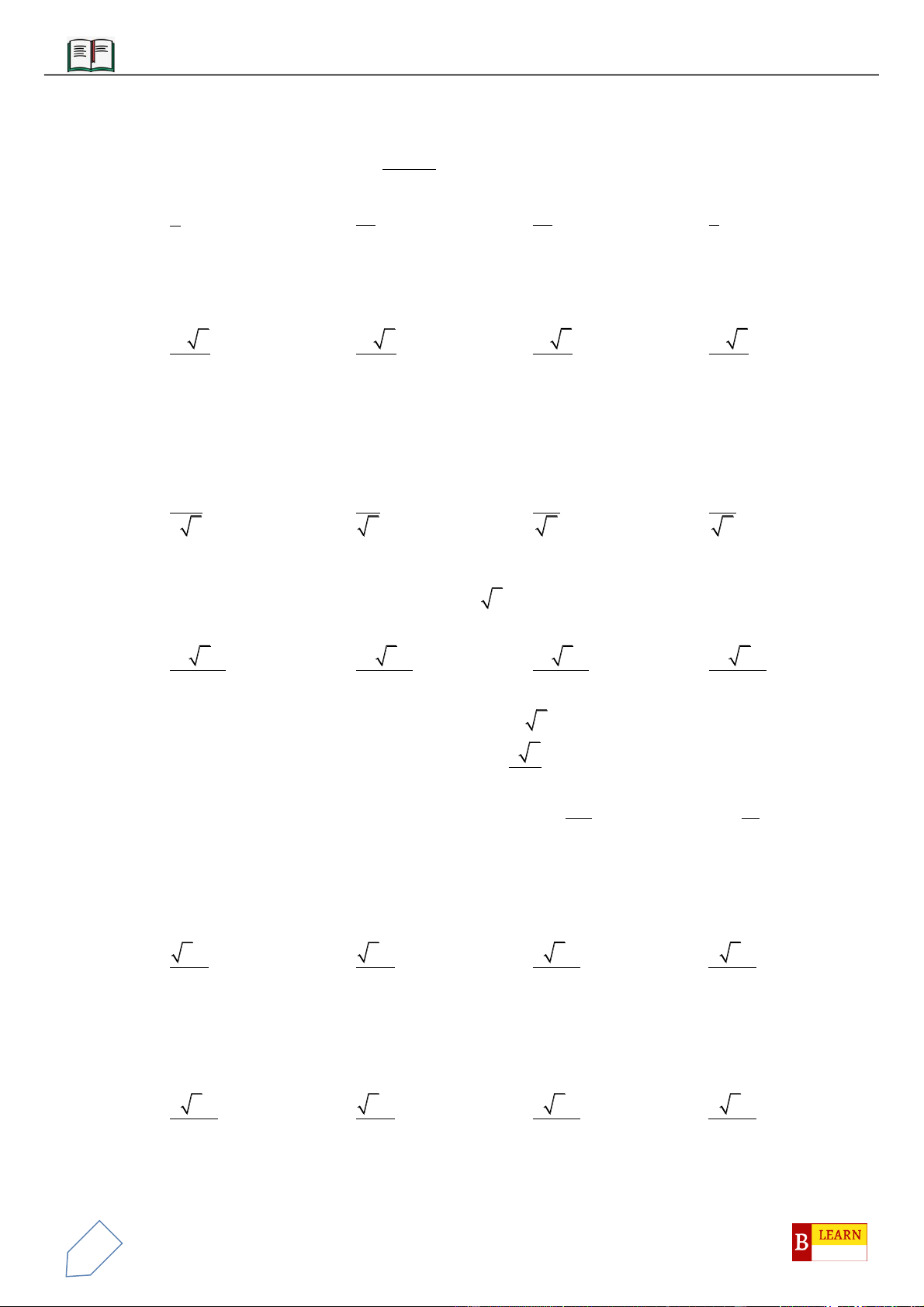
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

24

Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H là điểm trên cạnh SD sao cho

53SH SD=

, mặt phẳng

( )



qua B, H và song song với đường thẳng AC cắt hai cạnh SA, SC lần

lượt tại E, F. Tính tỉ số thể tích

.

C BEHF

S ABCD

V

A.

1

.

7

B.

3

.

20

C.

6

.

35

D.

1

.

6

Câu 17: Cho lăng trụ tam giác

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Độ dài cạnh bên bằng

4a

. Mặt

phẳng

( )

BCC B



vuông góc với đáy và

30B BC



=

. Thể tích khối chóp

.ACC B



là:

A.

3

2

a

. B.

3

12

a

. C.

3

18

a

. D.

3

6

a

.

Câu 18: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

. cạnh

2BC a=

và

60ABC =

. Biết tứ giác

BCC B



là hình thoi có

B BC



nhọn. Biết

( )

BCC B



vuông góc với

( )

ABC

và

( )

ABB A



tạo với

( )

ABC

góc

45

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

37

a

. B.

3

7

a

. C.

3

7

a

. D.

3

6

7

a

.

Câu 19: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

,

30ABC =

. Điểm

M

là trung

điểm cạnh

AB

, tam giác

MA C



đều cạnh

23a

và nằm trong mặt phẳng vuông góc với đáy. Thể

tích khối lăng trụ

.ABC A B C

  

là

A.

3

72 2

7

a

. B.

3

24 3

7

a

. C.

3

72 3

7

a

. D.

3

24 2

7

a

.

Câu 20: Cho lăng trụ tam giác đều

.ABC A B C

  

có

3AA a



=

. Gọi I là giao điểm của

AB



và

AB



. Biết

khoảng cách từ I đến mặt phẳng

( )

BCC B



bằng

3

2

a

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

3Va=

. B.

3

Va=

. C.

3

4

a

V =

. D.

3

4

a

V =

.

Câu 21: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có tất cả các cạnh bằng

a

. Gọi

M

,

N

lần lượt là

trung điểm của các cạnh

AB

và

BC



. Mặt phẳng

( )

A MN



cắt cạnh

BC

tại

P

. Tính thể tích của

khối đa diện

.MBP A B N



A.

3

24

a

. B.

3

12

a

. C.

3

73

96

a

. D.

3

73

32

a

.

Câu 22: Cho hình lăng trụ tam giác đều

.ABC A B C

  

có tất cả các cạnh bằng

a

. Gọi

,MN

lần lượt là

trung điểm của các cạnh

AB

và

BC



. Mặt phẳng

( )

A MN



cắt cạnh

BC

tại

.P

Thể tích khối đa

diện

.MBP A B N



bằng.

A.

3

73

68

a

. B.

3

32

a

. C.

3

73

96

a

. D.

3

73

32

a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

25

Câu 23: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình vuông cạnh

a

. Các cạnh bên tạo với

đáy một góc

o

60

. Đỉnh

A



cách đều các đỉnh

, , ,A B C D

. Trong các số dưới đây, số nào ghi giá trị

thể tích của hình lăng trụ nói trên?

A.

3

6

9

a

. B.

3

2

a

. C.

3

6

2

a

. D.

3

6

3

a

.

Câu 24: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



lên

mặt phẳng

( )

ABC

trùng với trung điểm cạnh

BC

. Góc giữa

BB



và mặt phẳng

( )

ABC

bằng

60

. Tính thể tích khối lăng trụ

.ABC A B C

  

.

A.

3

8

a

. B.

3

23

8

a

. C.

3

4

a

. D.

3

33

8

a

.

Câu 25: Cho hình lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

2a

, hình chiếu của

A



trên mặt phẳng

( )

ABC

là trung điểm cạnh

BC

. Biết góc giữa hai mặt phẳng

( )

ABA



và

( )

ABC

bằng

45

. Tính thể tích

V

của khối chóp

.A BCC B



.

A.

3

2

a

. B.

3

Va=

. C.

3

3a

. D.

3

23

3

a

.

Câu 26: Khối lăng trụ tam giác đều

. ' ' 'ABC A B C

có khoảng cách từ

A

đến mặt phẳng

( )

'A BC

bằng 3 và

góc giữa hai mặt phẳng

( )

'A BC

và

( )

ABC

bằng

0

60

. Tính thể tích

V

khối lăng trụ đã cho?

A.

24 3V =

. B.

83V =

. C.

83

3

V =

. D.

83

9

V =

.

Câu 27: Khối lăng trụ đứng

. ' ' 'ABC A B C

có đáy là tam giác vuông cân tại

A

. Biết khoảng cách từ

A

đến

mặt phẳng

( )

'A BC

bằng 3 và góc giữa hai mặt phẳng

( )

'A BC

và

( )

ABC

bằng

0

60

. Tính thể tích

V

khối lăng trụ đã cho?

A.

24 3V =

. B.

83V =

. C.

72V =

. D.

24V =

.

Câu 28: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Tính theo

a

thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

12

a

V =

. B.

3

a

V =

. C.

3

24

a

V =

. D.

3

6

a

V =

.

Câu 29: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

;3AB a AD a==

, góc giữa hai mặt phẳng

( )

''ADD A

và mặt phẳng

( )

'ACD

bằng

0

60

. Tính thể tích khối hộp chữ nhật đã cho.

A.

3

6

a

V =

. B.

3

2

4

a

V =

. C.

3

6

2

a

V =

. D.

3

32

4

a

V =

.

Câu 30: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên

mặt phẳng

( )

ABC

trùng với trọng tâm của tam giác

ABC

. Biết khoảng cách giữa hai đường thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ là

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

26

A.

3

24

a

. B.

3

12

a

. C.

3

36

a

. D.

3

6

a

.

Câu 31: Cho hình lăng trụ

.ABC A B C

  

, đáy

ABC

là tam giác đều cạnh

x

. Hình chiếu của đỉnh

A



lên

mặt phẳng

( )

ABC

trùng với tâm

ABC

, cạnh

2AA x



=

. Khi đó thể tích khối lăng trụ là:

A.

3

11

12

x

. B.

3

39

8

x

. C.

3

2

x

. D.

3

11

4

x

.

Câu 32: Cho hình hộp

.ABCD A B C D

   

có đáy là hình chữ nhật với

3, 7AB AD==

và cạnh bên bằng

1

. Hai mặt bên

( )

ABB A



và

( )

ADD A



lần lượt tạo với đáy các góc

45

và

60

. Thể tích khối

hộp bằng

A.

33

B.

77

C.

7

D.

3

Câu 33: Cho hình hộp

.ABCD A B C D

   

có đáy là hình chữ nhật với

3, 7AB AD==

và cạnh bên bằng

1

. Hai mặt bên

( )

ABB A



và

( )

ADD A



lần lượt tạo với đáy các góc

45

và

60

. Thể tích khối

hộp bằng

A.

33

B.

77

C.

7

D.

3

Câu 34: Cho hình lăng trụ

ABCA B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

A



lên

mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường thẳng

AA



và

BC

bằng

3

4

a

. Tính thể tích

V

của khối lăng trụ

.ABCA B C

  

A.

3

.

6

a

V =

B.

3

.

24

a

V =

C.

3

.

12

a

V =

D.

3

.

3

a

V =

Câu 35: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

)

5;2m−



. Hình chiếu vuông góc

của điểm

A



lên mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa

hai đường

AA



và

BC

bằng

3

4

a

. Tính thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

24

a

V =

. B.

3

12

a

V =

. C.

3

a

V =

. D.

3

6

a

V =

.

Câu 36: Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

3a

, hình chiếu của

'A

trên mặt phẳng

( )

ABC

trùng với tâm đường tròn ngoại tiếp tam giác

ABC

. Cạnh

'AA

hợp với mặt phẳng đáy

một góc

45

. Thể tích của khối lăng trụ

. ' ' 'ABC A B C

tính theo

a

bằng.

A.

3

9

4

a

. B.

3

27

4

a

. C.

3

4

a

. D.

3

27

6

a

.

Câu 37: Cho lăng trụ tam giác

.ABC A B C

  

. Các điểm

M

,

N

,

P

lần lượt thuộc các cạnh

AA



,

BB



,

CC



sao cho

1

2

AM

AA

=



,

2

3

BN

BB

=



và mặt phẳng

( )

MNP

chia lăng trụ thành hai phần có thể tích bằng

nhau. Khi đó tỉ số

CP

CC



là

A.

1

4

. B.

5

12

. C.

1

3

. D.

1

2

.

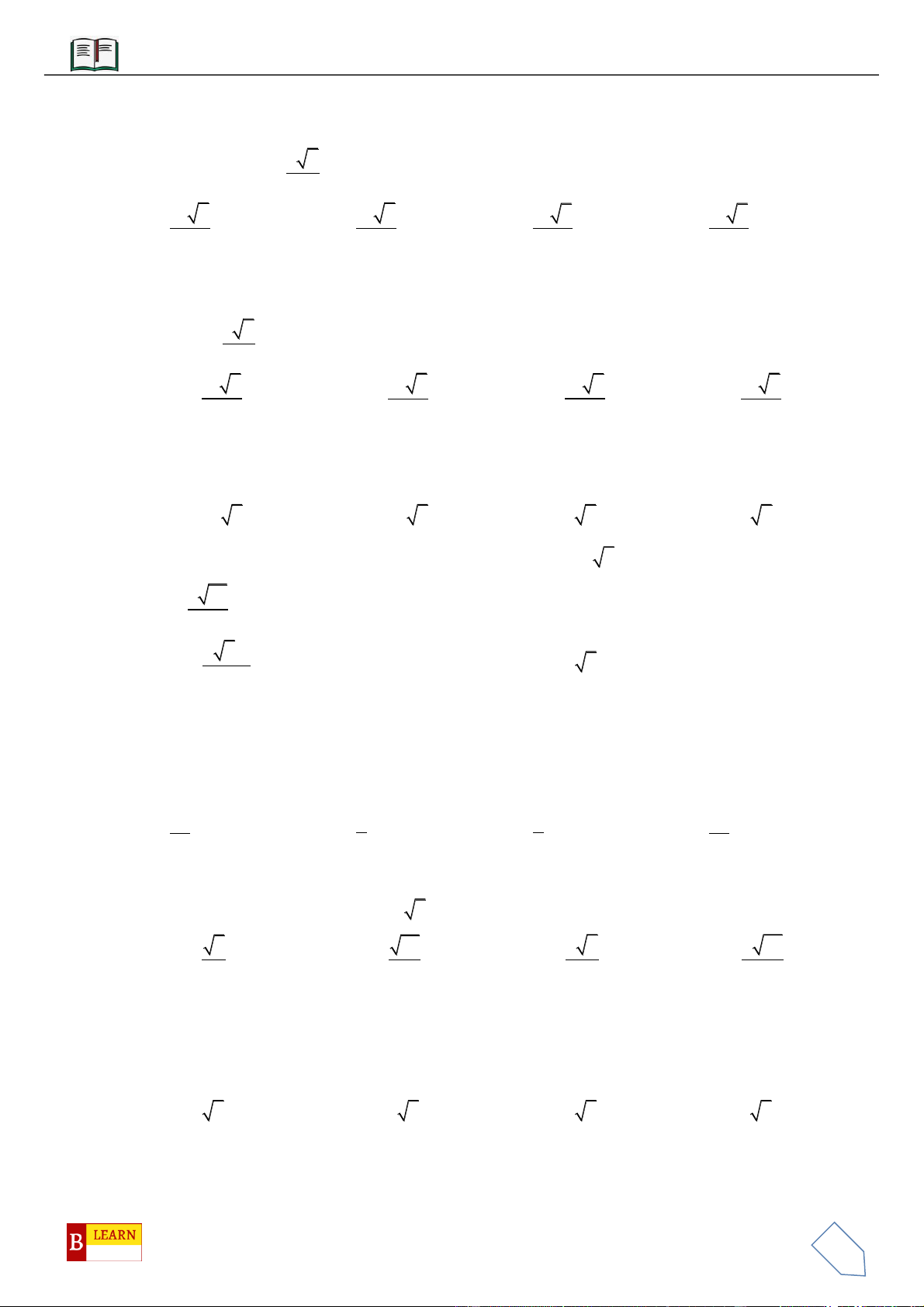
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

27

Câu 38: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên

mặt phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ là

A.

3

6

a

. B.

3

a

. C.

3

24

a

. D.

3

12

a

.

Câu 39: Cho hình lăng trụ

C

có đáy là tam giác đều cạnh

H

. Hình chiếu vuông góc của điểm

D

lên mặt

phẳng

M

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường thẳng

AA



và

BC

bằng

3

4

a

. Tính thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

12

a

V =

. B.

3

a

V =

. C.

3

24

a

V =

. D.

3

6

a

V =

.

Câu 40: Cho khối lăng trụ tam giác đều

1 1 1

ABCA B C

, góc giữa mặt phẳng

( )

1

A BC

và đáy bằng

30

, diện

tích tam giác

1

A BC

bằng 8. Tính thể tích

V

của khối lăng trụ đã cho.

A.

27 3V =

. B.

24 3V =

. C.

93V =

. D.

83V =

.

Câu 41: Cho khối hộp chữ nhật

.ABCD A B C D

   

có

,3AB a AD a==

, khoảng cách từ

A

đến

( )

A BD



bằng

15

5

a

. Tính thể tích

V

của khối hộp chữ nhật đã cho.

A.

3

23

3

a

V =

. B.

3

3Va=

. C.

3

23Va=

. D.

3

Va=

.

Câu 42: Cho hình chóp

.S ABCD

có thể tích

V

, đáy là hình chữ nhật, mặt phẳng song song với đáy cắt

các cạnh

SA

,

SB

,

SC

,

SD

lần lượt tại

M

,

N

,

P

,

Q

. Gọi

M



,

N



,

P



,

Q



lần lượt là hình

chiếu vuông góc của

M

,

N

,

P

,

Q

lên mặt đáy. Thể tích khối hộp chữ nhật

.MNPQ M N P Q

   

có giá trị lớn nhất là

A.

4

27

V

. B.

2

9

V

. C.

4

9

V

. D.

2

27

V

.

Câu 43: Cho hình hộp đứng

.ABCD A B C D

   

, đáy là một hình thoi. Biết diện tích của hai mặt chéo

ACC A



,

BDD B



lần lượt là 1 và

5

và

90BA D



=

. Tính thể tích

V

của khối hộp đã cho.

A.

5

2

V =

. B.

10

2

V =

. C.

25

5

V =

. D.

2 10

5

V =

.

Câu 44: Cho lăng trụ

.ABCD A B C D

   

với đáy

ABCD

là hình thoi,

2AC a=

,

0

120BAD =

. Hình chiếu

vuông góc của điểm

B

trên mặt phẳng

( )

A B C D

   

là trung điểm cạnh

AB



, góc giữa mặt phẳng

( )

AC D



và mặt đáy lăng trụ bằng

o

60

. Tính thể tích

V

của khối lăng trụ

.ABCD A B C D

   

.

A.

3

3Va=

. B.

3

63Va=

. C.

3

23Va=

. D.

3

33Va=

.

Câu 45: Cho khối lăng trụ tứ giác đều

.ABCD A B C D

   

có khoảng cách giữa hai đường thẳng

AB

,

AD



bằng 2 và độ dài đường chéo của mặt bên bằng 5. Tính thể tích

V

của khối lăng trụ đã cho, biết

độ dài cạnh đáy nhỏ hơn độ dài cạnh bên.

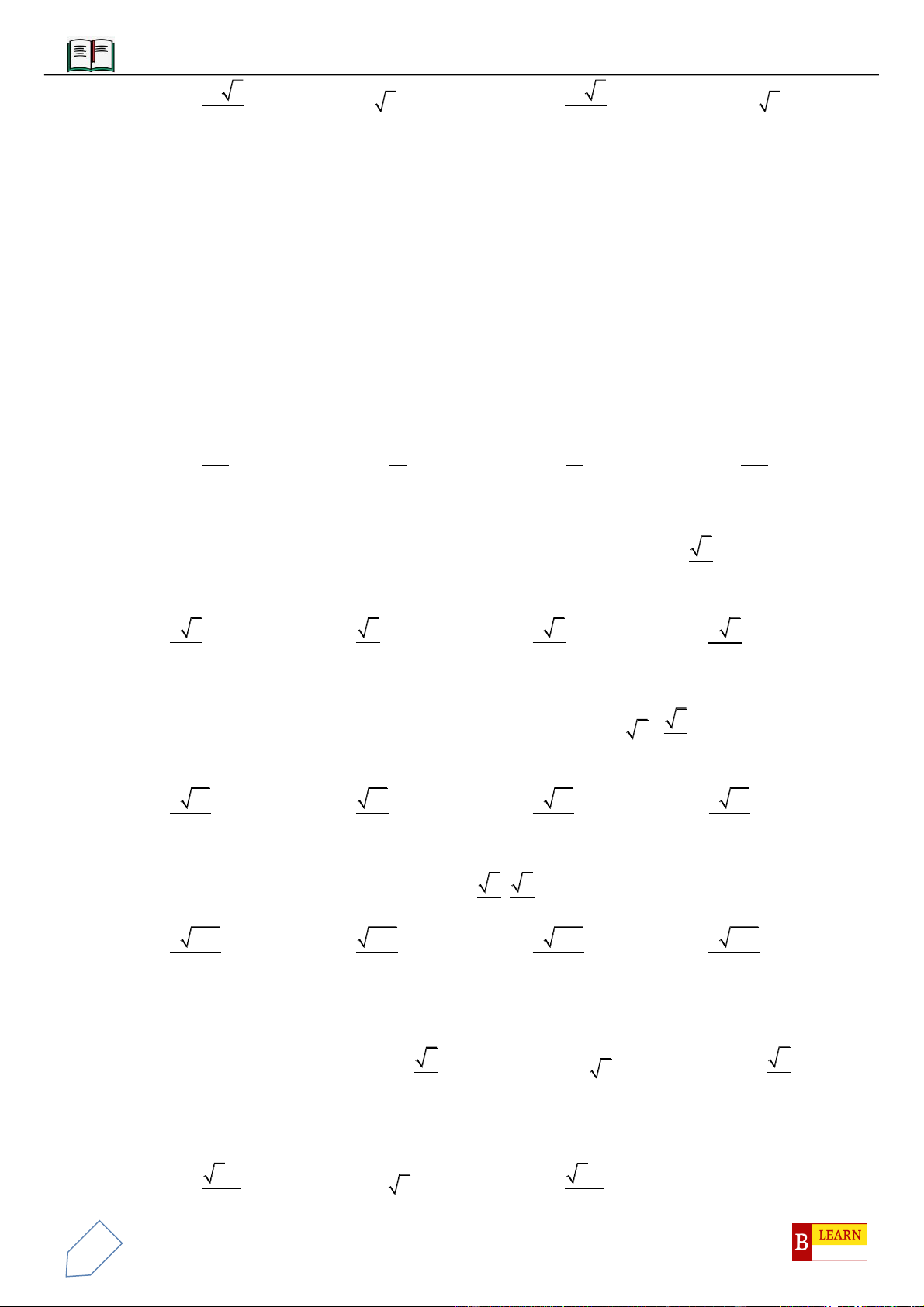
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

28

A.

10 5

3

V =

. B.

20 5

. C.

20 5

3

V =

. D.

10 5V =

.

Câu 46: Cho khối lập phương

( )

H

có cạnh bằng 1. Qua mỗi cạnh của

( )

H

dựng một mặt phẳng không

chứa các điểm trong của

( )

H

và tạo với hai mặt của

( )

H

đi qua cạnh đó những góc bằng nhau.

Các mặt phẳng như thế giới hạn một đa diện

( )

H



. Tính thể tích của

( )

H



.

A.

4

. B.

2

. C.

8

. D.

6

.

Câu 47: Một khối hộp chữ nhật có các kích thước thỏa mãn

a

,

b

,

c

1; 4 



và

6a b c+ + =

. Tìm giá trị

nhỏ nhất của diện tích toàn phần của khối hộp chữ nhật đó.

A.

18

. B.

24

. C.

9

. D.

12

.

Câu 48: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác cân

ABC

với

AB AC a==

, góc

120BAC =

, mặt phẳng

( )

AB C



tạo với đáy một góc

30

. Tính thể tích

V

của khối lăng trụ đã

cho.

A.

3

9

8

a

V =

. B.

3

6

a

V =

. C.

3

8

a

V =

. D.

3

8

a

V =

.

Câu 49: Cho khối lăng trụ tam giác đều

. ' ' 'ABC A B C

có khoảng cách từ điểm

'A

đến mặt phẳng

( )

''AB C

bằng

1

và

cosin

góc giữa hai mặt phẳng

( )

''AB C

và

( )

''ACC A

bằng

3

6

. Tính thể tích khối

lăng trụ

. ' ' 'ABC A B C

.

A.

32

2

. B.

2

. C.

32

4

. D.

32

8

.

Câu 50: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông tại

A

. Khoảng cách từ

A



đến các

đường thẳng

AB



,

AC



và mặt phẳng

( )

AB C



lần lượt bằng

1

;

2

;

3

2

. Tính thể tích khối lăng

trụ

.ABC A B C

  

.

A.

6 15

5

. B.

15

5

. C.

2 15

5

. D.

3 15

5

.

Câu 51: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông tại

A

. Khoảng cách từ

'A

đến các

đường thẳng

', ', ' 'AB AC B C

lần lượt bằng

32

1; ;

22

. Tính thể tích của khối lăng trụ

.ABC A B C

  

A.

6 210

35

. B.

210

35

. C.

2 210

35

. D.

3 210

35

.

Câu 52: Trong các khối lăng trụ đều

.ABC A B C

  

có diện tích tam giác

A BC



là

3

. Gọi



là góc giữa hai

mặt phẳng

( ) ( )

,A BC ABC



. Tính

tan



khi thể tích khối lăng trụ đạt lớn nhất.

A.

tan 2



=

. B.

2

tan

2



=

. C.

tan 2



=

. D.

2

tan

3



=

.

Câu 53: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông cân đỉnh

A

, mặt bên là hình vuông

''BCC B

, khoảng cách giữa

AB



và

CC



bằng

a

. Tính thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

2

3

a

V =

. B.

3

2Va=

. C.

3

2

a

V =

. D.

3

Va=

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

29

Câu 54: Cho khối lăng trụ tam giác đều

.ABC A B C

  

có

3AA a



=

. Gọi

I

là giao điểm của

AB



và

AB



Cho biết khoảng cách từ điểm

I

đến mặt phẳng

( )

BCC B



bằng

3

2

a

. Tính thể tích

V

của khối

lăng trụ

.ABC A B C

  

theo

a

.

A.

3

3Va=

. B.

3

Va=

. C.

3

4

a

V =

. D.

3

4

a

V =

.

Câu 55: Cho lăng trụ đứng

.ABCD A B C D

   

có đáy là hình bình hành. Các đường chéo

DB



và

AC



lần

lượt tạo với đáy góc

0

45

và

0

30

. Biết

0

60BAD =

, chiều cao hình lăng trụ bằng

a

. Tính thể tích

V

khối lăng trụ

.ABCD A B C D

   

.

A.

3

3Va=

. B.

3

2

a

V =

. C.

3

2

3

a

V =

. D.

3

2

a

V =

.

Câu 56: Cho lăng trụ đứng

. ' ' 'ABC A B C

đáy

ABC

là tam giác vuông cân tại

A

,

E

là trung điểm của

''BC

,

'CB

cắt

BE

tại

M

. Tính thể tích

V

của khối tứ diện

ABCM

, biết

3AB a=

và

'6AA a=

A.

3

8Va=

. B.

3

62Va=

. C.

3

6Va=

. D.

3

7Va=

.

Câu 57: Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông

ABC

vuông tại

A

,

AC a=

,

60ACB =

. Đường thẳng

BC



tạo với mặt phẳng

( )

A C CA



góc

30

. Tính thể tích khối lăng trụ

đã cho.

A.

3

6a

. B.

3

2

a

. C.

3

a

D.

3

23a

.

Câu 58: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác cân, với

AB AC a==

và góc

120BAC =

, cạnh bên

AA a



=

. Gọi

I

là trung điểm của

CC



. Cosin của góc tạo bởi hai mặt

phẳng

( )

ABC

và

( )

AB I



bằng

A.

33

11

. B.

10

. C.

30

10

. D.

11

.

Câu 59: Cho hình lăng trụ

.ABC A B C

  

có

AA



= 2, khoảng cách từ A đến các đường thẳng

BB



,

CC



lần

lượt bằng 1 và 2; khoảng cách từ C đến đường thẳng

BB



bằng

5

. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A. 2. B.

2

.

3

C. 4. D.

4

.

3

Câu 60: Cho khối lăng trụ

.ABC A B C

  

, khoảng cách từ C đến đường thẳng

BB



bằng

5

, khoảng cách từ

A đến đường thẳng

BB



và

CC



lần lượt bằng 1 và 2, hình chiếu vuông góc của A lên mặt phẳng

()ABC

  

là trung điểm M của

BC



và

A M 5



=

. Thể tích khối lăng trụ đã cho bằng

A.

25

.

3

B.

15

.

3

C.

5.

D.

2 15

.

3

Câu 61: Cho hình lăng trụ

.ABC A B C

  

, khoảng cách từ

A

đến các đường thẳng

,BB CC



lần lượt là

1

và

3

, khoảng cách từ

C

đến

BB



bằng

2

. Hình chiếu vuông góc của

A

lên mặt phẳng

( )

A B C

  

là trọng tâm

G



của tam giác

A B C

  

và

4

3

AG



=

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng:

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

30

A.

2

. B.

2

3

. C.

4

. D.

4

3

.

Câu 62: Cho khối hộp

.ABCD A B C D

   

có

AB



vuông góc với mặt phẳng

( )

ABCD

; góc giữa

AA



với

( )

ABCD

bằng

45

. Khoảng cách từ

A

đến các đường thẳng

,BB DD



cùng bằng

1

. Góc giữa

mặt phẳng

( )

BB C C



và mặt phẳng

( )

C CDD



bằng

60

. Thể tích của khối hộp đã cho bằng:

A.

23

. B.

2

. C.

3

. D.

33

.

Câu 63: Cho khối đa diện

. ' ' 'ABC A B C

có

'/ / '/ / 'AA BB CC

.

Biết khoảng cách từ A đến

'BB

bằng 1,

khoảng cách từ A đến

'CC

bằng

3

; Khoảng cách giữa hai đường thẳng

'BB

,

'CC

bằng 2 và

' 1, ' 2, ' 3AA BB CC= = =

.Thể tích khối đa diện

. ' ' 'ABC A B C

bằng

A.

3

2

. B.

33

2

. C.

1

2

. D.

3

.

Câu 64: Cho hình lăng trụ

. ' ' 'ABC A B C

.

Biết khoảng cách từ A đến

'BB

bằng 1, khoảng cách từ A đến

'CC

bằng

3

; góc giữa hai mặt bên của lăng trụ chung cạnh

'AA

bằng

90

o

. Hình chiếu của A

lên mặt phẳng

( )

' ' 'A B C

là trung điểm M của cạnh

''BC

và

23

'

3

AM=

.Thể tích khối đa diện

. ' ' 'ABC A B C

bằng

A. 2. B. 1. C.

3

. D.

23

3

.

---------------------------------HẾT-------------------------------

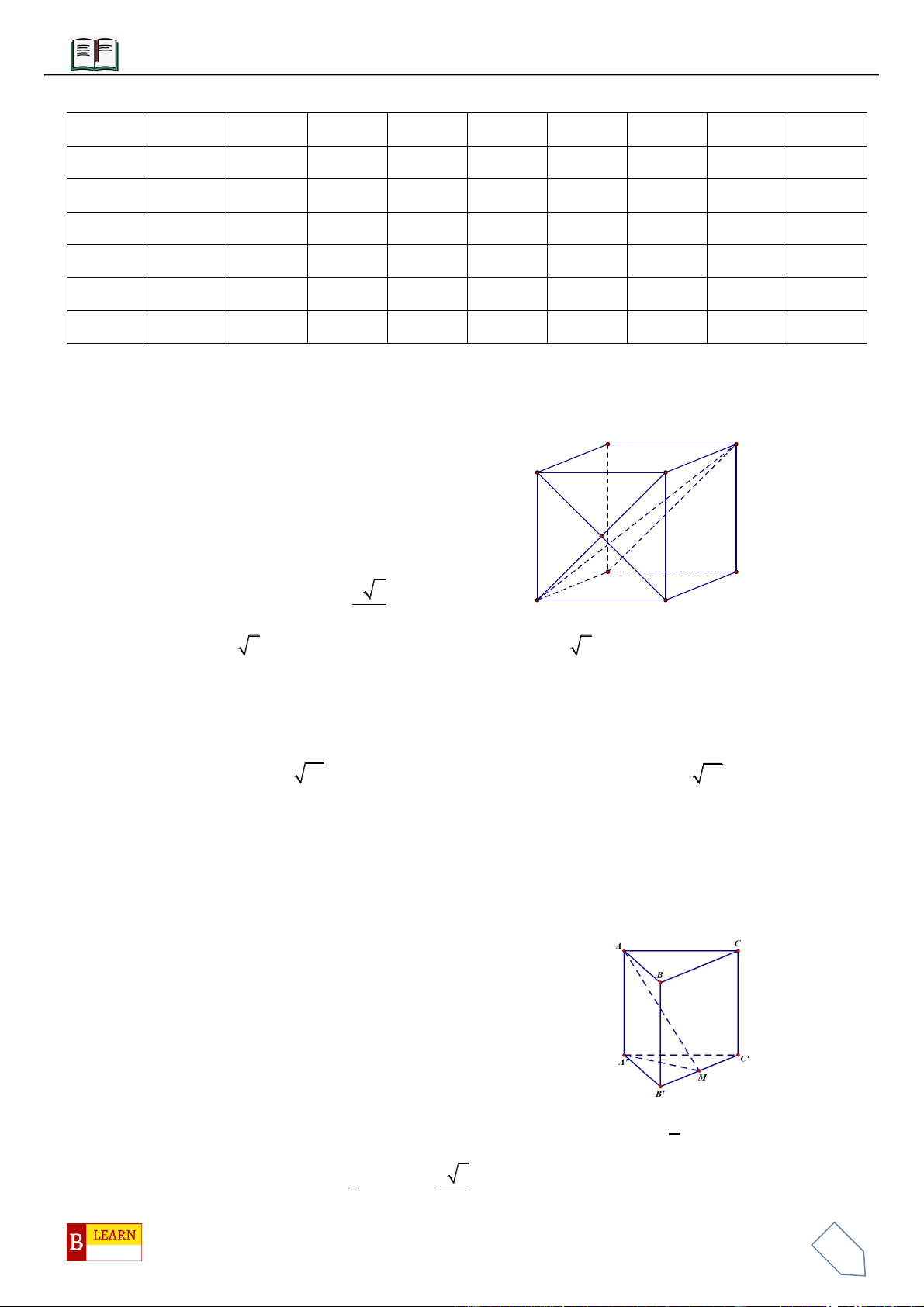
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

31

BẢNG ĐÁP ÁN

1.B

2.D

3.D

4.A

5.A

6.B

7.C

8.B

9.A

10.C

11.A

12.C

13.B

14.B

15.B

16.B

17.D

18.C

19.A

20.A

21.C

22.C

23.C

24.D

25.B

26.A

27.C

28.A

29.D

30.B

31.A

32.D

33.D

34.C

35.B

36.B

37.C

38.D

39.A

40.D

41.B

42.C

43.A

44.B

45.D

46.B

47.A

48.C

49.A

50.D

51.D

52.C

53.C

54.A

55.D

56.C

57.A

58.C

59.A

60.D

61.D

62.C

63.D

64.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn B

Đặt cạnh hình lập phương là

x

.

Gọi

O AD A D



=

, ta có

( )

D O DCB A

  

⊥

.

Ta có:

( )

//A C DCB A C D

    



nên

( ) ( )

( )

;;

2

;

2

d C D A C d C D DCB A

x

d D DCB A D O a

      

=

   

= = = =

.

Do đó,

2xa=

. Thể tích khối lập phương là:

33

22V x a==

.

Câu 2: Chọn D

Đặt độ dài các cạnh của hình hộp chữ nhật là

,,a b c

, ta có:

10

20 40 10

80

ab

bc abc

ca

=



=  =





=



. Thể tích của khối hộp chữ nhật là:

( )

3

40 10V abc cm==

.

Câu 3: Chọn D

Giả sử độ dài mỗi cạnh của khối hộp là

,,a b c

, thể tích khối hộp là

1

V abc=

.

Khi tăng độ dài mỗi cạnh lên 2 lần thì độ dài mỗi cạnh là

2 ,2 ,2a b c

và có thể tích là

21

2 .2 .2 8 8V a b c abc V= = =

Do đó, thể tích khối hộp chữ nhật tăng lên 8 lần.

Câu 4: Chọn A

Gọi M là trung điểm

BC



. Ta có

AM B C

A M B C





⊥



  

⊥



( ) ( )

( )

, 60AB C A B C A MA

     

 = = 

Tam giác

A MB



vuông tại M, có

60B A M



=

nên

cos60

2

a

A M a



=  =

.

(

)

.tanAA A M AMA

  

=

3

.tan60

22

aa

=  =

.

O

C'

B'

C

D'

A'

A

D

B

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

32

2

13

. .sin60

24

ABC

a

S AB AC=  =

. Vậy

3

.

8

ABC

a

V AA S



==

.

Câu 5: Chọn A

Ta có

AB BC a==

.

Thể tích lăng trụ đa cho là

3

1

. . . .

22

ABC

a

V S BB a a a





= = =

.

Câu 6: Chọn B

Ta có

AB BC

A B BC



⊥





⊥



( ) ( )

( )

' ' , 60A D BC ABCD A BA



 = = 

03

' .tan60 3 . . ' 3AA AB a V AB AAD AA a= =  = =

Câu 7: Chọn C

Dùng ảnh câu 6 nhé !

Ta có

( )

' , ' ' 30A C ABB A CA B



= = 

2 2 2 2

0

''

' .tan30 ' 2

33

a A A a A A

BC A B a A A a

++

= =  =  =

3

. . ' 2V AB AAD AA a==

Câu 8: Chọn B

Gọi

M

,

N

lần lượt là trung điểm

AB



,

CC



;

G

là trung điểm

MN

. Suy ra

G

là trọng tâm tứ diện

CA B C

  

.

( )

P

qua

G

và cắt các cạnh

AA



,

BB



,

CC



lần lượt tại

E

,

F

Q

thì

3

4

AE BF CQ AA



= = =

.

Thể tích khối lăng trụ là

.

ABC

V AA S



=

.

Thể tích tứ diện

CEFQ

là:

1 1 3 1 1

. . . 0,25

3 3 4 4 4

CEFQ

CEFQ EFQ ABC

V

V CQ S AA S V

V



= = =  = =

.

Câu 9: Chọn A

Gọi

O AC BD=

. Vì

12

. ; .S AC AA S BD AA



==

và

90

2

o

BD

BA D OA



=  =

Tam giác

A AO



vuông tại

A

có

2

2 2 2 2

4

AC

OA AA OA AA

  

= + = +

Suy ra

22

2

44

BD AC

AA



=+

hay

22

2

21

2

22

4

21

2

4

44

S

AA AA

AA A

S

A

S



=+

−

=



Do đó

( )

2

22

4

1 2 1

21

4.

1

22

ABCD

S S S S

V S AA AC BD AA

SS

AA



=  =   =

−

=



.

B'

A'

D'

D

B

C

A

C'

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

33

Câu 10: Chọn C

Mặt phẳng

( ) ( )

0

90 1 ,AMNP SC ANC SC AM⊥  = ⊥

.

Do

( ) ( ) ( )

0

90 2SAB BC BC AM AM SBC AM MC AMC⊥  ⊥  ⊥  ⊥  =

Tương tự ta có

( )

0

90 3APC =

Do

ABCD

là hình vuông nên từ

( ) ( ) ( )

1 , 2 , 3

suy ra

AC

là đường kính mặt cầu ngoại tiếp đa diện

ABCDMNP

.

Xét tam giác

SAC

có

( )

3

03

4

sin60 4 3 2 3 2 3 32 3

3

AC

AC a R a V a a

SC



=  =  =  = =

.

Câu 11: Chọn A

Gọi

2x

là cạnh của tam giác đều, Gọi

,OK

lần lượt là

trung điểm của

,AB BC

Kẻ

OCK C



⊥

Ta có

CH C O



⊥

và

CH AB⊥

nên

( )

CH ABC



⊥

và

( )

,'d C ABC CH a==

Suy ra:

2 2 2

1 1 1

CH CC CO

=+



hay

2 2 2

1 1 1

3a CC x

=+



(1)

Ta có hình chiếu vuông góc của tam giác

ABC



lên mặt

phẳng

( )

BCC B



là tam giác

'KBC

Do đó

'

1

cos

3

KBC

ABC

S





==

Ta có:

'

1

..

2

KBC

S x CC



=

và

2 2 2 2

'

11

. . . . 3

22

ABC

S AB C O AB CC CO x CC x



  

= = + = +

Do đó

2 2 2 2 2 2

11

. . 3 3 2 3 5 12

23

x CC x CC x CC CC x CC x

    

= +  = +  =

(2)

Từ

( ) ( )

1 , 2

ta có

22

2 2 2

1 1 4 3

59

5

a

CC a CC

a CC CC



= +  =  =



Suy ra

3

2

a

x =

. Vậy thể tích khối lăng trụ là

23

3 3 3 9 15

..

4 20

5

ABC

a a a

V S CC



= = =

.

H

K

O

A'

B'

C'

C

B

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

34

Câu 12: Chọn C

Gọi

M

là trung điểm cạnh

BC

,

H

là hình chiếu

vuông góc của

A

lên

'AM

ta có

( )

d C'; A'BC d A; A'BC AH==

.

Mà

22

AA' AM 4a

AH

3

A'A AM



==

+

22

AA' a 2 4a

AA' 4a

3

A'A 2a



 =  =

+

.

3

11

V AA' AB AC 4a 2a 2a 8a

22

=   =    =

.

Câu 13: Chọn B

Gọi

M

là trung điểm của

BC

, kẻ

( )

AH A M AH A BC



⊥  ⊥

( )

,AH d A A BC a



 = =

và góc giữa

( )

A BC



với

( )

ABC

là

A MA





=

.

Ta có

36

, 2 ,

sin sin sin

3

tan

cos

AH

AM BC AM

AA AM

  



= = = =



==

.

Khi đó

( )

2

1 27 27

. . .

2

sin .cos

1 cos .cos

V S h AM BC AA





= = = =

−

( )( )

3

2 2 2

222

27 2 27 2 81 3

2

2cos 1 cos 1 cos

3

  



=  =

−−



+ − + −





.

Dấu

""=

xảy ra

3

cos

3



=

.

Câu 14: Chọn B

Gọi

,KJ

lần lượt là trung điểm của

,AB BC

.

Gọi

x

là độ dài cạnh

AB

.

3

2

x

AJ CK==

.

Ta có

( )

CH ABC



⊥

( )

,d C ABC CH a



 = =

.

Mặt khác

( )

AJ BCC B



⊥

.

Nên

( ) ( )

(

)

,ABC BCC B

  

(

)

,CH AJ=



=

(

)

,CH AG=

(

cos sin



=

).

Ta có

1

sin

23

MG

AG



==

23

AG

MG=

2

3

3.2

AJ

==

3

6

2.3 3

xx

=

.

M

B

C

A'

B'

C'

A

H

M

G

J

K

C

B

A

C'

B'

A'

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

35

3 6 3 6

HC x a x

=  =

2xa=

mà

( )

,d C ABC CH a



==

.

22

.CH CK

CC

CK CH



=

−

( )

2

23

2

3

a

aa

=

−

6

2

a

=

. Vậy

2

3

.

4

x

V CC



=

( )

2

23

6

.

42

a

=

3

32

2

a

=

.

Câu 15: Chọn B

Từ

B

kẻ

BI AC⊥

( )

BI AA C C



⊥

.

Từ

I

kẻ

IH AA



⊥

( ) ( )

( )

, BIAA C C AA B B H

  

=





.

Theo giải thiết ta có

3AC =

.AB BC

BI

AC

=

2=

.

Xét tam giác vuông

BIH

có

tan

BI

BHI

IH

=

tan

BI

IH

BHI

=

42

3

IH=

.

Xét tam giác vuông

ABC

có

2

.AI AC AB=

2

AB

AI

AC

 = =

.

Gọi

M

là trung điểm cả

AA



, do tam giác

AA C



cân tại

C

nên

CM AA



⊥

//CM IH

.

Do

2

3

AI AH

AC AM

==

2

3

AH

AM

=

1

3

AH

AA

=



.

Trong tam giác vuông

AHI

kẻ đường cao

HK

ta có

42

9

HK =



chiều cao của lăng trụ

.ABCD A B C D

   

là

3h HK=

42

3

=

.

Vậy thể tích khối lăng trụ

.ABCD A B C D

   

là

.

..

ABCD A B C D

V AB AD h

   

=

42

63

3

=

8=

.

Câu 16: Chọn B

Đặt

.S ABCD

VV=

Trong tam giác SOD ta có:

3

. . 1 3 .

4

IS SI

IS BO HD SE SF

IO BD HS IO SO SA SC

=  =  = = =

Ta có:

.

33

.

5 10

S HBC

S DBC

V

SH V

V

V SD

= =  =

Mặt khác:

.

13

.

4 40

C FHB

C SHB

V

CF V

V

V CS

= =  =

Mà:

.

..

.

63

2.

40 20

C BEHF

C BEHF C FHB

S ABCD

V

VV

V

= =  =

M

C'

B'

D'

C

D

A

B

A'

I

H

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

36

Câu 17: Chọn D

Gọi

H

là hình chiếu của

B



trên

BC

. Từ giả thiết suy ra:

( )

B H ABC



⊥

.

1

. .sin

2

BB C

S BB BC B BC





=

1

4 . .sin30

2

aa=

2

a=

.

Mặt khác:

1

.

2

BB C

S B H BC



=

2

BB C

S

BH

BC



=

2

a

==

.

LT ABC

V B H S



=

2

3

2.

4

a

a=

3

2

a

=

.

..

1

2

A CC B A CC B B

VV

   

=

1 2 1

.

2 3 3

LT LT

VV==

3

13

.

32

a

=

3

6

a

=

.

Câu 18: Chọn C

Do

ABC

là tam giác vuông tại

,A

cạnh

2BC a=

và

60ABC =

nên

AB a=

,

3AC a=

.

Gọi

H

là hình chiếu vuông góc của

B



lên

BC



H

thuộc đoạn

BC

(do

B BC



nhọn)

( )

B H ABC



⊥

(do

( )

BCC B



vuông góc với

( )

ABC

).

Kẻ

HK

song song

AC

( )

K AB

HK AB⊥

(do

ABC

là tam giác vuông tại

A

).

( ) ( )

, 45 (1)ABB A ABC B KH B H KH



   

 = =   =





Ta có

BB H





vuông tại

H

22

4 (2)BH a B H



 = −

Mặt khác

HK

song song

AC

BH HK

BC AC

=

.2

(3)

3

HK a

BH

a

=

Từ (1), (2) và (3) suy ra

22

.2

4

3

B H a

a B H

a



−=

12

7

B H a



=

.

Vậy

3

. ' '

13

. . .

2

7

ABC A B C ABC

a

V S B H AB AC B H





= = =

.

Câu 19: Chọn A

Gọi

H

là trung điểm của

MC

.

Ta có

( ) ( )

( )

A H MC

A MC ABC A H ABC

A MC ABC MC





⊥





⊥  ⊥







=





Tam giác

MA C



đều cạnh

23a

23

3

MC a

A H a



=









=





60



2a

K

H

C'

B'

A'

C

B

A

a

C'

A'

B'

C

B

A

H

4

a

H

C'

B'

A'

C

B

M

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

37

Đặt

0AC x=

, tam giác

ABC

vuông tại

A

có

30ABC =

2

3

BC x

AB x



=







=





Áp dụng công thức tính độ dài trung tuyến ta có

2 2 2 2 2 2

22

4 3 4 3

12

2 4 2 4

7

CA CB AB x x x a

CM a x

++

= −  = −  =

.

Suy ra

2

1 1 12 4 3 24 3

. . .

2 2 7

77

ABC

a a a

S AB AC= = =

.

Do đó

3

.

72 3

.

7

ABC A B C ABC

a

V A H S

  



==

.

Câu 20: Chọn A

.ABC A B C

  

là khối lăng trụ đều nên

ABC

là tam giác đều và

3AA a



=

là chiều cao của khối này.

( ;( )) 3

2 ( ;( )) 2 ( ;( )) 2 3

( ;( )) 2

d A BCC B AB a

d A BCC B d I BCC B a

d I BCC B IB

  

   

= =  = = =

  

.

Gọi

H

là hình chiếu của

A

trên

BC

thì do

ABC

đều và

( ) ( )

ABC BCC B⊥



nên

H

cũng là

hình chiếu của

A

trên

( )

BCC B



và

H

là trung điểm của

BC

.

( ;( )) 3AH d A BCC B a



==

2

23

3

ABC

AH

BC a S a = =  =

.

Vậy thể tích của khối lăng trụ đều đã cho là

23

. 3. 3 3

ABC

V S a aA aA



= = =

.

Câu 21: Chọn C

Gọi

S

là giao điểm của

AM



và

BB



, khi đó

P

là giao điểm

SN

và

BC

.

Ta có

1

..

8

SMBP

SA B N

V

SM SB SP

V SA SB SN



==



.

77

88

MBP A B N SA B N

VV

   

 = =

.

1

.

3

SA B N A B N

V SB S

   





=

11

. . sin60

32

SB A B B N

   

=

1

2 . . sin60

62

a

aa=

3

12

a

=

.

3

.

7 7 3

8 96

MBP A B N SA B N

a

VV

   

 = =

.

P

S

M

N

C

B

A'

B'

C'

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

38

Câu 22: Chọn C

Gọi

Q

là trung điểm của

.BC

Suy ra

AQ A N MP AQ P





là

trung điểm của

BQ

.

Ta có

,,BB A M NP



đồng quy tại

S

và

B

là trung điểm của

BS



2SB a



=

.

23

.

33

8 12

A B N S A B N

aa

SV

   

=  =

.

1

8

SMNP SA B N

VV



=

3

7 7 3

8 96

MBPA B N SA B N

a

VV

   

 = =

.

Câu 23: Chọn C

Gọi

O

là tâm hình vuông

ABCD

.Từ giả thiết

A



cách đều các đỉnh

A

,

B

,

C

ta suy ra hình chiếu

của

A



trên mặt phẳng

ABCD

là

O

hay

AO



là đường cao của khối lăng trụ.

Trong tam giác

A OA



vuông tại

A

và

60A OA



=

, ta có:

6

.tan60 . 3

2

aa

A O OA



= = =

. Diện tích đáy

ABCD

là

2

ACDD

Sa=

.

Thể tích của khối lăng trụ là

3

6

..

2

ABCD

a

V B h S A O



= = =

. Vậy

3

6

2

a

V =

.

Câu 24: Chọn D

Gọi

H

là trung điểm cạnh

BC

. Theo đề ra:

( )

A H ABC



⊥

.

33

22

AB a

AH ==

.

( )

22

33

44

ABC

đvdt

AB a

S



==

.

Ta có:

( )

', '

' 60

', ', 60

AA ABC A AH

A AH

AA ABC BB ABC



=



 = 





= = 



.

Xét

A AH





vuông tại

H

:

3

.tan60

2

A H AH a



=  =

.

Vậy

( )

3

.

33

.

8

ABC A B C ABC

a

V tvA H S đt

  





==

60

°

C'

B'

A'

H

C

B

A

P

M

Q

N

B

C

A'

C'

B'

S

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

39

Câu 25: Chọn B

Ta có:

. . .ABC A B C A A B C A BCC B

V V V

       

=+

..A ABC A BCC B

VV

   

=+

.

Mà

..A BCC B A BCC B

VV

    

=

..A A B C A ABC

VV

   

=

.

Gọi

M

là trung điểm của

BC

,

I

là trung điểm của

AB

và

K

là trung điểm của

IB

. Khi đó:

( )

A M ABC



⊥

.

Mặt khác:

//MK CI

MK AB

CI AB



⊥



⊥



.

MK AB⊥

,

A M AB



⊥

A K AB



⊥

.

Góc giữa hai mặt phẳng

( )

ABA



và

( )

ABC

chính là góc giữa

AK



và

KM

và bằng

A KM



45=

nên tam giác

A KM



vuông cân tại

M

.

Trong tam giác

ABC

:

1 1 2 3 3

..

2 2 2 2

aa

MK CI= = =

Trong tam giác vuông cân

A KM



:

3

2

a

A M MK



==

và

..

1

.

3

A ABC ABC A B C

VV

   

=

.

. . .

1

3

A BCC B ABC A B C ABC A B C

V V V

        

 = −

.

2

3

ABC A B C

V

  

=

2

..

3

ABC

S A M





=

2

23

. 3.

32

a

a=

3

a=

.

Câu 26: Chọn A

Do lăng trụ

. ' ' 'ABC A B C

đều nên lăng trụ đã cho là lăng trụ

đứng.

Gọi

H

là trung điểm của

BC

,

K

là hình chiếu của

H

lên

'AH

.

Ta có

( ) ( ) ( )

''

'

BC AH

BC AA H ABC AA H

BC AA



⊥

 ⊥  ⊥



⊥



Mà

( ) ( )

( )

' ' , ' 3AK A H AK A BC d A A BC AK⊥  ⊥  = =

.

Ta có góc giữa

( )

'A BC

và

( )

ABC

là góc giữa

AH

và. Suy ra

0

' 60A HA =

.

Ta có

0

' .tan60 6

23

2.2 3

sin60

4

3

A A AH

AK

AH

AB



==



= = 



==





Thể tích khối lăng trụ là

. ' 4 3.6 24 3

ABC

V S AA= = =

.

Câu 27: Chọn C

Gọi

H

hình chiếu của

A

lên

BC

,

K

là hình chiếu của

H

lên

'AH

.

Ta có

( ) ( ) ( )

''

'

BC AH

BC AA H ABC AA H

BC AA



⊥

 ⊥  ⊥



⊥



Mà

( ) ( )

( )

' ' , ' 3AK A H AK A BC d A A BC AK⊥  ⊥  = =

.

45

°

K

I

C

2a

M

B

A

C

'

B

'

A

'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

40

Ta có góc giữa

( )

'A BC

và

( )

ABC

là góc giữa

AH

và. Suy ra

0

' 60A HA =

. Ta có

0

' .tan60 6

23

sin60

2 4 3; 2 6

A A AH

AK

AH

BC AH AB



==



= = 



= = =





Thể tích khối lăng trụ là

( )

2

1

. ' . 2 6 .6 72

2

ABC

V S AA= = =

.

Câu 28: Chọn A

Ta có

( )

A G ABC



⊥

nên

A G BC



⊥

;

BC AM⊥

( )

BC MAA



⊥

Kẻ

MI AA



⊥

;

BC IM⊥

nên

( )

3

;

4

a

d AA BC IM



==

Kẻ

GH AA



⊥

,

Ta có

2 2 3 3

.

3 3 4 6

AG GH a a

GH

AM IM

= =  = =

2 2 2

2 2 2 2

33

.

1 1 1 .

36

3

3 12

aa

AG HG a

AG

HG A G AG

AG HG a a



= +  = = =



−

22

.

33

..

3 4 12

ABC A B C ABC

a a a

V A G S

  



= = =

.

Câu 29: Chọn D

Gọi

H

là hình chiếu của

D

lên

'AD

.

Ta có

( ) ( ) ( )

( )

0

' ' ' , ' 60AD DHC ADD A ACD DHC⊥  = =

.

Có

0

3

.cot60

3

a

DH CD==

,

Suy ra

2 2 2

1 1 1 6

'

4

'

a

DD

DH DD DA

= +  =

.

Thể tích khối hộp là

3

32

.'

4

ABCD

a

V S DD==

.

Câu 30: Chọn B

Gọi

G

là trọng tâm của

ABC

,

M

là trung điểm

của

BC

.

( )

A G ABC



⊥

.

Trong

( )

AA M



dựng

MN AA



⊥

, ta có:

BC AM

BC A G



⊥





⊥



( )

BC AA G



⊥

BC MN⊥

.

N

H

B'

C'

M

A

C

B

A'

G

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

41

( )

,d AA BC MN



=

3

4

a

=

.

Gọi

H

là hình chiếu của

G

lên

AA



.

Ta có:

//GH MN

GH AG

MN AM

=

2

3

=

2

3

GH MN=

3

6

a

=

.

Xét tam giác

AA G



vuông tại

G

, ta có:

2 2 2

1 1 1

GH GA GA

=+



2 2 2

1 1 1

GA GH GA

 = −



22

11

33

63

aa

=−

   

   

   

2

27

3a

=

.

3

a

GA



=

.

Vậy thể tích của khối lăng trụ là:

.

ABC

V S A G



=

2

3

.

43

aa

=

3

12

a

=

.

Câu 31: ChọnA

Gọi

H

là hình chiếu vuông góc của

A



lên

( )

ABC

. Do

ABC

đều nên

H

là trọng tâm tam giác

ABC

. Ta có

3

2

x

AM =

23

33

x

AH AM = =

.

Xét tam giác vuông

AA H





,

có

22

33

3

x

A H AA AH



= − =

.

2

1 3 3

.

2 2 4

ABC

x

Sx



==

23

.

3 33 11

4 3 4

ABC A B C

x x x

V

  

=  =

.

Câu 32: Chọn D

Gọi

H

là hình chiếu của

A



trên

( )

ABCD

và

,KL

là hình

chiếu của

H

trên

,AB AD

.

Ta có các góc

45A KH



=

và

60A LH



=

.

Đặt

A H x



=

suy ra

3

;

3

x

HK x HL==

.

Do đó

2

2 2 2 2 2

3

x

AA AH A H x x



= + = + +

2

73

1

37

x

x =  =

.

Thể tích khối hộp bằng

3

. . . 3 7. 3

7

V B h AB AD A H



= = = =

.

Câu 33: Chọn D

Gọi

H

là hình chiếu của

A



trên

( )

ABCD

và

,KL

là hình chiếu của

H

trên

,AB AD

.

Ta có các góc

45A KH



=

và

60A LH



=

.

O

D'

B'

C'

C

B

A'

D

A

H

K

L

O

D'

B'

C'

C

B

A'

D

A

H

K

L

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

42

Đặt

A H x



=

suy ra

3

;

3

x

HK x HL==

.

Do đó

2

2 2 2 2 2

3

x

AA AH A H x x



= + = + +

2

73

1

37

x

x =  =

.

Thể tích khối hộp bằng

3

. . . 3 7. 3

7

V B h AB AD A H



= = = =

.

Câu 34: Chọn C

M

là trung điểm của

BC

thì

( )

BC AA M



⊥

.

Gọi

MH

là đường cao của tam giác

A AM



thì

MH A A



⊥

và

HM BC⊥

nên

HM

là khoảng cách

AA



và

BC

. Ta có

..A A HM A G AM



=

2

33

.

4 2 3

a a a

A A A A



=−

2 2 2

2 2 2 2

4 4 2

4 3 .

3 3 9 3

a a a a

A A A A A A A A A A



    

 = −  =  =  =





Đường cao của lăng trụ là

22

43

9 9 3

a a a

AG



= − =

. Thể tích

23

33

.

3 4 12

LT

a a a

V ==

.

Câu 35: Chọn B

Gọi

G

là trọng tâm tam giác

ABC

. Vì

( )

A G ABC



⊥

và tam giác

ABC

đều nên

A ABC



là hình chóp đều.

Kẻ

EF AA



⊥

và

( )

BC AA E



⊥

nên

( )

3

,

4

a

d AA BC EF



==

. Đặt

A G h



=

Ta có

2

3

a

A A h





=+





.

Tam giác

A AG



đồng dạng với tam giác

EAF

nên

A A AG A G

EA FA FE



==

2

3 3 3

. . . .

2 3 4 3

a a a a

A G EA A A FE h h h





 =  = +  =





.

Thể tích

V

của khối lăng trụ

.ABC A B C

  

là

23

33

..

3 4 12

ABC

a a a

V AG S= = =

.

Đặt

A H x H B x



=  =

.

Ta có

K

là trọng tâm tam giác

AA B



Suy ra

2

22

3 3 4

a

KB A B x



= = +

;

22

33

KA AH x a



= = +

.

H

G

M

B

C

A

C'

B'

A'

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

43

KAB

vuông tại

K

nên

2 2 2

KB KA AB+=

2

22

45

2

94

a

xa



 + =





2 2 2

8 5 9x a a + =

2

a

x=

.

Vậy

.

ABC

V S A H



=

2

32

.

42

aa

=

3

6

8

a

=

.

Câu 36: Chọn B

Gọi

AI

là đường cao,

H

là tâm của tam giác

ABC

( )

A H ABC



⊥

.

Vì

( )

AA ABC A

A H ABC





=









⊥





góc giữa

AA



và

( )

ABC

là

45A AH A AH



 = 

.

Ta có:

3 3 2

,3

23

a

AI AH AI a= = =

,

( )

2

33

93

44

ABC

a

S ==

.

.tan45 3A H AH AH a



=  = =

.

Thể tích của lăng trụ là:

23

9 3 27

. 3.

44

ABC

aa

V A H S a



= = =

.

Câu 37: Chọn C

Áp dụng công thức :

.

1

3

ABC MNP

ABC A B C

V

AM BN CP

V AA BB CC

  



= + +



  



.

Ta có :

..ABC MNP ABC A B C

VV

  

=

nên

11

32

AM BN CP

AA BB CC



+ + =



  



2

1

11

3

2

32

BB

AA

CP

AA BB CC







 + + =



  





1

3

CP

CC

=



.

Câu 38: Chọn D

Do

ABC

đều trọng tâm

G

và

( )

A G ABC



⊥

nên

.A ABC



là hình chóp đều.

Gọi

M

là trung điểm của

BC

, khi đó

3

2

a

AM =

3

a

AG=

.

Gọi

H

là hình chiếu của

M

trên

AA



. Khi đó do

( )

BC AA M



⊥

BC HM⊥

nên

HM

là đường vuông góc

chung của hai đường thẳng

AA



và

BC

. Do đó

3

4

a

HM =

Đặt

AA A B A C x

  

= = =

, khi đó

2

3

a

A G x



=−

.

I

B'

C'

A

B

C

H

A'

G

M

B'

C'

A'

A

C

B

H

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

44

Do

2 . .

AA M

S A G AM MH AA







==

2

33

..

2 3 4

a a a

xx − =

2

3

a

x=

.

Do

2

3

4

ABC

a

S



=

,

3

a

AG



=

3

.

3

.

12

ABC A B C ABC

a

V A G S

  





 = =

.

Câu 39: Chọn A

Gọi

M

là trung điểm của

BC

. Vẽ

MH AA



⊥

( )

H BC

.

Ta có

AM BC⊥

,

A G BC



⊥

( )

BC A AG



⊥

BC MH⊥

( )

,d AA BC MH



=

.

22

AH AM MH=−

22

33

4 16

aa

=−

3

4

a

=

.

Ta có

tan

MH A G

GAH

AH AG



==

.MH AG

AG

AH



=

33

.

43

3

4

aa

a

=

3

a

=

. Vậy

.

ABC

V S A G



=

2

3

.

43

aa

=

3

12

a

=

.

Câu 40: Chọn D

Đặt

BC x=

và gọi

K

là trung điểm của

BC

, ta có

1

30A KA =

.

Ta có

1

2

11

3

1

2

84

22

cos30

3

2

A BC

x

AK x

A K x S A K BC x



= = =  =  = =  =

Do đó

2

3 1 4 3

tan30 2 3 2 2 8 3

24

3

x

h V Sh



=  =  =  = =  =

.

Câu 41: Chọn B

Ta có

2 2 2 2

1 1 1 1

A

d AB AD AA

= + +



2 2 2

2

1 1 1 1

3

( 3)

15

5

AA a

a AA

a



 = + +  =







.

Vậy

3

3 3 3V a a a a=   =

.

Câu 42: Chọn C

Gọi

h

là chiều cao của khối chóp và

h MM



=

là chiều cao khối hộp

chữ nhật.

Theo Thales, ta có:

SM SN SP SQ MN NP

x

SA SB SC SD AB BC

= = = = = =

11

h AM SM

x

h AS SA



 = = − = −

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

45

Do đó

1

..

3

V AB BC h=

và

( ) ( )

22

. . . . . 1 3 1V MN NP h x AB BC x h x x V



= = − = −

.

Xét hàm số

( ) ( )

2 2 3

3 1 3 3f x x x x x= − = −

với

( )

0;1x

( ) ( )

2

0

6 9 0

2

3

x

f x x x f x

x



=





 = −  = 



=





.

Bảng biến thiên:

Vậy

( )

0;1

4

max

9

fx=

max

4

9

VV



=

.

Câu 43: Chọn A

Ta có:

( )

.

ACC A

BDD B

S

AC CC AC

CC DD

S BD DD BD







= = =



1

5

AC

BD AC

BD

 =  =

.

Ta có

2 2 2 2

22

5.

4 4 4 4

BD AC AC AC

AA OA OA AC



= − = − = − =

2

. 1 1

ACC A

S AC AA AC AC





 = = =  =

và

2

15

..

22

ABCD

S AC BD AC==

5

2

=

.

Vậy thể tích khối hộp đứng là

5

.1. 5

..

55

2

2 2 4 2

ABCD ACC A BDD B

S S S

V

   

= = = =

.

Câu 44: Chọn B

Gọi

H

là trung điểm

AB



, suy ra

( )

BH A B C D

   

⊥

.

Vì

A B C D

   

là hình thoi và

o

120B A D A B C

     

=  

là tam giác

đều cạnh

2a

.

Ta có:

( ) ( )

( )

o

, 60

AC D A B C D C D

HC C D

BC C D

AC D A B C D BC H



       

=



  

⊥





  

⊥



      

 = =

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

46

Có

A B C

  



đều cạnh

2a

nên

3

.2 3

2

C H a a



==

.

Xét tam giác

BHC



vuông tại

H

có:

oo

tan60 tan60 3

BH

BH C H a

CH



=  = =



.

( )

2

3

2 2. . 2 2 3

4

A B C D A B C

S S a a

      

= = =

.

Vậy,

23

.

. 3 .2 3 6 3

ABCD A B C D A B C

V BH S a a a

      

= = =

.

Câu 45: Chọn D

Dựng

'AK A D⊥

( )

CD AD

CD ADD A CD AK

CD DD



⊥



 ⊥  ⊥





⊥



Vậy

( )

AK CDA B



⊥

Ta có:

5AD



=

và

//AB CD

( )

//AB A B CD





( ) ( )

( )

, , 2d AB A D d A A B CD AK

  

 = = =

. Do đó với

AD a=

,

( )

AA b b a



=

, ta có:

22

25

2.5 10

5

b

ab

a



=

+=







==



=







2

10 5V a b = =

.

Câu 46: Chọn B

Ta có

( ) ( )

.

6

S ABCD

HH

V V V



=+

. Với

.S ABCD

là khối chóp tứ giác đều như hình vẽ.

Ta có

1

.tan45

2

SH HM HM=  = =

2

.

1

1.

1

2

36

S ABCD

V = =

. Do đó

( )

1

1 6. 2

6

H

V



= + =

.

Câu 47: Chọn A

Theo giả thiết có

a

,

b

,

c

1; 4  



và

6a b c+ + =

;

( )

2

tp

S ab bc ca= + +

.

a

,

b

,

c

1; 4  



( )( )( )

1 1 1 0

4 4 4 0

a b c



− − − 







− − − 





( ) ( )

10

64 16 4 0

abc a b c ab bc ca

a b c ab bc ca abc



+ + + − + + − 







− + + + + + − 





( ) ( )

63 15 3 0a b c ab bc ca − + + + + + 

( )

63 15 3 0ab bc ca − + + + 

90 63

9

3

ab bc ca

−

 + +  =

18

tp

S

.

Câu 48: Chọn C

M

C

B

A'

B'

C'

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

47

Gọi

M

là trung điểm của

BC



. Khi đó

A M B C

  

⊥

và

AM B C



⊥



góc giữa hai mặt phẳng

( )

AB C



và đáy là

30AMA



=

.

Trong tam giác vuông

''A MB

ta có

.cosA M A B B A M

    

=

2

a

=

.

Trong tam giác vuông

AA M



có:

3

tan30

6

a

AA A M h



=  = =

.

Diện tích tam giác

' ' 'A B C

là

2

3

4

a

S =

.

Câu 49: Chọn A

Đặt độ dài cạnh đáy bằng

a

và chiều cao bằng

h

. Ta có

2

3

4

ah

V =

.

Gọi

H

là trung điểm

''BC

và kẻ

'A H AH⊥

suy ra

( )

' ' 'A H AB C⊥

.

Vậy theo giả thiết ta có

2 2 2 2 2

1 1 1 1 4

1

13

3

2

h h a

a

= +  + =







.

Gọi

M

là trung điểm

''AC

và kẻ

'MN AC⊥

có

'MN AC⊥

và

''B M AC⊥

( ) ( ) ( )

( )

' ' 'C' , ' 'AC B MN AB ACC A MNB ⊥  =

.

Có

3'

cos tan 11 11

6

BM

MNB MNB

MN

=  =  =

22

3

2

11

2

a

ah

=

+

22

3 11a h h + =

trong đó

( )

22

1

', '

2

ah

MN d A AC

ah

==

+

.

Giải hệ trên ta được

6

2,

2

ah==

32

2

V=

.

Cách 2: chú ý

'AMC

là hình chiếu vuông góc của

''AB C

lên mặt phẳng

( )

''ACC A

Do đó

( ) ( )

( )

22

2

''

2

33

4

cos ' ' , ' ' 4 3

66

3

4

2

AMC

AB C

ah

S

AB C ACC A h h a

S

a

ah

=  =  = +

+

M

C

H

B

A

A'

B'

C'

K

N

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

48

Giải hệ trên ta được

6

2,

2

ah==

32

2

V=

.

Câu 50: Chọn D

Đặt

A B a



=

,

A C b



=

,

AA c



=

thì

1

2

ABC

S ab

  



=

.

1

2

ABC A B C

V abc

  

=

.

Ta có

( )

2 2 2

2

1 1 1

1

,

1 1 1 1

2

,

1 1 1 1 4

3

,

a c d A AB

b c d A AC

c b c

d A AB C





+ = =





+ = =







+ + = =

  





2

15

6

11

3

11

6

a

b

c



=



=





=





2 2 2

15

108

a b c

=

6 15

5

abc=

. Vậy

.

3 15

5

ABC A B C

V

  

=

.

Câu 51: Chọn D

Trong

( ' ')ACA C

kẻ

3

' ' '

2

A K AC A K⊥  =

.

Trong

( ' ')ABA B

kẻ

' ' ' 1A H AB A H⊥  =

.

Trong

( ' ' ')A B C

kẻ

2

' ' ' '

2

A E B C A E⊥  =

.

Đặt

' ' ; ' ' ; 'A B a A C b AA c= = =

.

Ta có

2 2 2

1 1 1

1

'

1 1 1 4

3

'

1 1 1

2

'

a c A H

b c A K

a b A E



+ = =



+ = =





+ = =





, Cộng theo vế ta có:

2 2 2

1 1 1 13

6

a b c

+ + =

2

6

15

5

6

1 7 6

67

11

6

a

b

c



=



=





 =  =





=









.

Vậy thể tích của khối lăng trụ

.

1 3 210

AA'. . .

2 35

ABC A B C

AB ACV

  

==

.

Câu 52: Chọn C

Gọi

I

là trung điểm

BC

( )

,A BC ABC A IA





 = =

.

Gọi

( )

2

6

0

A BC

S

BC x x A I

BC x



=   = =

.

244

22

3 36 3 144 3 144 3

2 4 2

2

x x x x

AI AA

x

xx

−−



=  = − = =

.

42

4

.

144 3 3 3

. . 144 3

2 4 8

ABC A B C ABC

xx

V AA S x x

x

  

−



 = = = −

.

A

B

C

C'

B'

A'

E

H

K

I

C'

A'

B'

C

A

B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

49

Đặt

( ) ( )

4

44

4

12

144 3 144 3 0 2

2 144 3

x

f x x x f x x x

x



= −  = − − =  =

−

.

( )

fx

đạt giá trị lớn nhất thì thể tích khối lăng trụ lớn nhất khi

2x =

.

6 , 3 tan 2

AA

AA AI

AI





 = =  = =

.

Câu 53: Chọn C

Ta có

( )

AA B B

//

CC AA

CC

AA



























nên khoảng cách giữa

'AB

và

'CC

là khoảng cách từ C đến mặt phẳng

( )

AA B B



.

Mặt khác

( )

AA B B

CA AB

CA

CA AA



⊥

⊥







⊥

suy ra khoảng cách từ

C

đến mặt phẳng

( )

AA B B



là

2

1

.

22

ABC

a

CA a AB AC a S AC AB



=  = =  = =

. Lại có tứ giác

''BCC B

là hình vuông nên

2CC BC a



==

. Vậy thể tích khối lăng trụ

23

. ' ' '

2

. 2.

22

ABC A B C ABC

aa

V CC S a





= = =

.

Câu 54: Chọn A

Đặt cạnh của đáy là

x

.

Gọi

I

là trung điểm

BC



, ta có

( )

3

;

2

x

d A BCC B A I

   

==

( )

1 3 3

; ; 2

2 4 2

xa

d I BCC B d A BCC B x a

    

= = =  =

.

( )

2

23

3

4

ABC

a

Sa

  



==

.

Thể tích khối lăng trụ:

23

3. 3 3V a a a==

Câu 55: Chọn D

Theo giả thiết ta có được đáy

ABCD

là hình bình hành, độ dài các đường chéo

0

, 3, 60BD a AC a BAD= = =

.

A'

D'

B'

C'

A

D

B

C

I

C

B

A'

C'

B'

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

50

Đặt

,AB x BC y==

, áp dụng định lý hàm số cosin cho hai tam giác

ABD

và

ABC

ta được.

2 2 2

2

2 2 2

3a x y xy

xy a

a x y xy



= + +



=



= + −





. Khi đó

3

0

3

. .sin60

2

a

V a xy==

Câu 56: Chọn C

Gọi

F

là trung điểm của

BC

,

''FC CB N N = 

là trung điểm của

MC

1

''

3

B M B C=

. Khi

đó ta có

( )

2

3

1 1 2 2.6 9

, . . ', . . 6

3 3 3 9 2

ABCM ABC ABC

aa

V d M ABC S d B ABC S a= = = =

.

Câu 57: Chọn A

Ta có

3AB a=

, dễ thấy góc giữa đường thẳng

BC



tạo với mặt

phẳng

( )

A C CA



là góc

30BC A



=

. Suy ra

3

tan30

a

AC

=



3AC a



=

22C C a



=

.

Vậy

.

1

2 2 . . 3

2

ABC A B C

V a a a

  

=

3

6a=

.

Câu 58: Chọn C

Ta có

2 2 2

2 . .cosBC AB AC AB AC BAC= + −

22

1

2. . .

2

a a a a



= + − −





2

3a=

3BC a=

.

Xét tam giác vuông

B AB



có

22

AB BB AB



=+

22

aa=+

2a=

.

Xét tam giác vuông

IAC

có

22

IA IC AC=+

2

4

a

a=+

5

2

a

=

.

Xét tam giác vuông

IB C



có

22

B I B C C I

   

=+

2

3

4

a

a=+

13

2

a

=

.

Xét tam giác

IB A



có

2

2 2 2

5

2

4

a

B A IA a



+ = +

2

13

4

a

=

2

BI



=

IB A





vuông tại

A

3a

6a

N

M

B

C

A

B'

A'

C'

E

F

a

3

a

I

C'

B'

A'

C

B

A

30

60

a

A'

B'

C

B

A

C'

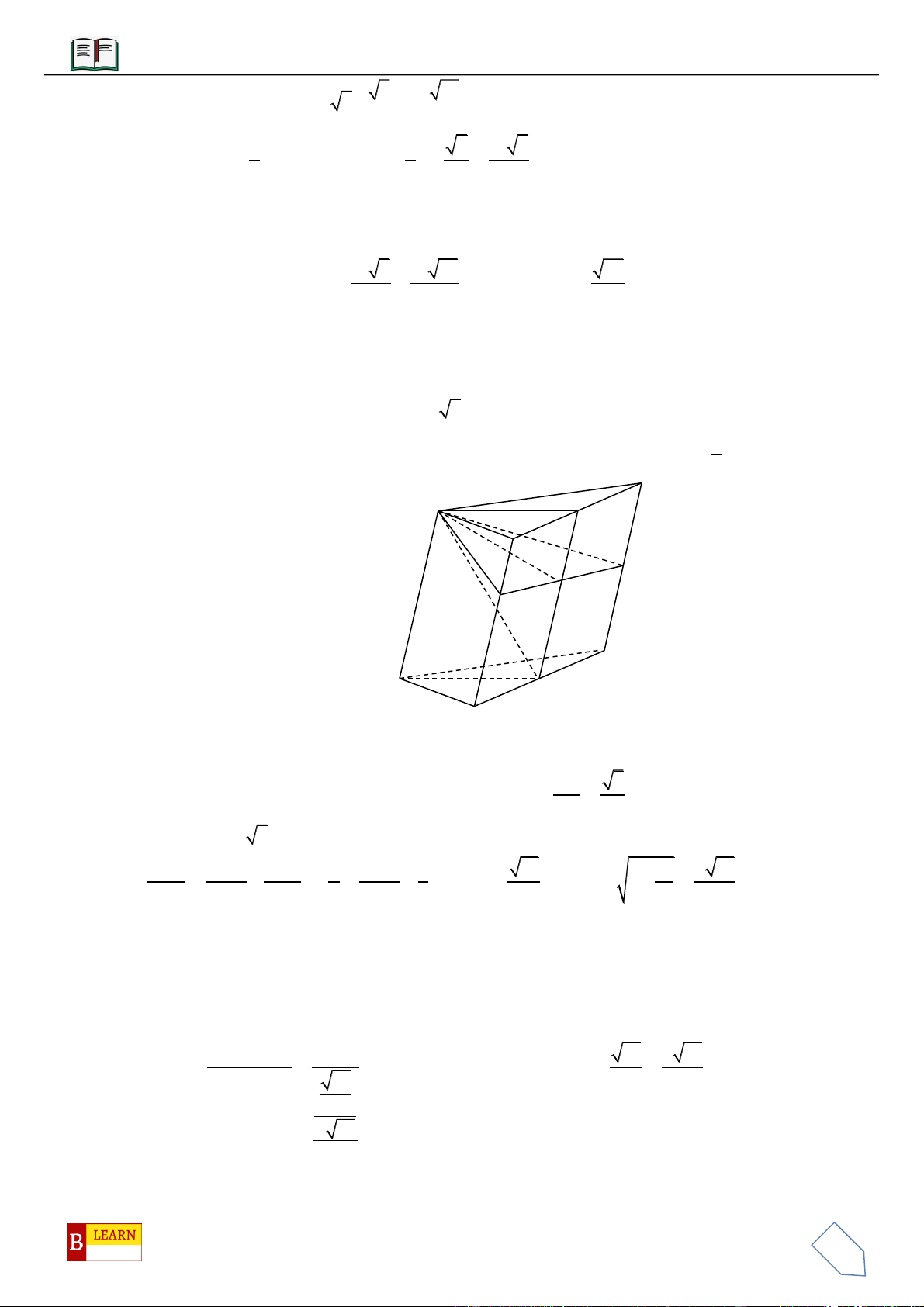
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

51



1

.

2

IB A

S AB AI



=

15

. 2.

22

a

a=

2

10

4

a

=

.

Lại có

1

. .sin

2

ABC

S AB AC BAC=

13

..

22

aa=

2

3

4

a

=

.

Gọi góc tạo bởi hai mặt phẳng

( )

ABC

và

( )

AB I



là



.

Ta có

ABC

là hình chiếu vuông góc của

AB I





trên mặt phẳng

( )

ABC

.

Do đó

.cos

ABC IB A

SS





=

22

3 10

.cos

44

aa



=

30

cos

10



=

.

Câu 59: ChọnA

Gọi H,K lần lượt là hình chiếu vuông góc của A lên BB’, CC’ ta có

( ) ( )

, 1; , 2AH d A BB AK d A CC



= = = =

và

AA //BB //CC ;AH BB ,AK CC

    

⊥⊥

( )

AHK AA



⊥

và

(C,BB) 5HK d



==

Tam giác AHK có

2 2 2

5AH AK HK AHK+ = =  

vuông tại A

1

.1

2

AHK

S AH AK = =

Vậy

.

.AA 2.

ABC A B C AHK

VS

  



==

Câu 60: Chọn D

Cách 1: Gọi N là trung điểm của BC,

EF MN AH MN(MN//AA').H =   ⊥

Ta có H là trung

điểm của EF và

2 2 2

+AF 5AE EF==

nên

5

.

22

EF

AH ==

Tam giác vuông AMN có

'

5AN A M==

và

'

2 2 2 2

1 1 1 4 1 1 15 15 2 15

AA 5 .

5 5 3 9 3

AM

AH AM AN AM

= +  = +  =  = + =

Mặt khác do

( ) AM

(( ),( )) ( ,AA ) = MAA .

( ) AA

ABC

A B C AEF AM

AEF

  

⊥



    

 = 





⊥



Tam giác AEF vuông tại A là hình chiếu vuông góc của tam giác A’B’C’ trên mặt phẳng (AEF)

Vì vậy theo định lý hình chiếu có

.

1

.1.2

15 2 15

2

2 . 2. .

cos 3 3

15

3

2 15

3

AEF

A B C ABC A B C A B C

S

S V S AM

MAA

        

= = =  = = =





Cách 2: Ta có thể tính thông qua công thức nhanh thể tích tứ diện như sau

A

N

C

B

F

E

A’

C’

B’

M

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

52

Có

..

2 . .sin((AA B ),(AA C ))

3

2 15

3

AA B AA C

ABC A B C A A B C

SS

V V AA

AA

   

     

   



= = = =



0

1 1 1

. ( , ) . ( , )

2 2 2

11

. (C , ) . ( ,CC )

22

(( ),(AA C )) 90

AA B

AA C

S AA d B AA AA d A BB AA

S AA d AA AA d A AA

AA B





     

= = =



     

= = =





   

=





Câu 61: Chọn D

Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

,BB CC



.

Suy ra

( )

AA AE

AA AEF

AA AF



⊥





⊥





⊥



.

Suy ra hình chiếu vuông góc của

ABC

  



lên mặt phẳng

( )

AEF

là

AEF

.

Gọi



là góc giữa hai mặt phẳng

( )

ABC

  

và

( )

AEF

.

Ta có

( )

.cos 1

cos

AEF

AEF A B C A B C

S

S S S





     

  

=  =

Mặt khác, ta có

( )

,

AA AEF

AA AG A AG

AG A B C





⊥





   

 = =



   

⊥





Suy ra

( )

cos cos . 2

AG

AG AA

AA







=  =



Từ

( )

1

và

( )

2

suy ra

.

..

A B C ABC A B C AEF

V AG S AA S

     





==

.

Ta có

1, 3AE AF==

,

( ) ( )

; ; 2d C BB d E BB EF EF



= =  =

. Suy ra

AEF

vuông tại

A

.

Suy ra

1 1 3

. . 3

2 2 2

AEF

S AE AF



= = =

.

Gọi

,MN

lần lượt trung điểm của

,BC B C



.

Giả sử

MN

cắt

EF

tại

H

. Suy ra

MN EF⊥

và

H

là trung điểm của

EF

nên

1

2

EF

AH ==

.

43

2

32

A G A M A G

    

=  = =

.

Xét hình bình hành

AA MN



có:

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

53

2

4 8 3

. . .2 1.

39

AA MN

S AG A M AH MN AA AA AA





    

= =  − =  =





.

Thể tích khối lăng trụ là:

.

8 3 3 4

..

9 2 3

A B C ABC AEF

V AA S

  





= = =

.

Câu 62: Chọn C

Gọi

,MN

lần lượt là hình chiếu vuông góc của

A

lên các cạnh

,BB DD



.

Ta có:

( )

BB AMN

AM BB AM AA

AA AMN

AN DD AN AA

DD AMN



⊥





⊥⊥







  ⊥ 

  



⊥⊥



⊥







Suy ra hình chiếu vuông góc của

ABD

  



lên mặt phẳng

( )

AMN

là

AMN

.

Gọi



là góc giữa hai mặt phẳng

( )

ABD

  

và

( )

AMN

Ta có

( )

.cos 1

cos

AMN

AMN A B D A B D

S

S S S





     

  

=  =

Mặt khác, ta có

( )

,

AA AMN

AA A B AA B

A B ABCD





⊥





  

 = =





⊥





Suy ra

( )

cos cos . 2

AB

A B AA

AA







=  =



Từ

( )

1

và

( )

2

suy ra

.

..

A B D ABD A B D AMN

V A B S AA S

     





==

Vậy thể tích khối hộp là:

..

2 2 .

ABCD A B C D ABD A B D AMN

V V AA S

      





==

.

Ta có

( ) ( )

( )

//

;;

//

BB C C ADD A

ADD A ABB A AM AN

C CDD ABB A

   





   

=



   





.

Suy ra

60MAN =

hoặc

120MAN =

.

13

. .sin

24

AMN

S AM AN MAN



==

Ta có

( )

; ; 45AA ABCD AA AB A AB A AB

   

= =  = 

. Suy ra

A AB





vuông cân tại

B

.

..

ABB A

S AM BB A B AB



==

. Suy ra

. . 2 2.1 2

22

AA AA

AM AA AA AM



=  = = =

.

Vậy

.

3

2.2. 3

4

ABCD A B C D

V

   

==

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

54

Câu 63: Chọn D

Ta hạ:

( )

'; ' '/ / '/ / 'AD BB AE CC ADE AA BB CC⊥ ⊥  ⊥

và

1; 3, 2AD AE DE= = =

.

Ta hạ:

( ) ( ) ( ) ( )

( )

ˆ

' ; : ' , ' , ' 'A H ABC Do AA ADE ABC ADE A H AA AA H⊥ ⊥  = =

Tam giác ADE là hình chiếu của tam giác ABC lên mp(ADE), do đó:

( )

'. ' '

.'

ˆ

.cos '

ˆ

'

cos '

1 1 1

. ' . . . ' ', ' ' .

3 3 3

ADE ADE

ADE ABC ABC

A ABC ABC ADE BCC B

S S AA

S S AA H S

AH

AA H

V A H S S AA d A BCC B S

=  = =

 = = =

Ta có:

( )

' ; 'BB ADE BB DE⊥⊥

.

Ta kẻ:

( )

' ' '⊥  ⊥  ⊥AK DE AK BB AK BCC B

( )

( ) ( )

'. ' '

. ' ' ' '. '. ' '

', ' ' , ' '

1 1 1

. . ' ' . . ' '

3 2 3

1 1 1

. . ' . . ' ' . . ' ' '

3 3 3

 = =

= + = +

 = + = + + = + +

A BCC B ADE

ABC A B C A ABC A BCC B ADE ADE ADE

d A BCC B d A BCC B AK

V AK DE BB CC S BB CC

V V V S AA S BB CC S AA BB CC

Tam giác ADE vuông tại A và

. ' ' '

3 ' ' ' 3 1 2 3

. . 3

2 3 2 3

ADE ABC A B C ADE

AA BB CC

S V S

+ + + +

=  = = =

Câu 64: Chọn A

Gọi E, F lần lượt là hình chiếu vuông góc của A lên BB’, CC’. Ta

có:

1, 2; '/ / '/ / 'AE AF AA BB CC==

Vậy:

( )

'; ' 'AF AA AE AA AEF AA⊥ ⊥  ⊥

Suy ra:

( ) ( )

( )

13

' ' , ' ' 90 .

22

= =  = =

O

AEF

EAF ABB A ACC A S AE AF

Gọi N là trung điểm BC, H là giao của EF và MN nên

( )

/ / 'AH MN MN AA⊥

.

Ta có H là trung điểm EF và

22

1

22

EF AE AF

AH

+

= = =

. Tam giác vuông AMN có:

23

'

3

AN A M==

và

2 2 2

1 1 1 4 3

2'

3

AM AA

AH AM AN

= +  =  =

.

Vậy

. ' ' '

3 4 3

. ' . 2

23

ABC A B C AEF

V S AA= = =

H

A

A'

C'

C

B

B'

E

F

M

N

A

C

C'

A'

B

B'

H

D

E

K

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

55

DẠNG 3. THỂ TÍCH KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY

Câu 1: Tính thể tích

V

của khối tứ diện đều có cạnh bằng

a

.

A.

3

12

a

V 

. B.

3

2

12

a

V 

. C.

3

4

a

V 

. D.

3

2

4

a

V 

.

Câu 2: Cho khối chóp tam giác đều

.S ABCD

có độ dài cạnh đáy bằng

,a

mặt phẳng chứa

BC

và vuông

góc với

SA

cắt khối chóp theo một thiết diện có diện tích bằng

2

.

4

a

Tính thể tích

V

của khối chóp

đã cho.

A.

2

.

24

a

V 

B.

3

2

.

12

a

V 

C.

3

.

36

a

V 

D.

3

.

72

a

V 

Câu 3: Cho khối chóp tứ giác đều

SABCD

có cạnh đáy bằng a. Gọi M,N lần lượt là trung điểm của

,SB SD

. Mặt phẳng

(AMN)

cắt

SC

tại

J

.Diện tích tứ giác

AMJN

bằng

2

5

6

a

. Tính thể tích của

khối chóp

SABCD

.

A.

3

2

3

a

V 

B.

3

2

6

a

V 

C.

3

a

V 

D.

3

6

a

V 

Câu 4: Bên cạnh con đường nước đi vào thành phố, người ta xây

một ngọn tháp hình chóp tứ giác đều

SABCD

có

600SA m

,

0

15ASB 

. Do sự cố đường dây điện tại

điểm

Q

( trung điểm của

SA

) bị hỏng nên người ta tạo ra

một con đường từ A đến Q gồm bốn đoạn

, , ,AM MN NP PQ

(như hình vẽ ). Để tiết kiệm chi phí, kỹ

sư đã nghiên cứu và có được chiều dài con đường từ A đến

Q nhỏ nhất. Tính tỉ số

AM MN

k

NP PQ







A.

2k 

B.

5

3

k 

C.

3

2

k 

D.

4

3

k 

Câu 5: Trong tất cả các khối chóp tam giác đều có diện tích toàn phần cho trước. Gọi a,b lần lượt là độ

dài cạnh đáy và độ dài cạnh bên của khối chóp. Tính tỉ số

a

b

khi thể tích của khối chóp đạt giá trị

lớn nhất.

A.

1

b

a



B.

2

b

a



C.

3

b

a



D.

2

b

a



Câu 6: Cho hình chóp

.S ABCD

có

1SA 

, tất cả các cạnh còn lại bằng

3

. Tính thể tích khối chóp

.S ABCD

.

A.

3

. B.

6

2

. C.

3

2

. D.

6

3

.

Câu 7: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

A

,

1AB 

,

2AC 

và

3SA SB SC  

.

Tính thể tích khối chóp

.S ABC

.

N

C

B

A

M

Q

D

P

S

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

56

A.

7

6

. B.

2

3

. C.

17

6

. D.

1

6

.

Câu 8: Cho hình chóp

.S ABC

có

135BAC 

,

1AB AC

và

2SA SB SC  

. Tính thể tích khối

chóp

.S ABC

.

A.

6 2 2

4



. B.

6 2 2

6



. C.

6 2 2

12



. D.

6 2 2

2



.

Câu 9: Cho khối chóp

.S ABC

có

6

,

3

a

SA SB AB AC a SC    

và mặt phẳng

 

SBC

vuông góc

với mặt phẳng

 

ABC

. Tính thể tích của khối chóp đã cho.

A.

3

14

36

a

. B.

3

14

12

a

. C.

3

21

36

a

. D.

3

21

12

a

.

Câu 10: Cho khối chóp

.S ABCD

có đáy là hình thang,

2,SA SB SC AD a AB BC CD a      

. Tính

thể tích của khối chóp đã cho.

A.

3

9

4

a

. B.

3

4

a

. C.

3

4

a

. D.

3

12

a

.

Câu 11: Trong các khối chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, chiều cao bằng

b

thỏa mãn

4 6 2ab

. Khối chóp có thể tích lớn nhất là.

A.

42

3

. B.

82

3

. C.

22

3

. D.

2

3

.

Câu 12: Cho khối chóp

.S ABCD

có

3SA SB SC SD a   

và

,2AB BC CD a AD a   

. Thể tích

của khối chóp

.S ABCD

bằng

A.

3

6

4

a

. B.

3

36

4

a

. C.

3

6

2

a

. D.

3

36

2

a

.

Câu 13: Cho hình chóp

.S ABC

có đáy là tam giác vuông,

1SA SB SC  

và cùng tạo với đáy một góc



. Tính

cos



khi thể tích của khối chóp

.S ABC

đạt giá trị lớn nhất.

A.

3

2

. B.

6

3

. C.

1

2

. D.

3

.

Câu 14: Cho hình chóp

.S ABC

có

3SA SB SC a  

,

2 , 3AB AC a BC a  

. Tính thể tích của khối

chóp

.S ABC

A.

3

5

2

a

. B.

3

35

2

a

. C.

3

35

6

a

. D.

3

25

7

a

.

Câu 15: Cho khối chóp

.S ABC

có đáy

ABC

đều cạnh

a

, cạnh bên

SA

vuông góc với đáy

 

ABC

và

góc giữa

SB

và mặt đáy bằng

30

. Tính thể tích

V

của khối chóp đã cho.

A.

3

4

a

V 

. B.

3

12

a

V 

. C.

3

4

a

V 

. D.

3

9

4

a

V 

.

Câu 16: Cho khối chóp

.S ABCD

có chiều cao

SA

bằng

a

. Mặt đáy

ABCD

là hình thoi cạnh

a

, góc

ABC

bằng

60

. Tính thể tích của khối chóp

.S ABCD

theo a.

A.

3

6

a

V 

. B.

3

4

a

V 

. C.

3

8

a

V 

. D.

3

12

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

57

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông với

2

a

AC 

. Cạnh bên

SA

vuông góc

với mặt phẳng

 

ABCD

, cạnh bên

SB

hợp với mặt phẳng

 

ABCD

một góc

60

. Tính thể tích

khối chóp

.S ABCD

.

A.

3

24

a

V 

. B.

3

33

24

a

V 

. C.

3

8

a

V 

. D.

3

33

8

a

V 

.

Câu 18: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

2AB a

,

60BAC 

. Cạnh bên

SA

vuông góc với mặt phẳng

 

ABC

và

3S A a

. Tính theo

a

thể tích khối chóp

.S ABC

.

A.

3

2Va

. B.

3

3Va

. C.

3

Va

. D.

3

4Va

.

Câu 19: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

B

,

SA a

,

30BAC 

,

45SCA 

. Cạnh

bên

SA

vuông góc với đáy. Thể tích khối chóp

.S ABC

là

V

. Tỉ số

3

V

a

gần giá trị nào nhất trong

các giá trị sau?

A.

0,01

. B.

0,05

. C.

0,08

. D.

1

.

Câu 20: Cho hình chóp

.S ABCD

, đáy

ABCD

là hình chữ nhật có

2,AB a AD a

. Hai mặt phẳng

 

SAB

và

 

SAD

cùng vuông góc với đáy và góc giữa hai mặt phẳng

 

SAB

,

 

SBD

là

45

. Thể

tích khối chóp

.S ABC

là

V

. Tỉ số

3

V

a

gần giá trị nào nhất trong các giá trị sau?

A.

0,25

. B.

0,5

. C.

0,75

. D.

1,5

.

Câu 21: Cho hình chóp

.S ABC

có cạnh bên

SA

vuông góc với đáy và

;2AB a AC a

và

0

120BAC 

.

Mặt phẳng

 

SBC

tạo với đáy một góc

0

60

. Tính thể tích khối chóp

.S ABC

A.

3

21

14

a

V 

. B.

3

21

13

a

V 

C.

3

2 21

14

a

V 

. D.

3

2 21

13

a

V 

.

Câu 22: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật có

3 ; 4AB a AD a

,

 

SA ABCD

, SC tạo

với đáy góc

0

45

. Tính theo a thể tích khối chóp

.S ABCD

A.

3

20Va

. B.

3

20 2Va

C.

3

30Va

. D.

3

30 2Va

.

Câu 23: Cho tứ diện

ABCD

có

 

AD ABC

và

3 ; 4 ; 5 ; 6AB a BC a AC a AD a   

. Thể tích khối tứ

diện

ABCD

là

A.

3

6Va

. B.

3

12Va

. C.

3

18Va

. D.

3

36Va

.

Câu 24: Cho khối tứ diện

SABC

có

 

SA ABC

. Hai mặt phẳng

 

SAB

và

 

SBC

vuông góc với nhau;

3SB a

,

0

45BSC 

,

0

30ASB 

. ThỂ tích khối tứ diện

SABC

là

V

. Tính tỉ số

3

a

V

.

A.

8

3

. B.

83

3

. C.

23

3

. D.

4

3

.

Câu 25: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang vuông tại

,AD

;

 

SD ABCD

;

; 3 ; 3AB AD a CD a SA a   

. Thể tích khối chóp

.S ABCD

là

A.

3

2

3

a

V 

. B.

3

4

3

a

V 

. C.

3

2

3

a

V 

. D.

3

22

3

a

V 

.

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

58

Câu 26: Cho hình chóp

.S ABCD

, đáy

ABCD

là hình vuông cạnh

a

. Hai mặt phẳng

()SAB

và

()SAD

cùng

vuông góc với đáy, góc giữa hai mặt phẳng

()SBC

và

()ABCD

là

0

30

. Thể tích khối chóp

.S ABCD

là

V

. Tính

3

3V

a

?

A.

3

. B.

3

4

. C.

3

2

. D.

3

6

.

Câu 27: Cho hình chóp

.S ABCD

,đáy

ABCD

là hình chữ nhật có

,3AB a BC a

. Hai mặt phẳng

()SAB

và

()SAD

cùng vuông góc với đáy, cạnh

SC

hợp với đáy một góc

0

60

. Thể tích khối chóp

.S ABCD

là?

A.

3

Va

. B.

3

2Va

. C.

3

3Va

. D.

3

23Va

.

Câu 28: Cho hình chóp

.S ABC

có tam giác.

ABC

.vuông tại

0

, , 60B AB a ACB

. Cạnh bên

SA

vuông

góc với mặt phẳng đáy và

SB

tạo với mặt đáy một góc bằng

0

45

. Thể tích khối chóp

.S ABC

là?

A.

3

6

a

V 

. B.

3

18

a

V 

. C.

3

9

a

V 

. D.

3

12

a

V 

.

Câu 29: Cho tứ

ABCD

có

ABC

là tam giác đều cạnh

a

.

AD

vuông góc với mặt phẳng

 

ABC

, góc giữa

BD

và mặt phẳng

 

DAC

là

0

30

. Thể tích khối tứ diện

ABCD

là

V

. Tính tỉ số

3

6a

V

.

A.

1

. B.

3

. C.

4

. D.

12

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

20cm

.

SA

vuông góc với mặt phẳng

đáy và

30SA cm

. Gọi

', 'BD

là hình chiếu của

A

lên

,SB SD

. Mặt phẳng

 

''AB D

cắt

SC

tại

'C

. Thể tích khối chóp

. ' ' 'S AB C D

là

A.

 

3

1466 cm

. B.

 

3

1500 cm

. C.

 

3

1400 cm

. D.

 

3

1540 cm

.

Câu 31: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

A

.

2BC a

.

SA

vuông góc với

mặt phẳng đáy. Mặt bên

 

SBC

tạo với đáy một góc

0

45

. Thể tich khối chóp

.S ABC

là

V

. Tính

tỷ số

3

6V

a

?

A.

3

4

. B.

3

6

. C.

2

. D.

32

2

.

Câu 32: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều. Cạnh bên

SA

vuông góc với mặt phẳng đáy.

Biết khoảng cách từ

A

đến mặt phẳng

()SBC

bằng

3

, góc giữa

()SBC

và mặt phẳng đáy bằng



. Tính

cos



khi khối chóp có thể tích nhỏ nhất.

A.

3

cos





B.

2

.

2

cos





C.

23

.

3

cos





D.

1

.

3

cos





Câu 33: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

, 8, 6B AB BC

. Biết

6SA 

và

vuông góc với mặt phẳng đáy

 

ABC

. Một điểm trong

M

của khối chóp cách đều tất cả các mặt

của khối chóp một đoạn bằng

h

. Mệnh đề nào dưới đây đng?

A.

4

3

h 

. B.

4

9

h 

. C.

2

3

h 

. D.

2

9

h 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

59

Câu 34: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

, 8, 6B AB BC

. Biết

6SA 

và

vuông góc với mặt phẳng đáy

 

ABC

. Một điểm

M

thuộc phần không gian bên trong của hình

chóp và cách đều tất cả các mặt của khối chóp. Tính thể tích khối tứ diện

.M ABC

.

A.

24V 

. B.

64

3

V 

. C.

32

3

V 

. D.

12V 

.

Câu 35: Cho khối chóp

.S ABC

có đáy là tam giác vuông cân tại

, 2 ,A AB a

SA

vuông góc với đáy,

khoảng cách từ

A

đến mặt phẳng

 

SBC

bằng

4

3

a

. Tính thể tích khối chóp

.S ABC

.

A.

3

8

3

a

V 

. B.

3

9

8

a

V 

. C.

3

8Va

. D.

3

27

8

a

V 

.

Câu 36: Cho hình chóp

.S ABC

có đáy là tam giác cân tại

A

,

2AB a

,

45BAC 

,

SA

vuông góc với

đáy, khoảng cách giữa hai đường thẳng

SB

,

AC

bằng

4

3

a

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

2

3

a

V 

. B.

3

2Va

. C.

3

42Va

. D.

3

42

3

a

V 

.

Câu 37: Cho hình chóp

.S ABC

có đáy là tam giác cân tại

A

,

BAC





 

30 90



   

,

6AB 

,

SA

vuông góc với đáy, khoảng cách giữa hai đường thẳng

SB

,

AC

bằng

3

. Tính

cos



khi khối

chóp

.S ABC

có thể tích nhỏ nhất.

A.

3

cos

2





. B.

1

cos

2





. C.

3

cos

3





. D.

2

cos

2





.

Câu 38: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB 

, cạnh bên

1SA 

và vuông góc

với mặt phẳng đáy

 

ABCD

. Kí hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di động

trên đoạn

CB

sao cho

45MAN 

. Thể tích nhỏ nhất của khối chóp

.S AMN

là?

A.

21

9



. B.

21

3



. C.

21

6



. D.

21

9



.

Câu 39: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB 

, cạnh bên

1SA 

và vuông góc

với mặt phẳng đáy

 

ABCD

. Ký hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di động

trên đoạn

CB

sao cho

30MAN 

. Thể tích nhỏ nhất của khối chóp

.S AMN

là?

A.

1

9

. B.

1

3

. C.

2

27

. D.

4

27

.

Câu 40: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông,

1AB 

, cạnh bên

1SA 

và vuông góc

với mặt phẳng đáy

 

ABCD

. Ký hiệu

M

là điểm di động trên đoạn

CD

và

N

là điểm di động

trên đoạn

CB

sao cho

60MAN 

. Thể tích nhỏ nhất của khối chóp

.S AMN

là?

A.

23

3



. B.

23

9



. C.

2 3 3

3



. D.

2 3 3

9



.

Câu 41: Cho tam giác

ABC

vuông cân tại

B

,

2AC 

. Trên đường thẳng đi qua

A

vuông góc với mặt

phẳng

 

ABC

lấy các điểm

,MN

khác phía với mặt phẳng

 

ABC

sao cho

.1AM AN 

. Tìm

thể tích nhỏ nhất của khối tứ diện

MNBC

.

A.

1

3

. B.

1

6

. C.

1

12

. D.

2

3

.

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

60

Câu 42: Cho hình chóp

.S ABC

có

SA

,

SB

,

SC

đôi một vuông góc,

I

là tâm đường tròn nội tiếp tam giác

ABC

. Mặt phẳng

 

P

thay đổi qua

I

cắt các tia

SA

,

SB

,

SC

lần lượt tại

A



,

B



,

C



. Biết

2SA SB

,

7SC 

. Hỏi thể tích của khối chóp

.S A B C

  

có giá trị nhỏ nhất là?

A.

243 7

256

. B.

7

3

. C.

81 7

256

. D.

27 7

256

.

Câu 43: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

C

,

2SA AB a

. Cạnh bên

SA

vuông góc với mặt phẳng đáy

 

ABC

. Gọi

H

,

K

lần lượt là hình chiếu vuông góc của

A

lên

SB

và

SC

. Tìm thể tích lớn nhất

max

V

của khối chóp

.S AHK

.

A.

3

max

2

6

a

V 

. B.

3

max

3

6

a

V 

. C.

3

max

3

a

V 

. D.

3

max

2

3

a

V 

.

Câu 44: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

, 2 ,B AB a SA

vuông góc với đáy. Gọi

M

là trung điểm cạnh

AB

, mặt phẳng

 

P

qua

SM

song song với

BC

cắt

AC

tại

N

. Tính thể

tích

V

của khối chóp

.S BCMN

biết góc giữa

 

SBC

và đáy bằng

0

60

.

A.

3

43

3

a

V 

. B.

3

a

V 

. C.

3

3Va

. D.

3

23

3

a

V 

Câu 45: Trong mặt phẳng

 

P

cho nửa đường tròn đường kính

2AB R

và điểm

C

thuộc nửa đường tròn

sao cho

0

30ABC 

. Trên đường thẳng vuông góc với mặt phẳng

 

P

tại

A

lấy điểm

S

sao cho

góc giữa hai mặt phẳng

   

,SAB SBC

bằng

0

60

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

6

12

R

V 

. B.

3

2

6

R

V 

. C.

3

6

4

R

V 

. D.

3

2

R

V 

Câu 46: Cho khối chóp

.S ABC

có đáy là tam giác cân tại

A

,

SA

vuông góc với đáy, độ dài đường trung

tuyến

AD a

, cạnh bên

SB

tạo với đáy một góc



và tạo với mặt phẳng

 

SAD

góc

 



. Tính

thể tích

V

của khối chóp đã cho.

A.

 

3

22

sin sin

3 cos sin

a

V







. B.

3

22

sin sin

cos sin

a

V







.

C.

 

3

22

sin sin

3 cos sin

a

V









. D.

3

22

sin sin

cos sin

a

V









Câu 47: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh bằng

2

,

2SA 

vuông góc với đáy. Gọi

,MN

là hai điểm lần lượt trên

,AB AD

sao cho

 

SMC

,

 

SNC

vuông góc với nhau. Tính tổng

22

11

T

AM AN



khi khối chóp

.S AMCN

đạt giá trị lớn nhất.

A.

5

4

. B.

2

. C.

23

4



. D.

13

9

.

Câu 48: Trong mặt phẳng

 

P

cho

XYZ

cố định; Trên đường thẳng

d

vuông góc với mặt phẳng

 

P

tại

điểm

X

và về 2 phía của

 

P

ta lấy 2 điểm

,AB

thay đổi sao cho hai mặt phẳng

 

AYZ

và

 

BYZ

luôn vuông góc với nhau. Hỏi vị trí của

,AB

thỏa mãn điều kiện nào sau đay thì thể tích

ABYZ

là nhỏ nhất

A.

2XB XA

. B.

2XA XB

. C.

2

.XA XB YZ

. D.

XA XB

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

61

Câu 49: Cho khối tứ diện

ABCD

có

2AB 

,

3AC 

,

4AD BC

,

25BD 

,

5CD 

. Tính thể tích

V

của khối tứ diện

ABCD

.

A.

15V 

. B.

15

2

V 

. C.

35

2

V 

. D.

95

2

V 

.

Câu 50: Cho tam giác đều

ABC

có cạnh bằng

a

. Trên đường thẳng



qua

A

vuông góc với mặt phẳng

 

ABC

lấy hai điểm

,MN

nằm khác phía với mặt phẳng

 

ABC

sao cho hai mặt phẳng

 

MBC

và

 

NBC

vuông góc với nhau. Thể tích khối tứ diện

MNBC

có giá trị nhỏ nhất bằng.

A.

3

4

a

. B.

3

8

a

. C.

3

4

a

. D.

3

8

a

.

Câu 51: Cho hình chữ nhật

ABCD

có

,AB a AD b

. Trên hai đường thẳng

,Ax Cy

cùng vuông góc với

mặt phẳng

 

ABCD

lần lượt lấy hai điểm

,MN

sao cho hai mặt phẳng

 

BDM

và

 

BDN

vuông góc với nhau. Thể tích khối tứ diện

BDMN

có giá trị nhỏ nhất bằng

A.

22

ab

ab

. B.

22

4ab

ab

. C.

22

4

3

ab

ab

. D.

22

3

ab

ab

.

Câu 52: Cho hình chóp

.S ABCD

có đáy là hình bình hành,

2 , BC aAB a

0

120ABC 

và

SD

vuông

góc với đáy. Sin góc giữa đường thẳng

SB

và mặt phẳng

 

SAB

bằng

1

4

. Thể tích khối chóp

.S ABCD

bằng

A.

3

a

. B.

3

2

a

. C.

3

3a

. D.

3

2

a

.

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

62

BẢNG ĐÁP ÁN

1.B

2.A

3.B

4.A

5.A

6.D

7.A

8.B

9.A

10.C

11.A

12.A

13.B

14.D

15.B

16.A

17.B

18.A

19.C

20.C

21.A

22.A

23.B

24.A

25.D

26.A

27.B

28.B

29.D

30.A

31.C

32.A

33.A

34.C

35.A

36.D

37.D

38.B

39.A

40.C

41.D

42.C

43.A

44.C

45.A

46.A

47.A

48.D

49.A

50.A

51.D

52.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn B

Cách tự luận. Gọi

G

là trọng tâm của

BCD

.

23

33

a

BG BM

,

22

6

3

a

AG AB BG  

.

23

1 1 3 6 2

..

3 3 4 3 12

ABCD BCD

a a a

V S AG



  





.

Cách trắc nghiệm. Ta nhớ trực tiếp kết quả “Tứ diện đều có

 

3

2

12

V canh

”.

Câu 2: Chọn A

Gọi

M

là trung điểm của

.BC

Gọi

O

là trọng tâm của

ABC

Gọi

I

là hình chiếu vuông góc của

M

lên

.SA

Ta có:

MI SA

và

BC SA

Suy ra

 

SA IBC

. Măt khác

2 2 2

11

..

4 2 4 2 4 2

IBC

a a a a

S MI BC MI a MI      

Ta có

22

2

;

2

a

AI AM MI  

.6

tan

6

MI SO MI AO a

MAI SO

AI AO AI

    

Vậy

23

1 3 6 2

. . .

3 4 6 24

SABC

a a a

V 

Câu 3:

Giả sử: độ dài cạnh bên là

x

Ta có: I là trung điểm của S0 nên

11

23

JS JS

JC SC

  

. Dựng OH //SC

I

D

N

C

J

A

M

0

B

S

C

A

0

H

I

J

S

G

M

B

D

C

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

63

Ta có:

00

0 0 1 2

..

0 0 2 3

00

AH

A IS H SJ SJ SJ x

AC JC

JC

AC I JC H JC JC

IS SJ

IH







      











Xét

AIC

:

2 2 2

2 2 2 2

2

4 2 2 4

2

2 . .cosC 2 2. 2. . (1)

9 3 3 9

a

x x a x

AJ AC CJ AI JC a a

x

       

22

1 5 1 2 5 10

. . (2)

2 6 2 2 6 3

AMJN

a a a a

S AJ MN AJ AJ     

Từ (1), (2) suy ra:

xa

.

2

22

aa

SO x  

nên

3

2

1 1 2 2

0. . .

3 3 2 6

ABCD

aa

V S S a  

.

Câu 4: Chọn A

Cắt ngọn tháp và trải đều trên mặt phẳng như hình vẽ

Do

0

15ASB 

nên khi trải ra ta thu được tam giác đều SAA

Để

AM MN NP PQ  

ngắn nhất thì A,M,N,P,Q thẳng hàng

Khi đó:

N SC AQ

là giao 2 đường trung tuyến nên N là

trọng tâm tam giác SAA. Do đó:

2

AM MN AN

k

NP PQ NQ



  



Câu 5: Chọn A

Đường cao mặt bên:

2

4

a

hb

. Diện tích toàn phần:

2

2 2 2 2 2

22

43

3

3 1 3 3 4

3.

4 2 4 4 4

tp

Sa

a

a a a a b a

S a b b













     

2

2 2 2

22

43

3

(2S 3 a )

13

. . 3.

3 4 3 12 4

66

Sa

a

aS

a a a

V b a













    

2

2 2 2 2 2 2 2

2

(2S 3 a ) 3 (2S 3 a )S 3 2 3

216 2

216 3 216 3 216 3

a S a S a S a S

V



   

   





Dấu “



” xảy ra:

22

3 2 3 3 1

b

a S a S a b a

a

       

Q

P

N

M

A

D

C

B

A

S

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

64

Câu 6: Chọn D

Gọi

O

là giao của

AC

và

BD

.

Ta có

SBD CBD  

nên

SO CO

.

Trong tam giác

SAC

có

1

2

SO CO AC

nên tam

giác

SAC

vuông tại

A

.

Suy ra

22

2AC SA SC  

.

Diện tích đáy

1

2 2. . 2 2

2

ABCD ABC

S S BO AC



  

.

Do

3SD SB S C  

nên hình chiếu vuông góc

H

của

S

trên

 

ABCD

thuộc cạnh

AC

.

Vì

SH

là đường cao của tam giác

SAC

nên

22

.3

.

2

SA SC

SH

SA SC





Vậy

.

1 1 3 6

. . .2 2

3 3 2 3

S ABCD ABCD

V SH S  

.

Câu 7: Chọn A

Trong tam giác

ABC

có

22

5BC AC AB  

.

Do

3SA SB SC  

nên hình chiếu vuông góc

H

của

S

trên

 

ABC

trùng với tâm đường tròn ngoại tiếp tam giác

ABC

. Khi đó

H

là trung điểm của

BC

.

Trong tam giác

SHB

có

22

57

3

42

SH SB HB    

.

Vậy

.

1 1 7 1 7

. . . .2.1

3 3 2 2 6

S ABC ABC

V SH S  

.

Câu 8: Chọn B

Ta có diện tích đáy

12

. .sin

24

ABC

S AB AC BAC





.

Trong tam giác

ABC

có

22

2 . .cos 2 2BC AB AC AB AC BAC    

.

Gọi

H

là tâm đường tròn ngoại tiếp tam giác

ABC

khi đó

22

21

2sin

2

BC

R

A



   

.

Do

3SA SB SC  

nên hình chiếu vuông góc của

S

trên

 

ABC

trùng với tâm đường tròn ngoại tiếp

H

của tam giác

ABC

.

Trong tam giác

SBH

có

 

22

4 2 1 3 2SH SB HB      

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

65

Vậy

.

1 1 2 6 2 2

. . 3 2 .

3 3 2 6

S ABC ABC

V SH S



   

.

Câu 9: Chọn A

Gọi

H

là trung điểm của

BC

ta có:

 

AH BC AH ABC  

Do

AS AB AC a  

nên là

H

tâm đường tròn ngoại tiếp tam giác

SBC

. Do đó

SBC

vuông tại

S

và

2

2 2 2 2

6 15 5 7

3 3 12 12

a a a

BC SB SC a AH a a



        





Suy ra

3

1 6 7 14

. . . .

6 3 12 36

aa

V a a

Câu 10: Chọn C

Do

2SA SB SC a  

suy ra hình chiếu vuông góc

H

của

S

lên mặt phẳng

 

ABCD

trùng Với

giải thiết

ABCD

là hình thang và

,2AB BC CD a AD a   

thì tứ giác

ABCD

là hình thang

cân và nội tiếp đường tròn tâm

H

có bán kính

Ra

.

Do đó chiều cao của khối chóp

22

3 3 3

4 3, .

44

d

aa

h a a a S V     

Câu 11: Chọn A

Ta có:

 

2

6 2 4

1

, 6 2 4 . .

33

aa

S a h b a V S h



      

Theo bất đẳng thức cô si ta có:

 

3

2 2 3 2 2 4 2

. . . 3 2 2 .

3 3 3 3

a a a

V a a a



  

   





Dấu bằng xảy ra khi:

3 2 2 2 2 2.a a a b     

Câu 12: Chọn A

3SA SB SC SD a   

nên tứ giác

ABCD

nội tiếp đường tròn

()O

bán kính

R

.

Do

,2AB BC CD a AD a   

nên

ABCD

là nửa lục giác đều. Suy ra

Ra

.

2 2 2 2

22h SA R a h a    

.

2

33

4

ABCD

a

S 

suy ra

3

.

16

.

34

S ABCD ABCD

a

V h S

Câu 13: Chọn B

H

D

A

B

C

B

A

S

C

H

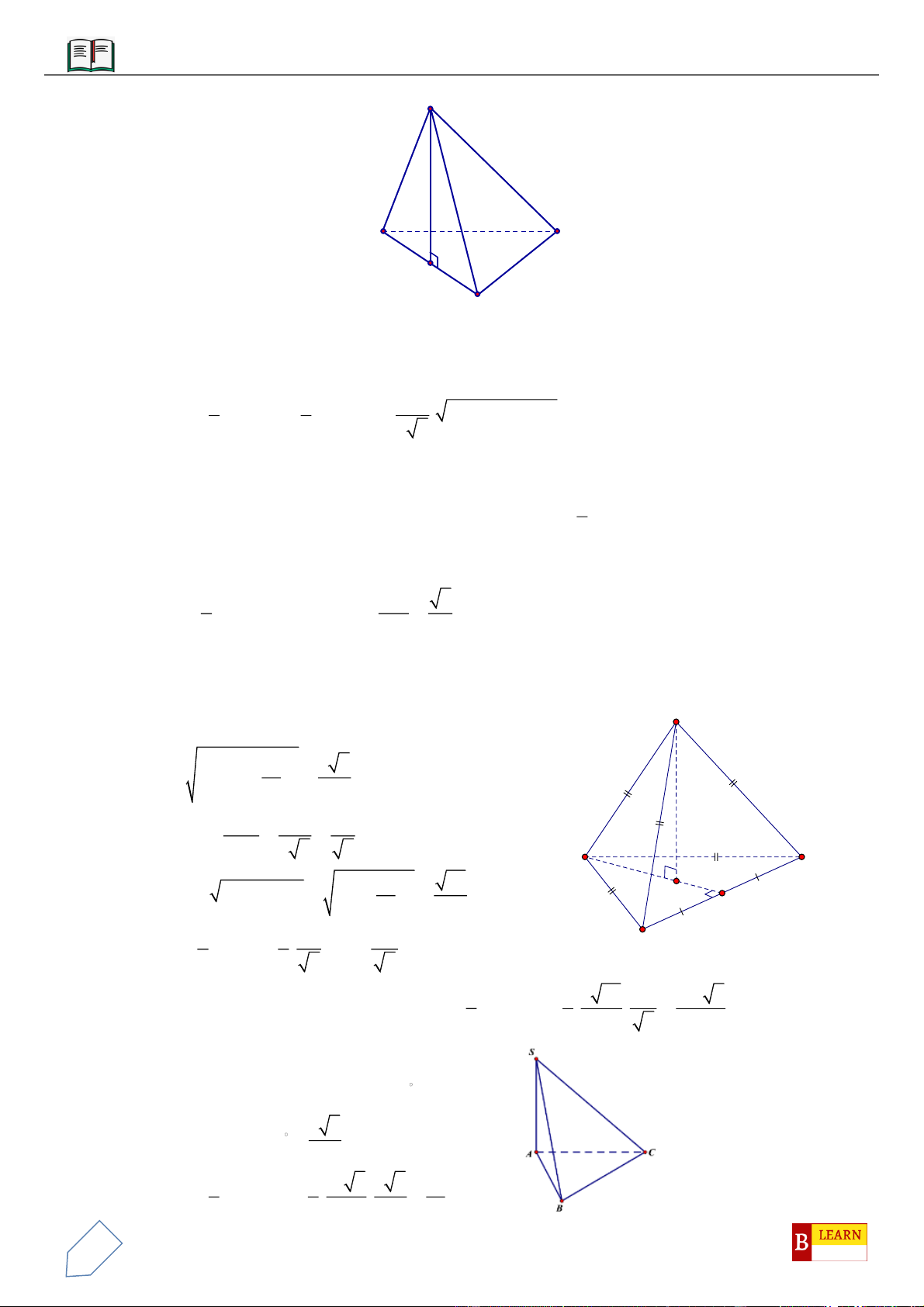
CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

66

Giả sử đáy là tam giác vuông tại

C

.

1SA SB SC  

nên hình chiếu vuông góc của

S

lên

()ABC

là trung điểm của

AB

.

2 2 2 2

.

1 1 1

. . . 2 . . .

33

32

S ABC ABC

V SH S SH HA SH SA SA  

Ta có:

2 2 2 2 2 2

2 2 2 2 2SH AH AH SH HA SA     

Vậy

222

2 . .SH SA SA

đạt GTLN khi

222

2

3

SH HA HA

Vậy

.S ABC

V

đạt GTLN khi tam giác

ABC

vuông cân và

2

26

cos cos

33

AH

HA SAH

SA



    

Câu 14: Chọn D

Gọi

O

là tâm đường tròn ngoại tiếp mặt đáy

 

ABC

.

SA SB SC

nên

 

SO ABC

.

 

2

37

2

22

aa

AI a



  





.

22

44

2

77

AC a

AO R a

AI

a

   

2 2 2 2

16 35

3

77

SO SA AO a a a     

.

2

1 1 4 6

. . .3

22

77

ABC

a

S AI BC a  

.

Vậy thể tích khối chóp cần tìm là:

.

1

.

3

S ABC ABC

V SO S

23

1 35 6 2 5

..

3 7 7

7

a a a



.

Câu 15: Chọn B

 

, , 30SB ABC SB AB SBA  

.

3

.tan30

3

a

SA AB  

.

23

.

1 1 3 3

. . . .

3 3 4 3 12

S ABC ABC

a a a

V S SA



  

S

A

B

C

H

I

O

C

B

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

67

Câu 16: Chọn A

Vì đáy ABCD là hình thoi có

22

33

60 2.

48

ABCD

aa

ABC S   

.

23

.

1 1 3 3

. . 2. .

3 3 4 6

S ABCD ABCD

aa

V S SA a



  





.

Câu 17: Chọn B

Vì

ABCD

là hình vuông với

2

2 2 4

ABCD

a a a

AC AB S    

.

 

3

, , 60 .tan60

2

a

SB ABCD SB AB SBA SA AB     

.

23

.

1 1 3 3

. . . .

3 3 4 2 24

S ABCD ABCD

a a a

V S SA  

.

Câu 18: Chọn A

ABC

vuông tại

B

:

.tan60 2 3BC AB a  

2

1

. 2 3

2

ABC

S AB BC a  

.

Vậy

23

.

11

. . . 3.2 3 2

33

S ABC ABC

V SA S a a a  

.

Câu 19: Chọn C

SAC

vuông cân tại

A

:

AC SA a

ABC

vuông tại

B

và

30BAC 

22

1

22

3

2

a

BC AC

a

AB AC BC











  





2

13

.

28

ABC

a

S AB BC  

.

Suy ra

3

.

13

.

3 24

S ABC ABC

a

V V SA S  

. Vậy

3

0,072

24

V

a



.

Câu 20: Chọn C

2

a

3

S

C

B

A

B

C

S

a

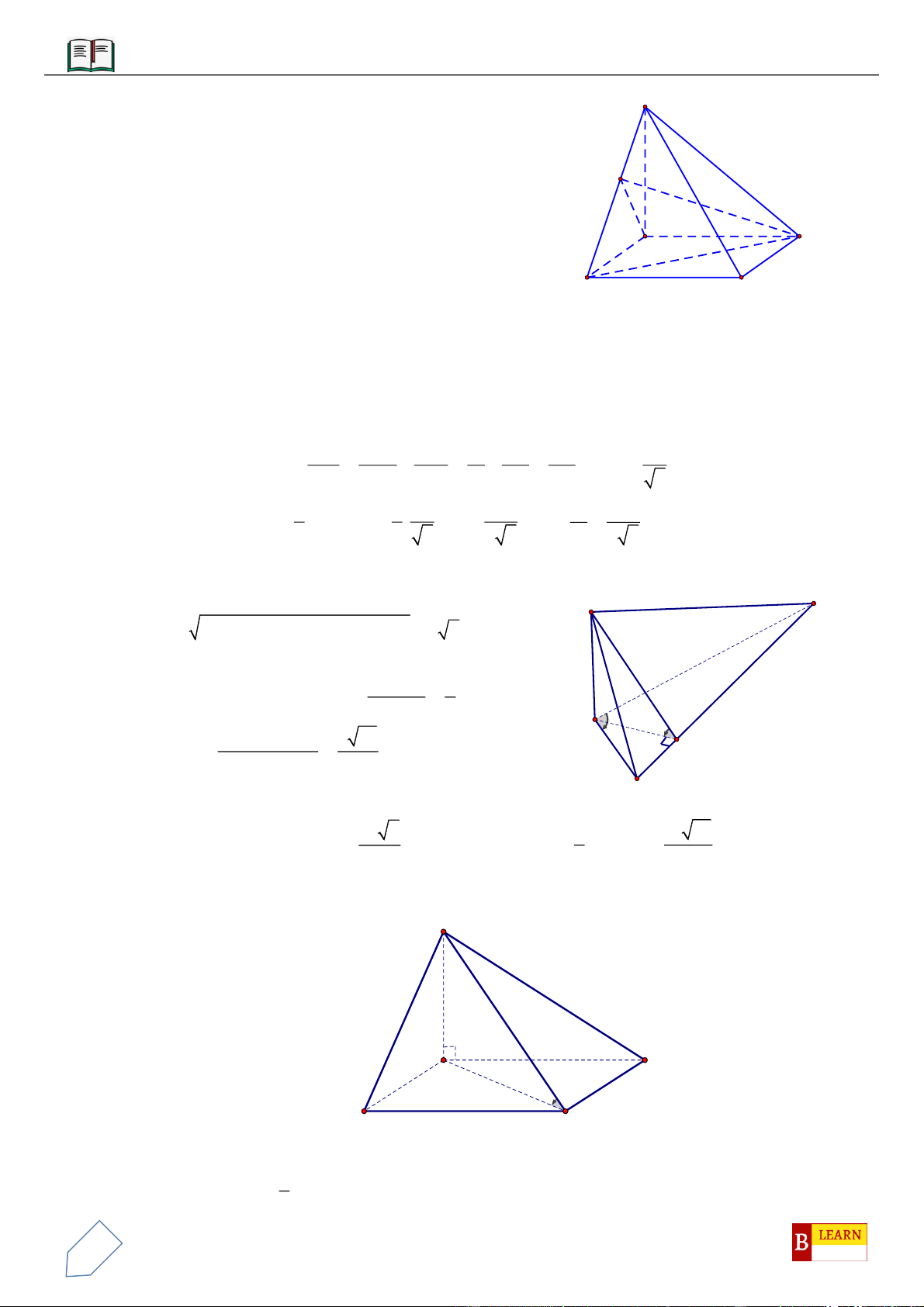
CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

68

Ta có:

   

 

SAB SAD SA

SAB ABCD SA ABCD

SAD ABCD







  











.

Gọi

H

là hình chiếu của

A

trên

SB

AH SB

.

Dễ thấy

 

AD SAB AD SB  

.

Do đó:

 

SB AHD S B HD  

.

Khi đó ta có:

   

 

; ; 45

;

SAB SBD SB

AH SB HD SB SAB SBD AHD

AH SAB HD SBD







     









.

Hay

AHD

vuông cân tại

A

AH AD a  

.

SAB

vuông tại

A

:

2 2 2 2 2 2

1 1 1 1 1 3 2

44

3

a

SA

SA AH AB a a a

      

.

Suy ra

3

2

.

1 1 2 4

. . .2

33

3 3 3

S ABC ABCD

aa

V V SA S a   

. Vậy

3

4

0,77

33

V

a



.

Câu 21: Chọn A

Tính cạnh

22

2 . .cos 7BC AB AC AB AC A a   

Kẻ AH vuông góc BC tại H,

diện tích tam giác

.1

. .sin

22

AH BC

AB AC A

. .sin 21

7

AB AC A a

AH

BC

  

Góc tạo bởi

 

mp MBC

và

 

mp ABC

là góc

0

60SHA 

.

Suy ra

 

0

37

.tan 60

7

a

SA AH

. Vậy thể tích

3

.

1 21

.

3 14

S ABC ABC

a

V SA S

Câu 22: Chọn A

Tính

5AC a

vì tam giác

SAC

suy ra

5SA a

Tính thể tích

3

1

. 20

3

ABCD

V SA S a

45

°

3a

4a

C

A

B

D

S

H

D

C

B

A

S

120

°

60

°

S

A

B

C

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

69

Câu 23: Chọn B

Ta có:

ABC

vuông tại

B

2

1

.6

2

ABC

S AB BC a



  

.

23

11

. .6 .6 12

33

SABC ABC

V S AD a a a



   

.

Câu 24: Chọn A

Ta có:

SBC

vuông tại

B

;

ABC

vuông tại

B

.

3

.cos

2

a

SA SB ASB

0

3

.sin30 ; 3

2

a

AB SB BC SB a   

.

1 1 1

. . . .

3 3 2

S ABC ABC

V S SA AB BC SA





3

1 3 3 3

. . 3.

6 2 2 8

a a a

a

3

8

3

a

V



.

Câu 25: Chọn D

Ta có:

 

.

11

. . .

3 3 2

S ABCD ABCD

AB CD AD

V S SD SD



  

 

3

3.

1 2 3

. . 3

3 2 3

a a a

a





.

Câu 26: Chọn A

Ta có góc tạo bởi

 

SBC

và

()ABCD

là

0

30SBA 

.

Xét tam giác

SAB

vuông tại

A

ta có

0

3

tan tan30

3

a

SA AB SBA a  

.

1

.

3

S ABCD ABCD

V S SA

3

2

1 3 3

..

3 3 9

aa

aV  

3

33

3

V

a



S

D

A

C

B

S

A

C

B

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

70

Câu 27: Chọn B

Xét tam giác

ABC

vuông tại

B

ta có

2 2 2 2 2 2

34AC AB BC a a a    

2AC a

.

Góc tạo bởi

SC

và đáy là góc

0

60SCA 

.

Xét tam giác

SAC

vuông tại

A

có

0

tan 2 tan60 2 3SA AC SCA a a  

3

.

11

. . 3.2 3 2

33

S ABCD ABCD

V S SA a a a a   

.

Câu 28: Chọn B

Xét tam giác

ABC

vuông tại

B

ta có

0

3

cot cot 60

3

a

BC AB BCA a  

2

1 1 3 3

. . .

2 2 3 6

ABC

aa

S AB BC a   

Do tam giác

SAB

vuông cân tại

A

suy ra

SA AB a

23

.

1 1 3 3

. . .

3 3 6 18

S ABC ABC

aa

V S SA a   

.

Câu 29: Chọn D

Gọi

H

là trung điểm của

AC

3

;

2

a

BH AC BH

.

Mà:

 

BH AC

BH ACD

BH AD





  







Hình chiếu của

B

xuống

 

DAC

là

H

.

Ta có:

   

 

0

; ; 30BD DAC D BD DAC BD DH BDH     

.

Xét tam giác

BHD

có:

0

3

tan30

2

tan30

BH BH a

HD

   

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

71

Xét tam giác

DAH

có:

22

2 2 2 2

9

22

44

aa

DA DH AH a DA a      

.

Thể tích khối tứ diện

ABCD

V

là:

22

1 3 6

. 2. .

3 4 12

ABCD

aa

Va

. Tỷ số

33

3

66

12

6

12

aa

V

a



.

Câu 30: Chọn A

Gọi

O

là giao điểm của

AC

và

BD

. Ta có:

 

SC SAC

.

Xét hai mặt phẳng

 

SAC

và

 

''AB D

có:

A

là điểm chung thứ nhất.

Trong

 

SBD

có:

''SO B D I

. Vậy

     

' ' ' ' 'SAC AB D AI SC AB D AI SC C      

.

Thể tích khôi chóp

SABCD

:

 

33

11

30.20 4000 cm

33

SABCD ABCD

V SA S     

.

Ta có:

2 2 2

2 2 2 2 2 2

30 9

17

30 20 20

SC SA SA

SC

SC SA AC



   

  

.

2 2 2

2 2 2 2 2

30 9

13

30 20

SD SA SA

SD

SD SA AD



   



.

 

3

2

9 9 81

4000 1466 cm

2 17 13 221

SAB C D SAC D

SABCD

SAB C D

SABCD SACD

VV

SA SC SD

VV

V V SA SC SD

    

  



          

.

Câu 31: Chọn C

Gọi

M

là trung điểm của

BC

12

22

a

AM BC  

.

2

11

2 4 2

ABC

a

S AM BC BC     

.

Ta có:

   

 

0

; 45

SBC ABCD BC

AM BC SBC ABCD SMA

SA ABCD







   









.

Xét tam giác

SAM

có:

2

.tan

2

a

SA AM SMA AM  

.

Thể tích của khối chóp là:

23

1 1 2 2

3 3 2 2 12

SABC ABC

a a a

V SA S      

. Tỷ số:

3

62

2

V

a



Câu 32: Chọn A

Gọi

I

là trung điểm

BC

. Vì chóp

.S ABC

có đáy

ABC

là tam giác đều và cạnh bên

SA

vuông góc

với mặt phẳng đáy nên

   

SAI SBC

theo giao tuyến

SI

. Kẻ

()AH SI AH SBC  

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

72

( ,( )) 3d A SBC AH  

. Giả sử

23AB x AI x  

.Trong tam giác vuông

SAI

có

2 2 2 2 2

1 1 1 1 1 1

9

3AH SA AI SA x

    

2

3

x

SA

x





(Điều kiện

 

3;x  

)

3

.

2

13

.

3

S ABCD ABC

x

V SA S

x

  



Xét hàm

 

3

2

( ) / 0;3

3

x

fx

x





có





4

22

2

23

2

33

(2 9)

3

()

3

x

xx

x

fx

x











0

3

( ) 0

2

3

2

x

f x x

x











   









. Lập bảng biến thiên suy ra GTNN của hàm số đạt tại

3

2

x 

Khi đó ta có

22

3

IH AI AH

cos

AI AI





  

Câu 33: Chọn A

Vì

M

điểm trong của khối chóp cách đều tất cả các mặt của khối

chóp một đoạn bằng

h

nên

M

là tâm mặt cầu nội tiếp hình chóp,

bán kính mặt cầu là

rh

.

Mặt khác mặt cầu bán kính

r

nội tiếp hình chóp thì thể tích khối

chóp là:

1

..

3

V S r

trong đó

S

là tổng diện tích tất cà các mặt của hình chóp.

Ta có

2 2 2 2

8 6 10;AC AB BC    

2 2 2 2

8 6 10SB AB SB    

Vì

()

BC AB

BC SAB BC SB

BC SA





   







ABC SAB SBC SAC

S S S S S

   

   

1 1 1 1

. . . . . . . . 108

2 2 2 2

AB BC SA AB SB BC SA AC    

1 1 1

. . . . .6.24 48

3 3 3

ABC

V S r SA S



   

3 3.48 4

.

108 3

V

rh

S

    

Câu 34: Chọn C

Vì điểm

M

thuộc phần không gian bên trong của hình chóp và cách đều tất cả các mặt của khối

chóp nên

M

là tâm mặt cầu nội tiếp hình chóp, bán kính mặt cầu là

r

.

Theo câu 31 ta có

4

3

rh

.

1 1 1 4 32

. . . .8.6. .

3 3 2 3 3

M ABC ABC

V S h



   

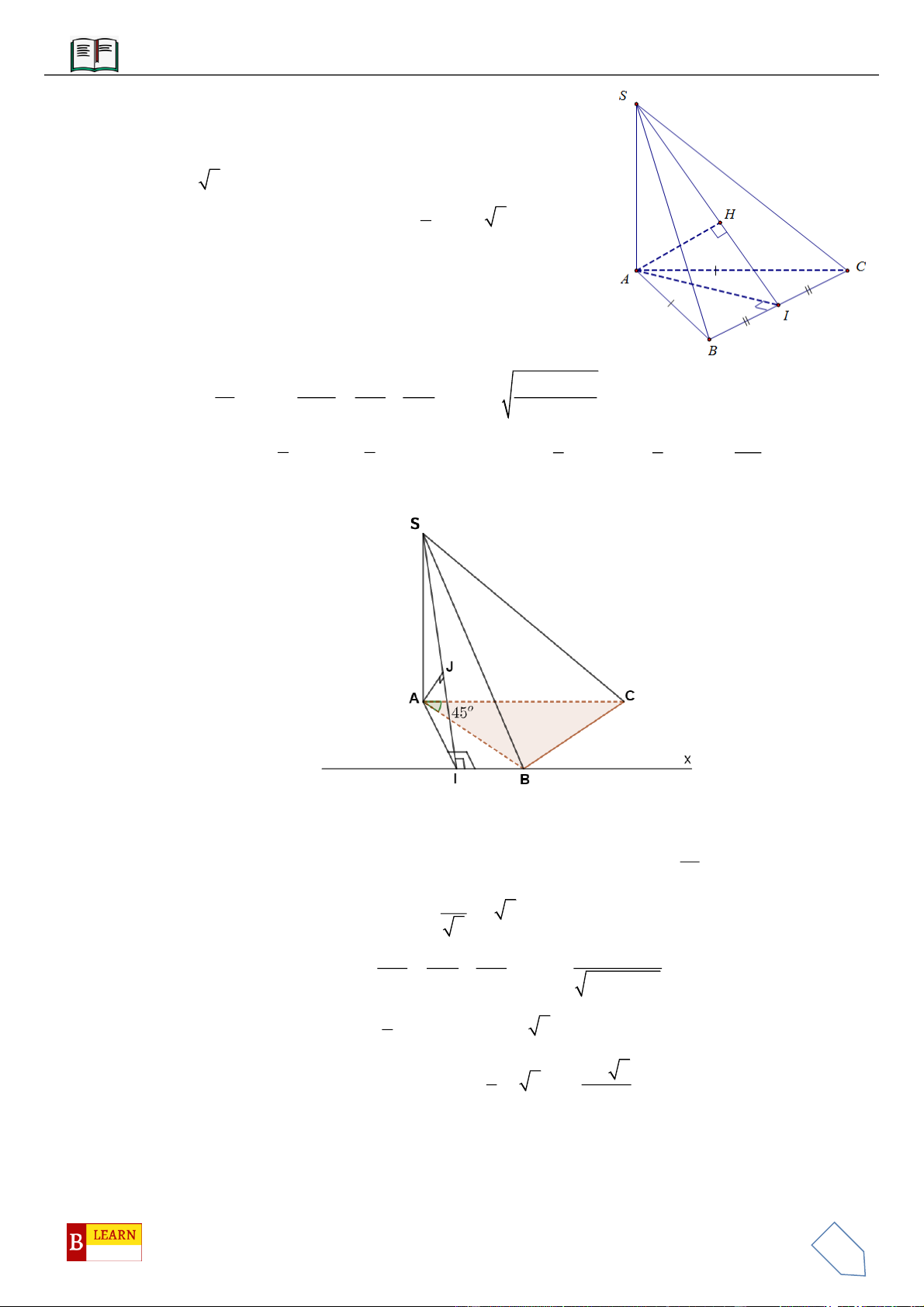
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

73

Câu 35: Chọn A

Vì

ABC

là tam giác vuông cân tại

, 2 ,A AB a

nên

22BC a

Gọi

I

là trung điểm

BC

suy ra

1

2.

2

AI BC a

Khi đó

 

.

BC AI

BC SAI

BC SA













Goi

H

là hình chiếu của

A

lên

SI

suy ra

AH

là khoảng

cách từ

A

đến mặt phẳng

 

SBC

.

4

3

a

AH

.

Ta có

22

2 2 2 2 2

1 1 1 .

4.

AI AH

SA a

AH AI SA AI AH

    



Mặt khác

2

11

. 2 .2 2 .

22

ABC

S AB AC a a a



  

3

2

.

1 1 8

. . .2 .4 .

3 3 3

S ABC ABC

a

V S SA a a



   

Câu 36: Chọn D

Kẻ

//Bx AC

     

, ,( ) ,( )d AC SB d AC SBx d A SBx  

.

Dựng

AI Bx

tại

I

,

AJ SI

tại

J

   

4

, ,( )

3

a

d AC SB d A SBx AJ   

.

Tam giác

AIB

vuông cân tại

I

2

AB

AI a  

.

Tam giác

SAI

vuông tại

A

2 2 2

22

1 1 1 .

4

AI AJ

SA a

AJ SA AI

AI AJ

     



.

Diện tích tam giác

ABC

là

2

1

.2 .2 .sin45 2

2

S a a a  

.



Thể tích

V

của khối chóp

.S ABC

là

3

2

1 4 2

. 2.4

33

a

V a a

.

Câu 37: Chọn D

Kẻ

//Bx AC

     

, ,( ) ,( )d AC SB d AC SBx d A SBx  

.

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

74

Dựng

AH Bx

tại

H

,

AI SH

tại

I

   

, ,( ) 3d AC SB d A SBx AI   

.

Tam giác

AHB

vuông tại

H



.sin 6.sinAH AB





.

Tam giác

SAH

vuông tại

A

2

2 2 2 2 2

1 1 1 1 1 4sin 1

9

36sin 36sinSA AI AH







     

.

2

6sin

4sin 1

SA







.

Thể tích khối chóp

2

22

1 1 6sin 1 36sin

. . . . .6.6.sin

3 3 2

4sin 1 4sin 1

ABC

V SA S







  



.

Ta có

 

2

2 2 2

9 4sin 1 9

36sin 1

9 4sin 1 18

4sin 1 4sin 1 4sin 1

V



  





     



  



.

min 18V

xảy ra khi

22

1

4sin 1 1 sin

2



   

2

cos

2





.

Câu 38: Chọn B

Thể tích khối chóp

.S AMN

nhỏ nhất



Diện tích tam

giác

AMN

nhỏ nhất.

Gọi

DM x

,

BN y

 

0 , 1xy

.

Khi đó ta có

tan tan

DAM x

BAN y



















.

 

tan tan

tan tan45 1

1 tan .tan 1

xy





      



12x y xy xy    

(1).

Đặt

 

01t xy t  

. (1)

2

2 1 0 2 1 2 1t t t         

.

Kết hợp điều kiện

0 2 1t   

0 3 2 2xy   

.

 

AMN ABCD ADM ABN CMN

S S S S S   

    

1 1 1 1

1 1 1 1 2 1

2 2 2 2

x y x y xy



         





.

Vậy

.

1 1 2 1

..

3 3 3

S AMN AMN AMN

V S SA S



  

21

min

3

V





.

Câu 39: Chọn A

D

B

A

C

S

M

N

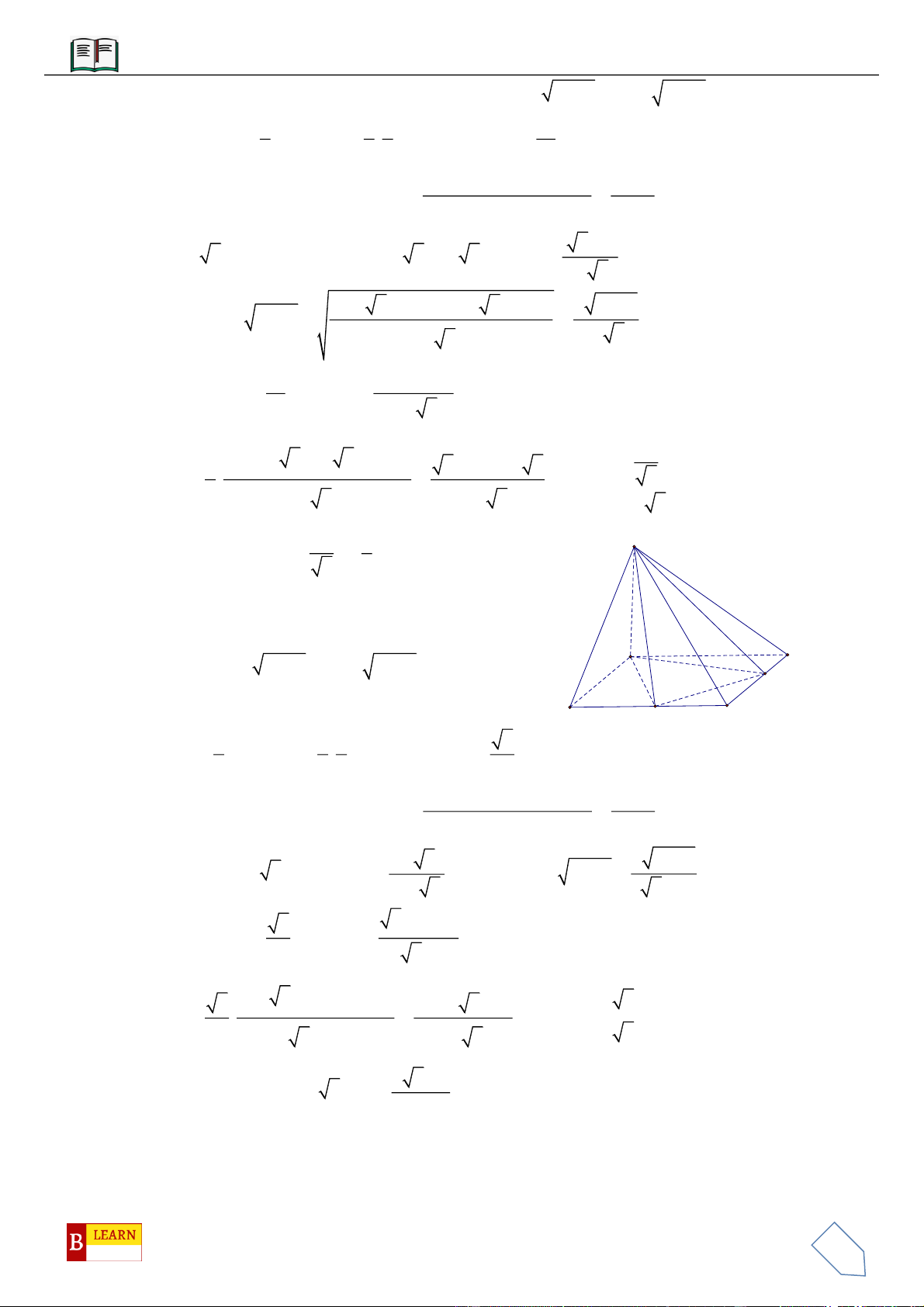
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

75

Đặt

,DM x BN y

với

0 , 1xy

. Khi đó

22

1, 1AM x AN y   

.

Ta có

.

1 1 1 1

. . . . . .sin30 . .

3 3 2 12

S AMN AMN

V SA S AM AN AM AN



   

.

Ta có





tan tan

tan60 tan

1

1 tan .tan

xy

DAM BAN

xy

DAM BAN



    



Suy ra

 

3

3 1 1 3 3

13

x

xy x y y x x y

x



        



.

Do đó

 

2 2 2

2

3 2 3 1 2 3 3 2 1

1

13

x x x x x

AN y

x

     

   



.

Suy ra

 

2

.

11

..

12

6 1 3

S AMN

x

V AM AN f x

x



  



.

 

   

 

2

22

1

2 . 1 3 3 1

1 3 2 3

3

.0

6

1 3 6 1 3

3

x x x

x TM

xx

fx

xx

xL



  









   











Suy ra

 

0; 1

11

Min

9

3

f x f









.

Câu 40: Chọn C

Đặt

,DM x BN y

với

0 , 1xy

.

Khi đó

22

1, 1AM x AN y   

.

Ta có

.

1 1 1 3

. . . . . .sin60 . .

3 3 2 12

S AMN AMN

V SA S AM AN AM AN



   

.

Ta có





tan tan

tan30 tan

1

1 tan .tan

xy

DAM BAN

xy

DAM BAN



    



Suy ra

 

13

3

x

xy x y y

x



    



. Do đó

2

21

1

3

x

AN y

x



  



.

Suy ra

 

2

.

31

3

..

12

63

S AMN

x

V AM AN f x

x



  



.

 

   

 

2

22

2 . 3 1

32

3 2 3 1

.0

6

32

3 6 1 3

x x x

x TM

xx

fx

xL

xx



  

  







   



  





Suy ra

 

0;1

2 3 3

Min 3 2

3

f x f



   

.

Câu 41: Chọn D

D

B

A

C

S

M

N

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

76

Ta có tam giác

ABC

vuông cân tại

B

,

2AC 

nên

2AB BC

.

   

..

1 1 1

. . . . . .

3 2 3

MNBC M ABC N ABC

V V V AM AB BC AN AB BC AM AN     

22

.

33

AM AN

, dấu bằng khi

1AM AN

.

Câu 42: Chọn C

Gọi

SA a





,

SB b





,

SC c





. Ta thấy

.

1

6

S A B C

V abc

  



.

Xét tứ diện

SABC

như hình vẽ. Gọi

H

là trung điểm của

AB

. Ta thấy

3CA CB

,

2AB 

và

2 2 2

3 1 2 2CH C HB B   

. Vậy tam giác

ABC

là tam giác cân tại

C

, suy ra điểm

I

thuộc vào đường cao

CH

của tam giác

CAB

, đồng thời

1

. 2 2

2

ABC

S CH AB

.

Gọi

r

là bán kính đường tròn nội tiếp tam giác

ABC

(

r IH

). Ta có

 

2 2 2

2

3 3 2 2

ABC

S

IH r

p

   



. Từ đây

2

7.

.7

2

4

22

IK IH SC IH

IK

SC CH CH

    

A

B

C

M

N

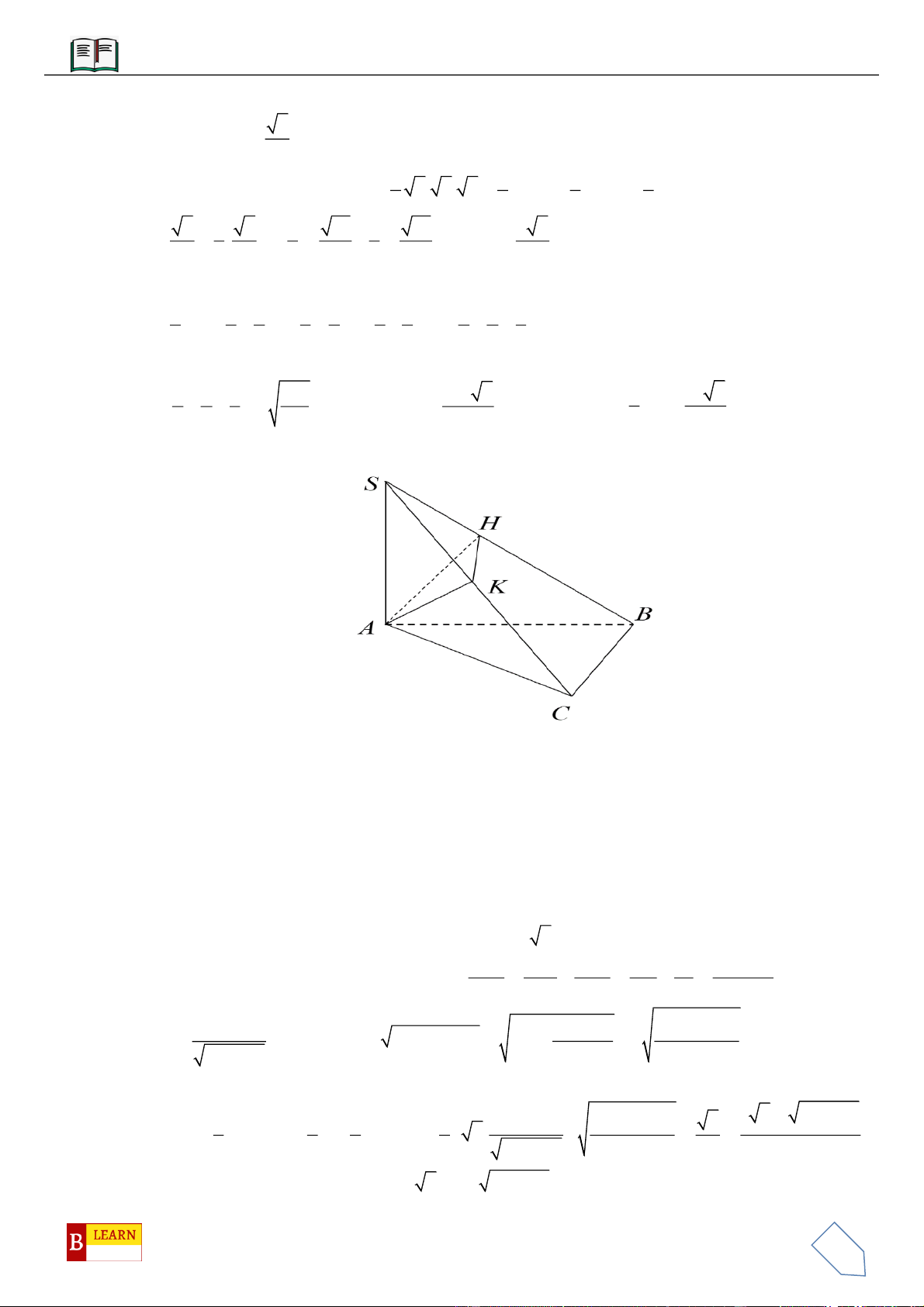
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

77

Gọi

x

,

y

,

z

lần lượt là khoảng cách từ

I

đến các mặt phẳng

 

SAB

,

 

SBC

,

 

SAC

. Dễ thấy

yz

,

7

4

x IK

. Đồng thời

. . . .

1 1 1 1

2. 2. 7 . . .

6 3 3 3

7 1 7 1 14 1 14 3 2

. .1 . . . .

3 3 4 3 2 3 2 8

S ABC I SAB I SAC I SBC SAB SBC SCA

V V V V x S y S z S

y z y z

      

      

Xét tứ diện

.S A B C

  

, ta thấy

. . . .S A B C I SA B I SA C I SB C

V V V V

        

  

1 1 1 1 1 1 1

. . . 1

6 3 2 3 2 3 2

y

xz

abc x ab y bc z ca

a b c

       

Theo bất đẳng thức Cauchy cho 3 số, ta có

3

243 7

3 27

128

1

y

xz

xyz

abc xyz

abca b c

 

. Từ đó

.

6

1

6

81 7

25

S A B C

V abc

  



Câu 43: Chọn A

Ta chứng minh được

 

BC SAC

, từ đó

 

AK SC

AK SBC AK KH

AK BC





   







.

Đồng thời

 

do

AH SB

SB AHK

AK SB AK SBC

















Vậy ta nhận thấy hình chóp

.S AHK

có

 

SH AHK

và tam giác

AHK

vuông tại

K

.

Gọi độ dài đoạn

AC x

(với

02xa

vì tam giác

ABC

vuông tại

C

với

2AB a

). Xét tam

giác vuông cân

SAB

ta có đường cao

2AH SH a

.

Trong tam giác vuông

SAC

ta có

22

2 2 2 2 2 2 2

1 1 1 1 1

44

4x

AK AS AC a a xx

a

   





. Khi đó

22

2

4

ax

x

AK

a





. Suy ra

 

22

2 2 2

2 2 2 2

24

4

2

44

a

H

x

K AH a a

x

AK

xxaa

 









Vậy thể tích

 

22

3

2 2 2

22

.

2

24

1 1 1 1 2 2

. . . 2. .

3 3 2 6 3

44

4

S AHK AHK

xa

a

ax

V SH S SH AK KH a a

x

a

aa

x

xx

a

















Áp dụng bất đẳng thức Cauchy cho

2x

và

22

4a x

ta có

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

78

 

2

22

24

4

24

22

x

xax

a

x

a





 



Từ đó suy ra

 

22

2 2 3

33

22

.

24

2 2 4 2

3 3 6

4

24

S AHK

x

V

x

xa

aa

a

x















.

Câu 44: Chọn C

Ta có tam giác

ABC

vuông tại

B

nên

2

11

. .2 .2 2

22

ABC

S AB BC a a a  

.

Mặt khác theo giả thiết ta có

   

 

0

, , 60 .SBC ABC SB AB SBA  

Do đó

0

.tan60 2 3SA AB a

. Nên

3

.

1 4 3

..

33

S ABC ABC

a

V SA S

.

Ta có

3

..

3

4

S BCMN S ABC

V V a

.

Câu 45: Chọn A

Kẻ

     

0

, , 60AH SB H SB AK SC K SC SB AHK AHK       

.

Ta có

2

sin 2 sin , cos 2Rcos S 2 sin cos

ABC

AC AB R BC AB R

     

     

.

Ta lại có

22

3 3 4

sin 2 3

2

AK

AHK AK AH

AH

AK AH

     

2 2 2 2 2

2

1 1 1 1 2 sin

3 4 .

4 sin 4

3 4sin

R

SA

SA R SA R



   

     

   

   



Do đó

3 2 3

.

2

1 4 sin cos 6

.

3 12

3 3 4sin

S ABC ABC

RR

V SA S





  



.

S

A

C

B

M

N

S

A

C

B

K

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

79

Câu 46: Chọn A

Ta có

 

,SB ABC SBA





.

Mặt khác ta có

   

 

,.

BD AD

BD SAD SB SAD BSD

BD SA







    







Giả sử

( 0).BD x x

Khi đó ta có

sin

xx

SB



  

.

Mặt khác ta có

cos sin

cos ,

sin sin

AB x x

AB SA

SB







   

.

Ta lại có

2

2 2 2 2

2

22

cos sin

1

sin

cos sin

a

AB x a x a x









      







.

Do đó

 

3

.

22

1 1 sin sin sin sin

. . . .

3 3 sin

3 cos sin

cos sin

S ABC

x a a

V SA AD BD a

   





  



.

Câu 47: Chọn A

Đặt

AM x

,

AN y

. Gọi

O AC DB

;

E BD CM

;

F BD CN

.

H

là hình chiếu vuông góc của

O

trên

SC

, khi đó:

CHO

đồng dạng

ASC

2

3

HO CO

HO

SA SC

   

.

Ta có:

 

BD SA

BD SAC

BD AC













Lại có:

 

SC OH SC HE

SC HBD

SC BD SC HF





  







.

S

A

B

C

D

E

F

O

A

D

B

C

E

M

N

H

K

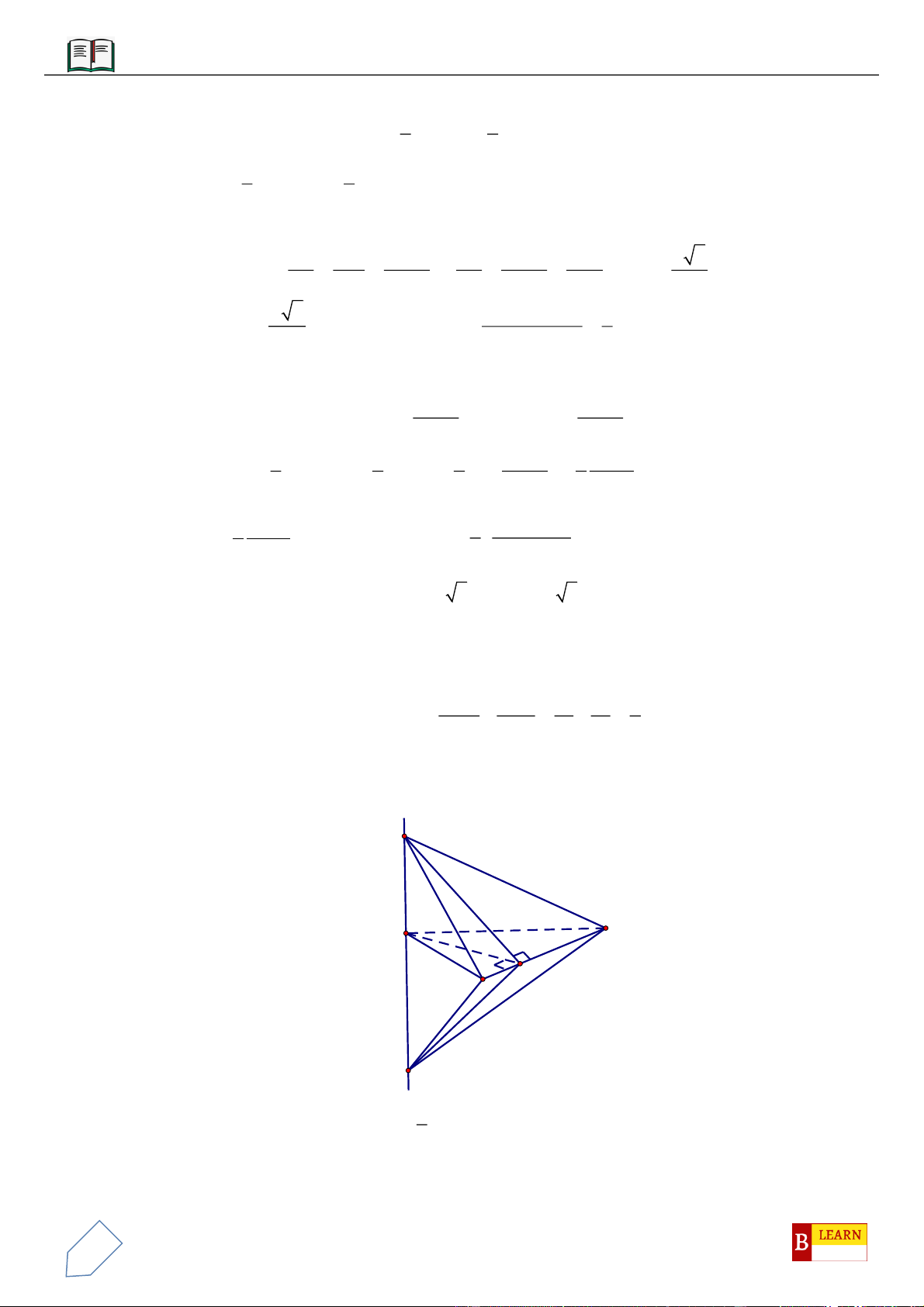
CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

80

Do đó góc giữa

 

SCM

và

 

SCN

bằng góc giữa

HE

và

HF

. Suy ra

HE HF

.

Mặt khác

11

..

22

AMCN ACN ACM

S S S CB AM CD AN x y



     

 

.

12

.

33

S AMCN AMCN

V SA S x y   

.

Ta có:

0x 

,

0y 

và nếu

2x 

,

2y 

thì gọi

K

là trung điểm của

AM

, khi

đó

//KO MC

nên

2

4 2 4 2 4 4

OE KM x OE EB OB x

OE

EB MB x x x x x

      

   

.

Tương tự:

2

4

y

OF

y





. Mà

  

2

.

3

44

xy

OE OF OH

xy

  



  

2 2 12xy   

Nếu

2x 

hoặc

2y 

thì ta cũng có

  

2

. 2 2 12OE OF OH x y    

.

Tóm lại:

  

2 2 12xy  

82

2

x

y

x







, do

2y 

nên

82

21

2

x



  



.

Do đó

 

2

.

1 2 2 8 2 2 8

.

3 3 3 2 3 2

S AMCD AMCN

xx

V SA S x y x

xx

   

     







.

Xét

 

2

28

32

x

fx

x







với

1; 2x   



,

 

2

2 4 8

3

2

xx

fx

x

















.

 

2

0 4 8 0 2 2 3f x x x x



        

;

2 2 3x   

(loại).

Lập BBT ta suy ra

     

0;2

max 1 2 2f x f f





  

.

Vậy

.

2 2 2 2

1

2

1 1 1 1 5

max 2

4

2

1

S AMCN

x

y

VT

AM AN x y

x

y

















       



















.

Câu 48: Chọn D

Thể tích khối tứ diện

ABYZ

là

1

.

3

XYZ

V AB S





.

Do diện tích tam giác

XYZ

không đổi nên thể tích tứ diện

ABYZ

là nhỏ nhất khi

AB

ngắn nhất.

d

X

Y

Z

B

A

F

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

81

Dựng

XF YZ

, do

YZ AB

nên

 

YZ ABF

, suy ra

   









, , 90AYZ BYZ FA FB AFB   

.

Xét tam giác vuông

ABF

có

FX

là đường cao không đổi (Do

XF

là đường cao của

XYZ

cố

định) nên

2

.XF XA XB

không đổi.

Có

2 . 2AB XA XB XA XB XF   

không đổi. Dấu bằng xảy ra khi và chỉ khi

XA XB

.

Vậy thể tích khối tứ diện

ABYZ

nhỏ nhất khi

X

là trung điểm

AB

hay

XA XB

Câu 49: Chọn A

Do

2 2 2

AB AD BD

ABD

vuông tại

A

;

2 2 2

AC AD CD

ACD

vuông tại

A

.

Lại có

2 2 2 2 2 2

2 3 4 1

cos

2. . 2.2.3 4

AB AC BC

BAC

AB AC

   

   

Sử dụng công thức giải nhan h: Cho chóp

.S ABC

có

SA a

,

SB b

,

SC c

và

AS B





,

BSC





,

ASC





. Thể tích khối chóp

.S ABC

là:

2 2 2

.

1 2 . .

6

S ABC

abc

V cos cos cos cos cos cos

     

    

.

Áp dụng: Thể tích khối tứ diện

ABCD

là

2

22

2.3.4 1 1

1 cos 90 cos 90 2. .cos90 .cos90 15

6 4 4

ABCD

V

   

          

   

   

.

Câu 50: Chọn A

Ta có:

2

13

.MN.S .

3 12

MNBC ABC

a

V MN

Gọi

D

là trung điểm cạnh

BC

ta có

()

BC AD BC DM

BC MDN

BC MN BC DN





  







Do đó

   

 

2

02

3a

, , 90 .

4

MBC NBC DM DN DM DN AM AN AD      

Khi đó theo bất đẳng thức AM – GM ta có:

2 . 3MN AM AN AM AN a   

Vì vậy

2 2 3

33

. . 3

12 12 4

MNBC

a a a

V MN a  

Câu 51: Chọn D

A

B

D

C

2

4

3

CHỦ ĐỀ 1: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

82

Ta có :

   

 

22

2 sin ,

2

3

MBD NBD

BDMN

S S MBD NBD

SS

V

BD

ab









Trong đó

22

BD a b

Và

   

 

0

sin , sin90 1MBD NBD 

Đặt

,AM x CN y

Ta có

   

 

   

 

   

 

0

, , , 180MBD ABCD NBD ABCD MBD NBD  

Do đó

   

 

   

 

0

, , 90MBD ABCD NBD ABCD

   

 

   

 

sin , ,MBD ABCD cos NBD ABCD

2

2 2 2 2 2

1 1 1 4

ABD ABD

MBD NBD

MBD NBD ABD

SS

a

SS

S S S a b



      





Theo định lý diện tích hình chiếu ta có

   

 

,

ABD

MBD

S

cos MBD ABCD

S



và

   

 

,

ABD

NBD

S

cos NBD ABCD

S



. Theo BĐT AM- GM ta có:

22

2 2 2 2 2 2

4 1 1 1 1 2 1

2 . .

.2

MBD NBD

MBD NBD MBD NBD

S S a b

SS

a b S S S S

     

. Vậy

22

3

BDMN

ab

V

ab





Câu 52: Chọn A

Đặt

SD h

, ta có

2 2 0

2 . .cos60 3BD AD AB AB AD a   

Suy ra

2 2 2 2

3SB SD BD h a   

Ta có

 

;;d B SAC d D SAC

và

 

2

2 2 2 2 2 2

2

1 1 1 1 1 7

; 4 3

;

DAC

AC

SD d D AC h S h a

d D SAC

     

 

22

3

;

37

ah

d D SAC

ah





( Do

2

22

1 3 3

7 ; .2 .

2 2 2

DAC

a

AC a S a a  

)

Do đó

 

22

3

;

1

37

sin SB; 3

4

3

ah

d B SAC

ah

SAC h a

SB

ha



    



Vậy

3

.S ABCD

Va

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

83

DẠNG 4: THỂ TÍCH KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY

BÀI TẬP VẬN DỤNG.

Câu 1. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

, mặt bên

 

SAD

là tam giác đều và nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích

V

của khối chóp đã cho.

A.

3

2

a

V 

. B.

3

6

a

V 

. C.

3

12

a

V 

. D.

3

4

a

V 

.

Câu 2. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

a

, mặt bên

 

SAD

là tam giác vuông cân tại

S

và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích

V

của khối chóp đã cho.

A.

3

6

a

V 

. B.

3

2

3

a

V 

. C.

3

2

6

a

V 

. D.

3

2

a

V 

.

Câu 3. Cho khối chóp

.S ABCD

có đáy là hình chữ nhật,

AB a

,

3AD a

, mặt bên

 

SAD

là tam

giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích

V

của khối chóp đã cho.

A.

3

a

V 

. B.

3

2

a

V 

C.

3

33

2

a

V 

. D.

3

6

a

V 

.

Câu 4. Cho khối chóp

.S ABCD

có đáy là hình chữ nhật,

AB a

,

3AD a

. Mặt bên

 

SAD

là tam

giác vuông cân tại

S

và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích

V

của khối chóp

đã cho.

A.

3

2

a

V 

. B.

3

2

a

V 

. C.

3

2

a

V 

. D.

3

2

a

V 

.

Câu 5. Cho hình chóp tứ giác

.S ABCD

có đáy là hình vuông cạnh bằng

2a

. Tam giác

SAD

cân tại

S

và mặt bên

 

SAD

vuông góc với mặt phẳng đáy. Biết thể tích khối chóp

.S ABCD

bằng

3

4

3

a

.

Tính khoảng cách

h

từ

B

đến mặt phẳng

 

SCD

.

A.

2

3

ha

. B.

4

3

ha

. C.

8

3

ha

. D.

3

4

ha

.

 Với các khối chóp có giả thiết mặt phẳng vuông góc với đáy ta sử dụng các định lý về gioa tuyến dưới

đây:

 Hai mặt phẳng cùng vuông góc với đáy thì đoạn giao tuyến của chúng vuông góc với đáy. Tính chất

này dựa trên định lí về giao tuyến của hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba.

Kí hiệu:

   

 

PR

Q R a R

P Q a







  











 Mặt bên nào vuông góc với đáy thì đường cao của mặt bên đó vuông góc với đáy. Tính chất này dựa

trên định lý sau:

   

 

,

PQ

P Q a d Q

d P d a







   











CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

84

Câu 6. Cho hình chóp

.S ABCD

có cạnh đáy là hình vuông cạnh bằng

2a

. Tam giác

SAD

cân tại

S

và

mặt bên

 

SAD

vuông góc với đáy. Biết khoảng cách

h

từ

B

đến mặt phẳng

 

SCD

bằng

4a

3

.

Tính thể tích của khối chóp

.S ABCD

.

A.

3

2a

3

V 

. B.

3

a

3

V 

. C.

3

8a

3

V 

. D.

3

4a

3

V 

.

Câu 7. Cho hình chóp

.S ABCD

có cạnh đáy là hình vuông cạnh bằng

a

. Tam giác

SAD

cân tại

S

và mặt

bên

 

SAD

vuông góc với đáy, biết

3a

2

SC 

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

a

3

V 

. B.

3

a

9

V 

. C.



3

4a

9

V

. D.

3

2a

9

V 

.

Câu 8. Cho hình chóp

.S ABCD

có đáy là hình chữ nhật

;3AB a AD a

. Tam giác

SAD

cân tại

S

và mặt bên

 

SAD

vuông góc với đáy, biết

2aSC 

. Tính thể tích của khối chóp

.S ABCD

.

A.

3

a3

6

V 

. B.

3

3a 3

2

V 

. C.

3

9a 3

2

V 

. D.

3

a3

2

V 

.

Câu 9. Cho hình chóp

.S ABCD

có đáy là hình thoi

;3AC a BD a

. Tam giác

SAB

là tam giác đều

và mặt bên

 

SAB

vuông góc với đáy. Tính thể tích của khối chóp

.S ABCD

.

A.

3

3a

4

V 

. B.

3

a

2

V 

. C.

3

a

4

V 

. D.

3

3a

2

V 

.

Câu 10. Cho hình chóp

.S ABCD

có đáy là hình thoi

;3AC a BD a

. Tam giác

SAB

là tam giác vuông

cân tại

S

và mặt bên

 

SAB

vuông góc với đáy. Tính thể tích của khối chóp

.S ABCD

.

A.

3

a3

4

V 

. B.

3

a3

6

V 

. C.

3

a3

12

V 

. D.

3

a3

2

V 

.

Câu 11. Trong các khối chóp

.S ABCD

có đáy là hình vuông, tam giác

SAD

cân tại

S

và mặt bên

 

SAD

vuông góc với đáy,

23SC 

. Khối chóp có thể tích lớn nhất là

A.

4 10

5

. B.

64

15

. C.

4 10

15

. D.

64

5

.

Câu 12. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

2a

, tam giác

SAB

vuông cân tại , tam giác

SCD

đều. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

6

12

a

V 

. B.

3

4

a

V 

. C.

3

6

a

V 

. D.

3

12

a

V 

.

Câu 13. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

, mặt bên

SAB

là tam giác cân tại

S

và

nằm trong mặt phẳng vuông góc với đáy. Biết

26

2

a

SC 

, tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

2

3

a

V 

. B.

3

4Va

. C.

3

4

3

a

V 

. D.

3

2Va

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

85

Câu 14. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

4, 6AB SC

và mặt bên

 

SAD

là tam giác cân tại

S

và nằm trong mặt phẳng vuông góc với mặt phẳng đáy

 

ABCD

. Thể tích

lớn nhất của khối chóp

.S ABCD

là

A.

40

3

. B.

40

. C.

80

. D.

80

3

.

Câu 15. Trong các khối chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

23AB 

, tam giác

SAB

vuông

cân tại

S

, tam giác

SCD

đều. Khối chóp

.S ABCD

có thể tích lớn nhất bằng

A.

6

. B.

63

. C.

23

. D.

62

.

Câu 16. Cho khối chóp

.S ABCD

có đáy là hình chữ nhật,

,3AB a AD a

. Gọi

H

là trung điểm của

cạnh

AB

, các mặt phẳng

   

,SHC SHD

cùng vuông góc với đáy và

SD

tạo với đáy góc

60

.

Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

13

2

a

V 

. B.

3

13

3

a

V 

. C.

3

3 13

2

a

V 

. D.

3

5 13

2

a

V 

.

Câu 17. Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

2a

, tam giác

SAB

cân tại

S

, mặt bên

 

SAB

vuông góc với đáy và

SC

tạo với đáy góc

60

. Tính thể tích

V

của khối chóp đã cho.

A.

3

Va

. B.

3

3Va

. C.

3

a

V 

. D.

3

a

V 

.

Câu 18. Cho khối chóp

.S ABC

có

SA SB AB AC a   

,

6

3

a

SC 

và mặt phẳng

 

SBC

vuông góc

với

 

ABC

. Tính thể tích

V

của khối chóp đã cho.

A.

3

14

36

a

. B.

3

14

12

a

. C.

3

21

36

a

. D.

3

21

12

a

.

Câu 19. Cho khối chóp

.S ABC

có

SA SB AB AC a   

,

SC x

và mặt phẳng

 

SBC

vuông góc với

 

ABC

. Tìm

x

để thể tích

V

của khối chóp đã cho lớn nhất.

A.

6

3

a

x 

. B.

6

2

a

x 

. C.

3

a

x 

. D.

3

2

a

x 

.

Câu 20. Cho khối chóp

.S ABCD

có đáy

ABCD

là một tứ giác lồi và góc tạo bởi các mặt bên

 

SAB

,

 

SBC

,

 

SCD

,

 

SDA

và mặt đáy tương ứng là

90 ,60 ,60 ,60

. Biết tam giác

SAB

vuông cân

tại

S

có

AB a

, chu vi tứ giác

ABCD

bằng

9a

. Tính thể tích

V

của khối chóp đã cho.

A.

3

3a

. B.

3

a

. C.

3

9

a

. D.

3

a

.

Câu 21. Cho khối tứ diện

ABCD

có tam giác

ABC

đều, tam giác

DBC

là tam giác vuông cân tại

D

.

2AD a

. Biết

 

ABC

vuông góc với mặt phẳng

 

DBC

. Thể tích

V

của khối tứ diện

ABCD

A.

3

12

a

V 

. B.

3

3Va

. C.

3

33

4

a

V 

. D.

3

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

86

Câu 22. Trong các khối tứ diện

ABCD

có tam giác

ABC

đều, tam giác

DBC

là tam giác cân tại

D

.

2AD a

. Biết

 

ABC

vuông góc với mặt phẳng

 

DBC

. Khối tứ diện có thể tích lớn nhất là

A.

3

42

9

a

V 

. B.

3

16

9

a

V 

. C.

3

16

27

a

V 

. D.

3

42

3

a

V 

.

Câu 23. Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

a

. Mặt bên

SAB

là tam giác đều và nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp

.S ABC

.

A.

3

8

a

V 

. B.

3

2

a

V 

. C.

3

8

a

V 

. D.

3

6

a

V 

.

Câu 24. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang vuông tại

A

và

D

. Gọi

I

là trung điểm

cạnh

AD

. Biết hai mặt phẳng

 

SIB

,

 

SIC

cùng vuông góc với mặt phẳng đáy

 

ABCD

, góc

giữa hai mặt phẳng

 

SBC

và

 

ABCD

bằng

0

60

. Biết thể tích khối chóp

.S ABCD

bằng

3 15

40

và

1AB AD

,

CD x

. Giá trị của

x

là

A.

2x 

. B.

1

4

x 

. C.

4x 

. D.

1

2

x 

.

Câu 25. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật với

2AB a

,

7AC a

. Mặt bên

SAB

là tam giác cân tại

S

và nằm trong mặt phẳng vuông góc với mặt phẳng đáy

 

ABCD

, góc

giữa

SC

và mặt đáy

 

ABCD

bằng

0

60

. Tính tỉ số

3

V

a

.

A.

3

4

V

a



. B.

3

22

V

a



. C.

3

6

V

a



. D.

3

12

V

a



.

Câu 26. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

. Mặt bên

SAD

là tam giác cân tại

S

và nằm trong mặt phẳng vuông góc với mặt phẳng đáy

 

ABCD

. Biết khoảng cách giữa hai

đường thẳng

SD

,

AC

bằng

4 33

33

a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

a

V 

. B.

3

4

3

a

V 

. C.

3

Va

. D.

3

2

3

a

V 

.

Câu 27. Cho khối chóp

.S ABCD

có

ABCD

là hình thang vuông tại

A

,

B

,

2AB AD a

,

BC a

. Gọi

I

là trung điểm cạnh

AB

, hai mặt phẳng

 

SIC

,

 

SID

cùng vuông góc với đáy, góc giữa

 

SCD

và đáy bằng

60

. Tính thể tích

V

của khối chóp đã cho.

A.

3

3 15

5

a

V 

. B.

3

15

5

a

V 

. C.

3

15

a

V 

. D.

3

9 15

5

a

V 

.

Câu 28. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

a

. Gọi

M

,

N

lần lượt là trung điểm các cạnh

AB

,

BC

. Hai mặt phẳng

 

SDM

,

 

SAN

cùng vuông góc với đáy và

 

SCD

tạo với đáy một

góc

60

. Tính thể tích

V

của khối chóp đã cho.

A.

3

73

10

a

V 

. B.

3

43

15

a

V 

. C.

3

73

30

a

V 

. D.

3

43

5

a

V 

.

Câu 29. Cho khối chóp

.S ABCD

có

ABCD

là hình thang vuông tại

A

,

B

,

2AB AD a

,

BC a

. Gọi

I

là trung điểm cạnh

AB

, hai mặt phẳng

 

SIC

,

 

SID

cùng vuông góc với đáy, khoảng cách từ

I

đến

 

SCD

bằng

4

3

a

. Tính thể tích

V

của khối chóp đã cho.

A.

3

36Va

. B.

3

18Va

. C.

3

12a

. D.

3

6a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

87

Câu 30. Cho hai mặt phẳng

 

P

,

 

Q

vuông góc với nhau, có giao tuyến là đường thẳng



. Trên



lấy

hai điểm

A

,

B

với

AB a

. Trong mặt phẳng

 

P

lấy điểm

C

, trong mặt phẳng

 

Q

lấy điểm

D

sao cho

AC

,

BD

cùng vuông góc với



và

AC BD AB

. Tính thể tích khối tứ diện

ABCD

A.

3

6

a

V 

. B.

3

2

a

V 

. C.

3

12

a

V 

. D.

3

2

12

a

V 

.

Câu 31. Cho tứ diện

ABCD

có tam giác

ABC

đều , tam giác

ABD

cân tại

D

, mặt phẳng

 

ABD

vuông

góc với mặt phẳng

 

ABC

,

23CD a

. Tính độ dài

AB

khi khối tứ diện

ABCD

có thể tích lớn

nhất.

A.

2AB a

. B.

26

3

a

AB 

. C.

46

3

a

AB 

. D.

23AB a

.

Câu 32. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

, 3 , 4B BA a BC a

. Mặt phẳng

 

SBC

vuông góc với mặt phẳng

 

ABC

. Biết

23SB a

và

30SBC 

.. Tính thể tích khối chóp

.S ABC

.

A.

3

3Va

. B.

3

Va

. C.

3

33Va

. D.

3

23Va

.

Câu 33. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh bằng

4

, tam giác

SAB

là tam giác đều nằm

trong mặt phẳng vuông góc với đáy. Gọi

M

,

N

,

P

lần lượt là trung điểm của các cạnh

SD

,

CD

BC

. Thể tích khối chóp

.S ABPN

là

x

, thể tích khối tứ diện

CMNP

là

y

. Giá trị

x

,

y

thỏa mãn

bất đẳng thức nào dưới đây?

A.

22

2 160x xy y  

. B.

22

2 2 109x xy y  

.

C.

24

145x xy y  

. D.

24

125x xy y  

.

Câu 34. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh bằng

a

, tam giác

SAB

là tam giác đều nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

a

V 

. B.

3

6

a

V 

. C.

3

6

a

V 

. D.

3

3Va

.

Câu 35. Cho tứ diện

ABCD

có

ABC

là tam giác đều,

BCD

là tam giác vuông cân tại

D

,

   

ABC BCD

và

AD

hợp với

 

BCD

một góc

60

,

AD a

. Tính thể tích

V

của tứ diện

ABCD

.

A.

3

9

a

V 

. B.

3

a

V 

. C.

3

24

a

V 

. D.

3

9

a

V 

.

Câu 36. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

, có

BC a

, mặt bên

SAC

vuông

góc với đáy, các mặt bên còn lại đều tạo với đáy một góc

0

45

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

12

a

V 

. B.

3

9

a

V 

. C.

3

12

a

V 

. D.

3

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

88

Câu 37. Cho hình chóp

.S ABC

có đáy

ABC

đều cạnh

a

, tam giác

SBC

vuông cân tại

S

và nằm trong

mặt phẳng vuông góc với

 

ABC

. Tính thể tích

V

của khối chóp

.S ABC

.

A.

3

9

a

V 

. B.

3

9

a

V 

. C.

3

36

a

V 

. D.

3

16

a

V 

.

Câu 38. Tứ diện

ABCD

có hai tam giác

ABC

và

BCD

là hai tam giác đều lần lượt nằm trong hai mặt

phẳng vuông góc với nhau, biết

AD a

. Tính thể tích

V

của khối tứ diện

ABCD

.

A.

3

6

9

a

. B.

3

9

a

. C.

3

36

a

. D.

3

6

36

a

.

Câu 39. Cho hình chóp

.S ABC

có

o

90BAC 

,

o

30ABC 

,

SBC

là tam giác đều cạnh

a

và

   

SBC ABC

. Tính thể

V

của khối chóp

.S ABC

.

A.

3

6

a

V 

. B.

3

16

a

V 

. C.

3

a

V 

. D.

3

9

a

V 

.

Câu 40. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông, gọi

M

là trung điểm của

AB

. Tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với đáy

 

ABCD

, biết

25SD a

,

SC

tạo

với đáy

 

ABCD

một góc

o

60

. Tính theo

a

thể tích của khối chóp

.S ABCD

.

A.

3

4 15

3

a

V 

. B.

3

15

3

a

V 

. C.

3

4

3

a

V 

. D.

3

a

V 

.

Câu 41. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

, , 3.A AB a BC a

Mặt bên

SAB

là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp

.S ABC

.

A.

3

26

.

3

a

B.

3

6

.

4

a

C.

3

6

.

6

a

D.

3

6

.

12

a

Câu 42. Cho hình chóp

.S ABCD

có đáy là hình chữ nhật

2AB a

,

AD a

. Tam giác

SAD

cân tại

S

và

nằm trong mặt phẳng vuông góc với mặt đáy lên mặt phẳng

 

ABCD

,

SB

hợp với đáy một góc

45

o

. Tính theo

a

thể tích

V

của khối chóp

.S ABCD

.

A.

3

17

3

a

V 

. B.

3

17

6

a

V 

. C.

3

17

9

a

V 

. D.

3

17

3

a

V 

.

Câu 43. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

.

SAB

là tam giác vuông cân tại

S

và nằm trong mặt phẳng vuông góc với đáy, góc giữa cạnh

SC

và mặt phẳng

 

ABCD

bằng

60

, cạnh

AC a

. Tính theo

a

thể tích

V

của khối chóp

.S ABCD

.

A.

3

4

a

V 

. B.

3

2

a

V 

. C.

3

a

V 

. D.

3

9

a

V 

.

Câu 44. Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

.a

Mặt bên

SAB

là tam giác vuông tại

S

và

nằm trong mặt phẳng vuông góc với đáy. Hình chiếu vuông góc của

S

trên đường thẳng

AB

là

điểm

H

thuộc đoạn

AB

sao cho

2.BH AH

Tính thể tích

V

của khối chóp

..S ABCD

A.

3

a

V 

B.

3

2

3

a

V 

C.

3

2

9

a

V 

D.

3

9

a

V 

Câu 45. Cho hình chóp

.S ABCD

có đáy là hình thoi,

SAB

đều và nằm trong mặt phẳng vuông góc với

đáy. Biết

2 , 4AC a BD a

. Tính theo a thể tích khối chóp

.S ABCD

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

89

A.

3

15

a

. B.

3

15

3

a

. C.

3

2 15

3

a

. D.

3

15

2

a

.

Câu 46. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

B

,

3 , 4BA a BC a

. Mặt phẳng

 

SBC

vuông góc với mặt phẳng

 

ABC

. Biết

23SB a

và

30SBC 

. Tính thể tích của khối

chóp

.S ABC

.

A.

3

Va

. B.

3

3Va

. C.

3

23Va

. D.

3

2Va

.

Câu 47. Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

A

,

,2AB a AC a

. Mặt phẳng

 

SBC

vuông góc với đáy, hai mặt phẳng

 

SAB

và

 

SAC

cùng tạo với mặt phẳng đáy góc

60

. Tính

thể tích

V

của khối chóp

.S ABC

theo

a

.

A.

3

a

V 

. B.

3

23

9

a

V 

. C.

3

9

a

V 

. D.

3

43

9

a

V 

.

Câu 48. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh bằng

a

,

2,SD a SA SB a  

và mặt phẳng

 

SBD

vuông góc với mặt phẳng

 

ABCD

. Tính theo

a

thể tích

V

của khối chóp

.S ABCD

A.

3

2

4

a

V 

. B.

3

2

6

a

V 

. C.

3

2

a

V 

. D.

3

2

8

a

V 

.

Câu 49. Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông

2a

,

,3SA a SB a

và mặt phẳng

 

SBA

vuông góc với mặt phẳng đáy. Gọi

,MN

lần lượt là trung điểm của các cạnh

AB

và

AC

. Tính theo

a

thể tích khối chóp

.BMNDS

A.

3

a

V 

. B.

3

a

V 

. C.

3

2

a

V 

. D.

3

2

3

a

V 

.

Câu 50. Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

SAC

cân tại

S

.

0

60SBC 

Mặt

phẳng

 

SAC

vuông góc

 

ABC

. Tính theo

a

thể tích khối chóp

.ABCS

A.

3

8

a

V 

. B.

3

32

8

a

V 

. C.

3

2

6

a

V 

. D.

3

2

8

a

V 

.

Câu 51. Cho hình chóp

.S ABC

có

   

SAC ABC

,

SAB

là tam giác đều cạnh

3, 3a BC a

, đường

thẳng

SC

tạo với đáy góc

60

. Thể tích khối chóp

.S ABC

bằng:

A.

3

a

. B.

3

26a

. C.

3

6

2

a

. D.

3

6

a

.

Câu 52. Cho khối chóp

.S ABCD

có đáy là một tứ giác lồi,

1, 13, 17BC CD DA  

. Tam giác

SAB

đều cạnh bằng

1

và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ

S

đến đường thẳng

,,BC CD DA

lần lượt bằng

1; 2; 5

. Thể tích khối chóp

.S ABCD

bằng

A.

31 3

12

. B.

43

3

. C.

31 3

24

. D.

23

3

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

90

Câu 53. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh bằng

1

, tam giác

,SAB SCD

là các tam giác

cân đỉnh

S

. Khoảng cách từ

S

đến các đường thẳng

,AB CD

lần lượt bằng

1; 3

. Tính thể tích

khối chóp

.S ABCD

A.

3

. B.

43

3

. C.

23

3

. D.

33

4

.

Câu 54. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

a

,

SA SB

,

SC SD

. Biết

   

SAB SCD

và tổng diện tích của hai tam giác

,SAB SCD

bằng

2

7

10

a

. Tính thể tích

V

của

khối chóp

.S ABCD

A.

3

4

75

a

. B.

3

4

15

a

. C.

3

4

25

a

. D.

3

12

25

a

.

Câu 55. Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

a

, tam giác

,SAB SCD

là các tam giác cân

đỉnh

S

. Góc giữa hai mặt phẳng

   

,SAB SCD

là

60

và tổng diện tích của hai tam giác

SAB

,

SCD

bằng

2

3

4

a

. Tính thể tích

V

của khối chóp

.S ABCD

.

A.

3

5

72

a

. B.

3

53

24

a

. C.

3

53

72

a

. D.

3

5

24

a

.

Câu 56. Cho hai tam giác đều

ABC

và

ABD

có độ dài cạnh bằng

1

và nằm trong hai mặt phẳng vuông

góc. Gọi

S

là điểm đối xứng của

B

qua đường thẳng

DE

. Tính thể tích của khối đa diện

ABDSC

.

A.

3

4

V 

. B.

3

8

. C.

1

2

. D.

1

4

.

Câu 57. Cho khối chóp S.ABC có các mặt phẳng

     

,,SAB SBC SCA

lần lượt tạo với đáy các góc

000

90 ,60 ,60

. Biết tam giác

SAB

vuông cân tại

, 2 ,S AB a

chu vi tam giác

ABC

bằng

10a

. Tính

thể tích khối chóp

.S ABC

.

A.

3

53

9

a

. B.

3

43

3

a

. C.

3

53

3

a

. D.

3

43

9

a

.

Câu 58. Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh a, các mặt bên

     

,,SBC SCA S AB

lần lượt

tạo với đáy các góc

0

90 ; ;



sao cho

0

90





. Thể tích khối chóp

.S ABC

có giá trị lớn nhất

bằng

A.

3

16

a

. B.

3

8

a

. C.

3

8

a

. D.

3

16

a

.

Câu 59. Cho khối chóp

.S ABC

có đáy là tam giác vuông tại

, 1, 2A AB AC

. Các mặt bên

     

,,S BC SCA SAB

lần lượt tạo với đáy các góc

90 ; ;





sao cho

90



  

. Thể tích khối

chóp

.S ABC

có giá trị lớn nhất bằng

A.

2

. B.

2

3

. C.

22

3

. D.

2

6

.

Câu 60. Cho khối tứ diện

ABCD

có

1, 2AB AC AD BD CD    

. Hai mặt phẳng

 

ABC

và

 

BCD

vuông góc với nhau. Tính thể tích

V

của khối tứ diện

ABCD

.

A.

2

4

V 

. B.

2

6

V 

. C.

2

12

V 

. D.

2

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

91

BẢNG ĐÁP ÁN

1.B

2.A

3.B

4.D

5.B

6.D

7.A

8.D

9.C

10.C

11.B

12.C

13.C

14.D

15.A

16.A

17.B

18.A

19.B

20.C

21.D

22.C

23.C

24.D

25.B

26.D

27.A

28.B

29.C

30.A

31.C

32.D

33.C

34.B

35.C

36.A

37.C

38.D

39.B

40.A

41.D

42.A

43.A

44.C

45.C

46.C

47.B

48.B

49.A

50.D

51.D

52.C

53.A

54.A

55.C

56.D

57.D

58.D

59.D

60.D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Chọn B

Gọi

H

là trung điểm

AD

3

2

a

SH

.

Ta có

   

SAD ABCD

SAD ABCD AD

SH AD



















 

SH ABCD

.

Vậy

3

.

13

..

36

S ABCD ABCD

a

V S SH

Câu 2. Chọn A

Gọi

H

là trung điểm

AD

22

AD a

SH  

.

Ta có

   

SAD ABCD

SAD ABCD AD

SH AD



















 

SH ABCD

.

Vậy

3

.

1

..

36

S ABCD ABCD

a

V S SH

Câu 3. Chọn B

Gọi

H

là trung điểm

AD

3

2

a

SH

. Ta có

   

SAD ABCD

SAD ABCD AD

SH AD



















 

SH ABCD

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

92

Vậy

3

.

1 1 3 3

. . . . 3.

3 3 2 2

S ABCD ABCD

aa

V S SH a a  

.

Câu 4. Chọn D

Gọi

H

là trung điểm

AD

3

22

AD a

SH  

.

Ta có

   

SAD ABCD

SAD ABCD AD

SH AD



















 

SH ABCD

. Vậy

3

.

1 1 3

. . . . 3.

3 3 2 2

S ABCD ABCD

aa

V S SH a a  

.

Câu 5. Chọn B

Gọi

H

là trung điểm

AD

.

Ta có

   

SAD ABCD

SAD ABCD AD

SH AD



















 

SH ABCD

.

Lại có

.

1

..

3

S ABCD ABCD

V S SH

.

3

2

S ABCD

ABCD

V

SH a

S

  

.

Kẻ

HK SD

tại

K

, khi đó ta chứng minh được

 

HK SCD

nên

 

;HK d H SCD

.

2 2 2

1 1 1

HK HD HS



2

3

a

HK

. Ta có

 

//AB SCD

nên

 

;;d B SCD d A SCD

.

 

AH SCD D

nên

 

;

2

;

d A SCD

AD

HD

d H SCD



. Vậy

 

4

; 2 ;

3

a

d B SCD d H SCD

.

Câu 6. Chọn D

Gọi

H

là trung điểm của

 

AD SH ABCD

.

Ta có

22

2 . 4a

2d 2 2a

3

A B H

SH HD

d d HK SH

SH HD

      



.

Vậy, thể tích của khối chóp

3

1 4a

.

33

SABCD ABCD

V SH S

.

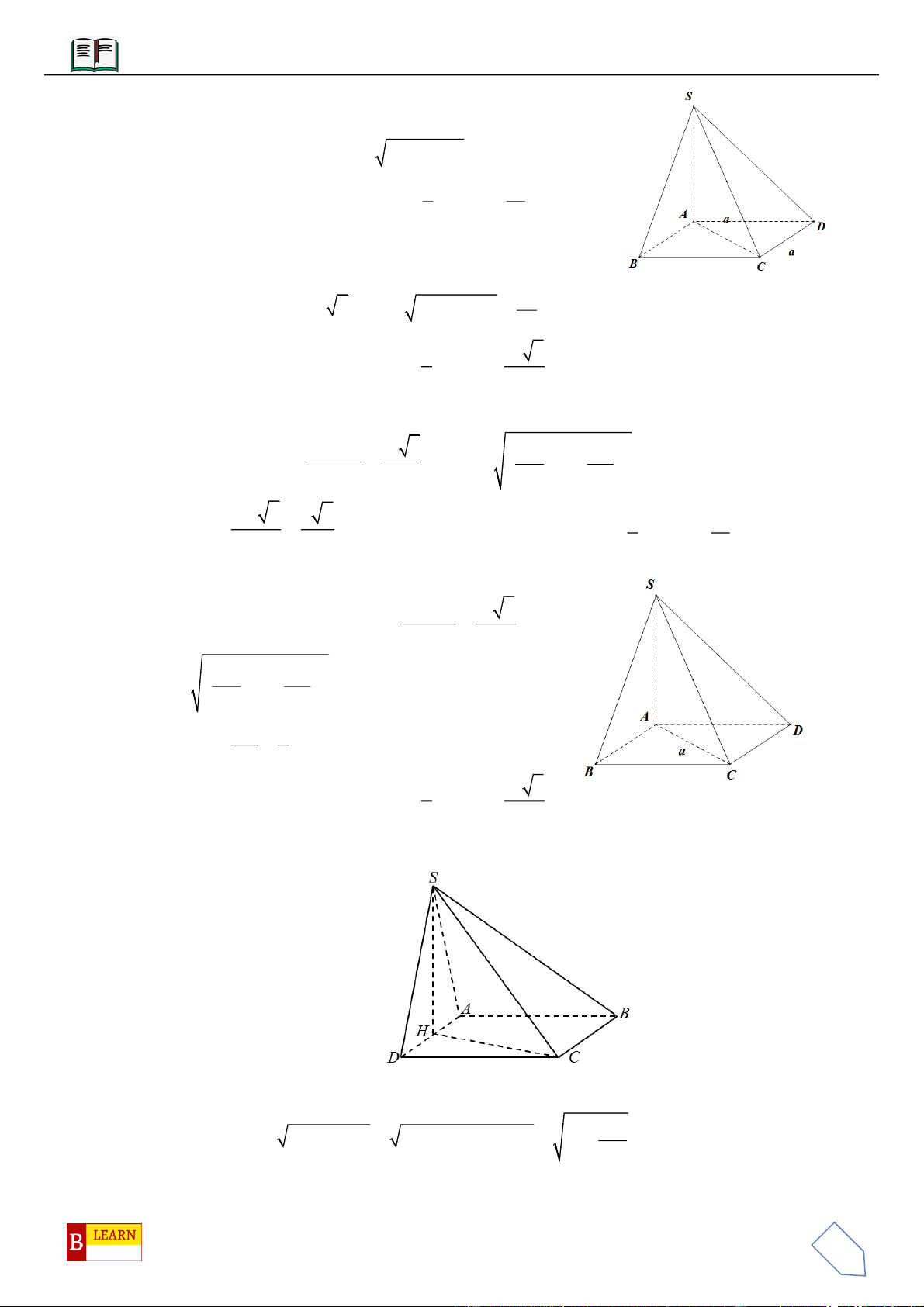
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

93

Câu 7. Chọn A

Diện tích đáy

2

ABCD

Sa

và

22

h SC HC a  

.

Vậy, thể tích của khối chóp

3

1a

.

33

SABCD ABCD

V h S

.

Câu 8. Chọn D

Diện tích đáy

2

3

ABCD

Sa

và

22

3a

2

h SC HC  

.

Vậy, thể tích của khối chóp

3

1 a 3

.

32

SABCD ABCD

V h S

.

Câu 9. Chọn C

Diện tích đáy

2

.

3

22

ABCD

AC BD

a

S 

và

2

22

BD

AC

AB a



  





.

Do đó:

3

22

AB

a

h 

. Vậy, thể tích của khối chóp

3

1a

.

34

SABCD ABCD

V h S

.

Câu 10. Chọn C

Diện tích đáy

2

.

3

22

ABCD

AC BD

a

S 

và

2

22

BD

AC

AB a



  





.

Do đó:

22

AB

a

h 

Vậy, thể tích của khối chóp

3

1 a 3

.

3 12

SABCD ABCD

V h S

.

Câu 11. Chọn B

Đặt

AB x

, Gọi

H

là trung điểm cạnh

AD

, ta có

 

SH ABCD

.

Ta có

2

2 2 2 2 2 2

5

, 12

4

x

S x h SC HC SC HD CD       

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

94

Vì vậy

 

2

1 1 5 4 10 64

12

3 3 4 5 15

x

V Sh f x x f



     





.

Câu 12. Chọn C

Ta có

2

2Sa

. Gọi

,MN

lần lượt là trung điểm của

,AB CD

ta có

     

;

//

SM AB SM CD

SM CD SMN CD SMN ABCD

AB CD SN CD

   

     







.

Gọi

H

là chân đường cao hạ từ

S

xuống

MN

ta có

 

SH ABCD

.

Mặt khác

2 2 2

26

, 2 ,

22

aa

SM MN a SN SM SN MN SM SN       

.

Vì vậy

2 2 2 2

1 1 1 8 6

4

3

a

h

h SM SN a

    

. Vậy

3

16

36

a

V Sh

.

Câu 13. Chọn C

Gọi

H

là trung điểm cạnh

AB

, ta có

 

SH ABCD

và theo Pitago ta có

22

2SH SC HC a  

. Vậy

3

14

.

33

ABCD

a

V S SH

.

Câu 14. Chọn D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

95

Đặt

AD x

, gọi

H

là trung điểm cạnh

AD

, ta có

 

SH ABCD

.

Khi đó

22

2 2 2 2

16 20

44

xx

HC HD DC SH SC HC        

.

Vì vậy

 

22

2

2 80

80

1 1 80

.4 . 20

3 3 4 3 3 3

xx

x

V Sh x





     

.

Dấu bằng xảy ra khi

22

80 2 10x x x   

.

Câu 15. Chọn A

Đặt

AD x

, gọi

,MN

lần lượt là trung điểm của

,AB CD

ta có

     

//

SM AB

SN CD CD SMN ABCD SMN

AB CD





    







.

Gọi

H

là chân đường cao hạ từ

S

xuống

MN

ta có

 

SH ABCD

.

Trong tam giác

SMN

ta có

13

3, 3,

22

CD

SM AB SN MN AD x     

.

Do đó

42

2

24 36

2

SMN

S

xx

h SH

MN x

  

  

.

Ta có

 

42

3 24 36

1 2 3 24 36

. 2 3 6

3 3 2 3

xx

x x x

V Sh f x f

x

  

     

Câu 16. Chọn A

Ta có

2

.3

ABCD

S AB AD a

.

Do các mặt phẳng

   

,SHC SHD

cùng vuông góc với đáy nên

 

SH ABCD

, suy ra góc giữa

SD

và

 

ABCD

là

60SDH 

.

H

D

B

C

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

96

Ta có

 

2

22

13

3

22

aa

HD AH AD a



    





,

39

tan60

2

a

SH HD  

Vậy

3

2

.

1 1 39 13

. . 3

3 3 2 2

S ABCD ABCD

aa

V SH S a  

.

Câu 17. Chọn B

Do tam giác

ABC

đều cạnh

2a

nên

 

2

3

23

4

ABC

S a a

.

Gọi

H

là trung điểm của

AB

, do tam giác

SAB

cân tại

S

nên

SH AB

.

Mặt khác, vì

   

SAB ABC

nên

 

SH ABC

, suy ra góc

giữa

SC

và

 

ABC

là

60SCH 

.

Vì tam giác

ABC

đều cạnh

2a

nên

3 tan 60 3CH a SH SH a    

.

Vậy

23

.

11

. 3 . 3 3

33

S ABCD ABC

V SA S a a a  

.

Câu 18. Chọn A

Gọi

H

là trung điểm cạnh

BC AH BC

.

Mà

     

ABC SBC AH SBC  

.

Mặt khác,

AS AB AC

H

là tâm đường tròn ngoại

tiếp

SBC

SBC

vuông tại

S

.

Khi đó,

2

16

.

26

SBC

a

S SB SC

;

22

15

3

a

BC SB SC  

;

22

7

12

AH AB BH a  

.

Vậy thể tích khối chóp

.S ABC

là

23

1 1 7 6 14

. . .

3 3 12 6 36

SBC

aa

V AH S a  

.

Câu 19. Chọn B

Gọi

H

là trung điểm cạnh

BC AH BC

.

Mà

     

ABC SBC AH SBC  

.

Mặt khác,

AS AB AC

H

là tâm đường tròn ngoại tiếp

SBC

SBC

vuông tại

S

.

H

B

C

S

A

H

A

B

C

S

H

B

C

S

A

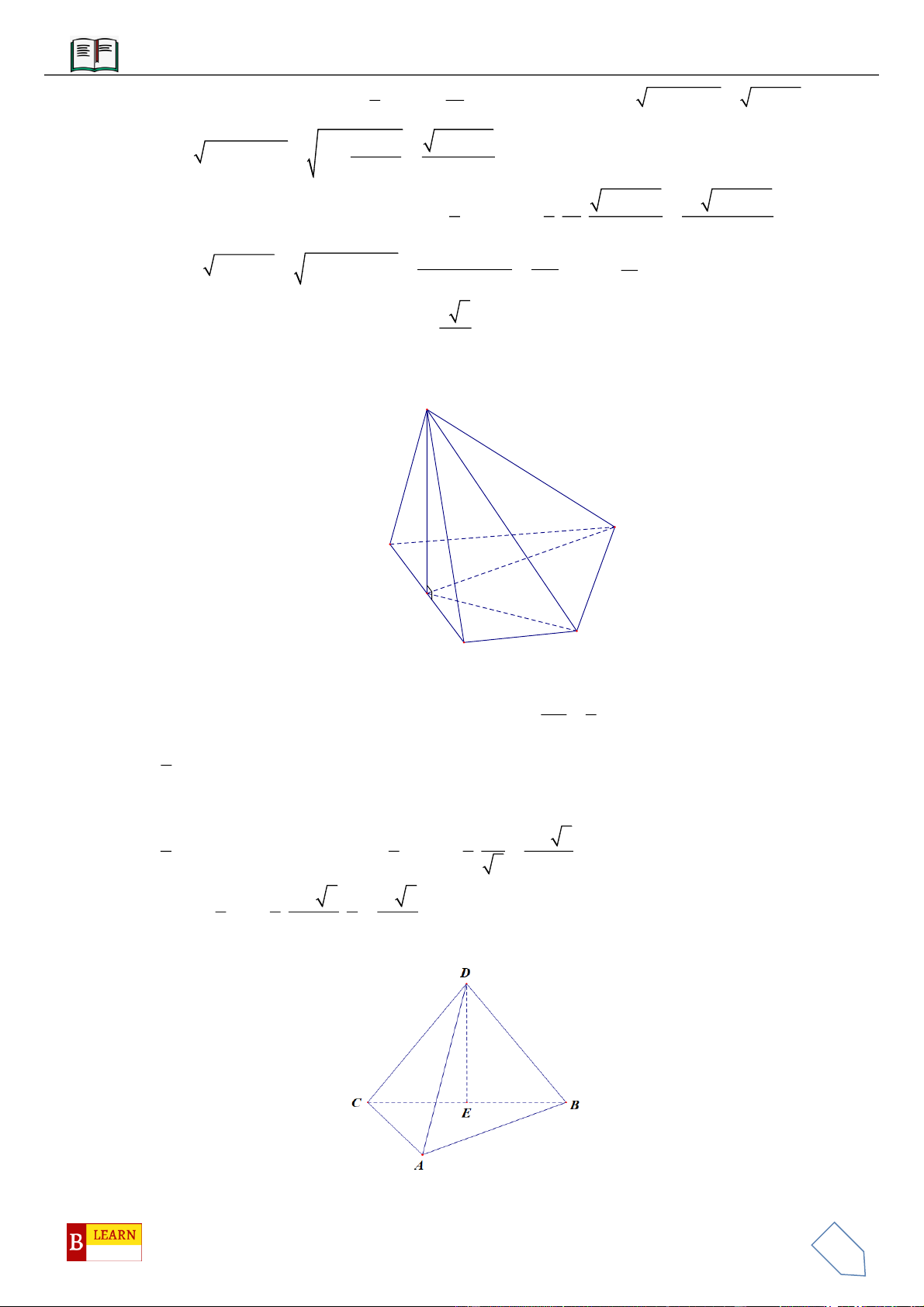
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

97

Khi đó,

1

.

22

SBC

ax

S SB SC

;

2 2 2 2

BC SB SC a x   

;

2 2 2 2

2 2 2

3

42

a x a x

AH AB BH a



    

.

Suy ra thể tích khối chóp

.S ABC

là

2 2 2 2

1 1 3 3

. . .

3 3 2 2 12

SBC

ax a x ax a x

V AH S



  

.

Ta có

 

2 2 2 2

2 2 2 2 2

33

22

x a x a

x a x x a x



    

3

8

a

V

.

Dấu “=” xảy ra khi

2 2 2

6

3

2

a

x a x x   

.

Câu 20. Chọn C

Gọi

H

là trung điểm cạnh

AB SH AB

.

Mà

     

SAB ABCD SH ABCD  

và

22

AB a

h SH  

. Ta có

HBC HCD HDA

S S S S  

 

1

. . .

2

BC HK CD HT DA HI  

( với

,,K T I

lần lượt là hình chiếu của

H

trên các đường thẳng

,,BC CD DA

).

 

1

. .cot60

2

BC CD DA h   

 

2

1 1 2 3

9 . .

2 2 3

3

aa

aa  

.

Vậy

23

1 1 2 3 3

. . .

3 3 3 2 9

a a a

V S h  

.

Câu 21. Chọn D

Gọi

E

là trung điểm của

BC

. Ta có

 

DE BC DE ABC  

.

H

A

B

S

C

D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

98

Đặt

13

;

2 2 2

xx

BC x DE CB AE    

; Ta có

2 2 2

2AE DE AD x a   

 

2

3

2 . 3

1 1 3

..

3 3 4 3

ABC

a

V S DE a  

.

Câu 22. Chọn C

Gọi

E

là trung điểm của

BC

. Ta có

 

DE BC DE ABC  

.

Đặt

3

2

x

BC x AE  

;

2

2 2 2

3

4

x

DE AD AE a   

 

22

2 2 3

2

33

3. . 16 3

1 1 3 3 16

22

. . . 4

3 3 4 4 36 27

ABC

xx

ax

x x a

V S DE a



    

.

Dấu bằng xảy ra khi

42

3

a

x 

.

Câu 23. Chọn C

Gọi

E

là trung điểm của

AB

. Ta có

 

SE AB SE ABC  

.

23

1 1 3 3

. . . .

3 3 4 2 8

SABC SBC

a a a

V S SE   

.

Câu 24. Chọn D

Ta có

   

 

SIB ABCD

SIC ABCD S I ABCD

SIB SIC SI







  











Gọi

H

là hình chiếu

I

lên

BC

IH BC

. Ta có

 

BC SIH BC SH  

   

 

; ; 60SBC ABCD IH SH SHI    

;

 

2

1 1 2 2BC x x x     

 

11

.

22

ABCD

x

S AB CD AD



  

;

1

;

44

IAB ICD

x

SS





1

4

IBC ABCD IAB ICD

x

S S S S

  



   

2

1

2 2 2

IBC

S

x

IH

BC

xx





  



CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

99

Ta có

 

2

31

.tan60

2 2 2

x

SI IH

xx



  



. Vậy

 

2

31

1 3 15

..

3 40

12 2 2

ABCD

x

V SI S

xx



  



1

2

x

.

Câu 25. Chọn B

Gọi

H

là trung điểm của

AB SH AB

Ta có

   

SAB ABCD AB

SAB ABCD

SH AB



















 

SH ABCD

Ta có

 

; ; 60SC ABCD SC HC SCH   

Ta có

22

3BC AC AB a  

,

22

2HC BC HB a  

Ta có

.tan60 a 6SH HC  

;

2

. 2 . 3 2 3

ABCD

S AB BC a a a  

.

1

.

3

S ABCD ABCD

V V SH S

2

1

.a 6.2 3

3

a

3

22a

3

22

V

a



.

Câu 26. Chọn D

Gọi

H

là trung điểm

AD

ta có:

 

SH ABCD

. Dựng hình bình hành

ACDE

ta có:

   

 

, ; ; 2 ; 2d AC SD d AC SDE d A SDE d H SDE HK   

Và

22

. 4 33

2 2.

33

HF SH a

HK

HF SH





vì

//HF DO

và

12

24

a

HF DO

. Do đó

2SH a

Vì vậy

3

2

1 1 2

. .2 .

3 3 3

ABCD

a

V SH S a a  

.

O

F

E

H

C

A

D

B

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

100

Câu 27. Chọn A

Ta có

2

.3

2

BC AD

S AB a





và

 

SI ABCD

.

Kẻ

IH CD

 

H CD

60SHI  

và

.tan 60 3h IH IH  

.

Tam giác

ICD

có

 

2

IBC IAD

ICD

S S S

S

IH

CD CD





3 3 15

5

aa

h  

.

Vậy

3

. 3 15

35

S h a

V 

.

Câu 28. Chọn B

Ta có:

 

2

dt ABCD a

. Gọi

     

H DM AN SH SDM S AN SH ABCD      

.

Kẻ

HE CD

 

E CD

60SEH  

. Ta cũng có

AN DM

.

Ta có:

2 2 2 2 2 2

1 1 1 1 1 5

2

AH AM AD a a

a

    







5

a

AH

,

5

2

a

AN 

2

5

AH

AN



.

và

22

55

DE AH a

DE DC

DC AN

   

.

Ta có:

2

2 2 2

2

5

aa

DH AD AH a    

22

4 4 4

5 25 5

a a a

HE DH DE     

.

Vì vậy

43

.tan60

5

a

h SH HE   

. Vậy

 

1

..

3

V SH dt ABCD

2

1 4 3

.

35

a

a

3

43

15

a



.

E

H

N

M

C

A

B

D

S

C

I

A

B

D

S

H

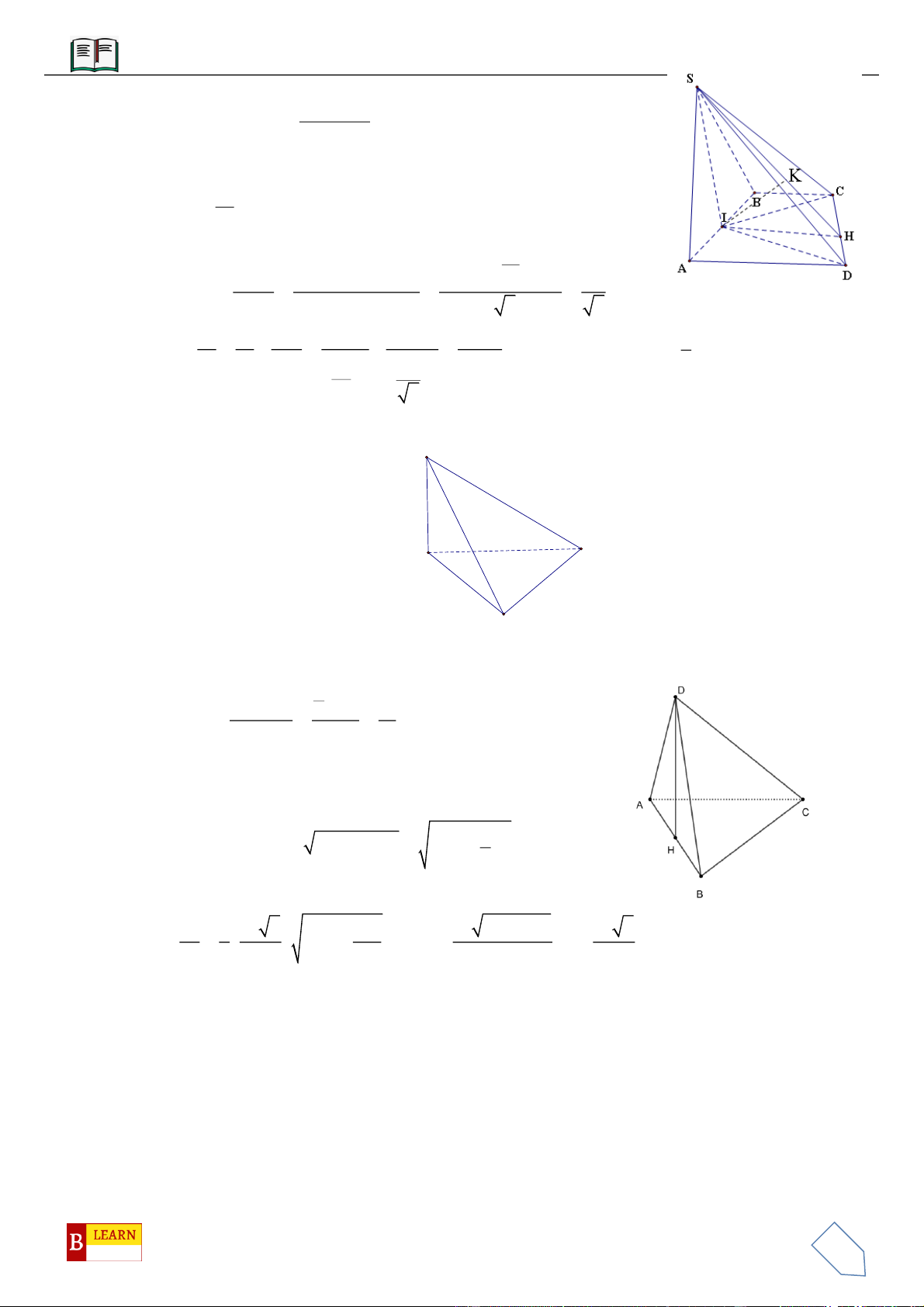
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

101

Câu 29. Chọn C

Ta có:

 

2

.3

2

AD BC

dt ABCD AB a





.

Kẻ

IH CD

 

H CD

,

IK SH

 

K HS

 

IK SCD

,

1

4

3

a

IK d

.

Ta có

 

2

22

23

2

3

55

IAB IAD

ICD

a

aa

S S S

S

a

IH

CD CD

a











   

.

Do đó

2 2 2 2 2 2

1

1 1 1 1 1 1

12

144

4

3

5

ha

h d IH a

a

      

   

   



. Do đó

 

3

1

. 12

3

V h dt ABCD a

.

Câu 30. Chọn A

Theo giả thuyết ta có

ABD

vuông tại

B

. Có

 

CA AB CA ABD  

.

Do đó

3

1

..

.

2

3 3 6

ABD

aaa

S CA

a

V   

.

Câu 31. Chọn C

Đặt

AB x

, gọi

H

là trung điểm của

AB

, ta có

 

DH ABC

và

2 2 2 2

3

12

4

h CD CH a x   

.

Vậy

2 2 2 2 2

2

1 3 3 16 4 6

12 ( )

3 3 4 4 8 3

Sh x x x a x a

V a f x f





       





.

C

A

B

D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

102

Dấu bằng đạt tại

46

3

a

x 

.

Câu 32. Chọn D

Kẻ

SH

vuông góc với

BC

suy ra

 

SH ABC

.

Có

.sin 3SH SB SBC a

và

2

1

.6

2

ABC

S BA BC a





.

Suy ra

3

1

. 2 3

3

SABC ABC

V S SH a





.

Câu 33. Chọn C

Gọi

H

là trung điểm của cạnh

AB

. Do

SAB

đều và

   

SAB ABCD

 

SH ABCD

.

Ta có

SAB

đều và cạnh bằng

4

23SH

.

Có

2

..

10

22

ABPN ABCD AND CPN

AD DN CN CP

S S S S AB      

.

Thể tích khối chóp

.S ABPN

là

1 20 3

.

33

ABPN ABPN

V SH S

20 3

3

x

.

Ta có

M

là trung điểm của

SD

 

11

, , 3

22

d M ABCD d S ABCD SH   

.

Thể tích khối tứ diện

MCPN

là

 

1 1 .CP 2 3

, , .

3 3 2 3

MCPN CPN

CN

V d M ABCD S d M ABCD  

23

3

y

.

Câu 34. Chọn B

Gọi

H

là trung điểm của cạnh

AB

. Do

SAB

đều và

   

SAB ABCD

 

SH ABCD

.

Ta có

SAB

đều và cạnh bằng

a

3

2

a

SH

. Có

22

ABCD

S AB a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

103

Thể tích khối chóp

.S ABCD

là

3

13

.

36

ABCD ABCD

a

V SH S

.

Câu 35. Chọn C

Gọi

H

là trung điểm của cạnh

BC

. Do

ABC

đều và

   

ABC BCD

 

AH BCD

.

Ta có

HD

là hình chiếu của

AD

lên

 

BCD

 

, , 60AD BCD AD HD ADH    

.

Có

3

.sin

2

a

AH AD ADH

,

.cos

2

a

HD AD ADH

.

Mà

BCD

vuông cân tại

D

nên

2BC DH a

.

Thể tích khối tứ diện

ABCD

là

3

1 1 . 3

..

3 3 2 24

ABCD BCD

BC DH a

V AH S AH  

.

Câu 36. Chọn A

Kẻ

SH AC

vì

     

SAC ABC SH ABC  

Gọi

,IJ

lần lượt là hình chiếu của

H

trên

AB

và

BC

suy ra

,SI AB SJ BC

Theo giả thiết

45SIH SIK

. Ta có

SHI SHJ HI HJ    

Tứ giác

HIBJ

là hình thoi nên

BH

là đường phân giác của

ABC

suy ra

H

là trung điểm

AC

2

a

HI HJ SH  

3

.

1

..

3 12

S ABC ABC

a

V S SH  

.

Câu 37. Chọn C

Gọi

H

là trung điểm

BC SH BC

.

Ta có

   

SBC ABC

và

 

SH BC SH ABC  

23

.

1 1 3 3

. . . .

3 3 4 2 24

S ABC ABC

a a a

V S SH  

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

104

Câu 38. Chọn D

Gọi

H

là trung điểm

BC AH BC

Ta có

     

,ABC BCD AH BC AH BCD   

Và

ABC BCD AH DH    

Do đó

AHD

vuông cân tại

H

2

a

AH

Mà

3 2 2

2

33

BC AH a

AH BC   

Do đó

2

3

.

1 2 3 6

. . .

3 4 36

23

S ABC

a a a

V









.

Câu 39. Chọn B

Gọi

H

là trung điểm của

BC

. Vì

SBC

là tam giác đều cạnh

a

nên

3

2

a

SH 

.Theo giả thiết ta

có

   

SBC ABC

nên

 

SH ABC

.

Ta có

BC a

nên

o

3

.cos30

2

a

AB BC

,

o

.sin30

2

a

AC BC

.

Suy ra

2

1 1 3 3

. . . .

2 2 2 2 8

ABC

a a a

S AB AC  

. Do đó

23

.

1 1 3 3

. . . .

3 3 2 8 16

S ABC ABC

a a a

V SH S  

.

Câu 40. Chọn A

Theo giả thiết ta có

 

SM ABCD

.

 

o

; ; 60SC ABCD SC MC SCM  

.

Trong tam giác vuông

SMC

và

SMD

ta có:

2 2 o

.tan 60SM SD MD MC  

mà

ABCD

là hình vuông

nên

MC MD

.

2 2 2

3 5 15SD MC MC MC a SM a      

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

105

Lại có

2

22

5

24

AB BC

MC BC



  





2

24

ABCD

BC a S a   

.

Vậy

3

.

1 4 15

.

33

S ABCD ABCD

a

V SM S

.

Câu 41. Chọn D

Do tam giác

SAB

đều cạnh

a

và nằm trong mặt phẳng

vuông góc với mặt phẳng đáy nên chiều cao của hình

chóp là

3

2

a

h 

.

Tam giác

ABC

vuông tại

A

22

2,AB BC AC a   

2

12

.

22

ABC

a

S AB AC

3

.

16

.

3 12

S ABC ABC

a

V h S  

.

Câu 42. Chọn A.

Gọi

E

trung điểm của

AD

. Khi đó

 

SE ABCD

1

.

3

ABCD

V S SE

,

2

ABCD

Sa

;

EB

là hình chiếu của

SB

lên mặt phẳng

 

ABCD

 

, 45 .

o

SB ABCD SBE SE BE    

;

2

2 2 2

17

4

22

aa

BE AE AB a



    





.

17

2

a

SE

.

Vậy

3

2

1 17 17

. .2

3 2 3

aa

Va

.

Câu 43. Chọn A

Gọi

I

là trung điểm của đoạn

AB

Suy ra,

     

SI ABmà SAB ABCD SI ABCD   

Nên

 





3

; 60 ,

2

a

SCI SC ABCD CI   

.

Suy ra,

3

.tan60

2

a

SI CI  

A

H

S

C

B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

106

Gọi

M

là trung điểm của đoạn

BC

,

N

là trung điểm của đoạn

BM

.

33

24

aa

AM IN  

Ta có

2 2 3

.

3 1 3 3 3

2

2 3 2 2 4

ABCD ABC S ABCD

a a a a

S S V



      

.

Câu 44. Chọn C

2

.

ABCD

Sa

( ) ( )

( ) ( ) ( ).

SAB ABCD

SAB ABCD AB SH ABCD

SH AB





   









Xét tam giác

SAB

vuông tại

S

có

SH

là đường cao.

2 2 2

12

. 2 2. .

93

a

SH BH AH AH a SH    

Thể tích của khối chóp

3

2

1 1 2 2

. : = . . . .

3 3 3 9

ABCD

aa

S ABCD V SA S a

Câu 45. Chọn C.

Ta có

2

.

4

2

ABCD

AC BD

Sa

. Gọi H là trung điểm

AB

. Ta có

SAB

đều

SH AB

Do

   

SAB ABCD

 

SH ABCD

;

22

5AB AO BO a  

3 15

22

AB a

SH 

.

2

.

1 1 15

. .4 .

3 3 2

S ABCD ABCD

a

V SH S a

3

2 15

3

a



.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

107

Câu 46. Chọn C

Gọi

H

là hình chiếu của

S

trên

BC

.

Vì

   

SBC ABC

theo giao tuyến

 

BC SH ABC

.

Ta có :

3

.

1

.sin60 3 . . 2 3

3

S ABC ABC

SH SB a V SH S a



     

.

Câu 47. Chọn B

Kẻ

 

SH BC SH ABC  

.

Kẻ

,HE AB HF AC

, ta có:

60SEH SFH  

và

. ot60 cot60HE SH c h   

,

. ot60 cot60HF SH c h   

Diện tích đáy bằng

2

1

..

2

S AB AC a

.

Mặt khác :

   

11

. . . .cot60 2 . .cot60

22

HAB HAC

S S S AB HE AC HF a h a h       

.

Vậy

3

2 2 1 2 3

..

2

39

3

33

S a a

h V S h

aa

    



. Chọn B.

Câu 48. Chọn B

AS AB AD SO BO DO    

hay

SBD

vuông tại

S

Ta có

 

AO BO

AO SBD

AO SO













2

2 2 2 2 2 2 2

3

2 3;

42

aa

BD SD SB a a a AO AB BO a         

3

1 1 1 1 2

. . . . . . . 2

3 3 2 6 2 12

ASBD SBD

aa

V AO S AO SB SD a a   

. Suy ra

3

.

2

6

S ABCD ASBD

a

VV

.

B

C

A

S

H

C

A

S

B

F

E

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

108

Câu 49. Chọn A

Kẻ

 

SH AB H AB

Mà

   

SAB ABCD

nên

 

SH ABCD

2 2 2

AB SA SB SAB   

vuông tại

H

.

.3

2

SA SB a

SH

AB



22

1

4 2. .2 2

2

BMND ABCD AMD NCD

S S S S a a a a     

Vậy thể tích khối chóp

.BMNDS

3

2

.

1 1 3 3

. . .2

3 3 2 3

S BMND BMND

aa

V SH S a  

.

Câu 50. Chọn D

Gọi

H

là trung điểm

AC

:

 

SH ABC

vì

   

SAC ABC

. Giả sử

 

0SH x x

Ta có

2

2 2 2 2

4

a

SC SH HC x   

;

2

2 2 2 2

3

4

a

SB SH HB x   

Áp dụng định lý cosin trong tam giác

 

SBC

2 2 2

2 2 2 2

2. . .cos

3 3 6

4 4 4 2

SC SB BC SB BC SBC

a a a a

x x a x a x

  

        

Vậy

23

.

1 1 6 3 2

. . . .

3 3 2 4 8

S ABC ABC

a a a

V SH S  

.

Câu 51. Chọn D

Có

3BA BS BC a  

nên hình chiếu vuông góc

H

của

B

lên

 

ABC

là tâm đường tròn

ngoại tiếp tam giác

ASC

. Mặt khác

   

BA BC

H

BAC SAC

















là trung điểm cạnh

AC

.

60

0

H

A

C

S

B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

109

Do đó tam giác

ASC

vuông tại

S

. Và cũng có

 

60 ,SCA SC ABC  

.

Vậy có

1

cot60 3 .

3

SC AS a a   

,

2

2 2 2

13

.

22

2

32

2

SAC

a

S SA SC

AC a

AC

BH BA a a a















    









. Vậy

23

1 3 6

. . 2

3 2 6

aa

Va

.

Câu 52. Chọn C

Gọi

H

là trung điểm

 

AB SH ABCD

và

3

2

h SH

.

Kẻ

,,HK BC HT CD HI DA  

ta có

,,SK BC ST CD SI DA  

và theo giả thiết có

1; 2; 5SK ST SI  

.

Vì vậy theo pitago cho các tam giác vuông

,,SHK SHT SHI

ta có:

22

31

1

42

HK SK SH    

.

22

3 17

5

42

HI SI SH    

.

Vì vậy, diện tích đáy của hình chóp là:

 

1

. . .

2

HBC HCD HDA

S S S S HK BC HT CD HI DA     

1 1 13 17 31

.1 . 13 . 17

2 2 2 2 4



   





.

Vậy thể thích khối chóp:

.

1 1 3 31 31 3

..

3 3 2 4 24

S ABCD ABCD

V SH S   

.

Câu 53. Chọn A

Gọi

,MN

lần lượt là trung điểm các cạnh

,AB CD

ta có

N

M

C

A

D

B

H

S

H

A

D

B

C

S

I

T

K

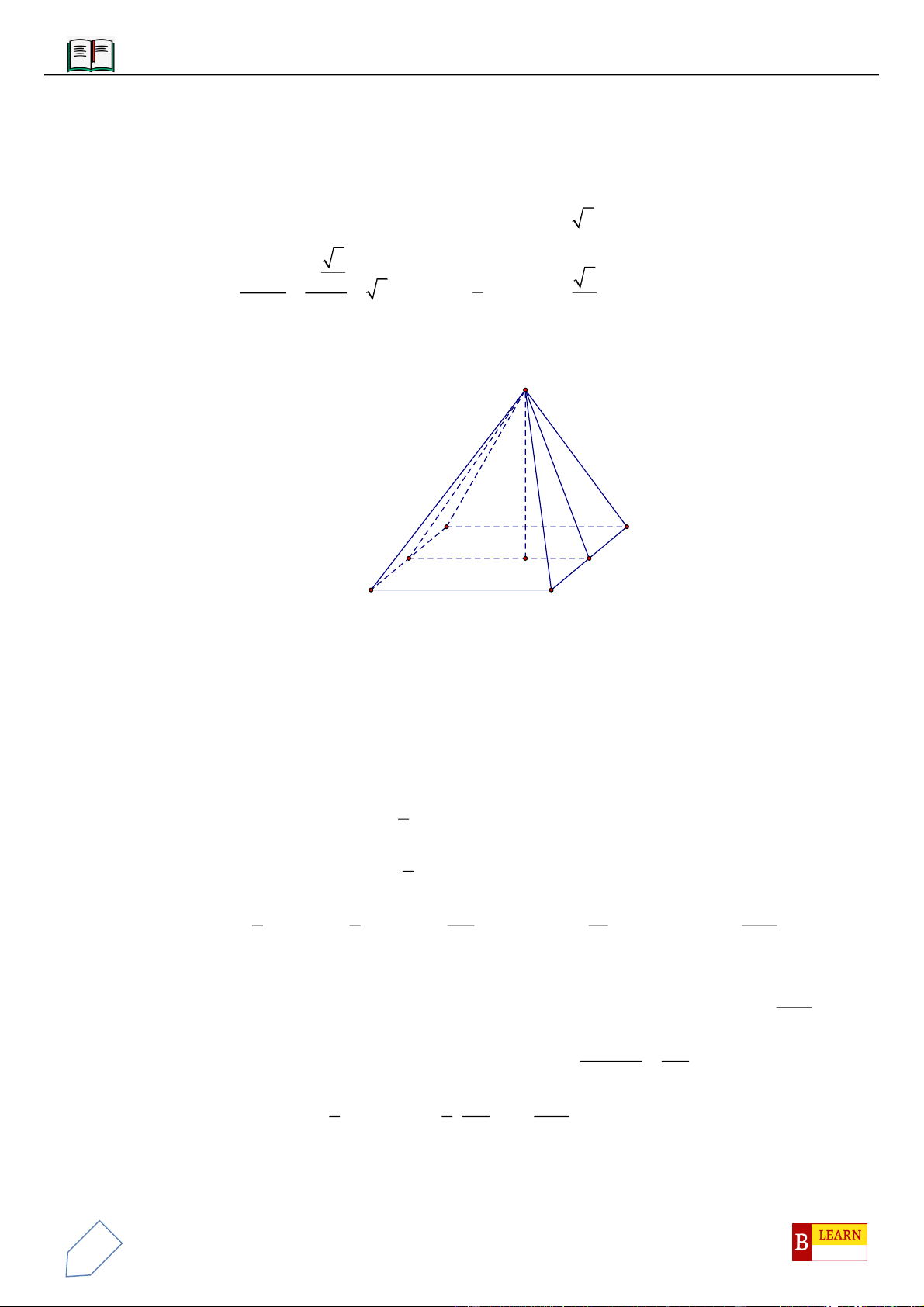
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

110

     

//

SM AB

SN CD CD SMN SMN ABCD

CD AB





    







.

Vì vậy, kẻ

 

SH MN H MN

ta có

 

SH ABC

.

Tam giác

SMN

có

 

,1SM d S AB

;

 

, 3, 1SN d S CD MN  

.

Do đó

3

2.

2

3

1

SMN

S

SH

MN

  

. Vậy

13

.

33

ABCD

V SH S

.

Câu 54. Chọn A

Gọi

,MN

lần lượt là trung điểm các cạnh

,AB CD

ta có

     

//

SM AB

SN CD CD SMN SMN ABCD

CD AB





    







.

Vì

   

SAB SCD

nên tam giác

SMN

vuông tại

S

.

Diện tích tam giác

SAB

là

1

2

SAB

S AB SM  

.

Diện tích tam giác

SCD

là

1

2

SCD

S CD SN  

.

Theo đề ta có

 

22

2

1 1 7 7 49

2 2 10 5 25

a a a

AB SM CD SN SM SN SM SN           

.

Mặt khác, vì tam giác

SMN

vuông tại

S

nên

 

2

2 2 2 2 2 2 2

12

2

25

a

SM SN MN SM SN a SM SN SM SN a SM SN            

.

Kẻ

 

SH MN H MN

ta có

 

SH ABC

, do đó

12

25

SM SN a

SH

MN





.

Suy ra thể tích

3

2

.

1 1 12 12

3 3 25 75

S ABCD ABCD

aa

V SH S a      

.

Câu 55. Chọn C

N

M

C

A

D

B

H

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

111

Gọi

,MN

lần lượt là trung điểm các cạnh

,AB CD

, khi đó góc giữa hai mặt phẳng

 

SAB

và

 

SCD

là góc giữa

SM

và

SN

, suy ra

 

, 60SM SN 

.

Kẻ

 

SH MN H MN

ta có

 

SH ABC

, do đó

sin60SM SN

SH

MN

  



 

*

.

Diện tích tam giác

SAB

là

1

2

SAB

S AB SM  

.

Diện tích tam giác

SCD

là

1

2

SCD

S CD SN  

.

Theo đề ta có

 

22

2

1 1 3 3 9

2 2 4 2 4

a a a

AB SM CD SN SM SN SM SN           

.

Theo định lý cosin trong tam giác

SMN

, ta có

 





2

2 2 2

2 cos 2 1 cosMN SM SN SM SN MSN SM SN SM SN MSN         

 





2

2 1 cos

SM SN MN

SM SN

MSN



  



.

Xét các trường hợp:

Trường hợp

60MSN 

, khi đó

22

55

12

1

81

2

aa

SM SN  









.

Thay vào

 

*

ta có

sin120 5 3

24

SM SN a

SH

MN

  



Suy ra thể tích

3

2

.

1 1 5 3 5 3

3 3 24 72

S ABCD ABCD

aa

V SH S a      

.

Trường hợp

120MSN 

, khi đó

22

55

4

1

81

2

aa

SM SN  









(vô lý vì

3

25

2

a

SM SN SM SN    

).

Câu 56. Chọn D

N

M

C

A

D

B

H

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

112

Gọi

,,I HI H

lần lượt là trung điểm của

, . , .CD ABCD AB

Ta có

 

..

13

, , .

34

ABDSC S ABD S ABC

V V V d S ABD d S ABC   

Trong đó.

 

3

, 2 , ,

2

d S ABD d I ABD d C ABD CH   

và

 

3

, 2 , , .

2

d S ABC d I ABC d D ABC DH   

Vậy

..

1 3 3 3

.

3 4 2

1

42

ABDSC S ABD S ABC

V V V



 













Câu 57. Chọn D

Gọi

H

là trung điểm cạnh

 

AB SH AB SH ABC   

Và

.

2

AB

SH a

Kẻ

0

( ) ( ), 60HM BC M BC HN CA N CA SMH SNH      

0

3

60

3

a

HM HN SHcot   

. Ta có

     

1 3 3 4 3

. . 10 2

2 6 6 3

ABC HAC HBC

a a a

S S S HM BC HN CA BC CA a a        

Vậy

3

43

49

Sh a

V 

.

Câu 58. Chọn D

.

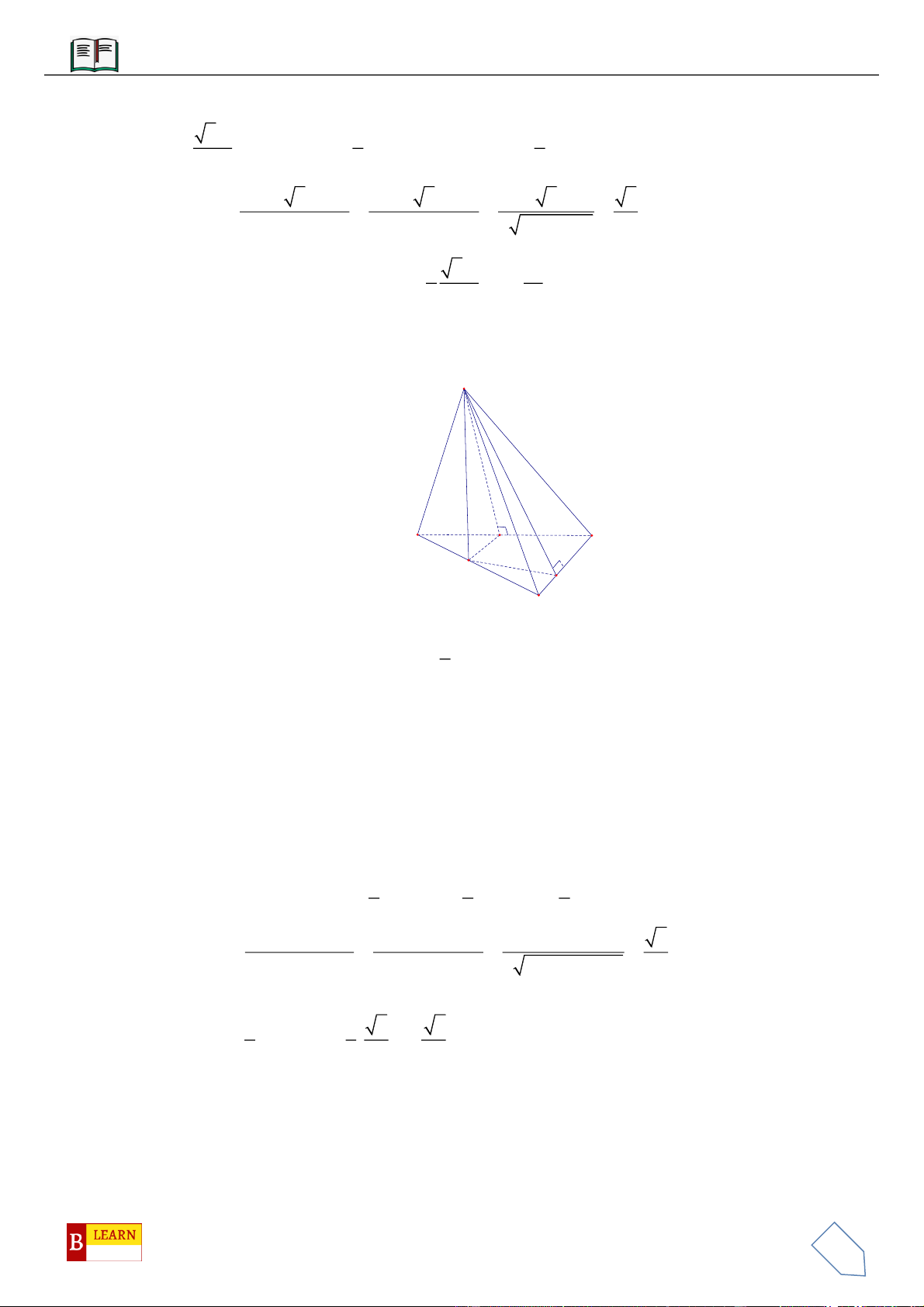
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

113

Kẻ

 

SH BC SH ABC  

và

,,HM AB HN CA SNH SMH



      

Ta có

   

2

31

..

4 2 2

HAB HCA

aa

S S AB HM AC HN SHcot SHcot



     

Do đó

   

3 3 3 3

.

2

4

2

.

SH

cot cot cot tan

cot tan

   



   



0

90 .tan cot

   

   

Vậy

23

13

.

3 4 16

aa

V SH

Câu 59. Chọn D

Tam giác

ABC

vuông tại

1

.1

2

ABC

A S AB AC



  

.

Gọi

 

SH H BC

là đường cao của

SBC

, theo giả thiết

     

SBC ABC SH ABC  

.

Gọi

,MN

lần lượt là hình chiếu của

S

trên

,AB AC

   

 

   

 

,

SMH SAB ABC

SNH SAC ABC

















SMH

SNH





















.

Ta có:

11

. . . .

22

ABC AHB AHC

S S S HM AB HN AC

  

    

 

1

. .cot 2. .cot

2

SH SH





Do đó:

2 2 2 2

cot 2.cot 2.cot tan 2

2 2.cot .tan

SH

   



   



(Vì

90



  

nên

cot tan





)

Vậy

.

1 1 2 2

. . . .1

3 3 2 6

S ABC ABC

V SH S



  

.

Câu 60. Chọn D

B

A

C

S

H

N

M

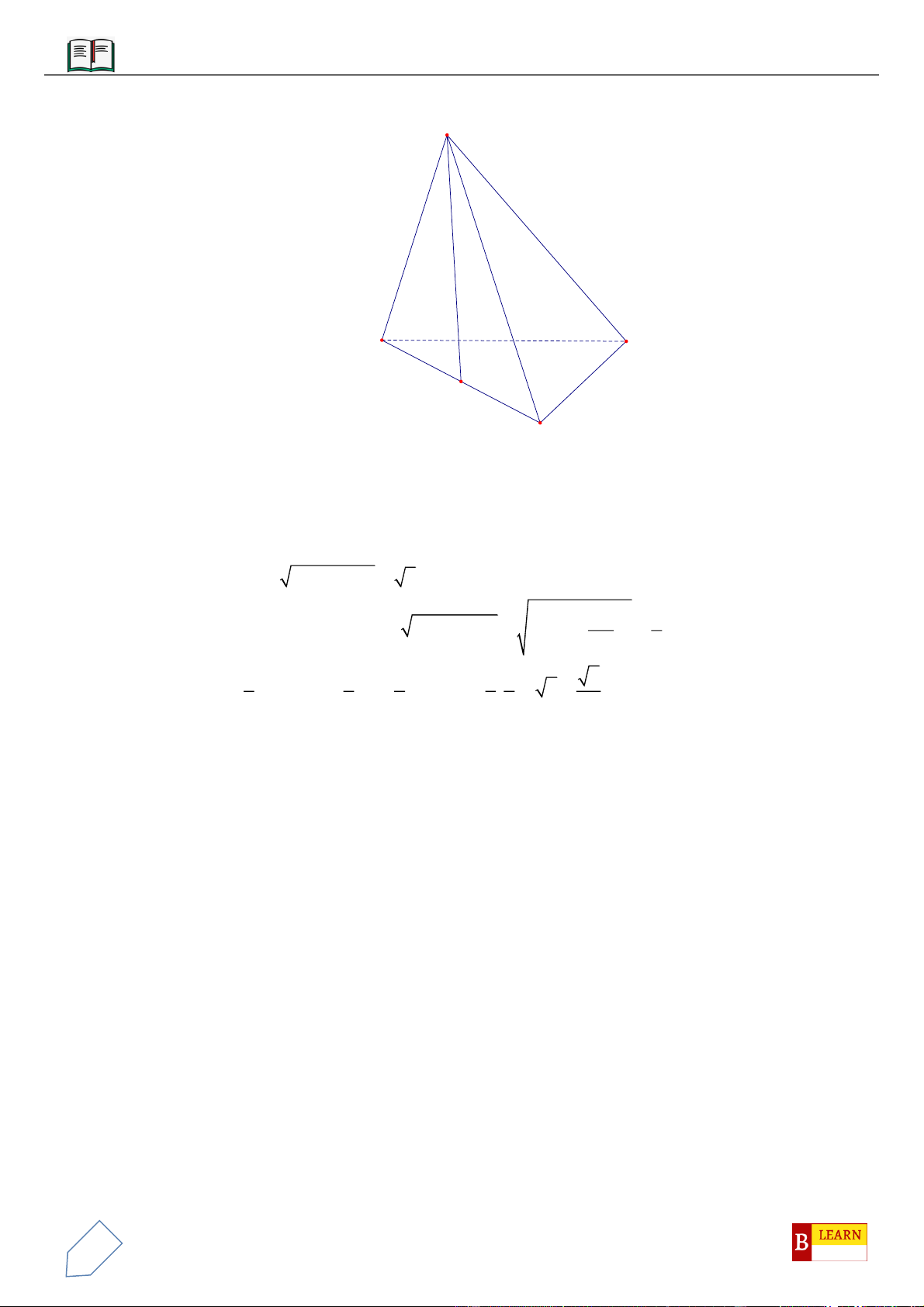
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

114

Gọi

H

là trung điểm cạnh

BC

.

ABC

cân tại

A AH BC

mà

     

ABC BCD AH BCD  

.

Lại có

AB AC AD

nên

H

là tâm đường tròn ngoại tiếp

BCD BCD  

vuông tại

D

.

Xét

22

:3BCD BC BD CD   

Xét

AHC

vuông tại

2

2 2 2

1

22

BC

H AH AC CH AC



     





.

Vậy

1 1 1 1 1 2

. . . . . . . .1. 2

3 3 2 6 2 12

ABCD BCD

V AH S AH DB DC   

.

H

B

D

C

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

115

DẠNG 5: THỂ TÍCH KHỐI CHÓP ĐỀU

Câu 1: Thể tích

V

của khối tứ diện đều có cạnh bằng

a

A.

3

12

a

V 

. B.

3

2

12

a

V 

. C.

3

4

a

V 

. D.

3

2

4

a

V 

.

Câu 2: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

, góc giữa mặt bên và mặt đáy bằng

60

Tính thể tích

V

khối chóp đã cho.

A.

3

48

a

V 

. B.

3

8

a

V 

. C.

3

24

a

V 

. D.

3

16

a

V 

.

Câu 3: Trong tất cả các hình chóp tam giác đều có cạnh bên bằng

3a

, khối chóp có thể tích lớn nhất là

A.

3

2

a

. B.

3

2

4

a

V 

. C.

3

6

2

a

V 

. D.

3

2

a

V 

Câu 4: Thể tích

V

của khối chóp tam giác đều có cạnh đáy bằng

a

và cạnh bên gấp đôi cạnh đáy

A.

3

11

12

a

V 

. B.

3

13

12

a

V 

. C.

3

11

4

a

V 

. D.

3

13

4

a

V 

.

Câu 5: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

, góc giữa cạnh bên và mặt đáy bằng

60

Tính thể tích

V

khối chóp đã cho.

A.

3

12

a

V 

. B.

3

4

a

V 

. C.

3

36

a

V 

. D.

3

6

a

V 

.

Câu 6: Khối chóp tam giác đều có cạnh bên bằng

23a

và thể tích bằng

3

43a

. Tính chiều cao

h

của

khối chóp đã cho.

A.

3ha

. B.

43

3

a

h 

. C.

2ha

. D.

43

9

a

h 

.

Câu 7: Trong tất cả các khối chóp tam giác đều

.S ABC

có khoảng cách từ

A

đến mặt phẳng

 

SBC

bằng

3a

, khối chóp có thể tích nhỏ nhất là?

A.

3

2

a

. B.

3

6

a

. C.

3

33

2

a

. D.

3

4

a

.

Câu 8: Khối chóp tam giác đều có cạnh đáy bằng

23a

và thể tích bằng

3

4a

. Tính chiều cao

h

của khối

chóp đã cho.

A.

43ha

. B.

43

3

a

h 

. C.

4ha

. D.

23

9

a

h 

.

Câu 9: Cho khối chóp tam giác đều

.S ABC

. Gọi

,MN

lần lượt là trung điểm của các cạnh

,SB SC

. Biết

mặt phẳng

 

AMN

vuông góc với mặt phẳng

 

SBC

, diện tích tam giác

AMN

bằng

2

10a

. Tính

thể tích

V

của khối chóp đã cho.

A.

3

85

3

a

. B.

3

85

9

a

. C.

3

85a

. D.

3

85

27

a

.

Câu 10: Thể tích

V

của khối chóp tứ giác đều có tất cả các cạnh đều bằng

a

.

A.

3

2

3

a

V 

. B.

3

2

6

a

V 

. C.

3

2a

. D.

3

2

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

116

Câu 11: Tính thể tích

V

của khối chóp tứ giác đều có cạnh đáy bằng

a

, cạnh bên có độ dài gấp đôi cạnh

đáy.

A.

3

2

a

V 

. B.

3

2

6

a

V 

. C.

3

14

2

a

V 

. D.

3

14

6

a

V 

.

Câu 12: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

. Gọi

,MN

lần lượt là trung điểm các

cạnh

,SB SC

. Biết mặt phẳng

 

AMN

vuông góc với mặt phẳng

 

SBC

. Tính thể tích

V

của khối

chóp đã cho.

A.

3

5

24

a

. B.

3

15

24

a

. C.

3

5

8

a

. D.

3

15

8

a

.

Câu 13: Thể tích

V

của khối bát diện đều có cạnh bằng

a

.

A.

3

2

6

a

. B.

3

2

3

a

. C.

3

2

a

. D.

3

2

4

a

.

Câu 14: Tính thể tích

V

của khối tứ diện đều

ABCD

, biết khoảng cách từ

A

đến mặt phẳng

 

BCD

bằng

6

.

A.

53V 

. B.

93

2

V 

. C.

27 3

2

V 

. D.

27 3V 

.

Câu 15: Một viên đá hình dạng khối tứ diện đều cạnh bằng

a

. Người ta cắt viên đá bởi mặt phẳng song

song với một mặt của khối tứ diện để chia viên đá thành

2

phần có thể tích bằng nhau. Tính độ

dài cạnh

x

của phần cắt ra có hình dạng khối tứ diện đều.

A.

3

2

a

x 

. B.

3

2

a

x 

. C.

3

2

a

x 

. D.

3

2

a

x 

.

Câu 16: Một viên đá hình dạng khối tứ diện đều cạnh bằng

a

. Người ta cắt viên đá bởi mặt phẳng song

song với một mặt của khối tứ diện để chia viên đá thành

2

phần có thể tích bằng nhau. Tính diện

tích thiết diện

S

của mặt cắt.

A.

2

3

16

a

S 

. B.

2

3

8

a

S 

. C.

2

3

44

a

S 

. D.

2

3

42

a

S 

.

Câu 17: Một viên đá hình dạng khối tứ diện đều cạnh bằng

a

. Người ta cắt viên đá bởi các mặt phẳng song

song với mặt của khối tứ diện để chia viên đá thành

5

phần, trong đó có

4

phần là các khối tứ

diện bằng nhau, tổng thể tích của

4

khối tứ diện này bằng một nửa thể tích của viên đá ban đầu.

Tính độ dài cạnh của

4

khối tứ diện đó.

A.

2

a

x 

. B.

3

2

a

x 

. C.

4

a

x 

. D.

3

4

a

x 

.

Câu 18: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

, , ,M N P Q

lần lượt là trọng tâm các mặt của

khối tứ diện đã cho. Tính thể tích

V

của khối tứ diện

MNPQ

.

A.

3

2

12

a

. B.

3

2

108

a

. C.

3

2

324

a

. D.

3

2

81

a

.

Câu 19: Cho khối tứ diện đều

ABCD

có chiều cao

h

. Từ ba đỉnh

,,A B D

của tứ diện người ta cắt ba khối

tứ diện đều có cùng chiều cao

h



. Biết rằng thể tích của khối đa diện còn lại bằng một nửa thể tích

của khối đa diện ban đầu. Mệnh đề nào dưới đây đúng?

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

117

A.

3

h





. B.

3

6

h





. C.

22

h





. D.

3

h





.

Câu 20: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

, góc giữa cạnh bên và mặt đáy bằng

0

60

Gọi

' ' '

;;A B C

lần lượt là các điểm đối xướng với

;;A B C

qua

S

. Tính thể tích của khối bát diện có

các mặt là

' ' ' ' ' ' ' ' ' ' '

; ; ; ; ; ; ; ;ABC ABC ABC ABC ABC ABC BAC CAB

A.

3

23

3

a

V 

. B.

3

23Va

. C.

3

43

3

a

V 

. D.

3

2

a

V 

.

Câu 21: Tính thể tích

V

của khối chóp lục giác đều có cạnh đáy bằng

a

, cạnh bên gấp đôi cạnh đáy.

A.

3

2

a

V 

. B.

3

4

a

V 

. C.

3

9

2

a

V 

. D.

3

2

a

V 

.

Câu 22: Kim tự tháp Ai Cập được xây dựng vào khoảng 2500 năm trước Công Nguyên. Kim tự tháp này

là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Thể tích của khối chóp đó

là

A.

3

2592100 m

. B.

3

7776300 m

. C.

3

2592300 m

. D.

3

3888150 m

.

Câu 23: Một viên đá hình dạng khối chóp tứ giác đều tất cả các cạnh bằng nhau và bằng

a

. Người ta khối

đá bởi mặt phẳng song song với đáy khối chóp để chia khối đá thành

2

phần có thể tích bằng

nhau. Tính diện tích

S

của mặt cắt.

A.

2

3

a

S 

. B.

2

3

2

a

S 

. C.

2

3

4

a

S 

. D.

2

4

a

S 

.

Câu 24: Tính thể tích V của khối chóp tứ giác đều có cạnh đáy bằng a và mặt bên tạo với mặt đáy góc

60

A.

3

6

2

a

V 

. B.

3

6

3

a

V 

. C.

3

6

a

V 

. D.

3

6

a

V 

.

Câu 25: Thể tích

V

của khối chóp tứ giác đều có các cạnh đều bằng

a

A.

3

6

2

a

B.

3

2

6

a

C.

3

2

a

D.

3

6

a

Câu 26: Tính thể tích

V

của khối chóp lục giác đều

.S ABCDEF

có

3, 5AB SA

.

A.

45 3V 

. B.

18 3V 

. C.

54 3V 

. D.

15 3V 

.

Câu 27: Tính thể tích V của khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên tạo với mặt đáy góc

60

.

A.

3

6

2

a

V 

. B.

3

6

3

a

V 

. C.

3

a

V 

. D.

3

6

a

V 

.

Câu 28: Khối tứ diện đều

ABCD

có thể tích

V

. Khối bát diện đều có các đỉnh là trung điểm các cạnh của

khối tứ diện đều có thể tích

V



. Tính tỉ số

V



.

A.

1

2

V





. B.

1

8

V





. C.

5

8

V





. D.

1

4

V





.

Câu 29: Tính thể tích

V

của khối chóp tứ giác đều có tất cả các cạnh bằng nhau và đường cao mặt bên

bằng

3a

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

118

A.

3

2Va

. B.

3

2

6

a

V 

. C.

3

42

3

a

V 

. D.

3

2

9

a

V 

.

Câu 30: Người ta gọt một khối lập phương có thể tích

V

để được một khối bát diện đều (tức là khối có

các đỉnh là tâm các mặt của khối lập phương đó) có thể tích

V



. Tính tỷ số

V



.

A.

1

4

V





. B.

1

6

V





. C.

1

8

V





. D.

1

12

V





.

Câu 31: Cho khối tứ diện đều

ABCD

. Gọi

M

,

N

,

P

,

Q

lần lượt là trung điểm các cạnh

AB

,

BC

,

CD

,

DA

. Biết tứ giác

MNPQ

có diện tích bằng

1

. Tính thể tích

V

của khối tứ diện đều đã cho.

A.

11

24

V 

. B.

22

3

V 

. C.

2

24

V 

. D.

11

6

V 

.

Câu 32: Một khối chóp tam giác đều có cạnh bên bằng

b

, chiều cao

h

. Tính thể tích

V

của khối chóp tam

giác đều đã cho.

A.

 

22

3

4

V b h h

. B.

 

22

3

4

V b h b

.

C.

 

22

3

8

V b h h

. D.

 

22

3

8

V b h b

.

Câu 33: Trong tất cả các khối chóp tứ giác đều có cạnh bên bằng

23a

, khối chóp có thể tích lớn nhất là?

A.

3

32

3

a

. B.

3

22a

. C.

3

62a

. D.

3

32a

.

Câu 34: Cho khối chóp tứ giác đều có cạnh bên bằng

23

, tính độ dài cạnh đáy khi khối chóp có thể tích

lớn nhất.

A.

3

. B.

23

. C.

4

. D.

2

.

Câu 35: Trong tất cả các khối chóp tứ giác đều

.S ABCD

có khoảng cách từ

A

đến mặt phẳng (SBC) bằng

23

. Khối chóp có thể tích nhỏ nhất là?

A.

18

. B.

54

. C.

9

. D.

27

.

Câu 36: Cho khối chóp tam giác đều

.S ABC

có tất cả các cạnh bằng

16

. Xét hình chữ nhật

MNPQ

nội

tiếp đáy

ABC

với

,M N BC

,

P AC

,

Q AB

. Thể tích khối chóp

.S MNPQ

có giá trị lớn

nhất là?

A.

512 2

3

. B.

512 6

3

. C.

512 3

3

. D.

512 3

2

.

Câu 37: Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

2

. Gọi

,MN

lần lượt là trung điểm của

,SB SC

. Tính thể tích

V

của khối chóp biết

CM BN

.

A.

26

3

. B.

26

. C.

26

6

. D.

26

2

.

Câu 38: Cho khối chóp tứ giác đều có tất cả các cạnh bằng nhau là

a

và có thể tích

3

2

6

a

. Tính chiều cao

h

của khối chóp tứ giác đều đã cho.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

119

A.

2

3

a

h 

. B.

3

2

a

h 

. C.

2

a

h 

. D.

3

a

h 

.

Câu 39: Cho khối chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

. Gọi

,MN

lần lượt là trung điểm các

cạnh

SC

và

SD

. Biết mặt phẳng

 

ABMN

vuông góc với mặt phẳng

 

SCD

. Tính thể tích

V

của khối chóp đã cho.

A.

3

2

6

a

V 

. B.

3

a

V 

. C.

3

2

3

a

V 

. D.

3

6

a

V 

.

Câu 40: Cho hình chóp tứ giác đều

.S ABCD

. Gọi

,MN

lần lượt là trung điểm các cạnh

SC

và

SD

. Biết

mặt phẳng

 

ABMN

vuông góc với mặt phẳng

 

SCD

, diện tích tứ giác

ABMN

bằng

2

23a

.

Tính thể tích

V

của khối chóp đã cho.

A.

3

32

9

a

V 

. B.

3

32

3

a

V 

. C.

3

16 3

9

a

V 

. D.

3

32 3

3

a

V 

.

Câu 41: Trong các hình chóp tam giác đều có khoảng cách giữa hai đường thẳng

SA

và

BC

là

d

. Khối

chóp có thể tích nhỏ nhất là?

A.

3

d

. B.

3

23

3

d

. C.

3

d

. D.

3

23

9

d

.

Câu 42: Gọi

12

,VV

lần lượt là thể tích tứ diện đều cạnh

a

, khối bất diện đều cạnh

a

. Tính tỉ số

1

2

V

.

A.

1

2

V



. B.

1

2

1

2

V



. C.

1

2

4

V



. D.

1

2

1

4

V



.

Câu 43: Cho khối chóp tam giác đều có chiều cao là

6a

, khoảng cách giữa hai đường thẳng

,SA BC

là

a

.

Thể tích

V

của khối chop là

A.

3

27 3

10

a

V 

. B.

3

81 3

40

a

V 

. C.

3

81 3

10

a

V 

. D.

3

27 3

40

a

V 

.

Câu 44: Cho tứ diện đều cạnh

a

. Gọi

h

là tổng khoảng cách từ một điểm trong của khối tứ diện lên các

mặt của nó. Tìm mệnh đề đúng.

A.

6

3

a

h 

. B.

6

12

a

h 

. C.

46

3

a

h 

. D.

26

3

a

h 

.

Câu 45: Cho khối bát diện đều cạnh

a

. Gọi

h

là tổng khoảng cách từ một điểm trong của khối tứ diện lên

các mặt của nó. Tìm mệnh đề đúng.

A.

6

a

h 

. B.

6

12

a

h 

. C.

46

3

a

h 

. D.

26

3

a

h 

.

Câu 46: Tìm Trong cách khối chóp tam giác đều

.S ABC

có cạnh bên là

23

, khối chóp có thể tích lớn

nhất là

A.

43

3

. B.

26

3

. C.

43

. D.

26

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

120

Câu 47: Trong cách khối chóp tam giác đều

.S ABC

có khoảng cách từ

A

đến

 

SBC

là

3

, khối chóp có

thể tích nhỏ nhất là

A.

3

8

. B.

9

2

. C.

3

2

. D.

33

2

.

Câu 48: Cho khối chóp tứ giác đều

.S ABCD

có tất cả các cạnh bằng a. Gọi

', ', ',D'A B C

lần lượt là các

điểm đối xứng của

, , ,DA B C

qua

S

. Tính thể tích

V

của khối đa diện có sáu mặt

           

, ' ' ' ' , , , ,ABCD A B C D BCA D ADB C CDB A ABD C

       

.

A.

3

22Va

. B.

3

2Va

. C.

3

42

3

a

V 

. D.

3

82

3

a

V 

.

Câu 49: Một khối bát diện dều cạnh a. Ngoại tiếp bát diện đều bởi một khối lập phương sao cho các đỉnh

của khối bát diện đều là tâm các mặt của khối lập phương. Tính thể tích khối lập phương.

A.

3

22

3

a

V 

. B.

3

22Va

. C.

3

42Va

. D.

3

42

3

a

V 

.

Câu 50: Cho khối tứ diện đều

 

H

có cạnh bằng 1. Qua mỗi cạnh của

 

H

dựng một mặt phẳng không

chứa các điểm trong của

 

H

và tạo với hai mặt phẳng của

 

H

đi qua cạnh đó những góc bằng

nhau. Các mặt phẳng như thế giới hạn một đa giác

 

H



. Tính thể tích của

 

H



.

A.

2

4

. B.

2

6

. C.

2

3

. D.

22

3

Câu 51: Khối tứ giác đều có tất cả các cạnh bằng 1. Khối lập phương có một mặt nằm trên mặt đáy của

khối chóp tứ giác đều và tất cả các cạnh còn lại của mặt đối diện nằm trên các mặt bên của khối

chóp tứ giác đều. Tính thể tích

V

của hình lập phương.

A.

5 2 7V 

. B.

6 3 10V 

. C.

5 2 7

3

V





. D.

6 3 10

3

V





.

Câu 52: Một khối tứ diện đều

 

H

có cạnh bằng 1. Khối lăng trụ tam giác đều có tất cả các cạnh bằng

nhau, có mặt đáy nằm trên một mặt của khối tứ diện

 

H

và tất cả các cạnh còn lại của mặt đối

diện nằm trên các mặt còn lại của khối tứ diện

 

H

. Tính thể tích của khối lăng trụ tam giác đều

đó.

A.

27 2 22 3

6

V





. B.

45 6 58 3

686

V





.

C.

27 2 22 3

2

V





. D.

9 6 22

2

V





.

Câu 53: Từ một miếng tôn hình vuông cạnh

50

cm, người ta cắt đi bốn tam

giác cân bằng nhau

MAN

,

NBP

,

PCQ

,

QDM

sau đó gò các tam

giác cân

ABN

,

BCP

,

CDQ

,

DAM

sao cho các đỉnh

M

N

,

P

,

Q

trùng nhau để được khối chóp tứ giác đuuè. Khối chóp tứ giác đều có

thể tích lớn nhất là

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

121

A.

15625

6

cm

3

. B.

15625

2

cm

3

. C.

4000 10

3

cm

3

. D.

4000 10

9

cm

3

.

Câu 54: Cho khối chóp tam giác đều

.S ABC

có độ dài cạnh đáy bằng

a

, mặt phẳng chứa

BC

và vuông

góc với

SA

cắt khối chóp theo một thiết diện có diện tích bằng

2

4

a

. Tính thể tích

V

của khối

chóp đã cho.

A.

3

2

24

a

V 

. B.

3

2

12

a

V 

. C.

3

36

a

V 

. D.

3

72

a

V 

.

Câu 55: Cho khối chóp tam giác đều

.S ABC

có góc giữa mặt bên và mặt đáy bằng



, khoảng cách từ

A

đến mặt phẳng

 

SBC

bằng

3

. Tính

tan



, khi thể tích khối chóp

.S ABC

đạt giá trị nhỏ nhất.

A.

1

tan

3





. B.

1

tan

2





. C.

tan 2





. D.

tan 3





.

Câu 56: Từ một tấm tôn hình vuông có cạnh bằng

13

, người ta cắt tấm tôn theo các tam giác cân bằng

nhau

, , , MAN NBP PCQ QDM

sau đó gò các tam giác cân

, , , ABN BCP CDQ DAM

sao cho

các đỉnh

, , , M N P Q

trùng nhau để được khối chóp tứ giác đều. Biết góc ở đỉnh của tam giác

cân bị cắt đi là

0

150

. Tính thể tích

V

khối chóp tứ giác đều tạo thành.

A.

3 6 5 2

24

V





. B.

2

3

V 

. C.

5 2 3 3

24

V





. D.

2

9

V 

.

Câu 57: Từ một tấm tôn hình vuông có cạnh bằng

a

, người ta cắt đi bốn tam giác cân bằng nhau

, , , MAN NBP PCQ QDM

sau đó gò các tam giác cân

, , , ABN BCP CDQ DAM

sao cho các

đỉnh

, , , M N P Q

trùng nhau để được khối chóp tứ giác đều. Khối chóp tứ giác đều có thể tích

lớn nhất là?

A.

3

48

a

. B.

3

16

a

. C.

3

4 10

375

a

. D.

3

4 10

125

a

.

Câu 58: Một khối chóp tứ giác đều

.S ABCD

có

m

là tan góc giữa cạnh bên và mặt đáy. Người ta tăng

cạnh hình vuông mặt đáy gấp đôi nhưng muốn giữ nguyên thể tích khối chóp nên đã thay đổi đồng

thời chiều cao cho phù hợp. Hỏi giá trị của

m

thay đổi như thế nào?

A. Giảm 2 lần. B. Tăng 2 lần. C. Giảm 8 lần. D. Tăng 8 lần.

Câu 59: Khối tứ diện đều

 

H

có cạnh bằng

1

. Khối lăng trụ tam giác đều có mặt đáy nằm trên một mặt

của khối tứ diện

 

H

và tất cả các cạnh còn lại của mặt đáy đối diện nằm trên các mặt còn lại của

khối tứ diện

 

H

. Tính thể tích lớn nhất của khối lăng trụ tam giác đều đó.

A.

2

27

. B.

2

48

. C.

2

18

. D.

2

16

.

Câu 60: Khối tứ diện đều

 

H

có tất cả các cạnh bằng

1

. Khối hộp chữ nhật

 

H



có một mặt nằm trên

mặt đáy của

 

H

và tất cả các cạnh còn lại của mặt đáy đối diện nằm trên các mặt bên của

 

H

Tìm thể tích lớn nhất của

 

H



.

A.

5 2 7

. B.

22

27

. C.

42

27

. D.

2

27

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

122

BẢNG ĐÁP ÁN

1.B

2. C

3. A

4. A

5. A

6.C

7. A

8. B

9. A

10.B

11. D

12.A.

13.B.

14.D.

15.D.

16.C

17.A.

18.C

19.B

20.A

21.D

22.A

23.C

24.C.

25.B

26.B

27.D

28.A

29.C

30.B

31.B

32.A

33.A

34.B

35.A

36.A

37.A

38.C

39.D

40.A

41.C

42.D

43.D

44.A

45.C

46.C

47.B

48.B

49.B

50.A

51.A

52.C

53.C

54.A

55.A

56.B

57.C

58.C

59.A

60.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn B

Gọi

H

là tâm của tam giác đều

ABC

. Ta có

 

SH ABC

và

2 2 3 3

3 3 2 3

BH AE a a  

.

22

6

3

SH SB BH a  

.

23

1 1 6 3 2

..

3 3 3 4 12

SABC ABC

V SH S a a a  

.

Câu 2: Chọn C

Ta có

   

 

; 60SBC ABC SHG  

3

.tan60 . 3

62

aa

SG GH    

.

Vậy

23

.

1 1 3 3

. . . .

3 3 4 2 24

S ABC ABC

a a a

V S SG  

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

123

Câu 3: Chọn A

Xét hình chóp tam giác đều

.S ABC

có cạnh bên

3S A a

, cạnh đáy

AB x

.

Ta có

2 2 2

SA SG AG

2

3

x

SG a  

22

9

3

ax



.

Do đó

2 2 2

1 3 9

..

3 4 3

x a x

V





2 2 2

1

.9

12

x a x

.

Xét hàm số

 

2 2 2

9f x x a x

trên

 

0; 3a

.

 

3

22

29

9

x

f x x a x

ax



  



23

22

18 3

9

a x x

ax







.

 

0

6

x

fx

xa

















.

   

0 3 0f f a

,

 

3

6 6 3f a a

.

Vậy thể tích khối chóp lớn nhất là

3

13

.6 3

12 2

a

Va

.

Câu 4: Chọn A

Gọi

H

là tâm của tam giác đều

ABC

. Ta có

 

SH ABC

và

2 2 3 3

3 3 2 3

BH AE a a  

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

124

22

33

3

SH SB BH a  

.

23

1 1 33 3 11

..

3 3 3 4 12

SABC ABC

V SH S a a a  

.

Câu 5: Chọn A

Ta có

 

; 60SA ABC SAG  

3

.tan60 . 3

3

a

SG AH a    

.

Vậy

23

.

1 1 3 3

. . . .

3 3 4 12

S ABC ABC

aa

V S SG a  

.

Câu 6: Chọn C

Gọi

x

là độ dài các cạnh đáy của tam giác

ABC

. Diện tích tam giác

ABC

là

2

3

4

x

B 

.

3

23

2

1 3 48

. 48

3

Va

V Bh h h x a

B

x

     

(1).

Gọi

G

là trọng tâm tam giác

ABC

 

SG ABC SGA   

vuông tại

G

,

3

x

AG 

 

2

2 2 2 2 2 2 2

12 3 12

3

x

h SG SA AG a h x a h         

(2).

Từ (1) và (2)

3 2 3

16 12 0 2a a h h h a    

.

Câu 7: Chọn A

A

B

C

S

G

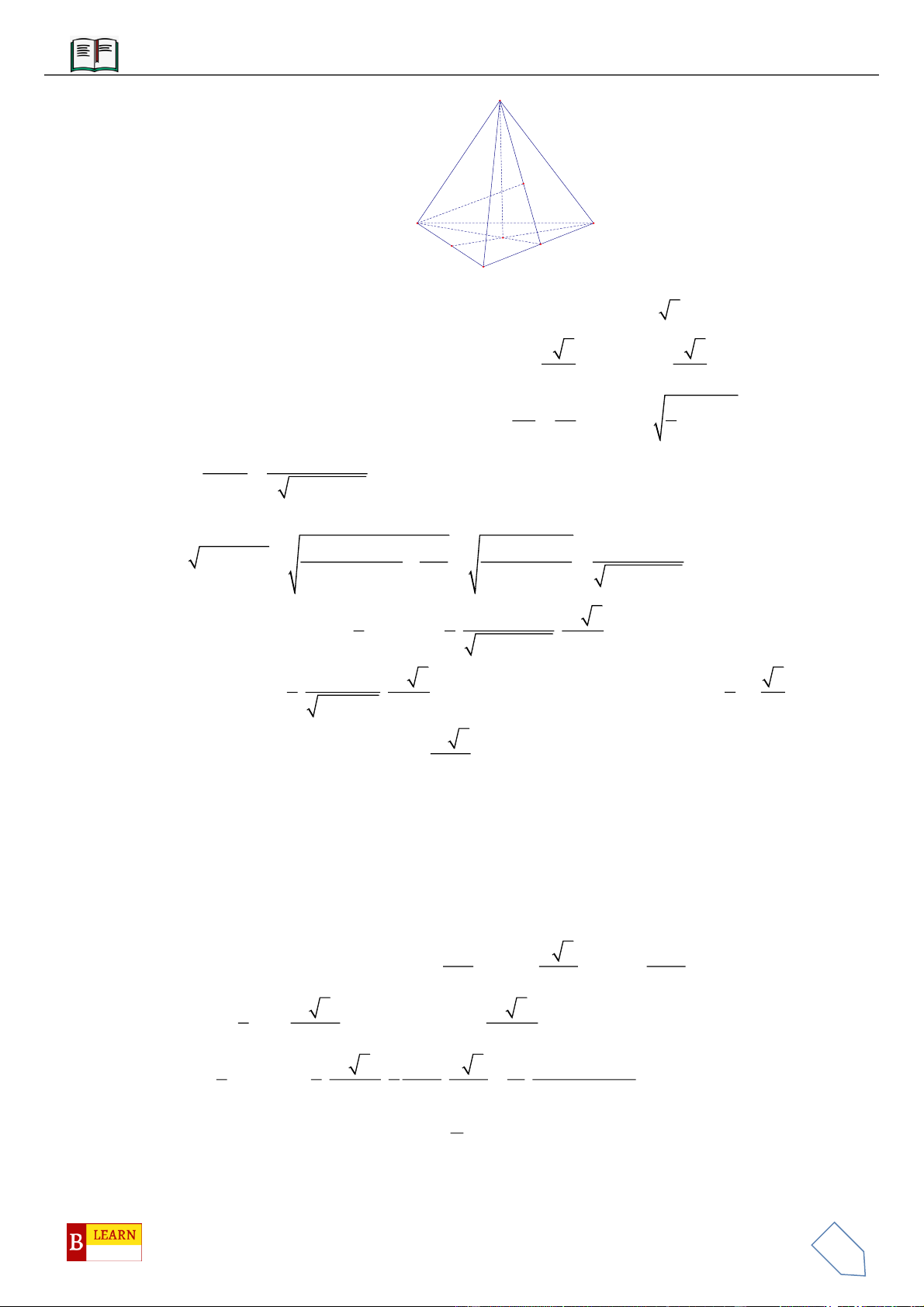
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

125

Cách 1: Gọi

I

là trung điểm của

BC

. Khi đó

 

,3d A SBC AH a

Gọi cạnh của tam giác đều

ABC

là

 

33

0;

23

xx

x x AI AO OB    

.

Tam giác

SOI

đồng dạng với tam giác

AHI

nên

IO IS

IH IA



mà

22

3

4

IH x a

2

22

.

2 3 12

IO IA x

SI

IH

xa

  



.

Xét tam giác

SOI

vuông tại

O

ta có:

   

4 2 2 2

22

2 2 2 2

22

3

36

4 3 12 3 12

3 12

x x x a xa

SO SI OI

x a x a

xa

     





.

Vậy thể tích khối chóp

2

22

1 1 3

. . .

3 3 4

3 12

ABC

xa x

V SO S

xa





.

Xét hàm số

2

13

( ) . .

34

3 12

xx

fx

x





trên khoảng

 

2; 4

ta có

53

min (x) ( )

22

ff

.

Vậy khối chóp có thể tích nhỏ nhất là

3

2

a

Cách 2: Gọi



là góc tạo bởi mặt bên và đáy

 

ABC

.

Gọi

O

là tâm tam giác

ABC

.

Gọi

I

là trung điểm của

BC 

góc

SAI

bằng



.

Gọi

H

là hình chiếu vuông góc của

A

lên

SI

 

AH SBC

 

A;d SBC AH

.

Xét tam giác vuông

AHI

ta có :

32

sin

sin sin

AH a a

AI BC

AI





    

.

Suy ra

13

3 3sin

a

OI AI





;

3

.tan

3cos

a

SO OI





nên suy ra

3

.

3

1 1 3 1 2 3 1

. . . . . .

3 3 3cos 2 sin sin 3

cos cos

S ABCD ABC

a a a a

V SO S

  



  



Để

 

3

min

cos cos , ;

2

V f o



   



   





đạt giá trị lớn nhất.

Đặt

     

32

cos 0;1 1 3 0t t f t t t f t t





         

O

A

C

B

S

I

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

126

3

t  

. Suy ra

 

3 2 3

max

39

f t f









.Vậy

3

min

93

.

32

23

a

Va

.

Câu 8: Chọn B

Diện tích tam giác đáy là

 

2

02

1

. 2 3 .sin60 3 3

2

B a a

.

Ta có:

3

1 3 12 4 3

33

V a a

V Bh h

B

a

    

.

Câu 9: Chọn A

Gọi

H

là tâm của tam giác

ABC

 

SH ABC

Gọi

I

là trung điểm của

BC

. Gọi

J MN SI

,

Giả sử

AB x

. Theo giả thiết

AJ SI

và

J

là trung

điểm của

SI

nên tam giác

SAI

cân tại

A

3

2

x

SB SA AI   

Tam giác

SBI

vuông tại

I

2

22

32

2 2 2

x x x

SI SB BI



     





Ta có

2

3 10

;

2 2 2 8 4

x SI x x x

MN AJ AI



     





2

1 1 10

. . . . 10 4

2 2 4 2

AMN

xx

S JA MN a x a    

Tam giác

SAH

vuông tại

H

 

2

22

4 2 15

23

3

aa

SH SA AH a



     





 

2

3

43

1 1 2 15 8 5

. . . .

3 3 3 4 3

ABC

a

aa

V SH S  

.

Câu 10: Chọn B

Giả sử

.S ABCD

là khối chóp tứ giác đều,

O

là tâm của hình vuông

ABCD

.

Khi đó:

2

ABCD

Sa

,

2

3

2 2 2 2

.

2 2 1 1 2 2

2 2 3 3 2 6

ABCD

a a a a

h SO SA AO a V S h a



         





.

Câu 11: Chọn D

Giả sử

.S ABCD

là khối chóp tứ giác đều,

O

là tâm của hình vuông

ABCD

.

Khi đó:

2

ABCD

Sa

,

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

127

 

2

3

2

2 2 2

.

2 14 1 1 14 14

2

2 2 3 3 2 6

ABCD

a a a a

h SO SA AO a V S h a



         





.

Câu 12: Chọn A

Gọi

H

là tâm của tam giác

ABC

 

SH ABC

Gọi

I

là trung điểm của

BC

3

2

a

AI

Gọi

J MN SI

, Theo giả thiết

AJ SI

và

J

là

trung điểm của

SI

nên tam giác

SAI

cân tại

A

Khi đó,

3

2

a

SA IA

.

Tam giác

SAH

vuông tại

H

2

22

3 15

26

3

a a a

SH SA AH



     





23

1 1 15 3 5

. . . .

3 3 6 4 24

ABC

a a a

V SH S  

.

Câu 13: Chọn B

Giả sử

SABCDE

là khối bát diện đều có cạnh bằng

a

và

O

là tâm của hình vuông

ABCD

.

Khi đó:

2

ABCD

Sa

,

 

2

3

2

2 2 2

..

2 2 1 1 2 2

2 2 3 3 2 6

S ABCD ABCD

a a a a

SO SA AO a V S SO a



        





.

33

.D

22

2. 2.

63

SABCDE S ABC

aa

VV   

.

Câu 14: Chọn D

Giả sử

ABCD

là khối tứ diện đều cạnh

a

và có khoảng cách từ

A

đến mặt phẳng

 

BCD

bằng

6

,

O

là tâm của tam giác

BCD

.

Ta có

2

2 2 2

36

6 3 6

33

aa

h AO AB BO a a



        





 

2

3 6 3

1 1 3 1

. . . . .6 27 3

3 3 4 3 4

BCD

a

V S AO AO    

.

Câu 15: Chọn D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

128

Thể tích viên đá ban đầu là

3

2

12

a

V 

.

Phần cắt ra có hình dạng khối tứ diện đều cạnh bằng

x

có thể tích

3

2

12

x

V





.

Theo giả thiết, ta có

2

V





33

22

12 24

xa



3

2

a

x

Câu 16: Chọn C

Thể tích viên đá ban đầu là

3

2

12

a

V 

.

Phần cắt ra có hình dạng khối tứ diện đều cạnh bằng

x

có

3

2

12

x

V





.

Theo giả thiết, ta có

2

V





33

22

12 24

xa



3

2

a

x

Do đó diện tích mặt cắt là

2

22

33

3 3 3

44

2 4 4

x a a

S



  





.

Câu 17: Chọn A

Gọi độ dài cạnh của

4

khối tứ diện nhỏ là

x

, thể tích của mỗi khối nhỏ này là

3

2

12

x

.

Theo giả thiết ta có

33

2 1 2

4

12 2 12 2

x a a

x

   

  

   

   

.

Câu 18: Chọn C

G

F

E

Q

P

N

M

a

C

a

D

B

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

129

Ta có

2 2 1

.

3 3 2 3

a

MN EF CB  

. Tương tự

6

a

MQ QN NP MP QP    

.

Xét tứ diện

ABCD

:

2

3 2 3 6

,

4 3 2 3

BCD

a a a

S h a



   





23

1 3 6 2

.

3 4 3 12

a a a

V  

3

2

3

2

12 324

MNPQ

a

V







  

Câu 19: Chọn B

Gọi

O

là tâm của

 

BCD AO BCD  

. Giả sử

AB x

.

Xét

ABO

có

2

22

3

x

hx



  





2

3

x



6

2

xh

. Ta có

33

23

12 8

ABCD

xh

V 

.

Tương tự, thể tích

3

khối tứ diện đều chiều cao

h



và

3

8

h

V











.

Theo giả thiết, ta có

3

26

6

V h h

  

    

Câu 20: Chọn A

Thể tích

V

của khối bát diện là

23

1 3 2 3

8 8 . . . 3

3 4 3

3

SABC

a a a

VV



  





.

Câu 21: Chọn D

Ta có:

22

3 3 3

6

42

aa

S









.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

130

Độ dài chiều cao của khối chóp

 

2

2a 3h a a  

.

Khi đó, thể tích

V

của khối chóp lục giác đều là

23

1 1 3 3 3

. . 3

3 3 2 2

aa

V S h a  

.

Câu 22: Chọn A

Đáy là hình vuông cạnh dài 230 m nên diện tích đáy là

 

22

230 52900Sm

.

Thể tích khối chóp là

 

3

11

. . .52900.147 2592100

33

V S h m  

.

Câu 23: Chọn C

Ta có

 

SO ABCD

Xét

SOD

có

2 2 2

SO SD OD

2

22

aa

a



  





2

a

SO

.

.ABCD

1

..

3

S ABCD

V V SO S

3

12

.

32

a

3

2

6

a

.

Phần cắt ra có hình dạng khối chóp tứ giác đều

.S MNPQ

có tất cả các cạnh bằng

x

có thể tích

3

2

6

x

V





. Ta có

33

22

2 6 12

V

V x a



  

3

2

a

x

. Diện tích

S

của mặt cắt là

2

3

4

a

S 

.

Câu 24: Chọn C

Xét khối chóp tứ giác đều S.ABCD, gọi O là tâm giao điểm AC và BD, M là trung điểm của AB. Ta có

 

SO ABCD

. Góc tạo bởi mặt bên (SAB) và mặt đáy là

60S MO 

.

Ta có

3

.tan .tan60

22

aa

SO MO SAC   

.

Thể tích khối chóp S.ABCD là

3

2

1 1 3 3

. . . .

3 3 2 6

ABCD

aa

V S SO a  

.

TYPS: Gọi



là góc tạo bởi mặt bên và mặt đáy, ta có

3

tan

6

a

V





.

M

O

C

A

D

B

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

131

Câu 25: Chọn B

Xét khối chóp tứ giác đều

.S ABCD

có

AB a

,

SA a

.

Gọi

O AC BD

, ta có

 

SO ABCD

.

22

SO SA OA

2

a









2

a



.

Thể tích của khối chóp

.S ABCD

là

.

1

..

3

S ABCD ABCD

V S SO

2

12

..

32

a

a

3

2

6

a



.

Câu 26: Chọn B

Gọi

O

là tâm lục giác

ABCDEF

. Ta có:

2 2 2 2

4SA SA OA SA AB    

.

Thể tich khối chóp là

2

1 1 3

. . .4.6. .3

3 3 4

ABCDEF

V SO V

18 3

.

Câu 27: Chọn D

Xét khối chóp tứ giác đều S.ABCD, gọi O là tâm giao điểm AC và BD. Ta có

 

SO ABCD

. Góc tạo

bởi cạnh bên SA và mặt đáy là

60SAO 

. Ta có

26

.tan .tan60

22

aa

SO AO SAC   

. Thể tích

khối chóp S.ABCD là

3

2

1 1 6 6

. . . .

3 3 2 6

ABCD

aa

V S SO a  

.

TYPS: Gọi



là góc tạo bởi cạnh bên và mặt đáy, ta có

3

2

tan

6

a

V





.

Câu 28: Chọn A

O

C

A

D

B

A

a

O

C

B

D

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

132

Gọi độ dài cạnh của tứ diện đều là

a

, suy ra thể tích khối tứ diện đều

3

2

12

a

V 

.

Ta có

1

22

a

MQ AD

là độ dài cạnh của bát diện đều. Suy ra

3

.2

2

3 24

a

V











.

Vậy

1

2

V





.

Câu 29: Chọn C

Theo giả thiết ta có

SBC

đều và

3

3 . 2

2

SM a BC BC a   

. Mặt khác

1

2

OM CD a

nên

từ tam giác vuông

 

2

2 2 2

32SOM SO SM OM a a a     

.

Vậy thể tích khối chóp

.S ABCD

là

 

3

2

1 4 2

. 2 . 2

33

a

V a a

.

Câu 30: Chọn B

Gọi cạnh hình lập phương là

a

. Suy ra thể tích khối lập phương là

3

Va

.

Ta có

1 1 2

.2

2 2 2

a

EJ A B a



  

là cạnh của bát diện đều.

Suy ra thể tích

3

2

36

a

V











nên ta có

1

6

V





.

Câu 31: Chọn B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

133

Do

ABCD

là tứ diện đều nên

MNPQ

là hình vuông.

Do diện tích

MNPQ

bằng

1

nên

1MN 



Tứ diện đều

ABCD

có độ dài các cạnh bằng

2

.

Gọi

I

là tâm đường tròn ngoại tiếp tam giác

BCD

ta có

 

1

.

3

V AI dt BCD

.

 

2

23

3

4

dt BCD 

,

2

2 2 2

2. 3 2

26

33

AI AB BI



    





.

Vậy thể tích của tứ diện

ABCD

là

1 2 6 2 2

3

3 3 3

V 

.

Câu 32: Chọn A

Giả sử hình chóp tam giác đều là

.A BCD

.

Gọi

I

là tâm đường tròn ngoại tiếp tam giác

BCD

ta có

 

1

.

3

V AI dt BCD

.

22

BI b h

, mà

22

3

3 3 3

3

BI BC BC BI b h    

.

 

22

2

3

44

bh

BC

dt BCD





 

22

3

4

V b h h  

Câu 33: Chọn A

Gọi độ dài cạnh đáy là

.S ABC

, ta có

2

Sx

và

 

2

22

2

24

23

22

x a x

ha





  





.

Do đó

 

3

2 2 2 2

2 2 2 3

48 2

3

24 32

3 6 6 3

32

x x a x

Sh x a x a

V



  







    

.

Dấu bằng đạt tại

2 2 2

48 2 4x a x x a   

.

Câu 34: Chọn B

Q

P

M

N

B

C

D

A

I

P

B

C

D

A

I

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

134

Gọi cạnh đáy là

 

0xx

khi đó chiều cao hình chóp

2

22

12

2

x

SO SD OD   

. Thể tích khối

chóp

 

2

2 2 4 2

.

1 1 1 1

. . . 12 . 24 144 12 2 2

3 3 2

3 2 3 2

S ABCD ABCD

x

V SO S x x x x        

.

Vậy thể tích khối chóp lớp nhất bằng

22

khi

2

12 0 2 3xx   

.

Câu 35: Chọn A

Gọi

H

là tâm mặt đáy và

a

là độ dài cạnh đáy. Ta có khoảng cách từ

H

đến mặt phẳng

 

SBC

là

3

2

A

H

d

d 

và

2 2 2 2 2

1 1 1 1 1 4

3

2

H

d h h a

a

    







2

22

2

4 12

33

3

h

a

hh

h

  



Do

23

2

4

()

33

3

Sh a h h

V f h

h

   



.

Có

 

2

4

0( )

4

( ) 0 3

3

()

6

x loai

h

f h x

h

i

h

x loa







   













Lập bảng biến thiên suy ra thể tích nhỏ nhất

(3) 18f 

.

Câu 36: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

135

Ta có

2

2 16 3 16 6

16 .

3 2 3

h



  





.

Đặt

tan60 3MB NC x MQ NP x x      

, và

16 2MN BC MB NC x    

.

Do đó

 

. 3 16 2S MN MQ x x  

.

 

16 6

3 16 2 .

32 8 2

512 2

3

3 3 3 3

xx

Sh

V



   

. Dấu bằng đạt được tại

4x 

.

Câu 37: Chọn A

Gọi

,OG

lần lượt là trọng tâm của tam giác

,ABC SBC

,

I

là trung điểm

BC

.

Đặt

SA SB SC x  

.

Ta có:

2 2 2

4 4 4 8

.

9 9 2 4 9

x x x

CG BG BN





    





.

Tam giác

BGC

vuông tại

G

nên

2

2 2 2

8

2. 4 10

9

x

GB GC BC x



     

.

2 2 2 3 2 3

.

3 3 2 3

AO AI  

;

2

22

2 3 78

10

33

SO SA AO



    





.

2

23

3

4

ABC

S





suy ra

1 1 78 26

. . . 3

3 3 3 3

ABC

V SO S



  

.

Câu 38: Chọn C

Ta có:

3

2

22

2

3.

1 3 2

6

.

32

a

Va

V a h h

aa

    

.

Câu 39: Chọn D

H

I

A

B

C

S

M

N

P

C

A

B

Q

G

N

M

O

I

A

C

B

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

136

Gọi

,,I J K

lần lượt là trung điểm của các cạnh

,,AB MN CD

và

O

là tâm hình vuông

ABCD

.

Ta có:

J

là trung điểm của

MN

và

IK

là hình chiếu của

IJ

trên mặt phẳng

 

ABCD

.

Mà

IK CD IJ CD IJ MN    

.

Xét tam giác

SIK

có

,IJ SO

là các đường trung tuyến đồng thời là các đường cao nên nó là tam giác

đều có cạnh

3

2

a

IK BC a SO   

. Ta có:

3

2

.

1 3 3

..

3 2 6

S ABCD

aa

Va

.

Câu 40: Chọn A

Gọi

,,I J K

lần lượt là trung điểm của các cạnh

,,AB MN CD

và

O

là tâm hình vuông

ABCD

.

Ta có:

J

là trung điểm của

MN

và

IK

là hình chiếu của

IJ

trên mặt phẳng

 

ABCD

.

Mà

IK CD IJ CD IJ MN    

.

Xét tam giác

SIK

có

,IJ SO

là các đường trung tuyến đồng thời là các đường cao nên nó là tam giác

đều có cạnh

 

3

0

2

x

IK BC x x SO IJ     

.

Ta có:

 

2

22

1 1 3 3 3 4 3

. 2 3 . 2 3

2 2 2 2 8 3

ABMN

x x x a

S AB MN IJ a x a x



        





2

3

.

43

.3

1 4 3 32

3

..

3 3 2 9

S ABCD

a

aa

V



  





.

O

A

D

B

C

S

M

N

I

J

K

O

A

D

B

C

S

M

N

I

J

K

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

137

Câu 41: Chọn C

Gọi là trọng tâm

ABC

ta có

 

SO ABC

.

Gọi

,MN

lần lượt là trung điểm của

,BC AB

.Ta có

 

BC S AM

tại

M

.

Dựng

MK SA

tại

K

ta có:

KM

là đoạn vuông góc

chung của hai đường thẳng

SA

và

BC

và

 

,d SA BC MK d

.

Đặt

 

0AB x x

. Dựng

OI SA

tại

22

33

d

I OI MK  

.

Ta có:

2 2 3 3

.

3 3 2 3

xx

OA AM  

.

Xét tam giác

SOA

vuông tại

O

có đường cao

2 2 2

1 1 1

OI

OI OA OS

  

2 2 2 2 2 2

23

.

. 2 . 3 2 3

33

3

4 3 3 4

39

dx

OI OA d x d

OS x

OA OI x d x d



    









Ta có:

23

.

2 2 2 2

1 3 2 3

..

34

3 3 4 6 3 4

S ABC

x dx dx

V

x d x d





.

Không mất tính tổng quát, đặt

1d 

, ta có

 

3

.

2

23

,

3

6 3 4

S ABC

x

V f x x

x

  



.

Ta có:

 





 





2 2 3

22

2

23

22

6

3 .6 3 4 6 .

2

2 3 4

02

36 3 4 3 4

x

x x x

xx

x

f x x

xx







    



Bảng biến thiên:

Vậy

.S ABC

V

nhỏ nhất bằng

3

d

khi

2xd

.

Cách 2: Đặt

,BC x SO h

, ta có:

2

2 2 2 2

3 3 2

,.

2 2 3 3

x x x

AM SA SO OA h h



      





.

O

A

C

B

S

M

N

K

I

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

138

Do đó:

2 . .

SAM

S SO AM SA MK

nên

2 2 2 2 2

2 2 2

33

2 3 4 3

xh x x h d x

d h d h    

2

2 2 2 2

3

43

d

x h d h



  





(

2

3

d

h 

) và

2 2 2 2 3

2

.

2 2 2 2

12 3 3

12

9 4 9 4

S ABC

d h x h d h

xV

h d h d

   



.

Xem

1d 

, xét hàm số

 

2

32

,

3

94

h

f h h

h





, ta có:

3

1

33

SABC

d

V 

.

Dấu bằng đạt tại

23

3

d

h 

.

Câu 42: Chọn D

Ta có:

2

3

2

1

1 3 3 2

..

3 4 3 12

a a a

Va



  





và

2

3

22

2

1 2 2

2. . .

3 2 3

aa

V a a



  





.

3

1

3

2

1

12

4

2

3

a

V

a

  

.

Câu 43: Chọn D

Dựng hình bình hành

ACBD

, ta có

     

 

33

, , , ,

22

BC SAD d BC SA d BC SAD d H SAD d G SAD GK a     

.

Suy ra

2 2 2

2 1 1 1 3 3 5

3 10

25

a a a

GK AG AB

AG KG SG

       

.

Thể tích khối chop là

23

1 3 27 3

..

3 4 40

AB a

V SG

.

Câu 44: Chọn B

Ta có thể tích của khối tứ diện đều cạnh

a

là

3

2

12

a

V 

, diện tích mỗi mặt là

2

3

4

a

S 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

139

Ta có

 

3

1 2 3 4

2

32

1 3 6

12

..

33

3

4

a

Va

V S h h h h h

S

a

       

.

Câu 45: Chọn C

Ta có thể tích của khối bát diện đều cạnh

a

là

3

2

3

a

V 

, diện tích mỗi mặt là

2

3

4

a

S 

.

Ta có

 

3

1 2 8

2

32

1 3 4 6

3

. . ...

33

3

4

a

Va

V S h h h h

S

a

      

.

Câu 46: Chọn C

Gọi cạnh đáy là

 

0xx

. Khi đó diện tích đáy là

2

3

4

x

S 

, chiều cao của hình chóp là

 

2

3 36

6

3

x

hx





.

Thể tích khối chóp là

 

22

2

23

. . 36

3 36

1 1 3 12

22

. . . 4 3

3 3 4 3 6 6

xx

x

V S h



    

.

Dấu bằng xảy ra khi

 

2

36 2 6

2

x

xx   

.

Câu 47: Chọn B

Gọi cạnh đáy là

 

0xx

. Khi đó

3

6

x

GH 

,

Ta có

 

, 3 , 3 3 1d A SBC d G SBC GK GK    

.

Có

 

2 2 2

22

2

12

23

12

12 12

x GH x

HK HG GK x SH

HK

x



      



.

Diện tích tam giác

SBC

là

3

2

11

..

2

43

12

SBC

x

S BC SH

x





Để thể tích khối chóp nhỏ nhất khi diện tích tam giác

SBC

nhỏ nhất. Khảo sát hàm số

 

3

2

12

x

fx

x





,

23x 

ta thấy giá trị nhỏ nhất của hàm số đạt được khi

32x 

.

Vậy

3

.

2

1 1 9

..

32

43

12

S ABC

x

MinV

x





.

Câu 48: Chọn B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

140

Khối đa diện tạo thành là một khối hộp chữ nhật có đáy là hình vuông cạnh a và chiều cao:

2

' 2 2 2

2

a

h HH SH a a



    





. Do đó

23

. 2 2V S h a a a  

.

Câu 49: Chọn B

Gọi

b

là độ dài các cạnh của khối lập phương, độ dài các cạnh của khối bát diện đều

2

b

a b a  

. Do đó

33

22V b a

Câu 50: Chọn A

Ta có

( ') ( ) .

4

H H S ABC

V V V

, trong đó

.S ABC

là khối chóp tam giác đều như hình vẽ.

Ta có

()

2

12

H

V 

và

2

6

16

3

1 tan 2 2

3

33

6

HD

HD HMD

HM



      





.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

141

Do đó

tan tan cot 2

22

HMD HMD

SMH







    





.

Do đó

36

SH HM.tan . 2

66

SMH  

.

Vì vậy

. ( ')

36

.

2 2 2 2

46

4.

3 24 12 24 4

S ABC H

VV     

.

Câu 51: Chọn A

Theo giả thiết thì khối lập phương có dạng như hình vẽ.

Chiều cao

h

của khối chóp tứ giác đều là

2

h 

.

Độ dài cạnh lập phương là

x

, theo Thales ta có

1 1 1 2 1

11

MN SM AM MK x x h

x

AD SA SA SH h h

           



. Do đó

 

3

2 1 5 2 7V    

Câu 52: Chọn C

Theo giả thiết ta có khối lăng trụ tam giác đều

. ' ' 'MNP M N P

như hình vẽ dưới đây.

Đặt

'MN MM x

, theo Thales ta có

'

11

MN AM BM MM

BC AB AB AH

    

.

Trong đó

6

' ,BC 1,AH

3

MN MM x   

, do đó

33

3 ( 6 2) 3 27 2 22 3

4 4 2

x

V



  

.

Câu 53: Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

142

Đặt

AD x

;

50a 

cm. Gọi

I

là trung điểm của

AB

, ta có

2

22

NQ AD a x

NI





.

Chiều cao khối chóp là

2

22

2 2 2

a x x a a x

h NI HI



   

    





. Do đó

   

2

3

0;

2

2 2 4 10 4000 10

2

max

3 3 5 375 3

a

a a x

x

Sh a a

V f x f x f











      





.

Câu 54: Chọn A

Gọi

M

là trung điểm của

BC

,

N

là hình chiếu vuông góc của

M

trên

SA

. Suy ra

 

SA BCN

do đó thiết diện là tam giác cân

NBC

.

2

2.

2

4

2

NBC

a

S

a

MN

BC a



  

.

Đặt

SH h

, ta có

..AM SH SA MN

2

3

22

a

ah





6

a

h

.

Vậy

2

23

6

3.

32

6

12 12 24

a

a h a

V   

.

Câu 55: Chọn A

Đặt

AB x

và

SH h

. Gọi

K

là hình chiếu vuông góc của

H

trên

SM

, Ta có

2 2 2

1 1 1

3

6

HK h

x









 

22

2

9 1 12

,

hx

d A SBC

  

2

12

1

h

x

h





.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

143

Do đó

 

23

2

0;

1 3 3 9

. . min 3

3 4 2

1

xh

V h f h f h f

h



     



.

Dấu bằng đạt tại

3h 

18x

31

tan

3

3 3 3

h

x



   

.

Câu 56: Chọn B

Ta có:

0 0 0

150 15 60MAN MNA ANB    

Suy ra khối chóp tứ giác đều có tất cả các cạnh bằng nhau và bằng

AM

.

Xét

MAN

ta có

0

2

75

MN

AM

sin



. Do đó:

3

22

63

AM

V 

.

Câu 57: Chọn C

Gọi

AD x

, ta có

2

22

NQ AD a x

NI





.

Gọi

H

là hình chiếu vuông góc của

S

trên

 

ABCD

.

Chiều cao khối chóp là:

2

22

2 2 2

a x x a a x

h NI HI



   

    





.

Diện tích đáy :

2

ABCD

Sx

Vậy thể tích :

2

.

1

2

. , 0;

33

2

ABCD

a a x

x

a

V S h x





  





.

Xét hàm số :

 

2

.

2

, 0;

3

2

a a x

x

a

f x x











CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

144

Có

   

22

2

1 5 2 4 2 2

, 0; 0

35

2

4

2

a x a x a a

f x x f x x

a a x













     











.

Suy ra

 

33

0;

2

2 2 4 10 4 10

5 375 375

a

a a a

maxf x f maxV









   





.

Câu 58: Chọn C

Ta có

 

SC ABCD C

SH ABCD















suy ra góc giữa cạnh bên SC

và đáy là góc

SCH





tan

22

aa

SH SCH m    

Ta có

2

3

2

3 3 6

8

(2 ) 2

36

a

am

Sh a m

V

m

S h a m

V







  









  







.

Câu 59: Chọn A

Theo giả thiết, ta có khối lăng trụ tam giác đều

.MNP M N P

  

như hình vẽ.

Đặt

MN x

,

MM h





;

1BC 

;

6

3

AH 

. Theo Thales, ta có

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

145

1

MN AM MM

BC AB AH



  

1

6

3

xh



  

 

6

1

3

hx



  

. Do đó

   

 

2

0;1

3 2 2 2

. 1 max

4 4 3 27

x

V h f x x x f x f





      





.

Câu 60: Chọn B

Theo giả thiết thì hình hộp chữ nhật

 

H



có dạng như hình vẽ.

Đặt

2

h SH

;

MN x

;

MK h





.

Theo Thales, ta có

11

MN SM AM MK

AD SA SA SH

    

1

xh

h



  

 

1h x h



  

. Do đó

 

   

 

2

22

21

2 2 2

1

2 3 27

H

xx

V x h x x h f x f









      





.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

146

DẠNG 6. THỂ TÍCH KHỐI TỨ DIỆN ĐẶC BIỆT

Câu 1: Cho hình chóp SABC có

1SA SB SC BA BC    

. Tìm thể tích lớn nhất của khối chóp

.S ABC

A.

1

6

. B.

2

12

. C.

1

8

. D.

3

12

.

Câu 2: Tính thể tích của khối chóp SABC có

60 , 90 , 120ASB BSC CSA     

và

, 2 , 4SA a SB a SC a  

A.

3

2

a

. B.

3

22

3

a

. C.

3

2a

. D.

3

32

2

a

.

Câu 3: Cho tứ diện

ABCD

có

4;AB a CD x

và các cạnh còn lại bằng

3a

. Tính

x

để thể tích khối tứ

diện

ABCD

là lớn nhất.

A.

2 10xa

. B.

10a

. C.

6a

. D.

3a

.

Câu 4: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc với nhau thỏa mãn

2 2 2

12OA OB OC  

. Thể tích lớn nhất của khối tứ diện bằng:

A.

8

. B.

4

3

. C.

4

. D.

8

3

.

Câu 5: Cho hình chóp

SABC

có thể tích bằng 3 và

3, 4, 5AB AC BC  

. Hình chiếu vuông góc của

đỉnh S lên mặt phẳng

 

ABC

nằm trong tam giác

ABC

. Góc giữa mặt phẳng

   

,SAB SAC

và

đáy lần lượt là

00

30 ;60

. Tính cotang góc giữa hai mặt phẳng

 

SBC

và

 

ABC

A.

24 13 3

15



. B.

8 5 3

5



. C.

24 13 3

15



. D.

8 5 3

5



.

Câu 6: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

B

,

8AB 

,

6BC 

. Biết

6SA 

và

vuông góc với mặt phẳng đáy

 

ABC

. Một điểm

M

thuộc phần không gian bên trong của hình

chóp và cách đều tất cả các mặt của hình chóp. Tính thể tích của khối tứ diện

MABC

.

A.

24V 

. B.

64

3

V 

. C.

32

3

V 

. D.

12V 

.

Câu 7: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

,

4AB a

,

3AC a

và hình chiếu

vuông góc của

S

lên mặt phẳng

 

ABC

là điểm

H

. Biết

,AH

nằm khác phía với đường thẳng

BC

và các mặt bên của hình chóp cùng tạo với mặt đáy góc

60

. Tính thể tích

V

của hình chóp

đã cho.

A.

3

23Va

. B.

3

12 3Va

. C.

3

63Va

. D.

3

36 3Va

.

Câu 8: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc; khoảng cách từ

O

đến mặt phẳng

 

ABC

bằng

1

. Thể tích nhỏ nhất của khối tứ diện

OABC

bằng

A.

9

2

. B.

3

6

. C.

3

2

. D.

3

2

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

147

Câu 9: Cho hình hộp

.ABCD A B C D

   

có tất cả các cạnh bằng

a

có các góc

 

00

0 90A AB BAD A AD





    

. Biết khối hộp đã cho có thể tích bằng

3

3 3 5

2

a 

A.

1

arccos

3





. B.

6







. C.

6

arccos

3





. D.

3



.

Câu 10: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc thỏa mãn

1 4 9

1

OA OB OC

  

. Khi

biểu thức

OA OB OC

đạt giá trị nhỏ nhất, tính thể tích khối tứ diện

OABC

.

A.

162

. B.

72

. C.

108

. D.

216

.

Câu 11: Cho khối hộp

. ' ' ' 'ABCD A B C D

có tất cả các cạnh bằng nhau và bằng

a

,

 

0

' ' 0 90A AB BAD A AD



    

. Tính thể tích khối hộp đã cho theo

a

và



.

A.

3

2 cos 1 2cos

2

Va





. B.

3

2 sin 1 2cos

2

Va





.

C.

32

2 cos 1 2cos

2

Va





. D.

32

2 sin 1 2cos

2

Va





.

Câu 12: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

. Hình chiếu vuông góc của

S

lên mặt

phẳng

 

ABC

nằm trong tam giác

ABC

và các mặt bên

     

,,SBC SCA SAB

tạo với mặt đáy

 

ABC

các góc lần lượt là

000

30 ,45 ,60

. Tính thể tích khối chóp đã cho.

A.

 

3

128 4 3

a

V 



. B.

 

3

8 4 3

a

V 



. C.

 

3

8 2 3 1

a

V 



. D.

 

3

128 2 3 1

a

V 



.

Câu 13: Cho hình chóp S.ABCD có đáy

ABCD

là một tứ giác lồi và góc tạo bởi các mặt bên

( ),( ),( ),( )SAB SBC SCD SDA

và mặt đáy tương ứng là

0000

90 ,60 ,60 ,60

. Biết tam giác

SAB

vuông

cân tại

S

có

AB a

, chu vi tứ giác

ABCD

bằng

9a

. Tính thể tích V của khối chóp đã cho.

A.

3

3Va

. B.

3

a

. C.

3

9

a

. D.

3

a

.

Câu 14: Cho khối lập phương

.ABCD A B C D

   

cạnh

a

. Các điểm

,MN

lần lượt di động trên các tia

,AC B D



sao cho

2AM B N a





. Thể tích khối tứ diện

AMNB



có giá trị lớn nhất là?

A.

3

2

6

a

. B.

3

12

a

. C.

3

2

12

a

. D.

3

6

a

.

Câu 15: Khối tứ diện

ABCD

có

2AB a

, tam giác

CAB

đều và tam giác

DAB

vuông cân tại

D

. Góc giữa

hai mặt phẳng

   

,CAB DAB

bằng

0

30

. Tính thể tích

V

của khối tứ diện

ABCD

.

A.

3

4

a

V 

B.

3

2

a

V 

C.

3

4

a

V 

D.

3

6

a

V 

Câu 16: Cho hai đường thẳng

,Ax By

chéo nhau và vuông góc với nhau có

2AB a

là đoạn vuông góc

chung. Các điểm

,MN

lần lươt di động trên

,Ax By

sao cho

23AM BN a

. Hỏi thể tích lớn

nhất của khối tứ diện

ABMN

là?

A.

3

2

3

a

. B.

3

8

a

. C.

3

4

a

. D.

3

2

a

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

148

Câu 17: Cho khối chóp

.S ABC

có

1AB 

,

2AC 

,

5BC 

. Các tam giác

,SAB SAC

lần lượt vuông tại

,BC

, góc giữa mặt phẳng

 

SBC

và đáy bằng

60

. Tính thể tích

V

của khối chóp đã cho.

A.

2 15

5

V 

. B.

23

3

V 

. C.

2 15

3

V 

. D.

2 15

15

V 

.

Câu 18: Cho khối tứ diện

ABCD

có

AB x

, tất cả các cạnh còn lại bằng nhau và bằng

2 x

. Hỏi có bao

nhiêu giá trị của

x

để khối tứ diện đã cho có thể tích bằng

2

12

.

A.

1

. B.

6

. C.

4

. D.

2

.

Câu 19: Khối tứ diện

ABCD

có

2AB a

, tam giác

CAB

đều và tam giác

DAB

vuông cân tại

D

. Góc

giữa hai mặt phẳng

 

CAB

,

 

DAB

bằng

30

. Tính thể tích

V

của khối tứ diện

ABCD

.

A.

3

4

a

V 

. B.

3

2

a

V 

. C.

3

4

a

V 

. D.

3

6

a

V 

.

Câu 20: Cho tứ diện

ABCD

có

2BD 

, hai tam giác

,ABD BCD

có diện tích lần lượt là

6

và

10

. Biết

thế tích của tứ diện

ABCD

bằng

16

, tính số đo góc giữa hai mặt phẳng

 

ABD

và

 

BCD

A.

4

arccos

5







. B.

4

arcsin

15







. C.

4

arcsin

5







. D.

4

arccos

15







.

Câu 21: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi hai đường chéo

AC

và

BD

vuông góc nhau, mặt

bên

SAD

là tam giác đều và tạo với mặt đáy góc

60

o

,

4, 6, 8AD AC BD  

. Tính thể tích

V

của khối

.S ABCD

A.

24V 

. B.

96

5

V 

. C.

48

5

V 

. D.

144

5

V 

.

Câu 50 : Cho khối lăng trụ

.ABC A B C

  

, khoảng cách từ

C

đến đường thẳng

BB



bằng

5

, khoảng cách

từ

A

đến đường thẳng

BB



và

CC



lần lượt bằng

1

và 2, hình chiếu vuông góc của

A

lên mặt

phẳng

 

A B C

  

là trung điểm

M

của

BC



và

5AM





. Thể tích khối lăng trụ đã cho bằng

A.

25

3

. B.

15

3

. C.

5

. D.

2 15

3

.

Câu 22: Cho khối tứ diện

OABC

có các cạnh

,,OA OB OC

đôi một vuông góc và tổng diện tích các mặt

 

OBC

,

 

OCA

,

 

OAB

bằng

3

. Diện tích mặt

 

ABC

bằng

1

. Tính thể tích

V

của khối tứ

diện đã cho.

A.

1

6

V 

. B.

4

12

9

V 

. C.

4

23

9

V 

. D.

4

3

9

V 

.

Câu 23: Cho khối lập phương

1 1 1 1

.ABCD A B C D

có độ dài các cạnh bằng

x

. Các điểm

,MN

lần lượt trên

các cạnh

11

,AA CC

sao cho

2AM CN a

. Tìm

x

biết thể tích khối tứ diện

BDMN

bằng

3

2a

.

A.

2xa

. B.

6xa

. C.

3xa

. D.

22xa

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

149

Câu 24: Cho khối tứ diện

ABCD

có tam giác

ABD

đều, tam giác

CAB

vuông cân tại

C

,

3AB a

. Gọi



là góc giữa hai mặt phẳng

   

,CAB ADB

. Tính

cos



khi thể tích khối tứ diện

ABCD

bằng

3

2

8

a

.

A.

2

cos

3





. B.

7

cos

3





. C.

3

cos

3





. D.

2

cos

2





.

Câu 25: Cho khối chóp

.S ABC

có

 

9AB cm

,

 

11BC cm

,

 

6CA cm

,

 

3SA cm

,

 

3SB cm

và

 

5SC cm

. Tính thể tích

V

của khối chóp.

A.

 

3

2159

6

V cm

. B.

 

3

241

2

V cm

. C.

 

3

2159

2

V cm

. D.

 

3

3 241

2

V cm

.

Câu 26: Cho khối lăng trụ tam giác

. ' ' 'ABC A B C

có đáy là tam giác vuông tại

A

,

1, 2AB BC

. Góc

00

' 90 , ' 120CBB ABB

. Gọi

M

là trung điểm của

'AA

. Biết

 

7

',

7

d AB CM 

. Tính thể tích

khối lăng trụ đã cho.

A.

22

. B.

42

9

. C.

42

. D.

42

3

.

Câu 27: Cho khối tứ diện

ABCD

có

3AB a

,

4AC a

,

90BAC 

và góc giữa các mặt phẳng

 

DAB

,

 

DBC

,

 

DCA

với mặt phẳng

 

ABC

bằng nhau và bằng

60

, hình chiếu vuông góc của

D

lên mặt phẳng

 

ABC

là điểm

H

sao cho

A

,

H

nằm về hai phía của đường thẳng

BC

. Tính thể

tích

V

của khối tứ diện

ABCD

.

A.

3

23Va

. B.

3

63Va

. C.

3

43Va

. D.

3

12 3Va

.

Câu 28: Cho khối tứ diện

ABCD

có

3AB a

,

4AC a

,

90BAC 

và góc giữa các mặt phẳng

 

DAB

,

 

DBC

,

 

DCA

với mặt phẳng

 

ABC

bằng nhau và bằng

60

, hình chiếu vuông góc của

D

lên mặt phẳng

 

ABC

là điểm

H

sao cho

C

,

H

nằm về hai phía của đường thẳng

AB

. Tính thể

tích

V

của khối tứ diện

ABCD

.

A.

3

23Va

. B.

3

63Va

. C.

3

43Va

. D.

3

12 3Va

.

Câu 29: Cho khối tứ diện

ABCD

có

3AB a

,

4AC a

,

90BAC 

và góc giữa các mặt phẳng

 

DAB

,

 

DBC

,

 

DCA

với mặt phẳng

 

ABC

bằng nhau và bằng

60

, hình chiếu vuông góc của

D

lên mặt phẳng

 

ABC

là điểm

H

sao cho

B

,

H

nằm về hai phía của đường thẳng

AC

. Tính thể

tích

V

của khối tứ diện

ABCD

.

A.

3

23Va

. B.

3

63Va

. C.

3

43Va

. D.

3

12 3Va

.

Câu 30: Cho khối tứ diện

ABCD

có

3 , 4 , 90AB a AC a BAC   

và góc giữa các mặt phẳng

     

,,DAB DBC DCA

và mặt phẳng

 

ABC

bằng nhau và bằng

60

, hình chiếu vuông góc của

D

lên mặt phẳng

 

ABC

là điểm

H

nằm trong tam giác

ABC

. Tính thể tích

V

của khối tứ diện

ABCD

:

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

150

A.

3

23Va

. B.

3

63Va

. C.

3

43Va

. D.

3

12 3Va

.

Câu 31: Cho khối hộp

.ABCD A B C D

   

có đáy là hình chữ nhật,

3, 7AB AD

. Hai mặt bên

   

, ' 'ABB A ADD A



tạo với đáy các góc lần lượt là

45

và

60

. Tính thể tích

V

của khối hộp

đã cho biết độ dài cạnh bên bằng

1

.

A.

3V 

. B.

7

3

V 

. C.

3V 

. D.

7V 

.

Câu 32: Cho khối tứ diện

ABCD

có

3 , 4 , 90AB a AC a BAC   

, góc giữa các mặt phẳng

   

,DAB DAC

và mặt phẳng

 

ABC

lần lượt là

45

và

60

. Tính thể tích

V

của khối tứ diện

ABCD

biết

6AD a

.

A.

3

12 5

5

a

V 

. B.

3

4 21

7

a

V 

. C.

3

45

5

a

V 

. D.

3

12 21

7

a

V 

.

Câu 33: Cho khối chóp

.S ABC

có đáy là tam giác vuông tại

A

,

2

a

AC BC a

. Hai mặt phẳng

   

,SAB SAC

cùng tạo với đáy góc

60

, tam giác

SBC

nhọn và mặt phẳng

 

SBC

vuông góc

với đáy. Tính thể tích

V

của khối chóp

.S ABC

.

A.

 

3

33

32

a

V





. B.

 

3

33

32

a

V





. C.

 

3

3 3 3

32

a

V





. D.

 

3

3 3 3

32

a

V





.

Câu 34: Cho hai đường thẳng chéo nhau

Ax

,

By

tạo với nhau góc

60

và

AB a

là độ dài đoạn vuông

góc chung. Hai điểm

M

,

N

di động trên

Ax

,

By

sao cho

2MN a

. Tìm thể tích lớn nhất của

khối tứ diện

ABMN

.

A.

3

16

a

. B.

3

4

a

. C.

3

36

a

. D.

3

12

a

.

Câu 35: Cho khối chóp

.S ABC

có

AB AC a

, các góc

120BAC 

,

90SBA SCA  

, góc giữa mặt

phẳng

 

SAC

và đường thẳng

SB

bằng

3

arcsin

8

và khoảng cách từ

S

đến

 

ABC

nhỏ hơn

2a

. Tính thể tích của khối chóp

.S ABC

.

A.

3

12

a

. B.

3

24

a

. C.

3

4

a

. D.

3

8

a

.

Câu 36: Cho hai đường thẳng

,ab

cố định chéo nhau. Gọi

AB

là đoạn vuông góc chung của 2 đường thẳng

,ab

;A a B b

. Trên

a

lấy điểm

M

khác

A

, trên

b

lấy điểm

N

khác

B

sao cho

;AM x BN y

. Biết

6AB 

, góc giữa hai đường thẳng

,ab

là

0

60

. Tính thể tích của tứ diện

ABMN

theo

x

và

y

.

A.

3

2

xy

. B.

3

4

xy

. C.

2

xy

. D.

3

6

xy

.

Câu 37: Cho khối chóp

.S ABCD

có đáy là hình vuông cạnh

a

,

SA SB

,

SC SD

. Biết rằng mặt phẳng

   

SAB SCD

và tổng diện tích của hai tam giác

SAB

,

SCD

bằng

2

7

10

a

. Tính thể tích

V

của

khối chóp

.S ABCD

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

151

A.

3

4

75

a

V 

. B.

3

4

15

a

V 

. C.

3

4

25

a

V 

. D.

3

12

25

a

V 

.

Câu 38: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh

2a

,

0

90SAB SCB

. Gọi

M

là trung điểm

cạnh

SA

. Biết khoảng cách từ điểm

A

đến mặt phẳng

 

BCM

bằng

2 21

7

a

. Thể tích khối chóp

đã cho bằng ?

A.

3

10 3

9

a

. B.

3

10 3

3

a

. C.

3

53

9

a

. D.

3

53

3

a

.

Câu 39: Cho khối chóp

.S ABC

có

SA BC x

,

SB CA y

,

SC AB z

và

2 2 2

12x y z  

. Thể

tích lớn nhất của khối chóp

.S ABC

bằng?

A.

22

3

. B.

42

3

. C.

22

9

. D.

42

9

.

Câu 40: Cho hình vuông

ABCD

và

ABEF

có cạnh bằng

1

, lần lượt nằm trên hai mặt phẳng vuông góc

với nhau. Gọi

S

là điểm đối xứng với

B

qua trung điểm của đoạn thẳng

DE

. Thể tích của khối

đa diện

ABCDSEF

bằng

A.

7

6

. B.

11

12

. C.

2

3

. D.

5

6

.

Câu 41: Cho hình vuông

ABCD

và

ABEF

có cạnh bằng

1

, lần lượt nằm trên hai mặt phẳng vuông góc

với nhau. Gọi

S

là điểm đối xứng với

B

qua đường thẳng

DE

. Thể tích của khối đa diện

ABCDSEF

bằng?

A.

7

6

. B.

11

12

. C.

2

3

. D.

5

6

.

Câu 42: Cho khối chóp tứ giác đều có cạnh đáy bằng , mặt bên tạo với đáy một góc . Mặt

phẳng chứa chứa đường thẳng và tạo với góc đáy một góc chia khối chóp

thành hai khối đa diện. Thể tích của khối đa diện chứa đỉnh bằng:

A. . B. . C. . D. .

Câu 43: Cho tứ diện có tam giác vuông tại , , . Mặt phẳng ,

, lần lượt tạo với mặt phẳng các góc , , trong đó .

Thể tích khối tứ diện có giá trị lớn nhất bằng:

A. . B. . C. . D. .

Câu 44: Cho khối đa diện

SABCD

bằng cách ghép hai khối chóp tam giác

.S ABD

và

.S BCD

lại với nhau ,

biết

4; 3; 2; 1SA SB SC SD   

và

0

60ASB BSC CSD DSA BSD    

. Thể tích khối đa

diện

SABCD

bằng

A.

32

. B.

32

2

. C.

72

6

. D.

42

3

.

.S ABCD

1

75

 

P

AB

45

.S ABCD

S

16 9 3

78



 

23

3 1 2



 

23

6 1 2



16 9 3

26



ABCD

ABC

A

3AB a

AC a

 

DBC

 

DAC

 

DAB

 

ABC

90





90



  

ABCD

3

4

a

3

13

a

3

32

10

a

3

8

a

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

152

Câu 45: Cho tứ diện đều

ABCD

có cạnh bằng

1

. Gọi

,MN

lần lượt là trung điểm của

,AB BC

; điểm

P

thuộc cạnh

CD

sao cho

2PD CP

, mặt phẳng

 

MNP

cắt

AD

tại

Q

. Tính thể tích khối đa diện

BMNPQD

.

A.

2

16

. B.

23 2

432

. C.

2

48

. D.

13 2

432

.

Câu 46: Cho tứ diện

ABCD

có

3AB a

;

15; 10; 4AC a BD a CD a  

. Biết góc giữa đường thẳng

AD

và

 

BCD

là

0

45

, khoảng cách giữa

AD

và

BC

là

5

4

a

. Hình chiếu vuông góc của

A

lên

 

BCD

nằm trong tam giác

BCD

. Tính độ dài đoạn

AD

.

A.

52

4

a

. B.

2a

. C.

22a

. D.

32

2

.

Câu 47: Cho hình lăng trụ

.ABC A B C

  

, khoảng cách từ

A

đến các đường thẳng

BB



,

CC



lần lượt bằng

1

và

3

; khoảng cách từ

C

đến đường thẳng

BB



bằng

2

. Hình chiếu vuông góc của

A

lên

mặt phẳng

 

A B C

  

là trọng tâm

G



của tam giác

A B C

  

và

4

3

AG





. Thể tích khối lăng trụ

.ABC A B C

  

bằng.

A.

2

. B.

2

3

. C.

4

. D.

4

3

.

Câu 48: Cho khối lăng trụ

.ABC A B C

  

có thể tích bằng

3

4

. Khoảng cách từ

A

đến các đường thẳng

BB



,

CC



lần lượt bằng

1

;

3

và

2AA





. Côsin góc giữa hai mặt phẳng

 

ABB A



và

 

ACC A



bằng.

A.

3

4

. B.

3

2

. C.

1

2

. D.

13

4

.

Câu 49: Cho khối chóp

.S ABC

có đáy là tam giác đều cạnh bằng

1

, khoảng cách từ

A

đến mặt phẳng

 

SBC

bằng

6

4

, khoảng cách từ

B

đến mặt phẳng

 

SCA

bằng

15

10

; khoảng cách từ

C

đến

mặt phẳng

 

SAB

bằng

30

20

. Hình chiếu vuông góc của

S

lên mặt phẳng

 

ABC

nằm trong tam

giác

ABC

. Thể tích khối chóp

.S ABC

bằng.

A.

1

36

. B.

1

48

. C.

1

12

. D.

1

24

.

Câu 50: Cho khối lăng trụ

.ABC A B C

  

có đáy là tam giác cân tại

A

,

1AB AC

,

30BAC 

. Các mặt

bên

 

ABB A



,

 

ACC A



lần lượt tạo với đáy các góc

45

,

60

và

1AA





. Tính thể tích khối

lăng trụ

.ABC A B C

  

bằng.

A.

3 31

124

. B.

93

372

. C.

31

124

. D.

93

124

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

153

Câu 51: Cho khối chóp

.S ABC

có

5( )AB cm

,

 

7AC cm

,

 

3SA cm

.

30CAB 

. Góc giữa hai mặt

phẳng

 

SAB

,

 

SAC

và đáy lần lượt là

45

,

30

. Tính thể tích

V

của khối chóp đã cho.

A.

35 29

116

V 

. B.

75

4

V 

. C.

21 5

4

V 

. D.

105 5

116

V 

.

Câu 52: Cho khối chóp

.S ABC

có đáy là tam giác vuông tại

A

,

3AB 

,

7AC 

. Hai mặt bên

 

SAB

,

 

SAC

lần lượt tạo với đáy góc

45

,

60

và

1SA 

. Tính thể tích

V

của khối chóp

.S ABC

bằng.

A.

1

2

V 

. B.

7

9

V 

. C.

3

V 

. D.

7

3

V 

.

Câu 53: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

A

,

1AB 

và

3AC 

. Các mặt bên

     

,,SBC SAC SAB

lần lượt tạo với đáy các góc

00

30 ,45

và

0

60

. Hình chiếu vuông góc của

điểm

S

lên mặt phẳng

 

ABC

nằm trong tam giác

ABC

. Tính thể tích khối chóp

.S ABC

A.

33

12



B.

33

20

C.

33

4



D.

3

20

Câu 54: Cho hình chóp

.S ABC

có thể tích bằng

3

12

, đáy làm tam giác vuông tại

A

và

1AB 

,

3AC 

. Các mặt bên

   

,SAC SAB

lần lượt tạo với đáy các góc

00

45 ,60

. Hình chiếu vuông góc của

S

lên mặt phẳng

 

ABC

nằm trong tam giác

ABC

. Cô-sin góc giữa mặt

 

SBC

và đáy bằng

A.

1

2

B.

3

2

C.

1

4

D.

3

4

Câu 55: Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

và

AB a

,

2AC a

. Mặt phẳng

 

SBC

vuông góc với đáy, hai mặt phẳng

 

SAB

và

 

SAC

cùng tạo với mặt phẳng đáy góc

0

60

. Tính thể tích

V

của khối chóp

.S ABC

theo

a

.

A.

3

a

V 

B.

3

23

9

a

V 

C.

3

9

a

V 

D.

3

43

9

a

V 

Câu 56: Cho khối chóp

.S ABCD

có đáy là hình thoi cạnh

a

, góc

0

120BAD 

. Các mặt bên

       

, , ,S AB SBC SCD SDA

lần lượt tạo với đáy các góc

0 0 0 0

90 ,30 ,45 ,60

. Thể tích khối chóp

.S ABCD

A.

 

3

4 3 3

26

a

V





B.

 

3

4 3 3

104

a

V





C.

 

3

12 3 9

26

a

V





D.

 

3

12 3 9

104

a

V





Câu 57: Cho hình hộp chữ nhật

.ABCD A B C D

   

có

1, 2, 3AB AD AA



  

. Mặt phẳng

 



thay đổi đi

qua

C



và cắt các tia

,,AB AD AA



lần lượt tại

,,M N P

. Khối tứ diện

AMNP

có thể tích nhỏ

nhất bằng

A.

27

B.

14

C.

11

D.

36

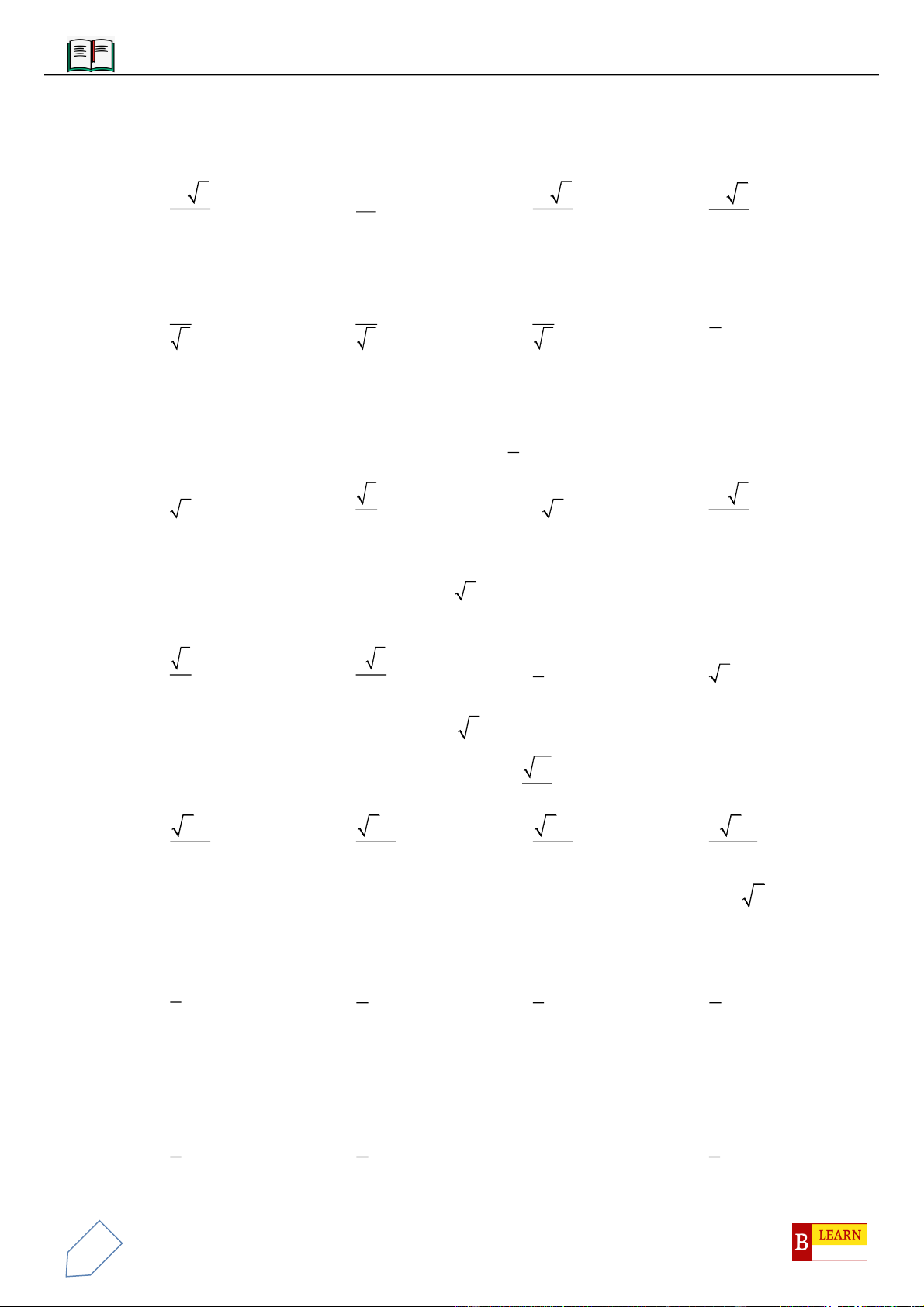
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

154

Câu 58: Cho hai đường thẳng chéo nhau

,Ax By

và hợp với nhau một góc bằng

0

60

. Biết

AB a

là đoạn

vuông góc chung. Lấy điểm

C

trên

By

sao cho

BC a

và gọi

D

là hình chiếu vuông góc của

C

lên

Ax

. Thê rtichs khối tứ diện

ABCD

bằng

A.

3

12

a

B.

3

12

a

C.

3

24

a

D.

3

6

a

Câu 59: Cho khối tứ diện

ABCD

có

1AB AC BD CD   

. Thể tích khối tứ diện

ABCD

đạt giá trị

lớn nhất thì khoảng cách giữa hai đường thẳng

AD

và

BC

bằng

A.

2

3

. B.

1

3

. C.

1

2

. D.

1

3

.

Câu 60: Trong không gian cho ba tia

,,Ox Oy Oz

đôi một vuông góc và các điểm

,,A B C

không trùng với

điểm

O

lần lượt thay đổi trên các tia

,,Ox Oy Oz

và luôn thỏa mãn điều kiện: Tỉ số diện tích tam

giác

ABC

và thể tích khối tứ diện

OABC

bằng

3

2

. Khối tứ diện

OABC

có thể tích nhỏ nhất bằng

A.

6

. B.

3

2

. C.

43

. D.

27 3

2

.

Câu 61: Cho khối đa diện

.ABC A B C

  

có

// //AA BB CC

  

. Biết khoảng cách từ điểm

A

đến

BB



bằng

1

, khoảng cách từ điểm

A

đến

CC



bằng

3

; khoảng cách giữa hai đường thẳng

,BB CC



bằng

2

và

1, 2, 3AA BB CC

  

  

. Thể tích của khối đa diện

.ABC A B C

  

bằng

A.

3

2

. B.

33

2

. C.

1

2

. D.

3

.

Câu 62: Cho hình chóp

.S ABC

có

, 3 , 2AB a AC a SB a  

và

0

90ABC BAS BCS  

, sin của góc

giữa đường thẳng

SB

và mặt phẳng

 

SAC

bằng

11

. Tính thể tích khối chóp

.S ABC

.

A.

3

6

a

. B.

3

6

3

a

. C.

3

9

a

. D.

3

23

9

a

.

Câu 63: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc và

2 , 1OA OB OC  

. Hai

điểm

,MN

lần lượt di động trên các cạnh

,AC BC

sao cho hai mặt phẳng

 

OMN

,

 

ABC

vuông góc với nhau. Khối đa diện

ABOMN

có thể tích lớn nhất bằng

A.

1

4

. B.

1

6

. C.

2

9

. D.

1

5

.

Câu 64: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc và

1OA 

,

2OB 

,

3OC 

. Gọi

G

là trọng tâm của

ABC

, mặt phẳng

 



qua trung điểm

I

của

OG

cắt các tia

,,OA OB OC

lần

lượt tại

,,D E F

. Thể tích khối tứ diện

ODEF

có giá trị lớn nhất bằng

A.

2

9

. B.

1

6

. C.

4

3

. D.

2

3

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

155

Câu 65: Cho khối lăng trụ

.ABC A B C

  

. Khoảng cách từ điểm

C

đến

BB



bằng

5

, khoảng cách từ

điểm

A

đến

,BB CC



lần lượt là

1

và

2

; hình chiếu vuông góc của

A

lên mặt phẳng

 

A B C

  

là trung điểm

M

của

BC



và

5AM





. Thể tích của khối lăng trụ đã cho bằng

A.

23

3

. B.

15

3

. C.

5

. D.

2 15

3

.

Câu 66: Cho hình lăng trụ

.ABC A B C

  

, khoảng cách từ

A

đến các đường thẳng

,BB CC



lần lượt là

1

và

3

; góc giữa hai mặt bên của lăng trụ chung cạnh

AA



bằng

0

90

. Hình chiếu vuông góc của

A

lên mặt phẳng

 

A B C

  

là trung điểm

M

của

BC



và

23

3

AM





. Thể tích khối lăng trụ

.ABC A B C

  

bằng

A.

2

. B.

1

. C.

3

. D.

23

3

.

Câu 67: Cho hình lăng trụ

.ABC A B C

  

có

.A ABC



là hình chóp tam giác đều,

AB a

. Biết khoảng cách

giữa hai đường thẳng chéo nhau

AA



và

BC

là

3

4

a

. Hãy tính thể tích của khối chóp

.A BB C C

  

A.

2

3

18

a

. B.

3

81

a

. C.

3

18

a

. D.

3

31

8

a

.

Câu 68: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

a

, khoảng cách từ điểm

A

đến mặt phẳng

 

SBC

bằng

15

5

a

, khoảng cách giữa hai đường thẳng

SA

và

BC

bằng

15

5

a

. Hình chiếu

vuông góc của

S

xuống mặt phẳng

 

ABC

nằm trong tam giác

ABC

. Thể tích khối chóp đã cho

bằng

A.

3

4

a

. B.

3

8

a

. C.

3

4

a

. D.

3

8

a

.

Câu 69: Cho hình chữ nhật

ABCD

và hình thang cân

ABEF

nằm trong hai mặt phẳng vuông góc với

nhau. Biết

AB a

,

2BC BE a

,

//AB EF

và

3EF a

. Thể tích khối đa diện

ABCDEF

bằng

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

156

A.

3

52

6

a

. B.

3

2a

. C.

3

2

3

a

. D.

3

32

2

a

.

Câu 70: Cho khối hộp

.ABCD A B C D

   

có

AB



vuông góc với mặt phẳng đáy

 

ABCD

; góc giữa

AA



với

 

ABCD

bằng

45

. Khoảng cách từ

A

đến các đường thẳng

;BB DD



cùng bằng

1

. Góc của

mặt phẳng

 

BB C C



và mặt phẳng

 

C CDD



bằng

60

. Thể tích khối hộp đã cho bằng

A.

23

. B.

2

. C.

3

. D.

33

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

157

BẢNG ĐÁP ÁN

1.C

2.B

3.B

4.B

5.A

6.C

7.B

8.C

9.B

10.D

11.D

12.B

13.C

14.B

15.D

16.B

17.D

18.D

19.D

20.C

21.A

22.D

23.B

24.D

25.B

26.A

27.A

28.D

29.C

30.B

31.A

32.A

33.D

34.A

35.B

36.A

37.A

38.C

39.A

40.A

41.D

42.D

43.A

44.A

45.B

46.B

47.D

48.D

49.D

50.B

51.D

52.A

53.D

54.A

55.B

56.A

57.A

58.C

59.B

60.C

61.D

62.A

63.A

64.A

65.D

66.A

67.C

68.B

69.A

70.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn C

Gọi SH là đường cao của hình chóp và I là trung điểm

của

AC

Vì

1SA SB SC  

nên H là tâm đường tròn ngoại tiếp

tam giác

ABC

. Do đó

H BI

.

Đặt

, 0 3AC x x  

.

Ta có

2

22

4

2

x

BI AB AI



  

.

Suy ra

2

14

.

24

ABC

xx

S BI AC





Mặt khác,

2

. . 1

4.

4

ABC

AB AC BC

HB

S

x





. Suy ra

2

22

2

3

4

x

SH SB BH

x



  



Khi đó,

22

2

1 1 1 3 1

. . . 3 .

3 12 12 2 8

SABC ABC

xx

V SH S x x



    

Vậy

 

1

max

8

SABC

V 

Câu 2: Chọn B

Trên các cạnh SB, SC lần lượt lấy các điểm M, N sao cho

SM SN a

.

N

M

A

B

C

S

K

I

H

A

M

N

S

1

I

A

B

C

H

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

158

Khi đó,

1

. 8.

8

SAMN

SABC SAMN

SABC

V

SM SN

VV

V SB SC

   

.

Xét khối chóp SAMN. Gọi SH là đường cao của hình chóp.

Tam giác SAM đều

AM a

Tam giác SMN vuông cân tại S

2MN a

Tam giác SAN cân tại S và

120NSA 

22

2 . .cos120 3AN SA SN SA SN a     

Từ đây suy ra tam giác AMN vuông tại M. Gọi I, K lần lượt là trung điểm của AM, MN. Khi đó:

()

AM SI

AM SHI AM HI

AM SH





   







Chứng minh tương tự, ta cũng có

MN HK

. Do đó H là trung điểm của AN.

Khi đó,

22

2

a

SH SA AH  

. Suy ra

3

12

.

3 12

SAMN AMN

a

V SH S

Vậy

3

22

8.

3

SABC SAMN SAMN

a

V V V  

.

Note: có thể sử dụng công thức giải nhanh:

3

2 2 2

. . 2 2

. 1 2cos .cos .cos cos cos cos

63

SABC

SA SB SC a

V ASB BSC CSA ASB BSC CSA     

Câu 3: Chọn B

Gọi

H

là trung điểm của

;AB CH AB DH AB  

.

   

22

3 2 5CH DH a a a   

.

Áp dụng công thức

   

 

12

. .sin ;

. .sin

22

..

33

ABC ABD

ABCD

S S ABC ABD

SS

VV

a AB



  

   

 

   

 

3

11

.2 . 5. .2 . 5.sin ;

25

22

. . .sin ;

3 4 6

ABCD

a a a a ABC ABD

V a ABC ABD

a



Do đó thể tích

ABCD

lớn nhất khi

   

 

   

sin ; 1ABC ABD ABC ABD  

.

Khi đó

2 2 2 2

10 10CH DH CD CH DH a CD a      

.

Câu 4: Chọn B

Ta có:

1

..

6

V OA OB OC

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

159

3

2 2 2

2 2 2 2

1 1 16 4

..

36 36 3 9 3

OA OB OC

V OA OB OC V





     





Câu 5: Chọn A

Gọi

H

là hình chiếu của S lên mặt phẳng đáy.



là góc giữa hai mặt phẳng

 

SBC

và

 

ABC

Ta có:

2 2 2

AB AC BC

nên tam giác

ABC

vuông tại

A

6.

ABC

S

và

33

2

ABC

V

SH

S



Từ H kẻ

;;HI AB HK AC HM BC  

00

3 3 3

;

22

tan30 tan60

SH SH

HI HK    

1 3 3 1 3 24 13 3

6 . .3 . .4

2 2 2 2 4

HBC ABC HAB HAC

S S S S



       

2

24 13 3

10

HBC

S

HM

BC



  

;

24 13 13

cot

15

HM

SH







.

Câu 6: Chọn C

Từ giả thiết ta có

,BC AB AS BC BS  

.

Xét tam giác vuông

ABC

ta có

22

10AC AB BC  

.

Xét tam giác vuông

SBA

ta có

22

10SB AS BA  

.

Gọi

h

là khoảng cách chung từ

M

đến các mặt của

hình chóp

.S ABC

.

Từ giả thiết ta có:

1

. . 48

6

SABC MABC MABS MCBS MACS

V SA BA BC V V V V     

 

1 1 1 1 1 1

. . . .

3 3 2 2 2 2

AS AS

ABC ABS ASC SBC

h S S S S h AB BC AC SB BC AB

   



       





36h

4

3

h

1 32

33

MABC ABC

V hS



  

.

Câu 7: Chọn B

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

160

Gọi

,,I J K

lần lượt là hình chiếu vuông góc của

H

lên các cạnh

,,AB AC BC

.

Khi đó

60SIH SJH SKH   

3

SH

HI HJ HK   

.

Ta có

 

1

2

3

ABC HAB HAC HBC

SH

S S S S AB AC BC

   

     

1

.2 .

2

3

SH

a

.

1

. . 6 3

2

3

SH

AB AC a SH a   

. Vậy

23

.

11

. .6 3.6 12 3

33

S ABC ABC

V SH S a a a



  

.

Câu 8: Chọn C

Đặt

,,OA a OB b OC c  

 

, , 0a b c 

.

Vẽ

 

AI BC I BC

,

OH AI

. Suy ra

 

OH ABC

 

,1d O ABC OH  

.

Ta có

11

. . .

36

OABC OBC

V OA S OA OB OC





6

abc



.

Xét tam giác

OAI

vuông tại

O

có

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 1

OH OA OI OA OB OC a b c

       

2 2 2

1 1 1

1

a b c

   

. Ta lại có

2 2 2

3

2 2 2

1 1 1 3

1

a b c

   

 

2

27 1 3

1

62

abc

   

.

Suy ra

3

2

OABC

V 

. Thể tích nhỏ nhất của khối tứ diện

OABC

bằng

3

2

khi

3a b c  

.

Câu 9: Chọn B

Áp dụng công thức nhanh ta có:

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

161

3

2 2 2 2 3

.

..

1 cos cos cos 2cos .cos .cos 1 3cos 2cos

66

A A BD

a a a a

V

       



       

.

3

3 2 3

.A B C D '. .

3 3 5

3 6 1 3cos 2cos

2

ABCD A ABCD A A BD

a

V V V a



    



     

.

 

2 3 2 3

2 1 3cos 2cos 3 3 5 4 1 3cos 2cos 3 3 5

   

         

.

32

3

8cos 12cos 3 3 9 0 cos

26



   

        

.

Câu 10: Chọn D

Áp dụng bất đẳng thức Cauchy- Schwarz

 

2

22

12

1 2 1 2

...

n

nn

a a a

a

aa

b b b b b b

  

   

  

, dấu “=” xảy ra khi

,

i j j i

a b a b i j  

Ta có

 

2

22

1 2 3

1 4 9 1 2 3 36

1

OA OB OC OA OB OC OA OB OC OA OB OC



       

   

36OA OB OC   

Suy ra

OA OB OC

nhỏ nhất bằng

36

khi

1 2 3

OA OB OC



.

Mà

1 4 9

1

OA OB OC

  

nên

6; 12; 18OA OB OC  

.

Vậy

11

. . .6.12.18 216.

66

OABC

V OA OB OC  

Câu 11: Chọn D

Gọi

,,H I J

lần lượt là hình chiếu của

A



lên mặt phẳng

 

ABCD

và các cạnh

,.AB AD

O

C

B

A

J

I

H

D

C

B

A

D'

C'

B'

A'

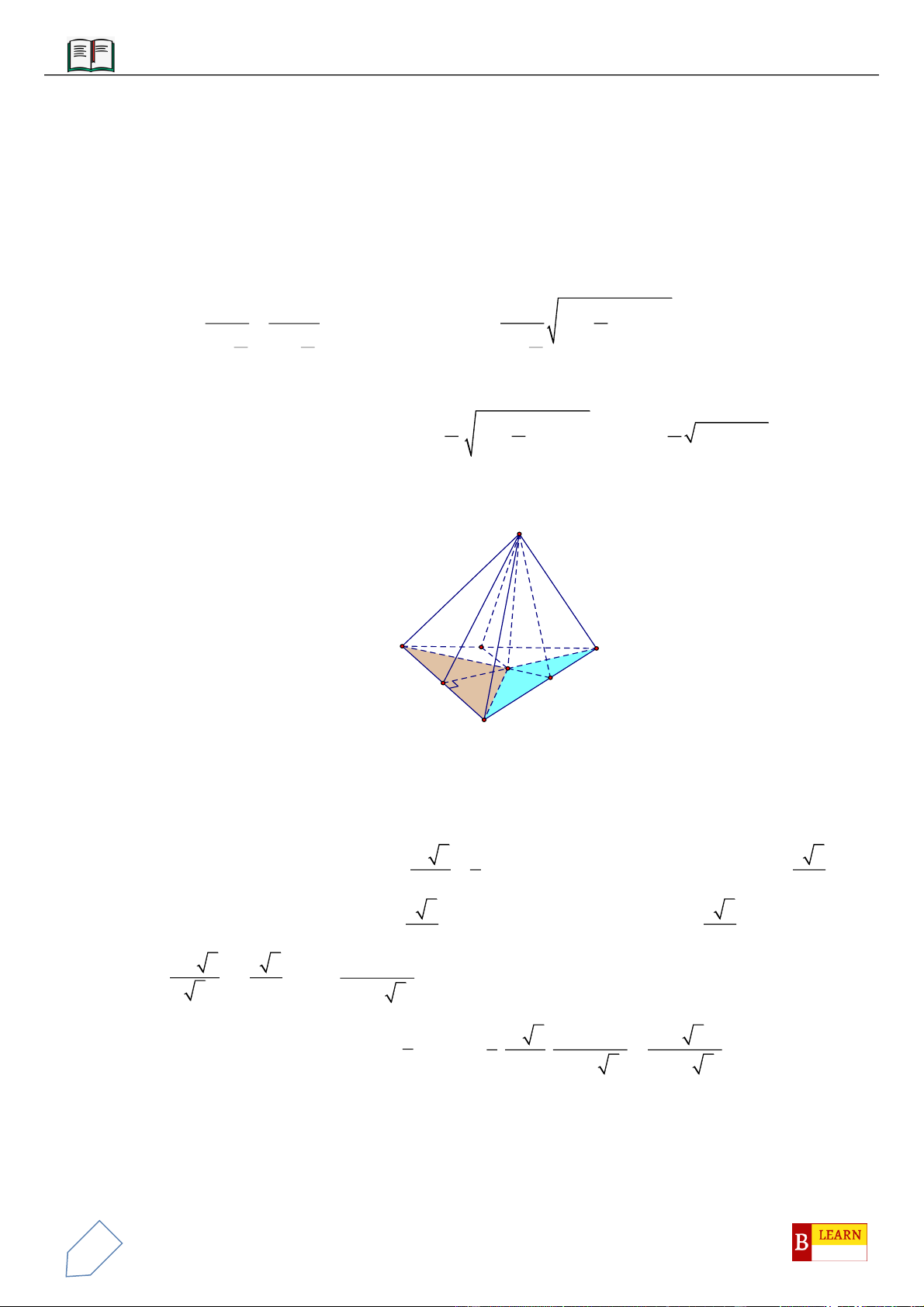
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

162

Ta có

 

.

A H AB

AB A HI AB HI

AI AB









   







Tương tự cũng có

.HJ AD

Xét hai tam giác vuông

A AI



và

A AJ



có

chungAA

A AI A AJ



















nên

.A AI A AJ



  

Suy ra

cos cos ,AI AJ AA a





  

do đó hai tam giác

,AHI AHJ

bằng nhau nên

.HI HJ

Vậy

H

cách đều

AB

và

AD

nên nằm trên phân giác góc

.BAD H AC

cos

,

cos cos

22

AI a

AH







2 2 2 2 2

cos cos .

2

cos

2

a

A H A A AH





   

Diện tích đáy

2

2 . .sin sin .

ABCD ABD

S S AB AD a



  

Vậy

3 2 2

.

. 2 sin . cos cos

22

ABCD A B C D ABCD

V A H S a





   



   

32

2 sin 1 2cos

2

a





.

Câu 12: Chọn B

Gọi

M

,

N

,

P

lần lượt là hình chiếu của

H

lên các cạnh

BC

,

AB

,

AC

;

h

là chiều cao của khối

chóp

.S ABC

.

Khi đó,

o

30SNH 

,

o

45SPH 

,

o

60SMH 

.

Mà

ABC HAB HAC HBC

S S S S

   

  

 

2

31

42

a

a HN NM HP   

3

2

a

HN NM HP   

.

 

ooo

3

tan30 tan45 tan60

2

a

h   

 

ooo

3

tan30 tan45 tan60

2

a

h   

4 3 3

2

3

a

h





 

3

2 4 3

a

h



.

Thể tích khối chóp

.S ABC

là

1

.

3

ABC

V S h





 

2

1 3 3

..

34

2 4 3

aa





 

3

8 4 3

a





.

h

a

N

B

A

S

C

H

M

P

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

163

Câu 13: Chọn C

Gọi

H

là trung điểm

AB

.

Theo giả thiết nên

()SH mp ABCD

,

2

a

SH 

và

8.BC CD DA a  

Gọi

,,M N P

là hình chiếu vuông góc của H

lần lượt lên lên

,,AD DC CB

.

Suy ra:

0

(( ,( ) 60SAD ABCD SMH

0

(( ,( ) 60SCD ABCD SNH

0

(( ,( ) 60 .SCB ABCD SPH

Từ đó:

23

a

HM HN HP  

.

Vậy:

1

.( )

.

3

V SH S S S

HAD

S ABCD HCD HCB

  





1

.

22

1

. ( . . . )

3

a

HM DA HN CD HP CB 

3

13

. . .8 .

2 2 9

23

1

.

3

a a a

a

Câu 14: Chọn B

Ta có:

 

0

, 90AM NB





.

 

,d AM B N a





. Gọi

 

0AM x x

.

Ta có:

   

 

2

3

2

1 1 1

. .sin , . , 2 . .

6 6 6 4 12

AMNB

a

V AM B N AM B N d AM B N x a x a a



  

    

.

Câu 15: Chọn D

Ta có:

 

2

22

12

23

2.

3;

42

CAB DAB

a

aa

S S a S S a



     

và

   

 

0

30 ,CAB DAB





Do đó

2 2 0

3

12

2 .sin

2. 3 . .sin30 3

3 3.2 6

SS

aa

Va

AB a



  

Câu 16: Chọn B

Áp dụng công thức tính thể tích của khối tứ diện

ABCD

1

. . ( ; ).sin( , ).

6

ABCD

V AB CD d AB CD AB CD

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

164

Đặt

 

, , 0AM x BN y x y  

. Từ giả thiết ta có

2 3 .x y a

Khi đó thể tích của khối tứ diện

ABMN

là:

11

. .d( ; ).sin( , ) . . . .sin90

6 6 3

ABMN

axy

V AM BN AM BN AM BN AM BN AB   

   

 

2

3

3 2 2

1 1 1 3

. 3 2 . . 3 2 .2 . .

3 6 6 4 8

a y y

a

a a y y a a y y a



     

Do đó,

3

max

3

8

a

V 

khi

3

2.

2

a

xy

Câu 17: Chọn D

Từ

S

vẽ

 

SH ABC

. Ta có

 

AB SB

AB SBH AB BH

AB SH





   







.

Chứng minh tương tự ta cũng có

AC CH

.

Tam giác

ABC

vuông tại

A

do

2 2 2

AC AB BC

. Vậy suy ra

ABHC

là hình chữ nhật.

Từ

H

vẽ

HE BC

thì

   

 

, 60SBC ABC SHE  

.3SH HE

.

Trong đó

22

. 2 5

5

HB HC

HE

HB HC





. Vậy

2 15

5

SH 

2 15

15

V

.

Câu 18: Chọn D

A

M

B

N

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

165

Gọi

,MN

lần lượt là trung điểm của

,AB CD

.

Các tam giác

,DAB CAB

cân nên ta có

 

DM AB

AB CMD AB MN

CM AB





   







.

Chứng minh tương tự ta cũng có

CD NM

.

Ta có

..

1 1 1

. . . .

3 3 6

ABCD A CDM B CDM CDM CDM

V V V AM S BM S AB CD NM    

.

Với

AB x

,

2CD x

và

2 2 2

22

2 2 2

CD AB CD

MN MD AD

     

    

     

     

 

22

2

2 2 12 12

2

2 2 2

x x x x

x

      

    

   

   

.

Suy ra

 

2

12

2 2 12 12

12 12

V x x x x    

 

2

2 2 12 12 2 2x x x x x      

.

Câu 19: Chọn D

Gọi

M

là trung điểm

AB

 

CM AB

AB CDM

DM AB





  







11

. . . .sin

36

CDM

V AB S AB CM DM CMD  

Trong đó

3

2 ; .2 3;

22

AB

AB a CM a a DM a    

. Vậy

3

13

.2 . 3. .sin30

66

V a a a a  

.

Câu 20: Chọn C

Ta có công thức:

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

166

   





   





   

2. . .sin ;

4

sin ;

3. 5

4

; arcsin

5

ABD ADC

S S ABD ADC

V ABD ADC

BD

ABD ADC



  









Câu 21: Chọn A

Ta có công thức diện tích đáy là

.

24

2

ABCD

AC BD

S 

   





2. . .sin ;

24

3.

ABCD SAD

S S ABCD ADC

V

AD





Câu 50 : Chọn D

Bổ đề : Cho lăng trụ tam giác

.ABC A B C

  

, mặt phẳng

 



vuông góc các cạnh của lăng trụ và

tạo với lăng trụ một thiết diện có diện tích

S

. Khi đó

.

LT A MN

V AA S





.

Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

trên

BB



và

CC



.

Gọi

M



là trung điểm của

BC

,

I

là giao điểm của

MM



và

EF I

là trung điểm của

EF

.

Ta có:

 

AE BB

BB AEF BB EF

AF BB do AF CC











   











   

, , 5d C BB d F BB EF



   

AEF

vuông tại

A

15

22

AI EF  

. Mà

MM AI





.

AMM





vuông tại

A

,

AI

là đường cao

22

. 15

3

AM AM

AI

AM AM



  





Tam giác

AA M



vuông tại

22

2 15

3

M AA AM A M



   

.

2 15 1 2 15

. . .1.2

3 2 3

ABC A B C AEF

V AA S

  



  

.

Câu 22: Chọn B

A'

B'

A

B

C

M

N

1

2

I

A

C

B

B'

C'

E

F

M

M'

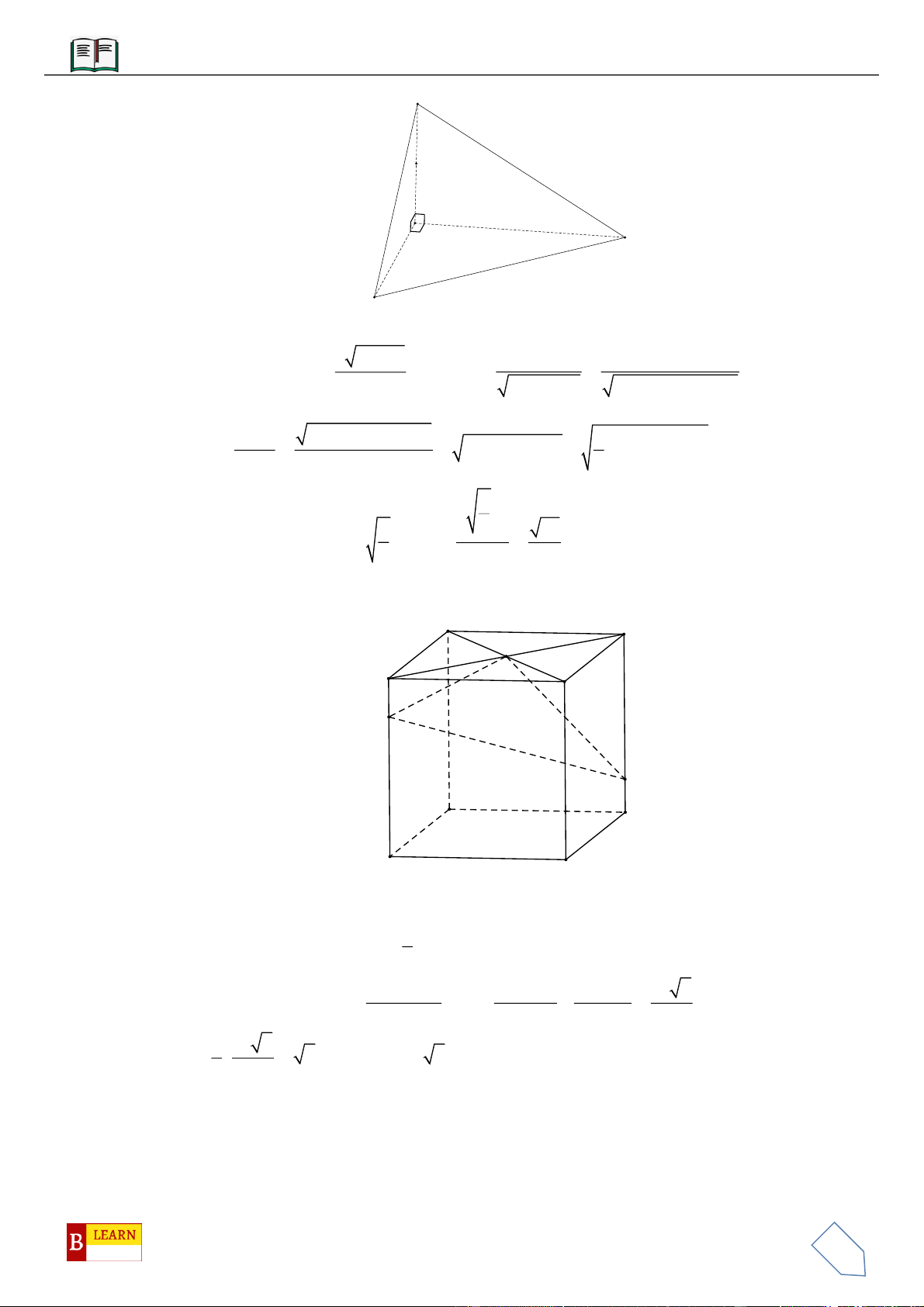
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

167

Ta có

1

2

3

2

S bc

S ca

S ab















;

22

tan

a b c

bc







2 2 2 2 2 2 2

1

cos

1 tan

bc

a b b c c a



  

  

.

Khi đó,

 

2 2 2 2 2 2

2

2 2 2

1

1 2 3 1 2 3

1

cos 2 3

S

a b b c c a

S S S S S S S





        

.

Dấu “=” xảy ra

4

3

a b c   

3

4

3

12

69

V







  

.

Câu 23: Chọn B

Đặt độ dài cạnh khối lập phương là

x

và

O

là tâm của hình vuông

ABCD

.

Ta có

 

BD ACNM

1

.

3

BDMN MON

V S BD

.

. . 2

2 2 2 2

OMN ACNM OAM OCN

AM CN AM OA CN OC ax

S S S S AC



       

3

12

2 2 6

32

BDMN

ax

V x a x a     

.

Câu 24: Chọn B

B

O

C

A

O

C'

B'

C

D'

A

A'

D

B

M

N

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

168

Ta có

 

2

1

33

44

ABD

a

SS  

,

22

2

3

44

CAB

AB a

SS  

Vì vậy,

22

33

12

3 3 3

2 sin

3 .sin 2

44

3 8 8

33

aa

SS

aa

V

AB

a



  

   

27

sin cos

33



   

.

Câu 25: Chọn A

Áp dụng công thức tổng quát khi biết độ dài

6

cạnh hoặc dùng công thức góc tại đỉnh

S

, ta có

2 2 2

23

cos

2 . 42

SA SB AB

ASB

SA SB



  

,

2 2 2

47

cos

2 . 70

SB SC BC

BSC

SB SC



  

2 2 2

1

cos

2 . 15

SA SC AC

ASC

SA SC



  

.

Vậy

 

2 2 2

3

3.5.7 23 47 1 23 47 1 2159

12

6 42 70 15 42 70 15 6

V cm

         

           

         

         

.

Câu 26: Chọn A

A

B

C

D

S

A

B

C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

169

Gọi

 

', / /I BM AB IN CM N BC  

có

 

/ / 'NCM AB

   

 

7

, ' , '

7

d CM AB d C AB N  

.

Lại có

11

' 2 2

IM AM NC IM

IB BB NB IB

    

 

27

, ' 2 , '

7

d B AB N d C AB N  

.

Ta có

1

cos

2

AB

ABN

BC



.

Đặt

'BB x

, thì

22

2

.'

1 4 1 1 1 1 2

.1. . . 1 2 . .0 0

6 3 2 2 2 2 9

B AB N

x

Vx

   

      

   

   

.

Mà

2

'1AB x x  

2

4 16

'

39

BN NB x   

,

22

13

2 . .cos

3

AN AB BN AB BN ABN   

.

   

22

13 16

1

99

32

cos '

2 13 1 2 13 1

3

x x x

x

B AN

x x x x



    









   

 

2

32

sin ' 1

52 1

x

B AN

xx



  



 

2

'

2

13 1

32

43 40 48

.1

6 12

52 1

AB N

xx

x

xx

S

xx







   



.

Do đó

 

.'

2

'

2

3

27

3

, ' 4

7

43 40 48

12

B AB N

ANB

x

V

d B AB N x

S

xx

    



.

Vậy

.'

42

9

B AB N

V 

và

BC AH

BC DM

BC AD













.

Câu 27: Chọn D

I

A'

B'

C'

A

B

C

M

N

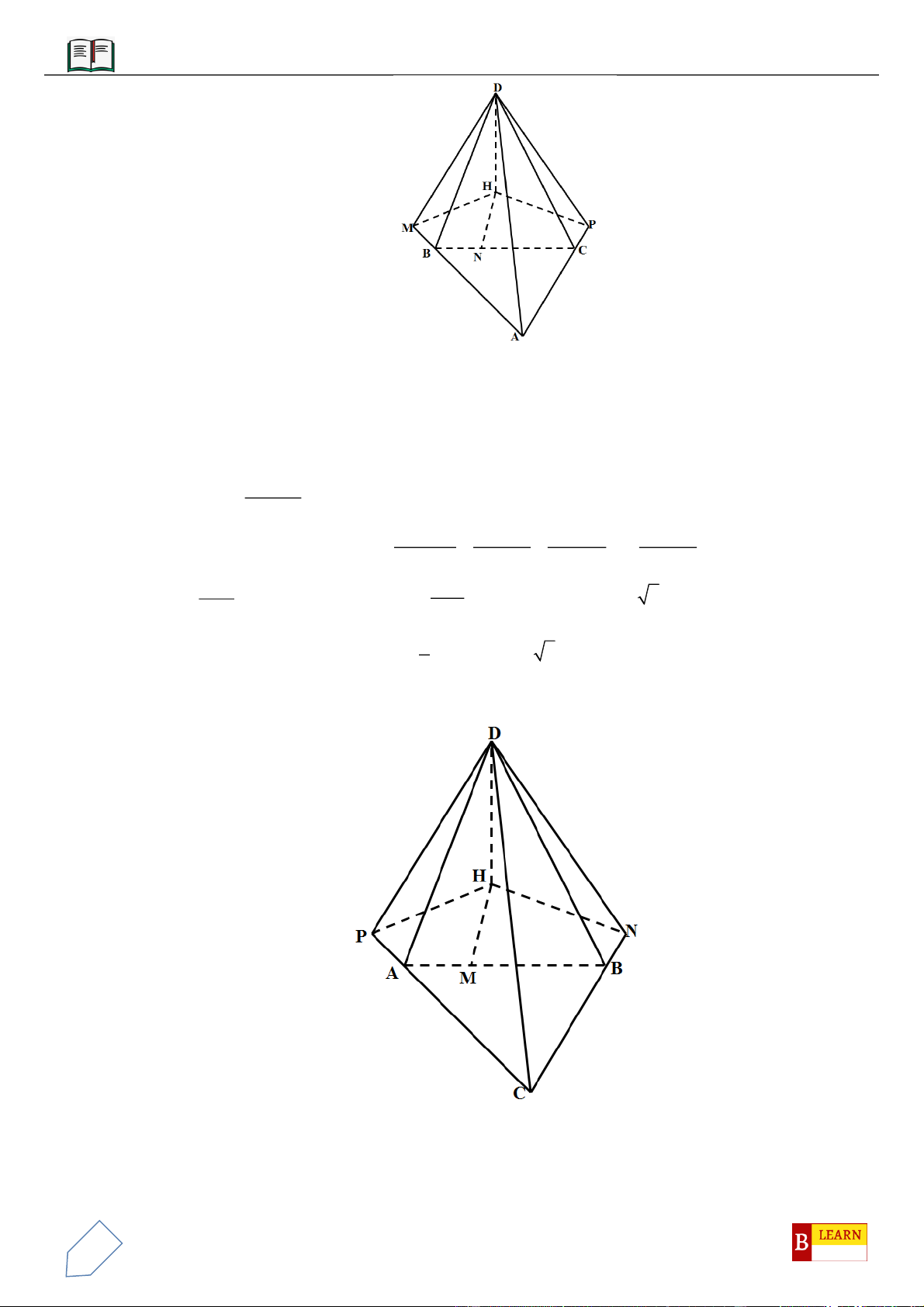
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

170

Gọi

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

H

lên các cạnh

AB

,

BC

,

CA

60DMH DNH DPH   

(góc của các mặt

     

,,DAB DBC DCA

với

 

ABC

)

HM HN HP  

H

là tâm đường tròn bàng tiếp góc

A

của tam giác

ABC

.

Gọi

a

r

là bán kính đường tròn bàng tiếp góc

A

a

r HM HN HP   

Ta có

2

.

6

2

ABC

AB AC

Sa

Ta có

 

. . .

2 2 2 2

ABC HAB HAC HBC a a

HM AB HP AC HN BC b c a

S S S S r r p a



        

6

ABC

a

S

ra

pa

  



. Lại có

tan

DH

DMH

HM



tan60 6 3

a

DH r a   

.

Thể tích khối tứ diện

ABCD

là

3

1

. 12 3

3

ABC

V DH S a

.

Câu 28: Chọn C

Gọi

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

H

lên các cạnh

AB

,

BC

,

CA

60DMH DNH DPH   

(góc của các mặt

     

,,DAB DBC DCA

với

 

ABC

)

HM HN HP  

H

là tâm đường tròn bàng tiếp góc

C

của tam giác

ABC

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

171

Gọi

c

r

là bán kính đường tròn bàng tiếp góc

C

c

r HM HN HP   

Ta có

2

.

6

2

ABC

AB AC

Sa

Ta có

 

...

2 2 2 2

ABC HAC HBC HAB c c

HP AC HN BC HM AB a b c

S S S S r r p c



        

2

ABC

c

S

ra

pc

  



. Lại có

tan

DH

DMH

HM



tan60 2 3

c

DH r a   

.

Thể tích khối tứ diện

ABCD

là

3

1

. 4 3

3

ABC

V DH S a

.

Câu 29: Chọn B

Gọi

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

H

lên các cạnh

AB

,

BC

,

CA

60DMH DNH DPH   

(góc của các mặt

     

,,DAB DBC DCA

với

 

ABC

)

HM HN HP  

H

là tâm đường tròn bàng tiếp góc

B

của tam giác

ABC

.

Gọi

b

r

là bán kính đường tròn bàng tiếp góc

B

b

r HM HN HP   

Ta có

2

.

6

2

ABC

AB AC

Sa

Ta có

 

. . .

2 2 2 2

ABC HAB HBC HAC b b

HM AB HN BC HP AC a c b

S S S S r r p b



        

3

ABC

b

S

ra

pb

  



. Lại có

tan

DH

DMH

HM



tan60 3 3

b

DH r a   

.

Thể tích khối tứ diện

ABCD

là

3

1

. 6 3

3

ABC

V DH S a

.

Câu 30: Chọn A

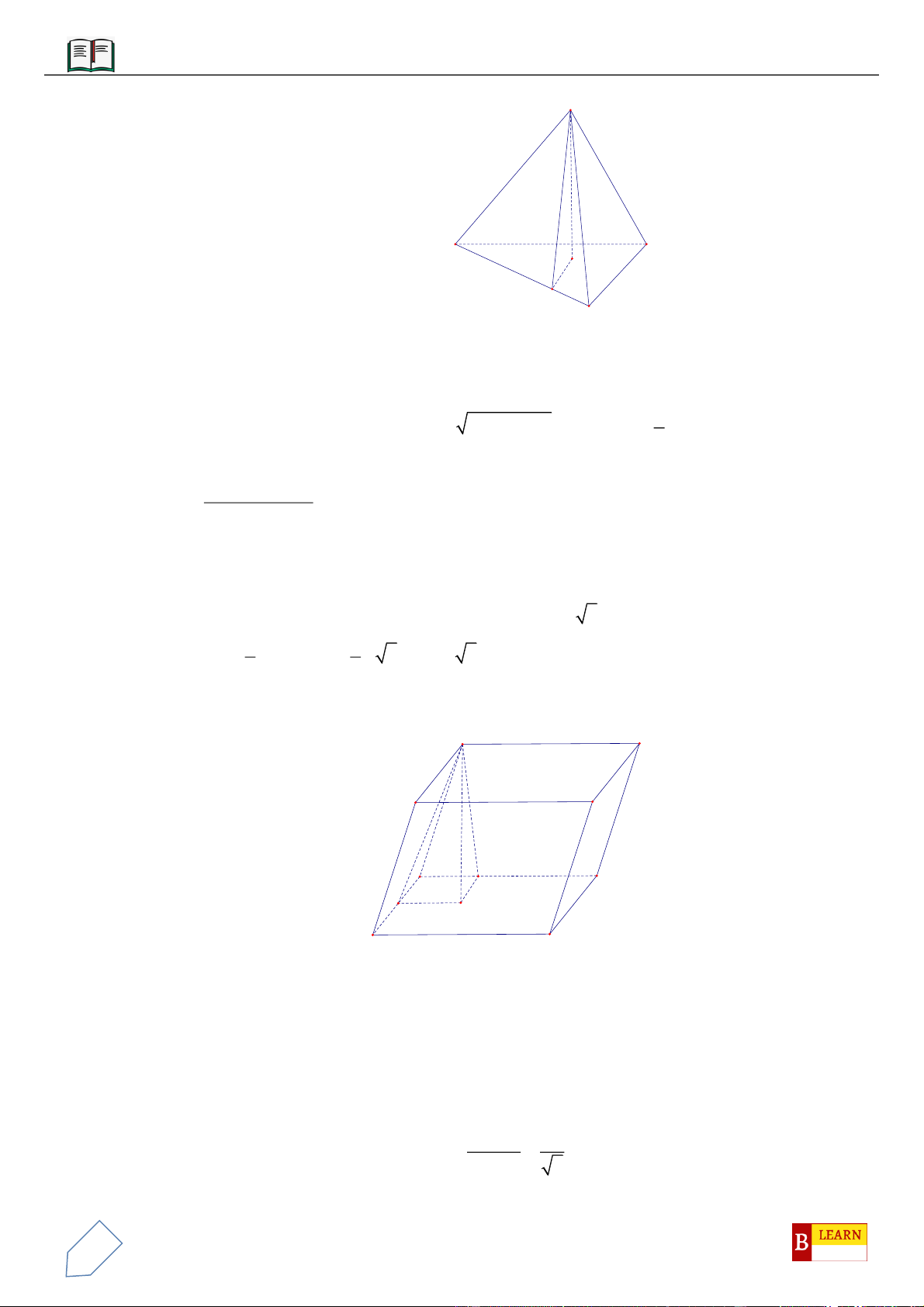
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

172

Vì góc giữa các mặt phẳng

     

,,DAB DBC DCA

và mặt phẳng

 

ABC

bằng nhau và

H

nằm

trong tam giác

ABC

nên

H

là tâm đường tròn nội tiếp tam giác

ABC

.

Tam giác

ABC

vuông tại

A

, ta có

2 2 2

1

5 ; . . 6

2

ABC

BC AB AC a S AB AC a



    

.

Gọi

r

là bán kính đường tròn nội tiếp tam giác

ABC

, ta có:

2

. 6 6 .

2

ABC

AB AC BC

S r a a r r a





    

.

Gọi

K

là hình chiếu của

H

trên cạnh

AB

, suy ra góc giữa mặt phẳng

 

DAB

và mặt phẳng

 

ABC

là

DKH

60DKH  

.

Tam giác

DHK

vuông tại

H

, ta có

.tan60 3DH HK a  

.

Vậy

23

11

. . . 3.6 2 3

33

ABCD ABC

V DH S a a a



  

.

Câu 31: Chọn A

Gọi

H

là hình chiếu của điểm

A

trên mặt đáy

 

A B C D

   

,

,MN

lần lượt là hình chiếu của

H

trên các cạch

,A B A D

   

suy ra góc giữa hai mặt bên

   

, ' 'ABB A ADD A



với đáy lần lượt là

, 45 , 60AMH ANH AMH ANH    

.

Đặt

AH x

Tam giác

AHM

vuông cân tại

H

, ta có

HM AH x

Tam giác

AHN

vuông tại

H

, ta có

tan60

3

AH x

HN 



B

C

A

H

D

K

C'

B'

A'

A

B

D

C

D'

H

M

N

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

173

Theo cách dựng ta có tứ giác

A MHN



là hình chữ nhật, suy ra

22

2

3

x

A H HN HM



  

Tam giác

AHA



vuông tại

H

, ta có

 

2

2 2 2 2

4 21

10

37

x

AA AH HA x x x



       

.

Vậy

.

21

. . 3. 7 3

7

ABCD A B C D ABCD

V AH S

   

  

.

Câu 32: Chọn D

Ta có

2

1

.6

2

ABC

S AB AC a





.

Hạ

   

 

   

, , DH ABC H ABC HK AB K AB HM AC M AC     

Theo định lí ba đường vuông góc chung, ta có

, 45 , 60AB DK AC DM DKH DMH      

Và tứ giác

HMAK

là hình chữ nhật với

AK HM

.

Đặt

h DH

, ta có

cot60

3

h

HM h  

.

Và

2

2 2 2 2 2

36 36 2

sin45

h

AK AD DK a a h



     







.

Vậy

3

22

108 12 21

36 2

7 3 7

3

h Sh a

a h h a V      

.

Câu 33: Chọn A

Kẻ

   

SH BC H BC SH ABC   

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

174

Kẻ

       

, ,HN AB M AB HN AC N AC AB SHM AC SHN      

và

60SNH SMH  

.

Ta có

2

13

..

2 2 2 2 8

ABAC a a a

Sa



   





. Với

h SH

và

cot60

3

h

HM HN h   

.

Ta có

 

2

1 3 3 3

..

2 2 2 8

23

2 3 1

HAB HAC

h a a a a

S S S AB HM AC HN h



        







.

Vậy

 

3

2

33

1 3 3

..

3 3 8 32

2 3 1

a

Sh a a

V



  



.

Câu 34: Chọn B

Đặt

AM x

,

BN y

. Ta có

3

. .sin60

6 12

axy

AM BN

V





.

Ta tìm mối quan hệ giữa

x

và

y

theo điều kiện

2MN a

.

Ta có

   

22

2

MN MN AM AN AM AB BN     

2 2 2

2 . 2 . 2 .AM BN AB AB AM AB BN AM BN     

2 2 2

2.x a y AM BN   

2 2 2 2

4x a y xy a    

.

2 2 2

32a x y xy xy xy xy      

3

4

a

V

.

Trong đó

 

2 . 2 . .cos ,AM BN AM BN AM BN xy  

.

Câu 35: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

175

Gọi

O

là tâm đường tròn ngoại tiếp tam giác

ABC

thì

OA OB OC AB a   

.

Gọi

D

là hình chiếu của

S

trên

()ABC

thì

, SD AB SD AC

.

,

90

AB SD SD AC

AB BD AC CD

SBA SCA







  



  





3, 2DB DC a AD a   

.

Đặt

SD x

. Điều kiện:

0 2 .xa

22

13

// d( ;( )) d( ;( )) d( ;( )) .

2

23

xa

OB AC B SAC O SAC D SAC

ax

   



2 2 2 2

3.SB SD DB a x   

.

Theo đề





3 ( ,( )) 3 3

sin ,(SAC) ( ,( )) .

8 8 8

d B SAC

SB d B SAC SB

SB

    

 

2 2 2 2

22

nhan

33

3 4 3 0 .

8

3 loai

23

xa

a x x ax a

xa

ax





      











Vậy thể tích của khối chóp

.S ABC

là

3

13

..

3 12

ABC

a

V S SD

Câu 36: Chọn A

Áp dụng công thức tính thể tích của khối tứ diện

ABCD

1

. . ( ; ).sin( , ).

6

ABCD

V AB CD d AB CD AB CD

Ta có thể tích của khối tứ diện

ABMN

là:

3

11

. .d( ; ).sin(a,b) . . . .sin30

6 6 2

ABMN

xy

V AM BN a b AM BN MN   

.

Câu 37: Chọn C

S

là điểm chung của

 

SAB

và

 

SCD

, đồng thời

//AB CD

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

176

Khi đó kẻ

/ / / /Sx AB CD

thì

Sx

là giao tuyến của

 

SAB

và

 

SCD

.

Gọi

,MN

lần lượt là trung điểm

,AB CD

.

,SAB SCD

là các tam giác cân tại

S

nên

SM AB

,

SN CD

.

Mặt khác

     

SM CD SM ABCD SMN ABCD    

theo giao tuyến

MN

.

Kẻ

   

SH MN H MN SH ABCD   

.

,SM Sx SN Sx

nên góc

     

0

; ; 90SAB SCD SM SN MSN



  



.

 

22

7 1 1 7 1 7

..

10 2 2 10 2 5

AB CD

SAB SCD

a a a

S S AB SM CD SN AB SM SN SM SN



         

.

 

2

22

2

2 2 2 2

12

.

2 25

SM SN SM SN

a

SM SN MN a SM SN

  

     

.

Vậy

3

.

12 1 4

.

25 3 25

ABCD

SM SN

aa

SH V S SH

MN

    

.

Câu 38: Chọn A

Gọi

H

là hình chiếu vuông góc của

S

lên mặt phẳng

 

ABC

. Ta có:

 

BC SC

BC SCH BC HC

BC SH





   







. Tương tự ta có

BA AH

.

Suy ra

H

thuộc đường tròn ngoại tiếp tam giác đều

ABC

. Do đó,

H

thuộc đường thẳng

BD

sao

cho

1

3

HD DB

, với

D

là trung điểm cạnh

CD

.

Ta có tứ giác

ABCH

nội tiếp đường tròn bán kính

BH

.

ABC

đều cạnh

23a BD a

.

Lại có:

3 4 4 2 3

3;

4 3 3 3

BD BD a

BH a HA

BH

    

.

Gọi

, G CM SD E BD SH   

thì

G

là trọng tâm

SAC

.

Áp dụng định lí Menelaus cho tam giác

SDH

với ba điểm

, , E G B

thẳng hàng, ta có

4 1 3

. . 1 . . 1

3 2 2

SE HB DG SE SE

EH BD GS EH EH

    

.

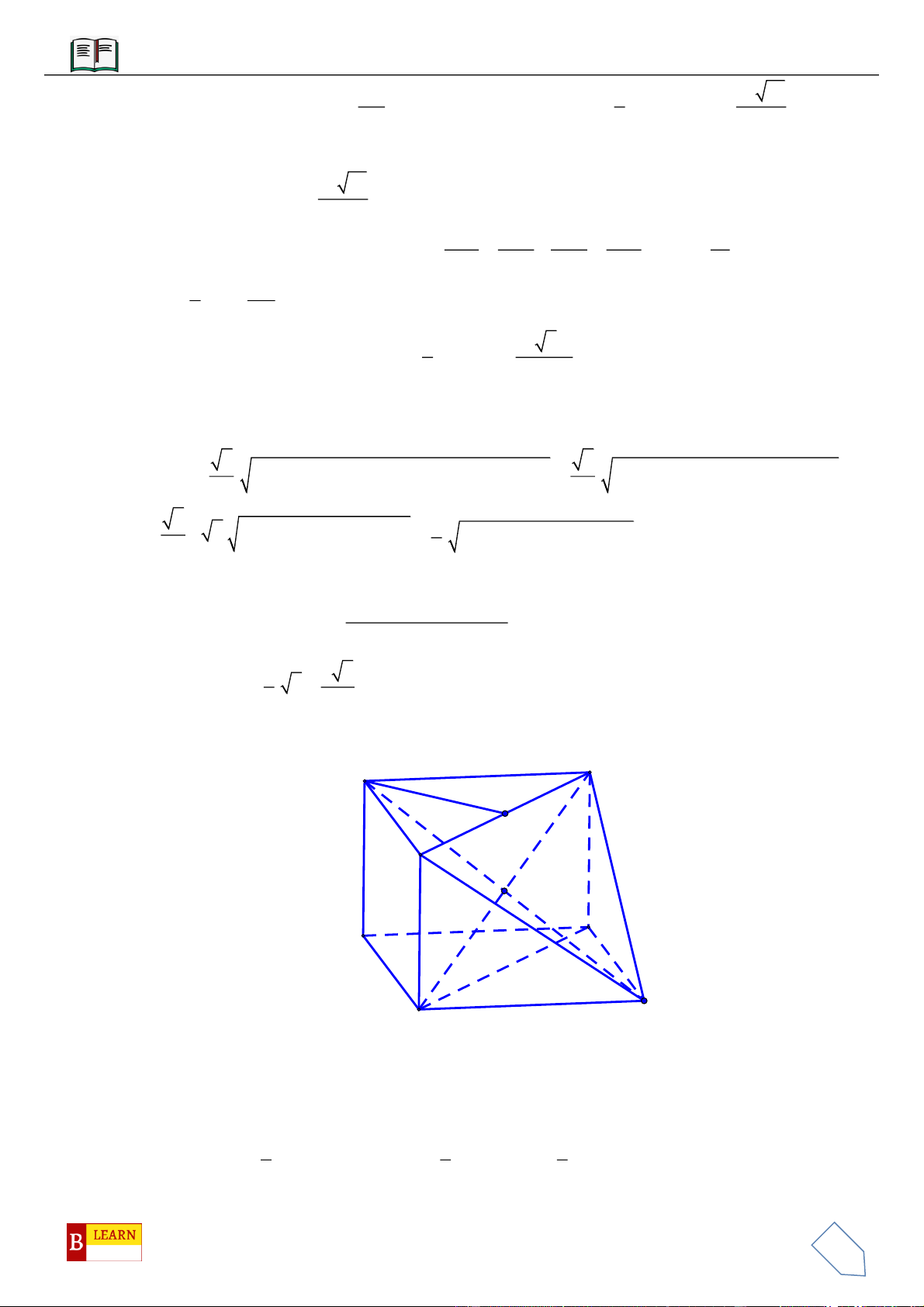
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

177

2 4 21

d( ;( ) d( ;( ) d( ;( ) d( ;( ) d( ;( ) .

3 21

SE a

A BCM S BCM H BCM H BCM A BCM

HE

    

Gọi

K

là hình chiếu của

H

trên

CE

thì

K

là hình chiếu của

H

trên

 

BCM

4 21

( ;( ) .

21

a

CK d H BCM  

HCE

vuông tại

,H

đường cao

2 2 2 2

1 1 1 9 4

3

16

a

HK HE

HE HK HC a

     

.

5 10

.

23

a

SH HE

Vậy thể tích của khối

.S ABC

là

3

1 10 3

..

39

ABC

a

V S SH

Câu 39: Chọn A

Áp dụng công thức tính thể tích của tứ diện gần đều, ta có:

   

2 2 2 2 2 2 2 2 2

.

2

.

12

S ABC

V x y z x z y y z x      

   

2 2 2

2

. 12 2 12 2 12 2

12

z y x   

   

2 2 2

2

.2 2. 6 6 6

12

z y x   

   

2 2 2

1

. 6 6 6

3

z y x   

Áp dụng bất đẳng thức Cauchy, ta có:

   

3

2 2 2

2 2 2 3

6 6 6

6 6 6 2 8

3

z y x



    

     





.

Do đó:

.

1 2 2

.8

33

S ABC

V 

. Dấu bằng xảy ra khi

2x y z  

.

Câu 40: Chọn D

Ta có

.ADE BCF

là một lăng trụ đứng có đáy

ADE

là tam giác vuông cân tại

A

với

1AD AE

, cạnh bên

1AB 

.

Gọi

I

là trung điểm

DE

thì

BI SI

nên

 

;;d S ADE d B ADE BH

.

Ta có

 

.

1 1 1

. , . . . .

3 3 3

S CDFE CDFE

V d S CDEF S BH CD CE  

.

H

S

I

F

D

E

C

A

B

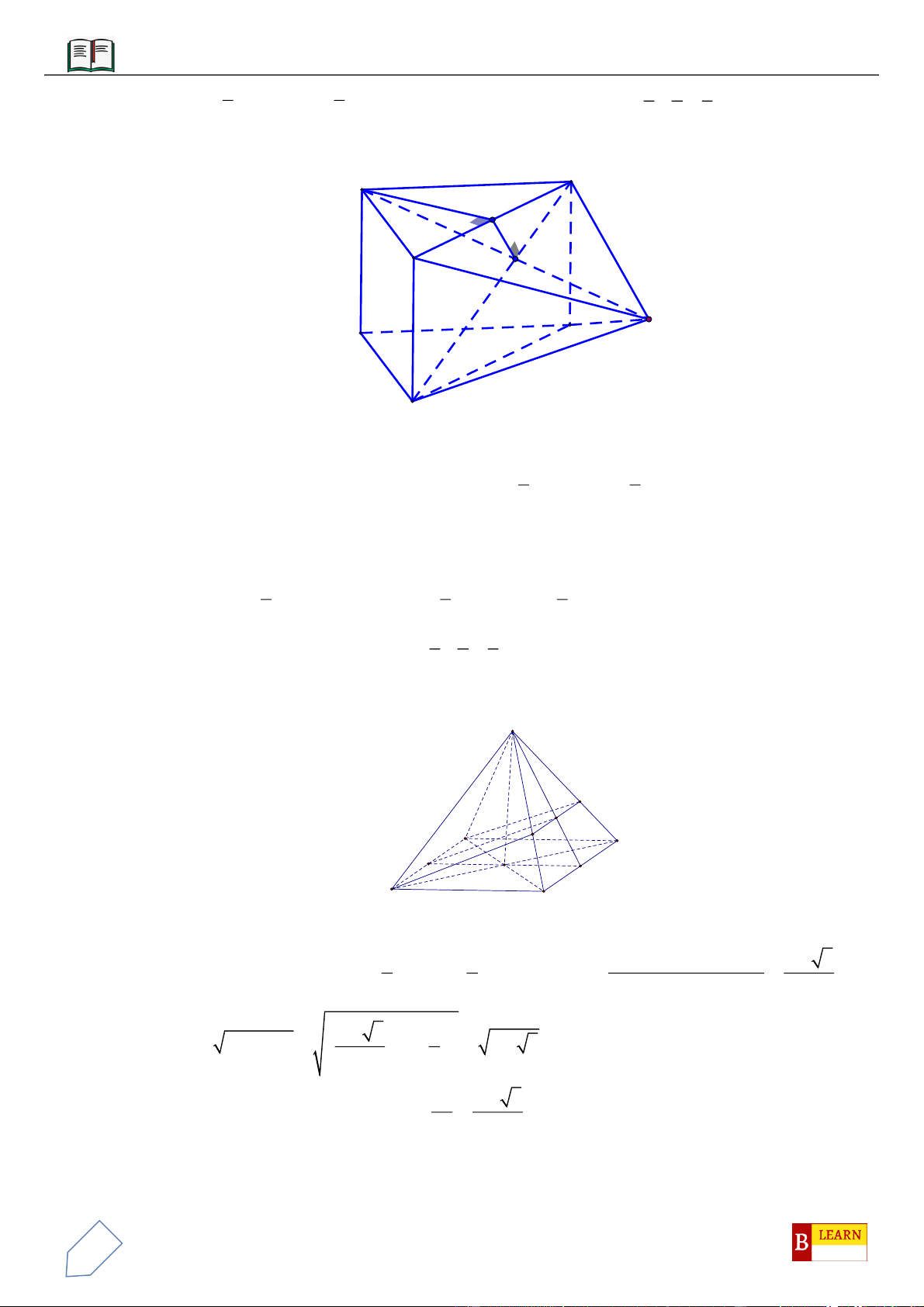
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

178

.

11

. . .

22

BCE ADF

V BC BE AB

. Khi đó:

..

1 1 5

3 2 6

ABCDSEF BCE ADF S CDEF

V V V    

.

Câu 41: Chọn D

Ta có

.ADE BCF

là một lăng trụ đứng có đáy

ADE

là tam giác vuông cân tại

A

với

1AD AE

, cạnh bên

1AB 

, do đó

.

11

. . .

22

BCE ADF

V BC BE AB

.

Gọi

H

là trung điểm

CE

và

I

là hình chiếu vuông góc của

H

trên

DE

, Khi đó ta có

BI

vuông

góc

DE

với tại

I

và

BI SI

nên

 

;;d S ADE d B ADE BH

.

Ta có

 

.

1 1 1

. , . . . .

3 3 3

S CDFE CDFE

V d S CDEF S BH CD CE  

.

Khi đó:

..

1 1 5

3 2 6

ABCDSEF BCE ADF S CDEF

V V V    

.

Câu 42: Chọn A

Gọi , lần lượt là trung điểm các cạnh , .

Chiều cao của khối chóp là .

Và .

Thể tích khối chóp tứ giác đều là .

Ta có . Kẻ sao cho khi đó và

   

// //P SCD HK CD AB

.

H

F

D

E

C

A

B

I

S

K

H

F

E

O

C

A

B

D

S

I

E

F

AB

CD

 

1 1 tan 45 tan30 2 3

tan75 tan 45 30

2 2 2 1 tan 45 tan30 2

h

  

       

  

2

22

2 3 1

23

22

SE h OE







     





0

23

36

Sh

V





 

SEF AB

EI SF I

45IEF 

   

P ABI

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

179

Trong tam giác

 

BD AC

BD SAC BD SH

BD SO





   







có:

.

Do đó theo tỉ số thể tích có:

.

Câu 43: Chọn A

Có , và áp dụng công thức thể tích tứ diện khi biết ba góc của mặt bên tạo

với đáy.

.

Câu 44: Chọn B

Ta có thể tích của khối tứ diện đều cạnh

1a 

là

3

22

12 12

a

V 

.

Ta có

.

. . 12 2

S ABD

V

SA SB SD V

V

   

và

.

2

. . 6

2

S CBD

V

SC SB SD V

V

   

.

Vậy

.

32

2

S ABCD

V 

.

Câu 45: Chọn B

1

2 3.

sin .sin30 3 5 2 3

2

1

.sin45 2 13

2

sin

1.

2

SEI

IEF

S

IS SEI SE SI

IF S FE SF

IEF





       



0 0 0 0 0

1 1 1 1 16 9 3

. . . . .

2 2 2 2 78

S

SH SK SI SI SI

V V V V V V

SC SD SF SF SF



   

     

   

   

10BC a

2

3

2

ABC

a

S 

 

2

3

2

3 cot cot cot

3 10 .0 cot 3 cot

a

S

V

a b c

a a a

  













 

3 3 3

2 cot 3tan 4

4 cot .3tan

a a a



  



CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

180

Ta có thiết diện của

 

MNP

và tứ diện là hình thang

MNPQ

trong đó

MN PQ

Có

. . .BMNPQD D BPQ B MNQ Q BNP

V V V V  

;

.

4

9

D BPQ ABCD

VV

 

.

1 1 1 1 1

. , . . ,

3 3 4 3 12

Q MBN MBN ABC ABCD

V S d Q MBN S d D ABC V  

 

.

1 1 1 2 1

. , . . ,

3 3 6 3 9

Q BPN PBN BCD ABCD

V S d Q PBN S d A PBN V  

23 23 2 23 2

.

36 36 12 432

BMNPQD ABCD

VV  

.

Câu 46: Chọn D

Ta có

2 2 2 2 2 2

0

22

AD AC CD AD AB BD

ADBC ADAC ADAB AD BC

   

      

Gọi

H

là hình chiếu của

A

lên

 

BCD

;

M DH BC

suy ra

M

nằm giữa

BC

.

Do

BC AH

BC DM

BC AD













.

Trong

 

ADM

dựng

MN AD

tại

N

suy ra

MN

là đoạn vuông góc chung của

,AD BC

5

4

a

MN

. Ta thấy góc giữa

AD

và

 

BCD

là

0

45ADH 

.

Ta có

22

5 2 110

2

44

aa

DM MN BM BD MN     

.

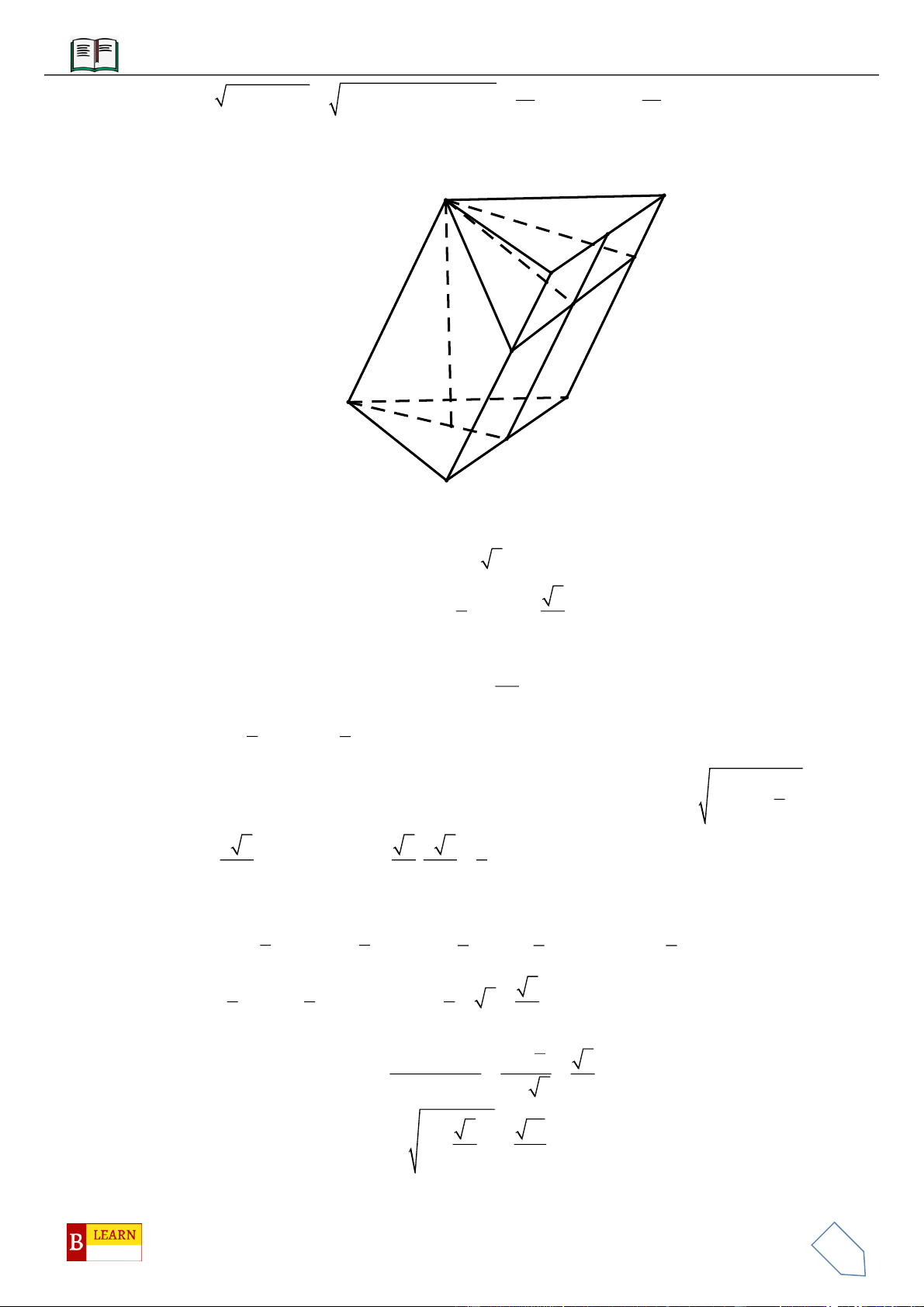
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

181

 

2 2 2 2 2

35

;

44

aa

AN AB BN AB BM MN DN MN        

.

Do đó

2AD AN DN a  

.

Câu 47: Chọn D

Kẻ

AE BB





,

AF CC





 

AEF AA





.

ABC A B C AEF

V AA S

  





.

Ta có

 

,1AE d A BB





,

 

,3AF d A CC





,

 

,2EF d C BB





.

Vì tam giác

AEF

vuông tại

A

và

13

.

22

AEF

S AE AF

.

Gọi

M

,

N

lần lượt là trung điểm các cạnh

BC



,

BC

và

H MN EF

AH MN

(do

//MN AA



) và

H

là trung điểm

EF

1

2

EF

AH  

.

Ta có

4

3

AG





3

2

A M A G

  

  

.

Hình bình hành

AA MN



có

.

AA MN

S AG A M







.AH MN

2

4

2 1.

3

AA AA





  





83

9

AA





. Vậy

.

3 8 3 4

.

2 9 3

ABC A B C

V

  



.

Câu 48: Chọn D

Ta có

..

11

34

A ABC ABC A B C

VV

   



và

 

1 1 1

. , .2.1 1

2 2 2

ABA ABB A

S S BB d A BB

  



   

.

Và

 

1 1 1 3

. . , .2. 3

2 2 2 4

ACA ACC A

S S CC d A CC

  



   

.

Vậy

   

 

.

1

3.2.

3.

3

4

sin ,

2. . 4

2.1. 3

A ABC

ABA ACA

AA S

ABB A ACC A

SS







   

  

.

Suy ra

   

 

2

3 13

cos , 1

44

ABB A ACC A



   

  





.

Câu 49: Chọn B

H

N

M

A'

C'

B'

B

C

A

E

F

G'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

182

Diện tích mặt đáy

3

4

S 

; diện tích các mặt bên

 

SBC

;

 

SCA

,

 

SAB

kí hiệu lần lượt là

1

S

,

2

S

,

3

S

. Gọi

H

là hình chiếu vuông góc của

S

lên mặt phẳng

 

ABC

và

M

,

N

,

P

lần lượt là

hình chiếu vuông góc của

H

lên

BC

,

CA

,

AB

. Khi đó các góc

SMH

,

SNH

,

SPH

lần lượt là

góc giữa các mặt bên

 

SBC

;

 

SCA

,

 

SAB

và đáy

 

ABC

.

Theo định lý diện tích hình chiếu vuông góc, ta có:

1

cos

HBC

S

SMC



1

..

2

BC HM

HM

SM



1

.

2

BC HM

1

2

SM

22

1

2

h HM

. Tương tự có

22

2

1

2

S h HN

,

22

3

1

2

S h HP

.

Mặt khác

 

1 2 3

3 . , . , . , . ,V S d S ABC S d A SBC S d B SCA S d C SAB   

.

Suy ra

 

2 2 2 2 2 2

3 6 15 30

1

4 8 20 40

h h HM h HN h HP     

.

Mặt khác

22

2

HBC HCA

HAB

SS

S

HM HN HP

BC CA AB

    

   

3

2 2 2

2

HBC HCA HAB

S S S S    

.

Kết hợp

   

1 , 2

suy ra

3

12

h 

và

1 1 3 3 1

. . . .

3 3 4 12 48

V S h  

.

Câu 50: Chọn D

Diện tích đáy

11

. .sin 30

24

S AB AC  

.

Chiều cao khối lăng trụ xác định bởi:

22

2 2 2

22

. .cot .cot

sin sin

cos

hh

d d h

a

dh



  





2 2 2

2

41

1 2 . 1

33

3

2

1

h h h

h

  





3

31

h

. Vậy

93

.

124

V S h

.

Câu 51: Chọn A

Diện tích đáy

1 35

. .sin30

24

S AB AC  

.

M

A

C

B

S

H

P

N

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

183

Chiều cao khối chóp xác định bởi:

22

2 2 2

22

. .cot .cot

sin sin

cos

hh

d d h

a

dh



  





2 2 2

2

3 9 2 . 9 4 3

2

9

h h h

h

  





3

29

h

. Vậy

1 35 29

..

3 116

V S h

.

Câu 52: Chọn A.

Diện tích đáy

1 21

.

22

S AB AC

.

Chiều cao khối chóp xác định bởi:

22

2 2 2

22

. .cot .cot

sin sin

cos

hh

d d h

a

dh



  





2 2 2

2

43

1 2 . 1

33

0

1

h h h

h

  





21

7

h

. Vậy

11

..

32

V S h

.

Câu 53: Chọn D

Có

 

2

0 0 0

3

2

23

20

3 .cot .cot .cot

3 2.cot30 3.cot45 1.cot 60

S

V

a b c

  







  



Câu 54: Chọn A

Có

 

2

3 .cot .cot .cot

S

V

a b c

  





2

3

2

3

2

1

3 2.cot 3

3



















11

cot cos

2

3



   

Câu 55: Chọn B

Kẻ

 

SH BC SH ABC  

, kẻ

,HE AB HF AC

Ta có:

0

60SEH SFH

và

00

.cot60 .cot60HE SH h

,

00

.cot60 .cot60HF SH h

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

184

Diện tích đáy bằng

2

1

.

2

S AB AC a

 

00

11

. . . .cot60 2 . .cot60

22

HAB HAC

S S S AB HE AC HF a h a h      

Vậy

22

2

3

33

Sa

h

aa





3

. 2 3

39

S h a

V  

Cách 2.

Có

 

2 4 3

2 2 2 3

9

3 .cot .cot .cot

11

3 5.0 2. . .

33

S a a

V

a b c

a a a

  

  











Câu 56: Chọn A

Có

 

2

3 .cot .cot .cot .cot

S

V

a b c d

   



  

 

2

3

2

4 3 3

2

26

1

3 .0 . 3 .1 .

3

a

a a a a













  





Câu 57: Chọn A

Khối tứ diện vuông

AMNP

có

1

. . .

6

AMNP

V AM AN AP

Theo quy tắc hình hộp, có:

'AC AB AD AA  

..

AB AD AA

AC AM AN AP

AM AN AP



   

1 2 3

AC AM AN AP

AM AN AP



   

Vì bốn điểm

, , ,M N P C



đồng phẳng nên

1 2 3

1

AM AN AP

  

Vì vậy theo bất đẳng thức

AM GM

, ta có:

3

1 2 3 1 1 1

1 3 . .

AM AN AP AM AN AP

   

. . 6.27AM AN AP

27

AMNP

V

Câu 58: Chọn C

Ta có

   

2

0

1 1 3

. . , .sin , . . . .sin60

6 6 12

ABCD

a

V AD BC d AD BC AD BC AD BC AB AD  

Ta đi tính độ dài đoạn thẳng

AD

dựa trên giả thiết

CD AD

,

 

0

, 60AD BC 

,

,AB AD AB BC

Có:

 

. . . .AD BC AD AC AB AD AC AD AB   

2 2 2 2 2 2 2 2 2 2

2 2 2

AD AC CD AD AB BD AC BD CD AB      

  

     

2 2 2 2 2 2 2

2

AB BC AB AD AC AD AB     



2 2 2 2

2

AB AD BC AC

AD

  



Và

 

.

. . .cos ,

2

a AD

AD BC AD BC AD BC

. Vậy

2

.

22

a AD a

AD AD  

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

185

Do đó:

3

24

ABCD

a

V 

Câu 59: Chọn B

Gọi

,EF

lần lượt là trung điểm của cạnh

,BC AD

. Ta có

 

BC AE BC EF

BC ADE

BC DE BC AD





  







.

 

,ABC DBC AE DE EF AD EF d AD BC        

.

Vậy

   

11

. . , .sin , . .

66

ABCD

V AD BC d AD BC AD BC AD BC FE

.

Ta có

2 2 2 2 2

22

1

4 4 4 4 4

AD BC AD BC AD

FE AE AB



       





.

Vậy

 

22

2 2 2 2

11

. . 1 . . 4

6 4 4 12

ABCD

BC AD

V AD BC AD BC AD BC     

3

2 2 2 2

1 4 2 3

12 3 27

AD BC AD BC



   







.

Dấu đẳng thức xảy ra

2 2 2 2

21

4

33

AD BC AD BC AD BC FE         

.

Câu 60: Chọn C

Ta có

 

3

2

, 3. 2

3

OABC

ABC

V

d O ABC

S

  

.

Vậy

 

3

2 2 2 2 2 2

2

1 1 1 1 1 1 1 1

3 . .

4

,

OA OB OC OA OB OC

d O ABC

    

.

Suy ra

3

1 12

. . 4 3

66

OABC

V OA OB OC  

.

Câu 61: Chọn D

E

D

A'

C'

B'

C

B

A

F

E

D

C

B

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

186

Hạ

AD BB





và

AE CC





suy ra

 

// //ADE AA BB CC

  



và

1, 3 , 2AD AE DE  

.

Ta có

.

3 3 1 2 3

. . 3

2 3 2 3

ADE ABC A B C ADE

AA BB CC

S V S

  

   

    

.

Câu 62: Chọn A

Gọi

D

là hình chiếu vuông góc của

S

lên

 

ABC

. Ta có

 

BA SA

BA SAD BA AD

BA SD





   







và

 

BC CS

BC SCD BC CD

BC SD





   







.

Vậy

ABCD

là hình chữ nhật tâm

O

và

2

.

1 1 2

. . . .

3 6 6

S ABC ABC

a

V S SD BA BC SD SD  

.

Đặt

SD x

ta có

 

,,d B SAC d D SAC

và tứ diện

DSAC

vuông tại

D

nên

 

2 2 2 2 2 2

2

22

1 1 1 1 1 1 1 2

,

2

,

32

xa

d D SAC

DC DA DS a a x

d D SAC

xa

       



và

 

22

2

,,

11

32

sin , 3

11

3

xa

d B SAC d D SAC

xa

SB SAC x a x a

SB SB

xa



      



.

Do đó

3

6

a

V 

.

Câu 63: Chọn A

Kẻ

,OH AB OK CH

suy ra

       

OK ABC ABC OMN OK OMN K MN      

.

O

D

S

C

A

B

H

K

N

M

C

B

A

O

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

187

Ta có

2

,

1

OA OB

HK

OC OH

















lần lượt là trung điểm của

,AB CH

.

Ta có

24

CA CB

CH CA CB CK CM CN

CM CN

    

.

Do

,,M K N

thẳng hàng nên

4

CA CB

CM CN



.

Vậy

1

4 2 . . 4 .

4

CA CB CA CB CA CB CM CN

CM CN CM CN CM CN CA CB

      

.

Vì vậy

3 3 1

1 1 .

4 4 4

OAMNB AMNB CMN

OAMNB OABC

OABC ABC CAB

V S S

CM CN

VV

V S S CA CB

        

.

Câu 64: Chọn A

Ta có

36

OA OB OC

OG OA OB OC OI OD OE OF

OD OE OF

      

1 2 3

6OI OD OE OF

OD OE OF

   

.

Do

,,,D E F I

đồng phẳng nên ta có

1 2 3

6

OD OE OF

  

.

Vậy

3

1 2 3 1 2 3 4 2

6 3 . . . .

39

ODEF

OD OE OF V

OD OE OF OD OE OF

       

.

Câu 65: Chọn D

Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

lên

,BB CC



.

Ta có

1, 2AE AF

và

// //AA BB CC

  

nên

F

E

D

I

G

C

B

A

O

H

M

N

F

E

A'

C'

B'

C

B

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

188

 

,AE AA AF AA EFA AA EF AA

   

     

. Do đó

 

,5FE d C BB





.

Gọi

N

là trung điểm của

BC

,

 

//H FE MN AH MN MN AA



   

.

Ta có

H

là trung điểm của

FE

và

2 2 2

5AE AF EF  

nên

5

22

FE

AH 

.

Tam giác vuông

AMN

có

AN A M





và :

2 2 2 2

1 1 1 4 1 1 15 15 2 15

5

5 5 3 9 3

AM AA

AH AM AN AM



          

.

Mặt khác do

 

   

 

0

, , 60

AM A B C

A B C AEF AM AA MAA

AA AEF



  





    

   











.

Tam giác

AEF

là hình chiếu vuông góc của tam giác

A B C

  

lên mặt phẳng

 

AEF

. Vì vậy theo

định lý hình chiếu ta có:

.

1

.1.2

15 2 15

2

2 . 2.

33

15

cos

3

2 15

3

AEF

A B C ABC A B C A B C

S

S V S AM

MAA

        

      



.

Câu 66: Chọn A

Gọi

,EF

lần lượt là hình chiếu vuông góc của

A

lên

,BB CC



.

Ta có

1, 2AE AF

và

// //AA BB CC

  

nên

 

,AE AA AF AA EFA AA

  

   

.

Do đó

   

 

0

13

, 90 .

22

AEF

EAF ABB A ACC A S AE AF

   

    

.

Gọi

N

là trung điểm của

BC

,

 

//H FE MN AH MN MN AA



   

.

Ta có

H

là trung điểm của

FE

và

22

1

22

EF AE AF

AH



  

.

Tam giác vuông

AMN

có

23

3

AN A M





và

2 2 2

1 1 1 4 3

2

3

AM AA

AH AM AN



     

. Vậy

.

3 4 3

. . 2

23

ABC A B C AEF

V S AA

  



  

.

Câu 67: Chọn C

H

M

N

F

E

A'

C'

B'

C

B

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

189

Gọi

H

là hình chiếu của

A



lên

 

ABC

H

là trọng tâm tam giác

ABC

.

N

là trung điểm

BC

, dựng hình bình hành

ACBE

.

Ta có

   

 

33

; ; ; ;

24

a

d AA BC d BC A AE d N A AE d H A AE

   

   

 

3

;

6

a

d H A AE





.

Kẻ

HK A A





, khi đó ta chứng minh được

 

HK A AE





nên

 

;d H A AE HK





.

Xét

A AH





có

2 2 2

1 1 1

3

a

AH

HK HA HA



   



.

Do đó

23

..

2 2 2 3 3

. . . .

3 3 3 3 4 18

A BB C C ABC A B C ABC

a a a

V V A H S

     





   

.

Câu 68: Chọn B

Gọi

M

là trung điểm

BC

,

D

là hình chiếu của

S

lên

BC

. Dựng hình chữ nhật

AMDF

.

Khi đó ta có

 

DF BC

BC SDF

SD BC













.

Từ

D

,

F

lần lượt kẻ

DK SF

 

K SF

,

FE SD

 

E SD

.

Ta cso

 

BC SDF BC EF  

. Mặt khác

 

;;EF SD d A SBC d E SBC EF   

.

Tương tự, ta có

   

 

;;d SA BC d D SAF DK

do

 

AF SDF

DK SF

DK AF

DK SF





















.

Theo giả thiết, ta có

15

5

a

EF DK

. Do đó

SDF

cân tại

S

.

Khi đó hình chiếu của

S

lên

 

ABC

là trung điểm

H

của

DF

hay ttrung điểm

AC

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

190

Xét hai tam giác đồng dạng

SDF

và

FDE

có

22

1

3

2

3

AM

SH DH a

SH

EF DE

DF EF

   



Vậy

23

.

1 1 3 3

. . . .

3 3 4 2 8

S ABC ABC

a a a

V S SH



  

.

Câu 69: Chọn A

Gọi

H

,

K

lần lượt là hình chiếu của

A

,

B

lên

EF

.

Khi đó

FH EK a

AH BK a  

.

Ta có

. . .ABCDEF D AHF C CEK DAH CAK

V V V V  

11

. . . .

33

AFH CEK BCK

DA S BC S AB S

  

  

3

1 1 1 1 1 5 2

. 2. . . . 2. . . . . . 2

3 2 3 2 2 6

a

a a a a a a a a a   

.

Câu 70: Chọn C

Hạ

AM BB





và

AN DD





 

AMN AA





Do đó

..

2 2 .

ABCD A B C D ABD A B D AMN

V V S AA

      





Vì

   

       

/

0

/

6

//

,,

BB C C ADD A

ABB A ADD A BB C C C CDD

C CDD ABB A

   



   



   

       



   

   





.

Khi đó

60MAN 

hoặc

120MAN 

1 3 1 3 3

. . .1.1.

2 2 2 2 4

AMN

S AM AN   

.

Hình bình hành

ABB A



có

. 1. . 2.

22

ABB A

S

A

AM BB

A AA

AAB AA AB A



  







.

Vậy

.

3

ABCD A B C D

V

   



.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

191

DẠNG 6. TỈ SỐ THỂ TÍCH

Câu 1: Cho tứ diện

ABCD

có các cạnh

AB

,

AC

và

AD

đôi một vuông góc. Các điểm

,,M N P

lần lượt

là trung điểm các đoạn thẳng

,,BC CD BD

. Cho biết

4 , 6 , 7AB a AC a AD a  

. Tính thể tích

V

của khối tứ diện

AMNP

.

A.

3

7Va

. B.

3

28Va

. C.

3

14Va

. D.

3

21Va

.

Câu 2: Cho hình chóp

.S ABCD

có đáy là hình bình hành và có thể tích là

V

. Gọi

M

là trung điểm của

SB

. P là điểm thuộc cạnh

SD

sao cho

2SP DP

. Mặt phẳng

 

AMP

cắt cạnh

SC

tại

N

. Tính

thể tích của khối đa diện

ABCDMNP

theo

V

A.

23

30

ABCDMNP

VV

. B.

19

30

ABCDMNP

VV

. C.

2

5

ABCDMNP

VV

. D.

7

30

ABCDMNP

VV

.

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

,

o

60BAD 

và

SA

vuông góc với

mặt phẳng

 

ABCD

. Góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

bằng

o

45

. Gọi

M

là điểm đối

xứng của

C

qua

B

và

N

là trung điểm của

SC

. Mặt phẳng

 

MND

chia khối chóp

.S ABCD

thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

S

có thể tích là

1

V

, khối còn lại có thể

tích là

2

V

. Tính tỉ số

1

2

V

.

A.

1

2

1

5

V



. B.

1

2

5

3

V



. C.

1

2

12

7

V



. D.

1

2

7

5

V



.

Câu 4: Cho khối lăng trụ

.ABC A B C

  

. Đường thẳng đi qua trọng tâm của tam giác

ABC

và song song

với

BC

cắt các cạnh

AB

,

AC

lần lượt tại

D

,

E

. Mặt phẳng

 

A DE



chia khối lăng trụ thành

hai phần, tính tỉ số thể tích của chúng.

A.

2

3

. B.

4

23

. C.

4

9

. D.

4

27

.

Câu 5: Cho tứ diện

ABCD

có thể tích

V

. Xét điểm

P

thuộc cạnh

AB

, điểm

Q

thuộc cạnh

BC

và điểm

R

thuộc cạnh

BD

sao cho

2

PA

PB



,

3

QB

BC



,

4

RB

RD



. Tính thể tích của khối tứ diện

BPQR

.

A.

5

V

. B.

4

V

. C.

3

V

. D.

6

V

.

Câu 6: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình bình hành. Các điểm

A



,

C



thỏa mãn

1

3

SA SA





,

1

5

SC SC





. Mặt phẳng

 

P

chứa đường thẳng

AC



cắt các cạnh

SB

,

SD

lần lượt

tại

B



,

D



và đặt

.

S A B C D

S ABCD

V

k

V

   



. Giá trị nhỏ nhất của

k

là?

A.

1

60

. B.

1

30

. C.

4

15

. D.

15

16

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

192

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

M

,

N

lần lượt là trung điểm của

các cạnh

AB

,

BC

. Điểm

I

thuộc đoạn

SA

. Biết mặt phẳng

 

MNI

chia khối chọp

.S ABCD

thành hai phần, phần chứa đỉnh

S

có thể tích bằng

7

13

lần phần còn lại. Tính tỉ số

IA

k

IS



?

A.

1

2

. B.

3

4

. C.

2

3

. D.

1

3

.

Câu 8: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình bình hành. Các điểm

A



,

C



thỏa mãn

1

3

SA SA





,

1

5

SC SC





. Mặt phẳng

 

P

chứa đường thẳng

AC



cắt các cạnh

SB

,

SD

lần lượt

tại

B



,

D



và đặt

.

S A B C D

S ABCD

V

k

V

   



. Giá trị lớn nhất của

k

là?

A.

4

105

. B.

1

30

. C.

4

15

. D.

4

27

.

Câu 9: Cho tứ diện đều có chiều cao

h

, ở ba góc của tứ diện người ta cắt đi các tứ diện bằng nhau có

chiều cao

x

để khối đa diện còn lại có thể tích bằng một nửa thể tích của khối đa diện đều ban

đầu. Tìm

x

.

A.

3

2

h

x 

. B.

3

h

x 

. C.

4

h

x 

. D.

3

6

h

x 

.

Câu 10: Cho lăng trụ

.ABC A B C

  

.Trên các cạnh

,AA BB



lần lượt lấy các điểm

,EF

sao cho

,AA kA E BB kB F

   



. Mặt phẳng

(C )EF



chia khối trụ đã cho thành hai khối đa diện bao gồm

khối chóp

( . )C A B FE

  

có thể tích

1

V

và khối đa diện

(ABCEFC )



có thế tích

2

V

. Biết rằng

1

2

7

V



tìm k.

A.

4k 

. B.

3k 

. C.

1k 

. D.

2k 

.

Câu 11: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

, tâm

O

. Hình chiếu vuông

góc của điểm

S

trên mặt phẳng

 

ABCD

là trung điểm

H

của đoạn thẳng

AO

. Biết mặt phẳng

 

SCD

tạo với mặt đáy

 

ABCD

một góc

60

. Thể tích khối chóp

.S ABCD

bằng

A.

3

93

4

a

. B.

3

4

a

. C.

3

4

a

. D.

3

33

4

a

.

Câu 12: Cho hình chóp tứ giác

.S ABCD

đáy

ABCD

là hình thoi cạnh

a

,

D 60BA 

và

SA

vuông góc

với mặt phẳng

 

ABCD

. Góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

là

45

. Gọi

M

là điểm

đối xứng của

C

qua

B

và

N

là trung điểm

SC

. Mặt phẳng

 

MND

chia khối chóp thành hai

khối đa diện, trong đó khối đa diện có đỉnh

S

có thể tích là

1

V

, khối đa diện còn lại có thể tích

2

V

. Tính tỉ số

1

2

V

A.

1

2

12

7

V



. B.

1

2

5

3

V



. C.

1

2

1

5

V



. D.

1

2

7

5

V



.

Câu 13: Cho hình lăng trụ

.ABC A B C

  

có thể tích bằng

3

48cm

. Gọi

,,M N P

theo thứ tự là trung

điểm các cạnh

,CC BC



và

BC



. Tính thể tích của khối chóp

.A MNP



.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

193

A.

3

8.cm

B.

3

12 .cm

C.

3

24 .cm

D.

3

16

.

3

cm

Câu 14: Cho hình chóp

.S ABC

có đáy là

ABC

vuông cân ở

,B

2,AC a

 

SA ABC

,

.SA a

Gọi

G

là trọng tâm của

SBC

,

 

mp



đi qua

AG

và song song với

BC

chia khối chóp thành hai

phần. Gọi

V

là thể tích của khối đa diện không chứa đỉnh

S

. Tính

V

.

A.

3

5

54

a

. B.

3

2

9

a

. C.

3

4

27

a

. D.

3

4

9

a

.

Câu 15: Cho tứ diện đều có chiều cao

h

, ở bốn góc của tứ diện người ta cắt đi các tứ diện đều bằng nhau

có chiều cao

x

để khối đa diện còn lại có thể tích bằng

3

4

thể tích của khối đa diện ban đầu. Tìm

x

.

A.

3

4

h

x 

. B.

3

16

h

x 

. C.

3

12

h

x 

. D.

3

6

h

x 

.

Câu 16: Cho khối hộp

.ABCD A B C D

   

. Lấy điểm

E

thuộc cạnh

BB



sao cho

4

BB

BE





, điểm

F

thuộc

cạnh

DD



sao cho

3

4

DD

DF





. Mặt phẳng qua ba điểm

,,A E F

chia khối hộp thành hai phần.

Tính tỉ số hai phần ấy.

A.

2

. B.

1

. C.

3

2

. D.

4

3

.

Câu 17: Cho khối lăng trụ tam giác

.ABC A B C

  

. Gọi

,MN

lần lượt thuộc các cạnh bên

,AA CC



sao

cho

;4MA MA NC NC





. Gọi

G

là trọng tâm tam giác

ABC

. Hỏi trong bốn khối tứ diện

,,GA B C BB MN ABB C

     

và

A BCN



, khối tứ diện nào có thể tích nhỏ nhất?

A. Khối

ABB C



. B. Khối

A BCN



. C. Khối

BB MN



. D. Khối

GA B C

  

.

Câu 18: Cho hình chóp tứ giác đều

.S ABCD

. Mặt phẳng

 

P

qua

A

và vuông góc

SC

cắt

SB

,

SC

,

SD

lần lượt tại

B



,

C



,

D



. Biết

C



là trung điểm

SC

. Gọi

1

V

,

2

V

lần lượt là thể tích hai khối chóp

.S AB C D

  

và

.S ABCD

. Tính tỉ số

1

2

V

.

A.

1

2

3

V



. B.

1

2

9

V



. C.

1

2

4

9

V



. D.

1

2

1

3

V



.

Câu 19: Cho hình chóp đều

.S ABC

, có đáy là tam giác đều cạnh bằng

a

. Gọi

,MN

lần lượt là trung điểm

của các cạnh

,SB SC

. Biết mặt phẳng

 

AMN

vuông góc với mặt phẳng

 

SBC

. Tính thể tích

V

của khối chóp

.A BCNM

.

A.

3

5

32

a

V 

. B.

3

2

16

a

V 

. C.

3

2

48

a

V 

. D.

3

5

96

a

V 

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

194

Câu 20: Cho hình chóp tam giác

.S ABC

. Gọi

M

là trung điểm của

SA

, lấy điểm

N

trên cạnh

SB

sao cho

2

3

SN

SB



. Mặt phẳng

 



qua

MN

và song song với

SC

chia khối chóp thành hai phần. Gọi

1

V

là thể tích của khối đa diện chứa đỉnh

A

,

2

V

là thể tích của khối đa diện còn lại. TÍnh tỉ số

1

2

.

V

A.

1

2

7

16

V



. B.

1

2

7

18

V



. C.

1

2

7

11

V



. D.

1

2

7

9

V



.

Câu 21: Cho khối hộp chữ nhật

. ' ' ' 'ABCD A B C D

có

4 ; 6 ; ' 7AB a AD a AA a  

. Các điểm

,,M N P

thỏa

mãn

2 ; 3 ; 4 'AM AB AN AD AP AA  

. Tính thể tích

V

của khối tứ diện

AMNP

.

A.

3

168Va

. B.

3

672Va

. C.

3

336Va

. D.

3

1008Va

.

Câu 22: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

'C

là trung điểm của

SC

. Mặt phẳng

 

P

chứa

'AC

cắt các cạnh

,SB SD

lần lượt tại

', 'BD

. Đặt

. ' ' '

.

S B C D

S ABCD

V

m

V



.Giá trị nhỏ nhất của

m

bằng

A.

2

27

. B.

4

27

. C.

1

9

. D.

2

9

.

Câu 23: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

C



là trung điểm cạnh

SC

. Mặt

phẳng

 

P

chứa đường thẳng

AC



cắt các cạnh

SB

,

SD

lần lượt tại

B



,

D



. Đặt

.

S B C D

S ABCD

V

m

V

  



.

Giá trị lớn nhất của

m

bằng

A.

1

9

. B.

1

8

. C.

3

8

. D.

4

9

.

Câu 24: Cho khối tứ diện đều

ABCD

. Gọi

, , , , ,M N P Q R S

lần lượt là trung điểm của các cạnh

, , , , ,AB AC AD BC CD DB

. Biết thể tích của khối bát diện đều

MQNPSR

bằng

3

9 2 cm

. Tính độ

dài cạnh của tứ diện đều

ABCD

.

A.

2 cm

. B.

3 cm

. C.

6 cm

. D.

3

2 cm

.

Câu 25: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,MN

lần lượt là các điểm trên cạnh

1

, : , 2

2

AM AN

AB AC

BM CN



. Mặt phẳng

 



chứa

MN

, song song với

AD

chia khối tứ diện

thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

A

có thể tích

V

. Tính

V

A.

3

42

108

a

V 

. B.

3

52

108

a

V 

. C.

3

42

81

a

V 

. D.

3

11 2

342

a

V 

Câu 26: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,MN

lần lượt là trung điểm các cạnh

,AB BC

và

E

là điểm thuộc tia đối của tia

DB

sao cho

BE

k

BD



. Tìm

k

để mặt phẳng

 

MNE

chia khối

tứ diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh

B

có thể tích

3

11 2

294

a

V 

A.

6

5

k 

. B.

6k 

. C.

4k 

. D.

5k 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

195

Câu 28: Cho hình chóp có đáy là hình bình hành. Trên cạnh lấy các điểm

,MN

sao cho

SM MN NA

. Hai mặt phẳng song song với

 

ABCD

và lần lượt đi qua

,MN

chia

khối chóp đã cho thành ba phần. Nếu phần trên có thể tích bằng

3

10 dm

thì phần ở giữa có thể

tích là

A. . B. . C. . D. .

Câu 29: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

,MN

lần lượt là trung điểm các

cạnh

,SA SD

. Mặt phẳng

 



chứa

MN

và cắt các tia

,SB SC

lần lượt tại

P

và

Q

. Đặt

SP

x

SB



,

1

V

là thể tích của khối chóp

.S MNQP

và

V

là thể tích khối chóp

.S ABCD

. Tìm

x

để

1

2VV

.

A.

1

2

x 

. B.

1 33

4

x





. C.

1 41

4

x





. D.

2x 

.

Câu 30: Cho lăng trụ đứng tam giác

. ' ' 'ABC A B C

. Gọi

, , ,M N P Q

là các điểm lần lượt thuộc các cạnh

', ', ', ' 'AA BB CC B C

thỏa mãn

1 1 1 ' 1

, , ,

' 2 ' 3 ' 4 ' ' 5

AM BN CP C Q

AA BB CC B C

   

. Gọi

12

,VV

lần lượt là thể

tích khối tứ diện

MNPQ

và khối lăng trụ

. ' ' 'ABC A B C

. Tính tỷ số

1

2

V

.

A.

1

2

11

30

V



. B.

1

2

11

45

V



. C.

1

2

19

45

V



. D.

1

2

22

45

V



.

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

M

,

N

lần lượt là trung điểm của

các cạnh

AB

,

BC

. Điểm

K

thuộc đoạn

SA

. Biết mặt phẳng

 

MNK

chia khối chóp

.S ABCD

thành hai phần, phần chứa đỉnh

S

có thể tích bằng

7

13

lần phần còn lại. Tính tỉ số

KA

t

KS



.

A.

1

2

t 

. B.

3

4

t 

. C.

1

3

t 

. D.

2

3

t 

.

Câu 32: Cho khối hộp chữ nhật

.ABCD A B C D

   

có thể tích bằng

2110

. Biết

A M MA





,

3DN ND





,

2CP C P





như hình vẽ. Mặt phẳng

 

MNP

chia khối hộp đã cho thành hai khối đa diện. Thể tích

khối đa diện nhỏ hơn bằng

A.

5275

6

. B.

5275

12

. C.

7385

18

. D.

8440

9

.

Câu 33: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

2AB a

,

BC a

,

2SA SB SC SD a   

.

Giả sử

E

thuộc cạnh

SC

sao cho

2SE EC

,

F

là điểm thuộc cạnh

SD

sao cho

1

3

SF FD

. Thể

tích khối đa diện

SABEF

bằng:

.S ABCD

SA

( ), ( )



3

70 dm

3

80 dm

3

180 dm

3

190 dm

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

196

A.

3

53

36

a

. B.

3

18

a

. C.

3

23

9

a

. D.

3

23

27

a

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Một mặt phẳng song song với đáy cắt

các cạnh bên

, , , SA SB SC SD

lần lượt tại

, , , M N P Q

. Gọi

, , , M N P Q

   

lần lượt là hình

chiếu của

, , , M N P Q

trên mặt phẳng đáy. Tìm tỉ số

SM

SA

để thể tích khối đa diện

.MNPQ M N P Q

   

đạt giá trị lớn nhất.

A.

3

4

. B.

2

3

. C.

1

2

. D.

1

3

.

Câu 35: Cho khối chóp

.S ABCD

có đáy là hình thang với hai đáy là

AB

và

CD

,

2AB CD

. Gọi

E

là

một điểm trên cạnh

SC

. Mặt phẳng

 

ABE

chia khối chóp

.S ABCD

thành hai khối đa diện có thể

tích bằng nhau. Tính tỉ số

SE

SC

.

A.

10 2

2



. B.

62

. C.

21

. D.

26 4

2



.

Câu 36: Cho hình chóp

.S ABC

. Một mặt phẳng song song với đáy

 

ABC

cắt các cạnh bên

, , SA SB SC

lần lượt tại

, , M N P

. Gọi

, , M N P

  

lần lượt là hình chiếu của

, , M N P

trên mặt phẳng đáy.

Tìm tỉ số

SM

SA

để thể tích khối đa diện

.MNP M N P

  

đạt giá trị lớn nhất.

A.

3

4

. B.

2

3

. C.

1

2

. D.

1

3

.

Câu 37: Cho hình chóp

.S ABC

. Một mặt phẳng

 

P

song song với đáy

 

ABC

cắt các cạnh bên

, , SA SB SC

lần lượt tại

, , M N P

. Tìm tỉ số

SM

SA

để

 

P

chia khối chóp đã cho thành hai khối

đa diện có thể tích bằng nhau.

A.

3

1

2

. B.

3

1

4

. C.

1

2

. D.

1

4

.

Câu 38: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông và

 

SA ABCD

. Trên đường thẳng

vuông góc với

 

ABCD

tại

D

lấy điểm

S



thỏa mãn

1

2

S D SA





và

S



,

S

ở cùng phía đối với mặt

phẳng

 

ABCD

. Gọi

1

V

là phần thể tích chung của hai khối chóp

.S ABCD

và

.S ABCD



. Gọi

2

V

là thể tích khối chóp

.S ABCD

. Tỉ số

1

2

V

bằng

A.

4

9

. B.

7

9

. C.

7

18

. D.

1

3

.

Câu 39: Cho hình chóp

.S ABC

có tất cả các cạnh đều bằng

a

, một mặt phẳng

 

P

song song với mặt đáy

 

ABC

cắt các cạnh bên

,,SA SB SC

lần lượt tại

,,M N P

. Tính diện tích tam giác

MNP

biết mặt

phẳng

 

P

chia khối chóp đã cho thành hai khối đa diện có diện tích bằng nhau.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

197

A.

2

3

8

MNP

a

S 

. B.

2

3

16

MNP

a

S 

. C.

2

3

42

MNP

a

S 

. D.

2

4

3

44

MNP

a

S 

.

Câu 40: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Trên đường thẳng qua

D

và song song

với

SA

lấy điểm

S



thỏa mãn

S D kSA





với

0k 

. Gọi

1

V

là phần thể tích chung của hai khối

chóp

.S ABCD

và

.S ABCD



. Gọi

2

V

là thể tích khối chóp

.S ABCD

. Tỉ số

1

2

V

bằng

A.

 

2

21

kk

k



. B.

 

2

32

21

k



. C.

 

2

32

21

kk

k



. D.

1

k

k 

.

Câu 41: Cho hình chóp tam giác đều

.S ABC

. Gọi

G

là trọng tâm tam giác

ABC

, biết góc tạo bởi

SG

và

 

SBC

bằng

30

. Mặt phẳng chứa

BC

và vuông góc với

SA

chia khối chóp đã cho thành hai

phần có thể tích

1

V

,

2

V

trong đó

1

V

là phần thể tích chứa điểm

S

. Tỉ số

1

2

V

bằng

A.

6

. B.

1

6

. C.

6

7

. D.

7

.

Câu 42: Cho hình chóp tam giác đều

.S ABC

có cạnh bên tạo với đường cao một góc

0

30

,

O

là trọng tâm

tam giác

ABC

. Một hình chóp tam giác đều thứ hai

.O A B C

  

có

S

là tâm của tam giác

A B C

  

và cạnh bên của hình chóp

.O A B C

  

tạo với đường cao một góc

0

60

sao cho mỗi cạnh bên

SA

,

SB

,

SC

lần lượt cắt các cạnh bên

OA



,

OB



,

OC



. Gọi

1

V

là phần thể tích chung của hai khối

chóp

.S ABC

và

.O A B C

  

. Gọi

2

V

là thể tích khối chóp

.S ABC

. Tỉ số

1

2

V

bằng

A.

9

16

. B.

1

4

. C.

27

64

. D.

9

64

.

Câu 43: Một viên đá có dạng khối chóp tứ giác đều có tất cả các cạnh bằng

a

. Người ta cưa viên đá theo

mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có thể tích bằng

nhau. Tính diện tích thiết diện viên đá bị cưa bởi mặt phẳng nói trên.

A.

2

3

4

a

. B.

2

3

2

a

. C.

2

a

. D.

2

3

22

a

.

Câu 44: Cho tứ diện

ABCD

có thể tích bằng

12

và

G

là trọng tâm tam giác

BCD

. Tính thể tích của khối

chóp

.AGBC

.

A.

3V 

. B.

4V 

. C.

6V 

. D.

5V 

.

Câu 45: Cho hình lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân tại

A

, cạnh

2AC a

. Biết

AC



tạo với mặt phẳng

 

ABC

góc

60

và

4AC





. Tính thể tích

V

của khối

đa diện

ABCB C



.

A.

8

3

V 

. B.

16

3

V 

. C.

83

3

V 

. D.

16 3

3

V 

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

198

Câu 46: Cho hình hộp

.ABCD A B C D

   

. Gọi

1

V

là phần thể tích chung của hai khối của hai khối tứ diện

A BC D



và

AB CD



. Gọi

2

V

là thể tích khối hộp

.ABCD A B C D

   

. Tỉ số

1

2

V

bằng

A.

1

2

. B.

1

6

. C.

1

3

. D.

1

4

.

Câu 47: Cho lăng trụ

.ABC A B C

  

, trên các cạnh

AA



,

BB



lấy các điểm

M

,

N

sao cho

3AA A M





,

3BB B N





. Mặt phẳng

 

C MN



chia khối lăng trụ đã cho thành hai phần. Gọi

1

V

là thể tích của

khối chóp

.C A B NM

  

,

2

V

là thể tích của khối đa diện

ABCMNC



. Tỉ số

1

2

V

bằng:

A.

1

2

4

7

V



. B.

1

2

7

V



. C.

1

2

1

7

V



. D.

1

2

3

7

V



.

Câu 48: Cho hình chóp

.S ABCD

đáy là hình bình hành. Gọi

,MN

lần lượt là trung điểm của

,SA SC

.

Mặt phẳng

()BMN

cắt

SD

tại

P

. Tỉ số

.

S BMPN

S ABCD

V

bằng:

A.

.

1

16

S BMPN

S ABCD

V



. B.

.

1

6

S BMPN

S ABCD

V



. C.

.

1

12

S BMPN

S ABCD

V



. D.

.

1

8

S BMPN

S ABCD

V



.

Câu 49: Cho tứ diện

ABCD

có thể tích bằng

54

, gọi

,,M N P

lần lượt là trọng tâm các tam giác

ABC

,

ACD

,

ADB

. Tính thể tích của khối tứ diện

AMNP

.

A.

27

2

V 

. B.

4V 

. C.

9V 

. D.

16V 

.

Câu 50: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh bằng

6

và góc nhọn bằng

45

,

cạnh bên của hình hộp bằng

10

và tạo với mặt phẳng đáy một góc

45

. Tính thể tích khối đa diện

ABCDD B



.

A.

180V 

. B.

60V 

. C.

90V 

. D.

120V 

.

Câu 51: Cho khối lăng trụ tam giác

.ABC A B C

  

, gọi

M

,

N

lần lượt thuộc các cạnh bên

AA



,

CC



sao

cho

MA MA





,

4NC NC





. Gọi

G

là trọng tâm tam giác

ABC

. Hỏi trong bốn khối tứ diện

GA B C

  

,

BB MN



,

ABB C



và

A BCN



, khối tứ diện nào có thể tích nhỏ nhất?

A. Khối

A BCN



. B. Khối

GA B C

  

. C. Khối

ABB C



. D. Khối

BB MN



.

Câu 52: Cho khối lăng trụ tam giác

.ABC A B C

  

có thể tích bằng

60

. Gọi

M

,

N

,

P

lần lượt thuộc các

cạnh bên

AA



,

BB



,

CC



sao cho

2MA MA





,

3NB NB





,

4PC PC





. Tính thể tích khối đa

diện

BCMNP

.

A.

40

. B.

30

. C.

31

. D.

85

3

.

Câu 53: Cho khối tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

M

,

N

lần lượt là trung điểm của các cạnh

AB

,

BC

và

E

đối xứng với điểm

B

qua

D

. Mặt phẳng

 

MNE

chia khối tứ diện

ABCD

thành

hai khối đa diện, trong đó khối đa diện chứa đỉnh

A

có thể tích

V

. Tính

V

.

A.

3

13 2

216

a

V 

. B.

3

72

216

a

V 

. C.

3

2

18

a

V 

. D.

3

11 2

216

a

V 

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

199

Câu 54: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành và có thể tích bằng

48

. Kí hiệu

M

,

N

lần lượt là các điểm thuộc cạnh

AB

,

CD

sao cho

MA MB

,

2ND NC

. Tính thể tích

V

của

khối chóp

.S MBCN

.

A.

40V 

. B.

8V 

. C.

20V 

. D.

28V 

.

Câu 55: Cho hình lăng trụ

. ' ' 'ABC A B C

có thể tích bằng V. Gọi M, N lần lượt là trung điểm của

' ',A B AC

và

P

là điểm thuộc cạnh

'CC

sao cho

2'CP C P

. Tính thể tích khối tứ diện

BMNP

theo V.

A.

2

9

V

. B.

3

V

. C.

5

24

V

. D.

4

9

V

.

Câu 56: Cho tứ diện đều

ABCD

có cạnh bằng

a

. Gọi

,MN

lần lượt là trọng tâm các tam giác

,ABD ABC

và

E

là điểm đối xứng với

B

qua

D

. Mặt

 

MNE

chia khối tứ diện

ABCD

thành hai khối đa

diện trong đó khối đa diện chứa đỉnh

A

có thể tích

V

. Tính

V

.

A.

3

92

320

a

V 

. B.

3

32

320

a

V 

. C.

3

2

96

a

V 

. D.

3

32

80

a

V 

.

Câu 57: Cho hình lăng trụ

.ABC A B C

  

có thể tích

V

. Các điểm

M

,

N

,

P

trên các cạnh

AA



,

BB



,

CC



sao cho

AM

x

AA





,

BN

y

BB





,

CP

z

CC





. Biết thể tích của khối đa diện

.ABC MNP

bằng

1

2

V

.

Mệnh đề nào sau đây đúng?

A.

1x y z  

. B.

2x y z  

. C.

3

2

x y z  

. D.

2

3

x y z  

.

Câu 58: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc và

1, 2, 3OA OB OC  

. Gọi

,,D E F

lần lươt là chân đường cao hạ từ đỉnh

O

xuống các cạnh

,,BC CA AB

. Thể tích khối tứ

diện

ODEF

bằng

A.

36

325

. B.

276

325

. C.

289

325

. D.

49

325

.

Câu 59: Cho tứ diện đều

ABCD

có cạnh bằng

1

. Gọi

,MN

lần lượt là trung điểm các cạnh

,AB BC

.

Điểm

P

trên cạnh

CD

sao cho

2PD CP

. Mặt phẳng

 

MNP

cắt

AD

tại

Q

. Tính thể tích khối

đa diện

BMNPQD

.

A.

2

16

. B.

23 2

432

. C.

2

48

. D.

13 2

432

.

Câu 60: Cho tứ diện

ABCD

đều cạnh bằng

1

. Gọi

,MN

lần lượt là trung điểm các cạnh

,AB BC

. Điểm

P

trên cạnh

CD

sao cho

2PC PD

. Mặt phẳng

 

MNP

cắt

AD

tại

Q

. Thể tích khối đa diện

BMNPQD

bằng

A.

11 2

216

. B.

2

27

. C.

52

108

. D.

72

216

.

Câu 61: Cho khối lăng trụ

.ABC A B C  

có thể tích bằng

1

. Gọi

,MN

lần lượt là trung điểm các đoạn

thẳng

AA

và

BB 

. Đường thẳng

CM

cắt đường thẳng

CA

tại

P

, đường thẳng

CN

cắt đường

thẳng

CB

tại

Q

. Thể tích của khối đa diện lồi

A MPB NQ

bằng

A.

1

. B.

1

3

. C.

1

2

. D.

2

3

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

200

Câu 62: Cho khối chóp tứ giác đều

.S ABCD

có tất cả các cạnh bằng

a

. Gọi

M

là điểm đối xứng của

C

qua

D

,

N

là trung điểm của cạnh

SC

. Mặt phẳng

 

BMN

chia khối chóp

.S ABCD

thành hai

khối đa diện. Tính thể tích

V

của khối đa diện chứa đỉnh

S

.

A.

3

15 2

144

a

V 

. B.

3

72

a

V 

. C.

3

11 2

144

a

V 

. D.

3

72

144

a

V 

.

Câu 63: Cho hình hộp

. ' ' ' 'ABCD A B C D

có đường cao bằng

8

và đáy là hình vuông cạnh bằng

6

. Gọi

, , ,M N P Q

lần lượt là tâm của các mặt

' ', ' ', ' ', ' 'ABB A BCC B CDD C DAA D

.Thể tích của khối đa

diện có các đỉnh là các điểm

, , , , , , , ,A B C D M N P Q

bằng

A.

108.

B.

168.

C.

96.

D.

120.

Câu 64: Cho hình chóp

.S ABCD

có

ABCD

là hình bình hành, M là điểm đối xứng với

C

qua

B

.

N

là

trung điểm

SC

. Mặt phẳng

 

MND

chia hình chóp thành hai khối đa diện. Gọi

1

V

là thể tích

khối đa diện chứa đỉnh

S

và

2

V

là thể tích khối đa diện còn lại. Tính tỉ số

1

2

V

?

A.

1

2

5

3

V



. B.

1

2

12

7

V



. C.

1

2

1

5

V



. D.

1

2

7

5

V



.

Câu 65: Cho lăng trụ

.ABC A B C

  

có thể tích bằng 2. Gọi

,MN

lần lượt là hai điểm nằm trên hai cạnh

AA



và

BB



sao cho

M

là trung điểm của

AA



và

2

3

B N BB





. Đường thẳng

CM

cắt đường

thẳng

AC



tại

P

và đướng thẳng

CN

cắt đường thẳng

BC



tại

Q

. Thể tích khối đa diện lồi

A MPB NQ



bằng

A.

13

18

. B.

23

9

. C.

7

18

. D.

5

9

.

Câu 66: Cho lăng trụ tam giác đều

.ABC A B C

  

cạnh đáy bằng

a

, chiều cao bằng

2a

. Mặt phẳng

 

P

qua

B



và vuông góc với

AC



chia lăng trụ thành hai khối. Biết thể tích của hai khối là

1

V

và

2

V

với

12

VV

. Tỉ số

1

2

V

bằng

A.

1

11

. B.

1

23

. C.

1

47

. D.

1

7

.

Câu 67:

Cho hình lăng trụ

.ABC A B C

  

và

,MN

là hai điểm lần lượt trên cạnh

,CA CB

sao cho

MN

song

song với

AB

và

CM

k

CA



. Mặt phẳng

()MNB A



chia khối lăng trụ

.ABC A B C

  

thành hai phần

có thể tích

1

V

và

2

V

sao cho

1

2

V



. Khi đó giá trị của

k

là

A.

15

2

k





. B.

1

2

k 

. C.

15

2

k





. D.

3

k 

.

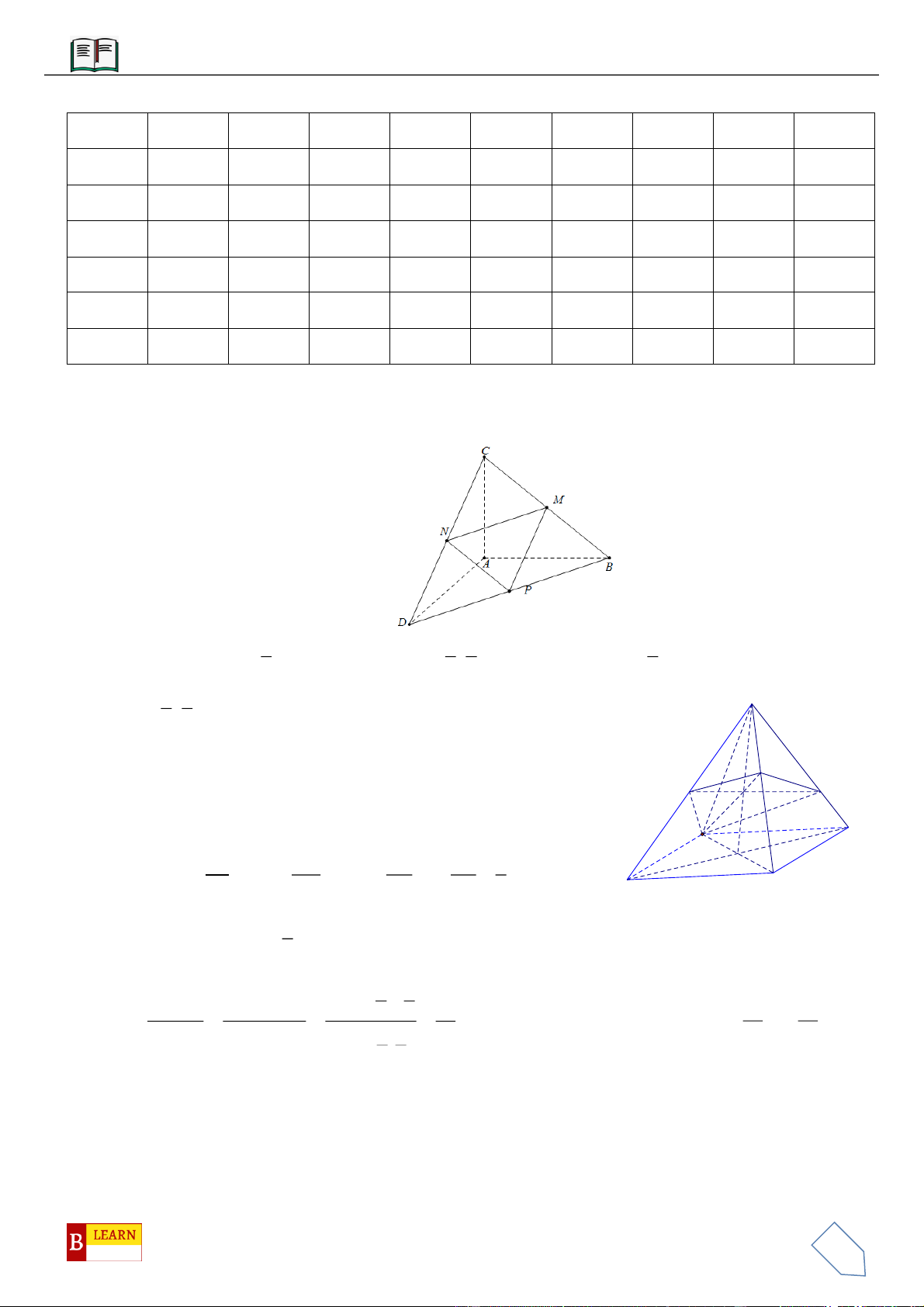
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

201

BẢNG ĐÁP ÁN

1.A

2.A

3.D

4.B

5.A

6.A

7.D

8.A

9.D

10.B

11.B

12.D

13.B

14.A

15.C

16.B

17.B

18.D

19.A

20.C

21.B

22.C

23.B

24.C

25.A

26.C

27.A

28.B

29.B

30.B

31.D

32.A

33.A

34.B

35.A

36.B

37.A

38.C

39.D

40.C

41.B

42.A

43.D

44.B

45.B

46.B

47.B

48.B

49.B

50.D

51.A

52.C

53.D

54.C

55.A

56.A

57.C

58.A

59.B

60.D

61.D

62.B

63.D

64.D

65.D

66.C

67.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn A

Ta có

 

.

1 1 1 1

,,

3 3 4 4

A MNP MNP BCD ABCD

V S d A MNP S d A MNP V       

3

11

7

46

AB AC AD a     

.

Câu 2: Chọn A

Gọi

O AC BD

,

I MP SO

,

N AI SC

Khi đó

..ABCDMNP S ABCD S AMNP

V V V

Đặt

1

SA

a

SA



,

2

SB

b

SM



,

SC

c

SN



,

3

2

SD

d

SP



ta có

5

2

a c b d c    

.

53

12

7

22

53

4 30

4.1.2. .

22

S AMNP

S ABCD

V

a b c d

V abcd

  

  

..

7 23

30 30

ABCDMNP S ABCD S AMNP

V V V V V V     

.

O

I

P

N

M

D

C

B

A

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

202

Câu 3: Chọn D

Trong tam giác

SMC

,

SB

và

MN

là hai trung

tuyến cắt nhau tại trọng tâm

K

2

3

SK

SB



.

BI

là đường trung bình của tam giác

MCD

I

là trung điểm

AB

.

1 . . .S AID S IKN S IND

V V V V  

Đặt:

.S ABCD

VV

.

1

.

4

S AID

VV

;

..

2 1 1 1

. . . .

3 2 4 12

S IKN S IBC

SK SN

V V V V

SB SC

  

;

..

1 1 1

. . .

2 2 4

S IND S ICD

SN

V V V V

SC

  

1

1 1 1 7

..

4 12 4 12

V V V



    





1

2

57

.

12 5

V

VV

V

   

.

Câu 4: Chọn B

Ta có

2

'.

'. . ' ' '

2

.

3

1

3

A ADE

ADE

A ABC ABC

A ABC ABC A B C

V

S

AD AE

V S AB AC

VV





   

















'. . ' ' '

4

27

A ADE ABC A B C

VV

Do đó

1

2

4

27

4

23

1

27

V





.

Câu 5: Chọn A

Ta có

.

1 3 4 1

..

3 4 5 5

B PQR

B ACD

V

BP BQ BR

VV

V BA BC BD

   

.

Câu 6: Chọn A

Đặt

SB

x

SB





,

SD

y

SD





. Ta có

SB SD SA SC

  

   

8xy  

.

Ta có

.

1

15

S A B C

S ABC

V

Vx

  



. . .

11

15 30

S A B C S ABC S ABCD

V V V

xx

  

  

.

Ta có

.

1

15

S A D C

S ADC

V

Vy

  



. . .

11

15 30

S A D C S ADC S ABCD

V V V

yy

  

  

.

Ta có

.

1 1 1

30

S A B C D

S ABCD

V

k

V x y

   



  





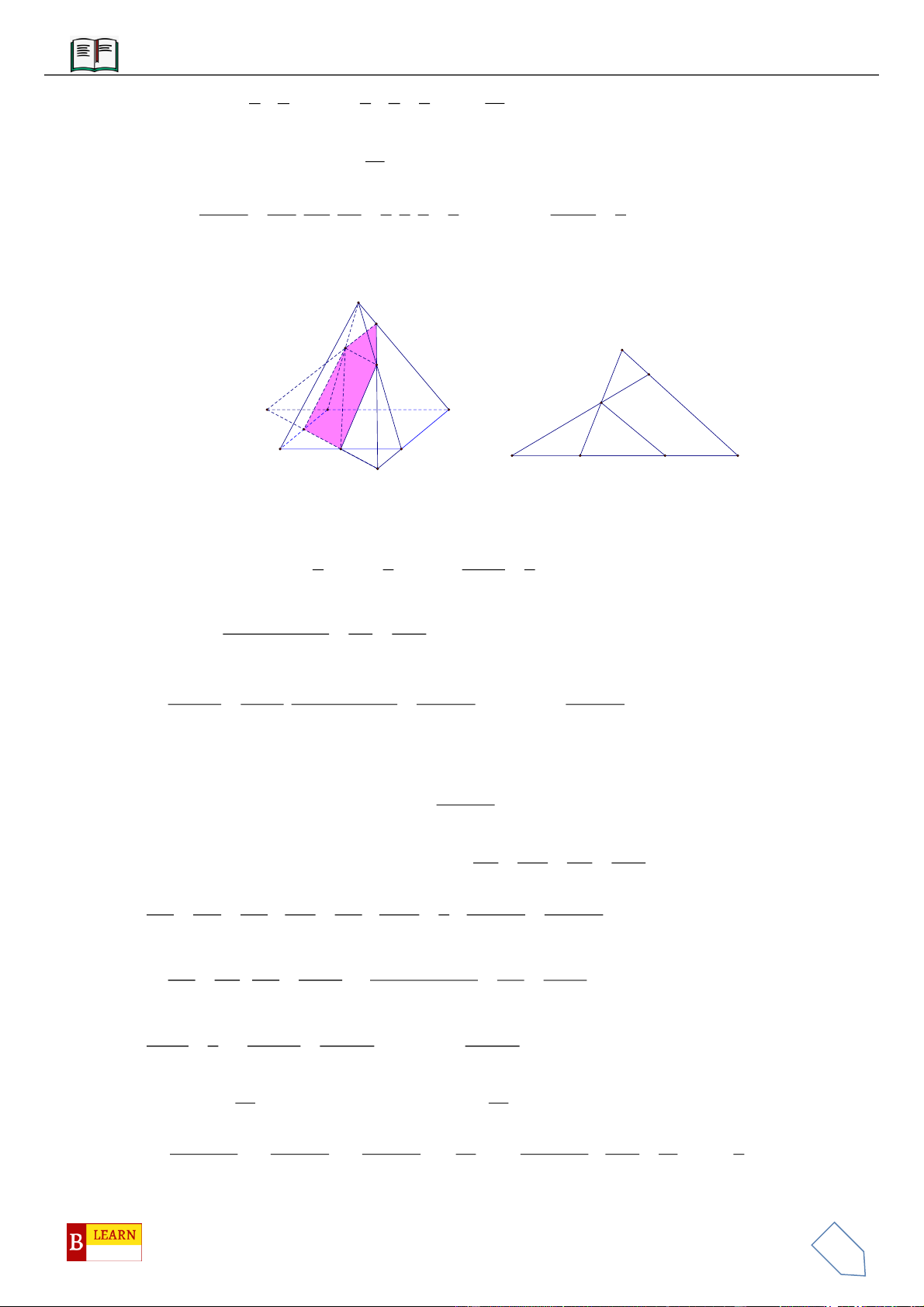
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

203

Ta có

 

11

4xy

xy



  





1 1 1

2xy

  

1

60

k

.

Vậy giá trị nhỏ nhất của

k

là

1

60

khi

4xy

.

Lại có:

..

.

1 2 1 1 6

. . . . 1

2 3 2 6 6 6

S MNP S ABC

S MNP

S ABC

VV

SM SN SP

V

V SA SB SC

      

.

Câu 7: Chọn C

Mặt phẳng

 

MNI

cắt khối chóp theo thiết diện như hình 1. Đặt

.S ABCD

VV

.

Ta có

1 1 1

4 8 8

APM

APM BMN ABC ABCD

ABCD

S

S S S S

S



  

    

.

Mặt khác:

 

,

1

,

d I ABCD

IA k

SA k

d S ABCD





.

 

   

.

,

.

8 1 8 1

,

I APM APM

I APM

S ABCD ABCD

d I ABCD

VS

kk

VV

VS

kk

d S ABCD



    



.

Do

   

 

/ / / / / / ; ;MN AC IK AC IK ABCD d I ABCD d K ABCD   

.

Mà

APM N CQ

SS





.

 

..

81

I APM K NCQ

k

V V V

k

  



.

Kẻ

//IH SD

(

H SD

) như hình 2. Ta có :

1

IH AH AI k

SD AD AS k

  



.

   

2 1 2 3 1

33

3 1 3 1

IH PH PA AH PA AH k k

ED PD PD PD PD AD

kk



       



.

3

:

31

ED IH ID k

SD SD ED k

  



 

,

3

31

,

d E ABCD

ED k

SD k

d S ABCD

  



.

9

8

PQD

ABCD

S





.

27 27

24 8 24 8

E PQD

S ABCD

V

kk

VV

V k k

   



.

. . .

13 13

20 20

EIKAMNCD E PDC I APM K NQC

V V V V V V    

       

27 13 27 13 2

20 1 5 3

8 3 1 8 1 8 1 2 3 1

k k k k k

V V V V k

k

k k k k

        



   

.

Câu 8: Chọn A

Hình 2

Hình 1

I

K

E

Q

P

N

M

D

A

B

C

S

A

D

S

I

P

E

H

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

204

Đặt

SB

x

SB





,

SD

y

SD





Ta có

SB SD SA SC

  

   

8xy  

8yx  

.

Ta có

.

1

15

S A B C

S ABC

V

Vx

  



. . .

11

15 30

S A B C S ABC S ABCD

V V V

xx

  

  

.

Ta có

.

1

15

S A D C

S ADC

V

Vy

  



. . .

11

15 30

S A D C S ADC S ABCD

V V V

yy

  

  

.

Ta có

.

1 1 1

30

S A B C D

S ABCD

V

k

V x y

   



  





4

15xy



 

4

15 8xx





 

2

4

15 8xx





.

Ta có

1 , 8xy

81x  

7x

.

Xét hàm số

 

2

8f x x x  

trên đoạn

1;7



.

 

28f x x



  

;

 

0fx





0 1;7

4 1;7

x



   







   







Tính

 

17f 

;

 

77f 

;

 

4 32f 

.

k

đạt giá trị lớn nhất khi

 

fx

đạt giá trị nhỏ nhất.

 

min 7fx



max

44

15.7 105

k 

.

Câu 9: Chọn D

Gọi cạnh của khối tứ diện đều ban đầu là

a

.

Ta có

22

AO AB BO

2

3

a









6

3

a



6

3

a

h

36

2

6

hh

a  

;

33

23

12 8

ABCD

ah

V 

.

Thể tích của ba khối tứ diện đều có chiều cao

x

được cắt ra là

33

3 3 3

3.

88

xx

V 

.

Ta có

33

3 3 1 3

8 2 8

xh



3

6

h

x

3

6

h

x

.

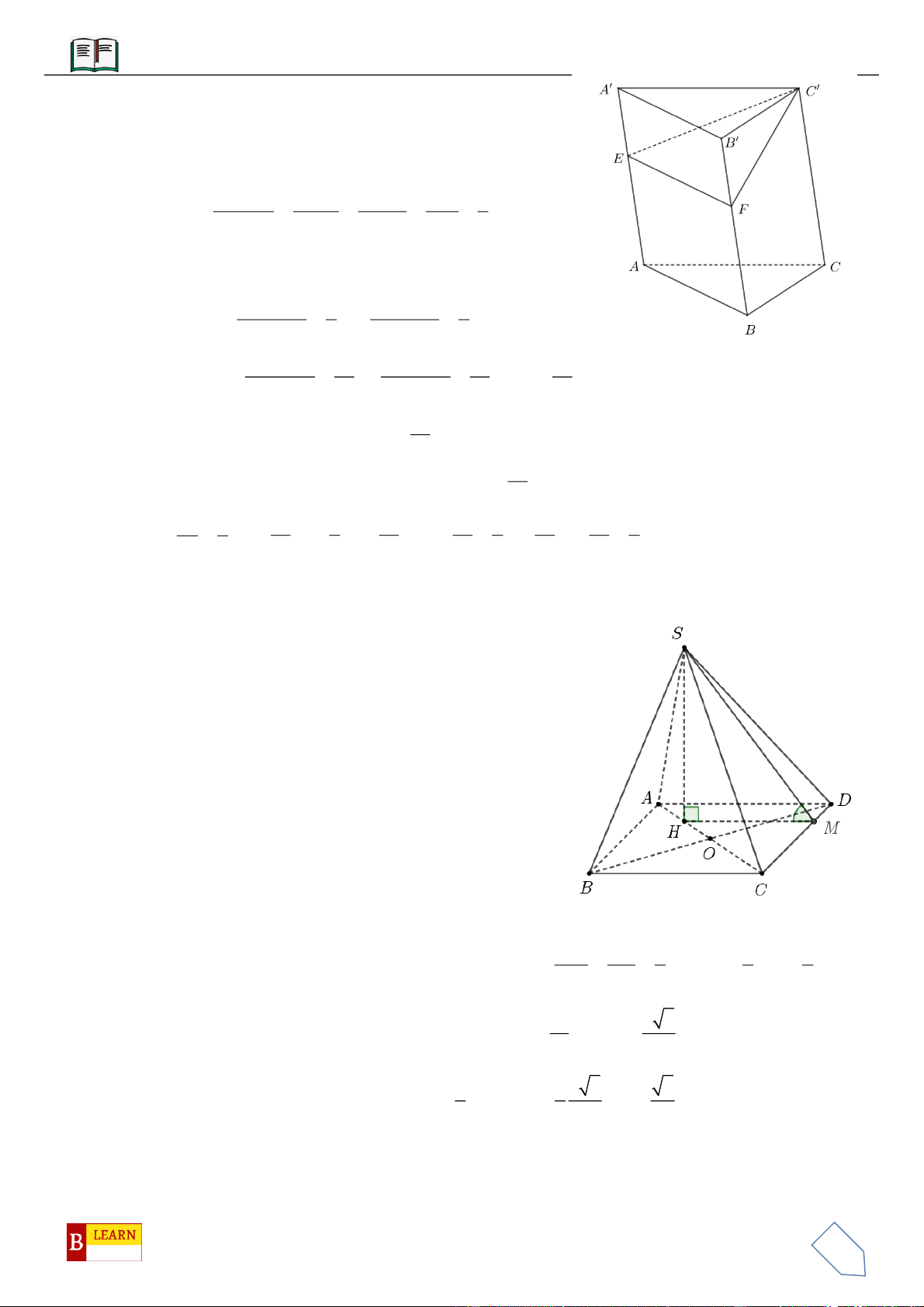
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

205

Câu 10: Chọn B

+) Do khối chóp

.C A B FE

  

và khối chóp

.C A B BA

  

có

chung đường cao hạ từ

C



nên

.

2

1

2

C A B FE

A B FE A B E

C A B BA A B BA A B A

V

SS

AE

V S S A A k

  

   

      



   



+) Do khối chóp

.C ABC



và khối lăng trụ

.ABC A B C

  

có chung đường cao hạ từ

C



và đáy là

ABC

nên

.

ABC.

1

3

C ABC

ABC

V



  



.

ABC.

2

3

C A B BA

ABC

V

  



Từ và suy ra

.

1

1 ABC.

ABC. ABC.

2 2 2

.

3 3 3

C A B FE

ABC

A B C A B C

V

VV

V k V k k

  

     

    

+) Đặt

ABC.ABC

VV

  



Khi đó

1

21

2

.

3

2

.

3

VV

k

V V V V V

k











   





Mà

1

2

7

V



nên

2 2 2 2 2 2 6 2

. ( . ) (1 ) 2 6 3

3 7 3 3 7 3 7 7

V V V k k

k k k k k

          

Câu 11: Chọn B

Dựng

HM CD

tại

M

.

Ta có

 

CD HM

CD SHM CD SM

CD SH





   







.

Khi đó

   

 

SCD ABCD CD

SCD SM CD

ABCD HM CD



















nên góc giữa

 

SCD

và

 

ABCD

là góc

SMH

.

Theo giả thiết ta có

60SMH 

.

Mặt khác ta lại có

CMH

đồng dạng với

CDA

nên

3 3 3

4 4 4

HM CH

HM AD a

AD CA

    

.

Xét

SMH

vuông tại

H

ta có

3 3 3

.tan tan60

44

a

SH HM SMH a   

.

Thể tích khối chóp

.S ABCD

là

23

.

1 1 3 3 3

..

3 3 4 4

S ABCD ABCD

V SH S a a a  

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

206

Câu 12: Chọn D

Gọi

;;O AC BD F DM AB K SB MN     

.

Ta có:

D 60BA 

nên tam giác

ADB

là tam giác

đều.

K

là trọng tâm

SCM

2

3

MK

MN



.

Xét:

.

..

.

2 1 1 1 1

. . . . .

3 2 2 6 6

M KFB

M KFB M NDC

M NDC

V

MK MF MB

VV

V MN MD MC

    

.

5

6

KFBNDC M NDC

VV

.

Mà:

..

2

M NDC B NDC

VV

và

..

1

2 2.

2

N BCD S BCD

VV

, vì

 

1

,,

2

d N BDC d S BDC

.

1

2

S ABCD

V

2 . .

55

6 12

KFBNDC M NDC S ABCD

V V V V   

1 . 1 .

7

12

SADFKN S ABCD S ABCD

V V V V V    

1

2

7

5

V



.

Câu 13: Chọn B

Gọi V là thể tích lăng trụ

.ABC A B C

  

.

Ta có:

   

1

4

',( ) ( '),( )

MNP BCC B

SS

d A MNP d A BCC B





















1

4

A MNP A BCC B

VV

   



Mặt khác:

12

33

A BCC B A ABC

V V V V V V

   

    

3

1 2 1 2

48 8 .

4 3 4 3

A MNP

V V cm



      

Câu 14: Chọn A

Trong mặt phẳng

 

SBC

, qua

G

kẻ đường thẳng song song với

BC

cắt

,SB SC

lần lượt tại

,MN

. Suy ra

 

//BC MAN

,

 

AG MAN

. Vì vậy

   

MAN





.

Ta có tam giác

ABC

vuông cân tại

B

,

2AC a AB BC a   

.

N

M

P

A'

C'

A

B

C

B'

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

207

3

11

. . .

3 2 6

SABC

a

V SA AB BC  

.

Gọi

E

là trung điểm của

BC

. Ta có

2

//

3

SM SN SG

MN BC

SB SC SE

   

.

Khi đó:

2 2 4

..

3 3 9

SAMN

SABC

V

SM SN

V SB SC

  

5

9

SABC

V



33

5 5 5

.

9 9 6 54

SABC

aa

VV   

.

Cách tính khác:

Gọi

H

là hình chiếu vuông góc của

A

trên

SB

. Ta chứng minh được

 

AH SBC

và

BMNC

là hình thang vuông tại

,BM

.

Khi đó

 

11

. . . .

32

ABMNC

V AH BM MN BC

3

1 2 1 2 2 5

. . . .

3 2 2 3 3 54

a a a a

a



  





.

Câu 15: Chọn C

Gọi cạnh của khối tứ diện đều ban đầu là

a

, ta có

2

32

33

a

h a a



  





3

2

ah

.

Thể tích của khối tứ diện ban đầu là

2

3

1 3 3

. . .

3 2 4 8

h

V h h









.

Do đó tổng thể tích của ba khối tứ diện đều có chiều cao

x

được cắt ra là

3

8

x

.

Theo giả thiết ta có

33

3

31

.

8 4 8

12

x h h

x  

.

Câu 16: Chọn B

Ta thấy thiết diện của

 

AEF

và hình hộp là tứ giác

'AFC E

.

Ta có

. ' . ' ' ' '

4

ABCD AFC E ABCD A B C D

x y z t

VV

  



trong đó

. ' . ' ' ' '

0 1 ' 3 1

0; ; 1;

' ' 4 ' ' 4 2

ABCD AFC E ABCD A B C D

BE CC DF

x y z t V V

AA BB CC DD

         

.

Vậy tỉ lệ thể tích của hai khối là 1.

Câu 17: Chọn B

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

208

Ta có

' ' '

' ' ' ' ' ' ' ' ' ' '

' ' ' ' ' ' ' '

' ' ' ' ' ' ' ' ' '

1

3

1 1 2 1

.

2 2 3 3

1 1 2 1

.

2 2 3 3

2 2 2 4

.

5 5 3 15

GA B C ABCA B C

BB MN A BB N A BCB C ABCA B C ABCA B C

ABB C ABCB C ABCA B C ABCA B C

A BCN A BCB C ABCA B C ABCA B C

VV

V V V V V

V V V V

  







   

  

Do đó thể tích của khối

A BCN



nhỏ nhất.

Câu 18: Chọn D

Do

.S ABCD

là hình chóp tứ giác đều nên hình chiếu của

S

lên mặt phẳng

 

ABCD

trùng với tâm

H

của hình

vuông

ABCD

.

C



là trung điểm của

SC

và

H

là trung điểm

AC

nên

I AC SH





là trọng tâm

SAC

2

3

SI SH

Ta có:

BD AC

,

BD SH

 

BD SAC

BD SC

 

//BD P

//BD B D





Mặt khác:

   

P SBD B D





,

 

I AC P





,

 

I SH SBD

I B D





Do đó:

2

3

SB SD SI

SB SD SH



  

Ta có:

.

..

1

2 . .

.

1

2 1 1

2

1

3 2 3

2

S AB C D

S AB C D S AB C

S ABCD S ABC

S ABCD

V

VV

V

V V V

V

  

    

     

.

Câu 19: Chọn A

Gọi

,EF

lần lượt là trung điểm của

,BC MN

. Gọi H là

trọng tâm

ABC

.

Ta có:

SBC

cân tại

S

SF MN

.

 

   

 

SF MN

MN SBC AMN

SBC AMN

















 

SF AMN

.

Ta có:

ASE

có

AF

vừa là đường cao vừa là đường

trung tuyến

ASE

cân tại

A

.

3

2

a

SA AE  

;

22

15

6

a

SH SA AH  

,

2

3

4

ABC

a

S





.

23

1 3 3 1 15 3 5

. . .

4 4 4 3 6 4 32

SAMN SABC SAMNCB SABC

a a a

V V V V    

.

G

N

M

A

C

B'

A'

B

C'

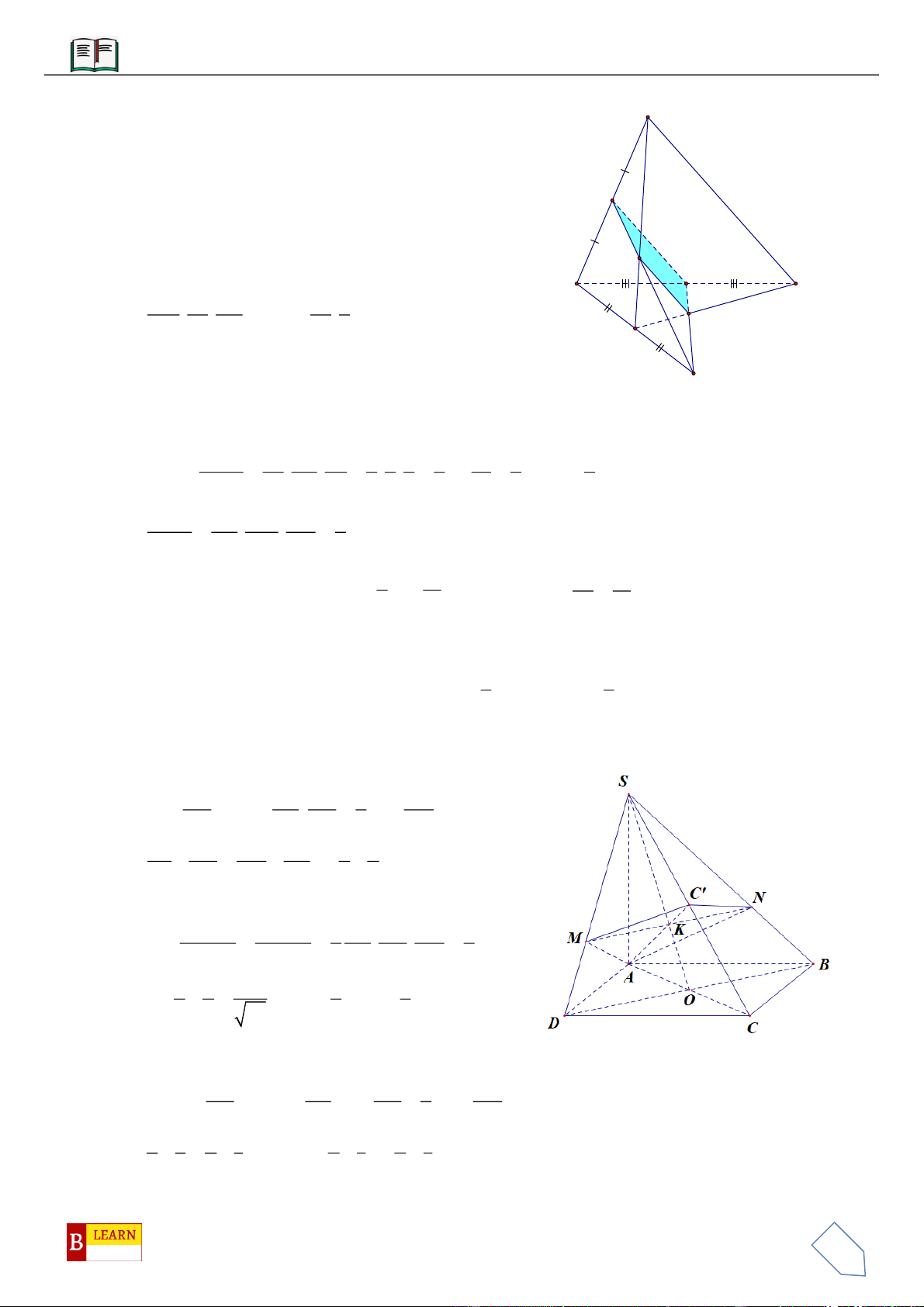
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

209

Câu 20: Chọn C

Kẻ

// , //MQ SC NP SC

ta được

 

MNPQ

chính là

mặt

phẳng

 



.

Ba mặt phẳng

     

,,SAB ABC



giao nhau theo ba

giao tuyến

,,MN AB PQ

đồng quy tại

.I

Xét trong tam giác

SAB

có

1

. . 1 1. . 1

2

MS IA NB IA

MA IB NS IB

  

nên

B

là trung điểm của

.IA

Các tam giác

,SAI IAC

lần lượt có các trọng tâm là

,.NP

Gọi thể tích khối chóp

IAMQ

là

.V

Ta có:

1

1 2 2 2 7 7

. . . .

2 3 3 9 9 9

IBNP

IAMQ

V

IB IN IP

VV

V IA IM IQ V

      

 

1

. 1 2

1

. . .2.2 2 2 2

2

ABSC

S ABC

AIMQ

V

AB AS AC

V V V V V

V AI AM AQ

       

 

2

Từ

 

1

và

 

2

suy ra

2

7 11

2

99

V V V V  

. Từ đó suy ra

1

2

7

11

V



.

Câu 21: Chọn D

Ta có tứ diện

AMNP

vuông tại

A

nên

3

11

. . ' .8 .18 .28 672

66

V AB AD AA a a a a  

.

Câu 22: Chọn C

Đặt

' ' ' 1 '

1; ; ;

2

SA SB SC SD

xy

SA SB SC SD

   

. Ta có

11

3

' ' '

SA SC SD SB

SA SC SD SB x y

     

Có

. ' ' ' . ' ' '

..

1 ' ' ' 1

..

2 2 4

S B C D S B C D

S ABCD S BCD

VV

SB SC SD

m xy

V V SB SC SD

   

.

1 1 2 4 1

3

99

xy m

xy

      

.

Câu 23: Chọn B

Đặt

1

SA

x

SA





;

SB

y

SB





;

1

2

SC

z

SC





;

SD

t

SD





. Ta có

1 1 1 1

x z y t

  

1 1 1 1

1 2 3

y t y t

      

.

P

N

Q

B

M

A

I

C

S

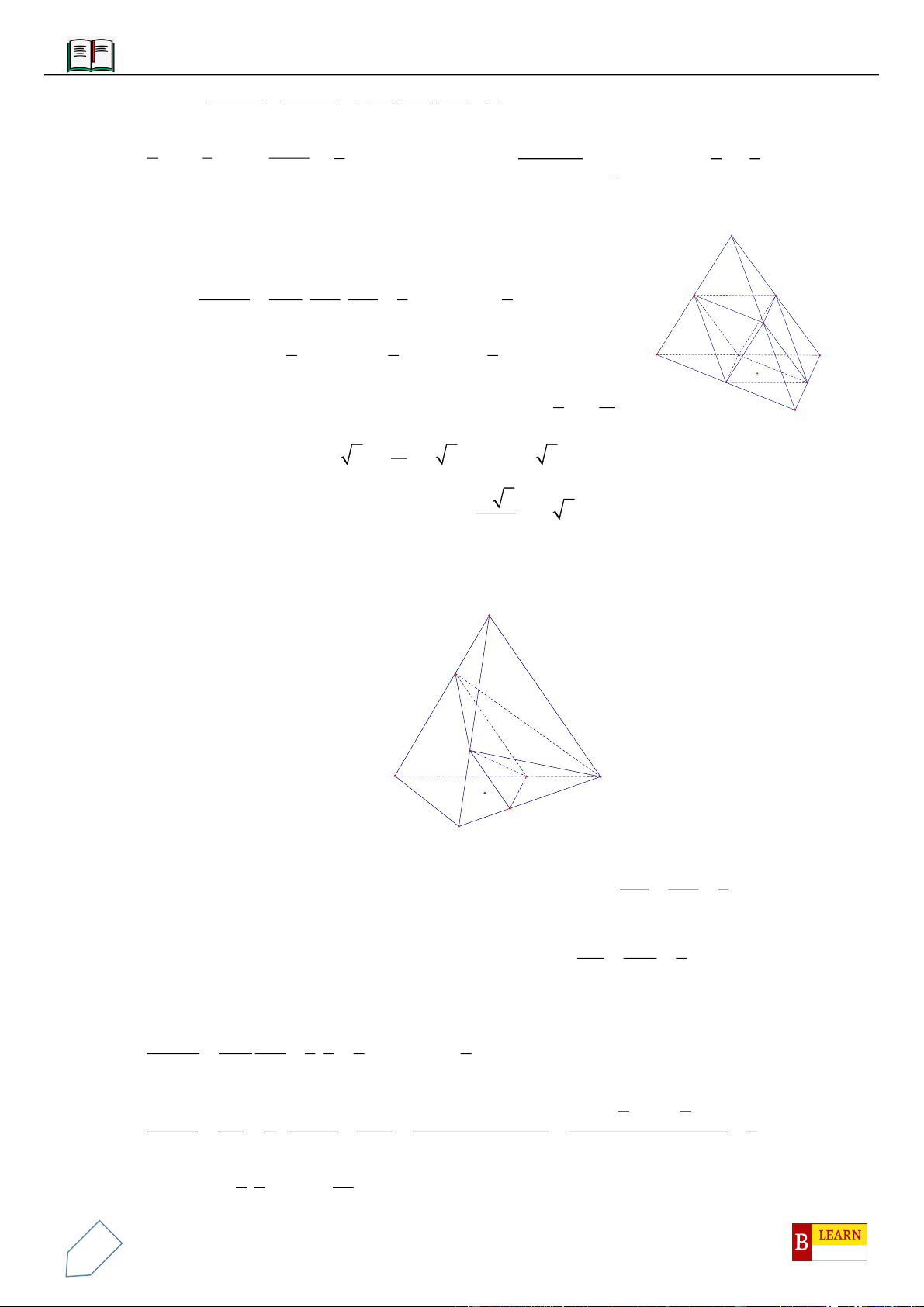
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

210

Mà

..

11

..

2 2 4

S B C D S B C D

S ABCD S BCD

VV

SB SC SD

m yt

V V SB SC SD

     

  

   

.

11

3

31

t

y

y t t

   



,

1

3

t









 

2

1

;1

3

11

max

28

4 3 1

t

m f t f t f

t











     







.

Câu 24: Chọn C

Gọi

.A BCD

VV

Ta có:

.

11

..

88

A MNP

A BCD

V

AM AN AP

VV

V AB AC AD

   

Tương tự

. . .

1 1 1

;;

8 8 8

B MQS C NQR D PRS

V V V V V V  

. . . .

1

4.

82

MQNPSR A MNP B MQS C NQR D PRS

V

V V V V V V V V       

Theo giả thiết

9 2 9 2 18 2

2

MQNPSR

V

VV    

.

Đặt độ dài cạnh của tứ diện là

a

, ta có:

3

2

18 2 6

12

a

Va   

. Vậy

6 cma 

.

Câu 25: Chọn A

Ta có

   

 

   

2

/ / ,

3

//

N ACD

DE AN

ACD NE AD E CD

DC AC

AD











     











   

 

   

1

/ / ,

3

//

M ABD

DF AM

ABD MF AD F BD

DB AB

AD











     











.

Như vậy thiết diện của tứ diện

ABCD

cắt bởi

 



là tứ giác

MNEF

.

..

.

1 2 2 2

.

3 3 9 9

A MND

A MND A BCD

A BCD

V

AM AN

VV

V AB AC

    

.

..

21

14

93

;

39

ABC ABC ABC

D MNF D MNB MNB ABC AMN BCN

D MNB D ABC ABC ABC ABC

S S S

V V S S S S

DF

V DB V S S S



     

. . .

1 4 4

.

3 9 27

D MNF A BCD A BCD

V V V  

.

F

E

A

C

D

B

M

N

P

N

M

S

Q

R

B

D

C

A

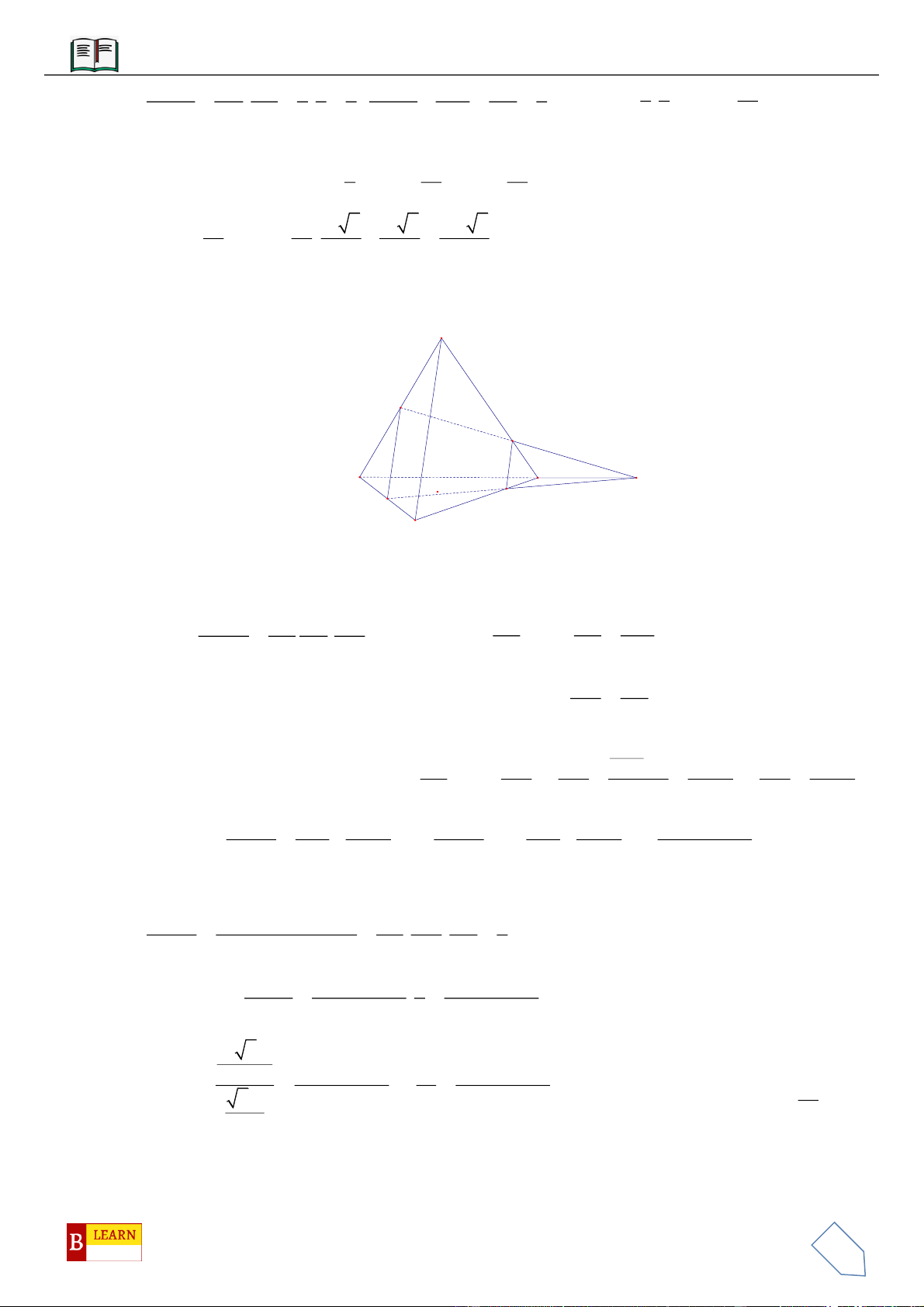
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

211

..

2 1 2 1

. . ;

3 3 9 3

D EFN D CBN CBN

D CBN D CBA CBA

V V S

DE DF CN

V DC DB V S CA

     

. . .

1 2 2

.

3 9 27

D EFN A BCD A BCD

V V V  

.

Cộng theo vế ta được:

. . . . . .

2 4 2

9 27 27

A MND D MNF D EFN A BCD A BCD A BCD

V V V V V V    

3 3 3

.

12 12 2 2 4 2

.

27 27 12 27 108

A BCD

a a a

VV    

.

Câu 26: Chọn C

Gọi

P EN CD

Q EM AD











suy ra thiết diện của tứ diện

ABCD

cắt bởi

 

MNE

là tứ giác

MNPQ

.

Ta có:

.

.BNM

.

E DPQ

E

V

ED EP EQ

V EB EN EM



. Theo giả thiết:

1BE ED k

k

BD EB k



  

;

Ta thấy:

   

//

/ / / /

MN AC

EQ EP

PQ MN AC

EMN ACD PQ

EM EN





  









Xét

EAB

có

EM

là trung tuyến

1

2 1 2 2

1

12

2 2 2 2 1

k

EB EM EM k EQ k

k

ED EQ EQ k EM k







       



Thay vào:

 

22

2

.

2

..

1 2 2 1 2 2 8 11 4

. 1 .

2 1 2 1

21

E DPQ

E BNM E BNM

V

k k V k k k k

V k k V k k

kk

         

    

   



   



.

Lại có:

 

.

,.

..

4

D, .

BMN

E BMN

D ABC

ABC

d E BMN S

V

EB BM BN k

V DB BA BC

d ABC S

  

Từ và suy ra

   

22

.

8 11 4 8 11 4

.

4

2 1 4 2 1

A BCD

V k k k k k

V

k k k

   





Như vậy

   

3

22

2

22

3

11 2

4

8 11 4 22 8 11 4

294

40 187 108 0

27

49

2

4 2 1 4 2 1

40

12

a

k

k k k k

kk

k

a

kk





   



       











Vậy

4k 

.

Câu 28: Chọn A

P

Q

M

N

B

D

C

A

E

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

212

Gọi

( ) , ( ) , ( ) , ( ) , ( ) , ( )P SD Q SC R SB E SD F SC G SB

     

           

thì theo đề ta có:

3

.

10 dm

S MPQR

V 

. . .

,

S NEFG S NEF S NGF

V V V

.

..

.

. . 2.2.2 8

S NEF

S NEF S MPQ

S MPQ

V

SN SE SF

VV

V SM SP SQ

   

,

.

..

.

. . 2.2.2 8

S NGF

S NEF S MRQ

S MRQ

V

SN SG SF

VV

V SM SR SQ

   

 

3

. . . . . . . .

8 8 8 8 80 dm .

S NEFG S NEF S NGF S MPQ S MRQ S MPQ S MRQ S MPQR

V V V V V V V V        

Vậy thể tích của khối chóp cụt

.NEFG MPQR

là

3

..

80 10 70 dm

S NEFG S MPQR

V V V    

.

Câu 29: Chọn B

Ta chứng minh

//PQ BC

.

Giải sử

   

SBC SAD d

khi đó ta có:

   

// //

//





















SBC SAD d

SBC ABCD BC

d BC, d AD.

SAD ABCD AD

BC AD

,MN

lần lượt là trung điểm các cạnh

,SA SD

nên ta có

MN / / AD, MN / / d.

Ta lại có:

   

//























SBC SAD d

SBC PQ

PQ / / MN PQ / / BC.

SAD MN

d MN

Xét tam giác

SBC

có

PQ / / BC,

SP

x

SB





SQ SP

= x.

SC SB

d

N

M

A

D

B

C

S

Q

P

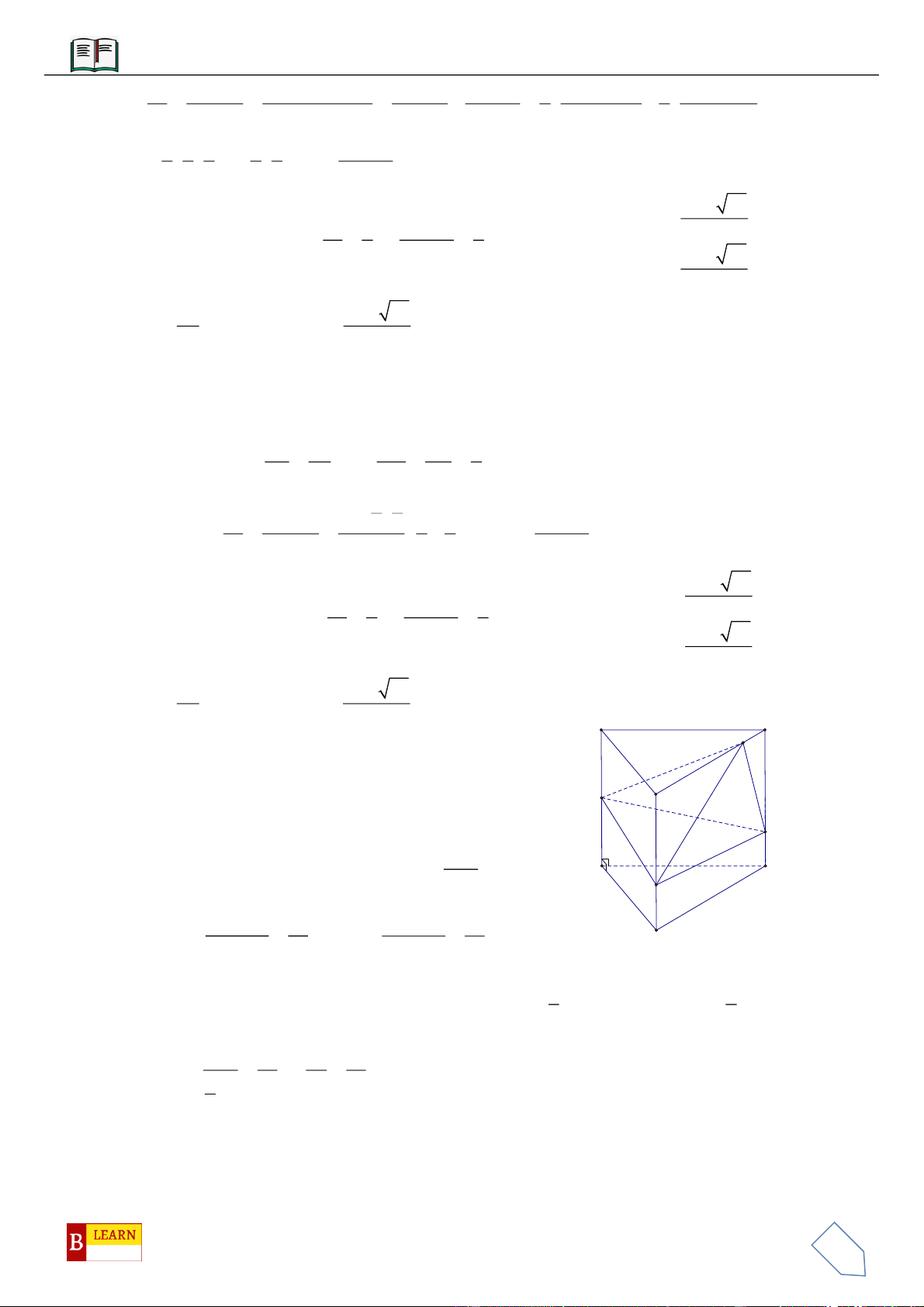
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

213

. . . .

.

1

. . . .

1 . . 1 . .

2 2 2 . . 2 . .

S MNQP S MNP S NQP S NQP

S MNP

S ABCD S ABCD S ABD S DCB

V V V V

V

SM SN SP SN SQ SP

V V V V V SA SB SD SD SC SB



       

2

1 1 1 1 1 2

2 2 2 2 2 8

xx

x x x



         

Theo bài ra:

2

1

1 33

1 2 1

4

2 2 4 0

2 8 2

1 33

4

x

V

xx

V V x x

V

x













         











Mà

1 33

0

4

SP

x x x

SB



     

Cch 2:

Sử dụng công thức tính nhanh tỉ lệ thể tích của khối chóp tứ giác như sau:

Cho chóp

.S ABCD

và mặt phẳng

 



cắt các cạnh

, , ,SA SB SC SD

của khối chóp tại các điểm

, , ,M P Q N

với



SQ SP

= x,

SC SB

1

2

SM SN

SA SD

  

Thì ta có:

2

.

1

.

11

.

1 1 2

22

48

S MNPQ

S ABCD

xx

V

xx

V V x x



  

      





Theo bài ra:

2

1

1 33

1 2 1

4

2 2 4 0 .

2 8 2

1 33

4

x

V

xx

V V x x

V

x













         











Mà

1 33

0

4

SP

x x x

SB



    

Câu 30: Chọn B

Đặt

,'BC a CC b

Diện tích tam giác

'NPQ

là:

 

' ' ' ' ' ' '

11

30

NPQ BCC B NB Q PC Q BCPN

ab

S S S S S    

Suy ra:

.'

'. ' '

11

30

M NPQ

A BCC B

V



. Tức là:

1

'. ' '

11

30

A BCC B

V



.

Mặt khác:

'. ' ' '. . ' ' ' '. ' ' 2 2 '. ' ' 2

12

33

A BCC B A ABC ABC A B C A BCC B A BCC B

V V V V V V V V      

Do đó:

11

2

11 11

2

30 45

3

VV

V

  

.

Câu 31: Chọn D

b

a

Q'

P

N

M

B'

C'

A

C

B

A'

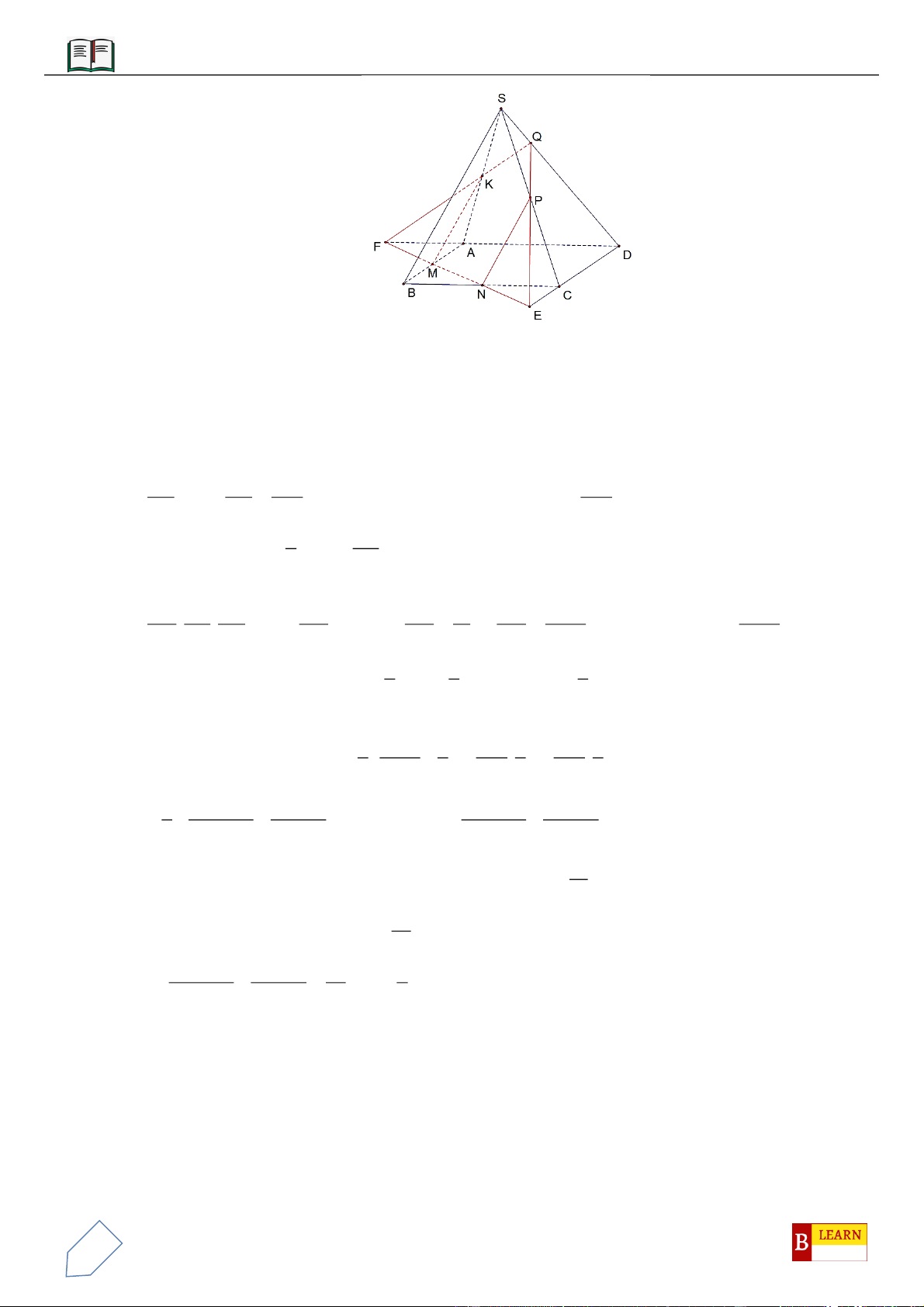
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

214

Trong mặt phẳng

 

ABCD

, kéo dài

MN

cắt

DA

,

DC

lần lượt tại

F

,

E

.

Trong mặt phẳng

()SAD

, gọi

FK SD Q

. Trong mặt phẳng

 

SCD

, gọi

QE SC P

.

Suy ra thiết diện là ngũ giác

MNPQK

và

// // MN AC PK

.

Đặt

 

,h d S ABCD

 

, , .

11

KA KA t t

t d K ABCD d P ABCD h

KS SA t t

     



Ta có:

1

3

2

FD

FA BN AD

FA

   

.

Áp dụng định lý Menelaus cho tam giác

SAD

, suy ra

 

1 3 3

. . 1 .3. 1 ,

3 3 1 3 1

QS FD KA QS QS QD t t

t d Q ABCD h

QD FA KS QD QD t SD t t

        



Mặt khác:

1 1 9

4 8 8

FAM NCE BMN ABC ABCD DEF ABCD

S S S S S S S     

Suy ra thể tích của khối đa diện không chứa đỉnh S là

1 3 9 1 1

...

3 3 1 8 1 8 1 8

QDEF KAMF PECN

t t t

V V V V h S S S

t t t



     



  



   

1 27 2

. . .

3

8 3 1 8 1

ABCD

tt

hS

tt











   

27 2

8 3 1 8 1

ABCD

tt

VV

tt



  







Phần thể tích của khối đa diện không chứa đỉnh

S

bằng

7

13

phần còn lại suy ra thể tích của khối

đa diện không chứa đỉnh S bằng

13

20

thể tích khối chóp

.S ABCD

   

27 2 13 2

20 3

8 3 1 8 1

tt

t

tt

    



.

Câu 32: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

215

Gọi

Q

là giao điểm của mặt phẳng

 

MNP

với

BB



.

Giả sử

AM

x

AA







,

CP

y

CC







,

DN

z

DD







,

BQ

t

BB







. Khi đó

x y z t  

.

3

A B D MQN

A B D ABD

V

x z t

V

  





.

6

A B D MQN

A B C D ABCD

V

x z t

V

  

   





.

3

C B D PQN

C B D CBD

V

y z t

V

  





.

6

C B D PQN

A B C D ABCD

V

y z t

V

  

   





.

1

2

nn

aa





.

1

2

MNPQ A D C B

ABCD A D C B

V

A M C P

V AA CC

   













1 1 1

2 2 3









5

12



. D.

5 5275

.

12 6

MNPQ A D C B ABC A D C B

VV

       

  

.

Câu 33: Chọn A

Vì

2SA SB SC SD a   

nên hình chiếu vuông góc hạ từ đỉnh

S

xuống đáy trùng với tâm

đường tròn ngoại tiếp đáy, tức là trùng với điểm

O AC BD

.

Ta có:

22

2 2 2

43

2

42

a a a

SO SA AO a



    

3

.

13

..

33

S ABCD ABCD

a

V SO S  

.

Ta có:

3 3 3

. . .

2 3 2 1 3 5 3

. . . . . .

3 6 3 4 6 36

S ABEF S ABE S AEF SABC SACD

SE SE SF a a a

V V V V V

SC SC SD

   

      

   

   

.

Câu 34: Chọn B

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

216

Đặt

 

01

SM

xx

SA

  

, kí hiệu

,Vh

lần lượt là thể tích và chiều cao của khối chóp đã cho.

Theo định l Ta-let, ta có:

MN NP PQ QM SM

x

AB BC CD DA SA

    

Và

 

,

1

,

d M ABCD

AM

x

SA

d S ABCD

  

 

,1d M ABCD x h  

.

Vì vậy

 

   

22

.

. . , . 1 . . 3 1

MNPQ M N P Q

V MN MQ d M ABCD x x h AB AD x x V

   

    

Theo BDT Co-si, ta có:

   

3

2

1 1 2 2 4

1 . . 2 2

2 2 3 27

x x x

x x x x x

    

    





.

Do đó,

.

4

9

MNPQ M N P Q

VV

   



. Dấu “=” xảy ra

2

22

3

x x x    

.

Câu 35: ChọnA

Ta có:

   

ABE SDC Ex

Ex DC AB

AB DC















.

Gọi

F Ex SD

,

 

, 0 1

SE

xx

SC

  

SF SE

x

SD SC

  

.

Do

ABCD

là hình thang có

2AB CD

nên

12

2 ; .

33

ACB ADC ADC ABCD ACB ABCD

S S S S S S

   

   

.

Ta có:

.

..

.

11

33

S ACD ACD

S ACD S ABCD

S ABCD ABCD

VS

VV

VS



   

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

217

.

..

.

22

33

S ABC ABC

S ABC S ABCD

S ABCD ABCD

VS

VV

VS



   

.

Lại có:

2 2 2

.

. . .

.

1

. . .

3

S AEF

S AEF S ACD S ABCD

S ACD

V

SE SF

x V x V x V

V SC SD

    

)

.

. . .

.

2

..

3

S ABE

S ABE S ABC S ABCD

S ABC

V

SE

x V x V x V

V SC

    

).

Theo bài ra mặt phẳng

 

ABE

chia khối chóp

.S ABCD

thành hai khối đa diện có thể tích bằng

nhau nên

.

1

2

S ABEF SABCD

VV

22

. . . . .

1 1 2 1 1 2 1

.0

2 3 3 2 3 3 2

S AEF S ABE S ABCD S ABCD S ABCD

V V V x x V V x x



         





2 10

2

2 10

2

x





















. Do

2 10

01

2

xx



   

.

Câu 36: Chọn B

Đặt

 

01

SM

xx

SA

  

, kí hiệu

,Vh

lần lượt là thể tích và chiều cao của khối chóp đã cho.

Theo định l Ta-let, ta có:

MN NP PQ SM

x

AB BC CD SA

   

Và

 

,

1

,

d M ABC

AM

x

SA

d S ABC

  

 

,1d M ABC x h  

.

Vì vậy

 

   

22

.

. , . 1 . 3 1

MNP M N P MNP ABC

V S d M ABCD x x h S x x V

  

    

Theo BDT Co-si, ta có:

   

3

2

1 1 2 2 4

1 . . 2 2

2 2 3 27

x x x

x x x x x

    

    





.

Do đó,

.

4

9

MNP M N P

VV

  



. Dấu “=” xảy ra

2

22

3

x x x    

.

Câu 37: Chọn A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

218

Đặt

 

01

SM

xx

SA

  

. Theo định l Ta-let, ta có:

SM SN SP

x

SA SB SC

  

Và

3

. . .

S MNP S ABC S ABC

SM SN SP

V V x V

SA SB SC



Theo giả thiết,

..

1

2

S MNP S ABC

VV

nên

3

11

2

xx  

Câu 38: Chọn C

Ta có

2

1

.

3

ABCD

V SA S

,

.2

11

.

32

S ABCD ABCD

V S D S V





.

Gọi

H S A SD





,

 

L S B S CD





khi đó thể tích chung của hai khối chóp

.S ABCD

và

.S ABCD



là thể tích khối

HLCDAB

. Do

//AB CD

nên giao tuyến

HL

của hai mặt

 

S AB



và

 

SCD

phải song song với

AB

.

1 . .HLCDAB S ABCD S HLCD

V V V V



  

;

11

23

S H S D S H

HA SA S A

  

   



.

. . .

.

. 1 1 1 1 1

.

. 3 3 9 9 18

S HLD

S HLD S ABD S ABCD

S ABD

V

S H S L

V V V

V SA SB



  





     

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

219

.

. . .

.

1 1 1

3 3 6

S LCD

S LCD S BCD S ABCD

S BCD

V

SL

V V V

V S B



  



    



. . . . . .

1 1 2

18 6 9

S HLCD S HLD S LCD S ABCD S ABCD S ABCD

V V V V V V

     

    

1 . . . 2

77

9 18

S ABCD S HLCD S ABCD

V V V V V

  

    

. Vậy

1

2

7

18

V



Câu 39: Chọn D

Mặt phẳng

 

P

song song với

 

ABC

và cắt các cạnh bên

,,SA SB SC

lần lượt tại

,,M N P

.

Theo Ta-let ta có:

0

SM SN SP

x

SA SB SC

   

.

Do đó

3

.

. . 0

S MNP

SABC

V

SM SN SP

x

V SA SB SC

  

.

Theo giả thiết:

3

.

3 3 3

1 1 1 1

22

2 2 2

S MNP

SABC

V

MN SM a

x x MN

V AB SA

         

.

Vì tam giác

ABC

đều cạnh

a

nên tam giác

MNP

là tam giác đều có cạnh bằng

3

2

a

.

Vậy

2

3

4

3

2

4

44

MNP

a

S









.

Câu 40: Chọn C

C

B

A

P

N

M

S

L

H

C

A

D

B

S

S'

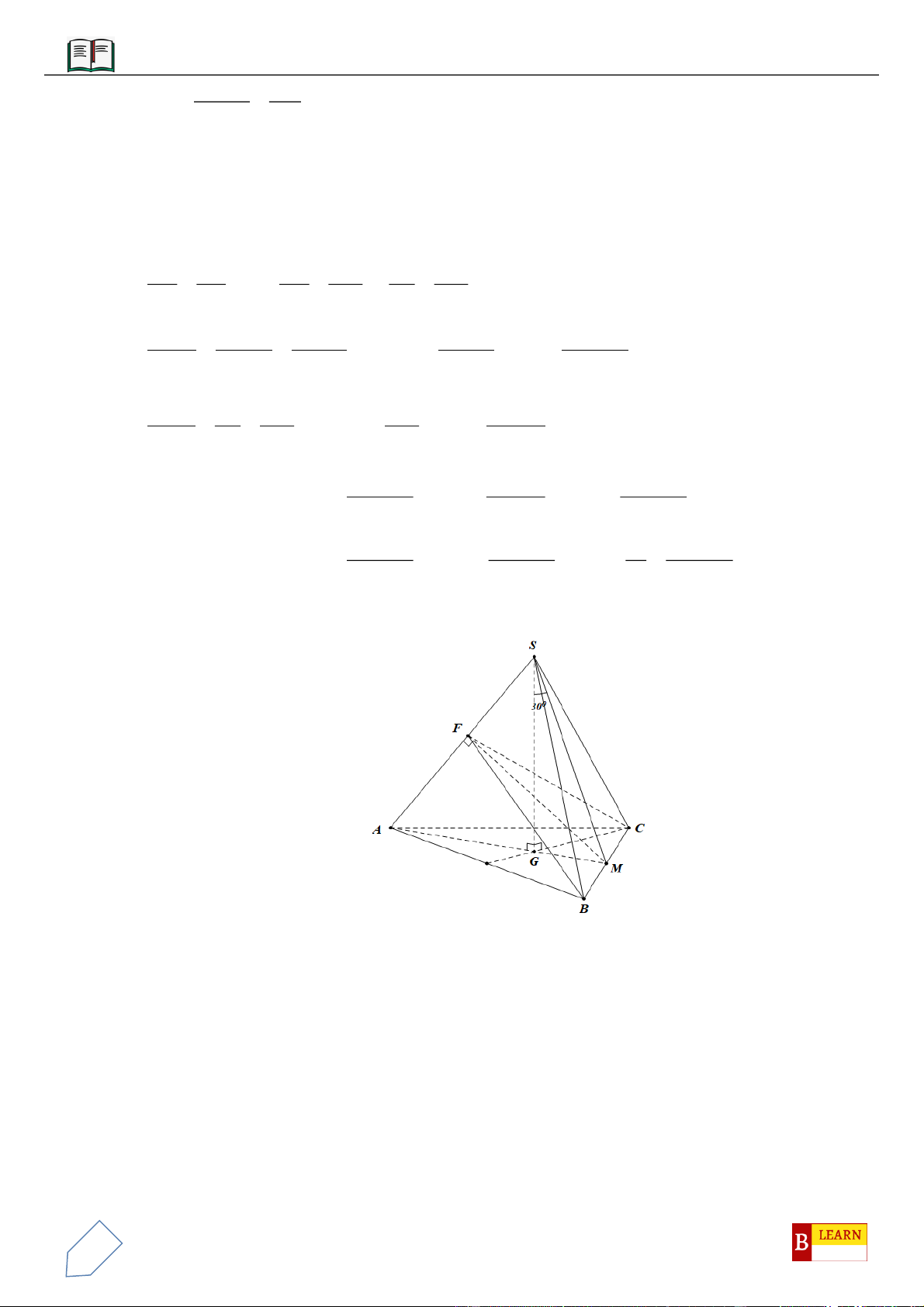
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

220

Ta có

.

2

'

S ABCD

V

SD

k

V SA





.

Gọi

H S A SD





,

 

L S B SCD





khi đó thể tích chung của hai khối chóp

.S ABCD

và

.S ABCD



là thể tích khối

HLCDAB

. Do

//AB CD

nên giao tuyến

HL

của hai mặt

 

S AB



và

 

SCD

phải song song với

AB

.

1 . .HLCDAB S ABCD S HLCD

V V V V



  

.

11

S H S D S H k S L k

k

HA SA S A k S B k

   

     





     

2 2 2

.

. . .

2 2 2

.

1 1 2 1

S HLD

S HLD S ABD S ABCD

S ABD

V

S H S L k k k

V V V

V SA SB

k k k



  





    

  

 

.

. . .

.

11

21

S LCD

S LCD S BCD S ABCD

S BCD

V

S L k k k

V V V

V S B k k

k



  



    







 

22

. . . . . .

22

2

21

2 1 2 1

S HLCD S HLD S LCD S ABCD S ABCD S ABCD

k k k k

V V V V V V

k

kk

     



    





   

2

1 . . . 2

22

3 2 3 2

2 1 2 1

S ABCD S HLCD S ABCD

k k k

V V V V V

kk

  



    



. Vậy

 

2

1

2

32

.

21

V

kk

V

k







Câu 41: Chọn B

Gọi

M

là trung điểm

BC

,

 

F SA





, trong đó

 



là mặt phẳng chứa

BC

và vuông góc

SA

,

H

là hình chiếu của

G

lên

SM

. Ta có:

 

SA





,

 

FM





nên

SA FM

.

Vì

.S ABC

là hình chóp tam giác đều nên

SG

là đường cao hình chóp ứng với đáy

 

ABC

và

ABC

là tam giác đều.

Ta có:

AM

vừa là đường trung tuyến, vừa là đường cao trong tam giác đều nên

AM BC

.

 

SG ABC

,

 

BC ABC

nên

SG BC

.

AM SG G

và

 

,AM SG SAM

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

221

Suy ra

 

BC SAM

BC GH

. Do đó:

 

,

GH SM

GH BC

GH SBC

SM BC M

SM BC SBC























.

Ta lại có:

 

SG SBC S

SH

SH SBC

















là hình chiếu vuông góc của

SG

lên

 

SBC

.

 









, , 30SG SBC SG SH GSH    

.

Giả sử cạnh của tam giác đều

ABC

là

a

.

Xét tam giác

SGM

vuông tại

G

, ta có:

3

cot30 . 3

62

aa

SG GM   

.

Xét tam giác

SAG

vuông tại

G

, ta có:

22

21

3 4 6

a a a

SA AG SG    

.

Trong tam giác

SAM

, ta có:

3

.

. 3 7

22

14

21

6

aa

SG AM a

MF

SA

a

  

.

Xét tam giác

AFM

vuông tại

F

, ta có:

22

3 3 7 21

2 14 7

a a a

FA AM FM

   

    

   

   

.

Suy ra

21

61

7

1 1 1

77

21

6

a

SF FA

SA SA

a

      

. Mà

.

1 . .

.

11

77

S FBC

S FBC S ABC

S ABC

V

SF

V V V

V SA

    

2.

6

7

S ABC

VV

. Do đó

1

2

1

6

V



.

Câu 42: Chọn A

Gọi

,,M N P

lần lượt là giao điểm của mỗi cạnh bên

SA

,

SB

,

SC

tương ứng với các cạnh bên

OA



,

OB



,

OC



. Phần chung của hai khối chóp

.S ABC

và

.O A B C

  

là khối đa diện

SMNPO

.

I

B'

C'

N

P

O

A

C

B

S

M

A'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

222

Từ giả thiết ta có

   

//ABC A B C

  

mà ta có

// //MN AB A B



,

// //NP AC A C



do đó

   

//ABC MNP

,

   

//A B C MNP

  

và

MNP

đều.

Xét các tam giác vuông

SMI

và

OMI

ta có

0

3

tan30

MI

SI MI

,

0

tan60

3

MI MI

OI 

suy ra

3

SI

OI



suy ra

3

4

SI MN

SO AB



,

1

' ' 4

OI MN

OS A B



.

Suy ra

3

AB





hay

2

.

.2

2

3 9 9

O A B C

V

VV

V

  

   

Do đó

33

.

2

3 27

4 64

S MNP

V

SI

V SO

   

  

   

   

33

O. O.

.2

1 1 9

4 64 64

MNP MNP

O A B C

VV

OI

V OS V

  

   

    

   

   

. Từ đó

1

22

27 9 9

64 64 16

OMNP SMNP

VV

V

VV



   

.

Câu 43: Chọn D

Giả sử cắt viên đá khối chóp tứ giác đều

.S ABCD

theo mặt phẳng

 

MNPQ

song song với

 

ABCD

như hình vẽ.

Theo Ta-let ta có:

0

SM SN SP SQ

x

SA SB SC SD

    

.

Theo giả thiết ta có:

. . . .

.

. . . .

1 1 1 1

.

2 2 2 2 2

S MNPQ S MNP S MPQ S MPQ

S MNP

S ABCD S ABC S ABC S ACD

V V V V

V

SM SP SN SQ

V V V V SA SC SB SD





        





.

3

3 3 3

1 1 1

2

4 4 4

MN SM a

x x MN

AB SA

        

.

Vì

ABCD

là hình vuông nên

MNPQ

là hình vuông cạnh

3

4

a

. Vậy

2

33

4 2 2

MNPQ

aa

S









.

Câu 44: Chọn B

O

D

C

B

A

S

Q

P

N

M

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

223

Ta có

.

1

3

A GBC GBC

A BCD BCD

VS



..

1

4

3

A GBC A BCD

VV  

.

Câu 45: Chọn B

Ta có

 

2

11

2 2 4

22

ABC

S AC  

và

 

, .sin60 2 3d C ABC C H AC

  

   

.

Khi đó,

..ABCB C ABC A B C A A B C

V V V

       



..

1

3

ABC A B C ABC A B C

VV

     



.

2

3

ABC A B C

V

  



2 16 3

.4.2 3

33



.

Câu 46: Chọn B

G

A

B

C

D

H

A

A'

C

C'

B

B'

N'

M'

P'

Q'

N

M

Q

P

O'

O

C

D

B

C'

A

B'

D'

A'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

224

Gọi

O

,

O



,

, , ,M N P Q

lần lượt là tâm của các hình chữ nhật

ABCD

,

A B C D

   

,

A B BA



,

BB C C



,

CC D D



,

AA D D



.

Ta có phần chung của hai khối tứ diện

A BC D



và

AB CD



là bát diện

OMNPQO



.

Gọi

, , ,M N P Q

   

lần lượt là trung điểm của

, , ,AB BC CD DA

. Ta có

1

4. .

1

8

2

ABCB ABCB

MNPQ M N P Q ABCB AM Q BM N CN P DP Q

ABCB ABCB ABCB ABCB

SS

S S S S S S S

S S S S

           



   

   

Ngoài ra, chiều cao của khối chóp

.O MNPQ

V

bằng

1

2

chiều cao của khối hộp

.ABCD A B C D

   

.

Suy ra

.

1

22

2

1 1 1 1

2. . . .

2 3 2 6

O MNPQ

V

VV

  

Câu 47: Chọn B

Đặt

.ABC A B C

VV

  



. Lấy điểm

E

trên

'CC

sao cho

3CC C E





.

Suy ra

1

3

A M B N C E

A A B B C C

  

  

  

   

//MNE ABC

.

Ta có:

..

1

3

C MNE A B C MNE

VV

   



1.

2

3

A B C MNE

VV

  



. Mặt khác:

.

1

3

A B C MNE

VV

  



.

Suy ra

1

2 1 2

.

3 3 9

V V V

2

27

99

V V V V   

1

2

7

V



.

Câu 48: Chọn B

N'

P'

Q'

M'

C

B

D

A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

225

Ta có

,MN

là trung điểm của

,SA SC

nên

1

2

SM SN

SA SC



.

Cách 1: Áp dụng định l Menelaus cho

SOD

ta có :

11

1 2 1 1

23

PS BD IO PS PS SP

PD BO IS PD PD SD

          

.

Cách 2: Kẻ

//OH BP

, ta có

O

là trung điểm của

BD

nên

H

là trung điểm của

PD

.

Ta có

//OH IP

mà

I

là trung điểm của

SO

nên

P

là trung điểm của

SH

.

Suy ra

SP PH HD

1

3

SP

SD



.

Theo công thức tỉ số thể tích ta có :

..

2

1 1 1

.

2 2 3 6

S BMPN S BMP

S ABCD S BAD

VV

SM SP

V V SA SD

     

Câu 49: Chọn B

Gọi

,,D E F

lần lượt là trung điểm các cạnh

,,BC CD DB

.

Ta có

33

2 2 1 2 2

. .54 4

3 3 4 27 27

AMNP ADEF ABCD ABCD

V V V V

   

    

   

   

.

Câu 50: Chọn D

N

P

M

F

D

E

A

B

C

D

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

226

Gọi

AH



là đường cao của hình hộp

Khi đó

 

; 45AA ABCD A AH



  

.sin45 5 2A H AA



   

.

2

6 .sin45 18 2

ABCD

S   

.Nên

.

. 180

ABCD A B C D ABCD

V S A H

   





.

..ABCDD B A BDD B C BDD B

V V V

     



. . .

2 2 2

. 120

3 3 3

ABD A B D BCD B C D ABCD A B C D

V V V

         

   

.

Câu 51: Chọn A

Đặt

.ABC A B C

VV

  



. Ta có

 

G ABC

nên

.

1

3

G A B C

VV

  



.

. . .

1 1 2 1

..

2 2 3 3

BB MN M BB N A BB N A BB C C

V V V V V V

    

    

;

.

1 1 2 1

.

2 2 3 3

ABB C A BB C C

V V V V

   

  

.

Ta có

4

5

CBN

CBC

S

CN

S CC







nên

4 4 1 4 1 2 4

. . .

5 5 2 5 2 3 15

A BCN A BCC A BCC B

V V V V V

     

   

Vậy khối tứ diện

A BCN



có thể tích nhỏ nhất.

Câu 52: Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

227

Gọi

d

là khoảng cách giữa

BB



và

CC



.

Ta có

 

1

.

2

BCPN

S CP BN d

1 3 4 1 31 31

. . . . .

2 4 5 2 20 40

BCC B

BB CC d BB d S





  

   





.

Do đó

. . .

31 31 2 31 2

. . . .60 31

40 40 3 40 3

BCMNP M BCPN M BCC B ABC A B C

V V V V

    

    

.

Câu 53: Chọn D

Gọi

P CD NE

,

Q AD ME

, khi đó

 

MNE

chia hình chóp là hai khối đa diện gồm

ACMNPQ

và

BMNDQP

.

Dễ dàng chứng minh được

P

,

Q

lần lượt là trọng tâm tam giác

EBC

và

EAB

. Khi đó:

2

3

EQ EP

EM EN



. Ta có

. . . .

1 2 2 2

. . . . .

2 3 3 9

E DQP E BMN E BMN E BMN

ED EQ EP

V V V V

EB EM EN

  

. . .

7

9

BMNDQP E BMN E DQP E BMN

V V V V   

.

Lại có

1

4

BMN ABC

SS





,

 

;

2

;

d E ABC

EB

DB

d D ABC



Nên

 

.

;.

11

2.

42

;.

BMN

E BMN

D ABC

ABC

d E ABC S

V

d D ABC S



  

suy ra

..

7 1 7

. . .

9 2 18

BMNDQP D ABC D ABC

V V V

33

..

11 11 2 11 2

..

18 18 12 216

ACMNPQ D ABC DMBDQP D ABC

aa

V V V V V      

.

Câu 54: Chọn C

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

228

Gọi

d

là khoảng cách giữa

AB

và

CD

.

Ta có

 

1 1 1 1 1 5 5

. . . . . . .

2 2 2 3 2 6 12

MBCN ABCD

S BM CN d AB CD d AB d S



     





.

Nên

..

55

.48 20

12 12

S MBCN S ABCD

VV  

.

Câu 55:Chọn A

Gọi

B

là diện tích tam giác

ABC

,

h

là độ dại đường cao của hình lăng trụ, suy ra

.V B h

. Gọi

Q

là trung điểm

AB

,

G

là trọng tâm tam giác

ABC

. Gọi

1

V

là thể tích khối chóp

BMNP

,

2

V

là thể tích khối chóp

MBNE

với

E QC MP

.

Ta có

2

3

PE CE PC

ME QF MQ

  

do

// PC MQ

và

2PC PC





nên

2

3

PC PC

MQ CC





.

Ta có

1

12

2

11

33

V

MP

VV

ME

V

   

.

Do

28

,2

33

GC QC CE QC GE GC CE QC     

.

Ta lại có

2

1

.

3

BNE

V S h

. Ta tính diện tích tam giác

BNE

theo diện tích tam giác

ABC

ta có

 

88

33

BNE BGE NGE NQC BQC QBNC

S S S S S S    

.

Mà

13

.

44

AQN

QBCN ABC

ABC

S

AQ AN

SS

AB AC

S

   

do đó

8

2

3

BNE QBNC

S S B

.

Nên

2

1 1 2

. .2 .

3 3 3

BNE

V

V S h B h  



12

39

V

VV

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

229

Câu 56: Chọn A

Gọi

, HK

lần lượt là trung điểm của

, BD BC

và

. I EM AB

Áp dụng định lí Menelaus cho

tam giác

AHB

ta được

3 2 3

. . 1 2. . 1

4 3 5

AM HE BI BI BI

AI AB

MH EB IA IA IA

      

32

53

AI AN

AB AK

   

Hai đường thẳng

IN

và

BC

cắt nhau, gọi giao điểm là

F

.

Gọi

. P EM AD

Vì

//MN CD

nên áp dụng định lí về giao tuyến của ba mặt phẳng

Ta có

// // .PQ EF CD

Áp dụng định lí Menelaus cho tam giác

ADB

ta được

12

. . 1 . . 1 3.

23

AP DE BI AP AP

PD EB IA PD PD

    

Có

ABCD

là tứ diện đều cạnh bằng

3

2

12

ABCD

a

aV

3

3 3 3 27 27 27 2

. . . . . .

4 4 5 80 80 80 12

APQI

APQI ABCD

ABCD

V

AP AQ AI a

VV

V AD AC AB

     

Vậy

3

92

320

APQI

a

V 

.

Câu 57: Chọn C

Ta có

. . .ABC NMP M ABC M BCPN

V V V

Trong đó

 

.

1

,.

33

M ABC ABC

x

V d M ABC S V

. . .

BCPN

M BCPN M BCC B A BCC B

BCC B

S

BP CN

V V V

S BB CC

   











2

.

1 1 3 3

y z y z

VV







.

Khi đó

.

3

ABC MNP

x y z

VV





.

Vậy

.

1 1 3

2 3 2 2

ABC MNP

x y z

V V V V x y z



      

.

Câu 58: Chọn A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

230

Ta có

2

91

10 10

CE CO AE

CA AC

CA

   

,

2

94

13 13

CD CO BD

CB BC

CB

   

,

2

14

55

AF AO BF

AB BA

AB

   

.

Ta có thể tích khối tứ diện

0

1

: . . 1

6

OABC V OA OB OC

.

Ta có:

. 0 0

1

..

50

A OEF

AO AE AF

V V V

AO AC AB



,

C. 0 0

81

..

130

OED

CO CE CD

V V V

CO CA CB



,

. 0 0

16

..

65

B ODF

BO BD BF

V V V

BO BC BA



. Vậy

00

1 81 16 36 36

1

50 130 65 325 325

ODEF

V V V



     





.

Câu 59: Chọn B

Có

   

// // //MN AC MNP ACD PQ MN AC  

. Ta chia khối đa diện thánh các khối tứ diện

. . .BMNPQD D PQB B MNQ B PQN

V V V V  

.

Thể tích khối tứ diện đều đã cho là

0

2

12

V 

.

Ta có

2

. 0 0 0

24

..

39

D PQB

DP DQ DB

V V V V

DC DA DB



  





.

Và

. . . 0 0 0

1 1 1 1

. . . .

4 4 4 12

ACQ

B MNQ B ACQ B ACQ

ACD

S

BM BN BQ AQ

V V V V V V

BA BC BQ S AD

    

.

Và

. . . 0 0 0

1 1 1 2 1

. . . .

2 2 2 9 9

PQC

B PQN B PQC B PQC

ADC

S

BP BQ BN

V V V V V V

BP BQ BC S

    

.

Vậy

0

4 1 1 23 2 23 2

.

9 12 9 36 12 432

BMNPQD

VV



    





.

Câu 60: Chọn D

C

O

B

A

D

E

F

M

N

A

C

B

D

P

Q

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

231

*Có

   

// //MN AC MNP ACD PQ MN  

. Ta chia khối đa diện thánh các khối tứ diện

. . .BMNPQD D PQB B MNQ B PQN

V V V V  

.

*Thể tích khối tứ diện đều đã cho là

0

2

12

V 

.

Ta có

2

. 0 0 0

11

..

39

D PQB

DP DQ DB

V V V V

DC DA DB



  





.

Và

. . . 0 0 0

1 1 1 1

. . . .

4 4 4 6

ACQ

B MNQ B ACQ B ACQ

ACD

S

BM BN BQ AQ

V V V V V V

BA BC BQ S AD

    

.

Và

. . . 0 0 0

1 1 1 2 1

. . . .

2 2 2 9 9

PQC

B PQN B PQC B PQC

ADC

S

BP BQ BN

V V V V V V

BP BQ BC S

    

.

Vậy

0

1 1 1 7 2 7 2

.

9 6 9 18 12 216

BMNPQD

VV



    





.

Câu 61: Chọn D

Ta có

A



là trung điểm của

PC



;

B



là trung điểm của

QC



. Do đó

. . . .

14

4 4.

33

C PQ

C C PQ C A B C C A B C ABC A B C

C A B

S

V V V V

S



         

  

   

.

Mặt khác

. . .

11

1

2

22

3 3 3

A B C MNC ABC A B C ABC A B C

A M B N C C

A A BB C C

V V V

        

  



  

  

.

M

N

A

C

B

D

P

Q

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

232

Do đó

..

4 2 2

3 3 3

A MPB NQ C C PQ A B C MNC

V V V

     

    

.

Câu 62: Chọn B

Gọi

O AC BD

 

SO ABCD

;

P MB AD

và

Q SD MN

suy ra

Q

là trọng tâm

của tam giác

SMC

1

3

QD

SD



 

,

1

3

,

d Q ABCD

d S ABCD



.

Mặt phẳng

 

BMN

chia khối chóp

.S ABCD

thành hai khối đa diện, trong đó khối đa diện chứa

đỉnh

S

là

SABPQN

.

Ta có

 

22

2

,

2

a

d S ABCD SO SA AO   

.

 

3

2

.

1 1 2

, . .

3 3 6

S ABCD ABCD

a

V d S ABCD S SO AB   

.

Có

 

3

.

1 1 1 . 2

, . . , .

3 3 2 2 12

N BCM BCM

MD BC a

V d N ABCD S d S ABCD  

.

Lạ có

 

3

.

1 1 1 . 2

, . . , .

3 3 3 2 72

Q DMP DMP

MD PA a

V d Q DMP S d S ABCD  

.

Mà

. . .SABPQN S ABCD Q DMP N BCM

V V V V  

3 3 3 3

2 2 2 7 2

6 72 12 72

SABPQN

a a a a

V    

.

Câu 63: Chọn D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

233

Thể tích khối hộp đã cho

2

6 .8 288.V 

Gọi

, , ,E F G H

lần lượt là trung điểm của

AA', ', ', 'BB CC DD

Ta có

 

. . . .ACBDMNPQ ABCDGH A MNQ B MFN C NGP D PHQ

V V V V V V    

. . . . . ' ' '

1 1 1 1 1 1

, . . . . . .

2 ' ' ' 2 2 2 6 48

ABCDGH A MNQ B MFN C NGP D PHQ D D C A

DH DP DQ

V V V V V V V V V

DD DC DA

      

Vậy

1 1 1 1 1 5

120

2 48 48 48 48 12

ACBDMNPQ

V V V V V V V



      





Câu 64: Chọn D

Ta có

1 . . .S ADQ S PQD S DNP

V V V V  

mà

 

.

1

. , .

1

3

1

4

. , .

3

AQD

S ADQ

S ABCD

ABCD

d S ABCD S

V

d S ABCD S





.

Và

.

..

S PQD

S BQD

V

SP SQ SD SP

V SB SQ SD SB



.

Áp dụng định lí Menelaus cho tam giác

SBC

với cát tuyến

MPN

ta có:

.PS.NC

12

.PB.NS

MB PS

MC PB

  

suy ra

2

3

SP

SB



Suy ra

.

2

3

S PQD

S BQD

V



mà

 

.B

.

1

. , .

1

3

1

4

. , .

3

BQD

S DQ

S ABCD

ABCD

d S ABCD S

V

d S ABCD S





nên

.

1

6

S PQD

S ABCD

V



.

Ta lại có:

.

. . 1

. . 3

S PND

S BCD

V

SP SN SD

V SB SC SD



mà

 

.

1

. , .

1

3

1

2

. , .

3

BCD

S BCD

S ABCD

ABCD

d S ABCD S

V

d S ABCD S





.

Suy ra

.

1

6

S PND

S ABCD

V



. Vậy

1.

7

12

S ABCD

VV

suy ra

1

2

7

5

V



Câu 65: Chọn D

Ta có:

 

. .g 2PA M CAM g c PA A C C P C A

      

      

.

P

M

Q

A

C

B

C'

B'

A'

N

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

234

22

3

33

QB B N

QB QC QC B C

QC C C



    

     



Ta có:

11

. .sin .2 .3 .sin 3

22

C PQ C A B

S C P C Q C C A B C C S

   

       

  

Suy ra:

.

. . .

.

3 3. 2

C C PQ C PQ

C C PQ C C A B ABC A B C

C C A B C A B

VS

V V V

VS



      

     

     

Mặt khác:

.

.ABC

12

1

13 13

23

3 3 18 9

A B C MNC

ABC

A M B N C C

V

A A B B C C

V

  

   

  

    

Ta có:

..

13 5

2

99

A MPB NQ C C PQ A B C MNC

V V V

     

    

. Chọn D

Câu 66: Chọn C

Gọi

E

,

I

,

K

lần lượt là trung điểm

AC



,

AC



và

AB



.

Ta có:

   

1B E ACC A B E A C

    

  

Trong

 

ABC



: từ

B



kẻ

B H A C





tại

H

.

Trong

 

AA C C



: gọi

F HE AA





.

Ta lại có

   

2

B H A C

B HF A C A C B F

B E A C







   

   









Từ

 

1

và

 

2

suy ra tam giác

B EF



là thiết diện của lăng trụ

.ABC A B C

  

khi cắt bởi mặt phẳng

 

P

.

Tam giác

CA B



cân tại

C

, ta có

19

2

5 2 5

a

CK A B a

CK A B B H A C B H

AC

a







    

      



Tam giác

'B HC

vuông tại

H

, ta có

22

9 9 1

10 4

25

a

CH B C B H CH CA A H HI

   

      

11

48

A F A H A F

HA F HIE

IE IH A A

  



      



.

Khi đó

.

. . . .

.

1 1 1 1 1

. . .

16 16 16 3 48

A B EF

A B EF A B C A ABC A B C ABC A B C

A B C A

V

A B A E A F

V V V V

V A B A C A A



          

  

   

     

    

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

235

Nên

11

.2

11

48 47

ABC A B C

VV

  

  

.

Câu 67:

Chọn A

Vì ba mặt phẳng

( ),( ),( )MNB A ACC A BCC B

     

đôi một cắt nhau theo ba giao tuyến phân biệt

,,A M B N CC

  

và

,A M CC



không song song nên

,,A M B N CC

  

đồng qui tại

S

.

Ta có

CM MN MN SM SN SC

k

CA AB A B SA SB SC

     

    

Từ đó

 

33

. . 1 . .

1

S MNC S A B C MNC A B C S A B C

V k V V V k V

        

    

.

Mặt khác

 

.

. ' ' '

3

31

ABC A B C

S A B C

SC SC

V

CC

k

V SC SC

  







   



 

.

31

ABC A B C

S A B C

V

k

  





Suy ra

 

2

.

3

.

1

1.

1

3

31

ABC A B C

k k V

V

Vk

k

  



  



.

Vì

1

2

V



nên

2

1.

2 1 2 1 5

1 0 ( 0)

3 3 3 2

ABC A B C

kk

V V k k k k

  

   

         

.

Vậy

15

2

k





.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

236

DẠNG 7: CÁC BÀI TOÁN THỂ TÍCH CHỌN LỌC

Câu 1: Cho hình chóp tứ giác đều có , côsin góc hợp bởi cạnh và

bằng . Thể tích của khối chóp bằng

A. . B. . C. . D. .

Câu 2: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

M

là trung điểm của

SB

,

N

là

điểm thuộc cạnh

SC

sao cho

2SN CN

,

P

là điểm thuộc cạnh

SD

sao cho

3SP DP

. Mặt

phẳng

()MNP

cắt

SA

tại

Q

. Biết khối chóp

.S MNPQ

có thể tích bằng

1

, khối đa diện

.ABCDQMNP

có thể tích bằng

A.

4

. B.

9

5

. C.

17

5

. D.

14

5

.

Câu 3: Cho lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

và

AB a

,

3AC a

,

mặt phẳng

 

A BC



tạo với đáy một góc

30

. Thể tích của khối lăng trụ

.ABC A B C

  

bằng

A.

3

12

a

. B.

3

a

. C.

3

33

4

a

. D.

3

4

a

.

Câu 4: Cho hình lăng trụ đều

. ' ' 'ABC A B C

có cạnh đáy bằng

23

3

a

. Đường thẳng

'BC

tạo với mặt

phẳng

 

''ACC A

góc



thỏa mãn

cot 2





. Thể tích khối lăng trụ

. ' ' 'ABC A B C

bằng

A.

3

4

11

3

a

. B.

3

1

11

9

a

. C.

3

1

11

3

a

. D.

3

2

11

3

a

.

Câu 5: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

,

3

2

a

AA





. Biết rằng hình

chiếu vuông góc của điểm

A



lên mặt phẳng

 

ABC

là trung điểm của cạnh

BC

. Tính thể tích

V của khối lăng trụ đó theo a.

A.

3

2

Va

. B.

3

2

3

a

V 

. C.

3

42

a

V 

. D.

3

Va

.

Câu 6: Cho hình lập phương

. ' ' ' 'ABCD A B C D

. Biết tích của khoảng cách từ điểm

'B

và điểm

D

đến

mặt phẳng

 

'D AC

bằng

 

2

60aa

. Giả sử thể tích của khối lập phương

. ' ' ' 'ABCD A B C D

là

2

ka

. Chọn mệnh đề đúng trong các mệnh đề sau.

A.

 

20;30k 

. B.

 

100;120k 

. C.

 

50;80k 

. D.

 

40;50k 

.

Câu 7: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác đều cạnh bằng

a

và

 

'A BC

hợp

với mặt đáy

ABC

một góc

30

. Tính thể tích

V

của khối lăng trụ

. ' ' 'ABC A B C

.

A.

3

8

a

V 

. B.

3

12

a

V 

. C.

3

24

a

V 

. D.

3

8

a

V 

.

.S ABCD

11SA a

SB

ABCD

1

10

.S ABCD

3

121

150

a

3

121

50

a

3

121

500

a

3

11

500

a

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

237

Câu 8: Cho khối chóp

.S ABCD

có đáy là hình thoi cạnh

a

,

0

60ABC 

. Hình chiếu vuông góc của đỉnh

S

trên mặt phẳng

 

ABCD

là trung điểm của cạnh

AB

. Góc giữa mặt phẳng

 

SCD

và mặt đáy

bằng

0

45

. Thể tích khối chóp đã cho bằng

A.

3

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

8

a

.

Câu 9: Cho hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

 

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường

AA



và

BC

bằng

3

4

a

. Tính thể tích

V

của khối lăng trụ

.ABC A B C

  

.

A.

3

6

a

V 

. B.

3

24

a

V 

. C.

3

12

a

V 

. D.

3

a

V 

.

Câu 10: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

. Hình chiếu vuông góc của đỉnh

A



lên đáy

ABC

trùng với trung điểm

I

của cạnh

BC

, cạnh bên

AA



tạo với đáy

ABC

góc

60

. Tính thể tích

V

của khối lăng trụ đã cho.

A.

3

33

8

a

V 

. B.

3

2

a

V 

. C.

3

33

16

a

V 

. D.

3

4

a

V 

.

Câu 11: Cho hình chóp đều

.S ABC

có cạnh bằng

a

, góc giữa đường thẳng

SA

và mặt phẳng

 

ABC

bằng

60

. Gọi

,,A B C

  

tương ứng là các điểm đối xứng của

,,A B C

qua

S

. Thể tích

V

của

khối bát diện có các mặt

, , , ,ABC A B C A BC B CA C AB

     

,,AB C BA C

   

,

CA B



là

A.

3

23Va

. B.

3

23

3

a

V 

. C.

3

43

3

a

V 

. D.

3

2

a

V 

.

Câu 12: Cho lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của điểm

A



lên mặt phẳng

 

ABC

trùng với trọng tâm tam giác

.ABC

Biết khoảng cách giữa hai đường

thẳng

AA



và

BC

bằng

3

4

a

. Khi đó thể tích của khối lăng trụ

.ABC A B C

  

là

A.

3

12

a

. B.

3

a

. C.

3

6

a

. D.

3

24

a

.

Câu 13: Cho lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

, hình chiếu vuông góc của

A



lên

 

ABC

trùng với trọng tâm của tam giác

ABC

. Một mặt phẳng

 

P

chứa

BC

và vuông góc

với

AA



cắt hình lăng trụ

.ABC A B C

  

theo một thiết diện có diện tích bằng

2

3

8

a

. Thể tích khối

lăng trụ

.ABC A B C

  

bằng

A.

3

4

a

. B.

3

23

3

a

. C.

3

10

a

. D.

3

12

a

.

Câu 14: Cho lăng trụ

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

'A

xuống

mặt phẳng

 

ABC

trùng với trọng tâm tam giác

ABC

. Biết khoảng cách giữa hai đường thẳng

'AA

và

BC

bằng

3

4

a

. Thể tích khối lăng trụ bằng

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

238

A.

3

12

a

. B.

3

4

a

. C.

3

37

14

a

. D.

3

37

28

a

.

Câu 15:

Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

a

,

3S A a

;

 

SA ABCD

.

Gọi

M

,

N

lần lượt là trung điểm của các cạnh

,SB SD

; mặt phẳng

 

AMN

cắt

SC

tại

I

. Tính

thể tích khối đa diện

.ABCDMNI

A.

3

53

18

a

V 

. B.

3

18

a

V 

. C.

3

53

6

a

V 

D.

3

13 3

36

a

V 

.

Câu 16: Cho tứ diện OABC có

OA a

,

OB b

,

OC c

và đôi một vuông góc với nhau. Gọi

r

là bán

kính mặt cầu tiếp xúc với cả bốn mặt của tứ diện. Giả sử

,a b a c

. Giá trị nhỏ nhất của

a

r

là

A.

13

. B.

23

. C.

3

. D.

33

.

Câu 17: Cho hình hộp chữ nhật

.ABCD A B C D

   

có

AB BC a

,

3AA a





. Gọi I là giao điểm của

AD



và

AD



; H là hình chiếu của I trên mặt phẳng

 

A B C D

   

; K là hình chiếu của B lên mặt

phẳng

 

CA B



. Tính thể tích của khối tứ diện

IHBK

.

A.

3

4

a

. B.

3

6

a

. C.

3

16

a

. D.

3

8

a

.

Câu 18: Cho hình hộp chữ nhật

.ABCD A B C D

   

. Khoàng cách giữa

AB

và

BC



là

25

5

a

, khoảng cách

giữa

BC

và

AB



là

25

5

a

, khoảng cách giữa

AC

và

BD



là

3

a

. Tính thể tích khối hộp.

A.

3

4a

. B.

3

3a

. C.

3

5a

. D.

3

2a

.

Câu 19: Cho hình hộp có thể tích bằng . Gọi lần lượt là tâm các

hình bình hành Thể tích khối đa diện

có các đỉnh bằng

A. . B. . C. . D. .

Câu 20: Cho hình chóp

.S ABC

có

39

3

a

SA SB SC  

. Tam giác

ABC

cân tại

A

có góc

120A 

,

2BC a

.

G

là trọng tâm tam giác

SAB

. Thể tích khối chóp

.G ABC

là

A.

3

2

9

a

. B.

3

a

. C.

3

a

. D.

3

9

a

.

Câu 21: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh bằng

1

. Biết khoảng cách từ

A

đến

mặt phẳng

 

SBC

là

6

4

, từ

B

đến mặt phẳng

 

SAC

là

15

10

, từ

C

đến mặt phẳng

 

SAB

là

30

20

và hình chiếu vuông góc của

S

xuống đáy nằm trong tam giác

ABC

. Thể tích khối chóp

.S ABC

bằng

. ' ' ' 'ABCD A B C D

V

, , , , ,M N P Q E F

, ' ' ' ', ' ', ' ', ' ', ' '.ABCD A B C D ABB A BCC B CDD C DAA D

, , , , ,M P Q E F N

4

V

2

V

6

V

3

V

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

239

A.

1

36

. B.

1

48

. C.

1

12

. D.

1

24

.

Câu 22: Cho hình lăng trụ

.ABCD A B C D

   

có đáy

ABCD

là hình chữ nhật

AB a

,

3AD a

. Hình

chiếu vuông góc của

A



trên mặt phẳng

 

ABCD

trùng với giao điểm của

AC

và

BD

. Góc giữa

hai mặt phẳng

 

ADD A



và

 

ABCD

bằng

60

. Tính thể tích khối tứ diện

ACB D



.

A.

3

2

a

. B.

3

6

a

. C.

3

a

. D.

3

2

a

.

Câu 23: Cho khối lăng trụ tam giác

.ABC A B C

  

. Gọi

G

là trọng tâm tam giác

ABC

.

M

,

N

,

P

lần

lượt là trung điểm của

CC



,

AC



,

AB



. Biết thể tích của khối

GMNP

bằng

5

, tính thể tích

khối lăng trụ

.ABC A B C

  

.

A.

72

. B.

21

. C.

18

. D.

17

.

Câu 24: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành. Gọi

N

là trung điểm

,SB

P

thuộc

đoạn

SC

sao cho

2,SP PC M

thuộc đoạn

SA

sao cho

4

.

5

SM MA

Mặt phẳng

 

MNP

cắt

SD

tại

.Q

NP

cắt

BC

tại

,E CQ

cắt

DP

tại

.R

Biết rằng thể tích khối chóp

EPQR

bằng

3

18 .cm

Thể tích khối chóp

SMNPQ

bằng

A.

3

65cm

. B.

3

260

9

cm

. C.

3

75cm

. D.

3

70cm

.

Câu 25: Cho khối lăng trụ tam giác

.ABC A B C  

có đáy là tam giác vuông tại

, 1, 2A AB BC

. Góc

00

' 90 , ' 120 .CBB ABB

Gọi

M

là trung điểm cạnh

AA

. Biết

 

7

', .

7

d AB CM 

Tính thể tích

khối lăng trụ đã cho.

A.

22

. B.

42

9

. C.

42

. D.

42

.

3

Câu 26: Cho khối lăng trụ

.ABC A B C

  

có thể tích

V

, đáy là tam giác cân,

AB AC

. Gọi

E

là trung

điểm cạnh

AB

và

F

là hình chiếu vuông góc của

E

lên

BC

. Mặt phẳng

 

C EF



chia khối lăng

trụ đã cho thành hai khối đa diện. Tính thể tích khối đa diện chứa đỉnh

A

.

A.

47

72

V

. B.

25

72

V

. C.

29

72

V

. D.

43

72

V

.

Câu 27: Cho khối đa diện lồi

 

H

gồm có

8

đỉnh là

, , , ,A B C D

, , ,M N P Q

; trong đó có hai mặt

 

ABCD

và

 

MNPQ

là hai hình vuông song song với nhau; hình chiếu vuông góc của

, , ,M N P Q

lên mặt phẳng

 

ABCD

lần lượt là trung điểm của các cạnh

, , ,AB BC CD DA

. Biết

rằng

3AM a

,

4AB a

. Thể tích khối đa diện

 

H

được tính theo

a

bằng

A.

3

40

3

a

. B.

3

40 5

3

a

. C.

3

20 5

3

a

. D.

3

18 3

5

a

.

Câu 28: Cho hình lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

a

. Hình chiếu vuông

góc của điểm

A

lên đáy

 

A B C

  

trùng với trung điểm

M

của cạnh

BC



. Góc nhị diện giữa

hai mặt phẳng

 

AA B



và

 

ABC

bằng

60

. Thể tích khối lăng trụ

.ABC A B C

  

bằng:

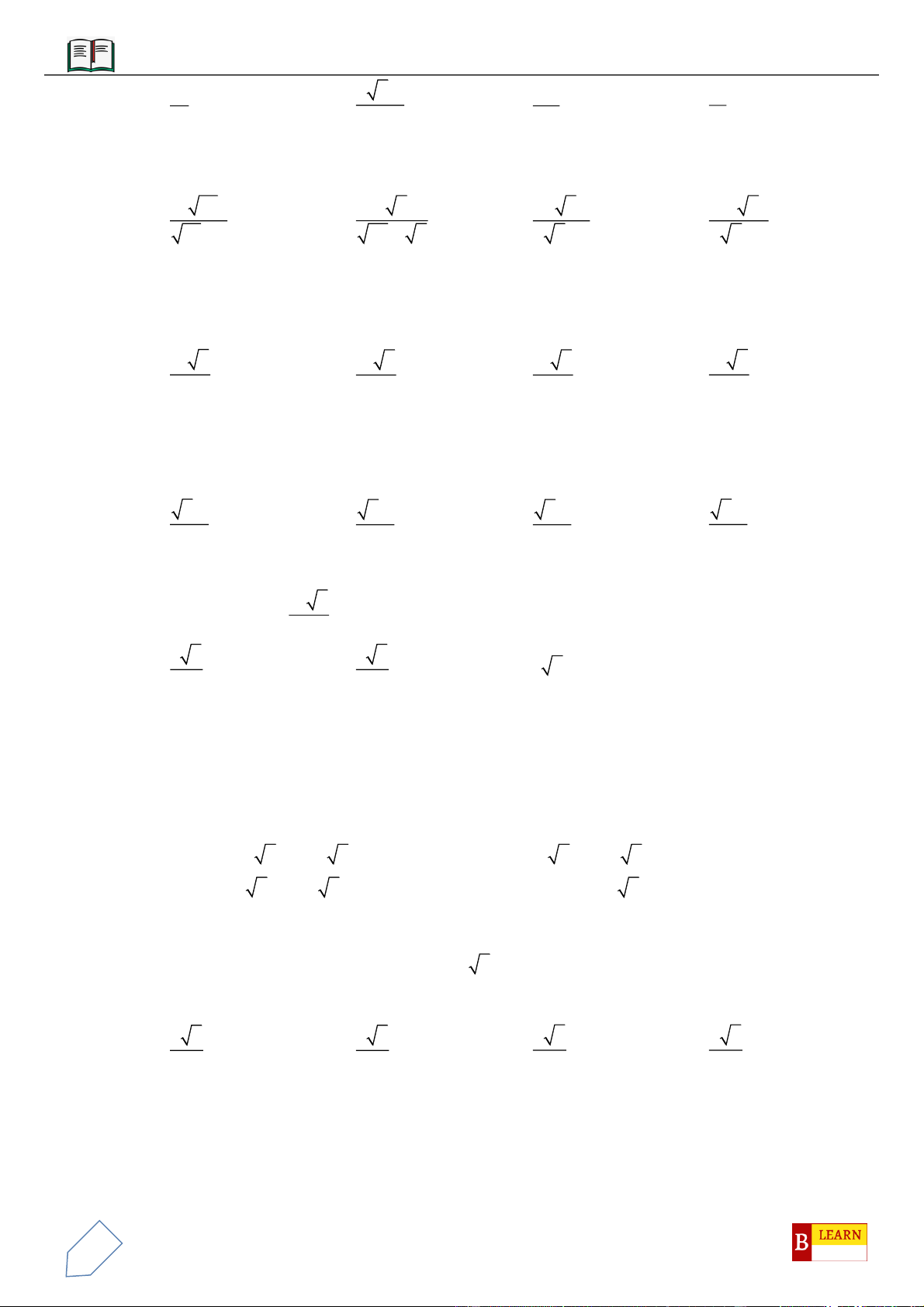
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

240

A.

3

.

16

a

B.

3

33

.

16

a

C.

3

.

8

a

D.

3

.

4

a

Câu 29: Cho hình chóp tứ giác đều

.S ABCD

cạnh đáy bằng

a

và cạnh bên bằng

2a

. Bán kính mặt cầu

nội tiếp hình chóp tứ giác

.S ABCD

tính theo

a

tương ứng bằng:

A.

14

15 3

a



. B.

7

30 2

a



. C.

6

2 5 1

a



. D.

23

4 7 3

a



.

Câu 30: Cho hình chóp

.DS ABC

có đáy

DABC

là hình vuông cạnh

a

và cạnh bên

SA

vuông góc với

đáy

 

DABC

. Biết góc tạo bởi hai mặt phẳng

 

DSB

và

 

DABC

bằng

0

60

. Thể tích khối chóp

.DS ABC

tương ứng bằng:

A.

3

6

3

a

. B.

3

6

4

a

. C.

3

6

12

a

. D.

3

6

a

.

Câu 31: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

và cạnh bên

SA

vuông góc với đáy

 

ABCD

. Biết góc tạo bởi hai mặt phẳng

 

SBD

và

 

ABCD

bằng

60

. Thể tích khối chóp

.S ABCD

bằng

A.

3

6

3

a

. B.

3

6

4

a

. C.

3

6

12

a

. D.

3

6

a

.

Câu 32: Cho hình lăng trụ tam giác đều

.ABC A B C

  

cạnh đáy bằng

a

. Biết thể tích khối lăng trụ

.ABC A B C

  

bằng

3

5

2

a

. Bán kính mặt cầu ngoại tiếp hình lăng trụ

.ABC A B C

  

là:

A.

3

2

a

. B.

5

2

a

. C.

2a

. D.

a

.

Câu 33: Cho khối đa diện lồi

 

H

gồm có

8

đỉnh là

, , , , , , ,A B C D M N P Q

; trong đó có hai mặt

 

ABCD

và

 

MNPQ

là hai hình vuông song song với nhau; hình chiếu vuông góc của

, , ,M N P Q

lên

mặt phẳng

 

ABCD

lần lượt là trung điểm của các cạnh

, , ,AB BC CD DA

. Biết rằng

4AM AB a

. Hãy tính theo

a

diện tích toàn phần của khối đa diện

 

H

?

A.

2 2 2

24 16 7 16 3.a a a

B.

2 2 2

7 16 3 36 .a a a

C.

2 2 2

24 8 7 16 3.a a a

D.

22

24 16 3.aa

Câu 34: Tỉ lệ diện tích xung quanh của hình lập phương

 

1

H

(tổng diện tích 4 mặt bên) so với diện tích

toàn phần của hình tứ diện đều

 

2

H

bằng

3

. Hỏi khi đó tỉ lệ thể tích của hình lập phương

 

1

H

so với thể tích hình tứ diện đều

 

2

H

bằng bao nhiêu?

A.

96

.

4

B.

33

.

4

C.

23

.

9

D.

25

.

5

Câu 35: Cho khối lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

, góc giữa cạnh bên với mặt đáy

của lăng trụ là

30

o

. Hình chiếu vuông góc của

A



lên đáy

 

ABC

trùng với trung điểm

H

của

cạnh

BC

. Thể tích của khối lăng trụ

.ABC A B C

  

là:

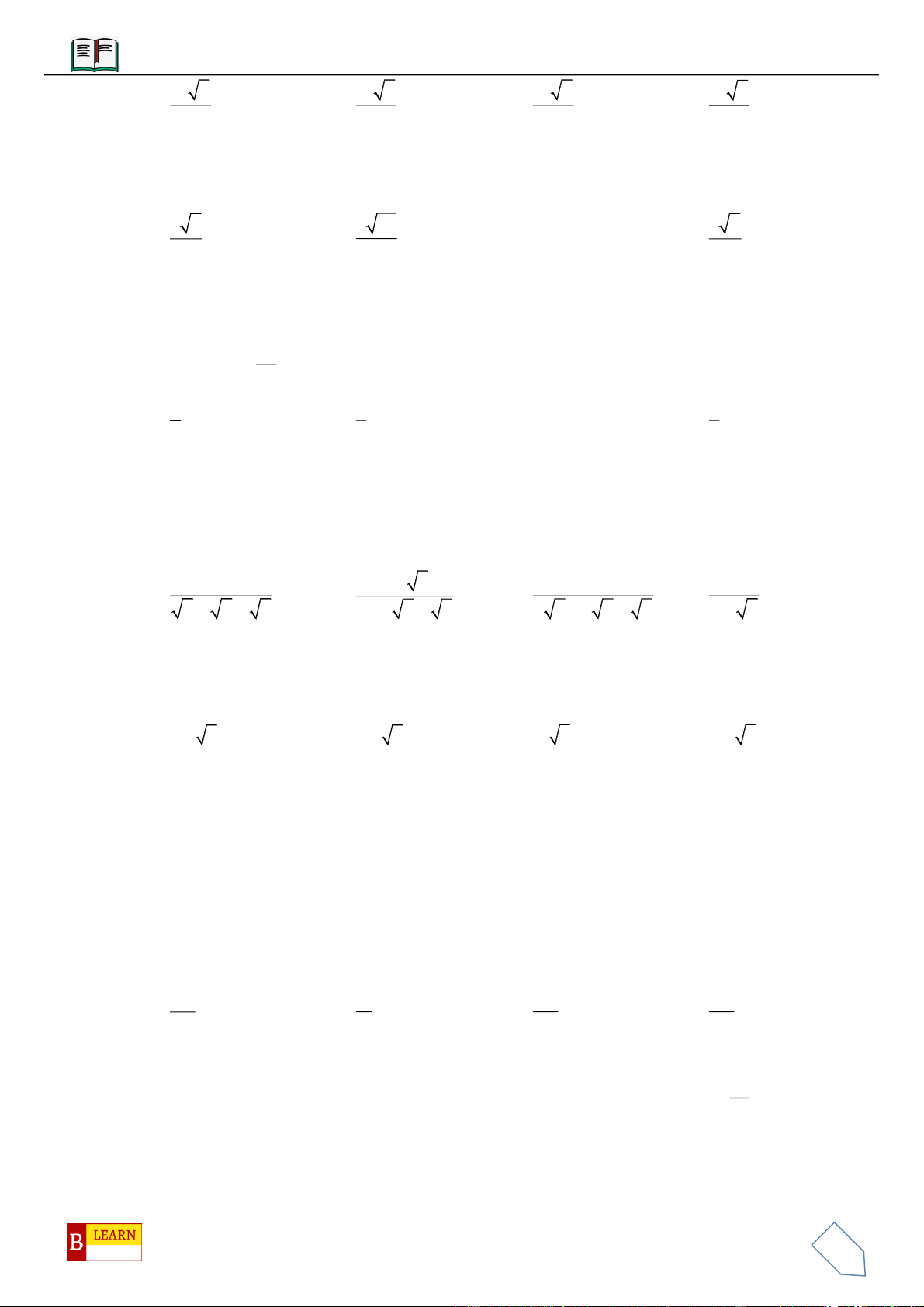
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

241

A.

3

2

.

3

a

B.

3

.

8

a

C.

3

2

.

9

a

D.

3

.

24

a

Câu 36: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

 

SA ABC

, góc giữa đường

thẳng

SB

và mp

 

ABC

bằng

60 .

Khoảng cách giữa hai đường thẳng

AC

và

SB

bằng:

A.

2

.

2

a

B.

15

.

5

a

C.

2.a

D.

7

.

7

a

Câu 37: Cho hình hộp

.ABCD A B C D

   

. Gọi

,,M N P

lần lượt là trung điểm của các cạnh

,,AA A D B C

    

. Mặt phẳng

 

MNP

chia khối hình hộp thành hai phần có thể tích là

1

V

và

2

V

, trong đó

12

VV

. Tỉ lệ thể tích

1

2

V

tương ứng bằng:

A.

1

.

7

B.

1

.

3

C.

1.

D.

1

.

8

Câu 38: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

A

với cạnh huyền

2BC a

.

Hình chiếu vuông góc của

S

lên mặt đáy

ABC

nằm trong tam giác

ABC

. Biết các mặt bên

 

SAB

,

 

SBC

,

 

SCA

lần lượt tạo với đáy các góc

60

o

,

60

o

,

45

o

. Thể tích của hình chóp

.S ABC

tính theo

a

tương ứng bằng:

A.

3

.

326

a



B.

3

23

.

2 3 2 6

a



C.

3

2

.

2 3 3 2 6

a



D.

3

6

.

23

a



Câu 39: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

có đáy

ABC

là tam giác vuông cân tại

A

có

2AC a

.

Đường thẳng

'BC

tạo với mặt phẳng

 

''ACC A

một góc

0

30

. Thể tích khối lăng trụ

. ' ' 'ABC A B C

bằng:

A.

3

22a

. B.

3

42a

. C.

3

3a

. D.

3

33a

.

Câu 40: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Biết rằng tam giác

SAC

vuông tại

đỉnh

S

và có diện tích bằng

2

2.a

Diện tích mặt cầu ngoại tiếp hình chóp

.S ABCD

có giá trị nhỏ

nhất là:

A.

2

8 a



. B.

2

4 a



. C.

2

6 a



. D.

2

12 a



.

Câu 41: Cho khối chóp

.S ABCD

có đáy

ABCD

là hình bình hành và có thể tích là

V

. Gọi

, , ,M N P Q

lần lượt là những điểm nằm trên các cạnh

, , ,SA SB SC SD

sao cho

, , 2 ,SM MA SN NB SP PC  

3.SQ QD

Thể tích khối đa diện lồi có 5 đỉnh

, , , ,S M N P Q

tính theo

V

bằng:

A.

5

24

V

. B.

8

V

. C.

7

16

V

. D.

7

32

V

.

Câu 42: Cho hình chóp

SABCD

có đáy

ABCD

là hình chữ nhật

22AB AD a

và cạnh

SA

vuông

góc với mặt phẳng đáy. Khoảng cách từ điểm

A

đến mặt phẳng

 

SBD

bàng

2

3

a

. Hãy tính theo

a

thể tích khối chóp

.SABCD

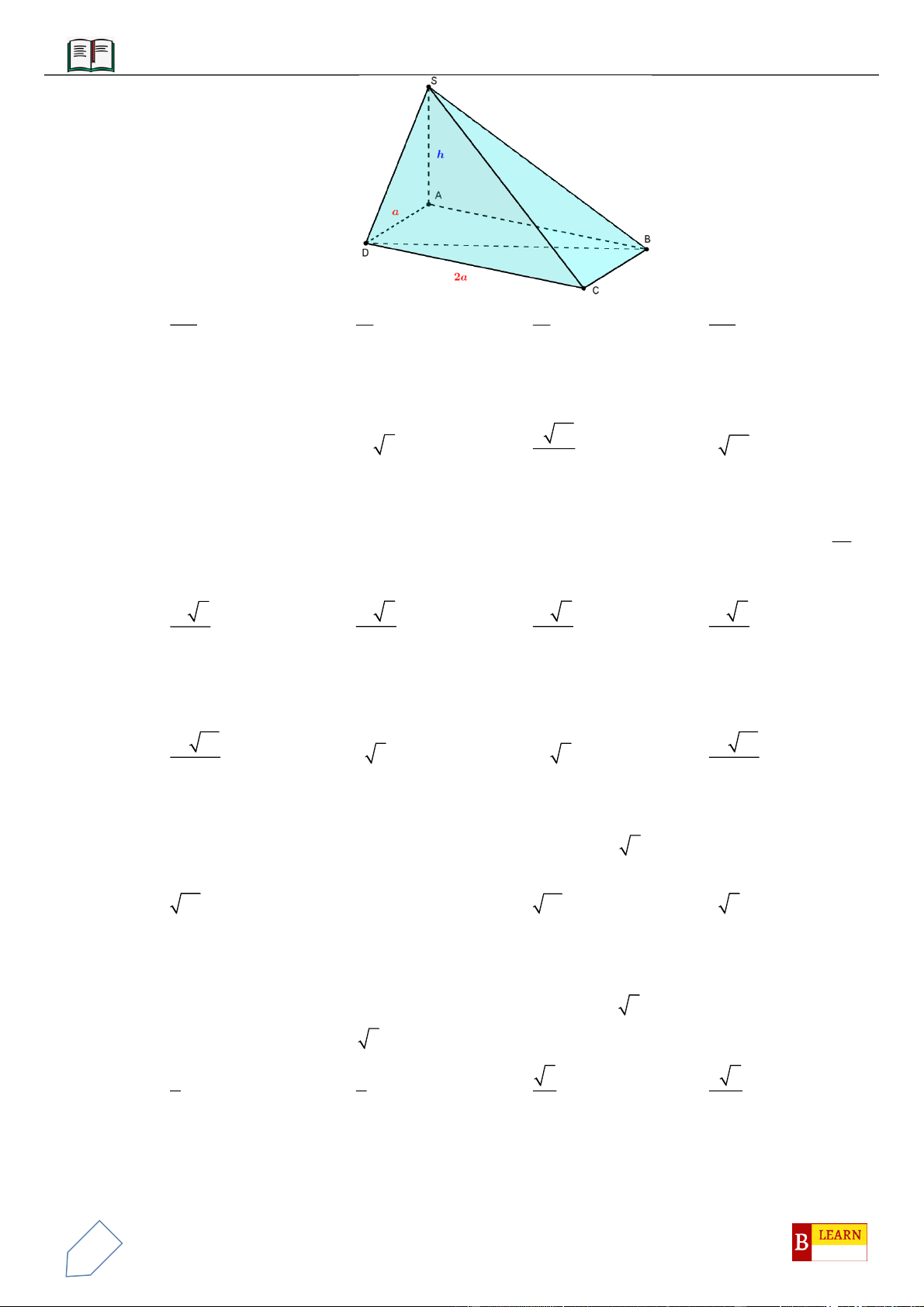
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

242

A.

3

2

3

a

B.

3

a

C.

3

6

a

D.

3

8

a

Câu 43: Cho lăng trụ đứng

. ' ' ' 'ABC A B C D

có

0

2, 4, 60 .AB AC BAC  

Gọi

M

là trung điểm của

'CC

và tam giác

'BMA

vuông tại

.M

Thể tích khối lăng trụ

. ' ' 'ABC A B C

bằng:

A.

24

B.

12 3

C.

2 42

3

D.

2 42

Câu 44: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

và

SA

vuông góc với đáy

( ).ABCD

Gọi

M

là trung điểm của

SC

và

N

nằm trên cạnh

SB

sao cho

2.NS NB

Biết rằng

2

.

3

a

MN 

Tính thể tích khối chóp

..S ABCD

A.

3

.

4

a

B.

3

.

3

a

C.

3

.

6

a

D.

3

5

.

6

a

Câu 45: Cho hình lăng trụ đứng

. ' ' ' 'ABCD A B C D

có mặt cầu ngoại tiếp là

 

S

, biết

 

S

có bán kính là

6

. Đáy

ABCD

là tứ giác có

0

60ABC 

và

4AD CD

. Thể tích tứ diện

'A ACD

:

A.

16 15

.

3

B.

8 5.

C.

16 3.

D.

12 15

.

5

Câu 46: Cho tứ diện

ABCD

có

 

ABC

vuông góc với

 

BCD

và

6BC 

,

0

90BAC BDC

. Chu vi

của đường tròn ngoại tiếp tam giác

ABC

và

DBC

lần lượt là

3a

và

a

. Bán kính mặt cầu

ngoại tiếp tứ diện

ABCD

tương ứng là?

A.

39

. B.

12

. C.

41

D.

23

Câu 47: Cho hình chóp

SABC

có đáy

ABC

là tam giác đều cạnh

1

. Gọi

M

là một điểm di động nằm

trên mặt phẳng

 

ABC

. Gọi

N

là điểm nằm trên đường thẳng

MS

sao cho

.3SM SN 

. Quỹ

tích điểm

N

khi

M

thay đổi là một mặt cầu có bán kính bằng

3

. Biết khoảng cách từ

S

đến

mặt phẳng

 

ABC

nhỏ hơn

3

. Thể tích hình chóp

SABC

tương ứng bằng

A.

1

6

. B.

1

8

. C.

3

6

. D.

22

15

.

Câu 48: Cho hình chóp

SABCD

có đáy

ABCD

là hình vuông cạnh

a

. Biết tâm của mặt cầu ngoại tiếp

hình chóp

SABCD

trùng với tâm

O

của hình vuông đáy

ABCD

và chân đường cao

H

hạ từ

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

243

đỉnh

S

xuống đáy

ABCD

trùng với trung điểm của đoạn thẳng

OA

. Thể tích hình chóp

SABCD

bằng:

A.

3

6

12

a

. B.

3

2

6

a

. C.

3

1

8

a

. D.

3

2

4

a

Câu 49: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi nhưng không là hình vuông,

AB SA SB SD a   

. Biết rằng thể tích khối chóp

.S ABCD

bằng

3

2

6

a

, khi đó góc giữa hai

mặt phẳng

 

SBC

và

 

SCD

bằng:

A.

30

. B.

45

. C.

60

. D.

90

.

Câu 50: Cho một hình lăng trụ

.ABC A B C

  

có đáy là tam giác đều cạnh

a

. Biết rằng

2AA AB a





và

hình chiếu vuông góc của

A

lên cạnh

BC



là điểm

M

sao cho

20MB MC





. Thể tích theo

a

của lăng trụ

.ABC A B C

  

bằng

A.

3

285

12

a

. B.

3

95

36

a

. C.

3

95

6

a

. D.

3

95

12

a

.

Câu 51: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Mặt phẳng

 



đi qua

,AB

và trung

điểm

M

của

SC

. Mặt phẳng

 



chia khối chóp đã cho thành hai phần có thể tích lần lượt là

1

V

,

2

V

với

12

VV

. Tỉ số

1

2

V

tương ứng bằng

A.

1

2

1

4

V



. B.

1

2

3

8

V



. C.

1

2

5

8

V



. D.

1

2

3

5

V



.

Câu 52: Cho hình chóp

.S ABCD

có đáy

ABCD

là nửa lục giác đều nội tiếp đường tròn đường kính

2AB a

. Có cạnh

SA

vuông góc với mặt phẳng

ABCD

và

3S A a

. Cosin của góc giữa hai

mặt phẳng

 

SAD

và

 

SBC

tương ứng bằng:

A.

2

. B.

2

3

. C.

2

4

. D.

2

5

.

Câu 53: Cho tứ diện

ABCD

có

9

2

AC 

và

2

3

AD 

. Gọi

M

là một điểm nằm trên cạnh

AB

sao cho

2MA MB

. Một mặt phẳng thay đổi

 



đi qua

M

cắt các cạnh

AC

và

AD

lần lượt tại

N

và

P

sao cho luôn thoả mãn

AMNP

ABCD

V

NC

V AN



. Giá trị nhỏ nhất của

AN AP

tương ứng bằng:

A.

3

. B.

64

.

15

C.

15

.

4

D.

263

.

120

Câu 54: Cho hình chóp

.S ABC

có

2SC a

, tam giác

SAB

đều cạnh

a

và tam giác

SAC

vuông tại

.A

Mặt phẳng

 

SBC

vuông góc với mặt phẳng

 

.ABC

Thể tích khối cầu ngoại tiếp hình chóp

.S ABC

là:

A.

3

4

3

a



. B.

3

6

a



. C.

3

4 a



. D.

3

2

a



.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

244

Câu 55: Cho hình chóp tứ giác

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng 6. Hình chiếu vuông

góc của đỉnh

S

trên mặt phẳng đáy là điểm

H

nằm trong đoạn

AC

sao cho

2HC HA

. Biết

góc giữa hai mặt phẳng

 

SBC

và

 

ABC

bằng

0

60

. Khoảng cách từ

A

đến mặt phẳng

 

SCD

bằng:

A.

42

3

. B.

33

. C.

42

. D.

53

.

Câu 56: Cho hình chóp

SABCD

có đáy

ABCD

là hình vuông cạnh

,a

cạnh bên

SA

vuông góc mặt

phẳng đáy và khoảng cách từ

A

đến mặt phẳng

 

SDM

bằng

,

2

a

trong đó

M

là một điểm nằm

trên đoạn

BC

sao cho

2BM MC

. Thể tích khối chóp

SABCD

tính theo

a

bằng:

A.

3

26

a

. B.

3

2

26

a

. C.

3

2 26

a

. D.

3

11

24

a

.

Câu 57: Cho một hình lăng trụ

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

.a

Hình chiếu vuông góc của

đỉnh

A

xuống đáy

 

' ' 'A B C

là trung điểm

M

của cạnh

''BC

, biết rằng

'2AA a

. Khoảng

cách từ

'C

đến mp

 

'ABA

bằng:

A.

39

55

a

. B.

13

6

a

. C.

15

10

a

. D.

39

16

a

.

Câu 58: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật có

22AB AD a

và

2SA SB a

.

Thể tích khối chóp

.S ABC

bằng

3

2

a

. Tính bán kính mặt cầu ngoại tiếp hình chóp

.S BCD

.

A.

3

6

a

. B.

2

3

a

. C.

16 2 3

3

a



. D.

85

3

a



.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

245

BẢNG ĐÁP ÁN

1.A

2.C

3.D

4.C

5.C

6.A

7.A

8.A

9.C

10.A

11.B

12.A

13.A

14.A

15.A

16.D

17.C

18.D

19.C

20.D

21.D

22.A

23.A

24.A

25.A

26.B

27.B

28.B

29.B

30.D

31.D

32.C

33.C

34.A

35.B

36.B

37.A

38.C

39.B

40.A

41.D

42.A

43.A

44.C

45.A

46.A

47.B

48.A

49.D

50.D

51.D

52.C

53.C

54.A

55.B

56.B

57.A

58.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn C

Gọi cạnh hình vuông đáy là ,góc hợp bởi cạnh và

là góc nhọn

.

Thể tích của khối chóp bằng

.

Câu 2: Chọn C

Gọi

;;O AC BD I SO PM Q IN SA     

.

Đặt

34

; 2 ; ;

23

SA SB SC SD

a b c d

SQ SM SN SP

      

. Ta có:

11

6

a c b d a    

.

Ta có:

.

5 22

4 22 5

S MNPQ

S ABCD

S BCDA

V

a b c d

V

V abcd

  

   

. Vậy

. . .

17

5

ABCD QMNP S ABCD S MNPQ

V V V  

.

Câu 3: Chọn D

x

SB

ABCD

SBO

1

cos

10

SMO

1

10

OB

SB

21

10

2. 11

x

a

11

52

xa

.S ABCD

1

.

3

ABCD

V SO S

2

22

1 11

.

3 25.2

SC OC a

22

2

11

100

.

3 50

aa

a

3

121

500

a

I

O

A

B

D

C

S

M

N

P

Q

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

246

Gọi

AH

là đường cao của tam giác

ABC

, ta có

 

BC AH

BC AA H BC A H

BC AA







   









nên góc giữa

mặt phẳng

 

A BC



và mặt phẳng

 

ABC

là góc

30AHA





. Ta có:

 

2 2 2 2 2 2

1 1 1 1 1 4 3

2

3

a

AH

AH AB AC a a

a

      

.

31

tan30 .tan30 .

22

3

AA a a

AA AH

AH





    

;

2

1 1 3

. . . . 3

2 2 2

ABC

a

S AB AC a a



  

. Do đó

23

.

33

..

2 2 4

ABC A B C ABC

a a a

V AA S

  





  

.

Câu 4: Chọn C

Gọi

I

là trung điểm

AC

, suy ra

BI AC

.

Mặt khác do

'BI CC

nên

 

''BI ACC A

.

Do đó

 

', ' ' ', ' 'BC ACC A BC IC BC I



  

.

Ta có:

2

2 3 3 3

.

3 4 3

ABC

aa

S











và

2 3 3

.

32

a

BI a

.

Theo đề bài:

'

cot 2 2 ' 2

CI

C I a

BI



    

.

Suy ra

2

2 2 2

33

' ' 4

33

aa

CC C I CI a    

.

Vậy thể tích khối lăng trụ

. ' ' 'ABC A B C

:

2

3

3 33 1

. ' . 11

3 3 3

ABC

aa

V S CC a



  

.

Câu 5: Chọn C

A'

A

B'

B

C'

C

H

α

I

C

B

A'

B'

C'

A

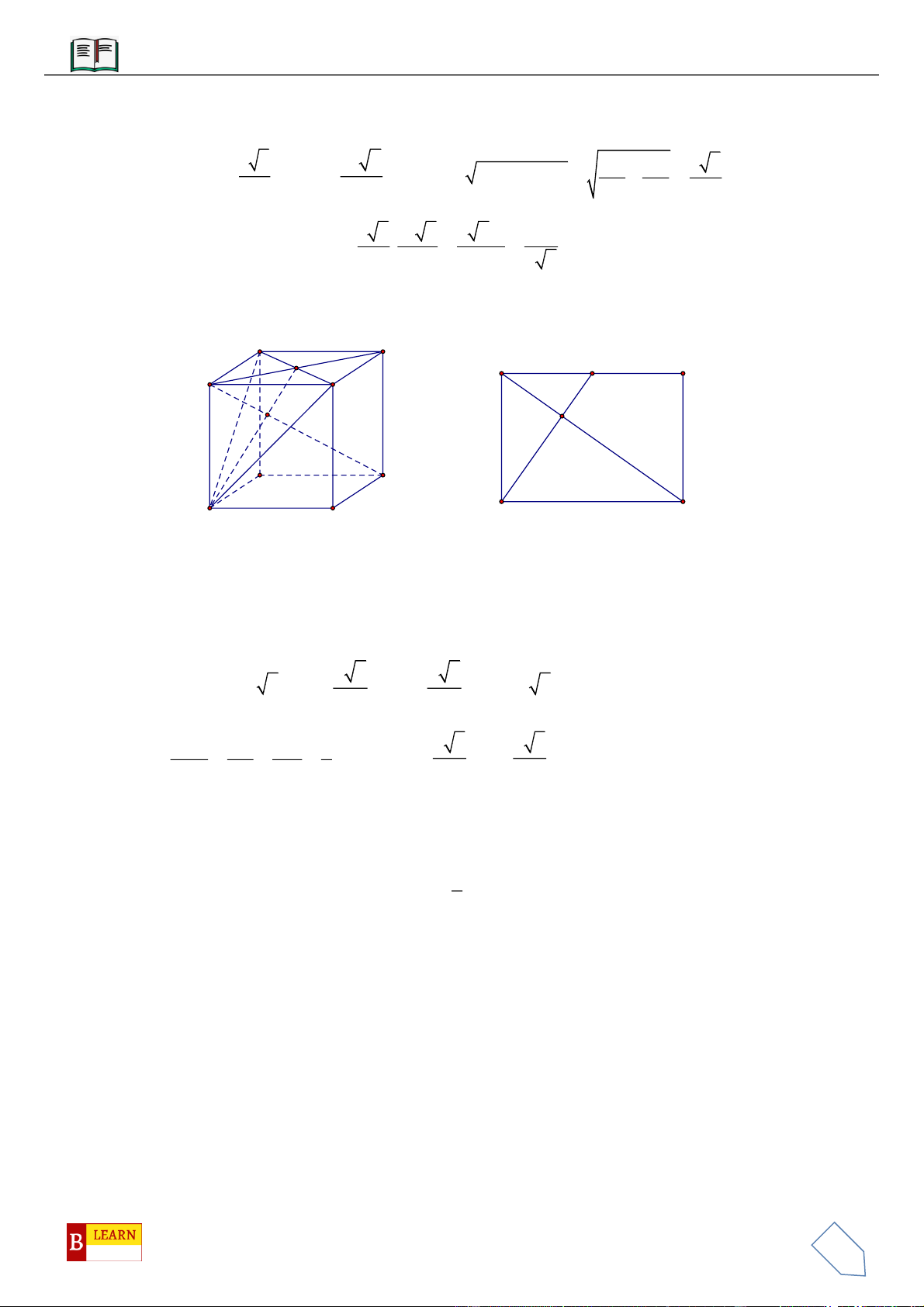
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

247

Gọi

H

là hình chiếu vuông góc của

A



lên

 

ABC

, suy ra

H

là trung điểm của

BC

và tam giác

A AH



vuông tại

H

.

Ta có

3

2

a

AH 

,

2

3

4

ABC

a

S 

.

22

9 3 6

4 4 2

a a a

A H AA AH



     

.

Vậy

2 3 3

.

6 3 3 2 3

.S .

2 4 8

42

ABC A B C ABC

a a a a

V A H

  



   

.

Câu 6: Chọn A

Gọi

O

là giao điểm của AC và BD,

I

là giao điểm của DB’ và D’O. Vì AC vuông góc với BD và

CC’ nên

 

''AC BDD B

.

Gọi x là độ dài cạnh hình lập phương

. ' ' ' 'ABCD A B C D

, khi đó hình chữ nhật

''BDD B

có

26

' ' 2; ; ' ; ' 3

22

xx

BD B D x DO OD BD x    

Vì

1

' ' ' ' 2

DO DI OI

B D B I D I

  

suy ra

36

;

36

xx

DI OI

do đó tam giác

; ' 'DIO D IB

là các tam

giác vuông.

Do

 

''AC BDD B

và

''DB D O

nên

 

22

2

', ' , ' ' . 6

3

d B ACD d D ACD B I DI x a   

nên

3xa

Lại có thể tích của

. ' ' ' 'ABCD A B C D

là

3

ka

nên

33

27 27ka a k  

Câu 7: CChọn A

I

O

C'

B'

B

A'

A

D'

D

C

I

O

B'

B

D'

D

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

248

Gọi

H

là hình chiếu vuông góc của

A

trên

BC

. Suy ra

AH BC

.

'A H BC

. Mà

   

'ABC A BC BC



Góc giữa

 

'A BC

và

 

ABC

bằng góc

 

; ' ' 30AH A H AHA  

.

Ta có:

ABC

là tam giác đều cạnh bằng

a

nên

3

2

a

AH 

,

' .tan30

2

a

A A AH  

.

Thể tích khối lăng trụ

. ' ' 'ABC A B C

là

23

33

'.

2 4 8

ABC

a a a

V A A S



   

.

Câu 8: Chọn A

Gọi

H

là trung điểm của

AB

 

SH ABCD

.

Tam giác

ABC

đều nên

CH AB

, mà

 

/ / 1CD AB CH CD

.

Có

     

2CD SCD ABCD

Có

 

3

CD CH

CD SC

CD SH













Từ đó suy ra

   

 

; ; 45SCD ABCD SC CH SCH   

.

Trong tam giác

SCH

có

3

.

2

a

SH HC

22

33

2 2.

42

ABCD ABC

aa

SS  

23

.

1 3 3

..

3 2 2 4

S ABCD

a a a

V  

.

Câu 9: Chọn C

H

D

B

C

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

249

Gọi

G

là trọng tâm tam giác

ABC

. Dễ thấy

AM BC

,

A G BC





 

BC A AM





.

Gọi

H

là hình chiếu của

M

lên

AA



.

Từ đó suy ra khoảng cách giữa hai đường

AA



và

BC

bằng

3

4

a

MH 

.

3

,

2

a

AM A G x





,

2

2 2 2

3

a

A A A G AG x



   

.

Ta có

2

33

. . . .

2 4 3 3

aa

A G AM HM A A x a a x x



     

.

Thể tích

V

của khối lăng trụ

.ABC A B C

  

là:

23

33

..

3 4 12

ABC

a a a

V A G S



  

.

Câu 10: Chọn A

Ta có:

 

A I ABC





;

AI

là hình chiếu vuông góc của

AA



lên mặt đáy

ABC

.

Do đó

 

, , 60AA ABC AA AI A AI

  

   

.

Tam giác

ABC

đều cạnh

a

nên

3

2

a

AI 

.

Trong tam giác vuông

A AI



, ta có:

33

.tan .tan60

22

aa

A I AI A AI



   

.

Thể tích

V

của khối lăng trụ đã cho là:

23

3 3 3 3

..

2 4 8

ABC

a a a

V A I S



  

.

Câu 11: Chọn B

H

N

M

G

B

C

A

C'

B'

A'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

250

Ta có:

. . .

2 2.4 8 8

A B C BC A SBC A SBC S ABC

V V V V V

   

   

.

Gọi

G

là trọng tâm

ABC

. Ta có

 

, , 60SA ABC SA AG SAG   

.

Xét

SAG

vuông tại

G

. Ta có

23

tan .tan . . 3

32

SG a

SAG SG AG SAG a

AG

    

.

23

.

1 1 3 3

. . . .

3 3 4 12

S ABC ABC

aa

V SG S a   

3

.

23

8

3

S ABC

a

VV  

.

Câu 12: Chọn A

Gọi

M

là trung điểm

BC

33

, , .

23

aa

AM BC AM AG   

Kẻ

 

/ / / / .Ax BC BC A Ax





Kẻ

 

' ' .GH AA GH A Ax  

   

 

3

, , , , .

2

d BC AA d BC AA x d M A Ax d G A Ax

   

   

3 3 3

.

4 2 6

aa

GH GH   

Ta có

2 2 2 2 2

1 1 1 1 27

3

a

GA

GH GA GA GA a



     



.

23

. ' ' '

33

..

3 4 12

ABC A B C ABC

a a a

V A G S



  

 

đvtt

Câu 13: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

251

Gọi

H

là trọng tâm tam giác

ABC

, ta có

 

A H ABC





.

AH BC I  

I

là trung điểm của

BC

và

AI BC

.

Ta có

3

.sin60

2

a

AI AB  

,

23

33

a

AH AI

,

2

13

..

24

ABC

a

S BC AI

Gọi

K

là hình chiếu của

I

trên đường thẳng

AA



. Khi đó

 

AA BCK





. Hay

   

P BCK

.

Ta có hình chiếu của tam giác

ABC

trên mặt phẳng

 

P

là tam giác

BCK

.

Ta có hai khả năng về vị trí điểm

K

.

Khả năng 1:

K

nằm trong đoạn

AA



thì thiết diện của

 

P

và lăng trụ là tam giác cân

BCK

.

Khả năng 2:

K

nằm ngoài đoạn

AA



thì thiết diện của

 

P

và lăng trụ là hình thang cân

BCDE

.

Trong cả hai khả năng trên ta đều có

thiÕtdiÖn

BCK

SS

.

Gọi

AIK





là góc giữa hai mặt phẳng

 

P

và

 

ABC

.

Ta có

2

thiÕtdiÖn

0

2

3

8

cos 30

2

3

4

BCK

ABC ABC

a

S

SS

a



     

90 60A AI





      

1 2 3

cos ' 2

2 cos 3

AH a

AA AH



     

và

3

cos

24

AI a

AK AI



  

.

Do đó

'AK AA

hay

K

phải nằm giữa

A

và

A



.

Ta có

2

1 1 3 3

..

2 2 8 4

BCK

aa

S BC KI a KI KI    

. Suy ra

3

sin 60

2

IK

A AI A AI

AI



    

3

.tan60 . 3

3

a

A H AH a



    

.

Do đó thể tích khối lăng trụ

.ABC A B C

  

là:

23

33

..

44

ABC

aa

V S A H a



  

.

Câu 14: Chọn A





H

I

B

A

A'

C'

B'

C

K





H

I

B

A

A'

C'

B'

C

K





J

E

D

H

I

B

A

C

B'

C'

A'

K





J

E

D

H

I

B

A

C

B'

C'

A'

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

252

Gọi

G

là trọng tâm

ABC

,

I

là trung điểm của cạnh

BC

và

H

là hình chiếu vuông góc của

I

trên

'AA

.

Ta có

 

'

BC AI

BC A AI BC IH

BC A G





   







.

Mặt khác

'IH AA

nên

IH

là đoạn vuông góc chung của

'AA

và

BC

suy ra

3

4

a

IH 

.

ABC

đều cạnh

a

suy ra

3 2 3

,

2 3 3

aa

AI AG AI  

. Diện tích

ABC

là

2

3

4

a

S 

.

AHI

vuông tại

H

có

3

2

a

AI 

và

3

4

a

IH 

suy ra

22

3

4

a

AH AI IH  

.

'GAA

đồng dạng với

HAI

nên ta có:

3

'3

4

' . .

3

33

4

a

GA HI HI a a

GA GA

a

GA HA HA

    

.

Vậy thể tích của khối chóp

. ' ' 'ABC A B C

là

23

33

.

4 3 12

a a a

V 

.

Câu 15: Chọn A

Trong mp

 

SBD

, gọi

P

là giao điểm của

MN

và

SO

Trong mp

 

SAC

, gọi

I

là giao điểm của

AP

và

SC

.

Theo định lý mendeleus ta có:

2 1 1 1

. . 1 . . 1 .

1 1 2 3

AC PO IS IS IS IS

AO PS IC IC IC SC

      

Ta có:

1 1 1 1 1 1

. . . . .

2 3 2 12 12 24

1 1 1 1 1 1

. . . . .

2 2 1 4 4 8

15

..

66

SMNI

SMNI SBCD SABCD

SBDC

SMNA

SMNA SBDA SABCD

SBDA

SAMNI SMNI SMNA SABCD MNIABCD SABCD

V

SM SI SN

V V V

V SB S C SD

V

SM SN SA

V V V

V SB SD SA

V V V V V V

     

     

3

2

1 1 3

. 3.

3 3 3

SABCD ABCD

a

V SA S a a  

33

5 5 3 5 3

. . .

6 6 3 18

ABCDMIN SABCD

V V a a   

Câu 16: Chọn D

H

I

G

C

B

A

C'

B'

A'

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

253

Ta có :

6

OABC

abc

V 

,





2 2 2 2 2 2

1

2

tp

S ab bc ac a b b c a c     

.

Gọi T là tâm mặt cầu nội tiếp tứ diện OABC, ta có:

11

( ) .

33

OABC TOAB TOAC TOBC TABC OAB OAC OBC ABC tp

V V V V V r S S S S r S        

(

r

là bán kính mặt

cầu nội tiếp tứ diện

OABC

)

2 2 2 2 2 2

3

OABC

tp

V

abc

r

S

ab bc ac a b b c a c

  

    

2 2 2 2 2 2 2 2

22

11

a ab bc ac a b b c a c a a a a

r bc c b

cb

    

       

1 1 1 1 1 1 3 3       

. Vậy

min

33

a

a b c

r



    





.

Câu 17: Chọn C

Gọi H là trung điểm của

 

//A D IH AA IH A B C D

      

  

và

3

22

AA a

IH





.

Gọi K là hình chiếu của B lên

CB BK CB





, mà

BK A B





nên

 

.BK CA B





BB C





có

22

.3

2

B B BC a

BK

B B BC









.

   

 

, , , , .d IH BK d IH BB C C d AA BB C C d A BB C C AB a

      

    

Gọi



là góc giữa

IH

và BK, mà

// 'IH BB

nên

B BK







.

Khi đó

13

cos sin

22

BK

BB



   



. Ta có

 

3

13

. . , .sin

6 16

IHBK

a

V IH BK d IH BK





.

Câu 18: Chọn D

I

A

B

D

C

A'

B'

C'

D'

H

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

254

Gọi độ dài các cạnh của hình hộp chữ nhật lần lượt là:

; ; ' zAB x AD y AA  

Ta có:

   

 

25

,,

5

a

d AB B C d AB B CD BH



  

(

H

là hình chiếu của

B

lên

BC



).

Xét tam giác

BCB



ta có:

2 2 2 2

1 1 1 5

4y z BH a

  

 

1

.

Ta có:

   

 

25

;;

5

a

d BC AB d BC ADB BK



  

(

K

là hình chiếu của

B

lên

AB



).

Xét tam giác

ABB



ta có:

2 2 2 2

1 1 1 5

4x z BK a

  

 

2

.

Dựng đường thẳng

d

đi qua

D



và song song với

AC



. Kéo dài

BC



cắt

d

tại

E



.

Ta có:

   

 

1

; ; ; ; B ;

2

d AC BD d AC BD E d C BD E d C BD E d BD E

          

   

.

Từ

 

1

và

 

2

xy



A B C D

   

là hình vuông.

 

23

;

3

a

E D B D d B BD E B I

       

    

(

I

là hình chiếu của

B



lên

BD



).

Xét tam giác

BB D



ta có:

 

2 2 2 2

1 1 1 3

4

2

z B I a

x

  



 

3

.

Từ

 

2

và

 

3

2

x a y a

za

   









. Vậy

3

.

. .2 2

ABCD A B C D

V a a a a

   



.

Câu 19: Chọn C

Gọi là thể tích khối đa diện có các đỉnh .

Gọi lần lượt là diện tích đáy và chiếu cao của hình hộp

.

Ta có

.

C'

A'

D'

C

D

B

A

B'

K

E'

H

I

1

V

, , , , ,M P Q E F N

,Sh

. ' ' ' 'ABCD A B C D

11

. .sin( , ) . .sin( , )

2 2 2

PQEF

S

S PE QF PE QF AB BC AB BC  

F

M

Q

N

E

P

C

D

B

C'

A'

D'

A

B'

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

255

Suy ra .

Phân tích:

+ Kiến thức trọng tâm của bài toán là công thức tính thể tích hình lăng trụ, hình chóp, diện tích

hình bình hành và khoảng cách từ một điểm đến một mặt phẳng.

+ Sử dụng quan hệ song song để tính tỷ số khoảng cách, tỷ số diện tích.

Câu 20: Chọn D

Gọi

H

là hình chiếu của

S

trên mặt đáy, vì

SA SB SC

nên

HA HB HC

hay

H

là tâm

đường tròn ngoại tiếp tam giác

ABC

23

2sin 3

BC a

HA HB HC

A

    

Gọi

O

là trung điểm

BC

, tam giác

ABC

cân tại

A

nên

60

AO BC

BAO CAO









  





Suy ra

23

3

sin

BO a

AB AC

BAO

  

Diện tích tam giác

ABC

là

2

13

. .sin120

23

ABC

a

S AB AC  

Đường cao của khối chóp là

22

39 12

3

99

aa

SH SA AH a    

Thể tích khối chóp

.S ABC

là

23

.

13

. . 3

3 3 3

S ABC

aa

Va

Do

G

là trọng tâm tam giác

SAB

nên

1

3

GM SM

 

1

d G, d ,

3

ABC S ABC

3

..

1

39

G ABC S ABC

a

VV  

.

Cách 2:

Gọi

H

là hình chiếu của

S

trên mặt đáy

 

ABC

, vì

SA SB SC

nên

HA HB HC

.

Gọi

O

là trung điểm

BC

HO BC

Tam giác

ABC

cân tại

A

nên

60

AO BC

BAO CAO









  





.

Vậy

H

nằm trên đường thẳng

AO

và

HAB

đều.

Ta có

. 3 2 2 3

23

3

AH BO a

BO AH AB    

.

Đường cao của khối chóp là

22

39 12

3

99

aa

SH SA AH a    

.

Diện tích tam giác

ABC

là

2

13

. .sin120

23

ABC

a

S AB AC  

 

1

11

( ,( ) ( ,( )

3 3 2 6

PQEF

SV

V S d M PQEF d N PQEF h   

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

256

Thể tích khối chóp

.S ABC

là

23

.

13

. . 3

3 3 3

S ABC

aa

Va

3

..

1

39

G ABC S ABC

a

VV  

.

Câu 21: Chọn B

Gọi

O

là chân đường cao hạ từ

S

xuống mặt phẳng

 

ABC

.

Đặt

 

,d BC aO

,

 

,d O AC b

,

 

,d O AB c

,

SO h

.

Ta có

 

3

1

2

ABC OBC OAC OAB

S S S S a b c

   

      

.

Mặt khác

 

,

2 2 6

,.

4

,

3 3 2

d O SBC

OM OI a a a

d O SBC

AM AK

d A SBC

     

.

Suy ra

2 2 2

2 1 1

ah

a h a

   

.

Tương tự

 

,

2 2 15

,.

10

,

3 3 5

d O SAC

d O AC

b b b

d O SAC

d

d SAC

    

B,AC

B

.

Suy ra

2 2 2

5 1 1

2bh

b h b

   

.

Tương tự

 

,

2 2 30

,.

20

C,

3 3 10

d O SAB

d O AB

c c c

d O SAC

d

d SAB

    

C,AB

.

Suy ra

2 2 2

10 1 1

3ch

c h c

   

.

 

3 3 1 1

1 2 3 . .

2 12 3 48

ABC

h h h h V SO S



        

.

Câu 22: Chọn A

Gọi

O AC BD

và

I

là trung điểm của

AD

.

Ta có

   

ADD A ABCD AD





,

OI AD

và

 

A O ABCD





nên góc giữa hai mặt phẳng

 

ADD A



và

 

ABCD

là

60A IO





.

Tam giác

A IO



vuông tại

O

nên

3

tan tan60

22

aa

A O IO A IO



    

.

a

60

°

I

B'

C'

D'

O

C

D

A

B

A'

a

B'

C'

D'

O

C

D

A

B

A'

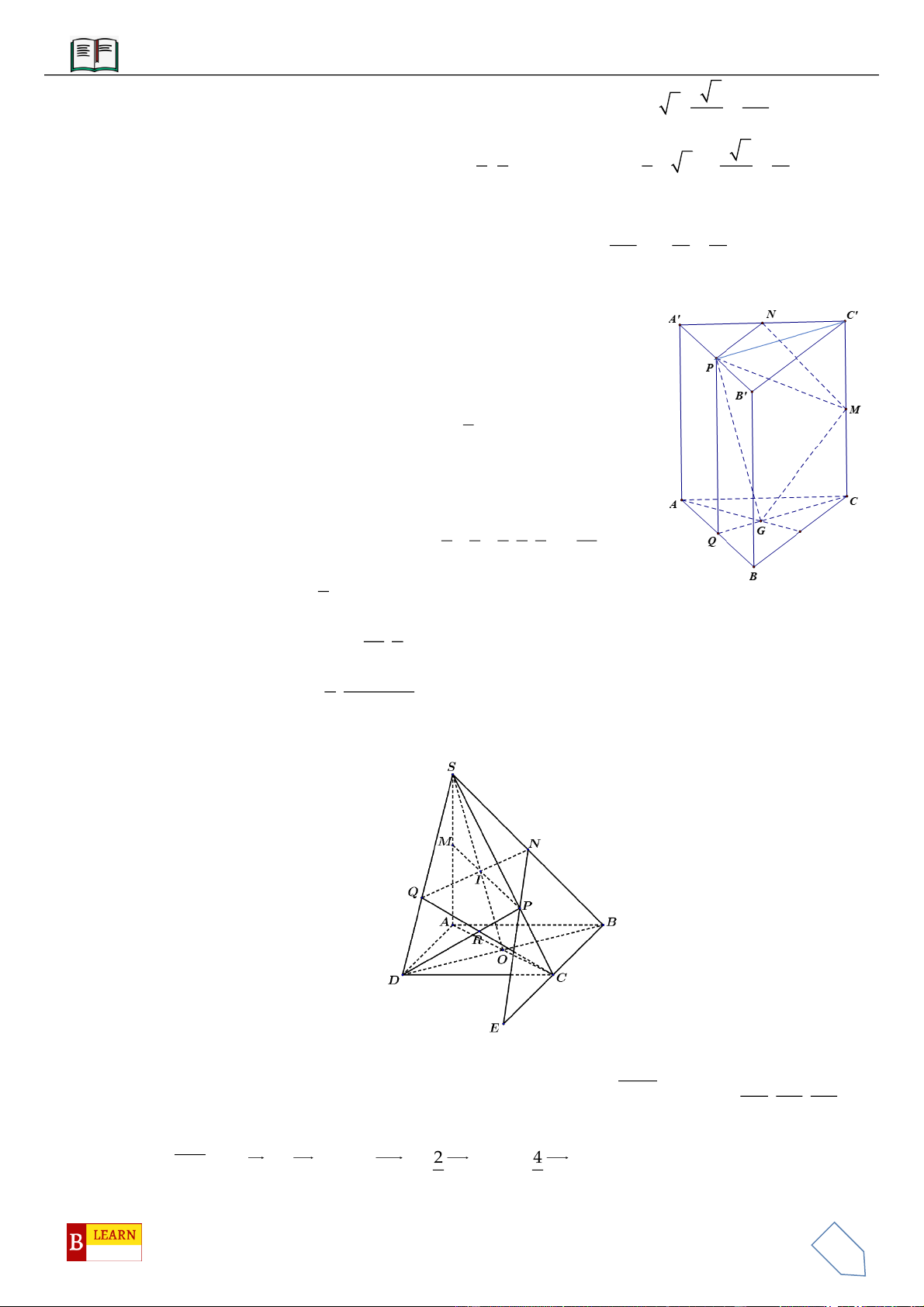
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

257

Thể tích của khối lăng trụ

.ABCD A B C D

   

là

3

33

. . . 3

22

aa

V AB AD A O a a



   

.

Dễ thấy

3

'

1 1 1 3

3

3 2 6 2 4

CC B D B ABC AA B D D ACD

aa

V V V V AD DC A O a a

      



            

.

Vậy thể tích khối tứ diện

ACB D



là

3 3 3

'

3

44

2 4 2

ACB D CC B D B ABC AA B D D ACD D ACD

a a a

V V V V V V V V

         

          

.

Câu 23: Chọn A

Gọi

Q

là trung điểm của

AB

.

Đặt

PQCC

SS





;

 

,h d A PQCC





.

Theo giả thiết

 

.

1

. , 5

3

N GMP GMP

V S d N GMP

 

. , 15

GMP

S d N GMP

.

Ta có

1 1 2 5

..

6 4 2 2 3 12

MPG PQCC PQG PMC MGC

S S S

S S S S S S S



        

.

Lại có

 

1

,,

2

d N GMP d A GMP





.

Suy ra:

 

5

. , .

12 2

GMP

Sh

S d N GMP 

. 72Sh

.

Mặt khác, vì

.

2

.

32

ABC A B C

A PQCC

V

  





nên

.

. 72

ABC A B C

V S h

  



.

Câu 24: Chọn A

Gọi

,O AC BD I MP SO Q NI SD      

ÁP dụng định lí Menelauyt cho tam giác

SBC

với cát tuyết

NPE

, ta được

. . 1

NB PS EC

NS PC EB



CE CB

Do

MIP

nên

24

(1 ) (1 )

39

SI xSP x SM x SC x SA     

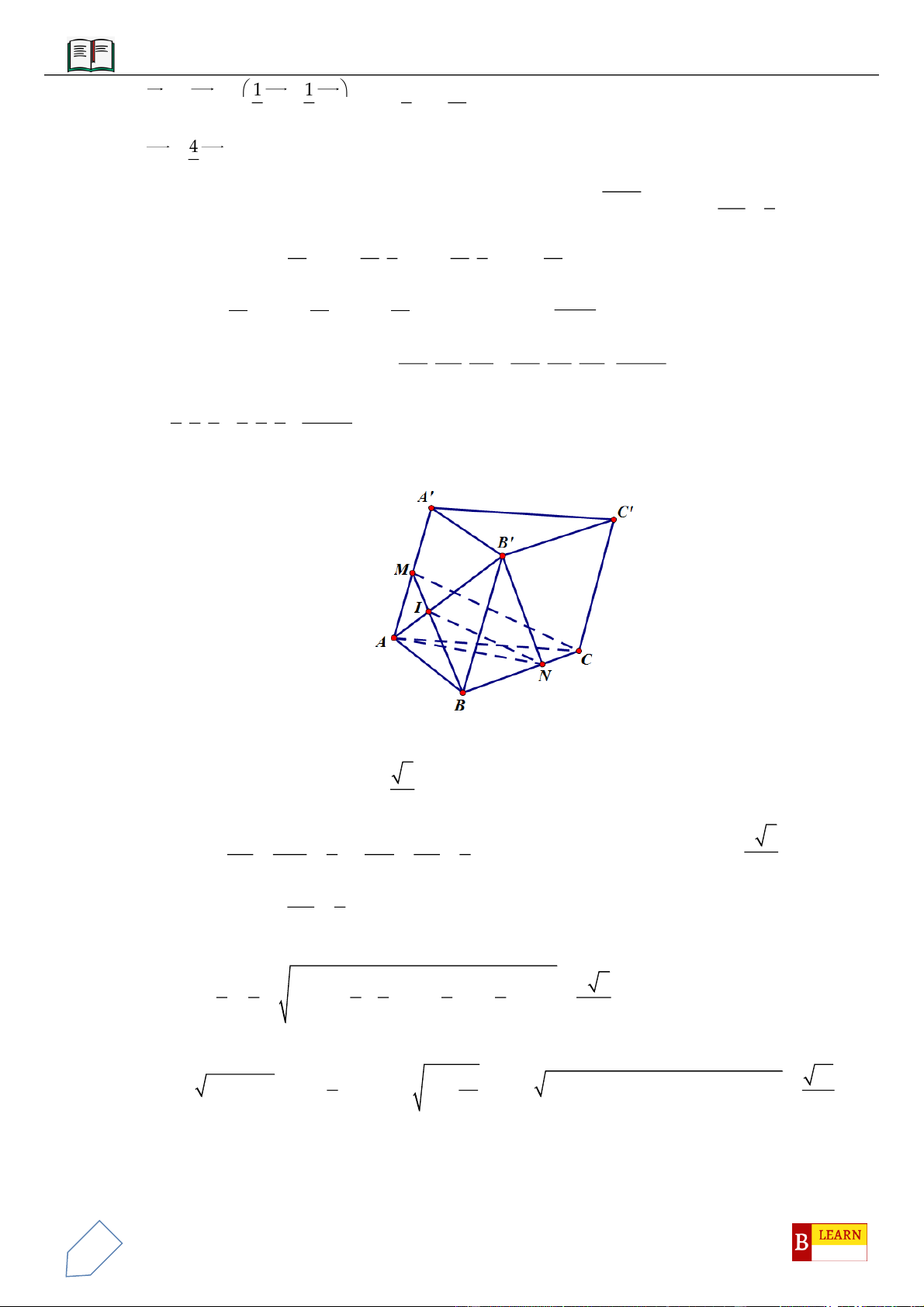
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

258

1 1 3 8

,

2 2 5 15

SI kSO k SC SA x k



     





. Tương tự với ba điểm thẳng hàng

,,N I Q

ta có

4

7

SQ SD

Áp dụng định lí Menelauyt cho tam giác

SCQ

với cát tuyết

PRD

, ta được

 

6

3

7

RQ

RC



Từ đó ta có

6 6 1 2 4 8

. . .

13 13 3 13 7 91

PRQ PQC SQC SDC SDC

S S S S S   

8 8 4

91 91 91

EPQR ESDC SBDC SABCD

V V V V   

18.91

4

SABCD

V

Do đó

. . . .

2

SABCD

SMNPQ SMNP SMPQ

V

SM SN SP SM SP SQ

V V V

SA SB SC SA SC SD



   





3

4 2 1 2 4 4

. . . . . 65cm

9 3 2 3 9 7 2

SABCD

V



  





Câu 25: Chọn A

Gọi

'; / / ( )I BM AB IN CM N BC  

. Khi đó:

/ /( ' )CM AB N

7

( , ' ) ( ,( ' )) .

7

d CM A B d C AB N  

Mặt khác:

11

' 2 2

IM AM NC IM

IB BB NB IB

    

27

( ,( ' )) 2 ( ,( ' )) .

7

d B AB N d C AB N  

Ta có:

1

cos .

2

AB

ABN

BC



Đặt

',BB x

áp dụng công thức thể tích khối chóp tam giác khi biết

ba cạnh chung đỉnh và ba góc tại đỉnh đó. Ta được:

22

2

.'

1 4 1 1 1 1 2

.1. . . 1 2. . .0 0 .

6 3 2 2 2 2 9

B AB N

x

Vx

     

       

     

     

Ta có:

2 2 2 2

4 16 13

' 1, ' , 2 . .cos .

3 9 3

AB x x BN NB x AN AB BN AB BN ABN          

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

259

22

13 16

1

99

32

cos '

2 13( 1) 2 13( 1)

3

x x x

x

B AN

x x x x



    









   

 

2

32

sin ' 1

52( 1)

x

B AN

xx



  



.

2

22

'

2

13( 1)

(3 2) 43 40 48

1

6 12

52( 1)

AB N

xx

x x x

S

xx



  

  



.

Do đó:

.'

2

'

2

3

27

3

( ,( ')) 4( 0).

7

43 40 48

12

B ANB

ANB

x

V

d B ANB x x

S

xx

     



Vậy

.'

42

9

B ANB

V 

và

. ' ' ' '. . '

3 9 4 2

3 3 . 2 2

2 2 9

ABC A B C B ABC B ANB

V V V



   





.

Câu 26: Chọn B

Gọi

M

là trung điểm của

BC

, vì

ABC

cân tại

A

nên

AM BC

. Lại có

//EF BC EF AM

.

ABC

có

E

là trung điểm của

AB

,

//EF AM

F

là trung điểm của

BM

EF

là đường

trung bình của

BAM

.

Kéo dài

FE

cắt tia

CA

tại

I

. Nối

CI



cắt

AA



tại

N

. Khi đó

 

C EF



cắt lăng trụ theo thiết diện

là tứ giác

EFC N



.

Gọi thể tích khối đa diện chứa đỉnh A là

1

V

.

Ta có:

2

//

3

AM CM

AM FI

FI CF

  

, mà

12

2

33

EF IE

AM EF

FI IF

    

.

Lại có:

1

3

IA FM

IC FC



;

IN IA

IC IC





nên

1

3

IN

IC





.

Từ

 

1

,

 

2

và

 

3

suy ra

.

2 1 1 2

. . . .

3 3 3 27

I EAN

I FCC

V

IE IA IN

V IF IC IC



  



.

Do đó

1

.

2 25

1

27 27

I FCC

V



  

. Dễ thấy

3

2

IC

AC



và

3

8

FCC

BCC B

S







, do đó

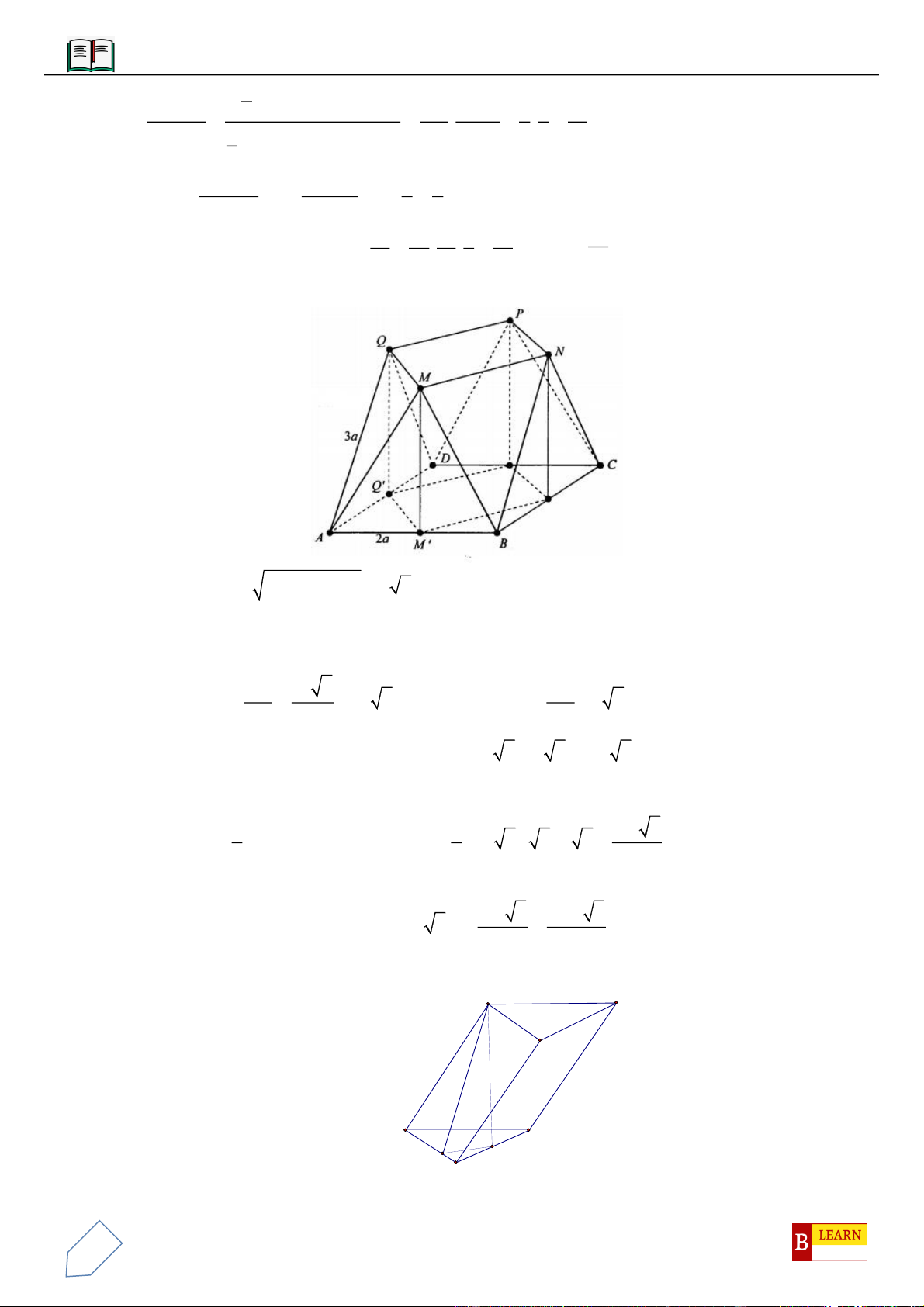
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

260

 

.

1

,.

3 3 9

3

..

1

2 8 16

,.

3

FCC

I FCC FCC

A BCC B BCC B

BCC B

d I FCC S

VS

IC

V AC S

d A BCC B S





   





   



.

Lại có

..

12

11

33

A BCC B A A B C

VV

    

    

.

Từ

 

4

,

 

5

và

 

6

, ta suy ra

1

25 9 2 25

..

27 16 3 72

V



.

1

25

72

VV

.

Câu 27: Chọn B

Ta có

   

22

3 2 5MM a a a



  

.

Chia khối đa diện đã cho thành khối lăng trụ đều có đáy là

MNPQ

và chiều cao là

MM



và 4

khối chóp tứ giác có đáy là hình chữ nhật dạng như

.A MQQ M



.

Ta có

 

42

2 2; , 2

2 2 4

AC a AC

MN a d A MQQ M a



    

.

Suy ta thể tích khối lăng trụ

 

2

3

.

2 2 . 5 8 5

MNPQ M N P Q

V a a a

   



.

Thể tích khối chóp tứ giác

.A MQQ M



là:

 

3

.

1 1 4 5

.d , . 2 2. 5 . 2

3 3 3

A MQQ M MQQ M

a

V S A MQQ M a a a

   



  

Suy ta thể tích khối đa diện đã cho là:

 

33

3

..

4 5 40 5

4 8 5 4.

33

MNPQ M N P Q A MQQ M

H

aa

V V V a

     

    

.

Câu 28: Chọn B

60

0

H

M

C'

B'

A'

A

B

C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

261

Hạ

HM

vuông góc với

''AB

tại điểm

H

. Khi đó góc nhị diện giữa hai mặt phẳng

 

AA B



và

 

ABC

cũng chính là góc giữa 2 mặt phẳng

 

''AA B

và

 

' ' 'A B C

và bằng

0

60AHM 

.

Xét tam giác vuông

'HB M

vuông tại H có

3

.sin60

24

aa

HM   

.

Xét tam giác vuông

AMH

vuông tại

M

có

3

.tan60

4

a

AM HM  

.

Thể tích khối lăng trụ

23

. ' ' '

3 3 3 3

..

4 4 16

ABC A B C ABC

a a a

V S AM  

Câu 29: Chọn B

Chiều cao hình chóp

2

2 2 2

14

4

22

aa

SO h SA OA a     

.

2

2 2 2

15

4

42

aa

SM SC MC a    

.

Cách 1: Gọi tâm mặt cầu nội tiếp là

I

, khi đó ta có

IO IN r

.

Từ hình vẽ ta có

 

IN SBC

,

SIN SOM∽

14

27

2

15 15 30 2

2

22

a

r

SI IN h r r r a

r

a

SM OM a

aa



       



.

Cách 2 Thể tích khói chóp

3

2

1 1 14 14

..

3 3 2 6

SABCD ABCD

aa

V S SO a  

.

Diện tích mặt bên

2

1 15

.

24

SBC

a

S BC SM

.

Áp dụng công thức

3

2

14

3.

3 3 7

6

.4

15 30 2

4.

4

tp ABCD SBC ABCD

a

V V a

r

S S S S

a

   



.

Câu 30: Chọn D

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

262

Gọi O là giao điểm của

AC

và

DB

. Ta có:

   

 

D , D 60SB ABC SOA

.

Xét tam giác

SOA

vuông tại

A

:

26

.tan .tan60

22

aa

h SA AO SOA   

.

3

2

. D D

1 1 6 6

. . . .

2 3 2 6

S ABC ABC

aa

V S SA a   

.

Câu 31: Chọn D

Gọi

O

là giao điểm của

AC

và

BD

.

Dễ dàng thấy được góc tạo bởi hai mặt phẳng

 

SBD

và

 

ABCD

là góc

SOA

suy ra

60SOA 

.

Xét tam giác

SOA

vuông tại

A

có

26

.tan .tan60

22

aa

h SA AO SOA    

.

Do đó thể tích khối chóp

.S ABCD

bằng

3

2

.

1 1 6 6

..

3 3 2 6

S ABCD ABCD

aa

V SA S a  

.

Câu 32: Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

263

Thể tích khối lăng trụ:

.

ABC

V S h





23

35

.

42

aa

h

2 15

3

a

h AA



  

.

Bán kính đáy lăng trụ

3

d

a

R 

.

Áp dụng công thức tính bán kính mặt cầu ngoại tiếp lăng trụ:

2

4

d

h

RR

2

2 15

3

34

a















2a

.

Câu 33: Chọn C

Hình vẽ minh họa

Ta dễ dàng tính được:

   

22

4 2 2 3MM a a a



  

.

Các cạnh hình vuông

MNPQ

là:

42

22

AC a

MN a  

.

Nếu ta gọi

A



là trung điểm của

MP

thì ta có

   

 

2

22

2

4 2 14AA AM MA a a a



    

Suy ra diện tích toàn phần của khối đa diện

 

H

là:

 

2

_

11

4 4. 4 2 2 4. .2 2. 14 4. .4 .2 3

22

ABCD MNPQ AMQ MAB

tp H

S S S S S a a a a a a



       

2 2 2

24 8 7 16 3a a a  

.

Câu 34: Chọn A

Gọi cạnh của hình lập phương và cạnh của tứ diện đều lần lượt là

,ab

.

Ta có:

 

1

2

22

2

4 4 2 3

3

33

3

4.

4

xq H

tp H

S

a

b a b a

S

b

     

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

264

Suy ra:

 

1

2

33

3

96

4

2

2 3 2

.

12

3 12

H

V

aa

V

b

a

  







.

Câu 35: Chọn B

Do góc giữa cạnh bên với mặt đáy của lăng trụ là

30

o

nên suy ra

00

31

30 .tan30 .

22

3

aa

A AH A H AH



     

.

Suy ra thể tích lăng trụ của khối lăng trụ

.ABC A B C

  

là

23

.

33

..

4 2 8

ABC A B C ABC

a a a

V S A H

  



  

.

Câu 36: Chọn B

Tam giác

SAB

vuông tại

A

và có

60 .tan60 3.SBA SA AB a     

Dựng hình bình hành

ABCD

, suy ra:

       

22

.

// ; ;( ) ;( ) .

SA AP

AC SBD d AC SB d AC SBD d A SBD AQ

SA AP

    



Trong đó

;.AP BD AQ SB

Tam giác

ABC

đều suy ra:

3

2

a

AP 

 

2 2 2

2

3

3.

. 15

2

;.

5

3

2

a

SA AP a

d AC SB AQ

SA AP

a

    











Câu 37: Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

265

Giao điểm của mặt phẳng

 

MNP

với cạnh

'BB

là trung điểm

Q

của

'BB

.

Khi đó thể tích

1

V

là phần thể tích khối lăng trụ

' . 'A MN B PQ

như hình vẽ.

Ta có:

' ' ' ' '

11

48

A MN A AD A MN A ADD

S S S S

   

  

' . ' . ' ' ' ' 1

1

88

A MN B PQ ABCD A B C D

V

V V V   

.

1

2

1

7

V



.

Câu 38: Chọn C

Gọi

H

là hình chiếu vuông góc của

S

lên

 

ABC

và

,,M N P

lần lượt là hình chiếu vuông góc

của

H

lên các cạnh

,,AB AC BC

. Khi đó góc tạo bởi các mặt phẳng

     

,,SAB SCA SBC

với

 

ABC

lần lượt là

,,SMH SNH SPH

. Suy ra

60 , 45

oo

SMH SPH SNH  

.

Đặt

SH h

.cot60

3

o

h

HM HP SH   

;

.cot45

o

HN SH h

.

Ta có

ABC ABH ACH CBH

S S S S

   

  

. . . .AB AC AB MH BC HP AC HN   

2

2 2. 2 . 2.

33

hh

a a a a h   

23

2 2 6

a

h



3

12

.

3

2 3 6 3 2

SABC ABC

a

V S h



  



.

Câu 39: Chọn B

D

P

N

Q

M

C

B

A

A'

D'

B'

C'

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

266

Ta có

 

AB AC

AB ACC A

AB AA

















, mà

 

BC ACC A C

   



nên góc tạo bởi đường thẳng

BC



và mặt phẳng

 

ACC A



là:

 









0

, , 30BC ACC A BC AC AC B

     

  

Ta có:

0

2 .cot30 2 3AB AC a AC AB a



    

Suy ra đường cao lăng trụ là

 

2

22

2 3 2 2 2h CC AC AC a a a



     

Thể tích lăng trụ là

 

2

3

1

. . 2 .2 2 4 2

2

ABC

V S CC a a a





  

.

Câu 40: Chọn A

Gọi

O AC BD

.

Ta có

SAC

vuông tại

S

nên

OS OA OB OC OD R    

. Vậy

O

là tâm mặt cầu ngoại tiếp

hình chóp

.S ABCD

bán kính

R

.

Đặt

,0SC x x

. Theo đầu bài, diện tích tam giác

SAC

là

2

2a

nên:

22

1 4 4

. 2 . 4

2

aa

SA SC a SA SC a SA

SC x

     

.

Suy ra

44

22

1 16 1 16

2 . 2.

22

AM GM

aa

R x x a

xx



   

Để diện tích mặt cầu ngoại tiếp hình chóp

.S ABCD

là nhỏ nhất thì bán kính

R

nhỏ nhất

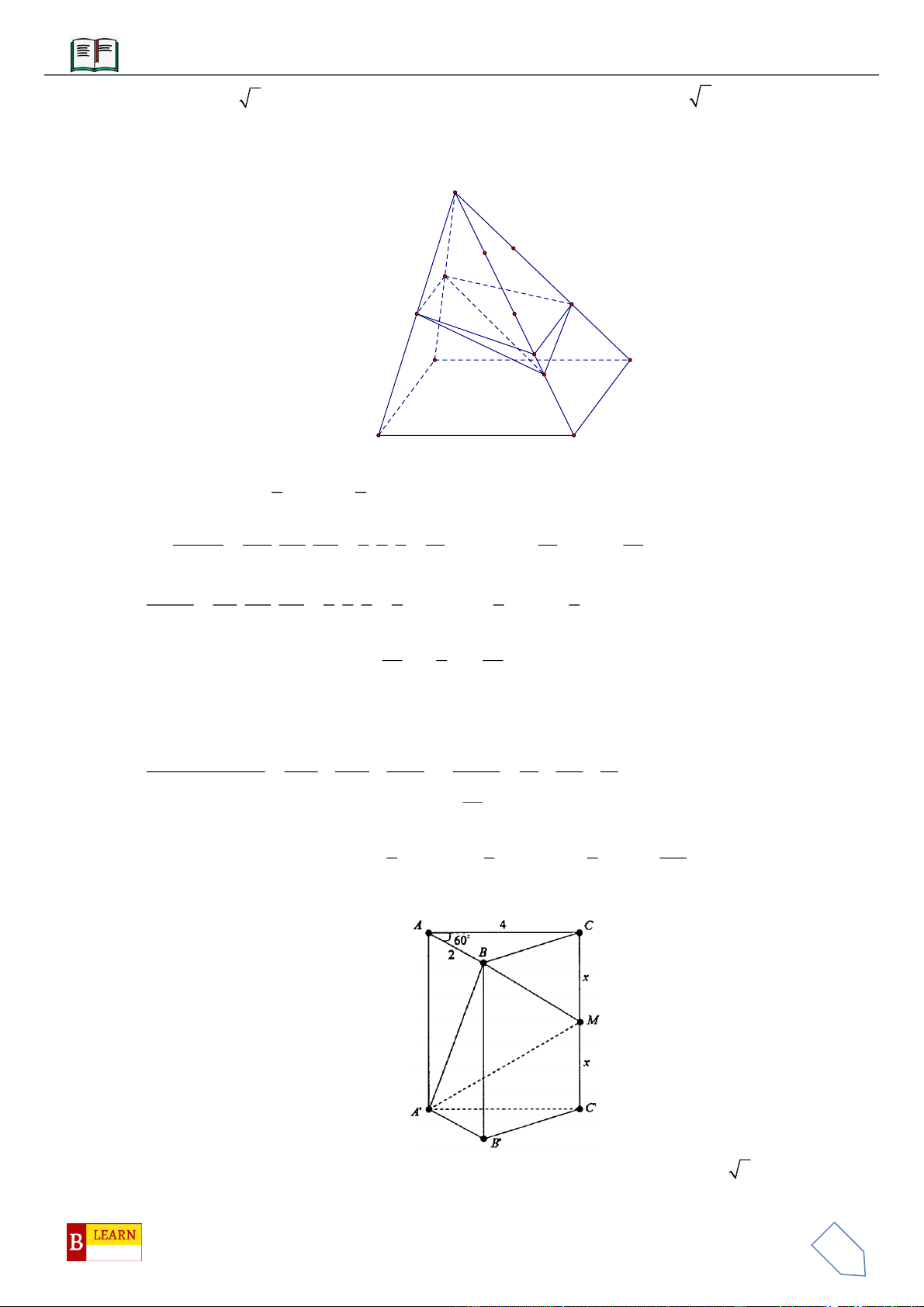
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

267

min 2Ra

. Vậy diện tích nhỏ nhất của mặt cầu là

 

2

22

4 4 2 8S R a a

  

  

.

Câu 41: Chọn D

Dễ thấy

. . .

11

22

S ABD S CBD S ABCD

V V V V  

.

Có

.

..

.

1 1 3 3 3 3

. . . .

2 2 4 16 16 32

S MNQ

S MNQ S ABD

S ABD

V

SM SN SQ

V V V

V SA SB SD

     

.

..

.

2 1 3 1 1 1

. . . .

3 2 4 4 4 8

S PNQ

S PNQ S CBD

S CBD

V

SP SN SQ

V V V

V SC SB SD

     

.

Vậy

..

3 1 7

32 8 32

SMNPQ S MNQ S PNQ

V V V V V V    

.

Câu 42: Chọn A

Gọi chiều cao của hình chóp là

h SA

. Khi đó ta có

 

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1

4

2

;

3

ha

AS AB AD h a a

a

d A SBD

        

   







Vậy thể tích khối chóp

3

1 1 1 2

. . .h 2 . .

3 3 3 3

SABCD ABCD

a

V S SA AB AD a a a   

Câu 43: Chọn A

Đặt

' 2 ,AA x

tam giác

ABC

có

2, 4AB AC

và

60 2 3.BAC BC    

K

P

Q

N

M

C

A

D

B

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

268

Ta có:

2

' 16

12

' 4 4

A M x

BM x

A B x



















Tam giác

'BMA

vuông tại

2 2 2

16 12 4 4 2 3 ' 4 3.M x x x x AA         

1

. . .sin60 2 3

2

ABC

S AB AC  

;

. ' ' '

. ' 24.

ABC A B C ABC

V S AA

Câu 44: Chọn C

Cách 1: Gọi

I

là trung điểm của

SB

Xét

MNI

vuông tại

,I

ta có:

22

47

9 4 6

a a a

NI MN MI    

1

7

6

IN SB SB a  

2 2 2 2

76SA SB AB a a a    

Thể tích của khối chóp

.S ABCD

là

3

22

1 1 6

. 6. .

3 3 3

a

V SA AB a a  

Cách 2: Gắn hệ trục tọa độ vào hình chóp với:

A

trùng với

,O

trục

Ox

dọc theo

,AD

trục

Oy

dọc theo

,AB

trục

Oz

dọc theo

.AS

Ta gán các giá trị

1.a 

Khi đó,

(0,0,0), (0,1,0), (1,1,0), (1,0,0), (0,0, ).A B C D S h   

11

, , ,

222

h

M







2

2 0 0, ,

33

h

NS NB N



  





222

2

1 1 2 10 2

06

2 2 3 2 3 6 2 3

h h h a a

MN h

      

          

     

     

Suy ra thể tích khối chóp

.S ABCD

là

33

2

1 1 1 . 6 6

. .1 .1. 6

3 3 3 3

ABCD

a

V S h   

Câu 45: Chọn A

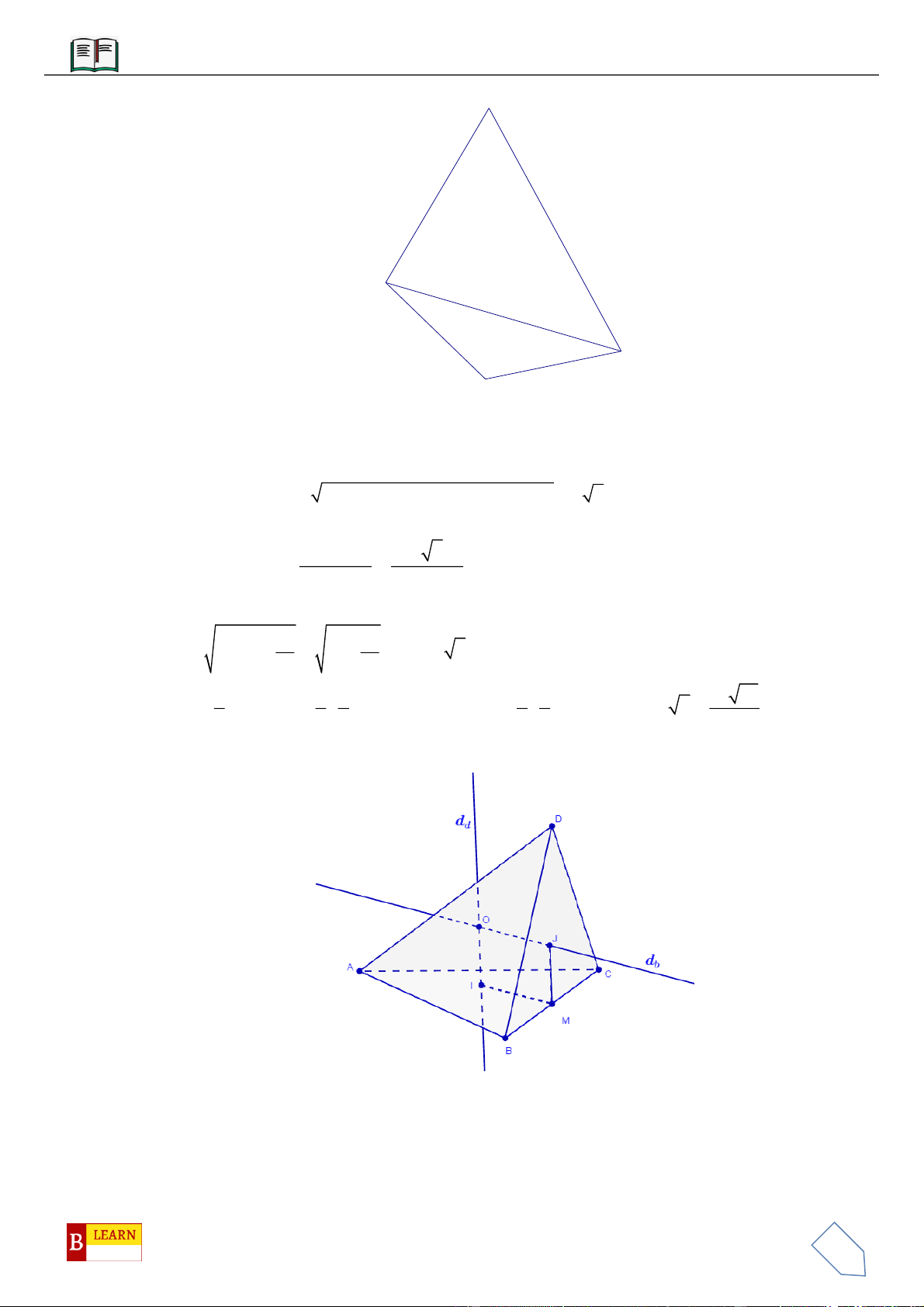
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

269

Vì lăng trụ đứng tồn tại mặt cầu ngoại tiếp nên bắt buộc đáy phải là tứ giác nội tiếp được đường

tròn. Suy ra

00

180 120ADC ABC  

Trong

:ADC

2 2 0

2. . . 120 4 3AC DA DC DA DC cos   

Khi đó bán kính đường tròn ngoại tiếp

ADC

( cũng là bán đường tròn ngoại tiếp tứ giác đáy

ABCD

) là:

00

43

4

2sin120 2sin120

ADC

AC

R





Nếu chiều dài cạnh bên ( cũng là chiều cao lăng trụ) là

'h AA

thì bán kính mặt cầu tiếp là:

22

6 4 4 5

44

ADC

hh

R R h



      

. Vậy thể tích tứ diện

'A ACD

là:

00

'

1 1 1 1 1 16 15

. ' . .sin120 . .4.4.sin120 .4 5 .

3 3 2 3 2 3

A ACD ACD

V S AA DA DC h

   

   

   

   

Câu 46: Chọn A

Gọi

,

db

RR

lần lượt là bán kính đường tròn ngoại tiếp tam giác

ABC

và

BCD

.

Gọi

,IJ

lần lượt là tâm đường tròn ngoại tiếp tam giác

ABC

và

BCD

.

,

db

R IC R JC  

.

Gọi

,

db

dd

lần lượt là trục đường tròn ngoại tiếp tam giác

ABC

và

BCD

.

60

°

120

°

4

C

D

B

A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

270

Gọi

O

là tâm của mặt cầu ngoại tiếp

ABCD

db

O d d

.

Gọi

M

là trung điểm

,BC MI MJ

là các đường trung trực của

BC

.

MIOJ

là hình chữ nhật.

2

2 2 2 2 2 2 2 2 2

4

db

GT

R OJ CJ IM CJ IC MC CJ R R R          

.

Đây là dạng hình chóp có hai mặt vuông góc với nhau. Khi đó công thức tính bán kính mặt cầu là

2

22

4

db

GT

R R R  

, trong đó

GT

là độ dài giao tuyến:

6GT BC

.

Bán kính đường tròn ngoại tiếp tam giác

ABC

và

DBC

là

2sin

ABC

BC

R

BAC





;

2sin

BDC

BC

R

BDC





.

Từ giả thiết suy ra

3 3. sin 3 sin

2sin 2sin

ABC DBC

BC BC

R R BDC BAC

BAC BDC



    

.

Lại có:

0

90BAC BDC

00

60 ; 30BDC BAC  

6, 2 3

ABC BDC

RR



  

.

Suy ra bán kính mặt cầu ngoại tiếp tứ diện

ABCD

là:

 

2

6

6 2 3 39

4

R    

.

Câu 47: Chọn B

Hạ đường cao

SH

vuông góc với

 

ABC

tại

H

(Vì

SABC

cố định nên

SH

cố định), trên

SH

lấy

điểm

K

sao cho

. . 3SH SK SM SN

. Suy ra điểm

K

cố định và được xác định bởi

3

SK

SH



.

Suy ra

SHM SNK∽

90SNK  

. Suy ra

N

nhìn

SK

(cố định) một góc vuông. Vì thế

M

chạy trên mặt phẳng

 

ABC

thì

N

nằm trên mặt cầu cố định có đường kính là

SK

.

Suy ra

33

2 2 3 . 2 3

2

23

SK R SH SK SH SH      

.

Diện tích tam giác

ABC

là

2

33

44

ABC

a

S





.

N

H

A

B

C

S

M

K

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

271

Suy ra

.

1 1 3 3 1

. . .

3 3 4 2 8

S ABC ABC

V S SH



  

.

Câu 48:

Chọn A

Tâm mặt cầu ngoại tiếp là điểm

O

cách đều các đỉnh:

2

a

OA OB OC OD OS    

.

Ta có

22

6

24

2 2 2 2 2

OA a a a a

OH SH SO OH

   

       

   

   

.

Suy ra thể tích của hình chóp

SABCD

là

3

2

1 1 6 6

..

3 3 4 12

SABCD ABCD

aa

V S SH a  

.

Câu 49: Chọn D

Cách 1:

Dễ thấy

3

2 2 2

.

21

. . 1 os os os 2 os . os . os

12 6

S ABD

a

V SA SB SD c ASB c ASD c BSD c ASB c ASD c BSD     

,

mặt khác

AB AD SA SB SD a    

nên

.S ABD

là tứ diện đều.

Suy ra

31

22

a

SO AC

, nên tam giác

SAC

vuông tại

S

.

Mặt khác: Dựng

OI SC

trong mặt phẳng

 

SAC

. Dễ dàng ta chứng minh được

 

SC BID

.

Nên:

 

   

 

   

11

1

22

; ; 2

OI SA BD

SBC SCD BI DI















.

H

O

D

B

C

A

S

O

H

I

B

C

D

A

S

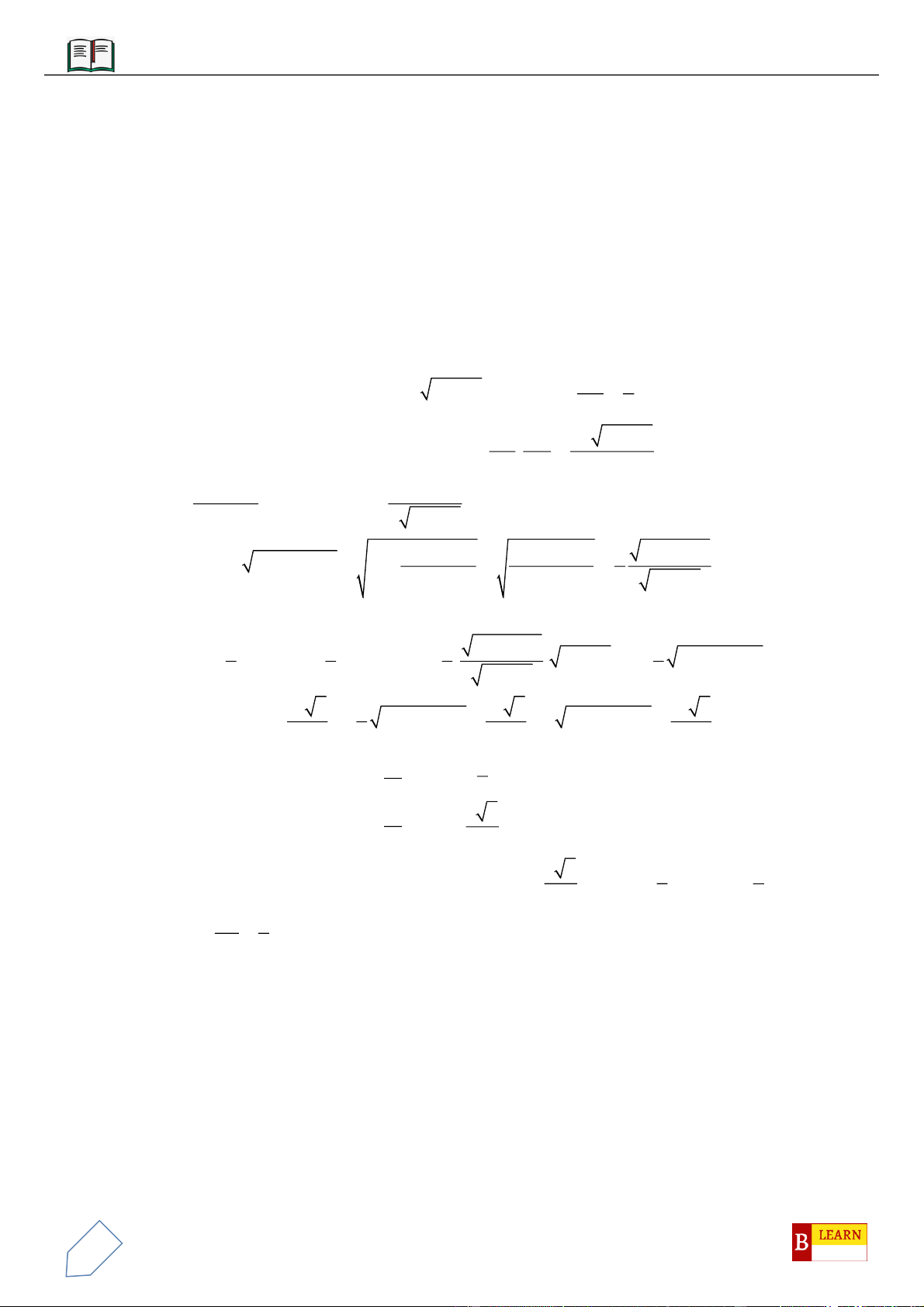
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

272

Từ

 

1 BID  

tại

I

. Từ

   

1 ; 2

suy ra

   

 

; ; 90SBC SDC BI DI  

.

Cách 2:

Gọi

O

là tâm của hình thoi

ABCD

. Ta có

, SCB SDC

là các tam giác cân lần lượt tại

,BD

.

Gọi

I

là trung điểm của

BI SC

SC

DI SC











.

Do đó góc giữa hai mặt phẳng

 

SBC

và

 

SDC

là góc giữa hai đường thẳng

BI

và

DI

.

SBC SDC BI DI IBD      

cân tại

I

.

Gọi

H

là hình chiếu của

S

lên mặt phẳng

 

ABCD

.

Do

SA SB SD HA HB HD H     

là tâm đường tròn ngoại tiếp của tam giác

ABD

.

Mà

ABD

cân tại

A

nên

H

nằm trên đường chéo

AC

của hình thoi

ABCD

.

Đặt

 

0OB x x a  

. Ta có

22

; sin

OB x

OA a x OAB

AB a

   

.

22

2

sin sin2 2sin .cos 2 .

OB OA x a x

BAD OAB OAB OAB

AB AB

a



   

.

Ta có

2

22

2

sin

2

BD a

AH AH

BAD

ax

  



.

Suy ra

   

4 4 2 2 2 2

2 2 2

2 2 2 2

22

3 4 3 4

2

44

a a a x a a x

SH SA AH a

a x a x

ax



     





.

Gọi

V

là thể tích của khối chóp

.S ABCD

.

Ta có

22

2 2 2 2 4

22

1 1 3 4

. . . . . .2 3 4

3 3 6 3

ABCD

a a x a

V SH S SH AO BD a x x a x x

ax



     



.

Theo giả thiết

3 3 2

2 2 4 2 2 4

2 2 2

3 4 3 4

6 3 6 2

a a a a

V a x x a x x      

.

2

4 2 2 4

2

4

8 6 0

2

a

x

x a x a

a

x







     









.

Do tứ giác

ABCD

không phải là hình vuông nên

2

a

x 

. Vậy

2

a

x 

hay

2

a

OB 

.

Mà

2

SA a

OI

a



. Suy ra

BIO

vuông cân tại

45 90O BIO BID     

.

Vậy góc giữa hai mặt phẳng

 

SBC

và

 

SCD

là

90

.

Câu 50: Chọn D

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

273

Gọi

N

là trung điểm

AB



AN A B





.

Gọi

H

là chân đường cao hạ từ

A

xuống mặt phẳng

 

A B C

  

HN A B





,

HM B C





.

Ta có:

2

3

3 cos30

3 3 3

2

a

a C M a

C M C H





    



.

3 2 5 3

2 18

33

a a a

HN C N C H



    

 

2

22

2

2 2 2 2 2

5 3 13 13 285

2

18 2 27 27 9

a a a a a

HB HN NB AH AB HB a



   

          





Suy ra thể tích lăng trụ là:

23

.

3 285 95

..

4 9 12

C ABA CBC A B

a a a

V S AH

  



  

  

.

Câu 51: Chọn D

Gọi

N

là giao điểm của mặt phẳng

 

ABM

với

SD

, đặt

.S ABCD

VV

.

Áp dụng công thức tỉ số thể tích cho khối chóp có đáy là hình bình hành:

SA SC SB SD SC SD

SA SM SB SN SM SN

    

, mà

22

SC SD

SM SN

  

.

1 1 2 2 3

4.1.1.2.2 8

4 . . .

S ABMN

S ABCD

SA SB SC SD

V

SA SB SM S N

SA SB SC SD

V

SA SB SM SN

  

  

.

Mặt phẳng

 

ABMN

chia hình chóp thành hai phần có thể tích theo tỉ lệ

3

và

5

.

D

A

B

C

S

M

N

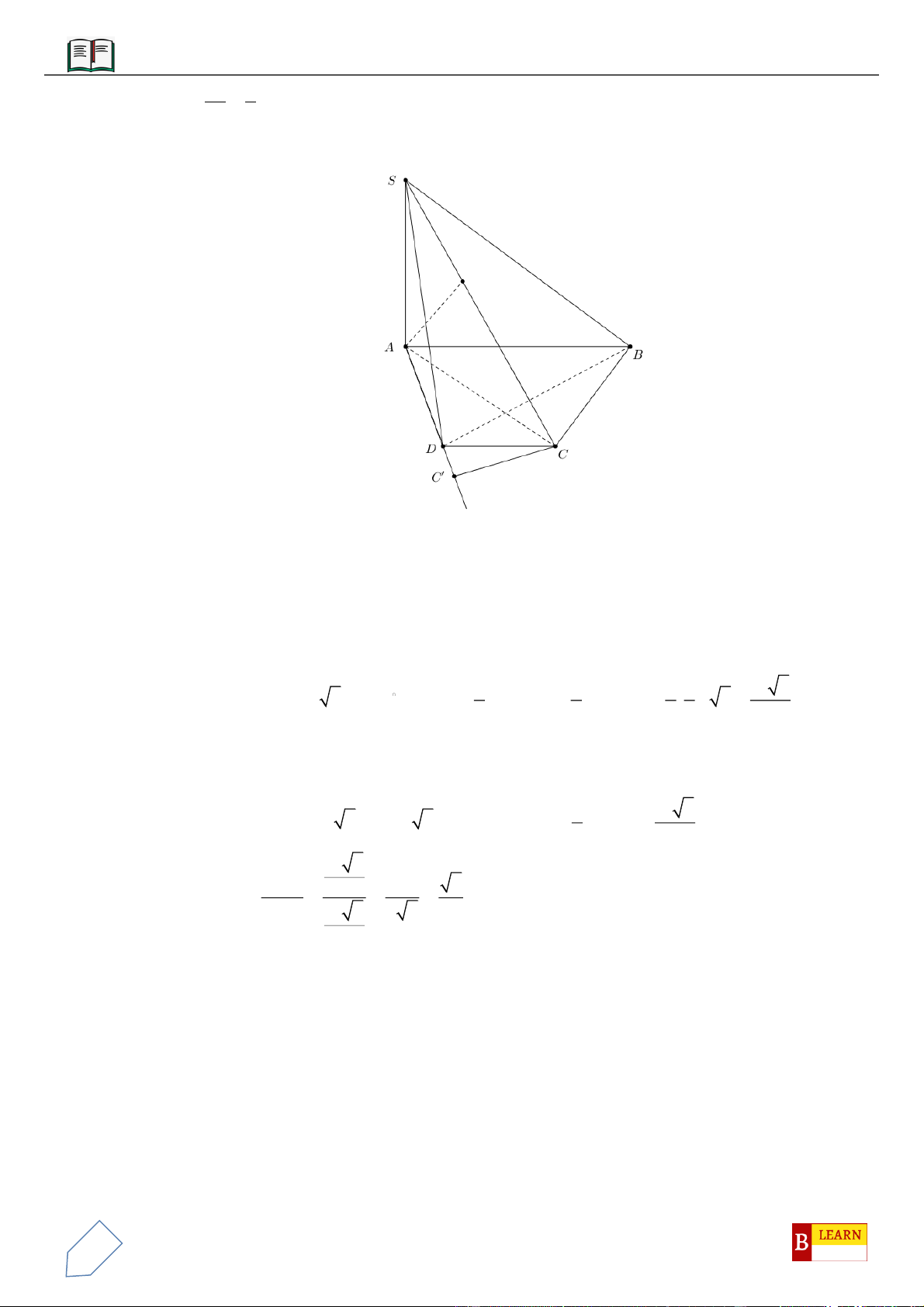
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

274

Suy ra:

1

2

3

5

V



.

Câu 52: Chọn C

Cách 1: Gọi góc giữa hai mặt phẳng

 

SBC

và

 

SAD

là



.

Dễ thấy

 

BD AD

BD SAD D

BD SA





  







là hình chiếu vuông góc của

B

lên mặt phẳng

 

SAD

Gọi

'C

là hình chiếu vuông góc của

C

lên mặt phẳng

 

SAD

.

Suy ra:

2

'

1 1 3

' .cos 3.cos30 ' . '. . . 3

2 2 2 2 4

SDC

a a a

AC AC CAD a DC S DC SA a



       

.

Suy ra

'SDC

là hình chiếu vuông góc của

SBC

lên mặt phẳng

 

SAD

.

Ta có:

 

CB AC CB SAC CB SC    

SBC

vuông tại

C

.

Tam giác

SBC

có

2

16

7; 6; . .

22

SBC

a

SB a SC a BC a S SC CB



     

.

Suy ra:

2

'

2

3

12

4

cos

4

6 2 2

2

SAC

SBC

a

S

a





   

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

275

Cách 2:

Ta chứng minh được

 

BD SAD

.

Dựng

SE SC

tại

E

 

SE SBC

.

Suy ra:

   

 

;;SAD SBC AE BD

.

Gọi

O AC BD

; dựng

OI SC I

   

/ / ; ;OI AE AE BD OI BD IOB   

OI

Cos IBO

OB



. Ta tính được:

66

2 3 6

a OE a

OE OI   

2 2 3

3

33

a

BD a BO BD   

. Suy ra:

2

4

Cos IOB 

.

Câu 53: Chọn C

Đặt

AN x

AP y











với

92

0 , 0

23

xy   

suy ra

9

2

NC x

.

..

AMNP

ABCD

V

NC AM AN AP NC

V AN AB AC AD AN

  

9

2

..

92

3

23

x

y

x





2

9

2

.

2

x

y

x





2

81 18

4

x

y

x





.

Suy ra

2

81 18

4

x

AN AP x y x

x



    

. Đặt

 

2

81 18

4

x

f x x

x





với

9

0

2

x

.

 

2 4 2

44

9 81 2 9 81

1

22

x x x x x

fx

xx

  



  

có

 

0

3

x

fx

x















.

Ta có bảng biến thiên:

A

B

D

C

M

N

P

I

O

E

C

A

B

D

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

276

Từ bảng biến thiên ta thấy

AN AP

nhỏ nhất bằng

15

4

khi

3x 

.

Câu 54: Chọn A

Từ giả thiết suy ra

22

AC SC SA a  

. Gọi

,HE

lần lượt là trung điểm

,BC BS

.

ABC

cân tại

,AH

là trung điểm

BC AH BC

.

   

 

,

ABC SBC

AH SBC AH BS

AH ABC AH BC cmt







   









.

, / /

BS AH

BS HE HE CS BS CS BSC

BS AE





     







vuông tại

S

.

AH

là trục đường tròn ngoại tiếp

BSC

tâm

O

của mặt cầu ngoại tiếp hình chóp

.S ABC

là

tâm đường tròn ngoại tiếp

ABC

.

Bán kính mặt cầu ngoại tiếp hình chóp

2

. . . . .

.:

4 2 .

2

4

ABC

AB AC BC AB AC BC AB AC

S ABC R OA OB OC a

S AH BC

BC

AB



      



.

Vậy thể tích khối cầu ngoại tiếp hình chóp

.S ABC

là:

3

4

3

a

V





.

Câu 55: Chọn B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

277

Kẻ

HK BC

tại

K

, suy ra

2

3

a

HK 

,

60SKH 

và

SHK

vuông tại

H

.

Suy ra

23

.tan60

3

a

SH h HK   

Kẻ

HP CD

tại

P

, hạ

HQ SP

tại

Q

. Suy ra

2

3

a

HP 

 

22

3 3 3 .

, , . . 3 3

2 2 2

SH HP

d A SCD d H SCD HQ

SH HP

   



Câu 56: Chọn B

Đây là dạng bài cơ bản về khoảng cách từ chân đường cao

A

đến mặt phẳng nghiêng có đỉnh

S

.

Hạ

AP

vuông góc với

DM

tại

P

, dựng

AQ

vuông góc với

SP

tại

Q

, khi đó khoảng cách từ

A

đến mặt phẳng

 

SDM

chính là

AQ

.

Ta có:

3

.cos . .

10 10

3

DC a a

AP AD AD a

DM

a



   

.

Có:

 

2 2 2 2 2 2

1 1 1 1 1 1 3

;

26

3

2

10

a

d A SDM AQ SA

AQ SA AP SA

a

        

   

   



.

Suy ra thể tích:

3

2

.

1 1 3

. . .

33

26 26

S ABCD ABCD

aa

V S SA a  

.

Câu 57: Chọn A

H

M

C

B

A'

B'

C'

A

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

278

Gọi

H

là hình chiếu vuông góc của điểm

M

trên

AB



và

K

là hình chiếu vuông góc của điểm

M

trên

AH

. Ta có

()MK ABA





, suy ra

 

,( )d M ABA MK





.

Tam giác

AA M



vuông tại

M

có

3

2

a

AM





và

2A A a





22

13

2

a

AM A A A M



   

.

Tam giác

HB M



vuông tại

H

, có

2

a

BM





và

0

60HB M





,

3

sin

4

HM a

HB M HM

BM



   



.

Tam giác

HAM

vuông tại

M

suy ra

22

. 39

2 55

HM AM a

KM

HM AM





.

Suy ra

   

39

,( ) 2 ,( )

55

d C ABA d M ABA a

  



.

Câu 58: Chọn C

Gọi

,MN

là trung điểm của

AB

và

CD

D thì ta có

 

,SM AB MN AB AB SMN   

.

Kẻ

,SH MN H MN

, khi đó

 

SH AB SH ABCD  

.

2

.

11

..

3 3 2

S ABC ABC

a

V S SH a SH  

3

2

a

SH

.

Có

3SM a

2

2 2 2

93

3

42

aa

MH SM SH a     



 

31

2

a

OH MH MO



  

.

Gọi

O AC BD

,

I

là tâm mặt cầu ngoại tiếp hình chóp

.S ABCD

suy ra

 

IO ABCD

//IO SH

. Kẻ

,IK SH K SH  

IOHK

là hình chữ nhật.

Bán kính mặt cầu ngoại tiếp

.S ABCD

là:

 

2

2 2 2

R IS IK KS OH S H IO     

 

2

31

3

42

a

IO





  





 

2

2 2 2 2

5

4

a

R ID IO OD OH SH IO IO       

 

2

31

3 5 4 3

4 2 4 6

a

aa

IO IO IO a



  

      





.

Suy ra bán kính:

2

2 2 2

4 3 5 16 2 3

6 4 3

a

R IO OD a a





    





O

N

M

B

D

C

A

S

H

I

K

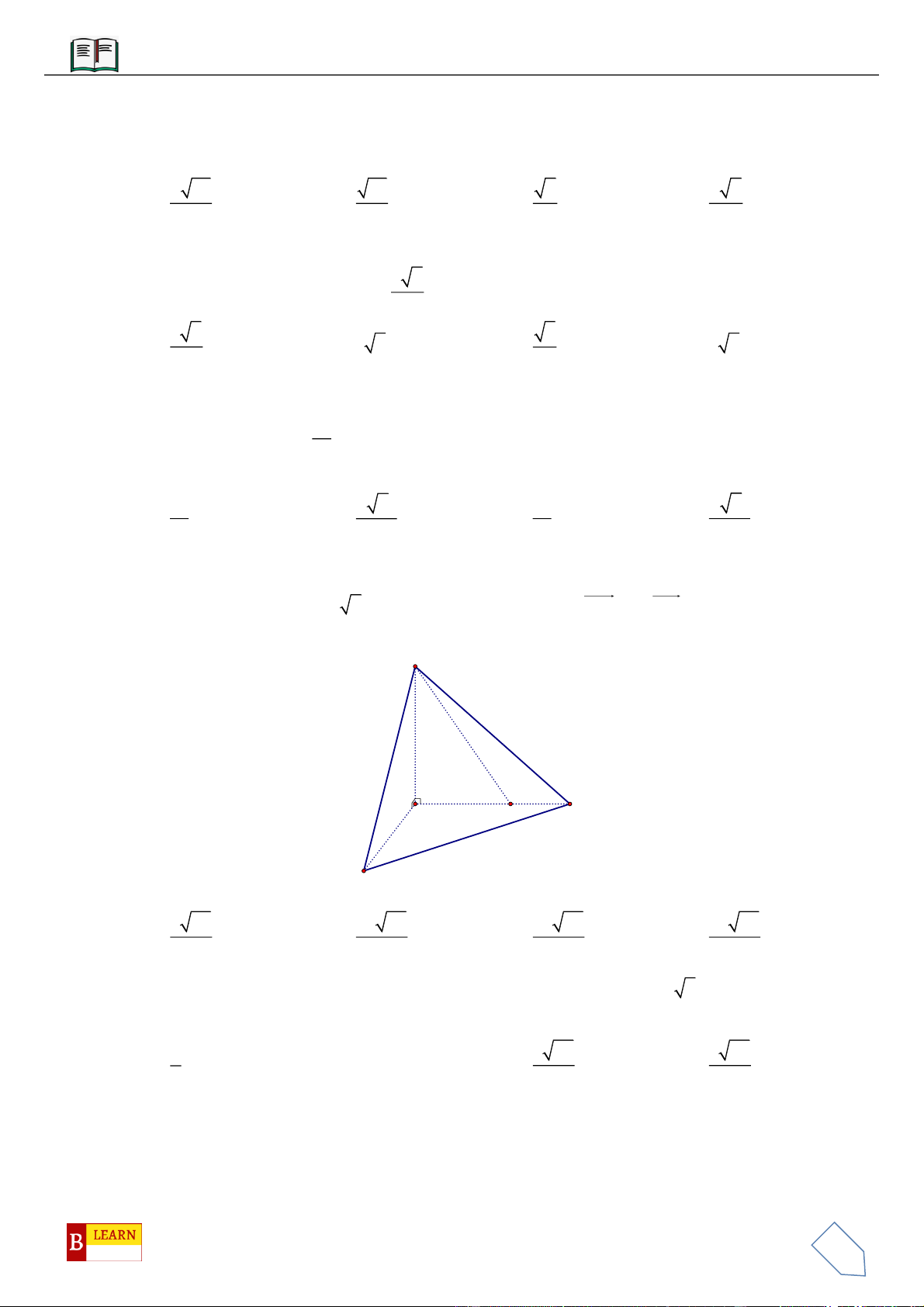
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

279

DẠNG 8: BÀI TOÁN GÓC – KHOẢNG CÁCH

Câu 1: Cho hình lập phương

. ' ' ' 'ABCD A B C D

có cạnh

3a

.

M

thuộc cạnh

’’AD

sao cho

'2A M a

.

Tính khoảng cách giữa

AM

và

'BD

theo

a

A.

3 14

14

a

. B.

14

a

. C.

7

a

. D.

37

7

a

.

Câu 2: Cho hình chóp

.S ABC

có mặt đáy là tam giác vuông tại đỉnh

A

,

AB AC a

. Đường thẳng

SA

vuông góc với

 

mp ABC

,



2

a

SA

. Tính khoảng cách giữa hai đường thẳng

AB

và

SC

A.

3

a

. B.

3a

. C.

3

a

. D.

33a

.

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi tâm

O

, cạnh

AB a

,

60BAD

,

 

SO ABCD

,



3

4

a

SO

. Gọi

M

là trung điểm của

CD

. Khoảng cách giữa hai đường thẳng

SM

và

BD

là

A.

3

8

a

. B.

37

14

a

. C.

8

3

a

. D.

27

3

a

.

Câu 4: Cho hình chóp

.S ABC

, tam giác

ABC

có

   6 , 3 , 120AB a AC a BAC

,

SA

vuông góc với

mặt phẳng đáy và

 2SA a

. Gọi

M

là điểm thỏa mãn

2MA MB

(Xem hình vẽ). Khoảng

cách giữa hai đường thẳng

SM

và

BC

bằng

A.

39

13

a

. B.

2 39

13

a

. C.

4 39

13

a

. D.

6 39

13

a

.

Câu 5: Cho

.S ABCD

có đáy là hình vuông cạnh

a

,

 

SA ABCD

và

 3SA a

. Gọi

M

là trung điểm

của

.AD

Khoảng cách giữa hai đường thẳng

BM

và

SD

bằng

A.

2

a

. B.

a

. C.

57

3

a

. D.

57

19

a

.

Câu 6: Cho hình chóp

.S ABC

có tam giác

ABC

đều cạnh 3a,

 

SA ABC

và

 2SA a

(minh họa như

hình vẽ). Gọi

M

là điểm trên cạnh

AB

sao cho

 2AM a

. Khoảng cách giữa hai đường thẳng

SM

và

BC

bằng

A

B

C

S

M

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

280

A.

21

7

a

. B.

21a

. C.

2 21a

. D.

2 21

7

a

.

Câu 7: Cho hình lăng trụ đứng

. ' ' 'ABC A B C

có đáy là tam giác vuông,

2BA BC a

, cạnh bên

'4AA a

,

M

là trung điểm của

BC

( minh họa như hình bên). Khoảng cách giữa hai đường

thẳng

'BC

và

AM

bằng

A.

27

7

a

. B.

6

a

. C.

a

. D.

6

3

a

.

Câu 8: Cho hình lăng trụ đứng

  

.ABC A B C

có đáy

ABC

là tam giác vuông tại

B

,

 3AB a

,

 2BC a

.

Gọi

M

là trung điểm của

BC

. Tính khoảng cách giữa hai đường thẳng

,'AM B C

biết

'2AA a

.

A.

10

a

. B.

2a

. C.

30

10

a

. D.

2a

.

Câu 9: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

,

SA

vuông góc với mặt phẳng đáy và

 3SA a

. Gọi

M

là điểm thuộc

AD

sao cho

 3AM MD

. Khoảng cách giữa hai đường thẳng

SM

và

BD

bằng

A.

35

a

. B.

3 35

35

a

. C.

2 35

35

a

. D.

9 35

35

a

.

Câu 10: Cho hình chóp

SABCD

, đáy

ABCD

là hình vuông, tam giác

SAB

cân tại

S

. Hình chiếu vuông

góc của

S

lên mặt đáy nằm trên miền trong hình vuông

ABCD

. Góc giữa đường thẳng

SA

và

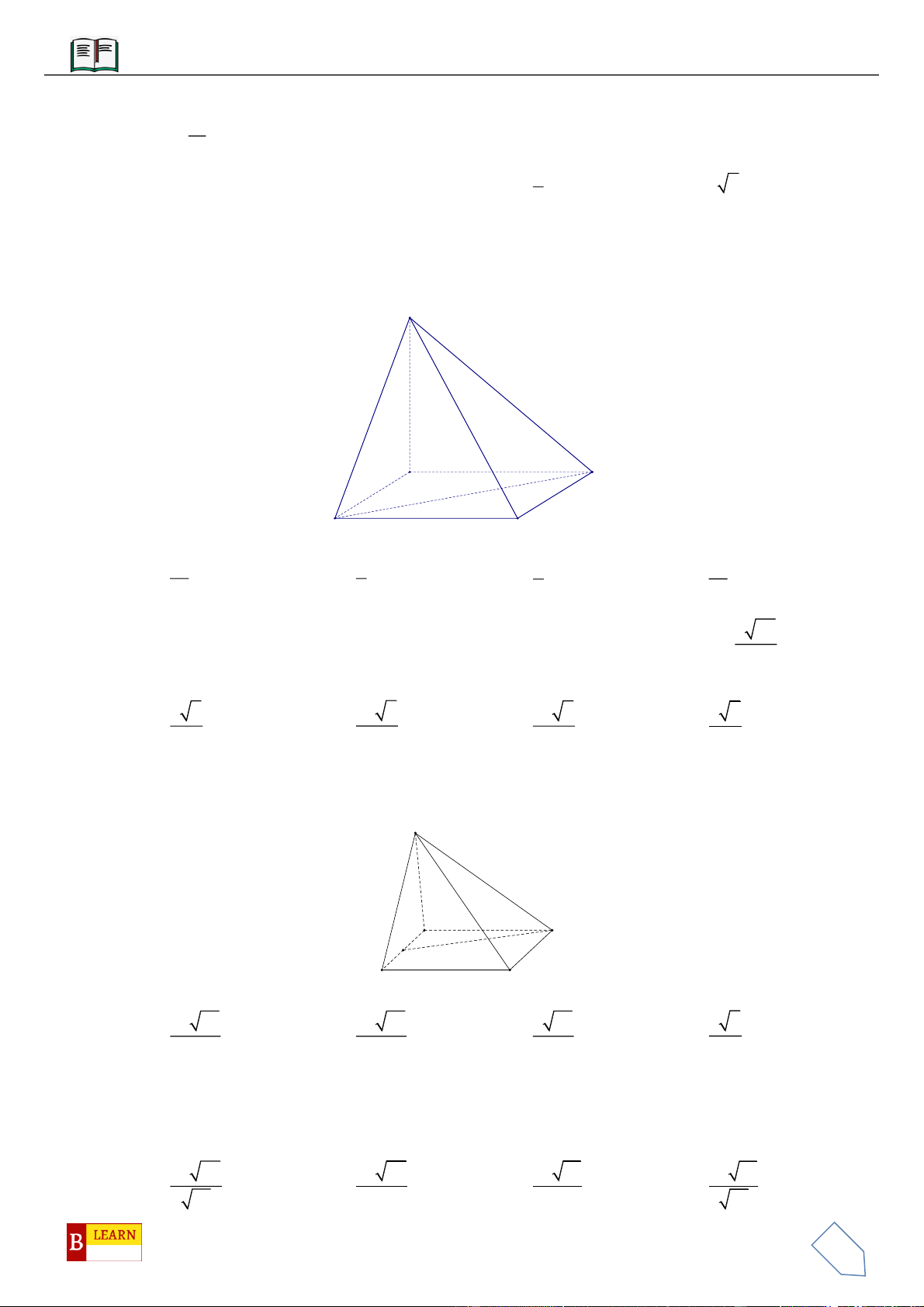
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

281

mặt đáy bằng

30

, góc giữa mặt phẳng

 

SAB

và mặt đáy bằng

45

. Thể tích hình chóp

SABCD

bằng

3

a

. Tính khoảng cách giữa hai đường thẳng

CD

và

SA

.

A.

2a

. B.

a

. C.

3

a

. D.

2a

.

Câu 11: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật;

AB a

,

 2AD a

. Cạnh bên

SA

vuông góc với đáy và

 2SA a

(hình vẽ minh họa). Tính theo

a

khoảng cách giữa hai đường thẳng

BD

và

SC

.

A.

2

3

a

. B.

3

a

. C.

2

a

. D.

3

4

a

.

Câu 12: Cho hình chóp tam giác đều

.S ABC

có cạnh đáy bằng

2a

và cạnh bên bằng

37

3

a

. Gọi

M

là

trung điểm cạnh

SA

. Tính khoảng cách giữa hai đường thẳng

AC

và

BM

.

A.

3

4

a

. B.

53

6

a

. C.

53

12

a

. D.

3

2

a

.

Câu 13: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật với

  ;2AB a AD a

,

 ()SA ABCD

và

 3SA a

. Gọi

M

là trung điểm

AB

, tính khoảng cách giữa hai đường thẳng

SC

và

DM

.

A.

4 21

21

a

. B.

2 21

21

a

. C.

21

a

. D.

6

3

a

.

Câu 14: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

có

2AB BC a

. Cạnh bên

SA

vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng

 

SBC

và

 

ABC

bằng

60

. Gọi

M

là

trung điểm của

AC

, tính khoảng cách giữa hai đường thẳng

AB

và

SM

theo

a

.

A.

2 39

13

a

. B.

2 39

13

a

. C.

2 11

13

a

. D.

2 11

13

a

.

C

B

D

A

S

M

C

A

D

B

S

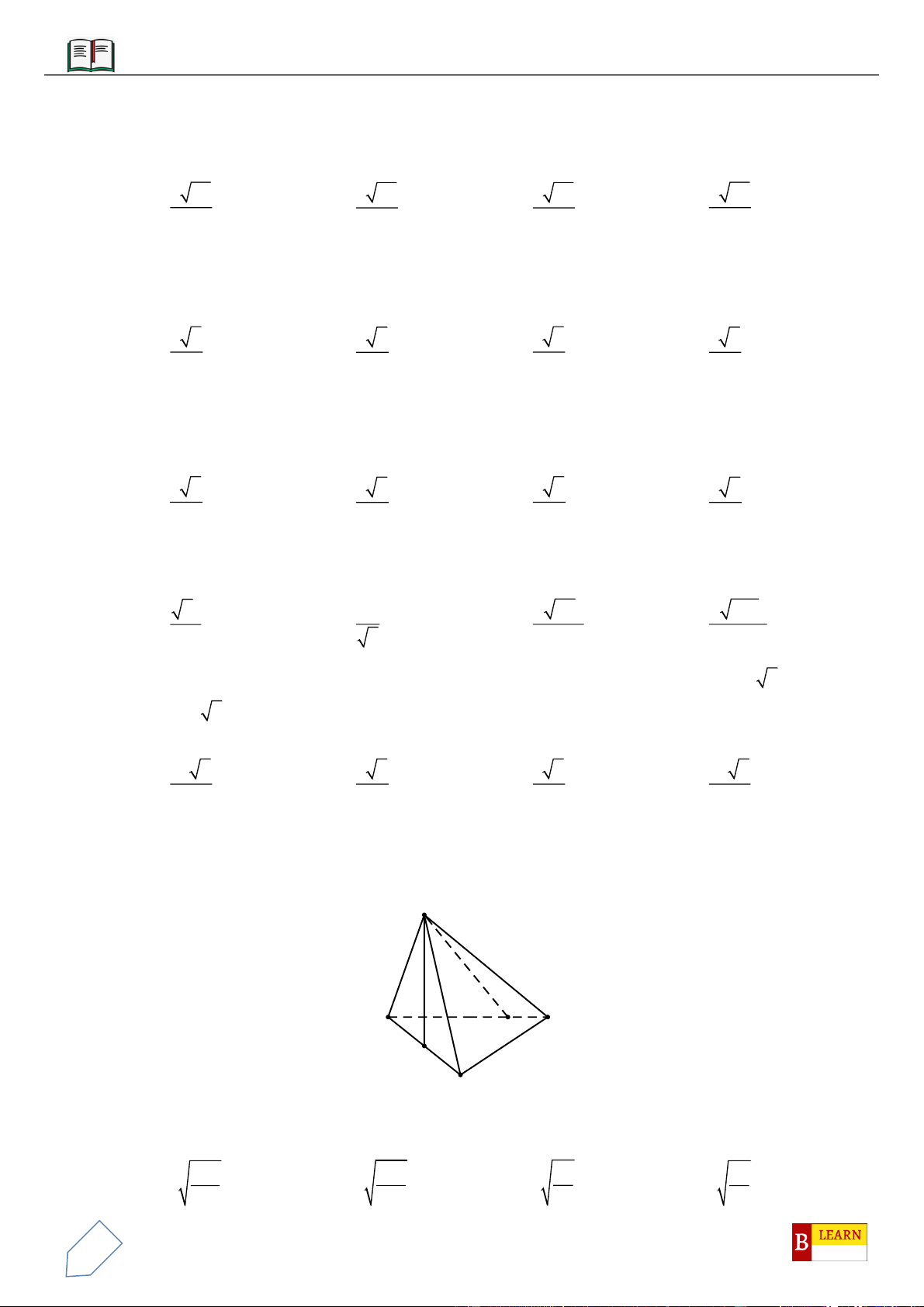
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

282

Câu 15: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

a

. Hình chiếu vuông góc của

S

trên mặt

phẳng

 

ABC

là điểm

H

thuộc cạnh

AB

sao cho

 2HA HB

. Góc giữa đường thẳng

SC

và mặt

phẳng

 

ABC

bằng

60

. Tính khoảng cách giữa hai đường thẳng

SA

và

BC

theo

a

.

A.

42

8

a

. B.

42

4

a

. C.

42

12

a

. D.

42

10

a

.

Câu 16: Cho hình lăng trụ

  

.ABC A B C

có đáy

ABC

là tam giác đều cạnh

a

. Biết hình chiếu vuông góc

của điểm

A

trên mặt phẳng

  

()A B C

là trọng tâm



G

của tam giác

  

A B C

và



AA a

. Ta có

khoảng cách giữa hai đường thẳng



AA

và



BC

là

A.

3

a

. B.

3

2

a

. C.

2

3

a

. D.

2

a

.

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, mặt bên

SAD

là tam giác đều và

   

SAD ABCD

. Gọi

M

là trung điểm của cạnh đáy

AB

. Ta có khoảng cách giữa hai đường

thẳng

SA

và

CM

là:

A.

2

3

a

. B.

5

4

a

. C.

3

a

. D.

3

4

a

.

Câu 18: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

AB a

,

 2BC a

,

SA

vuông góc với mặt phẳng

đáy. Tính khoảng cách giữa

AC

và

SB

, biết góc giữa

SC

và mặt phẳng

()ABCD

bằng

30

o

.

A.

5

.

2

a

B.

2

.

5

a

C.

2 37

.

185

a

D.

2 185

.

37

a

Câu 19: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành thỏa mãn

 6AB a

,

 3BC a

,

 3AC a

và

SA

vuông góc với mặt phẳng đáy,

 3SA a

.

M

là điểm thuộc cạnh

BC

sao cho

 2BM MC

. Khoảng cách giữa hai đường thẳng

AM

và

SD

là

A.

33

2

a

. B.

6

2

a

. C.

2

a

. D.

32

2

a

.

Câu 20: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

2a

. Hình chiếu vuông góc của đỉnh

S

lên mặt phẳng chứa đáy là trung điểm

H

của

AC

và

 2SH a

. Gọi điểm

M

thuộc cạnh

AB

sao

cho

 3AM MB

(tham khảo hình vẽ bên dưới).

Khoảng cách giữa

SM

và

BC

bằng

A.

12

259

a

. B.

259

12

a

. C.

67

12

a

. D.

12

67

a

.

M

H

A

B

C

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

283

Câu 21: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

đều cạnh

a

, tam giác

SBA

vuông tại

B

, tam giác

SAC

vuông tại

C

. Biết góc giữa hai mặt phẳng

 

SAB

và

 

ABC

bằng

60

. Tính khoảng cách

giữa

SC

và

AB

theo

a

.

A.

3

8

a

. B.

3

13

a

. C.

3

6

a

. D.

3

4

a

.

Câu 22: Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

. Hình chiếu vuông góc của

S

xuống

mặt phẳng

 

ABC

là trung điểm

H

của cạnh

AB

, góc giữa

SC

và đáy bằng

60

. Tính khoảng

cách giữa

SB

và

AC

.

A.

3

26

a

. B.

3

13

a

. C.

3

52

a

. D.

13

a

.

Câu 23: Cho hình chóp

.S ABCD

có đáy là nửa lục giác đều với

   2,AD a AB BC CD a

,

 3SA a

và

SA

vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng

SB

và

CD

theo

a

.

A.

2

3

a

. B.

6

5

a

. C.

14

7

a

. D.

15

5

a

.

Câu 24: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi G là trọng tâm tam giác ABC. Góc

giữa đường thẳng SA với mặt phẳng (ABC) bằng

0

60

. Khoảng cách giữa hai đường thẳng GC và

SA bằng:

A.

5

a

. B.

5

a

. C.

5

10

a

. D.

2

5

a

.

Câu 25: Cho hình chóp

.S ABCD

với đáy là nửa lục giác đều có

  AB BC CD a

,

 

SA ABCD

, góc

giữa

SC

và

 

ABCD

là

45

. Khoảng cách giữa

SB

và

CD

là

A.

15

3

a

. B.

15

5

a

. C.

3

5

a

. D.

5

3

a

.

Câu 26: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

4a

,

SAB

là tam giác đều và nằm trong

mặt phẳng vuông góc với đáy,



0

120BAD

. Gọi

M

là điểm trên cạnh

CD

sao cho

 3CM a

.

Khoảng cách giữa hai đường thẳng

SB

và

AM

bằng

A.

8 51

17

a

. B.

51

12

a

. C.

4 51

17

a

. D.

51

6

a

.

Câu 27: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

O

,

  2 , , 5AC a BC a DC a

,

SA

vuông góc với mặt phẳng đáy và

SA a

. Gọi

M

là trung điểm

OA

,

DM AB N

. Tính

 

d,N SBC

A.

2

3

a

. B.

45

15

a

. C.

1

2

a

. D.

5

a

.

Câu 28: Cho hình chóp

.S ABCD

có

 ()SA ABCD

, đáy

ABCD

là hình chữ nhật. Độ dài các cạnh

  3 , 4 , 5AB a AD a SA a

. Gọi

M

là điểm nằm trên cạnh

BC

và

 3BM a

. Khoảng cách giữa

hai đường thẳng

SB

và

MD

là

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

284

A.

15

259

a

. B.

29

245

a

. C.

39

245

a

. D.

45

259

a

.

Câu 29: Cho tứ diện đều

ABCD

cạnh bằng

a

. Gọi

M

là trung điểm của

CD

. Tính khoảng cách giữa hai

đường thẳng

AC

và

BM

.

A.

22

11

a

. B.

a 22

. C.

11

22

a

. D.

11a

.

Câu 30: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang vuông tại

A

và

B

với

AB BC a

,

 2AD a

,

SA

vuông góc với đáy và

SA a

. Khoảng cách giữa hai đường thẳng

AC

và

SD

bằng:

A.

2

6

a

. B.

3

a

. C.

6

3

a

. D.

2

9

a

.

Câu 31: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

 

SA ABC

, góc giữa đường thẳng

SB

và mặt phẳng

 

ABC

bằng

75

. Khoảng cách giữa hai đường thẳng

AC

và

SB

gần bằng giá

trị nào sau đây? (lấy 3 chữ số phần thập phân)

A.

0.833a

. B.

0.844a

. C.

0.855a

. D.

0.866a

.

Câu 32: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thang, với

//AB CD

 3,AB a

AD DC a

,



0

60BAD

, biết

SA

vuông góc với đáy và

 3SA a

. Gọi

M

là điểm thuộc cạnh

AB

sao cho

 3AB AM

. Khoảng cách giữa

SM

và

AD

bằng

A.

15

5

a

. B.

15

3

a

. C.

2

5

a

. D.

2

3

a

.

Câu 33: Cho hình chóp

.S ABCD

, có đáy

ABCD

là hình vuông cạnh

a

, tam giác

SAD

là tam giác đều,

()SAD

vuông góc với mặt phẳng đáy. Tính khoảng cách giữa

SA

và

BD

.

A.

15

5

a

. B.

5

a

. C.

21

10

a

. D.

21

7

a

.

Câu 34: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi cạnh

a

,



0

60ABC

,

 

SA ABCD

, góc giữa

đường thẳng

SD

và mặt phẳng

 

ABCD

bằng

0

30

. Tính khoảng cách giữa hai đường thẳng

SB

và

AD

.

A. . B. . C. . D. .

Câu 35: Cho hình chóp

.S ABCD

có đáy là hình thang,

   2,AB a AD DC CB a

,

SA

vuông góc với

mặt phẳng đáy và

 3SA a

. Gọi

E

là trung điểm

AD

,

F

nằm trên

AB

sao cho



1

4

AF AB

.

Khoảng cách giữa hai đường thẳng

SB

và

EF

bằng

A.

3

4

a

. B.

9

8

a

. C.

3 13

13

a

. D.

6 13

13

a

.

Câu 36: Cho hình chóp

.S ABCD

có

SD

vuông góc với

 

ABCD

,

 a5SD

. Đáy

ABCD

là hình thang

vuông tại

A

và

D

với

  2 2 2CD AD AB a

. Gọi

M

là trung điểm của

BC

. Tính khoảng cách

giữa hai đường thằng

AC

và

SM

.

39

13

a

3

13

a

2

13

a

39

3

a

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

285

A.

a

. B.

2

a

. C.

4

a

. D.

5

a

.

Câu 37: Cho hình chớp

.S ABCD

có đáy là hình thoi tâm

O

cạnh

a

,

60ABC

, mặt bên

SAB

là tam

giác đều. Hình chiếu vuông góc của

S

trên mặt phẳng

 

ABCD

trùng với trung điểm của

AO

.

Tính khoảng cách giữa hai đường thẳng

SA

và

CD

.

A.

560

112

a

. B.

560

10

a

. C.

560

5

a

. D.

560

28

a

.

Câu 38: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

D

,

 

SA ABCD

;

 2AB a

,

AD CD a

. Gọi

N

là trung điểm

SA

. Tính khoảng cách giữa

2

đường thẳng

SC

và

DN

,

biết rằng thể tích khối chóp

.S ABCD

bằng

3

6

2

a

.

A.

6

4

a

. B.

2

a

. C.

6

2

a

. D.

10

2

a

Câu 39: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

,



33

2

a

SD

. Hình chiếu vuông góc

H

của

S

lên mặt phẳng

 

ABCD

là trung điểm của đoạn

AB

. Gọi

K

là trung điểm của

AD

. Tính

khoảng cách giữa hai đường

SD

và

HK

theo

a

.

A.

399

.

19

a

B.

105

.

15

a

C.

399

.

57

a

D.

105

.

3

a

Câu 40: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

B

,

  ;2AB BC a AD a

.

SA

vuông góc với mặt phẳng đáy,

 2.SA a

Gọi

M

là trung điểm của

AD

. Tính khoảng cách giữa

SM

và

CD

.

A.

2

3

a

. B.

2 17

17

a

. C.

3

a

. D.

5

6

a

.

Câu 41: Cho hình chóp

.S ABC

có

ABC

vuông cân tại

B

,

AB a

,

  90SAB SCB

. Khoảng cách từ

điểm

A

đến mặt phẳng

 

SBC

bằng

3

a

. Thể tích khối chóp

.S ABC

bằng

A.

3

2

4

a

. B.

3

32

4

a

. C.

3

2

12

a

. D.

3

6

3

a

.

Câu 42: Cho hình chóp

.S ABC

có tam giác

ABC

vuông tại

A

,

 2,AB a

 4BC a

. Gọi

M

là trung điểm

của

BC

có



0

90SCB SMA

,

 







0

, 60SB ABC

. Thể tích khối chóp

.S ABC

bằng

A.

3

4 39

3

a

. B.

3

4 39a

. C.

3

39a

. D.

3

39

3

a

.

Câu 43: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

,

 43AC a

,

30ASB

. Góc giữa

hai mặt phẳng

 

SAB

và

 

ABC

bằng

30

. Biết

I

trung điểm

SA

là tâm mặt cầu ngoại tiếp hình

chóp

.S ABC

. Gọi



là góc giữa

IB

và mặt phẳng

 

SAC

. Khi





21

sin

7

thì khoảng cách giữa

hai đường thẳng

AC

và

SB

bằng

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

286

A.

14 3

5

a

. B.

83

3

a

. C.

33a

. D.

43a

.

Câu 44: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

,

 2AB a

,

AC a

,



0

90SBA SCA

, góc giữa

SA

và mặt phẳng

 

ABC

bằng

0

45

. Tính thể tích khối chóp

.S ABC

.

A.

3

5

3

a

. B.

3

5a

. C.

3

25

3

a

. D.

3

25a

.

Câu 45: Cho hình chóp

.S ABC

có

2 3 , 2 2SB a AB a

,



0

90SAB SCB

,

 





   







00

, 30 , , 60SB ABC SBC ABC

. Thể tích khối chóp

.S ABC

theo

a

bằng

A.

3

16 6

27

a

. B.

3

86

27

a

. C.

3

83

3

a

. D.

3

26

3

a

.

Câu 46: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,



0

90SBA SCA

, góc giữa đường

thẳng

SA

và mặt phẳng

 

ABC

bằng

0

60

.Thể tích của khối chóp

.S ABC

bằng

A.

3

3a

. B.

3

2

a

. C.

3

a

. D.

3

6

a

.

Câu 47: Cho hình chóp

.S ABC

có

AB BC a

,

 120ABC

, cosin góc giữa hai mặt phẳng

 

SAB

và

 

SBC

bằng

10

5

. Tính thể tích khối chóp

.S ABC

biết hình chiếu vuông góc của

S

lên mặt

phẳng

 

ABC

nằm trên tia

Cx AB

(cùng phía với

A

trong nửa mặt phẳng bờ

BC

) và nhìn cạnh

AC

dưới góc

60

.

A.

3

a

. B.

3

a

. C.

3

2

a

. D.

3

4

a

.

Câu 48: Cho hình chóp

.S ABC

có



0

135ABC

,

 ,AB a

 2BC a

,

 







,AC SAB



0

90SAB SBC

,

thỏa mãn





1

sin

5

. Thể tích khối chóp

.S ABC

theo

a

bằng

A.

3

12

a

. B.

3

4

a

. C.

3

5a

. D.

3

5

3

a

.

Câu 49: Cho hình chóp

.S ABC

có đáy là tam giác

ABC

cân tại

A

, cạnh

AB a

, góc

120BAC

. Tam

giác

SAB

vuông tại

B

, tam giác

SAC

vuông tại

C

. Góc giữa hai mặt phẳng

 

SAB

và

 

ABC

bằng

60

. Tính thể tích khối chóp

.S ABC

theo

a

.

A.

3

6

a

. B.

3

2

a

. C.

3

4

a

. D.

3

12

a

.

Câu 50: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

A

,

 2AB a

,

  90SBA SCA

góc giữa hai mặt phẳng

 

SAB

và

 

SAC

bằng

60

. Tính thể tích khối chóp

.S ABC

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

287

A.

3

4

6

a

. B.

3

a

. C.

3

4a

. D.

3

4

3

a

BẢNG ĐÁP ÁN

1.A

2.A

3.A

4.A

5.D

6.A

7.D

8.C

9.A

10.B

11.A

12.D

13.A

14.B

15.A

16.D

17.D

18.D

19.D

20.D

21.B

22.B

23.D

24.A

25.B

26.A

27.B

28.D

29.A

30.C

31.B

32.A

33.D

34.A

35.B

36.D

37.D

38.A

39.C

40.A

41.C

42.A

43.D

44.A

45.A

46.D

47.D

48.A

49.C

50.D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Chọn A.

Gọi

I

là trung điểm của

'BB

.

'N AI BA

thì

N

trọng tâm tam giác

'ABB

.

Khi đó

'MN BD

. Suy ra

 

'BD AMK

với

''K A B AI

và

'6A K a

.

Ta có

   

 

  

11

, ' ', . ', .

22

d AM BD d D AMK d A AMK d

.

Do

' , ' , 'A M A A A K

đôi một vuông góc nên

     

2 2 2 2 2

1 1 1 1 7 3 14

7

' ' ' 18

da

d A A A M A K a

. Vậy

 



3 14

,'

14

d AM BD a

.

Câu 2. Chọn A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

288

AC

là hình chiếu của

SC

lên

 

mp ABC

,

  AB AC AB SC

.

Trong mặt phẳng

 

SAC

dựng

AH SC

thì

AH

là đoạn vuông góc chung của hai đường thẳng

AB

và

SC

và

 

,d AB SC AH

  



2 2 2

2

.2

.3

2

3

2

4

aa

AC SA a

a

.

Câu 3. Chọn A

Gọi

N

là trung điểm của

OC

. Trong

 

SON

, kẻ

OH SN

 

H SN

.

 

1

Do

M

,

N

lần lượt là trung điểm của

CD

và

OC

nên

MN

là đường trung bình của

OCD

.

 //MN OD

hay

//MN BD

. Do đó

   

 

, , ,d BD SM d BD SMN d O SMN

.

Ta có









//MN BD

BD AC

nên

MN AC

hay

MN ON

.

Lại có

MN SO

(do

 

SO ABCD

) nên

 

  MN SON MN OH

.

 

2

Từ

 

1

và

 

2

suy ra

 

OH SMN

   

 

  ,,d BD SM d O SMN OH

.

Do

ABCD

là hình thoi nên

AB AD a

.

Lại có

60BAD

nên

ABD

là tam giác đều cạnh

a

.

Mà

AO

là đường cao của

ABD

nên

  

33

24

aa

AO ON

.

Xét

SON

vuông tại

O

có

      

2 2 2 2 2 2

1 1 1 16 16 64 3

8

3 9 9

a

OH

OH ON SO a a a

.

Vậy

 



3

,

8

a

d BD SM

.

Câu 4.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

289

Chọn A

Kẻ

//MN BC

, suy ra

 

//BC SMN

.

Ta có

   

 

  

1

, , , ,

2

d SM BC d BC SMN d B SMN d A SMN

.

Kẻ

,AI MN AH SI

, suy ra

 

AH SMN

,

 

,d A SMN AH

.

     

2 2 2

. .3 2

3 3 3

AN AM

AN AC a a

AC AB

.

   

    

22

2 4 2.2 .4 .cos120 2 7MN a a a a a

.



     

1 1 . .sin 4 .2 .sin120 2 21

. .sin .

2 2 7

27

AMN

AM AN BAC a a a

S AM AN BAC AI MN AI

MN

a

.

 

      







2 2 2 2 2 2

1 1 1 1 1 13 2 39

13

12

2 21

2

7

a

AH

AH SA AI a

a

.

Vậy

 



1 2 39 39

,.

2 13 13

aa

d SM BC

.

Câu 5. Chọn D

Gọi

N

là trung điểm của

SA

. Do

MN

là đường trung bình của tam giác

SAD

nên

//MN SD

.

Vậy

 

//SD BMN

vì vậy

   

 

   , , , ,d SD BM d SD BMN d D BMN d A BMN h

.

Do

.A BMN

là một góc tam diện vuông nên

     

2 2 2 2 2

1 1 1 1 19 57

19

3

a

h

h AB AM AN a

.

N

A

B

C

S

M

I

H

N

M

B

C

A

D

S

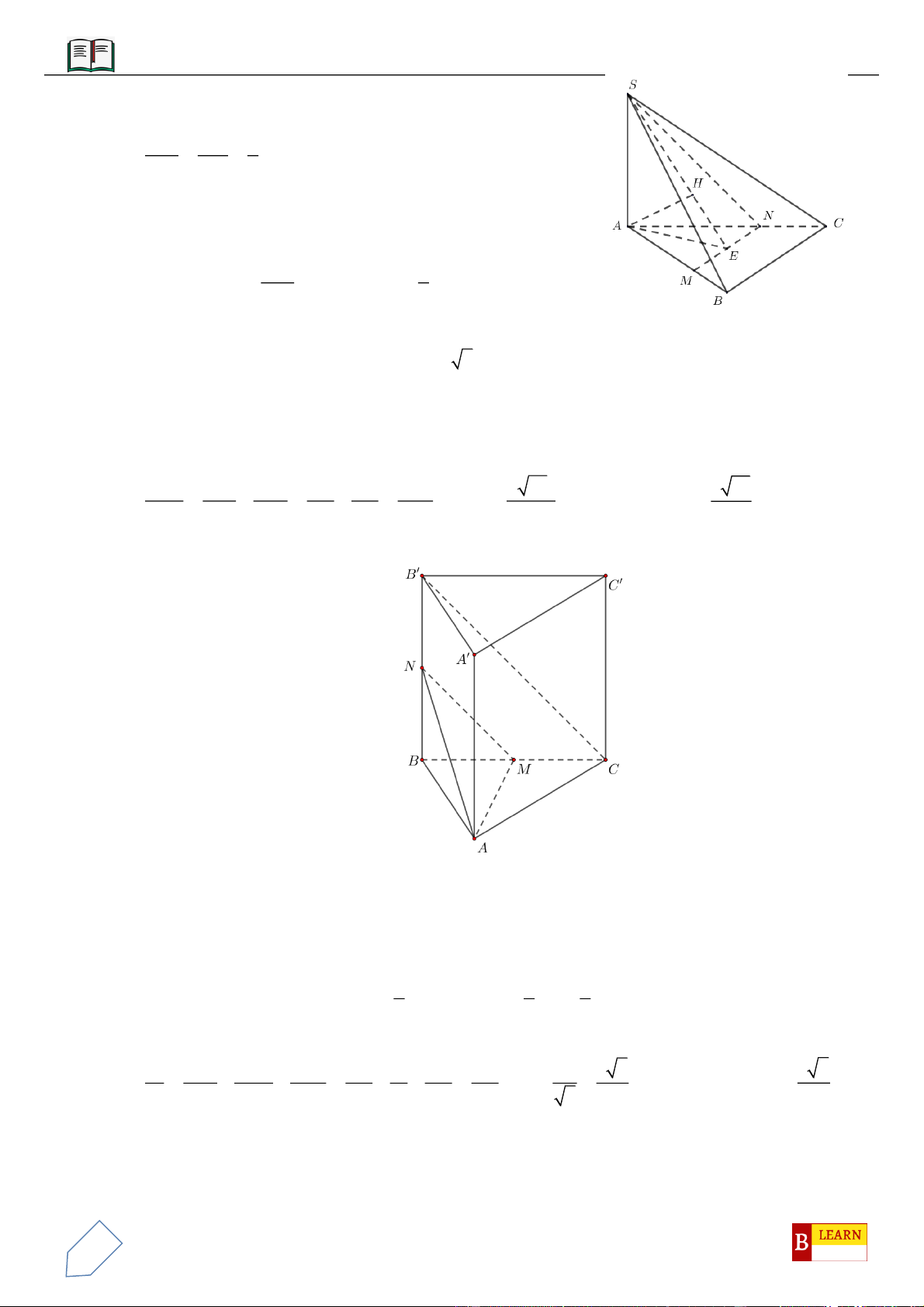
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

290

Câu 6.Chọn A.

Gọi

N

là điểm trên cạnh

AC

sao cho

 2AN a

, ta có:



2

3

AM AN

AB AC

 

// //MN BC BC SMN

.

Suy ra

   

 

,,d BC SM d BC SMN

 

 ,d B SMN

.

 

,d B S MN

 



1

. , ,

2

BM

d A SMN d A SMN

AM

.

Gọi

E

là trung điểm của

MN

, kẻ

AH SE

, (

H SE

) vì

tam giác

AMN

đều cạnh

2a

nên

 3AE a

.

Do













AE MN

MN AH

SA MN

. Mặt khác

AH SE

   

 

   ,AH SMN d A SMN AH

.

Áp dụng hệ thức lượng trong tam giác vuông

SAE

, ta có:

      

2 2 2 2 2 2

1 1 1 1 1 7 2 21

7

4 3 12

a

AH

AH AS AE a a a

. Vậy

 



21

,

7

a

d BC SM

.

Câu 7. Chọn D

Gọi

N

là trung điểm của

'BB

, khi đó

MN

là đường trung bình của

 'BCB

 

// ' ' //MN B C B C AMN

   

 

    , ' ' , , ,d AM B C d B C AMN d C AMN d B AMN h

Tính

 

,d B AMN

. Ta có

    

1 1 1

' 2 ; .2

2 2 2

BN BB a BM BC a a

Áp dụng công thức tính đường cao của tứ diện vuông ta có :

         

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 6 2 6

3

4 4 4

6

aa

h

h BA BM BN a a a a

. Vậy

 



6

,'

3

a

d AM B C

.

Câu 8. Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

291

Gọi

N

là trung điểm của

'BB

suy ra

/ / 'MN B C

.

Do đó

   

 

, ' ' , ,d AM B C d B C AMN d C AMN

.

Mà

M

là trung điểm của

BC

nên

 

,,d B AMN d C AMN

.

Ta có

, , BA BM BN

đôi một vuông góc với nhau nên

 

  

2 2 2

2

1 1 1 1

,

BA BM BN

d B AMN

.

Mặt khác

    

1

, 3, '

22

2

BC a

BM a AB a BN BB

.

Suy ra

 

   







2 2 2 2

2

1 1 1 1 10

3

,

3

2

aa

d B AMN

a

.

 

   

30 30

, , '

10 10

aa

d B AMN d AM B C

Câu 9. Chọn A

Gọi

N

là điểm thuộc

AB

sao cho

 3AN NB

 

// //MN BD BD SMN

,

   

 

, , ,d BD SM d BD SMN d O SMN

, (với

O

là tâm hình vuông

ABCD

).

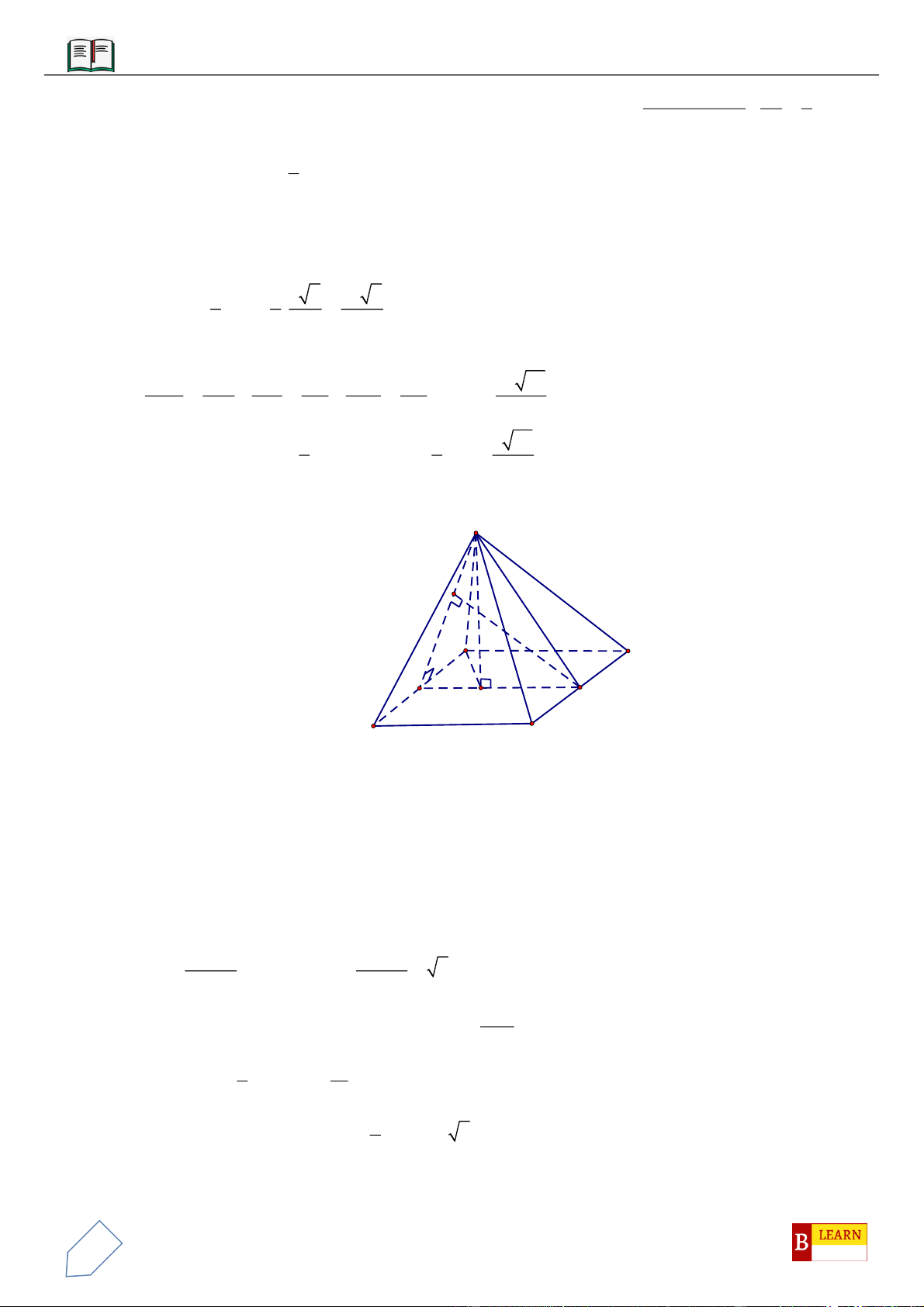
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

292

Gọi

I AO MN

, do

 

    

,

1

3

,

d O SMN

IO

AO SMN I

IA

d A SMN

\

 



1

,,

3

d O SMN d A SMN

. Trong

 

SAI

kẻ

AH SI

.

Ta có

 

     ,MN AI MN SA MN SAI MN AH

.

   

 

     ,,AH SI AH MN AH SMN d A SMN AH

.

Có

  

3 3 2 3 2

.

4 4 2 8

aa

AI AO

.

Tam giác

SAI

vuông tại

A

,

AH

là đường cao nên

      

2 2 2 2 2 2

1 1 1 1 64 35 3 35

35

3 18 9

a

AH

AH SA AI a a a

.

Vậy

 

  

1 1 35

,,

3 3 35

a

d O SMN d A SMN AH

.

Câu 10. Chọn B

.

Gọi

M

,

N

lần lượt là trung điểm

AB

và

CD

, suy ra

 

AB SMN

.

Kẻ

SH MN

,

H MN

, suy ra

 

SH ABCD

.

Khi đó

 

  , 30SA ABCD SAH

và

   

 

  , 45SAB ABCD SMH

.

Kẻ

NE SM

,

E SM

, suy ra

 

NE SAB

.

Ta có

   

 

  , , , .d CD SA d CD SAB d N SAB NE





2

sin30

SH

SA SH

;





2

sin45

SH

SM SH

.

Lại có

       

2

2 2 2 2 2 2 2

4 2 8 0

4

AB

SA SM AM SH SH SH AB

 

1

.

Và

   

3

2 2 3

1

..

33

SABCD

a

V SH AB SH AB a

 

2

.

Giải

 

1

và

 

2

ta được



2

a

SH

;

 2AB a

.

N

M

A

D

C

B

S

H

E

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

293

Xét tam giác

SMN

có

   

.2

2

..

2

a

SH MN NE SM NE a

a

.

Vậy khoảng cách giữa hai đường thẳng

CD

và

SA

bằng

a

.

Câu 11. Chọn A

Gọi

O

là giao điểm của

AC

và

BD

;

M

là trung điểm của cạnh

SA

.

Ta có

OM

là đường trung bình của tam giác

SAC

nên

// OM SC

. Suy ra

 

//SC MBD

.

Lúc đó

   

 

, , ,d SC BD d SC MBD d C MBD

. (1)

Mặt khác, do

AC

cắt

 

MBD

tại

O

và

OA OC

nên

 

,,d C MBD d A MBD AK

, với

K

là hình chiếu của

A

lên

 

MBD

. (2)

Xét tứ diện

.A MBD

có

AB

,

AD

và

AM

đôi một vuông góc, ta có

 

      

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 9

4

2

AK AB AD AM a a a

a

. Suy ra



2

3

a

AK

. (3)

Từ (1), (2) và (3) ta có

 



2

,

3

a

d SC BD

.

Câu 12. Chọn D

Cách 1:

Gọi

D

là đỉnh thứ tư của hình bình hành

ABDC

.

O

M

C

B

D

A

S

H

K

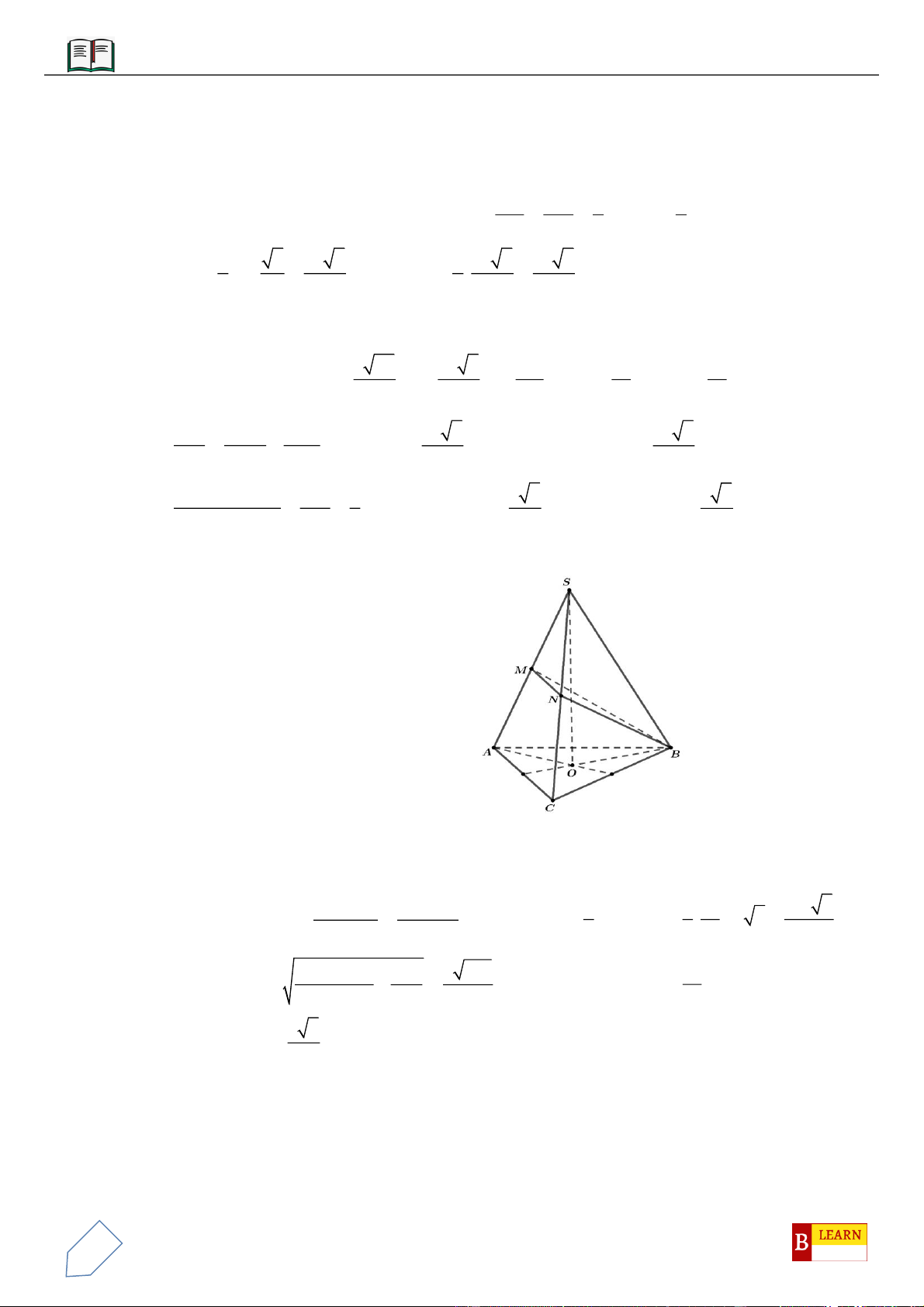
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

294

Khi đó,

     

 

   // // d , d , d ,AC BD AC MBD AC BM AC MBD A MBD

.

Gọi

O

là trọng tâm tam giác

ABC

. Suy ra

 

SO ABC

.

Gọi

H

là trung điểm

AO

. Suy ra

 

//MH SO MH ABC

.

Vẽ

HK BD

tại

K

. Suy ra

//HK BO

. Suy ra

   

45

54

BO OD

HK BO

HK HD

.

Mà



2 3 2 3

.2 .

3 2 3

a

BO a

suy ra



5 2 3 5 3

.

4 3 6

aa

HK

.

Vẽ

HI MK

tại

I

. Suy ra

 

d,H MBD HI

.

Ta có,

   

        

   

   

22

2 2 2

37 2 3 25 5 5

3 3 9 3 6

a a a a a

SO SA AO SO MH

.

Mà



2 2 2

1 1 1

HI MH HK

suy ra

 

   

5 3 5 3

d,

12 12

aa

HI H MBD HI

.

Mà

 

   

d,

53

d,

62

d,

H MBD

HD a

A MBD

AD

A MBD

. Vậy

 



3

d,

2

a

AC BM

.

Cách 2:

Gọi

M

là trung điểm

AC

.

Suy ra

   

 

  d , d , d , d ,AC BM AC BMN A BMN S BMN

.

Ta có,

 



..

3. 3.

d,

4.

S BMN S ABC

BMN BMN

VV

S BMN

SS

. Ta có

  

3

2

.

1 1 5 5 3

. . . . 3

3 3 3 9

S ABC ABC

aa

V SO S a

.

Ta có



   

2 2 2

109

2 4 6

BS BC SC a

BM BN

,

MN a

suy ra



5

6

BMN

a

S

.

Vậy

 



3

d,

2

a

AC BM

.

Câu 13. Chọn A

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

295

Gọi

G

là giao của

AC

và

DM

thì



1

2

GA MA

GC CD



1

3

AG

AC

.

Vẽ

//GH SC

thì



1

3

AH AG

AS AC

và

( ) //HDM SC

Do đó

     

, ,( ) ,( )d S C DM d SC HDM d C HDM

Xét tứ diện

.H ADM

thì ta thấy đây là tứ diện vuông, nên gọi

 

 ,( )h d A HDM

thì

        

   

   

   

2 2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 4 1

4

32

h AH AD AM AD a a a

SA AB



2 21

21

a

h

Vậy

     

   

2 21 4 21

, ,( ) ,( ) 2.

21 21

GC a a

d SC DM d C HDM d A HDM

GA

.

Câu 14. Chọn B

Gọi

N

là trung điểm của

BC

, khi đó

//AB MN

, vậy

 

//AB SMN

.

Khi đó

   

 

; ; ;d AB SM d AB SMN d A SMN

.

Dựng

AK MN

, dựng

AH SK

. Khi đó

 

;d A SMN AH

.

Góc giữa mp

 

SBC

và mp

 

ABC

bằng góc

SBA

, vậy

60SBA

.

Ta có

.tan 2 3SA AB SBA a

,

AK BN a

. Vậy







22

2 39

13

AK AS a

AH

AK AS

.

H

G

M

C

A

D

B

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

296

Câu 15. Chọn A

Áp dụng định lí cosin trong tam giác HBC ta có:



      





2

2 2 2 0

7

2 . cos 2. . cos60

3 3 3

a a a

HC HB BC HB BC HBC a a

Theo giả thiết ta có góc giữa đường thẳng

SC

và mặt phẳng

 

ABC

bằng

60

nên suy ra

 

  ; 60SCH SC ABC

Trong tam giác vuông SHC vuông tại H ta có:



0

21

tan60

3

a

SH HC

. Kẻ

Ax BC

.

Gọi

N

và

K

lần lượt là hình chiếu vuông góc của

H

trên

Ax

và

SN

.

Ta có

 

BC SAN

và



3

2

BA AH

nên

   

 



3

; , ,

2

d SA BC d B SAN d H SAN

.

Ta cũng có

 

Ax SHN

nên

Ax HK

. Do đó

   

 

  ,HK SAN d H SAN HK

      



22

2 3 . 42

, .sin60

3 3 12

a a SH HN a

AH HN AH HK

SH HN

Vậy

 



42

;

8

a

d SA BC

.

Câu 16. Chọn D

Do hình chiếu vuông góc của điểm

A

trên mặt phẳng

  

()A B C

là trọng tâm



G

của tam giác

  

A B C

, tam giác

  

A B C

là tam giác đều cạnh

a

và cạnh



AA a

nên tứ diện

  

AA B C

là tứ diện

đều.

Gọi

,HI

lần lượt là trung điểm của



BC

và



AA

, ta có các tam giác

  

,IB C HAA

là các tam

giác cân nên

  

,IH AA IH B C

. Do đó

  

( , )d AA B C IH

.

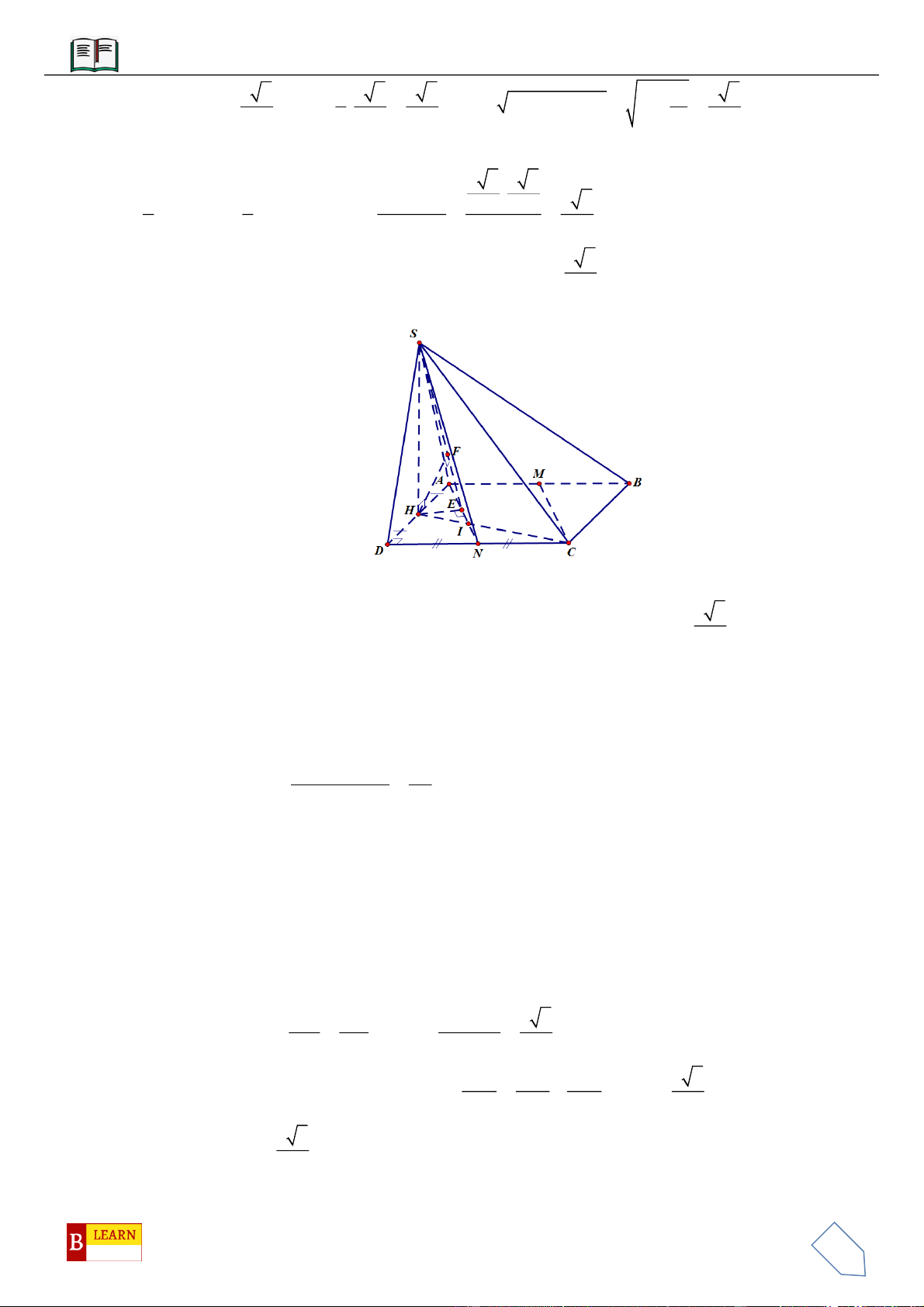
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

297

Ta có

      

       

2

2 2 2

3 2 3 3 6

, . , .

2 3 2 3 3 3

a a a a a

A H A G AG AA A G a

Áp dụng công thức tính diện tích tam giác



AA H

ta có:



  

    



63

.

1 1 . 2

32

..

2 2 2

aa

AG A H a

AG A H AA HI HI

AA a

.

Vậy khoảng cách giữa hai đường thẳng



AA

và



BC

là

2

a

.

Câu 17. Chọn D

Gọi

,NH

lần lượt là trung điểm của

AD

và

CD

. Ta có:

Tam giác

SAD

đều cạnh

a

,

H

là trung điểm của

  

3

,

2

a

AD SH AD SH

.

,MN

lần lượt là trung điểm

,AB CD

mà tứ giác

ABCD

là hình vuông

 //AN CM

.

 

 //CM SAN

   

 

  , , ,d SA CM d CM SAN d C SAN

.

Gọi

  I AN CH I

là trọng tâm tam giác

2ADC IC HI

.

 

      

,

2 , 2 ,

,

d C SAN

CI

HC SAN I d C SAN d H SAN

HI

d H SAN

.

Có

   

 







   











,

SAD ABCD

SAD ABCD AD SH ABCD

SH AD SH SAD

.

Trong

 

ABCD

kẻ

,HE AN E AN

.

Trong

 

SHE

kẻ

,HF SE F SE

   

 

    ,HF SAN h d H SAN HF

.

      

.5

10

HE HA HA DN a

AEH ADN HE

DN NA NA

∽

.

SHE

vuông tại

H

,

HF

là đường cao

    

2 2 2

1 1 1 3

8

a

HF

HF HS HE

.

 



3

,

4

a

d C SAN

.

Câu 18. Chọn D

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

298

Dựng

//BM AC

, khi đó

     

 

, ,( ) ,d AC SB d AC S BM d A SBM

.

Dựng

 

    ,AH MB AK SH AK SBM

 

,d A SBM AK

.

Hình chữ nhật

ABCD

,

   , 2 5AB a AD a AC a

.

   





    , 30

o

SA ABCD SC ABCD SCA SCA

.

Tam giác

SAC

vuông tại

A

,

   

5

5, 30

3

o

a

AC a SCA SA

.

Tam giác

ABM

vuông tại

A

,

    

. 2 . 2

55

AM AB a a a

AH BM AH

MB

a

.

Tam giác

SAH

vuông tại

A

,

     

2 2 2

1 1 1 2 185

37

a

AK SH AK

AK SA AH

.

Vậy

 



2 185

,

37

a

d AC SB

.

Câu 19. Chọn D

Dễ dàng chứng minh được

ABC△

vuông tại

A

. Do

 2BM MC

nên



1

3

MC BC a

.

Từ

  

22

. 3 . 3BC MC a a a AC

và

ABC△

vuông tại

A

ta suy ra được

AM BC

hay

AM AD

.

Vì

 

SA ABCD

nên

AM SA

, kết hợp

AM AD

suy ra

 

AM S AD

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

299

Trên mặt phẳng

 

SAD

, kẻ

AE

vuông góc với

SD

tại

E

. Khi đó ta có

AM AE

. Do vậy

 

,d AM SD AE

.

Ta có

3SA AD a

,

SA AD

suy ra



1 3 2

22

a

AE SD

.

Câu 20. Chọn D

Gọi

N

là trung điểm của

HC

, kết hợp với giả thiết ta có

// MN BC

. Suy ra

 

// BC SMN

.

Khi đó

   

 

  ; ; ; ;d SM BC d BC SMN d C SMN d H SMN

.

Trong mặt đáy, kẻ

,HE MN E MN

, suy ra

 

MN SHE

. Do đó hai mặt phẳng

 

SH E

và

 

SMN

vuông góc nhau và cắt nhau theo giao tuyến

SE

. Trong mặt phẳng

 

SHE

, kẻ

HK

vuông

góc với

SE

tại

K

ta được

 

 .HK d H SMN

Gọi

G

là trung điểm

BC

, suy ra

 AG BC

và

 3AG a

.

Ta thấy

HE

kéo dài cắt

BC

tại trung điểm

I

của

CG

và do đó

  

1 1 3

2 4 4

a

HE HI AG

.

Xét tam giác vuông

SHE

, ta có

   

2 2 2

1 1 1 12

67

HK a

HK HS HE

.

Vậy

 



12

;

67

d SM BC a

.

Câu 21. Chọn B

E

I

G

N

M

H

A

B

C

S

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

300

Gọi

D

là hình chiếu của

S

lên mặt phẳng

 

ABC

, suy ra

 

SD ABC

.

Ta có

SD AB

và

SB AB

 

gt

, suy ra

 

  AB SBD BA BD

.

Tương tự có

AC DC

hay tam giác

ACD

vuông ở

C

.

Dễ thấy

  SBA SCA

(cạnh huyền và cạnh góc vuông), suy ra

SB SC

.

Từ đó ta chứng minh được

  SBD SCD

nên cũng có

DB DC

.

Vậy

DA

là đường trung trực của

BC

, nên cũng là đường phân giác của góc

BAC

.

Ta có

30DAC

, suy ra



3

a

DC

. Ngoài ra góc giữa hai mặt phẳng

 

SAB

và

 

ABC

là

60SBD

, suy ra

    tan tan . 3

3

SD a

SBD SD BD SBD a

BD

.

Dựng hình bình hành

ABEC

, do tam giác

ABC

là tam giác đều nên tam giác

BEC

đều.

Có

      90 60 30CBD ABD ABC

nên

BD

là phân giác trong của góc

CBE

.

Gọi

I

là trung điểm của

EC

thì

BI EC

.

Kẻ

DH SI

tại

H

, ta có:

      







2 2 2 2 2 2

1 1 1 1 1 13

13

.

32

a

DH

DH SD DI a a

a

 

;

13

a

d D SCE

.

Có

     

 

    

3

// , ; ; ;

13

BI a

AB SEC d AB SC d AB SCE d B SCD d D SCE

DI

.

Câu 22. Chọn B

D

I

E

B

A

C

S

H

I

E

D

A

B

C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

301

Ta có

SH

vuông góc với

 

ABC

nên suy ra góc giữa

SC

và đáy

 

ABC

là góc

60SCH

.

     

33

.sin .tan60

22

aa

CH AC HAC SH CH

.

Kẻ

Bx

song song vớ

AC

suy ra

 

AC SBx

.

   

 

   , , , 2 ,d AC SB d AC SBx d A SBx d H SBx

.

Từ

H

kẻ

HK Bx

     

   Bx SHK SHK S Bx

.

   

     

 







    











,

SHK SBx

SHK SBx SK HI d H SBx

HI SK

.

  

3

.sin60

4

a

HK HB

,

      

2 2 2 2 2 2

1 1 1 4 16 52 3

9 3 9

52

a

HI

HI SH HK a a a

.

 

     

33

, , 2

52 13

aa

d H SBx HI d SB AC HI

.

Câu 23. Chọn D

Gọi

I

là trung điểm

AD

,

H

là giao điểm của

AC

và

BI

. Ta có

CD BI

nên

H

là trung điểm

của

AC

và

   

 

, , ,d CD SB d CD SBI d C SBI

 

 ,d A SBI

.

x

I

K

H

C

B

A

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

302

Kẻ

AK SH

tại

K

 

1

. Khi đó,











BI CD

BI AH

CD AC

.

Ta lại có,

BI SA

nên

 

  BI SAH BI AK

 

2

.

Từ

   

1 , 2

suy ra

 

AK SBI

nên

 

,d A SBI AK

.

       

2 2 2 2

3

2 . cos120 3 3

2

a

AC AB BC AB BC a AC a AH

.

    

2 2 2 2 2 2

1 1 1 1 4 5

3 3 3AK SA AH a a a

nên



15

5

a

AK

. Vậy

 



15

,

5

a

d CD SB

.

Câu 24. Chọn A

Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC. Gọi H là hình chiếu của G lên đường

thẳng đi qua A và song song với CG. GK là đường cao của tam giác GHS.

Khi đó,

( , ) ( ,( ))d GC SA d GC SAH GK

.

Ta có

AHGM

là hình chữ nhật và



3

a

AG

;





    

00

,( ) 60 .tan60 ,SA ABC SAG SG AG a



2

a

GH AM

, suy ra

  



22

.5

( , ) .

5

GS GH a

d GC SA GK

GS GH

Câu 25. Chọn B

Gọi

I

là trung điểm

AD

. Ta có

BCDI

là hình bình hành nên

//BI CD

.

Suy ra

 

//CD SBI

nên

   

 

d , d , d ,CD BI CD SBI D SBI

.

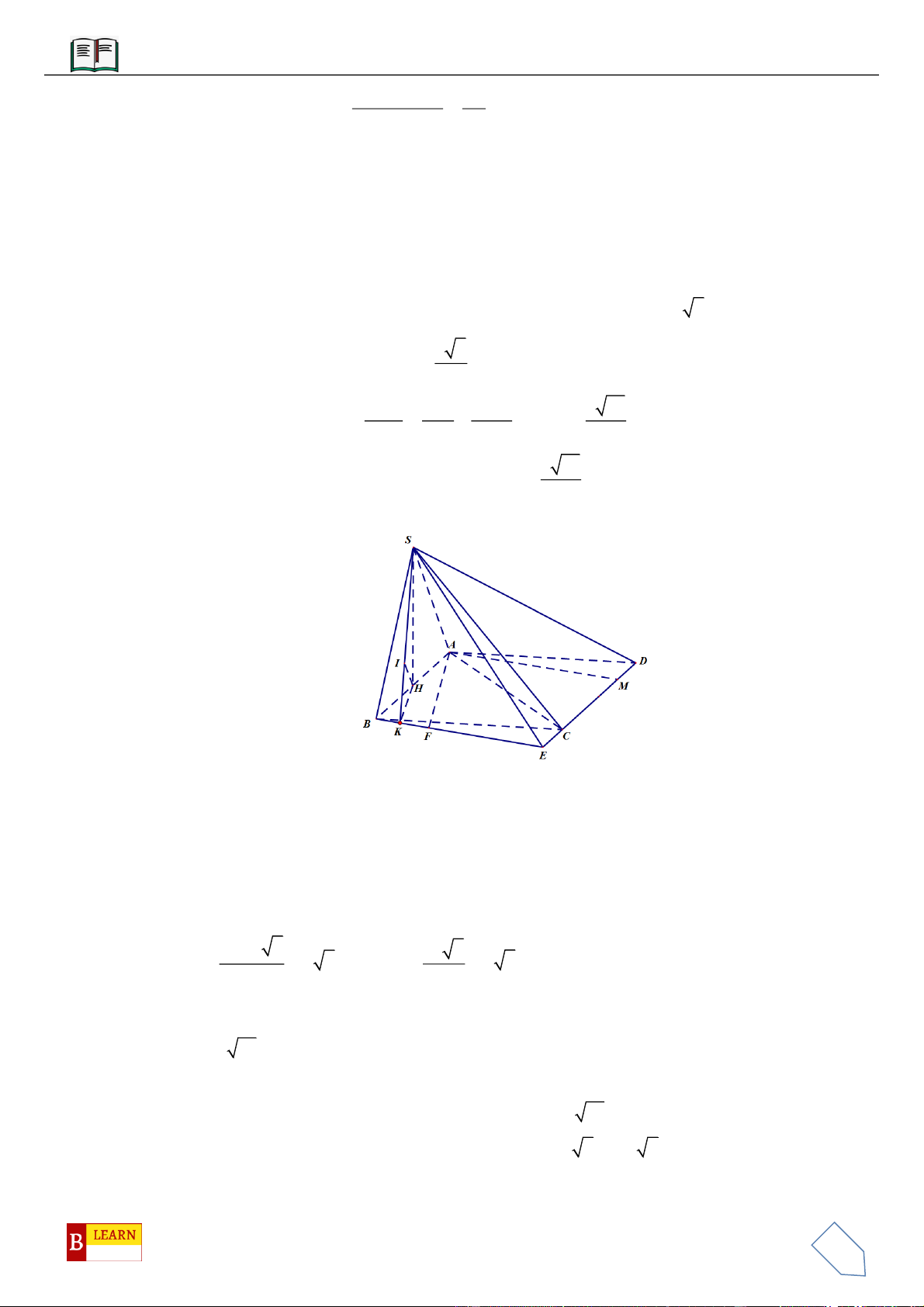
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

303

Ta có:

   

 

      

d,

1 d , d ,

d,

D SBI

DI

AD SBI I D SBI A SBI

AI

A SBI

.

Vì

ABCD

là nửa lục giác nội tiếp hình tròn tâm

I

nên

90ACD

AC CD

.

Suy ra

AM BI

, mà

SA BI

nên

     

  BI SAM SBI SAM

.

Ta lại có

   

SBI SAM SM

nên trong

 

SAM

kẻ

AH SM

thì

 

AH SBI

.

Vì

 

SA ABCD

nên hình chiếu của

SC

trên

 

ABCD

là

AC

.

 

         , D , 45 .tan60 a 3SC ABC SC AC SCA SA AC CD

.

Dễ thấy

ABI

đều cạnh

a

nên



3

2

a

AM

.

Trong

SAM

vuông tại

A

:

   

2 2 2

1 1 1 15

5

a

AH

AH SA AM

.

Vậy

   

 

   

15

d , d , d ,

5

a

CD BI D SBI A SBI AH

.

Câu 26. Chọn A.

Ta có:

   

 



















Trong ,

SAB ABCD

SAB ABCD AB

SAB SH AB

 

SH ABCD

.

Theo giả thiết ta có:

4AB BC a

và

    

0 0 0

120 30 60BAD ABD ABC

nên

ABC

là

tam giác đều, cạnh

4a

.

 

  

2

43

4

ABC

a

Sa

và



43

23

2

a

SH a

.

Ta có:

  

2 2 2

2 . .cosAM AD DM AD DM ADM

 

    

2

22

4 2.4 . .cos60 13a a a a a

.

13AM a

.

Trên tia đối của tia

CD

lấy điểm

E

sao cho

CE a

.

Khi đó, tứ giác

AMEB

là hình bình hành

   13BE AM a

.

Mặt khác,

  ADM BCE

    

22

2 2.4 3 8 3

AMEB ABCD ABC

S S S a a

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

304

Ta có:

 

















// //

AM SBE

AM BE AM SBE

BE SBE

.

Do đó

   

 

d , d , d ,AM S B AM SBE A SBE

.

Ta lại có:

 



d,

2

d,

A SBE

AB

HB

H SBE

 

d , 2d ,A SBE H SBE

.

Trong

 

ABCD

, gọi

K

và

F

lần lượt là hình chiếu của

H

và

A

lên

BE

.

  

11

.

22

AMEB

S

HK AF

EB



2

1 8 3 4 39

.

2 13

13

aa

a

(do

HK

là đường trung bình của

ABF

).

Ta có:

 







  













Do

,

BE HK

BE SH SH ABCD BE

HK SH SHK

HK SH H

 

BE SHK

.

Mà

     

  BE S BE SBE SHK

.

Ta lại có:

   

SBE SHK SK

Trong

 

SHK

, kẻ

 

HI SK I SK

 

HI SBE

 

d,H SBE HI

.

Tam giác

SHK

vuông tại

H

, đường cao

HI

nên

 

    







2 2 2 2 2 2

1 1 1 1 1 17

48

4 39

23

13

HI SH HK a

a

.

Do đó:



4 51

17

HI a

. Vậy

 



8 51

,

17

d AM SB a

.

Câu 27. Chọn B

Áp dụng định lý Menelaus cho

ABO

với cát tuyến

DMN

ta có:

 

      

1 2 2

. . 1 d , d ,

2 3 3

AM AN DO AN NB

N SBC A SBC

OM BN DB BN AB

Xét

ABC

có

      

2 2 2 2 2 2 2 2

5 ; 4 5AB CD a AC BC a a a ABC

vuông tại

C AC BC

 

SA ABCD SA BC

. Suy ra

 

BC SAC

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

305

Kẻ

AH SC

, ta có

 

BC SAC BC AH

nên

   

 

d,AH SBC AH A SBC

Xét

SAC

vuông tại

A

:

     



2 2 2

2 2 2 2

1 1 1 . .2 2

5

4

SA AC a a

AH a

AH SA AC

SA AC a a

Vậy

 

  

2 2 2 4 5

d , d , .

3 3 15

5

N SBC A SBC a a

.

Câu 28. Chọn D

Từ giả thiết ta có

 3BM a

, ta giải bằng cách gắn hệ trục tọa độ như sau:

Chọn hệ trục tọa độ đềcác vuông góc

Oxyz

thỏa

OA

, điểm

B

nằm trên

Ox

, điểm

D

nằm trên

Oy

, điểm

S

nằm trên

Oz

như hình vẽ:

Từ giả thiết ta có tọa độ các điểm

(3 ;0;0), (0;4 ;0), (0;0;5 )B a D a S a

và

(3 ;3 ;0)M a a

suy ra tọa độ

các vectơ

    (3 ;0; 5 ), ( 3 ; ;0), (0;3 ;0)SB a a MD a a BM a

Tích có hướng







2 2 2

, (5 ;15 ; 3 )SB MD a a a

Vận dụng công thức tính khoảng cách





  





3

2

,.

45 45

( , )

259 259

,

SB MD BM

aa

d SB MD

a

SB MD

.

Câu 29. Chọn A

Gọi

O

là tâm của tam giác

BCD

.

Qua

C

kẻ đường thẳng

d

song song với

BM

.

A

a

d

D

B

I

C

M

O

H

a

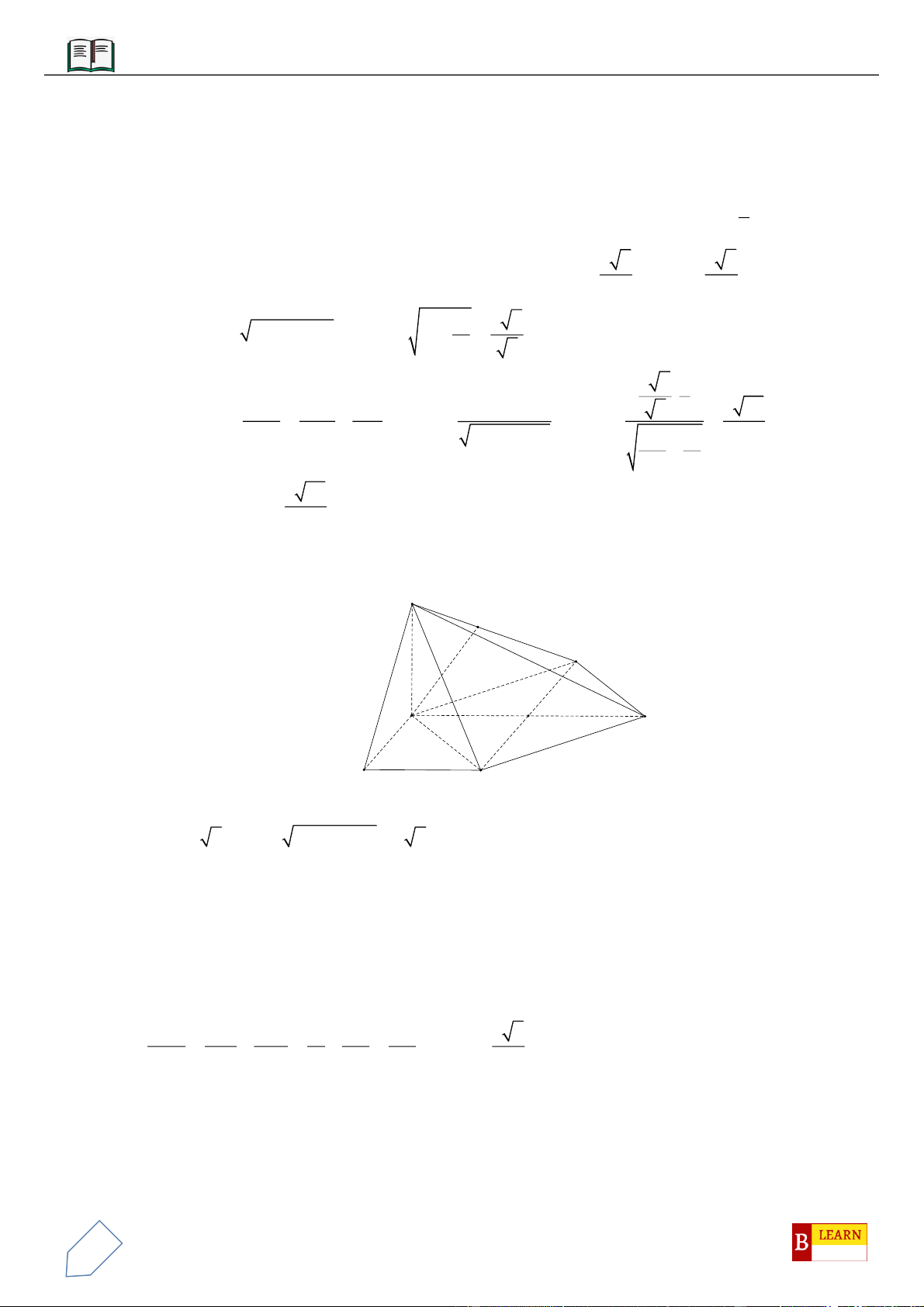
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

306

Khi đó

   

 

, , , , ,d AC BM d BM AC d d O AC d

.

Do tứ diện

ABCD

là tứ diện đều

 

AO BCD

.

Kẻ

OI d

và

Id

,

OH AI

và

H AI

 

,OH AC d

. Suy ra

 

, ,d O AC d OH

.

Ta có

// d BM

d CD

. Tứ giác

IOMC

là hình chữ nhật, suy ra



2

a

IO MC

.

BM

là đường cao trong tam giác đều cạnh bằng

a



3

2

a

BM



3

a

BO

.

Ta có



22

AO AB BO

   

2

3

aa

AO a

.

Do đó ta có



2 2 2

1 1 1

OH OA OI





22

.OA OI

OH

OA OI

  



22

2

.

2 22

3

11

2

34

aa

a

OH

aa

.

Vậy

 



22

,

11

a

d AC BM

.

Câu 30 Chọn C

Kẻ

CK AD

. Ta có

CK a

,

  AK BC a

KD a

.

 2AC a

,

  

22

2CD CK KD a

;

  

2 2 2

AC CD AD

ACD

vuông tại C.

Dựng hình chữ nhật

ACDE

, kẻ

AH SE

tại

H

.

Ta có

DE AE

và

DE SA

nên

 

DE SAE

DE AH

.

DE AH

và

SE AH

nên

 

AH SDE

tại

H

. Suy ra

 

,d A SDE AH

.

Ta có

 

//AC SDE

   

 

,,d AC SD d AC SDE

 

,d A SDE AH

.

Trong tam giác

SAE

vuông tại

A

, ta có

    

2 2 2 2 2 2

1 1 1 1 1 3

22AH SA AE a a a



6

3

a

AH

.

Câu 31.Chọn B

E

D

C

B

A

K

S

H

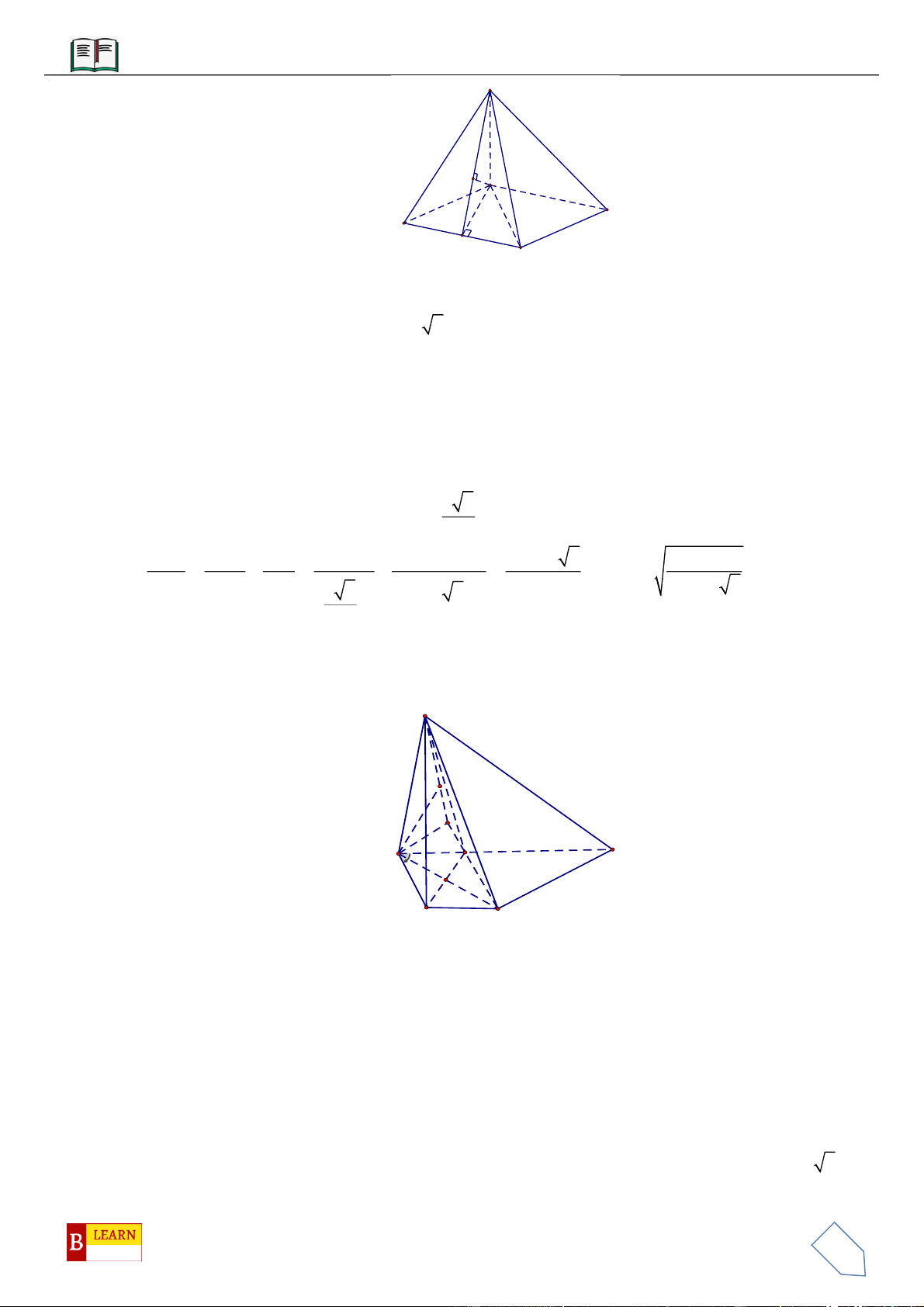
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

307

Vì

 

SA ABC

nên

 

,,SB ABC SB AB SBA

  75SBA

.

 

    .tan .tan75 2 3SA AB SBA a a

. Dựng hình bình hành

ACBD

, ta có

 

//AC SBD

nên:

   

 

, , ,d AC SB d AC SBD d A SBD

.

Gọi

M

là trung điểm

BD

, suy ra

BD AM

.

Từ

 

SA ABC

ta có

BD SA

, do đó

 

BD SAM

. Kẻ

AH SM

(

H SM

) thì

BD AH

Từ

 BD AH

và

AH SM

suy ra

 

AH SBD

nên

 

,d A SBD AH

.

Tam giác

ABD

đều cạnh

a

nên



3

2

a

AM

. Trong tam giác

SAM

vuông tại

A

, ta có

 







       











2 2 2 2 2 2

1 1 1 1 1 25 12 3 3

0.844

3

25 12 3

3

23

2

AH a a

AH AM SA a

a

.

Vậy

   

 

  , , 0.844d AC SB d A SBD AH a

.

Câu 32.Chọn A

Do

33AB AM a

nên

    AM a AD DC AM a

.

Do

//AM DC

và

  AM CD AD a

nên

AMCD

là hình thoi có cạnh bằng

a

.

Suy ra

     

 





   





/ / , , ,

//

CM a

AD SCM d AD SM d AD SCM d A SCM

AD CM

.

Kẻ

   

   , , ,AH CM H CM AK SH K SH

.

Ta có

 

  SA ABCD SA CM

mà

CM AH

suy ra

 

  CM SAH CM AK

.

Do

,AK AH AK CM

nên

   

 

   ,AK SMC AK d A SCM

.

Do

  

0

, 60AM AD a MAD

nên

MAD

là tam giác đều cạnh bằng

a

  23AC AI a

với

I

là tâm hình thoi

AMCD

.

M

B

S

A

C

D

H

I

M

A

D

C

B

S

H

K

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

308

Ta có



     

.3

1 1 . 3

2

. . .

2 2 2

AMC

a

MI AC a

S MI AC AH MC AH

MC a

.

Xét

SAH

vuông tại A có

AK SH

. Theo tính chất đường cao tam giác vuông,

Ta có

      

2 2 2 2 2 2

1 1 1 4 1 5 15

5

3 3 3

a

AK

AK AH SA a a a

.

Vậy

   

 

   

15

, , ,

5

a

d AD SM d AD SCM d A SCM AK

.

Câu 33.

Chọn D

Qua

A

kẻ đường thẳng

d

song song với

BD

. Gọi

O

là giao điểm

AC

và

BD

;

I

,

M

lần lượt là

trung điểm

AD

và

OD

;

N

là giao điểm

d

và

IM

. Nên

/ / / /( , )BD d BD SA d

  ( , ) ( ,( , )) ( ,( , ))d SA BD d BD SA d d M SA d

Trong

()mp SMN

kẻ

MH SN

(1),

()H SN

. Theo giả thiết :











( ) ( )

SI AD

SAD ABCD

   ()SI ABCD SI d

(*)

Mặt khác ta có :





  







//

d BD

BD AO d MN

AO MN

(**)

Từ (*),(**) suy ra

  ()d SMN d MH

(2). Từ (1),(2) suy ra

 ( , )MH SA d

.

Xét tam giác

SMN

có:



   

1 1 .

..

22

SMN

SI MN

S MH SN SI MN MH

SN

Với

        

22

3 2 1 2 14

,,

2 2 2 4 4

a a a a

SI MN AO IN MN SN SI IN

.

Do đó



. 21

.

7

SI NM a

MH

SN

Vậy



21

( , ) .

7

a

d SA BD

Câu 34.Chọn A

d

N

M

I

O

B

A

C

D

S

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

309

DAB C

là hình thoi nên

//AD BC

. Suy ra

 

//AD SBC

.

Khi đó

     

 

, ,( ) ,d SB AD d AD SBC d A SBC

(Gọi

K

là hình chiếu vuông góc của

A

lên

BC

,

H

là hình chiếu vuông góc của

A

lên

SK

).

Khi đó

 

AH SBC

, suy ra

 

,d A SBC AH

.

Tam giác

ABC

cân tại

B

và



0

60ABC

nên tam giác

ABC

là tam giác đều. Suy ra



3

2

a

AK

.

Ta có

  

3

.tan30

3

a

SA AD

. Vậy





22

. 39

13

AK SA a

AH

AK SA

.

Câu 35. Chọn B

Gọi

M

là trung điểm

AB

Ta có

BCDM

là hình bình hành (vì

CD

song song và bằng

BM

) nên



1

2

DM BC AB

suy ra

tam giác

ADB

vuông tại

D

. Tương tự tam giác

ACB

vuông tại

C

.

Vì

 









//

// //

//

EF DM

EF CB EF SBC

DM CB

   

 

   

3

, , , ,

4

d EF SB d EF SBC d F SBC d A SBC

Ta có

     





   







BC AC

BC SAC SBC SAC

BC SA

,

Gọi

H

là hình chiếu vuông góc của

A

lên

SC

thì

   

 

  ,AH SBC d A BC AH

.

K

A

D

B

S

C

H

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

310

Trong tam giác vuông

SAC

ta có

      

2 2 2 2 2 2

1 1 1 1 1 4 3

2

9 3 9

a

AH

AH SA AC a a a

Vậy

 



9

,

8

a

d SB EF

.

Câu 36. Chọn D

Gọi

N

là trung điểm của

AB

. Suy ra

MN

là đường trung bình của

ABC

.

   

 

  , , ,d AC SM d AC SMN d I SMN

( với

I DN AC

)

Ta có

 

    

,

1

5

,

d I SMN

IN

ID SMN N

DN

d D SMN

( do

    

11

//

45

IN AN IN

AN CD

ID CD DN

)

 



1

,,

5

d I SMN d D SMN

. Xét

ADN

và

DCA

có:

  90DA



1

2

AN AD

AD DC

 

    ADN DCA c g c”

ADN DCA

 

   DN AC MN SDN

.

Ta có

   

 







   











,

SMN SDN

SMN SDN SN d D SMN DH

Trong SDN DH SN

SDN

vuông tại

D

:

   

2 2 2

1 1 1

DH a

DH SD DN

 

  

1

,,

55

a

d I SMN d D SMN

.

Câu 37.Chọn D

Gọi

H

là trung điểm của

AO

. Theo giả thiết:

 

SH ABCD

.

Ta có:

 

// //CD AB CD SAB

   

 

  , , ,d SA CD d CD SAB d C SAB

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

311

Mặt khác:

 

   

,

4 , 4 ,

,

d C SAB

CA

d C SAB d H SAB

HA

d H SAB

.

Trong

 

ABCD

, kẻ

HI AB

tại

I

; kẻ

HK SI

tại

K

.

Khi đó:

 

,d H SAB HK

.

Tam giác

SHI

vuông tại

H

nên:



2 2 2

1 1 1

HK HS HI

 

1

Hình thoi có

60ABC

nên tam giác

ABC

đều

  

3

;

2

a

AC a BO

.

Tam giác

AIH

đồng dạng tam giác

AOB

     

3

.

.3

24

8

aa

IH AH OB AH a

IH

OB AB AB a

 

2

Tam giác

SAB

đều nên

  SA SB AB a

.

Tam giác

SAH

vuông tại

H

nên



    





2

2 2 2

15

44

aa

SH SA AH a

 

3

Thay

 

2

và

 

3

vào

 

1

ta được:

    

   

   

   

2 2 2 2

1 1 1 112 560

112

5

3 15

84

a

HK

HK a

aa

.

Vậy

 

  

560 560

, 4 , 4.

112 28

aa

d C SAB d H SAB

.

Câu 38.Chọn A

Ta có



.

1

.

3

S ABCD ABCD

V SA S

;

 

  

2

13

2.

22

ABCD

a

S a a a

Suy ra

  

3

.

2

3

3 6 2

.6

2

3

S ABCD

ABCD

V

a

SA a

S

a

.

Gọi

M

là trung điểm của

AB

,

O

là giao điểm của

AC

và

DM

.

Ta có tứ giác

ADCM

là hình vuông cạnh

a

.

Ta có

 

DNM

chứa

ON

và

//ON SC

nên

 

//SC DNM

.

Suy ra nên

   

 

  , , , ,d S C DN d SC DMN d C DMN d A DMN

.

Trong

 

SAC

kẻ

AH NO

. Ta có

DM AC

và

DM SA

nên

 

DM S AC

.

O

N

H

M

D

C

B

A

S

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

312

Khi đó ta có

 

















AH NO

AH DMN

AH DM DM SAC

 

,d A DMN AH

.



2 2 2

1 1 1

AH AN AO

;



6

2

a

AN

;



2

a

AO

     

2 2 2 2

1 1 1 8 6

4

33

2

a

AH

AH a a

a

.

Vậy

 



6

,

4

a

d SC DN

.

Câu 39.Chọn C

Ta có

     

 

   // // , , ,HK BD HK SBD d HK SD d HK SBD d H SBD

.

Dựng

HM BD

. Ta có

 













BD HM

BD SHM

BD SH

.

Dựng

HI SM

. Ta có

   

 





   







,.

HI SM

HI SBD d H SBD HI

HI BD

       

2 2 2 2

25

, , 7

2 4 2

AO a a

HM HD AH AD SH SD HD a

.

Xét

SHM

vuông tại

H

, ta có

 

      







2 2 2 2 2 2

1 1 1 1 1 57 399

57

7

2

7

4

a

HI

HI HS HM a

a

.

Vậy khoảng cách giữa hai đường thẳng

SD

và

HK

là

399

57

a

.

Câu 40.Chọn A

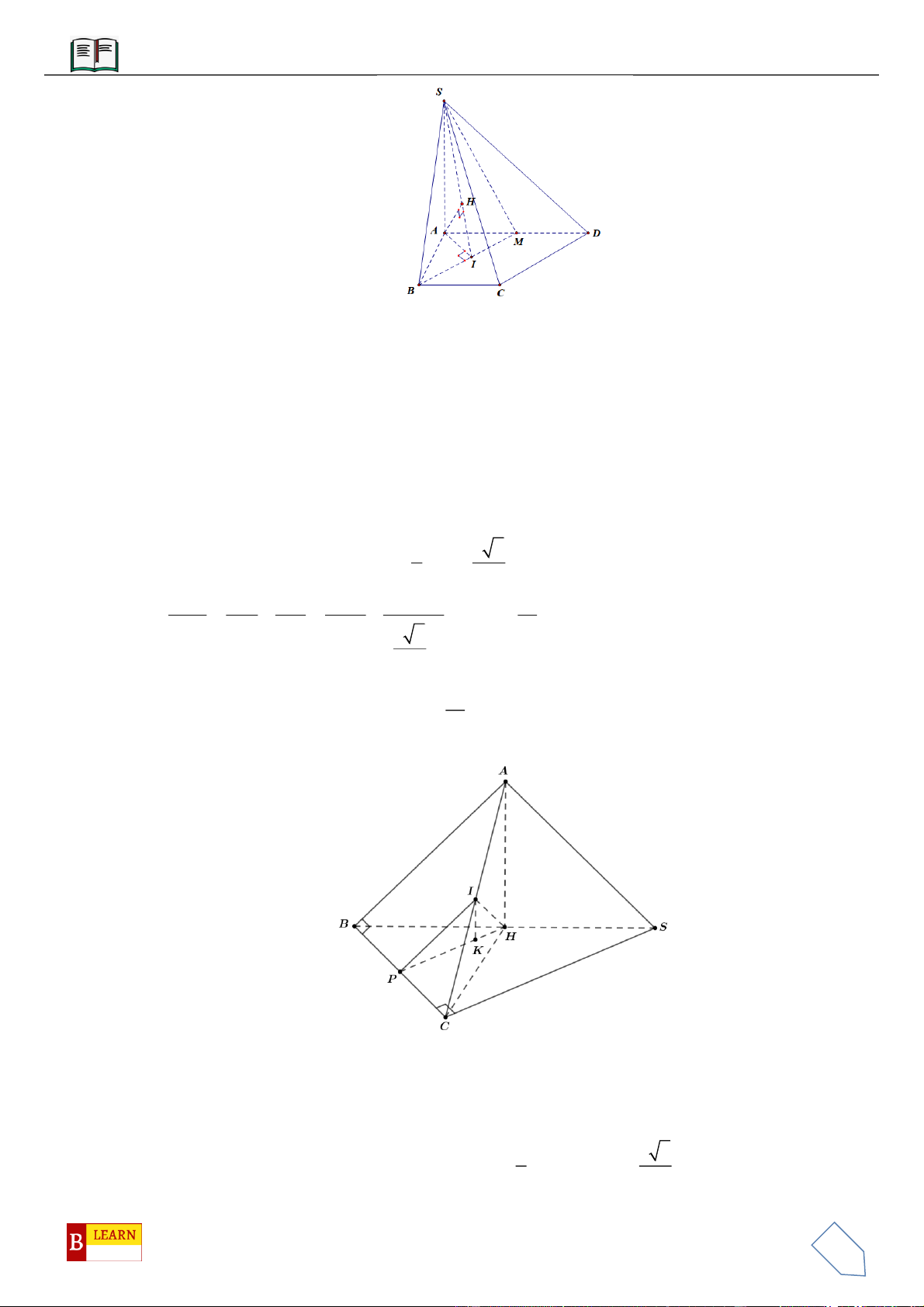
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

313

Do

ABCD

là hình thang có

  ;2AB BC a AD a

và

M

là trung điểm của

AD

nên ta có

 

// //BM CD CD SBM

.

Do đó

   

 

  , , , ,d SM CD d CD SBM d D SBM d A S BM

.

Ta kẻ

AI BM

, lại có

SA BM

   

SAI SBM

.

Ta có

   

SAI SBM SI

. Kẻ

 

  AH SI AH SBM

hay

 

,d A SBM AH

.

Xét tam giác

SAI

có

   

0

12

2 ; , 90

22

a

SA a AI BM SAI

.

 

      







2 2 2 2 2

1 1 1 1 1 2

3

2

a

AH

AH SA AI

a

.

Vậy

   

 

  

2

,,

3

a

d SM CD d A SBM AH

.

Câu 41. Chọn C

Gọi

I

là trung điểm của

AC

,

H

là trung điểm của

SB

,

P

là trung điểm của

BC

.

Ta có

SAB

,

SCB

vuông tại

A

và

C

nên

  HS HA HB HC

và

IA IB IC

.

Từ đó suy ra

 

  IH ABC IH BC

mà

IP BC

suy ra

 

BC IHP

.

Kẻ

   

 

      

13

,,

26

a

IK HP IK SBC IK d I SBC d A SBC

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

314

Ta có

     

2 2 2 2 2

1 1 1 1 8 2

4

a

IH

IK IH IP IH a

   

22

6

4

a

PH IP IH

.

Suy ra



6

2

a

SC PH



   

2

1 1 6 6

. . . .

2 2 2 4

SBC

aa

S BC SC a

.

Vậy

 



  

23

.

1 1 3 6 2

, . . . .

3 3 3 4 12

S ABC SBC

a a a

V d A SBC S

Câu 42. Chọn A.

Gọi

H

là hình chiếu vuông góc của

S

lên

 

ABC

. Suy ra

 







0

, 60SB ABC SBH

.

Do



0

90SCB SMA

nên

,BC CH AM MH

.

Ta có

ABM

đều cạnh

2a

và



0

90AMH

nên



0

30HMC

.

Từ đó



0

23

.tan30

3

a

CH CM

   

22

2 39

3

HB CH BC a

  

0

.tan60 2 13SH HB a

. Vậy



3

.

1 4 39

..

33

S ABC ABC

V SH S a

.

Câu 43. Chọn D

Ta có:

I

trung điểm

SA

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

   90SBA SCA

. Dựng

hình chữ nhật

ABDC

.

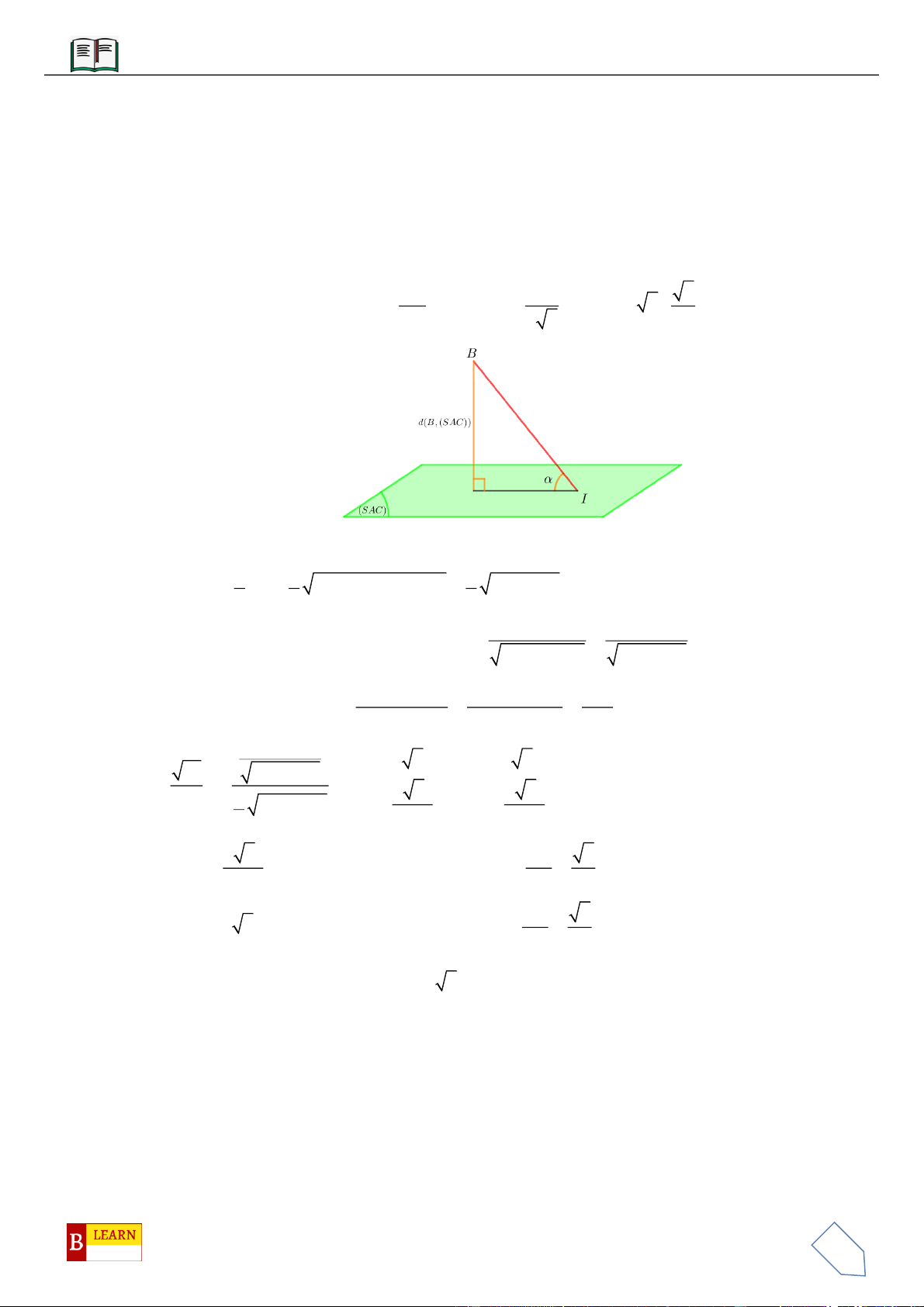
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

315

Mà

 





   







AB BD

AB SBD AB SD

AB SB

 

1

và

 





   







AC CD

AC SCD AC SD

AC SC

 

2

. Từ

 

1

và

 

2

suy ra

 

SD ABCD

.

Mặt khác:

   

 

   

 







      











, , , 30

,

SAB ABC AB

SB AB SB SAB SAB ABC SB BD SBD

BD AB BD ABC

.

Xét tam giác

SBD

có:

      

3

tan tan 30 4 3 . 4

3

43

SD SD

SBD SD a a

BD

.

Đặt

AB x

.

Ta có:

     

2 2 2 2 2

1 1 1

64

2 2 2

IB SA DB DC SD a x

.

Gọi

H

là hình chiếu của

D

lên

SC







2 2 2 2

. 4 .

16

SD DC a x

DH

SD DC a x

.

Mặt khác:

 

  

,,

sin ,

d B SAC d D SAC

DH

IB SAC

IB IB IB







22

4.

21

16

1

7

64

2

ax

a

ax



  







  





4 3 4 3

8 3 8 3

33

x a AB a

aa

x AB

.

Với



83

3

a

AB

,

 8SB a

, ta tính được

    

3

tan 30

3

AB

ASB ASB

SB

(Loại).

Với

 43AB a

,

 8SB a

, ta tính được

    

3

tan 30

2

AB

ASB ASB

SB

(Nhận).

Mà:

 





  







, 4 3

AB AC

d AC SB AB a

AB SB

.

Câu 44. Chọn A

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

316

Trong mặt phẳng

 

ABC

dựng hình chữ nhật

ABHC

, khi đó ta có

 













1

AB HB

AB SH

AB SB

và

 













2

AC CH

AC SH

AC SC

.

Từ (1) và (2) suy ra

 

SH ABC

.

Nên ta có

HA

là hình chiếu vuông góc của

SA

trên mặt phẳng

 

ABC

.

Do đó góc giữa

SA

và mặt phẳng

 

ABC

bằng góc giữa hai đường thẳng

,SA HA

và bằng góc

SAH

nên suy ra

45SAH

.

Theo cách dựng trên ta có

   

22

5HA BC AB AC a

và tam giác

SAH

vuông cân tại

H

nên

5SH HA a

.

Ta cũng có



  

2

11

. .2

22

ABC

S AB AC a a a

. Vậy



  

3

2

1 1 5

. . 5.

3 3 3

SABC ABC

a

V SH S a a

.

Câu 45. Chọn A.

Gọi

H

là hình chiếu vuông góc của

S

lên mặt phẳng

   

ABC SH ABC

    

00

90 90SAB SCB HAB HCB

,

 









   

00

, 30 , 30SB ABC SB HB SBH

Trong tam giác vuông

:SHB

   

00

.sin30 3; .cos30 3SH SB a HB SB a

,

   

22

HA HB AB a

Ta có

   









   

00

, 60 , 60SBC ABC HC SC SCH

   

0

.cot60 ; 2 2HC SH a CB a

.

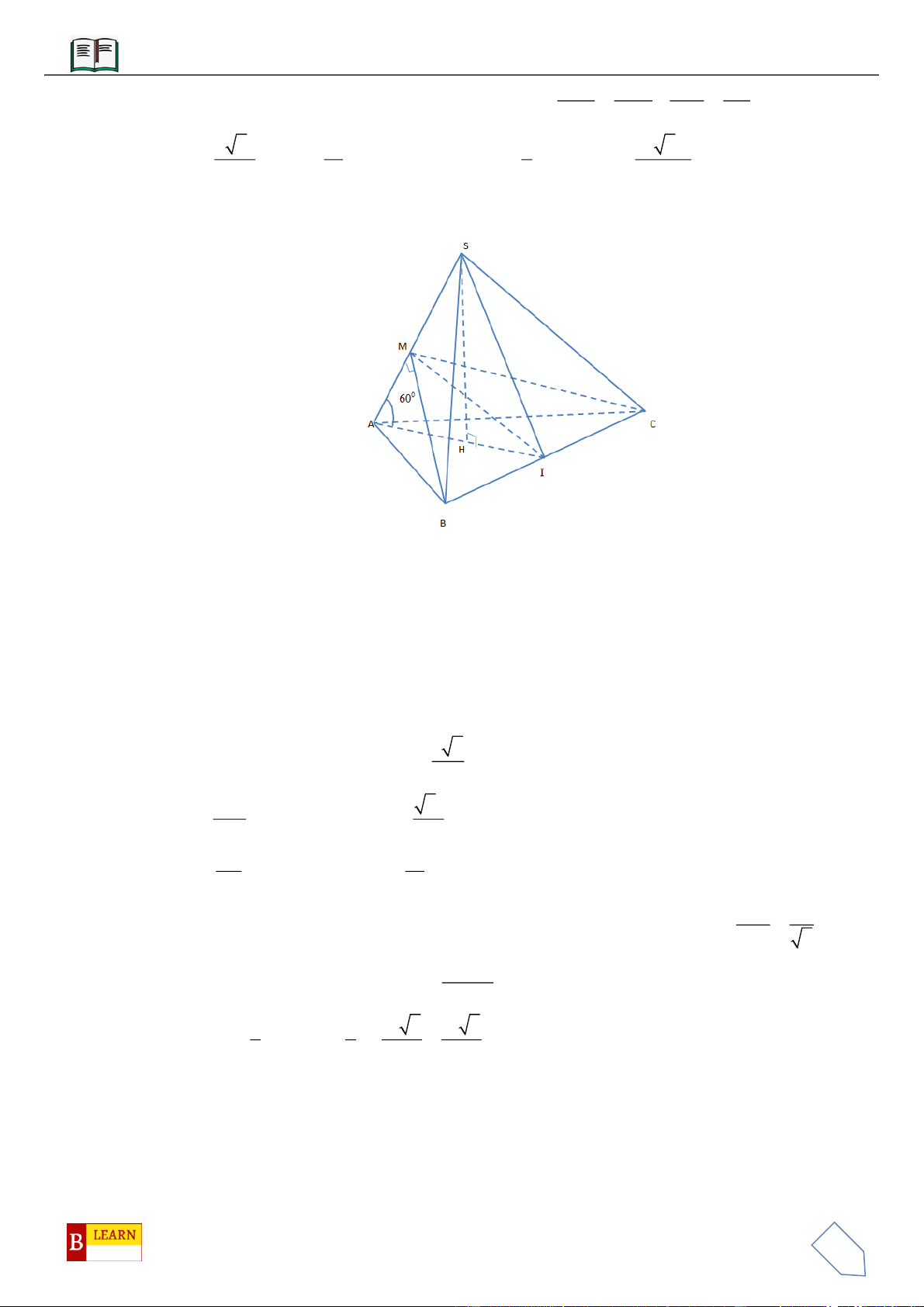
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

317

Gọi

O

là giao điểm của

,AC HB

; trong tam giác

:HAB

  

2 2 2 2

1 1 1 9

8AO AH AB a

   

2 2 8

33

aa

AO OB

. Vậy thể tích



3

.

1 16 6

..

3 27

S ABC

a

V OA OB SH

Câu 46. Chọn D

Dễ thấy

    SAB SAC SB SC

. Gọi

I

là trung điểm của

BC

.

Ta có:

 













AI BC

BC SAI

SI BC

. Kẻ

 

  SH AI SH ABC

.

Vậy

 





  

0

, 60SA ABC SAH SAI

Kẻ

BM SA

, do

 

  BC SAI BC SA

, vậy nên

 

SA MBC

.

Tam giác

IMA

vuông tại

M

có



3

2

a

IA

.

   

00

3

60 . 60 .

4

AM a

cos AM AI cos

AI

   

00

3

sin60 .sin60 .

4

IM a

IM AI

AI

Tam giác

SAB

vuông tại

B

,

BM

là đường cao. Ta có:

   

2

4

.

3

AB a

AB AM SA SA

AM

.

Xét

SAI

có:

   

.

. . 2

IM SA

SH AI IM SA SH a

AI

.

Vậy:

  

23

.

1 1 3 3

. . 2 . .

3 3 4 6

S ABC ABC

aa

V SH S a

Câu 47. Chọn D

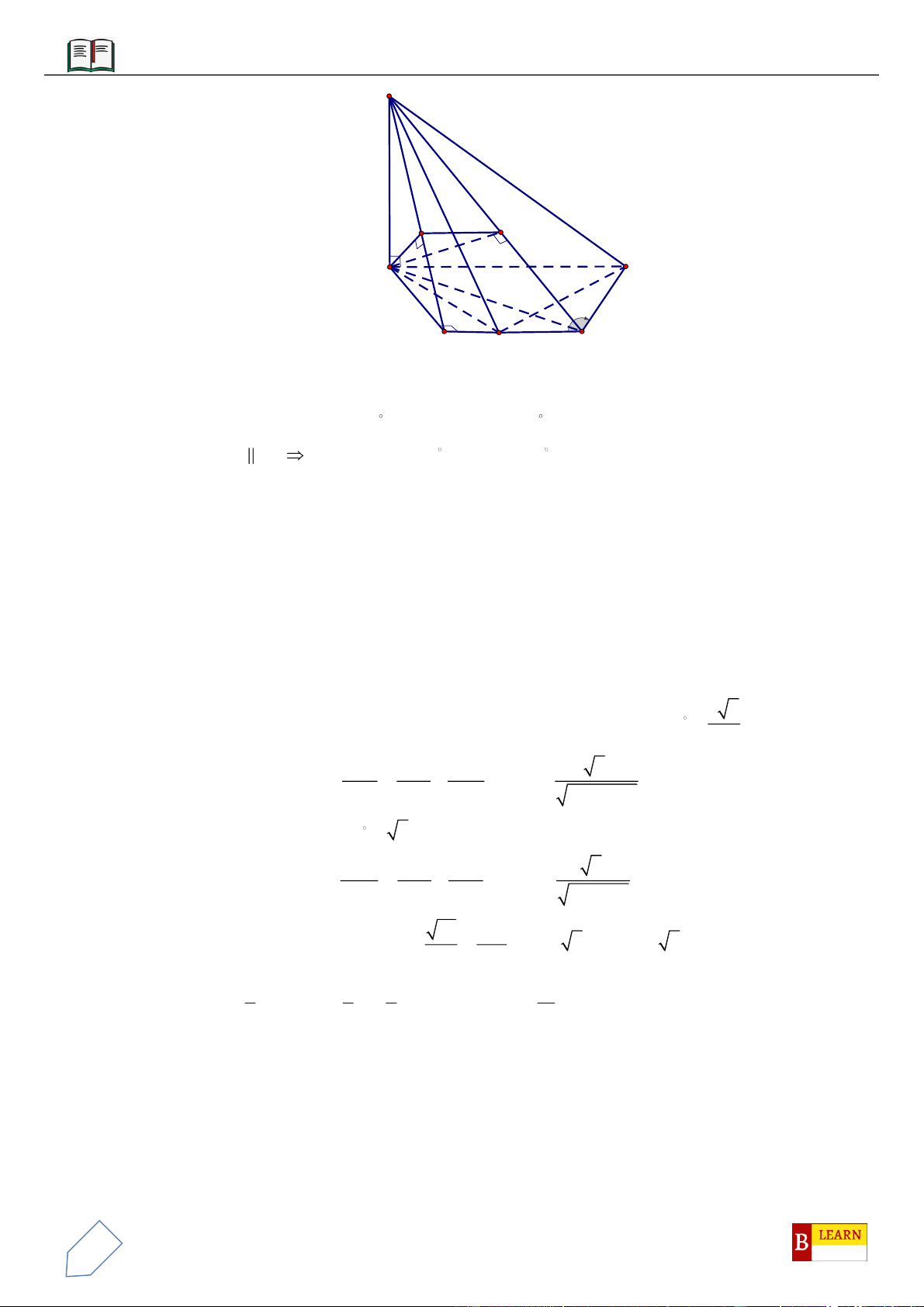
CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

318

Gọi

H

là hình chiếu vuông góc của

S

lên mặt phẳng

 

ABC

.

BAC

cân tại

B

và

 120ABC

   30ACB BAC

Theo bài

      30 60HC AB HCA CAB BCH AHC

ABCH

là hình thang cân.

Do đó

AH BC a

. Trong mp

 

ABCH

dựng

HK AB



 

AB SHK

.

Trong mp

 

SHK

kẻ

HP SK

 

   AB HP HP SAB

(1).

Trong mp

 

SHB

kẻ

HQ SB

. Dễ dàng chứng minh được

 

    BC HB BC SHB BC HQ

. Vì

 











HQ SB

HQ SBC

BC HQ

(2).

Từ (1) và (2) ta suy ra

   

 





,,SAB SBC HP HQ PHQ

. Đặt

SH x

Xét

AHK

vuông tại

K

:

   

3

.sin .sin .sin60 .

2

a

HK AH HAK AH AHC a

Xét

AHK

vuông tại

K

:

   



2 2 2

22

1 1 1 3.

34

ax

HP

HP SH HK

ax

.

  .tan .tan 60 3HB BC BCH a a

.

Xét

SHB

vuông tại

H

:

   



2 2 2

22

1 1 1 3.

3

ax

HQ

HQ SH HB

ax

.

HPQ

vuông tại

P

nên:

     

10

cos 3 3 .

5

HP

PHQ x a SH a

HQ

Vậy



  

3

.

1 1 1

. . . .sin

3 3 2 4

S ABC ABC

a

V SH S SH BA BC ABC

.

Câu 48. Chọn A.

Q

P

K

H

C

B

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

319

Ta có

   

2 2 0

2. . .cos135 5.AC AB BC AB BC a

.

Gọi

H

là hình chiếu vuông góc của

S

lên

 

ABC

,

  ,SH AB SH BC

Do



0

90SAB SBC

nên

   

,AB SHA BC SHB

  ,AB AH BC BH

.

Do



0

135ABC



0

45ABH

nên

ABH

vuông cân tại

A

. Từ đó

 2HB a

suy ra

HBC

vuông cân tại

B

. Suy ra



0

45BHC

 HC

//

AB

.

Gọi

K

là hình chiếu vuông góc của

H

lên

SA

, khi đó

 

HK SAB

nên

 

,,KH d H SAB d C SAB

.

Ta có

 



    

,

15

sin

55

d C SAB

HK

KH a

AC AC

.

Tam giác

SAH

vuông tại

A

có đưường cao

HK

. Ta có

      

2 2 2 2 2 2

1 1 1 5 1 4

2

a

HS

HS HK HA a a a

.

  

3

.

1 1 1

. . . . . 2.sin135

3 3 2 2 12

o

S ABC ABC

aa

V SH S a a

.

Câu 49. Chọn C

Gọi

H

là hình chiếu vuông góc của

S

lên

 

ABC

 

SH ABC

.

Ta có

 





   







AB SB

AB SBH AB BH

AB SH

.

CHUYÊN ĐỀ : KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

320

Ta có

   

 

   





 







      











, , , 60

,

SAB ABC AB

SB SAB SB AB SAB ABC SB BH SBH

BH ABC BH AB

.

Theo giả thiết,

ABC

cân tại

A

nên

            AB AC SAB SAC SB SC SHB SHC HB HC

.

Suy ra

HA

là đường trung trực của

BC

, suy ra

HA

là đường phân giác góc

BAC

,

suy ra

60HAB

.

Xét

HAB

vuông tại

B

suy ra

     tan .tan .tan60 3

BH

HAB BH BA HAB a a

BA

.

Xét

SHB

vuông tại

H

suy ra

     tan .tan 3.tan60 3

SH

SBH SH BH SBH a a

BH

.

Vậy



    

3

.

1 1 1 3

. . .3 . . . .sin . . .sin120

3 3 2 2 4

S ABC ABC

aa

V SH S a AB AC BAC a a

.

Câu 50. Chọn D

Gọi

H

là hình chiếu vuông góc của

S

lên

 

ABC

.

Theo bài ra, ta có

   





   







1

AC SC

AC SHC AC HC

AC SH

.

Tương tự

   





   







2

AB SB

AB SHB AB HB

AB SH

.

Mặt khác

90BAC

;

AB AC a

 

3

.

Từ

 

1

,

 

2

,

 

3

 ABHC

là hình vuông cạnh

a

.

Gọi

O HA BC

,

E

là hình chiếu vuông góc của

O

lên

SA

OE SA

 

4

.

Ta có

 





   







BC AH

BC SAH BC SA

BC SH

 

5

.

Từ

 

4

,

 

5

 





  







SA EB

SA BEC

SA EC

.

Từ đó, ta được: góc giữa

 

SAC

và

 

SAB

là góc giữa

EB

và

EC

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

321

Xét hai tam giác

BEC

,

BAC

ta có:

  BE CE BA AC

BEC BAC

.Vì



0

90CAB

nên

    90 120 .BEC BEC

Ta dễ dàng chỉ ra được

  60OEB OEC

.

Đặt

      



22

. 2.

8

AO SH a x

SH x SA x a OE

SA

xa

.

Xét tam giác vuông

OCE

ta có:

     



22

2.

tan60 2 : 3 2

8

OC a x

a x a

OE

xa

.

Vậy

  

3

2

..

1 1 1 4

. .2 .4

2 2 3 3

S ABC S HBAC

a

V V a a

.

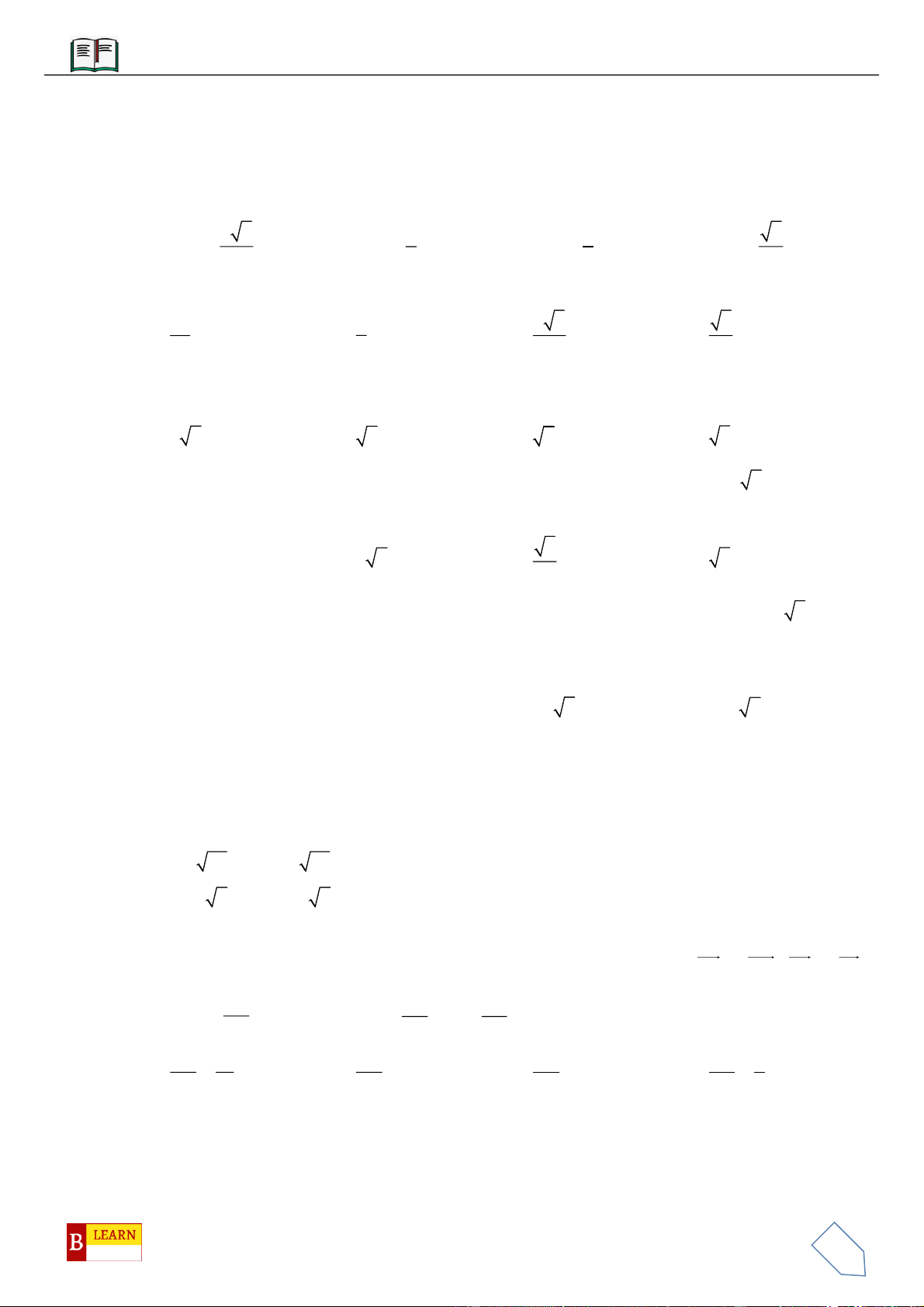
CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

321

DẠNG 9: CỰC TRỊ KHỐI ĐA DIỆN

Câu 1: Cho hình hộp chữ nhật

.ABCD A B C D

   

có

AB x

,

1AD 

. Biết rằng góc giữa đường thẳng

AC



và mặt phẳng

 

ABB A



bằng

30

. Tìm giá trị lớn nhất

max

V

của thể tích khối hộp

.ABCD A B C D

   

.

A.

33

4

max

V 

. B.

1

2

max

V 

. C.

3

2

max

V 

. D.

3

4

max

V 

.

Câu 2: Cho hình chóp

.S ABCD

đều, có cạnh bên bằng

1

. Thể tích lớn nhất của khối chóp

.S ABCD

bằng

A.

4

27

. B.

1

6

. C.

43

27

. D.

3

12

.

Câu 3: Cho hình chóp

.S ABCD

có

SA x

, các cạnh còn lại của hình chóp đều bằng 2. Giá trị của

x

để

thể tích khối chóp đó lớn nhất là

A.

22

. B.

2

. C.

7

. D.

6

.

Câu 4: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình thoi. Biết

SA x

với

 

0 2 3x

và tất cả các

cạnh còn lại đều bằng 2. Tìm

x

để thể tích của khối chóp

.S ABCD

đạt giá trị lớn nhất?

A.

2

. B.

22

. C.

6

2

. D.

6

.

Câu 5: Cho hình trụ có hai đường tròn đáy là

 

;OR

và

 

;OR



, chiều cao của hình trụ là

3R

. Giả sử

AB

là một đường kính cố định trên đường tròn

 

O

và

M

là điểm di động trên đường tròn

 

O



. Hỏi diện tích tam giác

MAB

đạt giá trị lớn nhất bằng bao nhiêu?

A.

2

2R

. B.

2

4R

. C.

2

3R

. D.

2

22R

.

Câu 6: Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích

3

72dm

, chiều cao là

3dm

Một vách ngăn ở giữa, chia bể cá thành hai ngăn, với các kích thước

,ab

như hình vẽ. Tính

,ab

để bể cá tốn ít nguyên liệu nhất, coi bề dày các tấm kính như nhau và không ảnh hưởng đến thể

tích của bể.

A.

24 dma 

;

24 dmb 

. B.

6dma 

;

4dmb 

.

C.

3 2 dma 

;

4 2 dmb 

. D.

4dma 

;

6dmb 

.

Câu 7: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình bình hành tâm

O

. Một mặt phẳng không qua

S

và cắt các cạnh

SA

,

SB

,

SC

,

SD

lần lượt tại

M

,

N

,

P

,

Q

thỏa mãn

2SA SM

,

3SC SP

.

Tính tỉ số

SB

SN

khi biểu thức

2

4

SB SD

T

SN SQ









đạt giá trị nhỏ nhất.

A.

11

2

SB

SN



. B.

5

SB

SN



. C.

4

SB

SN



. D.

9

2

SB

SN



.

Câu 8: Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên là một số

thực dương không đổi. Gọi



là góc giữa cạnh bên của kim tự tháp và mặt đáy. Khi thể tích của

kim tự tháp lớn nhất, tính

sin



.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

322

A.

6

sin

3





. B.

3

sin

3





C.

5

sin

3





. D.

3

sin

2





.

Câu 9: Cho hình chóp

.S ABC

có

SA SB SC AB AC a    

và

2BC x

. Tính thể tích lớn nhất

max

V

của hình chóp

.S ABC

A.

3

8

a

. B.

3

2

4

a

. C.

3

2

12

a

. D.

3

6

a

.

Câu 10: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

a

, cạnh bên hợp với đáy một góc

60

o

, gọi

M

là điểm đối xứng với

C

qua

D

;

N

là trung điểm của

SC

, mặt phẳng

 

BMN

chia khối chóp

.S ABCD

thành hai phần. Gọi

 

1

H

là phần đa diện chứa điểm

S

có thể tích

1

V

;

 

2

H

là phần đa

diện còn lại có thể tích

2

V

. Tính tỉ số thể tích

1

2

V

.

A.

31

5

. B.

7

3

. C.

7

5

. D.

1

5

.

Câu 11: Cho khối tứ diện

ABCD

có thể tích

1

6

V 

, góc

45ACB 

và

3

2

AC

AD BC  

. Hỏi độ dài

cạnh

CD

?

A.

23

. B.

3

. C.

2

. D.

2

.

Câu 12: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

P

đi qua điểm

 

9;1;1M

cắt các tia

,Ox

,Oy Oz

tại

,,A B C

(

,,A B C

không trùng với gốc tọa độ). Thể tích tứ diện

OABC

đạt giá trị nhỏ

nhất là bao nhiêu?

A.

81

2

B.

243

2

C.

81

6

D.

243

Câu 13: Cho tam giác đều

ABC

có cạnh bằng 2. Trên đường thẳng

d

đi qua

A

và vuông góc với mặt

phẳng

 

ABC

lấy điểm

M

sao cho

AM x

. Gọi

,EF

lần lượt là hình chiếu vuông góc của

C

lên

,.AB MB

Đường thẳng qua

,EF

cắt

d

tại

N

. Xác định

x

để thể tích khối tứ diện

BCMN

nhỏ nhất.

A.

2

x 

. B.

1x 

. C.

2x 

. D.

2x 

.

Câu 14: Cho lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều. Tam giác

ABC



có diện tích bằng

33

và nằm trong mặt phẳng tạo với đáy một góc bằng

, 0;

2













. Tìm



để thể tích khối lăng trụ

.ABC A B C

  

đạt giá trị lớn nhất.

A.

1

tan

6





. B.

tan 6





. C.

tan 2





. D.

3

tan

2





.

Câu 15: Cho hình chóp

.S ABC

, trong đó

()SA ABC

,

SC a

và đáy

ABC

là tam giác vuông cân tại

đỉnh

C

. Gọi



là góc giữa hai mặt phẳng

()SBC

và

()ABC

. Khi thể tích khối chóp

.S ABC

đạt

giá trị lớn nhất thì

sin2



bằng

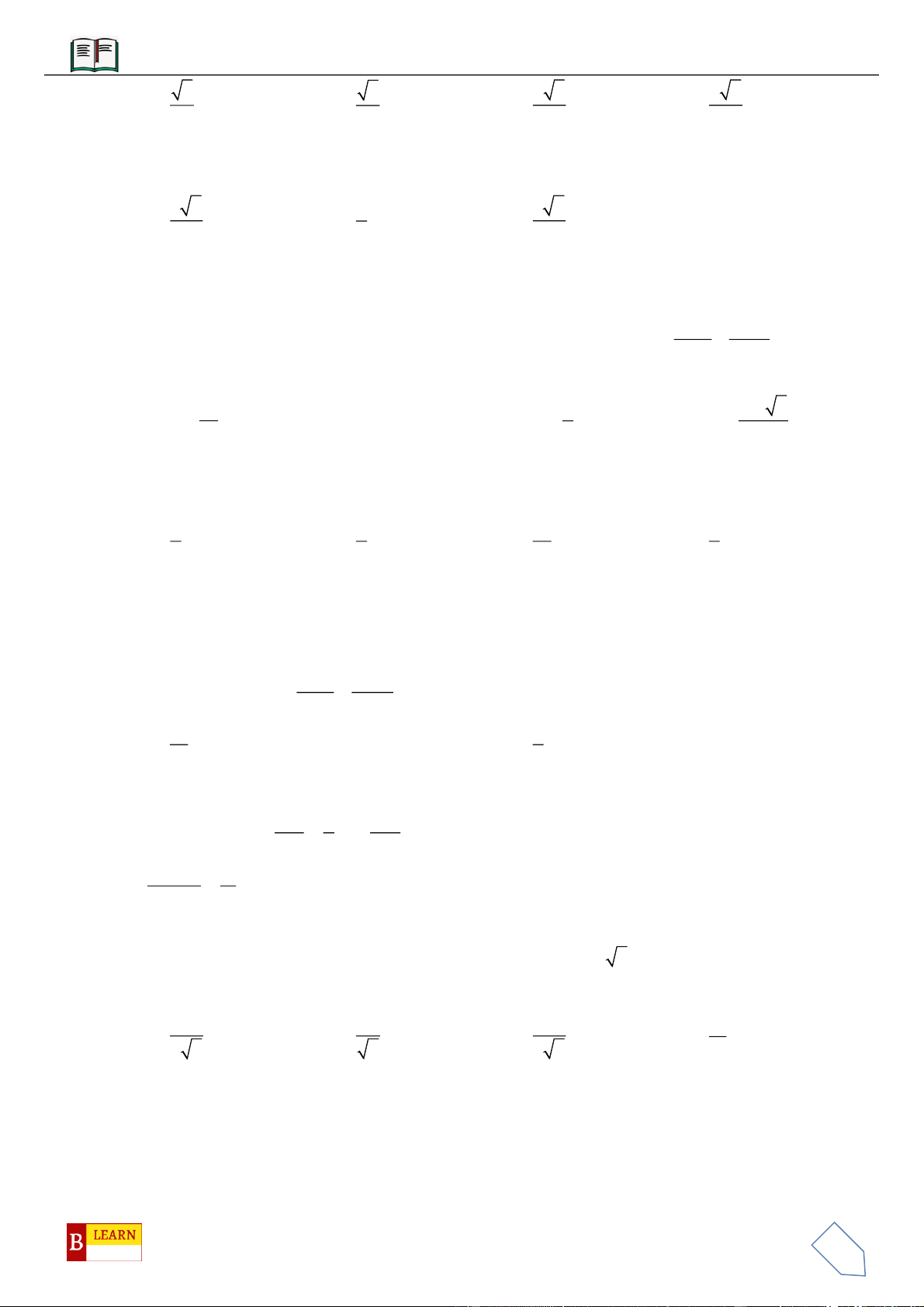
CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

323

A.

3

. B.

3

2

. C.

23

5

. D.

22

3

.

Câu 16: Cho hình chóp

.S ABC

có

SA x

, các cạnh còn lại của hình chóp đều bằng

a

. Để thể tích khối

chóp lớn nhất thì giá trị

x

bằng

A.

6

2

a

. B.

2

a

. C.

3

2

a

. D.

a

.

Câu 17: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

2

,

2SA 

và

SA

vuông góc

với mặt phẳng đáy

 

ABCD

. Gọi

M

,

N

là hai điểm thay đổi trên hai cạnh

AB

,

AD

sao cho

mặt phẳng

 

SMC

vuông góc với mặt phẳng

 

SNC

. Tính tổng

22

11

T

AN AM



khi thể tích

khối chóp

.S AMCN

đạt giá trị lớn nhất.

A.

13

9

T 

. B.

2T 

. C.

5

4

T 

. D.

23

4

T





.

Câu 18: Cho tứ diện

ABCD

có

AB x

,

CD y

, tất cả các cạnh còn lại bằng

2

. Khi thể tích tứ diện

ABCD

là lớn nhất tính

xy

.

A.

2

3

. B.

4

3

. C.

16

3

. D.

1

3

.

Câu 19: Cho hình chóp có đáy là hình vuông cạnh bằng , và vuông góc

với mặt phẳng đáy. Gọi , là hai điểm thay đổi trên hai cạnh , sao cho

mặt phẳng vuông góc với mặt phẳng . Khi thể tích khối chóp đạt giá trị

lớn nhất, giá trị của bằng

A. . B. . C. . D. .

Câu 20: Cho khối chóp

.S ABCD

có đáy là hình bình hành. Gọi

,MN

là hai điểm nằm trên hai cạnh

,SC SD

sao cho

1

2

SM

SC



và

2

SN

ND



, biết

G

là trọng tâm của tam giác

SAB

. Tỉ số thể tích

.

GMND

S ABCD

V

m

Vn



(

,mn

là các số nguyên dương và

 

,1mn 

). Giá trị của

mn

bằng

A.

17

. B.

19

. C.

21

. D.

7

.

Câu 21: Cho tứ diện

ABCD

có

o

90DAB CBD

,

AB a

,

5AC a

và

o

135ABC 

; Góc giữa hai

mặt phẳng

 

ABD

và

 

BCD

bằng

o

30

. Thể tích của tứ diện

ABCD

là

A.

3

23

a

. B.

3

2

a

. C.

3

32

a

. D.

3

6

a

.

Câu 22: Cho một cái hộp hình chữ nhật có kích thước ba cạnh lần lượt là

4cm

,

6cm

,

9cm

như hình vẽ.

Một con kiến ở vị trí

A

muốn đi đến vị trí

B

. Biết rằng con kiến chỉ có thể bò trên cạnh hay trên

bề mặt của hình hộp đã cho. Gọi

xcm

là quãng đường ngắn nhất con kiến đi từ

A

đến

B

. Khẳng

định nào sau đây đúng?

A.

 

15;16x 

. B.

 

13;14x 

. C.

 

12;13x 

. D.

 

14;15x 

.

.S ABCD

ABCD

2

2SA 

SA

M

N

AB

()AD AN AM

 

SMC

 

SNC

.S AMCN

22

1 16

AN AM



17

4

5

4

2

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

324

BẢNG ĐÁP ÁN

1.C

2.C

3.C

4.D

5.A

6.D

7.C

8.B

9.A

10.C

11.B

12.D

13.DC

14.

15.D

16.A

17.C

18.C

19.B

20.B

21.D

22.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn C

Vì

.ABCD A B C D

   

là hình hộp chữ nhật nên

 

BC ABB A





.

Suy ra:

 









; ; 30A C ABB A A C A B BA C

     

   

A BC





vuông tại

B

nên

3

tan30

BC

AB







.

A AB





vuông tại

A

nên

22

AA A B AB





2

3 x

.

Thể tích khối hộp:

 

..V x AB BC A A





2

3xx

với

 

0; 3x 

.

Có:

 

2

3

x

V x x

x



  



2

32

3

x







. Cho

 

0Vx





2

3 2 0x  

 

6

,0

2

xx  

.

Có bảng biến thiên:

Vậy

3

2

max

V 

khi

6

2

x 

.

Câu 2: Chọn C

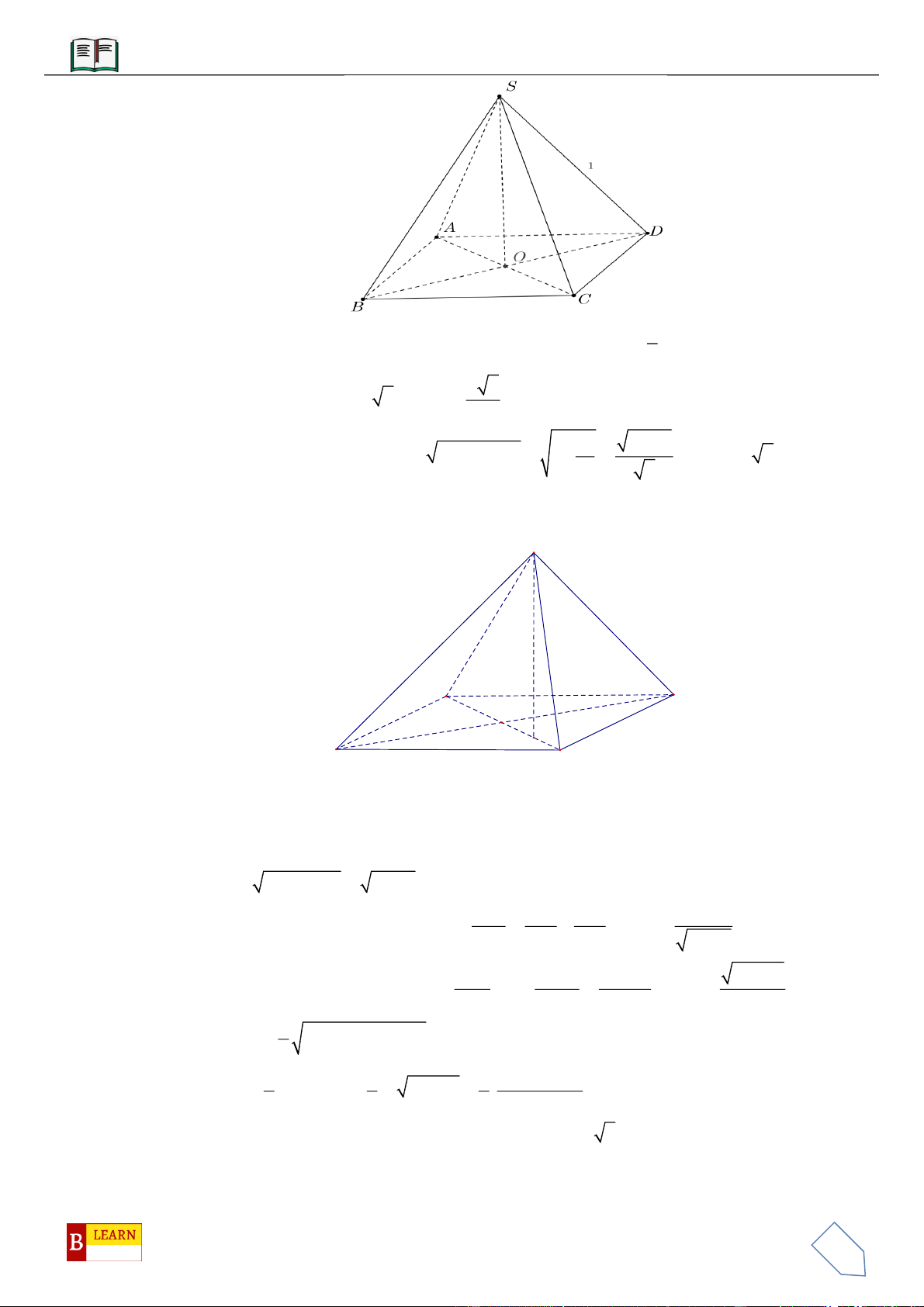
CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

325

Gọi

O

là giao điểm của

AC

và

BD

 

SO ABCD

.

1

..

3

S ABCD ABCD

V SO S

.

Đặt

AB x

 

0x 

2

x

BD x OD   

.

Tam giác

SOD

vuông tại

O

22

2

1

2

xx

SO SD OD



     

 

0; 2x

Câu 3: Chọn D

Vì

2SB SC SD  

nên hình chiếu

H

của

S

lên

ABCD

là tâm đường tròn ngoại tiếp tam giác

BCD

. Mà tứ giác

ABCD

có các cạnh bằng nhau nên tứ giác

ABCD

là hình thoi, do đó

H AC

;

SBD

;

CBD

;

ABD

có các cạnh tương ứng bằng nhau nên

SO AO CO

SAC

vuông

tại

S

2 2 2

4AC SA SC x    

.

SAC

vuông tại

S

, có đường cao

SH

nên

2 2 2

2

1 1 1 2

4

x

SH

SH SA SC

x

   



.

Lại có

2 2 2 2

2 2 2 2 2

4 12 12

4

4 4 4 2

AC x x x

OB OC BC OB BC OB

  

         

.

  

22

1

. 4 12

2

ABCD

S AC OB x x   

.

Ta có

22

2

.

1 1 1 12

. . . . 12 . 2

3 3 3 2

S ABCD ABCD

xx

V SH S x x



    

.

Dấu bằng xảy ra khi và chỉ khi

2 2 2

12 6 6x x x x     

.

Cách 2.

O

C

D

A

B

S

H

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

326

Theo giả thiết ta có hai tam giác

SBC

,

SCD

là hai tam giác đều bằng nhau.

Gọi

M

là trung điểm của

SC

suy ra

 

BM MC

MC MBD

DM MC













.

Ta có

. . .

2. 4.

S ABCD S BCD C MBD

V V V

.

Ta lại có

.

1 1 1 1

. . . . .sin sin

3 3 2 2

C MBD MBD

V MC S MB MD BMD BMD



  

,

 

1, 3MC MB MD  

.

Do đó để

.S ABCD

V

lớn nhất



.C MBD

V

lớn nhất



sin 1 90BMD BMD   

.

Xét

DMB

vuông tại

M

, khi đó

22

2. D D 6x SA MO B M MB     

.

Câu 4: Chọn D

Gọi

O

là tâm hình thoi

ABCD

và

H

là hình chiếu vuông góc của

S

lên

AC

Ta có

1

( ) SO OA OC

2

ABD CBD SBD c c c AC          

Mà

SO

là trung tuyến của

SAC

nên

SAC

vuông tại

S

.

Lại có

( ) ( ) ( ), (1)

BD AC

BD SAC ABCD SAC

BD SO





   







Và

( ) ( )SAC ABCD AC

;

, (2)SH AC

.

Từ

(1)

và

(2)

ta có

()SH ABCD

.

Trong

SAC

vuông tại

S

có

2

22

2

1 1 1 2

4;

4

x

AC x SH

SH x

x

     



.

M

O

B

D

A

C

S

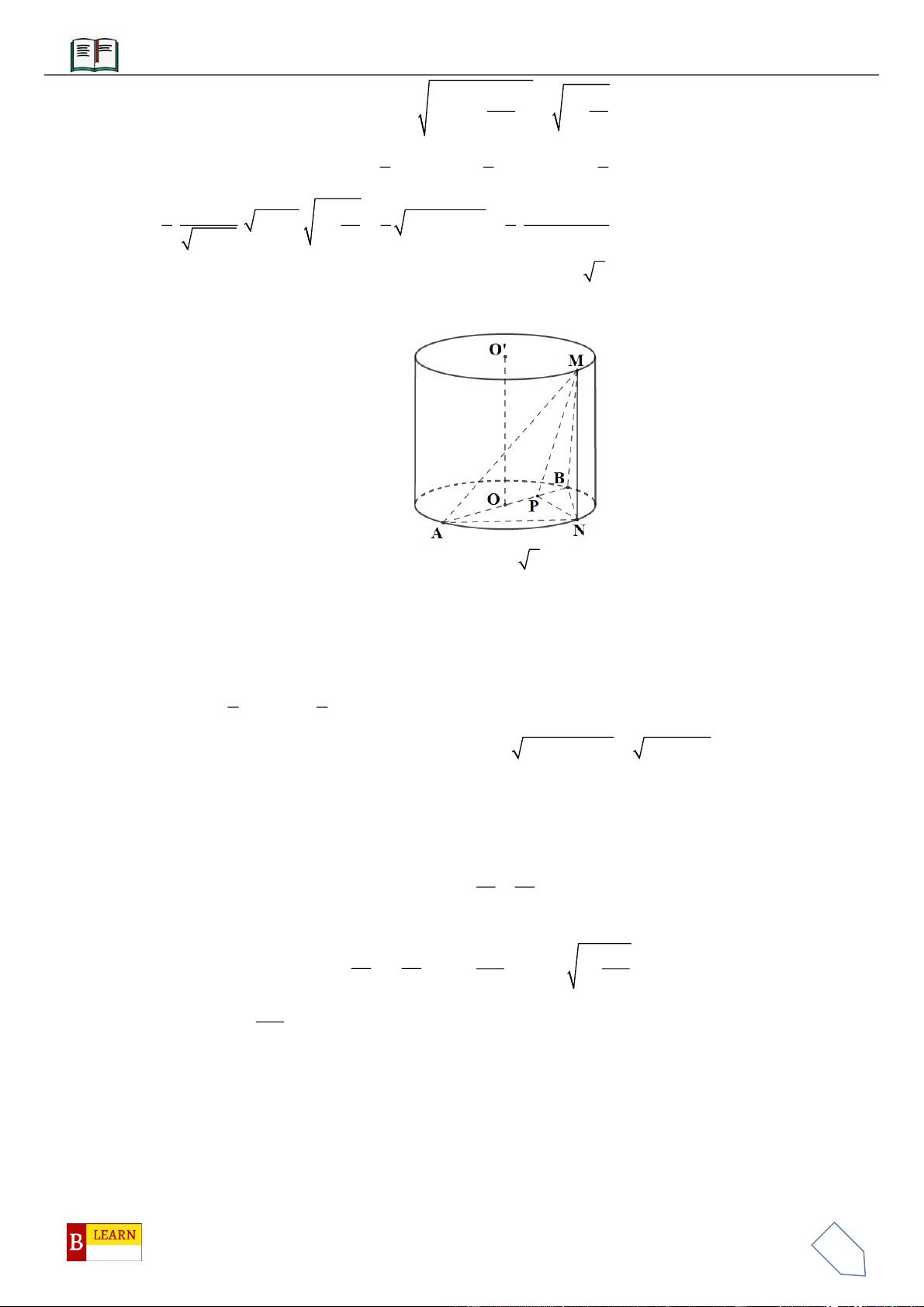
CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

327

Trong

OAB

vuông tại

O

có

2

3

24

AC x

OB AB



   





.

Thể tích hình chóp là

.

1 1 1

. . . .2. . . .

3 3 3

S ABCD ABCD ABC

V SH S SH S SH AC OB



  

2 2 2

2

1 2 1 1 12

. . 4. 3 (12 ) . 2

3 4 3 3 2

4

x x x x

x x x

x



      



.

.S ABCD

V

lớn nhất bằng

2

khi và chỉ khi

22

12 6x x x   

.

Câu 5: Chọn A

Gọi

N

là hình chiếu của

M

trên

 

O

3MN R

.

Gọi

P

là hình chiếu của

N

trên

AB

, khi

M

di chuyển trên

 

O

thì

0 NP R

.

Ta có:

 

MN ABN

MN AB

AB MNP AB MP

NP AB











    









.

11

. .2 . .

22

MAB

S AB MP R MP R MP



   

.

Mặt khác, tam giác

MNP

vuông tại

N

2 2 2 2

32MP MN NP R R R     

.

2

. .2 2

MAB

S R MP R R R



   

. Dấu “=” xảy ra khi

NP R

hay khi

MO AB





.

Vậy diện tích tam giác

MAB

đạt giá trị lớn nhất bằng

2

2R

.

Câu 6: Chọn D

Thể tích của bế cá:

3

72 24

3 72dm

3

V ab b

aa

    

, với

,0ab

.

Diện tích kính để làm bể cá như hình vẽ:

24 24

3.3 2.3 9 6. .S a b ab a a

aa

     

144 144

9 24 2 9 . 24aa

aa

    

96S

.

144

96 9 4 6S a a b

a

      

.

Vậy để bể cá tốn ít nguyên liệu nhất thì

4dma 

;

6dmb 

.

Câu 7: Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

328

Gọi

O

là tâm của hình bình hành

ABCD

, gọi

I MP AC

. Lấy điểm

N SB

,

NI SD Q

.

Do đáy

ABCD

là hình bình hành nên ta chứng minh được hệ thức sau:

SA SC S B SD

SM SP SQ SN

  

.

Đặt

SB

x

SQ



,

SD

y

SN



với

0; 0xy

. Theo bài ta được

2 3 5xy   

.

Theo bài, ta cần tìm giá trị nhỏ nhất của biểu thức

22

4T x y

với

0, 0xy

và

5xy

.

Áp dụng bất đẳng thức Bunhiacopxki, ta được:

 

22

2 2 2 2

11

5 1. .2 1 4

22

x y x y



   



    

   



   



suy ra

22

4 20xy

. Dấu bằng xảy ra khi và chỉ khi

2

44

1

51

2

5

y

x

x y x

x y y

xy

















  











.

Vậy giá trị nhỏ nhất của

T

là 20 đạt được khi

4x 

,

1y 

hay

4

SB

SN



.

Câu 8: Chọn B

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

329

Đặt

SC a

với

0a 

. Ta có:

()

SO ABCD

SC ABCD C











suy ra

SCO





.

Mặt khác:

.cos ; .sinOC a SO a





.

2 2 .cos ; 2.cos

2

AC

AC OC a AB a



   

;

2 2 2

2 .cos

ABCD

S AB a





.

3 2 3 2

.

1 2 2

. . .sin .cos .sin .(1 sin )

3 3 3

S ABCD ABCD

V SO S a a

   

   

Xét hàm

2

(1 )y t t

với

sin

01

t













Lập bảng biến thiên ta tìm được

3

t 

thì hàm số

y

đạt giá trị lớn nhất.

Câu 9: Chọn A

Gọi

O

là hình chiếu vuông góc của

S

lên mặt phẳng

()ABC

.

Vì

SA SB SC

nên

O

là tâm đường tròn ngoại tiếp tam giác

ABC

.

Tam giác

ABC

cân tại

A

. Gọi

A



là trung điểm của

BC

. Khi đó

AA



là đường trung trực của

tam giác

ABC

nên điểm

O

nằm trên đường thẳng

AA



.

Ta có:

2 2 2 2

AA AB BA a x



   

nên

2 2 2 2

11

.2

22

ABC

S BC AA x a x x a x



    

.

Lại có:

..

4

ABC

AB AC BC

S

R



22

2 2 2 2

. . .2

4

4 . 2

ABC

AB AC BC a x a

OA R

S

x a x a x

    



.

Trong tam giác vuông

SAO

, ta có:

4 2 2

2 2 2

2 2 2 2

34

2

4( ) ( )

a a a x

SO SA AO a

a x a x



    



.

Thể tích

22

2 2 2 2

.

22

1 1 3 4

. . .2 3 4

3 3 2 12

S ABC ABC

a a x a

V SO S x a x x a x

ax



    



.

Mặt khác:

2 2 2 2

22

4 3 4 3

2 3 4

22

x a x a

x a x



  

.

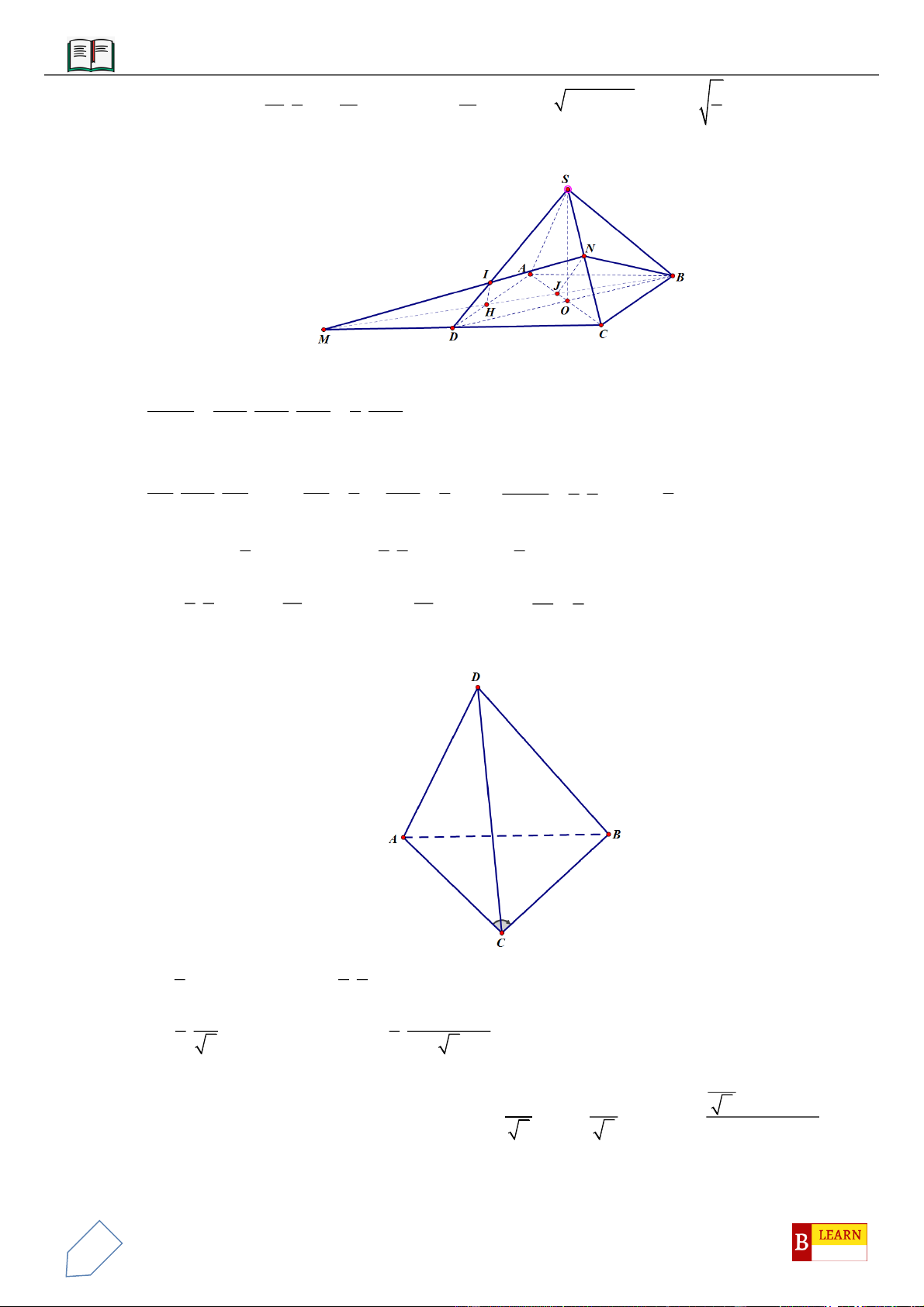
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

330

Do đó:

3

2

.

3

.

12 2 8

S ABC

aa

Va

. Vậy

3

8

max

a

V 

khi

22

3

2 3 4

8

x a x x a   

.

Câu 10: Chọn C

Áp dụng tỉ số thể tích cho khối chóp

.M CNB

ta có

1

. . .

4

MDIH

MCNB

V

MD MI MH MI

V MC MN MB MN



Định lý menelaus cho tam giác

MNC

với cát tuyến

DIS

ta có:

. . 1

SN CD MI

SC DM IN



12

23

IN MI

IM MN

   

. Vậy

12

.

43

MDIH

MCNB

V



2

5

6

MCNB

VV

Mà

 

;

1 1 1 1

. . . . .

3 3 2 2

MCNB MBC SABCD

N MBC

V d S SO DC BC V



  

21

5 1 5 7

.

6 2 12 12

SABCD SABCD SABCD

V V V V V   

. Vậy

1

2

7

5

V



.

Câu 11: Chọn B

 

1 1 1

. . , . . . .sin45 . ,

3 3 2

ABC

V S d D ABC CA CB d D ABC  

 

11

. . . ,

6

2

CA CB d D ABC

1 . .

.

6

2

CA CB AD



(1)

.

Áp dụng BĐT Cô-si cho 3 số dương

AD

,

BC

,

2

AC

, ta có

3

2

..

3

2

AC

BC AD

AC

BC AD













.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

331

Do đó,

3

11

2

.

6 3 6

AC

BC AD

V













(2)

.

Mặt khác ta có V =

1

6

, do đó để thõa mãn yêu cầu bài toán thì từ và, đẳng thức phải xảy ra, tức là

()

1

2

DA ABC

AC

BC AD







  





22

3

1 , 1, 2

CD AC DA

CD

BC AD AC







  



  





.

Câu 12: Chọn D

Ta có:

       

;0;0 , 0; ;0 , 0;0; , , 0A a B b C c a b c 

 

:1

y

xz

P

a b c

  

;

   

9 1 1

9;1;1 1MP

a b c

    

3

9 1 1 9 1 1

1 3 . . 243.

OABC

V abc

a b c a b c

      

Đẳng thức xảy ra khi

27, 3.a b c  

Câu 13: Chọn D

Do

 

MB FC

MB EFC FB EF

MB EC





   







. Xét các tam giác vuông:

, , .NAE BFE BAM  

Ta có

. . 2

NA AE

NAE BFE BAM AM AN AE BA

BA AM

       

.

   

2

1 1 2 3 2 3 2 6

. . . . . .

3 3 4 3 3

BCMN ABC

V S AM AN AM AN AM AN



     

Vậy

26

min

3

BCMN

V 

khi

2AM AN

hay

2.x 

Câu 14: Chọn C

E

A

C

M

N

B

F

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

332

Gọi

M

là trung điểm của

AB

. Khi đó

 

AB MCC







Góc giữa

 

ABC



và

 

ABC

là

CMC







. Đặt

,0AB x x

2

3

4

ABC

x

S

,

3

.tan tan

2

x

CC CM







23

.

3 3 3

. tan tan

4 2 8

ABC A B C

x x x

V



  

  

Ta lại có

cos 3 3 cos

ABC ABC

SS







2

3

3 3.cos 2 3cos

4

x



   

.

3

.24cos 3cos .tan 9 3.sin cos

8

ABC A B C

V

    

  

  

 

2

.

9 3. cos 1 c os

ABC A B C

V



  

  

Xét hàm số

 

23

( ) (1 ) , 0;1f t t t t t t    

. Ta có

2

( ) 1 3f t t







Hàm số đạt giá trị lớn nhất khi

1

3

t 

và

2

max ( )

33

ft

Khi đó

.

max 6

ABC A B C

V

  



1

cos tan 2

3



   

.

Câu 15: Chọn D

Đặt

AC BC x

,

22

SA a x

.

Ta có thể tích khối chóp

.S ABC

là

2 2 2 2 4 6

1 1 1 1

. . . .

3 3 2 6

ABC

V SA S a x x a x x



    

.

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

333

Xét hàm số

 

2 4 6

f x a x x

với

0 xa

.

 

2 3 5

0

4 6 0

6

3

x

f x a x x

a

x









   









.

Dựa vào bảng biến thiên, ta có thể tích khối chóp

.S ABC

đạt giá trị lớn nhất khi và chỉ khi

6

3

a

x 

. Khi đó

3

sin

3

a

SA

SC a



  

,

6

3

cos

3

a

AC

SC a



  

.

Vậy

3 6 2 2

sin2 2sin .cos 2. .

3 3 3

  

  

.

Câu 16: Chọn A

Cách 1:

Đặt

00

; 60 ; 60 .ABS ABC CBS

  

    

Ta có

3

2 2 2 2

.

. . 1 1

1 cos cos cos 2cos cos cos cos cos

6 6 2 2

B SAC

BA BC BS a

V

       

       

.B SAC

V

đạt GTLN khi

2

11

cos cos

22





đạt GTLN

1

cos

4





.

Với

1

cos

4





ta được

22

6

2 . .cos .

2

a

x BA BS BA BS



   

Cách 2:

A

S

C

B

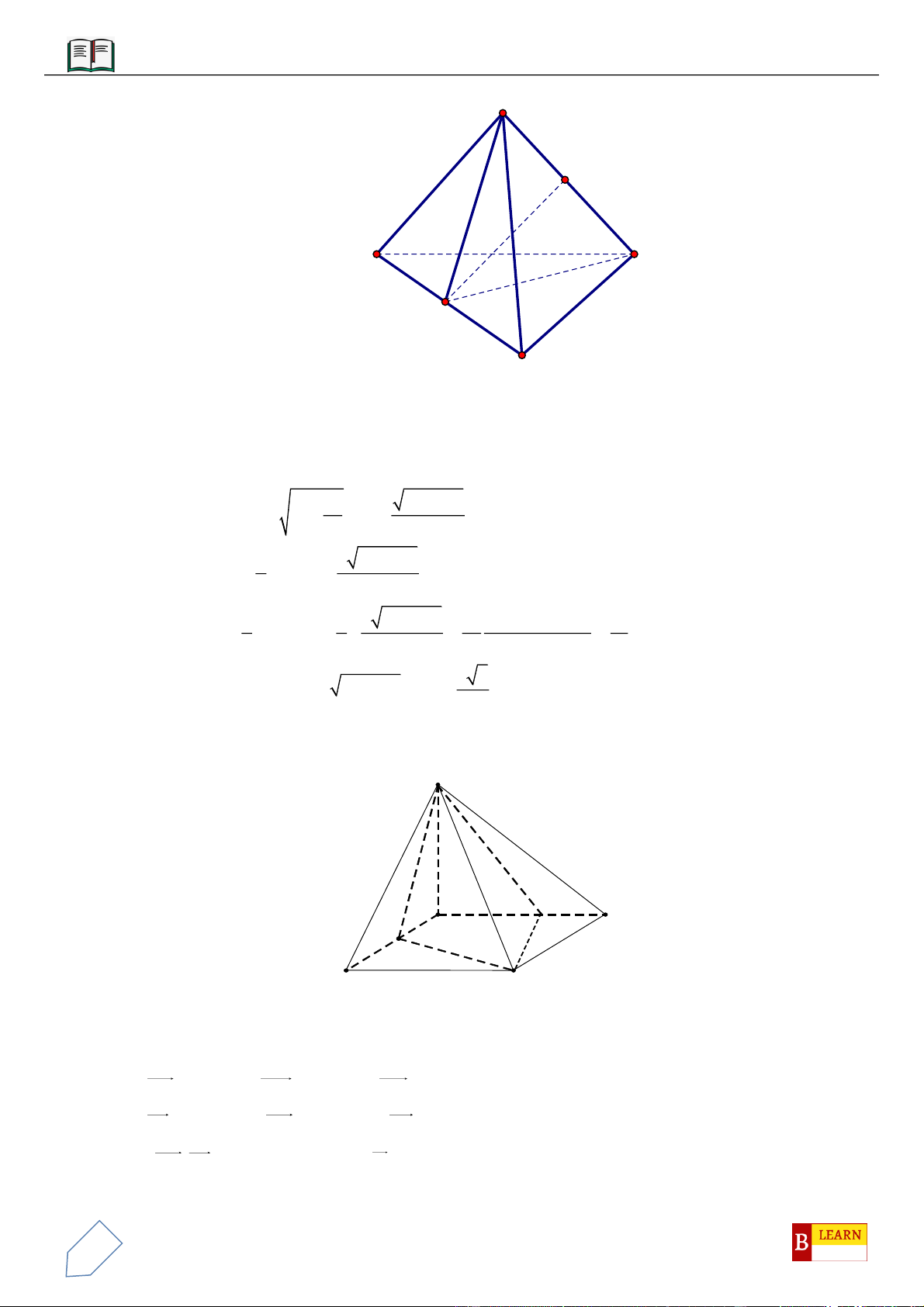
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

334

Gọi

,EF

lần lượt là trung điểm

SA

và

BC

.

Vì

BAS

và

CAS

lần lượt cân tại

B

và

C

nên

 

BE SA

SA BEC

CE SA











Ta có:

2 2 2

2

3

;

42

x a x

BE CE a EF



   

Suy ra

22

13

.

24

BEC

a a x

S BC EF







.

Vậy

 

2 2 2

2 2 3

3

1 1 3

..

3 3 4 12 2 8

SABC BEC

x a x

a a x a a

V SA S x







   

Dấu

""

xảy ra khi

22

6

3.

2

a

x a x x   

Câu 17: Chọn C

Chọn hệ trục tọa độ

Axyz

với:

 

0;0;0A

,

 

0;0; 2S

,

 

2;0;0B

,

 

2; 2;0C

,

 

0; 2;0D

¸

 

;0 ;0Ma

,

 

0; ;0Nb

 

, 0; 2ab  



 

2; 2;0AC 

,

 

;0;0AM a

,

 

0; ;0AN b

 

2; 2; 2SC 

,

 

;0; 2SM a

,

 

0; ; 2SN b

 

, 4; 2 4; 2SM SC a a









 

1

2; 2;n a a

là VTPT của mp

 

SCM

A

C

S

B

E

F

b

2

a

2

M

B

C

D

A

S

N

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

335

 

, 4 2 ; 4; 2SN SC b b



   





 

2

2 ; 2;n b b   

là VTPT của mp

 

SCN

       

1 2 1 2

. 0 2 2 2 2 0 8 2 2 0SCM SCN n n n n b a ab b a ab               

 

82

8 2 2 0

2

a

a b a b

a



      



Mà:

  

82

( 2;4]

0

82

2

0 2 1; 4

44

82

2

0 ; 2 1;

2

a

ba

a



















        











       

















Do đó:

1; 2a   



11

,,

22

AMCN AMC ACN

S S S AM AC AN AC



   

   

   

2

1 1 8 2 8

.2 .2

2 2 2 2

aa

a b a b a

aa



      



Xét hàm số

 

2

8

2

a

fa

a







trên

1; 2



 

2

48

'

2

aa

fa

a







;

 

2

2 2 3 1; 2

' 0 4 8 0

2 2 3

a

f a a a

a



     





     



  



Ta có:

 

13f 

khi

1, 2ab

;

 

23f 

khi

2, 1ab

 

2 3 4 4 3f     

khi

2 2 3, 2 2 3ab     

Khi đó:

 

0;2

2, 1

3

1, 2

a

ab

Max f a

ab



















.

1

..

3

S AMCN AMCN

V SA S

đạt giá trị lớn nhất 

AMCN

S

đạt giá trị lớn nhất

2, 1

1, 2

ab













2, 1ab

.

 

2;0;0 2AM AM  

,

 

0;1;0 1AN AN  

Vậy:

22

1 1 1 5

1

44

T

AN AM

    

.

1, 2ab

.

 

1;0;0 1AM AM  

,

 

0; 2;0 2AN AN  

Vậy:

22

1 1 1 5

1

44

T

AN AM

    

. Kết luận:

22

1 1 5

4

T

AN AM

  

.

Câu 18: Chọn C

CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

336

Gọi

,MN

lần lượt là trung điểm của

,AB CD

.

Tam giác

,ADB CAB

là hai tam giác cân cạnh đáy

AB

nên

DM AB

và

CM AB

. Suy ra

 

AB MCD

.

..

11

. . . .

33

ABCD B MCD A MCD MCD MCD

V V V BM S AM S   

.

3

MCD

x

S

.

Tam giác

 

..ABC ABD c c c  

nên

CM DM

MN CD

.

 

2 2 2 2 2

1 1 1

. . . .

2 2 2

MCD

S CD MN y MC CN y BC BM CN     

2

1

4

2 4 4

y

x

y  

 

22

1

16

4

y x y  

.

 

22

1

16 16 2 . . 16 2

12 12 12

ABCD

xy xy

V x y xy xy xy xy      

 

3

16 2

1 1 16

12 3 12 3

xy xy xy



  









.

Dấu bằng xảy ra khi

16

16 2

3

xy

xy xy

xy

























.

Vậy thể tích

ABCD

đạt giá trị lớn nhất khi

16

3

xy 

.

Câu 19: Chọn B

Cách 1: Chọn hệ trục tọa độ sao cho , , , .

Suy ra . Đặt , , , suy ra , .

, , .

, .

Do nên .

, do nên .

.

Oxyz

 

0;0;0A

 

2;0;0B

 

0;2;0D

 

0;0;2S

 

2;2;0C

AM x

AN y

 

, 0;2xy

;xy

 

;0;0Mx

 

0; ;0Ny

 

;0; 2SM x

 

2;2; 2SC 

 

0; ; 2SN y

 

1

, 4;2 4;2n SM SC x x



   



 

2

, 4 2 ; 4; 2n SN SC y y



    



   

SMC SNC

   

12

. 0 4 4 4 4 2 4 4 0n n y x xy      

 

28xy x y   

82

2

x

y

x







2y 

82

21

2

x



  



   

4 2 2

AMCN ABCD BMC DNC

S S S S x y x y         

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

337

Do đó .

Xét với , .

; .

Lập BBT ta suy ra .

Vậy .

Cách 2: Đặt , , .

Gọi ; ; .

là hình chiếu vuông góc của trên , khi đó: .

Ta có: .

Do đó góc giữa và bằng góc giữa và . Suy ra .

Mặt khác .

Tính , :

Ta có: , và nếu , thì gọi là trung điểm của , khi đó:

.

Tương tự: . Mà .

Nếu hoặc thì ta cũng có .

Tóm lại: .

Suy ra: .

Khảo sát hàm số ta được:

.

Cách 3. Đặt

Dựng .

 

.

12

.

33

S AMCD AMCN

V SA S x y  

2 8 2

32

x













2

28

32

x







 

2

28

32

x

fx

x







 

1;2x 

 

2

2 4 8

3

2

xx

fx

x









 

2

0 4 8 0f x x x



    

2 2 3x   

2 2 3x   

 

     

1;2

max 1 2 2f x f f  

.

1

2

max 2

2

1

S AMCN

x

y

V

x

y



































2

()

1

x

do x y

y













22

16 1

AM AN



22

16 1

5

xy

  

AM x

AN y

 

, 0;2xy

xy

O AC DB

E BD CM

F BD CN

H

O

SC

2

3

HO 

 

SC OH SC HE

SC HBD

SC BD SC HF





  







 

SCM

 

SCN

HE

HF

HE HF

 

.

12

.

33

S AMCN AMCN

V SA S x y  

OE

OF

0x 

0y 

2x 

2y 

K

AM

2

4 2 4 2 4 4

OE KM x OE EB OB x

OE

EB MB x x x x x

      

   

2

4

y

OF

y





  

2

. 2 2 12OE OF OH x y    

2x 

2y 

  

2

. 2 2 12OE OF OH x y    

  

2 2 12xy  

       

.

1 2 2 2 12

. 2 2 4 2 4

3 3 3 3 2

S AMCN AMCN

V SAS x y x y x

x



           











.

1

2

max 2

2

1

S AMCN

x

y

V

x

y



































2

()

1

x

do x y

y













22

16 1

AM AN



22

16 1

5

xy

  

, (0 2)AM m AN n n m    

, ( , )AP CM AQ CN P CM Q CN   

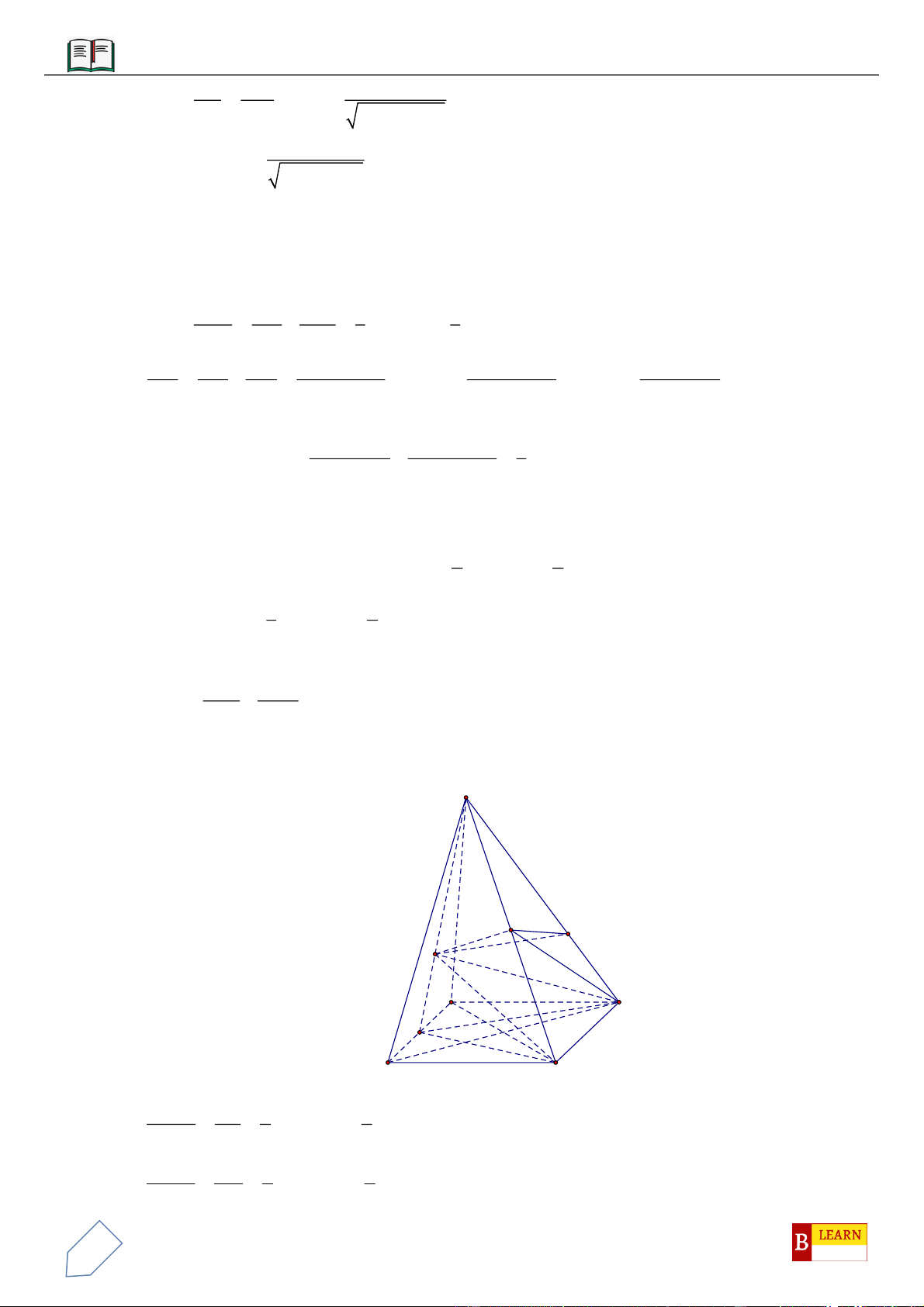
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

338

Ta có .

Tương tự .

Trong mặt phẳng dựng . Mặt phẳng cắt

tại .

Dựa vào điều kiện bài toán dễ dàng chứng minh được tứ giác là hình chữ nhật và

.

Ta có .

và .

Do hình chữ nhật nên

Do nên .

Do .

Ta có: .

Suy ra .

Dấu bằng xảy ra khi và chỉ khi .

Khi đó .

Câu 20: Chọn B

.

21

33

S GMN

GMND S GMD

S GMD

V

SN

VV

V SD

   

.

..

.

11

22

S GMD

S GMD S GCD

S GCD

V

SM

VV

V SC

   

2

4 (2 )

AP AM m

AP

BC CM

m

  



2

4 (2 )

n

AQ

n





()SAP

( ), (V )AL SP L SP AV SQ SQ   

()ALV

SC

H

ALHV

AH SC

2 2 2

1 1 1 3

8AH SA AC

  

2

8

3

AH

2

2 2 2 2

1 1 1 2 4

2

mm

AL SA SP m



  

2

24

m

AL

mm





2

24

n

AV

nn





22

2 2 2

22

2 2 8

( 4)( 2( ) 8) 0

2 4 2 4 3

nm

AV AL AH mn m n mn m n

n n m m

            

   

4 2 2 0mn m n mm m n        

2( ) 8mn m n  

0 2 ( 2)( 2) 0 2( ) 4 0 12 4( ) 0 3n m m n mn m n m n m n                  

D

11

4 .2.(2 ) .2.(2 )

22

ANCM ABC BMC DNC

S S S S m n m n         

12

. ( ) 2

33

SAMCN AMCN

V SAS m n   

2, 1mn

22

1 16

5

AN AM



G

E

N

M

D

B

C

A

S

CHUYÊN ĐỀ: KHỐI ĐA DIỆN - HÌNH HỌC KHÔNG GIAN.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

339

.

2

3

S GCD

S ECD

V

SG

V SE



.

Suy ra

. . . . .

1 1 1 2 1 1 1 1

. . . .

3 3 2 3 9 9 2 18

GMND S GMD S ECD S ECD S ABCD S ABCD

V V V V V V    

.

Suy ra

.

1

18

S GMND

S ABCD

V



. Do đó

1; 18 19m n m n    

.

Câu 21: Chọn D

Trong tam giác

ABC

có

2 2 2 o

2 . .cos135AC AB BC AB BC  

22

. 2 4 0BC BC a a   

2BC a

.

Gọi

K

là hình chiếu của

A

lên

BC

ta có

o

135ABC 

nên

o

45ABK 

. Suy ra tam giác

AKB

vuông cân tại

K

. Do đó

2

AB a

AK BK  

.

Gọi

,IH

lần lượt là hình chiếu của

A

lên

BD

và

 

ABCD

, ta có

KBIH

là hình chữ nhật.

Khi đó

   

 

o

; 30ABD BCD AIH

. Suy ra

o

6

.tan30

6

a

AH HI

.

Từ đó ta tính được

22

3

a

BI KH AK AH   

.

Tam giác

ABD

vuông tại

A

, đường cao

AI

nên

2

.AB BI BD

2

3

AB

BD a

BI

  

.

Vậy thể tích khối chóp

ABCD

là

3

1

..

66

a

V AH BD BC

Câu 22: Chọn B

Vì con kiến bò theo mặt của hình hộp từ

A

đến

B

nên khi ta vẽ hình khai triển của hình hộp chữ

nhật và trải phẳng như hình vẽ thì xem như con kiến bò trên một mặt phẳng.

K

I

H

135

°

a

5

a

A

B

D

C

9

6

4

N

R

A

T

M

B1

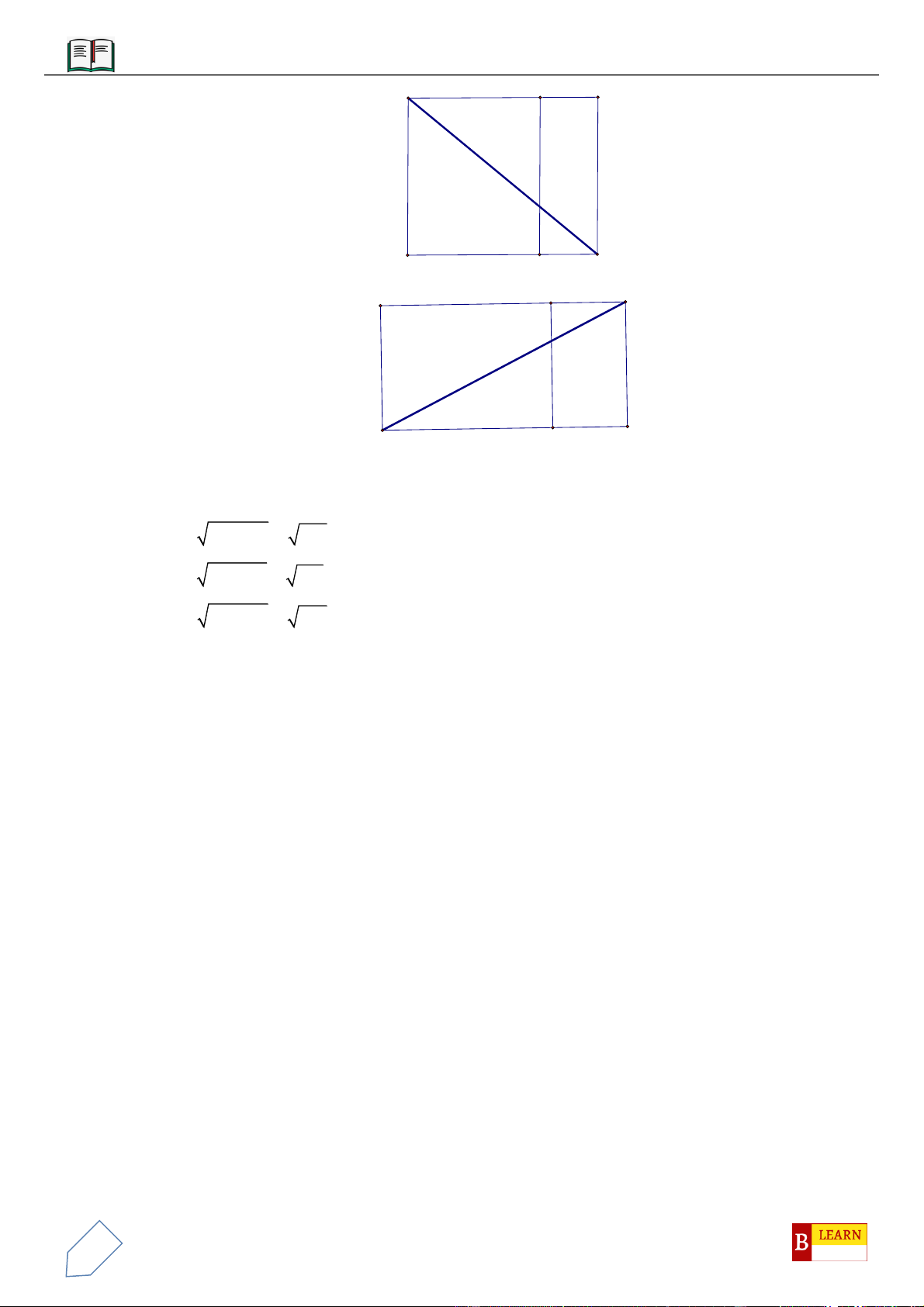
CHUYÊN ĐỀ: KHỐI ĐA DIỆN – HÌNH HỌC KHÔNG GIAN.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

340

Khi đó

B

sẽ được tách thành 3 vị trí là

1

B

;

2

B

và

3

B

. Quãng đường ngắn nhất sẽ là một trong ba

đoạn thẳng

1

AB

;

2

AB

hay

3

AB

. Ta có:

22

1

15 4 241AB   

.

22

2

9 10 181 13,45AB    

.

22

3

6 13 205AB   

.

Do đó quãng đường ngắn nhất là

 

2

13,45 13;14AB 

.

6

9

4

S

R

A

T

P

B2

6

9

4

B3

M

P

A

N

R

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

341

CHỦ ĐỀ : KHỐI NÓN, KHỐI TRỤ

 MẶT NÓN TRÒN XOAY VÀ KHỐI NÓN

1. Mặt nón tròn xoay

 Đường thẳng

,d 

cắt nhau tại

O

và tạo thành góc



với

00

0 90





. Mặt phẳng

 

P

chứa

,d 

và

 

P

quay quanh trục



với góc



không đổi thì tạo thành mặt nón tròn xoay đỉnh

O

.

Trong đó:





gọi là trục



d

được gọi là đường sinh

 Góc

2



được gọi là góc ở đỉnh

2. Khối nón

 Khối nón là phần không gian được giới hạn bởi một hình nón tròn xoay, kể cả hình nón đó.

 Đỉnh, mặt đáy, đường sinh của một hình nón cũng là đỉnh, mặt đáy, đường sinh của khối nón tương

ứng.

 Cho hình nón có chiều cao

h

, đường sinh

l

và bán kính đáy

r

. Khi đó, ta có các công thức sau:

 Diện tích xung quanh của hình nón:

..

xq

S r l





 Diện tích đáy của hình nón:

2

.

day

Sr





 Diện tích toàn phần của hình nón:

2

. . .

tp xq day

S S S r l r



   

 Thể tích của khối nón:

2

1

..

3

non

V r h





LÍ THUYẾT

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

342

 MẶT TRỤ TRÒN XOAY

1. Mặt trụ

 Trong mặt phẳng

 

P

cho hai đường thẳng



và

l

song song với nhau, cách nhau một khoảng

r

Khi quay mặt phẳng

 

P

xung quanh đường thẳng



thì đường thẳng

l

sinh ra một mặt tròn xoay

được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ. Trong đó:

 Đường thẳng



gọi là trục

 Đường thẳng

l

gọi là đường sinh



r

là bán kính của mặt trụ đó

2. Hình trụ tròn xoay và khối trụ tròn xoay

 Khối trụ tròn xoay hay khối trụ là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả

hình trụ tròn xoay đó.

 Mặt đáy, đường sinh, chiều cao, bán kính của một hình trụ cũng là mặt đáy, đuowngf sinh, chiều

cao, bán kính của khối trụ tương ứng.

 Cho hình trụ có chiều cao

h

, đường sinh

l

, bán kính đáy

r

. Khi đó ta có các công thức sau:

 Diện tích xung quanh:

2 . .

xq

S r l





 Diện tích toàn phần:

2

2 . . 2 .

tp

S r l r





 Thể tích của khối trụ:

2

..V r h





CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

343

 MẶT CẦU VÀ KHỐI CẦU

1. Mặt cầu

 Cho một điểm

I

cố định và một số thực dương

R

. Tập hợp tất cả các điểm

M

trong không gian

cách

I

một khoảng

R

được gọi là mặt cầu tâm

I

, bán kính

R

. Được kí hiệu là:

 

;S I R

.

 Khi đó

   

;/S I R M IM R

.

2. Công thức tính diện tích mặt cầu và thể tích khối cầu

 Cho mặt cầu

 

S

có tâm

I

, bán kính

R

. Khi đó, ta có các công thức như sau:

 Diện tích mặt cầu:

2

4.SR





 Thể tích của khối cầu:

3

4

.

3

VR





.

3. Một số công thức tính đặc biệt về khối tròn xoay

 Hình nêm loại 1

Thể tích :

3

2

. .tan

3

VR





 Hình nêm loại 2

Thể tích:

3

2

. .tan

23

VR













CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

344

Lời giải

Chọn C

.

Theo đề suy ra đường sinh

la

, và đường tròn đáy có bán kính

2

a

r 

. Khi đó

2

xq

a

S





, diện tích đáy

2

a

S





. Vậy

 

2

21

2

tp

a

S







.

Lời giải

Chọn A

.

VÍ DỤ MINH HỌA

VÍ DỤ 1: Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng

a

.

Tính diện tích

tp

S

toàn phần của hình nón đó:

A.

 

2

28

2

tp

a

S







. B.

2

tp

a

S





.

C.

 

2

21

2

tp

a

S







. D.

 

2

24

2

tp

a

S







.

VÍ DỤ 2: Một hình nón đỉnh

S

, đáy hình tròn tâm

O

và

SO h

. Một mặt phẳng

 

P

qua đỉnh

S

cắt

đường tròn

 

O

theo dây cung

AB

sao cho góc

90AOB 

, biết khoảng cách từ

O

đến

 

P

bằng

2

h

. Khi

đó diện tích xung quanh hình nón bằng.

A.

2

10

3

h



. B.

2

10

33

h



. C.

2

2 10

3

h



. D.

2

10

6

h



.

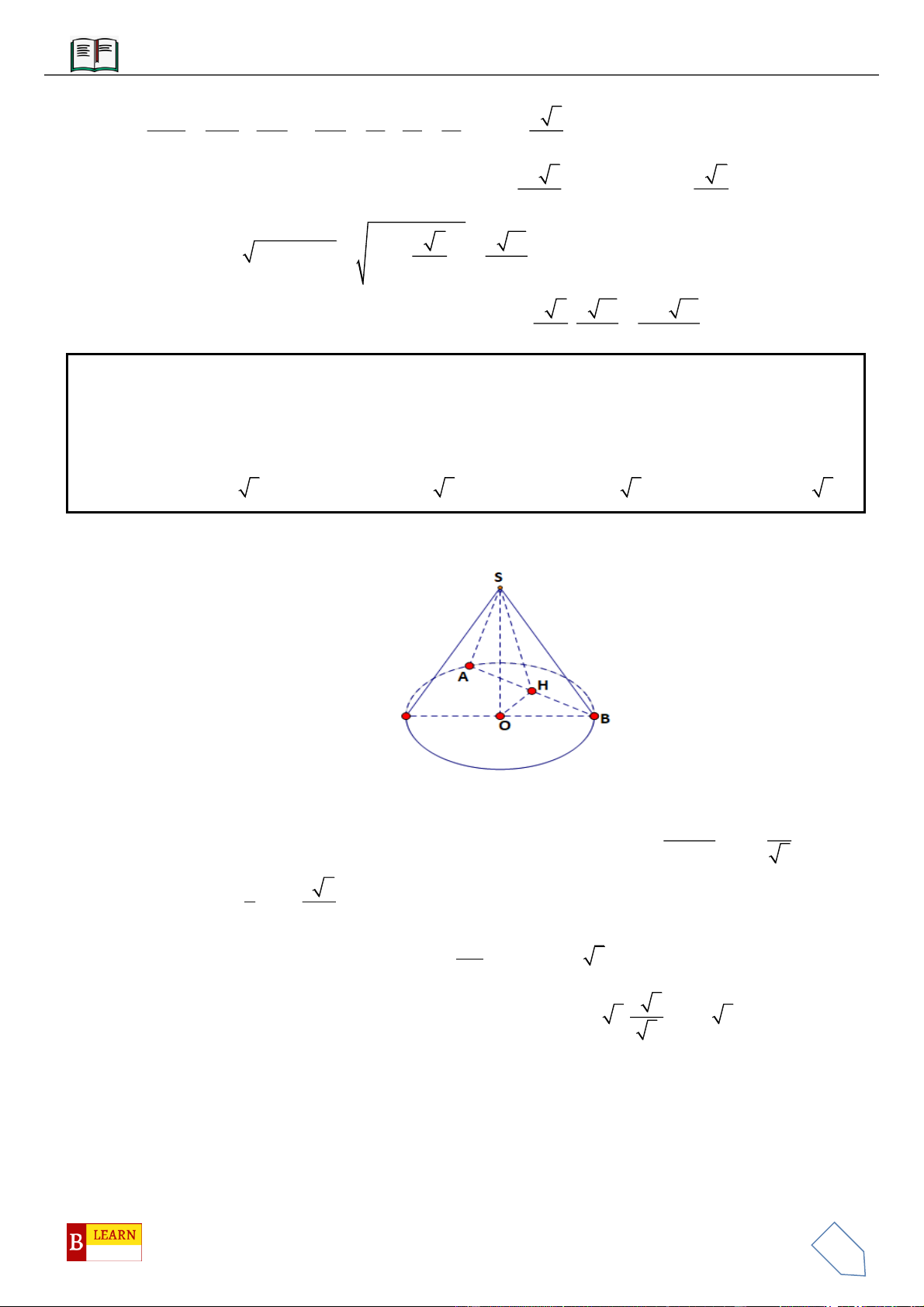
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

345

Gọi

I

là trung điểm của

AB

.

2 2 2 2 2 2 2

1 1 1 1 4 1 3

OH SO OI OI h h h

     

3

h

OI

.

Tam giác

OAB

vuông cân tại

O

nên:

23

2

3

h

AB OI

,

6

3

h

R OA OB  

.

Suy ra:

2

2 2 2

6 15

33

hh

SB SO OB h



    





.

Diện tích xung quanh của hình nón:

2

6 15 10

. . .

3 3 3

xq

h h h

S R SB





  

.

Hướng dẫn giải

Chọn B

Theo bài ra ta có tam giác

SAB

vuông tại

S

và

3OH 

; và

60BSO 

.

Gọi

r

là bán kính đường tròn đáy của hình nón thì đường sinh

2

sin60

3

rr

l SB l   



.

Suy ra

16

23

r

BH AB

.

Xét tam giác

OBH

vuông tại

H

, ta có

2

6

9 3 3

9

r

rr   

.

Diện tích xung quanh

xq

S

của hình nón

 

N

là

63

. . .3 3. 18 3

3

xq

S r l

  

  

.

VÍ DỤ 2: Hình nón

 

N

có đỉnh

S

, tâm đường tròn đáy là

O

, góc ở đỉnh bằng

120

. Một mặt phẳng qua

S

cắt hình nón

 

N

theo thiết diện là tam giác vuông

SAB

. Biết rằng khoảng cách giữa hai đường thẳng

AB

và

SO

bằng

3

. Tính diện tích xung quanh

xq

S

của hình nón

 

N

A.

27 3

xq

S





. B.

18 3

xq

S





. C.

93

xq

S





. D.

36 3

xq

S





.

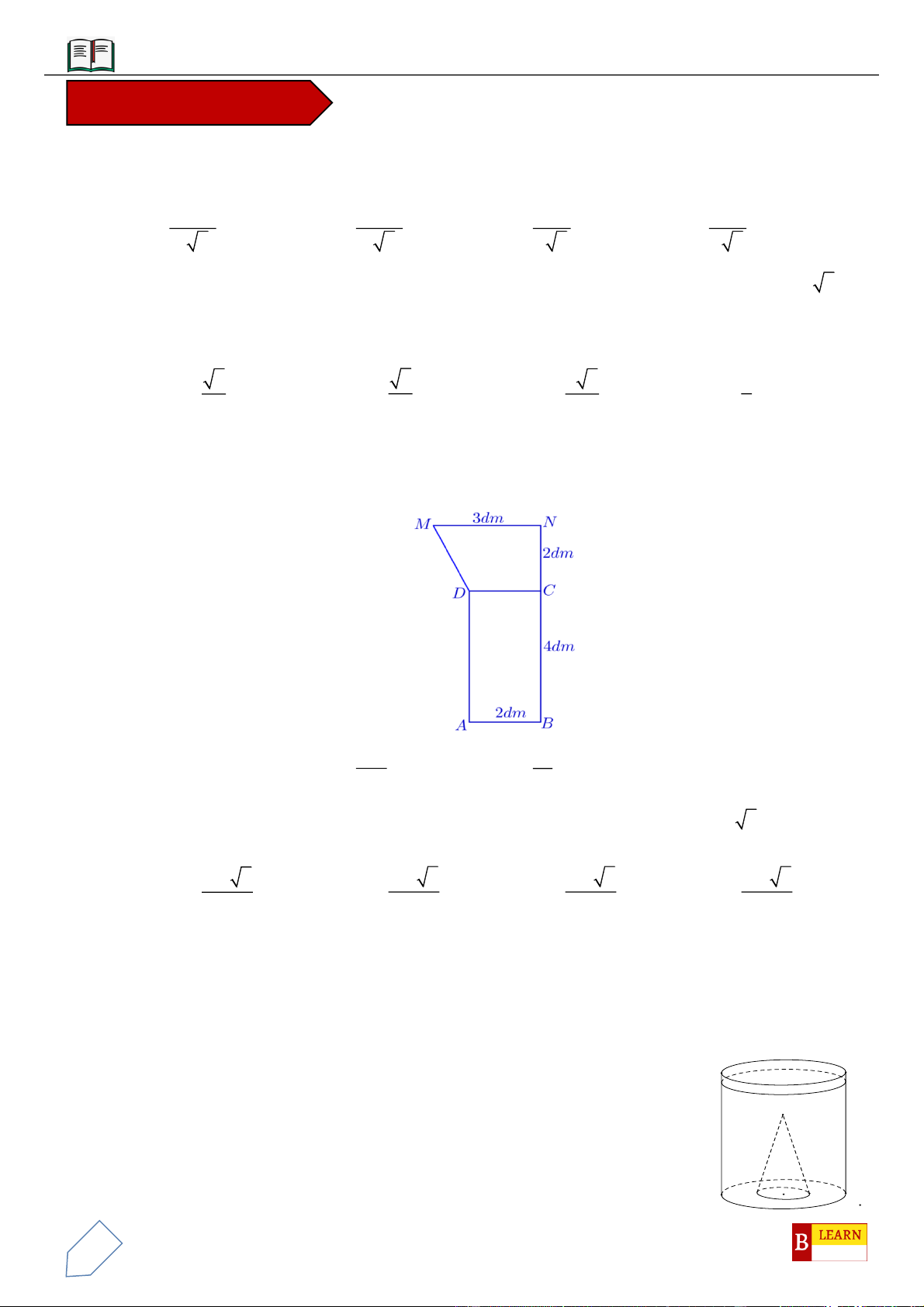
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

346

DẠNG 1: CÁC YẾU TỐ LIÊN QUAN ĐẾN KHỐI NÓN, KHỐI TRỤ

Câu 1: Một hình nón tròn xoay có đường sinh

2a

. Thể tích lớn nhất của khối nón đó là

A.



3

16

33

a

. B.



3

16

93

a

. C.



3

4

33

a

. D.



3

8

33

a

.

Câu 2: Cho đường tròn

 

C

có tâm

, I

bán kính

 .Ra

Gọi

M

là điểm nằm ngoài

 

C

và

 3;IM a

A

là điểm thuộc

 

C

và

MA

tiếp xúc với

 

C

;

H

là hình chiếu của

A

trên đường thẳng

.IM

Tính

theo

a

thể tích

V

của khối tròn xoay tạo bởi hình tam giác

MAH

quay xung quanh trục

.IM

A.





3

.

12

Va

B.





3

.

8

Va

C.





3

43

.

27

Va

D.





3

9

.

8

Va

Câu 3: Hình bên bao gồm hình chữ nhật

ABCD

và hình thang vuông

CDMN

. Các điểm

B

,

C

,

N

thẳng

hàng,

2dmAB CN

;

 4dm;BC

 3dmMN

. Quay hình bên xung quanh cạnh

BN

ta được

khối tròn xoay có thể tích bằng

A.



3

54 dm

. B.



3

86

dm

3

. C.

3

86

dm

3

. D.

3

54dm

.

Câu 4: Biết thiết diện qua trục của một hình nón là tam giác đều có diện tích bằng

2

3a

. Tính thể tích

của khối nón đã cho.

A.





3

2

a

V

. B.





3

6

a

V

. C.





3

6

a

V

. D.





3

a

V

.

Câu 5: Cho hình trụ

 

T

có chiều cao

 2,hm

bán kính đáy

 3.rm

Giả sử

 

L

là hình lăng trụ đều

n

cạnh

có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình trụ

 

T

. Khi n tăng lên vô hạn thì tổng diện

tích tất cả các mặt của của khối lăng trụ

 

L

có giới hạn là:

A.

 12S

. B.



 20S

. C.



30

. D.



12

.

Câu 6: Một khối nón làm bằng chất liệu không thấm nước, có khối lượng riêng lớn

hơ khối lượng riêng của nước, có đường kính đáy bằng

a

và chiều cao

12

, được đặt trong và trên đáy của một cái cốc hình trụ bán kính đáy

a

như

hình vẽ, sao cho đáy của khối nón tiếp xúc với đáy của cốc hình trụ. Đổ

nước vào cốc hình trụ đến khi mực nước đạt đến độ cao

12

thì lấy khối nón

ra. Hãy tính độ cao của nước trong cốc sau khi đã lấy khối nón ra.

BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

347

A.

11,37

. B.

11

. C.

63

. D.



37

2

.

Câu 7: Một hình trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ bằng



16

. Thể tích

V

của khối trụ bằng

A.



 32V

. B.



 64V

. C.



 8V

. D.



 16V

.

Câu 8: Cho hình nón tròn xoay có độ dài đường sinh là

2a

, góc ở đỉnh của hình nón bằng

60

. Thể tích

V

của khối nón đã cho là

A.





3

a

V

. B.





3

3Va

. C.





3

Va

. D.





3

a

V

.

Câu 9: Cho hình vuông

ABCD

cạnh

.a

Gọi

N

là điểm thuộc cạnh

AD

sao cho

 2.AN ND

Đường

thẳng qua

N

vuông góc với

BN

cắt

BC

tại

.K

Tính thể tích

V

của khối tròn xoay tạo thành khi

quay tứ giác

ANKB

quanh trục

BK

là

A.





3

7

6

Va

. B.





3

9

14

Va

. C.





3

6

7

Va

. D.





3

14

9

Va

.

Câu 10: Cho khối trụ có đáy là các đường tròn tâm

 

O

,

 



O

có bán kính là R và chiều cao

 2hR

. Gọi

A

,

B

lần lượt là các điểm thuộc

 

O

và

 



O

sao cho

OA

vuông góc với



.OB

Tỉ số thể tích của

khối tứ diện



OO AB

với thể tích khối trụ là:

A.



2

3

. B.



1

3

. C.



1

6

. D.



1

4

.

Câu 11: Người ta cần đổ một ống cống thoát nước hình trụ với chiều cao

2m

, độ dày thành ống là

10cm

.

Đường kính ống là

50cm

. Tính lượng bê tông cần dùng để làm ra ống thoát nước đó?

A.



3

0,08 ( )m

. B.



3

0,18 ( )m

. C.



3

0,5 ( )m

. D.



3

0,045 ( )m

.

Câu 12: Cho hình chữ nhật

ABCD

có

 2AB

,

 23AD

và nằm trong mặt phẳng

 

P

. Quay

 

P

một

vòng quanh đường thẳng

BD

. Khối tròn xoay được tạo thành có thể tích bằng

A.



28

9

. B.



28

3

. C.



56

9

. D.



56

3

.

Câu 13: Cho mặt cầu

 

S

có bán kính

3

. Trong tất cả các khối trụ nội tiếp mặt cầu

 

S

, khối trụ có thể

tích lớn nhất bằng bao nhiêu?

A.



33

2

. B.



4

. C.



3

. D.



43

3

.

Câu 14: Cho hình thang

ABCD

có

  90AB

,

AB BC a

,

 2AD a

. Tính thể tích khối tròn xoay

sinh ra khi quay hình thang

ABCD

xung quanh trục

CD

.

A.



3

72

6

a

. B.



3

72

12

a

. C.



3

7

6

a

. D.



3

7

12

a

.

Câu 15: Cho hình thang

ABCD

vuông tại

A

và

D

có

  2 2 4CD AB AD

. Thể tích của khối tròn xoay

sinh ra bởi hình thang

ABCD

khi quay xung quanh đường thẳng

BC

bằng

A.



28 2

3

. B.



20 2

3

. C.



32 2

3

. D.



10 2

3

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

348

Câu 16: Một khối trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của một hình lập phương cạnh

a

. Tính thể tích

V

của khối trụ đã cho.

A.





3

1

3

Va

. B.





3

1

4

Va

. C.





3

Va

. D.





3

1

2

Va

.

Câu 17: Một khối trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của một hình lập phương cạnh

a

. Tính thể tích

V

của khối trụ đã cho.

A.





3

1

3

Va

. B.





3

1

4

Va

. C.





3

Va

. D.





3

1

2

Va

.

Câu 18: Cho tứ diện

ABCD

có

DA

vuông góc với

 

mp ABC

,

   ,DB BC AD AB BC a

. Kí hiệu

1 2 3

,,V V V

lần lượt là thể tích của hình tròn xoay sinh bởi tam giác

ABD

khi quay quanh

AD

,

tam giác

ABC

khi quay quanh

AB

, tam giác

DBC

khi quay quanh

BC

. Trong các mệnh đề sau,

mệnh đề nào đúng?

A.



1 2 3

V V V

. B.



1 3 2

V V V

. C.



2 3 1

V V V

. D.



1 2 3

V V V

.

Câu 19: Một đội xây dựng cần hoàn thiện một hệ thống cột trụ tròn của một cửa hàng kinh doanh gồm 10

chiếc. Trước khi hoàn thiện mỗi chiếc cột là một khối bê tông cốt thép hình lăng trụ lục giác đều

có cạnh 20

cm

, sau khi hoàn thiện mỗi cột là một khối trụ có đường kính đáy bằng 42

cm

. Chiều

cao của mỗi cột trước và sau khi hoàn thiện là 4

m

. Biết lượng xi măng cần dùng chiếm 80%

lượng vữa và cứ một bao xi măng 50

kg

thì tương đương với

3

64000cm

xi măng. Hỏi cần ít nhất

bao nhiêu bao xi măng loại 50

kg

để hoàn thiện toàn bộ hệ thống cột đã cho?

A.

25

. B.

18

. C.

28

. D.

22

.

Câu 20: Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao

 1,5mh

gồm:

Phần dưới có dạng hình trụ bán kính đáy

 1mR

và có chiều cao bằng

1

;

3

h

Phần trên có dạng hình nón bán kính đáy bằng

R

đã bị cắt bỏ bớt một phần hình nón có bán kính

đáy bằng

1

2

R

ở phía trên ;

Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng

1

4

R

.

Thể tích của khối bê tông bằng

A.

3

2,815m

. B.

3

2,814 m

. C.

3

3,403m

. D.

3

3,109 m

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

349

Câu 21: Cho khối trụ

 

T

,

AB

và

CD

lần lượt là hai đường kính trên các mặt đáy của khối

 

T

. Biết góc

giữa

AB

và

CD

là

30

,

 6AB cm

và thể tích khối

ABCD

là

3

30cm

. Khi đó thể tích khối trụ

 

T

là

A.



3

90 cm

. B.



3

30 cm

. C.



3

45 cm

. D.



3

90 3

270

cm

.

Câu 22: Cho hình nón đỉnh

S

có đáy là đường tròn tâm

O

bán kính

R

. Trên đường tròn

 

O

lấy hai điểm

,AB

sao cho tam giác

OAB

vuông. Biết diện tích tam giác

SAB

bằng

2

2R

. Thể tích hình nón

đã cho bằng

A.



3

14

12

R

. B.



3

14

2

R

. C.



3

14

6

R

. D.



3

14

3

R

.

Câu 23: Một khối đá có hình là một khối cầu có bán kính

R

, người thợ thủ công mỹ nghệ cần cắt và gọt

viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của

viên đá cảnh sau khi đã hoàn thiện?

A.



3

43

9

R

. B.



3

43

3

R

. C.



3

43

6

R

. D.



3

33

12

R

.

Câu 24: Một hình thang cân có chiều cao

h

và độ dài hai đáy là

a

,

b

. Tính thể tích vật thể tròn xoay thu

được khi quay hình thang này quanh đường trung trực của hai đáy.

A.

 





22

1

3

h a ab b

. B.

 





22

1

6

h a ab b

.

C.

 





22

1

12

h a ab b

. D. Cả A, B, C đều sai.

Câu 25: Cho hình chóp

.S ABCD

có

SA

vuông góc với mặt phẳng

 

ABCD

, tứ giác

ABCD

là hình thang

vuông với cạnh đáy

, AD BC

.

33AD CB a

,

AB a

,

 3SA a

. Điểm

I

thỏa mãn

 3AD AI

,

M

là trung điểm

SD

,

H

là giao điểm của

AM

và

SI

. Gọi

, EF

lần lượt là hình

chiếu của

A

lên

, SB SC

. Tính thể tích

V

của khối nón có đáy là đường tròn ngoại tiếp tam giác

EFH

và đỉnh thuộc mặt phẳng

 

ABCD

.

A.





3

55

a

V

. B.





3

25

a

V

. C.





3

5

a

V

. D.





3

10 5

a

V

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

350

Câu 26: Cho hình trụ có hai đáy là hai hình tròn

 

;OR

và

 



;OR

.

AB

là một dây cung của đường tròn

 

;OR

sao cho tam giác



O AB

là tam giác đều và mặt phẳng

 



O AB

tạo với mặt phẳng chứa

đường tròn

 

;OR

một góc

60

. Tính theo

R

thể tích

V

của khối trụ đã cho.

A.





3

7

R

V

. B.





3

35

5

R

V

. C.





3

5

R

V

. D.





3

37

7

R

V

.

Câu 27: Có một miếng bìa hình chữ nhật

ABCD

với

 3AB

và

 6AD

. Trên cạnh

AD

lấy điểm

E

sao

cho

 2AE

, trên cạnh

BC

lấy điểm

F

là trung điểm

BC

.

Cuốn miếng bìa lại sao cho cạnh

AB

và

DC

trùng nhau để tạo thành mặt xung quanh của một

hình trụ. Khi đó tính thể tích

V

của tứ diện

ABEF

.

A.



π

3

V

. B.



2

93

2π

V

. C.



3

3π

2

V

. D.



2

3π

V

.

Câu 28: Cho hình chóp tứ giác đều

.S ABCD

có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình

nón có đáy là đường tròn ngoại tiếp tứ giác

ABCD

và chiều cao bằng chiều cao của hình chóp.

A.





9

2

xq

S

. B.





92

4

xq

S

. C.



 9

xq

S

. D.





92

2

xq

S

.

Câu 29: Một hình nón có chiều cao

2a

, bán kính đáy

2a

. Một phẳng phẳng đi qua đỉnh và tạo với mặt

đáy góc

60

. Tính diện tích thiết diện.

A.

2

52

3

a

. B.

2

43

3

a

. C.

2

53

3

a

. D.

2

42

3

a

.

Câu 30: Cho hình trụ có tâm hai đáy lần lượt là

O

và

'O

; bán kính đáy hình trụ bằng

a

. Trên hai đường

tròn

 

O

và

 

'O

lần lượt lấy hai điểm

A

và

B

sao cho

AB

tạo với trục của hình trụ một góc



30

và có khoảng cách tới trục của hình trụ bằng

3

2

a

. Tính diện tích toàn phần của hình trụ đã

cho

A.

 





2

2 3 1a

. B.

 





2

32

3

a

. C.

 





2

32a

. D.

 





2

33

3

a

.

Câu 31: Cho hình nón đỉnh

I

, đường cao

SO

và có độ dài đường sinh bằng

3cm

, góc ở đỉnh bằng

0

60

.

Gọi

K

là điểm thuộc đoạn

SO

thỏa mãn



3

2

IO IK

, cắt hình nón bằng mặt phẳng

()P

qua

K

và

vuông góc với

IO

, khi đó thiết diện tạo thành có diện tích là

S

. Tính

S

.

F

A

B

C

D

E

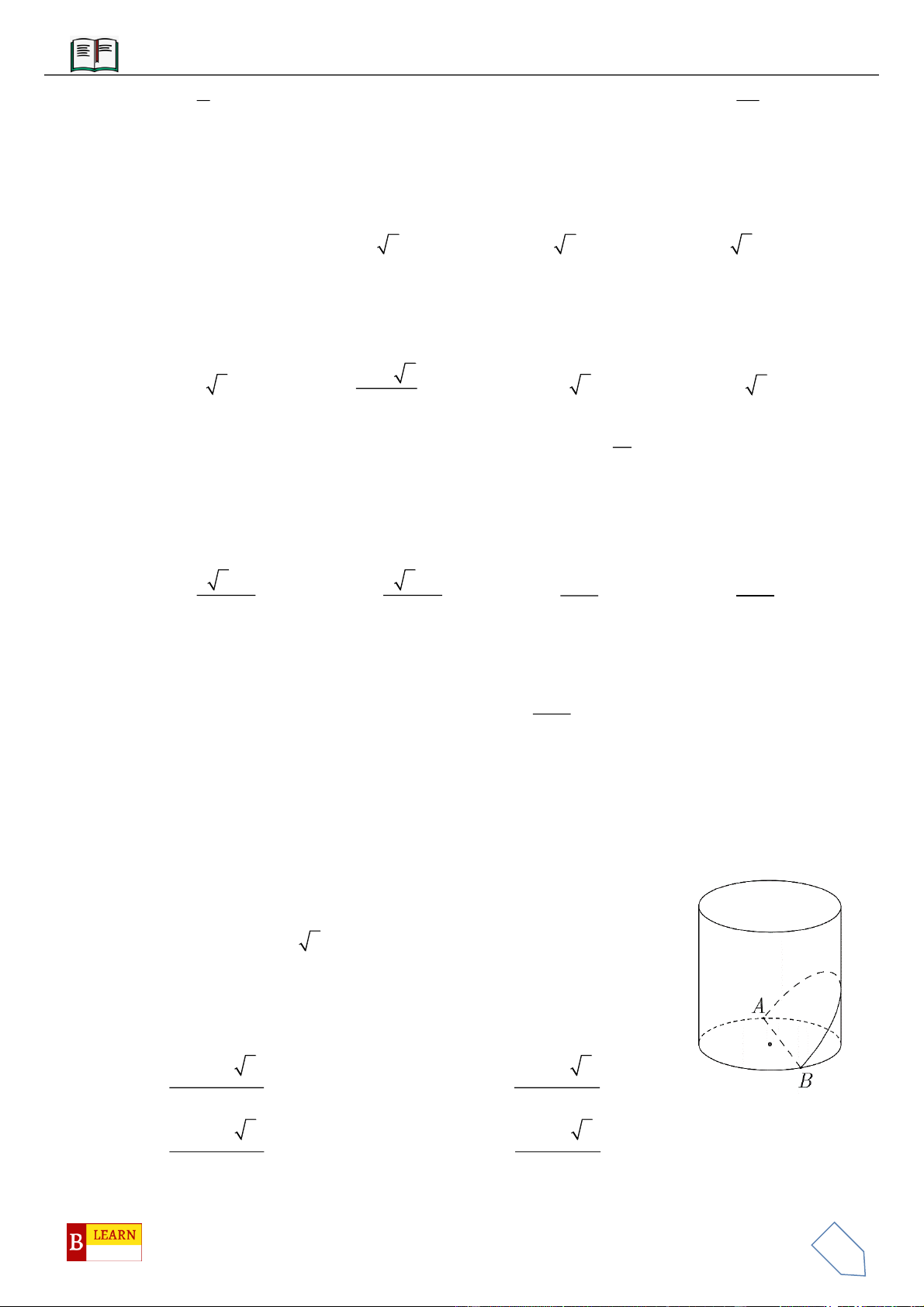
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

351

A.





2

()

3

S cm

. B.

 





2

S cm

. C.





2

3 ( )S cm

D.





2

()

3

S cm

Câu 32: Cho hình nón

 

N

có bán kính đáy bằng 6 và chiều cao bằng 12. Mặt cầu

 

S

ngoại tiếp hình nón

 

N

có tâm là

.I

Một điểm

M

di động trên mặt đáy của nón

 

N

và cách

I

một đoạn bằng 6.

Quỹ tích tất cả các điểm

M

tạo thành đường cong có tổng độ dài bằng

A.



6

. B.



6 2.

C.



3 7.

D.



4 6.

Câu 33: Cho hình nón đỉnh

S

, đường cao

SO

. Gọi

,AB

là hai điểm thuộc đường trò đáy của hình nón

sao cho khoảng cách từ

O

đến

AB

bằng

2,a



00

30 , 60 .SAO SAB

Diện tích xung quanh hình

nón đã cho bằng

A.



2

2 3.a

B.



2

32

.

4

a

C.



2

4 3.a

D.



2

3 2.a

Câu 34: Cho hình trụ có trục

'OO

, bán kính đáy

r

và chiều cao



3

2

r

h

. Hai điểm

,MN

di động trên

đường tròn đáy

 

O

sao cho

OMN

là tam giác đều. Gọi

H

là hình chiếu vuông góc của

O

lên

 

'O MN

. Khi

,MN

di động trên đường tròn

 

O

thì đoạn thẳng

OH

tạo thành mặt xung quanh

của một hình nón, diện tích

S

của mặt này.

A.





2

93

32

r

S

. B.





2

93

16

r

S

. C.





2

9

32

r

S

. D.





2

9

16

r

S

.

Câu 35: Cho tam giác

ABC

cân tại

A

, biết

 2AB a

và góc



o

30ABC

, cho tam giác

ABC

quay xung

quanh đường thẳng

AC

được khối tròn xoay. Khi đó thể tích khối tròn xoay bằng

A.

3

2πa

. B.

3

6πa

. C.

3

2π

3

a

. D.

3

2a

.

Câu 36: Một hộp đựng mỹ phẩm được thiết kế có thân hộp là hình trụ có bán kính hình tròn đáy

 5r cm

, chiều cao

 6h cm

và nắp hộp là một nửa hình cầu. Người ta cần sơn mặt ngoài của cái hộp đó

thì diện tích

S

cần sơn là

A.





2

80S cm

. B.





2

110S cm

. C.





2

160S cm

. D.





2

130S cm

.

Câu 37: Cho khối trụ có bán kính đáy bằng

 

4 cm

và chiều cao

 

5 cm

. Gọi

AB

là một dây cung đáy

dưới sao cho

 

 43AB cm

. Người ta dựng mặt phẳng

 

P

đi qua

hai điểm

A

,

B

và tạo với mặt phẳng đáy hình trụ một góc



60

như

hình vẽ. Tính diện tích thiết diện của hình trụ cắt bởi mặt phẳng

 

P

.

A.

 





2

8 4 3 3

3

cm

. B.

 





2

4 4 3

3

cm

C.

 





2

4 4 3 3

3

cm

. D.

 





2

8 4 3

3

cm

.

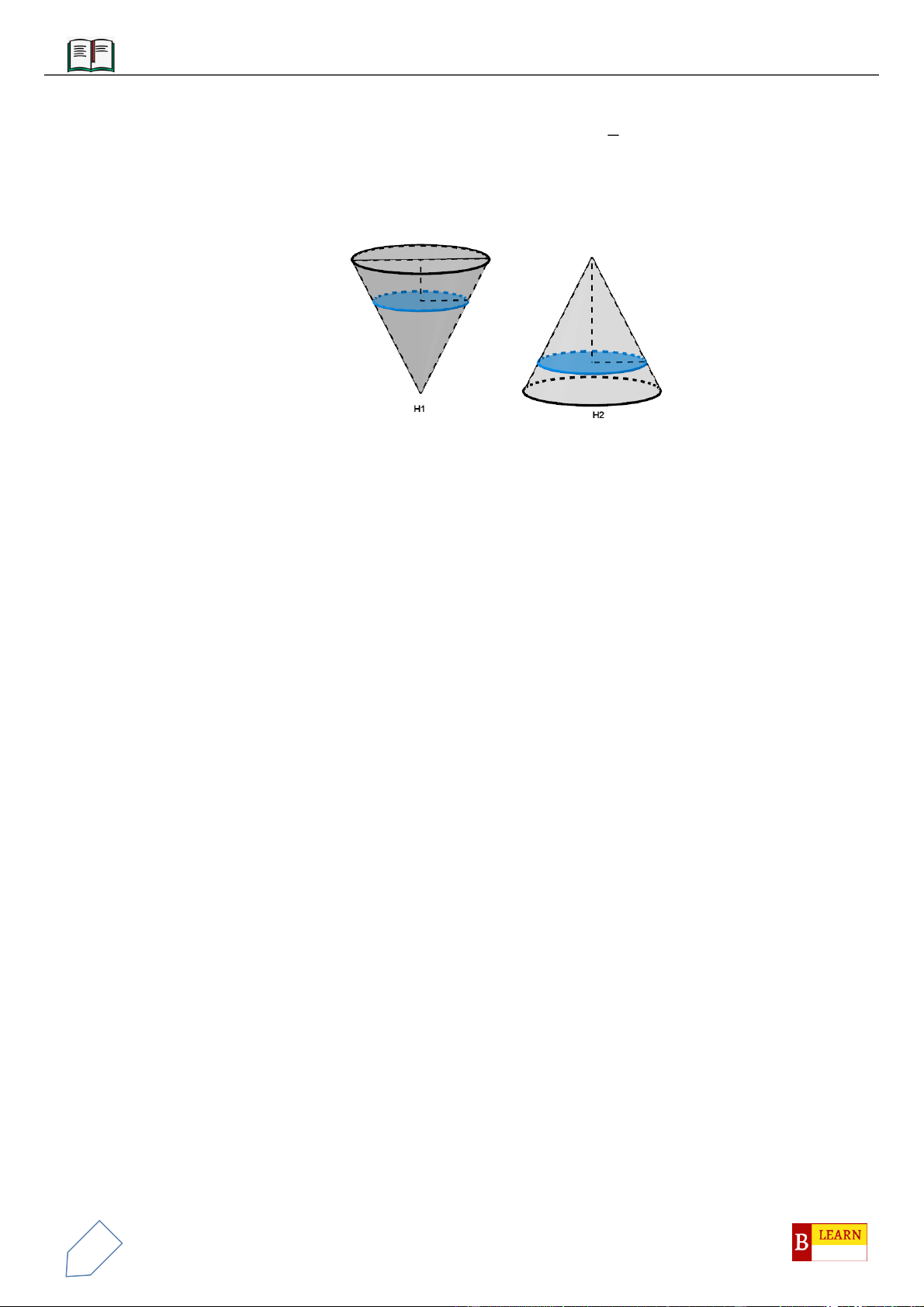
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

352

Câu 38: Một khối đồ chơi có dạng khối nón, chiều cao bằng

20cm

, trong đó có chứa một lượng nước. Nếu

đặt khối đồ chơi theo hình

1

H

thì chiều cao lượng nước bằng

2

3

chiều cao của khối nón. Hỏi nếu

đặt khối đồ chơi theo hình

2

H

thì chiều cao



h

của lượng nước trong khối đó gần với giá trị nào

sau đây?

A.

 

2,21 cm

. B.

 

5,09 cm

. C.

 

6,67 cm

. D.

 

5,93 cm

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

353

BẢNG ĐÁP ÁN

1.B

2.C

3.B

4.D

5.C

6.B

7.D

8.D

9.A

10.C

11.A

12.C

13.B

14.A

15.A

16.B

17.B

18.A

19.B

20.D

21.A

22.C

23.A

24.C

25.D

26.D

27.B

28.D

29.D

30.A

31.B

32.C

33.C

34.A

35.A

36.B

37.A

38.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn B

Gọi hình nón tròn xoay có đường sinh

 2la

có bán kính đáy là

R

và đường cao là

h

.

Thể tích khối nón:





2

1

3

V R h

. Ta có:



2 2 2

4R h a

.

Áp dụng bất đẳng thức Cô si:

     

2 2 4 2

2 2 2 2

3

43

2 2 4

R R R h

a R h h

.



   

42

6 2 3

64 1 16 3

4 27 3 27

Rh

a R h a

.

Đẳng thức xảy ra khi và chỉ khi



























2

2 2 2

23

3

2

26

4

3

R

ha

h

h R a

Ra

. Khi đó





3

max

16 3

27

Va

.

Câu 2: Chọn C

Tam giác

MAH

vuông tại

H

nên hình nón được tạo thành có

chiều cao

h MH

và bán kính đáy là

r AH

Có



2

.IH IM IA

   

22

33

IA a a

IH

IM

a

     

2

3

33

aa

MH IM IH a



2

22

..

3

33

a a a

AH IH MH

Vậy thể tích khối nón là

 

 

2

32

43

.

1 1 2 2

..

3 733

3

2

aa

V arh

Câu 3: Chọn B

Khi quay hình trên quanh cạnh

BN

ta được một khối tròn xoay

gồm một khối trụ có bán kính đáy bằng 2 dm, chiều cao bằng 4 dm

và một khối nón cụt có bán kính hai đáy lần lượt là 2dm và 3 dm,

chiều cao bằng 2 dm.

Do đó thể tích của khối tròn xoay là

 



    

      

3

2 86

4 .4 4 9 4 .9 dm

33

truï non cut

V V V

.

H

I

A

M

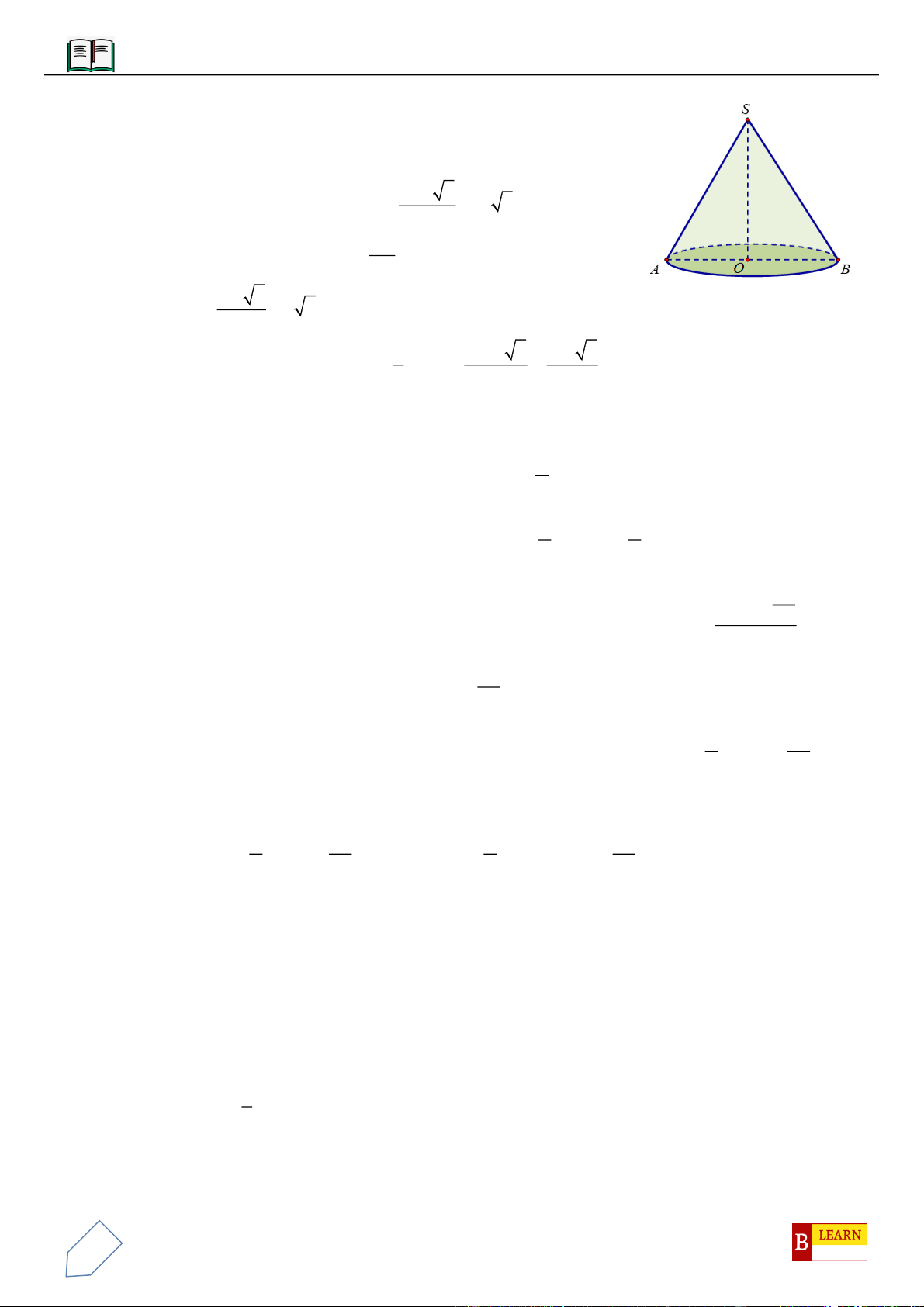
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

354

Câu 4: Chọn D

Gọi đỉnh của hình nón là

S

, tâm đường tròn đáy của hình nón là

O

,

AB

là một đường kính của đường tròn đáy. Khi đó

SAB

là

một thiết diện qua trục của hình nón đã cho.

Diện tích của tam giác

SAB

là:

  

2

3

32

4

AB

a AB a

.

Bán kính đường tròn đáy



2

AB

Ra

; Đường cao của hình nón là

  

3

2

AB

h SO a

.

Thể tích khối nón đã cho là:





  

23

2

1 . 3 3

3 3 3

a a a

V R h

.

Câu 5: Chọn C

Cách 1: Vì

 

L

là hình lăng trụ đều

n

cạnh có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình

trụ

 

T

nên độ dài mỗi cạnh của lăng trụ là



 2 .sinar

n

.

Do đó diện tích của n mặt bên là



  

1

2 .sin 12 .sinS nah nrh n

nn

Công thức diện tích của đa giác đều

n

cạnh, có độ dài mỗi cạnh là

a

là:





2

.sin

2

nr

n

s

.

Nên diện tích của hai đáy là:





2

2. 9 .sinS s n

n

.

Tổng diện tích tất cả các mặt của khối lăng trụ

 

L

là:

S



  

12

12 .sinS S n

n



2

9 .sinn

n

.

Khi

n

tăng lên vô hạn:













2

lim 12. .sin 9 .sin

x

nn





 

   

  

   

   

2

lim 12. .sin lim 9 .sin 30

xx

nn

.

Cách 2: Khi

n

tăng lên vô hạn, hình lăng trụ tiến dần tới hình trụ, do đó tổng diện tích tất cả các mặt

của của khối lăng trụ

 

L

bằng với diện tích toàn phần của hình trụ

 

T

và bằng

  



2

2 2 30rh r

Câu 6: Chọn B

Gọi

,,V R h

lần lượt là thể tích khối trụ (khối chứa phần nước trong cốc), bán kính đáy cốc và

chiều cao của lượng nước trong cốc khi chưa lấy khối nón ra. Suy ra:





2

V R h

(1)

Gọi

1 1 1

,,V R h

lần lượt là thể tích, bán kính đáy và chiều cao của khối nón.

Suy ra:





2

1 1 1

1

3

V R h

(2)

Gọi

22

,Vh

là thể tích lượng nước đổ vào và độ cao của nước trong cốc sau khi đã lấy khối nón ra.

Suy ra:





2

22

V R h

(3)

Từ (1),(2) và (3) ta có:

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

355

  



         

22

11

2 2 2 2 2 2

1 2 1 1 2 1 1 2 2

2

1

11

3

33

R h R h

V V V R h R h R h R h R h R h h

R

(4)

Thay

   

11

, , 12

2

a

R a R h h

vào (4) ta có:

  

2

11

12 . .12 11

34

h

.

Câu 7: Chọn D

Gọi

ABCD

là thiết diện qua trục của khối trụ.

Vì

ABCD

là hình vuông nên ta có:





1

2

OC OO

2hr

 

1

.

Diện tích xung quanh của khối trụ là:



 2

xq

S rh

 

2

.

Từ

 

1

và

 

2

suy ra:





2

24

xq

S rh r

.

Ta có:



 16

xq

S





2

4 16r





2

4 16r

.

Thể tích của khối trụ là:

   

   

2 3 3

2 2 .2 16V r h r

(đơn vị

thể tích).

Câu 8: Chọn D

Ta có

2l CB a

,

30BCA

.

Xét tam giác

ABC

vuông tại

A

có:

       

1

sin30 .sin30 2 .

2

AB r

r l a a

CB l

.

       

3

cos30 .cos30 2 . 3

2

CA h

h l a a

CB l

.

Suy ra





  

3

22

1 1 3

.3

3 3 3

a

V r h a a

.

Câu 9: Chọn A

Ta có

  

2

4 13

.

93

aa

NB a

ABN

đồng dạng

NKB

suy ra

    

22

13 3 13

.

9 2 6

AN NB NB a a

KB

NB KB AN a

Gọi

M

là điểm trên

BC

sao cho

 2BM MC

a

P

M

K

C

D

A

B

N

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

356

Suy ra



23

;.

32

aa

BM MK

Vậy

  

  

2 2 3

2 1 3 7

. . .

3 3 2 6

aa

V a a a

Câu 10: Chọn C

Thể tích khối trụ

  



2 2 3

1

. 2 2.R h R RVR

Khối tứ diện



BO OA

có



BO

là đường cao và đáy là tam giác

vuông



O OA

, do đó thể tích khối tứ diện là



 

    

3

2

3

1 1 2

. 2.

1

6

1

3 2

.

6

O OA

OA OO OV B R R RSB RO

Vậy





3

2

3

1

2

1

6 6

2 1

V

R

V

.

Câu 11: Chọn A

Bán kính ống cống là:

   

50

25 0.25

2

R AB cm m

.

Do lớp bê tông dày

10cm

nên bán kính phần được giới hạn bên trong là:

  15 0.15r AD cm m

Thể tích phần bê tông là:

     

  

    

2 2 2 2 3

. .2 0.25 0.15 0.08V h R r m

.

Câu 12: Chọn C

Cách 1:

Gọi

'A

,



C

lần lượt đối xứng với

A

,

C

qua

BD

,

'G BC AD

,



G

đối xứng với

G

qua

BD

.

'E AA BD

,

'F GG BD

 F

là trung điểm

BD

.

Gọi

V

là thể tích của khối tròn xoay tạo thành khi quay hình chữ nhật

ABCD

quanh đường thẳng

BD

.

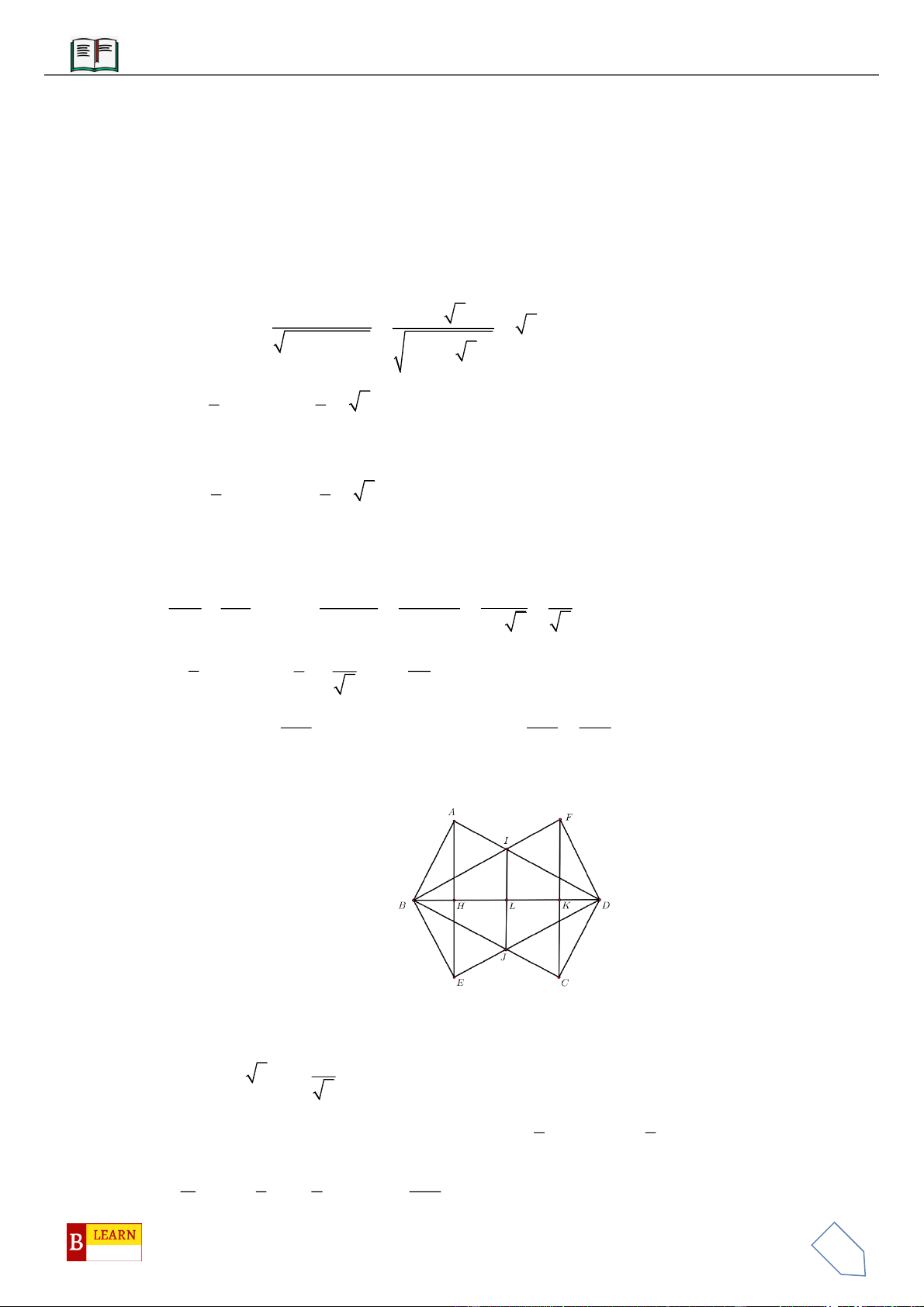
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

357

1

V

là thể tích của khối tròn xoay tạo thành khi quay tam giác

BAD

quanh cạnh

BD

(cũng là thể

tích của khối tròn xoay khi quay tam giác

BCD

quanh cạnh

BD

).



1

V

,



1

V

lần lượt là thể tích của khối tròn xoay tạo thành khi quay

BAE

,

EAD

quanh cạnh

BD

.

2

V

là thể tích khối tròn xoay tạo thành khi quay

BGD

quanh cạnh

BD

.



2

V

là thể tích của khối tròn xoay tạo thành khi quay

BGF

quanh cạnh

BD

.

Ta có



1

V

là thể tích của khối nón đỉnh

B

, bán kính đáy

AE

.

Tính được





22

.AB AD

AE

AB AD

 





2

2.2 3

2 2 3

 3

,

 4BD

,

 1BE

,

 3DE

.







2

1

..

3

V AE BE

 





2

1

3





.

Ta có



1

V

là thể tích của khối nón đỉnh

D

, bán kính đáy

AE

.







2

1

..

3

V AE DE

 





2

1

3 .3

3



 3

. Suy ra







1 1 1

V V V



3



 4

.

Ta có



2

V

là thể tích của khối nón đỉnh

B

, bán kính đáy

GF

.

Ta chứng minh được



 ~BGF BDC

(g – g).





GF BF

DC BC







.BF DC

GF

BC







.

2

BD DC

BC



4.2

2.2 3



2

3

.







2

1

..

3

V GF BF











2

12

. .2

3





8

9

.

Ta có





22

2VV





16

9

. Vậy



12

2V V V





16

2.4

9





56

9

.

Cách 2:

Gọi điểm như hình vẽ

12

,VV

lần lượt là thể tích khói nón, nón cụt nhận được khi quay tam giác

ABH

và tứ giác

AHLT

quay

BD

.

Ta có:

   

2

3,I , 1

3

AH L BH HL

.

Ta có:

 



12

2V V V

 





   





2 2 2

11

2 . . . . .

33

BH AH HL IL IL AH AH









    









1 1 4 56

2 .1. .3 .1. . 2 3

3` 3 3 9

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

358

Câu 13: Chọn B

Gọi bán kính mặt cầu là

R

và chiều cao của khối trụ là

20hx

.

Suy ra bán kính đáy trụ là



22

r R x

.

Thể tích khối trụ là

 



  

2 2 2

2V r h R x x

Theo bất đẳng thức Cauchy ta có:

 











   





3

2 2 2

26

2

2 2 2 2 2 2

22

16

2 .2 2

3 27

R x x

R

V R x x

Suy ra





3

43

9

R

V

. Đẳng thức xảy ra khi và chỉ khi

   

2 2 2

2

3

R

R x x x

Vậy





3

43

max

9

R

V

. Với

 3R

thì



max 4V

.

Câu 14: Chọn A

Gọi

E

là giao điểm của

AB

và

CD

. Gọi

F

là hình chiếu vuông góc của

B

trên

CE

.

Ta có:

  BCF BEF

nên tam giác

 BCF

và

 BEF

quay quanh trục

CD

tạo thành hai khối

nón bằng nhau có thể tích

1

V

.

  ADC AEC

nên tam giác

 ADC

và

 AEC

quay quanh trục

CD

tạo thành hai khối nón

bằng nhau có thể tích

V

.

Nên thể tích khối tròn xoay sinh ra khi quay hình thang

ABCD

xung quanh trục

CD

bằng:

 



  

22

1

2 2 2. . .

3

V V CD AC CF BF

 









  









3

2 7 2

2

36

2

aa

a

(đvtt).

Câu 15: Chọn A

Ta có:

2AB AD

,

  

22

22BD AB AD

,



  





2

1

22

2

BC AD CD

.

Tam giác

BCD

vuông cân tại

B

do



2 2 2

CD BD BC

và

22BD BC

.

Kéo dài

AD BC E

. Kẻ

AF BE

tại

F

. Khi đó

AF BD

.

O

R

x

I

'I

'M

M

r

O

R

x

I

'I

'M

M

r

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

359

Dễ chứng minh:

  BCD BED

,

  ABF AEF

,

  

1

2

AF BF BD

.

Thể tích khối tròn xoay sinh ra bởi tam giác

ECD

khi quay xung quanh đường thẳng

BC

bằng 2

lần thể tích khối nón sinh ra bởi tam giác

BCD

khi quay xung quanh đường thẳng

BC

(bán kính

đáy

BD

, đường cao

BC

):





2

1

1 32 2

2. .

33

V BD BC

.

Thể tích khối tròn xoay sinh ra bởi tam giác

ABE

khi quay xung quanh đường thẳng

BC

bằng 2

lần thể tích khối nón sinh ra bởi tam giác

ABF

khi quay xung quanh đường thẳng

BC

(bán kính

đáy

AF

, đường cao

BF

):





2

1 4 2

2. . .

33

V AF BF

.

Thể tích khối tròn xoay sinh ra bởi hình thang

ABCD

khi quay xung quanh đường thẳng

BC

là:



  

12

28 2

3

V V V

.

Câu 16: Chọn B

Gọi

O

là tâm của hình vuông

ABCD

. Kẻ

OE AB

tại

E

, khi đó bán kính của đường tròn nội

tiếp hình vuông

ABCD

là

OE

.

Ta có



22

AB a

OE

.

Diện tích hình tròn nội tiếp hình vuông

ABCD

là





22

1

.

4

S OE a

.

Gọi

h

là chiều cao của khối trụ, khi đó



h AA

.

Thể tích

V

của khối trụ đã cho là





   

23

11

. . .

44

V h S AA S a a a

.

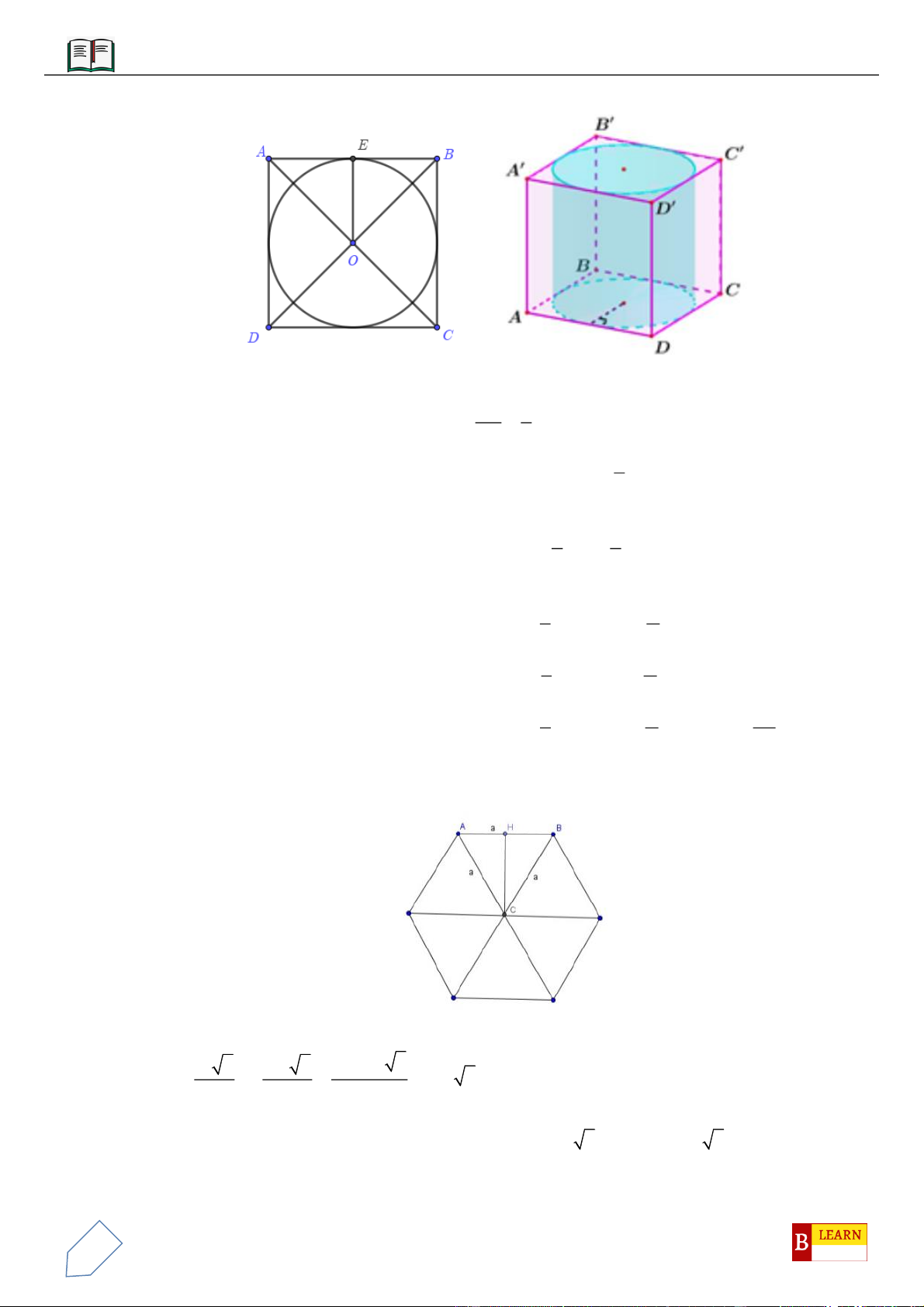
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

360

Câu 17: Chọn B

Gọi

O

là tâm của hình vuông

ABCD

. Kẻ

OE AB

tại

E

, khi đó bán kính của đường tròn nội

tiếp hình vuông

ABCD

là

OE

. Ta có



22

AB a

OE

.

Diện tích hình tròn nội tiếp hình vuông

ABCD

là





22

1

.

4

S OE a

.

Gọi

h

là chiều cao của khối trụ, khi đó



h AA

.

Thể tích

V

của khối trụ đã cho là





   

23

11

. . .

44

V h S AA S a a a

.

Câu 18: Chọn A

Quay tam giác

ABD

khi quay quanh

AD

ta có





23

1

..

33

V AD AB a

(đvtt).

Quay tam giác

ABC

khi quay quanh

AB

ta có





23

2

1

..

33

V AB BC a

(đvtt).

Quay tam giác

DBC

khi quay quanh

BC

ta có





  

2 2 3

3

12

BC. . .2

3 3 3

V BD AB AB a

(đvtt).

Vậy



1 2 3

V V V

.

Câu 19: Chọn B

Diện tích của một lục giác đều cạnh a là:

 



   





2

22

3 20 3

3 3 3

6 600 3

4 2 2

aa

S

2

(cm ).

Tổng thể tích 10 chiếc cột ban đầu là

  

6

1

10. . 10.600 3.400 2,4.10 . 3V S h

3

(cm ).

Tổng thể tích 10 khối trụ sau khi hoàn thiện là:

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

361

  



  





2

42

10. 10 . .400 1764000

2

V r h

3

(cm ).

Thể tích vữa cần dùng là



   

6

21

1764000 2,4.10 . 3V V V

3

(cm )

Số bao xi măng cần dùng là









  

6

0,8 1764000 2,4.10 . 3

0,8

17,3106.

64000 64000

V

n

Câu 20: Chọn D

Thể tích phần khối trụ phía dưới:





23

1

0,5 m

3

V R h

.

Thể tích phần khối nón cụt:







     









2

23

2

1 2 7

. . m

3 2 2 3 12

R R h

V R R

.

Thể tích phần trụ rỗng:











2

3

m

4 32

R

Vh

.

Thể tích khối bê tông:

  

3

1 2 3

3,109 mV V V

.

Câu 21: Chọn A

Gọi

h

,

V

lần lượt là chiều cao và thể tích khối trụ

 

T

   

,d AB CD h cm

.

Ta có:

 

  

2

11

.sin ; . . .sin30 .6

66

ABCD

V h AB CD AB CD h

 

  



2

6

10

sin30 .6

ABCD

V

h cm

.

 





  





2

3

. 90

2

T

AB

V h cm

.

Câu 22: Chọn C

Gọi

H

là trung điểm của đoạn

.AB

Nhận thấy:

Tam giác

OAB

vuông cân tại

O

.

Mặt khác:

OH AB

,

SH AB

nên góc giữa hai mặt phẳng

()SAB

,

()OAB

bằng



 SHO

.

Ta có:





 .cos

OAB SAB

SS





22

1

2.cos

2

RR





1

cos .

22

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

362

Mà





1

cos

22

OH

SH



2

1

2

22

R

SH

  

2

.2 2 2 .

2

R

SH R

  

22

SO SH OH









2

4

2

R



14

2

R

Vậy thể tích của khối nón bằng





  

3

22

1 1 14 14

. . .

3 3 2 6

RR

V R SO R

Câu 23: Chọn A

Gọi chiều cao của viên đá cảnh hình trụ là

 2hx

,

0 xR



bán kính đáy của khối trụ là:



22

Rx



   



   

2 2 2 3

2 2 .V R x x R x x

 



       

2

2 2 2

3

' 2 3 0 .

33

RR

V R x x x

Lập bảng biến thiên của hàm số V trên khoảng

 

0;R

ta được









3

max

3 4 3

.

39

RR

VV

Câu 24: Chọn C

Gọi

E

,

F

lần lượt là trung điểm của

AB

,

CD

.

Theo giả thiết, ta có



2

a

EB

,



2

b

FC

và

EF h

. Đặt

SE x

.

SEB SFC



SE EB

SF FC





xa

x h b





ah

x

ba

. Suy ra

  



ah bh

SF h

b a b a

.

Thể tích vật thể tròn xoay cần tìm là





22

11

. . . .

33

V SF FC SE EB





    







22

1

3 4 4

bh b ah a

b a b a

 

   



    



3 3 2 2

11

. . .

3 12

4

h

b a h a ab b

ba

.

Câu 25: Chọn D

Nhận xét: Tứ giác

ABCI

là hình vuông. Dễ chứng minh

 

BC SAB

và

BI SC

.

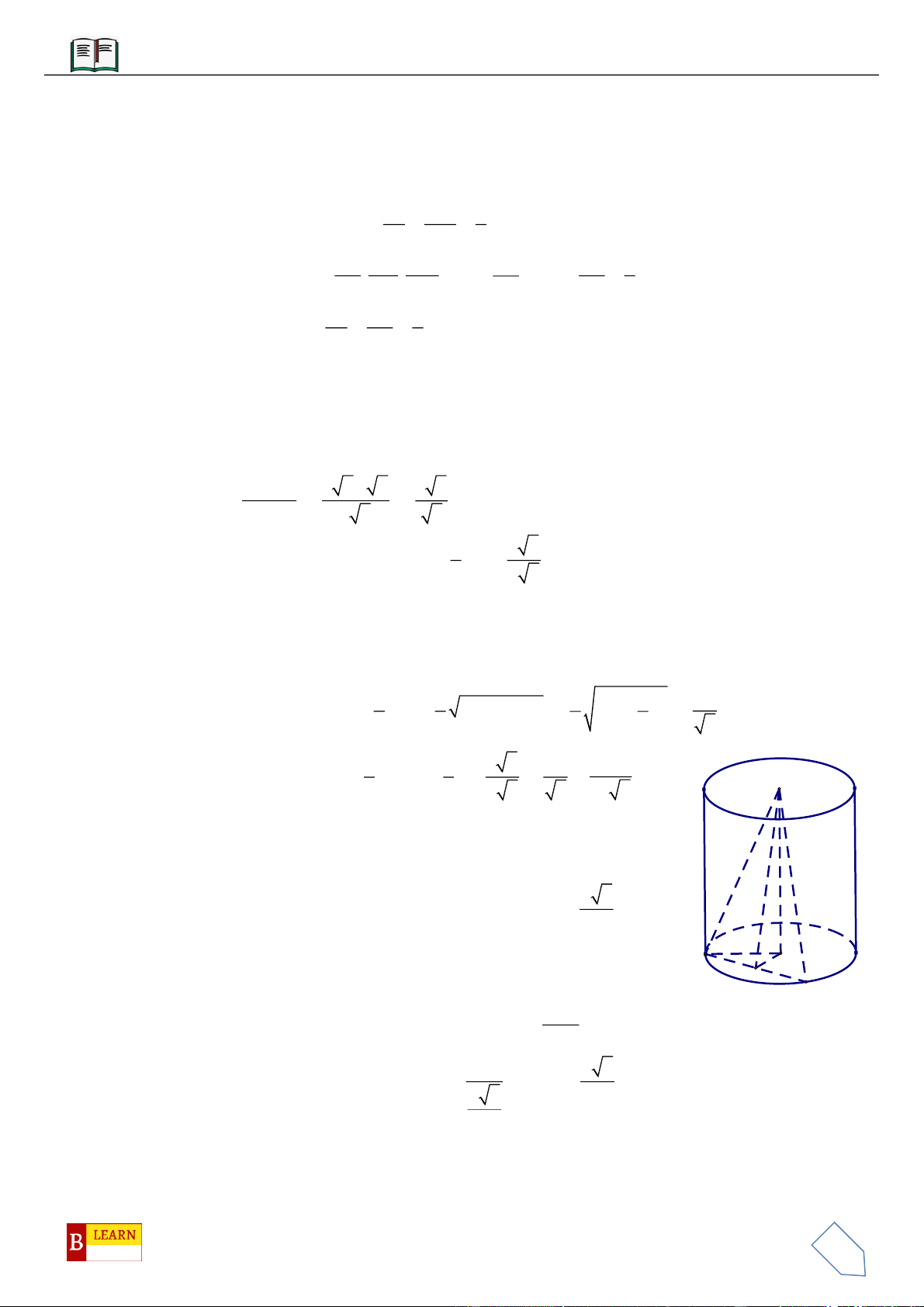
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

363

 













EA SB

EA SBC

EA BC

EA SC

.

 













EA SC

SC AEF

FA SC

.

Trong tam giác vuông

SAB

có



2

3

4

SE SA

SB

.

Trong tam giác

SAD

có

. . 1

HS AI MD

HI AD MS

3

HS

HI



3

4

SH

SI

.

Trong tam giác

SBI

có



3

4

SE SH

SB SI

 //EH BI

. Do

BI SC

nên

EH SC

.

Suy ra các điểm

, , , A E F H

cùng thuộc mặt phẳng đi qua

A

và vuông góc với

SC

.

Gọi

K

là trung điểm

AF

.

Vì











EA EF

AH FH

 K

là tâm đường tròn ngoại tiếp tam giác

EFH

.

Ta có:



.SA AC

AF

SC



3. 2

5

aa

a



6

5

a

.

Suy ra bán kính đáy của khối nón là



16

2

25

a

R AF

.

Gọi

O

là tâm hình vuông

ABCI

.

Do

 







  







//

SC EFH

OK EFH O

OK SC

là đỉnh của khối nón.

Chiều cao của khối nón là



1

2

h FC



22

1

2

AC AF



22

16

2

25

aa



5

a

.

Vậy thể tích khối nón là











2

1 1 6

. . . . .

33

2 5 5

aa

V R h





3

10 5

a

.

Câu 26: Chọn D

Đặt độ dài cạnh

AB x

 

 0x

và

M

là trung điểm

AB

.

Vì tam giác



O AB

đều nên



  O A O B AB x





3

2

x

OM

.

Vì mặt phẳng

 



O AB

tạo với mặt phẳng chứa đường tròn

 

;OR

góc

60

nên



60O MO

.

Xét tam giác



O OM

vuông tại

O

ta có:







cos

OM

O MO

OM

. Suy ra

   

3

cos60

4

3

2

OM x

OM

x

Xét tam giác

OAM

vuông ở

M

có:



2 2 2

OA OM AM

nên

M

B

A

O'

O

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

364



     





2

2 2 2

3 7 4 7

4 2 16 7

xx

R R x x R

Do đó:





3 2 21

27

x

O M R

và



3 21

47

x

OM R

.

Vì vậy, ta có



  

22

37

7

OO O M OM R

.

Vậy thể tích khối trụ là





   

3

22

3 7 3 7

..

77

R

V R h R R V

.

Câu 27: Chọn B

Từ giả thiết suy ra

BF

là đường kính đường tròn đáy của hình trụ.

Kẻ đường sinh

FK

, gọi

O

là trung điểm

AK

.

Gọi

r

là bán kính đáy, suy ra

  

3

2π6

π

rr

.

Đặt



AOE

(rad). Trong hình chữ nhật

ABCD

có

 2AE



      

22π

.2

3

AE

l r AOE

r



π

3

EOK

, suy ra tam

giác

EOK

là tam giác đều cạnh



3

π

r

. Gọi

H

là trung điểm

OK

EH AK

,

EH AB

   

 

     

3 3 3

,

22π

r

EH ABFK d E ABF EH

.

Diện tích tam giác

ABF

là

  

1 1 6 9

. . .3.

22ππ

S AB BF

.

Thể tích khối tứ diện

ABEF

là

 

  

2

1 1 9 3 3 9 3

. , . .

33π 2π

2π

ABF

V S d E ABF

.

Câu 28: Chọn D

Hình nón có bán kính của đáy là



32

22

AC

r

và độ dài đường

sinh

3l SA

.

Vậy diện tích xung quanh của hình nón là:





  

3 2 9 2

. .3

22

xq

S rl

.

Câu 29: Chọn D

Kí hiệu như hình vẽ

2

a

2a

O

S

B

A

M

H

O

A

K

B

F

E

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

365

Dễ thấy góc giữa mặt phẳng (SAB) và mặt đáy là góc



0

60S MO

.

Xét tam giác vuông

SOM

có



2

2 .cot60

3

a

OM a

;



24

sin60

3

aa

SM

;

Lại có

     

2

2 2 2

4 2 2

2. 2 2 2

3

aa

AB MB OB OM a

Vậy



  

2

1 1 4 2 2 4 2

. . .

2 2 3

33

ABC

a a a

S SM AB

.

Câu 30: Chọn A

Gọi

'A

là hình chiếu của

A

trên

 

'O

;

'B

là hình chiếu của

B

trên

 

O

.

Khi đó

'/ / 'OO AA

nên

   



  , ' , ' ' 30AB OO AB AA BAA

(do

 'ABA

vuông tại

B

).

Gọi

I

là trung điểm

'AB

. Do

 

'/ / ' 'OO AA BB

nên

   

 

   

3

', ', ' ' ', ' ' '

2

a

d OO AB d OO AA BB d O AA BB O I

.

Ta có



     





2

2 2 2

3

' 2 2 ' ' 2

2

a

A B BI O B O I a a

.



  ' ' ' .cot 30 3OO AA A B a

.

Diện tích toàn phần:

 

    

     

2 2 2

2 2 2 . 3 2 2 3 1

tp

S rh r a a a a

.

Câu 31: Chọn B

Xét tam giác

IOF

vuông tại

O

ta có:

 

  

0

2 2.sin 30 .3 3EF OF cm

.

Mặt khác thiết diện đi qua điểm

K

và vuông góc với

IO

nên

// MN EF

.

Ta xét tỉ lệ:

 

    

.2

.3 2

3

MN IK IK EF

MN cm

EF IO IO

.

Vậy bán kính của thiết diện là:

 

1

2

MN

KN cm

.

Suy ra:



 .S

Câu 32: Chọn C

M

O

I

A'

B'

O'

O

A

B

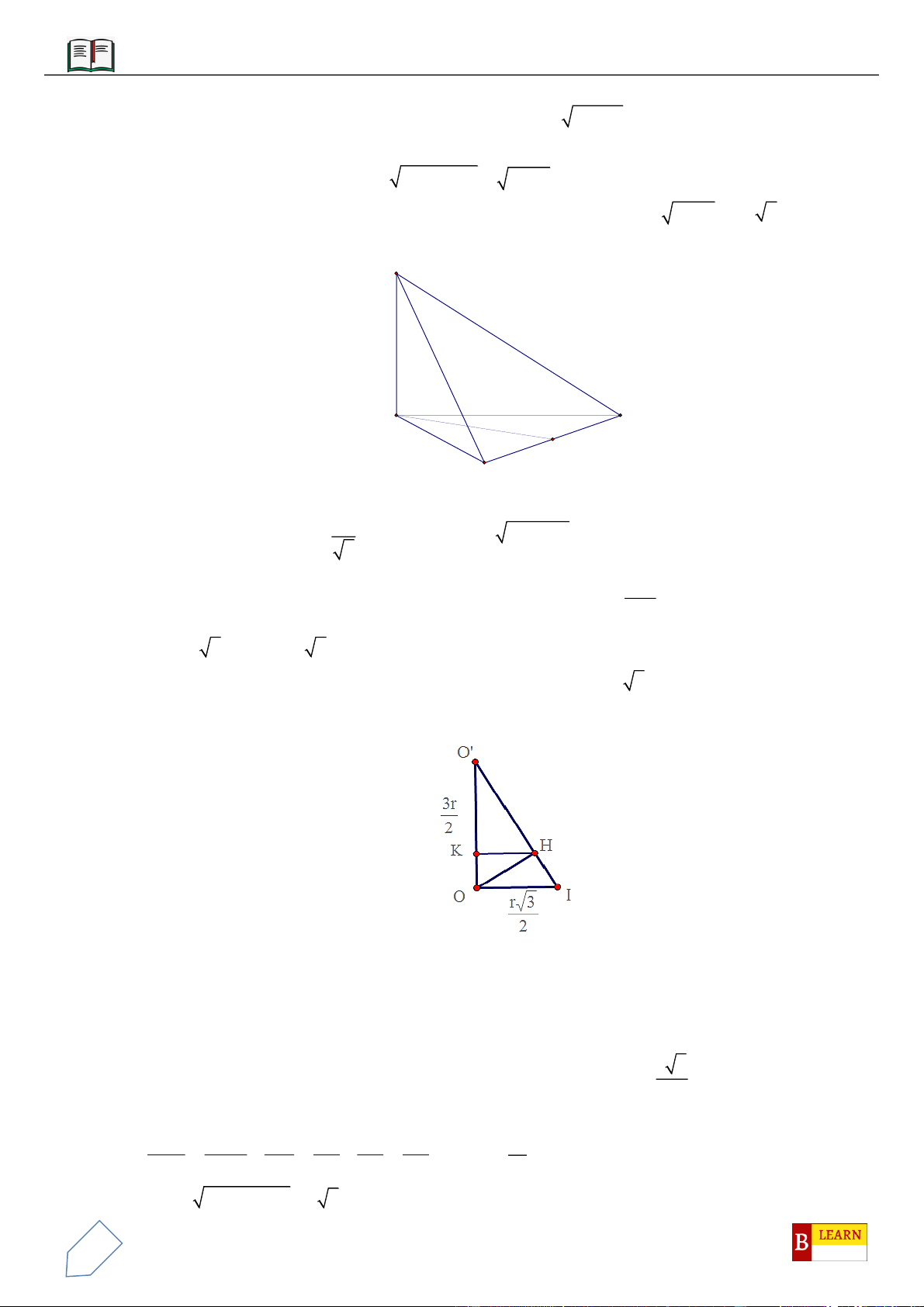
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

366

Gọi

O

là tâm của đáy. Đặt

   12OI a AI a

Để

I

là tâm mặt cầu ngoại tiếp hình nón thì

IA IB

     

22

6 12 4,5a a a

M

thuộc mặt đáy cách

I

một khoảng bằng

6

6IM

Xét

IOM

vuông tại

O

:

  

22

15,75OM IM IO

Suy ra tập hợp

M

là đường tròn tâm

O

bán kính

OM

. Chu vi là



2 15,75 3 7.

Câu 33: Chọn C

Đặt

OA R

. Gọi

C

là trung điểm của

.AB

Tam giác

OAB

cân tại

    2.O OC AB OC a

Ta tính được:



2

.

3

R

SA SB

và

  

22

2 2 4 .AB AC R a

Xét tam giác

SAB

có

















0

60

SA SB

SAB

đều

 

    

2

22

4

44

3

R

SA AB R a

   6 2 2R a SA a

.

Diện tích xung quanh của hình nón đã cho là:





2

. 4 3.S R SA a

Câu 34: Chọn A

Trong

 

O

kẻ

OI MN

tại

I

. Khi đó ta có

 

 'MN OO I

   

''OO I O MN

. Trong

 

'OO I

kẻ

 'OH O I

tại

H

 

'OH O MN

tại

H

nên

H

là hình chiếu vuông góc của

O

lên

 

'O MN

.

Tam giác

OMN

đều cạnh

r

, có

OI

là đường trung tuyến nên



3

2

r

OI

.

Tam giác

'O OI

vuông tại

O

, đường cao

OH

nên ta có

    

2 2 2 2 2 2

1 1 1 4 4 16

' 9 3 9OH O O OI r r r



3

4

r

OH

.

  

22

' ' 3O I O O OI r

.

C

O

A

B

S

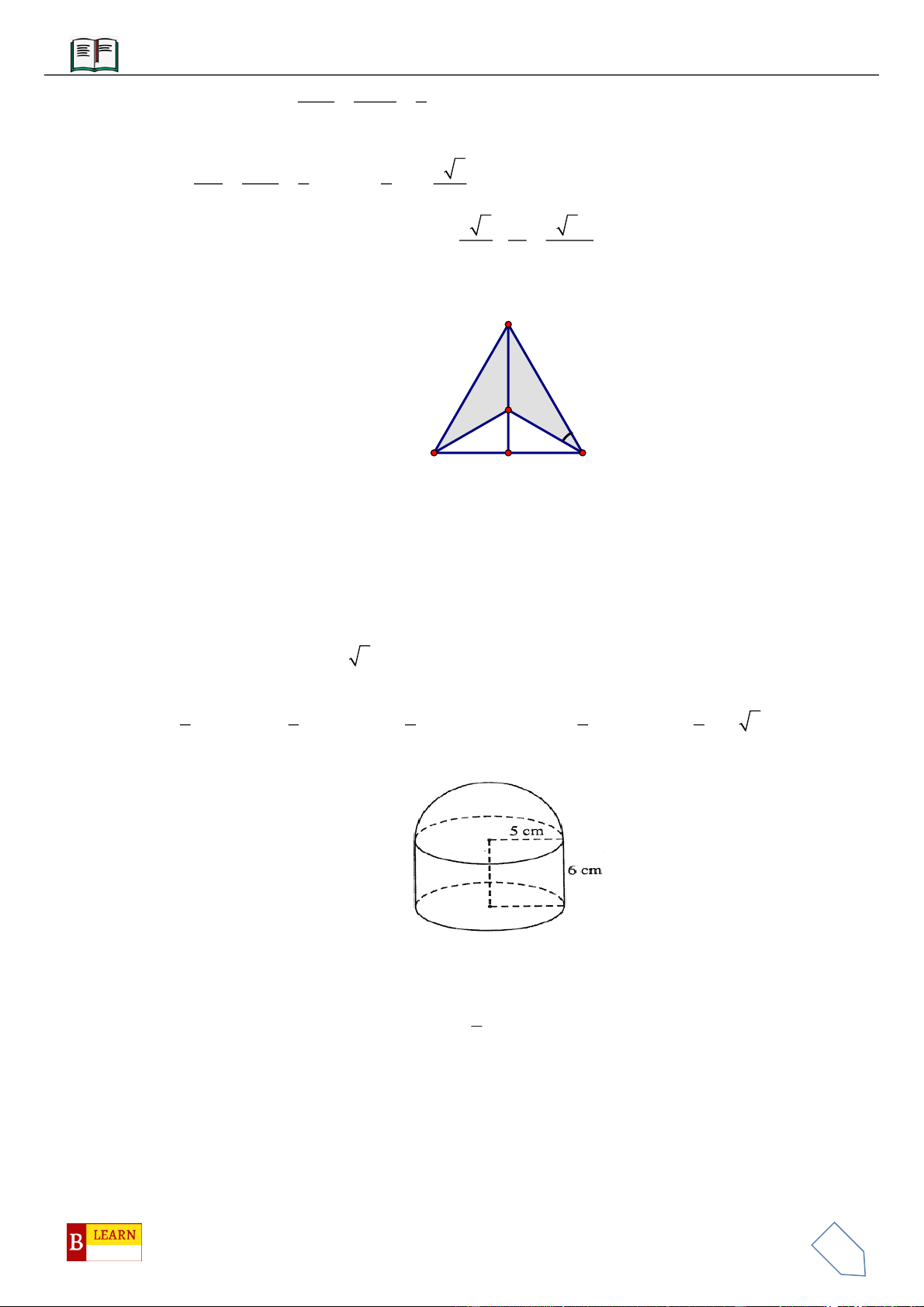
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

367

   

2

' ' 3

' ' . '

'4

'

O H O O

O O O H O I

OI

.

Kẻ

 'HK O O

tại

K

ta có

KH

là bán kính đáy của mặt nón.

Ta có

    

' 3 3 3 3

' 4 4 8

HK O H

HK OI r

OI O I

.

Diện tích

S

cần tính là



  

2

3 3 3 9 3

. . . .

8 4 32

rr

S HK OH r

.

Câu 35: Chọn A

Gọi

D

là hình chiếu vuông góc của

B

lên đường thẳng

AC

.

1

V

là thể tích khối nón tròn xoay sinh bởi tam giác vuông

CDB

khi quay quanh trục

CD

.

2

V

là thể tích khối nón tròn xoay sinh bởi tam giác vuông

ADB

khi quay quanh trục

AD

.

Khi đó thể tích khối tròn xoay cần tính là



12

V V V

.

Tam giác

ABC

cân tại

A

và

2AB a AC

,

  

oo

30 120ABC CAB

và



o

60DAB

.

Do đó



o

.sin60 3DB AB a

.

Vậy ta có



22

11

π. . π. .

33

V DB DC DB DA

 



2

1

π.

3

DB DC DA



2

1

π. .

3

DB AC

 



2

1

π. 3 .2

3

aa



3

2πa

Câu 36:

Chọn B

Diện tích xung quanh phần thân hộp là:

 





2

1

2 .5.6 60S cm

Diện tích xung quanh nửa hình cầu là:

 





22

2

1

.4 .5 50

2

S cm

Diện tích cần sơn là:

 



  

2

12

110S S S cm

.

Câu 37: Chọn A

D

B'

B

C

A

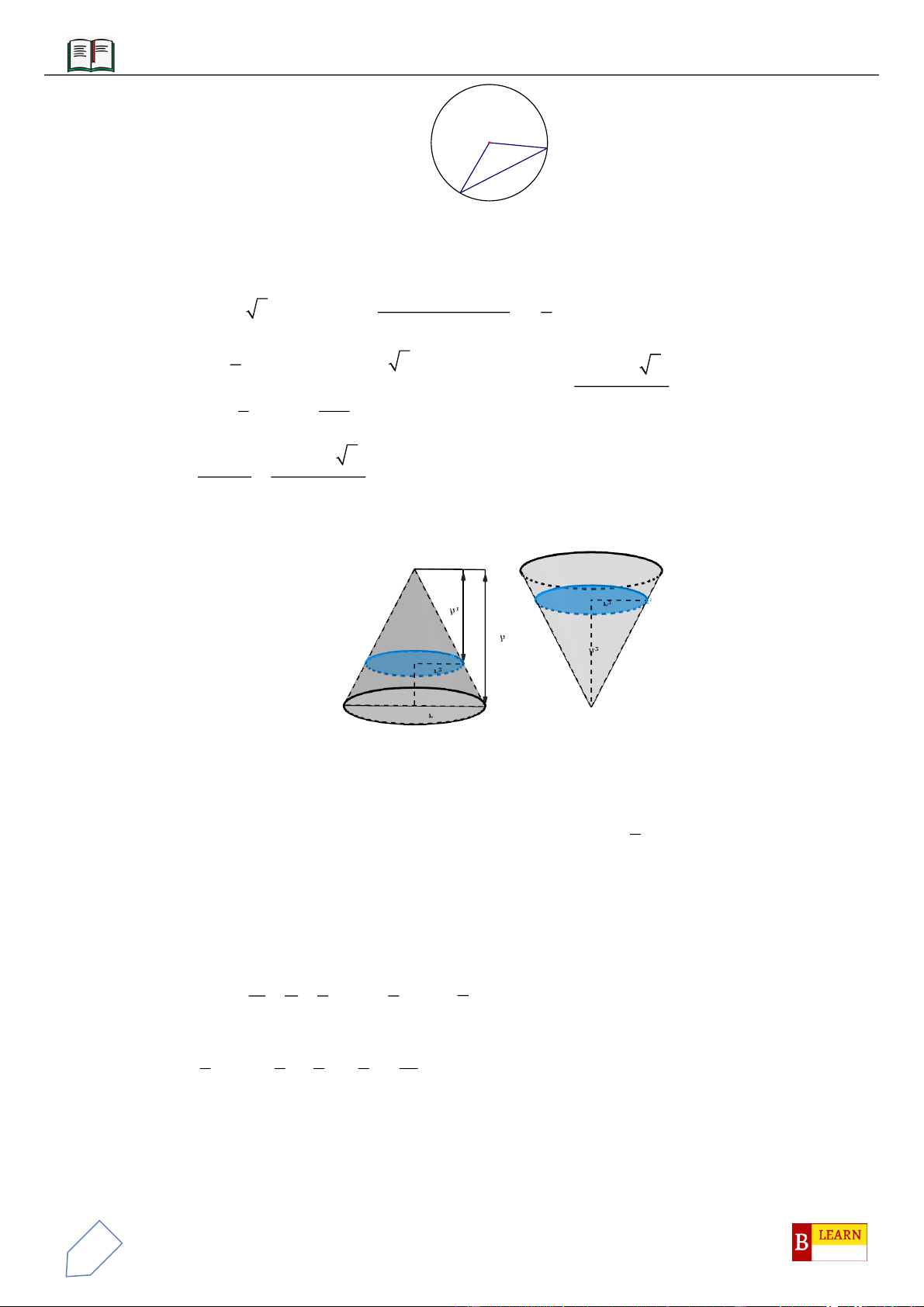
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

368

Gọi

S

là diện tích thiết diện,



S

là diện tích hình chiếu của thiết diện lên mặt phẳng

đáy. Khi đó



.cos60SS

.

Ta có



       

2 2 2

1

4 3 cos 120

2. . 2

OA OB AB

AB AOB AOB

OA OB



 





  







   











2

1

. .sin120 4 3

4 4 3 3

2

1 16

3

.

33

OAB

OAmB OAB

OAmB

S OA OB

S S S

S OA



 











8 4 3 3

cos60 3

S

.

Câu 38: Chọn A

Gọi

nuoc

V

,

V

lần lượt là thể tích của lượng nước trong đồ chơi và thể tích khối đồ chơi.

Gọi

h

,

r

lần lượt là chiều cao và bán kính đáy của khối đồ.





2

1

3

V r h

.

Xét khối đồ chơi đặt theo hình

1

H

.

Gọi

1

h

,

1

r

lần lượt là chiều cao và bán kính đáy của khối nón chứa lượng nước.

Khi đó ta có:

   

11

1

22

33

hr

hh

hr

,



1

2

3

rr

.

  



  





2

22

11

1 1 2 2 8

..

3 3 3 3 81

nuoc

V r h r h r h

.

 

*

Xét khối đồ chơi đặt theo hình

2

H

.

m

B

A

O

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

369

Gọi

2

h

,

2

r

lần lượt là chiều cao và bán kính đáy của khối nón không chứa nước trong khối đồ

chơi. Suy ra thể tích của khối nón không chứa nước:





2

22

1

3

non

V r h

.

Đặt:

   

22

2

.

hr

k h k h

hr

,



2

.r k r

.

 

    

       

2

2 2 2 2 3

22

1 1 1 1 1

. . . 1

3 3 3 3 3

nuoc non

V V V r h r h r h k r k h r h k

.

 

**

Từ

 

*

,

 

**

suy ra:

 



      

2 2 3 3

3

8 1 8 19

11

81 3 27 27

r h r h k k k

.

Vậy chiều cao lượng nước ở hình

2

H

:

   





        





3

2

19

. 1 20. 1 2,21

27

h h h h k h h k cm

.

CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

370

DẠNG 2: KHỐI TRÒN XOAY NỘI, NGOẠI TIẾP KHỐI ĐA DIỆN

Câu 1: Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng



2

36 a

. Tính thể tích

V

của lăng trụ lục giác đều nội tiếp hình trụ.

A.

3

27 3a

. B.

3

24 3a

. C.

3

36 3a

. D.

3

81 3a

.

Câu 2: Cho hình nón

1

N

đỉnh

S

đáy là đường tròn

 

;C O R

, đường cao

 40cmSO

. Người ta cắt nón

bằng mặt phẳng vuông góc với trục để được nón nhỏ

2

N

có đỉnh

S

và đáy là đường tròn

 

  

;COR

. Biết rằng tỷ số thể tích



2

1

8

N

V

. Tính độ dài đường cao nón

2

N

.

A.

20cm

. B.

5cm

. C.

10cm

. D.

49cm

.

Câu 3: Một hình tứ diện đều cạnh có một đỉnh trùng với đỉnh hình nón, ba đỉnh còn lại nằm trên đường

tròn đáy của hình nón. Diện tích xung quanh của hình nón bằng:

A. B. . C. . D. .

Câu 4: Cho lăng trụ tam giác đều

  

.ABC A B C

có độ dài cạnh đáy bằng

a

, góc giữa đường thẳng



AB

và mặt phẳng

 

ABC

bằng

60

. Tính thể tích

V

của khối trụ ngoại tiếp lăng trụ đã cho.

A.





3

3Va

. B.





3

43

3

a

V

. C.





3

9

a

V

. D.





3

a

V

.

Câu 5: Cho khối nón có độ dài đường sinh bằng

2a

và bán kính đáy bằng

a

. Thể tích của khối nón đã

cho bằng

A.



3

a

. B.



3

2

a

. C.



3

2

3

a

. D.



3

a

.

Câu 6: Cho khối nón có độ dài đường sinh bằng

2a

và chiều cao bằng

3a

. Thể tích khối nón đã cho

bằng

A.



3

a

. B.



3

2

3

a

. C.



3

a

. D.



3

2

3

a

.

Câu 7: Cho hình lập phương

   

.ABCD A B C D

có cạnh

a

. Một hình nón có đỉnh là tâm của hình vuông

ABCD

và đáy là hình tròn nội tiếp hình vuông

   

A B C D

. Kết quả diện tích toàn phần

tp

S

của

hình nón đó bằng

 





2

4

a

bc

với

b

và

c

là hai số nguyên dương và

 1b

. Tính

bc

.

A.

 7bc

. B.

 15bc

. C.

 8bc

. D.

 5bc

.

Câu 8: Cho hình vuông

ABCD

cạnh bằng

2

. Gọi

M

là trung điểm

AB

. Cho tứ giác

AMCD

và các

điểm trong của nó quay quanh trục

AD

ta được một khối tròn xoay. Tính thể tích khối tròn xoay

đó.

A.



7

3

. B.



7

6

. C.



14

3

. D.



14

9

.

Câu 9: Cho hình nón có bán kính đáy bằng

2

cm, góc ở đỉnh bằng

60

. Tính thể tích của khối nón đó.

a

2

3a

2

1

2

3

a

2

1

3

2

a

2

1

3

a

BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

371

A.



3

83

9

cm

. B.



3

83cm

. C.



3

83

3

cm

. D.



3

8

3

cm

.

Câu 10: Gọi

()H

là hình tròn xoay thu được khi cho tam giác đều

ABC

có cạnh

a

quay quanh

AB

, tính

thể tích khối tròn xoay giới hạn bởi

( ).H

A.



3

4

a

. B.



3

8

a

. C.



3

12

a

. D.



3

6

a

.

Câu 11: Gọi

()H

là hình tròn xoay thu được khi cho tam giác đều

ABC

có cạnh

a

quay quanh

AB

, tính

thể tích khối tròn xoay giới hạn bởi

( ).H

A.



3

4

a

. B.



3

8

a

. C.



3

12

a

. D.



3

6

a

.

Câu 12: Cho hình hộp chữ nhật

có , , . Thể tích khối nón có

đỉnh trùng với tâm của hình chữ nhật , đường tròn đáy ngoại tiếp là

A. . B. . C. . D. .

Câu 13: Thể tích của khối nón có thiết diện qua trục là tam giác đều cạnh a bằng

A.



3

48

a

. B.



3

24

a

. C.



3

8

a

. D.



3

.

12

a

Câu 14: Cho tam giác

ABC

vuông tại

A

,

6 , 8AB cm AC cm

. Gọi

1

V

là thể tích khối nón tạo thành khi

quay tam giác

ABC

quanh cạnh

AB

và

2

V

là thể tích khối nón tạo thành khi quay tam giác

ABC

quanh cạnh

AC

. Khi đó, tỷ số

1

2

V

bằng:

A.

3

4

. B.

4

3

. C.

16

9

. D.

9

16

.

Câu 15: Cho hình lăng trụ đều và một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt đáy của hình

lăng trụ. Gọi

12

,VV

lần lượt là thể tích khối lăng trụ và khối trụ. Tính

1

2

V

A.



32

4

. B.



35

4

. C.



52

4

. D.



33

4

.

Câu 16: Cắt hình nón

 

N

bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một tam giác đều

cạnh

2a

. Thể tích khối cầu ngoại tiếp hình nón

 

N

theo

a

là

A.



3

32 3

27

a

. B.



3

43a

. C.



3

16 2

27

a

. D.



3

43

27

a

.

Câu 17: Cho hình thang cân

ABCD

,

//AB CD

,

 6AB cm

,

 2CD cm

,

13AD BC cm

. Quay hình

thang

ABCD

xung quanh đường thẳng

AB

ta được một khối tròn xoay có thể tích là

A.

 



3

18 cm

. B.

 



3

30 cm

. C.

 



3

24 cm

. D.

 



3

12 cm

.

.ABCD A B C D

   

AB a

2AD a

3AA a





ABCD

A B C D

   

3

15

4

a



3

5

4

a



3

15 a



3

5 a



CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

372

Câu 18: Cho hình nón có đỉnh

S

, đáy là đường tròn tâm

O

sao cho

 5SO a

, một mặt phẳng



()

cắt

mặt nón theo hai đường sinh

, SA SB

. Biết khoảng cách từ

O

đến mặt phẳng



()

bằng

25

và

diện tích tam giác

SAB

bằng

360

. Thể tích khối nón bằng:

A.



1325 5

. B.



265 5

. C.

1325 5

. D.

265 5

.

Câu 19: Một hình hộp đứng có đáy là hình vuông chứa đồng hồ cát như hình vẽ. Tỉ số thể tích của đồng

hồ cát và phần còn lại giữa đồng hồ cát và hình hộp đứng là

A.



24 2

. B.



6

. C.



24

. D.



12

.

Câu 20: Cho khối nón

 

N

có chiều cao

 20h

cm, bán kính đáy

 25r

cm. Gọi

 



là mặt phẳng đi qua

đỉnh của

 

N

và cách tâm của mặt đáy

12

cm. Khi đó

 



cắt

 

N

theo một thiết diện có diện

tích là

A.

 300S

cm

2

. B.

 500S

cm

2

. C.

 406S

cm

2

. D.

 400S

cm

2

.

Câu 21: Cho hình trụ có hai đáy là hai đường tròn

 

;OR

và

 

';OR

, chiều cao bằng đường kính đáy. Trên

đường tròn đáy tâm

O

lấy điểm

A

, trên đường tròn đáy tâm

'O

lấy điểm

B

. Thể tích của khối

tứ diện

'OO AB

có giá trị lớn nhất bằng:

A.

3

2

R

. B.

3

R

. C.

3

6

R

. D.

3

R

.

Câu 22: Cho

ABC

đều cạnh

a

và nội tiếp trong đường tròn tâm

O

,

AD

là đường kính của đường tròn

tâm

O

. Thể tích của khối tròn xoay sinh ra khi cho phần tô đậm quay quanh đường thẳng

AD

bằng:

A.



3

24

a

. B.



3

20 3

217

a

. C.



3

23 3

216

a

. D.



3

43

27

a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

373

BẢNG ĐÁP ÁN

1.D

2.A

3.D

4.D

5.A

6.A

7.D

8.C

9.C

10..A

11..A

12.B

13.B

14.B

15.D

16.A

17.B

18.A

19.D

20.B

21.D

22.C

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn D

Ta có





2

36 2

xq

S a Rh

.

Do thiết diện qua trục là hình vuông nên ta có

2Rh

.

Khi đó



22

36ha

hay

 6ha

;

 3Ra

.

Diện tích của mặt đáy hình lăng trụ lục giác đều nội tiếp hình trụ là



22

3 27 3

6.

42

Ra

B

.

Thể tích

V

của lăng trụ lục giác đều nội tiếp hình trụ là



3

. 81 3V B h a

.

Câu 2: Chọn A

Ta có:





1

2

1

.

3

N

V R SO

,







2

1

.

3

N

V R SO

.

Mặt khác,



SO A

và

SOB

đồng dạng

nên





R SO

.

Suy ra:

  



  





2

1

3

2

.1

8

.

N

V

R SO SO

V SO

R SO

Suy ra



   

11

.40 20cm

22

SO

.

Câu 3: Chọn D

Do đáy hình chóp là tam giác đều nên bán kính đáy của hình nón

Đường sinh của hình nón có độ dài bằng cạnh của hình tứ diện đều

Vậy diện tích xung quanh hình nón là

Câu 4: Chọn D

Gọi

O

và



O

lần lượt là tâm đường tròn ngoại tiếp

ABC

và

  

A B C

.

3

ra

2

33

. .l . .

33

r a a a

a

O'

O

60

o

C'

B'

A'

C

B

A

R

R'

A

O

B

O'

S

CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

374

Do

  

.ABC A B C

là lăng trụ tam giác đều nên

ABC

là tam giác đều và

 



B B ABC

.



Góc giữa



AB

và mặt phẳng

 

ABC

chính là góc giữa



AB

và

AB

hay



60B AB

.



   .tan 60 3BB AB a

.

Lại có

ABC

là tam giác đều cạnh

a

nên



2 3 3

.

3 2 3

aa

OA

.

Mặt khác, hình trụ ngoại tiếp lăng trụ tam giác đều

  

.ABC A B C

có đường cao là



BB

, bán kính

đáy là

OA

.

Vậy thể tích khối trụ ngoại tiếp lăng trụ

  

.ABC A B C

là:









  





2

3

2

33

. . . . 3

33

aa

V OA BB a

.

Câu 5: Chọn A

Gọi khối nón đã cho có

S

là đỉnh,

O

là tâm đáy,

đường sinh

SA

. Ta có

 2SA a

,

OA a

.

 

    

2

2 2 2

23SO SA OA a a a

.

Thể tích của khối nón là:





  

3

22

1 1 3

. . . 3. .

3 3 3

a

V SO OA a a

.

Câu 6: Chọn A

Giả sử khối nón có đỉnh

S

, đường tròn đáy tâm

O

và bán kính

R OA

.

Ta có tam giác

SOA

vuông tại

O

nên

 

     

2

22

23R OA SA SO a a a

.

Thể tích khối nón là





  

3

22

1 1 3

. . 3

3 3 3

a

V R h a a

.

Câu 7: Chọn D

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

375

Hình nón có đáy là hình tròn nội tiếp hình vuông

   

A B C D

có cạnh là

a

nên đáy của hình nón là

hình tròn có bán kính



2

a

r

.

Hình nón có đỉnh là tâm của hình vuông

ABCD

nên chiều cao của hình nón bằng độ dài cạnh của

hình vuông. Suy ra:

ha

.

Khi đó: độ dài đường sinh của hình nón là:



     





2

2 2 2

55

.

2 4 2

a a a

l h r a

Diện tích toàn phần của hình nón là:

 







     





2

5

( ) 1 5

2 2 2 4

tp

a a a a

S r r l

.

Suy ra:

   5; 1 5b c bc

.

Câu 8: Chọn C

Cách 1

Gọi

S CM DA

. Vì

M

là trung điểm của

AB

, mà













//

1

2

AM CD

nên

AM

là đường trung

bình của

SCD

 A

là trung điểm của

SD

  24SD AD

.

Khi cho tứ giác

AMCD

và các điểm trong của nó quay quanh trục

AD

thì ta được một khối nón

cụt có chiều cao

 2AD

, hai đáy là hai đường tròn có bán kính lần lượt là



1

2R CD

,



2

1R AM

và có thể tích là

V

.

Tam giác

SCD

và các điểm trong của nó quay quanh trục

SD

sẽ tạo thành một khối nón tròn

xoay có chiều cao

 4SD

, bán kính đáy



1

2R CD

nên có thể tích là





2

11

1 16

.

33

V R SD

.

CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

376

Tam giác

SAM

và các điểm trong của nó quay quanh trục

SD

tạo thành một khối nón tròn xoay

có chiều cao

 2SA

, bán kính đáy



2

1R AM

nên có thể tích là





2

22

12

.

33

V R SA

.

Ta có



12

V V V





14

3

.

Cách 2 :

Áp dụng công thức tính nhanh thể tích khối nón cụt có chiều cao

h

, hai bán kính đáy là

12

,RR

 



  

22

1 2 1 2

1

.

3

V R R R R h

 



   

1 14

4 1 2 .2

33

.

Câu 9: Chọn C

Cắt hình nón bởi một mặt phẳng đi qua trục, ta được thiết diện là tam giác

ABC

cân tại đỉnh

A

của hình nón.

Do góc ở đỉnh của hình nón là

60BAC

, suy ra

30HAC

. Bán kính đáy

2R HC

cm.

Xét

AHC

vuông tại

H

, ta có



tan 30

HC

AH



2

1

3

 23

cm.

Thể tích của khối nón:





2

1

.

3

V R AH





83

3

cm

.

Câu 10: Chọn A

Khi cho tam giác đều

ABC

có cạnh

a

quay quanh

AB

ta thu được hai khối nón có cùng chiều

cao



22

AB a

h

và cùng bán kính đáy



3

.

2

B

a

rh

Do đó











2

3

13

2. . . .

3 2 2 4

a a a

V

Câu 11: Chọn A

Khi cho tam giác đều

ABC

có cạnh

a

quay quanh

AB

ta thu được hai khối nón có cùng chiều

cao



22

AB a

h

và cùng bán kính đáy



3

.

2

B

a

rh

Do đó











2

3

13

2. . . .

3 2 2 4

a a a

V

.

Câu 12: Chọn B

A

B

C

H

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

377

Gọi lần lượt là tâm hình chữ nhật và hình chữ nhật .

Ta có đường cao khối nón ; bán kính .

Vậy thể tích khối nón đã cho là .

Câu 13: Chọn B

Kí hiệu

,,h l r

lần lượt là độ dài đường cao, độ dài đường sinh và bán kính đáy của hình nón.

Theo giả thiết ta có







     









2

2 2 2

1

3

.

22

42

a

r MN

aa

h l r a

l SM a

Vậy





  

23

2

1 1 3 3

..

3 3 4 2 24

a a a

V r h

.

Câu 14: Chọn B

O'

C

A

C'

A'

D

B'

D'

B

O

,OO



ABCD

A B C D

   

3h OO AA a



  

 

2

15

2

22

a

r A O a a



   

2

3

2

1 1 5 5

3

3 3 2 4

aa

V r h a







  





h

=

CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

378

Ta có công thức tính thể tích khối nón có chiều cao

h

và bán kính

r

là





2

1

3

V r h

Khi quay tam giác

ABC

quanh cạnh

AB

thì:

6h AB cm

và

8r AC cm

thì





2

1

.8 .6 128

3

V

Khi quay tam giác

ABC

quanh cạnh

AC

thì:

8h AC cm

và

6r AB cm

thì





2

1

.6 .8 96

3

V

. Vậy:



1

2

4

3

V

Câu 15: Chọn D

Giả sử lăng trụ đều có cạnh đáy là a, chiều cao h. Khi đó, bán kính đáy của hình trụ là



2 3 3

.

3 2 3

aa

R

. Do đó,





2

1

2

3

.

33

4

..

3

a

h

V

a

h

.

Cách khác : đặc biệt hóa lăng trụ đã cho thành lăng trụ có tất cả các cạnh cùng bằng 1. Khi đó,











1

2

3

33

4

1

3

V

Câu 16: Chọn A

Giả sử thiết diện là tam giác

SAB

, với

S

là đỉnh của hình nón.

Gọi

,MN

lần lượt là trung điểm

, AB SA

.

Khi đó tâm mặt cầu ngoại tiếp hình nón nằm trên đường thẳng

SM

.

B'

C'

A'

B

C

A

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

379

Gọi

I

là trọng tâm tam giác

SBC

thì

IA IS

nên

I

là tâm mặt cầu ngoại tiếp hình nón

 

N

.

Bán kính mặt cầu là

   

2 2 3 2

. .2

3 3 2

3

a

R IS SM a

, từ đó thể tích khối cầu là:







  





3

4 4 2 32 3

..

3 3 27

3

aa

VR

.

Câu 17: Chọn B

Kẻ

 ,DH AB

CK AB

với

,H K AB

. Suy ra

 2HK cm

.

Do

ABCD

là hình thang cân,

 6AB cm

,

 2CD cm

nên

2AH BK cm

.

Do

 ,ADH

BCK

vuông nên

   13 4 3DH CK cm

.

Đoạn

DH

quay xung quanh

AB

tạo thành hình tròn

 

1

C

tâm

H

, bán kính



1

3R HD cm

.

Đoạn

CK

quay xung quanh

AB

tạo thành hình tròn

 

2

C

tâm

K

, bán kính



2

3R CK cm

.

Gọi

 

1

V

là thể tích khối nón đỉnh

A

, đáy là hình tròn

 

1

C

.

Gọi

 

2

V

là thể tích khối nón đỉnh

B

, đáy là hình tròn

 

2

C

.

Gọi

 

3

V

là thể tích khối trụ chiều cao

HK

và hai đáy là hai hình tròn

 

1

C

,

 

2

C

.

Ta có:

 

  

   

2 2 3

12

11

. . .3 .2 6

33

V V DH AH cm

.

 

  

  

2 2 3

3

. . .3 .2 18V DH HK cm

.

Khi hình thang

ABCD

quay xung quanh đường thẳng

AB

ta được một khối tròn xoay có thể tích

là:

 

   

      

3

1 2 3

6 6 12 30V V V V cm

.

Câu 18: Chọn A

I

O

S

A

B

H

CHUYÊN ĐỀ : KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

380

Kẻ

 



    , ,( ) 2 5OI AB OH SI OH d O

   

       

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 2

45

2 5 6 5

OH SO OI OI OH SO



3 10

2

OI

 



    





2

22

3 10 9 10

65

22

SI SO OI

     







1 360

. . . 8 10

2

9 10

2

SAB

S

S SI AB SI IA IA

SI

 



    





2

22

3 10 5 106

8 10

22

r OI IA











2

1 5 106

. . .6 5 1325 5

32

V

Câu 19: Chọn D

Gọi

     

,,

H DH CL

V V V

lần lượt là thể tích của hộp đứng, đồng hồ cát và phần còn lại.

Cho cạnh đáy hộp bằng 6, chiều cao hộp bằng 8. Đồng hồ cát tạo bởi 2 nón bằng nhau và chiều

cao nón bằng 4 ; bán kính đáy nón bằng 3 .

Ta có:

 



2

8.6 288

H

V

;

 





2

1

2. .4. .3 24

3

DH

V

;

     



   288 24

CL H DH

V V V

.

Theo đề thì đáp án bằng

 







24

288 24 12

DH

CL

V

.

Câu 20: Chọn B

Gọi

,SO

lần lượt là đỉnh và tâm đường tròn đáy của khối nón

 

N

.

Ta có mặt phẳng

 



cắt đường tròn đáy tâm

O

tại 2 điểm

,AB

.

Vậy mặt phẳng

 



cắt khối nón theo một thiết diện là

SAB

.

Kẻ

OI AB

,

OH SI

Ta có

 





   







OI AB

AB SOI AB OH

SO AB

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

381

Ta có

   







    









, 12

AB OH

OH SAB d O SAB OH

SI OH

cm.

Áp dụng hệ thức lượng cho

SOI

vuông tại

O

có đường cao

OH

     



2 2 2

2 2 2 2

1 1 1 1 1

15

1 1 1 1

12 20

OI

OH OI SO

OH SO

cm.

Xét

AOI

vuông tại

I

có:

       

2 2 2 2 2 2 2

25 15 20IA OI AO IA AO OI

cm.

Xét

SOI

vuông tại

O

có:

       

2 2 2 2 2 2 2

20 15 25SO IO SI SI SO IO

cm.

Vậy

   

1

. . 25.20 500

2

SAB

S SI AB S I IA

cm

2

.

Câu 21: Chọn D

Có

   

3

2

' ' ' ' ' '

1 1 1

2 . .sin '

2 3 6 3

BOO A BOO AA OAB O A B

R

V V V R R AOA





3

'

max

3

BOO A

R

V

.

Câu 22: Chọn C

Gọi thể tích của khối tròn xoay sinh ra do phần tô đậm quay quanh đường thẳng

AD

là

1

V

.

Gọi Thể tích của khối tròn xoay sinh ra do hình tam giác

ABC

quay quanh đường thẳng

AD

là

2

V

.

Gọi Thể tích của khối tròn xoay sinh ra do hình tròn đường kính

AD

quay quanh đường thẳng

AD

là

3

V

.

Khi đó:



   



      





3

2

3

32

1 3 2

4 1 4 3 1 3 23 3

. . . . . . . .

3 3 3 3 3 2 2 216

a a a a

V V V OA HC AH

.

A'

B'

O

O'

G

H

J

I

B

A

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

382

DẠNG 3: CỰC TRỊ VÀ TOÁN THỰC TẾ VỀ KHỐI TRÒN XOAY

Câu 1: Thể tích khối nón có bán kính đáy bằng

2a

và chiều cao bằng

3a

là

A.



3

4 a

. B.



3

12 a

. C.



3

2 a

. D.



3

a

.

Câu 2: Mặt tiền của một ngôi biệt thự có 8 cây cột trụ tròn, tất cả đều có chiều cao

4,2

m. Trong số các

cây đó có hai cây cột trước đại sảnh đường kính bằng

40

cm, sáu cây cột còn lại phân bổ đều hai

bên đại sảnh và chúng đều có đường kính bằng

26

cm. Chủ nhà thuê nhân công để sơn các cây

cột bằng một loại sơn giả đá, biết giá thuê là

2

380.000 / 1m

. Hỏi người chủ phải chi ít nhất bao

nhiêu tiền để sơn hết các cây cột nhà đó ?

A.

 15.642.000

. B.

 12.521.000

. C.

 10.400.000

. D.

 11.833.000

.

Câu 3: Lượng nguyên liệu cần dùng để làm ra một chiếc nón lá được ước lượng qua phép tính diện tích

xung quanh của mặt nón. Cứ

1kg

lá dùng để làm nón có thể làm ra số nón có tổng diện tích xung

quanh là

2

6,13m

. Hỏi nếu muốn làm ra

1000

chiếc nón lá giống nhau có đường kính vành nón

50cm

, chiều cao

30cm

thì cần khối lượng lá gần nhất với con số nào dưới đây?

A.

50kg

. B.

76kg

. C.

48kg

. D.

38kg

.

Câu 4: Người ta ngâm một loại rượu trái cây bằng cách xếp 6 trái cây hình cầu có cùng bán kính bằng

5cm vào một cái bình hình trụ sao cho hai quả nằm cạnh nhau tiếp xúc với nhau, các quả đều tiếp

xúc với tất cả các đường sinh của mặt xung quanh của hình trụ, đồng thời quả nằm bên dưới cùng

tiếp xúc với mặt đáy trụ, quả nằm bên trên cùng tiếp xúc với nắp của hình trụ, cuối cùng là đổ

rượu vào đầy bình. Số lít rượu tối thiểu cần đổ vào bình gần nhất với số nào sau đây:

A.

1,57

. B.

1,7

. C.

1570

. D.

1,2

.

Câu 5: Một khối đồ chơi gồm một khối trụ và một khối nón có cùng bán kính được chồng lên nhau, độ

dài đường sinh khối trụ bằng độ dài đường sinh khối nón và bằng đường kính của khối trụ, khối

nón . Biết thể tích của toàn bộ khối đồ chơi là

3

50 cm

, thể tích khối trụ gần với số nào nhất trong

các số sau

A.

3

36,5 cm

. B.

3

40,5 cm

. C.

3

38,2 cm

. D.

3

38,8 cm

.

Câu 6: Một con quạ bị khát nước, nó tìm thấy một bình đựng nước hình trụ, do mức

nước trong bình chỉ còn lại hai phần ba so với thể tích của bình nên nó không

thể thò đầu vào uống nước được. Nó liền gắp 3 viên bi ve hình cầu để sẵn bên

cạnh bỏ vào bình thì mực nước dâng lên vừa đủ đầy bình và nó có thể uống

nước. Biết 3 viên bi ve hình cầu đều có bán kính là 1cm và chiều cao của bình

hình trụ gấp 8 lần bán kính của nó. Diện tích xung quanh của bình hình trụ

nói trên gần với số nào nhất trong các số sau?

A.

2

65,8cm

. B.

2

61,6cm

.

C.

2

66,6cm

. D.

2

62,3cm

.

Câu 7: Người ta làm một dụng cụ sinh hoạt gồm hình nón và hình trụ như hình vẽ . Cần bao nhiêu

2

m

vật liệu để làm ?

BÀI TẬP RÈN LUYỆN

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

A.

2

5,6m

. B.

2

6,6m

. C.

2

5,2m

. D.

2

4,5m

.

Câu 8: Một khối đồ chơi gồm một khối hình trụ

()T

gắn chồng lên một khối hình nón

()N

, lần lượt có

bán kính đáy và chiều cao tương ứng là

1 1 2 2

, , ,r h r h

thỏa mãn



2 1 1 2

2 , 2r r h h

. Biết rằng thể tích

của khối nón

()N

bằng

3

20cm

. Thể tích của toàn bộ khối đồ chơi bằng

A.

3

140 cm

. B.

3

120 cm

. C.

3

30cm

. D.

3

50cm

.

Câu 9: Khi sản xuất hộp mì tôm các nhà sản xuất luôn để một khoảng trống dưới đáy hộp. Hình vẽ dưới

mô tả cấu trúc của hộp mì tôm. Thớ mì tôm có dạng hình trụ, hộp mì có dạng hình nón cụt được

cắt ra bởi hình nón có chiều cao

9cm

và bán kính đáy

6cm

. Nhà sản xuất tìm cách sao cho thớ

mì tôm có được thể tích lớn nhất vì mục đích thu hút khách hàng. Tìm thể tích lớn nhất đó.

A.



48

. B.



81

2

. C.



36

. D.



54

.

Câu 10: Tại trung tâm một thành phố người ta tạo điểm nhấn bằng cột trang trí hình nón có kích thước như

sau: chiều dài đường sinh

 10ml

, bán kính đáy

 5mR

. Biết rằng tam giác

SAB

là thiết diện

qua trục của hình nón và

C

là trung điểm

SB

. Trang trí một hệ thống đèn điện tử chạy từ

A

đến

C

trên mặt nón. Xác định giá trị ngắn nhất của chiều dài dây đèn điện tử.

A.

10m

. B.

15m

. C.

5 5 m

. D.

5 3 m

.

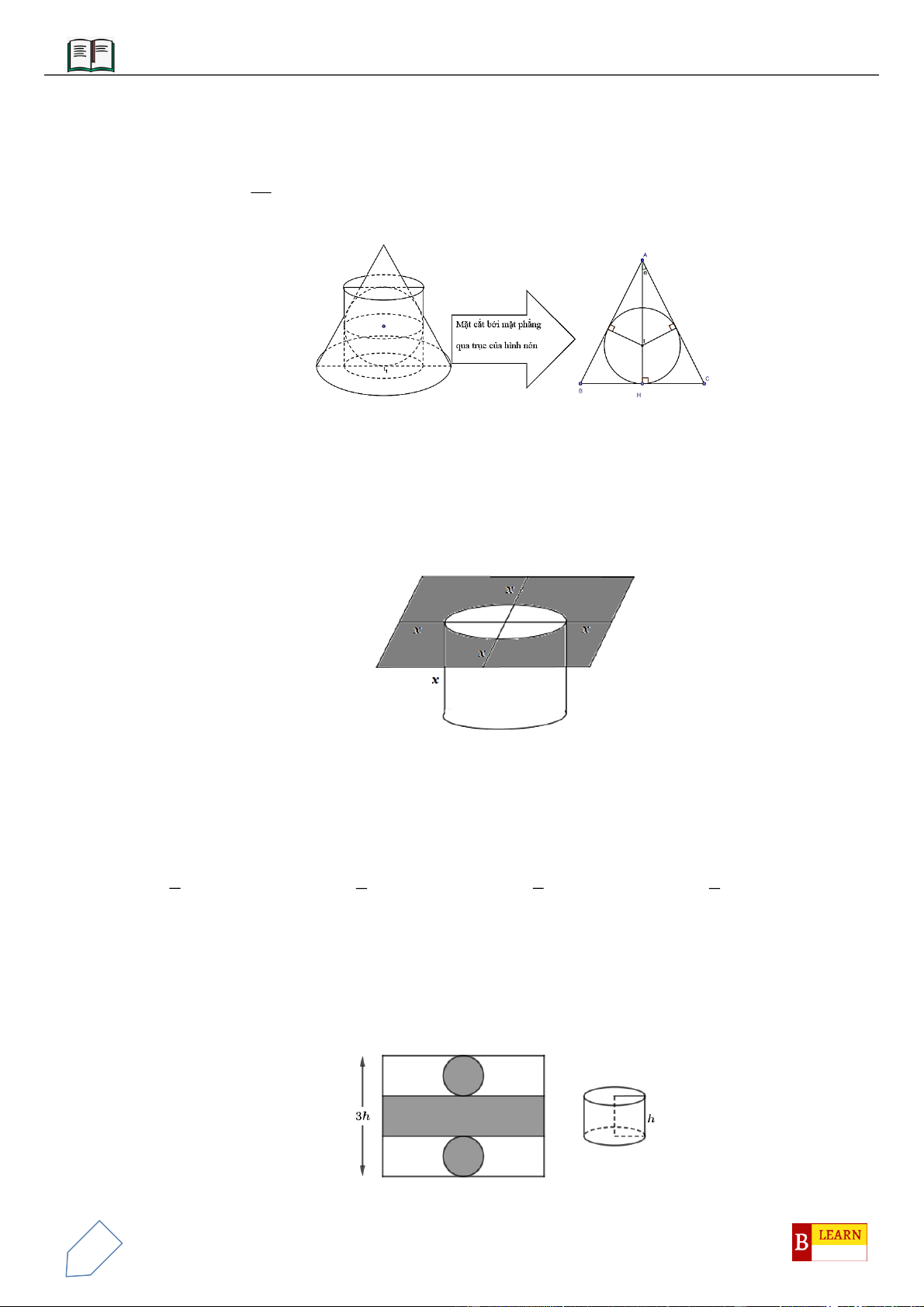
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

384

Câu 11: Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là



2

, bán kính đáy là

R

và chiều

cao là

h

. Một hình trụ ngoại tiếp hình cầu đó có đáy dưới nằm trong mặt phẳng đáy của hình nón

. Gọi

12

,VV

lần lượt là thể tích của hình nón và hình trụ, biết rằng



12

VV

. Gọi

M

là giá trị lớn

nhất của tỉ số

2

1

V

. Giá trị của biểu thức

48 25PM

thuộc khoảng nào dưới đây?

A.

(40;60)

. B.

(60;80)

. C.

(20;40)

. D.

(0;20)

.

Câu 12: Trên một mảnh đất hình vuông có diện tích

2

81m

người ta đào một cái ao nuôi cá hình trụ sao

cho tâm của hình tròn đáy trùng với tâm của mảnh đất. Ở giữa mép ao và mép mảnh đất người ta

để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao và mép mảnh đất là

 

xm

. Giả sử chiều sâu của ao cũng là

 

xm

. Tính thể tích lớn nhất

V

của ao.

A.

 





3

13,5V cm

. B.

 





3

27V cm

. C.

 





3

36V cm

. D.

 





3

72V cm

.

Câu 13: Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng

1

, chiều cao bằng

2

. Người ta khoét từ hai

đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối

cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là

A.

2

3

. B.

1

4

. C.

1

3

. D.

1

2

.

Câu 14: Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng

cách cắt ra hai hình tròn bằng nhau và một hình chữ nhật sau đó hàn kín lại, như trong hình vẽ

dưới đây. Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh của thùng đựng

dầu . Biết thùng đựng dầu có thể tích bằng

50,24

lít . Diện tích của tấm thép hình chữ nhật ban

đầu gần với giá trị nào sau đây nhất?

A.

 

2

1,2 m

. B.

 

2

1,8 m

. C.

 

2

2,2 m

. D.

 

2

1,5 m

.

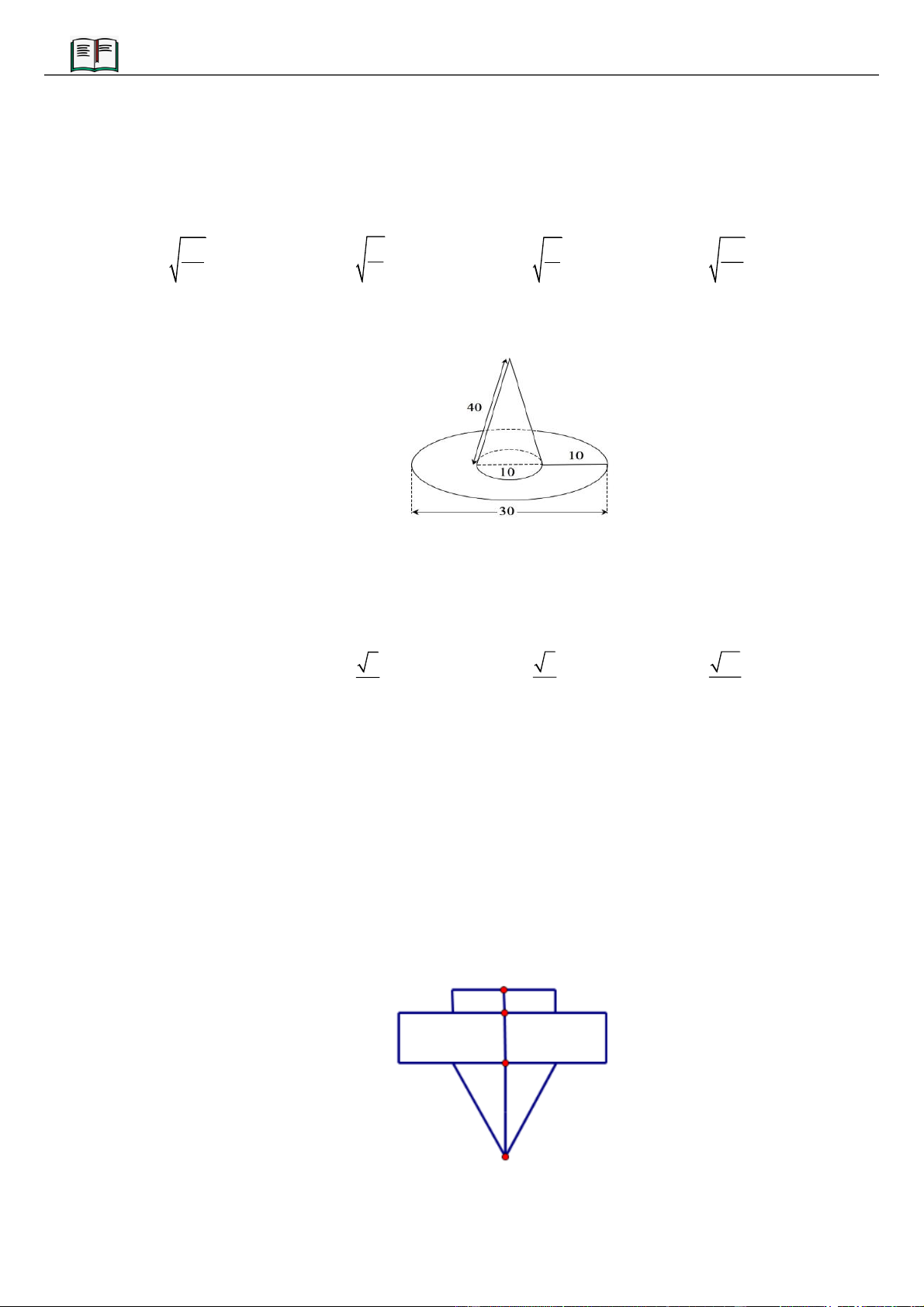
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Câu 15: Một thùng đựng nước hình trụ có bán kính đáy là

65cm

và chiều cao

160cm

. Hỏi thùng đó đựng

được tối đa bao nhiêu lít nước?

A.

 

10400 l

. B.

 

676 l

. C.

 

3265,6 l

. D.

 

2123,7 l

.

Câu 16: Cần sản xuất một vỏ hộp sữa hình trụ có thể tích

V

cho trước. Để tiết kiệm vật liệu nhất thì bán

kính đáy phải bằng

A.



3

2

V

. B.

3

2

V

. C.



3

V

. D.



3

V

.

Câu 17: Tính diện tích vải tối thiểu để may được chiếc mũ có hình dạng và kích thước được cho bởi hình

vẽ bên biết phía trên có dạng hình nón và phía dưới có dạng hình vành khăn.

A.

450π

. B.

500π

. C.

350π

. D.

400π

.

Câu 18: Cho hình trụ có bán kính bằng

r

và chiều cao cũng bằng

r

. Một hình vuông

ABCD

có hai cạnh

,AB CD

lần lượt là các dây cung của hai đường tròn đáy, còn cạnh

,BC AD

không phải là đường

sinh của hình trụ. Tan của góc giữa mặt phẳng chứa hình vuông và mặt đáy bằng

A.

1

. B.

6

2

. C.

6

3

. D.

15

5

.

Câu 19: Một ngôi biệt thự có 10 cây cột nhà hình trụ tròn, tất cả đều có chiều cao 4,2m. Trong đó, 4 cây

cột trước đại sảnh có đường kính 40cm và 6 cây cột còn lại bên thân nhà có đường kính 26cm.

Chủ nhà dùng loại sơn giả đá để sơn 10 cây cột đó. Nếu giá của một loại sơn giả đá là 380.000

đồng/m2 thì người chủ phải chi ít nhất bao nhiêu tiền để sơn 10 cây cột đó? .

A. 14.647.000. B. 13.627.000 . C. 16.459.000 . D. 15.844.000.

Câu 20: Một con xoay được thiết kế gồm hai khối trụ

1

()T

,

2

()T

chồng lên khối nón

(N)

. Khối trụ

1

()T

có

bán kính đáy

()r cm

, chiều cao

1

()h cm

. Khối trụ

2

()T

có bán kính đáy

2 ( )r cm

, chiều cao



21

2 ( )h h cm

. Khối nón

(N)

có bán kính đáy

()r cm

, chiều cao



1

4 ( )

n

h h cm

. Biết rằng thể tích

toàn bộ con xoay bằng

3

31( )cm

. Thể tích khối nón

(N)

bằng

A.

3

5( )cm

. B.

3

3( )cm

. C.

3

4( )cm

. D.

3

6( )cm

.

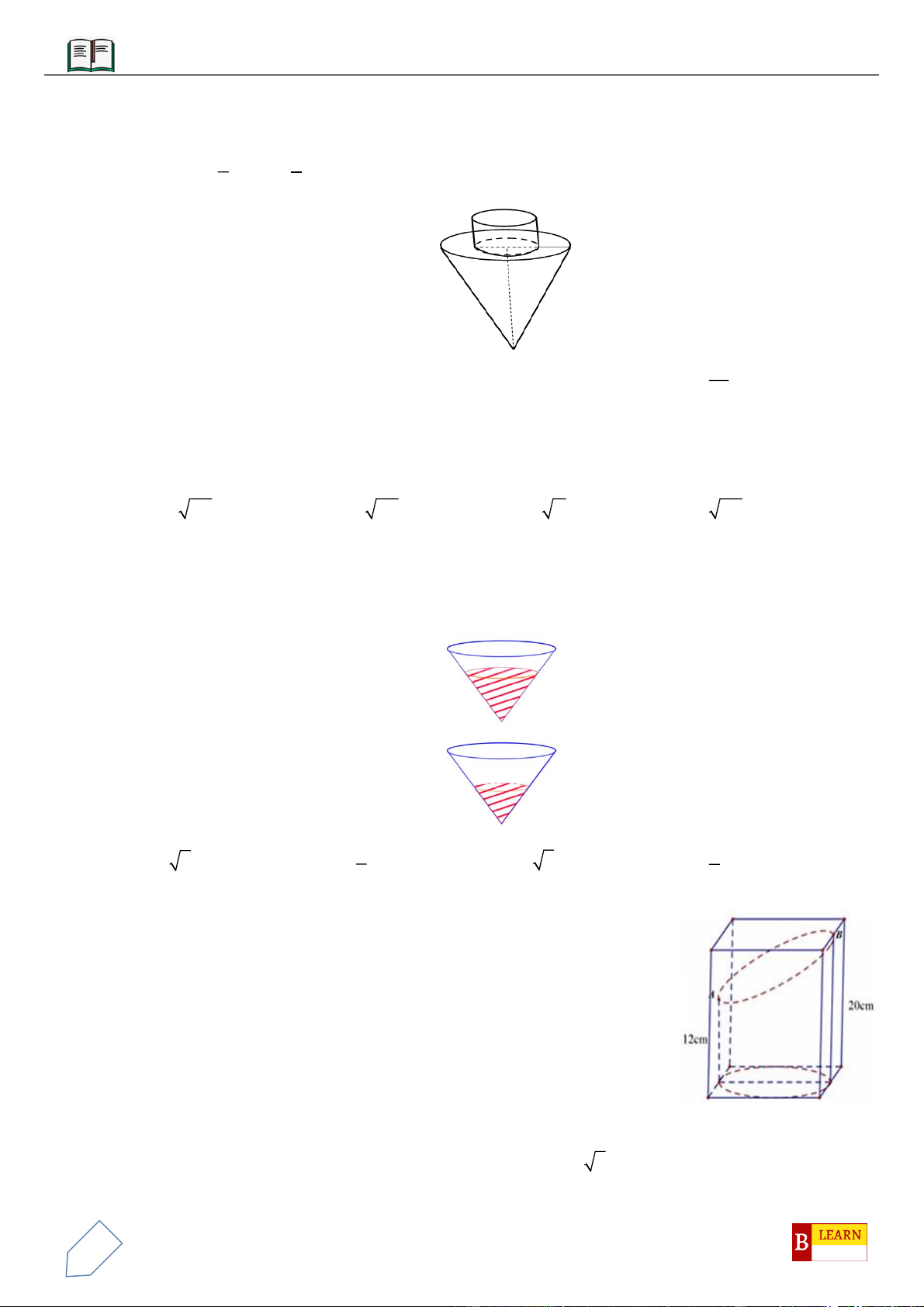
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

386

Câu 21: Một cái “cù” gồm hai khối: khối trụ

1

H

và khối nón

2

H

như hình bên. Chiều cao và bán kính

khối trụ lần lượt bằng

1

h

,

1

r

chiều cao và bán kính đáy của khối nón lần lượt bằng

2

h

,

2

r

thỏa

mãn



12

1

3

hh

,



12

1

2

rr

. Biết thể tích toàn khối là

3

30cm

, thể tích khối

1

H

bằng

A.

3

15cm

. B.

3

6cm

. C.

3

5cm

. D.

3

30

13

cm

.

Câu 22: Một nhà máy sản xuất bột trẻ em cần thiết kê bao bì cho một loại sản phẩm mới dạng khối trụ có

thể tích

3

1 dm

. Hỏi phải thiết kế hộp đựng này với diện tích toàn phần bằng bao nhiêu để tiết

kiệm nguyên vật liệu nhất.

A.



2

3

3 2 dm

. B.



2

3 2 dm

. C.



2

3

3 dm

. D.



2

3

4 dm

Câu 23: Hai hình nón bằng nhau có chiều cao bằng

2 dm

, được đặt như hình vẽ bên . Lúc đầu, hình nón

trên chứa đầy nước và hình nón dưới không chứa nước. Sau đó, nước được chảy xuống hình nón

dưới thông qua lỗ trống ở đỉnh của hình nón trên. Hãy tính chiều cao của nước trong hình nón

dưới tại thời điểm khi mà chiều cao của nước trong hình nón trên bằng

1

dm

.

A.

3

7

. B.

1

3

. C.

3

5

. D.

1

2

.

Câu 24: Một khúc gỗ hình trụ có bán kính

R

bị cắt bởi một mặt phẳng không

song song với đáy ta được thiết diện là một hình elip. Khoảng cách từ

điểm

A

đến mặt đáy là

12 cm

khoảng cách từ điểm

B

đến mặt đáy là

20 cm

. Đặt khúc gỗ đó vào trong hình hộp chữ nhật có chiều cao bằng

20 cm

chứa đầy nước sao cho đường tròn đáy của khúc gỗ tiếp xúc với

các cạnh đáy của hình hộp chữ nhật. Sau đó, người ta đo lượng nước

còn lại trong hình hộp chữ nhật là

2

lít. Tính bán kính của khúc gỗ

A. R = 5,2 cm. B. R = 4,8 cm. C. R = 6,4

cm. D. R = 8,2 cm.

Câu 25: Một khối nón có bán kính đáy bằng

2 cm

, chiều cao bằng

3 cm

. Một mặt phẳng đi qua đỉnh và

tạo với đáy một góc

0

60

chia khối nón làm

2

phần. Tính thể tích

V

phần nhỏ hơn .

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

A.



3

1,42cmV

. B.



3

2,36cmV

. C.



3

1,53cmV

. D.



3

2,47 cmV

.

Câu 26: Một quả tạ tập tay gồm ba khối trụ

 

1

H

,

 

2

H

,

 

3

H

gắn liền nhau lần lượt có bán kính và chiều

cao tương ứng là

11

,rh

,

22

,rh

,

33

,rh

thỏa mãn



13

rr

,



13

hh

;



21

1

3

rr

. Biết thể tích của toàn bộ

quả tạ bằng



60

và chiều dài quả tạ bằng

9

. Thể tích khối trụ

 

2

H

bằng?

A.

 







1

16 9 2

49

h

. B.

 







1

36 9 2

49

h

C.

 







1

60 9 2

49

h

D.

 







1

46 9 2

49

h

Câu 27: Một bình đựng nước dạng hình nón đựng đầy nước. Người ta thả vào đó một khối cầu có đường

kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là



3

18 dm

.Biết khối

cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu chìm trong nước.

Tính thể tích nước còn lại trong bình.

A.



3

27 dm

. B.



3

6 dm

. C.



3

9 dm

. D.



3

24 dm

.

Câu 28: Một ly nước hình trụ có chiều cao

20 cm

và bán kính đáy bằng

4 cm

. Bạn Nam đổ nước vào ly

cho đến khi mực nước cách đáy ly

17 cm

thì dừng lại. Sau đó, Nam lấy các viên đá lạnh hình cầu

có cùng bán kính

2 cm

thả vào ly nước. Bạn Nam cần dùng ít nhất bao nhiêu viên đá để nước trào

ra khỏi ly?

A. 4. B. 7. C. 5. D. 6.

Câu 29: Khi cắt hình nón có chiều cao

16 cm

và đường kính đáy

24 cm

bởi một mặt phẳng song song với

đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây?

A.

170

. B.

260

. C.

294

. D.

208

.

Câu 30: Cho tam giác

SAB

vuông tại

A

,

60ABS

. Phân giác của góc

ABS

cắt

SA

tại

I

. Vẽ nửa

đường tròn tâm

I

, bán kính

IA

. Cho miền tam giác

SAB

và nửa hình tròn quay xung quanh trục

SA

tạo nên các khối tròn xoay thể tích tương ứng là

12

;VV

. Khẳng định nào sau đây đúng?

A.



12

4

9

VV

. B.



12

3

2

VV

. C.



12

3VV

. D.



12

9

4

VV

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

388

Câu 31: Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là

5cm

, chiều

dài lăn là

23cm

. Sau khi lăn trọn

10

vòng thì trục lăn tạo nên tường phẳng lớp sơn có diện tích

là

A.



2

2300 cm

. B.



2

1150 cm

. C.



2

862,5 cm

. D.



2

5230 cm

.

Câu 32: Người ta thiết kế một thùng chứa hình trụ có thể tích

V

nhất định. Biết rằng giá của vật liệu làm

mặt đáy và nắp của thùng bằng nhau và gấp

1,5

lần so với giá vật liệu để làm mặt xung quanh của

thùng . Gọi chiều cao của thùng là

h

và bán kính đáy là

r

. Tính tỉ số

h

r

sao cho chi phí vật liệu

sản xuất thùng là nhỏ nhất?

A.

 2.

h

r

B.

 3.

h

r

C.

 3.

h

r

D.

 2 3.

h

r

Câu 33: Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là

5m

, có bán kính đáy

1m

, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đ rút dầu trong bồn tương ứng

với

0,5m

của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn .

A.

3

23,562 m

. B.

3

12,637 m

. C.

3

6,319 m

. D.

3

11,781 m

.

Câu 34: Từ một tấm tôn hình chữ nhật có kích thước

5 x40mm

, người ta làm hai thùng nước hình trụ có

cùng chiều cao

5m

, bằng cách cắt tấm tôn đó thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành

mặt xung quanh của một thùng .

Tổng thể tích của hai cái thùng hình trụ bằng

A.



3

1000 ( )m

. B.



3

2000 ( )m

. C.



3

2000

()m

. D.



3

1000

()m

.

5 m

0,5 m

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Câu 35: Một cái phễu có dạng hình nón. Người ta đổ một lượng nước vào phễu sao cho chiều cao của

lượng nước trong phễu bằng một phần ba chiều cao của phễu. Hỏi nếu bịt miệng phễu rồi lộn

ngược phễu lên thì chiều cao của nước bằng bao nhiêu? Biết chiều cao của phễu là

15

cm.

A.

0,5

cm. B.

0,216

cm. C.

0,3

cm. D.

0,188

cm.

Câu 36: Từ một tấm thép phẳng hình chữ nhật, người ta muốn làm một chiếc thùng đựng dầu hình trụ bằng cách

cắt ra hai hình tròn bằng nhau và một hình chữ nhật sau đó hàn kín lại, như hình vẽ dưới đây.

Hai hình tròn làm hai mặt đáy, hình chữ nhật làm thành mặt xung quanh của thùng đựng dầu . Biết

thùng đựng dầu có thể tích bằng

50,24

lít . Tính diện tích của tấm thép hình chữ nhật ban đầu?

A.

2

1,8062m

. B.

2

2,2012 m

. C.

2

1,5072m

. D.

2

1,2064m

.

Câu 37: Người ta xếp ba viên bi có bán kính bằng nhau và bằng

3

vào một cái lọ hình trụ sao cho các

viên bi đều tiếp xúc với hai đáy của lọ hình trụ và các viên bi này đôi một tiếp xúc nhau và cùng

tiếp xúc với các đường sinh của lọ hình trụ. Tính bán kính đáy của lọ hình trụ.

A.

1 2 3

. B.

23

. C.

3 2 3

2

. D.

23

.

Câu 38: Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là

V

, các nhà thiết kế luôn đặt mục tiêu sao cho

chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất.

Muốn thể tích khối trụ bằng

V

và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao

nhiêu?

A.





3

2

V

r

. B.



3

rV

. C.





3

2

V

r

. D.



3

2

V

r

.

Câu 39: Nam muốn xây một bình chứa hình trụ có thể tích

3

72m .

Đáy làm bằng bêtông giá 100 nghìn

đồng

2

/m ,

thành làm bằng tôn giá 90 nghìn đồng

2

/m ,

nắp bằng nhôm giá 140 nghìn đồng

2

/m .

Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

A.

 



3

m.

2

B.

 



3

m.

C.

 



3

m.

D.

 



3

2

m.

Câu 40: Một công ty sản xuất một loại cốc giấy hình nón không nắp có thể tích 27cm

3

. Với chiều cao h

và bán kính đáy là r. Tìm r để lượng giấy tiêu thụ ít nhất

A.

 





6

2

3

2

r cm

. B.

 





6

4

2

3

2

r cm

. C.

 





8

6

2

3

2

r cm

. D.

 





8

4

2

3

2

r cm

.

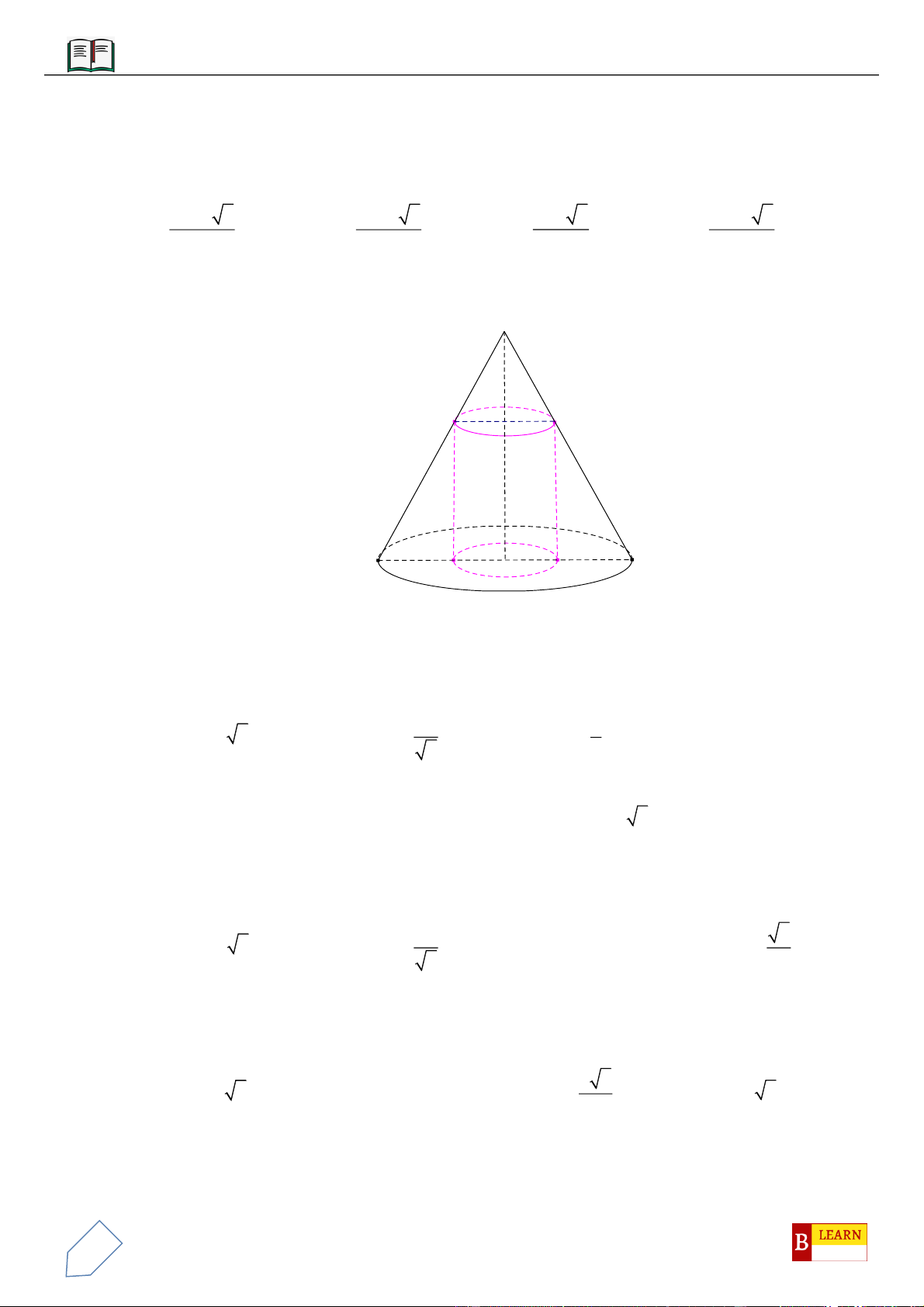
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

390

Câu 41: Cho hai mặt phẳng

()P

và

()Q

song song với nhau cắt khối cầu tâm

O

bán kính

R

tạo thành hai

hình tròn

1

()C

và

2

()C

cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình

tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó

thể tích khối trụ có hai đáy là hai hình tròn

1

()C

và

2

()C

bằng

A.



3

43

9

R

. B.



3

23

9

R

. C.



3

9

R

. D.



3

43

3

R

.

Câu 42: Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội

tiếp khối nón đ cho . Thể tích lớn nhất của khối trụ bằng

A.



6

. B.



10

. C.



4

. D.



8

.

Câu 43: Cho hình trụ có đáy là hai đường tròn tâm

O

và



O

, bán kính đáy bằng chiều cao và bằng

2a

.

Trên đường tròn đáy có tâm

O

lấy điểm

A

, trên đường tròn tâm



O

lấy điểm

B

. Đặt



là góc

giữa

AB

và đáy. Tính



tan

khi thể tích khối tứ diện



OO AB

đạt giá trị lớn nhất.

A.



tan 2

. B.





1

tan

2

. C.





1

tan

2

. D.



tan 1

.

Câu 44: Cho hình trụ có đáy là hai đường tròn tâm

O

và



O

, bán kính đáy bằng chiều cao và bằng

2a

.

Trên đường tròn đáy có tâm

O

lấy điểm

A

,

D

sao cho

 23AD a

; gọi

C

là hình chiếu vuông

góc của

D

lên mặt phẳng chứa đường tròn

 

'O

; trên đường tròn tâm



O

lấy điểm

B

(

AB

chéo

với

CD

). Đặt



là góc giữa

AB

và đáy. Tính



tan

khi thể tích khối tứ diện

CDAB

đạt giá trị

lớn nhất.

A.



tan 3

. B.





1

tan

2

. C.



tan 1

. D.





3

tan

3

.

Câu 45: Cho hình trụ có đáy là hai đường tròn tâm

O

và



O

, bán kính đáy bằng chiều cao và bằng

2a

.

Trên đường tròn đáy có tâm

O

lấy điểm

A

,

D

trên đường tròn tâm



O

lấy điểm

B

,

C

sao cho

//AB CD

và

AB

không cắt

'OO

. Tính

AD

để thể tích khối chóp

'.O ABCD

đạt giá trị lớn nhất.

A.

 22AD a

. B.

 4AD a

. C.



43

3

AD a

. D.

 2AD a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

BẢNG ĐÁP ÁN

1.A

2.D

3.A

4.A

5.D

6.B

7.B

8.D

9.A

10.C

11.B

12.A

13.C

14.D

15.D

16.D

17.D

18.C

19.D

20.C

21.B

22.A

23.A

24.D

25.C

26.C

27.B

28.C

29.D

30.D

31.B

32.C

33.B

34.D

35.D

36.C

37.D

38.C

39.B

40.C

41.A

42.D

43.B

44.D

45.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn A

Ta có

 

  

  

2

23

11

2 3 4

33

V R h a a a

.

Câu 2: Chọn D

Diện tích xung quanh của hai cây cột trước đại sảnh là:

 





1

2. 2 .0,2.4,2S

Diện tích xung quanh của sáu cây cột trước đại sảnh là:

 





2

6. 2 .0,13.4,2S

Số tiền người chủ phải trả để sơn hết các cây cột là:

 

  

12

380.000 11.833.000SS

.

Câu 3: Chọn A

50 0,5 ; 30 0,3cm m cm m

Theo đề ta có đường kính

 0,5AB m

, suy ra bán kính đáy

0,25

2

AB

rm

, đường cao

 0,3hm

Độ dài đường sinh

 

  

      

2 2 2

61 61 61

.0,25.

20 20 80

xq

l r h S rl m

Làm 1000 chiếc nón lá thì có diện tích xung quanh là:

 





2

61 25 61

1000. 1000. .

80 2

xq

Sm

.

Cứ

1kg

lá dùng để làm nón có thể làm ra số nón có tổng diện tích xung quanh là

2

6,13m

, suy ra

khối lượng lá để làm 1000 chiếc nón là:





25 61

. : 6,13 50

2

kg

.

Câu 4: Chọn A

Thể tích của

6

khối cầu là:

 

  

  

3 3 3

1

44

6. 6. .5 1000

33

V R cm

.

Thể tích của cái bình hình trụ là:

 

  

  

2 2 3

2

. .5 . 6.10 1500V R h cm

Thể tích rượu tối thiểu cần đổ vào bình là:

 

  

     

3

21

1500 1000 500 1,57V V V cm l

.

Câu 5: Chọn D

O

A

S

B

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

392

Gọi

 

cma

là độ dài đường kính khối trụ, khi đó thể tích khối trụ là:

 











2

3

cm

24

T

aa

Va

.

Dễ thấy chiều cao khối nón là

3

2

a

nên thể tích khối nón là:

 











2

3

1 3 3

cm

3 2 2 24

N

a a a

V

.

Thể tích của toàn bộ khối đồ chơi là:



NT

V V V



  

33

3

50

4 24

aa





  





3

1 50

46

a



  





3

1 50

6

T

V

 



   





3

50 : 1 38,8 cm

6

T

V

.

Câu 6: Chọn B

Gọi chiều cao của bình nước hình trụ là

 

h cm

Gọi bán kính của bình nước hình trụ là

 

R cm

Ta có chiều cao của bình nước thì gấp 8 lần bán kính của viên bi ve nên:

 

8.1 8h cm

Khi cho ba viên bi vào bình nước thì nước dâng lên đến miệng bình, nên ta có thể tích của ba viên

bi bằng một phần ba thể tích của bình nước

 





  





3

2

4 1 3

3 . . 1 . 8.

3 3 2

R R cm

Diện tích xung quanh của bình nước là:

 



  

2

3

2 2. . .8 61,6

2

xq

S Rh cm

Câu 7: Chọn A

Dựa vào hình vẽ ta có các kích thước như sau.

Bán kính đáy của hình nón và hình trụ



1,4

0,7

2

rm

.

Chiều cao của hình nón

  1,6 0,7 0,9hm

Suy ra độ dài đường sinh của hình nón

    

2 2 2 2

0,9 0,7 1,3l h r

.

Tổng vật liệu cần làm bằng diện tích xung quanh của khối hình.



   

..

2.

xq xq non xq tru tru

S S S rl r h

=



.0,7. 1,3 2.0,7 .0,7 5,586 5,6

Câu 8: Chọn D

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thể tích khối nón là





23

22

1

20

3

N

V r h cm

.

Thể tích khối trụ là





   





2

23

2

1 1 2

3

2 30

22

TN

r

V r h h V cm

.

Vậy thể tích của toàn bộ khối đồ chơi bằng

  

3

50

NT

V V V cm

.

Câu 9: Chọn A

Ta có mặt cắt qua trục hình nón như hình vẽ.

Đặt

r

là bán kính đáy hình trụ,

h

là chiều cao của hình trụ.

Thớ mì tôm có được thể tích lớn nhất khi khối trụ có thể tích lớn nhất.

Thể tích khối trụ là:





2

V r h

.

Ta có hai tam giác

SAI

và



SA I

đồng dạng

      

  



9 6 3

9

92

SI AI r

h

SI A I h r

.

Khi đó

  



     





3

2 2 2

33

. . . . 9 9

22

rr

V r h r r

.

Khảo sát hàm số

V

, biến số

 

06rr

;







  





2

9

18

2

r

Vr

.

 











     













2

0

9

0 18 0

2

4

rl

r

Vr

rn

.

Bảng biến thiên:

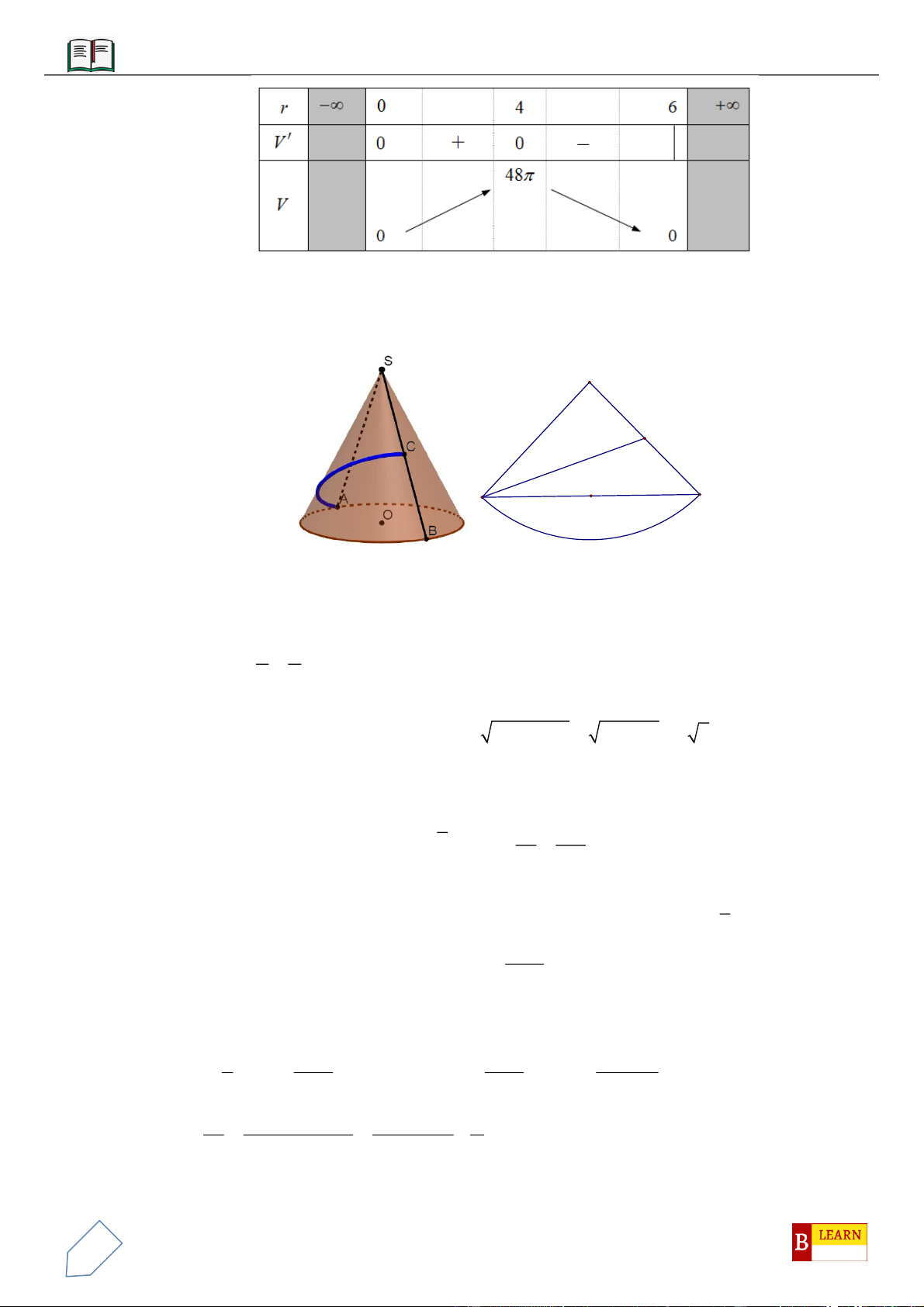
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

394

Dựa vào bảng biến thiên ta thấy





max

48V

khi

 4r

.

Vậy thớ mì tôm có thể tích lớn nhất là



48

.

Câu 10: Chọn C

Khi cắt mặt xung quanh hình nón bởi mặt phẳng

 

SAB

, rồi trải phẳng phần mặt xung quanh có

chứa hệ thống đèn trang trí ta được một hình quạt như trên.

Ta có độ dài cung quạt chính là nửa chu vi của đường tròn đáy hình nón:





1

5mlR

.

Khi đó





1

2

l

ASB

l

. Nên khi trải phẳng ta được tam giác

SAB

vuông tại

S

.

Chiều dài ngắn nhất của dây đèn trang trí chính là độ dài đoạn thẳng

AC

.

Do đó giá trị ngắn nhất của dây đèn là

    

2 2 2 2

10 5 5 5 mAC SA SC

.

Câu 11: Chọn B

Gọi

r

là bán kính hình cầu, khi đó

r

cũng là bán kính đường tròn đáy của hình trụ đ cho, chiều

cao của hình trụ bằng

2r

. Ta có



















2

3

1

2

1

2

1

6

3

.2

V R h

V

r

V

Rh

V r r

.

Xét mặt cắt qua trục của hình nón là 1 tam giác cân

ABC

có diện tích là



1

.2

2

S h R Rh

.

Tam giác cân có chiều dài cạnh bên





sin

R

AB AC

.

Mặt khác áp dụng công thức

S pr

với

p

là nửa chu vi tam giác,

r

là bán kính đường tròn nội

tiếp tam giác .

Ta có











1

22

2 sin

R

pR









    







.sin

sin sin 1

Rh

S Rh R r r

.

Khi đó













2

3 3 3

2

2 3 3

1

6 sin 6sin

.

(sin 1) (sin 1)

V

hh

VR

Rh

C

A

B

S

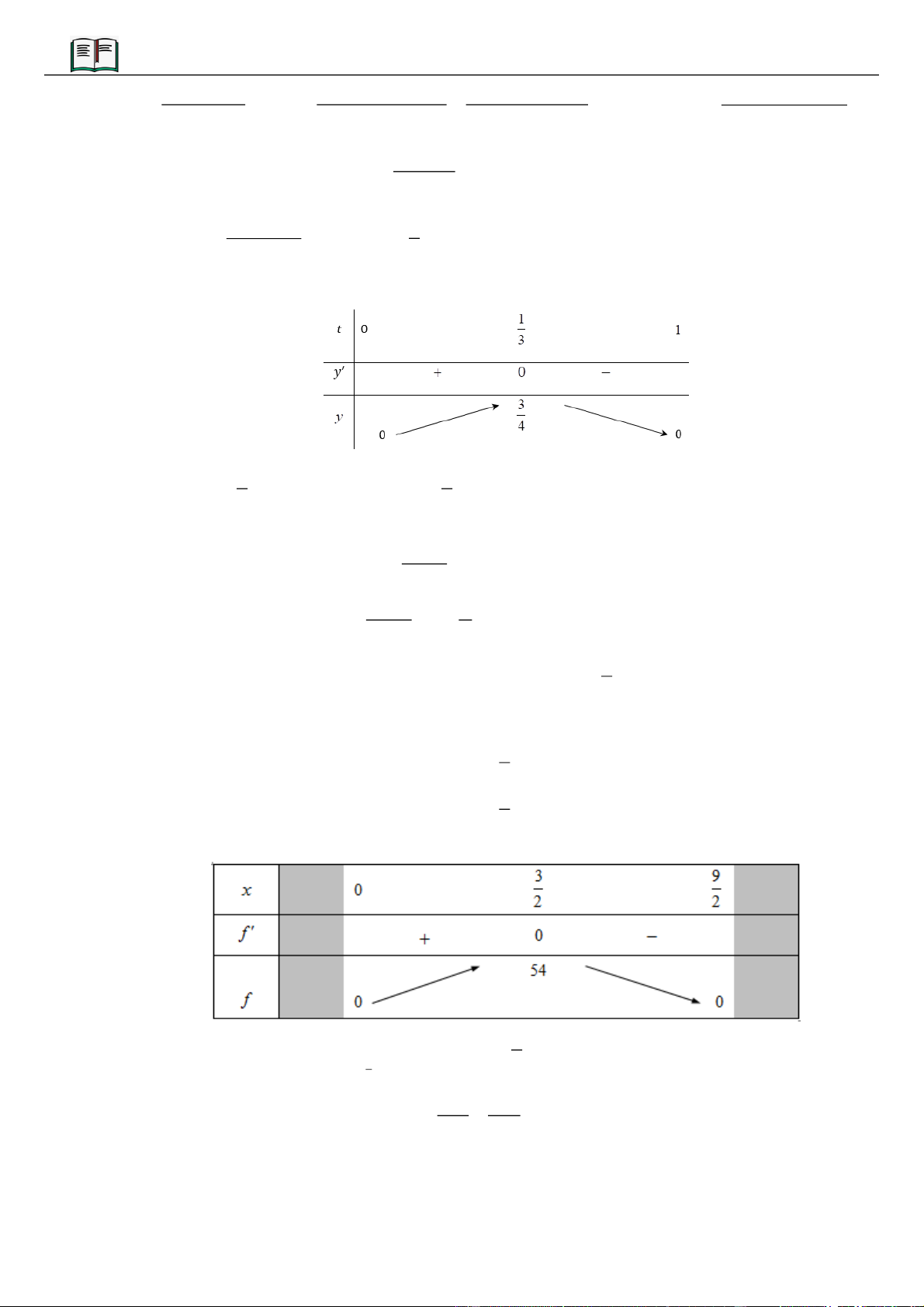
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

     

    



  



  

  

32

2

3 3 2

6sin 6sin (1 sin ) 6sin (1 sin )

.cot

sin 1 sin 1 sin 1

. Xét hàm số

 











2

6sin 1 sin

sin 1

y

.

Đặt



 sint

,

 

 0;1t

ta có

 







2

61

1

tt

y

t

,

 

 0;1t

.

Ta có

 









3

6 3 1

1

t

y

t

;



  

1

0

3

yt

.

Bảng biến thiên:

Suy ra



3

4

M

. Vậy

    

3

48 25 48. 25 61

4

PM

.

Câu 12: Chọn A

Ta có bán kính đáy hình trụ là





92

2

x

r

.

Thể tích ao là

 





  

   





2

92

24

x

V R h x x x

.

Xét hàm số

   

    

2

32

9 2 4 36 81f x x x x x x

với



9

0

2

x

.

Ta có

 



  

2

12 72 81f x x x

.

Khi đó

 









     









2

3

2

0 12 72 81 0

9

2

xn

f x x x

xl

.

Bảng biến thiên:

Từ bảng biến thiên suy ra:

 







  

9

0;

2

3

max 54

2

f x x

.

Vậy thể tích lớn nhất

V

của ao là

 





  

3

54 27

13,5

42

Vm

.

Câu 13: Chọn C

Theo bài toán ta có hình vẽ

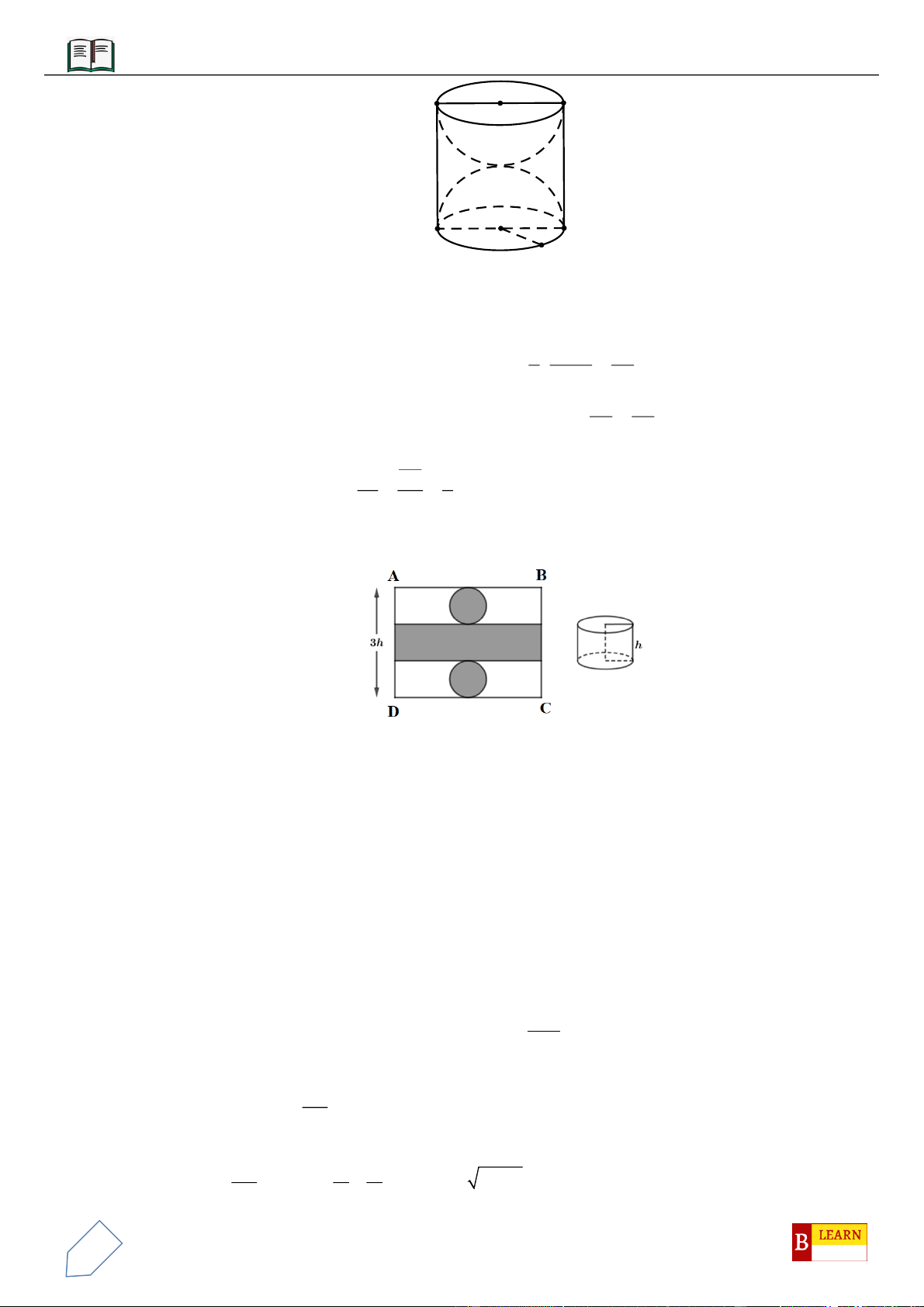
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

396

Thể tích của khối trụ là





2

.1 .2 2V

.

Vì đường tròn đáy của khối trụ là đường tròn lớn của mỗi nửa khối cầu nên bán kính của mỗi nửa

khối cầu là

 1R

.

Thể tích của hai nửa khối cầu bị khoét đi là



   

3

1

1 4 .1 4

2

2 3 3

V

.

Thể tích của phần còn lại của khối gỗ là





    

21

42

2

33

V V V

.

Vậy tỉ số thể tích cần tìm là





2

1

3

23

V

.

Câu 14: Chọn D

Gọi tấm thép hình chữ nhật ban đầu là

ABCD

,

r

là bán kính của hình tròn đáy.

Ta có

   3 4 2h r h h r

.

Thể tích của thùng đựng dầu là



  

2 2 3

. . 3,14. .2 6,28V r h r r r

   

      

33

50,24 6,28 8 2 0,2 .r r r dm m

Do đó

 

  3 6 1,2AD h r m

và

 



2 . 1,256AB r m

.

Vậy diện tích của tấm thép hình chữ nhật ban đầu là

 

  

2

. 1,2.1,256 1,5072 .S AB AD m

Câu 15: Chọn D

Thể tích khối trụ





2

V r h

 





2

6,5 .16 676

 

 2123,7 l

.

Câu 16: Chọn A

Giả sử vỏ hộp sữa có bán kính đáy là

R

, chiều cao là

h

(

,0Rh

).

Vì thể tích vỏ hộp là

V

nên ta có



  

2

V

V R h h

R

.

Để tiết kiệm vật liệu nhất thì hình trụ vỏ hộp sữa phải có diện tích toàn phần

  

   

22

2

2 2 2

tp

V

S Rh R R

R

nhỏ nhất.

Cách 1:

Ta có

  

     

3

2 2 2

2

2 2 3 2

tp

V V V

S R R V

R R R

.

2

1

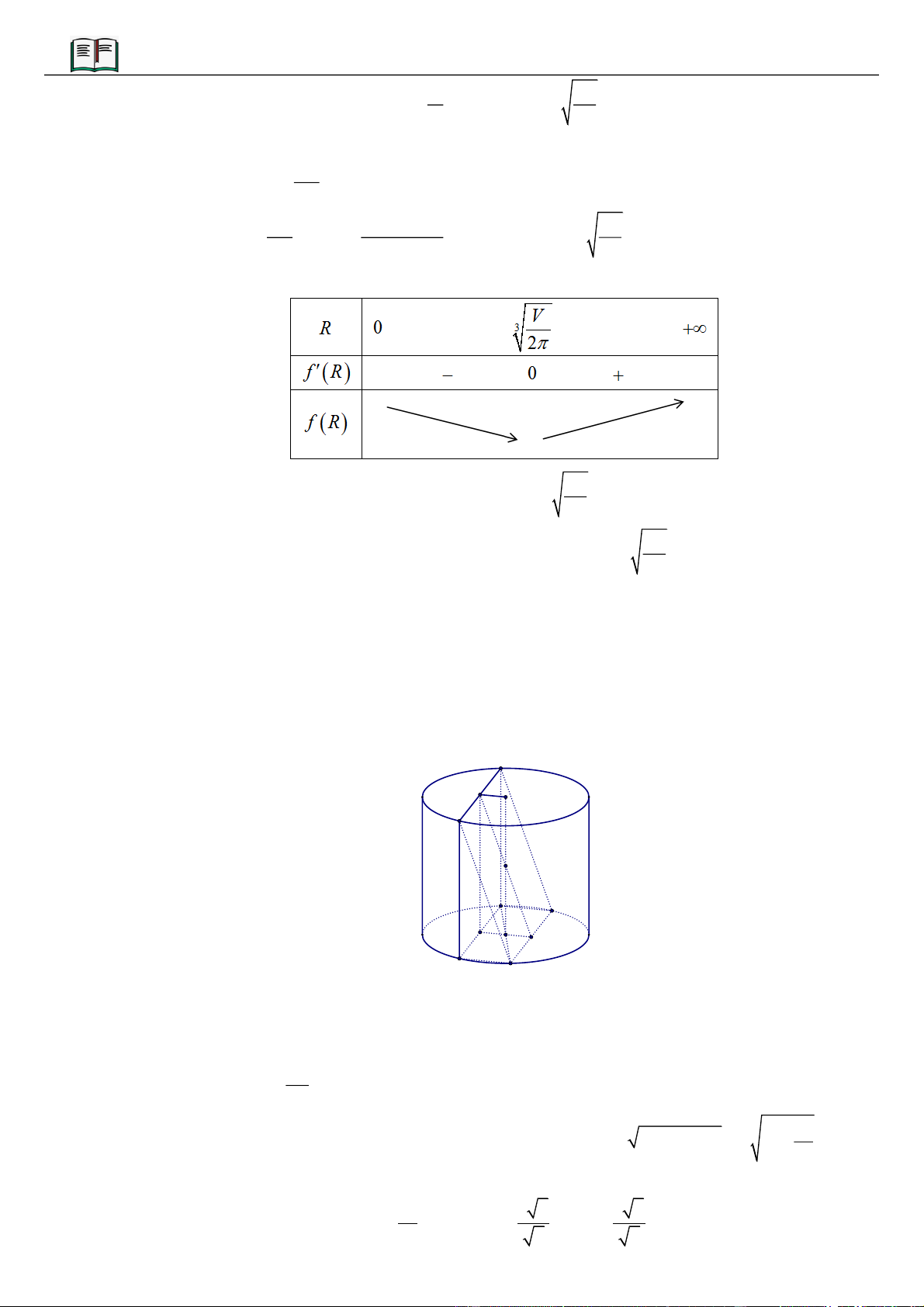
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

tp

S

đạt giá trị nhỏ nhất khi và chỉ khi



  

2

3

2

VV

RR

R

.

Cách 2:

Xét hàm số

 





2

V

f R R

R

trên khoảng

 

0;

.

Ta có

 







   

3

22

2 4 2

4

V R V

f R R

RR

.

 





  

3

0

2

V

f R R

.

Bảng biến thiên:

Từ bảng biến thiên ta thấy

 

fR

đạt nhỏ nhất khi





3

2

V

R

.

Vậy để tiết kiệm vật liệu nhất thì bán kính đáy vỏ hộp phải bằng



3

2

V

.

Câu 17: Chọn D

Gọi

12

,SS

lần lượt là diện tích xung quanh của hình nón phía trên và diện tích của hình vành khăn

phía dưới.

Ta có:



1

π.5.40 200πS

và

  

22

2

π.15 π.5 200πS

.

Khi đó: diện tích vải tối thiểu để may được chiếc mũ là

   

12

200π 200π 400πSS

.

Câu 18: Chọn C

Gọi

MN

là hình chiếu vuông góc của

AB

lên đường tròn đáy. Ta có

MNDC

là hình chữ nhật

và

NC MD O

là tâm đường tròn đáy. Gọi

,,H I K

lần lượt là trung điểm

,,AB MN CD

.

Lại có

, HK CD IK CD

, suy ra góc giữa mặt phẳng chứa hình vuông

ABCD

và mặt đáy là

tan

IH

HKI HKI

IK

.

Đặt

    ( 0)AB BC CD AD x x

. Ta có

     

2

2 2 2

4

x

MC IK OK OC CK r

.

Trong tam giác vuông

BMC

ta có



         





2

2 2 2 2 2 2

53

4

22

x r r

BM MC BC r r x x IK

.

I

N

M

D

C

K

H

O

B

A

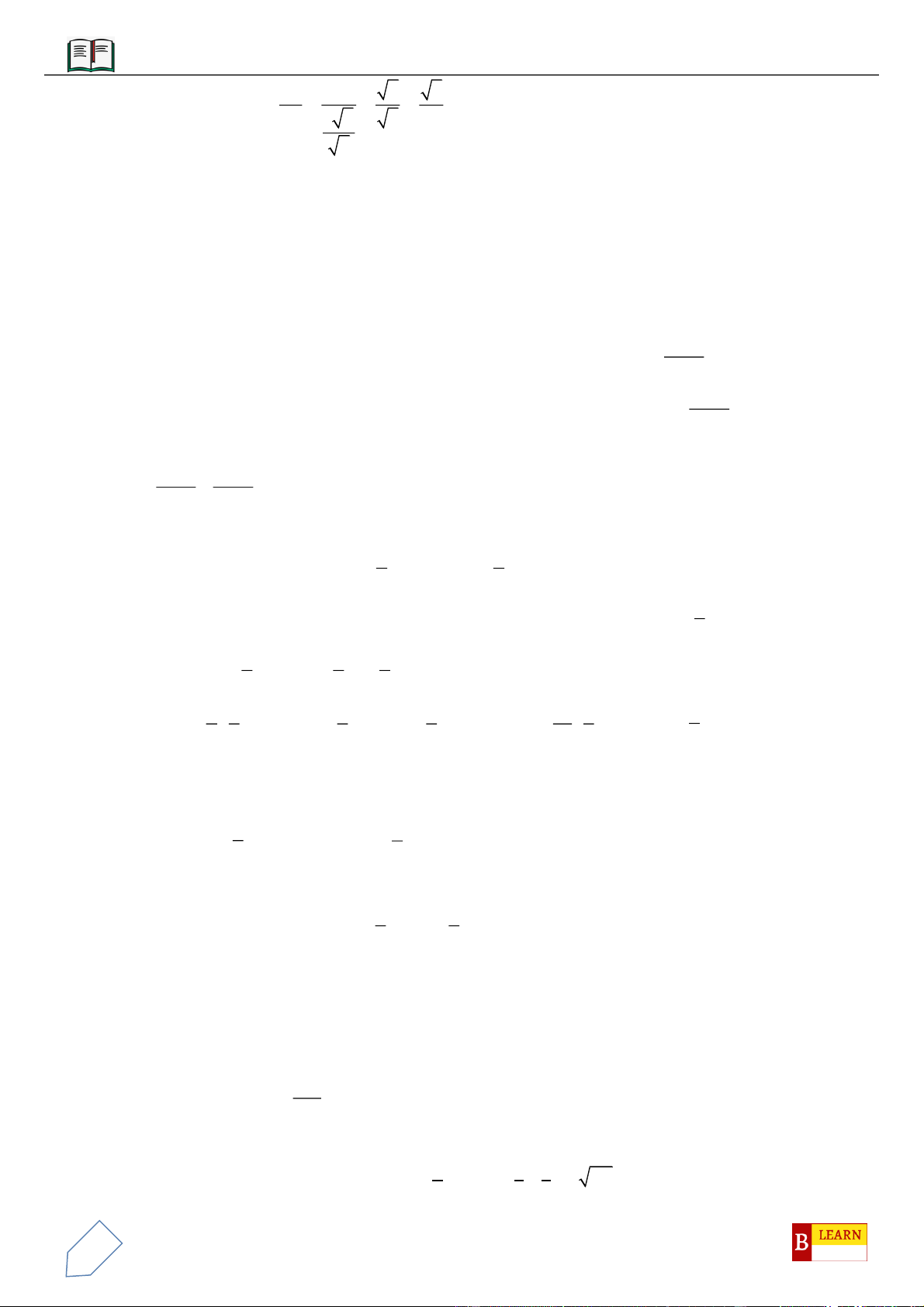
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

398

Suy ra

   

26

tan

3

33

2

IH r

HKI

IK

r

.

Câu 19: Chọn D

Diện tích cần sơn chính là tổng diện tích xung quanh của các cây cột có dạng hình trụ.

Gọi

12

,SS

lần lượt là tổng diện tích xung quanh của 4 cây cột nhà hình trụ có đường kính

40cm

và 6 cây cột nhà hình trụ có đường kính

26cm

.

Gọi

11

,rl

lần lượt là bán kính, độ dài đường sinh của 4 cây cột nhà hình trụ có đường kính

40cm

và

22

,rl

lần lượt là bán kính, độ dài đường sinh của 6 cây cột nhà hình trụ có đường kính

26cm

.

Khi đó:



1

20 0,2r cm m

,



1

4,2lm

nên

 





  

2

1 1 1

168

4.2 8 .0,2.4,2 .

25

S r l m

Lại có:



2

13 0,13r cm m

,



2

4,2lm

nên

 





  

2

2 2 2

819

6.2 12 .0,13.4,2

125

S r l m

.

Vậy số tiền người chủ biệt thự phải trả để sơn 10 cây cột nhà là





  





168 819

380.000 15.844.000

25 125

.

Câu 20: Chọn C

Theo bài ta có

    

1 1 2 1

11

4 ; 2

42

n n n

h h h h h h h

.

Thể tích toàn bộ con xoay là

  

     

12

2 2 2

( ) ( ) ( ) 1 2

1

. . .(2 ) . . .

3

T T N n

V V V V r h r h r h

  

   

2 2 2

1 1 1

31 . . .4 . . .

4 2 3

n n n

r h r h r h

   

     

     

     

     

2 2 2 2

3 1 1 1 31 1

31 . . 6 . . . . 31 . .

4 3 3 3 4 3

n n n n

r h r h r h r h





2

1

. . 4

3

n

rh

Vậy thể tích khối nón

()N

là:



3

()

4( )

N

V cm

.

Câu 21: Chọn B

Ta có:

  

1 2 2 1

1

3

h h h h

,

  

1 2 2 1

1

2

r r r r

.

Thể tích khối trụ

1

H

là:





2

1 1 1

V r h

.

Thể tích khối nón

2

H

là:

 

  

   

2

22

2 2 2 1 1 1 1 1

11

2 .3 4 4

33

V r h r h r h V

.

Thể tích toàn khối là:

        

1 2 1 1 1 1

30 4 30 5 6V V V V V V V

.

Vậy thể tích khối

1

H

bằng

3

6cm

.

Câu 22: Chọn A

Giả sử hộp trụ có bán kính đáy r, chiều cao là h. Theo giả thiết có



   

2

1

1.V r h h

r

Để tiết kiệm nguyên vật liệu nhất thì diện tích toàn phần phải nhỏ nhất:

    

         

2 2 2

3

2

2 1 1

2 2 2 2 3 2 .

tp xq day

S S S r rh r r

r r r

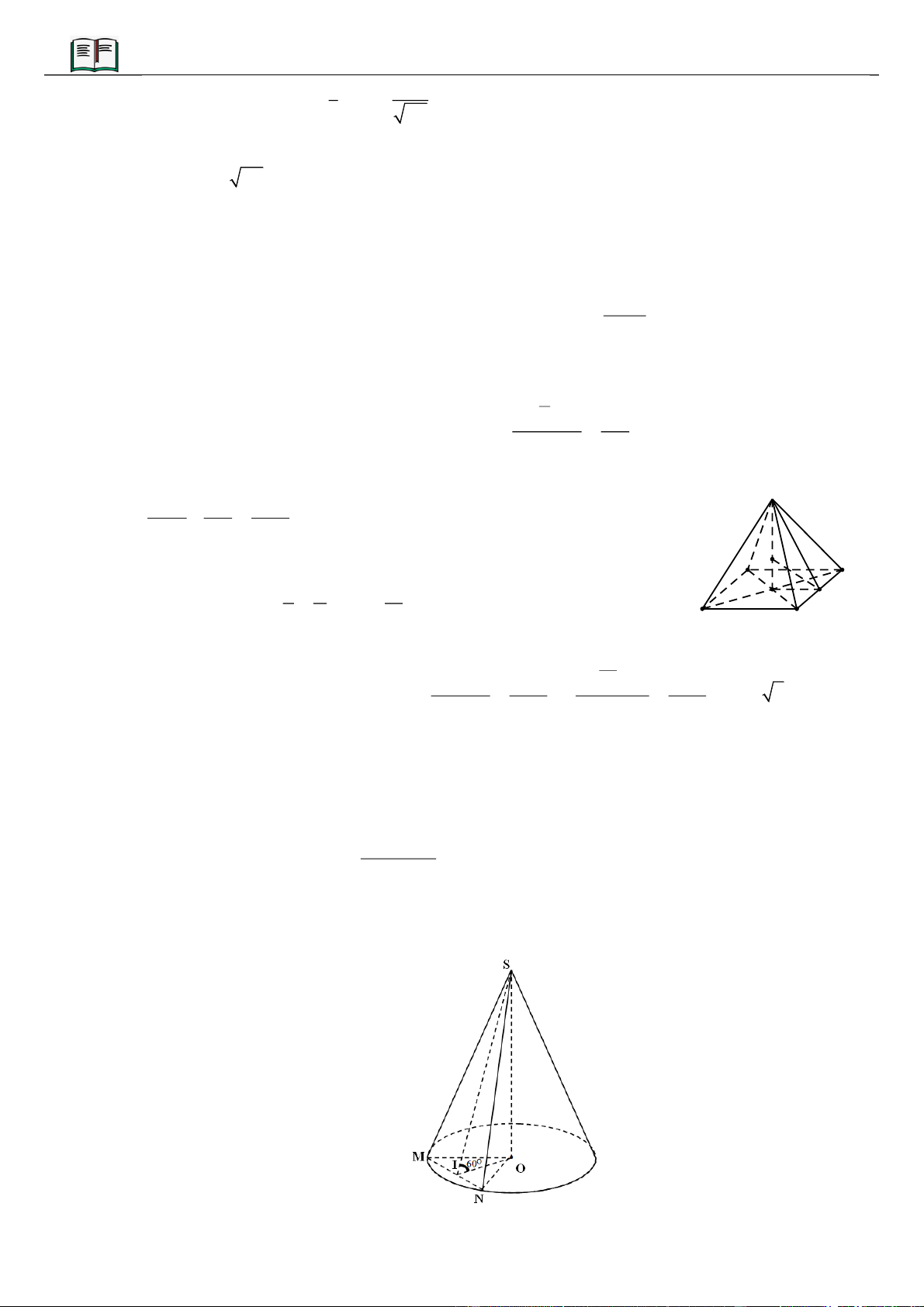
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Dấu bằng đạt tại



     

2

3

11

2 0,54 dm 1,084 dm

2

r r h

r

.

Vậy phải thiết kế một khối trụ có bán kính đáy

0,54 dm

và chiều cao

1,084 dm

.

Vậy





3

3 2 dm

tp

S

.

Câu 23: Chọn A

Gọi bán kính đáy của hình nón là

r

.

Khi đó thể tích nước trong khối nón phía trên lúc ban đầu là:



2

.2

3

r

Thể tích nước trong khối nón phía trên sau khi chảy xuống nón dưới tại thời điểm khi mà chiều

cao của nước trong hình nón trên bằng

1

dm

là:











2

. .1

2

3 12

r

Thể tích nước trong nón phía dưới sau khi nón trên chảy xuống là:

  



2 2 2

27

.

3 12 12

r r r

Gọi chiều cao nước trong nón dưới là

h

, bán kính đáy nước trong nón

dưới là



r

, khi đó:



   .

22

h r rh

r

Thể tích nước trong nón phía dưới là:

 













    

2

22

3

.

2

77

7.

3 12 3 12

rh

h

rh

rr

h

Câu 24: Chọn D

Giả sử

R

có đơn vị là

m

. Có

2 0.002l

 

3

m

.

Thể tích khối hộp bằng



22

4 .0,2 0,8RR

 

3

m

.

Thể tích khúc gỗ bằng



  







22

0,12 0,2

0,16

2

RR

 

3

m

.

Ta có

 



     

22

0,8 0,16 0,002 0,08201 8,2R R R m R cm

Câu 25: Chọn A

Cách 1:

O

I

M

S

A

B

C

D

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

400

Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc

60

cắt khối nón theo thiết diện là tam giác

SMN

như hình vẽ.

Gọi

I

là trung điểm

MN

. Khi đó

OI MN

và

SI MN

, suy ra góc giữa mặt phẳng

 

SMN

và mặt đáy là góc

60SIO

.

Xét tam giác

SIO

ta có:

  

0

3

1

tan60

tan

SO

OI

SIO

.

  

22

3IN ON OI

,

2 2 3MN IN

.





1

. . 3

2

OMN

S OI MN

.





.

1

. . 1

3

S OMN OMN

V SO S

;





2

/

1 4 3

. .2 . 3

33

k non

V

.



3

sin

2

IN

ION

ON

. Suy ra

60ION

,

  2. 120MON ION

.

Gọi

V

là thể tích cần tính. Ta có



    

3

/.

1 4 3

1 1,42cm

39

k non S OMN

V V V

.

Cách 2:

Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc

60

cắt khối nón theo thiết diện là tam giác

SMN

như hình vẽ.

Gọi

I

là trung điểm

MN

. Khi đó

OI MN

và

SI MN

, suy ra góc giữa mặt phẳng

 

SMN

và mặt đáy là góc



0

60SIO

.

Xét tam giác

SIO

ta có:

  

0

3

1

tan60

tan

SO

OI

SIO

.

  

22

3IN ON OI

  2 2 3MN IN

;





1

. . 3

2

OMN

S OI MN

.

Ta có



3

sin

2

IN

ION

ON

suy ra

60ION

,

  2. 120MON ION

.

Gọi

V

S

là diện tích hình viên phân tạo bởi dây

MN

và cung nhỏ

MN

.

Ta có





   

2

14

3

33

V OMN

S R S

Thể tích phần nhỏ cần tính là:



   

3

1 4 3

. 1 1,42cm

39

V

V SO S

.

Câu 26: Chọn C

Chiều dài quả tạ là

     

1 2 3 1 2

29l h h h h h

  

21

92hh

Thể tích quả tạ là

     

  

     

1 2 3

1 1 2 2 3 3

H H H

V V V V r h r h r h

  

  

1 1 2 2

2 60r h r h

  

1 1 2 2

2 60r h r h

 

   

2 1 2 1

6 9 2 60r h r h

 

  

21

9 4 60rh





2

1

60

94

r

h

Thể tích

 



  



2

2 2 1

1

60

92

94

H

V r h h

h

 









1

60 9 2

94

h

.

Câu 27: Chọn B

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Vì đúng một nửa khối cầu chìm trong nước nên thể tích khối cầu gấp 2 lần thể tích nước tràn ra

ngoài.

Gọi bán kính khối cầu là

R

, lúc đó:





33

4

=36 27

3

RR

.

Xét tam giác

ABC

có

AC

là chiều cao bình nước nên

 2AC R

Trong tam giác

ABC

có:

      

2

2 2 2 2 2 2

1 1 1 1 1 1 4

3

4

R

CB

CH CA CB R R CB

.

Thể tích khối nón:



  

   

2

2 3 3

1 1 4 8

. . . .2 . 24

3 3 3 9

n

R

V CB AC R R dm

.

Vậy thể tích nước còn lại trong bình:

  



3

24 18 6 dm

Câu 28:

Chọn C

Ta có thể tích phần không chứa nước





2

1

3. .4 48V

. Như vậy để nước trào ra ngoài thì số bi

thả vào cốc có tổng thể tích lớn hơn



48

.

Gọi n là số viên bi tối thiểu thả vào cốc khi đó tổng thể tích của n viên bi là





3

2

4 32

. .2

33

n

Vn

. Theo bài ra



  

32 9

48

32

n

. Vậy

 5n

.

Câu 29: Chọn D

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

402

Cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện là

một parabol.

Xét dây cung bất kỳ chứa đoạn

KH

như hình vẽ, suy ra tồn tại đường kính

AB KH

, trong tam

giác

SAB

,

/ / ,KE SA E SB

, Suy ra Parabol nhận

KE

làm trục như hình vẽ chính là một thiết diện

thỏa yêu cầu bài toán.

Đặt

BK x

.

Trong tam giác

ABH

có:

 

  

2

. 24HK BK AK x x

.

Trong tam giác

SAB

có:

    

5

.

6

KE BK BK x

KE SA KE

SA BA BA

.

Thiết diện thu được là một parabol có diện tích:



4

.

3

S KH KE

.

Ta có:

 

       

2

2 2 2 3 4 3 4

16 16 25 100 10

. . 24 . . 24 . 24

9 9 36 81 9

x

S KH KE x x x x S x x

Đặt

 



34

24f x x x

, với

0 24x

.

Ta có:

 



23

' 72 4f x x x

. Suy ra

 





    







23

0

' 0 72 4 0

18

x

f x x x

x

.

Bảng biến thiên:

Vậy thiết diện có diện tích lớn nhất là:



2

10

34992 207,8

9

cm

Câu 30: Chọn D

Đặt

AB x

 

 0x

. Tam giác

SAB

vuông tại

A

  .tan 3SA AB ABS x

.

IB

là phân giác trong góc

B

      30 tan30

3

x

IBA IA AB

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Quay miền tam giác

SAB

quanh

SA

ta được khối nón có chiều cao là

SA

, bán kính đáy là

AB





   

3

22

1

1 1 3

. . . . 3

3 3 3

x

V AB SA x x

.

Quay nửa hình tròn tâm

I

quanh

SA

ta được khối cầu tâm

I

bán kính

IA





   

33

3

2

4 4 4 3

.

3 3 27

33

xx

V IA



1

2

9

4

V

.

Câu 31: Chọn B

Khi lăn trọn một vòng thì trục lăn tạo trên tường phẳng lớp sơn có diện tích bằng diện tích xung

quanh của trục lăn là



 2.S R h





2

5

2 . .23 115 (cm )

2

.

Vậy sau khi lăn trọn

10

vòng thì trục lăn tạo nên tường phẳng lớp sơn có diện tích là





2

10 1150 (cm )S

.

Câu 32: Chọn C

Gọi giá của vật liệu làm mặt xung quanh là

,( 0)xx

, suy ra giá của vật liệu làm đáy và nắp là

1,5 .x

Tổng chi phí vật liệu sản xuất thùng:

     

    





   

        



   



   



2

2 2 2 2

3

2

23

3 2 3 3 . 3 3 . . 3 . .

V V V V V V

T x r x rh x r x r x r x

r r r r r

Dấu

""

xảy ra khi:





      

2

22

3 3 3 3.

V r h h

r r h r

r r r

Câu 33: Chọn B

Gắn hệ trục tọa độ

Oxy

vào đáy hình trụ như hình vẽ sau

Ta có

H

là trung điểm

OB

nên

OAB

là tam giác đều. Suy ra

60AOB

và

120AOC

nên

hình quạt chứa cung nhỏ

AC

có diện tích là





2

1

33

Sr

.

Khi đó diện tích phần tô đậm trên hình vẽ là



1 OAC

S S S





1

.0,5. 3

32





3

34

.

y

x

S

1

-1

1

C

A

0,5

B

O

H

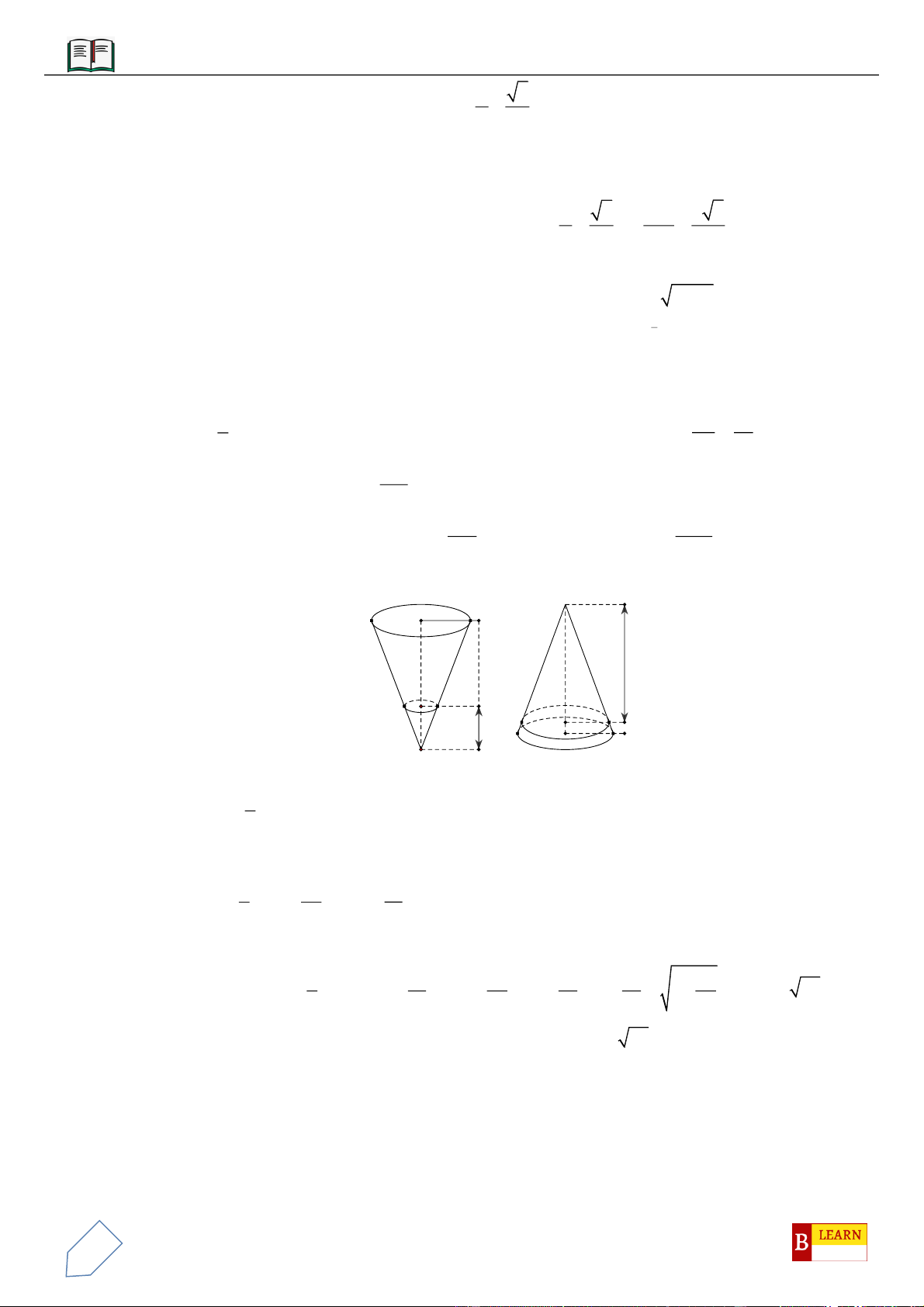
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

404

Và thể tích dầu được rút ra là





  





11

3

. 5.

34

V h S

.

Thể tích bồn chứa dầu hình trụ là





2

5V r h

.

Thể tích dầu còn lại trong bồn là



21

V V V





  





3

5 5.

34





10 5 3

34

 



3

12,637 m

.

Cách khác: Có thể tính diện tích phần tô đậm bằng tích phân





1

2

1

2

2 1 dS x x

.

Câu 34: Chọn D

Hai khối trụ có thể tích bằng nhau nên tổng thể tích bằng hai lần thể tích của một khối trụ.

Do



1

20

2

AE AB m

bằng chu vi của mặt đáy. Suy ra bán kính đáy





20 10

2

Rm

.

Diện tích mặt đáy là





22

100

()S R m

, chiều cao khối trụ là

 5AD m

.

Suy ra thể tích một khối trụ là





3

500

. ( )V S h m

.Vậy tổng thể tích là



3

1000

()m

.

Câu 35: Chọn D

Gọi

 15h

cm là chiều cao của phễu và

V

là thể tích của phễu hình nón.

Ký hiệu



1

5

3

hh

cm là chiều cao và

1

V

là thể tích của lượng nước trong phễu.

Gọi

2

h

,

2

V

là chiều cao và thể tích của phần không gian trống trong phễu khi lật ngược phễu lại.

Ta có









3

1

3 27

V

VV

,









3

2

h

VV

h

và



12

V V V

.

Khi đó,

   



            

   





   

33

3

2 2 2

3

1 2 2

1 1 1

1 1 5 26

3 27 15 15 27

h h h

V V V V V V h

h

.

Vậy chiều cao của nước khi lật ngược phễu lại là

   

3

2

15 5 26 0,188hh

cm.

Câu 36: Chọn C

Gọi tấm thép hình chữ nhật ban đầu là

ABCD

,

r

là bán kính của hình tròn đáy.

Diện tích hình chữ nhật

ABCD

là:

 ..S AB AD

Ta có

   3 4 2 .h r h h r

h

1

h

2

h

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thể tích của khối trụ



  

2 2 3

. . 3,14. .2r 6,28rV r h r

.

Theo bài ra

      

33

50,24 6,28 50,24 8 2.V r r r

Do



       2dm 0,2m 3 6 1,2m; 2 . 1,256m.r AD h r AB r

Vậy



2

1,2.1,256 1,5072(m ).S

Câu 37: Chọn D

Gọi

1 2 3

,,O O O

lần lượt là tâm của ba viên bi và

  

1 2 3

3r r r

là bán kính của ba viên bi đó.

Theo giả thiết thì ba đường tròn lớn của ba viên bi đôi một tiếp xúc với nhau, khi đó ba điểm

1 2 3

,,O O O

tạo thành một tam giác đều cạnh

23

. Gọi

O

là trọng tâm của tam giác

1 2 3

O O O

thì

   

1 2 3

23

.2 3. 2

32

OO OO OO

.

Cũng theo giả thiết thì ba viên bi tiếp xúc với các đường sinh của lọ hình trụ tại 3 điểm nằm trên

một đường tròn bằng đường tròn đáy của lọ hình trụ .

Vậy bán kính đáy của lọ hình trụ là

   

33

23OM OO O M

.

Câu 38: Chọn C

Ta có





2

đáy

Sr

;



 2

xq

S rh

.

Thể tích khối trụ



   

2

.

đáy

VV

V S h h

S

r

.

    



       

2 2 2

2

2 2 2 2 2 . 2

tp xqđáy

VV

S S S r rh r r r

r

.

Xét hàm số

 





2

V

f r r

r

, có

 







2

4

V

f r r

r

;

 





    

3

2

04

2

VV

f r r r

r

.

Từ đó suy ra giá trị nhỏ nhất của hàm số đạt tại





3

2

V

r

.

Vậy khi





3

2

V

r

thì diện tích toàn phần hình trụ đạt giá trị nhỏ nhất.

Câu 39: Chọn B

Gọi bán kính đáy của hình trụ là

R

và chiều cao là

h

.

Do thể tích khối trụ là

72

nên



  

2

72

72R h h

R

.

Diện tích đáy là



2

R

. Diện tích xung quanh là







2

72 144

2 2 .Rh R

R

.

Chi phí làm bình là:

  

    

    

2 2 2

22

3

144 12960

100. 90. 140. 240

6480 6480 6480 6480

240 3 240 . . 6480 .

T R R R

RR

R R R R

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

406

Dấu bằng xảy ra khi



   

2

3

6480 6480 3

240 .RR

RR

Câu 40: Chọn C

Ta có:



   

4

2

13

27

3

V r h h

r

. Độ dài đường sinh là



   

8

2 2 2

24

3

l h r r

r

Lượng giấy tiêu thụ ít nhất khi diện tích xung quanh nhỏ nhất.

Diện tích xung quanh của hình nón là

  



    

88

24

2 4 2 2

33

xq

S rl r r r

rr



  

   

8 8 16

4

3

2 2 2 2 4

3 3 3

3

2 2 4

r

rr

Dấu “=” xảy ra khi

 



  

88

4

6

2 2 2

33

22

r r cm

r

. Chọn đáp án C

Câu 41: Chọn A

Gọi

,,r h l

lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón và

12

,,IIO

lần lượt là

tâm của hai đường tròn

12

( ),( )CC

và mặt cầu.

Vì hai đường tròn

12

( ),( )CC

có bán kính bằng nhau nên dễ dàng suy ra:



12

2

h

OI OI

Ta có

      

22

2 2 2 2

3

44

hh

r R l h r R

.

Diện tích xung quanh hình nón là

   



       

2 2 2

2 2 2 2 2 2

32

. . 12 3 . 4 3

44

4 3 3

xq

h h R

S rl R R R h R h

.

xq

S

lớn nhất bằng



2

3

R

. Dấu

""

xảy ra khi và chỉ khi

    

2 2 2 2

2

12 3 4 3

3

R

R h R h h

.



6

3

R

r

.

Mà bán kính đáy và chiều cao của hình nón cũng chính là bán kính đáy và chiều cao hình trụ.

Vậy thể tích hình trụ





  

23

2

6 2 4 3

. . . .

99

3

R R R

V r h

.

Câu 42: Chọn D

Gọi bán kính của khối trụ là

 

03xx

, chiều cao của khối trụ là

 



  06h OO h

.

Khi đó thể tích khối trụ là:





2

V x h

.

Ta có:



SO N

đồng dạng với

SOB

nên có





     

6

62

36

O N SO x h

hx

OB SO

.

Suy ra

 

  

    

2 2 2 3

6 2 6 2V x h x x x x

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Xét hàm

   

   

23

6 2 , 0 3f x x x x

.

 





2

12 6f x x x

;

 

















0

2

xl

fx

xn

Bảng biến thiên:

Do đó

V

lớn nhất khi hàm

 

fx

đạt giá trị lớn nhất.

Vậy thể tích của khối trụ lớn nhất là



 8V

khi bán kính khối trụ bằng 2.

Câu 43: Chọn B

Cách 1:

Gọi

D

là hình chiếu vuông góc của

B

lên mặt phẳng

 

O

.

Kẻ

AH OD

,

H OD

.

Ta có thể tích của khối chóp



OO AB

:







1

.

3

OO AB OO B

V AH S



2

.

3

a

AH



2

.

3

a

AO



3

4

3

a

.

 





max

OO AB

V H O

. Suy ra

 22AD a

.

Suy ra:



tan tanBAD



1

2

.

Cách 2:

Nhận xét: Nên thêm giả thiết

AB

chéo với

'OO

để tứ diện



OO AB

tồn tại.

Gọi

D

là hình chiếu vuông góc của

B

lên mặt phẳng chứa đường tròn

 

O

.

Gọi

C

là hình chiếu vuông góc của

A

lên mặt phẳng chứa đường tròn

 

'O

.

Ta có

'.O CBOAD

là một hình lăng trụ đứng.

Ta có thể tích của khối chóp



OO AB

:





   

3

'.

1 1 1 4

2 . .2 . .2 .2 .sin

3 3 2 3

OO AB O BC OAD OAD

a

V V a S a a a AOD

.

 

   

0

'

max

90 2 2

O ABCD

V AOD AD a

. Suy ra:



tan tanBAD



1

2

.

Câu 44: Chọn D

Gọi

H

là hình chiếu vuông góc của

B

lên mặt phẳng chứa đường tròn

 

O

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

408

Gọi

K

là hình chiếu vuông góc của

A

lên mặt phẳng chứa đường tròn

 

'O

.

Ta có

.HAD BKC

là một hình lăng trụ đứng.

Ta có thể tích của tứ diện

CDAB

là

   



   

.

1 1 1 1 1 1

.2 . .2 . . . ; .2 . .2 3. ;

3 3 3 2 3 2

ABCD HAD BKC HAD

V V a S a AD d H AD a a d H AD

.

   

 



max

;

ABCD

V d H AD



H

là điểm chính giữa cung lớn

AD

của đường tròn

 

O

.

Theo định lý sin ta có

    

2 3 3

2.2 sin

4 4 2

sin

AD AD a

a AHD

aa

AHD

nên



0

60AHD

.

Do đó xảy ra khi

AHD

đều



23AH AD a

.

Suy ra:



   

23

tan tan

3

23

BH a

BAH

AH

a

.

Câu 45: Chọn A

Kẻ đường thẳng qua

'O

song song với

AB

cắt mặt phẳng chứa đường tròn

()O

tại

1

O

.

Lúc đó

1

.'AO D BO C

là một hình lăng trụ chiều cao bằng

2a

.

Vì

AD BC

nên





'BO C OAD

SS

Ta có thể tích của khối chóp

'.O ABCD

:



    

1

3

' . ' '

1 2 2 2 1 8

.2 . .2 . .2 . .2 .2 .sin

3 3 3 3 2 3

O ABCD AO D BO C BO C OAD

a

V V a S a S a a a AOD

.

 

   

0

'

max

90 2 2

O ABCD

V AOD AD a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

409

CHỦ ĐỀ: KHỐI CẦU NGOẠI TIẾP TỨ DIỆN

BÀI TẬP VẬN DỤNG

Câu 1: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác cân tại

A

với

AB AC a

, cạnh

SA SB a

và có

   

SBC ABC

. Tính

SC

để độ dài bán kính mặt cầu ngoại tiếp hình chóp bằng

a

.

A.

 2SC a

. B.

 3SC a

. C.

SC a

. D.

 2SC a

.

Câu 2: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. Cạnh bên

 6SA a

và vuông góc với đáy

 

ABCD

. Tính theo

a

diện tích mặt cầu ngoại tiếp khối chóp

.S ABCD

.

A.



2

8 a

. B.

2

2a

. C.



2

2 a

. D.

2

2a

.

 Định nghĩa: Mặt cầu ngoại tiếp khối đa diện là mặt cầu đi qua tất cả các đỉnh của khối đa diện

đó.

 Điều kiện cần và đủ để khối chóp có mặt cầu ngoại tiếp: có đáy là một đa giác nội tiếp.

 Cách xác định tâm mặt cầu ngoại tiếp khối đa diện:

Bước 1: Xác định trục của đường tròn ngoại tiếp đa giác đáy. Gọi tắt là trục của đáy ( là đường

thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

Bước 2: Xác định măt phẳng trung trực của một cạnh bên hoặc trục của đường tròn ngoại tiếp

một đa giác của mặt bên.

Bước 3: Giao điểm của trục của đáy và mặt phẳng trung trực của một cạnh bên ( hoặc trục của

đáy và trục của đường tròn ngoại tiếp một đa giác của mặt bên) là tâm mặt cầu ngoại tiếp khối

đa diện đó.

 Một số công thức tính nhanh bán kính mặt cầu ngoại tiếp

 Công thức 1: Mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với đáy:









2

d

h

RR

, trong đó

d

R

là bán kính đường tròn ngoại tiếp đáy,

h

là độ dài cạnh bên

vuông góc với đáy.

 Công thức 2: Khối tứ diện vuông (có các cạnh đôi một vuông góc):





2 2 2

2

OA OB OC

R

 Công thức 3: Mặt cầu ngoại tiếp khối chóp có mặt bên vuông góc với đáy:

  

2

22

4

db

a

R R R

, trong đó

d

R

là bán kính đường tròn ngoại tiếp đáy;

b

R

là bán kính đường

tròn ngoại tiếp của mặt bên và

a

tương ứng là độ dài đoạn giao tuyến của mặt bên và đáy.

 Công thức 4: Khối chóp có các cạnh bên bằng nhau:



2

a

R

h

, trong đó

a

là độ dài cạnh bên và

h

là chiều cao khối chóp và

h

được tính bằng

công thức



22

d

h a R

.

 Công thức 5: Khối tứ diện gần đều

ABCD

có

     ;;AB CD a AC BD b AD BC c





2 2 2

8

a b c

R

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

410

Câu 3: Một hình nón có độ dài đường sinh bằng đường kính đáy. Diện tích hình tròn đáy của hình nón

bằng



9

. Tính đường cao

h

của hình nón.

A.



3

2

h

. B.

 33h

. C.



3

h

. D.

 3h

.

Câu 4: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

,

SA

vuông góc với mặt phẳng

 

ABC

và

  2, 4, 5.AB AC SA

Mặt cầu đi qua các đỉnh của hình chóp

.S ABC

có bán kính

là

A.



5

2

R

. B.

 10R

. C.



10

2

R

. D.



25

2

R

.

Câu 5: Cho hình hộp chữ nhật

có , . Diện tích mặt cầu ngoại tiếp

hình hộp đã cho bằng

A. . B. . C. . D. .

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

2a, 3AB AD a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy, góc giữa

SD

và mặt phẳng đáy là

30

. Diện tích mặt cầu ngoại tiếp hình chóp

là:

A.



2

8 a

. B.



2

8

3

a

. C.



2

4 a

. D.



2

4

3

a

.

Câu 7: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật,

2a, 3AB AD a

, cạnh bên

SA

vuông góc

với mặt phẳng đáy, góc giữa

SD

và mặt phẳng đáy là

30

. Diện tích mặt cầu ngoại tiếp hình chóp

là:

A.



2

8 a

. B.



2

8

3

a

. C.



2

4 a

. D.



2

4

3

a

.

Câu 8: Cho hình chóp

.S ABC

có

 ()SA ABC

, tam giác

ABC

vuông tại

B

,

  3, 7SA BC AB

. Tính

bán kính

R

của mặt cầu ngoại tiếp hình chóp đã cho.

A.

 5R

. B.



5

2

R

. C.



5

2

R

. D.

 5R

.

Câu 9: Trong không gian, cho hình chóp

.S ABC

có

SA

,

AB

,

BC

đôi một vuông góc với nhau và

SA a

,

AB b

,

BC c

. Mặt cầu đi qua

S

,

A

,

B

,

C

có bán kính bằng

A.

 

2

3

a b c

. B.



2 2 2

a b c

. C.



2 2 2

2 a b c

. D.



2 2 2

1

2

a b c

.

Câu 10: Trong không gian

Oxyz

, cho bốn điểm

(1;2; 4)A

,

(1; 3;1)B

,

(2;2;3)C

,

(1;0;4)D

. Gọi

 

S

là

mặt cầu đi qua bốn điểm

, , , A B C D

. Tọa độ tâm

I

và bán kính

R

mặt cầu

 

S

là

A.

 

1;0; 2 , 21IR

. B.

 

2; 1; 0 , 26IR

.

C.

 

1; 0; 2 , 21IR

. D.

(2; 1;0), 26IR

.

.ABCD AB C D

   

AB a

2AD AA a





2

9 a



2

3

4

a



2

9

4

a



2

3 a



CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

411

Câu 11: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân ở

B

,

 2AC a

,

 

SA ABC

,

SA a

. Gọi

G

là trọng tâm tam giác

SBC

, mặt phẳng

 



đi qua

AG

và song song với

BC

cắt

SB

,

SC

lần

lượt tại

M

,

N

. Tính thể tích

V

của khối chóp

.S AMN

.

A.



3

9

a

V

. B.



3

2

27

a

V

. C.



3

2

9

a

V

. D.



3

6

a

V

.

Câu 12: Mặt cầu ngoại tiếp tứ diện vuông

.O ABC

có

  OA OB OC a

có bán kính bằng

A.

2

a

. B.

3

2

a

. C.

2

a

. D.

3

4

a

.

Câu 13: Cho khối trụ có đường sinh bằng

5

và thể tích bằng



45

. Diện tích toàn phần của khối trụ là

A.



18

. B.



33

. C.



48

. D.



39

.

Câu 14: Cho hình chóp

.S ABCD

có

 

SA ABCD

,

SA a

và đáy

ABCD

nội tiếp đường tròn bán kính

bằng

a

. Bán kính mặt cầu ngoại tiếp hình chóp

.S ABCD

là

A.

3

a

. B.

3

2

a

. C.

5

2

a

. D.

2

3

a

.

Câu 15: Một mặt cầu

 

S

ngoại tiếp tứ diện đều cạnh a. Diện tích mặt cầu

 

S

là:

A.



2

3

2

a

. B.



2

6 a

. C.



2

3

4

a

. D.



2

3 a

.

Câu 16: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

,

SA

vuông góc với mặt phẳng

 

ABC

và

 2,AB

 4,AC

 5SA

. Mặt cầu đi qua các đỉnh của hình chóp

.S ABC

có bán kính

là:

A.



25

2

R

. B.



5

2

R

. C.

 5R

. D.



10

3

R

.

Câu 17: Cho hình lập phương

   

.ABCD A B C D

có cạnh

a

.

Thể tích khối cầu ngoại tiếp hình lập phương là

A.



3

82

3

a

. B.



3

2

a

. C.



3

12 3

3

a

. D.



3

43

3

a

.

Câu 18: Tính bán kính

R

của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng

a

.

A.

3

2

a

. B.

a

. C.

23a

. D.

3a

.

Câu 19: Cho hình chóp S.ABC có

     

00

, 90 , 60 .SA SB SC a ASB ASC BSC

Tính diện tích mặt cầu

ngoại tiếp hình chóp đã cho.

A.



2

7

6

a

. B.



2

7

3

a

. C.



2

7

18

a

. D.



2

7

12

a

.

Câu 20: Cho hình trụ

 

T

có bán kính đáy

,a

trục



OO

bằng

2a

và mặt cầu

 

S

có tâm là trung điểm của

đoạn thẳng



OO

và đi qua điểm O. Tìm tỉ số giữa diện tích mặt cầu

 

S

và diện tích toàn phần

của hình trụ

 

T

.

A.

1

.

3

B.

2

.

3

C.

1.

D.

4

.

3

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

412

Câu 21: Cho hình chóp

.S ABC

có

 

SA ABC

,

ABC

là tam giác vuông tại

A

,

  3 ; 4 ; 5AB a AC a SA a

. Tìm bán kính mặt cầu mặt cầu ngoại tiếp hình chóp

.S ABC

?

A.

52

4

a

. B.

5

4

a

. C.

5

2

a

. D.

52

2

a

.

Câu 22: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt đáy và

SA a

. Mặt cầu ngoại tiếp hình chóp

.S ABCD

có bán kính bằng

A.

3a

. B.

6

2

a

. C.

3

a

. D.

3

2

a

.

Câu 23: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông, biết

2BA BC a

, cạnh bên

 22SA a

vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp theo

a

.

A.



2

8 a

. B.



2

16 a

. C.



2

4 a

. D.



2

64 a

.

Câu 24: Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính mặt cầu ngoại tiếp hình

nón đó là.

A.

23

. B.

23

3

. C.

3

2

. D.

3

.

Câu 25: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

2a

. Tam giác

SAC

vuông cân tại

S

và nằm

trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp

.S ABCD

.

A.



3

2

3

a

. B.



3

43a

. C.



3

4

3

a

. D.



3

4 a

.

Câu 26: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật với

 3AB a

,

 4BC a

,

 12SA a

và

SA

vuông

góc với đáy. Tính bán kính

R

của mặt cầu ngoại tiếp hình chóp

.S ABCD

.

A.



5

2

a

R

. B.



17

2

a

R

. C.



13

2

a

R

. D.

 6Ra

.

Câu 27: Cho tứ diện

ABCD

có tam giác

BCD

vuông tại

C

,

AB

vuông góc với mặt phẳng

 

BCD

,

 5AB a

,

 3BC a

và

 4CD a

. Tính bán kính

R

của mặt cầu ngoại tiếp tứ diện

ABCD

.

A.



52

3

a

R

. B.



53

3

a

R

. C.



52

2

a

R

. D.



53

2

a

R

.

Câu 28: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

3 2 ,a

cạnh bên bằng

5.a

Tính bán kính

R

của mặt cầu ngoại tiếp hình chóp

..S ABCD

A.

 3Ra

. B.

 2Ra

. C.



25

8

a

R

. D.

 2Ra

.

Câu 29: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác đều cạnh

a

,

SA

vuông góc với mặt phẳng

 

ABC

và

SA a

. Diện tích của mặt cầu ngoại tiếp hình chóp

.S ABC

bằng

A.



2

3

7

a

. B.



2

7

12

a

. C.



2

7

3

a

. D.



2

7

a

.

Câu 30: Cho mặt cầu tâm

O

và tam giác

ABC

có ba đỉnh nằm trên mặt cầu với góc



0

30BAC

và

BC a

Gọi

S

là điểm nằm trên mặt cầu, không thuộc mặt phẳng

 

ABC

và thỏa mãn

SA SB SC

, góc

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

413

giữa đường thẳng

SA

và mặt phẳng

 

ABC

bằng

0

60

. Tính thể tích

V

của khối cầu tâm

O

theo

a

.

A.





3

9

Va

. B.





3

32 3

27

Va

. C.





3

43

27

Va

. D.





3

15 3

27

Va

.

Câu 31: Cho hình

413

hop

.S ABCD

có

ABCD

là hình chữ nhật tâm

I

cạnh

 3AB a

,

 4BC a

. Hình

chiếu của

S

trên mặt phẳng

 

ABCD

là trung điểm của

ID

. Biết rằng

SB

tạo với mặt phẳng

 

ABCD

một góc

45

. Tính diện tích mặt cầu ngoại tiếp hình chóp

.S ABCD

.

A.



2

25

2

a

. B.



2

125

4

a

. C.



2

125

2

a

. D.



2

4 a

.

Câu 32: Cho tứ diện

ABCD

có

3AB CD

,

5AD BC

,

6AC BD

. Tính thê tích khối cầu ngoại

tiếp tứ diện

ABCD

.

A.



35

. B.

35

. C.



35 35

6

. D.



35 35

.

Câu 33: Cho hình chóp

.S ABC

, đáy

ABC

là tam giác đều cạnh

a

;

 

SA ABC

. Gọi

H

,

K

lần lượt là

hình chiếu vuông góc của

A

lên

SB

;

SC

. Diện tích mặt cầu đi qua 5 điểm

A

,

B

,

C

,

K

,

H

là

A.



2

4

9

a

. B.



2

3 a

. C.



2

4

3

a

. D.



2

3

a

.

Câu 34: Cho tứ diện đều

ABCD

cạnh

a

. Gọi

K

là trung điểm của

AB

,

, MN

lần lượt là hình chiều của

K

lên

AD

và

AC

. Tính theo

a

bán kính mặt cầu ngoại tiếp hình chóp

.K CDMN

?

A.

3

4

a

. B.

33

8

a

. C.

2

4

a

. D.

32

8

a

.

Câu 35: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

3a

. Hình chiếu vuông góc của

S

trên mặt

phẳng đáy

ABCD

là điểm

H

thuộc cạnh

AB

sao cho

 2HB HA

. Cạnh

SA

hợp với mặt phẳng

đáy góc

60

o

. Tính diện tích mặt cầu ngoại tiếp hình chóp

.S ABCD

A.



2

475

3

a

. B.



2

21 a

. C.



2

55

3

a

. D.



2

22 a

.

Câu 36: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

a

. Cạnh bên

 6SA a

và vuông góc với đáy

 

ABCD

. Tính theo

a

diện tích mặt cầu ngoại tiếp khối chóp

.S ABCD

.

A.



2

2 a

. B.



2

8 a

. C.

2

2a

. D.

2

2a

.

Câu 37: Cho khối chóp tứ giác đều có độ dài cạnh đáy bằng

2

, chiều cao bằng

22

. Gọi

O

là tâm mặt

cầu đường tròn ngoại tiếp khối chóp

.S ABCD

. Cosin góc giữa hai mặt phẳng

 

OAB

và

 

OCD

bằng:

A.

15

17

. B.

33

65

. C.

8

17

. D.

56

65

.

Câu 38: Cho hình lăng trụ đứng

  

.ABC A B C

có đáy

ABC

là tam giác vuông tại

A

,

 3AB a

,

 2BC a

đường thẳng



AC

tạo với mặt phẳng

 



BCC B

một góc

30

. Diện tích của mặt cầu ngoại tiếp

lăng trụ đã cho bằng:

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

414

A.



2

3 a

. B.



2

6 a

. C.



2

4 a

. D.



2

24 a

.

Câu 39: Cho hình chóp

.S ABC

có đáy là tam giác vuông tại

A

,

 1cmAB

,

 3 cmAC

. Tam giác

SAB

SAC

lần lượt vuông tại

B

và

C

. Khối cầu ngoại tiếp hình chóp

.S ABC

có thể tích bằng



55

6

3

cm

. Tính khoảng cách từ

C

tới

 

SAB

.

A.

5

cm

2

. B.

5

cm

4

. C.

3

cm

4

. D.

3

cm

2

.

Câu 40: Cho tam giác

ABC

vuông tại

B

và nằm trong mặt phẳng

()P

có

 2AB a

,

 23BC a

. Một

điểm

S

thay đổi trên đường thẳng vuông góc với

 

P

tại

A

()SA

. Gọi

,HK

lần lượt là hình

chiếu vuông góc của

A

lên

,SB SC

. Biết rằng khi

S

thay đổi thì 4 điểm

, , ,A B H K

thuộc một mặt

cầu cố định. Tính bán kính

R

của mặt cầu đó.

A.

 2Ra

. B.

 2Ra

. C.

Ra

. D.

 3Ra

.

Câu 41: Cho hình chóp

.S ABC

có

SA

vuông góc với

 

ABC

,

  

0

, 2 , 45AB a AC a BAC

. Gọi

', 'BC

lần lượt là hình chiếu vuông góc của

A

lên

,SB SC

. Thể tích khối cầu ngoại tiếp hình chóp

. ' 'A BCC B

.

A.



3

2

a

. B.



3

2a

. C.



3

4

3

a

. D.



3

2

3

a

.

Câu 42: Cho hình chóp

.S ABC

có



3

2

a

SA

, các cạnh còn lại cùng bằng

a

. Bán kính

R

của mặt cầu

ngoại tiếp hình chóp

.S ABC

là:

A.



13

2

a

R

. B.



3

a

R

. C.



13

3

a

R

. D.



13

6

a

R

.

Câu 43: Cho hình chóp

.S ABCD

có đáy

ABC

là tam giác vuông cân tại

B

,

 2BC a

, cạnh bên

SA

vuông

góc với đáy. Gọi

H

,

K

lần lượt là hình chiếu của

A

lên

SB

và

SC

, khi đó thể tích của khối cầu

ngoại tiếp hình chóp

AHKCB

là

A.



3

2 a

. B.



3

a

. C.



3

2

a

. D.



3

82

3

a

.

Câu 44: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

 3AB

,

 4AD

và các cạnh bên của

hình chóp tạo với mặt đáy một góc

60

. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

A.





250 3

3

V

. B.





125 3

6

V

. C.





50 3

3

V

. D.





500 3

27

V

.

Câu 45: Cho tứ diện

ABCD

có

 6AB a

,

 8CD a

và các cạnh còn lại bằng

74a

. Tính diện tích mặt cầu

ngoại tiếp tứ diện

ABCD

.

A.





2

S 25 a .

B.





2

S 100 a .

C.





2

100

S a .

3

D.





2

S 96 a .

Câu 46: Cho hình chóp

.O ABC

có

   OA OB OC a

,

60AOB

,

90BOC

,

120AOC

. Gọi

S

là trung điểm cạnh

OB

. Bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

415

A.

4

a

B.

7

4

a

C.

7

2

a

D.

2

a

Câu 47: Cho hai mặt phẳng

 

P

và

 

Q

vuông góc với nhau theo giao tuyến



. Trên đường thẳng



lấy

hai điểm

A

,

B

với

AB a

. Trong mặt phẳng

 

P

lấy điểm

C

và trong mặt phẳng

 

Q

lấy điểm

D

sao cho

AC

,

BD

cùng vuông góc với



và

AC BD AB

. Bán kính mặt cầu ngoại tiếp tứ

diện

ABCD

là:

A.

3

a

. B.

3

2

a

. C.

3a

. D.

23

3

a

.

Câu 48: Cho hình chóp

.S ABCD

có đáy là hình vuông cạnh

22

, cạnh bên

SA

vuông góc với mặt phẳng

đáy. Mặt phẳng

 



qua

A

và vuông góc với

SC

cắt cạnh

SB

,

SC

,

SD

lần lượt tại các điểm

M

,

N

,

P

. Thể tích

V

của khối cầu ngoại tiếp tứ diện

CMNP

bằng

A.





125

6

V

. B.





32

3

V

. C.





108

3

V

. D.





64 2

3

V

.

Câu 49: Cho hình chóp

.S ABC

có

 ,AC a

 3,AB a



0

150BAC

và

SA

vuông góc với mặt phẳng đáy.

Gọi

,M

N

lần lượt là hình chiếu vuông góc của

A

trên

SB

và

SC

. Thế tích khối cầu ngoại tiếp

hình chóp

.A BCNM

bằng

A.



3

47

3

a

. B.



3

28 7

3

a

. C.



3

20 5

3

a

. D.



3

44 11

3

a

.

Câu 50: Trong mặt phẳng

 

P

cho tam giác

ABC

đều cạnh bằng

8

cm và một điểm

S

di động ngoài mặt

phẳng

 

P

sao cho tam giác

MAB

luôn có diện tích bằng

16 3

cm

2

, với

M

là trung điểm của

SC

. Gọi

 

S

là mặt cầu đi qua bốn đỉnh

, , ,M A B C

. Khi thể tích hình chóp

.S ABC

lớn nhất, tính

bán kính nhỏ nhất của

 

S

:

A.

16 6

9

cm. B.

43

3

cm. C.

4 15

3

cm. D.

4 39

3

cm.

Câu 51: Cho mặt cầu

     

     

2 2 2

( ) : 2017 2018 2019 2020S x y z

. Xét mặt phẳng

 

P

thay đổi cắt

mặt cầu theo giao tuyến là đường tròn

 

.C

Hình nón

 

N

có đỉnh S nằm trên mặt cầu, đáy là

đường tròn

 

C

và có chiều cao

h

. Gọi V là thể tích của khối nón được tạo nên bởi

 

N

. Tính giá

trị lớn nhất

max

V

của V.

A.

 





3

max

.32. 2020

81

V

. B.

 





3

max

.8. 2020

81

V

.

C.

 





3

max

.16. 2020

81

V

. D.

 





3

max

.64. 2020

81

V

.

Câu 52: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. Tam giác

SAB

nằm trong mặt phẳng

vuông góc với mặt phẳng

 

ABCD

. Biết rằng

,3AB a AD a

và

60ASB

. Tính diện tích

khối cầu ngoại tiếp hình chóp

.S ABCD

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

416

A.





2

13

2

a

S

. B.





2

13

3

a

S

. C.





2

11

2

a

S

. D.





2

11

3

a

S

.

Câu 53: Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

B

,

32AB BC a

,



90SAB SCB

. Biết khoảng cách từ

A

đến mặt phẳng

 

SCB

bằng

23a

. Tính thể tích mặt

cầu ngoại tiếp hình chóp

.S ABC

.

A.



3

72 18 a

. B.



3

18 18 a

. C.



3

6 18 a

. D.



3

24 18 a

.

Câu 54: Cho hình chóp

.S ABC

có

    

6

,

3

a

SA SB SC AB a BC

và mặt phẳng

 

SAC

vuông góc với

mặt phẳng

 

ABC

. Tính diện tích xung quanh của mặt cầu ngoại tiếp hình chóp

.S ABC

.

A.



2

12

7

a

. B.



2

4

7

a

. C.



2

3

7

a

. D.



2

15

7

a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

417

BẢNG ĐÁP ÁN

1.A

2.A

3.B

4.A

5.A

6.A

7.A

8.C

9.D

10.B

11.B

12.B

13.C

14.C

15.A

16.B

17.B

18.A

19.B

20.B

21.D

22.D

23.B

24.B

25.C

26.C

27.C

28.C

29.C

30.B

31.B

32.C

33.C

34.D

35.C

36.B

37.B

38.B

39.D

40.A

41.D

42.C

43.D

44.D

45.B

46.C

47.B

48.B

49.B

50.C

51.A

52.B

53.D

54.A

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Chọn A

Gọi

H

là trung điểm của

BC AH BC

()AH SBC

.

Mà

  SA AB AC H

là tâm đường tròn ngoại

tiếp

SBC

    HS HB HC SBC

vuông tại

S

.

Gọi

I

là trung điểm

AC

,

 ,O AH

OI AC

O

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

. Đặt

HC x

. Ta có

AOI

đồng dạng

ACH

.

      



2

2 2 2 2

.

2

..

2

a

AI AC a

AO AH AI AC AO R

AH

a x a x

.

Lại có

Ra

         



2

2 2 2 2 2

22

3

2 4 4

2

aa

a a x a a x a x

ax

     

2 2 2 2

32SC BC SB a a a

.

Câu 2: Chọn A

Gọi

O AC BD

, đường chéo

 2AC a

.

Gọi

I

là trung điểm của

SC

.

Suy ra

OI

là đường trung bình của tam giác

SAC

. Suy ra

//OI SA

 

OI ABCD

.

Hay

OI

là trục đường tròn ngoại tiếp đáy

ABCD

.

Mà

IS IC



   IA IB IC ID IS

. Suy ra

I

là tâm

mặt cầu ngoại tiếp chóp

.S ABCD

.

Bán kính mặt cầu ngoại tiếp chóp

.S ABCD

:



   

22

2

22

SC SA AC

R SI a

.

Diện tích mặt cầu:





22

48S R a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

418

Câu 3: Chọn B

Gọi chiều cao, bán kính đáy, độ dài đường sinh của hình nón lần lượt là

,,h r l

.

Hình nón có độ dài đường sinh bằng đường kính đáy nên

 2lr

.

Diện tích hình tròn đáy của hình nón bằng



9

nên:



  

2

93rr

.

Suy ra

26lr

. Áp dụng định lý Pitago cho tam giác

OAH

ta được:

        

2 2 2 2 2 2 2

27 3 3.OH OA AH h l r h h

Vậy chiều cao

h

của hình nón là

33

.

Câu 4: Chọn A

Gọi

M

,

N

lần lượt là trung điểm của

BC

và

SA

. Do

tam giác

ABC

vuông tại

A

nên

M

là tâm đường tròn

ngoại tiếp tam giác

ABC

.

Gọi

a

là đường thẳng qua M và song song với

SA

mà

 ()SA ABC

nên

 ()a ABC

. Do đó

a

là trục đường

tròn ngoại tiếp tam giác

ABC

.

Trong mặt phẳng

()SAM

, gọi

b

là đường trung trực của

đoạn thẳng

SA

, gọi

I

là giao điểm của

a

và

b

.

Ta có

Ia

suy ra

IA IB IC

. Mặt khác,

Ib

suy ra

IA IS

.

Do đó

  IA IB IC IS

hay

I

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

.

Vậy bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là

   

       

2 2 2 2 2

22

5 4 16 5

4 4 4 4 2

AS BC AS AB AC

R IA AN AM

.

Câu 5: Chọn A

Mặt cầu ngoại tiếp hình hộp chữ nhật

có tâm là của hình hộp có bán kính

.

O

A

C

A'

C'

D'

B'

B

D

.ABCD AB C D

   

O

   

22

2 2 2 2

1 1 3

22

2 2 2

a

R AB AD AA a a a



      

b

a

I

N

M

A

B

C

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

419

Vậy diện tích mặt cầu ngoại tiếp hình hộp là .

Câu 6: Chọn A

Gọi

,OI

lần lượt là trung điểm của

,AC SC

. Ta có:

 

//IO SA IO ABCD

.

Mà:

   OA OB OC OD IO

là trục đường tròn ngoại tiếp đa giác đáy

   IA IB IC ID

.

Mặt khác

IS IC

nên mặt cầu ngoại tiếp hình chóp

.S ABCD

có tâm

I

và bán kính

 .

2

SC

R IS

Tam giác

SAD

vuông tại

A

và

     30 tan

SA

SDA SDA SA a

AD

.

  

22

7;AC AB AD a



   

22

2

22

SC SA AC

R IS a

. Vậy





22

48S R a

.

Câu 7: Chọn A

Gọi

,OI

lần lượt là trung điểm của

,AC SC

. Ta có:

 

//IO SA IO ABCD

.

Mà:

   OA OB OC OD IO

là trục đường tròn ngoại tiếp đa giác đáy

   IA IB IC ID

.

Mặt khác

IS IC

nên mặt cầu ngoại tiếp hình chóp

.S ABCD

có tâm

I

và bán kính

 .

2

SC

R IS

Tam giác

SAD

vuông tại

A

và

     30 tan

SA

SDA SDA SA a

AD

.

  

22

7;AC AB AD a



   

22

2

22

SC SA AC

R IS a

. Vậy





22

48S R a

.

Câu 8: Chọn C

Gọi

E

là trung điểm của AC,do tam giác

ABC

vuông tại

B

nên E là tâm đường tròn ngoại tiếp

tam giác

ABC

Gọi

I

và

M

lần lượt là trung điểm

SC

và

SA

,khi đó AMIE là hình chữ nhật

2

3

49

2

a

Sa











CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

420

/ / ( )IE SA IE ABC

mà E là tâm đường tròn ngoại tiếp tam giác ABC,nên

IA IB IC

Lại có

//IM AC IM SA

mà

M

là trung điểm SA nên

IM

là trục đối xứng của đoạn thẳng

SA, nên

IA IS

Từ 1,2

    IA IS IB IC R

hay

I

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

Xét tam giác vuông

ABC

có:

    

22

7 9 4AC AB BC

.

Xét tam giác vuông

IAM

có:

   

       

   

   

22

9 16 5

2 2 4 4 2

SA AC

R IA AM IM

Cách giải khác:

Ta có:





   







0

90

BC AB

BC SB SBC

BC SA

Mà



0

90SAC

nên các điểm

, , ,S A B C

thuộc mặt cầu đường kính

SC

.

Xét tam giác vuông

ABC

có:

    

22

7 9 4AC AB BC

.

Xét tam giác vuông

SAC

có:

   

22

1 1 5

.

2 2 2

R SC SA AC

.

Câu 9: Chọn D

Ta có:

SA

,

AB

,

BC

đôi một vuông góc

 

SA ABC

và

ABC

vuông tại

B

.

Gọi

I

là trung điểm của

AC I

là tâm đường tròn ngoại tiếp

ABC

.

Khi đó bán kính đường tròn tâm

I

ngoại tiếp

ABC

:

  

22

11

22

r AC b c

.

Gọi

O

là trung điểm

SC

O

là tâm mặt cầu ngoại tiếp hình

chóp

.S ABC



2

SA

OI

.

Khi đó bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là:

  

       





2

2 2 2

2 2 2 2

1

2 4 4 2

SA a b c

R OC r a b c

.

Câu 10: Chọn B

Giả sử

 

S

có phương trình dạng:

 

          

2 2 2 2 2 2

2 2 2 0 0 (1)x y z ax by cz d a b c d

.

Với tâm

 

;;I a b c

và bán kính

   

2 2 2

R a b c d

.

Vì

 

S

đi qua bốn điểm

, , , A B C D

nên tọa độ của các điểm

, , , A B C D

thỏa mãn. Từ đó ta có

hệ phương trình:



      



      





      



      



1 4 16 2 4 8 0

1 9 1 2 6 2 0

4 4 9 4 4 6 0

1 0 16 2 0 8 0

a b c d



   



   







   



   



2 4 8 21

2 6 2 11

4 4 6 17

2 0 8 17

a b c d















  



   



10 10 10

6 6 6

2 4 2 0

2 0 8 17

bc

a b c

a b c d























1

0

2

21

b

c

a

d

  ( 2; 1; 0), 26IR

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

421

Câu 11: Chọn B

Qua

G

, kẻ đường thẳng song song với

BC

, cắt

SB

tại

M

và cắt

SC

tại

N

. Gọi

H

là trung điểm

của

BC



2

3

SG

SH

. Ta có:

   

2

//

3

SM SN SG

MN BC

SB SC SH

.

Ta có:



2

AC

AB a

(

ABC

vuông cân tại

B

).

Có:



   

2 2 3

.

1 1 1 1 1 1

. . .

3 3 2 3 2 6

S ABC ABC

V SA S SA AB a a a

.

Theo công thức tỉ lệ thể tích ta có:

      

33

.

..

.

2 2 4 4 4 1 2

. . . .

3 3 9 9 9 6 27

S AMN

S AMN S ABC

S ABC

V

SA SM SN

V V a a

V SA SB SC

.

Câu 12: Chọn B

Trong

 

OBC

kẻ đường cao

OH

. Vì

OBC

là tam giác vuông cân nên

H

là tâm đường tròn

ngoại tiếp

OBC

và



2

a

OH

.

Qua H dựng đường thẳng

d

song song với

OA

 

d OBC

. Do đó,

d

là trục đường tròn của

OBC

.

Trong

 

,mp OA d

, dựng đường trung trực

OA

cắt

OA

,

d

lần lượt tai

,IN

. Khi đó

I

là tâm mặt

cầu ngoại tiếp tứ diện

.O ABC

.

Theo cách dựng ta có tứ giác

OHIN

là hình chữ nhật nên



2

a

NI OH

.



Bán kính



    





2

2 2 2

2

OA

R OI ON IN OH



  





2

23

2 2 2

a a a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

422

Chú ý: Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện vuông

.O ABC

là





2 2 2

2

OA OB OC

R

Câu 13: Chọn C

Ta có:





2

. 45V R h

. Suy ra:



45

3

5

R

.

Diện tích toàn phần khối trụ:

    

    

22

2 2 2 .3.5 2 .3 48

tp

S Rh R

.

Câu 14: Chọn C

Gọi điểm

O

là tâm đường tròn ngoại tiếp đáy.

I

là trung điểm

SA

.

J

là tâm mặt cầu ngoại tiếp.

Dễ thấy

AIJO

là hình chữ nhật. Do đó



    





2

2 2 2

5

22

aa

JA AO AI a

.

Câu 15:

Chọn A

Vì

.A BCD

là tứ diện đều nên tâm của mặt cầu ngoại tiếp hình chóp nằm trên đường cao

AO

trong đó

O

là trọng tâm của tam giác đều

BCD

.

Gọi M là trung điểm của cạnh

AB

. Từ

M

kẻ đường trung trực

MI

của đoạn

AB

cắt

AO

tại

I

.

Do đó

I

là tâm mặt cầu ngoại tiếp của hình chóp

.A BCD

Ta có

MI AB

nên hai tam giác vuông

IMA

và

BOA

đồng dạng.Từ đó suy ra:

    

2

1

.

2 2.

IA MA AB AB

IA R

BA OA OA AO

Ta có

        

22

2 2 2

66

3 3 2 4

a a AB a

AO AB BO a R IA

AO

Diện tích mặt cầu

 

S

là:





  

2

22

33

4 4 .

82

a

S R a

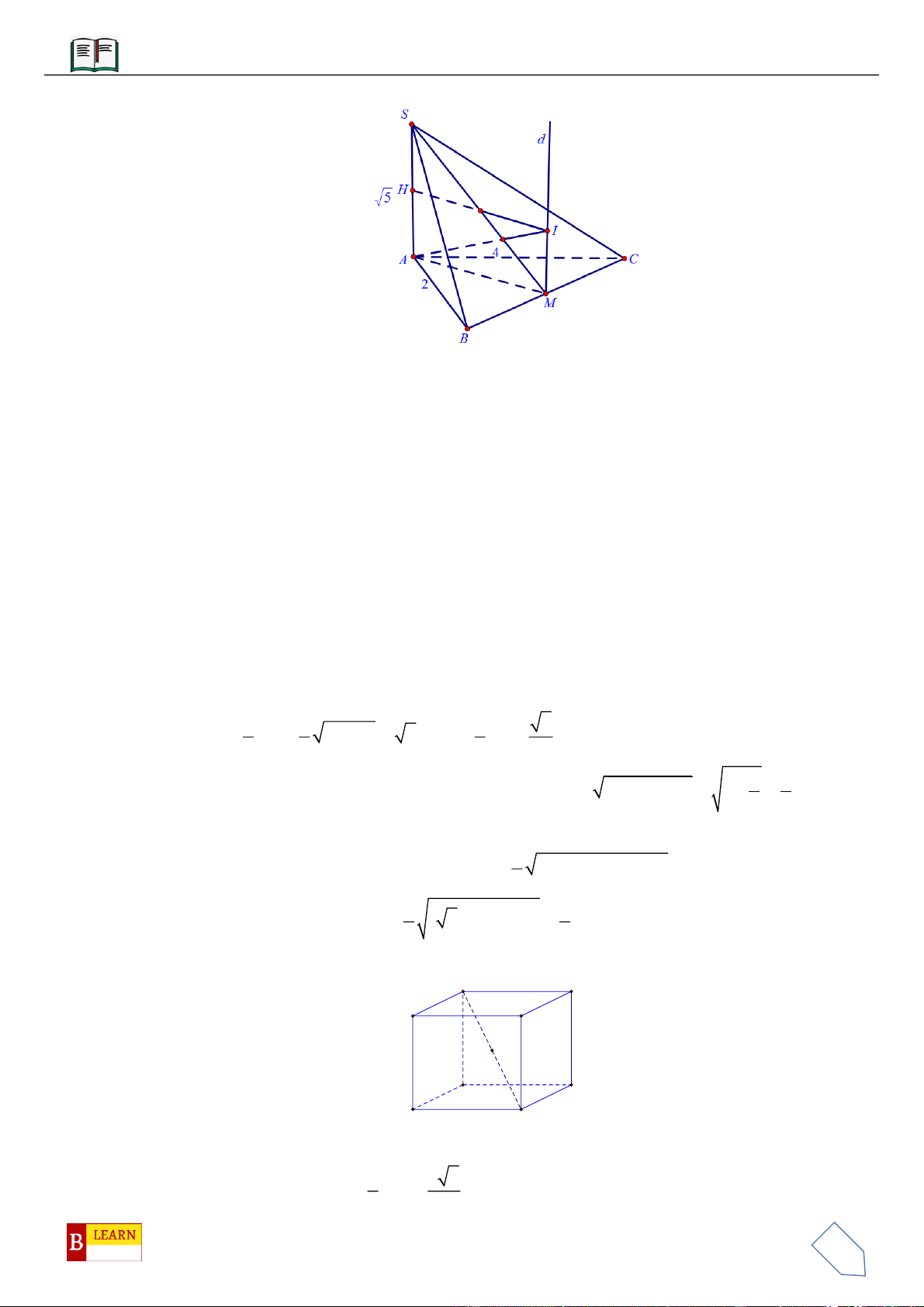
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

423

Câu 16: Chọn B

Cách 1.

Gọi

,MH

lần lượt là trung điểm

,SABC

.

Ta có tam giác

ABC

vuông tại

A

suy ra

M

là tâm đường tròn ngoại tiếp tam giác

ABC

.

Qua

M

kẻ đường thẳng

d

sao cho

 

d ABC

 d

là trục đường tròn ngoại tiếp tam giác

ABC

.

Trong mặt phẳng

 

SAM

kẻ đường trung trực



của đoạn

SA

, cắt

d

tại

I





    







IA IB IC

IA IB IC IS

IA IS

 I

là tâm mặt cầu ngoại tiếp hình chóp

..S ABC

●

 















HA ABC

IM ABC











//

HA AM

HA IM

;

 

















,,

HI SA

AM SA

HI SA AM SAM

 //HI AM

.

Suy ra tứ giác

HAMI

là hình chữ nhật.

Ta có

   

22

11

2 4 5

22

AM BC

,



15

22

IM SA

.

Bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là:

     

22

55

5

42

R AI AM IM

.

Cách 2. Sử dụng kết quả: Nếu

SABC

là một tứ diện vuông đỉnh

A

thì bán kính mặt cầu ngoại

tiếp tứ diện

SABC

được tính bởi công thức:

  

2 2 2

1

2

R AS AB AC

Áp dụng công thức trên, ta có

 

   

2

22

15

5 2 4

22

R

.

Câu 17: Chọn B

Gọi

I

là trung điểm



A C I

là tâm mặt cầu ngoại tiếp hình lập phương.

Bán kính mặt cầu là



  

13

22

a

R CI CA

.

I

C'

D'

A'

B

H

D

B

C

A

D

C

B'

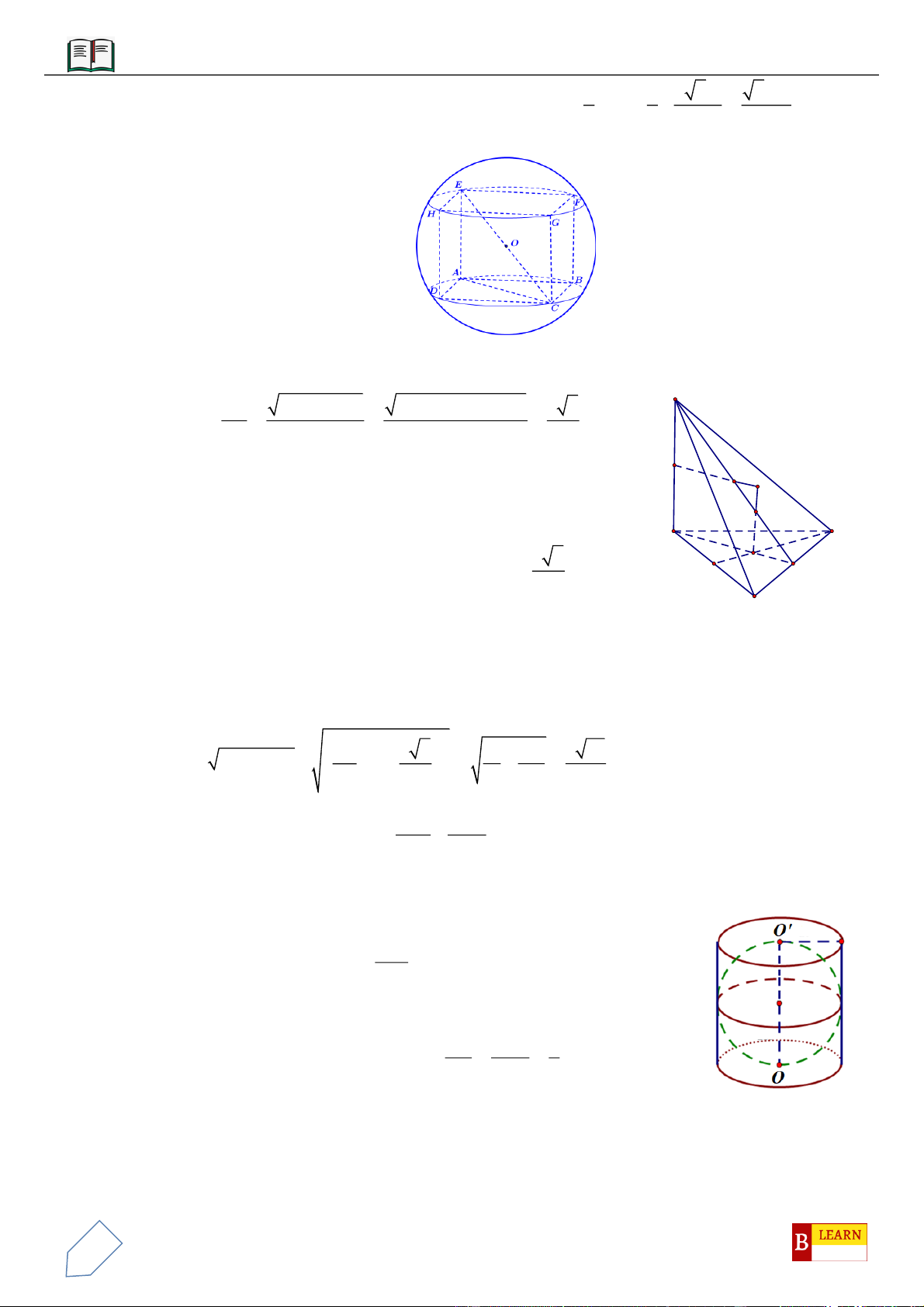
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

424

Suy ra thể tích khối cầu ngoại tiếp hình lập phương là





  

33

3

4 4 3 3 3

3 3 8 2

aa

VR

.

Câu 18: Chọn A

Gọi

O

là tâm của hình lập phương

.ABCD EFGH

.

Bán kính mặt cầu ngoại tiếp hình lập phương

.ABCD EFGH

là:

  

    

2 2 2 2 2

3

2 2 2 2

EC EA AC EA AB BC a

R OC

.

Câu 19: Chọn B

Ta có













( ).

SA SB

SA SBC

SA SC

Gọi

G

là trọng tâm tam giác đều SBC, suy ra



3

a

SG

.

Gọi

d

là đường thẳng qua G và vuông góc với. Suy ra d là trục của

đường tròn ngoại tiếp tam giác SBC.

Tâm I của mặt cầu ngoại tiếp hình chóp SABC là giao điểm của mặt phẳng trung trực đoạn SA và

d.



    





2

22

3

23

SA a

R SI SE SG

  

22

3 21

4 9 6

a a a

Diện tích mặt cầu





  

22

2

21 7

4 4 . .

36 3

aa

SR

Câu 20: Chọn B

Diện tích toàn phần của hình trụ là

  

  

22

()

2 2 .2 6 .

T

S a a a a

Diện tích mặt cầu là













2

()

4 4 .

2

S

OO

Sa

Tỉ số giữa diện tích mặt cầu

 

S

và diện tích toàn phần của hình trụ

 

T

là





2

()

2

()

42

.

3

6

S

T

S

a

S

a

Câu 21: Chọn D

Cách 1:

E

G

S

C

B

A

I

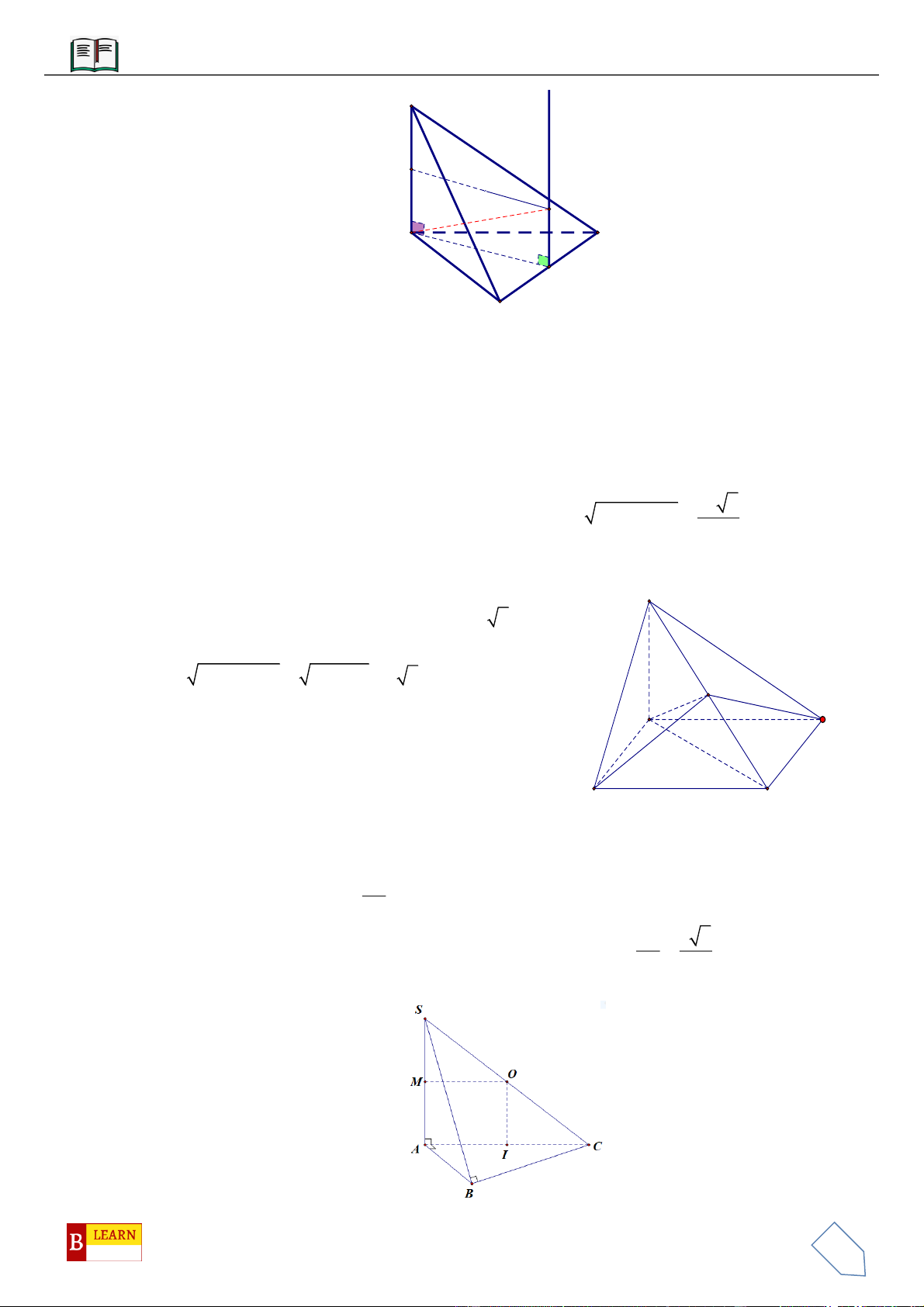
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

425

Gọi

E

là trung điểm của

BC

. Vì

ABC

vuông tại

A

nên

E

là tâm đường tròn ngoại tiếp

ABC

. Qua

E

dựng đường thẳng

d

song song với

SA

, vì

 

SA ABC

nên

d

là trục của

ABC

. Trong

mặt phẳng

 

;SA d

, dựng đường trung trực của

SA

cắt

d

tại

I

thì

I

là tâm mặt cầu ngoại tiếp

hình chóp

.S ABC

vì

   I d IA IB IC

, mặt khác

I

thuộc trung trực của

SA

nên

IS IA

.

Gọi

F

là trung điểm của

SA

. Trong mặt phẳng

 

;SA d

có

AE SA

,

FI SA

nên

// FI AE

lại

có

// EI AF

nên tứ giác

AFIE

là hình chữ nhật. Vậy

  

22

52

2

a

AI AE AF

.

Câu 22: Chọn D

Ta có

 

    , , .SA ABCD SA AC SA BC SA CD

Vì

ABCD

là hình vuông cạnh

a

nên

 2AC a

. Tam

giác

SAC

vuông tại

A

nên

    

2 2 2 2

23SC SA AC a a a

.

Ta có

 





   







BC AB

BC SAB BC SB

BC SA

;

 





   







CD AD

CD SAD CD SD

CD SA

.

Gọi

I

là trung điểm của

SC

. Vì

  ,,SBC SAC SDC

là các tam giác vuông có cạnh huyền là

SC

nên

    

2

SC

IS IC IA IB ID

.

Do đó bán kính của mặt cầu ngoại tiếp hình chóp

.S ABCD

là



3

22

SC a

R

.

Câu 23: Chọn B

E

F

I

C

B

A

S

I

C

A

D

B

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

426

Cách 1.

Gọi

I

là tâm đường tròn ngoại tiếp tam giác

ABC

, do tam giác

ABC

vuông tại

B

nên

I

là trung

điểm của

AC

. Qua

I

dựng đường thẳng

d

vuông góc với

 

ABC

. Suy ra

//d SA

.

Trong tam giác

SAC

, dựng đường trung trực của

SA

cắt

d

tại

O

là tâm mặt cầu ngoại tiếp hình

chóp

.S ABC

. Ta tính được

2 2 , 4AC a SC a

Bán kính mặt cầu

  

22

R OA OI OM

  

22

2 2 2a a a

.

Diện tích mặt cầu ngoại tiếp chóp

.S ABC

là

 





2

4 2 16S a a

.

Cách 2.

Ta có

   ,BC SA BC AB BC SB

. Ta có

  90SAC SBC

.

Khi đó 4 điểm

, , ,S A B C

nằm trên mặt cầu đường kính

SC

.

Bán kính mặt cầu

2

2

SC

Ra

.

Diện tích mặt cầu ngoại tiếp hình chóp

 





2

4 2 16S a a

.

Câu 24: Chọn B

Hình nón có đường sinh bằng đường kính đáy và bằng 2



Thiết diện qua trục hình nón là tam

giác đều có cạnh bằng 2 và bán kính mặt cầu ngoại tiếp bằng bán kính đường tròn ngoại tiếp tam

giác

SAB

.

Gọi

R

là bán kính mặt cầu, theo định lý sin trong tam giác

SAB

, ta có:

 2

sin

AB

R

S

.

   



2 2 3

2sin 2.sin60 3

AB

R

S

.

Câu 25: Chọn C

Gọi

O

là giao điểm của hai đường chéo

AC

và

BD

.

O

D

A

B

C

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

427

Ta có

90ABC

,

90ADC

và

90ASC

suy ra các đỉnh

B

,

D

,

S

cùng nhìn đoạn thẳng

AC

dưới một góc vuông nên

O

là tâm mặt cầu ngoại tiếp chóp

.S ABCD

và

  

2

AC

R OA a

.

Vậy





33

44

33

V R a

.

Câu 26: Chọn C

Ta có:

  

22

5AC AB BC a

. Vì

SA AC

nên

  

22

13SC SA AC a

Nhận thấy:













BC AB

BC SB

BC SA

.Tương tự:

CD SD

Do các điểm

,A

,B

D đều nhìn đoạn thẳng

SC

dưới một

góc vuông nên gọi

I

là trung điểm của đoạn thẳng

SC

thì

I

là tâm mặt cầu ngoại tiếp hình chóp

.S ABCD

. Vậy



13

22

SC a

R

.

Câu 27: Chọn C

Tam giác

BCD

vuông tại

C

nên áp dụng định lí Pitago, ta được

 5BD a

.

Tam giác

ABD

vuông tại

B

nên áp dụng định lí Pitago, ta được

 5 2.AD a

Vì

B

và

C

cùng nhìn

AD

dưới một góc vuông nên tâm mặt cầu ngoại tiếp tứ diện

ABCD

là

trung điểm

I

của

AD

. Bán kính mặt cầu này là:



52

.

22

AD a

R

Câu 28: Chọn C

Gọi

O

là tâm hình vuông

ABCD

,

G

là trung điểm

SD

,

,GI SD I SO

.

Ta có cạnh đáy bằng

32a

nên

3 2 . 2 6BD a a

,

 3OD a

.

Xét

SOD

vuông tại

O

ta có:

  

22

4SO SD OD a

Ta có

SOD SGI∽

, suy ra

 

    

2

1 25

4 . 5

28

SO SD a

a R a R

SG SI

.

Câu 29: Chọn C

12a

4a

3a

I

O

C

A

D

B

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

428

Đáy

ABC

là tam giác đều



tâm đường tròn ngoại tiếp là trọng tâm

G

.

Từ

G

kẻ đường thẳng

d

vuông góc với mặt phẳng đáy

 //d SA

và đường thẳng

d

là trục của

tam giác đáy.

Trong mặt phẳng

 

SAG

kẻ

'd

là đường trung trực của đoạn

SA

.

Trong mặt phẳng

 

SAG

hai đường thẳng

d

và

'd

cắt nhau tại

I



I

cách đều 4 đỉnh

, , ,CS A B

của hình chóp



I

là tâm của mặt cầu ngoại tiếp hình chóp

.S ABC

với

R AI

.

Tính bán kính

R

:

Tam giác

ABC

đều cạnh

a





3

2

a

AM





23

33

a

AG AM

.

N

là trung điểm

SA



  

1

22

a

AN SA GI

.

Xét tam giác vuông

AIG

:

   

22

21

6

a

AI AG GI R

.

Vậy diện tích của mặt cầu cần tìm là:

  



  





2

22

21 7

4 4 .

63

a

S R a

Câu 30: Chọn B

Gọi

H

là tâm đường tròn ngoại tiếp tam giác

ABC

, khi đó

 

SH ABC

và

SH

là trục đường

tròn ngoại tiếp đa giác đáy.

Góc giữa đường thẳng

SA

và mặt phẳng

 

ABC

là



0

60SAH

.

Gọi

N

là trung điểm

SA

, mặt phẳng trung trực của cạnh

SA

cắt

SH

tại

O

. Khi đó

  OS OA OB OC

nên

O

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

.

Khi đó bán kính đường tròn ngoại tiếp tam giác

ABC

là



0

.

2sin 30

BC

AH a



0

.tan60 3SH AH a

,

  

22

2SA SH AH a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

429

Bán kính mặt cầu là

   

2

. 2 3

23

SN SA SA

R SO a

SH SH

.

Thể tích của khối cầu tâm

O

là





33

4 32 3

3 27

V R a

.

Câu 31: Chọn B

Gọi

E

là trung điểm của

ID

,

F

là trung điểm của

SB

. Trong

mặt phẳng

 

SBD

, vẽ

IT

song song với

SE

và cắt

EF

tại

T

.

Ta có

 

SE ABCD

, suy ra

 



  



; D 45SBE SB ABC

. Suy ra

SBE

vuông cân tại

E

. Suy ra

EF

là trung trực của

SB

. Suy ra

TS TB

.

Ta có

IT SE

, suy ra

 

IT ABCD

. Suy ra

IT

là trục đường tròn ngoại tiếp hình chữ nhật

ABCD

. Suy ra

  TA TB TC TD

.

Từ và suy ra

T

là tâm mặt cầu ngoại tiếp hình chóp

.S ABCD

.

Do

ABCD

là hình chữ nhật nên

  

22

5BD AB BC a

, suy ra



5

2

IB ID a

.

Do

E

là trung điểm của

ID

nên



15

24

IE ID a

.

BEF

vuông tại

F

có

45EBF

nên

BEF

vuông cân tại

F

.

EIT

vuông tại

I

có

45IET

nên

EIT

vuông cân tại

I

. Suy ra



5

4

IT IE a

.

Do

BIT

vuông tại

I

nên

  

22

55

4

TB IB IT a

.

Vậy diện tích mặt cầu ngoại tiếp hình chóp

.S ABCD

là





22

125

4

S TB a

.

Câu 32: Chọn C

Gọi

M

,

N

,

I

lần lượt là trung điểm của

AB

,

CD

và

MN

.

Ta có

  ACD BCD

AN BN

ABN

cân

tại

N

, mà

AM

là đường trung tuyến



AM

là đường trung trực của

AB

  

2

MN

IA IB

.

Chứng minh tương tự ta có

  

2

MN

IC ID

.

Từ và suy ra

I

là tâm mặt cầu ngoại tiếp tứ diện

ABCD

.

Áp dụng công thức trung tuyến cho tam giác

ACD

ta

có





2

36 25 9

24

AN

Error! Not a valid embedded object..

Xét tam giác vuông Error! Not a valid embedded object. có: Error! Not a valid embedded object. Error!

Not a valid embedded object.Error! Not a valid embedded object.Error! Not a valid embedded object.Error!

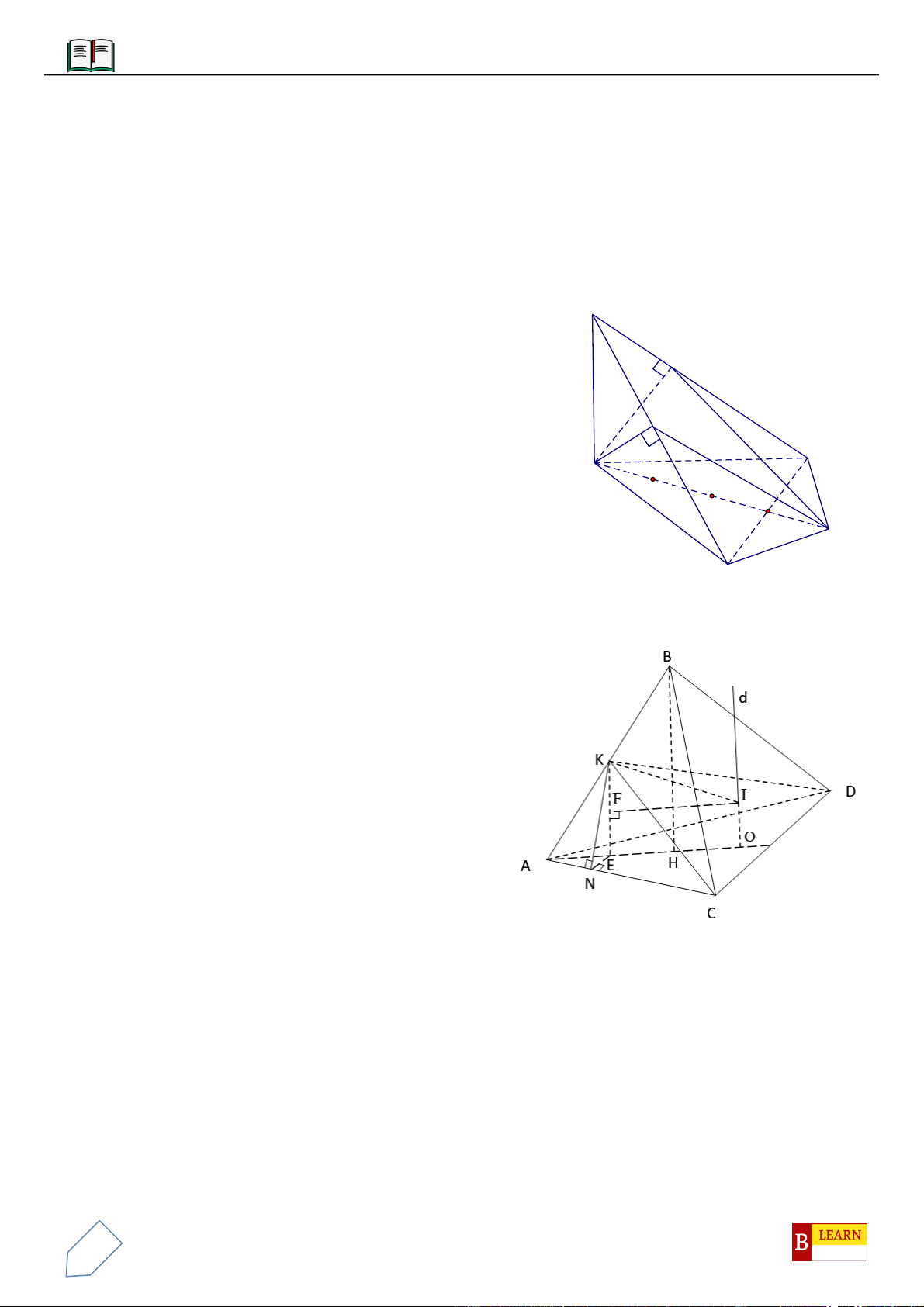
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

430

Not a valid embedded object.Error! Not a valid embedded object.Error! Not a valid embedded object.Error!

Not a valid embedded object..

Suy ra bán kính mặt cầu ngoại tiếp tứ diện Error! Not a valid embedded object. là Error! Not a valid

embedded object..

Vậy thê tích khối cầu ngoại tiếp tứ diện Error! Not a valid embedded object.là: Error! Not a valid

embedded object. Error! Not a valid embedded object..

Câu 33: Chọn C

Gọi Error! Not a valid embedded object. là đường kính

đường tròn ngoại tiếp Error! Not a valid embedded object..

Ta có Error! Not a valid embedded object..

Từ đó suy ra Error! Not a valid embedded object..

Chứng minh tương tự ta được Error! Not a valid

embedded object..

Từ,, ta suy ra 5 điểm Error! Not a valid embedded object.

cùng nằm trên mặt cầu đường kính Error! Not a valid

embedded object..

Gọi Error! Not a valid embedded object. là trung điểm của

Error! Not a valid embedded object., ta có Error! Not a valid

embedded object..

Vậy diện tích mặt cầu đi qua 5 điểm Error! Not a valid

embedded object. là: Error! Not a valid embedded

object..

Câu 34: Chọn D

Tứ diện Error! Not a valid embedded object. đều,

có độ dài cạnh là 1.

Gọi H là trọng tâm tam giác Error! Not a valid

embedded object. khi đó Error! Not a valid

embedded object.. Gọi E là trung điểm của

Error! Not a valid embedded object., suy ra Error!

Not a valid embedded object.. Từ E hạ EN vuông

góc xuống AC, Error! Not a valid embedded

object., suy ra Error! Not a valid embedded object.

Gọi Error! Not a valid embedded object. là tâm

đường tròn ngoại tiếp tam giác Error! Not a

valid embedded object.. Error! Not a valid

embedded object..

Ta tính được Error! Not a valid embedded object.. Dựng đường thẳng Error! Not a valid embedded object.

đi qua Error! Not a valid embedded object., vuông góc với Error! Not a valid embedded object.

Gọi I là tâm mặt cầu ngoại tiếp chóp Error! Not a valid embedded object., Error! Not a valid embedded

object. suy ra Error! Not a valid embedded object. là hình chữ nhật

Ta tính được: Error! Not a valid embedded object.; Error! Not a valid embedded object.; Error! Not a valid

embedded object.

Đặt Error! Not a valid embedded object. ta có

Error! Not a valid embedded object..

K

H

O

D

C

B

A

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

431

Mà Error! Not a valid embedded object. nên Error! Not a valid embedded object. suy ra Error! Not a valid

embedded object.. Vậy Error! Not a valid embedded object..

Câu 35: Chọn C

Hình chóp này có mặt bên vuông góc với mặt đáy. Nên ta có công thức tính bán kính mặt cầu

ngoại tiếp hình chóp Error! Not a valid embedded object. là: Error! Not a valid embedded object.,

với Error! Not a valid embedded object. là bán kính mặt cầu ngoại tiếp hình chóp Error! Not a valid

embedded object.,Error! Not a valid embedded object. là bán kính đường tròn ngoại tiếp đáy hình chóp

Error! Not a valid embedded object., Error! Not a valid embedded object. là bán kính đường tròn ngoại

tiếp tam giác Error! Not a valid embedded object..

Ta có: Do Error! Not a valid embedded

object. và Error! Not a valid embedded

object.. nên Error! Not a valid embedded

object..

Trong Error! Not a valid embedded object.

vuông tại Error! Not a valid embedded

object. ta có Error! Not a valid embedded

object..

Error! Not a valid embedded object.

Error! Not a valid embedded object., Error!

Not a valid embedded object.

Vậy Error! Not a valid embedded object.

Diện tích mặt cầu ngoại tiếp là: Error! Not a valid embedded object..

Câu 36: Chọn B

Dễ thấy các góc Error! Not a valid embedded object., Error! Not a valid embedded object., Error! Not a

valid embedded object. đều bằng Error! Not a valid embedded object.nên mặt cầu ngoại tiếp khối chóp

Error! Not a valid embedded object.có tâm là trung điểm Error! Not a valid embedded object. của Error!

Not a valid embedded object. và có bán kính Error! Not a valid embedded object. nên diện tích của mặt

cầu là:

Error! Not a valid embedded object..

Câu 37: Chọn B

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

432

Gọi Error! Not a valid embedded object. là tâm hình vuông Error! Not a valid embedded object.. Vì Error!

Not a valid embedded object. là hình chóp tứ giác đều nên Error! Not a valid embedded object. là giao

điểm của Error! Not a valid embedded object. và mặt phẳng trung trực cạnh bên Error! Not a valid

embedded object..

Khi đó Error! Not a valid embedded object. đi qua Error! Not a valid embedded object. và song song với

Error! Not a valid embedded object., Error! Not a valid embedded object..

Gọi Error! Not a valid embedded object., Error! Not a valid embedded object. lần lượt là trung điểm của

Error! Not a valid embedded object., Error! Not a valid embedded object..

Ta có Error! Not a valid embedded object.. Suy ra Error! Not a valid embedded object..

Mà: Error! Not a valid embedded object.

Xét hình vuông Error! Not a valid embedded object. có cạnh bằng Error! Not a valid embedded

object.Error! Not a valid embedded object.bán kính đáy hình vuông Error! Not a valid embedded object.

là Error! Not a valid embedded object..

Xét tam giác vuông

SAI

, ta có

    

22

1 8 3SA AI SI

.

Do đó cạnh bên hình chóp bằng

3

.

Bán kính mặt cầu ngoại tiếp hình chóp là:

  

2

9 9 2

2. 8

42

SA

R

SI

.

Khi đó



     





2

162 1 130

2 64 2 8

AB

OM ON R

,

2MN BC

.

Từ đó suy ra





  

2 2 2

130

2. 2

33

64

cos

130

2. . 65

2.

64

OM ON MN

MON

OM ON

.

Vậy cosin góc giữa hai mặt phẳng

 

OAB

và Error! Not a valid embedded object. bằng Error! Not a

valid embedded object..

Câu 38: Chọn B

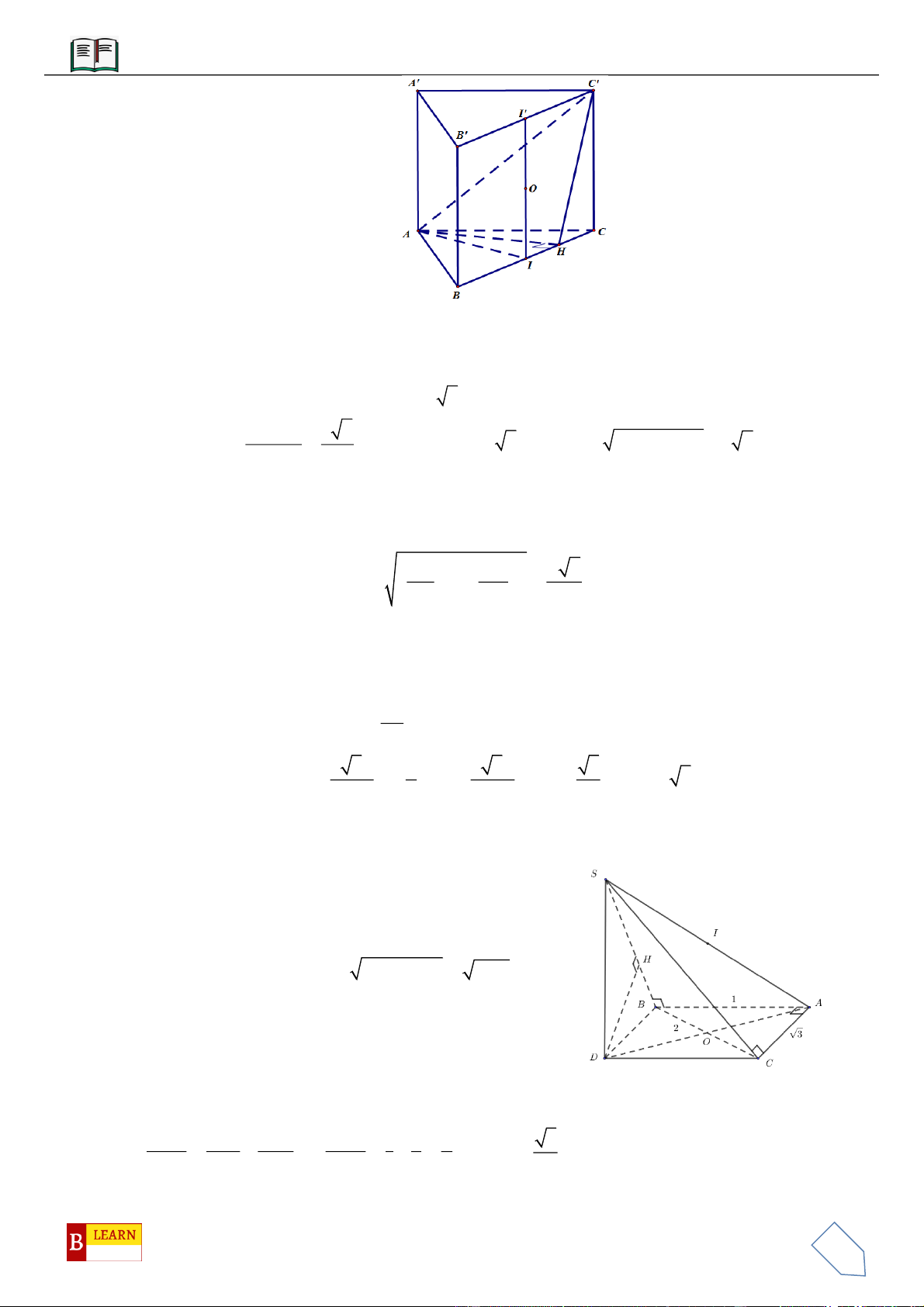
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

433

Gọi

H

là hình chiếu vuông góc của

A

trên

BC

 



AH BCC B

.

 

   

   , 30AC BCC B HC A

.

ABC

là tam giác vuông tại

A

,

 3AB a

,

 2BC a

suy ra

AC a

.

Ta có:



.3

2

AB AC a

AH

BC



  23AC AH a



   

22

2AA AC AC a

.

Gọi

I

,



I

lần lượt là trung điểm

BC

,



BC

. Dễ thấy

I

, .Error! Not a valid embedded object.. lần lượt

là tâm đường tròn ngoại tiếp

ABC

,

  

ABC

.

Gọi

O

là trung điểm của



II

suy ra

O

là tâm mặt cầu ngoại tiếp lăng trụ đã cho.

Bán kính mặt cầu là :

22

6

2 2 2



   

   

   

   

BC BB a

R OB

.

Diện tích của mặt cầu ngoại tiếp lăng trụ đã cho bằng:

22

46



S R a

.

Câu 39: Chọn D

Cách 1: Vì

90SBA SCA  

suy ra trung điểm

I

của cạnh

SA

là tâm mặt cầu ngoại tiếp hình

chóp

.S ABC

với bán kính

2

SA

R 

.

Thể tích khối cầu là

55

6

V 



3

4 5 5

36

R



5

2

R

5SA

.

Gọi

O

là trung điểm

BC

, điểm

D

đối xứng với

A

qua

O

nên tứ giác

ABDC

là hình chữ nhật.

Dễ thấy

CD SB

,

CD DB

CD SD

 

1

.

SC DB

,

CD DB

DB SD

 

2

.

Từ

 

SD ABDC

22

5 4 1SD SA AD     

.

Gọi

H

là chân đường vuông góc của

D

lên cạnh

SB

.

 

,,d C SAB d D SAB DH

.

Thật vậy

AB BD

;

AB SD

 

AB SDB

AB DH

;

DH SB

 

DH SAB

.

2 2 2

1 1 1

DH SD DB



2

1 1 1 4

1 3 3DH

   

3

2

DH

.

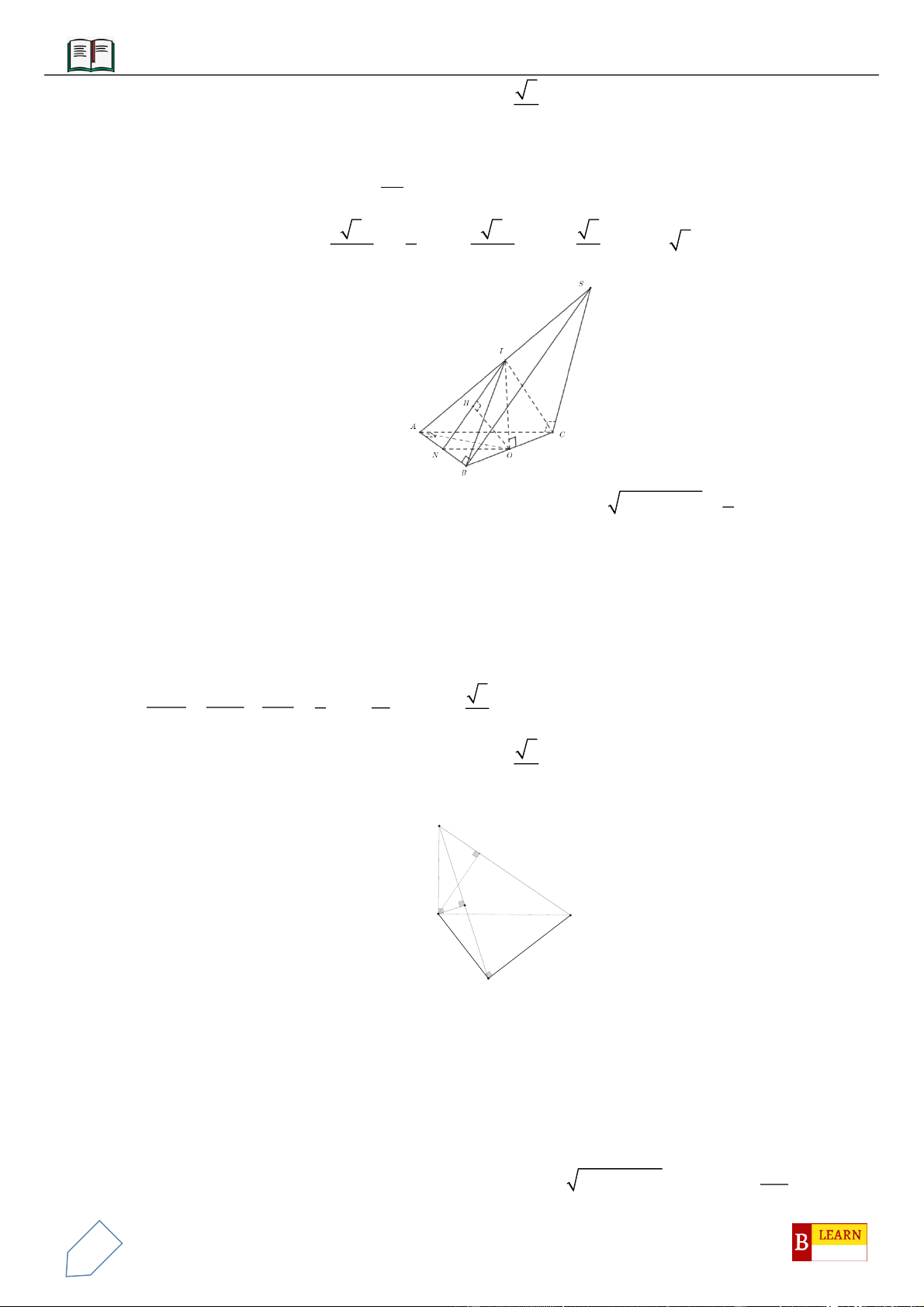
CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

434

Vậy khoảng cách từ

C

đến mặt phẳng

 

SAB

là

3

cm

2

.

Cách 2: Vì

90SBA SCA  

suy ra trung điểm

I

của cạnh

SA

là tâm mặt cầu ngoại tiếp hình

chóp

.S ABC

với bán kính

2

SA

R 

.

Thể tích khối cầu là

55

6

V 



3

4 5 5

36

R



5

2

R

5SA

.

Gọi

O

là trung điểm

BC

, vì

BIC

cân nên

OI BC

;

22

1

2

OI IC OC  

.

Mà

O

là tâm đường tròn ngoại tiếp

ABC

 

OI ABC

 

, 2 ,d C SAB d O ABI

.

Gọi

N

là trung điểm

AB

nên

ON AB

,

OI AB

 

AB ONI

.

   

ABI ONI

theo giao tuyến

IN

.

Kẻ

OH IN

 

OH ABI

 

, 2 , 2d C SAB d O ABI OH  

.

2 2 2

1 1 1

OH ON OI



4 16

4

33

  

3

4

OH

.

Vậy khoảng cách từ

C

đến mặt phẳng

 

SAB

là

3

cm

2

.

Câu 40: Chọn A

Ta có:

SA BC

(

Vì

()SA ABC

)

và

AB BC

()BC SAB

Ta lại có:

()AH SAB AH BC  

.

Và

AH SB

.

Từ và suy ra

()AH SBC

. Khi đó

AHC

vuông tại

H

.

Lại có

AKC

vuông tại

K

và

ABC

vuông tại

B

.

Suy ra

,,B H K

dều nhìn

AC

dưới góc vuông. Vậy bốn điểm

, , ,A B H K

đều thuộc mặt cầu

đường kính

AC

. Trong tam giác vuông

ABC

có:

22

4AC AB BC a  

2

AC

Ra  

.

C

B

A

K

H

S

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

435

Câu 41: Chọn D

Tam giác

ABC

có

0

, 2, 45AB a AC a BAC BC a    

suy ra tam giác

ABC

là tam giác

vuông cân tại

B

. Vậy điểm

B

nhìn

AC

dưới một góc vuông.

 

   

 

'

' ' ' ' ' .

' ' , ' '

BC SAB BC AB

AB SB

AB BCC B AB B C

SB BC B

SB BCC B BC BCC B

  









   











Suy ra

'B

nhìn

AC

dưới một góc vuông.

Do

'AC SC

nên

'C

nhìn

AC

dưới một góc vuông.

Từ,, và suy ra mặt cầu ngoại tiếp hình chóp

. ' 'ABCC B

là mặt cầu đường kính

AC

.

Bán kính mặt cầu ngoại tiếp hình chóp

. ' 'ABCC B

là:

2

22

AC a

R 

.

Suy ra thể tích của mặt cầu ngoại tiếp hình chóp

. ' 'ABCC B

là:

3

42

33

a

VR





.

Câu 42: Chọn D

Cách 1:

Gọi

,NM

lần lượt là trung điểm của

BC

và

AD

.

Ta có:

ABC

và

SBC

là các tam giác đều cạnh

a

3

2

a

AM SM  

.

SAM

là tam giác đều cạnh

3

2

a

.

O

N

F

M

A

C

B

S

E

I

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

436

Gọi

F

là trung điểm của

AM

SF AM

 

1

. Mặt khác

ABC

đều

AM BC

.

SBC

đều

SM BC

 

BC SAM

BC SF

 

2

.

Từ

 

1

và

 

2

 

SF ABC

.

Gọi

E

là trọng tâm

ABC

,

ABC

đều

E

là tâm đường tròn ngoại tiếp

ABC

.

Qua

E

kẻ đường thẳng

 

d

vuông góc với

 

mp ABC



 

d

là trục của đường tròn ngoại tiếp

ABC

. Vì

 

SF ABC

 

//d SF

.

Mặt khác

SAM

đều nên đường thẳng

MN

là đường trung trực đoạn

SA

.

Trong

 

mp SAM

, gọi

 

O d MN

;

 

O d OA OB OC   

.

O MN OS OA  

.

Vậy

O

là tâm mặt cầu ngoại tiếp hình chóp

.S ABC

, bán kính

22

R OA OE EA  

.

Trong

ABC

:

2 2 3 3

.

3 3 2 3

aa

AE AM  

,

13

36

a

EM AM

.

SAM

đều

MN

là đường phân giác trong góc

SMA

30OME  

.

Xét

OME

vuông tại

E

:

tan30

OE

EM



31

.

66

3

aa

OE  

.

Vậy

22

13

36 3 6

a a a

R OE EA    

.

Cách 2:

Gọi

H

là tâm đường tròn ngoại tiếp tam giác

SAB

,

E

là trung điểm của

SA

.

SAB

cân tại

B

nên

H BE

. Vì

CA CB CS a  

nên

()CH SAB

.



Đường thẳng

CH

là trục của đường tròn ngoại tiếp

SAB

.

Gọi

M

là trung điểm của

CB

, qua

M

dựng đường thẳng

 

d

vuông góc với

BC

.

 

d CH O

;

 

O d OB OC  

.

+

O CH OS OA OB   

.

Suy ra

O

là tâm mặt cầu ngoại tiếp hình chóp

SABC

, bán kính

R OC

.

Ta có

CMO CHB

CM CO

CH CB



2

.

2.

CM CB CB

CO

CH CH

  

.

B

S

A

H

C

E

M

O

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

437

Xét

SBE

ta có:

2

2 2 2

3 13

16 4

aa

BE SB SE a    

.

Ta có:

2

1 1 13 3 39

. . .

2 2 4 2 16

SAB

a a a

S BE SA



  

.

Bán kính đường tròn ngoại tiếp

SAB

là:

3

2

3

. . 2

2

4.

39 13

4.

16

SAB

a

SA SB AB a

BH

S

a



  

.

Xét

CHB

ta có:

2

2 2 2

43

13

aa

CH CB BH a    

.

Vậy

22

13

3

2. 6

2.

13

CB a a

R CO

a

CH

   

.

Câu 43: Chọn D

Gọi

M

là trung điểm

BC

.

ABC

vuông cân tại

B



1

2

MB MA MC AC  

.

KAC

vuông tại

K

1

2

MK AC

.

 

BC AB

BC SAB BC AH

AH SBC AH HC

BC SA

AH SB





   





   













.

AHC

vuông tại

H

1

2

MH AC

.

Từ

   

13



M

là tâm khối cầu ngoại tiếp hình chóp

AHKCB

.

Bán kính khối cầu cần tìm:

22

11

2

22

R AC AB BC a   

.

Thể tích khối cầu:

3

4 8 2

33

a

VR





.

Câu 44: Chọn D

Gọi

O

là tâm đáy, do các cạnh bên cùng tạo với đáy góc

60

nên

 

SO ABCD

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

438

Mặt phẳng trung trực của cạnh

SD

đi qua trung điểm

M

của

SD

và cắt

SO

tại

I

.

Ta có

I

là tâm mặt cầu ngoại tiếp hình chóp và bán kính mặt cầu

R IS

.

55

2 cos60 2

OD

BD OD SD SM       



;

53

sin60 3

SM

IS R  



.

Thể tích khối cầu tương ứng ngoại tiếp hình chóp bằng

3

4 500 3

3 27

VR





.

Câu 45: Chọn B

Gọi

,EF

thứ tự là trung điểm của

,AB CD

. Coi

1a 

, từ giả thiết ta có

74AC AD BC BD   

nên

 

,.AF CD BF CD ABF CD EF CD     

Chứng

minh tương tự

.EF AB

Khi đó

EF

là đường trung trực của

CD

và

.AB

Gọi

I

là tâm mặt cầu ngoại tiếp tứ diện

ABCD

ta có

IA IB IC ID R

nên

I

thuộc đoạn thẳng

EF

.

2 2 2 2 2

74 16 9 7.EF AF AE AD DF AE        

Đặt

7EI x FI x   

;

 

2 2 2

2

2 2 2

9

16 7 14 65

IA EA EI x

ID FI FD x x x



   





       





.

Ta có

IA ID

22

9 14 65x x x

9 14 65x

4x

Khi đó

2

95IA x  

. Do đó bán kính mặt cầu ngoại tiếp tứ diện là

5Ra

.

Vậy diện tích mặt cầu ngoại tiếp tứ diện là

22

4 4 .25S πR π a

2

100πa

.

Câu 46: Chọn C

Xét

AOB

đều nên cạnh

AB a

.

Xét

BOC

vuông tại O nên

2BC a

.

8a

6a

F

E

B

D

C

A

I

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

439

Xét

AOC

có.

2 2 0

2. . .cos120AC AO CO AO CO  

3a

.

Xét

ABC

có

2 2 2

AB BC AC

nên tam giác

ABC

vuông tại

B



tâm đường tròn ngoại tiếp

tam giác là trung điểm

H

của cạnh

AC

.

Lại có hình chóp

.O ABC

có

OA OB OC a  

nên

()OH ABC

.

Xét hình chóp

.S ABC

có

OH

là trục đường tròn ngoại tiếp đáy, trong tam giác

OHB

kẻ trung

trực của cạnh

SB

cắt

OH

tại

I

thì

I

là tâm mặt cầu ngoại tiếp hình chóp, bán kính

R IS

.

Xét

OHB

có

60HOB 

,cạnh

3

4

a

OB a OE  

33

.tan60

4

a

IE OE   

.

Xét

IES

vuông tại E:

2

22

3 3 7

4 4 2

a a a

IS IE ES



    





.

Câu 47: Chọn B

Có

   

 

,

PQ

P Q CA Q CA AD

CA CA P

  





    





  



nên

A

nhìn

DC

dưới một góc vuông.

Có

   

 

,

PQ

P Q DB P DB BC

DB DB Q

  





    





  



nên

B

nhìn

DC

dưới một góc vuông.

Do đó, đường kính mặt cầu ngoại tiếp tứ diện

ABCD

là

DC

.

Có

2 2 2 2

2BC AB AC a a a    

;

2 2 2 2

23DC BC DB a a a    

.

Vậy, bán kính mặt cầu ngoại tiếp tứ diện

ABCD

là:

13

22

a

R DC

.

Câu 48: Chọn B

Mặt phẳng

 



là mặt phẳng

 

AMNP

.

Do

 

, , .

,,

SC

AM SC AN SC AP SC

AM AN AP









   









CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

440

Có

 

,

BC AB

BC SA

BC SAB BC AM

AB SA SAB

AB SA A











   











.

Từ đó ta có

 

,

AM BC

AM SC

AM SBC AM MC

BC SC SBC

BC SC C











   











.

Tương tự ta có

 

,

CD AD

CD SA

CD SAD CD AP

AD SA SAD

AD SA A











   











.

Khi đó

 

,

AP CD

AP SC

AP SCD AP PC

CD SC SCD

CD SC C











   











.

Nhận xét:

,,AMC ANC APC  

là những tam giác vuông có cạnh huyền

AC

.

Nên tâm mặt cầu ngoại tiếp tứ diện

CMNP

là trung điểm

O

của

AC

.

2

22

AC AB

R OA    

. Vậy

3

4 32

33

VR





.

Câu 49: Chọn B.

Trong mp

 

ABC

, gọi



và

'

lần lượt là trung trực của các đoạn thẳng

AB

và

AC

.

Gọi

I

là giao điểm của



và

'

.

Vì

AB

SA











nên

 

AMB

, mà tam giác

AMB

vuông tại

M

suy ra



là trục đường tròn

ngoại tiếp tam giác

AMB

.

Có

I 



IA IB IM

Chứng minh tương tự ta được

'

là trục đường tròn ngoại tiếp tam giác

ANC

.

Do đó

IA IN IC

Từ và suy ra

IA IB IM IN IC   



I

là tâm mặt cầu ngoại tiếp hình chóp

.ABCNM

với bán

kính

R IA

.

Mặt khác trong tam giác

ABC

,

I

là giao điểm của hai đường trung trực nên

I

là tâm đường tròn

ngoại tiếp tam giác

ABC

.

Áp dụng định lý sin trong tam giác

ABC

22

0

2 . .cos 7

7.

2sin150

2sin 2sin

BC AB AC AB AC BAC

R IA a

BAC BAC



    

Vậy thể tích khối cầu ngoại tiếp hình chóp

.ABCNM

:

3

4 28 7

33

a

VR





.

Cách 2.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

441

Dựng

AD

là đường kính của đường tròn ngoại tiếp

ABC

.

Khi đó

0

90ABD ACD

;AB BD AC CD  

.

Ta có:

AB BD

SA BD











 

BD SAB

,

 

AM SAB

nên

BD AM

.

Mặt khác

 

AM MB AM MBD AM MD    

hay

0

90AMD 

.

Chứng minh tương tự:

0

90AND 

.

Hình chóp

.ABCNM

có các đỉnh cùng nhìn đoạn

AD

dưới một góc vuông nên khối cầu ngoại

tiếp hình chóp

.ABCNM

có đường kính là

AD

.

Vì vậy, bán kính của khối cầu ngoại tiếp hình chóp

.ABCNM

là bán kính

R

của đường tròn ngoại

tiếp

ABC

.

Áp dụng định lý sin trong tam giác

ABC

22

0

2 . .cos 7

7.

2sin150

2sin 2sin

BC AB AC AB AC BAC

Ra

BAC BAC



   

Vậy thể tích khối cầu ngoại tiếp hình chóp

.ABCNM

:

3

4 28 7

33

a

VR





.

Câu 50: Chọn C

Gọi

H

là trung điểm cạnh

AB

, ta có:

CH AB

.

Ta có:

 

, 2 , 2

SABC MABC

d S ABC d M ABC V V  

.

Mà

 

1 1 1

. , .16 3. , .16 3.

3 3 3

MABC CMAB MAB

V V S d C MAB d C MAB CH



   

.

Do đó,

.S ABC

V

lớn nhất khi và chỉ khi

 

;d C MAB CH

hay

 

CH MAB

.

Gọi

, JO

lần lượt là tâm hai đường tròn ngoại tiếp hai tam giác

MAB

và tam giác

ABC

.

Dựng hai trục của hai đường tròn ngoại tiếp hai tam giác

MAB

và tam giác

ABC

cắt nhau tại

I

. Khi đó

I

chính là tâm mặt cầu ngoại đi qua 4 điểm

, , ,A B C M

và bán kính mặt cầu đi qua bốn

điểm

, , ,A B C M

là

2

2 2 2

83

.

3

R OC OI JH



   





Do

 

16 3, 8 , 4 3

MAB

S AB d M AB



   

.

Chọn hệ trục tọa độ

Oxy

như hình vẽ, ta có

     

 

0;0;0 , 4;0 , 4;0 , ;4 3H A B M a

.

Đường trung trực của đoạn thẳng

AM

đi qua điểm

4

;2 3

2

a

N









và có một véc tơ pháp tuyến

 

4;4 3AM a

nên có phương trình là

 

4

4 4 3 2 3 0

2

a

a x y





    





2

32

0;

83

a

J











2

32 4 3

3

83

a

JH



  

. Do đó

22

min

8 3 4 3 4 15

.

3 3 3

R

   

  

   

   

Câu 51: Chọn A

Mặt cầu

 

S

có tâm

 

2017;2018;2019I

và bán kính

2020R 

.

Gọi

S

là đỉnh hình nón.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Thực hiện sưu tầm và biên soạn: nhóm admin luyện thi Đại học.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”

442

Gọi

H

là tâm đường tròn đáy của hình nón và

AB

là một đường kính của đáy.

Trường hợp 1: Xét trường hợp

SH R

.

Khi đó thể tích của hình nón đạt GTLN khi

SH R

. Lc đó

 

3

2020

3

V





.

Trường hợp 2:

 

SH R I

nằm trong tam giác

SAB

như hình vẽ trên.

Đặt

 

0IH x x R  

. Ta có

 

2 2 2

11

.

33

V HA SH R x R x



   

   

22

6

R x R x R x



   

 

3

32 2020

4

6 3 81

R











.

Dấu

""

xảy ra khi

2020

33

R

x 

.

Câu 52: Chọn B

Gọi I, J là tâm đường tròn ngoại tiếp của tứ giác ABCD và tam giác SAB. M là trung điểm của

AB và O là tâm của mặt cầu ngoại tiếp hình chóp.

Ta có:

JM AB

và

IM AB

và

   

mp SAB mp ABCD

nên

IM JM

, ngoài ra O là tâm

của mặt cầu ngoại tiếp hình chóp nên

 

OI ABCD OI IM  

;

 

OJ SAB OJ JM  

.

Do đó

, , ,O J M I

đồng phẳng và tứ giác

OJMI

là hình chữ nhật.

Gọi

,

b

RR

lần lượt là bán kính mặt cầu ngoại tiếp khối chóp và bán kính đường tròn ngoại tiếp

tam giác

SAB

.

Ta có:

2

2 2 2 2 2 2 2 2 2

4

b b b

AB

R SO SJ OJ R IM R IA AM R IA          

Áp dụng định lý Pytago:

2 2 2 2 2

22

3

4 4 4

BD AB AD a a

IA a IA a



     

.

Áp dụng định lý sin trong tam giác

SAB

:

2.sin60

3

2sin

b

AB a a

R

ASB

  



Do đó:

22

13

3 4 12

aa

R a a   

22

13

4

3

S R a



  

.

Nhận xét:

Xét hình chóp đỉnh

S

, có mặt bên

 

SAB

vuông góc với mặt phẳng đáy, mặt phẳng đáy nội tiếp

trong đường tròn bán kính

d

R

, bán kính mặt cầu ngoại tiếp tam giác

SAB

là

b

R

. Khi đó hình chóp

này nội tiếp trong 1 mặt cầu có bán kính

2

22

4

db

AB

R R R  

Câu 53: Chọn D

Ta ghép hình chóp

.S ABC

vào hình hộp đứng

.SRQP DABC

. Khi đó tâm

I

của mặt cầu ngoại

tiếp hình hộp đứng chính là tâm của hình chóp

.S ABC

.

Từ giả thiết

ABC

là tam giác vuông cân tại

B

nên đáy của hình hộp đứng là hình vuông.

 

, 2 , 2 3d A SBC d O SBC a

3OH a

.

CHUYÊN ĐỀ: KHỐI TRÒN XOAY NÓN – TRỤ - CẦU.

Sưu tầm và biên soạn bởi: nhóm admin TƯ DUY TOÁN HỌC 4.0.

Một sản phẩm của nhóm “TƯ DUY TOÁN HỌC 4.0”.

443

Xét tam giác vuông

OIK

có:

2 2 2

1 1 1

OH OI OK



 

22

2

1 1 1

32

3

2

OI

a

  







3OI a

.

Suy ra bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

là

22

R IB OI OB  

.

2

9 3 2

2

OI a a



  





18a

.

Thể tích mặt cầu ngoại tiếp hình chóp

.S ABC

là

3

4

3

VR





 

3

4

18

3

a





3

24 18 a





.

Câu 54: Chọn A

Gọi

H

là trung điểm của

 

AC SH ABC

;

I

là trung điểm của

6

26

BC a

AB HI  

Tam giác

SAB

đều cạnh

3

2

a

a SI

;

22

21

6

a

SH SI HI  

22

15

22

3

a

AC AH SA SH   

Gọi

,

bd

rr

lần lượt là bán kính đường tròn ngoại tiếp các tam giác

,SAC ABC

Gọi

R

là bán kính mặt cầu ngoại tiếp hình chóp

.S ABC

2

1 35 . . 21

.

2 12 4 7

SAC b

SAC

a SA SC AC a

S SH AC r

S



    

Theo công thức Hê-rông:

2

6 . . 15

6 4 6

ABC d

ABC

a AB AC BC a

Sr

S



   

2

22

21

47

bd

AC a

R r r   

Vậy:

2

21 12

4

77

mc

aa

S











Nắm trọn chuyên đề khối đa diện và khối tròn xoay

Chương 1: Khối đa diện 172 tài liệu

Toán 12 3.8 K tài liệu

Bình luận

Nắm trọn chuyên đề khối đa diện và khối tròn xoay