Nguyên tắc Dirichlet – toán rời rạc - lôgic

B1: Ở miền trong của một hình vuông cạnh bằng 1 có một tứ giác lồi diện tích lớn hơn

. Chứng minh rằng tồn tại một đoạn thẳng có hai đầu mút ở trên cạnh của tứ giác, song song với cạnh của hình vuông và có độ dài lớn hơn

B2: Mỗi ô vuông đơn vị của bảng kích thước 10 x 10 (10 dòng, 10 cột) đựơc ghi một số nguyên dương không vượt quá 10 sao cho bất kì hai số nào ghi trong hai ô chung một cạnh hoặc hai ô chung một đỉnh của bảng là hai số nguyên tố cùng nhau. Chứng minh rằng có số được ghi ít nhất 17 lần

B3: Cho hình vuông ABCD có AB = 14cm. Trong hình vuông có đánh dấu 76 điểm phân biệt. Chứng minh rằng tồn tại một đường tròn có bán kính 2cm chứa trong nó ít nhất 4 điểm trong số các điểm trên.

B4: Trong một giải đấu bóng đá, có 4 đội thi đấu vòng tròn một lượt (trong một trận, đội thắng đựơc 3 điểm, đội hoà được 1 điểm, đội thua đượưc 0 điểm). Khi kết thúc giải đấu, người ta thấy có 3 đội đạt được tổng số điểm lần lượt là 6 điểm, 5 điểm và 1 điểm. Hãy cho biết đội còn lại của giải có tổng số điểm là bao nhiêu và giải thích tại sao?

B5: Cho 13 số thực thoả mãn điều kiện tổng của 6 số bất kì đều nhỏ hơn tổng của 7 số còn lại. Chứng minh rằng tất cả 13 số đã cho đều dương

B6: Cho S là một tập hợp gồm ba số tự nhiên có tính chất: tổng hai phần tử bất kì tuỳ ý của S là một số chính phương (Ví dụ S = {5, 20, 44} hoặc S = {10, 54, 90} là các tập hợp thoả mãn điều kiện trên). C/m trong tập S không có quá một số lẻ.

B7: Cho một lưới vuông kích thước 5 x 5. Người ta điền vào mỗi ô của lưới một trong các số: -1; 0; 1. Xét tổng của các số được tính theo từng cột, theo từng hàng và theo từng đường chéo. C/m trong tất cả các tổng đó luôn tồn tại 2 tổng có giá trị bằng nhau

B8: Trong một hình chữ nhật có diện tích bằng 5 chứa chín hình chữ nhật nhỏ mà mỗi hình có diện tích bằng 1. Chứng minh tồn tại 2 hình chữ nhật nhỏ có diện tích phần chung không nhỏ hơn

B9: Đội bóng bàn của trường A thi đấu với đội bóng bàn của trường B, mỗi đấu thủ của trường này thi đấu với mọi đấu thủ của trường kia 1 trận. Biết rằng tổng số trận đấu bằng 4 lần tổng số đấu thủ của cả hai đội và số cầu thủ của trường B là số lẻ. Tìm số đấu thủ mỗi đội

B10: Cho A là tập hợp gồm 6 phần tử bất kì của tập hợp {0; 1; 2; …; 14}. Chứng minh rằng tồn tại hai tập hợp con B₁ và B₂ của tập hợp A (B₁ và B₂ khác nhau và khác rỗng) sao cho tổng tất cả các phần tử của hai tập này bằng nhau.

B11: Cho 33 điểm nằm trong hình vuông có độ dài cạnh bằng 4, trong đó không có ba điểm nào thẳng hàng. Người ta vẽ các đường tròn có bán kính bằng 2 và tâm là các điểm đã cho. Hỏi có hay không ba điểm trong các điểm đã cho sao cho chúng đều thuộc phần chung của ba hình tròn có tâm cũng chính là ba điểm đó? Ví sao?

B12: Chứng minh rằng luôn tồn tại một số tự nhiên N có không quá 2007 chữ số sao cho các chữ số của N chỉ là 9 hoặc 0 và N chia hết cho 10030.

B13: Trong mặt phẳng cho 2009 điểm, sao cho ba điểm bất kì trong chúng là ba đỉnh của một tam giác có diện tích không lớn hơn 1. Chứng minh rằng tất cả những điểm đã cho nằm trong một tam giác có diện tích không lớn hơn 4.

B14: Cho 3 điểm phâm biệt nằm trong hay trên cạnh một tam giác đều có cạnh băng 6cm. Chứng minh rằng luôn tồn tại hai điểm trong số 13 điểm đã cho mà khoảng cách giữa chúng không vượt quá 13 cm.

B15: Trong mặt phẳng cho 2010 điểm phân biệt sao cho không có ba điểm nào thẳng hàng và không có bốn điểm nào cùng nằm trên một đường tròn. Chứng minh rằng trong 2010 điểm đã cho, có thể dựng được một đường tròn đi qua ba điểm, chứa 1000 điểm và không chứa 1007 điểm còn lại.

B16: Trong một hình vuông cạnh 1, ta lấy 51 điểm tuỳ ý. Chứng minh rằng luôn tìm được ít nhất 3 điểm nằm trong một hình tròn bán kính R =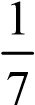

B17: Trong mặt phẳng cho hình vuông. Người ta vẽ 9 đường thẳng sao mỗi đường thẳng chia hình vuông thành 2 tứ giác có tỉ số diện tích 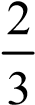. Chứng minh rằng tồn tại ít nhất 3 đường thẳng đồng quy

B18: Cho đa giác lồi n - cạnh (n  5) được đặt trong hệ toạ độ vuông góc. Biết 5 đỉnh của đa giác có toạ độ là những số nguyên, hãy chứng minh rằng ít nhất có một điểm thuộc miền trong hoặc trên cạnh của đa giác có toạ độ là các số nguyên

B19: Trên mặt phẳng cho 6 điển tuỳ ý, không có 3 điểm nào thẳng hàng. Người ta nối 2 trong các điểm đã cho với nhau bằng một đoạn thẳng có màu đỏ hoặc xanh. Chứng minh rằng tồn tại ít nhất một tam giác có 3 cạnh là 3 đoạn thẳng cùng màu.

B20: Một rừng thông mọc trên lô đất hình vuông cạnh 1 km. Biết rằng tất cả rừng có 4500 cây thông, mỗi cây có chu vi 50cm. Chứng minh rằng có thể chọn trong khu rừng đó 60 mảnh đất hình chữ nhật có kích thước 10m x 20m, mà trong đó không có một cây thông nào mọc

B21:Cho hai tập hợp A, B thoả mãn các điều kiện:

1. Mỗi tập hợp đều gồm các số nguyên dương khác nhau và nhỏ hơn 1990
2. Tổng số phần tử của A và B lớn hơn 1990

C/m tồn tại ít nhất một phần tử của A và một phần tử của B có tổng bằng 1990

B22: Với mỗi số nguyên dương r , xác định số nguyên nhỏ nhất h(r)  1 sao cho với mọi cách chia tập {1, 2, …, h(r) } thành r tập con đều tồn tại các số nguyên a  0, y  x  1 sao cho a + x, a + y + y thuộc cùng một tập con

B23: Cho n (n  2) em học sinh đứng thành hàng dọc. Sau mỗi lần cô giáo thổi còi, có hai em đổi chỗ cho nhau. Hỏi, sau một số lẽ lần thổi còi, ta có thể thấy tất cả các em học sinh đều đứng ở vị trí ban đầu của mình hay không?

B24: Cho bàn cờ vua n x n ô. Dán mép trái và mép phải của bàn cờ với nhau, sao cho mặt bàn cờ quay ra ngoài, ta thu được một bàn cờ hình trụ. Tiếp tục dán mép dưới của bàn cờ hình trụ ta sẽ thu được một bàn cờ hình xuyến. Hỏi trên bàn cờ hình xuyến ấy có thể xếp được tối đa bao nhiêu quân vua sao cho quân nọ không ăn được quân kia.

B25: Trên trang giấy có một vết mực có tổng diện tích bé hơn 1. Chứng minh rằng., có thể chia trang giấy thành các hình vuông đơn vị sao cho không có đỉnh nào của hình vuông rơi vào chỗ có mực

B26: Trên mặt bàn người ta dán một số hình tròn có bán kính bằng nhau sao cho không có hai hình nào giao nhau. Chứng minh rằng với 4 màu khác nhau ta có thể tô các hình tròn (mỗi hình tròn được tô bởi một màu) sao cho các hình tròn tiếp xúc nhau được tô bởi các màu khác nhau

B27: Cho một mảnh giấy hình vuông. Mảnh giấy này được cắt bởi đường cắt thẳng thành hai mảnh. Một trong hai mảnh nhặt đựơc, ta lại làm như vậy nhiều lần. Hỏi số lần cắt ít nhất phải là bao nhiêu để có thể nhận được 100 đa giác 20 cạnh

B28: Người rải 35 viên bi trên một mặt sàn hình vuông có cạnh bằng 10cm. Chứng minh rằng, khi các hòn bi đã đứng yên thì có thể tìm được trên mặt sàn ít nhất một hình chữ nhật có diện tích lớn hơn 3cm² không chứa viên bi nào (tức là không có điểm nào của hình chữ nhật là điểm tiếp xúc của một viên bi với mặt sàn)

B29: Chứng minh rằng không có cách xếp 5 hình cầu có cùng bán kính, sao cho mỗi hình cầu tiếp xúc với 4 hình cầu kia.

B30: Tìm tất cả các số nguyên dương k nhỏ nhất sao cho có thể phân chia tập hợp X = {1990, 1990 + 1, …., 1990 + k} thành hai tập con A, B thoả mãn các điều kiện: Tổng của tất cả các phần tử thuộc A bằng tổng tất cả các phần tử thuộc B

B31: Cho một hình phẳng có diện tích bằng 1, được phủ kín bởi một số hữu hạn các hình tròn. Chứng minh rằng trong số các hình tròn đó có thể chọn ra hoặc một hình có diện tích lớn hơn hoặc bằng , hoặc một số hình tròn đôi một rời nhau mà tổng diện tích của chúng lớn hơn hoặc bằng

B32: Cho tập hợp P gồm 10 điểm trong đó có một số cặp điểm được nối với nhau bằng đoạn thẳng. Số các đoạn thẳng có trong tập A nối từ điểm A đến các điểm khác gọi là bậc của điếm A. C/m bao giờ cũng tìm được 2 điểm trong tập hợp P có cùng bậc

B33: Có hay không 2003 điểm trên mặt phẳng mà bất kì 3 điểm nào trong chúng đều tạo thành một tam giác tù?

B34: Lấy 4 điểm ở miền trong của một tứ giác để cùng với 4 đỉnh ta được 8 điểm, trong đó không có 3 điểm nào thẳng hàng. Biết diện tích của tứ giác là 1, chứng minh rằng tồn tại một tam giác có 3 đỉnh lấy từ 8 đỉêm đã cho có diện tích không vượt quá 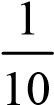. Tổng quát bài toán thành n – giác lồi

B35: Chứng minh rằng từ 8 số nguyên dương tuỳ ý không lớn hơn 20, luôn chọn được ba số x, y, z là độ dài ba cạnh của một tam giác.

B37: Trong một giải đấu bóng đá có k đội tham gia, thi đấu vòng tròn một lượt (2 đội bất kì đấu với nhau đúng 1 trận). Đội thắng được 3 điểm, đội hoà được 1 điểm và đội thua được 0 điểm. Kết thúc giải ta nhận thấy số trận thắng – thua gấp đôi số trận hoà và tổng số điểm của các đội là 176. Hãy tìm k.

B38: Cho hình vuông ABCD và 2005 đường thẳng đồng thời thoả mãn 2 điều kiện:

1. Mỗi đường thẳng đều cắt 2 cạnh đối của hình vuông
2. Mỗi đường thẳng đều chia hình vuông thành hai phần có tỉ số diện tích là 0,5Chứng minh trong 2005 đường thẳng có ít nhất 502 đường thẳng đồng quy

B39: Một đồi thông có 800 000 cây thông. Trên mỗi cây thông có không quá 500 000 chiếc lá. Chứng minh rằng ít nhất cũng có 2 cây thông có cùng số lá như nhau ở trên cây

B40: Một lớp học có 40 học sinh. Chứng minh rằng có ít nhất 4 học sinh có tháng sinh giống nhau

B41: Cho dăy số gồm 5 số tự nhiên bất ḱ a₁, a₂, a₃, a₄, a₅. Chứng minh rằng tồn tại một số chia hết cho 5 hoặc tổng của một số số liên tiếp trong dăy đă cho chia hết cho 5

B42: Với 39 số tự nhiên liên tiếp, hỏi rằng ta có thể t́m được một số mà tổng các chữ số của nó chia hết cho 11 hay không?

B43: Chứng minh rằng trong 52 số tự nhiên tùy ư, chí ít cũng có một cặp gồm hai số sao cho hoặc tổng hoặc hiệu của chúng chia hết cho 100

B44: Chứng minh rằng trong 19 số tự nhiên bất ḱ ta luôn luôn t́m được một số mà tổng các chữ số của nó chia hết cho 10

B45: Chứng minh rằng tồn tại lũy thừa của 29 mà các chữ số tận cùng của nó là 00001

B46: Chứng minh rằng trong hệ viết cơ số 10 có thể t́m được bội số của số 1995 mà trong đó các chữ số của nó chỉ là 0 và 1

B47 : Có 17 nhà toán học viết thư cho nhau trao đổi về 3 vấn đề khoa học, mỗi người viết thư cho một người về một vấn đề. Chứng minh rằng ít nhất cũng có 3 nhà toán học trao đổi với nhau về cùng một vấn đề

B48 : Người ta viết các số tự nhiên từ 1 đến 10 thành dng hàng ngang theo một thứ tự ̣ tùy ý, tiếp đó cộng mỗi một trong các số đă cho với số thứ tự chỉ vị trí mà nó đứng. Chứng minh rằng ít nhất cũng có hai tổng mà chữ số tận cùng của hai tổng đó là như nhau

B49: Trong 1 lớp học có 30 học sinh. chứng tỏ trong số học sinh, ta sẽ tìm thấy ít nhất 2 học sinh có tên bắt đầu bằng 1 chữ cái giống nhau

B50 : Chứng minh rằng trong bất kì 1 khối đa diện nào ta cũng có thể tìm đc 2 mặt có cùng số cạnh

Some problems about Principle Dirichlet

P1: (Putnam 1978) Let A be any set of 20 integers chosen from the arithmetic progression 1, 4, 7, …., 100. Prove that there must be two distinct integers in A whose sum is 104

P2: Show that amongst any seven distinct positive integers not exceeding 126, one can find two of them, say a and b, which safisfying b a  2b.

P3: Given any set of ten natural numbers between 1 and 99 inclusive, prove that there are two disjoint nonempty subsets of the set with equal sums of their elements

P4: No matter which fifty five integers may be selected from {1, 2, …, 100}, prove that one must select some two that differ by 10.

P5: (AHSME 1994) Label one disc “1”, two disc “2”, three disc “3”, …, fifty disc “50”. Put these 1 + 2 + 3 + … + 50 = 1275 labeled discs in a box. Discs are there drawn from the box at random without replacement. What is the minimun number of discs that must we drawn in order to guarantee drawing at least ten disc with the same label?

P6: (IMO 1964) Seventeen people correspond by mail with one other – each one with all the rest. In their letters only three different topics are discussed. Each pair of correspondents deals with only one of the these topics. Prove that there at least three people who write to each other about the same topic.

P7: Given any seven distinct real numbers x₁, …, x₇. prove that we can always find

two, say a and b with: 0 a b^  ¹

1ab 3

P8: (Canada MO 1981) Let a₁, a₂, …, a₇ be nongative real numbers with a₁+…+a₇ = 1. If M = max a_k + a_k+1 + a_k+2. Determine the minimum possible value that M can take

1k 5 as the a_k vary P9: (AHSME 1991) A circle table has excactly 60 chairs around it. There are N people seated at this table in such a way that the next person to be seated must sit next to some one. What is the smallest possible value of N. (Answer: 20)

P10: Show that if any five ponits are all in, or on, a square of side 1, then some pair of

them will be at most at distance ² . 2

P11: Prove that amongst 6 people in a room there are at least 3 who know one another, or at least 3 who do not know one other.

P12: Show that in any sum of non-negative real numbers there is always one number which is at least the average of the numbers and that there is always one menber that it is at most the average of numbers.

P13: 10 integers are chosen from 1 to 100 inclusively. Prove that we can find 2 disjoint non-empty subsets of the chosen integers such that the 2 subsets give the same sum of elements.

P14: 6 points are drawn on a plane. All edges between every points are painted in red or blue. Prove that there is a monochromatic triangle (i.e a triangle with its 3 edges painted in the same color)

P15: 9 people are in a club. Each of them can play one of the games among Bridge, Hearts and Mahjong. Prove that they can play at least one of the metioned games.

(note that all 3 games require 4 players)

P16: There are 17 mathemticians and 3 offical languages. Every pairs of mathemticians communicate in one of the offical languages. Prove that there are 3 mathemticians communicating in the same language pariwise.

P17: 27 points are aligned so that each row has 9 points and each column has 3 points. (A column is perpendicular to a row) Each point is painted red or blue. Prove that there exist a monochromatic rectangle (i.e 4 vertices are of the same colour) with its sides parallel to the rows and columns.

P18: 76 points are aligned so that each row has 19 points and each column has 4 ponits. (A column perpendicular to a row). Each point is painted red, blue of yellow. Prove that there exists a monochromatic rectangle (i.e 4 vertices are of the same colour) with its sides parallel to the rows and columns.

P19: There is a sequence of 100 integers. Prove that there is a sequence of consecutive terms such that the sum of these terms is divisible by 99.

P20: (IMO 1991) Let S = {1, 2, 3, …, 280}. Find the smallest integer n such that each n-elenment subset of S contains five numbe