Ôn tập giữa kì Vi tích phân 1C - Vi tích phân 1 | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
1. Tính giới hạn và khảo sát sự liên tục của hàm rẻ nhánh.
2. Tính đạo hàm cấp 1 bằng định nghĩa.
3. Tính đạo hàm cấp 1 bằng các quy tắc và công thức, đạo
hàm hàm hợp và hàm ẩn, Phương trình Ɵếp tuyến. Tính tốc độ biến thiên.
4. Xấp xỉ tuyến ơnh.
5. Khảo sát bài toán cực trị. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn: Vi tích phân 1 (MTH00005)
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
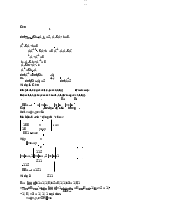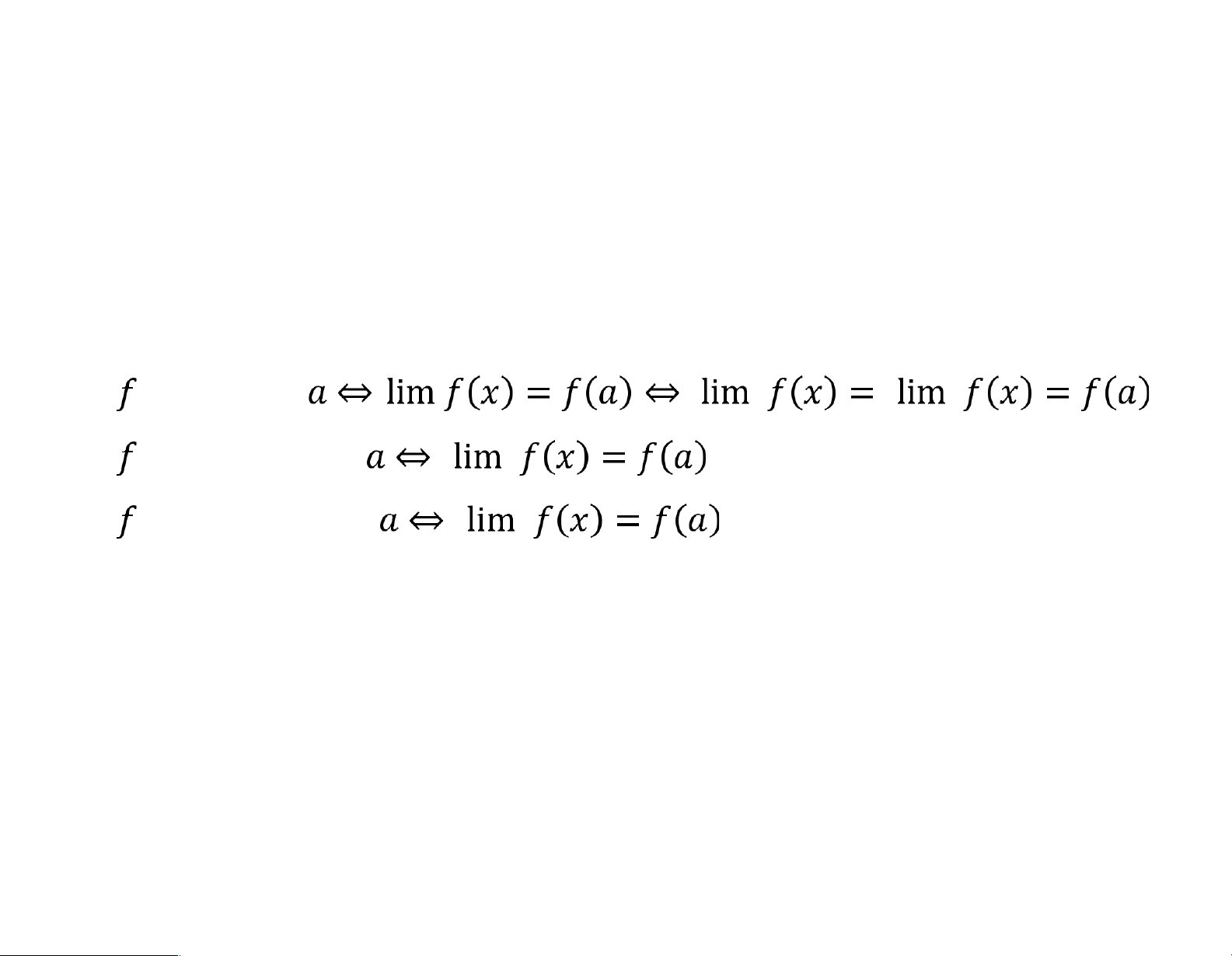
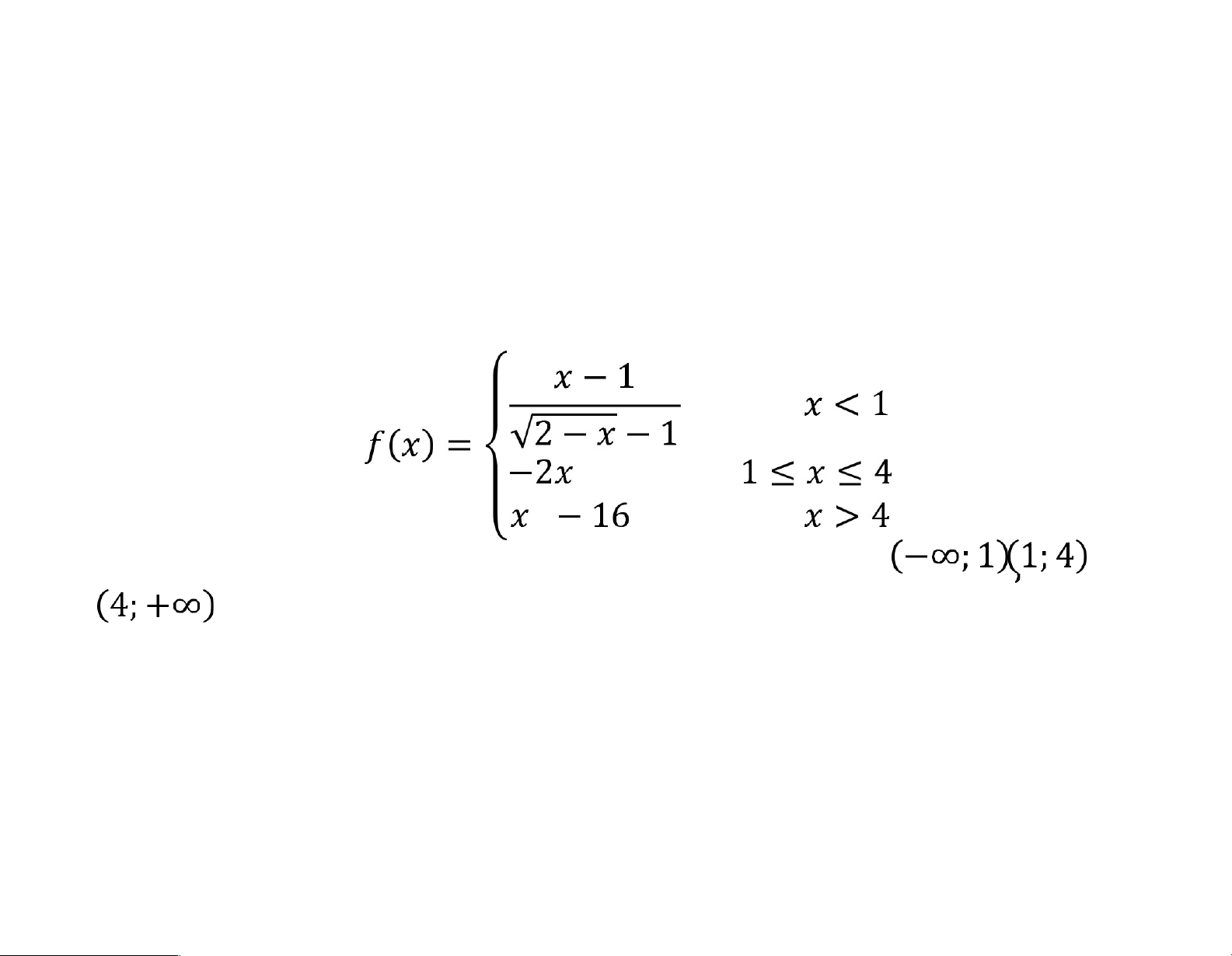
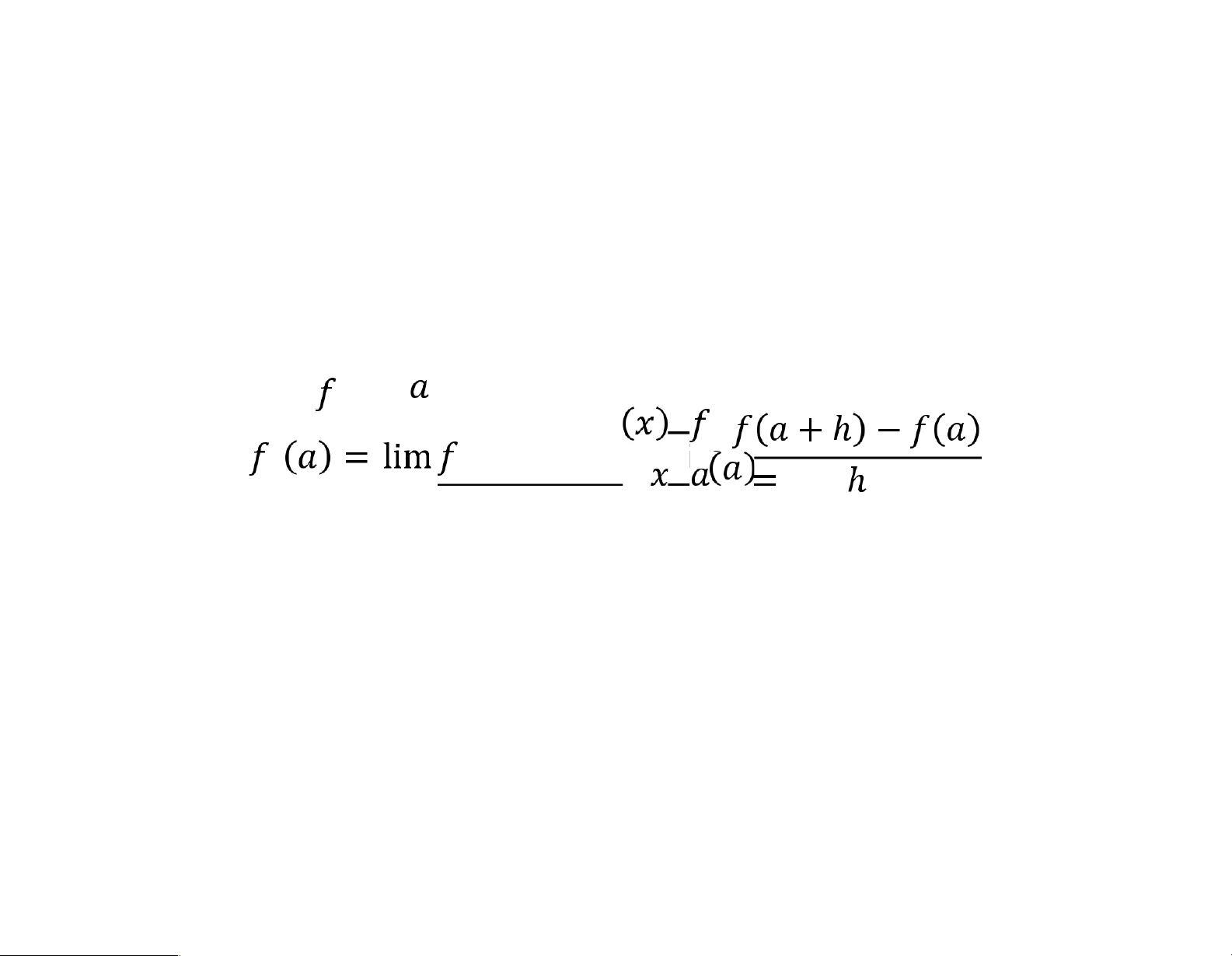
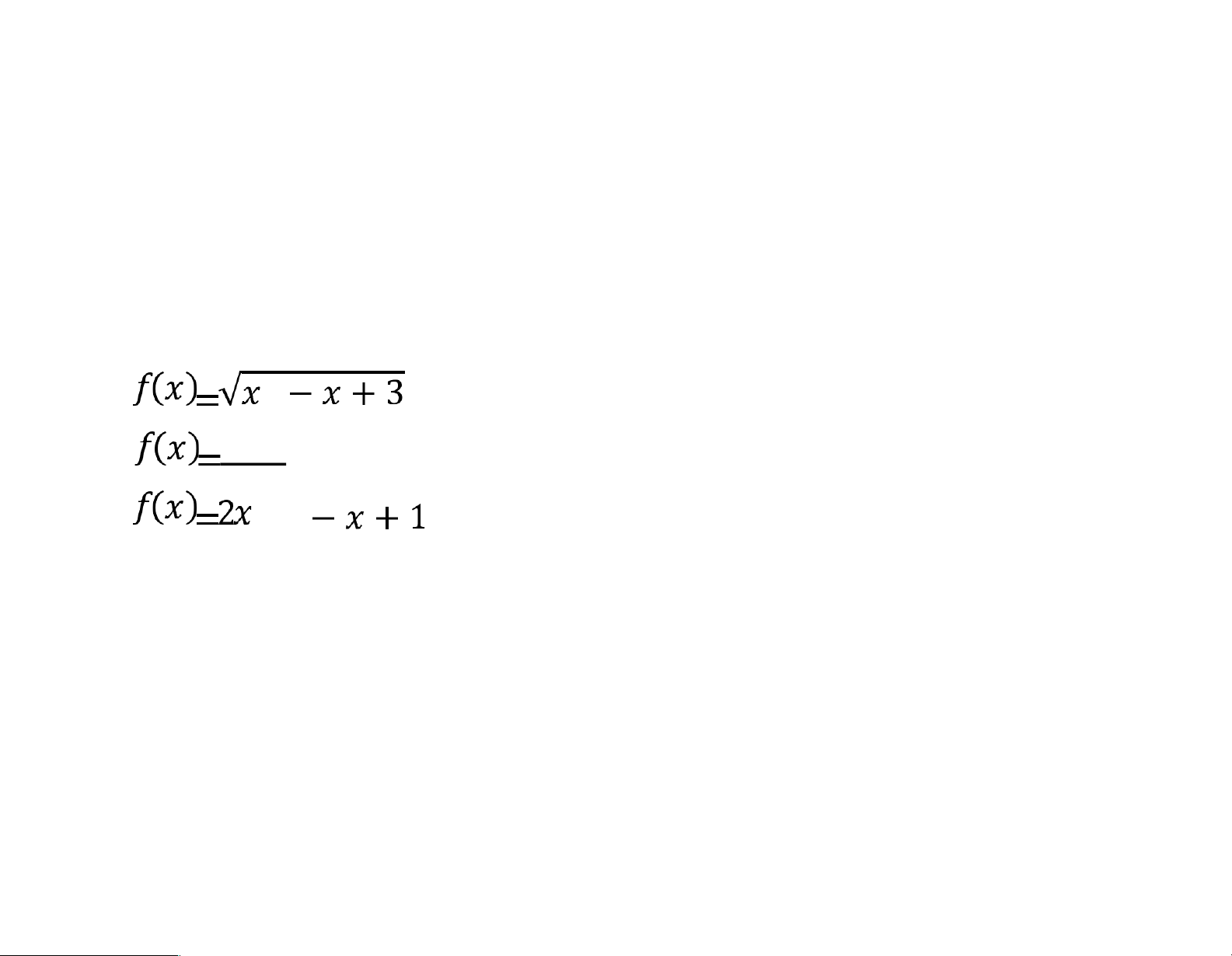
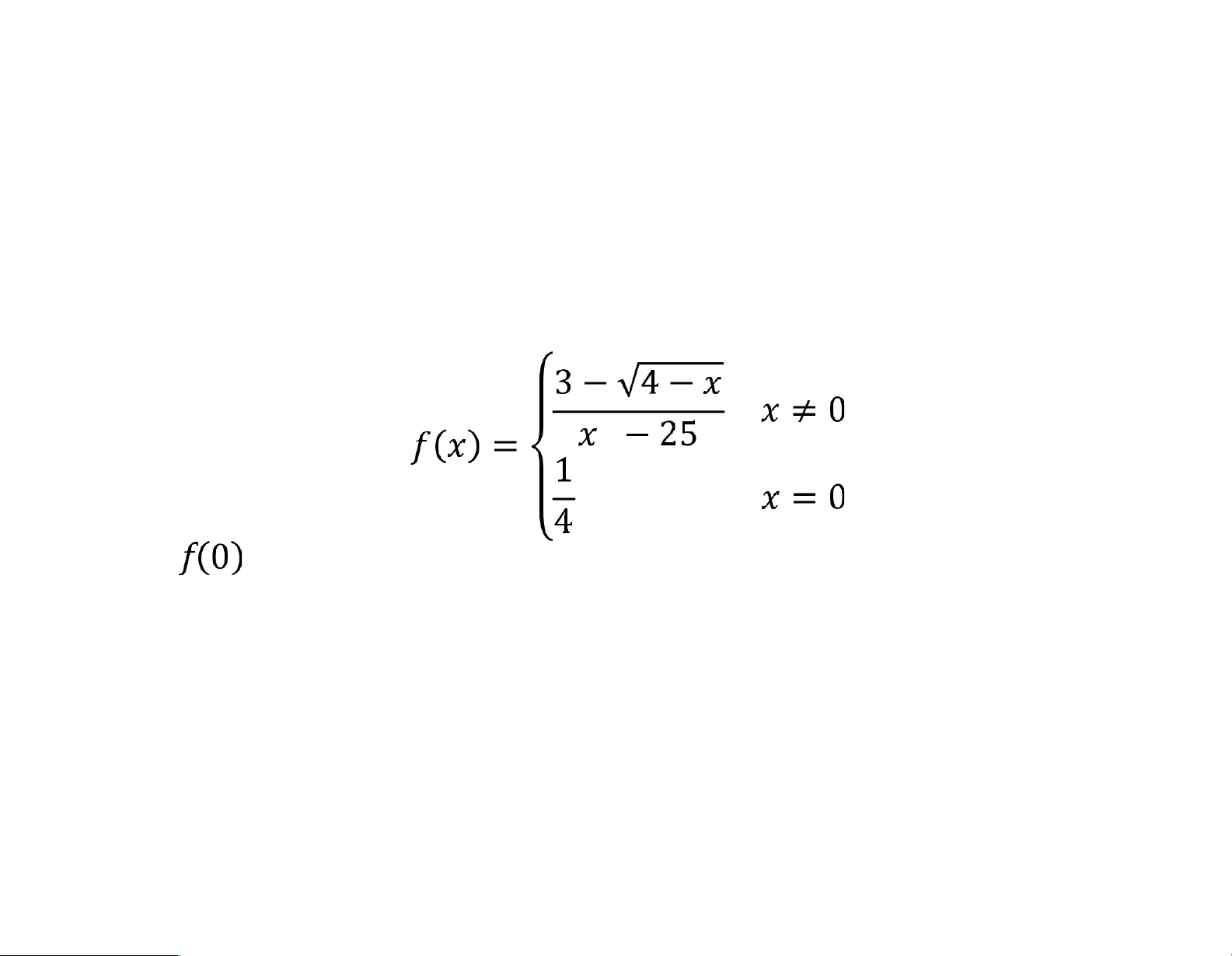
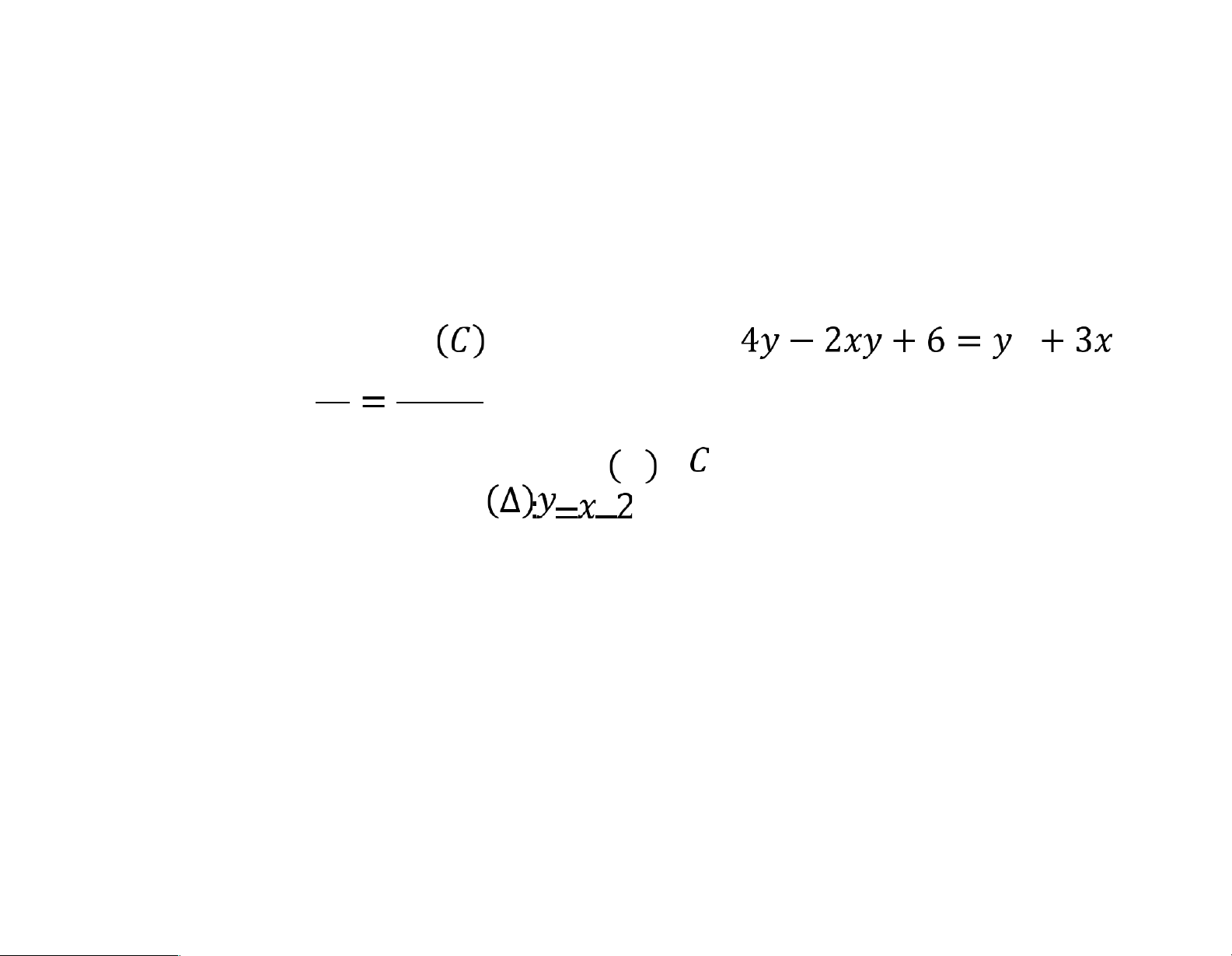
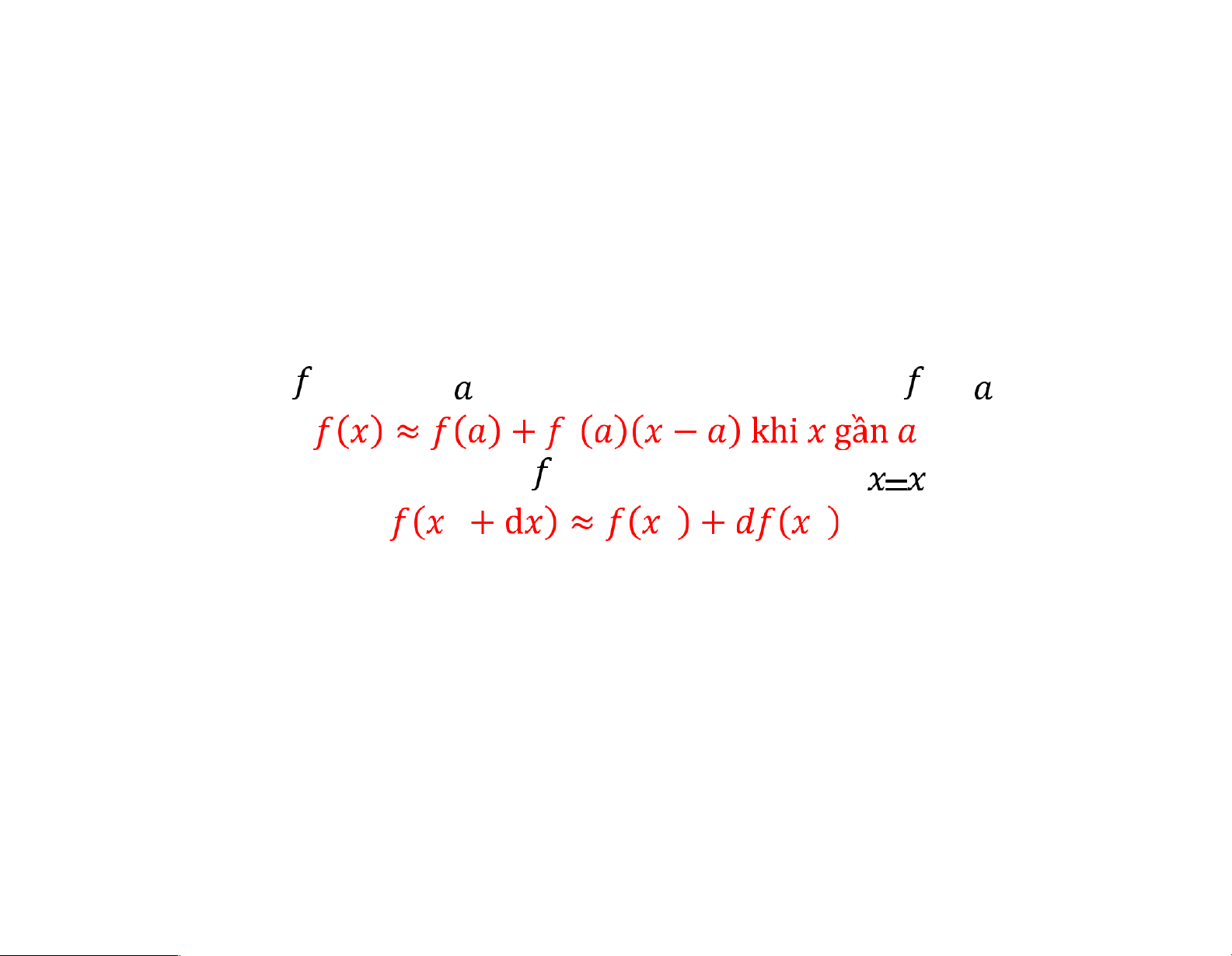
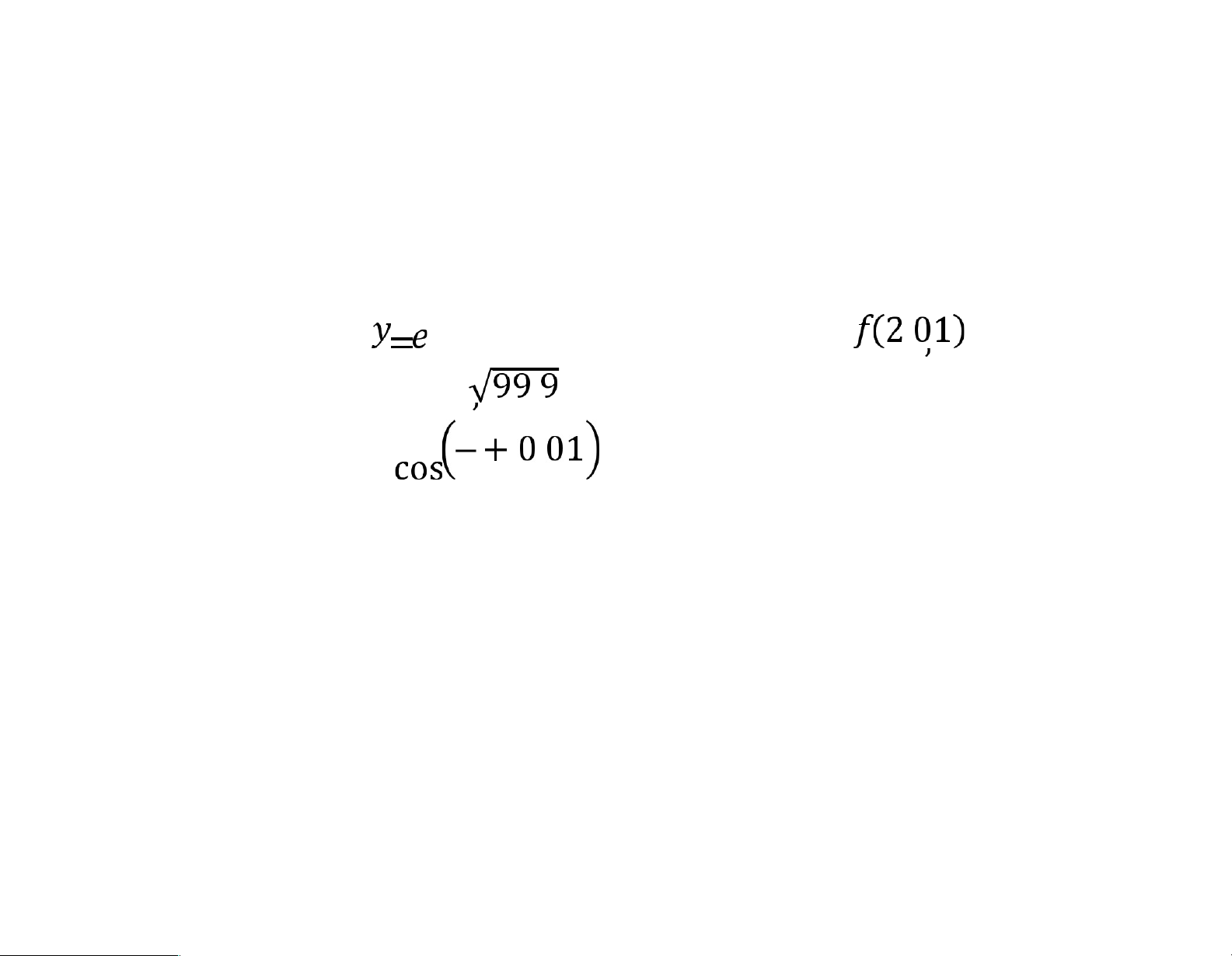
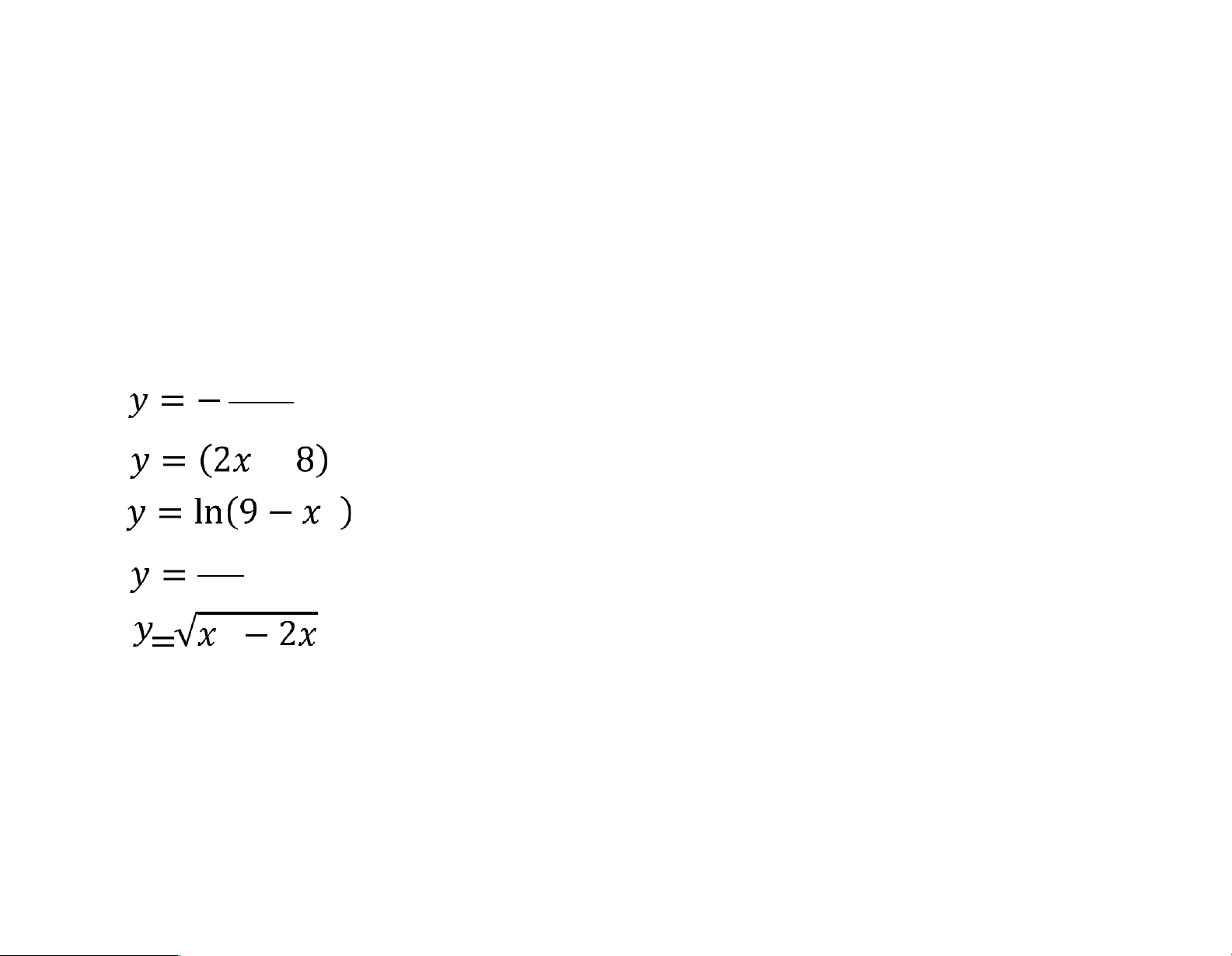
Preview text:
lOMoARcPSD|46342985 lOMoARcPSD|46342985 ÔN TẬP GIỮA KỲ VI TÍCH PHÂN 1C lOMoARcPSD|46342985 Nội dung ôn tập
1. Tính giới hạn và khảo sát sự liên tục của hàm rẻ nhánh.
2. Tính đạo hàm cấp 1 bằng định nghĩa.
3. Tính đạo hàm cấp 1 bằng các quy tắc và công thức, đạo
hàm hàm hợp và hàm ẩn, Phương trình ếp tuyến.
Tính tốc độ biến thiên. 4. Xấp xỉ tuyến nh.
5. Khảo sát bài toán cực trị. lOMoARcPSD|46342985
1. Khảo sát tính liên tục, liên tục trái-
phải của hàm rẽ nhánh Trọng tâm lý thuyết • liên tục tại •
liên tục trái tại → → → → •
liên tục phải tại →
• Mọi hàm số sơ cấp đều liên tục trên từng khoảng mà nó xác định. lOMoARcPSD|46342985
1. Khảo sát tính liên tục, liên tục trái-
phải của hàm rẽ nhánh Bài 1. Cho hàm số
a. Chứng minh hàm số đã cho liên tục trên các khoảng và
b. Tìm các điểm mà tại đó hàm số không liên tục, liên tục
trái hoặc liên tục phải. Phân loại điểm gián đoạn (Giải thích) lOMoARcPSD|46342985
1. Khảo sát tính liên tục, liên tục trái-
phải của hàm rẽ nhánh Bài 2. Cho hàm số
Tìm giá trị của tham số để liên tục trên . lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
Trọng tâm lý thuyết
• Đạo hàm của tại là → → lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến Trọng tâm lý thuyết
• Hàm số có đạo hàm tại
nó có đạo hàm tại ở cả hai bên và có cùng giá trị là .
• Các quy tắc tính đạo hàm (SV tự xem lại)
• Công thức đạo hàm của hàm số hợp. (SV tự xem lại)
• Bảng công thức đạo hàm (SV tự xem lại)
• Phương pháp tính đạo hàm hàm ẩn.
• Phương trình tiếp tuyến (SV tự xem lại) lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
Bài 1. Tìm biểu thức đạo hàm của các hàm số sau bằng định nghĩa a. b. c. lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến Bài 2. Cho hàm số Tính . lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
Bài 3. Tính đạo hàm của các hàm số sau a. b. c. d. lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
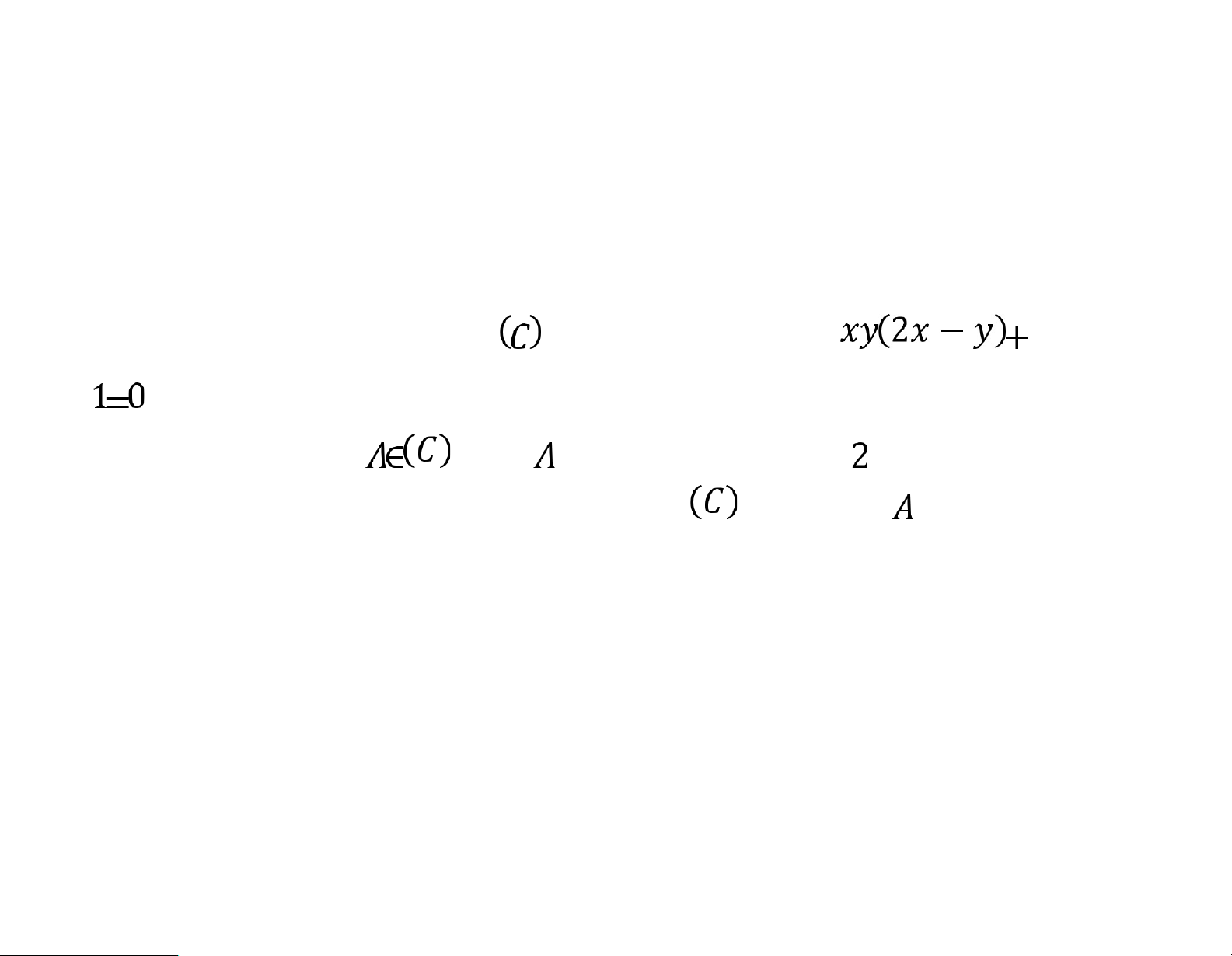
Bài 4. Cho đường cong có phương trình a. Tìm . b. Tìm toạ điểm
biết có tung độ bằng .
c. Viết phương trình tiếp tuyến với tại điểm . lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
Bài 5. Cho đường cong có phương trình . Tìm . lOMoARcPSD|46342985
2. Đạo hàm và phương trình tiếp tuyến
Bài 6. Cho đường cong có phương trình . a. Chứng minh .
b. Tìm phương trình tiếp tuyến với biết tiếp tuyến song
song với đường thẳng lOMoARcPSD|46342985
3. Xấp xỉ tuyến tính
Trọng tâm lý thuyết
• Nếu hàm số khả vi tại thì phép xấp xỉ tuyến tính của tại là
• Phép xấp xỉ vi phân của xung quanh điểm lOMoARcPSD|46342985
3. Xấp xỉ tuyến tính Bài 1. Cho hàm số
. Tính xấp xỉ tuyến tính cho
Bài 2. Tính xấp xỉ cho (bằng 2 cách)
Bài 3. Tính xấp xỉ (bằng 2 cách) lOMoARcPSD|46342985 4. Cực trị
Bài 1: Tìm điểm cực trị của các hàm số sau a. b. / c. d. e.