Ôn tập giữa kỳ: Rủi ro và Lý thuyết Hàm sản xuất Chương 3 & 4 | Môn Kinh tế vĩ mô 2 - Học viện Chính sách và Phát triển

lOMoAR cPSD| 59452058
Ôn tập giữa kỳ VI MO 2 (chương 3 & 4) Ch III: RỦI RO
1/ Các tiêu thức lựa chọn hđộng rro
• EMV; EU; VAR, độ lệch chuẩn; CV,CE....
• Xem lại 5 btap mẫu (Ở vở ghi)
2/ Các thái độ đối với rủi ro
Ghét rro Bàng quan với rro Thích rro
(Đồ thị đường quan hệ giữa lợi ích và thu nhập U(I)?)
4/ Giảm rro (Đa dạng hóa)
5/ Bài tập phí BH max và phí BH min.............................. Một số câu mẫu
1. Thái độ đối với rủi ro của người có hàm ích lợi phụ thuộc vào thu nhập U = 10I0,5 là: Ghét rủi ro- Đúng
2. Thái độ đối với rủi ro của người có hàm ích lợi phụ thuộc vào thu nhập U = 10I2 là: Thích rủi ro – Đúng
3. Thái độ đối với rủi ro của người có hàm ích lợi phụ thuộc vào thu nhập U = 10I là: Bàng quan với rủi ro- Đúng
4. Nếu sử dụng tiêu thức Hệ số biến thiên (CV), người ghét rủi ro sẽ chọn hành động có: CV nhỏ nhất
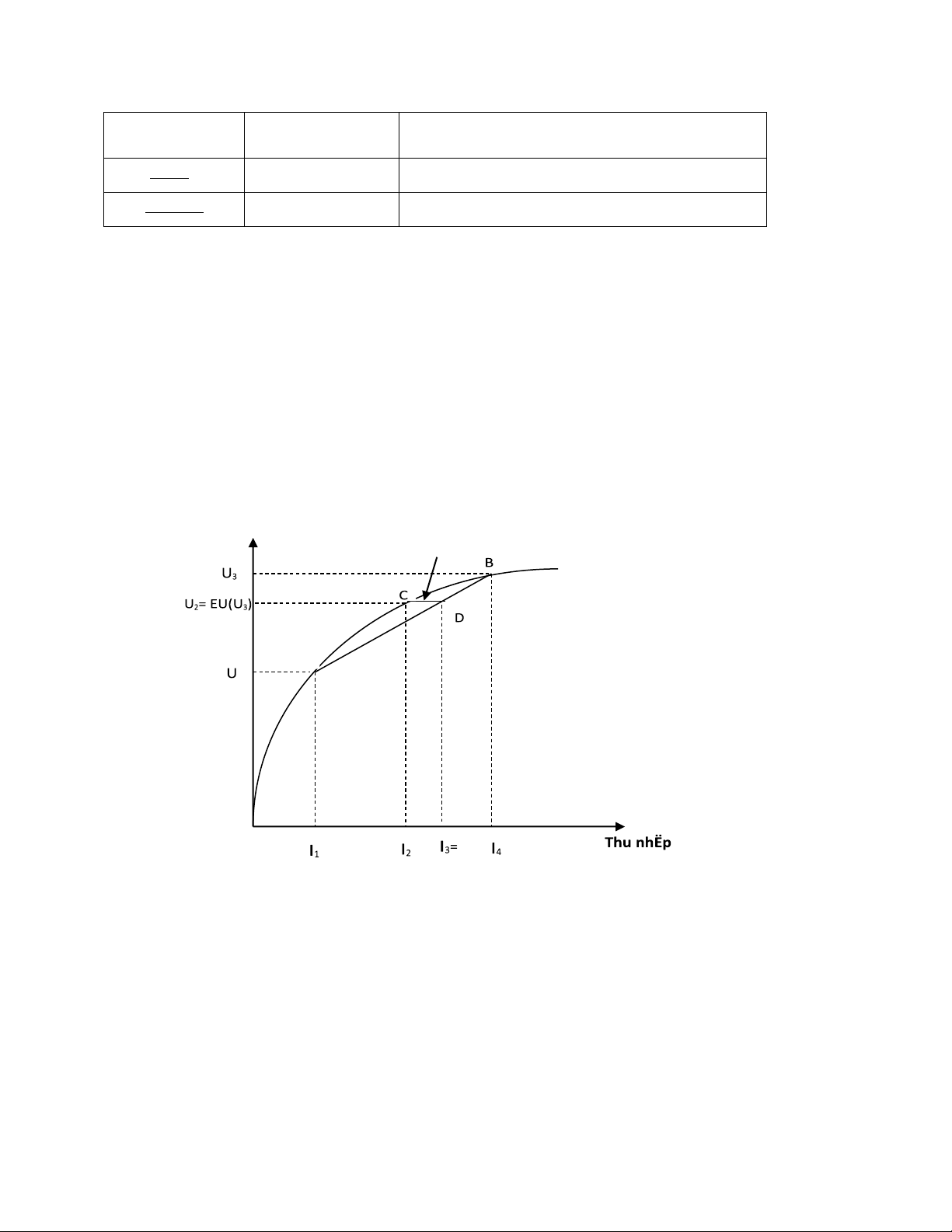
5. Đường biểu diễn quan hệ giữa ích lợi và thu nhập U(I) của người ghét rủi ro có dạng:
Cong lõm so với trục thu nhập
6. Đường biểu diễn quan hệ giữa ích lợi và thu nhập U(I) của người thích rủi ro có dạng:
Cong lồi so với trục thu nhập- Đúng
7. Đường biểu diễn quan hệ giữa ích lợi và thu nhập U(I) của người bàng quan với rủi ro
có dạng: Đường thẳng đi qua gốc tọa độ- Đúng
8. Khi U = EU có tương đương chắc chắn (CE)- Đúng........................................... lOMoAR cPSD| 59452058
Ch IV: Lý thuyết HÃNG/DN 1/ Hàm sx SR và LR
Đường Đồng lượng ( O
Hàm sx Coob- Douglas (Qui luật Năng suất cận biên giảm dần? Ý nghĩa các số mũ;
hiệu suất qui mô...) Đường Đồng lượng (ISOQ) ~IC
2/ Đường Đồng chi ph ( OC BL
Các đặc điểm của ISOC (xoay ?# dịch chuyển?)
3/ Kết hợp tối ưu: MPK/Pk = MPL/PL
Đường mở rộng/Đường phát triển DN (EP)
4/ Các đường Chi phí SR & LR ( UL Tính kte qui mô)
5/ Bài tập.............................. Một số câu mẫu
1. Hiệu suất tăng/giảm/ko đổi theo quy mô nghĩa là khi tất cả các đầu vào tăng lên n lần thì
Tổng sản lượng tăng lớn hơn/nhỏ hơn/ đúng bằng n lần.
2. Một hãng có hàm sản xuất Coob – Douglas dạng Q = K0,5L0,5 sẽ có hiệu suất giảm qui
mô: SAI mà là Không đổi- vì tổng 2 số mũ 0,5 + 0,5 =1
3. Một hãng có hàm sản xuất Coob – Douglas dạng Q = K0,8L0,5 khi đó co dãn của sản
lượng Q theo K là: 0,8- Đúng
4. Một hãng có hàm sản xuất Coob – Douglas dạng Q = K0,6L0,4 khi đó co dãn của sản
lượng Q theo L là: 0,4 - Đúng
5. Các đường ISOQ luôn có dạng Dốc xuống và cong lồi về gốc tọa độ trong khu vực sản
xuất – SAI vì có thể có dạng chữ L; tuyến tính
6. Đường ISOC có độ dốc là w/r luôn có dạng Đường thẳng dốc xuống - Đúng
7. Công thức để doanh nghiệp lựa chọn được kết hợp đầu vào tối ưu với 2 đầu vào K và L là MPK/ MPL = r / w - Đúng
8. Khi tổng chi phí là tối thiểu, tỷ lệ sản phẩm cận biên của lao động so với sản phẩm cận
biên của tư bản Bằng tỷ lệ giá của lao động so với giá của tư bản _Đúng lOMoAR cPSD| 59452058
9. Từ đường phát triển hay đường mở rộng của doanh nghiệp có thể suy ra trực tiếp được:
đường Tổng chi phí dài hạn LTC - Đúng 10.
Chi phí cận biên ngắn hạn (SMC) cắt các đường (SATC) và (SAVC) tại điểm cực tiểu của chúng- Đúng 11.
Khi chi phí trung bình dài hạn không đổi LAC = const, thì LAC = LMC - Đúng 12.
Tính kinh tế của quy mô tồn tại khi Chi phí sản xuất một đơn vị sản phẩm giảm xuống
khi sản lượng tăng - Đúng
13. Ước lượng Tính kinh tế của quy mô thực chất là xác định hình dạng của đường chi phí trung bình dài hạn (LAC)
14...................................................
Bài tập t nh toán Ch 3: RỦ RO
Bài số 2. Doanh nhân Trung có tổng tài sản là 5 tỷ đồng (trong đó bao gồm cả căn nhà có giá trị 2 tỷ, xác suất bị 0.5
cháy là 10%). Hàm ích lợi của Trung được cho bởi U(W) = W , ở đây W là giá trị tài sản.
a. Trung là người thích, ghét, hay trung tính với rủi ro?
b.Tính giá trị tài sản kỳ vọng của Trung nếu anh không mua bảo hiểm.
c. Hãy tính phần đền bù rủi ro của anh Trung.
d. Tính phí BH max mà doanh nhân Trung mua BH để tránh rủi ro và Phí BH min mà Cty BH có thể bán để có lợi nhuận Lời giải
a. Trung là người ghét rủi ro.
Cách 1: Vẽ đồ thị hàm lợi ích theo tài sản (đường U cong lõm với trục hoành w hay MUw w
giảm dần khi W tăng hay rủi ro tăng) 0.5
Cách 2: Tính đạo hàm bậc nhất và đạo hàm bậc hai của U(W) = W . -0,5 MUw = dU/dW = 0,5W > 0 2 2 -1,5
Đạo hàm (MUw) = d U/dW = - 0,25W < 0
(MUw nghịch biến với w hay lợi ích cận biên theo tài sản giảm dần)
b. Giá trị tài sản kỳ vọng được tính bằng trung bình quyền số của những kết quả có thể xảy ra: lOMoAR cPSD| 59452058 Xác suất (p) Giá trị tài sản (tỷ) Cháy 0,1
3 tỷ (= 5 – 2 cháy) ko cháy 0,9 5 (cháy = 0)
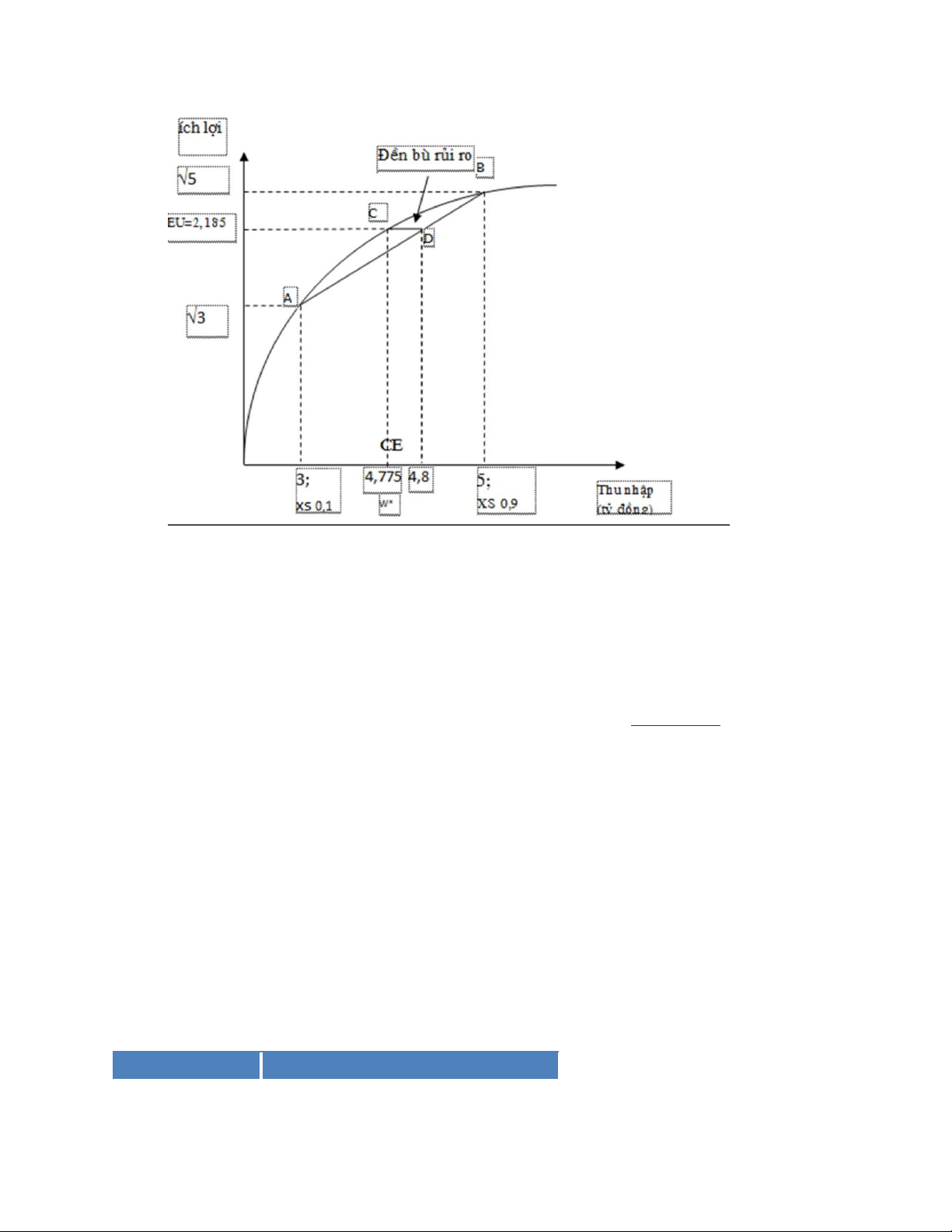
Giá trị tài sản kỳ vọng của Trung không mua bảo hiểm EMV = 0,1 x 3 tỷ + 0,9 x 5 = 4,8 (tỷ)
c. Đền bù rủi ro là số tiền mà một người ghét rủi ro sẵn sàng trả để tránh rủi ro; đó chính là số tiền
mà người đó sẵn sàng từ bỏ để không phải đắn đo giữa một hành động có rủi ro với thu nhập kì
vọng I3 và một hành động an toàn ko có rủi ro I2.
• Ngừơi ghét rủi ro; đường UI cong lõm với trục hoành (thu nhập)
• Người này bàng quan giữa công việc đem lại mức thu nhập I3 chắc chắn và công việc đem
lại thu nhập kỳ vọng tương đương (EMV = p1I1 + p2I4 = I3).
• Đền bù rủi ro được biểu thị qua đoạn CD = I3 – I2.
• CE = I2 vì (U(I2) = EU (p1I1 + p2I4 = I3) và rủi ro = 0
Í ch l ợ i
Đ ề n bù r ủ i ro A p X /s: p
1 I 1 + p 2 I 4 X / s : 1 p 2
Ích l ợ i kì v ọ ng khi ko mua BH là 0,5 0,5 EU
= 0,1 x U(3) + 0,9 x U(5) = 0,1 x (3) + 0,9 x (5) = 2,185 ko BH * *
Ở điểm C, U(W ) = 2,185, do đó W = 4,775 tỷ đồng = CE.
Đền bù rủi ro = 4,8 – 4,775 = 0,025 tỷ đồng = 25 triệu đồng.
• Phí BH max (gọi phí BH là X người mua BH trả) lOMoAR cPSD| 59452058 Xác suất (p)
Giá trị tài sản W (tỷ) Cháy 0,1
3 tỷ + được đền cháy (2 tỷ) – X = 5 - X ko cháy 0,9 5 - X
(Lưu ý X là tiền mua BH)
Giá trị tài sản kỳ vọng & Ích lợi kì vọng khi ko mua BH là
EMVBH = 0,1 x (5 - X) + 0,9 x (5 - X) = 5 - X
EU = 0,1 x (5 - X)0,5 + 0,9 x (5 - X)0,5 = (5 - x)0,5 BH
Người ghét rro chỉ mua BH khi EU > EU BH ko BH
Hay (5 - X)0,5 > 2,185 hay X < 0,225 suy ra phí BH max = 225 triệu
• Phí BH min mà Cty BH có thể bán để có lợi nhuận = (2 x 0,1) = 0,2 = 200 triệu
(theo nguyên tắc BH công bằng)
Cách 2 (giải bằng đại số): với Cty BH thì mục tiêu là phải có lợi nhuận kì vọng: π > 0 Xác suất (p)
Giá trị lợi nhuận π (tỷ) Cháy 0,1
đền cháy (2 tỷ ) + X = -2 + z ko cháy 0,9 z
(Lưu ý z là tiền bán BH)
Π kì vọng = 0,1 x (-2 + z) + 0,9 x z > 0 hay z > 0,2 do đó ta có phí BHmin = (200 triệu
Lưu ý: Phí BH max = Phí BH min + Đền bù rủi ro Đồ thị minh họa lOMoAR cPSD| 59452058 Bài số 3 2
Giám đốc công ty ABC có hàm ích lợi là U = 150M – M . Ông GĐ đang cân nhắc 2 phương án
cung cấp sản phẩm: tự sản xuất và thuê bên ngoài làm. Lợi nhuận (tính bằng tỷ đồng) từ 2 phương
án được cho ở bảng dưới đây:
a. Thái độ của giám đốc công ty này đối với rủi ro là gì? Giải thích. Ghét rủi ro, MU giảm dần. M
b. Tính ích lợi kỳ vọng của mỗi phương án kinh doanh cho giám đốc công ty này.
Tự làm: EU = 553,4, thuê ngoài: EU = 435
c. Tính tương đương chắc chắn của mỗi phương án kinh doanh cho giám đốc công ty này. (giải
điều kiện tìm tương đương chắc chắn chắn U = EU) 2 = Tự làm 150M – M
553,4 >>>CE = 3,8 Thuê ngoài: 150M – M
435 >>>>CE = 2,95 2 =
d. Giám đốc công ty ra quyết định theo tiêu thức tương đương chắc chắn, phương án nào sẽ được
chọn? Giải thích. (Phương án tự làm vì có CE cao hơn)
Tình hình thị trường lOMoAR cPSD| 59452058 Tốt (p = Xấu 0,4) (p = 0,6) Tự làm 2 5 Thuê ngoài làm 6 1
Lưu ý: Sv tự làm bài tập tính toán số 4 (trg 105) Sách HDTH vimo 2;
Bài 4 (tự làm : Giả sử hàm lợi ích của Phương là U(I) = I0,5, trong đó I là thu nhập hàng tháng
(tính bằng triệu đồng)
a) Phương là người thích rủi ro, trung tính với rủi ro hay ghét rủi ro? Vì sao?
b) Giả sử Phương hiện đang làm kiểm toán với mức lương 10 triệu đồng và chắc chắn kiếm
được mức thu nhập đó vào năm sau một cách chắc chắn. Phương đang được một chào mời
một cơ hội việc làm mà xác suất kiếm được 16 triệu đồng/1 tháng là 0,5 và xác suất chỉ
kiếm được 5 triệu đồng/1 tháng là 0,5. Vậy Phương có nên chấp nhận đề nghị mới này không?
c) Vẫn câu hỏi trên, nếu xác suất tương ứng bây giờ không phải là 50 - 50 mà là 70 - 30?
d) ở câu b), Phương có sẵn sàng mua bảo hiểm chống lại việc thu nhập thay đổi khi chuyển
sang công việc mới hay không? Nếu có, Phương sẵn sàng trả bao nhiêu cho bảo hiểm?
Bài tập t nh toán (Ch 4: LÝ THUYẾT HÃNG/DN)
Bài 1: Chi ph kinh tế và chi ph kế toán
Lan bỏ một công việc với mức lương 18.000$/năm và đầu tư 300.000$ của mình vào kinh doanh.
Trong năm đầu tiên cô không trả lương cho mình và thu được 52.000$ lợi nhuận tính toán. Lan hy
vọng rằng tình hình sẽ tiếp tục như năm đầu tiên. a.
Nếu lãi suất là 10%, lợi nhuận kinh tế là bao nhiêu? b.
Nếu tỷ lệ lãi suất là 20%, lợi nhuận kinh tế là bao nhiêu? c.
Lan có nên tự kinh doanh không, nếu lãi suất là 10%, nếu lãi suất là 20%? Lời giải:
a) Nếu lãi suất là 10%, với 300 000$ đầu tư vào kinh doanh sẽ có chi phí cơ hội là 10% x 300.000$ = 30.000$/năm.
Chi phí cơ hội của Lan nếu cô tự kinh doanh không đi làm cho công ty khác là:
30.000$ + 18.000$ = 48.000$/năm. lOMoAR cPSD| 59452058
Vậy Lợi nhuận kinh tế = Lợi nhuận tính toán – chi phí cơ hội = 52.000$ - 48.000$ = 4.000$/năm.
b) Nếu lãi suất là 20%, với 300 000 $ đầu tư vào kinh doanh sẽ có chi phí cơ hội là 20% * 300.000$ = 60.000$/năm.
Chi phí cơ hội của Lan nếu cô tự kinh doanh không đi làm cho công ty khác là:
60.000$ + 18.000$ = 78.000$/năm.
Trong trường hợp này Lợi nhuận kinh tế = Lợi nhuận tính toán – chi phí cơ hội = 52.000$ - 78.000$ = - 26.000$/năm.
c) Nếu lãi suất là 10%, Lan nên tự kinh doanh, vì lợi nhuận kinh tế là 4.000$ > 0
Nếu lãi suất là 20%, Lan không nên tự kinh doanh, vì lợi nhuận kinh tế là -26.000$ < 0
Bài 2: Lựa chọn đầu vào và chi ph dài hạn
Một doanh nghiệp có hàm sản xuất được cho bởi Q = K1/2L2/3. Giá của vốn là PK = r = 45$/đơn vị,
giá thuê lao động là PL = r =10$/đơn vị.
a. Hàm sản xuất này có hiệu suất tăng, giảm hay không đổi theo qui mô?
b. Với tổng chi phí C = 6720$, xác định số lượng vốn và lao động tối ưu để doanh nghiệp sản
xuất ra được mức đầu ra lớn nhất. Tính mức đầu ra lớn nhất đó.
c. Nếu muốn sản xuất được mức đầu ra là Q = 216 sản phẩm thì doanh nghiệp sẽ sử dụng kết
hợp đầu vào nào để tối thiểu hóa chi phí?
d. Minh họa các kết quả đã tính ở câu b và c trên cùng một đồ thị. Lời giải:
a. Vì 1/2 + 2/3 = 7/6 > 1 nên hàm sản xuất đã cho có hiệu suất tăng theo qui mô
b. MPK = 1/2 L2/3K-1/2 MPL = 2/3 K1/2 L-1/3
Để sản xuất ra mức đầu ra lớn nhất thì thỏa mãn điều kiện MPK/ PK = MPL/PL, hay 1/2 L2/3K-1/2 2/3 K1/2 L-1/3
-------------- = ---------------- suy ra L = 6K (1) 45 10
Để sản xuất với mức chi phí C = 6720 thì phương trình đường đồng phí 6720 = 45K + 10L (2)
Giải hệ phương trình gồm 2 phương trình (1) và (2), ta có: K = 64; L = 384
Vậy để sản xuất ra mức đầu ra lớn nhất với chi phí 840$, thì K = 64, L = 384 và mức đầu ra lớn nhất Q = 314 sản phẩm lOMoAR cPSD| 59452058
c. Để sản xuất ra Q = 216 sản phẩm thì ta có phương trình 216 = K1/2 L2/3 (3)
Bên cạnh đó để chi phí là ít nhất tức là thỏa mãn điều kiện MPK/ PK = MPL/PL, hay L = 6K (4).
Giải hệ gồm 2 phương trình (3) và (4), ta có: K = 36, L = 216.
Mức chi phí thấp nhất C min = 45K + 10L = 3780$ c. Hình vẽ K C 2 64 E 1 Q 1 = 314 E 2 Q C 1 2 = 216 216 384
Bài 3: Xu hướng vận động của các chi ph ngắn hạn
Cho hàm tổng chi phí TC = C0 + a Q3 - b Q2 + cQ
(trong đó C0- tượng trưng cho chi phí cố định)
a. Viết phương trình biểu diễn tổng chi phí bình quân (ATC)
b. Viết phương trình biểu diễn chi phí biến đổi bình quân (AVC)
c. Viết phương trình biểu diễn chi phí cố định bình quân (AFC)
d. Mức sản lượng đạt được chi phí biến đổi bình quân tối thiểu là bao nhiêu? lOMoAR cPSD| 59452058
e. Từ (AVC) hãy suy ra phương trình biểu diễn chi phí cận biên (MC).
f. Ở mức sản lượng nào chi phí biến đổi bình quân bằng chi phí cận biên.
g. Chứng minh rằng đường MC luôn cắt đường ATC tại điểm cực tiểu của ATC. Lời giải
Từ hàm tổng chi phí đã cho: TC = C0 + a Q3 - b Q2 + cQ
a. ATC = TC / Q = C0/Q + a Q2 - b Q + c (ATC có dạng chữ U)
b. AVC = VC / Q = (a Q3 - b Q2 + cQ) / Q = a Q2 - b Q + c (AVC có dạng chữ U)
c. AFC = FC/ Q = C0/Q (AFC ko có dạng chữ U mà là đường hypecbole tiệm cận trục Q))
d. AVCmin khi (AVC)'Q = (a Q2 - b Q + c)'Q = aQ - b tại mức sản lượng Q = b/a (dễ dàng kiểm tra
được điều kiện cực trị)
e. Để suy ra được chi phí cận biên (MC) từ (AVC) ta có chi phí biến đổi: VC = Q x AVC = (a Q2
- b Q + c) Q = a Q3 - b Q2 + cQ
Vậy: (MC) = (TC)'Q = (VC)'Q = 3a Q2 - 2bQ + c
f. Chi phí biến đổi bình quân bằng chi phí cận biên tại mức sản lượng AVCmin hay Q = b/a.
(Đường MC cắt AVC ở điểm đáy của AVC)
g. Tại điểm đáy của ATC khi AVCmin thì (ATC)'Q = 0 = - C0/Q2 + 2a Q- b
Ta có thể biến đổi tương đương như sau:
0 = [ - C0/Q2 - a Q + b - c/Q ] + [ 3a Q - 2b + c/Q] =
-1/ Q [(C0/Q + a Q2 – b Q + c) – (3a Q2 - 2bQ + c)] = -1/ Q (ATC - MC) = 0. Hay ATC = MC (đpcm)