


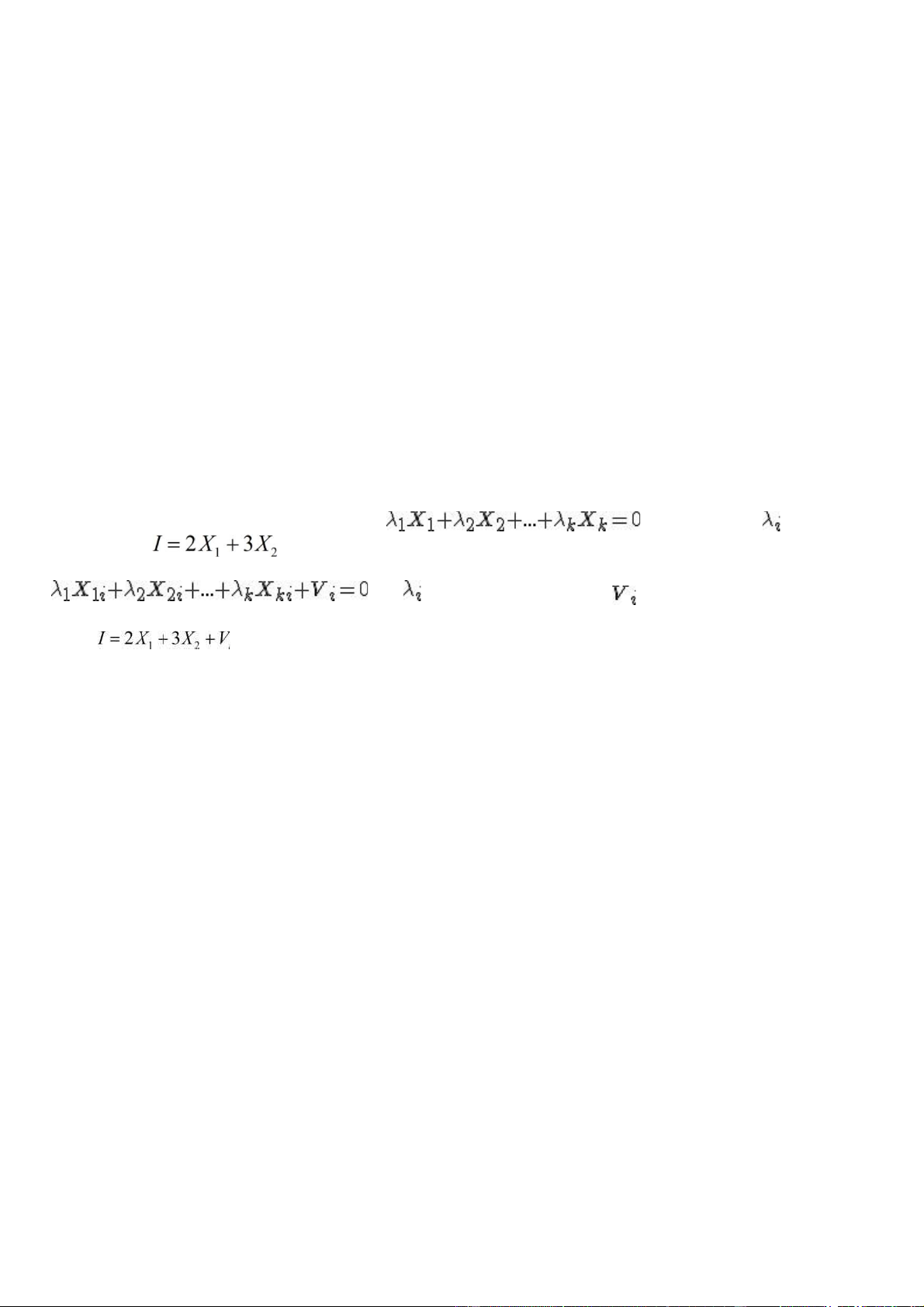















Preview text:
lOMoAR cPSD| 45876546
ÔN TẬP TÀI CHÍNH ĐỊNH LƯỢNG
Dữ liệu chuỗi thời gian, dữ liệu bảng và dữ liệu chéo là gì? Cho ví dụ
Dữ liệu chuỗi thời gian (time series): là dữ liệu phản ánh đặc trưng, đặc điểm c+ủa một chủ thể qua nhiều thời kỳ.
Ví dụ: Dữ liệu lợi nhuận của 1 công ty qua các năm/ báo cáo tài chính hợp nhất của công ty VNM qua từng năm
Dữ liệu bảng (panel data): là sự kết hợp giữa dữ liệu chuỗi thời gian và dữ liệu chéo. Nó thể hiện đặc điểm đặc trưng của nhiều
chủ thể qua nhiều thời kỳ.
Ví dụ: Lợi nhuận của các công ty trong ngành X/ dữ liệu về các chỉ số tài chính của 4 công ty top ngành điện qua khoảng thời gian là từ 2010 -2020.
Dữ liệu bảng bao gồm hai loại dữ liệu bảng cân đối (Balanced panel) và dữ liệu bảng không cân đối (Unbalanced panel).
+Dữ liệu bảng cân đối (Balanced panel): Khi các đơn vị dữ liệu chéo có cùng số quan sát theo thời gian.
+Dữ liệu bảng không cân đối (Unbalanced panel): Khi các đơn vị chéo không có cùng số quan sát theo thời gian.
Tầm quan trọng của dữ liệu bảng
Khi thảo luận các ưu điểm của dữ liệu bảng so với dữ liệu chéo thuần túy hoặc dữ liệu chuỗi thời gian thuần túy, Baltagi
liệt kê các yếu tố sau đây: -
Vì dữ liệu bảng liên quan đến các cá nhân, các công ty, các quốc gia, ... qua thời gian, nên chắc chắn có tính không -
đồngnhất (heterogeneity) trong các đơn vị này, mà tính không đồng nhất này thường không thể quan sát được. Các kỹ thuật
ước lượng dữ liệu bảng có thể tính đến tính không đồng nhất đó một cách rõ ràng bằng cách đưa vào các biến đặc thù theo chủ
thể (subject-specific), như chúng ta sắp thấy. Chúng ta sử dụng thuật ngữ ‘chủ thể’ ở đây có nghĩa chung nhất để bao gồm các
đơn vị vi mô như các cá nhân, công ty, hoặc các tiểu bang. -
Bằng cách kết hợp chuỗi thời gian của các quan sát chéo, dữ liệu bảng cho chúng ta “dữ liệu chứa nhiều thông tin hơn,
tínhbiến thiên cao hơn, ít có hiện tượng cộng tuyến giữa các biến hơn, nhiều bậc tự do hơn và hiệu quả cao hơn.” -
Bằng cách nghiên cứu các quan sát lăp đi lặp lại của các đơn vị chéo, dữ liệu bảng phù hợp hơn cho việc nghiên cứu
độngthái thay đổi theo thời gian của các đơn vị chéo này. Những tác động của thất nghiệp, tốc độ thay thế việc làm, độ dài của
sự thất nghiệp, và tính dịch chuyển của lao động được nghiên cứu tốt hơn với dữ liệu bảng.
Dữ liệu bảng có thể phát hiện và đo lường tốt hơn các ảnh hưởng không thể quan sát được trong dữ liệu chuỗi thời gian hay dữ
liệu chéo thuần túy. Vì thế ảnh hưởng của các luật về mức lương tối thiểu đối với việc làm và thu nhập có thể được nghiên cứu
tốt hơn nếu chúng ta theo dõi các đợt gia tăng liên tiếp trong các mức lương tối thiểu của liên bang và/hoặc tiểu bang. - Các
hiện tượng như lợi thế kinh tế theo quy mô và thay đổi công nghệ có thể được nghiên cứu tốt hơn với dữ liệu bảng so với dữ
liệu chéo hay dữ liệu chuỗi thời gian thuần túy.
Dưới đây là một số hạn chế và phát triển tiềm năng của dữ liệu panel trong lĩnh vực kinh tế: Hạn chế: 1.
Thiếu thông tin về biến chưa được quan sát: Trong một số trường hợp, dữ liệu panel có thể không bao gồm đầy đủ các
biếnquan trọng. Điều này có thể hạn chế khả năng phân tích và dự đoán hiệu quả. 2.
Độ rò rỉ thông tin giữa các đơn vị: Dữ liệu panel thường chứa thông tin về các đơn vị (ví dụ: công ty, hộ gia đình) theo
thờigian. Tuy nhiên, có thể xảy ra sự rò rỉ thông tin giữa các đơn vị, khiến việc đánh giá độc lập của dữ liệu trở nên khó khăn. 3.
Sự thay đổi trong cấu trúc dữ liệu: Trong dữ liệu panel, có thể xảy ra sự thay đổi trong cấu trúc dữ liệu, ví dụ như sự
thayđổi về số lượng đơn vị, đặc điểm của đơn vị hoặc chu kỳ quan sát. Điều này có thể tạo ra khó khăn trong việc xử lý và phân tích dữ liệu.
Phát triển tiềm năng: 1.
Mở rộng quy mô và phạm vi của dữ liệu panel: Một phát triển tiềm năng là mở rộng quy mô và phạm vi của dữ liệu
panelbằng cách thu thập thông tin từ nhiều quốc gia, ngành công nghiệp và lĩnh vực khác nhau. Điều này sẽ tạo ra cơ sở dữ
liệu lớn hơn và đa dạng hơn, giúp phân tích và dự đoán có sự phong phú hơn. 2.
Kết hợp với dữ liệu khác: Sự phát triển của dữ liệu panel có thể được kết hợp với dữ liệu từ các nguồn khác nhau,
chẳnghạn như dữ liệu địa lý, dữ liệu xã hội, hoặc dữ liệu từ các nguồn kinh tế khác. Việc kết hợp dữ liệu này có thể tạo ra thông
tin sâu hơn và nhìn nhận toàn diện hơn về các vấn đề kinh tế. 3.
Sử dụng các phương pháp phân tích tiên tiến: Sự phát triển của các phương pháp phân tích dữ liệu và máy học có thể
đượcáp dụng vào dữ liệu panel kinh tế, giúp phân tích và dự đoán hiệu quả hơn. Các phương pháp như mô hình hỗn hợp, học
sâu và học tăng cường có thể giúp hiểu rõ hơn về mối quan hệ giữa các biến và dự đoán tốt hơn trong tương lai.
Dữ liệu chéo (Cross-sectional data): là dữ liệu của một hay nhiều biến được thu thập cho nhiều đơn vị mẫu hoặc địa điểm
mẫu tại cùng một thời điểm.
Ví dụ: số bệnh viện tại thành phố HCM, Nha Trang, Đà Nẵng vào năm 2000/ Lợi nhuận trước Covid và sau Covid.
Ưu điểm của dữ liệu chéo là phù hợp cho những vấn đề nghiên cứu mang quy mô lớn, liên quan đến cá nhân, doanh nghiệp,
tỉnh thành, đất nước,…cần sự đặc trưng của từng cá thể.
Statistical description - Mô tả thống kê
Mean: giá trị trung bình, độ lớn của nó. Vd: giá trị trung bình càng nhỏ nếu đầu tư vào ăn nhiều hoặc không ăn.
Median: vị trí ở giữa của 1 dãy số=> cảm giác cơ hội của mình. Ví dụ 7đ=> sẽ có 50% cơ hội điểm cao tức trên 7đ. lOMoAR cPSD| 45876546
Expected value: E(x) trung bình của những khả năng nhận được. Vd: càng cao cơ hội nhận được trường tốt càng nhiều. Range
= Max-Min, lợi nhuận rủi ro thấp khi range nhỏ.
Standard deviation: độ lệch tb của những giá trị so với giá trị tb (càng lớn rủi ro càng lớn). Vd: điểm tb 5, độ lệch 1 thì sẽ có những điểm 4, 6 nhiều.
Distribution: phân phối cho biết xác suất xảy ra của những dãy số.
Skewness: độ nghiêng của phân phối, (lệch về những giá trị cao hơn hay thấp hơn giá trị tb)
Hồi quy OLS (Ordinary Least Square): chỉ chạy cho tuyến tính, phi tuyến tính không được. GLS (General Least Square) chạy được cả 2.
Trong mô hình 1 biến xuất hiện 2 lần khác nhau thì mới là không tuyến tính + Tuyến tính: y= + 12 + 22 +
+ Phi tuyến tính: y= + 12 + 22 + Mục tiêu là nhỏ để
ước lượng chính xác thực tế. Kiểm tra: +
Đặc thù dữ liệu: 3 loại dữ liệu (time series, panel data, cross-sectional data) +
Câu lệnh kiểm tra tính dừng + Thuật toán GLS, OLS
Kiểm tra giả định OLS
1) Hồi quy => dữ liệu có tuyến tính không?
Mô hình phải có các biến phù hợp, không có biến nào bị bỏ sót, mô hình phải có +εi 2) E(εi) = 0
Mean (ε) = 0 => dành cho mô hình định giá Được khắc phục bằng cách thêm một hằng số Ví dụ: y = 5+ 4x + ε với ε=3 => y= 5+3+ 4x+ε-3
=> y= 8+4x+ε’ (thay đổi hằng số để E(εi) = 0)
Ngoại sinh (Exogeneity)
Trong mô hình kinh tế, một biến được gọi là biến nội sinh nếu nó chịu tác động của các biến khác trong mô hình, và biến được
gọi là ngoại sinh (exogenous variable) nếu nó không chịu tác động của các biến khác trong mô hình. Như vậy, biến phụ thuộc
dĩ nhiên là biến nội sinh. Do nó chịu tác động của các biến độc lập.
Ví dụ: LN= size + inventory + doanh thu
Size và inventory là do suy nghĩ, không có tác động trực tiếp Doanh thu là nội sinh tác động trực tiếp Biến
độc lập không có liên hệ với biến Error (ε mang thông tin biến phụ thuộc).
Nội sinh (Endogeneity)
là biến (đáng lẽ là độc lập và giải thích cho biến phụ thuộc) trở thành biến phụ thuộc. Biến nội sinh là những biến có sự tương
quan với phần dư. sự xuất hiện biến nội sinh sẽ dẫn đến các trường hợp như bỏ biến, sai số trong biến, hoặc được xác định đồng
thời qua các biến giải thích khác Nguyên nhân:
Thiếu vắng biến độc lập trong mô hình và do đó phần giải thích của biến này sẽ nằm ở sai số (phần dư). Khi đó có mối tương
quan chặt giữa biến độc lập và phần dư. Ví dụ: sale= beta0 +beta1*price +εi => lỗi Sai số trong đo lường hay sai lệch do lựa
chọn, hệ số đi kèm không ý nghĩa. Vấn đề đồng thời và hệ phương trình đồng thời. Cách kiểm định:
Chắc chắn biến X bị nội sinh, Hồi quy OLS mô hình; sử dụng Hausman Test để xem xét vấn đề. Hồi quy OLS mô hình. Trích
phần dư và thực hiện hồi quy phần dư với biến độc lập. Sau đó sử dụng F-Test để kiểm định vấn đề nội sinh. Nếu có hiện tượng
nội sinh thì p value <= 10%
Xem xét việc không có biến công cụ yếu, Có nhiều cách để kiểm định khả năng mạnh – yếu của biến công cụ. Tất nhiên, không
có phương án nào là tốt nhất trong đánh giá này. Xem xét tiêu chí kiểm định cov(z,ui) = 0 để kết luận Hiệu lực của biến công
cụ: Thường sử dụng Sargan Test B1: Ước lượng mô hình 2SLS B2: Trích phần dư.
B3: Hồi quy phần dư với tất cả các biến ngoại sinh. Tính nR2 theo phân phối chi-bình phương.
B4: So sánh trong bảng phân phối chi bình phương với bậc tự do là số biến nội sinh. Nếu nR2 vượt qua giá trị tới hạn (critical
value) thì biến công cụ đạt hiệu lực tin cậy Cách giải quyết:
Chấp nhận sai lệch tiềm ẩn mà không làm gì cả. Có thể sử dụng thêm lệnh ước lượng vững (robust).
Ứng dụng dữ liệu bảng với một mô hình có thể giải quyết vấn đề nội sinh Tìm một biến proxy
khác phù hợp để giải quyết mô hình.
Sử dụng mô hình với biến công cụ: 2SLS, 3SLS, GMM … Thay biến khác
Không có tự tương quan (No Serial Correlation) lOMoAR cPSD| 45876546
Tự tương quan là việc dữ liệu (time series hay cross-section) tự tương quan với nhau, tự mình liên quan tạo ra dữ liệu phía sau,
tự tạo ra quy luật cho mình.
Giá chứng khoán thường có tự tương quan vì giá đóng cửa ngày hôm nay là giá mở cửa ngày hôm sau/ giá xăng dầu không có. Nguyên nhân:
Nguyên nhân do quán tính: Nét nổi bật của hầu hết các chuỗi thời gian trong kinh tế là quán tính mang tính chu kỳ. Hiện tượng mạng nhện
Các độ trễ: Trong phân tích chuỗi thời gian, chúng ta có thể gặp hiện tượng biến phụ thuộc ở thời kỳ t phụ thuộc vào chính biến
đó ở thời kỳ t -1 và các biến khác.
Xử lí số liệu: Trong phân tích thực nghiệm, số liệu thô thường được xử lý. Chẳng hạn trong hồi quy chuỗi thời gian gắn với các
số liệu quý, các số liệu này thường được suy ra từ các số liệu tháng bằng cách cộng 3 quan sát rồi chia cho 3. Việc lấy trung
bình này làm trơn các số liệu và làm giảm sự giao động trong số liệu tháng. Chính sự làm trơn này có thể dẫn đến sai số có hệ
thống trong các sai số ngẫu nhiên và gây ra sự tương quan Sai lệch do lập mô hình: Đây là nguyên nhân thuộc về việc lập mô hình. Hậu quả:
Các ước lượng OLS không còn BLUE
Phương sai ước lượng được của các ước lượng OLS là chệch
Kiểm định t và F không đáng tin cậy
Do công thức thông thường để tính phương sai của sai số là ước lượng chệch của thực, và trong một số trường hợp, nó dường
như là ước lượng thấp
Kết quả có thể là độ đo không đáng tin cậy cho thực
Các phương sai và sai số tiêu chuẩn của dự đoán đã tính được cũng có thể không hiệu quả Không tính ra Test ra vô nghĩa
Tính ra mức ý nghĩa bị biased do phương sai sai số lớn Kiểm
định tự tương quan: Giả thuyết H0:
H0 : Mô hình không xảy ra hiện tượng tự tương quan H1: Mô hình xảy ra hiện tượng tự tương quan
- Phương pháp đồ thị - Kiểm định Durbin –Watson Cách khắc phục: Dùng GLS
Chạy mô hình tự hồi quy Chạy hồi quy 2 lần
Phương sai sai số không thay đổi (Homoscedasticity)
Phương sai sai số thay đổi là hiện tượng mà tại đó phần dư (residuals) hoặc các sai số
của mô hình sau quá trình hồi quy không tuân theo phân phối ngẫu nhiên và phương sai không bằng nhau. Điều này vi phạm
giả thuyết của mô hình hồi quy tuyến tính là “phương sai thay đổi của các sai số phải giống nhau” Nguyên nhân:
Sai sót trong quá trình biến đổi chỉnh sửa dữ liệu, sai dạng hàm, bỏ sót biến.
Sử dụng các thang đo khác nhau cho các quan sát của cùng 1 biến trong mô hình hồi quy
Hậu quả: Mô hình OLS không còn là mô hình ước lượng tốt nhất nữa mà cần phải khắc phục trong các mô hình khác cao cấp
hơn. Ngoài ra, phương sai thay đổi làm chệch đi các kết quả của kiểm định T-test và F-test, khiến chúng ta đưa ra các kết luận sai lầm.
Kiểm định phương sai sai số thay đổi: có 2 cách
Cách 1: Vẽ đồ thị sai số thể hiện phương sai thay đổi
B1: Chạy hồi quy mô hình“reg BPT BĐL” B2: Vẽ đồ thị “rvfplot, yline(0)” lOMoAR cPSD| 45876546
Các chấm xanh là các sai số đối với từng giá trị ước lượng của các biến trong mô hình đa phần tập trung quanh đường trung
bình Tuy nhiên các sai số này có vị trí nằm không đối xứng với nhau nên có thể mô hình đang bị hiện tượng phương sai sai thay đổi.
Cách 2: Chạy kiểm định
Có 2 kiểm định có thể dùng là: Kiểm định Breusch-Pagan và kiểm định White, với giả thuyết là:
Ho: Mô hình không xảy ra hiện tượng phương sai thay đổi
H1: Mô hình có xảy ra hiện tượng phương sai thay đổi
Kiểm định White trong Stata với lệnh: estat imtest, white
Cả 2 kiểm định có cách đọc kết quả như nhau, là xem giá trị (Prob > chi2)
(Prob > chi2) > 0.05: Không có hiện tượng phương sai sai số thay đổi
(Prob > chi2) < 0.05: Có hiện tượng phương sai sai số thay đổi Cách
khắc phục phương sai sai số thay đổi:
Sử dụng mô hình WLS (Weighted Least Squares), mô hình khá tương tự với mô hình OLS giúp khắc phục phương sai sai số
thay đổi tuy nhiên cần phải sử dụng nhiều phép thử để chọn lọc ra được kết quả.
Biến đổi các biến thành dạng logarit để giảm bớt và khắc phục hiện tượng phương sai thay đổi.
Dùng mô hình phương sai sai số chuẩn (Standard Errors or Robust Standard Errors) để khắc phục phương sai sai số thay đổi.
=> code “reg BPT BĐL, robust”
Không có đa cộng tuyến hoàn hảo (No Perfect Multicollinearity)
Khái niệm: Hiện tượng đa cộng tuyến là hiện tượng mà các biến độc lập trong mô hình có mối quan hệ tuyến tính với nhau.
*Đa cộng tuyến hoàn hảo: Các biến độc lập
thỏa các giá trị không đồng thời bằng 0. Ví dụ: *Đa
cộng tuyến không hoàn hảo: nếu các biến độc lập thỏa
, các không đồng thời bằng 0 và là sai số ngẫu nhiên. Ví dụ:
với Vi là sai số ngẫu nhiên
*Nguyên nhân của đa cộng tuyến:
Khi chọn các biến độc lập mối quan có quan hệ nhân quả hay có tương quan cao vì đồng thời phụ thuộc vào một điều kiện khác.
Cách thu thập mẫu: mẫu không đặc trưng cho tổng thể Chọn
biến độc lập có độ biến thiên nhỏ.
*Hậu quả: Sai số chuẩn của các hệ số sẽ lớn. Khoảng tin cậy lớn và thống kê t ít ý nghĩa. Các ước lượng không thật chính xác.
Do đó chúng ta dễ đi đến không có cơ sở bác bỏ giả thiết "không" và điều này có thể không đúng. Cách nhận biết:
Cách 1: Như đã nói ở trên, nếu kết quả ước lượng có giá trị R2 rất cao nhưng rất ít biến độc lập có ý nghĩa thống kê thì khả
năng cao là các biến độc lập đã bị ảnh hưởng bởi đa cộng tuyến. Bởi vì, R2 thể hiện cho khả năng giải thích của biến độc lập
đến biến động trong biến phụ thuộc. Vậy nên, nếu biến độc lập không có ý nghĩa thống kê thì điều này cũng có nghĩa biến độc
lập cũng không có đóng góp gì vào hệ số R2.
Cách 2: Kiểm tra hệ số tương quan giữa các cặp biến (pairwise correlations)
Đây là hệ số tương quan giữa các cặp biến với nhau. Nếu hệ số này cao hơn 0.5 thì đó đã là điều đáng lo ngại rồi. Tuy nhiên,
chúng ta ko nên bỏ biến ra khỏi mô hình khi chỉ căn cứ vào hệ số này. Lý do là bởi vì khi hệ số này được ước tính, các biến
khác không được giữ nguyên (hold constant) nên có thể ảnh hưởng đến kết quả ước lượng.
Ở đây hệ số tương quan của roa và cpi là 0.4074 và sig < 0.05 nên ta kết luận giữa 2 biến có tương quan và tương quan dương.
Tương tự cho các biến còn lại, nếu tương quan dương < 0.5 thì không đáng lo ngại về đa cộng tuyến.
Cách 3: Kiểm tra hệ số tương quan từng phần (Partial correlation)
Hệ số tương quan này thực chất cũng được tính toán giữa các cặp biến, tuy nhiên các biến khác đã được giữ nguyên. Để dễ
phân biệt thì mình so sánh giữa hệ số tương quan pairwise và partial nhé. Giả sử chúng ta có 3 biến X1, X2, X3. Chúng ta sẽ
có 3 hệ số tương quan pairwise đó là r12, r13, r23. Chúng ta sẽ có 3 hệ số tương quan partial: r12.3, r13.2 và r23.1 Nếu biến
X1 có quan hệ tuyến tính với cả 2 biến X2 và X3 thì có khả năng hệ số tương quan pairwise r23 đã bị ảnh hưởng bởi X1 rồi.
Vậy nên, nếu chúng ta giữ X1 không đổi thì hệ số r23.1 sẽ phản ảnh tốt hơn mối tương quan giữa X2 và X3. Công thức câu
lệnh này như sau: pcorr biendoclap1 biendoclap2 biendoclap3. Cách 4: Hồi quy phụ trợ/hỗ trợ (Auxiliary regressions)
Chúng ta có thể hồi quy lần lượt từng biến độc lập lên các biến độc lập khác và kiểm tra kiểm định F của các mô hình hồi quy
phụ trợ này. Nếu như kiểm định F có ý nghĩa thống kê (P-value < 0.1 hoặc 0.05), kết quả này hàm ý là có hiện tượng đa cộng
tuyến giữa các biến độc lập. Ngược lại, nếu P-value của F lớn hơn 0.1 thì chúng ta có thể an tâm rằng không có hiện tượng đa
cộng tuyến trong mô hình
Cách 5: Dùng hệ số VIF (Variance Inflation Factor – hệ số phóng đại phương sai) hoặc TOF (Tolerance Factor – hệ số dung
sai) TOF thực chất chỉ là nghịch đảo của VIF mà thôi, nên các bạn dùng hệ số nào cũng được nhé. Đối với VIF, hệ số càng lớn lOMoAR cPSD| 45876546
thì có nghĩa là biến đó có nguy cơ cao gây ra hiện tượng đa cộng tuyến. Ngược lại, hệ số TOF càng nhỏ thì càng nguy hiểm.
Có rất nhiều tiêu chuẩn để lựa chọn hệ số VIF hay TOF Các giải pháp khắc phục đa cộng tuyến:
Giải pháp 1: Bỏ bớt biến độc lập(điều này xảy ra với giả định rằng không có mối quan hệ giữa biến phụ thuộc và biến độc lập bị loại bỏ mô hình).
Giải pháp 2: Bổ sung dữ liệu hoặc tìm dữ liệu mới,tìm mẫu dữ liệu khác hoặc gia tăng cỡ mẫu. Tuy nhiên nếu mẫu lớn hơn mà
vẫn còn multicollinearity thì vẫn có giá trị vì mẫu lớn hơn sẽ làm cho phương sai nhỏ hơn và hệ số ước lượng chính xác hơn so với mẫu nhỏ.
Giải pháp 3: Thay đổi dạng mô hình,mô hình kinh tế lượng có nhiều dạng hàm khác nhau. Thay đổi dạng mô hình cũng có
nghĩa là tái cấu trúc mô hình. Điều này thật sự là điều không mong muốn, thì lúc đó bạn phải thay đổi mô hình nghiên cứu.
Mô hình CAPM (Tuyến tính đơn biến)
Mô hình định giá tài sản vốn trong tiếng Anh là Capital asset pricing model, viết tắt là CAPM. Là mô hình định giá mô tả mối
quan hệ giữa rủi ro hệ thống và lợi nhuận kỳ vọng của tài sản, đặc biệt là cổ phiếu. (Theo: Investopedia)
Trong đó, rủi ro hệ thống là rủi ro cố hữu đối với toàn bộ thị trường hoặc phân khúc thị trường. Loại rủi ro này là không thể dự
đoán và không thể tránh hoàn toàn. Ví dụ như rủi ro thay đổi chính sách của chính phủ, rủi ro đến từ các điều kiện tự nhiên (bão lụt, hạn hán...)
Mô hình định giá tài sản vốn (CAPM) là một trong những đổi mới quan trọng nhất trong lý thuyết danh mục đầu tư. CAPM
được giới thiệu bởi William Sharpe, John Lintner, Jack Treynor và Jan Mossin và xây dựng dựa trên lý thuyết của Harry
Markowitz về đa dạng hóa danh mục đầu tư. Suất sinh lợi kỳ vọng:
Ri - Rf = α + β(RM – Rf) + ε
Hệ số beta: độ nhạy của chứng khoán đối với thay đổi trên thị trường
β =1: biến thiên bằng thị trường, rủi ro bằng mức thị trường β > 1: rủi ro cao hơn mức trung bình của thị trường
β <1: rủi ro thấp hơn mức trung bình của thị trường (biến thiên và độ lệch chuẩn thấp hơn thị trường)
Hệ số Beta là hệ số đo lường mức độ rủi ro hệ thống của 1 cổ phiếu (1 danh mục đầu tư), bằng cách so sánh mức độ biến động
giá của cổ phiếu đó so với mức độ biến động chung của toàn thị trường. Việc phân tích kỹ lưỡng về mức độ rủi ro và tỷ suất
sinh lời của các sản phẩm tài chính sẽ giúp cho NĐT xác định được đối tượng phù hợp với khả năng chịu rủi ro của họ Hệ số
Alpha cung cấp cho chúng ta một tiêu chuẩn hợp lý để đánh giá hoạt động quản lý quỹ. Kết quả của Alpha có thể giúp ta xác
định liệu người quản lý có đang giúp quỹ này tăng trưởng hoặc thậm chí kiếm thêm được những khoản lãi vượt ngoài mức lợi
nhuận cần thiết hay không. Không chỉ vậy, chỉ số này cũng giúp ta quyết định liệu mức phí quản lý đã phù hợp với kết quả kinh
doanh hay chưa. Việc mua (hoặc thậm chí nắm giữ) một quỹ đầu tư mà không cân nhắc đến yếu tố này sẽ giống như mua một
chiếc xe chỉ để đi lại mà không quan tâm đến hiệu suất nhiên liệu của nó.
Khi alpha > 0: đầu tư hiệu quả, càng cao thì càng hiệu quả.
Khi alpha < 0:đầu tư không hiệu quả, càng thấp càng không hiệu quả.
Giá trị tuyệt đối của Critical Value < Giá trị tuyệt đối của Test Statistic => là chuỗi dừng (không có vấn đề) Mô hình FAMA
Mô hình ba yếu tố Fama và French (tiếng Anh: Fama and French Three Factor Model) là mô hình định giá tài sản được phát
triển vào năm 1992, mở rộng mô hình định giá tài sản vốn (CAPM) bằng cách thêm các yếu tố rủi ro kích thước và rủi ro giá
trị vào yếu tố rủi ro thị trường trong mô hình định giá tài sản vốn CAPM
Mô hình này xem xét khía cạnh thực tế rằng cổ phiếu giá trị và cổ phiếu vốn hóa nhỏ thường xuyên có lợi nhuận vượt trội so
với thị trường. Bằng cách bao gồm hai yếu tố bổ sung này, mô hình sẽ điều chỉnh theo xu hướng vượt trội này, khiến nó trở
thành một công cụ tốt hơn để đánh giá hiệu suất của người quản lí. Công thức: lOMoAR cPSD| 45876546
Mô hình Fama và French có ba yếu tố: qui mô của các công ty, tỉ lệ sổ sách trên thị trường và lợi nhuận vượt mức trên thị
trường. Nói cách khác, ba yếu tố được sử dụng là SMB (nhỏ trừ lớn), HML (cao trừ thấp) và lợi nhuận của danh mục đầu tư ít
hơn tỉ lệ hoàn vốn phi rủi ro. SMB tính đến trường hợp các công ty giao dịch công chúng có giới hạn thị trường nhỏ tạo ra lợi
nhuận cao hơn, trong khi HML tính đến trường hợp các cổ phiếu giá trị với tỉ lệ sổ sách trên thị trường cao tạo ra lợi nhuận cao hơn. Cách đo lường biến:
Tính toán hai nhân tố SMB và HML:
SMB = (S/L+S/H)/2 – (B/L+B/H)/2 Chênh lệch suất sinh lợi tuần của các nhóm công ty có quy mô nhỏ so với nhóm công ty có quy mô lớn.
HML = (S/H+B/H)/2 – (S/L+B/L)/2 Chênh lệch suất sinh lợi tuần của nhóm công ty có tỷ số BE/ME cao so với nhóm công ty có tỷ số BE/ME thấp.
`7. Mô hình Logistics và Probit Outcome:
Ex: yes/no, success/ failure => chỉ tồn tại 2 thái cực. Mô hình logit
Hồi quy logistic (Logistic Regression) là một mô hình thống kê ở dạng cơ bản của nó sử dụng một hàm logistic để mô hình hóa
một biến phụ thuộc nhị phân , mặc dù tồn tại nhiều phần mở rộng phức tạp hơn . Trong phân tích hồi quy , hồi quy logistic (hay
hồi quy logit ) là ước lượng các tham số của mô hình logistic (một dạng của hồi quy nhị phân ). Về mặt toán học, mô hình
logistic nhị phân có một biến phụ thuộc với hai giá trị có thể có, chẳng hạn như đạt hoặc không đạt được đại diện bởi một biến
chỉ báo, trong đó hai giá trị được gắn nhãn “0” và “1”. Biến dữ liệu phân phối=> % xác suất=> chạy hồi quy
Logit nhận 1, 0 nên không chạy bình thường như OLS được
Trong đó, Pi= xác suất hút thuốc (tức là Yi=1) và
Xác suất của Y=0, nghĩa là một người không phải là người hút thuốc, được cho bởi:
Lấy log (tự nhiên) của phương trình (8.10), chúng ta có được một kết quả rất thú vị, đó là: lOMoAR cPSD| 45876546
Ví dụ ta có: Bộ dữ liệu gồm 200 quan sát cùng 2 biến phụ thuộc GUITK (Có gửi=1; Không gửi=0) và SOTIENGUI (nếu người
đó có gửi tiền). 9 biến độc lập gồm các biến nhân khẩu học như GIOITINH (1: Nam; 0: Nữ), TUOI (4 bậc tuổi), HONNHAN
(1: Đã kết hôn; 0: chưa), HOCVAN, THUNHAP (4 mức); các biến giải thích gồm KHOANGCACH, NGUOITHAN, THUONGHIEU. Kết luận
Tùy theo dạng biến phụ thuộc mà chúng ta những mô hình hồi quy tương ứng như sau:
Nếu biến phụ thuộc có dạng nhị phân (giá trị 0 và 1) thì mô hình phù hợp là mô hình logit hoặc mô hình probit.
Nếu biến phụ thuộc có dạng thứ tự (hạng 1, hạng 2, hạng 3...) thì mô hình phù hợp là mô hình logit thứ tự hoặc mô hình probit thứ tự.
Nếu biến phụ thuộc có dạng định danh thì mô hình sử dụng phù hợp là mô hình logit hoặc probit đa bậc, hoặc mô hình logit có điều kiện.
Các mô hình logit vs probit đều dựa trên phương pháp ước lượng hợp lí tối đa ML (Maximum likelihood). Ước lượng hợp lí tối
đa đòi hỏi một giả định về dạng hàm phân phối xác suất, chẳng hạn hàm logit và hàm bù log-log. Các mô hình Logit sử dụng
hàm phân phối Logit chuẩn trong khi các mô hình Probit giả định hàm phân phối chuẩn chuẩn hóaSự khác nhau giữa Logit vs
Probit chủ yếu tập trung ở hàm phân phối của các sai số nhiễu Mặc dù các mô hình biến phụ thuộc nhị phân có thể được ước
lượng bằng OLS, trong trường hợp này chúng được gọi là các mô hình xác suất tuyến tính (LPM), nhưng OLSkhông phải là
phương pháp ước lượng được ưa thích cho các mô hình như thế bởi vì hai hạn chế: (1) các xác suất ước lượng từ LPM không
nhất thiết nằm trong giới hạn 0 và 1 và (2) LPM giả định rằng xác suất của một phản ứng dương tăng tuyến tính với mức độ
của biến giải thích, điều này rất phản trực quan.
Mô hình dữ liệu bảng (OLS, FEM, REM) Mô hình OLS
Hồi quy tuyến tính (Linear Regression) được phát triển thành mô hình hồi quy tuyến tính – LRM (Liner Regression
Model) là 1 trong công cụ quan trọng trong Kinh tế lượng và là phương pháp thống kê giúp hồi quy và dự báo dữ liệu theo thuật
toán giữa một một giá trị liên tục với một hoặc nhiều các giá trị liên tục, định danh hay phân loại có liên quan. Hiểu 1 cách đơn
giản thì Hồi quy tuyến tính là phương pháp tiếp cận tuyến tính để dự đoán biến phụ thuộc Y (biến kết cục) trên trục tung Y dựa
trên các biến độc lập X (biến giải thích) trên trục hoành X trong mô hình.Phương pháp OLS sẽ lựa chọn các hệ số hồi quy alpha
và beta sao cho bình phương sai số của mô hình ước lượng là nhỏ nhất.
Giả định mô hình hồi quy tuyến tính:
• Sai số của phần dư (residuals errors) ở đường thẳng hồi quy có phân phối chuẩn hoặc xấp xỉ phân phối chuẩn. lOMoAR cPSD| 45876546
• Phương sai sai số đồng nhất theo tất cả các quan sát.
• Sai số ngẫu nhiên sẽ độc lập thống kê lẫn nhân. Đây là giả định về không tự tương quan.
• Dữ liệu không có chứa các điểm dị biệt (Xem thêm phát hiện điểm dị biệt).
• Biến phụ thuộc trong mô hình phải là biến liên tục (có thể dạng tỉ lệ, hoặc dạng khoảng)
Có mối quan hệ tuyến tính giữa biến phụ thuộc với các biến giải thích của mô hình. Nếu dữ liệu có dạng phi tuyến, thì
chúng ta thực hiện biến đổi biến thành biến mới qua một dạng hàm phù hợp sao cho biến mới này thỏa mãn giả định tuyến tính của mô hình hồi quy.
Không có sự đa cộng tuyến giữa các biến giải thích. Điều đó có nghĩa các biến giải thích trong mô hình không có sự tương quan cao với nhau.
Tính chất của ước lượng OLS
• Ước lượng OLS có những tính chất quan trọng sau:
• Không chệch (unbiasedness): giá trị trung bình của những tham số ước lượng sẽ bằng các tham số tổng thể hay E(bi)=βiE(bi)=βi
• Phù hợp (consistency): sự khác nhau giữa tham số ước lượng và tham số tổng thể sẽ giảm khi số quan sát của mẫu dữ
liệu tăng theo định lí giới hạn trung tâm.
• Hiệu quả (efficiency): phương sai của các tham số ước lượng sẽ nhỏ nhất so với các phương pháp ước lượng không chệch khác.
• BLUE (ước lượng không chệch tuyến tính tốt nhất): đây là sự kết hợp của các tính chất không chệch, tuyến tính, và
hiệu quả. Theo đó, những hệ số ước lượng bi sẽ là những ước lượng không chệch tốt nhất nếu có phương sai nhỏ nhất.
• Bình phương nhỏ nhất thông thường, (ordinary least squares –OLS) là phương pháp được sử dụng rộng rãi nhất để ước
lượng các tham số trong phương trình hồi quy. Để tối thiểu hoá tổng bình phương của các khoảng cách theo phương
thẳng đứng giữa số liệu thu thập được và đường (hay mặt) hồi quy.
Các kiểm định của OLS với dữ liệu bảng:
• Kiểm định đa cộng tuyến, nếu hệ số VIF của các biến < 10 thì không có hiện tượng đa cộng tuyến xảy ra.
• Kiểm định phương sai sai số thay đổi “imtest,white”
• kiểm định hiện tượng tự tương quan “xtserial BPT BĐL”
Mô hình FEM - Mô hình tác động cố định (Fixed Effect Model) Lý thuyết:
Xét một mối quan hệ kinh tế với biến phụ thuộc Y và 2 biến độc lập là X1 và X2. Chúng ta có dữ liệu bảng cho Y, X1, và X2,
gồm N-đối tượng và T-thời điểm, và vì vậy chúng ta có NxT quan sát. Mô hình hồi quy tuyến tính cổ điển không có hệ số cắt được xác định bởi:
Phương trình trên được gọi là mô hình hồi quy các ảnh hưởng cố định (FEM – fixed effects regression model). Thuật ngữ “các
ảnh hưởng cố định” là vì sự thật rằng mỗi hệ số cắt của biến độc lập, mặc dù khác nhau giữa các hệ số cắt của N-Đối tượng
khác nhau, nhưng không thay đổi qua thời gian (time – invariant).
Hiệu ứng cố định (FE) là một kỹ thuật bình phương nhỏ nhất tổng quát khả thi (FGLS) về mặt tiệm cận hiệu quả hơn so với mô
hình Pooled OLS tổng hợp khi các thuộc tính hằng số thời gian có mặt.
Nếu giả định rằng εi và các biến giải thích tương quan, thì mô hình FEM có thể là mô hình phù hợp
Thống kê của kiểm định này có phân phối 2 tiệm cận (tức mẫu lớn) với số bậc tự do df bằng số biến giải thích trong mô hình.
Như thường lệ, nếu giá trị Chi bình phương tính toán lớn hơn giá trị Chi bình phương phê phán ở bậc tự do df nhất định và một
mức ý nghĩa cho trước, thì chúng ta kết luận rằng mô hình REM là không phù hợp bởi vì các hạng nhiễu ngẫu nhiên i có thể
tương quan với một hoặc nhiều biến giải thích. Trong trường hợp này, mô hình FEM tốt hơn mô hình REM.
Biến phụ thuộc là Q và các biến độc lập là ERM, SIZE, LEVERAGE, SALESGROWTH, CASH, ROA và DIVIDENS.
Kiểm định phương sai thay đổi: Giả thuyết:
H0: Mô hình xảy ra hiện tượng phương sai thay đổi H1:
Mô hình không xảy ra hiện tượng phương sai thay đổi Kết quả:
Prob>chi2 = 0.0884 > Mức ý nghĩa 5%, α = 0.05 nên chấp nhận H0 và kết luận mô hình xảy ra hiện tượng phương sai thay đổi.
Kiểm định tự tương quan: lOMoAR cPSD| 45876546 Giả thuyết:
H0: Mô hình không xảy ra hiện tượng tự tương quan H1: Mô hình xảy ra hiện tượng tự tương quan Kết quả:
Prob>chi2 = 0.0749 > Mức ý nghĩa 5%, α = 0.05 nên chấp nhận H0 và kết luận mô hình không xảy ra hiện tượng tự tương quan. Mô hình REM
cú pháp: xtreg [Biến phụ thuộc] + [Biến độc lập,..], re
Điểm khác biệt giữa mô hình ảnh hưởng ngẫu nhiên (REM) và mô hình ảnh hưởng cố định (FEM) được thể hiện ở sự biến động giữa các đơn vị.
Nếu sự biến động giữa các đơn vị có tương quan đến biến độc lập – biến giải thích trong mô hình ảnh hưởng cố định thì trong
mô hình ảnh hưởng ngẫu nhiên sự biến động giữa các đơn vị được giả sử là ngẫu nhiên và không tương quan đến các biến giải thích.
Chính vì vậy, nếu sự khác biệt giữa các đơn vị có ảnh hưởng đến biến phụ thuộc thì REM sẽ thích hợp hơn so với FEM.
Trong đó, phần dư của mỗi thực thể (không tương quan với biến giải thích) được xem là một biến giải thích mới.
Mô hình hồi quy mẫu tác động ngẫu nhiên REM là:
Yit = β1Xit + β2Xit + μit với i = 1, 2, …, N và t = 1, 2, …, T; μit = εi + uit Trong đó: εi : Sai số
ngẫu nhiên có trung bình bằng 0 và phương sai là σ2 uit: Sai số thành phần kết hợp khác của cả
đặc điểm riêng theo từng đối tượng và theo thời gian.
Một giả định quan trọng trong mô hình tác động ngẫu nhiên là thành phần sai số μit không tương quan với bất kì biến giải thích nào trong mô hình.
Các hiệu ứng ngẫu nhiên điều chỉnh cho mối tương quan nối tiếp được tạo ra bởi các thuộc tính hằng số thời gian không quan sát được. Mô hình ARIMA
Dựa trên giả thuyết chuỗi dừng và phương sai sai số không đổi. Mô hình sử dụng đầu vào chính là những tín hiệu quá
khứ của chuỗi được dự báo để dự báo nó. Các tín hiệu đó bao gồm: chuỗi tự hồi quy AR (auto regression) và chuỗi trung bình
trượt MA (moving average). Hầu hết các chuỗi thời gian sẽ có xu hướng tăng hoặc giảm theo thời gian, do đó yếu tố chuỗi dừng
thường không đạt được. Trong trường hợp chuỗi không dừng thì ta sẽ cần biến đổi sang chuỗi dừng bằng sai phân. Khi đó tham
số đặc trưng của mô hình sẽ có thêm thành phần bậc của sai phân d và mô hình được đặc tả bởi 3 tham số ARIMA(p, d, q).
Trong mô hình ARIMA (AutoRegressive Integrated Moving Average), các thành phần chính của một chuỗi thời gian bao gồm: -
Thành phần Autoregressive (AR): Thành phần AR liên quan đến phụ thuộc của giá trị hiện tại trên các giá trị trước đó
trongchuỗi thời gian. Nó cho phép mô hình ước lượng giá trị hiện tại dựa trên giá trị của các điểm dữ liệu trước đó trong chuỗi thời gian. -
Thành phần Moving Average (MA): Thành phần MA liên quan đến phụ thuộc của giá trị hiện tại trên các giá trị sai số
trướcđó trong chuỗi thời gian. Nó giúp mô hình ước lượng giá trị hiện tại dựa trên sai số của các điểm dữ liệu trước đó trong chuỗi thời gian. -
Thành phần Integrated (I): Thành phần I thể hiện mức độ tích hợp cần thiết để chuỗi thời gian trở nên ổn định và có
tínhdừng. Quá trình tích hợp thường liên quan đến việc lấy sai số hoặc chênh lệch giữa các giá trị liền kề trong chuỗi thời gian
để tạo ra một chuỗi thời gian mới có tính dừng.
Để sử dụng mô hình ARIMA(p,d,q) trong dự báo cần nhận dạng ba thành phần p,d và q của mô hình. Thành phần d của
mô hình được nhận dạng thông qua kiểm định tính dừng của chuỗi thời gian. Nếu chuỗi thời gian dừng ở bậc 0 ta ký hiệu
I(d=0),nếu sai phân bậc 1 của chuỗi dừng ta ký hiệu I(d=1), nếu sai phân bậc 2 của chuỗi dừng ta ký hiệu I(d=2),...
Mô hình SARIMA (Seasonal ARIMA) là một biến thể của mô hình ARIMA, được sử dụng khi chuỗi thời gian hiển thị sự mô
hình hóa theo mùa hoặc chu kỳ thời gian. Điều này xảy ra khi có sự biến đổi chu kỳ hoặc mô hình trong chuỗi thời gian theo
một mô hình mùa vụ nhất định.
Phân tích khác biệt giữa ARIMA và SARIMA là như sau:
ARIMA: Mô hình ARIMA bao gồm các thành phần autoregressive (AR), moving average (MA) và integrated (I). ARIMA
không mô hình hóa các thành phần mùa vụ của chuỗi thời gian. Nó được sử dụng khi không có sự biến đổi chu kỳ hoặc mô
hình rõ ràng theo mùa trong dữ liệu.
SARIMA: Mô hình SARIMA mở rộng ARIMA bằng cách thêm các thành phần mô hình hóa theo mùa. Nó bao gồm các thành
phần autoregressive (AR), moving average (MA), integrated (I) và seasonal (S). Thành phần mùa (S) cho phép mô hình ước
lượng và dự đoán các biến động theo mùa trong chuỗi thời gian. SARIMA được sử dụng khi dữ liệu có sự biến đổi chu kỳ hoặc
mô hình theo mùa rõ ràng.
Trong SARIMA, có thêm các tham số khác để mô hình hóa thành phần mùa, bao gồm:
- P: bậc của thành phần AR mùa (Autoregressive Seasonal)
- D: bậc của thành phần I mùa (Integrated Seasonal)
- Q: bậc của thành phần MA mùa (Moving Average Seasonal) - m: độ dài chu kỳ mùa lOMoAR cPSD| 45876546
Với việc mô hình hóa thành phần mùa, SARIMA cung cấp một phương pháp linh hoạt hơn để dự đoán và mô hình hóa các
chuỗi thời gian có sự biến đổi chu kỳ.
GIẢI ĐỀ CUỐI KÌ NĂM NGOÁI Câu 1 (3 điểm):
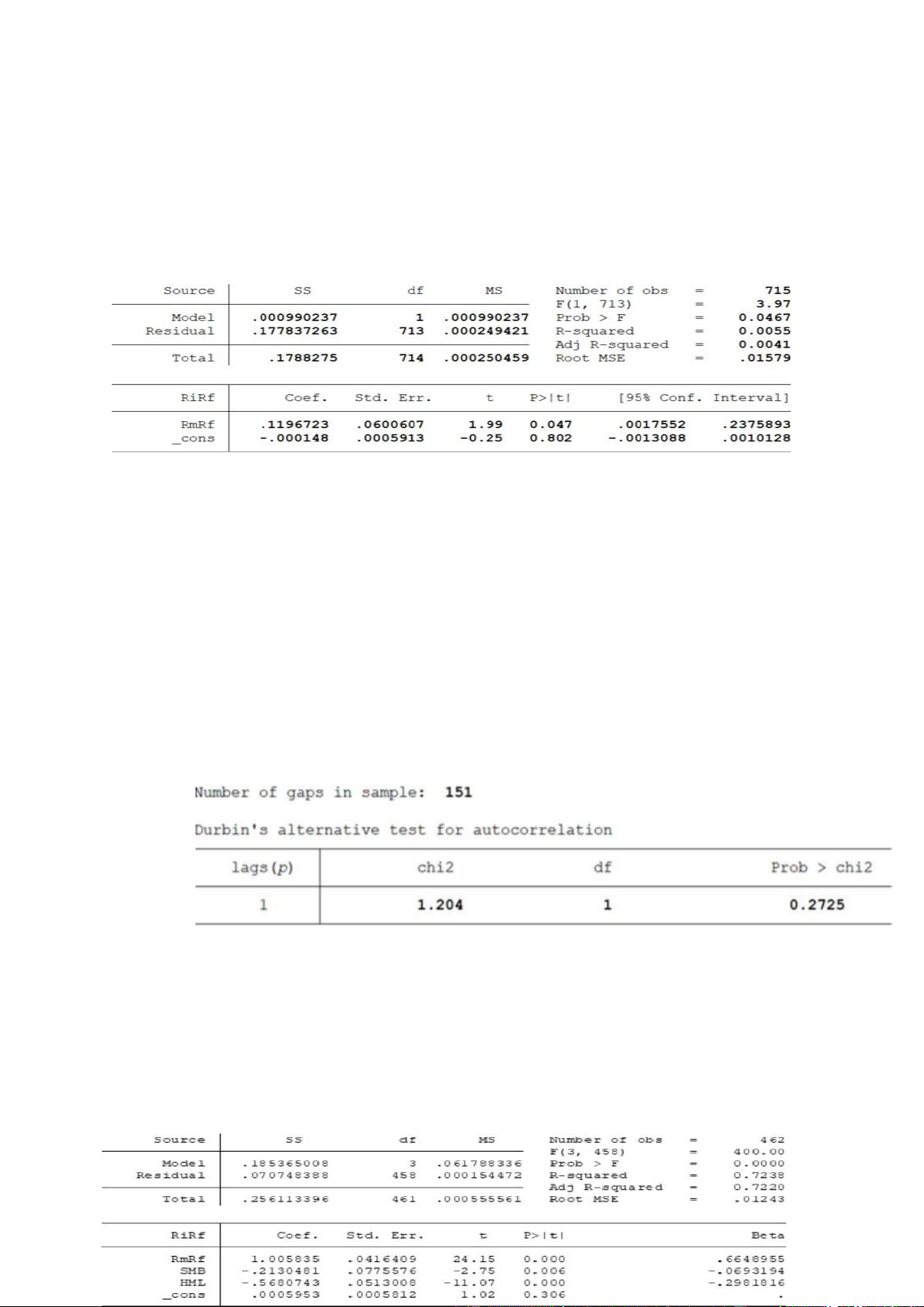
Cho mô hình CAPM, bảng kết quả hồi quy và bảng kiểm định như sau
Rit – Rf = α + βi(Rmt – Rf) + εit Trong đó,
Rit – Rf = RiRf: Phần bù tỷ suất lợi nhuận của cổ phiếu i trong giai đoạn t Rmt – Rf = RmRf: Phần bù thị trường trong giai đoạn t
Dựa vào bảng kết quả hồi quy, hãy cho biết hệ số nào có ý nghĩa và không có ý nghĩa. Hãy giải thích ý nghĩa của hệ số α trong mô hình CAPM trên.
Trong bảng hồi quy trên, hệ số Beta có ý nghĩa (P_Value=0,047 < 0.05), Alpha không có ý nghĩa (P_Value > 0.05). Trong
mô hình trên hệ số Alpha là hệ số phụ trội của lợi suất cổ phiếu:
Nếu Alpha > 0 thì cổ phiếu đang được định giá thấp.
Nếu Alpha = 0 thì cổ phiếu đang được định giá đúng.
Nếu Alpha < 0 thì cổ phiếu đang được định giá cao.
Ở đây, hệ số Alpha không có ý nghĩa => Alpha = 0 => Mô hình cân bằng, thị trường hiệu quả, định giá đúng.
Trong trường hợp giả định giá trị trung bình của phần dư khác 0 bị vi phạm, cụ thể là E(ε) = 2. Làm sao để giải quyết vấn đề vi
phạm trên, viết lại mô hình đúng. Ri – Rf = (0+2)+ 0.12*( Rmt – Rf )+ (ε -2)
= 2 + 0.12*( Rmt – Rf )+ v ✑ E(v)=0 c.
Dựa vào bảng kết quả kiểm định trên, hãy nêu giả thuyết và kết luận cho kiểm định trên. Giải thuyết:
H0 : Mô hình không xảy ra hiện tượng tự tương quan H1: Mô hình xảy ra hiện tượng tự tương quan
Nếu Prob > Chi2 > 0.05 => Chấp nhận H0
Prob > Chi2 > 0.05. Chấp nhận H0 => Mô hình không xảy ra hiện tượng tự tương quan.
Câu 2 (2 điểm): Cho mô hình Fama French 3 nhân tố, bảng kết quả hồi quy và kiểm định như sau:
Rit – Rf = α + β1t (Rmt – Rf) + β2t SMBt + β3t HMLt + εit Trong đó,
Rit – Rf : Phần bù tỷ suất lợi nhuận của cổ phiếu i trong giai đoạn t lOMoAR cPSD| 45876546
Rmt – Rf : Phần bù thị trường trong giai đoạn t
SMBt: chênh lệch tỷ suất lợi nhuận trung bình giữa nhóm cổ phiếu có quy mô nhỏ đối với quy mô lớn
HMLt: chênh lệch tỷ suất lợi nhuận trung bình giữa nhóm cổ phiếu có chỉ số BM (Book to Market) cao đối với chỉ số BM thấp
a. Hệ số nào có ý nghĩa và giải thích ý nghĩa của các hệ số?
Ba hệ số SMB, HML và RmRf đều có ý nghĩa do có P Value < 0.05. Hệ số Cons không có ý nghĩa do P Value > 0.05.
Hệ số Cons không có ý nghĩa nên Alpha = 0 => Mô hình cân bằng, thị trường hiệu quả, định giá đúng.
Rm-rf: nếu các yếu tố khác không nằm ngoài dự tính. Phần bù rủi ro thị trường tăng lên 1% thì phần bù tỷ suất lợi nhuận trung
bình của cổ phiếu tăng lên 1.005%.
SMB: nếu các yếu tố khác đúng như dự tính. Chênh lệch tỷ suất lợi nhuận trung bình giữa nhóm cổ phiếu có quy mô nhỏ đối
với quy mô lớn tăng lên 1% thì phần bù tỷ suất lợi nhuận trung bình của cổ phiếu giảm xuống 0.213%
HML: nếu các yếu tố khác đúng như dự tính. Chênh lệch tỷ suất lợi nhuận trung bình giữa doanh nghiệp có tỷ số giá trị sổ sách/
giá trị thị trường lớn so với doanh nghiệp có tỷ số giá trị sổ sách/ giá trị thị trường nhỏ tăng lên 1% thì phần bù tỷ suất lợi nhuận
trung bình của cổ phiếu giảm xuống 0.568%. b.
Bảng kết quả kiểm định trên là kiểm định cho giả thuyết nào trong các giả thuyết của phương pháp hồi quy OLS. Giả định đó
có bị vi phạm hay không?
Bảng kết quả trên là kiểm định cho tính tự tương quan. Ở đây ta có Prob > chi2 > 0.05
=> Chấp nhận H0 => Không xảy ra hiện tượng tự tương quan. (không vi phạm) Câu 3 (2 điểm):
Khi sử dụng biến giá chứng khoán trong mô hình định lượng, chúng ta thường kiểm định gặp vấn đề tự tương quan.
Nêu nguyên nhân gây ra vấn đề tự tương quan đối với biến giá chứng khoán? Hãy nêu một phương thức kiểm định hiện
tượng tự tương quan trong mô hình tuyến tính?
Nguyên nhân gây ra vấn đề tự tương quan vì giá tham chiếu chứng khoán ngày hôm sau là giá đóng cửa của ngày hôm trước.
Phương thức kiểm định tự tương quan là durbin’s alternative test Prob>chi2>0.05, chấp nhận giả thuyết H0 là không có hiện tượng tự tương quan
Phương sai thay đổi là gì và ảnh hưởng của nó đối với ước lượng hệ số β trong mô hình tuyến tính là gì?
Phương sai thay đổi: phương sai của phần dư thay đổi trong bộ dữ liệu. Khi dữ liệu của phần dư bị phân tán khiến cho phương
sai của phần dư thay đổi.
Ảnh hưởng: Phương sai thay đổi sẽ không làm cho ước lượng Beta bị sai, nhưng dẫn đến hệ số Beta không có ý nghĩa, đôi khi
xuất hiện kiểm định lỗi. Câu 4 (3 điểm):
Thế nào là đa cộng tuyến hoàn hảo, đa cộng tuyến một phần. Cho ví dụ cụ thể từng trường hợp?
Hiện tượng đa cộng tuyến là hiện tượng mà các biến độc lập trong mô hình có mối quan hệ tuyến tính với nhau.
*Đa cộng tuyến hoàn hảo: Các biến độc lập
thỏa các giá trị không đồng thời bằng 0. Ví dụ: *Đa
cộng tuyến không hoàn hảo: nếu các biến độc lập thỏa
, các không đồng thời bằng 0 và là sai số ngẫu nhiên. Ví dụ:
với Vi là sai số ngẫu nhiên vd: mô hình y= x1+ x2+ ε
ĐCT hoàn hảo: x1= 5x2 ĐCT 1 phần: x1=5x2 + ε
Hậu quả của đa cộng tuyến hoàn hảo và đa cộng tuyến một phần là gì? Hậu quả:
Đa cộng tuyến hoàn hảo: không tính toán được.
Đa cộng tuyến một phần: bị vi phạm, lỗi kiểm định. +
Phương sai và hiệp phương sai của các ước lượng OLS lớn. +
Khoảng tin cậy cho các hệ số ước lượng rộng hơn. lOMoAR cPSD| 45876546 +
Tỉ số t không có ý nghĩa. +
Dấu của các ước lượng của hệ số hồi quy có thể sai.
Hãy nêu một phương thức kiểm định hiện tượng đa cộng tuyến trong mô hình tuyến tính?
Sử dụng kiểm định hệ số: Dùng hệ số VIF (Variance Inflation Factor – hệ số phóng đại phương sai) Câu 1:
Trong phương pháp hồi quy OLS, nếu giả định phần dư độc lập với nhau bị vi phạm, hiện tượng gì sẽ xảy ra? Và ước
lượng hệ số beta sẽ bị ảnh hưởng như thế nào?
Nếu giả định phần dư độc lập với nhau bị vi phạm thì sẽ xảy ra hiện tượng đa cộng tuyến.
Nếu xảy ra đa cộng tuyến hoàn hảo thì không xác định được hệ số beta
Nếu xr đa cộng tuyến không hoàn hảo thì phương sai lớn => Khoảng tin cậy các hệ số beta lớn => vẫn xác định được beta
nhưng không chính xác, dấu có thể sai
Hãy nêu ít nhất 2 giả định chính của pp kiểm định Durbin-Watson?
Kiểm định Durbin-Watson dùng trong trường hợp:
Không có giá trị trễ của biến phụ thuộc là biến giải thích Không mất quan sát
Câu 2: Cho mô hình hồi quy tuyến tính Giải
thích ý nghĩa của các hệ số?
Liquid: Nếu Liquid tăng 1% thì tỷ suất lợi nhuận của Vinamilk tăng trung bình 0.6% với các điều kiện khác không đổi.
R(premium): Nếu R(premium) tăng 1% thì tỷ suất lợi nhuận của Vinamilk tăng trung bình 1.2% với các điều kiện khác không đổi.
Cons: Nếu hai hệ số Liquid, R(premium) không có giá trị thì tỷ suất lợi nhuận của Vinamilk đạt trung bình là 7.3%. ub.
Khi > 1.96, chúng ta có thể bác bỏ giả thiết Ho: Bo = 0 với
H1: B1#0. Do đó dựa vào bảng kết quả ta có βo và β2 có ý nghĩa và β1 không có ý nghĩa tại mức 5% Câu 3:
a.Thế nào là đa cộng tuyến hoàn hảo, đa cộng tuyến một phần. Cho ví dụ cụ thể từng trường hợp. -
Đa cộng tuyến hoàn hảo: Là khi 2 hoặc nhiều biến độc lập có quan hệ hoàn toàn với nhau thông qua một phương trình
cụ thể không tồn tại biến ngẫu nhiên. Ví dụ: X2 = X3ʎ -
Đa cộng tuyến một phần: Là khi 2 hoặc nhiều biến độc lập có quan hệ hoàn toàn với nhau thông qua một phương trình
cụ thể có tồn tại biến ngẫu nhiên. Ví dụ: X2 = X3 + ʎ ɛ
Hãy nêu một phương thức kiểm định đa cộng tuyến trong mô hình tuyến tính? VIF
Hậu quả của đa cộng tuyến hoàn hảo và đa cộng tuyến một phần là gì? -
Đa cộng tuyến hoàn hảo: Không thể ước lượng được mô hình -
Đa cộng tuyến một phần: +
Phương sai và hiệp phương sai của các ước lượng OLS lớn. +
Khoảng tin cậy cho các hệ số ước lượng rộng hơn. +
Tỉ số t không có ý nghĩa. +
Dấu của các ước lượng của hệ số hồi quy có thể sai.
Câu 4: Thế nào là mô hình tự hồi quy? Cho vd về mô hình tự hồi quy bậc 3 và cách kiểm định bậc tự hồi quy chính xác của nó?
- Mô hình tự hồi quy: Là mô hình có chứa 1 hay một số giá trị trễ của biến phụ thuộc trong số các biến độc lập.
VD mô hình tự hồi quy bậc 3 và cách kiểm định bậc tự hồi quy chính xác của nó:
Ví dụ: Mô hình AR(2): Xt = a0 + a1 Xt-1 + a2. Xt-2 + a3.Xt-3 + t
Để kiểm định bậc tự hồi quy chính xác ta dựa vào 2 dạng đồ thị SAC=f(t) và SPAC=f’(t): Đồ thị SAC giảm dần và đồ thị SPAC
có đỉnh tại p (bậc tự hồi qui)
Khi hồi quy mô hình theo phương pháp OLS, nếu giả định không có đa cộng tuyến hoàn hảo bị vi phạm, vấn đề gì sẽ xảy ra cho mô hình?
Đa cộng tuyến hoàn hảo xảy ra khi hai hoặc nhiều biến độc lập trong mô hình hồi quy thể hiện mối quan hệ tuyến tính xác định
(hoàn toàn có thể dự đoán hoặc không chứa ngẫu nhiên).
Nếu giả định “không có đa cộng tuyến hoàn hảo” bị vi phạm thì mô hình của bạn sẽ có hệ số hồi quy (regression coefficients)
không xác định và sai số chuẩn (standard errors) của chúng là vô hạn. Ý nghĩa của trị số p value
Ý nghĩa của p-value, sig là xác suất của dữ liệu xảy ra nếu giả thiết vô hiệu H0 là đúng. Nghĩa là có bao nhiêu phần trăm của
dữ liệu thỏa mãn trị số P. Giả sử P =2%, thì có 2% dữ liệu trong bộ số liệu thỏa mãn điều kiện nào đó.
Ví dụ: H0: Không có sự khác biệt giữa hai nhóm, không có mối tương quan giữa X và Y.
H0 thường được giả định đúng trong thủ tục kiểm định giả thuyết. Và người ta sẽ cố tìm cách để chứng minh H0 sai. Ví dụ một
tuyên bố của nhà sản xuất thường bị nghi ngờ và để trong phát biểu trong H0.
H1 là phát biểu ngược với H0 lOMoAR cPSD| 45876546
H1 được kết luận là đúng nếu H0 bị bác bỏ
Nhà nghiên cứu mong muốn ủng hộ H1 và nghi ngờ H0
EX: Xem xét một bị cáo trong phiên xử hình sự. Giả thuyết không là bị cáo “vô tội” và giả thuyết ngược lại và bị cáo “có tội”.
Giả định là bên bị đơn là vô tội và bên nguyên đơn phải chứng minh được rằng bên bị đơn là có tội, nghĩa là, thuyết phục ban
bồi thẩm bác bỏ giả thuyết không. Nếu ban bồi thẩm tuyên bố một người vô tội “không có tội” hoặc một người phạm tội “có
tội”, một quyết định đúng đã được thực hiện. Nếu một người vô tội bị tuyên bố có tội, ta phạm phải sai lầm loại I vì giả thuyết
đúng đã bị bác bỏ. Sai lầm loại II xảy ra khi một người có tội được tuyên bố trắng án.
Thủ tục kiểm định giả thuyết cổ điển là chọn giá trị cực đại cho sai lầm loại I chấp nhận được với người phân tích và sau đó
đưa ra quy tắc quyết định sao cho sai lầm loại II là thấp nhất. Trong ví dụ về phiên tòa hình sự, điều này có nghĩa là chọn quy
tắc ra quyết định sao cho số lần người vô tội bị kết tội không vượt qua một số phần trăm số lần nào đó (chẳng hạn, 1%) và cực
tiểu xác suất người có tội được thả tự do.
Mô hình CAMP, ý nghĩa alpha beta?
Hệ số Beta là hệ số đo lường mức độ rủi ro hệ thống của 1 cổ phiếu (1 danh mục đầu tư), bằng cách so sánh mức độ biến động
giá của cổ phiếu đó so với mức độ biến động chung của toàn thị trường. Việc phân tích kỹ lưỡng về mức độ rủi ro và tỷ suất
sinh lời của các sản phẩm tài chính sẽ giúp cho NĐT xác định được đối tượng phù hợp với khả năng chịu rủi ro của họ Hệ số
Alpha cung cấp cho chúng ta một tiêu chuẩn hợp lý để đánh giá hoạt động quản lý quỹ. Kết quả của Alpha có thể giúp ta xác
định liệu người quản lý có đang giúp quỹ này tăng trưởng hoặc thậm chí kiếm thêm được những khoản lãi vượt ngoài mức lợi
nhuận cần thiết hay không. Không chỉ vậy, chỉ số này cũng giúp ta quyết định liệu mức phí quản lý đã phù hợp với kết quả kinh
doanh hay chưa. Việc mua (hoặc thậm chí nắm giữ) một quỹ đầu tư mà không cân nhắc đến yếu tố này sẽ giống như mua một
chiếc xe chỉ để đi lại mà không quan tâm đến hiệu suất nhiên liệu của nó.
Câu hỏi: Hồi quy OLS là gì? Dựa trên nguyên tắc minimize epsilon, làm sao để giá trị thực tế và ước tính có
phương sai nhỏ nhất? Least square là gì?
là bình phương nhỏ nhất:
Là khái niệm chung để chỉ một nhóm các phương pháp kinh tế lượng phục vụ cho việc ước lượng tham số trong phương trình
hồi quy. Nói chung, mục đích của phương pháp bình phương nhỏ nhất là tối thiểu hóa tổng bình phương của các khoảng cách
theo phương thẳng đứng giữa số liệu thu thập được và đường hồi quy.
Phương pháp bình phương tối thiểu Khái niêṃ
Phương pháp bình phương tối thiểu trong tiếng Anh là Least Squares Method. Phương pháp bình phương tối thiểu là một dạng
phân tích hồi qui toán học được sử dụng để xác định đường biểu diễn phù hợp nhất cho một tập dữ liệu, cung cấp một phép
minh họa trực quan về mối quan hệ giữa các điểm dữ liệu trong tập dữ liệu.
Mỗi điểm dữ liệu biểu thị mối quan hệ giữa một biến độc lập đã biết và một biến phụ thuộc chưa biết. Đặc
điểm Phương pháp bình phương tối thiểu
Phương pháp bình phương tối thiểu cung cấp cơ sở lí luận chung cho việc sắp xếp tạo ra đường biểu diễn phù hợp nhất từ các
điểm dữ liệu đang được nghiên cứu.
Ứng dụng phổ biến nhất của phương pháp này là các phương pháp xác định đường tuyến tính, vẽ ra một đường thẳng
tối thiểu hóa tổng bình phương của các lỗi có thể xuất hiện trong các kết quả của các phương trình liên quan.
Chẳng hạn như như phần dư hay mức chênh lệch giữa giá trị quan sát và giá trị dự đoán bình phương.
Phương pháp phân tích hồi qui này được thực hiện bằng cách biểu diễn tập hợp các điểm dữ liệu trên biểu đồ gồm có trục x và trục y.
Sau đó, nhà phân tích sẽ xác định một đường biểu diễn phù hợp nhất giải thích mối quan hệ tiềm năng giữa các biến độc lập và phụ thuộc.
Trong phân tích hồi qui, các biến phụ thuộc được minh họa trên trục y hay trục hoành, trong khi các biến độc lập được minh
họa trên trục x hay trục tung.
Ngược lại với bài toán tuyến tính là bài toán bình phương tối thiểu phi tuyến tính không có kết quả cuối cùng mà được giải
quyết bằng cách lặp lại.
Nhà toán học và nhà khoa học người Đức, Carl Friedrich Gauss là người đã phát hiện ra phương pháp bình phương tối thiểu vào năm 1795.
Ví dụ về Phương pháp bình phương tối thiểu
Giả sử một nhà phân tích muốn kiểm tra mối quan hệ giữa lợi nhuận cổ phiếu của công ty A và lợi nhuận của chỉ số B mà cổ
phiếu công ty A là thành phần.
Trong ví dụ này, nhà phân tích tìm cách kiểm tra sự phụ thuộc của lợi nhuận cổ phiếu A vào lợi nhuận của chỉ số B. Để đạt được
điều này, tất cả các tỉ lệ lợi nhuận của cả cổ phiếu A và chỉ số B được biểu diễn trên biểu đồ. lOMoAR cPSD| 45876546
Với lợi nhuận của chỉ số B là biến độc lập và lợi nhuận của cổ phiếu A là biến phụ thuộc. Đường thẳng đúng nhất sẽ là đường
giải thích mối quan hệ giữa hai biến trên, cũng như cung cấp các hệ số giải thích mức độ phụ thuộc cho nhà phân tích.
Đường hồi qui bình phương tối thiểu
Đường biểu diễn phù hợp nhất được xác định bởi phương pháp bình phương tối thiểu có dạng phương trình tổng quát để cho
biết mối quan hệ giữa các điểm dữ liệu.
Nếu dữ liệu cho thấy mối quan hệ rõ ràng giữa hai biến nhất định, đường biểu diễn phù hợp nhất với mối quan hệ tuyến tính
này được gọi là đường hồi qui bình phương tối thiểu.
Đường hồi qui bình phương tối thiểu có khoảng cách sao cho giữa các điểm dữ liệu đến đường này bình phương nhỏ nhất.
Nguyên nhân cần phải bình phương khoảng cách giữa các điểm dữ liệu và đường hồi qui là để ngăn các điểm dữ liệu trái dấu triệt tiêu cho nhau.
Phương sai thay đổi?
Khái niệm: Phương sai thay đổi trong tiếng Anh là Heteroskedasticity hoặc Heteroscedasticity.Phương sai thay đổi là
một tình huống trong thống kê xảy ra khi lỗi tiêu chuẩn của một biến không đổi trong một khoảng thời gian cụ thể trong mô
hình hồi qui tuyến tính.
Phân loại phương sai thay đổi
Có 2 loại phương sai thay đổi: Không có điều kiện và có điều kiện Phương
sai thay đổi không có điều kiện xảy ra khi phương sai thay
đổi không tương quan với các biến độc lập trong hồi qui. Mặc dù, hình thức này vi phạm Giả định 4 (Phương sai của phần sai
số là giống nhau cho tất cả các quan sát) của mô hình hồi qui tuyến tính nhưng nó không tạo ra vấn đề lớn cho kết quả của thống kê.
Phương sai thay đổi có điều kiện xảy ra khi phương sai thay đổi có tương quan với các biến độc lập trong hồi qui. Đây là loại
gây ra nhiều vấn đề nhất cho kết quả của thống kê. Hậu quả của phương sai thay đổi
Phương sai thay đổi là một trường hợp của việc vi phạm các giả định của mô hình hồi qui tuyến tính. Do đó, nó có thể ảnh
hưởng đến kết quả khi phân tích kinh tế lượng hoặc mô hình tài chính như CAPM.
Mặc dù, phương sai thay đổi không ảnh hưởng đến tính nhất quán của việc ước lượng tham số hồi qui, nhưng nó có thể dẫn đến
lỗi trong kết luận. Khi lỗi phương sai thay đổi xảy ra, phép thử F (F-test) là không đáng tin cậy. Hậu quả trong thực tế có thể
nghiêm trọng nếu chúng ta sử dụng phân tích hồi qui trong việc phát triển các chiến lược đầu tư.
Ví dụ dưới đây cho thấy vấn đề này thậm chí còn ảnh hưởng đến sự hiểu biết của chúng ta về các mô hình tài chính:
MacKinlay và Richardson (1991) đã kiểm tra mức độ ảnh hưởng của phương sai thay đổi đến các thử nghiệm của mô hình định
giá tài sản vốn (CAPM). Tác giả lập luận rằng nếu CAPM là chính xác, họ sẽ không tìm thấy sự khác biệt đáng kể nào giữa tỉ
suất lợi nhuận có điều chỉnh rủi ro (risk-adjusted return) khi nắm giữ cổ phiếu nhỏ so với cổ phiếu lớn.
Để thực hiện thử nghiệm của mình, MacKinlay và Richardson đã nhóm tất cả các cổ phiếu trên Sàn giao dịch chứng khoán
New York và Sàn giao dịch chứng khoán Mỹ (ngày nay gọi là NYSE MKT) thành 10 nhóm theo giá trị thị trường và có sự sắp
xếp lại hàng năm. Sau đó, họ đã kiểm tra sự khác biệt có hệ thống trong tỉ suất lợi nhuận có điều chỉnh rủi ro của các danh mục
đầu tư chứng khoán dựa trên vốn hóa thị trường. Họ ước tính hồi qui sau:
ri,t = αi + βi x rm,t + εi,t Trong đó:
ri, t là lợi nhuận thặng dư (lợi nhuận cao hơn lãi suất phi rủi ro) của danh mục đầu tư i trong giai đoạn t rm,
t là lợi nhuận thặng dư của toàn bộ thị trường trong giai đoạn t
Công thức của CAPM đưa ra giả thuyết rằng lợi nhuận thặng dư của danh mục đầu tư được giải thích bởi lợi nhuận thặng dư
của toàn thị trường nói chung. Giả thuyết đó ngụ ý rằng αi = 0 cho mọi danh mục đầu tư i, trung bình, không có lợi nhuận
thặng dư tích lũy cho danh mục đầu tư khi tính đến rủi ro hệ thống (rủi ro thị trường) của nó.
Định nghĩa đa cộng tuyến là gì?
Trong mô hình hồi quy, nếu các biến độc lập có quan hệ chặt với nhau, các biến độc lập có mối quan hệ tuyến tính,
nghĩa là các biến độc lập có tương quan chặt, mạnh với nhau thì sẽ có hiện tượng đa cộng tuyến, đó là hiện tượng các biến độc
lập trong mô hình phụ thuộc lẫn nhau và thể hiện được dưới dạng hàm số. Ví dụ có hai biến độc lập A và B, khi A tăng thì B
tăng, A giảm thì B giảm…. thì đó là một dấu hiệu của đa cộng tuyến. Nói một cách khác là hai biến độc lập có quan hệ rất mạnh
với nhau, đúng ra hai biến này nó phải là 1 biến nhưng thực tế trong mô hình nhà nghiên cứu lại tách làm 2 biến. Hiện tượng
đa cộng tuyến vi phạm giả định của mô hình hồi qui tuyến tính cổ điển là các biến độc lập không có mối quan hệ tuyến tính với nhau.
Cách phát hiện đa cộng tuyến
Có hai cách: dựa vào hệ số phóng đại phương sai VIF, hoặc dựa vào ma trận hệ số tương quan. Tuy nhiên cách dùng ma trận
hệ số tương quan ít được sử dụng, chủ yếu sửa dụng cách nhận xét chỉ số VIF. Cách 1
Dựa vào VIF ,khi thực hiện hồi quy đa biến, ta nhấn vào nút Statistics , xong check vào Collinearity diagnostics. lOMoAR cPSD| 45876546
Ta cũng có thể xem xét giá trị Tolerance bằng công thức Tolerance=1/VIF . Hệ số này nằm cột bên trái của hệ số VIF. Tương
ứng là: nếu hệ số Tolerance bé hơn 0.5 thì có dấu hiệu đa cộng tuyến, đây là điều không mong muốn. Nếu giá trị Tolerance bé
hơn 0.1 thì chắc chắn có đa cộng tuyến. Cách 2
Nhận dạng Multicollinearity dựa vào hệ số tương quan,có hay không tương quan tuyến tính mạnh giữa các biến độc lập. Cách
làm: xây dựng ma trận hệ số tương quan cặp giữa các biến độc lập và quan sát để nhận diện độ mạnh của các tương quan giữa
từng cặp biến số độc lập. Cũng có thể nhìn vào kết quả hồi quy, ta thấy R2 cao( tầm trên 0.8) và thống kê t thấp. Tuy nhiên như
đã nói thì ít khi sử dụng cách hai này. Vì nó dựa vào phán đoán chủ quan hơn là công thức như cách 1.
Hậu quả của hiện tượng đa cộng tuyến:
Sai số chuẩn của các hệ số sẽ lớn. Khoảng tin cậy lớn và thống kê t ít ý nghĩa. Các ước lượng không thật chính xác. Do đó
chúng ta dễ đi đến không có cơ sở bác bỏ giả thiết "không" và điều này có thể không đúng.
Ba nguyên nhân gây ra hiện tượng đa cộng tuyến
Khi chọn các biến độc lập mối quan có quan hệ nhân quả hay có tương quan cao vì đồng thời phụ thuộc vào một điều kiện khác.
Cách thu thập mẫu: mẫu không đặc trưng cho tổng thể Chọn
biến độc lập có độ biến thiên nhỏ.
Các giải pháp khắc phục đa cộng tuyến
Giải pháp 1: Bỏ bớt biến độc lập (điều này xảy ra với giả định rằng không có mối quan hệ giữa biến phụ thuộc và biến độc lập bị loại bỏ mô hình).
Giải pháp 2: Bổ sung dữ liệu hoặc tìm dữ liệu mới,tìm mẫu dữ liệu khác hoặc gia tăng cỡ mẫu. Tuy nhiên nếu mẫu lớn hơn mà
vẫn còn multicollinearity thì vẫn có giá trị vì mẫu lớn hơn sẽ làm cho phương sai nhỏ hơn và hệ số ước lượng chính xác hơn so
với mẫu nhỏ. Giải pháp 3: Thay đổi dạng mô hình,mô hình kinh tế lượng có nhiều dạng hàm khác nhau. Thay đổi dạng mô hình
cũng có nghĩa là tái cấu trúc mô hình. Điều này thật sự là điều không mong muốn, thì lúc đó bạn phải thay đổi mô hình nghiên cứu.
Phân tích dữ liệu trong ngành tài chính ngân hàng sẽ bị ảnh hưởng gì khi tính chất và kích thước dữ liệu đang
thay đổi theo xu hương phát triển của công nghệ? So sánh giữ pp truyền thống và hiện đại?
Phương pháp truyền thống: Ưu điểm: 1.
Dễ hiểu và áp dụng: Phương pháp truyền thống thường được xây dựng dựa trên các nguyên tắc và quy tắc rõ ràng, dễ
hiểuvà dễ áp dụng trong nhiều trường hợp. 2.
Dựa trên giả định đơn giản: Phương pháp truyền thống thường dựa trên giả định đơn giản về dữ liệu và mô hình, giúp
đơngiản hóa quá trình phân tích và diễn giải kết quả.
Ví dụ: Sử dụng mô hình hồi quy tuyến tính truyền thống để dự đoán giá nhà dựa trên các biến như diện tích, vị trí và số phòng. Nhược điểm: 1.
Giới hạn về mô hình: Phương pháp truyền thống thường có giới hạn về mô hình, không thể mô hình hóa các mối quan
hệphức tạp và không tuyến tính giữa các biến. 2.
Không linh hoạt trong xử lý dữ liệu phi cấu trúc: Phương pháp truyền thống có thể gặp khó khăn khi xử lý và phân tích
dữliệu phi cấu trúc, như dữ liệu văn bản hoặc hình ảnh.
Phương pháp hiện đại: Ưu điểm: 1.
Linh hoạt và mô hình hóa phức tạp: Phương pháp hiện đại, chẳng hạn như học máy và học sâu, cho phép mô hình hóa
cácmối quan hệ phức tạp giữa các biến, cung cấp khả năng dự đoán và phân tích mạnh mẽ hơn. 2.
Xử lý dữ liệu phi cấu trúc: Phương pháp hiện đại có khả năng xử lý và phân tích dữ liệu phi cấu trúc, chẳng hạn như
dữ liệuvăn bản, hình ảnh và âm thanh, mở rộng khả năng phân tích và trích xuất thông tin từ các nguồn dữ liệu đa dạng.
Ví dụ: Sử dụng mạng nơ-ron học sâu để phân loại ảnh và nhận diện các đối tượng trong ảnh. Nhược điểm: 1.
Đòi hỏi lượng dữ liệu lớn: Phương pháp hiện đại thường đòi hỏi lượng dữ liệu lớn để huấn luyện mô hình và đảm bảo
độchính xác cao. Việc thiếu dữ liệu có thể làm giảm hiệu suất và độ tin cậy của phương pháp. 2.
Độ phức tạp tính toán: Phương pháp hiện đại thường yêu cầu tính toán mạnh mẽ và tài nguyên máy tính để huấn luyện
vàtriển khai mô hình, đòi hỏi hệ thống và tài nguyên kỹ thuật cao.
Ví dụ: Sử dụng mạng nơ-ron học sâu để dự đoán giá cổ phiếu dựa trên các biến kỹ thuật và tài chính.
Thảo luận về việc sử dụng mô hình dữ liệu panel trong phân tích dữ liệu ngân hàng tại Việt Nam. Những khó
khan có thể có khi sử dụng panel trong lĩnh vực này và làm thế nào để giải quyết chúng?
Ngân hàng Việt Nam có thể sử dụng mô hình phân tích dữ liệu panel trong việc phân tích dữ liệu ngân hàng để hiểu và
đưa ra các quyết định liên quan đến hoạt động ngân hàng và quản lý rủi ro. Dưới đây là một số ví dụ về cách mô hình phân tích
dữ liệu panel có thể được áp dụng: lOMoAR cPSD| 45876546 1.
Đánh giá tín dụng: Ngân hàng có thể sử dụng mô hình phân tích dữ liệu panel để đánh giá tín dụng của khách hàng.
Bằngcách xem xét dữ liệu về lịch sử tín dụng, thu nhập, tài sản và các yếu tố khác của khách hàng từ nhiều thời điểm khác
nhau, mô hình panel có thể đánh giá khả năng trả nợ và đưa ra quyết định về việc cấp tín dụng. 2.
Quản lý rủi ro tín dụng: Mô hình panel cũng có thể được sử dụng để quản lý rủi ro tín dụng trong ngân hàng. Bằng
cáchphân tích dữ liệu từ nhiều khách hàng và thời gian, mô hình có thể xác định các xu hướng và mô hình rủi ro trong danh
mục tín dụng của ngân hàng. Điều này giúp ngân hàng đưa ra các biện pháp phòng ngừa và quản lý rủi ro hiệu quả hơn. 3.
Dự báo thị trường tài chính: Mô hình phân tích dữ liệu panel cũng có thể được áp dụng để dự báo các biến thị trường
tàichính quan trọng. Bằng cách sử dụng dữ liệu từ nhiều thị trường, thời gian và các yếu tố liên quan, mô hình panel có thể dự
báo giá cổ phiếu, tỷ giá hối đoái, lãi suất và các biến khác, giúp ngân hàng có cái nhìn sâu hơn về xu hướng và biến động của thị trường. 4.
Điều chỉnh chính sách tín dụng: Dữ liệu panel cung cấp thông tin về khách hàng và hoạt động tín dụng từ nhiều thời
điểmkhác nhau. Ngân hàng có thể sử dụng mô hình panel để đánh giá hiệu quả của chính sách tín dụng hiện tại và điều chỉnh
chính sách để đáp ứng nhu cầu và mục tiêu kinh doanh.
Ví dụ về những khó khăn có thể gặp phải khi sử dụng dữ liệu panel trong phân tích dữ liệu ngân hàng tại Việt Nam và
cách giải quyết chúng là như sau: 1.
Thiếu dữ liệu hoặc dữ liệu không đầy đủ: Trong quá trình thu thập dữ liệu panel, có thể xảy ra tình trạng thiếu dữ liệu
hoặcdữ liệu không đầy đủ từ một số ngân hàng hoặc thời điểm. Ví dụ, một số ngân hàng có thể không cung cấp đầy đủ thông
tin hoặc có thời gian bỏ lỡ ghi nhận dữ liệu. Để giải quyết vấn đề này, có thể sử dụng phương pháp nội suy dữ liệu bị thiếu hoặc
áp dụng các kỹ thuật mô hình dự báo để dự đoán giá trị bị thiếu dựa trên các biến khác có sẵn. 2.
Non-stationarity: Trong dữ liệu panel, các biến có thể không tuân theo tính chất bất biến thống kê (non-stationarity),
tức làchúng có thể thay đổi theo thời gian. Điều này có thể làm ảnh hưởng đến hiệu quả của phân tích dữ liệu. Một cách để giải
quyết vấn đề này là áp dụng các phương pháp chuẩn hoá dữ liệu, chẳng hạn như chuyển đổi logarit hoặc chuyển đổi sai số để
đảm bảo tính bất biến thống kê và ổn định của dữ liệu. 3.
Endogeneity: Trong mô hình panel, có thể xảy ra vấn đề endogeneity khi mối quan hệ giữa các biến độc lập và phụ
thuộccó thể bị ảnh hưởng bởi các yếu tố không quan sát được. Để giải quyết vấn đề này, có thể sử dụng phương pháp
Instrumental Variables (IV) hoặc Fixed Effects (FE) để kiểm soát các yếu tố không quan sát được và đảm bảo tính chính xác
của kết quả phân tích. 4.
Dữ liệu không cân bằng: Trong dữ liệu panel, có thể xảy ra tình trạng không cân bằng về số lượng quan sát giữa các
ngânhàng hoặc thời điểm. Điều này có thể ảnh hưởng đến độ tin cậy và chính xác của kết quả phân tích. Một cách để giải quyết
vấn đề này là sử dụng các phương pháp re-weighting hoặc mô hình phân tích dữ liệu không cân bằng (unbalanced panel data
analysis) để đảm bảo tính đại diện của mẫu dữ liệu.
Rủi ro và cách xử lý dữ liệu thiếu trong dữ liệu panel, đưa ra ví dụ và giải thích cụ thể nơi áp dụng các kỹ thuật hiệu quả nhất
Rủi ro và cách xử lý dữ liệu thiếu trong dữ liệu panel là một vấn đề quan trọng trong phân tích dữ liệu. Dữ liệu thiếu có thể ảnh
hưởng đến tính chính xác và độ tin cậy của kết quả phân tích. Dưới đây là một số rủi ro phổ biến và cách xử lý dữ liệu thiếu
trong dữ liệu panel, cùng với ví dụ cụ thể và giải thích cách áp dụng các kỹ thuật hiệu quả nhất:
1.Thiếu dữ liệu ngẫu nhiên (Missing Completely at Random - MCAR). Đây là trường hợp khi việc thiếu dữ liệu
không liên quan đến giá trị thực tế hoặc các yếu tố khác trong dữ liệu.
Cách xử lý: Trong trường hợp MCAR, phương pháp nội suy (imputation) là phương pháp phổ biến để xử lý dữ liệu thiếu. Một
kỹ thuật phổ biến là nội suy toàn phần (Full Information Maximum Likelihood - FIML) hoặc Maximum Likelihood Estimation
(MLE). Phương pháp này cho phép xử lý dữ liệu thiếu bằng cách sử dụng tất cả thông tin có sẵn từ các biến khác trong dữ liệu panel.
Ví dụ: Giả sử bạn có dữ liệu panel về tăng trưởng GDP của các quốc gia trong 10 năm, nhưng một số quốc gia thiếu dữ liệu
cho một số năm. Bằng cách sử dụng phương pháp FIML, bạn có thể xây dựng mô hình tăng trưởng GDP và ước tính giá trị
thiếu dựa trên thông tin từ các quốc gia khác và các năm khác trong dữ liệu panel.
2.Thiếu dữ liệu có hệ thống (Missing at Random - MAR). Đây là trường hợp khi việc thiếu dữ liệu có mối quan hệ
với giá trị thực tế hoặc các yếu tố khác trong dữ liệu, nhưng không phụ thuộc vào giá trị bị thiếu.
Cách xử lý: Trong trường hợp MAR, một phương pháp phổ biến để xử lý dữ liệu thiếu là sử dụng phương pháp nội suy đa biến
(Multiple Imputation). Phương pháp này liên quan đến việc tạo ra nhiều bản sao của dữ liệu với các giá trị thiếu được nội suy
dựa trên mô hình dự báo và kết hợp các kết quả từ các bản sao này để tạo ra ước tính cuối cùng.
Ví dụ: Giả sử bạn đang nghiên cứu về tác động của thuế suất lãi suất trên lợi nhuận của các ngân hàng trong một dữ liệu panel.
Tuy nhiên, một số ngân hàng không báo cáo thuế suất lãi suất. Bằng cách sử dụng phương pháp nội suy đa biến, bạn có thể tạo
ra nhiều bản sao của dữ liệu với các giá trị thiếu được nội suy dựa trên mô hình hồi quy và kết hợp các kết quả từ các bản sao
này để ước tính tác động của thuế suất lãi suất.
3.Thiếu dữ liệu không ngẫu nhiên (Missing Not at Random - MNAR). Đây là trường hợp khi việc thiếu dữ liệu
phụ thuộc vào giá trị bị thiếu hoặc các yếu tố không quan sát được. lOMoAR cPSD| 45876546
Cách xử lý: Trong trường hợp MNAR, xử lý dữ liệu thiếu trở nên phức tạp hơn và không thể hoàn toàn đảm bảo tính chính xác.
Tuy nhiên, có thể áp dụng các phương pháp như mô hình hồi quy không tuyến tính, phương pháp M-estimation, hoặc sử dụng
các phân phối xấp xỉ để xử lý dữ liệu thiếu. lOMoAR cPSD| 45876546
Ví dụ: Giả sử bạn nghiên cứu về tỷ lệ nợ xấu của các khách hàng ngân hàng và một số khách hàng không cung cấp thông tin
tài chính cá nhân. Trong trường hợp MNAR, việc xử lý dữ liệu thiếu trở nên phức tạp hơn và có thể yêu cầu sự đánh giá kỹ
lưỡng từ phía nhà nghiên cứu để ước tính giá trị thiếu một cách chính xác.
Giải thích cụ thể Khái niệm adjusted R square và tầm quan trọng của nó trong mô hình hồi quy? 1. R-square:
R-square (R^2) là một phép đo thống kê được sử dụng để đánh giá mức độ phù hợp của mô hình hồi quy đối với dữ liệu.
Rsquare đo lường tỷ lệ biến thiên của biến phụ thuộc mà mô hình có thể giải thích được so với tổng biến thiên của biến phụ
thuộc. R-square có giá trị từ 0 đến 1, trong đó giá trị 1 đại diện cho mô hình hoàn hảo giải thích biến động của biến phụ thuộc,
và giá trị 0 đại diện cho mô hình không giải thích được biến động nào.
Tuy nhiên, R-square có một hạn chế khi số lượng biến độc lập trong mô hình tăng lên. R-square sẽ tăng dần mà không phản
ánh chính xác sự cải thiện của mô hình. Điều này là do R-square không điều chỉnh cho số lượng biến độc lập trong mô hình. 2. Adjusted R-square:
Adjusted R-square (R^2 điều chỉnh) là một biến thể của R-square được điều chỉnh cho số lượng biến độc lập trong mô hình.
Điều chỉnh R-square nhằm giảm độ phóng đại của R-square khi số lượng biến độc lập tăng lên mà không thực sự cải thiện mô
hình. Công thức tính Adjusted R-square là:
Adjusted R^2 = 1 - [(1 - R^2) * (n - 1) / (n - k - 1)]
Trong đó, n là số lượng quan sát trong dữ liệu và k là số lượng biến độc lập trong mô hình. Adjusted R-square giảm giá trị so
với R-square khi số lượng biến độc lập tăng lên, do việc điều chỉnh cho số lượng biến độc lập trong mô hình. Điều này giúp
đánh giá chính xác hơn hiệu quả của mô hình hồi quy và phân biệt được giữa mô hình đơn giản và mô hình phức tạp.
Tầm quan trọng của Adjusted R-square trong mô hình hồi quy là nó cung cấp một phép đo tổng quan về khả năng giải
thích của mô hình dựa trên số lượng biến độc lập và số lượng quan sát. Giá trị Adjusted R-square cao cho thấy mô hình có khả
năng giải thích tốt hơn biến động của biến phụ thuộc và được ưu tiên trong việc lựa chọn mô hình tốt nhất.
Phân tích điểm mạnh và điểm yếu của các mô hình arima, garch,... có điểm mạnh và điểm yếu gì khi so sánh
với các mô hình học máy trong phân tích dữ liệu để dự báo giá cổ phiếu: ARIMA: - Điểm mạnh: 1.
Mô hình ARIMA có khả năng mô hình hóa sự phụ thuộc thời gian trong dữ liệu. Nó có thể giúp xác định xu hướng,
môhình các yếu tố chuỗi thời gian như thành phần tự hồi quy (autoregressive) và thành phần trung bình trượt (moving average). 2.
ARIMA có thể áp dụng cho dữ liệu không phải chuỗi thời gian hoàn chỉnh, bằng cách sử dụng phép tích hợp
(integration)để chuyển đổi dữ liệu thành dữ liệu chuỗi thời gian có tính chất chuẩn xác hơn. - Điểm yếu: 1.
Mô hình ARIMA có giả định về tuyến tính và không xem xét các yếu tố phi tuyến tính hoặc phi tuyến tính phức tạp trongdữ liệu. 2.
ARIMA thường không xử lý được các yếu tố nhiễu (noise) phi tuyến tính trong dữ liệu, điều này có thể ảnh hưởng
đếnhiệu suất dự báo. GARCH: - Điểm mạnh: 1.
GARCH mô hình hóa tính biến động của dữ liệu và có thể xử lý được hiện tượng không đồng nhất về biến động(heteroskedasticity). 2.
Mô hình GARCH có thể mô hình hóa các yếu tố phi tuyến tính và không đồng nhất trong dữ liệu, giúp cải thiện chính xáccủa dự báo. - Điểm yếu:
1. GARCH yêu cầu có kiến thức chuyên môn về thống kê và tài chính để hiểu và sử dụng hiệu quả.
2. Mô hình GARCH thường phải ước lượng nhiều tham số, đòi hỏi nhiều dữ liệu để đạt được kết quả dự báo chính xác.So
sánh với các mô hình học máy: -
Mô hình ARIMA và GARCH thường được sử dụng trong phân tích chuỗi thời gian, trong khi các mô hình học máy
nhưRandom Forests, Support Vector Machines (SVM), hoặc Neural Networks thường được sử dụng trong phân tích dữ liệu
không phải chuỗi thời gian. -
Mô hình học máy có khả năng xử lý các yếu tố phi tuyến tính và phi tuyến tính phức tạp hơn, có thể học các mối quan
hệphức tạp giữa các biến đầu vào và biến mục tiêu. -
Mô hình học máy có thể mô hình hóa các mẫu phức tạp và tương tác giữa các yếu tố, trong khi ARIMA và GARCH
chỉ tậptrung vào phụ thuộc thời gian và biến động của dữ liệu. -
Tuy nhiên, mô hình học máy cũng đòi hỏi một lượng lớn dữ liệu huấn luyện và cần kiến thức sâu về lựa chọn và tinh
chỉnhcác thuật toán và siêu tham số để đạt được kết quả tốt. lOMoAR cPSD| 45876546
Trong phân tích dữ liệu panel, vấn đề nội sinh (endogeneity) là một vấn đề quan trọng cần được xem xét. Nội sinh xảy ra khi
biến giải thích (predictor) trong mô hình có tương quan hoặc ảnh hưởng đến biến phụ thuộc (dependent variable). Điều này gây
ra các vấn đề trong việc ước lượng và hiểu đúng mối quan hệ giữa các biến.
Hậu quả của vấn đề nội sinh trong phân tích dữ liệu panel có thể làm sai lệch kết quả ước lượng và dẫn đến kết luận sai về mối
quan hệ giữa các biến. Một số hậu quả chính của nội sinh bao gồm: 1.
Bị đảo ngược nhân quả (reverse causality): Nội sinh có thể dẫn đến tình huống khi biến phụ thuộc tác động lên biến
giảithích, thay vì ngược lại như dự đoán ban đầu. Điều này làm cho việc xác định mối quan hệ nhân quả trở nên khó khăn và
có thể dẫn đến kết quả sai. 2.
Điều chỉnh không chính xác (omitted variable bias): Nếu mô hình không bao gồm một biến quan trọng mà cũng ảnh
hưởngđến cả biến phụ thuộc và biến giải thích, thì việc bỏ qua biến này có thể dẫn đến hiệu ứng nội sinh. Kết quả là ước lượng
sai lệch và không chính xác. 3.
Sự chồng chéo (confounding): Nội sinh có thể tạo ra sự chồng chéo giữa biến giải thích và các biến ngoại lai khác, làm
choviệc xác định tác động riêng của biến giải thích trở nên khó khăn. Điều này ảnh hưởng đến tính chính xác và tin cậy của kết quả ước lượng.
Các vấn đề nội sinh trong phân tích dữ liệu panel có thể được khắc phục bằng cách sử dụng các phương pháp phân tích thích
hợp như GMM (Generalized Method of Moments), Pooled OLS (Ordinary Least Squares), Fixed Effects (FE), Random Effects
(RE) và Instrumental Variables (IV) để kiểm soát và ước lượng mối quan hệ một cách chính xác hơn giữa các biến trong mô hình panel.
Để giảm tác động của vấn đề nội sinh trong dữ liệu panel, có một số chiến lược và phương pháp sau đây có thể được áp dụng: 1.
Sử dụng biến công cụ (instrumental variables): Một phương pháp phổ biến để xử lý vấn đề nội sinh là sử dụng biến
công cụ(instrument) để ước lượng hiệu ứng. Biến công cụ là một biến không bị nội sinh và có mối quan hệ tương quan với biến
giải thích nhưng không có tác động trực tiếp đến biến phụ thuộc. Phương pháp GMM (Generalized Method of Moments) và
IV (Instrumental Variables) có thể được sử dụng để ước lượng hiệu ứng sử dụng biến công cụ. 2.
Mô hình hóa động lực (dynamic modeling): Trong một số trường hợp, nội sinh có thể xuất hiện do sự tương quan theo
thờigian. Trong trường hợp này, mô hình hóa động lực có thể được sử dụng để xem xét tác động của biến giải thích lên biến
phụ thuộc theo thời gian. 3.
Sử dụng phương pháp Fixed Effects (FE) và Random Effects (RE): Phương pháp FE và RE trong phân tích dữ liệu
panel cóthể giúp giảm tác động của nội sinh bằng cách kiểm soát các yếu tố cố định và các yếu tố ngẫu nhiên không quan sát
được. Phương pháp FE và RE có thể giúp xác định hiệu ứng của biến giải thích một cách chính xác hơn. 4.
Sử dụng thiết kế phân tán ngẫu nhiên (Randomized Control Trials): Trong một số trường hợp, việc thực hiện các
thửnghiệm điều tra ngẫu nhiên có thể giúp xác định tác động gây nên nội sinh một cách rõ ràng hơn. Thiết kế phân tán ngẫu
nhiên giúp tạo ra một nhóm kiểm soát ngẫu nhiên và một nhóm xử lý, từ đó xác định rõ ràng hiệu ứng của biến giải thích.
Nguồn tiềm năng của nội sinh trong dữ liệu panel có thể bao gồm: 1.
Lựa chọn biến: Nếu không chọn đúng các biến giải thích, có thể xảy ra nội sinh khi một biến có tác động lên cả biến
giảithích và biến phụ thuộc. 2.
Thiếu kiểm soát: Nếu không kiểm soát được các yếu tố cố định hoặc yếu tố ngẫu nhiên không quan sát được, nội sinh
cóthể xảy ra khi các yếu tố này tương quan với biến giải thích và biến phụ thuộc. 3.
Quan sát theo thời gian: Nếu không xử lý được tương quan theo thời gian và sự phụ thuộc qua lại giữa các quan sát
trongdữ liệu panel, nội sinh có thể ảnh hưởng đến ước lượng và hiểu đúng mối quan hệ giữa các biến. 4.
Thiếu biến công cụ: Nếu không sử dụng được biến công cụ (instrument) để ước lượng hiệu ứng, nội sinh có thể gây ra
cácvấn đề trong việc xác định mối quan hệ nhân quả.
Dưới đây là một số ví dụ về ứng dụng thực tế nơi mà vấn đề nội sinh đã được xử lý một cách hiệu quả: 1.
Ảnh hưởng của giáo dục lên thu nhập: Trong một nghiên cứu về ảnh hưởng của giáo dục lên thu nhập, vấn đề nội sinh
cóthể phát sinh do sự tương quan hai chiều giữa giáo dục và thu nhập. Tuy nhiên, để giảm tác động của nội sinh, nghiên cứu
có thể sử dụng phương pháp tự nhiên (natural experiment) như việc sử dụng các biến công cụ như chính sách ngẫu nhiên về
giáo dục bắt buộc để ước lượng tác động của giáo dục lên thu nhập một cách chính xác. 2.
Hiệu ứng của chương trình đào tạo công nghệ: Trong một nghiên cứu về hiệu ứng của chương trình đào tạo công nghệ
trênhiệu suất công việc, nội sinh có thể xuất hiện khi người tham gia chương trình cũng có mức hiệu suất công việc cao hơn.
Để xử lý vấn đề này, nghiên cứu có thể sử dụng phương pháp FE hoặc RE để kiểm soát các yếu tố cố định của từng cá nhân và
ước lượng hiệu ứng của chương trình một cách chính xác hơn. 3.
Tác động của quảng cáo lên doanh số bán hàng: Trong một nghiên cứu về tác động của quảng cáo lên doanh số bán
hàng,nội sinh có thể xảy ra khi các yếu tố khác như thị trường hoặc xu hướng tiêu dùng cũng ảnh hưởng đến cả quảng cáo và
doanh số bán hàng. Để xử lý vấn đề này, nghiên cứu có thể sử dụng các phương pháp mô hình hóa động lực hoặc biến công cụ
như sử dụng thông tin về thời gian và vị trí quảng cáo để ước lượng tác động riêng của quảng cáo trên doanh số bán hàng. lOMoAR cPSD| 45876546 4.
Tác động của chất lượng giáo dục lên kết quả học tập: Trong một nghiên cứu về tác động của chất lượng giáo dục lên
kếtquả học tập, nội sinh có thể xảy ra khi sự tương quan giữa chất lượng giáo dục và kết quả học tập là hai chiều. Để giảm tác
động của nội sinh, nghiên cứu có thể sử dụng các phương pháp như phân tích FE hoặc RE để kiểm soát các yếu tố cố định của
từng học sinh và ước lượng tác động của chất lượng giáo dục trên kết quả học tập một cách chính xác hơn.
Thảo luận về cách dữ liệu panel được dùng để hiểu và giải quyết các vấn đề kinh tế chính và đưa ra ví dụ về
những hạn chế và tiềm năng phát triển trong tương lai
Dữ liệu panel là một phương pháp thu thập dữ liệu trong nghiên cứu kinh tế, trong đó một nhóm cá nhân, hộ gia đình
hoặc doanh nghiệp được quan sát liên tục qua nhiều khoảng thời gian. Dữ liệu panel cung cấp thông tin về sự biến đổi của các
đối tượng quan sát theo thời gian và cho phép phân tích tương quan và tương quan nguyên nhân hiệu quả giữa các yếu tố kinh tế khác nhau.
Cách dữ liệu panel được sử dụng giúp hiểu và giải quyết các vấn đề kinh tế chính như sau: 1.
Phân tích tương quan: Dữ liệu panel cho phép phân tích tương quan giữa các biến theo thời gian. Điều này giúp xác
địnhmối quan hệ giữa các yếu tố kinh tế và nhận biết các yếu tố ảnh hưởng đến sự biến đổi của chúng. 2.
Xác định tương quan nguyên nhân: Dữ liệu panel giúp xác định mối quan hệ nguyên nhân giữa các yếu tố kinh tế.
Bằngcách quan sát sự biến đổi của các biến qua thời gian, chúng ta có thể phân biệt được yếu tố gây ra biến đổi và yếu tố bị
ảnh hưởng bởi biến đổi đó. 3.
Đưa ra dự báo và mô hình: Dữ liệu panel cho phép xây dựng các mô hình dự báo và mô phỏng để dự đoán sự biến đổi
củacác yếu tố kinh tế trong tương lai. Các mô hình này có thể hỗ trợ việc đưa ra quyết định và kế hoạch dựa trên thông tin thu
thập từ dữ liệu panel. 4.
Đánh giá tác động chính sách: Dữ liệu panel có thể được sử dụng để đánh giá tác động của các chính sách kinh tế. Qua
việcso sánh sự biến đổi trước và sau khi chính sách được áp dụng, chúng ta có thể đánh giá hiệu quả của chính sách đó.
Tuy nhiên, dữ liệu panel cũng có một số hạn chế và thách thức trong việc sử dụng và phát triển trong tương lai: 1.
Chi phí và thời gian: Thu thập và duy trì dữ liệu panel có thể đòi hỏi nhiều chi phí và thời gian. Việc tiếp tục theo dõi
các đối tượng trong một khoảng thời gian dài đòi hỏi sự cam kết và tài nguyên để thu thập và xử lý dữ liệu. 2.
Mất mát dữ liệu: Trong quá trình thu thập dữ liệu panel, có thể xảy ra mất mát dữ liệu do các lý do như thay đổi đối
tượngnghiên cứu, sự rời bỏ hoặc không tham gia của cá nhân hoặc doanh nghiệp. 3.
Sự đa dạng trong mẫu dữ liệu: Dữ liệu panel có thể bị ảnh hưởng bởi sự đa dạng trong mẫu dữ liệu, với sự thay đổi về
kíchcỡ, đặc điểm và sự biến động của các đối tượng quan sát. Điều này có thể ảnh hưởng đến tính khái quát và khả năng tổng
quát hóa của kết quả nghiên cứu.
Tuy nhiên, với sự phát triển của công nghệ và phương pháp nghiên cứu, dữ liệu panel cũng có tiềm năng phát triển trong tương lai: 1.
Mở rộng phạm vi và đa dạng hóa đối tượng nghiên cứu: Dữ liệu panel có thể mở rộng phạm vi và đa dạng hóa đối
tượngnghiên cứu, bao gồm cả các nhóm dân cư, khu vực địa lý và quốc gia khác nhau. Điều này giúp tăng tính đại diện và khả
năng tổng quát hóa của nghiên cứu. 2.
Ứng dụng của dữ liệu không gian và thời gian: Phát triển các phương pháp và công nghệ mới có thể tận dụng dữ liệu
panelđể xác định tương quan không gian và tương quan không gian-thời gian. Điều này có thể giúp hiểu rõ hơn về tương tác
giữa các yếu tố kinh tế trong không gian và thời gian. 3.
Kết hợp với các nguồn dữ liệu khác: Dữ liệu panel có thể được kết hợp với các nguồn dữ liệu khác như dữ liệu định
tính,dữ liệu xã hội và dữ liệu về môi trường để tạo ra thông tin phong phú và đa chiều. Sự kết hợp này có thể giúp tạo ra cái
nhìn toàn diện hơn về các vấn đề kinh tế.
Ví dụ về hạn chế và tiềm năng phát triển của dữ liệu panel trong tương lai:
Hạn chế: Một hạn chế của dữ liệu panel có thể là mất mát dữ liệu do sự thay đổi trong mẫu dữ liệu. Ví dụ, trong một nghiên
cứu panel về thu nhập hộ gia đình, nếu có sự rời bỏ của một số hộ gia đình giàu có, dữ liệu panel sẽ không thể đại diện đầy đủ
cho sự biến động thu nhập trong quần thể.
Tiềm năng phát triển: Với sự phát triển của công nghệ thu thập dữ liệu và phân tích, dữ liệu panel có tiềm năng phát triển bằng
cách tích hợp dữ liệu từ các nguồn khác nhau. Ví dụ, bằng cách kết hợp dữ liệu panel với dữ liệu về tình trạng môi trường,
chúng ta có thể tìm hiểu sự tương quan giữa hoạt động kinh tế và môi trường, từ đó đưa ra các giải pháp bền vững hơn cho phát triển kinh tế.
Những phân tích và phát triển trong tương lai có thể giúp tăng tính chính xác và khả năng áp dụng của dữ liệu panel
trong việc hiểu và giải quyết các vấn đề kinh tế quan trọng.
Để đưa ra ví dụ về ứng dụng cụ thể của dữ liệu panel trong việc hiểu và giải quyết các vấn đề kinh tế, hãy xem xét một
nghiên cứu panel về hiệu quả của chính sách giảm thuế thu nhập cá nhân.
Trong nghiên cứu này, một tập hợp các hộ gia đình được quan sát trong một khoảng thời gian dài, có thể là từ năm 2010
đến năm 2020. Dữ liệu panel được thu thập hàng năm về thu nhập cá nhân của các hộ gia đình, thuế thu nhập cá nhân và các
yếu tố kinh tế khác như lạm phát, tỷ lệ thất nghiệp và tăng trưởng kinh tế.




