













































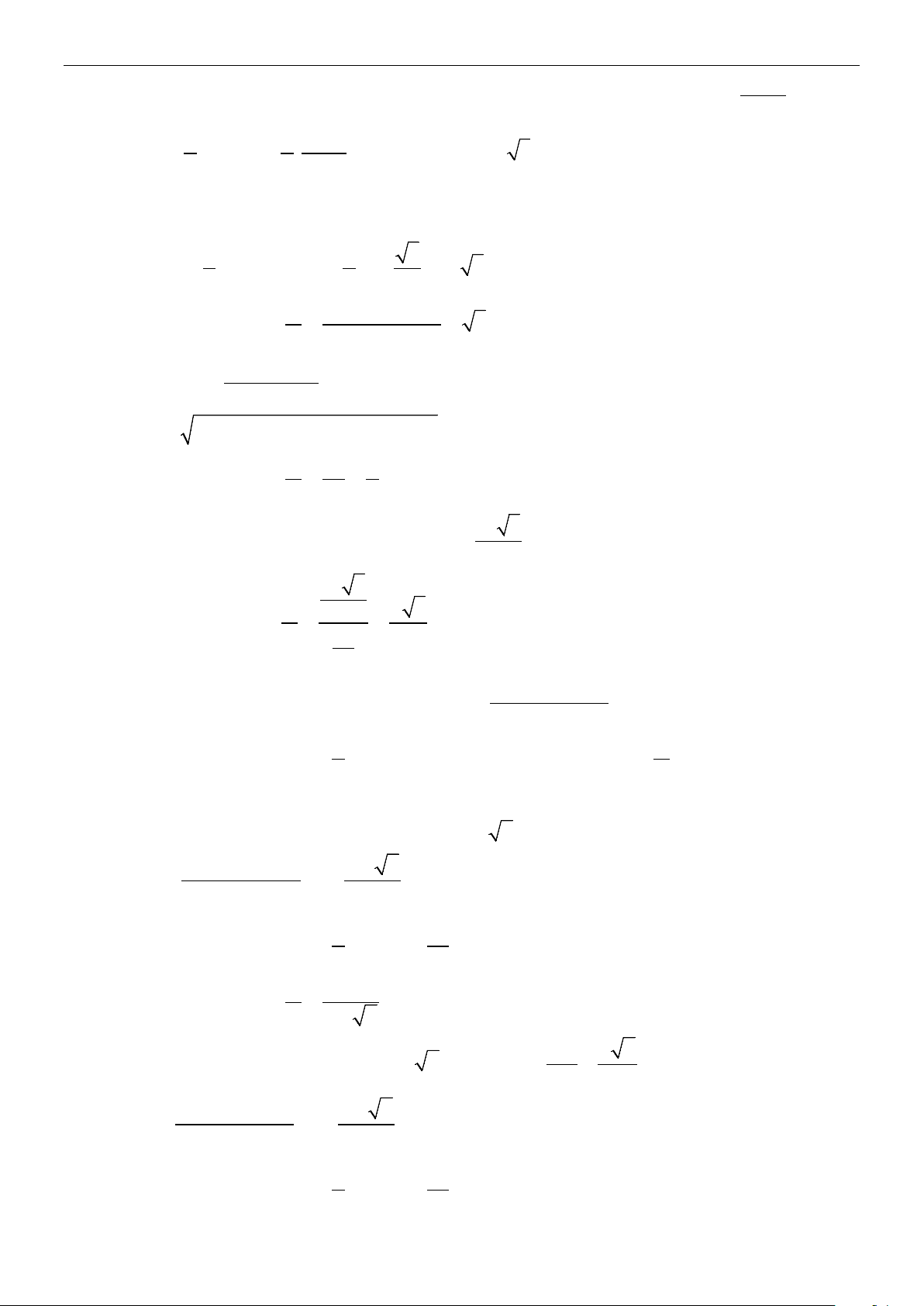









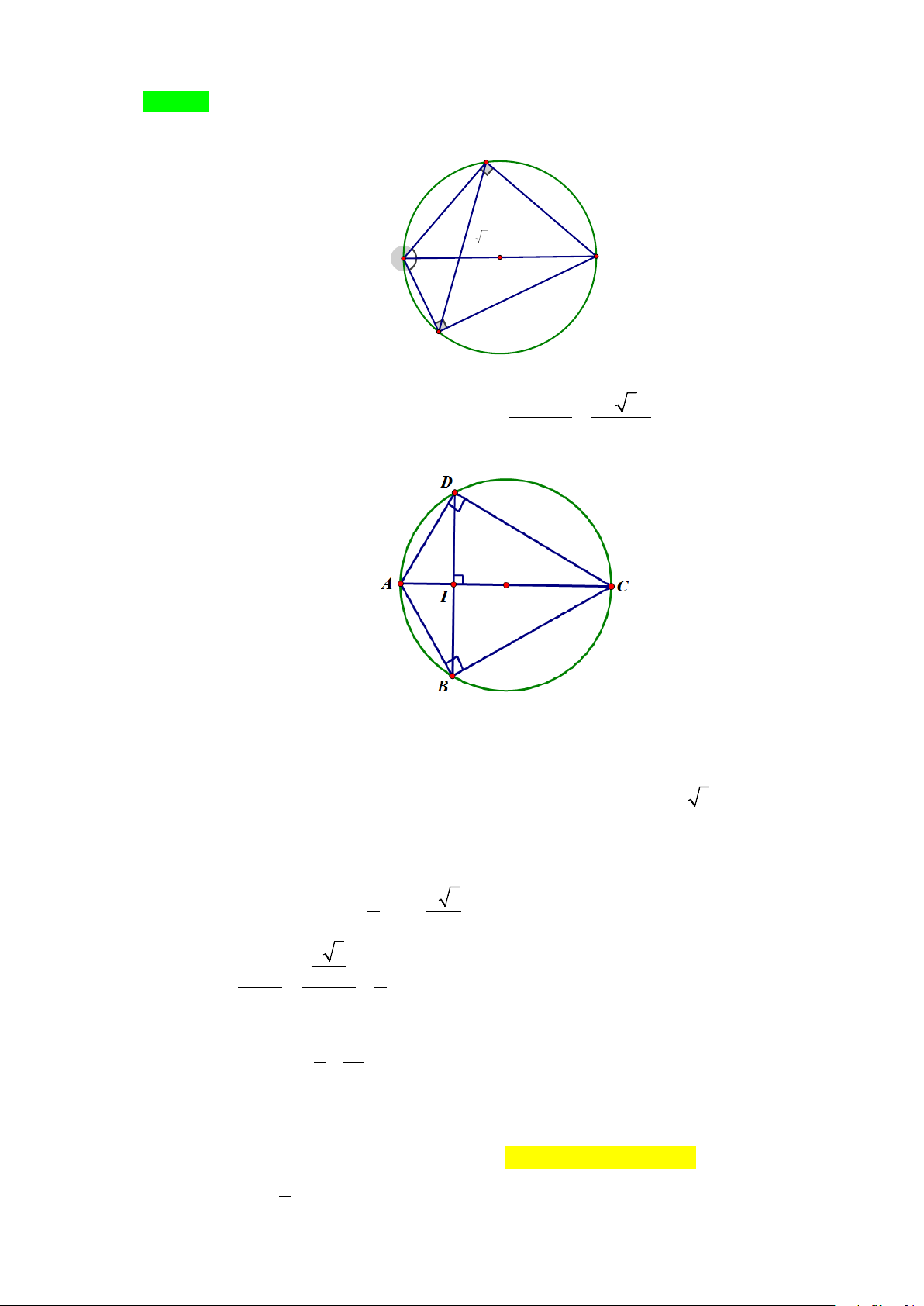






Preview text:
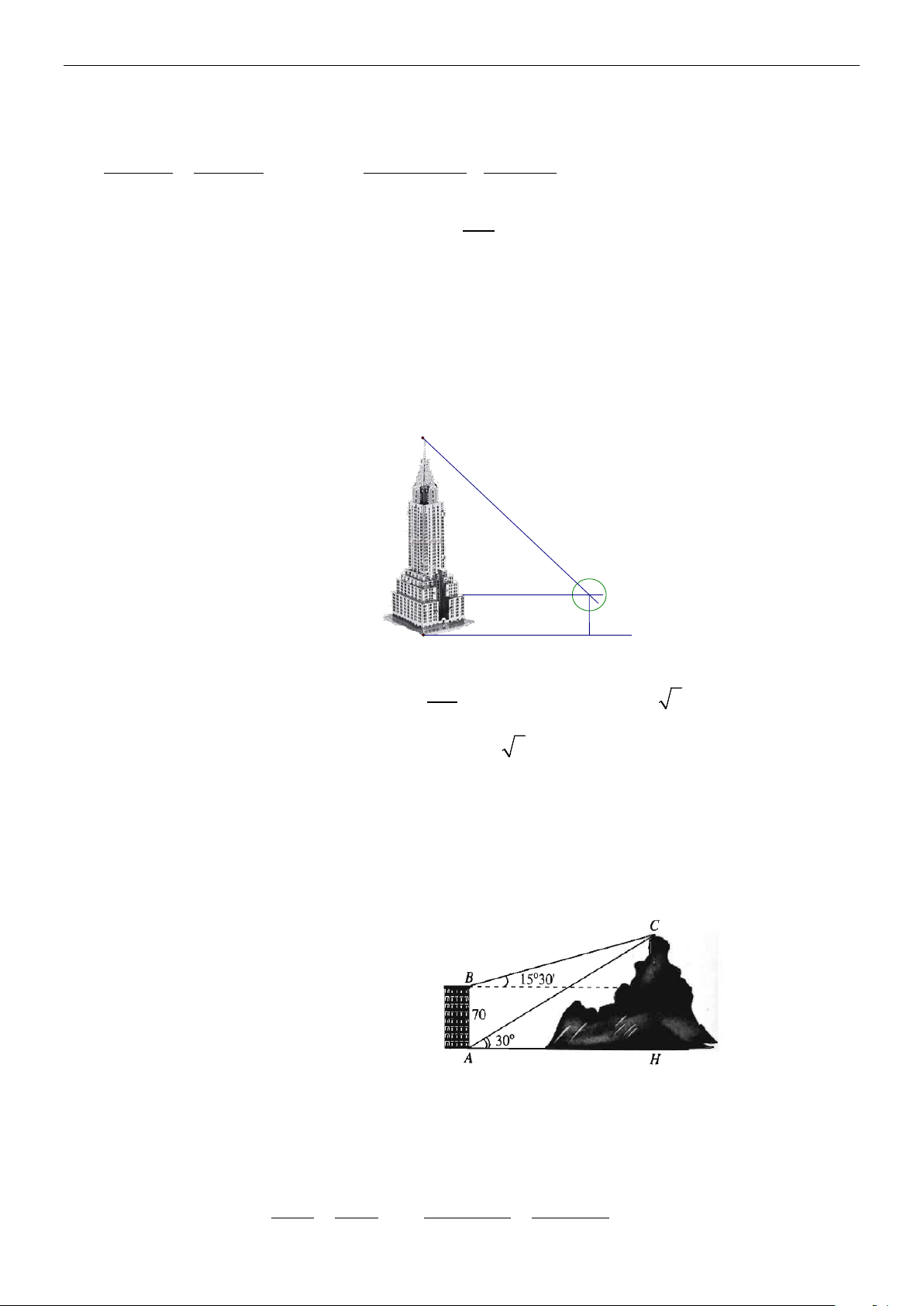
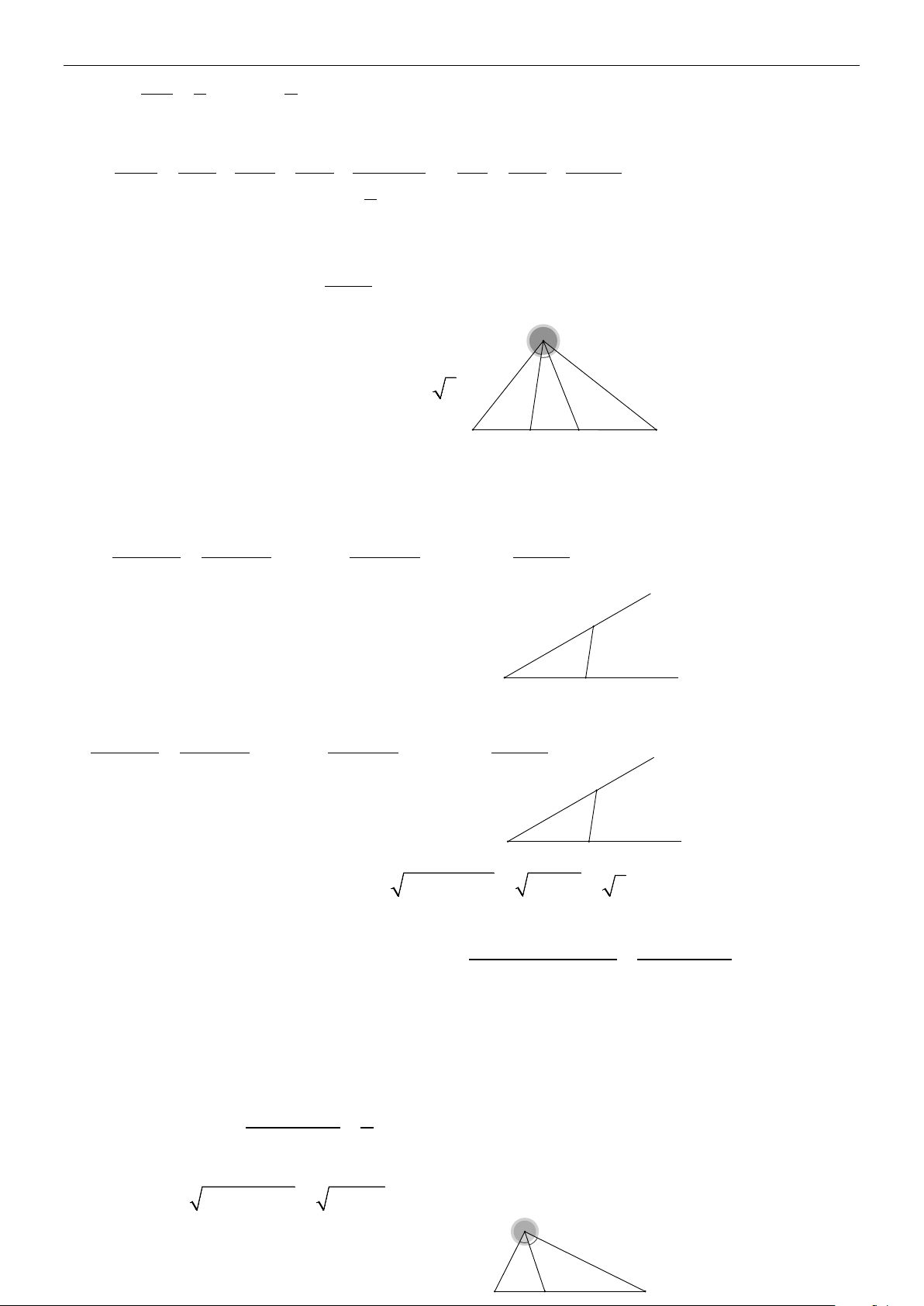
CHUYÊN ĐỀ 3: HỆ THỨC LƯỢNG TRONG TAM GIÁC
Chủ đề 1-GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 00 ĐẾN 0 180
A. TÓM TẮT LÝ THUYẾT. 1. Định nghĩa
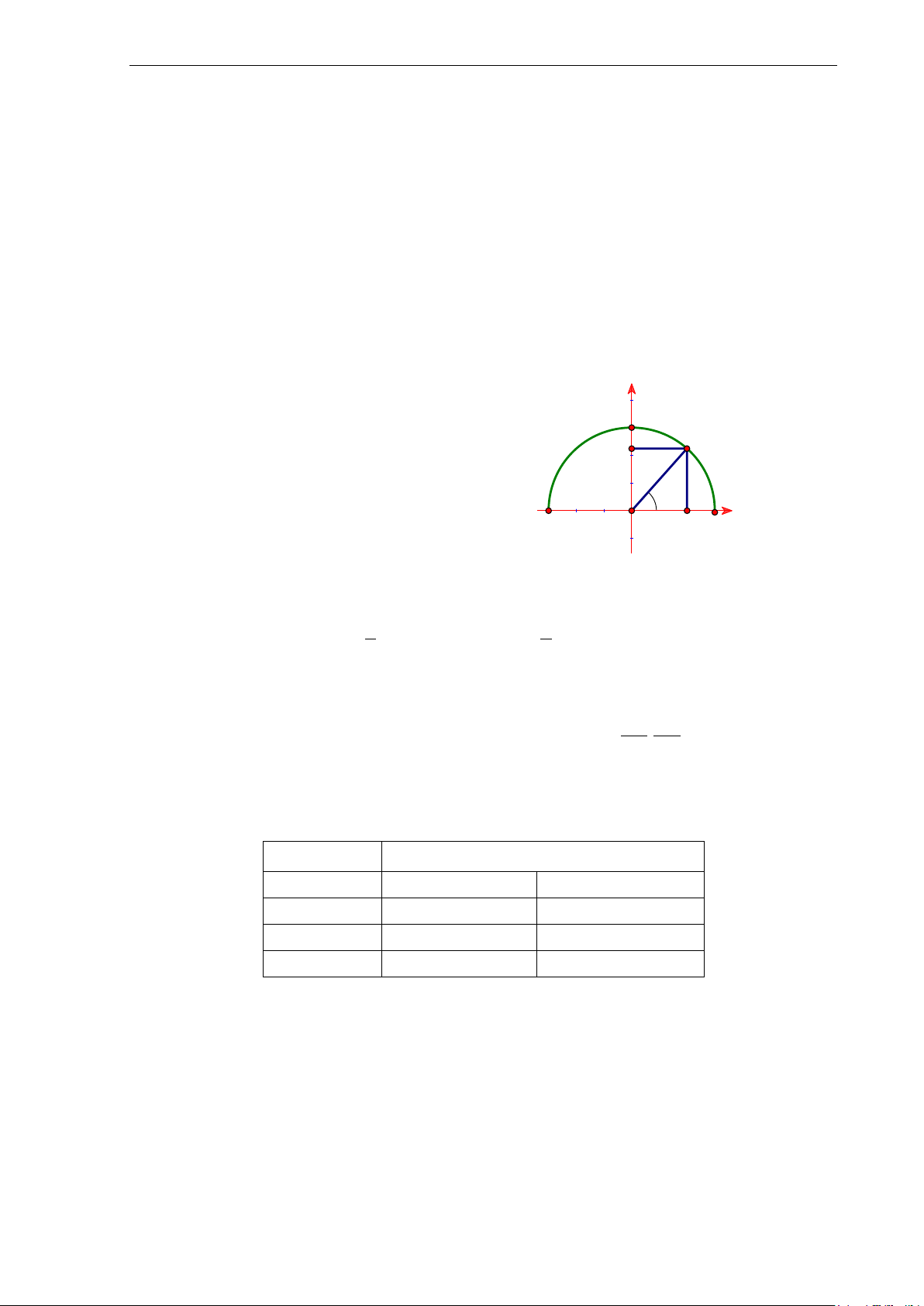
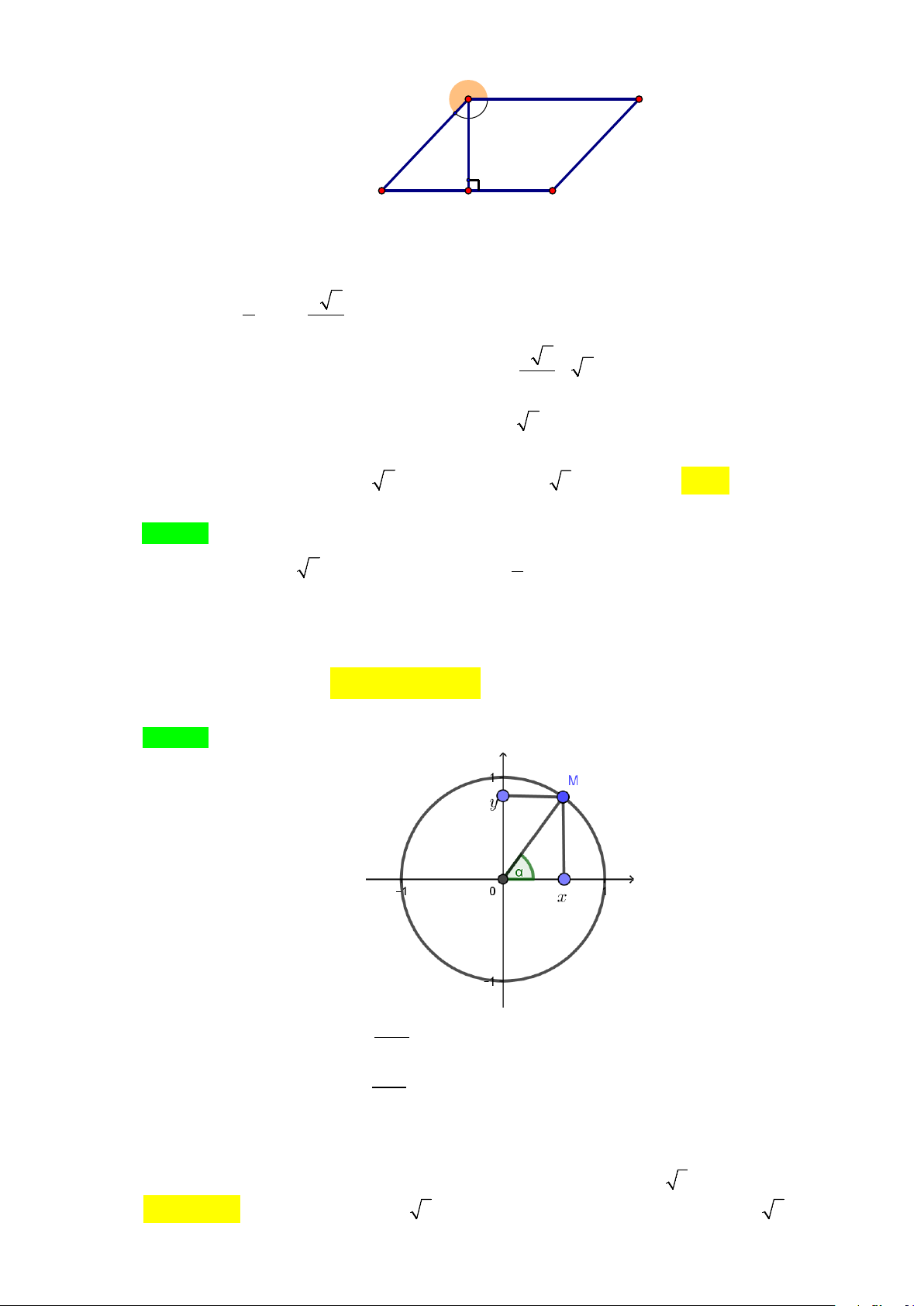
Trong mặt phẳng tọa độ Oxy .Với mỗi góc 0 0 0
180 , ta xác định điểm M
trên trên đường nửa đường tròn đơn vị tâm O sao cho
xOM . Giả sử điểm M có tọa độ x;y . Khi đó: y M ( x;y ) Q O P x Hình 2.1 y 0 x y
0 0 sin ; cos x; tan ( 90 ); cot ( 0 , 180 ) Các số x y sin , cos , tan ,
cot được gọi là giá trị lượng giác của góc .
Chú ý: Từ định nghĩa ta có:
Gọi P, Q lần lượt là hình chiếu của M lên trục Ox, Oy khi đó M OP;OQ . Với 0 0 0
180 ta có 0 sin 1; 1 cos 1
Dấu của giá trị lượng giác: Góc 0 0 0 90 0 180 sin + + co s + - tan + - cot + - b) Tính chất • Góc phụ nhau • Góc bù nhau 0
sin(90 ) cos 0
sin(180 ) sin 0 0
cos(90 ) sin
cos(180 ) cos 0
tan(90 ) cot 0
tan(180 ) tan 0
cot(90 ) tan 0
cot(180 ) cot
3. Giá trị lượng giác của các góc đặc biệt Trang 1/8
Góc 00 300 450 600 900 1200 1350 1500 1800 sin 0 1 2 3 1 3 2 1 0 2 2 2 2 2 2 co s 1 3 2 1 0 1 2 3 –1 2 2 2 2 2 2 tan 0 3 1 3 3 | 3 1 0 3 3 cot | 3 3 1 3 0 1 3 | 3 3
4. Các hệ thức lượng giác cơ bản sin 1) tan ( 0 90 ) ; cos cos 2) cot ( 0 0 0 ; 180 ) sin
3) tan .cot 1 ( 0 0 0 0 ; 90 ; 180 ) 2 4) sin 2 cos 1 1 5) 1 2 tan ( 0 90 ) 2 cos 1 6) 1 2 cot ( 0 0 0 ; 180 ) 2 sin Chứng minh:
- Hệ thức 1), 2) và 3) dễ dàng suy ra từ định nghĩa.
- Ta có sin OQ, cos OP 2 2 Suy ra 2
2 OQ OP OQ2 OP2 sin cos
+ Nếu 0 0 0 , 90 hoặc 0 180 thì dễ dàng thấy 2 2 sin cos 1
+ Nếu 0 0 0 , 90 và 0
180 khi đó theo định lý Pitago ta có 2
2 OQ2 OP2 OQ2 QM 2 OM 2 sin cos 1 Vậy ta có 2 2 sin cos 1 2 2 2 Mặt khác sin cos sin 1 2 1 tan 1 suy ra được 5) 2 cos 2 cos 2 cos 2 2 2 Tương tự cos sin cos 1 2 1 cot 1 suy ra được 6) 2 sin 2 sin 2 sin
B. PHƯƠNG PHÁP GIẢI TOÁN
Vấn đề 1:- Tính giá trị của một biểu thức-Hai góc phụ nhau, bù nhau
a)Phương pháp: Dùng bảng tỉ số lượng giác các góc đặc biệt và góc phụ nhau, bù nhau.
b) Ví dụ minh họa
I- BÀI TẬP TỰ LUẬN:
Ví dụ 1: Tính giá trị của các biểu thức sau: a) 2 0 2 0 2 0 2 0
A sin 45 cos 30 sin 0 cos 180 b) 0 0 2
B tan 30 cot 30 2.sin 180. Trang 2/8 c) 2 0 2 0 1
C = sin 45 + cot g 60 − 2 0 cos 135 ( 0 0 cot 44 + tan 46 ) 0 .cos 46 d) 0 0 D = − cot 72 .tan 72 0 cos 44 2 0 2 0 2 0 2 0 2 0 e)
sin 90 + cos 120 + cos 0 − tg 60 + cot g 135 E = 0 sin30 + 2 0 cos 60 Lời giải: 2 2 a) 2 3 9 2 0 2 0 2 0 2 0 2 2
A sin 45 cos 30 sin 0 cos 180 0 (1) 2 2 4 b) 3 4 3 0 0 2 2
B tan 30 cot 30 2.sin 180= 3 2.0 3 3 2 2 c) 2 0 2 0 1 2 3 1 1
C = cos 135 + cot 60 − = − + − = − . 2 0 2 sin 60 2 3 2 3 2 d) ( 0 0 cot 44 + tan 46 ) 0 0 0 0 .cos 46 0 0 2 tan 46 .cos 46 2sin 46 D = − cot 72 .tan 72 = −1 = −1 = 2 −1 =1. 0 0 0 cos 44 cos 44 cos 44 . 1 2 0 2 0 2 0 2 0 2 0 1+ +1− 3 +1 e)
sin 90 + cos 120 + cos 0 − tg 60 + cot g 135 4 1 E = = = . 0 sin30 + 2 0 cos 60 1 1 + 3 2 4
Ví dụ 2: Tính giá trị biểu thức của các biểu thức a) 2 O 2 O 2 O 2 sin 10 sin 20 sin 30 ... sin 80O P . b) 2 O 2 O 2 O 2
s 10 s 70 s 20 cos 80O Q co co co .
c) s0O s20O s 40O ... s160O cos180O R co co co co . d) 0 0 0 0
S tan1 tan 2 tan 3 ...tan 89 . e) E = 2 0 + 2 0 + 2 0 + 2 0 + 2 0 + 2 0 cos 12 cos 78 cos 1 cos 89 cos 17 cos 73 . f) 4 2 2 0 2 0 2 2 0
F 4a co s 60 2abcos 180 b co s 30 (a,b ). 3 c) G = 2 0 a + 2 0 b + 2 0 sin 90 cos90
c cos180 (a,b,c∈) Lời giải:
a) Do 10O 80O 20O 70O 30O 60O 40O 50O 90O
nên các cung lượng giác tương ứng
đôi một phụ nhau. Áp dụng công thức sin90O x cosx , ta được P 2 O 2
sin 10 cos 10O 2 O 2 sin 20 cos 20O 2 O 2
sin 30 cos 30O 2 O 2 sin 40 cos 40O 1111 4. b) 2 O 2 O 2 O 2 O 2 O 2 O 2 O 2
s 10 s 70 s 20 cos 80 ( s 10 sin 10 ) ( s 20 sin 20O Q co co co co co ) 11 2.
c) Sử dụng công thức s180O co x cos x ta được: Trang 3/8
R (co s 0O cos180O ) (co s 20O co s160O ) (co s 40O co s140O )
(co s 60O co s120O ) (co s80O cos100O ) 0
d) Áp dụng công thức tan x.tan90x tan x.cot x 1.Do đó S 1. e) E = 2 0 + 2 0 + 2 0 + 2 0 + 2 0 + 2 0 cos 12 cos 78 cos 1 cos 89 cos 17 cos 73 = 3. f)Ta có: 4 2 2 0 2 0 2 2 0
F 4a co s 60 2abcos 180 b co s 30 3 2 2 1 4 3 2 2 2 4a
2ab(1) b 2 3 2 2 2 2
a 2ab b (a b) . c) G = 2 0 a + 2 0 b + 2 0 c = 2 a − 2 sin 90 cos90 cos180 c .
Ví dụ 3: Cho là góc nhọn. Rút gọn các biểu thức sau: a) 0 0
A sin(90 ) 2cos 5co s(90 ). b) 0 0 0 0
B sin(90 ) co s(90 ) cot(180 ) tan(90 ) c) 0 0 0 0
C 2co s(180 ) sin(90 )cot(90 ).co t(180 ). 0 0 d)
2.cos(180 −α) + 5sin(90 −α) D = 0 sinα − 4cos(90 −α) 0 0 e) cos(90 −α) − cot(90 +α) 0 0 F =
− sin(180 −α)cot(180 −α). 0 cot(90 −α) Lời giải: a)Ta có: 0 0
A sin(90 ) 2cos 5co s(90 )
cos 2cos5sin 3cos 5sin . b) Ta có: 0 0 0 0
B sin(90 ) co s(90 ) cot(180 ) tan(90 )
co s sin cot co t
co s sin . c) Ta có: 0 0 0 0
C 2co s(180 ) sin(90 )cot(90 ).co t(180 )
2cos cos tan . co t 1co s . d) Ta có: 0 0
2.cos(180 −α) + 5sin(90 −α) D = . 0 sinα − 4cos(90 −α) 2 − cosα + 5cosα = = − cotα. sinα − 4sinα e) Ta có: Trang 4/8 0 0 cos(90 −α) − cot(90 +α) 0 0 F =
+ sin(180 −α)cot(180 −α). 0 cot(90 −α) 0 0
sinα − cot(180 − (90 −α)) = − sinα.cotα tanα sinα + tanα sinα = − cosα = +1− cosα =1. tanα tanα Ví dụ 4: Biết ,
A B, C là các góc nhọn của tam giác ABC . Hãy chứng minh
a) cosAC cosB. b) A C B sin cos . 2 2
c) sinA B 2CsinC.
d) B C 2A 3A tan cot . 2 2 Lời giải: a)Vì ,
A B, C là ba góc của một tam giác suy ra 0
A C 180 B. Do đó A C 0 cos
cos 180 B cos B. b) Vì A C B ,
A B, C là ba góc của một tam giác suy ra 0 0
A C 180 B 90 2 2 Do đó: A C 0 B B sin
sin(90 ) cos . 2 2 2 d)Ta có:
B C 2A 3 0 0 0 A
A B C 180 B C 2A 180 3A 90 2 2
B C 2A 3A 3 0 A tan tan(90 ) cot . 2 2 2
c) Ta có A B C 0 C C 0 sin 2 sin 180 2
sin 180 C sinC.
Ví dụ 5: Rút gọn các biểu thức sau:
a) A = cos10° + cos 20° + cos30° +...+ cos170° + cos180° ° −α − cot ° +α b) cos(90 ) (90 ) B =
+ sin(180° −α)cot(180° −α) cot(90° −α) Lời giải:
a)Ta có: cos170° = −cos10° ⇔ cos10° + cos170° = 0
cos160° = −cos 20° ⇔ cos 20° + cos160° = 0
cos150° = −cos30° ⇔ cos30° + cos150° = 0 cos90° = 0 cos180° = 1 − Vậy A = 1. −
b)Ta có: cos(90° −α) = sinα
cot(90° +α) = cot(180° +α − 90 ) ° = cot(α − 90 ) ° = −tanα cot(90° −α) = tanα sin(180° −α) = sinα cot(180° −α) = −co α t α + tanα Do đó sin B = + sinα(−co α t ) tgα Trang 5/8 B = sinαco α t +1− sinαco α t Vậy: B =1.
Ví dụ 6: Rút gọn các biểu thức sau:
a)C = cos 20° + cos 40° +...+ cos160° + cos180 .°
b) D = sin(90° −α) + sin(180° −α) − cosα + sinα Lời giải:
a)Ta có: cos 20° = −cos160° ⇔ cos 20° + cos160° = 0
cos 40° = −cos140° ⇔ cos 40° + cos140° = 0
cos60° = −cos120° ⇔ cos60° + cos120° = 0
cos80° = −cos100° ⇔ cos80° + cos100° = 0 cos180° = 1. − Vậy: C = 1. −
b)Ta có: sin(90° −α) = cosα sin(180° −α) = sinα
Vậy: D = cosα + sinα − cosα + sinα = 2sinα.
Ví dụ 7: Đơn giản biểu thức:
E = 2sinα − 3cos(90° −α) + tan(90° −α) + 2cot(180° −α) + 2sinα − 3cotα. Lời giải:
Ta có: cos(90° −α) = sinα ; tan( ° 90 −α) = c α
ot ; cot(180° −α) = −co α t
Vậy: E = 2sinα − 3sinα + co α t − 2co α t + 2sinα − 3co α t E = sinα − 4co α t .
Ví dụ 8: Đơn giản biểu thức: 2 2 2 2 2 2
T = sin 10° + sin 20° + sin 30° +...+ sin 70° + sin 80° + sin 90° Lời giải: Ta có: sin 90° =1 ⇒ 2 sin 90° =1 sin80° = cos10° ⇒ 2 2 2 2
sin 80° = cos 10° ⇒ sin 80° + sin 10° =1 sin 70° = cos 20° ⇒ 2 2 2 2
sin 70° = cos 20° ⇒ sin 70° + sin 20° =1 sin 60° = cos30° ⇒ 2 2 2 2
sin 60° = cos 30° ⇒ sin 60° + sin 30° =1 sin 50° = cos 40° ⇒ 2 2 2 2
sin 50° = cos 40° ⇒ sin 50° + sin 40° =1 Vậy 2 2 2 2
T = sin10° + sin 20° + sin 30° + sin 40° + cos 40° + cos 30° + cos 20° + cos 10° +1 T = 5.
Ví dụ 9: Đơn giản biểu thức: 2 2 2 2 2
T = cos 15° + cos 25° + cos 45° + cos 65° + cos 75 .° Lời giải: Ta có 2 cos 75° = sin15° ⇒ 2 2 cos 75° = sin 15° 2 cos 65° = sin 25° ⇒ 2 2 cos 65° = sin 25° 2 2 cos 45° = sin 45° ⇒ 2 2 2 1 cos 45° = sin 45° = = 2 2 Vậy 2 2 1 2 2 1 5
T = cos 15° + cos 25° + + sin 25° + sin 15° = 2 + = 2 2 2 Ví dụ 10: Cho ,
A B, C là 3 góc của một tam giác ABC. Chứng minh rằng:
a)sin B + A = cos C 2 2 Trang 6/8
b)sin A = sin(B + C)
c) cos A = −cos(B + C). Lời giải: a)Vì ,
A B, C là 3 góc của một tam giác nên A + B + C =180° ⇒ A B 180° C + = − = 90 C ° − 2 2 2 2 2
⇒ sin A + B sin 90 C = ° − = cos C . 2 2 2
b)Ta có: A + B + C =180° ⇒ A =180° − (B + C)
⇒ sin A = sin[180° − (B + C)] = sin(B + C). c)Ta có:
A + B + C =180° ⇒ A =180° − (B + C)
⇒ cos A = cos[180° − (B + C)] = −cos(B + C).
Ví dụ 11: Tính giá trị các biểu thức sau: a) 2 0 2 0 2 0
A = a sin 90 + b cos90 + c cos180 b) 2 0 2 0 2 0
B = 3− sin 90 + 2cos 60 − 3tan 45 c) 2 0 2 0 2 0 2 0 0 0
C = sin 45 − 2sin 50 + 3cos 45 − 2sin 40 + 4 tan 55 .tan 35 Lời giải: a) 2 2 2
A = a + b + c (− ) 2 2 .1 .0 . 1 = a − c 2 2 b) B = − ( )2 1 2 3 1 + 2 − 3 = 1 2 2 c) 2 0 2 0 C = + − ( 2 0 2 0 + ) 0 0
sin 45 3cos 45 2 sin 50 sin 40 + 4 tan 55 .cot 55 2 2 2 2 C = + − ( 2 0 2 0 + ) 1 3 3
2 sin 50 cos 40 + 4 = + − 2 + 4 = 4 2 2 2 2
Ví dụ 12: Tính giá trị các biểu thức sau: a) 2 0 2 0 2 0 2 0
A = sin 3 + sin 15 + sin 75 + sin 87 b) 0 0 0 0 0
B = cos0 + cos 20 + cos 40 +...+ cos160 + cos180 c) 0 0 0 0 0
C = tan 5 tan10 tan15 ...tan80 tan85 Lời giải: a) A = ( 2 0 2 0 + )+( 2 0 2 0 sin 3 sin 87 sin 15 + sin 75 ) = ( 2 0 2 0 + )+( 2 0 2 0 sin 3 cos 3 sin 15 + cos 15 ) = 1+1 = 2 b) B = ( 0 0 + )+( 0 0 + )+ +( 0 0 cos0 cos180 cos 20 cos160 ... cos80 + cos100 ) = ( 0 0 − )+( 0 0 − )+ +( 0 0 cos0 cos0 cos 20 cos 20 ... cos80 − cos80 ) = 0 c) C = ( 0 0 )( 0 0 ) ( 0 0
tan 5 tan85 tan15 tan 75 ... tan 45 tan 45 ) Trang 7/8 = ( 0 0 )( 0 0 ) ( 0 0
tan 5 cot 5 tan15 cot 5 ... tan 45 cot 5 ) = 1
Vấn đề 2: Dấu của một biểu thức lượng giác.
a) Phương pháp: Dùng dấu của các tỉ số lượng giác. b) Ví dụ minh họa I- BÀI TẬP TỰ LUẬN:
Ví dụ 1: Xét dấu biểu thức: P = cos .xsin x biết 0° < x < 90 .° Lời giải:
Ta có cos x > 0; sin x > 0 với 0° < x < 90 .° Do đó P = cos .xsin x > 0.
Ví dụ 2: Xét dấu biểu thức: 2
P = sin .xtan x biết 90° < x <180 .° Lời giải: Ta có 2,
sin x > 0;tan x < 0, với 90° < x <180 .° Do đó 2
P = sin .xtan x < 0
Ví dụ 3: Xét dấu biểu thức: P = (cos x −1)sin xtanx biết 0° < x < 90 .° Lời giải: Ta có: sin x 2 1
P = (cos x −1)sin x
= (cos x −1)sin x cos x cos x Ta có: 2
sin x ≥1; cos x −1< 0 ( vì 0° < x < 90° ) ⇔ 0 < cos x <1, cos x > 0 Ta có bảng tổng kết: x 0° 90° cos x −1 − cos x + P −
Vậy 0° < x < 90° thì P = (cos x −1)sin xtanx < 0.
Ví dụ 4: Xét dấu của 2 3
P = sin x cos xtanx, biết 45° < x <180 ,° x ≠ 90 .° Lời giải: Ta có: 2
sin x ≥ 0 vói 45° < x <180°
cos x ≥ 0 với 45° < x ≤ 90°
cos x < 0 với 90° < x <180°
tanx > 0 với 45° < x < 90°
tanx < 0 với 90° < x <180°
Ta có bảng dấu như sau: x 45° 90° 180° 3 cos x + 0 − tgx + − P + + Vậy 2 3
P = sin xcos xtanx luôn luôn dương khi 45° < x <180 ,° x ≠ 90°
Ví dụ 5: Xét dấu của 3 9
P = sin x cos x(1− sin x), biết 75° < x <125 .° Lời giải:
Ta có: sin x > 0 ⇒ 3
sin x > 0 với 75° < x <125° và 9 1− sin x ≥ 0 và
cos x ≥ 0 với 75° < x ≤ 90° Trang 8/8
cos x < 0 với 90° < x <125° Ta có bảng xét dấu: x 75° 90° 125° cos x + 0 − P + 0 − Vậy 3 9
P = sin x cos x(1− sin x) < 0 nếu 90° < x <125° 3 9
P = sin x cos x(1− sin x) ≥ 0 nếu 75° < x ≤ 90 .°
Ví dụ 6: Định x để P = sin xcos x > 0, biết 0° < x <180 .° Lời giải:
Vì 0° < x <180° ⇒ sin x > 0
Ta có: cos x ≥ 0 khi 0° < x ≤ 90°
cos x < 0 khi 90° < x <180° Ta có bảng xét dấu: x 0° 90° 180° sin x 0 + 1 + cos x + 0 −
P = sin x cos x + 0 −
Vậy để P = sin xcos x > 0 ⇔ 0° < x < 90 .°
Ví dụ 7: Định x để T = sin(115° − x) > 0, biết 0° < x <180 .° Lời giải:
Ta có: sin(115° − x) > 0 ⇒ 0° <115° − x <180° 0° <115° − x x <115° ⇔ ⇔ 115 ° − x <180° x > 65 − °
Vì giả thiết cho 0° < x <180° nên ta chọn 0° < x <115° thì T > 0.
Ví dụ 8: Định x để 2
P = sin x(1− cos x)cotgx > 0, biết 30° < x <160 ,° x ≠ 90 .° Lời giải: Ta có: 2
sin x > 0 và 1− cos x > 0 với 30° < x <160°
Ta chỉ cần xét dấu cotgx x 30° 90° 160° cotgx + 0 − P + 0 −
Vậy P > 0 khi 30° < x < 90 .°
Ví dụ 9: Tính theo hàm số lượng giác của các góc bé hơn 90 :
sin100 , sin160 , cos170 , tan10345', cot124 15 '. Lời giải:
sin100 = sin (180 −100 ) = sin80;
sin160 = sin (180 −160 ) = sin 20 ;
tan10345' = − tan (180 − 10345') = tan 76 15 ' cot124 15 ' = −cot (180 −124 15 ') = −cot5545' Trang 9/8
Vấn đề 3. Cho biết một giá trị lượng giác, tính các giá trị lượng giác còn lại hoặc tính
giá trị của một biểu thức lượng giác.
Phương pháp: dùng các hệ thức lượng giác cơ bản và dấu của các tỉ số lượng giác.
Ví dụ 1: Tính cosα, tanα, co α t . a)Biết 4 sinα = 5 b)Biết α nhọn và 3 sinα = 5
c) Biết 90° < α <180° và 12 sinα = . 13 Lời giải: a)Ta có: 2 2 16 9 cos α =1− sin α =1− = ⇒ 3 cosα = ± 25 25 5 4 Với 3 α cosα = thì sin 5 4 tanα = = = ; 1 3 co α t = = . 5 cosα 3 3 tanα 4 5 4 Với 3 α cosα = − thì sin 5 4 tanα = = = − ; 1 3 co α t = = − . 5 cosα 3 3 − tanα 4 5 b)Ta có: 2 2 9 16 cos α =1− sin α =1− = ⇒ 4 cosα = (α nhọn) 25 5 5 3 Ta có: sinα 5 3 tanα 1 4 = = = ; co α t = = . cosα 4 4 tanα 3 5 c)Ta có: 2 2 144 25 cos α =1− sin α =1− = 169 169 5
cosα = − (vì 90° < α <180 ) ° 13 12 Ta có: sinα 13 12 tanα 1 5 = = = − ; co α t = = − . cosα 5 5 − tanα 12 13 Ví dụ 2: Cho 2
sinα = và 90° < α <180 .° Tính cosα, tanα, co α t . 5 Lời giải:
Vì 90° < α <180° ⇒ cosα < 0 . Do đó 2 4 21
cosα = − 1− sin α = − 1− = − 25 5 Trang 10/8 2 α Ta có: sin 5 2 tanα = = = − ; 1 21 co α t = = − . cosα 21 21 tanα 2 − 5 Ví dụ 3: Cho 3
cosα = − . Tính sinα, tanα, co α t . 5 Lời giải: Vì 0° ≤ α ≤180° và 3
cosα = − ⇒ 90° ≤ α ≤180° 5 2 Ta có: 2 3 4 sinα = 1− cos α = 1− − = 5 5 4 sinα 5 4 tanα 1 3 = = = − ; co α t = = − . cosα 3 3 − tanα 4 5 Ví dụ 4: Cho 0 2 + 3 cos15 = . Tìm tan15ο 2 Lời giải: 1 4 tan 15 = −1 = −1 = (2− 3)2 2 0 0 ⇒ tan15 = 2 − 3 . 2 0 cos 15 2 + 3
Ví dụ 5: Tính các tỉ số lượng giác còn lại của góc α. a)Biết 1 cosα = − . 2 b)Biết 2 cosα = ( 3 −1). 4 c)Biết tanα = 2. d)Biết co α t = 3. − Lời giải: a)Ta có: 1
cosα = − = −cos60° = cos120° ⇒ α =120° 2 Do đó 3 sinα = sin120° = sin 60° = 2 tanα = t 120 an ° = −tan60° = − 3 3 co α t = co 120 t ° = −cot60° = − . 3 2 2 − + + b)Ta có: 2 2 6 2 8 − 2 12 sin α =1− cos α =1− 8 2 12 6 2 = 1− = = 4 16 16 4 ⇒ 6 2 sinα + = 4 2 α ⇒ sin 3 +1 ( 3 +1) 4 + 2 3 tanα = = = = = 2 + 3 cosα 3 −1 ( 3 −1)( 3 +1) 2 Trang 11/8 α − ⇒ cos 1 2 3 co α t = = = = 2 − 3. sinα 2 + 3 1 c)Ta có: 1 2 = 1+ tg α =1+ 4 = 5 ⇒ 2 1 cos α = 2 cos α 5 ⇒ 5 cosα =
(do tgα = 2 > 0 ⇒ α là góc nhọn) 5 ⇒ 2 2 1 4
sin α =1− cos α =1− = ⇒ 2 5 sinα = (vì α nhọn) 5 5 5 Ta có: 1 1 co α t = = . tanα 2
Chú ý: sinα có thể được tính theo công thức sau Ta có: sinα 2 5 tanα =
⇒ sinα = tanα.cosα = , cosα 5 d) 1 1 tanα = = − . cotα 3 Vì co α t = 3
− < 0 nên 90° < α <180° ⇒ sinα > 0, cosα < 0 Ta có: 1 2 = 1+ cot α =1+ 9 =10 ⇒ 2 1 sin α = 2 sin α 10 ⇒ 10 sinα = (vì 90° < α <180 ) ° 10 ⇒ 2 2 1 9 cos α =1− sin α =1− = ⇒ 3 10 cosα = − 10 10 10
Chú ý: cosα có thể được tính theo công thức sau Ta có: cosα 3 10 co tα =
⇒ cosα = co tα.sinα = − sinα 10 4
Ví dụ 6: Cho cosx =
. Tính giá trị của biểu thức 2 2
A= 3sin x − 4cos x −1.. 13 Lời giải: Ta có: 2 2 2
A= 3(1- cos x) − 4cos x −1= 2 − 7cos x 4 2 226 = 2 − 7( ) = . 13 169 1
Ví dụ 7: Cho sinx =
. Tính giá trị của biểu thức 4 4
A= 3sin x + cos x − 3.. 3 Lời giải: Ta có:
A= 3sin x + cos x − 3 = 3sin x + (cos x)2 4 4 4 2 − 3 2 4 = 3sin x + ( 2 1− sin x) − 3 4 2 1 1 20 = 3 + 1− − 3 = − 3 3 9 Trang 12/8 Ví dụ 8: Cho 3 α − α sinα = và 0 0
90 < α <180 . Tính giá trị của biểu thức cot 2 tan E = 5 tanα + 3cotα Lời giải: 4 cosα = Ta có 2 2 sin α + cos α =1 2 2 9 16 ⇒ cos α =1− sin α =1− = 5 ⇔ 25 25 4 cosα = − 5 Vì 0 0 90 < α <180 4 ⇒ cosα = − . Vậy 3 tanα = − và 4 cotα = − . 5 4 3 4 3 2. − − − cotα 2 tanα 3 4 − 2 E = = = − . tanα + 3cotα 3 4 57 − + 3. − 4 3 Ví dụ 9:a) Cho 2
cos . Tính giá trị của biểu thức tan 3 cot A . 3
tan cot b) Cho
sin cos
tan 3 . Tính giá trị của biểu thức B 3 3
sin 3 cos 2 sin c) Cho 3 α − α sinα = và 0 0
90 < α <180 . Tính giá trị của biểu thức cot 2 tan C = 5 tanα + 3cotα Lời giải: 1 1 tan 3 2 2 a) Ta có tan tan 3 2 A cos 2 1 2 cos 1 2 tan 1 1
tan tan 2 cos Suy ra 4 17 A 1 2. 9 9 sin cos tan 2
tan 1 2 tan 1 b) 3 3 cos cos B 3 3 sin 3 cos 2 sin 3
tan 3 2 tan 2 tan 1 3 3 3 cos cos cos
39 1 9 1 Suy ra 2 B 27 3 2.39 1 9 4 cosα = c) 2 2 sin α + cos α =1 ⇒ 2 2 9 16 cos α =1− sin α =1− = ⇔ 5 25 25 4 cosα = − 5 Vì 0 0 90 4
< α < 180 ⇒ cosα = − . Do đó: 3 tanα = − và 4 cotα = − . 5 4 3 4 3 2. − − − cotα − 2 tanα C − = . 3 4 = 2 = tanα + 3cotα 3 4 3. − + − 57 4 3 Trang 13/8 2 Ví dụ 10: α + α α Cho co α t sin sin cos = 2. Tính E = 2 2 sin α − cos α Lời giải: Vì co α t = 2 nên sinα ≠ 0 Chia tử và mẫu cho + co α 2 t sin α 1 1+ 2
≠ 0 , ta được: E = = = 1 − − 2. 2 1− cot α 1− 2 Ví dụ 11: Cho α + α
tanα = 2 . Tính giá trị của 3sin cos A = . sinα − cosα Lời giải: 3sinα + cosα 3tanα +1 A = = = 7 . sinα − cosα tanα −1 Ví dụ 12: Cho sinα tanα − cotα
= 2 −1 và 0° < α < 90 .° Tính 2 A = . cosα Lời giải:
Vì 0° < α < 90° ⇒ cosα > 0 Ta có: 2 2
cosα = 1− sin α = 1− ( 2 −1) = 2( 2 −1) α sin 2 −1 1 tanα = = = cosα 2( 2 −1) 2( 2 +1) 1 cotgα = = 2( 2 +1) tanα 1 − 2 2( 2 +1) 2( 2 +1) Do đó 4 2 + 3 A = = − . − 2 2( 2 1) Ví dụ 13: Cho α + α tanα = 2. − Tính cos sin T = . cosα − sinα Lời giải: Ta có: tanα = 2 − nên cosα ≠ 0
Ta chia tử và mẫu T cho cosα ≠ 0 cosα + sinα cosα + sinα cosα 1+ tanα 1− 2 1 T = = = = = − . cosα − sinα
cosα − sinα 1− tanα 1+ 2 3 cosα 2 2 Ví dụ 14: α − α
Tìm giá trị của biểu thức sin 5cos E = khi tanα = 3. 2 2
2sin α + 3sinα cosα + cos α Lời giải:
Vì tanα = 3 nên cosα ≠ 0
Ta chia tử và mẫu của E cho 2 cos α ≠ 0 Trang 14/8 2 2 sin α 5cos α − 2 2 2 α α tan α cos cos − 5 E = = 2 2 2 2sin α 3sinα cosα cos α 2tan α + 3tanα +1 + + 2 2 2 cos α cos α cos α 9 5 4 1 E − = = = . 18 + 9 +1 28 7 3 3 Ví dụ 15: α − α Cho tanα sin cos = 3. Tính E = . sinα − cosα Lời giải: 3 3 2 2 α − α α − α α + α α + α Ta có: sin cos (sin cos )(sin sin cos cos ) E = = sinα − cosα (sinα − cosα) 2 α + α α cos (1 sin cos ) =1+ sinα cosα = 2 cos α 1 1 1 2 = + tanα = (1+ tan α + tanα) 2 2 2 1+ tan α cos α 1+ tan α Do dó 1 1 E = (1+ 3+ 3) = (4 + 3). 1+ 3 4 2 Ví dụ 16: α − α α Cho co α t cos sin cos = 5. Tính A = 2 sin α Lời giải: Vì co α t = 5 ⇒ sinα ≠ 0 2 α α α cos sin cos 2 A = −
= cot α − cotg = 25 − 5 = 20. 2 2 sin α sin α Ví dụ 17:Cho 1 4 4
3 sin cos . Tính 4 4
A 2 sin cos . 2 Lời giải: Ta có 1 1 4 4
3 sin cos
⇔ 3 sin 1 sin 2 4 2 ⇔ 2 2 4 2 4 6 sin
2 1 2 sin sin 1 ⇔ 4 2
4 sin 4 sin 3 0 ⇔ 2 2 2 sin
1 2 sin 3 0 ⇔ 2
2 sin 1 0 (Do 2
2 sin 3 0 ) Suy ra 1 2 sin . 2 Ta lại có 1 1 2 cos 2
1 sin 1 2 2 2 2 Suy ra 1 1 1 A 2 = 2 2 4
Ví dụ 18: Biết sinx cosx m . Tính sinx cosx và 4 4
sin x cos x Lời giải: Ta có x x 2 sin cos 2 2
sin x 2 sin x cos x cos x 1 2 sin x cos x (*) Trang 15/8 2 Mặt khác m 1
sin x cos x m nên 2
m 1 2 sin cos hay sin cos 2 Đặt 4 4
A sin x cos x . Ta có A 2 2 x x 2 2 sin cos
sin x cos x = (sin x + cos x)(sin x − cos x) ⇒ A x x 2 x x 2 2 sin cos sin cos
1 2sinx cosx 1 2sinx cosx 2 2 2 4 3 2m m ⇒ m 1 m 1 2 A 1 1 2 2 4 2 4 Vậy 3 2m m A 2
Ví dụ 19: Biết sinα + co 2 sα = .Tinhs 2 2 tan α + cot α . 2 Lời giải: Ta có sinα + co 2 sα = ⇒ ( α + sα )2 sin co 1 = 1 ⇒ 1+ 2sinα cosα = 1 ⇒ sinα cosα = − 2 2 2 4 ⇒ ( α − α )2 1 6 sin cos
= 1− 2sinα cosα =1− 2 − = 6 ⇒ sinα − cosα = ± 4 4 2 ⇒ α + α = ( α + α ) 2 2 4 4 2 2 2 2 1 7 sin cos sin cos − 2sin α cos α =1− 2 − = 4 8 7 4 4 2 2 sin α + cos α 8 ⇒ tan α + cot α = = =14 2 2 2 sin α cos α 1 − 4
Vấn đề 4: Đơn giản một biểu thức lượng giác. Phương pháp:
• Dùng các công thức cơ bản.
• Dùng các công thức cung liên quan đặc biệt.
• Biến đổi đại số.
Ví dụ 1: Rút gọn biểu thức: 2
A = (1+ cosα)cot α(1− cosα). Lời giải: Ta có: 2 2 2
A = (1+ cosα)(1− cosα)cot α = (1− cos α)cot α 2 α 2 cos 2 A = sin α. = cos α. 2 sin α 3 3 3 3 Ví dụ 2: α + α α − α Rút gọn biểu thức: sin cos sin cos B = + . sinα + cosα sinα − cosα Lời giải: Ta có: 3 3 2 2
sin α + cos α = (sinα + cosα)(sin α − sinα cosα + cos α)
= (sinα + cosα)(1− sinα cosα) 3 3 α + α α + α − α α Suy ra sin cos (sin cos )(1 sin cos ) = =1− sinα cosα sinα + cosα (sinα + cosα) Trang 16/8 3 3 α − α α − α + α α Tương tự: sin cos (sin cos )(1 sin cos ) = =1+ sinα cosα sinα − cosα (sinα − cosα)
Do đó B = (1− sinα cosα) + (1+ sinα cosα) = 2 Vậy B = 2.
Ví dụ 3: Đơn giản các biểu thức: a) 2 2 2
E = cos a + cos acot a b) 2 2 2
F = sin a + sin atan a 2 c 2cos a −1 G = sin a + cos a d) 2 2
H = sin a(1+ co a
t ) + cos a(1+ tana) Lời giải: a) Ta có: 2 2 2 2 2
E = cos a + cos .
a cot a = cos a(1+ cot a) 2 1 2 E = cos . a = cot . a 2 sin a b) Ta có: 2 2 2 2 2
F = sin a + sin .
a tan a = sin a(1+ tan a) 2 1 2 F = sin . a = tan . a 2 cos a 2 2 2 2 c)Ta có:
2cos a −1 2cos a − cos a − sin a G = = sin a + cos a sin a + cos a 2 2
cos a − sin a (cos a + sin a)(cos a − sin a) G = = sin a + cos a (sin a + cos a)
G = cos a − sin . a d)Ta có: 2 cos a 2 sin sin 1 cos 1 a H a a = + + + sin a cos a 2 2 2
H = sin a + sin a cos a + cos a + sin a cos a = (sin a + cos a)
H = sin a + cos a .
Ví dụ 4: Rút gọn các biểu thức: 2 2 α α a) sin cos A =1− − 1+ cotgα 1+ tgα + α − α b) 1 cos 1 cos B = −
với 0° < α < 90 .° 1− cosα 1+ cosα Lời giải: 2 2 a) α α Ta có: sin cos A =1− cosα − sin 1+ 1 α + sinα cosα 3 3 3 3 α α α + α sin cos sin cos A =1− − = 1− sinα + cosα cosα + sinα sinα + cosα 2 2
A =1− (sin α − sinα cosα + cos α) = sinα.cosα. 2 2 b) + α − α + α − α Ta có: 1 cos 1 cos 1 (cos ) (1 cos ) B = − = − 2 2 1− cosα 1+ cosα sin α sin α 1+ cosα 1− cosα B = −
(vì 0° < α < 90° ⇒ cosα > 0, sinα > 0) sinα sinα Trang 17/8 1+ cosα −1+ cosα 2cosα B = = = 2tanα. sinα sinα
Ví dụ 5: Rút gọn biểu thức: 4 4 2 2
A = sin x + cos x + 2sin x cos x −1. Lời giải: Ta có: 4 4 2 2 2 2 2
A = (sin x + cos x + 2sin xcos x) −1 = (sin x + cos x) −1 A =1−1 = 0.
Vấn đề 5: Chứng minh một đẳng thức lượng giác.
Phương pháp: Chẳng hạn cần chứng minh A = B
• Cách 1: Dùng công thức lượng giác để biến đổi A bằng B.
• Cách 2: Dùng công thức lượng giác để biến đổi B bằng A.
• Cách 3: Dùng công thức lượng giác để biến đổi A = C, B = C.
• Cách 4: Thu gọn riêng từng vế rồi so sánh kết quả.
• Cách 5: Chứng minh A – B = 0.
• Cách 6: Chứng minh quy nạp nếu đẳng thức cần chứng minh phụ thuộc vào số nguyên
dương n (n∈N).
Ví dụ 1: Với điều kiện biểu thức đã cho có nghĩa, chứng minh: 2 2 2 2
a) tan α − sin α = tan α.sin α 2 2 2 2
b) cot α − cos α = cot α.cos α Lời giải: 2 a) Ta có 2 2 sin α 2 2 1 2 2 tan α − sin α = − sin α = sin α( −1) = tan α.sin α 2 2 cos α cos α 2 b) Ta có 2 2 cos α 2 2 1 2 2 cot α − cos α =
− cos α = cos α(
−1) = cot α.cos α. 2 2 sin α sin α
Ví dụ 2: Chứng minh: 1 2 2 1 − tan α + cot α = . 2 2 cos α sin α Lời giải: Ta có: 1 2 2 2 2 2
− tan α + cot α =1+ tan α − tan α + cot α 2 cos α 2 1 = 1+ cotg α = . 2 sin α 2
Ví dụ 3: Chứng minh: 1+ sin a 2 =1+ 2tan . a 2 1− sin a Lời giải: 2 2
Ta có: 1+ sin a 1+ sin a 1 2 2 2 2 = =
+ tan a =1+ tan a + tan a =1+ 2tan . a 2 2 2 1− sin a cos a cos a
Ví dụ 4: Chứng minh: cos a 1 + tana = . 1+ sin a cos a Lời giải: Ta có: cos a cos a sin a + tana = + = 1+ sin a 1+ sin a cos a 2 2
cos a + sin a + sin a 1+ sin a = = cos a(1+ sin a) cos a(1+ sin a) Trang 18/8 Vậy: cos a 1 + tana = . 1+ sin a cos a
Ví dụ 5: Chứng minh: sin a 1+ cos a 2 + = . 1+ cos a sin a sin a Lời giải: 2 2 Ta có: sin a
1+ cos a sin a +1+ 2cos a + cos a + = 1+ cos a sin a sin a(1+ cos a) 2(1+ cos a) 2 = =
sin a(1+ cos a) sin a Vậy: sin a 1+ cos a 2 + = . 1+ cos a sin a sin a 2
Ví dụ 6: Chứng minh: tanα cot α −1 . = 1. 2 1− tan α co α t Lời giải: 1 2 −1 tan cog − tan 2 α α α Ta có: 1 . tan α = 2 2 1 tan α co α t 1 tan α 1 − − tanα 2 1− tan α 2 tan 2 α tan α tanα 1− tan α tanα = = × × = 1. 2 2 2 1− tan α 1 1− tan α tan α 1 tanα
Ví dụ 7: Cho sin x + cos x = . a a) Tính 3 3
A = sin x + cos x theo a. b) Tính 4 4
B = sin x + cos x theo a. Lời giải: 2 Ta có: 2 2 2 − a a 1
= sin x + cos x + 2sin x cos x ⇔ = sin x cos x 2 a)Ta có: 3 3
A = sin x + cos x = (sin x + cos x)(1− sin x cos x) 2 − a 1 a 2 = a 1− = (3− a ). 2 2 b) Ta có: 4 4 2 2 2 2 2
B = sin x + cos x = (sin x + cos x) − 2sin x cos x 2 2 4 2 − a 1 −a + 2a +1 = 1− 2 = . 2 2
Ví dụ 8: Chứng minh các đẳng thức sau: a) 2 3 sin x + cos 1 x
+ tanx + tan x + tan x = 3 cos x b) 1 1 cos x cos x = + .
cos x 2 1 sin x 1 sin x + − Lời giải: 2 3 a)Ta có: 2 3 sin x sin x sin 1+ tan + tan + tan =1 x x x x + + + 2 3
cos x cos x cos x 3 2 2 3
cos x + sin xcos x + sin xcos x + sin x = 3 cos x Trang 19/8 3 3
(cos x + sin x) + sin xcos x(cos x + sin x) = 3 cos x 2 2
(cos x + sin x)(cos x − sin xcos x + sin x + sin xcos x) = 3 cos x Vậy: 2 3 sin x + cos 1 x
+ tanx + tan x + tan x = 3 cos x b) Ta có: cos x cos x
cos x(1− sin x) + cos x(1+ sin x) + = 2
1+ sin x 1− sin x 1− sin x
cos x − sin xcos x + cos x + sin xcos x = 2 cos x cos x cos x 2cos x 2 + = = 2
1+ sin x 1− sin x cos x cos x Suy ra: 1 cos x cos x 1 + = .
2 1 sin x 1 sin x + − cos x
Vấn đề 6: Chứng minh một biểu thức độc lập đối với x .
Phương pháp: Dùng các công thức lượng giác cơ bản và công thức góc phụ, góc bù để biến
đổi biểu thức cho thành một biểu thức không có . x
Ví dụ 1: Chứng tỏ biểu thức sau không phụ thuộc x : 6 6 4 2 2 2 2
M = cos x + 2sin x + sin x cos x + 4sin x cos x − sin . x Lời giải: Ta có: 6 6 2 2 3 2 2 2 2
sin x + cos x = (sin x + cos x) − 3sin xcos x =1− 3sin xcos x Ta có: 6 4 2 6 4 2 4
sin x + sin xcos x = sin x + sin x(1− sin x) = sin x Vậy: 2 2 4 2 2 2
M =1− 3sin x cos x + sin x + 4sin x cos x − sin x 2 2 4 2
=1+ sin x(1− sin x) + sin x − sin x 2 2 2 2
=1+ sin x(1− sin x) − sin x(1− sin x) M =1
Nên ta có M không phụ thuộc vào . x
Ví dụ 2: Chứng minh biểu thức sau đây độc lập đối với .x 1 2 2 1 P =
+ sin (180° − x) + cos(90° − x) − sin x + tan (90° − x) +1− . 2 2 1+ tan x sin x Lời giải: 2 2 2 1
P = cos x + sin x + sin x − sin x + cot x +1− 2 sin x Vậy ta có 1 1 P =1+ − = 1 2 2 sin x sin x
Vậy P độc lập đối với . x
Vì ta có sin(180° − x) = sin ;
x cos(90° − x) = sin ;
x tan(90° − x) = cot . x
Ví dụ 3: Chứng minh biểu thức sau đây độc lập đối với .x 2 2
P = (sin x + cos x) + (sin x − cos x) − 2. Lời giải: Ta có: 2 2 2 2
P = sin x + cos x + 2sin x cos x + sin x + cos x − 2sin x cos x − 2 Trang 20/8 P = 0.
Vậy P độc lập đối với .x
Ví dụ 4: Chứng minh biểu thức sau đây độc lập đối với .x 2 2 2 2
S = sin(90° − x) + cos(180° − x) + sin x + sin xtan x − tan (180° − x). Lời giải: Ta có: 2 2 2
S = cos x − cos x + sin x(1+ tan x) − tan x 2 1 2 2 2 S = sin x
− tan x = tan x − tan x = 0 2 cos x
Vậy S độc lập đối với .x
Ví dụ5: Chứng minh các biểu thức sau đây độc lập đối với .x a) 8 8 6 6 4
E = 3(sin x − cos x) + 4(cos x − 2sin x) + 6sin x b) 4 4 2 2 2 8 8
F = 2(sin x + cos x + sin x cos x) − (sin x + cos x). Lời giải: a)Ta có: 8 2 4 2 3 6 4
E = 3[sin x − (1− sin x) ]+ 4[(1− sin x) − 2sin x]+ 6sin x 8 2 4 6 8
= 3[sin x − (1− 4sin x + 6sin x − 4sin x + sin x]+ 2 4 6 6 4 4
+ [1− 3sin x + 3sin x − sin x − 2sin x]+ 6sin x 8 2 4 6 8
E = 3sin x − 3+12sin x −18sin x +12sin x − 3sin x + 4 − 2 4 6 4 1
− 2sin x +12sin x −12sin x + 6sin x E =1
Vậy E độc lập đối với .x b) 2 2 4 2 2 2 2 4 8
F = 2[(1− cos x) + cos x + (1− cos x)cos x] −[(1− cos x) + cos x] 2 4 4 2 4 2
= 2[1− 2cos x + cos x + cos x + cos x − cos x] − 2 4 6 8 8 [
− 1− 4cos x + 6cos x − 4cos x + cos x + cos x] 2 4 2 2 4 6 8
= 2[1− cos x + cos x] −[1− 4cos x + 6cos x − 4cos x + 2cos x] 4 8 2 6 4
= 2[1+ cos x + cos x − 2cos x − 2cos x + 2cos x]− 2 4 6 8 [
− 1− 4cos x + 6cos x − 4cos x + 2cos x] 4 8 2 6 4
= 2 + 2cos x + 2cos x − 44cos x − 4cos x + 4cos x −1+ 2 4 6 8 4
+ cos x − 6cos x + 4cos x − 2cos x F =1.
Ví dụ 6: Chứng minh biểu thức sau đây không phụ thuộc a : 4 4 6 6
T = 3(sin a + cos a) − 2(sin a + cos a). Lời giải: Ta có: 4 4 2 2 2 2 2 2 2
sin a + cos a = [sin a + cos a] − 2sin a cos a =1− 2sin a cos a 6 6 2 2 3 2 2 2 2
sin a + cos a = [sin a + cos a] − 3sin a cos a(sin a + cos a) 2 2
=1− 3sin a cos a Vậy: 2 2 2 2
T = 3− 6sin a cos a − 2 + 6sin a cos a =1
Nên T không phụ thuộc vào . a
II- BÀI TẬP TRẮC NGHIỆM Câu 1.
Đẳng thức nào sau đây đúng? A. ( o
tan 180 + a) = − tan a . B. ( o
cos 180 + a) = −cosa . C. ( o
sin 180 + a) = sin a . D. ( o
cot 180 + a) = −cot a . Trang 21/8 Lời giải Chọn B.
Lý thuyết “cung hơn kém 180°” Câu 2.
Trong các đẳng thức sau đây, đẳng thức nào đúng?
A. sin (180° −α ) = −sinα .
B. cos(180° −α ) = cosα
C. tan (180° −α ) = tanα .
D. cot (180° −α ) = −cotα Lời giải Chọn D.
Mối liên hệ hai cung bù nhau. Câu 3.
Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinα = sin β . B. cosα = −cos β .
C. tanα = − tan β . D. cotα = cot β . Lời giải Chọn D.
Mối liên hệ hai cung bù nhau. Câu 4.
Cho góc α tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα > 0. D. cotα < 0 . Lời giải Chọn D. Câu 5.
Điều khẳng định nào sau đây là đúng? A. sinα sin (180° = − −α ) . B. cosα cos(180° = − −α ). C. tanα tan (180° = −α ). D. cotα cot (180° = −α ) . Lời giải Chọn B.
Mối liên hệ hai cung bù nhau. Câu 6.
Hai góc nhọn α và β phụ nhau, hệ thức nào sau đây là sai? A. sinα = cos β . B. tanα = cot β . C. 1 cot β = . D. cotα cosα = −sin β . Lời giải Chọn D. cosα cos(90° = − β ) = sin β .
2- Tính giá trị lượng giác của một góc Câu 7.
Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ° 3 sin150 = − . B. ° 3 cos150 = . C. ° 1 tan150 = − . 2 2 3 D. cot150° = 3 Lời giải Chọn C.
Giá trị lượng giác của góc đặc biệt. Trang 22/8 Câu 8.
Bất đẳng thức nào dưới đây là đúng? A. sin 90° sin100° < . B. cos95° cos100° > . C. tan85° tan125° < . D. cos145° cos125° > . Lời giải Chọn B. Câu 9.
Giá trị của tan 45° cot135° + bằng bao nhiêu? A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn B. tan 45° cot135° + = 1−1 = 0 Câu 10.
Giá trị của cos30° sin 60° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1. 3 2 Lời giải Chọn C. ° ° 3 3 cos30 + sin 60 = + = 3 . 2 2 Câu 11.
Giá trị của E sin 36° cos6° sin126° cos84° = là A. 1 . B. 3 . C. 1. D. 1 − . 2 2 Lời giải Chọn A. E ° ° = ( ° ° + ) ( ° ° − ) ° ° ° ° ° 1
sin 36 cos6 sin 90 36 cos 90 6 = sin 36 cos6 − cos36 sin 6 = sin 30 = 2 Câu 12.
Giá trị của biểu thức 2 ° 2 ° 2 ° 2
A sin 51 sin 55 sin 39 sin 35° = + + + là A. 3. B. 4 . C. 1. D. 2 . Lời giải Chọn D. A ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 51 sin 39 sin 55 sin 35 sin 51 cos 51 sin 55 cos 55° = + + + = + + + ) = 2. Câu 13.
Giá trị của cos60° sin 30° + bằng bao nhiêu? A. 3 . B. 3 . C. 3 . D. 1 2 3 Lời giải Chọn D. Ta có ° ° 1 1 cos60 + sin 30 = + =1. 2 2 Câu 14.
Giá trị của tan 30° cot 30° + bằng bao nhiêu? A. 4 . B. 1+ 3 . C. 2 . D. 2 . 3 3 3 Lời giải Chọn A. Trang 23/8 ° ° 3 4 3 tan 30 + cot 30 = + 3 = . 3 3 Câu 15.
Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin 0° cos0° + = 1. B. sin 90° cos90° + = 1. C. sin180° cos180° + = 1 − . D. sin 60° cos60° + = 1. Lời giải Chọn D.
Giá trị lượng giác của góc đặc biệt. Câu 16.
Trong các khẳng định sau, khẳng định nào sai? A. cos60° sin 30° = . B. cos60° sin120° = . C. cos30° sin120° = . D. sin 60° cos120° = − . Lời giải Chọn B.
Giá trị lượng giác của góc đặc biệt. Câu 17.
Đẳng thức nào sau đây sai? A. sin 45° sin 45° + = 2 . B.sin 30° cos60° + = 1. C.sin 60° cos150° + = 0 . D. sin120° cos30° + = 0 . Lời giải Chọn D.
Giá trị lượng giác của góc đặc biệt. Câu 18.
Cho hai góc nhọn α và β (α < β ) . Khẳng định nào sau đây là sai? A. cosα < cos β . B. sinα < sin β .
C. tanα + tan β > 0. D. cotα > cot β . Lời giải Chọn B.
Biểu diễn lên đường tròn. Câu 19. Cho A
∆ BC vuông tại A , góc B bằng 30° . Khẳng định nào sau đây là sai? A. 1 cos B = . B. 3 sin C = . C. 1 cosC = . D. 3 2 2 1 sin B = 2 Lời giải Chọn A. ° 3 cos B = cos30 = . 2 Câu 20.
Tìm khẳng định sai trong các khẳng định sau: A. cos75° cos50° > . B. sin80° sin 50° > . C. tan 45° tan 60° < . D. cos30° sin 60° = . Lời giải Chọn A. Lý thuyết. Câu 21.
Cho biết sinα + cosα = a . Giá trị của sinα.cosα bằng bao nhiêu? A. 2 sinα.cosα = a .
B. sinα.cosα = 2a . Trang 24/8 2 2 C. 1 sin .cos a α α − = . D. a 1 sinα.cosα − = . 2 2 Lời giải Chọn D. 2 a ( α α )2 2 a 1 sin cos 1 2sinα cosα sinα cosα − = + = + ⇒ = . 2 Câu 22. Cho biết 2 α + α
cosα = − . Tính giá trị của biểu thức cot 3tan E = ? 3 2cotα + tanα A. 19 − . B. 19 . C. 25 . D. 25 − 13 13 13 13 Lời giải Chọn B. cotα + 3tanα 1+ 3tan α 3( 3 2 2 tan α ) − + − 2 2 1 2 2 cos α 3− 2cos α 19 E = = = = = = . 2 2cotα + tanα 2 + tan α 1+ ( 2 1+ tan α ) 2 1 1+ cos α 13 +1 2 cos α Câu 23.
Cho biết cotα = 5 . Tính giá trị của 2
E = 2cos α + 5sinα cosα +1? A. 10 . B. 100 . C. 50 . D. 101. 26 26 26 26 Lời giải Chọn D. 2 2 1 1 E = α α + α + = ( 2 101 sin 2cot 5cot 3cot α + 5cotα +1 = . 2 2 ) sin α 1+ cot α 26 Câu 24.
Đẳng thức nào sau đây là sai? A. ( x + x)2 + ( x − x)2 cos sin cos sin = 2, x ∀ . B. 2 2 2 2
tan x sin x tan xsin x, x 90° − = ∀ ≠ C. 4 4 2 2
sin x + cos x =1− 2sin xcos x, x ∀ . D. 6 6 2 2
sin x − cos x =1− 3sin xcos x, x ∀ Lời giải Chọn D. 6 6 x − x = ( 2 2 x − x)( 2 2 sin cos sin cos
1− sin x cos x). Câu 25.
Đẳng thức nào sau đây là sai? A. 1− cos x sin x =
(x ≠ 0°,x ≠180°). sin x 1+ cos x B. 1 tan x cot x (x 0°,90°,180° + = ≠ ) sin xcos x C. 2 2 1 tan x cot x 2 x 0°,90°,180° + = − ≠ 2 2 ( ) sin xcos x D. 2 2
sin 2x + cos 2x = 2 . Lời giải Chọn D. 2 2
sin 2x + cos 2x =1. Câu 26.
Trong các hệ thức sau hệ thức nào đúng? Trang 25/8 A. 2 2 α sin α + cosα =1. B. 2 2 sin α + cos = 1. 2 C. 2 2 sinα + cosα =1. D. 2 2 sin 2α + cos 2α =1. Lời giải Chọn D.
Công thức lượng giác cơ bản. Câu 27.
Trong các hệ thức sau hệ thức nào đúng? A. 2 2 α sin α + cosα =1. B. 2 2 sin α + cos = 1. C. 2 2 sinα + cosα =1. D. 2 2 2 sin α + cos α =1. Lời giải Chọn D.
Công thức lượng giác cơ bản. Câu 28. Cho biết 2 cosα = − . Tính tanα ? 3 A. 5 . B. 5 − . C. 5 . D. 5 − . 4 2 2 2 Lời giải Chọn D.
Do cosα < 0 ⇒ tanα < 0. Ta có: 2 1 1 5 + tan α = 2 5 ⇔ tan α = ⇒ tanα = − . 2 cos α 4 2 Câu 29.
Giá trị của biểu thức A tan1° tan 2° tan 3 .° .tan88° tan89° = là A. 0 . B. 2 . C. 3. D. 1. Lời giải Chọn D.
A (tan1.°tan89° ).(tan 2 .°tan88° ). .(tan 44 .°tan 46° ).tan 45° = = 1. Câu 30. Tổng 2 ° 2 ° 2 ° 2 ° 2 ° 2
sin 2 sin 4 sin 6 . . sin 84 sin 86 sin 88° + + + + + + bằng A. 21. B. 23. C. 22 . D. 24 . Lời giải Chọn C. 2 ° 2 ° 2 ° 2 ° 2 ° 2
S sin 2 sin 4 sin 6 . . sin 84 sin 86 sin 88° = + + + + + + ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 2 sin 88 sin 4 sin 86 ... sin 44 sin 46° = + + + + + + ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 sin 2 cos 2 sin 4 cos 4 ... sin 44 cos 44° = + + + + + + ) = 22. Câu 31.
Trong các hệ thức sau hệ thức nào đúng?
A. sin 2α + cos 2α =1. B. 2 2 sinα + cosα =1.C. 2 2 sin α + cosα =1. D. 2 2 sin α + cos α =1. Lời giải Chọn D.
Công thức lượng giác cơ bản. Câu 32.
Biết sin a + cos a = 2 . Hỏi giá trị của 4 4
sin a + cos a bằng bao nhiêu ? A. 3 . B. 1 . C. 1 − . D. 0 . 2 2 Trang 26/8 Lời giải Chọn B. Ta có: sin a 1 + cos a = 2 ⇒ = ( a + a)2 2 sin cos ⇒ sin . a cos a = . 2 a + a = ( a + a) 2 4 4 2 2 2 2 1 1 sin cos sin cos
− 2sin a cos a =1− 2 = . 2 2 Câu 33.
Biểu thức f (x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) có giá trị bằng: A. 1. B. 2 . C. 3 − . D. 0 . Lời giải Chọn A. • 4 4 2 2
sin x + cos x =1− 2sin xcos x . • 6 6 2 2
sin x + cos x =1− 3sin xcos x . f (x) = ( 2 2 − x x) − ( 2 2 3 1 2sin cos
2 1− 3sin x cos x) =1. Câu 34.
Biểu thức: f (x) 4 2 2 2
= cos x + cos xsin x + sin x có giá trị bằng A. 1. B. 2 . C. 2 − . D. 1 − . Lời giải Chọn A. f (x) 2 = x( 2 2 x + x) 2 2 2 cos cos sin
+ sin x = cos x + sin x =1. Câu 35. Biểu thức 2 2 2 2
tan xsin x − tan x + sin x có giá trị bằng A. 1 − . B. 0 . C. 2 . D. 1. Lời giải Chọn B. − + = ( − ) 2 2 2 2 2 2 2 2 sin tan sin tan sin tan sin 1 + sin x x x x x x x x = ( 2 − cos x) 2 + sin x = 0 . 2 cos x Câu 36.
Giá trị của A tan 5 .°tan10 .°tan15 ... ° tan80 .°tan85° = là A. 2 . B. 1. C. 0 . D. 1 − . Lời giải Chọn B.
A (tan5 .°tan85° ).(tan10 .°tan80° ). .(tan 40° tan50° ).tan 45° = = 1. Câu 37.
Chọn mệnh đề đúng? A. 4 4 2
sin x − cos x =1− 2cos x . B. 4 4 2 2
sin x − cos x =1− 2sin xcos x . C. 4 4 2
sin x − cos x =1− 2sin x . D. 4 4 2
sin x − cos x = 2cos x −1. Lời giải Chọn A. 4 4 x − x = ( 2 2 x − x)( 2 2 x + x) = ( 2 − x) 2 2 sin cos sin cos sin cos 1 cos
− cos x =1− 2cos x . Câu 38. Giá trị của 2 ° 2 ° 2 ° 2
B cos 73 cos 87 cos 3 cos 17° = + + + là A. 2 . B. 2 . C. 2 − . D. 1. Lời giải Chọn B. B ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 ° ) ( 2 ° 2 cos 73 cos 17 cos 87 cos 3 cos 73 sin 73 cos 87 sin 87° = + + + = + + + ) = 2. Trang 27/8 Câu 39. Cho 1 α + α
cotα = . Giá trị của biểu thức 3sin 4cos A = là: 3 2sinα − 5cosα A. 15 − . B. 13 − . C. 15 . D. 13. 13 13 Lời giải Chọn D.
3sinα + 4sinα.cotα 3+ 4cotα A = = =13 .
2sinα − 5sinα.cotα 2 − 5cotα Câu 40. Cho biết 2 α − α
cosα = − . Giá trị của biểu thức cot 3tan E = bằng bao nhiêu? 3 2cotα − tanα A. 25 − . B. 11 − . C. 11 − . D. 25 − . 3 13 3 13 Lời giải Chọn C.
cotα − 3tanα 1− 3tan α 4 − 3( 3 2 2 tan α + ) 4 − 2 1 2 cos α 4cos α − 3 11 E = = = = = = − . 2 2cotα − tanα 2 − tan α 3− ( 2 1+ tan α ) 2 1 3cos α −1 3 3− 2 cos α Câu 41.
Cho tanα + cotα = m . Tìm m để 2 2 tan α + cot α = 7 . A. m = 9 . B. m = 3 . C. m = 3 − . D. m = 3 ± . Lời giải Chọn D. = α + α = ( α + α )2 2 2 7 tan cot tan cot − 2 2
⇒ m = 9 ⇔ m = 3 ± . Câu 42. Biểu thức ( a + a)2 cot tan bằng A. 1 1 − . B. 2 2
cot a + tan a2 . C. 1 1 + . D. 2 2 sin α cos α 2 2 sin α cos α 2 2
cot a tan a + 2. Lời giải Chọn C. ( a + a)2 2 2 = a + a a +
a = ( 2 a + ) + ( 2 a + ) 1 1 cot tan cot 2cot .tan tan cot 1 tan 1 = + . 2 2 sin a cos a Câu 43.
Rút gọn biểu thức sau A = ( x + x)2 − ( x − x)2 tan cot tan cot A. A = 4 . B. A =1. C. A = 2 . D. A = 3 Lời giải Chọn A. A = ( 2 2 x + x x + x) −( 2 2 tan 2 tan .cot cot tan x − 2 tan .
x cot x + cot x) = 4. Câu 44.
Đơn giản biểu thức G = ( 2 − x) 2 2 1 sin
cot x +1− cot x . A. 2 sin x . B. 2 cos x . C. 1 . D. cos x . cos x Lời giải Chọn A. G = ( 2 − x) 2 2 2 2 2 1 sin
−1 cot x +1 = −sin .
x cot x +1 =1− cos x = sin x . Trang 28/8 Câu 45. Đơn giản biểu thức sin = cot x E x + ta được 1+ cos x A. sin x . B. 1 . C. 1 . D. cos x . cos x sin x Lời giải Chọn C. sin x cos x sin x
cos x(1+ cos x) + sin .xsin x E = cot x + = + =
1+ cos x sin x 1+ cos x sin x(1+ cos x) x( + x) + ( 2 cos 1 cos
1− cos x) cos x(1+ cos x) + (1+ cos x)(1− cos x) 1 = = = . sin x(1+ cos x) sin x(1+ cos x) sin x 2 2 Câu 46. Rút gọn biểu thức sau
cot x − cos x sin . x cos x A = + . 2 cot x cot x A. A =1. B. A = 2 . C. A = 3. D. A = 4 Lời giải Chọn A. 2 2 2
cot x − cos x sin . x cos x cos x sin . x cos x 2 2 A = + = 1− +
= 1− sin x + sin x =1. 2 2 cot x cot x cot x cot x Câu 47. Cho biết 1 tanα = . Tính cotα . 2 A. cotα = 2. B. cotα = 2 . C. 1 cotα = . D. 4 1 cotα = . 2 Lời giải Chọn A. 1
tanα.cotα =1⇒ cot x = = 2 . tan x Câu 48.
Trong các mệnh đề sau, mệnh đề nào sai? A.( x x)2 sin cos
= 12sin x cos x . B. 4 4 2 2
sin x + cos x =12sin x cos x . C. ( x + x)2 sin cos
= 1+ 2sin x cos x . D. 6 6 2 2
sin x + cos x =1sin xcos x . Lời giải Chọn D. x + x = ( x)3 + ( x)3 = ( x + x)3 6 6 2 2 2 2 − ( 2 2 x + x) 2 2 sin cos sin cos sin cos 3 sin cos .sin .xcos x 2 2 = 1− 3sin . x cos x . Câu 49.
Khẳng định nào sau đây là sai? A. 2 2 sin α + cos α =1. B. 2 1 1+ cot α = sinα ≠ 0 . 2 ( ) sin α C. tanα.cotα = 1 − (sinα.cosα ≠ 0) . D. 2 1 1+ tan α = cosα ≠ 0 . 2 ( ) cos α Lời giải Chọn C. Trang 29/8 sin x cos tanα.cotα = . x =1. cos x sin x 2 Câu 50. Rút gọn biểu thức 1− sin x P = ta được 2sin . x cos x A. 1 P = tan x . B. 1 P = cot x .
C. P = 2cot x . D. 2 2
P = 2 tan x . Lời giải Chọn B. 2 2 1− sin x cos x cos x 1 P = = = = cot x . 2sin . x cos x 2sin .
x cos x 2sin x 2 Trang 30/8
CHỦ ĐỀ 2: HỆ THỨC LƯỢNG TRONG TAM GIÁC
A. TÓM TẮT LÝ THUYẾT.
I. Các hệ thức lượng trong tam giác vuông:
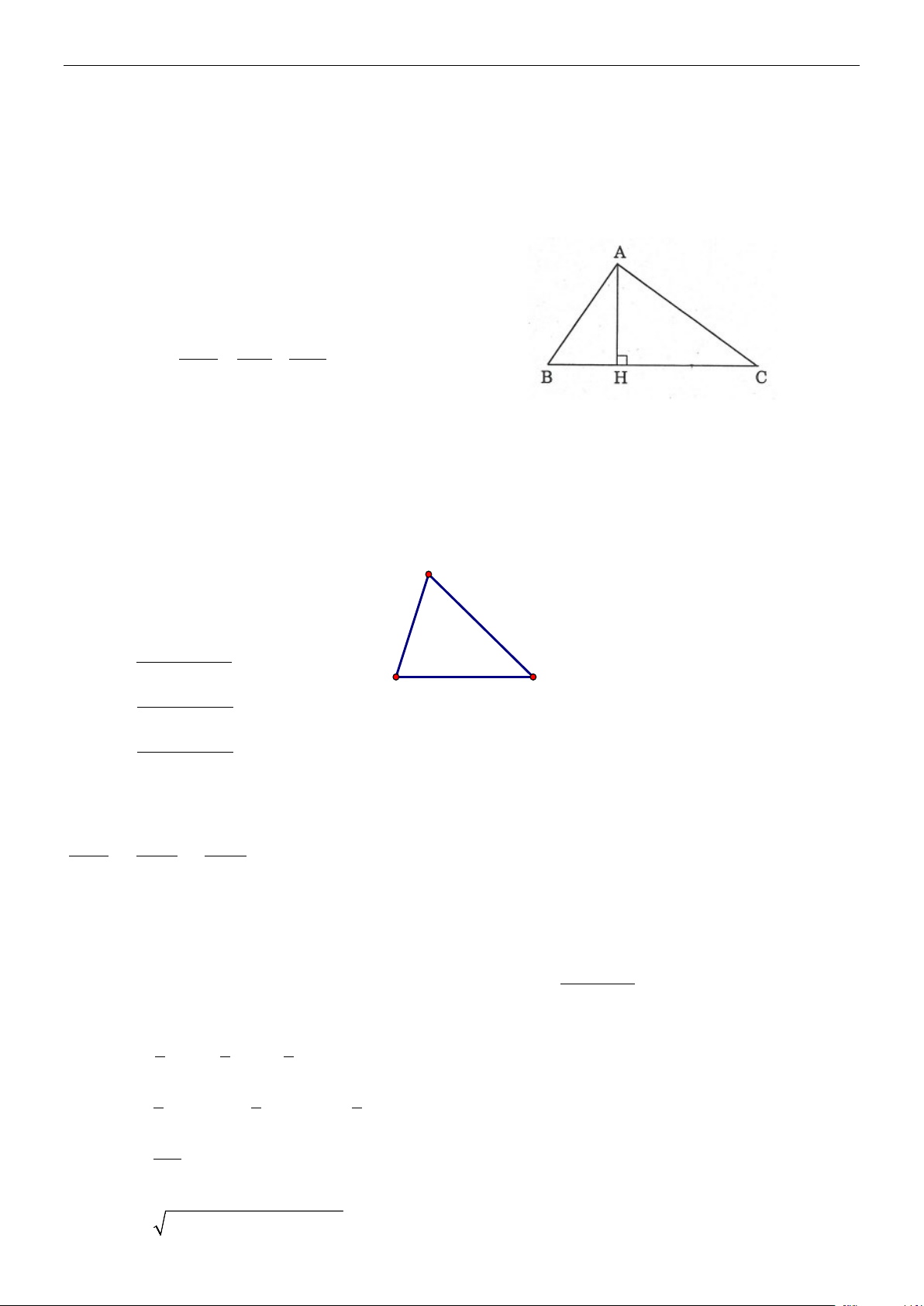
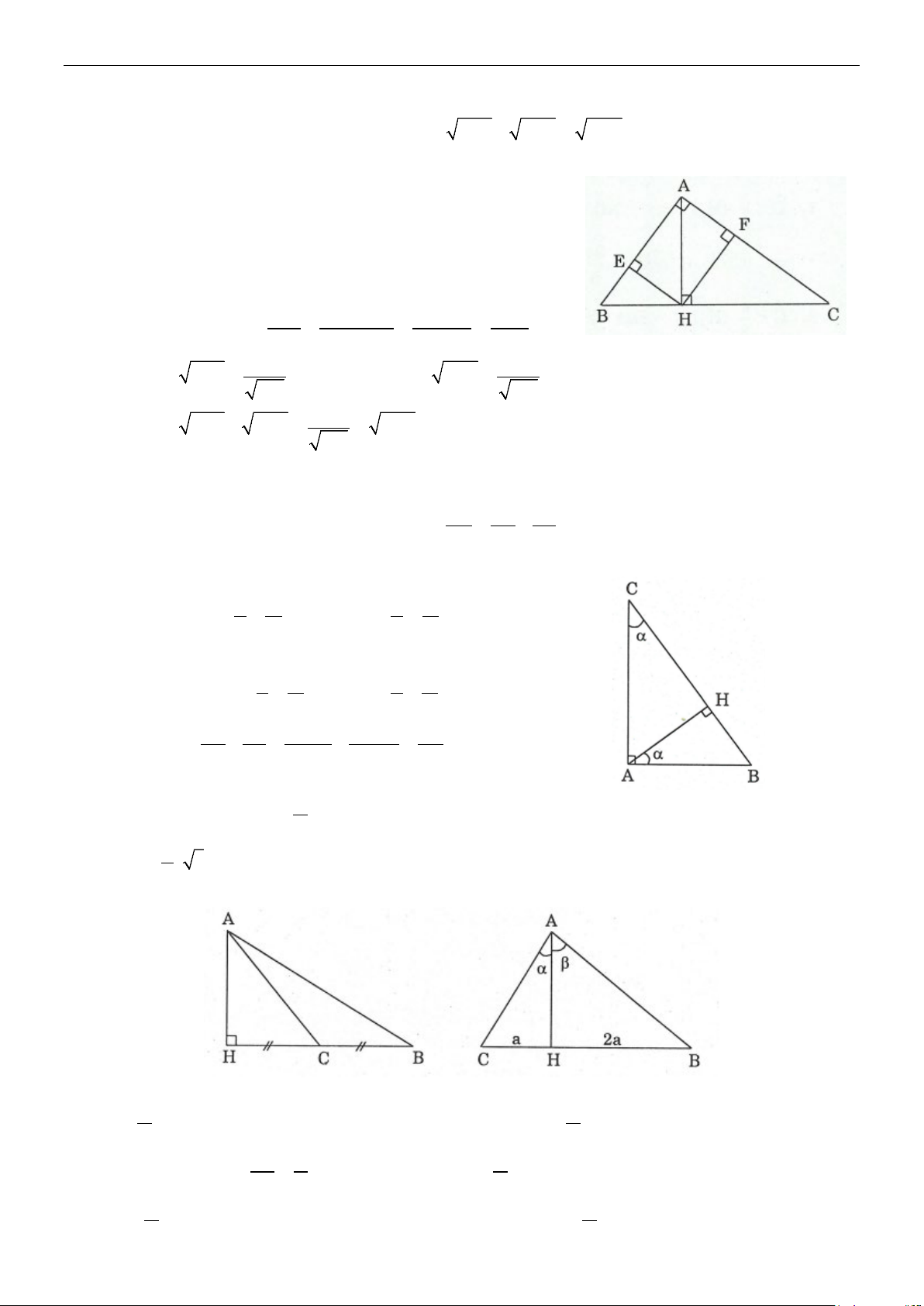
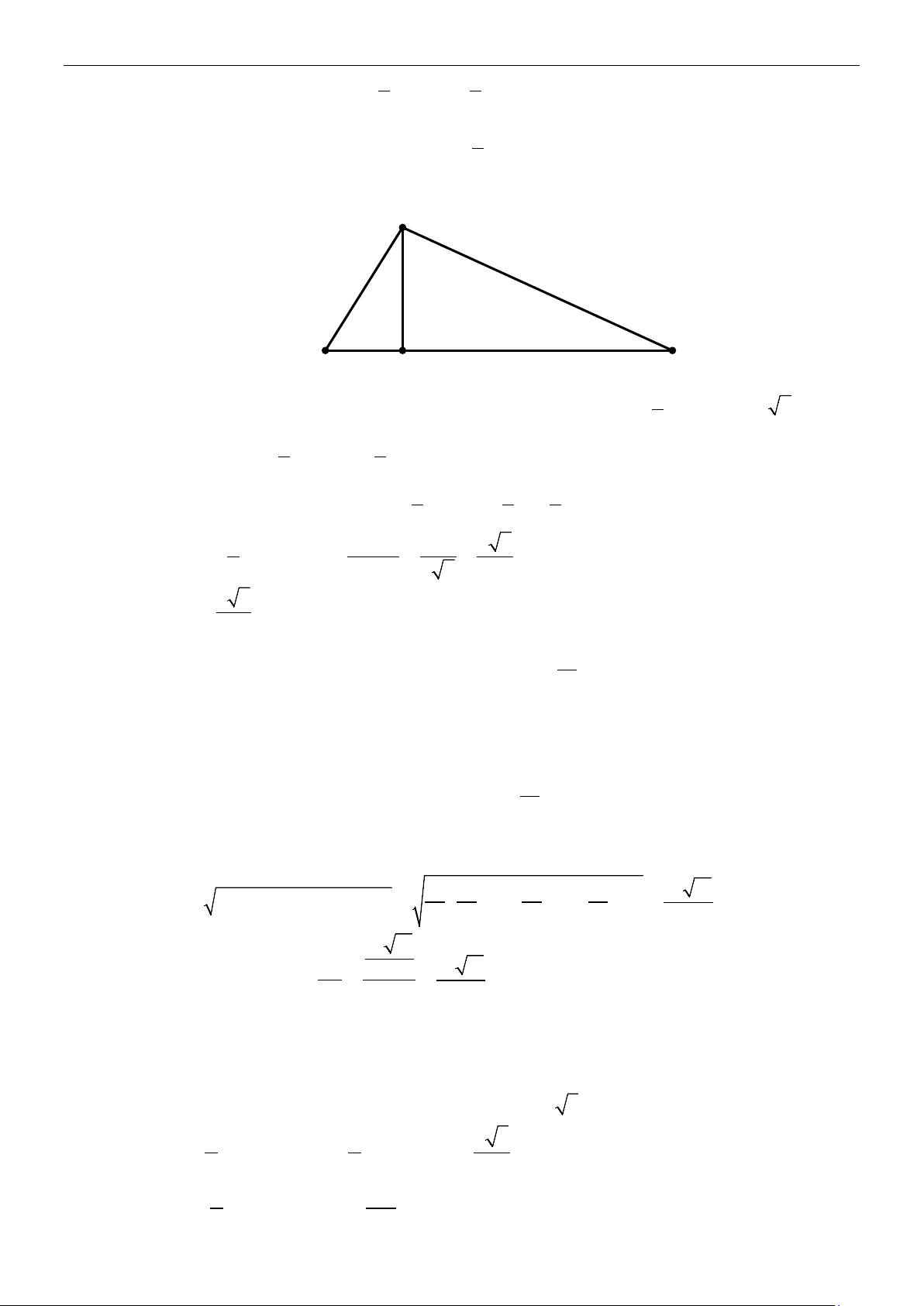
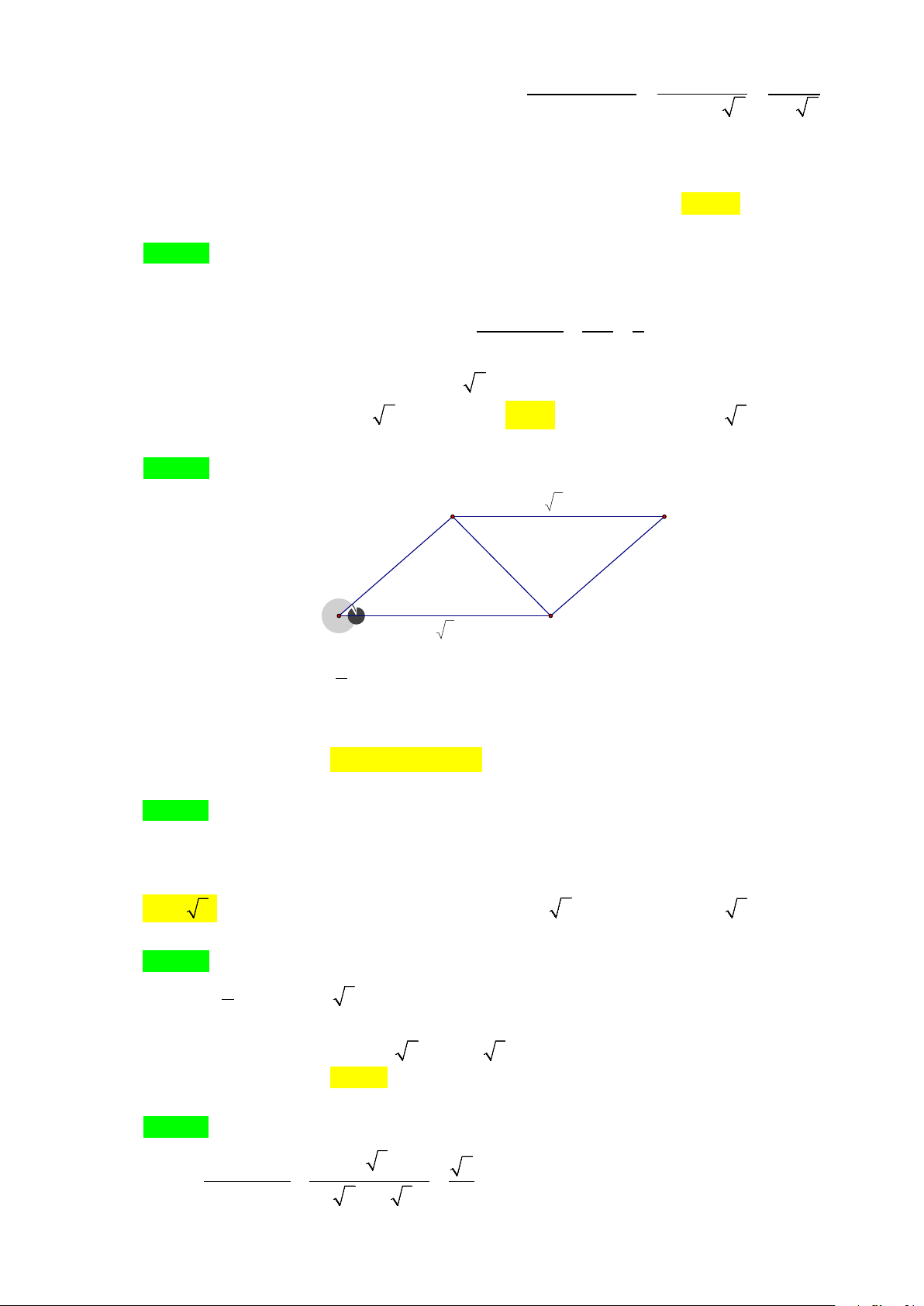
Cho tam giác ABC vuông tại ,
A AH là đường cao.
Ta có các hệ thức sau: 2 2 2
BC + AB + AC 2
AB = BH.BC 2
AC = CH.BC 2 AH = . HB HC
AH.BC = A . B AC 1 1 1 = + 2 2 2 AH AB AC
AC = BC.sin B ;
AB = BC.sin C
AC = BC.cosC ; AB = BC.cos B
AB = AC.tgC = AC.cotgB AC = A . B tgB = A . B cotgC
II. Các hệ thức lượng trong tam giác:
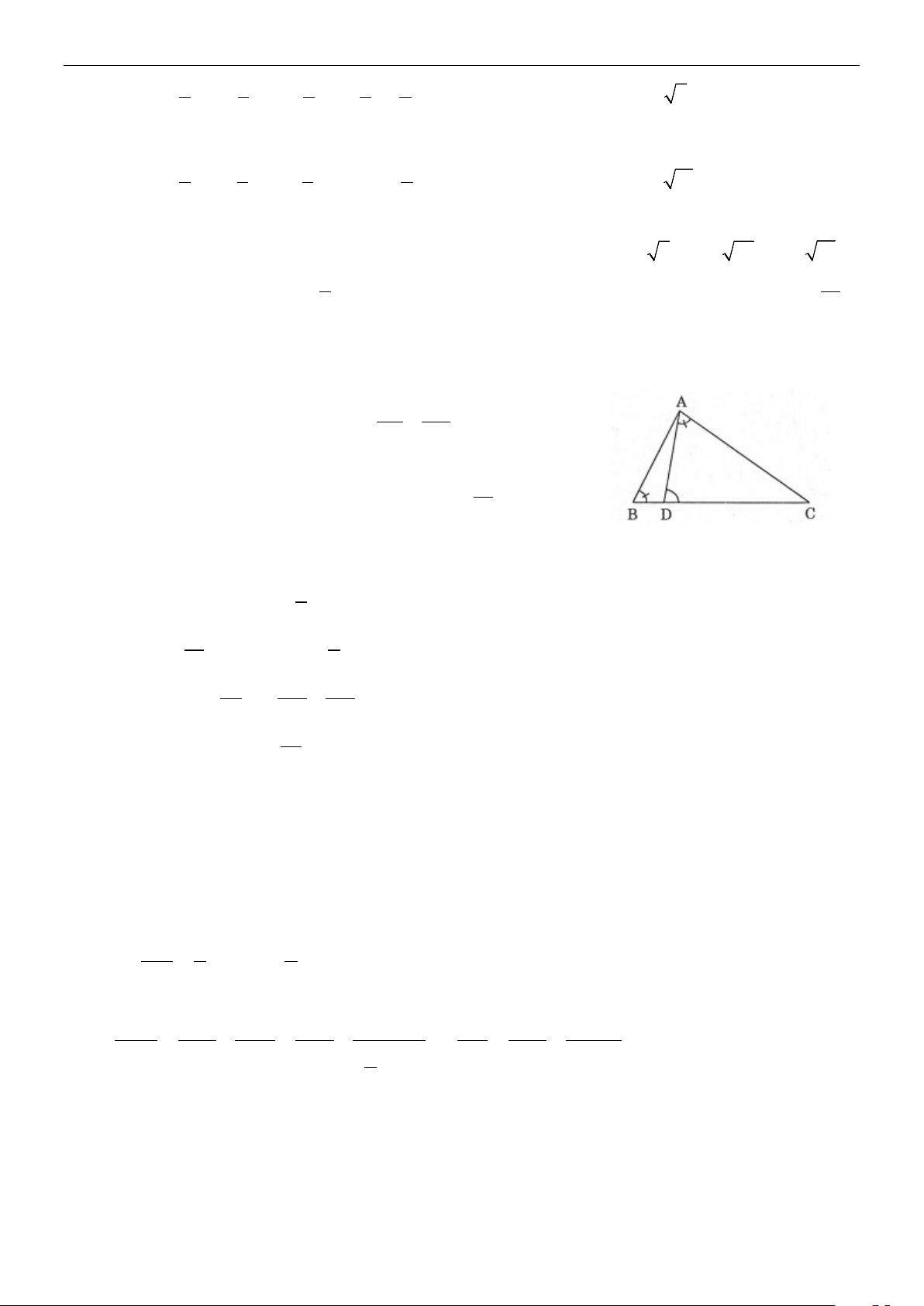
1. Định lí côsin: Trong tam giác ABC với BC a, AC b và AB c . Ta có :
a2 b2 c2 bc 2 .cos A A
b2 c2 a2 ca 2 .cos B
c2 a2 b2 ab 2 .cosC Hệ quả: c b
b2 c2 a2 cos A bc 2 C
c2 a2 b2 B a cos B ca 2 Hình 2.6
a2 b2 c2 cosC ab 2
b) Định lí sin : Trong tam giác ABC với BC a, AC b , AB c và R là bán kính đường tròn ngoại tiếp. Ta có : a b c R 2 sin A sin B sinC
c) Diện tích tam giác
Với tam giác ABC ta kí hiệu h , h , h là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, a b c AB; R, r
lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác;
a b c p
là nửa chu vi tam giác; S là 2
diện tích tam giác. Khi đó ta có: S = 1 1 1
ah bh ch a b c 2 2 2 = 1 1 1
bc sin A ca sin B ab sinC 2 2 2 = abc R 4 = pr
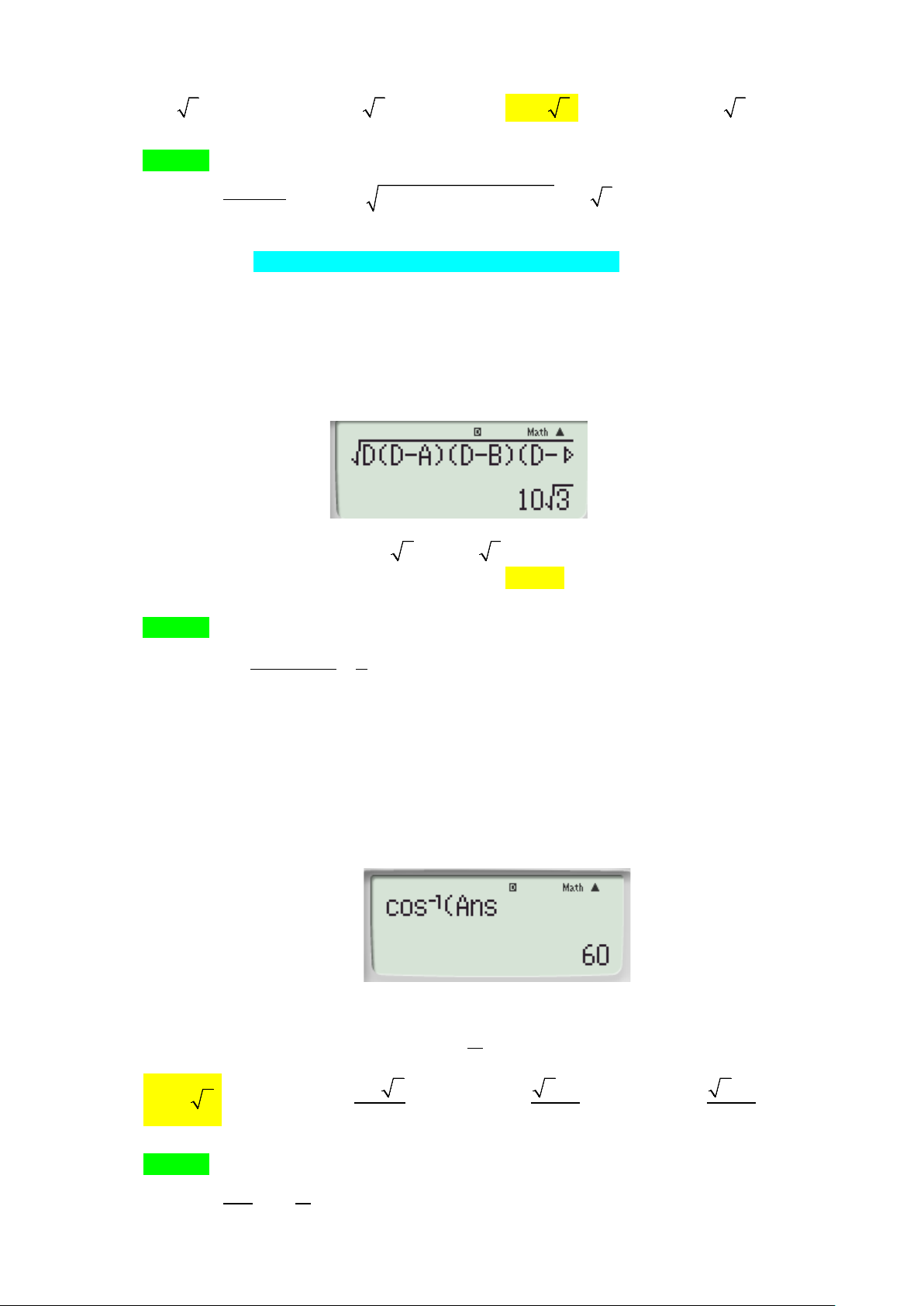
= p(p a)(p b)(p c) (công thức Hê–rông) Trang 1/9 B. VÍ DỤ MINH HỌA
Vấn đề 1. CÁC BÀI TOÁN VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài toán: Cho biết một số yếu tố của tam giác vuông. Tính các yếu tố còn lại
Phương pháp: Dùng các hệ thức lượng trong tam giác vuông
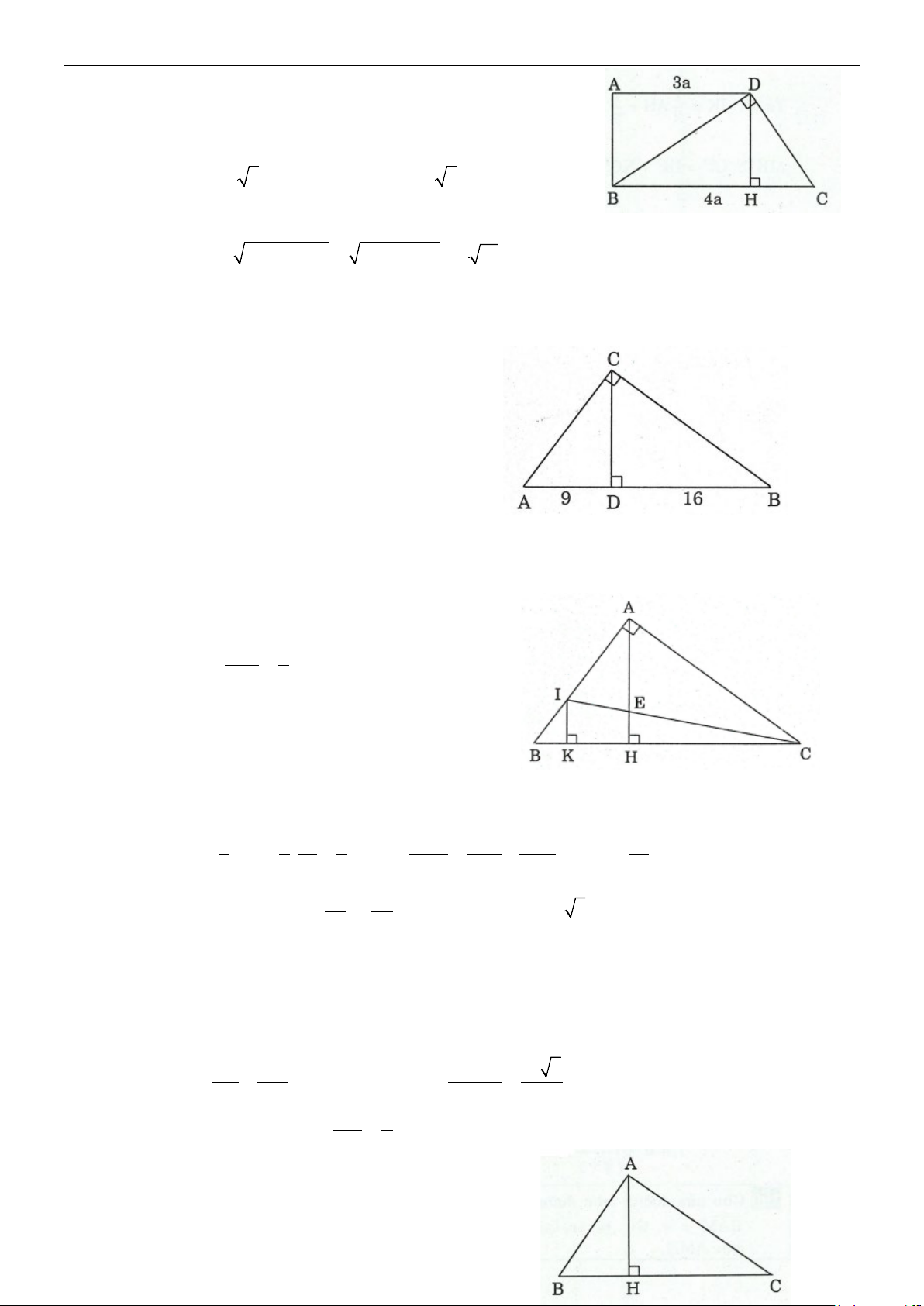
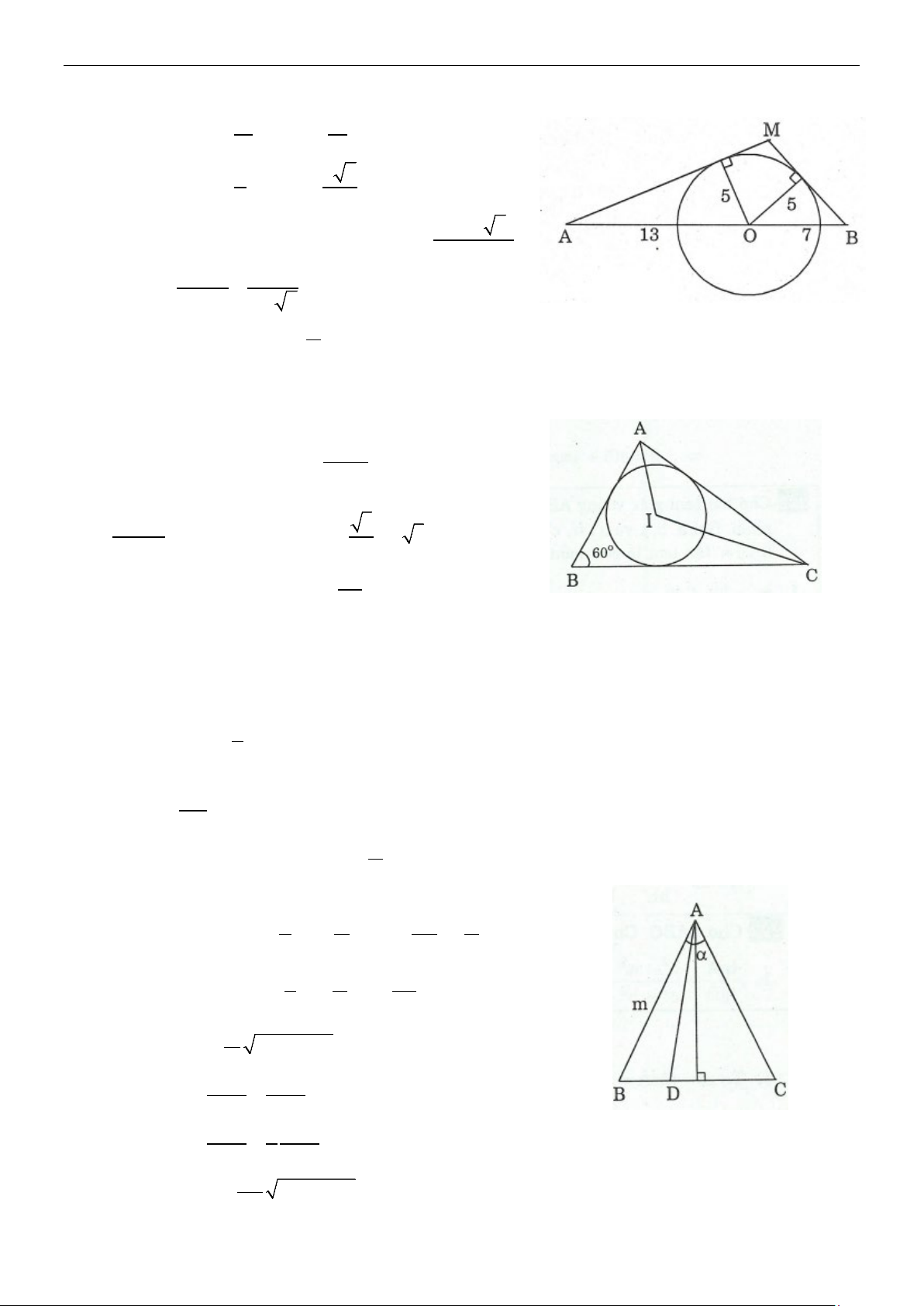
Ví dụ 1: Cho A ∆ BC vuông tại ,
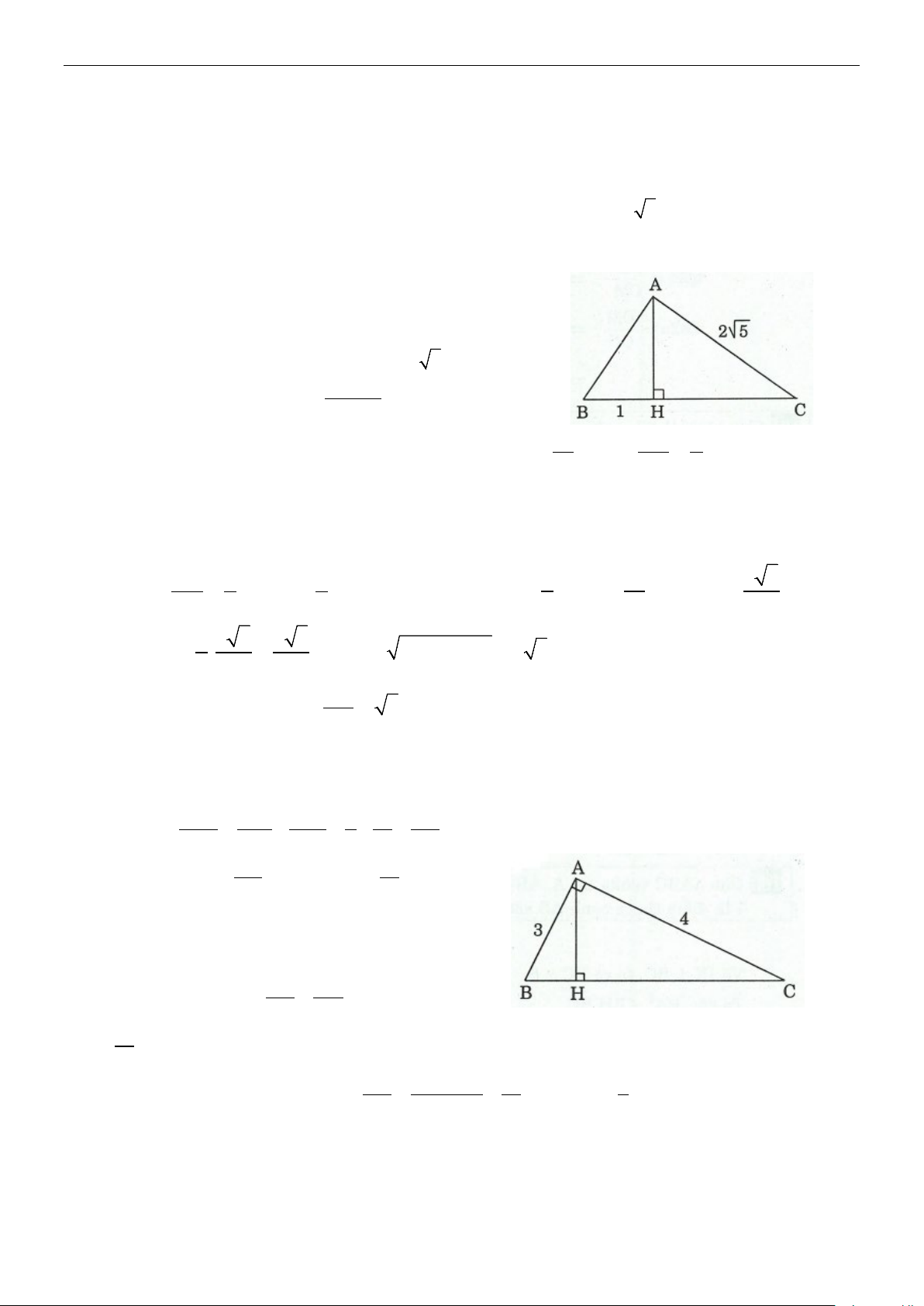
A AH là đường cao và có BH =1, AC = 2 5.
Tính AB, BC, AH. Lời giải Ta có: 2 CA = .
CB CH = CH (CH + HB) ⇒
20 = CH (CH +1) ⇒ CH = 4 ⇒
BC + BH + HC =1+ 4 = 5 2
AB = BH.BC ⇒ AB = 5 A . B AC AH = = 2. BC Ví dụ 2: AB
Tam giác ABC vuông tại A có đường cao 12 AH = cm và 3
= . Tính bán kính R 5 AC 4
của đường tròn ngoại tiếp tam giác ABC . Lời giải
Tam giác ABC vuông tại ,
A có đường cao AH ⇒ 2 . AB AC = AH (∗). 2 Mặt khác AB 3 3 3 12 8 3
= ⇔ AB = AC thế vào (∗), ta được 2 AC = ⇔ AC = . AC 4 4 4 5 5 Suy ra 3 8 3 6 3 2 2 AB = . =
⇒ BC = AB + AC = 2 3. 4 5 5
Vậy bán kính cần tìm là BC R = = 3 c . m 2
Ví dụ 3: Cho A ∆ BC vuông tại ,
A có đường cao AH ( H ở trên BC). Tính AH, CH, BH, BC nếu biết AB = 3, AC = 4. Lời giải Ta có: 1 1 1 1 1 25 = + = + = 2 2 2 AH AB AC 9 16 144 ⇒ 2 144 AH = ⇒ 12 AH = 25 5 Xét A ∆ HC : 2 2 2
AC = AH + HC ⇔ 2 2 2
HC = AC − AH ⇔ 2 144 256 HC =16 − = ⇒ 25 25 16 HC = 5 − A ∆ BH : 2 2 2 144 225 144 81
BH = AB − AH = 9 − = = ⇒ 9 BH = 25 25 5 5 Ta có: 2 2 2
BC = AB + AC = 9 +16 = 25 ⇒ BC = 5.
Ví dụ 4: Cho hình thang ABCD với đường cao A .
B Biết rằng AD = 3a, BC = 4a, BDC = 90 .° Tính
AB, CD, AC. Lời giải
Vẽ DH ⊥ BC ( H ở trên BC) thì ADHB là hình chữ nhật nên Trang 2/9
BH = AD = 3a và AB = DH
Xét tam giác vuông BDC, ta có: 2 2 DH = .
HB HC = HB(BC − BH ) = 3a(4a − 3a) = 3a ⇒ DH = a 3 ⇒
AB = DH = a 3 Ta lại có: 2 2
DC = CH.CB = .4 a a = 4a Suy ra DC = 2 . a Ta lại có: 2 2 2 2
AC = AB + BC = 3a +16a = a 19.
Ví dụ 5: Cho A
∆ BC vuông tại C, CD là đường cao, DA = 9, DB =16.
Tính CD, AC, BC. Lời giải Ta có: 2 DC = . DA DB = 9×16 =144 ⇒ DC =12 Ta có: 2 AC = A . B AD = 25×9 ⇒ AC = 5×3 =15 Ta có: 2 CB = A . B DB = 25×16 = 400 ⇒ CB = 20.
Ví dụ 6: Cho A ∆ BC vuông tại ,
A AB = 3, AC = 4, AH là đường cao (H ∈ BC). Gọi I là điểm thuộc
cạnh AB sao cho AI = 2BI, CI cắt AH tại E. Tính CE. Lời giải
Vẽ IK ⊥ BC, ta có BC = 5. Ta có: 2
BA = BH.BC 2 ⇒ BA 9 BH = = BC 5 Ta có:
∆ vuông BKI ∽ ∆ vuông BHA ⇒ BK BI 1 = = ⇒ BH 3 BK = = BH BA 3 3 5 Và 3 22
CK = CB − BK = 5 − = 5 5 Ta có: 1 1 12 4 IK = AH = . = 1 1 1 12 vì AH = + ⇒ = 3 3 5 5 2 2 2 AH AB AC 5 2 IK ∆ C : 2 2 2 16 22 CI IK KC = + = + = 20 ⇒ CI = 2 5 25 5 144 2 Ta lại có: 2
AH = BH.HC ⇒ AH 25 144 16 HC = = = = BH 9 5.9 5 5
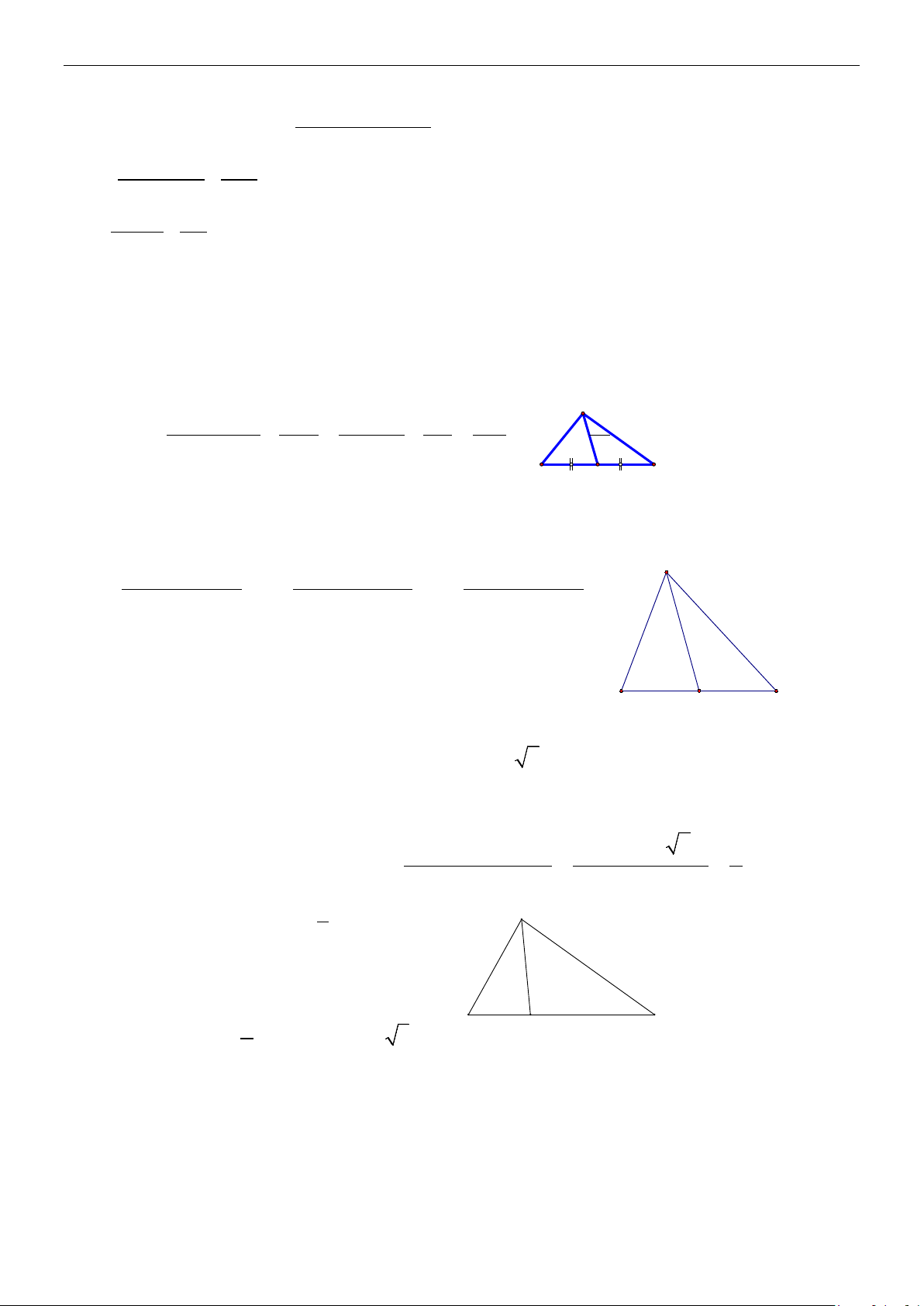
∆ vuông CHE ∽ ∆ vuông CKI nên ta có: CE CH = ⇒ CI.CH 16 5 EC = = . CI CK CK 11
Ví dụ 7: Cho A AB ∆ BC vuông tại , A 2
= . Đường cao AH = 6. AC 3
Tính HB, HC, AB, AC. Lời giải Ta có: 2 AB AH = = (vì A ∆ BC ∽ H ∆ C ) A 3 AC HC Trang 3/9 ⇒ 3 HC = AH = 9 2 Ta lại có: 2 AB BH = = 3 AC AH ⇒ 2 2
HB = AH = .6 = 4 3 3
AB = BH.BC = 4(4 + 9) = 2 13
AC = CH.BC = 9.13 = 3 13.
Ví dụ 8: Cho A
∆ BC vuông tại C, AD là đường phân giác trong, BD = x, CD = . y
Tính AB, BC, AC. Lời giải
Ta có: BC = a = x + y
Vì AD là phân giác nên ta có: 2 2 2 2 2 2 c x − − = ⇒ c x = ⇒ c b x y = b y 2 2 b y 2 2 b y 2 2 2 2 2 2 − + + ⇒ a x y = ⇒ 2 y (x y) y (x y) b = = 2 2 b y 2 2 x − y x − y ⇒ + = . x + y b y ; x x y c = b = x x − y y x − y
Vậy: BC = x + y ; x + y AC = y ; x − y x + y AB = x . x − y
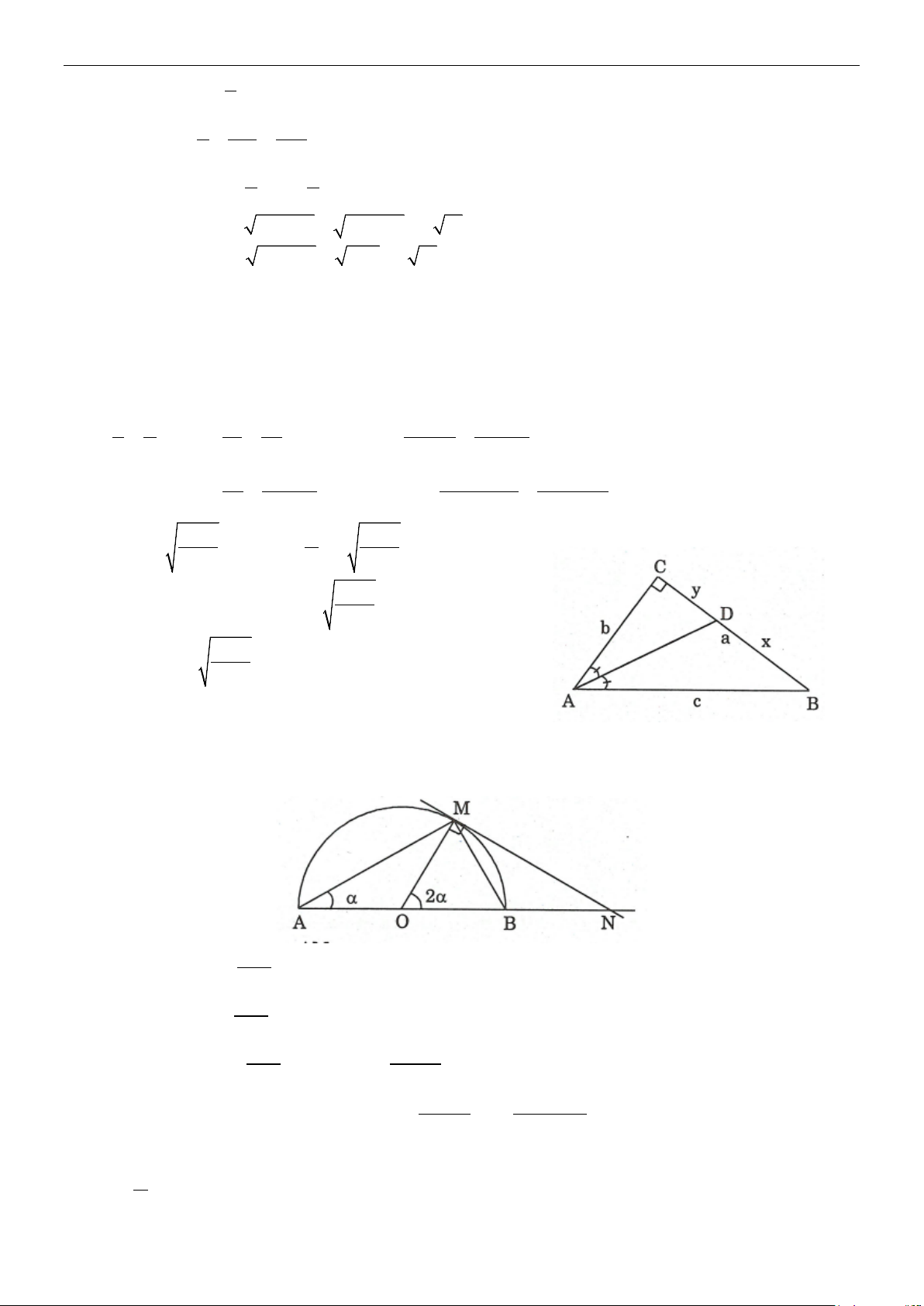
Ví dụ 9: Cho nửa đường tròn đường kính AB = 2R, m chạy trên đường tròn, đặt
BAM = α, tiếp tuyến
tại M cắt AB tại N. Hãy tính các cạnh của tam giác AMN. Lời giải Ta có: cos AM α =
⇒ AM = 2R cosα AB tg2 MN α =
⇒ MN = Rtg2α OM cos 2 OM α = ⇒ R ON = ON cos 2α + α ⇒ R 1 cos 2 AN R R = + = . cos 2α cos 2α
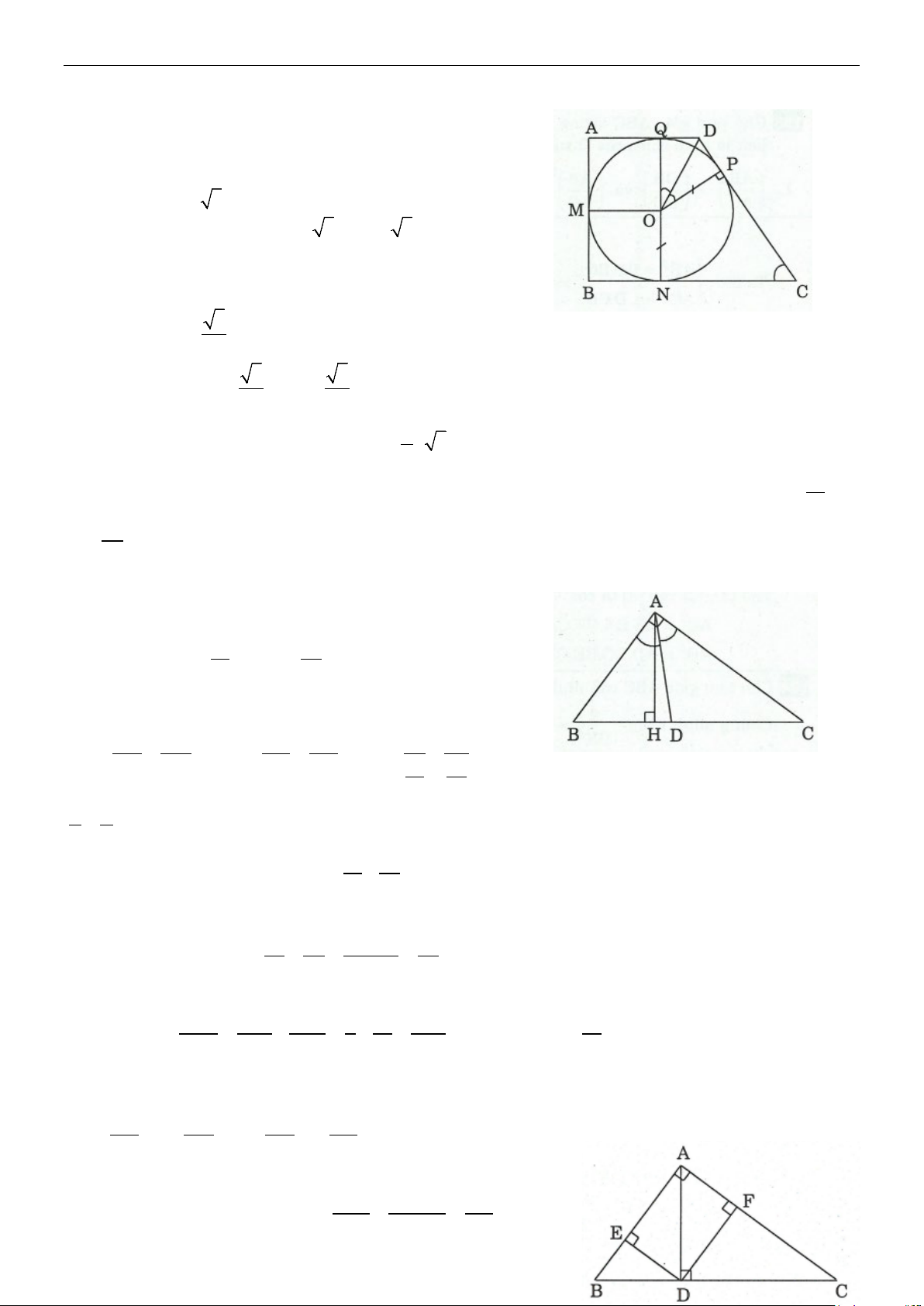
Ví dụ 10: Cho hình thang vuông ABCD, đường cao A .
B Ngoại tiếp đường tròn đường kính r, cho π
C = . Tính các cạnh của hình thang. 3 Lời giải Trang 4/9
Ta có: AB = 2r
Gọi M , N, P, Q là các tiếp điểm như hình vẽ. Vì ON = OP
⇒ OC là phân giác góc BCD ⇒ N
∆ OC là nửa tam giác đều ⇒ NC = r 3
⇒ BC = BN + NC = r + r 3 = r(1+ 3) Ta có:
ADC =120° (vì C = 60 ) ° ⇒ QDO ∆
là nửa tam giác đều (vì QDO = 60 ) ° ⇒ 3 QD = r ⇒ 3 3 3
AD = AQ + QD = r + r = r 1+ 3 3 Ta có: 4
DC = DP + PC = DQ + CN = r 3. 3
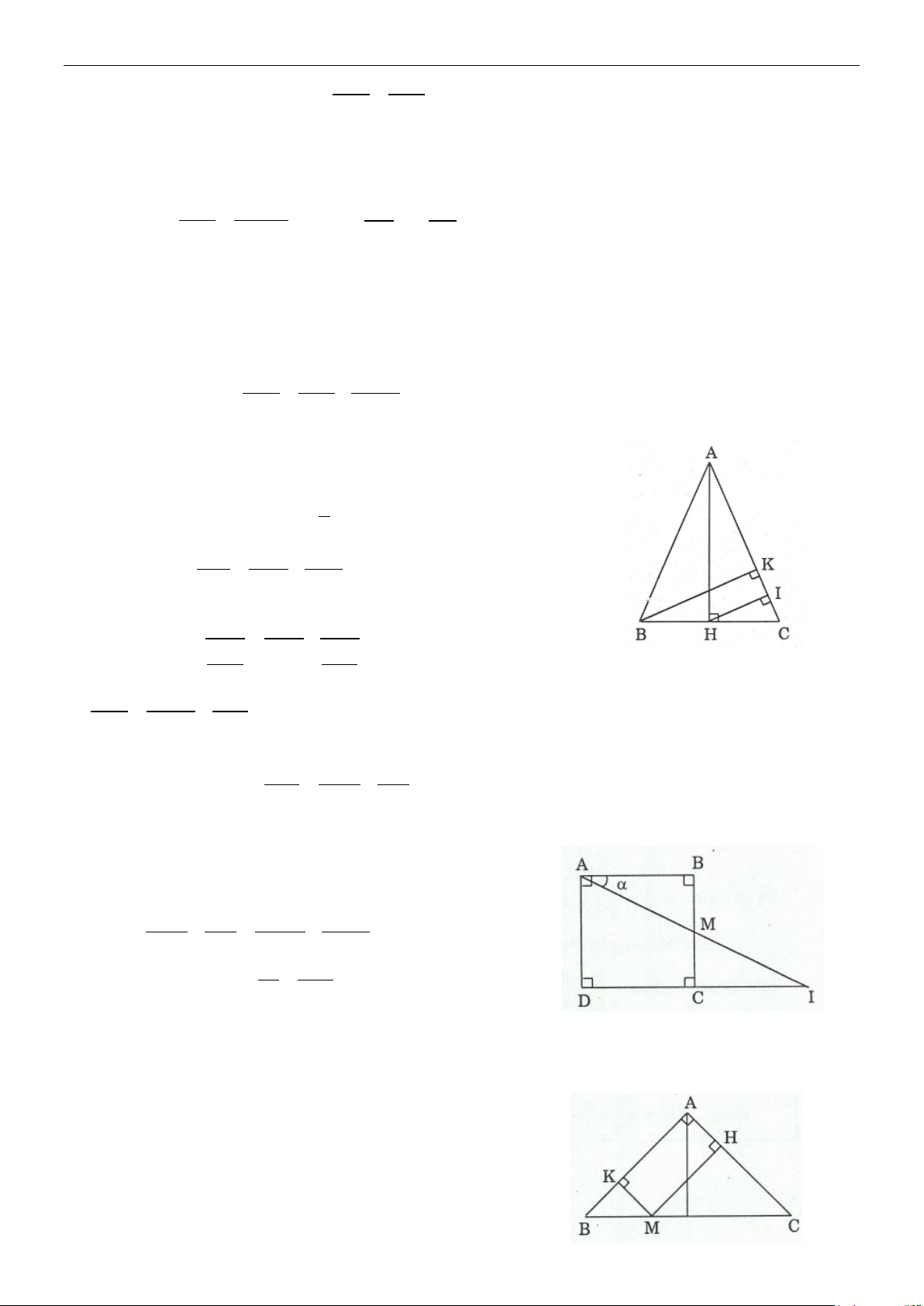
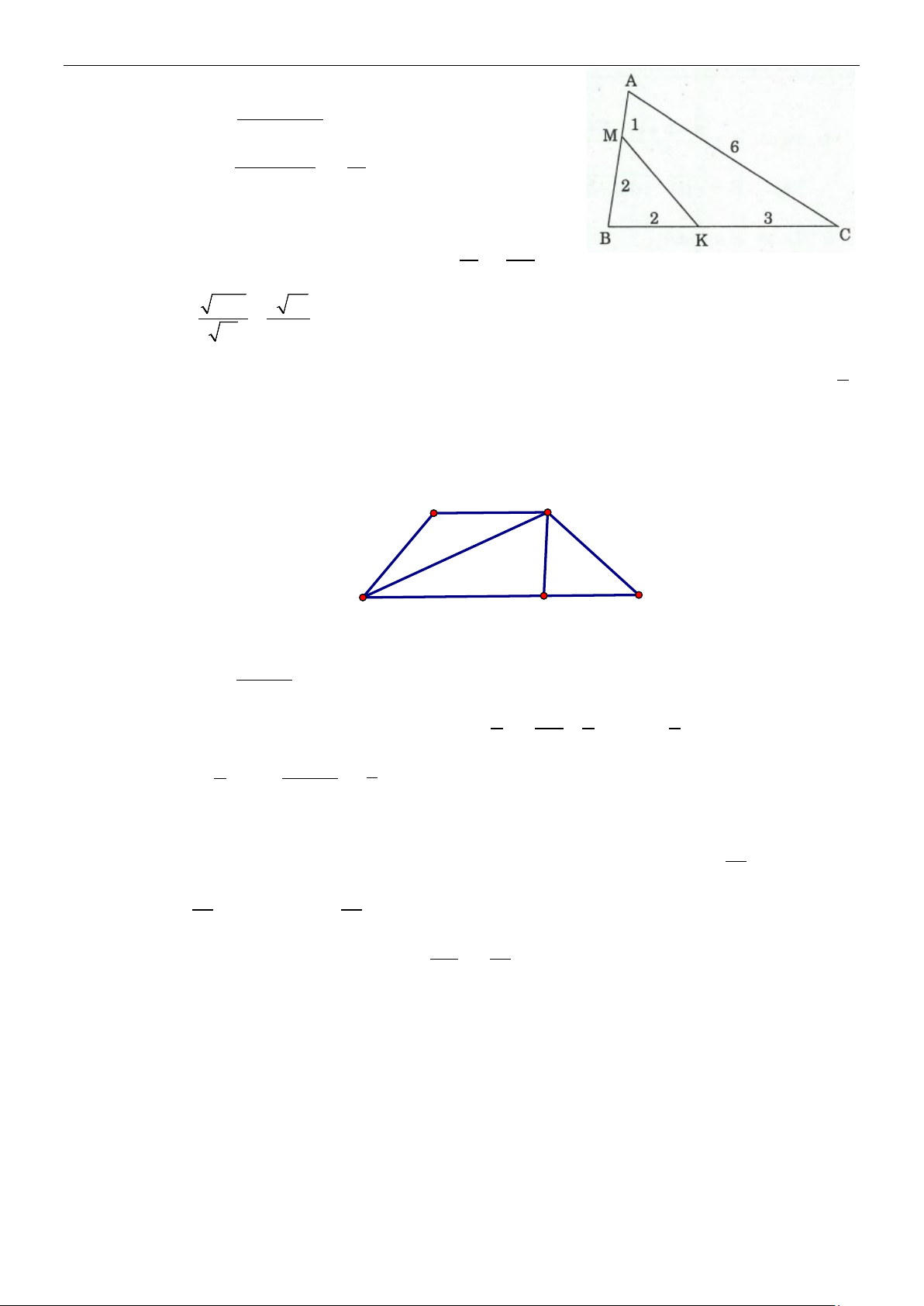
Ví dụ 11: Đường phân giác trong góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài bằng 15 và 7
20 . Tính các cạnh góc vuông và đường cao phát xuất từ đỉnh góc vuông. 7 Lời giải
Gọi AD là phân giác trong của góc A Giả sử 15 DB = ; 20 CD = . 7 7
Đặt AB = x ; AC = y (x, y > 0)
Do tính chất phân giác, ta có: AB DB = ⇒ AB AC = ⇒ x y = ⇒ AC DC BD CD 15 20 7 7 x y = (1) 3 4 Mặt khác 15 20
BC = BD + DC = + = 5 7 7 và 2 2 2
AB + AC = BC ⇒ 2 2 x + y = 25 (2) 2 2 2 2 2 x = 9 x = 3 Từ (1), (2) suy ra x y x + y 25 = = = =1 ⇒ ⇔ 9 16 25 25 2 y =16 y = 4
Do đó AB = 3 ; AC = 4 Ta có: 1 1 1 1 1 25 = + = + = Suy ra 12 AH = . 2 2 2 AH AB AC 9 16 9.16 5
Ví dụ 12: Cho tam giác ABC vuông tại ,
A D là hình chiếu của A lên BC, E, F lần lượt là hình chiếu
của D xuống AB và AC. Chứng minh rằng: 2 3 1. AB DB = AB BE và = b) 3
AD = BC.E . B CF. AC DC AC CF Lời giải 2 AB = B . D BC 2 Ta có: AB B . D BC BD ⇒ = = 2 AC = . CD CB 2 AC . CD CB CD Trang 5/9 4 2
Từ kết quả trên, ta suy ra: AB BD = 4 2 AC CD
Mặt khác, các tam giác vuông ADB và ADC cho ta: 2
DB = BE.BA (1) 2
DC = CF.CA (2) 4 3 Nên AB BE.BA = ⇒ AB BE = . 4 AC CF.CA AC CF
b) Tam giác vuông ABC cho: 2 AD = . DB DC ⇒ 4 2 2
AD = DB .DC (3)
Thế (1), (2) vào (3) ta có: 4
AD = BE.B .
ACF.CA = A .
B AC.BE.CF 4 AD = A .
D BC.BE.CF ⇒ 3
AD = BC.BE.CF.
Ví dụ 13: Cho tam giác ABC cân đỉnh .
A Vẽ các đường cao AH, BK. Chứng minh rằng: 1 1 1 = + . 2 2 2 BK BC 4AH Lời giải
Trong ∆ vuông AHC, vẽ đường cao HI
Xét tam giác vuông BKC, ta có: HI // BK ⇒ 1 HI = BK (1) HB = HC 2 Ta lại có: 1 1 1 = + (2) 2 2 2 HI AH HC Thế (1) vào (2) ta có: 1 1 1 = + ⇒ 2 2 2 BK AH BC 4 4 1 1 1 = + . 2 2 2 BK 4AH BC
Ví dụ 14: Cho hình vuông ABC .
D Đường thẳng qua ,
A cắt các cạnh BC tại M và đường thẳng CD tại
I. Chứng minh rằng: 1 1 1 = + . 2 2 2 AB AM AI Lời giải
Ta đặt AB = a; MAB = α
⇒ AM cosα = AB
và AI.sinα = AD 2 2 α α ⇒ 1 1 cos sin + = + 2 2 2 2 AM AI a a 1 1 = = (đpcm). 2 2 a AB
Ví dụ 15 Cho A
∆ BC vuông cân tại ,
A M là một điểm trên cạnh huyền BC. Chứng minh rằng: 2 2 2
MB + MC = 2MA . Lời giải
Ta dựng MH ⊥ AC; MK ⊥ AB Ta có: 2 2 2 2 2 2
MB + MC = KB + KM + HC + HM 2 2 2
= 2KM + 2HM = 2KH ⇒ 2 2 2
MB + MC = 2MA . Trang 6/9 Ví dụ 16: Cho A ∆ BC vuông tại ,
A dựng đường cao AH. Trong A
∆ HB dựng đường cao HE, trong A
∆ HC dựng đường cao HF. Chứng minh: 1. 2 2 2 2
BC = 3AH + BE + CF b) 3 2 3 2 3 2
BE + CF = BC . Lời giải 1. Ta có: 2 2
BC = (BH + HC) 2 2 = BH + HC + 2 . HB HC 2 2 2 2 2
= BE + HE + CF + HF + 2HA 2 2 2
= BE + CF + 3HA . 2 2 4 3 b) Ta có: 2 2 BA (BE.B ) = . A BH BH BE BE = = = 2 BA BH.BC BH.BC BC ⇒ 3 2 BH BE = , tương tự ⇒ 3 2 CH CF = 3 BC 3 BC ⇒ 3 2 3 2 BC 3 2 BE + CF = = BC . 3 BC
Ví dụ 17: Cho A ∆ BC, A ∆ ′B C
′ ′ đồng dạng, A ∆ BC vuông tại , A A ∆ ′B C
′ ′ vuông tại A .′ Hãy chứng minh:
1. aa′ = bb′ + cc′ b) 1 1 1 = + .
hh′ bb′ cc′ Lời giải ′ ′ Ta có: sin c c α = = ; cos b b α = = a a′ a a′ ⇒ 2 2
cc′ + bb′ = aa (′sin α + cos α) = aa′ ′ ′ Mặt khác: sin h h α = = ; cos h h α = = b b′ c c′ 2 2 α α ⇒ 1 1 sin cos 1 + = + = . bb′ cc′ . h h′ . h h′ hh′ Ví dụ 18: π Cho A
∆ BC có A = , AH là đường cao, BH = 2a, CH = .
a Chứng minh rằng: 3 1
AH = a ( 3 −1). 2 Lời giải
Ta chia làm 2 trường hợp: π π
a) C ≥ (H ) ⇒
AC > HC = CB ⇒ > CBA CAB = . 1 2 3 π π π ⇒ + 2 CBA CAB >
> . Mâu thuẫn với ACB ≥ 3 3 2 π π
b) C < (H ) Đặt AH = ; x HAC = α; HAB = β; α + β = 2 2 3 Trang 7/9 3a tgα + tgβ x 3 3 = tg(α + β ) ax = = = 2 2 2 1− tgαtgβ 2a x − 2 1 a − 2 x ⇒ 1
x = a ( 3 −1). 2
Ví dụ 19: Góc vuông
xOy, có Ox tiếp xúc với đường tròn (I; R) tại ,
A sao cho OA = a, Oy cắt đường
tròn đó tại B và C. Chứng minh rằng: a) 1 1 1 + = b) 2 2 2
AB + AC = 4R . 2 2 2 AB AC a Lời giải
a)Gọi B′ là điểm đối xứng của B qua . O Đường thẳng B A
′ cắt đường tròn tại điểm thứ hai là C .′ Ta có: = BAO ACB ⇒ C
∆ AB′ vuông tại A ⇒ 1 1 1 1 1 = + = + . 2 2 2 2 2 OA AC B A ′ AC BA
b) Ta có: = = ICA IAC BCA π Do
CAC′ = ⇒ C, I, C′ thẳng hàng 2 ⇒ 2 2 2 2 2 2
AB + AC = AC + C A ′ = C C ′ = 4R .
Vấn đề 2: HỆ THỨC LƯỢNG TRONG TAM GIÁC THƯỜNG 1-Định lí côsin
Bài toán 1: Biết hai cạnh và góc xen giữa, tính độ dài cạnh còn lại
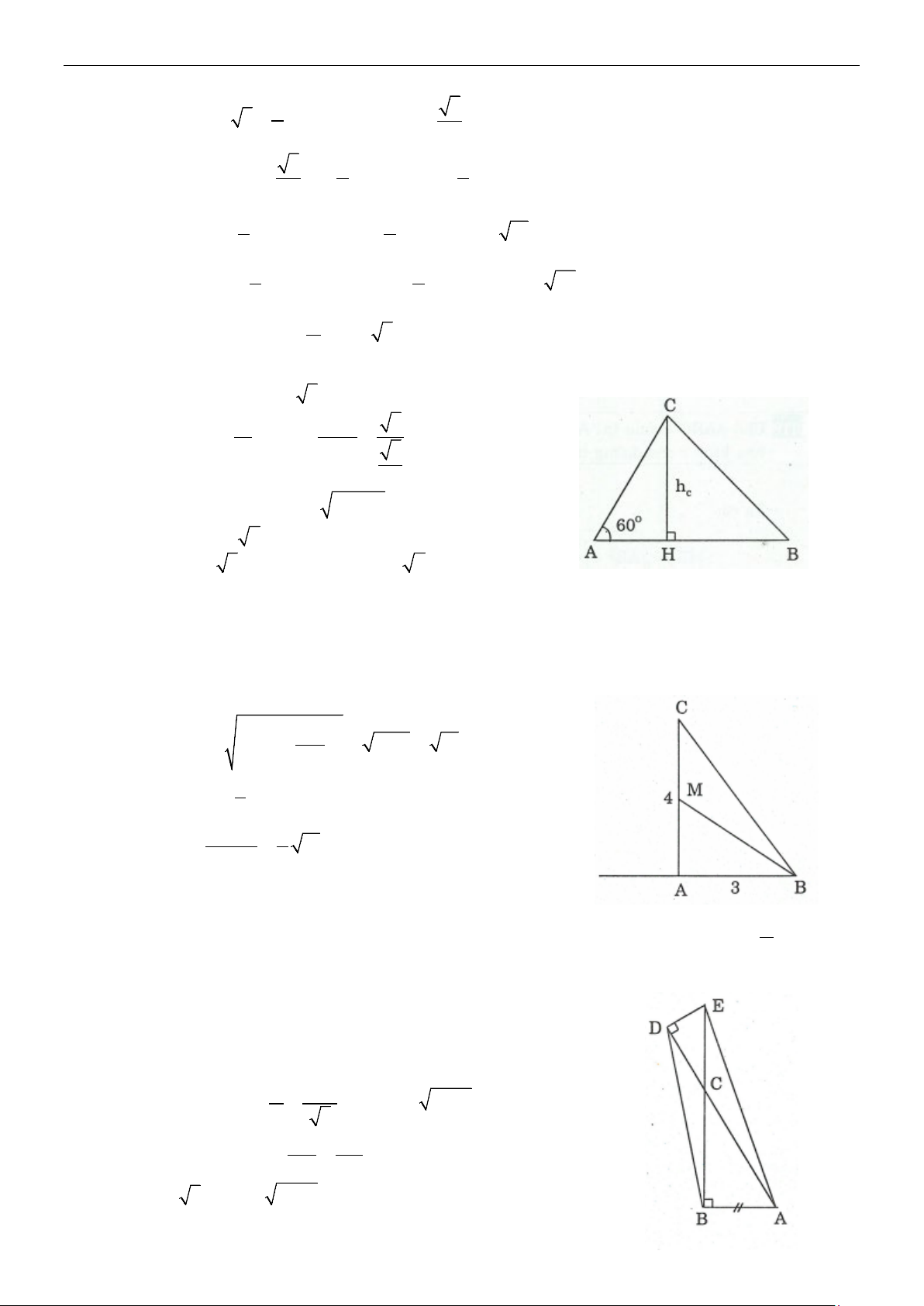
Phương pháp: Dùng định lí côsin Ví dụ 1: 4
ho tam giác ABC có AB = 2, AC = 5 và os
c A = . Tính cạnh BC . 5 Lời giải Ta có: 2 2 2
BC = AB + AC − 2A . B AC.cos A 4 2 2 = 2 + 5 − 2.5. = 21 5 ⇒ BC = 21
Ví dụ 2: Cho tam giác ABC có BC = 2, AC = 2 2 , 2 cos(A + B) = −
. Độ dài cạnh AB là 2 Lời giải Do 2 2 cos(A + B) = − ⇒ os c C= . 2 2
Áp dụng định lý côsin trong tam giác có: 2 2 2
AB = BC + AC − 2BC.AC.cosC = + ( )2 2 2 2 2 2 − 2.2.2 2. = 4 ⇒ AB = 2 . 2
Ví dụ 3: Cho tam giác ABC có ba góc nhọn và có AB = 3, BC = 3 3 , 1 sin B = . Tìm độ dài cạnh 3
AC ( chính xác đến hàng phần trăm) Lời giải Trang 8/9 2 Ta có cos B
> 0 ( vì B nhọn), do đó 2 1 6
cos B = 1− sin A = 1− = . 3 3
Áp dụng định lý côsin trong tam giác có: 2 2 2
AC = AB + BC − 2A . B BC.cos B AC = + ( )2 2 2 6 3 3 3 − 2.3.3 3.
= 36 −18 2 ⇒ AC 3,25 . 3
Ví dụ 4: : Tam giác ABC có a = 8, c = 3, B = 60°. Tính độ dài cạnh b Lời giải 2 2 2
b = a + c − 2accos B 2 2
= 8 + 3 − 2.8.3cos60° = 49 ⇒ b = 7 .
Ví dụ 5: Trong tam giác ABC có AB = 2cm , AC =1cm , A = 60°. Tính độ dài cạnh BC Lời giải Ta có 2 2 2
BC = AB + AC − 2A . B AC.cos A 2 2 2
⇒ BC = 2 +1 − 2.2.1.cos60° 2 ⇒ BC = 3 Vậy BC = 3 cm .
Ví dụ 6: Cho tam giác ABC có 0
C = 30 , cạnh a = 8, cạnh b = 6. Tính cạnh c ( làm tròn đến hàng phần trăm) Lời giải
Theo định lí côsin, ta có 2 2 2
c = a + b − 2 . ab cosC 2 2 0 = 8 + 6 − 2.8.6.cos30 2 2 0
c = 8 + 6 − 2.8.6.cos30 4,11.
Ví dụ 7: Cho hình thoi ABCD cạnh bằng 1 cm và có
BAD = 60° . Tính độ dài cạnh AC .
A. AC = 3. B. AC = 2. C. AC = 2 3. D. AC = 2. Lời giải B
Do ABCD là hình thoi, có = ° ⇒ BAD 60 ABC =120° .
Theo định lí côsin, ta có A C 2 2 2 = + − AC AB BC 2. . AB BC.cos ABC 2 2 D
= 1 +1 − 2.1.1.cos120° = 3 ⇒ AC = 3
Ví dụ 8: Cho A
∆ BC có 2 trung tuyến BM = 6; CN = 9 và hợp với nhau một góc 120 .°
Tính các cạnh A ∆ BC. Lời giải
Gọi G là trọng tâm của A ∆ BC. +Trường hợp 1: BGC =120°
Áp dụng định lí côsin trong GB ∆ C 2 2 2
BC = GB + GC − 2 . GB GC.cos120° 2 2 ⇒ 2 2 2 2 2 1 a 6 9 2 .6. 9 = + − − = 4.19 ⇒ a = 2 19 3 3 3 3 2 G ∆ MC : 2 2 2 = + − MC GM GC
2GM.GC.cosCGM 2 2 1 2 1 2 2 b = m + m − m m ° b c 2 b. c cos 60 4 3 3 9 Trang 9/9 2 2 1 2 1 2 4 1 b = 6 + 9 − 6.9 ⇒ 2 b = 7.16 ⇒ b = 4 7 4 3 3 9 2 B ∆ GN : 2 2 2 = + − NB GB GN 2B . G GN.cos BGN 2 2 1 2 1 1 1 c = 6 + 9 − 2.4.3. ⇒ 2 c = 4.13 ⇒ c = 2 13. 4 3 3 2 + Trường hợp 2: BGC = 60°
Giải tương tự như trên ta có kết quả: a = 2 7; b = 2 34; c = 2 19.
Ví dụ 9: Cho A ∆ BC có 5
cos A = . Điểm D thuộc cạnh BC sao cho =
ABC DAC, DA = 6, 16 BD = . 9 3 Tính chu vi A ∆ BC. Lời giải Do = ABC DAC ⇒ C ∆ AD ∽ C ∆ BA ⇒ CA CD = CB CA ⇒ 2 CA = . CB CD
Đặt: x = DC ⇒ 2 16 CA x x = + . 3
Theo định lí côsin ta có 2 2 2 = + − CA AD DC 2A .
D cos D (vì = D BAC ) 1 1 2 2 5
CA = 36 − x −12 . x 9 Vậy 2 16 2 + = + 36 − 20. x x x x ⇒ x = 3, 3 3 25 AC = 5, BC = , AD AC = ⇒ AB =10 3 AB BC Do đó chu vi 70 A ∆ BC = . 3
Ví dụ 10: Tam giác ABC vuông tại A, đường cao AH = 32 cm . Hai cạnh AB và AC tỉ lệ với 3
và 4. Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu? Lời giải
Do tam giác ABC vuông tại A, có tỉ lệ 2 cạnh góc vuông AB : AC là 3: 4 nên AB là cạnh nhỏ nhất trong tam giác. Ta có AB 3 4 = ⇒ AC = AB . AC 4 3 Trong ABC ∆
có AH là đường cao 1 1 1 1 1 1 1 9 ⇒ = + = + ⇔ = +
⇒ AB = 40. Chọn B. 2 2 2 2 2 2 2 AH AB AC AB 4 2 32 AB 16AB AB 3
Ví dụ 11: Tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc
MPE, EPF, FPQ bằng nhau. Đặt MP = q, PQ = ,
m PE = x, PF = y . Chứng minh 2 2 2
MF = q + y − y . q Lời giải Trang 10/9 Ta có = = MPQ = = ° ⇒ = MPE EPF FPQ 30 MPF EPQ = 60° . 3
Theo định lí côsin, ta có P 2 2 2 = + − ME AM AE
2.AM.AE.cos MAE 2 2 2 2 = q + x − 2 .
qx cos30° = q + x − qx 3 2 2 2 = + − MF AM AF
2AM.AF.cos MAF M E F Q 2 2 2 2 = q + y − 2 .
qy cos60° = q + y − qy 2 2 2 2 2
MQ = MP + PQ = q + m . Chọn C.
Ví dụ 12: Tam giác ABC vuông tại A, có AB = c, AC = b . Gọi là độ dài đoạn phân giác a trong góc
BAC . Tính theo b và c . a 2(b + c) 2 (b + c) A. 2bc bc = B. = C. 2 = D. = a . a . a . a . b + c bc b + c bc Lời giải Ta có 2 2 2 2
BC = AB + AC = b + c . A
Do AD là phân giác trong của BAC 2 2 AB ⇒ = . c = . c = .BC c b + c BD DC DC = . B + + D C AC b b c b c
Theo định lí hàm côsin, ta có 2 c ( 2 2 b + c 2 2 2 ) = + − 2 2 BD AB AD 2. . AB . AD cos ABD ⇔ = c + AD − 2 . c . AD cos45° (b + c)2 2 c ( 2 2 b + c ) 3 2 2 2 2 ⇒ − 2. + − = 0 ⇔ − 2. bc AD c AD c AD c AD + = 0. (b + c)2 (b + c)2 2bc ⇒ AD = hay 2bc = . Chọn A. b + c a b + c
Bài toán 2: Biết độ dài ba cạnh của một tam giác, tính các góc của tam giác
Phương pháp: Dùng hệ quả của định côsin
Ví dụ 1: Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 3, CA = 4 . Tính góc ABC Lời giải
Áp dụng hệ quả của định lý côsin trong tam giác ta có: 2 2 2 cos
BA + BC − AC ABC = 2 2 2 2 3 4 3 1 cos ABC + − − − ⇔ = = = . 2.B . A BC 2.2.3 12 4 Suy ra góc ABC 104 29 ° ′.
Ví dụ 2: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc A Lời giải Trang 11/9 b c a + ( + )2 2 2 2 6 1 3 − + − 4 2 cos A = = = ⇒ A = 45° . 2bc 2. 6.(1+ 3) 2
Ví dụ 3: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc B bằng Lời giải 2 2 2 Ta có
a + c − b 1 = = ⇒ cos B B = 60° . 2ac 2
Ví dụ 4: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện (a + b + c)(a + b − c) = 3ab . Tính số đo của góc C . Lời giải
Ta có: (a + b + c)(a + b − c) = 3ab ⇔ (a + b)2 2
− c = 3ab ⇔ 2 2 2
a + b − c = ab . 2 2 2 Mà
a + b − c 1 cosC = = ⇒ C = 60° . 2ab 2
Ví dụ 5: Tính góc A của A ∆ BC, biết rằng 2 2 2 2
b(b − a ) = c(a − c ). Lời giải Ta có: 2 2 2 2
b(b − a ) = c(a − c ) ⇔ 3 3 2
b + c = a (b + a) ⇔ 2 2 2
(b + c)(b + c − bc) = a (b + c) ⇔ 2 2 2
a = b + c − bc (1)
Theo định lí số côsin ta có: 2 2 2
a = b + c − 2bccos A (2) Từ (1) và (2) ta có: 1 cos A = ⇒ A = 60 .° 2 Ví dụ 6: Tam giác ABC có 6 2 AB
, BC 3, CA 2 . Gọi D là chân đường phân giác trong góc A . 2 Tìm số đo của ADB Lời giải
Theo định lí côsin, ta có: 2 2 2 A
AB + AC − BC 1 cos BAC = = − 2. . AB AC 2 ⇒ = ° ⇒ BAC 120 BAD = 60° 2 2 2 B D C
AB + BC − AC 2 = = ⇒ cos ABC ABC = 45° 2. . AB BC 2 Trong ABD ∆ có = ° = ° ⇒ BAD 60 , ABD 45 ADB = 75° .
Ví dụ 7: Tam giác ABC có AB = 8 cm , BC =10 cm , CA = 6 cm . Tìm độ dài đường trung tuyến AM của tam giác. A Lời giải Ta có B M C 2 2 2 cos
AB + BC − AC ABC = 2. . AB BC
Áp dụng định lí côsin trong tam giác ABM, ta được: Trang 12/9 2 2 2
AM = AB + BM − 2A . B BM.cosB 2 2 2 2 2 = + − 2 .
. AB + BC − AC AB BM AB BM 2.A . B BC 2 2 2 AB + AC BC = − 2 4 2 2 2 8 + 6 10 = − = 25 2 4 ⇒ AM = 5.
Ví dụ 8: Tam giác ABC có AB = 9cm, AC = 12 cm và BC =15cm. Tính độ dài đường trung
tuyến AM của tam giác đã cho. Lời giải
Áp dụng công thức ở ví dụ 7, ta được ta được: A 2 2 2 2 2 2 2 AC + AB BC 12 + 9 15 225 15 AM = − = − = ⇒ AM = . 2 4 2 4 4 2 B M C
Chú ý: Công thức tính độ dài đường trung tuyến: 2 2 2 b c 2 a
2 c a b
2 a b c A 2 2 2 2 2 2 2 2 2a m m m 4 b 4 c 4 b c ma C B M a
Ví dụ 9: Tam giác ABC có AB = 4, BC = 6, AC = 2 7 . Điểm M thuộc đoạn BC sao cho
MC = 2MB . Tính độ dài cạnh AM . Lời giải AB BC AC + − + − ( )2 2 2 2 2 2 4 6 2 7
Theo định lí hàm côsin, ta có : 1 cos B = = = . 2. . AB BC 2.4.6 2 A Do 1 MC = 2MB
→ BM = BC = 2. 3
Theo định lí hàm côsin, ta có 2 2 2 = + − AM AB BM 2. . AB BM.cos B B M C 2 2 1
= 4 + 2 − 2.4.2. =12 ⇒ AM = 2 3 2
Ví dụ 10: Cho A
∆ BC có a = 5, b = 6, c = 3. Trên đoạn AB, BC lấy lần lượt các điểm M , K sao cho
BM = 2, BK = 2. Tính MK. Lời giải Trang 13/9 A ∆ BC : 2 2 2
b = a + c − 2accos B 2 2 2 + − ⇒ cos a c b B = 2ac 25 + 9 − 36 1 = = − 2.5.3 15 MB ∆ K : 2 2 2 8 128
MK = BM + BK − 2BM.BK.cos B = 4 + 4 − − = 15 15 ⇒ 64.2 8 30 MK = = . 15 15
Ví dụ 11: Cho hình thang cân ABCD có đáy nhỏ AB , đáy lớn CD . Biết AB = CD và 3 tan BDC = . 4 Tính cos BAD . Lời giải A B D C E
Gọi E là hình chiếu vuông góc của B trên DC . Đặt AB = AD = BC = x . Ta có DC x EC − = ( ) 1 . 2
Trong tam giác vuông BDE ta có: 3 tan BDC = BE 3 3 ⇔ = ⇔ BE = ED 4 ED 4 4 3 ⇔ 3 DC x BE DC − = −
= (DC + x) (2) . 4 2 8
Trong tam giác vuông BEC ta có 2 2 2
BC = EC + BE (3) . Thay ( )
1 , (2) vào (3) biến đổi ta được: 2 2 39 25
x +14DC.x − 25DC = 0 ⇔ x = DC hay 39 39 DC = x . Khi đó 7 EC = x . 25 25 Mặt khác: cos BAD EC = − cos BCE 7 = − = − . BC 25 2-Định lí sin:
Bài toán 3: Biết độ dài một cạnh và số đo hai góc của một tam giác hoặc biết độ dài hai cạnh và một góc(
không xen giữa) tính độ dài cạnh còn lại; Phương pháp:
- Biết độ dài một cạnh và số đo hai góc của một tam giác Dùng định lí sin.
- Biết độ dài hai cạnh và một góc( không xen giữa) tính độ dài cạnh còn lại;
Cách 1: Dùng định lí sin.
Cách 2: Dùng định lí côsin
Ví dụ 1: Tam giác ABC có = °
B 60 , C = 45° và AB = 5. Tính độ dài cạnh AC . Trang 14/9 A. 5 6 AC = . B. AC = 5 3. C. AC = 5 2. D. AC =10. 2 Lời giải
Theo định lí hàm sin, ta có AB AC 5 AC 5 6 = ⇔ = ⇒ AC = . sinC sin B sin 45° sin 60° 2 Ví dụ 2: Cho A
BC có a 137,5cm , 0 0
B 83 ;C 57 .
Tính góc và độ dài các cạnh còn lại của tam giác( chính xác đến hàng phần mười) Lời giải A=1800- + (B C)=400 a b asin B b 211,6cm sin A sin B sin A
Tương tự: c 178,8 cm
Ví dụ 3: Tam giác ABC có AB 2, AC 3 và C 45 . Tính độ dài cạnh BC . Lời giải
Theo định lí hàm côsin, ta có = + − AB AC BC AC BC C ⇒ ( )2 = ( )2 2 2 2 2 2. . .cos 2
3 + BC − 2. 3.BC.cos45° 6 2 BC + ⇒ = . 2
Ví dụ 4: Tam giác ABC có = = ° AC 4, 30 BAC ,
ACB = 75°. Tính chu vi tam giác ABC ( làm
tròn đến hàng phần trăm) Lời giải Ta có 0 = − +
ABC 180 (BAC ACB) = ° = 75 ACB .
Suy ra tam giác ABC cân tại A nên AB = AC = 4.
Theo định lí hàm côsin, ta có 2 2 2 2 2 0
BC = AB + AC − 2A .
B AC.cos A = 4 + 4 − 2.4.4.cos30 = 32 −16 3 ⇒ BC = 32 −16 3.
Chu vi của tam giác ABC là
Ví dụ 5: Cho góc
xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB =1. Tìm độ dài lớn nhất của đoạn OB . Lời giải
Theo định lí hàm sin, ta có: OB AB AB = ⇔ = 1 = = OB .sinOAB
.sinOAB 2sinOAB sinOAB sin AOB sin AOB sin30° y
Do đó, độ dài OB lớn nhất khi và chỉ khi B = ⇔ sinOAB 1 OAB = 90° . Khi đó OB = 2 . x O Chọn D. A Trang 15/9 Ví dụ 6: Cho góc
xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB =1. Tìm độ dài của đoạn OA khi OB có độ dài lớn nhất. A. 3. B. 3. C. 2 2. D. 2. 2 Lời giải
Theo định lí hàm sin, ta có OB AB AB = ⇔ = 1 = = OB .sinOAB .sinOAB y 2sinOAB sinOAB sin AOB sin AOB sin30° B
Do đó, độ dài OB lớn nhất khi và chỉ khi = ⇔ sinOAB 1 OAB = 90° . x O A Khi đó OB = 2 .
Tam giác OAB vuông tại 2 2 2 2
A ⇒ OA = OB − AB = 2 −1 = 3 . Chọn B
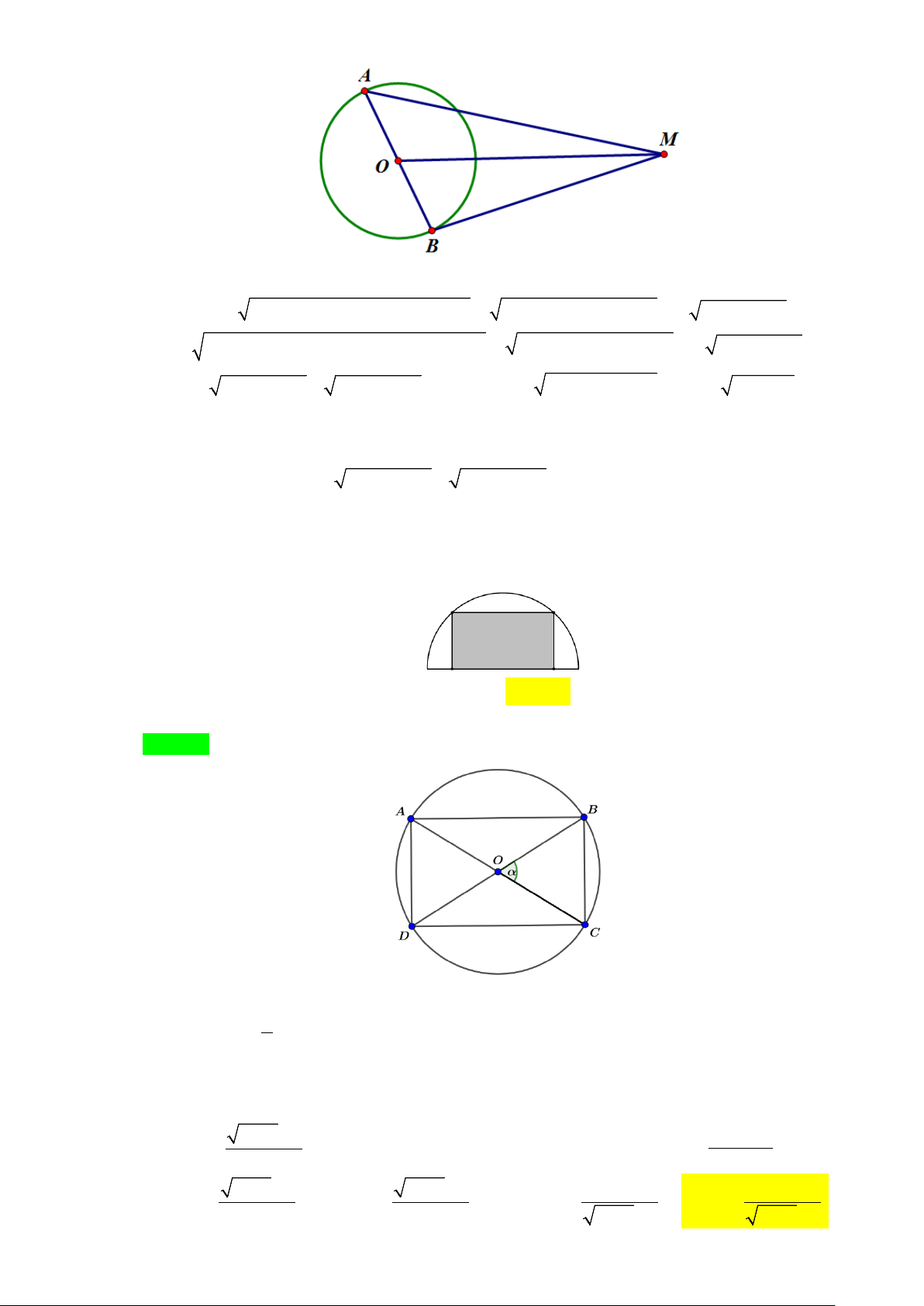
Ví dụ 7: Cho tứ giác lồi ABCD có = ABC ADC = 90° ,
BAD =120° và BD = a 3 . Tính AC . Lời giải Cách 1: B a 3 A C I D A
∆ BD nội tiếp đường tròn đường kính AC
Áp dụng định sin trong A ∆ BD , ta có BD a 3 AC = 2R = = = 2a . sin BAD sin120° Cách 2:
Đề không mất tính tổng quát ta có thể chọn BD ⊥ AC tại I . Ta có = ° − + +
C 360 (A B D) = 360°−(120°+90°+90°) = 60°. AB = AD Do BD ⊥ AC ⇒ . Suy ra B
∆ CD là tam giác đều cạnh bằng a 3 . CB = CD Trang 16/9 Ta có 3a CI = . 2 Xét A
∆ ID vuông tại I , 1 a 3 ID = BD = . 2 2 a 3 Suy ra ID 2 a AI = = = A . tan 60° 2 tan 2 Ta có a 3a
AC = AI + CI = + = 2a . 2 2 Vậy AC = 2a .
3-Diện tích tam giác
Bài toán Tìm diện tích của tam giác. Tiìm độ dài đường cao, tìm bán kính đường tròn nội-ngoại tiếp tam giác. Phương pháp:
3.1. Tìm diện tích tam giác
-Biết hai cạnh và góc xen giữa thì 1 1 1
S = bcsin A = casin B = absin C 2 2 2
-Biết độ dài ba cạnh thì S = p( p − a)( p − b)( p − c) ( a b c p + + = , nữa chu vi) 2 Ngoài ra 1 1 1 S = . a ha = . b hb = .chc 2 2 2 abc S = 4R
S = pr với a b c p + + =
, r là bán kính đường tròn nội tiếp 2
S = ( p − a)r = p − b r = p − c r a ( ) b ( ) c
r r r lần lượt là bán kính đường tròn bàng tiếp của các góc , A B, C. a , b , c
3.2 Tìm độ dài đường cao: 2S 2S 2S h = h = h = a , b , c . a b c
3. 3 Tìm bán kính đường tròn ngoại tiếp tam giác
-Biết độ dài cạnh và góc đối diện thì dùng định lí sin a b c a b c 2R R . sin A sin B sinC 2 sin A 2 sin B 2 sinC -Ngoài ra abc abc S = ⇒ R = 4R 4S
4.4Bán kính đường tròn nội tiếp: S 2S
S = pr ⇒ r = =
p a + b + c = ( − ) A tan = ( − ) B tan = ( − ) C r p a p b
p c tan . 2 2 2
3. 5.Bán kính đường tròn bàng tiếp: A r = ptan B r = ptan C r = ptan c . B ; a ; 2 2 2
Ví dụ 1: Cho A
∆ BC có a = 4, c = 5 , B =150°. Tính diện tích tam giác ABC . Lời giải Trang 17/9
Diện tích tam giác ABC là 1 = S acsin B 1 = .4.5sin150° = 5 . 2 2
Ví dụ 2: Cho tam giác ABC có b = 7 , c = 5 , 3
cos A = . Tìm độ dài đường cao h của tam giác ABC 5 a Lời giải A c b ha B H a C
Theo định lí hàm cos ta có 2 2 2
a = b + c − 2bccos A 3
= 49 + 25 − 2.7.5. = 32 ⇒ a = 4 2 . 5 Ta lại có: 3 cos A = 4 ⇒ sin A = . 5 5
Diện tích tam giác ABC là 1 S = 1 4 = .7.5. =14 . ∆ bc A ABC sin 2 2 5 Vì 1 S 28 = nên 2S ABC h ∆ = = 7 2 = ∆ a h ABC . 2 a a a 4 2 2 Vậy 7 2 h = . a 2
Ví dụ 3: Cho tam giác ABC có a = 5 cm , c = 9 cm , 1
cosC = − . Tính độ dài đường cao h hạ từ A 10 a của tam giác ABC . Lời giải
Áp dụng định lí côsin trong tam giác ABC ta có: b = 7 2 2 2
c = a + b − 2 . a . b cosC 2 1 81 25 b 2.5. . b ⇒ = + − − 2
⇔ b − b − 56 = 0 ⇔ 10 b = 8 −
Ta nhận được b = 7(cm)
Diện tích tam giác ABC là S = − − − 21 21 21 21 21 11 5 7 9 = − − − 2 = (cm ) ∆ p p a p b p c ABC ( )( )( ) 2 2 2 2 4 21 11 Độ dài đường cao 2S h = 2 = 21 11 = (cm) a a 5 10
Ví dụ 4: Tam giác ABC có = = AB 3, 6 AC ,
BAC = 60°. Tính độ dài đường cao h của tam giác. a Lời giải
Áp dụng định lý côsin, ta có 2 2 2
BC = AB + AC − 2 .
AB AC cos A = 27 → BC = 3 3 . Ta có 1 = 1 0 9 3 S = = . ∆ AB AC A ABC . . .sin .3.6.sin 60 2 2 2 Lại có 1 2S S = → = = ∆ BC h h ABC . . a a 3. 2 BC Trang 18/9
Ví dụ 5: Tam giác ABC có a = 8; b = 7 ; c = 5 . Tìm diện tích của tam giác ABC bằng Lời giải Ta có a b c p + + =
=10 , S = p( p − a)( p − b)( p − c) =10 3 . 2
Ví dụ 6: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD =135° . Tính diện tích của hình bình hành ABCD . Lời giải A D B E C Ta có ABC = 45° .
Gọi AE kà đường cao của tam giác ABC , khi đó tam giác AEB vuông cân tại E . Suy ra 1
AE = BC a 2 = . 2 2
Vậy diện tích hình bình hành ABCD là a 2 AE.BC = .a 2 2 = a . 2
Ví dụ 7: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD = 45°. Tính diện tích của hình bình hành ABCD . Lời giải B a 2 C a 45° A a 2 D Ta có: AD 1
= BC = a 2 nên S = S = 2. A . B A . D sin BAD 2 = a . ABCD 2. ABD ∆ 2
Ví dụ 8: Cho tam giác ABC có BC =10 , A = 30°. Tính bán kính đường tròn ngoại tiếp tam giác ABC . Lời giải
Trong tam giác ABC ta có: BC R = =10 . 2sin A
Ví dụ 9: Một tam giác có ba cạnh là 52, 56, 60 . Tính bán kính đường tròn ngoại tiếp tam giác Lời giải Ta có: 52 56 60 p + + = = 84 . 2
Áp dụng hệ thức Hê – rông ta có: S = 84(84 −52)(84 −56)(84 − 60) =1344 . Mặt khác abc S = abc ⇒ R = 52.56.60 = = 32,5. 4R 4S 4.1344 Trang 19/9
Ví dụ 10: Cho tam giác ABC có a = 2 , b = 6 , c = 3 +1. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . Lời giải 2 2 2 6 + 4 + 2 3 − 4 2 cos
b + c − a A = = = ⇒ 2 sin A = . 2bc 2 6 ( 3 + )1 2 2
Áp dụng định lý sin ta có a R = = 2 . 2sin A
Ví dụ 11: Tam giác đều cạnh a nội tiếp trong đường tròn (O). Tính bán bán kính R của đường tròn. Lời giải
Bán kính đường tròn ngoại tiếp tam giác đều cạnh a : 2 2 a 3 a 3 R = h = . = . 3 3 2 3
Ví dụ 12: Tam giác đều nội tiếp đường tròn bán kính R = 4 cm . Tính diện tích tam giác Lời giải
Ta có diện tích tam giác ABC là abc S =
. Do tam giác ABC đều nên ABC 4R 3 a ( R A)3 2 sin S = = 2 3 = 2R sin A 2 = 2.4 .(sin 60°)3 =12 3 2 cm . ABC 4R 4R
Ví dụ 13: Tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm . Tính bán kính đường tròn nội tiếp tam giác Lời giải
Do tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm nên 2 2
AB = BC − AC 2 2 = 10 − 6 = 8 .
Diện tích tam giác ABC là 1 S = = 24 . ∆ AB AC ABC . 2
Bán kính đường tròn nội tiếp tam giác ABC là 2S 2.24 ABC r ∆ = = = 2 .
AB + BC + CA 6 + 8 +10
Ví dụ 14: Tam giác ABC có AB = 5, 8 AC = và 0
BAC = 60 . Tính bán kính r của đường tròn
nội tiếp tam giác đã cho. A. r =1. B. r = 2. C. r = 3 . D. r = 2 3 .
Ví dụ 15: Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r là
bán kính đường tròn nội tiếp tam giác ABC . Tìm tỉ số R ? r Lời giải Ta có abc R = , S r = 4S P
Vì tam giác ABC vuông cân tại A nên b = c và 2 2
a = b + c = b 2
. a + b + c abc a(a + 2b) 2 2b (1+ 2) Xét tỉ số R . abc p = 2 = = = =1+ 2 . 2 r 4S 1 2 2 4. .( . b c)2 2b 2b 4
Ví dụ 16: Cho tam giác ABC. Tính đường cao vẽ từ A và bán kính đường tròn ngoại tiếp A ∆ BC. Trang 20/9 Biết:
a) CA = 8; AB = 5; A = 60°
b) BC = 21; CA =17; AB = 8. Giải a) *Ta có: 2 2 2
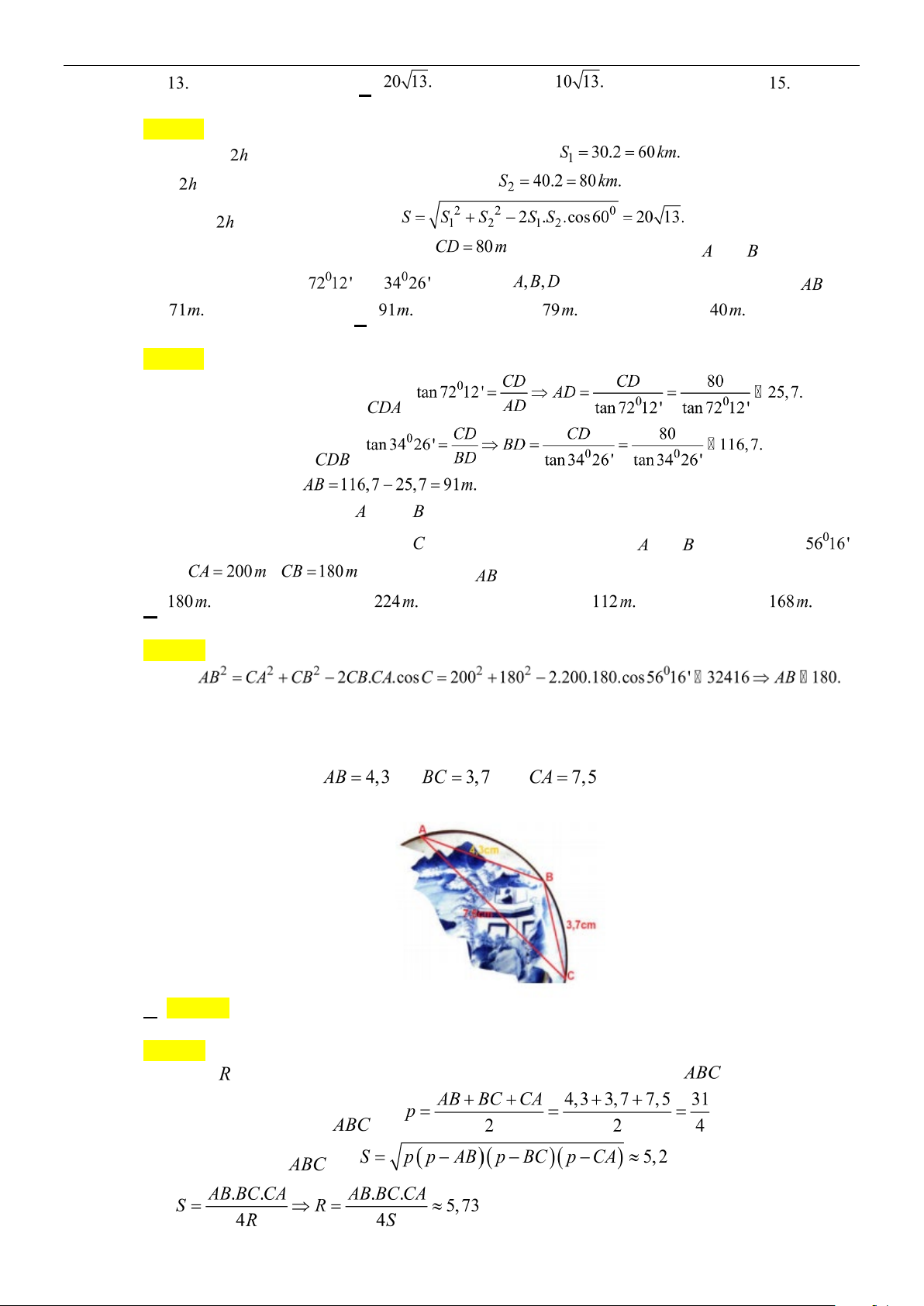
BC = AB + AC − 2A . B AC.cos A 2 1
BC = 25 + 64 − 2.5.8. = 49 Vậy: BC = 7. 2 * Ta có: 1 1 3 S = = = ∆ AB AC A ABC . .sin .5.8. 10 3 2 2 2 Ta lại có: 1 S = ⇔ 2S 2.10 3 20 3 h = = = ∆ BC h ABC . 2 a a BC 7 7 Ta lại có: A . B AC.BC S = ⇒ 5.7.8 7 7 3 R = = = . 4R 4.10 3 3 3 b) Ta có: AB AC CB 8 21 17 p + + + + = = = 23 2 2
S = p( p − a)( p − b)( p − c) = 23(23−12)(23−17)(23−8) = 6 115 A . B BC.CA 8.21.17 7.17 119 R = = = = 4S 4.6 115 115 115 1
S = BC.h ⇔ 2S 4 h = = a 115. 2 a BC 7
Ví dụ 17: Cho A
∆ BC có a = 5, b = 6, c = 7. Tính:
a) Diện tích S của A ∆ BC
b) Các đường cao h h h
a , b , c .
c) Các bán kính R, r. Giải a) Ta có: a b c 5 6 7 p + + + + = =
= 9; p − a = 4, p − b = 3, p − c = 2 2 2 Vậy
S = p( p − a)( p − b)( p − c) = 9.4.3.2 = 6 6. b) Ta có: 1 S = . a h ⇒ 2S 2.6 6 12 6 h = = = 2 a a a 5 5 1 S = . b h ⇒ 2S 2.6 6 h = = = b 2 6 2 b b 6 1 S = .ch ⇒ 2S 2.6 6 12 6 h = = = c . 2 c c 7 7 c) Ta có: abc S = ⇒ abc 5.6.7 35 6 R = = = 4R 4S 4.6. 6 24 S = pr ⇒ S 6 6 2 6 r = = = . p 9 3
Ví dụ 18: Tính các góc ,
A B và các độ dài h R của A ∆ BC, biết a ,
a) a = 6; b = 2; c = ( 3 +1)
b) a = 7; b = 5; c = 8. Giải 2 2 2 2 a) Ta có:
b + c − a 4 + ( 3 +1) − 6 2 + 2 3 1 cos A = = = = 2bc 2.2( 3 +1) 4(1+ 3) 2 ⇒ A = 60° Ta có: a b = sin A sin B Trang 21/9 3 2. ⇒ bsin A 2 1 2 sin B = = = = ⇒ B = 45 .° a 6 2 2 2 2 2 b) Ta có:
b + c − a 40 1 cos A = = = ⇒ A = 60° 2bc 80 2 Ta có: a b = ⇔ . b sin A 5 3 sin B = = . sin A sin B a 14 c) 1 3( 3 1) S . a h p p a p b p c + = = − − − = a ( )( )( ) 2 2 2 ( 3 +1) 2 h =
p p − a p − b p − c = a ( )( )( ) a 2 abc S = ⇒ abc R = = 2. 4R 4S
Ví dụ 19: Cho A∆BC có a=9, đường tròn nội tiếp, tiếp xúc với cạnh BC tại D sao cho AD= DC và 2 cosC = . 3 a) Tính ,
b c theo x với x = AD > 0 b) Suy ra giá trị . b Giải a) Ta có: a b c x + − = ; = cos cos b DAC C = 2 2x Vậy
b − c = 2x − 9; 4 b = x và 2 c = 9 − .x 3 3 2 2 b) Ta có: 2 2 2
c = a + b − 2abcosC ⇒ 2 2 4 4 2 9 − x = 9 + x − 2.9. . x 3 3 3 3
⇒ x = 3 và do đó b = 4; c = 7.
Ví dụ 20: Cho A∆BC có c=2, b=3, a=4, M là trung điểm A .B Tính bán kính r của đường tròn ngoại tiếp B ∆ CM. Giải
Áp dụng định lí đường trung tuyến. Ta có: 2 2 2 1 2
a + b = 2m + c c 2 ⇒ 23 m = c 2 2 2 2 + − A a c b 11 ∆ BC : cos B = = ⇒ 2ac 16 3 sin B = 15 16 23 B MC 2 16 23 ∆ MC : = 2r ⇔ r = = . sin B 3 15 3 30 16
Ví dụ 21: Cho A
∆ BC có c = 3, b = 4, S = Tính . a ABC 3 3. Giải Trang 22/9 Ta có: 2 2 2
a = b + c − 2bccos A = 25 − 24cos A Ta lại có: 1
S = 3 3 = bcsin A ⇒ 3 sin A = 2 2 2 ⇒ 2 3 1 cos A =1− = ⇒ 1 cos A = ± 2 4 2 * Nếu 1 cos A = ⇒ 2 1
a = 25 − 24. =13 ⇒ a = 13 2 2 * Nếu 1 cos A = − ⇒ 2 1 a 25 24. = − − = 37 ⇒ a = 37 2 2 Ví dụ 22: π Cho A
∆ BC có A = , h =
R = 5. Tính a, b, .c c 3, 3 Giải
Ta có: a = 2Rsin A = 5 3 ⇒ sin h h c A = ⇒ c 3 b = = = 2 b sin A 3 2 Ta có: 2 2
c = AH = HB =1+ a − h c c =1+ 6 2 Vậy: a = 5 3; b = 2; c =1+ 6 2.
Ví dụ 23: Cho A∆BC vuông tại ,A AB=3, AC =4, M là trung điểm của AC. Tính bán kính r của
đường tròn ngoại tiếp B ∆ CM. Giải Ta có: 2 2 AC MB AB = + = 9 + 4 = 13 2 3 sin C = ; 5 BM 5 r = = 13. 2sin C 6 Ví dụ 24: π Cho A
∆ BC vuông ở B kéo dài AC về phía C một đoạn CD = AB =1, CBD = . Tính 6 AC. Giải
Qua D, dựng đường thẳng vuông góc với DC, cắt BC tại E ⇒ = DBC DAE
Đặt AC = x >1 thì DA = x +1 π +1 = .tg x DE DA = ; 2 CB = x −1 6 3 CD ∆ E ∽ CB ∆ A ⇒ CD CB = ED AB ⇔ 2
3 = (x +1) x −1 ⇔ 4 3
x + 2x − 2x − 4 = 0 ⇔ 3 3
x(x − 2) + 2(x − 2) = 0 Trang 23/9 ⇔ 3
(x − 2)(x + 2) = 0 vì x > 0 ⇒ x + 2 > 0 ⇔ 3 x = 2 ⇔ 3 x = 2. Ví dụ 25: π π
Cho tứ giác ABCD có =
ABC ADC = , AB = a, AD = 3a,
BAD = . Tính AC . 2 3 Giải π Ta có: 2 2 2
DB = a + 9a − 2. .3 a a cos 3 2 2 DB = 7a
Suy ra DB = a 7
Vì ABCD nội tiếp trong một đường tròn nên ta có: AC BD = sin ABC sin π3 Suy ra a 7 21 AC = = 2a . 3 3 2 Ví dụ 26: π Cho ∆ A dt BPQ
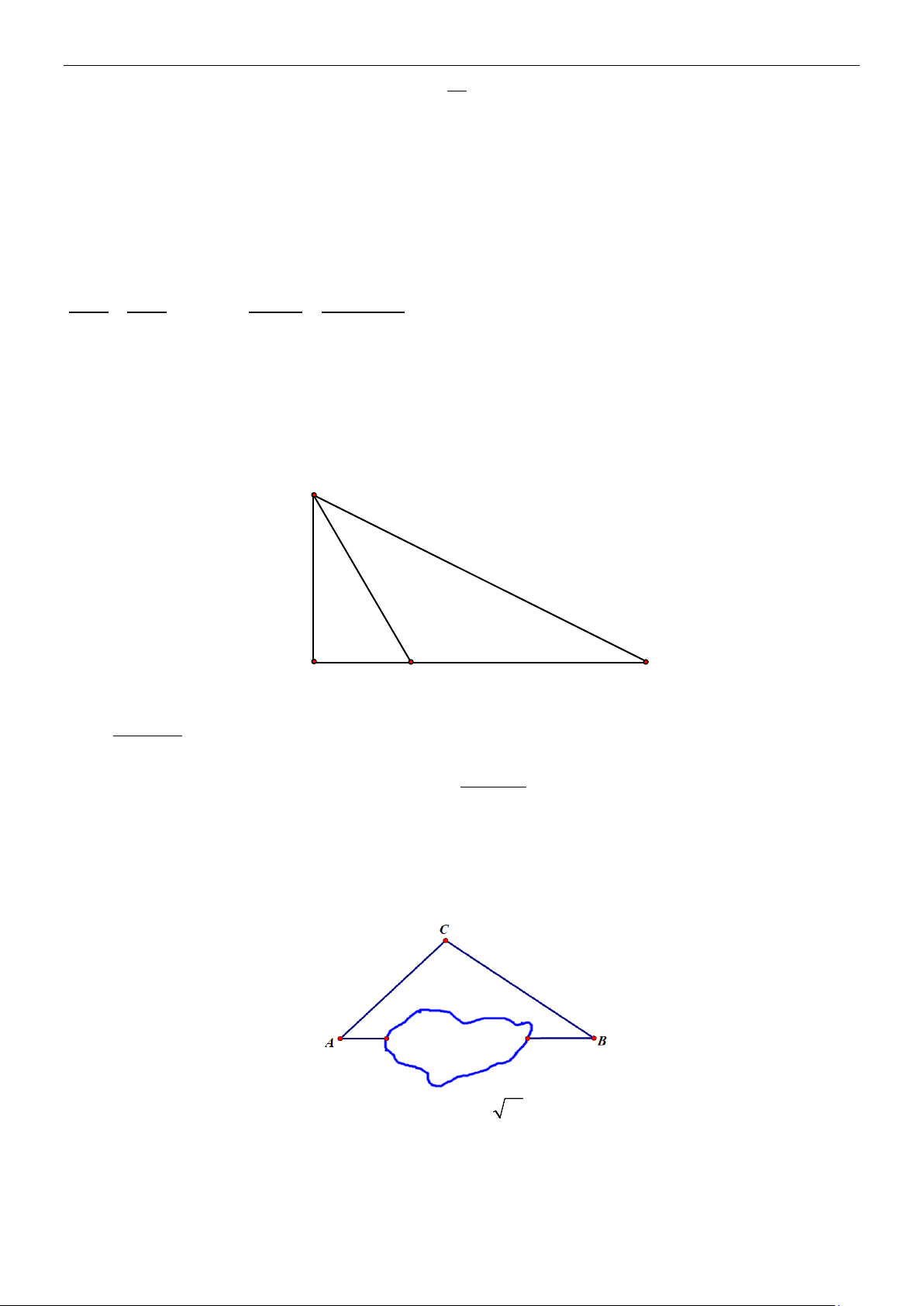
∆ BC có B < , AQ và CP là các đường cao và ( ) 1 = . 2 dt( A ∆ BC) 9 a) Tính cos . B
b) Cho PQ = 2 2. Tính bán kính R của đường tròn ngoại tiếp A ∆ BC. Giải a)Ta có: 1 dt( B ∆ PQ) = B . P BQsin ; B 1 dt( A ∆ BC) = B . A BC sin B 2 2
1 B .PBQsin B ⇒ dt( B ∆ PQ) 2 B . P BQ 1 = = = dt( A ∆ BC) 1 B . A BC 9 B . A BC sin B 2 ⇒ 2 1 cos B = ⇒ 1 cos B = . 9 3
b) Vì ACQP nội tiếp trong một đường tròn nên AC PQ PQ = = ⇒ PQ AC = sin 90° sin BAQ cos B cos B Mà AC PQ 2 2 9 R = = = = . 2sin B 1 2 2 2 2 2 sin B . 3 3 3
Ví dụ 27: Cho điểm O∈ đoạn AB, OA=13, OB=7. Dựng đường tròn tâm O, bán kính bằng 5. Từ ,
A B vẽ các tiếp tuyến với đường tròn, chúng cắt nhau tại M , các điểm tiếp xúc nằm về một phía cạnh Trang 24/9
A .B Tìm bán kính R của đường tròn ngoại tiếp A ∆ BM. Giải Ta có: 5 sin A = ; 12 cos A = 13 13 5 sin B = ; 2 6 cos B = 7 7 ⇒ 10(6 6)
sin(A B) sin Acos B sin B cos A + + = + = 91 ⇒ AB 91 R = = . 2sin C 6 + 6 Ví dụ 28: π Cho A
∆ BC có B = , R = 2, I là tâm đường tròn nội tiếp. Tìm bán kính r của đường 3 tròn ngoại tiếp A ∆ CI. Giải Ta có: 0 B = 60 ⇒ 0 AIC =120 (vì
AIC bù với A + C ) 2 Trong A ∆ BC : AC = 2R = 4 ⇒ 3 AC = 4. = 2 3 sin 60° 2 π Trong A ∆ IC : 2 AC = 2r.sin ⇒ 2 3
Ví dụ 30: Cho A ∆ BC cân tại ,
A A = α, AB = ,
m D là điểm trên cạnh BC, sao cho BC = 3B . D a) Tính BC.
b) Tính AD theo , m α.
c) Chứng tỏ rằng đường tròn ngoại tiếp các tam giác ABD, ACD bằng nhau. Tính cosα để bán kính
của chúng bằng 1 R ( R là bán kính đường tròn ngoại tiếp A ∆ BC). 2 Giải
a) Ta có: BC = A . B sinα 2 α ⇒ BC = 2A .
B sinα = 2msin . 2
b) Áp dụng định lí côsin: 2 2 2 2 α 2 α = + sin − 2 . m AD m m m sin cos B 3 2 3 2 2 2 2 8 α = 1 − sin m m = (5 + 4cosα) 9 2 2 ⇒ m AD = 5 + 4cosα . 3
c) • Đpcm ⇔ AD AD =
⇔ sin B = sin C (hiển nhiên) sin B sin C • Đpcm ⇔ AD 1 AC = ⇔ AC = 2AD sin B 2 sin B ⇔ 2m m = 5 + 4cosα 3 Trang 25/9 ⇔ 9 = 4(5 + 4cosα) ⇔ 11 cosα = − . 16
Bài toán 5 : Giải tam giác và các ứng dụng vào thực tế
Ví dụ 1: Giải tam giác ABC, biết = = 0
b 14,c 10, A =145 Lời giải
Xét ΔABC, theo định lý côsin, ta có: 2 2 2 2 2 0
BC = AB + AC − 2A .
B AC.cos A =14 +10 − 2.14.10.co 145 s 525.35 ⇒ BC 23. Theo định lí sin, ta có: 0 a b .
b sin A 14.sin145 = ⇒ = ⇒ 0 sin B 0.349 B 20 26' sin A sin B a 23 0 0
C =180 − (A + B) 14 34'
Ví dụ 2: Từ hai điểm A và B trên mặt đất người ta nhìn thấy đỉnh C và chân D của tháp CD dưới các góc nhìn là 72 12 ° ′ và 34 26
° ′ so với phương nằm ngang. Biết tháp CD cao 80 m . Tính khoảng cách AB Lời giải C 80 m D B A Ta có: DBC = 72 12 ° ′ , DAC = 34 26 ° ′ nên = − ACB DBC DAC = 37 46 ° ′ CD BC = 84 m . cos DBC
Áp dụng định lí sin trong tam giác BC ABC ta có = AB
.sin ACB 91 m . sin DAC
Ví dụ 3: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
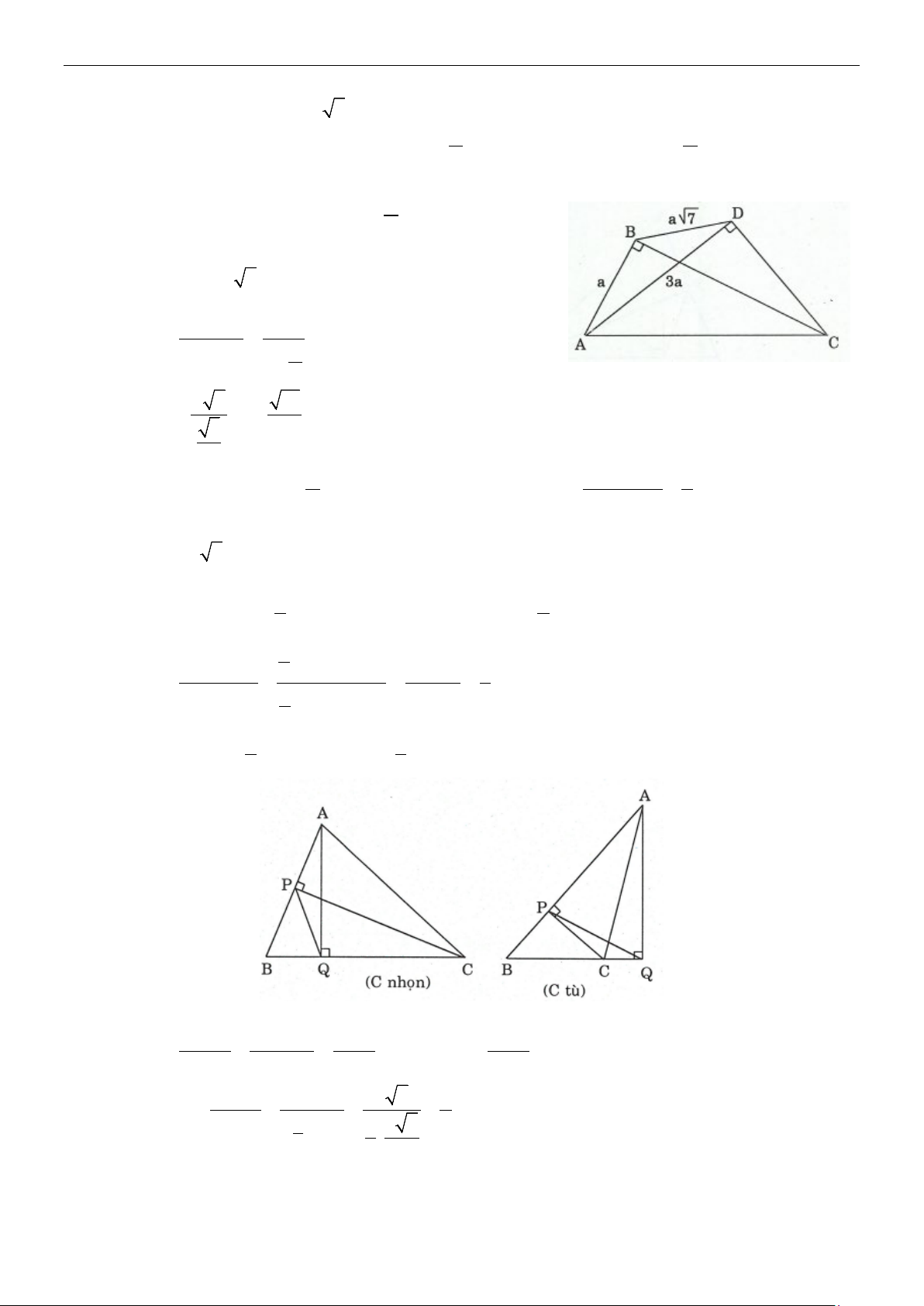
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết CA = 200(m) ,
CB =180(m) . Tính khoảng cách AB ? Lời giải 2 2 2
AB = CA + CB − 2 . CA .
CB cos60° = 36400 ⇒ AB = 20 91(m) .
Ví dụ 4:Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h.
Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao Trang 26/9
nhiêu kilômét (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định
lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không? Lời giải
a) Sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát là:
Trong đó vị trí A là vị trí là vị trí cảng Vân Phong.
b) Sau khi đi 1h theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí B, đi tiếp 0,5 giờ còn lại theo
hướng đông nam cũng với vận tốc 20km/h thì tàu đến vị trí C. Tiến hành đo đoạn AC ta thấy xấp xỉ 27,9 cm.
Vậy sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng vân phong 27,9 km. c)
Sau khi đi 1h theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí B, quãng đường AB là: 20.1 = 20 (km).
Còn 1h còn lại, tàu đi theo hướng nam với vận tốc 20km/h thì tàu đi đến vị trí B, quãng đường BC là: 20.1 = 20 (km).
Do hướng đông hợp với hướng nam một góc 900 nên B=900
Xét tam giác ABC vuông tại B, ta có: 2 2 2 2 2
BC = AB + AC = 20 + 20 = 800
⇒ BC = 800 = 20 2 28,28.
Ví dụ 5:Từ bãi biển Vũng Chùa, Quảng Bình ta có thể ngắm được Đảo yến. Hãy đề xuất cách xác định bề
rộng của hòn đảo (theo chiều ta ngắm được). Trang 27/9 Lời giải
Bước 1. Trên bờ, đặt một cọc ở vị trí A, một cọc ở vị trí B, một cọc ở vị trí C. Đo khoảng cách AB, AC.
Bước 2. Đứng tại A ngắm điểm B và điểm E để đo góc tạo bởi hai hướng ngắm đó là góc BAE . Đứng tại
B ngắm điểm E và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc EBA
Bước 3. Dựa vào định lí sin trong tam giác ABE ta tính được cạnh AE.
Bước 4. Đứng tại A ngắm điểm C và điểm D để đo góc tạo bởi hai hướng ngắm đó là góc DAC . Đứng
tại C ngắm điểm D và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc DCA
Bước 5. Dựa vào định lí sin trong tam giác ADC tính được AD.
Bước 6. Xét tam giác ADE, sử dụng định lí côsin để tính cạnh DE.
Vậy độ dài DE chính là chiều rộng của đảo.
Ví dụ 6:Trên biển, tàu B ở vị trí cách tàu A 53 km về hương 0
N34 E . Sau đó, tàu B chuyển động thẳng
đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn
50km/h để đuổi kịp tàu B.
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B? Lời giải
a) Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (h) (x > 0)
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km) Xét ΔABC, có: Trang 28/9
AC2 = BC2 + AB2 – 2AB.BC.cosB
⇔ 2500x2 = 900x2 + 532 – 2.53.30x.cos1240
⇔ 1600x2 – 1778x – 2809 = 0
⇔x≈1,99TM, x≈−0,88(KTM)
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B.
⇒ BC = 30.x = 30.1,99 = 59,7; AC = 50.x = 50.1,99 = 99,5 Ta lại có: a b 59,7 99,5 = ⇒ = ⇒ 0 A 29,83 0 sin A sin B sin A sin124
⇒ AC hợp với phương nam một góc 340 + 29,830 = 63,830
Vậy tàu A chuyển động theo hướng N63,830E
Ví dụ 7:Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và
dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa
phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều
cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)? Lời giải
Giả sử toà nhà là AB, AB = 18,5 m; giác kế AC = 1,5 m; chiều cao của cái cây là DE; khoảng cách từ tòa
nhà tới cây là BD = 30 m; góc tạo bởi phương quan sát gốc cây và phương nằm ngang là 0 FCD = 34 ,
góc tạo bởi phương quan sát ngọn cây và phương nằm ngang là 0
FCE = 24 . Ta cần tính DE. Hình vẽ mô phỏng:
Ta có: BC = BA + AC = 18,5 + 1,5 = 20 (m).
Tam giác BCD vuông tại B, áp dụng định lí Pythagore ta có: 2 2 2 2 2
CD = BC + BD = 20 + 30 =1300 ⇒ CD = 1300 =10 13 36,06. Lại có: = − 0 0 0
ECD FCD FCE = 34 − 24 =10 ⇒ = 0 CF / /BD CDB FCD = 34 (so le trong) ⇒ 0 0 0 = − = 0 CDB 90 34 56 ; CED =114 . 0 0 0 CDB = 90 − 34 = 56
Áp dụng định lí sin trong tam giác CDE ta có: CD DE = ⇒ DE 66 . m sin CED sin ECD
Vậy chiều cao của cây khoảng 6,6 m.
Ví dụ 10:Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm A và
B trên mặt đất có khoảng cách AB =12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân
của giác kế có chiều cao h =1,3m . Gọi D là đỉnh tháp và hai điểm A , B cùng thẳng hàng với C thuộc 1 1 1
chiều cao CD của tháp. Người ta đo được góc DAC = 49° và
DB C = 35° . Tính chiều cao CD của 1 1 1 1 Trang 29/9 tháp. Lời giải Ta có
C DA = 90° − 49° = 41°;
C DB = 90° − 35° = 55° , nên A DB =14° . 1 1 1 1 1 1
Xét tam giác A DB , có A B A D 12.sin 35 1 1 1 = A D ° ⇒ = ≈ 28,45m . 1 1 sin A DB sin A B D 1 sin14° 1 1 1 1
Xét tam giác C A D vuông tại C , có 1 1 1 1 sin C D C A D = ⇒ C D = A .
D sin C A D = 28,45.sin 49° ≈ 21,47 m 1 1 A D 1 1 1 1 1
⇒ CD = C D + CC ≈ 22,77 m . 1 1
Ví dụ 12:Cho đường tròn tâm O bán kính R và điểm M thỏa mãn MO = 3R . Một đường kính AB thay
đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức S = MA + MB . Lời giải Gọi = α ⇒ MOA MOB =180° −α . Ta có 2 2 2 2 2
MA = MO + AO − 2 . MO A .
O cosα = 9R + R − 6R cosα = R 10 − 6cosα . 2 2
MB = MO + BO − MO BO ( °−α ) 2 2 2 2 . .cos 180
= 9R + R + 6R cosα = R 10 + 6cosα .
Xét C = 10 − 6cosα + 10 + 6cosα 2 2
⇒ C = 20 + 2 100 − 36cos α ≥ 20 + 2 100 − 36 = 36 . cosα =1 α = 0°
Suy ra C ≥ 6 . Dấu " = " xẩy ra khi 2 cos α =1 ⇔ ⇔ . cosα 1 α = − =180°
Ta có S = MA + MB = R( 10−6cosα + 10+ 6cosα ) ≥ 6R.
Suy ra min S = 6R khi và chỉ khỉ A , O , B , M thẳng hàng.
Ví dụ 13: Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1 m , người ta cắt ra một hình chữ
nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu? Trang 30/9
Xét đường tròn bán kính 1, ta cắt trên đó một hình chữ nhật ABCD . Khi đó 1 S = AC BD α = 2sinα ≤ 2. ABCD . .sin 2
Dấu bằng xảy ra khi và chỉ khi α = 90° .
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng 1.
Ví dụ 14: Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 0
60 . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ.
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây? Lời giải
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có
AB = 40, AC = 30 và 0 A = 60 .
Áp dụng định lí côsin vào tam giác ABC, ta có 2 2 2
a = b + c − 2bccos A 2 2 0
= 30 + 40 − 2.30.40.cos60 = 900 +1600 −1200 =1300.
Vậy BC = 1300 ≈ 36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí. Chọn B.
Ví dụ 15:Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông,
người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta
đo được khoảng cách AB = 40m , 0 CAB = 45 và 0 CBA = 70 .
Tìm khoảng cách AC Lời giải
Áp dụng định lí sin vào tam giác ABC, ta có AC AB = sin B sinC 0 Vì sinC β = sin(α + β ) nên . AB sin 40.sin 70 AC = = ≈ Chọn C. sin(α + β ) 41,47 m. 0 sin115 Trang 31/9
Ví dụ 16:Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết = = 0 AH 4m, 20 HB m,
BAC = 45 . Tìm chiều cao của cây Lời giải
Trong tam giác AHB , ta có AH 4 1 = = = → 0 tan ABH ABH ≈11 19'. BH 20 5 Suy ra 0 = − 0 ABC 90 ABH = 78 41'. Suy ra 0 = − + ACB (BAC ABC) 0 180 = 56 19'.
Áp dụng định lý sin trong tam giác ABC , ta được AB CB . AB sin BAC = →CB = ≈17m. Chọn B. sin ACB sin BAC sin ACB
Ví dụ 17:Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , A B trên
mặt đất sao cho ba điểm ,
A B và C thẳng hàng. Ta đo được AB = 24 m , 0 = 0 CAD 63 , 48 CBD =
. Tìm chiều cao h của tháp Lời giải
Áp dụng định lí sin vào tam giác ABD, ta có AD AB = . sin β sin D
Ta có α = D + β nên 0 0 0
D = α − β = 63 − 48 =15 . 0 Do đó . AB sin β 24.sin 48 AD = = ≈ sin(α − β ) 68,91 m. 0 sin15
Trong tam giác vuông ACD, có h = CD = .
AD sinα ≈ 61,4 m. Chọn D.
Ví dụ 18:Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với
mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 0 50 và 0 40 so với
phương nằm ngang. Tìm chiều cao của tòa nhà gần nhất với giá trị nào sau đây? Lời giải Từ hình vẽ, suy ra 0 BAC =10 và Trang 32/9 0 = − + ABD (BAD ADB) 0 = − ( 0 0 + ) 0 180 180 50 90 = 40 .
Áp dụng định lí sin trong tam giác ABC , ta có 0 BC AC
BC.sin ABC 5.sin 40 = → AC = = ≈ 18,5 m . 0 sin BAC sin ABC sin BAC sin10
Trong tam giác vuông ADC , ta có CD = → = sinCAD
CD AC.sinCAD =11,9 m. AC
Vậy CH = CD + DH =11,9 + 7 =18,9 m. Chọn B.
Ví dụ 19:Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng
đứng cách chân tháp một khoảng CD = 60m, giả sử chiều cao của giác kế là OC =1m .
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy
đỉnh A của tháp. Đọc trên giác kế số đo của góc 0 AOB = 60 .
Tìm chiều cao của ngọn tháp A 60° B O 1m D 60m C Lời giải
Tam giác OAB vuông tại B, có AB 0 tan AOB =
⇒ AB = tan 60 .OB = 60 3 m. OB
Vậy chiếu cao của ngọn tháp là h = AB + OC = (60 3 + )1m. Chọn C.
Ví dụ 20:Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng
độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang góc 0
30 , phương nhìn BC
tạo với phương nằm ngang góc 0
15 30'. Tính độ cao của ngọn núi so với mặt đất.
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? Lời giải
Từ giả thiết, ta suy ra tam giác ABC có 0 = 0
CAB 60 , ABC =105 30′ và c = 70. Khi đó + + 0 = ⇔ 0 = − + A B C C (A B) 0 0 0 180 180
= 180 −165 30′ =14 30 .′
Theo định lí sin, ta có b c = hay b 70 = sin B sinC 0 0 sin105 30′ sin14 30′ Trang 33/9 0 ′ Do đó 70.sin105 30 AC = b = ≈ 269,4 m. 0 sin14 30′
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 0 30 nên AC 269,4 CH = = = 134,7 m. 2 2
Vậy ngọn núi cao khoảng 135 m. Chọn A.
Bài toán 6: Chứng minh các hệ thức trong tam giác
Phương pháp: Dùng các hệ thức lượng trong tam giác
Ví dụ 1:Cho tam giác ABC thỏa mãn hệ thức b + c = 2a . Chứng minh sin B + sin C = 2sin A .
a = 2R sin A Ta có a b c 2R b = = =
⇔ = 2Rsin B .
sin A sin B sin C c = 2Rsin C
Mà b + c = 2a ⇔ 2Rsin B + 2Rsin C = 4Rsin A ⇔ sin B + sin C = 2sin A.
Ví dụ 2:Cho tam giác ABC , các đường cao h , h , h thỏa mãn hệ thức 3h = h + h . Chứng minh a 2 a b c b c 3 2 1 = + . a b c
3h = h + h 6S 4S 2S ⇔ = + 3 2 1 ⇔ = + . a 2 b c a b c a b c
Ví dụ 3: Cho tam giác ABC , nếu 2h = h + h . Chứng minh 2 1 1 = + . a b c
sin A sin B sin C Lời giải
2h = h + h 4S 2S 2S ⇔ = + 4 2 2 ⇔ = + a b c a b c
2Rsin A 2Rsin B 2Rsin C 2 1 1 ⇔ = + .
sin A sin B sin C
Ví dụ 4:Diện tích S của tam giác chứng minh 2
8S = (a + b + c)(a + b − c)(a −b + c)(b + c − a) Lời giải
Áp dụng công thức Hê – rông S = p( p − a)( p −b)( p − c) 2
⇔ S = p( p − a)( p −b)( p − c) Nếu thay a b c p + + =
vào công thức Hê – rông thì ta 2 có: 2
8S = (a + b + c)(a + b − c)(a −b + c)(b + c − a).
Ví dụ 5:Cho hai tam giác vuông ABC, A′BC′′ vuông góc tại A và A′ đồng dạng với nhau. Gọi a, ,
b c và a ,′ b ,′ c′ lần lượt là độ dài các cạnh đối với các đỉnh, h và h′ lần lượt là các đường
cao xuất phát từ A và A .′ Chứng minh:
a) aa′ = bb′ + cc′ b) 1 1 1 = + .
hh′ bb′ cc′ Giải a) Ta có A ∆ BC ∽ A ∆ ′B C ′ ′ ⇒ BC AC AB = = ⇔ a b c = = B C
′ ′ A′C′ A′B′
a′ b′ c′ ′ ′ ′ ′ + ′ ⇔ aa bb cc bb cc = = = 2 2 2 2 2 a′ b′ c′ b′ + c′
Tam giác vuông A′B C ′ ′ ta có: 2 2 2
a′ = b′ + c′ Trang 34/9 ′ ′ + ′ Do đó aa bb cc = ⇒
aa′ = bb′ + cc .′ 2 2 a′ a′ b) Ta có A ∆ BC ∽ A ∆ ′B C ′ ′ nên ta có ah = bc ⇔ 1 a = h bc ′ a h ′ ′ = b c′′ ⇔ 1 a = h′ b c′′ ′ ′ + ′ Do đó 1 aa bb cc = = ⇒ hh′ . bc b c′′ . bc b c′′ 1 1 1 = + .
hh′ bb′ cc′
Ví dụ 6:Cho A∆BC. Chứng minh rằng: 2 2 2
a) tanA c + a − b = b) 1 2 2
S = (a sin 2B + b sin 2 ) A . 2 2 2
tanB c + b − a 4 Giải 2 2 2 a) Ta có: cos
b + c − a A = ; sin a A = 2bc 2R 2 2 2 cos
a + c − b B = ; sin b B = 2ac 2R 2 2 2
a .a +c −b
Ta có: tanA sin Acos B 2R 2ac = = 2 2 2
tanB sin B cos A
b .b +c −a 2R 2bc 2 2 2 tan
A a + c − b = . 2 2 2
tanB b + c − a 2 2 2 2 2 2 + − + −
b) Ta có: 1 2 b a c b 2 .2 + .2 a b c a a b 4 2R 2ac 2R 2bc 1 ab ( 2 2 2) ab a c b ( 2 2 2 b c a ) = + − + + − 4 2Rc 2Rc ab = ( 2 2 2 2 2 2 + − + + − ) ab 2 = .2 abc a c b b c a c = = S. 8Rc 8Rc 4R Ví dụ 7:Cho A
∆ BC có các cạnh là a, ,
b c và các đường trung tuyến xuất phát từ B, C là m m thỏa b , c c mb = ≠ 1. b mc
a) Chứng minh rằng: 2 2 2
2a = b + c
b) Suy ra rằng: 2cotgA = cotgB + cotgC. Giải 2 1 2 2 b a + c − 2 2 2 c 2 2 a) Ta có: c m c m b = ⇔ b = ⇔ = b m 2 2 b m 2 2 b c c 1 2 2 c a + b − 2 2 2 2 2 2 + − ⇔ c 2a 2c b = 2 2 2 2 b
2a + 2b − c ⇔ 2 2 2 2 4 2 2 2 2 4
2a c + 2b c − c = 2a b + 2b c − b ⇔ 4 4 2 2 2 2
c − b + 2a b − 2a c = 0 ⇔ 2 2 2 2 2
(c − b )(c + b − 2a ) = 0 Trang 35/9 ⇔ 2 2 2
c + b − 2a = 0 (vì 2 2
c ≠ b ⇒ c − b ≠ 0) ⇔ 2 2 2
2a = b + c . b) Ta có: 2 2 2
b + c = a + 2bccos A 2 Do đó (1) ⇔ 2 2
a + 2bccos A = 2a ⇔ cos a A = 2bc
Ta lại có: a = 2R ⇒ a = 2Rsin ;
A b = 2Rsin ;
B c = 2Rsin C sin A 2 2 Vậy a sin cos A A = = ⇔ 2cos A sin A =
2bc 2sin Bsin C sin A sin Bsin C + ⇔ sin( ) 2cotg B C A =
( A bù với B + C) sin Bsin C + ⇔ sin cos sin cos 2cotg B C C B A = sin Bsin C ⇔
2cotgA = cotgB + cotgC.
Ví dụ 8:Cho tứ giác lồi ABC .
D Gọi I, J lần lượt là trung điểm của AC và B . D
a) Chứng minh rằng 2 2 2 2 2 2 2
AB + BC + CD + DA = AC + BD + 4IJ .
b) Suy ra điều kiện cần và đủ để một tứ giác là hình bình hành. Giải
a) Áp dụng định lí trung tuyến đối với hai A ∆ BD và B ∆ CD, ta có 2 2 2 2 + = 2 BD AB AD AJ + (1) 2 2 2 2 2 + = 2 BD BC CD CJ + (2) 2
Cộng (1) và (2) vế theo vế ta có: 2 2 2 2 2 2 2
AB + AD + BC + CD = 2(AJ + CJ ) + BD (3)
Áp dụng định lí trung tuyến với A ∆ JC ta có: 2 2 2 2 + = 2 AC AJ CJ IJ + (4) 2
Thế (4) vào (3) ta được: 2 2 2 2 2 2 2
AB + AD + BC + CD = 4IJ + AC + BD .
b) ABCD là hình bình hành ⇔ I ≡ J ⇔ IJ = 0 ⇔ 2 2 2 2 2 2
AB + AD + BC + CD = AC + BD
Ta phát biểu: ABCD là hình bình hành khi và chỉ khi tổng bình phương các cạnh bằng tổng bình phương hai đường chéo.
Ví dụ 9:Ba cạnh của một tam giác có số đo là 2 2
x + x +1; 2x +1; x −1.
a) Tìm x để tồn tại một tam giác như trên. b) π
Khi đó chứng minh tam giác ấy có một góc là 2 . 3 Giải
a) Để tồn tại một tam giác có số đo ba cạnh như đề bài thì 2
2x +1> 0, x −1> 0 2 2 2 2 2
x + 3x + 2 > x −1, 2x + x > 2x +1, x + 2x > x + x +1 1
x > − , x < 1, − 1< x 2 ⇔ x >1. 1 x > 1,
− x < − ∨ x >1, x >1 2 Trang 36/9 b) Đặt 2
a = x + x +1; 2 b = x −1; c = 2x +1 2 2 2 2 π
b + c − a (2x +1)(1− x ) 1 cos A = = = − ⇒ 2 A = . 2 2bc 2(2x +1)(x −1) 2 3
Ví dụ 10: A∆BC vuông tại ,A AH là đường cao, r, r, r lần lượt là bán kính đường tròn nội tiếp các 1 2
tam giác ABC, AHB, AHC.
a) Chứng minh rằng r c r b 1 2 = , = . b) Suy ra 2 2 2
r = r + r . r a r a 1 2 Giải a) Ta có HB ∆ A ∽ HA ∆ C ⇒ r r r r BA c 1 2 1 = = ⇒ = = BA BC AC r BC a và r AC b 2 = = . r BC a 2 2 2 2
b) Suy ra r + r c + b 1 2 = = 1 ⇔ 2 2 r a 2 2 2
r = r + r . 1 2
Ví dụ 11:Cho A ∆ BC có 4 4 4
a = b + c . Chứng minh: a) 2 2 2
b + c > a ⇒ A ∆ BC nhọn. b) 2
2sin A = tanBtanC. Giải a > b A > B a) Ta có: 4 4 4
a = b + c ⇒ ⇒ a > c A > C Ta lại có: 4 4 4 2 2 2 2 2 2 2 2
a = b + c = (b + c ) − 2b c < (b + c ) Suy ra 2 2 2
a < b + c (đpcm) Hay 2 2 2 2
b + c − 2bccos A < b + c ⇒ cos A > 0 π
⇒ 0 < A < vì A > B, A > C ⇒ B, C nhọn 2 Kết luận: A ∆ BC nhọn. b) Ta có: 4 2 2 2 2 2
a = (b + c ) − 2b c ⇔ 4 2 2 2 2
a = (a + 2bc cos ) A − 2b c ⇔ 2 2 2 2 2 2
0 = 4b c cos A + 4a bccos A − 2b c ⇔ 2 2 0 = 2bc(1− sin )
A + 2a cos A − bc ⇔ 2 2
0 = (2sin Bsin C)(1− sin )
A − 2sin Acos(B + C) − sin Bsin C ⇔ 2
0 = sin Bsin C − 2sin Acos B cosC ⇔ 2
sin Bsin C = 2sin Acos B cosC ⇔ 2
tanBtanC = 2sin A (do chia 2 vế cho cos B cosC).
Ví dụ 12:Cho A
∆ BC , có các đường cong AA , BB , CC và , A B, C nhọn. 1 1 1
a) Chứng minh rằng A B + B C + C A = a cos A + bcos B + ccosC. 1 1 1 1 1 1
b) Chứng minh bán kính đường tròn ngoại tiếp A
∆ BC bằng hai lần bán kính đường tròn ngoại tiếp A ∆ B C . 1 1 1 Giải a) Ta có: A B 1 1 = AB ⇒
A B = AB cosC = . c cosC sin ACA 1 1 1 Tương tự B C = . a cos ; A C A = . b cos B 1 1 1 1 Do đó:
A B + B C + C A = a cos A + bcos B + ccosC. 1 1 1 1 1 1 Trang 37/9
b) Gọi R , R lần lượt là bán kính đường tròn ngoại tiếp A ∆ B C và A ∆ BC, ta có: 1 1 1 1 A B c cosC c cosC 1 1 2R = = = 1 + sin AC B
sin(A AC B BC) sin 2C 1 1 1 1 1 ⇒ 2 c R = = R (đpcm). 1 2sin C
Ví dụ 13:Cho A
∆ BC có độ dài các cạnh là a, ,
b c và bán kính đường tròn ngoại tiếp là . R Chứng minh rằng: 2 2 2 ( + + ) cot g + cot g + cot g a b c R A B C = . abc Giải 2 2 2
Áp dụng định lí hàm số côsin vào A + − ∆ BC, ta có: cos b c a A = 2bc
Áp dụng định lí hàm số sin, ta có: a = 2R ⇒ sin a A = sin A 2R 2 2 2 2 2 2 Do đó cos + − 2 2 (b + − ) cot g A b c a R R c a A = = × = sin A 2bc a 2bca 2 2 2 2 2 2 Tương tự ( + − ) cot g R a c b B + − = ; ( ) cotg R a b c C = abc abc Suy ra: 2 2 2 2 2 2 2 2 2 cotg + cotg + cotg R A B C =
b + c − a + a + c − b + a + b − c abc 2 2 2
(a + b + c ) = . R abc
Ví dụ 14:Chứng minh rằng A
∆ BC vuông nếu có S = p( p − a) với S là diện tích, p là nửa chu vi, a, ,
b c là độ dài 3 cạnh. Giải
Ta có: S = p( p − a) ⇔
p( p − a)( p − b)( p − c) = p( p − a)
Bình phương hai vế, ta có: 2 2
p( p − a)( p − b)( p − c) = p ( p − a)
Rút gọn 2 vế cho p( p − a) ⇒ ( p − b)( p − c) = p( p − a) ⇔ 2 2
p − pc − pb + bc = p − pa ⇔ pa − pb − pc + bc = 0 + +
⇔ p(b + c − a) − bc = 0
⇔ a b c (b + c − a) − bc = 0 2
⇔ [(b + c) + a][(b + c) − a]− 2bc = 0 ⇔ 2 2
(b + c) − a − 2bc = 0 ⇔ 2 2 2
b + c + 2bc − a − 2bc = 0 ⇔ 2 2 2
b + c − a = 0 ⇔ 2 2 2
a = b + c ⇔ A
∆ BC vuông tại A (đpcm).
Ví dụ 15:Cho A
∆ BC thỏa a = 2bc cosC. Hỏi A
∆ BC có đặc điểm gì ? Giải
Theo định lí hàm số côsin, ta có: 2 2 2 2 2 2 cos
a + b − c C + − = ⇒ = 2 cos = 2 . a b c a b C b 2ab 2ab ⇔ 2 2 2 2
a = a + b − c ⇔ 2 2 b − c = 0 ⇔ b = c Vậy A
∆ BC cân tại A nếu a = 2 . b cosC.
Ví dụ 16: Cho 2 đường tròn (O ; R) và (O ; r) cắt nhau tại ,
A B, tiếp xúc với một đường thẳng tại 1 2 C, .
D Gọi N là giao điểm của AB và CD ( B nằm giữa A và N). Đặt AO C = α; AO D = β. 1 2
a) Tính AC theo R và α, AD theo r, β.
b) Tính bán kính x của đường tròn ngoại tiếp A ∆ C . D Trang 38/9 Lời giải α β
a) Ta có: AC = 2Rsin ; AD = 2r sin . 2 2 β b) Mặt khác: =
AC 2xsin CDA = 2xsin 2 α AD = 2xsin 2 α β α β ⇒ 2
4Rr sin sin = 4x sin sin ⇒ 2 2 2 2 x = Rr.
Ví dụ 17:Tứ giác ABCD nội tiếp trong đường tròn đường kính AC.BD = ; a CAB = α; CAD = β. a) Tính AC.
b) Tính diện tích tứ giác ABCD theo a, α, β. Lời giải a) Ta có: BD a AC = = sin BAD sin(α + β )
b) Gọi I là giao điểm của AC và BD dt 1 = (ABCD) B . D AC.sin AIB 2 Ta có: = α + sin AIB sin( ABI) α π sin( ACD) sin α β = + = + − 2 ⇒
sin AIB = cos(β −α) 2 β −α Vậy dt a cos( ) (ABCD) = . 2sin(α + β )
C. BÀI TẬP TRẮC NGHIỆM
BÀI TẬP TRẮC NGHIỆM 1
Câu 1. Cho ∆ABC có = = 0
b 6,c 8, A = 60 . Độ dài cạnh a là: A. 2 13. B. 3 12. C. 2 37. D. 20. Lời giải Chọn A. Ta có: 2 2 2 0
a = b + c − 2bccos A = 36 + 64 − 2.6.8.cos60 = 52 ⇒ a = 2 13 .
Câu 2. Cho ∆ABC có S = 84,a =13,b =14,c =15. Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là:
A. 8,125. B. 130. C. 8. D. 8,5. Lời giải Chọn A. Ta có: . a . b c . a . b c 13.14.15 65 S ABC ∆ = ⇔ R = = = . 4R 4S 4.84 8
Câu 3. Cho ∆ABC có a = 6,b = 8,c =10. Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. Lời giải Chọn B. Trang 39/9 Ta có: Nửa chu vi a + b + c ABC ∆ : p = . 2
Áp dụng công thức Hê-rông: S = p( p − a)( p − b)( p − c) = 12(12 − 6)(12 −8)(12 −10) = 24 . Câu 4. Cho ABC ∆
thỏa mãn : 2cos B = 2 . Khi đó: A. 0 B = 30 . B. 0 B = 60 . C. 0 B = 45 . D. 0 B = 75 . Lời giải Chọn C. Ta có: 2 = ⇔ = ⇒ 0 2cos B 2 cos B B = 45 . 2
Câu 5. Cho ∆ABC vuông tại B và có 0
C = 25 . Số đo của góc A là: A. 0 A = 65 . B. 0 A = 60 . C. 0 A =155 . D. 0 A = 75 . Lời giải Chọn A. Ta có: Trong ABC ∆ + + 0 = ⇒ 0 = − − 0 0 0 0 A B C 180 A 180
B C =180 − 90 − 25 = 65 .
Câu 6. Cho ∆ABC có 0
B = 60 ,a = 8,c = 5. Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Lời giải Chọn A. Ta có: 2 2 2 2 2 0
b = a + c − 2accos B = 8 + 5 − 2.8.5.cos60 = 49 ⇒ b = 7 .
Câu 7. Cho ∆ABC có 0 = 0
C 45 , B = 75 . Số đo của góc A là: A. 0 A = 65 . B. 0 A = 70 C. 0 A = 60 . D. 0 A = 75 . Lời giải Chọn C. Ta có: + + 0 = ⇒ 0 = − − 0 0 0 0 A B C 180 A 180
B C =180 − 75 − 45 = 60 .
Câu 8. Cho ∆ABC có S =10 3 , nửa chu vi p =10. Độ dài bán kính đường tròn nội tiếp r của tam giác trên là: A. 3. B. 2. C. 2. D. 3. Lời giải Chọn D. Ta có: S 10 3
S = pr ⇒ r = = = 3. p 10
Câu 9. Cho ∆ABC có 0
a = 4,c = 5, B =150 .Diện tích của tam giác là: A.5 3. B. 5. C. 10. D. 10 3. Lời giải Chọn B. Ta có: 1 1 0 S ABC ∆ = . a .
c sin B = .4.5.sin150 = 5. 2 2
Câu 10. Cho tam giác ABC thỏa mãn: 2cos A =1. Khi đó: A. 0 A = 30 . B. 0 A = 45 . C. 0 A =120 . D. 0 A = 60 . Lời giải Chọn D. Ta có: 1 = ⇔ = ⇒ 0 2cos A 1 cos A A = 60 . 2
Câu 11. Cho tam giác ABC có b = 7; c = 5, 3
cos A = . Đường cao h của tam giác ABC là 5 a A. 7 2 . B. 8. C.8 3. D.80 3. 2 Trang 40/9 Lời giải Chọn A. Ta có: 2 2 2 2 2 3
a = b + c − 2bccos A = 7 + 5 − 2.7.5. = 32 ⇒ a = 4 2. 5 Mặt khác: 2 2 2 2 9 16 4
sin A + cos A =1⇒ sin A =1− cos A =1− =
⇒ sin A = (Vì sin A > 0 ). 25 25 5 4 7.5. Mà: 1 1 bcsin A 5 7 2 S ABC ∆ = . b . c sin A = . a h ⇒ h = = = . 2 2 a a a 4 2 2
Câu 12. Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 2 2 2 A. 2 b c a m + = + B. 2 a c b m + = − a . a . 2 4 2 4 2 2 2 2 2 2 C. 2 a b c m + = −
D. 2 2c 2b a m + − = a . a . 2 4 4 Lời giải Chọn D. 2 2 2 2 2 2 Ta có: 2 b + c a
2b + 2c − a a m = − = . 2 4 4
Câu 13. Cho tam giác ABC . Tìm công thức sai:
A. a = 2R. B. sin a A = .
C. bsin B = 2R. D. csin sin A C = . sin A 2R a Lời giải Chọn C. Ta có: a b c = = = 2 . R
sin A sin B sinC
Câu 14. Chọn công thức đúng trong các đáp án sau: A. 1
S = bcsin A. B. 1
S = acsin A. C. 1
S = bcsin B. D. 1
S = bcsin B. 2 2 2 2 Lời giải Chọn A. Ta có: 1 1 1
S = bcsin A = acsin B = absin C . 2 2 2
Câu 15. Cho tam giác ABC có a = 8,b =10 , góc C bằng 0
60 . Độ dài cạnh c là ? A. c = 3 21 . B. c = 7 2 . C. c = 2 11 . D. c = 2 21. Lời giải Chọn D. Ta có: 2 2 2 2 2 0
c = a + b − 2 . a .
b cosC = 8 +10 − 2.8.10.cos60 = 84 ⇒ c = 2 21 .
Câu 16. Cho tam giác ABC . Khẳng định nào sau đây là đúng ? A. 1 S a ABC ∆ = . a . b c . B. = R . 2 sin A 2 2 2 2 2 2 C. cos
b + c − a + − B = .
D. 2 2b 2a c m = . 2bc c 4 Lời giải Chọn D.
Câu 17. Cho tam giác ABC , chọn công thức đúng ? A. 2 2 2
AB = AC + BC − 2AC.AB cosC . B. 2 2 2
AB = AC − BC + 2AC.BC cosC . C. 2 2 2
AB = AC + BC − 2AC.BC cosC . D. 2 2 2
AB = AC + BC − 2AC.BC + cosC . Lời giải Chọn C. Trang 41/9
Câu 18. Cho tam giác ABC thoả mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng ?
A. cos B + cosC = 2cos . A
B.sin B + sinC = 2sin . A C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin . A 2 Lời giải Chọn B. Ta có: b + c a b c 2 = = = 2 b c b + c b + c R ⇒ = = ⇔ =
⇔ sin B + sinC = 2sin . A
sin A sin B sinC
sin A sin B sinC
2sin A sin B + sinC
Câu 19. Cho tam giác ABC. Đẳng thức nào sai ? A. B + C A
sin(A + B − 2C) = sin3C. B. cos = sin . 2 2 C. A + B + C C
sin(A + B) = sinC. D. 2 cos = sin . 2 2 Lời giải Chọn D. Ta có: 0
A + B + 2C 0 C B + C 0 180 90 cos cos 90 C cos B + C + + = ⇒ = + ⇒ = + ⇔ = − sin C A B C . 2 2 2 2 2 2 Câu 20. Gọi 2 2 2 S = a m + b m + c
m là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các
mệnh đề sau mệnh đề nào đúng ? A. 3 2 2 2
S = (a + b + c ) . B. 2 2 2
S = a + b + c . 4 C. 3 2 2 2
S = (a + b + c ) . D. 2 2 2
S = 3(a + b + c ) . 2 Lời giải Chọn A. 2 2 2 2 2 2 2 2 2 Ta có: 2 2 2 b + c a a + c b a + b c 3 2 2 2 S = a m + b m + c m = − + − + −
= (a + b + c ). 2 4 2 4 2 4 4
Câu 21. Độ dài trung tuyến c
m ứng với cạnh c của ABC ∆
bằng biểu thức nào sau đây 2 2 2 2 2 2 A. b + a c + − . B. b a c + . 2 4 2 4 2 2 2 C. 1 ( 2 2 b + a − 2b c + 2a ) 2 − c . D. . 2 4 Lời giải Chọn C. 2 2 2 2 2 2 Ta có: 2 b + a c b + a c 1 2 2 2 m = − ⇒ m = − =
b + a − c . c c (2 2 ) 2 4 2 4 2
Câu 22. Tam giác ABC có cosB bằng biểu thức nào sau đây? 2 2 2 2 2 2
A. b + c − a . B. 2 1 + − − sin B . C. a c b
cos(A + C). D. . 2bc 2ac Lời giải Chọn D. 2 2 2 Ta có: 2 2 2 = + − 2 cos ⇒ cos
a + c − b b a c ac B B = . 2ac
Câu 23. Cho tam giác ABC có 2 2 2
a + b − c > 0 . Khi đó : A. Góc 0 C > 90 B. Góc 0 C < 90 C. Góc 0 C = 90
D. Không thể kết luận được gì về góc C. Trang 42/9 Lời giải Chọn B. 2 2 2 Ta có: cos
a + b − c C = . 2ab Mà: 2 2 2
a + b − c > 0 suy ra: 0
cosC > 0 ⇒ C < 90 .
Câu 24. Chọn đáp án sai : Một tam giác giải được nếu biết : A. Độ dài 3 cạnh
B. Độ dài 2 cạnh và 1 góc bất kỳ C. Số đo 3 góc
D. Độ dài 1 cạnh và 2 góc bất kỳ Lời giải Chọn C.
Ta có: Một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một yếu tố
độ dài (tức là yếu tố góc không được quá 2).
Câu 25. Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu ? A. 84. B. 84 . C. 42. D. 168. Lời giải Chọn A. Ta có:
a + b + c 13 +14 +15 p = = = 21 . 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 21(21−13)(21−14)(21−15) = 84 .
Câu 26. Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là: A. 16. B. 8. C. 4. D. 4 2. Lời giải Chọn B. Ta có:
a + b + c 26 + 28 + 30 p = = = 42. 2 2 S
p( p − a)( p − b)( p − c)
42(42 − 26)(42 − 28)(42 − 30)
S = pr ⇒ r = = = = 8. p p 42
Câu 27. Một tam giác có ba cạnh là 52,56,60.Bán kính đường tròn ngoại tiếp là: A. 65. B. 40. C. 32,5. D. 65. 8 4 Lời giải Chọn C. Ta có:
a + b + c 52 + 56 + 60 p = = = 84. 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 84(84 − 52)(84 − 56)(84 − 60) =1344 . Mà abc abc 52.56.60 65 S = ⇒ R = = = . 4R 4S 4.1344 2
Câu 28. Tam giác với ba cạnh là 3,4,5. Có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ? A. 1. B. 2. C. 3. D. 2. Lời giải Chọn A. Ta có:
a + b + c 3 + 4 + 5 p = = = 6. 2 2 Suy ra: S
p( p − a)( p − b)( p − c) 6(6 − 3)(6 − 4)(6 − 5)
S = pr ⇒ r = = = =1. p p 6
Câu 29. Tam giác ABC có a = 6,b = 4 2,c = 2. M là điểm trên cạnh BC sao cho BM = 3 . Độ dài đoạn
AM bằng bao nhiêu ? A. 9 . B. 9. C. 3. D. 1 108. 2 Trang 43/9 Lời giải Chọn C.
Ta có: Trong tam giác ABC có a = 6 ⇒ BC = 6 mà BM = 3 suy ra M là trung điểm BC. 2 2 2 Suy ra: 2 2 b + c a AM = a m = − = 9 ⇒ AM = 3 . 2 4 Câu 30. Cho ABC ∆
, biết a = AB = (a ;a ) và b = AC = (b ;b ) . Để tính diện tích 1 2 1 2 S của ABC ∆ . Một
học sinh làm như sau: a b (I) Tính . cos A = a . b ( a.b )2 (II) Tính 2 sin A = 1− os c A = 1− ( 2 2 a . b ) 2 1 1 (III) 2 S = A . B AC.sinA =
a b − (a.b )2 2 2 1 (IV ) S = ( 2 2 a + a )( 2 2
b + b − a b + a b 1 2 1 2 ) ( 1 1 2 2)2 2 1 S = (a b + a b )2 1 2 2 1 2 1 S = ( 1 a 2 b − 2 a 1b) 2
Học sinh đó đã làm sai bắt đàu từ bước nào? A. (I) B. (II)
C. (III)
D. (IV ) Lời giải Chọn A. a.b
Ta có: cos A = . a . b
Câu 31. Câu nào sau đây là phương tích của điểm M (1;2) đối với đường tròn (C) . tâm I( 2 − ;1) , bán kính R = 2: A. 6. B. 8. C. 0. D. 5. − Lời giải Chọn A. Ta có: MI = ( 3 − ;1) ⇒ MI = 10 .
Phương tích của điểm M đối với đường tròn (C) tâm I là:
MI − R = ( − − + − )2 2 2 2 2 ( 2 1) (1 2) − 4 = 6.
Câu 32. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78o24' . Biết CA = 250 ,
m CB =120m . Khoảng cách AB bằng bao nhiêu ? A. 266 . m B. 255 . m C. 166 . m D. 298 . m Lời giải Chọn B. Ta có: 2 2 2 2 2 = +
− 2 . .cos = 250 +120 − 2.250.120.cos78o AB CA CB CB CA C
24' 64835 ⇒ AB 255.
Câu 33. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0
60 . Tàu thứ nhất chạy với tốc độ 30km / h , tàu thứ hai chạy với tốc độ 40km / h . Hỏi sau 2
giờ hai tàu cách nhau bao nhiêu km ? A. 13. B. 15 13. C. 10 13. D. 15. Lời giải Chọn Trang 44/9 Không có đáp án.
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: 1 S = 30.2 = 60k . m
Sau 2h quãng đường tàu thứ hai chạy được là: S2 = 40.2 = 80k . m
Vậy: sau 2h hai tàu cách nhau là: 2 2 0 S = 1 S + S2 − 2 1
S .S2.cos60 = 20 13.
Câu 34. Từ một đỉnh tháp chiều cao CD = 80m , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 72 12' và 0 34 26' . Ba điểm ,
A B, D thẳng hàng. Tính khoảng cách AB ? A. 71 . m B. 91 . m C. 79 . m D. 40 . m Lời giải Chọn B.
Ta có: Trong tam giác vuông CDA: 0 CD CD 80 tan 72 12' = ⇒ AD = = 25,7. 0 0 AD tan 72 12' tan 72 12'
Trong tam giác vuông CDB : 0 CD CD 80 tan34 26' = ⇒ BD = = 116,7. 0 0 BD tan34 26' tan34 26'
Suy ra: khoảng cách AB =116,7 − 25,7 = 91 . m
Câu 35. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 0 56 16' . Biết
CA = 200m , CB =180m . Khoảng cách AB bằng bao nhiêu ? A. 163 . m B. 224 . m C. 112 . m D. 168 . m Lời giải Chọn Không có đáp án Ta có: 2 2 2 2 2 0
AB = CA + CB − 2C . B C .
A cosC = 200 +180 − 2.200.180.cos56 16' 32416 ⇒ AB 180.
Câu 36. Cho đường tròn (C) đường kính AB với ( A 1; − 2
− ) ; B(2;1) . Kết quả nào sau đây là phương tích
của điểm M (1;2) đối với đường tròn (C) . A. 3. B. 4. C. 5. − D. 2. Lời giải Chọn D.
Ta có: AB = (3;3) ⇒ AB = 3 2 . Đường tròn −
(C) đường kính AB có tâm 1 1 I ;
là trung điểm AB và bán kính 2 2 AB 3 2 R = = . 2 2
Suy ra: phương tích của điểm M đối với đường tròn (C) là: 2 2 MI − R = 2.
Câu 37. Cho các điểm ( A 1; 2 − ), B( 2;
− 3),C(0;4). Diện tích ABC ∆ bằng bao nhiêu ? A. 13. B. 13. C. 26. D. 13. 2 4 Lời giải Chọn A. Ta có: AB = ( 3
− ;5) ⇒ AB = 34 , AC = ( 1
− ;6) ⇒ AC = 37 , BC = (2;1) ⇒ BC = 5 . Mặt khác
AB + AC + BC 37 + 34 + 5 p = = . 2 2 Suy ra: 13
S = p( p − AB)( p − AC)( p − BC) = . 2
Câu 38. Cho tam giác ABC có ( A 1; 1 − ), B(3; 3
− ),C(6;0). Diện tích ABC ∆ là A. 12. B. 6. C. 6 2. D. 9. Lời giải Chọn B. Ta có: AB = (2; 2
− ) ⇒ AB = 2 2 , AC = (5;1) ⇒ AC = 26 , BC = (3;3) ⇒ BC = 3 2 . Trang 45/9 Mặt khác .
AB BC = 0 ⇒ AB ⊥ BC . Suy ra: 1 S ABC ∆ = . AB BC = 6. 2
Câu 39. Cho a = (2; 3)
− và b = (5;m). Giá trị của m để a và b cùng phương là: A. 6. − B. 13 − . C. 12. − D. 15 − . 2 2 Lời giải Chọn D.
Ta có: a,b cùng phương suy ra 5 m 15 = ⇒ m = − . 2 3 − 2
Câu 40. Cho các điểm (
A 1;1), B(2;4),C(10; 2 − ). Góc
BAC bằng bao nhiêu? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 30 . Lời giải Chọn A.
Ta có: AB = (1;3) , AC = (9; 3) − . . AB AC Suy ra:
= = ⇒ 0 cos BAC 0 BAC = 90 . AB . AC
Câu 41. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là ? A. 6. B. 8. C. 13 . D. 11. 2 2 Lời giải Chọn C. Ta có: 2 2 2 13
5 +12 =13 ⇒ R = . (Tam giác vuông bán kính đường tròn ngoại tiếp bằng 1 cạnh 2 2 huyền ).
Câu 42. Cho tam giác ABC có a = 4,b = 6,c = 8 . Khi đó diện tích của tam giác là: A. 9 15. B. 3 15. C. 105. D. 2 15. 3 Lời giải Chọn B. Ta có:
a + b + c 4 + 6 + 8 p = = = 9. 2 2
Suy ra: S = p( p − a)( p − b)( p − c) = 3 15.
Câu 43. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu ? A. 2. B. 2 2. C. 2 3. D. 3. Lời giải Chọn A. Ta có: 5 +12 +13 p = =15 . Mà 2 2 2 1
5 +12 =13 ⇒ S = .5.12 = 30. 2 2 Mặt khác = . S
S p r ⇒ r = = 2. p
Câu 44. Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu ? A. 5. B. 4 2. C. 5 2. D. 6 . Lời giải Chọn A. Ta có: 2 2 2 10 6 + 8 =10 ⇒ R =
= 5. (Tam giác vuông bán kính đường tròn ngoại tiếp bằng 1 2 2 cạnh huyền ).
Câu 45. Cho tam giác ABC thoả mãn : 2 2 2
b + c − a = 3bc . Khi đó : Trang 46/9 A. 0 A = 30 . B. 0 A = 45 . C. 0 A = 60 . D. 0 A = 75 . Lời giải Chọn A. 2 2 2 Ta có:
b + c − a 3bc 3 0 cos A = = = ⇒ A = 30 . 2bc 2bc 2
Câu 46. Tam giác ABC có a =16,8 ; 0 B = 56 13'; 0
C = 71 . Cạnh c bằng bao nhiêu? A. 29,9. B. 14,1. C. 17,5. D. 19,9. Lời giải Chọn D.
Ta có: Trong tam giác ABC : + + 0 = ⇒ 0 0 0 0 A B C 180
A =180 − 71 − 56 13' = 52 47' . 0 Mặt khác a b c a c .
a sinC 16,8.sin 71 = = ⇒ = ⇒ c = = 19,9. 0
sin A sin B sinC sin A sinC sin A sin52 47'
Câu 47. Cho tam giác ABC , biết a = 24,b =13,c =15. Tính góc A? A. 0 33 34'. B. 0 117 49'. C. 0 28 37'. D. 0 58 24'. Lời giải Chọn B. 2 2 2 2 2 2 Ta có:
b + c − a 13 +15 − 24 7 0 cos A = = = − ⇒ A 117 49'. 2bc 2.13.15 15
Câu 48. Tam giác ABC có 0 A = 68 12' , 0
B = 34 44' , AB =117. Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Chọn A.
Ta có: Trong tam giác ABC : + + 0 = ⇒ 0 0 0 0 A B C 180
C =180 − 68 12'− 34 44' = 77 4'. 0 Mặt khác a b c AC AB .
AB sin B 117.sin34 44' = = ⇒ = ⇒ AC = = 68. 0
sin A sin B sinC sin B sinC sinC sin 77 4'
Câu 49. Tam giác ABC có = = 0
a 8,c 3, B = 60 . Độ dài cạnh b bằng bao nhiêu ? A. 49. B. 97 C. 7. D. 61. Lời giải Chọn C. Ta có: 2 2 2 2 2 0
b = a + c − 2accos B = 8 + 3 − 2.8.3.cos60 = 49 ⇒ b = 7 .
Câu 50. Cho tam giác ABC , biết a =13,b =14,c =15. Tính góc B ? A. 0 59 49'. B. 0 53 7'. C. 0 59 29'. D. 0 62 22'. Lời giải Chọn C. 2 2 2 2 2 2 Ta có:
a + c − b 13 +15 −14 33 0 cos B = = = ⇒ B 59 29'. 2ac 2.13.15 65
Câu 51: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy.
Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc . Biết
. Khoảng cách AB bằng bao nhiêu? A. B. C. D. Lời giải Chọn B Ta có:
Câu 52: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí , đi thẳng theo hai hướng tạo với nhau một góc
. Tàu thứ nhất chạy với tốc độ
, tàu thứ hai chạy với tốc độ . Hỏi
sau giờ hai tàu cách nhau bao nhiêu ? Trang 47/9 A. B. C. D. Lời giải Chọn B
Ta có: Sau quãng đường tàu thứ nhất chạy được là:
Sau quãng đường tàu thứ hai chạy được là:
Vậy: sau hai tàu cách nhau là:
Câu 53: Từ một đỉnh tháp chiều cao
, người ta nhìn hai điểm và trên mặt đất dưới các góc nhìn là và . Ba điểm
thẳng hàng. Tính khoảng cách ? A. B. C. D. Lời giải Chọn B
Ta có: Trong tam giác vuông : Trong tam giác vuông : Suy ra: khoảng cách
Câu 54: Khoảng cách từ đến không thể đo trực tiếp được vì phải qua một đầm lầy.
Người ta xác định được một điểm mà từ đó có thể nhìn được và dưới một góc . Biết , . Khoảng cách bằng bao nhiêu? A. B. C. D. Lời giải Chọn A Ta có:
Câu 55: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa
cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định
bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ ( cm; cm;
cm). Bán kính của chiếc đĩa này bằng.
A. 5,73 cm.
B. 6,01cm.
C. 5,85cm. D. 4,57cm. Lời giải Chọn A
Bán kính của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác . Nửa chu vi của tam giác là: cm. Diện tích tam giác là: cm2. Mà cm. Trang 48/9
BÀI TẬP TRẮC NGHIỆM 2
Câu 1. Tam giác ABC có AB = 5, BC = 7, CA = 8. Số đo góc A bằng: A. 30 .° B. 45 .°
C. 60 .° D. 90 .°
Câu 2. Tam giác ABC có AB = 2, AC =1 và A = 60°. Tính độ dài cạnh BC . A. BC =1. B. BC = 2. C. BC = 2. D. BC = 3.
Câu 3. Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và
ACB = 60° . Tính độ dài cạnh cạnh BC . A. BC = 3+ 3 6.
B. BC = 3 6 − 3. C. BC = 3 7.D. 3 3 33 BC + = . 2
Câu 4. Tam giác ABC có AB = 2, AC = 3 và C = 45°. Tính độ dài cạnh BC .
A. BC = 5. B. 6 2 BC + = . C. 6 2 BC − = . D. BC = 6. 2 2
Câu 5. Tam giác ABC có = °
B 60 , C = 45° và AB = 5. Tính độ dài cạnh AC . A. 5 6 AC = . B. AC = 5 3. C. AC = 5 2. D. AC =10. 2
Câu 6. Cho hình thoi ABCD cạnh bằng 1cm và có
BAD = 60° . Tính độ dài cạnh AC .
A. AC = 3. B. AC = 2. C. AC = 2 3. D. AC = 2.
Câu 7. Tam giác ABC có AB = 4, BC = 6, AC = 2 7 . Điểm M thuộc đoạn BC sao cho
MC = 2MB . Tính độ dài cạnh AM .
A. AM = 4 2. B. AM = 3.
C. AM = 2 3. D. AM = 3 2.
Câu 8. Tam giác ABC có 6 − 2 AB =
, BC = 3, CA = 2 . Gọi D là chân đường phân giác 2
trong góc A. Khi đó góc
ADB bằng bao nhiêu độ? A. 45 .° B. 60 .°
C. 75 .° D. 90 .°
Câu 9. Tam giác ABC vuông tại A, đường cao AH = 32 cm . Hai cạnh AB và AC tỉ lệ với 3 và
4. Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu? A. 38 c . m B. 40 c . m C. 42 c . m D. 45 c . m
Câu 10. Tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc
MPE, EPF, FPQ bằng nhau. Đặt MP = q, PQ = ,
m PE = x, PF = y . Trong các hệ thức sau, hệ thức nào đúng?
A. ME = EF = . FQ B. 2 2 2
ME = q + x − x . q C. 2 2 2
MF = q + y − y . q D. 2 2 2
MQ = q + m − 2q . m Câu 11. Cho góc
xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB = 1. Độ dài lớn nhất của đoạn OB bằng: A. 3. B. 3. C. 2 2. D. 2. 2 Trang 49/9 Câu 12. Cho góc
xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB =1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng: A. 3. B. 3. C. 2 2. D. 2. 2
Câu 13. Tam giác ABC có AB = c, BC = a, CA = b. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức ( 2 2 − ) = ( 2 2 b b a
c a − c ). Khi đó góc
BAC bằng bao nhiêu độ? A. 30 .° B. 45 .°
C. 60 .° D. 90 .°
Câu 14. Tam giác ABC vuông tại A, có AB = c, AC = b . Gọi là độ dài đoạn phân giác trong a góc
BAC . Tính theo b và c . a 2(b + c) 2 (b + c) A. 2bc bc = B. = C. 2 = D. = a . a . a . a . b + c bc b + c bc
Câu 15. Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 0
60 . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ.
Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào sau đây? A. 61 hải lí. B. 36 hải lí. C. 21 hải lí. D. 18 hải lí.
Câu 16. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người
ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo
được khoảng cách AB = 40m , 0 CAB = 45 và 0 CBA = 70 .
Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất
với giá trị nào sau đây? A. 53 m . B. 30 m. C. 41,5 m . D. 41 m .
Câu 17. Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết = = 0 AH 4m, 20 HB m, BAC = 45 .
Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m. B. 17m . C. 16,5m . D. 16m .
Câu 18. Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , A B trên
mặt đất sao cho ba điểm ,
A B và C thẳng hàng. Ta đo được AB = 24 m , Trang 50/9 0 = 0 CAD 63 , 48 CBD = .
Chiều cao h của tháp gần với giá trị nào sau đây? A. 18m . B. 18,5m . C. 60m . D. 60,5m.
Câu 19. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với
mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 0 50 và 0 40 so với phương nằm ngang.
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây? A. 12m . B. 19m . C. 24m . D. 29m .
Câu 20. Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng
đứng cách chân tháp một khoảng CD = 60m, giả sử chiều cao của giác kế là OC =1m .
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy
đỉnh A của tháp. Đọc trên giác kế số đo của góc 0 AOB = 60 .
Chiều cao của ngọn tháp gần với giá trị nào sau đây: A. 40m . B. 114m. A C. 105m . D. 110m. 60° B O 1m D 60m C
Câu 21. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng
độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang góc 0
30 , phương nhìn BC
tạo với phương nằm ngang góc 0 15 30'.
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? Trang 51/9 A. 135m. B. 234m. C. 165m . D. 195m .
Câu 22. Tam giác ABC có AB = 6cm, 8
AC = cm và BC =10cm . Độ dài đường trung tuyến
xuất phát từ đỉnh A của tam giác bằng: A. 4cm . B. 3cm . C. 7cm . D. 5cm .
Câu 23. Tam giác ABC vuông tại A và có AB = AC = a . Tính độ dài đường trung tuyến BM của tam giác đã cho. A. BM a = 1,5 .
a B. BM = a 2.
C. BM = a 3. D. 5 BM = . 2
Câu 24. Tam giác ABC có AB = 9cm, AC =12 cm và BC =15cm. Tính độ dài đường trung
tuyến AM của tam giác đã cho. A. 15 AM = cm.
B. AM =10cm. C. AM = 9 cm.D. 13 AM = cm. 2 2
Câu 25. Tam giác ABC cân tại C , có AB = 9cm và 15 AC =
cm . Gọi D là điểm đối xứng của 2
B qua C . Tính độ dài cạnh . AD
A. AD = 6 cm. B. AD = 9 cm.
C. AD =12cm. D. AD =12 2 cm.
Câu 26. Tam giác ABC có AB = 3, BC = 8. Gọi M là trung điểm của BC . Biết 5 13 cos AMB =
và AM > 3. Tính độ dài cạnh AC . 26
A. AC = 13 . B. AC = 7 . C. AC =13. D. AC = 7 .
Câu 27*. Tam giác .. có trọng tâm G . Hai trung tuyến BM = 6, CN = 9 và 0 BGC =120 . Tính độ dài cạnh AB .
A. AB = 11 . B. AB = 13 .
C. AB = 2 11. D. AB = 2 13 .
Câu 28**. Tam giác ABC có độ dài ba trung tuyến lần lượt là 9; 12; 15. Diện tích của tam giác ABC bằng: A. 24 . B. 24 2 .
C. 72. D. 72 2 .
Câu 29*. Cho tam giác ABC có AB = c, ,
BC = a CA = b. Nếu giữa a, , b c có liên hệ 2 2 2
b + c = 2a thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng: A. a 3 . B. a 3 . C. 2a 3 . D. 3a 3 . 2 3
Câu 30*. Cho hình bình hành ABCD có AB = a, ,
BC = b BD = m và AC = n . Trong các biểu
thức sau, biểu thức nào đúng: A. 2 2 m + n = ( 2 2 3 a + b ). B. 2 2 m + n = ( 2 2 2 a + b ). C. ( 2 2 + ) 2 2 2 m
n = a + b . D. ( 2 2 + ) 2 2 3 m
n = a + b .
Câu 31**. Tam giác ABC có AB = c, ,
BC = a CA = b. Các cạnh a, ,
b c liên hệ với nhau bởi đẳng thức 2 2 2
a + b = 5c . Góc giữa hai trung tuyến AM và BN là góc nào? A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Câu 32**. Tam giác ABC có ba đường trung tuyến m m m thỏa mãn 2 2 2
5m = m + m . Khi a , b , c a b c Trang 52/9
đó tam giác này là tam giác gì? A. Tam giác cân. B. Tam giác đều. C. Tam giác vuông.
D. Tam giác vuông cân.
Câu 33**. Tam giác ABC có AB = c, ,
BC = a CA = b. Gọi m m m là độ dài ba đường trung a , b , c
tuyến, G trọng tâm. Xét các khẳng định sau: (I). 2 2 2 3
m + m + m =
a + b + c . (II). a b c ( 2 2 2) 4 2 2 2 1
GA + GB + GC = ( 2 2 2
a + b + c ). 3
Trong các khẳng định đã cho có
A. (I) đúng. B. Chỉ (II) đúng. C. Cả hai cùng sai. D. Cả hai cùng đúng.
Câu 34. Tam giác ABC có BC =10 và O
A = 30 . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. R = 5. B. R =10. C. 10 R = . D. R =10 3 . 3
Câu 35. Tam giác ABC có AB = 3, 6
AC = và A = 60°. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. R = 3. B. R = 3 3 . C. R = 3 . D. R = 6 .
Câu 36. Tam giác ABC có BC = 21cm, CA =17cm, 10c AB =
m . Tính bán kính R của đường
tròn ngoại tiếp tam giác ABC . A. 85 R = cm . B. 7 R = cm. C. 85 R = cm . D. 7 R = cm. 2 4 8 2
Câu 37. Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R . Khi đó bán kính R bằng: A. a 3 R = . B. a 2 R = . C. a 3 R = . D. a 3 R = . 2 3 3 4
Câu 38. Tam giác ABC vuông tại A có đường cao 12 AH = cm và AB 3
= . Tính bán kính R 5 AC 4
của đường tròn ngoại tiếp tam giác ABC .
A. R = 2,5cm . B. R =1,5cm . C. R = 2cm . D. R = 3,5cm .
Câu 39. Cho tam giác ABC có AB = 3 3, 6 BC =
3 và CA = 9 . Gọi D là trung điểm BC .
Tính bán kính R của đường tròn ngoại tiếp tam giác . ABD A. 9 R = . B. R = 3. C. R = 3 3 . D. 9 R = . 6 2
Câu 40**. Tam giác nhọn ABC có AC = b, BC = a , BB' là đường cao kẻ từ B và CBB' = α .
Bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a, b và α là: 2 2 + − α 2 2 + + α A. a b 2abcos R = . B. a b 2abcos R = . 2sinα 2sinα 2 2 + + α 2 2 + − α C. a b 2abcos R = . D. a b 2abcos R = . 2cosα 2cosα
Câu 41. Tam giác A(1;3), B(5;− ) 1 có = = AB 3, 6 AC ,
BAC = 60°. Tính diện tích tam giác ABC . Trang 53/9 A. S = . B. 9 3 S = . C. S = .D. 9 S = . ABC ∆ 9 ABC ∆ 9 3 ABC ∆ 2 ABC ∆ 2
Câu 42. Tam giác ABC có = = ° AC 4, 30 BAC ,
ACB = 75°. Tính diện tích tam giác ABC . A. S = . B. S = . C. S = . D. S = . ABC ∆ 8 3 ABC ∆ 4 ABC ∆ 4 3 ABC ∆ 8
Câu 43. Tam giác ABC có a = 21, b =17, 10
c = . Diện tích của tam giác ABC bằng: A. S = . B. S = . C. S = . D. S = . ABC ∆ 84 ABC ∆ 24 ABC ∆ 48 ABC ∆ 16
Câu 44. Tam giác A(1;3), B(5;− ) 1 có = = AB 3, 6 AC ,
BAC = 60°. Tính độ dài đường cao h a của tam giác. A. h = . B. h = . C. h = . D. 3 h = . a 3 a 3 a 3 3 a 2
Câu 45. Tam giác ABC có = AC 4, 6
ACB = 0° . Tính độ dài đường cao h uất phát từ đỉnh A của tam giác.
A. h = 2 3 . B. h = 4 3 . C. h = 2. D. h = 4.
Câu 46. Tam giác ABC có a = 21, b =17, 10
c = . Gọi B' là hình chiếu vuông góc của B trên
cạnh AC . Tính BB' . A. BB' = 8. B. 84 BB' = . C. 168 BB' = . D. 84 BB' = . 5 17 17
Câu 47. Tam giác ABC có AB = 8cm, AC =18 cm và có diện tích bằng 64 2 cm . Giá trị sin A ằng: A. 3 sin A = . B. 3 sin A = . C. 4 sin A = . D. 8 sin A = . 2 8 5 9
Câu 48. Hình bình hành ABCD có AB = a, 2 BC = a và 0
BAD = 45 . Khi đó hình bình hành có diện tích bằng: A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 .
Câu 49*. Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE
cắt nhau tại G . Diện tích tam giác GFC bằng: A. 2 50 cm . B. 2 50 2 cm . C. 2 75 cm . D. 2 15 105 cm .
Câu 50*. Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng: A. 2 13 cm B. 2 13 2 cm C. 2 12 3 cm D. 2 15 cm .
Câu 51*. Tam giác ABC có BC = 2 3, 2
AC = AB và độ dài đường cao AH = 2. Tính độ dài cạnh AB . A. AB = 2 . B. 2 3 AB = . 3
C. AB = 2 hoặc 2 21 AB =
. D. AB = 2 hoặc 2 3 AB = . 3 3
Câu 52*. Tam giác ABC có BC = a, ,
CA = b AB = c và có diện tích S . Nếu tăng cạnh BC lên
2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích
của tam giác mới được tạo nên bằng: A. 2S . B. 3S . C. 4S . D. 6S .
Câu 53*. Tam giác ABC có BC = a và CA = b . Tam giác ABC có diện tích lớn nhất khi góc C bằng: Trang 54/9 A. 0 60 . B. 0 90 . C. 0 150 . D. 0 120 .
Câu 54*. Tam giác ABC có hai đường trung tuyến BM , CN vuông góc với nhau và có BC = 3, góc 0
BAC = 30 . Tính diện tích tam giác ABC . A. S = . B. S = . C. S = .D. 3 3 S = . ABC ∆ 9 3 ABC ∆ 6 3 ABC ∆ 3 3 ABC ∆ 2
Câu 55. Tam giác ABC có AB = 5, 8 AC = và 0
BAC = 60 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. r =1. B. r = 2. C. r = 3 . D. r = 2 3 .
Câu 56. Tam giác ABC có a = 21, b =17, 10
c = . Tính bán kính r của đường tròn nội tiếp tam giác đã cho.
A. r =16.
B. r = 7. C. 7 r = . D. r = 8. 2
Câu 57. Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a . A. a 3 r = . B. a 2 r = . C. a 3 r = . D. a 5 r = . 4 5 6 7
Câu 58. Tam giác ABC vuông tại A có AB = 6cm, BC =10cm. Tính bán kính r của đường
tròn nội tiếp tam giác đã cho.
A. r =1 cm. B. r = 2 cm. C. r = 2 cm. D. r = 3 cm.
Câu 59. Tam giác ABC vuông cân tại A, có AB = a . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. a r = . B. a r = . C. a r = . D. a r = . 2 2 2 + 2 3
Câu 60. Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r là
bán kính đường tròn nội tiếp tam giác ABC . Khi đó tỉ số R bằng: r A. 1 + − + + 2 . B. 2 2 . C. 2 1 . D. 1 2 . 2 2 2
ĐÁP ÁN VÀ LỜI GIẢI
Câu 1. Theo định lí hàm cosin, ta có 2 2 2 2 2 2
AB + AC − BC 5 + 8 − 7 1 cos A = = = . 2 . AB AC 2.5.8 2
Do đó, A = 60°. Chọn C.
Câu 2. Theo định lí hàm cosin, ta có 2 2 2 = + − 2 2 BC AB AC 2 .
AB AC.cos A = 2 +1 − 2.2.1.cos60° = 3 ⇒ BC = 3 . Chọn D. Câu 3.
Gọi M , N lần lượt là trung điểm của AB, BC . A
→MN là đường trung bình của ABC ∆ . M 1
→ MN = AC . Mà MN = 3 , suy ra AC = 6 . 2 B N C
Theo định lí hàm cosin, ta có Trang 55/9 2 2 2 = + − AB AC BC
2.AC.BC.cos ACB 2 2 2
⇔ 9 = 6 + BC − 2.6.BC.cos60° ⇒ BC = 3 + 3 6 Chọn A.
Câu 4. Theo định lí hàm cosin, ta có = + − AB AC BC AC BC C ⇒ ( )2 = ( )2 2 2 2 2 2. . .cos 2
3 + BC − 2. 3.BC.cos45° 6 2 BC + ⇒ = . Chọn B. 2
Câu 5. Theo định lí hàm sin, ta có AB AC 5 AC 5 6 = ⇔ = ⇒ AC = . sinC sin B sin 45° sin 60° 2 Chọn A. Câu 6. B
Do ABCD là hình thoi, có = ° ⇒ BAD 60 ABC =120° .
Theo định lí hàm cosin, ta có A C 2 2 2 = + − AC AB BC 2. . AB BC.cos ABC 2 2 D
= 1 +1 − 2.1.1.cos120° = 3 ⇒ AC = 3 Chọn A. Câu 7. AB BC AC + − + − ( )2 2 2 2 2 2 4 6 2 7
Theo định lí hàm cosin, ta có : 1 cos B = = = . 2. . AB BC 2.4.6 2 A Do 1 MC = 2MB
→ BM = BC = 2. 3
Theo định lí hàm cosin, ta có 2 2 2 = + − AM AB BM 2. . AB BM.cos B B M C 2 2 1
= 4 + 2 − 2.4.2. =12 ⇒ AM = 2 3 2 Chọn C. Câu 8.
Theo định lí hàm cosin, ta có: 2 2 2 A
AB + AC − BC 1 = = − cos BAC 2. . AB AC 2 ⇒ = ° ⇒ BAC 120 BAD = 60° 2 2 2 B D C
AB + BC − AC 2 = = ⇒ cos ABC ABC = 45° 2. . AB BC 2 Trong ABD ∆ có = ° = ° ⇒ BAD 60 , ABD 45 ADB = 75° . Chọn C.
Câu 9. Do tam giác ABC vuông tại A, có tỉ lệ 2 cạnh góc vuông AB : AC là 3: 4 nên AB là
cạnh nhỏ nhất trong tam giác. Trang 56/9 Ta có AB 3 4 = ⇒ AC = AB . AC 4 3 Trong ABC ∆
có AH là đường cao 1 1 1 1 1 1 1 9 ⇒ = + = + ⇔ = +
⇒ AB = 40. Chọn B. 2 2 2 2 2 2 2 AH AB AC AB 4 2 32 AB 16AB AB 3 Câu 10. Ta có = = MPQ = = ° ⇒ = MPE EPF FPQ 30 MPF EPQ = 60° . 3
Theo định lí hàm cosin, ta có P 2 2 2 = + − ME AM AE
2.AM.AE.cos MAE 2 2 2 2 = q + x − 2 .
qx cos30° = q + x − qx 3 2 2 2 = + − MF AM AF
2AM.AF.cos MAF M E F Q 2 2 2 2 = q + y − 2 .
qy cos60° = q + y − qy 2 2 2 2 2
MQ = MP + PQ = q + m . Chọn C.
Câu 11. Theo định lí hàm sin, ta có: OB AB AB = ⇔ = 1 = = OB .sinOAB
.sinOAB 2sinOAB sinOAB sin AOB sin AOB sin30° y
Do đó, độ dài OB lớn nhất khi và chỉ khi B = ⇔ sinOAB 1 OAB = 90° . Khi đó OB = 2 . x O Chọn D. A
Câu 12. Theo định lí hàm sin, ta có OB AB AB = ⇔ = 1 = = OB .sinOAB .sinOAB y 2sinOAB sinOAB sin AOB sin AOB sin30° B
Do đó, độ dài OB lớn nhất khi và chỉ khi = ⇔ sinOAB 1 OAB = 90° . x O A Khi đó OB = 2 .
Tam giác OAB vuông tại 2 2 2 2
A ⇒ OA = OB − AB = 2 −1 = 3 . Chọn B
Câu 13. Theo định lí hàm cosin, ta có 2 2 2 2 2 2 cos
AB + AC − BC
c + b − a BAC = = . 2. . AB AC 2bc Mà b( 2 2
b − a ) = c( 2 2 a − c ) 3 2 2 3 2
⇔ b − a b = a c − c ⇔ −a (b + c) + ( 3 3 b + c ) = 0 ⇔ (b + c)( 2 2 2
b + c − a − bc) 2 2 2
= 0 ⇔ b + c − a − bc = 0 (do b > 0, c > 0 ) 2 2 2
⇔ b + c − a = bc 2 2 2 Khi đó,
b + c − a 1 = = ⇒ cos BAC
BAC = 60°. Chọn C. 2bc 2 Câu 14. Ta có 2 2 2 2
BC = AB + AC = b + c . A
Do AD là phân giác trong của BAC Trang 57/9 B D C 2 2 AB ⇒ = . c = . c = .BC c b + c BD DC DC = . AC b b + c b + c
Theo định lí hàm cosin, ta có 2 c ( 2 2 b + c 2 2 2 ) = + − 2 2 BD AB AD 2. . AB . AD cos ABD ⇔ = c + AD − 2 . c . AD cos45° (b + c)2 2 c ( 2 2 b + c ) 3 2 2 2 2 ⇒ − 2. + − = 0 ⇔ − 2. bc AD c AD c AD c AD + = 0. (b + c)2 (b + c)2 2bc ⇒ AD = hay 2bc = . Chọn A. b + c a b + c
Câu 15. Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có
AB = 40, AC = 30 và 0 A = 60 .
Áp dụng định lí côsin vào tam giác ABC, ta có 2 2 2
a = b + c − 2bccos A 2 2 0
= 30 + 40 − 2.30.40.cos60 = 900 +1600 −1200 =1300.
Vậy BC = 1300 ≈ 36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí. Chọn B.
Câu 16. Áp dụng định lí sin vào tam giác ABC, ta có AC AB = sin B sinC 0 Vì sinC β = sin(α + β ) nên . AB sin 40.sin 70 AC = = ≈ Chọn C. sin(α + β ) 41,47 m. 0 sin115
Câu 17. Trong tam giác AHB , ta có AH 4 1 = = = → 0 tan ABH ABH ≈11 19'. BH 20 5 Suy ra 0 = − 0 ABC 90 ABH = 78 41'. Suy ra 0 = − + ACB (BAC ABC) 0 180 = 56 19'.
Áp dụng định lý sin trong tam giác ABC , ta được AB CB . AB sin BAC = →CB = ≈17m. Chọn B. sin ACB sin BAC sin ACB
Câu 18. Áp dụng định lí sin vào tam giác ABD, ta có AD AB = . sin β sin D
Ta có α = D + β nên 0 0 0
D = α − β = 63 − 48 =15 . 0 Do đó . AB sin β 24.sin 48 AD = = ≈ sin(α − β ) 68,91 m. 0 sin15
Trong tam giác vuông ACD, có h = CD = .
AD sinα ≈ 61,4 m. Chọn D.
Câu 19. Từ hình vẽ, suy ra 0 BAC =10 và 0 = − + ABD (BAD ADB) 0 = − ( 0 0 + ) 0 180 180 50 90 = 40 .
Áp dụng định lí sin trong tam giác ABC , ta có 0 BC AC
BC.sin ABC 5.sin 40 = → AC = = ≈ 18,5 m . 0 sin BAC sin ABC sin BAC sin10 Trang 58/9
Trong tam giác vuông ADC , ta có CD = → = sinCAD
CD AC.sinCAD =11,9 m. AC
Vậy CH = CD + DH =11,9 + 7 =18,9 m. Chọn B.
Câu 20. Tam giác OAB vuông tại B, có AB 0 tan AOB =
⇒ AB = tan 60 .OB = 60 3 m. OB
Vậy chiếu cao của ngọn tháp là h = AB + OC = (60 3 + )1m. Chọn C.
Câu 21. Từ giả thiết, ta suy ra tam giác ABC có 0 = 0
CAB 60 , ABC =105 30′ và c = 70. Khi đó + + 0 = ⇔ 0 = − + A B C C (A B) 0 0 0 180 180
= 180 −165 30′ =14 30 .′
Theo định lí sin, ta có b c = hay b 70 = sin B sinC 0 0 sin105 30′ sin14 30′ 0 ′ Do đó 70.sin105 30 AC = b = ≈ 269,4 m. 0 sin14 30′
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 0 30 nên AC 269,4 CH = = = 134,7 m. 2 2
Vậy ngọn núi cao khoảng 135 m. Chọn A. Câu 22. A 2 2 2
Áp dụng công thức đường trung tuyến 2 b c a m + = − ta được: a 2 4 2 2 2 2 2 2 AC AB BC B 2 8 6 10 M C m + + = − = − = a 25 2 4 2 4
⇒ m = Chọn D. a 5. Câu 23. AC a B
M là trung điểm của AC ⇒ AM = = . 2 2 Tam giác BAM ∆ vuông tại A C 2 A M 2 2 2 a a 5
⇒ BM = AB + AM = a + = . Chọn D. 4 2 Câu 24. 2 2 2 2 b c a A
Áp dụng hệ thức đường trung tuyến m + = − ta được: a 2 4 2 2 2 2 2 2 2 AC AB BC 12 9 15 225 m + + = − = − = a . B M C 2 4 2 4 4 15 ⇒ m = Chọn A. a . 2 Câu 25.
Ta có: D là điểm đối xứng của B qua C ⇒ C là trung điểm của . BD D
⇒ AC là trung tuyến của tam giác . DAB ∆
BD = 2BC = 2AC =15. C
Theo hệ thức trung tuyến ta có: B A Trang 59/9 2 2 2 2 2 AB AD BD AC + = − 2 2 BD 2 ⇒ AD = 2AC + − AB 2 4 2 2 2 2 ⇒ AD = 15 15 2 2. + − 9 =144 ⇒ AD = 12. Chọn C. 2 2 Câu 26.
Ta có: M là trung điểm của BC BC ⇒ BM = = 4. 2 Trong tam giác
AM + BM − AB ABM ta có: 2 2 2 cos AMB = 2AM.BM 2 ⇔ − 2 2 AM
2AM.BM.cos AMB + BM − AB = 0.
AM = 13 > 3 (thoaû maõn) 2 20 13 AM AM 7 0 ⇔ − + = ⇔ 7 13 13 AM = < 3 (loaïi) 13 ⇒ AM = 13. A Ta có: AMB và
AMC là hai góc kề bù. ⇒ = − 5 13 cos AMC cos AMB = − 26 B C Trong tam giác A ∆ MC ta có: M 2 2 2 = + − AC AM CM
2AM.CM.cos AMC 5 13 = 13 +16 − 2. 13.4.−
= 49 ⇒ AC = 7. Chọn D. 26 Câu 27*. Ta có: BGC và
BGN là hai góc kề bù mà 0 = ⇒ 0 BGC 120 BGN =120 .
G là trọng tâm của tam giác ABC ∆ 2 A BG = BM = 4. 3 ⇒ M N 1 G GN = CN = 3. 3 B C Trong tam giác BGN ∆ ta có: 2 2 2 = + − BN GN BG 2GN. . BG cos BGN 2 1
⇒ BN = 9 +16 − 2.3.4. =13 ⇒ BN = 13. 2
N là trung điểm của AB ⇒ AB = 2BN = 2 13. Chọn D. 2 2 2 2 b + c a m = − = a 81 2 4 2 a = 292 a = 2 73 2 2 2 + Câu 28**. Ta có: 2 a c b 2 m = − = ⇔ b = ⇒ b = 4 13 b 144 208 2 4 2 = 2 2 2 c =100 c 10 + 2 a b c m = − = c 225 2 4 Trang 60/9 2 2 2 Ta có:
b + c − a 208 +100 − 292 1 cos A = = = 2bc 2.4 13.10 5 13 2 2 1 18 13
sin A = 1− cos A = 1− = . Chọn C. 5 13 65 Diện tích tam giác 1 1 18 13 ABC ∆ : S = = = ∆ bc A ABC sin .4 13.10. 72 2 2 65 2 2 2
Câu 29*. Hệ thức trung tuyến xuất phát từ đỉnh b c a A của tam giác: 2 m + = − a 2 4 2 2 2 Mà: 2 2 2
b + c = 2a ⇒ 2 2a a 3a a 3 m = − = ⇒ m = Chọn A. a a . 2 4 4 2
Câu 30*. Gọi O là giao điểm của AC và . BD Ta có: 1 m BO = BD = . 2 2
BO là trung tuyến của tam giác ABC ∆ 2 2 2 2 2 2 2 2 BA BC AC BO + + ⇒ = − m a b n 2 2 ⇔ = − ⇔ m + n = ( 2 2
2 a + b ) . Chọn B. 2 4 4 2 4
Câu 31**. Gọi G là trọng tâm tam giác ABC ∆ . 2 2 2 2 2 2 4 2 b + c 2 2 ( 2 2) 2 Ta có: 2 AC AB BC b c a AM + + = − = − a ⇒ AG = AM = − 2 4 2 4 9 9 9 2 2 2 2 2 2 2 2 2 2 BA BC AC c a b BN + + = − = − 2 1 2 c a b GN BN + ⇒ = = − 2 4 2 4 9 18 36 Trong tam giác AGN ∆ ta có: 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b − + − − 2 2 2
AG + GN − AN 9 9 18 36 4 cos AGN = = 2. . AG GN 2( 2 2 b + c ) 2 2 2 2 2. a − . c + a b − 9 9 18 36 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b − + − − 2 2 2 9 9 18 36 4
10c − 2(a + b ) = = = 0 2( 2 2 b + c ) 2 2 2 2 2( 2 2 b + c ) 2 2 2 2 2. a − . c + a b − 36.2. a − . c + a b − 9 9 18 36 9 9 18 36 ⇒ 0
AGN = 90 . Chọn D. 2 2 2 2 b + c a m = − a 2 4 2 2 2
Câu 32**. Ta có: 2 a + c b m = − b 2 4 2 2 2 2 a + b c m = − c 2 4 2 2 2 2 2 2 2 2 2 + Mà: 2 2 2
5m = m + m ⇒ 5 b c a a + c b a + b c − = − + − a b c 2 4 2 4 2 4 2 2 2 2 2 2 2 2 2
⇔ 10b +10c − 5a = 2a + 2c − b + 2a + 2b − c Trang 61/9 2 2 2
⇔ b + c = a ⇒ tam giác ABC ∆ vuông. Chọn C. 2 2 2 2 b + c a m = − a 2 4 2 2 2
Câu 33**. Ta có: 2 a + c b 3 m = − 2 2 2
⇒ m + m + m =
a + b + c a b c ( 2 2 2) b 2 4 4 2 2 2 2 a + b c m = − c 2 4 2 2 2 4
GA + GB + GC = ( 2 2 2
m + m + m =
a + b + c =
a + b + c . Chọn D. a b c ) 4 3 ( 2 2 2) 1 . ( 2 2 2) 9 9 4 3
Câu 34. Áp dụng định lí sin, ta có BC BC 10 = 2R ⇒ R = = = 10. 0 sin BAC 2.sin A 2.sin30 Chọn B.
Câu 35. Áp dụng định lí Cosin, ta có 2 2 2 = + − BC AB AC 2 . AB AC.cos BAC 2 2 0 2 2 2 2
= 3 + 6 − 2.3.6.cos60 = 27 ⇔ BC = 27 ⇔ BC + AB = AC .
Suy ra tam giác ABC vuông tại B, do đó bán kính AC R = = 3. Chọn A. 2 Câu 36. Đặt AB BC CA p + + =
= 24. Áp dụng công thức Hê – rông, ta có 2 S = − − − = − − − = ∆ p p AB p BC p CA cm ABC ( )( )( ) ( ) ( ) ( ) 2 24. 24 21 . 24 17 . 24 10 84 .
Vậy bán kính cần tìm là . AB BC.CA .
AB BC.CA 21.17.10 85 S = ⇒ = = = ∆ R cm ABC . 4R 4.S ABC ∆ 4.84 8 Chọn C.
Câu 37. Xét tam giác ABC đều cạnh a, gọi M là trung điểm của BC. 2
Ta có AM ⊥ BC suy ra 1 1 2 2 a 3 S = = − = ∆ AM BC AB BM BC ABC . . . . . 2 2 4 3
Vậy bán kính cần tính là . AB BC.CA . AB BC.CA a a 3 S = ⇒ = = = ∆ R ABC . 2 4R 4.S ABC ∆ a 3 3 4. 4 Chọn C.
Câu 38. Tam giác ABC vuông tại ,
A có đường cao AH ⇒ 2 . AB AC = AH (∗). 2 Mặt khác AB 3 3 3 12 8 3
= ⇔ AB = AC thế vào (∗), ta được 2 AC = ⇔ AC = . AC 4 4 4 5 5 Suy ra 3 8 3 6 3 2 2 AB = . =
⇒ BC = AB + AC = 2 3. 4 5 5
Vậy bán kính cần tìm là BC R = = 3 c . m 2 2 2 2 Câu 39. Vì AB AC BC
D là trung điểm của BC ⇒ 2 AD + = − = 27 ⇒ AD = 3 3. 2 4
Tam giác ABD có AB = BD = DA = 3 3 ⇒ tam giác ABD đều. Trang 62/9
Nên có bán kính đường tròn ngoại tiếp là 3 3 R = AB = .3 3 = 3. Chọn B. 3 3 ′
Câu 40**. Xét tam giác BB C
′ vuông tại B ,′ có sin B C CBB′ = ⇒ B C ′ = . a sinα. BC Mà AB′ + B C
′ = AC ⇔ AB′ = b − . a sinα và 2 2 2
BB′ = a .cos α.
Tam giác ABB′ vuông tại B ,′ có 2 2
AB = BB′ + AB′ = (b − a α )2 2 2 .sin + a .cos α 2 2 2 2 2 2 2 = b − 2 .
ab sinα + a sin α + a cos α = a + b − 2absinα .
Bán kính đường tròn ngoại tiếp cần tính là 2 2 AB
a + b − 2absinα = 2R ⇔ R = . sin ACB 2cosα Câu 41. Ta có 1 = 1 0 9 3 S = = . Chọn B. ∆ AB AC A ABC . . .sin .3.6.sin 60 2 2 2 Câu 42. Ta có 0 = − +
ABC 180 (BAC ACB) = ° = 75 ACB .
Suy ra tam giác ABC cân tại A nên AB = AC = 4.
Diện tích tam giác ABC là 1 = S = Chọn C. ∆ AB AC BAC ABC . sin 4. 2 Câu 43. Ta có 21 17 10 p + + = = 24 . 2
Do đó S = p( p − a)( p − b)( p − c) = 24(24 − )
21 (24 −17)(24 −10) = 84. Chọn D.
Câu 44. Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC − 2 .
AB AC cos A = 27 → BC = 3 3 . Ta có 1 = 1 0 9 3 S = = . ∆ AB AC A ABC . . .sin .3.6.sin 60 2 2 2 Lại có 1 2S S = → = = Chọn C. ∆ BC h h ABC . . a a 3. 2 BC
Câu 45. Gọi H là chân đường cao xuất phát từ đỉnh A.
Tam giác vuông AHC , có AH = → = 3 sin ACH
AH AC.sin ACH = 4. = 2 3. AC 2 Chọn A. Câu 46. Ta có 21 17 10 p + + = = 24 . 2
Suy ra S = p( p − a)( p − b)( p − c) = 24(24 − ) 21 (24 −17)(24 −10) = 84. Lại có 1 1 168 S = .
b BB'←→84 = .17.BB' → BB' = . Chọn C. 2 2 17 Câu 47. Ta có 1 = 1 8 S ⇔ = ⇔ = Chọn D. ∆ AB AC BAC A A ABC . . .sin 64 .8.18.sin sin . 2 2 9
Câu 48. Diện tích tam giác 1 1 a ABD là = 2 0 S = = ∆ AB AD BAD a a ABD . . .sin . . 2.sin 45 . 2 2 2 Trang 63/9 2
Vậy diện tích hình bình hành ABCD là a 2 S = S = = Chọn C. ∆ a ABCD 2. ABD 2. . 2
Câu 49*. Vì F là trung điểm của AC ⇒ 1
FC = AC =15 c . m 2
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC. d ( ; B ( AC)) Khi đó BF 1 AB = = ⇒ = = = d ( 3
d (G; AC ) d ( ; B AC ) cm G;( AC)) ( ) ( ) 10 . GF 3 3
Vậy diện tích tam giác GFC là: 1 S = = = Chọn C. ∆ d G AC FC cm GFC . ( ;( )) 1 2 . .10.15 75 . 2 2
Câu 50*. Xét tam giác ABC đều, có độ dài cạnh bằng . a
Theo định lí sin, ta có BC a 0 = 2R ⇔
= 2.4 ⇔ a = 8.sin 60 = 4 3. 0 sin BAC sin 60
Vậy diện tích cần tính là 1 = 1 S = = ∆ AB AC BAC cm ABC . . .sin .(4 3)2 0 2 .sin 60 12 3 . 2 2 Chọn C. Câu 51*. Ta có AB BC CA 2 3 3AB p + + + = = . 2 2 + − − + Suy ra
3AB 2 3 3AB 2 3 2 3 AB 2 3 AB S = . 2 2 2 2 Lại có 1
S = BC.AH = 2 3. 2 + − − + Từ đó ta có
3AB 2 3 3AB 2 3 2 3 AB 2 3 2 3 AB = 2 2 2 2 ( 2 AB − )( 2 − AB ) AB = 2 9 12 12 12 ←→ = ←→ . 2 21 Chọn C. 16 AB = 3
Câu 52*. Diện tích tam giác ABC ban đầu là 1 = 1 = S
.AC.BC.sin ACB .a . b sin AC . B 2 2
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là 1 S = = = Chọn D. ∆ AC BC ACB AC BC ACB S ABC .(3 ).(2 ) 1 .sin 6. . . .sin 6 . 2 2
Câu 53*. Diện tích tam giác ABC là 1 = 1 = S ∆ AC BC ACB ab ACB ABC . . .sin . .sin . 2 2
Vì a, b không đổi và sin ACB ≤1, C ∀ nên suy ra ab S ≤ ABC ∆ . 2
Dấu " = " xảy ra khi và chỉ khi = ⇔ 0 sin ACB 1 ACB = 90 .
Vậy giá trị lớn nhất của diện tích tam giác ABC là ab S = . Chọn B. 2 Câu 54*. Vì 2 2 2 BM ⊥ CN
→5a = b + c . (Áp dụng hệ quả đã có trước) Trang 64/9 2
Trong tam giác ABC , ta có 2 2 2 2 2 = + − 2 .cos = 5 − 2 cos a a b c bc A a bc A →bc = . cos A 2 Khi đó 1 1 2a 2
S = bcsin A = .
.sin A = a tan A = 3 3 . Chọn A. 2 2 cos A
Câu 55. Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC − 2 .
AB AC cos A = 49 → BC = 7 . Diện tích 1 1 3 S = .
AB AC.sin A = .5.8. = 10 3 . 2 2 2 Lại có S 2 = . S S p r →r = = = 3 . Chọn C.
p AB + BC + CA Câu 56. Ta có 21 17 10 p + + = = 24 . 2 Suy ra S = 24(24 − )
21 (24 −17)(24 −10) = 84 . Lại có S 84 7 S = . p r →r = = = . Chọn C. p 24 2 2
Câu 57. Diện tích tam giác đều cạnh a bằng: a 3 S = . 4 2 a 3 Lại có S 4 a 3 S = pr →r = = = . Chọn C. p 3a 6 2
Câu 58. Dùng Pitago tính được AC = 8, suy ra AB BC CA p + + = = 12 . 2 Diện tích tam giác vuông 1 S = .
AB AC = 24 .Lại có = . S S p r →r = = 2 cm. 2 p Chọn C.
Câu 59. Từ giả thiết, ta có AC = AB = a và BC = a 2 . + + + Suy ra AB BC CA 2 2 p = = a . 2 2 2 Diện tích tam giác vuông 1 = . a S AB AC = . 2 2 Lại có = . S a S p r →r = = . Chọn C. p 2 + 2
Câu 60. Giả sử AC = AB = a
→ BC = a 2 . Suy ra BC a 2 R = = . 2 2 + + + Ta có AB BC CA 2 2 p = = a . 2 2 2 Diện tích tam giác vuông 1 = . a S AB AC = . 2 2 Trang 65/9 Lại có = . S a S p r →r = =
. Vậy R =1+ 2 . Chọn A. p 2 + 2 r Trang 66/9 ÔN TẬP CHƯƠNG 3 BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho tam giác ABC có B =120°, cạnh AC = 2 3 cm . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. R = 2 cm . B. R = 4 cm . C. R =1cm . D. R = 3 cm . Câu 2: Cho A
∆ BC có BC = a , CA = b, AB = c . Mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c − . bc cos A . B. 2 2 2
a = b + c − 2bc . 2 2 2 C. + − . b c a a sin A = . b sin B = . c sin C . D. cos A = . 2bc Câu 3: Cho A
∆ BC có BC = a ,
BAC =120° . Bán kính đường tròn ngoại tiếp A ∆ BC là A. a 3 R = . B. a R = . C. a 3 R = .
D. R = a . 2 2 3
Câu 4: Cho ∆ABC có các cạnh BC = a , AC = b , AB = c . Diện tích của ∆ABC là A. 1 S = ac C . B. 1 S = bc B . ∆ABC sin ∆ABC sin 2 2 C. 1 S = ac B . D. 1 S = bc C . ∆ABC sin ∆ABC sin 2 2
Câu 5: Cho tam giác ABC bất kỳ có BC = a , AC = b , AB = c . Đẳng thức nào sai? A. 2 2 2
b = a + c − 2accos B . B. 2 2 2
a = b + c − 2bccos A. C. 2 2 2
c = b + a + 2abcosC . D. 2 2 2
c = b + a − 2abcosC .
Câu 6: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 2 2 2 A. 2 b c a m + = + . B. 2 a c b m + = − . a 2 4 a 2 4 2 2 2 2 2 2
C. 2 2c 2b a m + − = . D. 2 a b c m + = − . a 4 a 2 4
Câu 7: Trong tam giác ABC với BC = a , AC = b , AB = c . Mệnh đề nào dưới đây sai? A. bsin A a = . B. sin sin c A C = .
C. a = 2Rsin A .
D. b = R tan B . sin B a
Câu 8: Cho α là góc tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα < 0. D. cotα > 0 .
Câu 9: Cho hai góc nhọn α và β trong đó α < β . Khẳng định nào sau đây sai? A. sinα < sin β . B. cosα < cos β .
C. cosα = sin β ⇔ α + β = 90°.
D. cotα + tan β > 0 .
Câu 10: Cho 0° < α < 90°. Khẳng định nào sau đây đúng?
A. cot (90° +α ) = tanα .
B. cos(90° +α ) = −sinα .
C. sin (90° +α ) = −cosα .
D. tan (90° +α ) = cotα .
Câu 11: Khẳng định nào sau đây là khẳng định đúng?
A. cosα = −cos(180° −α ) .
B. cotα = cot (180° −α ) .
C. tanα = tan (180° −α ) .
D. sinα = −sin (180° −α ) .
Câu 12: Cho tam giác ABC có BC =10 , A = 30° . Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. 10. B. 10 . C. 10 3 . D. 5. 3
Câu 13: Tam giác ABC vuông cân tại A có AB = AC = a . Đường trung tuyến BM có độ dài là A. 3 a . B. a 2 . C. a 3 . D. a 5 . 2 2
Câu 14: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R bằng A. a 3 . B. a 3 . C. a 2 . D. a 3 . 2 3 3 4
Câu 15 Bán kính đường tròn nội tiếp tam giác đều cạnh a bằng A. a 3 . B. a 2 . C. a 2 . D. a 5 . 6 5 4 7
Câu 16: Nếu tam giác ABC có 2 2 2
a < b + c thì: A. A là góc tù. B.
A là góc vuông. C. A là góc nhọn. D.
A là góc nhỏ nhất.
Câu 17: Trong tam giác ABC có:
A. a = 2R cos A.
B. a = 2Rsin A .
C. a = 2R tan A .
D. a = Rsin A.
Câu 18: Cho tam giác ABC có AB = 2 , AC = 2 2 , 2 cos(B + C) = −
. Độ dài cạnh BC là 2 A. 2 . B. 8 . C. 20 . D. 4 .
Câu 19: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD =135° . Diện tích của hình bình hành ABCD bằng A. 2 a . B. 2 a 2 . C. 2 a 3 . D. 2 2a .
Câu 20: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD = 45°. Diện tích của hình bình hành ABCD là A. 2 2a . B. 2 a 2 . C. 2 a 3 . D. 2 a .
Câu 21: Cho tứ giác lồi ABCD có = ABC ADC = 90° ,
BAD =120° và BD = a 3 . Tính AC .
A. AC = 2a .
B. AC = a 3 .
C. AC = a .
D. AC = a 5 .
Câu 22: Cho tam giác ABC thỏa mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos A .
B. sin B + sin C = 2sin A . C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin A. 2
Câu 23: Cho tam giác ABC có b = 7 , c = 5 , 3
cos A = . Đường cao h của tam giác ABC là 5 a A. 8 . B. 7 2 . C. 80 3 . D. 8 3 . 2
Câu 24: Một tam giác có ba cạnh là 52, 56, 60 . Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 . B. 40 . C. 32,5. D. 65,8 . 4
Câu 25: Cho tam giác ABC . Đẳng thức nào sai?
A. sin ( A+ B − 2C) = sin 3C .
B. cos B + C = sin A . 2 2 C. A + B + 2 cos C = sin C .
D. sin ( A+ B) = sinC . 2 2
Câu 26: Từ hai điểm A và B trên mặt đất người ta nhìn thấy đỉnh C và chân D của tháp CD dưới các góc nhìn là 72 12 ° ′ và 34 26
° ′ so với phương nằm ngang. Biết tháp CD cao 80 m . Khoảng cách AB gần đúng bằng A. 91 m. B. 71 m . C. 79 m. D. 40 m .
Câu 27: Tam giác ABC có a = 8, c = 3, B = 60°. Độ dài cạnh b bằng bao nhiêu? A. 49 . B. 97 . C. 7 . D. 61 .
Câu 28: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết CA = 200(m) ,
CB =180(m) . Khoảng cách AB bằng bao nhiêu? A. 228(m) . B. 20 91(m) . C. 112(m) . D. 168(m)
Câu 29: Cho tam giác ABC có a = 2 , b = 6 , c = 3 +1. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2 R = . B. 2 R = . C. R = 2 . D. R = 3 . 3 2
Câu 30: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện (a + b + c)(a + b − c) = 3ab . Tính số đo của góc C . A. 45°. B. 60°. C. 120°. D. 30° . Câu 31: Biết 2
sinα = , (90° < α <180°). Hỏi giá trị tanα là bao nhiêu? 3 A. 2. B. 2 − . C. 2 5 − . D. 2 5 . 5 5 Câu 32: Cho α − α tanα sin cos = 2 . Tính B = 3 3 sin α + 3cos α + 2sinα 3( 2 − )1 3( 2 − )1 A. B = . B. 3 2 1 B − = . C. B = . D. 3 2 1 B + = . 3+ 8 2 8 2 + 3 8 2 +1 8 2 −1 Câu 33: Cho A
∆ BC có a = 4, c = 5 , B =150°. Tính diện tích tam giác ABC . A. S =10 . B. S =10 3 . C. S = 5. D. S = 5 3 . Câu 34: Biết 1
sinα = (90° < α <180°). Hỏi giá trị của cotα bằng bao nhiêu? 4 A. 15 − . B. − 15 . C. 15 . D. 15 . 15 15
Câu 35: Cho cotα = − 2 , (0° ≤ α ≤180°). Tính sinα và cosα . A. 1 sinα = , 6 cosα = . B. 1 sinα = , 6 cosα = − . 3 3 3 3 C. 6 sinα = , 1 cosα = . D. 6 sinα = , 1 cosα = − . 2 3 2 3 Câu 36: Cho 1
sin x + cos x = . Tính P = sin x − cos x . 5 A. 3 P = . B. 4 P = . C. 5 P = . D. 7 P = . 4 5 6 5
Câu 37: Tính giá trị biểu thức P = sin 30°cos60° + sin 60°cos30°. A. P =1. B. P = 0 . C. P = 3 . D. P = − 3 .
Câu 38: Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 3, CA = 4 . Tính góc ABC (chọn kết quả gần đúng nhất). A. 60°. B. 104 29 ° ′ . C. 75 31 ° ′ . D. 120°.
Câu 39: Cho một hình bình hành ABCD có AB = a , BC = b . Công thức nào dưới đây là công thức tính
diện tích của hình bình hành đó? A. 2 2 a + b . B. absin ABC . C. ab .
D. 2(a + b).
Câu 40: Tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm . Đường tròn nội tiếp tam giác đó có bán kính r là A. 1 cm . B. 2 cm . C. 2 cm . D. 3 cm .
Câu 41: Tam giác ABC có: a = 3 cm , b = 2 cm , c =1 cm . Đường trung tuyến m có độ dài là a A. 1 cm . B. 1.5 cm . C. 5 cm . D. 3 cm. 2 2
Câu 42: Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích là A. 2 12 3 cm . B. 2 13 2 cm . C. 2 13 cm . D. 2 15 cm .
Câu 43: Tam giác ABC vuông cân tại A có AB = a . Đường tròn nội tiếp tam giác ABC có bán kính r bằng A. a . B. a . C. a . D. a . 2 2 2 + 2 3
Câu 44: Tam giác ABC có ba cạnh thoả mãn điều kiện (a + b + c)(a + b − c) = 3ab . Khi đó số đo của C là A. 120°. B. 30° . C. 45°. D. 60°.
Câu 45: Hình bình hành ABCD có AB = a , BC = a 2 và
BAD = 45°. Khi đó hình bình có diện tích là A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 . A. 2 2 2
a = b + c − 3bc . B. 2 2 2
a = b + c + bc . C. 2 2 2
a = b + c + 3bc . D. 2 2 2
a = b + c − bc .
Câu 46: Tam giác ABC có
A =120° thì câu nào sau đây đúng A. 2 2 2
a = b + c − 3bc . B. 2 2 2
a = b + c + bc . C. 2 2 2
a = b + c + 3bc . D. 2 2 2
a = b + c − bc .
Câu 47: Tam giác ABC có
A = 60° ; b =10 ; c = 20 . Diện tích của tam giác ABC bằng A. 50 3 . B. 50. C. 50 2 . D. 50 5 .
Câu 48: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc A là A. 30° . B. 45°. C. 68°. D. 75°.
Câu 49: Cho tam giác ABC , các đường cao h , h , h thỏa mãn hệ thức 3h = h + h . Tìm hệ thức a 2 a b c b c
giữa a , b , c A. 3 2 1 = − .
B. 3a = 2b + c .
C. 3a = 2b − c . D. 3 2 1 = + . a b c a b c
Câu 50: Cho tam giác ABC , nếu 2h = h + h thì a b c A. 2 1 1 = + .
B. 2sin A = sin B + sin C .
sin A sin B sin C
C. sin A = 2sin B + 2sin C . D. 2 1 1 = − .
sin A sin B sin C
Câu 51: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. 2
S = p( p − a)( p −b)( p − c) II. 2
16S = (a + b + c)(a + b − c)(a −b + c)(b + c − a) A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có.
Câu 52: Trong tam giác ABC có AB = 2cm , AC =1cm , A = 60°. Khi đó độ dài cạnh BC là A. 1cm . B. 2cm . C. 3 cm . D. 5 cm .
Câu 53: Tam giác ABC có: a = 5 ; b = 3 ; c = 5 . Số đo của góc BAC là A. A > 60° . B. A = 30°. C. A = 45° . D. A = 90°.
Câu 54: Tam giác ABC có a = 8; b = 7 ; c = 5 . Diện tích của tam giác ABC bằng A. 5 3 . B. 8 3 . C. 10 3 . D. 12 3 .
Câu 55: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc B bằng A. 115°. B. 75°. C. 60°. D. 53 32 ° ′ .
Câu 56: Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r là bán
kính đường tròn nội tiếp tam giác ABC . Khi đó tỉ số R bằng r A. 1+ 2 . B. 2 + 2 . C. 2 −1 . D. 2 +1 . 2 2 2
Câu 57: Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm A và B
trên mặt đất có khoảng cách AB =12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân
của giác kế có chiều cao h =1,3m . Gọi D là đỉnh tháp và hai điểm A , B cùng thẳng hàng với C thuộc 1 1 1
chiều cao CD của tháp. Người ta đo được góc DAC = 49° và
DB C = 35° . Tính chiều cao 1 1 1 1 CD của tháp. A. 22,77 m . B. 21,47 m . C. 20,47 m . D. 21,77 m .
Câu 58: Trên nóc một tòa nhà có cột ăng-ten cao 5m . Từ vị trí quan sát A cao 7 m so với mặt
đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương
nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là A. 21,2m . B. 14,2m . C. 11,9m. D. 18,9m .
Câu 59: Cho tam giác ABC có a = 5 cm , c = 9 cm , 1
cosC = − . Tính độ dài đường cao h hạ từ A 10 a của tam giác ABC . A. 462 h = cm . B. 462 h = cm . C. 21 11 h = cm . D. 21 11 h = cm . a 40 a 10 a 40 a 10
Câu 60: Cho đường tròn tâm O bán kính R và điểm M thỏa mãn MO = 3R . Một đường kính AB thay
đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức S = MA + MB .
A. min S = 6R .
B. min S = 4R .
C. min S = 2R .
D. min S = R .
Câu 61: Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1 m , người ta cắt ra một hình chữ
nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu? A. 2 1,6 m . B. 2 2 m . C. 2 1 m . D. 2 0,8 m . Câu 62: Biết 2017 1 α sinα + =
, 90° < α <180° . Tính giá trị của biểu thức sin M = cotα + . 2018 1+ cosα A. 2017 1 M + = − . B. 2017 1 M + = . C. 2018 M = − . D. 2018 M = . 2018 2018 2017 +1 2017 +1
Câu 63: Cho hình thang cân ABCD có đáy nhỏ AB , đáy lớn CD . Biết AB = CD và 3 tan BDC = . 4 Tính cos BAD . A. 17 . B. 7 − . C. 5 . D. 17 − . 25 25 25 25 HƯỚNG DẪN GIẢI
Câu 1: Cho tam giác ABC có B =120°, cạnh AC = 2 3 cm . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. R = 2 cm . B. R = 4 cm . C. R =1cm . D. R = 3 cm . Lời giải Chọn A.
Áp dụng định lý sin trong tam giác có: AC AC 2 3 = 2R ⇒ R = = = 2 (cm) . sin B 2sin B 2sin120° Câu 2: Cho A
∆ BC có BC = a , CA = b, AB = c . Mệnh đề nào sau đây đúng? A. 2 2 2
a = b + c − . bc cos A . B. 2 2 2
a = b + c − 2bc . 2 2 2 C. . a sin A = .
b sin B = .csin C . D. cos
b + c − a A = . 2bc Lời giải Chọn D. Câu 3: Cho A
∆ BC có BC = a ,
BAC =120° . Bán kính đường tròn ngoại tiếp A ∆ BC là A. a 3 a R = . B. R = . C. a 3 R = .
D. R = a . 2 2 3 Lời giải Chọn D.
Theo định lý sin trong tam giác ta có 2 BC R = 1 a a 3 ⇒ R = . = . sin BAC 2 sin120° 3
Câu 4: Cho ∆ABC có các cạnh BC = a , AC = b , AB = c . Diện tích của ∆ABC là A. 1 S = ac C . B. 1 S = bc B . ∆ABC sin ∆ABC sin 2 2 C. 1 S = ac B . D. 1 S = bc C . ∆ABC sin ∆ABC sin 2 2 Lời giải Chọn C. Ta có: 1 S = ac B . ∆ABC sin 2
Câu 5: Cho tam giác ABC bất kỳ có BC = a , AC = b , AB = c . Đẳng thức nào sai? A. 2 2 2
b = a + c − 2ac cos B . B. 2 2 2
a = b + c − 2bc cos A. C. 2 2 2
c = b + a + 2abcosC . D. 2 2 2
c = b + a − 2abcosC . Lời giải Chọn C.
Theo định lí hàm số cosin, 2 2 2
c = b + a − 2abcosC nên C sai.
Câu 6: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: 2 2 2 2 2 2 A. 2 b c a m + = + . B. 2 a c b m + = − . a 2 4 a 2 4 2 2 2 2 2 2
C. 2 2c 2b a m + − = . D. 2 a b c m + = − . a 4 a 2 4 Lời giải Chọn C. 2 2 2 2 2 2
Theo công thức đường trung tuyến ta có 2 b c a 2b 2c a m + + − = − = . a 2 4 4
Câu 7: Trong tam giác ABC với BC = a , AC = b , AB = c . Mệnh đề nào dưới đây sai? A. bsin A a = . B. sin sin c A C = .
C. a = 2Rsin A .
D. b = R tan B . sin B a Lời giải Chọn D.
Theo định lý sin ta có a b c = = = 2R
sin A sin B sin C bsin A ⇒ a = , sin sin c C C =
, a = 2Rsin A , nên các mệnh đề A, B, C đúng. sin B a
Vậy mệnh đề D là mệnh đề sai. Câu 8: + Cho tan x = 1
− . Tính giá trị của biểu thức sin x 2cos x P = . cos x + 2sin x A. 1 − . B. 1. C. 2 . D. 2 − . Lời giải Chọn A. sin x + + 2 + Ta có: sin x 2cos x P − + = cos x tan x 2 1 2 = = = = 1 − . cos x + 2sin x sin 1+ 2
x 1+ 2tan x 1+ 2.(− ) 1 cos x
Câu 9: Cho α là góc tù. Điều khẳng định nào sau đây là đúng? A. sinα < 0 . B. cosα > 0 . C. tanα < 0. D. cotα > 0 . Lời giải Chọn C. si nα > 0 α là góc tù suy ra : ⇒ tanα < 0 . cosα < 0
Câu 10: Cho hai góc nhọn α và β trong đó α < β . Khẳng định nào sau đây sai? A. sinα < sin β . B. cosα < cos β .
C. cosα = sin β ⇔ α + β = 90°.
D. cotα + tan β > 0 . Lời giải Chọn B. si n x > 0 tan x > 0
α và β là hai góc nhọn ⇒ ⇒
⇒ tan x + cot x > 0 . cos x > 0 cot x > 0
α + β = 90° ⇒ sin β = sin (90° −α ) = cosα . si nα < sin β
Với α < β , biểu diễn trên nửa đường tròn đơn vị. Suy ra: . cosα > cos β
Câu 11: Cho 0° < α < 90°. Khẳng định nào sau đây đúng?
A. cot (90° +α ) = tanα .
B. cos(90° +α ) = −sinα .
C. sin (90° +α ) = −cosα .
D. tan (90° +α ) = cotα . Lời giải Chọn B.
Câu 12: Khẳng định nào sau đây là khẳng định đúng?
A. cosα = −cos(180° −α ) .
B. cotα = cot (180° −α ) .
C. tanα = tan (180° −α ) .
D. sinα = −sin (180° −α ) . Lời giải Chọn A.
Với hai góc bù nhau ta có cosα = −cos(180° −α ) .
Câu13: Cho tam giác ABC có BC =10 , A = 30°. Tính bán kính đường tròn ngoại tiếp tam giác ABC . A. 10. B. 10 . C. 10 3 . D. 5. 3 Lời giải Chọn A.
Trong tam giác ABC ta có: BC R = =10 . 2sin A
Câu 14: Tam giác ABC vuông cân tại A có AB = AC = a . Đường trung tuyến BM có độ dài là A. 3 a . B. a 2 . C. a 3 . D. a 5 . 2 2 Lời giải Chọn D. A a M B C 2 2 2 2 a a 5
BM = AB + AM = a + = . 4 2
Câu 15: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R bằng A. a 3 . B. a 3 . C. a 2 . D. a 3 . 2 3 3 4 Lời giải Chọn B.
Bán kính đường tròn ngoại tiếp tam giác đều cạnh a : 2 2 a 3 a 3 R = h = . = . 3 3 2 3
Câu 16: Bán kính đường tròn nội tiếp tam giác đều cạnh a bằng A. a 3 . B. a 2 . C. a 2 . D. a 5 . 6 5 4 7 Lời giải Chọn A.
Bán kính đường tròn nội tiếp tam giác đều cạnh a : 1 1 a 3 a 3 r = h = . = . 3 3 2 6
Câu 17: Nếu tam giác ABC có 2 2 2
a < b + c thì: A. A là góc tù. B.
A là góc vuông. C. A là góc nhọn. D.
A là góc nhỏ nhất. Lời giải Chọn C. 2 2 2 Ta có 2 2 2 + − a b c a
= b + c − 2bc cos A ⇒ cos A = < + nên cos A > 0 2bc do 2 2 2 a b c
⇒ A là góc nhọn.
Câu 18: Trong tam giác ABC có:
A. a = 2R cos A.
B. a = 2Rsin A .
C. a = 2R tan A .
D. a = Rsin A. Lời giải Chọn B.
Định lý sin trong tam giác.
Câu 19: Cho tam giác ABC có AB = 2 , AC = 2 2 , 2 cos(B + C) = −
. Độ dài cạnh BC là 2 A. 2 . B. 8 . C. 20 . D. 4 . Lời giải Chọn A. Do 2 B + C = − ⇒ A = − (B +C) 2 cos( ) cos cos = . 2 2
Áp dụng định lý cosin trong tam giác có: 2 2 2
BC = AB + AC − 2A . B AC.cos A = + ( )2 2 2 2 2 2 − 2.2.2 2. = 4 ⇒ BC = 2. 2
Câu 20: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD =135° . Diện tích của hình bình hành ABCD bằng A. 2 a . B. 2 a 2 . C. 2 a 3 . D. 2 2a . Lời giải Chọn A. A D B E C Ta có ABC = 45° .
Gọi AE kà đường cao của tam giác ABC , khi đó tam giác AEB vuông cân tại E . Suy ra 1
AE = BC a 2 = . 2 2
Vậy diện tích hình bình hành ABCD là a 2 AE.BC = .a 2 2 = a . 2
Câu 21: Cho hình bình hành ABCD có AB = a , BC = a 2 và
BAD = 45°. Diện tích của hình bình hành ABCD là A. 2 2a . B. 2 a 2 . C. 2 a 3 . D. 2 a . Lời giải Chọn D. Ta có: AD 1
= BC = a 2 nên S = S = 2. A . B A . D sin BAD 2 = a . ABCD 2. ABD ∆ 2
Câu 22: Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn lượng giác tâm O . Điểm M trên đường
tròn sao cho sđ(Ox,OM ) = α . Tọa độ của điểm M là A. M (α;0) .
B. M (cosα;sinα ). C. M (sinα;cosα ). D. M (1;0). Lời giải Chọn B. cos x α = x = cosα Gọi M ( ; x y) . Khi đó OM ⇔ (vìOM =1 ). = α si n y α y sin = OM
Vậy M (cosα;sinα ).
Câu 33: Cho tứ giác lồi ABCD có = ABC ADC = 90° ,
BAD =120° và BD = a 3 . Tính AC .
A. AC = 2a .
B. AC = a 3 .
C. AC = a .
D. AC = a 5 . Lời giải Chọn A. Cách 1: B a 3 A C I D A
∆ BD nội tiếp đường tròn đường kính AC
Áp dụng định sin trong A ∆ BD , ta có BD a 3 AC = 2R = = = 2a . sin BAD sin120° Cách 2:
Đề không mất tính tổng quát ta có thể chọn BD ⊥ AC tại I . Ta có = ° − + +
C 360 (A B D) = 360°−(120°+90°+90°) = 60°. AB = AD Do BD ⊥ AC ⇒ . Suy ra B
∆ CD là tam giác đều cạnh bằng a 3 . CB = CD Ta có 3a CI = . 2 Xét A
∆ ID vuông tại I , 1 a 3 ID = BD = . 2 2 a 3 Suy ra ID 2 a AI = = = A . tan 60° 2 tan 2 Ta có a 3a
AC = AI + CI = + = 2a . 2 2 Vậy AC = 2a .
Câu 34: Cho tam giác ABC thỏa mãn hệ thức b + c = 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. cos B + cosC = 2cos A .
B. sin B + sin C = 2sin A . C. 1
sin B + sin C = sin A .
D. sin B + cosC = 2sin A. 2 Lời giải Chọn B.
a = 2R sin A Ta có a b c 2R b = = =
⇔ = 2Rsin B .
sin A sin B sin C c = 2Rsin C
Mà b + c = 2a ⇔ 2Rsin B + 2Rsin C = 4Rsin A ⇔ sin B + sin C = 2sin A.
Câu 35: Cho tam giác ABC có b = 7 , c = 5 , 3
cos A = . Đường cao h của tam giác ABC là 5 a A. 8 . B. 7 2 . C. 80 3 . D. 8 3 . 2 Lời giải Chọn B. A c b ha B H a C
Theo định lí hàm cos ta có 2 2 2
a = b + c − 2bccos A 3
= 49 + 25 − 2.7.5. = 32 ⇒ a = 4 2 . 5 Ta lại có: 3 cos A = 4 ⇒ sin A = . 5 5
Diện tích tam giác ABC là 1 S = 1 4 = .7.5. =14 . ∆ bc A ABC sin 2 2 5 Vì 1 S 28 = nên 2S ABC h ∆ = = 7 2 = ∆ a h ABC . 2 a a a 4 2 2 Vậy 7 2 h = . a 2
Câu 36: Một tam giác có ba cạnh là 52, 56, 60 . Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 . B. 40 . C. 32,5. D. 65,8 . 4 Lời giải Chọn C. Ta có: 52 56 60 p + + = = 84 . 2
Áp dụng hệ thức Hê – rông ta có: S = 84(84 −52)(84 −56)(84 − 60) =1344 . Mặt khác abc S = abc ⇒ R = 52.56.60 = = 32,5. 4R 4S 4.1344
Câu 37: Cho tam giác ABC . Đẳng thức nào sai?
A. sin ( A+ B − 2C) = sin3C .
B. cos B + C = sin A . 2 2 C. A + B + 2 cos C = sin C .
D. sin ( A+ B) = sinC . 2 2 Lời giải Chọn C. Do A + B + 2 π π cos
C cos A+ B C C C C = + = cos − + C = cos + = −sin 2 2 . 2 2 2 2 2
Câu 38: Từ hai điểm A và B trên mặt đất người ta nhìn thấy đỉnh C và chân D của tháp CD dưới các góc nhìn là 72 12 ° ′ và 34 26
° ′ so với phương nằm ngang. Biết tháp CD cao 80 m . Khoảng cách AB gần đúng bằng A. 91 m. B. 71 m . C. 79 m. D. 40 m . Lời giải Chọn A. C 80 m D B A Ta có: DBC = 72 12 ° ′ , DAC = 34 26 ° ′ nên = − ACB DBC DAC = 37 46 ° ′ CD BC = 84 m . cos DBC
Áp dụng định lí sin trong tam giác BC ABC ta có = AB
.sin ACB 91 m . sin DAC
Câu 39: Tam giác ABC có a = 8, c = 3, B = 60°. Độ dài cạnh b bằng bao nhiêu? A. 49 . B. 97 . C. 7 . D. 61 . Lời giải Chọn C. 2 2 2
b = a + c − 2accos B 2 2
= 8 + 3 − 2.8.3cos60° = 49 ⇒ b = 7 .
Câu 40: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta
xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60°. Biết CA = 200(m) ,
CB =180(m) . Khoảng cách AB bằng bao nhiêu? A. 228(m) . B. 20 91(m) . C. 112(m) . D. 168(m). Lời giải Chọn B. 2 2 2
AB = CA + CB − 2 . CA .
CB cos60° = 36400 ⇒ AB = 20 91(m) .
Câu 41: Cho tam giác ABC có a = 2 , b = 6 , c = 3 +1. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2 R = . B. 2 R = . C. R = 2 . D. R = 3 . 3 2 Lời giải Chọn C. 2 2 2 6 + 4 + 2 3 − 4 2 cos
b + c − a A = = = ⇒ 2 sin A = . 2bc 2 6 ( 3 + )1 2 2
Áp dụng định lý sin ta có a R = = 2 . 2sin A
Câu 42: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện (a + b + c)(a + b − c) = 3ab . Tính số đo của góc C . A. 45°. B. 60°. C. 120°. D. 30° . Lời giải Chọn B.
Ta có: (a + b + c)(a + b − c) = 3ab ⇔ (a + b)2 2
− c = 3ab ⇔ 2 2 2
a + b − c = ab . 2 2 2 Mà
a + b − c 1 cosC = = ⇒ C = 60° . 2ab 2 Câu 43: Biết 2
sinα = , (90° < α <180°). Hỏi giá trị tanα là bao nhiêu? 3 A. 2. B. 2 − . C. 2 5 − . D. 2 5 . 5 5 Lời giải Chọn C. Vì 4
90° < α <180° ⇒ cosα < 0 2
⇒ cosα = − 1− sin α = − 1− 5 = − . 9 3 Vậy sinα tanα = 2 5 = − . cosα 5 Câu 44: Cho α − α tanα sin cos = 2 . Tính B = 3 3 sin α + 3cos α + 2sinα 3( 2 − )1 3( 2 − )1 A. B = . B. 3 2 1 B − = . C. B = . D. 3 2 1 B + = . 3+ 8 2 8 2 + 3 8 2 +1 8 2 −1 Lời giải Chọn A. 1 1 sinα − cosα tanα. − 2 2 2 2
tanα (1+ tan α ) −(1+ tan α ) B = cos α cos α = = 3 3 sin α + 3cos α + 2sinα 3 2 3 1 tan α + 3+ 2 tanα.
tan α + 3+ 2 tanα (1+ tan α ) 2 cos α ( 2 1+ tan α )(tanα − ) 1 3( 2 − )1 = = . 3 3tan α + 2 tanα + 3 8 2 + 3 Câu45: Cho A
∆ BC có a = 4, c = 5 , B =150°. Tính diện tích tam giác ABC . A. S =10 . B. S =10 3 . C. S = 5. D. S = 5 3 . Lời giải Chọn C.
Diện tích tam giác ABC là 1 = S acsin B 1 = .4.5sin150° = 5 . 2 2 Câu 46: Biết 1
sinα = (90° < α <180°). Hỏi giá trị của cotα bằng bao nhiêu? 4 A. 15 − . B. − 15 . C. 15 . D. 15 . 15 15 Lời giải Chọn B. Ta có 2 1 1 cot α = −1 = −1 =15 . 2 2 sin α 1 4
Do 90° < α <180° nên cotα = − 15 .
Câu 47: Cho cotα = − 2 , (0° ≤ α ≤180°). Tính sinα và cosα . A. 1 sinα = , 6 cosα = . B. 1 sinα = , 6 cosα = − . 3 3 3 3 C. 6 sinα = , 1 cosα = . D. 6 sinα = , 1 cosα = − . 2 3 2 3 Lời giải Chọn B.
Ta thấy cotα = − 2 < 0 nên suy ra 90° < α <180° . Và: 2 1 1 1 1 sin α = = = ⇔ sinα = ± . 2 1+ cot α 1+ 2 3 3 Do 0° ≤ α ≤180° nên 1 sinα > 0 ⇒ sinα = . 3 α Mà: cos 1 6 cotα =
⇒ cosα = cotα.sinα = − 2. = − . sinα 3 3 Câu 48 Cho 1
sin x + cos x = . Tính P = sin x − cos x . 5 A. 3 P = . B. 4 P = . C. 5 P = . D. 7 P = . 4 5 6 5 Lời giải Chọn D. Ta có: 2
P = (sin x − cos x)2 =1− 2sin .xcos x . Theo giả thiết: 1 1 = x + x ⇒ = ( x + x)2 1 24 sin cos sin cos ⇒ = 1+ 2sin .
x cos x ⇒ 2sin . x cos x = − . 5 25 25 25 Do đó: 2 24 49 7 P =1+ =
⇒ P = (Vì P ≥ 0). 25 25 5
Câu 49: Tính giá trị biểu thức P = sin 30°cos60° + sin 60°cos30°. A. P =1. B. P = 0 . C. P = 3 . D. P = − 3 . Lời giải Chọn A. Ta có 2 2
P = sin 30 .°sin 30° + cos30 .°cos30° = sin 30° + cos 30° =1.
Câu 50: Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 3, CA = 4 . Tính góc ABC (chọn kết quả gần đúng nhất). A. 60°. B. 104 29 ° ′ . C. 75 31 ° ′ . D. 120°. Lời giải Chọn B. + −
Áp dụng định lý cosin trong tam giác ta có: 2 2 2 cos BA BC AC ABC = 2.B . A BC 2 2 2 2 3 4 3 1 cos ABC + − − − ⇔ = = = . 2.2.3 12 4 Suy ra góc ABC =104 29 ° ′ .
Câu 51: Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 5 , CA = 6. Tính độ dài đường trung
tuyến MA , với M là trung điểm của BC . A. 15 . B. 55 . C. 110 . D. 55 . 2 2 2 Lời giải Chọn B.
Áp dụng công thức tình độ dài trung tuyến ta có: 2 2 2 AB AC BC 2 2 2 MA + + = − 2 6 5 55 = − = 2 4 2 4 2
Câu53: Cho một hình bình hành ABCD có AB = a , BC = b . Công thức nào dưới đây là công thức tính
diện tích của hình bình hành đó? A. 2 2 a + b . B. absin ABC . C. ab .
D. 2(a + b). Lời giải Chọn B. S = S 1 = = absin ABC . ABCD 2 ABC 2. .A . B BC sin ABC 2
Câu 54: Tam giác ABC có AB = 8 cm , BC =10 cm , CA = 6 cm . Đường trung tuyến AM của tam giác đó có độ dài bằng A. 4 cm . B. 5 cm . C. 6 cm . D. 7 cm . Lời giải Chọn B.
Cách 1: Áp dụng công thức tính độ dài đường trung tuyến ta có 2 2 2 2 2 2 2 AB AC BC AM + + = − 6 8 10 = − = 25 ⇒ AM = 5 cm . 2 4 2 4 Cách 2: Do 2 2 2
AB + AC = BC nên tam giác ABC vuông tại 1
AM = BC = 5 cm . 2
Câu 55: Tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm . Đường tròn nội tiếp tam giác đó có bán kính r là A. 1 cm . B. 2 cm . C. 2 cm . D. 3 cm . Lời giải Chọn C.
Do tam giác ABC vuông tại A có AC = 6 cm , BC =10 cm nên 2 2
AB = BC − AC 2 2 = 10 − 6 = 8 .
Diện tích tam giác ABC là 1 S = = 24 . ∆ AB AC ABC . 2
Bán kính đường tròn nội tiếp tam giác ABC là 2S 2.24 ABC r ∆ = = = 2 .
AB + BC + CA 6 + 8 +10
Câu 56: Tam giác ABC có: a = 3 cm , b = 2 cm , c =1 cm . Đường trung tuyến m có độ dài là a A. 1 cm . B. 1.5 cm . C. 5 cm . D. 3 cm. 2 2 Lời giải Chọn D.
Áp dụng công thức tính độ dài đường trung tuyến ta có 2 2 2 2 2 2 2 b c a + m + 2 1 3 = − = − 3 = 3 ⇒ m = . a cm a 2 4 2 4 4 2
Câu 57: Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích là A. 2 12 3 cm . B. 2 13 2 cm . C. 2 13 cm . D. 2 15 cm . Lời giải Chọn A.
Ta có diện tích tam giác ABC là abc S =
. Do tam giác ABC đều nên ABC 4R 3 a ( R A)3 2 sin S = = 2 3 = 2R sin A 2 = 2.4 .(sin 60°)3 =12 3 2 cm . ABC 4R 4R
Câu 58: Tam giác ABC vuông cân tại A có AB = a . Đường tròn nội tiếp tam giác ABC có bán kính r bằng A. a . B. a . C. a . D. a . 2 2 2 + 2 3 Lời giải Chọn C.
Tam giác ABC vuông cân tại A có AB = a nên BC = a 2 . 2
Diện tích tam giác ABC là 1 S = AB AC a = . ABC . 2 2 2
Bán kính đường tròn nội tiếp tam giác ABC là 2S a a ABC r = = = .
AB + BC + CA a + a + a 2 2 + 2
Câu 59 Tam giác ABC có ba cạnh thoả mãn điều kiện (a + b + c)(a + b − c) = 3ab . Khi đó số đo của C là A. 120°. B. 30° . C. 45°. D. 60°. Lời giải Chọn D.
Ta có: (a + b + c)(a + b − c) = ab ⇔ (a + b)2 2 2 2 2 3
− c = 3ab ⇔ a + b − c = ab . 2 2 2
Theo hệ quả của định lí hàm cosin:
a + b − c ab 1 = = = ⇒ cos C C = 60° . 2ab 2ab 2
Câu 60: Hình bình hành ABCD có AB = a , BC = a 2 và
BAD = 45°. Khi đó hình bình có diện tích là A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 . Lời giải Chọn C. B a 2 C a 45° A a 2 D Ta có: 1 2 S = S = AB AD ° = a . ABCD 2 ABD 2. . . .sin 45 2
Câu 61 Tam giác ABC có
A =120° thì câu nào sau đây đúng A. 2 2 2
a = b + c − 3bc . B. 2 2 2
a = b + c + bc . C. 2 2 2
a = b + c + 3bc . D. 2 2 2
a = b + c − bc . Lời giải Chọn B. Ta có 2 2 2 2 2 2 2
a = b + c − 2 .
ab cos A = b + c − 2 .
ab cos120° = b + c + ab .
Câu 62: Tam giác ABC có
A = 60° ; b =10 ; c = 20 . Diện tích của tam giác ABC bằng A. 50 3 . B. 50. C. 50 2 . D. 50 5 . Lời giải Chọn A. Ta có 1 S = .
bc sin A = 50 3 . 2
Câu 63: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc A là A. 30° . B. 45°. C. 68°. D. 75°. Lời giải Chọn B. b c a + ( + )2 2 2 2 6 1 3 − + − 4 2 cos A = = = ⇒ A = 45° . 2bc 2. 6.(1+ 3) 2
Câu 64: Cho tam giác ABC , các đường cao h , h , h thỏa mãn hệ thức 3h = h + h . Tìm hệ thức a 2 a b c b c
giữa a , b , c A. 3 2 1 = − .
B. 3a = 2b + c .
C. 3a = 2b − c . D. 3 2 1 = + . a b c a b c Lời giải Chọn D.
3h = h + h 6S 4S 2S ⇔ = + 3 2 1 ⇔ = + . a 2 b c a b c a b c
Câu 65: Cho tam giác ABC , nếu 2h = h + h thì a b c A. 2 1 1 = + .
B. 2sin A = sin B + sin C .
sin A sin B sin C
C. sin A = 2sin B + 2sin C . D. 2 1 1 = − .
sin A sin B sin C Lời giải Chọn A.
2h = h + h 4S 2S 2S ⇔ = + 4 2 2 ⇔ = + a b c a b c
2Rsin A 2Rsin B 2Rsin C 2 1 1 ⇔ = + .
sin A sin B sin C
Câu 66: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. 2
S = p( p − a)( p −b)( p − c) II. 2
16S = (a + b + c)(a + b − c)(a −b + c)(b + c − a) A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có. Lời giải Chọn A.
Áp dụng công thức Hê – rông S = p( p − a)( p −b)( p − c) 2
⇔ S = p( p − a)( p − b)( p − c) Nếu thay a b c p + + =
vào công thức Hê – rông thì ta có: 2 2
8S = (a + b + c)(a + b − c)(a −b + c)(b + c − a).
Câu 67: Trong tam giác ABC có AB = 2cm , AC =1cm , A = 60°. Khi đó độ dài cạnh BC là A. 1cm . B. 2cm . C. 3 cm . D. 5 cm . Lời giải Chọn C. Ta có 2 2 2
BC = AB + AC − 2A . B AC.cos A 2 2 2
⇒ BC = 2 +1 − 2.2.1.cos60° 2 ⇒ BC = 3 Vậy BC = 3 cm .
Câu 68: Tam giác ABC có: a = 5 ; b = 3 ; c = 5 . Số đo của góc BAC là A. A > 60° . B. A = 30°. C. A = 45° . D. A = 90°. Lời giải Chọn A. 2 2 2 2 2 2 Ta có cos
b + c − a 1 A = 3 5 5 3 cos A + − ⇒ = = ⇒ < ⇒ cos A A > 60° . 2bc 2.3.5 10 2
Câu 69: Tam giác ABC có a = 8; b = 7 ; c = 5 . Diện tích của tam giác ABC bằng A. 5 3 . B. 8 3 . C. 10 3 . D. 12 3 . Lời giải Chọn C. Ta có a b c p + + =
=10 , S = p( p − a)( p − b)( p − c) =10 3 . 2 Cách 2 (Bấm máy)
Gán biến nhớ: (Cài font ES03 để đọc được kí tự phím máy tính) 8qJz 7qJx 5qJc aJz+Jx+JcR2qJj Tính diện tích sJj(JjpJz)(JjpJx)(JjpJc)= .
Câu 70: Cho tam giác ABC có a = 2 ; b = 6 ; c =1+ 3 . Góc B bằng A. 115°. B. 75°. C. 60°. D. 53 32 ° ′ . Lời giải Chọn C. 2 2 2 Ta có
a + c − b 1 = = ⇒ cos B B = 60° . 2ac 2 Cách 2 (Bấm máy) Gán biến nhớ: 2qJz s6qJx 1+s3qJc Tính góc aJzd+JcdpJxdR2JzJc=qkM= .
Câu 71: Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r là bán
kính đường tròn nội tiếp tam giác ABC . Khi đó tỉ số R bằng r A. 1+ 2 . B. 2 + 2 . C. 2 −1 . D. 2 +1 . 2 2 2 Lời giải Chọn A. Ta có abc R = , S r = 4S P
Vì tam giác ABC vuông cân tại A nên b = c và 2 2
a = b + c = b 2
. a + b + c abc a(a + 2b) 2 2b (1+ 2) Xét tỉ số R . abc p = 2 = = = =1+ 2 . 2 r 4S 1 2 2 4. .( . b c)2 2b 2b 4
Câu 72: Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm A và
B trên mặt đất có khoảng cách AB =12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân
của giác kế có chiều cao h =1,3m . Gọi D là đỉnh tháp và hai điểm A , B cùng thẳng hàng với C thuộc 1 1 1
chiều cao CD của tháp. Người ta đo được góc DAC = 49° và
DB C = 35° . Tính chiều cao CD của 1 1 1 1 tháp. A. 22,77 m . B. 21,47 m . C. 20,47 m . D. 21,77 m . Lời giải Chọn A. Ta có
C DA = 90° − 49° = 41°;
C DB = 90° − 35° = 55° , nên A DB =14° . 1 1 1 1 1 1 Xét tam giác 12.sin 35 A DB , có A B A D 1 1 1 = A D ° ⇒ = ≈ 28,45m . 1 1 sin A DB sin A B D 1 sin14° 1 1 1 1
Xét tam giác C A D vuông tại C , có 1 1 1 1 sin C D C A D = ⇒ C D = A .
D sin C A D = 28,45.sin 49° ≈ 21,47 m 1 1 A D 1 1 1 1 1
⇒ CD = C D + CC ≈ 22,77 m . 1 1
Câu 73: Trên nóc một tòa nhà có cột ăng-ten cao 5m . Từ vị trí quan sát A cao 7 m so với mặt đất, có
thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang (như
hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là A. 21,2m . B. 14,2m . C. 11,9m. D. 18,9m . Lời giải Chọn D.
Ta có chiều cao của tòa nhà chính là đoạn BH .
Mà BH = CD + DH = CD + 7.
Xét tam giác ACD vuông tại D có CD AC = sin 40°
Xét tam giác ABD vuông tại D có 5 CD AB + = sin 50°
Xét tam giác ABC có: 2 2 2 = + − BC AB AC 2A . B AC.cos BAC 1 1 2cos10° 2 10 10cos10° 25 ⇔ + − CD + − CD + − 25 = 0 2 2 2 2
sin 50° sin 40° sin 40°sin 50°
sin 50° sin 40°sin 50° sin 50° ⇔ CD ≈11,9
⇒ BH ≈ 7 +11,9 ≈18,9 (m). Vậy tòa nhà cao 18,9 m .
Câu 74 Cho tam giác ABC có a = 5 cm , c = 9 cm , 1
cosC = − . Tính độ dài đường cao h hạ từ A 10 a của tam giác ABC . A. 462 h = cm . B. 462 h = cm . C. 21 11 h = cm . D. 21 11 h = cm . a 40 a 10 a 40 a 10 Lời giải Chọn D.
Áp dụng định lí cosin trong tam giác ABC ta có: b = 7 2 2 2
c = a + b − 2 . a . b cosC 2 1 81 25 b 2.5. . b ⇒ = + − − 2
⇔ b − b − 56 = 0 ⇔ 10 b = 8 −
Ta nhận được b = 7(cm)
Diện tích tam giác ABC là S = − − − 21 21 21 21 5 7 9 = − − − ∆ p p a p b p c ABC ( )( )( ) 2 2 2 2 21 11 2 = (cm ) 4 21 11 Độ dài đường cao 2S h = 2 = 21 11 = (cm) a a 5 10
Câu 75: Cho đường tròn tâm O bán kính R và điểm M thỏa mãn MO = 3R . Một đường kính AB thay
đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức S = MA + MB .
A. min S = 6R .
B. min S = 4R .
C. min S = 2R .
D. min S = R . Lời giải Chọn A. Gọi = α ⇒ MOA MOB =180° −α . Ta có 2 2 2 2 2
MA = MO + AO − 2 . MO A .
O cosα = 9R + R − 6R cosα = R 10 − 6cosα . 2 2
MB = MO + BO − MO BO ( °−α ) 2 2 2 2 . .cos 180
= 9R + R + 6R cosα = R 10 + 6cosα .
Xét C = 10 − 6cosα + 10 + 6cosα 2 2
⇒ C = 20 + 2 100 − 36cos α ≥ 20 + 2 100 − 36 = 36 . cosα =1 α = 0°
Suy ra C ≥ 6 . Dấu " = " xẩy ra khi 2 cos α =1 ⇔ ⇔ . cosα 1 α = − =180°
Ta có S = MA + MB = R( 10−6cosα + 10+ 6cosα ) ≥ 6R.
Suy ra min S = 6R khi và chỉ khỉ A , O , B , M thẳng hàng.
Câu 76: Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1 m , người ta cắt ra một
hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu? A. 2 1,6 m . B. 2 2 m . C. 2 1 m . D. 2 0,8 m . Lời giải Chọn C.
Xét đường tròn bán kính 1, ta cắt trên đó một hình chữ nhật ABCD . Khi đó 1 S = AC BD α = 2sinα ≤ 2. ABCD . .sin 2
Dấu bằng xảy ra khi và chỉ khi α = 90° .
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng 1. α Câu 77: Biết 2017 1 sinα + =
, 90° < α <180° . Tính giá trị của biểu thức sin M = cotα + . 2018 1+ cosα A. 2017 1 M + = − . B. 2017 1 M + = . C. 2018 M = − . D. 2018 M = . 2018 2018 2017 +1 2017 +1 Lời giải Chọn D. sinα α α + α M = cotα + cos sin = + 1 cos = 1 = 2018 = . 1+ cosα sinα 1+ cosα sinα (1+ cosα ) sinα 2017 +1
Câu 78: Cho hình thang cân ABCD có đáy nhỏ AB , đáy lớn CD . Biết AB = CD và 3 tan BDC = . Tính 4 cos BAD . A. 17 . B. 7 − . C. 5 . D. 17 − . 25 25 25 25 Lời giải Chọn B. A B D C E
Gọi E là hình chiếu vuông góc của B trên DC . Đặt AB = AD = BC = x . Ta có DC x EC − = ( ) 1 . 2
Trong tam giác vuông BDE ta có: 3 tan BDC = BE 3 3 ⇔ = ⇔ BE = ED 4 ED 4 4 3 ⇔ 3 DC x BE DC − = −
= (DC + x) (2) . 4 2 8
Trong tam giác vuông BEC ta có 2 2 2
BC = EC + BE (3) . Thay ( )
1 , (2) vào (3) biến đổi ta được: 2 2 39 25
x +14DC.x − 25DC = 0 ⇔ x = DC hay 39 39 DC = x . Khi đó 7 EC = x . 25 25 Mặt khác: cos BAD EC = − cos BCE 7 = − = − . BC 25
Document Outline
- 1. Giá trị lượng giác của một góc từ 0 - 180 độ
- CHUYÊN ĐỀ 3: HỆ THỨC LƯỢNG TRONG TAM GIÁC
- Chủ đề 1-GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ ĐẾN
- 2. Hệ thức lượng trong tam giác
- CHỦ ĐỀ 2: HỆ THỨC LƯỢNG TRONG TAM GIÁC
- ôn tập chương 3




