












Preview text:
Dạy cho ngày mai – Học cho tương lai
CHƯƠNG I: SỐ HỮU TỈ
BÀI 1: TẬP HỢP CÁC SỐ HỮU TỈ
A. KIẾN THỨC CẦN NHỚ a
Số hữu tỉ là số viết được dưới dạng phân số với , a b , b 0 . b
Tập hợp các số hữu tỉ được ký hiệu là . a a Chú
ý: Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ là số hữu tỉ . b b
* Ta có thể so sánh hai số hữu tỉ bất kỳ bằng cách viết chung dưới dạng phân số rồi so sánh hai phân số đó. *
Với hai số hữu tỉ a,b bất kỳ, ta luôn có hoặc a b hoặc a b hoặc a b
Cho ba số hữu tỉ a, ,
b c . Nếu a b và b c thì a c (tính chất bắc cầu)
* Trên trục số, nếu a b thì điểm a nằm trước điểm b Trên
trục số điểm biểu diễn số hữu tỉ a được gọi là điểm a . Ta
thường chọn phân số tối giản để biểu diễn số hữu tỉ trên trục số. *
Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương *
Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ dương *
Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
B. PHÂN LOẠI CÁC BÀI TẬP I. Số hữu tỉ 3
Câu 1: Trong các phân số sau những phân số nào biểu diễn số hữu tỉ ? 4 12 15 24 2 0 2 7 ; ; ; ; 15 20 3 2 28 36 4 8 32 64
Câu 2: Các phân số ; ; ;
biểu diễn cho số hữu tỉ nào? 2 4 16 32 1
Câu 3: Các số sau đây có phải là số hữu tỉ hay không: 0,6; 1, 25; 1 ; 5 ? 3
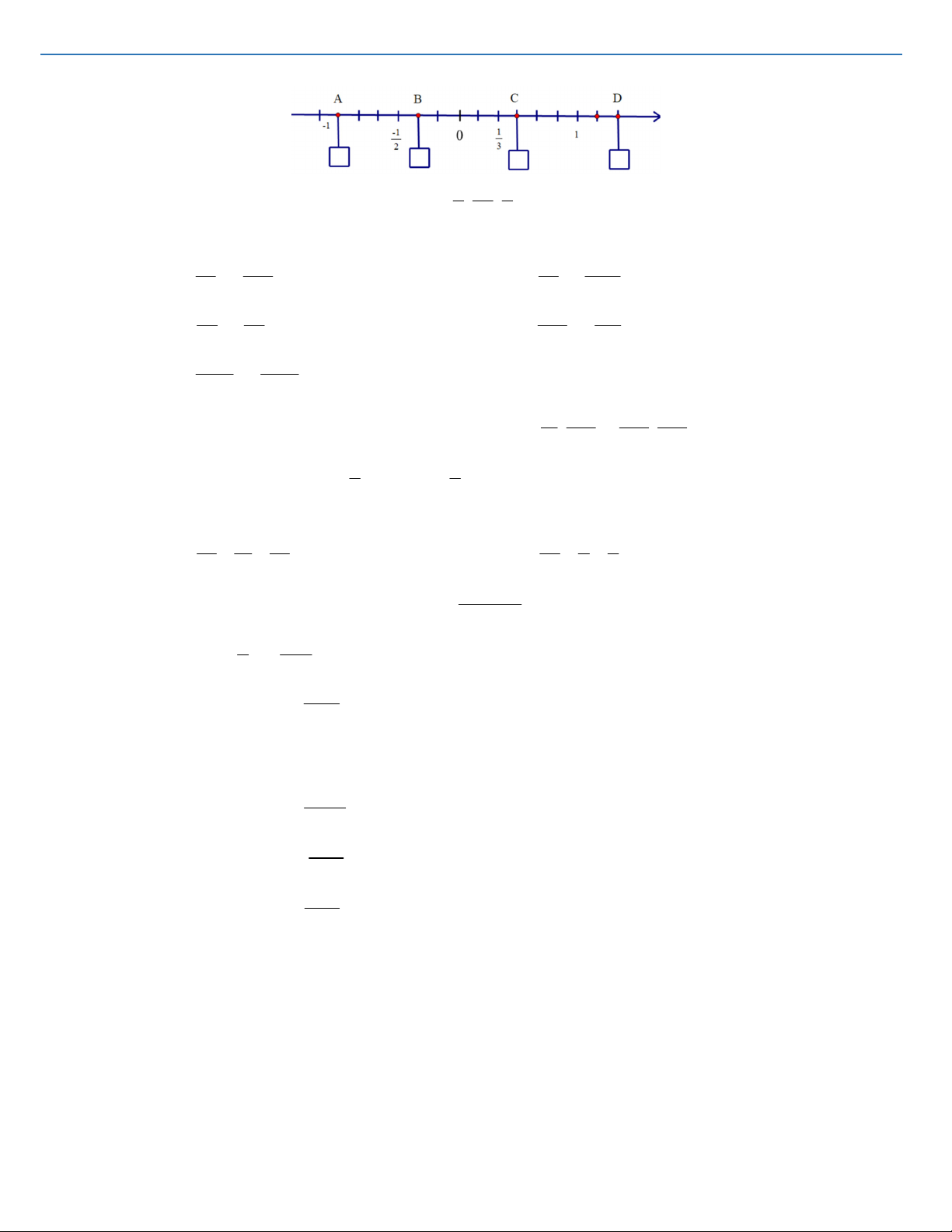
Câu 4: Điền kí hiệu ; ;
thích hợp vào ô trống: 3 ; 3 ; 3 ; 2 2 ; ; ; 3 3
II. Biểu diễn số hữu tỉ trên trục số 3 5
Câu 5: Biểu diễn các số ; trên trục số. 4 3 6 11 10 4
Câu 6: Biểu diễn các số sau trên cùng một trục số: ; ; ; 3 11 15 3
III. So sánh hai số hữu tỉ
Câu 7: So sánh các cặp số sau 1 2 3 a) 0, 4 và b) và 2 7 11 Trang 1
Dạy cho ngày mai – Học cho tương lai 21 3 18 c) và d) 2, 4 và 2, 15 300 25 a
Câu 8: So sánh số hữu tỉ a,b ;
b 0 với số 0 khi a,b cùng dấu và khi a,b khác dấu. b a b a b
Câu 9: Giả sử x ; y
(a,b Z;m 0) và x y . Hãy chứng tỏ rằng nếu chọn z thì ta có m m 2m
x z y . a a b Hướng dẫn: Chứng tỏ với a b m m 3 1
Câu 10: Tìm ba phân số nhỏ hơn và lớn hơn ? 7 5
Hướng dẫn: Quy đồng mẫu thức hai phân số đã cho. a c
Câu 11: Cho hai số hữu tỉ và
b 0;d 0. Chứng tỏ rằng: b d a c a c a) Nếu thì ad . bc b)
Nếu ad bc thì . b d b d a c a a c c
Câu 12: a) Chứng tỏ rằng nếu
(b 0, d 0) thì . b d b b d d 1 1
b) Hãy viết ba số hữu tỉ xen giữa và . 3 4 *
Hướng dẫn: Áp dụng Câu 11. a a 2001 Câu 13: Cho ,
a b , b 0 . Hãy so sánh hai số hữu tỉ và ? b b 2001 a a n Câu 14: So sánh * và
b 0;n N b b n *
Hướng dẫn: Xem lời giải Câu 11 và 12. 5 2
Câu 15: a) Tìm phân số có mẫu bằng 7, lớn hơn và nhỏ hơn . 9 9 10 10
b) Tìm phân số có tử bằng 7, lớn hơn và nhỏ hơn . 13 11 * Hướng dẫn 2 5 a a) Quy đồng các phân số: ;
; (a là tử số cần tìm) 9 9 7
Câu 16: So sánh các phân số sau? 1 1 267 1 347 a) và b) ; 5 1000 26 8 1343 13 29 18 18 1818 c) và d) và 38 88 31 313131 17 23 e) và 21 27 C. BÀI TẬP
Câu 1.1. Điền kí hiệu ( ;
; ) thích hợp vào ô trống: 5 3 2 ; 2 ; 2 ; ; ; 5 5 Trang 2
Dạy cho ngày mai – Học cho tương lai
Câu 1.2. Điền số hữu tỉ thích hợp vào ô trống: 2 4 7
Câu 1.3. Biểu diễn các số hữu tỉ sau trên trục số: ; ; 5 5 5 Câu 1.4. So sánh 5 15 1 1 a) và d) và 3 9 25 1225 5 2 215 104 b) và e) và 7 3 216 103 788 789 c) và 789 788 9 3 0 1 4 1 2
Câu 1.5: Hãy sắp xếp các số hữu tỉ sau theo thứ tự tăng dần: ; ;0; ; ? 11 40 18 8 1 1
Câu 1.6: Tìm ba phân số lớn hơn và nhỏ hơn 4 2
Câu 1.7: Tìm a , sao cho: 3 a 3 5 a 1 a) . b) . 7 14 5 10 5 2 62 8628
Câu 1.8: Viết dạng chung của các số hữu tỉ bằng . 942942 a a 1 Câu 1.9: So sánh và
a,b,b 0 . b b 1 a 4
Câu 1.10: Cho số hữu tỉ x
. Với giá trị nào của a thì 5 a) x là số dương? b) x là số âm ? 2
Câu 1.11: Cho số hữu tỉ: x
. Tìm a để x ? 2a 1 a 3
Câu 1.12: Cho số hữu tỉ: x
. Tìm a để x ? a a 2
Câu 1.13: Cho số hữu tỉ x
. Tìm a để x ? 2a
BÀI 2: CỘNG TRỪ NHÂN CHIA SỐ HỮU TỈ
A. KIẾN THỨC CẦN NHỚ
Ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.
Nếu hai số hữu tỉ được viết dưới dạng số thập phân thì ta áp dụng quy tắc cộng và trừ đối với số thập phân. Trang 3
Dạy cho ngày mai – Học cho tương lai
Trong tập các số hữu tỉ , ta cũng có quy tắc dấu ngoặc tương tự như trong tập các số nguyên .
Đối với một tổng trong , ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng
một cách tuỳ ý như các tổng trong .
Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia
đối với số thập phân.
B. PHÂN LOẠI CÁC BÀI TẬP
I. Thực hiện phép cộng, trừ số hữu tỉ Câu 1: Tính: 1 1 8 15 5 2 a) b) c) 0,75 d) 3,5 21 28 18 27 12 7 Câu 2: Tính: 3 5 3 4 2 3 a) b) 7 2 5 3 5 2 4 2 7 2 7 1 3 c) d) 5 7 10 3 4 2 8 5
Câu 3: Viết số hữu tỉ
là tổng của hai số hữu tỉ âm và là hiệu của hai số hữu tỉ dương. 16 1 1 1 Câu 4: a) Chứng minh đẳng thức: * n . nn 1 n n 1
b) Áp dụng đẳng thức trên để tính tổng 1 1 1 1 1 A ... 1.2 2.3 3.4 98.99 99.100 Câu khác: 1 1 1 1 1 1 1 1 Tính: P 2 6 12 20 30 42 56 72 1 1 1 1 1 1 1 1 1 A . 90 72 56 42 30 20 12 6 2 Câu 6: Tính 1 1 1 a) A 1 1 ... 1 1.2 2.3 2015.2016 3 5 7 9 11 b) B . 1.4 4.9 9.16 16.25 25.36
II. Tìm số chưa biết trong đẳng thức
Câu 7: Tìm x , biết: 1 3 2 5 2 6 4 1 a) x b) x c) x d) x . 3 4 5 7 3 7 7 3 Trang 4
Dạy cho ngày mai – Học cho tương lai
Hướng dẫn: “Chuyển vế, đổi dấu”
Câu 8: Tìm x , biết: 17 7 7 3 3 2 a) x b) x . 6 6 4 35 5 7
Câu 9: Tìm tập hợp các số nguyên x , biết: 1 1 1 1 1 1 3 5 x 2 1 a) x b) 1 . 2 3 4 48 16 6 4 6 12 3 4
III. Nhân, chia số hữu tỉ Câu 10: Tính: 2 21 6 5 7 a) b) . c) ( 2 ) 7 8 25 4 2 3 5 d) : 6 e) : ( 2 ) 25 23
Hướng dẫn: Áp dụng quy tắc nhân, chia phân số Câu 11: Tính: 3 12 25 38 7 3 a) . . b) ( 2 ) 4 5 6 21 4 8 11 33 3 7 8 45 c) : d) 12 16 5 23 6 18
Hướng dẫn: Thực hiện các phép tính trong ngoặc trược; nhân chia trước, cộng trừ sau. Câu 12: Tính: 2 3 4 1 4 4 5 1 5 5 1 2 a) : : b) : : 3 7 5 3 7 5 9 11 22 9 15 3
Hướng dẫn: A : C B : C A B :C . Câu 13: Tính: 3 3 3 3 1 1 1 a) 5 7 9 11 A b) 9 39 63 B 8 8 8 8 1 1 1 5 7 9 11 12 52 84
17 17 17 1 17 1 1 ... 1 2 3 19
Câu 14: Tính: A
19 19 19 1 19 1 1 ... 1 2 3 17 Câu 15: Tính: Trang 5
Dạy cho ngày mai – Học cho tương lai 1 1 1 1 1 1 a) A 2 3 3 4 9 10 1 1 1 1 b) B 1 1 1 1 2 3 9 10 1 1 1 1 1 c) C 1 1 1 1 1 4 9 16 81 100 1.1 1 1 1 Hướng dẫn: ; . v v 2.3 2.3 2 3 Câu 16: Tính: 1 1 1 1 1 1 a) A b) B 2.5 5.8 98.101 1.5 5.9 41.43 Hướng dẫn: 1 1 1 1 1 1 1 1 a) ; v.v... b) ; v.v.. 2.5 3 2 5 1.5 4 1 5
Câu 17: Tìm x , biết: 2 1 3 1 1 2 a) x (2x 1) 5
b) x (x 1) 0 3 3 2 2 3 5 2 1 8 c) x : 9 5 10
Câu 18: Tìm x , biết: 1 3 a) x x 0 b) 2x 1 2x 3 0 2 4 Hướng dẫn: .
A B 0 A 0 hoặc B 0 .
Câu 19: Tìm x , biết: 2x 1 4 3x a) 0 b) 0 3x 2 2x 5
Câu 20: Tìm các giá trị x , biết: x 2 a) x 1 x 2 0 b) x 2 2 x 0 c) 0 3 3x 2
Hướng dẫn: Tích hai số khác dấu là một số âm; tích hai số cùng dấu là một số dương. 5
Câu 21: a) Tìm x để biểu thức P
nhận giá trị âm? 2x 5
b) Tìm x để biểu thức 2
P 2x 5x nhận giá trị dương? Trang 6
Dạy cho ngày mai – Học cho tương lai
Hướng dẫn: Tích hai số khác dấu là một số âm, tích hai số cùng dấu là một số dương.
Câu 22: Tìm hai số hữu tỉ x và y sao cho a) x y .
x y x : y y 0 b) x y .
x y x : y y 0 C. BÀI TẬP: 1 2 2 5 5 4
Câu 1.14: Cho A 3 2 5 2 3 3 2 2 3
Hãy tính giá trị của A theo 2 cách
Cách 1: Bỏ dấu ngoặc rồi nhóm các số hạng thích hợp.
Cách 2: Trước hết tính giá trị của từng biểu thức trong ngoặc đơn.
Câu 1.15: Tính nhanh: 1 3 3 1 2 1 1 a) A 3 4 5 72 9 36 15 1 3 5 1 7 9 7 2 5 3 1 b) B 5 7 9 11 13 16 13 11 9 7 5 x 1 1
Câu 1.16: Tìm các số nguyên , x y ; biết: 6 y 2 1 1 1 1 1
Câu 1.17. Chứng tỏ ...
không phải là một số nguyên. 11 12 13 18 19
Câu 1.18. Tìm x, biết: 11 2 2 5 4 2 4 a) x b) x 12 5 3 2 5 3 7 1 8 x 3 5
Câu 1.19. Tìm x , biết: 1 4 9 36 8 6
Câu 1.20. Tính tổng: 3 3 3 a) S ... 1 1.4 4.7 100.103 3 6 9 12 15 18 b) S 2
1.4 4.7 10.19 19.31 31.46 46.64 Câu 1.21: Tính 1 9 1 2 1 a) 2 1 . b) 1 . 5 11 14 5 1 1 2 Trang 7
Dạy cho ngày mai – Học cho tương lai
5 1 1 5 9 c) :1 : .
3 4 5 8 4 Câu 1.22: Tính 3 3 3 3 1 1 1 a) 4 5 7 13 P . b) M 1 1 1 . 11 11 11 11 2 3 2014 4 5 7 13
Câu 1.23: Tìm x , biết: x 3 x 1 x 3 a) 0 b) 0 c) 0 2 x 1 x 1 2
Câu 1.24: Cho hai số hữu tỉ có tổng bằng và tích bằng
. Tính tổng các số nghịch đảo của hai số đó. 3 9
Câu 1.25: Tìm x , y , z , biết: x x y z 5
; y x y z 9; zx y z 5. Câu 1.26: Tính: 1 1 1 1 a) A 1 1 ... 1 1 , * n . 2 3 n 1 n 1 1 1 b) B 1 ... , * n . 2 2 2 2 1 3 n 1 9 8 7 1 ... Câu 1.27: Tính: 1 2 3 9 P 1 1 1 1 ... 2 3 4 10 Câu 1.28: Tìm * x , biết: 1 1 1 1 49 a) ... . 1.4 4.7 7.10
x x 3 148 1 1 1 13 b) ... . 5.6 6.7 x x 1 90
Câu 1.29: Tìm x , biết: 7 11 13 x a) .
x 3 x 10 x 10 x 2 1
x 2 1x 34 x 3x 34 3 6 15 1 1 b) .
x 4 x 7 x 7 x 13 x 13 x 28 x 28 20
BÀI 3: LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN CỦA MỘT SỐ HỮU TỈ
A. KIẾN THỨC CẦN NHỚ Trang 8
Dạy cho ngày mai – Học cho tương lai
* Lũy thừa bậc n của một số hữu tỉ x , là tích của n thừa số x . Kí hiệu n
x , là tích của n thừa số
x ( n là số tự nhiên lớn hơn 1) n x . x . x ... x x (x ,
n , n 1) nthua so n
x đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x
x gọi là cơ số, n gọi là số mũ Quy ước: 0
x x 1 1 0 ; x x
* Tích và thương của hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ. m. n m n x x x
Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia
trừ số mũ của lũy thừa chia. m n m– : n x x x
x 0,m n
* Lũy thừa của lũy thừa
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ. n m m.n x x
B. PHÂN LOẠI CÁC BÀI TẬP
I. Các phép toán về lũy thừa 4 3 1 1 Câu 1: Tính ; 2 ; 0, 22 ; 5 ,50 3 4 2 3 4 5
1 1 1 1 Câu 2: Tính: ; ; ;
2 2 2 2 16 Câu 3: Viết số
dưới dạng một lũy thừa 81 Câu 4: Tính 21 6 3 9 a) 3 2 25 : 5 ; b) : 7 49 2 3 4 .4 7 3 2 .9 4 4 5 .20 c) ; d) ; e) 10 2 5 2 6 .8 5 5 25 .4 Câu 5: Tính Trang 9
Dạy cho ngày mai – Học cho tương lai 2 3 1 2 3 5 5 4 10 6 a) ; b) ; c) . 7 2 4 6 3 5 2 2 1 4 3 2 1 2 d) 1 ; e) 2 : 3 4 5 4 2 3
II. Tìm số chưa biết trong một lũy thừa
Câu 6: Ta thừa nhận tính chất sau đây: Với a 0;a 1 , nếu m n
a a thì m n
Tìm số tự nhiên n biết: 1 n 1 343 7 n 16 a) b) c) 2 2 32 125 5 2n 3n d) 27
e) 8n : 2n 4 81
Câu 7: Tìm x biết: 2 1 2 1 1 a) x 0 b) x 2 2 1 c) x 3 2 1 8 d) x 2 2 16
Câu 8: Tìm x biết: 7 x 8 x 3 1 1 5 7 3 3 a) 27 b) 729 c) x : d) .x 81 9 2 2 4 4
Câu 9: Tìm n , biết: a) 2.16 2n 4 b) 9.27 3n 243 c) n 1 125 5 25
Câu 10: a) Tìm x , biết: x 2 y 2 1 1 0 b) Tìm ,
x y , biết: x 1
2 .3y 12x
III. Lũy thừa của lũy thừa Câu 11: Tính 6 2 3 1 2 1 a) 3 3 2 b) c) 2 2 n
Hướng dẫn: m . m n a a
Câu 12: Viết dưới dạng lũy thừa của một số hữu tỉ 5 7 1 1 a) 4 8 25 .2 b) . 9 27
Câu 13: Viết các số 27 2 v à 18
3 dưới dạng các lũy thừa có số mũ 9 .Từ đó hãy só sánh 27 2 v à 18 3 Trang 10
Dạy cho ngày mai – Học cho tương lai Câu 14: So sánh: a) 91 2 và 35 5 b) 332 2 và 223 3 b) 20 99 và 10 9999 d) 20 10 và 10 20 e) 23 2 và 32 2 Câu 15: So sánh: 0 1 10
A 2 2 ... 2 và 11 B 2 Câu 16: Số 7 5
2 .5 có bao nhiêu chữ số? C. BÀI TẬP
Câu 1.30: Viết các số 8 0, 25 và 4
0,125 dưới dạng luỹ thừa của có số 0,5 .
Câu 1.31: Viết các biểu thức số sau dưới dạng n a ; ( a ; n ) 1 1 2 2 2 1 1 a) 3 2 9.3 . .3 b) 5 3 4.2 : 2 . c) 2 5 3 .2 . d) 2 . .9 81 16 3 3 3
Câu 1.32: Tìm x , biết: 2 1 1 a) x 2 2 1 b) x 3 2 1 27 c) x 2 4 d) x 2 9 2 3 e) x 3 8 3 1 121 27
Câu 1.33: Tìm x , biết: 3 1 1 5 7 3 3 12 x a) 2 x : b) .x 4x x 0 5 2 2 4 4 x d) 10 8 x 25x e) x 1 x3 3 3 810
Câu 1.34: a) Chứng minh 6 7 10 5 chia hết cho 59 b) Chứng minh 7 18 8 2 chia hết cho 14 11 10 9 9 9 9 c) Chứng minh 639 d) Chứng minh 2 10
2 2 ... 2 chia hết cho 3 Câu 1.35: Tính: 1 1 1 1 1 1 1 1 a) A ... 3 3 3 3
125 1 125 2 125 3 125 5 b) 2 2 2 2
B 2 4 6 ... 20 , biết 2 2 2 1 2 ...10 385 Câu 1.36: So sánh Trang 11
Dạy cho ngày mai – Học cho tương lai a) 30 2 v à 20 3 b) 32 2 v à 2 3 2
Câu 1.37: Tìm chữ số tận cùng của a) 10 3 b) 25 7 c) 2009 2010 2011 3 .7 .13
Câu 1.38: Tìm n : a) 27 3n 3.81 b) 15 15 n n 16 16 4 .9 2 .3 18 .2 Câu 1.39: Cho 13 7 a 2 .5 Tìm
số có các chữ số của số a
BÀI 4: THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH VÀ QUY TẮC CHUYỂN VẾ
A.KIẾN THỨC CẦN NHỚ
1. * Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực
hiện các phép tính từ trái qua phải.
* Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:
Lũy thừa Nhân và chia Cộng và trừ
* Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau. Theo thứ tự: ... ... ...
2. Quy tắc chuyển vế
Khi chuyển vế một hạng tử từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng
đó: dấu “ ” đổi thành dấu “ ” và dấu “ ” đổi thành dấu “ ”
Nếu A B C thì A C B
Nếu A B C thì A C B
B. PHÂN LOẠI CÁC BÀI TẬP
I. Thực hiện các phép tính Câu 1: Tính 4 2 7 2 7 1 3 a) b) 5 7 10 3 4 2 8 4 5 4 16 c)1 0,5 23 21 23 21
Hướng dẫn: Thực hiện trong ngoặc trước
Câu 2: Thực hiện phép tính 2 9 2 7
a) 0, 75 1,5
b) 0,8 5,9 0, 6 3,5 : 5 3 3 Trang 12
Dạy cho ngày mai – Học cho tương lai Câu 3: Tính 4 3 2 2 5 2 4 a) 1 : 0,5 b)1 : 5 5 3 9 3 27 3 5 1 1 5 5 c) 6 4
d) 0,8 : 0,2 7 8 12 3 6 21 14
II. Quy tắc chuyển vế
Câu 4: Tìm x biết 1 5 9
a) x 0, 25 b) x 2 7 14 5 7 9 1 7 c) x d) 2x 4 5 20 2 9 3 7 e) 6x 4 13
Hướng dẫn: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức ta phải đổi dấu số hạng đó. III. TOÁN THỰC TẾ
Câu 5: Ông A gửi tiền tiết kiệm 200000000 đồng vào ngân hàng theo thể thức kì hạn 1 năm. Hết thời
hạn ông A nhận được cả vốn lẫn lãi là 214 400000 đồng.Tính lãi suất ngân hàng theo thể thức này?
Hướng dẫn: Tính tiền lãi một năm
Tìm lãi suất theo tỉ số phần trăm Bài toán khác:
Ông A gửi tiền tiết kiệm 200000000 đồng vào ngân hàng với lãi suất một năm 7, 2 %. Hỏi
sau hai năm ông A nhận được cả vốn lẫn lãi là bao nhiêu tiền?
Câu 6: Một người đi quãng đường từ địa điểm A đến địa điểm B với vận tốc 30km / h mất 3,5 giờ. Từ
địa điểm B quay trở về dịa điểm A, người đó đi với vận tốc 36km / h . Tính thời gian đi từ địa
điểm B quay về địa điểm A của người đó?
Câu 7: Vào dịp tết nguyên đán, bà của An gói bánh chưng cho gia đình. Nguyên liệu để làm bánh gồm
gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,8kg khoảng
gồm 0,5kg gạo; 0,125kg đậu xanh, 0,04kg lá dong, còn lại là thịt. Hỏi khối lượng thịt trong
mỗi cái bánh là khoảng bao nhiêu?
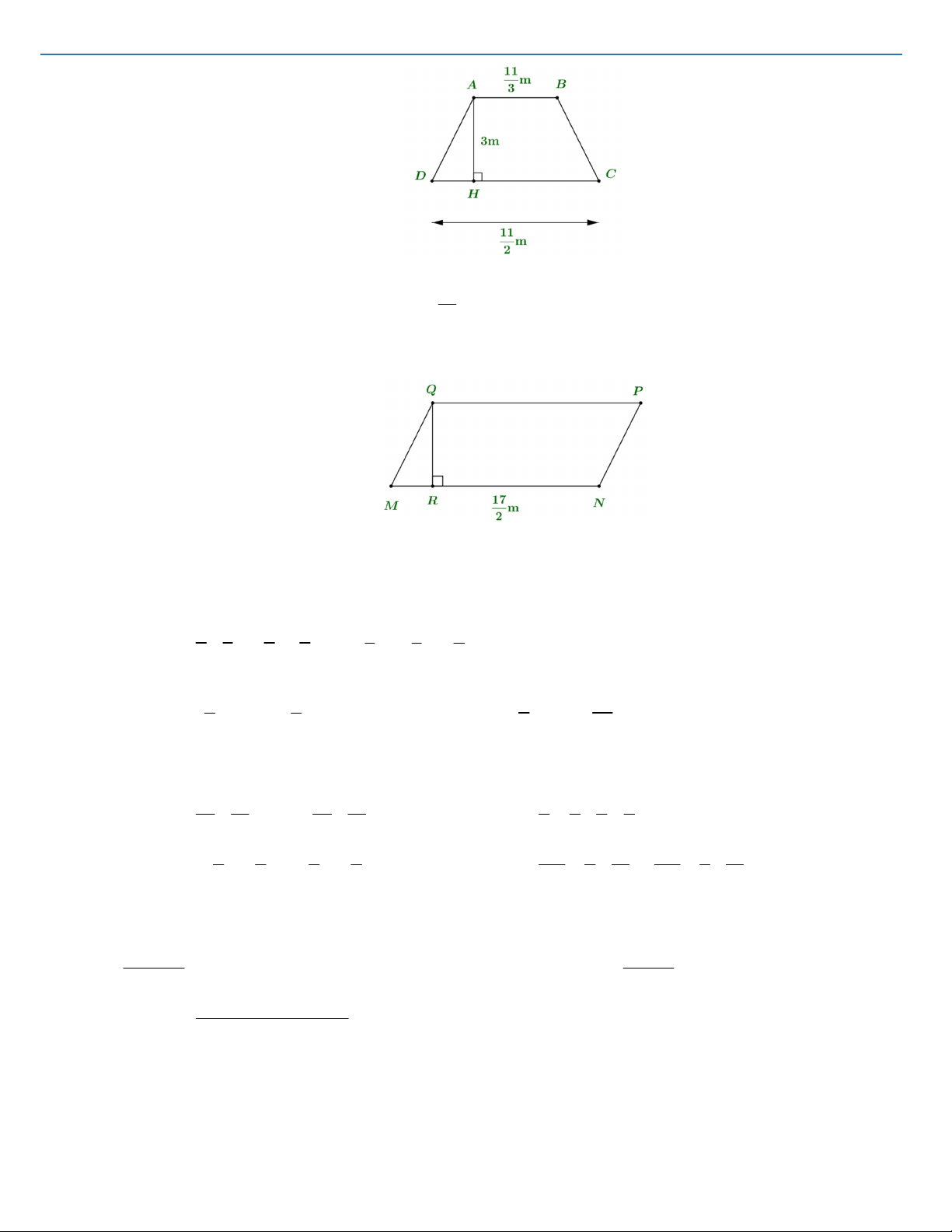
Câu 8: a) Tính diện tích hình thang ABCD có kích thước như hình sau: Trang 13
Dạy cho ngày mai – Học cho tương lai 17
b) Hình bình hành MNPQ có MN
m và diện tích bằng hình thang ABCD (câu a). Tính 2
đường cao QR của hình bình hành? C. BÀI TẬP
Câu 1.41: Thực hiện phép tính 2 3 3 1 2 1 1 3 a) : b) 2 5 5 2 2 3 3 2 2 7 5 c) 0, 25 : 0,75 d) 3 5 0,75 2 :1,5 8 6 2 4 Câu 1.42: 5 7 5 10 3 2 3 1 a) 0,25 b) 2 1 23 17 23 17 7 3 7 2 1 4 1 4 100 3 7 23 9 7 c) 13 : 17 : d) : : 4 7 4 7
123 4 12 123 5 15
Câu 1.43: Thực hiện phép tính: 16 7 5 27 3 3 2 27 a) b) 2 (0, 2) 5 5 11 125 9 6 5 4 9 6 2 3 3 2 5 2 25 2 125 c) 6 26.5
Câu 1.44: Tìm x , biết: Trang 14
Dạy cho ngày mai – Học cho tương lai 3 12 3 3 1 a) x b) x 1 5 25 5 4 2 2 3 3 1 2 c) : x 0,5 d) x 1 5 5 4 2 3 2 1 2 1 5 e) 2 : 5x 2 g) 2 x : 3 15 3 5 9 3
Câu 1.45. Tìm x , biết: 2 5 3 2 1 a) : x 0,5 b) x 1 9 6 4 3 3 1 2 5 5 3 4 c) 1 : x 0,75 d) x : 4 3 6 4 2 3
Câu 1.46. Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các 1
cạnh mảnh vườn, người ta trồng các khóm hoa, cứ m trồng một khóm hoa. Tính số khóm hoa 4 cần trồng?
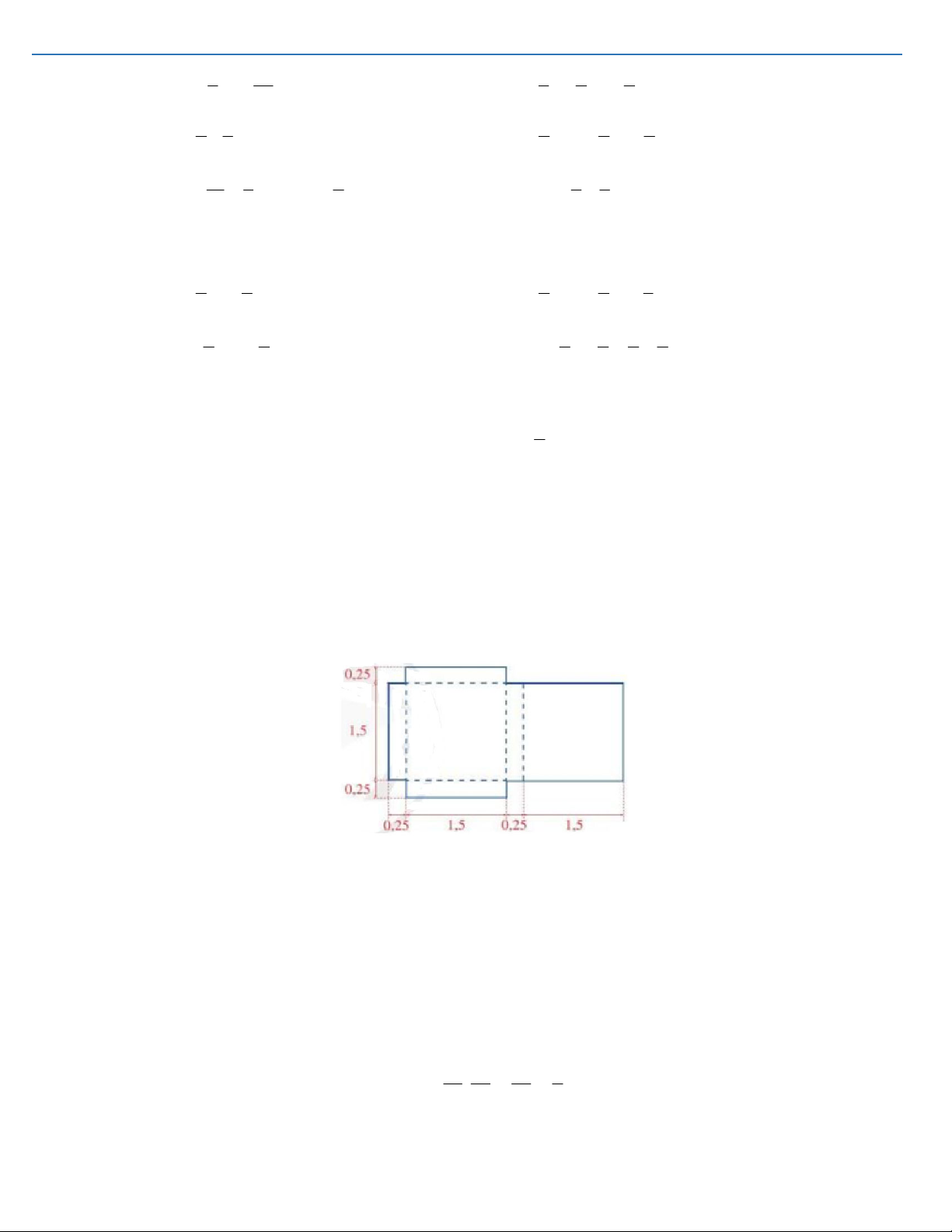
Câu 1.47. Cho miếng bìa có kích thước như hình vẽ bên dưới (các số đo trên hình tính theo đơn vị đề-xi- mét).
a) Tính diện tích miếng bìa?
b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó?
Câu 1.48. Trong đợt tri ân khách hàng, một cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách
mua hàng. Cửa hàng vẫn lãi được 20% của giá nhập về đối với mỗi chiếc xe bán ra. Tính giá
nhập về và giá niêm yết của một chiếc xe đạp, biết rằng với mỗi chiếc xe đạp bán ra như thế, cửa
hàng vẫn lãi được 600.000 đồng?
BÀI TẬP CUỐI CHƯƠNG I Câu 1. Hình
vẽ mô phỏng vị trí của năm điểm , A , B C, ,
D E so với mực nước biển. Biết rằng độ cao (tính
theo đơn vị ki- lô- mét) so với mực nước biển của mỗi điểm là một trong các số sau: 33 79 25 5 ; ; ; ;0 12 30 12 6 Trang 15
Dạy cho ngày mai – Học cho tương lai
Quan sát hình và cho biết độ cao của mỗi điểm?
Câu 2. Tính giá trị của các biểu thức sau: 12 15 3 3 2 1 2 a) b) 2 : 0,125 .8 124 3 3 4 : 6 3 1 3 2 3
Câu 3. Tính một cách hợp lí: 5 7 6 7 a) 3, 7 6,3 b) 2,8. 7, 2 2,8. 12 12 13 13 Câu 4. Tính 4 4 6 2 1 3 5 a) 0,3 : . 1 b) : 0,53 .4 9 3 5 3 8 2 2 1 1 8 c) 1 2 : ( 2 ,25) d) 0,5 2 : 2 3 6 4 3
Hướng dẫn: Lũy thừa, nhân và chia; cộng và trừ.
Câu 5. Tìm x , biết 1 3 1 4 2 1 a) x 2, 25 b) 2x c) x 2 5 3 9 3 3
Hướng dẫn: Áp dụng quy tắc chuyển vế.
Câu 6. Tìm x , biết a) x 2 4 2 1 b) x 3 1 3 1 9 8 HẾT Trang 16
Dạy cho ngày mai – Học cho tương lai ĐÁP ÁN THAM KHẢO
CHƯƠNG I: SỐ HỮU TỈ
BÀI 1: TẬP HỢP CÁC SỐ HỮU TỈ 3
Câu 1: Trong các phân số sau những phân số nào biểu diễn số hữu tỉ ? 4 12 15 24 2 0 2 7 ; ; ; ; 15 20 3 2 28 36 Lời giải
Hướng dẫn: Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ.
Các phân số đã cho cần rút gọn để được phân số tối giản. 12 4 1 5 3 24 3 2 0 5 27 3 Ta có: ; ; ; ; 15 5 20 4 3 2 4 28 7 36 4 4 8 32 64
Câu 2: Các phân số ; ; ;
biểu diễn cho số hữu tỉ nào? 2 4 16 32 Lời giải 4 8 32 64 Ta có: 2 2 4 16 3 2 Chú
ý: 1
Câu 3: Các số sau đây có phải là số hữu tỉ hay không: 0,6; 1, 25; 1 ; 5? 3 a
Hướng dẫn: Các số có dạng * ;a ;
b là các số hữu tỉ b Lời giải 6 3 5 1 4 Ta có: 0,6 ; 1, 25 ; 1 ; 5 10 5 4 3 3
Câu 4: Điền kí hiệu ; ;
thích hợp vào ô trống: 3 ; 3 ; 3 ; 2 2 ; ; ; 3 3 Lời giải 3 ; 3 ; 3 ; 2 2 ; ; 3 3 3 5
Câu 5: Biểu diễn các số ; trên trục số. 4 3 Lời giải 3 3 Ta có: 4 4 3 Biểu diễn số
trên trục số bởi điểm A 4 Trang 17
Dạy cho ngày mai – Học cho tương lai 5
Biểu diễn số trên trục số bởi điểm A 3
Câu 6: Biểu diễn các số sau trên cùng một trục số: 6 11 10 4 ; ; ; 3 11 15 3 Lời giải 6 11 10 2 4 Ta có: 2; 1; ; 3 11 15 3 3
Biểu diễn trên cùng một trục số. 2 4 Các số 2; 1; ;
lần lượt được biểu diễn bởi các điểm ; A ; B C; D . 3 3 4 2
Nhận xét: Có thể sắp xếp các số hữu tỉ đã cho theo thứ tự tăng dần: 1 2 3 3
Câu 7: So sánh các cặp số sau 1 2 3 a) 0, 4 và b) và 2 7 11 213 18 c) và d) 2, 4 và 2, 15 . 300 25 Lời giải
Hướng dẫn: Đưa về so sánh các phân số (với hai số thập phân ta không cần đưa về dạng phân số). 4 1 5 a) 0, 4 ; 10 2 10 4 5 Vì 4 5 10 10 1 Vậy 0, 4 . 2 2 2 2 3 2 1 b) ; 7 77 11 77 Vì 21 22 21 22 3 2 77 77 11 7 18 21 6 c) Ta có: 25 300 213 216 213 18 Vì 21 3 2 16 . 300 300 300 25 d) 2, 4 2 ,15 . Trang 18
Dạy cho ngày mai – Học cho tương lai a
Câu 8: So sánh số hữu tỉ a,b ;
b 0 với số 0 khi a,b cùng dấu và khi a,b khác dấu. b Lời giải
Hướng dẫn: So sánh hai phân số khi đưa phân số về mẫu số dương (xem Câu 7). a Ta có
thể coi phân số a,b ; b 0 b a 0 a
Với a,b cùng dấu, b 0 a 0 0 b b b a a a
Vậy 0 khi a,b cùng dấu; 0 khi a,b trái dấu; 0 khi a 0 ; a,b ; b 0 . b b b a b a b
Câu 9: Giả sử x ; y
(a,b Z;m 0) và x y . Hãy chứng tỏ rằng nếu chọn z thì ta có m m 2m
x z y . a a b Hướng dẫn: Chứng tỏ với a b m m Lời giải a 2a Ta có: m 2m a b Vì x và y
mà x y a b m m 2a a b
a a a b hay 2a a b
,vậy x z . 2m 2m
Chứng minh tương tự: z y
Nhận xét: giữa hai số hữu tỉ khác nhau luôn tìm được một số hữu tỉ “ nằm giữa ” hai số hữu tỉ đó. 1 2 1 1 2 2 1 3 2 1 1 2 Chẳng hạn: hay 3 3 3 2.3 3 3 6 3 3 2 3 1 1 2 3 2 2 3 3 1 5 1
Lại có : hay 3 2 6 6 6 12 6 3 12 2 3 1
Câu 10: Tìm ba phân số nhỏ hơn và lớn hơn ? 7 5
Hướng dẫn: Quy đồng mẫu thức hai phân số đã cho. Lời giải 3 15 Ta có: 1 7 BCNN 5,7 35 và 5 35 7 35 a 7 a 15 Ta tìm phân số sao cho b 35 b 35 a 8 a 9 a 10 Suy ra hoặc hoặc b 35 b 35 b 35
Nhận xét: Có thể áp dụng Câu 9 a c
Câu 11: Cho hai số hữu tỉ và b 0;d 0 . Chứng tỏ rằng: b d a c a) Nếu thì ad . bc b d a c b)
Nếu ad bc thì . b d * Hướng dẫn: Trang 19
Dạy cho ngày mai – Học cho tương lai a) Quy
đông mẫu thức hai phân số (xem Câu 10). b)
Viết theo thứ tự ngược lại của bài toán a). Lời giải a c ad cb a) Ta có:
vì b 0;d 0 ad bc . b d bd db ad bc a c b)
Ngược lại, nếu: ad bc . bd bd b d
Nhân xét: Ta có thể viết: a c
Với b 0 và d 0 , ta có ad bc . b d Câu 12: a c a a c c a) Chứng tỏ rằng nếu
(b 0, d 0) thì . b d b b d d 1 1
b) Hãy viết ba số hữu tỉ xen giữa và . 3 4 *
Hướng dẫn: Áp dụng Câu 11. Lời giải a a c a c a) Ta chứng minh , biết . b b d b d a c Theo Câu 11: ad bc b d
a a c ad ab bc ab a b d b a c b b d a c a c c a a c c Tương tự: . Vậy: b d b d d b b d d
b) Áp dụng phần a), ta có: 1 1 1 1 1 1 1 2 1 * hay 3 4 3 3 4 4 3 7 4 1 2 1 1 2 2 1 3 2 * hay 3 7 3 3 7 7 3 10 7 1 3 1 1 3 3 1 4 3 * hay 3 10 3 3 10 10 3 13 10 1 4 3 2 1 Vậy 3 13 10 7 4
Câu 13: Cho a,b , b 0 . a a 2001
Hãy so sánh hai số hữu tỉ và ? b b 2001 Lời giải Ta có: a b 2
001 ab 2001a ba 2
001 ab 2001b -
Trường hợp 1: Nếu a b 2001a 2001b a a 2001
ab 2001a ab 2001b b b 2001 Trang 20




