


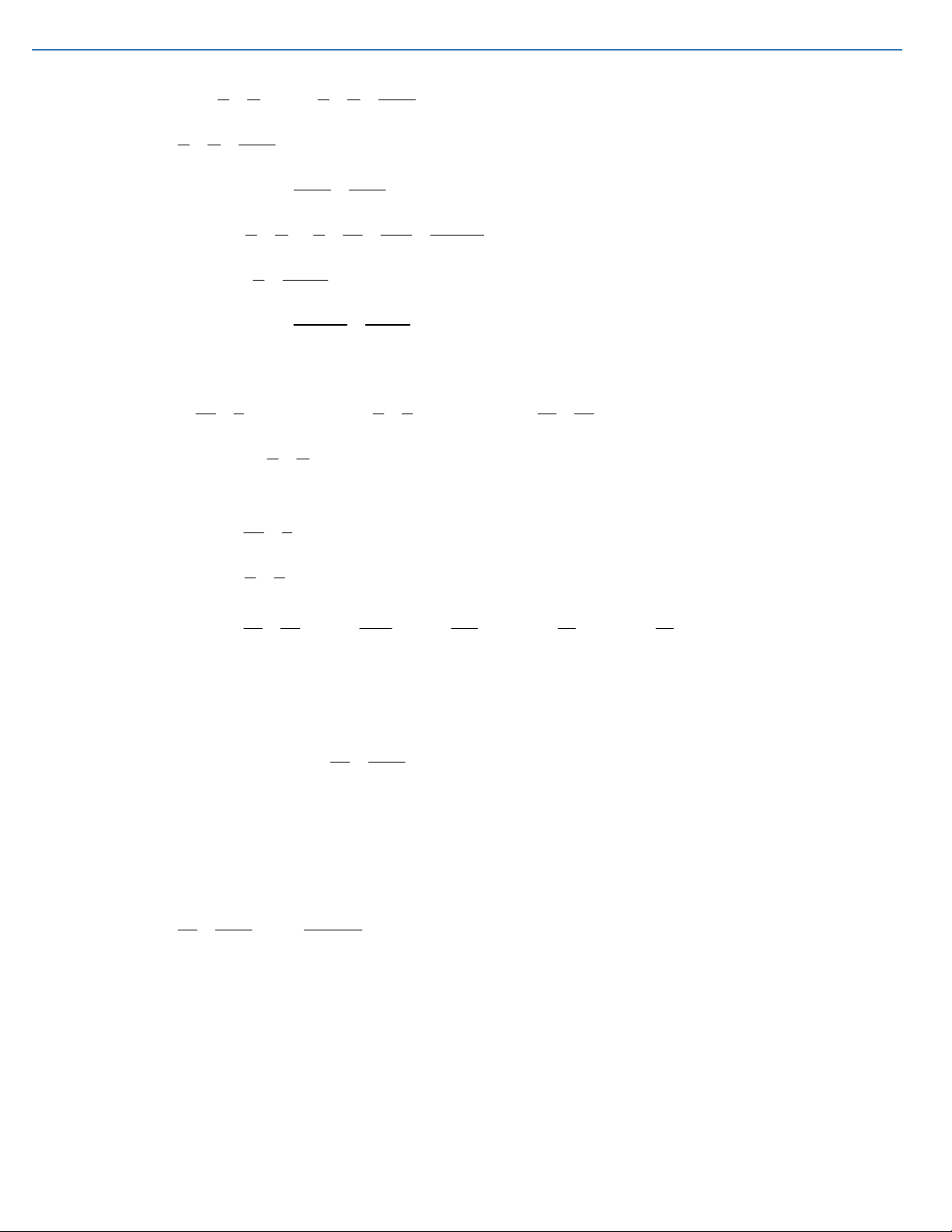












Preview text:
Dạy cho ngày mai – Học cho tương lai
Chương VI. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
BÀl 20: TỈ LỆ THỨC
A. KIẾN THỨC CẦN NHỚ a c
Tỉ lệ thức là đẳng thức của hai tỉ số:
(có thể viết a : b c : d ) b d
Tính chất của tỉ lệ thức a c Nếu
thì ad bc . b d a c a b d c d b
Nếu ad bc thì
(với a, b , c , d 0 ); ; ; . b d c d b a c a
B. PHÂN LOẠI CÁC BÀI TOÁN I. Lập tỉ lệ thức
Bài toán 1. Lập tất cả các tỉ lệ thức có thể được từ các đả̉ng thức sau: a) 6.63 9.42 b)
0, 24 1, 61 0,84 0, 46 15 35 1 1 c) d) 6 : (27) 6 : 29 5,1 11,9 2 4
Huớng dẫn: Xem sơ đồ phần A a c a b b d d c ad bc
; ; ; (với a,b,c, d 0 ) b d c d a c b a
Bài toán 2: Lập các tỉ lệ thức có thể được từ chữ số: 5; 25; 125; 625.
Bài toán 3: Tìm các tỉ số bằng nhau trong các tỉ số sau đây rồi lập các tỉ lệ thức: 1 1 2
28 :14; 2 : 2;8 : 4; : ;3:10; 2,1: 7;3 : 0,3 2 2 3 a c
Bài toán 4: Từ tỉ lệ thức . Hãy suy ra: b d a b c d a c a) b)
( a b 0;c d 0 ) b d a b c d a b a b a c d c a c a c Hướng dẫn: 1;
1. Từ đó ta viết lại: 1 1. b b b b d d b d b d
Bài tập tương tự: a c 1. Cho . Hãy suy ra: b d a a c a b c d a c 2 2 ac a c a) b) c) d) b b d a c a b c d 2 2 bd b d a c Bài toán 5: Cho . Chứng minh: b d a b c d 3a 2c a 3c a) b) a b c d 3b 2d b 3d
Huớng dẫn: Xem bài toán 4. (phần bài tập tương tự)
Dạy cho ngày mai – Học cho tương lai
II. Tìm số hạng chưa biết
Bài toán 6: Tìm x trong tỉ lệ thức sau: 2x 5 x 5 2 x 24 a) b) c) 6 3 8 4 6 25 a c Hướng dẫn: . a d . b c b d
Bài toán 7: Để pha nước muối sinh lí, người ta cần pha theo đúng tỉ lệ. Biết rằng cứ 3l nước tinh khiết thì
pha với 27g muối. Hỏi nếu có 45g muối thì cần pha với bao nhiêu lít nước tinh khiết để được nước muối
Hướng dẫn: Gọi x (gam) là số nước cần dùng x 3000
Ta có 3l 3000 g và 45 27 Từ đó tìm x .
Bài toán 8: Để cày hết một cánh đồng trong 14 ngày phải sử dụng 18 máy cày. Hỏi muốn cày hết cánh
đồng đó trong 12 ngày thì phải sử dụng bao nhiêu máy cày (biết năng suất của các máy cày là như nhau)?
Hướng dẫn: Gọi x (máy) là số máy cày cần dùng
Theo đề bài, ta thấy nếu dùng 1 máy sẽ mất: 1418 252 (ngày)
Vậy số máy cần dùng là 252 :12 21. x y Bài toán 9: Tìm , x y biết: và xy 112 . 4 7 x y
Huớng dẫn: Đặt
k x 4k; y 7k 4 7 Ta có: 2
xy 112; x 4k; y 7k 4k.7k 112 k 4 Từ đó tìm k và ; x y C. BÀl TẬP
6.1. Tìm x , biết: 26 12 a) x : 7,5 2,5 : 7,5 b) . x 42
6.2. Tìm x , biết: 5 15 4 2 x 1 1 a) b)
: x 0, 4 c) x 2 6 9 3 8 x 1
6.3. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 2 phần dầu với 7 phần xăng. Hỏi cần
bao nhiêu lít xăng để trộn hết 8 lít dầu theo cách pha nhiên liệu như trên?
6.4. Hãy viết một tỉ lệ thức từ đẳng thức 2a b .
6.5. Hai máy xúc (cùng năng suất) làm xong một công việc trong 4 ngày. Hỏi nếu có 4 máy xúc như thế
sẽ làm xong công việc trong bao lâu?
Dạy cho ngày mai – Học cho tương lai ĐÁP ÁN THAM KHẢO
BÀl 20: TỈ LỆ THỨC
B. PHÂN LOẠI CÁC BÀI TOÁN I. Lập tỉ lệ thức
Bài toán 1. Lập tất cả các tỉ lệ thức có thể được từ các đẳng thức sau: a) 6.63 9.42 b)
0, 24 1, 61 0,84 0, 46 15 35 1 1 c) d) 6 : (27) 6 : 29 5,1 11,9 2 4
Huớng dẫn: Xem sơ đồ phần A a c a b b d d c ad bc
; ; ; (với a,b,c, d 0 ) b d c d a c b a Lời giải 6 42 6 9 63 9 63 42 a) 6.63 9.42 ; ; ; 9 63 42 63 42 6 9 6 0, 24 0,84 1, 61 0,84 0, 24 0, 46 1, 61 0, 46
b) 0, 24 1,61 0,84 0 46 ; ; ; 0, 46 1,61 0, 46 0, 24 0,84 1, 61 0,84 0, 24 15 35 15 5,1 11,9 3 5 11,9 5,1 c) ; ; 5,1 11,9 3 5 11,9 5,1 15 35 15 1 1 1 1 1 1 d) 6 : (27) 6 : 29 6 : 6 (27) : 29 ; (27) : 6 29 : 6 ; 2 4 2 4 4 2 1 1 29 : (27) 6 : 6 4 2
Bài toán 2: Lập các tỉ lệ thức có thể được từ chữ số: 5; 25; 125; 625. Lời giải 5 125 5 25 625 125 625 25 Ta có: 5.625 25.125 ; ; ; . 25 625 125 625 25 5 125 5
Bài toán tương tự: Cho 1,5 ; 2; 3,6 ; 4,8 ta lập các tỉ lệ thức sau: 1,5 3,6 1,5 2 4,8 2 4,8 3, 6 Ta có: 1,5.4,8 2.3,6 ; ; ; . 2 4,8 3,6 4,8 3,6 1,5 2 1,5
Bài toán 3: Tìm các tỉ số bằng nhau trong các tỉ số sau đây rồi lập các tỉ lệ thức: 1 1 2
28 :14; 2 : 2;8 : 4; : ;3:10; 2,1: 7;3 : 0,3 2 2 3 Lời giải 28 14 8 4 4 14
Ta có: 28 :14 8 : 4( 2) ; ; 8 4 28 14 8 28 3 10 2,1 7 10 7 Ta có: 3:10 2,1: 7 ; ; 2,1 7 3 10 3 2,1
Bài toán khác: Từ các tỉ số: 3 2 a) 3,5 : 5, 25 và 14 : 21 b) 39 : 52 và 2,1: 3,5 10 5 2 c) 0,51:1,19 và 3: 7 d) 7 : 4 và 0,9 : (0,5) 3
Có thể lập được tỉ lệ thức không?
(Hướng dẫn: 3,5 : 5, 25 14 : 21( 2 : 3);0,51:1,19 3 : 7 ) a c
Bài toán 4: Từ tỉ lệ thức . Hãy suy ra: b d
Dạy cho ngày mai – Học cho tương lai a b c d a c a) b)
( a b 0;c d 0 ) b d a b c d a b a b a Hướng dẫn: 1; b b b b c d c a c a c
1 từ đó ta viết lại: 1 1. d d b d b d Lời giải a c a c a b c d a) Ta có: 1 1 b d b d b d a c b d b d b) Ta có: 1 1 b d a c a c b a d c a c a c a b c d a c a b a b Cách khác: b d c d c d a c Suy ra: . a b c d
Bài tập tương tự: a c Cho . Hãy suy ra: b d a a c a b c d a) b) b b d a c a c 2 2 ac a c c) d) a b c d 2 2 bd b d Lời giải a c a)
ad bc ab ad ab bc b d a a c
a(b d) b(a c) b b d a c b d b d a b c d b) 1 1 b d a c a c a c a c c) ad bc b d a ad bc bc bc c a b
d(a b) ad bd bc bd
b(c d) c d a c d) Đặt
t a bt;c dt b d 2 ac bt dt bd t 2 t (1) bd bd bd 2 a c (bt) (dt) t 2 2 2 2 2 2 b d 2 t (2) 2 2 2 2 2 2 b d b d b d 2 2 ac a c
Vậy, từ (1) và (2) suy ra . 2 2 bd b d a c Bài toán 5: Cho . Chứng minh: b d a b c d 3a 2c a 3c a) b) a b c d 3b 2d b 3d
Huớng dẫn: Xem bài toán 4. (phần bài tập tương tự)
Dạy cho ngày mai – Học cho tương lai Lời giải a c a c a c a) Vì , ta có: (1) b d b d b d a c a c (2) b d b d a c a c Từ (1) và (2) . b d b d a c a 3a 2c 3a 2c b) Ta có: (1) b d b 3b 2d 3b 2d a a 3c Tương tự: (2) b b 3d 3a 2c a 3c Từ (1) và (2) . 3b 2d b 3d
II. Tìm số hạng chưa biết
Bài toán 6: Tìm x trong tỉ lệ thức sau: 2x 5 x 5 2 x 24 a) b) c) 6 3 8 4 6 25 a c Hướng dẫn: . a d . b c b d Lời giải 2x 5 a) Ta có:
(2x) 3 6.5 6x 6.5 x 5 . 6 3 x 5
b) Ta có: 4x 8.5 x 2.5 x 10 8 4 2 2 x 24 6.24 144 12 12 c) Ta có: 2 2 2 x x x x . 6 25 25 25 5 5
Bài toán 7: Để pha nước muối sinh lí, người ta cần pha theo đúng tỉ lệ. Biết rằng cứ 3l nước tinh khiết thì
pha với 27g muối. Hỏi nếu có 45g muối thì cần pha với bao nhiêu lít nước tinh khiết để được nước muối
Hướng dẫn: Gọi x (gam) là số nước cần dùng x 3000
Ta có 3l 3000 g và 45 27 Từ đó tìm x . Lời giải 3l 3000 g
Gọi x g là số lượng nước cần dùng x 0
Người ta pha đúng tỉ lệ nên ta có: x 3000 3000.45 x x 5000 45 27 27 5000 5 g l Đáp số: 5l
Bài toán 8: Để cày hết một cánh đồng trong 14 ngày phải sử dụng 18 máy cày. Hỏi muốn cày hết cánh
đồng đó trong 12 ngày thì phải sử dụng bao nhiêu máy cày (biết năng suất của các máy cày là như nhau)?
Hướng dẫn: Gọi x (máy) là số máy cày cần dùng
Theo đề bài, ta thấy nếu dùng 1 máy sẽ mất: 1418 252 (ngày)
Vậy số máy cần dùng là 252 :12 21. Lời giải
Gọi x là số máy phải sử dụng để cày hết cánh đồng trong 12 ngày ( x *)
Dạy cho ngày mai – Học cho tương lai 14.18
Nếu dùng 1 máy phải mất: 14.18 12.x (ngày) x x 21 12
Đáp số: Số máy phải sử dụng là 21 (máy).
Chú ý: Ở lớp 5, ta thường gọi là phương pháp “quy về đơn vị”. x y
Bài toán 9: Tìm x, y biết: và xy 112 . 4 7 x y
Huớng dẫn: Đặt
k x 4k; y 7k 4 7 Ta có: 2
xy 112; x 4k; y 7k 4k.7k 112 k 4 Từ đó tìm k và ; x y Lời giải x y
k x 4k; y 7k 4 7 Vậy 2
xy 112 4k.7k 112 k 4 k 2 hoặc k 2
+ Nếu k 2 x 8 và y 14 + Nếu k 2 x 8 và y 14
Đáp số: x 8 và y 14 hoặc x 8 và y 14 C. BÀl TẬP
6.1. Tìm x , biết: 26 12
a) x : 7,5 2,5 : 7,5 b) . x 42 Lời giải x a) x : 7,5 2,5 2,5 : 7,5 x 2,5 7,5 7,5 26 12 b) 26 2 x 91 x 42 x 7
6.2. Tìm x , biết: 5 15 4 2 x 1 1 a) b)
: x 0,4 c) x 2 6 9 3 8 x 1 Lời giải 5 15 1 1 a)
x 2 2 x 4 x 2 6 x 2 2 4 2 4 2 4
b) : x 0,4
2 x 0, 4 x 9 3 3 x 0, 4 3 15 x 1 1 c) x 1 x 1 8 8 x 1 2
x x x 1 8 2
x 9 x 2 2
3 x 3 hoặc x 3
6.3. Người ta pha nhiên liệu cho một loại động cơ bằng cách trộn 2 phần dầu với 7 phần xăng. Hỏi cần
bao nhiêu lít xăng để trộn hết 8 lít dầu theo cách pha nhiên liệu như trên? Lời giải
Gọi số lít xăng cần pha là x (lít và x 0 ) x 8
Ta có: x 28 (lít) 7 2
Đáp số: Số xăng cần tìm là 28 lít.
6.4. Hãy viết một tỉ lệ thức từ đẳng thức 2a b . Lời giải a b
Ta có: 2a b hay 2a 1 b 1 2
Dạy cho ngày mai – Học cho tương lai
6.5. Hai máy xúc (cùng năng suất) làm xong một công việc trong 4 ngày. Hỏi nếu có 4 máy xúc như thế
sẽ làm xong công việc trong bao lâu? Lời giải
Hướng dẫn: Xem bài toán 8. Đáp số: 2 ngày
Dạy cho ngày mai – Học cho tương lai
BÀI 21: TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU.
A. KIẾN THỨC CẦN NHỚ. a c a c a c a c Từ tỉ lệ thức suy ra
(giả thiết các tỉ số đều có nghĩa) b d b d b d b d
Mở rộng tính chất cho dãy tỉ số bằng nhau
Tính chất trên còn được mở rộng cho dãy tỉ số bằng nhau, chẳng hạn: a c e a c e
a c e
a c e
Từ dãy tỉ số bằng nhau suy ra (giả thiết các tỉ b d f b d f
b d f
b d f số đều có nghĩa) a c e Nếu
, ta còn nói các số a,c,e tỉ lệ với các số b, d, f b d f
Khi đó ta cũng viết a : c : e b : d : f
B. PHÂN LOẠI CÁC BÀI TOÁN
Các bài toán trong phần này với giả thiết các tỉ số đều có nghĩa. I. Tìm các số. x y
Bài toán 1: Tìm hai số , x y biết:
và x y 16 . 3 5 Lời giải
Từ tính chất của dãy tỉ số bằng nhau, ta có: x y x y
mà x y 16 3 5 3 5 x y 16 x y 2
2 và 2 x 6 và y 10 3 5 8 3 5
Bài toán 2: Tìm hai số x, y biết: x : 2 y : 5
và x y 7 Lời giải
Từ tính chất của dãy tỉ số bằng nhau, ta có: x y x y
mà x y 7 2 5 2 5 x y 7 x y 1 1
và 1 x 2 và y 5 2 5 7 2 5
Bài toán 3: Tìm hai số x, y biết: x 3
a) 7x 3y và x y 16 b)
và x y 20 y 2 Lời giải x y x y
a) Ta có: 7x 3y 3 7 3 7
Dạy cho ngày mai – Học cho tương lai x y x y mà x y 16 16 4 4 và 4 x 1 2 và y 28 3 7 4 3 7 x 3 x y b) Ta có: y 2 3 2
theo tính chất dãy tỉ số bằng nhau, ta suy ra: x y x y 20 x y 4
4 và 4 x 12 và y 8 3 2 3 2 5 3 2 x y z
Bài toán 4: Tìm ba số x, y, z biết:
và z x 6 2 3 4 Lời giải
Theo tính chất của dãy tỉ số bằng nhau ta có: x y z z x 6 3 2 3 4 4 2 2 x y z
3; 3; 3 x 6; y 9; z 12 2 3 4 x y z
Bài toán tương tự: Tìm ba số x, y, z biết:
và x 2y 3z 12 2 3 4 x y z x 2 y 3z Hướng dẫn: 2 3 4 2 2.3 3.4 Lời giải x y z x 2 y 3z Ta có: 2 3 4 2 6 12
Theo tính chất của dãy tỉ số bằng nhau ta có: x 2 y 3z
x 2 y 3z 12 3 2 6 12 2 6 12 4 x y z
3; 3; 3 x 6; y 9; z 12 2 3 4
Bài toán 5: Tìm các số a,b, c, d biết rằng: a : b : c : d 2 : 3: 4 : 5 và a b c d 42 a b c d
Hướng dẫn: a : b : c : d 2 : 3 : 4 : 5 2 3 4 5 Lời giải a b c d
Từ giả thiết: a : b : c : d 2 : 3: 4 : 5 , ta suy ra: 2 3 4 5 a b c d
a b c d
Theo tính chất của dãy tỉ số bằng nhau ta có: mà 2 3 4 5 2 3 4 5
a b c d 42 a b c d 42 a b c d 3
3; 3; 3 ; 3 2 3 4 5 14 2 3 4 5
Dạy cho ngày mai – Học cho tương lai
a 6;b 3;c 12;d 15 a b c
Bài toán 6: Tìm các số a,b,c biết rằng: và 2 2 2
a b 2c 108 2 3 4 2 2 2 a b c a b c
Hướng dẫn: 2 3 4 4 9 16 Lời giải 2 2 2 2 2 2 a b c a b c a b 2c Ta có: 2 3 4 4 9 16 4 9 32 2 2 2 2 2 2 a b 2c
a b 2c
Theo tính chất của dãy tỉ số bằng nhau ta có: , mà 4 9 32 4 9 32 2 2 2
a b 2c 108 2 2 2 a b 2c 108 4 2 2 2
a 16;b 36;c 64 a 4 ;b 6 ;c 8 4 9 32 27 a b c Vì
a,b,c cùng dấu, nên ta có: a 4;b 6;c 8 hoặc a 4;b 6;c 8 2 3 4
II. Bài toán chứng minh một đẳng thức. a b c a
Bài toán 7: Chứng minh rằng nếu: 2
a bc (với a b và a c ) thì a b c a Hướng dẫn: 2 a b a b a b a bc c a c a c a Lời giải Ta có: 2 a b a bc c a a b a b a b
Theo tính chất của dãy tỉ số bằng nhau ta có: c a c a c a a b a b a b c a Vậy: c a c a a b c a a c a c Bài toán 8: Cho . Chứng minh: b d 3a b 3c d Lời giải a c a b a 3a b Ta có: b d c d c 3c d
Theo tính chất của dãy tỉ số bằng nhau ta có: a 3a b 3a b a 3a b a c c 3c d 3c d c 3c d 3a b 3c d a c 2 2 . a b a b Bài toán 9: Cho . Chứng minh: b d 2 2 . c d c d Lời giải
Dạy cho ngày mai – Học cho tương lai a c a b Ta có: b d c d . a b a b Xét: , với điều kiện . c d c d 2 2 . a b a b a a b b . a b a b . . . 2 2 . c d c d c c d d . c d c d 2 2 2 2 2 2 . a b a b a b . a b a b
Theo tính chất của dãy tỉ số bằng nhau ta có: 2 2 2 2 2 2 . c d c d c d . c d c d 2 a c . a b a b
Nhận xét: Với giả thiết
, ta cũng chứng minh được b d . c d c d2 Hướng dẫn giải a c a b a b b d c d c d ab a b
a b a b a b2 . . cd c d
c d c d c d 2 bz cy cx az ay bx a y z Bài toán 10: Cho . Chứng minh . a b c x b c Lời giải bz cy cx az ay bx bxz cxy cxy ayz ayz bxz 0 Ta có: 0 a b c ax by cz
ax by cz z y (1) 0 c b bz cy bz cy a z
cx az 0 cx az (2) a c
ay bx 0 ay bx y x (3) b a x y x Từ (1); (2) và (3) a b c x y z x Bài toán 11: Cho . Tính ? y z z x x y y z a c e
a c e
Hướng dẫn: Tính chất của dãy tỉ số bằng nhau: b d f
b d f Lời giải
Theo tính chất của dãy tỉ số bằng nhau ta có: x y z
x y z
x y z
x y z 1 y z z x x y
y z z x x y 2x 2y 2z 2x y z 2
Dạy cho ngày mai – Học cho tương lai x 1 Vậy: y z 2 a b c 3
a b c a
Bài toán 12: Cho . Chứng minh rằng: b c d
b c d d Lời giải a b c
a b c
Theo tính chất của dãy tỉ số bằng nhau ta có: b c d
b c d 3 a . a . b c a b c
a b c a b c a b c
a b c Vậy: . . . . d . b . c d b c d
b c d b c d b c d
b c d III. TOÁN ĐỐ.
Bài toán 13: Có 64 tờ giấy bạc loại 2000 đồng; 5000 đồng; 10000 đồng. Biết rằng tổng giá trị của mỗi
loại giấy bạc trên đều bằng nhau. Hỏi mỗi loại tiền có bao nhiêu tờ. Lời giải
Gọi số tờ giấy bạc loại 2000 đồng; 5000 đồng; 10000 đồng theo thứ tự là x, y, z (x, y, z * )
Theo bài ra ta có: 2000x 5000 y 10000z và x y z 64
BCNN(2000,5000,10000) 10000 2000x 5000 y 10000z x y z
x y z Ta có: 64 8 10000 10000 10000 5 2 1 5 2 1 8
(theo tính chất của dãy tỉ số bằng nhau)
x 8.5 40; y 8.2 16; z 8.1 8
Vậy có 40 tờ giấy bạc loại 2000 đồng, 16 tờ giấy bạc loại 5000 đồng và 8 tờ giấy bạc loại 10000 đồng.
Em hãy giải bài toán sau: Cho 2x 3y 4z và x y z 35 .
Tìm x, y, z Hướng dẫn giải 2x 3y 4z
2x 3y 4z
; trong đó 12 BCNN2;3;4 12 12 12 x y z
x y z 35
7 x 42; y 28; z 21 6 4 3 6 4 3 5
Bài toán 14: Một lớp có 35 học sinh. Sau khảo sát chất lượng được xếp thành ba loại: giỏi, khá, trung
bình. Số học sinh giỏi và khá tỉ lẹ với 2 và 3 ; số học sinh khá và trung bình tỉ lệ với 4 và 5 .
Tính số học sinh mỗi loại. Lời giải
Gọi x, y, z lần lượt là số học sinh giỏi, khá, trung bình ( x, y, z *)
Dạy cho ngày mai – Học cho tương lai x y y z
Theo bài ra ta có: ; và x y z 35 2 3 4 5 x y y z x y y z x y z Ta lại có: và và 2.4 3.4 4.3 5.3 8 12 12 15 8 12 15
Theo tính chất của dãy tỉ số bằng nhau ta có: x y z
x y z 35 1 8 12 15 8 12 15 35 x y z 1; 1;
1 x 8; y 12; z 15 8 12 15
Vậy số học sinh giỏi, khá, trung bình lần lượt là 8;12;15 (học sinh)
Bài toán 15: Số học sinh khối 6,7,8,9 tỉ lệ với các số 9,8, 7,6 . Biết rằng số học sinh khối 9 ít hơn số
học sinh khối 7 là 70 học sinh. Tính số học sinh mỗi khối. Lời giải
Gọi số học sinh khối 6,7,8,9 theo thứ tự là a, ,
b c, d a, ,
b c, d * a b c d Ta có:
và b d 70 9 8 7 6
Theo tính chất của dãy tỉ số bằng nhau ta có: a b c d b d 70 35 9 8 7 6 8 6 2 a b c d
35; 35; 35; 35 9 8 7 6
a 315;b 280;c 245;d 210
Vậy số học sinh khối 6,7,8,9 lần lượt là 315; 280; 245; 210 (học sinh)
Bài toán 16: Vườn rau nhà bạn An có diện tích trồng bắp cải, su hào và cà chua lần lượt tỉ lệ với 9;5; 4 .
Diện tích trồng cà chua ít hơn diện tích trồng bắp cải là 2
100m . Tính diện tích vườn rau nhà bạn An? Lời giải
Gọi diện tích trồng bắp cải, diện tích trồng su hào và diện tích trồng cà chua lần lượt là x 2 m y 2 ; m ; 2
z m x, y, z 0 x y z Ta có:
và x z 100 9 5 4
Ta phải tìm x y z ?
Theo tính chất của dãy tỉ số bằng nhau ta có: x z x z 100 x y z x y z x y z 20 20 9 4 9 4 5 9 5 4 9 5 4 18
Vậy diện tích vườn rau nhà bạn An là: x y z 2 20.18 360 m
Dạy cho ngày mai – Học cho tương lai C. BÀI TẬP x y
6.6. Tìm hai số x và y , biết:
và x y 40 9 11 x y
6.7. Tìm hai số x và y , biết:
và x y 8 17 21
6.8. Tìm x và y , biết: x 5 x 9
a) và x y 16
b) và x y 15 y 3 y 4 2 3 c) và xy 96 x y
6.9. Tỉ số của số học sinh của hai lớp 7A và 7B là 0,95. Hỏi mỗi lớp có bao nhiêu học sinh, biết số học
sinh của một lớp nhiều hơn lớp kia là 2 em?
6.10. Người ta định làm một con đường trong 15 ngày. Một đội công nhân 45 người làm trong 10 ngày
mới được một nửa công việc. Hỏi phải bổ sung thêm bao nhiêu người nữa để có thể hoàn thành
công việc đúng hạn (biết năng suất lao động của mỗi người như nhau)?
6.11. Tìm x, y, z biết:
a) 3x 2 y;7 y 5z và x y z 32 2x 3y 4z b)
và x y z 49 3 4 5 x y z
6.12. Tìm x, y, z biết: và xyz 810 2 3 5 6.13. Cho 2 2 2
a b c a b c 1 và x : y : z a : b : c
Chứng minh rằng: 2 2 2 2
x y z x y z 2 2 2 2 x y x 2y
6.14. Tìm x, y biết: và 4 4 x y 81 10 7 a b c
6.15. So sánh các số a,b, c biết rằng: b c a
HƯỚNG DẪN GIẢI BÀI TẬP x y
6.6. Tìm hai số x và y , biết:
và x y 40 9 11 Lời giải x y x y 40
2 x 18; y 22 9 11 9 11 20 x y
6.7. Tìm hai số x và y , biết:
và x y 8 17 21 Lời giải
Dạy cho ngày mai – Học cho tương lai x y x y 8
2 x 34; y 4 2 17 21 17 21 4
6.8. Tìm x và y , biết: x 5 x 9
a) và x y 16 ;
b) và x y 15 ; y 3 y 4 2 3 c) và xy 96 . x y Lời giải x 5
a) và x y 16 y 3 x 5 x y x y 16
2 x 10; y 6 y 3 5 3 5 3 8 x 9
b) và x y 15 y 4 x 9 x y x y 1 5 3 x 2 7; y 1 2 y 4 9 4 9 4 5 2 3 c) và xy 96 x y 2 3 Đặt k . x y 2 3
Ta có: x ; y . k k 2 3 6 1 1
Mà: xy 96 . Do đó ta có: 2 . 96 k k . k k 96 16 4 1 1 1
Với k ta có: x 2 : 8; y 3 : 12 4 4 4 1 1 1
Với k ta có: x 2 : 8; y 3: 1 2 4 4 4
6.9. Tỉ số của số học sinh của hai lớp 7A và 7B là 0,95. Hỏi mỗi lớp có bao nhiêu học sinh, biết số học
sinh của một lớp nhiều hơn lớp kia là 2 em? Lời giải
Gọi a,b theo thứ tự là số học sinh của lớp 7A, 7B a,b * a
a b vì 0,95 1 b a a 19 a b b a 2 Ta có: 0,95
2 a 38;b 40 b b 20 19 20 20 19 1
Dạy cho ngày mai – Học cho tương lai
6.10. Người ta định làm một con đường trong 15 ngày. Một đội công nhân 45 người làm trong 10 ngày
mới được một nửa công việc. Hỏi phải bổ sung thêm bao nhiêu người nữa để có thể hoàn thành
công việc đúng hạn (biết năng suất lao động của mỗi người như nhau)? Lời giải
45 người làm trong 10 ngày mới được một nửa công việc nên 45 người làm xong công việc
phải mất 10.2 20 ngày.
Ta có: 15 10 5 (ngày)
Bài toán đưa về tìm số người để làm một nửa công việc trong 5 ngày hay tìm số người làm
xong công việc trong 2.5 10 (ngày)
Gọi x là số người cần làm xong công việc trong 10 ngày.
Ta có: 45.20 10x x 90 (xem lời giải bài toán 8)
Khi đó, ta có: 90 45 45
Vậy cần phải bổ sung thêm 45 người.
6.11. Tìm x, y, z biết:
a) 3x 2 y;7 y 5z và x y z 32 2x 3y 4z b)
và x y z 49 3 4 5 Lời giải x y y z
a) 3x 2 y và 7 y 5z và 2 3 5 7 y y
BCNN3,5 15 (3 và 5 là hai mẫu số và ) 3 5 x y y z x y z x y z 32 và 2 10 15 15 21 10 15 21 10 15 21 16
x 20; y 30; z 42 2x 3y 4z x y z
x y z 49 b) 12 3 4 5 3 4 5 3 4 5 49 2 3 4 2 3 4 12
x 18; y 16; z 15 x y z
6.12. Tìm x, y, z biết: và xyz 810 2 3 5 Lời giải
Hướng dẫn: Xem bài toán 8. Bài 1: Tỉ lệ thức. x y z Đặt
k x 2k; y 3k; z 5k 2 3 5
Thay x, y, z vào đẳng thức xyz 810 ta có: 3 3
30k 810 k 27 k 3
Dạy cho ngày mai – Học cho tương lai
Từ đó ta tìm được: x 6; y 9; z 15 6.13. Cho 2 2 2
a b c a b c 1 và x : y : z a : b : c
Chứng minh rằng: 2 2 2 2
x y z x y z Lời giải x y z
x y z Ta có:
x y z (vì a b c 1) a b c
a b c 2 2 2 x y z
x y z2 2 2 2 a b c 2 2 2 2 2 2 x y z
x y z Lại có: 2 2 2
x y z (vì 2 2 2
a b c 1) 2 2 2 2 2 2 a b c
a b c Vậy: 2 2 2 2
x y z x y z 2 2 2 2 x y x 2y
6.14. Tìm x, y biết: và 4 4 x y 81 10 7 Lời giải 2 2 x y x 2y
x y 2 2 2 2 2 2 x 2y 2 2 2 2 2
x y x 2y 3y Ta có: 2 y 10 7 10 7 3 3 2 2 x y Vậy: 2 2 2 2 2 2
y x y 10y x 9y 10 Thay 2 2
x 9y vào đẳng thức 4 4
x y 81, ta được y 2 2 4 8 8 9
.y 81 81y 81 y 1 y 1
Ta tìm được: x 3; y 1 hoặc x 3; y 1 hoặc x 3; y 1 hoặc x 3; y 1 a b c
6.15. So sánh các số a,b, c biết rằng: b c a Lời giải a b c
a b c a b c Ta có:
1 1; 1; 1 a b c b c a
b c a b c a
Dạy cho ngày mai – Học cho tương lai
BÀI 22: ĐẠI LƯỢNG TỈ LỆ THUẬN
A. KIẾN THỨC CẦN NHỚ
Nếu đại lượng y liên hệ với đại lượng x theo công thức y ax (với a là hằng số khác 0) thì ta
nói y tỉ lệ thuận với x theo hệ số tỉ lệ a.
Nếu đại lượng y tỉ lệ thuận với đại lượng x thì:
+ Tỉ số hai giá trị tương ứng của chung luôn không đổi (và bằng hệ số tỉ lệ): y y y 1 2 3 ... a x x x 1 2 3
+ Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia: y x y x 1 1 , 2 2 ,… y x y x 2 2 3 3
Giải toán về đại lượng tỉ lệ thuận
Để giải bài toán về đại lượng tỉ lệ thuận, ta cần nhận biết hai đại lượng tỉ lệ thuận trong bài toán.
Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.
B. PHÂN LOẠI CÁC BÀI TẬP I. Hệ số tỉ lệ
Bài toán 1. Cho biết hai đại lượng x và y tỉ lệ thuận với nhau và khi x 6 thì y 4 .
a) Tìm hệ số tỉ lệ k của y đối với x .
b) Biểu diễn y theo x.
c) Tính giá trị của y khi x 9 .
Hướng dẫn: Áp dụng công thức: y kx .
Bài toán 2. Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào ô trống: x 3 1 1 2 5 y 4 y
Hướng dẫn: k . x
Bài toán 3. Cho biết x tỉ lệ thuận với y theo hệ số tỉ lệ 0,8 và y tỉ lệ thuận với z theo hệ số tỉ lệ 5 .
Hãy chứng tỏ x tỉ lệ thuận với z và tìm hệ số tỉ lệ.
Hướng dẫn: Đại lượng y tỉ lệ thuận với đại lượng x hay y tỉ lệ thuận với x , ta có 1 1
y kx x
y và ta nói x tỉ lệ thuận với y theo hệ số tỉ lệ . k k
Bài toán 4. Tính các giá trị tương ứng của t và s được cho trong bảng sau: t 2 1 1 2 3 4 s 90 45 45 90 135 18 0 s t
a) Điền số thích hợp vào ô trống ở bảng trên.
b) Hai đại lượng s và t có tỉ lệ thuận với nhau hay không? Tìm hệ số tỉ lệ của s đối với t .
Bài toán 5. Cho y tỉ lệ thuận với x theo hệ số tỉ lệ k ; với x , x có giá trị tương ứng y , y và 1 2 1 2
x x 4; y y 8 . Tìm hệ số tỉ lệ k . 1 2 1 2
Dạy cho ngày mai – Học cho tương lai
Bài toán 6. Cho hai số có tổng bằng 32 và hai số đó tỉ lệ với 3 và 5. Tìm hai số.
Hướng dẫn: Gọi hai số là a,b , ta có: a 3 3
a : 3 b : 5
hay a tỉ lệ thuận với b theo hệ số k . Ta thấy bài toán quen thuộc về b 5 5
“tổng, tỉ” là nói về hai đại lượng tỉ lệ thuận.
Các tính chất về tỉ lệ thức, dãy tỉ số bằng nhau có thể áp dụng để giải các bài toán về đại lượng tỉ lệ thuận.
Bài toán 7. Cho x và y là hai đại lượng tỉ lệ thuận, biết x x 2 và hai giá trị tương ứng y và y có 1 2 1 2 y y 1
. Biểu diễn y theo x. 1 2
Bài toán 8. Chu vi và cạnh hình vuông có phải là hai đại lượng tỉ lệ thuận với nhau không?
Hướng dẫn: Cạnh hình vuông là x chu vi là 4x II. Toán đố
Bài toán 9. Để làm nước mơ, người ta thường ngâm mơ theo công thức 2 kg quả mơ ngâm với 2,5kg
đường. Hỏi cần bao nhiêu kilôgam đường để ngâm 5 kg quả mơ.
Hướng dẫn: Mơ và đường là hai đại lượng tỉ lệ thuận.
Bài toán 10. Biết rằng 17 lít dầu hỏa nặng 13,6 kg. Hỏi 12 kg dầu hỏa có chứa được vào hết can 16 lít không? 17 5
Hướng dẫn: Thể tích dầu và khối lượng là hai đại lượng tỉ lệ thuận, hệ số tỉ lệ là . Em 13,6 4
tự lập bảng tóm tắt như bài toán 9.
Bài toán 11. 5m dây đồng nặng 43 gam. Hỏi 10kg dây đồng như thế nặng bao nhiêu ki-lô-gam.
Hướng dẫn: Lập bảng tóm tắt: Số mét về trọng lượng dây đồng là hai đại lượng tỉ lệ thuận.
Bài toán 12. Chu vi hình chữ nhật là 64m. Tính chiều dài và chiều rộng hình chữ nhật biết chúng tỉ lệ với 5 và 3.
Bài toán 13. Ba đơn vị kinh doanh góp vốn theo tỉ lệ 3;5;7 . Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi,
nếu tổng số lãi là 450 triệu đồng và tiền lãi được chia theo tỉ lệ thuận với số vốn đã đóng.
Bài toán 14. Biết độ dài các cạnh của một tam giác tỉ lệ với 3;4;5. Tính độ dài mỗi cạnh của tam giác đó,
biết rằng cạnh lớn nhất dài hơn cạnh nhỏ nhất là 6m .
Bài toán 15. Tam giác ABC có số đo các góc ; A ;
B C tỉ lệ với 3;5;7 . Tính số đo các góc của tam giác ABC .
Hướng dẫn:
A B C 180
Bài toán 16. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 24 cây xanh. Lớp 7A có 32 học
sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao
nhiêu cây xanh, biết rằng số cây tỉ lệ thuận với số học sinh. BÀI TẬP
Bài 6.16. Hai đại lượng x và y có tỉ lệ thuận với nhau hay không, nếu: a) x 1 2 3 4 5 y 9 18 27 36 45 b)
Dạy cho ngày mai – Học cho tương lai x 1 2 5 6 9 y 12 24 60 72 90
Bài 6.17. Thay cho việc đo chiều dài của các cuộn dây thép người ta thường cân chúng. Cho biết mỗi mét dây nặng 25 gam.
a) Giả sử x mét dây nặng y gam. Hãy biểu diễn y theo x .
b) Cuộn dây dài bao nhiêu mét. Biết rằng nó nặng 4,5kg ?
Bài 6.18. Hạnh và Vân định làm mứt dẻo từ 2,5kg dâu. Theo công thức, cứ 2kg dâu thì cần 3kg đường.
Hạnh bảo cần 3,75kg đường, còn Vân bảo cần 3, 25kg đường. Theo em ai đúng và vì sao?
Bài 6.19. Đố em tính được trên một chiếc đồng hồ khi kim giờ quay được một vòng thì kim phút kim giây
quay được bao nhiêu vòng?
Bài 6.20. Đồng bạch là một loại hợp kim của Niken, kẽm và đồng, khối lượng của chúng lần lượt tỉ lệ với
3;4 và 13 . Hỏi cần bao nhiêu ki-lô-gam niken, kẽm và đồng để sản xuất 150 kg đồng bạch? 1 1
Bài 6.21. Ba lớp 7 trồng được 36 cây. Sau khi lớp 7A trồng được số cây, lớp 7B trồng được số cây 5 3 3
và 7C trồng được số cây thì số cây còn lại của ba lớp bằng nhau. Tính số cây của mỗi lớp đã 7 trồng được.
Bài 6.22. Tìm số có ba chữ số, biết rằng số đó là bội của 18 và các chữ số tỉ lệ với 1: 2 : 3 .
Bài 6.23. Ba đơn vị kinh doạnh góp vốn theo tỉ lệ 2, 3, 4 . Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi
nếu tổng số tiền lãi là 135 triệu đồng và tiền lãi được chia tỉ lệ thuận với số vốn đóng góp.
Bài 6.24. Số 184 được viết thành tổng của ba số sao cho số hạng thứ nhất và số hàng thứ hai tỉ lệ thuận với
3 và 2 ; số hạng thứ nhất và số hạng thứ ba tỉ lệ thuận với 5 và 7 . Tìm ba số hạng.




