







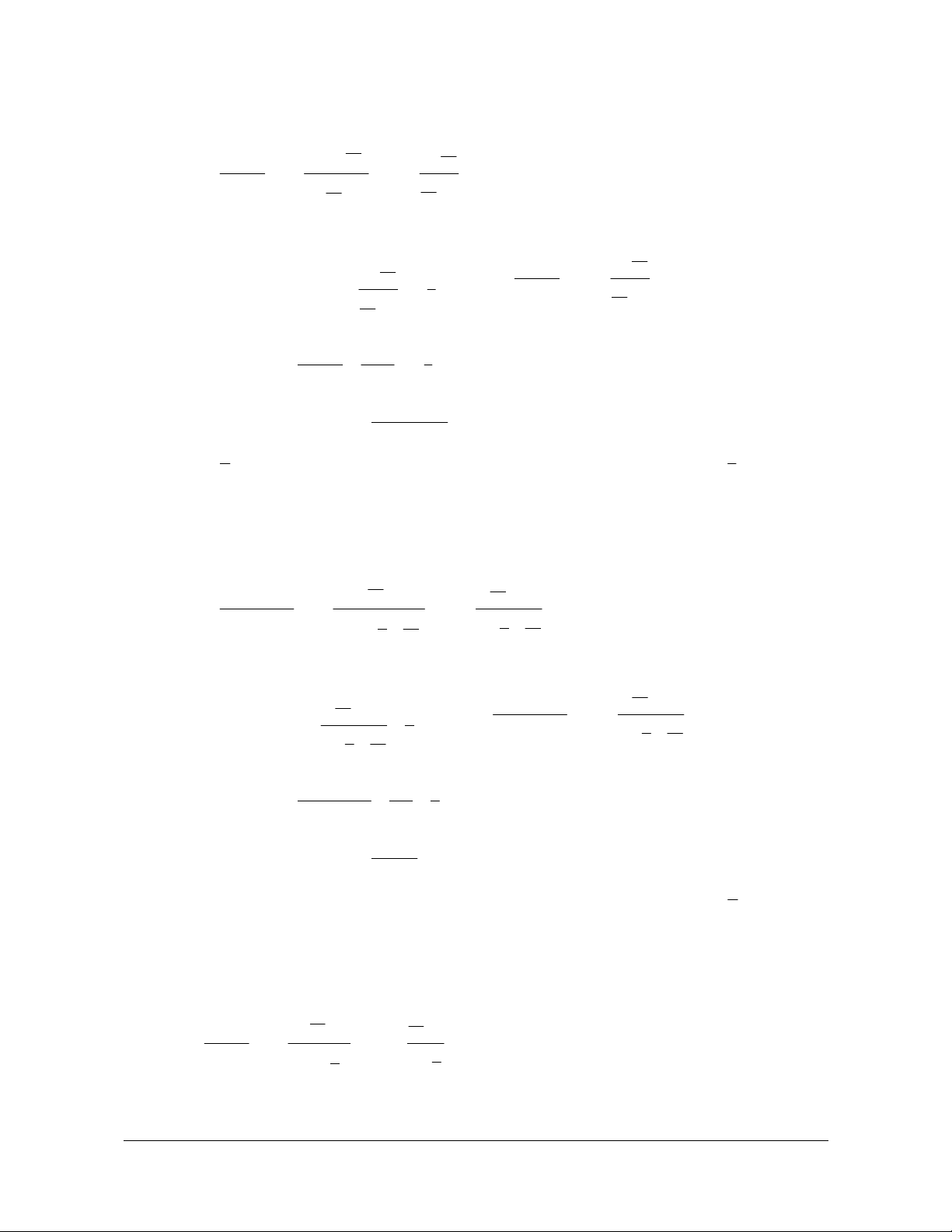





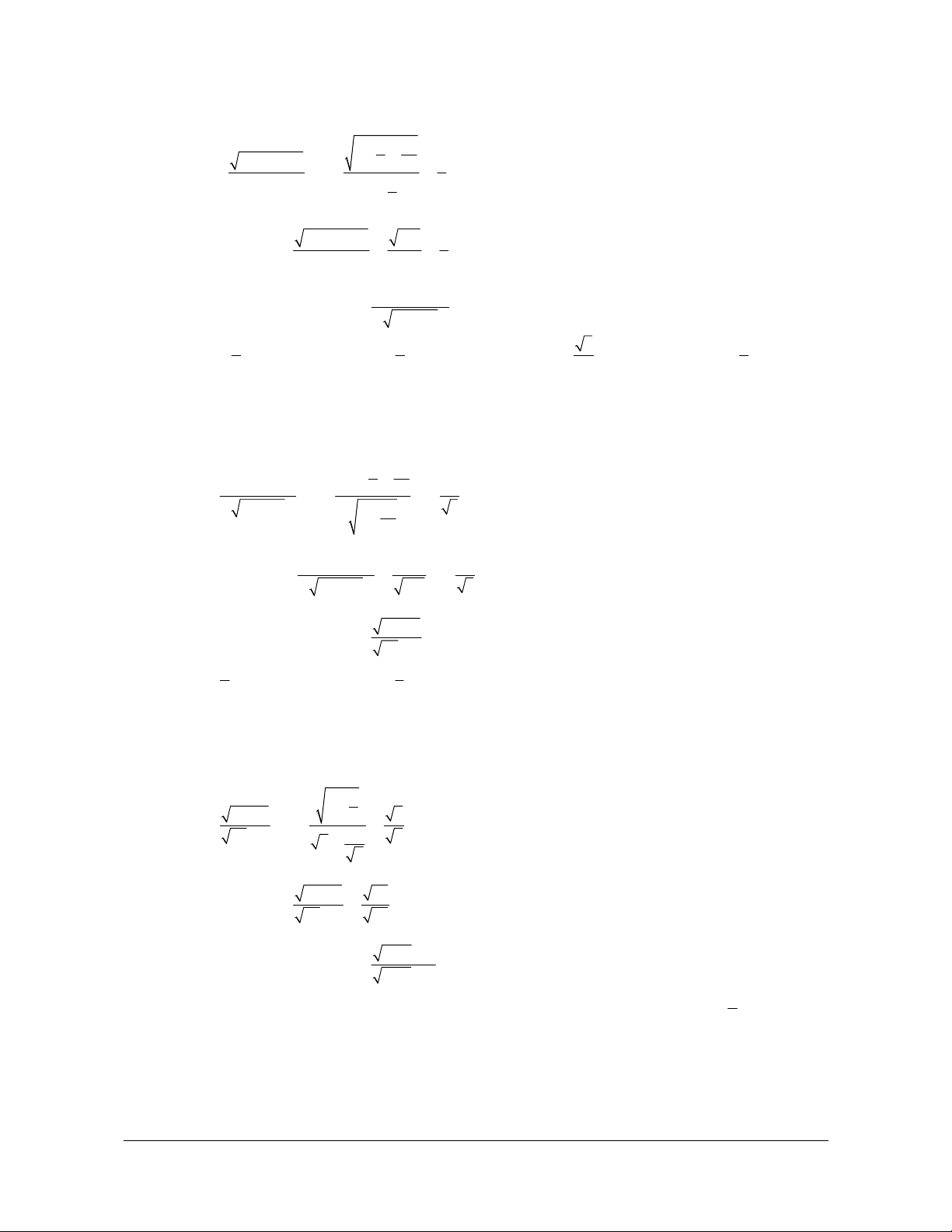
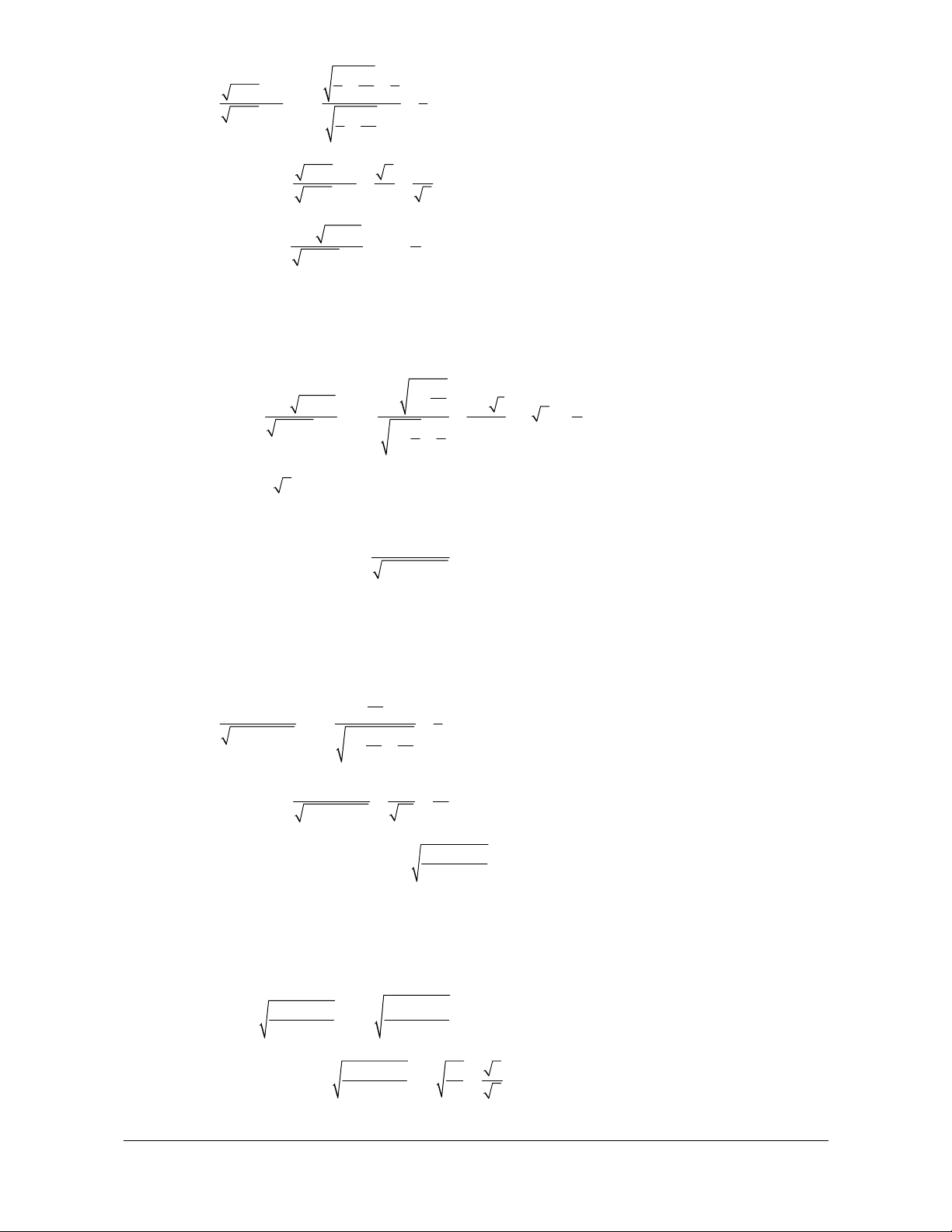


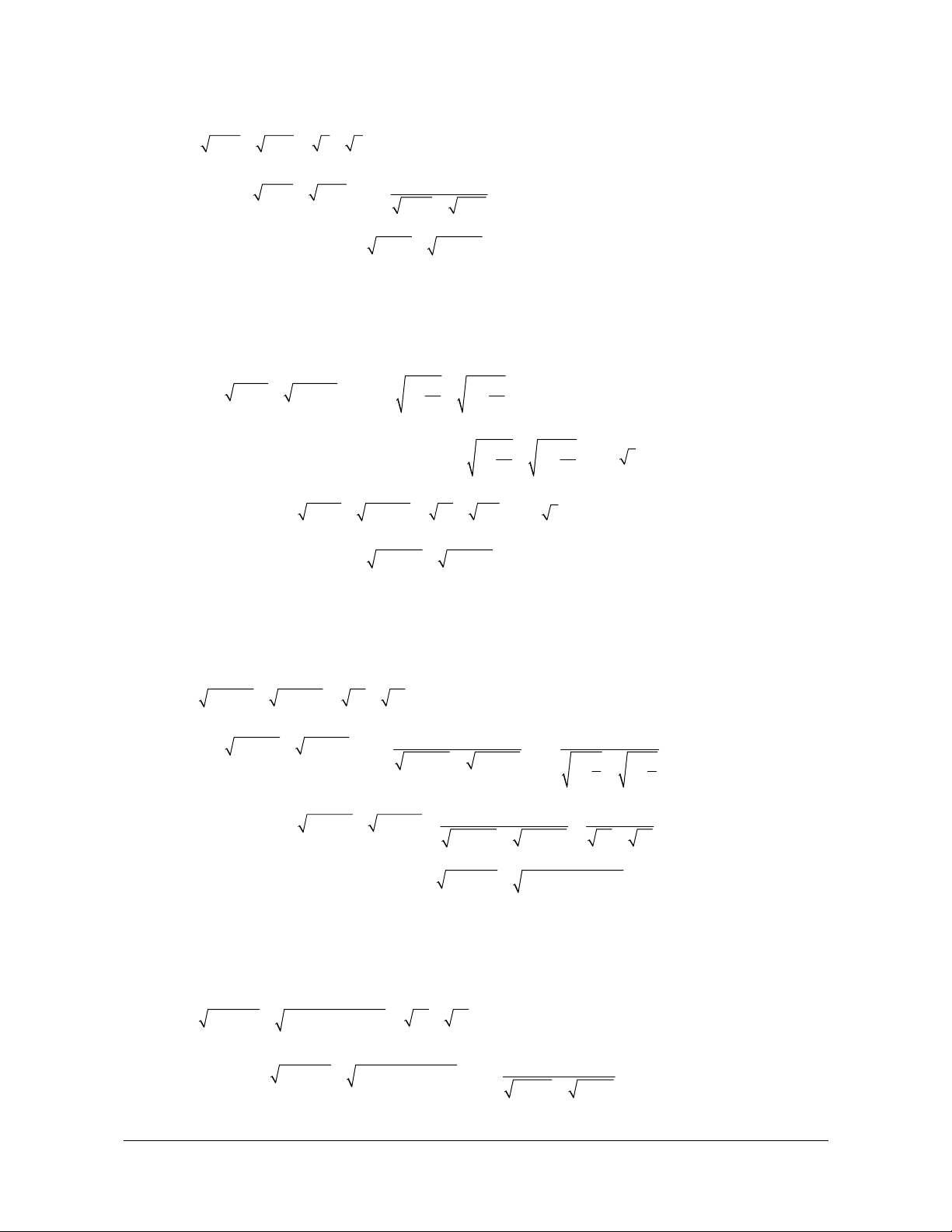














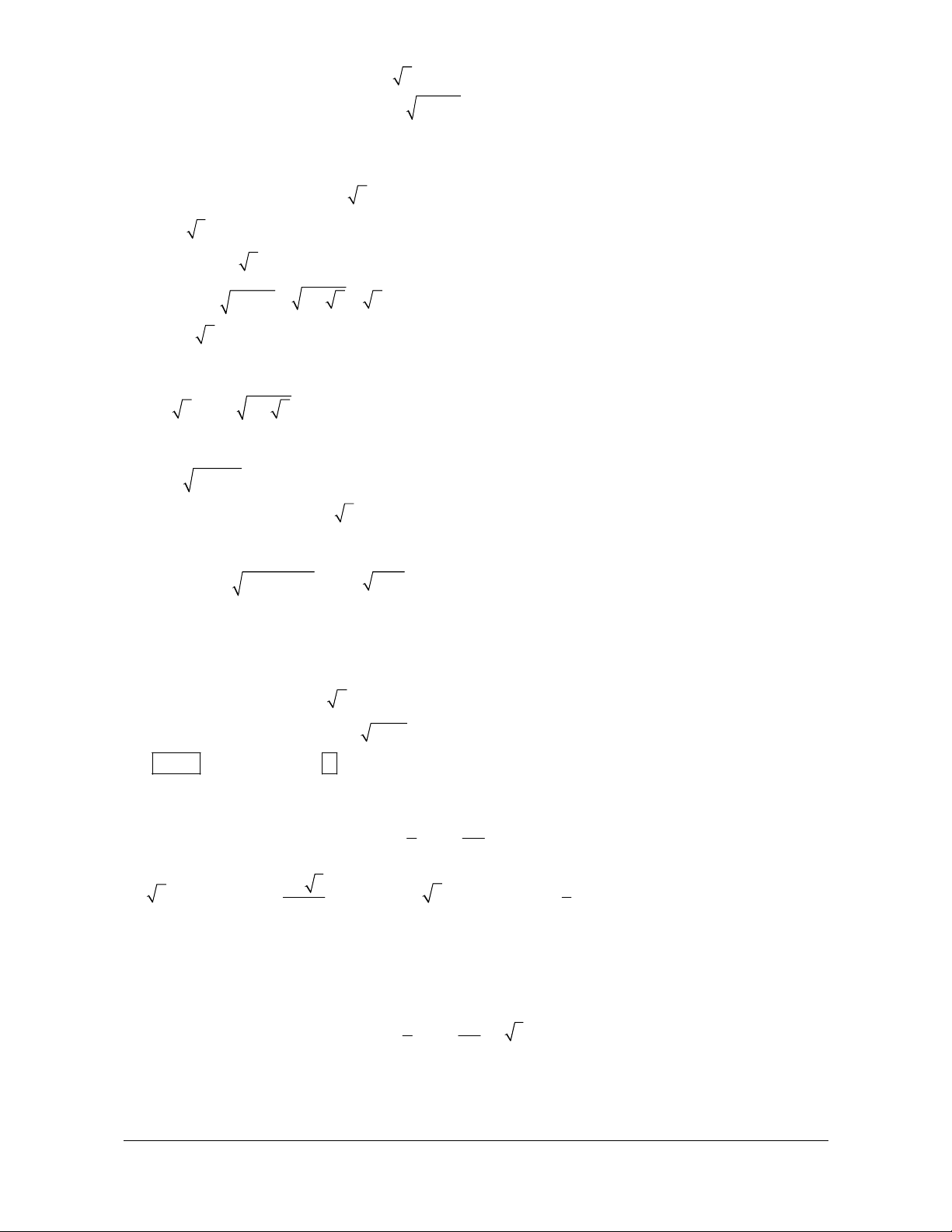



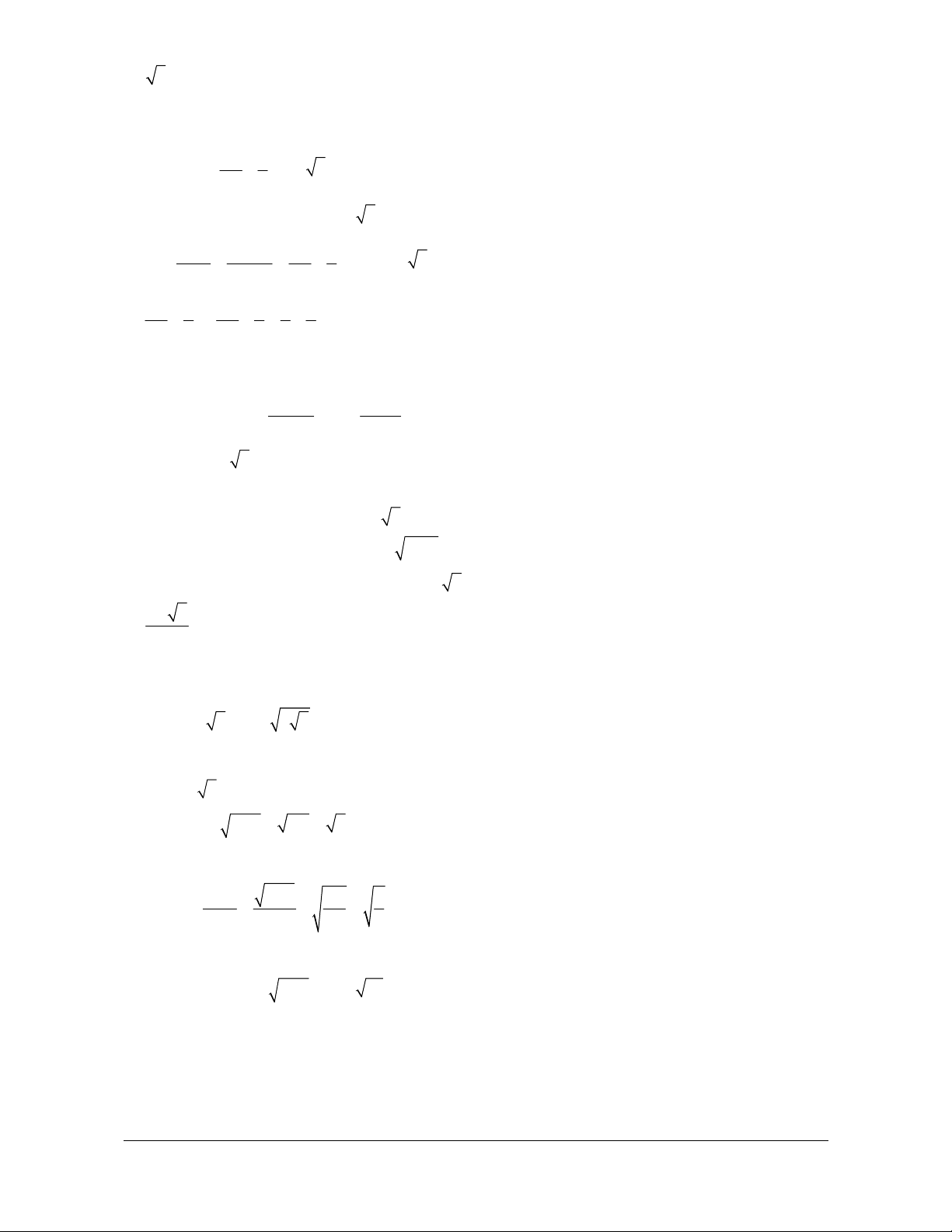







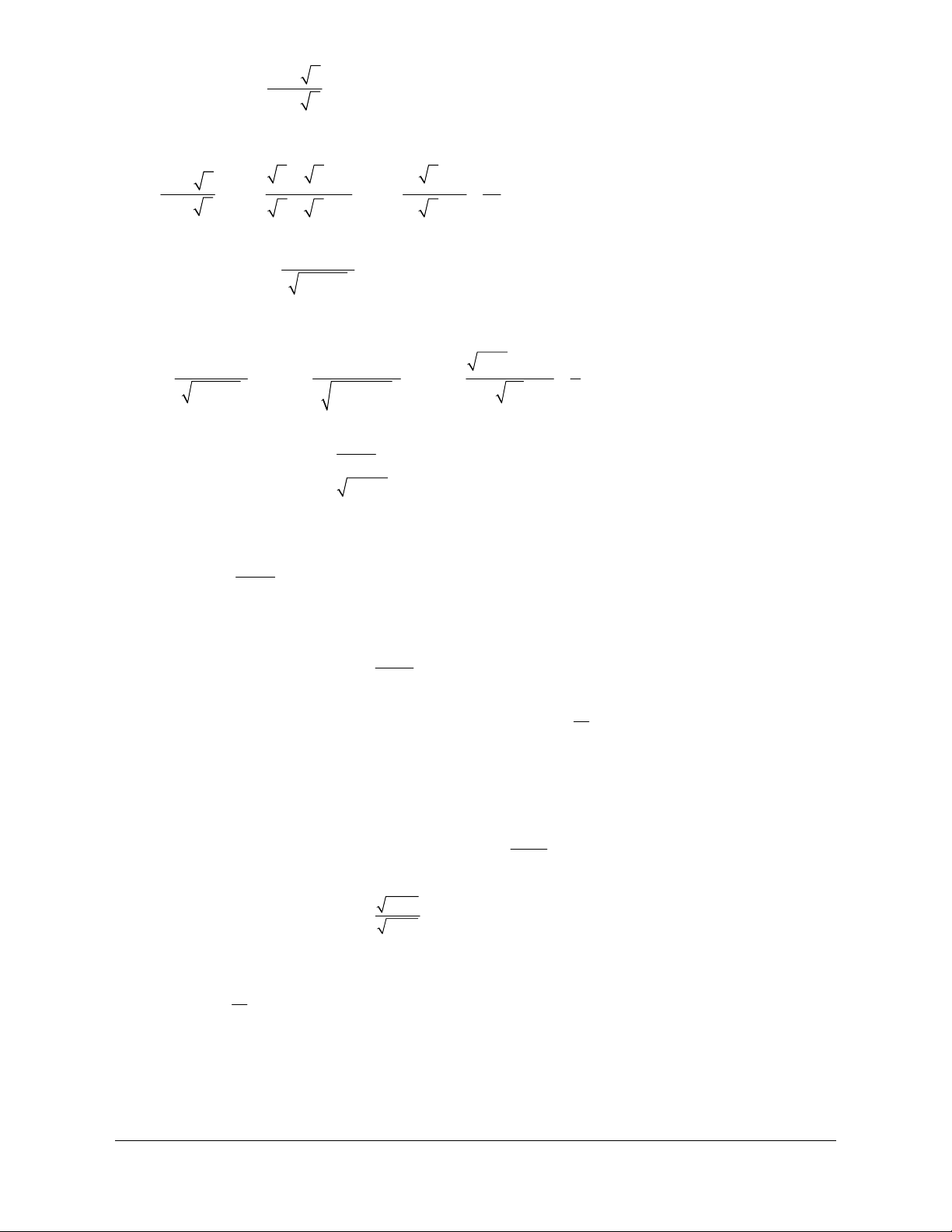



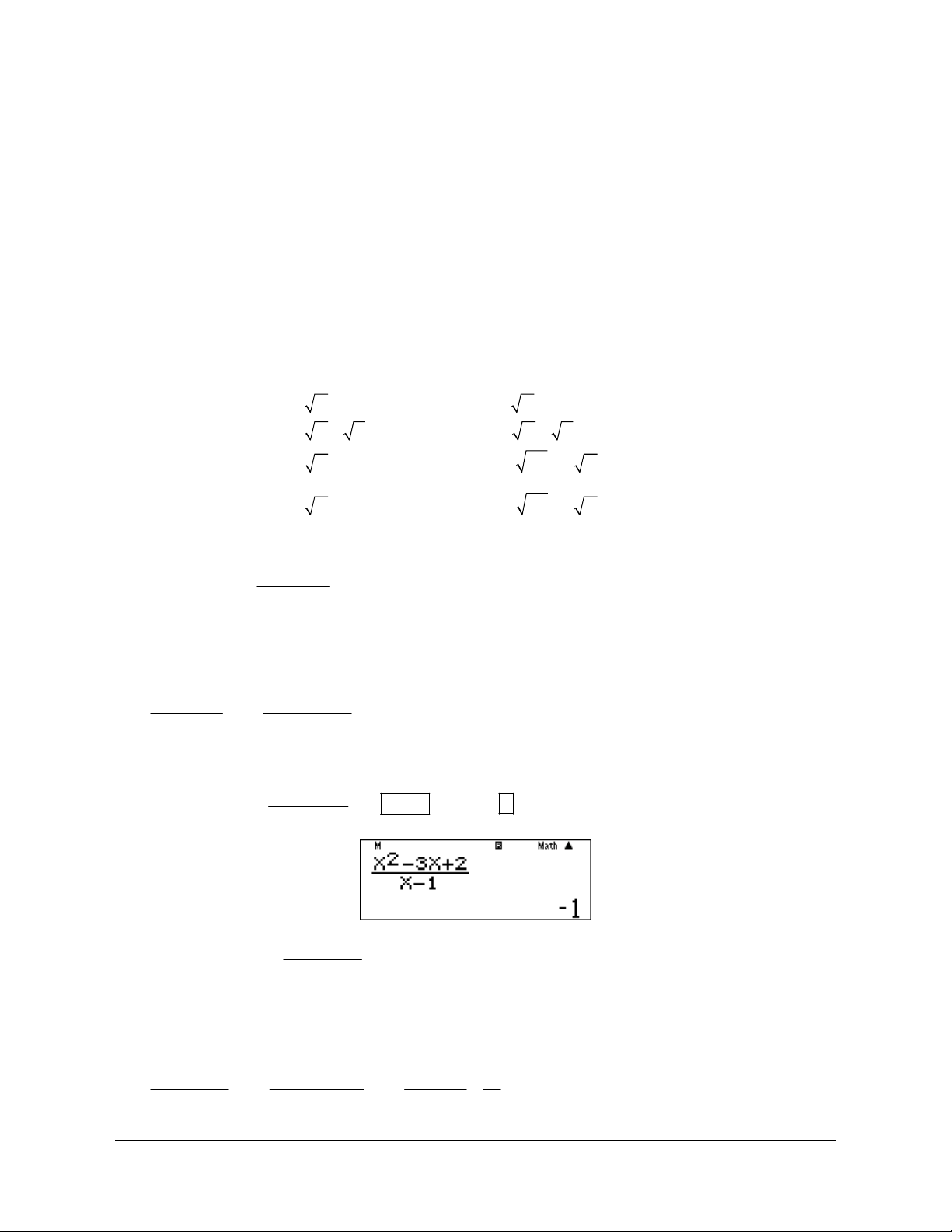
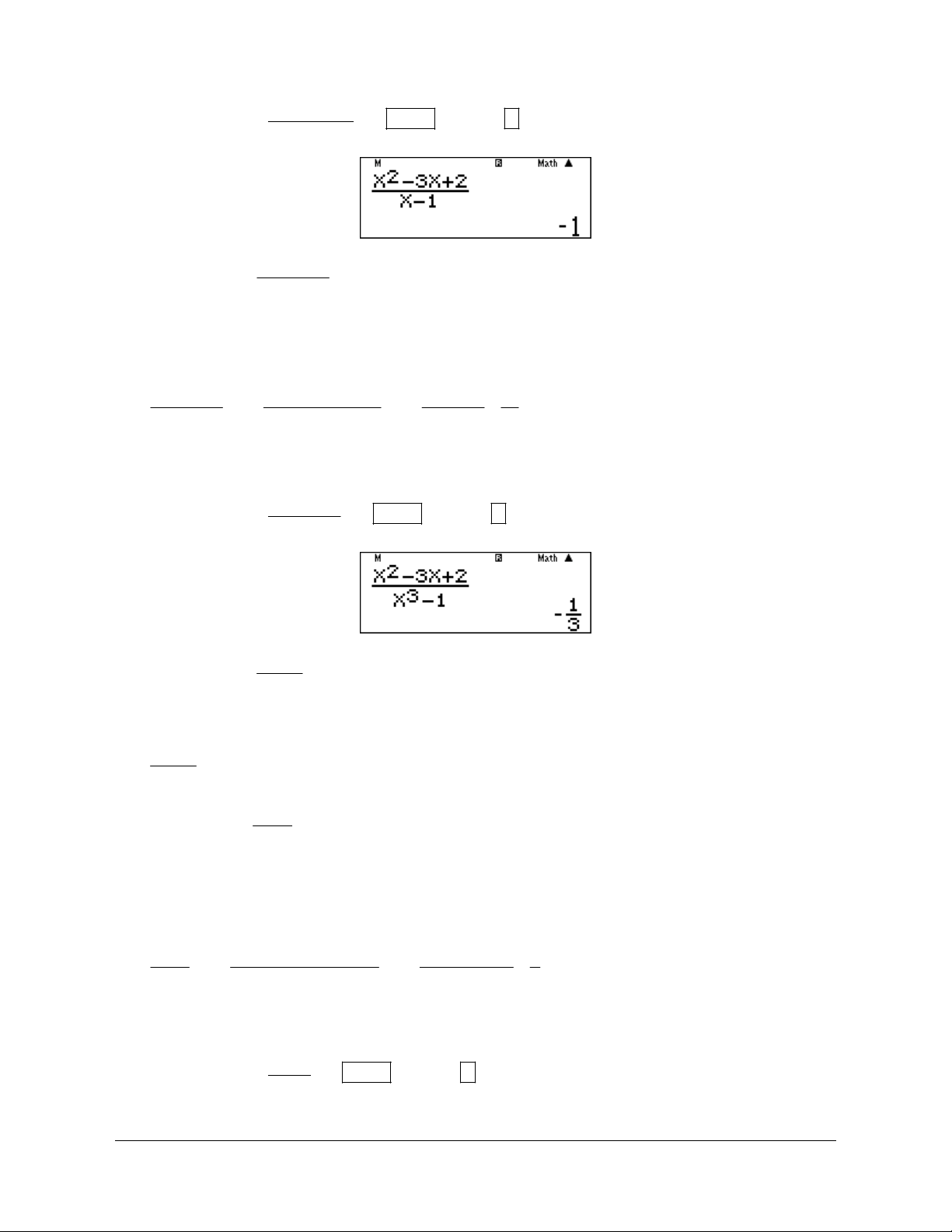
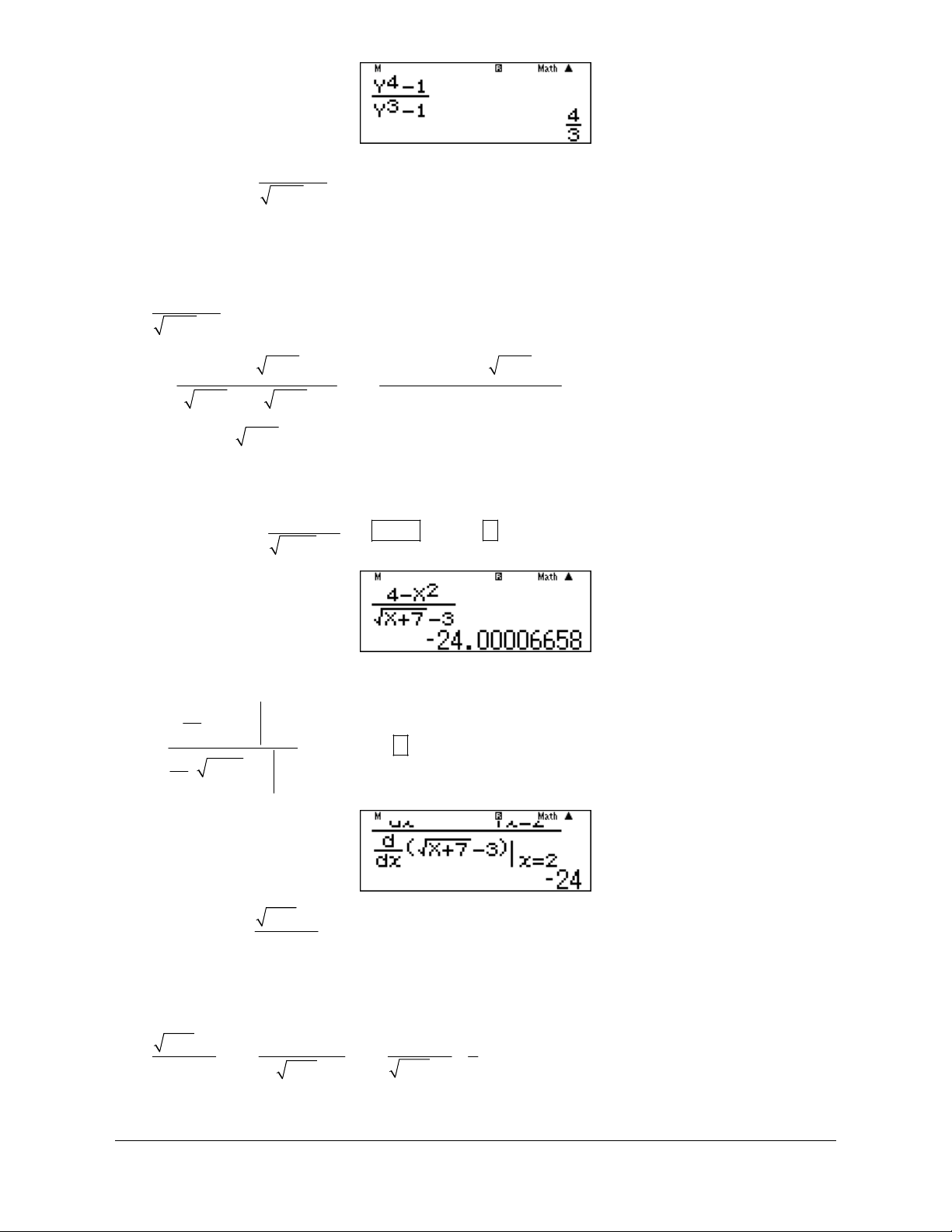
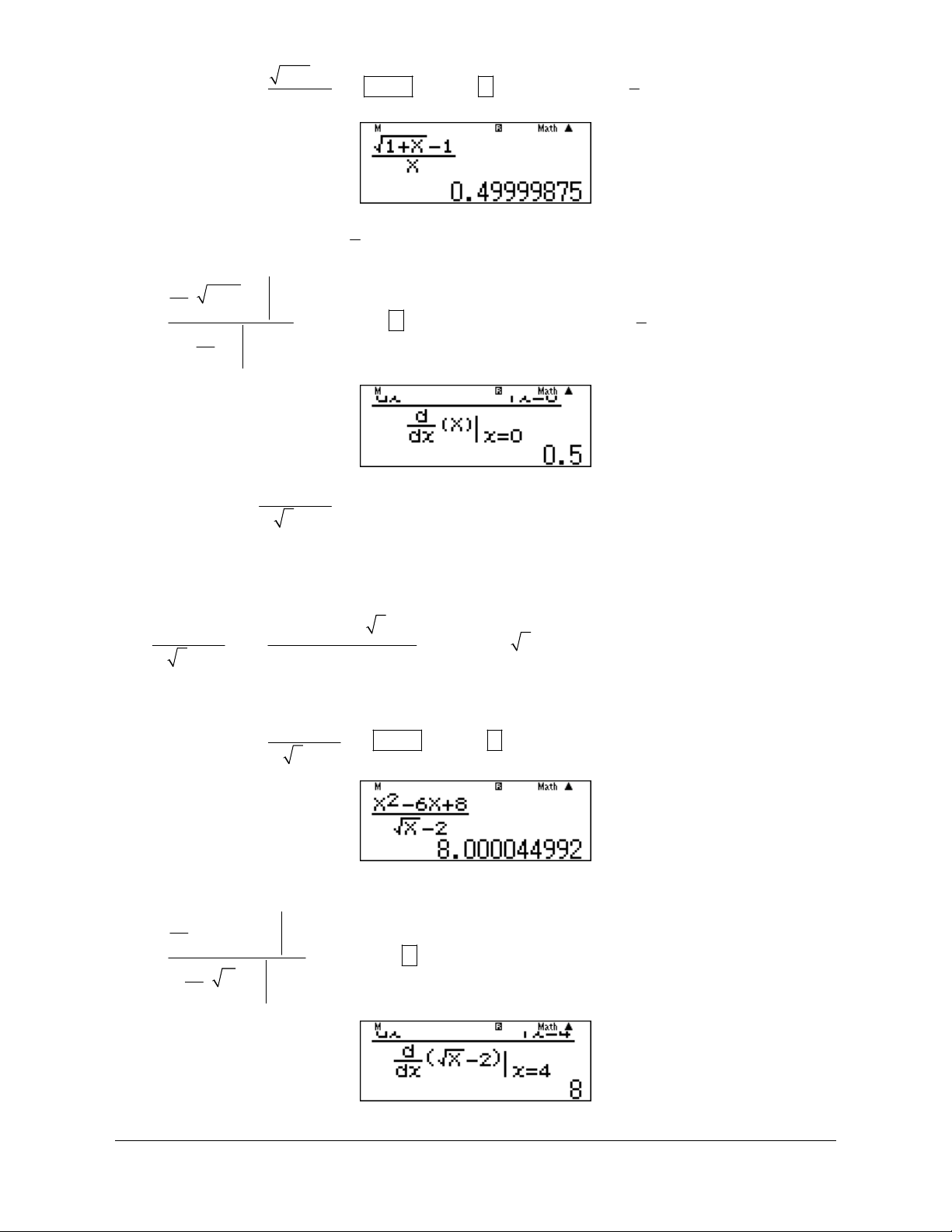





























Preview text:
CHƯƠNG 4. GIỚI HẠN
BÀI 1. GIỚI HẠN DÃY SỐ
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – GIỚI HẠN HỮU HẠN CỦA DÃY SỐ 1. Định nghĩa Định nghĩa 1
Ta nói dãy số (u có giới hạn là 0 khi n dần tới dương vô cực, nếu u có thể nhỏ hơn một số dương n ) n
bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim u = 0 hay u 0 khi n + . ¥ n n n +¥ Định nghĩa 2
Ta nói dãy số (v có giới hạn là a (hay v dần tới a ) khi n + ,
¥ nếu lim (v -a = n ) 0. n ) n n+¥
Kí hiệu: lim v = a hay v a khi n + . ¥ n n n +¥
2. Một vài giới hạn đặc biệt a) 1 lim = 0; 1 lim
= 0 với k nguyên dương; n+¥ n k n+¥ n b) lim n
q = 0 nếu q < 1; n+¥
c) Nếu u = c ( c là hằng số) thì lim u = lim c = .c n n n +¥ n+¥
Chú ý: Từ nay về sau thay cho lim u = a ta viết tắt là lim u = a . n n n +¥
II – ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN Định lí 1
a) Nếu lim u = a và lim v = b thì n n
· lim (u + v ) = a+ b · lim (u -v ) = a-b n n n n æ ö li · m ( u ç ÷ a u .v ) = . a b · lim n
ç ÷ = (nếu b ¹ 0 ). n n ç ÷ çèv ÷ø b n ìïlim = ìï b) Nếu u a ï = n u a í thì lim ï n í . u ï ³ 0, "n ïî a ïï ³ 0 n î
III – TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
Cấp số nhân vô hạn (u có công bội q , với q <1 được gọi là cấp số nhân lùi vô hạn. n )
Tổng của cấp số nhân lùi vô hạn:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 279
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 u
S = u + u + u +¼+ u +¼ = q < 1 . 1 2 3 n ( ) 1-q
IV – GIỚI HẠN VÔ CỰC 1. Định nghĩa
· Ta nói dãy số (u có giới hạn là +¥ khi n +¥ , nếu u có thể lớn hơn một số dương bất kì, kể n ) n
từ một số hạng nào đó trở đi.
Kí hiệu: lim u = +¥ hay u +¥ khi n + . ¥ n n
· Dãy số (u có giới hạn là -¥ khi n +¥ , nếu lim ( u - ) = +¥ n ) n .
Kí hiệu: lim u = -¥ hay u -¥ khi n + . ¥ n n
Nhận xét: u = +¥ lim ( u - ) = - . ¥ n n
2. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau a) lim k
n = +¥ với k nguyên dương; b) lim n
q = +¥ nếu q >1 . 3. Định lí 2 a) Nếu u lim u =
a và limv = ¥ thì lim n = 0 . n n vn b) Nếu u lim u = a 0
> , limv = 0 và v > 0, "n > 0 thì lim n = + . ¥ n n n vn
c) Nếu lim u = +¥ và lim v = a > 0 thì lim u .v = . +¥ n n n n
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Sử dụng nguyên lý kẹp 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng (- ) 1 n
Ví dụ 1 : Cho hai dãy số ( 1 u và (v có u = và v =
. Khi đó lim (u +v có giá trị bằng: n n ) n ) n ) n 2 n +1 n 2 n + 2 A. 3. B. 0. C. 2. D. 1. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 280
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 1 1 0 ï £ u £ £ 0 ï n 2 Ta có ïï n +1 n í ¾¾
limu = lim v = 0 ¾¾ lim u + v = n n ( n n ) . 0 ï 1 1 0 ïï £ v £ £ 0 n 2 ïîï n + 2 n æ ö
Ví dụ 2: Kết quả của giới hạn sin 5 lim n çç -2÷÷ ç bằng: è 3 ÷ n ø A. -2. B. 3. C. 0. D. 5. 3 Lời giải Chọn A æ ö Ta có sin 5n 1 0 £ £ , mà 1 n lim = 0 nên sin 5 lim n = 0, do đó sin 5 limçç -2÷÷ = 2. - 3 ç ÷ n n n 3n è 3n ø
Nhận xét : Có thể dùng MTCT để tính (có thể chính xác hoặc gần đúng) giới hạn như sau
(các bài sau có thể làm tương tự) : sin(5X ) Nhập -2. 3X
Bấm CALC và nhập 9999999999 (một số dòng MTCT khi bấm nhiều số « 9 » thì nó báo lỗi,
khi đó ta cần bấm ít số « 9 » hơn.
Bấm « = » ta được kết quả (có thể gần đúng), sau đó chọn đáp án có giá trị gần đúng với
kết quả hiện trên MTCT.
Ví dụ 3 : Kết quả của giới hạn 3sin n + 4 cos lim n bằng: n +1 A. 1. B. 0. C. 2. D. 3. Lời giải Chọn B Ta có 3sin n + 4cos n 7 7 3sin n + 4cos 0 £ £ £ 0 ¾ ¾ lim n = 0. n +1 n +1 n n +1
3. Bài tập trắc nghiệm æç ( )n ö - Câu 1: 1 ÷
Giá trị của giới hạn lim çç4 ÷ + ÷ bằng: ç ÷ ç n +1 ÷ è ø A. 1. B. 3. C. 4. D. 2. Lời giải Chọn C (- ) 1 n 1 1 (- ) 1 n æç ( )1n ö - Ta có ÷ 0 £ £ £ 0 ¾¾ lim = 0 ¾¾ limçç4 ÷ + ÷ = 4. + + + ç ÷ n 1 n 1 n n 1 ç n +1 ÷ è ø k 1 n - 2 n cos Câu 2: 1
Có bao nhiêu số tự nhiên chẵn k để lim n = . 2n 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 281
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 0. B. 1. C. 4. D. Vô số. Lời giải Chọn A k 1 k 1 n - 2 n cos n cos Ta có 1 n n = - . 2n 2 n k 1 n cos
Điều kiện bài toán trở thành lim n = 0. n Ta có 1
lim cos = cos 0 = 1 nên bài toán trở thành tìm k sao cho n k k 1 n - k 2 lim = lim n
= 0 -1 < 0 k < 2 ¾¾¾¾ không tồn tại *
k (do k nguyên dương và k Î , k =3 n 2 l chẵn). æ ö Câu 3: n cos 2n
Kết quả của giới hạn lim 5 ç ÷ ç - ÷ bằng: 2 ç ÷ è n +1 ø A. 4. B. 1 . C. 5. D. -4. 4 Lời giải Chọn C Ta có n cos 2n n 1 n cos 2n æ n cos 2 ö 0 £ £ £ 0 ¾¾ lim = 0 ¾¾ lim 5 n ç ÷ ç - ÷ = 5. 2 2 2 2 ç ÷ n +1 n +1 n n +1 è n +1 ø æ ö Câu 4: np
Kết quả của giới hạn 2 3 lim ççn sin -2n ÷÷ ç là: è 5 ÷ø A. . -¥ B. -2. C. 0. D. . +¥ Lời giải Chọn A æ ö æ ö Ta có np 1 sin p 2 3 3 limçç sin -2 ÷÷ = lim çç . n n n n -2÷÷. ç è 5 ÷ø ç ÷ èn 5 ø Vì 3 3 li ìï m n = +¥ l ìï im n = +¥ ï ï ï ï æ1 sin p ö ï ï 3 n í 1 sin ¾¾ í æ ö ¾¾ ç ÷ np 1 1 sin np lim n ç . - 2÷ = - . ¥ 0 ï £ . £ 0 l ï imç ï ï ç . - 2÷÷ = -2 < 0 ç ÷ èn 5 ø ï ï ç ÷ n 5 n èn 5 ø ïî ïî
Dạng 2. Giới hạn hữu tỉ 1. Phương pháp
Chú ý : Cho P(n), Q(n) lần lượt là các đa thức bậc ,
m k theo biến n :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 282
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 P(x) m m 1
= a n + a n - ++ a n + a a = / 0 m m 1 - 1 0 ( m ) Q(n) k k 1
= b n + b n - ++ b n +b b = / 0 k k 1 - 1 0 ( k ) P(n) m P(n) m Khi đó a n a n lim = lim m , viết tắt m
, ta có các trường hợp sau : Q(n) k b n Q(n) k b n k k P(n)
Nếu « bậc tử » < « bậc mẫu ( m < k ) thì lim = 0. Q(n) P(n)
Nếu « bậc tử » = « bậc mẫu ( a m = k ) thì lim m = . Q(n) bk P(n) ì+¥ ï khi a b > 0
Nếu « bậc tử » > « bậc mẫu ( ï m k
m > k ) thì lim = í . Q(n) ï-¥ khi a b < 0 ïî m k
Để ý rằng nếu P(n), Q(n) có chứa « căn » thì ta vẫn tính được bậc của nó. Cụ thể 1 m k k
n tì có bậc là . Ví dụ n có bậc là 3 4
, n có bậc là 4 ,... n 2 3
Trong các bài sau ta có thể dùng dấu hiệu trên để chỉ ra kết quả một cách nhanh chóng !
2. Các ví dụ rèn luyện kĩ năng 3 3n 2 5n 1 Ví dụ 1. Tính lim 3 . 2n 2 6n 4n 5 Giải 5 1 3 3 3n 2 5n 3 1 n n 3 lim lim 3 2n 2 6n 4n 5 6 4 5 2 2 2 3 n n n 2 Ví dụ 2: Tính n + 2 lim n 3 n + 3n -1 Lời giải 1 2 2 + Ta có 2 n + 2n 0 lim = lim n n = = 0. 3 n + 3n -1 3 1 1 1+ - 2 3 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0.
Ví dụ 3 : Cho dãy số ( n + b u với 2 u =
trong đó b là tham số thực. Để dãy số (u có giới hạn hữu n ) n ) n 5n + 3
hạn, giá trị của b bằng bào nhiêu Lời giải 2 b + Ta có 2n + b 2 lim = lim = lim n u = "b Î n ( ) 5n + 3 3 5 5 + n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 283
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Giải nhanh : 2n + b 2n 2 = với mọi b Î . 5n + 3 5n 5 2
Ví dụ 4: Cho dãy số ( 4n + n + 2 u với u =
. Để dãy số đã cho có giới hạn bằng 2 , giá trị của a n ) n 2 an + 5 bằng bao nhiêu Lời giải 1 2 2 4 + + 2 4n + n + 2 4 2 = lim = lim = lim n n u = (a =
/ 0) a = 2. n 2 an + 5 5 a a + 2 n 2 2 Giải nhanh : 4n + n + 2 4n 4 2 = a = 2. 2 2 an + 5 an a ( 2 n + 2n)( 3 2n + ) 1 (4n +5)
Ví dụ 5 : Tính giới hạn L = lim ( . 4 n -3n - ) 1 ( 2 3n -7) Lời giải æ 2öæ 1 öæ 5ö ( ç ÷ ç + ç ÷ ÷ç + ç ÷ 2 ÷ç + ÷ n + 2n)( 3 2n + ) 1 (4n + ) 1 2 4 ç ÷ 3 5 è øç ÷ è øç ÷ n n è nø 1.2.4 8 L = lim ( = lim = = . 4 n - 3n - ) 1 ( 2 3n -7) æ 3 1 öæ 7 ö 1.3 3 1 ç ÷ ç - - ÷ 3 ç ÷ ç ÷ç - ÷ 3 4 2 è øç ÷ n n è n ø ( 2 n + 2n)( 3 2n + ) 1 (4n + ) 2 3 5 Giải nhanh: n .2n .4n 8 ( = . 4 n - 3n - ) 1 ( 2 3n -7) 4 2 n .3n 3
3. Bài tập trắc nghiệm Câu 1: -3
Giá trị của giới hạn lim là: 2 4n - 2n +1 A. 3 - . B. . -¥ C. 0. D. -1. 4 Lời giải Chọn C -3 Ta có 2 -3 0 lim = lim n = = 0. 2 4n - 2n +1 2 1 4 4- + 2 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0. 3 Câu 2: 3n -2n +1
Giá trị của giới hạn lim là: 4 4n + 2n +1 A. . +¥ B. 0. C. 2 . D. 3 . 7 4 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 284
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 2 1 3 - + Ta có 2 4 3n - 2n +1 0 lim = lim n n n = = 0. 4 4n + 2n +1 2 1 4 4 + + 3 4 n n
Giải nhanh : Dạng « bậc tử » < « bậc mẫu » nên kết quả bằng 0. Câu 3: v
Cho hai dãy số (u ) và (v có 1 u = và 2 v =
. Khi đó lim n có giá trị bằng: n ) n n n +1 n n + 2 un A. 1. B. 2. C. 0. D. 3. Lời giải Chọn A 1 1+ Ta có v n +1 1 lim n = lim = lim n = =1. u n + 2 2 1 n 1+ n
Giải nhanh : n +1 n = 1. n + 2 n Câu 4: + Cho dãy số ( an u với 4 u =
trong đó a là tham số thực. Để dãy số (u có giới hạn n ) n ) n 5n + 3
bằng 2 , giá trị của a là: A. a = 10. B. a = 8. C. a = 6. D. a = 4. Lời giải Chọn A 4 a + Ta có an + 4 lim = lim = lim a n u = . Khi đó n 5n + 3 3 5 5 + n lim = 2 a u
= 2 a = 10 n 5 Giải nhanh : an + 4 2 an a = a = 10. 5n + 3 5n 5 2 Câu 5: n + n + 5
Tính giới hạn L = lim . 2 2n +1 A. 3 L = . B. 1 L = . C. L = 2. D. L = 1. 2 2 Lời giải Chọn B 1 5 2 1+ + Ta có 2 n + n + 5 1 = lim = lim n n L = 2 2n +1 1 2 2 + 2 n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 285
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2
Giải nhanh: n + n +5 n 1 = . 2 2 2n +1 2n 2 2 3 Câu 6: n -3n
Tính giới hạn L = lim . 3 2n + 5n -2 A. 3 L = - . B. 1 L = . C. 1 L = . D. L = 0. 2 5 2 Lời giải Chọn A 1 2 3 -3 n - 3n -3 = lim = lim n L = 3 2n + 5n - 2 5 2 2 2 + - 2 3 n n 2 3 3
Giải nhanh: n -3n 3 - n 3 = - . 3 3 2n + 5n- 2 2n 2 2 4 Câu 7: 5n -3
Tìm tất cả các giá trị của tham số an a để L = lim > 0. (1-a) 4 n + 2n +1
A. a £ 0;a ³1.
B. 0 < a <1.
C. a < 0; a >1.
D. 0 £ a <1. Lời giải Chọn C 5 2 4 -3a 2 5n -3an -3a éa < 0 = lim = lim n L = > 0 ê . (1-a) 4 n + 2n +1 - ê (1 > -a) 2 1 (1 a) a 1 + + ë 3 4 n n ( 3 2n -n )( 2 3n + ) 1
Câu 8: Tính giới hạn L = lim . (2n - ) 1 ( 4 n -7) A. 3 L = - . B. L = 1. C. L = 3. D. L = + . ¥ 2 Lời giải Chọn A Ta có æ 2 ö æ 1 ö æ 2 öæ 1 ö ( ç ÷ ç - ç ÷ ÷ ç + ç ÷ ÷ ç - ç ÷ 2 ÷ç + ÷
n - n )(3n + ) 3 2 3 2 n 1 .n 3 1 3 2 ç ÷ 2 è ø ç ÷ 2 è ø ç ÷ 2 1 è øç ÷ n n n è n ø -1.3 3 L = lim = lim = lim = = - . (2n- ) 1 ( 4 n - 7) æ 1ö æ ö æ öæ ö 4 7 1 7 2.1 2 nçç2 ÷ - ÷.n 1 ç ÷ ç - ç ÷ ç2 ÷ - ÷ 1 ç ÷ ç - ÷ ç ÷ 4 è ø ç ÷ è ø ç ÷ 4 è øç ÷ n n n è n ø ( 3 2n - n )( 2 3n + ) 3 2 1 Giải nhanh: n - .3n 3 = - . (2n- ) 1 ( 4 n - 7) 4 2 . n n 2 3 Câu 9: n - 2n
Kết quả của giới hạn lim là: 2 1-3n A. 1 - . B. . +¥ C. . -¥ D. 2 . 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 286
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn C æ ö 3 2 ç ÷ 2 n 1 ç - ÷ 3 - 2 1 - ç ÷ 2 n 2 è ø lim n = lim n = lim . n n . Ta có 2 1-3n æ 1 ö 1 2 n çç -3÷÷ -3 2 2 ç ÷ èn ø n li ìï m n = +¥ ïï 2 ï 2 3 1- ï 2 ï 1- n - 2n n 2 í 1 ¾¾ im = lim . n = -¥ n 2 li ï m = - < 0 1-3n 1 ïï 1 -3 3 2 ï -3 n ï 2 ïî n 3 3
Giải nhanh : n -2n n 1 = - n ¾¾ - . ¥ 2 2 1-3n 3 - n 3 3 Câu 10: 2n + 3n
Kết quả của giới hạn lim là: 2 4n + 2n +1 A. 3 . B. . +¥ C. 0 D. 5. 4 7 Lời giải Chọn B æ ö 3 2 ç ÷ 2 n ç + 3÷ 3 + 2 3 + ç ÷ 2 2n 3 è ø lim n = lim n = lim . n n . Ta có 2 4n + 2n +1 æ 2 1 ö 2 1 2 n çç4 ÷ + + ÷ 4 + + 2 2 ç ÷ è n n ø n n li ìï m n = +¥ ïï 2 ï 2 3 + 3 ï 2 ï + 3 2n + 3n n 2 í 3 ¾¾ im = lim . n = + . ¥ n 2 li ï m = > 0 4n + 2n +1 2 1 ïï 2 1 4 4 + + 2 ï 4 + + n n ï 2 ïî n n 3 3
Giải nhanh : 2n +3n 3n 3 = .n ¾¾ + . ¥ 2 2 4n + 2n +1 4n 4 4 Câu 11: 3n -n
Kết quả của giới hạn lim là: 4n -5 A. 0. B. . +¥ C. . -¥ D. 3 . 4 Lời giải Chọn C æ ö 4 3 ç ÷ 3 n ç -1÷ 4 - 3 1 - ç ÷ 3 3n n èn ø 3 lim = lim = lim . n n . Ta có 4n -5 æ 5ö 5 nçç4 ÷ - ÷ 4- ç ÷ è nø n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 287
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 li ìï m n = +¥ ïï 3 ïï 3 4 -1 3 ï 3 ï -1 n - n 3 n 3 í 1 ¾¾ lim = l lim n . = - . ¥ li ï m n = - < 0 4n -5 5 ïï 5 4 4 - ïï 4- n ïî n 4 4
Giải nhanh : 3n-n n - 1 3 = - .n ¾¾ - . ¥ 4n-5 4n 4
Câu 12: Trong các giới hạn sau đây, giới hạn nào bằng 0? 3 2 3 2 4 A. 3 + 2 2n -3 2n -3 2n -3 lim n . B. lim . C. lim n . D. lim n . 2 2n -1 3 2 - n -4 2 2 - n -1 4 2 2 - n + n Lời giải Chọn B
. Theo dấu hiệu ở đã nêu ở phần Chú ý trên thì ta chọn giới hạn nào rơi vào trường hợp
« bậc tử » < « bậc mẫu » ! 3 3+ 2 lim
n = +¥ : « bậc tử » > « bậc mẫu » và a b = 2.2 = 4> 0. 2 2n 1 - m k 2 2n -3 lim
= 0 : « bậc tử » < « bậc mẫu ». 3 2 - n -4 3 2n-3 lim
n = +¥ : « bậc tử » > « bậc mẫu » và a b = - - > n k ( ) 3 ( . ) 2 0. 2 2 - n 1 - 2 4 2n -3n 3 - 3 - lim =
= : « bậc tử » = « bậc mẫu » và a 3 3 m = = . 4 2 2 - n + n 2 - 2 b -2 2 k
Câu 13: Dãy số nào sau đây có giới hạn là -¥ ? 3 2 4 2 A. 1+ 2n n + 2n -1 2n -3n n - 2n . B. u = . C. u = . D. u = . 2 5 n n n n + 5n 3 n - + 2n 2 3 n + 2n 5n +1 Lời giải Chọn C
Ta chọn đáp án dạng « bậc tử » = « bậc mẫu » và a b < 0. m k 2 4 2n -3n u =
: « bậc tử » > « bậc mẫu » và a b = -3.2 = -6 < 0 ¾¾ lim u = - . ¥ n 2 3 n + 2n m k n ì+¥ ï khi a > 0 Chú ý : (i) lim( m m 1 - ï n a n + a n
++ a n + a = í . m n 1 - 1 0 ) ï-¥ khi a < 0 ïî n
(ii) Giả sử q > max{ q : i =1;2¼;m thì i } ìïa khi q <1 ï 0 ï lim( . n n n ï
a q + a q ++ a q + a = +
í ¥ khi a > 0, q >1. m m 1 1 0 )
ïïï-¥ khi a<0, q>1 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 288
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta dùng « dấu hiệu nhanh » này để đưa ra kết quả nhanh chóng cho các bài sau.
Câu 14: Tính giới hạn L = ( 2
lim 3n + 5n - 3). A. L = 3. B. L = - . ¥ C. L = 5. D. L = + . ¥ Lời giải Chọn D 2 li ìï m = +¥ æ ö n ï . ïï L = lim( 5 3 2 3n + 5n - ) 2 3 = lim n çç2 ÷ + - ÷ = +¥ vì í æ 5 3 ö . 2 ç ÷ è n n ø li ï mç ï ç2 ÷ + - ÷ = 2 > 0 2 ï ç ÷ è n n ø ïî Giải nhanh : 2 2
3n +5n-3 3n ¾¾ + . ¥
Câu 15: Có bao nhiêu giá trị nguyên của tham số a thuộc khoảng ( 10 - ;10) để L = ( n- ( 2a - ) 3 lim 5 3 2 n )= -¥ . A. 19. B. 3. C. 5. D. 10. Lời giải Chọn B æ ö Ta có lim (5n-3( 5 2 a - 2) 3 n ) 3 = lim n çç -3( 2 a - 2 ÷÷ = -¥ 2 ) ç ÷ èn ø æ 5 ö lim çç -3( 2 a - 2) 2
÷÷= a -2 < 0 - 2 < a < 2 ¾¾¾¾¾a = 1 - ; 0; 1. 2 ç ÷ a , a ( 10;10) èn Î Î - ø
Câu 16: Tính giới hạn ( 4 2
lim 3n + 4n - n + ) 1 . A. L = 7. B. L = - . ¥ C. L = 3. D. L = + . ¥ Lời giải Chọn D Ta có 4 li ìï m = +¥ æ ö n ïï lim( 4 1 1 4 2 3 ï
n + 4n - n + ) 4 1 = lim n 3 ç ÷ ç + - + ÷ = +¥ vì í æ 4 1 1 ö . 2 3 4 ç ÷ è n n n ø li ï m 3 ç ÷ ï ç + - + ÷ = 3 > 0 2 3 4 ï ç ÷ è n n n ø ïî Giải nhanh : 4 2 4
3n + 4n -n +1 3n ¾¾ + . ¥ Câu 17: 2 n
Cho dãy số (u với u = 2 + + +
Mệnh đề nào sau đây đúng ? n ( 2) ... ( 2) . n ) A. lim u = - . ¥ B. 2 lim u = . C. lim u = + . ¥ D. Không tồn tại n n 1- 2 n lim u . n Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 289
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Vì ( )2 n 2,
2 , ¼ ,( 2) lập thành cấp số nhân có u = 2 = nên 1 q n 1-( 2) ìï n é ù a = 2 - 2 > 0 ï u = 2. = - ê - ú ¾¾ u = +¥ vì í . n (2 2) ( 2) 1 lim 1- 2 n êë úû ïïq = 2 >1 ïî 1 3 +1+ +... n +
Câu 18: Giá trị của giới hạn 2 2 2 lim bằng: 2 n +1 A. 1. B. 1. C. 1 . D. 1 . 8 2 4 Lời giải Chọn D 1 3 n 1 1 n(n + ) Ta có 1
+1+ +...+ = (1+ 2 ++ n) = . . Do đó 2 2 2 2 2 2 1 3 +1+ +... n + 2 n + n 1 2 2 2 lim = lim
= (“bậc tử” = “bậc mẫu”). 2 2 n +1 4n + 4 4 æ - ö Câu 19: 1 2 1
Giá trị của giới hạn lim çç + +... n ÷ + ÷ bằng: 2 2 2 ç ÷ èn n n ø A. 0. B. 1. C. 1 . D. 1. 3 2 Lời giải Chọn C 1 2 n -1 1 1 (n - ) 1 (1+ n- ) 2 1 Ta có - + +...+ = (1+ 2++ n- ) 1 = . n n = . Do đó 2 2 2 2 2 2 n n n n n 2 2n 2 æ 1 2 n -1ö n - n 1 limçç + +... ÷ + ÷ = lim = . 2 2 2 ç ÷ 2 èn n n ø 2n 2 1 æ +3+5++(2n + ) 1 ö Câu 20: ç ÷
Giá trị của giới hạn lim ç ÷ ç bằng: 2 ÷ çè 3n + 4 ÷ø A. 0. B. 1. C. 2 . D. 1. 3 3 Lời giải Chọn B n(1+ 2n - ) Ta có 1+3+5+ ( 2n - ) 1 2 1 = = n nên 2 1 æ +3+5++(2n + ) 2 1 ö ç ÷ n 1 limç ÷ = ç ÷ lim = ¾¾ 2 2 çè 3n + 4 ÷ø 3n + 4 3 æ ö Câu 21: ç 1 1 1 ÷
Giá trị của giới hạn lim ç + +... + ÷ ç ÷ là: çè1.2 2.3 n(n + ) 1 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 290
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1 . B. 1. C. 0. D. . -¥ 2 Lời giải Chọn B Ta có æç 1 1 1 ö÷ æ 1 1 1 1 1 ö æ 1 ö limç + +...+ ÷ ç ÷ = lim 1 ç ÷ ç - + - ++ - ÷ = lim 1 ç ÷ ç ÷ è + ç ÷ ç - ÷ =1. 1.2 2.3 ø è + ø ç ÷ n(n ) 1 2 2 3 n n 1 è n +1ø æ ö Câu 22: ç 1 1 1 ÷
Giá trị của giới hạn lim ç + +... + ÷ ç ÷ bằng: çè1.3 3.5 (2n - ) 1 (2n + ) 1 ÷ø A. 1 . B. 1 . C. 1. D. 2. 2 4 Lời giải Chọn A æ ö Với mọi * 1 1 1 1 k Î thì = ç ÷ ç - ÷ , do đó (2 ç ÷ k - ) 1 (2k + ) 1
2 è2k -1 2k +1ø æç 1 1 1 ö÷ 1 é 1 1 1 1 1 ù limç + +...+ ÷ ç ÷ = lim 1 ê - + - + - ú 1 çè .3 3.5 (2n- ) 1 (2n + ) 1 ÷ø 2 êë 3 3 5 2n 1 - 2n +1úû 1 é 1 ù 1 = lim 1 ê - ú = . 2 êë 2n +1úû 2 é ù Câu 23: 1 1 1
Giá trị của giới hạn lim ê ...... ú + + + ê bằng: 1.4 2.5 ú n ê (n +3) ë úû A. 11 . B. 2. C. 1. D. 3 . 18 2 Lời giải Chọn A Ta có 1 1 1 1 é 1 1 1 1 1 1 1 ù + +......+ = 1 ê - + - + - ++ - ú 1.4 2.5 n(n + ) 3 3 êë 4 2 5 3 6 n n + 3úû 1 éæ 1 1 1ö æ1 1 1 1 ùö = ê 1 ç ÷ ç + + ++ ÷-ç ÷ ç + + ++ ú÷ 3 çêè 2 3 ÷ø ç ÷ n è4 5 6 n + 3 ú ø ë û 1æ 1 1 1 1 1 ö = 1 ç ÷ ç + + - - - ÷ 3çè 2 3 ÷ n +1 n + 2 n + 3ø 1 11 æ 1 1 1 ö = ç ÷ ç - - - ÷ 3çè 6 ÷ n +1 n + 2 n + 3ø æ ö ç ÷ æ ö Do đó 1 1 1 1 11 1 1 1 11 limç + +......+ ÷ ç ÷ = lim ç ÷ ç - - - ÷ = . 1. çè 4 2.5 ÷ + ç ÷ n(n ) 3 ø 3è 6 n +1 n + 2 n + 3ø 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 291
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 Câu 24: 1 + 2 +... +
Giá trị của giới hạn lim n bằng: n ( 2 n + ) 1 A. 4. B. 1. C. 1 . D. 1. 2 3 Lời giải Chọn D 3 2
2n -3n + n n(n - ) 1 (2n + ) 1 Đặt P(n)= = thì ta có 6 6 2 2 2 2
1 + 2 + 3 ++ n = (P(2)- P( ) 1 )+(P( )
3 - P(2))++(P(n + ) 1 - P(n)) n(n + ) 1 (2n + )
= P(n + )- P( ) 3 1 1 = 6 2 2 2 1 + 2 +...+ n n(n + ) 1 (2n + ) Do đó 3 2 1 lim = = = n( lim . 2 n + ) 1 6n( 2 n + ) 1 6 3 ìï 1 ï = ï 1 u ï Câu 25: 2
Cho dãy số có giới hạn ( ï u xác định bởi í . Tính lim u . n ) ï 1 n u ïï = , n ³1 n 1 + ï 2-u ïî n A. lim u = 1 - . B. lim u = 0. C. 1 lim u = . D. lim u =1. n n n 2 n Lời giải Chọn D
Giả sử limu = a thì ta có n 1 1 a ìï =/ 2 ìïa =/ 2 ï ï a = lim u = lim = í í a =1. n 1 + 2-u 2-a a ï (2-a) 2 =1 ï ïî ïa -2a +1= 0 n î u ìï = 2 1 ï
Câu 26: Cho dãy số có giới hạn ( ï u xác định bởi í u +1 . Tính lim u . n ) n n u ï = , n ³ ï 1 n 1 + ïî 2 A. lim u =1. B. lim u = 0. C. lim u = 2. D. lim u = + . ¥ n n n n Lời giải Chọn A
Giả sử limu = a thì ta có n u +1 a +1 a = lim u = lim n = a = 1 ¾¾ n 1 + 2 2 2 Câu 27: 9n -n +1
Kết quả của giới hạn lim bằng: 4n -2 A. 2 . B. 3 . C. 0. D. 3. 3 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 292
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B 1 1 - + 2 9 2 . 9n - n +1 n n 3 lim = lim = 4n - 2 2 4 4- n 2 2
Giải nhanh: 9n -n +1 9n 3 = . 4n - 2 4n 4 2 Câu 28: n - + 2n +1
Kết quả của giới hạn lim bằng: 4 3n + 2 A. 2 - . B. 1 . C. 3 - . D. 1 - . 3 2 3 2 Lời giải Chọn C 2 1 2 -1+ + 2 n - + 2n +1 1 lim = lim n n = - 4 3n + 2 2 3 3+ 4 n 2 2 Giải nhanh : n - + 2n +1 n - 1 = - . 4 4 3n + 2 3n 3 Câu 29: n +
Kết quả của giới hạn 2 3 lim là: 2n +5 A. 5 . B. 5. C. . +¥ D. 1. 2 7 Lời giải Chọn D 3 2 + 2n + 3 n 2 lim = lim = = 1. 2n + 5 5 2 2 + n
Giải nhanh: 2n +3 2n =1. 2n + 5 2n Câu 30: + -
Kết quả của giới hạn n 1 4 lim bằng: n +1 + n A. 1. B. 0. C. -1. D. 1 . 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 293
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 4 + - 2 n +1 - 4 n n n 0 lim = lim = = 0 n +1 + n 1 1 1 + +1 2 n n
Giải nhanh: n +1-4 n 1 = ¾¾ 0. n +1 + n n n 2 Câu 31: n + n +1 p Biết rằng lim = a sin + . b Tính 3 3
S = a + b . 2 - - 4 n n 2 A. S = 1. B. S = 8. C. S = 0. D. S = -1. Lời giải Chọn B 1 1+ 1+ 2 2 Ta có n + n +1 n 1+ 1 p lim = lim = = 2 2 sin 2 n - n - 2 1 2 1 4 1- - n n ìïa = ï 2 2 ¾¾ í ¾¾ S = 8 ïïb = î 0 Câu 32: 10
Kết quả của giới hạn lim là: 4 2 n + n +1 A. . +¥ B. 10. C. 0. D. . -¥ Lời giải Chọn C 10 2 10 0 lim = lim n = = 0. 4 2 n + n +1 1 1 1 1+ + 2 4 n n Giải nhanh: 10 10 10 = ¾¾ 0. 2 4 2 4 + +1 n n n n Câu 33: 2n + 2
Kết quả của giới hạn lim (n + ) 1 là: 4 2 n + n -1 A. . +¥ B. 1. C. 0. D. . -¥ Lời giải Chọn C 2n + 2 2(n + )3 1 lim(n + ) 1 = lim
= 0 (“bậc tử” < “bậc mẫu”). 4 2 4 2 n + n -1 n + n -1 Giải nhanh: ( + n + ) 2n 2 2n 2 1 . n = ¾¾ 0. 4 2 4 n + n -1 n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 294
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 3 2 Câu 34: an + 5n -7 Biết rằng lim
= b 3 + c với , a ,
b c là các tham số. Tính giá trị của biểu thức 2 3n -n + 2 a + c P = . 3 b
A. P = 3. B. 1 P = . C. P = 2. D. 1 P = . 3 2 Lời giải Chọn B 5 7 3 + - 3 3 2 a 3 3 3 Ta có an + 5n -7 lim = lim n n b a = = 3 2 3n -n + 2 1 2 3 3 3- + 2 n n ìï3 b ï a = ï 1 = b 3 + c í 3 P = . ï 3 c ïï = 0 î
Câu 35: Kết quả của giới hạn 5 5 2
lim 200 -3n + 2n là: A. . +¥ B. 1. C. 0. D. . -¥ Lời giải Chọn D Ta có li ìï m = +¥ æ n ï ç 200 2 ö ï 5 5 2 ÷ ï 5
lim 200-3n + 2n = lim nç -3+ ÷ ç ÷ = -¥ vì æç 200 2 ö í . 5 3 ç ÷ è n n ÷ø 5 ï 5 limç -3+ ÷ ï ç ÷ = - 3 < 0 5 3 ï ç ï è n n ÷ø î Giải nhanh: 5 5 2 5 5 5
200-3n + 2n -3n = - 3.n ¾¾ - . ¥
Dạng 3. Dãy số chứa căn thức 1. Phương pháp
Nếu biểu thức chứa căn thức cần nhân một lượng liên hiệp để đưa về dạng cơ bản. A B
löôïng lieân hieäp laø: A B A B
löôïng lieân hieäp laø: A B
A B löôïng lieân hieäp laø: A B 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B
2. Các ví dụ rèn luyện kĩ năng 2 2
Ví dụ 1. Tính lim n 7 n 5 Giải 2 2 2 2 n 7 n 5 2
lim n 7 n 5 lim lim 0 2 2 2 2 n 7 n 5 n 7 n 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 295
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2
Ví dụ 2. Tính lim n 3n n Giải 2 2 3n 3 3
lim n 3n n lim lim 2 2 n 3n n 3 2 1 1 n Ví dụ 3. Tính ( 2 lim
n -n +1 -n) Lời giải . 2 2
n - n +1 - n n - n = 0 ¾¾
nhân lượng liên hợp : 1 - + - + lim( 1 n 1 1 2 - +1- )= lim = lim n n n n = - 2
n - n +1 + n 1 1 2 1- + +1 2 n n Giải nhanh : n - +1 n - 1 2
n - n +1 - n = = - . 2 2 - + + + 2 n n 1 n n n Ví dụ 4. Tính (3 2 3 lim
n -n + n) Lời giải 3 2 3 3 3
n - n + n n - + n = 0 ¾¾
nhân lượng liên hợp :
lim( n -n + n) 2 3 n 1 1 2 3 = lim = lim = . ( 2 3 n - n )2 2 3 2 3 2 3 3
- n n - n + n æ1 ö 1 3 ç ÷ 3 ç -1÷ - -1 +1 ç ÷ èn ø n 2 2 Giải nhanh : 3 n n 1 2 3
n - n + n = = . ( 2 3 - )2 3 6 3 3 2 3 2 3 2 - - + 3 3 n n n n n n
- n n - n + n
Ví dụ 5. Tính lim é ù n ê ( n+1- n)ú ë û Lời giải
n ( n +1- n) n ( n - n) = 0 ¾¾
nhân lượng liên hợp :
n ( n + - n) n 1 1 lim 1 = lim = lim = n +1 + n 1 2 1+ +1 n
Giải nhanh : n ( n+ - n) n n 1 1 = = . n +1 + n n + n 2
3. Bài tập trắc nghiệm
Câu 1: Giá trị của giới hạn lim ( n +5 - n +1) bằng: A. 0. B. 1. C. 3. D. 5.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 296
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn A
n +5 - n +1 n - n = 0 ¾¾
nhân lượng liên hợp : ( n+ - n+ ) 4 lim 5 1 = lim = 0 n + 5 + n +1
Câu 2: Giá trị của giới hạn ( 2 2 lim
n -1 - 3n + 2 ) là: A. -2. B. 0. C. . -¥ D. . +¥ Lời giải Chọn C æ ö lim( ç 1 2 2 2 ÷ n 1
- - 3n + 2)= limnç 1- - 3+ ÷ ç ÷ = -¥ vì 2 2 çè n n ÷ø æç 1 2 ö lim ÷ n = + , ¥ limç 1- - 3+ ÷ ç ÷ =1- 3 < 0. 2 2 çè n n ÷ø Giải nhanh : 2 2 2 2
n -1 - 3n + 2
n - 3n = (1- 3)n ¾¾ - . ¥
Câu 3: Giá trị của giới hạn ( 2 2 lim
n + 2n - n -2n ) là: A. 1. B. 2. C. 4. D. . +¥ Lời giải Chọn B 2 2 2 2
n + 2n - n - 2n n - n = 0 ¾¾
nhân lượng liên hợp : lim( 4n 4 2 2
n + 2n - n - 2n ) = lim = lim = 2. 2 2
n + 2n + n - 2n 2 2 1+ + 1- n n Giải nhanh : 4n 4 2 2 + 2 - - 2 n n n n n = = 2. 2 2 2 2
n + 2n + n - 2n n + n
Câu 4: Có bao nhiêu giá trị của a để ( 2 2 2 lim
n + a n - n +(a + 2)n +1)= 0. A. 0. B. 2. C. 1. D. 3. Lời giải Chọn B 2 2 2
n + a n - n +(a + ) 2 2
2 n +1 n - n = 0 ¾¾
nhân lượng liên hợp: 2
a - a - 2 n -1 Ta có lim ( 2 2 2
n + a n - n +(a + 2)n +1) ( ) = lim 2 2
n + n + n +1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 297
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 1 a - a - 2 - 2 a - a - 2 éa = -1 = lim n = = 0 ê . 1 1 2 êa = 2 1 1 ë + + + 2 n n
Câu 5: Giá trị của giới hạn ( 2 2 lim
2n -n +1 - 2n -3n + 2) là: A. 0. B. 2 . C. . -¥ D. . +¥ 2 Lời giải Chọn B 2 2 2 2
2n - n +1- 2n -3n + 2 2n - 2n = 0 ¾¾
nhân lượng liên hợp : - lim( 2n 1 2 2
2n - n +1- 2n -3n + 2)= lim 2 2
2n - n +1 + 2n -3n + 2 1 2- 1 = lim n = . 1 1 3 2 2 2- + + 2- + 2 2 n n n n Giải nhanh : 2n -1 2n 1 2 2
2n - n +1- 2n -3n + 2 = = . 2 2 2 2
2n - n +1 + 2n -3n + 2 2n + 2n 2
Câu 6: Giá trị của giới hạn ( 2 2 lim
n + 2n -1 - 2n + n ) là: A. -1. B. 1- 2. C. . -¥ D. . +¥ Lời giải Chọn C Giải nhanh : 2 2 2 2
n + 2n -1 - 2n + n
n - 2n = (1- 2)n ¾¾ - . ¥ æ ö Cụ thể : lim( ç 2 1 1 2 2 ÷ n + 2n 1
- - 2n + n)= lim .nç 1+ - - 2+ ÷ ç ÷ = -¥ vì 2 çè n n n ÷ø æç 2 1 1 ö lim ÷ n = + , ¥ limç 1+ - - 2 + ÷ ç ÷ =1- 2 < 0 2 çè n n n ÷ø
Câu 7: Có bao nhiêu giá trị nguyên của a thỏa ( 2 2 lim
n -8n -n + a )= 0 . A. 0. B. 2. C. 1. D. Vô số. Lời giải Chọn B Nếu 2 2 2
n -8n - n + a n - n = 0 ¾¾
nhân lượng liên hợp :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 298
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2a -8 n Ta có - lim ( 2a 8 2 2
n -8n - n + a ) ( ) = lim = lim 2 n + n + n 1 1+ +1 n 2
= a -4 = 0 a = 2 .
Câu 8: Giá trị của giới hạn ( 2 lim
n - 2n + 3 - n) là: A. -1. B. 0. C. 1. D. . +¥ Lời giải Chọn A 2 2
n - 2n + 3 - n n - n = 0 ¾¾
nhân lượng liên hợp : 3 - + - + lim( 2 2n 3 2 - 2 + 3 - )= lim = lim n n n n = -1 2
n - 2n + 3 + n 2 3 1- + +1 2 n n Giải nhanh : 2 - n +3 2 - 2 - 2 + 3 n n n -n = = 1 - . 2 2
n - 2n + 3 + n n + n
Câu 9: Cho dãy số (u với 2 2 u =
n + an + 5 - n +1 , trong đó a là tham số thực. Tìm a để n ) n lim u = 1 - . n A. 3. B. 2. C. -2. D. -3. Lời giải Chọn C 2 2 2 2
n + an + 5 - n +1 n - n = 0 ¾¾
nhân lượng liên hợp : + -1= lim = lim an u
n + an + - n + = n ( 4 2 2 5 1) lim 2 2
n + an + 5 + n +1 4 a + = lim a n = a = -2. a 5 1 2 1+ + + 1+ 2 2 n n n Giải nhanh : an + 4 2 2 -1 + + 5 - +1 an a n an n = = a = 2 - . 2 2 2 2 + + + + + 2 n an 5 n 1 n n
Câu 10: Giá trị của giới hạn lim (3 3 3 3
n +1 - n + 2 ) bằng: A. 3. B. 2. C. 0. D. 1. Lời giải Chọn C 3 3 3 3 3 3 3 3 n +1 - n + 2 n - n = 0 ¾¾
nhân lượng liên hợp :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 299
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 - lim( 1 3 3 3 3
n +1- n + 2) = lim = 0. 3 (n + )2 3 3 3 3 3 3
1 + n +1. n + 2 + ( 3 n + 2)
Câu 11: Giá trị của giới hạn (3 3 2 lim
n -2n -n) bằng: A. 1. B. 2 - . C. 0. D. 1. 3 3 Lời giải Chọn B 3 3 2 3 3
n - 2n - n n - n = 0 ¾¾
nhân lượng liên hợp : - -
lim( n -2n -n) 2 3 2n 2 2 3 2 = lim = lim = - . ( 3 2 n - 2n )2 2 3 3 2 2 3 3 + .
n n - 2n + n æ 2ö 2 3 ç ÷ 3 1 ç - ÷ + 1- +1 ç ÷ è n ø n 2 2 Giải nhanh : - - 3 2n 2n 2 3 2
n - 2n - n = = - . ( 3 2 - 2 )2 3 6 3 3 2 3 3 2 2 n + . + 3 3 + . - 2 n n n n n n n n + n
Câu 12: Giá trị của giới hạn lim é ù n ê
( n+1- n-1)ú là: ë û A. -1. B. . +¥ C. 0. D. 1. Lời giải Chọn D
n ( n +1- n - )
1 n ( n - n) = 0 ¾¾
nhân lượng liên hợp :
n ( n + - n - ) 2 n 2 lim 1 1 = lim = lim =1 n +1 + n -1 1 1 1+ + 1- n n Giải nhanh : ( + - - ) 2 n 2 1 1 n n n n = = 1. n +1 + n -1 n + n Câu 13: é ù
Giá trị của giới hạn ên( 2 2 lim
n +1 - n -3)ú bằng: ë û A. -1. B. 2. C. 4. D. . +¥ Lời giải Chọn B n( 2 2
n + - n - ) n( 2 2 1 3 n - n ) = 0 ¾¾
nhân lượng liên hợp : lim n( 4n 4 2 2
n +1 - n - 3) = lim = lim = 2 2 2 n +1 + n - 3 1 3 1+ + 1- 2 2 n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 300
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Giải nhanh : ( 4n 4 2 2 +1- -3) n n n n = = 2. 2 2 2 2 n +1 + n -3 n + n Câu 14: é ù
Giá trị của giới hạn ên( 2 2 lim
n + n +1 - n + n - 6 )ú là: ë û A. 7 -1. B. 3. C. 7 . D. . +¥ 2 Lời giải Chọn C n( 2 2
n + n + - n + n - ) n( 2 2 1 6 n - n )= 0 ¾¾
nhân lượng liên hợp : lim ( 7 2 2 + +1- + -6)= lim n n n n n n 2 2
n + n +1 + n + n - 6 7 7 = lim = . 1 1 1 6 2 1+ + + 1+ - 2 2 n n n n
Giải nhanh : n( 7n 7n 7 2 2
n + n +1 - n + n - 6) = = . 2 2 2 2 + + + + - + 2 n n 1 n n 6 n n Câu 15: 1
Giá trị của giới hạn lim là: 2 2 n + 2 - n + 4 A. 1. B. 0. C. . -¥ D. . +¥ Lời giải Chọn C 2 2 2 2
n + 2 - n + 4 n - n = 0 ¾¾
nhân lượng liên hợp : 1 1 é æ ùö lim = lim ê ç ÷ú - + + + = - ç + + + ÷ ê ç ÷ = -¥ ú 2 ( 1 2 4 2 2 n 2 n 4) lim .n 1 1 2 2 2 + - + 2 2 2 4 ç ê è n n ÷ n n ø ë úû é æ ùö vì 1 ê ç 2 4 lim ÷ú n = + , ¥ lim - ç 1+ + 1+ ÷ ê ç ÷ = 1 - < 0 2 2 2 ú ç ê è n n ÷ø ë úû Giải nhanh : 1 1 = - + + + - + = - ¾¾ -¥ 2 ( 1 2 2 n 2 n 4) ( 2 2 n n n . 2 ) + - + 2 2 n 2 n 4 2 Câu 16:
9n -n - n + 2
Giá trị của giới hạn lim là: 3n -2 A. 1. B. 0. C. 3. D. . +¥ Lời giải Chọn A 2 2
9n - n - n + 2 9n = 3n = / 0 ¾¾ giải nhanh :
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 301
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2
9n - n - n + 2 9n = 1 3n - 2 3n 1 1 2 - - + 2 9 2 Cụ thể :
9n - n - n + 2 n n n 9 lim = lim = = 1. 3n - 2 2 3 3- n Câu 17: 1
Giá trị của giới hạn lim là: 3 3 n +1 - n A. 2. B. 0. C. . -¥ D. . +¥ Lời giải Chọn B 3 3 3 3 n +1 - n n - n = 0 ¾¾
nhân lượng liên hợp : lim( 1 3 3 n +1 - n) = lim = 0 3 (n + )2 3 3 3 2 1 + n n +1 + n
Dạng 4. Dãy số chứa hàm lũy thừa 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng n n 1 + Ví dụ 1: Tính 3 -2.5 lim n 1 2 + + 5n Lời giải n n 1 + n 1 + Giải nhanh : 3 -2.5 2 - .5 = 10 - n 1 2 + +5n 5n æ3 n ö ç ÷ ç ÷ -10 n n 1 + - ç ÷ Cụ thể : 3 2.5 è5ø lim = lim = -10. n 1 2 + + 5n æ2 n ö 2.ç ÷ ç ÷ +1 çè5÷ø n n 1 + Ví dụ 2: Tính 3 -4.2 -3 lim 3.2n + 4n Lời giải 1 n n n+ n - - æ ö Giải nhanh : 3 4.2 3 3 3 = ç ÷ ç ÷ ¾¾ 0. 3.2n + 4n 4n çè4÷ø æ3 n ö æ1 n ö æ1 n ö ç ÷ ç ÷ -8.ç ÷ - - ç ÷ ç ÷ -3.ç ÷ è ø ç ÷ ç ÷ n n 1 + è ø ç ÷ Cụ thể : 3 4.2 3 4 2 è4ø 0 lim = lim = = 0. 3.2n + 4n æ1 n ö 1 3.ç ÷ ç ÷ +1 çè2÷ø n 5n1 1 2 Ví dụ 3: Tính lim 5n2 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 302
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải
Cách 1: Giải bằng tự luận n 5n 1 n 1 2 n 2 2 Ta có: lim lim 1 . 0. 5n 2 3 9 3
Cách 2: Mẹo giải nhanh n 5n 1 5n 1 2 n 2 1 . 0. 5n 2 3 3 n n 1 3 4.2 3 Ví dụ 4: Tính lim . n n 3.2 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 n 2 n 3 4.2 n n1 3 4.2 3 4 4 4 n 4 Ta có:
(chia tử và mẫu cho n ). n 3.2 n 4 2 n 3. 1 4 n n 1 3 4.2 3 0 Suy ra lim 0. n n 3.2 4 1
Cách 2: Mẹo giải nhanh n n n 1 n 3 4.2 3 3 3 0. n n n 3.2 4 4 4 2
Ví dụ 5: Có bao nhiêu giá trị nguyên của an -1 1
a thuộc (0;20) sao cho lim 3 + - là một số nguyên. 2 3 + n 2n Lời giải ìï 1 ï 2 a - ï 2 ï an -1 ïlim = lim n = a ï 2 2 ï 3 + n 3 Ta có an -1 1 ï +1 í 2 lim 3 + - = 3 + a. 2 ï n 3 + n 2n ïïï 1 æ1 n ö ïïlim = limç ÷ ç ÷ = 0 ïï 2n çè2÷ø î a ìï (0;20), a Ta có ï Î Î ïí ¾¾ a Î {1;6;1 } 3 . ïï a+3 ïî Î
3. Bài tập trắc nghiệm n+2 Câu 1: 2 -5
Kết quả của giới hạn lim bằng: 3n + 2.5n A. 25 - . B. 5 . C. 1. D. 5 - . 2 2 2 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 303
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ1 n ö 2ç ÷ ç ÷ - 25 n+2 - ç ÷ Cụ thể : 2 5 è5ø 25 lim = lim = - . 3n + 2.5n æ3 n ö 2 ç ÷ ç ÷ + 2 çè5÷ø n+2 n+2 Giải nhanh : 2-5 5 - 25 = - 3n + 2.5n 2.5n 2 n Câu 2: -
Kết quả của giới hạn 3 1 lim bằng: 2n -2.3n +1 A. -1. B. 1 - . C. 1 . D. 3 . 2 2 2 Lời giải Chọn B n n Giải nhanh : 3 1 - 3 1 = - 2n -2.3n +1 2 - .3n 2 æ1 n ö 1-ç ÷ ç ÷ n - ç ÷ Cụ thể : 3 1 è3ø 1 lim = lim = - . 2n - 2.3n +1 æ2 n ö æ1 n ö 2 ç ÷ ç ÷ - 2 +ç ÷ ç ÷ çè3÷ø çè3÷ø æçç ( n ö 5) n 1 -2 + +1 2 ÷ + ÷ Câu 3: 2n 3 a 5 Biết rằng lim ç ÷ ç + ÷ = + c với , a , b c Î .
Tính giá trị của biểu thức + ÷ çç - ÷ n ç + è ( )n 1 2 n 1 5.2 5 -3 b ÷÷ø 2 2 2
S = a + b + c . A. S = 26. B. S = 30. C. S = 21.
D. S = 31. Lời giải Chọn B æç 2 n 1 n ö æ ö æ ö ÷ æçç ( )n ö ç ç ÷ ç ÷ 3 ÷ - - + ÷ ç ç ÷ + n 1 + 1 2. ç ÷ + ÷ ç ç ÷ ç ÷ + ÷ 2 2 5 2 1 ÷ 2 2 ÷ n 3 è ç ÷ ç 5 ø è 5 ø ÷ lim ç ++ ÷ = lim n ÷ ç + ÷ n+ ÷ ç ç n n ÷ çç5.2 - ÷ n + è ( 5) 1 2 n 1 - ÷ ç æ ö æ ö 1 3 ÷ ç 2 1 ø ç ÷ ç ÷ 1 ÷ ç5.ç ÷ + 5 -. - ÷ çç ç ÷ ç ÷ 2 ÷ ÷ ç ÷ ÷ è è 5 ø è 5 ÷ n ø ÷ø 1 5 = + 2 = + 2. 5 5 Giải nhanh : ( )n ì 1 n ï = n+ a 1 5 -2 +1 2 ï n + ( 5 2 3 ) 2 2n 1 5 ï 2 2 + + = + = + ¾¾ b í = 5. n+ n+ 5.2 - ï n +( 5) 1 2 n 1 -3 ( 5) 1 2 n 5 5 ïc ï = 2 ïî Vậy 2 2 2
S = 1 + 5 + 2 = 30. n n 2n Câu 4: p +3 + 2
Kết quả của giới hạn lim là: n n 2n+2 3p -3 + 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 304
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1. B. 1. C. . +¥ D. 1 . 3 4 Lời giải Chọn D n n 2n n n n n Giải nhanh: p +3 + 2 p +3 + 4 4 1 = = n n 2n+2 3p -3 + 2 3 n
p -3n + 4.4n 4.4n 4 n æpö æ3 n ö ç ÷ ç ÷ +ç ÷ ç ÷ +1 n n 2n + + ç ÷ è ø ç ÷ Cụ thể : p 3 2 4 è4ø 1 lim = lim = . n n 2n+2 3p -3 + 2 n æpö æ3 n ö 4 3.ç ÷ ç ÷ -3.ç ÷ ç ÷ + 4 çè 4÷ø çè4÷ø Câu 5: é ù
Kết quả của giới hạn lim ê3 - 5n n ú là: ë û A. 3. B. - 5. C. . -¥ D. . +¥ Lời giải Chọn D
Giải nhanh : Vì 3> 5 nên 3 5n n 3n - ¾¾ + . ¥ li ìï m3n = +¥ n æ ö æ ö ï é ù ç ÷ ï Cụ thể : n ç ç ÷ ï n n 5 lim ê3 - 5 ú = lim 3 1 ÷ ç -ç ÷ ÷ n í æ ö ç ç ÷ = +¥ vì . ë û ï ç 5 ç ç ÷ ç è 3 ÷ ÷ ÷ ø ÷ è ø li ï m1-ç ÷ ï ç ÷ =1> 0 ç ï è 3 ÷ø ïî
Câu 6: Kết quả của giới hạn ( 4 n 1
lim 3 .2 + -5.3n ) là: A. 2 . B. -1. C. . -¥ D. 1. 3 3 Lời giải Chọn C Giải nhanh : 4 n 1 3 .2 + -5.3n 5 - .3n = -¥ ( 5 - < ) 0 . li ìï m3n = +¥ ï n æ ö æ ö ï Cụ thể : ç ÷ lim( ï n+ n n 2 4 1 3 .2 -5.3 ) = lim3 1 ç 62.ç ÷ ç ç ÷ -5÷÷ = -¥ vì æ í ç 2 n ö æ ö . ç çè ÷ 3÷ø ÷÷ è ø l ï im 162 ç .ç ÷ ï ç ç ÷ -5÷÷ = 5 - < 0 ï ç çè3÷ø ÷÷ ï è ø ïî n n 1 + Câu 7: 3 - 4.2 -3
Kết quả của giới hạn lim là: 3.2 + 4n n A. 0. B. 1. C. . -¥ D. . +¥ Lời giải Chọn A 1 n n n+ n - - æ ö Giải nhanh : 3 4.2 3 3 3 = ç ÷ ç ÷ ¾¾ 0. 3.2 + 4n 4n ç ÷ n è4ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 305
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 n n 1 + 1 n n+ n n 1 + - - æ ö Cụ thể : 3 4.2 3 8.3 3 3 -4.2 -3 0 £ £ = 24.ç ÷ ç ÷ 0 ¾¾ lim = 0. 3.2 ç ÷ n + 4n 4n è4ø 3.2n + 4n n 1 + Câu 8: 2 +3n +10
Kết quả của giới hạn lim là: 2 3n -n + 2 A. . +¥ B. 2 . C. 3 . D. . -¥ 3 2 Lời giải Chọn A ìï n ï ï n n(n - ) 1 (n - 2) 0 3 n . Ta có n ï n k n 3 ï2
2 = åC 2 ³ C = í . Khi đó: n n ï k = 6 6 n 0 2 ïï +¥ ï 2 ïîn ìï 2n li ïï m = +¥ n æ1 n ö 2 ï 2 + 3. +10.ç ÷ ç ÷ ï n ï n 1 2 + + 3n +10 2n 2n çè2÷ø ï n lim = lim . = +¥ vì ï n æ1ö í + + ç ÷ . 2 2 3 2 3. 10. ï ç ÷ n - n + 2 n 1 2 ç ÷ 3- + ï 2n è2ø 2 2 li ï m = > 0 n n ïï 1 2 3 ï 3- + ï 2 ïî n n n n 1 + Câu 9: 4 + 2 1
Tìm tất cả giá trị nguyên của a thuộc (0;2018) để 4 lim £ . 3n + 4n+a 1024 A. 2007. B. 2008. C. 2017. D. 2016. Lời giải Chọn B æ1 n ö 1+ 2.ç ÷ ç ÷ n n 1 4 + 2 + çè2÷ø 1 1 1 4 lim = lim = = = . + 4 3n + 4n a æ3 n ö 4a a ç ÷ (2 )2 2a a ç ÷ + 4 çè4÷ø n n 1 + n Giải nhanh: 4 + 2 4 1 1 4 a 10 4 = £
2 ³1024 = 2 a ³10. n n+2 3 + 4 4n+a 2a 1024 Mà a Î(0; )
2018 và a Î nên a Î {10;2017} ¾¾ có 2008 giá trị . a æ 2 ö ç n + 2n (- )n Câu 10: 1 ÷
Kết quả của giới hạn lim ç ÷ ç + ÷ bằng: çç 3 ÷ n -1 3n ÷ è ø A. 2 . B. -1. C. 1. D. 1 - . 3 3 3 Lời giải Chọn C æ 2 ö ç n + 2n (- )n 2 1 ÷ n + 2n (- )n . Ta có 1 limç ÷ ç + ÷ = lim + lim . Ta có çç 3 ÷ n -1 3n ÷ 3n -1 3n è ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 306
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 2 ïï + 2 1 ï n + 2n ï n 1 li ï m = lim = ïï 3n -1 1 æ 2 3 n ö ï 3- ç n + 2n (- ) 1 ÷ 1 í limç ÷ ç + ÷ = . n ï ç ï ç 3 ÷ n -1 3n ÷ 3 è ø ïï (- ) 1 n æ1ö (- ) 1 n n 0 ïï £ £ ç ÷ ç ÷ 0 lim = 0 ïï 3n çè3÷ø 3n ïî æç 3 ö n +(- )n Câu 11: 1 cos 3n ÷
Kết quả của giới hạn lim ç ÷ ç ÷ bằng: ç ÷ çè n -1 ÷ø A. 3 . B. 3. C. 5. D. -1. 2 Lời giải Chọn B æç 3 ö æ ö n +(- ) 1 n cos 3n÷ ç 3n (- )n . 1 cos 3n÷ limç ÷ ç ÷ = limç ÷ Ta có : ç ÷ ç + ÷. ç - ÷ ç ÷ è n 1 ÷ø çè n -1 n ÷ø ìï 3n 3 li ïï m = = 3 ïï n -1 1 æ ï ç 3 ö n +(- ) 1 n cos 3n÷ í limç ÷ ç ÷ = 3. ïï (- ) 1 n cos 3 1 (- ) 1 n ç ÷ n cos 3n çè n -1 ÷ 0 ï £ £ 0 lim = 0 ø ïï n -1 n -1 n -1 ïî
Câu 12: Kết quả của giới hạn lim 2.3n -n +2 là: A. 0. B. 2. C. 3. D. . +¥ Lời giải Chọn D n Ta có n æ ö n n 1
lim 2.3 - n + 2 = lim 3 . 2- + 2.ç ÷ ç ÷ . Vì 3n çè3÷ø üïïïïïï lim 3n ï = +¥ ïï li ìï ï ï m 3n = +¥ ï ï n n n 2 ï ï 0 0 lim n = 0 £ £ = = ý ¾¾ n í , n 2 3 æ ö C n(n - ) n - ï ï n 1 1 n 1 3 ï ï - + ç ÷ n lim 2 2. ï ï ç ÷ = 2 > 0 ï ï 3n çè3÷ 2 ï ïî ø ïï æ1 n ö ï limç ÷ ç ÷ = 0 ïï çè3÷ ï ø ïþ
do đó lim 2.3n -n + 2 = + . ¥
Dạng 5. Tổng của cấp số nhân lùi vô hạn 1. Phương pháp
Cấp số nhân lùi vô hạn là cấp số nhân vô hạn và có công bội là q 1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 307
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Tổng các số hạng của một cấp số nhân lùi vô hạn (un) 1 u S 1
u u2 ... un ... 1q
Mọi số thập phân đều được biểu diễn dưới dạng luỹ thừa của 10 n 1 a a2 3 a a X N, 1 a a2 3 a ...an... N ... ... 2 3 n 10 10 10 10
2. Các ví dụ rèn luyện kĩ năng n 1 1 1 1 1
Ví dụ 1: Tính tổng của cấp số nhân lùi vô hạn 1, , , ,..., ,... 2 4 8 2 Hướng dẫn giải 1 Theo đề cho ta có: 1 u 1, q . 2 1 u 1 2 S . 1 q 1 3 1 2
Ví dụ 2: Cho số thập phân vô hạn tuần hoàn a 0,212121... (chu kỳ là 21). Tìm a dưới dạng phân số. Hướng dẫn giải
Cách 1: Giải bằng tự luận Ta có: a 0,212121...
0,21 0,0021 0,000021 ... 1 1 1 21 ... 2 4 6 10 10 10 1 1 1 1 1 Tổng S ... u , q . 2 4 6
là tổng cấp số nhân lùi vô hạn có 10 10 10 1 2 2 10 10 1 u 2 1 10 1 1 7 S . A 21. . 1 Do đó q 1 99 1 99 33 2 10
Cách 3: Giải nhanh bằng máy tính 7
Nhập vào màn hình 0,2
1 và ấn phím ta được kết quả . 33 2 3 n 1
Ví dụ 3: Tổng Sn 1 0,9 0,9 0,9 ... 0,9
... có kết quả bằng bao nhiêu? Hướng dẫn giải 2 3 n 1 S 1 0,9 0,9 0,9 ... 0,9 ...
Đây là tổng của cấp số nhân lùi vô hạng có 1 u 1, q 0,9.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 308
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 u 1 S 10. 1 q 1 0,9 2 3
Ví dụ 4: Cho S 1 q q q ..., q 1 T 1 Q 2 Q 3 Q ..., Q 1 E 1 qQ 2 2 q Q 3 3 q Q ...
Biểu thị biểu thức E theo S,T Hướng dẫn giải 2 3
S 1 q q q ..., q 1 là tổng của cấp số nhân lùi vô hạn, có 1 u 1, q q. Khi đó: 1 u 1 S 1 S q . 1 q 1 q S (1) 1 T 1 Tương tự: T Q . 1 (2) Q T 2 2 3 3
E 1 q.Q q .Q q .Q ... là tổng của cấp số nhân lùi vô hạng công bội qQ (vì qQ 1, và 1 u 1). 1 u E 1qQ (3) Thay (1), (2) vào (3): 1 u ST E E . T 1 S 1 S T 1 1 . T S 1
Ví dụ 5: Tìm số hạng 1
U của cấp số nhân lùi vô hạn, biết S 4; q . 2 Hướng dẫn giải u u Ta có: 1 S q 1 1 4 1 u 2. 1 q 1 1 2
Ví dụ 6: Tìm công bội của cấp số nhân lùi vô hạn, biết S 6 ; 1 U 3 . Hướng dẫn giải 3 1 Ta có: 1 u S q 1 6 q . 1 q 1 q 2
3. Bài tập trắc nghiệm
Câu 1: Tổng của một cấp số nhân lùi vô hạn bằng 2 , tổng của ba số hạng đầu tiên của cấp số nhân bằng 9 . Số hạng đầu 4 1
u của cấp số nhân đó là: A. 9 u = 3. B. u = 4. C. u = . D. u = 5. 1 1 1 2 1 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 309
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi q là công bội của cấp số nhân, ta có : ìï ì 1 u ï 1 ï = 2 ï u ìï = 2 1-q ïq = - ï - ï 1 ( ) 1 ï q ï ï ï 2 ï ï í í í . 3 ïï 1- q 9 ïï2( 9 3 1- q ) ï æ = 1ö ï ï = = ï ï = ç ÷ S u . u 2 1 ï ïî ç + ÷ = 3 3 1 4 1 ï 1 ï ç ÷ - q 4 è ï ï 2ø î î Câu 2: 1 1 1
Tính tổng S = 9 +3+1+ + ++ + . 3 3 9 3n- A. 27 S = . B. S = 14. C. S = 16. D. S = 15. 2 Lời giải Chọn A Ta có æ ö ç ÷ æ ö ç ÷ ç ÷ ç ÷ 1 1 1 ç 1 1 1 1 ÷ ç ÷ ç 1 ÷÷ 27 ç = + + + + ++ += ç + + + ++ + ÷÷ = ç ÷ S 9 3 1 9 1 9 ÷ = ç . n 3 - 2 4 n 1 3 9 3 çç 3 3 3 3 - ÷ ç
÷ 1 ÷÷ 2 ç ÷ 1 ç ÷ ç ÷ ç - ÷ 1 ç ÷ ç ÷ è ø
CSN lvh: u = q= ÷ 3 1 1, è ø 3 æ ö Câu 3: Tính tổng 1 1 1 1 S = 2 1 ç ÷ ç + + + ++ + ÷ ç . è 2 4 8 2n ÷ø A. S = 2 +1. B. S = 2. C. S = 2 2. D. 1 S = . 2 Lời giải Chọn C Ta có æ ö ç ÷ æ ö ç ÷ ç ÷ ç ÷ ç 1 1 1 1 ÷ ç ÷ ç 1 ÷÷ ç = ç + + + ++ + ÷÷ = ç ÷ S 2 1 2 ÷ = 2 2. ç ç ç 2 4 8 2n ÷ ç 1 ÷
÷ ÷ ç ÷ 1 ç ç ÷ ç - ÷÷ 1 ç ç ÷ è ø CSN lv : h u = q= ÷ 2 1 1, è ø 2 n Câu 4: Tính tổng 2 4 2 S = 1+ + ++ + . 3 9 3n A. S = 3. B. S = 4. C. S = 5. D. S = 6. Lời giải Chọn A Ta có 2 2 4 2n 2 æ2ö æ2 n ö 1 S = 1+ + ++ + =1+ +ç ÷ ç ÷ ++ç ÷ ç ÷ + = 3. 3 9 3n 3 çè3÷ = ø çè3÷ø 2
1- 2 = = 3 CSN lvh: 1 u 1, q 3 + 1 1 1 (- )n 1 1
Câu 5: Tổng của cấp số nhân vô hạn ,- , ,..., ,... bằng: n 1 2 6 18 2.3 -
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 310
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 3 . B. 8. C. 2 . D. 3. 4 3 3 8 Lời giải Chon D . Ta có : æ ö ç ÷ æ ö ç ÷ + + ç ÷ ç ÷ 1 1 1 (- )n 1 1 1 ç 1 1 (- )n 1 1 ÷÷ 1çç 1 ÷÷ 3 ç = - + ++ += ç - + ++ ÷÷= ç ÷ S 1 ÷ = ç . n 1 - 2 n 1 2 6 18 2.3 2 çç 3 3 3 - ÷
÷ 2 ç 1 ÷÷ 8 ç ÷ 1 ç ÷ ç ÷ ç + ÷ 1 ç ÷ ç ÷ è ø CSN lvh:u = q=- ÷ 3 1 1, è ø 3 æ ö æ ö æ ö Câu 6: Tính tổng 1 1 1 1 1 1 S = ç ÷ ç - ÷+ç ÷ ç - ÷+... +ç ÷ ç - ÷+... ç . è2 3÷ø çè4 9÷ø çè2n 3n ÷ø A. 1. B. 2 . C. 3 . D. 1 . 3 4 2 Lời giải Chọn D Ta có æ1 1ö æ1 1ö æ 1 1 ö S = ç ÷ ç - ÷+ç ÷ ç - ÷+...+ç ÷ ç - ÷+... çè2 3÷ø çè4 9÷ø çè2n 3n ÷ø æ ö æ ö ç ÷ ç ÷ ç ÷ ç ÷ 1 1 ç ÷ ç ÷ ç ÷ 1 1 1 ÷ ç1 1 1 ÷÷ 1 1 = çç + ++ + ÷ ç 2 3 ÷ -ç + ++ + ÷÷ = - = - = ç 1 . ç2 4 2n ÷ ç
÷ ç3 9 3n ÷ 1 1 ç
÷ ç÷ 2 2 ç ÷ 1- 1- 1 ÷ ç 1 ç ÷ ÷÷ CSN lvh: ÷ è ø ç 2 3 1 u =q= CSN lv : h 1 u =q= è ø 2 3 2 n Câu 7:
1+ a + a +... + a
Giá trị của giới hạn lim
a < 1, b <1 bằng: 2 ( ) 1+b +b +... n +b A. -b -a 0. B. 1 . C. 1 . D. Không tồn tại. 1-a 1-b Lời giải Chọn B Ta có 2 1+ + +... n a a
+a là tổng n +1 số hạng đầu tiên của cấp số nhân với số hạng đầu là 1 và 1.( n 1 1 a + ) n 1 + - công bội là -a n 1 a , nên 2
1+ a + a +... + a = = . 1-a 1-a 1( n 1 1 b + ) n 1 + - Tương tự: -b n 1 2
1+ b + b +... + b = = . 1-b 1-b n 1 1-a + 2 n n 1 + Do đó
1+ a + a +... + a 1- 1-b 1-a 1- lim = lim = lim . b a =
a <1, b < 1 . 2 n n 1 + n 1 + ( )
1+ b + b +... +b 1-b 1-a 1-b 1-a 1-b Câu 8: Rút gọn 2 4 6 2 S = 1+ cos +cos +cos ++cos n x x x
x + với cos x ¹ 1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 311
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 1 1 S = sin x. B. 2 S = cos x. C. S = . D. S = . 2 sin x 2 cos x Lời giải Chọn C Ta có n 1 1 2 4 6 2
S = 1+ cos x + cos x + cos x ++ cos x + = = .
2 2 1-cos x sin 2 x CSN lvh: 1 u 1 = , q=cos x Câu 9: Rút gọn 2 4 6 = - + - ++(- )n 2 1 sin sin sin 1 . sin n S x x x
x + với sin x ¹ 1. A. 2 1 S = sin x. B. 2 S = cos x. C. S = . D. 2 S = tan x. 2 1+ sin x Lời giải Chọn C Ta có n n 1 2 4 6
S = 1-sin x + sin x -sin x ++(- ) 2 1 .sin x += . 2
1+ sin x 2 CSN lv : h 1 u 1 = , q=-sin x Câu 10: p Thu gọn 2 3
S = 1- tan a + tan a - tan a +¼ với 0 < a < . 4 A. 1 a a S = . B. cos S = . C. tan S = . D. 2 S = tan . a 1- tan a æ pö 1+ tan a 2 sin a ç ÷ ç + ÷ çè 4 ÷ø Lời giải Chọn B æ ö Ta có p tan a Î(0 )
;1 với mọi a Îçç0; ÷÷, ç do đó è 4÷ø 1 cos a cos a 2 3
S = 1- tan a + tan a - tan a +¼ = = = .
+ + æ ö = =- a a a p a 1 tan sin cos CSN lv : h ç ÷ 1 u 1, q tan 2 sin a ç + ÷ çè 4 ÷ø
Câu 11: Cho m, n là các số thực thuộc ( 1 - ; ) 1 và các biểu thức: 2 3
M = 1+ m + m + m + 2 3
N = 1+ n + n + n + 2 2 3 3
A = 1+ mn + m n + m n +
Khẳng định nào dưới đây đúng? A. MN MN A = . B. A = . C. 1 1 1 A = + - . D. M + N -1 M + N +1 M N MN 1 1 1 A = + + . M N MN Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 312
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A ìï 1 ìï 1 ïM = ïm =1- ï ï Ta có ïï 1- m ï M í í , khi đó ï 1 ï 1 ï ï ïN = ïn = 1- ïïî 1 n ï - ïî N 1 1 MN A = = = . 1- mn æ 1 öæ 1 ö M + N -1 1- 1 ç ÷ ç - ÷ 1 ç ÷ ç - ÷ ç ÷ è øç ÷ M è N ø
Câu 12: Số thập phân vô hạn tuần hoàn 0,5111 được biểu diễn bởi phân số tối giản a . Tính tổng b T = a + . b A. 17. B. 68. C. 133. D. 137. Lời giải Chọn B Ta có 2 - 3
0,5111= 0,5 +10 +10- ++10-n + Dãy số -2 3
10 ;10- ;...;10-n ;... là một cấp số nhân lùi vô hạn có số hạng đầu bằng -2 u = 10 , công 1 2 - bội bằng - u 10 1 1 q = 10 nên 1 S = = = . -1 1-q 1-10 90 46 23 a ìï = 23 Vậy 0,5111... 0,5 ï = +S = = ¾¾ í ¾¾ T
= a +b = 68. 90 45 b ï = 45 ïî
Câu 13: Số thập phân vô hạn tuần hoàn A = 0,353535... được biểu diễn bởi phân số tối giản a . Tính b T = a . b A. 3456. B. 3465. C. 3645. D. 3546. Lời giải Chọn B Ta có 35 2 35 35 35 ìïa = 35 10 ï
A = 0,353535... = 0, 35 + 0, 0035 + ... = + +... = = í T = 3465. . 2 4 10 10 1 99 b ï = 99 1 ï - î 2 10
Câu 14: Số thập phân vô hạn tuần hoàn B = 5,231231... được biểu diễn bởi phân số tối giản a . Tính b T = a - . b A. 1409. B. 1490. C. 1049. D. 1940. Lời giải Chọn A Ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 313
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B = 5, 231231... = 5 + 0, 231+ 0, 000231+... 231 3 231 231 231 1742 ìïa =1742 10 5 ... 5 5 ï = + + + = + = + = ¾¾ í T =1409 3 6 10 10 1 999 333 b ï = 333 1- ïî 3 10
Câu 15: Số thập phân vô hạn tuần hoàn 0,17232323¼ được biểu diễn bởi phân số tối giản a . Khẳng b
định nào dưới đây đúng? A. 15 a -b > 2 . B. 14 a -b > 2 . C. 13 a -b > 2 . D. 12
a -b > 2 . Lời giải Chọn D Ta có æ 1 1 1 ö 0,17232323¼= 0,17 + 23ç ÷ ç + + ÷ 4 6 8 1 çè 0 10 10 ÷ø 1 17 17 23 1706 853 10000 = + 23. = + = = . 100 1 100 100.99 9900 4950 1-100 ìïa = 853 ï 12 13 ¾¾ í
2 < T = 4097 < 2 . b ï = 4950 ïî
Dạng 6: Giới hạn dãy số có quy luật công thức, dãy cho bởi hệ thức truy hồi 1. Phương pháp
Dãy tăng và bị chặn trên hoặc giảm và bị chặn dưới thì tồn tại giới hạn.
Phương pháp quy nạp thường được sử dụng.
2. Các ví dụ rèn luyện kĩ năng 1 1 1 Ví dụ 1: Cho u ... lim u n 1.2 2.3 . Tính nn 1 n Hướng dẫn giải 1 1 1 Ta luôn có: áp dụng vào u : kk 1 k k 1 n 1 1 1 1 u ... n 1.2 2.3 3.4 nn 1
1 1 1 1 1 1 1 1 1
... 1
1 2 2 3 3 4 n n 1 n 1 1 Do đó: lim un lim1 1. n 1 1 1 1 1 Ví dụ 2: Cho u lim u n ... Tính . 3.5 5.7 7.9 2n 1 2n 1 n Hướng dẫn giải 1 1 1 1 Ta luôn có: 2k 1 2k . 1 2 2k 1 2k 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 314
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 1 1 un ... 3.5 5.7 7.9 2n 12n 1
1 1 1 1 1 1 1 1 1 1 1 1
... 2
3 5 2 5 7 2 7 9 2 2n 1 2n 1 1 1 1 . 2 3 2n 1 1 1 1 1 Do đó lim un lim . 2 3 2n 1 6 1 2 3 ... n Ví dụ 3: lim 2 bằng bao nhiêu? 2n Hướng dẫn giải nn 1 1 2 3 ... n nn 1 1
Vì 1 2 3 ... n lim lim . 2 nên: 2 2 2n 4n 4 1 1 1
Ví dụ 4: Tính giới hạn: lim 1 1 ...1 . 2 2 2 2 3 n Hướng dẫn giải 1 1 1 2 2 2 1 3 2 1 n 1 Ta có: 1 1 ...1 . ... 2 2 2 3 2 n 2 2 2 2 3 n
2 1.2 1.3 1.3 1...n 1n 1 n1 . 2 2 2 2 .3 ...n 2n 1 1 1 1 Vậy lim 1 1 ...1 . 2 2 2 2 3 n 2 1 U 2
Ví dụ 5: Tìm giới hạn của dãy: U 1 . n * Un 1 ; n 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận
Ta chứng minh dãy Un là bị chặn: 1 Un 2.
Dãy Un là dãy giảm. U 1 Thật vậy ta xét U U n 2U U 1 U 1 k U 1 k k 2 k k k (đúng).
Vậy dãy Un có giới hạn. Đặt lim U n a . U 1 a 1 Ta có: lim n Un lim a a 1. 1 2 hay 2
Cách 2: Giải nhanh bằng máy tính
Khai báo: 1 X {biến đếm}; 2 A {giá trị 1 u } A 1
Ghi vào màn hình: X X 1: A 2
Ấn CALC và lặp lại phím , quan sát ta thấy dãy giảm và bị chặn dưới bởi 1. Vậy lim Un 1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 315
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 U 2
Ví dụ 6: Tìm giới hạn của dãy: . * U n 1 2 Un ; n Hướng dẫn giải
Cách 1: Giải bằng tự luận
Ta sẽ chứng minh dãy bị chặn: 2 U n
2 (bằng phương pháp quy nạp). 1 U 3 (đúng). Giả sử Uk 2, k 1.
Ta có: Uk 1 2 Uk 2 2 2 k 1 . * Vậy Uk 2 n . * Tương tự: Un 2 n
. Ta chứng minh dãy Un là dãy tăng (bằng phương pháp quy nạp). + 1 U 2; U2 2 2 1 U U2. + Giả sử U U k k 2 1 k . Ta xét U U ; k * k k 1 U 2 U 2 U 2 U 2 U U 2 k m k k k k 0 1 U k
2 (luôn đúng vì 2 U 2, k * k )
Vậy dãy Un tăng; bị chặn trên nên có giới hạn, gọi a lim U n limUn1. 2
Ta có: lim U 2 LimU a 2 a a 2 n n a a 2 (nhaän) 2
a a 2 0 a 1(loaïi)
Cách 2: Giải nhanh bằng máy tính
Khai báo: 1 X {biến đếm}; 2 A {giá trị 1 u }
Ghi vào màn hình: X X 1: A 2 A
Ấn CALC và lặp lại phím , quan sát ta thấy dãy tăng và bị chặn dưới bởi 2. Vậy lim Un 2. 1 U 3
Ví dụ 7: Tìm giới hạn của dãy: 1 3 * . U n 1 U n ; n 2 U n 1 3 3 A. 2. B. . . 2 C. 3. D. 2 Hướng dẫn giải ĐÁP ÁN C Ta có: U 0, n * n . 1 3 *
Theo bất đẳng thức Cô‐si, ta có: Un 1 U n 3, n . 2 U n
Vậy Un là dãy bị chặn dưới.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 316
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 3 2 2 1 U Vì U 3 U 3 U n n n 1 U n U n 2 U 2 n U n n 1 U U * n n Un , n . 2
Dãy đã cho là giảm. Vậy dãy có giới hạn. Đặt limUn 1 limUn a. 1 3 Ta có: lim U lim n U n 2 U n 1 3 2
a a a 3 a 3. 2 a
3. Bài tập trắc nghệm
1 3 5 ... 2n 1
Câu 1: Tính giới hạn: lim . 2 3n 4 1 2 A. 0. B. . . 3 C. 3 D. 1. Lời giải ĐÁP ÁN B Ta có:
2 1 3 5 ... 2n 1 n 1 .
1 3 5 ... 2n 1 n 2 1 Vậy: lim lim 2 3n 2 4 3n 4 2 1 2 1 2 n 2n 1 n n 1 lim lim . 2 3n 4 4 3 3 2 n 1 1 1
Câu 2: Tính giới hạn: lim ... . 1.2 2.3 n n 1 A. 0. B. 1. 3 C. . 2
D. Không có giới hạn. Lời giải ĐÁP ÁN B 1 1 1 1 1 1 1 1 Ta có: lim ... lim 1 ... 1.2 2.3 nn 1 2 2 3 n n 1 1 lim1 1. n 1 1 1 1
Câu 3: Tính giới hạn: lim ... . 1.3 3.5 n 2n 1 2n 1 1 A. 1. B. 0. C. . 2 D. 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 317
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải ĐÁP ÁN C. 1 1 1 Ta có: lim ... 1.3 3.5 n2n 1 2n 1 1 1 1 1 1 1 1 1 1
lim1 ... lim1 . 2 3 3 5 2n 1 2n 1 2 2n 1 2 1 1 1
Câu 4: Tính giới hạn: lim ... . 1.3 2.4 n n 2 3 2 A. . . 4 B. 1. C. 0. D. 3 Lời giải ĐÁP ÁN A 1 1 1 Ta có: ... 1.3 2.4 nn 2 1 1 1 1 1 1 1 1 1 1
1 ... 2 3 2 4 3 5 n 1 n 1 n n 2 1 1 1 1 1 2 2 n 1 n 2 1 1 1 3 Vậy lim ... n n 2 . 1.3 2.4 4 1 1 1
Câu 5: Tính giới hạn: lim ... . 1.4 2.5 n n 3 11 3 A. . . 18 B. 2. C. 1. D. 2 Lời giải ĐÁP ÁN A 1 1 1 Ta có: ... 1.4 2.5 nn 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
... 3 1 4 2 5 3 6 4 7
n 3 n n 2 n 1 n 1 n 2 n n 3 vậy: 1 1 1 1 1 1 1
3 2 3 n 1 n 2 n 3 1 1 1 11 lim ... n n 3 . 1.4 2.5 18 1 2 3 ... n
Câu 6: Cho dãy un với un . 2
Mệnh đề nào sau đây là mệnh đề đúng? n 1 1 A. lim un 0. B. lim un . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 318
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. lim un 1.
D. lim un không tồn tại. Lời giải ĐÁP ÁN B
Dãy số 1, 2, 3, …, n là cấp số cộng có số hạng đầu là 1
u 1 số hạng cuối cùng u n n , công sai d 1. n 1 u n nn 1 Khi đó n
S 1 2 3 . . n . 2 2 nn 1 Viết lại: u n 2 2 n 1 1 2 n 1 n n 1 n 1 lim un lim 2 lim lim . 2 n 1 2 2 2 n 2 2 n 1 1 U 2
Câu 7: Tìm giới hạn của dãy: . 2 1 Un * Un 1 ; n 2 2 A. 2. B. 1. C. 2.
D. Không có giới hạn. Lời giải ĐÁP ÁN B 1 5 57 Ta có: U ; U ; U 1 2 3 ;... 2 8 64
Ta chứng minh: U 1 n * n
(bằng phương pháp quy nạp). Vậy dãy bị chặn trên.
Ta chứng minh Un là dãy tăng. Thật vậy: 2 1 U Ta có: U U n n U 1 n n 2 2 U 2U 1 0 U 1 n n U n 2 2
1 0 luôn đúng * n , vì n .
Vậy dãy có giới hạn. Đặt a lim U n limUn1. 2 2 1 Un 1 a 2 Ta có: lim U lim n a 2a 1 a 1 2 2 2 2 2
a 2a 1 0 a 1. 1 U 5
Câu 8: Tìm giới hạn của dãy: 2 2 U . n * Un 1 ; n 2U n A. 1. B. 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 319
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. 3.
D. Không có giới hạn. Lời giải ĐÁP ÁN B 1 1 Ta có: U U n 2 U 0 U 1 n U
). Vậy n là dãy bị chặn dưới. n 2
(theo bất đẳng thức Cô‐si với n *
Dấu “=” không xảy ra, nên Un 2, n . U 2 2 U 1 1 2 Lại có: n1 n . Vì U 2 U 2 2 2 U n n n 2U U 2 n n 1 1 1 1 1 1 * 1 U U , n . 2 2 n 1 n U 2 U 2 2 2 n n
Vậy dãy giảm, khi đó Un có giới hạn. Đặt limU lim U n a a 0 1 n . 2 2 U 2 2 a Ta có: lim U n lim a 2 2a 2 2 n a 1 2Un 2a 2
a 2 a 2 (vì a 0 ). U 1 2
Câu 9: Tìm giới hạn của dãy: U 2.U ; n * n 1 n A. 2. B. 1 2. 1 7 C. . 2
D. Không có giới hạn. Lời giải ĐÁP ÁN A Ta có: U 2; U 1 2 2 2 ;… Ta sẽ chứng minh U n 2 ; * n
(bằng phương pháp quy nạp). n 1, U 2 U 2, k 1 1 2 . Giả sử k . Ta có: Uk 1 2Uk 2.2 4 2. * Vậy U 2, n n . Lại có: Un 0, n . U 2U 2 2 n 1 n Lại có: 1 Un Un Un 2 dãy tăng.
Vậy dãy đã cho có giới hạn. Đặt lim U lim U a a 0 n 1 n 2 Ta có: lim Un 1 lim 2Un a 2a a 2a a 2.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 320
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. GIỚI HẠN HÀM SỐ
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM 1. Định nghĩa
Cho khoảng K chứa điểm x y f x 0 và hàm số
xác định trên K hoặc trên K \{x0}. Ta nói hàm số
y f x có giới hạn là số L khi x dần đến x0 nếu với dãy số xn bất kì,
xn K \{x0} vaø xn x0,tacoù f(xn) L.
Kí hiệu: lim f(x) L hay f(x) L khi x x0 xx0 lim f(x) L (x
n),xn K \{x0},xn x0 f(xn) L xx0
2. Định lí về giới hạn hữu hạn:
Ta thừa nhận định lý sau:
a)Giaûi söû lim f(x) L vaø lim g(x) M.Khi ñoù: xx xx 0 0
* lim f(x) g(x) L M; x x0 * lim f(x).g(x) L.M; x x0 f(x) L * lim neáuM 0. xx0 g(x) M
b)Neáuf(x) 0 vaø lim f(x) L thì :L 0 vaø lim f(x) L. xx xx 0 0
Daáu cuûa f(x) ñöôïc xaùc ñònh treân khoaûng ñang tìm giôùi haïn, vôùi x x0
3. Giới hạn một bên * Định nghĩa:
Cho hàm số y f x xác định trên khoảng x0;b.
Số L được gọi là giới hạn bên phải của hàm số y f x khi x x0 nếu với dãy số xn bất kì,
x0 xn b vaø xn x0 ta coù: f(xn) L. Kí hiệu: lim f(x) L x x 0
lim f(x) L xn ,x0 xn b,xn x0 f(xn) L x x 0
Cho hàm số y f x xác định trên khoảng a;x0 . Số L được gọi là giới hạn bên trái của hàm
số y f x khi x x0 nếu với dãy số xn bất kì, a xn x0 vaø xn x0 ta coù: f(xn) L. Kí hiệu: lim f(x) L. x x 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 321
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
lim f(x) L xn ,a xn x0,xn x0 f(xn) L. x x 0 * Định lí
lim f(x) L lim f(x) lim f(x) L. xx0 xx xx 0 0
II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC * Định nghĩa
Cho hàm số y f x xác định trên khoảng (a;). Ta nói hàm số y f x có giới hạn là số L
khi khi x nếu với mọi dãy số xn bất kì, xn a vaø xn ta coù: f(xn) L..
Kí hiệu: lim f(x) L hay f(x) L khix . x
lim f(x) L xn ,xn a,xn f(xn) L. x
Cho hàm số y f x xác định trên khoảng ( ;
a). Ta nói hàm số y f x có giới hạn là số L
khi khi x nếu với mọi dãy số xn bất kì, xn a vaø xn ta coù: f(xn) L.
Kí hiệu: lim f(x) L hay f(x) L khix . x
lim f(x) L xn ,xn a,xn f(xn) L. x
III. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ
1. Giới hạn vô cực
Các định nghĩa về giới hạn ( hoặc ) của hàm số được phát biểu tương tự các định nghĩa 1,2
hay 3 ở trên. Chẳng hạn, giới hạn của hàm số y f x khi x dần đến dương vô vực được định nghĩa như sau:
* Định nghĩa: Cho hàm số y f x xác định trên khoảng a;.
Ta nói hàm số y f x có giới hạn là khi x nếu với mọi dãy số (xn) bất kì,
xn a vaø xn , ta coù: f(xn) .
Kí hiệu: lim f(x) hay f(x) khi x x lim f(x) (
xn),xn a,xn f(xn) . x
Nhận xét: lim f(x) lim f(x) . x x
2. Các giới hạn đặc biệt
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 322
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 c 1. lim c c lim
0 vôùi c laø haèng soá x x x 2. lim x x k neáu k nguyeân döông 3. lim x x 0 neáu k nguyeân aâm k neáu k chaün 4. lim x x neáu k leû
3. Một vài quy tắc về giới hạn vô cực:
a) Quy tắc tìm giới hạn của tích f(x).g(x)
Nếu lim f(x) L 0 vaø lim g(x) hoaëc thì lim f(x)g(x) được tính theo quy tắc trong xx xx xx 0 0 0 bảng sau: lim f(x) lim g(x) lim f(x).g(x) xx0 xx0 xx0 L 0 L 0 - + f(x)
b) Quy tắc tìm giới hạn của tích g(x) lim f(x) lim g(x) Dấu của g(x) f(x) xx lim 0 xx0 xx0 g(x) L Tuỳ ý 0 + L 0 - 0 + L<0 -
Các quy tắc trên vẫn đúng cho các trường hợp x x
0,x x0,x ,x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 323
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Dãy số có giới hạn hữu hạn 1. Phương pháp
Nếu hàm số f x xác định trên K x0 thì lim f x f x0 . xx0
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính lim 2 x x 7. x 1 Hướng dẫn giải lim 2
x x 7 11 7 9. x 1 4 5 3x 2x Ví dụ 2: Tính lim 4 6 x 1 5x 3x 1 Hướng dẫn giải 4 5 3x 2x 3 2 1 lim . 4 6 x 1
5x 3x 1 5 3 1 9 Ví dụ 3: Tính 3 lim 4x 2x 3 là: x 1 Hướng dẫn giải ĐÁP ÁN A 3 lim 4x 2x 3 4 2 3 5. x 1 3 x 1 Ví dụ 4: Tính lim x 1 3 2 x 3 2 Hướng dẫn giải 3 x 1 1 1 lim 0. x1 3 3 2 x 3 2 4 2 4 2 x 4x 3 Ví dụ 5: Tính lim 2 x 2 7x 9x 1 Hướng dẫn giải 4 2 x 4x 3 16 16 3 1 lim . 2 x 2 7x 9x 1 28 18 1 3
3. Bài tập trắc nghiệm
Câu 1: Giá trị của giới hạn lim ( 2 3x +7x +1 ) 1 là: x 2 A. 37. B. 38. C. 39. D. 40. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 324
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A lim( 2 3x + 7x +1 ) 2 1 = 3.2 + 7.2 +11= 37 x2
Câu 2: Giá trị của giới hạn 2 lim x - 4 là: x 3 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B lim x - 4 = ( 3)2 2 - 4 =1 x 3 Câu 3: 1 Giá trị của giới hạn 2 lim x sin là: x 0 2 A. 1 sin . B. . +¥ C. . -¥ D. 0. 2 Lời giải Chọn D Ta có 1 1 2 lim x sin = 0.sin = 0 x0 2 2 2 Câu 4: x -3
Giá trị của giới hạn lim là: 3 x 1 - x + 2 A. 1. B. -2. C. 2. D. 3 - . 2 Lời giải Chọn B x -3 (- )2 2 1 -3 lim = = 2 - 3 x- x + 2 (- )3 1 1 + 2 3 Câu 5: x - x
Giá trị của giới hạn lim là: x (2x - ) 1 ( 4 1 x -3) A. 1. B. -2. C. 0. D. 3 - . 2 Lời giải Chọn C 3 3 x - x 1-1 lim = = 0 x (2x - ) 1 ( 4 x - ) 3 (2.1- ) 1 ( 4 1 1 - ) 3 Câu 6: x -1
Giá trị của giới hạn lim là: 4
x -1 x + x -3 A. 3 - . B. 2 . C. 3 . D. 2 - . 2 3 2 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 325
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D x -1 1 - 1 - Ta có 2 lim = = - 4 x 1 - x + x -3 1-1-3 3 2 Câu 7: 3x +1 - x
Giá trị của giới hạn lim là: x -1 x -1 A. 3 - . B. 1 . C. 1 - . D. 3 . 2 2 2 2 Lời giải Chọn A 2 Ta có 3x +1- x 3+1 +1 3 lim = = - x-1 x -1 -1-1 2 2 Câu 8: 9x - x
Giá trị của giới hạn lim là: x (2x - ) 1 ( 4 3 x -3) A. 1. B. 5. C. 1 . D. 5. 5 5 Lời giải Chọn C 2 2 9x - x 9.3 -3 1 lim = = x (2x- ) 1 ( 4 x - ) 3 (2.3- ) 1 ( 4 3 3 - ) 3 5 2 Câu 9: x - x +1 Giá trị của giới hạn 3 lim là: 2 x 2 x + 2x A. 1 . B. 1 . C. 1. D. 1. 4 2 3 5 Lời giải Chọn B 2 2 x - x +1 2 - 2 +1 1 3 lim = = 2 2 x2 x + 2x 2 + 2.2 2 3 2 Câu 10: 3x - 4 - 3x -2
Giá trị của giới hạn lim là: x 2 x +1 A. 3 - . B. 2 - . C. 0. D. . +¥ 2 3 Lời giải Chọn C 3 2 3 Ta có: 3x - 4 - 3x - 2 12- 4 - 6- 2 0 lim = = = 0 x2 x +1 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 326
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 2. giới hạn một bên 1. Phương pháp
Ta cần nắm các tính chất sau
lim f(x) L xn ,x0 xn b, lim xn x0 lim f(xn) L n n x x 0
lim f(x) L xn ,a xn x0, lim xn x0 lim f(xn) L n n x x 0
lim f(x) lim f(x) L lim f(x) L xx xx xx 0 0 0
2. Các ví dụ rèn luyện kĩ năng x 3 Ví dụ 1: Tính lim x 3 2x 6 Hướng dẫn giải
Cách 1: Giải bằng tự luận x 3 x 3 1 lim lim . x 3 2x 6 x 3 2x 3 2
Cách 2: Giải nhanh bằng máy tính x 3 Nhập vào màn hình và ấn 5 CALC 3 10 ta được kết quả 2x 6 3 1 x Ví dụ 2: Tính lim 2 x 1 3x x Hướng dẫn giải 3 1 x 0 lim 0. 2 x 1 3x x 4 3 x 2x 3 Ví dụ 3: Tính lim 2 x 2 x 2x Hướng dẫn giải ĐÁP ÁN D
Tử số có giới hạn là 1
, mẫu số có giới hạn 0 và khi x 2 thì 2 x 2x 0. 3 x 2x 3 Do đó lim . 2 x 2 x 2x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 327
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2x x Ví dụ 4: Tính lim x 0 5x x Hướng dẫn giải x 2 x 1 2 x 1 2x x 1 lim lim lim 1 . x 0 5x x x 0 x 5 x 1 x 0 5 x 1 1 2 x 4x 3 Ví dụ 5: Tính lim 3 2 x 1 x x Hướng dẫn giải 2 x 4x 3 x 1x 3 x 1x 3 0 lim lim lim 0. 3 2 x x 2 x x 1 2 1 x 1 x 1 x 1 x 2 x 1 vôùi x 1
Ví dụ 6: Cho hàm số f x 1 x
. Khi đó lim f x bằng bao nhiêu? x 1 2x 2 vôùi x 1 Hướng dẫn giải 2 x 1 lim f x lim
vì tử số có giới hạn là 2, mẫu số có giới hạn 0 và 1 x 0 với x 1. x 1 x 1 1 x
3. Bài tập trắc nghiệm Câu 1: x -15
Kết quả của giới hạn lim là: x 2+ x - 2 A. . -¥ B. . +¥ C. 15 - . D. 1. 2 Lời giải Chọn A ìï lim (x-1 ) 5 = 1 - 3 < 0 ï . Vì ïx2+ x -15 í ¾¾ lim = - . ¥ ï lim (x-2) x2
= 0 & x - 2 > 0, "x > ï 2 + x - 2 ïîx2+ Câu 2: x + 2
Kết quả của giới hạn lim là: x 2+ x - 2 A. . -¥ B. . +¥ C. 15 - .
D. Không xác định. 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 328
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìï lim x + 2 = 2 > 0 ïïx2+ x + 2 í ¾¾ lim = + . ¥ ï x2
ï lim x - 2 = 0 & x - 2 > 0, "x > 2 + x - 2 ïîx2+ 3x + 6
Câu 3: Kết quả của giới hạn lim là: x ( 2)+ - x + 2 A. . -¥ B. 3. C. . +¥
D. Không xác định. Lời giải Chọn B
Ta có x + 2 = x + 2 với mọi x > -2, do đó : 3x + 6 3 x + 2 3(x + 2) lim = lim = lim = lim 3 = 3 x ( 2)+ x + 2 x ( ) 2 + x + 2 x ( 2)+ x + 2 x ( ) 2 + - - - - Câu 4: 2 - x
Kết quả của giới hạn lim là: - 2
x 2 2x - 5x + 2 A. . -¥ B. . +¥ C. 1 - . D. 1. 3 3 Lời giải Chọn C Ta có 2 - x 2 - x 1 1 lim = lim = lim = - . - 2 x 2 - + x 2 2x 5x 2
- (2 - x )(1- 2x ) x 2- 1-2x 3 2 Câu 5: x +13x + 30
Kết quả của giới hạn lim là: x 3+ - (x +3)( 2 x + 5) A. -2. B. 2. C. 0. D. 2 . 15 Lời giải Chọn C
Ta có x +3> 0 với mọi x > -3, nên: 2 x +13x + 30 (x + ) 3 (x +10) x + 3 ( . x +10) 3 - + 3( 3 - + 7) lim = lim = lim = = 0 . x 3+ (x + ) 3 ( 2 x + ) x 3 5 + (x + ) 3 ( 2 x + ) x 3+ - - - 2 5 x + 5 (- )2 3 + 5 ìï 2x ï víi x < 1 ï
f (x) = ïí 1- x . ïï 2 ï Câu 6: 3x 1 víi x 1 Cho hàm số ï + ³ î
Khi đó lim f (x) là: x 1+ A. . +¥ B. 2. C. 4. D. . -¥ Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 329
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 lim f (x) 2 2
= lim 3x +1 = 3.1 +1 = 2 x 1+ x 1+ 2 ìïx +1 ïï víi x < 1
Câu 7: Cho hàm số f (x) = ïí 1- x
. Khi đó lim f (x) là: ïï x 1-
ï 2x 2 víi x ³1 ïî - A. . +¥ B. -1. C. 0. D. 1. Lời giải Chọn A ì 2 2 + ïlim + = ï - (x )1 2 f (x) x 1 lim = lim = +¥ vì ïx 1 í . x 1- x 1- 1- x
ïïlim (1- x)= 0 & 1- x > 0 ("x < ) 1 ïîx 1- 2 ìï Câu 8: x - ï 3 víi x ³ 2
Cho hàm số f (x) = í
. Khi đó lim f (x) là:
ïïx-1 víi x < 2 î x2 A. -1. B. 0. C. 1. D. Không tồn tại. Lời giải Chọn C
ìï lim f (x)= lim - = ï + + ( 2 x ) 3 1 Ta có ïx2 x2 í
lim f (x) = lim f (x) =1 lim f (x) = 1.
ïïlim f (x)= lim (x- ) x2+ x2- x2 1 = 1 ïîx2- x2- ìï Câu 9: x - + víi x ³
Cho hàm số f (x) 2 3 2 = ïí
. Tìm a để tồn tại lim f (x). ax ïï -1 víi x < 2 î x 2 A. a = 1. B. a = 2. C. a = 3. D. a = 4. Lời giải Chọn B
ìï lim f (x)= lim (ax- ) 1 = 2a -1 ï Ta có x2- x2- ïí .
ïïlim f (x)= lim - + = + + ( x 2 )3 3 ïîx2 x2
Khi đó lim f (x) tồn tại lim f (x)= lim f (x) 2a 1 - = 3 a = 2. x2 x 2- x 2+ 2
ìïx -2x +3 víi x > 3 ï Câu 10: ï
Cho hàm số f (x) = 1 ïí
víi x = 3. Khẳng định nào dưới đây sai? ïï 2 3 ï - 2x víi x < 3 ïî
A. lim f (x)= 6.
B. Không tồn tại lim f (x). x 3+ x3
C. lim f (x)= 6.
D. lim f (x)= 1 - 5. x 3- x 3- Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 330
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïlim f (x)= lim x - x + = ï + + ( 2 2 ) 3 6 Ta có ïx3 x3 í ¾¾
lim f (x) ¹ lim f (x)
ïïlim f (x)= lim x x - x = - - - ( 2 3 2 ) 3+ 3 15 - ïîx3 x3 ¾¾
không tồn tại giới hạn khi x 3.
Vậy chỉ có khẳng định C sai.
Dạng 3. Giới hạn tại vô cực 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 11: Giá trị của giới hạn ( 3 lim x - x + ) 1 là: x -¥ A. 1. B. . -¥ C. 0. D. . +¥ Lời giải Chọn D 3 ìï lim x = -¥ æ ö ïx-¥ ï lim ( 1 1 3 x - x + ) 3 1 = lim x çç -1 ÷ + ÷ = +¥ vì ïí . 2 3 ç ÷ æ 1 1 ö x-¥ x-¥ è x x ø ïï lim çç -1 ÷ + ÷ = -1< 0 2 3 ï ç ÷ x-¥ ï è x x ø î Giải nhanh: 3
x - x + (- ) 3 1 1 x ¾¾ +¥ khi x - . ¥
Câu 12: Giá trị của giới hạn ( 3 2
lim x + 2x + 3 x ) là: x -¥ A. 0. B. . +¥ C. 1. D. -¥ . Lời giải Chọn B Ta có æ ö lim ( 3 2 3 2
x + 2x +3 x ) = lim ( 3 2 x - + 2x -3x) 3 = lim x çç 1 ÷ - + - ÷ = + . ¥ 2 ç ÷ x -¥ x -¥ x -¥ è x x ø Giải nhanh: 3 3 2
x + 2x + 3 x x +¥ khi x - . ¥
Câu 13: Giá trị của giới hạn ( 2 lim x +1 + x) là: x +¥ A. 0. B. . +¥ C. 2 -1. D. -¥ . Lời giải Chọn B Giải nhanh: 2 2
x +¥ : x +1 + x x + x = 2x +¥ .
Đặt x làm nhân tử chung:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 331
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï lim x = +¥ æ ö ïx+¥ ï lim ( ç 1 2
x +1 + x) = lim xç 1+ +1÷÷ ï ç ÷ = +¥ vì í . 2 x+¥ x+¥ çè x ÷ø ï 1 ï lim 1+ +1 = 2 > 0 ï + 2 x 2 ïî x
Câu 14: Giá trị của giới hạn (3 3 2 lim
3x -1 + x + 2) là: x +¥ A. 3 3 +1. B. . +¥ C. 3 3 -1. D. -¥ . Lời giải Chọn B Giải nhanh: 3 3 2 3 3 2 x +¥ x - + x + x + x = (3 : 3 1 2 3 3 + ) 1 x + . ¥
Đặt x làm nhân tử chung: æ ö lim ( ç 1 2 3 3 2 3x -1 + x + 2) ÷ 3 = lim xç 3- + 1+ ÷ ç ÷ = +¥ vì 3 2 x+¥ x+¥ çè x x ÷ø ìï lim x = +¥ ïx+¥ ïïí æ ö . ï ç 1 2 ÷ 3 3 ï lim ç 3- + 1+ ÷ ï ç ÷ = 3 +1> 0 3 2 x+¥ ç ï è x x ÷ø ïî
Câu 15: Giá trị của giới hạn x + + là: +¥ ( 2 lim 4x 7x 2x x ) A. 4. B. . -¥ C. 6. D. +¥ . Lời giải Chọn D Đặt 2
x làm nhân tử chung: 2 ìï lim x = +¥ æ ö ïx+¥ ïï lim x ç ÷ + + = ç + + ÷ ï ç ÷ = +¥ vì í æ ö . +¥ ( 7 2 4x 7x 2x) 2 lim x 4 2 ï ç 7 x x+¥ çè x ÷ø ï lim ç 4 + + 2÷÷ ï ç ÷ = 4 > 0 x+¥ ï çè x ÷ø ïî
Giải nhanh: x +¥ x( 2
x + x + x) x( 2 x + x) 2 : 4 7 2 4 2 = 4x + . ¥ 0
Dạng 4. Dạng vô định 0 1. Phương pháp 0 u(x)
Nhận dạng vô định : lim
khi lim u(x) lim u(x) 0. 0 xx v(x) xx xx 0 0 0
Phân tích tử và mẫu thành các nhân tử và giản ước u(x) (x x0)A(x) A(x) A(x) lim lim lim vaø tính lim .
xx v(x) xx (x x )B(x) xx B(x) xx o o 0 o o B(x)
Nếu phương trình f x 0 có nghiệm là x0 thì f x x x0 .gx Đặc biệt:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 332
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2
f(x) ax bx c,maø f(x) 0 coù hai nghieäm phaân bieät x ,x
Nếu tam thức bậc hai 1 2
thì f(x) ñöôïc phaân tích thaønhf(x) ax - 1 x x -x2
Phương trình bậc 3: 3 2
ax bx cx d 0 (a 0)
a b c d 0 thì pt coù moät nghieäm laø x 1, ñeå phaân tích 1
thaønh nhaân töû ta duøng pheùp chia ña thöùc hoaëc duøng sô ñoà Hooc-ner
a b c d 0 thì pt coù moät nghieäm laø x 1 , ñeå phaân tích 1
thaønh nhaân töû ta duøng pheùp chia ña thöùc hoaëc duøng sô ñoà Hooc-ner
Nếu ux và vx có chứa dấu căn thì có thể nhân tử và mẫu với biểu thức liên hiệp, sau đó
phân tích chúng thành tích để giản ước. A B
löôïng lieân hieäp laø: A B. A B
löôïng lieân hieäp laø: A B.
A B löôïng lieân hieäp laø: A B. 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B . 3 3 2 3 2 A B
löôïng lieân hieäp laø: A B A B .
2. Các ví dụ rèn luyện kĩ năng 2 x 3x 2 Ví dụ 1: Tính lim x 1 x 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 x 3x 2 x 1x 2 lim lim limx 2 1 . x 1 x 1 x 1 x 1 x
Cách 2: Giải nhanh bằng máy tính 2 X 3X 2 Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả X 1 2 2x 3x 1
Ví dụ 2: Tính L lim . 2 x 1 1 x Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 2x 3x 1 2x 1x 1 2x 1 1 lim lim lim . 2 x 1 x 1 1 x 1 x1 x x 1 1 x 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 333
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Cách 2: Giải nhanh bằng máy tính 2 2X 3X 1 Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả 2 1 X 2 x 3x 2 Ví dụ 3: Tính lim 3 x 1 x 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 x 3x 2 x 1x 2 x 2 1 lim lim lim . 3 x 1 x 1 x 1 x 1 2 x x 2 x 1 1 x x 1 3
Cách 2: Giải nhanh bằng máy tính 2 x 3x 2 Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả 3 x 1 4 4 t a Ví dụ 4: Tính lim ta t a Hướng dẫn giải 4 4 t a lim lim 3 2 2 3 t t a ta a 3 4a . ta t a ta 4 y 1
Ví dụ 5: Tính lim 3 y 1 y 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận y 1 y 1 3 2 4 y y y 1 3 2 y y y 1 4 lim lim lim . 3 y 1 y 1 y 1
y 1 2y y 2 y 1 1 y y 1 3
Cách 2: Giải nhanh bằng máy tính 4 Y 1 Nhập vào màn hình ấn 10 CALC 1 10 ta được kết quả 3 Y 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 334
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 4 x Ví dụ 6: Tính lim x2 x 7 3 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 4 x lim x2 x 7 3 2 x 4 x 7 3
x 2x 2 x 7 3 lim lim
x2 x2 x 7 9 x 7 3 x 7 3 lim x 2 x 7 3 24. x2
Cách 2: Giải nhanh bằng máy tính 2 4 X Nhập vào màn hình ấn 5 CALC 1 10
ta được kết quả 24. X 7 3
Lưu ý: Để ra kết quả chính xác 24
ta có thể tính theo quy tắc Lô-pi-tan như sau: d 2 4 X dx Nhập x2
rồi ấn phím ta được kết quả chính xác 24. d X7 3 dx x2 1 x 1 Ví dụ 7: Tính lim x0 x Hướng dẫn giải
Cách 1: Giải bằng tự luận 1 x 1 1 x 1 1 1 lim lim lim . x0 x
x0 x 1 x x0 1 1 x 1 2
Cách 2: Giải nhanh bằng máy tính
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 335
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 x 1 1 Nhập vào màn hình ấn 5 CALC 0 10
ta được kết quả . x 2 1
Lưu ý: Để ra kết quả chính xác ta có thể tính theo quy tắc Lô-pi-tan như sau: 2 d 1X 1 dx 1 Nhập
x0 rồi ấn phím ta được kết quả chính xác 0,5 . d 2 X dx x0 2 x 6x 8 Ví dụ 8: Tính lim x4 x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2
x 2x 4 x 2 x 6x 8 lim lim
lim x 2 x 2 24 8. x4 x4 x 2 x 4 x4
Cách 2: Giải nhanh bằng máy tính 2 x 6x 8 Nhập vào màn hình ấn 5 CALC 4 10
ta được kết quả 8. x 2
Lưu ý: Để ra kết quả chính xác 8 ta có thể tính theo quy tắc Lô-pi-tan như sau: d 2X 6X8 dx Nhập
x4 rồi ấn phím ta được kết quả chính xác 8. d X 2 dx x4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 336
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 2 x 4 2 Ví dụ 9: Tính lim b x2 2 4 2x 8 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 x 4 2 E lim x2 2 4 2x 8
Nhân tử và mẫu hai lượng liên hợp: 2 3 2 3 2 2 x 4 2 x 4 4 4 2x 8 2 3 2 3 2 3 2 2 x 4 2 x 4 2 x 4 44 2x 8 E lim x2 2 2 2 3 2 3 2
4 2x 8 4 2x 8 x 4 2 x 4 4 2x 4 8 2 4 2x 8 lim x2 2 16 2x 8 2 3 2 3 2
x 4 2 x 4 4 2x 4 2 4 2x 8 lim x2 2 2 x 4 2 3 2 3 2
x 4 2 x 4 4 2 4 2x 8 8 1 lim . x2 2 24 3 3 2 3 2
2 x 4 2 x 4 4
Cách 2: Giải nhanh bằng máy tính 3 2 x 4 2 1 Nhập vào màn hình ấn 5 CALC 4 10
ta được kết quả . 2 4 2x 8 3
Lời bình: Nếu ta dùng quy tắc Lô-pi-tan d 3 2 x 4 2 dx Nhập
x2 rồi ấn phím ta được kết quả 1 0, 3 . d 2 3 4 2x 8 dx x2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 337
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 4 2 x 12 2 Ví dụ 10: Tính lim 2 x2 x 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận 4 2 x 12 2 E lim 2 x 2 x 4 4 2 4 2 x 12 2 x 12 2 lim x2 2x 44 2 x 12 2 2 x 12 4 0 lim
(vẫn còn dạng vô định ) x 2 2x 44 2 0 x 12 2 2 2 x 12 4 x 12 4 lim x 2 2x 44 2 2 x 12 2 x 12 4 2 x 12 16 lim x 2 2x 44 2 2 x 12 2 x 12 4 1 1 lim . x 2 4 2 2 32
x 12 2 x 12 4
Cách 2: Giải nhanh bằng máy tính Ta dùng quy tắc Lô-pi-tan d 4 2 x 12 2 dx 1 Nhập x 2
rồi ấn phím ta được kết quả 0,03125 . d 2 32 x 4 dx x 2 6 x 1 Ví dụ 11: Tính lim 2 x 1 x 1 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 338
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Cách 1: Giải bằng tự luận 6 x 1 E lim 2 x 1 x 1 6 x 6 2 6 1 x x 1 lim x 1 2x 6 2 6 1 x x 1 x 1 0 lim (Vẫn dạng vô định ) x 1 2x 6 2 6 1 0 x x 1 x 1 x 1 lim x 1 x 1x 6 2 6 1 x x 1 x 1 1 1 lim . x 1 6 2 6 12 x 1 x x 1 x 1
Cách 2: Giải nhanh bằng máy tính Ta dùng quy tắc Lô-pi-tan d 6 X 1 dx Nhập x 1
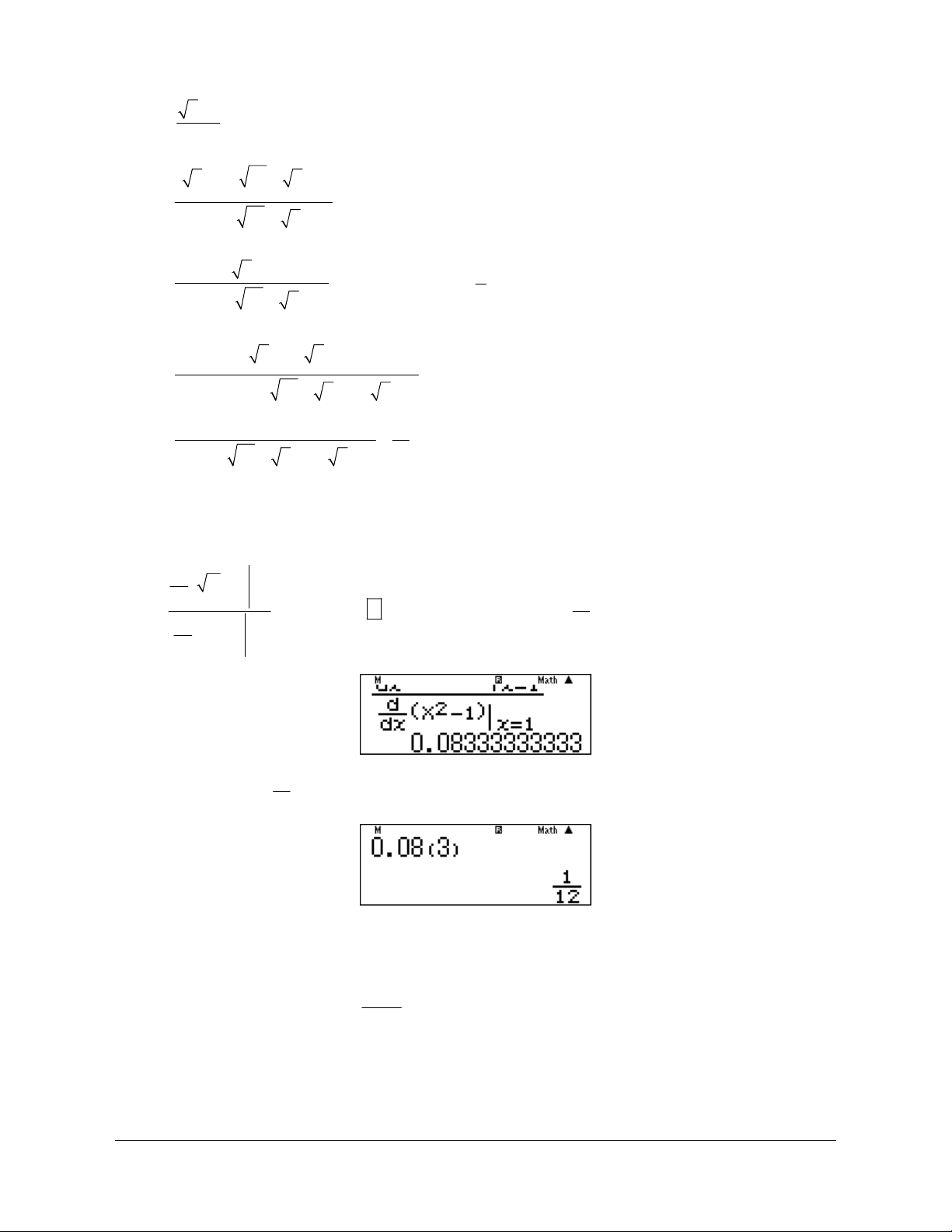
rồi ấn phím ta được kết quả 1 0,08 3 . d 2 12 x 1 dx x 1 Để chuyển 1 0,08 3 ta bấm như sau 0.08Qs3= 12
3. Bài tập trắc nghiệm 3 Câu 1: x -8
Giá trị của giới hạn lim là: 2 x 2 x - 4 A. 0. B. . +¥ C. 3.
D. Không xác định. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 339
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C 3 2 2 Ta có x -8
(x -2)(x + 2x + 4) x + 2x + 4 12 lim = lim = lim = = 3 2 x 2 x 2 x 2 x - 4 (x -2)(x + 2) x + 2 4 5 Câu 2: x +1
Giá trị của giới hạn lim là: 3 x 1 - x +1 A. 3 - . B. 3. C. 5 - . D. 5. 5 5 3 3 Lời giải Chọn D (x + ) 1 ( 4 3 2 5
x - x + x - x x + + ) 4 3 2 1 1
x - x + x - x +1 5 lim = lim = lim = . 3 x - x +1 x - (x + ) 1 ( 2 1 1 x - x + ) 2 x -1 1 x - x +1 3 3 Câu 3: 2x + 6 3 Biết rằng lim = a 3 + . b Tính 2 2 a +b . 2 x- 3 3- x A. 10. B. 25. C. 5. D. 13. Lời giải Chọn A 2 2 3 3
(x + 3)( 2x - 3x + )3 2( 2 3 x - 3x x + + )3 Ta có lim = lim = lim 2 x - 3 - x - 3 3 x ( 3-x)( 3 +x) x - 3 3 - x é ù 2 (ê- 3)2 - 3.(- 3)+3ú êë úû 18 a ìï = 3 ï 2 2 = = = ¾¾ í a + b = . 3 -(- 3) 3 3 10 2 3 b ï = 1 ïî 2 Câu 4: x - - x + 6
Giá trị của giới hạn lim là: 2 x -3 x + 3x A. 1. B. 2 . C. 5. D. 3. 3 3 3 5 Lời giải Chọn C 2 x - - x + 6 (x +3)(x -2) x -2 3 - -2 5 lim = lim = lim = = . 2 x 3 - x 3 x + 3x - x (x +3) x -3 x 3 - 3 Câu 5: 3- x
Giá trị của giới hạn lim là: x 3- 3 27 - x A. 1. B. 0. C. 5. D. 3. 3 3 5 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 340
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có 3- x > 0 với mọi x < 3, do đó: 3- x 3- x lim = lim x 3- 3 x 3 27 - x - (3- x)( 2 9 + 3x + x ) 3- x 3-3 = lim = = 0. x 3- 2 2 9 + 3x + x 9 + 3.3 + 3 ( 2 21 x + p )7 21 1-2x -p
Câu 6: Giá trị của giới hạn lim là: x 0 x 21 21 21 21 A. 2p 2p 2p 1-2p - . B. - . C. - . D. . 7 9 5 7 Lời giải Chọn A Ta có ( 2 21 x + p ) 7 21 1-2x -p ( 2 21
x + p )(7 1-2x - ) 1 21 2p lim = lim + lim x = - . x 0 x 0 x 0 x x 7 2 Câu 7: x + x - x
Giá trị của giới hạn lim là: + 2 x 0 x A. 0. B. . -¥ C. 1. D. . +¥ Lời giải Chọn D x x x ( 2 2 x + x)- + - x Ta có 1 lim = lim = lim = +¥ + 2 x 0 x 0+ 2 x x ( 2
x + x + x ) x 0+ 2 x + x + x vì 1> 0 ; lim ( 2
x + x + x = và 2
x + x + x > 0 với mọi x > 0. + ) 0 x 0 3 Câu 8: x -1
Giá trị của giới hạn lim là: x 1 3 4x + 4 -2 A. -1. B. 0. C. 1. D. . +¥ Lời giải Chọn C (x -1) x + + x + + x -1 (3 4 4 2 4 4 4 3 ( )2 3 ) Ta có lim = lim x 1 3 x 1 4x + 4 -2 (4x + 4 -8)(3 2 3 x + x + ) 1 (3(4x+4)2 3 + 2 4x + 4 + 4) 12 = lim = = 1. x 1 (3 2 3 x + x + ) 12 4 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 341
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 Câu 9: 2 1+ x - 8 - x
Giá trị của giới hạn lim là: x 0 x A. 5 . B. 13 . C. 11. D. 13 - . 6 12 12 12 Lời giải Chọn B 3 æ 3 ö Ta có 2 1+ x - 8 - x ç2 1+ x -2 2 - 8 - x lim = lim ÷ ç + ÷ ç ÷ x 0 x 0 x çè x x ÷ø æ ö çç 2 1 ÷÷ 1 13 = lim ç ÷ + ç ÷ = 1+ = . x 0 ÷ ç + + 3 ç x 1 1 3
4 + 2 8 - x + (8- x)2 ÷ 12 12 ÷ è ø 3 Câu 10: ax +1 - 1-bx
Biết rằng b > 0, a + b = 5 và lim
= 2 . Khẳng định nào dưới đây sai? x 0 x
A. 1 < a < 3. B. b >1. C. 2 2 a +b >10.
D. a-b < 0. Lời giải Chọn A 3 æ 3 ö Ta có ax +1 - 1-bx
ç ax +1 -1 1- 1-bx lim = lim ÷ ç + ÷ ç ÷ x 0 x 0 x è x x ø æ ax bx ö = lim ç ÷ ç + ÷ ç ÷
x 0 çççè (3 ( + )2 3 + + + ) x(1+ 1 1 1 1 - x x x x )÷÷÷ø æ a b ö a b = lim ç ÷ ç + ÷ = + = 2. ç ÷
x 0 çççè(3 ( + )2 3 + + + ) (1+ 1 1 1 1 - x x x )÷ 3 2 ÷÷ø ìïa +b = ï 5 ìïa +b = Vậy ta được: ï ï 5 ía b í
a = 3, b = 2 ï + = 2 ï2a +3b = ï ïî 12 ïî3 2 ¥
Dạng 5. Dạng vô định ¥ 1. Phương pháp
Nhận biết dạng vô định u(x) lim
khi lim u(x) , lim v(x) . xx v(x) xx xx 0 0 0 u(x) lim
khi lim u(x) , lim v(x) . x v(x) xx xx 0 0
Chia tử và mẫu cho n
x với n là số mũ cao nhất của biến ở mẫu ( Hoặc phân tích thành tích chứa nhân tử n x rồi giản ước)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 342
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Nếu u(x) hoặc v(x) có chứa biến x trong dấu căn thì đưa xk ra ngoài dấu căn (Với k là mũ cao
nhất của biến x trong dấu căn), sau đó chia tử và mẫu cho luỹ thừa cao nhất của x (thường là bậc cao nhất ở mẫu).
Cách tính giới hạn dạng này hoàn toàn tương tự giới hạn dãy số.
2. Các ví dụ rèn luyện kĩ năng 4 3 2 2x x 2x 3 Ví dụ 1: Tính lim 4 x x 2x Hướng dẫn giải
Cách 1: Giải bằng tự luận 1 2 3 4 3 2 2 2 4 2x x 2x 3 x x x lim lim 1. 4 x x x 2x 1 2 3 x
Cách 2: Mẹo giải nhanh 4 3 2 4 2x x 2x 3 2x 1. 4 4 x 2x 2 x
Cách 3: Giải nhanh bằng máy tính 4 3 2 2x x 2x 3 Nhập vào màn hình ấn 15
CALC 10 ta được kết quả 1. 4 x 2x 2
Lời bình: “Bậc tử bằng bậc mẫu” nên kết quả 1. 2 4 5 3x 2x Ví dụ 2: Tính lim 4 x 5x 3x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 4 5 3x 2x 3 2x lim lim 4 x x 5x 3x 2 3 2 5 3 4 x x 3 2 lim 5
5 0; lim 3 2x . 3 4 x x x x 4 5 3x 2x Do đó: lim . 4 x 5x 3x 2
Cách 2: Mẹo giải nhanh
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 343
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 4 5 5 3x 2x 2x 2 x . 4 4 5x 3x 2 5x 5
Cách 3: Giải nhanh bằng máy tính 4 5 3x 2x Nhập vào màn hình ấn 15
CALC 10 ta được kết quả . 4 5x 3x 2
Lời bình: Bậc tử lớn hơn bậc mẫu nên kết quả là . 4 5 3x 2x Ví dụ 3: Tính lim 4 6 x 5x 3x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 4 5 2 3x 2x x x 0 lim lim 0. 4 6 x x 5x 3x 2 5 2 3 3 2 6 x x
Cách 2: Mẹo giải nhanh 4 5 5 3x 2x 2x 2 1 . 0. 4 6 6 5x 3x 2 3x 3 x
Cách 3: Giải nhanh bằng máy tính 4 5 3x 2x Nhập vào màn hình ấn 15
CALC 10 ta được kết quả 0. 4 6 5x 3x 2
Lời bình: “Bậc tử bé hơn bậc mẫu” nên kết quả là 0. 4 5 3x 4x 2 Ví dụ 4: Tính lim 5 4 x 9x 5x 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận 3 2 4 5 4 5 3x 4x 2 x x 2 lim lim . 5 4 x x 9x 5x 4 5 4 3 9 5 x x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 344
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Cách 2: Mẹo giải nhanh 4 5 5 3x 4x 2 4x 4 2 . 5 4 5 9x 5x 4 9x 9 3
Cách 3: Giải nhanh bằng máy tính 4 5 3x 4x 2 Nhập vào màn hình ấn 15
CALC 10 ta được kết quả 0. 5 4 9x 5x 4 2 x 2x 3x
Ví dụ 5: Tính L lim . x 2 4x 1 x 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 2 2 x 1 3x 1 3 x 2x 3x x x 2 lim lim lim . x 2 x x 4x 1 x 2 1 1 2 3 x 4 x 2 4 1 2 2 x x x
Cách 2: Giải nhanh bằng máy tính 2 x 2x 3x 2 Nhập vào màn hình ấn 15
CALC 10 ta được kết quả . 2 4x 1 x 2 3 2 4x 1 x 5 Ví dụ 6: Tính lim x 2x 7 Hướng dẫn giải
Cách 1: Giải bằng tự luận 1 1 5 2 4 2 2 4x 1 x 5 x x x 2 0 lim lim 1. x 2x 7 x 7 2 0 2 x
Cách 2: Giải nhanh bằng máy tính 2 4x 1 x 5 Nhập vào màn hình ấn 25
CALC 10 ta được kết quả 2x 7
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 345
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 x
Ví dụ 7: Tính lim x 5 3 x x 1 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 5 2 1 lim x 5 x xx 5 x lim lim 1. 3 3 x x x x 1 x 1 1 1 3 x
Cách 2: Giải nhanh bằng máy tính x
Nhập vào màn hình x 5 ấn 25
CALC 10 ta được kết quả 3 x 1
x 3112x94 2
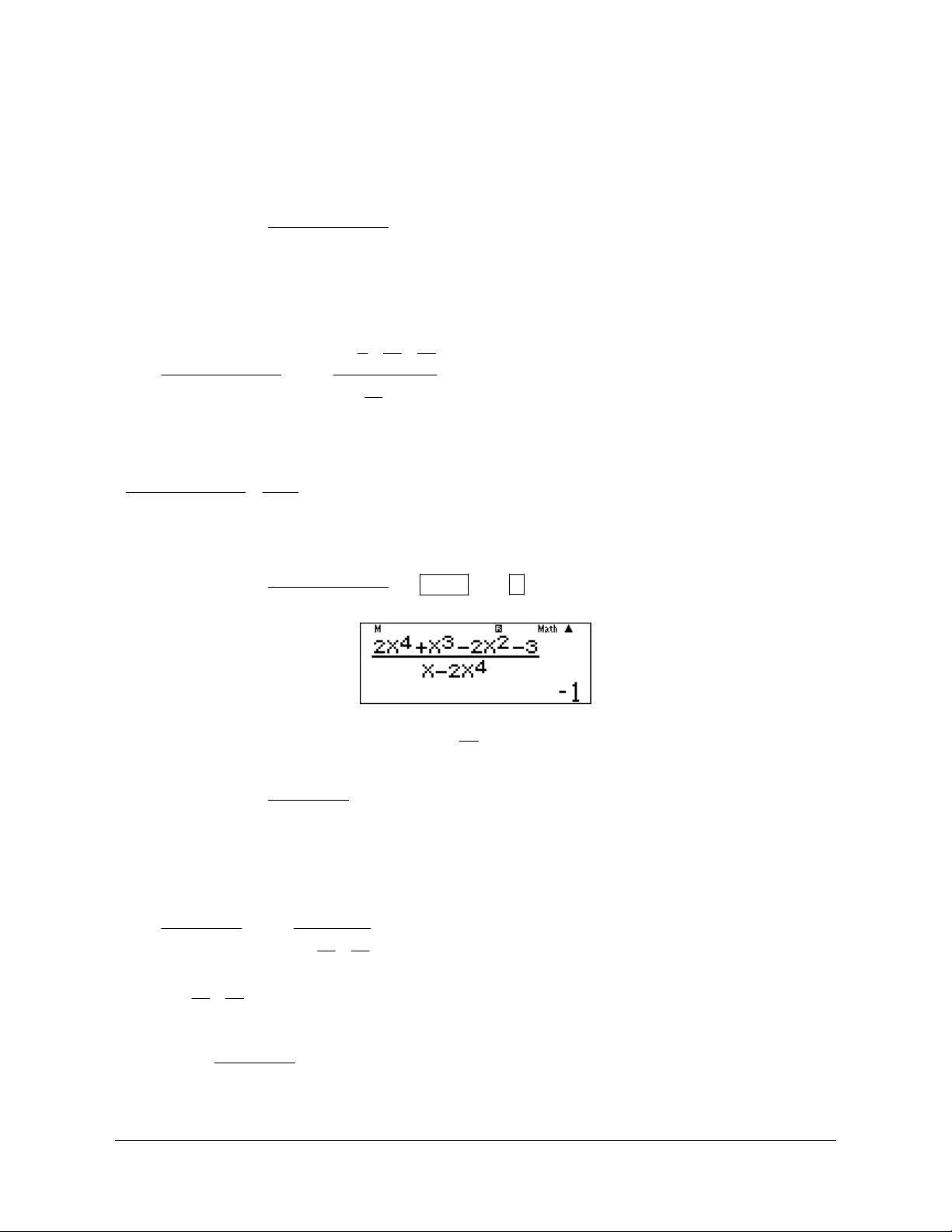
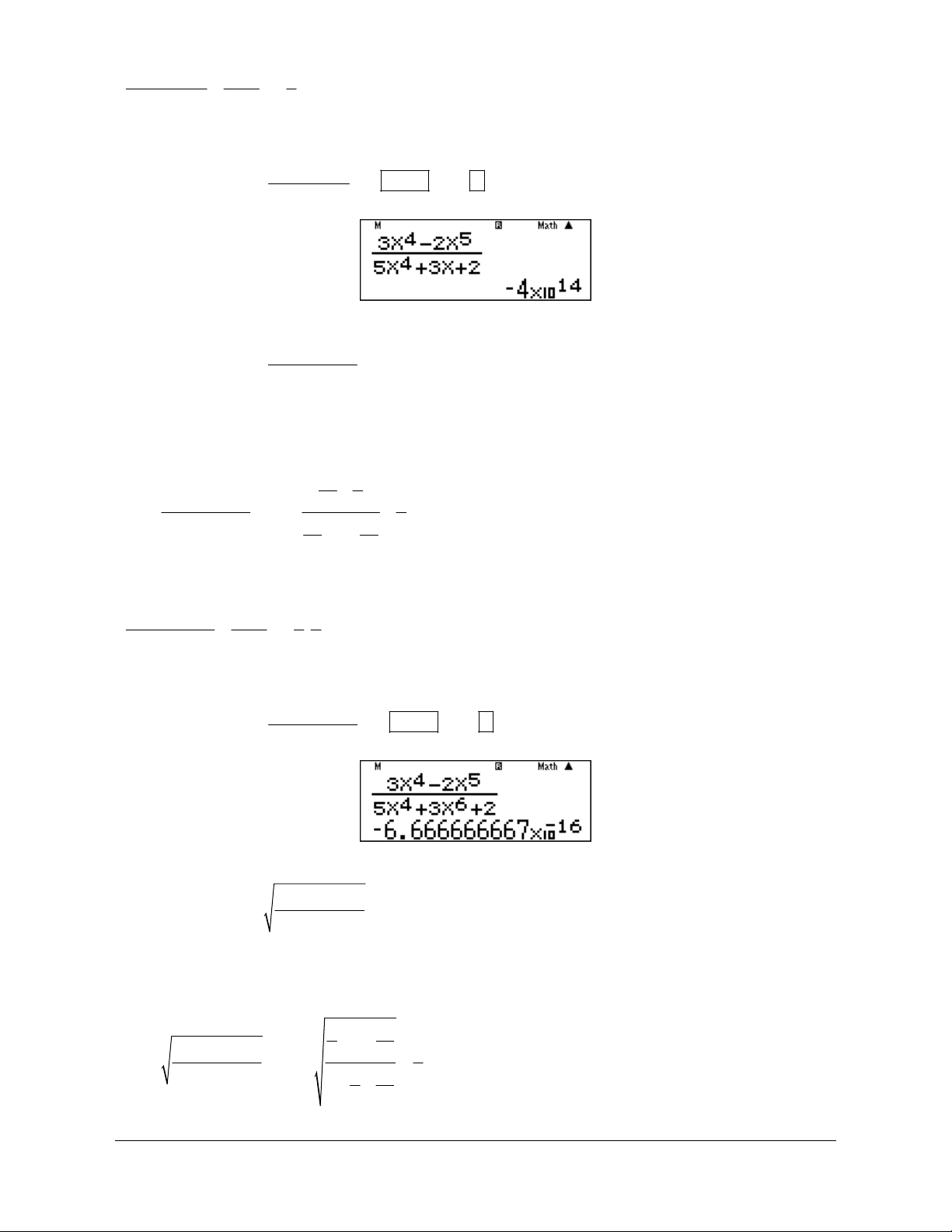
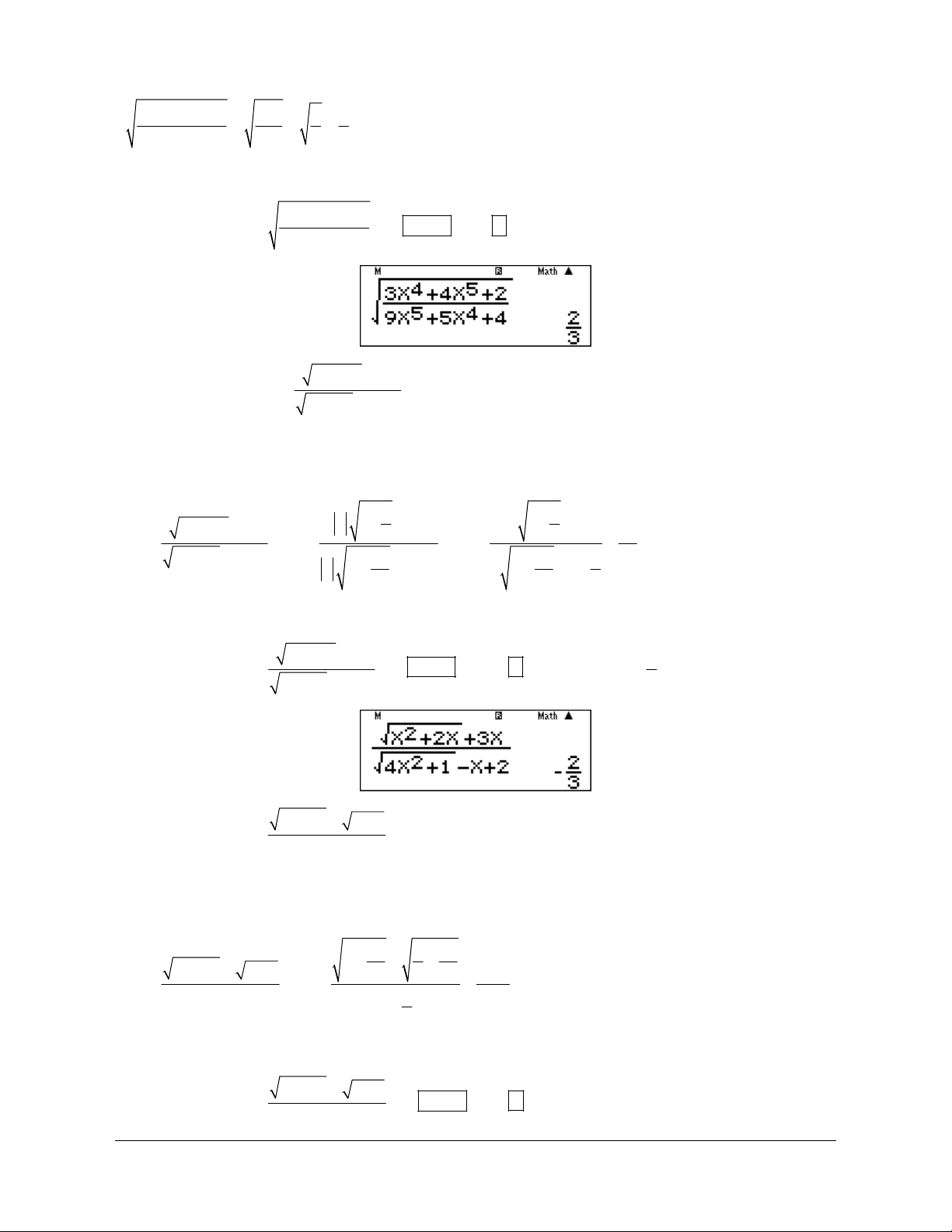
Ví dụ 8: Tính lim 100 x 2x 3 Hướng dẫn giải 3 94 3 1 1 2 94 2 x 1 x 2 x 1 1 2x 2 x x E lim lim 100 x x 2x 3 100 3 x 2 100 x 94 3 6 1 94 1 x 1 x 2 2 x x lim x 100 3 x 2 100 x 3 94 1 1 1 2 x x 3 1 . 2 94 2 lim 93 2 . x 3 2 2 100 x
3. Bài tập trắc nghiệm 2 Câu 1: 2x +5x -3
Kết quả của giới hạn lim là: 2
x -¥ x + 6x + 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 346
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. -2. B. . +¥ C. 3. D. 2 . Lời giải Chọn D 5 3 2 2 + - Ta có 2 2x + 5x -3 lim = lim x x = 2 . 2
x -¥ x + 6x + 3 x +¥ 6 3 1+ + 2 x x 2 2 Giải nhanh : khi 2x + 5x -3 2x x -¥ thì : = 2. 2 2 x + 6x +3 x 3 2 Câu 2: 2x +5x -3
Kết quả của giới hạn lim là: 2 x -¥ x + 6x +3 A. -2. B. . +¥ C. . -¥ D. 2 . Lời giải Chọn C 5 3 3 2 2 + - Ta có: 3 2x + 5x -3 lim = lim . x x x = - . ¥ 2 x -¥ x + 6x + 3 x -¥ 6 3 1+ + 2 x x 3 2 3 Giải nhanh : khi 2x + 5x -3 2x x -¥ thì : = 2x - . ¥ 2 2 x + 6x + 3 x 3 2 Câu 3: 2x -7x +11
Kết quả của giới hạn lim là: 6 5
x -¥ 3x + 2x -5 A. -2. B. . +¥ C. 0. D. . -¥ Lời giải Chọn C 2 7 11 3 2 - + Ta có: 3 4 6 2x -7x +11 0 lim = lim x x x = = 0. 6 5
x -¥ 3x + 2x -5 x -¥ 2 5 3 3 + - 6 x x 3 2 3 Giải nhanh : khi 2x -7x +11 2x 2 1 x -¥ thì : = . 0. 6 5 6 3 3x + 2x -5 3x 3 x Câu 4: 2x -3
Kết quả của giới hạn lim là: x -¥ 2 x +1 - x A. -2. B. . +¥ C. 3. D. 1 - . Lời giải Chọn D
. Khi x -¥ thì 2 2 2 x = x - ¾¾
x +1 - x x - x = x - - x = 2 - x = / 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 347
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 2 - 2x -3 ¾¾
chia cả tử và mẫu cho x , ta được lim = lim x = -1 . x -¥ 2 x +1 x - x -¥ 1 - 1+ -1 2 x (2-a)x -3 Câu 5: Biết rằng
có giới hạn là +¥ khi x +¥ (với a là tham số). Tính giá trị nhỏ 2 x +1 - x nhất của 2
P = a -2a + 4. A. P = 1. B. P = 3. C. P = 4. D. P = 5. min min min min Lời giải Chọn B Khi x +¥ thì 2 2 2 x = x ¾¾
x +1 - x x - x = x - x = 0 ¾¾
Nhân lượng liên hợp: (2-a)x -3 æ æ ö ö Ta có lim = lim ( ( 2-a)x - ) 3 x + + x = x çç -a ç ÷ ÷ - ç ÷ + + ÷ ç ç ÷ ÷ x +¥ x +¥ ( 3 1 2 1 ) 2 lim 2 1 1 . 2 2 +1 x +¥ è - x øçè x x x ÷ø 2 ìï lim x = +¥ ïx+¥ ïï (2-a) - Vì x 3 ïí æ ö lim ï ç 1 = +¥ ÷ x +¥ 2 ï lim ç 1+ +1÷ ï ç ÷ = 4 > 0 x +1 - x 2 x +¥ ï çè x ÷ø ïî æ 3 ö lim çç2-a ÷
- ÷ = 2-a > 0 a < 2 ç ÷ . x +¥è x ø Giải nhanh : ta có 2x -3 x +¥ ¾¾ 2 x +1 - x = (
( -a)x - )( 2x + +x)( -a)x ( 2 2 3 1 2 .
x + x)= 2(2-a)x +¥ a < 2 . Khi đó 2
P = a - 2a + 4 = (a - )2
1 + 3 ³ 3, P = 3 a = 1 < 2 P = 3. min 2 Câu 6: 4x - x +1
Kết quả của giới hạn lim là: x -¥ x +1 A. -2. B. -1. C. -2. D. . +¥ Lời giải Chọn C 2 2 Giải nhanh: khi 4x - x +1 4x -2x x -¥ ¾¾ = = -2. x +1 x x 1 1 - 4 - + 2 2 Cụ thể: 4x - x +1 x x - 4 lim = lim = = -2. x -¥ x +1 x -¥ 1 1 1+ x 2 Câu 7:
4x -2x +1 + 2 - x
Kết quả của giới hạn lim là: x +¥ 2
9x -3x + 2x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 348
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1 - . B. . +¥ C. . -¥ D. 1 . 5 5 Lời giải Chọn D Giải nhanh : khi 2 2
4x -2x +1 + 2 - x 4x - x 2x - x 1 x +¥ ¾¾ = = . 2 2
9x -3x + 2x 9x + 2x 3x + 2x 5 2 1 2 4 - + + -1 2 2 Cụ thể :
4x -2x +1 + 2 - x x x x 1 lim = lim = . x +¥ 2 9x -3x + 2 x x +¥ 3 5 9 - + 2 x 2 Câu 8:
4x -2x +1 + 2 - x Biết rằng L = lim
> 0 là hữu hạn (với ,
a b là tham số). Khẳng định x -¥ 2
ax -3x + bx nào dưới đây đúng. A. a ³ 0. B. 3 L = - C. 3 L = D. b > 0. a + b b- a Lời giải Chọn B Ta phải có 2
ax -3x > 0 trên ( ;
-¥ a) a ³ 0. Ta có 2 2 x -¥ ¾¾
4x -2x +1 + 2 - x 4x - x = 3 - x = / 0. 2
Như vậy xem như “tử” là một đa thức bậc 1. Khi đó
4x -2x +1 + 2 - x lim > 0 khi và x -¥ 2
ax -3x + bx chỉ khi 2
ax -3x +bx là đa thức bậc 1. Ta có 2 2
ax -3x + bx ax + bx = (- a + ) b x ¾ ¾ - a + b = / 0. 2
Khi đó 4x -2x +1 +2- x 3 - x 3 =
= L > 0 b- a > 0 b > a. 2
ax -3x +bx
(- a + )bx b- a 3 3 2 Câu 9: x + 2x +1
Kết quả của giới hạn lim là: x -¥ 2 2x +1 A. 2 . B. 0. C. 2 - . D. 1. 2 2 Lời giải Chọn C 3 3 2 3 3 Giải nhanh: x + 2x +1 x x 1 x -¥ ¾¾ = = - . 2 2 2x +1 2x - 2x 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 349
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 1 3 1+ + 3 3 2 3 Cụ thể: x + 2x +1 x x 1 lim = lim = - . x -¥ 2 2x +1 x -¥ 1 2 - 2 + 2 x
Câu 10: Tìm tất cả các giá trị của a để + + là . +¥ -¥( 2 lim 2x 1 ax x ) A. a > 2. B. a < 2. C. a > 2. D. a < 2. Lời giải Chọn B Giải nhanh: 2 2 x -¥ ¾¾
2x +1 + ax 2x + x
= - 2x + ax = (a- 2)x +¥ a- 2 < 0 a < 2. æ ö Cụ thể: vì ç 1 lim x = -¥ nên lim x + + ax = x ç- + + a÷÷ ç ÷ = +¥ x -¥ ( 2 2 1 ) lim 2 x -¥ 2 x -¥ çè x ÷ø æç 1 ö lim ç- 2 + + a÷÷ ç
÷ = a- 2 < 0 a < 2. 2 x -¥ çè x ÷ø
Dạng 6. Dạng vô định ¥ -¥ , 0.¥ 1. Phương pháp
Nếu biểu thức chứa biến số dưới dấu căn thì nhân và chia với biểu thức liên hợp
Nếu biểu thức chứa nhiều phân thức thì quy đồng mẫu và đưa về cùng một biểu thức.
Thông thường, các phép biến đổi này có thể cho ta khử ngay dạng vô định ;0 . hoặc 0
chuyển về dạng vô định ; 0
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính lim x 1 x 3 x Hướng dẫn giải 4 x 1 x 3 x lim x 1 x 3 lim lim 0. x x x x 1 x 3 1 3 1 1 x x Ví dụ 2: Tính 2 lim x x 5 x x Hướng dẫn giải 2 2 2 x 5 x 5 5
lim x x 5 x lim x lim . x x 2 x x 5 x 5 2 1 1 2 x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 350
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ví dụ 3: Tính 2 lim x x 5x x Hướng dẫn giải 2 E lim x x 5x x Nhân và chia liên hợp 2 x x 5x 2 2 x x 5x x x 5x 2 2 x x 5x E lim lim x 2 x x x 5x 5 x x 1 x 5x lim (Vì lim x lim x ) x 5 x x x x 1 x 5 5 5 lim . x 5 1 1 0 2 1 1 x 1 1 Ví dụ 4: Tính lim 1 x 0 x x 1 Hướng dẫn giải 1 1 E lim
1 (Dạng vô định 0. ) x 0 x x 1 1 x 1 1 lim lim 1. x 0 x x 1 x 0 x 1 1 Ví dụ 6: Tính 2 lim x 5 0. x x Hướng dẫn giải 1 2 5 lim x 5 lim 1 1. x x x x
Ví dụ 7: Tính 2 lim x x 2 x x Hướng dẫn giải 2 2 2 x 2 x 2 2
lim x x 2 x lim x lim 1. x x 2 x x 2 x 2 2 1 1 2 x 2 x 1 x x 1 Ví dụ 8: Tính lim x0 x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 351
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải 2 2 x 1 x x 1 x 1 x x 1 lim lim x0 x x0 2 x 1 x x 1 x 0 lim 0 x0 2 2 x 1 x x 1
Ví dụ 9: Tính lim x 5 x 7 x Hướng dẫn giải x 5 x 7 12 lim x 5 x 7 lim lim x x x x 5 x 7 x 5 x 7 12 x 0 lim 0. x 5 7 2 1 1 x x 2 Ví dụ 8: Tính 2
lim x 5x x . x 5 Hướng dẫn giải 2 2 2 x x x 5 x
lim x 5x x lim lim x x 2 x 2 x 5x x x 5x x 5 5 lim . x 5 2 1 1 x 1 Ví dụ 8: Tính 2 lim x 5 1. x x Hướng dẫn giải 5 5 2 x . 1 x 1 2 2 x 5 x x 5 lim lim lim lim 1 1 . 2 x x x x x x x x
3. Bài tập trắc nghiệm
Câu 1: Giá trị của giới hạn ( 3 2
lim 2x - x ) là: x -¥ A. 1. B. . +¥ C. -1. D. -¥ . Lời giải Chọn D Giải nhanh : 3 2 3 x -¥ ¾¾
2x - x 2x - . ¥
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 352
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 3 ìï lim x = -¥ æ ö ïx-¥ ï Cụ thể: lim ( 1 3 2 2x - x ) 3 = lim x çç2 ÷ - ÷ = -¥ ï ç ÷ vì í . æ 1 ö x -¥ x -¥ è x ø ïï lim çç2 ÷ - ÷ = 2 > 0 ï ç ÷ x -¥ ï è x ø î æ ö Câu 2: 1 1
Giá trị của giới hạn lim ç ÷ ç - ÷ là: - 2 ç ÷ x 2 è x - 2 x -4ø A. . -¥ B. . +¥ C. 0. D. 1. Lời giải Chọn A æ ö æ + - ö æ + ö Ta có 1 1 x 2 1 x 1 lim ç ÷ ç - ÷ = lim ç ÷ ç ÷ = lim ç ÷ ç ÷ = -¥ - 2 ç ÷ - 2 è - - ø ç ÷ - 2 è - ø ç ÷ x 2 x 2 x 2 x 2 x 4 x 4 è x -4ø Vì lim (x + ) 1 = 3 > 0; lim - = và 2
x -4 < 0 với mọi x Î( 2; - 2). - - ( 2 x 4) 0 x 2 x 2 æ a b ö æ b a ö lim ç ÷ ç - ÷ = ç ÷ ç ÷ L lim ç - ÷ ç ÷
Câu 3: Biết rằng a +b = 4 và 3 x 1
è1- x 1- x ø hữu hạn. Tính giới hạn 3 x 1 è1- x 1- x ø. A. 1. B. 2. C. 1. D. -2. Lời giải Chọn C 2 2 æ ö Ta có a b
a + ax + ax -b
a + ax + ax -b lim ç ÷ ç - ÷ = lim = lim . 3 ç ÷ 3 x è1- x 1- ø x x 1 x - x (1- x )( 2 1 1 1 1+ x + x ) æ ö Khi đó a b lim ç ÷ ç - ÷ hữu hạn 2 1+ . a 1+ .
a 1 -b = 0 2a-b = 1 - . 3 ç ÷ x 1 è1- x 1- x ø ìï + = ìï = æ ö Vậy ta có a b 4 a 1 a b ï ï í í L = -lim ç ÷ ç - ÷ 3 ï - = - ï ç ÷ x 1 2a b 1 b = 3 è1- x 1- x ø ïî ïî 2 x + x -2 -(x + 2) = -lim = -lim = 1 . x (1- x )( 2 1 1+ x + x ) 2 x 1 1+ x + x
Câu 4: Giá trị của giới hạn ( 2 lim
1+ 2x - x) là: x +¥ A. 0. B. . +¥ C. 2 -1. D. -¥ . Lời giải Chọn B æ ö Ta có lim ( ç 1 2
1+ 2x - x) = lim x ç + 2 -1÷÷ ç ÷ = +¥ 2 x +¥ x +¥ çè x ÷ø æ ö Vì ç 1 lim x = + ; ¥ lim ç + 2 -1÷÷ ç ÷ = 2 -1> 0. 2 x +¥ x +¥ çè x ÷ø Giải nhanh : 2 2 x +¥ ¾¾
1+ 2x - x 2x - x = 2x - x = ( 2 - ) 1 x + . ¥
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 353
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 5: Giá trị của giới hạn + - là: +¥( 2 lim x 1 x x ) A. 0. B. . +¥ C. 1 . D. -¥ . 2 Lời giải Chọn A . 2 2 x +¥ ¾¾
x +1 - x x - x = x - x = 0 ¾¾
Nhân lượng liên hợp. Giải nhanh: 1 1 1 2 x +¥ ¾¾ x +1 - x = = 0. 2 2 x +1 + x x + x 2x 1 Cụ thể: lim x x + - x = = = = x +¥ ( 1 0 2 1 ) lim lim 0. x +¥ 2 x +1 x + x +¥ 1 2 1+ +1 2 x x + x + x = a +b x -¥( 2 lim 5 2 5) 5 . Câu 6: Biết rằng
Tính S = 5a + . b A. S = 1. B. S = -1. C. S = 5. D. S = 5. - Lời giải Chọn A 2 2 x -¥ ¾¾
5x + 2x + x 5 5x + x 5 = - 5x + x 5 = 0 ¾¾
Nhân lượng liên hợp: Giải nhanh: 2 x -¥ ¾¾
5x + 2x + x 5 2x 2x 2x 1 = = = - . 2 2
5x + 2x + x 5 5x - x 5 -2 5x 5 Cụ thể: Ta có x lim x + x + x = x -¥ ( 2 2 5 2 5) lim x -¥ 2
5x + 2x + x 5 ìï 1 2 2 1 1 a ï = - lim 5 ï = = = - = - ¾¾ í 5 S = 1 - . x -¥ 2 -2 5 5 5 ï - 5 + + 5 b ïï = 0 î x
Câu 7: Giá trị của giới hạn + - + là: +¥( 2 2 lim x 3x x 4x x ) A. 7 . B. 1 - . C. . +¥ D. . -¥ 2 2 Lời giải Chọn B . Khi 2 2 2 2 x +¥ ¾¾
x +3x - x + 4x x - x = 0 ¾¾
Nhân lượng liên hợp:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 354
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Giải nhanh: 2 2 x +¥ ¾¾
x +3x - x + 4x -x -x -x 1 = = = - . 2 2 2 2
x + 3x + x + 4x x + x 2x 2 Cụ thể: + - + = +¥( 2 2 lim x 3x x 4x x ) -x -1 1 lim = lim = - . x +¥ 2 2
x + 3x + x + 4 x x +¥ 3 4 2 1+ + 1+ x x
Câu 8: Giá trị của giới hạn (3 3 2 lim
3x -1 + x + 2) là: x -¥ A. 3 3 +1. B. . +¥ C. 3 3 -1. D. -¥ . Lời giải Chọn D æ ö lim (3 ç 1 2 3 2 3x -1 + x + 2) ÷ 3 = lim x ç 3- - 1+ ÷ ç ÷ = -¥ 3 2 x -¥ x -¥ çè x x ÷ø æ ö Vì ç 1 2 ÷ 3 3 lim x = - , ¥ lim ç 3- - 1+ ÷ ç ÷ = 3 -1> 0. 3 2 x -¥ x -¥çè x x ÷ø Giải nhanh: 3 3 2 3 3 2 x -¥ ¾¾ x - + x + x + x = (3 3 1 2 3 3 - ) 1 x - . ¥
Câu 9: Giá trị của giới hạn + - - là: +¥ ( 2 3 3 2 lim x x x x x ) A. 5 . B. . +¥ C. -1. D. -¥ . 6 Lời giải Chọn A Khi 2 3 3 2 2 3 3 x +¥ ¾¾
x + x - x - x x -- x = x - x = 0 ¾¾
Nhân lượng liên hợp: + - - = + - + - - +¥ ( 2 3 3 2 x x x x ) +¥( 2 3 3 2 lim lim x x x x x x x x ) æ ö ç 2 ÷ ç x x ÷ ç ÷ 1 1 5 = lim ç + ÷÷ = + = . x +¥ ç 2 ÷ ç 2 3 x +1 + x ç x + x x -1 + è ( 3 ÷ 2 3 6 3 x - )2 3 1 ÷ø Giải nhanh: 2 3 3 2 + - - = ( 2 + - )+( 3 3 2 x x x x x x x
x - x - x ) 2 2 x x x x = + + 2 2 3 x +1 + x + -1 + ( 3 3 - )2 2 2 3 3 6 6 3 1 x + x
x + x x + x x x x x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 355
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 5 = + = (x +¥). 2 3 6
Câu 10: Giá trị của giới hạn (3 3 lim
2x -1 - 2x +1) là: x +¥ A. 0. B. . +¥ C. -1. D. -¥ . Lời giải Chọn A 3 3 3 3 x +¥ ¾¾
2x -1 - 2x +1 2x - 2x = 0 ¾¾
nhân lượng liên hợp: - lim ( 2 3 3
2x -1 - 2x +1) = lim = 0. x +¥ x +¥ (2x - )2 3 1 + (2x - ) 1 (2x + ) 1 + (2x + )2 3 3 1 Giải nhanh: 3 3 2x -1 - 2x +1 = 2 - 2 - -2 = 0. 3 (2x - )2 3
1 + 4x -1 - (2x + )2 3 2 3 2 3 2 3 2 3 2 1
4x + 4x + 4x 3 4x é æ ùö Câu 11: 1
Kết quả của giới hạn lim êx 1 ç ÷ ç - ú÷ là: ê ç ÷ x 0 è x úø ë û A. . +¥ B. -1. C. 0. D. +¥ . Lời giải Chọn B é æ ùö Ta có 1 lim êx 1 ç ÷ ç - ú÷ = lim (x - ) 1 = 0 -1 = -1. ê ç ÷ x 0 è úø x 0 x ë û Câu 12: x
Kết quả của giới hạn lim (x -2) là: + 2 x 2 x - 4 A. 1. B. . +¥ C. 0. D. -¥ . Lời giải Chọn C Ta có ( - x - ) x x 2. x 0. 2 lim 2 = lim = = 0 . + 2 x 2 - x 2 x 4 + x + 2 2 Câu 13: 2x +1
Kết quả của giới hạn lim x là: 3 2 x +¥ 3x + x + 2 A. 2 . B. 6 . C. . +¥ D. -¥ . 3 3 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 356
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 2 + 2x +1 x ( x + ) 2 2 1 6 lim = lim = lim x x = . 3 2 3 2 x +¥ 3x + x + 2 x +¥ 3x + x + 2 x +¥ 1 2 3 3 + + 3 x x Giải nhanh: 2x +1 2x 6 1 6 1 6 x +¥ ¾¾ x x. = .x. = .x. = . 3 2 2 2 3x + x + 2 3x 3 3 x 3 x æ ö Câu 14: 1
Kết quả của giới hạn 2 lim x ççsin px ÷ - ÷ là: 2 ç ÷ x 0 è x ø A. 0 . B. 1 - . C. . p D. . +¥ Lời giải Chọn B æ ö Ta có 1 2 lim x ççsin px ÷ - ÷ = lim ( 2
x sin px -1 = -1. 2 ) ç ÷ x 0 x 0 è x ø Câu 15: x
Kết quả của giới hạn lim + là: + ( 3 x ) 1 x ( - ) 2 1 x -1 A. 3. B. . +¥ C. 0. D. -¥ . Lời giải Chọn C . Với x x Î( 1;
- 0) thì x +1> 0 và > 0 . x -1 Do đó x x lim + = + - + + ( 3 x ) 1 lim (x ) 1 + ( 2 x x 1 2 ) x (- ) 1 x -1 x (- ) 1 (x - ) 1 (x + ) 1 x = lim x +1 - + = + ( 2 x x ) 1 0 x ( - ) 1 x -1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 357
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. HÀM SỐ LIÊN TỤC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM Định nghĩa 1
Cho hàm số y = f (x) xác định trên khoảng K và x Î K . 0
Hàm số y = f (x) được gọi là liên tục tại x nếu lim f (x)= f (x . 0 ) 0 x x0
II – HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG Định nghĩa 2
Hàm số y = f (x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f (x) được gọi là liên tục trên đoạn [ ;
a b] nếu nó liên tục trên khoảng ( ; a ) b và
lim f (x) = f (a), lim f (x) = f ( ) b . + - x a x b
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một '' đường liền '' trên khoảng đó. y y x a b a x O O b
Hàm số liên tục trên khoảng ( ; a )
b Hàm số không liên tục trên khoảng ( ; a ) b
III – MỘT SỐ ĐỊNH LÍ CƠ BẢN Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng. Định lí 2
Giả sử y = f (x) và y = g(x) là hai hàm số liên tục tại điểm x . Khi đó: 0
a) Các hàm số y = f (x)+ g(x) , y = f (x)- g(x) và y = f (x).g(x) liên tục tại x ; 0 f (x ) b) Hàm số
liên tục tại x nếu g(x ¹ 0 . 0 ) 0 g(x ) Định lí 3
Nếu hàm số y = f (x) liên tục trên đoạn [ ;
a b] và f (a). f (b) < 0, thì tồn tại ít nhất một điểm c Î ( ; a b)
sao cho f (c)= 0 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 358
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f (x) liên tục trên đoạn [ ;
a b] và f (a). f (b) < 0, thì phương trình f (x ) = 0 có ít nhất
một nghiệm nằm trong khoảng ( ; a ) b .
B. CÂU HỎI TRẮC NGHIỆM
Dạng 1. Xét tính liên tục của hàm số 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1: Hàm số f (x) 1 = 3- x + liên tục trên: x + 4 A. [ 4; - 3]. B. [ 4; - 3). C. ( 4; - 3]. D. [ ; -¥ 4 - ]È[3;+ ) ¥ . Lời giải Chọn C ìï - ³ ìï > - Điều kiện: 3 x 0 x 4 ï ï TXD í í ¾¾¾ D = (-4; ] 3 ¾¾
hàm số liên tục trên ( 4; - ) 3 . Xét tại ïx + 4 > 0 ïx £ -3 ïî ïî x = 3, ta có æ ö ç ÷ f (x) 1 1 lim = lim ç 3- x + ÷ = = f ç ÷ ( ) 3 ¾¾
Hàm số liên tục trái tại x = 3. - - x3 x3 ç è x + 4 ÷ø 7
Vậy hàm số liên tục trên (-4; ] 3 . 3 Câu 2:
x + x cos x + sin x
Hàm số f (x) = liên tục trên: 2 sin x +3 æ ö A. [ 1; - ] 1 . B. [1;5]. C. 3 ç- ç ; ÷ +¥÷. ç D. . è 2 ÷ø Lời giải Chọn D
Vì 2sin x +3 =/ 0 với mọi TXD x Î ¾¾¾ D = ¾¾
Hàm số liên tục trên . 2 Câu 3: x -3x + 2
Cho hàm số f (x) xác định và liên tục trên với f (x) =
với mọi x =/1. Tính x -1 f ( ) 1 . A. 2. B. 1. C. 0. D. -1. Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 359
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vì f (x) liên tục trên nên suy ra 2 - + f ( ) = f (x) x 3x 2 1 lim = lim = lim(x- ) 2 = 1 - . x 1 x 1 x 1 x -1 Câu 4: x + - - x
Cho hàm số f (x) xác định và liên tục trên [ 3; - ] 3 với f (x) 3 3 = với x ¹ 0 . x Tính f (0). A. 2 3 . B. 3 . C. 1. D. 0. 3 3 Lời giải Chọn B
Vì f (x) liên tục trên [ 3; - ] 3 nên suy ra + - - f ( ) = f (x) x 3 3 x 2 1 0 lim = lim = lim = . x0 x0 x0 x x + 3 + 3- x 3 Câu 5: x
Cho hàm số f (x) xác định và liên tục trên (-4;+ ) ¥ với f (x) = với x ¹ 0 . x + 4 - 2 Tính f (0). A. 0. B. 2. C. 4. D. 1. Lời giải Chọn C
Vì f (x) liên tục trên ( 4; - +¥) nên suy ra (0)= lim ( )= lim x f f x = lim( x + 4 + ) 2 = 4. x0 x0 x0 x + 4 - 2
Dạng 2. Hàm số liên tục tại một điểm 1. Phương pháp
Ta cần phải nắm vững định nghĩa:
Cho hàm số y f x xác định trên khoảng K và x0 K. Hàm số y f x gọi là liên tục tại x0 nếu
lim f(x) f(x0) lim f(x) lim f(x) f(x0). xx0 xx xx o o
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho x 2 2 x f x f 0 x với x
0. Phải bổ sung thêm giá trị bằng bao nhiêu thì
hàm số liên tục tại x 0? Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 360
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 x 2 2 x x 2 2 x lim f x lim lim x0 x0 x
x0 x 2 2 x 2 1 lim .
x0 x 2 2 x 2
Như vậy để hàm số liên tục tại x 0 thì phải bổ sung thêm giá trị 1 f 0 . 2
Ví dụ 2: Cho hàm số 2 a x vôùi x 1 vaø a f x
. Giá trị của a để f x liên tục tại x 1 là bao 3 vôùi x 1 nhiêu? Hướng dẫn giải TXĐ: D . Ta có: lim f x lim 2 a x a 1. x 1 x 1
Để hàm số liên tục tại x 1 lim f x f
1 a 1 3 a 4. x 1 2 x 1 vôùi x 3 vaø x 2
Ví dụ 3: Cho hàm số f x 3 . x x 6
Tìm b để f x liên tục tại x 3. b 3 vôùi x 3 vaø b TXĐ: D . Ta có: 2 x 1 3 lim f x lim ; f 3 b 3. 3 x3 x3 x x 6 3 3 2 3
Để hàm số liên tục tại x 3 lim f x f 3 b 3 b . x3 3 3 a 2 kh i x 2
Ví dụ 4: Cho hàm số f x
. Với giá trị nào của a thì hàm số liên tục tại x 2. sin khi x 2 x Hướng dẫn giải TXĐ: D . Ta có f 2 sin 1 2
lim f x lim a 2 a 2 x 2 x 2
lim f x lim sin 1 x 2 x 2 2
Hàm số liên tục tại x 2 khi a 1 2 a 3.
Ví dụ 5: Tìm số a để hàm số sau liên tục tại điểm x0. 3 3x 2 2 neáu x 2 f x x 2 ; x0 2. ax 2 neáu x 2 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 361
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 TXĐ: D . Ta có: 3 3x 2 2 3x 2 1 lim f x lim lim . x 2 2 x 2 x 2 x 2 3 3 4 x 2 3x 2 2 3x 2 4
lim f x ax 2 2a 2. x 2
Lại có: f 2 2a 2 . 1 7
Hàm số liên tục tại x0 2 nếu 2a 2 a . 4 8
Ví dụ 6: Xét tính liên tục của hàm số sau tại x0. x 3 2 neáu x 1 x 1 1 f x neáu x 1 x 0, x 1. 4 ; 0 0 2 x 1 neáu x 1 2 x 6x 7 Hướng dẫn giải x 3 2 x 1 1 Ta có: lim f x lim lim . x 1 x 1 x 1 x 1 4 x 1 x 3 2 2 x 1 x 1 1 1 lim f x lim lim ; f 1 . 2 x 1 x 1 x 6x 7 x 1 x 7 4 4 1
Vậy lim f x lim f x f
1 , nên hàm số liên tục tại x0 1. x 1 x 1 4 2 x 1 1
Dễ thấy lim f x lim f 0 2
nên hàm số liên tục tại x 0. x0 x0 x 6x 7 7
Ví dụ 7: Xét tính liên tục của hàm số sau tại x0.
f x x 2 ; x0 2, x0 1. Hướng dẫn giải x 2 ne áu x 2
Ta có: f x x 2 x 2 ne áu x 2
Ta có: lim f x limx 2 3; f 1 3. x 1 x 1
Vậy lim f x f
1 , nên hàm số liên tục tại tại x 1. x 1 0
Lại có: lim f x lim x 2 0; lim f x 0; f 2 0. x 2 x 2 x 2
Vậy lim f x lim f x lim f 2
0 nên hàm số liên tục tại x 2. x 2 0 x 2 x 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 362
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 x 2 vôùi 5 x 4 x 5
Ví dụ 8: Cho hàm số f x mx 2 vôù i x 4
. Tìm giá trị của m để f x liên tục tại x 4 . x vôùi x 4 3 Hướng dẫn giải x 2 2 x 2 Ta có: lim f x lim ; lim . x 4 x 4 x 5 3 x 4 3 3 Và f 4 4m 2
Để hàm số liên tục tại x 4 thì lim f x lim f x f 4 x 4 x 4 2 1
4m 2 m . 3 3 2 x 8 3 neáu x 1 2
Ví dụ 9: Cho hàm số f x x 4x 3
. Tìm giá trị của a để f x liên tục tại x 1. 1 2 cos x a x neáu x 1 6 Hướng dẫn giải TXĐ: D . 1 1 f 2 2
1 cos a 1 a 1. 6 6 1 1 lim f x 2 2 lim cos x
a x a 1. x 1 x 1 6 6 2 2 2
x 8 3 x 8 3 x 8 3 lim f x lim lim 2 x 4x 3 2x 4x3 2 x 1 x 1 x 1 x 8 3 2 x 8 9 x 1x 1 lim lim 2 x 4x 3 2 x 8 3 x 1x 3 2 x 1 x 1 x 8 3 x 1 1 lim . 2 x 1 6 x 3 x 8 3
Để hàm số liên tục tại x 1 lim f x lim f x f 1 x 1 x 1 1 2 1
a 1 a 1 . 6 6
3. Bài tập trắc nghiệm 2 ìïx - x -2 ï Câu 1: ï khi 2 x ¹
Tìm giá trị thực của tham số ï
m để hàm số f (x ) = í x - 2
liên tục tại x = 2. ïïm ï khi 2 x ïî = A. m = 0. B. m =1. C. m = 2. D. m = 3.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 363
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D
. Tập xác định: D = , chứa x = 2 . Theo giả thiết thì ta phải có 2 - - m = f ( ) = f (x) x x 2 2 lim = lim = lim(x + ) 1 = 3. x2 x2 x2 x - 2 3 2
ìïx - x +2x -2 ï Câu 2: ï khi 1 x ¹
Tìm giá trị thực của tham số ï
m để hàm số f (x ) = í x -1 liên tục tại ï3 ïï x +m khi x = 1 ïî x = 1. A. m = 0. B. m = 2. C. m = 4. D. m = 6. Lời giải Chọn A
. Hàm số xác định với mọi x Î . Theo giả thiết ta phải có
x - x + x - (x- ) 1 ( 2 3 2 x + 2 2 2 ) 3+ m = f ( )
1 = lim f (x) = lim = lim = lim( 2
x + 2) = 3 m = 0. x 1 x 1 x 1 x 1 x -1 x 1 - ìï x -1 ï Câu 3: ï khi 1 ¹
Tìm giá trị thực của tham số x
k để hàm số y = f (x) = í x -1
liên tục tại x = 1.
ïïïk +1 khi x =1 ïî A. 1 k = . B. k = 2. C. 1 k = - . D. k = 0. 2 2 Lời giải Chọn C
Hàm số f (x) có TXĐ: D =[0;+ )
¥ . Điều kiện bài toán tương đương với Ta có: - k + = y( ) x 1 1 1 1 1 1 = lim y = lim = lim = k = - . x 1 x 1 x 1 x -1 x +1 2 2 ìï 3- x ï khi 3 ¹ Câu 4: x ï
Biết rằng hàm số f (x)= í x +1-2
liên tục tại x = 3 (với ï
m là tham số). Khẳng ïm ï khi 3 x ïî =
định nào dưới đây đúng? A. m Î( 3; - ) 0 . B. m £ -3. C. m Î[0; ) 5 . D. m Î[5;+ ) ¥ . Lời giải Chọn B
Hàm số f (x) có tập xác định là ( 1 - ;+ )
¥ . Theo giả thiết ta phải có (3- x) 3 + + - x ( x 1 )2 m = f ( )
3 = lim f (x) = lim = lim = -lim( x +1+ ) 2 = -4. x3 x3 x3 x3 x +1 - 2 x -3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 364
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 1 2 ï Câu 5: x sin khi 0 x ¹
Tìm giá trị thực của tham số ï
m để hàm số f (x ) = í x
liên tục tại x = 0. ïm ïï khi 0 x = î A. m Î( 2; - - ) 1 . B. m £ -2. C. m Î[ 1; - 7). D. m Î[7;+ ) ¥ . Lời giải Chọn C
Với mọi x =/ 0 ta có 0 £ f (x) 1 2 2 = x sin
£ x 0 khi x 0 ¾¾
lim f (x) = 0. x x0
Theo giải thiết ta phải có: m = f (0)= lim f (x)= 0. x0 ìïtan x ï Câu 6: sin khi 0 x ¹ Biết rằng lim x =1. Hàm số ï
f (x ) = í x
liên tục trên khoảng nào sau đây? x0 x ï0 ïï kh i x = 0 î æ ö æ ö æ ö A. p ç p p p ç0; . ÷÷ ç ÷ ç ÷ ç B. ç ; -¥ ÷. C. - ç ; ÷. D. ( ; -¥ ) +¥ . è 2 ÷ø çè 4 ÷ø çè 4 4÷ø Lời giải Chọn A Tập xác định: ìïp ü ï ï æp 3p ö
æ p pö æp 3pö ï
D = í + kp | k Î ý = ç ç +k ; p + kp÷÷ = Èç- ç ; ÷÷Èç ÷ ç + ÷È ïïî2 ï ç ÷ ï è ø ç ÷ è ø ç ÷ è ø þ k Î 2 2 2 2 2 2 Ta có f (x) tan x sin x 1 1 lim = lim = lim . = 1. = 1= / 0 = f (0) ¾¾
f (x) không liên tục tại x0 x0 x0 x x cos x cos 0 x = 0. ìïsin px ï Câu 7: sin khi 1 x Biết rằng lim
x =1. Tìm giá trị thực của tham số ï ¹
m để hàm số f (x ) = í x -1 x0 x ïm ïï khi 1 x = î
liên tục tại x = 1. A. m = p - .
B. m = p. C. m = 1. - D. m =1. Lời giải Chọn A
Tập xác định D = .
Điều kiện bài toán tương đương với = ( ) = ( ) sin p 1 lim =lim x m f f x x 1 x 1 x -1
sin(px -p + p) -sin p(x - ) 1 é sin p(x - )ù (ê p) 1 lim lim lim . ú = = = - ( ) * . ê ú x 1 x 1 x 1 x -1 x -1 p(x - ê ) 1 ë úû Đặt sin t
t = p(x - )
1 thì t 0 khi x 1. Do đó (*) trở thành: m = lim( p - ). = - . p t 0 t
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 365
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Câu 8: sin Biết rằng lim
x =1. Tìm giá trị thực của tham số m để hàm số x0 x 1 ìï + cos x ï khi x ¹ p ïï
f (x ) = í (x - p)2
liên tục tại x = . p ïïm ï khi x = p ïî A. p p m = . B. m = - . C. 1 m = . D. 1 m = - . 2 2 2 2 Lời giải Chọn C
. Hàm số xác định với mọi x Î . Điều kiện củz bài toán trở thành: 2 æ ö é æ öù x p p 2 x x 2 2cos 2sin ç ÷ ç - ÷ êsinç ÷ + ç ÷ ç - ÷ú è ø ê ç ÷ è øú
m = f (p) = lim f (x) 1 cos x 2 2 2 1 2 2 = lim = lim = lim = lim ê ú ( ) * xp
xp ( -p)2
xp ( -p)2 xp ( -p)2
2 xp ê æ x x x x pö ú ê ç ÷ ç - ÷ ú ê çè2 2÷ø ú ë û 2 æ ö Đặt x p 1 sin t 1 1 t =
- 0 khi x 1. Khi đó (*) trở thành: 2 m = limç ÷ ç ÷ = .1 = . 2 2 ç ÷ t0 2 è t ø 2 2 3 ìï khi x = 1 ï - ïï 4 Câu 9: x + x
Hàm số f (x)= ïí khi x ¹ 1
- , x ¹ 0 liên tục tại: 2 ï x + x ïï1ïï khi x = 0 ïî
A. mọi điểm trừ x = 0, x =1.
B. mọi điểm x Î .
C. mọi điểm trừ x = -1.
D. mọi điểm trừ x = 0. Lời giải Chọn B
Hàm số y = f (x) có TXĐ: D = .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng ( ; -¥ - ) 1 ,( 1 - ;0) và (0; ) +¥ .
(i) Xét tại x = -1 , ta có + x(x + ) 1 ( 2 4 x - x x x + ) 1 lim f (x) = lim = lim = lim ( 2
x - x +1 = 3 = f 1 - . 2 ) ( ) x 1 - x 1 - x 1 x + x - x(x + ) x 1 1 - ¾¾
hàm số y = f (x) liên tục tại x = -1 .
(ii) Xét tại x = 0 , ta có x(x + ) 1 ( 2 4 x - x x x + + )1 lim f (x) = lim = lim = lim( 2
x - x +1 = 1 = f 0 . 2 ) ( ) x0 x0 x0 x + x x(x + ) x0 1 ¾¾
hàm số y = f (x) liên tục tại x = 0 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 366
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 0, ìï 5 khi x = -1 ïïïïx(x+ )1
Câu 10: Số điểm gián đoạn của hàm số ï f (x ) = í
khi x ¹ -1, x ¹ 1 là: 2 ï x -1 ïï1ï khi x = 1 ïïî A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B
. Hàm số y = f (x) có TXĐ D = . x (x + ) 1
Hàm số f (x) =
liên tục trên mỗi khoảng ( ; -¥ - ) 1 , (-1; ) 1 và (1;+¥) . 2 x -1 x(x + ) 1 (i) Xét tại x 1
x = -1 , ta có lim f (x) = lim = lim = = f (- ) 1 ¾¾ Hàm số liên tục 2 x 1 - x-1 x-1 x -1 x -1 2 tại x = -1. ìï x(x + ) 1 ïïlim ( )= lim = lim x f x = +¥ + + 2 + ï (ii) Xét tại x 1 x 1 ï - x 1 x 1 x -1 x = 1 , ta có í ¾¾
Hàm số y = f (x) gián ï x(x + ï ) ï ( ) 1 lim = lim = lim x f x = -¥ ï - - 2 - ïx 1 x 1 î - x 1 x 1 x -1 đoạn tại x = 1 .
Dạng 3. Hàm số liên tục trên một khoảng 1. Phương pháp
Hàm số y f x được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Hàm số y f x được gọi là liên tục trên đoạn a,b
nếu nó liên tục trên a,b và
lim f(x) f(a), lim f(x) f(b .) x a x b
2. Các ví dụ rèn luyện kĩ năng x 1
Ví dụ 1: Cho hàm số f x 2 . f x 2
Khi đó liên tục trên các khoảng nào sau đây? x 5x 6 A. 3;2. B. 3;. C. ;3 . D. 2;3. Hướng dẫn giải ĐÁP ÁN D 2 x 1 f x f x 2;3 . 2 không liên tục tại x 2; x
3, suy ra liên tục trên khoảng x 5x 6
Ví dụ 2: Hàm số nào dưới đây liên tục trên ? 3x 1 A. y . 2 B. y 3 tan x. 1 x 4 x 3 2x C. y . D. y . 2 2 1 x 1 sin x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 367
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải ĐÁP ÁN C
Ta có định lí: Mọi hàm sơ cấp đều liên tục trên từng khoảng xác định.
Do đó: Phương án A sai vì tập xác định là \ 1; 1 .
Phương án B sai vì tan x chỉ xác định khi x k , k . 2
Phương án D sai vì 1 sin x 0 , nghĩa là hàm số chỉ xác định khi x k2 , k . 2
Phương án C đúng vì hàm số có tập xác định là D nên nó liên tục trên .
Ví dụ 3: Hàm số nào dưới đây liên tục trên 0;? sin x 2 3 2x 2 A. y x 1. B. y . y . y x x. 2 C. D. x 1 x 1 Hướng dẫn giải ĐÁP ÁN C
Tập xác định của hàm số y x 1 là 1;
suy ra y không liên tục trên 0;. sin x 2
Tập xác định của hàm số y \ 1;1 0; . 2 là
suy ra y không liên tục trên x 1 3 2x
Tập xác định của hàm số y
là 1;. Suy ra y liên tục trên 1;. Mặt khác x 1
1; 0; nên y cũng liên tục trên 0;. 2
Tập xác định của hàm số y x x là ;0 1 ;
. Suy ra y không liên tục trên 0;.
Ví dụ 4: Hàm số y tan x.cot x liên tục trên khoảng nào dưới đây? A. 0; . B. ; . C. 0;. D. ; . 2 2 2 Hướng dẫn giải ĐÁP ÁN A x 1 k
Hàm số y tan x.cot x xác định khi ; 1 k ,k2 . x k2 2
Do đó trong bốn khoảng của đề bài thì chỉ có 0; 2 thỏa điều kiện xác định của hàm số y
tanx.cot x.Nghĩa là nó liên tục trên 0; . 2 tanx vôùi x 0
Ví dụ 5: Cho hàm số f x x
. Hàm số f x liên tục trên các khoảng nào sau đây? 0 vôùi x 0 A. 0; . B. ; . C. ; .. D. ; . 2 4 4 4 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 368
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ĐÁP ÁN A tan x lim
1 f 0 0. Hàm số f x gián đoạn tại x 0 và x k ,
suy ra f x liên tục trên x0 x 0 0 2 khoảng 0; . 2 2 2 a x vôùi x 2, a
Ví dụ 6: Cho hàm số f x
Giá trị của a để f x liên tục trên là: 2 a . 2 x vô ùi x 2 A. 1 và 2. B. 1 và 1 . C. 1 và 2. D. 1 và 2. Hướng dẫn giải ĐÁP ÁN D lim f x 2
2a lim f x 22 a f 2 x 2 x 2 2 2 a 1
a 2 a a a 2 0 . a 2
3. Bài tập trắc nghiệm 2 2 ìï £ Câu 1: m x khi 2 x
Có bao nhiêu giá trị thực của tham số ï
m để hàm số f (x ) = liên tục ( íï 1-m ï )x khi x > 2 î trên ? A. 2. B. 1. C. 0. D. 3. Lời giải Chọn A
. TXĐ: D = . Hàm số liên tục trên mỗi khoảng ( ;2 -¥ ); (2; ) +¥ .
Khi đó f (x) liên tục trên f (x) liên tục tại x = 2
lim f (x) = f (2) lim f (x) = lim f (x) = f (2). ( ) * x 2 + - x 2 x 2 ìïï f (2) 2 = ï 4m é ï m = -1 ï ê
Ta có ïílim f (x)= lim (é1-m)xù = 2(1-m) ¾¾ ( ) 2
* 4m = 2(1-m) ê + + 1 . ë û ïx2 x 2 êm = ïï êë ï f ï (x) 2 2 2 2 lim = lim m x = 4m - - ïîx2 x 2 ìï Î Câu 2: x khi x 0;4 Biết rằng hàm số ï f (x ) [ ] = í
tục trên [0;6]. Khẳng định nào sau đây đúng? 1 ï +m khi x Î ï (4;6] î A. m < 2.
B. 2 £ m < 3.
C. 3 < m < 5. D. m ³ 5. Lời giải Chọn A
Dễ thấy f (x) liên tục trên mỗi khoảng (0;4) và (4;6) . Khi đó hàm số liên tục trên đoạn
[0;6] khi và chỉ khi hàm số liên tục tại x = 4, x = 0, x = 6 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 369
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïïlim f (x)= f (0) + ïx0 ï
Tức là ta cần có ïïílim f (x)= f (6) . ( ) * - ïx6
ïïïlim f (x)= lim f (x)= f (4) ï - + ïîx4 x 4 ìïlim f ï (x)= lim x = 0 + + ïx0 x 0 · í ; ïï f (0)= 0 = 0 ïî
ìïlim f (x)= lim (1+m)=1+m ï - - ïx6 x 6 · í ; ïï f (6)=1+m ïî ìïlim f ï (x) = lim x = 2 - ïx4 - x 4 ïï li
· í m f (x) = lim (1+ m) = 1+ m ; + + ïx4 x 4 ïïïf (4)=1+m ïïî Khi đó ( )
* trở thành 1+ m = 2 m = 1 < 2. 2 ìïx -3x + 2 ïï khi x ¹ 1
Câu 3: Có bao nhiêu giá trị của tham số ï
a để hàm số f (x ) = í x -1 liên tục trên ïïaï khi x = 1 ïî . A. 1. B. 2. C. 0. D. 3. Lời giải Chọn C
Hàm số f (x) liên tục trên ( ) ;1 -¥
và (1;+¥). Khi đó hàm số đã cho liên tục trên khi
và chỉ khi nó liê tục tại x =1, tức là ta cần có
lim f (x) = f ( )
1 lim f (x) = lim f (x) = f ( ) 1 . ( ) * x 1 + - x 1 x 1
ìïx -2 khi x>1 ì ï
ïlim f (x) = lim (2 - x) = 1 ï ï Ta có - - ï ï f (x ) x 1 x 1 = a í khi 1 x = ¾¾ í ¾¾ ( ) * không tỏa mãn với ï ï ï
lim f (x) = lim (x -2) = - ï 1 2
ï - x kh i x <1 + + ïîx 1 x 1 ïî mọi a Î .
Vậy không tồn tại giá trị a thỏa yêu cầu. 2 ìï x -1 ïï khi 1 ¹ Câu 4: x Biết rằng ï
f (x ) = í x -1
liên tục trên đoạn [0; ] 1 (với ï
a là tham số). Khẳng định ïa ï khi 1 x ïî =
nào dưới đây về giá trị a là đúng?
A. a là một số nguyên. B. a là một số vô tỉ. C. a > 5. D. a < 0. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 370
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hàm số xác định và liên tục trên [ )
0;1 . Khi đó f (x) liên tục trên [0; ] 1 khi và chỉ khi
lim f (x) = f ( ) 1 . ( ) * - x 1 ìï f ( ) 1 = a ï Ta có ïï 2 í - ¾¾ * a = 4. ï é ù ï f (x ) x 1 lim = lim = lim (x + ê ) 1 + = ú - - - ( x ) ( ) 1 4 ïx 1 x 1 x 1 ïî x 1 ë û - ìï x -1 ï khi 1 < Câu 5: x ï
Xét tính liên tục của hàm số f (x)= í 2- x -1
. Khẳng định nào dưới đây đúng? ï- ïï 2x khi x ³1 ïî
A. f (x) không liên tục trên .
B. f (x) không liên tục trên (0;2).
C. f (x) gián đoạn tại x = 1.
D. f (x) liên tục trên . Lời giải Chọn D ìïïïïïf ( )1=-2 ïï
Ta có ïílim f (x)= lim (-2x)= 2 - ¾¾
f (x) liên tục tại x = 1. + + ïx 1 x 1 ïïï - ï é ù ï f (x ) x 1 lim = lim = lim - - + = - ê ú - - - ( 2 x )1 2 ïx 1 x 1 x 1 ïî 2 x 1 ë û - -
Vậy hàm số f (x) liên tục trên . 2 ìï x -5x +6 ïï khi 3 > Câu 6: x
Tìm giá trị nhỏ nhất của ï
a để hàm số f (x ) = í 4x -3 - x
liên tục tại x = 3 . ïï 2 1 ï a x khi x 3 ïî - £ A. 2 - . B. 2 . C. 4 - . D. 4 . 3 3 3 3 Lời giải Chọn A
Điều kiện bài toán trở thành: lim f (x)= lim f (x)= f (3). ( ) * + - x 3 x 3 ìï f (3) 2 = 1-3a ïïïï 2 ï (x -2) ï - + ( 4x -3 5 6 + x x x )
Ta có ílim f (x)= lim = lim = -3 + + + ïx3 x 3 x 3 ï 4x -3 - x 1- x
ïïïlim f (x)= lim - = - ï - - ( 2 1 a x) 3 1 3a . ïx3 x 3 î ¾¾ ( ) 2 2 * a = ¾¾ a = - . min 3 3 ì 3 ï 3x + 2 -2 ïï khi 2 x > ï
Câu 7: Tìm giá trị lớn nhất của ï x - 2
a để hàm số f (x ) = í
liên tục tại x = 2. ïï 1 2 a ï x + khi 2 x £ ïïî 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 371
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. a = 3. B. a = 0. C. a = 1. D. a = 2. max max max max Lời giải Chọn C
Ta cần có lim f (x)= lim f (x)= f (2). ( ) * + - x 2 x 2 ìïï f (2) 7 2 = 2a - ïï 4 ïïï 3 Ta có ï + - ïí f (x ) 3x 2 2 1 lim = lim = ¾¾ ( ) * a = 1 ¾¾ a = 1. + + max ïx2 x 2 x - 2 4 ïïï æ ö ïïlim f (x) 1 7 2 2 = lim ç ï ça x ÷ + ÷ = 2a - - - ç ÷ ïx2 x 2 è 4 ø 4 ïî 1 ìï -cos x khi x £ 0
Câu 8: Xét tính liên tục của hàm số ï f (x ) = í
. Khẳng định nào sau đây đúng? ïï x +1 khi x > 0 î
A. f (x) liên tục tại x = 0.
B. f (x) liên tục trên (-¥ ) ;1 .
C. f (x) không liên tục trên .
D. f (x) gián đoạn tại x = 1. Lời giải Chọn C
Hàm số xác định với mọi x Î .
Ta có f (x) liên tục trên ( ;0 -¥ ) và (0; ) +¥ . ìïïïf (0)=1 ïï
Mặt khác ïílim f (x)= lim (1-cos x)=1-cos0 = 0 ¾¾
f (x) gián đoạn tại x = 0. - - ïx0 x 0
ïïïïlim f (x)= lim x+1= 0+1=1 + + ïîx0 x 0 ìï px ï £ Câu 9: x
Tìm các khoảng liên tục của hàm số ï f (x ) cos khi 1 = í 2
. Mệnh đề nào sau đây là
ïïïx -1 khi x >1 ïî sai?
A. Hàm số liên tục tại x = -1 .
B. Hàm số liên tục trên các khoảng ( , -¥ - ) 1 ; (1;+ ) ¥ .
C. Hàm số liên tục tại x = 1 .
D. Hàm số liên tục trên khoảng (-1, ) 1 . Lời giải Chọn A
Ta có f (x) liên tục trên ( ; -¥ - ) 1 , ( 1 - ; ) 1 , (1;+ ) ¥ .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 372
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï æ pö ïï f (- ) 1 = cosç ÷ - ç ÷ = 0 ï ç ÷ · Ta có è 2 ø í ¾¾
f (x) gián đoạn tại x = -1. ïï lim f ï (x)= lim (x - ) 1 = -2 - - ïx ( - ) 1 x ( - ) 1 ïî ìïï p ï f ( ) 1 = cos = 0 ïï 2 ï
· Ta có ïílim f (x) = lim (x - ) 1 = 0 ¾¾
f (x) liên tục tại x = 1. + + ïx 1 x 1 ïïï p ïïlim x f (x ) = lim cos = 0 - - ïx 1 x 1 ïî 2
Câu 10: Hàm số f (x) có đồ thị như hình bên không liên tục tại y
điểm có hoành độ là bao nhiêu? 3 A. x = 0. 1 x B. x = 1. O 1 2 C. x = 2. D. x = 3. Lời giải Chọn B
Dễ thấy tại điểm có hoành độ x = 1 đồ thị của hàm số bị '' đứt ''
nên hàm số không liên tục tại đó.
Cụ thể: lim f (x)= 0 =/ 3 = lim f (x) nên f (x) gián đoạn tại x =1. + - x 1 x 1 2 ìïx ïï khi 1 x < , x ¹ 0 ïï x Câu 11: ï Cho hàm số ï f (x ) = 0 í k hi x = 0
. Hàm số f (x) liên tục tại: ïïïï x khi 1 x ³ ïïïî
A. mọi điểm thuộc . B. mọi điểm trừ x = 0 .
C. mọi điểm trừ x = 1 . D. mọi điểm trừ x = 0 và x = 1 . Lời giải Chọn A
Hàm số y = f (x) có TXĐ: D = .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng ( ;0 -¥ ),(0; ) 1 và (1; ) +¥ .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 373
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïïïf (0)=0 ïïï 2 ï
Ta có ïílim ( )= lim x f x = lim x = 0 ¾¾
f (x) liên tục tại x = 0. - - - ïx0 x 0 x 0 x ïï 2 ïïïlim ( )= lim x f x = lim x = 0 ï + + + ïx0 x 0 x 0 î x ìïï f ( )1=1 ïï 2 ï
Ta có ïílim ( )= lim x f x = lim x = 1 ¾¾
f (x) liên tục tại x = 1. - - - ïx 1 x 1 x 1 x
ïïïïlim f (x)= lim x =1 ï + + ïîx 1 x 1
Vậy hàm số y = f (x) liên tục trên . 2 ìïx -1 ïï
khi x < 3, x ¹ 1 ïï x -1 Câu 12: ï Cho hàm số ï f (x ) = í4 khi x = 1
. Hàm số f (x) liên tục tại:
ïïïï x+1 khi x ³3 ïïïî
A. mọi điểm thuộc . B. mọi điểm trừ x = 1 .
C. mọi điểm trừ x = 3 . D. mọi điểm trừ x = 1 và x = 3 . Lời giải Chọn D
Hàm số y = f (x) có TXĐ: D = .
Dễ thấy hàm số y = f (x) liên tục trên mỗi khoảng (-¥ ) ;1 ,(1; ) 3 và (3; ) +¥ . ìï f ( ) 1 = 4 ï Ta có ï 2 í ¾¾ f (x) -
gián đoạn tại x = 1. ïï f (x ) x 1 lim = lim = lim (x + ) 1 = 2 ï x 1 x 1 x 1 ïî x -1 ìï f (3)= 2 ï Ta có ï 2 í ¾¾ f (x) -
gián đoạn tại x = 3. ïï f (x ) x 1 lim = lim = lim (x + ) 1 = 4 - - - ïx3 x 3 ïî - x 3 x 1 2
ìï x khi x < 0 ï Câu 13: ï
Số điểm gián đoạn của hàm số ï h(x ) 2
= íx +1 khi 0 £ x £ 2 là:
ï3ïïx -1 khi x >2 ïî A. 1. B. 2. C. 3. D. 0. Lời giải Chọn A
Hàm số y = h(x) có TXĐ: D = .
Dễ thấy hàm số y = h(x) liên tục trên mỗi khoảng ( ;0 -¥ ),(0;2) và (2; ) +¥ .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 374
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 h ìï (0)=1 Ta có ïí ¾¾
f (x) không liên tục tại x = 0 .
ï lim h(x) = lim 2x = 0 ï - - ïîx0 x 0 ìïh ï (2)= 5 ïï
Ta có ïïílim h(x)= lim + = ¾¾
liên tục tại x = 2 . - - ( 2 x ) 1 5 f (x ) ïx2 x 2
ïïïlim h(x)= lim (3x- )1=5 ï + + ïîx2 x 2 2 ìïx + x khi 1 x < ï Câu 14: ï Tính tổng ï
S gồm tất cả các giá trị m để hàm số f (x ) = 2 í
khi x = 1 liên tục tại x = 1 . ïï 2 m ï x +1 khi x > 1 ïî A. S = -1. B. S = 0. C. S =1. D. S = 2. Lời giải Chọn B
Hàm số xác định với mọi x Î .
Điều kiện bài toán trở thành lim f (x)= lim f (x)= f ( ) 1 . ( ) * + - x 1 x 1 ìïïïf ( )1=2 ïï
Ta có ïílim f (x)= lim + = + ¾¾ + = + + ( 2 m x ) 2 1 m 1 ( ) 2 * m 1 2 ïx 1 x 1
ïïïïlim f (x)= lim + = - - ( 2 x x ) 2 ïîx 1 x 1 m = 1 ¾¾ S = 0. ì-
ï x cos x khi x < 0 ïïï 2 Câu 15: ï x Cho hàm số ï f (x ) = í
khi 0 £ x <1. Hàm số f (x) liên tục tại: 1 ï + x ïïï 3 ïx khi x ³1 ïî
A. mọi điểm thuộc x Î .
B. mọi điểm trừ x = 0.
C. mọi điểm trừ x = 1. D. mọi điểm trừ x = 0; 1 x = . Lời giải Chọn C
Hàm số y = f (x) có TXĐ: D = .
Dễ thấy f (x) liên tục trên mỗi khoảng ( ;0 -¥ ),(0; ) 1 và (1; ) +¥ . ìïïïïïf (0)=0 ïï
Ta có ïílim f (x)= lim (-x cos x)= 0 ¾¾
f (x) liên tục tại x = 0 . - - ïx0 x 0 ïï 2 ïïïlim ( )= lim x f x = 0 ï + + x 0 x 0 ïî 1+ x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 375
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïï f ( )1=1 ïïï 2 ï Ta có ïí f (x ) x 1 lim = lim = ¾¾
f (x) không liên tục tại x = 1 . - - ïx 1 x 1 1+ x 2
ïïïï lim f (x) 3 = lim x = 1 ï + + x 1 ïî x 1
Dạng 4. Số nghiệm của phương trình trên một khoảng 1. Phương pháp
Chứng minh phương trình f x 0 có ít nhất một nghiệm
- Tìm hai số a và b sao cho f a.f b 0
- Hàm số f x liên tục trên đoạn a;b
- Phương trình f x 0 có ít nhất một nghiệm x0 a;b
Chứng minh phương trình f x 0 có ít nhất k nghiệm
- Tìm k cặp số ai,bi sao cho các khoảng ai;bi rời nhau và
f(ai)f(bi) 0, i 1,...,k
- Phương trình f x 0 có ít nhất một nghiệm xi ai;bi .
Khi phương trình f x 0 có chứa tham số thì cần chọn a, b sao cho : -
f a, f b không còn chứa tham số hoặc chứa tham số nhưng dấu không đổi.
- Hoặc f a, f b còn chứa tham số nhưng tích f(a).f(b) luôn âm.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tìm m để phương trình sau có nghiệm: m x
1 x 2 2x 1 0. Hướng dẫn giải
Đặt f x m x 1 x 2 2x 1.
Tập xác định: D nên hàm số liên tục trên . Ta có: f
1 3; f 2 3 f 1 .f 2 0.
Vậy phương trình đã cho có nghiệm với mọi m. 2 x 4 x 0;2
Ví dụ 2: Cho hàm số f x
. Phương trình f x 7 có bao nhiêu nghiệm?
x 42 6 x2;4 Hướng dẫn giải 2
Xét phương trình: x 4 7 trên 0;2 2 2 x 3 (nhaän)
Ta có: x 4 7 x 3 x 3 (loaïi)
Xét phương trình: 2
x 4 6 7 trên 2;4 x 3 (nhaän) Ta có: 2 2
x 4 6 7 x 8x 15 0 x 5 (loaïi)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 376
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy phương trình f x 7 có đúng hai nghiệm.
3. Bài tập trắc nghiệm
Câu 1: Cho hàm số f (x) 3 = 4
- x + 4x -1. Mệnh đề nào sau đây là sai?
A. Hàm số đã cho liên tục trên .
B. Phương trình f (x)= 0 không có nghiệm trên khoảng (-¥ ) ;1 .
C. Phương trình f (x)= 0 có nghiệm trên khoảng (-2;0). æ ö
D. Phương trình f (x)= 0 có ít nhất hai nghiệm trên khoảng 1 çç 3; - . ÷÷ ç è 2÷ø Lời giải Chọn B
(i) Hàm f (x) là hàm đa thức nên liên tục trên ¾¾ A đúng. ìï f (- ) 1 = 1 - < 0 (ii) Ta có ïí ¾¾
f (x) = 0 có nghiệm -2;1 , mà ï 1 x trên ( ) f (-2) = 23 > ï 0 î ( 2 - ;- ) 1 Ì( 2; - ) 0 Ì(- ; ¥ ) 1 ¾¾
B sai và C đúng ìï f (0)= -1< 0 ï æ ö (iii) Ta có ïïí æ ç ÷ 1ö 1 ¾¾
f (x) = 0 có nghiệm ç
÷ Kết hợp với (1) suy ra ï 2 x thuộc 1 0; . ç ÷ ï f ç ÷ ç ÷ = > 0 è 2ø ï çè2÷ø 2 ïî 1
f (x) = 0 có các nghiệm x , -3 < x < 1 - < 0 < < ¾¾ D đúng. 1 2 x thỏa: 1 2 x 2
Câu 2: Cho phương trình 4 2
2x -5x + x +1 = 0. Mệnh đề nào sau đây là đúng?
A. Phương trình không có nghiệm trong khoảng ( 1; - ) 1 .
B. Phương trình không có nghiệm trong khoảng (-2;0).
C. Phương trình chỉ có một nghiệm trong khoảng ( 2; - ) 1 .
D. Phương trình có ít nhất hai nghiệm trong khoảng (0;2). Lời giải Chọn D Hàm số f (x) 4 2
= 2x -5x + x +1 là hàm đa thức có tập xác định là nên liên tục trên . Ta có ìï f (0)=1 (i) ïí f (- ) 1 . f (0)< 0 ¾¾
f (x) = 0 có ít nhất một nghiệm 1 - ;0 . ï 1 x thuộc ( ) ï f (- ) 1 = 3 - î ìï f (0)=1 (ii) ïí f ( ) 0 . f ( ) 1 < 0 ¾¾
f (x) = 0 có ít nhất một nghiệm 0;1 . ï 2 x thuộc ( ) f ( ) 1 = 1 - ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 377
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï f ( ) 1 = 1 - (iii) ïí f ( ) 1 . f (2)< 0 ¾¾
f (x) = 0 có ít nhất một nghiệm 1;2 . ï 3 x thuộc ( ) f (2) = ï 15 î
Vậy phương trình f (x)= 0 đã cho có các nghiệm x , x , 1 2 3 x thỏa
-1< x < 0 < x <1< x < 2 1 2 3 Câu 3: Cho hàm số 3
f (x ) = x - 3x -1 . Số nghiệm của phương trình f (x ) = 0 trên là: A. 0. B. 1. C. 2. D. 3. Lời giải Chọn D Hàm số f (x) 3
= x -3x -1 là hàm đa thức có tập xác định là nên liên tục trên . Do đó
hàm số liên tục trên mỗi khoảng ( 2; - - ) 1 , ( 1 - ;0), ( 0;2). Ta có ìï f ( 2 - ) = -3 · ïí f ( 2 - ) f (- ) 1 < 0 ¾¾ ( )
1 có ít nhất một nghiệm thuộc ( 2; - - ) 1 . ï f (- ) 1 = ï 1 î ìï f (- ) 1 = 1 · ïí f (- ) 1 f (0)< 0 ¾¾ ( )
1 có ít nhất một nghiệm thuộc ( 1; - 0). ï f (0)= 1 - ïî ìï f (2)=1 · ïí
f (2) f (0)< 0 ¾¾ ( )
1 có ít nhất một nghiệm thuộc (0;2). ïï f (0)= -1 î Như vậy phương trình ( )
1 có ít nhất ba thuộc khoảng (-2;2) . Tuy nhiên phương trình
f (x) = 0 là phương trình bậc ba có nhiều nhất ba nghiệm. Vậy phương trình f (x ) = 0 có đúng nghiệm trên .
Cách CASIO. (i) Chọn MODE 7 (chức năng TABLE) và nhập: 3
F ( X ) = X - 3X -1.
(ii) Ấn “=” và tiếp tục nhập: Start « 5
- (có thể chọn số nhỏ hơn).
End « 5 (có thể chọn số lớn hơn).
Step «1 (có thể nhỏ hơn, ví dụ 1 ). 2
(iii) Ấn “=” ta được bảng sau:
Bên cột X ta cần chọn hai giá trị a và b (a < b) sao cho tương ứng bên cột F(X ) nhận
các giá trị trái dấu, khi đó phương trình có nghiệm ( ;
a b) . Có bao nhiêu cặp số a, b như
thế sao cho khác khoảng ( ;
a b) rời nhau thì phương trình f (x) = 0 có bấy nhiêu nghiệm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 378
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 4: Cho hàm số f (x) liên tục trên đoạn [-1;4] sao cho f (- )
1 = 2 , f (4) = 7 . Có thể nói gì về
số nghiệm của phương trình f (x)= 5 trên đoạn [-1;4]: A. Vô nghiệm.
B. Có ít nhất một nghiệm. C. Có đúng một nghiệm.
D. Có đúng hai nghiệm. Lời giải Chọn B
Ta có f (x)= 5 f (x)-5 = 0 . Đặt g(x)= f (x)-5. Khi đó ìïg(- ) 1 = f (- ) 1 -5 = 2 -5 = 3 - ïí g(- ) 1 g(4)< 0.
ïg(4)= f (4)-5 = 7-5 = ï 2 î
Vậy phương trình g(x)= 0 có ít nhất một nghiệm thuộc khoảng (1;4) hay phương trình
f (x ) = 5 có ít nhất một nghiệm thuộc khoảng (1; 4) .
Câu 5: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-10;10) để phương trình 3 2
x -3x +(2m -2) x + m -3 = 0 có ba nghiệm phân biệt x , x , x < -1 < < 1 2 x thỏa mãn 3 1 x2 x3 ? A. 19. B. 18. C. 4. D. 3. Lời giải Chọn C
Xét hàm số f (x) 3 2
= x -3x +(2m -2)x +m -3 liên tục trên .
● Giả sử phương trình có ba nghiệm phân biệt x , x , x < -1 < < . Khi đó 1 2 x sao cho 3 1 x2 x3
f (x) = (x - x - - . 1 )(x x2 )(x x3 ) Ta có f (- ) 1 = ( 1 - - x -1- x
-1- x > 0 (do x < -1 < < ). 1 )( 2 )( 3 ) 1 x2 x3 Mà f (- ) 1 = m - -5 nên suy ra m
- -5 > 0 m < -5.
● Thử lại: Với m < -5 , ta có
▪ lim f (x)= -¥ nên tồn tại a < -1 sao cho f (a)< 0 . ( ) 1 x -¥
▪ Do m < -5 nên f (- ) 1 = m - -5 > 0 . (2)
▪ f (0)= m -3 < 0 . ( ) 3
▪ lim f (x)= +¥ nên tồn tại b > 0 sao cho f ( ) b > 0 . (4) x +¥ Từ ( )
1 và (2) , suy ra phương trình có nghiệm thuộc khoảng ( ; -¥ - ) 1 ; Từ (2) và (3), suy
ra phương trình có nghiệm thuộc khoảng ( 1;
- 0) ; Từ (3) và (4) , suy ra phương trình có nghiệm thuộc khoảng (0; ) +¥ .
Vậy khi m < -5 thỏa mãn mÎ
¾¾¾¾ m Î {-9;-8;-7;-6}. m ( Î -10;10)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 379
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133




