Phân Tích Thị Trường Gas và Độc Quyền môn Kinh tế vi mô | Trường Đại học Kinh Tế Quốc Dân

CTHH & ĐQUYỀN
1. Thành phố X có 100 hãng bán gas. Cung, cầu của thị trường hàng ngày về gas được cho bởi:
P = Qs / 25000 và P = 2,4 - Q /25000 d
a/ Vẽ đường cung và đường cầu về gas của mỗi hãng, giả định rằng thị trường gas được coi là cạnh tranh hoàn hảo.
b/ Giả sử thị trường bị độc quyền hoá (chẳng hạn một tập đoàn độc quyền lớn được hình thành
và quyết định giá cả, sản lượng như một nhà độc quyền và sau đó phân bổ mức sản xuất đều
nhau cho mỗi thành viên). Xác định mức sản lượng và giá bán cân bằng trong độc quyền.
c/ Tại sao có thể nói rằng trong độc quyền các nguồn lực được sử dụng kém hiệu quả hơn trong
trong cạnh tranh hoàn hảo? Khoản mất không (DWL) mà độc quyền gây ra cho xã hội là bao nhiêu?
d/ Vẽ đồ thị minh hoạ các kết quả ở câu b và c. Lời giải:
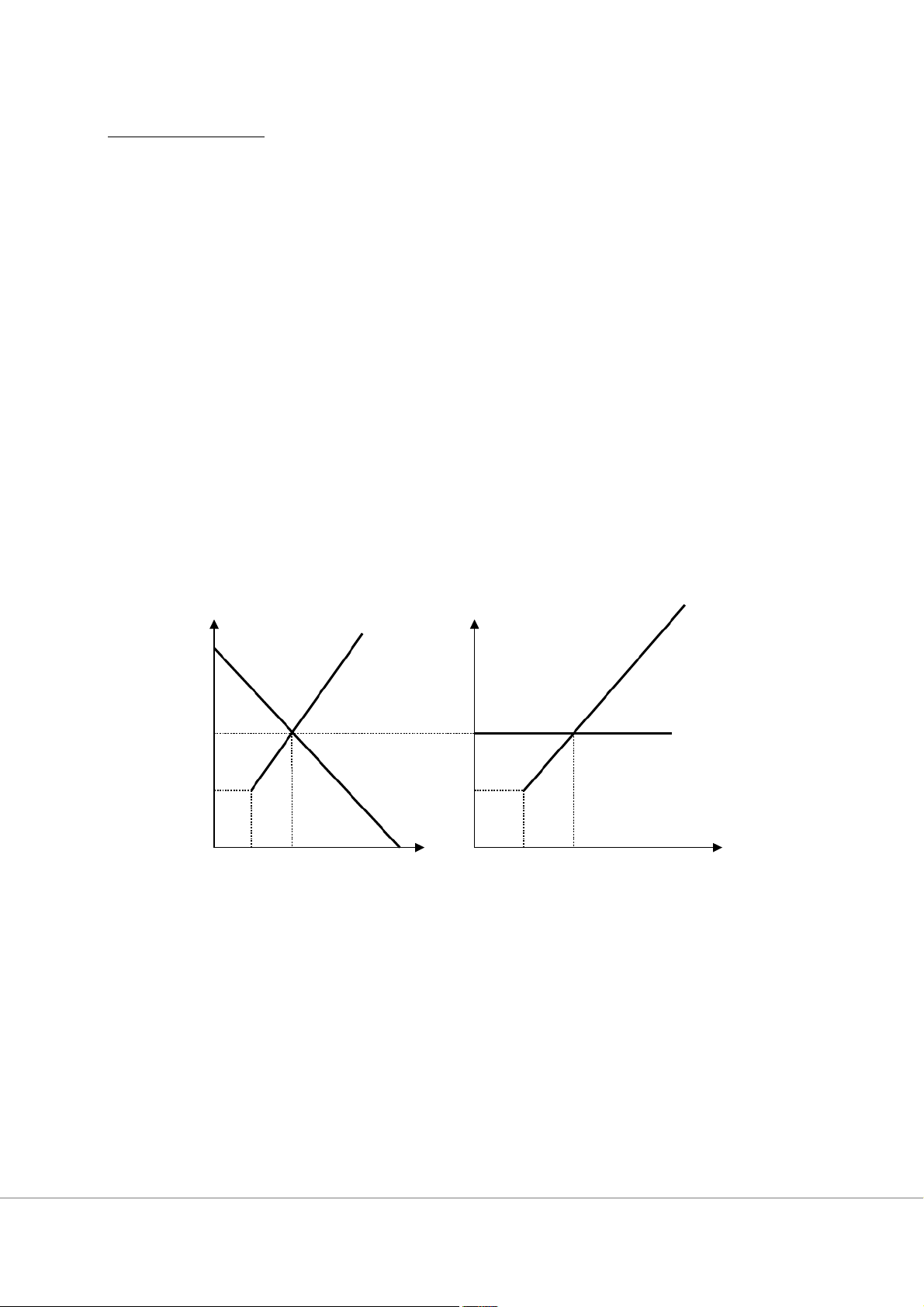
a. PE, QE: 60.000 - 25.000P = 25.000P PE = 1,2$ QE = 30.000 gallon b. Vẽ: Cầu cá nhân hãng P = 1,2$
Cung cá nhân qS = 250P = QS/ 100 MC Shãng P S 2,4 E d MR 1,2 D 1,2 0,6 0,6 0 15000 30000 60000 Q 0150300 q QE
c. Cung, cầu của hãng và của thị trường trong thị trường CTHH
+ Cầu cá nhân là đường cầu nằm ngang và doanh nghiệp chấp nhận giá thị trường (do cung, cầu
quyết định) P = 1,2$. Đường cầu thị trường vẫn dốc xuống.
+ Cung cá nhân giống nhau và được xác định bằng đường cung thị trường (cung thị trường bằng tổng cung cá nhân)
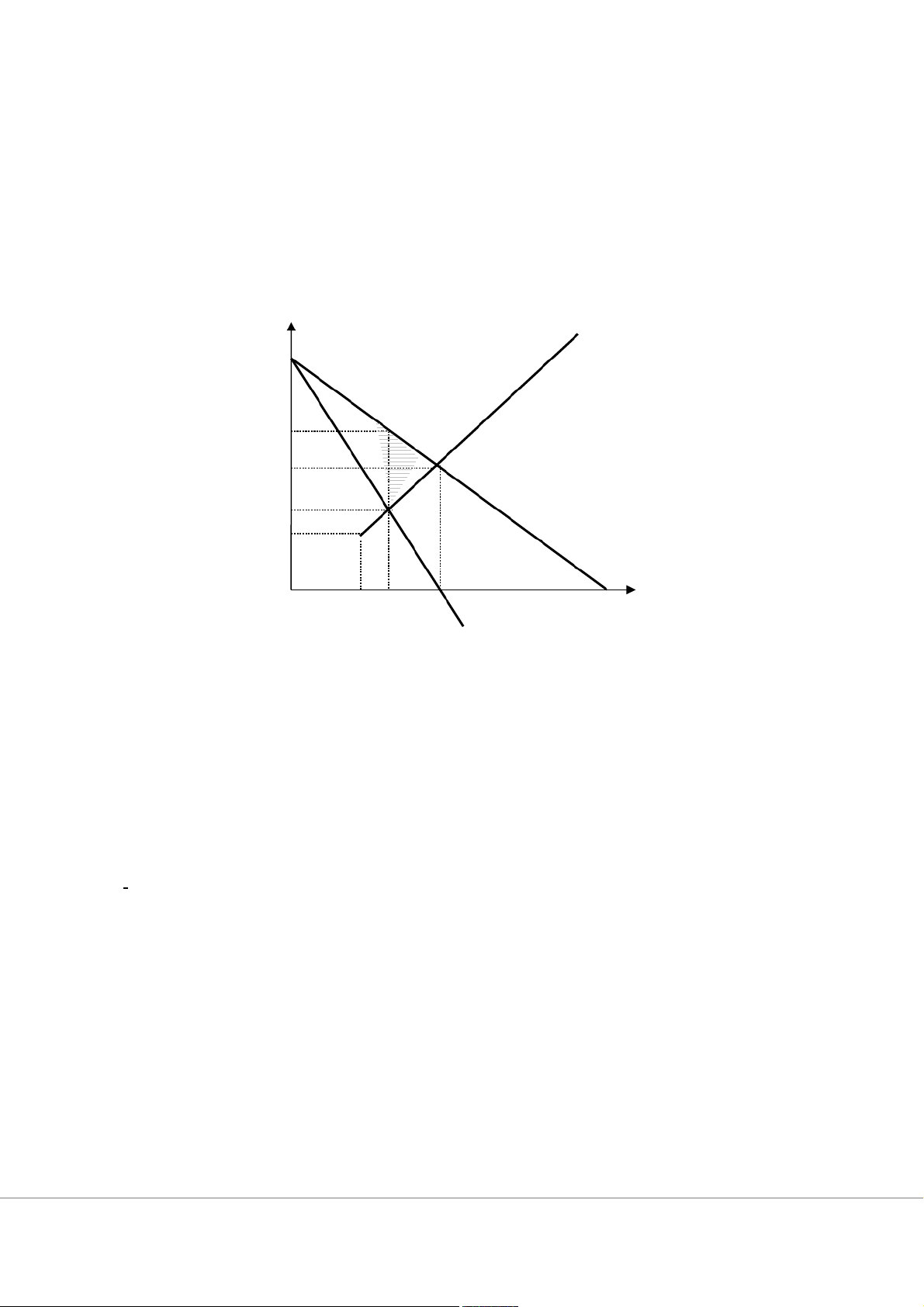
d. Thị trường bị độc quyền hoá (1 độc quyền tập đoàn lớn được hình thành và quyết định P, Q
chung sau đó mức sản lượng được chia đều cho mỗi thành viên). MR = 2,4 -0,0008Q vì P = 2,4 - 0,0004Q.
Cung thị trường chính là MC của nhà độc quyền. MR = MC QM = 20.000 PM = 1,6$ MC P 2,4 1,6 1,2 0,8 0,6 D 0 15000 20000 30000 60000 Q MR
e. Công suất của một trạm xăng: 300 gallon
Số trạm xăng nhà độc quyền sẽ cho hoạt động là
m = QM/ 300 = 20000/300 = 67 trạm
f. Có thể khẳng định trong độc quyền các nguồn lực được sử dụng kém hiệu quả hơn so với
trong CTHH : giá bán cao hơn, sản lượng nhỏ hơn
( định giá không theo nguyên tắc chi phí cận biên) DWL = S
= (1,6 - 0,8) * (30000 - 20000)/2 = 4000 ABE
2. (Kiểm soát giá độc quyền)
Giả sử một nhà độc quyền gặp phải đường cầu P = 30 – 0,5 Q, trong đó P là giá tính bằng
đôla ($) cho một đơn vị sản phẩm và Q là sản lượng tính bằng ngàn đơn vị. Nhà độc quyền
có chi phí bình quân không đổi bằng 14$.
a) Cho biết chi phí cận biên của hãng là bao nhiêu?
b) Mức sản lương tối ưu của hãng là bao nhiêu? Nhà độc quyền này sẽ đặt giá bao
nhiêu ? Tính lợi nhuận lớn nhất đó. Hãy sử dụng chỉ số Lenrer, tính mức độ của sức mạnh độc quyền bán.
c) Mức giá và sản lượng tối ưu cho xã hội đối với hãng này là bao nhiêu? Tính mất
không (Deadweight loss) do hãng độc quyền này gây ra.
d) Giả sử Chính phủ quy định giá bán của nhà độc quyền là 18$ một đơn vị sản phẩm.
Khi đó sản lượng nào sẽ được sản xuất ra? Lợi nhuận của hãng sẽ là bao nhiêu?
e) Minh họa các kết quả trên bằng đồ thị. Lời giải
a) Với ATC = 14 thì TC = Q.ATC = 14Q vậy MC = 14
b) Nguyên tắc tối đa hóa lợi nhuận là MC = MR hay 14 = 30  Q vậy Q* = 16 (ngàn
đơn vị) và P* = 22 và lợi nhuận cực đại là 128( = 16 x (22 - 14))
Mức độ của sức mạnh độc quyền là: P  MC 22 1   4  3 , 0 6 p 22
c)Mức giá và sản lượng tối ưu cho xã hội xảy ra ở điểm B khi MC gặp đường cầu hay
14 = 30 0,5 Q suy ra Q opt = 32, P opt = 14
Để tối đa lợi nhuận nhà độc quyền đã hạn chế sản lượng thấp hơn mức sản lượng tối ưu
cho xã hội và gây ra mất không là :  32  16  .(22  ) 14 98 DWL = 2
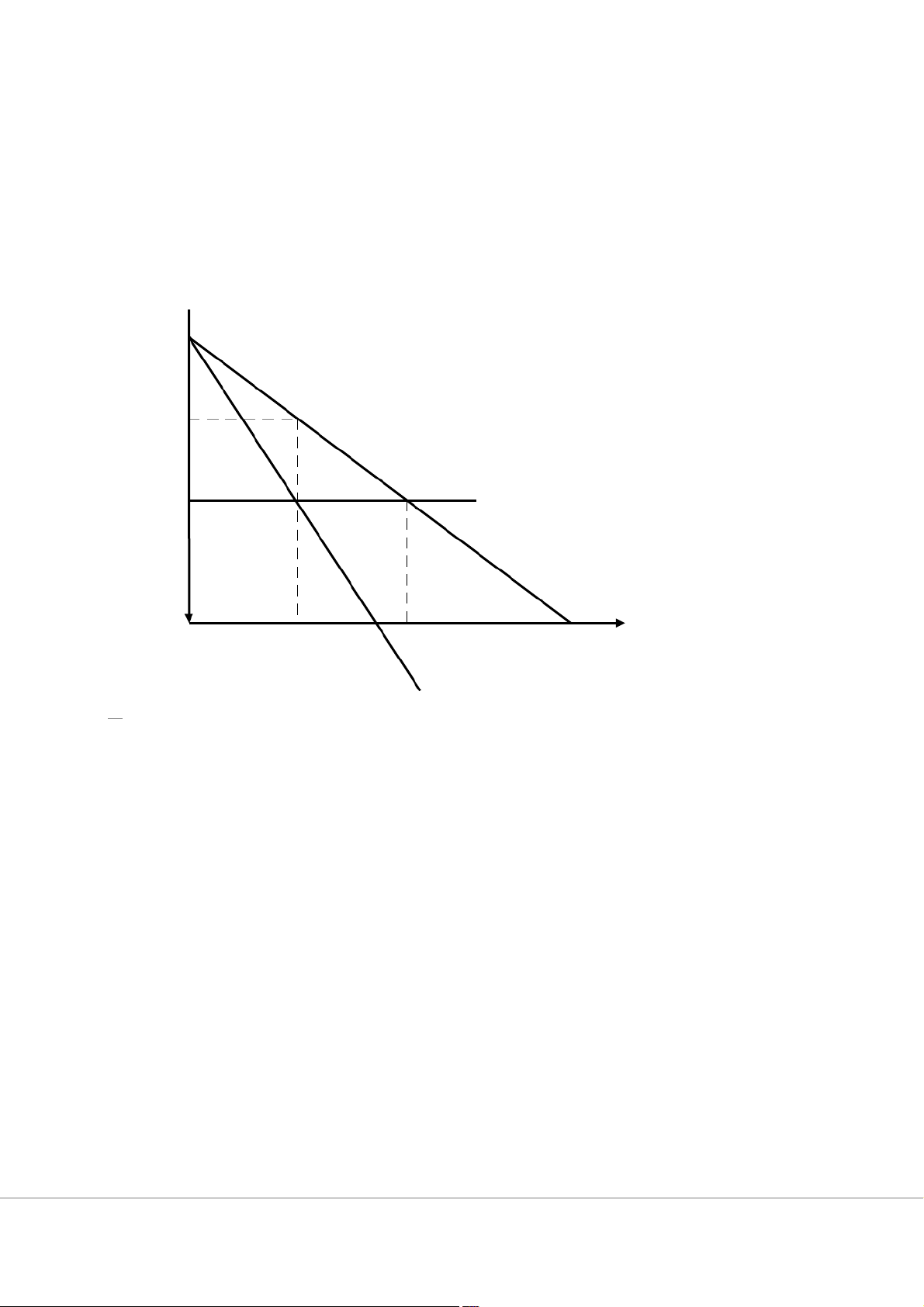
d) Với trần giá P c = 18 đường doanh thu biên của nhà độc quyền gãy khúc và có đoạn
trống (không liên tục) IJ. Sản lượng mà hãng sản xuất là 24 đơn vị và lợi nhuận là 96$.
3. (Phân biệt giá hoàn hảo)
Một hãng có hàm cầu ($)P = 200 - 0,5Q trong đó Q là sản lượng tính bằng đơn vị. Hãng sản
xuất với chi phí bình quân không đổi ATC = 100 $.
a. Quyết định sản xuất của hãng nếu hãng là người sản xuất duy nhất trên thị trường.
b. Tính chỉ số LERNER và mất không của xã hội ở mức giá mà nhà độc quyền tối đa hoá lợi nhuận.
c. Nếu hãng thực hiện phân biệt giá hoàn hảo thì lợi nhuận thu được sẽ là bao nhiêu? Minh hoạ
các kết quả trên đồ thị. Lời giải
a. Hãng tối đa hoá lợi nhuận, quyết định sản xuất tại MR = MC khi P = 200 - 0,5 Q  MR = 200 - Q
ATC = 100  TC = 100 Q  MC = 100  200 - Q = 100  Q = 100 và P = 150
 = TR - TC = 150 x100 – 100 x100 = 5000$ b. L = (P - MC)/ P = 1/3 DWL = (50 x 100)/ 2 = 2500
CS = (200 – 150) x100/2 = 2500
a. Phân biệt giá hoàn hảo
Sản lượng khi phân biệt giá cấp I: QI = 200
Tổng doanh thu khi phân biệt giá cấp I: TRI = (200 +100) x 200/2 =30000
Lợi nhuận khi phân biệt giá cấp I: I = TRI – TC(QI) = 30000 – 20000= 10000 hay I =  +
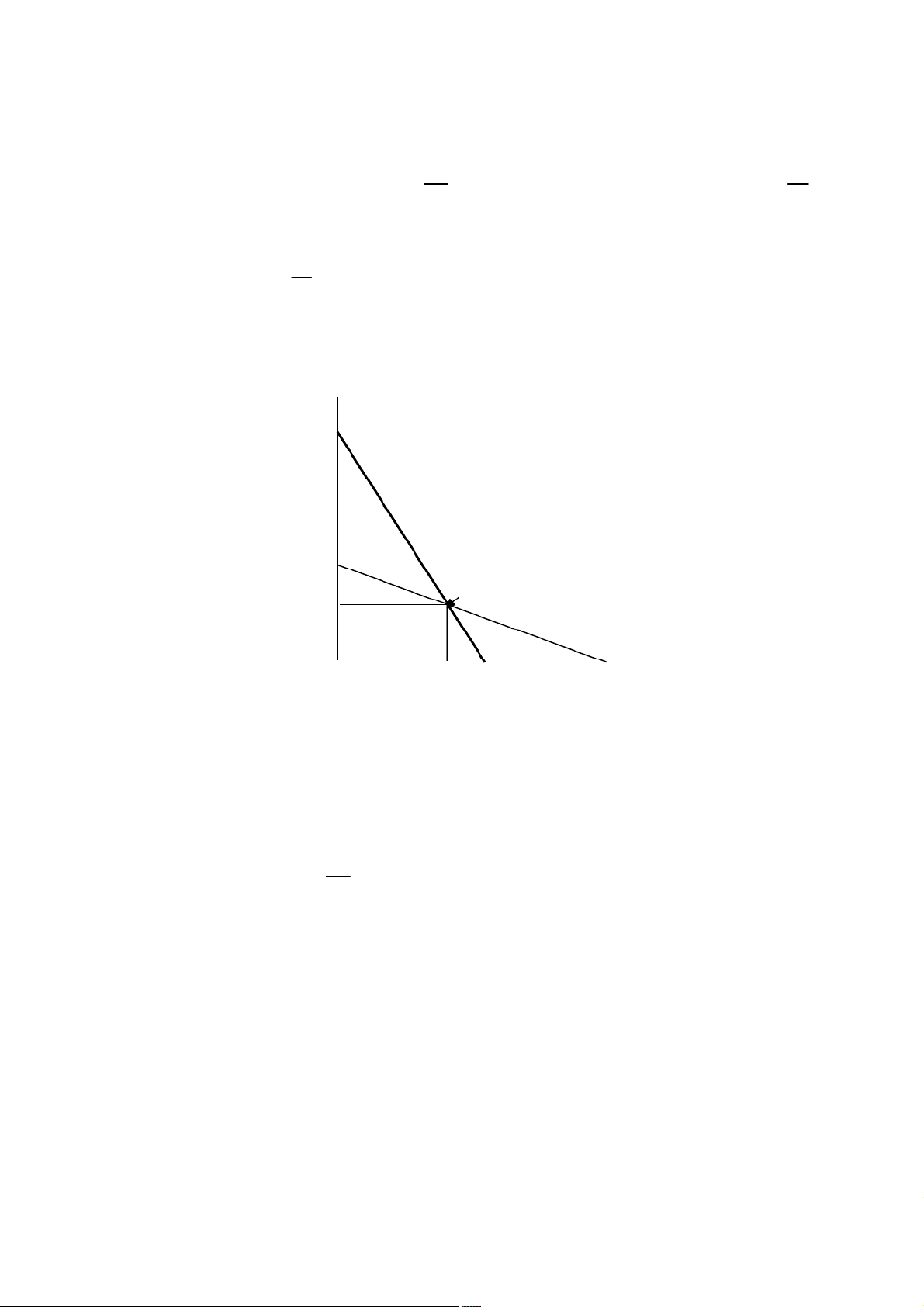
CS + PS = 5000 + 2500 + 2500 = 10000 P 20 0 A 15 0 E ATC = MC = 100 10 0 B 0 100 200 400 MR Q
4. (Phân biệt giá cấp III)
Công ty thực phẩm Sagavina bán một loại thực phẩm đông lạnh trực tiếp cho người tiêu dùng và
các khách sạn. Hàm cầu D và hàm doanh thu cận biên của công ty trên thị trường 1 (thị trường
người tiêu dùng) và thị trường 2 (thị trường khách sạn) là:
Q1 = 160 - 10P1và MR1 = 16 - 0,2Q1
Q2 = 200 - 20P2và MR2 = 10 - 0,1Q2
Hàm tổng chi phí của Sagavina là: TC = 120 + 4Q. Vẽ hình chỉ ra:
a. Đường cầu D, MR, MC của hãng.
b. Sản lượng tối đa hoá lợi nhuận. Hãng sẽ phân phối sản lượng trên các thị trường như thế nào
để tối đa hoá lợi nhuận với hình thức phân biệt giá cấp 3.
c. Giá và tổng doanh thu của hãng trên mỗi thị trường với sự phân biệt giá cấp ba.
d. Lợi nhuận đơn vị và tổng lợi nhuận theo phân biệt giá cấp 3.
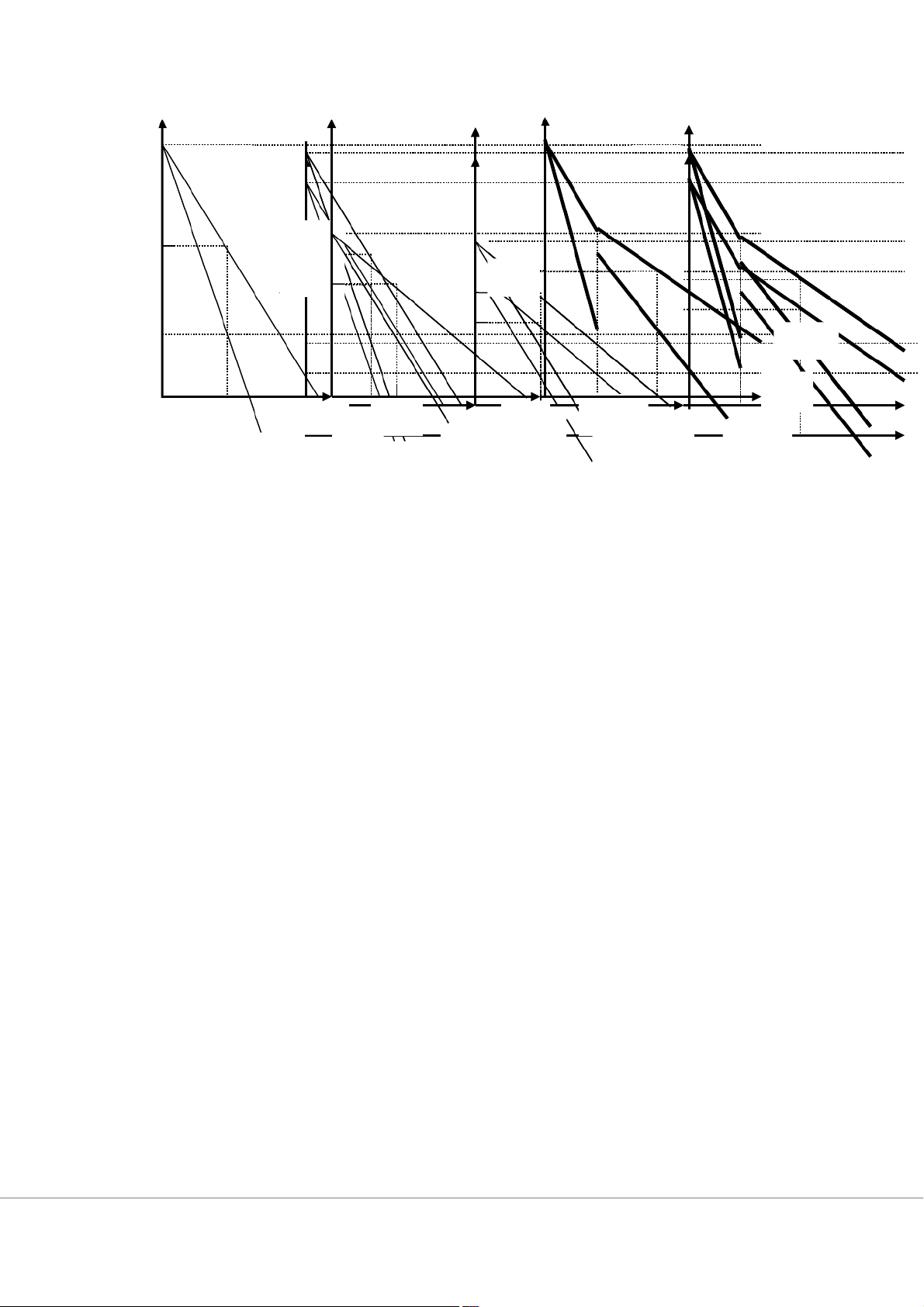
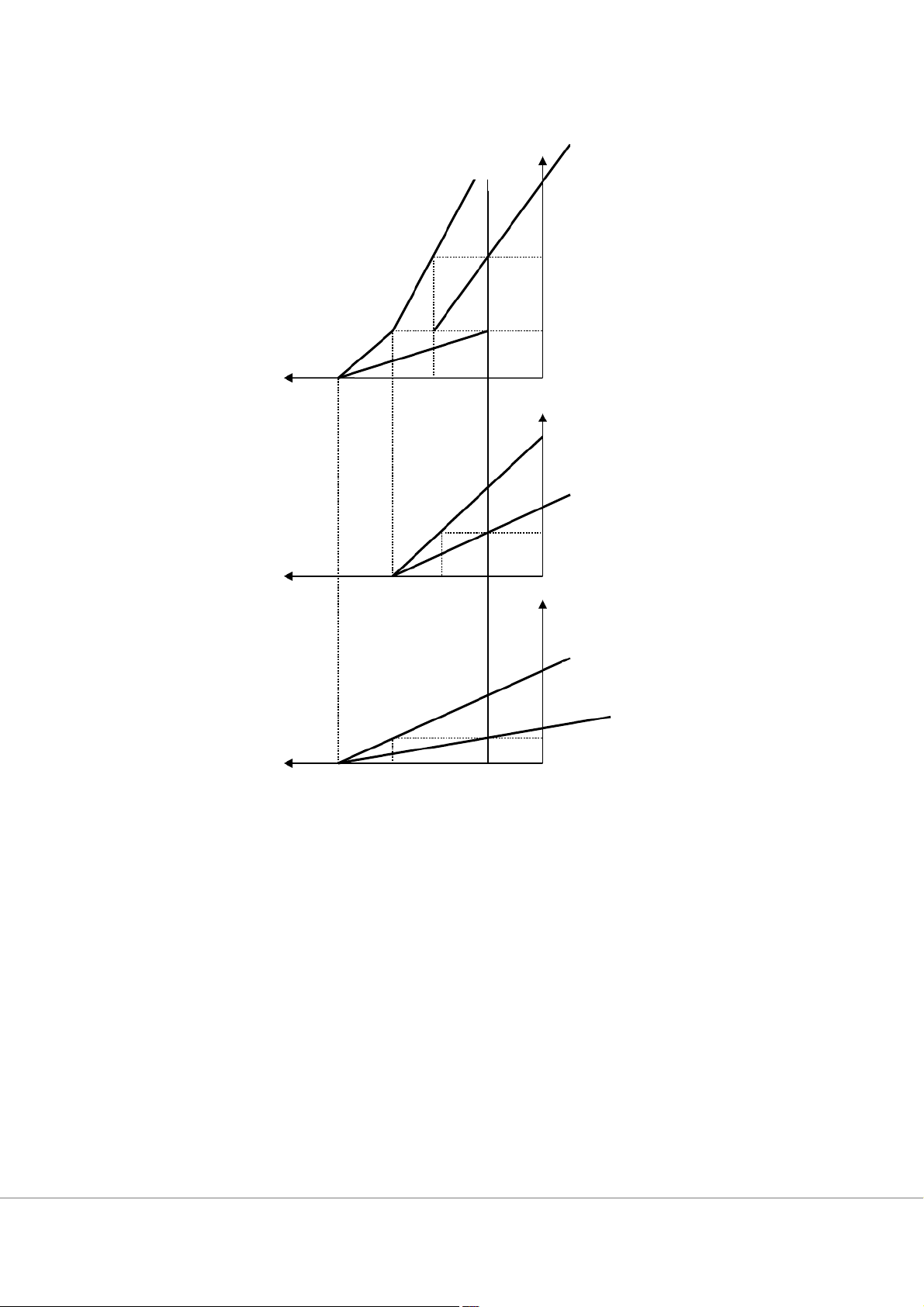
a. Sản lượng, giá, doanh thu, lợi nhuận nếu không phân biệt giá. Lời giải P P P P P P 40 40 P P P 25 25 24 2 16,5 19 2 16,5 19 16,5 19 MC Q Q 16 17 15 Q2 Q1 16 15 Q2 Q1 Q 33 MR2MRT MR1 MR 33 2MRT 16 17 15 Q2 MR1
a. D thị trường: Q = Q + Q 33 1 = 360 2
ay P = 12 - Q/30 với Q MR2MRT MR1
Điểm gãy A ứng với Q = 60 P= 10
Phương trình đường cầu chung có thể viết P = 16 - 0,1Q với Q < 60 P = 12 -Q/30 Với Q 60
Phương trình đường doanh thu biên tương ứng gồm 2 đoạn (có phần gián đoạn) MR = 16 - 0,2Q với Q < 30 MR = 12 - Q/15 với Q 30
b. Sản lượng tối đa hoá lợi nhuận: MR = MC - Nếu Q < 30: 16 - Q/5 = 4 Q* = 60 (loại) -
Nếu Q 30 12 - 2q/30 = 4 Q* = 120 P* = 8$
Nguyên tắc phân phối sản lượng trên các thị trường khi phân biệt giá cấp 3 MR1 = MR = MR 2 T = MCT = 4 MR1 =MC Q*1 = 60, P* =10$ 1 MR2 =MC Q*2 = 60, P* =7$ 2 c. TR1= 60* 10 = 600$ TR2 = 60 * 7 = 420$ d. Thị trường 1:
Lợi nhuận = 300$, lợi nhuận đơn vị =5$ Thị trường 2:
Lợi nhuận = 120$, lợi nhuận đơn vị = 2$ Tổng lợi nhuận = 420$
Lưu ý: ATC/Q* = 4 + 120/120 = 5
e. Nếu không phân biệt giá MR = MC, Q = 120, P= 8$ Q1 = 80TR = 640 1 Q2 = 40 TR = 320 2
 = 360 < 420 khi phân biệt giá P P P 16 16 10 10 10 8 7 DT 4 MC D1D2 Q 60 60 60 12 MR Q Q 1MR2 0 MRT
5. Một công ty bán thịt bò cho người tiêu dùng và các nhà sản xuất thịt bò khô. Hàm cầu D và
hàm doanh thu cận biên của công ty trên thị trường 1 (thị trường người tiêu dùng) và thị trường 2
(thị trường nhà máy) là: Q1 = 40 - P1và MR = 40 - 2Q 1 1 Q2 = 50 - 2P2và MR2 = 25 - Q2
Hàm tổng chi phí của công ty là: TC = 100 + 8Q
a. Vẽ hình chỉ ra: Đường cầu D, MR, MC của hãng.
b. Sản lượng tối đa hoá lợi nhuận. Hãng sẽ phân phối sản lượng trên các thị trường như thế
nào để tối đa hoá lợi nhuận với hình thức phân biệt giá cấp 3.
c. Giá và tổng doanh thu của hãng trên mỗi thị trường với sự phân biệt giá cấp ba là bao
nhiêu? Lợi nhuận khi hãng phân biệt giá là bao nhiêu?
d. Sản lượng, giá, doanh thu, lợi nhuận nếu không phân biệt giá. Lời giải
a. D thị trường: Q = Q + Q 1 = 90 - 3P hay 2 P = 30 - Q/3 với Q  15.
Điểm gãy A ứng với Q = 15 và P = 25.
Phương trình đường cầu chung có thể viết P = 40 - Q Với Q < 15 P = 30 - Q/3 Với Q 15
Phương trình đường doanh thu biên tương ứng gồm 2 đoạn để đơn giản chỉ xét có 1 điểm gãy - hình ở dưới MR = 40 - 2Q với Q < 15
MR = 30 - Q/1,5 với Q 15
b. Sản lượng tối đa hoá lợi nhuận: MR = MC - Nếu Q < 15: 40 - 2Q = 8 Q* = 16 (loại) -
Nếu Q 15: 30 – Q/1,5 = 8 Q* = 33 ; P* = 19
Nguyên tắc phân phối sản lượng trên các thị trường khi phân biệt giá cấp 3 MR1 = MR = MR 2 T = MCT = 8 MR1 = MC Q*1 = 16, P* = 24 1 MR2 = MC Q*2 = 17, P* =16,5 2
c. Thị trường 1: TR = 16 x 24 = 384 1
Thị trường 2: TR = 17 x 16,5 = 280,5 2 Tổng lợi nhuận = 300,5
d. Nếu không phân biệt giá MR = MC, Q = 33, P = 19;
 = 263 < 300,5 khi phân biệt giá P P P 40 25 24 16,5 19 MC Q 16 17 15 Q2 Q1 MR 33 2MRT MR1 CTĐQ & ĐQTĐ
1.Một hãng cạnh tranh độc quyền gặp đường cầu về sản phẩm của mình là P = 9 - Q. Trong đó
sản lượng tính bằng nghìn đơn vị, giá tính bằng nghìn đồng/đơn vị. Tổng chi phí ngắn hạn của
hãng là TC = 2 + 3Q + Q . Đường chi phí trung bình dài hạn của hãng là LAC = 5Q - Q 2 .2
a. Tìm giá, sản lượng và lợi nhuận cho hãng trong ngắn hạn.
b. Tìm giá, sản lượng và lợi nhụân cho hãng trong ngắn hạn.
c. Vẽ đồ thị minh họa các kết quả. Lời giải
a. Trong ngắn hạn hãng sẽ sản xuất ở mức sản lượng có chi phí cận biên ngắn hạn bằng doanh
thu cận biên ngắn hạn. Từ hàm tổng chi phí ngắn có thể xác định được chi phí cận biên ngắn hạn
là MC = TC' = 3 + 2Q. Từ đường cầu có thể xác định được doanh thu cận biên là MR = 9 - 2Q.
Đặt MC = MR, giải tìm được Q = 1,5. Thay mức sản lượng này vào đường cầu ta tìm được giá là
P = 7,5. Lúc đó lợi nhuận của hãng là  = 7,5.1,5 - 2 - 3.1,5 - (1,5) = 2,5. 2
b. Hãng đạt cân bằng dài hạn ở điểm tiếp xúc của đường cầu với đường chi phí trung bình dài
hạn. Vì thế có thể sử dụng đường cầu và đường chi phí trung bình dài hạn để tìm sản lượng và
giá sản phẩm của hãng. Ta có 9 - Q = 5Q - Q . Hay 2 Q -
2 6Q + 9 = 0. Giải phương tình này tìm
được Q = 3, thay Q = 3 vào đường cầu ta tìm được P = 6. Lúc đó lợi nhụân của hãng là  = 0.
(lợi nhuận kinh tế bằng 0 hay bị cạnh tranh hết) c. Đồ thị tự vẽ
2. Công ty Big One hoạt động trong thị trường độc quyền tập đoàn có hàm cầu được cho bởi: P = 7 - Q/30 Với 0 P = 9 - Q/10 Với Q≥30
Hàm tổng chi phí của công ty là : TC = Q(Q + 210)/60
a. Vẽ đường cầu, doanh thu cận biên, chi phí cận biên và chi phí bình quân trên một đồ thị.
b. Giải thích vì sao đường cầu và đường doanh thu biên của công ty lại có dạng như vậy?
c. Tính khoảng của đường doanh thu cận biên mà trong đó chi phí cận biên có thể dịch chuyển
nhưng không làm thay đổi giá và sản lượng tối ưu của công ty.
d. Giá, sản lượng tối ưu và lợi nhuận của công ty sẽ thay đổi như thế nào nếu tổng chi phí của
công ty được cho bởi TC = Q(Q + 140)/40
Lời giải: (MH đường cầu gãy)
D1: Q = 210 - 30P hay P = 7 - Q/30
D2 : Q’ = 90 - 10P hay P = 9 - Q/10 a. Để tìm điểm gãy: 210 - 30P = 90 -10P P = 6, Q = 30 MR1 = 7 - Q/15 MR E = 5 (Q<30) MR2 = 9 - Q/5 MRF = 3 (Q>30) b. MC = 3,5+ Q/30 Q* = 30 P* = 6
Lợi nhuận đơn vị = P - ATC = 6 - 4 =2
Tổng lợi nhuận = 2 * 30 = 60
c. EF lớp đệm chi phí MC’ (3,5)
d. Nếu tổng chi phí của công ty được cho bởi TC = Q(Q + 140)/40 thì MC 1 = 3,5 + Q/20
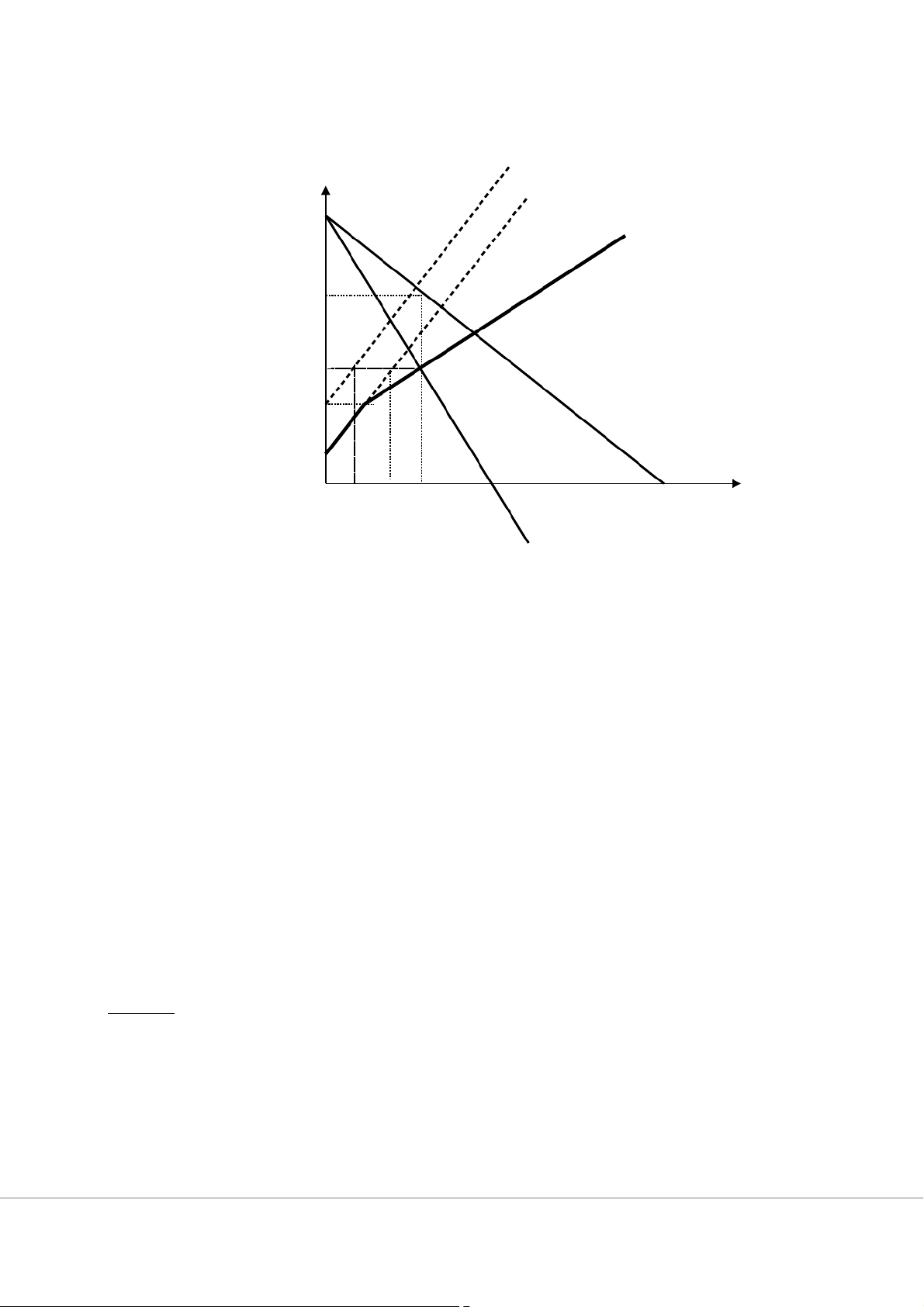
Giá, sản lượng tối ưu của công ty sẽ không thay đổi và lợi nhuận giảm MC MC1 P 9 Điểm gãy ATC 7 6 5 E 4,5 3,5 F 3 D 30 45 90 210 Q MR 0
5. (Mô hình Cournot-Stackelberg)
Có 2 hãng độc quyền. cầu thị trường cho bởi P = 10 - Q trong đó Q = Q 1+ Q 2
Chi phí của 2 hãng này là C 1(Q1) = 4 + 2Q 1 và C 2(Q2) = 3 + 3Q 2
a) Giả sử cả 2 hãng đều đã ra nhập ngành. Sản lượng cân bằng và lợi nhuận của mỗi
hãng là bao nhiêu nếu hai hãng hành động theo lối không hợp tác?
b) Hãy sử dụng mô hình Cournot vẽ các đường phản ứng của các hãng và chỉ ra cân bằng.
c) Hãng 1 là người ra quyết định trước thì Sản lượng cân bằng và lợi nhuận của mỗi
hãng là bao nhiêu theo mô hình Stackelberg Lời giải:
a). Nếu các hãng ứng xử theo cách không hợp tác thì hãng 1 phải cân nhắc sản lượng
của hãng 2, Q 2 . Hàm lợi nhuận của câu a sẽ trở thành
1 = (10  Q 1  Q 2)Q1  4  2Q 1 = 4 + 8Q 1  Q 12  Q 2 Q1 .
Đặt độ dốc của hàm lợi nhuận này theo Q 1 bằng không, ta tìm được hàm phản ứng của Q2 1 Q hãng 1 là 8  Q 2 2
2  2Q 1 = . Hay Q 1 = 4 
. Hàm phản ứng của hãng 2 là Q 2 = 3,5  .
Các hàm phản ứng này phù hợp với các sản lượng độc quyền đã tìm được ở câu a. Để
tìm ra cân bằng Cournot ta thay hàm phản ứng của hãng 2 vào hàm phản ứng của hãng 1 Q
1: Q1 = 4 – 1/2.(3,5 – 2 ). Do đó Q 1 = 3. Thay giá trị này vào hàm phản ứng của hãng
2 ta tìm được Q 2 =2. Khi đó giá bằng 5, lợi nhuận của hãng 1 là 3 x 5 - 4 - 2 x 3 = 5 và
lợi nhuận của hãng 2 là 2 x 5 - 3 - 3 x 3 = 1. b) Q2 8 Q1 = 4 - Q2/2 Cân bằng Cour not 3,5 Q2 = 5,5 - Q1/2 2 3 4 7 Q1
c). Tuy nhiên hãng 1 có thể có khả năng thực hiện mục đích tối đa hoá lợi nhuận của
mình bằng việc hành động như người dẫn đầu Stackelberg. Nếu hãng 1 biết hàm phản
ứng của hãng 2 nó có thể xác định sản lượng tối đa hoá lợi nhuận bằng việc thay Q 2 vào
hàm lợi nhuận của mình: 0 2 II 4  8 1  1 Q  1
Q  Q 2Q1 2 Q1 4 8 Q Q   5 , 3 (  ) 1 1 Q 1 2 2  4 5 , 4 Q 1 Q1 2
Độ dốc của hàm lợi nhuận này theo Q 1 là 4,5 – Q 1. Cho bằng không ta được Q 1 = 1,5. ở
mức sản lượng này hãng 2 sẽ sản xuất 3,5 – 4,5/2 = 1,25. Giá sẽ là 4,25, lợi nhuận của
hãng 1 sẽ là 4,25 x 4,5 – 4 – 2 x 4,5 = 6,125 và lợi nhuận của hãng 2 là 1,25 x 1,25 – 3 – 3 x 1,25 = -1,4375.
6. (Cartel phân chia sản lượng)
Một tập đoàn độc quyền gồm 2 hãng thành viên sản suất kim cương cho ngành có hàm cầu như
sau: Q = 120 - 10P hoặc P = 12 - 0,1 Q
Hàm MC và ATC của mỗi hãng là MC1 = 4+0,2Q 1 và ATC1 = 4+0,1 Q1 MC2 = 2+0,2Q 2 và ATC2 = 2+0,1Q2
a. Vẽ hình chỉ ra mức sản lượng và giá bán tối ưu của tập đoàn.
b. Sản lượng của mỗi hãng thành viên là bao nhiêu để tối thiểu hoá tổng chi phí cho tập đoàn.
c. Tính toán lợi nhuận đơn vị và tổng lợi nhuận cho mỗi hãng. Lời giải:
Mô hình cartel tập trung : n = 2 hãng Hàm cầu
P = 12 - 0,1Q do đó MR = 12- 0,2Q MC1 = 4 + 0,2Q1 Q = -20 + 5MC 1 T MC2 = 2 + 0,2Q2 Q = -10 + 5MC 2 T Q = Q + Q 1 = -30 + 10 2
MC hay MCT = 3 + 0,1Q (với Q 10) cho MC = -4 2
Mức sản lượng và giá bán tối ưu của tập đoàn:
MR = MCT = 2 + 0,2Q với Q<10
12 - 0,2Q = 3 + 0,1Q với Q10 Q<10 : Q* =25 (loại) Q 10 : Q* = 30, P* = 9 Cách 1: MC1 = MC = 2 MC = MRT =6
Q*1 xác định bởi 6 = 4 + 0,2Q* 1  Q*1 = 10
Q*2 xác định bởi 6 = 2 + 0,2Q* 2  Q*2 = 20 1 = TR - TC 1 = 40 1  đơn vị = 4 2 = TR - TC 2 = 100 2  đơn vị = 5
Cách 2: tính bằng đại số sản lượng của mỗi hãng nhỏ bằng bao nhiêu để tối thiểu hoá tổng chi phí cho tập đoàn. ATC1 = 4 + 0,1Q 1  TC = 4Q 1 + 0,1 Q 1 12 ATC2 = 2 + 0,1Q 2  TC = 2Q 2 + 0,1 Q 2 22 Do đó TC = TC1 + TC2 = 4Q1 +0.1 Q 2 1 + 2Q2 + 0,1 Q2 2  Min
điều kiện ràng buộc Q = Q + Q 1 = 30 2
Lập hàm Lagrange L = 4Q + 0,1 Q 1 12 + 2Q + 0,1 Q 2 22 +  (Q + Q 1 2 - 30)  Min
∂L =4+0,2Q1+λ=0 ∂Q1
∂L =2+0,2Q2+λ=0 ∂Q2 ∂L
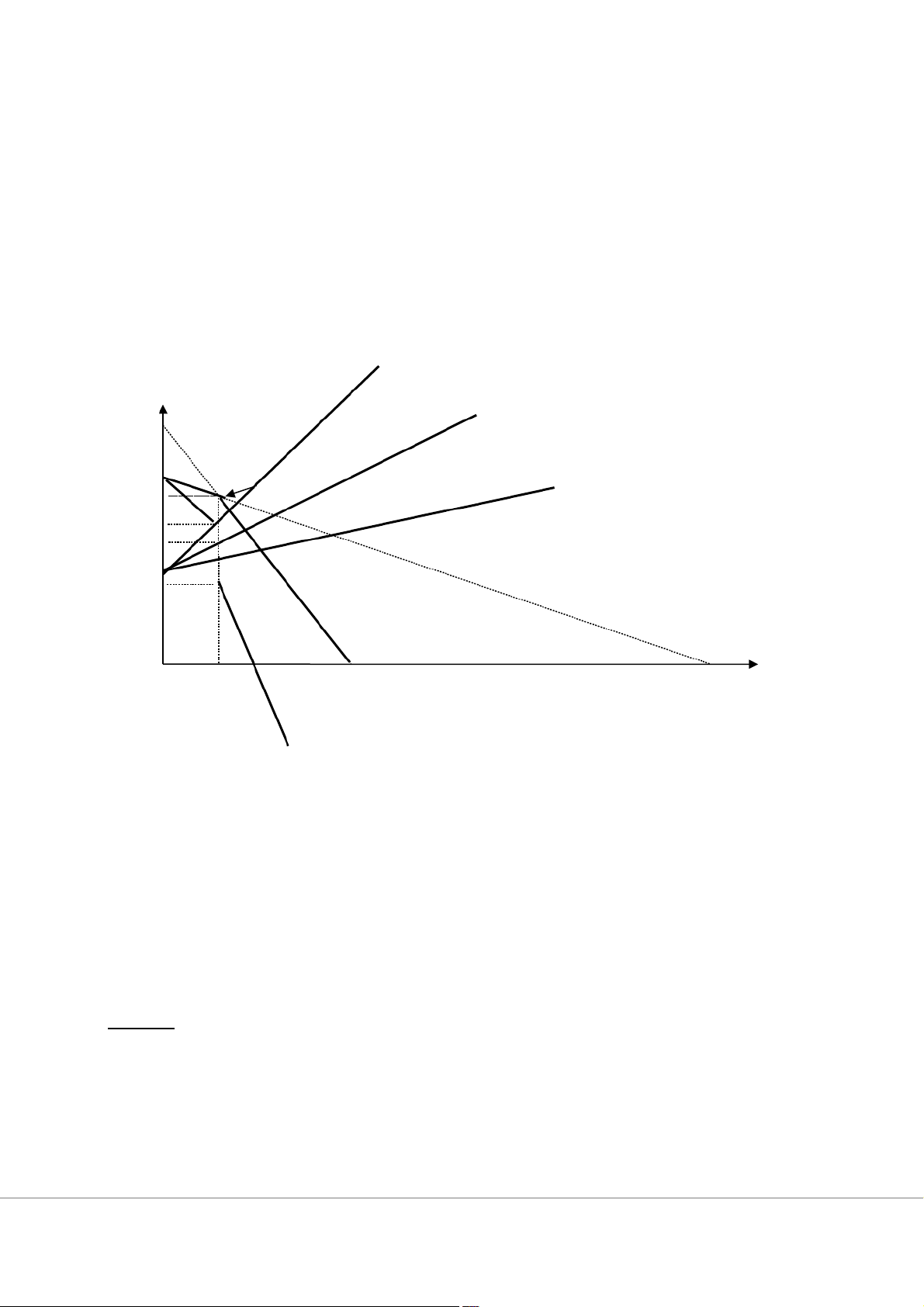
∂λ=Q1+Q2−30=0 Giải ra ta được Q1* = 10, Q*2 = 20, MC1  = -6 MC2 P MCT 9 E 6 4 D 2 10 20 3060 120 Q 0 Q*1 Q*2 Q* MR
7.(Chỉ đạo giá- Hãng trội)
ở thành phố Hồ Chí Minh có một cửa hàng lớn chuyên chăm sóc sắc đẹp và một số cửa hàng
nhỏ khác. Cầu thị trường về dịch vụ đó mỗi ngày là Q = 180 -10P (P tính theo ngàn đồng).
Hàm chi phí biên của tất cả các cửa hàng nhỏ hơn là MCF = 4 + 0,1Q và của hãng lớn là MCL = 7 + 0,1Q
a. Vẽ hình chỉ rõ DT, MCF , MCL, , DL , MRL, MRT và đường tổng theo chiều ngang của MCF và MCL,
b.Xác định mức sản lượng và giá bán tối ưu của hãng lớn và các hãng nhỏ nếu như hãng lớn giữ vai trò chỉ đạo giá.
c. Nếu tất cả tập hợp hình thành nên một tập đoàn giá và sản lượng tối ưu là bao nhiêu. Hãng lớn
sẽ sản xuất bao nhiêu và các hãng nhỏ sẽ cung ứng bao nhiêu nếu tập đoàn muốn tối thiểu hoá
tổng chi phí để sản xuất ra mức sản lượng tối ưu cho tập đoàn.
d. Mức giá và sản lượng cân bằng là bao nhiêu nếu hãng lớn không tồn tại và các hãng nhỏ hoạt
động như trong thị trường cạnh tranh hoàn hảo.
e. Giá và sản lượng cân bằng là bao nhiêu nếu hãng lớn vẫn tồn tại cùng với các hãng nhỏ hoạt
động trong thị trường cạnh tranh hoàn hảo. Lời giải:
Bài tập: Hãng trội và chỉ đạo giá
D thị trường: Q = 180 - 10P , MR = 18 - 0,2 Q MCF = 4 + 0.1Qf Qf = 10MCF - 40 MCL = 7 + 0.1QLQL = 10MCL - 70 Q = Qf + QL = 20MCT -110
MCT = MCL + MCF = [5.5 +0.05Q (Q>30) cho MCF = 7 [ 4 +0.1Q (Q30)
MCF cắt DT ở F : QE = 70 , PE = 11
MCF + MCL cắt DT ở F : QF = 83.33 , PF = 9.66
DL : P = 11- Q/20 với Q < 140
P = 18 - Q/ 10 với Q140 MRL = 11- 0,1Q với Q < 140 = 18 - 0,2 Q với Q140
Nếu hãng lớn giữ vai trò chỉ đạo giá
* Mức sản lượng và giá bán tối ưu của hãng trội là: MCL = MRL Q* = 20 P* = 10$
* ở giá 10$ cả thị trường bán là QT = 80 (tại F’) do đó các hãng nhỏ bán là QF = 60
c. Nếu tất cả các hãng hình thành một tập đoàn, giá và sản lượng chung là: MCT = MRT Q* = 50 ; P* =13
Nếu muốn tối thiểu hoá chi phí để sản xuất ra mức sản lượng tối ưu cho tập đoàn thì:
Cách 1: MCL =  MCF = MCT = MRT =8$ . Để xác định QL đặt: 8 = MCLQL = 10 (điểm I)
Để xác định  QF đặt 8 =  MCF QF = 40 (điểm J)
Cách 2: giải quyết bằng đại số: Lập hàm Lagrange TCL = 7QL + 0.05QL + FC 2 L TCf = 4QF + 0.05QF + FC 2 F TC = TCL + TCF  Min
L = TC = TCL + TCF +  ( QL + QF -50)  Min
với điều kiện ràng buộc QL + QF =50
QL = 10 ;  QF = 40 ;  = -8
d. Nếu không có hãng lớn và các hãng nhỏ hoạt động như trong thị trường CTHH thì giá và sản
lượng cân bằng là: Cung thị trường = cầu thị trường:  MCF = Dt ; QE = 70; PE =11
e. Nếu hãng lớn vẫn tồn tại cùng với các hãng nhỏ hoạt động trong thị trường CTHH thì giá và
sản lượng cân bằng sẽ là MCT =  MCF + MCL = DT ;. QF = 83.33; PE =9.66
8.Thị trường hàng hoá dịch vụ X được cung cấp bởi một hãng lớn và 10 hãng nhỏ khác. Cầu thị
trường về dịch vụ đó mỗi ngày là Q = 180 - 10P.
Hàm chi phí biên của hãng lớn là MCL = 4 + 0,1q.
Hàm MC của mỗi hãng nhỏ là MC = q + 7.
a. Vẽ các đường chỉ rõ DT, MCN, MCL, DL L và MR
b. Giả sử hãng lớn giữ vai trò chỉ đạo giá, xác định Q*,P của hãng lớn và các hãng nhỏ. *
c. Nếu tất cả hợp thành một cartel, xác định mức Q*,P *của cả cartel, của hãng lớn và của các
hãng nhỏ nếu tập đoàn muốn tối thiểu hoá chi phí để sản xuất ra mức sản lượng tối ưu cho cả tập đoàn. Lời giải:
a. Cung của hãng nhỏ MC = q + 7  q = MC - 7.
Vậy tổng cung của 10 hãng nhỏ là
Q = 10MC - 70  MCN = 7 + 0,1Q
Đường cầu của hãng lớn P = 12,5 - 0,05q ( q≤ 110) MRL = 12,5 - 0,1q (q≤ 110) P = 18 - 0,1 q ( q> 110) MRL = 18 - 0,2q ( q>110) Vẽ hình 18 MCN MCL 12,5 10,375 8 7 4 DT 33,75 42,5 76,25 110 MRL Q
b. Nếu hãng lớn giữ vai trò chỉ đạo giá
Mức sản lượng và giá bán tối ưu của hãng lớn là MCL = MRL
12,5 - 0,1q = 4 + 0,1q (q≤ 110) QL* = 42,5
18 - 0,2q = 4 + 0,1q ( q>110) QL* =46,67 (loại)
Giá bán tối ưu hãng lớn đưa ra là P = 10,375
Lượng bán của hãng nhỏ QN = 33,75 *
Lượng bán của cả thị trường Q = QL + Q * N = 76,25 *
c. Nếu tất cả các hãng hình thành một cartel thì chi phí biên của cartel là MCCT = 4 + 0,1 q ( q≤ 30)
MCCT = 5,5 + 0,05 q ( q >30)
Giá và sản -lượng tối ưu của Cartel đạt ở mức MCCT = MR = 18 - 0,2 q Vậy Q = 50 và P * = 13 *
Nếu tập đoàn muốn tối thiểu hoá chi phí sản xuất cho cả tập đoàn thì phân chia sản lượng sản
xuất sao cho MCL = MCN = MCCL = 8
Các hãng nhỏ sản xuất 7 + 0,1q = 8  q* = 10 1
Hãng lớn sản xuất 4 + 0,1q = 8  q* = 40 2