1 CHƯƠNG
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ BÀI 5.
PHÉP BIẾN ĐỔI ĐỒ THỊ
Cho hàm số y = f(x) có đồ thị (C) và a > 0, khi đó
 Đồ thị hàm số y = f(x + a) có được bằng cách tịnh tiến đồ thị (C) sang trái a đơn vị theo trục Ox.
 Đồ thị hàm số y = f(x − a) có được bằng cách tịnh tiến đồ thị (C) sang phải a đơn vị theo trục Ox.
 Đồ thị hàm số y = f(x) + a có được bằng cách tịnh tiến đồ thị (C) lên phía trên a đơn vị theo trục Oy.
 Đồ thị hàm số y = f(x) − a có được bằng cách tịnh tiến đồ thị (C) xuống phía dưới a đơn vị theo trục Oy.
 Đồ thị hàm số y = −f(x) có được bằng cách lấy đối xứng với đồ thì (C) qua Ox.
 Đồ thị hàm số y = f(−x) có được bằng cách lấy đối xứng với đồ thì (C) qua Oy.
 Đồ thị hàm số y = |f(x)| có được bằng cách sau: giữ lại phần đồ thị (C) phía trên Ox, phần
phía dưới Ox bỏ và lấy đối xứng qua Ox.
 Đồ thị hàm số y = f(|x|) có được bằng cách sau: giữ lại phần đồ thị (C) phía bên phải Oy
(bỏ phần bên trái Oy), sau đó lấy đối xứng qua Oy.  u(x)  nếu  u(x) ≤ 0   Đồ thị |u(x)| v(x) y = = . v(x) u(x)  nếu  − u(x) < 0  v(x) VÍ DỤ VÍ DỤ 1.
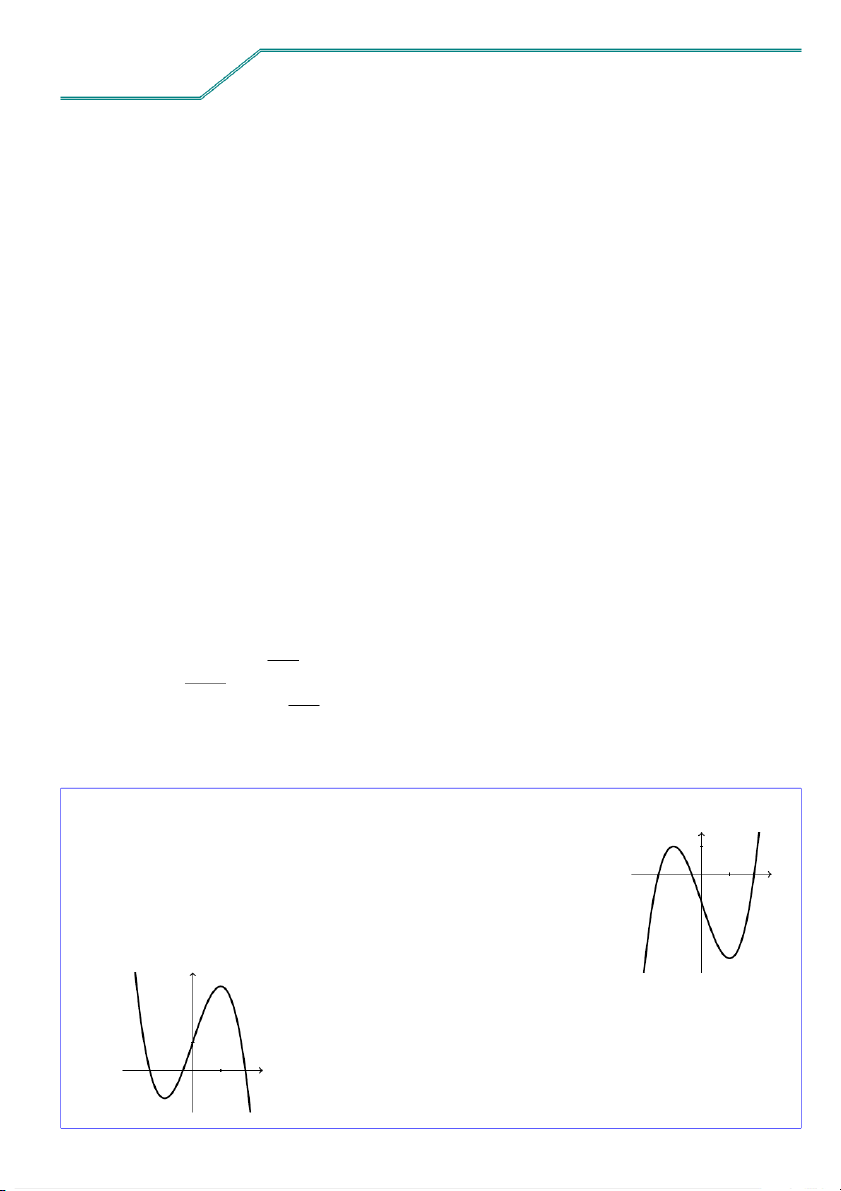
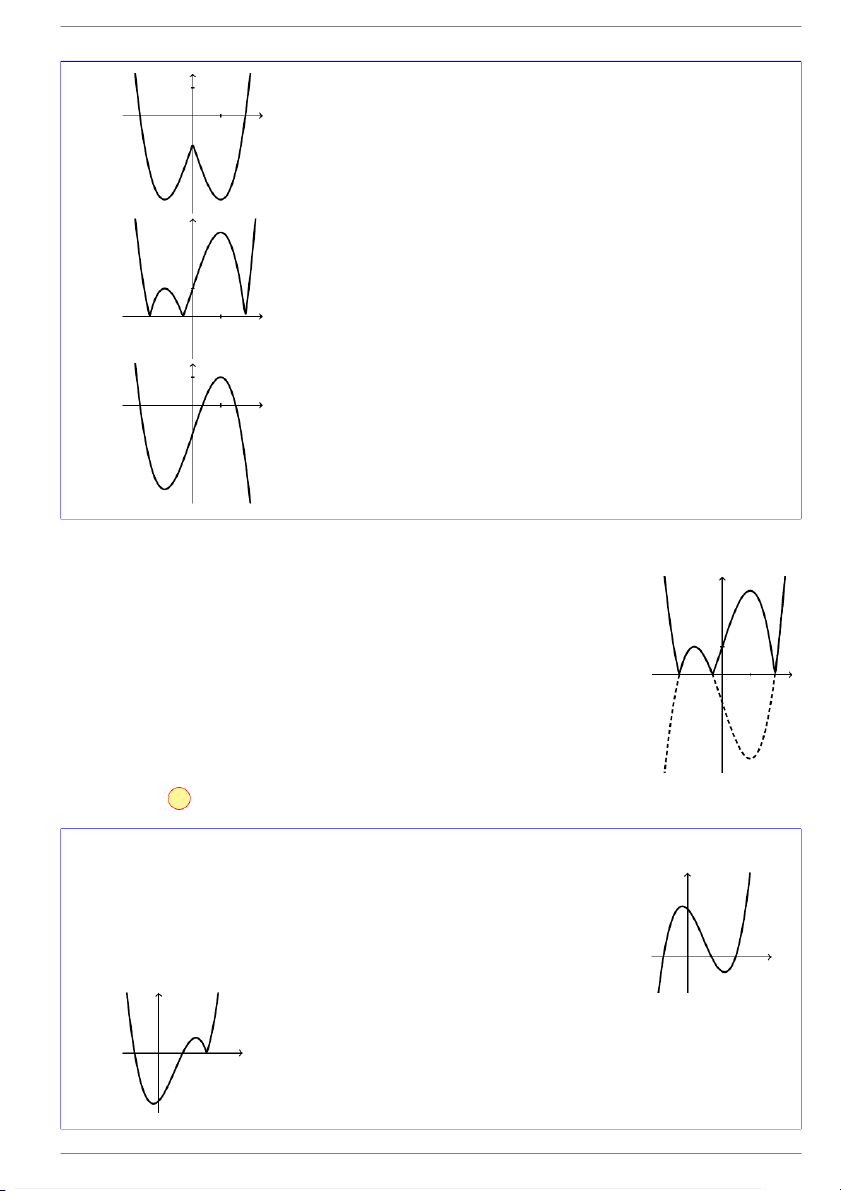
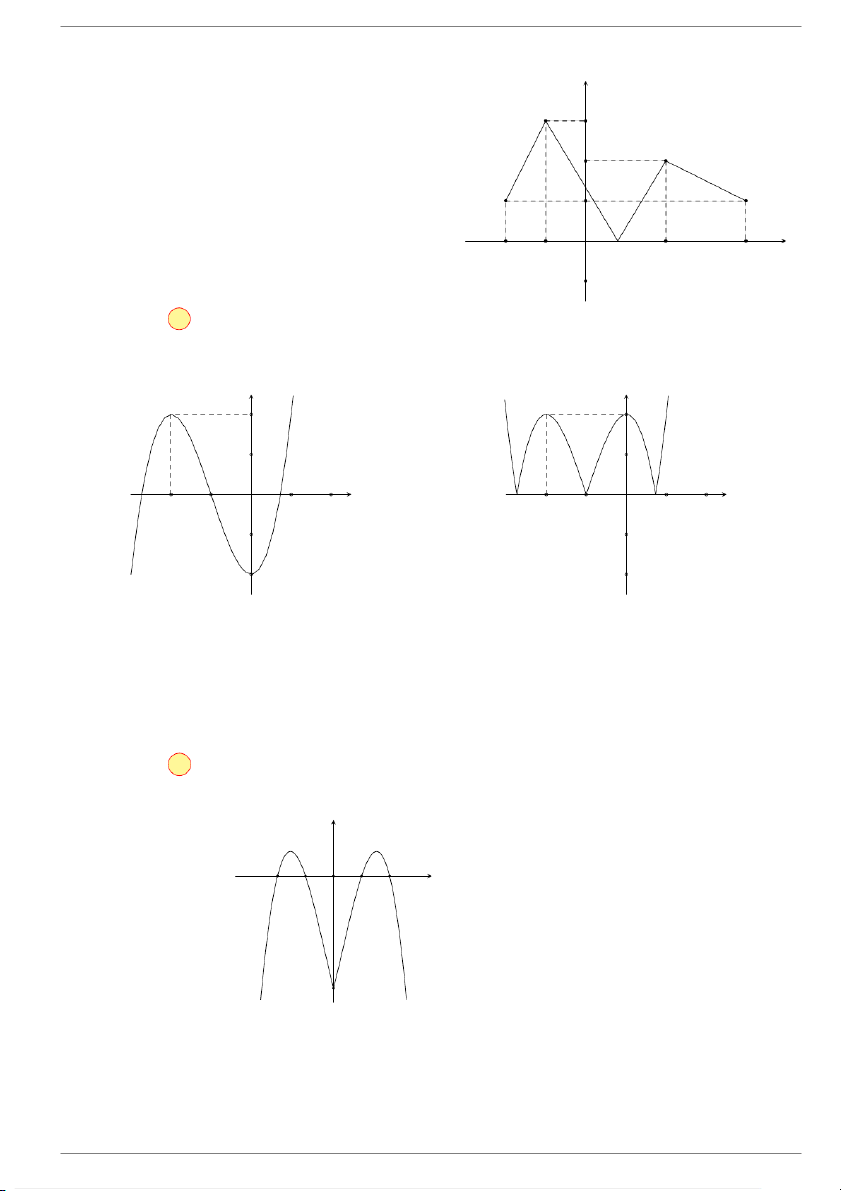
Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị như y
hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số 1 y = f (−x)? x O 1 y 1 x O 1 A. . 1
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 1 x O 1 B. . y 1 x O 1 C. . y 1 x O 1 D. . Lời giải.
Đồ thị (C1) của hàm số y = f(−x) được suy ra từ đồ thị (C) của hàm số y 1
y = f (x) bằng cách lấy đối xứng đồ thị (C) qua trục Oy. x O 1 Chọn đáp án D  VÍ DỤ 2.
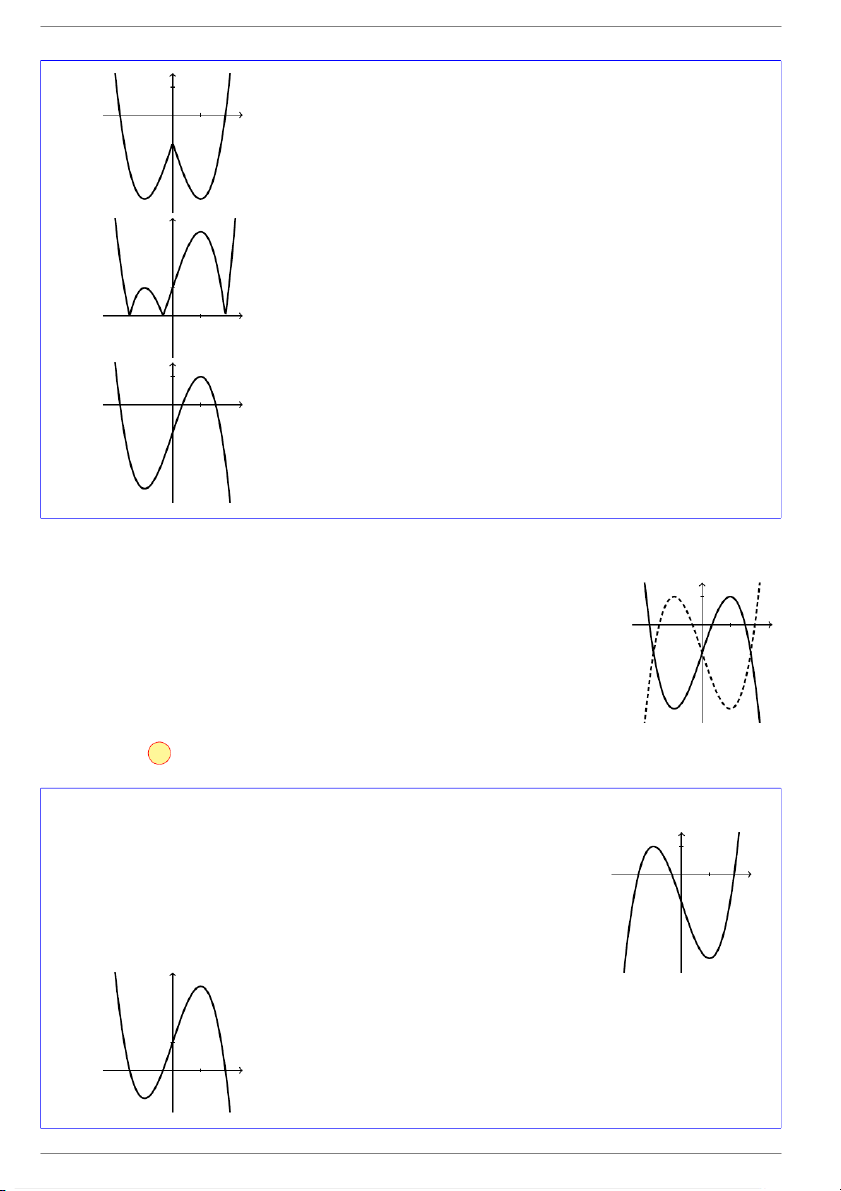
Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị như y
hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số 1 y = −f (x)? x O 1 y 1 x O 1 A. .  GV: Đỗ Trung Lai 2 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 1 x O 1 B. . y 1 x O 1 C. . y 1 x O 1 D. . Lời giải.
Đồ thị (C1) của hàm số y = −f(x) được suy ra từ đồ thị (C) của hàm số y
y = f (x) bằng cách lấy đối xứng đồ thị (C) qua trục Ox. 1 x O 1 Chọn đáp án A  VÍ DỤ 3.
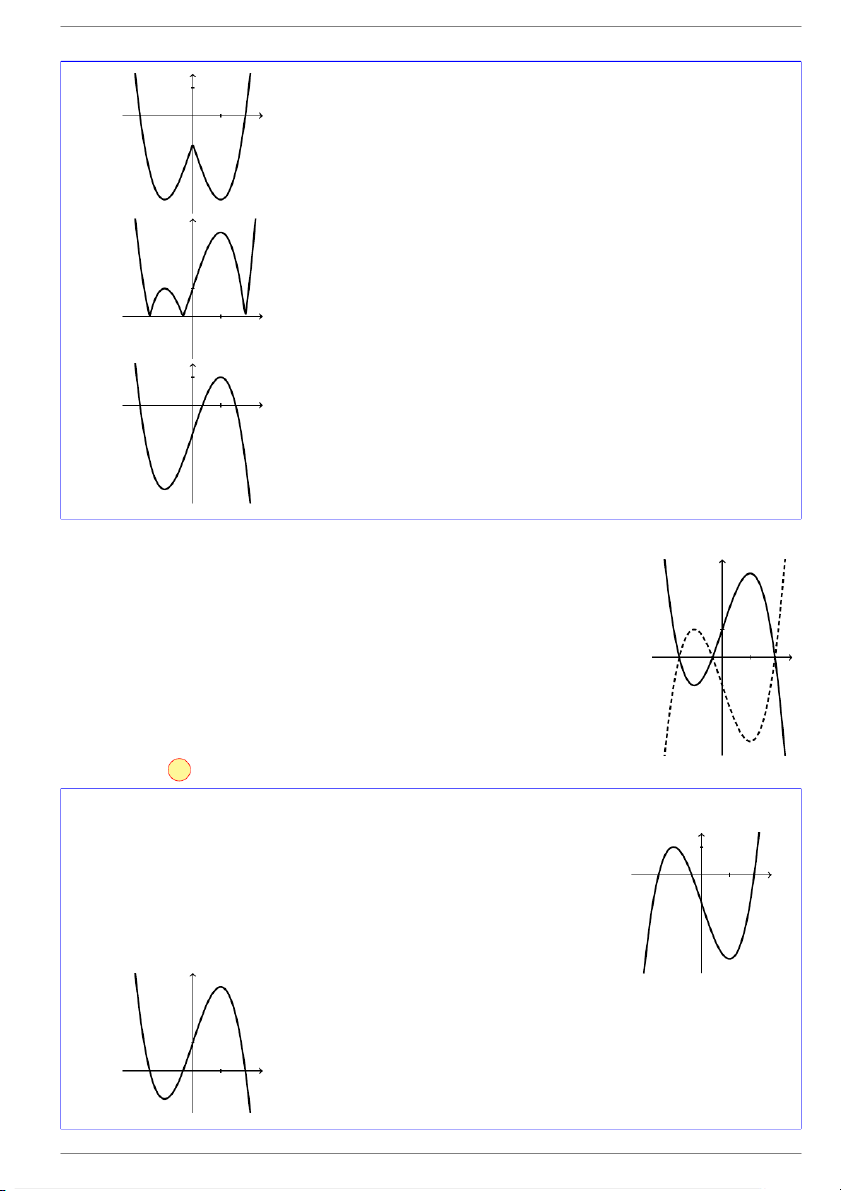
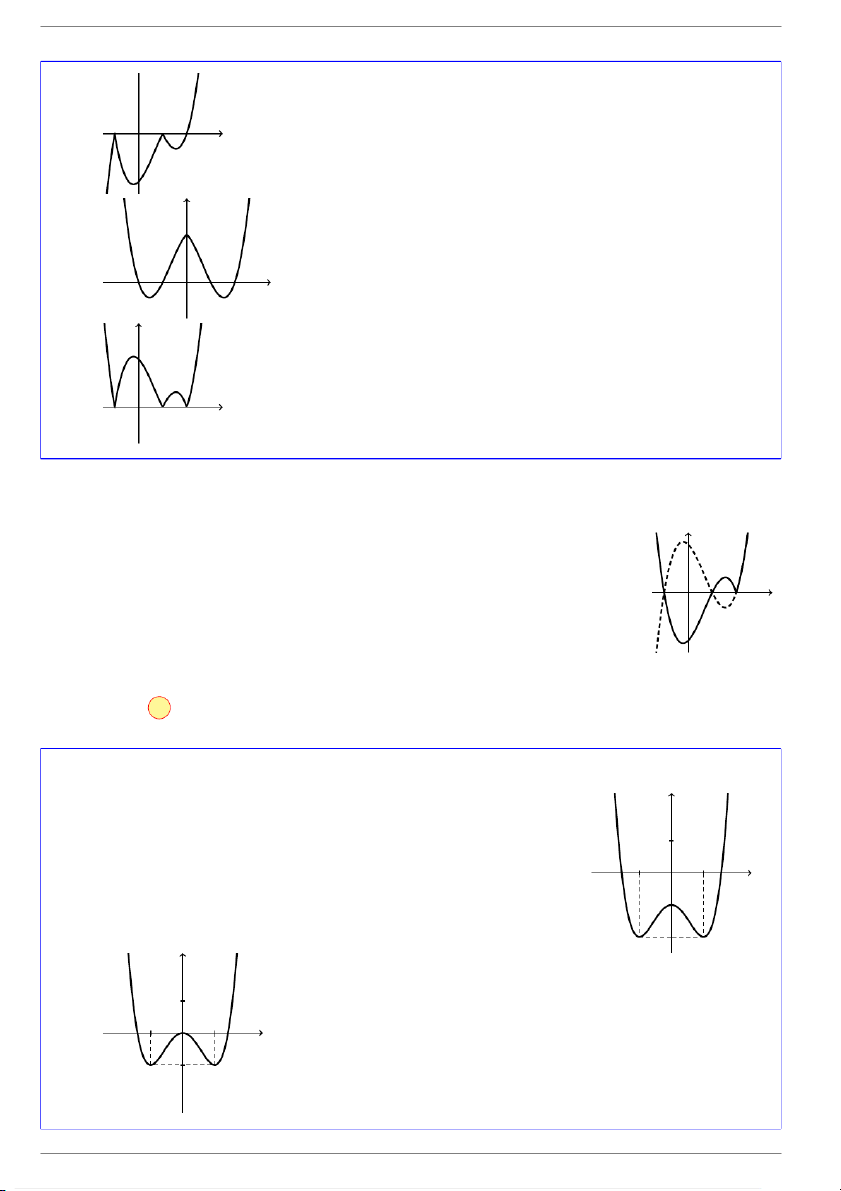
Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị như y
hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = f(|x|)? 1 x O 1 y 1 x O 1 A. .  GV: Đỗ Trung Lai 3 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 1 x O 1 B. . y 1 x O 1 C. . y 1 x O 1 D. . Lời giải.
Đồ thị (C1) của hàm số y = f(|x|) được suy ra từ đồ thị (C) của hàm số y y = f (x) bằng cách: 1 x
- Giữ lại phần đồ thị (C) nằm bên phải trục Oy. O
- Lấy đối xứng phần giữ lại qua trục 1 Oy. Chọn đáp án B  VÍ DỤ 4.
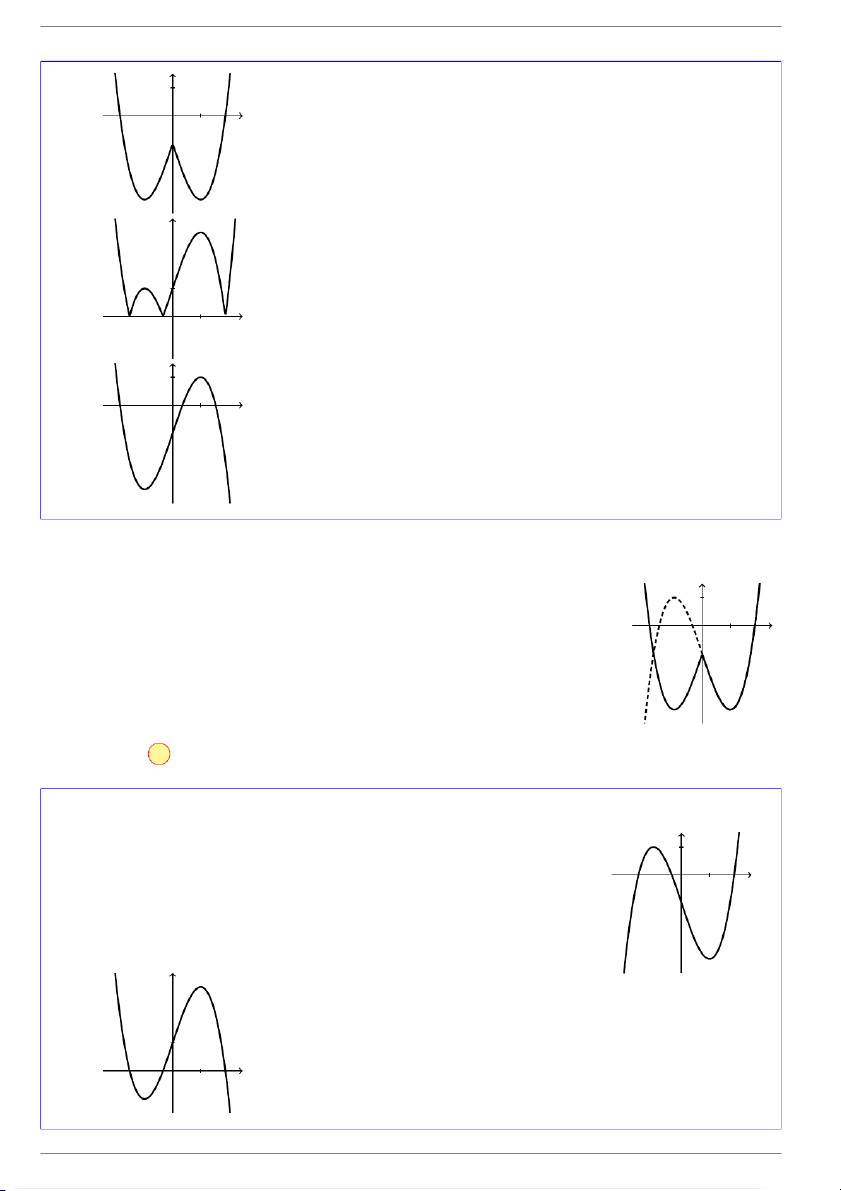
Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị như y
hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = |f(x)|? 1 x O 1 y 1 x O 1 A. .  GV: Đỗ Trung Lai 4 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 1 x O 1 B. . y 1 x O 1 C. . y 1 x O 1 D. . Lời giải.
Đồ thị (C1) của hàm số y = |f(x)| được suy ra từ đồ thị (C) của hàm số y y = f (x) bằng cách:
- Giữ nguyên phần đồ thị (C) nằm phía trên trục Ox.
- Lấy đối xứng phần còn lại qua trục Ox. 1 x O 1 Chọn đáp án C  VÍ DỤ 5.
Cho hàm số y = (x − 2)(x2 − 1) có đồ thị như hình vẽ bên. Hình nào y
dưới đây là đồ thị của hàm số y = |x − 2|(x2 − 1)? x O y x O A. .  GV: Đỗ Trung Lai 5 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y x O B. . y x O C. . y x O D. . Lời giải.
Ta có: y = (x − 2)(x2 − 1). y Khi đó y−nế y u nếxu −x 2 ≥ − 2 0< 0 ( . 1)(2) y x 1 = |x − 2|(x2 − 1) =
Do đó đồ thị hàm số (C1) được suy ra từ đồ thị hàm số (C) như sau: O
- Giữ nguyên phần đồ thị của (C) nằm trên miền x − 2 ≥ 0 (do (1)).
- Lấy đối xứng qua trục hoành phần đồ thị (C) nằm trên miền x − 2 < 0. (do (2)). Chọn đáp án A  VÍ DỤ 6.
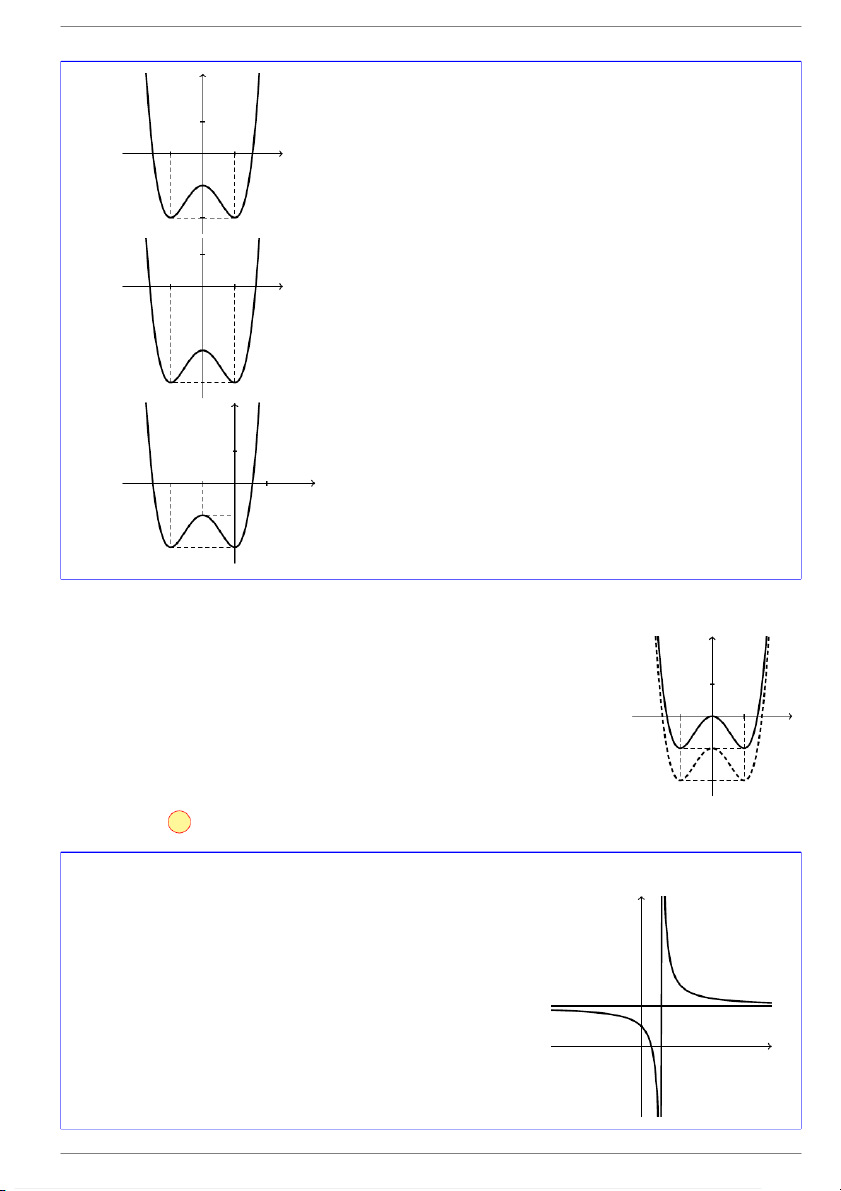
Cho hàm số y = f(x) xác định và liên tục trên R và có đồ thị như y
hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = f(x)+1? 1 x −1 O 1 −2 y 1 x −1 O 1 −1 A. .  GV: Đỗ Trung Lai 6 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 1 x −1 O 1 B. −2 . y 1 x −1 O 1 −2 C. . y 1 x −1 O 1 D. −2 . Lời giải.
Đồ thị (C1) của hàm số y = f(x) + 1 được suy ra từ đồ thị (C) của hàm y
số y = f(x) bằng cách tịnh tiến lên phía trên theo phương trục Oy 1 đơn vị. 1 x −1 O 1 −2 Chọn đáp án A  VÍ DỤ 7.
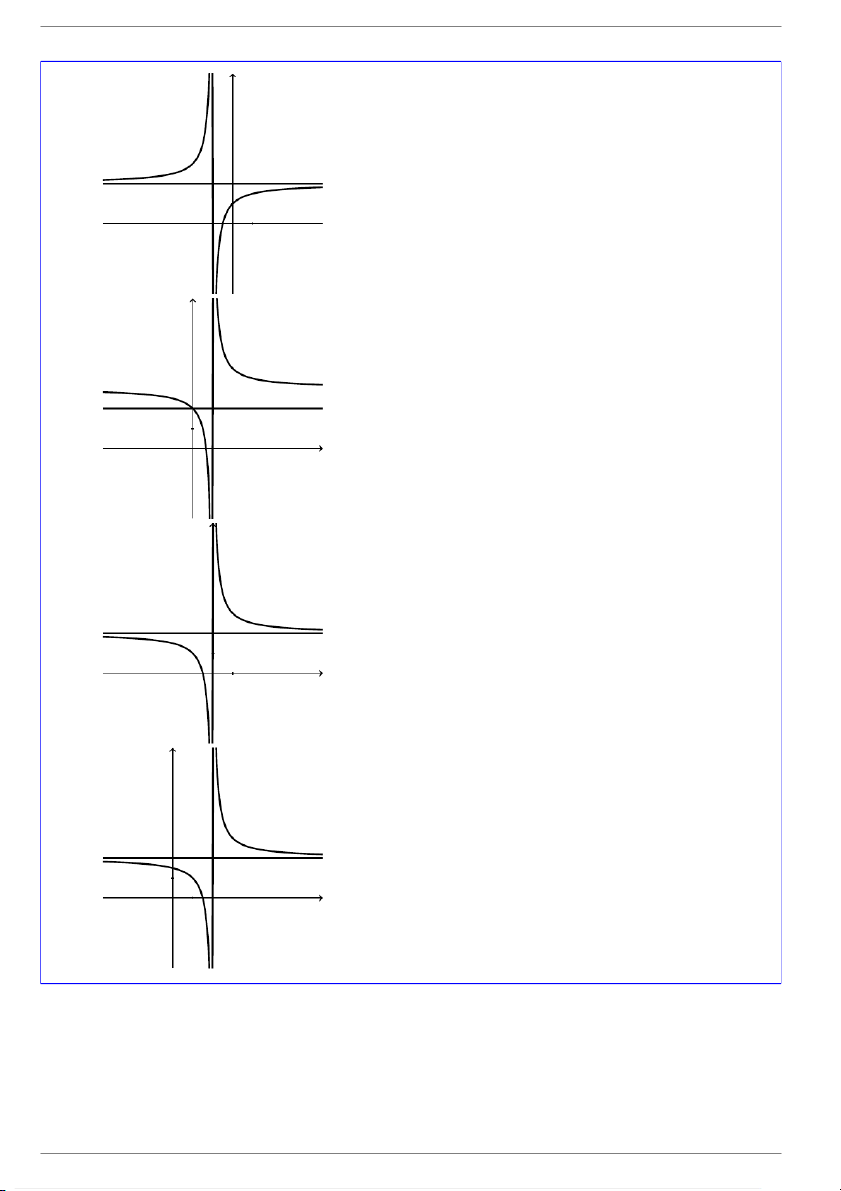
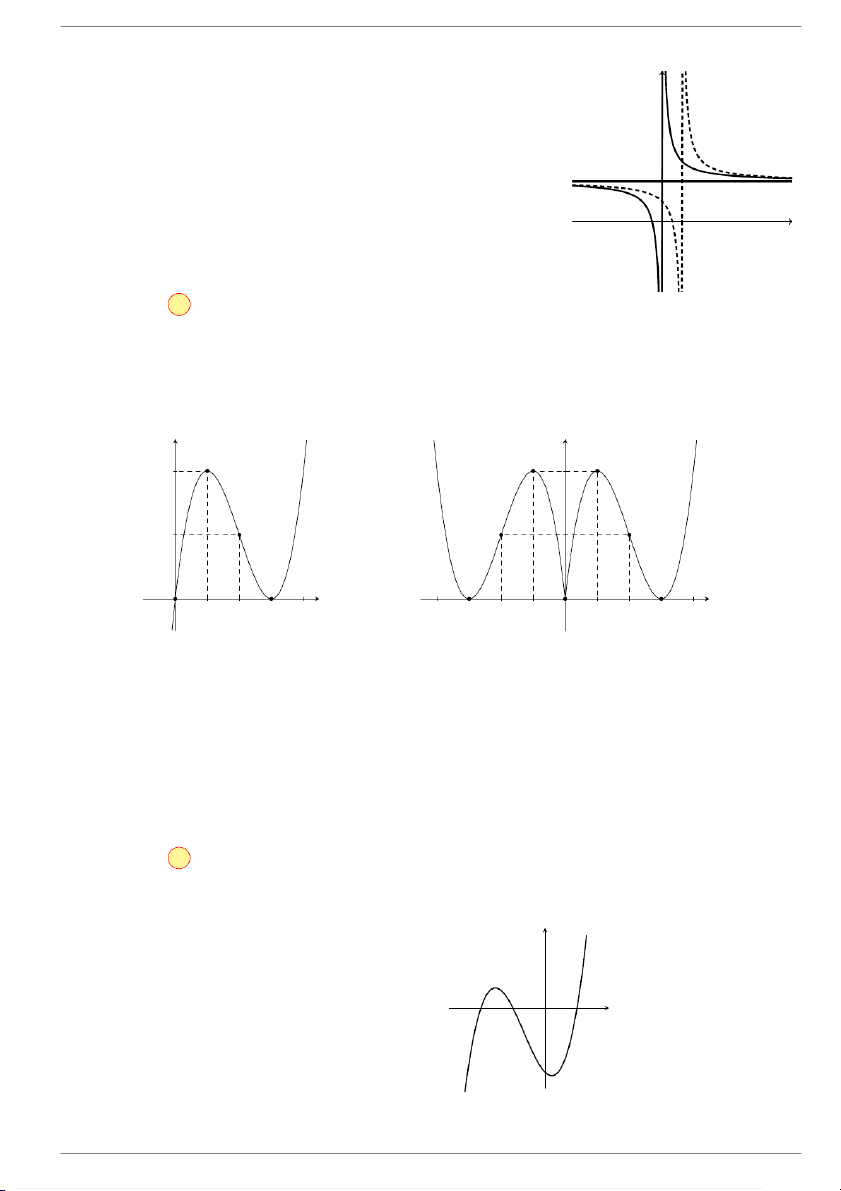
Cho hàm số y = f(x) xác định và liên tục trên R \ {1} và y
có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = f(x + 1)? 2 1 x O 1  GV: Đỗ Trung Lai 7 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị y 2 1 x 1 O A. . y 2 1 x O 1 B. . y 2 1 x O 1 C. . y 2 1 x O 1 D. . Lời giải.  GV: Đỗ Trung Lai 8 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị
Đồ thị (C1) của hàm số y = f(x + 1) được suy ra từ đồ thị (C) y
của hàm số y = f(x) bằng cách tịnh tiến sang trái theo phương trục Ox 1 đơn vị. 2 1 x O 1 Chọn đáp án C  BÀI TẬP TRẮC NGHIỆM
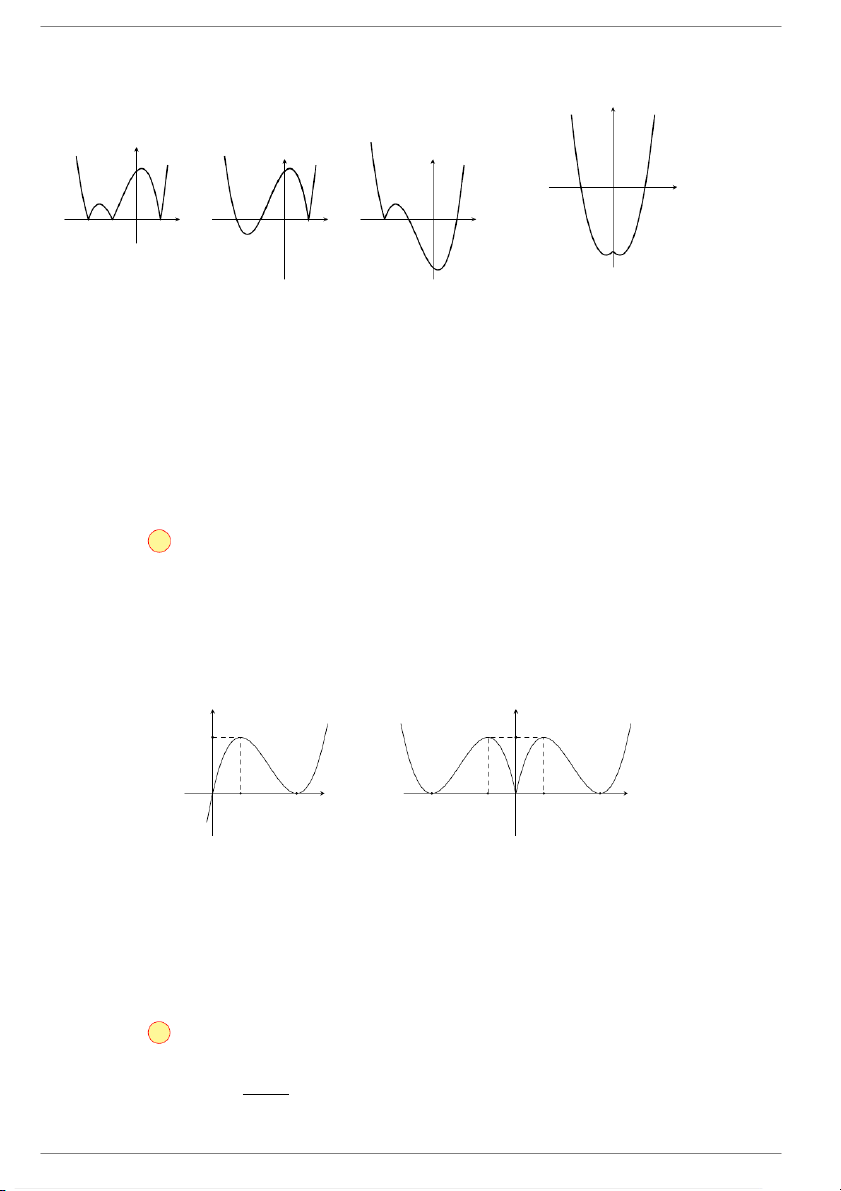
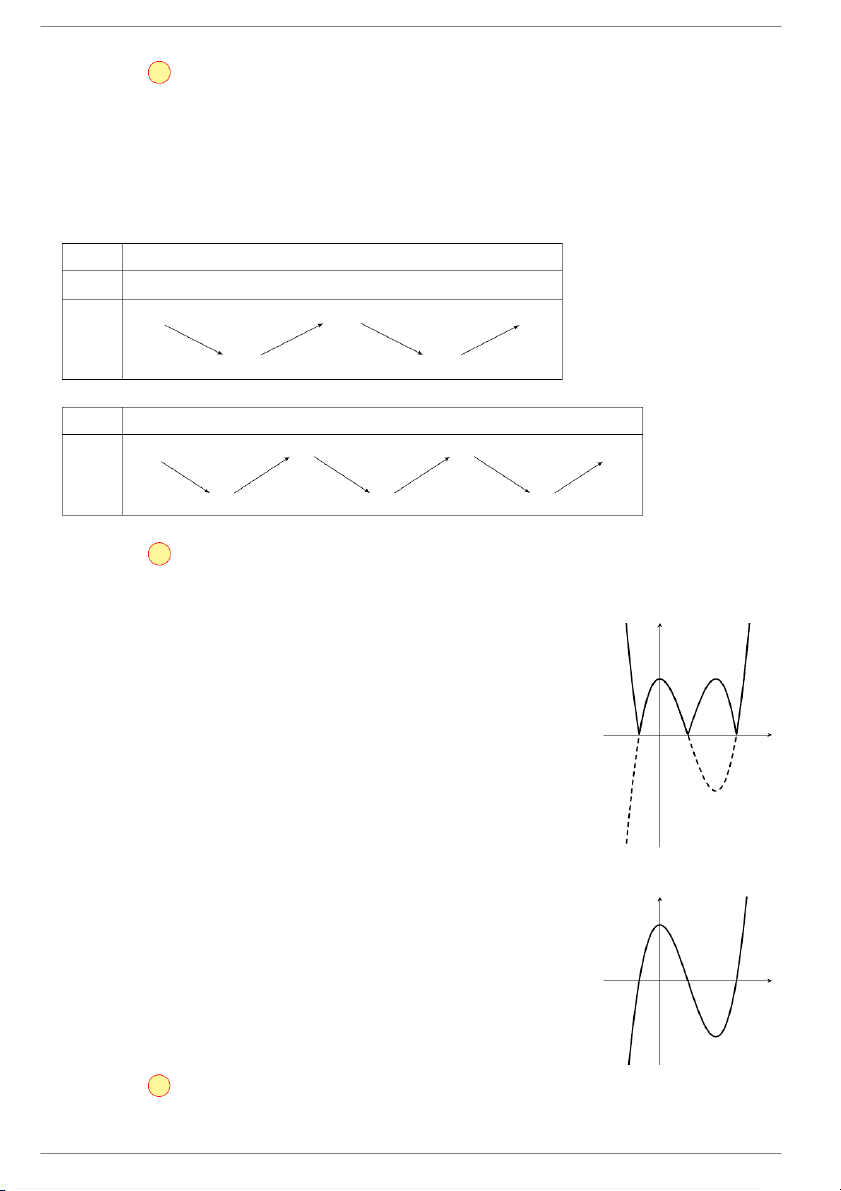
Câu 1. Cho hàm số y = x3 − 6x2 + 9x có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây? O O A. y = |x|3 + 6x2 + 9 |x|. B. y = |x|3 − 6x2 + 9 |x|. C. y = −x3 + 6x2 − 9x. D. y =  . x3 − 6x2 + 9x  Lời giải.
Từ đồ thị hàm số y = x3 − 6x2 + 9x suy ra đồ thị hàm số y = |x|3 − 6x2 + 9 |x|, ta làm theo cách sau
Bước 1. Giữ nguyên phần đồ thị nằm bên phải trục tung của hàm số y = x3 − 6x2 + 9x. Xóa bỏ
phần đồ thị nằm bên trái trục tung.
Bước 2. Lấy đối xứng phần đồ thị nằm bên phải trục tung qua trục tung.
Đồ thị nhận được chính là hình 2. Chọn đáp án B  Câu 2.
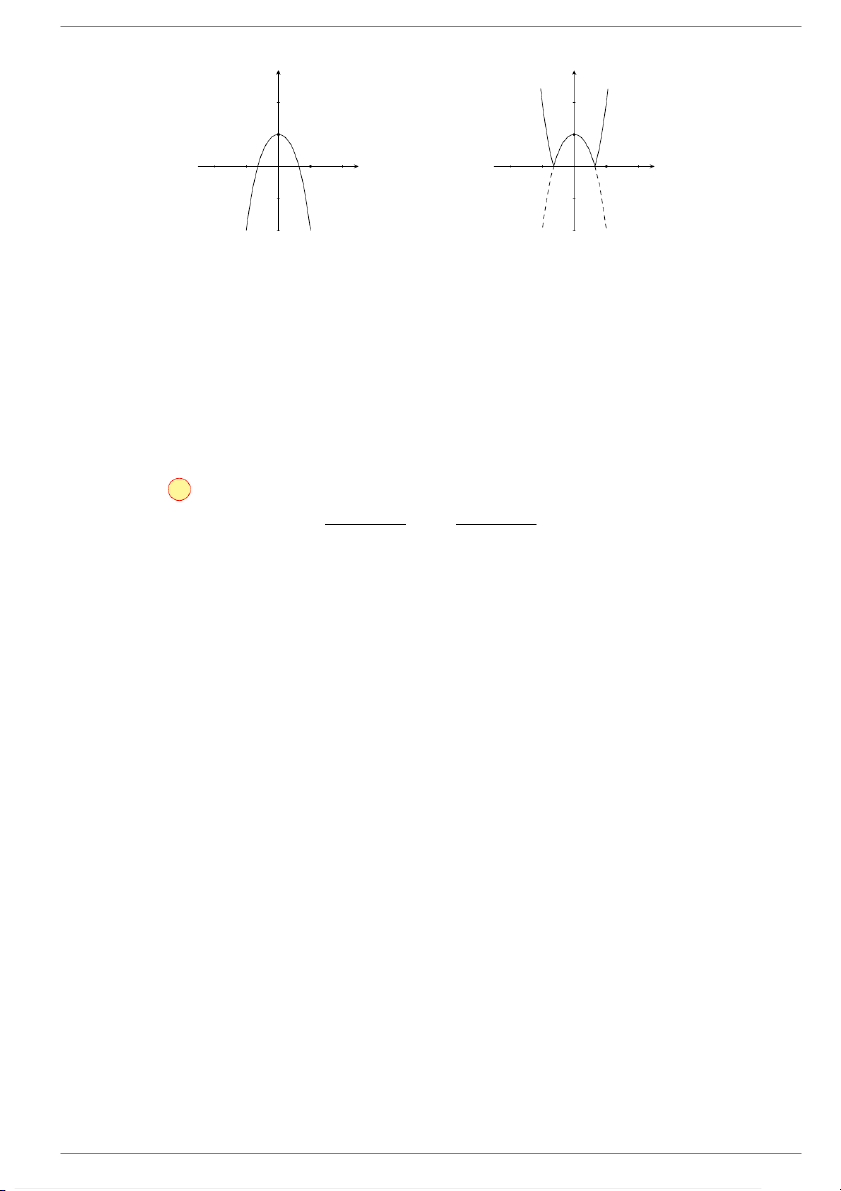
Cho hàm số y = x3 + 2x2 − x − 2 có đồ thị (C) như hình vẽ bên y x O  GV: Đỗ Trung Lai 9 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị
Đồ thị của hàm số y = 
là một trong các hình dưới, đó là hình nào? x3 + 2x2 − x − 2  y y y y x O x x x O O O Hình 1 Hình 2 Hình 4 Hình 3 A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. Lời giải.
Theo cách vẽ đồ thị hàm số |f(x)|, ta làm như sau:
- Giữ nguyên phần đồ thị phía trên trục hoành.
- Bỏ phần đồ thị dưới trục hoành.
- Lấy đối xứng qua trục hoành phần đồ thị nằm bên dưới trục hoành.
Ta được hình cần tìm là hình 1. Chọn đáp án D 
Câu 3. Cho hàm số y = x3 − 6x2 + 9x có đồ thị như Hình 1. Khi đó, đồ thị Hình 2 là của hàm số nào dưới đây? A. y = −x3 + 6x2 − 9x . B. y = |x3 − 6x2 + 9x|. C. y = |x|3 − 6x2 + 9|x|. D. y = |x|3 + 6|x|2 + 9|x|. Lời giải.
Đồ thị hình 2 có được từ phép suy đồ thị y = f(|x|) trong đó f(x) = x3 − 6x2 + 9x.
Vậy hàm số có đồ thị như hình 2 là y = |x|3 − 6x2 + 9|x|. Chọn đáp án C  Câu 4. Cho hàm số x y =
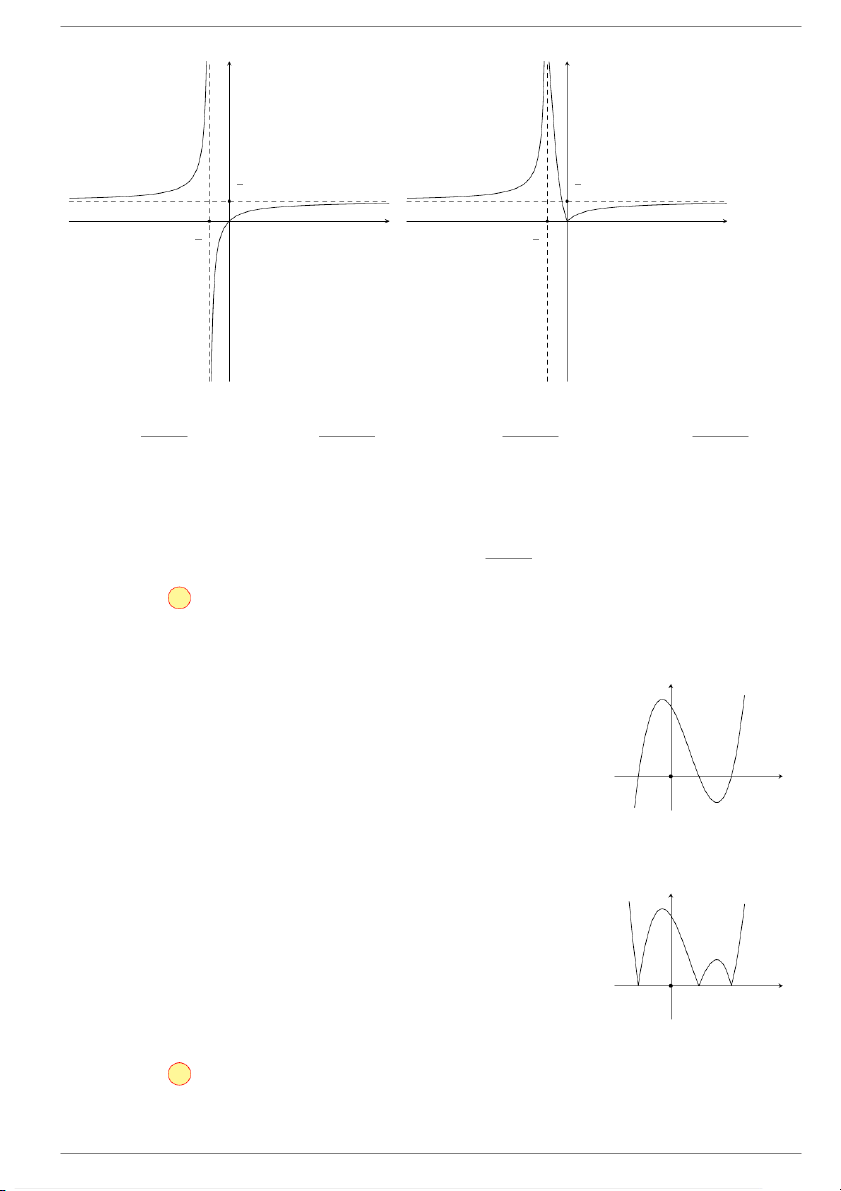
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào trong 2x + 1 các đáp án dưới đây?  GV: Đỗ Trung Lai 10 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị Hình 1 Hình 2   A.  x  |x| x |x| y =    . B. y = . C. y = . D. y = .    2x + 1 2|x| + 1 2|x| + 1  2|x| + 1  Lời giải.
Ta thấy đồ thị của hình 2 được tạo ra từ đồ thị của hình 1 như sau:
Giữ nguyên phần đồ thị hàm số ứng với y > 0, lấy đối xứng qua trục Ox phần đồ thị nằm phía dưới trục  x 
Ox. Do đó đồ thị hình 2 là của hàm số y =  .  2x + 1  Chọn đáp án A  Câu 5.
Cho hàm số y = f(x) có đồ thị trên một khoảng K như hình vẽ bên.
Trên K, hàm số y = |f(x)| có bao nhiêu cực trị? A. 3. B. 2. C. 4. D. 5. Lời giải.
Ta vẽ đồ thị hàm số y = |f(x)| bằng cách giữ nguyên phần đồ thị
hàm số y = f(x) nằm phía trên trục hoành và lấy đối xứng qua trục
hoành phần đồ thị nằm phía dưới trục hoành.
Dựa vào đồ thị hàm số y = |f(x)| ta thấy hàm số này có 5 cực trị. Chọn đáp án D  Câu 6.  GV: Đỗ Trung Lai 11 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị
Đồ thị hình bên là đồ thị của hàm số nào trong bốn hàm số cho dưới đây? A. 2x − 3 y = . B. x − 1 2x − 3 y = . |x − 1| C. |2x − 3| y = . D. x − 1    2x − 3 y = .    x − 1  Lời giải.
Đồ thị hàm số đi qua điểm 2x − 3 |2x − 3|
(0, 3) nên các đồ thị hàm số y = và y = không thỏa |x − 1| x − 1 mãn. Với 3 2x − 3  3 1 < x <
đồ thị hàm số có giá trị dương mà y = < 0 với ∀x ∈ 1; . 2 x − 1 2 Chọn đáp án D 
Câu 7. Cho hàm số y = f(x) có bảng biến thiên sau x −∞ −1 3 +∞ y + 0 − 0 + 5 +∞ y −∞ 1
Hàm số y = |f(x)| có bao nhiêu cực trị? A. 4. B. 3. C. 5. D. 2. Lời giải.
Dựa vào bảng biến thiên ta thấy đồ thị hàm số của hàm y = |f(x)| nhận được bằng cách lấy
đối xứng phần bên dưới trục hoành qua trục hoành có 3 điểm cực trị. Chọn đáp án B  Câu 8.
Cho hàm số y = f(x) có đồ thị trên đoạn [−2; 4]
như hình vẽ. Tìm max|f(x)|. [ 2;4] A. 2. B. |f(0)|. C. 3. D. 1. Lời giải.  GV: Đỗ Trung Lai 12 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị
Từ đồ thị hàm số f(x) ta có đồ thị của hàm số |f (x)| như hình bên.
Ta thấy max|f(x)| = 3 khi x = −1. [ 2 4] Chọn đáp án C 
Câu 9. Cho hàm số y = x3 + 3x2 − 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Hình 1 Hình 2 A. y =  2 2 x3  + 3x − 2. B. y = −x3 − 3x + 2. C.  y =  . D. . x3  + 3x2 − 2  y =  x3 + 3x2 − 2  Lời giải.
Ta có y = x3 + 3x2 − 2
. Do vậy, dựa vào đồ thị chọn
x3 + 3x2 − 2 nếu 0 ≤ x3 + 3x2 − 2
− (x3 + 3x2 − 2) nếu x3 + 3x2 − 2 < 0  = đáp án D. Chọn đáp án D 
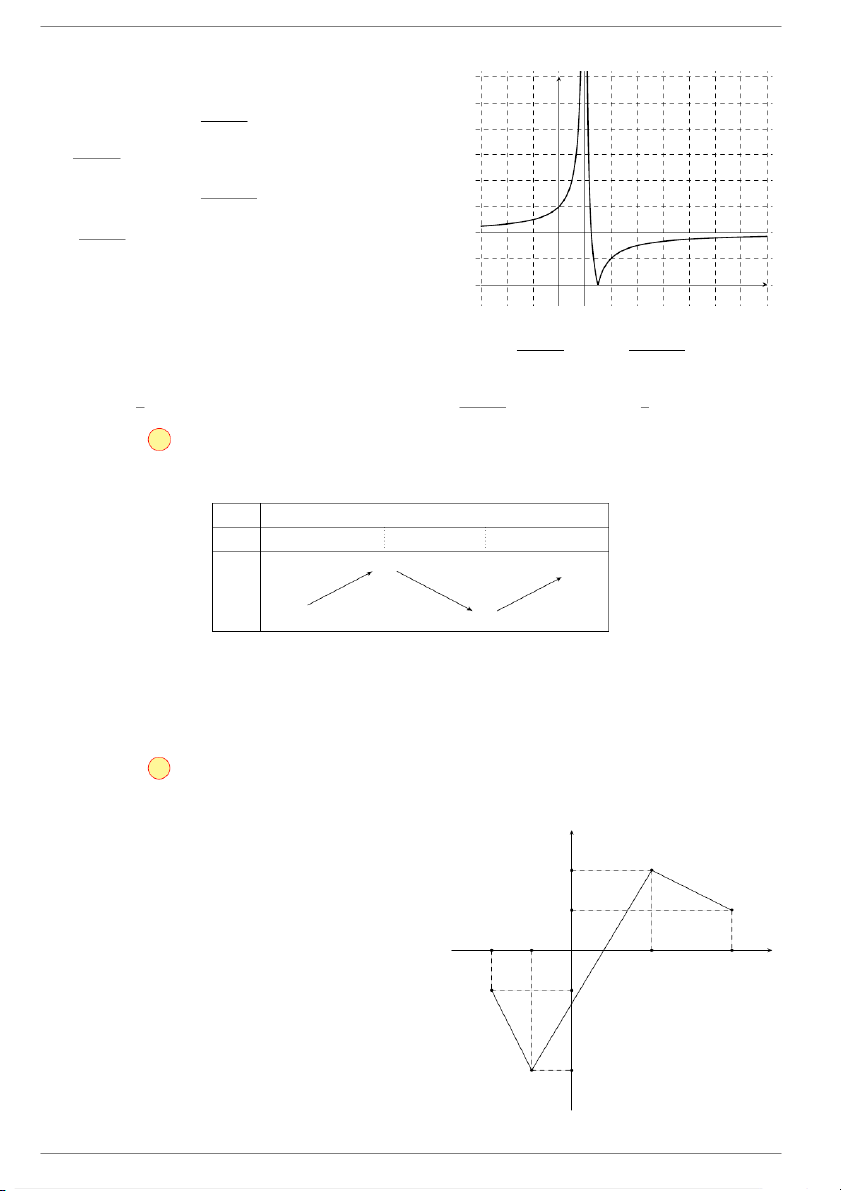
Câu 10. Cho hàm số y = f(x) có đồ thị hàm số y = f (|x|) như hình vẽ. Chọn kết quả đúng trong các kết quả sau
A. f(x) = −x3 + x2 + 4x − 4.
B. f(x) = x3 − x2 − 4x + 4.
C. f(x) = −x3 − x2 + 4x + 4.
D. f(x) = x3 + x2 − 4x − 4.
Lời giải.. Đồ thị hàm số y = f (|x|), trùng với đồ thị hàm số y = f(x) khi x ≥ 0.
Dựa vào đồ thị, ta thấy đồ thị hàm số y = f(x) = ax3 + bx2 + cx + d có hệ số a < 0, d = −4, suy
ra f(x) = −x3 + x2 + 4x − 4.  GV: Đỗ Trung Lai 13 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị Chọn đáp án A 
Câu 11. Cho hàm số y = |x4 − 2x2 − 3|. Số điểm cực trị của đồ thị hàm số là A. 1. B. 2. C. 3. D. 5. Lời giải.
Xét hàm số y = f(x) = x4 − 2x2 − 3.
Ta lập được bảng biến thiên của hàm số như sau
f (x) = 4x3 − 4x = 0 ⇔ x = 0, x = ±1. x −∞ −1 0 1 +∞ f (x) − 0 + 0 − 0 + +∞ −3 +∞ f (x) −4 −4
Từ đó ta suy ra được bảng biến thiên của hàm số y = |f(x)| = |x4 − 2x2 − 3| là x −∞ x1 −1 0 1 x2 +∞ +∞ 4 4 +∞ |f (x)| 0 3 0
Dựa vào bảng biến thiên ta có đồ thị hàm số y = |x4 − 2x2 − 2| có 5 điểm cực trị. Chọn đáp án D  Câu 12.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Đồ thị bên là của hàm số A. y = f(x) = −x3 + 3x2 + 2.
B. y = f(x) = |x3 − 3x2 + 2|. C. y = f(x) = |x3 − 3x2|.
D. y = f(x) = | − x3 − 3x2 + 2|. Lời giải.
Ta có đồ thị hàm số g(x) = x3 − 3x2 + 2 như hình vẽ. Giữ nguyên phần
đồ thị hàm số g(x) nằm phía trên trục hoành và lấy đối xứng phần đồ
thị hàm số g(x) nằm dưới trục hoành qua trục hoành ta được đồ thị
hàm số y = f(x) = |x3 − 3x2 + 2| như trong đề bài. Chọn đáp án B 
Câu 13. Biết đồ thị hàm số y = f(x) có dạng như Hình (1).  GV: Đỗ Trung Lai 14 dotrunglai@gmail.com
Trường THPT Tân Châu − An Giang Phép biến đổi đò thị
Đồ thị ở Hình (2) là của hàm số nào trong các hàm số sau? A. y = |f(x)|. B. y = f(|x|). C. y = −f(x). D. y = −f(|x|). Lời giải.
Đồ thị ở Hình (2) gồm 2 phần:
 Phần 1 là phần đồ thị nằm trên trục hoành của Hình (1).
 Phần 2 là phần nhận được bằng cách lấy đối xứng phần đồ thị nằm dưới trục hoành của Hình (1) qua Ox.
Do đó, đồ thị ở Hình (2) là của hàm số y = |f(x)|. Chọn đáp án A  HẾT  GV: Đỗ Trung Lai 15 dotrunglai@gmail.com