











Preview text:
MỤC LỤC phiếu khảo bài 12 – hk1 Trang hÌNh hỌC
PhiÕu 1.1. Gãc gi÷a ®êng th¼ng & mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
PhiÕu 1.2. Gãc gi÷a ®êng th¼ng & mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
PhiÕu 2.1. Gãc gi÷a ®êng th¼ng & mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
PhiÕu 2.2. Gãc gi÷a ®êng th¼ng & mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
PhiÕu 3.1. Gãc gi÷a hai mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
PhiÕu 3.2. Gãc gi÷a hai mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
PhiÕu 4.1. Kho¶ng c¸ch tõ mét ®iÓm ®Õn mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
PhiÕu 4.2. Kho¶ng c¸ch tõ mét ®iÓm ®Õn mÆt ph¼ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
PhiÕu 5.1. Kho¶ng c¸ch gi÷a hai ®êng th¼ng chÐo nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
PhiÕu 5.2. Kho¶ng c¸ch gi÷a hai ®êng th¼ng chÐo nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
PhiÕu 6.1. DiÖn tÝch cña 10 h×nh thêng gÆp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
PhiÕu 6.2. DiÖn tÝch cña 10 h×nh thêng gÆp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
PhiÕu 7.1. C«ng thøc thÓ tÝch khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
PhiÕu 7.2. C«ng thøc thÓ tÝch khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
PhiÕu 8. ThÓ tÝch khèi chãp cã c¹nh bªn vu«ng gãc víi mÆt ®¸y . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
PhiÕu 9. ThÓ tÝch khèi chãp cã c¹nh mÆt vu«ng gãc víi mÆt ®¸y . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
PhiÕu 10. ThÓ tÝch khèi chãp ®Òu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
PhiÕu 11. ThÓ tÝch khèi l¨ng trô . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
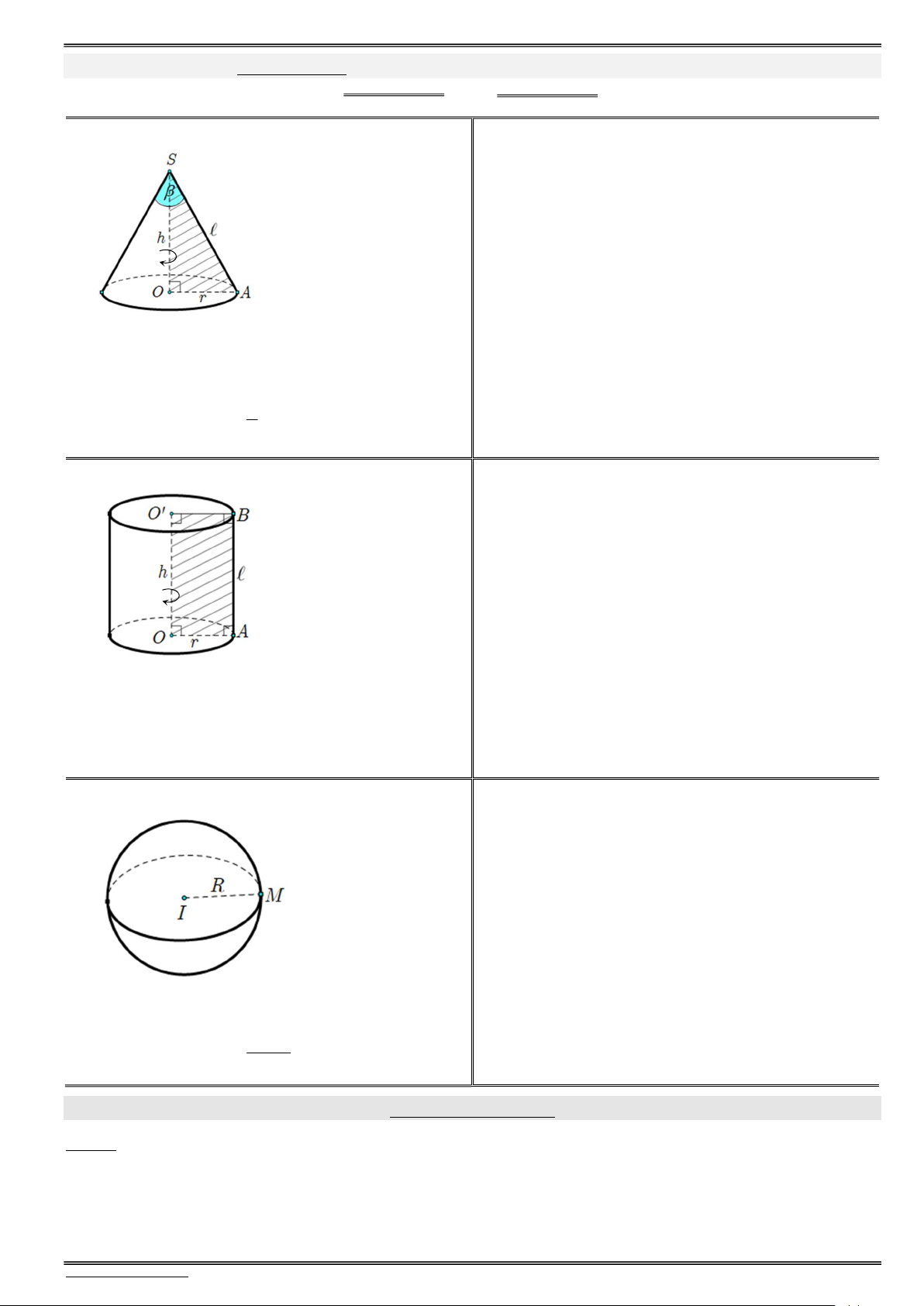
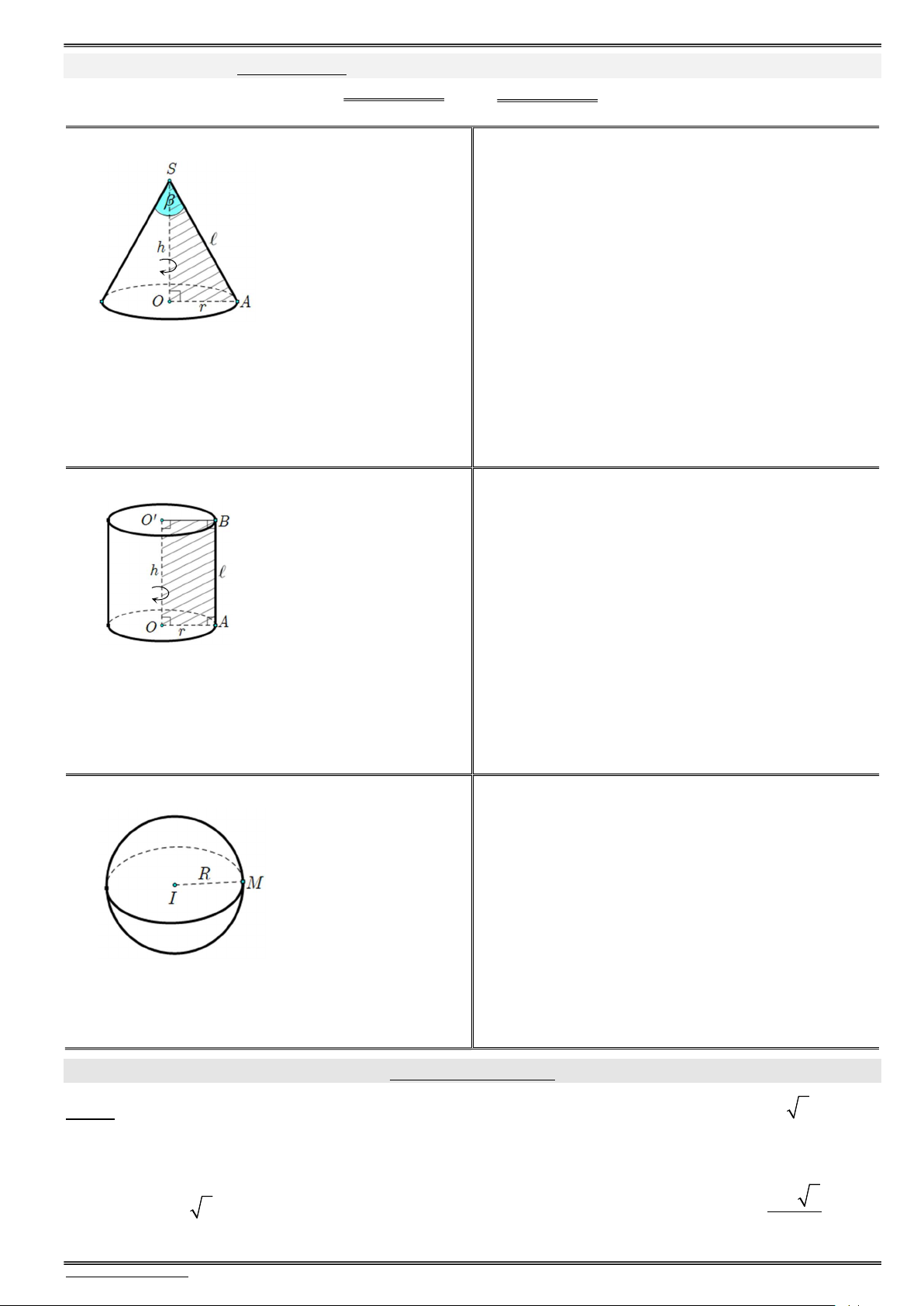
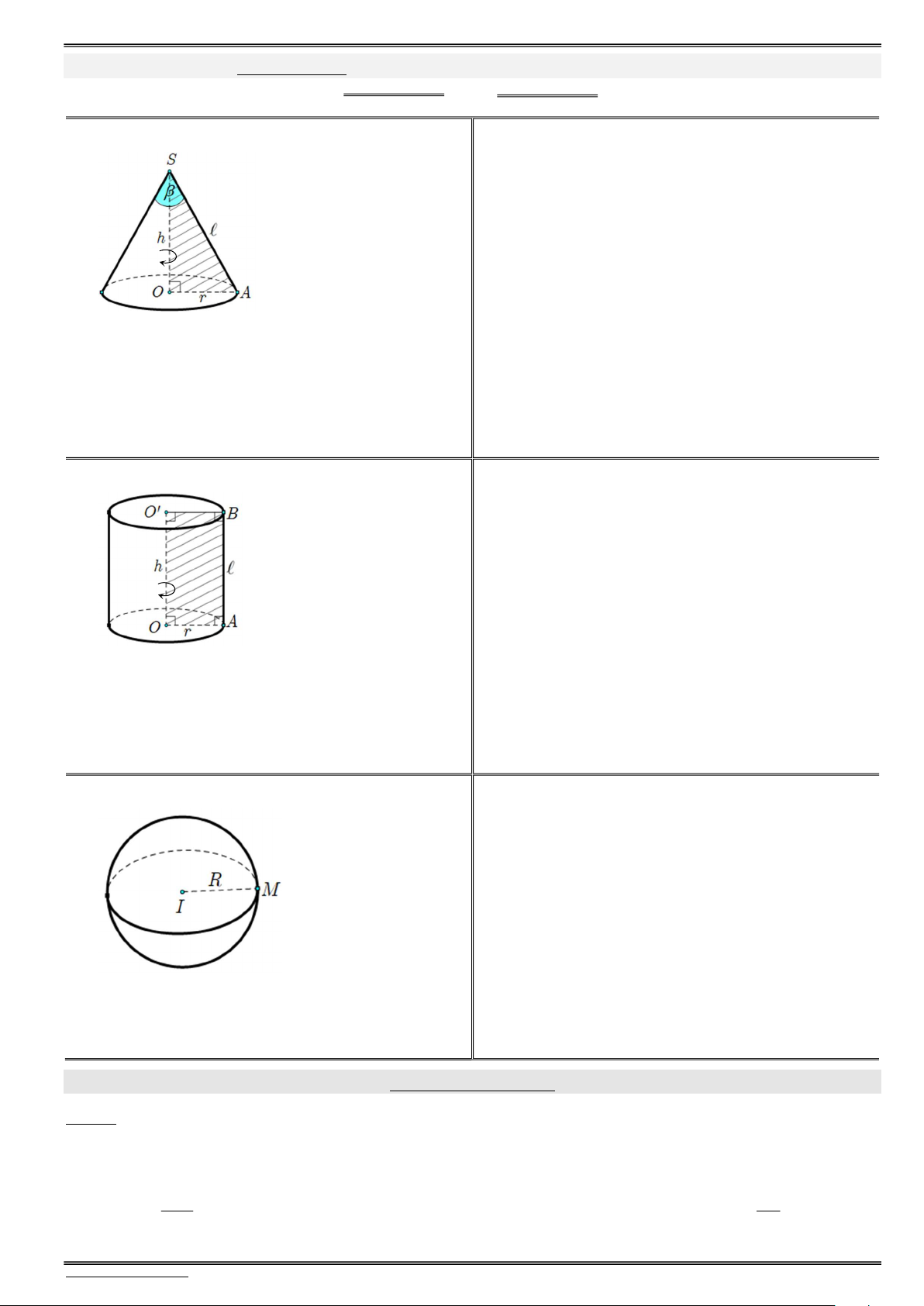
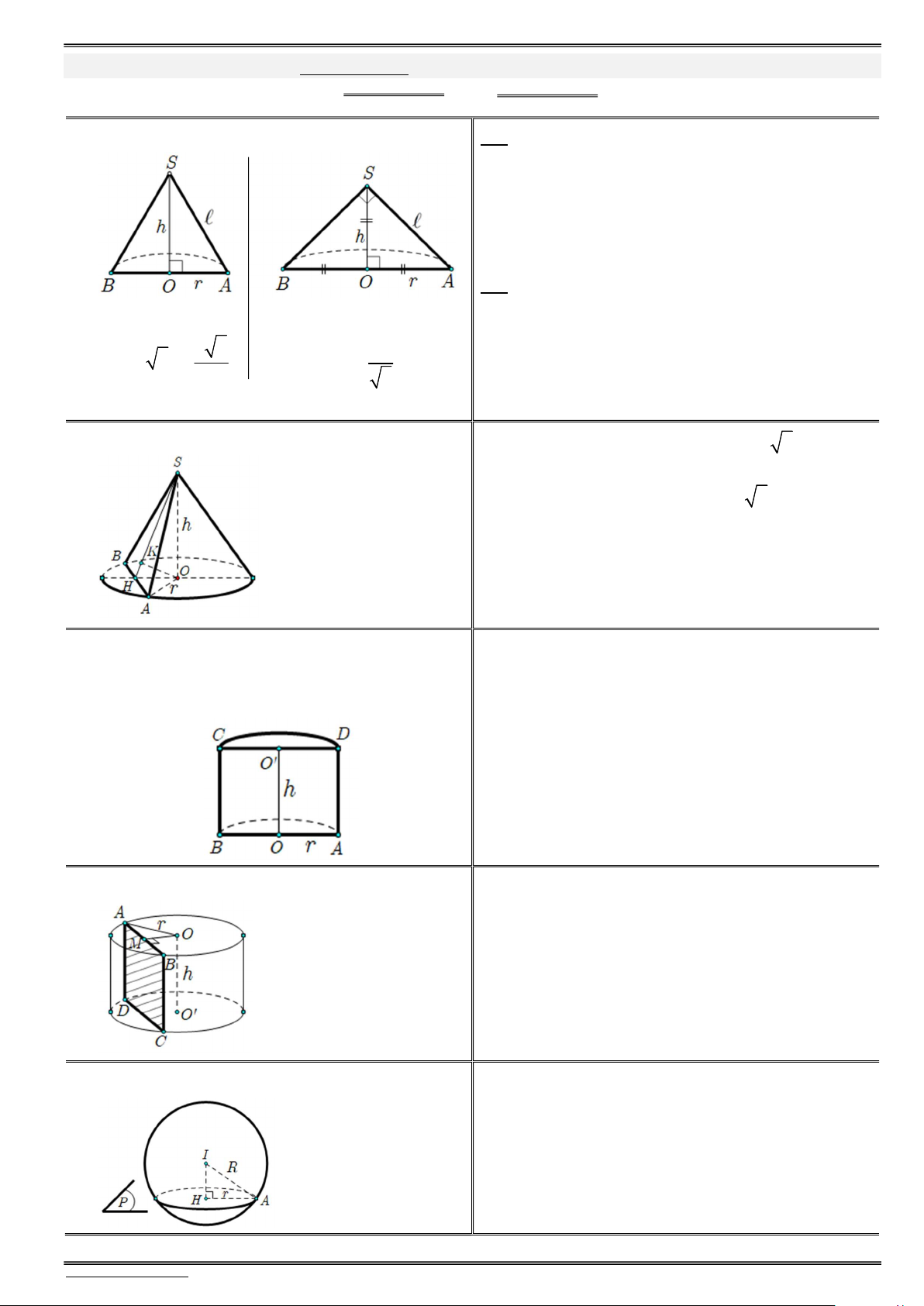
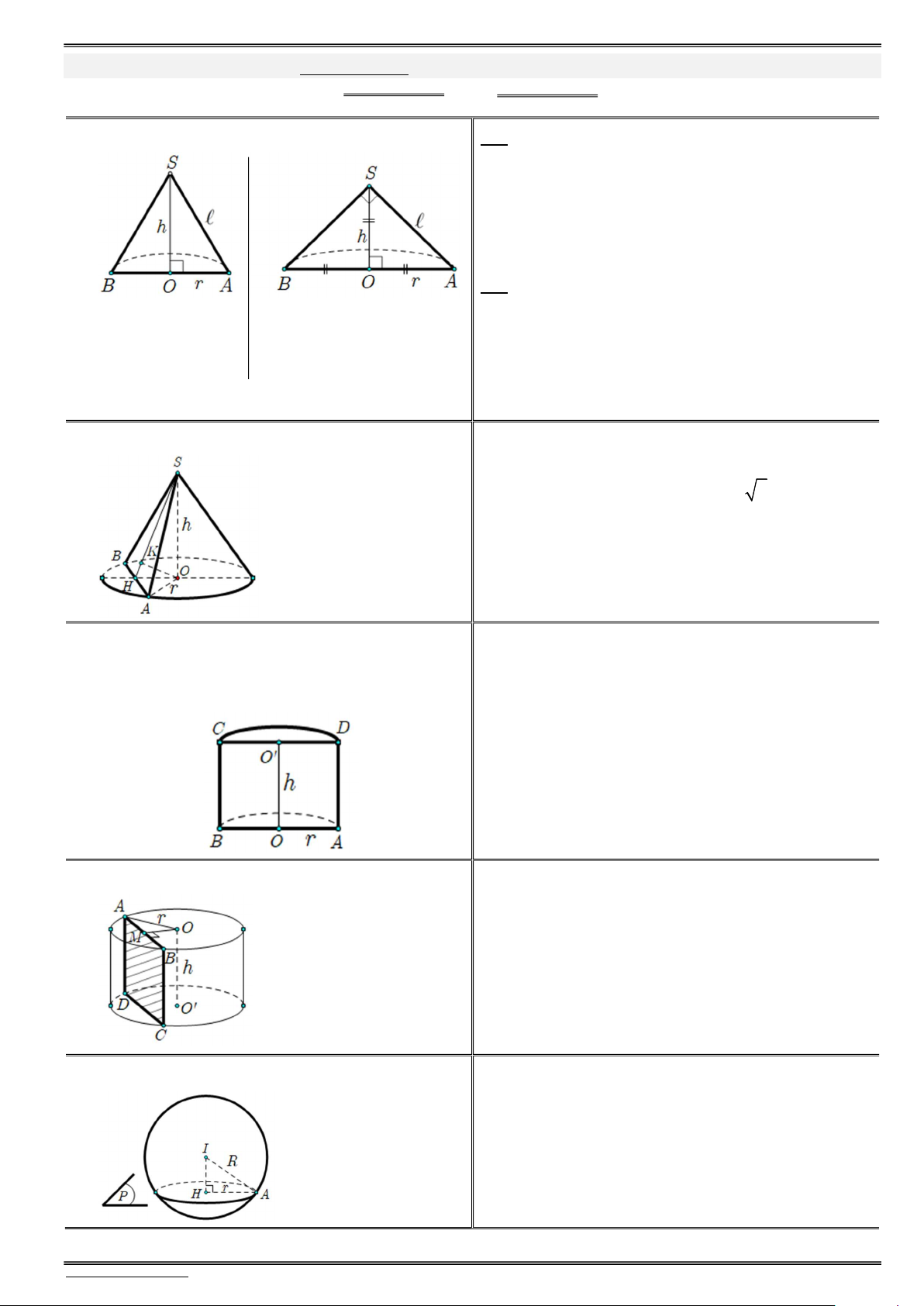
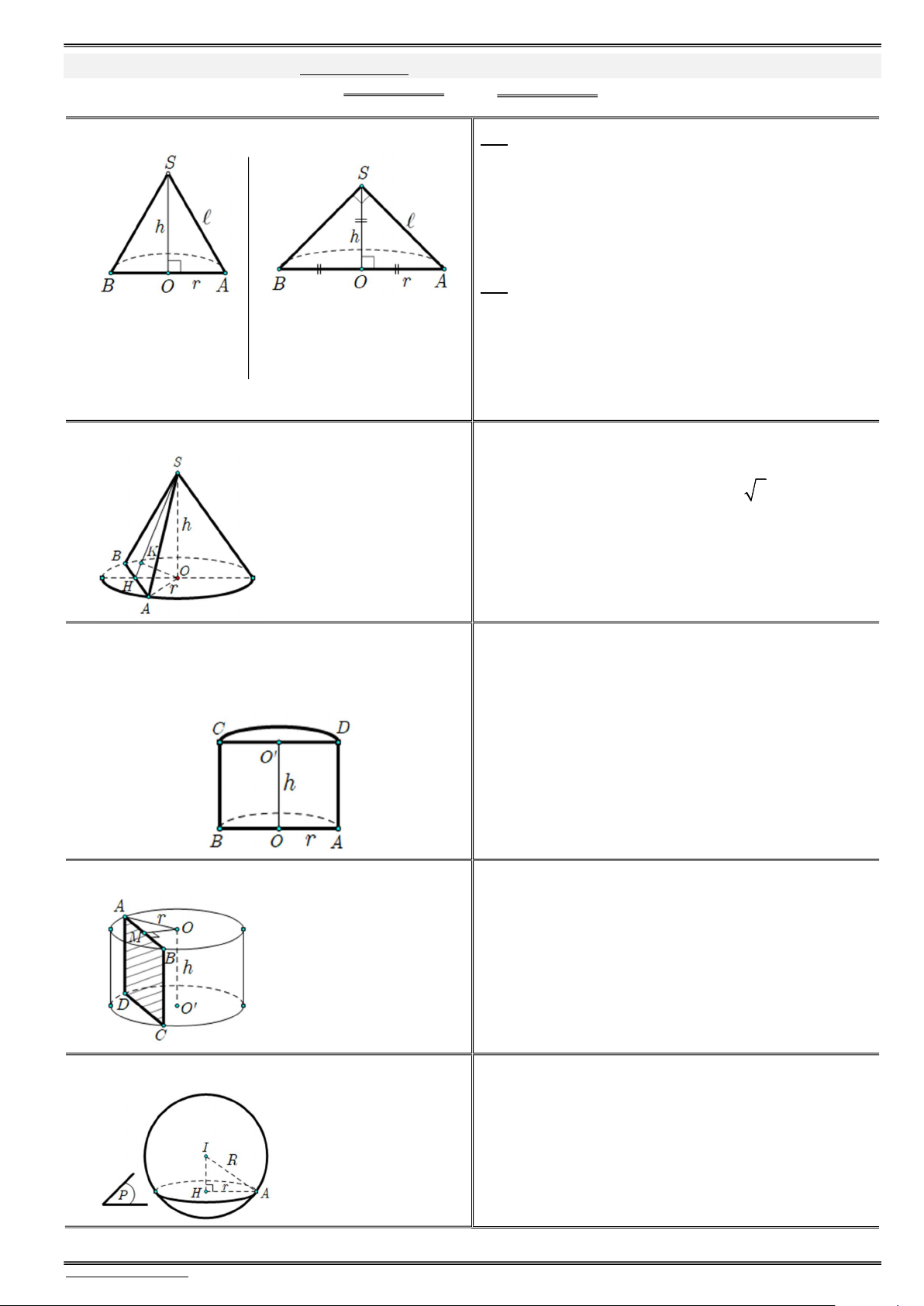
PhiÕu 12.1. Nãn trô cÇu (c«ng thøc & xoay h×nh) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
PhiÕu 12.2. Nãn trô cÇu (c«ng thøc & xoay h×nh) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
PhiÕu 12.3. Nãn trô cÇu (c«ng thøc & xoay h×nh) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
PhiÕu 13.1. Nãn trô cÇu (thiÕt diÖn) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
PhiÕu 13.2. Nãn trô cÇu (thiÕt diÖn) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
PhiÕu 13.3. Nãn trô cÇu (thiÕt diÖn) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
PhiÕu 14.1. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
PhiÕu 14.2. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
PhiÕu 14.3. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
PhiÕu 15.1. Khèi cÇu ngo¹i tiÕp khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
PhiÕu 15.2. Khèi cÇu ngo¹i tiÕp khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
PhiÕu 15.3. Khèi cÇu ngo¹i tiÕp khèi ®a diÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 1.1 – K§D – Gãc gi÷a hai ®êng th¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 1.1. Gãc gi÷a hai ®êng th¼ng («n líp 11, nÒn líp 12)
Phương pháp: Dựng thêm đường thẳng song song.
Chẳng hạn dựng đường thẳng c b và c cắt a tại I (hoặc tịnh tiến cả hai đường). I Khi đó
(a;b) (a;c) như hình vẽ.
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc . BÀI TẬP ÁP DỤNG
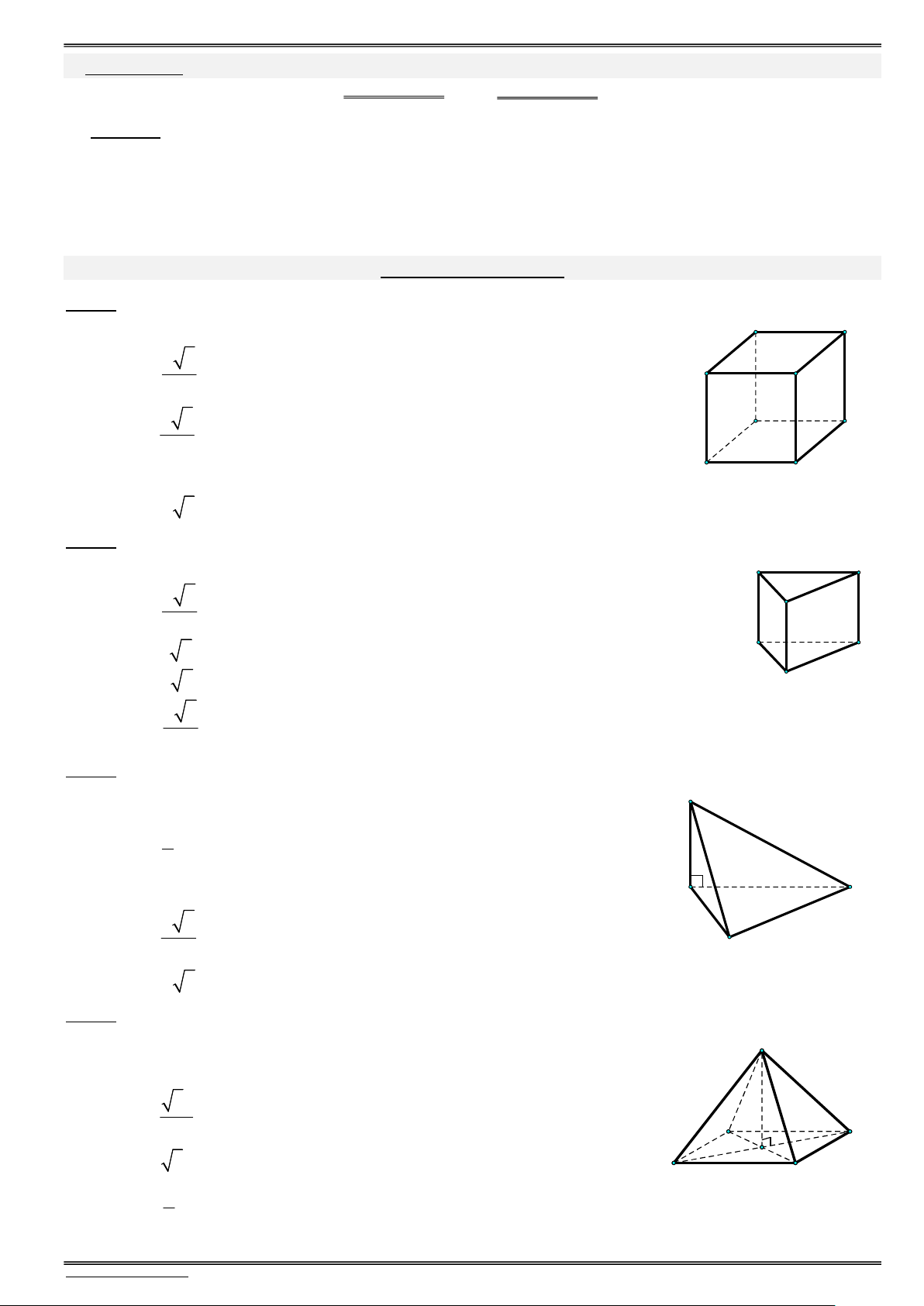
Câu 1. Cho hình lập phương ABCD.AB C D có cạnh bằng .
a Khi đó góc giữa AB và B C bằng A' D' A. 0. Giải. Ta có AB D C (AB,B C ) (D C ,B C ) D C B . B'
B. 45. Hình lập phương là hình có 6 mặt là 6 hình vuông bằng nhau nên C'
C. 60. 6 đường chéo tương ứng bằng nhau, hay có B C CD D B . A D D. 90. B C D đều D C
B 60 Chọn đáp án C. B C
Câu 2. Cho hình lập phương ABC . D AB C D
. Góc giữa hai đường thẳng BA và CC bằng A'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D'
A. 30 . ................................................... B' B. C' 45 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C. D 60 .
D. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 3. Cho hình lập phươngABCD.AB C D có cạnh bằng . a Góc giữa B D và AD bằng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A' D' A. 45 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' B. 30 . C'
C. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
D. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 4. Cho hình lập phương ABCD.AB C D
(tham khảo hình vẽ dưới), góc giữa hai đường thẳng AB và B C bằng A' D'
A. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C'
B. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D C. 30 .
D. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 5. Cho hình lập phương ABCD.AB C D
(hình vẽ). Góc giữa hai đường thẳng BA và CD bằng A'
A. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D'
B. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C'
C. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
D. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình thoi góc
ABC 120. Gọi M, N lần lượt là
trung điểm của SA và SC . Góc giữa hai đường thẳng MN và BC bằng S
A. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C. C 45 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D. 90 . D
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 1 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 1.1 – K§D – Gãc gi÷a hai ®êng th¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 2 , a BC .a Các cạnh bên
của hình chóp cùng bằng a 2. Góc giữa hai đường thẳng AB và SC bằng S
A. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
C. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D O B
D. 75. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
Câu 8. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2 ,
a SA (ABC) và SA 6a. Gọi D là trung điểm của S S .
B Góc giữa hai đường thẳng SA và DC bằng
A. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D
B. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
C. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. 75. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
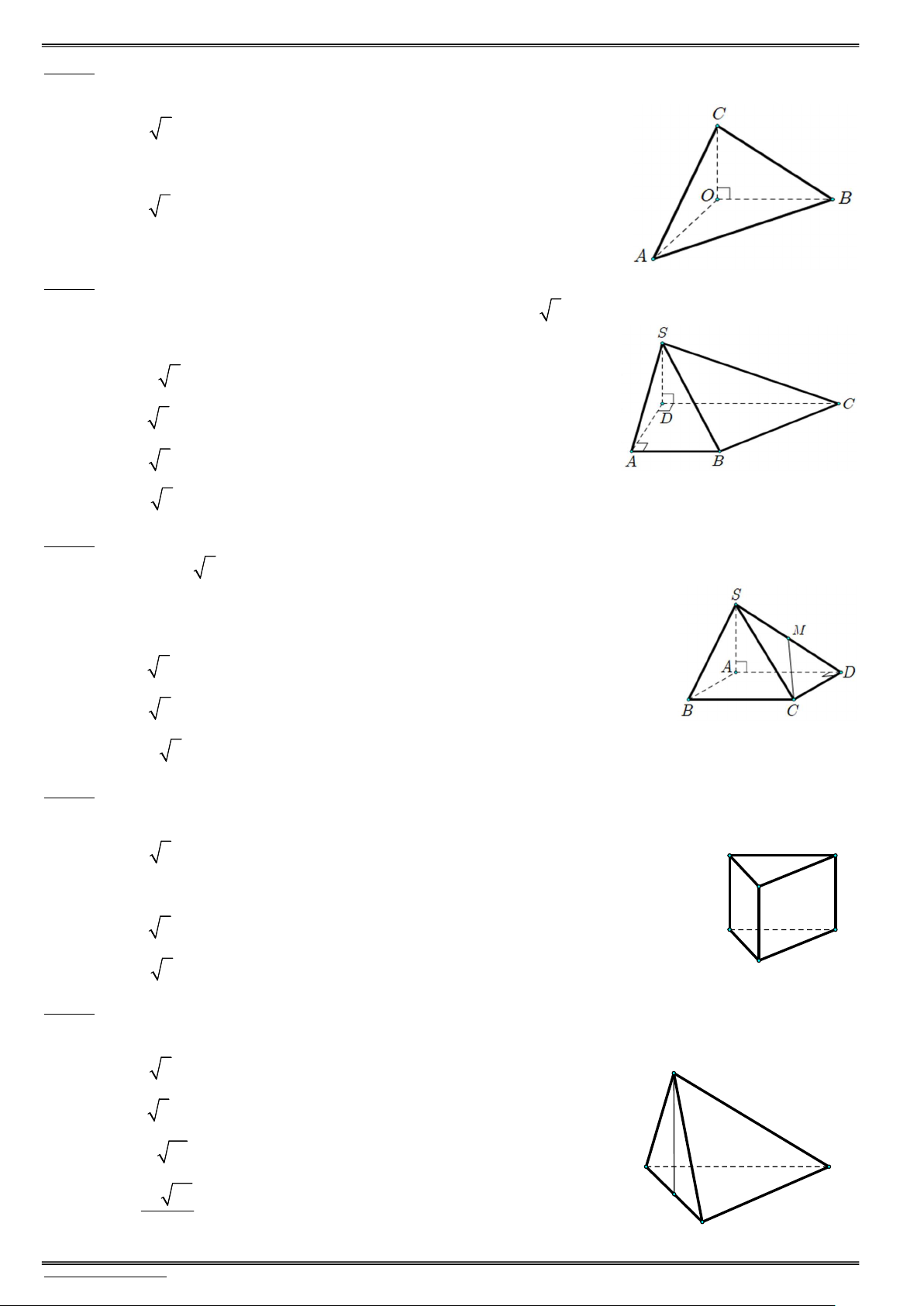
Câu 9. Cho lăng trụ đều ABC.AB C
có tất cả các cạnh bằng a (lăng trụ đều là lăng trụ đứng có đáy là
đa giác đều). Gọi M, N lần lượt là trung điểm của các cạnh A , B B C
và là góc giữa hai
đường thẳng AC, MN (tham khảo hình vẽ). Giá trị của tan bằng A' C' N
A. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. 1. B'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A 2 C
D. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . M B
Câu 10. Cho hình hộp chữ nhật ABC . D AB C D
có AB AD 2 và AA 2 (tham khảo hình vẽ).
Côsin góc giữa hai đường thẳng AB và CD bằng A' D'
A. 1/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C'
B. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 1/6. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D D. 5/6. B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
Câu 11. Cho hình lăng trụ tam giác đều ABC.AB C
có tất cả các cạnh bằng . a Côsin góc giữa hai
đường thẳng AB và AC bằng A' C'
A. 1/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
B. 5/6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C. 5/8. C
D. 3/4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 12. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC. Gọi M
là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C A. 45.
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O B
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 2 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 1.2 – K§D – Gãc gi÷a hai ®êng th¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 1.2. Gãc gi÷a hai ®êng th¼ng («n líp 11, nÒn líp 12)
Phương pháp: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chẳng hạn xét (a,b), ta dựng: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Khi đó
(a;b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Để tính góc ,
ta sử dụng: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho hình lập phương ABCD.AB C D
(tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng AC và AD bằng D' C'
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A'
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' D
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
Câu 2. Cho hình hộp chữ nhật ABC . D AB C D
có AB AD 2, AA 2 (tham khảo hình vẽ bên
dưới). Côsin góc giữa hai đường thẳng AB và CD bằng A' D' 1 C'
A. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A 1 D C. 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D.
6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3. Cho lăng trụ đứng ABC.AB C
có tất cả các cạnh bằng nhau (lăng trụ đứng là lăng trụ có các
cạnh bên vuông với các cạnh đáy). Góc giữa đường thẳng AA và BC bằng A' C'
A. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
B. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
D. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 4. Cho hình lập phương ABCD.AB C D
(tham khảo hình vẽ bên dưới), góc giữa hai đường thẳng AB và B C bằng D' C'
A. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A ' B'
B. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D C
D. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
Câu 5. Cho hình lập phương ABCD.AB C D
(hình vẽ). Góc giữa hai đường thẳng BA và CD bằng D' C'
A. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A'
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D C
D. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 3 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 1.2 – K§D – Gãc gi÷a hai ®êng th¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 6. Cho lăng trụ đều ABC.AB C
có tất cả các cạnh bằng a (lăng trụ đều là lăng trụ đứng có đáy là
đa giác đều). Gọi M, N lần lượt là trung điểm của các cạnh A , B B C
và là góc giữa hai
đường thẳng AC, MN (tham khảo hình vẽ). Giá trị của tan bằng A' C' N
A. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. 1. B'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C 2 M
D. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 7. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC. Góc
giữa hai đường thẳng A , B BC bằng C
A. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 120. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O B
C. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
D. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC. Gọi M
là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O B
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
Câu 9. Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau và cùng bằng a (tham khảo hình vẽ bên
dưới). Góc giữa đường thẳng SA và CD bằng S
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O B C
D. 75. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB 2 , a BC .
a Các cạnh bên của hình S
chóp cùng bằng a 2 (hình vẽ). Góc giữa hai đường thẳng AB và SC bằng
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O B C
D. 75. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11. Cho hình lăng trụ tam giác đều ABC.AB C
có AB a và AA 2a (tham khảo hình vẽ bên
dưới). Góc giữa hai đường thẳng AB và BC bằng A' C'
A. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
B. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
C. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 4 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.1 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
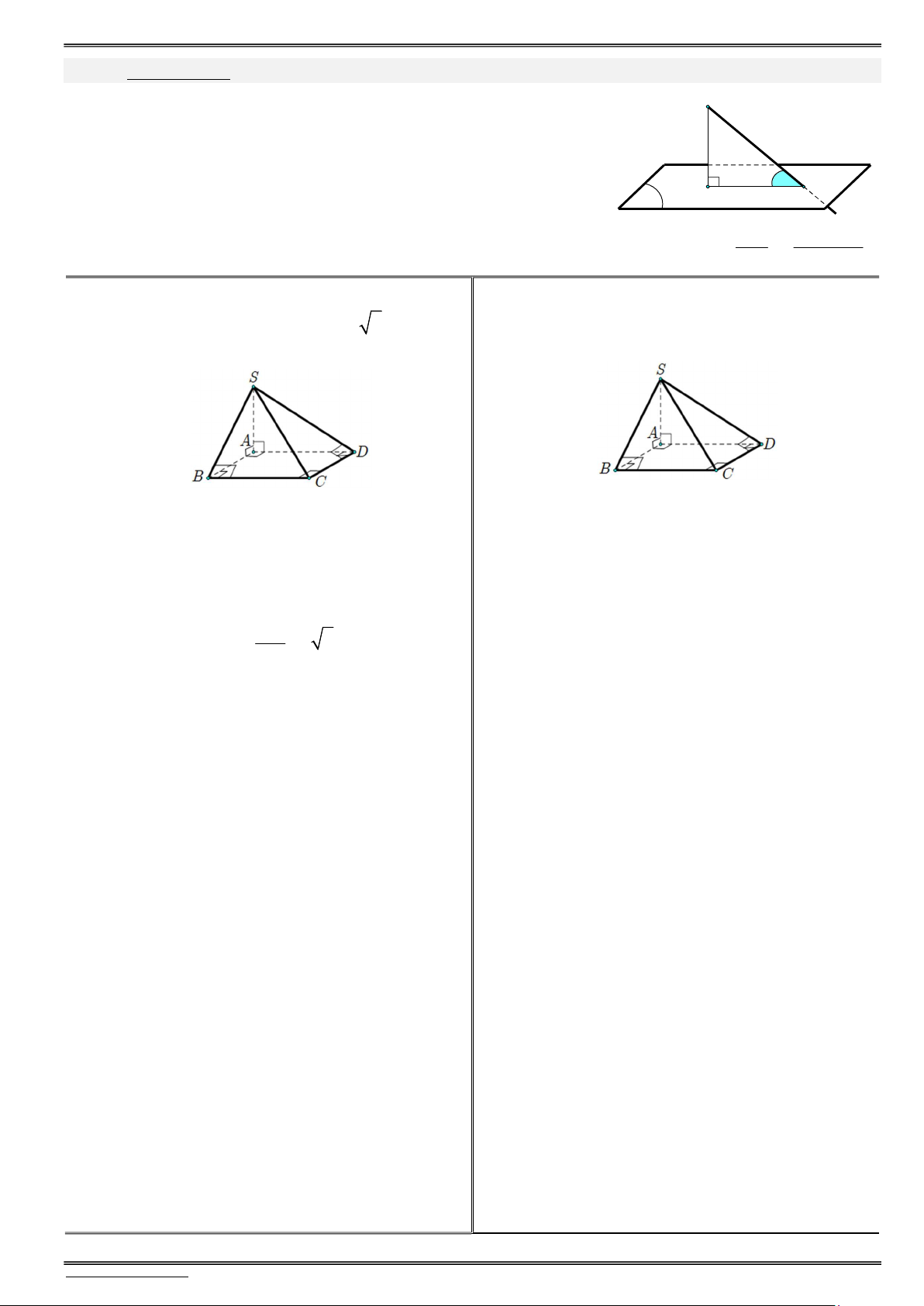
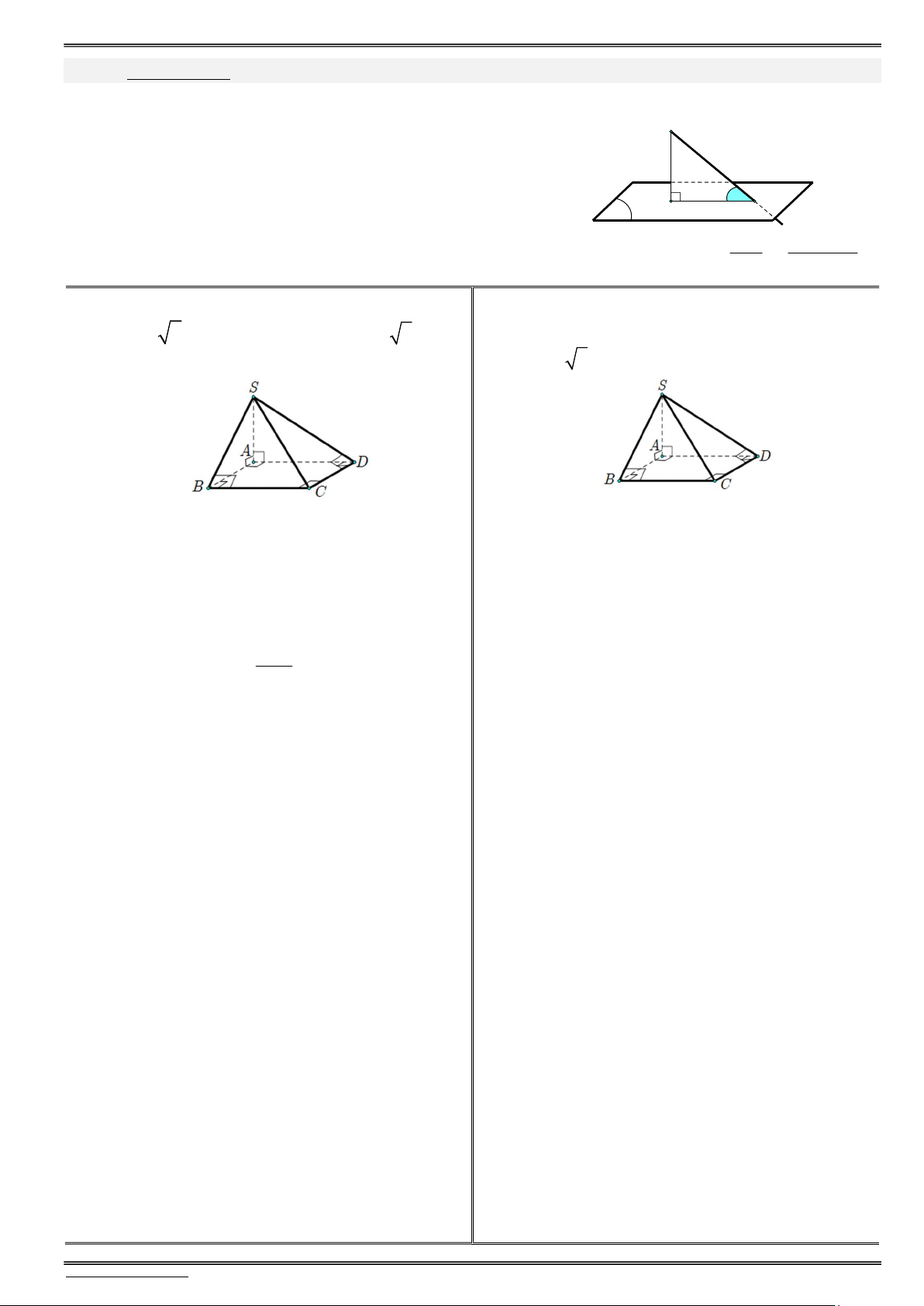
PhiÕu 2.1. Gãc gi÷a ®êng th¼ng vµ mÆt ph¼ng («n líp 11, nÒn líp 12) A
Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó.
Tìm góc giữa đường thẳng AB và mặt phẳng (P) ? A B (P) B Ta có:
(AB,(P)) (AB,BH ) ABH . H B A H (P) H P t¹i
Trong trường hợp khó tách phẳng đưa về định nghĩa, sử dụng khoảng cách, tức ( ,( )) sin AH d A P AB AB
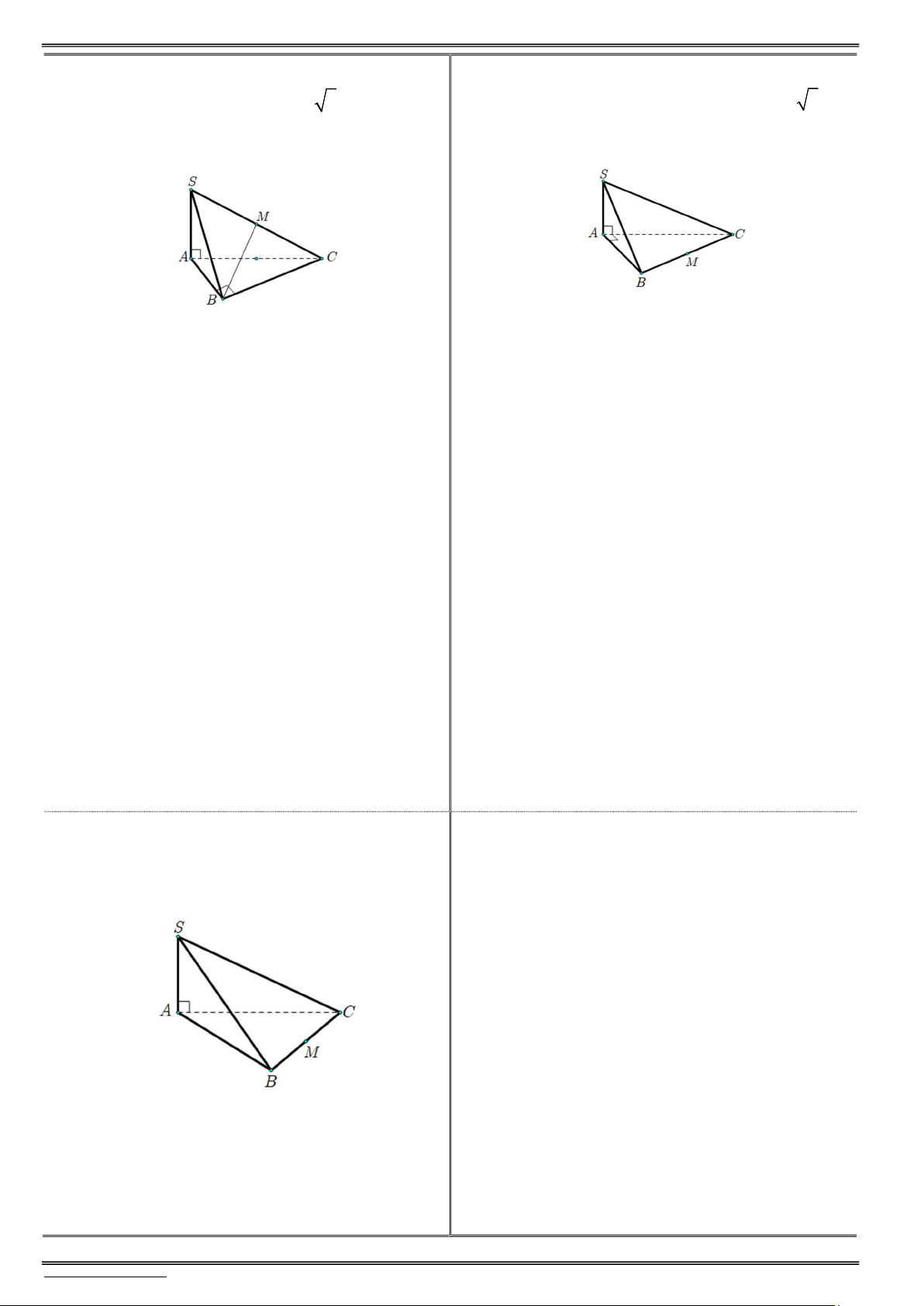
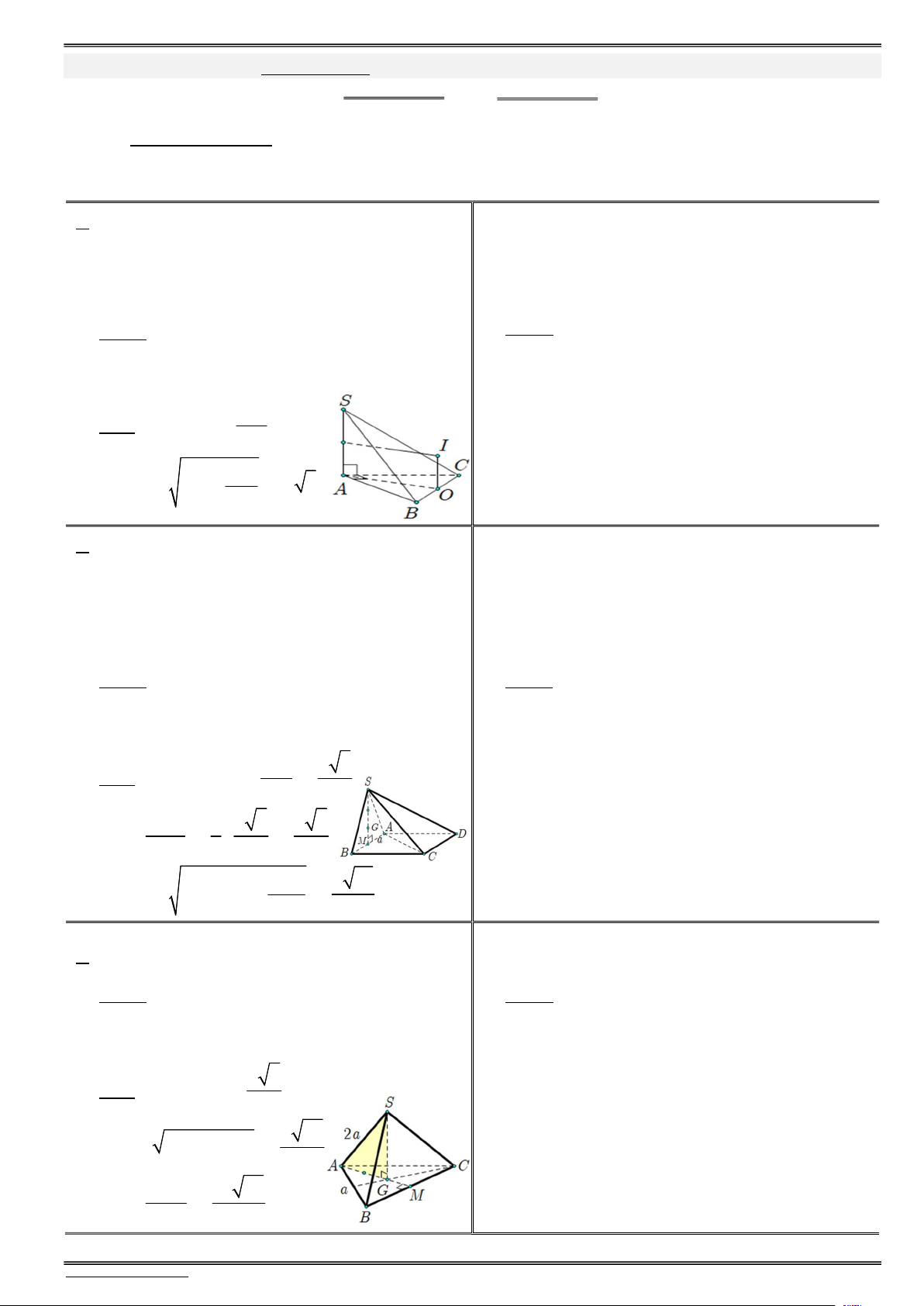
1) Cho hình chóp S.ABCD có đáy là hình vuông 1) Cho hình chóp S.ABCD có đáy là hình chữ
cạnh a, SA (ABCD), SA a 3. Tính góc
nhật, AB 3a, AD 4a, SA (ABCD) và
giữa đường thẳng và mặt phẳng sau đây ?
SA 4a. Tính góc giữa đường và mặt sau ? a) (S ,
B (ABCD)) ? (học sinh trình bày như mẫu) a) (S ,
D (ABCD)) ? . . . . . . . . . . . . . . . . . . . . . . . . S B (ABCD) B Ta có:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S A (ABCD) A t¹i
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(SB,(ABCD)) (SB,AB) SB . A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SAB SA tanSBA
3 SBA 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . t ¹i A AB
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) (SC,(ABCD)) ?
b) (SC,(ABCD)) ? . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c) (S , D (SAC)) ?
c) (SC,(SAD)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d) (S ,D(SBC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
d) (SC,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 5 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.1 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
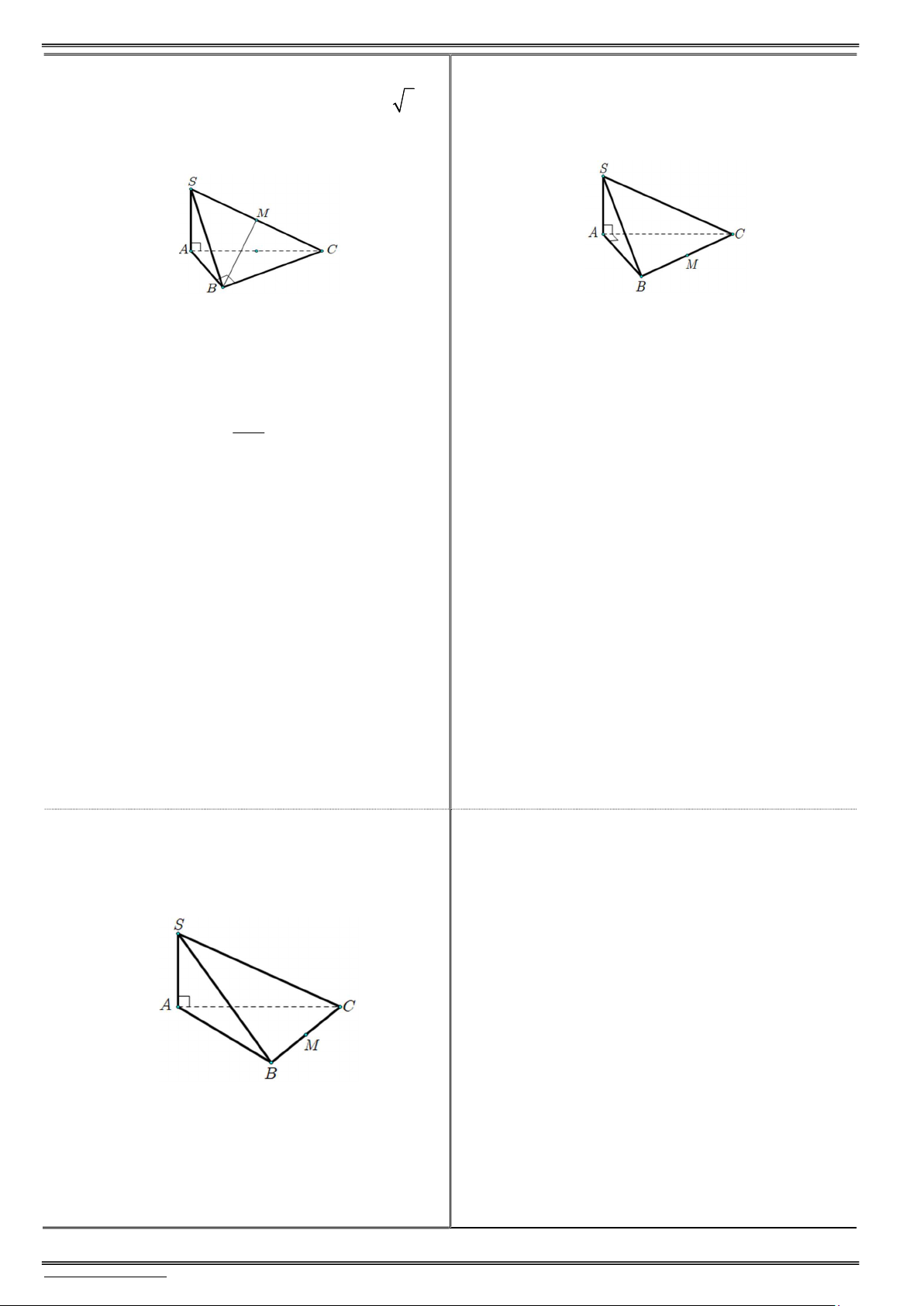
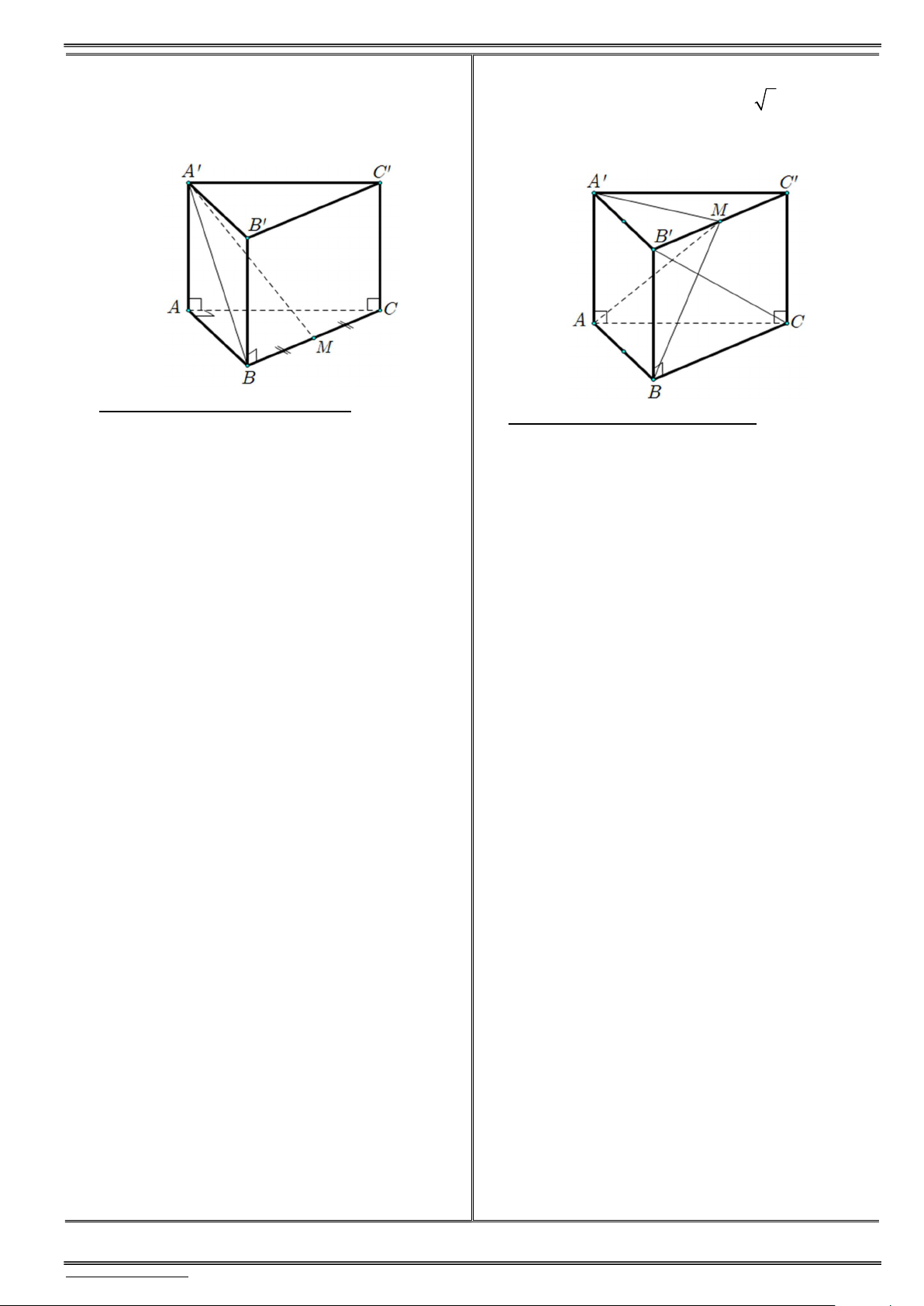
2) Cho hình chóp S.ABC có đáy ABC là tam 2) Cho hình chóp S.ABC có đáy là tam giác
giác vuông cân tại B, AB a, SA a 2 và vuông cân tại , A có AB , a SA 2a và
SA (ABC). Gọi M là trung điểm của SC.
SA (ABC). Gọi M là trung điểm của BC.
Xác định và tính góc giữa đường và mặt ?
Xác định và tính góc giữa đường và mặt sau ? S C (ABC) C
a) (SM,(ABC )) ? . . . . . . . . . . . . . . . . . . . . . . . .
a) (SC,(ABC)) ? Ta có: S A (ABC) A t¹i
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (SC,(ABC )) (SC,C ) A SC . A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SAC tan SA SCA 1 SCA 45 . t ¹i A AC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) (SC,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . . b) (S ,
A (SBC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) (BM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . c) (SM,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Cho hình chóp S.ABC có đáy ABC là tam b) (SM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
giác đều cạnh a, SA 2a và SA (ABC ).
Gọi M là trung điểm của BC. Xác định và . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
tính góc giữa đường thẳng và mặt phẳng ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c) (S ,
A (SBC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a) (S ,
B (ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . d) (SM,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 6 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.1 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
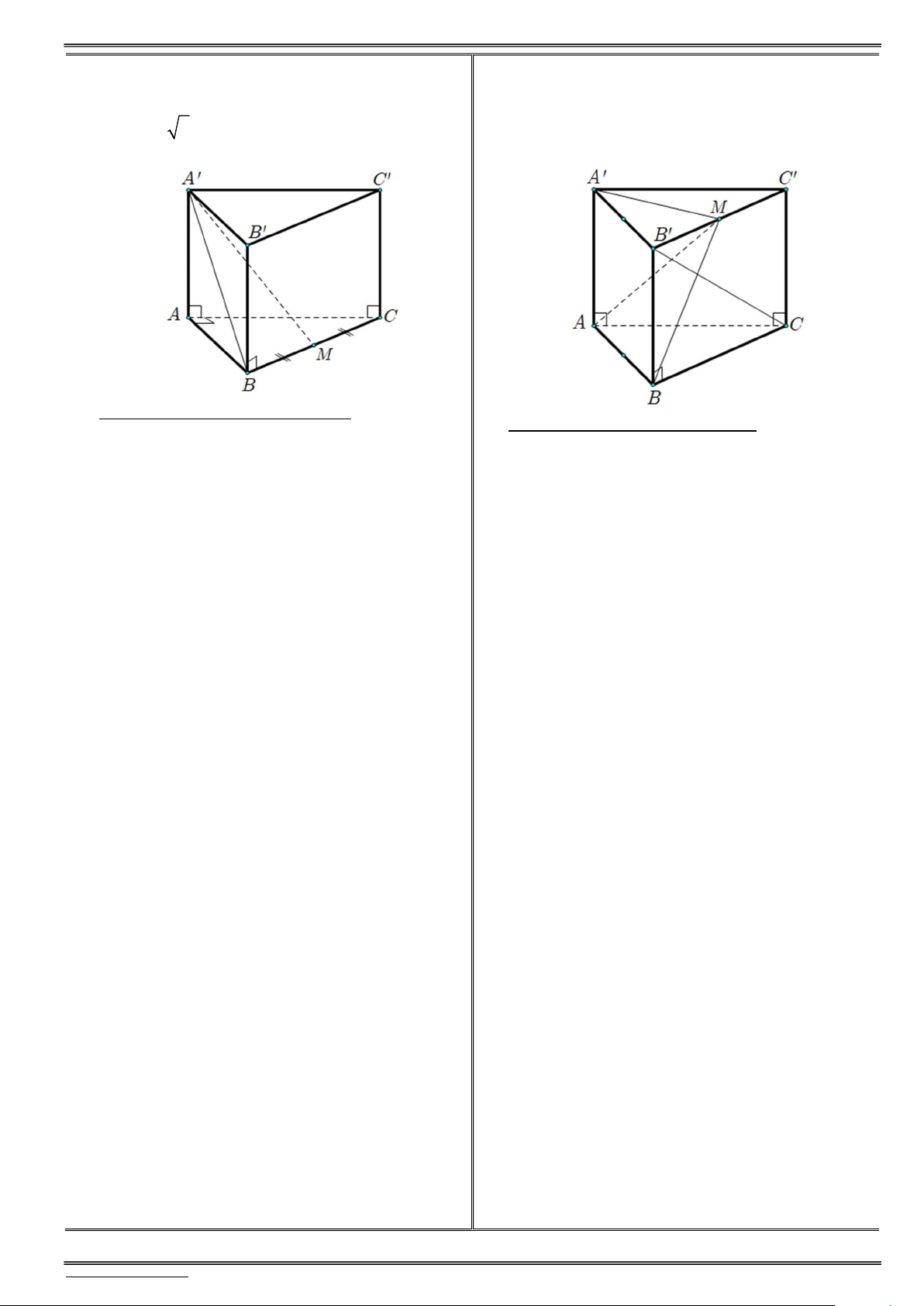
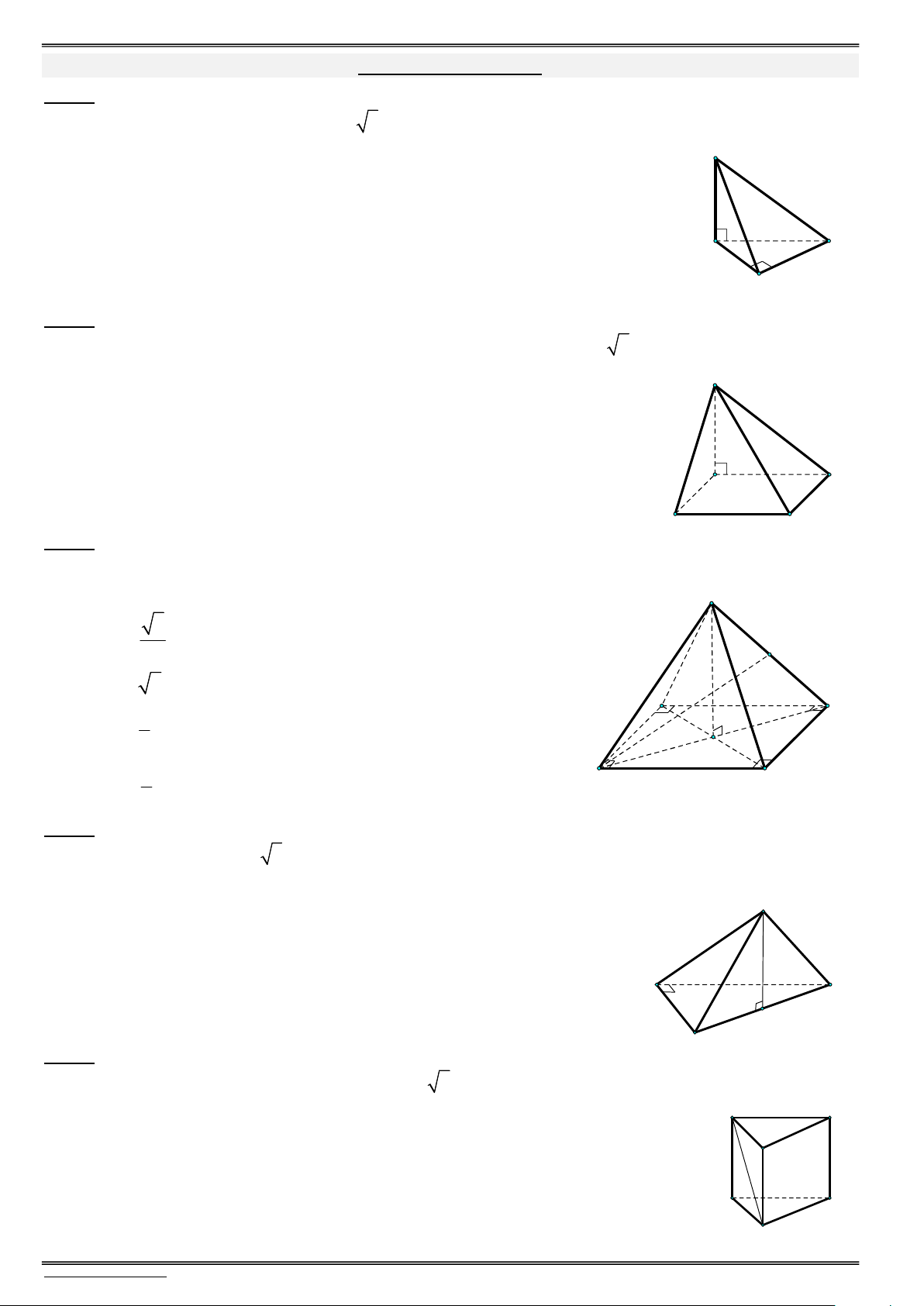
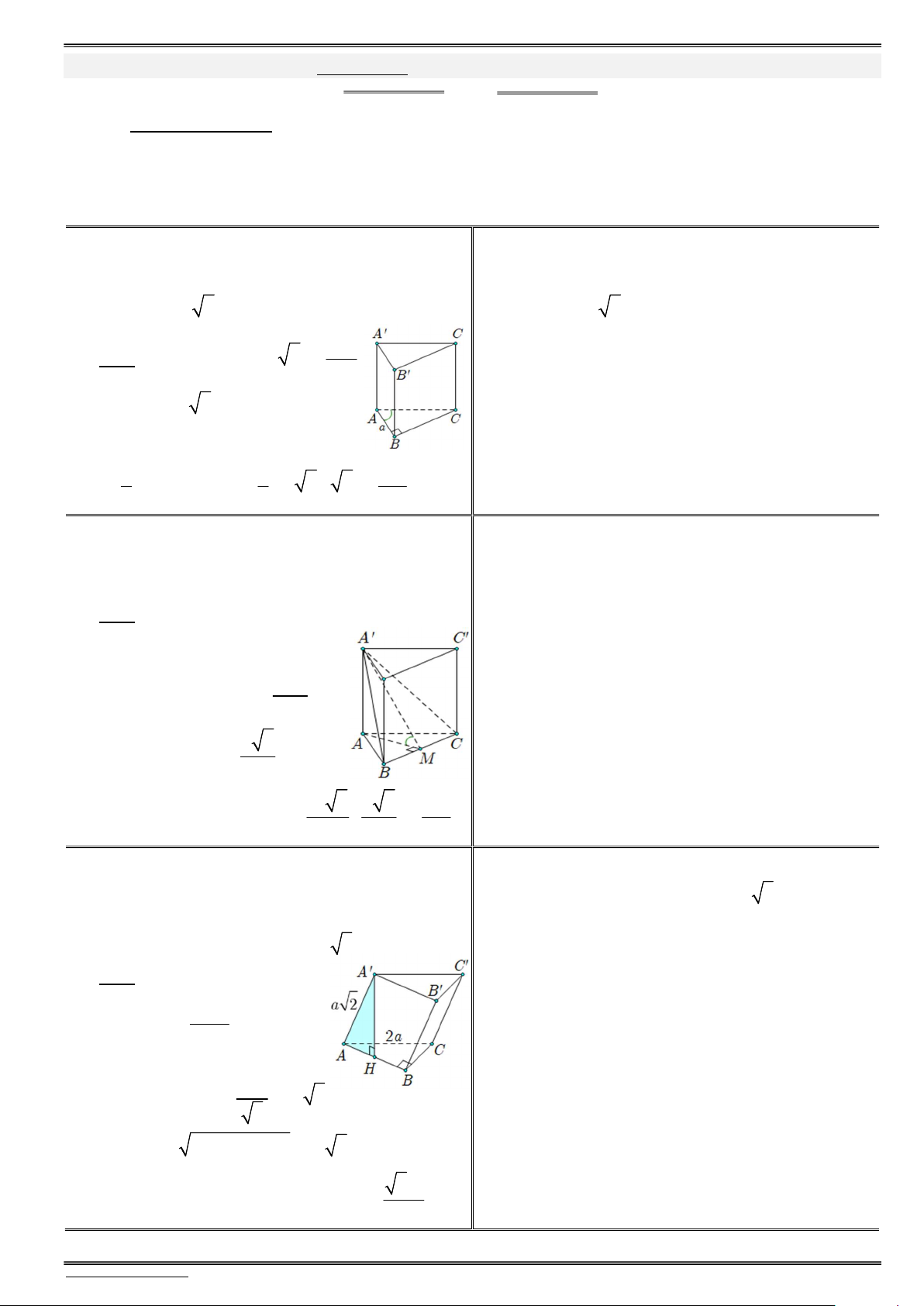
4) Cho hình lăng trụ đứng ABC.AB C
có đáy 3) Cho hình lăng trụ đều ABC.AB C có cạnh
ABC là tam giác vuông cân tại , A AB a và
đáy bằng a, cạnh bên bằng 2a. Gọi M là
AA a 3. Gọi M là trung điểm của BC. trung điểm của B C
. Xác định và tính góc
Xác định và tính góc giữa đường và mặt sau:
giữa đường và mặt sau ?
Cần nhớ về hình lăng trụ đứng:
Cần nhớ về hình lăng trụ đều: Hình lăng trụ Hai đáy (ABC)(AB C ).
đều là một hình lăng trụ đứng, có đáy là một đa
Chiều cao AA BB CC các mặt bên là
giác đều Có đầy đủ tính chất của một hình lăng các hình chữ nhật (ABB A , B CC B ,. .). trụ đứng. a) (A , B (AB C
)) ? . . . . . . . . . . . . . . . . . . . . . . . a) (AM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) (A , B (AAC C
)) ? . . . . . . . . . . . . . . . . . . . . . . b) (AM,(BCC B
)) ? . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) (AM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . c) (B C ,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d) (AM,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . . d) (AM,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 7 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.1 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
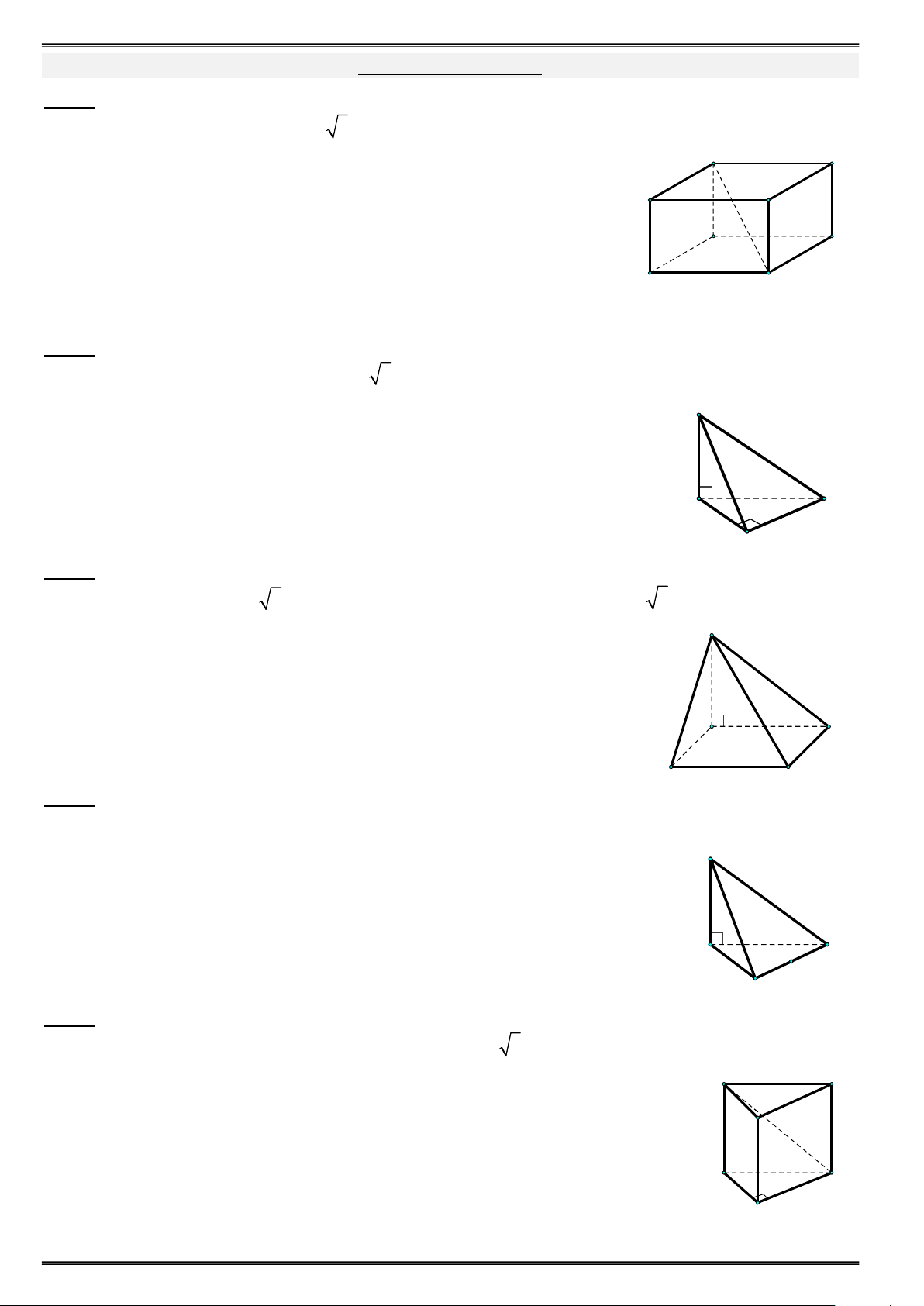
Câu 1. (Đề tham khảo – Bộ GD & ĐT năm 2021) Cho hình hộp chữ nhật ABCD.AB C D có
AB AD 2 và AA 2 2 (tham khảo hình vẽ bên dưới). Góc giữa đường thẳng AC và mặt phẳng (ABCD) bằng A' B' A. 30. D' C'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D C
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2. (Đề thi TN THPT năm 2020 – Mã đề 102 – Câu 27) Cho hình chóp S.ABC có đáy là tam giác
vuông tại B, AB 3a, BC a 3, SA vuông góc với mặt phẳng đáy và SA 2a (tham khảo
hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng đáy bằng S
A. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 3. (Đề tham khảo – Bộ GD & ĐT năm 2020 lần 1 – Câu 17) Cho hình chóp S.ABCD có đáy là
hình vuông cạnh a 3, SA vuông góc với mặt phẳng đáy và SA a 2 (minh họa như hình bên).
Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng S
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 60. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 4. (VTED – Đề số 16) Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với
mặt phẳng đáy và 2SA 3a. Gọi M là trung điểm của BC (tham khảo hình vẽ), góc giữa đường
thẳng SM và mặt phẳng (ABC ) bằng S
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 60. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C D. 90. M
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 5. (THPT Chuyên Lê Quý Đôn – Bình Định) Cho hình lăng trụ đứng ABC.A B C có đáy ABC
là tam giác vuông cân tại B có AB a, AA a 2 (tham khảo hình vẽ). Góc giữa đường thẳng AC với mặt phẳng (AA B B ) bằng A' C'
A. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
B. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 8 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.2 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 2.2. Gãc gi÷a ®êng th¼ng vµ mÆt ph¼ng («n líp 11, nÒn líp 12)
Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó. A
Tìm góc giữa đường thẳng AB và mặt phẳng (P) ? A B (P) B Ta có:
(AB,(P)) (AB,BH) ABH . A H (P) H H B t¹i P
Trường hợp khó nhìn tách phẳng đưa về định nghĩa, sử dụng khoảng cách, tức ( ,( )) sin AH d A P AB AB
1) Cho hình chóp S.ABCD có đáy là hình vuông 1) Cho hình chóp .
S ABCD có đáy là hình chữ
cạnh a 3, SA (ABCD), SA a 3. Tính
nhật, AB a, AD 2a, SA (ABCD) và
góc giữa đường thẳng và mặt phẳng sau đây ?
SA a 3. Tính góc giữa đường và mặt sau ? a) (SB,(ABCD)) ? a) (S ,
D (ABCD)) ? . . . . . . . . . . . . . . . . . . . . . . . .
.. . .. . . .. . .. . .. . .. . .. . .. . .. . .. . ..
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có:
.. . .. . . .. . .. . .. . .. . .. . .. . .. . .. . ..
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(SB,(ABCD)) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SAB . . .. tanSBA . . . SBA . . . t ¹i A . . ..
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) (SC,(ABCD)) ?
b) (SC,(ABCD)) ? . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c) (SD,(SAC )) ?
c) (SC,(SAD)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d) (SB,(SCD)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
d) (SC,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 9 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.2 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
2) Cho hình chóp S.ABC có đáy ABC là tam 2) Cho hình chóp S.ABC có đáy là tam giác
giác vuông cân tại B, AB a 2, SA 2a và vuông cân tại ,
A có AB a, SA a 2 và
SA (ABC). Gọi M là trung điểm của SC.
SA (ABC ). Gọi M là trung điểm của BC.
Xác định và tính góc giữa đường và mặt ?
Xác định và tính góc giữa đường và mặt sau ?
... .. ... .. . . . .. ... . . a)
(SM,(ABC)) . . . . . . . . . . . . . . . . . . . . . . . . . .
a) (SC,(ABC)) ? Ta có:
... .. ... .. . . . .. ... . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(SC,(ABC )) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SAC
tanSCA . . . . . . . . . . . . . . . . . . . . . . . t ¹i A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) (SC,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . . b) (S ,
A (SBC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) (BM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . c) (SM,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Cho hình chóp S.ABC có đáy ABC là tam b) (SM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . . . giác đều cạnh ,
a SA a và SA (ABC ). Gọi
M là trung điểm của BC. Xác định và tính góc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
giữa đường thẳng và mặt phẳng ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c) (S ,
A (SBC )) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a) (SB,(ABC )) ? . . . . . . . . . . . . . . . . . . . . . . . . . d) (SM,(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 10 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.2 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
4) Cho hình lăng trụ đứng ABC.AB C
có đáy 3) Cho hình lăng trụ đều ABC.AB C có cạnh
ABC là tam giác vuông cân tại , A AB 2a
đáy bằng a, cạnh bên bằng a 2. Gọi M là
và AA 3a. Gọi M là trung điểm của BC . trung điểm của B C
. Xác định và tính góc
Xác định và tính góc giữa đường và mặt sau:
giữa đường và mặt sau ?
Cần nhớ về hình lăng trụ đứng:
Cần nhớ về hình lăng trụ đều: Hình lăng trụ
Hai đáy (ABC) (AB C ).
đều là một hình lăng trụ đứng, có đáy là một đa
Chiều cao AA BB CC các mặt bên là
giác đều Có đầy đủ tính chất của một hình lăng các hình chữ nhật (ABB A , BCC B ,...). trụ đứng. a) (AB,(AB C
)) ? . . . . . . . . . . . . . . . . . . . . . . . a) (AM,(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) (AB,(AAC C
)) ? . . . . . . . . . . . . . . . . . . . . . . b) (AM,(BCC B
)) ? . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) (AM,(ABC )) ? . . . . . . . . . . . . . . . . . . . . . . . . c) (B C ,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d) (AM,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . . d) (AM,(ABB A
)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 11 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 2.2 – K§D – Gãc gi÷a ®êng vµ mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. (Đề thi THPT QG năm 2018 – Mã đề 103 – Câu 20) Cho hình chóp S.ABC có đáy là tam giác
vuông tại C, AC a, BC 2a, SA vuông góc với mặt phẳng đáy và SA a (tham khảo
hình vẽ). Góc giữa đường thẳng SB và mặt phẳng đáy bằng S
A. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
D. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
Câu 2. (Sở GD & ĐT Ninh Bình) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a và AD 2 .
a Biết SA vuông góc với mặt phẳng đáy và SB a 5 (tham khảo hình vẽ). Góc giữa
đường thẳng SD và mặt phẳng (ABCD) bằng S
A. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
D. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
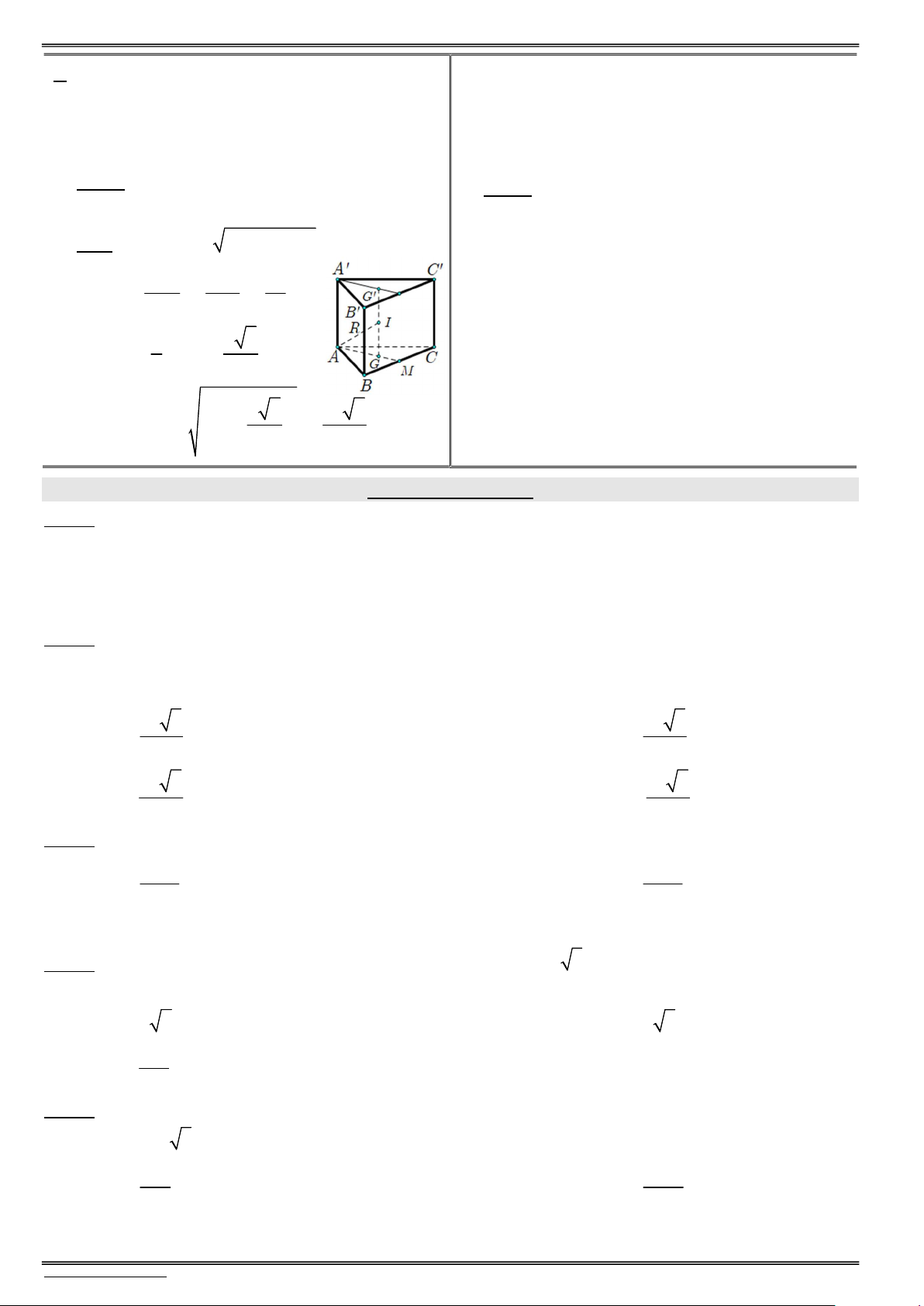
Câu 3. (Đề tham khảo – Bộ GD & ĐT năm 2018 – Câu 25) Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng .
a Gọi M là trung điểm của SD (tham khảo hình vẽ). Tang của góc giữa đường
thẳng BM và mặt phẳng (ABCD) bằng S
A. 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 M
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 O
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 1 a B C 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
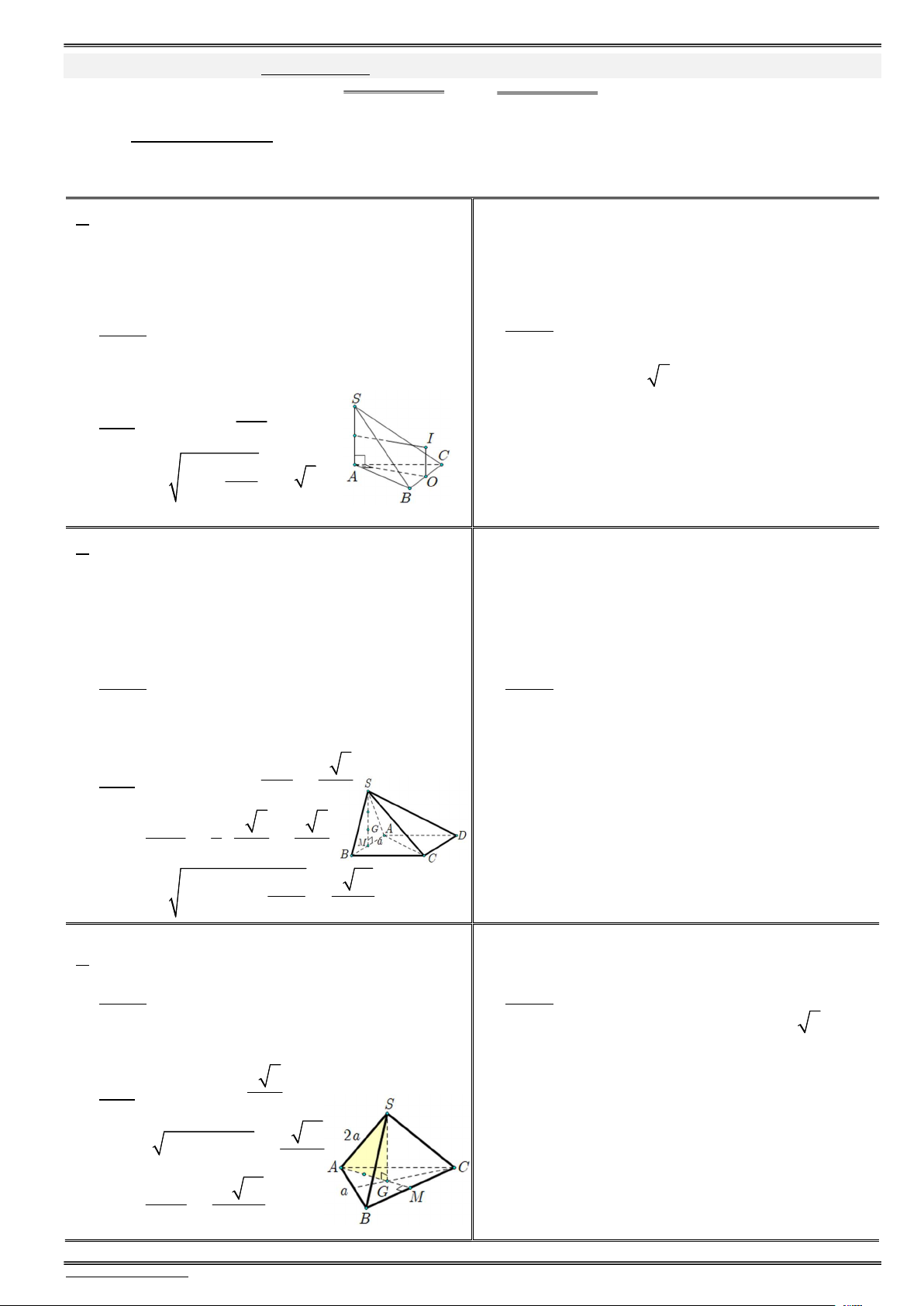
Câu 4. (THPT Hoàng Hoa Thám – Đà Nẵng) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại , A BC a 2 và SB .
a Hình chiếu vuông góc của S lên mặt phẳng (ABC) trùng
với trung điểm M của BC (tham khảo hình vẽ). Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng S A. 30 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. 60 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .A C. 45 . C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 75. M B
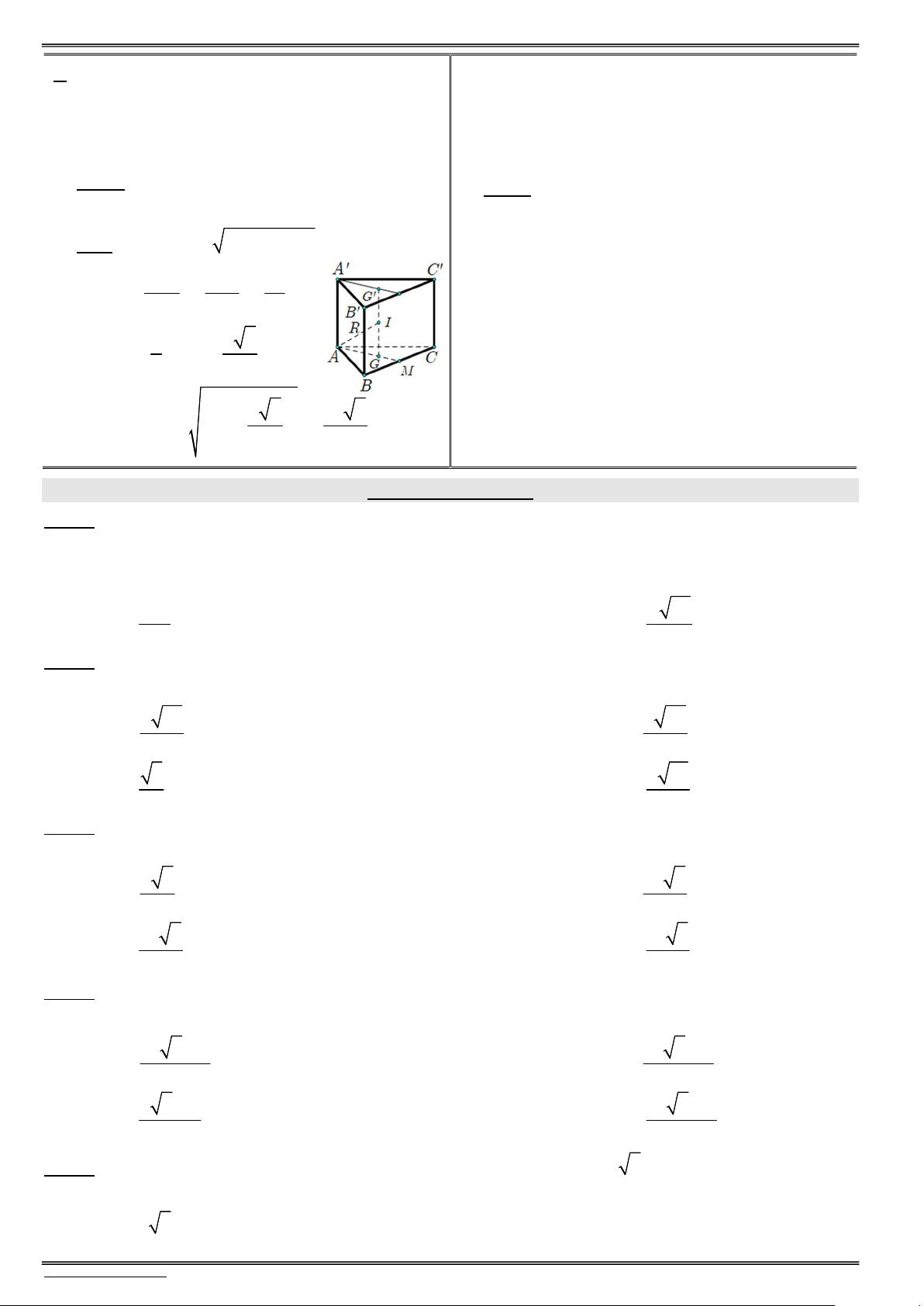
Câu 5. (THPT Chuyên Thái Bình – Thái Bình) Cho hình lăng trụ đứng tam giác ABC.AB C . Biết
tam giác ABC đều cạnh a và AA a 3 (tham khảo hình vẽ). Góc giữa đường thẳng AB và mặt phẳng (AB C ) bằng A C A. 60 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B B. 45 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 30 . A'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C' D. 90 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 12 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.1 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 3.1. Gãc gi÷a hai mÆt ph¼ng («n líp 11, nÒn líp 12) u ( P )(P ) u d2 d 1 2 1 Ta có: u d (P ) (
(P ),(P )) (d ,d ) . 1 1 1 2 1 2 P 2 P 1 u d (P ) 2 2
Với u là giao tuyến của hai mặt phẳng (P ) và (P ). Có hai loại giao tuyến: hai điểm chung và song song. 1 2
Góc giữa hai mặt phẳng là góc nhọn, nếu tìm ra 90 góc cần tìm là 180 .
1) Cho hình chóp S.ABCD có đáy là hình vuông 1) Cho hình chóp tứ giác đều S.ABC . D Gọi E là
và SA (ABCD). Xác định góc giữa hai mặt: trung điểm S .
B Xác định góc giữa hai mặt: a) ((SBC ),(ABCD)) ?
a) ((SBC ),(ABCD)) ? . . . . . . . . . . . . . . . . . . . . ( SBC)(ABCD) BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có: B C SB (SBC)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C AB (ABCD)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
((SBC ),(ABCD)) (SB,AB) SB . A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) ((SCD)),(ABCD)) ? . . . . . . . . . . . . . . . . . . . . b) ((ACE)),(ABCD)) ? . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) ((SBD)),(ABCD)) ? . . . . . . . . . . . . . . . . . . . . c) ((SAB)),(SCD)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d) ((SAD)),(SBC)) ? . . . . . . . . . . . . . . . . . . . . . . d) ((SBC )),(SAD)) ?. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 13 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.1 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt 2) Cho hình chóp S.ABC có A
BC vuông cân 2) Cho hình chóp S.ABC có đáy là tam giác đều
tại B và SA (ABC). Xác định góc giữa:
và SA (ABC ). Xác định góc giữa:
a) ((SBC),(ABC)) ? . . . . . . . . . . . . . . . . . . . . . . a) ((SBC),(ABC)) ? . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) ((SBC),(SAB)) ? . . . . . . . . . . . . . . . . . . . . . . . b) ((SAC),(SBC)) ? . . . . . . . . . . . . . . . . . . . . . .
Cách 1. Tìm đường thẳng cắt hai mặt phẳng, đồng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
thời vuông góc với giao tuyến.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dựng BH AC và HK SC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ta có: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3) Cho hình chóp S.ABC có đáy ABC là tam
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . giác vuông tại , A AB a, AC 2a và
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SA (ABC ), SA a 3. Xác định và tính
Cách 2. Tìm hai đường thẳng vuông góc với hai
góc giữa hai mặt phẳng (SBC) và (ABC).
mặt phẳng. Khi đó góc giữa hai đường
thẳng chính là góc giữa hai mặt phẳng.
Dựng AE SB và AF SC.
Ta có: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cách 3. Tách phẳng đưa về khoảng cách, sau đó . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
nhìn hình ban đầu tính toán.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Từ hình tách phẳng:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ta có: ((SBC ),(SAB)) với:
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . sin AE d( , A (SBC))
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AF d( , A SC)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 14 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.1 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. (THPT Hoa Lư – Ninh Bình) Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc và OB OC a 6, OA .
a Góc giữa hai mặt (ABC ) và (OBC) bằng A
A. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O C
C. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
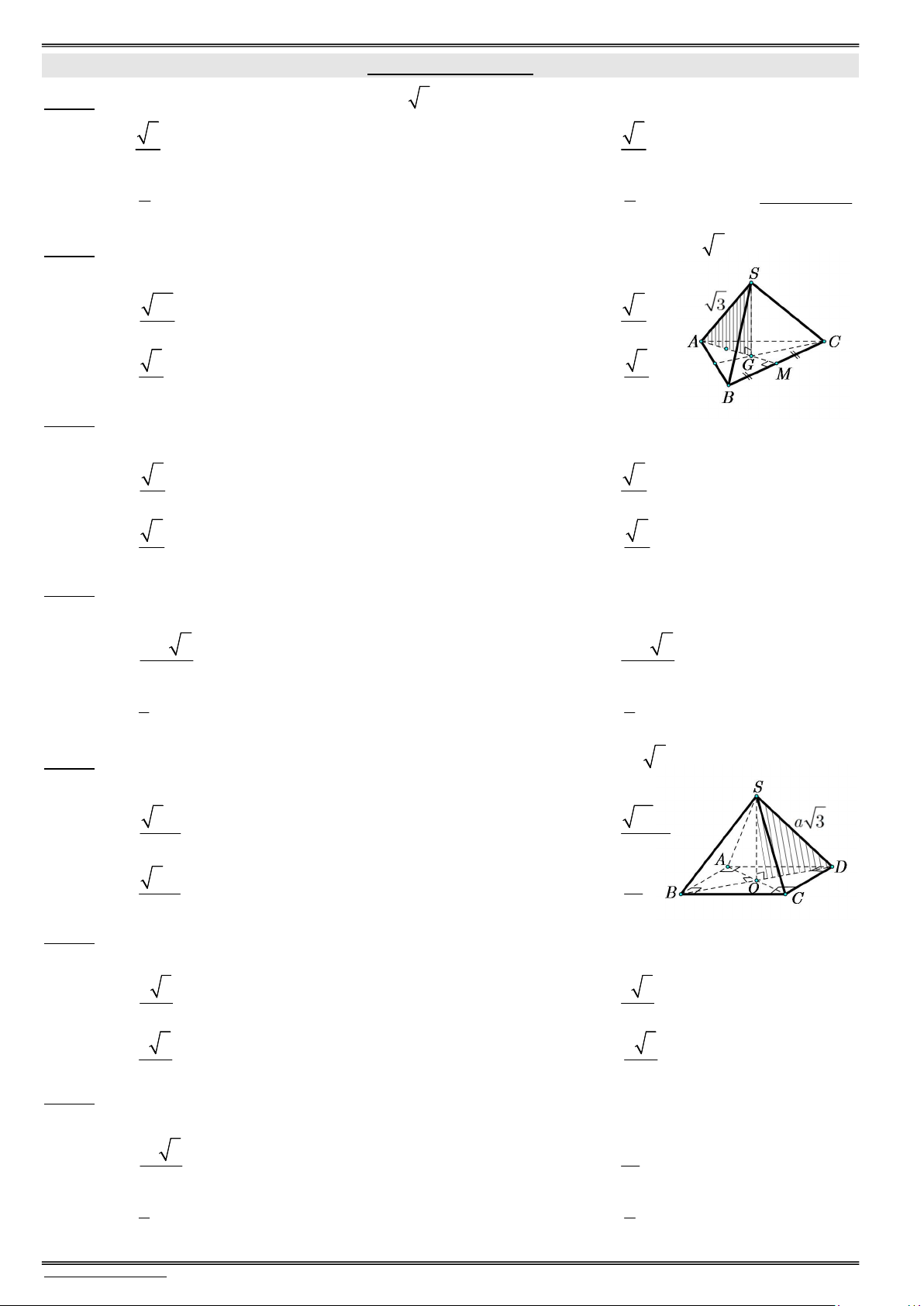
Câu 2. (VTED – Đề số 02) Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh bằng a, cạnh
bên SA (ABC) và SA a (tham khảo hình vẽ). Tang của góc giữa hai mặt phẳng (SBC) và (ABC ) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. 1.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. 2 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C C. 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3. (VTED – Đề số 05) Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 3a. Cạnh
bên SA 3a và vuông góc với đáy (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBC) và (ABC) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C C. 30 .
D. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 4. (THPT Hàn Thuyên – Bắc Ninh) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và
cạnh bên bằng a 5/2. Góc giữa (SAB) và (ABCD) bằng S
A. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D A
C. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O
D. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C B
Câu 5. (THPT Việt Trì – Phú Thọ) Cho hình lăng trụ đều ABC.AB C
có cạnh đáy bằng 2a, cạnh
bên bằng a (tham khảo hình vẽ). Góc giữa hai mặt phẳng (AB C ) và (AB C ) bằng
A. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C B
B. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A' C'
D. 90 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B'
Câu 6. (THPT Hàn Thuyên – Bắc Ninh) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và
cạnh bên bằng a 5/2. Góc giữa (SAB) và (ABCD) bằng S
A. 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D A
C. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 60 . O
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C B
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 15 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.1 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 7. (THPT Lê Xoay – Vĩnh Phúc) Cho hình chóp S.ABC có tam giác ABC vuông cân tại B,
AB BC a, SA a 3 và SA (ABC) (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBC) và (ABC ) bằng S
A. 45 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 90 . A C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 30 . B
Câu 8. (VTED – Đề số 08) Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên
SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng S
A. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 9. (THPT Nguyễn Khuyến – Nam Định) Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật với AB a và AD 2a. Cạnh bên SA vuông góc với đáy (ABCD), SA 2a (tham khảo
hình vẽ). Tang của góc giữa hai mặt phẳng (SBD) và (ABCD) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. 5 5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. 5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C D. 5 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 10. (VTED – Đề số 02) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng a,
cạnh bên SA (ABC) và SA a (tham khảo hình vẽ). Tang của góc giữa hai mặt phẳng (SBC) và (ABC) bằng S 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
B. 2 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 B C. 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11. (Sở GD & ĐT Phú Thọ) Cho hình hộp chữ nhật ABCD.AB C D có AB , a BC 2a và
AA 3a. Gọi là góc giữa hai mặt phẳng (ACD ) và (ABCD) (tham khảo hình vẽ). Giá trị của tan bằng A' D'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C' A. 6 5 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 3 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D 2 C. 3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
D. 3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 16 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.2 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 3.2. Gãc gi÷a hai mÆt ph¼ng («n líp 11, nÒn líp 12) u
. . . . . . . . . .. . . . . d2 d 1
Ta có: . . . . . . . . . .. . . . . (
(P ),(P )) . .. .. .. . .. .. .. . .. .. . .. 1 2 P
. . . . . . . . . .. . . . . 2 P 1 S
. . .. . . . . . . . . . . . . . . . .
Ta có: . . .. . . . . . . . . . . . . . . . . (ABC),(SBC
) . .. . .. .. .. . . . . . .. .. . .. A C
. . .. . . . . . . . . . . . . . . . . M B
1) Cho hình chóp S.ABCD có đáy là hình vuông 1) Cho hình chóp S.ABCD có đáy là hình chữ cạnh ,
a SA (ABCD) và SA a 3. Xác nhật, AB , a AD 2 , a SA (ABCD) và
định và tính góc giữa các mặt phẳng sau đây ? SA 2 .
a Tìm góc giữa các mặt phẳng sau ? a)
((SBC),(ABCD)) . . . . . . . . . . . . . . . . . . . a)
((SCD),(ABCD)) . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b)
((SBD)),(ABCD)) . . . . . . . . . . . . . . . . . . b)
((SBD)),(ABCD)) . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Cho hình chóp S.ABC có đáy ABC là tam 2) Cho hình chóp S.ABC có đáy là tam giác
giác đều cạnh 2a, SA 2a và SA (ABC). vuông cân tại , B có AB SA a 3 và
Xác định và tính góc giữa hai mặt phẳng ?
SA (ABC). Xác định và tính góc giữa: a)
((SBC),(ABC)) . . . . . . . . . . . . . . . . . . . . . a)
((SBC),(ABC)) . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b)
((SBC),(SAB)) . . . . . . . . . . . . . . . . . . . . . b)
((SBC),(SAC)) . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 17 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 3.2 – K§D – Gãc gi÷a hai mÆt ph¼ng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. (THPT Lê Xoay – Vĩnh Phúc) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB BC ,
a SA a 3 và SA (ABC) (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBC) và (ABC) bằng S
A. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 60. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 90. A C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 30. B
Câu 2. (VTED – Đề số 08 năm 2021) Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a,
cạnh bên SA a 2 và vuông góc với đáy (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng S
A. 30. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 45. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. 60. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D
D. 90. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Câu 3. (THPT Nguyễn Khuyến – Nam Định) Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật với AB a và AD 2 .
a Cạnh bên SA vuông góc với đáy (ABCD), SA 2a (tham khảo
hình vẽ). Tang của góc giữa hai mặt phẳng (SBD) và (ABCD) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. 5 5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. 5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C D. 5 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. (VTED – Đề số 02) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh bằng , a
cạnh bên SA (ABC) và SA a (tham khảo hình vẽ). Tang của góc giữa hai mặt phẳng (SBC) và (ABC) bằng S A. 1.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 A C C. 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5. (Sở GD & ĐT Phú Thọ) Cho hình hộp chữ nhật ABCD.AB C D
có AB a, BC 2a và
AA 3a. Gọi là góc giữa hai mặt phẳng (ACD ) và (ABCD) (tham khảo hình vẽ). Giá trị của tan bằng A' D'
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C' A. 6 5 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 3 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D 2 C. 3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
D. 3 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 18 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 4.1 – K§D – Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 4.1. Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt ph¼ng («n líp 11, nÒn líp 12)
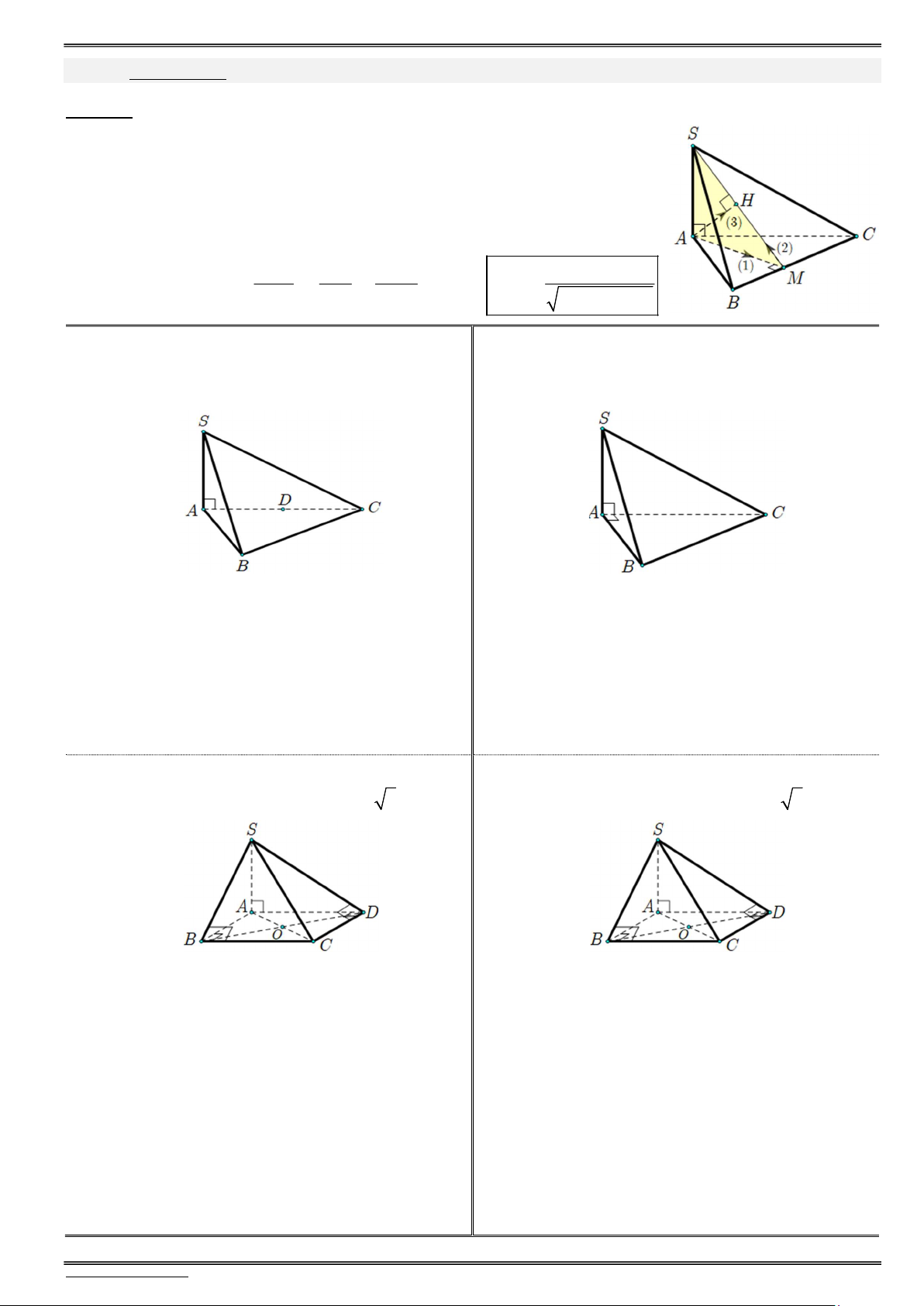
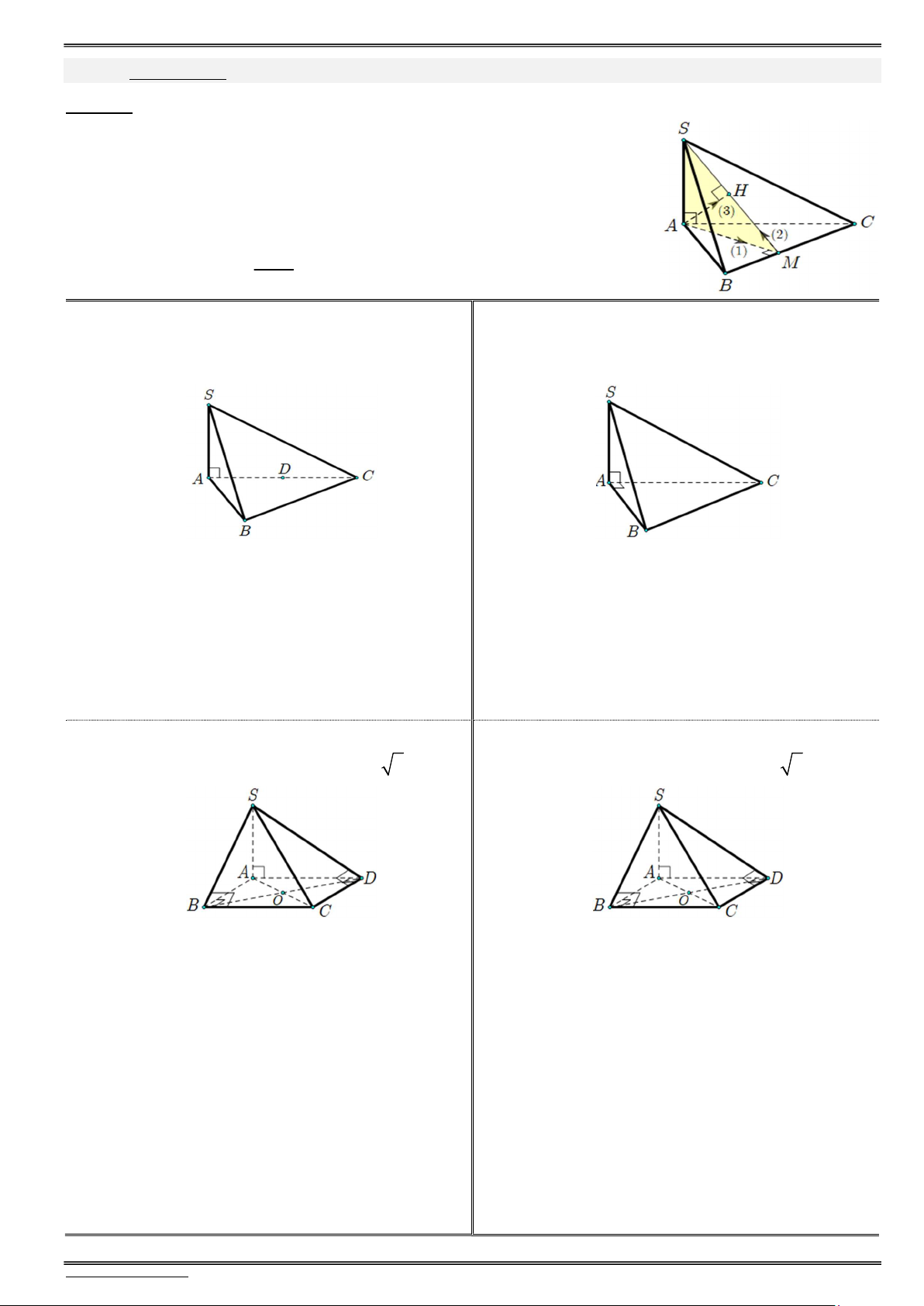
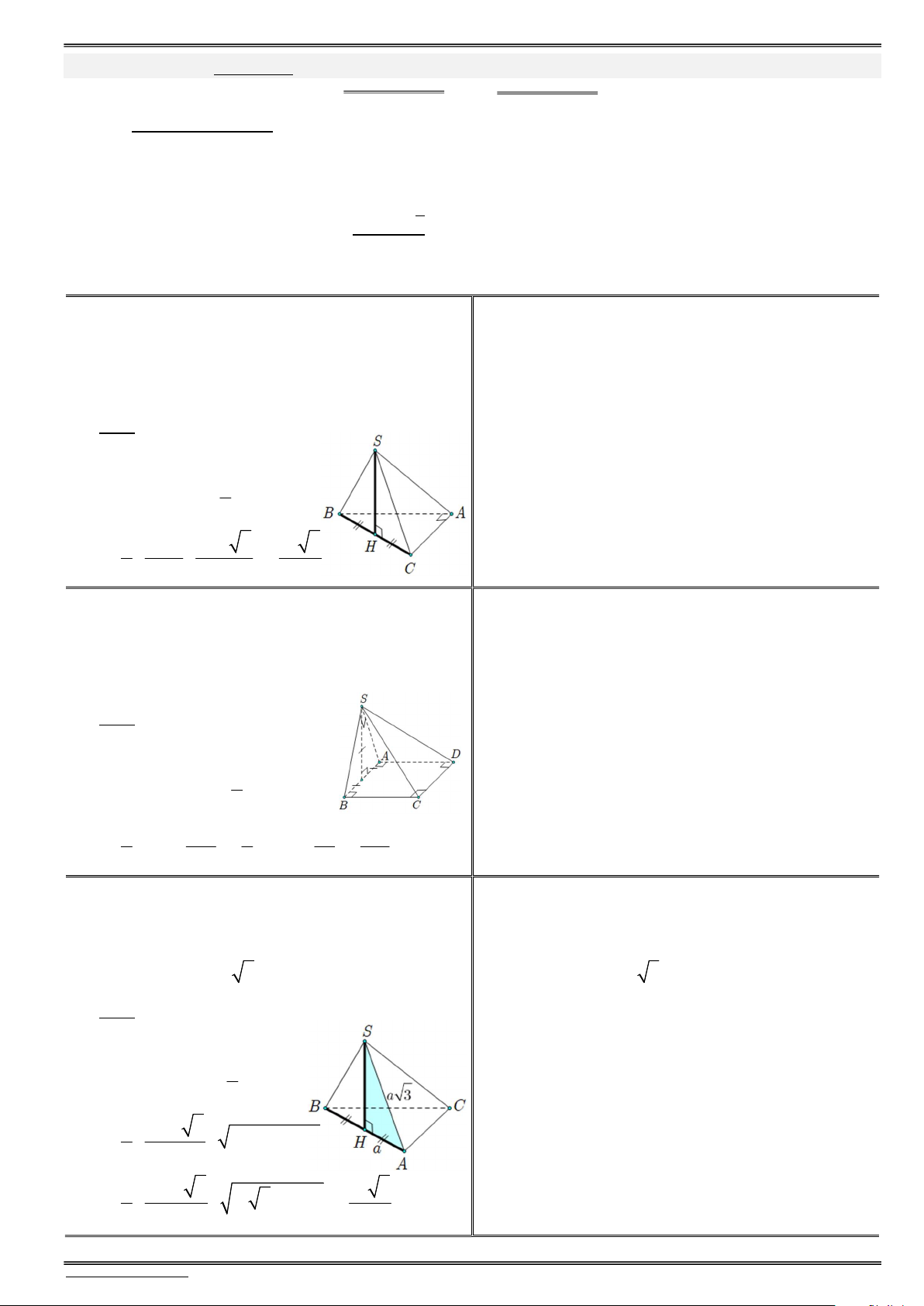
Bài toán. Cho hình chóp S.ABC có SA (ABC). Xác định khoảng cách từ chân chiều cao A đến mặt phẳng bên (SBC) ?
Xác định giao tuyến của mặt bên và mặt đáy là BC (SBC) (ABC).
Dựng 3 đường cơ bản: từ A dựng AM BC, nối SM, kẻ AH SM.
Dễ dàng chứng minh AH (SBC) d( , A (SBC)) AH. Tính SAM AH 1 1 1 SAAM AH 2 2 2 AH SA AM 2 2 SA AM
1) Cho hình chóp S.ABC có đáy ABC là tam 1) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2 , a SA a và SA (ABC). giác vuông cân tại , A BC 2 , a SA (ABC)
Gọi D là trung điểm AC. Tính:
và SA a. Gọi D thỏa DA 2DC. Tính: a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Cho hình chóp S.ABCD có đáy là hình vuông 2) Cho hình chóp S.ABCD có đáy là hình vuông cạnh ,
a SA (ABCD) và SA a 2. Tính: cạnh ,
a SA (ABCD) và SA a 2. Tính: a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . a) d( ,
A (SCD)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
B (SCD)) . . . . . . . . . . . . . . . . . . . . . . . .
c) d(C,(SBD)) . . . . . . . . . . . . . . . . . . . . . . . .
c) d(C,(SBD)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 19 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 4.1 – K§D – Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. (Đề thi THPT QG năm 2018 – Mã đề 104 – Câu 18) Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, BC ,
a SA vuông góc với mặt phẳng đáy và SA a (tham khảo hình vẽ).
Khoảng cách từ A đến mặt phẳng (SBC) bằng S
A. 2a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
C. 2 2a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. 3a. C
Câu 2. (Đề thi TN THPT năm 2021 lần 1 – Mã đề 101 – Câu 33) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông cân tại B, AB 2a và SA vuông góc với mặt phẳng đáy (tham khảo hình vẽ).
Khoảng cách từ C đến mặt phẳng (SAB) bằng S
A. 2a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. . a A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
D. 2 2a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
Câu 3. (THPT Chuyên Lê Hồng Phong – Tp. Hồ Chí Minh) Cho hình chóp S.ABCD có đáy ABCD
là hình vuông cạnh a, SA a 3 và vuông góc với mặt phẳng đáy (tham khảo hình vẽ). Khoảng
cách từ A đến mặt phẳng (SBC) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. a 3
2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. . a D A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. a B 3 C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. (THPT Trường Xuân – Nam Định) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình
vẽ). Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. a 21 7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. . a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A D
C. a 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . M D. a 3. B C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5. (THPT Chuyên Hùng Vương – Phú Thọ) Cho hình chóp đều S.ABCD có AB 2 , a SO a
với O là giao điểm của AC và BD (tham khảo hình vẽ). Khoảng cách từ A đến (SCD) bằng A. a 3. S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a
C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 A D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. a 2 O 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 20 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 4.2 – K§D – Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 4.2. Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt ph¼ng («n líp 11, nÒn líp 12)
Bài toán. Cho hình chóp S.ABC có SA (ABC). Xác định khoảng cách từ chân chiều cao A đến mặt phẳng bên (SBC) ?
Xác định giao tuyến của mặt bên và mặt đáy là . . . . . . . . . . . . . . . . . . . . . .
Dựng 3 đường cơ bản: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dễ dàng chứng minh AH (SBC) . . . . . . . . . . . . . . . . . . . . . . . . . Tính SAM AH
1 . . . . . . . . . . . . . . AH . . . . . . . . . . . . . . . . 2 AH
1) Cho hình chóp S.ABC có đáy ABC là tam 1) Cho hình chóp S.ABC có đáy ABC là tam
giác đều cạnh a, SA a và SA (ABC). giác vuông cân tại , A BC 4 , a SA (ABC)
Gọi D là trung điểm AC. Tính:
và SA 2a. Gọi D thỏa DC 2D . A Tính: a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Cho hình chóp S.ABCD có đáy là hình vuông 2) Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 ,
a SA (ABCD) và SA a 3. Tính: cạnh ,
a SA (ABCD) và SA a 3. Tính: a) d( ,
A (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . a) d( ,
A (SCD)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
D (SBC)) . . . . . . . . . . . . . . . . . . . . . . . . b) d( ,
B (SCD)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) d(C,(SBD)) . . . . . . . . . . . . . . . . . . . . . . . .
c) d(C,(SBD)) . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 21 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 4.2 – K§D – Kho¶ng c¸ch tõ ®iÓm ®Õn mÆt
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. (THPT Cổ Loa – Hà Nội) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , A biết SA (ABC) và AB 2 ,
a AC 3a, SA 4a (tham khảo hình vẽ). Khoảng cách từ điểm A
đến mặt phẳng (SBC) bằng S
A. 12a 61 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 B. 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 43 B 12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 6a 29 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Câu 2. (Sở GD & ĐT Phú Thọ) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2 , a
SA (ABC) và SA a (tham khảo hình vẽ). Khoảng cách từ A đến (SBC) bằng S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. a 3 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 2. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C a 2a D.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 B
Câu 3. (THPT Kinh Môn 2 – Hải Dương) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a. Biết SA vuông góc với đáy và SA a (tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng (SBD) bằng S
A. 2a 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. a 3 A 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 3 B C 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. a 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Câu 4. (Đề thi TN THPT năm 2019 – Mã đề 104 – Câu 40) Cho hình chópS.ABCD có đáy ABCD là
hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt
phẳng đáy (tham khảo hình vẽ). Khoảng cách từ B đến mặt phẳng (SAC) bằng S
A. a 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 21 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 A D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . M C. a 21 7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. a 21
14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 22 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 5.1 – K§D – Kho¶ng c¸ch gi÷a hai ®êng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 5.1. Kho¶ng c¸ch gi÷a hai ®êng th¼ng chÐo nhau («n líp 11, nÒn líp 12)
Cần nhớ: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung.
Nếu hai đường thẳng chéo nhau và vuông góc nhau dựng đường vuông góc chung.
Nếu hai đường thẳng chéo nhau và không vuông góc nhau Dựng song song để tìm đường vuông
góc chung (đưa về bài toán khoảng cách từ chân đường cao đến mặt phẳng bên).
1) Cho hình chóp S.ABC có đáy ABC là tam 2) Cho hình chóp S.ABC có đáy là tam giác
giác đều cạnh a, SA a và SA (ABC). vuông cân tại , A AB , a M là trung điểm
Tính khoảng cách giữa các đường thẳng sau:
của AC, SA (ABC) và SA 2a. Tính: a) d(S ,
A BC) ? Phân tích: nhận thấy hai đường a) d(S ,
A BC) ? . . . . . . . . . . . . . . . . . . . . . . . . . . .
SA và BC chéo nhau và vuông góc nhau do . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SA (ABC) nên tìm đoạn vuông góc chung. Lời giải tham khảo
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gọi M là trung điểm của BC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Do là tam giác đều nên AM BC. b) d(A ,
B SC) ? . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vì SA (ABC) nên SA AM.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A M SA Vậy a 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
M BC d(S ,ABC) AM 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
b) d(AC,SB) ? Phân tích: nhận thấy hai đường c) d(BC,SM) ? . . . . . . . . . . . . . . . . . . . . . . . . . .
AC và SB chéo nhau nhưng không vuông nhau. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lời giải tham khảo
Ta có cạnh bên SB (ABC) . B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Từ B dựng Bx AC, trên Bx lấy điểm D.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Do AC (SBD) d(AC,SB) d(AC,(SBD))
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d( ,
A (SBD)) (khoảng cách từ chân đến mặt bên).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dựng 3 đường cơ bản: AH D ,
B nối SH lại và . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . dựng AK SH d( , A (SBD)) AK.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Suy ra . ( , ) SAAH d AC SB AK
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 SA AH
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Để dễ nhìn và tìm AH, ta vẽ hình phẳng đáy và . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
có: AH BN, với N là trung điểm của AC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Suy ra: a 21 d(AC,SB) AK
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
(Lời giải trên là tự luận để học sinh dễ hiểu, khi thực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
chiến chỉ dựng hình và tính toán, không chứng minh) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 23 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 5.1 – K§D – Kho¶ng c¸ch gi÷a hai ®êng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP VẬN DỤNG
Câu 1. [MĐ2 – KĐD – LVĐ] Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc nhau và
OB a/2, OA 2OB, OC 2O .
A Khoảng cách giữa hai đường thẳng OB và AC bằng A
A. 2a 3/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2a 5/5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C O
C. a 3/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. 3a 5/10. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2. [MĐ2 – KĐD – LVĐ] Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA a và
vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
A. a 3/4. .................................................
B. a 6/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A C. a/2. D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. a 6/6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .B . . . . . . . . . . . . . C . . . . . .
Câu 3. [MĐ2 – KĐD – LVĐ] Cho tứ diện đều ABCD cạnh a. Khoảng cách giữa hai đường thẳng AB
và CD bằng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A. a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. a/2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. a 3/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. a 2/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. [MĐ3 – KĐD – LVĐ] Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, BC 2a,
SA vuông góc với mặt phẳng đáy và SA a. Khoảng cách giữa hai đường thẳng AC và SB bằng
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A. 6a/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2a/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. a/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5. [MĐ3 – KĐD – LVĐ] Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh , a
SO vuông góc với mặt phẳng (ABCD) và SO .
a Khoảng cách giữa hai đường thẳng SC và
AB bằng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A. a 3/15. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 2a 3/15. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 2a 5/5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 24 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 5.2 – K§D – Kho¶ng c¸ch gi÷a hai ®êng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 5.2. Kho¶ng c¸ch gi÷a hai ®êng th¼ng chÐo nhau («n líp 11, nÒn líp 12)
Cần nhớ: Khoảng cách giữa hai đường thẳng chéo nhau là . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nếu hai đường thẳng chéo nhau và vuông góc nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nếu hai đường thẳng chéo nhau và không vuông góc nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP VẬN DỤNG
Câu 1. [MĐ2 – KĐD – LVĐ] Cho hình lập phương ABCD.AB C D
có cạnh bằng a (tham khảo hình
vẽ). Khoảng cách giữa hai đường thẳng CC và BD bằng A' D'
A. a 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B' C' 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A a D B. 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C C. a.
D. a 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2. [MĐ2 – KĐD – LVĐ] Cho hình lăng trụ đứng ABC.AB C
có tất cả các cạnh bằng a (tham
khảo hình vẽ). Khoảng cách giữa AB và CC bằng A' C' B'
A. a 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B. a 3. C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 3. B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. a 3 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3. [MĐ2 – KĐD – LVĐ] Cho hình chóp S.ABC có đáy là tam giác cân tại , A AB a, góc S
ABC 30. Biết SA (ABC). Khoảng cách giữa SA và BC bằng
A. a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B. A a. C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 3 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B
D. a 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. [MĐ2 – KĐD – LVĐ] Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng 2 , a O là tâm của
đáy (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng SO và CD bằng S
A. a. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. 2a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A 2 D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . O C. 2a. B C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D. a 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 25 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 5.2 – K§D – Kho¶ng c¸ch gi÷a hai ®êng
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 5. [MĐ2 – KĐD – LVĐ] Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và
OA OB OC a (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng OA và BC bằng
A. a 3/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. a 2/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 3a/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6. [MĐ2 – KĐD – LVĐ] Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và , D SD
vuông góc với mặt đáy (ABCD), AD 2a và SD a 2 (tham khảo hình vẽ). Khoảng cách giữa
đường thẳng CD và SA bằng
A. 2a 3/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 2/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. a 3/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 7. [MĐ3 – KĐD – LVĐ] Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA (ABCD)
và SA a 3. Gọi M là trung điểm SD (tham khảo hình vẽ). Khoảng cách giữa hai đường AB và CM bằng
A. 3a/4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 3/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. a 3/4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. 2a 3/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8. [MĐ3 – KĐD – LVĐ] Cho hình lăng trụ đứng ABC.AB C
có đáy là tam giác vuông tại , A
AB AC a và có cạnh bên bằng a. Khoảng cách giữa hai đường thẳng AB và BC bằng
A. a 2/2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A' C' B' B. a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C. a 3/3. A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C D. a 3. B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 9. [MĐ3 – KĐD – LVĐ] Cho chóp S.ABC có đáy là tam giác đều cạnh 2 , a tam giác SAC vuông
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa SC và AB bằng
A. a 6/6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B. a 2/3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
C. 2a 21/7. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A B
D. 2a 30 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 26 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 6.1 – K§D – DiÖn tÝch cña 10 h×nh thêng gÆp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 6.1. DiÖn tÝch cña 10 h×nh thêng gÆp («n líp 8,9,10, nÒn líp 12) 1) 1 1) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . thêng S
chiÒu cao c¹nh ®¸y t¬ng øng thêng . 2 Ví dụ. Tính diện tích A BC, biết BC 5 và Ví dụ. Tính diện tích A BC, biết BC 4 và chiều cao AH 4. chiều cao AH 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2) 1 2) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vu«ng S tÝch hai c¹nh gãc vu«ng vu«ng . 2
Ví dụ. Tính diện tích của tam giác vuông tại Ví dụ. Tính diện tích A BC vuông tại , A có , A có AB 4, BC 6. AB 2a, A C 4a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3) (c¹nh huyÒn) 1 S AB.AC. 3) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vu«ng c©n vu«ng c©n 4 2
Ví dụ. Cho tam giác ABC vuông cân tại , A có
Ví dụ. Tính diện tích của tam giác ABC
cạnh huyền BC 2a. Tính S ? vuông cân tại ,
A với cạnh huyền BC 3a. ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 4) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®Òu 4) (c¹nh) . 3 c¹nh. 3 S ChiÒu cao ®Òu 4 2
Ví dụ. Tính diện tích và chiều cao AH của tam
Ví dụ. Tính diện tích và chiều cao AH của tam
giác giác đều ABC, có cạnh bằng a 3.
giác đều ABC, có cạnh bằng 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
AH . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5) 1 S tÝch hai c¹nh sin gãc kÑp 5) S
. . . . . . . . . . . . . . . . . . . . . . . . . . cho 2 c¹nh, 1 gãc cho 2 c¹nh, 1 gãc 2
Ví dụ. Tính diện tích của tam giác ABC có
Ví dụ. Tính diện tích của tam giác ABC có AB , a A
AB 2a, BC 3a và góc ABC 120 . C 2a và góc BAC 60.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 27 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 6.1 – K§D – DiÖn tÝch cña 10 h×nh thêng gÆp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt 6) S
chiÒu cao c¹nh ®¸y t¬ng øng h×nh b×nh hµnh 6) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . h×nh b×nh hµnh Hoặc S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . h×nh b×nh hµnh 2.S . ABCD ABD
Ví dụ. Tính diện tích hình bình hành ABCD
Ví dụ. Tính diện tích hình bình hành ABCD có AB , a B C 2a và góc BAD 60.
có AB 2a, BC 3a và góc ABC 120 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7) 2 S
c¹nh) Đường chéo cạnh 2. 7) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh vu«ng H×nh vu«ng (
Ví dụ. Tính diện tích và đường chéo của hình
Ví dụ. Tính diện tích và đường chéo BD của
hình vuông ABCD có cạnh bằng 2a.
vuông ABCD có cạnh bằng a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
AC . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8) S dµi réng H×nh ch÷ nhËt . 8) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh ch÷ nhËt
Ví dụ. Tính diện tích hình chữ nhật ABCD có AB 2a,
Ví dụ. Tính diện tích hình chữ nhật ABCD có BC 4a. AB 2a, AD 3a. S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9)
(®¸y lín ®¸y bÐ) chiÒu cao S 9) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh thang H×nh thang 2
Ví dụ. Tính diện tích hình thang ABCD
Ví dụ. Tính diện tích hình thang ABCD vuông tại ,
A B có AB BC 2, AD 4. vuông tại ,
A B có AB BC a, AD 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
. . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10) 1 S tÝch hai ®êng chÐo 10)S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh thoi H×nh thoi . 2
Ví dụ. Tính diện tích hình thoi ABCD có cạnh
Ví dụ. Tính diện tích hình thoi ABCD có cạnh bằng a và góc ABD 60. bằng 2a và góc ABC 120 . S . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 28 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 6.2 – K§D – DiÖn tÝch cña 10 h×nh thêng gÆp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 6.2. DiÖn tÝch cña 10 h×nh thêng gÆp («n líp 8,9,10, nÒn líp 12) 1) 1 1) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . thêng S
chiÒu cao c¹nh ®¸y t¬ng øng thêng . 2 Ví dụ. Tính diện tích A BC, biết BC 8 và Ví dụ. Tính diện tích A BC, biết BC 4 và chiều cao AH 4. chiều cao AH 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2) 1 2) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vu«ng S tÝch hai c¹nh gãc vu«ng vu«ng . 2
Ví dụ. Tính diện tích của tam giác vuông tại Ví dụ. Tính diện tích A BC vuông tại , A có , A có AB 3, BC 5. AB 2a, A C 4a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3) (c¹nh huyÒn) 1 S 3) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vu«ng c©n vu«ng c©n AB.AC. 4 2
Ví dụ. Cho tam giác ABC vuông cân tại , A có
Ví dụ. Tính diện tích của tam giác ABC
cạnh huyền BC 2a. Tính S ? vuông cân tại ,
A với cạnh huyền BC a 5. ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 4) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ®Òu 4) (c¹nh) . 3 c¹nh. 3 S ChiÒu cao ®Òu 4 2
Ví dụ. Tính diện tích và chiều cao AH của tam
Ví dụ. Tính diện tích và chiều cao AH của tam
giác giác đều ABC, có cạnh bằng a 3.
giác đều ABC, có cạnh bằng 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
AH . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5) 1 S tÝch hai c¹nh sin gãc kÑp 5) S
. . . . . . . . . . . . . . . . . . . . . . . . . . cho 2 c¹nh, 1 gãc cho 2 c¹nh, 1 gãc 2
Ví dụ. Tính diện tích của tam giác ABC có
Ví dụ. Tính diện tích của tam giác ABC có AB , a A
AB 2a, BC 3a và góc ABC 120 . C 2a và góc BAC 60.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 29 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 6.2 – K§D – DiÖn tÝch cña 10 h×nh thêng gÆp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt 6) S
chiÒu cao c¹nh ®¸y t¬ng øng h×nh b×nh hµnh 6) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . h×nh b×nh hµnh Hoặc S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . h×nh b×nh hµnh 2.S . ABCD ABD
Ví dụ. Tính diện tích hình bình hành ABCD
Ví dụ. Tính diện tích hình bình hành ABCD có AB , a B C 2a và góc BAD 60.
có AB 2a, BC 3a và góc ABC 120 .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7) 2 S
c¹nh) Đường chéo cạnh 2. 7) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh vu«ng H×nh vu«ng (
Ví dụ. Tính diện tích và đường chéo của hình
Ví dụ. Tính diện tích và đường chéo BD của
hình vuông ABCD có cạnh bằng 2a.
vuông ABCD có cạnh bằng a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
AC . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8) S dµi réng H×nh ch÷ nhËt . 8) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh ch÷ nhËt
Ví dụ. Tính diện tích hình chữ nhật ABCD có AB 2a,
Ví dụ. Tính diện tích hình chữ nhật ABCD có BC 4a. AB 2a, AD 3a. S . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9)
(®¸y lín ®¸y bÐ) chiÒu cao S 9) S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh thang H×nh thang 2
Ví dụ. Tính diện tích hình thang ABCD
Ví dụ. Tính diện tích hình thang ABCD vuông tại ,
A B có AB BC 2, AD 4. vuông tại ,
A B có AB BC a, AD 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
. . . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10) 1 S tÝch hai ®êng chÐo 10)S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H×nh thoi H×nh thoi . 2
Ví dụ. Tính diện tích hình thoi ABCD có cạnh
Ví dụ. Tính diện tích hình thoi ABCD có cạnh bằng a và góc ABD 60. bằng 2a và góc ABC 120 . S . . . . . . . . . . . . ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 30 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 7.1 – K§D – C«ng thøc thÓ tÝch khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 7.1. C«ng thøc thÓ tÝch khèi ®a diÖn 1) Thể tích khối chóp: 1 V Bh với B là
1) Thể tích khối chóp: . . . . . . . . . . . . . . . . . . . . . . 3
diện tích đáy và h là chiều cao hình chóp.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Cho hình chóp S.ABC có đáy ABC là
Ví dụ. Tính thể tích khối chóp S.ABC có đáy tam giác vuông tại , A AB 2 , a AC 3a. là tam giác vuông tại , B BA 4 , a B C 3a
Biết SA (ABC), SA a 3. Tìm V ? và SA (ABC), SA a 2. S.ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. Ta có: 1 V S .SA S.ABC 3 ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 3
AB.AC.SA .2a.3a.a 3 a 3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2 6
2) Thể tích chóp có ba cạnh S , A S , B SC đôi
2) Thể tích khối chóp có ba cạnh S , A S , B SC đôi một vuông góc với nhau: S . ASB.SC V
một vuông góc nhau là V 6
Ví dụ. Tính thể tích của khối chóp S.ABC có
Ví dụ. Tính thể tích khối tứ diện OABC có các cạnh SA 2 , a SB 3 , a SC 4a đôi OA , a O B 2 , a O C 3a đôi một vuông một vuông góc với nhau. góc với nhau. Giải. S . ASB.SC 2a.3a.4a 3 V 4a .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABC 6 6 3 (c¹nh) . 2
3) Thể tích tứ diện đều: V
3) Thể tích tứ diện đều: V tø diÖn ®Òu tø diÖn ®Òu 12
Ví dụ. Tính thể tích của khối tứ diện đều có
Ví dụ. Tính thể tích của khối tứ diện đều có cạnh bằng 4. cạnh bằng a 2. 3 3 Giải. (c¹nh) . 2 4 . 2 16 2 V
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . tø diÖn ®Òu 12 12 3
4) Thể tích khối lăng trụ: V B.h , với B là
4) Thể tích khối lăng trụ: V . . . . . . . . . . . . . . .
diện tích đáy và h là chiều cao lăng trụ.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tính thể tích khối lăng trụ tam giác đều
Ví dụ. Tính thể tích khối lăng trụ tam giác đều có cạnh đáy bằng , a cạnh bên bằng 2a. có cạnh đáy bằng 2 , a cạnh bên bằng a 5.
Giải. Diện tích đáy là tam giác đều cạnh a là
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 a 3 3 B , chiều cao a 3 h 2a V 4 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5) Khối lập phương: 3 V c¹nh)
5) Thể tích khối lập phương: V . . . . . . . . . . . . LËp ph¬ng (
Ví dụ. Tính thể tích khối lập phương có cạnh
Ví dụ. Tính thể tích khối lập phương có cạnh bằng bằng 2a 3 3 V (2a) 8a .
a 2 V . . . . . . . . . . . . . . . . . . . .
6) Khối hộp chữ nhật: V dµi réngcao
6) Thể tích khối hộp chữ nhật V . . . . . . . . . . .
Ví dụ. Tính thể tích khối hộp chữ nhật có ba
Ví dụ. Tính thể tích khối hộp chữ nhật có ba kích thức là 3 a,
kích thức là 2, 3, 5 V . . . . . . . . . . . . . . . .
2a, 3a V a.2a.3a 6a .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 31 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 7.1 – K§D – C«ng thøc thÓ tÝch khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Cho khối chóp có đáy là hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối chóp đã cho bằng A. 4 3 a . B. 2 3 a . 3 3 C. 3 2a . D. 3 4a .
Câu 2. Thể tích của khối lập phương cạnh 2 bằng A. 6. B. 8. C. 4. D. 2.
Câu 3. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối lăng trụ đã cho bằng A. 3 4a . B. 3 16a . C. 4 3 a . D. 16 3 a . 3 3
Câu 4. Cho khối hộp chữ nhật có ba kích thước 3; 4; 5. Thể tích của khối hộp đã cho bằng A. 10. B. 20. C. 12. D. 60.
Câu 5. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OB OC a 6 và
OA a. Thể tích khối tứ diện đã cho bằng A. 3 3a . B. 3 2a . C. 3 6a . D. 3 a .
Câu 6. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc đáy là
SA 2 3a. Thể tích của khối chóp S.ABC bằng 3 3 A. 3a B. 3 2a 2 2 C. 3 a . D. 3 0,5a .
Câu 7. Cho khối chóp S.ABC có đáy là tam giác vuông cân tại B, SA vuông góc với đáy và
SA AB 6a. Thể tích khối chóp S.ABC bằng A. 3 72a . B. 3 36a . C. 53 3 a . D. 19 3 a . 3 3
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB , a AD 2 , a SA vuông
góc với đáy và SA 3a. Thể tích khối chóp S.ABCD bằng 3 3 A. 5a B. 8a 2 3 C. 3 2a . D. 3 a .
Câu 9. Thể tích của tứ diện đều cạnh 6a bằng A. 3 54 2a . B. 3 18 2a . C. 2 3 a . D. 3 36 2a . 12
Câu 10. Cho lăng trụ đứng ABC.AB C
có đáy là tam giác vuông cân tại ,
A BC 2a, AB 3a. Thể
tích của khối lăng trụ ABC.AB C bằng 3 A. 2a B. 3 7a . 3 C. 3 2a . D. 3 6a .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 32 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 7.2 – K§D – C«ng thøc thÓ tÝch khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 7.2. C«ng thøc thÓ tÝch khèi ®a diÖn
1) Thể tích khối chóp: . . . . . . . . . . . . . . . . . . . . . . 1) Thể tích khối chóp: . . . . . . . . . . . . . . . . . . . . . .
Với . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Với . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Cho hình chóp S.ABC có đáy ABC là
Ví dụ. Tính thể tích khối chóp S.ABC có đáy tam giác vuông tại , A AB 2 , a AC 3a. là tam giác vuông tại , A BA 5 , a B C 4a
Biết SA (ABC), SA a 3. Tìm V ? và SA (ABC), SA 6a. S.ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Thể tích chóp có ba cạnh S , A S ,
B SC đôi một 2) Thể tích khối chóp có ba cạnh S , A S , B SC
vuông góc với nhau: V
đôi một vuông góc nhau là V
Ví dụ. Tính thể tích của khối chóp S.ABC có
Ví dụ. Tính thể tích khối tứ diện OABC có các cạnh SA 2 , a SB 3 , a SC 4a đôi một OA , a O B 3 , a O C 4a đôi một vuông vuông góc với nhau. góc với nhau.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3)
Thể tích tứ diện đều V
3) Thể tích tứ diện đều: V tø diÖn ®Òu tø diÖn ®Òu
Ví dụ. Tính thể tích của khối tứ diện đều có
Ví dụ. Tính thể tích của khối tứ diện đều có cạnh bằng 4. cạnh bằng 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4) Thể tích khối lăng trụ: . . . . . . . . . . . . . . . . . . . . 4) Thể tích khối lăng trụ: V . . . . . . . . . . . . . . .
Với . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tính thể tích khối lăng trụ tam giác đều
Ví dụ. Tính thể tích khối lăng trụ tam giác đều có cạnh đáy bằng , a cạnh bên bằng 2 . a có cạnh đáy bằng 2 , a cạnh bên bằng 4a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5) Khối lập phương: V
. . . . . . . . . . . . . . 5) Thể tích khối lập phương: V . . . . . . . . . . . . LËp ph¬ng
Ví dụ. Tính thể tích khối lập phương có cạnh
Ví dụ. Tính thể tích khối lập phương có cạnh bằng 2a V
. . . . . . . . . . . . . . . . . . . . . .
bằng 2 2a. V . . . . . . . . . . . . . . . . . . .
6) Khối hộp chữ nhật: V . . . . . . . . . . . . . . . . . . 6) Thể tích khối hộp chữ nhật V . . . . . . . . . . .
Ví dụ. Tính thể tích khối hộp chữ nhật có ba
Ví dụ. Tính thể tích khối hộp chữ nhật có ba
kích thức là a, 2a, 3a V . . . . . . . . . . . . . .
kích thức là 2, 3, 5 V . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 33 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 7.2 – K§D – C«ng thøc thÓ tÝch khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Cho khối chóp có diện tích đáy 2
B 3a và chiều cao h 6a. Thể tích của khối chóp bằng A. 3 3a . B. 3 6a . C. 3 9a . D. 3 18a .
Câu 2. Thể tích khối hộp chữ nhật ABC . D AB C D
có AB a, AD 2a, AA 3a bằng A. 3 2a . B. 2 6a . C. 3 6a . D. 2 2a .
Câu 3. Cho khối chóp S.ABC có SA (ABC ), tam giác ABC vuông cân tại , A BC 4a và
SA a 3. Thể tích khối chóp đã cho bằng 3 3 A. 2a 3 B. 4a 3 3 3 C. 3 4a 3 D. 3 2a 3.
Câu 4. Tính thể tích của khối lập phương ABCD.AB C D , biết AC a. 3 A. 3 3 3a . B. 3a 3 3 3 C. a D. 3a 27 9
Câu 5. Cho khối lăng trụ đứng ABC.AB C
có đáy là tam giác đều cạnh a và AA 2a. Thể tích
của khối lăng trụ đã cho bằng 3 3 A. 6a B. 6a 4 6 3 3 C. 6a D. 6a 12 2
Câu 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a. Thế tích của khối chóp đã cho bằng 3 3 A. 4a B. 4 7a 3 9 3 C. 4 7a D. 3 4 7a . 3
Câu 7. Cho hình chóp S.ABC có đáy là tam giác vuông tại C. Tam giác SAB đều nằm trong mặt
phẳng vuông góc với đáy. Biết AB a 3 và AC a. Thể tích của khối chóp S.ABC bằng 3 3 A. a 2 B. a 4 2 3 3 C. a 3 D. a 2 2 2
Câu 8. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60. Thể tích
của khối chóp đó bằng 3 3 A. a 3 B. a 3 12 6 3 3 C. a 3 D. a 3 36 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 34 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 8 – K§D – ThÓ tÝch chãp cã c¹nh bªn vu«ng ®¸y
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 8. ThÓ tÝch khèi chãp cã c¹nh bªn vu«ng gãc ®¸y
1) Cho hình chóp S.ABC có đáy là tam giác đều 1) Cho hình chóp S.ABC có đáy là tam giác đều
cạnh a 3, cạnh bên SB vuông góc với mặt
cạnh a 3, cạnh bên SC vuông góc với mặt
phẳng đáy (ABC) và SA a 6. Tính thể tích
phẳng đáy (ABC) và SB a 5. Tính thể tích của khối chóp đã cho. của khối chóp đã cho.
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Cho hình chóp S.ABC có đáy là tam giác 2) Cho hình chóp S.ABC có đáy là tam giác
vuông tại C, AB 5, BC 3, cạnh bên SB vuông tại ,
A AB 6, BC 10, cạnh bên SA
vuông góc với mặt phẳng đáy (ABC) và
vuông góc với mặt phẳng đáy (ABC) và
SC 6. Tính thể tích của khối chóp đã cho.
SC 12. Tính thể tích của khối chóp đã cho.
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Cho hình chóp S.ABCD có đáy là hình vuông 3) Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a 3, SA (ABCD) và SD a 6. Tính cạnh ,
a SA (ABCD) và SB a 5. Tính
thể tích của khối chóp đã cho.
thể tích của khối chóp đã cho.
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4) Cho hình chóp S.ABCD có đáy là hình chữ 4) Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, BC 2 , a SA (ABCD) và nhật, AB a, BC 2 , a SA (ABCD) và
SB a 15. Tính thể tích của khối chóp.
SD a 10. Tính thể tích của khối chóp.
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 35 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 8 – K§D – ThÓ tÝch chãp cã c¹nh bªn vu«ng ®¸y
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
BÀI TẬP ÁP DỤNG (học sinh vẽ hình góc phải ngoài cùng, trình bày ở giữa – hình như câu 1)
Câu 1. Cho hình chóp S.ABC có SA (ABC). Tam giác ABC vuông tại C, BC a 2, AC a,
SA 2a. Thể tích của khối chóp S.ABC bằng S 3 3 A. 6a B. 6a 6 4 3 3 A B C. 2a D. 10a 3 6 C
Câu 2. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại ,
A AC 2a 3, cạnh bên SB vuông
góc với đáy (ABC ) và SB a 5. Thể tích khối chóp đã cho bằng 3 A. 3 2a 5. B. a 5 6 3 C. 3 3a 5. a 5 D. 3
Câu 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a 3, cạnh bên SB vuông góc với mặt
phẳng đáy (ABC ) và SA a 6. Thể tích khối chóp đã cho bằng A. 3 3 a . B. 3 a . 4 C. 1 3 a . a 2 D. 3 3.
Câu 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA (ABCD), SA a. Thể tích
của khối chóp S.ABCD bằng A. 3 3 a . B. 1 3 a . 2 3 3 3 C. 3a D. 2a 3 3
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, BC 2a, SA (ABCD)
và SC a 11. Thể tích khối chóp đã cho bằng 3 3 A. 11a B. 2 11a 3 3 3 3 C. 6a 2 6a 3 D. 3
Câu 6. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc
ABC 60. Biết SA (ABCD) và
SA a 6/6. Thể tích của khối chóp S.ABCD bằng A. 1 3 a . B. 1 3 a . 12 4 3 3 C. 2a D. 2a 12 6
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB BC a và
AD 2a. Biết SA (ABCD) và SA a. Thể tích khối chóp S.ABCD bằng A. 1 3 a . B. 3 a . 2 C. 3 3 a . D. 3 2a . 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 36 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 9 – K§D – ThÓ tÝch chãp cã mÆt bªn vu«ng ®¸y
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 9. ThÓ tÝch khèi chãp cã mÆt bªn vu«ng gãc ®¸y
Học sinh cần nhớ:
Nếu mặt bên vuông góc với mặt đáy thì chiều cao của hình chóp chính là chiều cao của mặt bên.
Đặc biệt nếu mặt bên là tam giác cân hoặc đều thì chân đường cao là trung điểm của giao tuyến.
Đường cao trong tam giác đều bằng ạ × √
Đường trung tuyến xuất phát từ góc vuông trong tam giác vuông (vuông cân) bằng ½ cạnh huyền.
1) Cho hình chóp S.ABC có đáy ABC là tam 1) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại , A BC 2a. Mặt bên SBC giác vuông cân tại , A BC 4a. Mặt bên SBC
là tam giác đều và nằm trong mặt phẳng
là tam giác đều và nằm trong mặt phẳng
vuông góc với mặt đáy. Tính V ?
vuông góc với đáy. Tính V ? S.ABC S.ABC
Giải. Gọi H là trung điểm BC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SH (ABC).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có 1 V S .SH
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABC 3 ABC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1 BC BC. 3 3 a 3 3 4 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) Cho hình chóp S.ABCD có đáy là hình vuông 2) Cho hình chóp S.ABCD có đáy là hình chữ cạnh 2 ,
a mặt bên SAB là tam giác vuông cân
nhật, AB 2, AD 4. Mặt bên SAB là tam
tại S và nằm trong mặt phẳng vuông góc với
giác vuông cân và nằm trong mặt phẳng vuông đáy. Tính V ? góc với đáy. Tính V ? S.ABCD S.ABCD
Giải. Gọi H là trung điểm AB.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SH (ABCD).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có: 1 V S .SH
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABCD 3 ABCD 3 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 AB 1 2 2a 4 . (2 ) a AB a 3 2 3 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Cho hình chóp S.ABC có đáy ABC là tam 3) Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2 ,
a mặt bên SAB là tam giác
giác đều cạnh 4a, mặt bên SAB là tam giác
cân và nằm trong mặt phẳng vuông góc với
cân và nằm trong mặt phẳng vuông góc với
đáy, biết SA a 3. Tính V ?
đáy, biết SA 2 2a. Tính V ? S.ABC S.ABC
Giải. Gọi H là trung điểm AB.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SH (ABCD).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có 1 V S SH
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABCD 3 ABCD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1 AB 3 2 2 SA AH 3 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1 (2a) 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 (a 3) a a 6 3 4 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 37 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 9 – K§D – ThÓ tÝch chãp cã mÆt bªn vu«ng ®¸y
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a 3, mặt bên SAC là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy (ABC ). Thể tích khối chóp đã cho bằng 3 3 A. 3a B. 3a 3 8 4 A B 3 3 C. a 3 3a 3 D. 8 C
Câu 2. Cho hình chóp S.ABC có đáy là tam giác vuông tại ,
A AB 3a, BC 5a, mặt bên SAB là
tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC ). Thể
tích khối chóp đã cho bằng 3 3 A. 3a B. 10a 2 3 3 C. 7a a 2 D. 3 3 .
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABCD bằng 3 A. a 3 B. 3 a 3. 6 3 3 C. a 3 D. a 3 2 3
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD 2a. Tam giác SAB
vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khi đó thể tích của khối chóp S.ABCD bằng 3 3 A. 3a B. 2a 3 3 3 3 C. 2 3a D. a 3 3
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc 45. Khi đó
thể tích của khối chóp S.ABCD bằng 3 3 A. 4 3a B. 4 5a 3 3 3 3 C. 2 5a D. 2 3a 3 3
Câu 6. Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, BC 2a. Tam giác SAB
cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SCD) và mặt
phẳng đáy (ABCD) bằng 60. Thể tích khối chóp S.ABCD bằng 3 3 A. 8 3a B. 4 3a 9 9 3 3 C. 8a D. 4 3a 9 3
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 38 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 10 – K§D – ThÓ tÝch chãp ®Òu
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 10. ThÓ tÝch khèi chãp ®Òu
Học sinh cần nhớ:
Hình chóp tam giác đều có đáy là tam giác đều và chân chiều cao trùng với trọng tâm G của A BC.
Hình chóp tứ giác đều có đáy là hình vuông và có chân chiều cao trùng với tâm O AC BD.
1) Tính thể tích khối chóp tam giác đều có cạnh 1. Thể tích khối chóp tam giác đều có cạnh đáy
đáy bằng a, cạnh bên bằng 2a.
bằng 2a, cạnh bên gấp đôi cạnh đáy.
Giải. Gọi G là trọng tâm A BC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có: 2 2 a 3 a 3 AG AM 3 3 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 SG SA AG a 33 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 1 a 3 a 33 a 11 V
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABC 3 4 3 12
2) Tính thể tích khối chóp tứ giác đều có cạnh đáy 2. Tính thể tích khối chóp tứ giác đều có cạnh đáy
bằng a, cạnh bên gấp đôi cạnh đáy.
bằng 2a, cạnh bên bằng 3a.
Giải. Gọi O AC BD SO (ABCD).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ta có: BD a 2 OD 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 SO SD OD a 14 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 1 V S .SO a 14
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S.ABCD 3 ABCD 6
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 39 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 10 – K§D – ThÓ tÝch chãp ®Òu
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Thể tích khối tứ diện đều có cạnh là a 2 bằng A. 2 3 a . B. 2 3 a . Học sinh ghi công 12 3 thức: C. 1 3 a . D. 1 3 a . 3 6 Vtø diÖn ®Òu
Câu 2. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 1 và cạnh bên bằn g 3. Tính thể tích V của khối chóp S.ABC. A. 35 B. 3 24 6 C. 2 D. 2 6 2
Câu 3. Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 30. Thể tích
của khối chóp đã cho bằng A. 6 3 a . B. 3 3 a . 36 36 C. 3 3 a . D. 3 3 a . 48 12
Câu 4. Cho hình chóp tam giác đều có cạnh đáy bằng 2a và mặt bên tạo với mặt đáy một góc 45. Thể
tích của khối chóp đó bằng 3 3 A. 8a 3 B. 4a 3 9 3 C. 1 3 a . D. 1 3 a . 2 3
Câu 5. Cho khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng a 3. Thể tích của khối chóp đã cho bằng 3 3 A. 2a B. 10a 3 6 3 3 C. 3a D. a 6 2
Câu 6. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 3. Cạnh bên tạo với đáy một góc bằng
60. Thể tích của khối chóp đó bằng A. 3 2 B. 9 6 2 2 C. 9 3 D. 3 6 2 2
Câu 7. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, mặt bên tạo với mặt đáy một góc 45.
Thể tích của khối chóp S.ABCD bằng 3 3 A. a 2 B. a 6 6 C. 1 3 a . D. 1 3 a . 3 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 40 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 11 – K§D – ThÓ tÝch khèi l¨ng trô
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 11. ThÓ tÝch khèi l¨ng trô
Học sinh cần nhớ:
Hình lăng trụ đứng: có các mặt bên vuông góc với đáy Chiều cao là các cạnh bên.
Hình lăng trụ đều: là hình lăng trụ đứng, có đáy là đa giác đều Chiều cao là các cạnh bên.
Hình lăng trụ xiên: cần xác định chân chiều cao (hình chiếu), vẽ từ chân thẳng lên sẽ tìm được đỉnh.
1) Cho lăng trụ đứng ABC.AB C
có đáy ABC 1) Cho lăng trụ đứng ABC.AB C có đáy ABC là tam giác vuông tại , B BAC 60 , AB a là tam giác vuông tại , B BAC 30 , AB a và AA a 3. Tính V và AA a 3. Tính V ? ? ABC .A B C ABC .A B C
Giải. Ta có: tan 60 3 BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BC a 3.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Khi đó V S .AA ABC .A B C A BC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1 1 3 . . . . 3. 3 a AB BC AA a a a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2
2) Tính thể tích khối lăng trụ đều ABC.AB C
2) Tính thể tích khối lăng trụ đều ABC.AB C
có cạnh đáy bằng a. Biết góc giữa (ABC) và
có cạnh đáy bằng 2a. Biết góc giữa (ABC) và đáy bằng 45. đáy bằng 60.
Giải. Gọi M là trung điểm của BC.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
((ABC),(ABC)) AM . A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Khi đó tan 45 1 AA
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AM
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . a 3 AA AM
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 a 3 a 3 3 . a V S AA ABC .A B C A BC 4 2 8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) Cho hình lăng trụ ABC.AB C
có đáy là tam 3) Cho hình lăng trụ ABC.AB C có đáy là tam
giác vuông cân tại B và AC 2a. Hình chiếu
giác vuông cân ở A và AB a 2. Hình chiếu
vuông góc của A trên (ABC ) là trung điểm
vuông góc của A trên (ABC ) là trung điểm
H của cạnh AB và AA a 2. Tính V ?
H của BC và AA 4a. Tính V ? ABC.A B C
Giải. Ta có: AH (ABC).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 AC 2 S a .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A BC 4 Do ABC vuông cân
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . tại AC B AB a 2 2AH.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2
AH AA AH a 6/2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 6a V
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S A H ABC .A B C A C B 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 41 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 11 – K§D – ThÓ tÝch khèi l¨ng trô
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Thể tích khối lăng trụ tam giác đều có cạnh đáy là a 3, cạnh bên là a 5 bằng A' 3 3 C' A. 3 15a B. 15a B' 4 4 3 3 A C. 3 5a 3 3a D. C 4 4 B
Câu 2. Thể tích khối lăng trụ tứ giác đều có cạnh đáy là a 3, cạnh bên là a 5 bằng 3 A. 15a B. 3 5 3a . 3 3 C. 5 3a a 3 D. 3 3 5 .
Câu 3. Cho khối lăng trụ đứng tam giác ABC.AB C
có đáy là một tam giác vuông cân tại , A AB 2 ,
a góc giữa thẳng AC và (ABC) bằng 30. Thể tích khối lăng trụ đã cho bằng 3 3 A. 2 3a B. 4 3a 9 9 3 3 C. 2 3a 4 3a 3 D. 3
Câu 4. Cho khối lăng trụ đứng tam giác ABC.AB C
có đáy là một tam giác vuông cân tại , A
AB 3a, góc giữa (ABC) và đáy bằng 45. Thể tích khối lăng trụ đã cho bằng 3 3 A. 3 6a B. 3 3a 4 4 3 3 C. 3 6a 3 3a 2 D. 2
Câu 5. Cho hình lăng trụ ABC.AB C
có đáy ABC là tam giác vuông cân tại A và AC 2a. Hình
chiếu vuông góc của A trên mặt phẳng (ABC) là trung điểm H của cạnh BC và AA 5a.
Thể tích của khối lăng trụ đã cho bằng A' 3 A. 2 23a B. 3 2 23a . 3 A C 3 C. 10a D. 3 10a . H 3 B
Câu 6. Cho hình lăng trụ ABC.AB C
có đáy ABC là tam giác vuông tại , A AB a 2, BC a 3.
Hình chiếu vuông góc của A trên mặt phẳng (ABC) trùng với tâm đường tròn ngoại tiếp tam
giác ABC và AA a 11. Thể tích của khối lăng trụ đã cho bằng 3 3 A. a 246 B. a 11 2 2 3 3 C. a 82 a 66 4 D. 4
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 42 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.1 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 12.1. Nãn trô cÇu (c«ng thøc & xoay h×nh) 1) KHỐI NÓN 1) KHỐI NÓN : đường sinh.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . h : chiều cao.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . r : bán kính đáy.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . : góc ở đỉnh.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Liên hệ: 2 2 2 h r .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Diện tích xung quanh: S r . xq ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích toàn phần: 2 S r r .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . tp ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Thể tích: 1 2 V r h. () 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2) KHỐI TRỤ 2) KHỐI TRỤ Khi quay hình chữ nhật
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . OO A B quanh trục OO
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ta thu được mặt trụ.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . h : chiều cao.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . r : bán kính đáy.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Diện tích xung quanh: S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C 2 r h. xq ( )
Diện tích toàn phần: 2 S
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C 2 r h 2 r . tp ( ) Thể tích: 2 V
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C r h. ( ) 3) KHỐI CẦU 3) KHỐI CẦU Tập hợp các điểm M trong không
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . gian cách điểm I cố
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . định một khoảng R không đổi gọi là mặt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . cầu ( ) tâm I, bán
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . kính , R kí hiệu là
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S(I; ) R hay Diện tích: 2 S 4 R .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . {M | IM } R . () 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Thể tích: 4 R V () 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. (Đề tham khảo lần 2 – Bộ GD & ĐT năm 2020 – Câu 8) Cho khối nón có chiều cao h 3 và
bán kính đáy r 4. Thể tích của khối nón đã cho bằng A. 16 . B. 48 . C. 36 . D. 4 .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 43 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.1 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 2. (Đề thi TN THPT năm 2020 lần 1 – Mã đề 101 – Câu 3) Cho hình trụ có bán kính đáy r 4 và
độ dài đường sinh 3. Diện tích xung quanh của hình trụ đã cho bằng A. 48 . B. 12 . C. 16 . D. 24 .
Câu 3. (Đề tham khảo lần 2 – Bộ GD & ĐT năm 2020 – Câu 9) Cho mặt cầu có bán kính R 2. Diện
tích của mặt cầu đã cho bằng A. 24 . B. 8 . C. 16 . D. 4 .
Câu 4. (Đề thi TN THPT năm 2020 – Mã đề 101 – Câu 8) Cho khối cầu có bán kính r 4. Thể tích của khối cầu đã cho bằng A. 256 B. 64 3 3 C. 64 . D. 256 .
Câu 5. (Đề thi THPT QG năm 2017 – Mã đề 104 – Câu 18) Cho hình nón có bán kính đáy r 3 và
độ dài đường sinh 4. Tính diện tích xung quanh của hình nón đã cho. A. 12 . B. 4 3 . C. 39 . D. 8 3 .
Câu 6. (Đề thi TN THPT năm 2020 lần 2 – Mã đề 104 – Câu 13) Cho khối trụ có bán kính đáy r 3
và chiều cao h 5. Thể tích của khối trụ đã cho bằng A. 45 . B. 5 . C. 15 . D. 30 .
Câu 7. (Đề tham khảo – Bộ GD & ĐT năm 2019 – Câu 25) Cho khối nón có độ dài đường sinh bằng
2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng 3 3 a 3 3 a A. B. 3 2 3 3 C. 2 a D. a 3 3
Câu 8. (Đề thi TN THPT năm 2020 lần 1 – Mã đề 102 – Câu 36) Cho hình nón có bán kính bằng 5 và
góc ở đỉnh bằng 60. Diện tích xung quanh của hình nón đã cho bằng A. 50 . B. 100 . 50 3 100 3 C. D. 3 3
Câu 9. (Đề minh họa – Bộ GD & ĐT năm 2017 – Câu 39) Trong không gian, cho tam giác ABC vuông tại ,
A AB a và AC 3a. Khi quay tam giác ABC quanh trục AB tạo thành hình nón có đương sinh bằng A. 3a. B. 2a. C. a. D. 2a.
Câu 10. (Sở GD & ĐT Cần Thơ năm 2020) Trong không gian cho hình chữ nhật ABCD có AB a,
AC a 5. Diện tích xung quanh của hình trụ khi quay xung quanh trục AB bằng A. 2 2 a . B. 2 4 a . C. 2 2a . D. 2 4a .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 44 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.2 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 12.2. Nãn trô cÇu (c«ng thøc & xoay h×nh) 1) KHỐI NÓN 1) KHỐI NÓN
: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
h : . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
r : . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Liên hệ: . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Diện tích xung quanh: S . . . . . . . . . . xq ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích toàn phần: S . . . . . . . . . . . . tp ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Thể tích: V . . . . . . . . . . . . . . . . . . . . . . . . ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2) KHỐI TRỤ 2) KHỐI TRỤ Khi quay hình chữ nhật
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . OO A B quanh trục OO
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ta thu được mặt trụ (C).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
h : . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
r : . . . . . . . . . . . . . . . . Diện tích xung quanh: S . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C xq ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích toàn phần: S . . . . . . . . . . . . C tp ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Thể tích: V
. . . . . . . . . . . . . . . . . . . . . . . . C ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3) KHỐI CẦU 3) KHỐI CẦU Tập hợp các điểm M trong không
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . gian cách điểm I cố
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . định một khoảng R không đổi gọi là mặt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . cầu ( ) tâm I, bán
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . kính , R kí hiệu là
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích: S . . . . . . S(I;R) hay ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . {M | IM } R .
Thể tích: V . . . . . . . ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. (Đề thi THPT QG năm 2017 – Mã đề 102 – Câu 19) Cho khối nón có bán kính đáy r 3 và chiều
cao h 4. Thể tích của khối nón đã cho bằng A. 12 . B. 4 . C. 16 3. D. 16 3 3
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 45 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.2 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 2. (Đề thi TN THPT năm 2021 lần 1 – Mã đề 101 – Câu 24) Cho khối hình trụ có bán kính đáy
r 6 và chiều cao h 3. Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 .
Câu 3. (Đề thi TN THPT năm 2020 lần 2 – Mã đề 103 – Câu 13) Cho mặt cầu có bán kính r 4. Diện
tích của mặt cầu đã cho bằng A. 16. B. 64. C. 64 D. 256 3 3
Câu 4. (Sở GD & ĐT Thanh Hóa) Cho khối cầu (S) có thể tích bằng 3
36cm . Diện tích mặt cầu bằng A. 2 12cm . B. 2 18cm . C. 2 36cm . D. 2 27cm .
Câu 5. (Đề tham khảo – Bộ GD & ĐT năm 2018 – Câu 14) Cho hình nón có diện tích xung quanh bằng 2 3 a
và có bán kính đáy bằng .
a Độ dài đường sinh của hình nón đã cho bằng A. 2 2a. B. 3a. C. 2a. D. 3a/2.
Câu 6. (Đề thi THPT QG năm 2017 – Mã đề 103 – Câu 25) Cho hình trụ có diện tích xung quanh bằng
50 và độ dài đường sinh bằng đường kính của đường tròn đáy. Bán kính r của đường tròn đáy bằng A. 5 . B. 5. C. 5 2 D. 5 2 2 2
Câu 7. (Đề thi TN THPT năm 2020 lần 1 – Mã đề 101 – Câu 35) Cho hình nón có bán kính đáy bằng 2
và góc ở đỉnh bằng 60. Diện tích xung quanh của hình nón đã cho bằng A. 8 . B. 16 . C. 8 3 D. 16 3 3 3
Câu 8. (Sở GD & ĐT Hải Phòng) Diện tích toàn phần của hình trụ có bán kính đường tròn đáy là 3, chiều cao là 6 3 bằng A. 9 36 3. B. 18 36 3. C. 18 18 3. D. 6 36 3.
Câu 9. (Đề thi THPT QG năm 2017 – Mã đề 103 – Câu 40) Trong không gian cho tam giác ABC vuông tại , A AB a và
ACB 30 . Thể tích khối nón khi quay tam giác quanh cạnh AC bằng 3 3 A. 3 a B. 3 a 3 9 C. 3 3 a . D. 3 a .
Câu 10. (Sở GD & ĐT Bắc Giang) Cho hình chữ nhật ABCD có AB ,
a AD 2a. Thể tích của khối
trụ tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB bằng 3 A. 3 4 a . B. 4 a 3 C. 3 2a . D. 3 a .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 46 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.3 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 12.3. Nãn trô cÇu (c«ng thøc & xoay h×nh) 1) KHỐI NÓN 1) KHỐI NÓN
: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
h : . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
r : . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Liên hệ: . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Diện tích xung quanh: S . . . . . . . . . . xq ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích toàn phần: S . . . . . . . . . . . . tp ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Thể tích: V . . . . . . . . . . . . . . . . . . . . . . . . ()
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2) KHỐI TRỤ 2) KHỐI TRỤ Khi quay hình chữ nhật
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . OO A B quanh trục OO
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ta thu được mặt trụ (C ).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
h : . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
r : . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Diện tích xung quanh: S . . . . . . . . . . C xq ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diện tích toàn phần: S . . . . . . . . . . . . C tp ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Thể tích: V
. . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C ( ) 3) KHỐI CẦU 3) KHỐI CẦU Tập hợp các điểm M trong không
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . gian cách điểm I cố
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . định một khoảng R không đổi gọi là mặt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . cầu () tâm I, bán
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . kính , R kí hiệu là
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S(I;R) hay
Diện tích: S . . . . . . . c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . {M | IM } R .
Thể tích: V . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c BÀI TẬP ÁP DỤNG
Câu 1. (Đề thi TN THPT năm 2020 lần 1 – Mã đề 102 – Câu 10) Cho khối nón có bán kính đáy r 4
và chiều cao h 2. Thể tích của khối nón đã cho bằng A. 32 . B. 8 . C. 32 D. 8 3 3
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 47 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 12.3 – K§D – Nãn trô cÇu (c«ng thøc, xoay h×nh) Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 2. (Đề thi TN THPT năm 2020 lần 1 – Mã đề 102 – Câu 7) Cho hình trụ có bán kính đáy R 8 và
độ dài đường sinh 3. Diện tích xung quanh của hình trụ đã cho bằng A. 24 . B. 192 . C. 48 . D. 64 .
Câu 3. (Đề thi TN THPT năm 2020 lần 2 – Mã đề 104 – Câu 16) Cho mặt cầu bán kính r 5. Diện tích
của mặt cầu đã cho bằng A. 500 B. 100 3 3 C. 25 . D. 100 .
Câu 4. (Sở GD & ĐT Phú Thọ) Nếu diện tích mặt ngoài của mặt cầu bằng 36 thì thể tích của khối cầu bằng A. 9 . B. 36 . C. D. 9 3
Câu 5. (Đề thi TN THPT năm 2020 lần 2 – Mã đề 101 – Câu 25) Cho hình nón có bán kính đáy r 2
và độ dài đường sinh 5. Diện tích xung quanh của hình nón đã cho bằng A. 10 B. 20 3 3 C. 10 . D. 20 .
Câu 6. (Đề thi THPT QG năm 2017 – Mã đề 101 – Câu 11) Tính thể tích của khối trụ có bán kính đáy
r 4 và chiều cao h 4 2. A. 128 . B. 64 2 . C. 32 . D. 32 2 .
Câu 7. (Đề thực nghiệm – Bộ GD & ĐT năm 2017 – Câu 39) Cho khối ( )
có bán kính đáy bằng 3 và
diện tích xung quanh bằng 15 .
Thể tích của khối nón ( ) bằng A. 12 . B. 20 . C. 36 . D. 60 .
Câu 8. (Sở GD & ĐT Cần Thơ) Diện tích toàn phần của hình trụ có bán kính đáy là a và đường cao là a 3 bằng A. 2 2 a ( 3 1). B. 2 a 3. C. 2 a ( 3 1). D. 2 2 a ( 3 1).
Câu 9. (Đề tham khảo lần 2 – Bộ GD & ĐT năm 2020 – Câu 32) Trong không gian, cho tam giác ABC vuông tại ,
A AB a và AC 2a. Khi quay tam giác ABC quanh cạnh góc vuông AB thì
đường gấp khúc ACB tạo thành một hình nón. Diện tích xung quanh của hình nón đó bằng A. 2 5 a . B. 2 10 a . C. 2 2 5 a . D. 2 5 a .
Câu 10. (Sở GD & ĐT Hà Nội) Cho hình vuông ABCD quay quanh cạnh AB tạo ra hình trụ có độ dài
của đường tròn đáy bằng 4 a
. Thể tích của hình trụ này bằng A. 3 2 a . B. 3 4 a . 3 C. 3 8 a . D. 8 a 3
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 48 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.1 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 13.1. Nãn trô cÇu (thiÕt diÖn)
1) KHỐI NÓN KHI CẮT QUA TRỤC S . O
1.1. Cắt hình nón bởi mặt phẳng qua trục được
thiết diện là tam giác đều cạnh 2a. Tính thể tích của khối nón ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Cắt hình nón bởi mặt phẳng qua trục được S AB đều S AB vuông cân ở S.
thiết diện là tam giác vuông cân có cạnh
huyền bằng 2a. Tính thể tích khối nón ? 3 h r 3 h r 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) KHỐI NÓN KHI CẮT QUA ĐỈNH S.
2. Cho hình nón có chiều cao bằng 2 5. Cắt hình
nón bởi mặt phẳng qua đỉnh được thiết diện là Thiết diện: S AB cân.
tam giác đều, diện tích bằng 9 3. Tính V ? () H là trung điểm A . B d( , O (SAB)) OK.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ((SAB);(O)) SHO.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) KHỐI TRỤ KHI CẮT QUA TRỤC OO .
3. Cắt một khối trụ bởi mặt phẳng qua trục, ta
Thiết diện là hình chữ nhật (hoặc hình vuông)
được thiết diện là một hình chữ nhật ABCD ABC ,
D với h BC AD và r O . A có A ,
B CD thuộc hai đáy của trụ, AB 2a, BC 3a. Tính V ? (T)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4) KHỐI TRỤ KHI CẮT SONG SONG TRỤC. 4. Cho hình trụ có chiều cao 6a. Cắt hình trụ song
song với trục và cách trục một khoảng 3a, thiết Thiết diện: ABCD là
diện thu được là hình vuông. Tính
hình chữ nhật (hoặc hv) V ? (T) M là trung điểm A . B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d(OO ,(P)) OM.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Pitago O AM r.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5) THIẾT DIỆN CỦA (P) VỚI MẶT CẦU (S). 5. Mặt phẳng (P) cắt khối cầu tâm I, bán kính bằng 4 và d( ,
O (P)) 3. Tìm bán kính cầu ?
Thiết diện: là đường tròn giao tuyến (H,r).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d(I,(P)) IH d.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 R r d .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 49 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.1 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Cho hình nón có thiết diện qua trục của hình nón là tam giác vuông cân có cạnh góc vuông bằng
a 2. Diện tích xung quanh của hình nón bằng 2 2 A. a 2 B. a 2 3 2 C. 2 2 2 a . D. 2 2 a .
Câu 2. Thiết diện qua trục của một hình nón là một tam giác đều có cạnh 8cm. Diện tích xung quanh của hình nón đó là A. 32 2 cm . B. 2 16cm . 3 C. 2 32cm . D. 2 64cm .
Câu 3. Cắt hình trụ có bán kính đáy bằng 5, bởi mặt phẳng qua trục thu được hình chữ nhật có chu vi
bằng 32. Diện tích xung quanh của hình trụ bằng A. 110 . B. 55 . C. 60 . D. 150 .
Câu 4. Một hình trụ có thiết diện qua trục là là một hình vuông có cạnh bằng 6cm. Bán kính đáy của hình trụ đó bằng A. 36cm. B. 6cm. C. 12cm. D. 3cm.
Câu 5. Cho hình cầu đường kính 2a 3. Mặt phẳng (P) cắt hình cầu theo thiết diện là hình tròn có bán
kính bằng a 2. Khoảng cách từ tâm hình cầu đến (P) bằng A. a. B. a 10. C. a D. a 10 2 2
Câu 6. Cho hình nón đỉnh S có chiều cao bằng bán kính đáy và bằng 2a. Mặt phẳng (P) đi qua S cắt
đường tròn đáy tại A và B sao cho AB 2 3a. Khoảng cách từ tâm của đáy đến (P) bằng A. a 5. B. a. C. a 2 D. 2a 5 2 5
Câu 7. Cho hình trụ có chiều cao bằng 6 ,
a Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng song
song với trục và cách trục một khoảng bằng 3a, thiết diện thu được là một hình vuông. Thể tích
của khối trụ được giới hạn bởi hình trụ đã cho bằng A. 3 216 a . B. 3 150 a . C. 3 54 a . D. 3 108 a .
Câu 8. Cho hình trụ có chiều cao bằng 5 3. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng 1, thiết diện thu được có diện tích bằng 30. Diện tích xung quanh
của hình trụ đã cho bằng A. 10 3 . B. 5 39 . C. 20 3 . D. 10 39 .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 50 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.2 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 13.2. Nãn trô cÇu (thiÕt diÖn)
1) KHỐI NÓN KHI CẮT QUA TRỤC S . O
1.1. Cắt hình nón bởi mặt phẳng qua trục được
thiết diện là tam giác đều cạnh 2a. Tính thể tích của khối nón ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Cắt hình nón bởi mặt phẳng qua trục được S AB đều S AB vuông cân ở S.
thiết diện là tam giác vuông cân có cạnh
huyền bằng 3a. Tính thể tích khối nón ? h . . . . . . . . . . .
h . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) KHỐI NÓN KHI CẮT QUA ĐỈNH S.
2. Cho hình nón có chiều cao bằng 2. Cắt hình
nón bởi mặt phẳng qua đỉnh được thiết diện là
Thiết diện: . . . . . . . . . .
tam giác đều, diện tích bằng 4 3. Tính V ? ()
H là trung điểm . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d( , O (SAB)) . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ((SAB);(O)) . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) KHỐI TRỤ KHI CẮT QUA TRỤC OO .
3. Cắt một khối trụ bởi mặt phẳng qua trục, ta
Thiết diện là hình chữ nhật (hoặc hình vuông)
được thiết diện là một hình vuông ABCD có ABC ,
D với h . . . . . . . . . và r . . . ..
có cạnh bằng 4a. Tính V ? (T)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4) KHỐI TRỤ KHI CẮT SONG SONG TRỤC. 4. Cho hình trụ có chiều cao 8a. Cắt hình trụ song
song với trục và cách trục một khoảng 4 , a thiết Thiết diện: ABCD là
diện thu được là hình vuông. Tính
hình chữ nhật (hoặc hv) V ? (T)
M là trung điểm . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d(OO ,(P)) . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Pitago O AM r.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5) THIẾT DIỆN CỦA (P) VỚI MẶT CẦU (S). 5. Mặt phẳng (P) cắt khối cầu tâm I, bán kính bằng 13 và d( ,
O (P)) 5. Tìm bán kính cầu ?
Thiết diện: là đường tròn giao tuyến (H,r).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d(I,(P)) . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
R . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 51 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.2 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG
Câu 1. Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng a 2. Diện tích xung
quanh của hình nón đó bằng 2 2 A. a 3 B. a 2 3 2 2 2 C. a 2 D. a 2 6 3
Câu 2. Hình nón có thiết diện qua trục là tam giác đều cạnh 3a. Diện tích toàn phần của hình nón bằng 2 2 A. 27 a B. 9 a 4 4 C. 2 4 a . D. 2 9 a .
Câu 3. Cho khối trụ có đường cao gấp đôi bán kính đáy. Một mặt phẳng qua trục của khối trụ cắt khối
trụ theo thiết diện là hình chữ nhật có diện tích bằng 2
16a . Thể tích của khối trụ đã cho bằng A. 3 16 a . B. 3 4 a . C. 22 3 a . D. 16 3 a . 3 3
Câu 4. Cắt hình trụ (T) bởi một mặt phẳng đi qua trục của nó, ta được thiết diện là một hình vuông
cạnh bằng 7. Diện tích xung quanh của (T) bằng A. 49 B. 49 4 2 C. 98 . D. 49 .
Câu 5. Mặt phẳng (P) cắt khối cầu tâm O theo đường tròn có bán kính bằng 4cm và khoảng cách từ
O đến mặt phẳng (P) bằng 3cm. Bán kính R của mặt cầu bằng A. 3 3cm. B. 5cm. C. 3 2cm. D. 6cm.
Câu 6. Cho hình nón đỉnh S, đáy là hình tròn tâm ,
O bán kính, R 3cm, góc ở đỉnh hình nón là 120.
Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SA , B trong đó , A B thuộc
đường tròn đáy. Diện tích tam giác SAB bằng A. 2 3 3cm . B. 2 6 3cm . C. 2 6cm . D. 2 3cm .
Câu 7. Một khối trụ có bán kính đáy r 5, khoảng cách giữa hai đáy h 4. Mặt phẳng (P) song
song với trục cắt khối trụ theo một thiết diện là hình vuông. Khoảng cách từ trục đến (P) bằng A. 3. B. 41. C. 29. D. 21.
Câu 8. Cho hình trụ có chiều cao bằng 4 2. Cắt hình trụ đã cho bởi mặt phẳng song song với trục và
cách trục một khoảng bằng 2, thiết diện thu được có diện tích bằng 16. Diện tích xung quanh
của hình trụ đã cho bằng A. 24 2 . B. 8 2 . C. 12 2 . D. 16 2 .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 52 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.3 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 13.3. Nãn trô cÇu (thiÕt diÖn)
1) KHỐI NÓN KHI CẮT QUA TRỤC S . O
1.1. Cắt hình nón bởi mặt phẳng qua trục được
thiết diện là tam giác đều cạnh 3a. Tính thể tích của khối nón ?
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Cắt hình nón bởi mặt phẳng qua trục được S AB đều S AB vuông cân ở S.
thiết diện là tam giác vuông cân có cạnh
huyền bằng 4a. Tính thể tích khối nón ? h . . . . . . . . . . .
h . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2) KHỐI NÓN KHI CẮT QUA ĐỈNH S.
2. Cho hình nón có chiều cao bằng 4. Cắt hình
nón bởi mặt phẳng qua đỉnh được thiết diện là
Thiết diện: . . . . . . . . . .
tam giác đều, diện tích bằng 6 3. Tính V ? ()
H là trung điểm . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . d( , O (SAB)) . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ((SAB);(O)) . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3) KHỐI TRỤ KHI CẮT QUA TRỤC OO .
3. Cắt một khối trụ bởi mặt phẳng qua trục, ta
Thiết diện là hình chữ nhật (hoặc hình vuông)
được thiết diện là một hình vuông ABCD có ABC ,
D với h . . . . . . . . . và r .. .. . .
có cạnh bằng 2a. Tính V ? (T)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4) KHỐI TRỤ KHI CẮT SONG SONG TRỤC. 4. Cho hình trụ có chiều cao 4a. Cắt hình trụ song
song với trục và cách trục một khoảng 2 , a thiết Thiết diện: ABCD là
diện thu được là hình vuông. Tính
hình chữ nhật (hoặc hv) V ? (T)
M là trung điểm . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d(OO ,(P)) . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Pitago O AM r.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5) THIẾT DIỆN CỦA (P) VỚI MẶT CẦU (S). 5. Mặt phẳng (P) cắt khối cầu tâm I, bán kính bằng 10 và d( ,
O (P)) 6. Tìm bán kính cầu ?
Thiết diện: là đường tròn giao tuyến (H,r).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
d(I,(P)) . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
R . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 53 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 13.3 – K§D – Nãn trô cÇu (thiÕt diÖn)
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt BÀI TẬP ÁP DỤNG Câu 1. Cho hình nón ( )
có thiết diện qua trục là một tam giác vuông cân có diện tích bằng 9. Khối nón sinh bởi ( ) có thể tích bằng A. 6 . B. 3 . C. 9 . D. .
Câu 2. Cho hình nón có bán kính đáy bằng 2cm và thiết diện qua trục của hình nón đó là một tam giác
đều. Thể tích của khối nón đã cho bằng A. 16 3 3 cm . B. 8 3 3 cm . 3 3 C. 3 8 3cm . D. 3 16 3cm .
Câu 3. Một hình trụ có bán kính đáy bằng ,
a mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng 2
8a . Diện tích xung quanh của hình trụ bằng A. 2 4 a . B. 2 8 a . C. 2 16 a . D. 2 2 a .
Câu 4. Cắt một hình trụ (T) bởi một mặt phẳng qua trục của nó được thiết diện là hình vuông cạnh
2a. Diện tích toàn phần của (T) bằng A. 2 2 a . B. 2 4 a . C. 2 8 a . D. 2 6 a .
Câu 5. Cho mặt cầu (S) tâm I. Một mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi 8 ,
biết khoảng cách từ I đến mặt phẳng (P) bằng 3. Diện tích của mặt cầu bằng A. 25 . B. 100 . C. 75 . D. 50 .
Câu 6. Cho hình nón tròn xoay có chiều cao h 20cm, bán kính đáy r 25cm. Một thiết diện đi qua
đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là 12cm. Diện tích
của thiết diện đó bằng A. 2 500cm . B. 2 400cm . C. 2 300cm . D. 2 406cm .
Câu 7. Khi cắt khối trụ bởi một mặt phẳng song song với trục và cách trục của trụ một khoảng bằng
a 3 ta được thiết diện là hình vuông có diện tích bằng 2
4a . Thể tích của khối trụ bằng A. 3 7 7 a . B. 7 7 3 a . 3 C. 3 3 a . D. 3 8 a .
Câu 8. Cho hình trụ có chiều cao bằng 3 2. Cắt hình trụ bởi mặt phẳng song song với trục và cách trục
một khoảng bằng 1, thiết diện thu được có diện tích bằng 12 2. Diện tích xung quanh của hình trụ đã cho bằng A. 6 10 . B. 6 34 . C. 3 10 . D. 3 34 .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 54 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.1 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 14.1. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn
Tâm và bán kính R của đường tròn ngoại tiếp Tâm O và bán kính r của đường tròn nội tiếp 1. Hình vuông 1. Hình vuông Tâm: O AC B . D Tâm: O AC B . D Bán kính: Bán kính: M AC R AO r OM c¹nh 2 2 2. Hình chữ nhật 2. Tam giác đều Tâm: O AC B . D
Tâm: G là trọng tâm của tam giác Bán kính: ABC. Bán kính: AC R AO 2 AM c¹nh. 3 M r GM 3 6 3. Tam giác đều 3. Hình thoi
Tâm: G là trọng tâm của tam giác ABC. Tâm: O AC B . D Bán kính: Bán kính: O . AOB 2AM R AG c¹nh 3 r OH AB 3 3 4. Tam giác vuông 4. Tam giác vuông
Tâm: O là trung điểm của
Tâm: O là giao điểm của cạnh huyền BC. hai đường phân giác. Bán kính: b c a BC Bán kính: r R AO c¹nh huyÒn 2 2 2 BÀI TẬP ÁP DỤNG
Câu 1. Cho hình hộp chữ nhật ABC . D AB C D
có đáy là hình vuông cạnh a và cạnh bên bằng 2a.
Diện tích xung quanh của hình nón có đỉnh là tâm O của hình vuông AB C D và đáy là hình
tròn nội tiếp hình vuông ABCD bằng 2 A. a 17 B. 2 a 17. 2 2 C. a 17 D. 2 2 a 17. 4
Câu 2. Cho hình lập phương ABC . D AB C D
có cạnh bằng a. Một hình nón có đỉnh là tâm hình vuông AB C D
và có đường tròn đáy ngoại tiếp hình vuông ABCD. Diện tích xung quanh hình nón bằng 2 2 A. 3 a B. 2 a 3 2 2 2 C. 3 a D. 6 a 2 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 55 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.1 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 3. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh bằng 1.
Thể tích của khối trụ đó bằng A. B. 2 4 C. . D. 3
Câu 4. Cho hình hộp chữ nhật ABC . D AB C D có AB 2 ,
a AD 3a và AA 4a. Thể tích của
khối trụ ngoại tiếp hình hộp chữ nhật ABC . D AB C D bằng 3 A. 144 a B. 3 13 a . 13 C. 3 24 a . D. 3 13a .
Câu 5. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA 2a. Thể tích của khối
nón có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC bằng 3 3 A. a B. a 33 6 27 C. 3 a . D. 3 2 a .
Câu 6. Cho hình lăng trụ tam giác đều ABC.AB C
có độ dài cạnh đáy bằng a, chiều cao là h. Thể
tích của khối trụ ngoại tiếp hình lăng trụ bằng 2 A. a h B. 2 3 a h. 9 2 C. 2 a h. D. a h 3
Câu 7. Cho hình lăng trụ đứng ABC.AB C
có đáy là tam giác vuông cân tại , A AB a 2 và
AA a 6. Diện tích xung quanh hình trụ ngoại tiếp hình lăng trụ bằng A. 2 4 a 6. B. 2 4 a . C. 2 2 a 6. D. 2 a 6.
Câu 8. Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh của hình trụ có một đường
tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện. A. 16 2 B. 8 2 . 3 C. 16 3 D. 8 3 . 3
Câu 9. Cho hình chóp tứ giác đều S.ABCD có các cạnh đều bằng a 2. Thể tích khối nón có đỉnh S
và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD bằng S 2 3 A. 2 a B. 2 a 6 2 D A 3 C. 3 a . D. a M O 6 C B
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 56 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.2 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 14.2. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn
Tâm và bán kính R của đường tròn ngoại tiếp Tâm O và bán kính r của đường tròn nội tiếp 1. Hình vuông 1. Hình vuông
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
M Bán kính: . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 2. Hình chữ nhật 2. Tam giác đều
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . M 3. Tam giác đều 3. Hình thoi
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . 4. Tam giác vuông 4. Tam giác vuông
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho hình lập phương ABC . D AB C D
cạnh 2a. Thể tích khối nón có đỉnh là tâm hình vuông AB C D
và đáy là đường tròn nội tiếp hình vuông ABCD bằng A. 4 3 a . B. 1 3 a . 3 3 C. 2 3 a . D. 3 2 a . 3
Câu 2. Cho hình hộp chữ nhật ABC . D AB C D
có AB 6, AD 8, AA 12. Một hình nón có
đỉnh là tâm hình chữ nhật AB C D
và có đường tròn đáy ngoại tiếp hình chữ nhật ABCD.
Thể tích hình khối nón tương ứng bằng A. 125 . B. 175 2 C. 100 . D. 225 2
Câu 3. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh bằng
a 2. Thể tích của khối trụ đó bằng
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 57 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.2 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt 3 3 A. 2a B. 2a 6 2 3 3 C. 2a D. a 3 2
Câu 4. Thể tích của khối trụ ngoại tiếp hình lập phương có cạnh là a bằng 3 3 A. a B. a 6 2 3 C. 3 a . D. a 4
Câu 5. Cho tứ diện đều SABC cạnh a. Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy
là đường tròn ngoại tiếp tam giác ABC bằng 2 A. 3 a B. 3 2 a . 6 3 C. 2 a . D. 2 2 3 a . 3 Câu 6. a 3
Cho một khối lăng trụ tam giác đều có thể tích là
Thể tích của khối trụ ngoại tiếp lăng 2 trụ đã cho bằng 3 3 A. a . 3 B. 2 a . 3 3 3 3 3 C. a D. 2 a 3 3
Câu 7. Cho lăng trụ đứng ABC.AB C
có cạnh bên AA 2a. Tam giác ABC vuông tại A có cạnh
huyền BC 2a 3. Thể tích của khối trụ ngoại tiếp khối lăng trụ này bằng 3 3 A. 13 a B. 16 a 3 3 C. 3 6 a . D. 3 4 a .
Câu 8. Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng 3. Diện tích xung quanh của hình
trụ có một đường tròn đáy là đường tròn nội tiếp tam giác ABC và chiều cao bằng chiều cao
hình chóp S.ABC đỉnh S bằng A. 3 2. B. 8 3 . C. 16 2 D. 16 3 3 3
Câu 9. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a. Tam giác SAB có diện tích là 2 2a . Thể
tích của khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng S 3 3 A. a 7 B. a 15 4 24 D A 3 a 7 3 a 7 M C. D. O C B 7 8
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 58 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.3 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 14.3. Nãn trô cÇu ngo¹i tiÕp, néi tiÕp khèi ®a diÖn
Tâm và bán kính R của đường tròn ngoại tiếp Tâm O và bán kính r của đường tròn nội tiếp 1. Hình vuông 1. Hình vuông
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
M Bán kính: . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 2. Hình chữ nhật 2. Tam giác đều
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . M 3. Tam giác đều 3. Hình thoi
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . 4. Tam giác vuông 4. Tam giác vuông
Tâm: . . . . . . . . . . . . . . . .
Tâm: . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
Bán kính: . . . . . . . . . . . .
Bán kính: . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho hình hộp chữ nhật ABCD.AB C D
có đáy là hình vuông cạnh a và cạnh bên bằng 2a.
Diện tích xung quanh của hình nón có đỉnh là tâm O của hình vuông AB C D và đáy là hình
tròn nội tiếp hình vuông ABCD bằng 2 A. a 17 B. 2 a 17. 2 2 C. a 17 D. 2 2 a 17. 4
Câu 2. Cho hình lập phương ABCD.AB C D
có cạnh bằng a. Một hình nón có đỉnh là tâm hình vuông AB C D
và có đường tròn đáy ngoại tiếp hình vuông ABCD. Diện tích xung quanh hình nón bằng 2 2 A. 3 a B. 2 a 3 2 2 2 C. 3 a D. 6 a 2 2
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 59 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 14.3 – K§D – Nãn, trô, cÇu néi, ngo¹i tiÕp
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
Câu 3. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh bằng 1.
Thể tích của khối trụ đó bằng A. B. 2 4 C. . D. 3
Câu 4. Cho hình hộp chữ nhật ABCD.AB C D có AB 2 ,
a AD 3a và AA 4a. Thể tích của
khối trụ ngoại tiếp hình hộp chữ nhật ABCD.AB C D bằng 3 A. 144 a B. 3 13 a . 13 C. 3 24 a . D. 3 13a .
Câu 5. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên SA 2a. Thể tích của khối
nón có đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC bằng 3 3 A. a B. a 33 6 27 C. 3 a . D. 3 2 a .
Câu 6. Lăng trụ tam giác đều ABC.AB C
có cạnh đáy bằng a, cạnh bên bằng 3a và có hai đáy là
hai tam giác nội tiếp hai đường tròn đáy của hình trụ (T). Khi đó V ? (T) 3 A. 2 a 6 B. 3 3 a . 3 C. 3 a . D. 3 3 3 a .
Câu 7. Cho hình lăng trụ đứng ABC.AB C có A BC vuông cân tại , A AB a 2 và cạnh bên
BB a 6. Diện tích xung quanh hình trụ ngoại tiếp hình lăng trụ bằng A. 2 4 a 6. B. 2 4 a . C. 2 2 a 6. D. 2 a 6.
Câu 8. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng 4. Tính diện tích xung quanh
của hình trụ có một đường tròn đáy là đường tròn nội tiếp tứ giác ABCD và chiều cao bằng
chiều cao hình chóp S.ABCD đỉnh S. A. 8 2 . B. 16 2 3 C. 16 3 . D. 23 3 3
Câu 9. Cho hình lăng trụ đều ABC.AB C
có cạnh đáy bằng a, cạnh bên bằng 2a. Thể tích của hình
trụ có hai đáy nội tiếp hình lăng trụ bằng 3 A. a B. 3 a . 18 3 3 C. a D. a 12 6
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 60 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.1 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 15.1. MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Học sinh cần nhớ: Mặt cầu S(I;R) ngoại tiếp hình chóp S.ABC là mặt cầu đi qua các đỉnh của
hình chóp, tức tâm I cách đều các đỉnh S, , A , B C
hay IS IA IB IC R . c
1. Hình chóp có cạnh bên vuông góc đáy
1) Hình chóp có cạnh bên vuông góc đáy 2 2 ( R R chiÒu cao) .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trong đó R là bán c c 1 4 1
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
kính đường tròn ngoại tiếp đáy.
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
chóp S.ABC có ABC đều cạnh a, SA 2a
chóp S.ABC có đáy ABC là tam giác vuông và SA (ABC). cân tại , A BC 2 , a SA (ABC), SA 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. Ta có BC R a. 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 SA R R a 2. c 1 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Hình chóp có mặt bên vuông với đáy
2) Hình chóp có mặt bên vuông với đáy 2 2 2 (
R R R giao tuyÕn) .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Trong đó c c 1 2 4
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
R , R là bán kính đường tròn ngoại tiếp đáy 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . và mặt bên.
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
chóp S.ABCD có đáy là hình chữ nhật, với
chóp S.ABCD có đáy là hình vuông cạnh a, AB , a BC 2 ,
a mặt bên SAB là tam giác
mặt bên SAB là tam giác đều và vuông đáy.
vuông cân tại S và vuông góc với mặt đáy. Giải. AC a 2 R R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 ABCD 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2SM 2 a 3 a 3 R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 2 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 AB R R R a 21 c 1 2 4 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3. (c¹nh bªn) Hình chóp đều: R
3) Hình chóp đều: R . . . . . . . . . . . . . . . . . . . . . c 2chiÒu cao c
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
chóp tam giác đều có cạnh đáy bằng a và cạnh
chóp tứ giác đều có cạnh đáy bằng a, cạnh bên
đáy gấp đôi cạnh đáy. gấp đôi cạnh đáy.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. Ta có a 3 AG 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 a 33 SG SA AG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 SA 2a 33 R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c 2.SG 11
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 61 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.1 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
4. Lăng trụ, hình hộp chữ nhật và lập phương
4) Lăng trụ, hình hộp chữ nhật và lập phương
Tâm của mặt cầu là trung điểm của OO với
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , O O
là tâm ngoại tiếp của hai đáy. Bán kính
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
là R IA IB IC . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp lăng
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
trụ tam giác đều có cạnh đáy a, cạnh bên 2a.
lăng trụ đứng ABC.AB C
có đáy là tam giác Giải. 2 2 R IA IG AG ( ) vuông cân tại , A BC 2a và AA 3a. c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GG AA 2a IG a. 2 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 a 3 AG AM 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . () 2 a 3 2a 3 R a c 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB 3 ,
a BC 4a, SA 12a và SA
vuông góc với đáy. Bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. 4a. B. 6a. C. 13a D. 17a 2 2
Câu 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại .
A Tam giác SAB vuông tại S
và nằm trong mặt phẳng vuông góc với đáy và AB a. Thể tích của khối cầu ngoại tiếp hình chóp S.ABC bằng 3 3 A. a . B. a 2 . 3 3 C. 3 5a 2 . D. 3 2a 2 .
Câu 3. Cho hình chóp tam giác đều có cạnh đáy bằng 6 và chiều cao h 1. Diện tích của mặt cầu
ngoại tiếp của hình chóp đó bằng A. 9 . B. 6 . C. 5 . D. 27 .
Câu 4. Cho khối cầu ngoại tiếp khối hộp chữ nhật có ba kích thước lần lượt là , a 2 , a 2a. Thể tích của khối cầu bằng A. 3 36 a . B. 3 18 a . 2 3 C. 9 a D. 9 a 2 2
Câu 5. Cho khối lăng trụ đứng tam giác ABC.AB C
có đáy ABC là tam giác vuông tại A và AB , a
AC a 3, AA 2a. Bán kính của mặt cầu ngoại tiếp khối lăng trụ đó bằng A. a 2 B. a 5 2 2 C. a 2. D. 2a 2.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 62 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.2 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 15.2. MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Học sinh cần nhớ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Hình chóp có cạnh bên vuông góc đáy
1) Hình chóp có cạnh bên vuông góc đáy
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c c
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
chóp S.ABC có đáy ABC là tam giác vuông
chóp S.ABCD có đáy là hình vuông cạnh 2a, cân tại , A BC 2 , a SA (ABC), SA 2a. SA (ABCD) và SA 2a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. Ta có BC R a. 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 SA R R a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c 1 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Hình chóp có mặt bên vuông với đáy
2) Hình chóp có mặt bên vuông với đáy
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c c
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm diện tích mặt cầu ngoại tiếp chóp
chóp S.ABCD có đáy là hình vuông cạnh a,
S.ABC có đáy là tam giác đều cạnh a, mặt
mặt bên SAB là tam giác đều và vuông đáy.
bên là tam giác vuông cân tại S và vuông đáy.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. AC a 2 R R 1 ABCD 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2SM 2 a 3 a 3 R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 2 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 AB R R R a 21 c 1 2 4 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. Hình chóp đều: R . . . . . . . . . . . . . . . . . . . . . 3) Hình chóp đều: R . . . . . . . . . . . . . . . . . . . . . c c
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm thể tích khối cầu ngoại tiếp hình
chóp tam giác đều có cạnh đáy bằng a và cạnh
chóp tứ giác đều có cạnh đáy bằng 2a, mặt bên
đáy gấp đôi cạnh đáy.
tạo với mặt đáy một góc 45. Giải. Ta có a 3 AG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 a 33 SG SA AG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2 SA 2a 33
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . R c 2.SG 11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 63 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.2 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
4. Lăng trụ, hình hộp chữ nhật và lập phương
4) Lăng trụ, hình hộp chữ nhật và lập phương
Tâm của mặt cầu là trung điểm của OO với
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , O O
là tâm ngoại tiếp của hai đáy. Bán kính
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
là R IA IB IC ... .. .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp lăng
Ví dụ. Tìm thể tích khối cầu ngoại tiếp hình
trụ tam giác đều có cạnh đáy a, cạnh bên 2a.
lăng trụ đứng có đáy là tam giác vuông tại , A Giải. 2 2 R IA IG AG ( ) AB , a BC 2a và AA 2a. c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GG AA 2a IG a. 2 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 a 3 AG AM 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . () 2 a 3 2a 3 R a c 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho tứ diện OABC có O , A O ,
B OC đôi một vuông góc nhau và OA , a OB 2 , a OC 3a.
Diện tích S của mặt cầu ngoại tiếp tứ diện OABC bằng A. 2 8 a . B. 2 14 a . C. 2 12 a . D. 2 10 a .
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB , a AD 2a. Mặt bên SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Bán kính R của mặt
cầu ngoại tiếp hình chiếu hình chóp S.ABCD bằng A. 2a 2 B. 3a 2 3 2 C. 3a 3 D. 2a 3 2 3
Câu 3. Diện tích của mặt cầu ngoại tiếp hình tứ diện đều cạnh a bằng 2 2 A. 3 a B. 3 a 4 2 C. 2 6 a . D. 2 3 a .
Câu 4. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 3 2 ,
a cạnh bên bằng 5a. Bán kính của
mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. a 3. B. a 2. C. 25a D. 2a. 8
Câu 5. Cho hình lăng trụ đứng ABC.AB C
có đáy là tam giác vuông cân tại , A biết AB AC , a
AA 2a. Thể tích khối cầu ngoại tiếp hình tứ diện AB A C bằng 3 3 A. a B. 4 a 3 3 C. 3 a . D. 3 4 a .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 64 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.3 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
PhiÕu 15.3. MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Học sinh cần nhớ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Hình chóp có cạnh bên vuông góc đáy
1) Hình chóp có cạnh bên vuông góc đáy
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c c
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
chóp S.ABC có đáy ABC là tam giác vuông
chóp S.ABC có đáy là tam giác vuông tại , A cân tại , A BC 2 , a SA (ABC), SA 2a.
AB a, AC a 3, SA (ABC), SA a. Giải. Ta có BC R a.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 SA R R a 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c 1 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2. Hình chóp có mặt bên vuông với đáy
2) Hình chóp có mặt bên vuông với đáy
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c c
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Trong đó: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm diện tích mặt cầu ngoại tiếp hình
chóp S.ABCD có đáy là hình vuông cạnh a,
chóp S.ABCD có đáy là hình vuông cạnh 2a,
mặt bên SAB là tam giác đều và vuông đáy.
mặt bên SAB là tam giác đều và vuông đáy.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Giải. AC a 2 R R 1 ABCD 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2SM 2 a 3 a 3 R
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3 2 2 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 2 AB R R R a 21 c 1 2 4 6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. Hình chóp đều: R . . . . . . . . . . . . . . . . . . . . . 3) Hình chóp đều: R . . . . . . . . . . . . . . . . . . . . . c c
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp hình
Ví dụ. Tìm thể tích khối cầu ngoại tiếp hình
chóp tam giác đều có cạnh đáy bằng a và cạnh
chóp tứ giác đều có cạnh đáy bằng a 2, cạnh
đáy gấp đôi cạnh đáy.
bên tạo với đáy một góc 45 . Giải. Ta có a 3 AG
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 a 33 SG SA AG 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 SA 2a 33
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . R c 2.SG 11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 65 -
PhiÕu kh¶o bµi ®Çu giê – PhiÕu 15.3 – K§D – MÆt cÇu ngo¹i tiÕp khèi ®a diÖn
Nh÷ng bµi to¸n thêng gÆp trong kú thi Tn Thpt
4. Lăng trụ, hình hộp chữ nhật và lập phương
4) Lăng trụ, hình hộp chữ nhật và lập phương
Tâm của mặt cầu là trung điểm của OO với
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , O O
là tâm ngoại tiếp của hai đáy. Bán kính
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
là R IA IB IC .........
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ví dụ. Tìm bán kính mặt cầu ngoại tiếp lăng
Ví dụ. Tìm diện tích mặt cầu ngoại tiếp hình
trụ tam giác đều có cạnh đáy a, cạnh bên 2a.
lập phương có cạnh bằng 3a. Giải. 2 2 R IA IG AG ( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . GG AA 2a IG a. 2 2 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 a 3 AG AM
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 ( ) 2 a 3 2a 3 R a
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . c 3 3
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . BÀI TẬP ÁP DỤNG
Câu 1. Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, ba cạnh S , A S , B SC đôi một
vuông góc với nhau và SA 3, SB 3, SC 5. Diện tích của mặt cầu bằng A. 2 43 . B. 43 . C. 59 D. 59 2 2
Câu 2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAB là tam giác đều mà (SAB) vuông
góc với (ABCD). Thể tích của khối cầu ngoại tiếp S.ABCD bằng A. 7 24 3 a . B. 5 30 3 a . 24 27 C. 2 3 a . D. 7 21 3 a . 3 54
Câu 3. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Biết góc tạo bởi cạnh bên và mặt đáy bằng
60. Bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD bằng A. a 6 B. 5a 3 3 12 C. 5a 3 D. 2a 6 6 3
Câu 4. Cho hình lăng trụ tam giác đều ABC.AB C
có độ dài cạnh đáy bằng a và chiều cao bằng 2a.
Thể tích của khối cầu ngoại tiếp hình lăng trụ ABC.AB C bằng 3 3 A. 32 3 a B. 32 3 a 27 9 3 3 C. 8 3 a D. 32 3 a 27 81
Câu 5. Đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng a 3 bằng A. 6a. B. 2a. C. a 3. D. 3a.
Biªn so¹n & gi¶ng d¹y: Ths. Lª V¨n §oµn – 0933.755.607 – 0929.031.789 Trang - 66 -




