PHONG-TỎA-TOÁN-THỰC-TẾ-ÔN-THI-HỌC-KỲ-1

HỆ THỐNG GIÁO DỤC EDUPRIME
TỔNG ÔN TOÁN THỰC TẾ HỌC KỲ 1 LỚP TOÁN THẦY CHINH
PAGE : LỚP TOÁN THẦY CHINH
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Dân số Nam Định năm 2022 là 1.876.854 người. Theo thống kê trung bình mỗi năm dân số Nam
Định tăng khoảng 2,2% so với năm trước. Dự kiến dân số Nam Định năm 2032 là A. 2.331.053 người. B. 2.289.762 người. C. 2.333.133 người. D. 2.200.000 người.
Câu 2. Một công ty xây dựng mua một chiếc máy ủi với giá 5 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị
của chiếc máy ủi này lại giảm 15% so với giá trị của nó trong năm liền trước đó. Tìm giá trị còn lại của
chiếc máy ủi đó sau 10 năm sử dụng (làm tròn đến hàng phần nghìn với đơn vị tỉ đồng) A. 0,974 tỉ đồng. B. 0,985 tỉ đồng. C. 0,986 tỉ đồng. D. 0,984 tỉ đồng.
Câu 3. Một người gửi 10 triệu đồng vào một ngân hàng với lãi suất là 7% một năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng cứ sau một năm số tiền lại được nhập vào vốn ban đầu. Nếu người đó không rút
tiền ra và lãi suất ngân hàng không thay đổi thì sau 12 năm người đó nhận được số tiền gần nhất với số tiền nào sau đây? A. 21,2 triệu đồng. B. 20,4 triệu đồng. C. 22,5 triệu đồng. D. 18,6 triệu đồng.
Câu 4. Bác An gửi Ngân hàng 100 triệu đồng với lãi suất 5,05% trên 1 năm, sau mỗi năm tiền lãi nhập
vào tiền vốn cho năm sau (lãi kép). Hỏi nếu bác An không rút lãi và gốc thì sau 5 năm bác An rút về được bao nhiêu tiền? A. 127932322 đồng. B. 127930000 đồng. C. 127000000 đồng. D. 128000000 đồng.
Câu 5. Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày. Tính khối lượng còn lại của 10
gam poloni 210 sau 1380 ngày. A. 4,8828125. 10 gam. B. 9,765625. 10 gam. C. 0,01953125 gam. D. 9,8828125.10 gam.
Câu 6. Cho ba số 2, −4 và 𝑥 theo thứ tự lập thành cấp số nhân. Giá trị của 𝑥 bằng A. −8. B. 8. C. 1. D. −1.
Câu 7. Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các
cạnh của tam giác đó là A. ; 1; . B. ; 1; . C. ; 1; . D. ; 1; .
Câu 8. Một cái thang có chiều dài thanh ngang của bậc cuối cùng đến bậc đầu lần lượt là
80𝑐𝑚, 76𝑐𝑚, 72𝑐𝑚, . . . ,36𝑐𝑚. Cái thang có bao nhiêu bậc? A. 8. B. 10. C. 12. D. 14.
Câu 9. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để làm.
Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ hai trở đi, giá của mỗi mét khoan
tăng thêm 50.000 đồng so với giá của mét khoan trước đó. Biết cần phải khoan sâu xuống 50 mét mới có
nước. Hỏi phải trả bao nhiêu tiên để khoan được giếng nước đó?
LỚP TOÁN THẦY CHINH, Trang 1/29 A. 4.000.000 đồng. B. 5.250.000 đồng. C. 4.245.000 đồng. D. 10.125.000 đồng.
Câu 10. Vào năm 2020, dân số của một thành phố là khoảng 1,2 triệu người. Giả sử mỗi năm dân số của
thành phố này tăng thêm khoảng 30 nghìn người. Hãy ước tính dân số của thành phố này vào năm 2030. A. 1,4 triệu người. B. 1,5 triệu người. C. 1,7 triệu người. D. 1,6 triệu người.
Câu 11. Bà chủ quán trà sữa 𝑋 muốn trang trí cho đẹp nên quyết định thuê nhân công xây một bức tường
bằng gạch với xi măng (như hình vẽ bên), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít
hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là
bao nhiêu viên? (hình ảnh dưới đây là hình ảnh minh họa hàng gạch dưới cùng có 5 viên) AnhvabiAnh1.hide A. 125250. B. 12550. C. 250500. D. 25250.
Câu 12. Độ cao các bậc cầu thang so với mặt sàn tầng 1 của một căn nhà theo thứ tự lập thành một cấp số
cộng với công sai 𝑑 = 16 cm, bậc thứ nhất có độ cao 𝑢 = 16 cm. Bậc thứ năm có độ cao so với mặt sàn tầng 1 bằng A. 21 cm. B. 80 cm. C. 96 cm. D. 64 cm.
Câu 13. Chiều cao (centimét) của một đứa trẻ 𝑛 tuổi (𝑛 ∈ ℕ∗) phát triển bình thường được cho bởi công
thức 𝑥 = 75 + 5(𝑛 − 1). (Nguồn: http://bibabo.vn). Một đứa trẻ phát triển bình thường có chiều cao năm 4 tuổi là A. 80 cm. B. 85 cm. C. 90 cm. D. 95 cm.
Câu 14. Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu ℎ(𝑚) của mực nước trong
kênh tính theo thời điểm 𝑡(ℎ) được cho bởi công thức ℎ = 3cos +
+ 12. Thời gian sớm nhất để
mực nước của kênh là cao nhất là khi nào? A. 𝑡 = 14(h). B. 𝑡 = 10(h). C. 𝑡 = 22(h). D. 𝑡 = 15(h).
Câu 15. Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu ℎ (m) của con kênh
tính theo thời gian 𝑡 (giờ) trong một ngày được cho bởi công thức: ℎ = cos + + 3. Thời điểm
mực nước của kênh cao nhất là A. 𝑡 = 16. B. 𝑡 = 13. C. 𝑡 = 15. D. 𝑡 = 14.
Câu 16. Số giờ có ánh sáng mặt trời của một thành phố 𝑋 ở vĩ độ 40∘ Bắc trong ngày thứ 𝑡 của năm
2015 được cho bởi hàm số 𝑦 = 2sin
(𝑡 − 70) + 13 với 𝑡 ∈ ℤ và 0 < 𝑡 ≤ 365. Thành phố 𝑋 có
đúng 11 giờ có ánh sáng mặt trời vào ngày thứ bao nhiêu trong năm? A. 340. B. 300. C. 180. D. 70.
Câu 17. Độ sâu ℎ (m) của mực nước ở một cảng biển vào thời điểm 𝑡 (giờ) sau khi thuỷ triều lên lần đầu
tiên trong ngày được tính xấp xỉ bởi công thức ℎ(𝑡) = 0,8 ⋅ cos0,5𝑡 + 5.
(Theo https://noc.ac.uk/files/documents/business/an-introduction-to-tidalmodelling.pdf) Một con tàu cần
mực nước sâu tối thiểu 4,6m để có thể di chuyển ra vào cảng an toàn. Hỏi có bao nhiêu thời điểm trong
vòng 12 tiếng sau khi thuỷ triều lên lần đầu tiên trong ngày tàu có thể hạ thuỷ. A. 1. B. 2. C. 4. D. 3.
LỚP TOÁN THẦY CHINH, Trang 2/29
Câu 18. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu ℎ (mét) của mực nước
trong kênh được tính tại thời điểm 𝑡 (giờ) trong một ngày bởi công thức ℎ = 4cos + + 14. Mực
nước của kênh cao nhất khi A. 𝑡 = 13 (giờ). B. 𝑡 = 14 (giờ). C. 𝑡 = 15 (giờ). D. 𝑡 = 12 (giờ).
Câu 19. Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu ℎ(𝑚) của mực nước trong
kênh tính theo thời gian 𝑡(ℎ) được cho bởi công thức ℎ = 3cos +
+ 12. Thời điểm gần nhất trong
ngày mà mực nước của kênh là cao nhất là A. 𝑡 = 22(ℎ). B. 𝑡 = 10(ℎ). C. 𝑡 = 14(ℎ). D. 𝑡 = 15(ℎ).
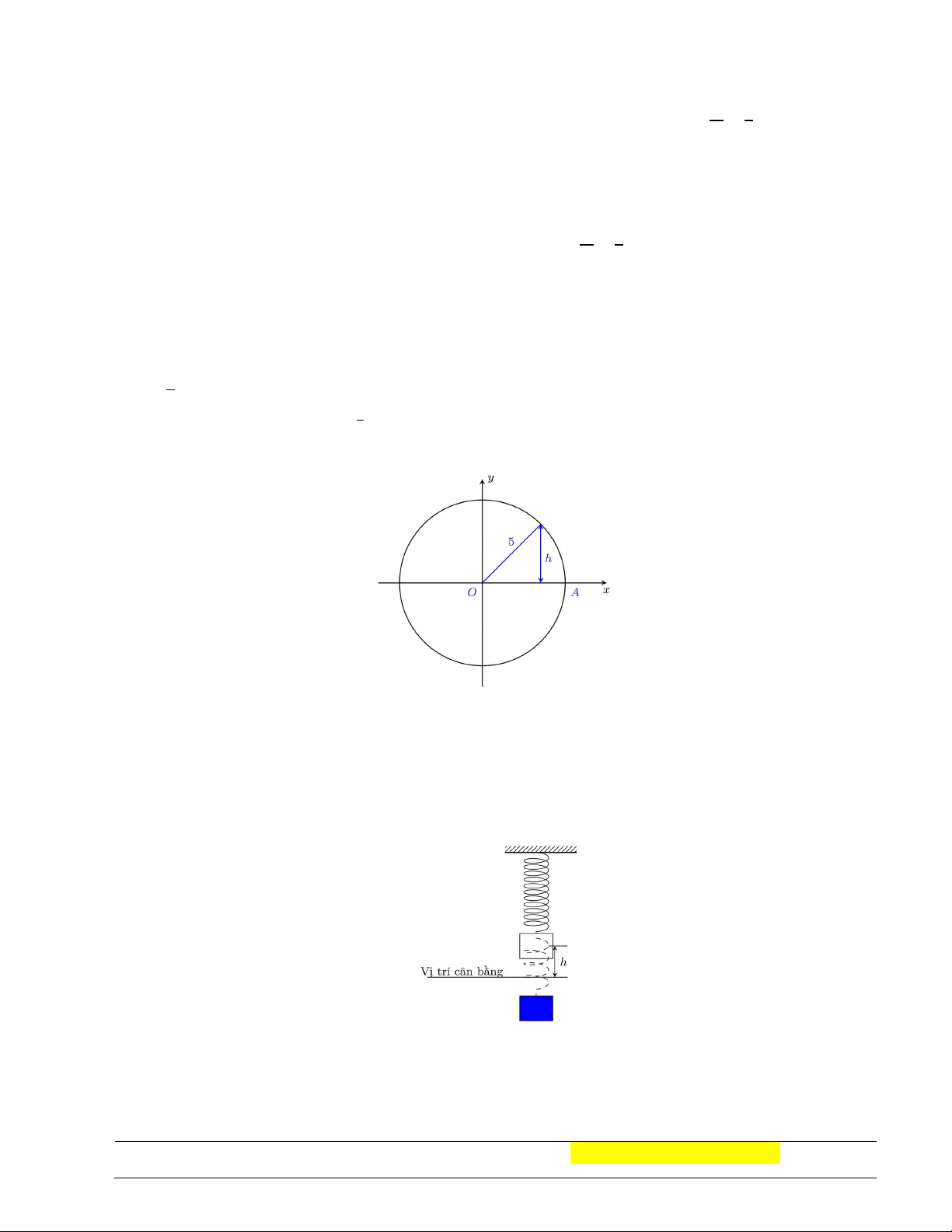
Câu 20. Một chất điểm chuyển động theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm.
Khoảng cách ℎ cm từ chất điểm đến trục hoành được tính theo công thức ℎ = |𝑦|, trong đó 𝑦 = 5sin
𝑡 với 𝑡 là thời gian chuyển động của chất điểm tính bằng giây (𝑡 ≥ 0) và chất điểm bắt đầu
chuyển động từ vị trí A. Khi 𝑡 = giây thì khoảng cách ℎ bằng A. ℎ = 2,5 cm. B. ℎ = 5 cm. C. ℎ = 2 cm. D. ℎ = 0,5 cm.
Câu 21. Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí cân bằng. Khoảng cách
ℎ từ vật đến vị trí cân bằng ở thời điểm 𝑡 giây được tính theo công thức ℎ = |𝑑| trong đó 𝑑 = 5sin6𝑡 −
4cos6𝑡 với 𝑑 được tính bằng centimet. Hỏi trong giây đầu tiên, có bao nhiêu thời điểm vật ở xa vị trí cân bằng nhất? A. 0. B. 4. C. 1. D. 2.
Câu 22. Hàng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu ℎ (mét) của mực nước
trong kênh tính theo thời gian 𝑡 (giờ) trong một ngày (0 ≤ 𝑡 ≤ 24) cho bởi công thức ℎ =
LỚP TOÁN THẦY CHINH, Trang 3/29 2sin 1 − 4sin
+ 12. Hỏi trong một ngày có bao nhiêu lần mực nước trong kênh đạt độ sâu 13 mét? A. 5 lần. B. 11 lần. C. 7 lần. D. 9 lần.
Câu 23. Trong dịp hội trại hè 2017 bạn An thả một quả bóng cao su từ độ cao 3 m so với mặt đất, mỗi lần
chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng đường quả
bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng A. 16 m. B. 14 m. C. 13 m. D. 9 m.
Câu 24. Trong dịp hội trại hè 2017 bạn A thả một quả bóng cao su từ độ cao 3 m so với mặt đất, mỗi lần
chạm đất quả bóng lại nảy lên một độ cao bằng hai phần ba độ cao lần rơi trước. Tổng quãng đường quả
bóng đã bay (từ lúc thả bóng cho đến lúc bóng không nảy nữa) khoảng: A. 15 m. B. 16 m. C. 13 m. D. 14 m.
Câu 25. Từ hình vuông đầu tiên có cạnh bằng 2 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có
hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông
thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem hình dưới). Kí hiệu 𝑆 là tổng diện
tích của 𝑛 hình vuông đầu tiên. Tìm lim𝑆 A. lim𝑆 = 8. B. lim𝑆 = 6. C. lim𝑆 = 4. D. lim𝑆 = 2.
Câu 26. Tại một nhà máy, người ta đo được 80% lượng nước sau khi sử dụng được xứ lí và tái sử dụng.
Với 6m ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xứ lí và tái sử dụng được lặp lại mãi
mãi, tổng lượng nước nhà máy cần xử lí và tái sử dụng là bao nhiêu lít? A. 3000 lít. B. 30 lít. C. 300 lít. D. 30000 lít.
Câu 27. Một tháp 12 tầng có diện tích sàn của tầng dưới cùng là 12288m . Biết rằng diện tích mặt sàn
mỗi tầng bằng nửa diện tích mặt sàn ngay bên dưới. Gọi 𝑎 là tổng diện tích mặt sàn của 12 tầng, 𝑏 là diện
tích mặt sàn tầng trên cùng. Giá trị của 𝑎 − 𝑏 bằng A. 12282. B. 12294. C. 24564. D. 24570.
Câu 28. Số giờ ánh sáng mặt trời của thành phố 𝐴 trong ngày thứ 𝑡 của 1 năm được cho bởi hàm số 𝑑(𝑡) = 3sin
(𝑡 − 80) + 12, 𝑡 ∈ ℤ, 0 < 𝑡 ≤ 365. Gọi 𝑇 là ngày trong năm mà thành phố 𝐴 có 9 giờ
ánh sáng mặt trời trong một ngày. Hỏi 𝑇 thuộc những tháng nào trong năm? A. Tháng 12. B. Tháng 12 và tháng 1. C. Tháng 2. D. Tháng 1 và tháng 11.
Câu 29. Trong hình bên khi được kéo ra khỏi vi trí cân bằng ở điểm 𝑂 và buông tay, lực đàn hồi của lò
xo khiến vật 𝐴 gắn ở đầu lò xo dao động quanh điểm 𝑂. Tọa độ 𝑠(cm) của 𝐴 trên trục 𝑂𝑥 vào thời điểm
𝑡(giây) sau khi buông tay được xác định bởi công thức 𝑠 = 5cos
. Thời điểm nào sau đây thì 𝑠 = 5cm?
LỚP TOÁN THẦY CHINH, Trang 4/29 A. 𝑡 = 25 giây. B. 𝑡 = 36 giây. C. 𝑡 = 20 giây. D. 𝑡 = 23 giây.
Câu 30. Mực nước cao nhất tại một cảng biển là 14 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều
xuống thấp thì mực nước thấp nhất là 10 m. Biết chiều cao của mực nước ℎ (m) theo thời gian 𝑡 (h)
(0 ≤ 𝑡 ≤ 24) được cho bởi công thức ℎ = 𝑎cos
𝑡 + 𝑏 với 𝑎, 𝑏 là các số thực dương cho trước. Tìm
thời điểm trễ nhất trong ngày khi chiều cao của mực nước là 12 m. A. 16ℎ. B. 18ℎ. C. 20ℎ. D. 21ℎ.
Câu 31. Hàng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu ℎ (m) của mực nước
trong kênh tính theo thời gian 𝑡 (giờ) trong một ngày 0 ≤ 𝑡 ≤ 24 cho bởi công thức ℎ = 3cos + 1 +
12. Tìm thời gian 𝑡 để độ sâu của mực nước là 9m.
A. 10,23 giờ và 22,23 giờ.
B. 4,09 giờ và 16,09 giờ.
C. 10,09 giờ và 22,09 giờ.
D. 9,09 giờ và 22,09 giờ.
Câu 32. Số giờ có ánh sáng Mặt trời của thành phố 𝐴 trong ngày thứ 𝑡 của năm 2023 được cho bởi hàm số 𝑦 = 4sin
(𝑡 − 60) + 10 với 𝑡 ∈ ℕ và 0 < 𝑡 ≤ 365. Vào ngày nào trong năm thì thành phố 𝐴 có
nhiều giờ có ánh sáng Mặt trời nhất? A. 30 tháng 5. B. 31 tháng 5. C. 29 tháng 5. D. 28 tháng 5.
Câu 33. Số giờ có ánh sáng mặt trời của một thành phố B trong ngày thứ 𝑡 (ở đây 𝑡 là số ngày tính từ
ngày 1 tháng giêng) của một năm không nhuận được mô hình hoá bỏi hàm số 𝐿(𝑡) = 12 + 2,83sin
(𝑡 − 80) , (𝑡 ∈ ℤ) và 0 < 𝑡 ≤ 365. Hỏi vào ngày nào trong năm thì thành phố B có ít giờ
ánh sáng mặt trời nhất?
A. Ngày thứ 352 của năm.
B. Ngày thứ 333 của năm.
C. Ngày thứ 353 của năm.
D. Ngày thứ 253 của năm.
Câu 34. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là 100000 đồng
và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30000 đồng so với giá của mét khoan ngay
trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu 20 mét lấy
nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu? A. 7400000 đồng. B. 7700000 đồng. C. 8000000 đồng. D. 15400000 đồng.
Câu 35. Chu vi của một đa giác là 158cm, số đo các cạnh của nó lập thành một cấp số cộng với công sai
𝑑 = 3cm. Biết cạnh lớn nhất là 44cm. Khi đó số cạnh của đa giác đó là A. 5. B. 4. C. 6. D. 3.
Câu 36. Ông 𝐴 dự định mua một cây đàn piano có giá 142 triệu đồng. Trong tháng đầu tiên, ông 𝐴 để
dành được 20 triệu đồng. Trong các tháng tiếp theo, mỗi tháng ông 𝐴 để dành hơn tháng trước 3 triệu
đồng. Hỏi ít nhất vào tháng thứ bao nhiêu thì ông 𝐴 mới có đủ tiền để mua cây đàn piano đó? A. 43. B. 40. C. 41. D. 42.
Câu 37. Độ cao các bậc cầu thang so với mặt sàn tầng 1 của một căn nhà theo thứ tự lập thành một cấp số
cộng với công sai 𝑑 = 16 cm, bậc thứ nhất có độ cao 𝑢 = 16 cm. Bậc thứ năm có độ cao so với mặt sàn tầng 1 bằng
LỚP TOÁN THẦY CHINH, Trang 5/29 A. 96 cm. B. 21 cm. C. 64 cm. D. 80 cm.
Câu 38. Số giờ ánh sáng mặt trời của nột thành phố B trong ngày thứ 𝑡 (ở đây 𝑡 là số ngày tính từ ngày 1
tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số 𝐿(𝑡) = 12 + 2,83sin (𝑡 −
80) , (𝑡 ∈ ℤ) và 0 < 𝑡 ≤ 365. Hỏi vào ngày nào trong năm thì thành phố B có ít giờ ánh sáng mặt trời nhất?
A. Ngày thứ 353 của năm.
B. Ngày thứ 253 của năm.
C. Ngày thứ 352 của năm.
D. Ngày thứ 333 của năm.
Câu 39. Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có
đường kính là 189 cm và bánh xe trước có đường kính là 90 cm. Hỏi khi xe chạy trên đoạn đường thẳng,
bánh xe sau lăn được 10 vòng thì xe đi được bao xa và bánh xe trước lăn được mấy vòng? A. 10. B. 21. C. 15. D. 20.
Câu 40. Độ sâu ℎ(m) của mực nước ở một cảng biển vào thời điểm 𝑡 (giờ) sau khi thuỷ triều lên lần đầu
tiên trong ngày được tính xấp xỉ bởi công thức ℎ(𝑡) = 0,8 ⋅ cos0,5𝑡 + 5. (Theo
https://noc.ac.uk/files/documents/business/an-introduction-to-tidalmodelling.pdf) Một con tàu cần mực
nước sâu tối thiểu 4,6m để có thể di chuyển ra vào cảng an toàn. Hỏi có bao nhiêu thời điểm trong vòng
12 tiếng sau khi thuỷ triều lên lần đầu tiên trong ngày tàu có thể hạ thuỷ? A. 1. B. 3. C. 4. D. 2.
Câu 41. Trên đồng hồ tại thời điểm đang xét kim giờ 𝑂𝐺 chỉ đúng số 3, kim phút 𝑂𝑃 chỉ đúng số 12. Số
đo góc lượng giác mà kim giờ quét được từ lúc xét đến khi kim phút và kim giờ gặp nhau lần đầu tiên bằng A. 𝛼 = . B. 𝛼 = − . C. 𝛼 = − . D. 𝛼 = − .
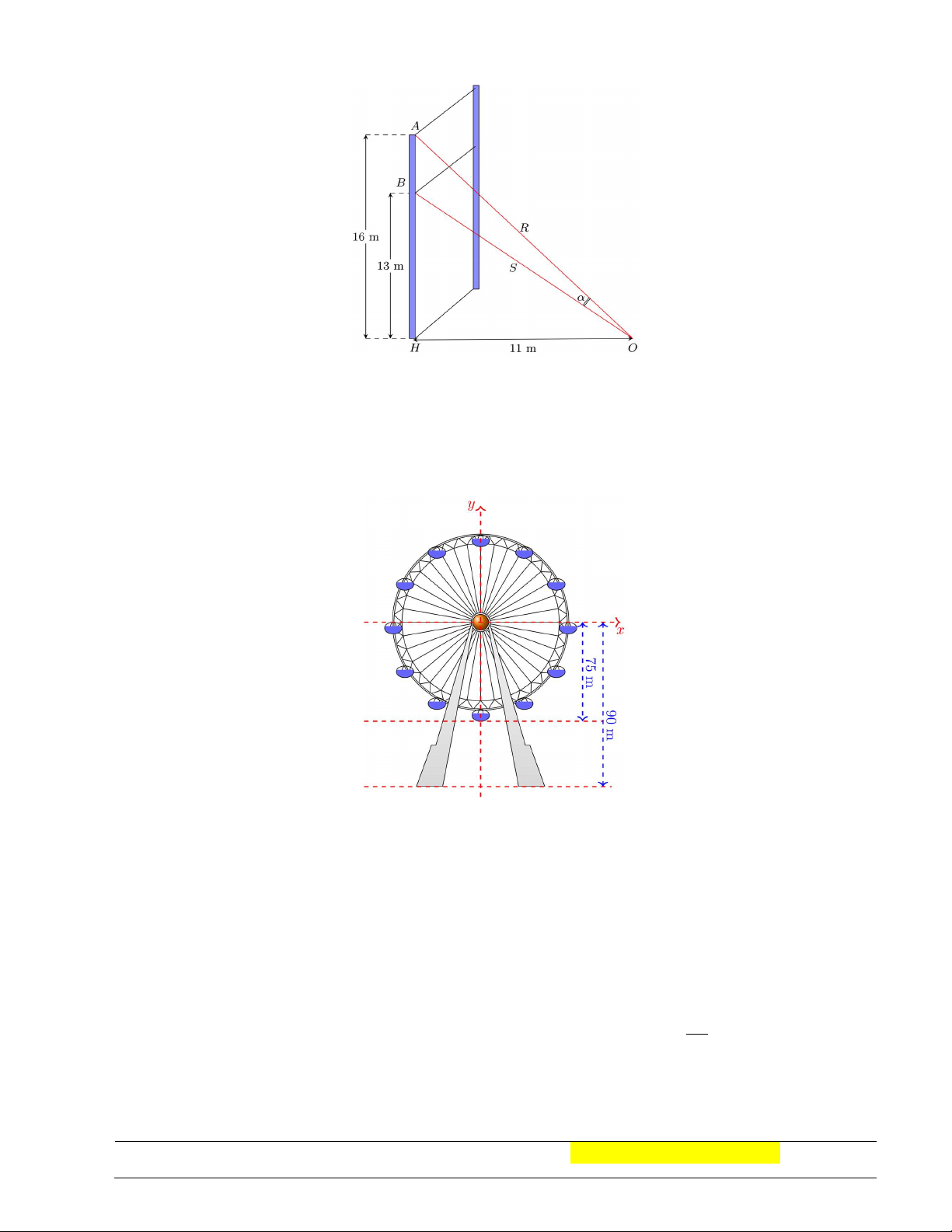
Câu 42. Một sợi cáp 𝑅 được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 16m. Một sợi cáp 𝑆 khác
cũng được gắn vào cột đó ở vị trí cách mặt đất 13m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất
tại một vị trí cách chân cột 11m (như hình vẽ). Tính số đo góc 𝛼 = 𝐴𝑂𝐵.
LỚP TOÁN THẦY CHINH, Trang 6/29 A. 7∘21″5″. B. 5∘43′40″. C. 6∘43′40″. D. 5∘21′54″.
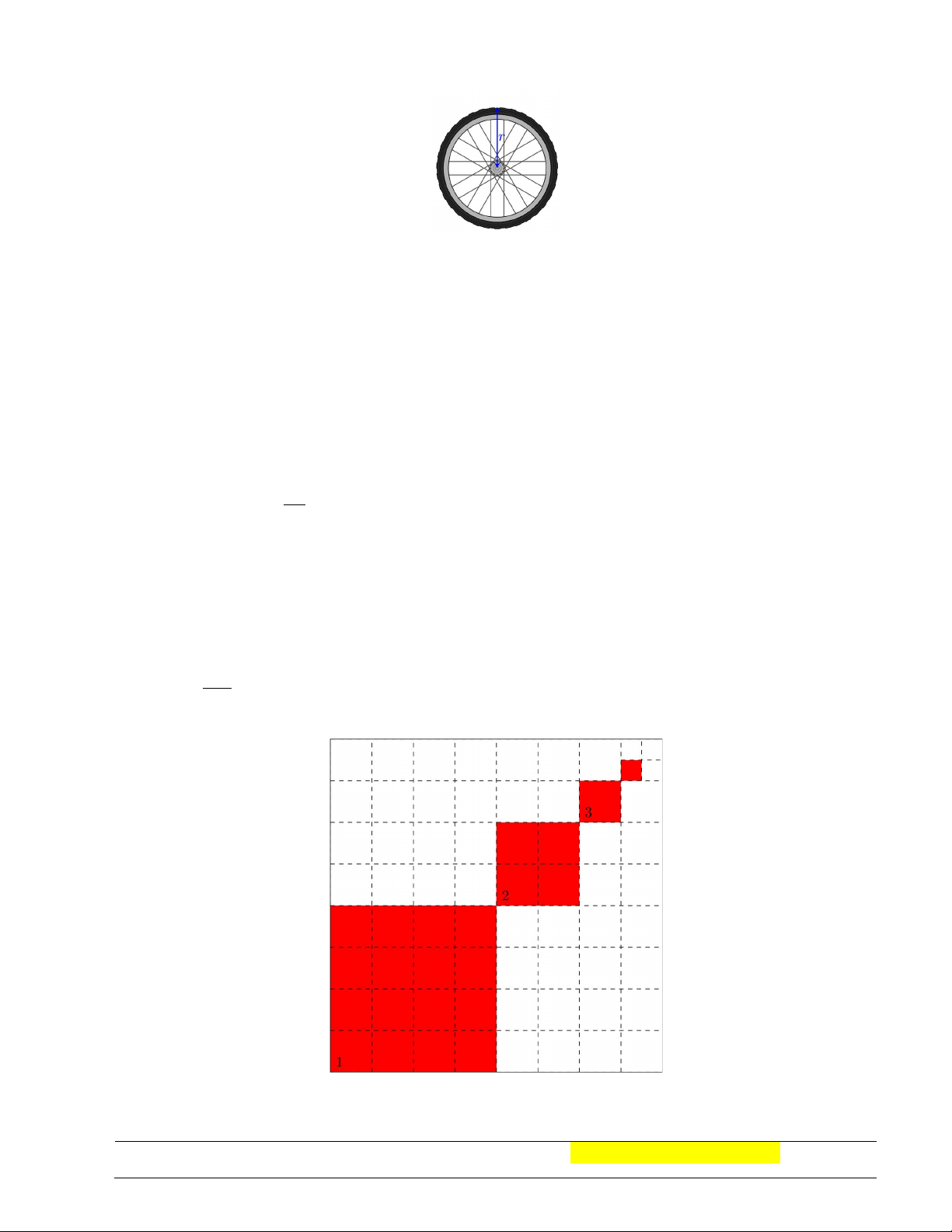
Câu 43. Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (tham khảo hình vẽ).
Thời gian quay hết 1 vòng của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng
quay thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? A. 155m. B. 75m. C. 165m. D. 127,5m.
Câu 44. Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho dân với theo hình
thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số thứ 11
đến số 20, bậc 3 từ số thứ 21 đến số thứ 30, … Bậc 1 có giá là 800 đồng/1 số, giá của mỗi số ở bậc thứ
𝑛 + 1 tăng so với giá của mỗi số ở bậc thứ 𝑛 là 2,5%. Gia đình ông A sử dụng hết 347 số trong tháng 1,
hỏi tháng 1 ông A phải đóng bao nhiêu tiền? (đơn vị là đồng, kết quả được làm tròn đến hàng phần trăm). A. 𝑥 ≈ 415481,84. B. 𝑥 ≈ 433868,89. C. 𝑥 ≈ 402832,28. D. 𝑥 ≈ 402903,08.
Câu 45. Người ta đo được trong 5 giây bánh xe của một xe gắn máy quay được vòng. Biết rằng
đường kính bánh xe gắn máy bằng $40\rm cm$, độ dài quãng đường xe gắn máy đã đi được trong vòng
40 phút gần nhất với kết quả nào sau đây (lấy 𝜋 = 3,1416)
LỚP TOÁN THẦY CHINH, Trang 7/29 A. $24{,}56\rm km$. B. $49{,}12\rm km$. C. $4912\rm km$. D. $2456\rm km$.
Câu 46. Trong giờ sinh hoat lớp ngày 16 tháng 10 năm 2023, lớp 11𝐴 lập ra kế hoạch quyên góp tiền để
chuẩn bi 52 phần ăn trưa cho các bệnh nhân ở bệnh viện Trưng Vương, mỗi phần trị giá 50.000 đồng với
kế hoạch thưc hiên như sau: Ngày hôm đó, tất cả hoc sinh đều thống nhất mỗi bạn bỏ 2.000 đồng vào heo
đất, từ ngày thứ hai trở đi mỗi bạn bỏ vào heo đất hơn ngày liền trước là 1.000 đồng. Biết rằng lớp 11𝐴
có sĩ số 40 học sinh, các thành viên trong lớp đều bỏ heo đất đều đặn theo kế hoạch đã thống nhất. Hỏi
vào ngày mấy thì tập thể lớp 11𝐴 có vừa đủ số tiền (không góp dư) để thực hiện kế hoạch từ thiện của mình. A. Ngày 24 tháng 10. B. Ngày 25 tháng 10. C. Ngày 26 tháng 10. D. Ngày 27 tháng 10.
Câu 47. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ 𝑡 của năm 2017 được cho bởi một hàm số 𝑦 = 4sin
(𝑡 − 60) + 10 với 𝑡 ∈ ℤ và 0 < 𝑡 ≤ 365. Vào ngày nào trong năm thì thành
phố A có nhiều giờ có ánh sáng mặt trời nhất? A. 31 tháng 5. B. 28 tháng 5. C. 29 tháng 5. D. 30 tháng 5.
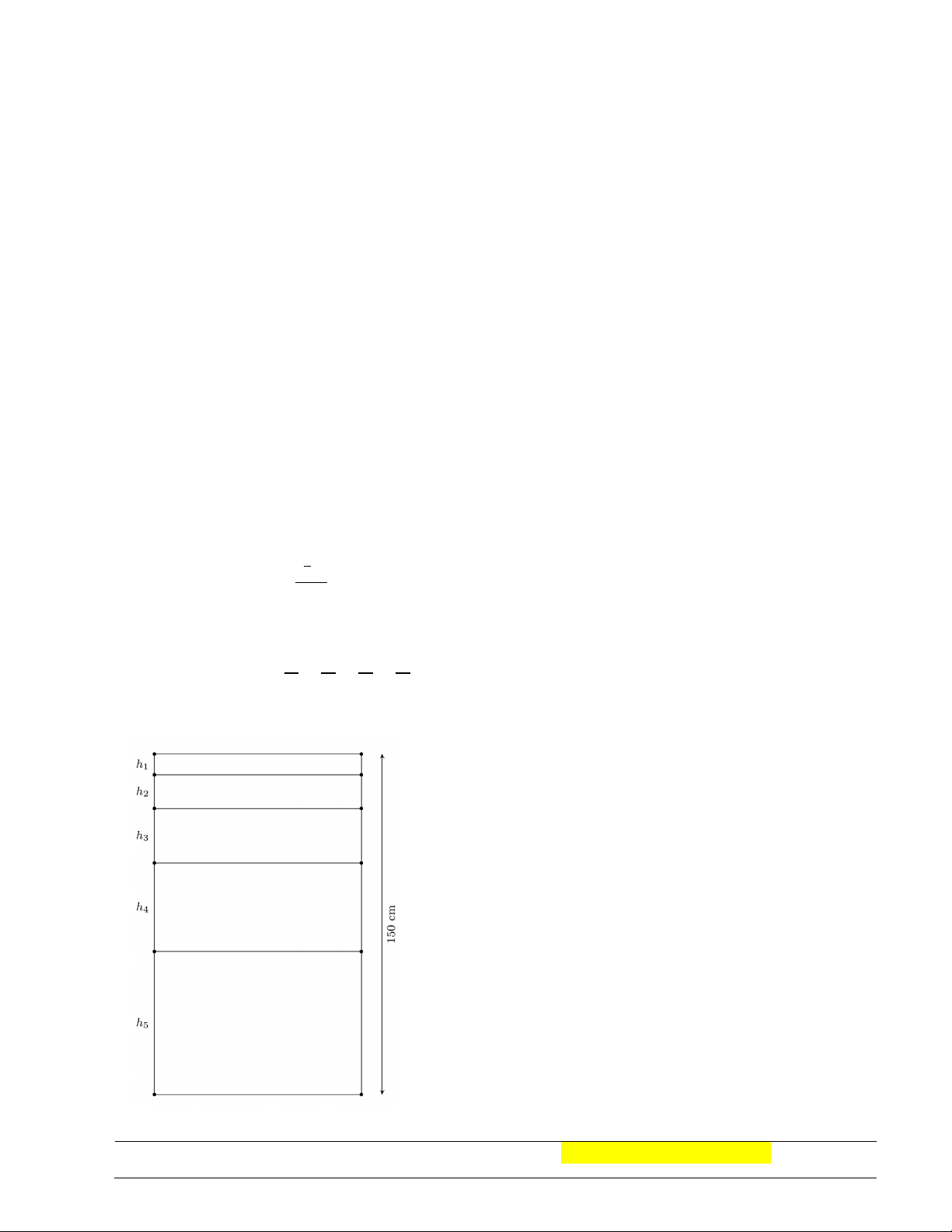
Câu 48. Để trang hoàng cho căn hộ của mình, bạn Việt quyết định tô màu một miếng bìa hình vuông
cạnh bằng 1. Bạn ấy tô màu đỏ các hình vuông nhỏ được đánh số lần lượt là 1,2,3, … , 𝑛, … trong đó cạnh
của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (hình vẽ). Giả sử quy trình tô màu của
Việt có thể tiến ra vô hạn. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô nhỏ hơn ? A. 3. B. 4. C. 5. D. Không tồn tại.
LỚP TOÁN THẦY CHINH, Trang 8/29
Câu 49. Có 1 kg chất phóng xạ độc hại. Biết rằng cứ sau một khoảng thời gian 𝑇 = 24000 năm thì một
nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe con người (𝑇 được
gọi là chu kì bán rã). Gọi 𝑢 là khối lượng chất phóng xạ còn lại sau chu kì thứ 𝑛. Cho biết chất phóng xạ
này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn 10 g. Trong các khẳng định
dưới đây, khẳng định nào đúng?
A. lim𝑢 = 0 và sau 720000 năm khối lượng chất phóng xạ không còn độc hại đối với con người.
B. lim𝑢 = 0 và sau 696000 năm khối lượng chất phóng xạ không còn độc hại đối với con người.
C. lim𝑢 = 0 và khối lượng chất phóng xạ không bao giờ hết độc hại đối với con người.
D. lim𝑢 = 0 và sau 30 năm khối lượng chất phóng xạ không còn độc hại đối với con người.
PHẦN II. Câu trắc nghiệm đúng sai
Câu 1. Anh Bình mua một chiếc ô tô mới trị giá 900 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị
còn lại của chiếc xe giảm đi 6\% so với năm ngay trước đó. Xét tính đúng sai của các khẳng định sau.
a) Giá trị còn lại của chiếc xe sau một năm sử dụng bằng 846 triệu đồng.
b) Gọi 𝑢 là giá trị còn lại của chiếc xe sau 𝑛 năm sử dụng (𝑛 ∈ ℕ∗) thì dãy số (𝑢 ) là một cấp số nhân.
c) Giá trị còn lại của chiếc xe sau 𝑛 năm sử dụng là 900 ⋅ (0,94) .
d) Giá trị còn lại của chiếc xe sau mười năm sử dụng xấp xỉ 484,754 triệu đồng.
Câu 2. Một bệnh nhân hằng ngày phải uống 150 mg thuốc kháng sinh đặc trị bệnh bạch hầu. Sau một
ngày bệnh nhân uống thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể vẫn còn 6% lượng thuốc của
ngày hôm trước. Xét tính đúng sai của các khẳng định sau.
a) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu còn trong cơ thể sau ngày đầu tiên uống thuốc là 9 mg.
b) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ 2 là 159 mg.
c) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ 4 là 170 mg.
d) Ước tính lượng thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể nếu bệnh nhân sử dụng thuốc
trong một thời gian 30 ngày là 159,57 mg.
Câu 3. Tục truyền rằng nhà Vua Ấn Độ cho phép người phát minh ra bàn cờ Vua được lựa chọn một
phần thưởng tùy theo sở thích. Người đó chỉ xin nhà Vua thưởng cho số thóc bằng số thóc được đặt lên
64 ô của bàn cờ vua như sau: Đặt lên ô thức nhất của bàn cờ một hạt thóc, tiếp đến ô thứ hai hai hạt,... cứ
như vậy, số hạt thóc ở ô sau gấp đôi số hạt thóc ở ô liền trước cho đến ô cuối cùng. Xét tính đúng sai của các khẳng định sau.
a) Ô thứ ba có 4 hạt thóc.
b) Gọi 𝑢 là số hạt thóc ở ô thứ 𝑛 thì dãy số (𝑢 ) là một cấp số nhân.
c) Số hạt thóc ở ô thứ 10 bằng 1024 hạt.
d) Số hạt thóc để làm phần thưởng là 2 − 1.
Câu 4. Một cái tháp có 11 tầng. Diện tích của mặt đáy tháp bằng 12288 (m ), kể từ mặt sàn tầng hai trở
đi, mỗi mặt sàn tầng trên có diện tích bằng một nửa diện tích của mặt sàn ngay trước nó. Gọi 𝑢 là diện
tích của mặt sàn tầng thứ 𝑛, (𝑛 ∈ ℕ, 1 ≤ 𝑛 ≤ 11). Xét tính đúng sai của các khẳng định sau.
a) Dãy số (𝑢 ) là một cấp số nhân với số hạng đầu là 12288 và công bội bằng .
b) Diện tích của mặt sàn tầng thứ ba là 376 (m ).
c) Diện tích của mặt sàn tháp trên cùng bằng 12 (m ).
d) Tổng diện tích tất cả các mặt sàn xấp xỉ bằng 24576 (m ).
LỚP TOÁN THẦY CHINH, Trang 9/29
Câu 5. Để trang trí cho một viên gạch lót nền hình vuông cạnh 𝑎 người ta làm như sau. Cho hình vuông
𝐻 có cạnh bằng 𝑎. Chia mỗi cạnh của hình vuông này thành bốn phần bằng nhau và nối các điểm chia
một cách thích hợp để có hình vuông 𝐻 có các đỉnh không trùng với trung điểm của hình vuông 𝐻 . Lặp
lại cách làm như trên với hình vuông 𝐻 để được hình vuông 𝐻 như hình vẽ dưới đây.
Tiếp tục quá trình trên ta nhận được dãy hình vuông 𝐻 , 𝐻 , 𝐻 , …, 𝐻 , … Gọi 𝑠 là diện tích của hình
vuông 𝐻 . Xét tính đúng sai của các khẳng định sau.
a) Khi 𝑎 = 2 thì tổng diện tích các hình vuông 𝐻 , 𝐻 bằng 6,5. b) Khi 𝑎 = 4 thì 𝑠 = .
c) Dãy các diện tích 𝑠 ; 𝑠 ; 𝑠 ; … ; 𝑠 ; … lập thành một cấp số nhân lùi vô hạn với công bội là 𝑞 = .
d) Khi 𝑎 = 2 thì tổng diện tích tất cả các hình vuông được tạo thành là .
Câu 6. Số giờ có ánh sáng mặt trời của một thành phố ven biển 𝐴 trong ngày thứ 𝑡 của một năm không
nhuận được cho bởi hàm số 𝑑(𝑡) = 3sin
(𝑡 − 70) + 10 với 𝑡 ∈ ℤ và 0 < 𝑡 ≤ 365. Cánh đồng muối
𝐵 (thuộc địa phận của thành phố 𝐴) có thể hoạt động nếu trong ngày nắng nhiều hơn 10 giờ. Xét tính
đúng sai của các khẳng định sau.
a) Ngày có nhiều giờ ánh sáng nhất là 13 giờ.
b) Số giờ có ánh sáng giảm liên tục trong tháng 7.
c) Cánh đồng muối B có thể hoạt động 213 ngày mỗi năm.
d) Ngày thứ 70 trong năm, thành phố có 10 giờ có ánh sáng.
Câu 7. Khi kí kết hợp đồng lao động với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau
+) Phương án 1: Năm thứ nhất, tiền lương là 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền
lương được tăng 20 triệu đồng.
+) Phương án 2: Quý thứ nhất, tiền lương là 24 triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý tiền lương
được tăng 2 triệu đồng.
Xét tính đúng sai của các khẳng định sau.
a) Với phương án 1, tiền lương người lao động nhận được ở năm thứ hai là 140 triệu đồng.
b) Với phương án 2, tổng số tiền lương người lao động nhận được ở năm thứ nhất là 106 triệu đồng.
c) Với phương án 1, để người lao động nhận được tổng số tiền lương trên 1 tỷ đồng thì người lao động
đó phải làm việc cho doanh nghiệp ít nhất 6 năm.
d) Nếu người lao động kí hợp đồng với doanh nghiệp 4 năm thì người lao động nên kí hợp đồng theo
phương án 1 để tổng tiền lương nhận được cao hơn.
Câu 8. Litva sẽ tham gia vào cộng đồng chung châu Âu sử dụng đồng Euro là đồng tiền chung vào ngày
01 tháng 01 năm 2015. Để kỷ niệm thời khắc lịch sử này, chính quyền đất nước này quyết định dùng
122550 đồng tiền xu Litas Lithuania cũ của đất nước để xếp một mô hình kim tự tháp. Biết rằng tầng
dưới cùng có 4901 đồng và cứ lên thêm một tầng thì số đồng xu giảm đi 100 đồng. Xét tính đúng sai của các khẳng định sau.
a) Theo nội dung mô tả trong đề bài, đồng tiền xu Litas Lithuania cũ xếp thành một mô hình kim tự
tháp, gồm n tầng, số đồng xu các tầng tạo thành cấp số cộng có số hạng đầu bằng 4901 (tầng dưới
cùng) và công sai bằng −100.
b) Tầng 40 của kim tự tháp trên có 2097 đồng xu.
c) Tổng số đồng xu được dùng để xếp cho 10 tầng đầu tiên (tính từ tầng dưới cùng) của kim tự tháp trên là 90097 đồng xu.
d) Mô hình Kim tự tháp này có tất cả 50 tầng.
Câu 9. Anh 𝑋 nhận hợp đồng làm việc cho một công ty 𝑌 với lương tháng đầu là 6 triệu. Trong điều
LỚP TOÁN THẦY CHINH, Trang 10/29
khoản về lương, nếu anh 𝑋 hoàn thành nhiệm vụ thì cứ sau 6 tháng được tăng 15% so với mức lương
trước đó. Trong suốt quá trình làm việc, anh 𝑋 đều hoàn thành nhiệm vụ của mình và được tăng lương đúng kỳ hạn.
a) Mức lương của anh 𝑋 ở tháng thứ 11 kể từ khi ký hợp đồng lao động là 6,9 triệu đồng.
b) Coi mỗi 6 tháng anh 𝑋 nhận lương như nhau là một kỳ và 𝑢 là lương mỗi tháng của kỳ thứ 𝑛, khi
đó (𝑢 ) là một cấp số cộng với công sai 𝑑 = 1,15.
c) Tổng số tiền anh 𝑋 nhận được từ tiền lương của công ty 𝑌 sau 4 năm kể từ ngày ký hợp đồng (làm
tròn đến hàng phần trăm) là 494,17 triệu đồng.
d) Khi nhận lương hàng tháng, nếu anh 𝑋 phải đóng bảo hiểm thất nghiệp 1,5% số tiền lương được
nhận thì sau 10 năm kể từ ngày ký hợp đồng anh 𝑋 đã đóng số tiền bảo hiểm thất nghiệp (làm tròn đến
hàng phần trăm) là 55,32 triệu đồng.
Câu 10. Hàng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Chiều cao ℎ(𝑚) của mực
nước theo thời gian 𝑡 (giờ) trong một ngày được cho bởi công thức ℎ = 14 + 8sin 𝑡 với 0 ≤ 𝑡 ≤ 24.
Xét tính đúng sai của các khẳng định sau.
a) Lúc 6 giờ sáng thì chiều cao của mực nước tại bến cảng là cao nhất.
b) Chiều cao của mực nước tại bến cảng thấp nhất vào lúc 12 giờ.
c) Mực nước tại bến cảng cao 18 (m) vào lúc 2 giờ và 10 giờ.
d) Biết tàu chỉ vào được cảng khi mực nước trong cảng không thấp hơn 18 (m). Vậy thời gian tàu vào
được cảng là từ 10 sáng hôm trước đến 2 giờ sáng hôm sau.
PHẦN III. Câu trắc nghiệm trả lời ngắn
Câu 1. Xác định số đo góc giữa kim giờ và kim phút vào lúc 1 giờ 0 phút. (Kết quả tính theo đơn vị độ và
làm tròn đến hàng đơn vị)
Câu 2. Tại một nhà máy, người ta đo được 90% lượng nước sau khi sử dụng được xứ lí và tái sử dụng.
Với 20 m ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xứ lí và tái sử dụng được lặp lại mãi
mãi, tổng lượng nước nhà máy cần xử lí và tái sử dụng là bao nhiêu m ?
Câu 3. Bạn Hoa thả quả bóng cao su từ độ cao 15 m so với mặt đất bằng phẳng theo phương thẳng đứng.
Mỗi lần chạm đất quả bóng lại nảy lên theo phương thẳng đứng với độ cao bằng độ cao lần rơi trước đó.
Biết tổng quãng đường quả bóng đi được từ lúc thả đến lúc quả bóng không nảy lên nữa là ℎ mét. Tìm giá
trị của ℎ. (Viết kết quả làm tròn đến chữ số thập phân hàng phần chục)
Câu 4. Giả sử số tiền gốc là 𝐴, lãi suất là 𝑟%/ kì hạn gửi (có thể là tháng, quý hay năm) thì tổng số tiền
nhận được cả gốc và lãi sau 𝑛 kì hạn gửi là 𝐴(1 + 𝑟) . Bà Hạnh gửi 100 triệu vào tài khoản định kỳ tính
lãi kép với lãi suất là 8%/ năm. Hỏi số tiền lãi thu được sau 8 năm là bao nhiêu triệu đồng? (Kết quả làm
tròn đến hàng đơn vị)
Câu 5. Một quần thể sinh vật có 3000 cá thể. Biết mỗi năm quần thể sinh vật đó tăng thêm 11% số lượng
cá thể. Hỏi sau 5 năm thì quần thể đó tăng thêm bao nhiêu cá thể? (Kết quả làm tròn đến hàng đơn vị)
(Làm tròn đến hàng phần chục)
Câu 6. Một bệnh nhân hàng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống,
hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng
thuốc trong một thời gian dài (kết quả làm tròn đến hàng đơn vị).
Câu 7. Anh Huy quyết định vay tín dụng ngân hàng để mua xe máy. Hợp đồng tín dụng giữa đại diện
ngân hàng và anh Huy có hai điều khoản sau: Tổng số tiền ngân hàng cho vay một lần là 20 triệu đồng;
thời hạn cho vay là 24 tháng tính từ ngày anh Huy nhận được khoản tiền vay trên. Lãi suất cho vay là
9\%/năm và không thay đổi trong suốt thời gian hợp đồng (là 24 tháng). Hỏi khi kết thúc hợp đồng, anh
Huy phải trả cho ngân hàng tổng cộng bao nhiêu tiền? (làm tròn đến hàng phần chục của triệu đồng)
LỚP TOÁN THẦY CHINH, Trang 11/29
Câu 8. Tỉ lệ vàng 𝜑 = √
là một khái niệm phổ biến trong toán học và có nhiều ứng dụng trong thực tế.
Trong thiết kế nội thất, người ta thường áp dụng tỉ lệ vàng để có được sự cân bằng hài hoà và tính thẩm
mĩ cao. Một người thợ mộc thiết kế một cái tủ đựng quần áo bằng gỗ như hình vẽ bên dựa vào tỉ lệ vàng
này. Biết rằng chiều cao của cái tủ này là 150𝑐𝑚 và nếu gọi ℎ , ℎ , ℎ , ℎ , ℎ (cm) là chiều cao các ngăn đựng quần áo thì = = =
= 𝜑. Hỏi chiều cao ℎ của ngăn đựng quần áo trên cùng bằng bao
nhiêu centimét (làm tròn kết quả đến hàng phần chục của đơn vị centimét).
Câu 9. Sau một tháng thi công, công trình xây dựng lớp học từ thiện cho học sinh vùng cao đã thực hiện
được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 tháng nữa công
trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp thời đưa vào sử dụng, đơn vị xây dựng quyết
định từ tháng thứ hai tăng 4% khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở
tháng thứ mấy sau khi khởi công?
Câu 10. {<}br/{>}Ông Sang đầu mỗi tháng đều đặn gửi tiết kiệm vào ngân hàng 10 triệu đồng với lãi
suất 0,4%/ tháng theo hình thức lãi kép (tức là sau mỗi tháng mà không rút tiền về thì tiền lãi của những
tháng trước đó được gộp vào tiền gốc để tính lãi cho tháng tiếp theo). Nếu sau 24 tháng kể từ ngày gửi
đầu tiên mà ông Sang rút tiền thì sẽ thu được tất cả gốc và lãi là bao nhiêu triệu đồng. (Kết quả làm tròn đến hàng đơn vị) {<}br/{>} {<}br/{>} {<}br/{>}
Câu 11. Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi, biết rằng sau 5 phút người ta đếm được có
64000 con. Hỏi sau bao nhiêu phút thì có được 2048000 con?
Câu 12. {<}br/{>}Ông Bình cần khoan một cái giếng sau nhà. Biết rằng giá của một mét khoan đầu tiên
là 200000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 8% so với giá của mét
khoan ngay trước đó. Hỏi nếu khoan 20 mét thì ông Bình phải trả số tiền là bao nhiêu nghìn đồng? (Kết
quả làm tròn đến hàng đơn vị) {<}br/{>} {<}br/{>} {<}br/{>}
Câu 13. Cho hình vuông 𝐶 có cạnh bằng 1. Gọi 𝐶 là hình vuông có các đỉnh là trung điểm các cạnh của
LỚP TOÁN THẦY CHINH, Trang 12/29
hình vuông 𝐶 ; 𝐶 là hình vuông có các đỉnh là trung điểm của các cạnh của hình vuông 𝐶 ;… Cứ tiếp tục
quá trình như trên, ta được dãy các hình vuông 𝐶 ; 𝐶 ; 𝐶 ; … ; 𝐶 ; … Diện tích của hình vuông 𝐶 có dạng . Tìm 𝑎.
Câu 14. Một quả bóng được thả thẳng đứng từ độ cao 10m rơi xuống đất và nảy lên. Giả sử sau mối một
lần rơi xuống, nó nảy lên được một độ cao bằng 75% độ cao vừa rơi xuống. Tính tổng quãng đường quả
bóng di chuyển được kể từ lúc thả xuống đến khi quả bóng chạm đất lần thứ 10 (làm tròn kết quả đến
hàng phần mười của mét).
Câu 15. Một tam giác đều có cạnh bằng 4 cm. Chia tam giác đều đó thành 4 tam giác đều bằng nhau và
tô màu tam giác ở trung tâm. Với mỗi tam giác nhỏ chưa được tô màu, lại chia thành 4 tam giác đều bằng
nhau và tô màu tam giác ở trung tâm (Hình 1). Cứ như thế, quá trình trên được lặp lại. Tính tổng diện tích
phần đã được tô màu ở hình tô thứ 5 (đơn vị: cm , làm tròn kết quả đến hàng phần trăm). Hình 1
Câu 16. Cho hình vuông 𝐶 có cạnh bằng 4cm. Người ta chia mỗi cạnh hình vuông 𝐶 thành bốn phần
bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông 𝐶 . Từ hình vuông 𝐶 lại làm tiếp
tục như trên để có hình vuông 𝐶 . Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông
𝐶 , 𝐶 , 𝐶 , … , 𝐶 , … như Hình 2. Tính diện tích của hình vuông thứ 6 (đơn vị: cm , làm tròn kết quả đến hàng phần trăm).
LỚP TOÁN THẦY CHINH, Trang 13/29
Câu 17. Ông Minh gửi số tiền 100 triệu đồng vào một ngân hàng với hình thức lãi kép kì hạn 12 tháng,
lãi suất 7%/năm. Giả sử trong khoảng thời gian gửi tiền, ông Minh không rút tiền ra và lãi suất không
thay đổi. Sau 10 năm, tổng số tiền cả vốn lẫn lãi mà ông nhận được là ≈ 𝑎9𝑏7𝑐5000 với 𝑎; 𝑏; 𝑐 là các số
tự nhiên và đơn vị: đồng, kết quả gần đúng đến hàng nghìn. Tính 𝑆 = 𝑎 + 𝑏 + 𝑐.
Câu 18. Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi
tam giác ở giữa bỏ đi1tam giác có diện tích .
Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại
bỏ đi3tam giác, mỗi tam giác có diện tích .
Cứ tiếp tục quá trình như vậy ở bước thứ𝑛, bỏ đi3
tam giác, mỗi tam giác có diện tích .
Tổng diện tích các tam giác đã bỏ đi bằng bao nhiêu? \par
Câu 19. Tỉ lệ vàng 𝜑 = √
là một khái niệm phổ biến trong toán học và có nhiều ứng dụng trong thực
tế. Trong thiết kế nội thất, người ta thường áp dụng tỉ lệ vàng để có được sự cân bẳng hài hòa và tính
thẩm mĩ cao. Một người thợ mộc thiết kế một cái tủ đựng quần áo bằng gỗ như hình vẽ bên dự vào tỉ lệ
vàng này. Biết rằng, chiều cao của cái tủ này là 150 cm và nếu gọi ℎ , ℎ , ℎ , ℎ , ℎ cm là chiều cao của
các ngăn đựng quần áo thì = = =
= 𝜑. Hỏi chiều cao ℎ của ngăn đựng quần áo trên cùng
LỚP TOÁN THẦY CHINH, Trang 14/29
bằng bao nhiêu xentimét (làm tròn kết quả đến hàng phần chục của đơn vị xentimét)?
Câu 20. Chỉ số giá tiêu dùng (hay được viết tắt là CPI), là chỉ số tính theo phần trăm để phản ánh mức
thay đổi tương đối của giá hàng tiêu dùng theo thời gian. Đây là chỉ tiêu được sử dụng phổ biến nhất để
đo lường mức giá và sự thay đổi của mức giá chính là lạm phát (theo Wikipedia). Ở Việt Nam, theo số
liệu của Tổng cục Thống kê, chỉ số giá tiêu dùng (CPI) năm 2023 tăng 3,25% so với năm trước. Giả sử
chỉ số giá tiêu dùng này không thay đổi trong các năm tiếp theo và giá của một mặt hàng A tại năm 2023
là 120 nghìn đồng/kg. Hỏi đến năm 2030, mặt hàng A này có giá là bao nhiêu nghìn đồng một kilogram
(kết quả làm tròn đến hàng đơn vị)? \par
Câu 21. Tỉ lệ tăng dân số mỗi năm của một tỉnh A từ năm 2010 đến năm 2019 là 0,4%. Vì thực hiện
chính sách về dân số nên tỉnh A dự kiến từ năm 2020 đến 2035 tỉ lệ tăng dân số mỗi năm chỉ còn lại
0,35%. Theo thống kê số dân tỉnh A năm 2021 nhiều hơn năm 2017 là 40500 người. Ước tính số dân
tỉnh A vào năm 2035 (làm tròn kết quả đến hàng nghìn) là bao nhiêu nghìn người?
Câu 22. Cho hình vuông 𝐶 có cạnh bằng 1. Gọi 𝐶 là hình vuông có các đỉnh là trung điểm các cạnh của
hình vuông 𝐶 ; 𝐶 là hình vuông có các đỉnh là trung điểm của các cạnh của hình vuông 𝐶 ;… Cứ tiếp tục
quá trình như trên, ta được dãy các hình vuông 𝐶 ; 𝐶 ; 𝐶 ; … ; 𝐶 ; … Diện tích của hình vuông 𝐶 có dạng . Tìm 𝑎.
Câu 23. Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số 11 đến số 20,\ldots
Bậc 1 có giá là 800 đồng/số, giá của mỗi số ở bậc thứ 𝑛 + 1 tăng so với giá của mỗi số ở bậc thứ 𝑛 là
2,5%. Gia đình ông An sử dụng hết 347 số trong tháng 1, hỏi số tiền điện ông An phải đóng trong tháng
1 là bao nhiêu tiền? (Kết quả tính theo đơn vị nghìn đồng và làm tròn đến hàng đơn vị)
Câu 24. Thẻ tín dụng ngân hàng cho phép người dùng chi tiêu trước và thanh toán sau. Giả sử vào ngày
15/8, chị Lan sử dụng thẻ tín dụng để thanh toán hóa đơn mua sắm quần áo tổng giá trị 8 triệu đồng. Chu
kỳ thanh toán là từ ngày 15/8 đến ngày 15/9 với mức lãi suất 22%/năm và phí giao dịch mua sắm qua
thẻ là 1,5%. Chị Lan chỉ thanh toán toàn bộ số tiền này vào ngày 20/9. Tính tổng chi phí mà chị Lan
phải trả cho ngân hàng sau khi thanh toán hóa đơn mua sắm là bao nhiêu nghìn đồng? (kết quả làm tròn đến hàng đơn vị).
Câu 25. Tình trạng nắng nóng, hạn hán, thiếu nước đã làm cho các hồ thủy điện ảnh hưởng nghiêm trọng,
nguồn điện sản xuất không đáp ứng đủ nhu cầu tiêu thụ của người dân. Nhằm muốn người dân tiết kiệm
điện, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo hình thức lũy tiến (bậc thang).
Mỗi bậc gồm 10 số điện (với 1 số điện bằng 1 kWh); bậc 1 từ số điện thứ 1 đến số điện thứ 10; bậc 2 từ
số điện thứ 11 đến số điện thứ 20; bậc 3 từ số điện thứ 21 đến số điện thứ 30; … Giá của mỗi số điện ở
bậc 1 là 1500 đồng/1 số điện, giá của mỗi số điện ở bậc thứ 𝑛 (𝑛 ∈ ℕ, 𝑛 ≥ 2) tăng 2,5 so với giá của mỗi
số điện ở bậc thứ 𝑛 − 1. Biết rằng trong tháng 1, gia đình ông Hưng sử dụng hết 330 số điện, hỏi gia đình
ông Hưng phải trả bao nhiêu tiền điện (đơn vị: nghìn đồng) trong tháng này (làm tròn kết quả đến hàng đơn vị)?
Câu 26. Thẻ tín dụng ngân hàng cho phép người dùng chi tiêu trước và thanh toán sau. Giả sử vào ngày
15/8, chị Lan sử dụng thẻ tín dụng để thanh toán hóa đơn mua sắm quần áo tổng giá trị 8 triệu đồng. Chu
kỳ thanh toán là từ ngày 15/8 đến ngày 15/9 với mức lãi suất 22%/năm và phí giao dịch mua sắm qua
thẻ là 1,5%. Chị Lan chỉ thanh toán toàn bộ số tiền này vào ngày 20/9. Tính tổng chi phí mà chị Lan
phải trả cho ngân hàng sau khi thanh toán hóa đơn mua sắm là bao nhiêu nghìn đồng? (kết quả làm tròn đến hàng đơn vị).
Câu 27. Tình trạng nắng nóng, hạn hán, thiếu nước đã làm cho các hồ thủy điện ảnh hưởng nghiêm trọng,
nguồn điện sản xuất không đáp ứng đủ nhu cầu tiêu thụ của người dân. Nhằm muốn người dân tiết kiệm
điện, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo hình thức lũy tiến (bậc thang).
Mỗi bậc gồm 10 số điện (với 1 số điện bằng 1 kWh); bậc 1 từ số điện thứ 1 đến số điện thứ 10; bậc 2 từ
số điện thứ 11 đến số điện thứ 20; bậc 3 từ số điện thứ 21 đến số điện thứ 30; … Giá của mỗi số điện ở
bậc 1 là 1500 đồng/1 số điện, giá của mỗi số điện ở bậc thứ 𝑛 (𝑛 ∈ ℕ, 𝑛 ≥ 2) tăng 2,5 so với giá của mỗi
LỚP TOÁN THẦY CHINH, Trang 15/29
số điện ở bậc thứ 𝑛 − 1. Biết rằng trong tháng 1, gia đình ông Hưng sử dụng hết 330 số điện, hỏi gia đình
ông Hưng phải trả bao nhiêu tiền điện (đơn vị: nghìn đồng) trong tháng này (làm tròn kết quả đến hàng đơn vị)?
Câu 28. Một người muốn gửi tiền vào ngân hàng để đến ngày 24/5/2028 rút được khoản tiền là 60 triệu
dồng (cả vốn ban đầu và lãi). Lãi suất ngân hàng là 6%/năm, tính theo thể thức lãi kép với kỳ hạn 1
tháng. Hỏi vào ngày 24/4/2025 người đó phải gửi ngân hàng số tiền là bao nhiêu triệu đồng để đáp ứng
nhu cầu trên, giả sử lãi suất không thay đổi trong thời gian người đó gửi tiền (làm tròn kết quả đến hàng đơn vị)?
Câu 29. Cuối mỗi tháng anh Bình đều gửi tiết kiệm 1 triệu đồng vào ngân hàng với lãi suất 8%/năm theo
phương thức tính lãi kép với kì hạn 1 tháng. Hỏi sau bao nhiêu tháng anh Bình có đủ 21 triệu đồng để
mua được một chiếc xe máy?
Câu 30. Trang trại 𝑋 dự trữ thức ăn cho cá, với mức tiêu thụ mỗi ngày không đổi như dự định thì lượng
thức ăn dự trữ đủ cho 90 ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng tiêu thụ thức ăn của cá tăng
thêm 1% so với ngày trước đó. Hỏi lượng thức ăn dự trữ của trang trại X thực tế chỉ đủ cho cá ăn trong bao nhiêu ngày?
Câu 31. Vào ngày 01/04/2023, ông An vay ngân hàng 300 triệu đồng với lãi suất 8%/năm. Ông dùng
toàn bộ số tiền vay mua cổ phiếu mã GK với giá 50 nghìn đồng/1 cổ phiếu. Đúng sau 2 năm, để trả nợ
ngân hàng ông An bán toàn bộ cổ phiếu đó với giá mỗi cổ phiếu là 59,5 nghìn đồng. Số tiền còn lại của
ông An sau khi đã trả nợ cho ngân hàng là bao nhiêu triệu đồng?
Câu 32. Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân
tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn trước đó. Lượng thuốc trong máu ở ngày thứ nhất
trong máu là 50 mg , và mỗi ngày sau đó giảm chỉ còn một nữa so với ngày kề trước đó. Tính tổng lượng
thuốc (tính bằng mg) đã được đưa vào trong máu của bệnh nhân khi dùng thuốc trong 10 ngày liên tiếp
(kết quả làm tròn đến hàng phần mười).
Câu 33. Một bà mẹ muốn cho con vào học một trường quốc tế sau khi tốt nghiệp THPT. Để chủ động
việc đóng học phí cho con, vào cùng một thời điểm mỗi năm trong 5 năm liển tiếp, bà mẹ gửi tiền vào
một tài khoản có lãi suất kép hàng năm. Các khoản tiền gửi lần lượt là 100 triệu đồng, 120 triệu đồng, 150
triệu đồng, 160 triệu đồng, 180 triệu đồng. Hỏi rằng sau lần gửi tiền cuối cùng, tổng số tiền trong tài
khoản là bao nhiêu biết lãi suất là 6% / năm? (kết quả làm tròn đến hàng triệu, đon vị là triệu đồng)?
Câu 34. Phương thức tính lãi kép là việc tính tiền lãi bằng cách lấy số tiền lãi của kì trước nhập vào vốn
để tính lãi cho kì tiếp theo. Tỉ lệ lạm phát được tính bằng tỉ lệ phần trăm sụ thay đổi giá của hàng hóa,
dịch vụ trong một khoảng thời gian (thường là một năm). Nếu tỉ lệ lạm phát của năm sau so với năm truớc
là i thì 𝐴 đồng của năm trước có giá trị tương đương với 𝐴(1 + 𝑖) đồng của năm sau. Một người đầu tư
bằng cách góp vốn 1 tỉ đồng vào công ty 𝑋 trong 2 năm với lãi suất không đổi 8% /năm theo phương thức
tính lãi kép. Giả sử trong 2 năm đó, tỉ lệ lạm phát mỗi năm lần lượt là 3,7% và 4,2%. Gọi 𝑎 (triệu đồng)
là số tiền cả vốn lẫn lãi người đó nhận được sau 2 năm đầu tư. Gọi 𝑏 (triệu đồng) là giá trị tương đương
của số tiền vốn 1 tỉ đồng sau 2 năm có tính đến yếu tố lạm phát. Tính giá trị của 𝑎 − 𝑏. (làm tròn kết quả đến hàng phần mười)
Câu 35. Cô Lan gửi 120 triệu đồng vào ngân hàng với kỳ hạn năm có lãi kép với lãi suất 6%/ năm. Sau 3
năm, cô rút ra 40 triệu để mua xe máy, và phần còn lại tiếp tục gửi và không rút ra cho đến khi được ít
nhất 150 triệu. Hỏi cô Lan cần gửi ngân hàng ít nhất bao nhiêu năm kể từ lần gửi đầu tiên?
Câu 36. Để tiết kiệm tiền sau này cho việc học đại học của con, cô Bình quyết định gửi 1,5 triệu đồng
cuối mỗi tháng vào ngân hàng với lãi suất mỗi tháng là 0,3% theo hình thức lãi kép. Cô bắt đầu gửi tiền
khi con cô tròn 3 tuổi. Cô Bình sẽ tiết kiệm được bao nhiêu tiền vào thời điểm con cô tròn 18 tuổi nếu cô
không rút lãi và lãi suất ngân hàng không thay đổi trong suốt quá trình gửi tiết kiệm? (Kết quả làm tròn
đến hàng đơn vị theo triệu đồng)
Câu 37. Lạm phát là sự tăng mức giá chung một cách liên tục của hàng hóa và dịch vụ theo thời gian, tức
là sự mất giá trị của một loại tiền tệ nào đó. Chẳng hạn, nếu lạm phát là 5% mỗi năm thì sức mua của 1
triệu đồng sau một năm chỉ còn là 950 nghìn đồng (vì đã giảm mất 5% của 1 triệu đồng, tức là 50000
LỚP TOÁN THẦY CHINH, Trang 16/29
đồng). Nếu tỉ lệ lạm phát là 7% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại bao
nhiêu? (số tiền tính theo triệu đồng và làm tròn đến hàng đơn vị)
Câu 38. Một người muốn gửi tiền vào ngân hàng để đến ngày 24/5/2028 rút được khoản tiền là 60 triệu
dồng (cả vốn ban đầu và lãi). Lãi suất ngân hàng là 6%/năm, tính theo thể thức lãi kép với kỳ hạn 1
tháng. Hỏi vào ngày 24/4/2025 người đó phải gửi ngân hàng số tiền là bao nhiêu triệu đồng để đáp ứng
nhu cầu trên, giả sử lãi suất không thay đổi trong thời gian người đó gửi tiền (làm tròn kết quả đến hàng đơn vị)?
Câu 39. Cuối mỗi tháng anh Bình đều gửi tiết kiệm 1 triệu đồng vào ngân hàng với lãi suất 8%/năm theo
phương thức tính lãi kép với kì hạn 1 tháng. Hỏi sau bao nhiêu tháng anh Bình có đủ 21 triệu đồng để
mua được một chiếc xe máy?
Câu 40. Anh Minh kí hợp đồng lao động có thời hạn ở một công ty với phương án trả lương như sau:
Quý thứ nhất, tiền lương là 27 triệu. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng 2,1 triệu.
Tổng số tiền lương anh nhận được trong các năm đã đi làm là 684 triệu đồng. Hỏi anh Minh đã làm ở
công ty đó bao nhiêu năm?
Câu 41. Anh Nam vay tiền ngân hàng 1 tỷ đồng theo phương thức trả góp với lãi suất 0,5\%/tháng. Nếu
cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Nam trả 30 triệu đồng. Hỏi sau bao nhiêu tháng anh Nam trả hết nợ?
Câu 42. Để đầu tư dự án trồng rau sạch theo công nghệ mới, bác Thảo đã làm hợp đồng xin vay vốn ngân
hàng số tiền là 500 triệu đồng với lãi suất 𝑟% (𝑟 < 0) cho kỳ hạn một năm. Điều kiện kèm theo của hợp
đồng là số tiền lãi năm trước sẽ được tính làm vốn để sinh lãi cho năm sau (theo thể thức lãi kép). Sau hai
năm thành công với dự án rau sạch của mình, bác đã thanh toán hợp đồng ngân hàng với số tiền là
599823000 đồng. Tính giá trị của 𝑟 (làm tròn kết quả đến hàng phần chục).
Câu 43. Tỉ lệ vàng 𝜑 = √
là một khái niệm phổ biến trong toán học và có nhiều ứng dụng trong thực
tế. Trong thiết kế nội thất, người ta thường áp dụng tỉ lệ vàng để có được sự cân bằng hài hoà và tính
thẩm mĩ cao. Một người thợ mộc thiết kế một cái tủ đựng quần áo bằng gỗ như hình vẽ bên dựa vào tỉ lệ
vàng này. Biết rằng chiều cao của cái tủ này là 150𝑐𝑚 và nếu gọi ℎ , ℎ , ℎ , ℎ , ℎ (cm) là chiều cao các ngăn đựng quần áo thì = = =
= 𝜑. Hỏi chiều cao ℎ của ngăn đựng quần áo trên cùng bằng
bao nhiêu centimét? (Làm tròn kết quả đến hàng phần chục của đơn vị centimét).
Câu 44. Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với lãi suất 0,5% /tháng theo hình thức lãi
LỚP TOÁN THẦY CHINH, Trang 17/29
kép. Sau khi gửi được 3 tháng, ông rút toàn bộ gốc và lãi rồi gửi tiếp số tiền đó với lãi suất 6% /năm cũng
theo hình thức lãi kép. Tổng số tiền ông An thu được sau 4 năm 3 tháng kể từ lúc bắt đầu tiết kiệm là bao
nhiêu triệu đồng (kết quả làm tròn đến hàng đơn vị)?
Câu 45. Dân số trung bình sơ bộ năm 2021 của tỉnh Hải Dương là 1936780 người, tăng 1,04% so với
năm 2020. Hỏi với tốc độ tăng dân số được duy trì mức 1,04% một năm thì đến năm bao nhiêu dân số
tỉnh Hải Dương lần đầu vượt 3041975 người
Câu 46. Trong điều kiện nuôi cấy thích hợp, cứ 20 phút vi khuẩn E.Coli lại phân đôi một lần. Giả sử lúc
đầu có 5 vi khuẩn và sau 𝑛 phút (𝑛 ∈ ℕ) có hơn 2.000 vi khuẩn. Giá trị nhỏ nhất của 𝑛 là bao nhiêu?
(làm tròn đến hàng đơn vị).
Câu 47. Một người gửi 60 triệu đồng vào ngân hàng với lãi suất 0,5%/tháng. Biết rằng nếu không rút tiền
ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (hay gọi là lãi kép). Giả
sử trong nhiều tháng liên tiếp kể từ khi gửi tiền, người đó không rút tiền ra và lãi suất không thay đổi. Hỏi
từ tháng thứ mấy trở đi, người đó có hơn 66 triệu đồng?
Câu 48. Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện
tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp
(có diện tích là 12288 m ). Tính diện tích mặt trên cùng.
Câu 49. Một siêu thị chạy chương trình khuyến mãi cho nước tăng lực có giá niêm yết là 9000 (đồng/lon) như sau:
• Nếu mua 1 lon thì không giảm giá.
• Nếu mua 2 lon thì lon thứ hai được giàm 500 đồng.
• Nếu mua 3 lon thì lon thứ hai được giàm 500 đồng và lon thứ ba được giảm giá 10%.
• Nếu mua trên 3 lon thì lon thứ hai được giảm 500 đồng, lon thứ ba được giảm 10% và những lon thứ tư
trở đi đều được giảm thêm 2% trên giá đã giảm của lon thứ ba.
Hòa phải trả 422500 đồng để thanh toán khi mua những lon nước tăng lực trên. Hòa đã mua bao nhiêu lon nước?
Câu 50. Một người muốn thuê khoan cái giếng sâu 32 (mét) nên đã tham khảo giá ở hai cơ sở khoan
giếng A và B. Cơ sở A, có giá mét khoan đầu tiên là 75 (nghìn đồng) và kể từ mét khoan thứ hai, giá của
mỗi mét sau tăng thêm 15 (nghìn đồng) so với giá của mét khoan ngay trước đó. Cơ sở B, giá của mét
khoan đầu tiên là 75 (nghìn đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 10%
so với giá của mét khoan ngay trước đó. Hỏi chênh lệch giá tiền ở hai cơ sở khoan giếng là bao nhiêu
nghìn đồng? (Kết quả làm tròn đến hàng đơn vị) (Làm tròn đến hàng phần chục)
Câu 51. Giá của một chiếc xe ô tô lúc mới mua là 950 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc
xe ô tô giảm 80 triệu đồng. Giá trị còn lại của chiếc xe sau 9 năm sử dụng là bao nhiêu triệu đồng. (Kết
quả làm tròn đến hàng đơn vị)
Câu 52. Ông Sơn trồng cây trên một mãnh đất hình tam giác theo quy luật: ở hàng thứ nhất có 1 cây, ở
hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây, {\dots}, ở hàng thứ 𝑛 có 𝑛 cây. Biết rằng ông đã trồng hết
11325 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
Câu 53. Trong sân vận động có tất cả 20 dãy ghế, dãy đầu tiên có 30 ghế, các dãy liền sau nhiều hơn dãy
trước 2 ghế, hỏi sân vận động đó có tất cả bao nhiêu ghế?
Câu 54. Người ta trồng 1275 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 2
cây, hàng thứ ba có 3 cây,\ldots , hàng thứ 𝑛 có 𝑛 cây. Người ta có thể trồng bao nhiêu hàng cây với cách trồng này?
Câu 55. Một cuộn túi nilon có dạng hình trụ gồm 105 túi nilon giống nhau nối tiếp liền nhau được cuốn
quanh một lõi rỗng hình trụ bán kính đáy của phần lõi là 𝑟 = 2,5 cm, bán kính đáy của cả cuộn nilon là
𝑅 = 4,20 cm. Biết độ dày mỗi túi nilon là 0,01 cm. Tính chiều dài mỗi túi nilon. (Kết quả tính theo đơn
vị mm và làm tròn đến hàng đơn vị)
Câu 56. Một Rạp hát có 1287 ghế ngồi được xếp thành nhiều hàng với số ghế tăng dần, hàng kề sau
nhiều hơn hàng trước 3 ghế. Biết số ghế ở hàng thứ 6 là 27 ghế. Tính tổng số ghế ở 7 hàng cuối của Rạp
LỚP TOÁN THẦY CHINH, Trang 18/29 hát. Câu 57.
Một Rạp hát có 1872 ghế ngồi được xếp thành nhiều hàng với số ghế tăng dần, hàng kề sau nhiều hơn
hàng trước 2 ghế. Biết số ghế ở hàng thứ 6 là 20 ghế. Tính số ghế ở hàng thứ 13.
Câu 58. Khi một vận động viên nhảy dù nhảy ra khỏi máy bay, giả sử quãng đường người ấy rơi tự do
(tính theo feet) trong mỗi giây liên tiếp, theo thứ tự trước khi bung dù lần lượt là: 10; 40; 70; 100; 𝑙𝑑𝑜𝑡𝑠
(các quãng đường này tạo thành cấp số cộng). Tính tổng chiều dài quãng đường người đó rơi trong 5 giây đầu tiên.
Câu 59. Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, … , cứ tiếp tục trồng như thế cho đến khi hết số cây. Tính số hàng cây đã trồng.
Câu 60. Một tấm đề can hình chữ nhật được cuộn tròn lại theo chiều dài tạo thành một khối trụ có đường
kính 50 cm. Người ta trải ra 250 vòng để cắt chữ và in tranh cổ động, phần còn lại là một khối trụ có
đường kính 45 cm. Hỏi phần đã trải ra dài bao nhiêu mét? (Kết quả làm tròn đến hàng đơn vị)
Câu 61. Người ta trồng 15050 cây theo dạng một hình tam giác bậc thang như sau: hàng thứ nhất trồng 2
cây, hàng thứ hai trồng 5 cây, hàng thứ ba trồng 8 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Tính số hàng cây được trồng.
Câu 62. Một hội trường A của một trường đại học có 600 chỗ ngồi và các hàng ghế được xếp theo dạng
bậc thang, hàng ghế đầu tiên có 15 chỗ ngồi và cao 0,3m so với mặt nền. Mỗi hàng ghế sau có thêm 3
chỗ ngồi và cao hơn 0,2m so với hàng ghế ngay trước nó. Hỏi hàng ghế cuối cùng của hội trường đó sẽ
cao bao nhiêu mét (m) so với mặt nền. (Kết quả làm tròn đến hàng phần chục)
Câu 63. Một chú cò khát nước, chú tìm thấy một chiếc bình đựng nước nhưng cổ bình vừa cao lại vừa bé
nên chú không thể uống được. Chú bèn nhặt những hòn sỏi bỏ vào bình để nước dâng lên, phút đầu tiên
chú bỏ được 5 viên sỏi, do quen việc nên từ phút thứ hai mỗi phút chú lại bỏ nhiều hơn phút trước đó 4
viên sỏi (trong phút thứ 2 bỏ được 9 viên). Sau 10 phút thì nước đã dâng lên để chú có thể uống được.
Hỏi chú cò đã phải nhặt tổng cộng bao nhiêu viên sỏi để bỏ vào bình?
Câu 64. Một đội hình học sinh có 15 hàng, hàng đầu tiên có 9 học sinh, mỗi hàng sau hơn hàng trước 5
học sinh. Hỏi đội văn nghệ có tất cả bao nhiêu học sinh?
Câu 65. Để chuẩn bị vốn từ vựng cho kì thi IELTS sắp tới, ngày đầu tiên, ban An học 3 từ vựng mới và
ngay sau học nhiều hơn ngày trước đó 2 từ mới. Hỏi để có vốn từ mới tối thiểu là 2000 từ, bạn An cần
phải học ít nhất bao nhiêu này?
Câu 66. Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là 100 nghìn
đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn đồng so với giá của mét khoan
ngay trước đó. Một người cần khoan một giếng sâu 20 m để lấy nước dùng cho sinh hoạt của gia đình.
Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
Câu 67. Khi kí kết hợp đồng với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:
Phương án 1: Năm thứ nhất, tiền lương là 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền lương
được tăng 18 triệu đồng.
Phương án 2: Quý thứ nhất, tiền lương là 24 triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng 1,8 triệu đồng.
Tìm 𝑛 (với 𝑛 ∈ ℕ∗) để từ năm thứ 𝑛 trở đi thì tổng số tiền lương nhận được trong 𝑛 năm đi làm ở phương
án thứ hai nhiều hơn ở phương án thứ nhất?
Câu 68. Một nhà thi đấu có 20 hàng ghế dành cho khán giả. Hàng thứ nhất có 30 ghế, hàng thứ hai có 31
ghế, hàng thứ ba có 32 ghế,... Cứ như thế, số ghế ở hàng sau nhiều hơn số ghế ở hàng ngay trước là 1
ghế. Trong một giải thi đấu, ban tổ chức đã bán được hết số vé phát ra và số tiền thu được từ bán vé là
63200000 đồng. Tính giá tiền của mỗi vé (đơn vị: nghìn đồng), biết số vé bán ra bằng số ghế dành cho
LỚP TOÁN THẦY CHINH, Trang 19/29
khán giả của nhà thi đấu và các vé là đồng giá.
Câu 69. Một công ty kí hợp đồng một kỹ sư để làm việc cho công ty trong 12 tháng với thỏa thuận như
sau: tháng đầu tiên kỹ sư sẽ được nhận số tiền là 𝐴 đồng. Sau đó mỗi tháng công ty sẽ tăng thêm cho kỹ
sư 300000 đồng vào số lương của tháng trước. Đồng thời công ty này trả trước cho kỹ sư tổng số tiền
lương 12 tháng làm việc là 187800000 đồng. Nhưng khi làm việc đến hết tháng thứ mười thì do sức
khỏe không đảm bảo nên kỹ sư xin nghỉ việc. Hỏi kỹ sư phải trả lại công ty bao nhiêu triệu đồng nếu
công ty vẫn đồng ý trả lương cho kỹ sư trong mười tháng làm việc theo thỏa thuận ban đầu và không phạt hợp đồng?
Câu 70. Anh Hải muốn tiết kiệm tiền để mua một đôi giày chơi bóng rổ giá 3840000 đồng. Do đó, anh
Hải quyết định bắt đầu mỗi ngày tiết kiệm với ngày đầu 5000 đồng, ngày sau cao hơn ngày trước 2000
đồng. Hỏi anh Hải phải tiết kiệm bao nhiêu ngày thì đủ tiền mua đôi giày đó?
Câu 71. Trong hội chợ tết Mậu Tuất 2018, một công ty sữa muốn xếp 900 hộp sữa theo số lượng
1,3,5, … từ trên xuống dưới (số hộp sữa trên mỗi hàng xếp từ trên xuống là các số lẻ liên tiếp). Hàng dưới
cùng có bao nhiêu hộp sữa?
Câu 72. Tam giác 𝐴𝐵𝐶 có số đo một góc là 120∘ và độ dài ba cạnh của nó là ba số hạng liên tiếp của một
cấp số cộng. Xác định chu vi của tam giác 𝐴𝐵𝐶 biết diện tích tam giác đó là √ (cm ).
Câu 73. Người ta thiết kế số ghế ngồi trên khán đài một sân vận động bóng đá như sau. Hàng ghế đầu
tiên gần sân bóng đá nhất có 1600 ghế. Kể từ hàng thứ hai trở đi, mỗi hàng liền sau hơn hàng liền trước
400 ghế. Muốn sức chứa trên khán đài có ít nhất 222000 ghế thì cần phải thiết kế ít nhất bao nhiêu hàng ghế?
Câu 74. Tại lễ Sơ kết Học kì 1 của một trường THPT, Ban thi đua đã phát thưởng cho 5 lớp có kết quả
thi đua xuất sắc hạng nhất, nhì, ba, tư và năm. Tổng giá trị tiền thưởng phát cho 5 lớp là 2,5 triệu đồng.
Biết rằng lớp có xếp hạng cao hơn lớp liền kề thì nhận tiền thưởng nhiều hơn là 200 nghìn đồng và không
có lớp nào đồng hạng. Lớp nhận được tiền thưởng 300 nghìn đồng thì có kết quả thi đua hạng mấy?
Câu 75. Một doanh nghiệp hỗ trợ cho người dân bị thất nghiệp ở một khu phố với tiền lương trong mỗi
tháng được tính như sau:
• Người thất nghiệp của khu phố làm việc tạp vụ cho doanh nghiệp trong nhiều ngày.
• Sau ngày đầu tiên, doanh nghiệp trả cho 110 nghìn đồng/người.
• Bắt đầu từ ngày thứ hai, mỗi ngày tăng thêm 20 nghìn đồng/người so với ngày hôm trước.
Mỗi người thất nghiệp phải làm cho doanh nghiệp đó ít nhất bao nhiêu ngày để có được ít nhất 5 triệu đồng/tháng?
Câu 76. Người ta trồng 15050 cây theo dạng một hình tam giác bậc thang như sau: Hàng thứ nhất trồng
2 cây, hàng thứ hai trồng 5 cây, hàng thứ ba trồng 8 cây, …, cứ tiếp tục trồng cho đến khi hết số cây và
hàng cuối cùng có đủ số cây theo quy luật này. Tính số hàng cây được trồng.
Câu 77. Một rạp hát có 18 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 17 ghế, hàng thứ hai có 20
ghế, hàng thứ ba có 23 ghế …, cứ thế tiếp tục cho đển hàng cuối cùng. Tính tổng số ghế của rạp?
Câu 78. Giá của một chiếc xe ô tô lúc mới mua là 950 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc
xe ô tô giảm 70 triệu đồng. Tính giá trị còn lại của chiếc xe sau 7 năm sử dụng. (Kết quả tính theo đơn vị
triệu đồng và là tròn đến hàng đơn vị)
Câu 79. Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, ..., cứ tiếp tục trồng như thế cho đến khi hết số cây. Số hàng cây được trồng là
Câu 80. Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết
rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm,
41 cm, … ,31 cm. Tính chiều dài thanh gỗ mà người đó cần mua, giả sử chiều dài các mối nối (phần gỗ bị
cắt thành mùn cưa) là không đáng kể. (Kết quả tính theo đơn vị cm và làm tròn đến hàng đơn vị)
Câu 81. Nền nhà của tầng một có độ cao 1.5 m so với mặt đất. Từ nền nhà tầng 1 lên nền nhà tầng 2 có
LỚP TOÁN THẦY CHINH, Trang 20/29