








Preview text:
Gv. ThS Nguyễn Vũ Minh
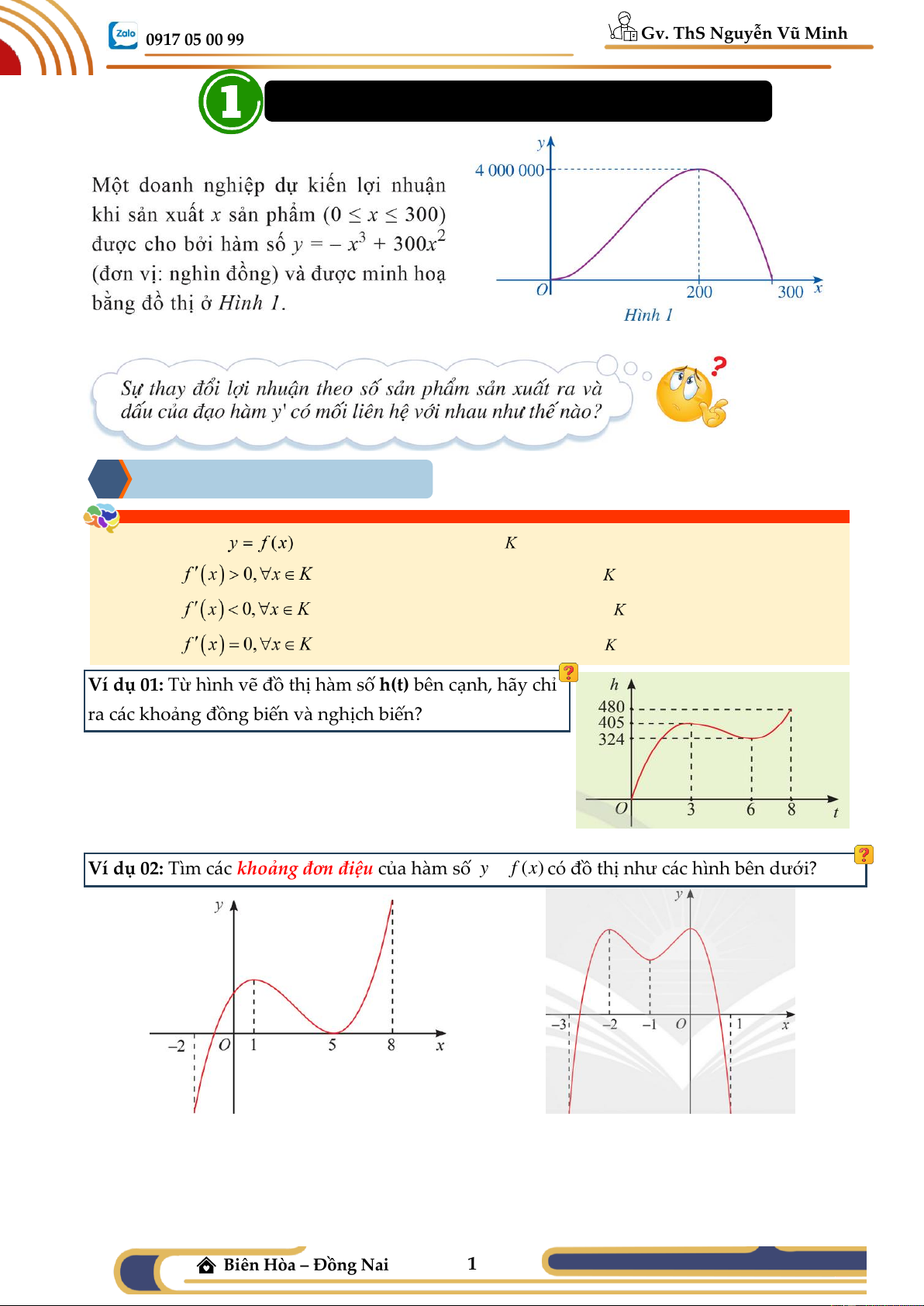
0917 05 00 99 (Toán – Vật Lí THPT) TÍNH ĐƠN ĐIỆU
VÀ CỰC TRỊ CỦA HÀM SỐ
1 Tính đơn điệu của hàm số Cho hàm số
có đạo hàm trên khoảng . ● Nếu
thì hàm số đồng biến trên khoảng . ● Nếu
thì hàm số nghịch biến trên khoảng . ● Nếu
thì hàm số không đổi trên khoảng .
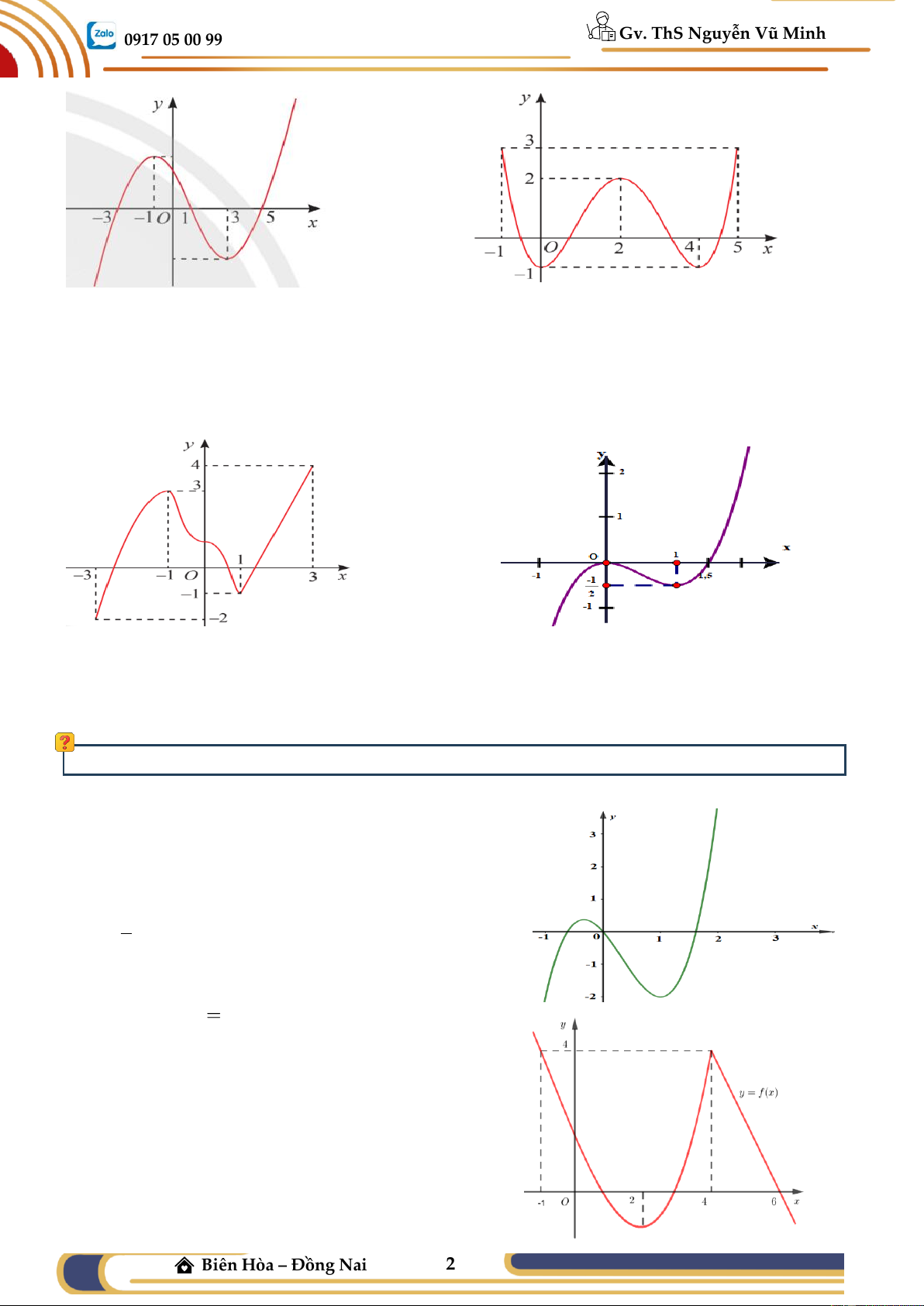
Ví dụ 01: Từ hình vẽ đồ thị hàm số h(t) bên cạnh, hãy chỉ
ra các khoảng đồng biến và nghịch biến?
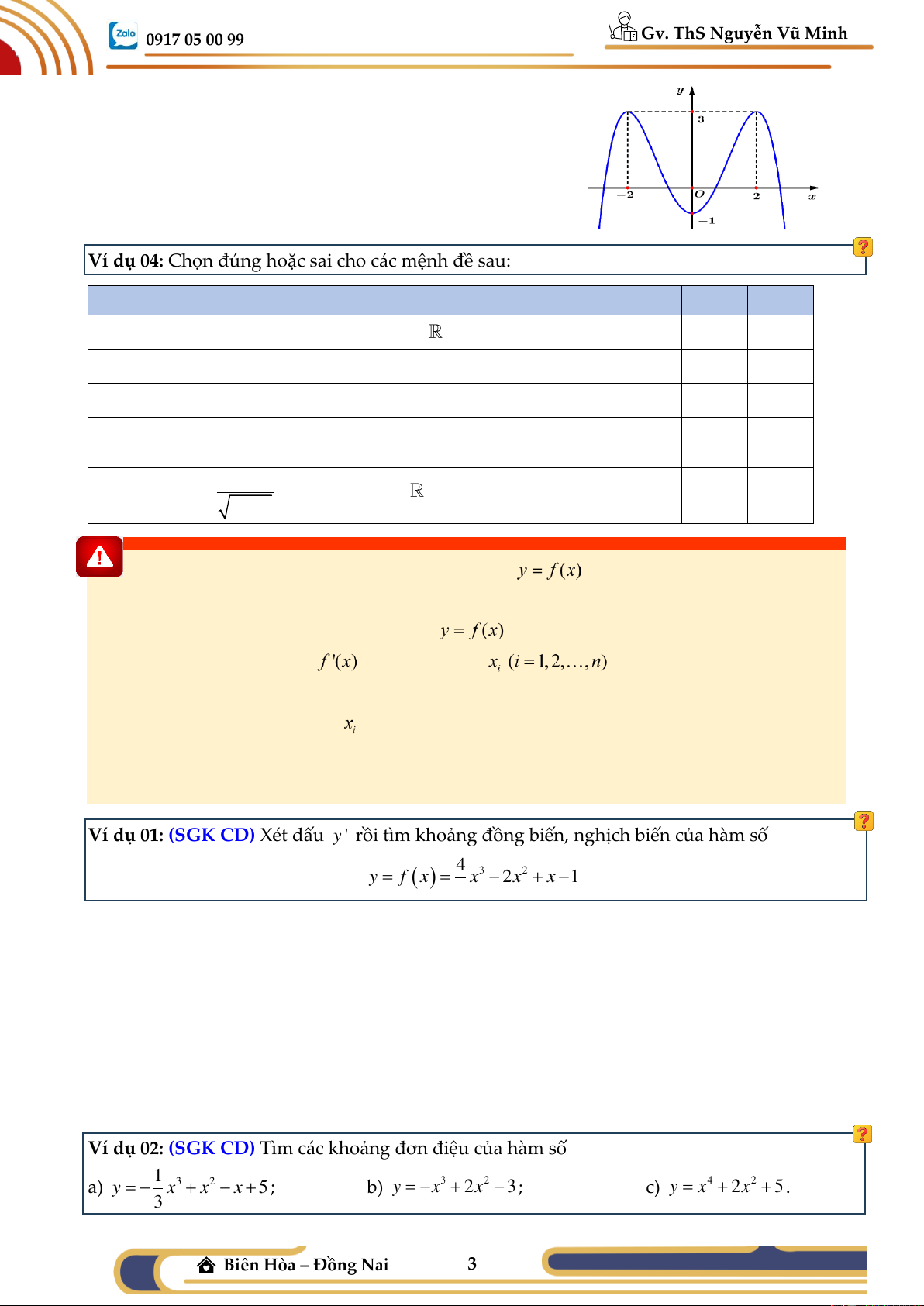
Ví dụ 02: Tìm các khoảng đơn điệu của hàm số y = f (x)
có đồ thị như các hình bên dưới?
Biên Hòa – Đồng Nai 1
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 03: Chọn đáp án đúng
a) Đường cong trong hình vẽ bên là đồ thị của hàm số có dạng 3 2
y = ax + bx + cx + d (a 0) .
Hàm số nghịch biến trong khoảng nào dưới đây? A. (− ; − 2). B. (1; 2) . 1 C. 0; . 2 D. (0; 3) . b) Cho hàm số y
f x có đồ thị như hình vẽ bên
dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (2;6) . B. (0; 4) . C. (3;4) . D. ( 1 − ;4) .
Biên Hòa – Đồng Nai 2
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
c) Cho hàm số y = f ( x) có đồ thị như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (0;+) . B. (− ; 2 − ). C. ( 2 − ;0) . D. ( 2 − ;2) .
Ví dụ 04: Chọn đúng hoặc sai cho các mệnh đề s au:
Xét các mệnh đề sau Đúng Sai a) Hàm số 3 y = (
− x −1) nghịch biến trên . b) Hàm số = ( ) x y
f x = e + 2x .
c) Hàm số y = f ( x) = sin x + 5x . x
d) Hàm số y = ln(x −1) −
đồng biến trên tập xác định của nó. x −1 x e) Hàm số y = đồng biến trên . 2 x +1
Để xét tính đồng biến, nghịch biến của hàm số
, ta có thể thực hiện các bước sau:
Bước 1: Tìm tập xác định của hàm số .
Bước 2: Tính đạo hàm . Tìm các điểm
mà tại đó hàm số có đạo
hàm bằng 0 hoặc không tồn tại.
Bước 3: Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ 01: (SGK CD) Xét dấu y ' rồi tìm khoảng đồng biến, nghịch biến của hàm số
y = f ( x) 4 3 2
= x − 2x + x −1 3
Ví dụ 02: (SGK CD) Tìm các khoảng đơn điệu của hàm số 1 a) 3 2 y = −
x + x − x + 5 ; b) 3 2
y = −x + 2x − 3 ; c) 4 2
y = x + 2x + 5 . 3
Biên Hòa – Đồng Nai 3
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 03: Xét tính đơn điệu của các hàm số sau đây: x − x + 3x +1 2x −1
a) y = f ( x) 2 2025 = y = f x = y = ; d) y = . x + ; b) ( ) 1 1 3 − ; c) x 2 − x x + 2
Biên Hòa – Đồng Nai 4
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) 2 x − 2x 2 x + 4
Ví dụ 04: Tìm các khoảng đơn điệu của mỗi hàm số sau: a) y = ; b) y = . x +1 x 2x +1
Ví dụ 05: (SGK CTST) Chứng minh rằng hàm số y =
nghịch biến trên từng khoảng xác x − 3 định của nó.
Ví dụ 06: Xét tính đơn điệu của hàm số 2
y = 8 + 2x − x ?
Biên Hòa – Đồng Nai 5
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 07: Chọn đáp án đúng x − 3
a) THPT Sóc Sơn 2023) Cho hàm số y =
. Mệnh đề nào dưới đây đúng? x +1
A. Hàm số đồng biến trên \ 1 − .
B. Hàm số nghịch biến trên (− ; − ) 1 .
C. Hàm số đồng biến trên (− ; + ).
D. Hàm số đồng biến trên (− ; − ) 1 . x + 2 b) Cho hàm số y =
Mệnh đề nào dưới đây đúng? x −1
A. Hàm số nghịch biến trên (− ;1 ) (1;+).
B. Hàm số nghịch biến trên \ {1}.
C. Hàm số nghịch biến trên ( ;1 − ) và (1;+).
D. Hàm số nghịch biến trên với x 1.
Ví dụ 08: (SGK CD) Chứng minh rằng hàm số 2 y =
x +1 nghịch biến trên nửa khoảng ( ;
− 0] và đồng biến trên nửa khoảng [0;+) .
Ví dụ 09: Chứng minh rằng: a) Hàm số 2 y =
x − 4 nghịch biến trên khoảng (− ; 2
− ) và đồng biến trên khoảng ( 2;+ ). b) Hàm số y = ( 2 ln x + )
1 nghịch biến trên khoảng ( ;
− 0) và đồng biến trên khoảng ( 0;+ ). 2 c) Hàm số 2 2 x x y − + =
đồng biến trên khoảng ( ;1
− ) và nghịch biến trên khoảng (1;+ ).
Biên Hòa – Đồng Nai 6
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 10: (SBT CD) Dùng đạo hàm của hàm số, hãy giải thích: a) Hàm số x
y = a đồng biến trên
khi a 1, nghịch biến trên khi 0 a 1.
b) Hàm số y = log x đồng biến trên khoảng (0; +) khi a 1, nghịch biến trên khoảng a
(0; +) khi 0 a 1.
Ví dụ 11: Cho hàm số ( ) = ( 2 − 3 − 3)ex f x x x
. Các phát biểu dưới đây là đúng (Đ) hay sai (S)?
a) Hàm số đã cho xác định với mọi x .
b) Giá trị f (0) = − e 3 .
c) Phương trình f ( x) = 0 có hai nghiệm phân biệt.
d) Hàm số f ( x) đồng biến trên khoảng ( 2 − ;3) . 1
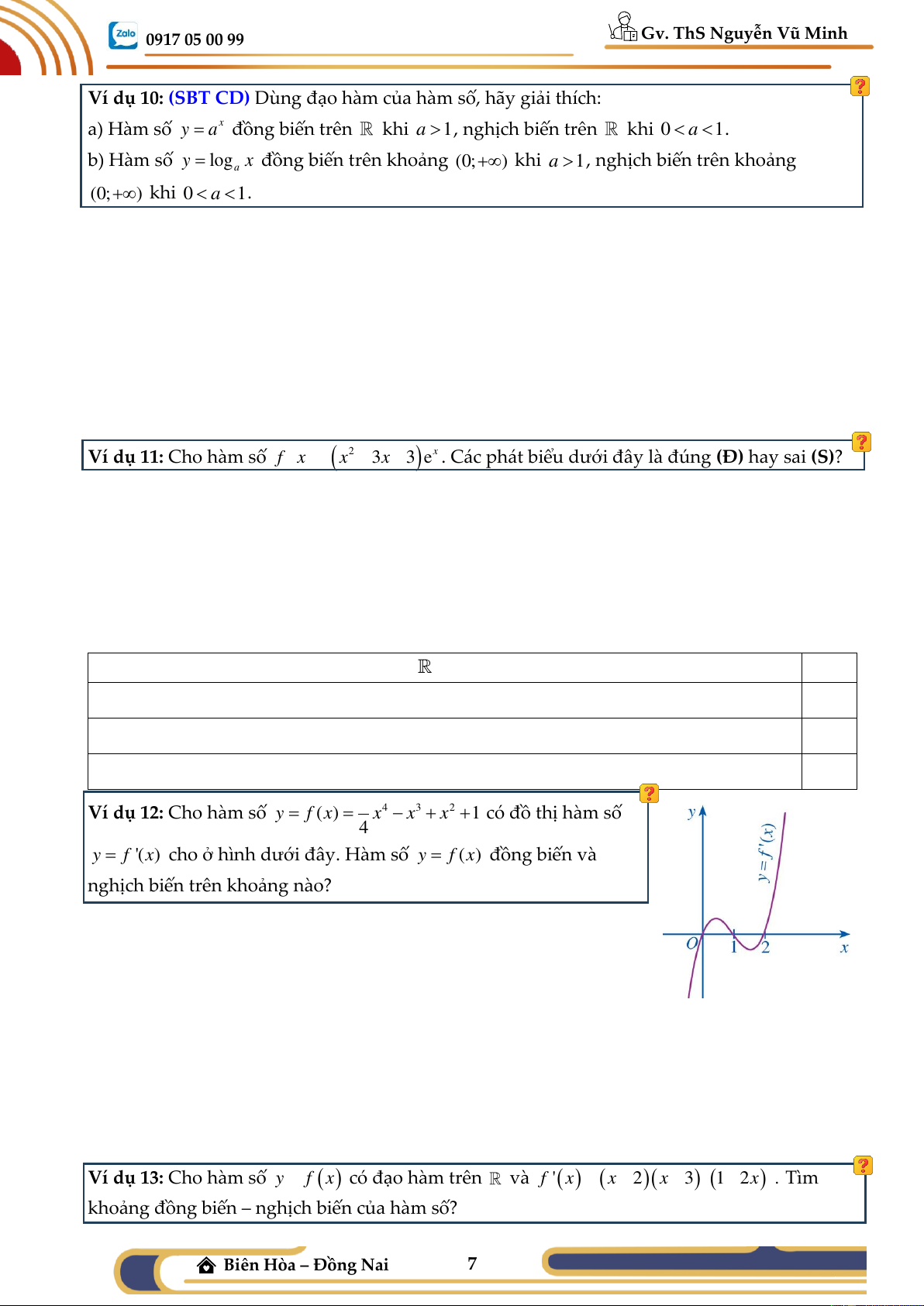
Ví dụ 12: Cho hàm số 4 3 2
y = f (x) =
x − x + x +1 có đồ thị hàm số 4
y = f '(x) cho ở hình dưới đây. Hàm số y = f (x) đồng biến và
nghịch biến trên khoảng nào?
Ví dụ 13: Cho hàm số 4 3
y = f ( x) có đạo hàm trên và f '( x) = ( x − 2)( x + 3) (1− 2x) . Tìm
khoảng đồng biến – nghịch biến của hàm số?
Biên Hòa – Đồng Nai 7
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
13.1 (sở GD Hải Dương 2023) Cho hàm số y = f ( x) liên tục trên và f ( x) 2
= x (x + 2)(1− x) . Hàm số đã cho nghịch biến trên khoảng A. (2;3) . B. ( 1 − ; ) 1 . C. (0; 2) . D. ( ) ;1 − .
13.2 (Sở GD Ninh Thuận 2023) Cho hàm số y = f ( x) có đạo hàm
f ( x) = ( x + )( x − )2023 1 3
với mọi x . Hàm số đã cho nghịch biến trên khoảng nào? A. ( 3 − ; ) 1 . B. (− ; − ) 1 . C. ( 1 − ;3) . D. ( 1 − ;+) .
13.3 (sở GD Bắc Ninh 2023) Cho hàm số y = f ( x) có đạo hàm
f ( x) = x ( x − )2 ( x + )3 1
1 ( x − 2) . Hàm số y = f ( x) đồng biến trên khoảng nào dưới đây? A. (− ; − ) 1 . B. (0 ) ;1 . C. ( 1 − ;0) . D. (1; +) .
13.4 (sở GD Bắc Giang 2023) Cho hàm số f ( x) có f ( x) 2 = x ( 2 x − ) 1 với x
. Hàm số y = f ( x) nghịch biến trên khoảng nào dưới đây? A. ( ;0 − ). B. ( ) ;1 − . C. ( 1 − ;+) . D. ( 1 − ; ) 1 .
Biên Hòa – Đồng Nai 8
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
13.5 Cho hàm số f ( x) có đạo hàm xác định và liên tục trên thoả mãn f ( x) + .
x f ( x) = x ( x − ) 1 ( x − 2) , x
. Hàm số g (x) = .x f (x) đồng biến trên khoảng nào? A. ( ;0 − ). B. (1;2) . C. (2;+) . D. (0; 2) .
2 Điểm cực trị, giá t
rị cực trị của hàm số Giả sử hàm số liên tục trên khoảng chứa điểm
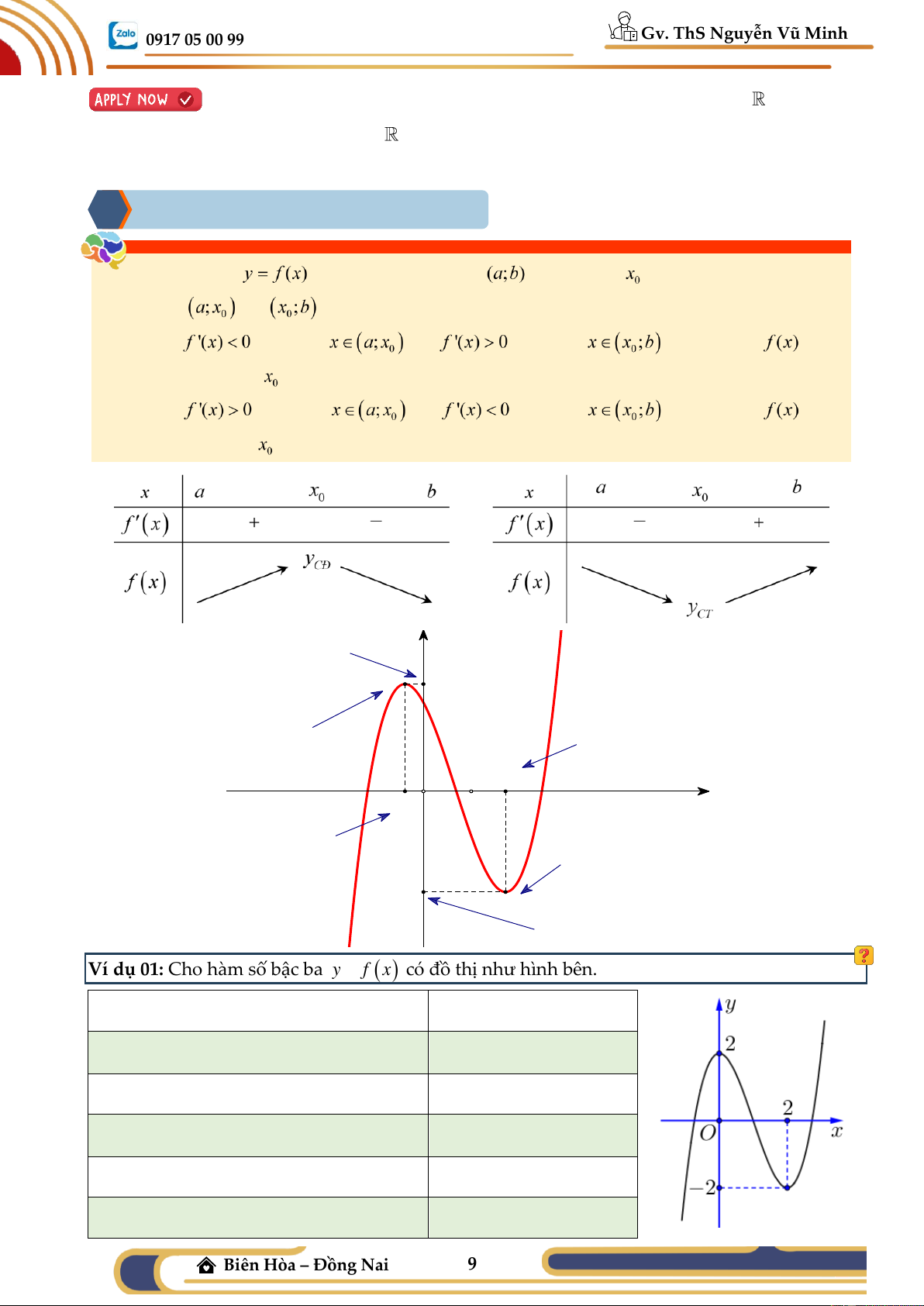
và có đạo hàm trên các khoảng và . Khi đó a) Nếu với mọi và với mọi thì hàm số đạt cực tiểu tại điểm . b) Nếu với mọi và với mọi thì hàm số đạt cực đại tại điểm . y giá trị cực đại của hàm số A y CĐ điểm cực đại của đths điểm cực tiểu của hàm số x x CT x O CĐ điểm cực đại của hàm số điểm cực tiểu của đths yCT B giá trị cực tiểu của hàm số
Ví dụ 01: Cho hàm số bậc ba y = f ( x) có đồ thị như hình bên.
Giá trị cực đại của hàm số đã cho là:
Giá trị cực tiểu của hàm số đã cho là:
Điểm cực đại của hàm số là:
Điểm cực tiểu của hàm số là:
Điểm cực đại của đồ thị hàm số là:
Điểm cực tiểu của đồ thị hàm số là:
Biên Hòa – Đồng Nai 9 y = f'(x)
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
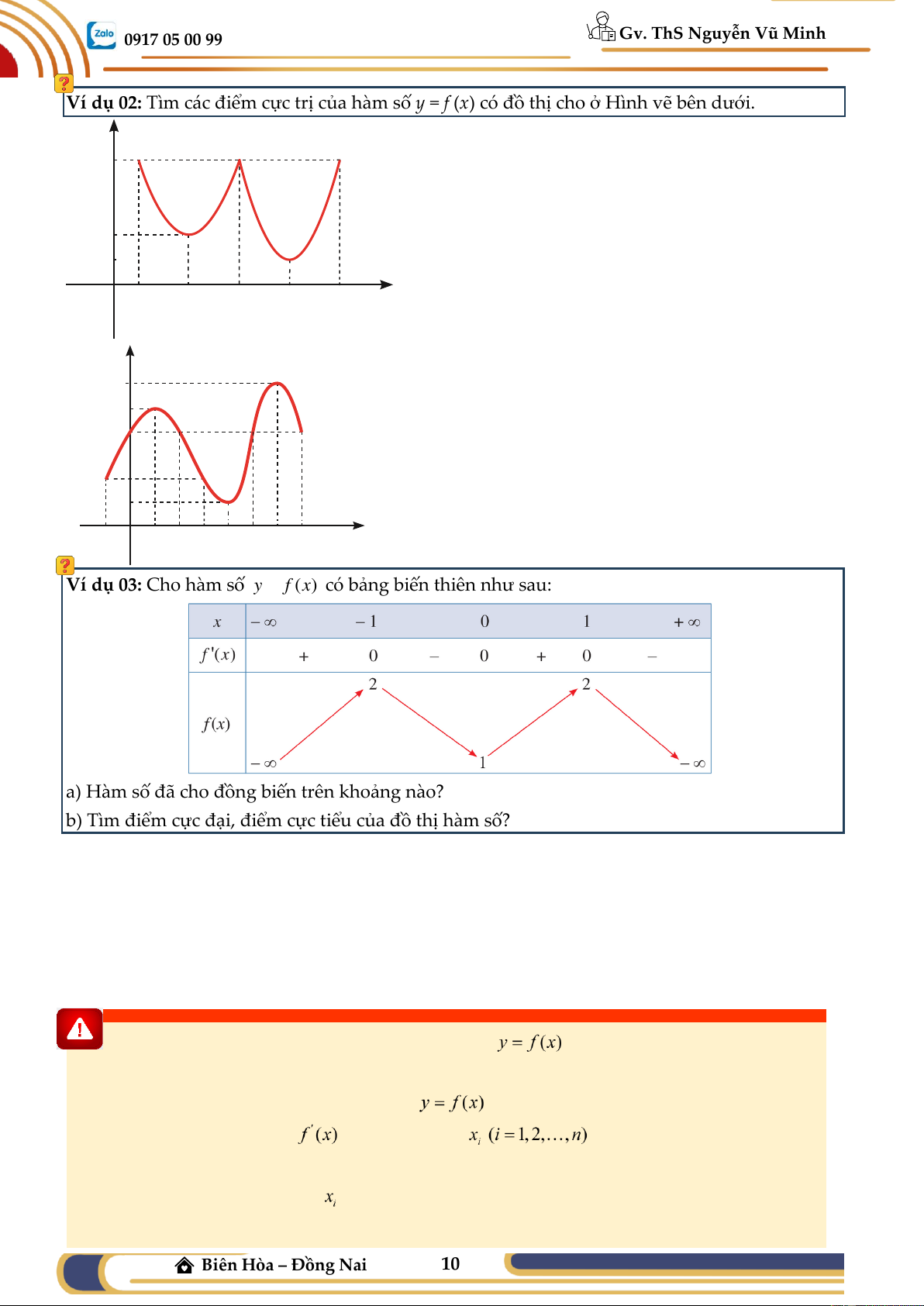
Ví dụ 02: Tìm các điểm cực trị của hàm số y = f ( x) có đồ thị cho ở Hình vẽ bên dưới. y 5 2 1 O 1 3 5 7 9 x y 6 5 4 2 1 –1 O 1 2 3 4 5 6 7 x
Ví dụ 03: Cho hàm số y = f (x) có bảng biến thiên như sau:
a) Hàm số đã cho đồng biến trên khoảng nào?
b) Tìm điểm cực đại, điểm cực tiểu của đồ thị hàm số?
Để xét tính đồng biến, nghịch biến của hàm số
, ta có thể thực hiện các bước sau:
Bước 1: Tìm tập xác định của hàm số .
Bước 2: Tính đạo hàm . Tìm các điểm
mà tại đó hàm số có đạo
hàm bằng 0 hoặc không tồn tại.
Bước 3: Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên, nêu kết luận về các cực trị của hàm số
Biên Hòa – Đồng Nai 10
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) Chú ý a) Nếu và
không đổi dấu khi qua điểm thì hàm số không có cực trị tại b) Nếu
không đổi dấu trên khoảng
thì không có cực trị trên khoảng đó.
Ví dụ 01: Tìm cực trị các hàm số sau: a) 3 2
y = −x + 6x +1 b) 3 2 y = 2
− x + 3x +12x − 5 c) 3 2
y = 2x + 3x − 36x −10 d) 4 y = −3x + 5
Ví dụ 02: Tìm cực trị của hàm số 2 ( ) x g t = e + 2026 t −1
Biên Hòa – Đồng Nai 11
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) 2 x +1
Ví dụ 03: Tìm cực trị các hàm số sau: a) y = ; b) y = . 3 − x 5 + 3x +
Cần nhớ: Hàm số nhất biến dạng = ( ) ax b y f x =
…………………………………… cx + d
Ví dụ 04: Tìm điểm cực trị của mỗi hàm số sau: a) 3 2
y = 2x + 3x − 36x −10 ; b) 4 2
y = −x − 2x + 9 ; c) 4 2
y = x − 2x + 9 .
Biên Hòa – Đồng Nai 12
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) 2 x + x + 4
Ví dụ 05: (SGK CTST) Tìm cực trị của hàm số g (x) = . x +1
5.1 Tìm cực trị của các hàm số dưới đây 2 x − 2x − 7 2 x − 8x +10 2 x + x + 4 1 a) y = ; b) y = ; c) y = ; d) y = x + . x − 4 x − 2 x − 3 x
Biên Hòa – Đồng Nai 13
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
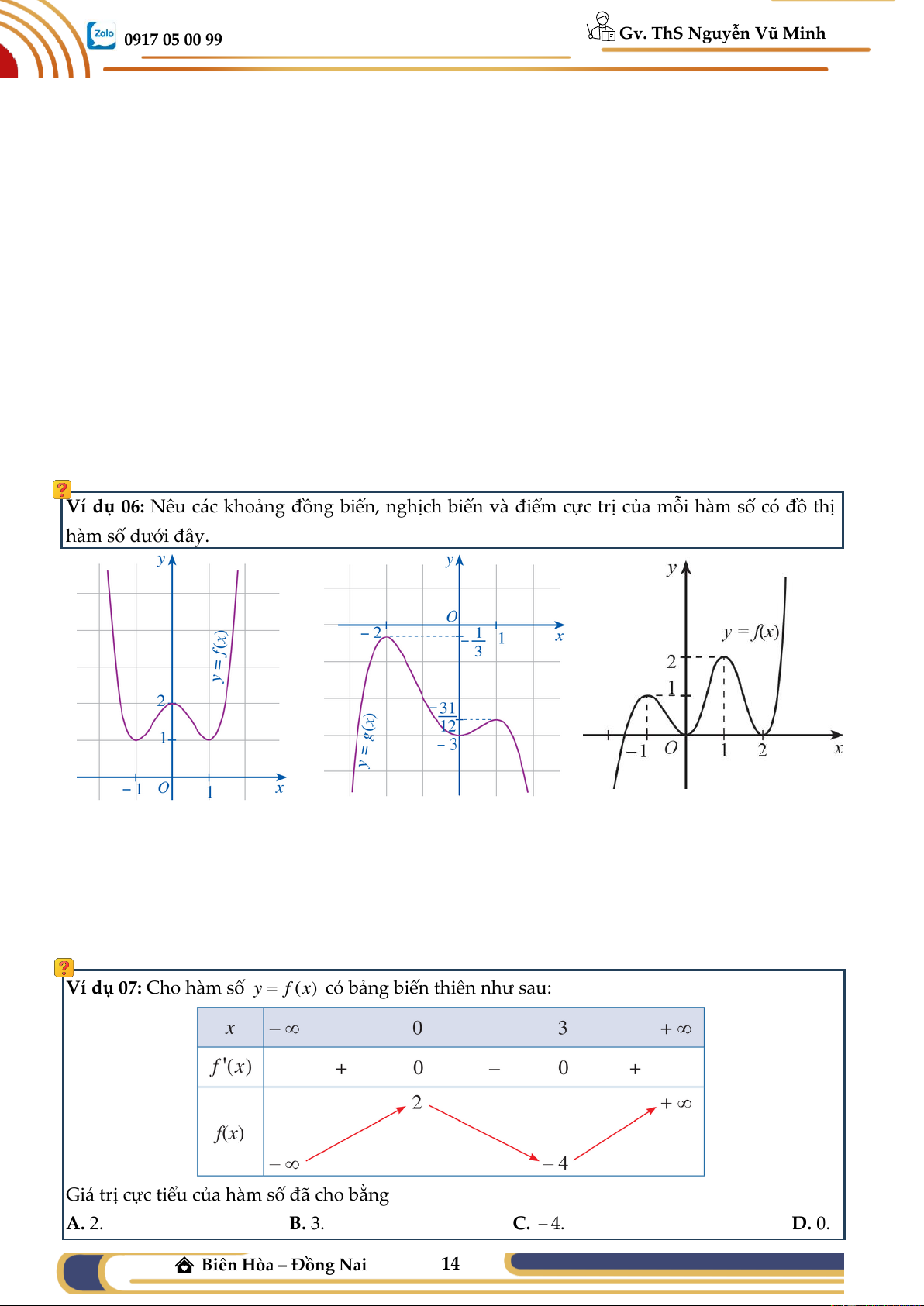
Ví dụ 06: Nêu các khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số có đồ thị hàm số dưới đây. a) b) c)
Ví dụ 07: Cho hàm số y = f (x) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2. B. 3. C. − 4. D. 0.
Biên Hòa – Đồng Nai 14
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 08: Máng trượt của một cầu trượt cho trẻ em (Hình minh họa a) được uốn từ một tấm
kim loại có bề rộng 80 cm, mặt cắt có dạng hình chữ nhật được mô tả ở hình b. Nhà thiết kế
khuyến cáo, diện tích của mặt cắt càng lớn thì càng đảm bảo an toàn
a) Gọi S là diện tích mặt cắt. Tìm điều kiện của x và viết công thức tính S theo x.
b) Với x đạt giá trị bằng bao nhiêu thì cầu trượt đảm bảo an toàn nhất cho trẻ em?
Ví dụ 09: Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: a) 3 2
y = 4x + 3x − 36x + 6 ; b) 3 2
y = 2x + 3x − 36x +1; c) 2 y = −x + 4 .
Biên Hòa – Đồng Nai 15
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
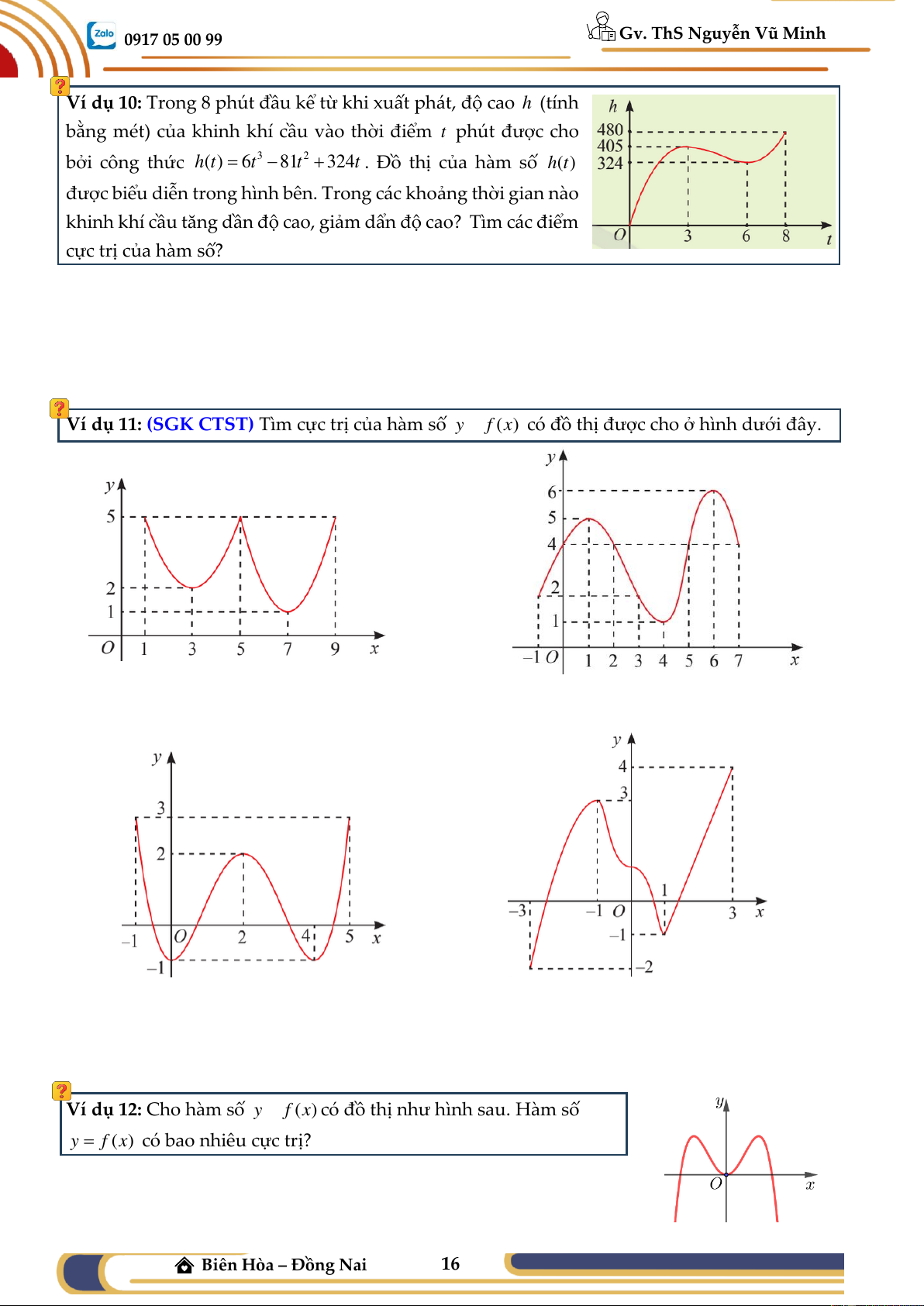
Ví dụ 10: Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính
bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức 3 2
h(t) = 6t − 81t + 324t . Đồ thị của hàm số h(t)
được biểu diễn trong hình bên. Trong các khoảng thời gian nào
khinh khí cầu tăng dần độ cao, giảm dẩn độ cao? Tìm các điểm cực trị của hàm số?
Ví dụ 11: (SGK CTST) Tìm cực trị của hàm số y = f (x) có đồ thị được cho ở hình dưới đây.
Ví dụ 12: Cho hàm số y = f (x) có đồ thị như hình sau. Hàm số
y = f (x) có bao nhiêu cực trị?
Biên Hòa – Đồng Nai 16
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 13: (SGK KNTT) Một vật được phóng thẳng đứng lên trên từ độ cao 2 m với vận tốc
ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h
(mét) của vật sau t (giây) được cho bởi công thức 2
h(t) = 2 + 24,5t − 4,9t . Hỏi tại thời điểm nào
thì vật đạt độ cao lớn nhất?
Ví dụ 14: Cho hàm số y = f ( x) 2
= x + 4ln(3− x) . Tì
m giá trị cực đai y của hàm số đã cho. CÐ
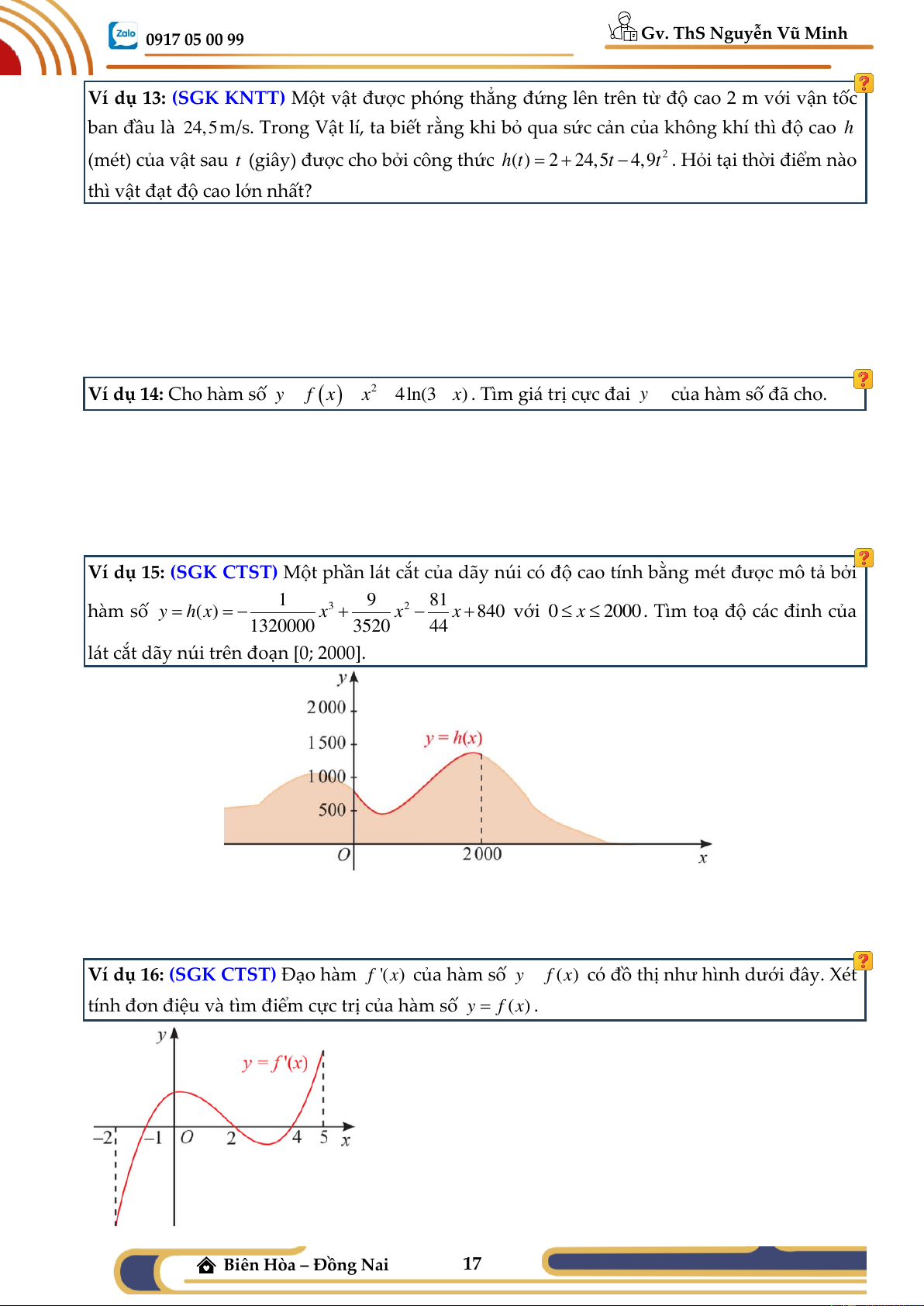
Ví dụ 15: (SGK CTST) Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi 1 9 81 hàm số 3 2
y = h(x) = − x + x − x + 8
40 với 0 x 2000. Tìm toạ độ các đỉnh của 1320000 3520 44
lát cắt dãy núi trên đoạn [0; 2000].
Ví dụ 16: (SGK CTST) Đạo hàm f '(x) của hàm số y = f (x) có đồ thị như hình dưới đây. Xét
tính đơn điệu và tìm điểm cực trị của hàm số y = f (x) .
Biên Hòa – Đồng Nai 17
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
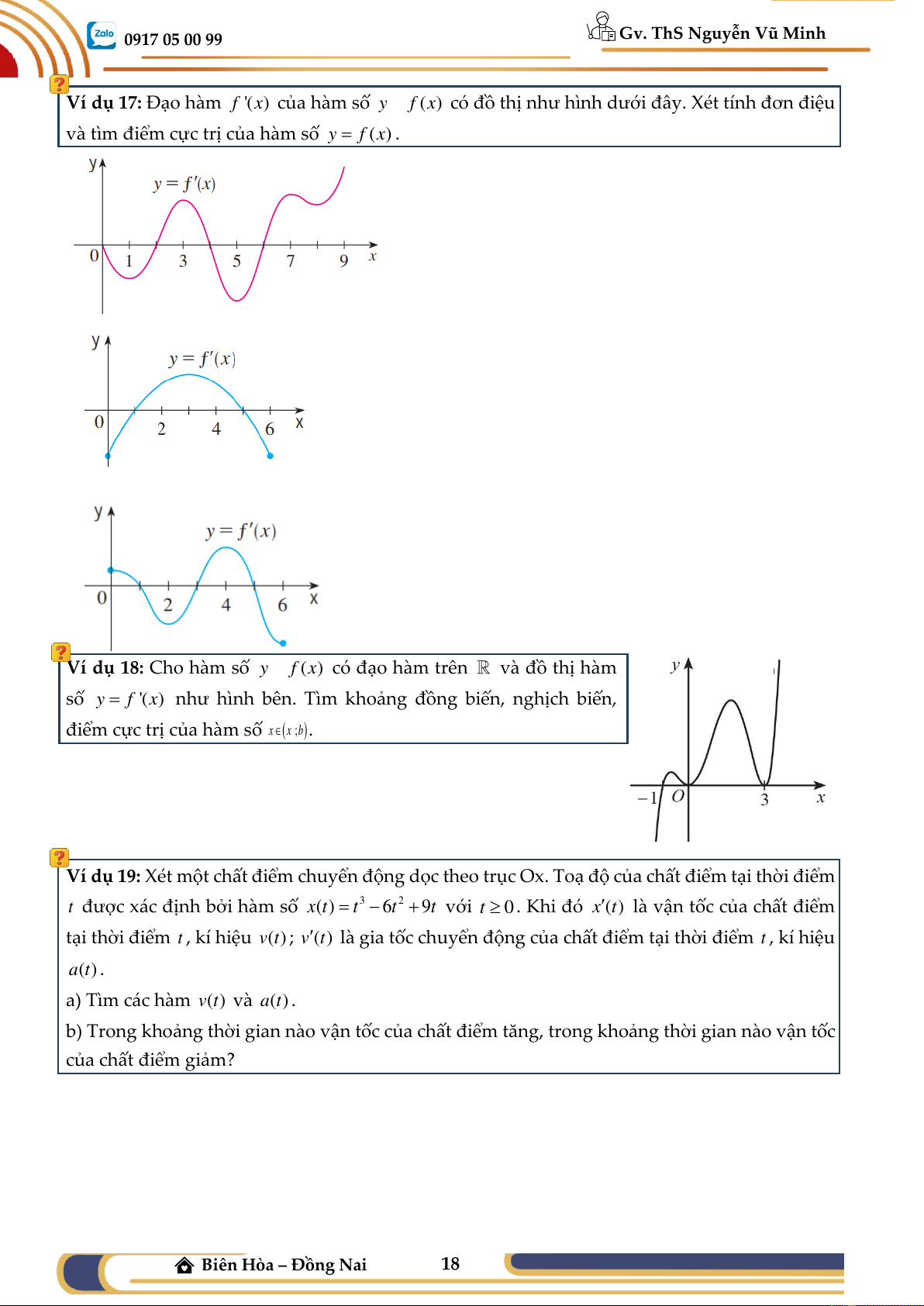
Ví dụ 17: Đạo hàm f '(x) của hàm số y = f (x) có đồ thị như hình dưới đây. Xét tính đơn điệu
và tìm điểm cực trị của hàm số y = f (x) . a) b) b)
Ví dụ 18: Cho hàm số y = f (x) có đạo hàm trên và đồ thị hàm
số y = f '(x) như hình bên. Tìm k
hoảng đồng biến, nghịch biến,
điểm cực trị của hàm số x(x ;b . 0 )
Ví dụ 19: Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm
t được xác định bởi hàm số 3 2
x(t) = t − 6t + 9t với t 0 . Khi đó x (
t) là vận tốc của chất điểm
tại thời điểm t , kí hiệu v(t) ; v (
t) là gia tốc chuyển động của chất điểm tại thời điểm t , kí hiệu a(t) .
a) Tìm các hàm v(t) và a(t) .
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Biên Hòa – Đồng Nai 18
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 20: (SBT CD) Cho hàm số f (x) có đạo hàm 2 2
f '(x) = x (x +1) (x −1)(x + 2), x . Tìm
điểm cực đại của hàm số đã cho? 2 x + 2mx + 2
Ví dụ 21: (THPT Việt Nam – Ba Lan 2025) Cho hàm số y =
. Tính tổng tất các giá x + 1
trị nguyên dương của tham số m để hàm số có cực đại và cực tiểu.
Ví dụ 22: (Sở Hải Dương 2022) Tìm m để hàm số 3
y = x + (m − ) 2
1 x − mx +1 đạt cực tiểu tại x = 1.
Biên Hòa – Đồng Nai 19
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
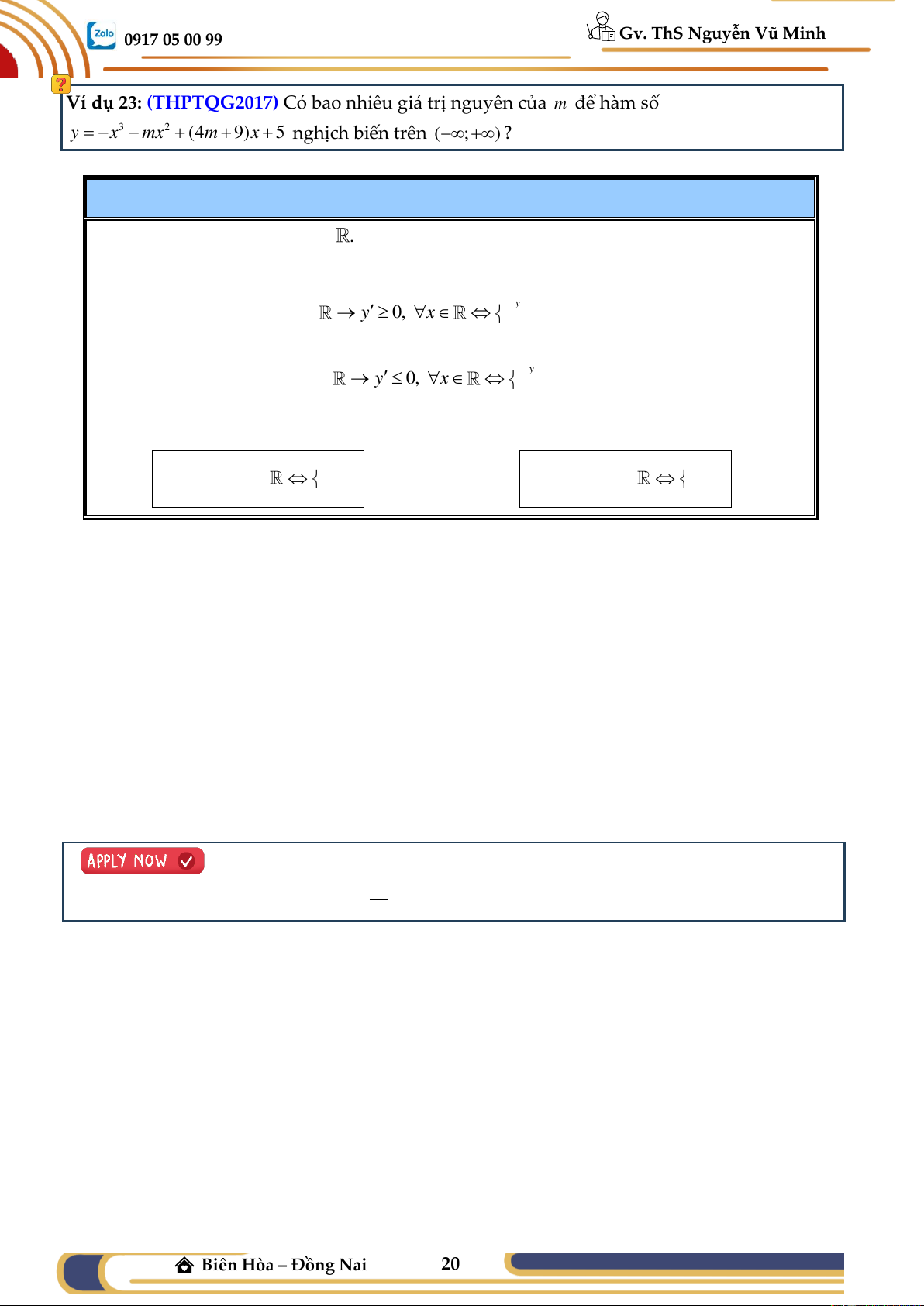
Ví dụ 23: (THPTQG2017) Có bao nhiêu giá trị nguyên của m để hàm số 3 2
y = −x − mx + (4m + 9)x + 5 nghịch biến trên (− ; +) ?
(Đơn diệu hàm số tìm m – dạng mở rộng)
Tìm tham số m để hàm số bậc ba 3 2
y = ax + bx + cx + d đơn điệu trên tập xác định
● Bước 1: Tập xác định: D = . Tính đạo hàm 2
y = 3ax + 2bx + . c
● Bước 2: Ghi điều kiện để hàm đơn điệu, chẳng hạn: a 0 y
Để f (x) đồng biến trên
→ y 0, x m ? 0 y a 0 y
Để f (x) nghịch biến trên
→ y 0, x m ? 0 y
Lưu ý: Dấu của tam thức bậc hai 2
f (x) = ax + bx + . c a 0 a 0
f (x) 0, x
f (x) 0, x 0 0
Tìm m để các hàm số sau luôn tăng trên từng khoảng xác định: 3 x
y = f ( x) = − ( − ) 2 x + ( 2 m 1 2 m + 2) x − 4 3
Biên Hòa – Đồng Nai 20




