lOMoARcPSD| 36991220
Nhập môn Kỹ thuật Truyền thông
Bài 3: Các hệ thống truyền thông
kỹ thuật số PGS. Tạ Hải Tùng
1. Các khái niệm cơ bản về các hệ
thống truyền thông kỹ thuật số
Giới thiệu các hệ thống truyền thông kỹ thuật số
Hệ thống truyền thông kỹ thuật số:
Truyền các chuỗi ký hiệu thuộc về một «bảng
chữ cái» rời rạc. lOMoARcPSD| 36991220 Ví dụ:
- Chữ viếtHuman writing
- Mã điện báo Morse - GSM - CD/DVD
Introduction to digital transmission systems
Chúng ta sẽ tập trung vào các hệ thống được đặc
trung bởi 2 tính chất sau:
1. Bảng chữ cái rời rạc = Bảng chữ cái nhị phân {0,1}
Các chuỗi dữ liệu nhị phân lOMoARcPSD| 36991220
2. Kênh truyền = kênh không dây hoặc có dây
Introduction to digital transmission systems
Nếu các thông tin tương tự cần truyền (ví dụ: voice, video)
Lấy mẫu và lượng tử hóa (mã hóa nguồn)
Các chuỗi dữ liệu nhị phân
Introduction to digital transmission systems
Các hệ thống truyền thông kỹ thuật số: lOMoARcPSD| 36991220  GSM/UMTS  Telephone Modem  Optical Fibers  Wired and Wireless LAN  GPS/Galileo ...
Một số đại lượng chính đặc trưng các
hệ thống truyền thông kỹ thuật số
 Tốc độ truyền bit (bit-rate)
 Băng thông (bandwidth) lOMoARcPSD| 36991220
 Công suất (power)
 Xác suất lỗi (error probability)
 Đô phức tạp (complexity)
Tốc độ truyền dòng bit (bit-rate)
Các chuỗi dữ liệu nhị phân được đặc trưng bởi
“tốc độ” của nó
BIT-RATE Rb [bps]
= số bit được truyền trong 1 giây lOMoARcPSD| 36991220
Băng thông (bandwidth)
Các chuỗi dữ liệu nhị phân
Muốn được truyền qua một kênh có dây hay
không dây thì đều phải được chuyển sang
một dạng sóng s(t) lOMoARcPSD| 36991220 Băng thông
Dạng sóng s(t) được đặc trưng bởi
phổ mật độ công suất của nó Gs(f)
BANDWIDTH B [Hz] = Khoảng tần số chứa
“phần có ý nghĩa quan trọng” của Gs(f) lOMoARcPSD| 36991220 Công suất
Công suất tín hiệu nhận được S [W] [dBm]
Phụ thuộc vào công suất truyền tín hiệu
Và được đặc trưng bởi tỷ số công suất tín hiệu
/ công suất tạp âm (signal-to-noise ratio) tại phía bộ thu lOMoARcPSD| 36991220
Xác suất xảy ra lỗi
Các chuỗi dữ liệu nhị phân uT=(uT[i])
Dạng sóng truyền s(t)
Dạng sóng nhận r(t) s(t) (trong các kênh thực tế, không lý tưởng)
Các chuỗi dữ liệu nhị phân nhận được uR=(uR[i]) lOMoARcPSD| 36991220
Xác suất xảy ra lỗi
Các chuỗi dữ liệu nhị phân truyền uT=(uT[i])
Các chuỗi dữ liệu nhị phân nhận được uR=(uR[i])
Xác xuất xảy ra lỗi bit P(uR[i] uT[i])
Độ phức tạp (complexity)
COMPLEXITY = Độ phức tạp về mặt kỹ thuật
của một phương án thực hiện cụ thể lOMoARcPSD| 36991220
Các đại lượng khác
Độ trễ D [s]
Sự khác nhau giữa các thời điểm truyền và nhận
Vào (bộ phát, transmitter - TX) Ra (bộ thu, receiver, RX)
Ví dụ thực tế
Xây dựng một hệ thống truyền thông kỹ thuật số
với các điều kiện: lOMoARcPSD| 36991220
• tốc độ truyền BIT-RATE Rb=34 Mbps
• trên vùng tần số có độ rộng BANDWIDTH B=20
MHz, có tần số trung tâm f0=18 GHz
• đảm bảo tối thiểu BER = 10-7 trong điều kiện công
suất tín hiệu nhận được POWER S=-40 dBm
• với độ trễ tối đa DELAY D=500 ms
• với tối thiểu độ phức tạp COMPLEXITY (chi phí)
2. Chùm tín hiệu, gán nhãn,
và dạng sóng truyền
Các chuỗi dữ liệu nhị phân: khái niệm lOMoARcPSD| 36991220
Bảng chữ cái nhị phân Z2 = {0,1} Các
chuỗi dữ liệu nhị phân: uT
(uT [0],uT [1],...,u iT [ ],...) i N u iT [ ] Z2 u T (1101001...) Ví dụ: u T
(uT [0],uT [1],...,u iT [ ],...)
Tốc độ dòng bit Rb [bps] lOMoARcPSD| 36991220
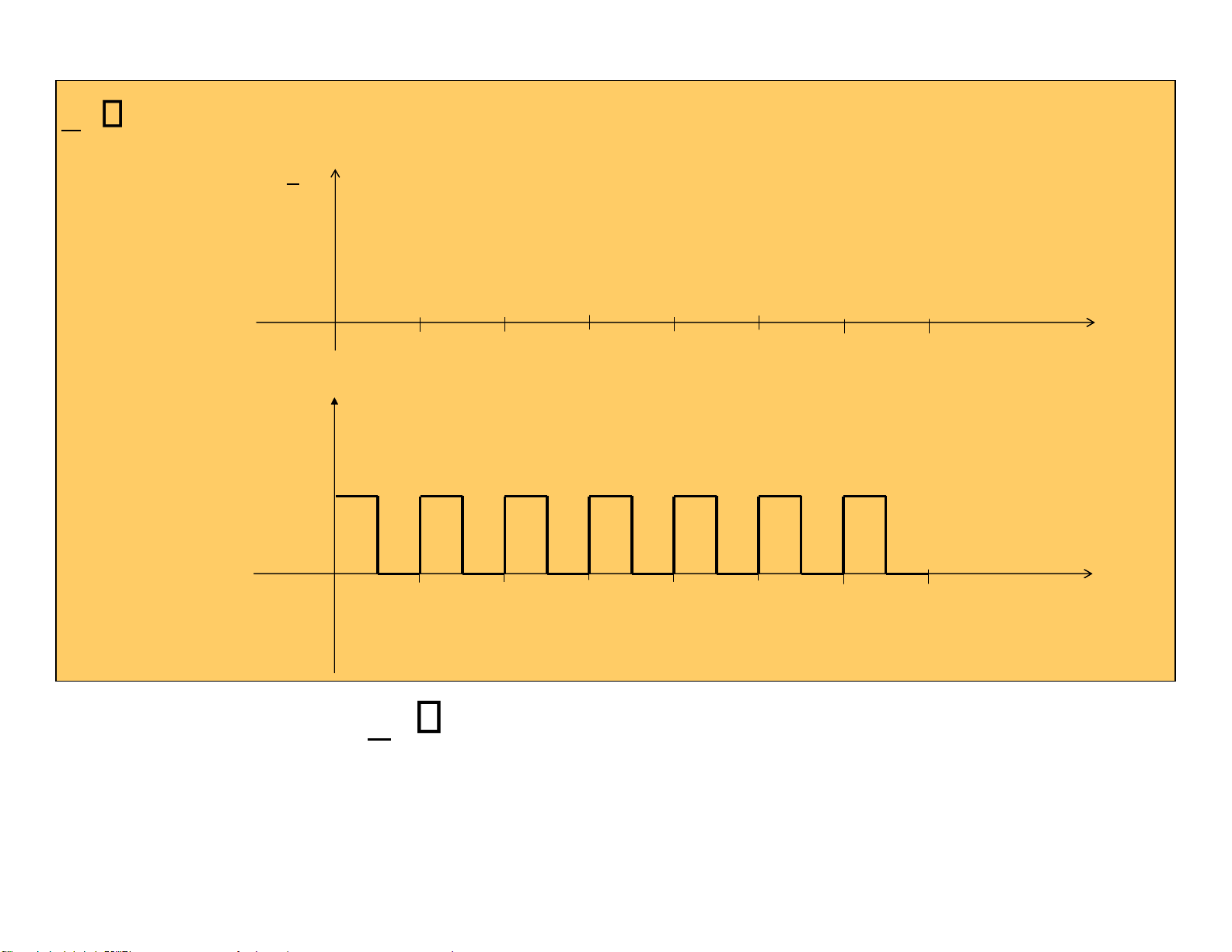
Mỗi bit uT[i] sẽ tồn tại trong khoảng Tb=1/Rb giây ( iT b
t < (i+1)Tb) u T Ví dụ: u (1101001...) T 1 1 0 1 0 0 1 T 2 T 3 T 4 T 5 T 6 T 7 T b b b b b b b
Một chuỗi dữ liệu nhị phân u được đặc trưng như sau:T
• Các bit dữ liệu của nó u iT [ ]
• Xung đồng hồ truyền, với tần số Rb Ví dụ lOMoARcPSD| 36991220 u (1101001...) T uT 1 1 0 1 0 0 1 T T T 7T t b 2 T 3 T 4T 6 b b 5 b b b b CLOCK t T T T 7T b 2 T 3 T 4 T 5 6 b b b b b b u T
(uT [0],uT [1],...,u iT [ ],...) lOMoARcPSD| 36991220
Các chuỗi dữ liệu nhị phân ngẫu nhiên lý tưởng
• Các bit của nó độc lập thống kê với nhau P(uT[i] |(uT[j] )=P(uT[i])
• Xác suất bit 0 và bit 1 là tương đồng P(uT[i] = 0) = P(uT[i] = 1) i
Các dạng sóng truyền (transmitted waveforms)
Chuỗi dữ liệu nhị phân: uT
Dạng sóng truyền thực sự s(t) lOMoARcPSD| 36991220
= hàm thực theo thời gian Ví dụ
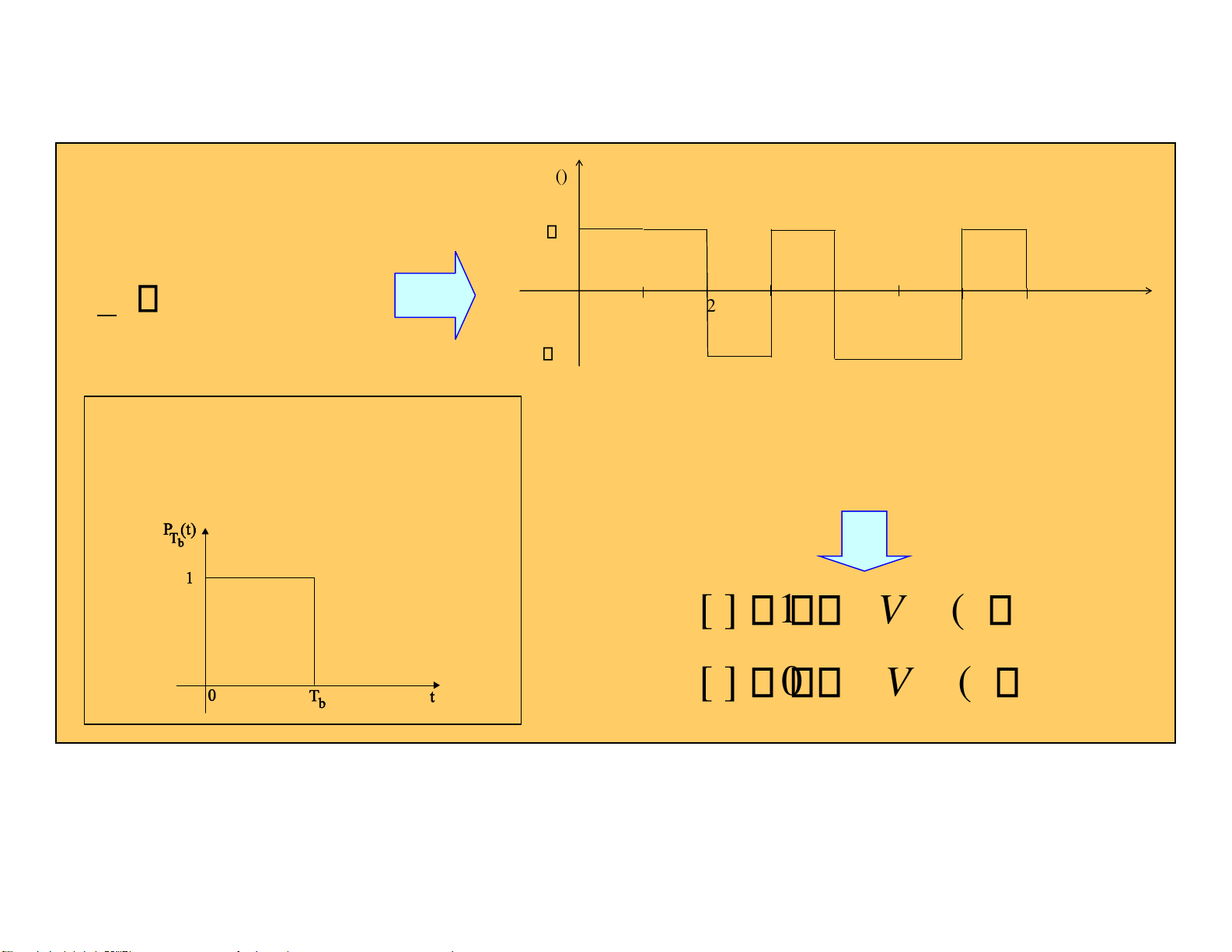
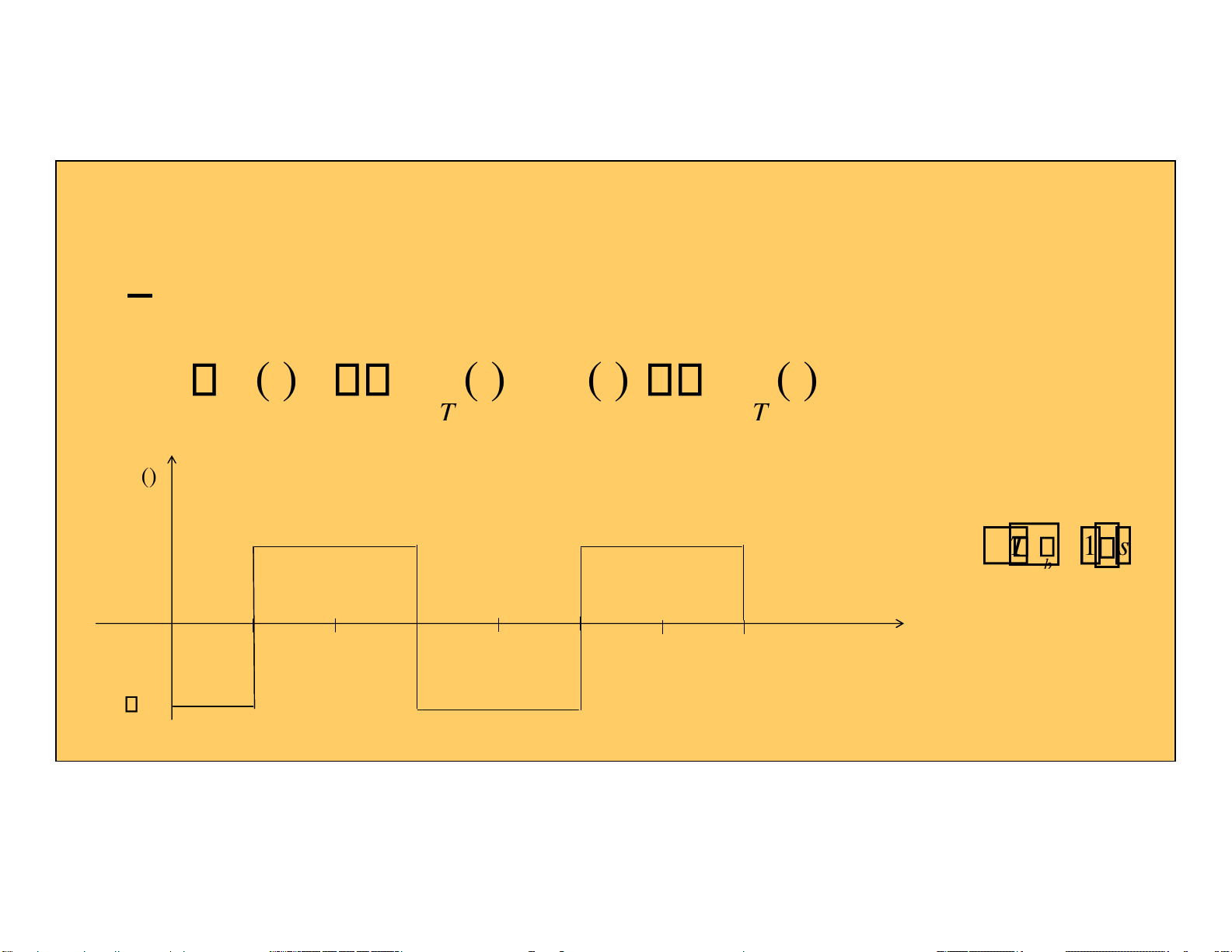
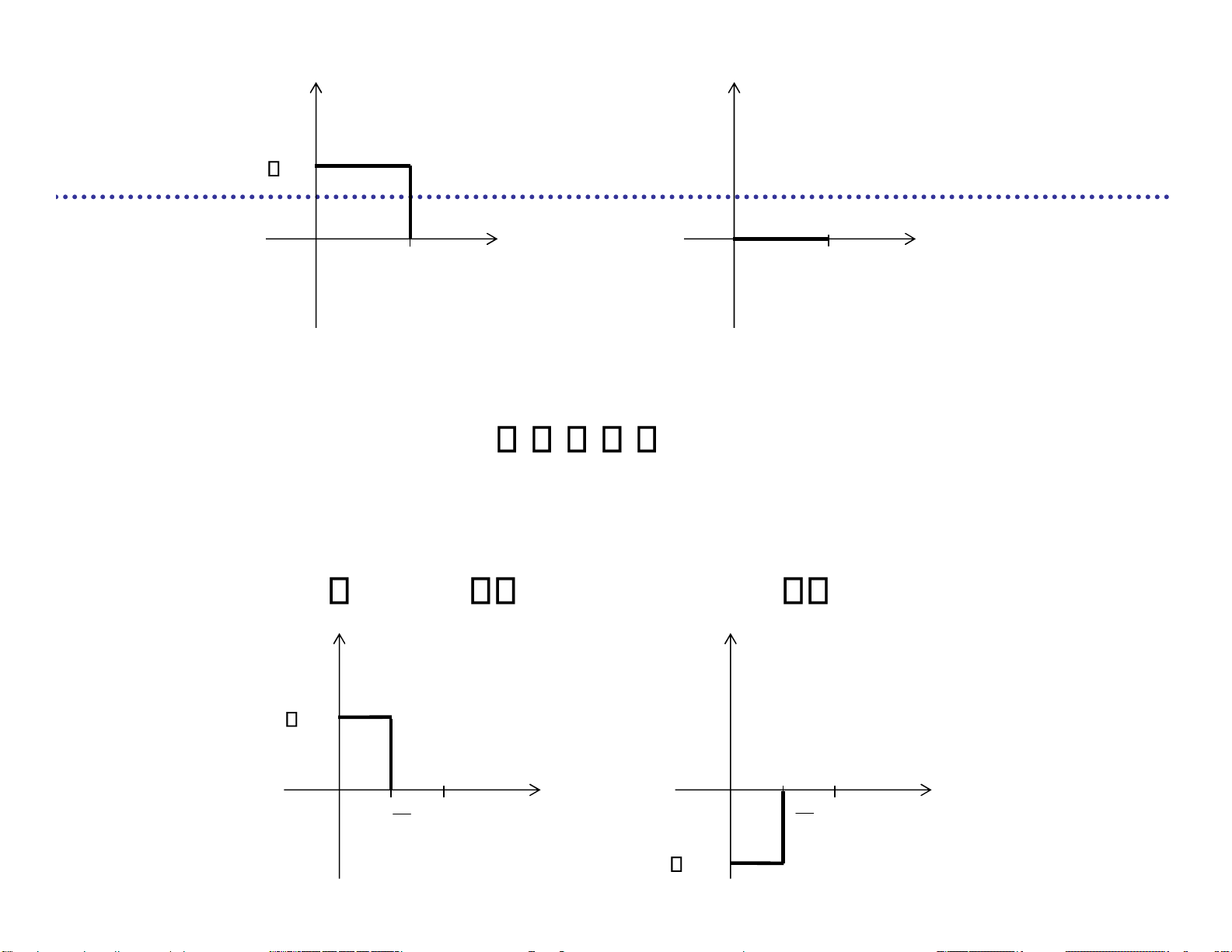
Biểu diễn NRZ lưỡng cực uT (1101001...)
bit '1’  tín hiệu +V u T
bit ‘0’  tín hiệu-V 1 1 0 1 0 0 1 T T 6 T 7 T b 2 T 3 T 4 T 5 b b b b b b () st V T T 6 T 7 T b 2 T 3 T 4 T 5 b b b b b b V lOMoARcPSD| 36991220 Ví dụ () st V u (1101001...) T T T 6 T 7 T b 2 T 3 4 T 5 b b b b b b T V
Hình chữ nhật trong
Hai tín hiệu tồn tại
khoảng thời gian T b [ ] u i 1 ( VP t iT ) T b T b [ ] u i 0 ( VP t iT ) T b T b
Chùm tín hiệu lOMoARcPSD| 36991220
Chùm tín hiệu M
M = { s1(t) , … , si(t), …, sm(t) }
Số phần tử: |M|=m=2k tín hiệu lOMoARcPSD| 36991220
M = { s1(t) , … , si(t), …, sm(t) }
Giả thiết: tất cả tín hiệu si(t) có miền thời gian hữu hạn
0 t < T = kTb Ví dụ lOMoARcPSD| 36991220 M { ( )s t1 VP t s tT ( ), 2( ) VP tT ( )} m 2 M { ( )s t1
VP tT ( )cos(2 f t s t0 ), 2( ) VP tT (
)sin(2 f t0 ), s t3( )
VP tT ( )cos(2 f t s t0 ), 4( )
VP tT ( )sin(2 f t0 )} m 4 lOMoARcPSD| 36991220
Không gian Hamming
Vector nhị phân k-bit v
(u0,...,ui ,...uk 1) ui Z2 Không gian Hamming Hk
{v (u0,...,ui ,...,uk 1) ui Z2}
Số phần tử: |Hk|=2k vectors lOMoARcPSD| 36991220 Ví dụ H1 = { (0) (1) } = Z2
H2 = { (00) (01) (10) (11) }
H3 = { (000) (001) (010) (011) (100) (101) (110) (111) }
Gán nhãn nhị phân
Chùm tín hiệu M: số tín hiệu thuộc chùm là: 2k lOMoARcPSD| 36991220
Không gian Hamming Hk: số phần tử 2k Ánh xạ 1-1 Gán nhãn nhị phân e: H k M
v Hk s t( ) e( )v M Ví dụ lOMoARcPSD| 36991220 M { ( )s t1 VP t s tT ( ), 2( ) VP tT ( )} m=2 k=1 H1 = { (0) , (1) } e H: 1 M (0) s t1( ) (1) s t2( ) Ví dụ lOMoARcPSD| 36991220
M { ( )s t1 VP tT ( )cos(2 f t s t0 ), 2( ) VP tT ( )sin(2 f t0 ), s t3( )
VP tT ( )cos(2 f t s t0 ), 4( ) VP tT ( )sin(2 f t0 )} m=4 k=2 e H: 2 M H (00) s t1( )
2 = { (00) , (01) , (11) , (10) } (01) s t2( ) (10) s t3( ) (11) s t4( )
Dạng sóng truyền Giả thiết: lOMoARcPSD| 36991220  Chuỗi nhị phân uT
 Chùm tín hiệu M
 Gán nhãn nhị phân e
Xây dựng dạng sóng truyền s(t)
là một nhiệm vụ khá đơn giản M
có số phần tử 2k e H: k M
chia uT thành các vector k-bit u T
(uT [0],uT [1],...,u iT [ ],...) lOMoARcPSD| 36991220 uT
vT [0],vT [1],...,v nT [ ],... Vector [0]
vT[0]=(uT[0],…, uT[k-1]) Vector [n]
vT[n]=(uT[nk],…, uT[(n+1)k-1])
Mỗi bit tồn tại trong Tb giây
Mỗi vector k-bit tồn tại trong kTb=T giây uT
(vT[0] ,vT[1] ,..., v nT[ ] ,...) lOMoARcPSD| 36991220 T T T
Mỗi tín hiệu si(t) M tồn tại trong T giây 0 t < T = kTb
Transmitted waveform
Gán nhãn nhị phân e H: k M u T
( vT[0] , vT[1] , ... , v nT[ ] , ... ) T T T e e e lOMoARcPSD| 36991220
st() ( s[0]()t , s t[1]() , ... , sn t[ ]() , ... )
Dóng hàng đúng(Correct alignment): s n t[ ]( ) e( [ ])vT n ???
Vấn đề: chùm tín hiệu
M = { s1(t) , … , si(t), …, sm(t) } Được định nghĩa trong
0 t < T = kTb
Nhưng chỉ có vector nhị phân đầu tiên được biểu diễn u T
( vT[0] , vT[1] , ... , v nT[ ] , ... ) lOMoARcPSD| 36991220 e T e e T T
st() ( s[0]()t , s t[1]() , ... , sn t[ ]() , ... )
Dóng hàng chính xác đạt đượ c
s n t[ ]( ) T en ( (vT [ ])n Nếu
T y tn ( ( )) y t(nT)
Gán nhãn nhị phân e H: k M lOMoARcPSD| 36991220 u T
( vT[0] , vT[1] , ... , v nT[ ] , ... ) T T T e e e
st() ( s[0]()t , s t[1]() , ... , sn t[ ]() , ... )
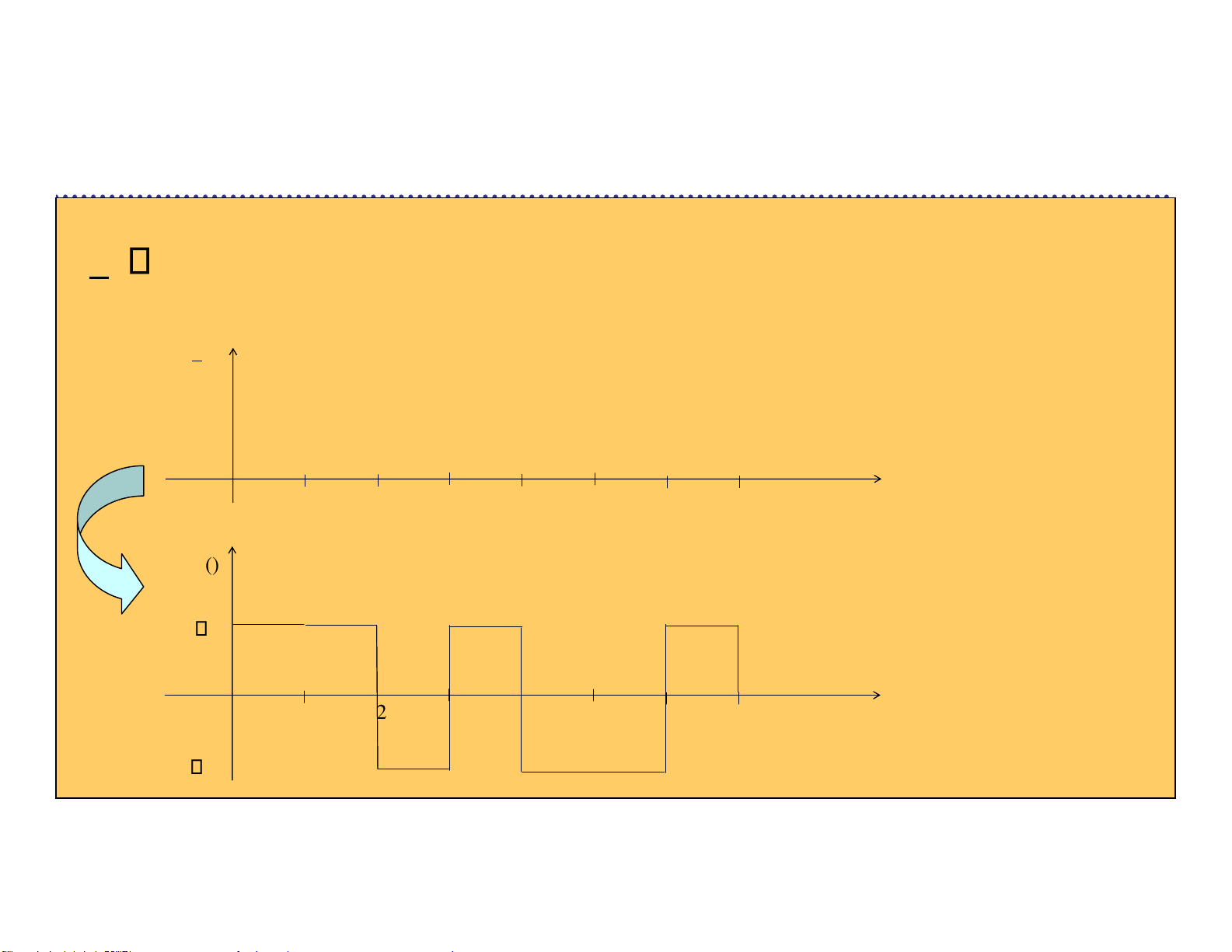
s n t[ ]( ) T en ( (vT [ Dóng hàng đúng ])n lOMoARcPSD| 36991220 Ví dụ:
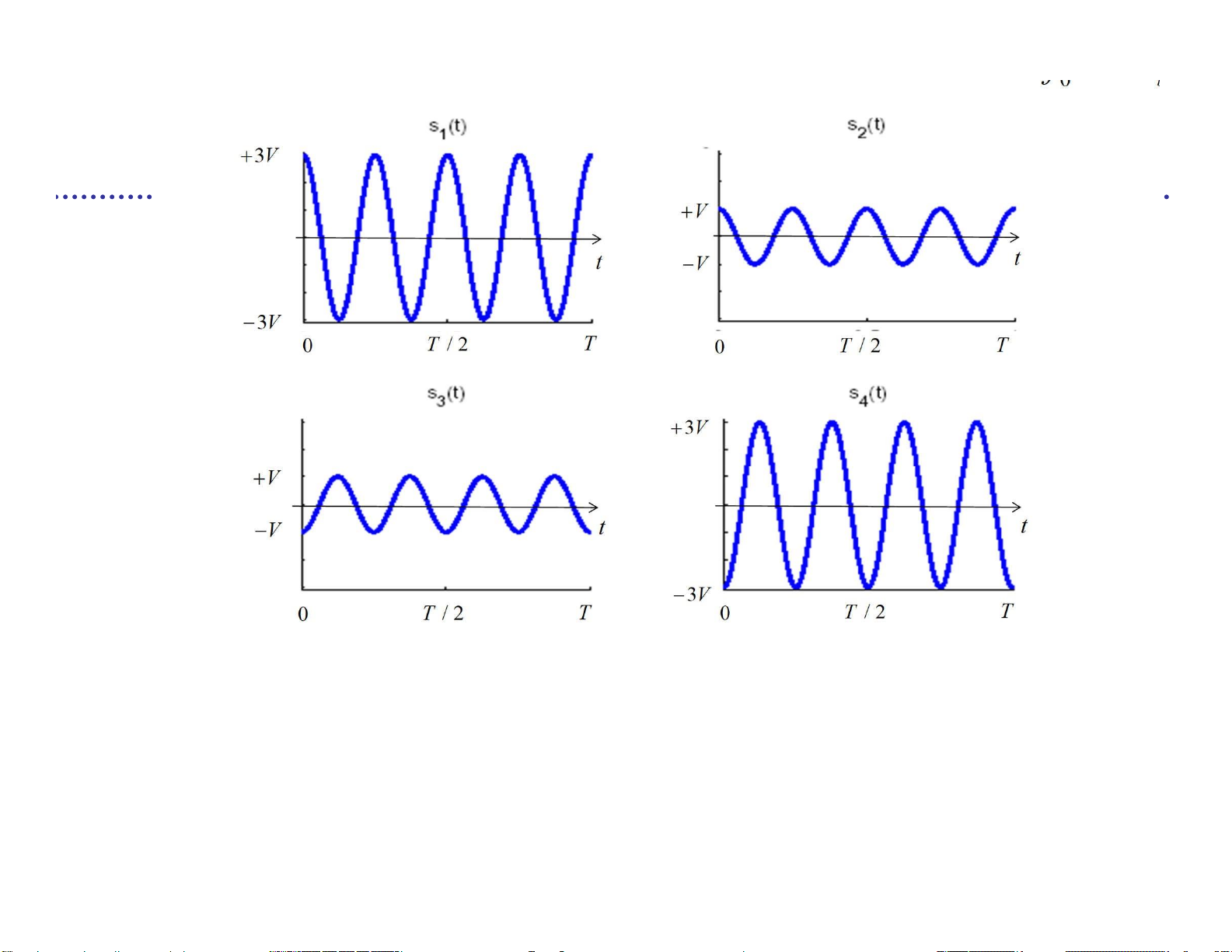
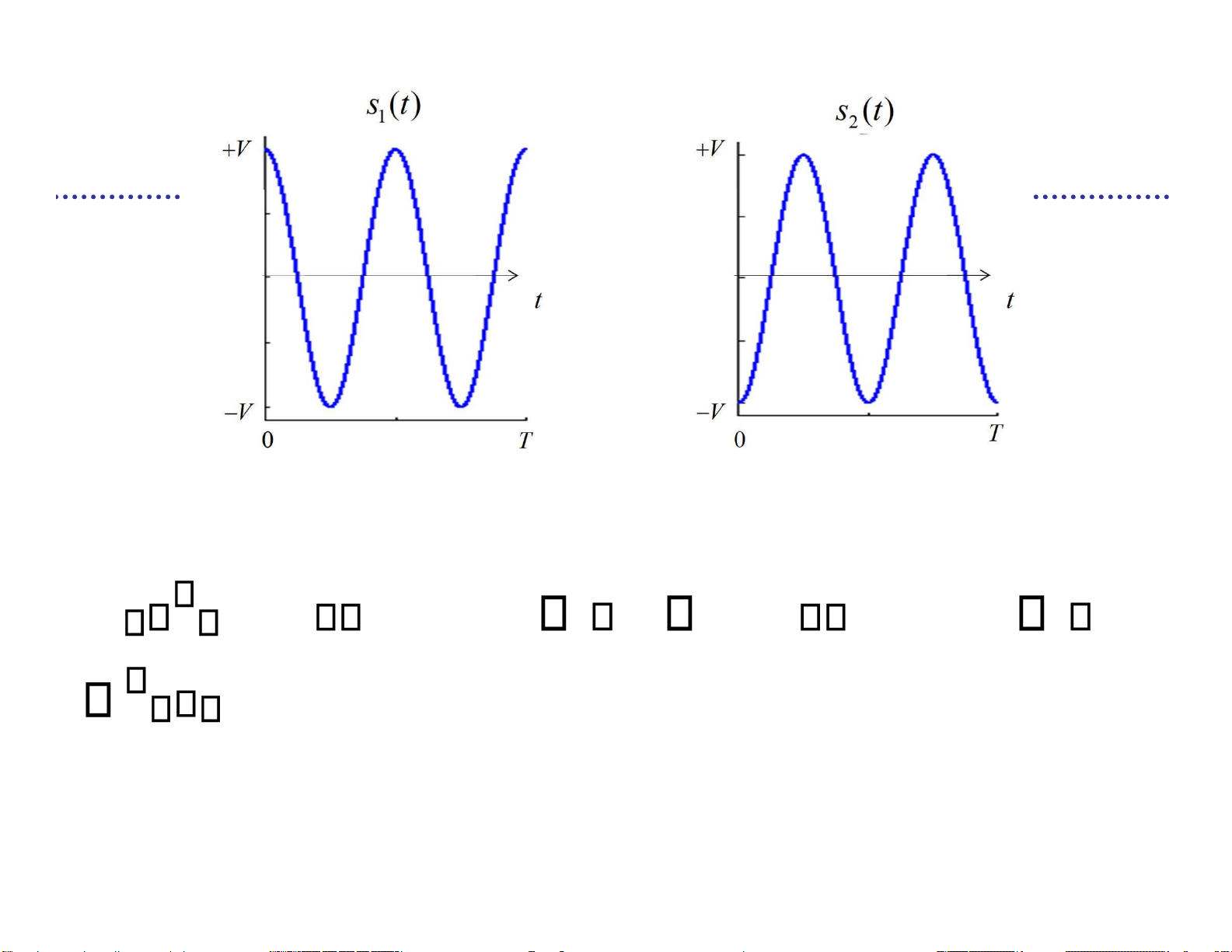
u =(0110011…) R =1 Mbps T b M { ( ) s t VP ( ) t , ( ) s t VP ( )} t 1 T 2 T () st V T T 1 s b T 2 T 3 T 4 T 5 T 6 T 7 T V lOMoARcPSD| 36991220 Bài tập
uT=(10011100…) Rb=1 Mbps
M { ( )s t1 VP tT ( )cos(2 f t s t0 ), 2( ) VP tT ( )sin(2 f t0 ), s t3( )
VP tT ( )cos(2 f t s t0 ), 4( ) VP tT ( )sin(2 f t0 )} ( f0=1MHz )
Ví dụ các chùm tín hiệu trong thực tế lOMoARcPSD| 36991220
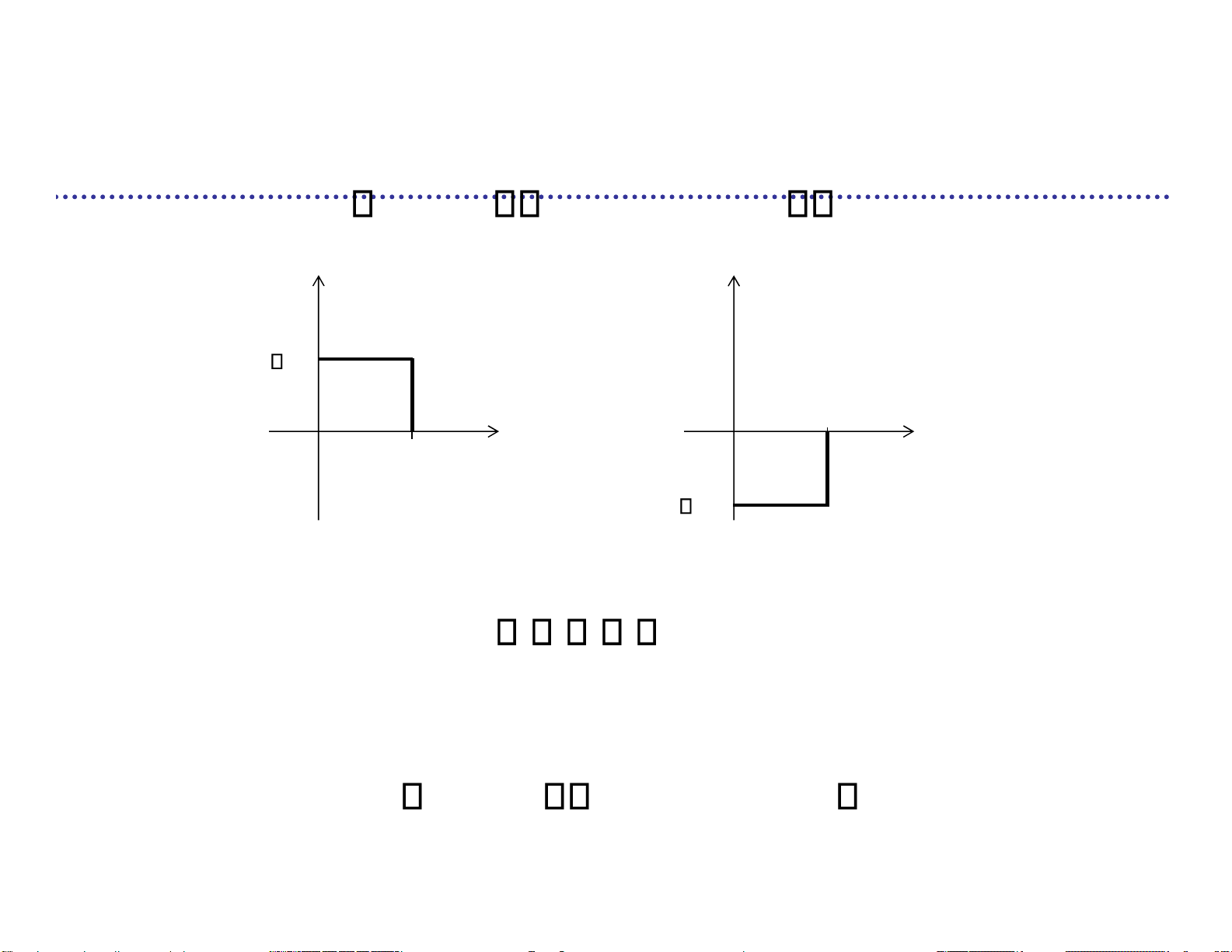
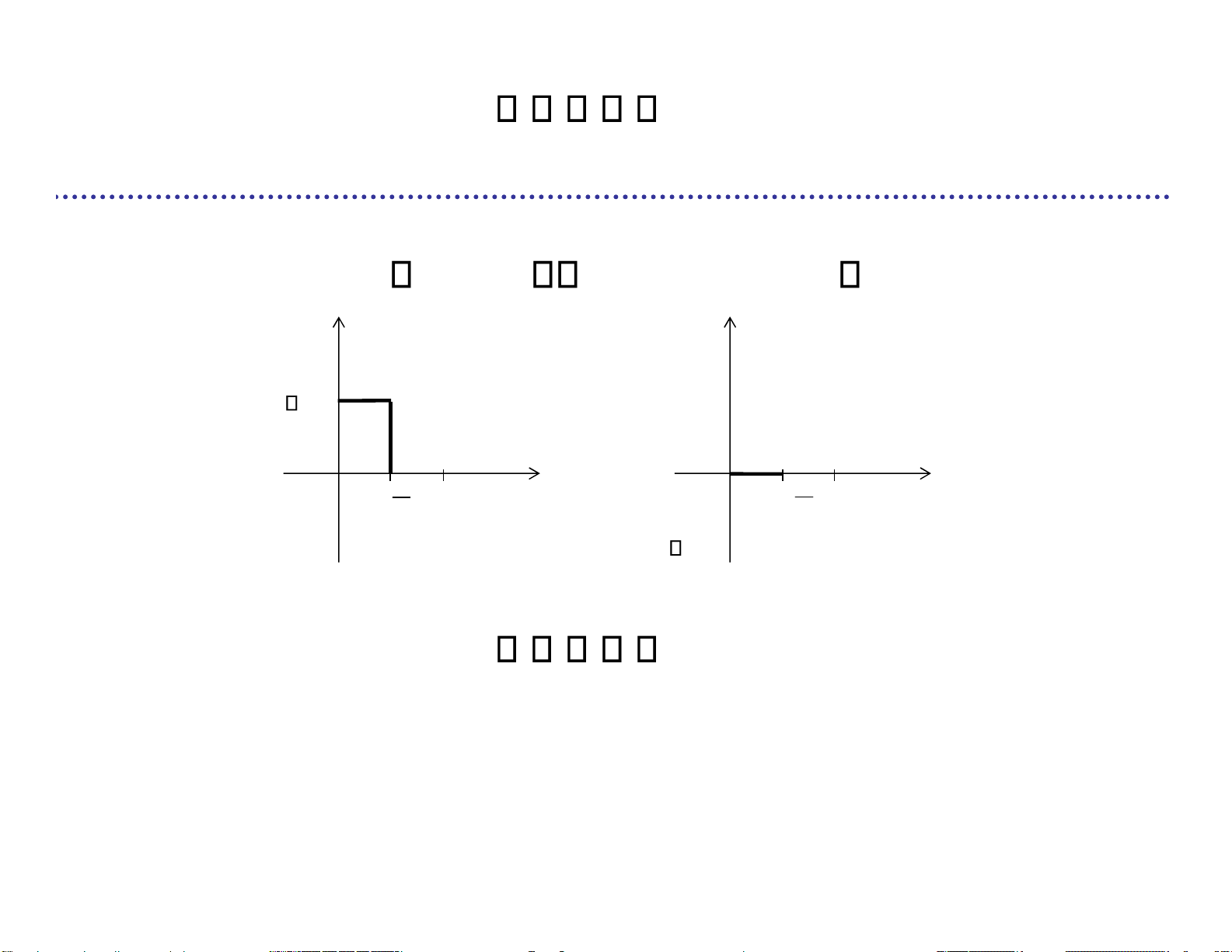
NRZ lưỡng cực (Non Return to Zero) M { ( )s t1 VP t s tT ( ), 2( ) VP tT ( )} s t s t 1 () 2 () V T T t V t m 2k 1 T Tb
NRZ đơn cực (Non Return to Zero) M { ( )s t1 VP t s tT ( ), 2( ) 0} lOMoARcPSD| 36991220 s t s t 1 () 2 () V T T t t m 2k 1 T Tb
RZ lưỡng cực (Return to Zero) M { ( )s t1
VPT /2 ( )t s t, 2 ( ) VPT /2( )}t s t s t 1 () 2 () V T T t T T t 2 2 V lOMoARcPSD| 36991220 m 2k 1 T Tb
RZ đơn cực (Return to Zero) M { ( )s t1
VPT /2( )t s t, 2 ( ) 0} s t s t 1 () 2 () V T T t T T t 2 2 V m 2k 1 T Tb
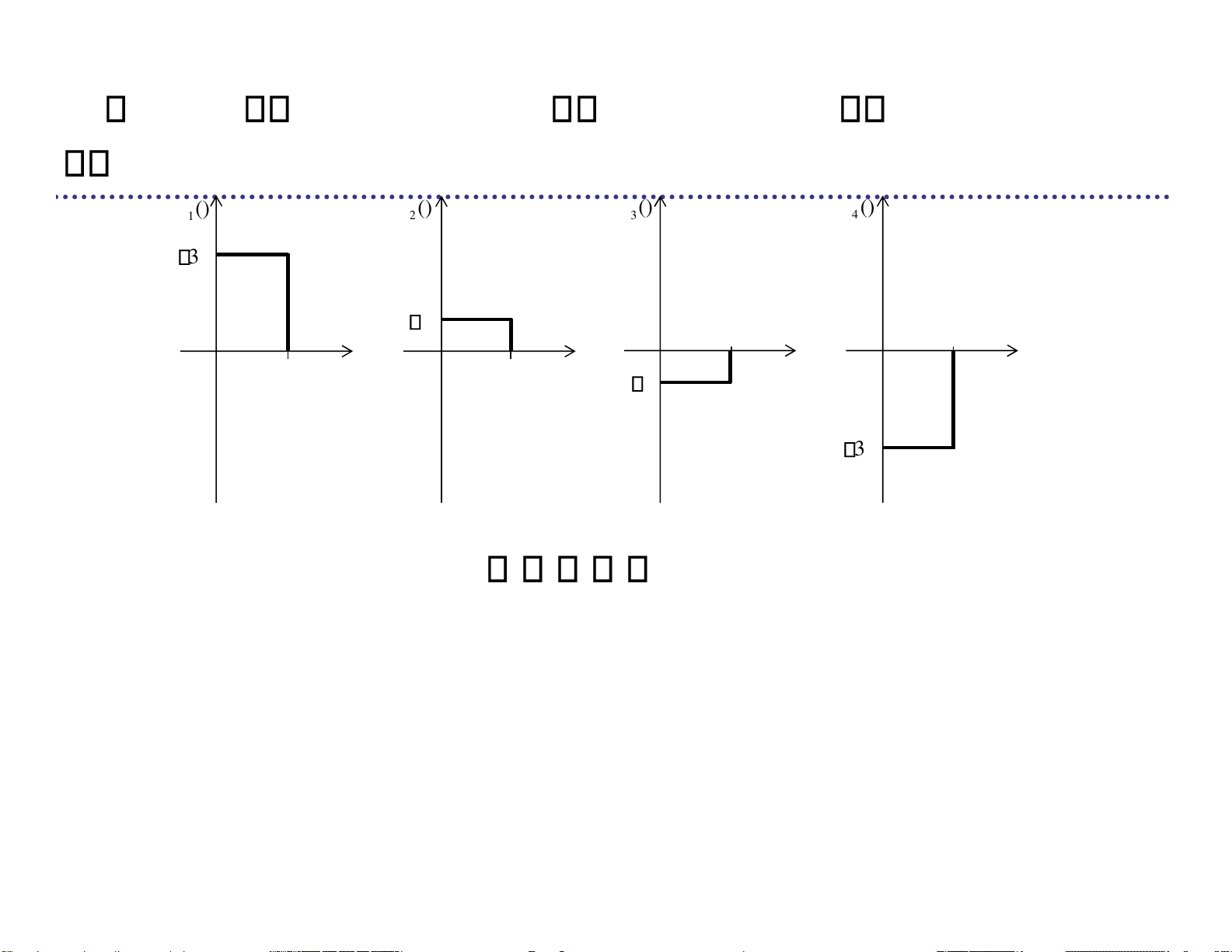
m-PAM (Pulse Amplitude Modulation)
điều chế biên độ xung Ví dụ: 4-PAM lOMoARcPSD| 36991220 M { ( )s t1 3VP t s tT ( ), 2( ) VP t s tT ( ), 3( ) VP t s tT ( ), 4( ) 3VP tT ( )} st st st st 1 () 2 () 3 () 4 () 3 V V T T T T V 3 V t t t t m 4k 2 T 2Tb
m-ASK (Amplitude Shift Keying)
Điều chế dịch biên độ Ví dụ: 4-ASK lOMoARcPSD| 36991220 M { ( )s t1
3VP tT ( )cos 2 f t0 ,s t2( ) VP tT (
)cos 2 f t0 , s t3( )
VP tT ( )cos 2 f t0 ,s t4( )
3VP tT ( )cos 2 f t0 } m 4k 2 T 2Tb 4-ASK f 0 2Rb lOMoARcPSD| 36991220
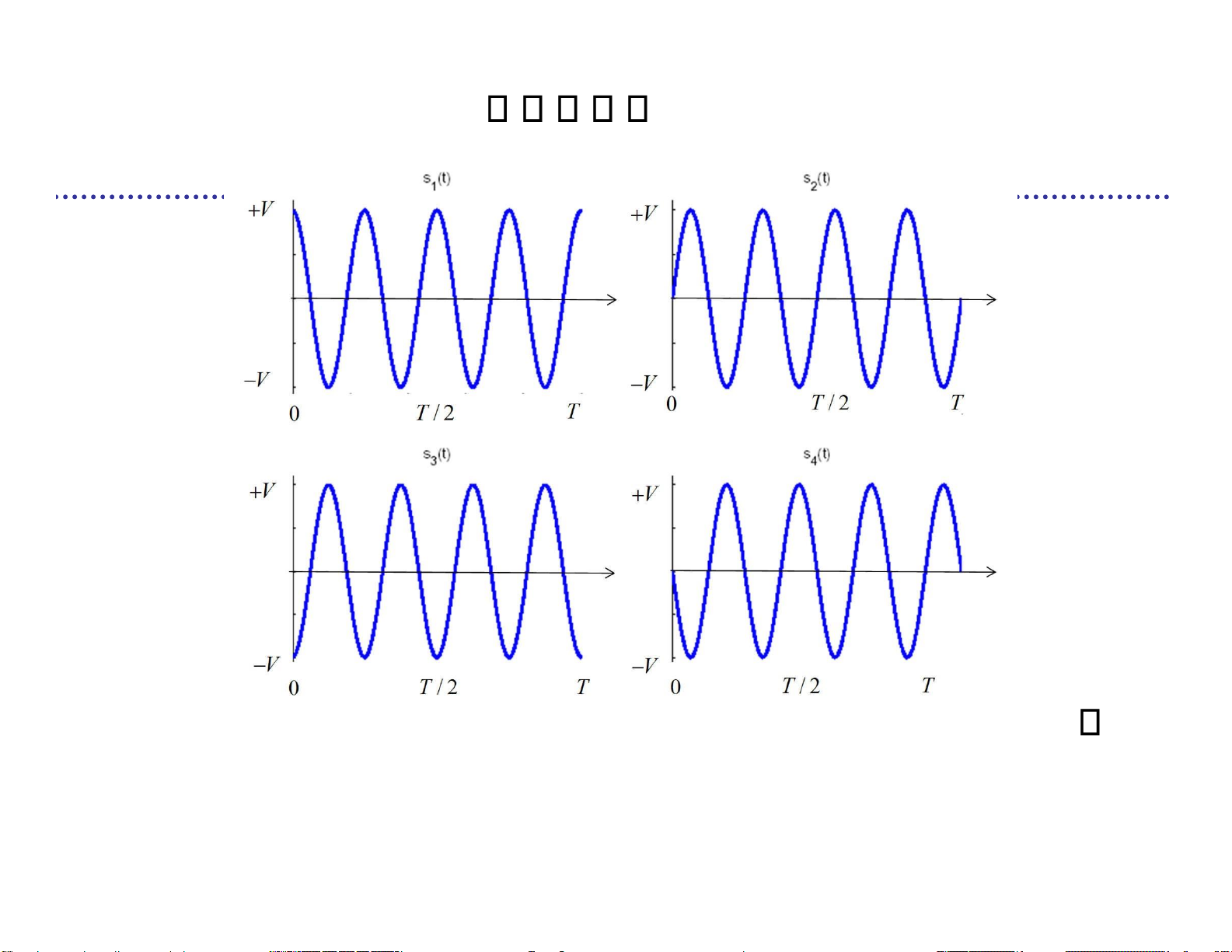
m-PSK (Phase Shift Keying) Example: 2-PSK lOMoARcPSD| 36991220 M { ( )s t1
VP tT ( )cos 2 f t0 ,s t2( )
VP tT ( )cos 2 f t0 } { ( )s t1
VP tT ( )cos 2 f t0 ,s t2( )
VP tT ( )cos 2 f t0 } m 2k 1 T Tb 2-PSK f 0 2Rb lOMoARcPSD| 36991220 Example: 4-PSK M s t1( )
VP tT ( )cos 2 f t0 ,s t2( )
VP tT ( )sin 2 f t0 , lOMoARcPSD| 36991220 s t 3( )
VP tT ( )cos 2 f t0 ,s t4( )
VP tT ( )sin 2 f t0 s t1( )
VP tT ( )cos 2 f t0 ,s t2( ) VP tT ( )cos 2 f t0 2 , s t3( ) VP tT ( )cos 2 f t 3 0
,s t4( ) VP tT ( )cos 2 f t0 2 lOMoARcPSD| 36991220 m 4k 2 T 2Tb 4-PSK f 0 2Rb lOMoARcPSD| 36991220
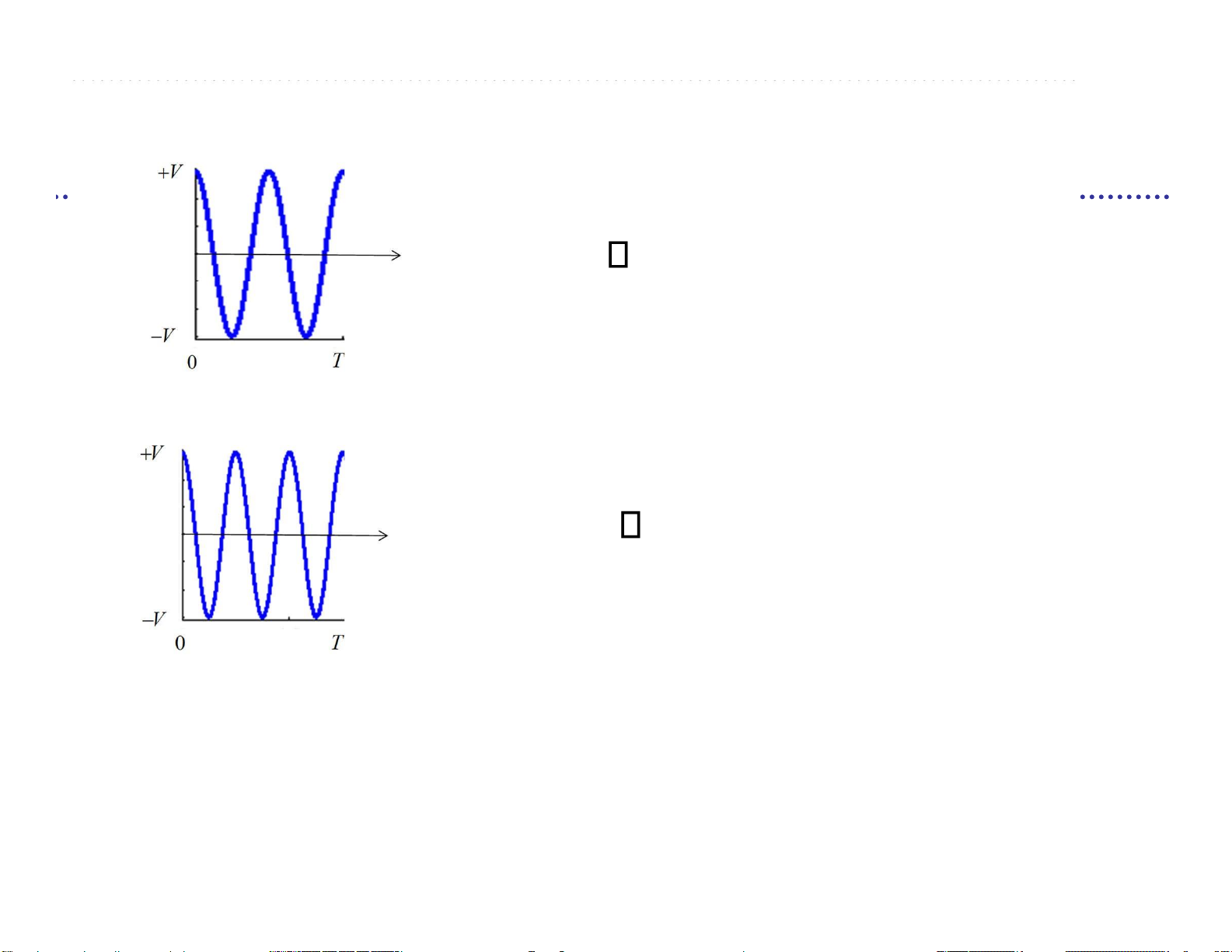
m-FSK (Frequency Shift Keying)
Điều chế dịch tần số Ví dụ: 2-FSK M { ( )s t1
VP tT ( )cos 2 f t1 ,s t2( )
VP tT ( )cos 2 f t2 } m 2k 1 T Tb lOMoARcPSD| 36991220 2- FSK f 2R 1 b f 3R 2 b lOMoARcPSD| 36991220 Bài tập
uT=(10011100…) Rb=1 Mbps
Vẽ dạng sóng của tất cả các chùm tín hiệu đã liệt kê vừa rồi