lOMoARcPSD| 36991220
Nhập môn Kỹ thuật Truyền thông
Bài 4: Lý thuyết ra quyết định
4.1 Biểu diễn không gian tín hiệu PGS. Tạ Hải Tùng 1 lOMoARcPSD| 36991220
4.1 Lý thuyết ra quyết định: biểu diễn không gian tín hiệu lOMoARcPSD| 36991220
Truyền thông trên kênh (channel transmission)
Chuỗi dữ liệu nhị phân uT Dạng sóng s t( )
Được truyền qua kênh để đến điểm đích lOMoARcPSD| 36991220 Mô hình kênh: Kênh Tạp âm trắng cộng Gauss có tính
(Additive White Gaussian Noise - AWGN) Channel transmission
Kênh AWGN có đặc tính
 Tuyến tính và bất biến theo thời gian Đáp
ứng tần số lý tưởng H(f)=1
 Tạp âm Gauss có tính cộng n(t) lOMoARcPSD| 36991220 Channel transmission
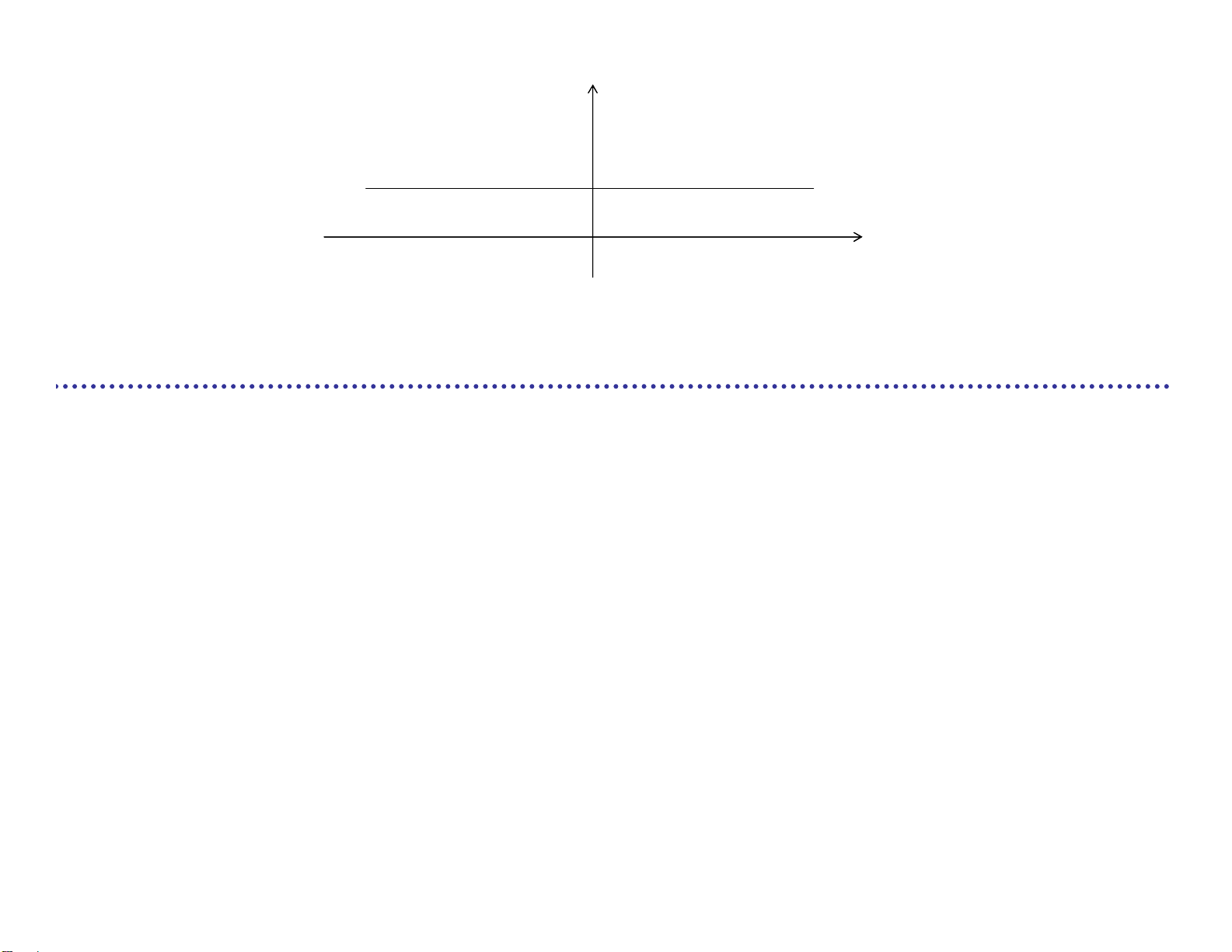
Tạp âm Gauss trắng n(t)
• Tiến trình ngẫu nhiên ergodic
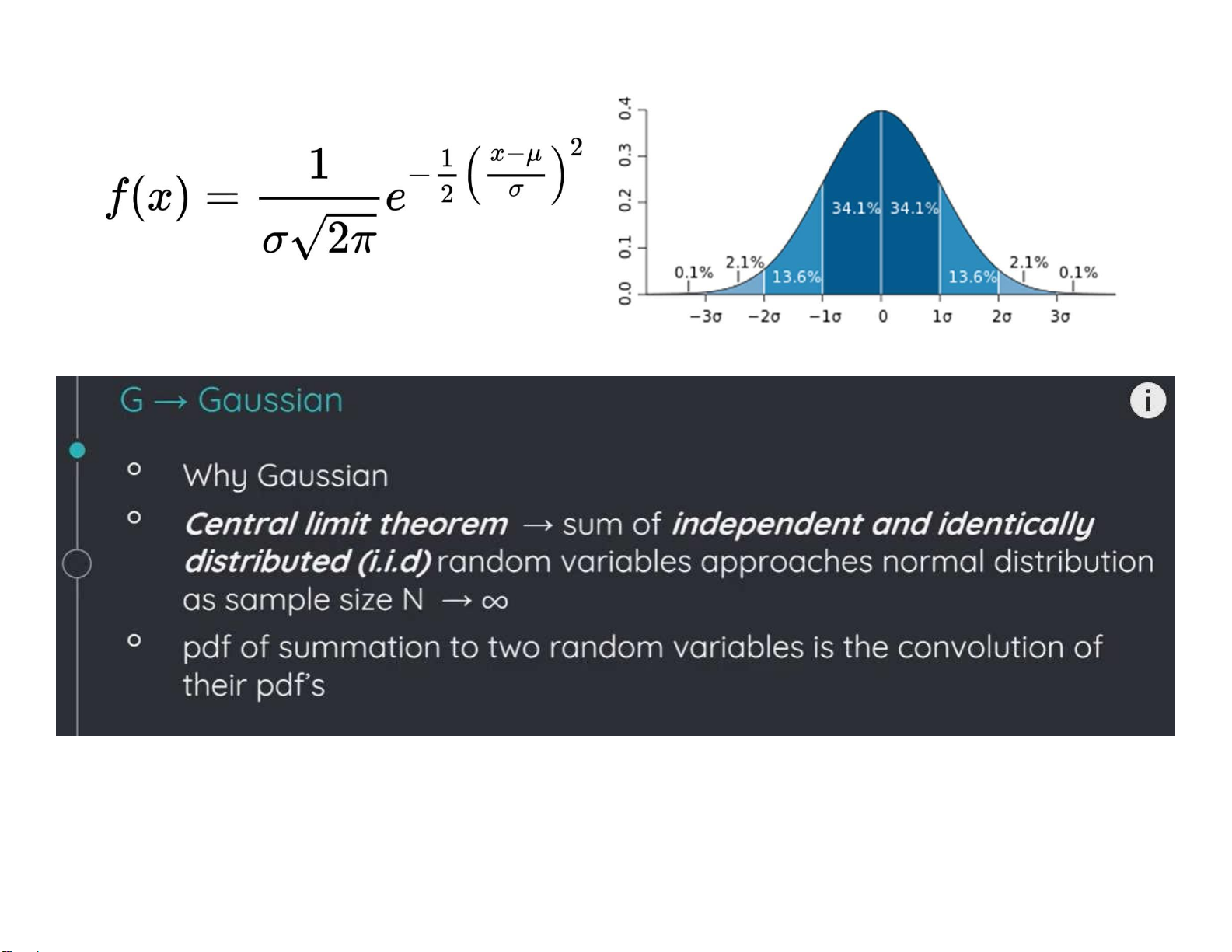
• Mỗi biến ngẫu nhiên tuân theo Phân bố chuẩn Gauss
với giá trị trung bình bằng 0
• Mật độ công suất phổ tín hiệu là hằng số Gn(f)=N0/2 G ( )f lOMoARcPSD| 36991220 n N 0 /2 f
Quá trình ngẫu nhiên có tính chất ergodic
• Quá trình ngẫu nhiên được gọi là ergodic nếu các
đặc trưng thống kê của nó có thể suy ra được từ
một chuỗi các mẫu đủ dài của nó. lOMoARcPSD| 36991220
Tại sao tạp âm có phân bố Gaussian? lOMoARcPSD| 36991220 lOMoARcPSD| 36991220
• Noise (tạp âm tổng cộng) là tổng hợp của nhiễu từ nhiều nguồn khác nhau.
Ví dụ: Loa Bluetooth nhận tín hiệu từ máy tính xách tay của bạn, có các nhiễu (tạp âm) sau:
– lò vi sóng có tần số vô tuyến tương tự, lỗi cảm biến do quá nhiệt, nhiễu
vật lý khi bạn nhấc loa lên, v.v.
– Làm thế nào để tạp âm tổng cộng tuân theo Gauss??? lOMoARcPSD| 36991220
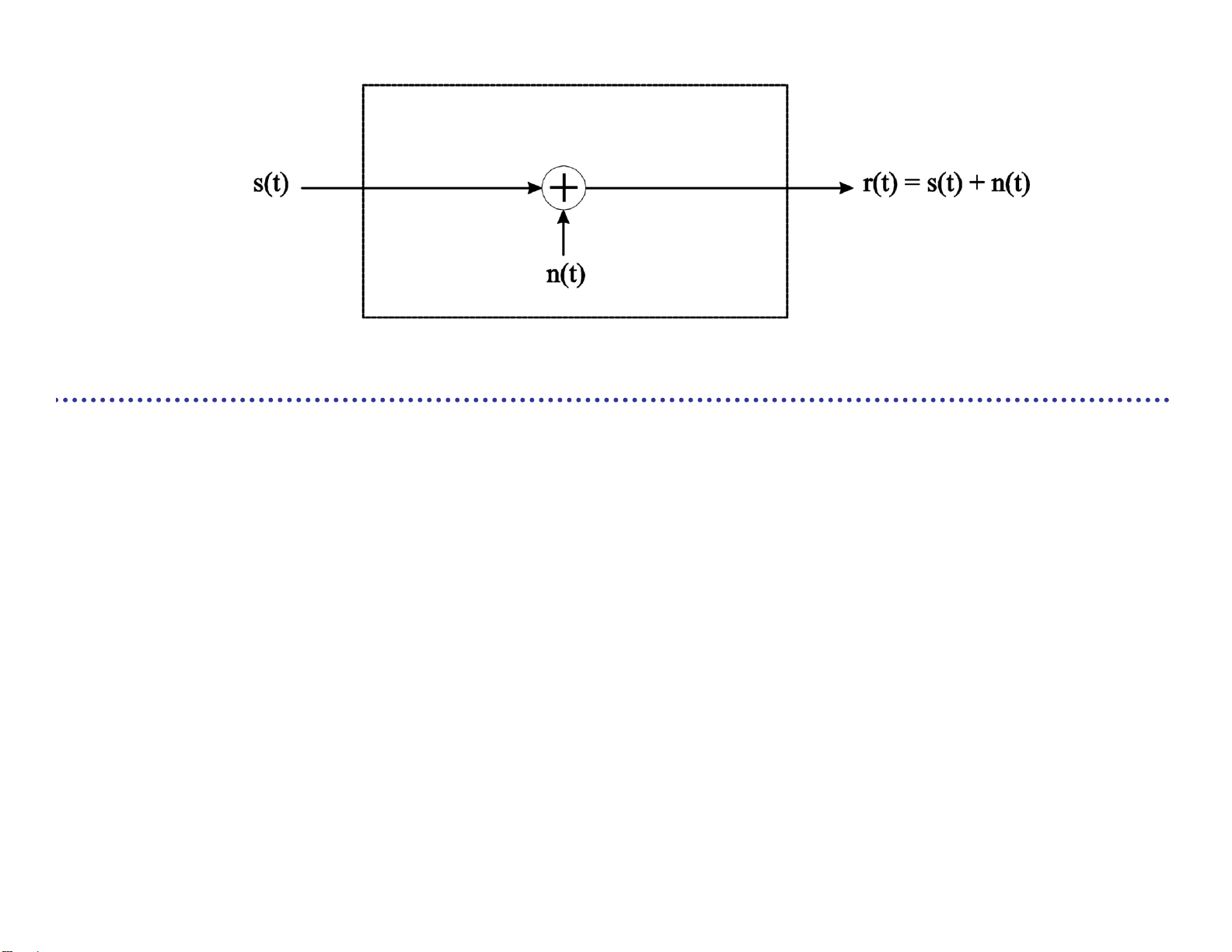
Truyền thông trên kênh
Chuỗi dữ liệu nhị phân uT
Dạng sóng được truyền s t( ) Kênh AWGN
Dạng sóng nhận được r t( ) s t( ) n t( ) uT s( )t
r( )t s( )t n( )t lOMoARcPSD| 36991220
Vấn đề tại phía bộ thu uT s( )t
r( )t s( )t n( )t
Vấn đề: nhận được r(t) khôi phục uT uT s( )t
r( )t s( )t n( )t lOMoARcPSD| 36991220
Vấn đề: nhận được r(t) khôi phục uT Chia thành 2 bước:
1. Nhận được r(t), khôi phục s(t): (vấn đề khó)
2. Nhận được s(t), khôi phục uT: (vấn đề dễ: gán nhãn là ánh xạ 1-1) uT s t( )
r t( ) s t( ) n t( )
Vấn đề: nhận được r(t) khôi phục s(t) lOMoARcPSD| 36991220
Thay vì xử lý trên dạng sóng thật
Đơn giản hơn nếu xử lý trên VECTORS
Cho chùm tín hiệu M = { s1(t) , … , si(t), …, sm(t) }
 Xây dựng cơ sở trực chuẩn B
 Xử lý trên không gian tín hiệu S sinh bởi B
 Mỗi tín hiệu thuộc S có thể được biểu diễn là một phối hợp
tuyến tính (linear combination) của các thành phần cơ sở lOMoARcPSD| 36991220
mỗi tín hiệu của S tương ứng với một vector thực (=
các hệ số của phối hợp tuyến tính đó) Cơ sở B Cho chùm tín hiệu:
M = { s1(t) , … , si(t), …, sm(t) }
Chúng ta phải tìm được cơ sở trực chuẩn:
B = { b1(t) , … , bj(t), …, bd(t) } (d m)
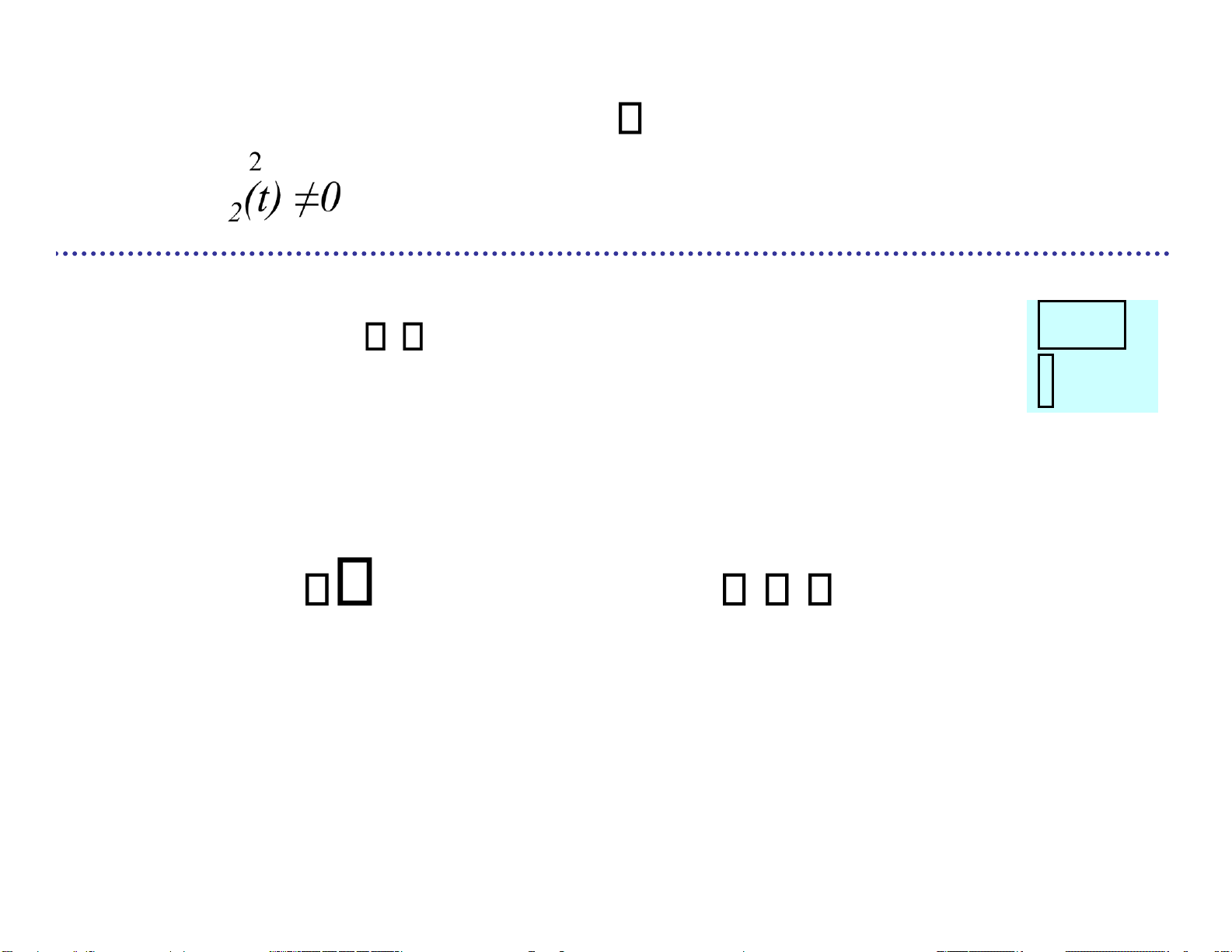
B = tập hợp các tín hiệu lOMoARcPSD| 36991220 T 1. Trực giao lẫn nhau j i b t b t dtj ( ) ( when )i 0 0 Cho chùm tín hiệu:
M = { s1(t) , … , si(t), …, sm(t) }
Chúng ta phải tìm được cơ sở trực chuẩn:
B = { b1(t) , … , bj(t), …, bd(t) } (d m)
B = tập hợp các tín hiệu lOMoARcPSD| 36991220 T
2. Với năng lượng đơn vị
b2 j ( )t dt 1 0 Cho chùm tín hiệu:
M = { s1(t) , … , si(t), …, sm(t) }
Chúng ta phải tìm được cơ sở trực chuẩn:
B = { b1(t) , … , bj(t), …, bd(t) } (d m)
B = tập hợp các tín hiệu
3. Số phần tử của cơ sở d là nhỏ nhất đủ để biểu diễu mỗi tín hiệu
của M là một phối hợp tuyến tính lOMoARcPSD| 36991220 d s ti ( ) s b t sij R ij j ( ) j 1 Cơ sở B
Cho chùm tín hiệu: M = { s1(t) , … , si(t), …, sm(t) }
Chúng ta có thể xây dựng được cơ sở :
B = { b1(t) , … , bj(t), …, bd(t) } (d m)
B = tập các tín hiệu T lOMoARcPSD| 36991220
b12 j ( )t dt 1 0 d s ti ( sij R ) s b tij j ( )
1 . Với năng lượng đơn vị: T j b t b t dt i j ( ) ( when )i 0 0
2 . Số phần tử của cơ sở d là nhỏ nhất đủ để biểu diễu mỗi tín hiệu
của M là một phối hợp tuyến tính lOMoARcPSD| 36991220 j 1 Xây dựng cơ sở B
Cho M, làm thế nào để xây dựng B ?
Với các chùm tín hiệu đơn giản, không khó để xây dựng B một cách trực tiếp 1 . Trực giao lOMoARcPSD| 36991220
Trong trường hợp chung ta có thể sử dụng thuật toán sau để xây dựng B từ M: Thuật toán Gram-Schmidt
Thuật toán Gram-Schmidt
M = { s1(t) , … , si(t), …, sm(t) } Bước 1
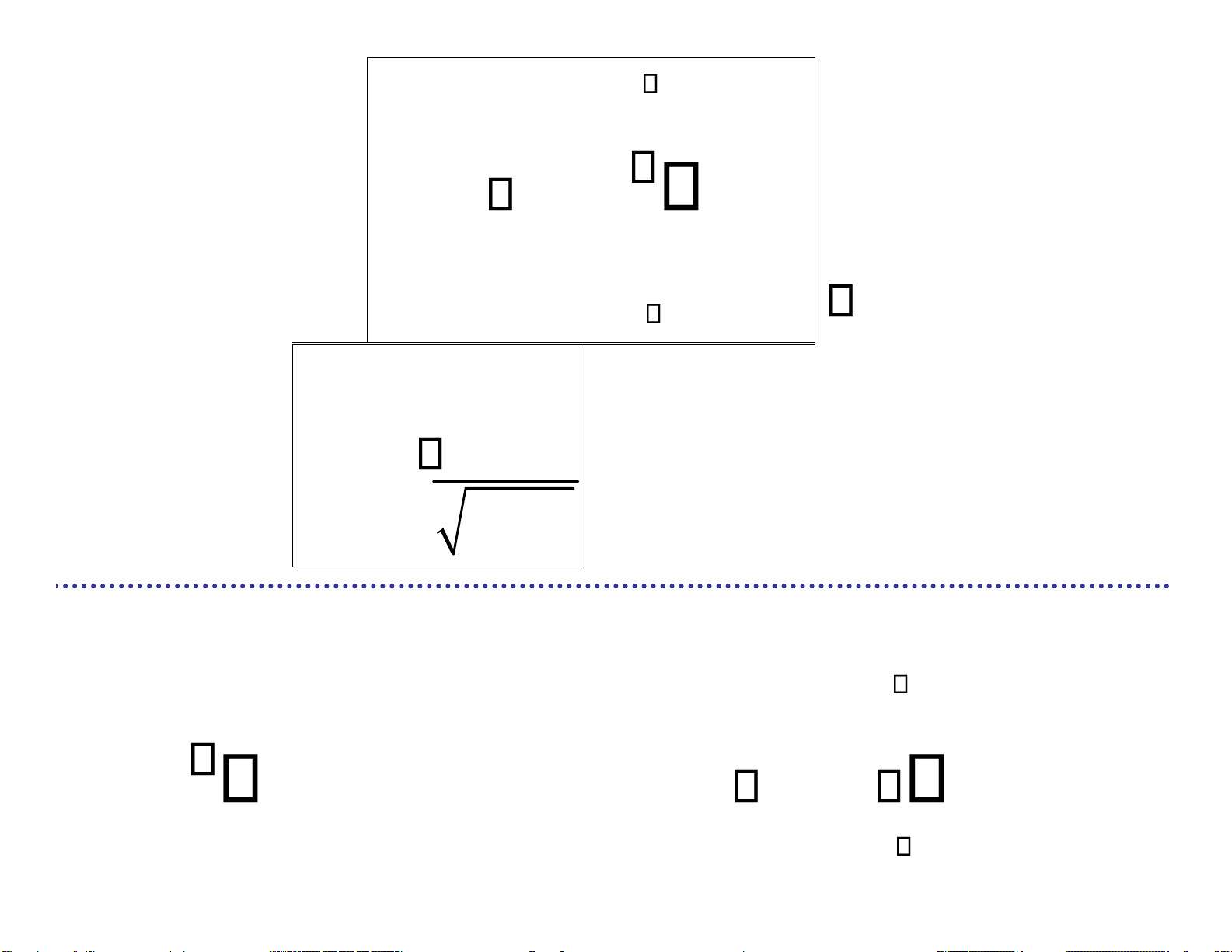
Cho s1(t) tính versor thứ nhất Định nghĩa tính b t * 1 ( ) s t1( ) lOMoARcPSD| 36991220 b t* (Nếu b t * 1 ( )
0 b1(t) = 0 ) b t1( ) 1 ( )* E b( )1 Cho s Bước
2(t), tìm versor thứ 2. 2
Tính phép chiếu của lên versor đầu tiên T s21 s t b t dt2( ) ( )1 0 Định nghĩa b t * 2 ( )
s t2( ) s b t21 1( ) lOMoARcPSD| 36991220 Tính b t* b ( Nếu b t * 2 ( ) 0 b2(t) = 0 t2( ) 2( )* ) E b( )2 T * s21 s t b t dt2( ) ( )1
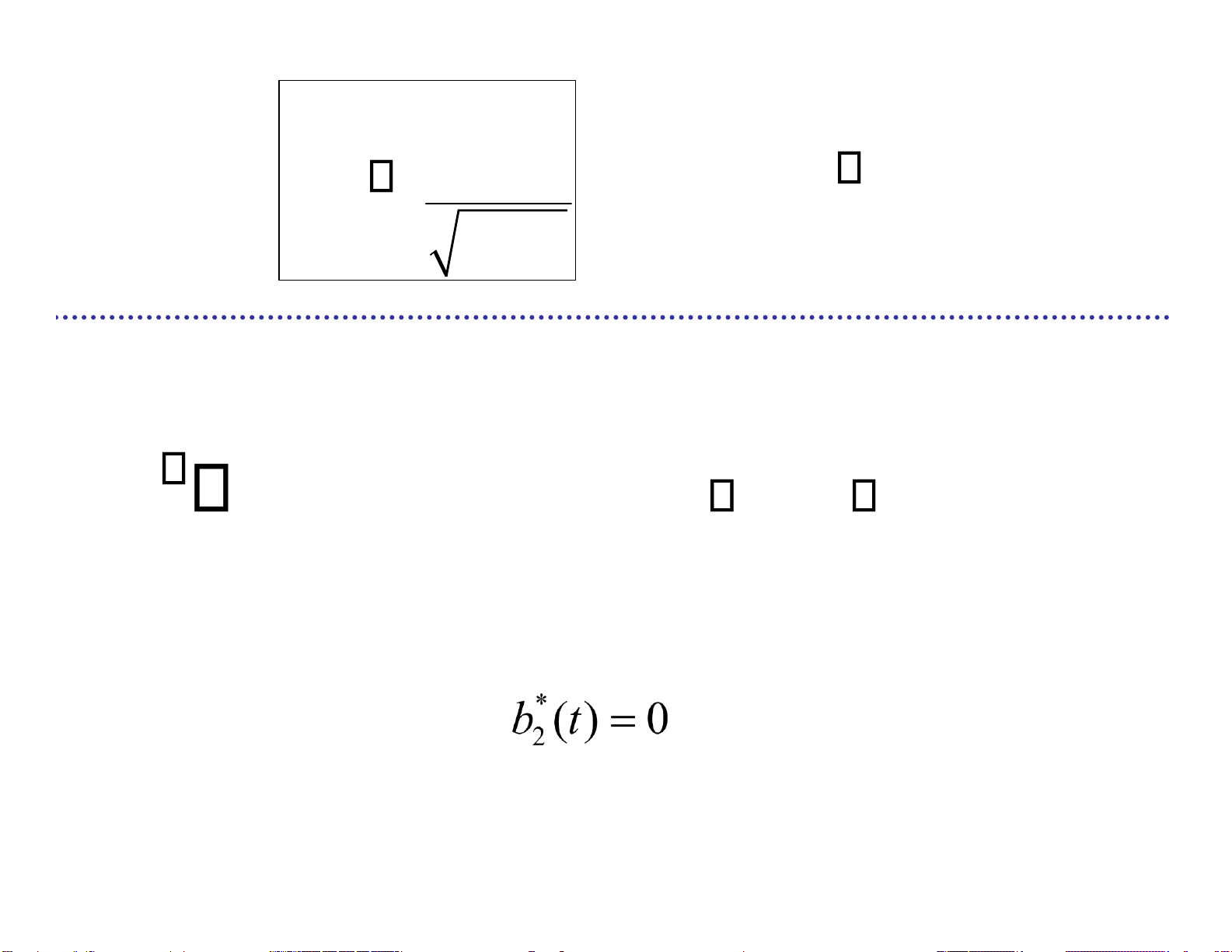
b t2 ( ) s t2( ) s b t21 1( ) 0 Lưu ý: • Nếu (
s2 (t) tỷ lệ với b1(t) )
 b2(t)=0 và không có versor mới nào lOMoARcPSD| 36991220
• Nếu (b t*( ) 0 s2 (t) không tỷ lệ với b1(t) )  b
và versor mới được tìm thấy Given s STEP i(t) 3 i m i
Tính phép chiếu lên các versor trước: T sij
s t b t dti ( ) ( )j 1 ji 1 o lOMoARcPSD| 36991220 Định nghĩa i 1 b t * i ( ) s ti ( ) s b tij j Tính ( ) j 1
0 bi(t) = 0 ) b t* b ti ( ) i ( )* E b( ) * i ( If b t1 ( ) i T 1 * sij
s t b t dti ( ) ( )j
b ti ( ) s ti ( ) s b tij j ( ) o j 1 lOMoARcPSD| 36991220 Lưu ý:
• Nếu (b t *i( ) 0 si (t) là phối hợp tuyến tính của các versor )
 bi(t)=0 và không có versor mới
• Nếu (b t *i( ) 0 si (t) không phải là phối hợp tuyến tính)
 bi(t) ≠0 và một versor mới tìm được lOMoARcPSD| 36991220 Bước cuối
• Loại bỏ tất cả bi(t) = 0
• Đánh lại chỉ số icho các versor khác 0 bi(t) • Ta có cơ sở B:
B = { b1(t) , … , bj(t), …, bd(t) } (d m) Bài tập lOMoARcPSD| 36991220 Cho chùm tín hiệu: M { ( )s t1 P t s tT ( ), 2( ) P tT ( )}
Xây dựng cơ sở trực chuẩn B? Xây dựng cơ sở lOMoARcPSD| 36991220
Như đã đề cập, với các chùm tín hiệu đơn giản, có thể xây dựng
trực tiếp Bmà không cần áp dụng Gram Schmidt.
Chỉ cần tìm ra d tín hiệu thỏa mãn các điều kiện của một cơ sở trực chuẩn: 1. Trực giao 2. Năng lượng đơn vị
3. Số phần d là nhỏ nhất và đủ để biểu diễn mỗi tín hiệu của M là một phối hợp tuyến tính Bài tập Cho chùm tín hiệu: lOMoARcPSD| 36991220 M { ( )s t 1 0,s t2( ) P tT ( )}
Xây dựng cơ sở trực chuẩn B? lOMoARcPSD| 36991220 Bài tập Cho chùm tín hiệu: M { ( )s t1
P tT ( )cos(2 f t s t0 ), 2( )
P tT ( )cos(2 f t0 )}
Xây dựng cơ sở trực chuẩn B? lOMoARcPSD| 36991220
Không gian tín hiệu S
Với cơ sở trực chuẩn B
B = { b1(t) , … , bj(t), …, bd(t) }
Không gian S được biểu diễn qua B là: d S a t( )
a b tjj ( ) aj R j 1
(tập tất cả các tín hiệu có thể được biểu diễn như là các phối hợp
tuyến tính của các tín hiệu cơ sở) lOMoARcPSD| 36991220 Bài tập Cho cơ sở B B b t1( ) 1 P tT ( ) T
Không gian tín hiệu S là gì? lOMoARcPSD| 36991220 Bài tập Cho cơ sở B B b t1( 2 ) P tT( T )cos 2 f t0
Không gian tín hiệu S là gì? lOMoARcPSD| 36991220 Biểu diễn vector
Cho trước B, với mỗi tín hiệu a(t) S ta có a t( ) d a b tj j ( ) j 1
Tín hiệu a(t) tương ứng với một vector thật với d thành phần (các
hệ số aj của phối hợp tuyến tính), và ngược lại: lOMoARcPSD| 36991220
a t( ) a (a1 ,...,aj ,...,ad ) Biểu diễn vector
1. Từ vector a tới tín hiệu a(t)
a (a1 ,...,aj ,...,ad ) a t( ) a b tj j ( )
2. Từ tín hiệu a(t) tương ứng vector a j 1 d
Phép chiếu lên versor bj(t) T lOMoARcPSD| 36991220 a t( ) aj
a t b t dt( ) ( )j 0
a (a1 ,...,aj ,...,ad )
Biểu diễn vector chùm tín hiệu Ta có M S
Mỗi tín hiệu si(t) S tương ứng với một vector thật với d thành phần và ngược lại: lOMoARcPSD| 36991220 s t i ( )
si (si1 ,...,sij ,...sid )
Chùm tín hiệu M là một tập tín hiệuM = { s1(t) , … , si(t), …, sm(t) }
Chùm tín hiệu M là một tập vector M = { s1 , … , si , …, sm }
1. Từ vector si tới tín hiệu si(t) d si
(si1 ,...,sij ,...,sid ) s ti ( ) s b tij j ( ) j 1
2. Từ tín hiệu si(t) tới vector si
Phép chiếu lên versor bj(t) T lOMoARcPSD| 36991220 s ti ( ) sij
s t b t dti ( ) ( )j 0 s i
(si1 ,...,sij ,...,sid )
Lưu ý: đối với các chùm tín hiệu đơn giản, các thành phần của
vector có thể được suy ra trực tiếp thay vì tính phép chiếu. Ta viết: lOMoARcPSD| 36991220 s t i ( )
s b ti1 1( ) ...s b tijj ( ) ...s b tid d ( )
Các tín hiệu cơ sở bi(t) đã biết.
Ta tìm tập các hệ số sij có thể thỏa mãn phương trình trên.
Lời giải (nghiệm) là duy nhất.
Không gian tín hiệu S là đẳng cấu (đồng hình) với không gian Euclid Rd
(tập hợp của tất cả các vector với các thành phần thực d)
Ta có thể vẽ trong không gian Đề-các)
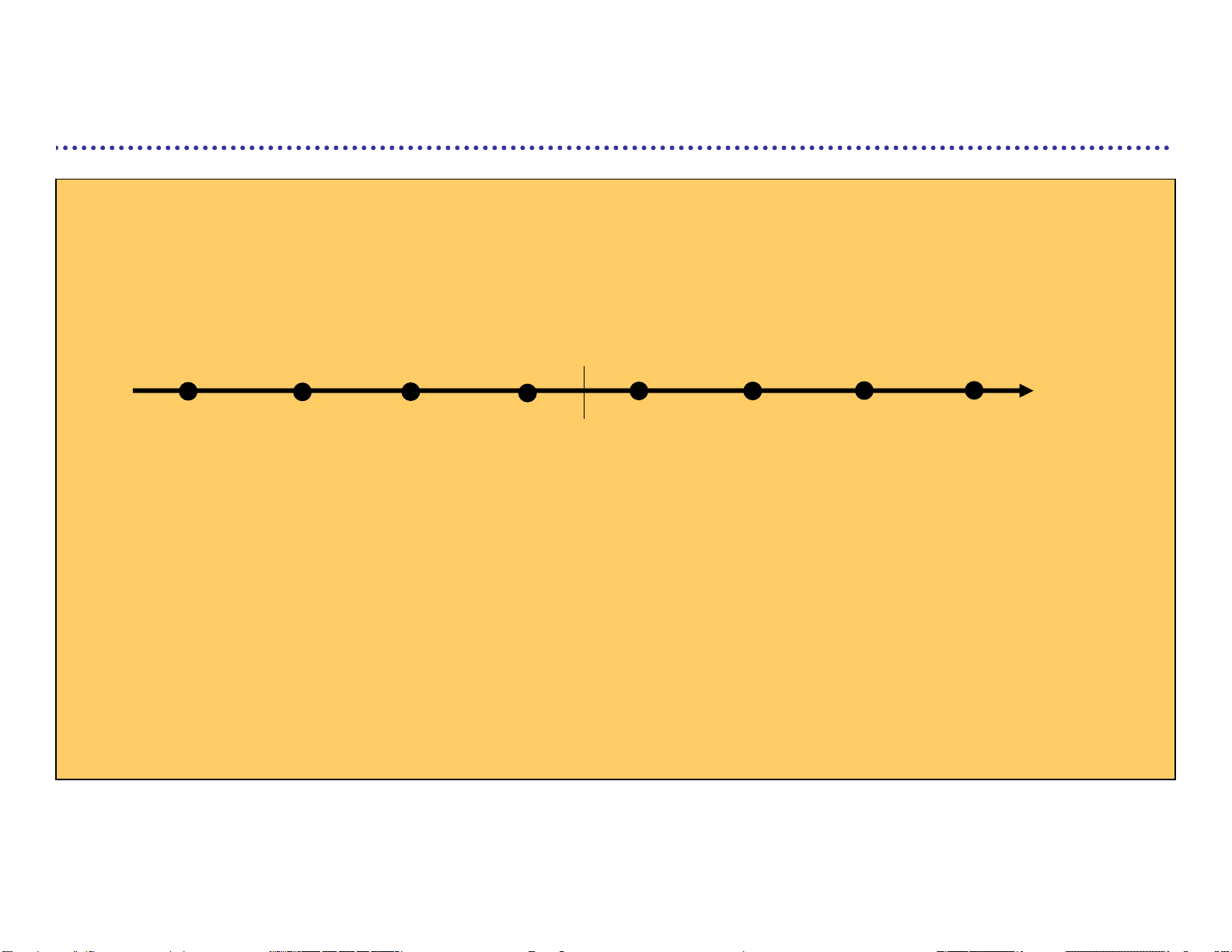
If d=1, S ≈ R và có thể vẽ như một đường thẳng 1-D
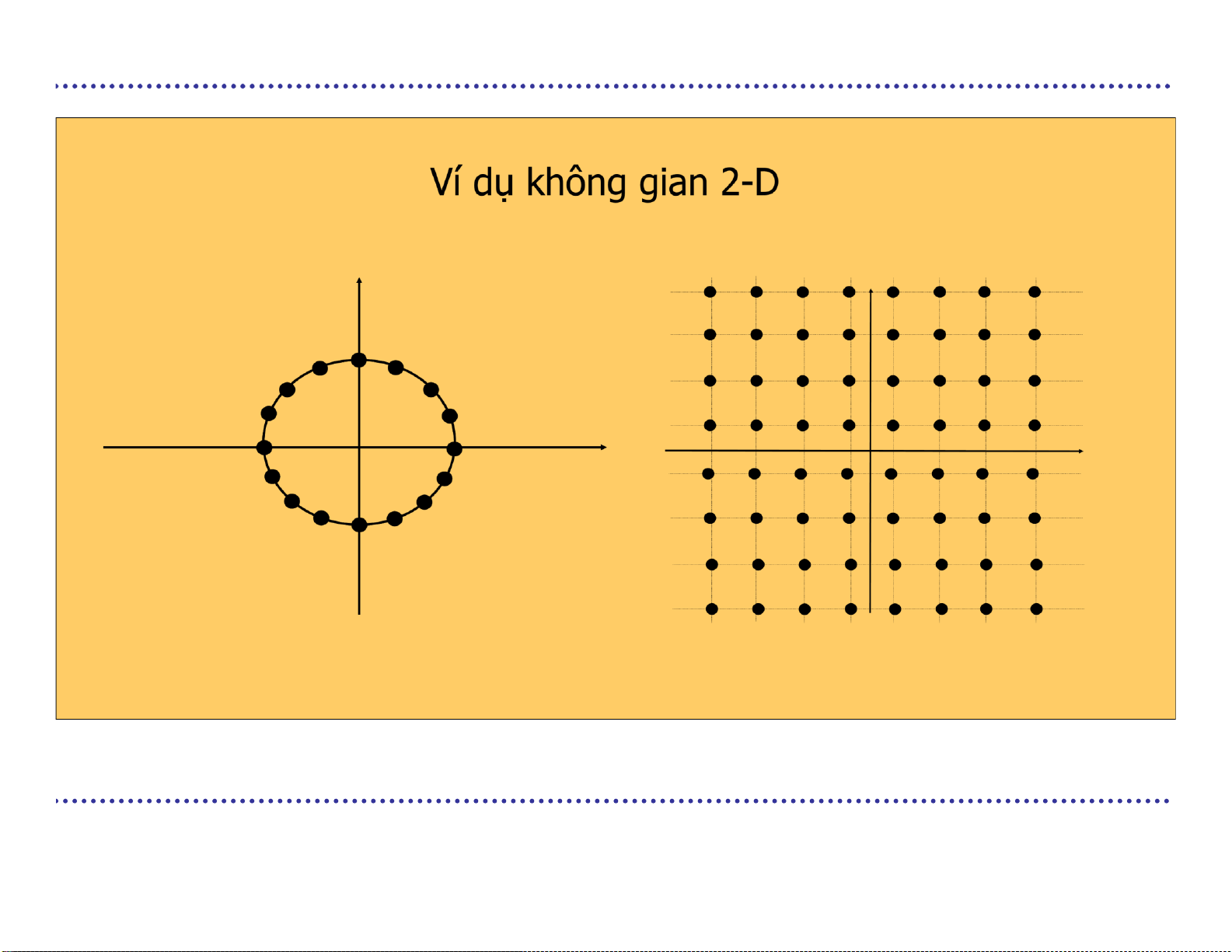
If d=2, S ≈ R2 và có thể vẽ như một mặt phẳng 1-D
If d=3, S ≈ R3 và có thể vẽ như một không gian 1-D lOMoARcPSD| 36991220 Ta sẽ viết M R d
(Một chùm là một tập m điểm trong không gian Euclid Rd ) lOMoARcPSD| 36991220 Ví dụ Ví dụ không gian 1-D 0 lOMoARcPSD| 36991220
Năng lượng tín hiệu lOMoARcPSD| 36991220
Với một tín hiệu a(t) S T Năng lượng của nó là: E a( ) a t dt2( ) 0
Nếu biểu diễn vector của nó là: a t( )
(a1,...,aj ,...ad )
Thì năng lượng được tính như sau: (Parseval identity) d E a( ) a2j j 1 lOMoARcPSD| 36991220 d Trong thực tế, vì a t( ) a b tjj ( ) j 1 T T d 1 d 1 T d 1 E a( ) a t dt2( ) [
a b tjj ( )]2 dt a2j b t dt2j ( ) a2j 0 0 j 0 j 0 0 j 0
Trong đó đã sử dụng tính chất trực giao T
b t b t dtj ( ) ( )i 0 se i j 0 lOMoARcPSD| 36991220
Năng lượng chùm tín hiệu M
s1,...,si ,...,sd Rd si
(si1 ,...,sij ,...,sid ) Cho chùm tín hiệu Với d Ta có: E s( )i sij2 j 1
Năng lượng chùm (trung bình): m lOMoARcPSD| 36991220 Es
P s E s( ) ( )i i i 1
Với P(si) là xác suất truyền si
Năng lượng chùm tín hiệu
Các chuỗi dữ liệu nhị phân: ngẫu nhiên lý tưởng lOMoARcPSD| 36991220 Các vector nhị phân
có xác suất tương đương v Hk Gán nhãn ánh xạ 1-1 e H: k M
Các tín hiệu trong chùm có xác su
ất tương đươngsi M P s( ) 1 1 m i m
Chùm tín hiệu có năng lượng: Es E s( )i
Năng lượng trên từng bit m i 1
Năng lượng cần để truyền một bit qua M lOMoARcPSD| 36991220 E b ES k lOMoARcPSD| 36991220 Bài tập lOMoARcPSD| 36991220 Bài tập
Cho một chùm tín hiệu NRZ lưỡng cực: M { ( )s t1 VP t s tT ( ), 2( ) VP tT ( )}
• Xây dựng cơ sở trực chuẩn.
• Biểu diễn dạng vector của chùm tín hiệu.
• Vẽ trên không gian Euclid.
• Xác định không gian tín hiệu S ?
• Tính Es và Eb. lOMoARcPSD| 36991220 Bài tập
Cho một chùm tín hiệu NRZ đơn cực: M { ( )s t1 VP t s tT ( ), 2( ) 0}
• Xây dựng cơ sở trực chuẩn.
• Biểu diễn dạng vector của chùm tín hiệu.
• Vẽ trên không gian Euclid.
• Xác định không gian tín hiệu S ?
• Tính Es và Eb. lOMoARcPSD| 36991220 Bài tập
Cho một chùm tín hiệu 2-PSK: M { ( )s t1
AP tT ( )cos(2 f t s t0 ), 2( )
AP tT ( )cos(2 f t0 )}
• Xây dựng cơ sở trực chuẩn.
• Biểu diễn dạng vector của chùm tín hiệu.
• Vẽ trên không gian Euclid.
• Xác định không gian tín hiệu S ?
• Tính Es và Eb. lOMoARcPSD| 36991220 Bài tập lOMoARcPSD| 36991220 Bài tập: lOMoARcPSD| 36991220
Cho một chùm tín hiệu 4-PSK: M { ( )s t1
AP tT ( )cos(2 f t s t0 ), 2( ) AP tT (
)sin(2 f t0 ), s t3( )
AP tT ( )cos(2 f t s t0 ), 4( )
AP tT ( )sin(2 f t0 )}
• Xây dựng cơ sở trực chuẩn.
• Biểu diễn dạng vector của chùm tín hiệu.
• Vẽ trên không gian Euclid.
• Xác định không gian tín hiệu S ?
• Tính Es và Eb.
Gợi ý: Acos(2 f t 0 ) Acos cos(2 f t0 ) Asin sin(2 f t0 ) lOMoARcPSD| 36991220 Bài tập:
Lặp lại với tất cả các chùm tín hiệu sau:
• NRZ (bipolar and unipolar) • RZ (bipolar and unipolar) • 4-PAM • 4-ASK • 2-PSK • 4-PSK • 2-FSK