Sổ tay lý thuyết đại số chương 1 | Đại học Bách khoa Hà Nội

SỔ TAY LÝ THUYẾT ĐẠI SỐ
CHƯƠNG 1: TỔ HỢP – LOGIC – ÁNH XẠ – SỐ PHỨC 1. LOGIC
Các phép logic thường gặp Phép phủ định Phép hội Phép tuyển A = 1− A A  B = min{ ; A } B A  B = max{ ; A } B Kéo theo Tương đương
A → B = max{1− ; A } B
A = B  A  B = 1
A  B  A  B = 0
 Quy ước 1 = đúng; 0 = sai
📌 Để chứng minh các mệnh đề ta sử dụng cách lập bảng chân lý (*) Các tính chất
- Tính giao hoán: A  B  B  ;
A A  B  B  A .
- Tính kết hợp: (A  B)  C  A  (B  C)
(A  B)  C  A (B  C)
- Tính phân phối: A  (B  C)  (A  B)  (A  C)
A  (B  C)  (A  B)  (A  C)
 Công thức quan trọng
A → B  A  B
A  B  (A → B)  (B → ) A
📌Để chứng minh mệnh đề bằng biến đổi tương đương dựa vào các công thức và tính chất trên.
 Phủ định mệnh đề < Phần này phụ thuộc vào người đọc; đề bài >
Các kí hiệu thường gặp  = ;   = ;
  = ;  =  ;  = ;   = ;   = ; 
P(x) = P(x),.....
Ví dụ: Cho mệnh đề A: " Tồn tại một phần tử x của X có tính chất P ( x) ". 1
Tìm mệnh đề phủ định? Giải:
A = {x  X , P(x)}  A = {x  X ; P(x)}.
Vây mệnh đề A ta: " Mọi phần tử x của X không có tính chất P ( x) " 2. TỔ HỢP
 Các phép tổ hợp thường gặp Phép hợp Phép giao Phép trừ x  A x  A x  A
x  A  B  
x  A  B  
x  A \ B   x  B x  B x  B
Phép lấy phần bù : Nếu A  X  A = X \ A gọi là phần bù của A trong X x  A Phép nhân: ( ,
x y)  A B   [Mở rộng] y  B
Ví dụ về phép nhân: A = {1, 2}; B = {X ,Y}
 A B = {(1, X );(1,Y );(2, X );(2,Y )}
 Các tính chất :
- Tính giao hoán: A  B  B  , A 
- Tính kết hợp: (A  B)  C  A  (B  C),
- Tính Phân phối: A  (B  C)  (A  B)  (A  C)
- Công thức quan trọng (*): Công thức trừ: Nếu ,
A B  X thì A \ B = A  B
Công thức DeMoorgan: A  B = A  B;A = A i i
A  B = A  B;A = A i i
Bài toàn chính của phần này chính là đi chứng minh mệnh đề
Nếu mệnh đề đó Đúng → Phương pháp phần tử (*)
Phương pháp biến đổi tổ hợp
Sai → Phương pháp phản chứng 2 3. ÁNH XẠ
Xét ánh xạ f : X → Y . Với Xlà tập nghịch ảnh, Ylà tập ảnh của ánh xạ f . Tìm ảnh: f ( )
A = { f (x) Y ∣ x  } A Tìm nghịch ảnh: 1 − f ( )
A = {x  X ∣ f (x)  } A Tìm ánh xạ ngược: 1 −
f (x) : Y → X
* Điều kiện để tồn tại ánh xạ ngược là f là song ánh * Cách tìm 1 − 1 y f (x) x f ( y) − =  =
 y = f (x) là hàm ngược cần tìm
 Các loại ánh xạ
- Đơn ánh  f (x) = a(a Y ) có nhiều nhất một nghiệm (❗)
 giả sử x ; x  X thỏa mãn f ( x = f x  x = x (🔹) 1 ) ( 2 ) 1 2 1 2
- Toàn ánh  f (x) = a(a Y ) có ít nhất một nghiệm (❗)
giả sử aY , cho f (x) = a tìm được x = g(a) a Y (🔹)
- Song ánh  f (x) = a(a Y ) có duy nhất một nghiệm (❗)
 f (x) vừa đơn ánh, vừa toàn ánh.(🔹)
(❗) Ánh xạ f có dạng là hàm số, tập ,
X YR ; (🔹) Ánh xạ f có dạng là khác. 4. SỐ PHỨC
Các dạng số thức thường gặp:
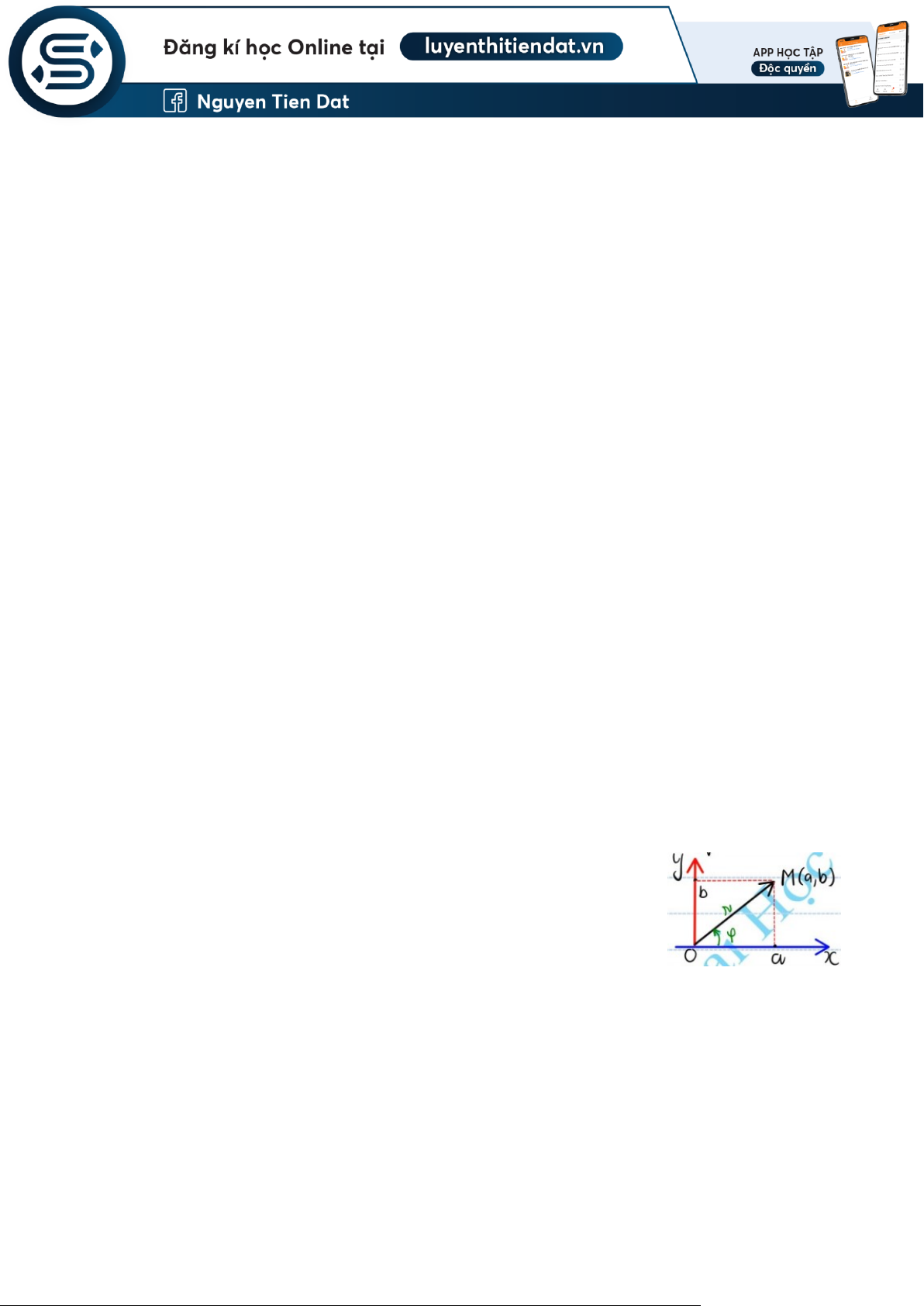
z = a + bi = r 
 = r(cos + isin) → dạng lượng giác ✓ r |
= z | : độ dài hay môdum số phức z
✓  = arg z : góc argment của số phức z
✓ a = Re(z) : phần thực.
✓ b = Im(z) : phần ảo.
Các phép số phức lượng giác cần biết: z = r 
 = r cos + isin 1 1 1 1 ( 1 1 ) z = r  
= r cos + isin 2 2 2 2 ( 2 2 )
Phép nhân : z  z = r  r 
 + = r  r cos  + + isin  + 1 2 1 2 1 2 1 2 ( ( 1 2) ( 1 2)) 3 z r r Phép chia : 1 1 1 =   − =
cos  − + isin  − 1 2 ( ( 1 2) ( 1 2)) z r r 2 2 2
Phép lũy thừa : n = n  = n z r n r cos  n + i sin  n 1 1 1 1 ( ( 1) ( 1))    + k2    + k2  Phép khai căn : n n 1 1 z = r cos + i sin
, k = 0,1,.., n −1. 1 1        n   n 
📌 Phép khai căn sẽ tồn tại n số phức thỏa mãn
Giải thích: z =  n n x
x = z (PT phức bậc n) Tồn tại n nghiệm thỏa mãn 1 1
📌Trong trường số phức phương trình bậc n sẽ có n nghiệm
Phương trình bậc 2 ẩn phức, hệ số phức: 2
az + bz + c = 0  −b + 1 z =    = − = ( ) 1 2 2 2 4   a b ac 1 −b −   1 z = 2  2a arg()
Tìm  bằng casio  = |  | . 1 1 2 4