




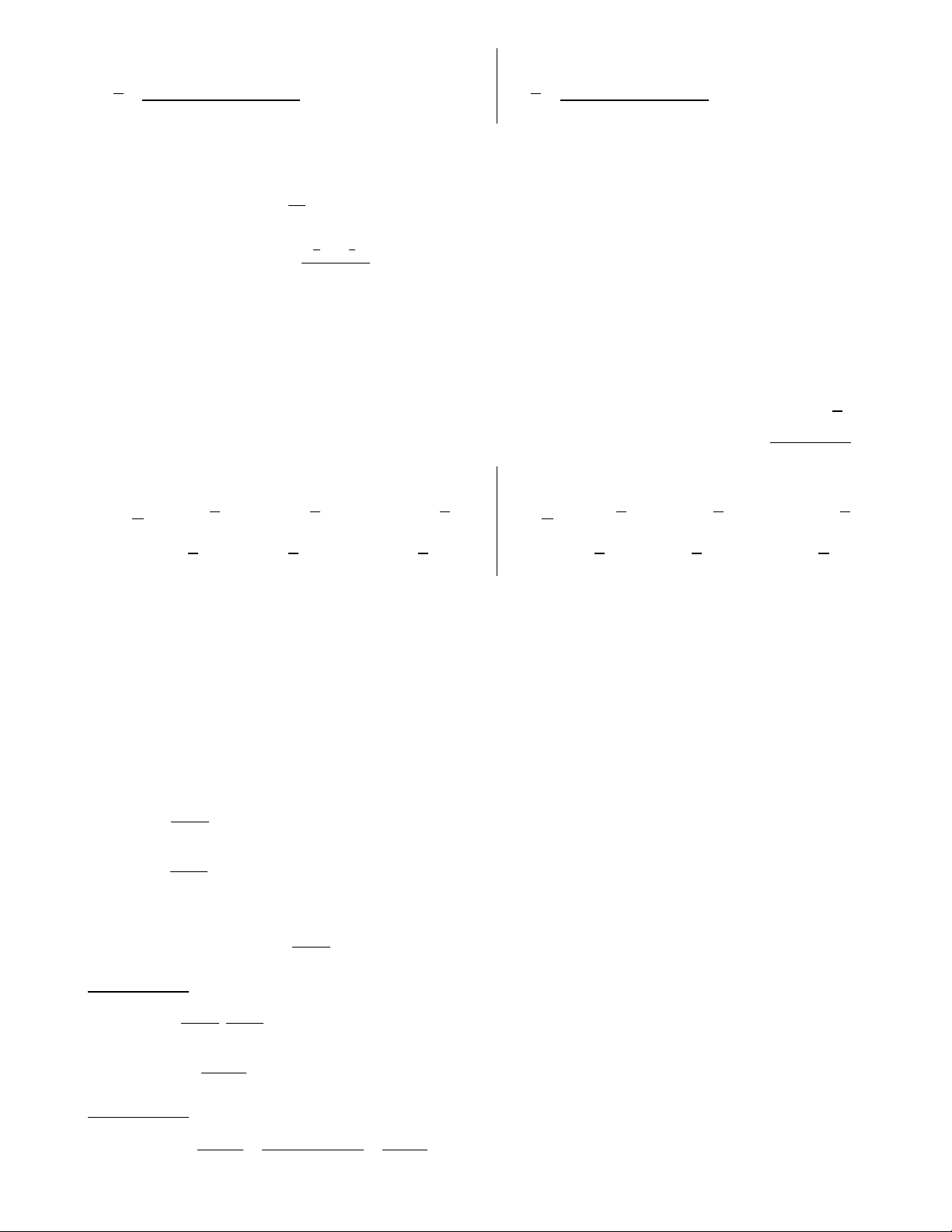








Preview text:
LỚP TOÁN THẦY CƯỜNG
Liên hệ: 0967453602 – Facebook: ThayCuongToan
SỔ TAY TRA CỨU NHANH KIẾN THỨC
MÔN TOÁN LỚP 10 – HỌC KÌ II
Họ và tên: ………………………………………………………………………
Trường: …………………………………… Lớp: ……………………………..
TÀI LIỆU LƯU HÀNH NỘI BỘ
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan Mục lục
PHẦN ĐẠI SỐ................................................................................................................................................................ 4
Chương IV. BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH .................................................................................. 4
I. BẤT ĐẲNG THỨC ................................................................................................................................................ 4
1. Tính chất của bất đẳng thức ............................................................................................................................ 4
2. Bất đẳng thức Cô si ........................................................................................................................................... 4
3. Bất đẳng thức có chứa dấu giá trị tuyệt đối.................................................................................................. 4
4. Một số bất đẳng thức thường dùng khác ...................................................................................................... 4
II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN ................................... 4
1. Dấu của nhị thức bậc nhất ............................................................................................................................... 4
2. Bất phương trình bậc nhất .............................................................................................................................. 5
3. Hệ bất phương trình bậc nhất một ẩn ........................................................................................................... 5
III. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN ................................... 5
1. Bất phương trình bậc nhất hai ẩn .................................................................................................................. 5
2. Hệ bất phương trình bậc nhất hai ẩn ............................................................................................................ 5
IV. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN ................................................................................................ 6
1. Dấu của tam thức bậc hai ................................................................................................................................ 6
2. Bất phương trình bậc hai một ẩn ................................................................................................................... 6
3. Một số phương trình và bất phương trình quy về bậc hai ......................................................................... 6
Chương V. THỐNG KÊ ................................................................................................................................................ 7
I. KHÁI QUÁT ........................................................................................................................................................... 7
II. BẢNG PHÂN BỐ TẦN SỐ VÀ TẦN SUẤT ................................................................................................... 7
III. BIỂU ĐỒ .............................................................................................................................................................. 7
1. Biểu đồ hình cột ................................................................................................................................................ 7
2. Biểu đồ đường gấp khúc .................................................................................................................................. 8
3. Biểu đồ hình quạt .............................................................................................................................................. 8
IV. SỐ TRUNG BÌNH CỘNG ................................................................................................................................. 8
V. SỐ TRUNG VỊ ...................................................................................................................................................... 9
VI. MỐT ...................................................................................................................................................................... 9
VII. PHƯƠNG SAI .................................................................................................................................................... 9
VIII. ĐỘ LỆCH CHUẨN ......................................................................................................................................... 9
Chương VI. LƯỢNG GIÁC .......................................................................................................................................... 9
I. CÔNG THỨC LƯỢNG GIÁC ............................................................................................................................. 9
1. Công thức cơ bản............................................................................................................................................... 9
Hệ quả của công thức cơ bản ................................................................................................................................ 9
2. Công thức cộng ................................................................................................................................................ 10
Hệ quả của công thức cộng ................................................................................................................................. 10
3. Công thức biến đổi tổng thành tích ............................................................................................................. 11
4. Công thức biến đổi theo f (x) = asinx +bcosx ......................................................................................... 11
5. Công thức biến đổi theo tan x = t ............................................................................................................... 12 2
II. GÓC VÀ CUNG LƯỢNG GIÁC ĐẶC BIỆT ................................................................................................. 12
1. Góc và cung lượng giác .................................................................................................................................. 12 2
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
2. Giá trị của góc và cung lượng giác đặc biệt ................................................................................................. 12
3. Giá trị lượng giác của các góc (cung) lượng giác đặc biệt ......................................................................... 13
PHẦN HÌNH HỌC ...................................................................................................................................................... 14
Chương III. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG Oxy .............................................................. 14
I. HỆ TỌA TRỤC TỌA ĐỘ TRONG MẶT PHẲNG TỌA ĐỘ Oxy .............................................................. 14
1. Hệ trục tọa độ ................................................................................................................................................... 14
2. Tọa độ véc-tơ .................................................................................................................................................... 14
3. Tọa độ điểm ...................................................................................................................................................... 14
4. Liên hệ giữa tọa độ véc-tơ và tọa độ điểm ................................................................................................... 15
II. ĐƯỜNG THẲNG TRONG MẶT PHẲNG TỌA ĐỘ Oxy .......................................................................... 15
1. Véc-tơ pháp tuyến và véc-tơ chỉ phương của đường thẳng ...................................................................... 15
2. Các dạng phương trình của đường thẳng.................................................................................................... 15
3. Cách viết nhanh phương trình của đường thẳng ....................................................................................... 15
4. Vị trí tương đối giữa đường thẳng với điểm và đường thẳng.................................................................. 16
5. Góc giữa hai đường thẳng .............................................................................................................................. 16
6. Khoảng cách từ điểm tới đường thẳng ........................................................................................................ 17
III. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ Oxy ............................................................................ 17
1. Các dạng phương trình của đường tròn ...................................................................................................... 17
2. Cách viết nhanh phương trình của đường tròn ......................................................................................... 17
3. Vị trí tương đối của đường tròn với điểm, đường thẳng và đường tròn ............................................... 17
4. Phương trình tiếp tuyến với đường tròn ..................................................................................................... 18
IV. ELIP TRONG MẶT PHẲNG TỌA ĐỘ Oxy ................................................................................................ 19
1. Định nghĩa đường elip .................................................................................................................................... 19
2. Phương trình chính tắc của elip .................................................................................................................... 19
3. Các thông tin của elip ..................................................................................................................................... 19 3
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan PHẦN ĐẠI SỐ
Chương IV. BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH
I. BẤT ĐẲNG THỨC
1. Tính chất của bất đẳng thức
• a > b ⇔ a + c > b + c.
• c > 0 ⇒ a > b ⇔ ac > bc c <
; 0 ⇒ a > b ⇔ ac < bc. a > b
a > b > 0 •
⇒ a + c > b + d ⇒ ac > ; bd. c > d c > d > 0 • 2n+1 2n+
a > b ⇔ a > 1 b n∈* , . •
> > ⇒ > ⇔ 2n > 2n a b a b a b n∈* 0 , .
• a > b > 0 ⇒ a > b ⇔ a > b.
• a > b ⇔ 3 a > 3 b.
2. Bất đẳng thức Cô si
• Nếu a và b là hai số thực không âm thì a + b ≥ 2 ab (Dấu “=” xảy ra ⇔ a = ). b
• Nếu có n số không âm a ,a ,...,a thì a + a + .. + a ≥ n
n a a a (Dấu “=” xảy ra ⇔ a = a = ... = a n ). n ... 1 2 n 1 2 1 2 n 1 2
3. Bất đẳng thức có chứa dấu giá trị tuyệt đối
• ∀x ∈ : x ≥ 0 x ≥ x x ≥ − ; ; x.
• x ≤ a ⇔ −a ≤ x ≤ a (a > 0). x ≤ −a
• x ≥ a ⇔ (a > 0). x ≥ a
• a − b ≤ a + b ≤ a + b .
4. Một số bất đẳng thức thường dùng khác
• Bất đẳng thức Bunhiacopxki:
• Áp dụng cho bộ hai số a, b và x, y ta được: + ≤ ( 2 + 2 )( 2 + 2 ax by a b x
y ) (Dấu “=” xảy ra ⇔ a = b). x y
• Áp dụng cho bộ n số a ,a ,...,a b b b ta được: n và , ,..., 1 2 1 2 3
a b + a b + ... + a b ≤ a a a b b
b (Dấu “=” xảy ra ⇔ a a a 1 = 2 = ... = n n n
( 2 + 2 +...+ 2n)( 2 + 2 +...+ 2 ). 1 1 2 2 1 2 1 2 n ) b b b 1 2 n
• Bất đẳng thức Svác-xơ: a b ( + )2 2 2 a b
• Áp dụng cho bộ hai số a, b và x, y ta được + ≥
(Dấu “=” xảy ra ⇔ a = b ). x y x + y x y
• Áp dụng cho bộ n số a ,a ,...,a b b b ta được: n và , ,..., 1 2 1 2 3 2 2 a a a
(a +a +...+a a a a 1 2 n 1 2 n )2 2 + + ... + ≥
(Dấu “=” xảy ra ⇔ 1 = 2 = ... = n ). b b b b + b + b b b b n ... + 1 2 1 2 n 1 2 n
II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
1. Dấu của nhị thức bậc nhất
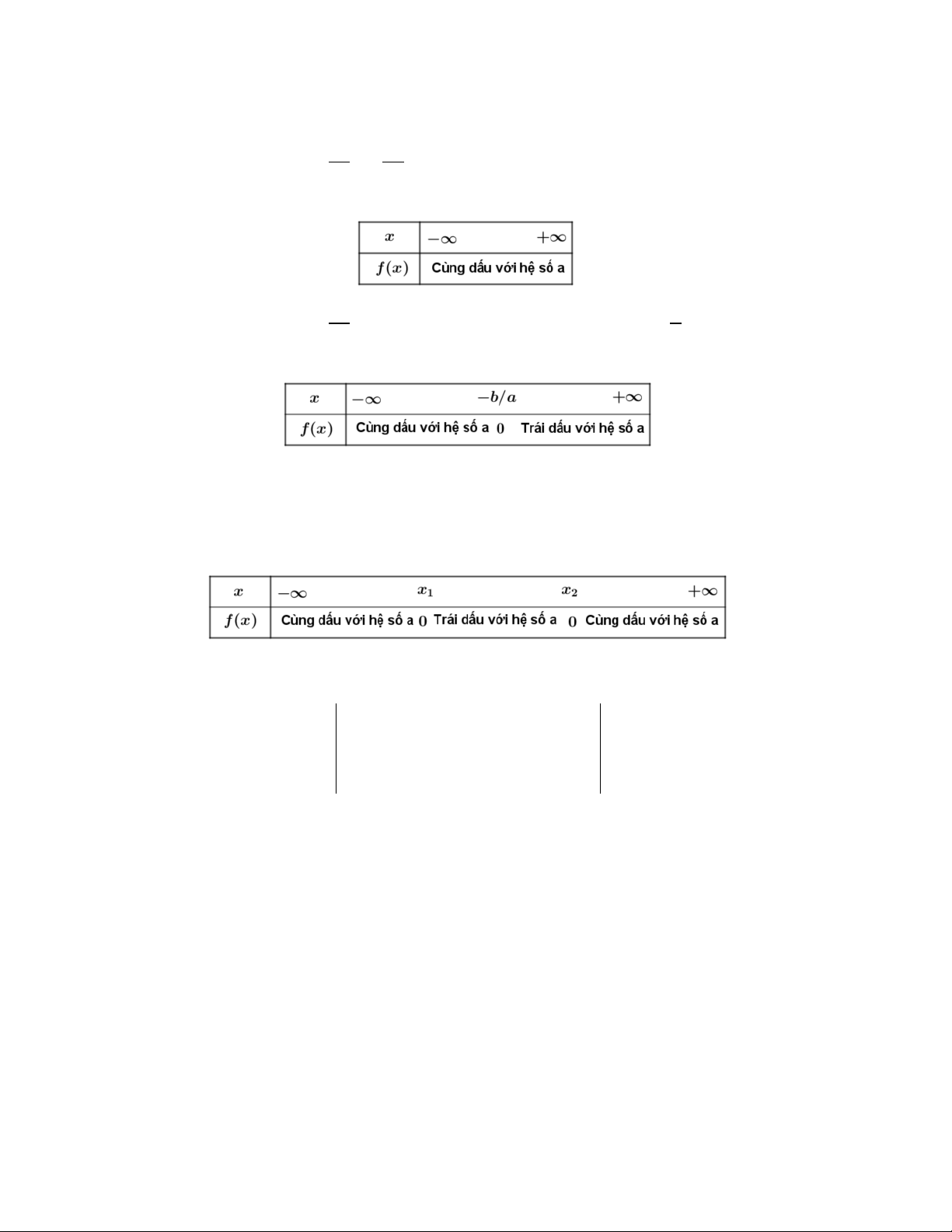
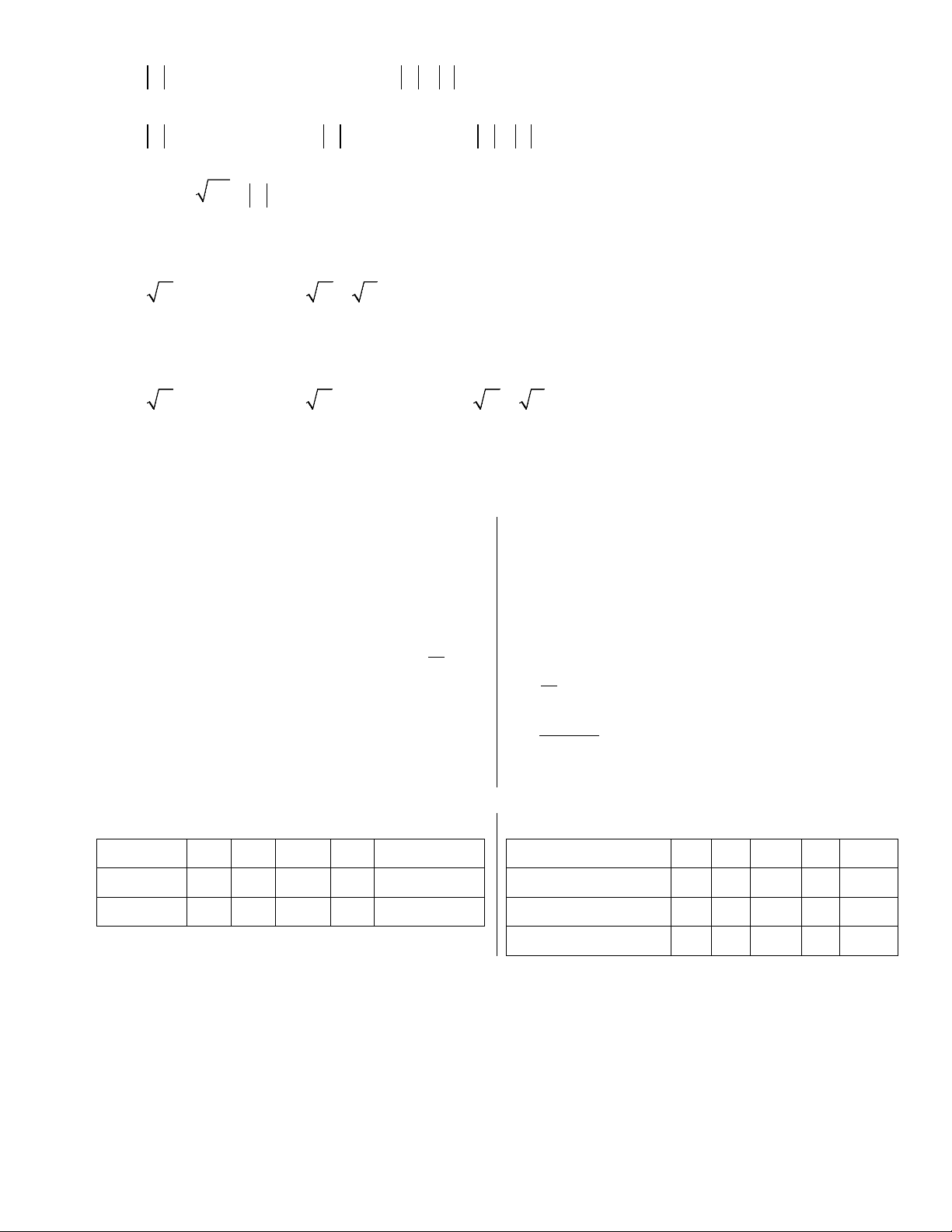
• Xét nhị thức bậc nhất f (x) = ax + b (a ≠ 0) ta có bảng xét dấu: x −∞ − b +∞ a f (x)
Trái dấu với hệ số a 0
Cùng dấu với hệ số a 4
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
Cách nhớ: Trái trái – Phải cùng.
• Từ bảng xét dấu ta có kết luận:
• Dấu của f (x) cùng dấu với hệ số a khi và chỉ khi > − b x . a
• Dấu của f (x) trái dấu với hệ số a khi và chỉ khi < − b x . a
2. Bất phương trình bậc nhất
• Giải và biện luận bất phương trình ax + b > 0 (1)
• TH1. Nếu a > 0 thì (1) ⇔ > − b x
. Vậy tập nghiệm của (1) là b S = − ;+∞ . a a
• TH2. Nếu a < 0 thì (1) ⇔ < − b x
. Vậy tập nghiệm của (1) là b S = −∞;− . a a
• TH3. Nếu a = 0 thì (1) ⇔ 0.x < − . b Khi đó:
+ Nếu b ≥ 0 thì (1) vô nghiệm. Vậy tập nghiệm của (1) là S = ∅.
+ Nếu b < 0 thì (1) có nghiệm đúng với mọi x. Vậy tập nghiệm của (1) là S = .
• Các bất phương trình ax + b < 0; ax + b ≥ 0; ax + b ≤
0 có các giải và biện luận tương tự như trên.
3. Hệ bất phương trình bậc nhất một ẩn
• Hệ bất phương trình bậc nhất một ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất một ẩn.
• Để giải hệ bất phương trình bậc nhất một ẩn thì ta giải từng bất phương trình để tìm nghiệm của từng bất
phương trình rồi tìm giao của hai tập nghiệm.
• Trong quá trình tìm giao của hai tập nghiệm thì ta nên vẽ trục số để việc giải trở nên thuận lợi và dễ dàng.
III. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Bất phương trình bậc nhất hai ẩn
• Để giải bất phương trình ax + by + c > 0 (1) thì ta làm như sau:
• Bước 1: Vẽ đường thẳng ∆ : ax + by + c = 0 trên hệ trục tọa độ Oxy.
• Bước 2: Chọn điểm M (x ; y bất kì không thuộc đường thẳng ∆ 0 0 ) .
• Bước 3: Tính giá trị biểu thức T = ax + by + c và xét dấu của nó để thu được miền nghiệm của bất 0 0
phương trình đã cho trên mặt phẳng hệ trục tọa độ Oxy, bằng cách:
+ Nếu T > 0 tức là cùng dấu với (1) thì miền nghiệm của (1) là nửa mặt phẳng không kể bờ ∆ chứa điểm M.
+ Nếu T < 0 tức là trái dấu với (1) thì miền nghiệm của (1) là nửa mặt phẳng không kể bờ ∆ không chứa điểm M.
• Nếu bất phương trình có chứa dấu “=” thì khi kết luận miền nghiệm là nửa mặt phẳng kể cả bờ.
• Các bất phương trình ax + by + c < 0; ax + by + c ≥
0; ax + by + c ≤
0 có cách giải như trên.
2. Hệ bất phương trình bậc nhất hai ẩn
• Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai phương trình trở lên.
ax + by + c > 0
• Giả sử giải hệ bất phương trình thì ta làm như sau:
a'x + b' y + c' > 0
• Bước 1: Vẽ các dường thẳng ∆ : ax + by + c = 0 và ∆':a'x + b' y + c' = 0 .
• Bước 2: Xác định tọa độ giao điểm (nếu có) của ∆ v ∆ à '.
• Bước 3: Xác định miền nghiệm của mỗi bất phương trình và tìm phần giao điểm của chúng, ta được
miền nghiệm của hệ. 5
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
IV. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
1. Dấu của tam thức bậc hai
• Xét tam thức bậc hai f x = 2
( ) ax + bx + c (a ≠ 0) có biệt thức ∆ = 2
b − 4ac , ta có các trường hợp sau: 2 TH1. b ∆
Nếu ∆ < 0 thì f (x) = a x + −
cùng dấu với hệ số a với mọi x ∈. 2a 4a Bảng xét dấu: 2
TH2. Nếu ∆ = 0 thì b
f (x) = a x + b
cùng dấu với hệ số a với mọi x ∈ \ − . 2a a Bảng xét dấu:
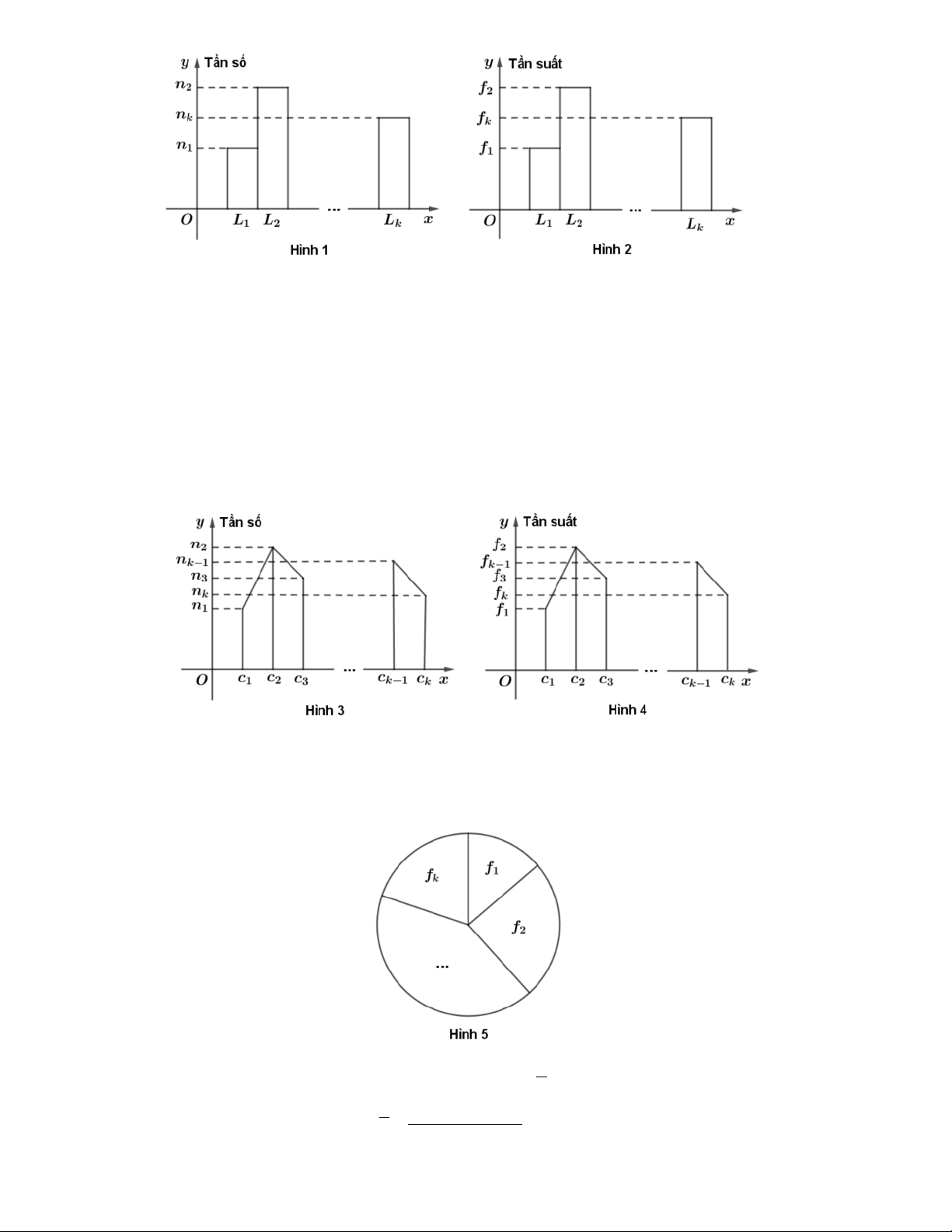
TH3. Nếu ∆ > 0 với x < x là nghiệm của phương trình f x = 2
( ) ax + bx + c = 0 thì 1 2
+ f (x) = a(x − x )(x − x cùng dấu với hệ số a với mọi x ∈(−∞;x ) ∪(x ;+∞ . 1 2 ) 1 2 )
+ f (x) = a(x − x )(x − x trái dấu với hệ số a với mọi x ∈(x ;x . 1 2 ) 1 2 ) Bảng xét dấu:
• Định lí đảo của tam thức bậc hai f x = 2
( ) ax + bx + c (a ≠
0) trong trường hợp ∆ = 2
b − 4ac > 0 và x < x 1 2
là nghiệm của phương trình f x = 2
( ) ax + bx + c = 0 thì: ∆ > 0 ∆ > 0 x x α < < ⇔ . a f ( ) 0. α
< x < x ⇔ . a f ( ) 0.
x < α < x ⇔ . a f α ( ) < 0. 1 2 α > 1 2 α > 1 2 S < α 2 S > α 2
2. Bất phương trình bậc hai một ẩn
• Ta dùng tam thức bậc hai để giải. a > 0
• Bất phương trình f x = 2
( ) ax + bx + c > 0 có nghiệm đúng với mọi x ∈ ⇔ . ∆ < 0 a < 0
• Bất phương trình f x = 2
( ) ax + bx + c < 0 có nghiệm đúng với mọi x ∈ ⇔ . ∆ < 0 a > 0
• Bất phương trình f x = 2
( ) ax + bx + c ≥ 0 có nghiệm đúng với mọi x ∈ ⇔ . ∆ ≤ 0 a < 0
• Bất phương trình f x = 2
( ) ax + bx + c ≤ 0 có nghiệm đúng với mọi x ∈ ⇔ . ∆ ≤ 0
3. Một số phương trình và bất phương trình quy về bậc hai
• Phương trình và bất phương trình chứa dấu giá trị tuyệt đối: 6
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội A B A B • A = B ( ĐK : B ≥ 0) = = ⇔ A = ; B ⇔ . A = −B A = − B A > B
• A < B ⇔ −B < A < A A > B ⇔ A > B ⇔ 2 A > 2 ; ; B . A < − B , A khi A ≥ 0 • Chú ý 2 A = A = . , A khi A < 0
• Phương trình và bất phương trình chứa căn thức: A ≥ 0 B ≥ 0 • A = B ⇔ A = B ⇔ ; 0 B . 2 ≥ A = B A = B B < 0 A ≥ 0 A ≥ A ≥ 0 0 •
A < B ⇔ B > 0 A > B ⇔ ;
A > B ⇔ B ≥ ; 0 . B ≥ 0 2 A < B A > B 2 A > B
Chương V. THỐNG KÊ I. KHÁI QUÁT
Phân bố tần số và tần suất rời rạc
Phân bố tần số và tần suất ghép lớp
Giả sử dãy n số liệu thống kê đã cho có k giá trị khác Giả sử dãy n số liệu thống kê đã cho được phân vào k
nhau (n ≤ k) : x ,x ,...,x Số lần suất hiện giá trị lớp (n < k) : L ,L ,...,L Mỗi lớp là một nửa khoảng k . k . 1 2 1 2 x i
k trong dãy số liệu đã cho được gọi là đóng bên trái. Số n các số liệu thống kê thuộc lớp i ( = 1,2,..., ) i L i
k được gọi là tần số của lớp đó. Tỉ số i ( = 1,2,..., )
tần số của giá trị x kí hiệu là n Tỉ số f = ni được i . i , i n n
gọi tần suất của giá trị x
f = i được gọi tần suất của lớp L Trung điểm i . i i . nx +x i i+ c =
1 của nửa khoảng xác định lớp L được i 2 i
gọi là giá trị đại diện của lớp L i .
II. BẢNG PHÂN BỐ TẦN SỐ VÀ TẦN SUẤT
Phân bố tần số và tần suất rời rạc
Phân bố tần số và tần suất ghép lớp Giá trị x x x L L L 1 2 … k Cộng Lớp 1 2 … k Cộng Tần số n n n n n n n n 1 2 … k Tần số 1 2 … k Tần suất f f f f f f 1 2 … k 100% Tần suất 1 2 … k 100% Giá trị đại diện c c c 1 2 … k III. BIỂU ĐỒ
1. Biểu đồ hình cột
• Dùng được cho cả tần số và tần suất. • Cách vẽ:
• Chọn hệ tọa độ vuông góc. Trên mỗi nửa khoảng xác định lớp dựng một hình chữ nhật với đáy là nửa
khoảng đó và chiều cao bằng tần số của lớp đó ta có biểu đồ tần suất hình cột (Hình 1).
• Nếu lấy dơn vị trên trục tung là phần trăm và trên mỗi đoạn xác định lớp ta dựng một hình chữ nhật
với đáy là đoạn đó và chiều cao bằng tần suất của lớp đó ta có biểu đồ tần suất hình cột (Hình 2). 7
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
2. Biểu đồ đường gấp khúc
• Dùng được cho cả tần số và tần suất • Cách vẽ:
• Gọi c là giá trị đại diện và n là tần số của lớp L Trên mặt phẳng tọa độ ta xác định các điểm (c n i ; i ) i . i i
với i = 1,2,...,k. Vẽ đoạn thẳng nối điểm (c n với điểm (c n với i = 1,2,...,k −1. Ta thu được i ; +1 i+1 ) i ; i )
một đường gấp khúc và được gọi là đường gấp khúc tần số (Hình 3).
• Nếu lấy đơn vị trên trục tung là phần trăm và nối các điểm (c f với i = 1,2,...,k. Trong đó f là tàn i ; i ) i
suất của lớp L tương tự như trên ta thu được một đường gấp khúc và được gọi là đường gấp khúc tần i suất (Hình 4).
3. Biểu đồ hình quạt
• Chỉ dùng cho tần suất
• Cách vẽ: Vẽ một đường tròn và chia hình tròn đó thành những hình quạt. Mỗi hình quạt tương ứng với
một lớp có diện tích tỉ lệ với tần suất của lớp đó ta có biểu đồ hình quạt (Hình 5).
IV. SỐ TRUNG BÌNH CỘNG
Số trung bình của một dãy số gồm n số liệu x ,x ,...,x kí hiệu là x và được tính theo công thức: 1 2 n x + x + ... + x = x 1 2 n . n 8
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
Phân bố tần số và tần suất rời rạc
Phân bố tần số và tần suất ghép lớp
n x + n x + ... +
n c + n c + ... + x = n x n c 1 1 2 2
k k = f x + f x + ... + f x x = 1 1 2 2
k k = f c + f c + ... + f c 1 1 2 2 k k n 1 1 2 2 k k n V. SỐ TRUNG VỊ
Kí hiệu là M của một dãy số gồm n số liệu sắp xếp theo thứ tự không giảm x ≤ x ≤ ... ≤ x là: e 1 2 n
+ Nếu n là số lẻ thì M = x e n . +1 2 x + x n n+1
+ Nếu n là số chẵn thì M = 2 2 e . 2 VI. MỐT
Cho dãy số liệu dưới dạng bảng phân bố tần số. Mốt được kí hiệu là M là giá trị có tần số lớn nhất. Một bảng 0
phân bố tần số có thể có hai hay nhiều mốt. VII. PHƯƠNG SAI
∑n(x − x i )
Phương sai của dãy gồm n số liệu x ,x ,...,x kí hiệu là 2s, được tính theo công thức: 2 i= s = 1 n , . 1 2 n
Phân bố tần số và tần suất rời rạc
Phân bố tần số và tần suất ghép lớp s = 1 n x x n x x ... n x x s = 1 n c x n c x ... n c x 1 ( − 1 )2 + 2( − 2 )2 + + k ( − k )2 2 1 ( − 1 )2 + 2( − 2 )2 + + k ( − k )2 2 n n
= f (x − x )2 + f (x − x )2 +... + f x x = f c x f c x ... f c x 1 ( − 1 )2 + 2( − 2 )2 + + k ( − k )2 k ( − k )2 1 1 2 2 VIII. ĐỘ LỆCH CHUẨN
Độ lệch chuẩn là căn bậc hai của phương sai và được kí hiệu là s. Khi số liệu có đơn vị như mét, ki-lô-gam, …
thì độ lệch chuẩn có cùng đơn vị với số liệu. Đơn vị của phương sai là bình phương đơn vị của số liệu.
Chương VI. LƯỢNG GIÁC
I. CÔNG THỨC LƯỢNG GIÁC 1. Công thức cơ bản 2 sin a = 1− 2 cos a [1] 2 sin a + 2 cos a = 1⇒ . 2 cos a = 1− 2 sin a [2] = sin tan a a
⇒ sina = tanacos . a cosa [3] = cos cot a a
⇒ cosa = cotasin . a sina
Hệ quả của công thức cơ bản [4] a a = ⇒ a = 1 tan cot 1 cot . tana Chứng minh: = sina cos tan cot . a a a = 1⇒ dp . cm cosa sina [5] + 2 a = 1 1 tan . 2 cos a Chứng minh: 2 2 sin a cos a + 2 + 2 = + = sin a a = 1 1 tan 1 ⇒ dp . cm 2 2 2 cos a cos a cos a 9
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan [6] + 2 a = 1 1 cot . 2 sin a Chứng minh: 2 2 cos a sin a + 2 + 2 = + = cos a a = 1 1 cot 1 ⇒ dp . cm 2 2 2 sin a sin a sin a 2. Công thức cộng
[7] cos(a −b) = cosacosb + sinasin . b
[8] cos(a + b) = cosacosb − sinasin . b
[9] sin(a −b) = sinacosb −sinbcos . a
[10] sin(a + b) = sinacosb + sinbcos . a [11] ( ) tana − − = tan tan b a b . 1+ tanatanb [12] ( ) tana + + = tan tan b a b . 1− tanatanb
Hệ quả của công thức cộng
a. Công thức nhân hai [13] a = 2 a − 2 a = 2 a − = − 2 cos2 cos sin 2cos 1 1 2sin . a Chứng minh:
cos2a = cos(a + a) = cosacosa − sinasina = 2 cos a − 2 sin a ⇒ dpc . m cos2a = 2 cos a − 2 sin a = 2 cos a − (1− 2 cos a) = 2
2cos a −1⇒ dpc . m cos2a = 2 cos a − 2 sin a = (1− 2 sin a) − 2 sin a = 1− 2 2sin a ⇒ dp . cm
[14] sin2a = 2sinacos . a Chứng minh:
sin2a = sin(a + a) = sinacosa + sinacosa = 2sinacosa ⇒ dpc . m [15] = 2tan tan2 a a . 1− 2 tan a Chứng minh: ( ) tana + = + = tana = 2tan tan2 tan a a a a ⇒ dp . cm
1− tanatana 1− 2 tan a
Hệ quả của công thức nhân hai
Công thức hạ bậc 1+ [16] 2 = cos2 cos a a . 2 Chứng minh: 1+ Từ công thức nhân hai = 2 − ⇔ 2 = cos2 cos2 2cos 1 cos a a a a ⇒ dp . cm 2 1− [17] 2 = cos2 sin a a . 2 Chứng minh: 1− Từ công thức nhân hai = − 2 ⇔ 2 = cos2 cos2 1 2sin sin a a a a ⇒ dp . cm 2 10
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
b. Công thức biến đổi tích thành tổng [18] a b = 1 cos .cos
cos(a −b) + cos(a + b). 2 Chứng minh:
Cộng vế với vế [7] và [8] ta được cos(a −b) + cos(a + b) = 2cos .
a cosb ⇒ dp . cm [19] a b = 1 sin .cos
sin(a −b) + sin(a + b). 2 Chứng minh:
Cộng vế với vế [9] và [10] ta được sin(a −b) + sin(a + b) = 2sin .
a cosb ⇒ dp . cm [20] a b = 1 sin .sin
cos(a −b) − cos(a + b). 2 Chứng minh:
Trừ vế với vế [7] và [8] ta được cos(a −b) − cos(a + b) = 2sin .
a sinb ⇒ dp . cm c. Công thức nhân ba [21] a = 3 cos3 4cos a − 3cos . a Chứng minh:
cos3a = cos(2a + a) = cos2acosa − sin2asina = 3
2cos a − cosa − (2sinacosa)sina = ( 2 2cos a − ) 1 cosa − 2 2sin acosa = 3
2cos a − cosa − 2(1− 2 cos a)cosa = 3
4cos a − 3cosa ⇒ dp . cm [22] a = a − 3 sin3 3sin 4sin . a Chứng minh:
sin3a = sin(2a + a) = sin2acosa + sinacos2a = (2sinacosa)cosa + sina(1− 2 2sin a) = 2
2sinacos a + sina − 3
2sin a = 2sina(1− 2
sin a) + sina − 3
2sin a = 3sina − 3 4sin a ⇒ dpc . m 3tana − 3 [23] = tan tan3 a a . 1− 2 3tan a Chứng minh: 2tana + tana 3 2
tan3a = tan(2a + a) tan2a + tana 1− tan a 3tana − = = = tan a ⇒ dp . cm 1− tan2atana 2tana 1− 2 − 3tan 1 tan a a 1− 2 tan a
3. Công thức biến đổi tổng thành tích a + b a − [24] cos + cos = 2cos cos b a b . 2 2 a + b a − [25] cos − cos = −2sin sin b a b . 2 2 a + b a − [26] sin + sin = 2sin cos b a b . 2 2 a + b a − [27] sin − sin = 2cos sin b a b . 2 2
4. Công thức biến đổi theo f (x) = asinx +bcosx Ta có f x = a x + b x = 2 a + 2 ( ) sin cos
b sin(x +α ) với tanα = b . a
Cách bấm máy để tìm nhanh α như sau: 11
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
Bước 1: Bấm qw4 để chuyển về đơn vị góc là radian (rad).
Bước 2: Bấm ql giá trị b a giá trị a = để thu được kết quả. Chứng minh: a b f (x) = 2 a + 2 b sinx + cosx = 2 a + 2
b (sinxcosα + sinα cosx) = 2 a + 2 b sin(x +α ) 2 a + 2 2 b a + 2 b Trong đó cosα = a và sinα = b , suy ra tanα = b . 2 a + 2 2 b a + 2 b a
Từ công thức trên, ta có thể tính một số công thức thường gặp sau: π π π
sinx ± cosx = 2 sin x ±
sinx ± 3 cosx = 2sin x ±
3sinx ± cosx = 2sin x ± 4 3 6
5. Công thức biến đổi theo tan x = t 2 2t 1− 2
Nếu đặt tan x = t thì sin = và cos = t x x . 2 1+ 2 t 1+ 2 t Chứng minh: x x 2tan = = x x = x x x = x 2 x = 2 sin sin 2 2sin cos 2tan cos cos 2tan cos = 2t x . 2 2 2 2 2 2 2 2 2 x 1+ 2 1+ tan t 2 1− 2 x x tan x 2 2 1− 2 cos = cos 2 = 2 2cos −1 = −1 = = t x . 2 2 2 x 2 x 1+ 2 1+ tan 1+ tan t 2 2 sinx 2t cosx 1− 2
Từ đó ta suy ra công thức của tanx và cot x theo t là tan = = và cot = = t x x . cosx 1− 2 t sinx 2t
II. GÓC VÀ CUNG LƯỢNG GIÁC ĐẶC BIỆT
1. Góc và cung lượng giác
• Đơn vị đo của góc và cung gồm độ (α°) và radian (α rad) . π • 180 1° = rad và 1rad = ° . 180 x
• Ta có bảng chuyển đổi: Độ 30° 45° 60° 90° 120° 135° 150° 180° 270° 360° π π π π π π π Radian 2 3 5 π π 3 π 2 6 4 3 2 3 4 6 2 πα
• Độ dài cung tròn l có bán kính R và số đo α° là: = R l . 180
2. Giá trị của góc và cung lượng giác
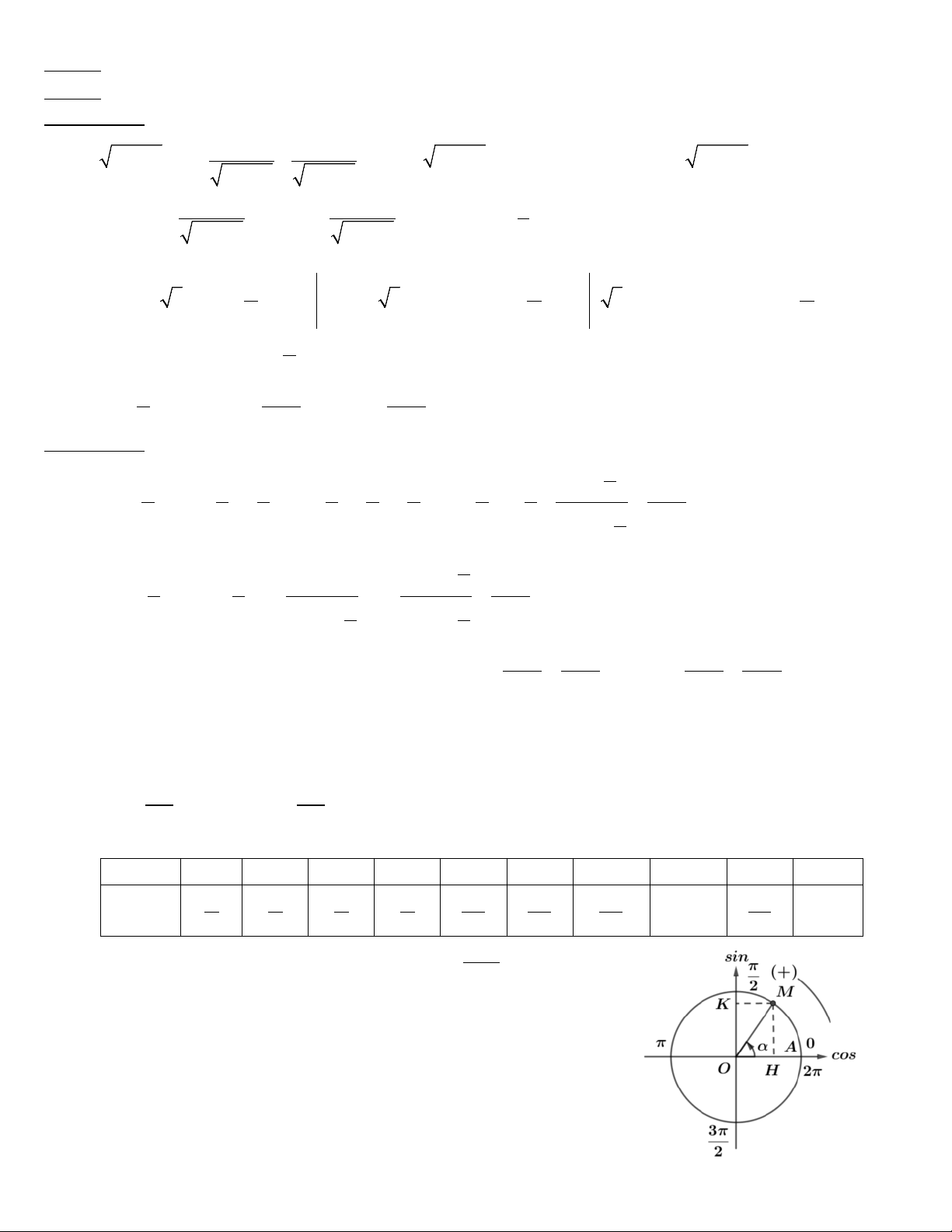
• Đường tròn lượng giác gắn với hệ trục tọa độ: là đường tròn định hướng
có tâm là gốc tọa độ và bán kính bằng 1. Điểm A(1;0) là điểm gốc. Với
mỗi điểm M mà α = ( ,
OA OM) rad ta nói M định ra một góc và cung α.
Ngược lại, với mỗi số thực α luôn tôn tại điểm M trên đường tròn lượng giác mà α = ( , OA OM) = AOM rad. 12
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
• Giá trị lượng giác của góc và cung α : Trên đường tròn lượng giác gắn với hệ trục tọa độ cho cung lượng giác
AM có số đo α. Tọa độ điểm M (x; y). Khi đó:
cosα = ; sinα = ; tanα = y ( ≠ 0); cotα = x x y x (y ≠ 0). x y
• Các kết quả được thừa nhận: • sin(α + k π
2 ) = sinα,∀k ∈ và cos(α + k π
2 ) = cosα,∀k ∈. • tan(α + π
k ) = tanα,∀k ∈ và cot(α + π
k ) = cotα,∀k ∈. • −1 ≤ sinα ≤ 1, α
∀ và −1 ≤ cosα ≤ 1, α ∀ . π
• tanα xác định với mọi α ≠ + π
k ,k ∈ và cotα xác định với mọi α ≠ π k ,k ∈. 2 • Nếu góc α = ( , OA OM) =
AOM tạo bởi điểm cuối M của cung lượng giác
AM nằm ở góc phần thứ nhất
(I) thì hình chiếu vuông góc của M xuống trục hoành (Trục côsin) là điểm H nên dấu của cosα > 0 (nằm
bên trên số 0) còn hình chiếu vuông góc của M xuống trục tung (Trục sin) là điểm K nên dấu của sinα > 0
(nằm bên trên số 0). Như vậy, để biết dấu của các giá trị lượng giác của góc α thì ta xác định điểm M nằm
ở góc phần tư nào rồi tìm hình chiếu vuông góc xuống các trục côsin và sin để tìm dấu của các giá trị đó
tại góc phần tư đó. Từ đó, ta có bảng dấu của các giá trị lượng giác của góc α phụ thuộc vào điểm cuối M của cung lượng giác AM là: π π π 3 π 3 Góc phần tư thứ I 0 → II → π III π → IV → π 2 2 2 2 2 cosα + − − + sinα + + − − tanα + − + − cotα + − + −
• Bảng giá trị lượng giác của các góc và cung lượng giác đặc biệt: α π π π π 0 6 4 3 2 cosα 0 1 2 3 1 2 2 2 sinα 1 3 1 2 0 2 2 2 tanα 0 3 1 3 || 3 cotα || 3 1 3 0 3
3. Giá trị lượng giác của các góc (cung) có liên quan đặc biệt
• Hai góc đối nhau α và −α : sin( α − ) = −sinα cos( α − ) = cosα tan( α − ) = −tanα cot( α − ) = −cotα
• Hai góc bù nhau α và π −α :
sin(π −α ) = sinα
cos(π −α ) = −cosα
tan(π −α ) = −tanα
cot(π −α ) = −cotα π
• Hai góc phụ nhau α và −α : 2 13
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan π π π π sin α − = cosα cos −α = sinα tan −α = cotα cot −α = tanα 2 2 2 2
Ta có thể thấy, giá trị lượng giác của các cung và góc đặc biệt là hệ quả của công thức cộng, vì:
• Với hai góc đối nhau: sin( α
− ) = sin(0 −α ) = sin0cosα −sinα cos0 = −sinα ⇒ dp . cm
• Với hai góc bù nhau: sin(π −α ) = sinπ cosα −sinα cosπ = sinα ⇒ dp . cm π π π
• Với hai góc phụ nhau: sin
−α = sin cosα − sinα cos = cosα ⇒ dp . cm 2 2 2
Hoàn toàn tương tự với các giá trị lượng giác cos, tan và cot. PHẦN HÌNH HỌC
Chương III. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG Oxy
I. HỆ TỌA TRỤC TỌA ĐỘ TRONG MẶT PHẲNG TỌA ĐỘ Oxy 1. Hệ trục tọa độ
• Gồm 2 trục Ox (là trục hoành – nằm ngang) và Oy (là trục tung – thẳng đứng) vuông góc với nhau và cắt
nhau tại điểm O (là gốc tọa độ – O(0; 0)).
• Ta gọi i (1;0) và j (0 )
;1 là các véc-tơ đơn vị của trục Ox và Oy, khi đó ta có các kết qủa sau: • i .j = 0. • i = j = 1. 2. Tọa độ véc-tơ
• Tọa độ véc-tơ a có hoành độ bằng a và tung độ bằng b trong mặt phẳng tọa độ Oxy được viết là:
a(a;b) hoặc a = (a;b) hoặc a = . a i + . b j.
• Trong mặt phẳng tọa độ Oxy, cho hai véc-tơ a(a;b) và b (c;d) , khi đó:
• Tổng hiệu của hai véc-tơ: a ± b = (a ± c;b ± d).
• Tích vô hướng của hai véc-tơ: a.b = . a c + . b d = const.
• Tích của véc-tơ với một số:
k.a = k(a;b) = (ka;kb) (k = const). a = c
• Hai véc-tơ bằng nhau: a = b ⇔ . b = d
• Hai véc-tơ cùng phương: a,b cùng phương (song song hoặc trùng nhau) ⇔ a = kb (k = const) .
• Độ dài của véc-tơ: a = 2 a + 2 b > 0. . a c +
• Góc giữa hai véc-tơ: ( ) =α ⇔ α = . , cos b d a b ( 0° ≤α ≤180°). 2 a + 2 2 b . c + 2 d 3. Tọa độ điểm
• Tọa độ điểm M có hoành độ bằng a và tung độ bằng b trong mặt phẳng tọa độ Oxy được viết là:
M (a;b) hoặc M = (a;b) hoặc OM = (a;b) hoặc OM = . a i + . b j.
• Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(x y B x y C x y , khi đó:
A ; A ), ( B ; B ), ( C; C )
x + x y + y
• Tọa độ trung điểm M của đoạn thẳng AB là: M A B ; A B . 2 2
x − kx y − ky
• Tọa độ điểm M thuộc đoạn thẳng AB thỏa mãn MA = kMB (k ≠ ) 1 là: M A B ; A B . 1− k 1− k 14
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
x + x + x y + y + y
• Tọa độ trọng tâm G của tam giác ABC là: G A B C ; A B C . 3 3
4. Liên hệ giữa tọa độ véc-tơ và tọa độ điểm
Trong mặt phẳng tọa độ Oxy, cho các điểm A(x y B x y C x y , khi đó:
A ; A ), ( B ; B ), ( C; C )
• Tọa độ véc-tơ đi qua hai điểm A và B là: AB = (x − x y y B A ; − B A ).
• Độ dài của đoạn thẳng AB là: AB = AB = (x − x y y B A )2 + ( − B A )2 > 0.
2 • 2
Liên hệ giữa véc-tơ AB và độ dài của AB : AB AB = AB = AB = 2 . AB .
• Ba điểm A, B, C thẳng hàng ⇔ AB = kAC (k = const) .
• Ba điểm A, B, C tạo một thành tam giác ⇔ AB ≠ kAC (k = const) .
II. ĐƯỜNG THẲNG TRONG MẶT PHẲNG TỌA ĐỘ Oxy
1. Véc-tơ pháp tuyến và véc-tơ chỉ phương của đường thẳng
• Véc-tơ pháp tuyến (VTPT – thường kí hiệu là n ) của đường thẳng có giá vuông góc với đường thẳng đó.
• Véc-tơ chỉ phương (VTCP – thường kí hiệu là u ) của đường thẳng có giá song song hoặc trùng với đường thẳng.
• Một đường thẳng có vô số VTPT và VTCP.
• VTPT và VTCP có giá vuông góc với nhau nên . n u = 0 , khi đó:
• Nếu biết được tọa độ VTPT là n = (a;b) thì tọa độ VTCP là u( ;
b −a) hoặc u(− ; b a).
• Nếu biết được tọa độ VTCP là u = (a;b) thì tọa độ VTPT là n( ;
b −a) hoặc n(− ; b a).
• Khi biết mối quan hệ của đường thẳng ∆ với một đường thẳng khác hoặc với điểm thì ta tìm VTPT n ∆
hoặc VTCP u của đường thẳng ∆ như sau: ∆
• Nếu ∆ ⊥ d thì ∆ nhận VTCP của d làm VTPT và nhận VTPT của d làm VTCP.
• Nếu ∆ d thì ∆ nhận VTPT của d làm VTPT và nhận VTCP của d làm VTCP.
• Nếu ∆ đi qua 2 điểm A và B thì ∆ nhận AB làm VTCP.
2. Các dạng phương trình của đường thẳng
• Nếu đường thẳng ∆ đi qua điểm M (x ; y và có VTPT n = (a;b) thì có phương trình tổng quát là: 0 0 )
∆ : a(x − x ) +b( y − y ) = 0 Hay ∆ : ax +by + c = với c = −(ax +by . 0 0 ) 0 0 0
• Nếu đường thẳng ∆ đi qua điểm M (x ; y và có VTCP u = (a;b) thì có phương trình tham số là: 0 0 )
x = x + at ∆ : 0 (t ∈). y = y + bt 0
• Nếu đường thẳng ∆ đi qua điểm
M (x ; y và có VTCP u = (a;b) thì có phương trình chính tắc là: 0 0 ) x − x y − ∆ y 0 = 0 : (ab ≠ 0). a b
• Nếu đường thẳng ∆ đi qua điểm M (x ; y và có hệ số góc k thì có phương trình có hệ số góc là: 0 0 )
∆ : y = k(x − x ) + y = kx + h với h = y − kx . 0 0 0 0
• Nếu đường thẳng ∆ đi qua điểm A(a;0) và B(0;b) thì có phương trình đoạn chắn là:
∆ : x + y = (ab ≠ 1 0). a b
3. Cách viết nhanh phương trình của đường thẳng
• Để viết được phương trình của đường thẳng thì ta cần biết 2 yếu tố: 15
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
• Yếu tố 1: Tìm tọa độ điểm mà đường thẳng đi qua.
• Yếu tố 2: Tìm tọa độ VTPT hoặc VTCP hoặc hệ số góc của đường thẳng.
• Từ đó, ta có quy trình 3 bước để viết phương trình đường thẳng như sau:
• Bước 1: Xác định tọa độ điểm mà đường thẳng đi qua.
• Bước 2: Xác định VTPT (nếu viết theo phương trình tổng quát) hoặc VTCP (nếu viết theo phương
trình tham số hoặc chính tắc) hoặc hệ số góc (nếu viết theo phương trình hệ số góc) bằng cách xét xem
đường thẳng cần tìm có vuông góc hay song song hay đi qua thêm 1 điểm nào nữa không mà từ đó xác định được.
• Bước 3: Áp dụng công thức dạng phương trình để viết.
4. Vị trí tương đối giữa đường thẳng với điểm và đường thẳng
• Vị trí tương đối giữa đường thẳng và điểm:
• Điểm A(x y thuộc đường thẳng ∆ : ax + by + c = khi và chỉ khi ax + by + c = , ngược lại điểm A A 0 A ; A ) 0
A(x y không thuộc đường thẳng ∆ : ax +by + c = khi và chỉ khi ax +by + c ≠ A A 0. A ; A ) 0
• Hai điểm A(x y
B x y nằm cùng phía so với đường thẳng ∆ : ax +by + c = khi và chỉ khi
A ; A ) và ( B ; B ) 0
(ax +by +c ax by c
, ngược lại hai điểm A(x y
B x y nằm khác phía so với
A ; A ) và ( B ; B ) A A )( + + B B ) > 0
đường thẳng ∆ : ax + by + c = 0 khi và chỉ khi (ax + by + c ax by c A A )( + + B B ) < 0.
• Vị trí tương đối giữa đường thẳng với đường thẳng:
Để xét vị trí tương đối của hai đường thẳng ∆ : a x + b y + c = 0 và ∆
: a x + b y + c = 0 ta chọn một trong 1 1 1 1 2 2 2 2 các cách sau:
a x + b y + c = 0
• Cách số 1: Xét số nghiệm của hệ phương trình 1 1 1
(I) với số nghiệm chính là số giao
a x + b y + c = 0 2 2 2
điểm của hai đường thẳng, khi đó:
+ Hệ (I) vô nghiệm ⇔ ∆ ∩ ∆ (hai đường thẳng cắt nhau). 1 2
+ Hệ (I) có nghiệm duy nhất ⇔ ∆
(hai đường thẳng song song nhau). 1 ∆2
+ Hệ (I) có vô số nghiệm ⇔ ∆ ≡ ∆ (hai đường thẳng trùng nhau). 1 2
• Cách số 2: Xét tỉ số giữa các hệ số khi a b c ≠ 0 , khi đó: 2 2 2 + a b a b c a b c 1 ≠ 1 ⇔ ∆ ∩ ∆ + 1 = 1 ≠ 1 ⇔ ∆ + 1 = 1 = 1 ⇔ ∆ ≡ ∆ 1 ∆ 1 2 a b 2 a b c 1 2 a b c 2 2 2 2 2 2 2 2
• Cách số 3: Xét hệ số góc của hai đường thẳng bằng cách chuyển phương trình về dạng ∆ : y = k x + h 1 1 1 và ∆
: y = k x + h với k và k lần lượt là hệ số góc của ∆ và ∆ , khi đó: 2 2 2 1 2 1 2 k = k k = k
+ k ≠ k ⇔ ∆ ∩ ∆ + 1 2 ⇔ ∆ + 1 2 ⇔ ∆ ≡ ∆
+ k .k = −1 ⇔ ∆ ⊥ ∆ 1 ∆ 1 2 1 2 h ≠ 2 h h = 1 2 h 1 2 1 2 1 2 1 2
5. Góc giữa hai đường thẳng
• Góc giữa hai đường thẳng ∆ và ∆
lần lượt có VTPT là n a ;b và n a ;b được xác định bởi công 2 ( 2 2 ) 1 ( 1 1 ) 1 2 thức: ( n n a a b b , ) cos( n ,n ) . . + . cos ∆ ∆ = = 1 2 = 1 2 1 2 . 1 2 1 2 2 n . n a + 2 2 b . a + 2 1 2 b 1 1 2 2
• Góc giữa hai đường thẳng ∆ và ∆
lần lượt có VTCP là u a ;b và u a ;b được xác định bởi công 2 ( 2 2 ) 1 ( 1 1 ) 1 2 thức: 16
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội ( u u a a b b , ) cos( u ,u ) . . + . cos ∆ ∆ = = 1 2 = 1 2 1 2 . 1 2 1 2 2 u . u a + 2 2 b . a + 2 1 2 b 1 1 2 2
• Góc giữa hai đường thẳng ∆ và ∆
lần lượt có hệ số góc là k và k được xác định bởi công thức: 1 2 1 2 tan( , ) k − ∆ ∆ = k 1 2 . 1 2 1+ k .k 1 2
6. Khoảng cách từ điểm tới đường thẳng
• Khoảng cách từ điểm M (x ; y đến đường thẳng ∆ ax +by + c = ( 2 a + 2 : b > 0 0) là: 0 0 ) ( ax by c d M, ) + + ∆ = 0 0 > 0. 2 a + 2 b
• Khoảng cách giữa hai đường thẳng song song ∆ : ax + by + c = 0 và ∆ : ax + by + d = 0 (c ≠ d là: 1 2 ) ( c d d , 0. 1 2 ) − ∆ ∆ = > 2 a + 2 b
• Phương trình hai đường phân giác của các góc tạo bởi hai đường thẳng cắt nhau ∆ : a x + b y + c = 0 1 1 1 1 và ∆
: a x + b y + c = 0 là: 2 2 2 2
a x + b y + c
a x + b y + c
a x + b y + c
a x + b y + c 1 1 1 = 2 2 2 1 1 1 và = − 2 2 2 . 2 a + 2 2 b a + 2 2 b a + 2 2 b a + 2 b 1 1 2 2 1 1 2 2
III. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ Oxy
1. Các dạng phương trình của đường tròn
• Có loại phương trình của đường tròn (C) như sau:
• Dạng 1: (C) (x − a)2 + ( y −b)2 = 2 : R
⇒ Đường tròn (C) có tâm I (a;b) và có bán kính . R
• Dạng 2: (C) 2 x + 2 :
y − 2ax − 2by + c = 0
⇒ Đường tròn (C) có tâm I (a;b) và có bán kính R = 2 a + 2 b − c.
• Điều kiện để 2 phương trình trên là phường trình của đường tròn là R > 0 , khi đó điều kiện để phương
trình dạng 2 là phương trình của tròn là: 2 a + 2 b − c > 0.
2. Cách viết nhanh phương trình của đường tròn
• Để viết phương trình của đường tròn ta cần biết hai yếu tố sau:
• Yếu tố 1: Tìm tọa độ tâm của đường tròn.
• Yếu tố 2: Tìm độ dài bán kính của đường tròn.
• Từ đó, ta có quy trình 3 bước để viết phương trình của đường tròn như sau:
• Bước 1: Tìm tọa độ tâm của đường tròn.
• Bước 2: Tìm độ dài bán kính của đường tròn.
• Bước 3: Áp dụng công thức viết phương trình của đường tròn theo dạng 1 hoặc 2.
3. Vị trí tương đối của đường tròn với điểm, đường thẳng và đường tròn
Cho đường tròn (C) (x − a)2 + ( y −b)2 = 2 :
R có tâm I (a;b) và có bán kính . R
• Với điểm M (x ; y : 0 0 )
• Điểm M nằm trong đường tròn ⇔ IM < R ⇔ (x − a)2 + ( y −b)2 < 2 R . 0 0
• Điểm M nằm trên đường tròn ⇔ IM = R ⇔ (x − a)2 + ( y −b)2 = 2 R . 0 0 17
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
• Điểm M nằm ngoài đường tròn ⇔ IM > R ⇔ (x − a)2 + ( y −b)2 > 2 R . 0 0
• Với đường thẳng ∆ : Ax + By + C = 0 : Aa Bb C
• Đường thẳng ∆ không cắt đường tròn (C) d(I, ) + + ⇔ ∆ > R ⇔ > . R 2 A + 2 B Aa Bb C
• Đường thẳng ∆ tiếp xúc đường tròn (C) d(I, ) + + ⇔ ∆ = R ⇔ = . R 2 A + 2 B Aa Bb C
• Đường thẳng ∆ cắt đường tròn (C) d(I, ) + + ⇔ ∆ < R ⇔ < . R 2 A + 2 B
• Với đường tròn (C') có tâm I ' và bán kính R' > R :
• (C) và (C’) đồng tâm ⇔ II ' = 0.
• (C) và (C’) dựng nhau ⇔ II ' < R'− . R
• (C) và (C’) tiếp xúc nhau ⇔ II ' = R'− . R
• (C) và (C’) cắt nhau tại 2 điểm ⇔ R'− R < II ' < R'+ . R
• (C) và (C’) tiếp xúc ngoài ⇔ II ' = R'+ . R
• (C) và (C’) ở ngoài nhau ⇔ II ' > R'+ . R Chú ý:
• Đường thẳng ∆ tiếp xúc đường tròn (C) tại M thì IM ⊥ ∆. 2
• Đường thẳng ∆ cắt đường tròn (C) tại A và B thì AB R = + d(I,∆ 2 2 ) . 2
4. Phương trình tiếp tuyến với đường tròn
• Phương trình tiếp tuyến ∆ của đường tròn (C) tại điểm M (x ; y : 0 0 )
Vì IM ⊥ ∆ nên đường thẳng ∆ nhận IM = (x − a; y −b làm VTPT. 0 0 )
Phương trình của đường thẳng ∆ đi qua điểm M (x ; y và có VTPT n = IM = x − a; y −b là: ∆ ( 0 0 ) 0 0 )
∆ : (x −a)(x − x ) + ( y −b)( y − y ) = 0. 0 0 0 0
• Phương trình tiếp tuyến ∆ của đường tròn (C) đi qua điểm A(a;b) :
Gọi phương trình tiếp tuyến ∆ của đường tròn (C) tại điểm M (x ; y có dạng: y = kx + h 0 0 )
Vì A(a;b)∈∆ : y = kx + h nên b = ka + h ⇒ h = b − ka
Khi đó ∆ : y = kx + b − ka ⇔ kx − y + b − ka = 0 (lúc này phương trình tiếp tuyến ∆ chỉ còn duy nhất ẩn k)
kx − y + b − ka
Mà ∆ là tiếp tuyến của đường tròn (C) nên d(I,∆) = R ⇔ I I = R (1) k + (− )2 2 1
Giải phương trình duy nhất ẩn k ta tìm được phương trình tiếp ∆ cần tìm.
• Phương trình tiếp tuyến ∆ của đường tròn (C) song song hoặc vuông góc hoặc tạo góc với đường thẳng
d : ax + by + c = 0 :
• TH1: Tiếp tuyến ∆ d : ax + by + c = 0
Khi đó phương trình tiếp tuyến ∆ có dạng ∆ : ax + by + d = 0 (c ≠ d) ax by d
Vì ∆ là tiếp tuyến của đường tròn (C) nên d(I, ) + + ∆ = R ⇔ I I = R (1) 2 a + 2 b
Giải phương trình duy nhất ẩn d ta tìm được phương trình tiếp ∆ cần tìm.
• TH2: Tiếp tuyến ∆ ⊥ d : ax + by + c = 0 18
Địa chỉ: Số 24, ngõ 266/36/6 (Quán trà sữa Dingtea), Nguyễn Văn Cừ, Long Biên, Hà Nội
Khi đó phương trình tiếp tuyến ∆ có dạng ∆ : bx − ay + d = 0
bx − ay + d
Vì ∆ là tiếp tuyến của đường tròn (C) nên d(I,∆) = R ⇔ I I = R (1) b + (−a)2 2
Giải phương trình duy nhất ẩn d ta tìm được phương trình tiếp ∆ cần tìm.
• TH3: Tiếp tuyến ∆ tạo với đường thẳng d : ax + by + c = 0 một góc bằng α, tức là (∆,d) =α
Gọi phương trình tiếp tuyến ∆ có dạng: y = kx + h ⇔ kx − y + h = 0
Khi đó VTPT của đường thẳng ∆ và d lần lượt là n = k;−1 và n = a b d ( ; ) ∆ ( ) n .n k.a + (− ) 1 .b Vì (∆,d) =α nên cosα ∆ = d = (1) 2 n . n ∆ 2 d k + (− ) 2 1 . a + 2 b
Giải phương trình duy nhất ẩn k ta tìm được ẩn k nên phương trình tiếp tuyến ∆ chỉ còn duy nhất ẩn h.
kx − y + h
Vì ∆ là tiếp tuyến của đường tròn (C) nên d(I,∆) = R ⇔ I I = R (2) k + (− )2 2 1
Giải phương trình duy nhất ẩn h ta tìm được phương trình tiếp ∆ cần tìm.
• Phương trình tiếp tuyến ∆ là tiếp tuyến chung của hai đường tròn (C) và (C’):
d(I,∆) = R
∆ là tiếp tuyến chung của hai đường tròn (C) và (C’) ⇔ .
d(I ',∆) = R'
IV. ELIP TRONG MẶT PHẲNG TỌA ĐỘ Oxy
1. Định nghĩa đường elip
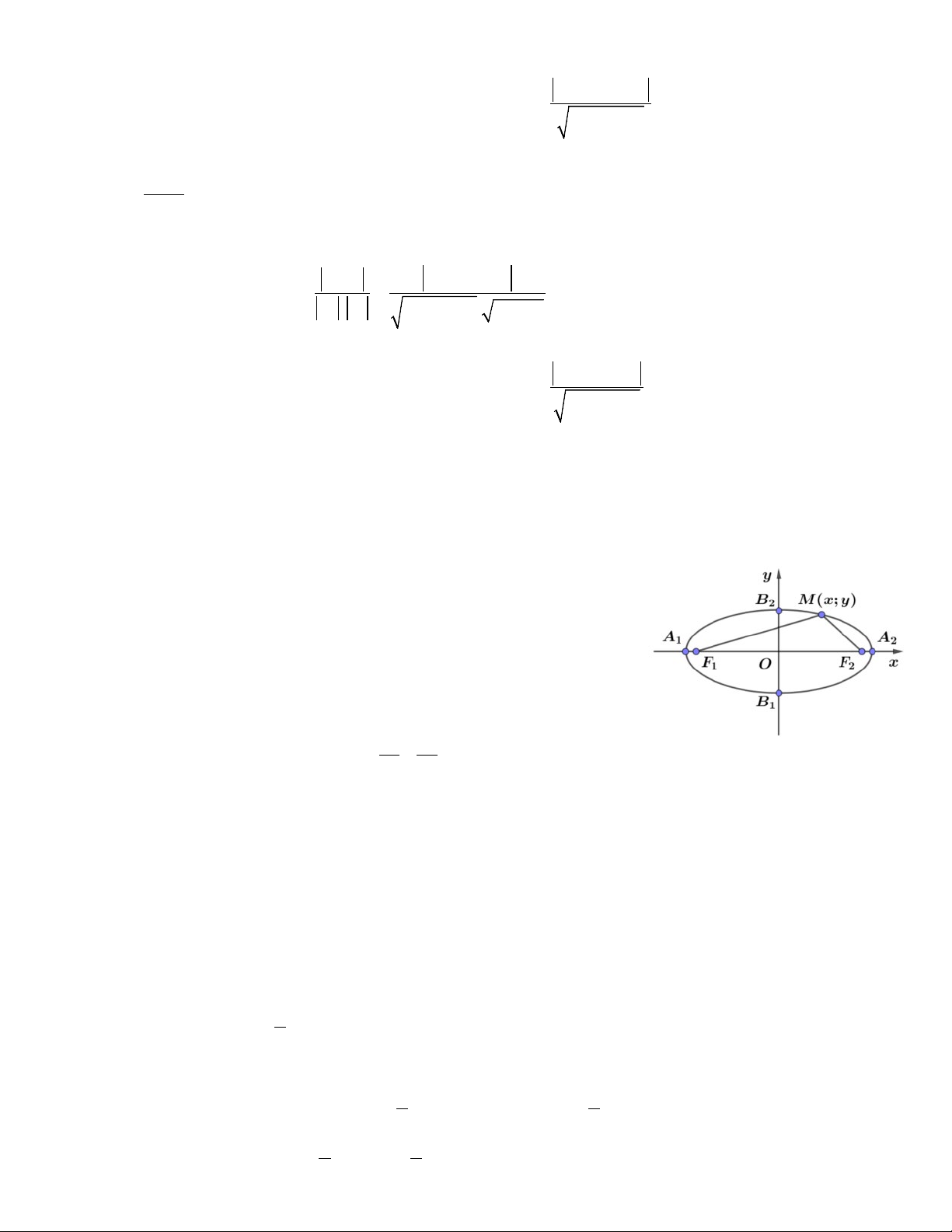
Trong mặt phẳng tọa độ Oxy, cho hai điểm F (−c;0 và F c;0 và độ dài 2 ( ) 1 )
không đổi a thỏa mãn a > c > 0. Elip (E) là tập hợp các điểm M thỏa mãn MF + MF = 2 .
a Các điểm F ,F được gọi là các tiêu điểm của elip (E) và 1 2 1 2
a gọi là bán trục lớn của elip (E).
2. Phương trình chính tắc của elip 2 2
Phương trình chính tắc của elip (E) là: x + y = 1, trong đó 2 b = 2 a − 2 c . 2 2 a b
3. Các thông tin của elip
• Hai tiêu điểm: F (−c;0 ,F c;0 . 1 ) 2( )
• Bốn đỉnh: A (−a;0),A (a;0),B (0;−b ,B 0;b . 1 2 1 ) 2( )
• Độ dài trục lớn: A A = 2a và độ dài trục bé: B B = 2 . b 1 2 1 2
• Tiêu cự: F F = 2c. 1 2
• Elip nhận gốc độ O làm tâm đối xứng và nhận trục hoành Ox và trục tung Oy làm hai trục đối xứng.
• Bốn đường thẳng x = −a,x = a, y = − ;
b y = b tạo thành hình chữ nhật được gọi là hình chữ nhật cơ sở của
Elip. Hình chữ nhật có chiều dài là 2a và chiều rộng là 2b.
• Tâm sai của elip: = c e ( 0 < e < )1. a
• Biểu thức tính bán kính qua tiêu cự MF và MF của điểm M (x y nằm trên elip là: M ; M ) 1 2 = + c = + c MF a x a ex MF a x a ex M M , = − = − M M . 1 2 a a
• Đường chuẩn của elip: + a = 0 và − a x x
= 0 lần lượt ứng với tiêu điểm F (−c;0 và F c;0 . 1 ) 2 ( ) e e 19
Giáo viên: NGUYỄN MẠNH CƯỜNG – Điện thoại: 0967453602 – Facebook: ThayCuongToan
Phải có thời gian để nhìn nhận lại bản thân. Xem mình đã ngã
chỗ nào thì phải đứng dậy ở chỗ đó. Đặc biệt không được tự ti,
tự phụ mà phải tự tin vào bản thân mình. Bởi lẽ người thành
công không bao giờ nói “không” với bất kì khó khăn nào. Có
như vậy thì thành công sẽ đến với bạn trong tương lai gần.
Thầy Nguyễn Mạnh Cường 20
Document Outline
- PHẦN ĐẠI SỐ
- Chương IV. BẤT ĐẲNG THỨC – BẤT PHƯƠNG TRÌNH
- I. BẤT ĐẲNG THỨC
- 1. Tính chất của bất đẳng thức
- 2. Bất đẳng thức Cô si
- 3. Bất đẳng thức có chứa dấu giá trị tuyệt đối
- 4. Một số bất đẳng thức thường dùng khác
- II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
- 1. Dấu của nhị thức bậc nhất
- 2. Bất phương trình bậc nhất
- 3. Hệ bất phương trình bậc nhất một ẩn
- III. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
- 1. Bất phương trình bậc nhất hai ẩn
- 2. Hệ bất phương trình bậc nhất hai ẩn
- IV. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- 1. Dấu của tam thức bậc hai
- 2. Bất phương trình bậc hai một ẩn
- 3. Một số phương trình và bất phương trình quy về bậc hai
- I. BẤT ĐẲNG THỨC
- Chương V. THỐNG KÊ
- I. KHÁI QUÁT
- II. BẢNG PHÂN BỐ TẦN SỐ VÀ TẦN SUẤT
- III. BIỂU ĐỒ
- 1. Biểu đồ hình cột
- 2. Biểu đồ đường gấp khúc
- 3. Biểu đồ hình quạt
- IV. SỐ TRUNG BÌNH CỘNG
- V. SỐ TRUNG VỊ
- VI. MỐT
- VII. PHƯƠNG SAI
- VIII. ĐỘ LỆCH CHUẨN
- Chương VI. LƯỢNG GIÁC
- I. CÔNG THỨC LƯỢNG GIÁC
- 1. Công thức cơ bản
- Hệ quả của công thức cơ bản
- 2. Công thức cộng
- Hệ quả của công thức cộng
- a. Công thức nhân hai
- Hệ quả của công thức nhân hai
- Công thức hạ bậc
- b. Công thức biến đổi tích thành tổng
- c. Công thức nhân ba
- 3. Công thức biến đổi tổng thành tích
- 4. Công thức biến đổi theo
- 5. Công thức biến đổi theo
- II. GÓC VÀ CUNG LƯỢNG GIÁC ĐẶC BIỆT
- 1. Góc và cung lượng giác
- 2. Giá trị của góc và cung lượng giác
- 3. Giá trị lượng giác của các góc (cung) có liên quan đặc biệt
- I. CÔNG THỨC LƯỢNG GIÁC
- PHẦN HÌNH HỌC
- Chương III. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG Oxy
- I. HỆ TỌA TRỤC TỌA ĐỘ TRONG MẶT PHẲNG TỌA ĐỘ Oxy
- 1. Hệ trục tọa độ
- 2. Tọa độ véc-tơ
- 3. Tọa độ điểm
- 4. Liên hệ giữa tọa độ véc-tơ và tọa độ điểm
- II. ĐƯỜNG THẲNG TRONG MẶT PHẲNG TỌA ĐỘ Oxy
- 1. Véc-tơ pháp tuyến và véc-tơ chỉ phương của đường thẳng
- 2. Các dạng phương trình của đường thẳng
- 3. Cách viết nhanh phương trình của đường thẳng
- 4. Vị trí tương đối giữa đường thẳng với điểm và đường thẳng
- 5. Góc giữa hai đường thẳng
- 6. Khoảng cách từ điểm tới đường thẳng
- III. ĐƯỜNG TRÒN TRONG MẶT PHẲNG TỌA ĐỘ Oxy
- 1. Các dạng phương trình của đường tròn
- 2. Cách viết nhanh phương trình của đường tròn
- 3. Vị trí tương đối của đường tròn với điểm, đường thẳng và đường tròn
- 4. Phương trình tiếp tuyến với đường tròn
- IV. ELIP TRONG MẶT PHẲNG TỌA ĐỘ Oxy
- 1. Định nghĩa đường elip
- 2. Phương trình chính tắc của elip
- 3. Các thông tin của elip
- I. HỆ TỌA TRỤC TỌA ĐỘ TRONG MẶT PHẲNG TỌA ĐỘ Oxy




