Soạn bài tuần 7 Môn Cơ lý thuyết 1 | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58675420 I.
Soạn nội dung bài học:
Ta lần lượt có các công thức tính như sau: Lực hấp dẫn: 𝑮𝒎𝟏𝒎𝟐 |𝜶|
⃗𝑭⃗⃗⃗⃗⃗⃗𝒉𝒅⃗⃗⃗ = −⃗𝒆⃗⃗⃗⃗⃗⃗𝒓
𝒓𝟐 = −⃗𝒆⃗⃗⃗⃗⃗⃗𝒓 𝒓𝟐 Lực Cu-lông:
⃗𝑭⃗⃗⃗⃗⃗⃗𝑪𝑳⃗⃗ = −⃗𝒆⃗⃗⃗⃗⃗⃗𝒓 𝒌
𝒒𝒓𝟏𝟐𝒒𝟐 = −⃗𝒆⃗⃗⃗⃗⃗⃗𝒓 | 𝒓𝜷𝟐| Xác định khối tâm.
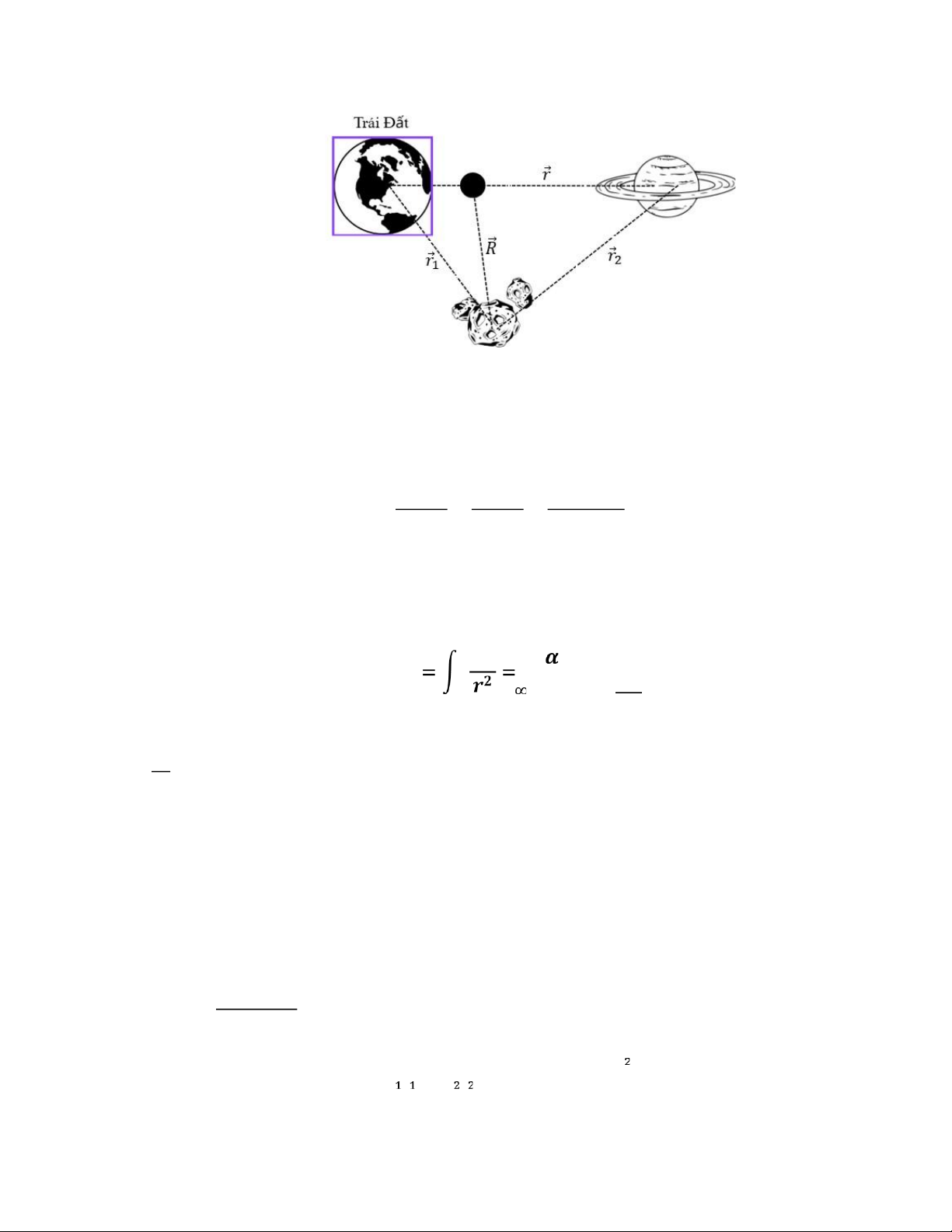
⃗𝑹⃗⃗⃗⃗⃗⃗⃗⃗𝑮 = 𝒎𝟏⃗𝒓⃗⃗⃗𝟏 +𝒎𝟐⃗𝒓⃗⃗𝟐⃗ 𝒎𝟏 +𝒎𝟐
Xét một hệ ngoài không gian có các hành tinh, ta xét các hành tinh như là các hạt chuyển
động với nhau. Lúc này bài toán của ta là bài toán nhiều hạt (Hệ nhiều hành tinh ở hình
bên dưới là một hệ có 6 chiều).
• Cách để giải bài toán nhiều hạt:
- Cố gắng đưa bài toán về các đại lượng cùng đối xứng với nhau.
- Đưa về hệ quy chiếu khối tâm. lOMoAR cPSD| 58675420 G
Ta có công thức xác định như sau: ⃗ ⃗
𝒎𝟏 𝒓⃗⃗⃗𝟐𝟏 𝒎𝟐 𝒓⃗⃗⃗𝟐𝟐 |𝜶| 𝓛𝑷𝑻𝑵 = 𝜶 + 𝜶
+|⃗𝒓⃗⃗⃗𝟏 −⃗𝒓⃗⃗⃗𝟐 |
Ta lại có công thức thế năng 𝑈 là: 𝒓 | | |𝜶| 𝑼 𝒓 |𝛼|
Với 𝑟 trường thế xuyên tâm giảm được số chiều chuyển động.
Ta phải đưa bài toán về dạng như sau:
(⃗𝑹⃗⃗⃗⃗⃗⃗⃗⃗𝟏 ,⃗𝒓⃗⃗⃗𝟐 ) = (⃗𝑹⃗⃗⃗⃗⃗ ,𝒓⃗⃗ )
Ta sẽ rút ra từ công thức khối tâm:
⃗𝑅⃗⃗⃗⃗⃗⃗𝐺 = 𝑚
1𝑚⃗𝑟⃗⃗⃗11 ++𝑚𝑚22⃗𝑟⃗⃗⃗2⃗ và 𝑟⃗ = ⃗𝑟⃗⃗2 −⃗𝑟⃗1⃗ ( với 𝑚1 +𝑚2 = μ)
𝑚 𝑟⃗⃗⃗⃗ 𝑚 𝑟⃗⃗⃗⃗ 𝑟⃗⃗⃗1 = 𝑅⃗⃗⃗⃗⃗⃗ − 𝑚𝑟⃗⃗ lOMoAR cPSD| 58675420 μ 1
⟹ ⃗𝑅⃗⃗⃗⃗⃗ = + với {
𝑅⃗⃗⃗⃗⃗⃗ + 𝑚 ⃗𝑟⃗ ⃗𝑟⃗⃗2 = Ta thay vào công thức: ℒ = 𝑚
1 (⃗𝑅⃗⃗⃗⃗⃗ −𝑚 𝑟⃗ )2 +𝑚2 (⃗𝑅⃗⃗⃗⃗⃗ +𝑚 ⃗𝑟 )2 +|𝛼| 𝛼 𝛼 𝑟 μ 1 𝑚 𝑚2 𝑚 𝑚2 |𝛼|
= ⃗𝑅⃗⃗⃗⃗⃗⃗2 + (+)𝑟⃗ + 𝛼 𝛼 𝑟 μ 1 𝑚 𝑚2 𝑚 𝑚2 |𝛼|
= ⃗𝑅⃗⃗⃗⃗⃗⃗2 + (+)𝑟⃗ + 𝛼 𝛼 𝑟
μ⃗𝑅⃗⃗⃗⃗⃗⃗2 + 1𝑚1𝑚2 ⃗𝑟 +|𝛼| = 𝛼 𝛼 μ 𝑟 Với:
• 𝑀 𝛼 ⃗𝑅⃗⃗⃗⃗⃗⃗2 = (𝑅⃗⃗⃗⃗ ,𝑟⃗ ) Khối tâm chuyển động với 𝑀 của hạt chuyển động tự do được đặt ngay tại khối tâm
• 𝛼1 𝑚1𝑀𝑚2 : Chuyển động tương đối của 2 vật với nhau 𝑚1,𝑚2
• |𝑟𝛼 | trường thế xuyên tâm giảm được số chiều.
Từ đây ta có phương trình Langrange cho 𝑅⃗⃗⃗𝑖 lOMoAR cPSD| 58675420 𝜕𝛼 𝑑 𝜕𝛼
−= 0 ⟹ 𝑅⃗⃗⃗⃗ = 𝑐𝑜𝑛𝑠𝑡 𝜕𝑅⃗⃗⃗ 𝑑𝑡𝜕𝑅⃗⃗⃗𝑖
có phương trình Langrange cho 𝑟 : 𝑀 𝑟 |𝛼| 𝛼 =
+ ( đây là không gian 3 chiều ) 𝛼 2
Lúc này bậc vẫn đang là 𝛼 ta cũng thể nào giải được bài toán. Nên ta tiếp tục hạ bậc để tìm
các đại lượng bảo toàn. 𝑚1𝑚2 μ = < 𝑚1 𝑚2 𝑚1 +𝑚2 1 1 ⟺= + 𝑚1 𝑚2
𝐿⃗⃗ = 𝑐𝑜𝑛𝑠𝑡 sẽ có hướng và độ lớn: 𝐿⃗⃗ 𝑟 × 𝐿⃗ 𝑟 × 𝑣
Ta đưa về tọa độ cực: 2 +𝑟2𝜑̇ 2)+|𝛼| 𝐿⃗ =(𝑟 𝑟
Lúc này ta có phường trình Langrange cho 𝜑̇:
𝜕𝑓 − 𝑑 𝜕𝛼 𝑣ớ𝑖 𝐿⃗ = 𝑐𝑜𝑛𝑠𝑡 = μ𝑟2𝜑̇ = 𝐿⃗ 𝜕𝜑̇ 𝑑𝑡𝜕𝜑̇ lOMoAR cPSD| 58675420 𝐿⃗ ⟹ 𝜑̇ = μ 𝑟2 Nhận xét:
- Μoment không đổi
- Nghiệm đúng định luật Keepler
Chứng Minh Giả sử định luật Keepler là đúng: 𝐴 = 𝑟2𝜑̇
Ta lấy đạo hàm theo 𝑑𝑡 ta được:
𝑑𝐴2𝜑̇ = 𝐿⃗ = 𝑐𝑜𝑛𝑠𝑡 =𝑟 𝑑𝑡 2μ
Định luật II Keepler là hệ quả của moment động lượng vận tốc quay luôn bằng hằng số đều
phải phụ thuộc bán kính 𝑟
Giải tiếp phần đầu phương trình Langrange cho 𝑟 𝜕𝑓 𝑑 𝜕𝐿⃗ = 𝜕𝜑̇ 𝑑𝑡𝜕𝑟 Ta được như sau:
μ𝑟 = 𝑎𝑟𝜑̇ 2 +𝐹ℎ𝑑 lOMoAR cPSD| 58675420 𝐿⃗2 ⟺ μ𝑟 = 𝑀 𝑟3 +𝐹ℎ𝑑
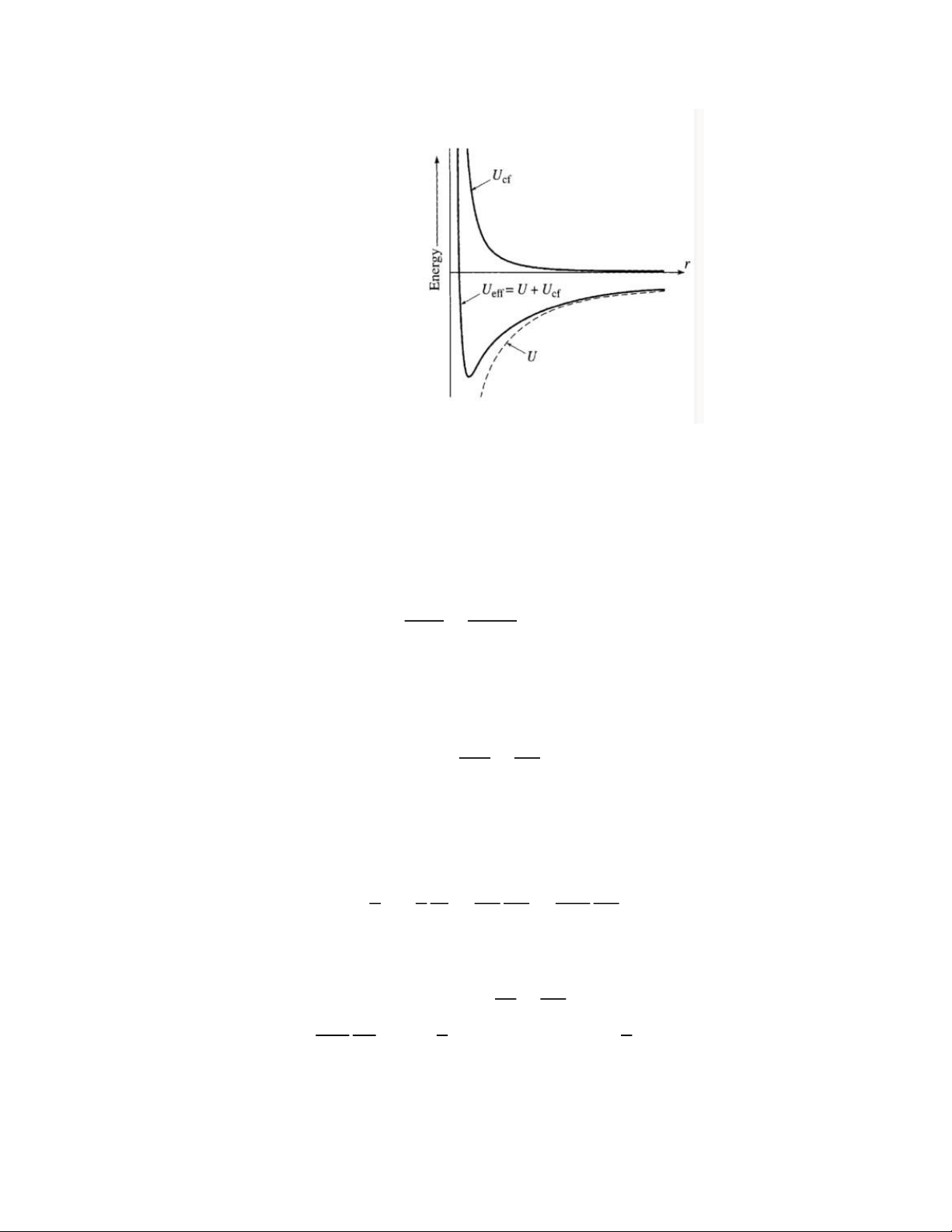
Nhận xét các thành phần biểu thức trên: Với:
𝐹ℎ𝑑: là thành phần lực hút vào 𝐿⃗2
3: là lực li tâm do chuyển động quay đẩy ra 𝑀𝑟
𝑚1 ⃗𝑃⃗⃗⃗⃗1⃗2 𝑚2 ⃗𝑃⃗⃗⃗⃗2⃗2 |𝛼| 6𝐷 𝐿⃗𝑝𝑡𝑛 = 2 + 2 +|𝑟⃗⃗1 −⃗𝑟⃗2 | |
= 𝑈(𝑟 2 +𝑟2𝜑̇2 )+ 𝛼| 𝑟
2𝜑̇ = 𝑐𝑜𝑛𝑠𝑡 rút ra ta được 𝜇𝑟 = 𝜇𝐿⃗𝑟23
+𝐹ℎ𝑑 Ta có 𝐿⃗ = 𝜇𝑟 − 𝑟 2 𝑈 μ 3 𝑑𝑟 𝐸 𝑈𝑒𝑔𝑔(𝑟) 𝛼 lOMoAR cPSD| 58675420
Chỉ 1 quỹ đạo 𝑟 thõa mãn 𝑟𝑒𝑞 và là quỹ đạo tròn. Quỹ đạo sẽ thay đổi từ 𝑟min đến 𝑟𝑚𝑎𝑥 và
quỹ đạo có hình elip hay còn gọi là quỹ đạo quay đầu: −|𝐿⃗| 𝐿⃗2 𝑈𝑒𝑓𝑓(𝑟) = 𝑟 +𝛼𝑚𝑟2 = 𝐸
Tính 𝑟𝑚𝑖𝑛 và 𝑟𝑚𝑎𝑥 𝐿⃗2 |𝛼| 𝑢𝑟 = 𝜇𝑟3 − 𝑟 Với 1 1 d d dφ L d
u = r ⟹ μdt = dφ dt = Μr2 dφ 𝑟 =
μr𝐿⃗2 𝑑𝑞𝑑 1u 𝐿⃗μ 𝑢1 𝑑𝑢 𝐿⃗ ′𝜑̇ ( ) =𝑢(− 2 −𝑑𝜑̇) = −μ𝑢 Mà lOMoAR cPSD| 58675420 𝑑 𝐿⃗𝑢2 𝑑 𝐿⃗ du L2𝑢2𝑢′′ 𝑟 = 𝑑𝑡 𝑟 = − μ𝐫𝟐 𝑑𝑞μdφ = μ2 Nên ta được: 𝐿⃗2 |𝛼| L2𝑢2𝑢′′ L2𝑢3
𝑢𝑟 = 𝑢 𝑟3 − 𝑟 ⟹ μ2 = μ ′′ = −𝑢+|𝛼𝑟|2𝑢 𝑢 II.
Giải các bài tập:
Exersise 4: Hai vật có khối lượng 𝒎𝟏 và 𝒎𝟐 chuyển động trong một mặt phẳng và
tương tác với nhau thông qua thế năng 𝑼(𝒓) = 𝟏 𝒌𝒓𝟐. Hãy viết Lagrangian của hệ
𝟐 theo vị trí của khối tâm 𝑹⃗⃗⃗⃗ và vị trí
tương đối 𝒓, đồng thời tìm phương trình chuyển động cho các tọa độ 𝑿,𝒀 và 𝒙,𝒚. Mô
tả chuyển động và tìm tần số của chuyển động tương đối. Bài làm
Xét 𝑟1(𝑥1;𝑦1) và 𝑟2 = (𝑥2;𝑦2) Vị trí khối tâm 𝑂 là: 𝑚1𝑟1 +𝑚2𝑟2 𝑅⃗⃗⃗ = 𝑚1 +𝑚2 Vị trí tương đối là:
𝑟 = 𝑟1 −𝑟2 ⇒ 𝑟2 = 𝑟1 −𝑟
Thay vào biểu thức 𝑅⃗⃗⃗ ta có:
𝑚1𝑟1 +𝑚2(𝑟1 −𝑟) 𝑀𝑟1 −𝑚2𝑟 𝑅⃗⃗⃗ = = 𝑀 𝑀 Suy ra: 𝑚2 𝑟1 = 𝑅⃗⃗⃗+ 𝑟 lOMoAR cPSD| 58675420 𝑀
Vì 𝑟2 = 𝑟1 −𝑟 nên: 𝑚1 𝑟2 = 𝑅⃗⃗⃗− 𝑟 𝑀 Động năng của hệ là: 2 1 2 𝑇 = 𝑚1𝑟1 + 𝑚2𝑟2 2 1 𝑚 2 𝑇 = 𝑚1 (𝑅⃗⃗⃗ +
2 𝑟 ) +1 𝑚2 (𝑅⃗⃗⃗ −𝑚 1 𝑟 )2 2 𝑀 2 𝑀
𝑇 = 1 𝑀𝑅⃗⃗⃗ 2 +1 𝑚1𝑚2 𝑟 2 2 2 𝑀
Gọi 𝜇 = 𝑚1𝑚2 là khối lượng rút gọn của hệ 𝑀 2 +1𝜇𝑟 2 𝑇 =𝑀𝑅⃗⃗⃗ 2 Larangian của hệ là: 1 1 1
𝐿⃗ = 𝑇−𝑈 = 𝑀𝑅⃗⃗⃗ 2 + 𝜇𝑟 2 − 𝑘𝑟2 2 2
2 +𝑌̇ 2)+1𝜇(𝑥2 +𝑦 2)−𝑘(𝑥2 +𝑦2) 𝐿⃗ =𝑀(𝑋̇ 2 2
Áp dụng phương trình Euler – Larange: • Với 𝑋̇ 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑋̇ 𝜕𝑋̇ 𝑑 (𝑀𝑋̇ ) = 0 𝑑𝑡 lOMoAR cPSD| 58675420 𝑀𝑋̇ = 0 𝑋̇ = 0 • Với 𝑌̇ 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑌̇ 𝜕𝑌̇ 𝑑 (𝑀𝑌̇ ) = 0 𝑑𝑡 𝑀𝑌̇ = 0 𝑌̇ = 0 • Với 𝑥 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑥 𝜕𝑥 𝑑 (𝜇𝑥 )+𝑘𝑥 = 0 𝑑𝑡 𝜇𝑥 +𝑘𝑥 = 0
⇒ 𝑥 = 𝐴cos(𝜔𝑡+𝜑̇𝑥) • Với 𝑦 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑦 𝜕𝑦 𝑑 (𝜇𝑦 )+𝑘𝑦 = 0 𝑑𝑡 𝜇𝑦 +𝑘𝑦 = 0
⇒ 𝑦 = 𝐵cos(𝜔𝑡+𝜑̇𝑦) 𝑘 Với 𝜔 = √ 𝑢
Dao động của khối tâm là dao động thẳng đều do gia tốc bằng 0, dao động của hệ là dao
động điều hòa hai chiều 𝑥,𝑦. lOMoAR cPSD| 58675420 Excersise 5:
Xét hai hạt có khối lượng bằng nhau 𝑚1 = 𝑚2, được nối với nhau bằng một lò xo nhẹ, thẳng
(có độ cứng 𝑘 và chiều dài tự nhiên 𝐿⃗), và có thể trượt tự do trên một mặt bàn ngang không ma sát. (a)
Viết Lagrangian của hệ theo tọa độ 𝑟1 và 𝑟2, sau đó viết lại theo tọa độ khối tâm 𝑅⃗⃗⃗
và vị trí tương đối 𝑟, sử dụng tọa độ cực (𝑟,𝜙) cho 𝑟. (b)
Viết phương trình Lagrange cho các tọa độ khối tâm𝑋̇,𝑌̇. (c)
Viết phương trình Lagrange cho 𝑟 và 𝜙. Giải phương trình này trong các trường hợp
đặc biệt: khi 𝑟 không đổi và khi 𝜙 không đổi. Mô tả các chuyển động tương ứng. Đặc biệt,
chứng minh rằng tần số dao động trong trường hợp thứ hai là 𝜔 . Bài giải
(a) Viết Lagrangian theo 𝒓𝟏, 𝒓𝟐, và sau đó đổi sang 𝑹⃗⃗⃗⃗, 𝒓 sử dụng tọa độ cực Ta có: 𝑚1 = 𝑚2 = 𝑚
Vị trí khối tâm 𝑂 là: 𝑚1𝑟1 +𝑚2𝑟2 1 𝑅⃗⃗⃗ = = (𝑟1 +𝑟2) 𝑚1 +𝑚2 2 Vị trí tương đối là:
𝑟 = 𝑟1 −𝑟2 ⇒ 𝑟2 = 𝑟1 −𝑟
Thay vào biểu thức 𝑅⃗⃗⃗ ta có:
𝑅⃗⃗⃗ = (𝑟1 +𝑟1 −𝑟) = 𝑟1 − 𝑟 Suy ra: 𝑟1 = 𝑅⃗⃗⃗+ 𝑟
Vì 𝑟2 = 𝑟1 −𝑟 nên: 𝑟2 = 𝑅⃗⃗⃗− 𝑟 Động năng của hệ là 𝑇 = 𝑚1𝑟12 +1 𝑚2𝑟22 2 1 2 1 1 2 𝑇
= 𝑚(𝑅⃗⃗⃗ + 𝑟 ) + 𝑚(𝑅⃗⃗⃗ − 𝑟 ) lOMoAR cPSD| 58675420 2 2 2 2 +1𝑚𝑟 2 𝑇 = 𝑚𝑅⃗⃗⃗ 4
Chuyển sang tọa độ cực:
𝑟 2 = 𝑟 2 +𝑟2𝜑̇ 2 Vậy:
𝑇 = 𝑚(𝑋̇ 2 +𝑌̇ 2)+ 𝑚(𝑟 2 +𝑟2𝜑̇ 2) Lò xo
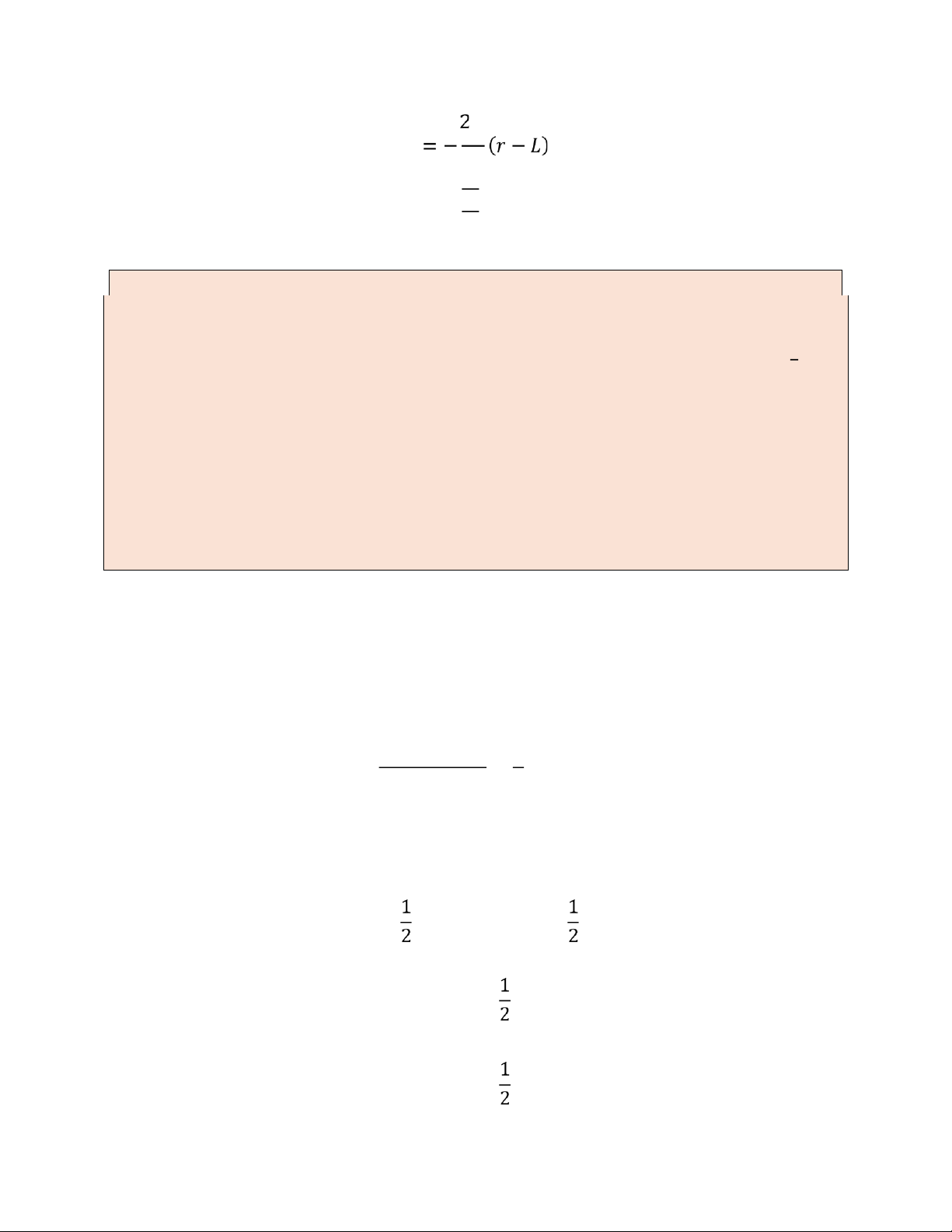
có độ cứng 𝑘, chiều dài tự nhiên 𝐿⃗, nên: 𝑈 = 𝑘(𝑟−𝐿⃗)2 Laragian là
𝐿⃗ = 𝑇−𝑈 = 𝑚(𝑋̇ 2 +𝑌̇ 2)+ 𝑚(𝑟 2 +𝑟2𝜑̇ 2)− 𝑘(𝑟−𝐿⃗)2
b) Phương trình Lagrange cho 𝑿,𝒀 • Với 𝑋̇ 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑋̇ 𝜕𝑋̇ 𝑑 (𝑚𝑋̇ ) = 0 𝑑𝑡 𝑋̇ = 0 • Với 𝑌̇ 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑌̇ 𝜕𝑌̇ 𝑑 (𝑚𝑌̇ ) = 0 𝑑𝑡 𝑌̇ = 0
c) Phương trình Lagrange cho 𝒓 và 𝝋 Với 𝒓: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0
𝑑𝑡 𝜕𝑟 𝜕𝑟 Ta có lOMoAR cPSD| 58675420
𝜕𝐿⃗2 −𝑘(𝑟−𝐿⃗) =𝑚𝑟𝜑̇ 𝜕𝑟 𝜕𝐿⃗ 𝑑 𝜕𝐿⃗ =𝑚𝑟 ⇒ ( ) = 𝑚𝑟 𝜕𝑟 𝑑𝑡 𝜕𝑟 Vậy:
2 −𝑘(𝑟−𝐿⃗) ⇒ 𝑟 = 𝑟𝜑̇ 2 −2𝑘(𝑟−𝐿⃗) 𝑚𝑟 =𝑚𝑟𝜑̇
𝑚 Với 𝝋: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝜑̇ 𝜕𝜑̇ 𝜕𝐿⃗
= 0  hệ có đối xứng quay  bảo toàn moment động lượng 𝜕𝜑̇ 𝑑 𝜕𝐿⃗ ( ) = 0 𝑑𝑡 𝜕𝜑̇ Vậy:
𝑚𝑟2𝜑̇ = 𝑐𝑜𝑛𝑠𝑡
Trường hợp đặc biệt
Trường hợp 1: 𝒓 = 𝒄𝒐𝒏𝒔𝒕 (lò xo không giãn)
 𝑟 = 𝑟 = 0 Từ phương trình 𝑟 = 𝑟𝜑̇ 2 − 2 𝑘 (𝑟−𝐿⃗), suy ra: 𝑚 2 = 2𝑘(𝑟−𝐿⃗) 𝜑̇ 𝑚 𝑟
Đây là chuyển động quay tròn đều nếu 𝑟 > 𝐿⃗
Trường hợp 2: 𝝋 = 𝒄𝒐𝒏𝒔𝒕 (quay ngừng → chuyển động thẳng) 𝜑̇ = 0 Khi đó phương trình lOMoAR cPSD| 58675420 𝑘 𝑟 𝑚 2 𝑘
Đây là dao động điều hòa với tần số 𝜔 = √ 𝑚 Excersise 6:
Hai hạt có khối lượng bằng nhau 𝑚1 = 𝑚2 chuyển động trên một mặt phẳng ngang không
ma sát, gần một tâm lực cố định, với các thế năng lần lượt là 𝑈1 = 12 𝑘𝑟12 và 𝑈2 = 12 𝑘𝑟22.
Ngoài ra, chúng còn tương tác với nhau thông qua thế năng 𝑈12 = 12 𝛼𝑘𝑟2, trong đó 𝑟là
khoảng cách tương đối giữa hai hạt, và 𝛼, 𝑘 là các hằng số dương. (a)
Tìm Lagrangian của hệ theo vị trí khối tâm 𝑅⃗⃗⃗ và vị trí tương đối 𝑟 = 𝑟1 −𝑟2. (b)
Viết và giải các phương trình Lagrange cho các tọa độ 𝑋̇,𝑌̇ của khối tâm và 𝑥,𝑦của
vị trí tương đối. Mô tả chuyển động. Bài giải
a) Tìm Lagrangian của hệ theo vị trí khối tâm 𝑹⃗⃗⃗⃗ và vị trí tương đối 𝒓 = 𝒓𝟏 −𝒓𝟐. Ta có: 𝑚1 = 𝑚2 = 𝑚
Vị trí khối tâm 𝑂 là: 𝑚1𝑟1 +𝑚2𝑟2 1 𝑅⃗⃗⃗ = = (𝑟1 +𝑟2) 𝑚1 +𝑚2 2 Vị trí tương đối là:
𝑟 = 𝑟1 −𝑟2 ⇒ 𝑟2 = 𝑟1 −𝑟
Thay vào biểu thức 𝑅⃗⃗⃗ ta có:
𝑅⃗⃗⃗ = (𝑟1 +𝑟1 −𝑟) = 𝑟1 − 𝑟 Suy ra: 𝑟1 = 𝑅⃗⃗⃗+ 𝑟
Vì 𝑟2 = 𝑟1 −𝑟 nên: 𝑟2 = 𝑅⃗⃗⃗− 𝑟 lOMoAR cPSD| 58675420 Động năng của hệ là 𝑇 = 𝑚1𝑟12 +1 𝑚2𝑟22 2 1 2 1 1 2 𝑇 =
𝑚(𝑅⃗⃗⃗ + 𝑟 ) + 𝑚(𝑅⃗⃗⃗ − 𝑟 ) 2 2 2 2 +1𝑚𝑟 2 𝑇 = 𝑚𝑅⃗⃗⃗ 4 Thế năng của hệ là 1 1 1
𝑈 = 𝑘𝑟12 + 𝑘𝑟22 + 𝛼𝑘𝑟2 2 2 2 𝑈
=𝑘(𝑅⃗⃗⃗ +1𝑟)2 +1 1 2 1 2
𝑘(𝑅⃗⃗⃗−𝑟) +𝛼𝑘𝑟 2 2 2 2 1 𝛼
𝑈 = 𝑘𝑅⃗⃗⃗2 +( + )𝑘𝑟2 4 2 Larangian là: 2 +𝑌̇
2)+1𝑚(𝑥 2 +𝑦 2)−𝑘(𝑋̇2 +𝑌̇2)−(1+𝛼)𝑘(𝑥2 +𝑦2) 𝐿⃗ = 𝑇−𝑈 = 𝑚(𝑋̇ 4 4 2
b) Viết và giải các phương trình Lagrange cho các tọa độ 𝑿,𝒀 của khối tâm và 𝒙,𝒚
của vị trí tương đối. Mô tả chuyển động. Với 𝑋̇: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑋̇ 𝜕𝑋̇ 𝑑
(2𝑚𝑋̇ )+2𝑘𝑋̇ = 0 𝑑𝑡 2𝑚𝑋̇ +2𝑘𝑋̇ = 0 𝑘 lOMoAR cPSD| 58675420 𝑋̇ = − 𝑋̇ 𝑚 Với 𝑌̇: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑌̇ 𝜕𝑌̇ 𝑑
(2𝑚𝑌̇ )+2𝑘𝑌̇ = 0 𝑑𝑡 2𝑚𝑌̇ +2𝑘𝑌̇ = 0 𝑘 𝑌̇ = − 𝑌̇ 𝑚 Với 𝑥: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑥 𝜕𝑥 𝑑 1 1
( 𝑚𝑥 )+( +𝛼)𝑘𝑥 = 0 𝑑𝑡 2 2 1
𝑚𝑥 +( +𝛼)𝑘𝑥 = 0 2 𝑘 𝑥 = −(1+2𝛼) 𝑥 𝑚 Với 𝑥: 𝑑 𝜕𝐿⃗ 𝜕𝐿⃗ ( )− = 0 𝑑𝑡 𝜕𝑦 𝜕𝑦 𝑑 1 1
( 𝑚𝑦 )+( +𝛼)𝑘𝑦 = 0 𝑑𝑡 2 2 1
𝑚𝑦 +( +𝛼)𝑘𝑦 = 0 2 𝑘 𝑦 = −(1+2𝛼) 𝑦 lOMoAR cPSD| 58675420 𝑚
Mô tả chuyển động
Theo phương trình của 𝑋̇,𝑌̇ ta thấy rằng đây là dao động điều hòa. Do đó, khối tâm dao 𝑘
động điều hòa quanh gốc tọa độ với tần số góc 𝜔 = √ 𝐶𝑀 𝑚
Theo phương trình của 𝑥,𝑦 ta thấy rằng đây là dao động điều hòa. Do đó, hệ dao động điều
hòa với tần số góc 𝜔 = √(1+2𝛼) 𝑘 𝑚 Exercise 7: 𝑘𝑟2
Consider two particles interacting by a Hooke’s law potential energy 𝑈 = , where 𝑟 = 2
𝑟1 −𝑟2 is their relative position. The system is subjected to no external forces. Show that
the orbit is an ellipse. Hence show that both particles move on similar ellipses around their common CM. Dịch đề: 𝑘𝑟2
Xét hai hạt tương tác với nhau thông qua một thế năng tuân theo định luật Hooke: 𝑈 = 2
với 𝑟 = 𝑟1 − 𝑟2 là vector vị trí tương đối giữa hai hạt. Hệ không chịu bất kỳ lực ngoài nào.
Chứng minh rằng quỹ đạo là một elip. Từ đó, chứng minh rằng cả hai hạt đều chuyển động
trên các elip đồng dạng quanh tâm khối chung (CM). Bài làm: Ta gọi:
- 𝑚1,𝑚2: là khối lượng của hạt
- 𝑟1,𝑟2: vị trí của hạt
- 𝑟 = 𝑟1 −𝑟2: vector vị trí tương đối
- 𝑅⃗⃗⃗ = 𝑚1𝑟1+𝑚2𝑟2: vị trí khối tâm 𝑚1+𝑚2 - 𝜇 =
𝑚1𝑚2 : khối lượng rút gọn (Reduce mass) 𝑚1+𝑚2 lOMoAR cPSD| 58675420
Do không có lực ngoài → khối tâm 𝑹⃗⃗⃗⃗ chuyển động thẳng đều.
Ta xét phương trình chuyển động của vector 𝑟: 𝑘 𝜇𝑟 𝑘𝑟 ⇒ 𝑟 = − 𝑟 𝜇 𝑘 Đặt 𝜔 = √ 𝑢
Đây là phương trình dao động điều hòa hai chiều, có nghiệm tổng quát:
𝑟(𝑡) = Acos(𝜔𝑡)+Bsin(𝜔𝑡)
Với A,B là 2 vector điều kiện ban đầu. Đây là phương trình tham số của elip. Ta có: 𝑚1𝑟1 +𝑚2𝑟2 𝑅⃗⃗⃗ = ;𝑟 = 𝑟1 −𝑟2 𝑚1 +𝑚2
Ta biến đổi 𝑟1,𝑟2 theo 𝑅⃗⃗⃗,𝑟: 𝑚2 𝑚1 𝑟1 = 𝑅⃗⃗⃗ +𝑟 ;𝑟2 = 𝑅⃗⃗⃗−𝑟 𝑚1 +𝑚2 𝑚1 +𝑚2
Vì 𝑟(𝑡) là elip, và hệ số tỉ lệ là hằng số nên 𝑟1,𝑟2 cũng nằm trên các elip đồng dạng, quay quanh 𝑅⃗⃗⃗ . lOMoAR cPSD| 58675420 Exercise 9
Consider a particle of reduced mass µ orbiting in a central force with 𝑈 = 𝑘𝑟𝑛 where 𝑘𝑛 > 0. (a)
Explain what the condition 𝑘𝑛 > 0 tells about the force. Sketch the effective potential
energy for the cases that 𝑛 = 2,−1,−3. (b)
Find the radius at which the particle (with given angular momentum l) can orbit at a
fixed radius. For what values of n is this circular orbit stable? (c)
For the stable case, show that the period of small oscillations about the circular orbit is: 𝜏𝑜𝑠𝑏 𝜏𝑜𝑠𝑐 . Argue that if
is a rational number, these orbits are closes. Sketch them for the
cases that n = 2,−1,7 Dịch đề:
Xét một hạt có khối lượng rút gọn µ chuyển động quay quanh tâm trong một lực thế trung
tâm với thế năng: 𝑈 = 𝑘𝑟𝑛 với 𝑘𝑛 > 0.
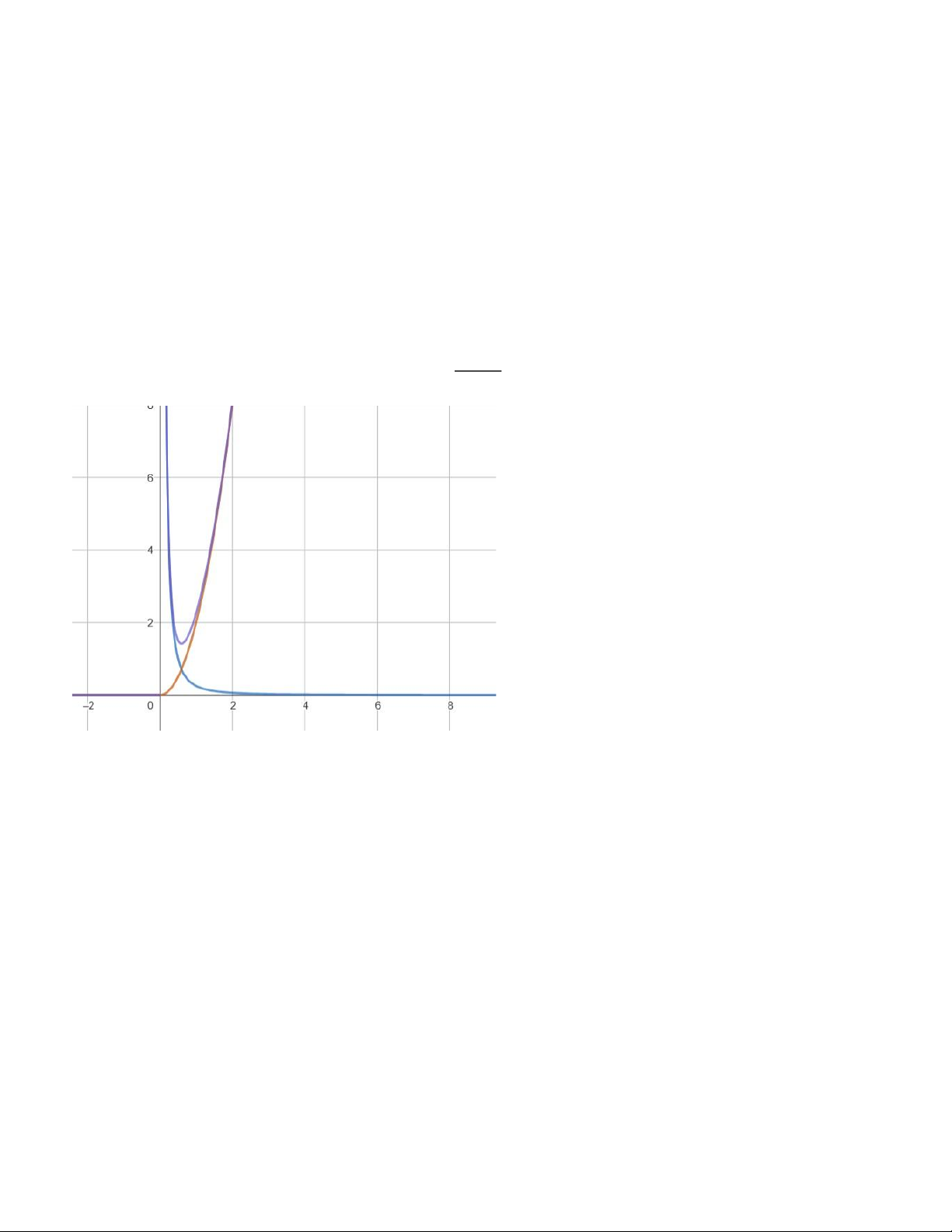
a.Giải thích điều kiện 𝑘𝑛 > 0 nói gì về lực. Vẽ đồ thị thế năng hiệu dụng cho các trường hợp: 𝑛 = 2,−1,−3.
b.Tìm bán kính tại đó hạt (với một moment động lượng 𝑙 đã cho) có thể chuyển động
tròn đều. Với giá trị nào của 𝑛, quỹ đạo tròn đó là ổn định?
c.Với trường hợp ổn định, hãy chứng minh rằng chu kỳ dao động nhỏ quanh quỹ đạo tròn là: 𝜏𝑜𝑠𝑏 𝜏𝑜𝑠𝑐 Lập luận rằng nếu
là một số hữu tỉ thì quỹ đạo là kín. Vẽ các trường hợp 𝑛 = 2,−1,7 Bài làm: Ta có thế năng: 𝑑𝑈
𝑈(𝑟) = 𝑘𝑟𝑛 ⇒ 𝐹(𝑟) = − = −𝑘𝑛𝑟𝑛−1 𝑑𝑟 lOMoAR cPSD| 58675420 Với 𝑘𝑛 > 0: •
𝐹(𝑟) < 0 với 𝑛 > 0: lực hướng về gốc (lực hút) •
𝐹(𝑟) > 0 𝑣ớ𝑖 𝑛 < 0: lực đẩy ra ngoài
Dù là lực hút hay đẩy, điều kiện 𝑘𝑛 > 0 đảm bảo rằng lực luôn có chiều nhất định. Ta có: 𝑈𝑒𝑓𝑓(𝑟) = 2 𝜇𝑙2𝑟2 +𝑘𝑟𝑛 Với 𝑛 = 2 Với 𝑛 = 1: