









Preview text:
Business Horizons (2014) 57, 595—605
Available online at www.sciencedirect.com ScienceDirect www.elsevier.com/locate/bushor Supply chain analytics Gilvan C. Souza
Kelley School of Business, Indiana University, Bloomington, IN 47405, U.S.A. KEYWORDS Abstract
In this article, I describe the application of advanced analytics techniques Supply chain
to supply chain management. The applications are categorized in terms of descrip- management;
tive, predictive, and prescriptive analytics and along the supply chain operations Analytics;
reference (SCOR) model domains plan, source, make, deliver, and return. Descriptive Optimization;
analytics applications center on the use of data from global positioning systems Forecasting
(GPSs), radio frequency identification (RFID) chips, and data-visualization tools to
provide managers with real-time information regarding location and quantities of
goods in the supply chain. Predictive analytics centers on demand forecasting at
strategic, tactical, and operational levels, all of which drive the planning process in
supply chains in terms of network design, capacity planning, production planning, and
inventory management. Finally, prescriptive analytics focuses on the use of mathe-
matical optimization and simulation techniques to provide decision-support tools
built upon descriptive and predictive analytics models.
# 2014 Kelley School of Business, Indiana University. Published by Elsevier Inc. All rights reserved.
1. Why analytics in supply chain
analytical approaches to make decisions that better management? match supply and demand.
Well-planned and implemented decisions con-
The supply chain for a product is the network of
tribute directly to the bottom line by lowering
firms and facilities involved in the transformation
sourcing, transportation, storage, stockout, and
process from raw materials to a product and in
disposal costs. As a result, analytics has historically
the distribution of that product to customers. In
played a significant role in supply chain manage-
a supply chain, there are physical, financial, and
ment, starting with military operations during and
informational flows among different firms. Supply
after World War II–—particularly with the develop-
chain analytics focuses on the use of information
ment of the simplex method for solving linear pro-
and analytical tools to make better decisions regard-
gramming by George Dantzig in the 1940s. Supply
ing material flows in the supply chain. Put
chain analytics became more ingrained in decision
differently, supply chain analytics focuses on
making with the advent of enterprise resource plan-
ning (ERP) systems in the 1990s and more recently
with ‘big data’ applications, particularly in descrip-
tive and predictive analytics, as I describe with
E-mail address: gsouza@indiana.edu some examples in this article.
0007-6813/$ — see front matter # 2014 Kelley School of Business, Indiana University. Published by Elsevier Inc. All rights reserved.
http://dx.doi.org/10.1016/j.bushor.2014.06.004 596 G.C. Souza
The Supply Chain Operations Reference (SCOR)
pallets (even at the product level), and transactions
model developed by the Supply Chain Council
involving barcodes. Information is derived from the
(www.supply-chain.org) provides a good framework
vast amounts of data collected from these sources
for classifying the analytics applications in supply
through data visualization, often with the help of
chain management. The SCOR model outlines four
geospatial mapping systems. RFID is a significant
domains of supply chain activities: source, make,
improvement over barcodes because it does not
deliver, and return. A fifth domain of the SCOR
require direct line of sight. Accurate inventory re-
model–—plan–—is behind all four activity domains.
cords are critical in supply chains as they trigger
Furthermore, a key input of the supply chain plan-
regular replenishment orders and emergency orders
ning process is demand forecasting at all time
when inventory levels are too low. Although RFID
frames: long, mid, and short term with planning
technology helps in significantly reducing the fre-
horizons of years, months, and days, respectively.
quency of manual inventory reviews, such reviews
Table 1 illustrates different decisions in each of the
are still needed because of data inaccuracy due to,
four SCOR domains that can be aided by analytics.
for example, inventory deterioration or damage or
These decisions are further classified into strategic, even tag-reading errors.
tactical, and operational according to their time
Predictive analytics in supply chains derives de- frame.
mand forecasts from past data and answers the
Analytics techniques can be categorized into
question of what will be happening.
three types: descriptive, predictive, and prescrip-
Prescriptive analytics derives decision recom-
tive. Descriptive analytics derives information from
mendations based on descriptive and predictive
significant amounts of data and answers the ques-
analytics models and mathematical optimization
tion of what is happening. Real-time information
models. It answers the question of what should be
about the location and quantities of goods in the
happening. Arguably, the bulk of academic re-
supply chain provides managers with tools to make
search, software, and practitioner activity in supply
adjustments to delivery schedules, place replenish-
chain analytics focuses on prescriptive analytics.
ment orders, place emergency orders, change trans-
In Table 2, I provide a summary of analytics
portation modes, and so forth. Traditional data
techniques–—descriptive, predictive, and prescrip-
sources include global positioning system (GPS) data
tive–—used in supply chains in terms of the four SCOR
on the location of trucks and ships that contain
domains of source, make, deliver, and return. I
inventories, radio frequency identification (RFID)
elaborate on Table 1 and Table 2 in the next
data originating from passive tags embedded in sections. Table 1.
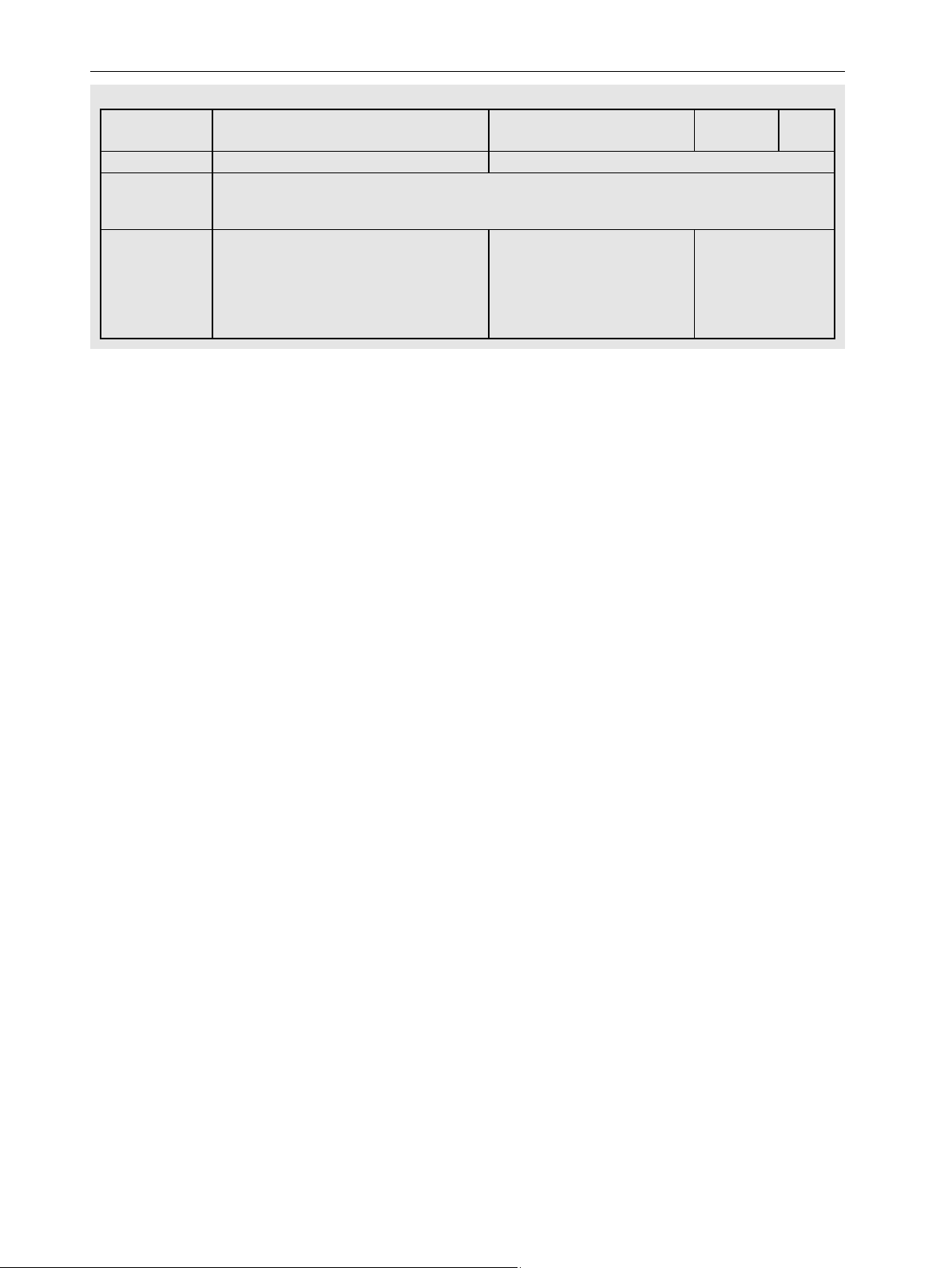
SCOR model and examples of decisions at the three levels SCOR Domain Source Make Deliver Return Activities Order and receive Schedule and Receive, schedule, Request, approve, and materials and manufacture, repair, pick, pack, and determine disposal of products remanufacture, or ship orders products and assets recycle materials and products Strategic Strategic Location of plants Location of Location of return (time frame: sourcing Product line mix distribution centers centers years) Supply chain at plants Fleet planning mapping Tactical
Tactical sourcing Product line Transportation and Reverse distribution (time frame: Supply chain rationalization distribution planning plan months) contracts Sales and Inventory policies operations planning at locations Operational Materials Workforce scheduling Vehicle routing Vehicle routing (for (time frame: requirement Manufacturing, order (for deliveries) returns collection) days) planning tracking, and scheduling and inventory replenishment orders Plan
Demand forecasting (long term, mid term, and short term) Supply chain analytics 597 Table 2.
Analytic techniques used in supply chain management Analytics Source Make Deliver Return Techniques Descriptive Supply chain mapping Supply chain visualization Predictive
Time series methods (e.g., moving average, exponential smoothing, autoregressive models)
Linear, non-linear, and logistic regression
Data-mining techniques (e.g., cluster analysis, market basket analysis) Prescriptive Analytic hierarchy process Mixed-integer linear Network flow
Game theory (e.g., auction design, programming (MILP) algorithms contract design) Non-linear programming MILP Stochastic dynamic programming
2. Plan: Demand forecasting using
are derived from time-based demands for the predictive analytics
SKUs that use those parts, so parts have dependent
demand. In contrast, SKUs have independent
Demand forecasting is a critical input to supply
demand. Demand forecasts for items subject to inde-
chain planning. Different time frames for demand
pendent demand require predictive analytics techni-
forecasting require different analytics techniques.
ques, whereas forecasts for dependent demand items
Long-term demand forecasting is used at the stra-
are obtained directly from the MRP system. Demand
tegic level and may use macro-economic data, de-
forecasts for independent demand items are also used
mographic trends, technological trends, and
to plan for inventory safety stocks at other locations,
competitive intelligence. For example, demand fac-
such as distribution centers and retailers.
tors for commercial aircraft at Boeing include ener-
Demand forecasting for independent demand
gy prices, discretionary spending, population
items is usually performed using time-series methods,
growth, and inflation, whereas demand factors for
for which the only predictor of demand is time. Time-
military aircraft include geo-political changes, con-
series methods include moving average, exponential
gressional spending, budgetary constraints, and
smoothing, and autoregressive models. For example,
government regulations (Safavi, 2005). Causal fore-
Winter’s exponential smoothing method incorporates
casting methods–—called such because they analyze
both trend and seasonality and can be used for both
the underlying factors that drive demand for a
short-term and mid-term forecasting. In an autore-
product–—are used at this level. Analytics causal
gressive model, demand forecast in one period is a
forecasting methods include linear, non-linear,
weighted sum of realized demands in the previous and logistic regression. periods.
To illustrate demand forecasting for tactical and
Mid-term forecasting can also benefit from
operational supply chain decisions, consider the
causal forecasting methods, especially in non-
production planning process for an original equip-
manufacturing industries or the manufacturing of
ment manufacturer (OEM) such as Whirlpool. At the
non-discrete items. For example, in order to fore-
product family level (e.g., refrigerators), the sales
cast monthly demand for truckload (TL) freight
and operations planning (S&OP) process uses aggre-
services, Fite, Taylor, Usher, English, and Roberts
gate demand forecasts in monthly time buckets to
(2002) considered 107 economic indexes as poten-
establish aggregate production rates, aggregate
tial predictors, including the purchasing manager’s
levels of inventories, and workforce levels. The
index, the Dow Jones stock index, the consumer
aggregate plan is revised on a rolling basis as new
goods production index, automotive dealer sales,
data is available. The S&OP plan, as well as more
U.S. exports, the producer commodities price index
refined demand forecasts at the stock-keeping unit
for construction materials and equipment, interest
(SKU) level, is used to derive the master production
rates, and gasoline production. They used stepwise
schedule (MPS), which details weekly production
regression to identify the most relevant indexes and
quantities at the SKU level for a typical planning
found parsimonious models for predicting TL de-
horizon of 8—12 weeks. The MPS and the bill of
mand for specific industries and regions. Their mod-
materials are then used to plan production and
el only predicts industry-wide demand for TL
sourcing at the part level through a materials re-
services (nationally or by region); the connection
quirement planning (MRP) system that is embedded
to demand forecasts at the firm level was made
in most ERP software. Time-based demands for parts
using historical market shares. 598 G.C. Souza
Data mining has also been used for demand fore-
Firms are very familiar with their first-tier sup-
casting in conjunction with traditional forecasting
pliers (i.e., those that directly supply them) and
techniques (Rey, Kordon, & Wells, 2012). Usually,
perhaps their second-tier suppliers (i.e., those that
the data-mining step precedes the use of causal
supply first-tier suppliers), but some of their lower-
forecasting techniques by finding appropriate de-
tier suppliers may be unknown. A recent example is
mand drivers (i.e., independent variables) for a
the November 2012 fire at the Bangladesh factory
product that can be used in regression analysis.
that killed more than 100 workers. An audit of the
For example, Dow Chemical uses a combination of
factory by Walmart in 2011 ruled it out as a supplier.
data mining and regression techniques to forecast
However, one of Walmart’s suppliers continued to
demand at the strategic and tactical levels (e.g.,
subcontract work to that factory (Tsikoudakis,
identifying demand trends), which is useful for its
2013). The threat of disruptions like natural disas-
pricing strategy and for configuring and designing its
ters, social and political unrest, and major strikes
supply chain to respond to these trends (Rey & Wells,
makes it imperative for firms to map their supply
2013). Data-mining methods usually involve cluster-
chains. For example, Cisco (2013) uses supply chain
ing techniques. So, if a retailer finds out, for exam-
mapping and enterprise social networking to iden-
ple, that demand for cereal is strongly related to
tify its vulnerabilities to supply chain disruptions as
milk sales, then the retailer may build a causal
well as to collaborate with its suppliers and part-
forecasting model that predicts cereal sales with
ners. The open source tool sourcemap.com, devel-
milk sales as one of the predicting variables. Market
oped at the Massachusetts Institute of Technology,
basket analysis is a specific data-mining technique
allows one to visualize and map a supply chain; the
that provides an analysis of purchasing patterns at
tool can also be used for purposes such as carbon
the individual transaction level, so a retailer can
footprint estimation. An example is shown in
analyze the frequency with which two product cat- Figure 1.
egories (e.g., DVDs and baby products) are pur-
chased together. Lift for a combination of items is
3.2. Source: Tactical decisions
equal to the actual number of times the combina-
tion occurs in a given number of transactions divided
In contrast to strategic sourcing, tactical sourcing
by the predicted number of times the combination refers to the process of achieving specific
occurs if items in the combination were indepen-
objectives–—such as determining costs for parts,
dent. Lift values above 1 indicate that items tend to
materials, or services–—through structured procure-
be purchased together. This kind of analysis can be
ment mechanisms like auctions. The central prob-
useful when building causal regression models for
lem in procurement auctions centers on mechanism
demand forecasting. It can also aid in promotion
design: How should one structure the rules of an
activities because the retailer can predict how much
auction so that bidders (i.e., suppliers) behave in a
sales of Product 1 would increase if there is a
manner that results in minimal procurement cost
promotion for Product 2 if the two products are
(and desired performance) for the buyer? Auctions often purchased together.
can be open (i.e., bidders can view and respond to
bids) or sealed and one shot or dynamic (which occur 3. Source
over several rounds of bidding). Government auc-
tions tend to be one-shot, sealed auctions, whereas
3.1. Source: Strategic decisions
open, dynamic auctions are common in industrial
procurement (Beil, 2010). Buyers must consider the
Strategic sourcing is the process of evaluating and
total procurement cost as bidders usually bid on
selecting key suppliers. There is limited use of
contract payment terms only (e.g., unit cost). Ad-
analytics for strategic sourcing in practice even
ditional logistics costs, if paid by the buyer, must be
though academics prescribe the use of sophisticated
taken into account in the bid price. The prescriptive
multi-criteria decision-making techniques such as
analytics used here is centered on game theory,
analytic hierarchic process (AHP). AHP decomposes
which is used to determine auction rules. Procure-
a complex problem (e.g., selecting a supplier among
ment auctions are widely used in practice.
a diverse set) into more easily comprehended sub-
A commonly used payment contract in sourcing is
problems that can be analyzed separately. In the
wholesale price, via which the buyer (i.e., retailer)
supplier-selection problem, these sub-problems
pays the seller (i.e., manufacturer) a fixed price per
might include distinct evaluations of factors like
unit. Under this contract, retailers are exposed to
cost, quality, delivery speed, delivery reliability,
demand risk: they bear the entire costs of over-
volume flexibility, product mix flexibility, and sus-
stocking and therefore have an incentive to stock
tainability. These evaluations are then weighed.
less than what is optimal for the supply chain as a Supply chain analytics 599 Figure 1.
Example of supply chain mapping using sourcemap.com
Source: free.sourcemap.com/view/6585/
whole. Recognizing this, academics have used a
problem can be illustrated when deciding where to
combination of game theory and statistics to pre-
build DCs that serve as intermediary stocking
scribe more sophisticated contracts that will im-
and shipping points between existing plants and
prove product availability in retailers. For example,
retailers. This problem is formulated as a mixed-
in a buy-back contract, retailers can return unsold
integer linear program (MILP). Data requirements
units to the manufacturer and receive a partial
include yearly aggregate demands for the product
refund. Although such contracts can improve supply
family at each retailer, plant capacities, unit ship-
chain performance, the wholesale price contract is
ping costs between each pair of locations, and the
still widely used, perhaps due to its simplicity.
annual fixed cost of operating a DC at each potential
location. Decision variables include the quantity to
ship between locations and binary variables that 4. Make
indicate if each DC should be open or closed. The
objective function minimizes total shipping and 4.1. Make: Strategic decisions
fixed DC costs. Constraints ensure that demand is
met at all locations, that companies only ship prod-
Network design determines the optimal location and
ucts from a DC if it is open, and that all plant
capacity of plants, distribution centers (DCs), and
capacities are respected. The solution provides
retailers. The simplest form of the network design
the location (i.e., where to open the DCs) as well 600 G.C. Souza
as the allocation of plants to the DCs, the allocation
meets fluctuating demand by producing at a constant
of DCs to retailers, and the capacity of each DC.
rate and holding inventory to meet the peak demand.
Variations of this simple MILP formulation include
Alternatively, the firm can use a chase strategy,
multiple products, transportation capacities between
adjusting workforce levels monthly to meet fluctuat-
locations, multiple transportation modes between
ing demand. Firms frequently use a hybrid strategy
locations, a multi-year planning horizon, multiple between chase and level.
echelons (i.e., tiers in the supply chain), demand
Product proliferation and mass customization have
uncertainty, supply uncertainty, and reverse flows
been widely documented (e.g., Rungtusanatham &
(e.g., the collection of used products for recycling
Salvador, 2008). For product proliferation and mass
and remanufacturing). When the problem incorpo-
customization, the plant must adapt from a mass
rates multiple products, the analysis also provides the
production environment–—designed for economies
product mix at each plant. When many of the varia-
of scale, with fewer products produced in dedicated
tions above are incorporated and the problem is large
lines and setup costs spread over long production
(e.g., thousands of retailers and potential DC and
runs–—to a flexible production environment. This
plant locations), the problem may become too diffi-
adaptation is made possible with the aid of flexible
cult to solve to optimality using off-the-shelf optimi-
manufacturing technology or changes in the product
zation software. Therefore, many researchers have
and process design that support a postponement
proposed well-performing heuristics, such as genetic
strategy (Lee, 1996). In a postponement strategy, algorithms, that ensure good–—and sometimes
the step in the manufacturing process in which prod-
optimal–—solutions. Genetic algorithms use a divide
uct differentiation occurs–—from gray boxes to
and conquer (the feasible region) approach to finding
SKUs–—is located closer to the customer, which allows
a good solution to the MILP as opposed to optimal
the firm to carry inventory of gray boxes instead of
branch and bound algorithms, which are combinato-
SKUs, and thus lessens differentiation time. Post- rial in nature.
ponement mitigates the negative impacts of in-
Some of the data necessary to perform such
creased product proliferation, such as increased
analysis requires a preliminary level of analysis so
forecasting uncertainty at the SKU level; increased
it can be extracted, cleaned, and aggregated from
inventory costs; and complexity costs, such as re-
ERP systems. Network design, however, is only per-
search and development, testing, tooling, returns,
formed infrequently for each firm, including during
and obsolescence. Postponement requires changes in
mergers and acquisitions. As a result, it is not part of
product and process design, and it may not be feasi-
standard ERP software. Specialized software makes
ble for products like automobiles, for which strict
it easy to input this data, specify the constraints,
quality guidelines in final assembly preclude signifi-
perform the optimization, and visualize the results,
cant customization at dealers. As an alternative, especially for large problems.
firms may increase supply chain performance through
product rationalization using analytics, as shown in 4.2. Make: Tactical decisions Table 3.
We have previously described the S&OP process,
4.3. Make: Operational decisions
which is used for planning aggregate workforce
and inventory levels on a medium planning horizon
Manufacturing scheduling is the last step in the
based on demand forecasts, underlying costs, and
planning process after MRP plans are released. An
actual sales. Academics have proposed MILP models
MRP plan specifies quantities and due dates for all
for this process. For each month in the planning
parts. Scheduling then sequences the jobs (i.e.,
horizon, decision variables include the amount to
parts) by the different resources necessary for
produce for each product family using regular time,
manufacturing the part in order to meet the due
overtime, and subcontracting and the number of
dates. In general, there are n jobs to be scheduled in
workers to be hired and laid off. The objective
m different resources, and the processing time, due
function minimizes total cost, which comprises total
date, and weight (i.e., priority) of each job in each
production cost (i.e., regular time, overtime, and
resource are known. This problem takes different
subcontracting), total inventory cost, total wages,
forms depending on the decision maker’s objective,
total hiring cost, and total layoff cost. Constraints
the number of resources, and how the jobs are
may come from, among others, inventory and work-
processed with the resources. An objective function force balancing, regular production capacity,
minimizes the maximum completion time, or the
and overtime production. Many practitioners use
maximum lateness, across all jobs. There can be
rules-based heuristics. For example, one heuristic
precedence relationships, setup times, or even
is a level production strategy, via which the firm
sequence-dependent setup times (i.e., when the Supply chain analytics 601 Table 3.
Product rationalization at Hewlett-Packard
Hewlett-Packard (HP) has developed optimization tools for product rationalization (Ward et al., 2010). One tool
requires proposed new product line extensions to meet minimum complexity return-on-investment (ROI)
thresholds. Complexity ROI is defined as the incremental margin minus variable complexity costs, divided by fixed
complexity costs. Variable complexity costs are largely driven by forecasting uncertainty and resulting increased
inventory costs, whereas fixed complexity costs are driven by criteria such as research and development, tooling,
and manufacturing setup costs. With another tool, HP uses a maximum flow algorithm on an existing product line to
perform product rationalization. The tool acknowledges that in firms with configurable product lines, some
products, such as power supplies, may generate little revenue on their own but are critical components for high-
revenue orders and for overall order fulfillment. Order coverage is defined as the percentage of a given set of past
orders that can be met from the rationalized product portfolio. Similarly, revenue coverage is the smallest portfolio
of products that covers a given percentage of historical order revenue. This optimization tool revealed how HP can
offer only 20% of previously offered features in laptops and reach 80% revenue coverage. After implementing the
recommendations, HP realized significantly reduced inventory costs and increased gross margins.
setup time for a job at a resource depends on the
The decision maker needs demand forecasts for
previous job there, such as in processing industries
each time block (e.g., 12 p.m.—1 p.m. on Monday),
like the chemical industry). Scheduling problems
which can be obtained through predictive forecast-
can be formulated as MILPs, and the combinatorial
ing models. This problem can be formulated as an
nature of these problems makes them very hard to
MILP in which decision variables include the number
solve to optimality for large problems. As a result,
of employees assigned to each tour and the number
significant effort has been devoted to finding good
of employees necessary to meet demands within
solutions through heuristics because other compli-
each time block. The objective function minimizes
cations arise in practice, such as adding new jobs to
total labor costs. Complications, such as workers’
the existing pool of processing jobs as well as chang-
preferences, multiple locations, task assignments,
ing priorities and preferences. In terms of software,
and so forth, increase the size of the MILP model to
some ERP systems have scheduling modules (e.g.,
such an extent that heuristics are almost certainly
the Applied Planning and Optimization module in
needed. Some ERP vendors have workforce sched-
SAP) that use genetic algorithms to provide good
uling modules for specific applications like retail and
solutions to MILPs found in determinist scheduling.
hospitality. There are also vendors for industry-spe-
These algorithms can provide good solutions to fairly
cific software, such as call centers and health care
large problems, such as 1 million jobs over 1,000
providers. Many airlines, which are heavy analytics
resources (Pinedo, 2008). There are a few compa-
users, have developed their own scheduling algo-
nies such as Taylor (www.taylor.com) that specialize rithms.
in providing scheduling software with many function-
alities not present in ERP systems. Although the
discussion above has centered on manufacturing 5. Deliver and return
scheduling, some of the same algorithms can be used
in other scheduling problems like assigning gates at
5.1. Deliver and return: Strategic
an airport or trucks at a cross-docking location. decisions
Workforce scheduling can be challenging for ser-
vice industries, such as call centers, hospitals, and
In Section 4, I presented the network design problem
airlines, in which there is seasonal demand, not only
of planning the location of DCs and return centers.
for time of the year (common in manufacturing), but
Another strategic decision here is fleet planning,
also for day of the week and hour of the day. A
which can be described as the dynamic acquisition
common way of modeling these problems is
and divestiture of delivery vehicles to meet the
by defining tours. A tour is a combination of time
demand for deliveries or returns collection. This
blocks within a day and within days of the week that
problem is formulated as an MILP, or dynamic pro-
add up to the necessary work hours per employee. gramming, as in Table 4.
An example of a tour would be Monday, 8 a.m.—1
p.m.; Tuesday, 1 p.m.—6 p.m.; Thursday, 8 a.m.—6
5.2. Deliver and return: Tactical decisions
p.m.; and Friday, 8 a.m.—6 p.m. Tours should be
feasible; for example, it is not very convenient for
In transportation and distribution planning, the firm
most people to work from 8 a.m.—10 a.m. and
distributes a set of products from source nodes (i.e.,
then from 3 p.m.—5:00 p.m. on the same day.
supply points such as factories) to sink nodes 602 G.C. Souza Table 4.
Fleet planning for Coca-Cola Enterprises
Coca-Cola Enterprises (CCE) has started replacing some of its fleet of diesel delivery trucks with diesel-electric
hybrid vehicle (HEV) trucks. How the company chooses to invest those dollars depends on volatile fuel costs, usage-
based deterioration, and seasonal demand. Wang, Ferguson, Hu, and Souza (2013) have provided a prescriptive
analytics model that takes into consideration CCE’s historical maintenance costs, purchasing costs for both diesel
and HEV trucks, CCE demand data, and historical diesel price data to calibrate a stochastic model that simulates
diesel prices dynamically. Using dynamic programming, the optimal policy is obtained, at each period of a planning
horizon and for each realization of diesel prices, that determines how many trucks of each type (diesel and HEV)
CCE should acquire and/or divest. Wang et al. found that at the current outlook of diesel prices, CCE should include
both HEV (54%) and diesel trucks (46%) in its capacity portfolio. In this regard, CCE could use HEV trucks to meet its
average baseline demand and then deploy diesel trucks to supplement the delivery fleet during peak demand seasons.
(i.e., demand points such as retail locations)
replenishment lead times are variable. Data re-
through intermediary storage nodes (e.g., DCs). This
quirements include historic demand and forecasting
problem is solved using a multi-commodity network
data, replenishment lead times, the desired service
flow model, which is a linear programming formula-
level (i.e., a desired fill rate or stock-out probabili-
tion with a special structure. In the network formu-
ty), holding cost, and the fixed cost of placing a
lation, there can be multiple arcs between each pair
replenishment order. The inventory policy parame-
of nodes. Each arc represents a shipping mode with a
ters–—reorder point and order quantity–—can be
given capacity, such as rail, truckload (TL), less than
computed using exact algorithms or approximate
truckload (LTL), and air. The amount to ship in each
formulas, which are embedded in most supply chain
arc in the network for each commodity and time
software, including in some ERP systems modules.
period is considered. Constraints include capacity at
More often, the supply chain has multiple stocking
each arc, time period, and node, as well as flow-
points for the same product. For example, a product
balancing at each node. Data requirements include
can be stocked at a DC and multiple different retailers
shipping costs in each arc, forecasts of supply avail-
in different regions. Although one can set inventory
able at each source node (provided by the S&OP
policies at each location that use only local demand
plan), point forecasts for demand at each sink node
and replenishment lead-time information, this ‘local
(from predictive analytics models), and arc capaci-
optimization’ approach is not optimal for the supply
ties. Economies of scale in shipping can also be
chain. Due to risk pooling, it may be optimal to have
incorporated. Problems of realistic size have thou-
some level of inventory at the DC so that higher-than-
sands of nodes, resulting in millions of decision
normal demand in one retailer can be balanced against
variables. However, such problems can be solved
lower-than-normal demand at another retailer. This
efficiently with numerical algorithms based on the
situation calls for an integrated inventory policy for
network simplex method, which is embedded in
the entire supply chain; the theory that prescribes
supply chain optimization software. Despite exten-
these inventory policies is called multi-echelon inven-
sive planning, disruptions (e.g., traffic, weather)
tory theory. The complication in multi-echelon inven-
and demand uncertainty often require plan modifi-
tory theory arises when the DC does not have sufficient
cation, and descriptive analytics tools can be quite
inventory to meet all incoming orders from retailers at
valuable. For example, the Control Tower descrip-
a given period. In that case, the optimal inventory-
tive analytics system allows Procter & Gamble (P&G)
rationing policy is complex, and even more so if there
to see all the transportation occurring in its near
are more than two echelons. There are, however,
supply chain (i.e., inbound, outbound, raw materi-
several well-performing heuristics that are computa-
als, and finished product). With this technology,
tionally simple, such as the guaranteed service level
P&G has reduced deadhead movement (i.e., when
heuristic (Graves & Willems, 2000), which has been
trucks travel empty or not optimally loaded) by 15%
implemented in software like Optiant. An example of
and thus has reduced costs (McDonald, 2011).
successful application is provided in Table 5. Another important decision is determining
supply levels at nodes in a distribution network–—
5.3. Deliver and return: Operational
that is, setting inventory policies. The science for decisions
setting inventory policies (i.e., reorder point and
order-up-to level or order quantity) for a product
The vehicle routing problem (VRP) optimizes the
at a single location, such as a DC, is mature, even
sequence of nodes to be visited in a route, for
when demand is uncertain and non-stationary and
example, for a parcel delivery truck, for a returns Supply chain analytics 603 Table 5.
Multi-echelon inventory management at P&G
Before 2000, P&G used only single-location inventory models, which optimize inventory levels locally given that
location’s own replenishment lead time. However, starting in 2005—2006, P&G started implementing multi-echelon
inventory models based on the guaranteed service level heuristic in its more complex supply networks. At a
particular stage in the supply chain, inventory is set to meet a desired service level based on a guaranteed delivery
time to the customer (S), its own replenishment lead time when ordering from a preceding stage (SI), and its
processing time (T). Essentially, the method sets safety stock levels as if it was a single location with a
replenishment lead time of SI + T - S. Note that SI for a stage is equal to S for a preceding stage. Through dynamic
programming, the method finds the optimal S for each stage to minimize holding costs across the supply chain. The
multi-echelon supply chain approach to inventory management was implemented at 30% of P&G’s locations using
Optiant software and consequently saved the company $1.5 billion in inventory costs in 2009 compared to the
single-location models previously in place (Farasyn et al., 2011). Table 6.
Vehicle routing at Waste Management, Inc.
Waste Management, Inc. (WM) is a leading provider of solid waste collection and disposal services. It has a fleet of
more than 26,000 vehicles running nearly 20,000 routes. In 2003, the company implemented the WasteRoute
vehicle-routing software, which included GIS capabilities and navigational capabilities, and integrated it with a
relational database containing customer information. An origin-destination matrix was then developed that
considered constraints such as time and distance traveled between any two points, speed limits, and one-way
streets. By implementing the combined prescriptive and descriptive analytics software, the firm saved $44 million in 2004. Source: www.informs.org
collection truck, or for both. The optimal sequence
to match their fixed capacity through prices and
takes into account the distances between each pair
other mechanisms that will be described next. This
of nodes; expected traffic volume; left turns; and
is known as revenue management.
other constraints placed on the routes, such as
Revenue management started in the airline in-
delivery and pickup time windows. Known as the
dustry after deregulation, with the problem of allo-
travelling salesman problem (TSP), the classical VRP
cating seats in a flight to fare classes. Allocation
problem only takes into account the distances be-
policies are nested. For instance, suppose there are
tween each pair of nodes: In what sequence should
two fare classes: $150 (Fare Class 1) and $90 (Fare
nodes be visited, ending at the same starting point?
Class 2). The decision maker sets a booking limit for
This problem can be formulated as an MILP. The TSP
Fare Class 2 and then determines the booking limit
problem is combinatorial in nature, and is hard
of Fare Class 1 based on the capacity of the flight.
to solve beyond a few thousand nodes (Funke &
Data requirements for the computation of booking
Gruenert, 2005). Among others, complications such
limits include demand forecasts for the different
as multiple vehicles, vehicle capacities, tour-length
classes (as a probability distribution) at different
restrictions, and delivery and pickup time windows
times before departure, cancellation probabilities,
result in an MILP that is very difficult to solve, thus
up-selling probabilities (i.e., the probability that a
requiring heuristic approaches. In addition to heu-
customer will buy a higher fare if the lower fare is
ristic approaches, vehicle-routing software incorpo-
unavailable), and fare values. The problem is sig-
rates descriptive analytics, as shown in Table 6.
nificantly more complex in a network. For example,
one passenger goes from Indianapolis (IND) to
New York (JFK), whereas another passenger goes 6. Modulating demand to match
from IND to Rochester (ROC) via JFK. In this case, capacity: Revenue management
heuristic approaches, such as bid-price controls, are
used. The bid price for a resource (e.g., a seat in a
The SCOR model implicitly assumes that managers
specific flight IND-JFK) is the marginal cost to the
plan their operations–—source, make, deliver, and
network of consuming one unit of that resource.
return–—based on demand forecasts. Therefore, the
When a customer demand arises (e.g., IND-ROC via
SCOR model plans capacity to match a given de-
JFK), then the demand’s revenue is compared
mand. Industries with perishable capacities, like
against the sum of bid prices for all resources asso-
airlines, hospitality, and transportation, must take
ciated with the demand request (i.e., bid prices for
a reverse approach, so firms modulate their demand
a seat IND-JFK and for a seat JFK-ROC). The demand 604 G.C. Souza Table 7. Additional information on analytics
research, particularly linear programming and
techniques for supply chain management
optimization. For example, inventory theory is more
than 50 years old, and there were significant
General overview: Snyder and Shen (2011)
contributions to production planning in the 1980s. Network design: Funaki (2009)
Therefore, analytics in supply chain management is Auctions: Krishna (2002)
not new. More recent applications include the inte-
Sales and operations planning: Jacobs, Berry, Whybark, and Vollmann (2011)
gration of price analytics and supply chain manage-
Transportation and distribution planning: Ahuja,
ment in the field of revenue management, for which Magnanti, and Orlin (1993)
the problem revolves around managing demand in
Inventory management: Zipkin (2000)
an environment with fixed and perishable capacity.
Dynamic pricing and revenue management: Talluri
Revenue management research and practice (par- and Van Ryzin (2004)
ticularly in manufacturing) is relatively new because
Manufacturing scheduling: Pinedo (2008)
many demand models can only be calibrated with
Workforce scheduling: Campbell (2009)
significant amounts of data, which just recently
became available from modern ERP systems and web technologies.
With big data, new opportunities arise. I have
is accepted if the revenue is higher than the sum of
heard consultants praising the potential of harness-
bid prices. Bid prices can be approximated through
ing social networks for supply chain management, linear programming.
for example, by detecting local trends in demand to
In capacity allocation, fare prices are given as
adjust inventories and prices. There is indeed po-
they are determined by market forces. Another way
tential there, although many firms still struggle to
to manage uncertain demand for fixed capacity–—be
match basic supply and demand in a world with
it flight seats, hotel rooms, rental cars, or inventory
increased product proliferation, competition, and
in a retail environment–—is through pricing. As ar-
globalization (i.e., longer lead times). Among other
gued by Talluri and Van Ryzin (2004, p. 175), ‘‘the
benefits, big data has the potential to improve
distinction between quantity and price controls is
demand forecasting methods, detect supply chain
not always sharp (for instance, closing the availabil-
disruptions, and improve communications in supply
ity of a discount class can be considered equivalent
chains that are often global (see Table 7).
to raising the product’s price to that of the next
highest class).’’ However, using price as a direct
mechanism to match demand with capacity is an References
important enough practical problem to merit special
treatment. Dynamic pricing has gained significant
Ahuja, R., Magnanti, T., & Orlin, J. (1993). Network flows:
traction lately, particularly in retailing (i.e., mark-
Theory, algorithms, and applications. Upper Saddle River,
down pricing), e-commerce, and even manufactur- NJ: Prentice Hall.
ing (e.g., Ford’s offering of incentives at its auto
Beil, D. (2010). Procurement auctions. In J. J. Hasenbein (Ed.),
dealers). The key is to find a good predictive demand
2010 tutorials in operations research: Risk and optimization
in an uncertain world. Linthicum, MD: INFORMS.
model: At price p, what is the expected demand
Campbell, G. (2009). Overview of workforce scheduling software.
d( p) for the product? Demand models may be linear
Production and Inventory Management Journal, 45(2), 7—22.
(d( p) = a-bp), exponential (i.e., constant elastici-
Cisco. (2013). Building a collaboration architecture for a global
ty), logit (i.e., S-curve), or discrete-choice. There
supply chain. Retrieved June 14, 2013, from http://www.
are many vendors of dynamic pricing software, and
cisco.com/en/US/solutions/collateral/ns340/ns858/c22- 613680_sOview.html
software calibrates the demand models using histor-
Farasyn, I., Humair, S., Kahn, J., Neale, J., Rosen, O., Ruark, J.,
ical point-of-sale data. In addition, data on available
et al. (2011). Inventory optimization at Procter & Gamble:
inventories is necessary for the price-optimization
Achieving real benefits through user adoption of inventory
algorithm. Different price-optimization algorithms
tools. Interfaces, 41(1), 66—78.
are embedded in these packages based on non-linear
Fite, J., Taylor, G., Usher, J., English, J., & Roberts, J. (2002).
Forecasting freight demand using economic indices. Interna- and dynamic programming.
tional Journal of Physical Distribution and Logistics Manage- ment, 32(4), 299—308.
Funaki, K. (2009). State of the art survey of commercial software 7. Conclusion
for supply chain design. Retrieved June 18, 2013, from http://
www.scl.gatech.edu/research/supply-chain/GTSCL_ scdesign_software_survey.pdf
Supply chain management is a fertile area for the
Funke, B., & Gruenert, T. (2005). Local search for vehicle routing
application of analytics techniques, which has his-
and scheduling problems: Review and conceptual integration.
torically been the case through the use of operations
Journal of Heuristics, 11(4), 267—306. Supply chain analytics 605
Graves, S., & Willems, S. P. (2000). Optimizing strategic safety
inertia, and transition hazard. Production and Operations
stock placement in supply chains. Manufacturing and Service Management, 17(3), 385—396.
Operations Management, 2(1), 68—83.
Safavi, A. (2005). Forecasting demand in the aerospace and
Jacobs, R., Berry, W., Whybark, D. C., & Vollmann, T. (2011).
defense industry. Journal of Business Forecasting, 24(1),
Manufacturing planning and control for supply chain manage- 2—7. ment. New York: McGraw-Hill.
Snyder, L. V., & Shen, Z-J. M. (2011). Fundamentals of supply
Krishna, V. (2002). Auction theory. New York: Academic Press.
chain theory. Hoboken, NJ: John Wiley & Sons Inc.
Lee, H. (1996). Effective inventory and service management
Talluri, K., & Van Ryzin, G. (2004). The theory and practice of
through product and process redesign. Operations Research,
revenue management. New York: Springer. 44(1), 151—196.
Tsikoudakis, M. (2013, January 13). Supply chain disasters and
McDonald, R. (2011, November). Inside P&G’s digital revolution.
disruptions can cause lasting reputation damage. Business
McKinsey Quarterly. Available at http://www.mckinsey.com/
Insurance. Retrieved June 14, 2013, from http://www.
insights/consumer_and_retail/inside_p_and_ampgs_digital_
businessinsurance.com/article/20130113/NEWS06/ revolution 301139968
Pinedo, M. (2008). Scheduling theory, algorithms and systems
Wang, W., Ferguson, M., Hu, S., & Souza, G. C. (2013). Dynamic (3rd ed.). New York: Springer.
capacity investment with two competing technologies.
Rey, T., Kordon, A., & Wells, C. (2012). Applied data mining for
Manufacturing and service operations management, 15(4),
forecasting using SAS. Cary, NC: SAS Institute. 616—629.
Rey, T., & Wells, C. (2013, March 7). Integrating data mining and
Ward, J., Zhang, B., Jain, S., Fry, C., Olavson, H., Amaral, J.,
forecasting. Analytics. Retrieved June 17, 2013, from http://
et al. (2010). HP transforms product portfolio management
www.analytics-magazine.org/march-april-2013/765-
with operations research. Interfaces, 40(1), 17—32.
integrating-data-mining-and-forecasting
Zipkin, P. (2000). Foundations of inventory management.
Rungtusanatham, M. J., & Salvador, F. (2008). From mass produc- New York: McGraw-Hill.
tion to mass customization: Hindrance factors, structural
Document Outline
- Supply chain analytics
- Why analytics in supply chain management?
- Plan: Demand forecasting using predictive analytics
- Source
- Source: Strategic decisions
- Source: Tactical decisions
- Make
- Make: Strategic decisions
- Make: Tactical decisions
- Make: Operational decisions
- Deliver and return
- Deliver and return: Strategic decisions
- Deliver and return: Tactical decisions
- Deliver and return: Operational decisions
- Modulating demand to match capacity: Revenue management
- Conclusion
- References




