Tài liệu Bài tập phương trình vi phân | Đại học Bách khoa Thành phố Hồ Chí Minh
Tài liệu Bài tập phương trình vi phân | Đại học Bách khoa Thành phố Hồ Chí Minh. Tài liệu gồm 65 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi. Mời bạn đọc đón xem!
Môn: Giải tích
Trường: Đại học Bách khoa Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Tài liệu liên quan:
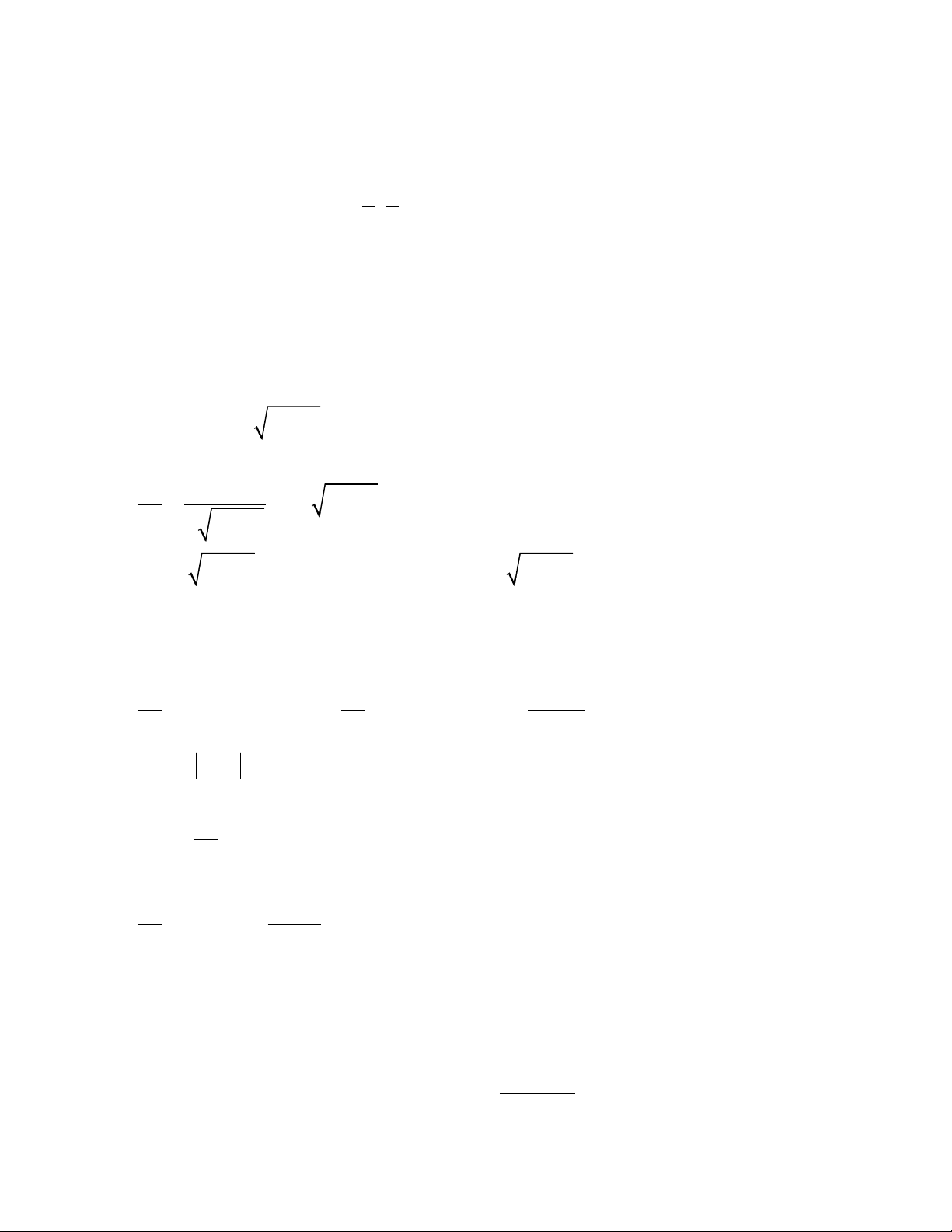
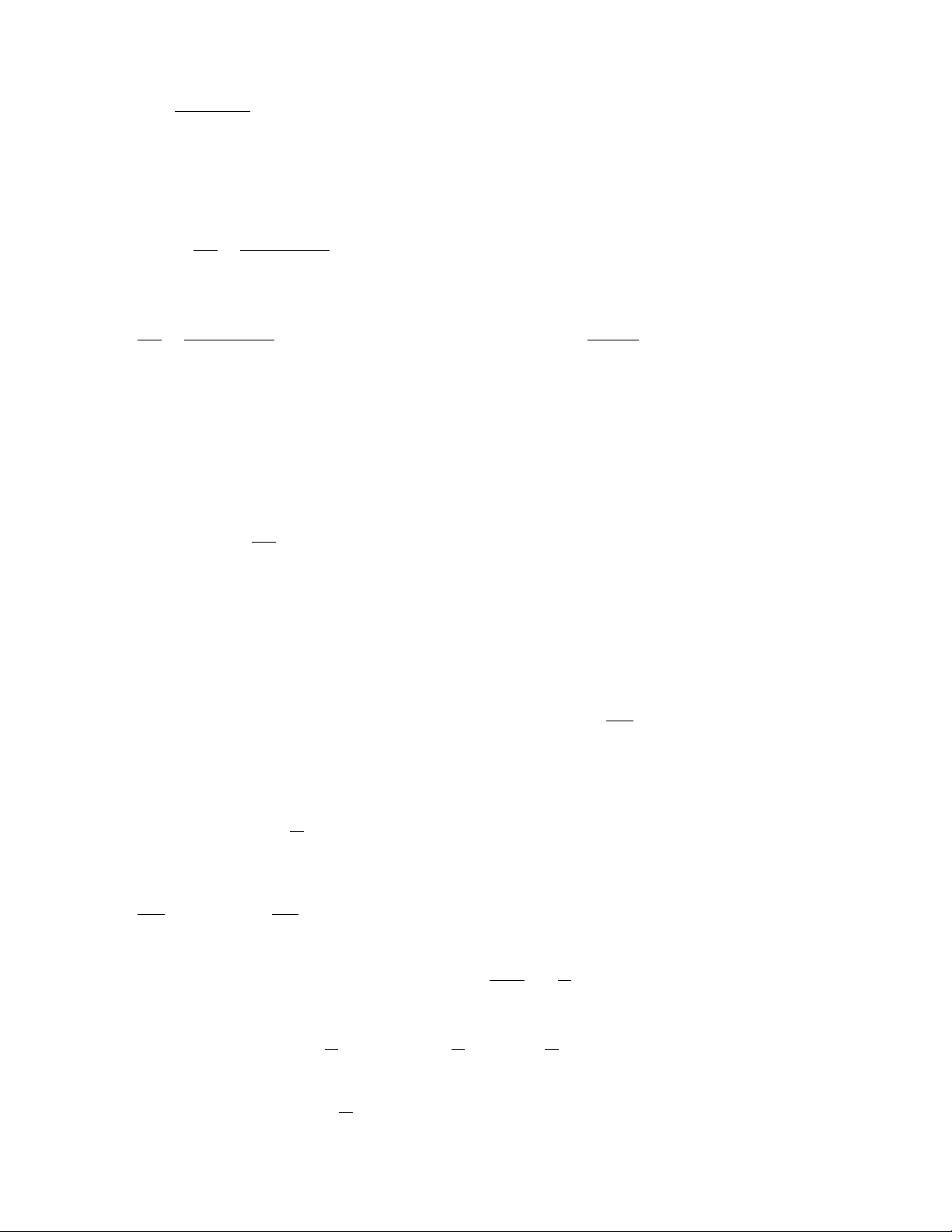
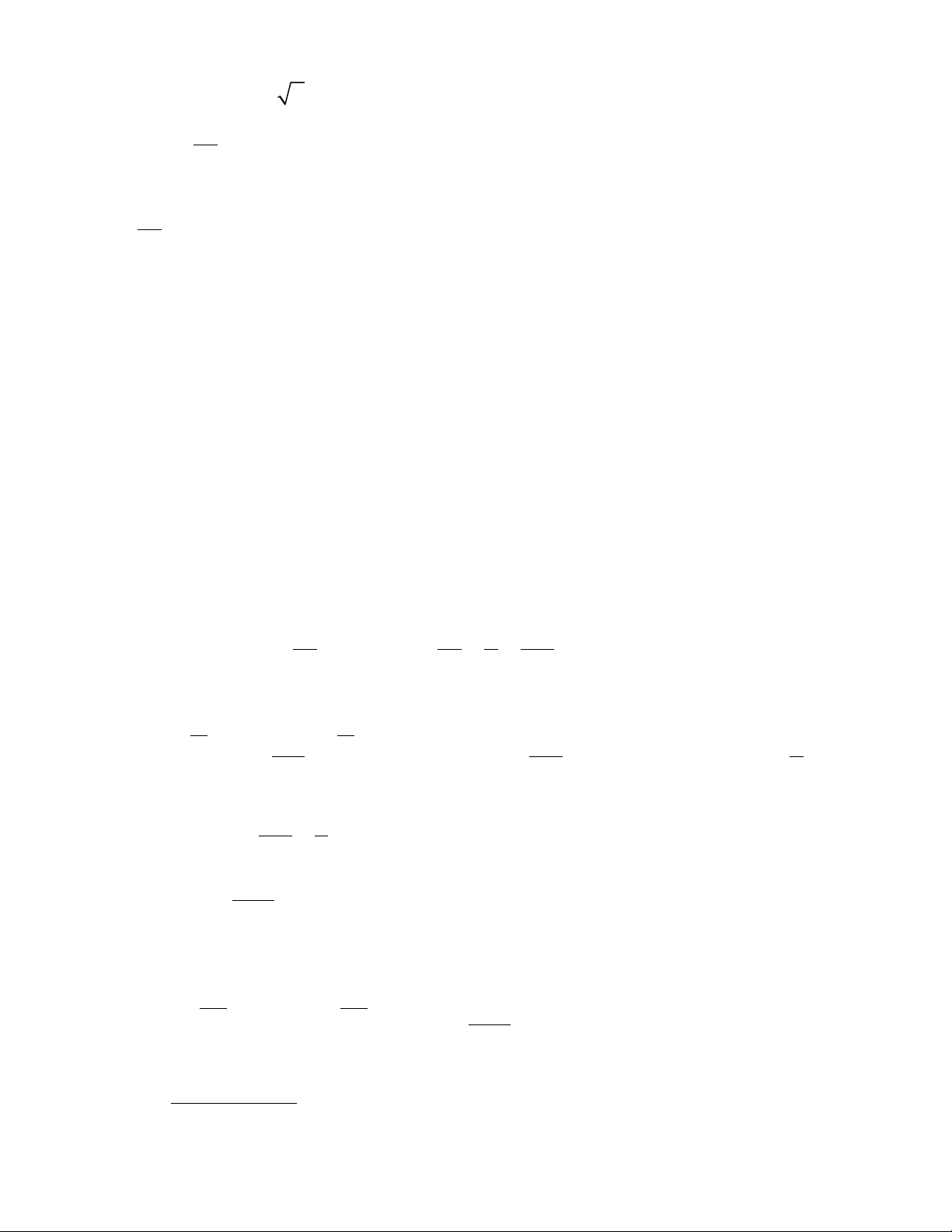
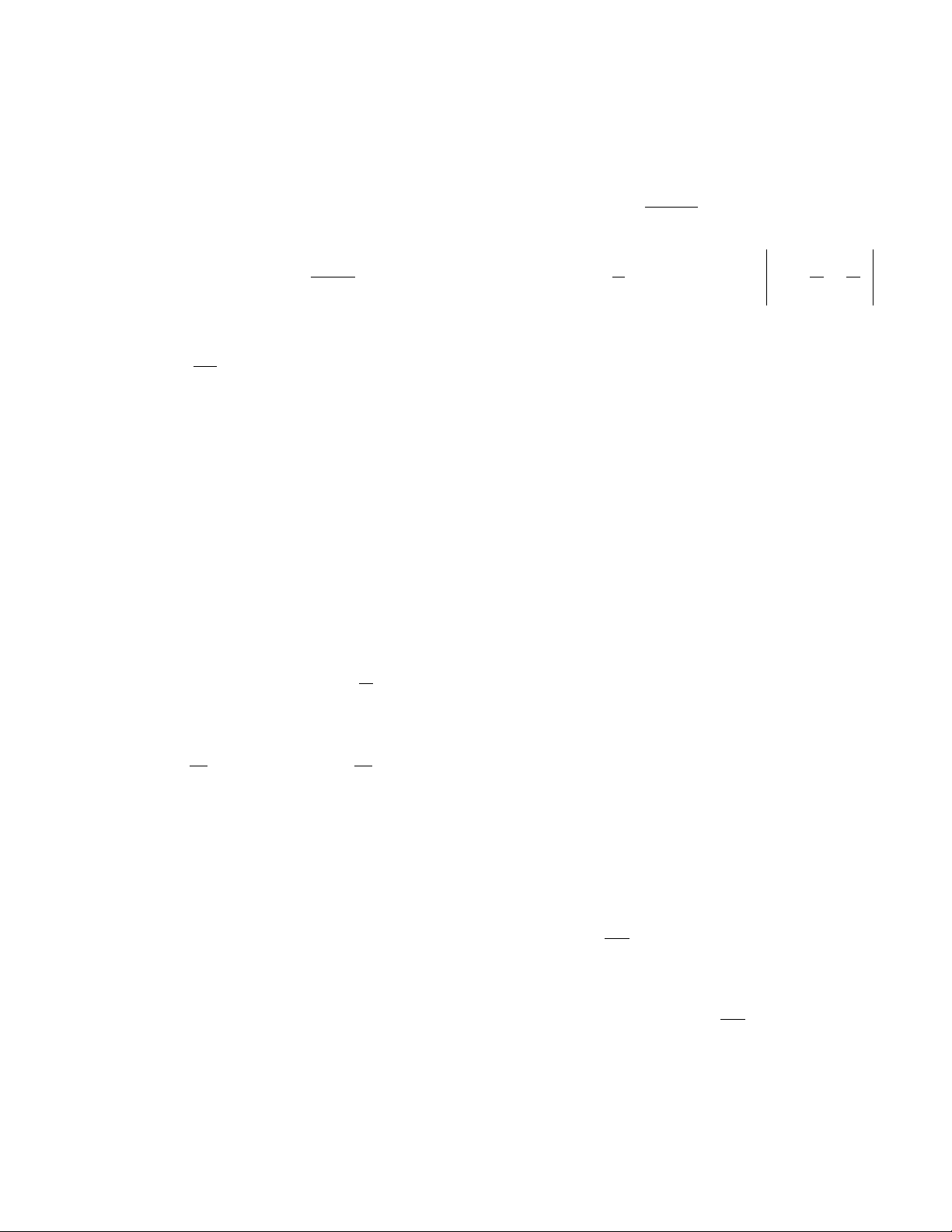
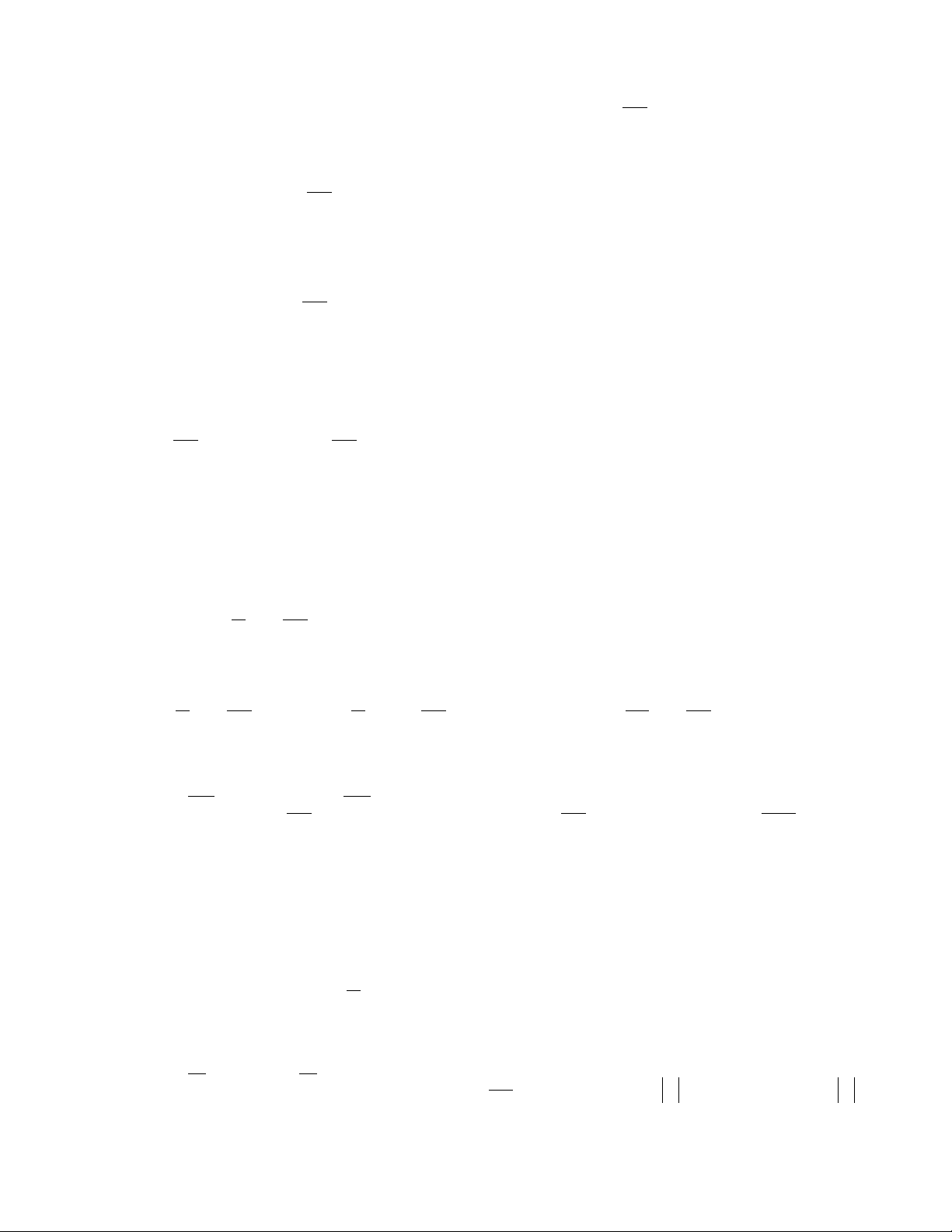
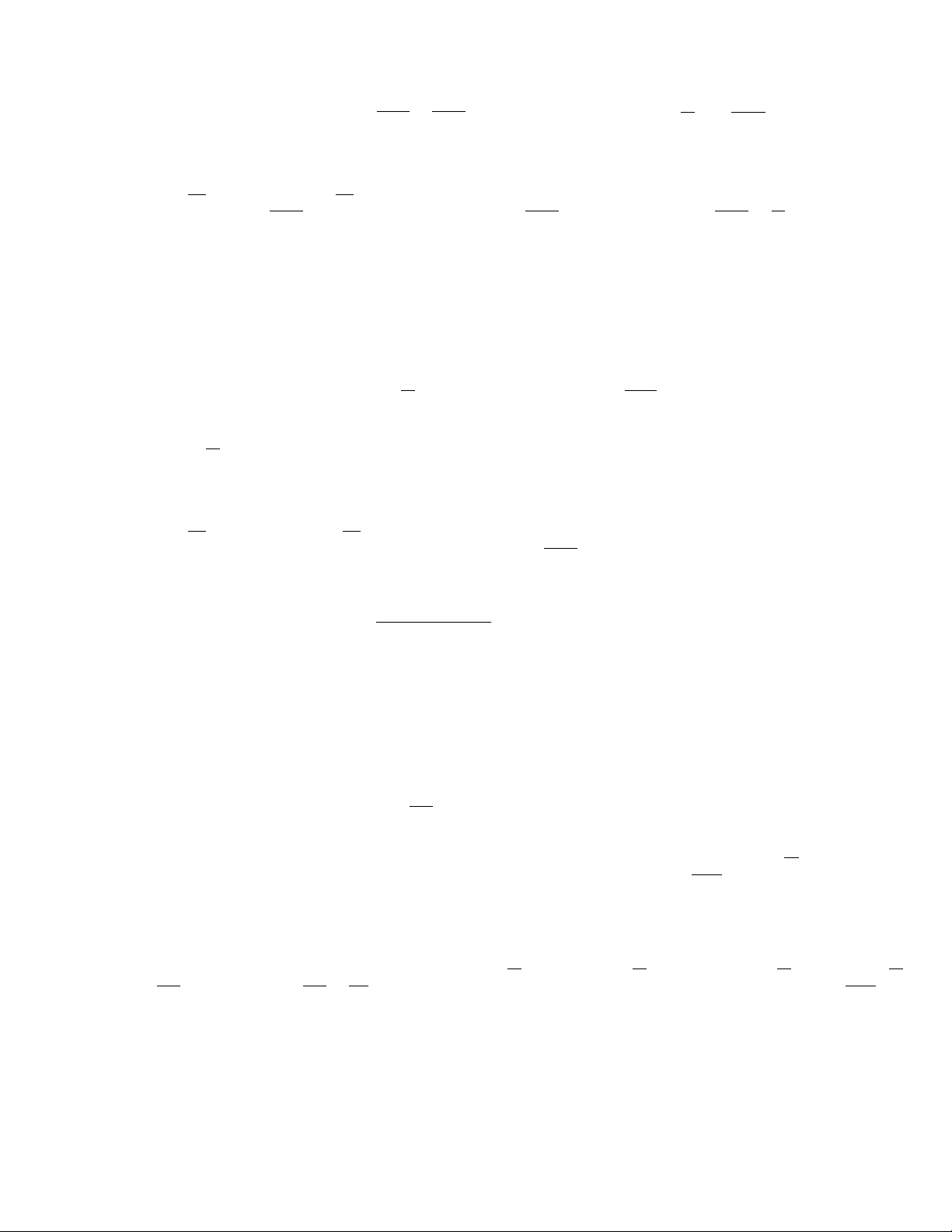
Preview text:
PHƯƠNG TRÌNH VI PHÂN
1) Kiểm tra rằng y = cos x(sin x − 1) là nghiệm của bài toán 2 y + y tan x = cos x giá trị ban đầu
y(0) = −1 trên khoảng − , 2 2 Lời giải: 2
y = −sin x(sin x − 1) + cos x 2 2
y + y tan x = −sin x(sin x − 1) + cos x + sin x(sin x − 1) = cos x
2) Giải các phương trình tách biến x dy xe a. = dx 2 y 1 + y Lời giải: x dy xe 2 x = y 1+ y dy = xe dx dx 2 y 1 + y 2 x 2 2 x y 1 + y dy = xe dx + + + = − + 1 C (1 y ) 1 y 3(x 1)e C du b. = 2 + 2u + t + tu dt Lời giải: du du du = 2 + 2u + t + tu = (1 + u)(2 + t) = (2 + t)dt dt dt (1 + u) 2 2ln 1+ u = 4t + t + C
3) Tìm nghiệm của PTVP thoả mãn điều kiện ban đầu dy a. 2 =1+ y , y(1) = 0; dx Lời giải: dy 2 dy =1+ y
= dx arctan y = x + C với y(1) = 0 thì C = 1 − 2 dx 1 + y
nghiệm của phương trình : arctan y = x − 1 + − b. x y x y y = e + e , y(0) = 1; Lời giải: y x + y x − y y 2y x e dy x y = e + e e y = (e +1)e = e dx 2y (e +1) 1 y e dy x y x
= e dx + C arctan e = e + C 2y (e +1)
với y(0) = 1 thì C = arctan e −1 nghiệm của phương trình : y x arctan e = e + arctan e −1 2 du 2t + sec t c. = , u(0) = 5 − . dt 2u Lời giải: 2 du 2t + sec t 2 1 2 = 2udu = (2t + sec t)dt 2t + dt = u + C 2 dt 2u cos t 2 2 t + tan t = u + C với u(0) = 5 − thì C = 2
− 5 nghiệm của phương trình 2 2 t + tan t = u − 25
4) Tìm phương trình đường cong thoả mãn 3
y = 4x y và cắt trục Oy tại 7. Lời giải: 4 3 dy 3 x y = 4x y
= 4x dx y = Ce ,từ giả thiết thì y(0) = 7 nên C = 7 y
Đó là đường cong có phương trình 4 x y = 7e
5) Dung dịch glucose được truyền theo đường tĩnh mạch vào máu với vận tốc
không đổi r. Khi glucose được đưa vào, nó chuyển thành các chất khác và bị đẩy khỏi
máu với vận tốc tỷ lệ thuận với nồng độ tại thời điểm đó. Như vậy, mô hình biểu diễn dC
nồng độ C = C(t) của dung dịch glucose trong máu là
= r − kC , trong đó k là hằng dt
số dương.Giả sử nồng độ tại thời điểm t = 0 là 0
C . Xác định nồng độ tại thời điểm
tuỳ ý bằng cách giải PTVP nói trên. r Giả sử rằng C 0
, tìm giới hạn lim C(t) và diễn giải đáp án của bạn. k t → Lời giải: dC dC − kdt = r − kC + kC = r C(t) = e ( kdt A + r e dt dt dt ) − − re r − C(t) = e (A+r e dt ) kt kt kt kt kt = e A + = + Ae k k r r r − Tại t = 0 A = C − C(t) = + C − e 0 .Vậy kt 0 k k k r
a. Giả sử rằng C 0
, tìm giới hạn lim C(t) và diễn giải đáp án của bạn. k t → 2 Lời giải: r r − r Hiển nhiên kt lim C(t) = + lim C − = 0 e t → k t → k k
Khi dung dịch glucose được truyền theo đường tĩnh mạch vào máu với vận tốc không
đổi,và thời gian truyền vô hạn thì nồng độ glucose của dung dịch glucose trong máu coi như không đổi.
6) Lượng cá bơn halibut Thái bình dương được mô hình hoá bởi PTVP dy y = ky 1 − ,trong đó dt K
y(t) là sinh khối (khối lượng tổng cộng của các cá thể trong quần thể) theo kilogram
tại thời điểm t (đo theo năm), dung lượng cực đại được ước lượng bởi 7 K = 8 10 kg và k = 0,71 theo năm. a. Nếu 7
y(0) = 2 10 kg , tìm sinh khối một năm sau.
b. Bao lâu nữa sinh khối đạt được 7 4 10 kg ? Lời giải: 2 dy y ky − − k − − k Từ 2 1 = ky 1− y − ky = − y y − ky = − ( 1 y ) 1 + ky = dt K K K K k z + kz = K kt kt − kdt k kdt −kt e −kt e − z = e C + e dt = e C + ye C + =1 với 1 z = y K K K kt Ke y = kt KC + e 7 7 − 8 10 3 10 Khi 7 y(0) = 2 10 kg thì 7 7 2 10 = 810 C +1= 4 C = 7 8 10 C + 1 8 7 kt 8 10 e y = kt 3 + e 7 0,71 8 10 e
a) Sinh khối một năm sau được xác định: 7 y = 3,2310 0,71 3 + e 7 kt 8 10 e ln 3
b) Ta cần tìm t sao cho 7 kt = 4 10 e = 3 t = . kt 3 + e 0,71 3 ln 3 Vậy sau t =
1,547 năm sinh khối đạt được 7 4 10 kg . 0,71
7) Trong mô hình sinh trưởng theo mùa, một hàm tuần hoàn theo thời gian được
đề nghị để tính đến những biến đổi có tính mùa vụ liên quan đến vận tốc sinh
trưởng. Những biến đổi ấy có thể, chẳng hạn, gây ra do những thay đổi có tính chất
mùa vụ về nguồn thức ăn.Tìm nghiệm của mô hình sinh trưởng theo mùa dP = kPcos(rt − ) P(0) = , trong đó k, r và φ 0 P
là những hằng số dương. dt Lời giải: dP k = k kP cos(rt − ) ln P = sin(rt − ) + C với P(0) = = − + 0 P ln 0 P sin C dt r r + + k sin r ln P k k sin r ln P 0 C = 0 ln P = sin(rt − ) + r r r P k k ln = sin(rt − ) + sin P(t) = − + 0 P exp sin(rt ) sin 0 P r r
8) Giải PTVP thuần nhất hoặc bài toán ban đầu: a. 2 2 (x − 3y )dx + 2xydy = 0 ; Lời giải: 2 2 − 2 2 dy x 3y x 3y (x − 3y )dx + 2xydy = 0 = − = − + khi xy 0 dx 2xy 2y 2x Đặt 1 2udu dx
y = xu y = u + xu 2u + 2xu = 3u − = 2 u u − 1 x 2 2 2
u − 1 = Cx y = (1 + Cx)x ; x , y y b. xy + x tan − y = 0 y(1) = ; x 2 Lời giải: y xy + x tan − y = 0 y y y + tan − = 0 x x x Đặt cos u dx C
y = xu y = u + xu u + xu + tan u − u = 0 du = − sin u = sin u x x y C ta có sin
= với y(1) = thì C =1 nghiệm của phương trình y x sin =1 x x 2 x y y c. y x sin + x = ysin ; x x Lời giải: 4 y y y y y y x sin + x = ysin y sin +1 = sin x x x x x
Đặt y = xu y = u + xu (u + xu )
sinu +1= usinu xusinu +1= 0 y cos dx −sin udu = cosu = ln Cx x Cx = e x y y d. y = + sin y(1) = ; x x 2 Lời giải:
Đặt y = xu y = u + xu u + xu = u + sin u xu = sin u u d tan du dx 2 u = ln Cx = = ln tan sin u x u 2 tan 2 u y ln Cx = ln tan Cx = tan với y(1) = thì C = 1 y x = tan 2 2x 2 2x e. 2 (x − y)ydx − x dy = 0 Lời giải: 2 với xy 0 ta có 2 y x
(x − y)ydx − x dy = 0 1 − = y x y Đặt 2 du dx C
y = xu y = u + xu u + xu = u − u − = = ln x 2 u x u
nghiệm của phương trình Cx = yln x , ngoài ra x = 0;y = 0 thỏa mãn phương
trình nên x = 0; y = 0 là nghiệm kì dị của phương trình
9) Xét xem phải chăng phương trình là tuyến tính: a. x 2 5 y + ye = x y Lời giải: Từ x 2 5 5 − 4 − x 2 + = + = ( 4− ) 4 − x 2 y ye x y y y y e x y − 4 y e = 4 − x x 2 u − 4ue = 4 − x Giả sử 1
y (x) và y2(x) là hai nghiệm của phương trình,tức là x 2 5 + = x 2 5 + = nhưng x + + + 1 y 1 y e x 1 y y2 y2e x y2 (a 1 y by2 ) (a 1 y by2)e 5 = a ( x y + y e ) + b( x y + y e ) 2 5 + 1 1 2 2 x (a 1 y
by2) đó không phải là phương trình vi
phân tuyến tính .Xong đó là phương trình Becnuli nên có thể đưa phương trình về phương tr −
ình vi phân tuyến tính bằng cách đặt 4 u = y . b. 2 xy + ln x − x y = 0 Lời giải: Từ 2 ln x
xy + ln x − x y = 0 y + xy =
đó là phương trình vi phân tuyến tính cấp một. x c. 4 x y = y + sin x Lời giải: Từ 4 y sin x
x y = y + sin x y − =
đó là phương trình vi phân tuyến tính cấp một. 4 4 x x d. 2 xy − y = x sin x Lời giải: Từ 2 y
xy − y = x sin x y −
= xsin x đó là phương trình vi phân tuyến tính cấp một. x 10) Giải các PTVP: a. x y + 2y = 2e ; Lời giải:
phương trình đã cho là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định − ( + = C + 2 e e dx ) 3x 2dx 2dx x C 2e y e = 1 2x 3e 2x 3x 3ye
= C + 2e là nghiệm phương trình b. xy + y = x ; Lời giải: y 1 xy + y = x y + = x x
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định dx dx − 1 1 x = x y e + = + 1 C e dx y ( 1C x dx ) x x 6
3yx = C + 2x x là nghiệm phương trình. dy c. 2 + 2xy = x ; dx Lời giải: dy 2 2
+ 2xy = x y + 2xy = x đó là phương trình vi phân tuyến tính cấp một,nên dx 2 2 − 2xdx 2xdx −
nghiệm được xác định = ( 2 + ) x = ( 2 x y e C x e dx y e C + x e dx ) d. 2 2 y + 3x y = 6x ; Lời giải: 2 2
y + 3x y = 6x đó là phương trình vi phân tuyến tính cấp một,
nên nghiệm được xác định 2 − ( 2 = + ) 3 − = ( 3 3x dx 3x dx 2 x x 3 y e C 6x e dx y e C + 2 e dx ) 3 3 3 − − x = ( x + ) x y e C 2e y = Ce + 2 e. y = xy + yln y ; Lời giải: coi x = x(y) dx y = x + ln y dx x ln y − =
đó là phương trình vi phân tuyến dy dy y y
tính cấp một,nên nghiệm được xác định dy dy − y ln y y ln y x e C e dy = + = + = − x y C dy 1 x y C ln yd y 2 y y ln y 1 x = y C − − 1+ x + ln y = C y y y 1 f. 2 y + y = x ; x + 1 Lời giải:
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định dx dx − 2 1 y = e + C + x e + dx y = ( 2 x 1 x 1 + + 1 1 C x (x 1)dx ) x + 1 4 3 C + 3x + 4x y = 12(x + 1) 7 g. 2 y + y tan x = sin x . Lời giải:
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định − 2 tan xdx sin x y = e ( tan xdx 2 + = + 1 C sin xe dx ) y cosx 1C dx cos x dx y = cos x + − 1 x = − + + 1 C cos xdx y Ccos x sin 2x cos x ln tan cos x 2 2 4
11) Giải bài toán giá trị ban đầu: 2 dv a. 2 t − 2tv = 3t e v(0) = 5 ; dt Lời giải:
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định ( 2 − = + ) 2 = ( + ) 2 2tdt 2tdt 2 t t 2 t = ( 3 v e C 3t e e dt v e C 3t dt v e C + t ) với v(0) = 5 C = 5 2 t = ( 3 v e 5 + t ) b. 2 xy = y + x sin x y( ) = 0 . Lời giải: 2 y
xy = y + x sin x y −
= xsin x đó là phương trình vi phân tuyến tính cấp x
một,nên nghiệm được xác định dx dx − x = x y e C + x sin xe dx y = x (C+ sinxdx )y = x(C−cosx) với y( ) = 0 C = 1 − y = −x(1 + cos x)
12) Những nhà tâm lý quan tâm đến lý luận học tập khảo sát đường cong học.
Đường cong học là đồ thị của hàm số P(t), hiệu quả của một ai đó học một kỹ năng đượ dP
c coi là hàm của thời gian huấn luyện t. Đạo hàm
thể hiện vận tốc mà tại đó dt
hiệu suất học được nâng lên. dP a.
Bạn nghĩ P tăng lên nhanh nhất khi nào? Điều gì xảy ra với khi t tăng lên? dt Giải thích. Lời giải:
P tăng lên nhanh nhất khi thời gian huấn luyện ít nhất 8 Khi t tăng, tứ dP
c là thời gian huấn luyện tăng lên dẫn đến giảm đi dt
b. Nếu M là mức cực đại của hiệu quả mà người học có khả năng đạt được,giải dP thích tại sao PTVP
= k(M − P) , k là hằng số dương là mô hình hợp lý cho việc dt học. Lời giải: dP Khi = thì = m P ax M 0 dt c.
Giải PTVP để tìm ra một biểu thức của P(t).Dùng lời giải của bạn để vẽ đồ thị
đường cong học.Giới hạn của biểu thức này là gì? Lời giải: Từ dP dP −kt − = k(M − P) + kP = kM P = e ( kt C + kM e dt ) kt P = M + Ce dt dt
Từ giả thiết của bài toán ta có − P(0) = 0 C = −M kt P = M − Me − kt lim P = lim (M + Ce ) = M t → t →
13) Giải PTVP Bernoulli: 3 2 y a. y + y = ; 2 x x Lời giải: 3 2 y 3 − 2 2 − 1 − 4z 2 y + y = y y + y = ,đặt 2 z = y z − = − 2 2 x x x x 2 x x
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định 4dx 4dx 2 − 4 2 4 2 x = x z e − = − = + 1 C e dx z x 1 C dx z x 1 C 2 6 5 x x 5x 5 2 5x = (C x + 2)y b. 2 xy + y = −xy ; Lời giải: đặt −1 z = y ta được z z −
=1 đó là phương trình vi phân tuyến tính cấp một, x
nên nghiệm được xác định dx dx − dx x = x z e C + e dx z = x C + z = x
(C + ln x ) 1= xy(C + ln x ) x 9 c. 2 (2xy − y)dx + xdy = 0 ; Lời giải: 2 y 2
(2xy − y)dx + xdy = 0 y − = 2 − y x đặt −1 z = y ta được z z +
= 2 đó là phương trình vi phân tuyến tính cấp một, x
nên nghiệm được xác định dx dx − 1 z = e C + e dx z = (C + xdx ) 2 1 x x x = + 2 = + 1 1 z 1 C x y(C x ) x x 2 d. 2 2xyy − y + x = 0 ; Lời giải: 2 − + = ( 2 ) 2 z 2xyy y x 0 y + x − y = 0 đặt 2 z = y z − = 1 − đó là phương x
trình vi phân tuyến tính cấp một,nên nghiệm được xác định dx dx − dx x = x z e C + e dx z = x C + z = x (C + ln x ) 2 y = x (C + ln x ) x 2x e. y = ; 2 x cos y + 4sin 2y Lời giải: 2 dx x cos y + 4sin 2y coi x = x(y) = ( 2 x ) 2 − x cos y = 4sin 2y dy 2x đặt 2
z = x z − z cos y = 4sin 2y đó là phương trình vi phân tuyến tính cấp một,
nên nghiệm được xác định cos ydy ( − cos ydy = + ) sin y = ( − sin y z e C 4sin 2ye dy z e C − 8 sin ye d(−sin y) ) sin y = ( − sin y − + ) sin y z e C 8(1 sin y)e z = Ce − 8(1 + sin y) 2 sin y x = Ce − 8(1 + sin y) f. 2 xy + y = y ln x ; Lời giải: 10 1 − 2 2 − y ln x − z ln x xy + y = y ln x y y + = đặt 1 z = y z − = − đó là x x x x
phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định dx dx ln x − ln x ln x 1 x = x z e C − e dx z = x C − dx z = x C + + 2 x x x x y(Cx + ln x + ) 1 = 1 g. 2 xy + 2xy ln x + y = 0 . Lời giải: − y + + = + = − ( − ) 1 2 2 1 y − xy 2xy ln x y 0 y 2y ln x y − = 2ln x đặt 1 z = y x x z z − = 2ln x x
đó là phương trình vi phân tuyến tính cấp một,nên nghiệm được xác định dx dx − ln x x = x z e C + 2ln xe dx z = x C + 2 dx z = x (C+ 2 lnxd(lnx) ) x = ( 2 1 z x C + ln x ) y = x ( 2 C + ln x )
14) Một vật khối lượng m rơi xuống từ trạng thái nghỉ và chúng ta giả sử rằng sức
cản không khí tỷ lệ thuận với vận tốc của vật. Nếu S(t) là khoảng cách rơi được sau t
giây thì vận tốc là v = S (
t) và gia tốc là a = v (t). Nếu g là gia tốc trọng trường thì
lực hướng xuống dưới tác động lên vật là mg − cv , trong đó c là hằng số dương, Định dv
luật Newton thứ hai dần đến m = mg − cv . dt ct mg −
a. Giải PT này khi coi nó là PT tuyến tính để chỉ ra rằng = m v 1 − e . c Lời giải: c c ct ct − dt dt dv dv c − mg m = − + = = m + m = m m mg cv v g v e A g e dt v e A + e dt dt m c 11 ct ct − mg mg
Khi vật không rơi tức v(0) = 0 ,từ m = m v e A + e = − ta có A c c ct mg − = m v 1 − e c
b. Vận tốc giới hạn là bao nhiêu? Lời giải: ct mg − mg = m lim v lim 1 − e = t → c t→ c c.
Tính quãng đường vật rơi được sau t giây. Lời giải: ct ct − − 2 mg mg m = m g m − m S(t) 1 e dt = t + e + A từ S(0) = 0 A = − c c c 2 c ct 2 − mg m m g m S(t) = t + e − 2 c c c − 15)
Tìm các quỹ đạo trực giao của họ các đường cong 1 y = (x + k) . Vẽ một vài
đường của mỗi họ trên cùng một hệ trục. Lời giải: −
Quỹ đạo trực giao của họ các đường cong 1
y = (x + k) là quỹ tích của tọa độ khúc
tâm của chính đường cong đó,và tọa độ đó được xác định 2 2 (1 + y )y 1 + y X = x − ;Y = y + y y − 1 2 Từ 1 y = (x + k) 2 3 y = −y = − ; y = 2y = 2 3 (x + k) (x + k) 2 2 4 4 4 y ( 1+ y ) y (1 + y ) 1 1 + y 3 + y X = x − = x + X + k = + X + k = 3 y ; 2y y 2y 2y 4 4 4 1 + y 1 + 3y 3 (3 + y ) 4 3(X + k) 4 Y = y + = = − = − 3 3 2 3 2 3 2y 2y y 2y y y y + 4 + 3(X k) 4 3 y Y = − và X + k = 2 3 y y 2y
16) Giải các PTVP toàn phần: 12 2 (x + y )dx − 2xydy a. = 0 ; 2 x Lời giải: 2 (x + y )dx − 2xydy Nhận thấy = 0 là PTVP toàn phần vì 2 x 2 + x y 2 − xy 2y = = 2 2 2 x x x x y 2 (x + y )dx − 2xydy nên
không phụ thuộc đường lấy tích phân 2 x AB
Do vậy ta chọn A(1,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định 2 x y (x + y )dx − 2xydy dx 2ydy 2 = − = y C ln x − = C 2 x x x x 1 0 AB b.
(2x − y + 1)dx + (2y − x − 1)dy = 0 ; Lời giải:
Nhận thấy (2x − y + 1)dx + (2y − x − 1)dy = 0 là PTVP toàn phần vì (2x − y + 1) = − − = − y (2y x 1)x 1 nên
(2x − y + 1)dx + (2y − x − 1)dy
không phụ thuộc đường lấy tích phân AB
Do vậy ta chọn A(0,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x y
(2x − y + 1)dx + (2y − x − 1)dy = (2x + 1)dx + (2y − x − 1)dy = C 0 0 AB 2 2
x + x + y − xy − y = C c. ( 2 2 + + ) +( 2 2 1 x x y dx x + y − ) 1 ydy = 0 ; Lời giải: Nhận thấy ( 2 2 + + ) +( 2 2 1 x x y dx x + y − )
1 ydy = 0 là PTVP toàn phần vì ( 2 2 + + ) = ( 2 2 + − ) xy 1 x x y y x y 1 = 2 2 y x x + y nên ( 2 2 1 + x x + y )dx + ( 2 2 x + y −
)1ydy không phụ thuộc đường lấy tích phân AB 13
Do vậy ta chọn A(0,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x ( 2 1 + x ) y dx + ( 2 2 x + y − ) 1 ydy = C 0 0 3 2 x y 1 x + − + ( x + y ) x + y ) y 2 2 2 2 = C 3 2 3 y =0 2 y 1 x − + ( 2 2 x + y ) 2 2 x + y = C 2 3 1 d. (x + y)dx + x + dy = 0 . y Lời giải: 1 Nhận thấy (x + y)dx + x + dy = 0 là PTVP toàn phần vì y 1 (x + y) = + = y x 1 y x 1 nên (x + y)dx + x + dy
không phụ thuộc đường lấy tích phân y AB
Do vậy ta chọn A(0,1) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x y 1 1 (x + y)dx + x + dy = (x + 1)dx + x + dy = C y y 0 1 AB 2 x + x + (xy + ln y ) y = C y 1 2 = 2 x + xy + ln y = C 2
17) Giải các PTVP dùng thừa số tích phân: x x a. 1 + dx + −1 dy = 0 ; y y Lời giải: x x Nhận thấy y 1 + dx + y −1 dy = 0 là PTVP toàn phần y y 14 x x nên y 1 + dx + y −1 dy
không phụ thuộc đường lấy tích phân y y AB
Do vậy ta chọn A(0,1) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x y x x y 1 + dx + y
−1 dy = (x + 1)dx + (x − y)dy = 1 C y y 0 1 AB 2 2 x y 1 + x − + xy − x + = − + = 1 C 2 2 x y 2xy C 2 2 2 2 2 x − y + 2xy = C b. 2 2
(1 − x y)dx + x (y − x)dy = 0 ; Lời giải: P − Q 2 y x 2 − = − = − − = − y P Qx 2x 2xy 2x(y x)
khi đó thừa số tích phân Q x 1 2 − (1 x y)dx (x) = .Ta được
+ (y − x)dy = 0 là PTVP toàn phần 2 x 2 x 2 (1 − x y)dx nên + (y − x)dy
không phụ thuộc đường lấy tích phân 2 x AB
Do vậy ta chọn A(1,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định 2 x y 2 (1 − x y)dx dx 1 y + (y − x)dy = + (y − x)dy = − + − + = 1 C 1 xy 1 C 2 2 x x x 2 1 0 AB 2 2 y x − 2x y − 2 = C x c. 2 2
y(1 + x y)dx + x(2 + yx )dy = 0 ; Lời giải: P − Q 2 y x 1 − = − − − = = y P Qx 1 x y
khi đó thừa số tích phân (y) y P y Ta được 2 2 2
y (1 + x y)dx + xy(2 + yx )dy = 0 là PTVP toàn phần nên 2 2 2 y (1 + x y)dx + xy(2 + yx )dy
không phụ thuộc đường lấy tích phân AB
Do vậy ta chọn A(0,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x y 3 3 2 2 2 2 2 x y
y (1 + x y)dx + xy(2 + yx )dy = 0dx + xy(2 + yx )dy = + = 1 C xy 1 C 3 0 0 AB 15 2 3 3 3xy + x y = C d. 2 2
(sin y − x )dx − x sin 2ydy = 0 ; Lời giải: − y P Q 2 − = = − 1 = y P Qx 2sin 2y
khi đó thừa số tích phân (x) Q x 2 x 2 2 − Ta được (sin y x )dx sin 2ydy − = 0 là PTVP toàn phần 2 x x 2 2 (sin y − x )dx sin 2ydy nên −
không phụ thuộc đường lấy tích phân. 2 x x AB
Do vậy ta chọn A(1,0) ; B(x, y) ,khi đó nghiệm của phương trình được xác định 2 2 x y (sin y − x )dx sin 2ydy sin 2ydy cos 2y − = − dx − = − + = 1 C 1 x 1 C 2 x x x 2x 1 0 AB 2 2x + C x = cos 2y e. 2 (2xy − y)dx + xdy = 0 . Lời giải: − y P Qx 2 − = − − = − 1 = y P Qx 4xy 2
khi đó thừa số tích phân (y) P y 2 y − Ta được (2xy 1)dx xdy + = 0 là PTVP toàn phần 2 y y (2xy − 1)dx xdy nên +
không phụ thuộc đường lấy tích phâ 2 y y AB
Do vậy ta chọn A(0,1) ; B(x, y) ,khi đó nghiệm của phương trình được xác định x y (2xy − 1)dx xdy xdy x 2 + = (2x −1)dx + = C x − = C 2 yx − x = C y 2 2 y y y y 0 1 AB 18) Giải các PTVP a. 2 xy = 1 + y ; Lời giải: dz dx Đặt 2 2 z = y xz = 1 + z = z + 1+ z = Cx 2 x 1 + z 2 2 2 2 1+ z = z − 2zxC + C x 16 2 2 − 2 2 2 − C x 1 C x 1 Cx ln x z = y = dx + D y = − + D 2xC 2xC 4 2C b. 2 2 (1 + x )y + 1 + y = 0 . Lời giải: Đặ dz dx t z = y 2 2 (1 + x )z + 1 + z = 0 = − arctan z = − 1 C arctan x 2 2 1 + z 1 + x − C x z = 1 + xC − C x x 1 y = dx + = + − + + + 1 D ln 1 xC ln 1 xC 1 D 2 1 + xC C C 1 x y = 1 + ln 1 + xC − + 1 D 2 C C 2
Cy = (1 + C )ln 1 + xC − Cx + D 19) Giải các PTVP a. 4y + y = 0 ; Lời giải: Phương trình đặc trưng 2 4k + k = 0 x −
nghiệm tổng quát của phương trình 4 y = + 1 C C2e b. y − 2y − y = 0 ; Lời giải:
Phương trình đặc trưng 2 k − 2k − 1 = 0 → = 1 k ,2 1 2
nghiệm tổng quát của phương trình + − (1 2)x (1 2)x y = + 1 C e C2e c. y + 8y + 41y = 0; Lời giải:
Phương trình đặc trưng 2 k + 8k + 41 = 0 → = − 1 k ,2 4 5i −
nghiệm tổng quát của phương trình 4x y = e ( + 1 C cos5x C2 sin5x) d. y + y + y = 0 . Lời giải: 17 − Phương trình đặc trư 1 i 3 ng 2 k + k + 1 = 0 → = 1 k ,2 2 x − x 3 x 3
nghiệm tổng quát của phương trình 2 y = e + 1 C cos C2 sin 2 2
20) Giải bài toán giá trị ban đầu: a. 2y + 5y + 3y = 0 y(0) = 3, y (0 ) = 4 − ; Lời giải: Phương trình đặc trưng 2 3 2k + 5k + 3 = 0 → = − = − 1 k 1;k2 nghiệm tổng quát 2 3x − − của phương trình x 2 y = + = − = 1 C e C2e .Từ điều kiện y (0) 4, y(0) 3 ta có + = 1 C C2 3 3 C = 2;C =1 + = 2 1 1 C C2 4 2 3x − −
nghiệm riêng của phương trình thỏa mãn điều kiện đầu: x 2 y = e + 2e b. 4y − 4y + y = 0 y ( 0) = 1 − ,5; y(0) =1; Lời giải: Phương trình đặc trưng 2 1 4k − 4k + 1 = 0 → = 1 k ,2
nghiệm tổng quát của phương 2 trình x 2 y = ( + = − = 1 C
C2x)e .Từ điều kiện y (0) 1,5; y(0) 1 ta có = 1 C 1 1 3 = − = 2 C 2; 1 C 1 C + = − 2 1 C 2 2 x
nghiệm riêng của phương trình thỏa mãn điều kiện đầu: 2 y = (1 − 2x)e 21) Giải các PTVP a. 4y + y = 0 y(0) = 3, y ( ) = 4 − , ; Lời giải: Phương trình đặc trưng 2 i 4k + 1 = 0 → = 1 k ,2
nghiệm tổng quát của phương 2 trình 18 x x y = + = = − 1 C cos
C2 sin .Từ điều kiện y(0) 3, y ( ) 4, ta có 2 2
(xem lại điều kiện) b. y − 6y + 25y = 0 y ( ) = 2, y(0) =1; Lời giải:
Phương trình đặc trưng 2 k − 6k + 25 = 0 →
= nghiệm tổng quát của 1 k ,2 3 4i phương trình 3x y = e ( + = = 1 C cos 4x
C2 sin 4x).Từ điều kiện y ( ) 2, y(0) 1 ta có = 3 − 1 C 1 e 3 C =1; C = − 3 1 2 (4C + = 2 4 2 3 1 C )e 2
nghiệm riêng của phương trình thỏa mãn điều kiện đầu: 3 − e 3 3x y = e ( + C = 1; C = − 1 C cos 4x C2 sin 4x) với 1 2 2 4 22) Giải các PTVP a. 2 y + 3y + 2y = x ; Lời giải:
Phương trình đặc trưng 2 k + 3k + 2 = 0 → = − = − 1 k 1;k2
2 nghiệm tổng quát của phương trình thuầ − − n nhất x 2x y = + 1 C e C2e
nghiệm riêng của phương trình 2
y + 3y + 2y = x có dạng * 2 y = ax + bx + c ,thay 2a =1
vào phương trình ta được 2 2
2a + 3(2ax + b) + 2(ax +bx + c) = x 3 a + b = 0 2a + 3b + 2c = 0 ( ) 1 3 7 a, b,c = , − , 2 2 4 − − 1
nghiệm tổng quát của phương trình đã cho x 2x 2 y = + + − + 1 C e C2e (2x 6x 7) 4 − b. x y − 4y + 5y = e ; Lời giải:
Phương trình đặc trưng 2 k − 4k + 5 = 0 → = 1
k ,2 2 i nghiệm tổng quát của
phương trình thuần nhất 2x y = e ( + 1 C cos x C2 sin x) 19 − * −
nghiệm riêng của phương trình x y − 4y + 5y = e có dạng x y = ae ,thay vào phương trình ta được 1 a =
nghiệm tổng quát của phương trình đã cho 10 −x 2x = ( e y e + + 1 C cos x C2 sin x) 10 c. x y − y = xe y ( 0) =1, y(0) = 2 ; Lời giải:
Phương trình đặc trưng 2 k − k = 0
nghiệm tổng quát của phương trình thuần nhất x y = + 1 C C2e
nghiệm riêng của phương trình x
y − y = xe có dạng * x y = x(ax + b)e ,thay vào
phương trình ta được 2ax + 2a + b = x 1 a = ;b = 1
− nghiệm tổng quát của 2 phương trình đã cho x 1 x y = + + − = = 1 C C2e x(x
2)e .Từ điều kiện y (0) 1, y(0) 2 ta có 2 = 1 C 0 1
nghiệm riêng thỏa mãn điều kiện đầu: x x y = 2e + x(x − 2)e C = 2 2 2 d. y − 2y = sin 4x ; Lời giải:
Phương trình đặc trưng 2 k − 2k = 0
nghiệm tổng quát của phương trình thuần nhất 2x y = + 1 C C2e
nghiệm riêng của phương trình y − 2y = sin 4x có dạng y* = a cos 4x + bsin 4x −b − 2a = 0
,thay vào phương trình và rút gọn ta được 1 1 a = ;b = − 8 a −16b =1 40 20 1 1
nghiệm tổng quát của phương trình đã cho 2x y = + + − 1 C C2e cos 4x sin 4x 40 20 e. x y − 3y + 2y = ( 12 − x + 4)e Lời giải:
Phương trình đặc trưng 2 k − 3k + 2 = 0
nghiệm tổng quát của phương trình thuần nhất x 2x y = + 1 C e C2e
nghiệm riêng của phương trình x y − 3y + 2y = ( 12 − x + 4)e có dạng * x
y = x(ax + b)e ,thay vào phương trình và rút gọn ta được 2 − ax + 2a − b = 1 − 2x + 4 20