


















Preview text:
1
Giải tích toán học Tập 1 Lê Văn Trực
NXB Đại học quốc gia Hà Nội 2007.
Từ khoá: Giải tích toán học, giải tích, tập hợp, số thực, ánh xạ, Hàm liên tục, Điểm
gián đoạn, liên tục, liên tục đều, hàm sơ cấp, Giới hạn, giới hạn dãy số, giới hạn hàm
số, dãy số, hàm số, nguyên lý Cantor, nguyên lý Cauchy, giới hạn trên, giới hạn dưới,
vô cùng bé, vô cùng lớn, hàm số hợp, hàm số ngược, Phép tích vi phân, Đạo hàm, vi
phân, Công th c Taylor, Khai triển Maclaurin, Quy tắc L’hospital, tích phân không
xác định, tích phân, nguyên hàm, Phép thế Euler, Điều kiện khả tích, Hàm khả tích,
Diện tích, thể tích, Tích phân suy rộng, Nguyên lí Canto, Tập compact, Hàm nhiều
biến, Liên tục, giới hạn, liên tục đều, Đạo hàm, cực trị hàm nhiều biến, Phép tích vi phân, Sự hội tụ.
Tài liệu trong Thư viện điện tử ĐH Khoa học Tự nhiên có thể được sử dụng cho mục
đích học tập và nghiên cứu cá nhân. Nghiêm cấm mọi hình thức sao chép, in ấn phục
vụ các mục đích khác nếu không được sự chấp thuận của nhà xuất bản và tác giả. Mục lục
Chương 1 Tập hợp và số thực ............................................................................................... 7 1.1 Khái
niệm về tập hợp ................................................................................................. 7
1.2 Số thực........................................................................................................................ 9 1.3 Ánh
xạ ...................................................................................................................... 14 1.4 Bài
tập chương 1 ...................................................................................................... 16 2
Chương 2 Giới hạn c a dãy số và hàm số .......................................................................... 19
2.1 Giới hạn c a dãy số .................................................................................................. 19
2.1.1 Định nghĩa dãy số................................................................................................. 19
2.1.2 Các tính chất c a dãy hội tụ ................................................................................. 21
2.1.3 Giới hạn vô hạn .................................................................................................... 24 2.2 Tiêu
chuẩn hội tụ...................................................................................................... 25 2.2.1 Các
định lý ........................................................................................................... 25
2.2.2 Số e....................................................................................................................... 26
2.2.3 Nguyên lý Cantor về dãy các đoạn thẳng lồng nhau và thắt lại ........................... 27
2.2.4 Sự hội tụ c a dãy bị chặn ..................................................................................... 28
2.2.5 Nguyên lý Cauchy về sự hội tụ c a một dãy số ................................................... 29
2.2.6 Giới hạn trên và giới hạn dưới ............................................................................. 30 2.3 Khái
niệm về hàm số một biến số ............................................................................ 32
2.3.1 Định nghĩa ............................................................................................................ 32
2.3.2 Đồ thị c a hàm số................................................................................................. 32 2.3.3 Hàm
số hợp .......................................................................................................... 34 2.3.4 Hàm
số ngược ...................................................................................................... 34
2.3.5 Các hàm lượng giác ngược................................................................................... 36
2.3.6 Các hàm số hypebol ............................................................................................. 38
2.3.7 Các hàm hypebol ngược....................................................................................... 39
2.4 Giới hạn c a hàm số................................................................................................. 41 2.4.1 Lân
cận c a một điểm .......................................................................................... 41 2.4.2 Các
định nghĩa giới hạn........................................................................................ 42
2.4.3 Giới hạn một phía................................................................................................. 45
2.4.4 Giới hạn vô cùng .................................................................................................. 46
2.4.5 Các tính chất c a giới hạn .................................................................................... 47 2.4.6 Tiêu
chuẩn tồn tại giới hạn c a hàm số................................................................ 47
2.4.7 Vô cùng bé. Vô cùng lớn...................................................................................... 48 2.4.8 Các
giới hạn đáng nhớ.......................................................................................... 51 2.5 Bài
tập chương 2 ...................................................................................................... 54
Chương 3 Hàm liên tục một biến số .................................................................................... 61
3.1 Định nghĩa sự liên tục c a hàm số tại một điểm .......................................................... 61 3.1.1 Các
định nghĩa...................................................................................................... 61
3.1.2 Hàm liên tục một phía, liên tục trên một khoảng, một đoạn kín.......................... 62 3.1.3 Các
định lý về những phép tính trên các hàm liên tục ......................................... 63
3.1.4 Điểm gián đoạn c a hàm số ................................................................................. 65 3.2
Các tính chất c a hàm liên tục ................................................................................. 68 3.2.1 Tính
chất bảo toàn dấu lân cận một điểm ......................................................... 68 3.2.2 Tính
chất c a một hàm số liên tục trên một đoạn ................................................ 68 3.3
Điều kiện liên tục c a hàm đơn điệu và c a hàm số ngược ..................................... 72
3.3.1 Điều kiện liên tục c a hàm đơn điệu.................................................................... 72 3.3.2 Tính liên
tục c a hàm ngược ................................................................................ 73 3.4 Khái
niệm liên tục đều ............................................................................................. 74
3.4.1 M đầu ................................................................................................................. 74
3.4.2 Định nghĩa ............................................................................................................ 74 3.4.3 Liên
tục c a các hàm số sơ cấp ............................................................................ 76 3.5 Bài
tập chương 3 ...................................................................................................... 77 3
Chương 4 Phép tính vi phân c a hàm một biến ................................................................ 81
4.1 Đạo hàm và cách tính ..................................................................................................... 81
4.1.1 Định nghĩa đạo hàm ................................................................................................ 81
4.1.2 Công th c đối với số gia c a hàm số ...................................................................... 81
4.2 Các qui tắc tính đạo hàm ................................................................................................ 82
4.2.1 Các qui tắc tính đạo hàm ......................................................................................... 82
4.2.2 Đạo hàm c a hàm số hợp ........................................................................................ 82
4.2.3 Đạo hàm c a hàm số ngược .................................................................................... 84
4.2.4 Đạo hàm theo tham số............................................................................................. 85
4.2.5 Đạo hàm một phía ................................................................................................... 85
4.2.6 Đạo hàm vô cùng..................................................................................................... 87
4.2.7 Đạo hàm các hàm số sơ cấp .................................................................................... 87
4.3 Vi phân c a hàm số ........................................................................................................ 88
4.3.1 Định nghĩa ............................................................................................................... 88
4.3.2 Các qui tắc tính vi phân........................................................................................... 89
4.3.3 Vi phân c a hàm số hợp .......................................................................................... 89
4.3.4 ng dụng c a vi phân ............................................................................................ 90
4.4 Các định lí cơ bản c a hàm khả vi ................................................................................. 90
4.4.1 Cực trị địa phương................................................................................................... 90
4.5 Đạo hàm và vi phân cấp cao........................................................................................... 96
4.5.1 Định nghĩa đạo hàm cấp cao ................................................................................... 96
4.5.2 Các công th c tổng quát đối với đạo hàm cấp n ..................................................... 97
4.5.3 Vi phân cấp cao ....................................................................................................... 97
4.6 Công th c Taylor ........................................................................................................... 98
4.6.1 Công th c Taylor .................................................................................................... 99
4.6.2 Khai triển Maclaurin ............................................................................................. 101
4.7 Qui tắc L’hospital để khử dạng vô định ....................................................................... 103
4.7.1 Dạng vô định ......................................................................................................... 103
4.7.2 Dạng vô dịnh ......................................................................................................... 105
4.8 Khảo sát hàm số ........................................................................................................... 108
4.8.1 Khảo sát đư ng cong cho dưới dạng phương trình hiện ....................................... 108
4.8.2 Đư ng cong cho dưới dạng tham số ..................................................................... 110
4.8.3 Khảo sát đư ng cong trong tọa độ cực.................................................................. 114
4.9 Bài tập chương 4 .......................................................................................................... 117
Chương 5 Tích phân không xác định ............................................................................... 123 5.1
Tích phân không xác định ...................................................................................... 123
5.1.1 Định nghĩa nguyên hàm ..................................................................................... 123
5.1.2 Các tính chất....................................................................................................... 123
5.1.3 Định nghĩa tích phân không xác định................................................................. 123
5.1.4 Các tính chất c a tích phân không xác định....................................................... 123
5.1.5 Bảng các tích phân cơ bản.................................................................................. 124 5.2
Cách tính tích phân không xác định ....................................................................... 125
5.2.1 Dựa vào bảng các tích phân cơ bản.................................................................... 125
5.2.2 Tính tích phân nh phép đổi biến....................................................................... 126
5.2.3 Phương pháp tính tích phân từng phần............................................................... 127 5.2.4 Công
th c truy hồi.............................................................................................. 129 5.3
Tích phân các phân th c hữu tỉ .............................................................................. 130 4
5.3.1 Tích phân các phân th c hữu tỉ đơn giản nhất ................................................... 130
5.3.2 Tích phân c a các phân th c hữu tỉ.................................................................... 132 5.4
Tích phân các biểu th c ch a hàm lượng giác và các hàm hypebol ...................... 134
5.4.1 Tích phân các biểu th c ch a hàm lượng giác................................................... 134
5.4.2 Tích phân các biểu th c ch a hàm hypebol ....................................................... 136 5.5
Tích phân một vài lớp hàm vô tỉ ............................................................................ 137 ax + b I = ( R , m x )dx 5.5.1 Tích phân dạng ∫ cx + d
............................................................................ 137 p r ⎡ ax b ax b ⎤ + + I = R ⎢ ,( x ) q ,( )s ⎥ d , x ∫ 5.5.2 Tích phân dạng cx ⎢ + d cx + d ⎥ ⎣ ⎦
.................................................................... 138
5.5.3 Tích phân các nhị th c vi phân .......................................................................... 138 2 5.6
Tích phân các biểu th c dạng R( , x
ax + bx + c) với a ≠ 0 ...................................... 139 5.6.1 Phép
thế Euler th nhất ..................................................................................... 140 5.6.2 Phép
thế Euler th hai ........................................................................................ 140 5.6.3 Phép
thế Euler th ba ......................................................................................... 141
5.6.4 Tích phân eliptic................................................................................................. 142
5.7 Bài tập chương 5 .................................................................................................... 143
Chương 6 Tích phân xác định........................................................................................... 145 6.1
Định nghĩa tích phân xác định................................................................................ 145
6.1.1 Bài toán diện tích hình thang cong..................................................................... 145
6.1.2 Bài toán tính khối lượng..................................................................................... 146
6.1.3 Định nghĩa tích phân xác định............................................................................ 146 6.1.4 Ý
nghĩa hình học c a tích phân xác định ........................................................... 148 6.2
Điều kiện khả tích .................................................................................................. 148
6.2.1 Điều kiện cần để hàm khả tích ........................................................................... 148 6.2.2 Các
tổng Darboux............................................................................................... 149
6.2.3 Các tính chất c a tổng tích phân Darboux ......................................................... 150
6.2.4 Dấu hiệu tồn tại c a tích phân xác định ............................................................. 151 6.3 Các
lớp hàm khả tích.............................................................................................. 152 6.4
Các tính chất cơ bản c a tích phân......................................................................... 154
6.4.1 Các tính chất c a tích phân xác định.................................................................. 154 6.4.2 Các
định lí giá trị trung bình .............................................................................. 158 6.5
Nguyên hàm và tích phân xác định ........................................................................ 159 6.5.1 Các
định nghĩa.................................................................................................... 160
6.5.2 Tích phân xác định như hàm c a cận trên.......................................................... 160 6.6
Tính tích phân xác định.......................................................................................... 162 6.6.1 Phép
đổi biến trong tích phân xác định.............................................................. 162 6.6.2 Phép
lấy tích phân từng phần ............................................................................. 164 6.6.3 Tính
gần đúng tích phân xác định ...................................................................... 168
6.7 Một số ng dụng hình học, vật lý c a tích phân xác định...................................... 172 6.7.1 Tính
diện tích hình phẳng................................................................................... 172 6.7.2 Tính
độ dài đư ng cong phẳng........................................................................... 177 6.7.3 Tính
thể tích vật thể............................................................................................ 180
6.7.4 Diện tích mặt tròn xoay...................................................................................... 183 6.8
Tích phân suy rộng................................................................................................. 186
6.8.1 Tích phân suy rộng loại 1................................................................................... 186
6.8.2 Tích phân suy rộng loại 2................................................................................... 195 6.8.3 Thay
biến số trong tích phân suy rộng ............................................................... 199 5
6.9 Bài tập chương 6 ..................................................................................................... 200
Chương 7 Hàm số liên tục trong n ............................................................................... 206 n 7.1 Tập hợp trong
.................................................................................................. 206 n 7.1.1 Khoảng cách trong
...................................................................................... 206 7.1.2 Lân
cận c a một điểm ........................................................................................ 207
7.1.3 Điểm trong, điểm biên, điểm tụ c a tập hợp ...................................................... 208
7.1.4 Tập m , tập đóng................................................................................................ 210
7.1.5 Tập liên thông..................................................................................................... 210 n 7.2 Sự hội tụ trong
, các khái niệm cơ bản c a hàm số nhiều biến số................... 211 n 7.2.1 Sự hội tụ trong
............................................................................................. 211 7.2.2 Dãy
cơ bản.......................................................................................................... 212
7.2.3 Nguyên lí Canto ................................................................................................. 213 7.2.4 Chú
ý .................................................................................................................. 213
7.2.5 Tập hợp compact ................................................................................................ 214
7.2.6 Định nghĩa hàm nhiều biến số............................................................................ 214
7.2.7 Tập xác định c a hàm nhiều biến số .................................................................. 214
7.2.8 Đư ng m c và mặt m c..................................................................................... 215 n
7.3 Giới hạn c a hàm số trong
............................................................................... 216
7.3.1 Giới hạn c a hàm số tại một điểm...................................................................... 216
7.3.2 Giới hạn lặp ........................................................................................................ 217 7.3.3 Quan
hệ giữa giới hạn theo tập hợp các biến và các giới hạn lặp ...................... 218 7.3.1 Chú
ý .................................................................................................................. 219 7.4 Hàm
số nhiều biến số liên tục ................................................................................ 221 7.4.1 Hàm
số liên tục tại một điểm ............................................................................. 221 7.4.2 Hàm
số liên tục đều............................................................................................ 222 7.4.3 Liên
tục theo từng biến....................................................................................... 223 7.5
Phép tính vi phân c a hàm số nhiều biến số .......................................................... 224
7.5.1 Đạo hàm riêng và vi phân cấp một..................................................................... 224
7.5.2 Đạo hàm và vi phân cấp cao............................................................................... 230 7.6
Đạo hàm c a hàm số ẩn.......................................................................................... 233 7.6.1 Khái
niệm về hàm số ẩn một biến số ................................................................. 233 7.6.2 Khái
niệm hàm số ẩn c a hai biến số ................................................................. 235 7.7
Đạo hàm theo hướng .............................................................................................. 237
7.7.1 Đạo hàm theo hướng .......................................................................................... 237
7.7.2 Gradien ............................................................................................................... 238 7.8 Công
th c Taylor. Cực trị c a hàm số nhiều biến số ............................................. 239 7.8.1 Công
th c Taylor ............................................................................................... 239
7.8.2 Cực trị c a hàm nhiều biến số ............................................................................ 241 7.8.3 Giá
lớn nhất và nhỏ nhất c a hàm số nhiều biến số trên compac ...................... 244
7.9 Cực trị có điều kiện ................................................................................................ 245
7.9.1 Định nghĩa:......................................................................................................... 245
7.9.2 Phương pháp tìm cực trị ..................................................................................... 245 7.10
ng dụng c a phép tính vi phân trong hình học .................................................... 250
7.10.1 Tiếp tuyến c a đư ng cong ............................................................................ 250
7.10.2 Mặt phẳng tiếp xúc c a mặt cong................................................................... 251 6 7.10.3
Độ cong .......................................................................................................... 253 7.10.4
Bao hình c a một họ đư ngcong ................................................................... 255 7.11 Bài
tập chương 7 .................................................................................................... 258
7.12 Hướng dẫn giải bài tập và đáp số ........................................................................... 262
Tài liệu tham khảo............................................................................................................ 302 7 Chương 1
Tập hợp và số thực
1.1 Khái niệm về tập hợp 1.1.1 Tập hợp
Cho tập hợp M, để chỉ x là phần tử c a tập M ta viết x ∈ M (đọc là x thuộc M), để chỉ x
không phải là phần tử c a tập M ta viết x ∉ M (đọc là x không thuộc M).
Tập hợp M chỉ có một phần tử a, kí hiệu là { } a .
Tập hợp M không có phần tử nào gọi là tập rỗng, ký hiệu là ∅ .
Cho hai tập A và B. Nếu mỗi phần tử c a A đều là phần tử c a B ta nói rằng A là tập con
c a B và ta viết A ⊆ B .
Nếu A là tập con c a B và A ≠ B ta nói rằng A là tập hợp con thực sự c a tập hợp B và
viết là A ⊂ B . Trong trư ng hợp này tồn tại ít nhất một phần tử trong B mà không phải là
phần tử c a A. Ví dụ như tập hợp các số nguyên là tập con c a tập hợp các số hữu tỷ .
Cho A, B, C là ba tập hợp. Khi đó có tính chất sau: a) ∅ ∈ A (1.1.1)
b) A ⊆ B vµ B ⊆ A ⇒ A = B ( 1.1.2)
c) A ⊂ B v
µ B ⊂ C ⇒ A ⊂ C. ( 1.1.3)
1.1.2 Một số tập hợp thường gặp
Trong các giáo trình đại số trư ng phổ thông trung học ta đã làm quen với tập hợp các số tự nhiên ʼ
ʼ ={ 0,1,2,…, n,…} (1.1.4)
ʼ *={1,2,… n,…}. (1.1.5)
Để xét nghiệm c a phương trình x+n = 0 trong đó n∈ʼ ta đưa thêm tập các số nguyên ¦ : ¦ = {0, 1 ± ,±2,...,±n, } ... . (1.1.6)
Để xét nghiệm c a phương trình mx + n = 0 trong đó ,
m n ∈ ¦ ta đưa thêm tập các số hữu tỷ 8 ⎧ m ⎫ ˜ = x | ⎨ x = , n ≠
0, m,n ∈ ¦⎬ . (1.1.7) ⎩ n ⎭
Ta đã biết bốn phép toán cơ s (cộng, trừ, nhân, chia) c a số hữu tỷ và cách sắp xếp
chúng theo độ lớn (nếu a, b là hai số hữu tỷ, thì một trong chúng bé hơn số th hai). Tổng a
a+b, hiệu a - b, tích a.b, thương
(b ≠ 0) c a hai số hữu tỷ a,b lại là số hữu tỷ, nhưng với b
các phép toán khác nếu chỉ xét trên tập các số hữu tỷ, ta thấy những điều nêu trên không còn
đúng nữa. Ví dụ phép lấy căn là phép toán như vậy. Ta hãy tìm căn bậc hai c a số 2, t c là
tìm một số x mà bình phương c a nó bằng 2. Ta khẳng định rằng không có số hữu tỷ nào mà
bình phương c a nó bằng 2. Giả sử rằng số hữu tỷ x như vậy tồn tại, ta có thể viết dưới dạng p 2 p phân số tối giản
, trong đó p và q chỉ có ước số chung là 1 ± . Khi đó 2 2 = 2; 2 p = q cho q 2 q
nên p2 là số chẵn và do đó p cũng là số chẵn, p = 2m, trong đó m là số nguyên, do đó
4m2=2q2, 2m2=q2 cho nên q2 là số chẵn và vì thế q là số chẵn. Như vậy p,q là các số chẵn,
điều này mâu thuẫn với giả thiết là p,q chỉ có ước chung là ±1. Mâu thuẫn nhận được ch ng minh khẳng định trên.
Từ nguyên nhân này, trong toán học ta đưa thêm vào những số mới, đó là các số vô tỷ. Ví
dụ vể số vô tỷ là 2, 3, lg3, π , sin20o…
Tập các số hữu tỷ và các số vô tỷ được gọi là tập các số thực và kí hiệu là { . Như vậy ta có bao hàm th c: ⊂ ⊂ ⊂ . (1.1.8)
1.1.3 Các phép toán trên tập hợp
a) Hợp A ∪ B c a tập hợp A và tập hợp B, đọc là “A hợp B” là tập hợp được định nghĩa b i:
A ∪ B = {x | x ∈ A hoÆc x ∈ } B . (1.1.9)
b) Giao A ∩ B c a hai tập hợp A và B, đọc là “A giao B” là tập hợp định nghĩa b i:
A ∩ B = {x | x ∈ A vµ x ∈ B }. (1.1.10)
c) Hiệu A| B = {x| x A
∈ vµ x ∉ B} . (1.1.11)
Ta nói rằng các tập A và B là r i nhau nếu A ∩ B = Φ .
d) Bổ sung CAB c a B trong A ( B ⊆ A ) là tập hợp định nghĩa b i
C B = {x| x ∈ A vµ x ∉ B} (1.1.12) A
Phép giao, hợp và bổ sung có các tính chất sau:
i) ( A ∩ B) ∩ C = A ∩ (B ∩ C) (1.1.13)
ii) ( A ∪ B) ∪ C = A ∪ (B ∪ C) (1.1.14)
iii) ( A ∩ B) ∪ C = ( A ∪ C) ∩ (B ∪ C) (1.1.15)
iv) ( A ∩ B) ∪ C = ( A ∩ C) ∪ (B ∩ C) (1.1.16) 9 v) A \ ∅ = A, ∅ \ A=∅ (1.1.17) vi) C ( B B C B C B (1.1.18) A ∪ ) = A ∩ 1 2 1 A 2 vii) C ( B B C B C B . (1.1.19) A ∩ ) = A ∪ 1 2 1 A 2 1.1.4 Tích Đề các
Cho hai tập hợp A,B không rỗng. Tích Đề các c a hai tập hợp A và B, kí hiệu là A× B là
tập hợp các cặp (x,y) trong đó x ∈ A, y ∈ B , đồng th i (x,y)= (a,b) khi và chỉ khi x = a, y = b. Như vậy
A× B ={(x,y)| x ∈ A, y ∈ B } (1.1.20)
Thay cho A× A ta viết là A2
Ví dụ: {1,2}× {2,3,4} = {(1,2); (1,3); (1,4); (2,2); (2,3); (2,4)}
Ngoài ra {1,2}2 ={(1,1); (1,2); (2,1); (2,2)}.
1.1.5 Các kí hiệu lôgic
Bây gi giả sử M là một tập hợp và t là một tính chất nào đó c a các phần tử c a tập M.
Nếu phần tử x ∈ M có tính chất t ta viết t(x). Gọi c(t) là tập hợp c a tất cả các phần tử c a tập
M có tính chất t:
c(t) ={ x ∈ M |x có tính chất t} (1.1.21) hay
c(t) ={ x ∈ M |t(x)} (1.1.22) khi đó nếu c(t) = M
thì mọi phần tử c a M đều có tính chất t, ta nói rằng “với mọi x ∈ M , x có tính chất t” và ta viết x
∀ ∈ M : t(x) hay ∀ t(x) . x M ∈
Ký hiệu ∀ gọi là ký hiệu phổ biến. Nếu (
c t ) ≠ ∅ , thì có ít nhất một phần tử x ∈ M , x có tính chất t” và viết x
∃ ∈ M : t(x) hay ∃ t(x) x M ∈
Ký hiệu ∃ gọi là ký hiệu tồn tại. 1.2 Số thực
1.2.1 Phép cộng và nhân các số thực
Xét tập hợp các số thực
. Ta có thể xác định phép cộng và nhân hai số thực bất kì a và
b. Phép toán cộng cho tương ng hai số thực a và b với số thực được ký hiệu là a+b, phép 10
nhân cho tương ng hai số thực a và b với số thực được kí hiệu là a.b sao cho thoả mãn các
tính chất sau: Với mọi số thực a,b và c.
a) a+b = b+a (tính chất giao hoán),
b) a+(b+c) = (a+b)+c (tính chất kết hợp),
c) a.b = b.a (tính chất giao hoán ),
d) a(b.c) = (a.b).c (tính chất kết hợp),
e) (a+b).c = a.c+b.c (tính chất phân phối),
f) Tồn tại duy nhất số 0 sao cho a+0 = a ∀a ∈ ,
g) Với mọi a, tồn tại số – a sao cho a + (− a) = 0,
h) Tồn tại duy nhất số 1 ≠ 0 sao cho a.1 = a ∀a ∈ , 1
i) Với mọi số a ≠ 0, tồn tại số a-1 sao cho a.a-1= 1, số a-1 còn được kí hiệu là . a
Chú ý: Số (− a) và số a-1 nói trong tính chất g) và i) là duy nhất. Thật vậy, ví dụ như nếu tồn tại
số b ≠ − a thoả mãn điều kiện a+b =0, thì a+b+ (− a)= − a, từ đây a+ (− a)+b=− a hay 0+b = −
a và b= − a, mâu thuẫn.
1.2.2 So sánh hai số thực a và b
Cho hai số thực bất kì a và b. Khi đó chỉ có thể xảy ra một trong ba trư ng hợp sau:
a = b (a bằng b), a > b (a lớn hơn b) hay b > a (b lớn hơn a).
Mệnh đề “=” có tính chất: nếu a=b và b=c thì a=c.
Mệnh đề “>” có tính chất sau: Với mọi số thực a,b và c.
a) Nếu a > b và b > c thì a > c
b) Nếu a > b thì a+c > b+c.
c) Nếu a > 0, b > 0 thì ab > 0.
Mệnh đề a ≥ b nghĩa là hoặc a=b, hoặc a>b.
Các mệnh đề a < b, a ≤ b, a > b, a ≥ b được gọi là các bất đẳng th c. Các bất đẳng th c
a < b, a > b được gọi là các bất đẳng th c thực sự.
Số thực a thoả mãn bất đẳng th c a>0 được gọi là số dương.
Số thực a thoả mãn bất đẳng th c a<0 được gọi là số âm.
1.2.3 Tính liên tục c a tập hợp số thực
Định lí 1.2.1 Giả sử X và Y là hai tập hợp các số thực thoả mãn điều kiện sau: x ≤ y x ∀ ∈ X, y ∀ ∈ Y . (1.2.1)
Khi đó tồn tại một số c sao cho
x ≤ c ≤ y ∀
x ∈ X, ∀y ∈ Y . (1.2.2) 11
Chú ý rằng chỉ có tập hợp các số thực mới có tính chất này. Ví dụ như, giả sử
X = {x hữu tỉ | x < 2 } và
Y = {y hữu tỉ | y > 2 }.
Khi đó đối với mọi x ∈ X với mọi y ∈ Y thoả mãn x ≤ y, nhưng không tồn tại số hữu tỉ c
nào sao cho x ≤ c ≤ y . Thật vậy, số như vậy chỉ có thể là 2 , nhưng 2 không phải là số hữu tỉ.
Trong lý thuyết số vô tỉ ngư i ta ch ng minh được rằng với hai số thực bất kì α,β trong
đó α < β luôn luôn tìm được một số thực và đặc biệt một số hữu tỉ r nằm giữa hai số đó (và
thành thử có một tập vô số các số vô tỉ như vậy nằm giữa α và β ).
1.2.4 Cận c a tập hợp số
Giả sử M là tập hợp số (t c là tập hợp mà các phần tử c a nó là những số thực). Tập hợp
M được gọi là bị chặn trên nếu tồn tại một số thực k sao cho x ≤ k x ∀ ∈ M . (1.2.3)
Số k bất kì có tính chất như vậy được gọi là cận trên c a tập M. Do đó tập hợp M là bị
chặn trên nếu có ít nhất một cận trên. Nếu tập M có một cận trên thì nó có vô hạn cận trên, b i
vì nếu số k là cận trên thì bất kì số l nào lớn hơn k là cận trên. Một câu hỏi được đặt ra là liệu
có tồn tại số nhỏ nhất trong các cận trên c a tập M. Số nhỏ nhất như vậy gọi là cận trên đúng
c a tập M và kí hiệu là sup M.
Cận trên đúng c a tập M có tính chất sau: ∀ε > 0, ∃
x ∈ M sao cho
x > supM - ε .
Thật vậy, nếu số x như vậy không tồn tại thì số supM − ε cũng là cận trên và khi đó số
supM không phải là cận trên đúng c a tập M. Nói một cách khác, tính chất này nói lên supM
là số nhỏ nhất trong số các cận trên c a M.
Ví dụ 1: Tìm cận trên đúng c a tập 1 1 1 M = {1, , ,..., ,...}. 2 3 n 1
Giải: Ta thấy 0 <
≤ 1 ∀n ∈ * , vì thế tập hợp M bị chặn trên, dễ thấy số 1 là cận n
trên. Ta hãy ch ng minh số 1 là cận trên đúng c a M. Thật vậy ε
∀ > 0 , ta phải tìm được số 1 tự nhiên n sao cho
> 1 − ε . Số n này, ví dụ là n = 1. n
Ví dụ 2: sup(0,1) = sup[0,1] = 1.
Bây gi ta có thể định nghĩa cận trên đúng c a tập M một cách khác như sau:
Số supM được gọi là cận trên đúng c a tập M bị chặn trên nếu
a) x ≤ sup M ∀ x ∈ M (1.2.4) b) ∀ε > 0, ∃ x ∈ M sao cho sup x > M - ε (1.2.5) 12
Tập hợp số M được gọi là bị chặn dưới, nếu tồn tại số g sao cho x ≥ g x ∀ ∈ M . (1.2.6)
Mọi số g có tính chất này gọi là cận dưới c a tập hợp M. Do đó tập M bị chặn dưới, nếu
nó có ít nhất một cận dưới.
Số lớn nhất trong các cận dưới c a tập M gọi là cận dưới đúng c a M và được kí hiệu là inf M.
Ví dụ 3: Xét tập M=(a,b)
Hiển nhiên số a và số bất kì bé hơn a là cận dưới c a M. Hiển nhiên số a là cận dưới
đúng c a tập M, t c là a= inf M.
Tương tự như đối với cận trên đúng, cận dưới đúng có tính chất sau:
∀ε, ∃x ∈ M sao cho x < inf M + ε . (1.2.7) 1 1 1
Ví dụ 4: Xét tập M = {1, , ,..., ,...} 2 3 n
Ta ch ng minh rằng số 0 là cận dưới đúng c a tập M. Thật vậy, ε
∀ > 0 , ta phải tìm được số tự nhiên n sao cho 1 < 1 1 0 + ε, hay < ε ⇒ n > . n n ε
Điều này nghĩa là số 0 là cận dưới đúng c a tập M, t c là inf M = 0.
Ví dụ 5: inf(0,1) = inf[0,1] = 0.
Trong các ví dụ trên, ta thấy sup M, inf M có thể thuộc M, cũng có thể không thuộc M.
Định lí 1.2.2 Tập hợp số không rỗng bất kì bị chặn trên (dưới) có cận trên (dưới) đúng.
Ch ng minh: Giả sử X là tập hợp số không rỗng bị chặn trên. Khi đó tập hợp Y các số là
cận trên c a tập X không rỗng. Theo định nghĩa c a cận trên suy ra rằng đối với bất kì x ∈ X
và bất kì y ∈ Y ta có bất đẳng th c. x ≤ y .
Dựa vào tính chất liên tục c a tập hợp các số thực, tồn tại một số c sao cho
x ≤ c ≤ y ∀
x ∈ X, ∀y ∈ Y . (1.2.8)
Từ bất đẳng th c th nhất trong (1.2.8) suy ra số c chặn trên tập hợp X, từ bất đẳng th c
th hai trong (1.2.8) suy ra c là số bé nhất trong các cận trên c a X, t c là cận trên đúng c a tập X.
Ví dụ 6: Ch ng minh rằng tập hợp các số nguyên
X= {…,−3, −2, −1,0,1,2,3,…}
không bị chặn trên, cũng không bị chặn dưới, t c là
supX= + ∞ và inf X= − ∞ .
Thật vậy, giả sử ngược lại, tập hợp X bị chặn trên. Khi đó theo định lí trên, nó có cận trên đúng 13 c = sup X.
Theo tính chất c a cận trên đúng, đối với ε = 1 , ta tìm được một số nguyên x ∈ X sao cho x > c – 1
nhưng khi đó x+1> c. B i vì x + 1 ∈ X , điều này có nghĩa là c không phải là cận trên đúng
c a tập hợp X, mâu thuẫn với điều nói trên.
Ví dụ 7: Giả sử X và Y là hai tập hợp số. Hãy ch ng minh rằng nếu Y ⊂ X thì supX ≥ supY.
Giải: Giả sử supX = A, supY = B. Ta phải ch ng minh B ≤ A. Giả sử ngược lại B > A. Khi
đó dựa vào tính chất cận trên đúng, ε
∀ > 0,∃y∈ Y sao cho y > B − ε .
B i vì: B− A >0, nên ta có thể lấy ε = B − A . Ta nhận được y >B −ε = B –B +A, t c là y > A.
Nhưng y ∈ Y và Y ⊂ X nên y ∈ X , theo định nghĩa sup suy ra y ≤ A . Mâu thuẫn nhận
đựơc ch ng tỏ rằng B ≤ A .
Ta có thể ch ng minh khẳng định trên bằng cách khác như sau:
B i vì Y ⊂ X nên x ∀ ∈ X và y ∀ ∈ Y ta có
x ≤ sup X, y ≤ sup X và y ≤ sup Y .
Nhưng supY là số thực nhỏ nhất trong các cận trên c a Y và supX là một trong số cận trên c a Y nên
sup Y ≤ sup X.
Nếu tập M đồng th i bị chặn dưới và bị chặn trên, ta gọi là tập bị chặn.
Cuối cùng nếu tập M không bị chặn trên, thì ta nói rằng cận trên đúng c a tập đó là + ∞ ,
sup M = + ∞ . Tương tự nếu tập M không bị chặn dưới, ta nói rằng cận dưới đúng c a tập đó là
−∞ , inf M=− ∞ .
Ví dụ như sup(0,+ ∞ ) = + ∞ , inf(− ∞ ,0)= − ∞ .
Giả sử M là tập hợp các số thực, nếu tồn tại một phần tử lớn nhất trong các phần tử c a
tập M, thì ta kí hiệu phân tử đó là maxM. Tương tự ta kí hiệu phân tử nhỏ nhất c a tập M là minM.
Ví dụ như max{2, –3, –5,0} = 2, min{2,–3, –5,0}=–5,
|x|=max {(–x,x)} x ∀ .
1.2.5 Trục số thực
Bây gi ta tìm cách biểu diễn hình học tập các số thực.
Ta lấy một đư ng thẳng nằm ngang và trên đó ta lấy một điểm 0 nào đó làm gốc. Ta chon
một độ dài thích hợp làm đơn vị và đặt độ dài đó liên tiếp nhau từ điểm 0 sang trái và sang
phải sao cho trải khắp đư ng thẳng. Ví dụ như số 2 được biểu diễn bằng “điểm 2”, t c là điểm
bên phải điểm 0 với khoảng cách 2 đơn vị.
Ta gọi đư ng thẳng nói trên là đư ng thẳng thực hay trục số. Bất kỳ một số thực nào
cũng được ng với một điểm trên đư ng thẳng thực và ngược lại, bất kì một điểm nào trên 14
đư ng thẳng thực cũng được ng với một số thực. Số thực a ng với điểm M trên trục số được
gọi là toạ độ c a điểm M. Thông thư ng ngư i ta không phân biệt “điểm a” nằm trên đư ng
thẳng thực và số thưc a (là toạ độ c a điểm đó). Tập hợp
không có phần tử cực đại và phần tử cực tiểu, b i vì đối với một số thực x bất
kì luôn luôn tồn tại hai số y và z sao cho y< x< z (ví dụ y = x −1, z = x+1). Vì thế ta hãy bổ sung vào tập
hai phần tử mới mà ta ký hiệu là + ∞ , − ∞ và ta gọi chung là các điểm vô tận
c a trục thực. Ta ký hiệu tập mới xuất hiện như vật là *. Như vậy là *= ∪ {− ∞ , + ∞ }. (1.4.2)
Tập hợp R* ta sẽ gọi là trục thực m rộng. Cuối cùng ta chú ý thêm là
−∞ < a < +∞ , ∀a ∈ . (1.4.3) 1.3 Ánh xạ
Trong phần này chúng ta sẽ trình bày một vài khái niệm về ánh xạ mà nó rất có ích cho
việc nghiên c u lý thuyết hàm số sau này. 1.3.1 Định nghĩa
Cho hai tập hợp A và B. Ánh xạ từ tập hợp A tới tập hợp B là một quy luật f cho tương
ng mỗi phần tử x ∈ A với một và chỉ một phần tử y ∈ B .
Ví dụ 1: Cho A = B = .
Qui luật y = x3 cho tương ng mỗi x ∈
với một và chỉ một y ∈ , nên qui luật trên là một ánh xạ từ tới .
Ví dụ 2: Cho A = B = {x | x ∈ , x ≥ 0 }.
Qui luật y = x cho tương ng mỗi x ∈ A với một và chỉ một y ∈ B , nên là một ánh xạ từ A tới B
Để diễn tả f là ánh xạ từ tập hợp A tới tập hợp B ta viết f: A →B hay ⎯⎯ f A →B và gọi
A là tập xác định c a ánh xạ f.
Phần tử y ∈ B tương ng với x ∈ A b i qui luật f gọi là ảnh c a x và x được gọi là
nghịch ảnh c a y và ta viết:
y = f (x ) hay x
y = f (x) . Ta gọi tập
f ( A) = { y| y = f (x), x ∈ A} (1.3.1) hay
f ( A) = { y| ∃x ∈ A, y = f (x)} (1.3.2)
là ánh xạ c a tập A qua ánh xạ f.
Chú ý rằng ta luôn có f ( A) ⊆ B . Nếu f(A)=B, ta nói rằng f là ánh xạ từ tập hợp A lên tập
hợp B hay ánh xạ f : A → B là một toàn ánh. 15
Ví dụ 3: Ánh xạ cho b i qui luật f (x) = sin ,
x x ∈ là ánh xạ tập tới tập và đồng th i
ánh xạ tập lên tập hợp tất cả các số thực y sao cho 1 − ≤ y ≤ 1. Nếu như M ⊂
⊂ A thì f (M ) ⊆ f ( ) . (1.3.3)
1.3.2 Đơn ánh, song ánh
Ánh xạ f : A → B gọi là ánh xạ đơn ánh nếu
f ( x ) = f (x ) ⇒ x = x (1.3.4) 1 2 1 2 π
ví dụ như ánh xạ được cho b i sinx là đơn ánh từ tập hợp { x ∈ | 0 < x < } lên tập hợp 2
{ y ∈ | 0 < y < 1} .
Ví dụ 4: Xét ánh xạ cho b i qui luật 2
y = x . Vì phương trình y = 2
x , y ∈ có hai nghiệm
khác nhau x1 và x2 nếu y > 0, có nghĩa là f(x1) = f(x2) nhưng x ≠ x , vậy ánh xạ này không 1 2 phải là đơn ánh.
Ánh xạ f : A → B gọi là một song ánh nếu nó vừa là đơn ánh vừa là toàn ánh.
Ví dụ 5: Ánh xạ f : → cho b i qui luật 3
y = x là một song ánh
Ví dụ 6: Ánh xạ f : + → cho b i qui luật 2
y = x không phải là song ánh, nhưng ánh xạ f : + + → cho b i qui luật 2
y = x là một song ánh.
Ví dụ 7: Cho x ∈ , [x] ký hiệu phần nguyên c a x (nghĩa là [x] là số nguyên lớn nhất không
lớn hơn x chẳng hạn [−4,5] = −4; [2] = 2; [2,5] = 2; [2,7] = 2). Ta có [x] ≤ x ≤ [x]+1. Ánh xạ f :
→ cho b i qui luật y=[x] không phải là song ánh.
1.3.3 Ánh xạ ngược
Giả sử f là một ánh xạ tập hợp A lên tập hợp B. Khi đó ng với mỗi phần tử có một và chỉ
một x ∈ A sao cho y = f (x) . Ánh xạ cho tương ng phần tử y ∈ B với phần tử x ∈ A sao
cho y = f (x) gọi là ánh xạ ngược c a ánh xạ f kí hiệu là f 1 − . Như vậy f 1 − : B → A f 1
− ( y) = x ⇔ f (x) = y (với x ∈ A , y∈ B ). (1.3.5) 16 Hình 1.3.1
Ví dụ 8: Nếu A là tập hợp các vòng tròn đồng tâm nằm trên cùng một phẳng và f(x) là bán
kính c a vòng tròn x, khi đó f là ánh xạ đơn trị tập A lên tập các số thực dương. Khi đó ánh xạ
ngược f −1 tương ng một số thực dương x với vòng tròn nằm trong tập A mà bán kính c a nó là x.
1.3.4 Hợp (tích) c a hai ánh xạ Cho hai ánh xạ:
g : M → A
vµ f : A → B .
Xét ánh xạ từ tập M tới tập hợp B được xác định như sau:
x ∈ M → z = f ( (
g x)) ∈ B . (1.3.6)
Ánh xạ này gọi là hợp c a ánh xạ g và ánh xạ f (hay tích c a g và f ), ký hiệu là f g Như vậy f
g : M → B f ( g x) = f ( (
g x)), x ∈ M . (1.3.7)
Ví dụ 9: Ánh xạ cho b i qui luật sinx2, x ∈ R là hợp c a ánh xạ trong cho b i qui luật x2,
x ∈ và ánh xạ ngoài được cho b i qui luật siny, y ∈
Ánh xạ sin2x, x ∈
là hợp c a ánh xạ trong cho b i sinx, x ∈ và ánh xạ ngoài cho b i y2, y ∈ .
1.4 Bài tập chương 1
1.1 Cho a là số vô tỉ, r là số hữu tỉ
1) Hãy ch ng minh rằng a+r và a− r là các số vô tỉ a r
2) Giả sử r ≠ 0 hãy ch ng minh rằng các số ar, , là các số vô tỉ. r a
1.2 Cho a,b∈ , gọi số 17 d( , a b) | = a − |
b là khoảng cách giữa hai điểm a và b c a trục số Hãy ch ng minh rằng 1) d(a,a) = 0
2) d(a,b)>0 khi a ≠ b
3) d(a,b) =d(b,a)
4) d(a,b) + d(b,c) ≥ d( , a ) c .
1.3 Hãy ch ng minh mệnh đề “tập hợp M ⊂
là bị chặn khi và chỉ khi tồn tại số thực r>0
sao cho: |x| ≤ r x ∀ ∈ M . 1.4 Cho X ⊂
. Định nghĩa: (−X) = {−x|x∈X} Hãy ch ng minh:
1) inf(−X) = −sup X
2) sup(−X)= −inf X
1.5 Cho X ,Y ⊂ . Định nghĩa
X+Y = { a ∈ R| ∃x ∈ X ,∃y ∈ Y , a = x + y }
XY = {a ∈ R| ∃x ∈ X ,∃y ∈ Y , a = xy}
Nghĩa là X+Y là tập hợp các số thực có dạng x+y với x ∈ X, y ∈ Y , còn XY là tập hợp
các số thực có dạng xy với x ∈ X , y ∈ Y .
1) Giả sử X,Y bị chặn trên, ch ng minh:
sup(X+Y) = supX+ supY
2) Giả sử X, Y bị chặn dưới, ch ng minh:
inf(X+Y) = inf X + inf Y
3) Giả sử X, Y bị chặn trên, + + X ⊂ ,Y ⊂ .
Ch ng minh: sup(XY)= (sup X)(sup Y)
4) Giả sử X, Y bị chặn dưới, + X , + ⊂ Y ⊂ .
Ch ng minh: inf(XY) = (inf X)(inf Y). 1.6 Giả sử φ ≠ ⊂ ⊂ * M . Ch ng minh rằng: inf M ≤ inf ≤ sup ≤ sup M . 1.7 Cho A ⊂
và F = { f | f : A → A} . Ch ng minh rằng nếu f,g,h∈F và i là ánh xạ đồng
nhất trên tập A, t c là i(x) =x, ∀ x∈A thì: 1) ( f
g) h = f ( g h) , 2) f i = f .
1.8 Cho F là tập hợp nói trên và 18 *
F = { f | f : A → A và f là đơn ánh}
Ch ng minh rằng nếu f,g∈F* thì 1) f g ∈ F* 2) 1 f f − = i 19 Chương 2
Giới hạn c a dãy số và hàm số
2.1 Giới hạn c a dãy số
2.1.1 Định nghĩa dãy số Cho
* ={1,2,3,…} là tập hợp các số tự nhiên. Một ánh xạ f: * → được gọi là
một dãy số thực. Nếu đặt xn= f(n) thì ta có thể biểu diễn dãy số dưới dạng:
x , x , x ,..., x ,... (2.1.1) 1 2 3 n
Phần tử xn được gọi là số hạng th n c a dãy số.
Để cho gọn ta sẽ ký hiệu dãy số bằng {xn}. Chỉ số n trong số hạng xn chỉ vị trí c a số
hạng này trong dãy (2.1.1).
Trước hết ta hãy nêu ra một vài ví dụ về dãy: ⎧1 ⎫ 1 1 1 1 :
⎨ ⎬ x = 1, x = , x = ,x = ,...,x = ,... (2.1.3) 1 2 3 4 n 2 3 4 ⎩ ⎭ n n ⎧ n ⎫ 1 2 n : ⎨
⎬ x = , x = ,...,x = ,... (2.1.4) 1 2 ⎩n +1 2 3 ⎭ n n + 1 ⎧ 1 1 ⎫ 1 1 1 1 , : ⎨
⎬ x = , x = 1, x = ,..., x = , x = ,... (2.1.5) 1 2 3 2 1 − 2 2n 2 ⎩ n − 1 2 4 2n 2 ⎭ n n n − 1
Ta thấy rằng các số hạng c a dãy (2.1.3) và dãy (2.1.5) gần 0 tuỳ ý khi n tăng, các số
hạng c a dãy (2.1.4) gần 1 tuỳ ý khi n tăng. Ta nói rằng dãy (2.1.3) và dãy (2.1.5) có giới hạn
0, còn dãy (2.1.4) có giới hạn 1.
Bây gi ta đưa ra định nghĩa chính xác về giới hạn c a dãy.
Định nghĩa 1: Ta nói rằng số a là giới hạn c a dãy {xn} nếu đối với mọi số dương ε bé tuỳ
ý đều tìm được một số ∈ * p
sao cho ∀n > p n ∈ * , ta đều có:
|xn − a|< ε , t c là a− ε < xn < a+ε . (2.1.6)
Nếu a là giới hạn c a dãy {xn} thì ta viết:
lim x = a hay x → a khi n . (2.1.7) n n → ∞ n →∞
Ta chú ý rằng số p trên nói chung phụ thuộc vào việc chọn ε . Để nhấn mạnh điều đó
đôi khi thay cho p ta sẽ viết pε . 20
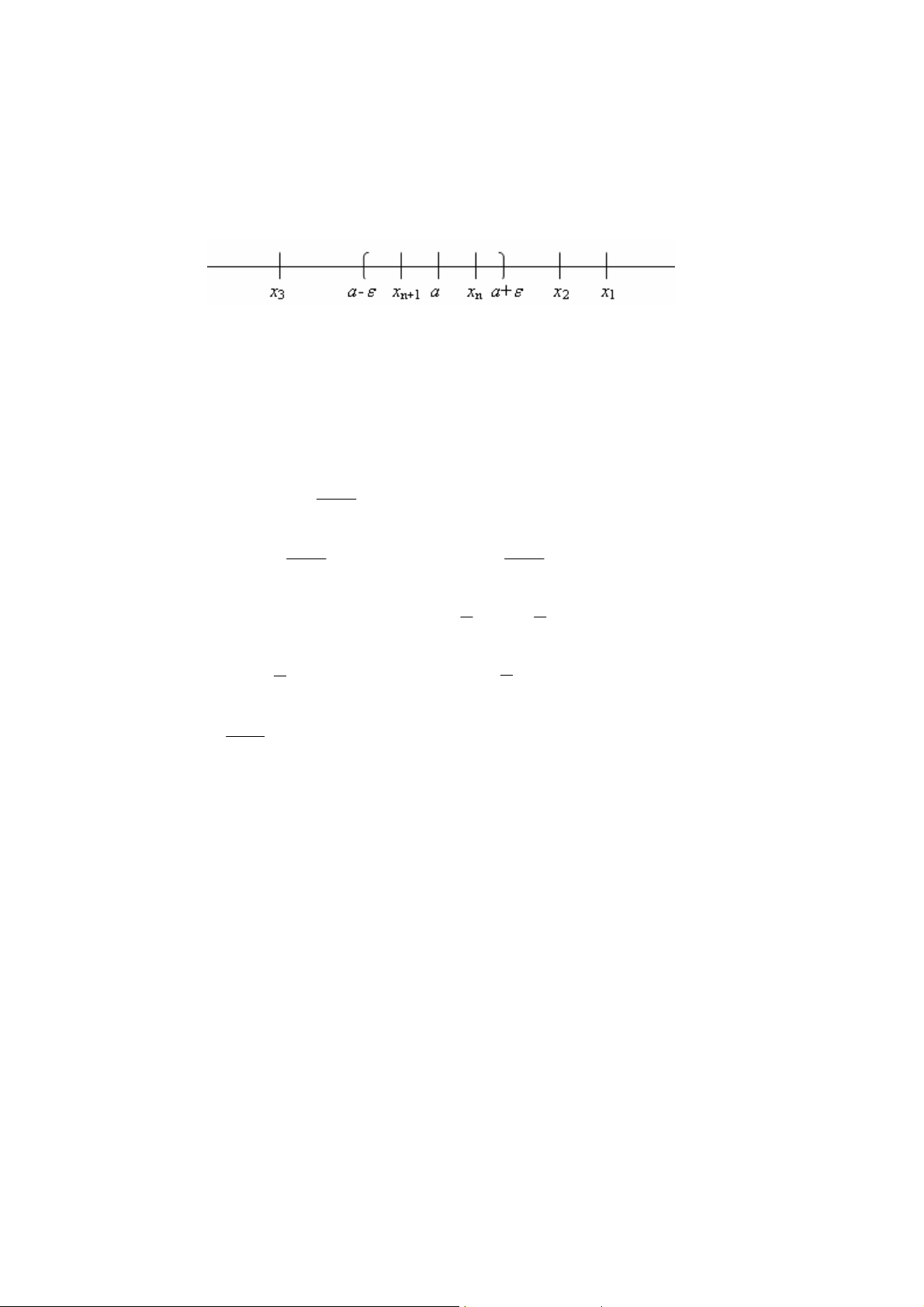
Khoảng m (a−ε , a+ε ) có tâm tại điểm a được gọi là lân cận c a điểm a. Như vậy, để a
là giới hạn c a dãy {xn} thì với lân cận bé bất kỳ c a điểm a tất cả các phần tử xn c a dãy
bắt đầu từ một chỉ số nào đó cần phải rơi vào trong lân cận đó (t c là ngoài lân cận đó chỉ
có thể có một số hữu hạn các phần tử xn). Hình 2.1.1
Nếu dãy (2.1.1) có giới hạn, ta nói rằng nó hội tụ, nếu không có giới hạn được gọi là phân kỳ. Ví dụ 1 ⎧ n ⎫ Hãy ch ng minh dãy ⎨ ⎬ có giới hạn là 1. ⎩n +1⎭ 1 1 Ta có: | x . Với mọi ε cho trước < ε n − 1| = n +1 n + 1 1 1
⇔ n +1 > ⇔ n > −1 ε ε . ⎡1 ⎤ 1 Nếu ta lấy p = −1 +1 ε ⎢ ⎥ 1 ∀ > ta có: |x ⎣ε (phần nguyên c a ( ⎦ ε − )) thì n pε n− 1|< ε . n Do đó lim = 1. n→∞ n + 1 Ví dụ 2 Hãy chỉ ra rằng dãy: {( 1 − )n } : 1, − 1, 1, − ..., (2.1.8) không có giới hạn.
Giả sử rằng dãy có giới hạn là a. Khi đó với ε =1, tồn tại số p sao cho với n>p ta có |xn – a|< ε =1.
Ta hãy chọn n lớn hơn p, khi đó n+1>p, cho nên
|xn+1 – a|<1.
Từ đó ta suy ra với n>p
|xn – xn+1|= |(xn − a)+ ( a −xn+1)| ≤ | xn − a|+| xn+1 − a|n< 1+1 = 2
điều này mâu thuẫn với tính chất c a các số hạng c a dãy (2.1.8) là: | xn – xn+1|= 2 ∀ ∈ * n .




