





















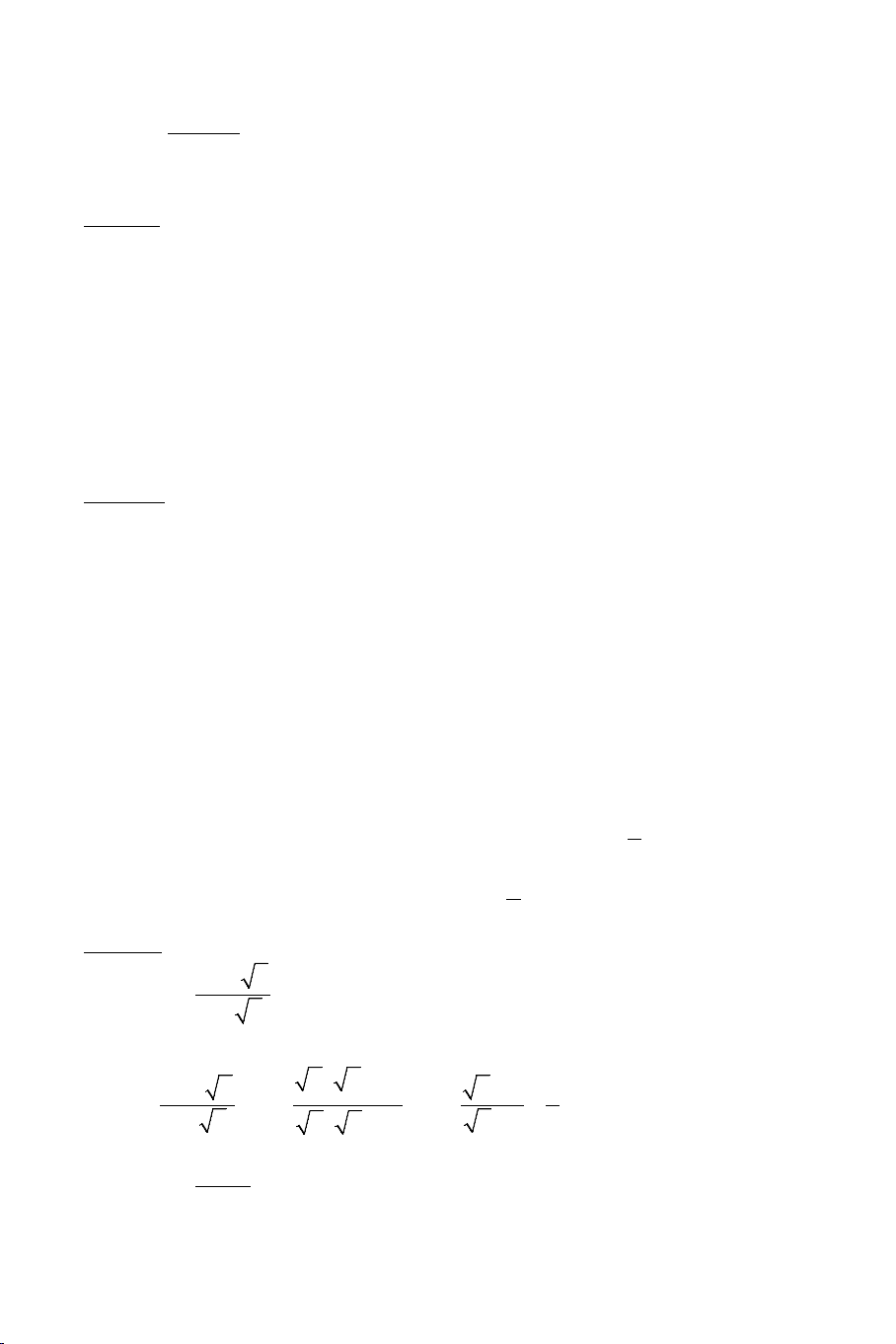





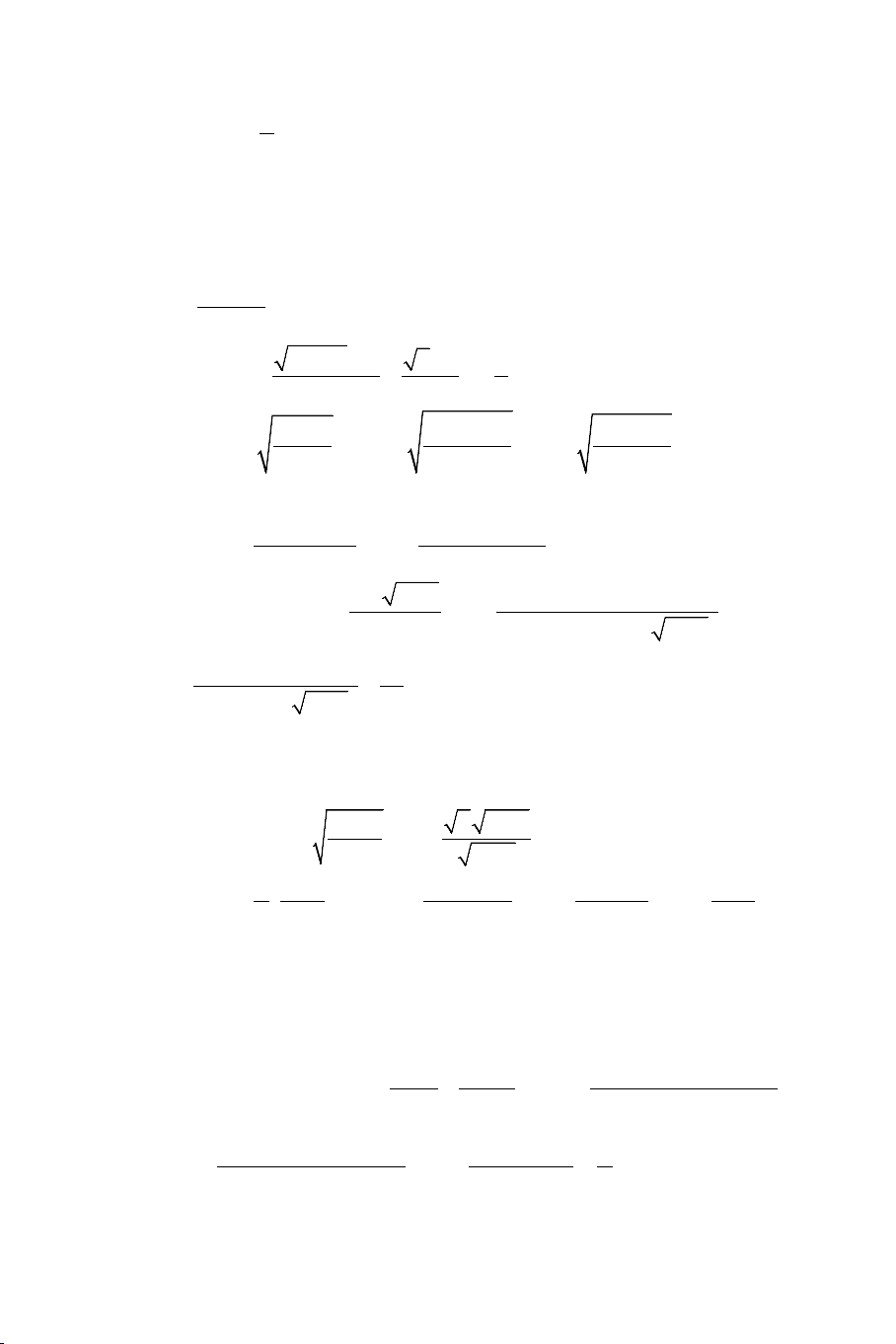
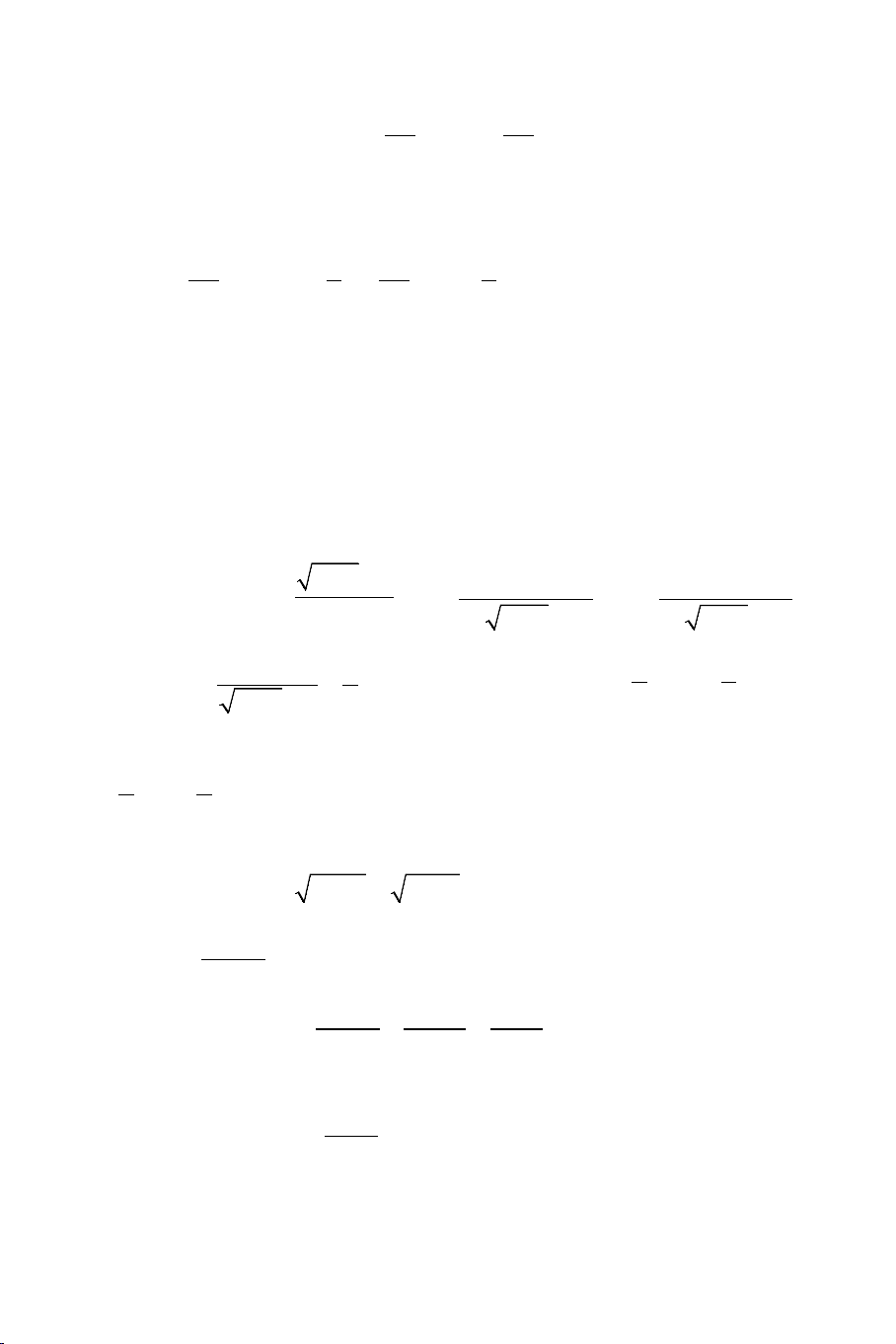












































Preview text:
Chương III:
GIỚI HẠN. HÀM SỐ LIÊN TỤC
Bài 1 GIỚI HẠN DÃY SỐ
A. TÓM TẮT LÝ THUYẾT.
I. Giới hạn hữu hạn của dãy số.
1. Giới hạn 0 của dãy số
- Ta nói dãy số (u có giới hạn 0 khi u n )
n dần tới dương vô cực, nếu n
nhỏ hơn một số dương bất kì cho trước, kể từ một số hạng nào đó trở
đi. Kí hiệu lim u = hay u → khi n → + .
∞ Ta còn viết là limu = n 0. n 0 n 0 n→+∞ - Nhận xét: • 1 lim
= 0, với k nguyên dương bất kì. k n • lim n
q = 0, với q là số thực thỏa mãn q <1.
2. Giới hạn hữu hạn của dãy số
• Ta nói dãy số (u có giới hạn hữu hạn là số u dần tới n ) a (hay n a ) khi n
dần tới dương vô cực, nếu lim(u − a = Khi đó, ta viết lim u = a hay n ) 0. n n→+∞
limu = a hay u → a khi n → + . ∞ n n
Chú ý: Nếu u = c ( u = c = c n
c là hằng số) thì lim n lim .
II. Các phép toán về giới hạn hữu hạn của dãy số.
Cho limu = a v = b và n , lim n
c là hằng số. Khi đó:
• lim(u + v = a + b . n n ) • lim( . c u = c a . n ) . • lim u a n = (b ≠ 0) . v b n
• lim(u − v = a − b . n n )
• lim(u v = a b . n . n ) . • Nếu u ≥ n ∀ ∈
thì a ≥ 0 và lim u = a n 0, * n
III. Tổng của cấp số nhân lùi vô hạn.
• Cấp số nhân vô hạn (u có công bội q thỏa mãn q <1 được gọi là cấp n )
số nhân lùi vô hạn.
Cấp số nhân lùi vô hạn này có tổng là: u1
S = u + u + ...+ u + = n .... . 1 2 1− q
IV. Giới hạn vô cực. 5
• Ta nói dãy số (u có giới hạn là +∞ khi n → +∞ nếu u lớn hơn một số n ) n
dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu limu = +∞ hay n
u → +∞ khi n → +∞ . n
• Ta nói dãy số (u có giới hạn là −∞ khi n → +∞ nếu lim( u − = +∞ ,kí n ) n )
hiệu limu = −∞ hay u → −∞ khi n → +∞ . n n
Chú ý: Ta có các kết quả sau:
• limu = +∞ khi và chỉ khi lim( u − = −∞ . n ) n
• Nếu limu = +∞ hoặc limu = −∞ thì 1 = . n n lim 0 un
• Nếu limu = và u > với mọi = +∞ . n 0 n 0 n thì 1 lim un • lim k
n = +∞ (k ∈, k ≥1) . • lim n
q = +∞ (q >1) . B. CÁC DẠNG TOÁN. DẠNG 1:
TÍNH GIỚI HẠN CỦA DÃY SỐ Phương pháp:
+ Nắm vững khái niệm cơ bản.
Ví dụ 1. Tính các giới hạn sau: 2 a) n +1 lim . b) 5 + 3 − 7 lim n n . 2n + 3 2 n 2 c) 9n − n +1 lim . d) n + 7 lim . 4n − 2 2 4 + n Lời giải 1 1 n1+ 1+ a) n +1 n n 1 lim = lim = lim = . 2n + 3 3 3 2 n2 + 2 + n n 2 3 7 n 5 + − 2 2 b) 5n + 3n − 7 n n 3 7 lim = lim = lim 5 + − = 5. 2 2 2 n n n n 6 2 1 1 1 1 n 9 − + 2 2 n 9 − + 2 c) 9n − n +1 lim lim n n = = lim n n 4n − 2 2 2 n 4 n4 − − n n 1 1 9 − + 2 n n 3 = lim = . 2 4 4 − n 7 1+ d) n + 7 1 lim = lim . n = 0. 2 4 + n n 4 +1 2 n DẠNG 2:
TÍNH TỔNG CỦA CÁC CẤP SỐ NHÂN LÙI VÔ HẠN Phương pháp:
+ Tìm số hạng đầu và công bội của cấp số nhân.
+ Sau đó áp dụng công thức tổng của cấp số nhân lùi vô hạn: u1
S = u + u + ...+ u + = n .... . 1 2 1− q
Ví dụ 2. Tính tổng của các cấp số nhân lùi vô hạn: a) 1 1 1 S =1+ + + + ... 2 4 8 n b) 1 1 1 1 T 1 ... = − + − + + − + ... 4 16 64 4 Lời giải
a) S là tổng của cấp số nhân lùi vô hạn có u =1 và 1 1 q = . 2 Do đó 1 S = = 2 1 . 1− 2
b) T là tổng của cấp số nhân lùi vô hạn có u =1 và 1 1 q = − . 4 Do đó 1 4 T = = . 1 5 1− − 2
C. BÀI TẬP TỰ LUYỆN.
Bài 1: Tính các giới hạn sau: 7 2 2 5 4 a) 4n − n −1 − − lim . b) (2n n) 4n 2) l ( im . 2 3 + 2n 6 2 4
20n (2n − 3n +1) 2 3 c) n − n + 3 lim . d) 2n −11n +1 lim . 3 n + 2n 2 n − 2 2 e) n + 2n − 2 lim . f) ( 2
lim 2n − 3n + n − 4) . 2
2n − n + n g)
1+ 3 + 5 + 7 +(2n +1) lim . 2 3n + 4 h) 1 1 1 1 1 lim + + + ++ . 1.2 2.3 3.4 4.5 n(n 1) +
Bài 2: Tính tổng của cấp số nhân lùi vô hạn 5 5 5 S = 5 + + + ...+ + .... 6 36 6n
Bài 3: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số: a) 2,( ) 21 = 2,212121...; b) 5,(205) = 5,205205205....
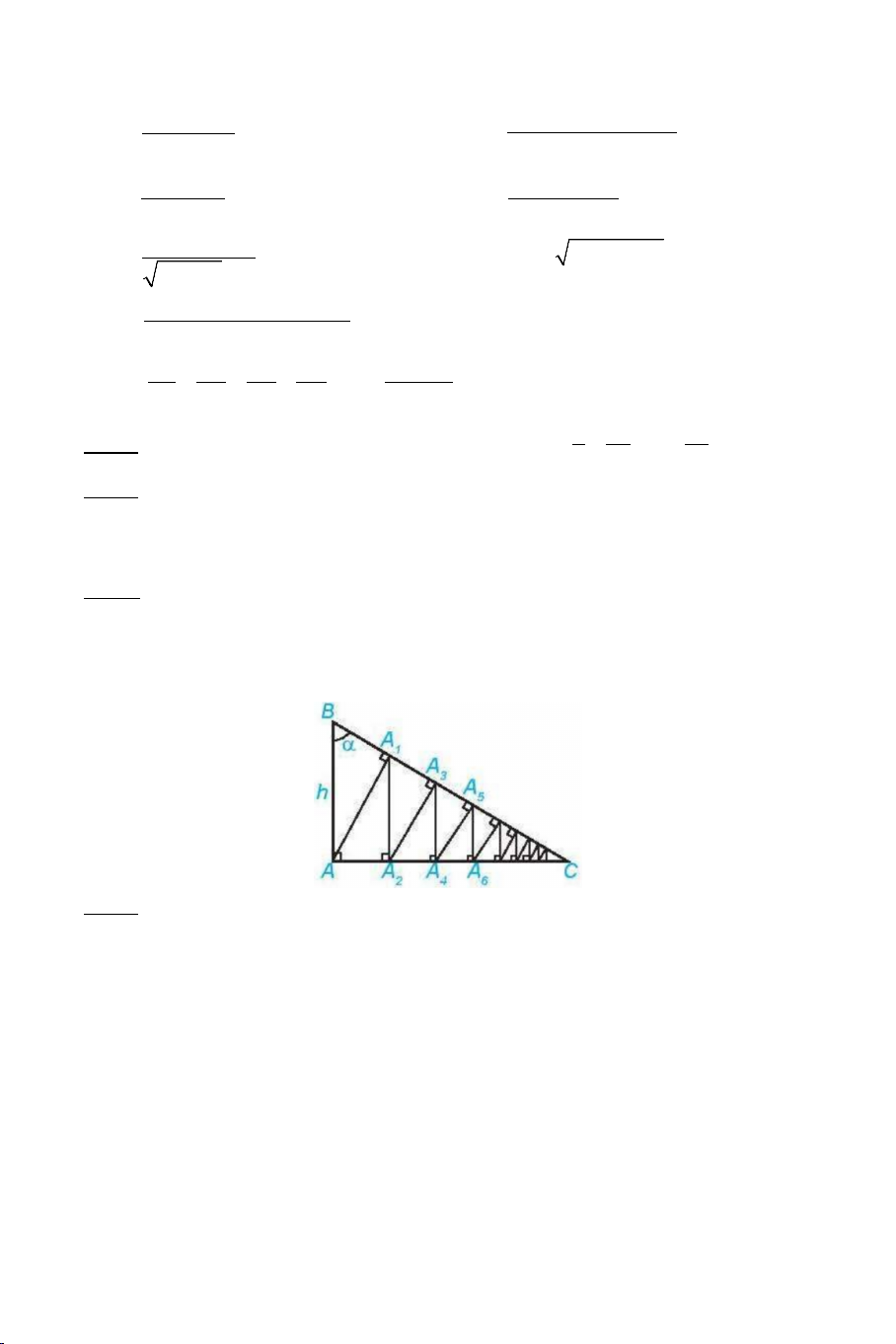
Bài 4: Cho tam giác ABC vuông tại A , có AB =10 cm và góc B bằng 60°
(H 5.3). Từ A kẻ AA ⊥ BC , từ A kẻ A A ⊥ AC , sau đó lại kẻ 1 1 1 2
A A ⊥ BC . Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn 2 3
AA A A ... .Tính độ dài đường gấp khúc này. 1 2 3
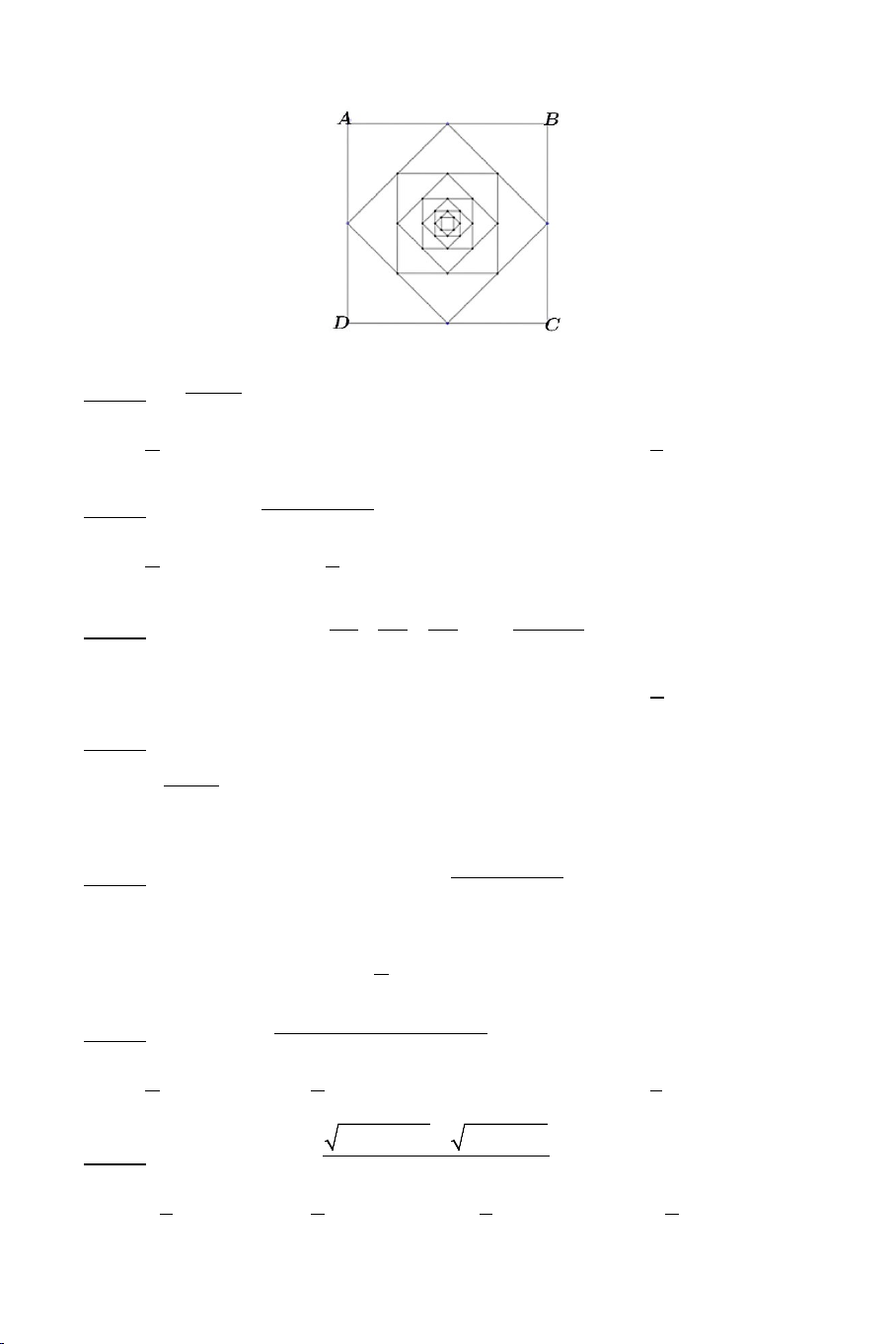
Bài 5: Cho hình vuông ABCD có cạnh bằng 5 cm. Lấy trung điểm bốn cạnh
của hình vuông nối lại được một hình vuông mới nhỏ hơn A . Tiếp tục 1
làm như vậy tới vô hạn. Tính tổng diện tích các hình vuông A , A ,... 1 2
(tham khảo hình vẽ dưới đây). 8
D. BÀI TẬP TRẮC NGHIỆM Câu 1: 1 lim bằng: 2n + 5 A) 1 . B) 0 . C) +∞ . D) 1 . 2 5 2 3 Câu 2: Tìm 7n − 2n +1 I = lim . 3 2 3n + 2n +1 A) 7 . B) 2 − . C) 0 . D) 1. 3 3
Câu 3: Tính giới hạn 1 1 1 1 lim + + + ...+ . 1.2 2.3 3.4 n (n )1 + A) 0 . B) 2 . C) 1. D) 3 . 2
Câu 4: Gọi S là tập hợp các tham số nguyên a thỏa mãn 3n + 2 2 lim a 4a + − =
0 . Tổng các phần tử của S bằng n + 2 A) 4 . B) 3 . C) 5 . D) 2 . 2 2 Câu 5: Cho + + a∈ an a n 1 sao cho giới hạn 2 lim
= a − a +1. Khi đó khẳng (n + )2 1
định nào sau đây là đúng?
A) 0 < a < 2 . B) 1
0 < a < . C) 1 − < a < 0 .
D) 1< a < 3. 2 2 2 2 2 2 Câu 6: Giới hạn 1 + 2 + 3 + 4 + ... lim
+ n có giá trị bằng? 3 n + 2n + 7 A) 2 . B) 1 . C) 0 . D) 1 . 3 6 3 2 2
Câu 7: Tính giới hạn
4x + x +1 − x − x + 3 lim : x→−∞ 3x + 2 A) 1 − . B) 2 . C) 1 . D) 2 − . 3 3 3 3 9
Câu 8: Giới hạn lim n ( n + 4 − n + 3) bằng : A) 0 . B) +∞ . C) 7 . D) 1 . 2 2 n 1 + n Câu 9: 100 + 3.99 lim là : 2n n 1 10 − 2.98 + A) +∞ . B) 100 . C) 1 . D) 0 . 100
Câu 10: Tổng vô hạn sau đây 2 2 2 S = 2 + + + ...+
+ ... có giá trị bằng : 2 3 3 3n A) 8 . B) 3 . C) 4 . D) 2 . 3
Câu 11: Số thập phân vô hạn tuần hoàn 3,15555... = 3, ( 1 5) viết dưới dạng hữu tỉ là : A) 63 . B) 142 . C) 1 . D) 7 . 20 45 18 2
Câu 12: Từ độ cao55,8m của tháp nghiêng Pisa nước Italia người ta thả một
quả bóng cao su chạm xuống đất. Giả sử mỗi lần chạm đất quả bóng lại
nảy lên độ cao bằng 1 độ cao mà quả bóng đạt trước đó. Tổng độ dài 10
hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó nằm
yên trên mặt đất thuộc khoảng nào trong các khoảng sau đây?
A) (67m ; 69m) . B) (60m ; 63m). C) (64m ; 66m) . D) (69m ; 72m) . E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN
Bài 1: Tính các giới hạn sau: 2 1 1 1 1 n 4 − − 2 2 4 − − 2 a) 4n − n −1 l n n n n 4 − 0 − 0 im = lim = lim = = 2 . 2 3+ 2n 3 3 2 0 + 2 n + 2 + 2 2 2 n n 10 5 4 2 1 2
n 2 − n 4 − 2 5 4 b)
(2n − n) 4n − 2) l ( im lim n n = 6 2 4
20n (2n − 3n +1) 4 6 2 3 1 20n n 2 − + 2 n n 5 4 5 4 10 1 4 2 1 2 n 2 n 4 2 4 − − − − n n n n 128 = lim = lim = . 4 4 3 1 3 1 5 6 8 20n n 2 − + 202 − + 2 2 n n n n 2 1 3 1 3 n 1 − + 2 2 1− + − + 2 c) n n 3 n n 1 n n 1− 0 + 0 lim = lim = lim ⋅ = 0⋅ = 0 . 3 n + 2n 2 n 2 3 + + 1+ 0 n 1 1 2 2 n n 3 11 1 11 1 n 2 − + 3 3 2 − + 3 d) 2n −11n +1 lim lim n n = = lim .lim n n n = +∞ . 2 n − 2 2 2 2 n 1− 1− 2 2 n n 2 2 2 1+ − 2 e) n + 2n − 2 lim = lim n n = +∞ . 2
2n − n + n 2 1 1 − + 2 3 n n n f) ( 2
n − n + n − ) = ( 2 lim 2 3 4
lim 2n − 3n + n − 4) 1 4 = lim . n lim 2 − 3+ − = +∞ . 2 n n
g) Xét cấp số cộng 1,3,5,7,9,…,2n +1 có số hạng đầu tiên u = 1, công sai d = 2 và 1
số hạng cuối cùng là u = n + ta có: m 2 1
u + (m −1)d = 2n +1 ⇔ 1+ 2(m −1) = 2n +1 ⇔ m = n +1. 1
Vậy cấp số cộng có n +1 số hạng. Suy ra tổng
= 1+ 3 + 5 + 7 ++ 2 +1 m = ( n + S n u + u =
+ n + = n + n + . m ) 1 2 (1 2 1) 2 1 1 2 2 2 2 1 2 1 n 1+ + 2 2 1+ + 2 Vì thế n + 2n +1 n n n n 1+ 0 + 0 1 L = lim = lim = lim = = . 2 3n + 4 4 4 2 3+ 0 3 n 3+ 3+ 2 2 n n h) Số hạng tổng quát 1 1 1 = − ;( k
∀ = 1,2,…,n) do đó k(k +1) k k +1 1 1 1 1 1 1 1 1 L lim 1 = − + − + − + −+ − 2 2 3 3 4 4 n n +1 11 1 n 1 1 = lim 1− = lim = lim = = 1. n +1 n +1 1 1+ 0 1+ n
Nhận xét: Phân tích 1 a b = + vói 1 1 a = = 1;b = = 1 − .
k(k +1) k k +1 k +1 = k k 0 k = 1 −
Bài 2: S là tổng của cấp số nhân lùi vô hạn với 1 u = 5;q = . 1 6 Do đó u 5 1 S = = = 6 . 1− q 1 1− 6 Bài 3 : a) Ta có ( ) 21 21 21 2, 21 = 2,212121... = 2 + + + + ... . 2 4 6 10 10 10 Dãy số 21 21 21 ; ;
;... là một cấp số nhân lùi vô hạn với 21 u = , công bội 2 4 6 10 10 10 1 2 10 1 q = . 2 10 21 2 Suy ra 21 21 21 10 7 + + + = = . 2 4 6 10 10 10 1 33 1− 2 10 Vậy ( ) 7 73 2, 21 = 2,212121... = 2 + = . 33 33 b) Ta có ( ) 205 205 205 5, 205 = 5,205205205... = 5 + + + + . 3 6 9 10 10 10 Dãy số 205 205 205 ; ;
;... là một cấp số nhân lùi vô hạn với 205 u = , công bội 3 6 9 10 10 10 1 3 10 1 q = . 3 10 205 3 Suy ra 205 205 205 10 205 + + + = = . 3 6 9 10 10 10 1 999 1− 3 10 Vậy ( ) 205 5200 5, 205 = 5,205205205... = 5 + = . 999 999
Bài 4 : Ta có: AA = 10sin 60° , 2
A A = AA sinα = 10sin 60° ,..., A = ° . − A 10sinn n n 60 1 1 2 1 1
Độ dài đường gấp khúc AA A ...A bằng: 1 2 n 2 n
AA + A A +...+ A = ° + ° + + ° − A n n 10sin 60 10sin 60 ... 10sin 60 1 1 2 1 ( n n 1 − ) 1− sin 60 10sin 60 1 sin 60 ... sin 60 10sin 60 . ° = ° + ° + + ° = ° 1− sin 60°
Khi n ra vô hạn, ta có: 12 1− sinn 60° sin 60° AA ...A = ° = = + . n .... lim 10sin 60 10 30 20 3 1 n→∞ 1− sin 60° 1− sin 60° n (Do 3 sin 60° = nên n 3 lim sin 60° = lim = 0 ). 2 n→∞ n→∞ 2
Bài 5 : Cạnh của hình vuông A bằng cạnh của hình vuông ABCD nhân với 1 . 1 2
Tương tự, ta có cạnh của hình vuông A bằng cạnh của hình vuông ABCD n n nhân với 1 . 2
Do đó, công thức diện tích của hình vuông A là 1 S = . n 25. n 2n
Tổng của n hình vuông đầu tiên là: 1 1 1 1 1 − 1 1 1 n S S ... S 25 + + + = + + + = + + + 2 = . n 25. 25. ... 25. 25. .1 .. 1 2 2 n n 1 2 2 2 2 2 2 − 2 1 1− 2
Cho n ra vô hạn, ta có tổng diện tích của các hình vuông là: 1 1 − n S = lim ( 25 2 25 1 S +...+ S = = = . n lim . . 25 1 ) n→∞ n→∞ 2 1 − 2 1 1 2 2
BÀI TẬP TRẮC NGHIỆM 1.B 2.B
3.C 4.A 5.A 6.D 7.A 8.D 9.B 10B 11.B 12.A
Câu 1: Chọn B. Ta có: 1 lim 1 1 = lim . = 0 . 2n + 5 n 5 2 + n 7 1 2 3 − 2 + 3
Câu 2: Chọn B. Ta có 7n − 2n +1 n n 2 I = lim = lim = − . 3 2 3n + 2n +1 2 1 3 3+ + 3 n n
Câu 3: Chọn C. Ta có: 1 1 1 1 + + + ...+ 1.2 2.3 3.4 n(n + ) 1 1 1 1 1 1 1 1 1 = − + − + 1 + − + − = 1− . 1 2 2 3 n −1 n n n +1 n +1 Vậy 1 1 1 1 lim 1 + + + ...+ = lim 1− = 1 . 1.2 2.3 3.4 n (n ) 1 + n +1 13 ( 2 a − a + ) 2 4
3 n + 2 + 2a −8a
Câu 4: Chọn A. Ta có: 3n + 2 2 lim a 4a + − = lim n 2 + n + 2 2 + − 2 2 2a 8 − 4 + 3 a a a + n 2 = lim
= a − 4a + 3. 2 1 + n Theo giả thiết: 3n + 2 2 2 lim
+ a − 4a = 0 ⇔ a − 4a + 3 = 0 ⇔ a = 3∨ a = 1. n + 2 Vậy S = {1; } 3 ⇒ 1+ 3 = 4 . 2 a 1 2 2 2 2 a + + 2
Câu 5: Chọn A. Ta có an + a n +1 an + a n +1 lim = lim = lim n n = a . (n + )2 2 1 n + 2n +1 2 1 1+ + 2 n n 2
a − a +1 = a 2
⇒ a − 2a +1 = 0 ⇒ a = 1 . n(n + ) 1 (2n + ) 1
Câu 6: Chọn D. Ta có kết quả quen thuộc 2 2 2 2 1 + 2 + 3 +...+ n = . 6 2 2 2 2 2 n(n + ) 1 (2n + ) 1 Do đó 1 + 2 + 3 + 4 +... lim + n = lim 3 n + 2n + 7 6( 3 n + 2n + 7) 1 1 1 2 + + n n 1.2 1 = lim = = . 2 7 6 3 6 1+ + 2 3 n n 1 1 1 3 2 2 −x 4 + + + x 1− + 2 2
Câu 7: Chọn A.
4x + x +1 − x − x + 3 lim = lim x x x x x→−∞ 3x + 2 x→−∞ 3x + 2 1 1 1 3 − 4 + + + 1− + 2 2 = lim x x x x 1 = − . x→−∞ 2 3+ 3 x
Câu 8: Chọn D.
n ( n + − n + ) 1 lim 4 3 = lim n n + 4 + n + 3 1 1 = lim = . 4 3 2 1+ + 1+ n n 99 n + n+ n 100 3. 1
Câu 9: Chọn B. 100 + 3.99 100 lim lim = = 100 . 2n n 1 10 − 2.98 + 98 n 1 2. − 100 14
Câu 10: Chọn B. Ta có 2 2 2
2; ; ;...; ;... là một cấp số nhân lùi vô hạn với công bội 2 3 3 3n 1 q 2 2 2 1 = < 1 . S = 2 + + + ...+ + ... = 2. = 3 . 3 2 3 3 3n 1 1− 3 1
Câu 11: Chọn B. 3,15555... = 3,1(5) 2 1 1 10 142 = 3,1+ 5 + + ... = 3,1+ 5. = . 2 3 10 10 1 45 1− 10
Câu 12: Chọn A. Theo đề, mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng 1 10
độ cao mà quả bóng đạt trước đó và sau đó lại rơi xuống từ độ cao thứ hai. Do
đó độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến:
+ Thời điểm chạm đất lần thứ nhất là d = 55,8m . 1
+ Thời điểm chạm đất lần thứ 2 là 55,8 d = 55,8 + 2. . 2 10
+ Thời điểm chạm đất lần thứ 3 là 55,8 55,8 d = 55,8 + 2. + 2. . 3 2 10 10
+ Thời điểm chạm đất lần thứ 4 là : 55,8 55,8 55,8 d = 55,8 + 2. + 2. + 2. . 4 2 3 10 10 10 …
+ Thời điểm chạm đất lần thứ n , (n > ) 1 là : 55,8 55,8 55,8 d = + + + + . n 55,8 2. 2. ... 2. 2 n 1 10 10 10 −
Do đó độ dài hành trình của quả bóng được thả từ lúc ban đầu cho đến khi nó
nằm yên trên mặt đất là: 55,8 55,8 55,8 d = 55,8 + 2. + 2. + ...+ 2. + ... (mét). 2 1 10 10 10n− + Vì 55,8 2. , 55,8 2. , 55,8 2. , …, 55,8 2.
,…, là một cấp số nhân lùi vô hạn với 10 2 10 3 10 1 10n− 55,8 1 2. 55,8 55,8 55,8 q = , 10 2. + 2. + ...+ 2. + ... = = 12,4 . 10 2 n 1 10 10 10 − 1 1− 10 Vậy 55,8 55,8 55,8 d = 55,8 + 2. + 2. + ...+ 2.
+ ... = 55,8 +12,4 = 68,2 . 2 1 10 10 10n− 15 Chương II.
GIỚI HẠN. HÀM SỐ LIÊN TỤC Bài 2 GIỚI HẠN HÀM SỐ
A. TÓM TẮT LÝ THUYẾT.
I. GIỚI HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Giới hạn hữu hạn của hàm số tại một điểm
Cho điểm x thuộc khoảng K và hàm số y = f (x) xác định trên K hoặc 0 K { \ x . 0}
Ta nói hàm số y = f (x) có giới hạn hữu hạn là số L khi x dần đến x nếu với 0
dãy số (x bất kì, x ∈K {
\ x và x → x thì f (x L n ) → n 0} n ) n 0
Kí hiệu: lim f (x) = L hay f (x) → L khi x → x x→ 0 0 x
Nhận xét và lưu ý:
- Giới hạn của hàm số được định nghĩa thông qua khái niệm giới hạn của dãy số.
- Hàm số không nhất thiết phải xác định tại x . 0
- Trong giải bài tập ta thường áp dụng các định lí và phương pháp để tiện
cho việc tính toán thay vì việc đưa về giới hạn của dãy số.
2. Định lí và các phép toán về giới hạn hữu hạn của hàm số tại một điểm
a) Giả sử lim f (x) = L và lim (
g x) = M . Khi đó: x→ 0 x x→ 0 x
• lim f (x) ± (
g x) = L ± M . x→ 0 x
• lim f (x) ( g x) = . L M . x→ 0 x
f (x) L • lim = với M ≠ 0 . x→ 0
x g(x) M
• lim cf (x) =
c lim f (x) với c ∈ , nếu tồn tại lim f (x)∈ . x→x x→ x→ 0 0 x 0 x
• Nếu f (x) ≥ 0 và lim f (x) = L thì L ≥ 0 và lim f (x) = L . x→ 0 x x→ 0 x
b) Một số giới hạn đặc biệt: • lim x = x . 0 x→ 0 x • lim k k
x = x với k nguyên dương. 0 x→ 0 x 5
• lim c = c với c là hằng số . x→ 0 x
3. Giới hạn một phía
• Cho hàm số y = f (x) xác định trên khoảng (x ;b . 0 )
Ta nói hàm số y = f (x) có giới hạn bên phải là số L khi x dần tới x nếu với 0
dãy số (x bất kì x < x < b và x → x thì f (x → L . n ) n ) 0 n n 0
Kí hiệu lim f (x) = L . x x+ → o
• Cho hàm số y = f (x) xác định trên khoảng (a;x . 0 )
Ta nói hàm số y = f (x) có giới hạn bên trái là số L khi x dần tới x nếu với 0
dãy số (x bất kì a < x < x và x → x thì f (x → L . n ) n ) n 0 n 0
Kí hiệu lim f (x) = L . x x− → o
Ta cũng có thể hiểu và biểu diễn giới hạn một bên như sau: x x+ →
nghĩa là x → x và x > x . 0 0 0 x x− →
nghĩa là x → x và x < x . 0 0 0 Lưu ý:
a) Tính chất được thừa nhận của giới hạn một bên:
lim f (x) = lim f (x) = L ⇔ lim f (x) = L . x x− + → o x→xo x→xo
lim f (x) ≠ lim f (x)thì không tồn tại lim f (x) . x x− + → o x→xo x→xo
b) Các phép toán và định lí về giới hạn tại một điểm vẫn đúng khi ta
thay x → x bằng x x+ → và x x− → . 0 0 0
c) Một số giới hạn một bên thường dùng: • 1 lim 1 = +∞ ; lim = −∞ . x x+ → x − x − − o x→x x x 0 o 0
4. Giới hạn vô cực của hàm số tại một điểm
Cho hàm số y = f (x) xác định trên khoảng (x ;b . 0 )
+ Ta nói hàm số y = f (x) có giới hạn bên phải là +∞ khi x → x về bên phải 0
nếu với dãy số (x bất kì, x < x < b và x → x thì f (x . n ) → +∞ n ) 0 n n 0
Kí hiệu: lim x = +∞ hay f (x) → +∞ khi x → x . x→ 0 0 x 6
+ Ta nói hàm số y = f (x) có giới hạn bên phải là −∞ khi x → x về bên phải 0
nếu với dãy số (x bất kì, x < x < b và x → x thì f (x . n ) → −∞ n ) 0 n n 0
Kí hiệu: lim x = −∞ hay f (x) → −∞ khi x → x . x→ 0 0 x
Ta có các giới hạn thường dùng sau: 1 lim 1 = +∞ và lim = −∞ với x ∈ . 0 + x→x x x − x x x x o − o − → 0 0
5. Quy tắc về giới hạn vô cực
a) Quy tắc 1: Quy tắc tìm giới hạn của tích
L = lim f (x) lim ( g x) lim f (x) ( g x) x→ 0 x x→ 0 x x→ 0 x +∞ +∞ L > 0 −∞ −∞ +∞ −∞ L < 0 −∞ +∞
b) Quy tắc 2: Quy tắc tìm giới hạn của thương
L = lim f (x) lim ( g x) f (x) Dấu của ( g x) lim x→ 0 x x→ 0 x x→ 0 x ( g x) L ±∞ Tùy ý 0 + +∞ L > 0 0 - −∞ + −∞ L < 0 0 - +∞ 7
II. GIỚI HẠN CỦA HÀM SỐ TẠI VÔ CỰC
1. Giới hạn hữu hạn của hàm số tại vô cực
a) Cho hàm số y = f (x) xác định trên khoảng (a;+∞).
Ta nói hàm số y = f (x) có giới hạn hữu hạn là số L khi x → +∞ nếu với dãy
số (x bất kì, x > a và x → +∞ thì f (x → L . n ) n ) n n
Kí hiệu lim f (x) = L . x→+∞
b) Cho hàm số y = f (x) xác định trên khoảng (−∞;b).
Ta nói hàm số y = f (x) có giới hạn hữu hạn là số L khi x → −∞ nếu với dãy
số (x bất kì, x < a và x → −∞ thì f (x → L . n ) n ) n n
Kí hiệu lim f (x) = L . x→−∞
Với c là hằng số và k là số nguyên dương, ta luôn có:
lim f (x) = c và lim c = 0 . x→±∞ →±∞ k x x
Các phép toán trên giới hạn hàm số vẫn đúng khi thay x → x bằng 0
x → +∞ và x → −∞ .
2. Giới hạn vô cực tại vô cực
a) Cho hàm số y = f (x) xác định trên khoảng (a;+∞) . lim f(x) = +∞ x→+∞
với mọi dãy số (x ), x > a và x → +∞ ta đều có lim f(x) = +∞ . n n n
Các định nghĩa: lim f (x) = −∞, lim f (x) = +∞, lim f (x) = −∞ được phát x→+∞ x→−∞ x→−∞
biểu hoàn toàn tương tự.
b) Ta có các giới hạn thường dùng sau: • lim k
x = +∞ với k nguyên dương; x→+∞ • lim k
x = +∞ nếu k là số chẵn; x→−∞ • lim k
x = −∞ nếu k là số lẻ. x→−∞ 8 B. CÁC DẠNG TOÁN. PHÂN LOẠI:
Các bài toán giới hạn của hàm số có 3 dạng lớn: giới hạn tại một điểm, giới
hạn một phía và giới hạn tại vô cực. Trong hai dạng này thì ta thường gặp
các 4 dạng đặc biệt hay còn gọi là 4 dạng vô định là: 0 0. ; ; ∞ ∞
và ∞ − ∞ . 0 ∞ PHƯƠNG PHÁP CHUNG:
+ Nắm vững khái niệm cơ bản.
+ Nhập hàm số vào máy tính cầm tay (MTCT) để kiểm tra kết quả có ở
dạng vô định hay không? Nếu có thì mỗi dạng vô định đều có phương
pháp giải riêng sẽ được hướng dẫn chi tiết ở dưới.
DẠNG 1: GIỚI HẠN HÀM SỐ TẠI MỘT ĐIỂM x → x 0
DẠNG 1.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
Nhận dạng chung: Nhập hàm số vào máy tính cầm tay (MTCT) sau đó cho
x = x . Nếu kết quả là một số thực thì ra sử dụng các phép toán tổng, hiệu, 0
tích, thương hoặc các định lí và tính chất được thừa nhận để giải.
Ví dụ 1. Cho hàm số f (x) 2 x + 1 =
. Khi đó lim f (x) bằng: 2 x x→3 A. +∞ . B. 0. C. 5 3 . D. 1 . 3 2 Lời giải 2 2 2 x + 1 3 + 1 3 + 1 5 3
[TL] Ta có lim f (x) = lim = lim = = . x→3 x→3 x→3 2 x 2 3 2 3 3 Chọn đáp án C.
[TN] Nhập biểu thức của hàm số f (x) 2 x + 1 =
vào MTCT. Bấm phím CALC 2 x
, máy hỏi X? nhập 3 =. Máy hiển thị kết quả : 5 3 . 3 Chọn đáp án C.
Ví dụ 2. Tìm các giới hạn sau: a) lim ( 2 x − 7x + 5) x 4 →− Lời giải
lim (x − 7x + 5) = lim x − lim 7x + lim 5 = ( 4 − )2 2 2
− 7 lim x + 5 = 16 − 7.( 4 − ) + 5 = 49 x 4 →− x 4 →− x 4 →− x 4 →− x 4 →− 9 b) lim − − → ( 3 x 2x 6 x 8 ) Lời giải 3
lim x − 2x − 6 = 3
lim x− lim 2x − lim6 = 3 8 − 2 lim x − 6 = 2 − 2. 8 − 6 = −8 x→8 ( ) x→8 x→8 x→8 x→8 2
2 x + 1 − 5 x − 3 c) lim x 2 →− 2x + 3 Lời giải 2 2
2 x + 1 − 5 x − 3 2 lim x + 1 − 5lim x − 3 − x→− x→− 2 5 2 2 lim = = = 3 . x 2 →− 2x + 3 lim 2x + 3 1 − x 2 →−
DẠNG 1.2: CÁC VÔ ĐỊNH THƯỜNG GẶP
Nguyên tắc : Là phải triệt tiêu được yếu tố làm cho hàm số bị vô định.
KHỬ VÔ ĐỊNH 0 TẠI MỘT ĐIỂM 0 Nhận dạng chung: f (x)
+ Dấu hiệu 1: Hàm số có dạng phân thức
hoặc biểu thức có căn thức. g(x)
+ Dấu hiệu 2: Ta thế x = x vào hàm số cần tính giới hạn (có thể sử dụng 0
MTCT để kiểm tra trước là hàm số có thuộc dạng vô định hay không) và
nhận thấy với x = x lần lượt làm tử và mẫu đều bằng 0. 0 Phương pháp giải: f (x)
+ Đối với hàm phân thức: có dạng lim x→ 0 x g(x)
f (x) (x − x . f x 0 ) 1 ( ) Ta phân tích =
. Khi đó x − x là thừa số làm hàm số bị vô
g(x) (x − x .g x 0 0 ) 1 ( )
định sẽ bị triệt tiêu.
Một số phương pháp kết hợp có thể sử dụng:
+ Các hằng đẳng thức, nhóm hạng tử chung, chia đa thức; chia Hóc – ne.
+ Phân tích thừa số bậc 2: Cho biểu thức 2
ax + bx + c ta có thể phân tích thành dạng nhân tử nếu 2
ax + bx + c = 0 có hai nghiệm x ; x . Khi đó: 1 2 2
ax + bx + c = a(x − x x x . 1 )( − 2 )
+ Hẳng đẳng thức mở rộng (áp dụng những câu khó): n n a b
(a b)( n−1 n−1 n−1 2 2 n−3 n−2 n− − = −
a + a b + a b + + a a + ab + 1 . . ... b ). 10
+ Đối với biểu thức chứa căn: ta nhân lượng liên hợp để khử căn thức và tạo
ra thừa số x − x để triệt tiêu đại lượng làm hàm số vô định. 0
Một số dạng liên hợp thường sử dụng: 2 3 • A − B A ± B = A ± B • 3 A ± B = A B (3 A)2 3 2 . B A + B − • A B A ± B = A B • 3 3 A ± B A ± B = ( A )2 3 . A B + ( B)2 3 3
Ví dụ 1. Tính giới hạn của các hàm số sau: 3 − a) x 8 lim 2 x→2 x − 4 Lời giải x (x − 2)( 2 3 x + 2x + − 4 8 ) 2 x + 2x + 4 lim = lim = lim = 3 . x→ 2 2 x→ x − 2 4 (x − 2)(x + 2) x→2 x + 2 2 b) x − 5x + 4 lim x→4 x − 4 Lời giải 2 x − 5x + 4
(x −1)(x − 4) lim = lim
= lim(x −1) = 4 −1 = 3 . x→4 x→4 x→4 x − 4 x − 4 x = 1
[Cách biến đổi, ta bấm phương trình 2
x − 5x + 4 = 0 ⇔ . x = 4 Khi đó 2
x − 5x + 4 = (x −1)(x − 4) ]. 2 c) 2x − x + 15 lim x→3 3 − x Lời giải 2 2x − x − 15
(2x + 5)(x − 3) lim = lim
= lim(−2x − 5) = −11 . x→3 x→3 x→ 3 − x 3 − 3 x 5 x − =
[Cách biến đổi, ta bấm phương trình 2
2x − x − 15 = 0 ⇔ 2 . x = 3 Khi đó 2 5 2x x 15 2 x − − = +
(x − 3) = (2x + 5)(x − 3)]. 2 11 3 d) 2x − 2x −12 lim x→2 2x − 4 Lời giải 2x − 2x −12 (x − 2)( 2 3 2x + 4x + 6) lim = lim = lim( 2 x + 2x + 3) =11. x→2 x→2 2x − 4 2(x − 2) x→2
[Cách biến đổi, ta bấm phương trình 3
2x − 2x − 12 = 0 ⇔ x = 2 . Khi đó 3 x − x − = (x − )( 2 2 2 12
2 2x + 4x + 6) có thể dùng phương pháp
chia đa thức hoặc chia Hóc – ne để đưa về dạng nhân tử].
CÁC BÀI TẬP VẬN DỤNG TƯƠNG TỰ 2 1. 2x − 75x +175 lim Đáp án: 13 2
x→35 3x − 95x − 350 23 3 2. x −1 lim Đáp án: 3 2 x 1 → x −1 2 4 3. x −16 lim Đáp án: 8 − 3 2 x 2 →− x + 2x 4 2 (x − ) 1 (x + ) 1 ( 2 x − 2) 4. x − 3x + 2 − lim (Gợi ý: ) Đáp án: 2 3 x 1 → x + 2x − 3 (x − ) 1 ( 2 x + x + 3) 5 3 2 2 5.
x − x − x +1 (x − ) 1 (x + ) 1 lim (Gợi ý: ) Đáp án: 0 2 x 1 → x − 3x + 2 (x − ) 1 (x − 2)
Ví dụ 2. Tính giới hạn của các hàm số sau: a) 3 lim − x x→9 9 − x Lời giải 3 (3− x)(3+ − x x ) 9 − x 1 1 lim = lim = lim = lim = . x→9 x→ 9 − 9 x
(9 − x)(3+ x) x→9 (9−x)(3+ x) x→9 3+ x 6 b) 4x +1 − 3 lim 2
x→2 3x − 4x − 4 Lời giải 4x +1 − 3 4x +1− 9 4(x − 2) lim = lim = lim 2 x→2 x→2 3x − 4x − 4 ( 2
3x − 4x − 4)( 4x +1 + 3) x→2 (x − 2)(3x + 2)( 4x +1 + 3) 4 4 1 = lim = = .
x→2 (3x + 2)( 4x +1 + 3) (3.2 + 2)( 4.2 +1 + 3) 12 12 2 −x + 5x + 6 c) lim x→6 2x −8 −1 Lời giải x x (− 2 2
x + 5x + 6)( 2x − 8 + 2)
(x +1)(6 − x)( 2x−8 + − + + 2 5 6 ) lim = lim = lim x→6 x→6 x→ 2x − 8 − 2 2x − 8 − 6 4 2x − 12
(x +1)( 2x−8 + 2) (6+1)( 2.6−8 + 2) = lim = = −14 . x→6 −2 −2 2 d) x + x − 2 3 lim x→3 x − 3 Lời giải 2 x + x − 2 2 3 x + x − 12 (x − 3)(x + 4) lim = lim = lim x→3 x→ x − 3 3
(x − 3)( 2x + x +2 3) x→3 (x−3)( 2x + x +2 3) x + 4 3 + 4 7 3 = lim = = . x→3 2 x + x + 2 2 3 3 + 3 + 2 3 12 3 2 e) 8 + x − 2 lim 2 x→0 x Lời giải 3 8 + 2 x − 2 8 + 2 x − 8 lim = lim x→ 2 0 x→0 x 2 2 x ( 2 8 x ) + 3 + 3 2 8 + 2 x + 4 1 1 = lim = . x→ ( 2 0 12 8 + 2 x )3 + 3 2 8 + 2 x + 4
CÁC BÀI TẬP VẬN DỤNG TƯƠNG TỰ 1. x + 3 − 2 lim Đáp số: 1 x 1 → x −1 4 2 2. 1+ x −1 lim
Đáp số: 3 + 2 3 3 2
x→ 3 2x − 3x 9 2 3.
x − 3x + 4 − 2 3 − lim Đáp số: x→0 x 4 2 4. x + x − 2 3 lim
Đáp số: 7 3 x→3 x − 3 12 13 3 5. x − 2 +1 1 lim Đáp số: 2 x 1 → x − x 3
Ví dụ 3. Tính các giới hạn sau [sử dụng phương pháp thêm bớt đại lượng] 2 3 a)
x + x + 2 − 7x + 1 lim x→1 2 (x −1) Lời giải
Nhận thấy bài toán có 2 căn thức khác bậc nên ta tính trước ngoài nháp giới hạn của 2
lim x + x + 2 = 2 và 3
lim 7x + 1 = 2 nên ta thêm bớt 2 và -2 vào tử x→1 x→1
để thành dạng A − B và 3
B − A . Khi đó: x x x
( 2x +x+2 −2)+(2− 3 2 3 7x + + + − + 1 2 7 1 ) lim = lim x→1 2 (x −1) x→1 2 (x −1) 2 x + x + 2 − 2 2 − 3 7x + 1 = lim + lim = I + J . x→1 2 (x −1) x→1 2 (x −1) 2 2 x + x + 2 − 2 x + x + 2 − 4 * Tính I = lim = lim x 1 → 2 (x −1) x 1 →
2 (x −1)( 2x + x+ 2 + 2) (x −1)(x + 2) x + 2 3 = lim = lim = . x→1
2 (x −1)( 2x + x + 2 + 2) x→1 2( 2x + x + 2 + 2) 4 2 3 2 − 7x + 1 8 − 7x − 1 * Tính J = lim = lim x→1
2 (x −1) x→1 2(x−1) 3 4 + 2 7x + 1 + (3 7x+1)2 7 − 7 lim − = = . x→1 3 + x + + (3 x + )2 12 2 2 4 2 7 1 7 1 2 3
x + x + 2 − 7x + 1 2 Do đó lim = I + J = . x→1 2 (x −1) 12 3 b) + − − 2 1 x 8 lim x x→0 x Lời giải 14 + − − (2 1+x −2)+( 3 3 2 − 8 2 1 8 − x x x ) lim = lim x→0 x→0 x x 2( 1+ x −1) 3 2 − 8 − x 2 1 = lim + = lim + lim x→0 x→0 x→0 x x 1+ x + 1
4 + 2 8 − x + (8 − x)2 3 3 2 1 1 13 = + = 1 + = .
1+ 0 + 1 4 + 2 8 − 0 + (8 −0)2 3 3 12 12
CÁC BÀI TẬP VẬN DỤNG TƯƠNG TỰ 2 1.
x + 3 + x + x + 2 − 4 lim Đáp số: 1 x→1 x − 1 3 2.
8x + 11 − x + 7 7 lim Đáp số: x→2 x − 2 54 3 3. 3x + 1 − 1+ 2 lim x Đáp số: 0 2 x→0 x
BÀI TẬP TRẮC NGHIỆM: GIỚI HẠN TẠI MỘT ĐIỂM
Câu 1: Cho các giới hạn: lim f (x) = 2 ; lim g(x) = 3 , hỏi lim 3
f ( x) − 4g ( x) x → 0 x x→ 0 x x→ 0 x bằng: A. 5. B. 2 . C. 6 − . D. 3.
Câu 2: Giá trị của lim( 2 2x −3x + ) 1 bằng? x 1 → A. 2 . B. 1. C. +∞ . D. 0 . 2 Câu 3: Giới hạn x − 2x + 3 lim bằng? x 1 → x +1 A. 1. B. 0 . C. 3 . D. 2 . Câu 4: Giới hạn 2 lim x − 4 bằng? x→ 3 A. 5 − . B. 1. C. 5 . D. 1 − . 2 x + − x − Câu 5: Giới hạn 2 1 5 3 lim bằng: x 2 →− 2x + 3 1 1 A. . B. . C. 7 . D. 3 . 3 7 Câu 6: Biểu thức sin lim x bằng: π x→ x 2 15 2 π A. 0 . B. . C. . D. 1. π 2 2( 3x +1− )1 2 x − x −
Câu 7: Cho I = lim và 2 J = lim
. Tính I − J . x→0 x x→ 1 − x +1 A. 6 . B. 3. C. 6 − . D. 0. 2
x − 3x + 2 a a
Câu 8: Cho giới hạn lim
= trong đó là phân số tối giản. Tính 2 x→2 x − 4 b b 2 2
S = a + b .
A. S = 20 .
B. S =17 .
C. S =10 .
D. S = 25 . 4 2 x − x + Câu 9: Tìm 3 2 lim . 3 x 1 → x + 2x − 3 5 2 1 A. − . B. − . C. . D. +∞ . 2 5 5 2 + + − Câu 10: Cho x ax b 1 lim =
a,b∈ . Tổng 2 2
S = a + b bằng: 2 ( ) x 1 → x −1 2
A. S =13.
B. S = 9.
C. S = 4. D. S =1. 2
x − 3x + 4 − 2
Câu 11: Giới hạn lim bằng: x→0 x 1 1 3 2 A. − . B. . C. − . D. − . 2 2 4 3 x +1 − 2 a a Câu 12: Biết lim =
( là phân số tối giản). Tính a + b + 2018. 2 x→3 x −3 b b A. 2021. B. 2023. C. 2024 . D. 2022 .
x +1− 5x +1 a a
Câu 13: Giới hạn lim =
, với a,b∈ Z,b > 0 và là phân số x→3 x − 4x − 3 b b
tối giản. Giá trị của a − b là: 8 1 A. 1. B. 1 − . C. . D. . 9 9 3 2 8 + x − 2 Câu 14: Tính lim . 2 x→0 x 1 1 1 1 A. . B. . C. . D. . 12 4 3 6 16 + x − − x
Câu 15: (*) Cho hàm số y = f ( x) 3 2 1 8 =
. Tính lim f ( x). x x→0 1 13 10 A. . B. . C. +∞ . D. . 12 12 11
HƯỚNG DẪN GIẢI : GIỚI HẠN TẠI MỘT ĐIỂM
Câu 1: Ta có lim 3 f (x) − 4g (x) = lim 3 f (x) − lim 4g (x) = 6 − Chọn C. x→ 0 x x→ 0 x x→ 0 x Câu 2: Ta có: lim( 2 2x − 3x + ) 1 = 0 . Chọn D. x 1 → 2 2 x − + − + Câu 3: Ta có: 2x 3 1 2.1 3 lim = = 1. Chọn A. x 1 → x +1 1+1 Câu 4: Dễ thấy 2
lim x − 4 = 3− 4 =1. Chọn B. x→ 3 2
2 x +1 − 5 x − 3 2 − 5 Câu 5: Ta có lim = = 3. Chọn D. x 2 →− 2x + 3 1 − Câu 6: Vì π sin x 2 sin =1 nên lim = . Chọn B. 2 π x→ x π 2 Câu 7: Ta có: 2( 3x +1 − )1 6x 6 I = lim = lim = lim = 3 . x→0 x→0 x
x( 3x +1 + ) x→0 1 3x +1 +1 2 x − x − 2 (x + )1(x − 2) J = lim = lim = lim (x − 2) = 3 − . x 1 →− x 1 →− x 1 x +1 x +1 →−
Khi đó I − J = 6 . Chọn A. 2 x − 3x + 2
(x −1)(x − 2) x −1 1 Câu 8: lim = lim = lim = . 2 x→2 x→2 x→2 x − 4 (x + 2)(x − 2) x + 2 4 Do đó a =1; 4 b = suy ra 2 2 S =1 + 4 =17. Chọn B. 4 2 x − x +
(x − )1(x + )1( 2x −2) Câu 9: 3 2 lim = lim 3 x 1 →
x + 2x − 3 x→ (x − )1( 2 1 x + x + 3)
(x + )1( 2x −2) 2 = lim = − . Chọn B. 2 x 1 → x + x + 3 5
Câu 10: Vì hàm số có giới hạn hữu hạn tại x =1 nên biểu thức tử nhận x =1
làm nghiệm, hay 1+ a + b = 0 .
Áp dụng vào giả thiết, được: 17 2
x + ax −1− a 1 − (x − ) 1 (x +1+ a) 1 lim = ⇔ lim = − . 2 x 1 → x 1 x −1 2 → (x − ) 1 (x + ) 1 2 x +1+ a 1 2 + a 1 ⇔ lim = − ⇔ = − ⇔ a = 3 − . Suy ra b = 2 . x 1 → x +1 2 2 2 Vậy 2 2 a + b =13. Chọn A. 2
x − 3x + 4 − 2 2 Câu 11: lim
x − 3x + 4 − 4 = lim x→0 x
x→0 x ( 2x − 3x + 4 + 2) x − 3 3 = lim = − . Chọn C. x→0 2 x − 3x + 4 + 2 4 x +1 − 2 − 1 Câu 12: lim x 3 = lim 1 = lim = . x→3 x −3
x→3 (x − 3)( x +1 + 2) x→3 x +1 + 2 2 2
Suy ra a =1;b = 2 .
a + b + 2018 =1+ 2 + 2018 = 2021. Chọn A. x x x 2
1 5x 1x 4x3 1 5 1 Câu 13: Ta có lim lim x 3 x 3 x 4x3 2 x 4x
3 x1 5x 1
2x 3xx 4x3
xx 4x3 lim lim x 3 2 x 4x
3 x1 5x x 3 1 x
1 x1 5x 1 18 9 . Chọn A. 16 8 3 2 8 + x − 2 2 8 + x − 8 Câu 14: Ta có: lim = lim . 2 x→0 x x→0 2 3 x ( 2 8 + x )2 3 2 + 2 8 + x + 4 1 1 = lim = . Chọn A. x→0 3 ( 2 + x )2 3 2 12 8 + 2 8 + x + 4 3
2 1+ x − 8− x ( + x − )+( 3 2 1 2 2 − 8 − x ) Câu 15: Ta có: = x x 2( 1+ x − )1 3 2 − 8 − x 2 1 = + = + x x
1+ x +1 4+ 2 8− x + (8− x)2 3 3 18 Do vậy: 2 1
lim f ( x) lim = + x→0
x→0 1+ x +1 3 3
4 + 2 8 − x + (8− x)2 2 1 1 13 = lim + lim =1+ = . Chọn B. x→0 x→0 1+ x +1 3 3
4 + 2 8 − x + (8 − x)2 12 12
DẠNG BÀI 2: GIỚI HẠN MỘT PHÍA x x+ ; x x− → → 0 0
DẠNG 2.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
Phương pháp giải: Tương tự như giải giới hạn tại một điểm nếu bài toán
không gặp dạng vô định.
Ngoài ra: Có thêm một vài giới hạn đặc biệt thường dùng: 1 lim 1 = +∞ và lim = −∞ + x→x x x − x x x x o − o − → 0 0
Lưu ý: Ta cũng có thể hiểu và biểu diễn giới hạn một bên như sau để xét dấu
hiệu số x − x tiện cho việc nhớ công thức ở trên. 0 x x+ →
nghĩa là x → x và x > x . 0 0 0 x x− →
nghĩa là x → x và x < x . 0 0 0
Ví dụ 1. Dùng định nghĩa, tính các giới hạn sau: a) 3x + 5 lim x 2− → x + 1 Lời giải lim + + + − ( 3x 5) 3lim x 5 Ta có: 3x 5 + x→ x − → 3.2 5 11 2 2 lim = = = = . x→2− x + 1 lim + + + − ( x 1) lim x 1 2 1 3 x→2 x→2− b) 1 lim x 4− → 4 − x Lời giải Ta có: x 4− →
⇔ x < 4 ⇔ 4 − x > 0 Khi đó 1 lim = +∞ . x 4− → 4 − x x − 5 c) lim x − → (x − 4)2 4 Lời giải Ta có: x − →
⇔ x < ⇔ x − < ⇒ (x − )2 4 4 4 0 4 > 0 . 1 Khi đó lim
= +∞ và lim − = − = − . − ( x 5) 4 5 1 x − → (x − 4)2 4 x→4 19 x − 5 Vậy lim = + . ∞ ( 1 − ) = −∞ . x − → (x − 4)2 4 4 2
x − 6x − x khi x ≥ 1
Ví dụ 2. Cho hàm số f (x) =
. Tính lim f (x và lim f (x − ) + ) 3
x − 3x khi x < 1 x→1 x→1
. Hỏi hàm số có giới hạn tại x = 1 hay không? Lời giải
Ta có: lim f (x) = lim( 4 2
x − 6x − x = − − = − . + + ) 4 2 1 6.1 1 1 x→1 x→1
lim f (x) = lim( 3 x − 3x = − = − . + + ) 31 3.1 2 x→1 x→1
=> lim f (x) ≠ lim f (x nên không tồn tại lim f (x) . + − ) x→1 x→1 x→1
Ví dụ 3. Cho hàm số − ≥ f (x) 2 x 3 khi x 2 =
. Tính lim f (x và lim f (x . − ) + )
x − 1 khi x < 2 x→2 x→2
Hỏi hàm số có giới hạn tại x = 2 hay không? Lời giải Ta có: lim f = − = − = . +
(x) lim+( 2x 3) 22 3 1 x→2 x→2 lim f = − = − = . −
(x) lim+(x 1) 2 1 1 x→2 x→2
=> lim f (x) = lim f (x nên lim f x = 1. 1 ( ) + − ) x→2 x→2 x→2
DẠNG 2.2: CÁC DẠNG VÔ ĐỊNH THƯỜNG GẶP
DẠNG 2.2.1: KHỬ DẠNG VÔ ĐỊNH 0 0
Phương pháp giải: Tương tự dạng vô định 0 của giới hạn tại một điểm. 0
Ví dụ 1. Tính các giới hạn sau: x + x a) 2 lim x 0+ → x − x Lời giải x x + x ( x +2 2 ) x + 2 2 lim = lim = lim = . x 0+ x 0 x − x +
x ( x −1) x 0+ → → → x − 1 1 2 b) 4 lim − x x 2− → 2 − x 20 Lời giải 2 4 − x (2 − x)(2 + x) lim = lim = lim + = . − − − ( 2 x) 4 x→2 2 − x x→2 2 − x x→2 2
3x − 3 + x − 1 5x + 4 c) lim − 2 x→1 x − 2x + 1 Lời giải Khi x 1− →
→ x < 1 ⇔ x − 1 < 0 → x − 1 = 1− x . Khi đó :
3(x −1) + (1− x) 2 5x + 2 4 9 − 3 − 5x + 4 ( 2 5x + 4) lim = lim = lim − x 1 (x −1)2 − − → x→1 x − x→ 1 1 (x −1)(3+ 2 5x + 4 ) 5(1− 2 x ) −5(1+ x) −5(1+ 1) −5 = lim = lim = = . − x 1 (x −1)(3+ 2 5x + 4 ) − → x→1 3 + 2 5x + 4 3 + 2 5.1 + 4 3
BÀI TẬP VẬN DỤNG TƯƠNG TỰ 2
2x − 2x + x − 1 x + 3 1. lim Đáp số: 7 − 2 x→1 x − 2x + 1 4 2 − x 2. lim Đáp số: 1 − − 2
x→2 2x − 5x + 2 3
x − 1+ 4 x − 1 3. lim Đáp số: 4 x 1+ → 1− x + x − 1
Ví dụ 2. Tính các giới hạn sau: 2 a) 3x + 1 − 2 lim x x 1+ → x − 1 Lời giải 2 3x + 1 − 2 2x 3x + 1− 2 4x − 2 x + 1 lim = lim = lim + + x 1 x − 1 x 1 (x −1)( 2 3x + 1 + 2x) + → → x→1 (x −1)( 2 3x + 1 + 2x)
−(x −1)(x + 1) −(x + 1) −(1+ 1) −1 lim = lim = lim = . + x 1 (x − )( 2 x + + x) + x 1 ( 2 x + + x) + → → x→1 ( 2 + + ) 2 1 3 1 2 3 1 2 3.1 1 2.1 b) 4x +1 − 3 lim + 2
x→2 3x − 4x − 4 Lời giải 21 4x +1 − 3 4x +1− 9 4(x − 2) lim = lim = lim + 2
x 2 3x − 4x − 4 x 2+ ( 2
3x − 4x − 4)( 4x +1 + 3) x 2+ → → →
(x − 2)(3x + 2)( 4x +1+3) 4 4 1 = lim = = . x 2+ →
(3x + 2)( 4x +1 +3) (3.2+ 2)( 4.2+1 +3) 12 x + 1− 5x + 1 c) lim x 3− → x − 4x − 3 Lời giải x x
( 2x −3x)(x+ 4x− + − + 3 1 5 1 ) lim = lim − − x→3 x→ x − 4x − 3 3
( 2x −4x+3)(x+1+ 5x+1)
x(x + 4x − 3) 3.6 9 = lim = = . −
x→3 (x − 1)(x +1+ 5x +1) 2.8 8
Ví dụ 3. Tính các giới hạn sau: 2 − x 2 − x 2 − x a) lim và lim
từ đó cho kết luận về lim . − 2
x→2 2x − 5x + 2 + 2
x→2 2x − 5x + 2 2
x→2 2x − 5x + 2 Lời giải Ta có: x 2− →
⇒ x < 2 ⇔ 2 − x > 0 . 2 − x 2 − x 1 − 1 − 1 − Khi đó lim = lim = lim = = . − 2
x 2 2x − 5x + 2
x 2− (x − 2)(2x − 1) x 2− → → → 2x − 1 2.2 − 1 3 Ta có: x 2+ →
⇒ x > 2 ⇔ 2 − x < 0 . 2 − x − Khi đó x 2 1 1 1 lim = lim = lim = = . + 2
x 2 2x − 5x + 2
x 2− (x − 2)(2x − 1) x 2− → → → 2x − 1 2.2 − 1 3 2 − x 2 − x 2 − x Ta thấy lim ≠ lim vậy lim không tồn − 2 + 2
x→2 2x − 5x + 2
x→2 2x − 5x + 2 2
x→2 2x − 5x + 2 tại. b) 2x + 1 lim và 2x + 1 lim
từ đó cho kết luận về 2x + 1 lim . x 3+ → x − 3 x 3− → x − 3 x→3 x − 3 Ta có: x 3+ →
⇒ x > 3 ⇔ x − 3 > 0 . => 1 lim 2x + 1 = +∞ và lim + = + = > => lim = +∞ . + ( 2x 1) 2.3 1 7 0 x 3+ → x − 3 x→3 + x→3 x − 3 Ta có: x 3− →
⇒ x < 3 ⇔ x − 3 < 0 . => 1 lim 2x + 1 = −∞ và lim + = + = > => lim = −∞ . − ( 2x 1) 2.3 1 7 0 x 3− → x − 3 x→3 + x→3 x − 3 22 Ta thấy 2x + 1 2x + 1 lim 2x + 1 ≠ lim vậy lim không tồn tại. x 3+ x − 3 x 3− → → x − 3 x→3 x − 3
DẠNG 2.2.2: KHỬ DẠNG VÔ ĐỊNH 0.∞
Nhận dạng: khi thay thử x = x vào giới hạn ta thấy kết quả sẽ ra 0.∞ . 0
Phương pháp giải: Thường ta dùng các phép biến đổi toán học để đưa về
dạng 0 sau đó áp dụng phương pháp giải khử dạng vô định 0 đã đề cập. 0 0
Ví dụ 1. Tính các giới hạn sau: a) + − − ( x) 2x 1 lim 4 3 x→4 x − 64 Lời giải Ta có: x − →
⇒ x < ⇔ − x > → − x = ( − x)2 4 4 4 0 4 4 . 2 x x x x x lim ( 2 1 2 1 4 2 1 4 4 − x) + ( + )( − ) ( + )( − ) = lim = lim = 0 . − 3 − x 64 − x x
(4 − x)(16 + 4x + 2 4 4 x ) − → → x→ 2 4 x + 4x + 16 b) + − + ( x ) 2 x 1 lim 2 1 4 3 1
2x − x + 8x − 4 x→ 2 Lời giải + Ta có: 1 1 x →
⇒ x > ⇔ 2x > 1 ⇔ 2x − 1 > 0 → 2x − 1 = (2x − 1)2 2 2 x ( 2 2 x + 1) 2x − 2 + 1 1 lim 2x − 1 = lim + ( ) ( ) 4 3 −
2x − x + 8x − 4 x x x x 2 − 3 1 1 1 + 4 → → ( )( ) 2 2 ( 2x +1)(2x−1) = lim = 0 . − 3 1 x + 4 x→ 2
BÀI TẬP VẬN DỤNG TƯƠNG TỰ 1. 1 1 lim − Đáp số: −∞ − 2
x→3 x − 3 x − 9 2. 1 12 lim − Đáp số: 1 + 3
x→2 x − 2 x − 8 2 3. lim − Đáp số: 0 + ( 2) x x 2 x→2 x − 4 23
BÀI TẬP TRẮC NGHIỆM: GIỚI HẠN MỘT PHÍA
1. SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
Câu 1: Trong các mệnh đề sau, mệnh đề nào sai? A. 1 lim 1 = +∞ . B. 1 lim = −∞ . C. 1 lim = +∞ . D. lim = +∞ . x 0+ → x x 0+ → x + 5 x→0 x x 0+ → x Câu 2: Giới hạn 2 − x +1 lim bằng: x 1+ → x −1 2 1 A. +∞. B. −∞. C. . D. . 3 3 2 3x +1 − x
Câu 3: Giới hạn lim bằng? x ( ) 1 + → − x −1 1 1 3 3 A. . B. − . C. D. − . 2 2 2 2 x
Câu 4: Giới hạn lim ( x − 2) bằng: + 2 x→2 x − 4 1 A. +∞ . B. 0 . C. .
D. Kết quả khác. 2 2 x − 2x − 3
Câu 5: Giới hạn lim bằng: x 1 →− x +1 A. 0 . B. 4 − . C. 3 − . D. 1. 2 − x + 3 khi x ≠ 1
Câu 6: Cho hàm số y = f (x) 2 x −1 =
. Tính lim f (x) . 1 x 1− → khi x =1 8 1 1 A. . B. +∞ . C. 0 . D. − . 8 8 5
x + 2 khi x ≥ 1
Câu 7: Cho hàm số f (x) =
. Khẳng định nào dưới đây là 2
x -3 khi x < 1 đúng ?
A. lim f (x) = 8 .
B. lim f (x) = 2 − . x 1 → x 1 →
C. lim f (x) = 7 .
D. lim f (x) = 7 . x 1− → x 1+ → x
Câu 8: Giới hạn lim ( x − 2) bằng: + 2 x→2 x − 4 24 1 A. +∞ . B. 0 . C. . D. Kết quả khác. 2 Câu 9: Giới hạn 1 1 lim 1 − bằng : x 0− → x x +1 A. 0. B. -1. C. 1. D. −∞ .
2. BÀI TẬP BIỆN LUẬN THEO THAM SỐ m 1 1 − khi x > 2
x − 2 x −8
Câu 10: Cho hàm số f (x) 3 = . Với giá trị nào của 2 m x +
− 2m khi x ≤ 2 2
tham số m thì hàm số có giới hạn tại x = 2 .
A. m = 3 hoặc m = 2 − .
B. m =1 hoặc m = 3 .
C. m = 0 hoặc m =1.
D. m = 2 hoặc m =1. 2 x + ax + x > Câu 11: Tìm 1 khi 2
a để hàm số f (x) =
có giới hạn tại x = 2. 2
2x − x +1 khi x ≤ 2 A. 1 − . B. 2 − . C. 2 . D. 1. x + 4 − 2 khi 0 x >
Câu 12: Cho hàm số ( ) x f x =
, m là tham số. Tìm giá 1 mx + m + khi 0 x ≤ 4
trị của m để hàm số có giới hạn tại x = 0 . 1 1 A. m = . B. m =1.
C. m = 0 .
D. m = − . 2 2 2
x − 5 khi x ≥ 3 (1)
Câu 13: Cho hàm số f (x) = 2 x −5 . khi x < 3 (2) x + 2
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f ( x)
có giới hạn khi x → 3 ? A. 19. B. 1. C. 1 − .
D. Không có số nào thỏa mãn.
BÀI GIẢI THAM KHẢO
1. SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN 25 1
Câu 1: Ta có: lim = +∞ do lim x = 0 và x > 0 . Vậy đáp án A đúng. x 0+ → x x 0+ → Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A. Chọn B. Câu 2: Ta có lim ( 2 − x + ) 1 = 1
− < 0, lim (x − )
1 = 0 và x −1 > 0 khi x 1+ → . x 1+ → x 1+ → − + Suy ra 2x 1 lim = −∞ . Chọn B. x 1+ → x −1 2 Câu 3: Ta có: 3x +1 − x 4 +1 3 lim = = − . Chọn D. x ( ) 1 + → − x −1 1 − −1 2 2 x(x − 2) (x − 2)x Câu 4: lim( − 2) x x = . lim = lim = 0 . Chọn B. + 2 x→2 x − 4 + 2 x 2 x − x 2 4 + → → x + 2 2 x − 2x − 3 (x + )1(x −3) Câu 5: Ta có lim = lim = lim (x − 3) = 4 − . Chọn B. x 1 →− x 1 →− x 1 x +1 x +1 →− − x + − x − Câu 6: Ta có f (x) 2 3 4 3 lim = lim = lim . − − 2 x 1 x 1 x −1 x 1− → → → ( x − ) 1 (x + ) 1 (2 + x + 3) 1 − 1 lim − = = Chọn D. x 1− → (x + ) 1 (2 + x + 3) 8
Câu 7: Ta có lim f (x) = lim (5x + 2) = 5.1+ 2 = 7 . Chọn D x 1+ x 1+ → → Ta có : Câu 8: Ta có (x − ) x x x − 2 lim 2 = lim = 0 . Chọn B. + 2 x 2 x − 4 x 2+ → → x + 2 1 1 1− (x +1) −x 1 − Câu 9: Ta có lim ( −1) = lim = lim = lim = 1 − . x 0− + x 0− + x 0− + x 0 x x 1 x(x 1) x(x 1) − → → → → x +1 Chọn B.
2. BÀI TẬP BIỆN LUẬN THEO THAM SỐ m Câu 10: 2 1 12 x + 2x −8
Ta có : lim f ( x) = lim − = lim + + 3 x x
x − 2 x −8 + → → x→ (x − 2)( 2 2 2 2 x + 2x + 4) (x − 2)(x + 4) x + 4 1 = lim = = . + x→ (x − 2)( lim 2 2 x + 2x + 4) + 2
x→2 x + 2x + 4 2 26 2 2 lim ( ) = lim m + − 2 m f x x m = − 2m + 2 . x 2− x 2− → → 2 2
Hàm số có giới hạn tại x = 2 khi chỉ khi lim f (x) = lim f (x) x 2− x 2+ → → 2 m 1 2 m = 3 ⇔ − 2m + 2 = m 3 ⇔ − 2m + = 0 ⇔ . Chọn B. 2 2 2 2 m = 1
Câu 11: Xét: lim f ( x) = lim x + ax + = a + + + ( 2 )1 2 5. x→2 x→2
lim f (x) = lim x − x + = − − ( 2 2 )1 7. x→2 x→2
Hàm số y = f (x) có giới hạn tại x = 2 khi và chỉ khi
lim f (x) = lim f (x) ⇔ 2x + 5 = 7 ⇔ a =1. Chọn D. x 2+ x 2− → → Câu 12: Ta có: 2 f (x) x + 4 − 2 lim (x + 4) = lim − 2 = lim = lim x x 0+ x 0+ → → x x 0+ →
x( x + 4 + 2) x 0+ → x( x + 4 + 2) 1 1 1 1 = lim
= . lim f ( x) = lim mx + m + = m + x 0+ →
x + 4 + 2 4 x 0− x 0− → → 4 4
Hàm số đã cho có giới hạn tại x = 0 khi và chỉ khi lim f ( x) = lim f ( x) x 0+ x 0− → → 1 1
⇔ = m + ⇔ m = 0. Chọn C. 4 4
Câu 13: Hàm số đã cho các định trên \{ } 2 .
Ta có lim f ( x) 2 2
= lim x − 5 = 3 − 5 = 2 . x 3+ x 3+ → → 2 x − m Đặt f ( x) =
khi x < 3 ( m là tham số, m > 0 ). x + 2 2 2
x − m 3 − m 9 − m
Ta có lim f ( x) = lim = = = . x 3− x 3− → → x + 2 3+ 2 5
Để hàm số f ( x) có giới hạn khi x → 3 thì ( ) = ( ) 9 lim lim − m f x f x ⇔ = 2 ⇔ m = 1 − . Chọn C. x 3+ x 3− → → 5 27
DẠNG BÀI 3: GIỚI HẠN HÀM SỐ TẠI VÔ CỰC
DẠNG 3.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
Ví dụ 1. Tính giới hạn của các hàm số sau: a) 2 lim x + 2x + 2 x→+∞ Lời giải Ta có 2
lim x = +∞ và 2 2 lim 1 + + = 1 . 2 x→+∞ x→+∞ x x Nên 2 2 2 2
lim x + 2x + 2 = lim x 1 + + = +∞ . 2 x→+∞ x→+∞ x x b) 2
lim 4x + 4x + 2023 x→+∞ Lời giải 2 2 4 2023 4 2023
lim 4x + 4x + 2023 = lim x 4 + + = lim x 4 + + 2 x→+∞ x→+∞ x→+∞ x x 2 x x 4 2023 = lim x 4 + + = +∞ . x→+∞ 2 x x c) 2
lim 9x − 5x + 2023 x→−∞ Lời giải 2 2 5 2023 5 2023
lim 9x − 5x + 2023 = lim x 9 − + = lim x 9 − + 2 2 x→−∞ x→−∞ x→−∞ x x x x 5 2023 = − lim x 9 − + = +∞ . 2 x→−∞ x x d) 3 6 4 2
lim 5x + 2x + x + x − 2023 x→+∞ Lời giải 3 6 4 2 6 2 1 1 2023
lim 5x + 2x + x + x − 2023 = lim 3 x 5 + + + − 2 4 5 6 x→+∞ x→+∞ x x x x 2 1 1 2023 = 2 3 lim x . 5 + + + − = +∞ . x→+∞ 2 4 5 6 x x x x
DẠNG 3.2: CÁC DẠNG VÔ ĐỊNH THƯỜNG GẶP
Nguyên tắc: Khử được yếu tố làm giới hạn bị vô định. 28
DẠNG 3.2.1: KHỬ DẠNG VÔ ĐỊNH ∞ TẠI VÔ CỰC ∞ f (x)
Vô định ∞ thường có dạng phân thức . ∞ g(x)
Phương pháp giải: Đặt nhân tử chung n x và m
x ra ngoài với n và m là số
mũ lớn nhất của f (x) và g(x).
Ví dụ 1. Tính giới hạn của các hàm số sau: 3 + + a) x 3x 1 lim 3 2 x→+∞ 6 − x − 6x + 2 Lời giải 3 3 1 x + + 3 1 1 3 2 3 1+ + x + 3x + 1 x x 2 3 − x x 1 lim = lim = lim = . x→+∞ 3 2 x→+∞ x→+∞ −6x − 6x + 2 6 2 6 2 3 6 x −6 − + −6 − + 3 x x 3 x x 3 2 − + − b) x 2x 3x 5 lim 2 x→+∞ 2x + 1 Lời giải 3 2 3 5 2 3 5 x 1 − + − x 1 − + − 3 2 2 3 2 3
x − 2x + 3x − 5 x x x x x x lim = lim = lim x→+∞ 2 x→+∞ x→+∞ 2x + 1 2 1 1 x 2 + 2 + 2 2 x x − 2 + 3 − 5 1 2 3 lim . lim x x x x = +∞ . x→+∞ x→+∞ + 1 2 2 x 2 − c) 2x 5 lim 5 2
x→−∞ 3x − 4x + x + 1 Lời giải 2 5 x 2 − 2 2 2x − 5 x lim = lim x→−∞ 5 2 x→−∞
3x − 4x + x + 1 5 4 1 1 x 3 − + + 3 4 5 x x x 29 − 5 2 2 1 x 2 = lim . lim = 0. = 0 .
x→−∞ 3 x→−∞ x − 4 + 1 + 1 3 3 3 4 5 x x x
(2x − 3)10 .(4x +1)12 d) lim x→+∞ (x − 5)22 Lời giải 10 3 10 12 1 12
(2x 3)10 (4x 1)12 x 2 − x 4 + 12 − + x x lim = lim x→+∞ (x − 5)22 x→+∞ 5 22 22 x 1 − 22 x 3 10 1 12 2 − 4 + 12 x x (2 −0)10 (4 + 12 0) = lim = = 34 2 x→+∞ 5 22 (1−0)22 1− 22 x e) 5x + 1 lim x→+∞ 2 3x + 4x + 1 Lời giải 5x + 1 5x + 1 5x + 1 lim = lim = lim x→+∞ 2 x→+∞ x→+∞ 3x + 4x + 1 3x + x 4 + 1 3x + x 4 + 1 2 2 x x 1 x 5 + 1 5 + x x 5 + 0 = lim = lim = = 1 . x→+∞ x→+∞ 1 1 3 + 4 + 0 x 3 + 4 + 3 + 4 + 2 2 x x f) 5x + 1 lim x→−∞ 3x + 2 4x + 1 Lời giải 5 1 5 1 3 . x 8 − + 3 3 3 2 . x 8 − + 8x − 5x + 3 3 1 lim = lim x x = lim x x x→−∞ 2 x→−∞ x→−∞ 4x + 4x + 1 4x + x 4 + 1 4x − x 4 + 1 x x 30 5 1 3 8 − + 3 3 x x 8 − 0 + 0 2 1 = lim = = = . x→−∞ 1 4 + 4 + 0 6 3 4 − 4 + x
DẠNG 3.2.2: KHỬ DẠNG VÔ ĐỊNH ∞ − ∞ và 0.∞ TẠI VÔ CỰC
Phương pháp giải: + Đặt nhân tử chung .
+ Quy đồng mẫu phân thức.
+ Nhân chai lượng liên hợp để khử căn.
+ Chuyển về dạng 0 hoặc ∞ đã biết. 0 ∞
Ví dụ 1. Tính giới hạn của các hàm số sau: 1. 2
lim x − 2x + 1 x→+∞ Lời giải 2 2 2 1
lim x − 2x + 1 = lim x 1 − + = +∞ . 2 x→+∞ x→+∞ x x 2. 2
lim 9x + 5x + 2023 x→−∞ Lời giải 2 2 5 2023 5 2023
lim 9x + 5x + 2023 = lim x 9 + + = lim x 9 + + 2 2 x→−∞ x→−∞ x→−∞ x x x x 5 2023 = − lim x 9 + + = +∞ . 2 x→−∞ x x 3. 3 6 4 3
lim 5x + 2x − x − x − 2023 x→+∞ Lời giải 3 6 4 3 6 2 1 1 2023 lim 5x 2x x x 2023 lim + − − − = 3 x 5 + − − − 2 3 5 6 x→+∞ x→+∞ x x x x 2 2 1 1 2023 = 3 lim x . 5 + − − − = +∞ . 2 3 5 6 x→+∞ x x x x
Ví dụ 2. Tính giới hạn của các hàm số sau: a) 2
lim x + 3 − x x→+∞ Lời giải ( 2 2 x + 3) − 2x 2 3 3
lim x + 3 − x = lim = lim = lim x→+∞ x→+∞ 2 x→+∞ 2 x→+∞ x + 3 + x x + 3 + x x 1+ 3 + 1 2 x x 31 1 3 3 = lim . lim = 0. = 0 . x→+∞ x→+∞ x 3 1 1+ 0 + + + 0 1 2 x x b) x x x x ( 2 lim − +1 + − 2 →−∞ ) Lời giải
x − x + + x − − x +
x − x + + x − = = x→−∞ ( ) 2 1 2 2 ( )2 3 5 lim 1 2 lim lim x→−∞ 2
x − x +1 − (x − 2) x→−∞ 2
x − x +1 − x + 2 5 5 x 3 x 3 − + − + lim x lim x = = x→−∞ 1 1 x→−∞ 1 1 2 x 1− + − x + 2 −x 1− + +1− 2 2 x x x x x 5 3 − + x 3 − + 0 3 lim − = = = x→−∞ 1 1 2 1− 0 + 0 +1− 0 2 1− + +1− 2 x x x c) 2 2
lim x + x − 4 + x x→+∞ Lời giải ( 2 2 2
x + x ) −( 4 + 2x ) 2 x + x − (4 + 2 x 2 2 )
lim x + x − 4 + x = lim = lim x→+∞ x→+∞ 2 2 x→+∞ x + x + 4 + 2 x x + x + 4 + 2 x 4 4 x 1− 1− x − 4 x x 1 = lim = lim = lim = x→+∞ 2 2 x→+∞ x→+∞ x + x + 4 + x 1 4 1 4 2 x 1+ + + 1 1 + + + 1 x x x x d) 2 2
lim 4x − x − 5 + 4x x→−∞ Lời giải 32 2
4x − x − (5 + 2 4x 2 2 ) −x − 5
lim 4x − x − 5 + 4x = lim = lim x→−∞ x→−∞ 2 2 x→−∞ 4x − x + 5 + 2 4x 4x − x + 5 + 2 4x 5 5 −x 1 + −x 1 + 5 1+ x x = lim = lim = lim x x→−∞ x→−∞ x→−∞ 1 5 1 5 1 5 x 4 − + + 4 −x 4 − + + 4 4 − + + 4 2 2 2 x x x x x x 1+ 0 1 = = . 4 − 0 + 0 + 4 4
Ví dụ 2. Tính giới hạn của các hàm số sau: x −1 a) lim ( x + 2) 3 x→+∞ x + x Lời giải x − x − x + x − lim (x + 2) 1 = lim (x+2) 1 ( 2) 1 = lim 3 x→+∞ x→+∞ 3 x→+∞ 3 x + x x + x x + x 2 1 2 1 x 1+ x 1− 1+ 1− x x x x (1+ 0) 1− 0 = lim = lim = = 1. x→+∞ x→+∞ 3 1 1 1+ 0 2 x 1+ 1+ 1 1 2 2 x x 3 2x + x b) lim x 5 2 x→−∞ x − x + 3 Lời giải 3 1 1 x 2 + 3 3 2 + 3 2 lim x + x lim x = = lim x x x x 5 2 x→−∞
x − x + 3 x→−∞ 5 1 3 x→−∞ 2 1 3 x 1 x 1 − + − + 3 5 3 5 x x x x 1 1 2 + 2 + 3 3 = lim x x = lim x . lim x = − 2 . x→−∞ x 1 3 x→−∞ x −x →−∞ 1 3 1− + 1− + 3 5 3 5 x x x x
BÀI TẬP TƯƠNG TỰ 1. x x x Đáp số: 2 − x ( 2 lim 4 + 8 +1 + 2 →−∞ ) 33 2. + + + + Đáp số: 3 →−∞ ( 2 lim x x 2 x 2 x ) 2 3. 2 2
lim x − 4x + 1 − x − 9x Đáp số: 5 x→+∞ 2 4. − − − Đáp số: 0 →+∞ ( 3 3 lim 2x 8x 5x 1 x ) 4x −1 5. lim (2x + 3) Đáp số: 3 0 x→+∞ 16x + 2x
BÀI TẬP TRẮC NGHIỆM GIỚI HẠN HÀM SỐ TẠI VÔ CỰC
Câu 1: Chọn kết quả đúng của ( 5 3 lim 4
− x − 3x + x + 1) . x→−∞ A. 0 . B. +∞ . C. −∞ . D. 4 − . Câu 2: Giới hạn ( 3 2
lim 3x + 5x − 9 2x − 2023 bằng: x→−∞ ) A. −∞ . B. 3 . C. 3 − . D. +∞ .
Câu 3: Tính giới hạn 2x −1 lim . x→+∞ 4x + 2 1 1 − 1 − A. . B. 1. C. . D. 2 4 2 2 x − 2023x + 3
Câu 4: Tính giới hạn lim được: 2
x→+∞ 2x + 2023x 1 1 A. 2023. B. . C. 2. D. . 2 2023 5 3 x − x + Câu 5: Giới hạn 2 3 1 lim bằng: 3 4 5
x→+∞ 4x − 2x − x − 3 1 3 A. 2 − . B. . C. 3 − . D. . 2 2 3 4 4x +1 2x +1
Câu 6: Cho hàm số f (x) ( ) ( ) =
. Tính lim f (x) . (3+ 2x)7 x→−∞ A. 2 . B. 8 . C. 4 . D. 0. (x − )10 1 (x + 2)6 Câu 7: lim bằng: x→−∞ (x +9)8 2 2 1 A. . B. 1. C. 1 − . D. − . 9 9 −
Câu 8: Giá trị của 2x 1 lim bằng: x→−∞ 2 x +1 −1 34 A. 0 . B. 2 − . C. −∞ . D. 2 . 1+ 3x
Câu 9: Chọn kết quả đúng của lim . x→+∞ 2 2x + 3 3 2 2 3 2 2 A. − . B. − . C. . D. . 2 2 2 2 2 x + 2 − 2
Câu 10: Giới hạn lim bằng : x→+∞ x − 2 A. −∞ . B. 1. C. +∞ . D. -1 Câu 11: Cho ( 2
lim 9x + ax + 3x) = 2
− . Tính giá trị của a . x→−∞ A. 6 − . B. 12. C. 6 . D. 12 −
Câu 12: Tìm giới hạn = ( 2 2 M lim
x − 4x − x − x Ta được M bằng: x ). →−∞ 3 1 3 1 A. − . B. . C. . D. − . 2 2 2 2 Câu 13: Biết ( 2
lim 5x + 2x + x 5) = a 5 + b với a, b∈ . Tính S = 5a + b . x→−∞ A. ( 2 2 lim
x − 4x − x − x B. S = 1
− . C. S =1. D. S = 5 →−∞ ). x Câu 14: Tìm x x . x ( 3 3 lim +1− + 2 →+∞ ) A. 1 − . B. −∞ . C. +∞ . D. 1.
BÀI GIẢI THAM KHẢO:
TRẮC NGHIỆM GIỚI HẠN HÀM SỐ TẠI VÔ CỰC Câu 1: Ta có ( 5 3 lim 4
− x − 3x + x + ) 1 5 3 1 1 lim x . lim 4 = − − + + x→−∞ 2 4 5 x→−∞ x→−∞ x x x = +∞ . 3 1 1 lim 4 − − + + = 4 − < 0. Vì 2 4 5 x→−∞ x x x Chọn B. 5 lim x = − . ∞ x→−∞ Câu 2: ( 3 2 lim 3x 1 1 2023
+ 5x − 9 2x − 2023 3 lim x . lim 3 5 9 2 = + − − x→−∞ ) 2 3 x→−∞ x→−∞ x x x = −∞ . Chọn A. 35 1 2 2x 1 − − x 1 Câu 3: Ta có lim = lim = . Chọn A. x→+∞ 4x + 2 x→+∞ 2 2 4 + x 2023 3 2 x − 2023x + 3 1− + 2 1 Câu 4: lim = lim x x = . Chọn B. 2
x→+∞ 2x + 2023x x→+∞ 2023 2 + 2 x3 1 5 3 x − x + 2 − + 2 5 Câu 5: 2 3 1 lim = lim x x = 2 − . Chọn A. 3 4 5
x→+∞ 4x − 2x − x − 3 x→+∞ 4 2 3 − −1− 2 5 x x x 3 4 1 1 3 4 4 + 2 4x 1 2x 1 + + +
Câu 6: lim f (x) ( ) ( ) lim lim x x = = = 8 x→−∞ x→−∞ (3+ 2x)7 7 x→−∞ 3 2 + x Chọn B. 10 6 1 2 ( − + x − )10 1 (x + 2)6 1 1 Câu 7: lim lim x x = = 1. Chọn B. x→−∞ (x +9)8 2 8 x→−∞ 9 1 + 2 x 1 − − 2x −1 2 Câu 8: Ta có: 2x 1 lim = lim = lim x = 2 − x→−∞ 2
x +1 −1 x→−∞ 1 x→−∞ 1 1 −x 1+ −1 − 1+ − 2 x 2 x x Chọn B 1 1 x + 3 + 3 + 3 2 Câu 9: Ta có 1 3 lim x lim x = = lim x = . x→+∞ 2 2x + 3 x→+∞ 3 x→+∞ 3 2 x 2 + 2 + 2 2 x x Chọn C 2 2 2 2 x 1+ − 2 1+ − 2 2 x + 2 − 2 Câu 10: lim = lim x = lim x x =1. Chọn B. x→+∞ x − 2 x→+∞ x − 2 x→+∞ 2 1− x 36 Câu 11: Ta có: lim ax a a
x + ax + x = = = − . x→−∞ ( 2 9 3 ) lim lim x→−∞ 2
9x + ax − 3 x x →−∞ a 6 − 9 + − 3 x a ⇒ − = 2 − ⇔ a =12. 6 Chọn B. − Câu 12: Ta có: = − − − = x x x x x x→−∞ ( 2 2 ) 3 M lim 4 lim x→−∞ 2 2
x − 4x + x − x 3 − x 3 3 = lim = lim = . Chọn C. x→−∞ 4 1 x→−∞ 4 1 2 x . 1− + 1− 1− + 1− x x x x 2x 2 Câu 13: lim x + x + x = = x→−∞ ( 2 5 2 5) lim lim x→−∞ 2
5x + 2x − x 5 x→−∞ 2 − 5 + − 5 x 1 = − 5 1
. Suy ra: a = − , b = 0. Vậy S = 1 − . Chọn B. 5 5 2 −
Câu 14: Ta có: lim + x − x + = + x→+∞ ( 3 3 1 2) lim 1 x→+∞ 2 3
x + x x + 2 + x ( 3+2)2 3 3 −2 − 2 2 lim 1+ = lim 1 x + = 1 2 2 x→+∞ 2 2 x→+∞ 2 2 2 + 3 + + 3 + + 3 + + 3 x 1 1 1 1 1 1+ 3 3 3 3 x x x x Vậy lim + − + = . Chọn D. →+∞ ( 3 3 x 1 x 2) 1 x 37 Chương III.
GIỚI HẠN. HÀM SỐ LIÊN TỤC Bài 3 HÀM SỐ LIÊN TỤC A. TÓM TẮT LÝ THUYẾT.
I. Hàm số liên tục tại một điểm x . 0
Cho hàm số y = f (x) xác định trên khoảng K và x ∈ K . 0
- Hàm số y = f (x) được gọi là liên tục tại điểm x nếu lim f (x) = f (x . 0 ) 0 x→ 0 x
- Nếu y = f (x) không liên tục tại x thì gọi là hàm số gián đoạn tại x . 0 0
Chú ý: Nếu hàm số y = f ( x) không xác định tại x thì hàm số y = f ( x) 0
không liên tục tại x . 0
II. Hàm số liên tục tại trên một khoảng, trên một đoạn.
- Hàm số y = f (x) xác định khoảng ( ; a b) .
Hàm số y = f (x) được gọi là liên tục trên khoảng ( ;
a b) nếu f (x) liên tục
tại mọi điểm trên khoảng ấy.
- Hàm số y = f (x) xác định trên đoạn [a;b] .
Hàm số y = f (x) được gọi là liên tục trên đoạn [a;b] nếu f (x) liên tục trên khoảng ( ;
a b) và lim f (x) = f (a) , lim f (x) = f (b). x a+ → x b− →
- Nếu hàm số y = f (x) liên tục đoạn [ ;
a b] và f (a). f (b) < 0 thì luôn tồn tại
ít nhất một điểm c∈(a;b)sao cho f (c) = 0.
III. Một số kết quả được thừa nhận.
1) Hàm số đa thức y = P(x) , các hàm số lượng giác y = sin x, y = cos x liên tục trên R. 2) Hàm phân thức P(x) y =
, hàm số căn thức y = P(x) và các hàm số Q(x)
lượng giác y = tanx, y = cotx liên tục trên từng khoảng của tập xác định của chúng.
3) Cho hai hàm số y = f (x), y = g (x) liên tục tại x . 0
• Khi đó y = f (x) + g (x) , y = f (x) − g (x) , y = f (x).g (x) liên tục tại x . 0 5 f (x) 4) Hàm số y =
liên tục tại x nếu g (x ≠ 0 . 0 ) g (x) 0 B. CÁC DẠNG TOÁN. DẠNG 1:
g x khi x ≠ x
Xét tính liên tục của hàm số f (x) ( ) 0 = tại x = x a khi x = 0 x0 2 x + x − 2 ≠
Ví dụ 1: Cho hàm số f (x) khi x 1 2 = x −1 . 2 khi x =1
Xét tính liên tục của hàm số tại điểm x =1. 0 Giải:
Ta có: f (x = f 1 = 2 . 0 ) ( )
Với mọi x ≠1 ta có: 2 + − − + + + f (x) x x 2 (x ) 1 (x 2) x 2 1 2 3 lim = lim = lim = lim = = ≠ f 1 . 2 x 1 → x 1 → x 1 x −1 → ( x − ) 1 (x + ) ( ) x 1 1 → x +1 1+1 2
Vậy hàm số f (x) không liên tục tại điểm x =1. 0 2
x + 3x khi x ≠ 3 − 2
Ví dụ 2: Cho hàm số f (x) x + 4x + 3 = . 3 khi x = 3 − 2
Xét tính liên tục của hàm số tại điểm x = 3 − . 0 Giải: Ta có: f ( 3 x = f 3 − = . 0 ) ( ) 2 Với mọi x ≠ 3 − ta có: 2 + + − f (x) x 3x x(x 3) x 3 3 lim = lim = lim = lim = = = f 3 − 2 x 3 →− x 3 →− x 3 x + 4x + 3 →− ( x + ) 1 (x + 3) ( ) x 3 →− x +1 3 − +1 2
Vậy hàm số f (x) liên tục tại điểm x = 3 − . 0 DẠNG 2:
g x khi x > x
Xét tính liên tục của hàm số f (x) ( ) 0 = tại x = x h 0
( x) khi x ≤ x0 6 2 x − 4
Ví dụ 1: Cho hàm số < f (x) khi x 2 = x − 2 .
3x − 2 khi x ≥ 2
Xét tính liên tục của hàm số tại điểm x = 2 . 0 Giải:
Ta có: f (x = f 2 = 3.2 − 2 = 4 . 0 ) ( ) Với x > 2 ta có:
lim f (x) = lim (3x − 2) = 3.2 − 2 = 4 . x 2+ x 2+ → → Với x < 2 ta có: 2 x − x − x + lim f (x) 4 ( 2)( 2) = lim = lim
= lim ( x + 2) = 2 + 2 = 4 . x 2−
x 2− x − 2 x 2− x − 2 x 2− → → → →
Do đó: f (2) = lim f (x) = lim f (x) = 4 . x 2+ x 2− → →
Vậy hàm số f (x) liên tục tại điểm x = 2 . 0 2 3
x + x − 2 khi x < 1
Ví dụ 2: Cho hàm số f (x) = . 2
x + 3x −1 khi x ≥1
Xét tính liên tục của hàm số tại điểm x =1. 0 Giải:
Ta có: f (x ) = f ( ) 2 1 = 1 + 3.1−1 = 3 . 0 Với x >1ta có:
lim f (x) = lim x + x − = + − = . + x + → → ( 2 3 1) 2 1 3.1 1 3 x 1 1 Với x <1 ta có: lim f (x) = lim + − = + − = − − ( 2 3x x 2 ) 2 3.1 1 2 2 x 1 → x 1 → Do đó: f ( )
1 = lim f (x) ≠ lim f (x) . x 1+ x 1− → →
Vậy hàm số f (x) không liên tục tại điểm x =1. 0 DẠNG 3: g x khi x ≠ x
Tìm m để hàm số f (x) ( ) 0 =
liên tục tại x = x h 0 (m) khi x = x0 7 2
x − x − 2
Ví dụ 1: Cho hàm số ≠ − f (x) khi x 1. = x +1
2m +5 khi x = 1. −
Tìm m để hàm số liên tục tại điểm x = 1 − . 0 Giải:
Ta có: f (x = f 1 − = 2m + 5. 0 ) ( ) Với mọi x ≠ 1 − ta có: 2
x − x − x + x − lim f (x) 2 ( )1( 2) = lim = lim
= lim ( x − 2) = 1 − − 2 = 3 − . x 1 →− x 1 →− x 1 →− x 1 x +1 x +1 →−
Để hàm số f (x) liên tục tại điểm x = 1 − thì: 0 f (− )
1 = lim f (x) ⇔ 2m + 5 = 3 − ⇔ m = 4 − . x 1 →− 3 2
x − x + 2x − 2 ≠
Ví dụ 2: Cho hàm số f (x) khi x 1 = x −1 . 3x + m khi x =1
Tìm m để hàm số liên tục tại điểm x =1. 0 Giải:
Ta có: f (x = f 1 = 3 + m . 0 ) ( )
Với mọi x ≠1 ta có: 3 2 2 2
x − x + x −
x x − + x −
x − x + lim f (x) 2 2 ( )1 2( )1 ( )1( 2) = lim = lim = lim x 1 → x 1 → x 1 → x 1 x −1 x −1 → x −1 = lim( 2 x + 2) 2 =1 + 2 = 3 . x 1 →
Để hàm số f (x) liên tục tại điểm x =1 thì: 0 f ( )
1 = lim f (x) ⇔ 3 + m = 3 ⇔ m = 0 . x 1 → DẠNG 4: g x khi x ≤ x
Tìm m để hàm số f (x) ( ) 0 =
liên tục tại x = x h 0 ( x,m) khi x > x0 3 3x + 2 − 2 khi x > 2
Ví dụ 1: Cho hàm số f (x) x − 2 = . 1 mx + khi x ≤ 2 4
Tìm m để hàm số liên tục tại điểm x = 2 . 0 Giải: 8 Ta có: f ( 1
x = f 2 = 2m + . 0 ) ( ) 4 Với x > 2 ta có 3 + − ( 3 3x + 2 − 2) x ( 33x+2)2 3 2 + 2. 3x + 2 + 2 3 2 2 )
lim f (x) = lim = lim x + → x + → x 2 − x + → (x − 2) ( 33x+2)2 2 2 2 3 2
+ 2. 3x + 2 + 2 ) ( 3 3x + 2)3 3 − 2 3x + 2 − 8 = lim = lim x + → (x − 2) ( 33x+2)2 3 2
+ 2. 3x + 2 + 2 ) x + → (x − 2) ( 33x+2)2 2 2 3 2 + 2. 3x + 2 + 2 ) 3(x − 2) = lim 3 lim = x→2+ (
x − 2)( 3 3x + 2)2 3 2
+ 2. 3x + 2 + 2 ) x 2+ → ( 3 3x + 2 )2 3 2 + 2. 3x + 2 + 2 3 1 = ( = . 3 + )2 3 2 4 3.2 2 + 2. 3.2 + 2 + 2 Với x < 2 ta có: f (x) 1 1 lim = lim mx + = 2m + . x 2− x 2− → → 4 4
Để hàm số f (x) liên tục tại điểm x = 2 thì: 0 f ( ) = f (x) = f (x) 1 1 2 lim lim
⇔ 2m + = ⇔ m = 0 . x 2+ x 2− → → 4 4 x −1
Ví dụ 2: Cho hàm số f (x) khi x >1 = x −1 . 3 mx +1 khi x ≤1
Tìm m để hàm số liên tục tại điểm x =1. 0 Giải:
Ta có: f (x = f 1 = 3m +1. 0 ) ( ) Với x >1ta có: − − f (x) x 1 x 1 1 1 lim lim lim = = = lim = . x 1+ x 1+ x −1 x 1+ ( x − )
1 ( x + ) x 1 1 + → → → → x +1 2 Với x <1 ta có:
lim f (x) = lim (3mx + ) 1 = 3m +1. x 1− x 1− → → 9
Để hàm số f (x) liên tục tại điểm x =1 thì: 0 f ( ) = f (x) = f (x) 1 1 1 lim lim
⇔ 3m +1 = ⇔ m = − . x 1+ x 1− → → 2 6
DẠNG 5: CHỨNG MINH PHƯƠNG TRÌNH CÓ NGHIỆM
Nếu hàm số f (x) liên tục trên đoạn [a;b] và f (a). f (b) < 0 thì tồn tại ít
nhất một điểm c∈(a;b) sao cho f (c) = 0 .
Ví dụ 1: Chứng minh phương trình: 3
2x − 6x +1= 0 có ít nhất 2 nghiệm. Giải: Đặt f (x) 3
= 2x − 6x +1 thì f (x) liên tục trên R.
Ta có: f (0) =1; f ( ) 1 = 3 − ; f (2) = 5 . f (0). f ( ) 1 =1.− 3 = 3
− < 0 do đó ∃x ∈ 0;1 sao cho f (x = 0 nên phương 0 ) 0 ( )
trình đã cho có nghiệm trên khoảng (0; ) 1 . f ( ) 1 . f (2) = 3.5 − = 15
− < 0 do đó ∃x ∈ 1;2 sao cho f (x = 0 nên phương 0 ) 0 ( )
trình đã cho có nghiệm trên khoảng (1;2) .
Vậy phương trình đã cho có ít nhất 2 nghiệm.
Ví dụ 2: Chứng minh rằng phương trình: 2 x .cos x + .
x sinx +1 = 0 có ít nhất
một nghiệm thuộc khoảng (0;π ). Giải: Đặt f (x) 2 = x .cos x + .
x sinx +1 liên tục trên đoạn [0;π ] .
Ta có: f ( ) = > f (π ) 2 0 1 0;
=1−π < 0 do đó ∃x ∈ 0;π sao cho f (x = 0 . 0 ) 0 ( )
Vậy phương trình đã cho có nghiệm trên khoảng (0;π ). 10
C. BÀI TẬP TỰ LUYỆN.
3x +10 − x − 4 khi x ≠ 2 −
Bài 1: Cho hàm số f (x) x + 2 = . 1 − khi x = 2 − 4
Xét tính liên tục của hàm số tại điểm x = 2 − . 0 2 4 − x + 2x + 8 khi x < 2
Bài 2: Cho hàm số f (x) 2 x − 3x + 2 = . 19 2x − khi x ≥ 2 4
Xét tính liên tục của hàm số tại điểm x = 2 . 0 3 − x khi x ≠ 3
Bài 3: Cho hàm số f (x) = x +1 − 2 3 m − 2 khi x = 3
Tìm m để hàm số liên tục tại điểm x = 3. 0 4 2 x − 5x + 4 <
Bài 4: Cho hàm số f (x) khi x 2 3 = x −8 . 2 mx + x + 2 khi x ≥ 2
Tìm m để hàm số liên tục tại điểm x = 2 . 0
Bài 5: Chứng minh rằng phương trình: mx(x − ) 4
2 + x − 2 = 0 luôn có nghiệm với mọi m.
D. BÀI TẬP TRẮC NGHIỆM. 1+ 2x −1
Bài 1: Cho hàm số f (x) khi x > 0 = x
. Với giá trị nào của a
3x + a −1 khi x ≤ 0
thì hàm số đã cho liên tục tại x = 0 . 0 A. a =1. B. a = 2 . C. a = 4 . D. a = 3. 2 Bài 2: Cho hàm số + f (x) x 1 =
. Khi đó hàm số y = f (x) liên tục trên 2 x + 5x + 6 khoảng nào? A. ( 2; − +∞) . 11 B. ( 2; − 3) . C. (− ; ∞ 2 − ) . D. (− ;3 ∞ ) . 3 2
2x − 7x + 7x − 2 khi x ≠ 1 3 2
Bài 3: Cho hàm số f (x) x − 3x + 7x − 5 = . Với giá trị nào của x + m khi x =1 2
tham số m thì hàm số liên tục tại x =1. 0 A. 1 m= − . 4 B. m= 2 . C. 3 m= . 4 D. 3 m= − . 4 Bài 4: Cho hàm số − f (x) x 1 =
. Phát biểu nào sau đây đúng? x −1
(I) f (x) gián đoạn tại x =1.
(II) f (x) liên tục tại x =1. (III) f (x) 1 lim = . x 1 → 2 A. Chỉ (I). B. Chỉ (II). C. Chỉ (I) và (III). D. Chỉ (II) và (III).
Bài 5: Chọn giá trị f (0) để hàm số + − f (x) 2x 1 1 = liên tục tại điểm x(x +1) x = 0 . 0 A. 1. B. 2. C. 3. D. 4. x +1 − x
Bài 6: Tìm m để hàm số f (x) khi x > 0 = x liên tục trên R. 2
2x + 3m +1 khi x ≤ 0 A. m=1.. 12 B. 1 m= − . 6 C. m= 2 . D. m= 0 . x +1 khi x < 2
Bài 7: Tìm m để hàm số f (x) 2
= x − 2mx + 3m + 2 liên tục trên R. 2x − 4 +3 khi x ≥ 2 A. m=1. B. 1 m= − . 6 C. m= 5 . D. m= 0 . 2 x + 4x − 5 ≠ −
Bài 8: Cho hàm số f (x) khi x 5 = x + 5 . Với giá trị nào của 2a − 4 khi x = 5 −
tham số a thì hàm số liên tục tại x = 5 − . 0 A. a = 5. B. a = 10 − . C. a = 6 − . D. a = 1 − . 3x +1 − 2 khi x >1 2 Bài 9: Tìm x −1
a để hàm số f (x) =
liên tục tại x =1. a( 2 x − 0 2) khi x ≤1 x −3 A. 1 . 2 B. 1 . 4 C. 3 . 4 D. 1. 2 + >
Bài 10: Cho hàm số f (x) x 1 khi x 0 =
. Mệnh đề nào dưới đây sai? x khi x ≤ 0
A. lim f (x) =1. x 0+ → 13 B. f (0) = 0 .
C. lim f (x) = 0 . x→0
D. f (x) liên tục tại x = 0 . 0
E. HƯỚNG DẪN GIẢI
BBÀI TẬP TỰ LUYỆN Bài 1: Giải: Ta có: f ( 1 x = f 2 − = − . 0 ) ( ) 4 Với mọi x ≠ 2 − ta có: x + − x − x + − x + lim f (x) 3 10 4 3 10 ( 4) = lim = lim x 2 →− x 2 →− x 2 x + 2 →− x + 2
( 3x +10 −(x + 4))( 3x +10 +(x + 4)) lim = x 2 →−
(x 2)( 3x 10 (x 4)) + + + +
( 3x +10 )2 − ( x + 4)2 2
−x − 5x − 6 lim lim = = x 2 →−
( x 2)( 3x 10 (x 4)) x 2 →− (x 2)
( 3x 10 (x 4)) + + + + + + + +
−(x + 2)(x + 3) −(x + 3) lim = = lim x 2
→− ( x + 2)( 3x +10 + (x + 4)) x 2 →− 3x +10 + (x + 4) −( 2 − + 3) 1 = = − = f ( 2 − ) . 3.− 2 +10 + ( 2 − + 4) 4
Vậy hàm số f (x) liên tục tại điểm x = 2 − . 0 Bài 2: Giải: Ta có: f ( 19 3
x = f 2 = 2.2 − = − . 0 ) ( ) 4 4 Với x > 2 ta có: f (x) 19 19 3 lim = lim 2x − = 2.2 − = − . x 2+ x 2+ → → 4 4 4 Với x < 2 ta có: 14 x x − + + ( 2
4 − x + 2x + 8)( 2 2 4 + x + 2x + 8 4 2 8 )
lim f (x) lim lim = = − − 2 − + x→2 x→2 x 3x 2 x→2−
( x − 2)( x − ) 1 ( 2
4 + x + 2x + 8) 4 ( x 2x 8)2 2 2 − + + 2 −x − 2x + 8 lim lim = =
x→2− (x − 2)(x − ) 1 ( 2
4 + x + 2x + 8) x→2−
( x − 2)( x − ) 1 ( 2
4 + x + 2x + 8)
−(x − 2)(x + 4) −(x + 4) = lim lim =
x→2− (x − 2)(x − )
1 (4 + 2x + 2x +8) x 2− → ( x − ) 1 ( 2
4 + x + 2x + 8) −(2 + 4) 3 = = − . ( − )( 2 + + + ) 4 2 1 4 2 2.2 8 Do đó: f ( ) = f (x) = f (x) 3 2 lim lim = − . x 2+ x 2− → → 4
Vậy hàm số f (x) liên tục tại điểm x = 2 . 0 Bài 3: Giải:
Ta có: f (x = f 3 = 3m − 2 . 0 ) ( )
Với mọi x ≠ 3 ta có: (3− x) + + x ( x 1 2) (3− x) ( x+1+ − 2 3 ) lim f (x) = lim = lim = x→ x→ x x → + −
( x + − )( x + + ) lim 1 2 1 2 1 2 x→ ( x +1)2 3 3 3 3 2 − 2
(3− x)( x +1+ 2)
(3− x)( x +1+ 2) lim lim = = = lim − x +1 + 2 x→3 + − x→3 − − x→3 ( ( ) x 1 4 (3 x) = −( 3+1 + 2) = 4 − .
Để hàm số f (x) liên tục tại điểm x = 3 thì: 0 f ( ) = f (x) 2 3 lim ⇔ 3m − 2 = 4 − ⇔ m = − . x→3 3 Bài 4: Giải:
Ta có: f (x = f 2 = 4m + 4 . 0 ) ( ) Với x > 2 ta có: 15 lim f (x) = lim + + = + . + + ( 2 mx x 2 ) 4m 4 x→2 x→2 Với x < 2 ta có: x − 5x + 4
(x − 2)(x + 2)( 2x − )1 (x + 2)( 2 4 2 x − ) lim f (x) 1 = lim = lim = lim − − 3 x→ x→ x − 8 x − → (x − 2) ( 2 2 2 2 x + 2x + 4) − 2
x→2 x + 2x + 4 (2 + 2)( 22 − )1 = =1. 2 2 + 2.2 + 4
Để hàm số f (x) liên tục tại điểm x = 2 thì: 0 f ( ) = f (x) = f (x) 3 2 lim lim
⇔ 4m + 4 =1 ⇔ m = − . x 2+ x 2− → → 4 Bài 5: Giải:
Đặt f (x) = mx(x − ) 4
2 + x − 2 liên tục trên R. Ta có: f (0) = 2; − f (2) =14 .
f (0). f (2) = 2.14 − = 28
− < 0 do đó ∃x ∈ 0;2 sao cho f (x = 0 nên phương 0 ) 0 ( )
trình đã cho có nghiệm trên khoảng (0;2) .
Hay phương trình đã cho luôn có nghiệm với mọi m.
BÀI TẬP TRẮC NGHIỆM 1.B 2.A 3.D 4.C 5.A 6.B 7.C 8.D 9.C 10.D Bài 1: Chọn B.
Để hàm số f (x) liên tục tại điểm x = 0 thì: 0
f (0) = lim f (x) = lim f (x) ⇔ a −1=1⇔ a = 2 . x 0+ x 0− → → Bài 2: Chọn A. 2 Hàm số + f (x) x 1 =
có tập xác định D = (− ; ∞ 3 − ) ∪ ( 3 − ; 2 − ) ∪ ( 2 − ;+∞). 2 x + 5x + 6
Nên hàm số y = f (x) liên tục trên khoảng ( 2; − +∞) . Bài 3: Chọn D.
Để hàm số f (x) liên tục tại điểm x =1 thì: 0 f ( ) = f (x) 1 1 3 1 lim
⇔ m + = − ⇔ m = − . x 1 → 2 4 4 Bài 4: Chọn C. Bài 5: Chọn A. 16
Để hàm số f (x) liên tục tại điểm x = 0 thì: 0
f (0) = lim f (x) =1. x→0 Bài 6: Chọn B.
Để hàm số f (x) liên tục tại điểm x = 0 thì: 0 f ( ) = f (x) = f (x) 1 1 0 lim lim
⇔ 3m +1 = ⇔ m = − . x 0+ x 0− → → 2 6 Bài 7: Chọn C.
Để hàm số f (x) liên tục tại điểm x = 2 thì: 0 f ( ) = f (x) = f (x) 3 2 lim lim ⇔ = 3 ⇔ m = 5 . x 2+ x 2− → → −m + 6 Bài 8: Chọn D.
Để hàm số f (x) liên tục tại điểm x = 5 − thì: 0 f ( 5
− ) = lim f (x) ⇔ 2a − 4 = 6 − ⇔ m = 1 − . x 5 →− Bài 9: Chọn C.
Để hàm số f (x) liên tục tại điểm x =1 thì: 0 f ( ) = f (x) = f (x) a 3 3 1 lim lim ⇔ = ⇔ m = . x 1+ x 1− → → 2 8 4 Bài 10: Chọn D.
f (0) = lim f (x) = 0 ≠1= lim f (x) nên hàm số f (x) không liên tục tại điểm x 0− x 0+ → → x = 0 . 0 17 Chương III
GIỚI HẠN. HÀM SỐ LIÊN TỤC ÔN TẬP CHƯƠNG
A. TÓM TẮT LÝ THUYẾT.
1. Giới hạn của dãy số.
2. Giới hạn của hàm số. 3. Hàm số liên tục. B. CÁC DẠNG TOÁN.
1. Tính giới hạn của dãy số, hàm số.
2. Tính tổng của cấp số nhân lùi vô hạn.
3. Tính liên tục của hàm số.
C. BÀI TẬP TỰ LUYỆN.
Bài 1. Tìm các giới hạn sau: 5 4 3 6 3 1)
n + n − n − 2 − − − + lim . 2) n 7n 5n 8 lim . 3 2 4n + 6n + 9 n +12 2 ( 2n + )1(2n+3) 3) 9n + 2n − 3 lim n . 4) lim . 4n + 3 4 2 n − n +1 5) ( 2
lim 4n + 2n − 2n).
6) lim( 2n + 3 − n +1). n n 7) ( 2 3 2 3 lim −
n + 2n + 3 − n + n ) 8) 3 2.5 lim . 7 + 3.5n ( 3 − )n − 6n 2 n 9) lim . 10) 1+ 2 + 2 + ...+ 2 lim . ( 3 − )n 1+ n 1 + 5 + 2 1+ 3 + 3 + ...+ 3n
Bài 2. Tìm các giới hạn sau: 2 1) x − 5x + 4 lim . 2) x − 2x −1 lim x→4 x − 4 2 x 1 → x + x − 2 3) 2x − x + 3 lim . 4) x +1− 5x +1 lim 2 x 1 → x −1 x→3 x − 4x − 3
3 x + 7 +10(x − ) 2 1 − 5 − x 3 5) lim 6) 4x + 5 − 7 + 6 lim x . x 1 → 5(x − ) 1 x→− (x + )2 1 1 (x − ) 1 3 x − 27 , khi x ≠ 3 2
Bài 3 : Cho hàm số f (x) x − x − 6 = 27 , khi x = 3 5
Xét tính liên tục của hàm số tại điểm x = 3 5 4 2 x − 5x + 4 khi x < 1 −
Bài 4. Cho hàm số f (x) 3 = x +1 2 2
m x + 2mx − 5 khi x ≥ 1 −
Tìm m để hàm số liên tục tại điểm x = 1 − .
Bài 5. Chứng minh phương trình 2
x sin x + xcos x +1 = 0 có ít nhất một nghiệm.
D. BÀI TẬP TRẮC NGHIỆM Câu 1. Tính 1−19 lim n bằng : 18n +19 A. 19 − . B. 1 . C. +∞ . D. 1 − . 18 18 2 Câu 2. Tính 3n − 5 L = lim . 3 n +1 A. L =1. B. L = 0. C. L = 3. D. L = 5. − Câu 3. Tính ( n 2 lim 3 2 n − ) là: A. −∞ B. 1 C. 3 D. +∞ n n 1 + Câu 4. Giới hạn 4.3 + 7 lim là : 2.5n + 7n A. 4. B. 2. C. 7. D. 6. − Câu 5. Tính ( 2
lim n − 3n +1 − n) bằng : A. 3 − . B. +∞ . C. 0 . D. 3 − . 2 Câu 6. Giới hạn ( 2 lim 2n − n + ) 1 bằng : A. − . ∞ B. 2. C. 2. − D. + . ∞
Câu 7. Giá trị của ( 3 2
lim −n + 2n + 2) bằng : A. − . ∞ B. 3. − C. 3. D. + . ∞ Câu 8. Giới hạn 2
lim 2n − 3n − 8 bằng : A. 2 2. B. 3. C. 2. D. + . ∞
Câu 9. Giá trị của 3 3
lim 1+ 2n − n bằng : A. − . ∞ B. 3 2. C. 1. − D. + . ∞ 6
Câu 10. Gọi S là tập hợp các tham số nguyên a thỏa mãn 5n + 2 2 lim a 4a + − =
0 . Tổng các phần tử của S bằng : 2 − n A. 4 . B. 3 . C. 5 . D. 2 . Câu 11. Cho 1 1 1 S =1+ + + ...+
+ ....Chọn đáp án đúng. 2 2 2 2n A. S ∈( ;2 1 ) . B. S ∈( ;3 2 ) . C. S ∈[ ;2 1 ) . D. S ∈[ ;3 2 ) . Câu 12. Giới hạn 1 1 1 lim + + ...+ bằng 2.4 4.6 2n(2n 2) + A. 1. B. 1 − . C. 2. D. 1 . 3 2 4 Câu 13. Cho hàm số u(x)
y = f (x) =
trong đó limu(x) = 2024 và v(x) x→2
limv(x) = 0 đồng thời v(x) > 0 với x
∀ ∈(0;2) . Khi đó lim f (x) = ? x→2 x→2 A. 0. B. + . ∞ C. − . ∞ D. 2019.
Câu 14. Tìm giới hạn 3
lim (3x − x + 2) . Kết quả đúng là : x→+∞ A. − . ∞ B. + . ∞ C. 0. D. 3.
Câu 15. Cho hàm số y = f (x) = u(x).v(x) trong đó lim u(x) = a > 0 và x→−∞
lim v(x) = −∞ .Khi đó khẳng định nào sau đây là đúng? x→−∞
A. lim f (x) = 0. B. lim f (x) = + . ∞ x→−∞ x→−∞
C. lim f (x) = − .
∞ D. lim f (x) = 2020. x→−∞ x→−∞ 2
Câu 16. Tìm giới hạn x − 2024 lim . x 2+ → x − 2 A. + . ∞ B. − . ∞ C. 0. D. 1. −
Câu 17. Kết quả đúng của giới hạn 1 2x + 3 lim − là : x 4+ → x − 4 x + 5 − 3 A. + . ∞ B. −∞ . C. 2. D. 1. −
Câu 18. Giá trị của giới hạn lim( 4 2 x − 4x + ) 1 bằng : x 1 → A. +∞ . B. −∞ . C. 2. D. 2. − 2 Câu 19. Biết x + x +1 lim
= a + b 2 (với ;
a b∈). Giá trị của a + b bằng : x 1 → x +1 A. 1. B. 2 . C. 3 . D. 4 . 7 2 Câu 20. Biết x − m x + 4 lim
= 2 . Khẳng định nào sau đây đúng? x→0 x + 2 A. m∈( 3 − ;− ) 1 . B. m∈( 5 − ;0) . C. m∈( 1; − ) 1 . D. m∈(1;3) . 2020
Câu 21. Giá trị của x + x − 2 lim
bằng a (với a là phân số tối giản). Tính 2019 x 1 → x + x − 2 b b giá trị của 2 2 a − b . A. 4039 . B. 4041. C. 4041 − . D. 4039 − . 2 3 Câu 22. Biết
x + x + 2 − 7x +1 a 2 lim = + c (với ; a ;
b c∈ và a tối giản). x 1 → 2 (x − ) 1 b b
Giá trị của a + b + c bằng A. 37 . B. 13. C. 5 . D. 51. f (x) +1
Câu 23. Cho f (x) là hàm đa thức thỏa mãn lim = a và tồn tại x→2 x − 2
f (x) + 2x +1 − x lim
= T . Đẳng thức nào sau đây đúng? 2 x→2 x − 4 A. a − 2 + − + T = . B. a 2 T = . C. a 2 T = . D. a 2 T = . 16 16 8 8 2
Câu 24. Giá trị của giới hạn 3x + 5 lim x bằng: 2 x→+∞ 2x +1 A. +∞ . B. −∞ . C. 3 . D. 1. 2
Câu 25. Giá trị của giới hạn 2x + 5 lim bằng: 2 x→+∞ 3x +1 A. 2 . B. −∞ . C. +∞ . D. 0 . 3 2
Câu 26. Giá trị của giới hạn 4x − 7x +12 lim bằng: x→−∞ 3 x −17 A. 2 − . B. 2 . C. 4 . D. 1 . 17 3 3 3 4 5
Câu 27. Giá trị của giới hạn 3x + 4x + 2 lim bằng: 5 4 x→+∞ 9x + 5x + 4 A. 2 . B. −∞ . C. 4 . D. 0 . 3 9
Câu 28. Cho hàm số f (x) xác định trên [a;b] . Trong các mệnh đề sau, mệnh đề nào đúng? 8
A. Nếu hàm số f (x) liên tục trên ( ;
a b) và f (a). f (b) < 0 thì phương
trình f (x) = 0 có nghiệm trong ( ; a b) .
B. Nếu hàm số f (x) liên tục trên [ ;
a b] và f (a). f (b) < 0 thì phương
trình f (x) = 0 có nghiệm trong ( ; a b) .
C. Nếu hàm số f (x) liên tục trên [ ;
a b] và f (a). f (b) < 0 thì phương
trình f (x) = 0 vô nghiệm trong ( ; a b) .
D. Nếu hàm số f (x) liên tục trên [ ;
a b] và phương trình f (x) = 0 có nghiệm trong ( ;
a b) thì f (a). f (b) < 0.
Câu 29. Phương trình nào dưới đây có nghiệm trong khoảng (0; ) 1 ? A. 2
2x − 3x + 4 = 0 . B. (x − )2017 2019 1 − x − 2 = 0 . C. 4 2
3x − 4x + 5 = 0 . D. 2019 3x − 8x + 4 = 0 .
Câu 30. Cho phương trình ( 2 m + )(x − )( 2 x − ) 3 3 1 4 − x + 3 = ( ) 0 1 , với m là
tham số. Khẳng định nào sau đây về phương trình ( ) 1 là khẳng định đúng? A. ( )
1 có đúng 4 nghiệm phân biệt. B. ( ) 1 vô nghiệm. C. ( )
1 có ít nhất 2 nghiệm phân biệt. D. ( ) 1 có đúng một nghiệm.
a + c > b +1
Câu 31. Cho các số thực a,b,c thỏa mãn . Tìm số giao điểm
a + b + c +1< 0 của đồ thị hàm số 3 2
y = x + ax + bx + c và trục hoành. A. 3 . B. 2 . C. 1. D. 0 .
Câu 32. Cho hàm số f (x) = 2x −1 . Khẳng định nào sai trong các khẳng định sau?
A. Hàm số f (x) liên tục tại 1 x = − . 0 2
B. Hàm số f (x) liên tục tại x =1. 0
C. Hàm số f (x) gián đoạn tại x = 1 − . 0 9
D. Hàm số f (x) gián đoạn tại 1 x = − . 0 2 Câu 33. Hàm số 2x −1 y =
gián đoạn tại điểm nào dưới đây? 5 − x + 50 A. x = 5. B. x =10. C. x = 5. − D. x =11. x + 2a khi 0 x <
Câu 34. Tìm a để các hàm số f (x) =
liên tục tại x = 0 . 2
x + x +1 khi x ≥ 0 A. 1 . B. 1 . C. 0. D. 1. 2 4
Câu 35. Hàm số có đồ thị như hình bên gián đoạn tại điểm có hoành độ bằng bao nhiêu? A. 0. B. 1. C. 2. D. 3. 3x +1 − 2 khi x >1 2
Câu 36. Tìm a để các hàm số x −1 f (x) =
liên tục tại x =1. 2
a(x − 2) khi x ≤1 x −3 A. 1 . B. 1 . C. 3 . D. 1. 2 4 4 2
ax − (a − 2)x − 2 khi x ≠1
Câu 37. Cho hàm số f (x) = x + 3 − 2 . Có tất cả bao nhiêu 2 8
+ a khi x =1
giá trị của a để hàm số liên tục tại x =1? A. 2 . B. 0 . C. 3 . D. 1. 2 Câu 38. Cho hàm số + f (x) x 1 =
. Khi đó hàm số y = f (x) liên tục trên 2 x + 5x + 6 khoảng nào sau đây? 10 A. (− ; ∞ 3) B. ( 3 − ;2) C. (2;3) D. [ 2; − +∞) 2 x − 3x + 2 Câu 39. Cho hàm số > f (x) khi x 2 = x − 2 3
x + a khi x ≤ 2
Với giá trị nào của a thì hàm số đã cho liên tục trên . A. 0. B. 1. C. -5. D. 3.
Câu 40. Tìm giá trị của tham số m để phương trình ( 2
m − x + )(x + )2019 ( 2020 5 6 5 x
+ 2x) + 2x −1= 0 có nghiệm A. m∈{2; } 3 B. m∈ \{2; } 3 C. m∈∅ D. m∈
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN Hướng dẫn giải
Bài 1. Tìm các giới hạn sau : 5 1 1 2 n 1 1 2 1 + − − 5 4 4 5 1+ − − 1)
n + n − n − 2 4 5 lim lim n n n = 2 = lim .lim n n n n 3 2 4n + 6n + 9 6 9 3 6 9 n 4 + + 4 + + 3 n n 3 n n 1 1 2 1 + − − Mà 2 limn = +∞ và 4 5 n n n 1 lim = > 0 6 9 + + 4 4 3 n n 5 4 Nên
n + n − n − 2 lim = + . ∞ 3 2 4n + 6n + 9 3 6 3 2)
− n − 7n − 5n + 8 lim n +12 2 7 5 8 − 7 5 8 3 n . 1− − + 3 1− − + 3 5 6 3 5 6 = lim n n n = lim(− ).lim n n n n 12 12 n 1 + 1+ n n 11 7 5 8 3 1− − + 3 5 6
Mà lim(−n) = −∞ và n n n 1 lim = =1 > 0 12 1 1+ n 3 6 3 Nên
− n − 7n − 5n + 8 lim = − . ∞ n +12 2 2 n 9 + − 3n 3) 9n + 2n − 3 lim n = lim n 4n + 3 4n + 3 2 9 + − 3 n 9 + 0 − 3 0 = lim = = = 0 3 4 + 0 4 4 + n 1 3 1 3 ( n + ) 1 (2n + 3) 3 2 n 1+ 2 + 1+ 2 + 2 2 4) lim lim n
n lim .lim n n n = = = +∞ 4 2 n − n +1 2 1 1 1 1 n 1− + 1− + 2 4 2 4 n n n n 1 3 1 2 + + 2 (Vì lim n
n = 2 > 0 vàlimn = +∞) 1 1 1− + 2 4 n n 5) ( + − ) 2 2 2
4n + 2n − 4n 2 lim 4 2 2 = lim = lim n n n n 2
4n + 2n + 2n 2 n 4 + + 2 n 2 1 = lim = . 2 2 4 + + 2 n 6) ( n+ − n+ ) 3 1 lim 2 3
1 = lim n.lim 2 + − 1+ . n n Do lim n = +∞ và 3 1
lim 2 + − 1+ = 2 −1> 0. n n
Nên lim( 2n + 3 − n +1) = +∞. 7) ( 2 3 2 3
n + n + − n + n ) = ( 2n + n + − n) + ( 3 2 3 lim 2 3 lim 2 3
lim n − n + n ). 12 Mà 3
n + 2n + 3 − n 2 +
lim( n + 2n + 3 − n) 2 2 2 = lim = lim n =1. 2
n + 2n + 3 + n 2 3 1+ + +1 2 n n 3 2 3
n − n + n lim( 3 2 3
n − n + n ) ( ) = lim 2 2 3 n + . n n + n + ( 2 3 n + n )2 3 3 1 − 1 − 1 = lim = = − . 2 1+1+1 3 1 1 + 3 + + 3 1 1 +1 n n Vậy ( 2 3 2 3
n + n + − n + n ) 1 2 lim 2 3 =1− = . 3 3 3 n − n n 2 8) 3 − 2.5 5 0 − 2 2 lim = lim = = − . 7 + 3.5n 1 n 7.0 + 3 3 7. + 3 5 1 n (− )n n − − 1 3 − 6 9) 2 lim lim = . ( 3 − )n 1+ n 1 + 5 + 1 n 5 n 3 5 − + 2 6 n n n Do 1 1 5 lim 1 1 0;lim 3 5 − − = − < − + = 0 và 2 2 6 n 1 n 5 n ( 3 − ) − 6n 3 5 − + > 0 . Nên lim = − . ∞ 2 6 ( 3 − )n 1+ n 1 + 5 + n 1 + n 1 2 1 + − 2 n n 1 + 10) 1+ 2 + 2 + ...+ 2 2 −1 3 3 lim lim lim2. = = = 0. 2 n n 1 + n 1 1+ 3 + 3 + ...+ 3 3 −1 1 + 1 2 − 3
Bài 2. Tìm các giới hạn sau : 2 x − 5x + 4
(x − )1(x − 4) 1) lim = lim = lim(x − ) 1 = 4 −1= 3 x→4 x→4 x→4 x − 4 x − 4 13 2 2) x − 2x −1 x − 2x +1 x −1 lim = lim = lim = 0 2 x 1 → x 1 x + x − 2 → ( x − )
1 (x + 2)(x + 2x −1) x 1
→ ( x + 2)(x + 2x −1) 3) x x
(2x− x+3)(2x+ x+ − + 3 2 3 ) 2 4x − x − 3 lim = lim = lim 2 x 1 → x 1 x −1 → (x − ) 1 (x + )
1 (2x + x + 3) x 1 → (x − ) 1 (x + ) 1 (2x + x + 3) (x − ) 1 (4x + 3) 4x + 3 7 = lim = lim = x 1 → ( x − ) 1 (x + )
1 (2x + x + 3) x 1 → ( x + ) 1 (2x + x + 3) 8 x x
( 2x −3x)(x+ 4x− + − + 3 1 5 1 ) 4) lim = lim x→3 x→3 x − 4x − 3
( 2x −4x +3)(x+1+ 5x+1)
x(x + 4x −3) 3.6 9 = lim = = x→3 (x − )
1 (x +1+ 5x +1) 2.8 8
3 x + 7 +10(x − ) 2 1 − 5 − x 5) lim x 1 → 5(x − ) 1 (3 x+7 −2) 2 2 − 5 − x 10x −10 lim + lim + lim 1 1 127 = + + 2 = x 1 → 5(x − ) x 1 1 → 5(x − ) x 1 1 → 5( x − ) 1 60 10 60 3
4x + 5 − (2x + 3) (2x + 3) 3 − 7 + 6x 6) 4x + 5 − 7 + 6 lim x = lim + lim x→− (x + )2 1 1 (x − ) 1 x→− (x + )2 1 (x − ) 1 x→− (x + )2 1 1 1 (x − ) 1 =1+ ( 2 − ) = 1 −
Bài 3: Hàm số xác định trên Ta có f ( ) 27 3 = 5 x − 27 (x −3)( 2 3 x + 3x + 9) 2 + + f (x) x 3x 9 27 lim = lim = lim = lim = 2 x→3 x→3 x→3 x − x − 6 (x −3)(x + 2) x→3 x + 2 5
Ta thấy lim f (x) = f (3) nên hàm số liên tục tại x = 3. x→3
Bài 4: Hàm số xác định trên x − 5x + 4 (x − ) 1 ( 2 4 2 x − 4)
Ta có: lim f (x) = lim = lim = 2 − − 3 − 2 x 1 →− x 1 →− x +1 x 1 →− x − x +1 lim f (x) = lim + − = − − + + ( 2 2 m x 2mx 5) 2 m 2m 5 x 1 →− x 1 →− f (− ) 2
1 = m − 2m − 5 14
Hàm số liên tục tại x = 1 − khi và chỉ khi
lim f (x) = lim f (x) = f (− ) 1 2
⇔ m − 2m − 5 = 2 ⇒ m =1± 2 x 1+ x 1− →− →− Bài 5.
Ta có hàm số f (x) 2
= x sin x + xcos x +1 liên tục trên .
f (0). f (π ) = π − +1< 0
Suy ra phương trình f (x) = 0 có ít nhất một nghiệm thuộc (0; π ).
BÀI TẬP TRẮC NGHIỆM 1. A 2. B 3. A 4. C
5. D 6. D 7. A 8. D 9. A 10. A
11. D 12. D 13. D 14. B 15. C 16. B 17. B 18. D 19. A 20. B
21. B 22. B 23. B 24. C 25. D 26. B 27. A 28. B 29. D 30. C
31. A 32. A 33. B 34. A 35. B 36. C 37. A 38. C 39. C 40. D Câu 1. Chọn A. 1 −19 Ta có 1−19n n 19 lim = lim = − . 18n +19 19 18 18 + n Câu 2. Chọn B. 3 5 2 − Ta có 3 3n − 5 n n 0 lim = lim = = 0 . 3 n +1 1 1 1+ 3 n Câu 3. Chọn A. n Ta có ( n 3 n 2
lim 3 2 n ) lim(3n 4n − = − ) lim4 lim = − 1 = −∞ . 4 Câu 4. Chọn C. 15 3 n + n n+ 4. 7 1 4.3 + 7 7 ilm lim = = 7 . 2.5n + 7n n 2. 5 + 1 7 Câu 5. Chọn D. − + Ta có ( 2 lim 3n 1 n 3
− 3n +1 − n) = lim = − . 2
n − 3n +1 + n 2 Câu 6. Chọn D. lim( 2 2n − n + ) 1 1 2 1 = lim 2 − + .lim n = +∞ . 2 n n Câu 7. Chọn A. lim( 3 2 −n + 2n + 2) 2 2 3 = lim 1 − + + .n = −∞ . 3 n n Câu 8. Chọn D. 2 3 8
lim 2n − 3n − 8 = lim 2 − − .lim n = +∞ . 2 n n Câu 9. Chọn A. 3 3 1 2
lim 1+ 2n − n = lim + −1.limn = −∞ . 3 2 n n Câu 10. Chọn A. Ta có: 5n + 2 2 5n + 2 2 lim
+ a − 4a = 0 ⇔ lim + a − 4a = 0 . 2 − n 2 − n a = 1 − 2
a − 4a − 5 = 0 ⇔ . Vậy S = { 1; − } 5 ⇒ 1 − + 5 = 4 . a = 5 Câu 11. Chọn D. Ta thấy 1 1 1
;1 ; ;...; ;.... là một cấp số nhân lùi vô hạn với công bội 1 q = 2 2 2 2n 2
và số hạng đầu u =1. Do đó 1 S = = 2 ⇒ S ∈[2;3). 1 1 1− 2 Câu 12. Chọn D. Ta có : 16 1 1 1 1 1 1 1 1 1 1 lim ... + + + = − + − + + − n ( n + ) lim ... 2.4 4.6 2 2 2 2 2 4 4 6
2n 2n + 2 1 1 1 1 = lim − = . 2 2 2n + 2 4 Câu 13. Chọn B.
Áp dụng quy tắc tìm giới hạn vô cực có kết quả. Câu 14. Chọn B. Ta có: 3 3 1 2 lim (3x x 2) lim x lim 3 − + = − + . 2 3 x→+∞ x→+∞ x x Mặt khác : 3 1 2 3 lim x = +∞, lim 3 − + =
1 > 0 ⇒ lim (3x − x + 2) = +∞ . 2 3 x→+∞ x→+∞ x x x →+∞ Câu 15. Chọn C.
Áp dụng quy tắc tìm giới hạn vô cực có kết quả. Câu 16. Chọn B. Ta có lim − = − < . + ( 2 x 2024) 2020 0 x→2 2 lim (x −
− 2) = 0, x → 2+ ⇒ x > 2 ⇒ x − 2 > 0 nên x 2024 lim = − . ∞ x→2+ x 2+ → x − 2 (2x + 3) x ( x+5 + + 3 1 2 3 1 ) Câu 17. Chọn B. lim lim − = − x 4+ x − 4 x 4 x + 5 − 3 + → → x − 4 x − 4
1− (2x + 3)( x + 5 + 3) = lim . x 4+ → x − 4 Ta có lim 1 − (2x + 3) + + = − < + ( x 5 3) 55 0. x→4
lim (x − 4) = 0, x → 4+ ⇒ x > 4 ⇒ x − 4 > 0. x→4+
1− (2x + 3)( x + 5 + 3) Suy ra lim = −∞ . x 4+ → x − 4 Câu 18. Chọn D. Ta có lim( 4 2 x − 4x + ) 4 2 1 =1 − 4⋅1 +1= 2 − . x 1 → Câu 19. Chọn A. 2 Ta có
x + x +1 1+ 2 1 1 1 lim =
= + ⋅ 2 ⇒ a = b = . x 1 → x +1 1+1 2 2 2 17
Do vậy a + b =1. Câu 20. Chọn B 2 Ta có x − m x + 4 2 lim = 2 − m ⇔
= 2 ⇒ −m = 2 ⇔ m = 2 − . x→0 x + 2 2 Suy ra m∈( 5 − ;3) . Câu 21. Chọn B. Ta có : n x −1 (x − ) 1 ( n 1− n−2 x + x ++ ) 1 lim = lim = lim( n 1− n−2 x + x ++ ) 1 = n . x 1 → x 1 → x 1 x −1 x −1 → Câu 22. Chọn B. Ta có 2020 2020 2019 2018 x + x − 2 x −1+ x −1 (x + x
+ . .+1)(x −1) + x −1 lim = lim = lim 2019 2019 2018 2017 x 1 → x 1 → x 1 x + x − 2 x −1+ x −1 → (x + x
+ . .+1)(x −1) + x −1 . 2019 2018 x + x + ...+1+1 2020 +1 2021 = lim = = 2018 2017 x 1 → x + x + ...+1+1 2019 +1 2020 Suy ra 2 2
a = 2021; b = 2020 ⇒ a − b = 4041. Câu 23. Chọn B. Ta có 2 3 2 3
x + x + 2 − 7x +1 x + x + 2 − 2 2 − 7x +1 lim = lim + lim 2 = . x 1 → 2 (x − ) x 1 1 → 2 (x − ) x 1 1 → 2 (x − ) 1 12
Suy ra a =1; b =12;c = 0 ⇒ a + b + c =13 . Câu 24. Chọn C. 5 2 3 + Ta có 3x + 5x x 3 lim = lim = . 2 x→+∞ 2x +1 x→+∞ 1 2 2 + 2 x Câu 25. Chọn D. 2 5 + Ta có 2 2x + 5 x x 0 lim = lim = = 0 . 2
x→+∞ 3x +1 x→+∞ 1 3 3 + 2 x Câu 26. Chọn B. 7 12 2 x 4 − + 2 Ta có: 4x − 7x +12 lim = lim x x x→−∞ 3 x −17 x→−∞ 3 x −17 18 7 12 7 12 −x 4 − + − 4 − + 2 2 x x x x 2 = lim = lim = . x→−∞ 3 − x −17 x→−∞ 17 3 3 − − x Câu 27. Chọn A. 3 2 4 5 + 4 + 5 Ta có 3x + 4x + 2 x x 4 2 lim = lim = = . 5 4 x→+∞
9x + 5x + 4 x→+∞ 5 4 9 3 9 + + 5 x x Câu 28. Chọn B. Câu 29. Chọn D.
Xét hàm số f (x) 2019 = 3x
− 8x + 4 liên tục trên .
Vì hàm số liên tục trên đoạn [0; ]
1 và f (0). f ( ) 1 = 4.(− ) 1 < 0 nên tồn tại
x ∈ 0;1 sao cho f (x ) = 0 0 ( )
. Vậy phương trình có nghiệm trong khoảng 0 (0; )1 . Câu 30. Chọn C.
Đặt f (x) = ( 2 m + )(x − )( 2 x − ) 3 3 1
4 − x + 3 liên tục trên . Ta có f ( ) 3 1 = 1
− + 3 = 2 > 0 ; f ( ) 3 2 = 2 − + 3 = 5 − < 0; f ( ) = ( 2 m + ) 2 3 10
3 − 24 =10m + 6 > 0, m ∀ ∈ . Vì f ( )
1 . f (2) < 0 nên phương trình f (x) = 0 có ít nhất một nghiệm c ∈ 1;2 1 ( ) .
Vì f (2). f (3) < 0 nên phương trình f (x) = 0 có ít nhất một nghiệm c ∈ 2;3 1 ( ) . Vậy phương trình ( )
1 có ít nhất 2 nghiệm phân biệt. Câu 31. Chọn A.
Phương trình hoành độ giao điểm 3 2
x + ax + bx + c = 0( ) 1 . Đặt ( ) 3 2
f x = x + ax + bx + c liên tục trên .
Theo giả thiết f (− ) 1 > 0; f ( ) 1 < 0 . 19
+ Vì lim f (x) = −∞ nên tồn tại số c < 1
− sao cho f (c < 0 . 1 ) x→−∞ 1
f (c . f 1
− < 0 nên phương trình ( )
1 có ít nhất một nghiệm thuộc (c ;−1 . 1 ) 1 ) ( ) + f (− ) 1 . f ( )
1 < 0 nên phương trình ( )
1 có ít nhất một nghiệm thuộc ( 1; − ) 1 .
+ Vì lim f (x) = +∞ nên tồn tại số c >1 sao cho f (c > 0. 2 ) x→+∞ 2 f ( )
1 . f (c < 0 nên phương trình ( )
1 có ít nhất một nghiệm thuộc (1;c . 2 ) 2 ) Vì phương trình ( )
1 là phương trình bậc ba nên có nhiều nhất là 3 nghiệm. Vậy phương trình ( )
1 có 3 nghiệm phân biệt. Câu 32. Chọn A.
Hàm số f (x) có tập xác định là 1 D ; = +∞ 1 1 . x = − ∉ ;+∞ nên hàm số 2 0 2 2 đã cho gián đoạn tại 1 x = − . o 2 Câu 33. Chọn B. Ta có 5
− x + 50 ≠ 0 ⇔ x ≠ 10 . Vậy hàm số gián đoạn tại x =10. Câu 34. Chọn A. Ta có : 2
lim f (x) = lim (x + x +1) =1. x 0+ x 0+ → →
lim f (x) = lim(x + 2a) = 2a . Và f (0) =1. x 0− x 0− → → Hàm số liên tục tại 1
x = 0 ⇔ 2a =1 ⇔ a = . 2 Câu 35. Chọn B.
Dựa vào hình vẽ đồ thị ta thấy hàm số gián đoạn tại điểm x =1. Câu 36. Chọn C. Ta có : 3x +1 − 2 3 lim f (x) = lim = + + 2 x 1 → x 1 → x −1 8 20 2 a(x − 2) lim ( ) = lim a f x = và ( ) 1 a f = . x 1− x 1− → → x − 3 2 2 Hàm số liên tục tại a 3 3
x =1⇔ lim f (x) = lim f (x) = f (1) ⇔ = ⇔ a = . x 1+ x 1− → → 2 8 4 Câu 37. Chọn A.
Tập xác định: D = [ 3 − ;+ ∞) . 2
ax − (a − 2) x − 2
(x − )1(ax + 2)( x +3 + 2) lim f (x) = lim = lim x 1 → x 1 → x + 3 − 2 x 1 → x −1 = lim(ax + 2) + +
= 4(a + 2) . Và f ( ) 2 1 = 8 + a . → ( x 3 2) x 1
Hàm số đã cho liên tục tại x =1 khi lim f (x) = f ( ) 1 ⇔ (a + ) 2 4 2 = 8 + a x 1 → a = 0 ⇔ . a = 4
Vậy có 2 giá trị của a để hàm số đã cho liên tục tại x =1. Câu 38. Chọn C. x = 2 − Nhận xét: 2
x + 5x + 6 = 0 ⇔
⇒ f (x) có TXĐ D = \{ 2; − − } 3 nên x = 3 −
f (x) liên tục trên (− ; ∞ 3 − ),( 3 − ; 2 − ),( 2
− ,+∞) ⇒ f (x) liên tục trên (2;3) Câu 39. Chọn C. TXĐ : D = 2
Nhận xét: Khi x∈(2;+∞) ⇒ − +
f (x) x 3x 2 =
xác định nên f (x) liên tục x − 2 trên (2;+∞) . Khi x∈(− ;2
∞ ) ⇒ f (x)= 3x + a xác định nên f (x) liên tục trên (− ;2 ∞ ) .
Xét tại x = 2 lim f (x)= lim (x − )
1 =1 ; lim f (x)= lim (3x + a)= a + 6. x 2+ x 2+ → → x 2− x 2− → → f (2) = a + 6
Để hàm số liên tục tại x = 2 thì 21
lim f (x)= lim f (x)= f (2)⇔ a+ 6 =1⇔ a = 5 − . x 2+ x 2− → → Câu 40. Chọn D.
Đặt f (x) = ( 2
m − x + )(x + )2019 ( 2020 5 6 5 x
+ 2x) + 2x −1.
Hàm số f (x) liên tục trên . m = 2 Xét 2
m − 5m + 6 ⇔
. Khi đó phương trình trở thành 1
2x −1= 0 ⇔ x = m = 3 2 m ≠ 2 Xét 2
m − 5m + 6 ≠ 0 ⇒ . m ≠ 3
Hàm f (x) có bậc cao nhất là 2019 + 2020 = 4039 là đa thức bậc lẻ nên
f (x) = 0 có ít nhất một nghiệm với m ∀ ∈ .
ĐỀ KIỂM TRA CUỐI CHƯƠNG IV
(Thời gian làm bài: 45 phút)
A. PHẦN TRẮC NGHIỆM (7 điểm) Câu 1. 3 − 2 lim n bằng 2 n +1 A.3. B. 2. − C. 0. D. 1. n n Câu 2. 4 − 2.5 lim bằng 3n + 2.5n A.1. B. 0. C. 1. − D. 2. − Câu 3. ( 2
lim 5n − 4n + 2) bằng A. − . ∞ B. 4. − C. 5. D. + . ∞ 2 Câu 4. 4x − 3x +1 lim bằng 2 x→−∞ 2 − 2x A. 1 . B. 1 − . C. 2. D. 2. − 2 2 2 Câu 5. 3
lim x + x bằng x ( ) 1 − → − 1− x A. − . ∞ B. 0. C. 1. D. + . ∞ 22 2 Câu 6. −x + x − 2 lim bằng x 2 →− 2 − x A. 2. − B. 0. C. 8. − D. 2. Câu 7. ( 3
lim 1− 2x + 3x ) bằng x→−∞ A. − . ∞ B. 3. C. 2. − D. + . ∞ Câu 8. 1− 4 lim x bằng 2
x→+∞ x − 4x
A. 1. B. 0. C. 4. − D. 1. −
Câu 9. Phương trình nào sau đây có nghiệm trên khoảng(1;2) ? A. 2
2x − 7x + 6 = 0. B. 2 x − 9 = 0. C. 2
x − x +1 = 0. D. 2
2x − 5x + 2 = 0. n 1 − Câu 10. Tính tổng 1 1 1 1 S 1 ... = − + − + + − + ... 4 16 64 4 A. 3 − S = . B. 4 S = . C. 3 S = . D. 4 S = − . 4 5 4 5 3 Câu 11. x − 2x +1 lim bằng 2 x→−∞ −x + 4 A. − . ∞ B. 1. − C. 2. D. + . ∞ Câu 12. x − 2 lim bằng 2 x→2 4 − x A. 1 . B. 1 − . C. 4. D. 4. − 4 4 2 Câu 13.
x − x − 2x + 8 lim bằng x→−∞ 2x + 3 A. 1. − B. 1. C. 0. D. 2. Câu 14. 2x − 2 lim bằng x 2+ → 2 − x A. 2. B. 0. C. − . ∞ D. + . ∞
Câu 15. Phương trình 6 3
x − x − x −12 = 0 có ít nhất bao nhiêu nghiệm thuộc khoảng( 2; − 2) ? A. 2. B. 1. C. 0. D. 3. 23
Câu 16. Tìm giá trị của tham số m để hàm số 2 x + 6x + 5 ≠ − f (x) , khi x 1 = 2x + 2
liên tục tại x = 1 − 2 3 − m x −10, khi x = 1 − A. m = 2.
± B. m = 2. C. m = 4.
± D. m = 4.
Câu 17. Tìm giá trị của tham số m để hàm số 8 − x + 3x , khi x < 1 − f (x) x +1 =
liên tục tại x = 1 − 2 5 m + mx + , khi x ≥ 1 − 6
A. m =1;m = 2. B. m = 1; − m = 2. C. m = 1; − m = 2 − .
D. m =1;m = 2.
Câu 18. Tính S = − +
( a là hằng số ) ? →−∞ ( 2 lim 2x ax 2x x ) A. a 2 S = . B. a 2 S = . 4 2 C. −a 2 − S = . D. a 2 S = . 4 2 3
Câu 19. Tính = lim x − a a S
( a là hằng số và a > 0 ) ? 2 x→ a x − a A. 3a − − S = . B. 3a S = . C. 3 a S = . D. 3 a S = . 2 2 2 2 Câu 20. Biết ( + x + ) 3x 1 lim 9 2
= a 6 + b .Tính giá trị của biểu thức x→+∞ (2x + )3 1
S = 4a − b A. S = 9. −
B. S = 9. C. 9 S = . D. 9 S = − . 2 2
B. PHẦN TỰ LUẬN (3 điểm)
Câu 1 (1điểm). Tính giới hạn : 3 − 5 lim x .
x→−∞ 2x + 4
Câu 2 (1điểm). Tính giới hạn : x − 4 lim . x→4 2 − x
Câu 3 (1điểm). Tính giới hạn : − + − + . →−∞ ( 2 lim 4x x 3 1 2x x )
-----------------HẾT------------------ 24 ĐÁP ÁN
A.TRẮC NGHIỆM(7 điểm) Câu 1 2 3 4 5 6 7 8 9 10 Đáp án C C D D C A A B A B Câu 11 12 13 14 15 16 17 18 19 20 Đáp án D B B C A A B A C B
B.TỰ LUẬN( 3điểm) 3 −5 Câu 1 (1điểm). 3 − 5x x 5 lim = lim = − .
x→−∞ 2x + 4 x→−∞ 4 2 2 + x (x − 4)(2 4 + − x x ) Câu 2 (1điểm). lim = lim = lim( 2 − − x = − . → ) 4 x→4 x→4 2 − x 4 − x x 4 Câu 3 (1điểm). − + − + =
x − x + + x − x→−∞ ( 2 lim 4 3 2 ) lim 1 →−∞ ( 2 lim 4x x 3 1 2x x ) x→−∞ 2 2
4x − x + 3 − 4 −x + 3 = lim x −1 = lim −1 x→−∞ 2
4x − x + 3 − 2x x→−∞ 1 3 x 4 − + − 2x 2 x x 3 1 − + = lim x −1 1 3 = −1 = − . x→−∞ 1 3 4 4 − 4 − + − 2 2 x x 25
Document Outline
- Bài 1. GIỚI HẠN DÃY SỐ - 15T
- Bài 2. GIỚI HẠN HÀM SỐ
- A. Tóm tẮT lý thuyẾt.
- I. GIỚI HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
- 1. Giới hạn hữu hạn của hàm số tại một điểm
- 2. Định lí và các phép toán về giới hạn hữu hạn của hàm số tại một điểm
- 3. Giới hạn một phía
- 4. Giới hạn vô cực của hàm số tại một điểm
- 5. Quy tắc về giới hạn vô cực
- II. GIỚI HẠN CỦA HÀM SỐ TẠI VÔ CỰC
- 1. Giới hạn hữu hạn của hàm số tại vô cực
- 2. Giới hạn vô cực tại vô cực
- I. GIỚI HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
- B. CÁC DẠNG TOÁN.
- DẠNG 1: GIỚI HẠN HÀM SỐ TẠI MỘT ĐIỂM
- DẠNG 1.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
- DẠNG 1.2: CÁC VÔ ĐỊNH THƯỜNG GẶP
- BÀI TẬP TRẮC NGHIỆM: GIỚI HẠN TẠI MỘT ĐIỂM
- HƯỚNG DẪN GIẢI : GIỚI HẠN TẠI MỘT ĐIỂM
- DẠNG BÀI 2: GIỚI HẠN MỘT PHÍA
- DẠNG 2.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
- DẠNG 2.2: CÁC DẠNG VÔ ĐỊNH THƯỜNG GẶP
- BÀI TẬP TRẮC NGHIỆM: GIỚI HẠN MỘT PHÍA
- BÀI GIẢI THAM KHẢO
- DẠNG BÀI 3: GIỚI HẠN HÀM SỐ TẠI VÔ CỰC
- DẠNG 3.1: SỬ DỤNG ĐỊNH NGHĨA VÀ TÍNH CHẤT CƠ BẢN
- DẠNG 3.2: CÁC DẠNG VÔ ĐỊNH THƯỜNG GẶP
- BÀI TẬP TRẮC NGHIỆM GIỚI HẠN HÀM SỐ TẠI VÔ CỰC
- BÀI GIẢI THAM KHẢO:
- DẠNG 1: GIỚI HẠN HÀM SỐ TẠI MỘT ĐIỂM
- A. Tóm tẮT lý thuyẾt.
- Bài 3. HÀM SỐ LIÊN TỤC
- Bài 4. ÔN TẬP CHƯƠNG




