THỰC HÀNH VẬT LÝ HẠT NHÂN I MỤC LỤC
Bài 1: THỐNG KÊ SỐ ĐẾM KHI GHI NHẬN BỨC XẠ HẠT NHÂN .................. 0
BÀI SỐ 2: ĐẶC TRƯNG ĐẾM CỦA ỐNG ĐẾM GEIGER-MULLER ............... 10
BÀI 3: XÁC ĐỊNH THỜI GIAN CHẾT CỦA ỐNG ĐẾM GEIGER – MULLER 15
BÀI 4: PHỔ KẾ GAMMA NHẤP NHÁY ............................................................... 18
THÍ NGHIỆM 1. XÂY DỰNG ĐƯỜNG CHUẨN NĂNG LƯỢNG ............. 26
THÍ NGHIỆM 2. XÁC ĐỊNH NĂNG LƯỢNG NGUỒN CHƯA BIẾT ....... 31
BÀI 5: HẾ SỐ HẤP THỤ TUYẾN TÍNH ................................................................ 31
BÀI 6: QUY LUẬT BÌNH PHƯƠNG KHOẢNG CÁCH ....................................... 37
Bài 1: THỐNG KÊ SỐ ĐẾM KHI GHI NHẬN BỨC XẠ HẠT NHÂN 1. Mục đích
Nắm được đặc điểm của phân bố Poisson và điều kiện để một đại lượng ngẫu
nhiên tuân theo phân bố Poisson. Khảo sát quy luật phân bố của số đếm N mà thiết
bị ghi nhận được, xác định tốc độ đếm và đánh giá sai số thống kê. 2. Lý thuyết
Phương pháp thống kê là phương pháp cần thiết khi nghiên cứu các hiện tượng
của thế giới vi mô. Đặc biệt trong vật lý hạt nhân thực nghiệm, các bài toán thường
liên quan đến việc ghi nhận các bức xạ hạt nhân, cụ thể là tốc độ đếm n của các
thiết bị hạt nhân.Thông thường, chùm bức xạ hạt nhân phát ra từ nguồn phóng xạ
là một đại lượng ngẫu nhiên.Vì vậy, phép thống kê kết quả ghi nhận bức xạ hạt
nhân là một trong những nội dung quan trọng của vật lý hạt nhân thực nghiệm. Để
khảo sát bài toán cơ bản của phân bố Poisson, ta xác định hàm phân bố của số bức
xạ hạt nhân phát ra từ một nguồn phóng xạ trong khoảng thời gian t xác định.
2.1. Bài toán cơ bản của phân bố Poisson
Phân bố Poisson là một phân bố gián đoạn, hàm phân bố xác suất có dạng: Pk = (1) ! lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Trong đó µ là giá trị trung bình của đại lượng ngẫu nhiên, Pklà xác suất để đại
lượng ngẫu nhiên nhận giá trị k.
Phân bố Poisson được xác định hoàn toàn khi ta biết đại lượng . Giá trị vừa là
kỳ vọng toán học vừa là độ phân tán của đại lượng ngẫu nhiên.
Trong phân bố Poisson người ta quan tâm đến xác suất để xảy ra k sự kiện
trong khoảng thời gian theo dõi t với các giả thiết sau:
- Việc xảy ra hay không xảy ra sự kiện tại thời điểm t không phụ thuộc
vào lịch sử xảy ra sự kiện trước thời điểm t.
- Xác suất để xảy ra sự kiện riêng biệt trong khoảng thời gian δt đủ nhỏ, tỷ lệ với δt.
- Xác suất để hai hay nhiều hơn hai sự kiện xảy ra trong khoảng thời gian
δtđủ nhỏ là bằng không.
Vì giả thiếtthứ ba do đó phân bố Poisson là phân bố xác suất hiếm.
Từ các giả thiết trên bằng cách giải phương trình vi phân đối với Pk(t), để tìm
xác suất để xảy ra k sự kiện trong khoảng thời gian từ 0 đến t, ta thu được hàm
phân bố của Pk(t): Pk(t) = (2)
Trong đó nt trong công thức (2) chính là số sự kiện trung bình xảy ra trong
khoảng thời gian từ 0 đến t.
Nếu ký hiệu = và Pk(t) = Pk công thức (2) chuyển thành: Pk(t) = (3) !
Công thức (3) là hàm phân bố Poisson.
Xét bài toán vật lý hạt nhân sau:
Bộ môn Vật lý Hạt nhân 1 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Có một nguồn phóng xạ trung bình phát ra nt hạt trong khoảng thời gian từ 0
đến t. Tìm xác suất để nguồn đó phát ra k hạt trong khoảng thời gian t. Điều kiện
t << chu kỳ bán rã để trong thời gian đo cường độ phóng xạ của nguồn là không đổi.
Ta hãy chia khoảng thời gian t thành m khoảng bằng nhau. Như vậy trung bình
xác suất để một hạt phát ra trong một khoảng thời gian trên là p = (nt)/m. Bài toán
của ta đưa về bài toán phân bố nhị thức sau: Xác suất để cho một hạt phát ra trong
một khoảng là p. Tìm xác suất Pm(k) để tìm thấy k hạt rơi vào m khoảng trên. Xác suất đó là:
Pm(k) = .pk (1 – p)m-k (4)
Giá trị trung bình của phân bố nhị thức (4) là = mp = nt. Như đã biết khi giá
trị trung bình của phân bố nhị thức đủ lớn, phân bố nhị thức chuyển thành phân bố Poisson: Pk(t) = (5) !
Với một nguồn phóng xạ, là tập hợp số lớn nguyên tố phóng xạ, số hạt bức xạ
phát ra trong một thời gian t rất lớn. Vậy ta có thể kết luận: Số hạt bức xạ k phát
ra từ nguồn phóng xạ, trong khoảng thời gian t << T1/2 là đại lượng ngẫu nhiên
tuân theo phân bố Poisson.
Do số bức xạ phát ra từ nguồn bức xạ là đại lượng ngẫu nhiên tuân theo phân
bố Poisson nên số bức xạ hạt nhân bay vào thể tích nhạy của Detector cũng tuân
theo phân bố Poisson. Số xung mà thiết bị hạt nhân ghi nhận được N, trong khoảng
thời gian t, tỷ lệ với số hạt bức xạ hạt nhân k, bay vào Detector trong khoảng thời gian trên.
Bộ môn Vật lý Hạt nhân 2 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
2.2. Phân bố số đếm từ nguồn được ghi nhận bởi detector
2.2.1. Điều kiện thực nghiệm để số đếm trong khoảng thời gian t tuân
theo phân bố Poisson.
Trong các phép đo thường ta dùng các ống chuẩn trực hoặc thay đổi khoảng
cách từ nguồn đến Detector sao cho thời gian trung bình giữa hai bức xạ liên tiếp
đi đến Detector lớn hơn thời gian chết của Detector. Gọi n là tốc độ đếm, khoảng
thời gian trung bình để ghi một xung là 1/n. Ta có: 1/n >>τc, thường 1/n ≥ 10τc.
Khi điều kiện 1/n >τc việc ghi nhận bức xạ đi vào Detector tại thời điểm trước
sẽ không ảnh hưởng đến việc ghi nhận các bức xạ tiếp theo đi vào Detector. Giả
thiết thứ nhất của phân bố Poisson được thực hiện.
Với các bài toán để xác định tốc độ đếm, thực nghiệm tiến hành xác định số
đếm N trong khoảng thời gian t. Thường t << T1/2, do đó trong khoảng thời gian
đo t, cường độ bức xạ bay vào Detector không đổi, số xung ghi nhận được trong
khoảng thời gian tỷ lệ với tốc độ đếm n và thời gian t, ta có N = nt. Giả thiết thứ
hai của phân bố Poisson được thực hiện.
Với bất kỳ một Detector nào cũng có thời gian chết là τc, sau khi ghi nhận được
một bức xạ, trong khoảng thời gian τc nếu có bức xạ hạt nhân khác bay vào
Detector thì thiết bị không thể ghi nhận được. Như vậy xác suất để xuất hiện đồng
thời 2 xung trở lên hay chính xác để thiết bị đếm được 2 xung, trong khoảng thời
gian δt cỡ τc bằng không. Giả thiết thứ 3 được thực hiện.
Ba điều kiện thực nghiệm vừa nêu luôn được thực hiện trong các phép đo vật
lý hạt nhân. Vậy ta có thể kết luận số xung N mà thiết bị hạt nhân ghi nhận được
trong khoảng thời gian t, đối với số lượng lớn các sự kiện hiếm, ta thấy rằng xác
suất ghi nhận số đếm N tuân theo phân bố Poisson.
Bộ môn Vật lý Hạt nhân 3 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
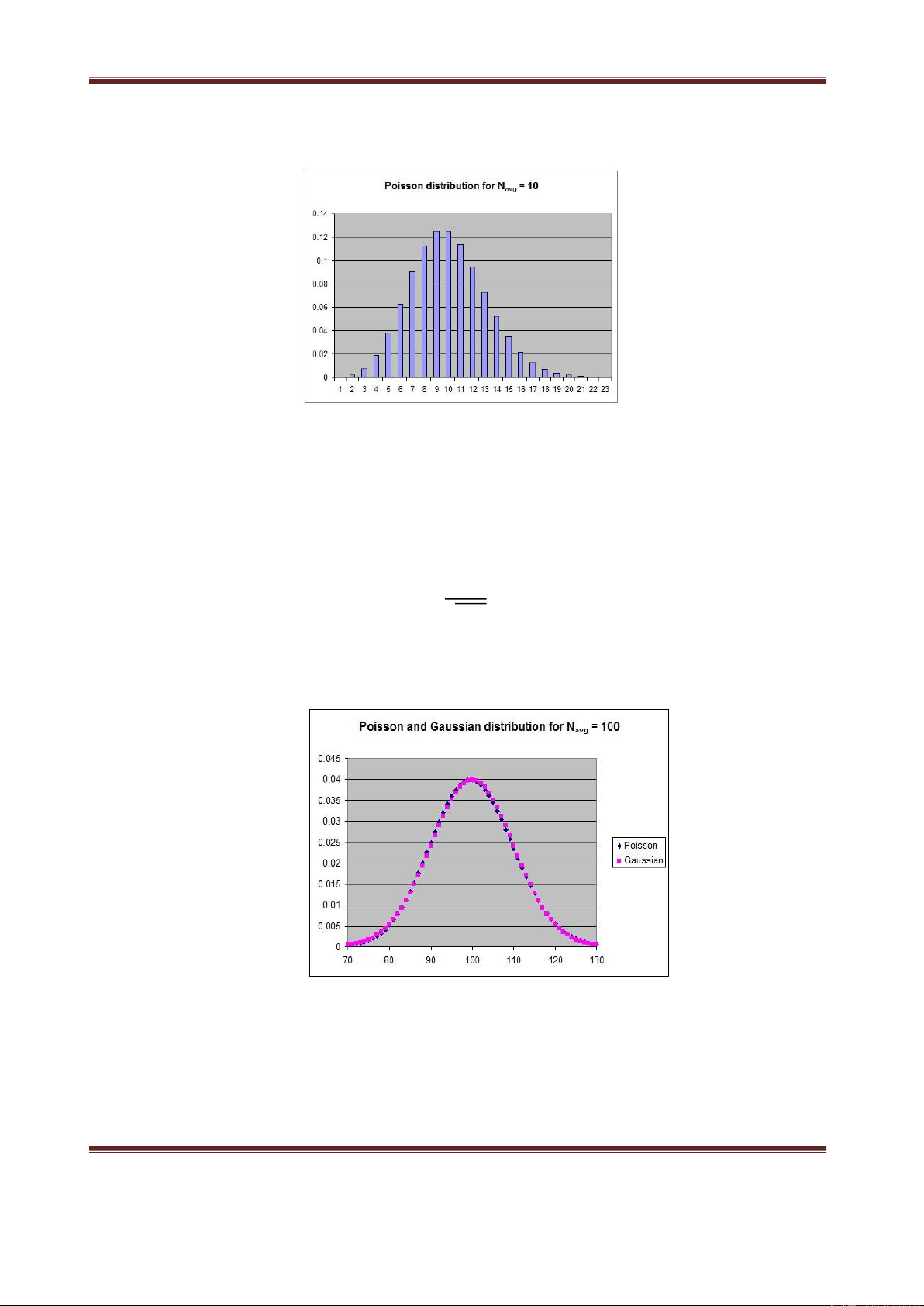
Hình 1. Phân bố Possion đối với số đếm trung bình bằng 10
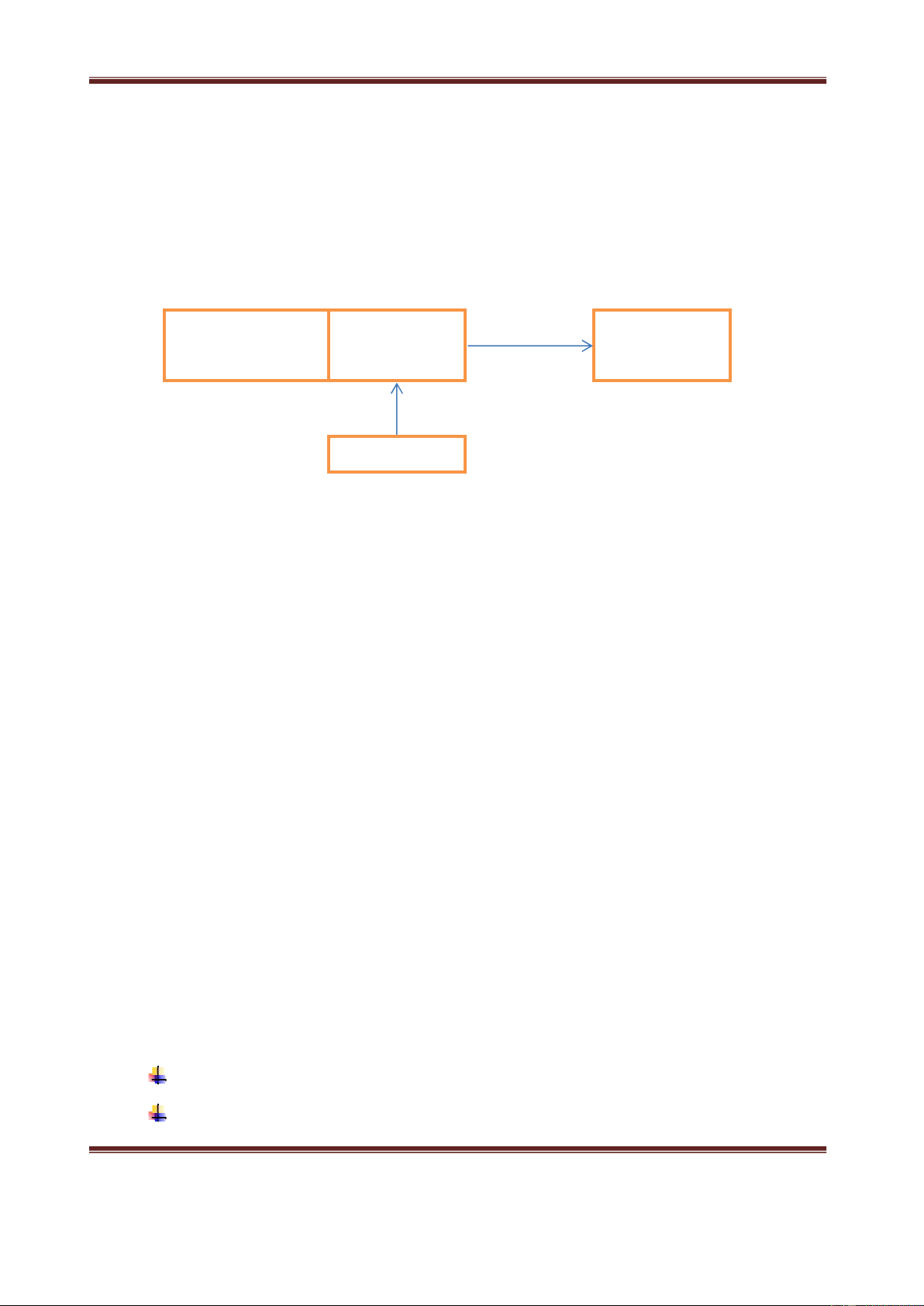
Đối với số lượng lớn các sự kiện xảy ra thường xuyên, ta thấy rằng, xác suất
ghi nhận số đếm N tuân theo phân bố Gaussian PN(t) = ( ) /( ) √
Hay nói cách khác, số đếm trung bình lớn, phân bố Poisson tiệm cận đến phân bố Gaussian.
Hình 2. Phân bố Possion đối với số đếm trung bình bằng 100
Bộ môn Vật lý Hạt nhân 4 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
2.2.2. Sai số thống kê khi ghi nhận bức xạ
Do đặc điểm ngẫu nhiên, số xung N mà thiết bị hạt nhân đếm được trong
khoảng thời gian t cho trước không phải là một đại lượng xác định, mà là đại lượng
ngẫu nhiên tuân theo phân bố Poisson. Vì vậy để nâng cao độ chính xác, giảm sai
số của kết quả đo, thực nghiệm phải tiến hành nhiều phép đo. Giả sử tiến hành m
phép đo trong cùng một thời gian t. Như vậy, thực nghiệm thu được mẫu có thể tích m: {N} = N1, N2, …, Ni,…, Nm
Trong đó Ni là số đếm thu được trong phép đo thứ i, 1 <iTheo các định luật thống kê toán học, trung bình của mẫu: = ∑ (6)
Giá trị chính là đánh giá thống kê của kỳ vọng toán học của đại lượng ngẫu
nhiên N. Đại lượng SN được xác định theo công thức: SN = ∑( ) (7)
SN đánh giá độ phân tán của đại lượng N.
Độ lệch chuẩn của đại lượng ngẫu nhiên N được tính theo công thức: (8)
Theo tính chất của phân bố Poisson, xác suất để đại lượng ngẫu nhiên nhận giá
trị trong khoảng từ (µN – σN, µN + σN) là 68%. Đại lượng σN liên quan đến sai số
trung bình của mỗi phép đo, thực chất σN là sai số trung bình của mỗi phép đo.
Bộ môn Vật lý Hạt nhân 5 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Như đã biết trong phân bố Poisson kỳ vọng toán học µN cũng chính bằng độ phân tán của mẫu. Do đó: σN = √ ≈ (9)
Từ công thức (9) trong vật lý hạt nhân nếu ta tiến hành phép đo có giá trị là N,
sai số thống kê của nó được tính theo công thức: σN = ΔN = √ (10)
Sai số tương đối của phép đo là: = (11) √
Độ chính xác thống kê: (12)
Nếu số phép đo m lớn, thể tích lớn, phân bố của mẫu tiến tới phân bố thực của
đại lượng ngẫu nhiên.
Tuy nhiên, như đã nói ở trên để xác định số xung đếm được N trong khoảng
thời gian t, để giảm sai số ta tiến hành m phép đo. Giá trị trung bình của mẫu là
được tính theo công thức số (6). Với thể tích m lớn, theo định lý giới hạn trung
tâm, trung bình của mẫu tiến tới phân bố chuẩn với kỳ vọng toán bằng kỳ vọng
toán của của đại lượng ngẫu nhiên. Độ phân tán của mẫu nhỏ hơn độ phân tán của
đại lượng ngẫu nhiên m lần. Vậy ta có: = (13)
Bộ môn Vật lý Hạt nhân 6 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Độ lệch của giá trị trung bình của mẫu so với kỳ vọng toán học µN được tính theo công thức: (14)
Từ công thức (8) ta có độ lệch chuẩn của giá trị trung bình mẫu được tính như sau: (15)
Với độ tin cậy β đại lượng µN được xác định theo công thức: µN = ± (16) hay - tβ ≤ ≤ + tβ
Đại lượng tβ được tra trong bảng phân bố Student với độ tin cậy β tương ứng. 2.2.3. Tốc độ đếm
Nếu phép đo tiến hành trong thời gian t, số xung thiết bị ghi nhận được N, tốc
độ đếm n được tính theo công thức: n = (17)
Theo công thức chuyển sai số ta có: (δn)2 = + = + = ( ) +
Thường thời gian dt/t ~ 0 nên: (δn)2 = =
Sai số của tốc độ đếm được tính theo công thức:
Bộ môn Vật lý Hạt nhân 7 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I Δn = (18)
Với t ≠ 1 ta có δn2 ≠ n. Vậy tốc độ đếm không tuân theo phân bố Poisson. Tiến
hành m phép đo ta có: Trung bình của mẫu được tính theo công thức (6)
và độ phân tán của là Δ = =
Tốc độ đếm n = theo công thức truyền sai số ta có, sai số của tốc độ đếm được tính theo công thức sau: Δn = (19)
Từ công thức (19) nhận thấy rằng để giảm sai số cần tiến hành nhiều phép đo
(m lớn), thời gian mỗi phép đo lớn (t lớn). Nói cách khác thời gian tiến hành cho
toàn bộ phép đo T = mt lớn. Khi thời gian đo càng dài, số xung ghi nhận được
càng tăng, sai số tương đối càng giảm, độ chính xác thống kê tăng. 3. Thực hành
3.1. Nội dung thực hành
Lấy thống kê số đếm Nmà thiết bị hạt nhân ghi nhận được trong khoảng thời
gian t xác định. Tiến hành m phép đo, xác định mẫu {Ni}.
Xây dựng hàm phân bố xác suất của đại lượng N đo được, hay xây dựng
hàm phân bố xác suất của mẫu từ tập hợp số liệu thựcnghiệm.
Đánh giá các giá trị trung bình của mẫu, độ phân tán của đại lượng ngẫu
nhiên N và độ phân tán của mẫu. 3.2. Thiết bị 1. Thiết bị đếm xung
Bộ môn Vật lý Hạt nhân 8 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I 2. Nguồn nuôi 3. Detector 4. Nguồn phóng xạ
5. Buồng chì bảo vệ, che chắn nguồn phóng xạ
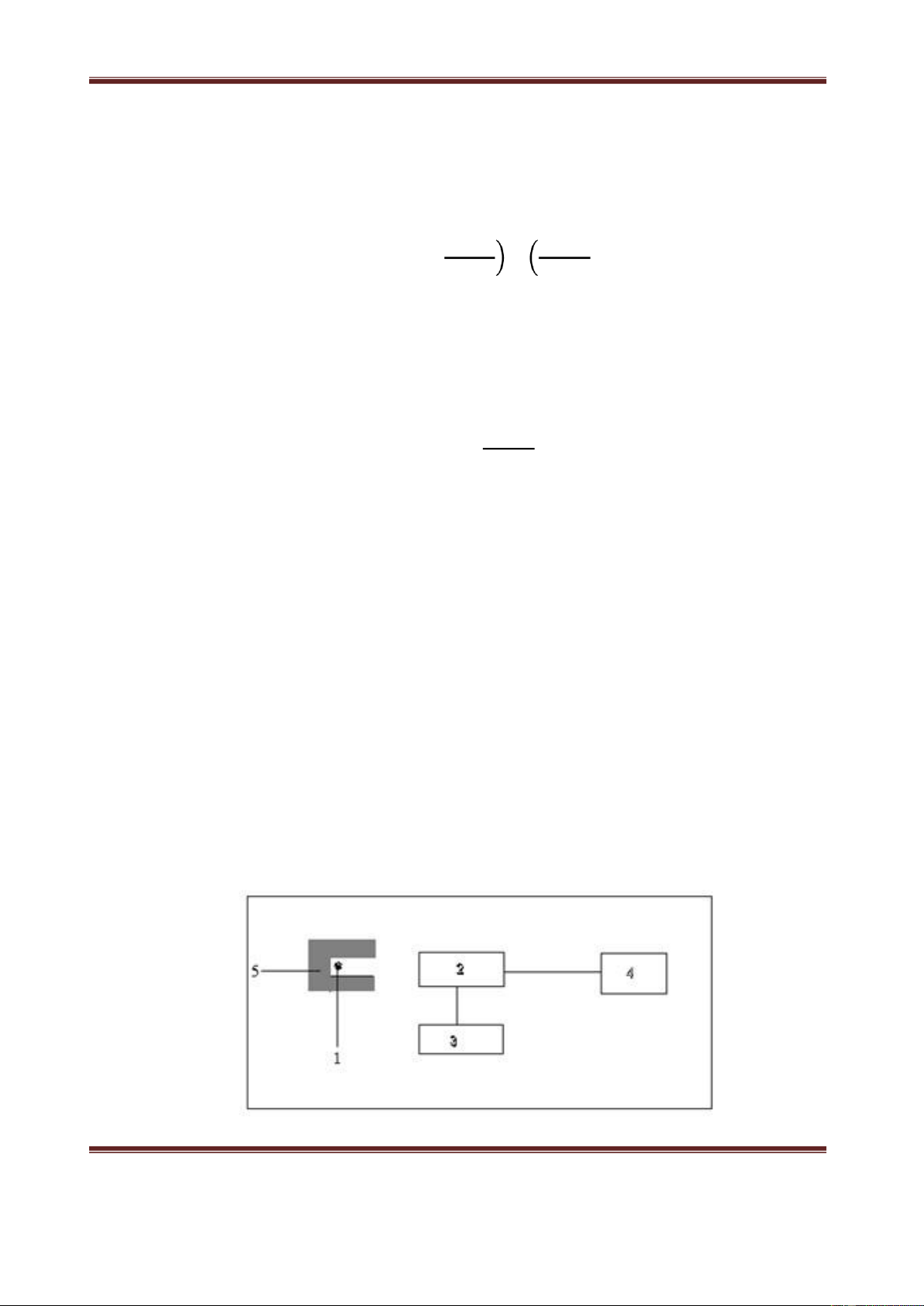
3.3. Sơ đồ thí nghiệm Geiger Muller biến đổi Máy đếm xung xung Cao thế
Hình 1.1. Sơ đồ khối hệ đo sử dụng ống đếm Geiger Muller Nguồn
phóng xạ dùng trong bài này có thể là nguồn β hoặc γ tùy thuộc vào hệ đo detector
sử dụng là detector đobức xạ β hay bức xạ γ tương ứng. Nguồn phóng xạ phải có
chu kỳ bán rã T1/2 lớn. Các nguồn sử dụng có thể là: Cs137,Co60, Ba133…
Ống đếm hay Detector có thể là ống đếm chứa khí Geiger Muller hoặc ống đếm nhấp nháy.
Nguồn nuôi cho Detector là nguồn cao áp, điện áp có thể thay đổi được.
Thường nguồn nuôi cao áp được đặt trong máy đo.
Thiết bị đếm xung: cho phép ghi nhận các xung điện lối ra ở Detector có biên
độ lớn hơn ngưỡng của thiết bị đếm. Thường trong máy đếm phóng xạ có bộ đếm
thời gian đi kèm cho phép đặt trước khoảng thời gian t cần đo xác định.
Buồng chì bảo vệ: có nhiệm vụ che chắn các bức xạ phát ra theo các hướng
khác nhau, trừ hướng các bức xạ bay đến Detector. Thông thường để giảm phông
cả ống đếm được đặt trong buồng bảo vệ.
3.4. Các bước tiến hành
Bật máyđếm (G-M counter)
Tăng thế đến thế làm việc của Detector (600 V)
Bộ môn Vật lý Hạt nhân 9 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Thay đổi khoảng cách từ nguồn đến Detector, hoặc kích thước ống chuẩn
trực, xác định nhanh tốc độ đếm n trong 10 s, kiểm tra điều kiện ≥ 100τc
(Giá trị thời gian chết τccủa ống đếm do cán bộ hướng dẫn cung cấp)
Xác định khoảng thời gian t cần đo
Sử dụng nguồn Cs137để tiến hành ghi nhận sốđếm
Đo khoảng 250 - 300 phépđo và ghi lại giá trị sốđếm sau mỗi lầnđo để xác định mẫu {Ni}.
4. Xử lý số liệu
a. Tính trung bình của mẫu theo công thức (6).
b. Xác định độ lệch chuẩn trung bình
của đại lượng N theo công thức (9) và
so sánh với kết quả tính từ công thức (8).
c. Xác định độ lệch của giá trị trung bình mẫu theo công thức (15).
d. Vẽ đồ thị biểu diễn tần số xuất hiện các giá trịNivới 10 khoảng chia.
e. Vẽ đồ thị biểu diễn phân bố xác suất theo các giá trị Nivới 10 khoảng chia .
f. Xác định số phép đo m* có giá trị nằm trong khoảng từ – σN đến + σN, tính P
= m*/m, so sánh với giá trị lý thuyết Plt = 0,68.
g. Xác định tốc độ đếm theo công thức (17) và (18).
BÀI SỐ 2: ĐẶC TRƯNG ĐẾM CỦA ỐNG ĐẾM GEIGER-MULLER 1. Mục đích
Mục đích của thí nghiệm này là xác định vùng thế Plateau củaống đếm G – M
và tìm ra điểm làm việc hợp lý nhất cho ống đếm. 2. Lý Thuyết
Ống đếm Geiger-Muller là loại ống đếm chứa khí làm việc trong vùng phóng
điện tự lập.Cũng giống như các loại ống đếm chứa khí khác, ống đếm GeigerMuller
có dạng hình trụ. Anot là một sợi dây ở chính giữa trụ, cathot là lớp kim loại mỏng
Bộ môn Vật lý Hạt nhân 10 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
được phủ ở thành trong của ống đếm. Với ống đếm beta và alpha, ống đếm phải có
cửa sổ mỏng để cho bức xạ bay vào vùng nhạy của nó.
Để sử dụng sự phóng điện tự lập trong chất khí ghi nhận các bức xạ hạt nhân,
cần dập tắt quá trình phóng điện thứ cấp trong ống đếm. Tín hiệu ở lối ra của ống đếm
là kết quả của thác lũ ban đầu do các hạt bức xạ gây ra, hay sự phóng điện sơ cấp. Có
hai cách dập tắt sự phóng điện tự lập trong ống đếm:
- Cách thứ nhất là dùng điện trở tải lớn mắc ở mạch anot. Gọi C là điện dung dò
của mạch anot. Điện trở tải R ở mạch anot có giá trị sao cho hằng số thời gian
ở mạch ngoài anot τ = RC rất lớn so với thời gian chuyển động của các ion từ
anot về cathot. Đây là nguyên tắc làm việc của ống đếm Geiger-Muller không
tự tắt. Thời gian chết τc của ống đếm Geiger-Muller loại này rất lớn cỡ 10-1
10-2 giây. Ống đếm Geiger-Muller không tự tắt ít được sử dụng để ghi nhận bức xạ.
- Cách dập tắt sự phóng điện thứ hai là cho một lượng tạp chất hơi hữu cơ đa
nguyên tử vào trong ống đếm. Với lượng tạp chất thích hợp, sự phóng điện thứ
cấp được dập tắt ngay trong ống đếm. Đây là nguyên tắc làm việc của ống đếm
Geiger-Muller tự tắt. Điện trở tải ở mạch ngoài của ống đếm này thường được
chọn nhỏ hơn điện trở ngoài của ống đếm Geiger-Muller không tự tắt cỡ 2 bậc.
Thời gian chết của ống đếm Geiger-Muller cỡ 10-4giây.
Tính chất cơ bản của ống đếm Geiger-Muller là biên độ xung lối ra không phụ
thuộc vào độ ion hóa ban đầu. Tất cả các xung có độ lớn như nhau, biên độ cỡ hàng
vôn. Ống đếm Geiger-Muller không sử dụng để xác định năng lượng của bức xạ mà
được sử dụng để xác định cường độ bức xạ của nguồn.
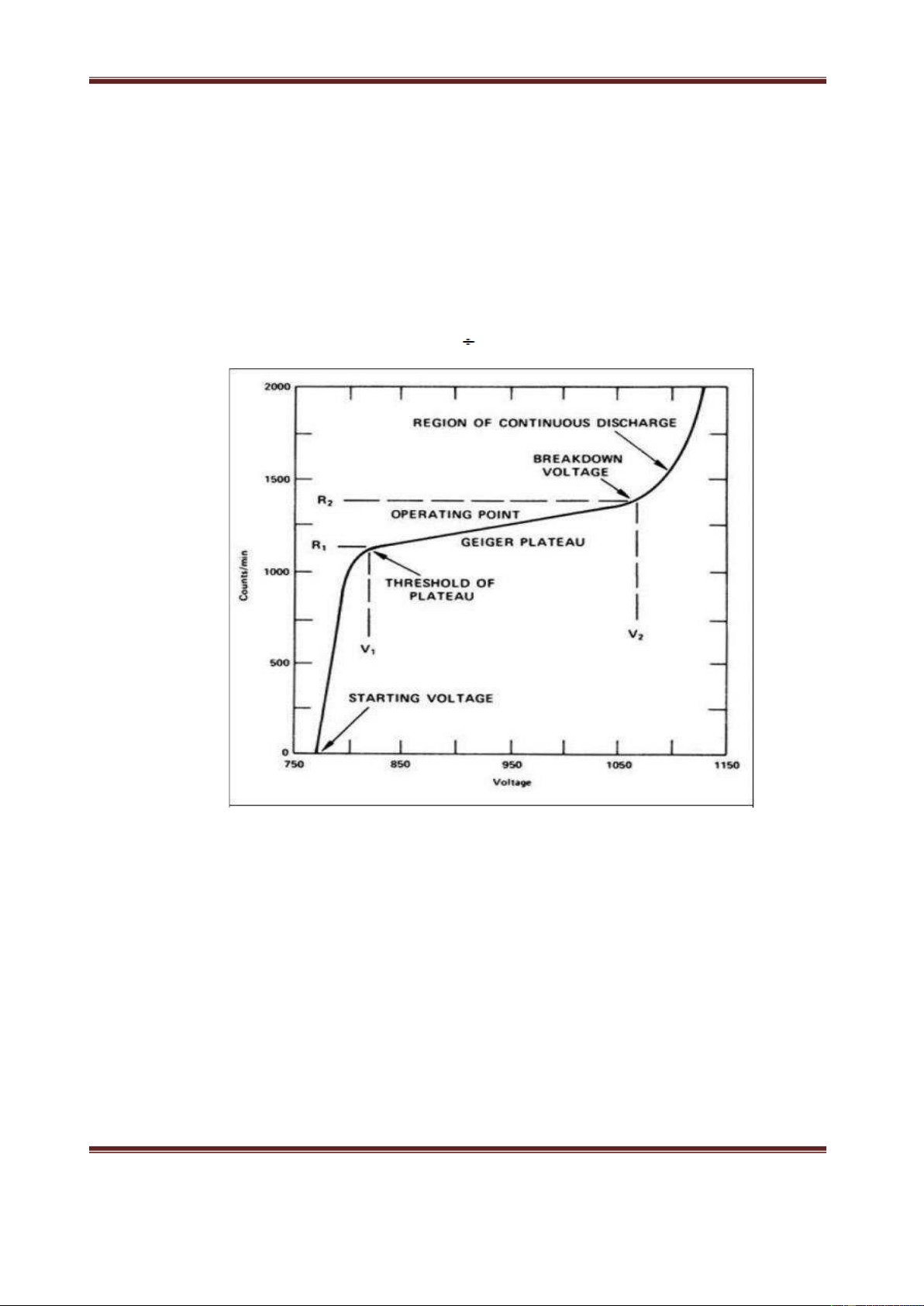
Đặc trưng đếm là một đặc trưng cơ bản của ống đếm Geiger-Muller. Đặc trưng
đếm là sự phụ thuộc của tốc độ đếm vào thế nuôi của ống đếm khi ống đếm được
chiếu bằng chùm bức xạ cường độ không đổi. Trên hình 1 là dạng đặc trưng đếm của
các loại ống đếm Geiger-Muller.
Khi thế nuôi V nhỏ hơn Vm, biên độ xung lối ra còn nhỏ hơn ngưỡng của máy
đếm, tốc độ ghi bằng không. Vm gọi là hiệu điện thế mồi. Khi Vmtăng khi thế nuôi tăng. Khi thế nuôi nằm trong khoảng Vm đến V1, tuy đã có hiện
tượng phóng điện tự lập trong ống đếm, do thăng giáng khác nhau trong quá trình
thác lũ sơ cấp và quá trình dập tắt sự phóng điện nên xung lối ra có biên độ khác nhau.
Bộ môn Vật lý Hạt nhân 11 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Khi thế mồi tăng, xác suất để xung có biên độ lớn hơn ngưỡng đếm của máy đếm
tăng, tốc độ đếm tăng.
Khi thế nuôi ống đếm đạt tới giá trị V1, các xung lối ra đều có biên độ như nhau
(và lớn hơn ngưỡng). Với mỗi ống đếm có hiệu suất ghi xác định, khi chùm bức xạ
chiếu vào ống đếm không đổi, số xung xuất hiện ở lối ra ống đếm không đổi, tốc độ
đếm không đổi khi thế nuôi tăng. Vùng V1 V2 gọi là vùng Plateau. Số đế m/ Ngưỡng của ph Plateau út Thế mồi V m Thế
Hình 1. Đặc trưng đếm của ống đếm G-M
Tuy nhiên ngoài các xung xuất hiện do hiện tượng phóng điện sơ cấp khi có
hạt bức xạ vào ống đếm gây ra, còn có các xung giả. Các xung giả xuất hiện là do các
điện tử phát ra từ cathot. Khi chuyển động về anot do hiện tượng phóng điện trong
ống đếm ở lối ra cũng xuất hiện một xung. Xung giả cũng có thể là kết quả của quá
trình dập tắt quá trình phóng điện thứ cấp không triệt để. Khi thế nuôi tăng sự xuất hiện xung giả tăng.
Khi thế nuôi V tăng đến giá trị nào đó, xác suất xuất hiện xung giả tăng, tốc độ
đếm tăng nhanh khi thế nuôi tăng, lúc này tốc độ đếm không còn phụ thuộc đơn trị
vào cường độ bức xạ chiếu vào ống đếm.
Bộ môn Vật lý Hạt nhân 12 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Độ dốc vùng Plateau được tính bởi công thức sau, với R1, R2 lần lượt là tốc độ
đếm tại các điểm V1, V2. Độ dốc q (%)= x x 100%
Để giảm ảnh hưởng của sự không ổn định thế nuôi ống đếm tới kết quả xác
định tốc độ đếm R, điểm làm việc của ống đếm được chọn với thế nuôi: Vp =
Ống đếm có độ dốc vùng Plateau càng nhỏ càng tốt. Khi q nhỏ, trong trường
hợp nếu thế nuôi ống đếm thăng giáng nhưng chưa ra khỏi vùng plateau thì tốc độ
đếm thay đổi nhỏ hơn q%. 3. Thực Hành
3.1. Các việc cần tiến hành
1. Xây dựng đặc trưng đếm của một ống đếm Geiger-Muller
2. Xác định vùng plateau và điểm làm việc Up.
3. Xác định độ dốc của vùng plateau.
3.2. Các thiết bị cần sử dụng
Sơ đồ thực nghiệm như hình vẽ 2:
Bộ môn Vật lý Hạt nhân 13 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
Hình 2: Sơ đồ bố trí thí nghiệm
1. Nguồn phóng xạ gamma có thể là 137Cs, 60Co,…
2. Ống đếm Geiger-Muller đo bức xạ gamma.
3. Nguồn nuôi cao thế nuôi ống đếm, có thể thay đổi hiệu điện thế ở lối ra. 4. Máy đếm phóng xạ. 5. Buồng chì che chắn.
3.3. Thứ tự công việc thực hiện.
1. Bật máy đếm và nguồn nuôi cao thế
2. Đặt nguồn phóng xạ vào vị trí 1.
3. Đặt máy đếm ở chế độ đếm thời gian .
4. Đặt thế nuôi từ 200V, quan sát xem máy đếm có đếm hay không.
Nếu không tăng dần thế nuôi mỗi nấc 50V, cho đến khi máy đếm bắt đầu đếm.
5. Tìm giá trị thế Vm bằng cách cho thế nuôi về nấc trước khi máy
đếm bắt đầu đếm, tăng dần thế nuôi 5V một. Ghi giá trị Vm.
6. Tăng thế nuôi ống đếm 5V một bắt đầu từ Vm. Tiến hành lấy số
đếm trong thời gian sao cho sai số thống kê nhỏ hơn 3%, số xung lớn hơn
900 xung. Tăng thế nuôi đến khi bắt đầu xảy ra hiện tượng tự phóng điện V>V2 thì dừng lại.
7. Lập bảng: Sự phụ thuộc của tốc độ đếm vào thế nuôi. V t N R = N/t ± Δn
Bộ môn Vật lý Hạt nhân 14 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
8. Vẽ đồ thị đặc trưng của ống đếm G-M.
9. Xác định vùng plateau của ống đếm và điểm làm việc Vp.
10. Xác định độ dốc vùng plateau: qo = q ± Δq
11. Đưa ra kết luận và nhận xét hoặc đề nghị nếu có.
BÀI 3: XÁC ĐỊNH THỜI GIAN CHẾT CỦA ỐNG ĐẾM GEIGER – MULLER 1. Mục đích
Ống đếm Geiger Muller (G-M ) khá chậm để ghi nhận các sự kiện (cần khoảng
micro giây để ống đếm ghi nhận sự kiện tia gamma hoặc hạt mang điện tới và cần cớ
hàng trăm micro giây để ống đếm phục hồi độ nhạy hoàn toàn cho sự kiện tiếp theo).
Khái niệm thời gian chết trong ống đếm G-M là thời gian sau khi quá trình phóng
điện xảy ra, ống đếm không thể phản ứng với bất kỳ bức xạ ion hóa nào đó đến ngay
sau đó, cho tới khi ống đếm bắt đầu có thể phản ứng với sự kiện tiếp theo. Nhưng hệ
điện tử của ống đếm G-M chỉ đếm khi xung có thế vượt qua giá trị ngưỡng xác định.
Do đó, thời gian phân giải bao gồm thời gian chết và thời gian phục hồi (đạt tới độ
lớn nhất định để ngưỡng của bộ tách xung có thể ghi nhận) của detector. Trên thực tế,
hai khái niệm thời gian phân giải và thời gian chết rất dễ bị nhầm lẫn nên thời gian
phân giải thường được ghi là thời gian chết.
Thời gian chết lớn của ống đếm G-M làm ảnh hưởng tới độ chính xác của tốc độ
đếm đo được với tốc độ đếm trên 500 xung/phút. Do đó, việc xác định thời gian chết
của ống đếm G-M để giá trị tốc độ đếm thực là cần thiết đối với ống đếm loại này.
Việc đo thời gian chết sẽ được thực hiện với phương pháp sử dụng hai nguồn phóng
xạ và thời gian chết đo được sẽ được dùng để hiệu chỉnh tốc độ đếm của tất cả các phép đo sau này. 2. Lý thuyết
Sự phóng điện trong ống đếm dẫn đến việc tạo thành điện tích không gian dương
xung quanh điện cực trung tâm. Điện trường giữa điện tích trong không gian và anot
bị suy giảm đến mức, những hạt mới tới, không thể tạo thành thác lũ. Thời gian ống
đếm hoàn toàn không nhạy với bức xạ được gọi là thời gian chết. Khi các iôn dương
Bộ môn Vật lý Hạt nhân 15 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
rời khỏi anot tới cathot, điện trường ở gần anot dần dần được phục hồi trở lại độ lớn
ban đầu. Nó tăng dần theo phương dịch chuyển của các iôn dương về cathot và đạt
giá trị cực đại khi điện tích dương về tới bề mặt cathot. Khoảng thời gian này gọi là thời gian phục hồi.
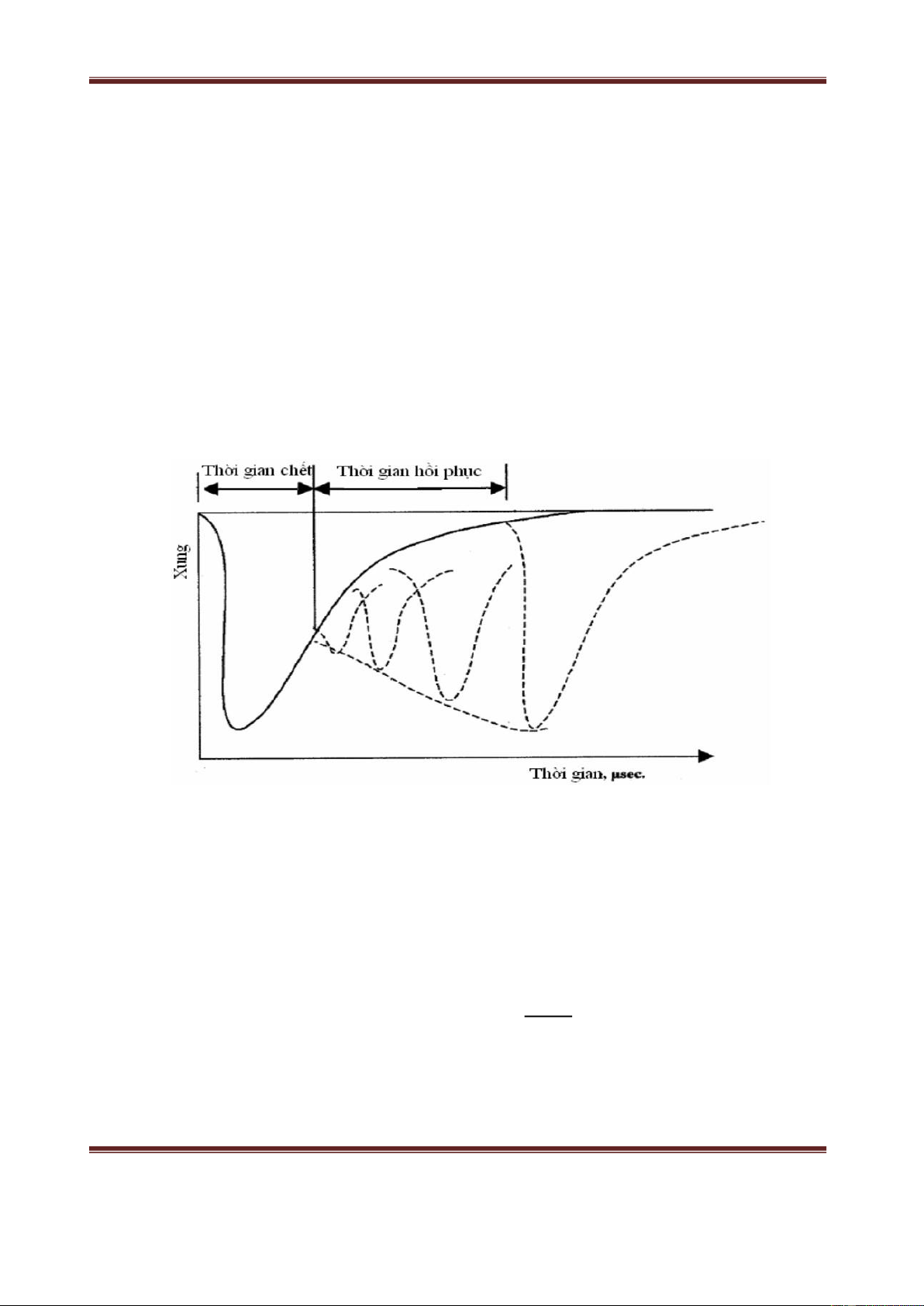
Khả năng đếm cực đại của ống đếm được xác định bằng hai đặc điểm đó là 8
thời gian chết9 và 8thời gian hồi phục9. Cả hai đặc điểm này đều liên quan trực tiếp
đến thời gian phóng điện của ống đếm. Thời gian phân giải là thời gian khoảng thời
gian nhỏ nhất có thể phân biệt được sự bay vào của hai hạt liên tiếp nhau và có thể
ghi nhận chúng riêng biệt. Thời gian phân giải của ống đếm G-M cỡ 10-4s.
Hình 1: Đặc trưng thời gian chết và hồi phục của ống đếm G – M
Thời gian chết của mỗi quá trình phóng điện sẽ giới hạn tốc độ đếm cực đại vì
các sự kiện bức xạ gây ion hóa có thể xảy ra trong khoảng thời gian chết sẽ không
được ghi nhận. Mối liên hệ giữa thời gian chết với tốc độ đếm R đo được từ ống đếm là: R= (1)
Với r là tốc độ đếm thực của ống đếm
Một cách khác để xác định thời gian chết của ống đếm đó là phương pháp sử
dụng hai nguồn phóng xạ. Giả sử trong cùng một cấu hình đo ta thu được tốc độ đếm
Bộ môn Vật lý Hạt nhân 16 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
của nguồn một, nguồn hai và cả hai nguồn lần lượt là , và ( lưu ý < + ). Khi đó thời
gian chết của ống đếm được xác định theo công thức: = [ ( )( )]/ (2)
Một cách gần đúng, công thức (2) có thể biến đổi thành: = (3)
3.Các bước tiến hành
1. Kiểm tra kết nối: đầu ra của ống đếm kết nối với đầu vào của bộ đếm
2. Cài đặt cao thế cho ống đếm : 550 V – 700 V
3. Sử dụng hai nguồn 137Cs và 133Ba
4. Đặt nguồn 137Cs vào vị trí đặt mẫu phía bên phải trong buồng chì
5. Tiến hành đo số đếm của 137Cs
6. Đặt nguồn 133Ba vào vị trí đặt mẫu phía bên trái trong buồng chì
7. Tiến hành đo số đếm của cả hai nguồn
8. Bỏ nguồn 137Cs ra khỏi buồng chì
9. Tiến hành đo số đếm của nguồn 133Ba
10. Mỗi phép đo tiến hành 5 lần để tính sai số
11. Xác định thời gian chết và tốc độ đếm thực của ống đếm dựa vào công thức (3) và (1).
Bộ môn Vật lý Hạt nhân 17 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
BÀI 4: PHỔ KẾ GAMMA NHẤP NHÁY 1. Mục đích
Mục đích của thí nghiệm này là để cho sinh viên làm quen với một vài kỹ thuật
cơ bản được sử dụng trong đo đạc tia gamma sử dụng detector NaI (Tl). 2. Lý thuyết 2.1 Bức xạ gamma
Hầu hết các nguồn gamma được sử dụng là từ các đồng vị phân rã beta. Các
đồng vị sau khi phân rã beta biến thành hạt nhân mới ở trạng thái kích thích, các mức
kích thích này đặc trưng cho từng nguyên tố khác nhau. Sau đó chúng phát ra tia
gamma để trở về trạng thái cơ bản. Tia beta thường sẽ bị hấp thụ trong vật liệu bao
quanh và không đi vào Detector nhấp nháy. Phần hấp thụ này có thể làm bằng nhôm, hay là nhựa (polyme).
Thông thường có hai đặc trưng mà chúng ta cần phải nghiên cứu về nguồn
gamma. Thứ nhất là xác định các năng lượng của các tia gamma phát ra từ nguồn.
Thứ hai là xác định số photon phát ra từ nguồn trong một đơn vị thời gian. Trong thí
nghiệm này sinh viên sẽ làm quen với một vài phép đo cơ bản với Detector NaI(Tl)
liên quan đến việc xác định gamma phát ra từ đồng vị phóng xạ.
Bộ môn Vật lý Hạt nhân 18 lOMoAR cPSD| 49669324
Thực tập Vật lý Hạt nhân I
2.2 Tương tác của bức xạ gamma với vât chất
1. Hiệu ứng quang điện (Photoelectric absorption)
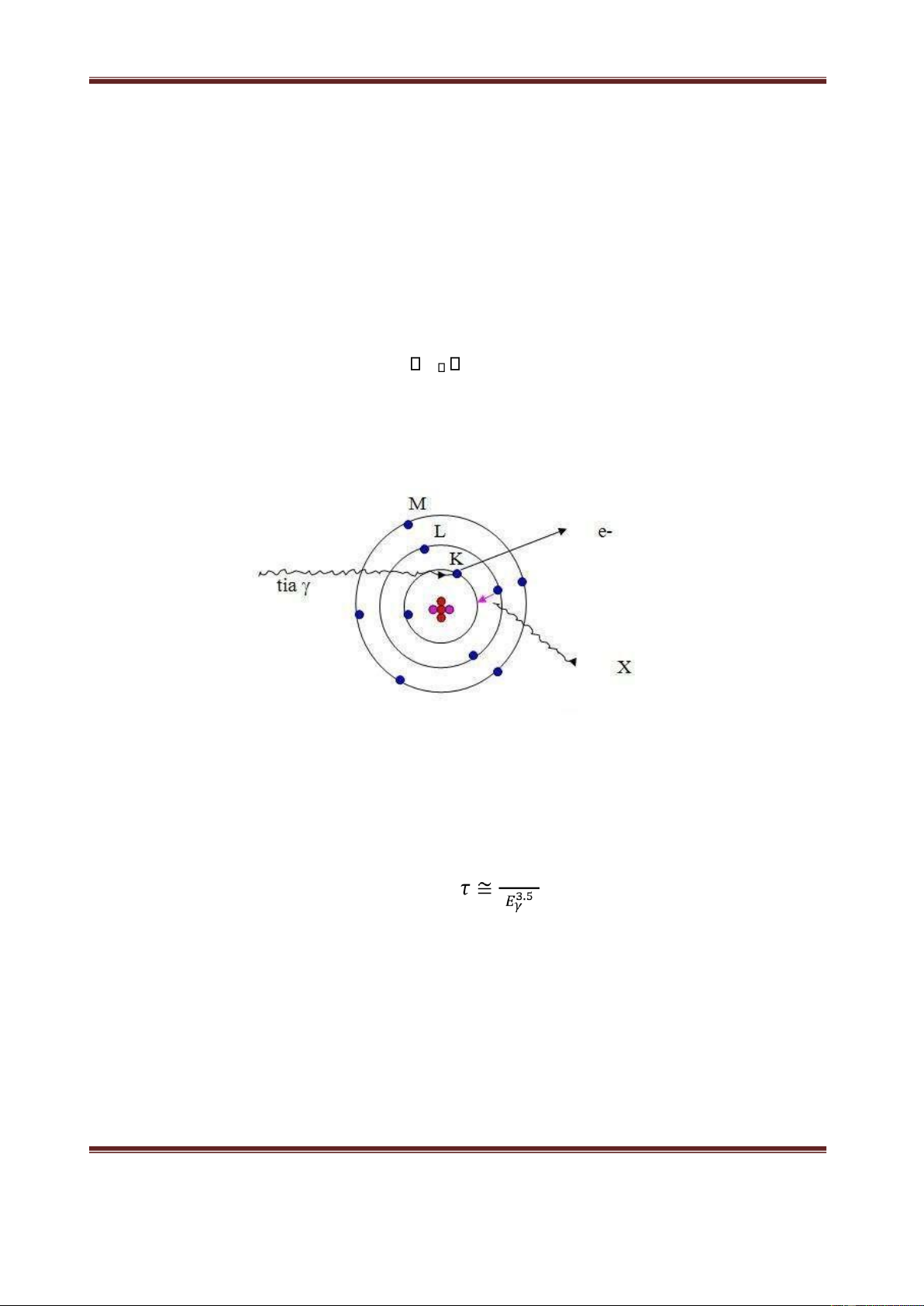
Hiệu ứng quang điện là quá trình tương tác mà photon tới bị một electron nguyên tử
hấp thụ hoàn toàn, khi đó photon biến mất và một electron bứt ra khỏi nguyên tử còn
gọi là electron quang điện hay quang electron. Động năng của quang electron bật ra
được tính theo công thức: E e E E i (1.1)
trong đó:Ee là động năng quang electron
Eᵧ là năng lượng của tia Gamma tới
Ei là năng lượng liên kết của electron với nguyên tử ở lớp i (i=K, L, M,…)
Hình 1. Hiệu ứng quang điện
Từ công thức (1.1) ta thấy rằng hiệu ứng quang điện chỉ xảy ra khi photon tới có
năng lượng lớn hơn năng lượng liên kết của electron trong nguyên tử.
Xác suất để một photon bị hấp thụ quang điện có thể được biểu diễn qua tiết diện hấp thụ τ với: × (1.2)
với a là hằng số, Z là nguyên tử số của môi trường, Eγ là năng lượng của tia gamma,
số mũ n thay đổi từ 4 đến 5 trong vùng năng lượng gamma quan tâm.
2. Hiệu ứng tán xạ Compton (Compton scattering)
Tán xạ Compton là quá trình tương tác của photon tới với một electron của môi
trường hấp thụ được xem như tự do. Tán xạ này là tán xạ đàn hổi của gamma với các
electron chủ yếu ở quỹ đạo ngoài cùng của nguyên tử.Sau tán xạ, photon truyền một
phần năng lượng của nó cho electron và bị lệch đi một góc θ so với hướng ban đầu.
Bộ môn Vật lý Hạt nhân 19