lOMoARcPSD|45315597 lOMoARcPSD|45315597
Tài liệu chỉ phục vụ ôn thi, các bạn dùng tài liệu để quay cóp, page không chịu trách nhiệm. #bún ĐỀ CƯƠNG ÔN TẬP
Câu 1: Nêu khái niệm về môn học, nhiệm vụ, vai trò của Trắc địa trong quy hoạch, xây dựng?
Lịch sử phát triển của Trắc địa:
- Trắc địa xuất hiện từ 3000 năm trước công nguyên. Từ thế kỷ 16 – 17
đã thành lập bản đồ cho các khu vực rộng lớn. Trắc địa là một trong
những ngành cổ xưa nhất, xuất hiện từ thực tiễn của con người.
- Hiện nay, nhờ có sự phát triển rất nhanh của các ngành khoa học ứng dụng,
đặc biệt là lĩnh vực điện tử, tin học, trắc địa nói chung và trắc địa công
trình nói riêng cũng có những bước tiến mới, nhiều máy móc, công nghệ đo
đạc ra đời, nhiều quá trình được tự động hóa đáp ứng yêu cầu thực tế sản
xuất cũng như nghiên cứu khoa học,…
Khái niệm: Trắc địa là môn khoa học chuyên nghiên cứu về các phương pháp,
phương tiện đo đạc và xử lý số liệu để xác định vị trí, hình dạng, kích thước của
các đối tượng đo và biểu thị bề mặt quả đất dưới dạng bản đồ và số liệu, phục
vụ cho các mục đích nghiên cứu khoa học, đáp ứng các nhu cầu của các ngành
kinh tế quốc dân và quốc phòng. Nhiệm vụ:
- Tiến hành đo đạc các yếu tố cần thiết như góc, cạnh, độ cao xử lý số liệu và
thể hiện chúng dưới dạng bình đồ, bản đồ, mặt cắt…
- Nghiên cứu hình dạng, kích thước Trái đất và biểu diễn bề mặt Trái đất
dưới dạng bình đồ hoặc bản đồ.
- Sử dụng những thành quả, dụng cụ, phương pháp đo cơ bản trong Trắc địa
để ứng dụng trong quy hoạch, thiết kế, thi công công trình xây dựng, lĩnh
vực kinh tế và quân sự.
Một số ngành hẹp của Trắc địa: + Trắc địa cao cấp; + Trắc địa công trình; + Trắc địa phổ thông;
+ Trắc địa bản đồ, viễn thám và GIS;
+ Trắc địa ảnh, địa hình. Vai trò:
- Là ngành điều tra cơ bản, có vai trò quan trọng đối với nền kinh tế quốc dân
và quốc phòng; đặc biệt đối với ngành xây dựng cơ bản, trắc địa luôn giữ vị 1 lOMoARcPSD|45315597
trí quan trọng hàng đầu. Số liệu Trắc địa là cơ sở cho việc thiết kế,
quy hoạch, thi công xây dựng cho đến khi sử dụng công trình.
- Giai đoạn khảo sát, thiết kế và quy hoạch: đáp ứng mọi yêu cầu về mặt bằng
(bình đồ, bản đồ), các mặt cắt ngang, dọc, độ cao, sâu,…. các số liệu khảo
sát kể cả về địa chất công trình và thủy văn. Cung cấp tư liệu cơ sở lập bình
đồ, bản vẽ thiết kế quy hoạch mặt bằng và độ cao, tính toán các số liệu san lấp, diện tích khu vực.
- Giai đoạn thi công: Trắc địa đảm bảo bố trí công trình trên thực địa đúng như
thiết kế. Cung cấp mạng lưới các điểm tọa độ và độ cao chính xác. Tiến hành
đo vẽ hoàn công để đánh giá chất lượng (hình dạng, kích thước), xác định sai
lệch so với thiết kế để có những biện pháp khắc phục kịp thời.
- Giai đoạn khai thác và sử dụng công trình: Theo dõi ổn định của công trình
theo thời gian hoặc tác động của con người và thiên nhiên. Phát hiện được
nguyên nhân và dự báo sự phát triển của biến dạng… nhằm đạt được hiệu quả
kinh tế và tránh được sự cố đáng tiếc.
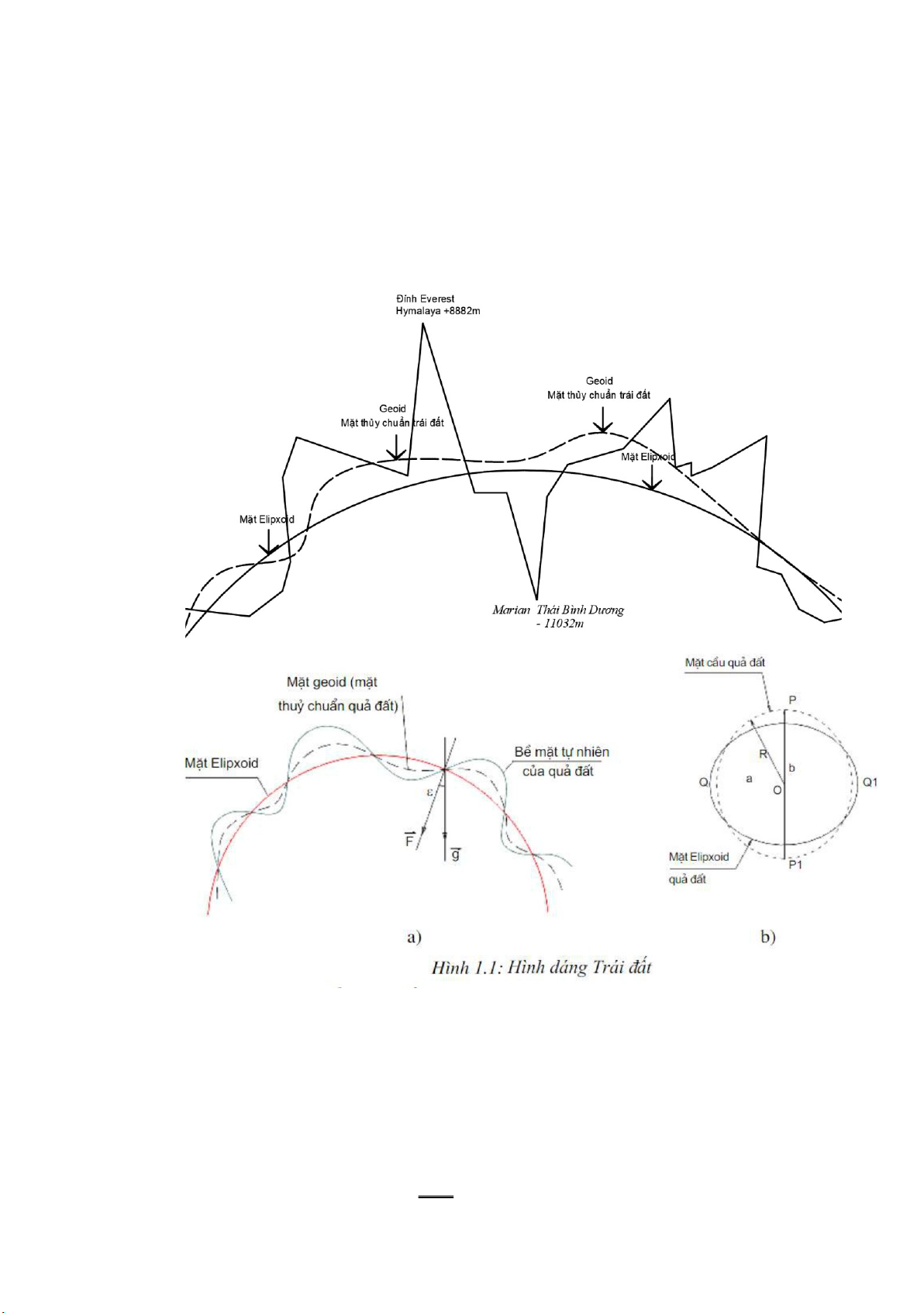
Câu 2: Khái niệm về hình dạng và kích thước của Trái đất, mặt nước gốc quả
đất và các lần khái quát tiếp theo (vẽ hình minh họa); ý nghĩa của những lần khái quát đó?
- Quả đất có hình dạng quả cầu, hơi dẹt về phía hai cực.
- Bề mặt vật lý của quả đất lồi lõm, gồ ghề có tổng diện tích khoảng 510 triệu
km2; trong đó bề mặt đại dương chiếm tới 71%; còn lại 29% là lục địa, đất
liền. Độ cao trung bình của đất liền so với mặt biển chỉ bằng khoảng 780m, độ
sâu trung bình của đại dương đạt tới 3800m, chênh lệch giữa nơi cao nhất và
nơi thấp nhất của vỏ quả đất cũng chỉ xấp xỉ 20km. Nếu đem so sánh với kích
thước quả đất có đường kính khoảng 12000 km thì sự lồi lõm của bề mặt quả đất là không đáng kể.
(Nơi cao nhất là đỉnh Everest Hymalaya = 8882m; nơi thấp nhất là
Marian-Thái Bình Dương = - 11032m)
Khái quát lần 1: Trái đất có hình dạng mặt nước gốc quả đất (geoid)
Mặt nước gốc quả đất (Geoid):
- Khái niệm: Là mặt đại dương yên tĩnh kéo dài xuyên qua lục địa tạo thành một
mặt cong khép kín. Tâm và trục quay của mặt Geoid trùng với tâm và trục quay của Trái đất. - Đặc điểm:
+ Luôn nằm ngang tại mọi điểm, tức là tại mọi điểm phương của đường
pháp tuyến luôn trùng với phương dây dọi. lOMoARcPSD|45315597
+ Sự phân bố vật chất không đều của cấu tạo vỏ Trái đất nên ngay cả
ở trạng thái yên tĩnh Geoid có một hình dạng rất phức tạp.
+ Mặt Geoid là mặt vật lý (được dùng làm mặt quy chiếu xác định độ cao)
Khái quát lần 2: Trái đất là một Elipxoid / Elipxoidtròn xoay chính tắc toán
học nhằm giải được các bài toán liên quan đến các CT toán học Mặt Elipxoid:
- Là mặt toán học, nhận được bằng cách xoay hình elip quanh trục nhỏ PP1 của nó.
- Kích thước Elipxod quả đất được xác định bằng các đại lượng bán trục lớn a,
a b+ Thể tích bằng thể tích tráibántrụcnhỏbvàđộdẹt:α= a đất.
- Mặt Elipxoid có những tính + Mặt phẳng xích đạo chất:
trùng với mặt phẳng xích
+ Tâm trùng với tâm trái đất. đạo trái đất. lOMoARcPSD|45315597
+ Tổng bình phương chênh cao
giữa mặt Eipxoid trái đất và mặt Geoid là nhỏ nhất.
+ Tại mọi điểm trên bề mặt trái đất,
phương của pháp tuyến đều vuông góc với mặt Elipxoid trái đất.
Mặt Elipxoid tham khảo là mặt được xác định riêng cho từng quốc gia, và được
định vị trong quả đất sao cho nó gần trùng nhất với bề mặt Geoid của quốc gia đó.
Việt Nam đã và đang sử dụng 2 mặt Elipxoid:
- Trước đây, nước ta vẫn sử dụng Elipxoid Krasovski của Nga
- Hiện nay, nước ta đang sử dụng hệ tọa độ VN-2000, hệ quy chiếu toàn
cầu WGS-84 và Elipxoid tham khảo GRS-80.
Khái quát lần 3: Trái Đất là mặt cầu tâm O có bán kính TB Rtb = 6371,1 km
Khái quát lần 4: Coi phạm vi mặt cầu có bán kính khu vực ≤ 20km là mặt phẳng.
Câu 3: Nguyên tắc biểu diễn bề mặt trái đất trong phạm vi hẹp lên
mặt phẳng? Khái niệm bình đồ, bản đồ và mặt cắt?
a. Nguyên tắc biểu diễn bề mặt trái đất trong phạm vi hẹp lên mặt phẳng:
+ Sử dụng phương pháp chiếu thẳng góc (phương pháp chiếu bằng) + Phạm vi: không quá 20 km
+ Hệ quy chiếu: Mặt phẳng ngang
+ Phương chiếu: Phương dây dọi
+ Mục đích là các điểm trên mặt đất được chuyển lên mặt phẳng ngang theo những
đường thẳng đứng song song với nhau và vuông góc với mặt phẳng ngang.
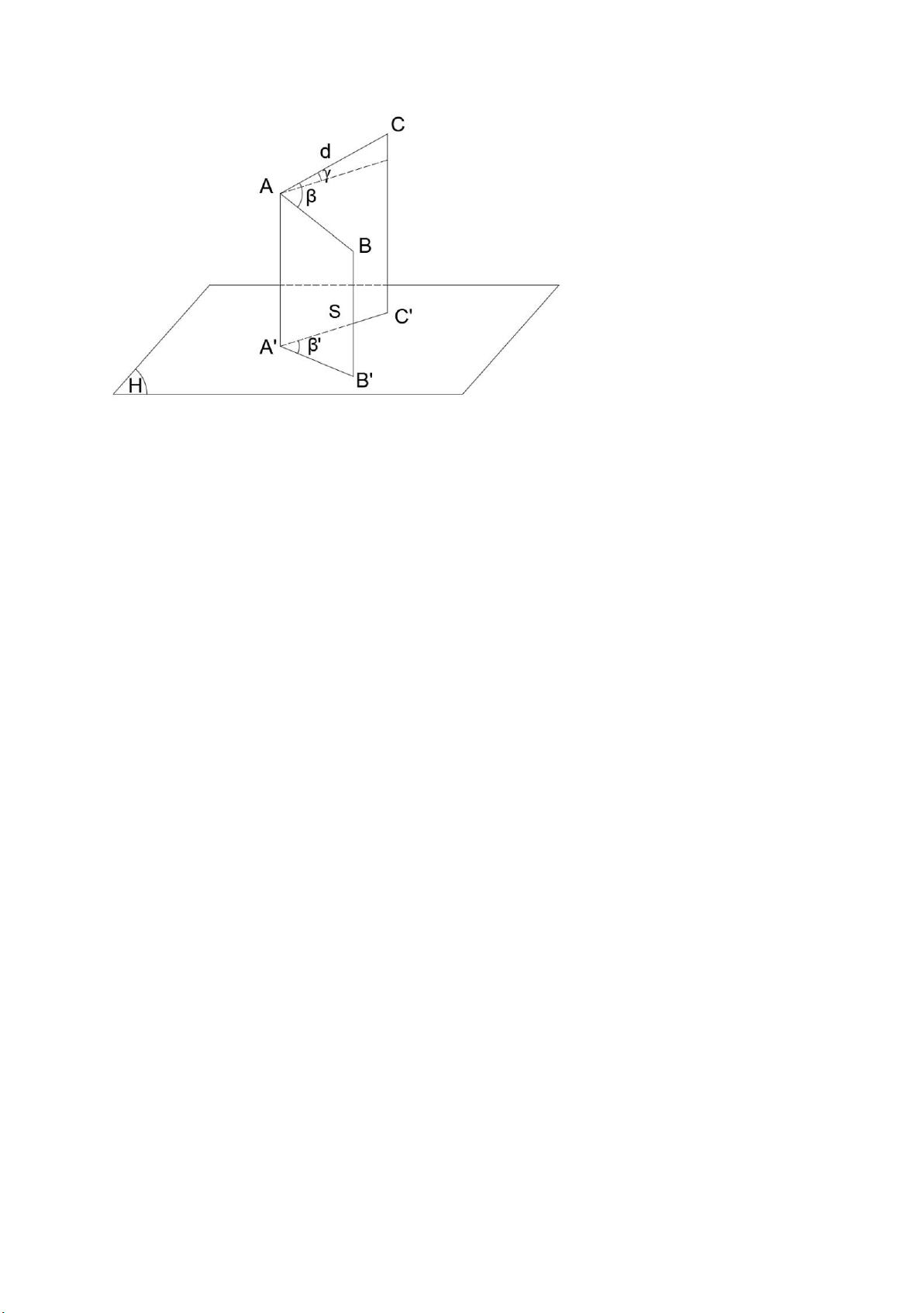
- Biểu diễn: Giả sử 3 điểm A, B, C có độ cao khác nhau trên thực địa.
Nhiệm vụ: Chiếu 3 điểm A, B, C lên mặt phẳng nằm ngang
Thực hiện: Giả sử A/,B/,C/ nằm trên mặt bằng nằm ngang là hình chiếu của các điểm.
S: khoảng cách ngang của các điểm β: góc ngang trên mp(H) β=β’ S=α cos v lOMoARcPSD|45315597 lOMoARcPSD|45315597
Trong đó: A’, B’, C’ là hình
chiếu bằng của các điểm A, B, C.
A’B’, B’C’, C’A’: hình chiếu bằng cả các cạnh AB, BC, CA (còn gọi là khoảng cách ngang S). S=d.cosγ
γ: góc nghiêng đo ngoài thực địa;
d: khoảng cách nghiêng đo ngoài thực địa. β : góc trên thực địa
β’: hình chiếu bằng của các góc tương ứng trên thực địa (còn gọi là góc ngang) β= β’
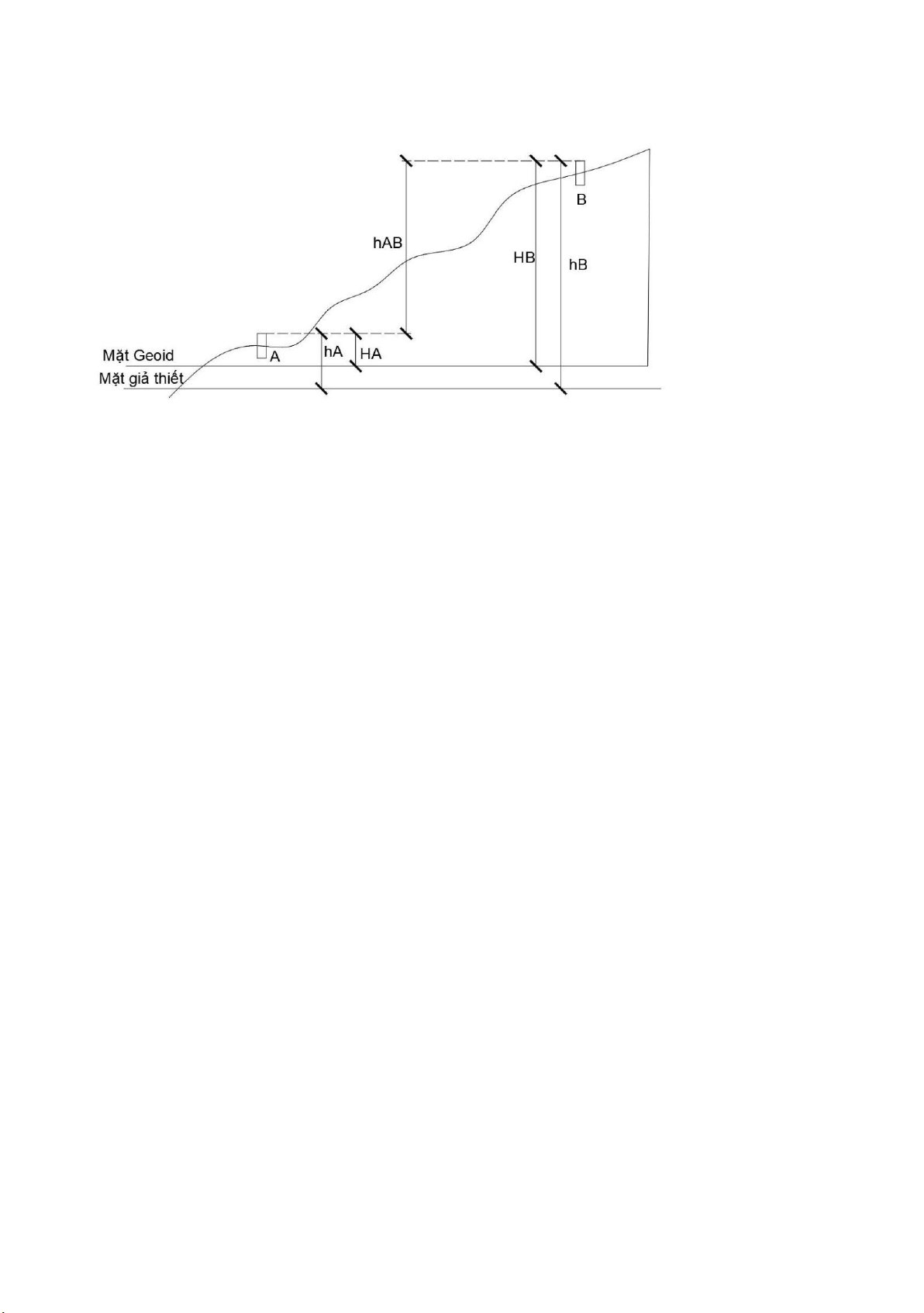
- Một điểm được thể hiện dưới 2 dạng độ cao:
+ Độ cao tuyệt đối (H) của một điểm: là khoảng cách thẳng đứng từ
điểm đó đến mặt nước gốc quả đất.
+ Độ cao tương đối (h) của một điểm: là khoảng cách từ điểm đó đến
mặt bất kỳ (mặt giả định) song song với mặt nước gốc.
- Chênh lệch độ cao (tuyệt đối hoặc giả định) giữa 2 điểm được gọi là chênh cao
giữa 2 điểm đó và được kí hiệu là h: hAB= HB-HA = hB-hA lOMoARcPSD|45315597
b. Khái niệm bình đồ, bản đồ và mặt cắt:
Bình đồ là biểu diễn thu nhỏ bề mặt thực địa trên một phạm vi hẹp lên mặt
phẳng theo phép chiếu bằng không tính đến ảnh hưởng của độ cong quả đất;
mọi điểm biểu diễn thu nhỏ đều đồng dạng với thực địa và thực tế không bị biến dạng.
Có 2 loại bình đồ: + Bình đồ địa vật (không thể hiện độ cao)
+ Bình đồ địa hình (có thể hiện độ cao) lOMoARcPSD|45315597
Bản đồ: là biểu thị toàn bộ mặt đất hoặc một phần lớn của mặt đất (như biểu thị
trọn vẹn 1 lục địa, một nước, một miền, một vùng). Bản đồ là biểu diễn khái
quát thu nhỏ và có biến dạng do độ cong quả đất một khu vực rộng lớn bề mặt
trái đất lên mặt phẳng trong 1 phép chiếu bản đồ nhất định.
Mặt cắt: là biểu diễn thu nhỏ hình chiếu bề mặt quả đất theo một hướng nhất
định nào đó lên mặt phẳng đứng. Trong thực tế thường sử dụng phổ biến 2
loại mặt cắt là mặt cắt dọc và mặt cắt ngang.
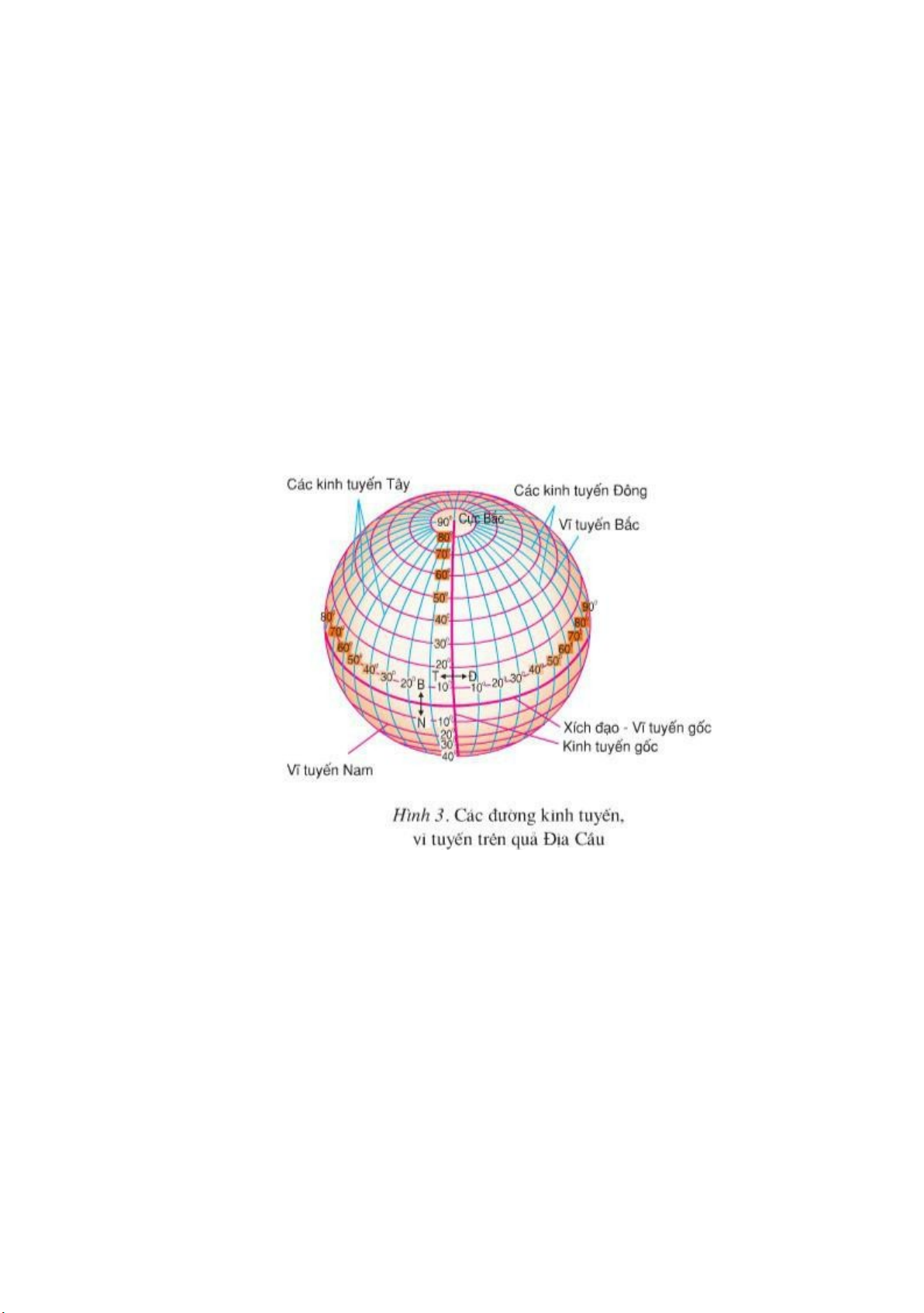
Câu 4: Khái niệm về hệ tọa độ địa lý, khái niệm về kinh độ và vĩ độ của một
điểm (vẽ hình địa cầu và chỉ rõ các yếu tố)? Căn cứ vào đâu để xác định tọa
độ địa lý của một điểm trên bản đồ?
Hệ tọa độ địa lý là một hệ tọa độ cho phép tất cả mọi điểm trên Trái Đất đều
có thể xác định được bằng một tập hợp các số có thể kèm ký hiệu. Các tọa độ
thường gồm số biểu diễn vị trí thẳng đứng, và hai hoặc ba số biểu diễn vị trí
nằm ngang. Hệ tọa độ địa lý được quy định chung và thống nhất cho toàn bộ quả đất.
Đường thẳng gốc: -Kinh tuyến gốc -Vĩ tuyến gốc
Tọa độ địa lý của một điểm là đại lượng đặc trưng cho vị trí địa lý của
điểm đó trên bề mặt quả địa cầu.
Kinh tuyến là giao tuyến giữa mặt phẳng chứa trục quay của trái đất (BN) với
mặt cầu (mặt Geoid). Mặt phẳng chứa đường kinh tuyến và trục quay của trái
đất (BN) gọi là mặt phẳng kinh tuyến.
- Đường kinh tuyến gốc là kinh tuyến đi qua đài thiên văn Greenwich ở
gần thủ đô London của Anh.
Vĩ tuyến là giao tuyến của mặt phẳng vuông góc với trục quay của trái đất
và mặt cầu (mặt Geoid). Mặt phẳng chứa đường vĩ tuyến và vuông góc với
trục quay của trái đất gọi là mặt vĩ tuyến.
- Đường vĩ tuyến gốc là đường xích đạo, mặt phẳng xích đạo đi qua tâm O
của trái đất và vuông góc với trục quay của trái đất.
Khái niệm về kinh độ và vĩ độ của 1 điểm:
- Kinh độ địa lý của điểm M là góc nhị diện
tạo bởi giữa mặt phẳng chứa M
đường kinh tuyến đi qua M với mặt phẳng kinh tuyến gốc. lOMoARcPSD|45315597 00≤≤1800 M
Mặt phẳng kinh tuyến gốc chia trái đất thành 2 nửa phía Đông và phía
Tây, tương ứng với kinh độ Đông và kinh độ Tây. lOMoARcPSD|45315597
- Vĩ độ của điểm M là góc φM tạo bởi phương của đường dây dọi đi qua
điểm đó với mặt phẳng xích đạo. 00≤φM≤900
Mặt phẳng xích đạo chia Trái đất thành 2 nửa phía Bắc và phía Nam,
tương ứng với vĩ độ Bắc và vĩ độ Nam.
Để xác định tọa độ địa lý của một điểm M nào đó trên bản đồ, ta cần căn cứ vào
các yếu tố sau: Kinh tuyến và vĩ tuyến của điểm M đó.
- Để xác định được kinh tuyến và vĩ tuyến của điểm M đó, ta cần các yếu tố: + Tâm của trái đất
+ Trục quay của trái đất + Mặt phẳng xích đạo
+ Mặt phẳng kinh tuyến gốc.
Câu 5. Anh/chị hãy vẽ hình và thuyết minh nội dung của phép chiếu bản đồ UTM?
Hệ tọa độ vuông góc quốc gia trên bản đồ? (có vẽ hình minh họa) Pháp chiếu Gauss:
Mục đích: biểu diễn bề mặt TĐ lên mặt phẳng với độ biến dạng nhỏ nhoi
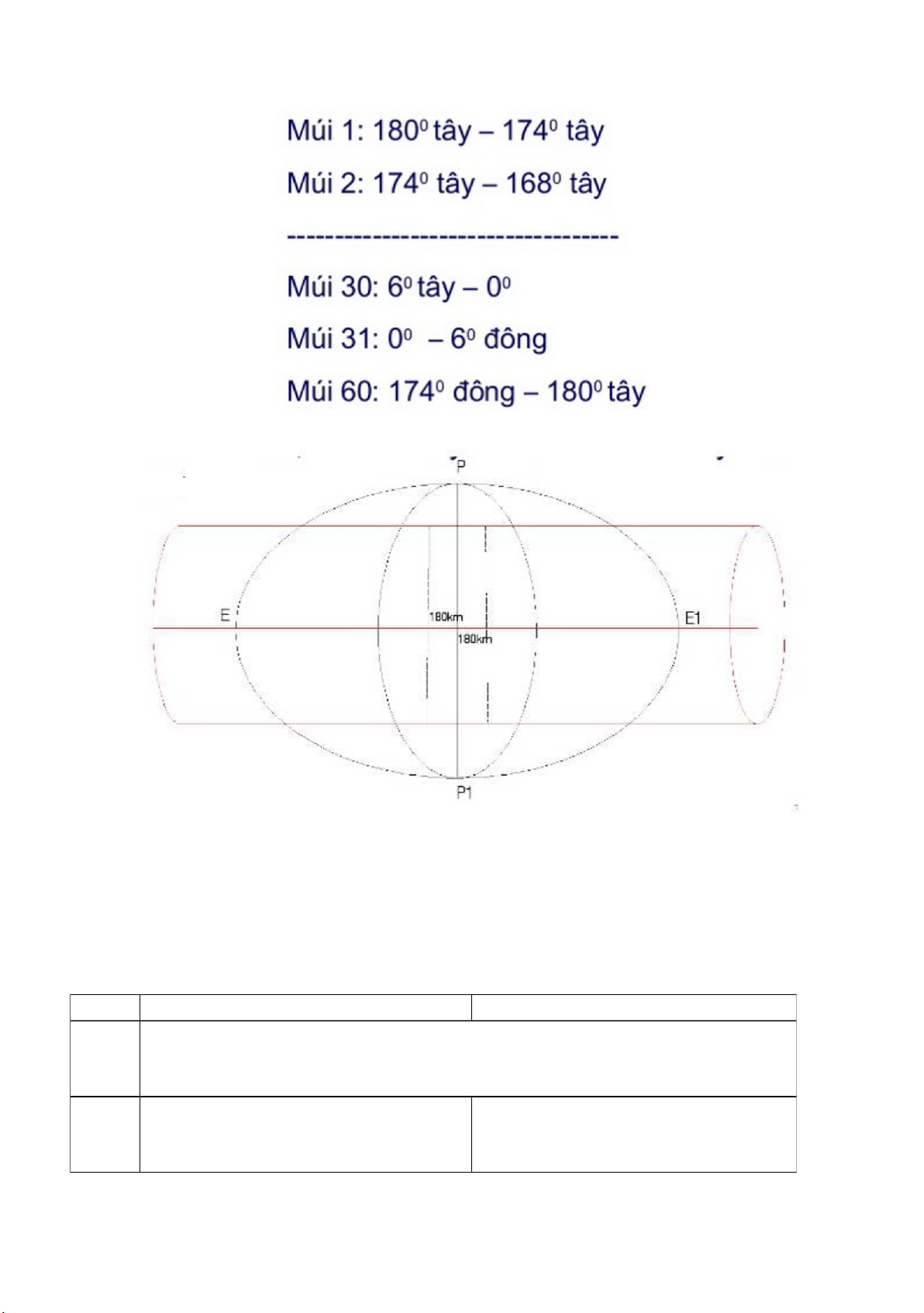
Nội dung: chia TĐ thành 60 múi, dọc kinh tuyến mỗi múi 60 Kí hiệu:n
2 kinh tuyến giới hạn 1 múi là kinh tuyến biên
-Kinh tuyến qua giữa múi chia làm hai nửa đối xứng bằng nhau gọi là kinh tuyến trục
+Đặt nội tiếp quả cầu vào trong hình trụ nằm ngang, kinh tuyến trục tiếp xúc mặt bên hình trụ.
+Trục hình trụ thuộc mặt phẳng xích đạo lOMoARcPSD|45315597
+Cắt theo hai đường sinh của hình trụ trải ra mặt phẳng ta được 60 múi
-Kinh tuyến trục cuông góc với xích đạo
-Độ dài kinh tuyến giữa không đổi (k=1) các đường thẳng khác độ dài biến dạng, tăng về
hai biên, góc được bảo toàn.
-Diện tích múi trên bản đồ lớn hơn diện tích thực trên mặt đất
Phép chiếu bản đồ UTM( Universal Trasverse Mercator) cũng thực hiện với tâm chiếu là
tâm quả đất và với từng múi 6 độ, nhưng khác với phép chiếu hình Gauss để giảm độ
biến dạng về chiều dài và diện tích, trong phép chiếu UTM sử dụng hình trụ ngang có
bán kính nhỏ hơn bán kính quả đất, nố cắt mặt cầu theo hai đường cong đối xứng và
cách kinh tuyến giữa khoảng 180km. Kinh tuyến giữa năm phía ngoài mặt trụ còn hai
kinh tuyến biên nằm phía trong mặt trụ
Chia trái đất thành 60 múi (6 độ) đánh số từ 1-60 lOMoARcPSD|45315597
Như vậy, hai đường cong cắt mặt trụ không bị biến dạng chiều dài(k=1), tỷ lệ chiếu k
của kinh tuyến giữa múi nhỏ hơn 1 (k=0.9996 với múi chiếu 3 độ) còn trên kinh tuyến
biên tỷ lệ chiếu lớn hơn 1
ưu điểm là độ biến dạng được phân bố đều hơn và có trị số nhỏ hơn nhưng khi xử lý số
liệu lại rất phức tạp Gauss UTM Giốn g nhau
Chia TĐ thành 60 múi mỗi múi 60 đánh số từ 1-60 thành vòng khép kín Cách
Từ 1-60 bắt đầu từ kinh tuyến gốc
Từ 1-60 bắt đầu từ kinh tuyến 1800 đánh
00 vòng qua Tây bán cầu rồi trở lại
ngược chiều kim đồng hồ khép lại số kinh tuyến gốc ở kinh tuyến lOMoARcPSD|45315597
Hệ tọa độ vuông góc quốc gia trên bản đồ
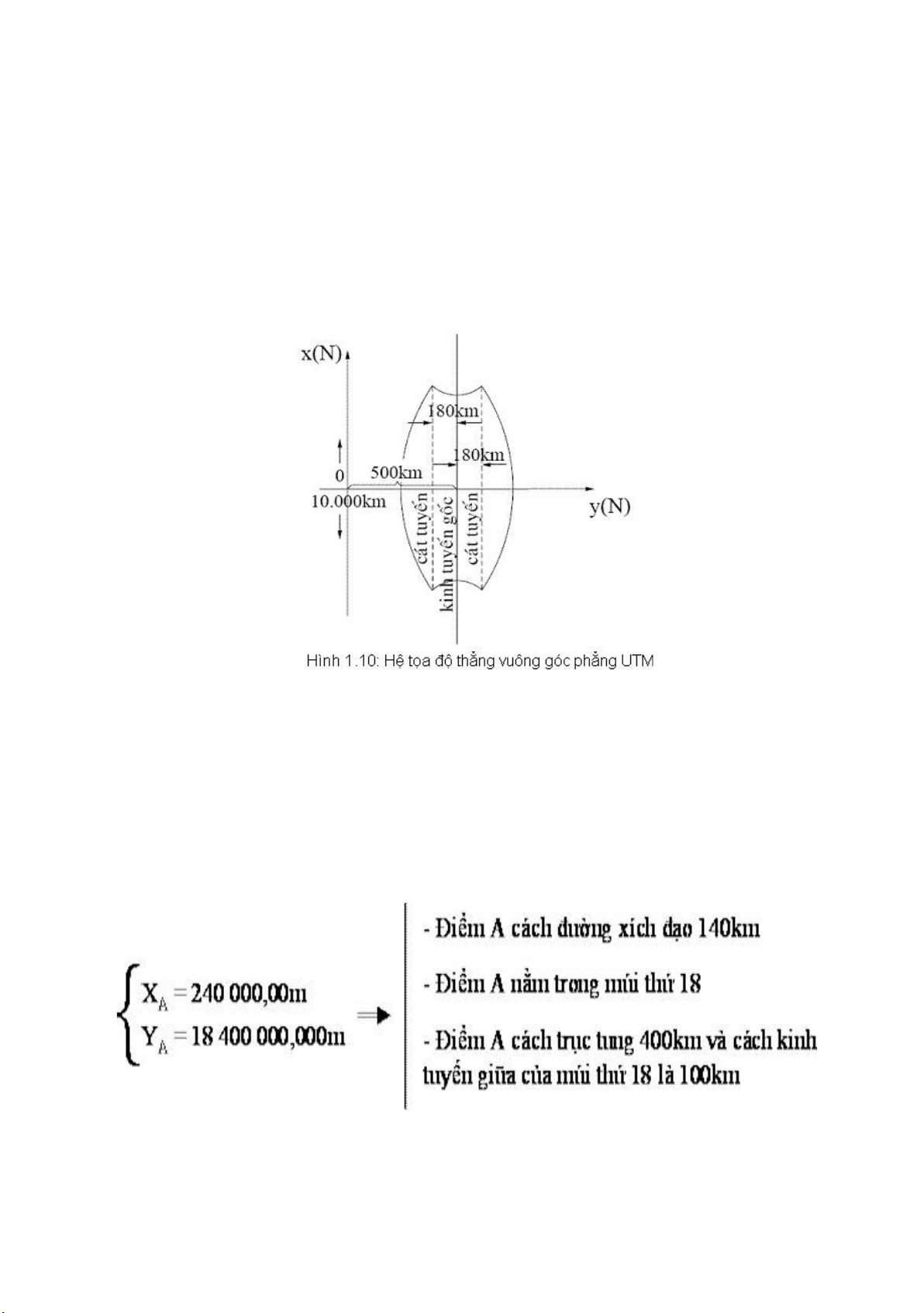
Trong hệ tọa độ vuông góc phẳng UTM có trục tung được ký hiệu là X hoặc N (viết tắt
của chữ North là hướng Bắc), trục hoành được ký hiệu là Y hoặc E (viết tắt của chữ East là hướng Đông).
Trục hoành Oy: - Hình chiếu của xích đạo
-Chiều dương hướng sang phía đông
Trục tung Ox: - Tịnh tiến kinh tuyến trục sang tây 500km
- Chiều dương hướng lên phía Bắc
Để trị số hoành độ Y không âm, Trong hệ tọa độ thẳng vuông góc UTM trục tung được
ký hiệu là X hoặc N (viết tắt của chữ North là hướng Bắc), trục hoành được ký hiệu là Y
hoặc E (viết tắt của chữ East là hướng Đông). Hệ tọa độ này cũng qui ước chuyển trục X về bên trái cách kinh tuyến trục 500km (Hình 1.10), khi ghi
hoành độ Y có ghi kèm sốthứ tự của múi chiếu ở phía trước. Còn trị số qui ước của gốc
tung độ ở bắc bán cầu cũng là 0, ở nam bán cầu là 10.000km, có nghĩa là gốc 0 tung độ ở
nam bán cầu được dời xuống đỉnh nam cực. Ví dụ:
+ Ở bắc bán cầu một điểm A có tọa độ là:
+ Còn nếu ở nam bán cầu một điểm B có tọa độ là: lOMoARcPSD|45315597
Bắt đầu từ năm 2000 nước ta chính thức đưa vào sử dụng hệ tọa độ quốc gia VN–2000
thay cho hệ tọa độ HN-72. Hệ tọa độ quốc gia VN–2000 sử dụng phép chiếu UTM,
Ellipsoid WGS-84 và điểm gốc toạ độ quốc gia: Điểm N00 đặt tại Viện Nghiên cứu Địa
chính thuộc Tổng cục Địa chính, đường Hoàng Quốc Việt, Hà Nội.
Câu 6: Anh/chị hãy nêu khái niệm về định hướng đường thẳng và các góc
phương vị? Mối quan hệ giữa ba loại góc phương vị (có vẽ hình minh họa)?
Định hướng đường thẳng là xác định hướng của đường thẳng ấy so với một
hướng nào đó được chọn làm gốc. Thực chất của việc định hướng đường thẳng
là xác định góc giữa hướng gốc đi qua điểm đầu của đường thẳng và hướng của
bản thân đường thẳng đó.
- Trong Trắc địa, sử dụng 3 hướng gốc:
+ Hướng Bắc của kinh tuyến thực: góc phương vị thực
+ Hướng Bắc của kinh tuyến từ: góc phương vị từ
+ Hướng Bắc của kinh tuyến trục: góc phương vị định hướng.
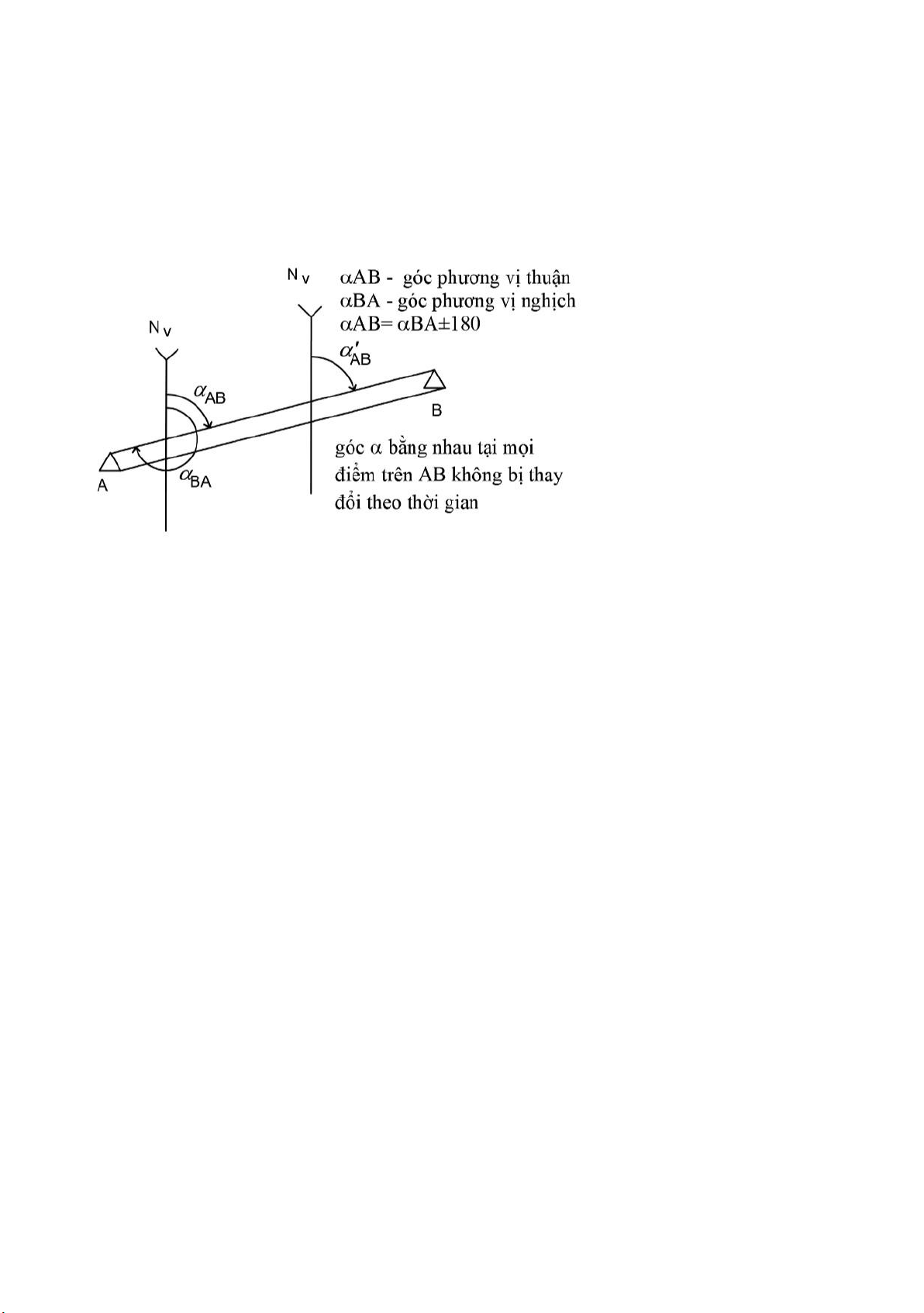
Các góc phương vị:
- Góc phương vị thực: là góc phẳng tính từ hướng Bắc của kinh tuyến thực theo
chiều kim đồng hồ đến đường thẳng cần xác định . 00 ≤ Ath ≤ 3600
Vì các kinh tuyến ở các điểm khác nhau không song song mà cắt nhau ở 2 cực
của quả đất nên phương vị thực của cùng một đường thẳng nhưng ở các điểm khác
nhau trên đường thẳng đó sẽ có những giá trị khác nhau. lOMoARcPSD|45315597
- Góc phương vị từ: lấy kinh tuyến từ làm gốc, là góc phẳng được tính từ hướng
Bắc của kinh tuyến từ theo chiều kim đồng hồ đến đường thẳng cần xác định. 00 ≤ Am ≤ 3600
Tại mỗi điểm, góc phương vị từ thay đổi theo thời gian: A  Am   (δ: độ lệch từ thông)
- Góc phương vị định hướng: lấy kinh tuyến trục làm gốc, là góc phẳng tính từ
hướng Bắc của kinh tuyến trục của mỗi múi hoặc từ hướng dương của trục Ox lOMoARcPSD|45315597
(hướng song song với trục Ox) theo chiều kim đồng hồ đến đường thẳng cần xác định. 0 0 0 360 0    '180 lOMoARcPSD|45315597
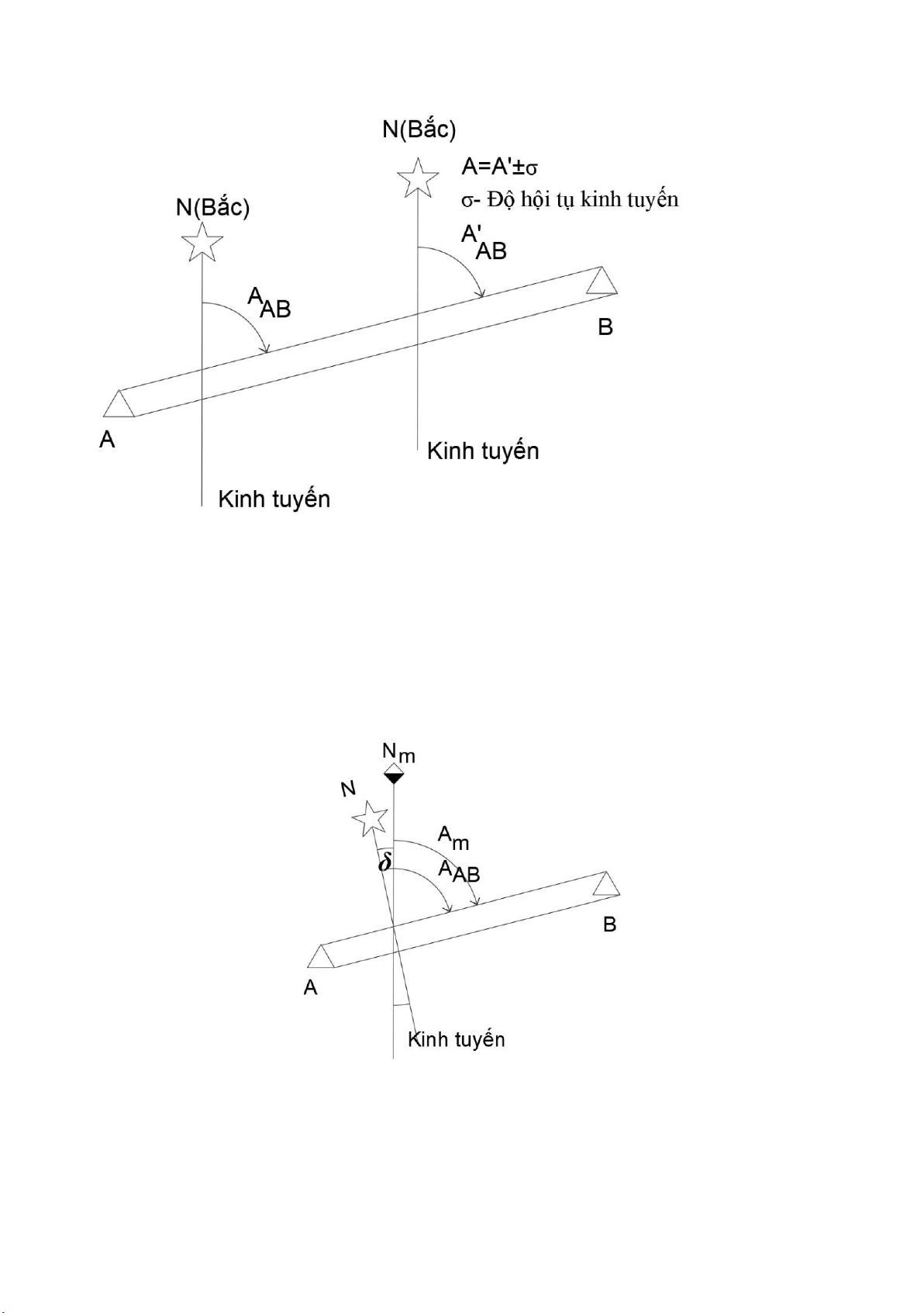
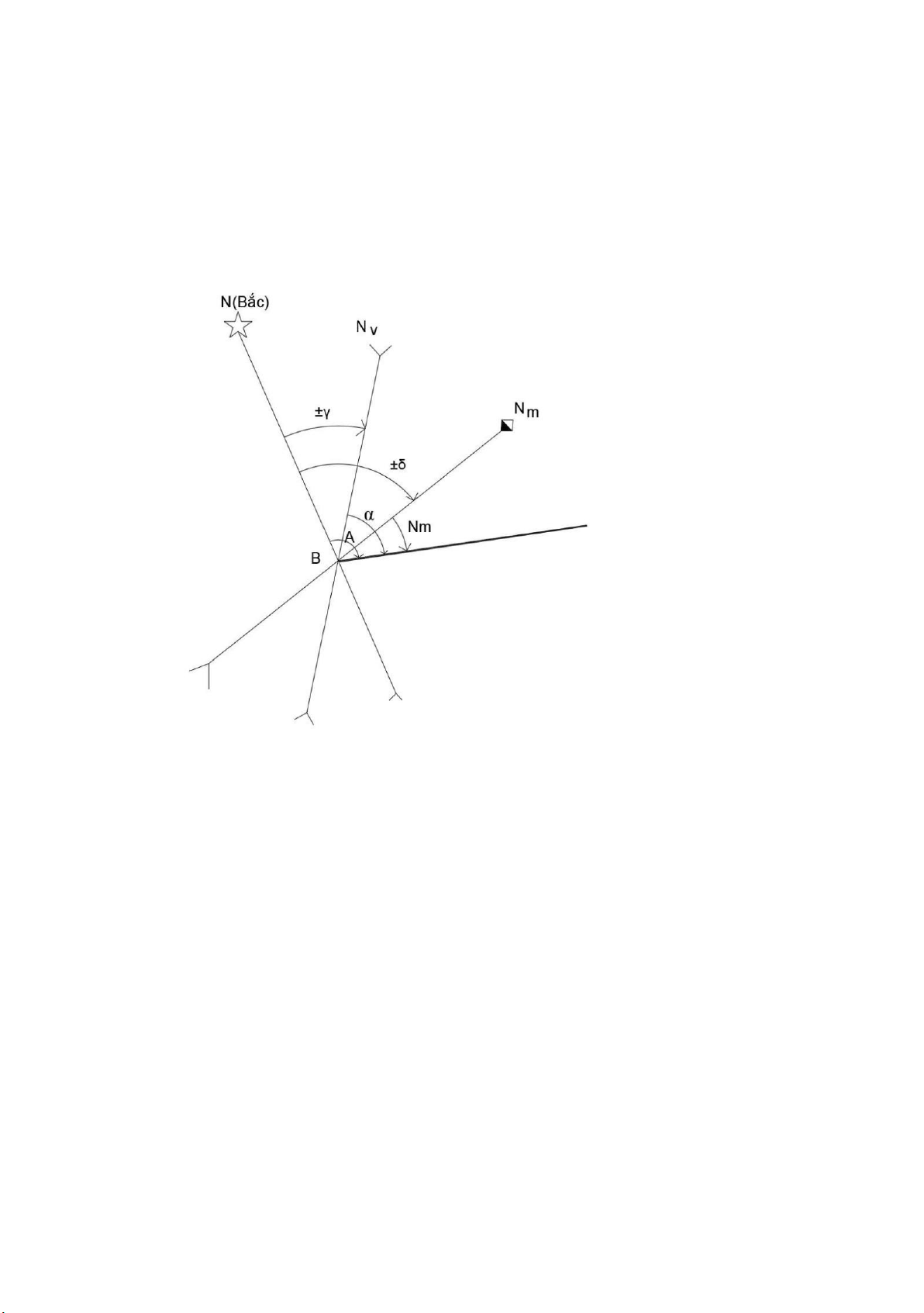
Mối quan hệ giữa các góc phương vị: A= Am ± δ A=α±γ Trong đó:
+ BN là kinh tuyến thực;
+ BNv là đường song song với kinh tuyến trục;
+ BNm là hướng của kinh tuyến từ
+ Góc NBNv= γ: là độ hội tụ kinh tuyến ;
+ Góc NBNm= δ: là độ lệch từ
Khi tính toán, dấu +/- được chọn theo dấu cụ thể của δ và γ cho trên từng mảnh bản đồ.
Câu 7 . Anh/chị hãy nêu mối quan hệ giữa phương vị định hướng của hai cạnh liên
tiếp nhau – Nội dung và ý nghĩa của bài toán chuyền phương vị? (vẽ hình, cho ví dụ cụ thể)
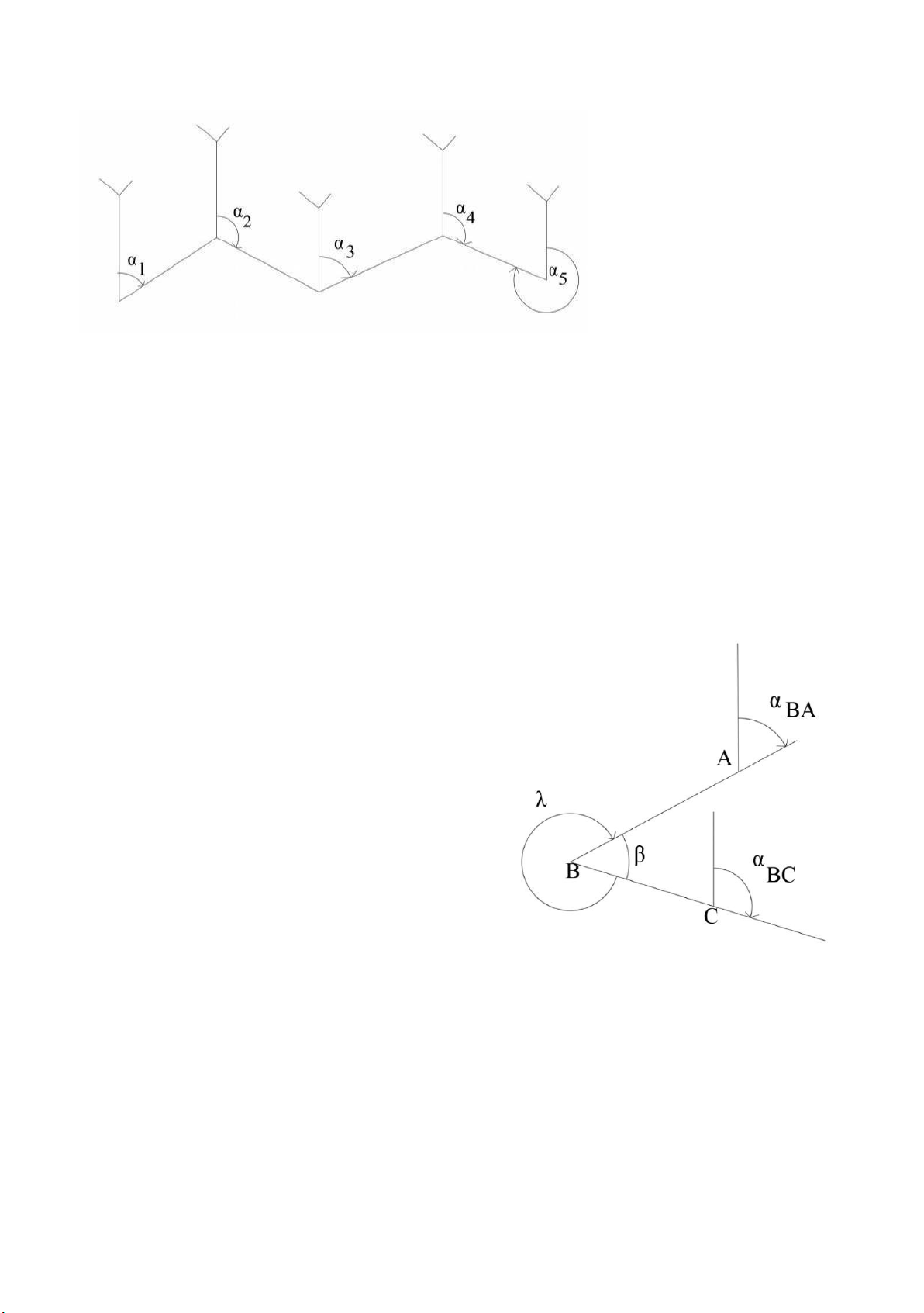
Mối liên hệ giữa phương vị định hướng α của hai cạnh liên tiếp nhau lOMoARcPSD|45315597
Vì βtr =360- λph (βtr+λp=3600) => λph=3600 - βtr
Mà α2= α1+180- λph= α1+1800 – 3600+ βtr= α1 - 1800 + βtr Tổng quát: αi+1= αi – 1800 – β αi+1= αi + 1800 – λ
Bài toán chuyền phương vị: Nội dung:
Cho hai đường thẳng AB,AC góc αAB=
α1, hai góc ngang xác định αBC= α2 Th1: Biết β Ta có: αAB=αBA 1800 (1) αBA = αAB + 1800 (2) Tại B: αBC=αAB + β (3) =>αBC = αAB 1800 + β (4) =>α2 = α1 1800 +β (5) TH2: Biết λ
λ +β =3600 =>λ = 3600 – β => β= 3600 – λ
=>αBC = αAB 1800 +(3600 – λ) =>αλBC= αAB 1800 - λ lOMoARcPSD|45315597 => α2= α1 1800 – λ Tổng quát: αi+1=( αi 1800 ) + βi (1) αi+1= ( αi 1800 ) – λi(2) (1) (+) αi < 1800 (2) (+) αi +1800 > λi (-) αi > 1800 (-) αi – 1800 > λi
Câu 8: Nêu nội dung và ý nghĩa của hai bài toán trắc địa cơ bản: Bài toán
thuận và bài toán ngược (có vẽ hình minh họa cho 2 bài toán).
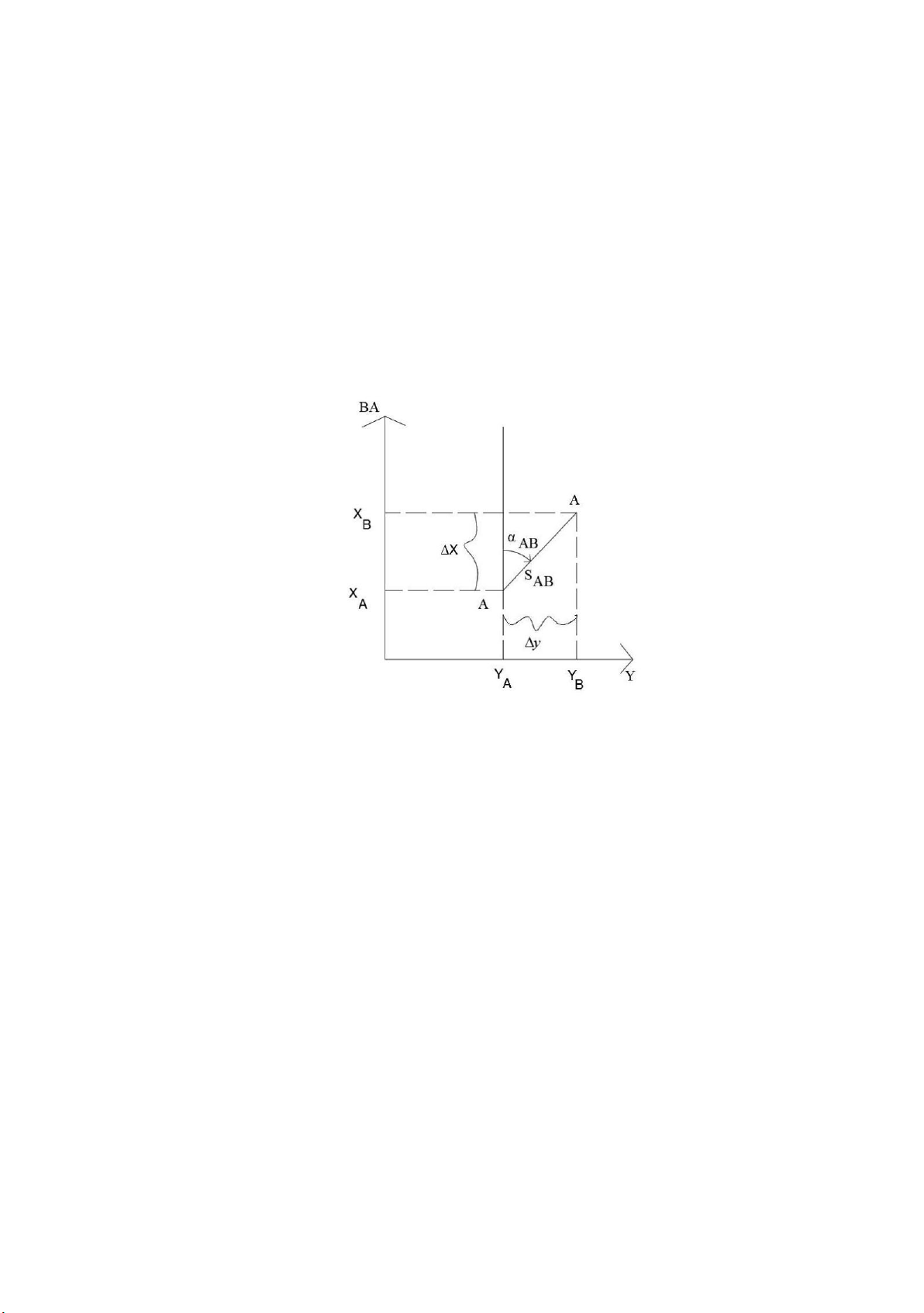
a. Bài toán thuận (bài toán chuyền tọa độ)
Biết tọa độ điểm 1 (x1; y1), biết khoảng cách giữa hai điểm 1 và 2 là S,
biết góc phương vị định hướng α của cạnh 1-2. Tìm tọa độ điểm 2.
- Gọi ∆x và ∆y là các gia số tọa độ . Như vậy, ta có: x2  x1 x y2  y1 y
- Mặt khác: ∆x=S.cosα; ∆y=S.sinα.
Từ đó ta được: x2=x1+S.cosα y2=y1+S.sinα
Ý nghĩa: Dựa vào tọa độ điểm thứ nhất, khoảng cách từ điểm thứ nhất đến
điểm thứ hai và phương vị định hướng của cạnh đó có thể xác định được tọa độ của điểm thứ hai.
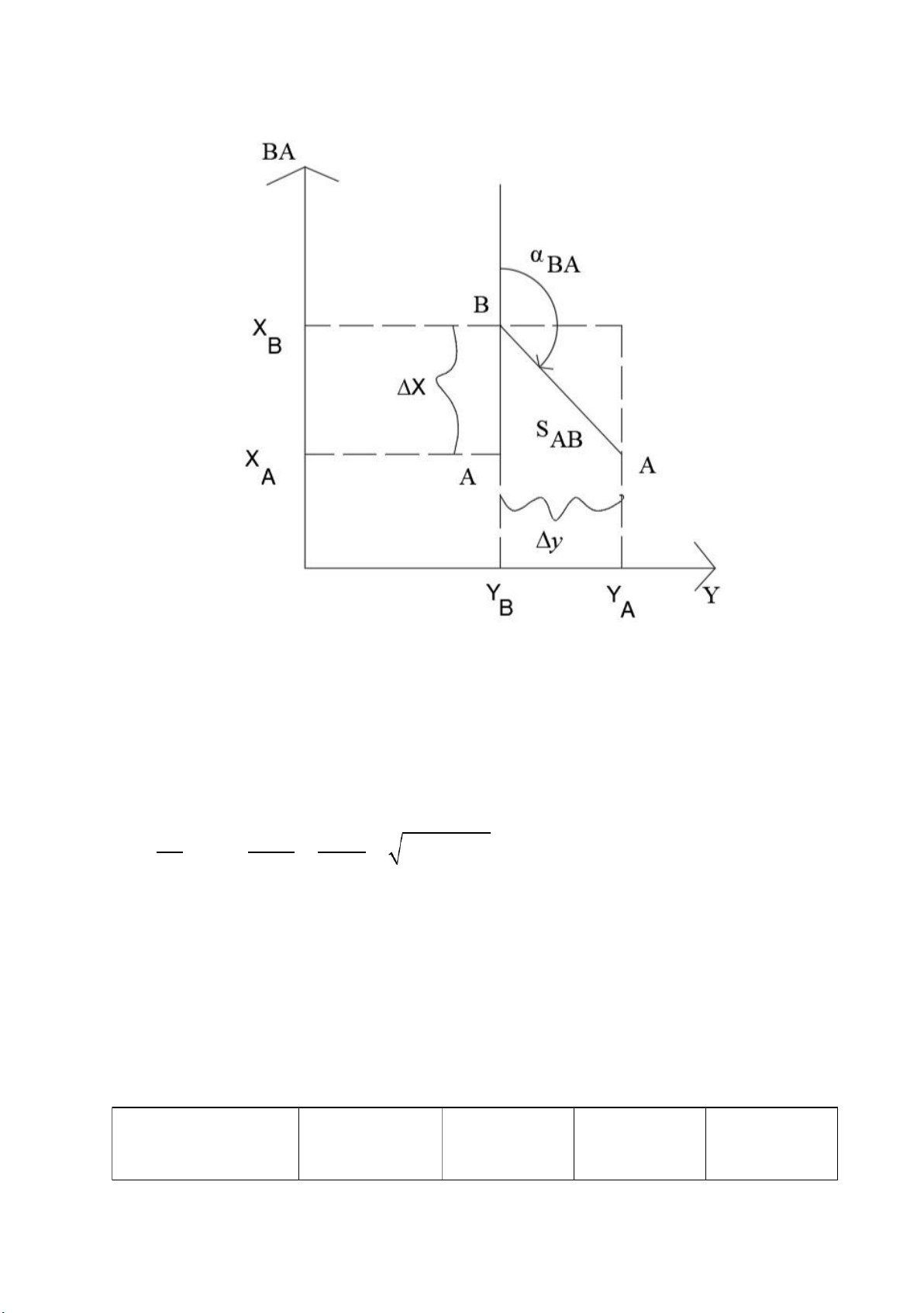
b. Bài toán ngược trong trắc địa: lOMoARcPSD|45315597
- Bài toán ngược cho biết tọa độ vuông góc của hai điểm 1 và 2 lần lượt là
x1, y1; x2, y2. Xác định góc phương vị α12 và khoảng cách ngang S12 giữa hai điểm đó
- Khi đó ta có: x  x2 x1
y  y2 y1 tg y ;S y x 2 x 2 y 1 2 x 1 2 sin cos
Ý nghĩa: Khi biết tọa độ 2 điểm có thể xác định được phương vị định hướng của
cạnh và khoảng cách giữa 2 điểm đó.
Giá trị của góc α thay đổi từ 00 đến 3600 nên ta tính giá trị góc hai phương r
cũng như lấy dấu của số gia tọa độ tùy thuộc vào giá trị của các góc phương vị α: Góc α 00 - 900 - 1800 - 2700 -