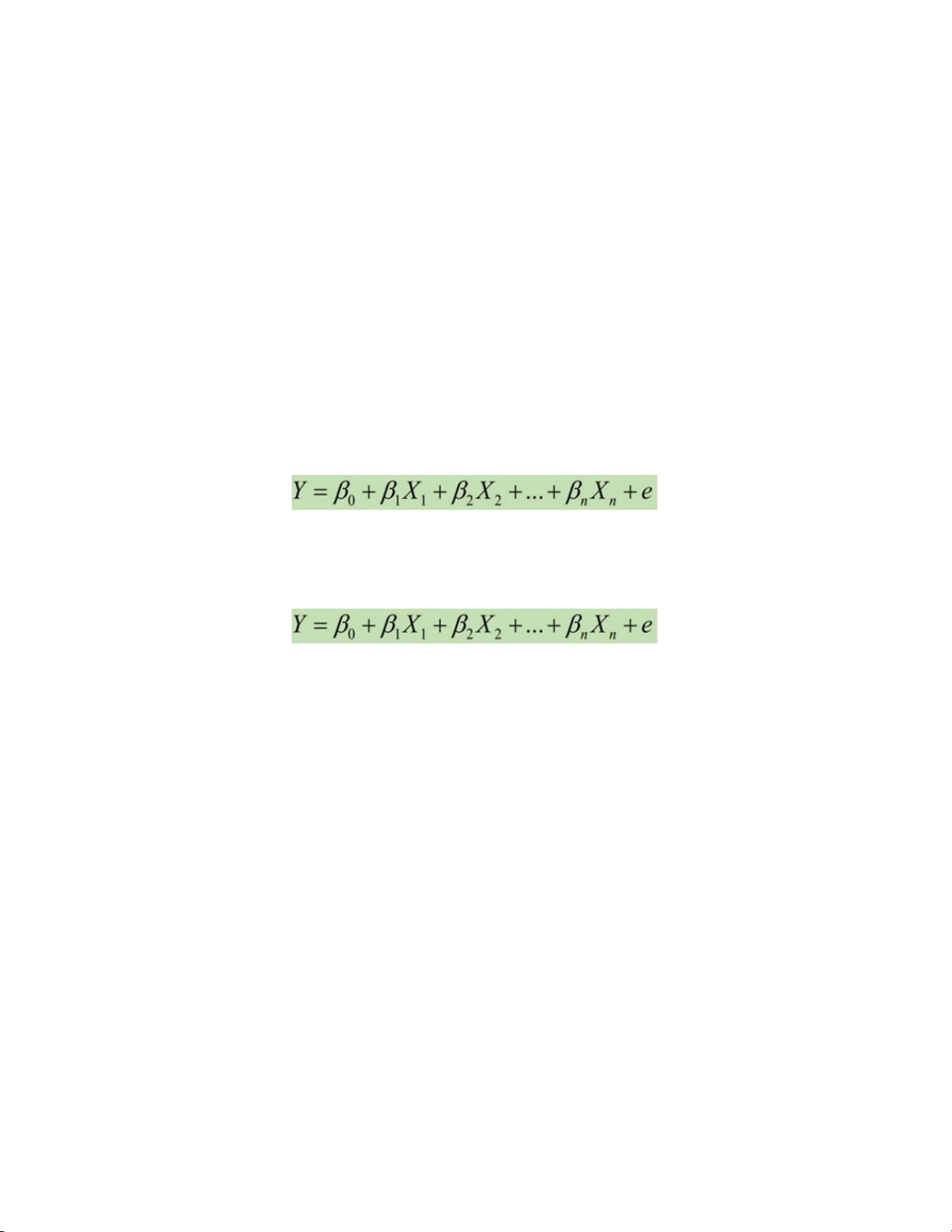








Preview text:
ĐẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
KHOA HỆ THỐNG THÔNG TIN BÁO CÁO CUỐI KỲ
PHÂN TÍCH DỮ LIỆU KINH DOANH
Giảng Viên: PGS.TS. Nguyễn Đình Thuân
Hướng Dẫn: Nguyễn Thị Viết Huơng Nguyễn Minh Nhựt Mã lớp : IS403.N22.HTCL Nhóm thực hiện : Nhóm 6 Dương Nhật Minh 20520242 Hồ Thị Hằng 20521285 Nguyễn Hòang Ngọc Hạnh 20521287 Hồ Chí Minh, tháng 4 2023 1 lOMoAR cPSD| 59285474 NHẬN XÉT CỦA GIÁO VIÊN
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
…………………………………………………………………………………………
………………………………………………………………………………………… 2 lOMoAR cPSD| 59285474 Nội dung
1. Giải thích và lấy ví dụ ............................................................................................................................. 4
1.1 Hồi quy tuyến tính đa biến ............................................................................................................... 4
1.1.1 Giải thích .................................................................................................................................... 4
1.1.2 Ví dụ ............................................................................................................................................ 5
1.2 Hồi quy phi tuyến đa biến ................................................................................................................ 7
1.2.1 Giải thích .................................................................................................................................... 7
1.2.2 Ví dụ ............................................................................................................................................ 7
1.3 Hồi quy Logistic ................................................................................................................................ 8
1.3.1 Giải thích .................................................................................................................................... 8
1.3.2 Ví dụ .......................................................................................................................................... 10
2. Thực hành.............................................................................................................................................. 14
2.1 Dùng MS Excel, ngôn ngữ R và ngôn ngữ Python thực hiện các phép tính hồi quy tuyến tính
đa biến với tập tin dữ liệu Colleges and Universities ........................................................................ 14
2.1.1 Phát biểu bài toán .................................................................................................................... 14
2.1.2 Sử dụng MS Excel .................................................................................................................... 14
2.1.3 Sử dụng ngôn ngữ R ................................................................................................................ 19
2.1.4 Sử dụng ngôn ngữ Python ....................................................................................................... 23
2.1.5 Kết luận .................................................................................................................................... 24
2.2 Dùng MS Excel, ngôn ngữ R và ngôn ngữ Python thực hiện phép tính Hồi quy phi tuyến đa
biến với dữ liệu thực tế tùy chọn về/của Việt Nam ............................................................................ 25
2.2.1 Giới thiệu tập dữ liệu ............................................................................................................... 25
2.2.2. Phát biểu bài toán ................................................................................................................... 27
2.2.3. Sử dụng MS Excel ................................................................................................................... 28
2.2.4 Sử dụng ngôn ngữ R ................................................................................................................ 30
2.2.5 Sử dụng Python ........................................................................................................................ 34
2.3 Dùng MS Excel, ngôn ngữ R và ngôn ngữ Python thực hiện các phép tính hồi quy logistic với
dữ liệu tùy chọn về Việt Nam ............................................................................................................... 37
2.3.1 Giới thiệu tập dữ liệu ............................................................................................................... 37
2.3.2 Phát biểu bài toán .................................................................................................................... 37
2.3.3 Sử dụng MS Excel .................................................................................................................... 38
2.3.4 Sử dụng ngôn ngữ R ................................................................................................................ 44
2.3.5 Sử dụng ngôn ngữ Python ....................................................................................................... 45
2.3.6 Kết luận .................................................................................................................................... 47
BẢNG PHÂN CÔNG CÔNG VIỆC........................................................................................................ 48
TÀI LIỆU THAM KHẢO ........................................................................................................................ 48 3 lOMoAR cPSD| 59285474 1.
Giải thích và lấy ví dụ
1.1 Hồi quy tuyến tính đa biến 1.1.1 Giải thích
Hồi quy tuyến tính đa biến là một kỹ thuật phân tích dữ liệu, dùng để dự đoán
giá trị của một biến dựa trên giá trị của hai hoặc nhiều biến khác. Biến muốn dự đoán
được gọi là biến phụ thuộc. Các biến sử dụng để dự đoán giá trị của biến phụ thuộc được
gọi là biến độc lập.
Mô hình hồi qui tuyến tính đa biến là phương trình mô tả mối quan hệ giữa biến
phụ thuộc y với các biến độc lập x1 , x2 , . . . xp và sai số ngẫu nhiên e
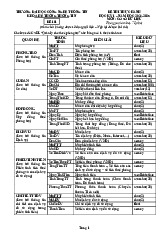
Phương trình hồi qui tuyến tính đa biến là phương trình mô tả mối quan hệ giữa
biến phụ thuộc y với các biến độc lập x1 , x2 , . . . xp Trong đó, + Y là biến phụ thuộc
+ X1, X2,..Xn là biến độc lập
+ β0 là hằng số hồi quy
+ β1, β2,… βn là các hệ số hồi quy
+ e là sai số ngẫu nhiên
Ta có thể sử dụng hồi quy tuyến tính đa biến để:
+ Lập mô hình mối quan hệ giữa các biến phức tạp, như:
- Lượng mưa, nhiệt độ và tần suất sử dụng phân bón đối với cây ăn quả. 4 lOMoAR cPSD| 59285474
- Thu nhập, số thành viên đối với chi tiêu trong gia đình
+ Tính giá trị của biến phụ thuộc tại một giá trị cụ thể của các biến độc lập, như:
- Giá nhà của 1 căn có số phòng, diện tích và độ tuổi ngôi nhà nhất định 1.1.2 Ví dụ
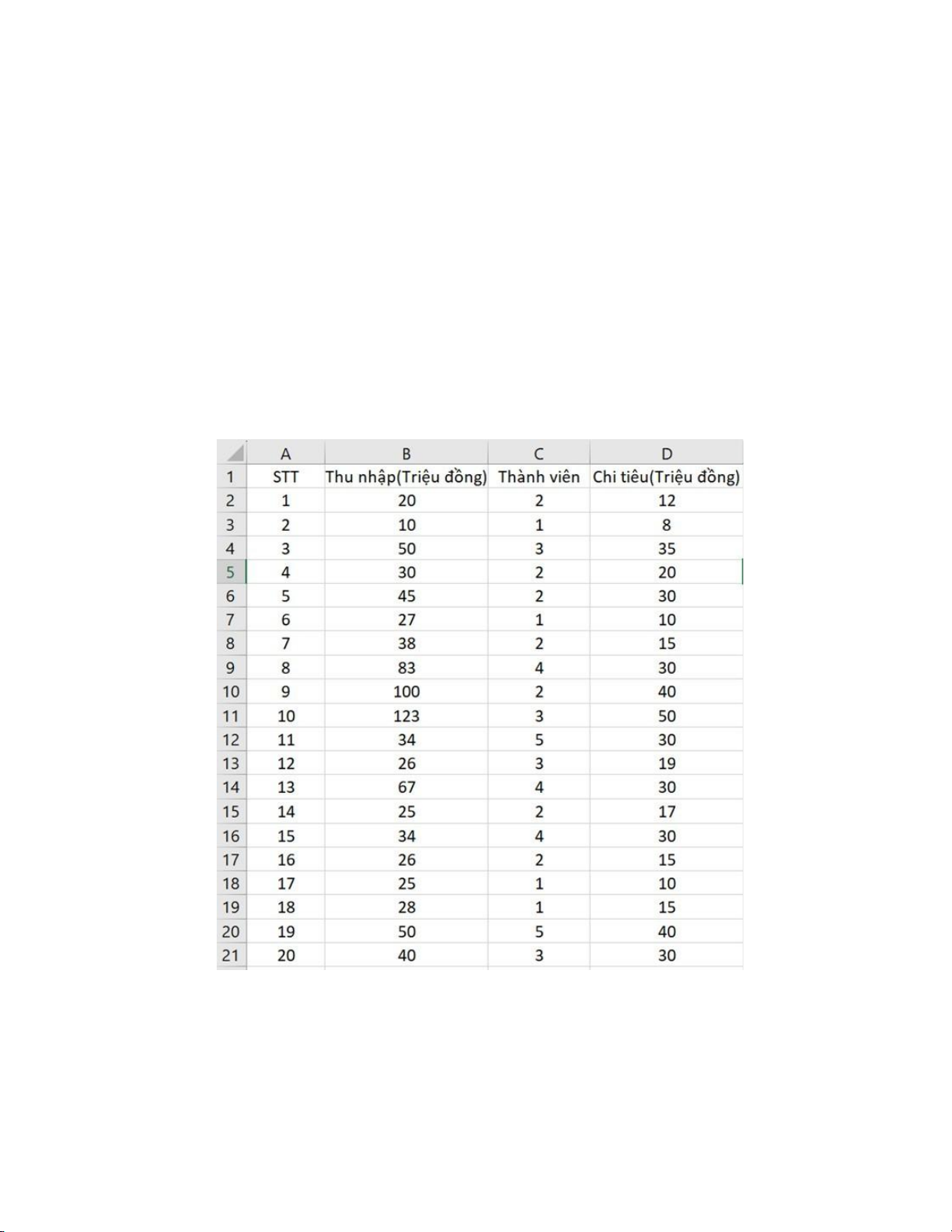
Khảo sát mức chi tiêu trong 1 tháng của 20 hộ gia đình trong vùng dựa trên tổng thu
nhập và số thành viên trong gia đình. Sử dụng phân tích hồi quy để xác định xem chi
tiêu có mối quan hệ như thế nào với thu nhập và số thành viên.
Mức chi tiêu, thu nhập và số thành viên của 20 hộ gia đình được trình bày như sau:
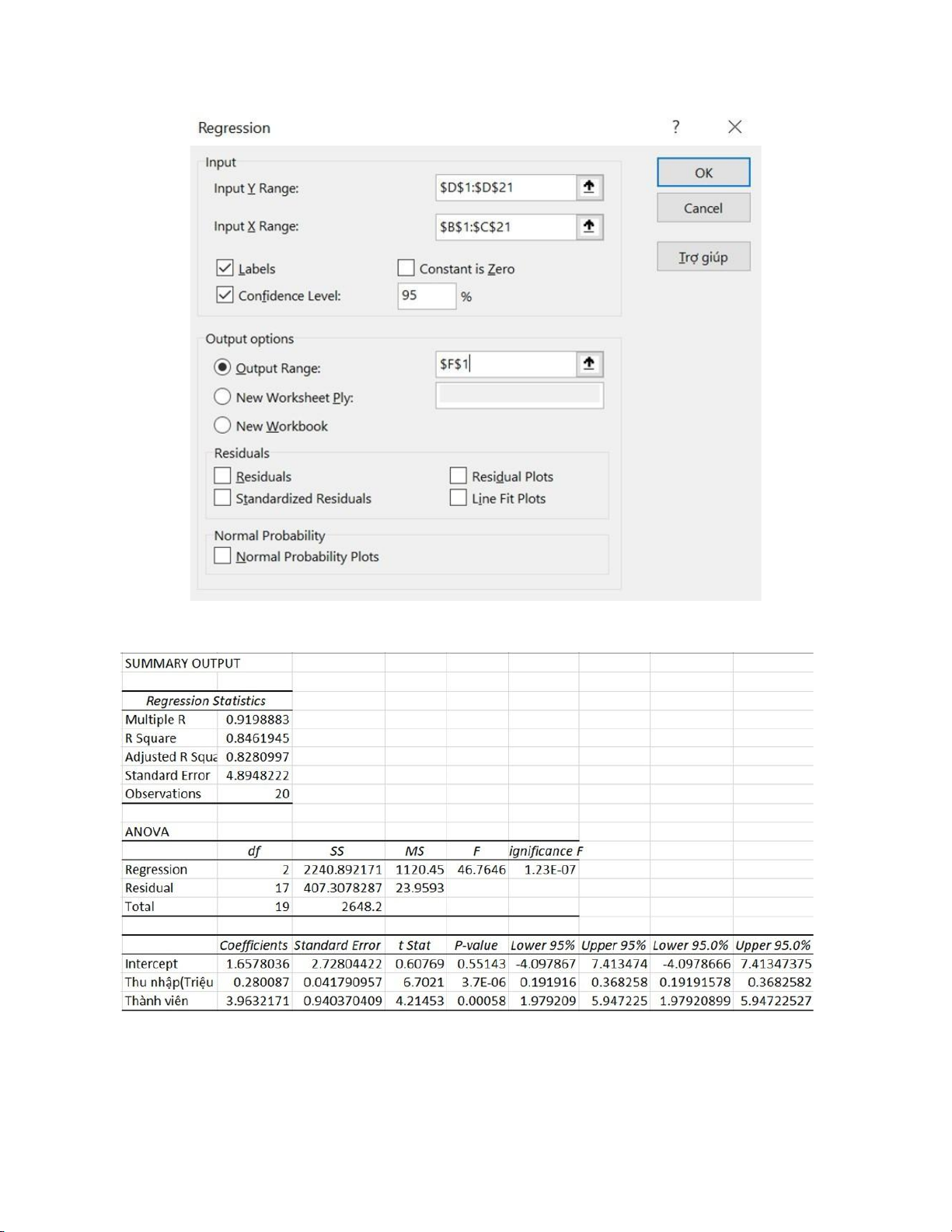
Thực hiện hồi quy bằng công cụ Data Analysis: 5 lOMoAR cPSD| 59285474
Kết quả hồi qui trên Excel:
Dựa vào kết quả phân tích, ta có phương trình hồi quy:
Chi tiêu = 1.658 + 0.28 * [Thu nhập] + 3.963 * [Thành viên] 6 lOMoAR cPSD| 59285474
1.2 Hồi quy phi tuyến đa biến 1.2.1 Giải thích
Hồi quy phi tuyến đa biến (Multivariate Nonlinear Regression) là một phương pháp
phân tích hồi quy để dự đoán một biến mục tiêu (biến phụ thuộc) dựa trên nhiều biến độc
lập. Nhưng với mối quan hệ phi tuyến giữa chúng, mối quan hệ giữa biến phụ thuộc và
các biến độc lập là hàm phi tuyến tính.
Các bước chính để thực hiện hồi quy phi tuyến tính đa biến là:
B1: Thu thập dữ liệu cho các biến độc lập và biến phụ thuộc.
B2: Kiểm tra giả thiết về phân phối và tương quan giữa các biến.
B3: Xác định hàm mục tiêu (hàm phi tuyến) dựa trên mối quan hệ giữa các biến
độc lập và biến phụ thuộc.
B4: Ước tính các tham số của hàm mục tiêu bằng các phương pháp tối ưu hóa.
B5: Đánh giá mô hình và kiểm tra tính chính xác của nó. 1.2.2 Ví dụ
• Giả sử: xây dựng một mô hình để dự đoán giá trị nhà dựa trên nhiều yếu tố, bao gồm
diện tích, số lượng phòng ngủ và độ tuổi của căn nhà. Ta có thể sử dụng mô hình hồi
quy phi tuyến đa biến để mô hình hóa mối quan hệ giữa các yếu tố này và giá trị nhà.
• Để thực hiện việc này, ta có thể sử dụng công thức sau:
Giá trị nhà = β0 + β1Diện tích + β2Số phòng ngủ + β3*Độ tuổi + ε Trong đó:
+ β0, β1, β2 và β3 là các tham số mô hình
+ ε là sai số ngẫu nhiên 7 lOMoAR cPSD| 59285474
• Công thức trên cho phép ta tính toán giá trị nhà dựa trên các yếu tố diện tích, số
lượng phòng ngủ và độ tuổi của căn nhà. 1.3 Hồi quy Logistic 1.3.1 Giải thích
Mô hình hồi quy logistic dùng để mô tả mối liên quan giữa biến phân loại (thường có
2 giá trị nên đây là biến nhị phân) và biến tiên lượng (có thể là biến phân loại hay biến
liên tục), từ đó phân loại và phân tích dự đoán. Ngoài ra, mô hình còn giúp kiểm soát
các biến nhiều và phát triển mô hình tiên lượng.
Một số khái niệm liên quan:
- p (probability): xác suất của biến cố xảy ra trong một thời gian 0 <= p <= 1
- Odds: tỉ số giữa xác suất biến cố xảy ra và biến cố không xảy ra.
Odds là một biến liên tục
• Nếu ODDs > 1: xác suất biến cố xảy ra cao hơn biến cố đối của nó.
• Nếu ODDs < 1 xác suất biến cố xảy ra thấp hơn biến cố đối của nó.
• Nếu ODDs = 1 xác suất biến cố xảy ra khả năng bằng biến cố đối của nó.
- Odds ratio: tỉ số của 2 odds
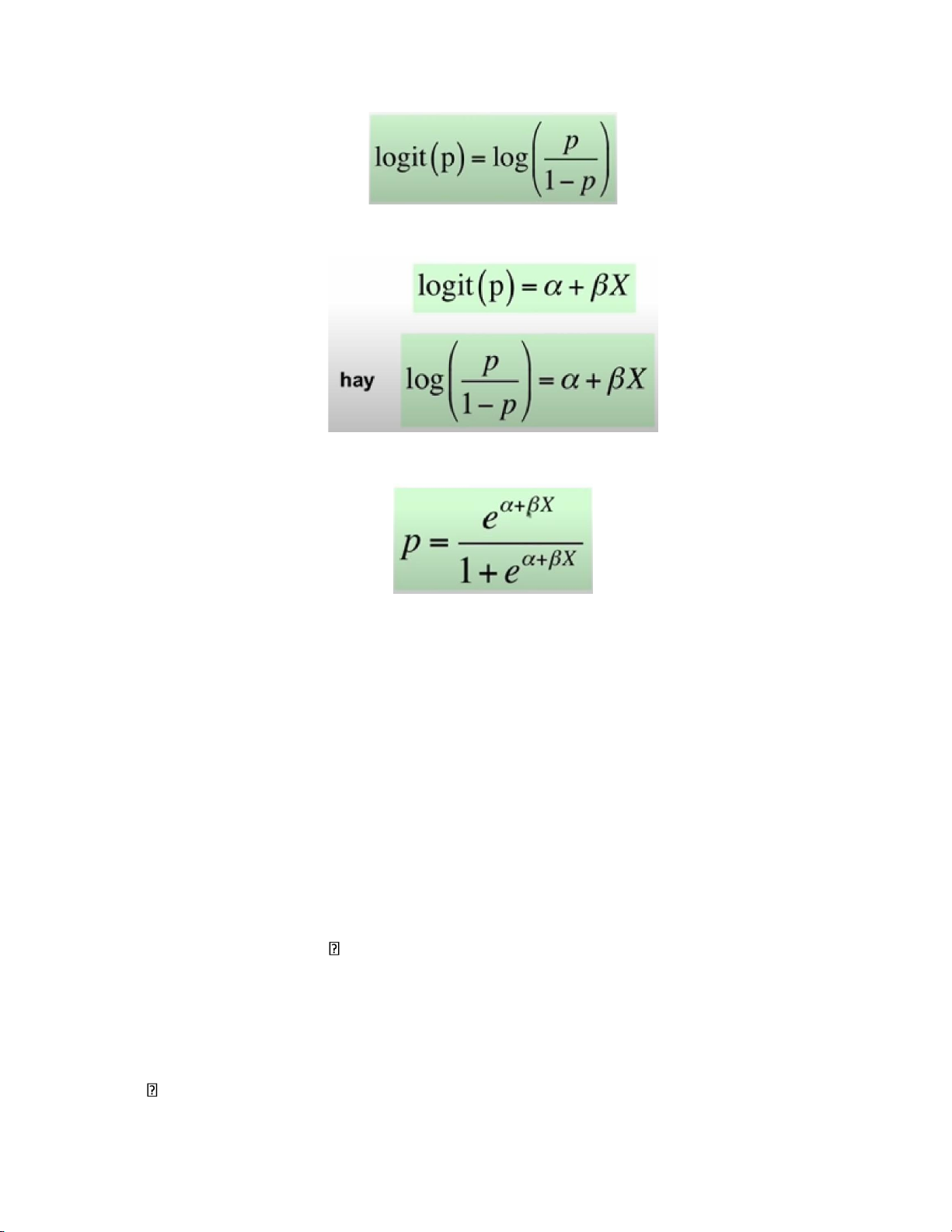
- Logit: gọi logit = log odds: 8 lOMoAR cPSD| 59285474
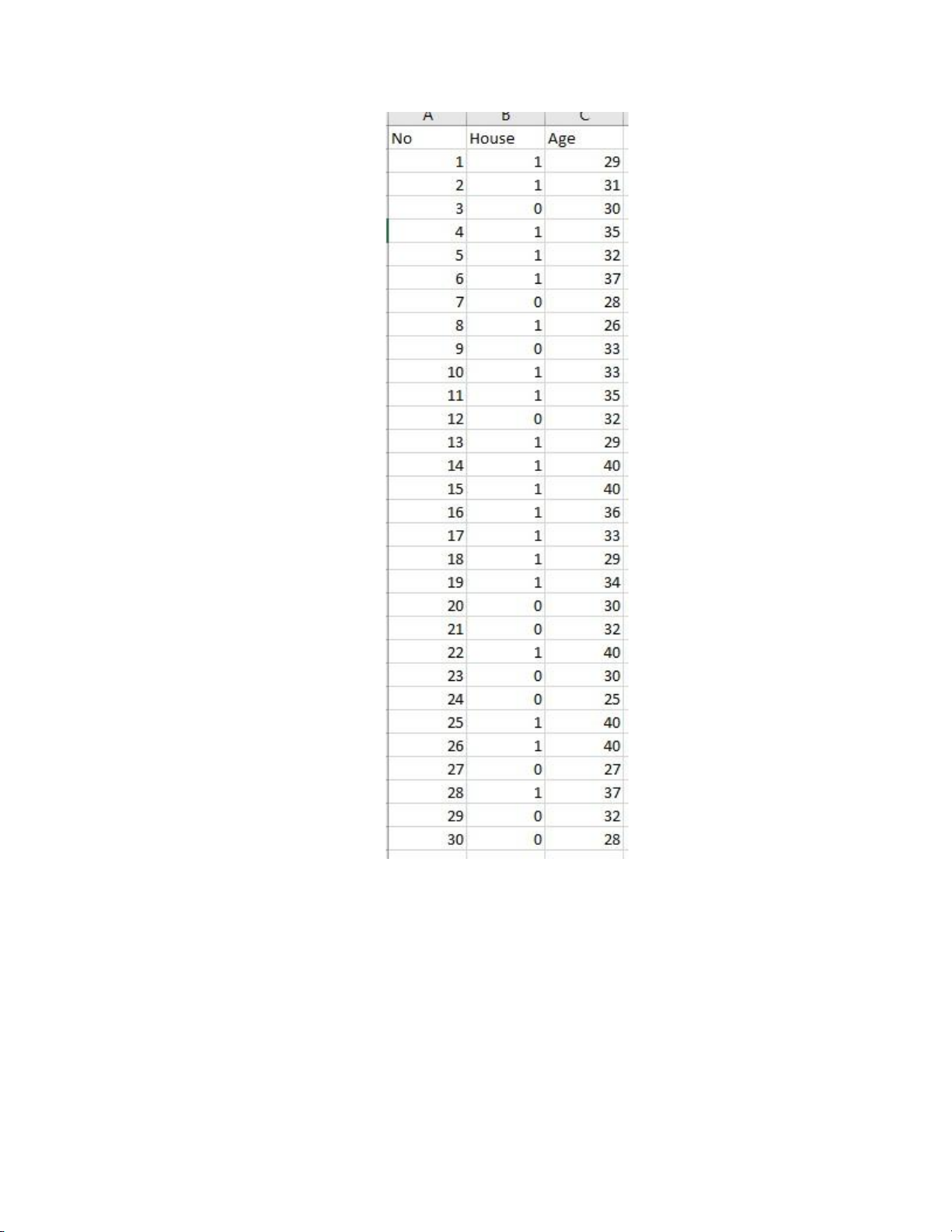
Mô hình hồi quy logistic được dựa trên khái niệm logit phát biểu rằng: Tương đương trong đó:
- α: log odds của biến phân loại khi biến tiên lượng X = 0
- β: log odds ratio liên quan với một đơn vị tăng của biến tiên lượng X - Odds ratio = eβ
Cách mô hình hồi quy hoạt động: khá giống với mô hình hồi quy tuyến tính, có thể viết như sau: p = α + βX
p là xác suất vế trái chạy giá trị từ 0 đến 1
Nhưng vế phải là biến liên tục có thể vượt qua khoảng 0 đến 1, nên ta đổi
vế trái thành odds ratio để vế trái cũng là một biến liên tục p/(1-p) = α + βX 9 lOMoAR cPSD| 59285474
Vì odds ratio luôn là một số dương, nên ta chuyển vế trái thành logarit
log(p/(1-p)) = α + βX
Để được p như ban đầu, ta áp dụng hà mũ cho cả 2 vế
elog(p/(1-p)) = eα + βX ~p/(1-p) = eα + βX
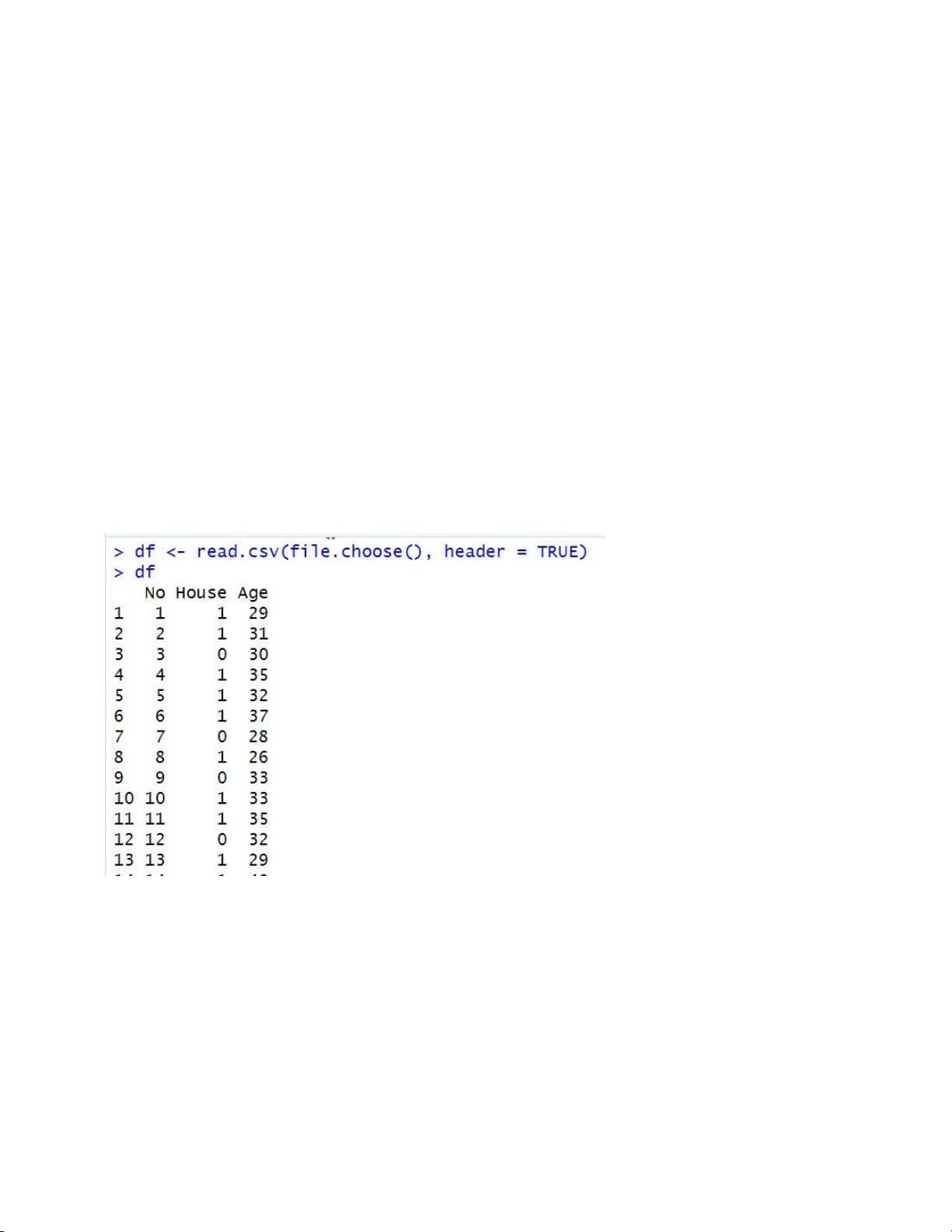
Sau vài phép biến đổi đơn giản ta thu được:
p = eα + βX/((1+ eα + βX)
Mô hình hồi quy logistic rất quan trọng vì nó biến đổi các tính toán phức tạp
xung quanh thành một bài toán số học đơn giản hơn nhờ các ứng dụng thống kê
hiện đại tự động ngày nay. 1.3.2 Ví dụ
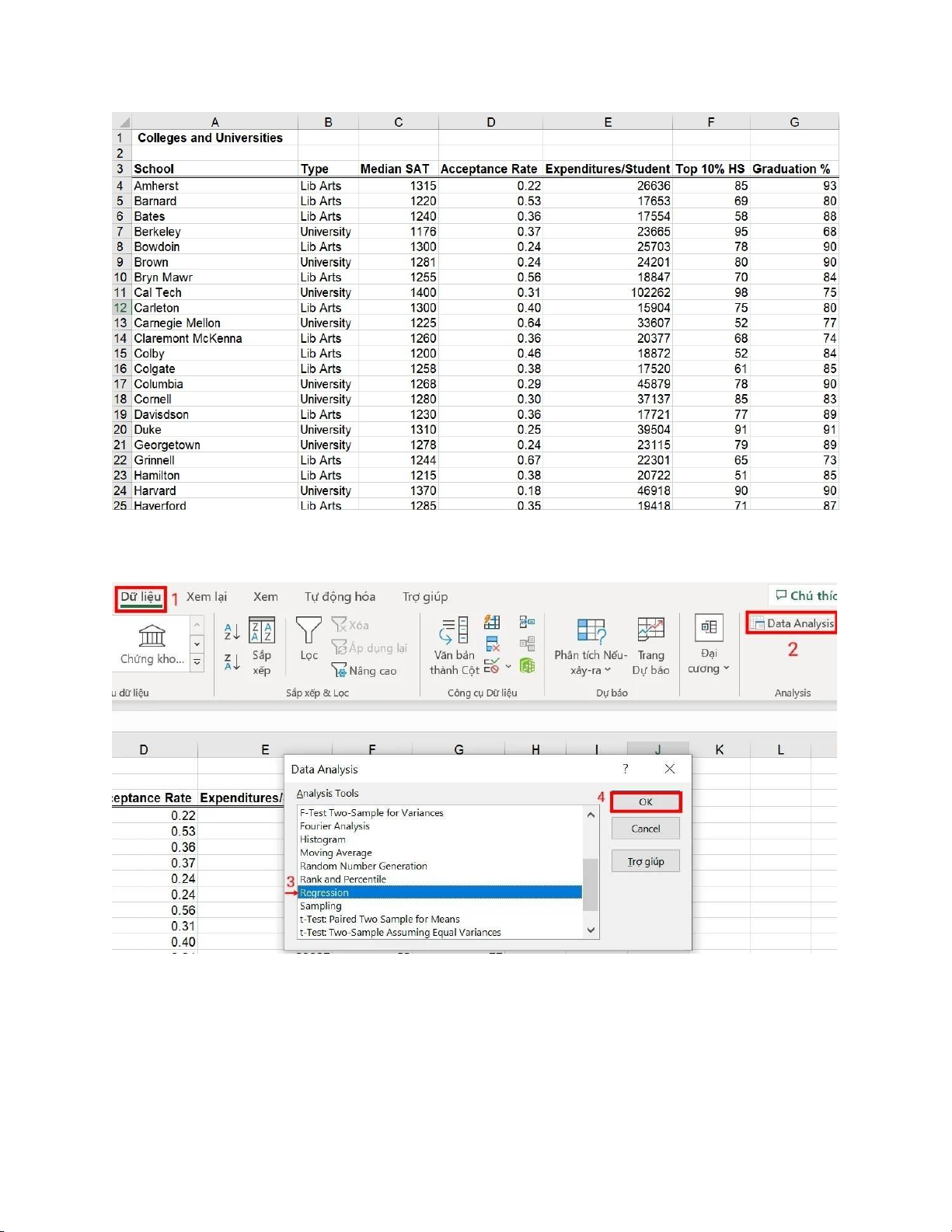
Hãy dự đoán khả năng mua nhà của nhóm người thông qua độ tuổi qua bộ dữ liệu: 10 lOMoAR cPSD| 59285474
Gọi: biến phân loại “House” là y (y=1: có khả năng mua nhà, y=0: không có khả năng mua nhà). Dự báo P(y=1) P(y=0) = 1 – P(y=1)
Biến tiên lượng “Age” là X thể hiện độ tuổi. 11 lOMoAR cPSD| 59285474
Dạng tuyến tính của phương trình hồi quy logistic: Y = β0 + β1X Với:
- Y: biến phân loại nhị phân - X: biến tiên lượng
Do Y là biến nhị phân tuân theo luật phân phối nhị thức nên mô hình hồi quy tuyến
tính không thể áp dụng được.
Bài toán đặt ra: Kiểm tra xem độ tuổi có ảnh hưởng đến khả năng mua nhà hay không?
Bước 1: Import dữ liệu vào RStudio
Bước 2: Dùng hàm glm() để phân tích hồi quy logistic với tham số family = binomial 12 lOMoAR cPSD| 59285474
Từ kết quả trên ta được phương trình hồi quy: p Age
Ta suy ra được kết quả: p
−10.9095+0.3593∗Age =e 1−p
Tỉ số: OR = eβ=e0.3593 ≈1.4323
Ta có thể hiểu: cứ tuổi (Age) tăng lên 1 đơn vị thì khả năng mua nhà tăng lên 1.4323 lần. 13 lOMoAR cPSD| 59285474 2. Thực hành
2.1 Dùng MS Excel, ngôn ngữ R và ngôn ngữ Python thực hiện các phép tính hồi
quy tuyến tính đa biến với tập tin dữ liệu Colleges and Universities
2.1.1 Phát biểu bài toán
Giả sử, với độ tin cậy là 95%, có thể tìm ra mối quan hệ giữa Graduation % với
Median SAT, Acceptance Rate, Expenditures/Student và Top 10% HS được hay không?
Ta có phương trình hồi quy như sau:
Graduation % = β0 + β1 * Median SAT + β2 * Acceptance Rate + β3 *
Expenditures/Student + β4 * Top 10% HS Ta cần,
+ Tìm hằng số β0 và các hệ số β1, β2 , β3 , β4
+ Phân tích kết quả, từ đó kết luận xem mô hình có phù hợp hay không?
2.1.2 Sử dụng MS Excel
Bước 1: Mở tập dữ liệu Colleges and Universities.xlsx và đổi dữ liệu sang dạng số các
cột cần đổi, ta được kết quả như hình dưới: 14 lOMoAR cPSD| 59285474
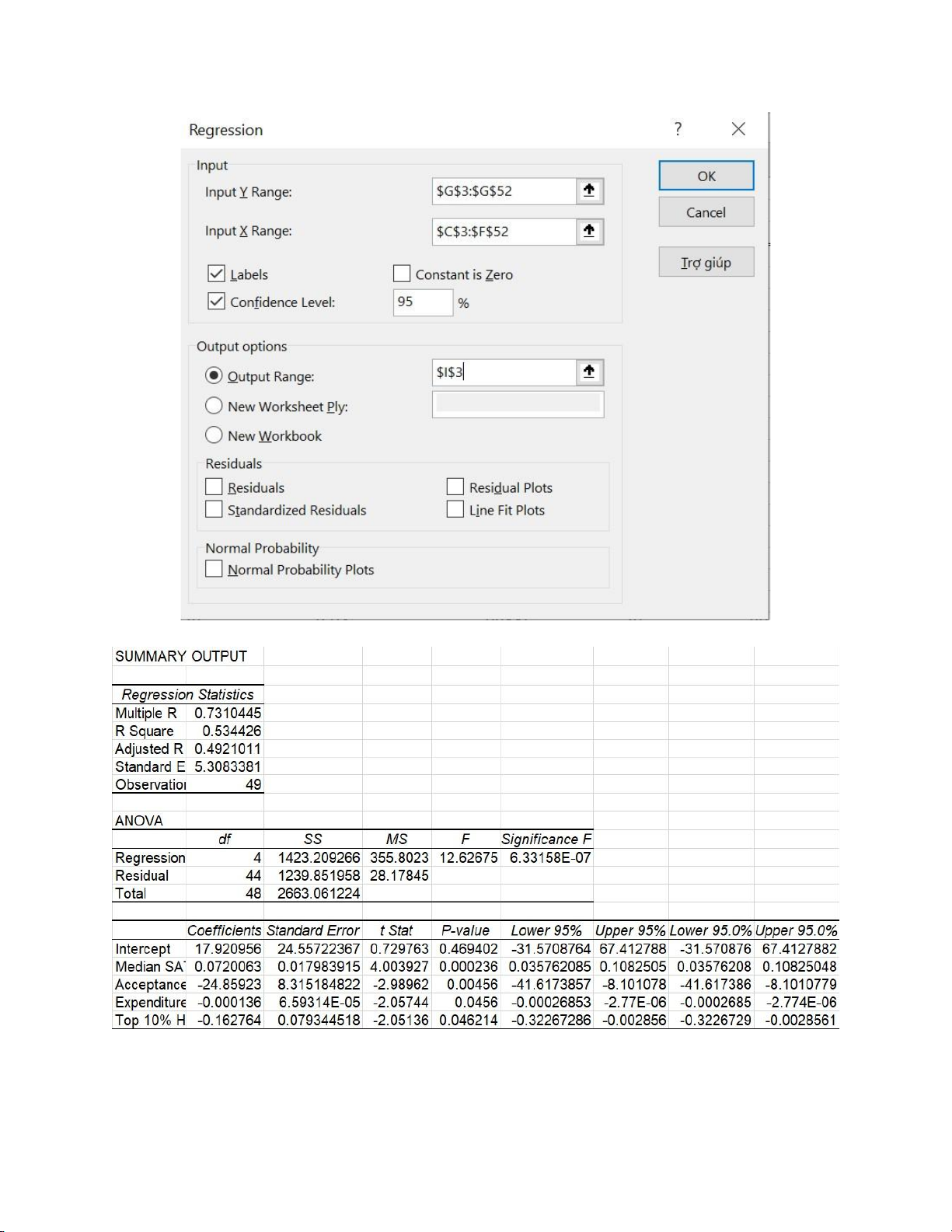
Bước 2: Thực hiện phân tích trên Excel theo các bước như hình dưới
Bước 3: Chọn Input Y Range: “Graduation”, Input X Range: “Median SAT”,
“Acceptance Rate”, “Expenditures/ Student” và Top 10% HS và nhấn OK 15 lOMoAR cPSD| 59285474
Bước 4: Sau khi nhấn OK, ta được kết quả như sau:
Bảng tóm tắt SUMMARY OUTPUT: 16 lOMoAR cPSD| 59285474
+ Dựa vào kết quả Regression Statistics, ta thấy các thông số của mô hình hồi quy như sau:
- Multiple R: Hệ số tương quan bội(0<=R<=1), cho thấy mức độ chặt chẽ
của mối liên hệ tương quan bội.
- R Square: Hệ số xác định R bình phương. Cho biết trong 100% sự biến
động của biến phụ thuộc Y thì có bao nhiêu % sự biến động là do các
biến độc lập X ảnh hưởng, còn lại là do sai số ngẫu nhiên.
- Adjusted R Square: R bình phương hiệu chỉnh. Giá trị này phản ánh sát
mức độ phù hợp của mô hình hồi quy. Ở bài toán này giá trị này bằng
0.492, nghĩa là các biến độc lập giải thích được 49,2% sự biến thiên của
biến phụ thuộc, phần còn lại 50,8% được giải thích bơi các bên ngoài
mô hình và sai số ngẫu nhiên.(Mô hình này được đánh giá là chưa tốt)
- Standard Error: Sai số chuẩn của Y do hồi quy.
- Observation: Số mẫu quan sát.
+ Bảng phân tích phương sai ANOVA:
- Regression: Do hồi quy
- Residual: Do ngẫu nhiên - Total: Tổng cộng
- Df (Degree of freedom): Số bậc tự do
- SS (Sum of Square): Tổng bình phương của độ lệch giữa các giá trị
quan sát của Y và giá trị trung bình của chúng
- MS (Mean of Square): Phương sai hay số trung bình của tổng bình
phương độ lệch kể trên 17 lOMoAR cPSD| 59285474
- F: Tiêu chuẩn F, dùng làm căn cứ để kiểm định độ tin cậy về mặt khoa
học (thống kê) của toàn bộ phương trình hồi quy
- Significance F: F lý thuyết.
+ Bảng phân tích hồi quy
- Coefficients: Cột giá trị của các hệ số hàm hồi quy:
Intercept: Hệ số hồi quy, hệ số này cho thấy xuất phát điểm của đường hồi quy
Median SAT, Acceptance Rate, Expenditures/Student, Top 10% HS:
Các hệ số hồi quy của các biến độc lập tương ứng Standard Error:
Độ lệch chuẩn t-Stat: Tiêu chuẩn t dùng làm căn cứ để kiểm định độ
tin cậy về mặt khoa học (thống kê) của mối liên hệ giữa X và Y.
P-value: Trong bài toán này ta thấy giá trị P-value của các biến độc lập
đều <0.05, nên ta chấp nhận tất cả các biến độc lập này
Lower 95%, Upper 95%, Lower 95%, Upper 95%: Là cận dưới và cận
trên của khoảng ước lượng cho các tham số với độ tin cậy 95% và độ tin cậy 95%.
Dựa vào kết quả bảng ANOVA ta thấy:
+ Significance F <0.05, nên mô hình này phù hợp
Dựa vào bảng kết quả Coefficients, ta thấy:
+ Mỗi biến độc lập đều có p-value < 0.05. Nên ta chấp nhận tất cả các biến này
Vậy ta có phương trình hồi quy:
Graduation % = 17.921 + 0.072 * Median SAT – 24.859 * Acceptance Rate -
0.000136 * Expenditures/Student - 0.163 * Top 10% HS 18 lOMoAR cPSD| 59285474
2.1.3 Sử dụng ngôn ngữ R
Bước 1: Import dữ liệu, attach dữ liệu, và xem các trường dữ liệu
Bước 2: Gán mô hình bằng hàm lm, gõ thêm lệnh summary(reg)
R-squared = 0,5344, Adjusted R-square = 0,4921 => Có 49.21% dữ liệu phù hợp với mô
hình và < 50% nên mô hình này được đánh giá là chưa tốt.
Vì giá trị p-value = 6.332e-07 < 0.05. Nên ta thấy mô hình hồi quy này là phù hợp 19 lOMoAR cPSD| 59285474
Dựa vào bảng kết quả Coefficients. Ta có mỗi biến độc lập đều có Pr(>|t|) < 0.05. Nên ta
chấp nhận tất cả các biến độc lập.
Vậy ta có phương trình hồi quy:
Graduation = 1.792e+01 + 7.201e-02 * Median.SAT – 2.486e+01 * Acceptance.Rate
- 1.356e-04 * Expenditures.Student – 1.628e-01 * Top10% HS
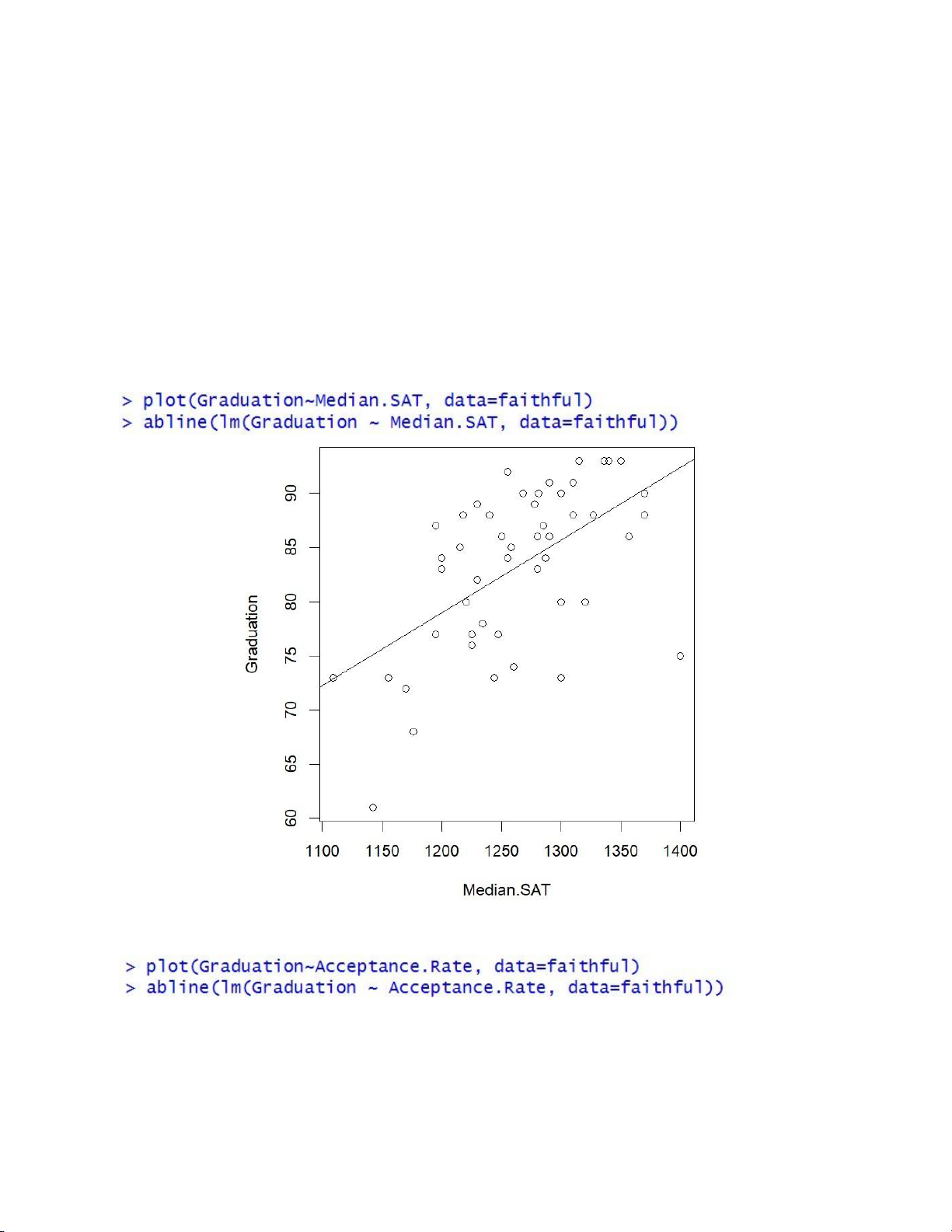
Bước 3: Biểu diễn phương trình hồi quy giữa biến phụ thuộc và các biến độc lập
+ Graduation và Median.SAT
+ Graduation và Acceptance.Rate 20