Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
Bài 1: THÍ NGHIỆM KÉO MẪU THÉP
I. Mục đích thí nghiệm:
Tìm sự liên hệ giữa lực và biến dạng của vật liệu khi kéo mẫu, từ đó xác định đặc
trưng cơ tính của vật liệu bao gồm: -
Giới hạn chảy σch -
Giới hạn bền σb -
Độ dãn dài tương đối khi đứt δ % -
Độ thắt tương đối ψ %
II. Cơ sở lý thuyết:
Thanh chịu kéo hay nén đúng tâm là thanh mà trên mọi mặt cắt ngang chỉ có một
thành phần nội lực là lực dọc Nz.
Các giả thuyết làm cơ sở cho thanh chịu kéo đúng tâm:
- Giả thuyết mặt cắt ngang: Mặt cắt ngang ban đầu là phẳng và thẳng góc với
trục của thanh thì sau khi biến dạng vẫn phẳng và thẳng góc với trục của thanh.
- Giả thuyết về các thớ dọc: Trong quá trình biến dạng, các thớ dọc không ép lên
nhau, cũng không đẩy nhau, các thớ dọc của thanh trước và sau khi biến dạng vẫn song song với nhau.
- Dưới tác dụng của lực kéo hay nén đúng tâm, trên mặt cắt ngang chỉ có một
thành phần ứng suất pháp σ Z P
- Quan hệ giữa ứng suất và lực: σ = (kg/mm2, N/mm2) Z F
III. Chuẩn bị thí nghiệm: - Đo kích thước
• Đường kính mẫu thép trước khi kéo: d0 = 12 (mm) π. 2 d π 0 ( 2 1 ) 2 • 2
Tiết diện mẫu thép trước khi kéo: F = = 113 (mm ) 0 = 4 4
• Chiều dài mẫu thép trước khi kéo: L0 = 10d0 = 120 (mm) - Khắc vạch trên mẫu Vạch trung tâm < d0 d0 > d0 d0 L ả 0 = 10d0 = 10 kho ng chia
Phạm Thanh Luân – Phạm Văn Sang Trang 1
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM Sơ bộ P Sơ bộ B Sơ bộ σ = (1 ) 2 2 π - Dự đoán tải trọng : B F => PB = 60. = 6786 (Kg) 0 4
- Điều chỉnh cấp tải trọng, điều chỉnh kim đồng hồ về 0
- Điều chỉnh hai ngàm kẹp của máy kéo – nén thích hợp với hai đầu kẹp mẫu
- Đặt mẫu vào ngàm kẹp và kẹp chặt mẫu, kiểm tra kim chỉ lực
IV. Tính toán kết quả:
Pđh = 5760 (Kg); Pch = 5800 (Kg); Pb = 6700 (kg) P 5760 dh - Giới hạn đàn hồi: σ = = = 50 2 dh (kg / mm ) F 113 0 P 5800 ch - Giới hạn chảy: σ = = = 51 2 ch (kg / mm ) F 113 0 P 6700 b - Giới hạn bền: σ = = = 59 2 b (kg / mm ) F 113 0 ả đầ 4 khoảng chia đầ 4 kho ng chia u u Các khoảng chia còn lại
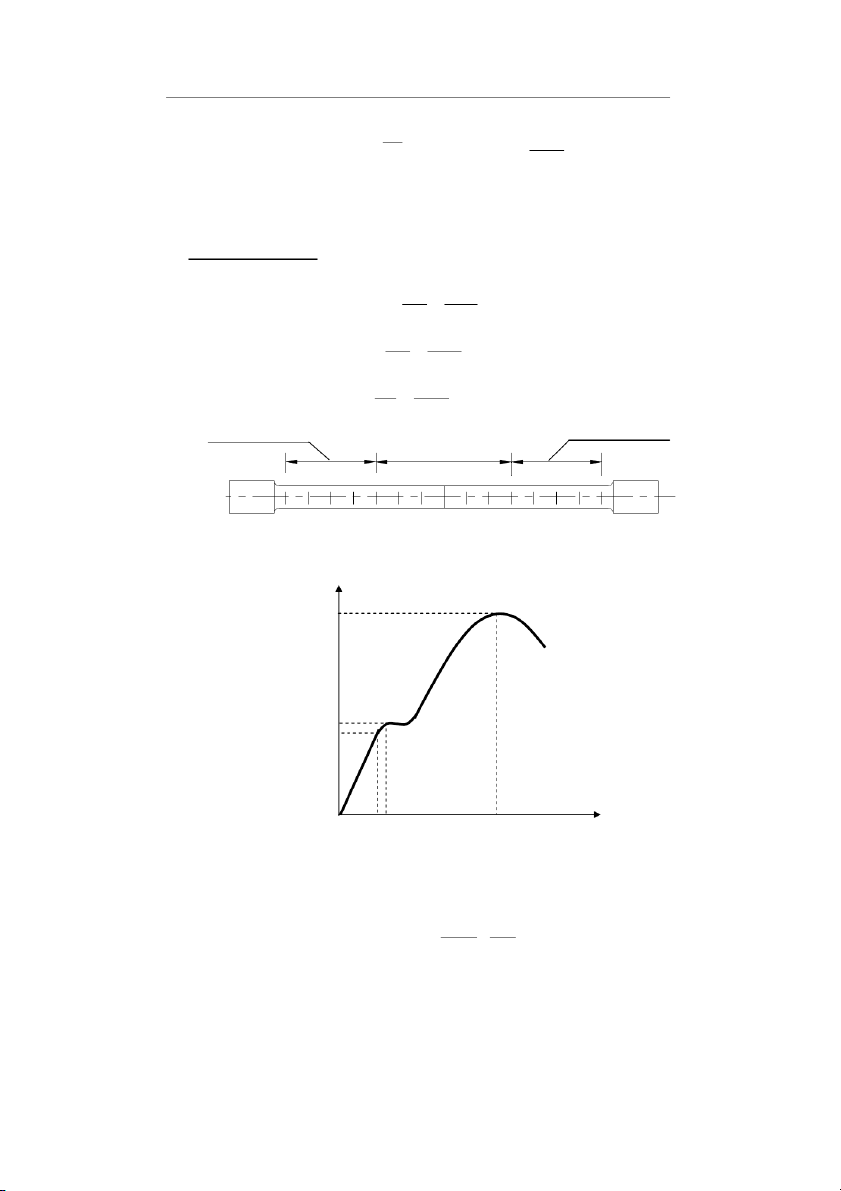
* Đồ thị biểu diễn mối quan hệ giữa lực P và biến dạng ∆ L P C 6700 D B 5800 5700 A O ∆ L
* Mẫu đứt nằm trong các khoảng chia còn lại. Đo được:
• Chiều dài mẫu thép sau khi kéo là: L1 = 155 (mm)
• Đường kính mẫu thép sau khi kéo là: d1 = 8 (mm) π(d π 1 )2 8 . 2
• Tiết diện mặt cắt sau khi kéo là: F1= = ≈50 (mm2) 4 4
Phạm Thanh Luân – Phạm Văn Sang Trang 2
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
+ Độ dãn dài tương đối khi bị đứt: L − L 155 −120 δ % 1 0 = ×100 = ×100 = 29 1 , % 7 L 120 0
+ Độ thắt tương đối: F − F 113− 50 ψ % 0 1 = ×100 = ×100 = 55 % 8 , F 113 0 V. Nhận xét: Trên đồ thị
- OA : Giai đoạn đàn hồi, tương quan giữa P và ∆L là bậc nhất. Lực lớn nhất
trong giai đoạn này là lực tỉ lệ (hay lục đàn hồi)
- AB : Giai đoạn chảy, lực kéo không tăng nhưng biến dạng tăng liên tục. Lực
kéo tương ứng là lực chảy.
- BCD : Giai đoạn củng cố (tái bền), tương quan giữa lực P và ∆L là đường
cong. Lực lớn nhất là lực bền.
Tiết diện chỗ bị đứt nhỏ hơn so với tiết diện ban đầu (hình thành cổ thắt) do chịu tác
dụng của tải trọng cao nhất P ạ ả ế ạ ụ ộ đ ả
b, trong kim lo i x y ra bi n d ng c c b . Lúc ó tuy t i
trọng tác dụng giảm đi mà biến dạng vẫn tăng, kim loại ở chổ biến dạng cục bộ bị đứt
và đi đến phá hủy ở điểm D (như trên đồ thị).
Phạm Thanh Luân – Phạm Văn Sang Trang 3
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
Bài 2: THÍ NGHIỆM NÉN MẪU GANG
I. Mục đích thí nghiệm:
Tìm sự liên hệ giữa lực và biến dạng của vật liệu khi nén mẫu, từ đó xác định đặc
trưng cơ tính của vật liệu:
- Giới hạn bền σb đối với gang.
II. Cơ sở lý thuyết:
Thanh chịu kéo hay nén đúng tâm là thanh mà trên mọi mặt cắt ngang chỉ có một
thành phần nội lực là lực dọc Nz.
Các giả thuyết làm cơ sở cho thanh chịu nén đúng tâm:
- Giả thuyết mặt cắt ngang: Mặt cắt ngang ban đầu là phẳng và thẳng góc với
trục của thanh thì sau khi biến dạng vẫn phẳng và thẳng góc với trục của thanh.
- Giả thuyết về các thớ dọc: Trong quá trình biến dạng, các thớ dọc không ép lên
nhau, cũng không đẩy nhau, các thớ dọc của thanh trước và sau khi biến dạng vẫn song song với nhau.
- Dưới tác dụng của lực kéo hay nén đúng tâm, trên mặt cắt ngang chỉ có một
thành phần ứng suất pháp σ Z P
- Quan hệ giữa ứng suất và lực: σ = (kg/mm2, N/mm2) Z F
III. Chuẩn bị thí nghiệm: - Đo kích thước
• Đường kính mẫu gang trước khi nén: d0 = 20 (mm)
• Tiết diện mặt cắt ngang của mẫu gang trước khi nén: π. 2 d π 0 ( 2 2 ) 0 F 2 0 = = = 314 (mm ) 4 4
• Chiếu cao mẫu gang trước khi nén: h = 35 (mm) Sơ bộ Sơ bộ PB σ =
- Dự đoán tải trọng thích hợp B F 0 Sơ bộ h
=> PB = 110 × 314 = 34540 (Kg)
- Điều chỉnh cấp tải trọng, điều chỉnh kim đồng hồ về 0
- Điều chỉnh hai ngàm kẹp của máy kéo – nén thích hợp ề ủ ẫ d0 với chi u cao c a m u
- Đặt mẫu vào ngàm nén, chú ý đặt mẫu sao cho nén được đ Mẫu thí nghiệm
úng tâm, kiểm tra kim chỉ lực.
Phạm Thanh Luân – Phạm Văn Sang Trang 4
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
IV. Tính toán kết quả:
Sau khi tiến hành thí nghiệm ta có P ớ ạ ề ủ
B = 26600 (kg), gi i h n b n c a gang khi nén là: PB 26600 σ = = ≈ 85 B (kg/mm2) F 314 0
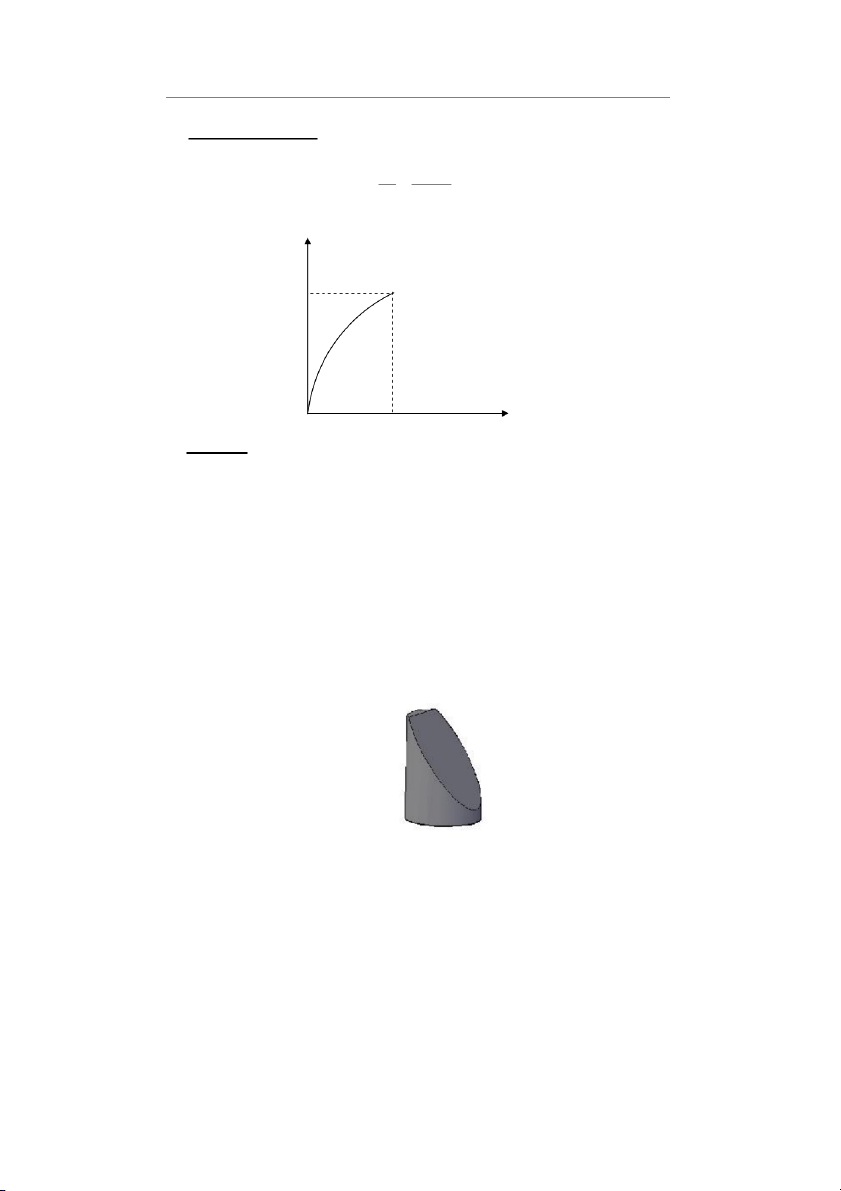
* Đồ thị biểu diễn mối quan hệ giữa lực P và biến dạng ∆L P 26600 O ∆ L V. Nhận xét:
* Đối với vật liệu dòn (gang) không có bất kì biến dạng dẻo nào, ngoài thể hiện biến
dạng đàn hồi. Một đặc trưng của phá hủy dòn là 2 mặt vỡ có thể ghép lại với nhau để
khôi phục nguyên dạng vật liệu ban đầu. Đường cong ứng suất biến dạng đối với vật
liệu dòn có dạng tuyến tính.Thử cơ tính đối với nhiều mẫu như nhau sẽ có nhiều kết
quả ứng suất phá hủy khác nhau.
Độ bền kéo rất nhỏ so với độ bền nén và nó thường được cho là bằng 0 đối với nhiều
ứng dụng. Có thể giải thích là do Hệ số cường độ ứng suất gắn với các khuyết tật trong vật liệu.
* Khi P đạt đến giá trị P ẫ ị ỡ ề ặ ế ữ ẫ
B thì m u b phá v , do trên b m t ti p xúc gi a m u và bàn
nén không có bôi trơn nên vết nứt nghiêng một góc 450 so với phương của trục. Tiết
điện mặt cắt bị phá hỏng trong thí nghiệm trên là một hình elíp.
Phạm Thanh Luân – Phạm Văn Sang Trang 5
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
Bài 3: XÁC ĐỊNH MÔĐUN ĐÀN HỒI TRƯỢT G
I. Mục đích thí nghiệm:
Nhằm xác định môđun đàn hồi trượt G của thép và đồng, kiểm nghiệm định luật Hooke.
II. Cơ sở lý thuyết:
Khi xoắn thuần túy thanh mằt cắt ngang hình tròn, góc xoắn tương đối giữa hai mặt
cắt ngang A và B cách nhau một đoạn LAB là: M L M .L AB . Z AB Z AB ϕ = → G = G.J AB ϕ J . P P Trong đó: M ắ Z : mômen xo n. J độ ự ủ ặ ắ P : mômen quán tính c c c c a m t c t ngang. Nếu xác định được M đ đượ AB ϕ Z, JP, LAB và o c
thì có thể suy ra môđun đàn hồi trượt G.
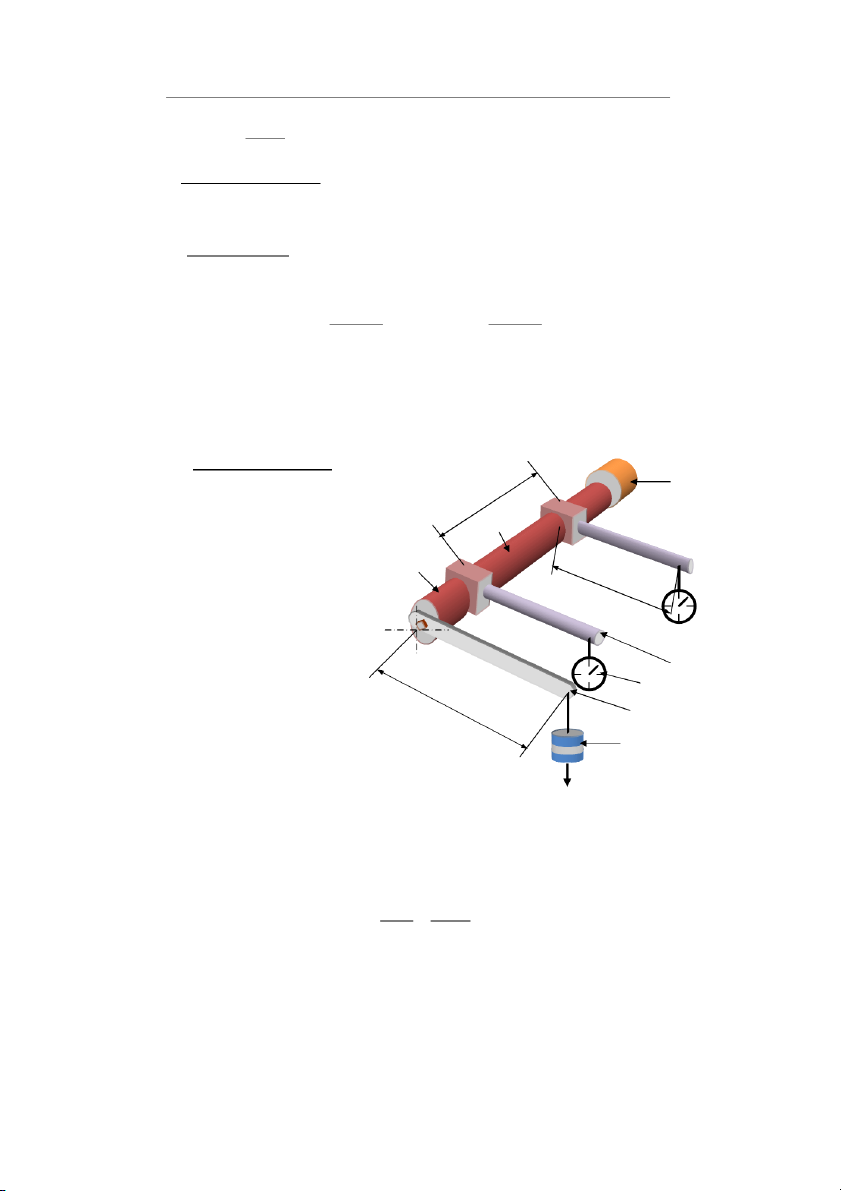
III. Chuẩn bị thí nghiệm: 7 L 1. Quả cân. AB B 2. Thanh treo quả cân. 6 3. Ổ lăn. B’ A 4. Đồng hồ so. 3 a 5. Thanh ngang. 6. Dầm. A’ 7. Ngàm. 5 4 b 2 1 P
Mô hình thí nghiệm - Đo các kích thước:
• Đường kính mẫu d = 26 (mm)
• Khoảng cách LAB = 129,5 (mm); a = 169 (mm); b = 350 (mm). π. 4 d π 2 . 64 J = = ≈ 44864 P 32 32
Phạm Thanh Luân – Phạm Văn Sang Trang 6
Báo cáo Thí nghiệm Cơ học Trường Đại học Sư Phạm Kỹ Thuật TP.HCM
- Đặt các chuyển vị kế tựa vào thanh ngang.
- Bảng ghi kết quả thí nghiệm: Lần
Số đọc trên chuyển vị kế r Ai’- r Bi’ đặt Tải trọng r Ai’ r Bi’ tải Pi (Kg) Thép Đồng Thép Đồng Thép Đồng thứ i 1 0,5 0,03 0,08 0,02 0,04 0,01 0,04 2 1 0,07 0,15 0,04 0,08 0,03 0,07 3 1,5 0,10 0,24 0,07 0,13 0,03 0,11 4 2 0,14 0,31 0,09 0,17 0,05 0,14
IV. Tính toán kết quả: Ta có: M .L P .b.L 32 . P . a . b L 32 G Z AB i AB = = . i AB = . i AB AB 4 ' ' 4 ϕ .J ϕ π.d A ∆ − B ∆ π .d i P i i i
- Ứng với mỗi tải trọng Pi suy ra: Môđun Tải trọng Pi đàn hồi Thép Đồng (Kg) Gi G1 0,5 8536,9 2134,2 G2 1 5691,3 2439,1 G3 1,5 8536,9 2328,3 G4 2 6829,5 2439,1 -
Vậy môđun đàn hồi trượt G của thép là: 4 ∑Gi G = i=1 = 2 thép 7398,7 (Kg/mm ) 4 -
Vậy môđun đàn hồi trượt G của đồng là: 4 ∑Gi G i=1 2 đồ = ng = 2335,2 (Kg/mm ) 4
Phạm Thanh Luân – Phạm Văn Sang Trang 7