

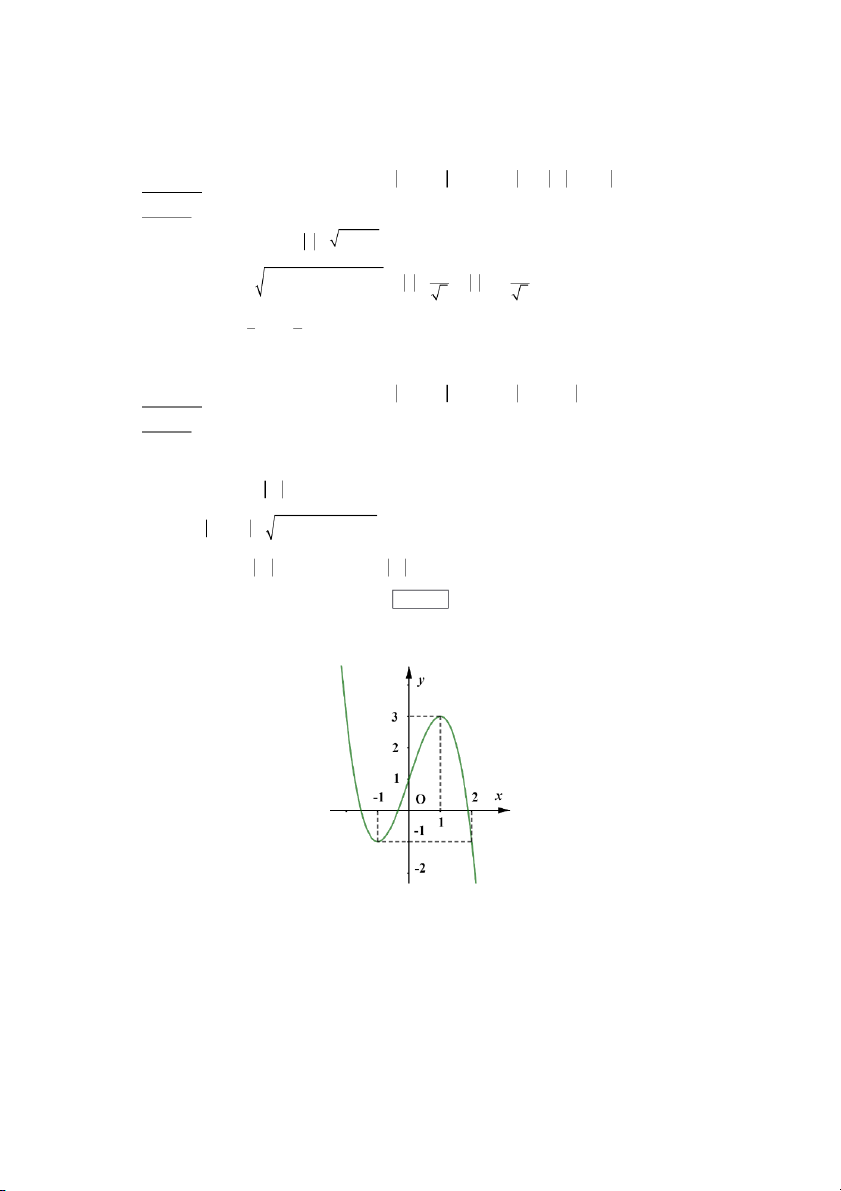
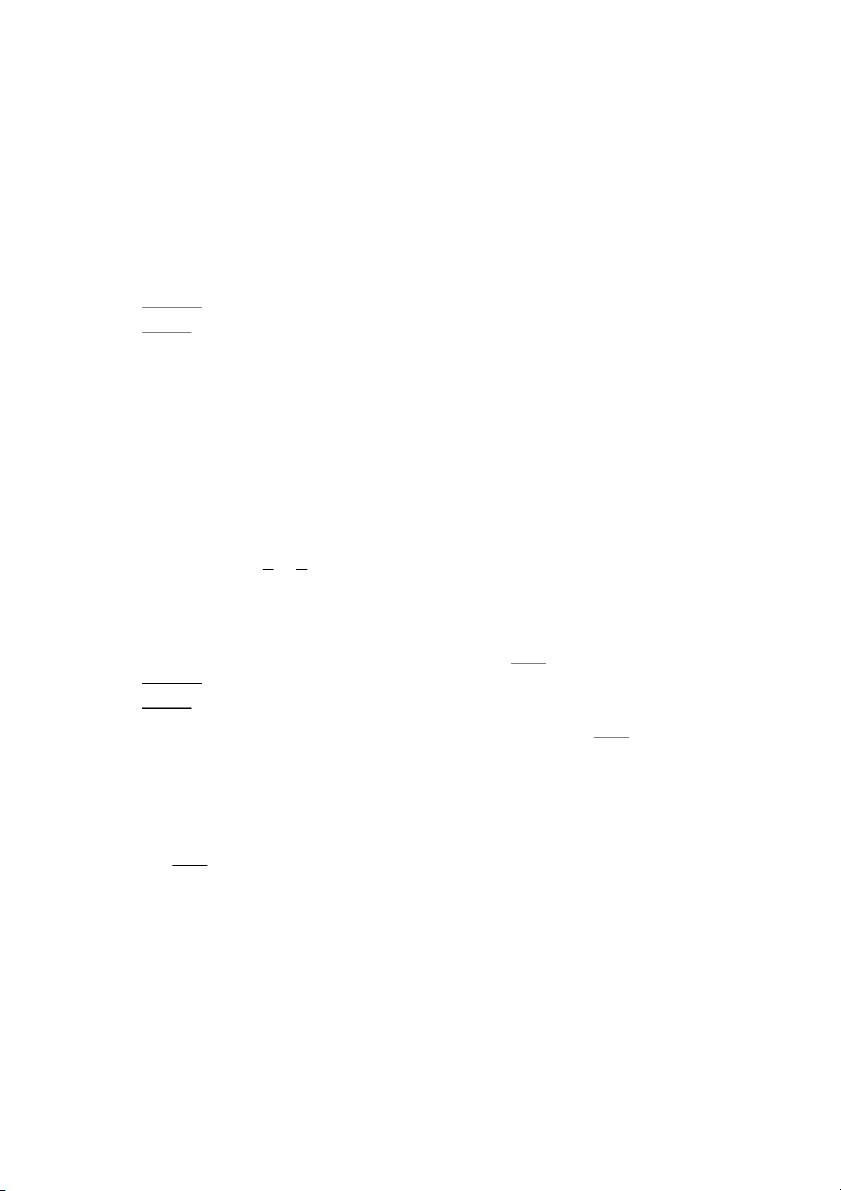

Preview text:
TÍCH PHÂN f x 0; 1 f Câu 6. Cho hàm số
có đạo hàm liên tục trên đoạn thoả mãn 1 0 , 1 1 1 1
f ' x 2 dx 7 2 d x f x x f x d . x 3 0 và 0 . Tính tích phân 0 7 7 . . A. 5 B. 1. C. 4 D. 4. f x 0; 1 f Câu 6a. Cho hàm số
có đạo hàm liên tục trên đoạn thoả mãn 1 3 , 1 1 7 1 f x 2 4 ' dx 4
x f x dx f x d . x 11 11 0 và 0 . Tính tích phân 0 35 65 23 9 . . . . A. 11 B. 21 C. 7 D. 4 f x 0; f Câu 6b. Cho hàm số
có đạo hàm liên tục trên đoạn 1 thoả mãn 1 3 , 1 1 7 f x 2 4 ' dx 4
x f x dx 11 11 f 1 f 2 . 0 và 0 . Tính giá trị A. 19. B. 19. C. 17. D. 17. f x 0;1 f Câu 6c. Cho hàm số
có đạo hàm liên tục trên đoạn thoả mãn 1 1 , 1 1 2 2 f x 2 9 ' dx
f x dx
f x ln x d . x 5 5 0 và 0 . Tính tích phân 1 15 2 ln 2 . 15 4 ln 2 . 1 ln 2 . 1 ln 2 . A. 16 B. 16 C. 16 D. 16
Lời giải và phân tích Câu 6: Lời giải: u f x du f ' x dx 1 1 1 2 3x f x 3 dx x . f x 3 x f ' x dx 2 3 0 Đặt dv 3 x dx v x , khi đó 0 0 1 1 1 f 1 3 x f ' x dx 3 x f
' x dx 1. Ta có 0 suy ra 0 2 b b b f
x g x 2 x f x 2 d dx g xd .x
Áp dụng bất đẳng thức tích phân a a a
f x k g x
Dấu bằng xảy ra khi và chỉ khi
với k là hằng số. 2 1 1 1 1 7 1 ' d d ' 2 3 6 d 7 x x f x x x x f x x 1 Ta có 7 0 0 0 0 .
Dấu bằng xảy ra khi và chỉ khi f 3 ' x k
x với k là hằng số. 1 1 3 x f
' x dx 1 6 kx dx 1 Mà 0 hay 0 suy ra k 7. 7 7 f x 4 x C
f x 4 1 x f 1 0 Vậy f 3 ' x 7x nên 4 mà nên 4 , suy ra 1 f x 7 dx . 5 0 Câu 6a: 1 1 1 f '
x 2dx 7 2 d x f x x f 1 0 , 3
Phân tích: Thay các giả thiết 0 , 0 thành 1 1 7 f x 2 4 ' dx 4
x f x dx f 1 3 , 11 11 0 , 0 . Lời giải:
du f ' x dx u f x 1 1 1 5 1 1 7 4 4 5 5 d d x v x x x f
x dx x .f x x f ' x v dx Đặt 5 , khi đó 5 5 11 0 0 0 1 2 5
x f ' x dx 11 0 1 1 10 x dx Ta có 11 0 nên 1 1 1 f ' x 2 5
dx 4 x f ' x 10 dx 4 x dx 0 0 0 0 1 f '
x2x 2 5 dx 0
f ' x 5 2x 0 6 f x x 10 C C 3 3 f 1 0 (do ) 1 1 6 f x x 10 23 dx dx . 3 3 7 0 0 Câu 6b: 1 1 1
f ' x 2 dx 7 2 d x f x x f 1 0 , 3
Phân tích: Thay các giả thiết 0 , 0 thành 1 1 7 f x 2 4 ' dx 4
x f x dx f 1 3 , 11 11 0 , 0
. Thay yêu cầu bài toán thành tính giá trị f 1 f 2 . Lời giải: du f ' x dx u f x 1 5 1 1 1 1 7 4 4 5 5 d d x v x x v
x f x dx x . f x
x f ' x dx Đặt 5 , khi đó 5 5 11 0 0 0 1 2 5
x f ' x dx 11 0 1 1 10 x dx Ta có 11 0 nên 1 1 1 f ' x 2 5
dx 4 x f ' x 10 dx 4 x dx 0 0 0 0 1 f '
x2x 2 5 dx 0
f ' x 5 2x 0 6 f x x 10 C C 3 3 (do f 1 0 ) 6 f x 10 x Do đó 3
3 . Vậy f 1 f 2 1 18 1 9 . Câu 6c: 1 1 1
f ' x 2 dx 7 2 d x f x x f 1 0 , 3
Phân tích: Thay các giả thiết 0 , 0 thành 1 1 2 f x 2 9 ' dx
f x dx f 1 1 , 5 5 0 , 0
. Thay yêu cầu bài toán thành tính tích phân 1 f x l n x d . x 0 Lời giải: Đặt 2
t x x t dx 2
tdt. Đổi cận x 0 t 0 ; x 1 t 1 . 1 1 1 1 2 2t.f t dt t
. f t 1 2 2 t . f '
t dt f 1 2 t . f ' t 2 dt 1 t . f ' tdt 0 Ta có: 5 0 0 0 0 1 3 1 3 2
t .f 't dt 2 x . f '
xdx . 1 5 5 0 hay 0 1 1 1 f x2 9 ' dx 2 4 x dx . 3 Mặt khác ta có 5 5 0 và 0 1 1 1 1 f
' x 3x 2 2 dx f ' x 2 2
dx 6 x . f ' x 4
dx 9 x dx 9 3 1 6. 9. 0. Xét tích phân 0 0 0 0 5 5 5
f x x 2 2 ' 3 0 , x 0; Mà
1 . Vậy f x 2 ' 3x .
Do đó f x 3 x C C
0 (do f 1 1). Vậy f x 3x. dx d ln u u x x 3 4
dv x dx x v Đặt 4 , khi đó 2 2 2 2
x f x 3 x x x 1 4 x x x 1 3 x x 15 ln d .ln d .ln d 4 ln 2 . 4 4 16 1 1 1 1 SỐ PHỨC z 1 2i 2
Câu 10. Cho số phức z thoả mãn
. Tìm môđun lớn nhất của số phức z . A. 9 4 5 . B. 11 4 5 C. 6 4 5 . D. 5 6 5 .
z 2 4i z 2i .
Câu 10a. Trong các số phức thoả mãn điều kiện Tìm môđun nhỏ nhất
của số phức z 2 .i A. 5 . B.3 5 . C.3 2 . D.3 2 .
z 3i z 2 i .
Câu 10b. Trong các số phức thoả mãn điều kiện Tìm số phức có môđun nhỏ nhất. 1 2 1 2 z .i z .i A. z 1 2 .i B. 5 5 C. 5 5
D. z 1 2 .i
2z 3 4i 1 0
Câu 10c. Cho số phức z thoả mãn
. Gọi M và m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của z . Khi đó M m bằng A. 5. B. 15. C. 10. D. 20.
Lời giải và phân tích Câu 10: Lời giải: z 1 2i a
bi z a
1 b 2 . 2 2 a b 4 . 1 Đặt
i Từ giả thiết ta có 1 Khi đó theo
và bất đẳng thức Bunhiacopxki ta có: 2 z
a 2 b 2 a b 2 2 2 2 1 2 9 2 4 9 2 4 a b 9 4 5. 2 5 2 2 a b 4 a 5 . a b 4 5 2 4 b Hay ta có z 9 4 5 max đạt được khi 5 Câu 10a: z i z
i z i
Phân tích: Thay đổi giả thiết bài toán từ 1 2 2 thành 2 4 2 . Lời giải: 2 2
Đặt z 2i a
bi z a
b 2i , ta cần tìm min của T a b .
Thay z vào giả thiết ta có a
b i a b i a 2 b 2 a b 2 2 2 6 4 2 6 4 a b 6 . 1 2 2
T a b
a b2 3 2 Từ đó ta có 2
đạt được tại a b 3 . Câu 10b: z 1 2i 2
z 3i z 2 i .
Phân tích: Thay đổi giả thiết bài toán từ thành Lời giải: 2 2 2 2 Gọi z a
bi a b 2 2 , ,
z a b . Từ giả thiết ta có a b 3 a 2 b 1 . a
b 2 2 2 2 a b 1 1 1 2 1 2 z z min Suy ra 5 5 đạt được tại a 2b 1 1 2
a ,b . 2a b 5 5 Câu 10c: z i z i
Phân tích: Thay đổi giả thiết bài toán từ 1 2 2 thành 2 3 4 10. Lời giải: 2 2
Đặt 2z 3 4i a
bi 2z a
3 b 4 i và a b 1 00. 1 2 2 2
Khi đó từ 1 ta có 2z
a 3 b 4 125 2 3a 4b . 2
a b 2 2 2 2 3 4 3 4 a b 5 0 50 3 a 4b 5 0. 3 Mặt khác 2 125 100 2z 1
25 100 5 2z 1
5 2 M m Suy ra 15 5 10 M m 5. ĐỒ THỊ Câu 4.
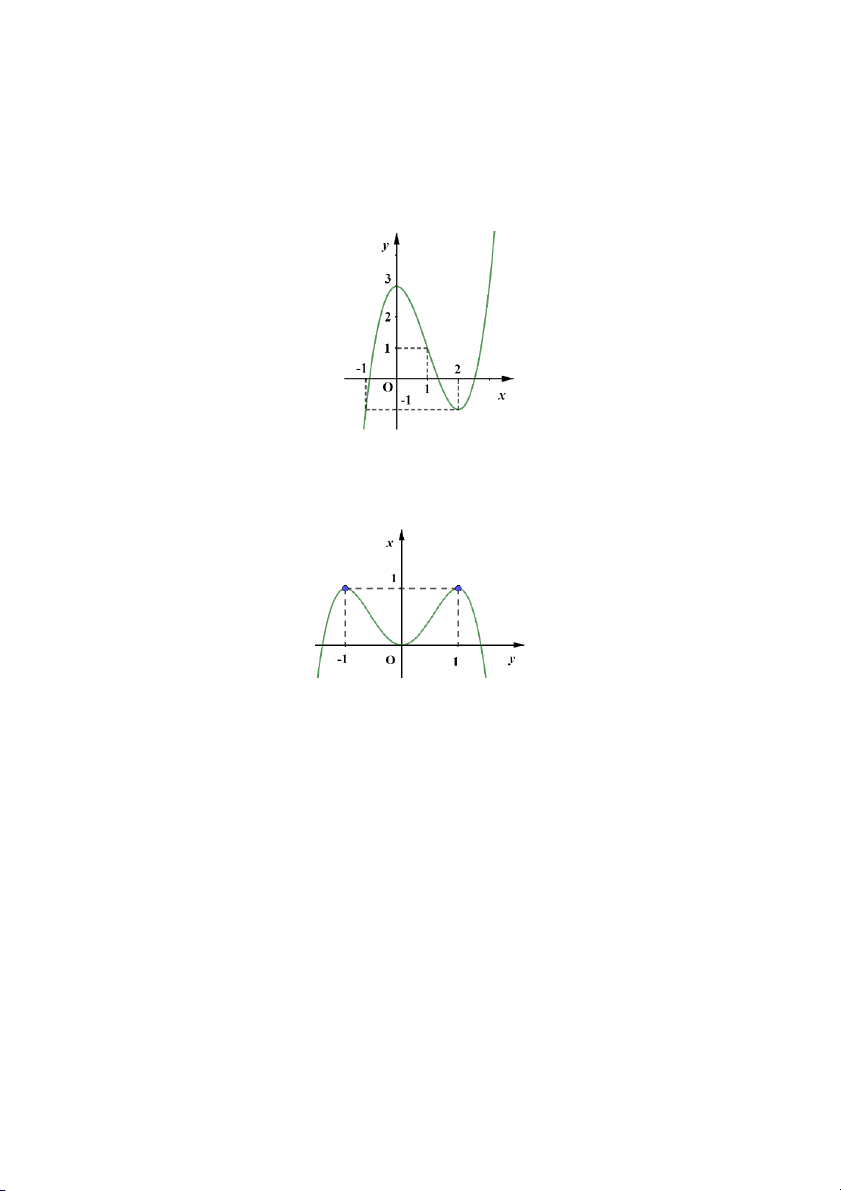
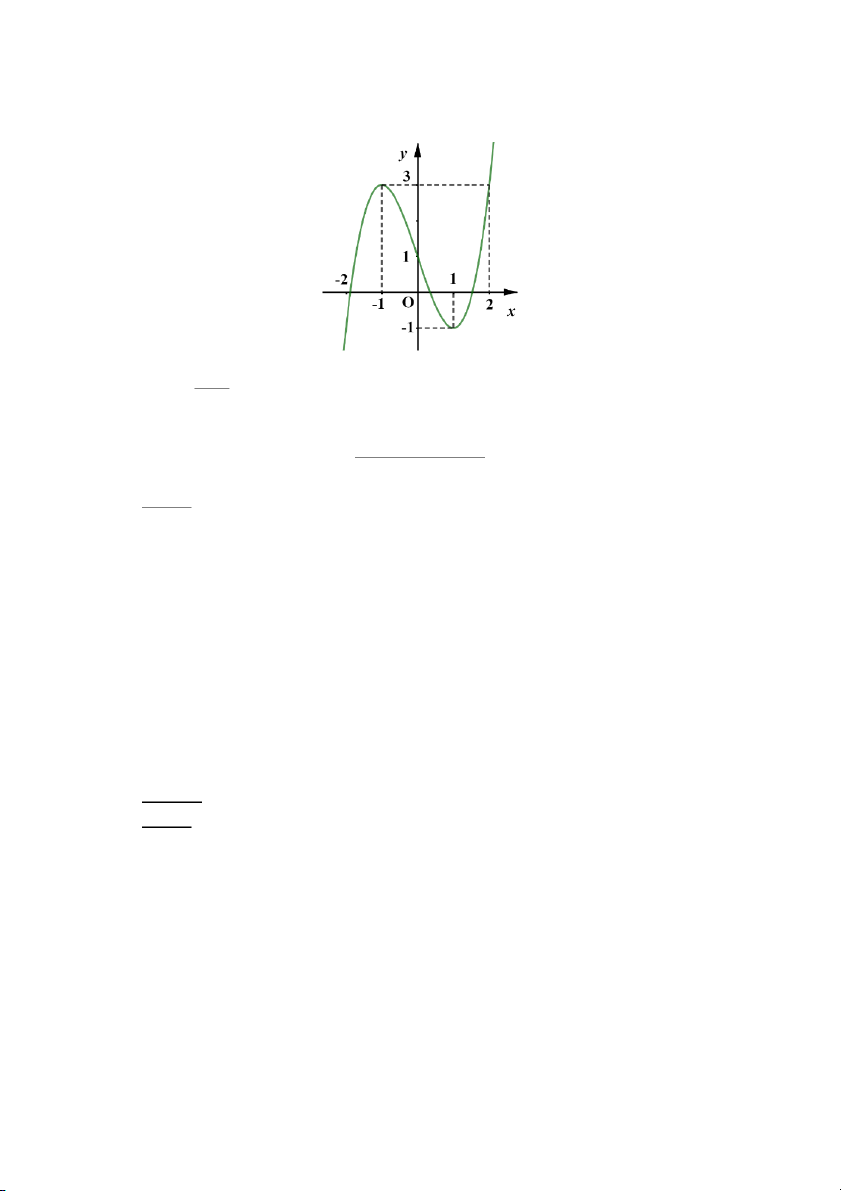
y f x Cho hàm số
liên tục trên và có đồ thị như hình vẽ dưới đây.
Số nghiệm phân biệt của phương trình f f x 1 là A. 6. B. 7. C. 8. D. 9.
Câu 4a. Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ dưới đây.
f x 2 2 f 2 1 x 1 2 0
Số nghiệm của phương trình là: A. 1. B. 4. C. 3. D. 5.
y f x Câu 4b. Cho hàm số
liên tục trên và có đồ thị như hình vẽ dưới đây.
Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn nghiệm của phương trình f f cos 2x 0 ? A. 1 điểm. B. 3 điểm. C. 4 điểm. D. Vô số điểm.
Câu 4c. Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ dưới đây.
Số các giá trị nguyên của tham số m không vượt quá 5 để phương trình 2 f m x 1 0 8
có hai nghiệm phân biệt là A. 4. B. 5. C. 6. D. 7.
Lời giải và phân tích Câu 4: Lời giải: t a
2 a 1 f t 1 t 0 t b 1b
Đặt t f x , khi đó 2 .
f x a
2 a 1
f x 0 f
x b 1 b 2 Khi đó ta có .
Dựa vào đồ thị ta có phương trình f x a
có 1 nghiệm, phương trình f x 0 có 3 f x nghiệm và phương trình b có 3 nghiệm.
Vậy phương trình f f x 1 có 7 nghiệm. Câu 4a: 2 2 2
f f x 1 f x 1 f x 1 2 0
Phân tích: Thay phương trình thành . Lời giải: Đặt 2
t x 1 t 1
. Ta thấy ứng với t 1
cho ta một giá trị của x và ứng với mỗi giá trị
t 1 cho hai giá trị của . x f t 2 f t f t 1
2 0 f t . 2
Phương trình đã cho trở thành
y f t 1; f t Từ đồ thị hàm số trên suy ra phương trình
1 có 1 nghiệm t 2 f t và phương trình
2 có 1 nghiệm t 2 do đó phương trình đã cho có 4 nghiệm. Câu 4b: f f x 1 f f cos 2x 0
Phân tích: Thay phương trình thành . Lời giải: x 1;1 y 0;1 .
Dựa vào đồ thị ta thấy khi thì t 1;1
f cos 2x 0;1 .
Do đó nếu đặt t c os 2x thì , khi đó
f cos 2x 0 f f cos 2x 0 f cos2x a a 1 lo¹i
f cos2x b b
Dựa vào đồ thị, ta có 1 lo¹i cos 2x 0 f cos2x 0 cos 2x a a 1 lo¹i cos2x b b 1 lo¹i Phương trình
cos 2x 0 x k k . 4 2
Vậy phương trình đã cho có 4 điểm biểu diễn trên đường tròn lượng giác. Câu 4c: f m x 2 1 0 f f x 1 Phân tích: : Thay phương trình thành 8 . Lời giải: 2 f t m 1 . * Đặt x t
. Điều kiện t 0. Khi đó phương trình đã cho trở thành 8 Vì với mỗi nghiệm *
t 0 của phương trình
cho đúng một nghiệm x l og t của
phương trình * nên * có hai nghiệm phân biệt khi và chỉ khi * có đúng hai nghiệm 0; phân biệt trêm
. Dựa vào đồ thị ta thấy điều này xảy ra khi và chỉ khi 2 m 1 1 1. 8 m m m5 m5
m 2; 1;0;1; 2 . 2 m 1 3 m 3 1 1
Yêu cầu bài toán tương đương 8
Vậy có 5 số nguyên thoả mãn.




