Chương 5 không gian Euclide - Môn đại số tuyến tính | Học viện nông nghiệp
Đại học Y dược Cần Thơ với những kiến thức và thông tin bổ ích giúp các bạn định hướng và học tập dễ dàng hơn. Mời bạn đọc đón xem. Chúc bạn ôn luyện thật tốt và đạt điểm cao trong kì thi sắp tới.
Môn: Đại số tuyến tính (HVNG) 5 tài liệu
Trường: Học viện Nông nghiệp Việt Nam 2 K tài liệu
Tác giả:
Preview text:
ĐẠI SỐ TUYẾN TÍNH NÂNG CAO
LỚP: CAO HỌC LÝ THUYẾT XÁC SUẤT VÀ THÔNG KÊ TOÁN KHÓA 27
CHƯƠNG 5 – KHÔNG GIAN EUCLIDE
u=( u,u ,u , v= v,v ,v Î ¡ 1 2 3 ) ( 1 2 3) 3
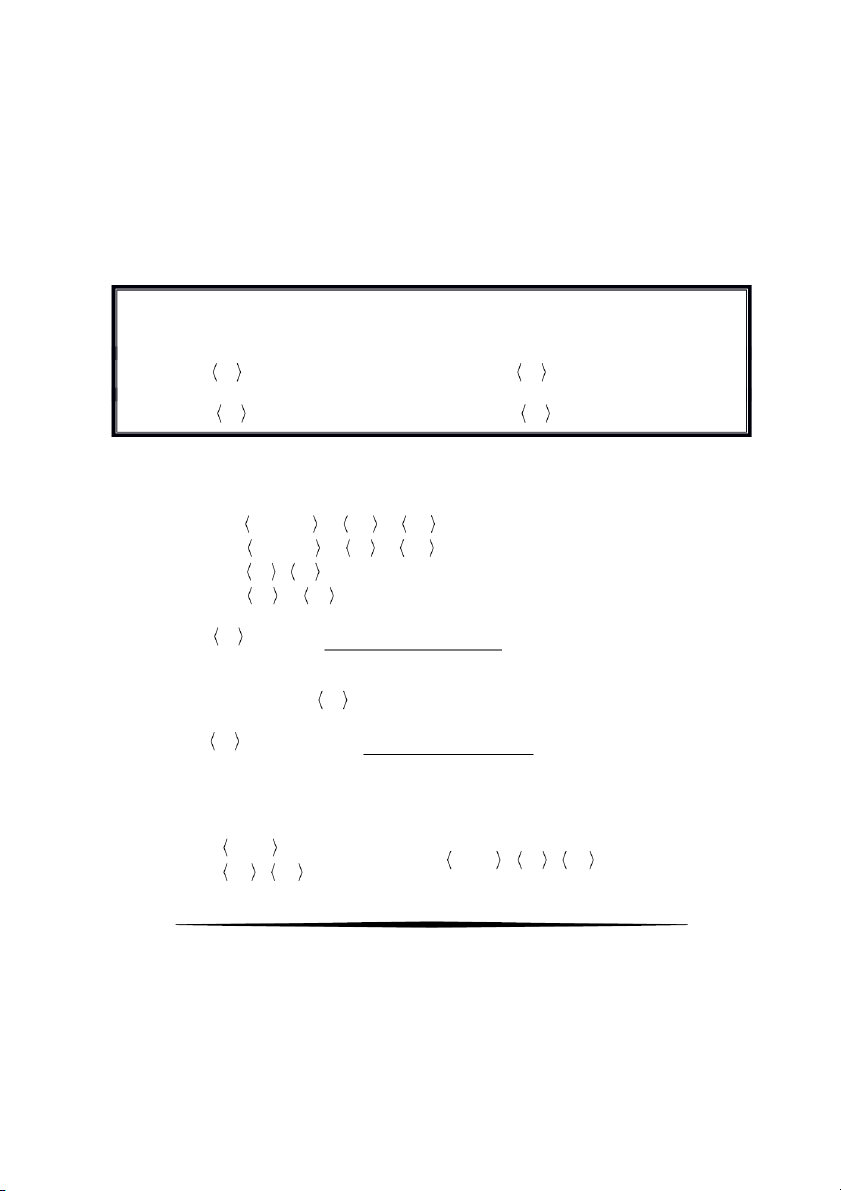
Bài 1. Xét hai vectơ
. Các biểu thức dưới đây
có thể là tích vô hướng trong 3 ¡ không? Giải thích? 2 2 2 2 2 2 a) ,
u v := uv +uv ,
u v := u v +u v +u v 1 1 3 3 b) 1 1 2 2 3 3 c) ,
u v := 2uv +uv +4uv ,
u v := uv - uv +uv 1 1 2 2 3 3 d) 1 1 2 2 3 3 Giải
Thỏa mãn các tính chất sau:
TVH1: u v,w
u, w v, w TVH2 : , u v w , u v , u w
TVH3: u, v , v u TVH4 : ,
u u 0, u, u 0 u
,với , và với mọi u, , v w V a) Biểu thức ,
u v := uv +uv 1 1
3 3 không thể là tích vô hướng vì chỉ thoả tính chất TVH1, TVH2,
TVH3, không thỏa tính chất TVH4. u= (0,1, ) Xét
0 . Khi đó ,uu =0 nhưng u¹ q 2 2 2 2 2 2 b) Biểu thức ,
u v := u v +u v +u v 1 1 2 2 3
3 không thể là tích vô hướng vì không thỏa tính chất (TVH1) của tích vô hướng. u v 1,3, Xét u=(1,2, )
3 ,v=( 0;1; )1 ,w=(1,0, )1 . Khi đó: 4 2 2 2 2 2 u+ , v w =1.1 +3.0+4.1 =17ü
ïïýÞ u+ ,vw ¹ ,uv + ,vw , u w + , v w =10 1 + =11 ï Khi đó: ïþ 1 c) Biểu thức ,
u v := 2uv +uv +4uv 1 1 2 2
3 3 là tích vô hướng vì thỏa mãn 4 tính chất của tích vô hướng
Với mọi a, b Î ¡ và với mọi , u , v wÎ V au+ b , v w = ( 2 au + v b
w + au +bv w + 4 au + v b w 1 )1 1 ( 2 )2 2 ( 3 )3 3
= a( 2uw +uw +4uw +b 2vw +vw +4vw 1 1 2 2 3 3 ) ( 1 1 2 2 3 3 ) TVH1: = a , u w + b , v w , u av+ w b = 2u av + w b +u av + w b +4u av + w b 1 ( 1 1 ) 2 ( 2 2) 3 ( 3 3) TVH2: =2auv +2 u b w a + uv + u
b w +4auv +4 u b w 1 1 1 1 2 2 2 2 3 3 3 3 a = ( 2uv u + v 4 + uv b + 2uw u + w 4 + uw 1 1 2 2 3 )3 ( 1 1 2 2 3 )3 a = , u v b + , u w TVH3: ,
u v = 2uv +u v +4uv = 2vu +v u + 4vu = , v u 1 1 2 2 3 3 1 1 2 2 3 3 2 2 2 ,
u u = 2u u +u u + 4u u = 2u +u + 4u ³ 0 TVH4: 1 1 2 2 3 3 1 2 3 2 2 2 và ,
u u = 0Û 2u +u +4u = 0Û u = u = u = 0Þ u= q 1 2 3 1 2 3 d) Biểu thức ,
u v := uv - uv +uv 1 1 2 2
3 3 không thể là tích vô hướng vì không thỏa mãn tính chất TVH4 của tích vô hướng u= (0,1, ) Xét
0 . Khi đó: ,uu =- 1<0
Bài 2. Với giá trị nào của λ các ánh xạ dưới đây xác định một tích vô hướng trong không gian 3
a) x, y x y 10x y 6λx y x y x y x y 1 1 2 2 1 2 3 3 2 3 3 2 . x, y 2
x y 7x y 7x y 8x y 3λx y λx y x y b) 1 1 1 2 2 1 2 2 3 3 2 3 3 2 . Giải
a) x, y x y 10x y 6λx y x y x y x y 1 1 2 2 1 2 3 3 2 3 3 2 . x 0,1,0 Với và y ( 1, 0, 0). 2 ,x y 0 , x y , y x y,x 6 Ta có: .
Vậy ánh xạ đã cho không phải là tích vô hướng λ . b) x, y 2
x y 7x y 7x y 8x y 3λx y λx y x y 1 1 1 2 2 1 2 2 3 3 2 3 3 2 . x 0,0, 1
x, x 3 0 Với . Ta có: .
Vậy ánh xạ đã cho không phải là tích vô hướng λ .
Bài 3. Cho V M , , m n
với ,ABV , ta định nghĩa: , :
V x V ,
A B Tr T B A
Chứng minh V là không gian Euclide. Giải
* Chứng minh V là không gian véc-tơ.
(Ta dễ dàng kiểm tra 8 tiên đề của không gian véc-tơ).
* Chứng minh <,> là một tích vô hướng trên V a a ... a b b ... b 11 12 1n 11 12 1n a a ... a
b b ... b 21 22 2n A 21 22 2n B , ... ... ... ... ... ... ... ... Với mọi ,
A B,C V giả sử
a a ... a
b b ... b 1 m 1 m mn , m 1 m 1 mn , ta có:
i) A B,C T
r A BT C T r T T
A C B C T r T A C T r T B C
A ,C B ,C . i ) i ,
A B C Tr T
A B C Tr T T
A B A C T r T A B T r T A C
A,B A,C . 3 m m ii )i , A B T r T
A B a b , j=1, n và , B A T r TB A b a n a b b a ij ij , j=1, vì ij ij ij ij ij ij i 1 i 1 nên ,
A B B, A . m i ) v , A A T r T A 2 A a 0 , j=1, n ij i 1 m 2 , A A 0 a 0
, j=1, n a 0 , i=1, m, j=1, . n ij ij và i 1
Vậy V là không gian Euclide. M R n
Bài 4. Cho không gian vector
gồm các ma trận vuông cấp n trên trường số thực .
A a M R T Tr AA ij n a) Với , tính vết
theo aij . Qua đó chứng minh rằng T Tr A nTr AA , T A B Tr AB
b) Chứng minh rằng ánh xạ
xác định một tích vô hướng trong không gian M R n . Giải T Tr AA a) * Tính vết . A M R n Ta có: nên : a a ... a a a ... a 11 12 1n 11 21 1 n a a ... a a a ... a 21 22 2n T 12 22 n 2 A A a a ... a a a ... a n1 n 2 nn 1n 2n nn 2 2 2
a a ... a n * 11 12 1 T AA 2 2 2 * a a a n n ... 1 2 nn 4 Tr T AA 2 2 a . .. a a a
a a n 2 2 ... n ... 2 2 ... 11 1 21 2 n1 nn n n n n n n n 2 2 2
a a a a a a a a j j ... nj 2 2 2 j j ... nj 2 2 1 2 1 2 ij ij Do đó: j 1 j 1 j 1 j 1 j 1 i 1 i,j 1 T Tr A nTr AA *Chứng minh
Ta viết lại đẳng thức chứng minh có dạng: 2 n n
Tr A nTr T AA 2 2 a n a ii ij * i 1 i, j 1 *
Ta chứng minh bất đẳng thức n n n n 2 2 2 2 a a a a ij ii ij ii 1 i , j 1 i 1 i, j 1 i 1 Ta có: i j
Mặt khác, theo bất đẳng thức cauchy-Schwarz, ta có:
1.a 1.a ... 1.a
a a a nn 2 2 2 1 1 ... 1 2 2 2 ... 11 22 11 22 nn
a a ... a n a a a nn 2 2 2 ... 11 22 11 22 nn n Tr 2
A n a ii 3 i 1 n Tr A 2
n a Tr A nTr T AA ij Từ 1 , 2 i ,j 1 b) Xét ánh xạ: , : M R M R R n n
A,B Tr T AB
Ta chứng minh , là một tích vô hướng trong M R n A
,B,C M R n và
, R , ta có: 5
i) A B,C T
r A B T C T r T T
AC BC T r T
AC Tr T BC T r T AC T r T BC ,
A C B,C ii) ,
A B C Tr A B C T Tr A T T
B C T r T T
AB AC T r T
AB Tr T AC , A B , A C iii) A,B
Tr AB Tr AB T Tr B T T T T T A T r T
BA B,A n n iv) A, A T r T AA 2 2
a 0; A,A 0 a 0 a 0 A 0 ij ij ij ,i j 1 ,i j 1
( A là ma trận không). M R n
Vậy , là một tích vô hướng trong
Bài 5. Chứng minh rằng tích vô hướng trong V thỏa: ,
u v = 0,"vÎ V Û u= 0. Giải u,v 0 ,vV Giả sử
, ta chứng minh u
Thật vậy, v V
u,u v u,u u,v Ta có
Do u,u v 0 , u,v 0 nên u,u 0 u Giả sử u
. Ta chứng minh u,v 0 ,v 0 ,vV Thật vậy: v
V ta có: ,v
, v ,v ,v 0,v 0 , v V
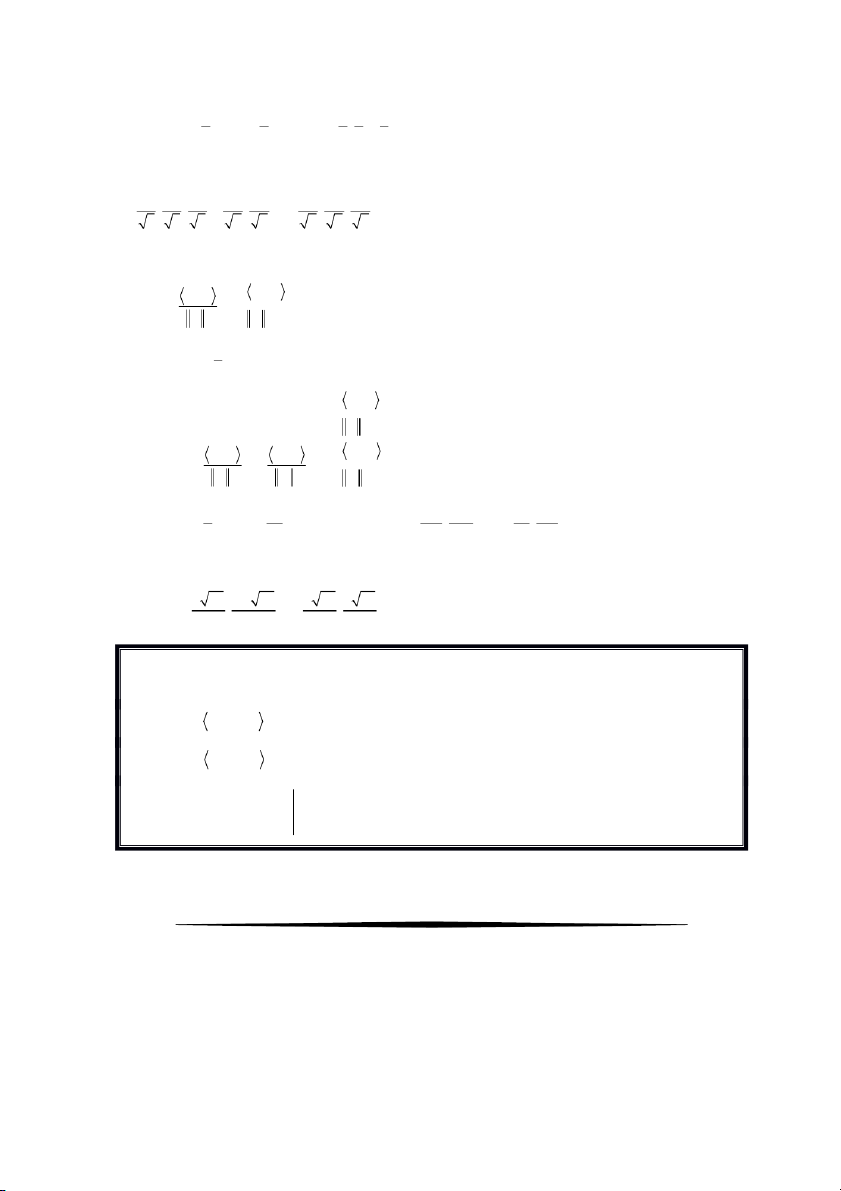
Bài 6. Với tích vô hướng Euclide trong 4
¡ , hãy tìm hai vectơ có chuẩn bằng 1 và trực giao với
các vectơ sau u =( 2,1,- 4, ) 0 ,v =( - 1,- 1,2, ) 2 , w =( 3,2,5, ) 4 Giải
Gọi là vectơ cần tìm. Ta có: vectơ x trực giao với các vec tơ u,v,w ìï x ^u ìï < , x u>= 0 ï ï ï ï í x v Þ ^ Þ í < , x v>= 0 ï ï ïï x w ï ^ ï < , x w >= 0 ïî ïî 6 ìï
2x + x - 4x = 0 1 2 3
ïïïí - x- x +2x +2x =0 1 2 3 4 ïï
Suy ra ta có hệ phương trình thuần nhất sau ï 3x +2x +5x +4x = 0 ï 1 2 3 4 î (1) 2 æ 1 - 4 0ö æ - 1 - 1 2 2ö æ- 1 - 1 2 2ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ A ç = - ç 1 - 1 2 2÷ ÷ ç ® ÷ ç 0 - 1 0 4 ÷ ÷ ç ® ÷ ç 0 - 1 0 4÷ ÷ ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ è ø çè - ÷ ø ç ÷
Ma trận hệ số của hệ này là 3 2 5 4 0 1 11 10 è 0 0 11 6ø ìï 34 ï x =- t ï 1 ï 11
ìï - x - x + 2x + 2x = 0 ï 1 2 3 4 ï ï ï ï x = 4 ( ) t 2 1 ï Û í - x + 4x = 0 ï Û í ,tÎ ¡ 2 4 ï ï 6 ïï 11x +6x = 0 ïï x =- t ïî 3 4 3 ï 11 ï æ 34 6 ö ï ç ÷ ï Þ x = - ç , t 4 , t - , t t÷ ç ÷ Suy ra ï x = t è 11 11 ø 4 î 2 2 æ 34 ö æ ö x =1Û ç- t÷+ ç ÷ ( )2 6 t +ç- t÷+ ç ÷ ç ÷ ( )2 11 4 t =1Û t = ± ç ÷ Mà è 11 ø è 11 ø 57 æ-34 44 - 6 11ö 34 æ - 44 6 - 11ö x = ç , , , , ÷ ç ÷x = ç , , , ÷ ç ÷ 1 2 ç ÷ è ø ç ÷ Vậy 57 57 57 57 5
è 7 57 57 57 ø là hai vec tơ cần tìm. Bài 7. Trong 3
¡ xét tích vô hướng Euclide. Hãy áp dụng quá trình Gram-Smidt để biến cơ sở { u,u,u 1 2
}3 thành cơ sở trực chuẩn:
u = 1;1;1 ,u = - 1;1;0 ;u = 1;2;1
u = 1;0;0 ,u = 3;7;- 2 ,u = 0;4;1 1 ( ) 2 ( ) 3 ( ) 1 ( ) 2 ( ) 3 ( ) a) b) Giải { u,u,u 1 2 3 }
a) Áp dụng quá trình trực giao hoá Gram-Smidt để biến cơ sở
thành cơ sở trực chuẩn.
Đặt v = u = (1,1,1) 1 1 u ,v u ,v 0 2 1 2 1 v =u - v 2 2 2 1 2 v v 3 1 1 0 v 1,1, 0 1,1,1 1,1,0 2 3 u , v 4 3 1 2 v 3 1 u ,v u ,v u , v 1 3 2 3 1 3 2 v =u - v - v 3 3 2 1 2 2 2 v v v 2 1 2 2 7 4 1 1 1 1 v 1, 2,1 1,1,1 1,1,0 , , 3 3 2 6 6 3
Chuẩn hóa cơ sở trực giao { v,v ,v 1 2 3 }
ta được cơ sở trực chuẩn là ìï 1 æ 1 1 öæ- 1 1 ö 1 æ 1 - 2 ü öï ï ç í ç , , , ÷çç , ,0 ,÷ç ÷ ÷ç , , ï÷ ÷ ý ï çè 3 3 3÷ øçè 2 2 ÷ ø çè 6 6 6÷ï ø ïî ïþ
b) Đặt v =u =(1,0,0) 1 1 u ,v u ,v 3 2 1 2 1 v =u - v 2 2 2 1 v 2 v 1 1 1 3 v 3,7, 2
1,0,0 3,7, 2 3,0,0 0,7, 2 2 1 u , v 0 3 1 2 v 1 1 u ,v u ,v u , v 26 3 2 3 1 3 2 v = u - v - v 3 3 2 1 2 2 2 Đặt v v v 53 1 2 2 0 26
182 52 30 105 v 0,4,1 1, 0,0 0,7, 2 0,4,1 0, , 0, , 3 1 53 53 53 53 53 { v,v,v 1 2 3 }
Chuẩn hóa cơ sở trực giao
ta được cơ sở trực chuẩn là ìï æ öæ ü ö - ï ïí( ) 7 53 2 53 ç ÷ 2 53 7 53 1,0,0 , 0 ç , , , 0 ç ÷ç , , ÷ï ÷ ç ÷ ý ï ç ï è 53 53 ç ÷ øçè 53 53 ÷ ÷ï ÷ ø î ïþ
Bài 8. Xét tích vô hướng Eulide trong 4
tìm một cơ sở trực giao và một cơ sở trực chuẩn của
không gian con U trong 4
trong các trường hợp:
U u ,u ,u u 1,1,0,0
u 1,1,1,1 u 0, 1,0,1 3 2 1 a) 1 2 3 với , , .
U u ,u ,u
u 1, 2,2, 1 u 1,1, 5,3 u 3,2,8, 7 3 2 1 b) 1 2 3 với , , .
x x x U
x , x , x , x 0 1 2 4 1 2 3 4
x x x 0 c) 2 3 4 Giải
a) Xây dựng cơ sở trực giao B 8 v u 1,1,0,0 1 1 Đặt u ,v 2 2 1 v u
.v 1,1,1,0 . 1,1,0,0 0,0,1,0 2 2 2 1 v 2 1 . u ,v u ,v 3 1 3 2 1 0 1 1 v u .v .v 0, 1,0,1 1,1,0,0 0,0,1,0 , ,0,1 3 3 2 1 2 2 v v 2 1 2 2 1 2 . 1 1 B v
1,1,0,0 ,v 0,0,1,0 ,v , ,0,1 1 2 3
Vậy cơ sở trực giao là 2 2 .
Đơn vị hóa các vector trực giao B Ta có: v 1 1 1 1 w . 1,1,0,0 , ,0,0 1 v 2 2 2 1 v 1 2 w . 0,0,1, 0 0,0,1,0 2 v2 1 v 1 1 1 6 6 6 3 w . , ,0,1 , ,0, 3 v 6 2 2 6 6 3 3 2 1 1 6 6 6 P w , ,0,0 ; w 0,0,1,0 , w , ,0, 1 2 3 2 2 6 6 3 Cơ sở trực chuẩn là v u 1;2;2; 1 1 1 b) Đặt . u ,v 2 1 v u λv , λ 1
v 2;3; 3;2 2 2 1 1 2 2 v1 . u ,v 3 2 v u
λ v λ v , λ 1
v 5;5;5; 5 3 3 1 2 2 3 2 2 3 v2 . 1;2;2;
1 ; 2;3; 3;2 ; 5;5;5; 5 là một cơ sở trực giao của U . 1 1 1
u ,u ,u 1;2;2; 1 ; 2;3; 3;2 ; 5;5;5; 5 1 2 3 10 26 10
là một cơ sở trực chuẩn của U . 9 x a 1 x x x 0 x x x 0
x a b 1 2 4 1 2 4 2 ,a b
x x x 0 x x 0 x a 2 3 4 1 3 3
c) Xét hệ phương trình: x b 4 .
u 1,1,1,0 ,u 0,1,0,1 1 2 Suy ra là cơ sở của U . v 3 3 3 1 v u ; e , , ,0 1 1 1 v 3 3 3 Đặt 1 . u ,v 2 1 1 2 1 v 15 2 15 15 15 2 v u v , , ,1 ; e , , , 2 2 2 1 2 v 3 3 3 v 15 15 15 5 2 1 . v ,v e ,e 1 2 1 2
Vậy cơ sở trực giao của U là
và cơ sở trực chuẩn của U là .
Bài 9. Xét tích vô hướng Euclide trong 4
R . Hãy bổ sung chúng để được một cơ sở trực giao của 4 R
a) u 1,1,1,1 , u 1,0, 1,0 1 2
u 0,0,1,1 , u 1,1,1, 1 1 2 b) . Giải u 0,0,1,0 u 0,0,0,1
u ,u ,u ,u 1 2 3 4 4 3
a) Ta bổ sung 2 véctơ và để hệ là một cơ sở của 4 R . Xây
v ,v ,v ,v 1 2 3 dựng cơ sở trực giao 4 . Đặt v u 1,1,1,1 1 1 u ,v 2 1 v u v u 1, 0, 1,0 . 2 2 1 2 v ,v 1 1 u , v u , v 1 1 1 3 1 3 2 v u v v 0, 0,1,0 1,1,1,1
1,0, 1, 0 1, 1,1, 1 . 3 2 1 2 v , v v , v 4 2 4 1 1 2 2 v ' 1, 1, , 1 1 3 Chọn lại u ,v u ,u u , v 4 1 4 2 4 3 v u v v v 4 4 1 2 3 v ,v v ,v v ,v 1 1 2 2 3 3 10 1 0 1 1 0,0,0,1 1,1,1,1 1,0, 1,0
1, 1,1, 1 0, 1, 0,1 4 2 4 2
Chọn lại v ' 0, 1,0,1 4 . u 0,0, , 1 0 , u 0,0,0,1
v ,v ,v' ,v' 1 2 3 3 4 Vậy ta bổ sung 2 véctơ thì hệ 4
là một cơ sở trực giao của 4 R .
b) Ta bổ sung 2 véctơ u 0,1,0,0 u 0,0,0,1
u ,u ,u , u 3 và 4
thì để hệ 1 2 3 4 là một cơ sở của 4 R
.Xây dựng cơ sở trực giao v ,v ,v , v 1 2 3 4 . v u 0,0,1,1 1 1 Đặt u ,v 2 1 v u
v u 1,1,1, 1 2 2 1 2 v ,v 1 1 u ,v u ,v 0 1 1 3 1 3 2 v u v v 0,1, 0,0 0,0,1,1 1,1,1, 1 1,3, 1,1 3 3 1 2 v ,v v ,v 2 4 4 1 1 2 2
v ' 1,3, 1,1 3 Chọn lại u , v u , u u ,v 1 1 1 1 4 1 4 2 4 3 v u u v v v 0,0,0,1 0,0,1,1 1,1,1, 1
1,3, 1,1 2,0, 1,1 4 4 4 1 2 3 v ,v v ,v v ,v 2 4 12 6 1 1 2 2 3 3 v' 2,0, , 1 1 4 Chọn lại
Vậy ta bổ sung 2 véctơ u 0,1,0,0 , u 0,0,0,1
v , v , v ' , v ' 3 4
thì hệ 1 2 3 4 là một cơ sở trực giao của 4 R .
Bài 10. Xét tích vô hướng Euclide trong 4
. Hãy tìm hình chiếu trực giao của vectơ x
lên không gian con U của 4 với x
1; 1;1;0 ,U u ,u ,u ;u 1,1,0,0 ,u 1,1,1,1 ,u 0, 1,0,1 1 2 3 1 2 3 a)
x x x
x 1,0,1, 2 ,U
x , x , x , x 0 1 2 4 1 2 3 4
x x x 0 b) 2 3 4 Giải a) Đặt v u 1,1,0,0 1 1 u ,v 2 1 2 v u .v 1,1,1,1 1,1,0,0 0,0,1,1 2 2 2 1 v 2 Ta có: 1 11 u ,v u ,v ' 3 2 3 1 1 1 1 v u .v .v 0, 1,0,1 0,0,1,1 1,1,0,0 1, 1, 1,1 3 3 2 2 2 1 v v 2 2 2 2 1 v 1, 1, 1,1 3 Chọn
U : v 1,1,0,0 ,v 0,0,1,1 ,v 1, 1, 1,1 1 2 3
Suy ra cơ sở trực giao của v 1 1 v 1 1 v 1 1 1 1 1 2 3 e , ,0,0 ; e 0,0, , ; e , , , 1 2 3 v 2 2 v 2 2 v 2 2 2 2 1 2 3
Suy ra cơ sở trực chuẩn của U : 1 1 1 1 1 1 1 1 W e , ,0,0 , e 0,0, , , e , , , 1 2 3 2 2 2 2 2 2 2 2
Hình chiếu trực giao của vectơ x lên không gian con U của 4
pr x x,e e x,e e x,e e w 1 1 2 2 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 3 0 , ,0,0 0,0, , , , , , , , 2 2 2 2 2 2 2 2 2 2 4 4 4 4 x b 1 x x x 0 x a b 1 2 4 2
U u 0,1,0,1 ,u 1,1,1,0 1 2
x x x 0 x b 2 3 4 3 x a b) 4 v u 0,1,0,1 . 1 1 Đặt Ta có: u ,v 1 1 1 ' 2 1 v u .v 1,1,1,0 0,1,0,1 1, ,1, v 2,1,2, 1 2 2 2 1 2 v 2 2 2 1
U : v 0,1,0,1 ,v 2,1,2, 1 1 2
Suy ra cơ sở trực giao của v 1 1 v 2 1 2 1 1 2 e 0, ,0, ; e , , , 1 2 v 2 2 v 10 10 10 10 1 2
Suy ra cơ sở trực chuẩn của U : 1 1 2 1 2 1 W e 0, ,0, , e , , , 1 2 2 2 10 10 10 10 12
Hình chiếu trực giao của vectơ x lên không gian con U của 4
pr x x,e e x,e e w 1 1 2 2 2 1 1 2 2 1 2 1 2 6 2 4 0, ,0, , , , , , , 2 2 2 10 10 10 10 10 5 5 5 5
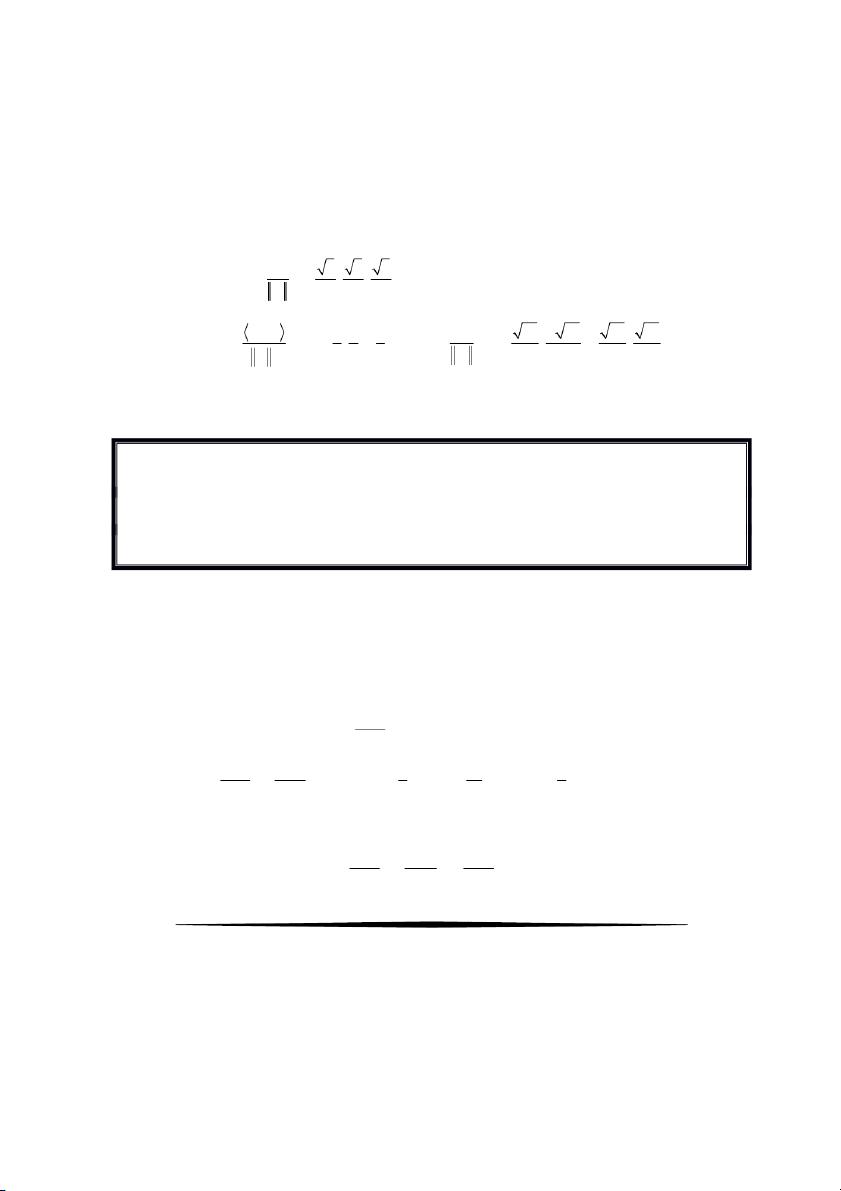
Bài 11. Xét không gian Euclide n
R với tích vô hướng chính tắc. Chứng minh rằng với mọi số thực 2 n n 2 x n .x
x ,x ,... ..,x i i 1 2
n . Chứng minh rằng i 1 i 1 Giải Xét không gian n
R với tích vô hướng Euclide.
Với x= (x ,x ,.. ...,x ) y= 1 2 n
được lấy tùy ý, ta chọn (1,1,......,1). n Þ < , x y>= . x 1+ x.1 . + .+ x.1= x å 1 2 n i i 1 =
Áp dụng bất đẳng thức Cauchy – Schwarzt cho tích vô hướng của hai vectơ trên ta được: 2 n n n 2 n n 2 2 x x .1 2
x .n x i i i i i 1 i 1 i 1 suy ra i 1 i 1
Bài 12.Xét không gian Euclide 3
¡ với tích vô hướng chính tắc
a) Cho P là mặt phẳng trong 3
¡ được xác định bởi phương trình x - 2x + x = 0 1 2 3 và p là
phép chiếu trực giao của 3
¡ xuống P. Hãy viết ma trận biểu diễn của p trong cơ sở chính tắc.
u = 1,0,1 , u = 2,1,0 , u = 1,1,1
B ={ u ,u ,u 1 2 3} 1 ( ) 2 ( ) 3 ( ) b) Cho các vectơ . Chứng minh rằng là cơ sở của 3
¡ . Xét xem B có phải là cơ sở trực chuẩn không. Nếu B không phải là cơ sở trực chuẩn
thì hãy sử dụng quá trình trực chuẩn hoá Gram – Schmidt để xây dựng từ B một cơ sở trực chuẩn
B ' ={e ,e ,e . 1 2 3 } Giải
a) Ta thực hiện qua các bước sau:
1- Tìm cơ sở của P .
2- Sử dụng quá trình Gram- Smidt để tìm cơ sở trực chuẩn của P . 13
3- Tìm hình chiếu của các vectơ trong cơ sở chính tắc lên mặt phẳng P , từ đó xác định B0 .
Bước 1 : Tìm cơ sở của P.
ìï x = 2a - b 1 ïïïí x = a 2 ïï
P được xác định bởi 1 x 2 2 x 3 x 0 Û ï x = b ïî a b Î ¡ 3 , Þ B 1
v 2,1,0,v2 1,0,1 là 1 cơ sở của P .
Bước 2 : Tìm cơ sở trực chuẩn của P. u ,v 2 1' 2 l =- = 2 1 u 1 v 2,1,0 u 5 Đặt ; u2 2 v 1 u ; 1' 1 2 u , ,1 , Þ 2 5 5 3 u 1,2,5 chọn .
Þ 2,1,0 , 1,2,5 là 1 cơ sở trực giao của P . ìï 2 æ 1 ö æ 1 2 5 ü öï B
ïíu çç ; ;0 ,u ÷ ç Þ = = ÷ = - ç ; ; ï÷ ÷ ý 0 1 2 ï çè 5 5 ÷ ø çè 30 30 30÷ï ø ïî
ïþ là một cơ sở trực chuẩn của P .
Bước 3: Tìm hình chiếu của các vectơ trong cơ sở chính tắc lên mặt phẳng P. æ ö æ ö æ ö
pr e = e u u + e u u ç ÷ ç ÷ = ç - ÷ - ç =ç ÷ ÷ ç ÷ ç ÷ ç - ÷ P ( 2 2 1 1 1 2 5 5 1 1 , , ; ;0 , , ; ; 1 ) 1 1 1 1 2 2 5è 5 5 ø 30 è 30 30 30÷ ø 6 çè 3 6÷ ø æ ö æ ö æ ö
pr e = e u u + e u u ç ÷ ç ÷ = ç + ÷ - ç =ç ÷ ÷ ç ÷ ç ÷ ç ÷ P ( 1 2 1 2 1 2 5 1 1 1 , , ; ;0 , , ; ; 2 ) 2 1 1 2 2 2 5è 5 5 ø 30è 30 30 30÷ ø 3 çè 3 3÷ ø æ ö æ ö æ ö
pr e = e u u + e u u ç ÷ ç ÷ = ç + ÷ - ç =ç ÷ ÷ - ç ÷ ç ÷ ç ÷ P ( 2 1 5 1 2 5 1 1 5 , , 0 ; ;0 , , ; ; 3 ) 3 1 1 3 2 2 è 5 5 ø 30è 30 30 30÷ ç ø è 6 3 6÷ ø 5 æ 1 1ö ç ÷ ç - ÷ ç 6 3 6÷ ç ÷ ÷ ç ÷ ç ÷ [ ] 1 1 1 ç ÷ p ç = ÷ ç ÷ 0 B ç 3 3 3 ÷ ç ÷ ç ÷ 1 1 5 ÷ ç ÷ ç- ÷ ç ÷ ç ÷ Vậy : è 6 3 6 ø
b) Chứng minh B là một cơ của 3 ¡
u = 1;0;1 , u = 2;1;0 u = 1;1;1 3 ( ) 1 ( ) 2 ( ) Với các vectơ và
Xét ma trận A lập bởi các vectơ u ,u ,u 1 2 3 . Ta có 14 1 2 1 det A = 0 1 1 = 2 ¹ 0 1 0 1
Do đó u ,u ,u 1 2
3 là các vectơ độc lập tuyến tính. Vậy B là một cơ sở của 3 ¡ .
*Xét tính trực chuẩn của B. u ;u = 2 ¹ 0 Ta có 1 2
nên B không phải là cơ sở trực chuẩn
*Xây dựng cơ sở trực chuẩn B1 : a =u = 1;0;1 1 1 ( ) Đặt u , a 2 2 1 l = - = - = - 1 1 2 a 2
Þ a = - a +u = 1;1;- 1 2 1 2 ( ) Ta có : a l = a +u 2 1 1 2 với 1 Ta có a = l a l + a +u 3 2 1 3 2 3 với : u ,a 2 u ,a 3 1 3 2 1 l = - = - = - 1; l = - = - 2 2 3 2 a 2 a 3 1 2 a = 1;- 2;- 1 3 ( ) Do a , a l a 1 2 vẫn trực giao với
3 , với l Î ¡ nên ta có thể chọn Đặt : a 1 1 e = = 1;0;1 1 ( ) a1 2 a 1 2 e = = 1;1;- 1 2 ( ) a 3 2 a 1 3 e = =- 1; - 2;- 1 3 ( ) a 6 3
Vậy ta có cơ sở trực chuẩn B1 cần xây dựng là : ìï 1 1 1 ü ï B ïí e 1;0;1 , e 1;1; 1 , e 1; 2; 1 ï = = = - =- - - ý 1 1 ( ) 2 ( ) 3 ( ) ïî 2 3 6 ï ï ïþ
Bài 13. Trong không gian Euclide với tích vô hướng chính tắc cho các vector u ( 2,1, 2,4), u (
2,1, 1, 6),u ( 2,3, 4, 8)
W u , u ,u 1 2 3 . Gọi 1 2
3 là không gian con của sinh
ra vởi các vector và W là không gian con của trực giao với W
a) Tìm một cơ sở của mỗi không gian W và W .
b) Cho . Tìm hình chiếu trực giao pr d u,W
W(u) của u lên W và tính khoảng cách từ u đến W . Giải
a) Lập ma trận A là ma trận vectơ dòng của hệ {u ,u ,u } 1 2 3 15 2 æ 1 - 2 4 ö 2 æ 1 - 2 4 ö 2 æ 1 - 2 4 ö ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ ç ÷ A ç = - ç 2 1 - 1 - 6÷® 0 ç ÷ ç 2 - 3 - 2÷® 0 ç ÷ ÷ ÷ ç 2 - 3 - 2÷ ÷ ÷ ç ÷ ç ÷ ç ÷ çç-è 2 3 - 4 - 8÷ø 0 ççè 4 - 6 - 4÷ø 0 ççè 0 0 0 ÷ ÷ ÷ ÷ ø
r(A) = 2 < 3 nên hệ {u ,u ,u } phụ thuộc tuyến tính, do đó cơ sở của W là B = {u } 1 2 3 1 2 ,u
ìï x =a - 5b ï 1
ïïïx =6a +2b 2 ï Û í ; , a b Î ¡ ìï , x u = 0
ìï - 2x +x - x - 6x =0 ï x = 4a ï ^ ï 1 3
x= (x ,x ,x ,x )Î W Û í 1 2 3 4 ï Û í ï 1 2 3 4 ï ï ïï x =2b Gọi , x u = 0
- 2x +3x - 4x - 8x =0 2 ïî ïî 1 2 3 4 4 ïî W^ { = (a- 5 , b 6a 2 + , b 4 , a 2 ) b | , a b Î ¡ }= ( < 1,6,4,0),(- 5,2,0,2) >
Hệ B'={(1,6,4,0),(- 5,2,0,2)} độc lập tuyến tính nên nó là cơ sở của W^.
b) Tìm cơ sở trực chuẩn của W
v = u = 2;1;- 2;4 1 1 ( ) Đặt u, v 2 1 l =- 2
Ta có v = u +l v; v ^ v | v | 2 2 1 sao cho 2 1 . Ta suy ra : 1 2
Với u ,v =- 25; | u | = 25Þ l =1Þ v = (0,2,- 3,- 2) 2 1 1 2
Ta có v =5; v = 17 1 2 ìï 2 æ 1 - 2 4ö æ 2 - 3 - 2 ü öï B ïí e ç = =ç ; ; ; ,e ÷ ÷ = 0 çç ; ; ; ï÷ ÷ý 1 2 ï ç ÷ è ø ç ÷
Vậy cơ sở trực chuẩn của W là 5 5 5 5 è î 17 17 17 ï ø ï ïþ * Tìm pr (u) w Ta có , u e =5; , u e = 17 1 2 Vậy pr ( ) u = , u e e + , u e e = (2,3,- 5,2) W 1 1 2 2 Suy ra ( d , u )
W = u- pr ( )
u = (3,2,2,- 1) = 18= 3 2 w
Bài 14. Cho A M K n , chứng minh rằng:
a) A trực giao khi và chỉ khi T A trực giao.
b) A trực giao khi và chỉ khi 1 A trực giao. 16 c) ,
A B trực giao thì AB trực giao.
d) A trực giao thì A 1 hoặc A 1 . Giải T T T T T A T A T A T T
A I A
a) Ta có: A trực giao A A AA I n n trực giao.
b) Ta có: A trực giao T T
A A AA I n T A A 1 T AA 1 In T
A 1 A A T A 1 1 1 In
A T A 1 A 1 1 1
A T In 1 A trực giao. T T T T c) Vì ,
A B trực giao nên ta có: A A AA B B B B I n. Do đó, ta có:
ABT AB T T B A T
AB B T A A T B B T
BB B T B B T BB In .
AB AB T AB T T B A A T BB T
A A T A A T A T A A T AA I n . Vậy, AB trực giao.
d) Vì A trực giao nên ta có: 2 A 1 T T A A I A A I 1 T A A 1 A 1 n n A 1 .
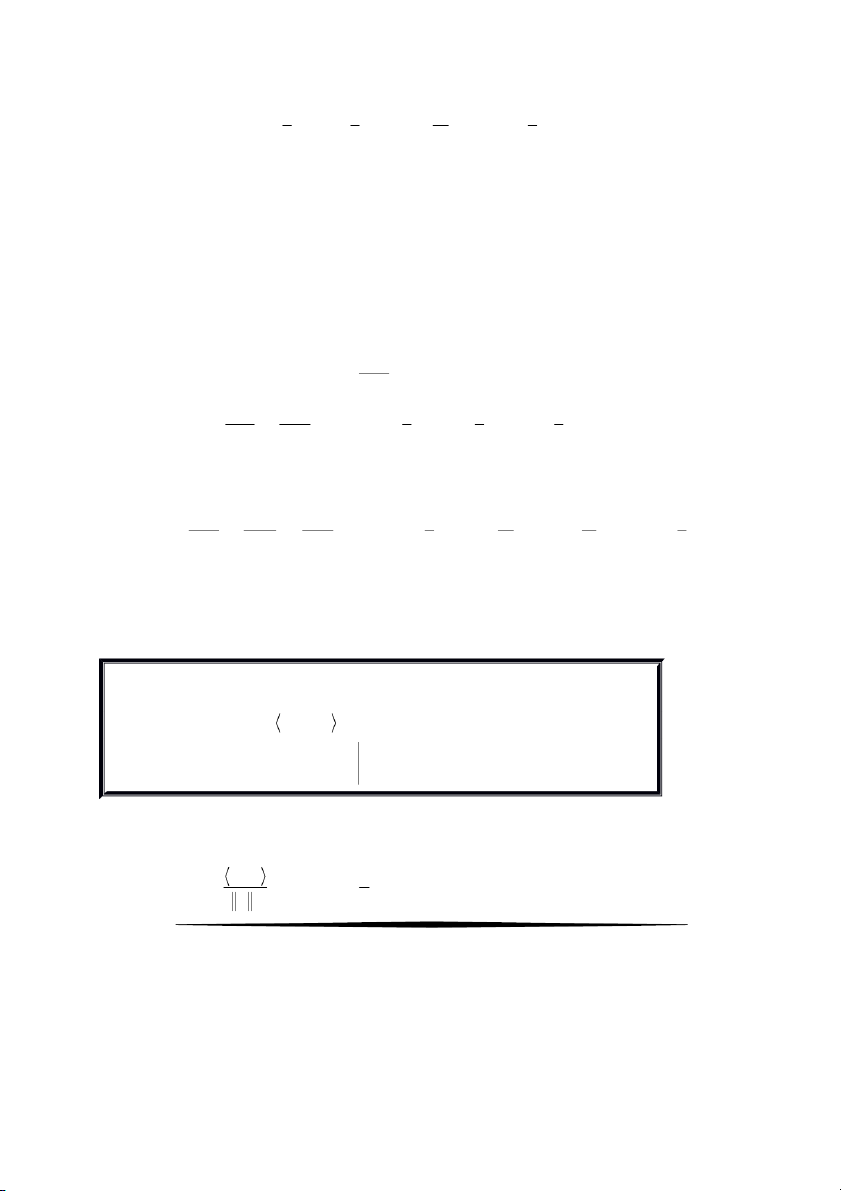
Bài 17. Tính góc giữa u= 3t- 1 và 2 v 2
t t 1 trong không gian các đa thức P3 với tích vô hướng 1 f,g = f ( ) t . ( g ) t dt ò-1 . Giải 17 8 = 1 3 , u v = (3t- ) 1 ( 2 2t +t- ò ) 1 dt Theo đề bài - 1 . 1 2 2 u
P P =<u,u >= (3t - 1) dt =8
Trong không gian đa thức P ta có: ò 3 - 1 . Þ Pu = P 8 . 1 8 2 2 2 v P P = v < ,v >= (2t t + - 1) dt = ò Tương tự - 1 5 . 8 Þ Pv = P 5 .
Góc giữa hai vecto u và v là: 8 u ,v 5 3 cos j = = = u . v 8 3 8. 5 0 Þ j » 41 48' 1 2 1 2 , x y x y x y .
Bài 18. Chứng minh rằng 4 4 Giải
Xét tích vô hướng , :V V , R x
, y V ta có: 2 2 1 1 VP
x y ,x y
x y ,x y 4 4 1 1
x y,x y
x y,x y 4 4 1
x x y x x y y y 1 , , , ,
x,x y,x x, y y, y 4 4 1 1 .2 , x y .2 , x y 4 4 , x y VT .
Bài 19. Cho V ,1 V2 là hai không gian con của không gian Euclide V . Chứng minh rằng ( ^ ^ V V V^ V^ + = Ç V V V^ V . ^ Ç = + 1 )2 1 2 và ( 1 2) 1 2 Giải 18 ^ ^ ^
a) Ta chứng minh ( V+ V = V Ç V 1 2) 1 2 ^ ^ ^
Chứng minh ( V+ V Ì V Ç V 1 2) 1 2 ^
" xÎ ( V+ V ," yÎ V+ V
"v Î V, "v Î V 1 2) 1 2 ta có = 0. Ta xét 1 1 2 2 ta có ìï á , x v ñ=á ,
x v +qñ=qdo v +qÎ V V + ìï x v ^ ìï x Î V^ 1 1 1 1 2 1 1 ^ ï ï ï í Û í Û í
Û xÎ V^Ç V ^ hay "xÎ V +V Þ xÎ V^Ç V ^ ^ 1 2 ( 1 )2 1 2 ï á , x v ñ=á , x v q + ñ q = do v q + Î V V + ï x v ^ ï x Î V 2 2 2 1 2 2 2 ïî ïî ïî ^ ^ ^
Vậy ( V+ V Ì V Ç V 1 )2 1 2 (1) ^ ^ ^ + É Ç Chứng minh ( V V V V 1 2) 1 2 ìï xÎ V^
ìï x ^v "v Î V ìïá , x vñ= 0 ^ ^ 1 1 ( 1 1 ) ï ï 1 x V V ï ï Î Ç Û í Û í Û í Þ á , x vñ+á , x vñ= 0Þ á , x v + vñ= 0 1 2 ï xÎ V^ ï ïî
ï x ^v ( "v Î V) 1 2 1 2 ïá , x v ñ= 0 2 ï 2 2 2 2 ïî î Þ á , ^
x yñ=0, "y=v +v Î V +V Þ x Î V +V 1 2 1 2 ( 1 2) ^ ^ ^ ^ ^ ^
Vậy ( V+ V É V Ç V
V+ V = V Ç V 1 )2 1
2 (2) Từ (1) và (2) ta có ( 1 2) 1 2 ^ ^ ^
b) Ta chứng minh ( VÇ V = V + V 1 2) 1 2 ^ ^ ^
Chứng minh ( VÇ V Ì V + V 1 2) 1 2 ^
"xÎ ( V Ç V ,"yÎ V Ç V
"v Î V, " v Î V 1 2)
( 1 2) ta có = 0. Ta xét 1 1 2 2 ta có ìï Î ìï xÎ V^ Do y ( V V ) y V1 ï Î Ç Û í 1 ïí
Û xÎ ( V^ Ç V^ ^ 1 2 ) 1 2 ï yÎ V ï xÎ V 2 ïî mà = 0 nên 2 ïî x V^
V ^ do V^ V ^ V^ V ^ Þ Î + Ç Ì + 1 2 ( 1 2 ) ( 1 2 ) ^ ^ ^
Vậy ( VÇ V Ì V + V 1 )2 1 2 (1) ^ ^ ^ Ç É + Chứng minh ( V V V V 1 )2 1 2 ìï x á ,vñ=0," Î ( ^ ^ ) ( v V x V V x x x x V^ , x V^) 1 1 1 1 ï Î + Þ = + " Î " Î Þ í 1 2 1 2 1 1 2 2 ï x
á ,vñ= 0," v Î V ï 2 2 2 2 î ìï x á , yñ=0
y V V y V1 1 ï 1 2 íï Ta có yV x á ,yñ= 0 2 ï nên từ trên ta có 2 î á , ^ x yñ= x
á +x ,yñ= x á ,yñ+ x
á ,yñ= 0+0= 0Þ xÎ V Ç V 1 2 1 2 ( 1 2 ) Do đó 19 ^ ^ ^
Vậy ( VÇ V É V + V 1 )2 1 2 (2) ^ ^ ^
Từ (1) và (2) ta có ( VÇ V = V + V . 1 2) 1 2
Bài 20. Xét không gian con V của 4
R được cho bởi hệ phương trình
2x x 3x x 0 1 2 3 4
3x 2x 2x 0 1 2 4
3x x 9x x 0 1 2 3 4 .
Tìm hệ phương trình xác định V . Giải
*Tìm cơ sở của không gian V
2x x 3x x 0 1 2 3 4
3x 2x 2x 0 1 2 4
3x x 9x x 0 1 2 3 4 . x 6b 1 x x 3x x 0 x 9 b a 1 2 3 4 2 ,( , a b ).
x 9x x 0 x b 2 3 4 3 Phương trình trở thành: x a 4
v 0;1;0;1 ,v 6;9;1;0 1 2 Cơ sở của V là: . x
x ; x ; x ; x . 1 2 3 4 *Xét vectơ 4 x R nên , x v 0 1 x x 0 2 4 , x v 0
6x 9x x 0 Để x V
thì x V nên 2 1 2 3
là hệ phương trình xác định V .
Bài tập 24. Cho là một toán tử trực giao 3
với ma trận biểu diễn theo cơ sở chính tắc 2 2 1 1 A 2 1 2 3 1 2 2
Hãy viết ma trận chính tắc Jordan của và tìm một cơ sở trực chuẩn để có dạng chính tắc Jordan Giải 20