Tiểu luận Giải bài tập các chương trong giáo trình bài giảng môn Kỹ thuật số | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58737056
B ộ GiÆo d ục và Đào t ạ o H
Ọ C VI Ệ N C NG NGH Ệ BƯU CHÍNH VIỄ N THNG
CƠ SỞ T Ạ I THNH PH Ố H Ồ CH˝ MINH
Khoa: Cng Ngh ệ Thng Tin 2
Ngnh: Cng Ngh ệ Thng Tin
Gi ả i bi t ập các chương trong Giáo trình Bi Gi
ả ng K ỹ Thu ậ t S ố
Gi ả ng viên hướ ng d ẫ n Th ự c hi ệ n b ở i Nhóm 1 Nguyễ
n Lan Anh D21CQCN01-N
Nguy ễ n Ph ạ m M ẫ n Uy
Nguy ễ n Duy B ả o
Võ Gia B ả o
Nguy ễn Đứ c Kh ả i Hoàn
Ph ạm Văn Hùng
Nguy ễ n Nh ậ t Minh Tr ầ n Th ị Thu ỳ Ngân
Nguy ễn Bình Phương
Tr ầ n Vi ệ t Quang
Nguy ễ n Ng ọ c Quý
T ạ Hoàng Trung Sơn
Tr ầ n Thi ệ n T ấ n
Lê Đứ c Thái Lưu Văn Thành
Dương Hoàng Thiệ n
Đào Nguyễ n Duy Tiên
Nguy ễ n Ng ọ c Thiên Phúc (N
hóm trưở ng) LỜI MỞ ĐẦU
Cùng với sự tiến bộ của khoa học và công nghệ, các thiết bị iện tử ang và sẽ tiếp tục ược ứng
dụng ngày càng rộng rãi và mang lại hiệu quả cao trong hầu hết các lĩnh vực kinh tế kỹ thuật
cũng như ời sống xã hội. Việc xử lý tín hiệu trong các thiết bị iện tử hiện ại ều dựa trên cơ sở
nguyên lý số. Bởi vậy việc hiểu sâu sắc về iện tử số là iều không thể thiếu ược ối với kỹ sư
ngành Điện - Điện tử, Điện tử - Viễn thông, cũng như Công nghệ thông tin. Nhu cầu hiểu biết
về Điện tử số không phải chỉ riêng ối với các kỹ sư các ngành nói trên mà còn cần thiết ối với
nhiều cán bộ kỹ thuật các chuyên ngành khác có ứng dụng iện tử.
Bài tập của 4 chương ược bố cục như sau: Chương 1: Hệ ếm Chương 2: Cổng logic
Chương 3: Mạch logic tổ hợp
Chương 4: Mạch logic tuần tự
Nhằm mục ích ưa ến càng nhiều cách giải và cách tiếp cận các bài toán trong môn Kỹ thuật số,
chúng em hy vọng bài tiểu luận này sẽ giúp ích cho mọi người nhiều hơn trong việc học và giải bài tập Kỹ thuật số.
Tuy rằng chúng em ã rất cố gắng, song các thiếu sót còn tồn tại trong bài tiểu luận là iều khó
tránh khỏi. Chúng em rất mong sự óng góp ý kiến của cô cùng bạn bè. Chúng em xin chân thành cảm ơn! Mục lục:
Chương 1: Hệ đếm ............................................................................................ 1 lOMoAR cPSD| 58737056
C u 1: .............................. 1
C u 5: .............................. 5
C u 9: ............................... 8
C u 2: .............................. 2
C u 6: .............................. 6
C u 10:: ........................... 9
C u 3: .............................. 2
C u 7: .............................. 7
C u 11: ............................. 9
Chương 2: Cổng logic ............................................................................................12
C u 4: .............................. 5
C u 8: .............................. 7
C u 12: ........................... 11
C u 1: ............................ 12
C u 10: .......................... 20
C u 19: ........................... 28
C u 2: ............................ 13
C u 11: .......................... 20
C u 20: ........................... 28
C u 3: ............................ 14
C u 12: .......................... 21
C u 21: ........................... 30
C u 4: ............................ 16
C u 13: .......................... 22
C u 22: ........................... 31
C u 5: ............................ 17
C u 14: .......................... 23
C u 23: ........................... 32
C u 6: ............................ 17
C u 15: .......................... 24
C u 24: ........................... 33
C u 7: ............................ 18
C u 16: .......................... 24
C u 25: ........................... 34
C u 8: ............................ 18
C u 17: .......................... 26
C u 26: ........................... 36
C u 9: ............................ 20
C u 18: .......................... 27
Chương 3: Mạch logic tổ hợp ...............................................................................37
C u 1: ............................ 37
C u 7: ............................ 39
C u 13:. .......................... 43
C u 2: ............................ 37
C u 8: ............................ 39
C u 14:. .......................... 44
C u 3:……. ...................... 37
C u 9:. ........................... 40
C u 15: ........................... 44
C u 4: ............................ 37
C u 10: .......................... 41
C u 16: ........................... 45
C u 5: ............................ 38
C u 11: .......................... 41
C u 17:. .......................... 47
C u 6:. ........................... 39
C u 12:. ......................... 42
C u 18:. .......................... 49
Chương 4: Mạch logic tuần tự ..............................................................................50
C u 1: ............................
C u 5: ............................
C u 10: .......................... 58 C 50 52
u 11: ........................... 58
C u 2: ............................
C u 12: ........................... 59 50
C u 6:. ........................... 53
C u 13: ........................... 60
C u 3: ............................
C u 7: ............................ 53
C u 14: ........................... 60 51
C u 8:. ........................... 54
C u 15: ........................... 61
C u 4: ............................
C u 9: ............................ 57 51
Chương 1: Hệ ếm
Câu 1: Phân biệt các hệ ếm nhị phân, hệ thập phân, hệ 8 và hệ 16. Hệ thập phân Hệ nhị phân Hệ 8 Hệ 16
Downloaded by Bao Ngoc (baongoc32@gmail.com) Cơ số
Hệ cơ số 10, có Hệ cơ số hai, chỉ
Hệ 8 gồm 8 ký Hệ gồm 16 ký 10 ký hiệu từ 0
gồm hai ký hiệu hiệu: 0, 1, 2, 3, ến 9. hiệu là 0, 1, 2, 3, 0 và 1 4, 5, 6 và 7 nên
cơ số của hệ là 8 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Là hệ cơ số 16. Trọng số/ biểu 10n là trọng số Trọng số của hệ Mỗi ký hiệu diễn trong hệ nhị của hệ Mỗi ký hiệu là 2n trong hệ 8 có thể phân. trong hệ 8 có thể thay thế bằng 3
bit trong hệ nhị thay thế bằng 4 phân bit trong hệ nhị phân Ưu iểm
Tiện dụng, ược Dễ thể hiện bằng Biểu diễn các số nhị phân rất lớn sử dụng trong các thiết bị cơ, ời sống hàng iện
ngày biểu diễn ngôn ngữ của gọn các mạch logic, các thiết bị tính toán hiện ại - ngôn ngữ máy. Nhược iểm Hệ biểu diễn dài Do có nhiều ký hiệu nên việc thể hiện bằng thiết bị kỹ thuật sẽ khó khăn và phức tạp.
Câu 2: Hãy viết lại 16 trạng thái ầu tiên của hệ ếm nhị phân. Hệ thập lục ph n Hệ thập ph n Hệ nhị ph n 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 A 10 1010 B 11 1011 C 12 1100 D 13 1101 E 14 1110 F 15 1111
Câu 3: Đổi các số thập phân sau sang các hệ khác: a) N10 = 75
Đổi số 75 10 sang hệ nhị phân 75 : 2 = 37 dư 1 37 : 2 = 18 dư 1 18 : 2 = 9 dư 0 9 : 2 = 4 dư 1 4 : 2 = 2 dư 0 2 : 2 = 1 dư 0 1 : 2 = 0 dư 1  7510 =1001011 2 Đổi số 75 10 sang hệ 8 75 : 8 = 9 dư 3 9 : 8 = 1 dư 1 1 : 8 = 0 dư 1  7510 =113 8
Đổi số 75 10 sang hệ 16 75 : 16 = 4 dư 11B 4 : 16 = 0 dư 4B  7510 =BBH
b) N10 = 157 Đổi số 157 10 sang hệ nhị phân 157 : 2 = 78 dư 1 78 : 2 = 39 dư 0 39 : 2 = 19 dư 1 19 : 2 = 9 dư 1 9 : 2 = 4 dư 1 4 : 2 = 2 dư 0 2 : 2 = 1 dư 0 1 : 2 = 0 dư 1  15710 =10011101 2
Đổi số 157 10 sang hệ 8 157 : 8 = 19 dư 5 19 : 8 = 2 dư 3 2 : 8 = 0 dư 2  15710 =235 8
Đổi số 157 10 sang hệ 16 157 : 16 = 9 dư 13  D 9 : 16 = 0 dư 9  7510 =9DH 16 c) N10 = 1976;
• Đổi sang hệ nhị phân 1976 : 2 = 988 dư 0 988 : 2 = 494 dư 0 494 : 2 = 247 dư 0 247 : 2 = 123 dư 1 123 : 2 = 61 dư 1 61 : 2 = 30 dư 1 30 : 2 = 15 dư 0 15 : 2 = 7 dư 1 7 :2 = 3 dư 1 3 : 2 = 1 dư 1 1 : 2 = 0 dư 1  111 1011 1000 B
• Đổi sang hệ thâp lục phân 1976 : 16 = 123 dư 8 123 : 16 = 7 dư 11 => B 7 : 16 = 0 dư 7  7B8 H d) N10 = 2711 Giải:
• Đổi sang hệ nhị phân 2711 : 2 = 1355 dư 1 1355 : 2 = 677 dư 1 677 : 2 = 338 dư 1 338 : 2 = 169 dư 0 169 : 2 = 84 dư 1 84 : 2 = 42 dư 0 42 : 2 = 21 dư 0 21 : 2 = 10 dư 1 10 : 2 = 5 dư 0 5 :2 = 2 dư 1 2 : 2 = 1 dư 0 1 :2 = 0 dư 1  1010 1001 0111 B
• Đổi sang hệ thập lục phân 2711 : 16 = 169 dư 7 169 : 16 = 10 dư 9 10 : 16 = 0 dư 10  A97 H
Câu 4: Đổi các số nhị phân sau sang hệ thập phân: a) N2 = 1011010;
N2 = 1011010 = 26 + 24 + 23 + 21 = 90  10110102 -> 9010 b) N2 = 111000111;
N2 = 111000111 = 28 + 27 + 26 + 22 + 21 +20 = 455  1110001112 -> 45510 c) N2 = 100001111; N = = + + + + + + + + =8 7 6 5 2
100001111 2 0 0 0 0 2 2 2 2 256 8 4 2 1 2712 4 3 2 1 0
+ + + + = 10 d) N2 = 101010101; N = = + + + + + + + + =8 7 6 5 4 2
101010101 2 0 2 0 2 0 2 0 1 256 64 16 4 1 3412 3 2 1 0+ + + + = 10
Câu 5: Đổi số nhị phân sau sang dạng bát phân:
a) 0101 1111 0100 1110 Binary 0101 1111 0100 1110 Hexadecimal 5 F 4 E Đáp án: 5F4E (H)
b) 1010 1100 1001 1000 Binary 1010 1100 1001 1000 Hexadecimal A C 9 8 Đáp án: AC98 (H)
c) 1111 1010 1101 1001 Binary 0101 1111 0100 1110 Hexadecimal F A D 9 Đáp án: FAD9 (H)
d) 001 000 110 111 000 011 001 1 0000 1106 1117 0000 0111
Vậy 1000110111000011 2 =107601 8
Câu 6: Thực hiện phép tính hai số hệ 16 sau:
a) 132,4416 + 215,0216. 132,4416 + 215,0216 347,4616 b) 13E16 + 2FD16 13E16 + 2FD16 43B16 c) 3B916 + 7A316. 3B916 * B + A = 21 + 7A316 21 16 5 1 B5016
3 + 7 = 10 -> nhớ 1 => 11 = B d) 9B516 + 6D816. 11 + ↓9B516 * B + D = 24 6D816 24 16 8 1 16 16 0 1
108D16 9 + 6 = 15 -> nhớ 1 => 16 ->
Câu 7: Thực hiện phép tính hai số hệ 8 phân sau: a) 132,448 + 215,028 Giải 132,44 +215,02 347,46
-Ta có các tổng số ều nhỏ hơn bằng 7 nên cộng trực tiếp như hệ thập phân b) 6378 + 2458 637
-Ta có 7+5=12 không có trong hệ 8 nên ta phải chia cho 8 ược 1 dư 4 viết 4 xuống tổng nhớ 1.
Tương tự ta có 3+4+1=8 không có trong hệ 8 nên chia cho 8 ược 1 dư 0 ghi 0 nhớ 1. Ta có
6+2+1=9 không có trong hệ 8 nên chia cho 8 ược 1 dư 1 ghi vào tổng c) 4108 + 7238 410
Ta có 4+7 =11 không có trong hệ 8 do ó ta chia 8 ược 1 dư 3. Ghi 13 vào tổng tương ứng với trọng số ó d) 2158 + 6548. 215
Câu 8: Thực hiện phép cộng hai số có dấu sau theo phương pháp bù 1:
a) 0.101 11112 + 0.100 11102 0 1 0 1 1 1 1 1 + 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 1
Kiểm tra: 0.101 11112 = 9510 0.100 11102 = 7810
0.101 11112 + 0.100 11102 = 0. 101011012 = 17310 Lại
có: 9510 + 7810 = 17310 => Kết quả úng.
b) 1.010 11002 + 1.001 10002 1 0 1 0 1 1 0 0 + 1 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 0 Bù tròn → + 1 0 1 0 0 0 1 0 1
c) 1.111 10102 + 1.101 10012 1 1 1 1 1 0 1 0 + 1 1 0 1 1 0 0 1 1 1 1 0 1 0 0 1 1 Bù tròn → + 1 1 1 0 1 0 1 0 0
d) 1.000 11012 + 1.100 00112 1 0 0 0 1 1 0 1 + 1 1 0 0 0 0 1 1 1 0 1 0 1 0 0 0 0 Bù tròn → + 1 0 1 0 1 0 0 0 1
Câu 9: Thực hiện phép cộng hai số có dấu sau theo phương pháp bù 2:
a) 0.101 11112 + 0.100 11102 ->0.0101 11112 (+9510 ) + ->0.0100 11102 (+7810)
0.101011012 (+17310) (Kết quả úng)
b) 1.010 11002 + 1.001 10002 𝑏ù 2
1.010 11002(-8410 ) → 0.10101002(+8410 ) -> 0010101002(+8410 ) + + + 𝑏ù 2
1.001 10002(-10410 )→ 0.11010002(+10410 ) ->0011010002(+10410 )
1.01111002(kết quả sai) 0101111002(+18810 )
c) 1.111 10102 + 1.101 10012 Ta có: 1.111 10102 =-610 1.101 10012=-3910 -6-39=-4510 Có 1.111 10102 bù -2 0000 0110 +0010 0111 + 1.101 10012 bù -2 1101 0011 0010 1101 =4510
Có : bù -2(1101 0011)= bù -1(1101 0011 ) +1 = 0010 1100 +1 = 0010 11012 =4510  1. 101 00112 = 4510
d) 1.000 11012 + 1.100 00112 1000 1101 (-115) + 1100 0011 (-61) 101010000 (-176)
Câu 10: Hãy viết 4 số kế tiếp trong các dãy số sau:
a) 110012 110102 110112 …. …. …. ….
Các số kế tiếp là: 111002 , 111012 , 111102 , 111112 ( 2710 , 2810 , 2910 , 3010 )
b) 6248 6258 6268 …. …. …. …. Các
số kế tiếp là: 627, 630, 631, 632
c) 9D16 9E16 9F16 …. …. …. …. Các
số kế tiếp là: A0, A1, A2, A3
Câu 11: Hãy chuyển ổi các số sau sang biểu diễn tương ương khác:
a.Z16 = 24AE16 → A10 → A2
A10 = 24AE16 = 2.163+4.162+10.16+14.160=939010 A2 9390 : 2 = 4695 dư 0 4695 : 2 = 2347 dư 1 2347 : 2 = 1173 dư 1 1173 : 2 = 586 dư 0 586 : 2 = 293 dư 0 293 : 2 = 146 dư 1 146 : 2 = 73 dư 0 73 : 2 = 36 dư 1 36 : 2 = 18 dư 0 18 :2 = 9 dư 0 9 : 2 = 4 dư 1 4 :2 = 2 dư 0 2 :2 = 1 dư 0 1 :2 = 0 dư 1  100100101011102 B
b. Z16 = A6F216 → A10 → A2
Z16 =A6F216=10.163+6.162+15.16+2.160=4273810 Z16 =A6F216 Có : A16=10102 616=01102 F16=11112 216=00102
 A6F216 =1010 0110 1111 00102
c.A10 = 311810 → Z16 → A2 Z16 : 3118 : 16 = 194 dư 14  E 194 : 16 = 12 dư 2 12 : 16 = 0 dư 12  311810 =C2E 16 C2E16 = 1100 0010 11102
d.A10 = 978510 → Z16 → A2 9785 : 16 = 611 dư 9 611 : 16 = 38 dư 3 38 : 16 = 2 dư 6 2 : 16 = 0 dư 2  Z16 =2639 9875 : 2 = 4892 dư 1 4892 : 2 = 2446 dư 0 2446 : 2 = 1223 dư 0 1223 : 2 = 611 dư 1 611 : 2 = 305 dư 1 305 : 2 = 152 dư 1 152 :2 = 76 dư 0 76 : 2 = 38 dư 0 38 :2 = 19 dư 0 19 :2 = 9 dư 1 9 : 2 = 4 dư 1 4 :2 = 2 dư 0 2 : 2 = 1 dư 0 1 :2 = 0 dư 1 A2=1001 1000 111001
Câu 12: Hãy tính hiệu hai số nhị phân sau và kiểm tra lại kết quả ở dạng thập phân:
a) 11 0101 – 10 0101 - 11 0101 10 0101 ( Hệ 2 ) 01 0000
Đổi sang hệ 10 : 11 0101 = 20 + 22 + 24 + 25 = 53 10 0101 = 20 + 22 + 25 = 37 01 0000 = 24 = 16 Vậy 53 – 37 =16 ( úng )
b) 1001 0110 - 10 0110 0 1 1 1 0 0 0 0 11210 1 0 0 1 0 1 1 0 - 15010 1 0 0 1 1 0 - 3810
Chương 2: Cổng logic
Câu 1: Chuyển các hàm logic sau sang
dạng chuẩn của minterm?
a) A.B.(CD+A.B)
A.B.(̅C. D +̅̅̅̅̅AB̅̅)
= A.B(C. D̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅. A. B̅̅)=A.B.̅CD̅̅̅̅̅̅̅̅̅̅=A.B.C̅̅̅̅̅+ABD̅̅̅̅̅
= A.B.C̅̅̅̅̅(D + D̅̅̅̅̅)+A.B.D̅̅̅̅̅(C+C̅̅̅̅̅)
= A.B.C̅̅̅̅̅. D + A. B. C̅̅̅̅̅. D̅̅̅̅̅+A.B.C, D̅̅̅̅̅+A.B.C̅̅̅̅̅. D̅̅̅̅̅
b) A.(B+A.C).(A+B.C)
A(B+̅A. C̅̅̅)(A + B. C̅̅̅̅̅̅) = A(B+A̅̅̅̅̅+C).(A̅̅̅̅̅. B. C̅̅̅)=0
c) A.B.A.C.A.D+B.C.B.C+C.D
A. B. A. C. AD̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + ̅B. C. B. C̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + CD̅̅̅̅̅̅̅̅̅̅= ̅A. B. A. C. AD̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + ̅B. C̅̅̅̅̅̅̅̅̅̅ + B. C̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + CD̅̅̅̅̅̅̅̅̅̅=1
= A+A̅̅̅̅̅ = A(B+B̅̅̅̅̅)(C+C̅̅̅̅̅)(D + D̅̅̅̅̅) + A̅̅̅̅̅(B+B̅̅̅̅̅)(C+C̅̅̅̅̅)(D + D̅̅̅̅̅)
= A.B.C.D+A.B. C̅̅̅̅̅.D+A. B̅̅̅̅̅. C. D+A. B̅̅̅̅̅. C̅̅̅̅̅. D+A.B.C. D̅̅̅̅̅+A.B. C̅̅̅̅̅. D̅̅̅̅̅+A.B. C̅̅̅̅̅. D̅̅̅̅̅ + A.B̅̅̅̅̅.C.D+A. B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅+A̅̅̅̅̅. B. C.
D+A̅̅̅̅̅. B. C̅̅̅̅̅. D+A̅̅̅̅̅. B̅̅̅̅̅. C. D+A̅̅̅̅̅. B̅̅̅̅̅. C̅̅̅̅̅. D+A̅̅̅̅̅. B. C. D̅̅̅̅̅ + A.̅ B. C̅̅̅̅̅. D̅̅̅̅̅ + A̅̅̅̅̅. B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅
d) (A+B).(B+C).(C+D)
(A+B̅̅̅̅̅)(B+C̅̅̅̅̅)(C+D̅̅̅̅̅) = A.B.C + A.B. D̅̅̅̅̅ + A. C̅̅̅̅̅. D ̅+ B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅
= A.B.C(D+D̅̅̅̅̅) + A.B. D̅̅̅̅̅(C + C̅̅̅̅̅) + A. C̅̅̅̅̅. D̅̅̅̅̅. (B + B̅̅̅̅̅) + B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅(A + A̅̅̅̅̅)
= A.B.C.D + A.B.C. D̅̅̅̅̅ + A. B. C̅̅̅̅̅. D̅̅̅̅̅ + A. B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅ + A̅̅̅̅̅. B̅̅̅̅̅. C̅̅̅̅̅. D̅̅̅̅̅
Câu 2: Chuyển các hàm logic sau sang dạng chuẩn của maxterm a) AB CD AB. .( + . )
`p dụng định l Dermogan ta c : =AB CD A B. .( + + ) =ABCD A B..( + ) =AB C D.( + )
= +(A BB CC DD B AA CC DD C D AA BB+ + )( + + + )( + + + )
= + +(A B CC DD A B CC DD B A CC DD B A CC DD+ )( + + + )( + + + )( + + + )
(C D A BB C D A BB+ + + )( + + + )
= + + +(A B C DD A B C DD A B C DD A B C DD)( + + + )( + + + )( + + + )
(B A C DD B A C DD B A+ + + )( + + +
)( + + +C DD B A C DD)( + + + )
(C D A B C D A B C D A B C D A B+ + + )( + + + )( + + + )( + + + )
= + + +(A B C D A B C D A B C D A B C D A B C D)( + + + )( + + + )( + + + )( + + + )
(A B C D A B C D A B C D B A C D B A C D+ + + )( + + + )( + + + )( + + + )( + + + )
(B A C D B A C D C D A B C D A B C D A B+ + + )( + + + )( + + + )( + + + )( + + + ) (A B C D+ + + )
=M0.M M M M M M M M M M M M1.2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 15
= (0,1,2,3,4,5,6,7,8,9,10,11,15) b) A(B+AC)(A+BC) = A(B+A+C)A(B+C ) = A(B+C)A(B+C ) = A(B+C+AA)A(B+C+AA ) =(A+BB+CC )(AA+B+C)(A+BB+CC)(B+C+AA )
=( A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C )
( A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C )
=( A+B+C)(A+B+C)(A+B + C)(A+B+C)(A+B+C)(A+B+C)(A+B+C)(A+B+C) = (0 ,1,2,3,4,5,6, 7) c)
ABACAD BCBC CD. . + . +
M BCBC. = 0nŒn BCBC. =1
Ta được : ABACAD BCBC CD. . + . +
=ABACAD.. + +1 CD=1 = F ABC D( , , ,
) = (0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15) d) (A+B)(B+C)(C+D)
=(A+B+CC+DD)(AA+B+C+DD)(AA+BB+C+D)
=(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)
(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)
=(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)
(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D)(A+B+C+D) = (1,2,3,4,5,6,7,9,10,11,13)
Câu 3: Rút gọn hàm sau theo phương pháp dùng bảng Cácnô?
a) F (A, B, C, D) = ∏ (1, 4, 6, 9, 10, 11, 14, 15)
F (A, B, C, D) = (A+C)(A+B+D)(B+C+D)
b) F (A, B, C, D) = ∑ (3, 7, 8, 9, 11, 12)
F (A, B, C, D) = ACD+ABC+ABD+ACD
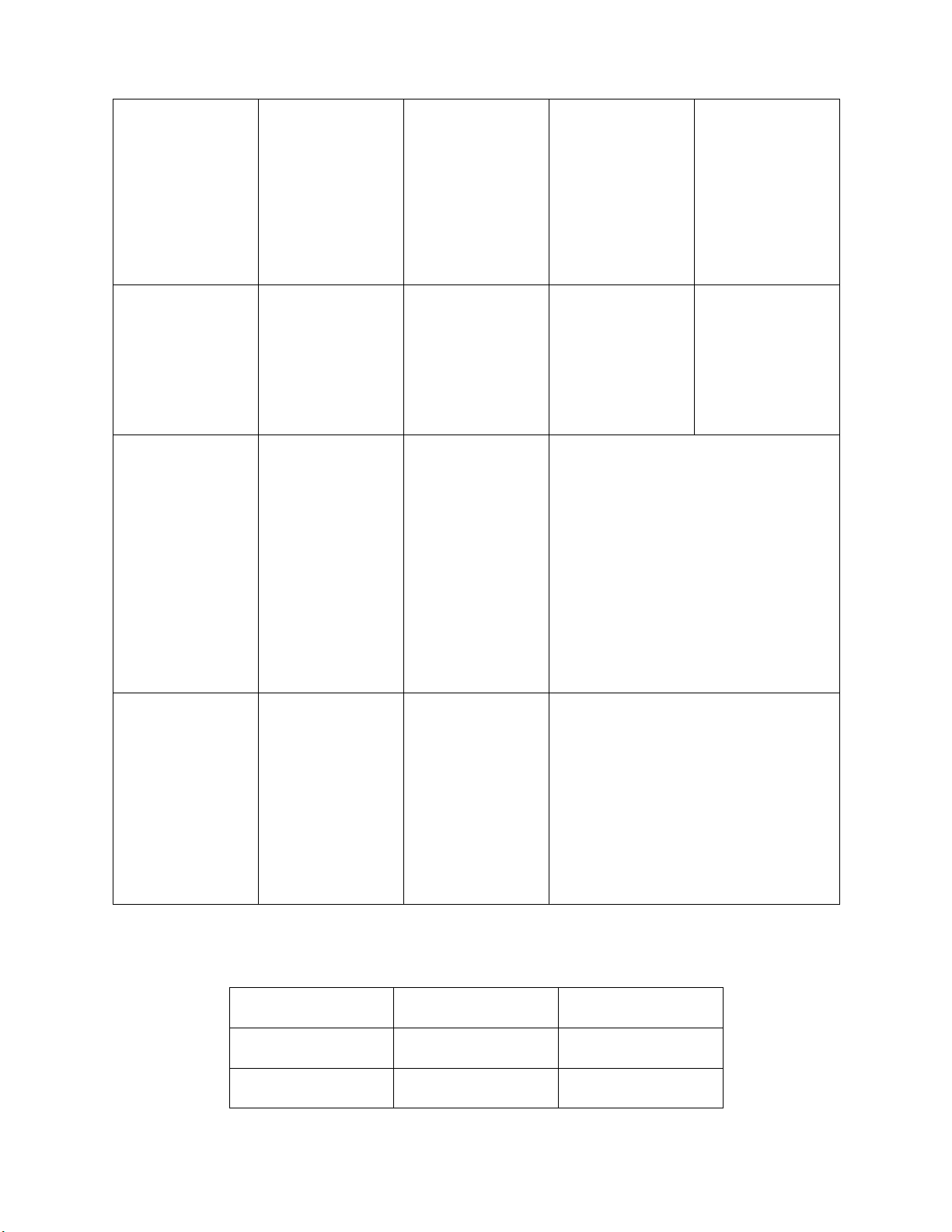
c) F (A, B, C, D) = ∑ (3, 6, 8, 9, 11, 12) + ∑d (0, 1, 2, 13, 14, 15)
F (A, B, C, D) = AB+BCD+AC+AD
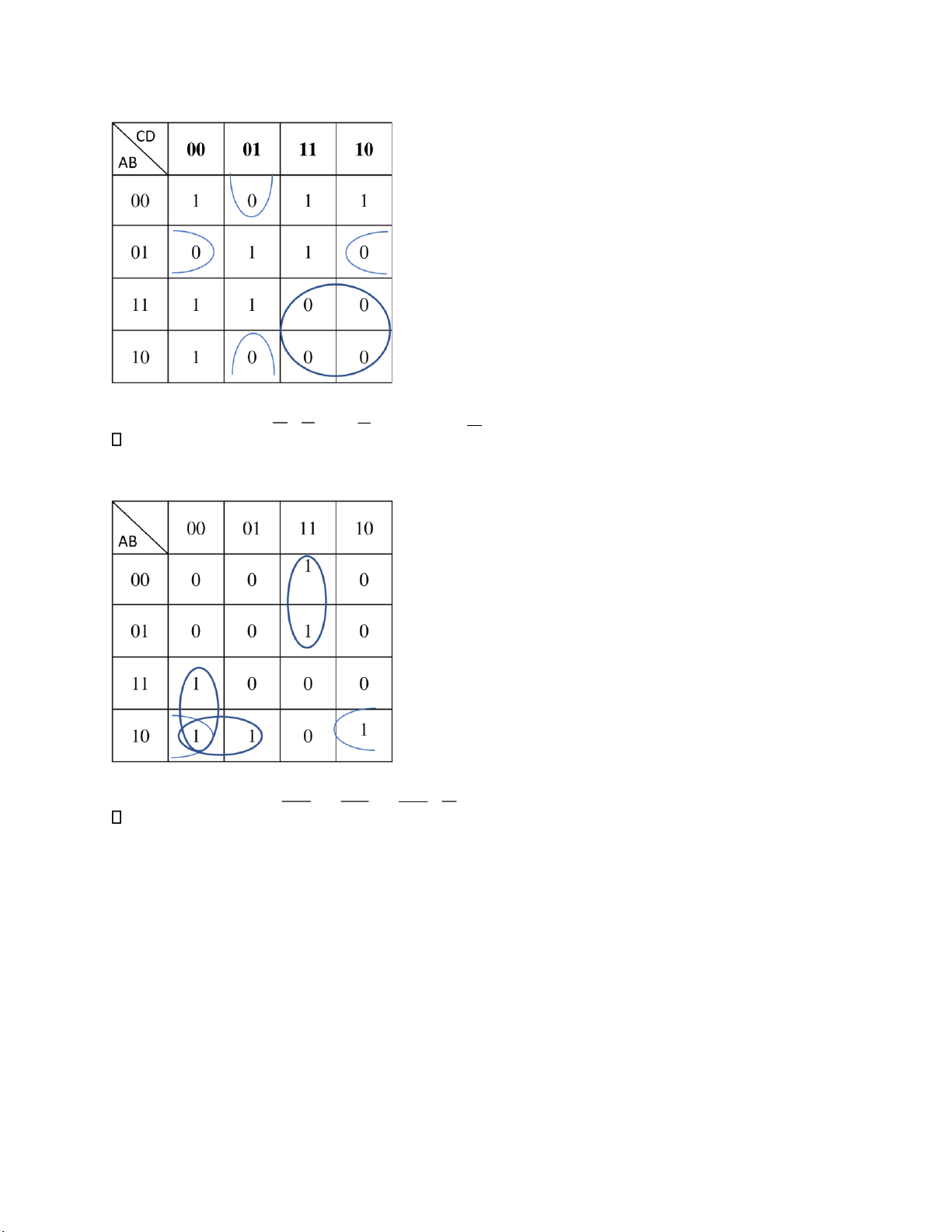
d) F (A, B, C, D) = ∑ (0, 1, 4, 9, 12, 13) + ∑d (2, 3, 6, 10, 11, 14)
F (A, B, C, D) = AB+ACD+ABC+ABD
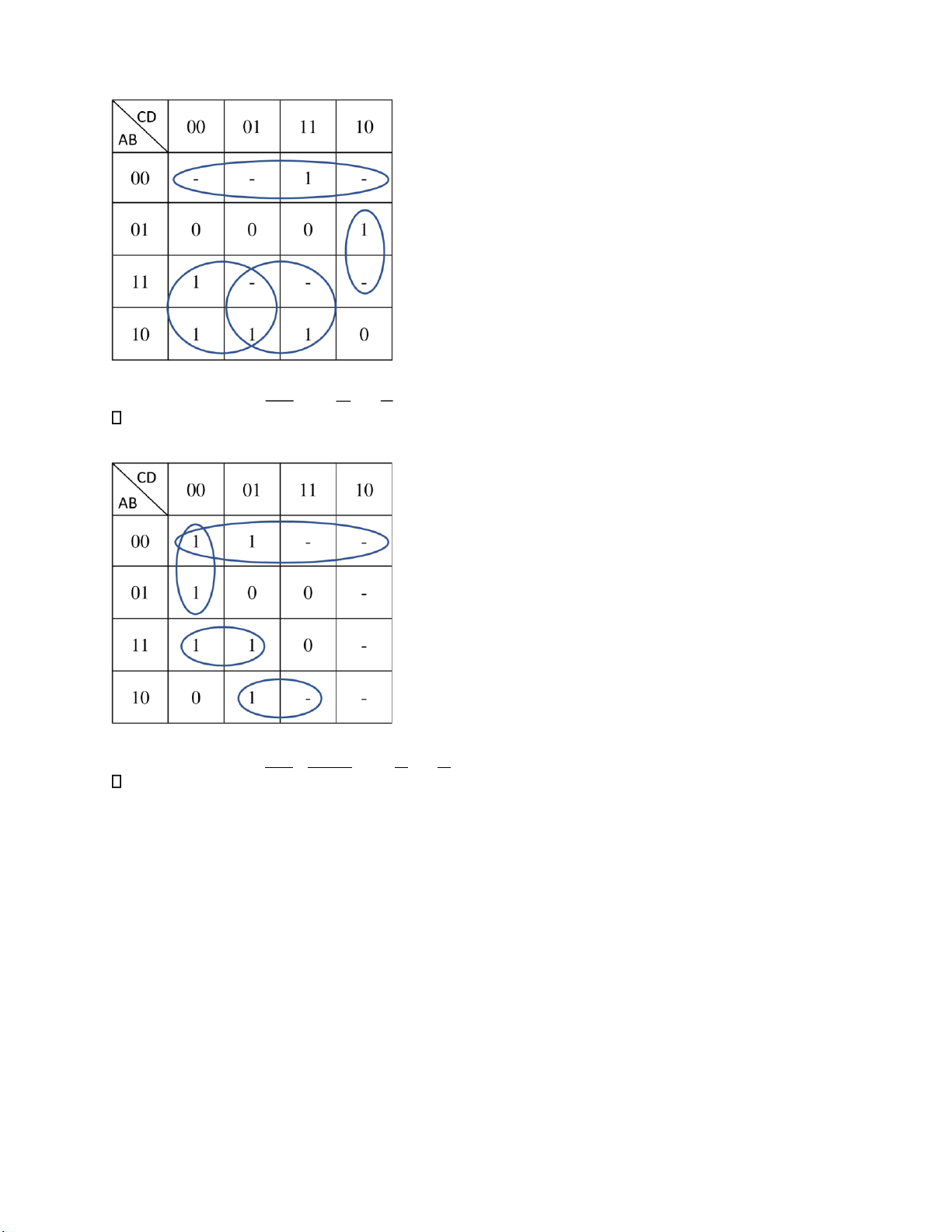
Câu 4: Rút gọn hàm sau theo phương pháp dùng bảng Cácnô?
a) F (A, B, C, D) = ∑ (3, 6, 8, 9, 11, 12) + ∑d (0, 1, 2, 13, 14, 15)