Tìm giới hạn bằng máy tính cầm tay – Nguyễn Văn Phép

TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY
GIẢI PHÁP THỰC HIỆN BẰNG MÁY TÍNH CẦM TAY (MTCT)
ĐỂ TÍNH GIỚI HẠN
Kiến thức giới hạn dãy số và giới hạn hàm số là cơ sở của của hai phép tính
đạo hàm và tích phân ở phổ thông trung học .Kiến thức vế giới hạn không những
khó đối với người học mà còn khó đối với người dạy .Trong tình hình hiện nay để
cập nhật phù hợp thi trắc nghiệm .Để giúp giăm bớt khó khăn nên tôi soạn đề tài này.
Giải pháp thực hiện bằng máy tính cầm tay (MTCT) để tính giới hạn Dãy số:
Quy ước : trong máy tính không có biến n nên ta ghi x thay cho n .
• Gặp hằng số : C 10 10 ,C 20
10 …. đọc là (dấu của C) nhân vô cực với C
là hằng số ( chú ý có thể lớn hơn 10). ví dụ -5 10
10 ( đọc là âm vô cực ghi  )
• Gặp hằng số C 12 10 
đọc là 0 ( Chú ý số mũ có thể nhỏ hơn – 10 ). ví dụ: 15 12 10  đọc là 0
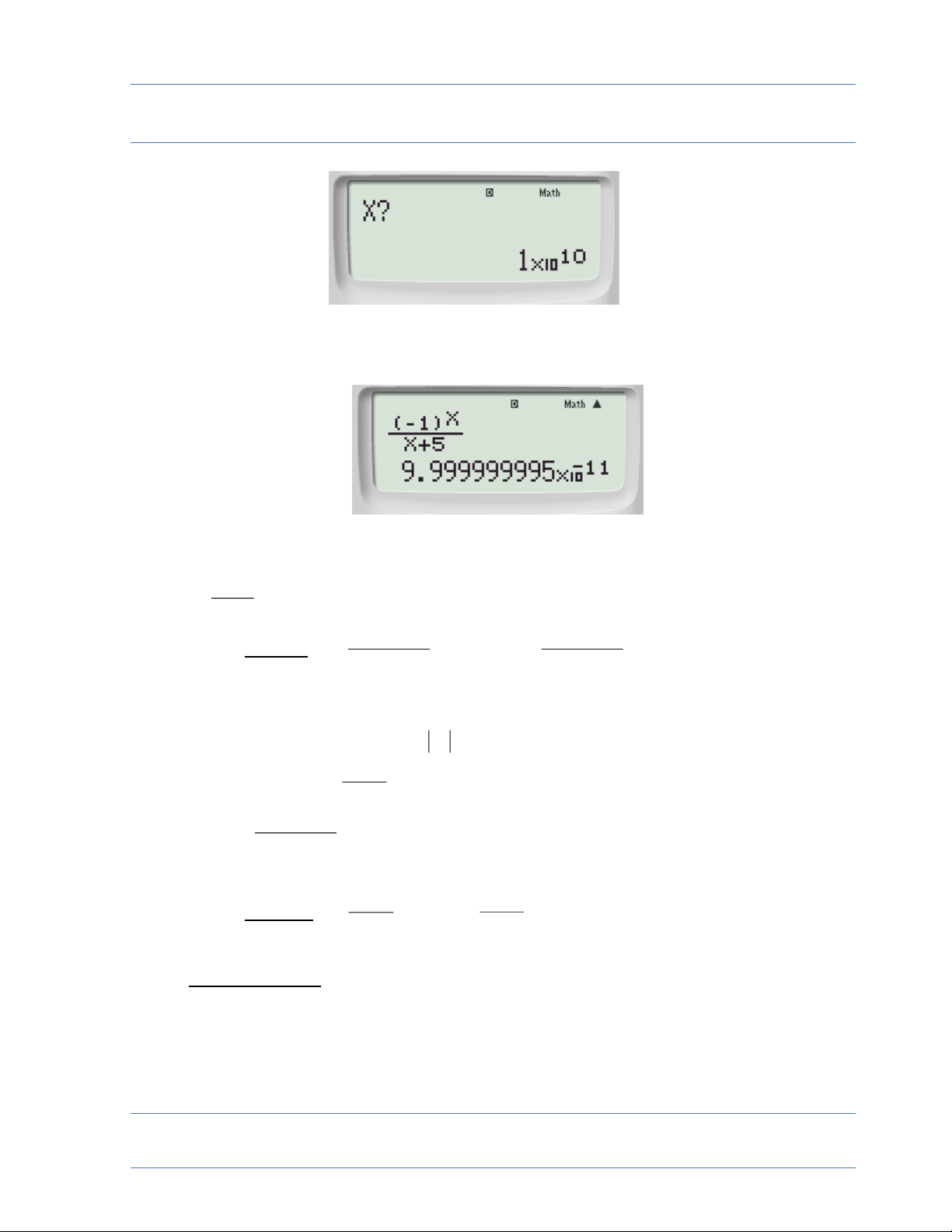
A. Dãy có giới hạn là 0 n x •  1  1 Ví dụ 1: lim máy ghi : calc x ? nhập 10 10  n  5 x  5 Kq : 11 9 . 9 9999995 10  ta đọc là 0 Cách bấm máy:
 Nhập vào máy tính: (sau khi đã mở máy) a(z1)^Q)RQ)+5
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác ở
dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)
Giáo viên thực hiện: Nguyễn Văn Phép Trang 1
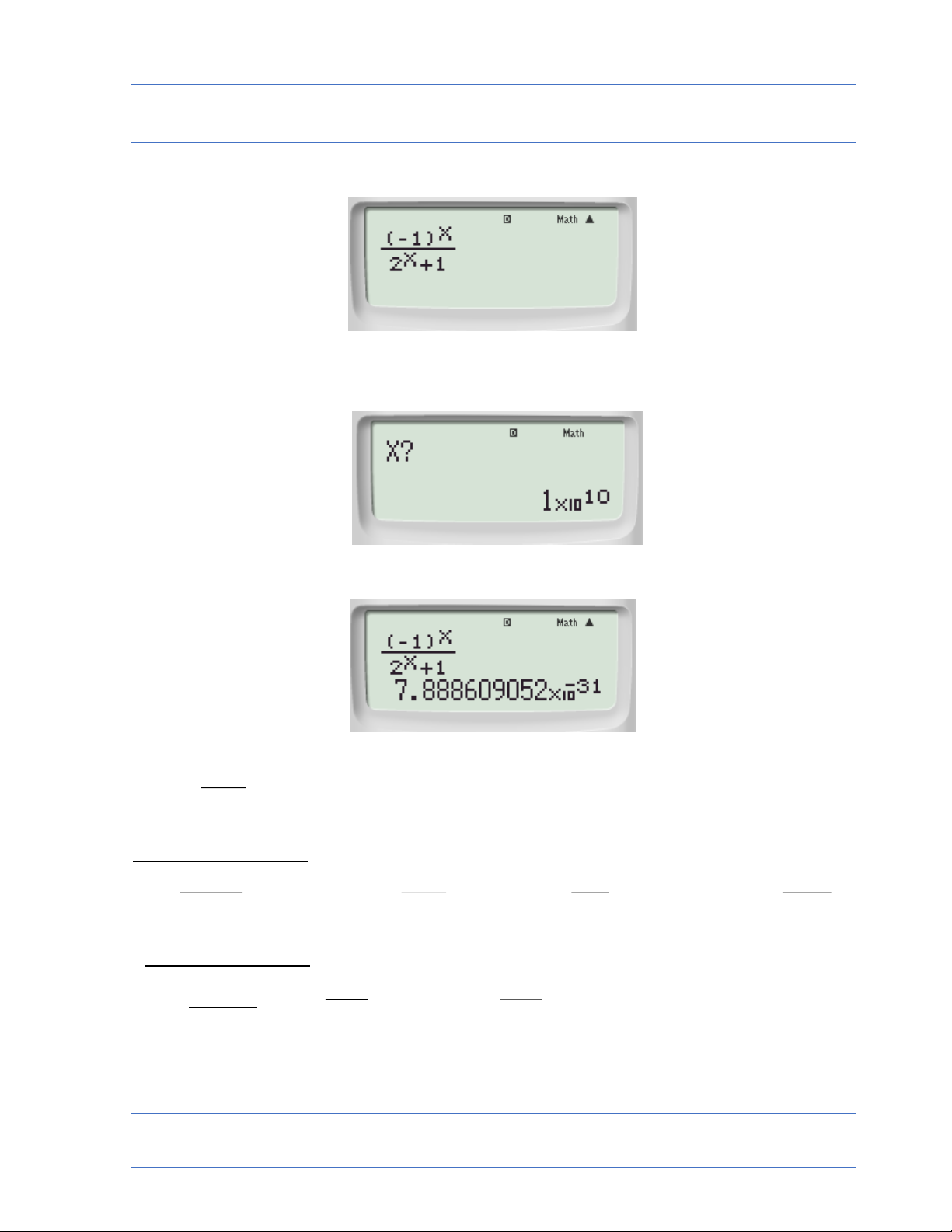
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  Ta nhập tiếp: 10^10=
Màn hình sẽ xuất hiện: Kq : 11 9 . 9 9999995 10  ta đọc là 0  n Vậy 1 lim  0 n  5 n x • ( ) 1 cosn ( ) 1 cos x Ví dụ 2: lim nếu nhập
calc như trên máy sẽ 2 n  1 2 x  1 Math ERROR
- Vận dụng định lý 1 Nếu u  v với mọi n và lim v  0 thì lim u  0. n n n n - 1 Ta chỉ cần ghi calc x ? nhập 10 10  kết quả 20 1 10  đọc là 0 2 x  1  n Vậy ( ) 1 cosn lim  0 2 n  1 n x •  1 ( ) 1 Ví dụ 3: lim máy ghi calc x ? 100 kq: 31 8 . 3 4430 26 ... 10 x 2n  1 2 x  1 đọc là 0 Cách bấm máy:
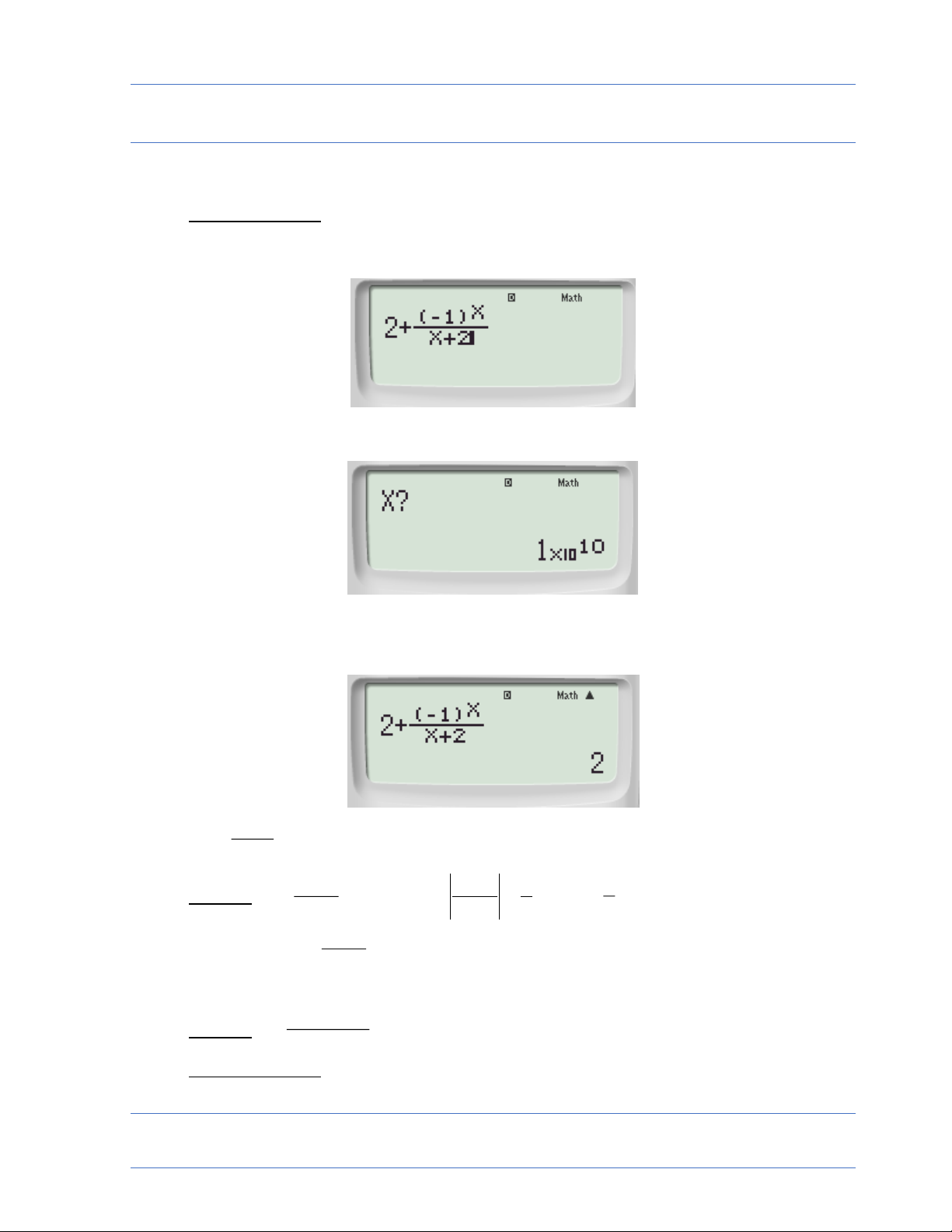
 Nhập vào máy tính: (sau khi đã mở máy) a(z1)^Q)R2^$Q)+1
Giáo viên thực hiện: Nguyễn Văn Phép Trang 2
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác ở
dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)  Ta nhập tiếp: 100=
Màn hình sẽ xuất hiện:  x Vậy 1 lim  0 2 x  1
BÀI TẬP TƯƠNG TỰ : Tìm các giới hạn   n 1. (n  ) 1 ( ) 1 sin n cos2n lim 2. lim 3. lim 4. lim 2 n 2n  1 n  5 3 n  1
B.Giới hạn hữu hạn : n n •   1   1
Ví dụ 1: lim 2   máy ghi: 2   n  2  n  2 calc x ? nhập 10 10  kq là 2
Giáo viên thực hiện: Nguyễn Văn Phép Trang 3
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY Cách bấm máy:
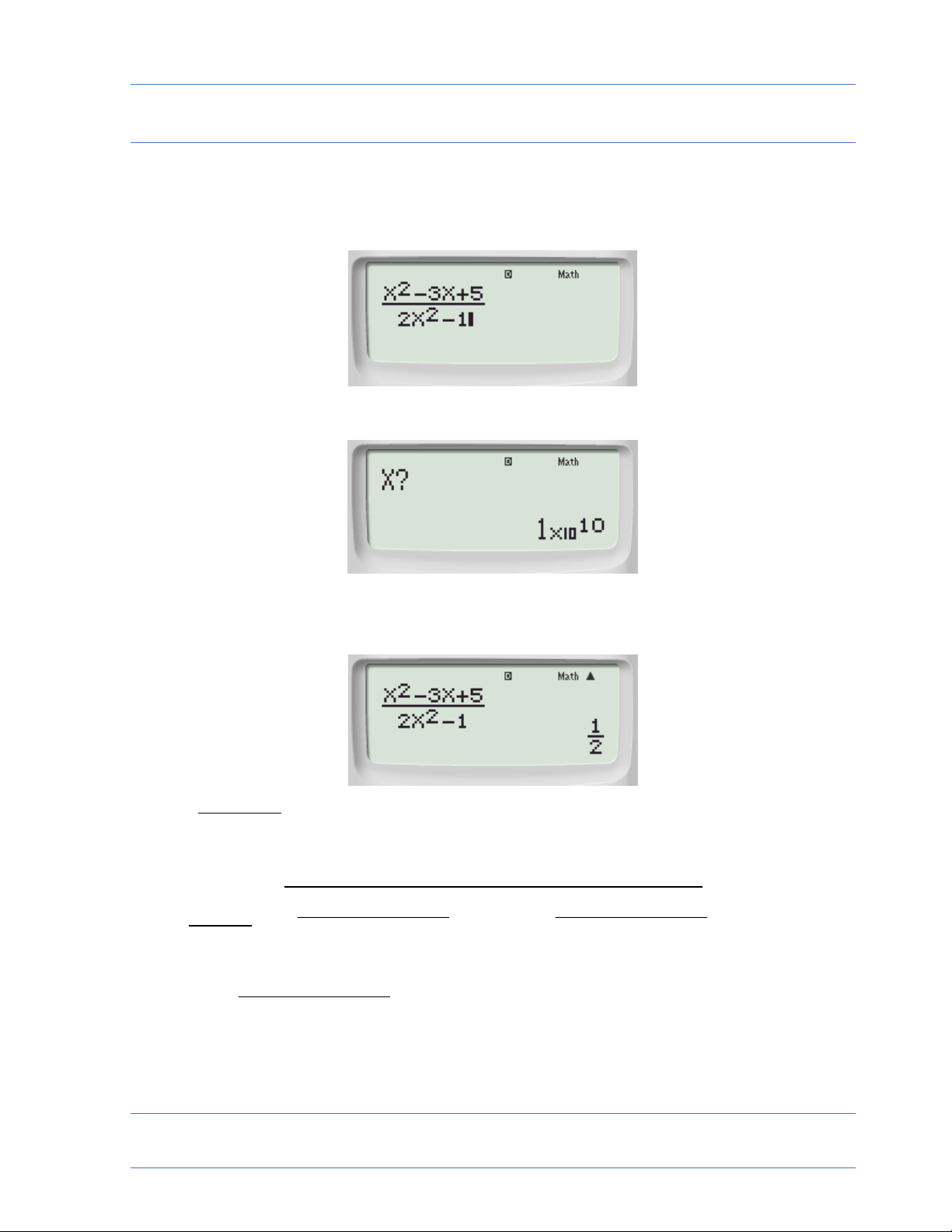
 Nhập vào máy tính: 2+a(z1)^Q)RQ)+2
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác ở
dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)  Ta nhập tiếp: 10^10=
Màn hình sẽ xuất hiện:   1n  vậy lim 2   =2  n  2  •  sin 3n  sin n 3 1 1 Ví dụ 2: lim 1  1  vì
 mà lim  0 khi đó lim (-1)=-1  4n  4n n n  n  nên sin 3 lim  1  1   4n  2 • n  3n  5 Ví dụ 3 lim 2 2 n 1 Cách bấm máy:
Giáo viên thực hiện: Nguyễn Văn Phép Trang 4
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  Nhập vào máy tính: aQ)^2$p3Q)+5R2Q)^2$p1
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác
ở dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)  Ta nhập tiếp: 10^15=
Màn hình sẽ xuất hiện: 2 n  n  vậy 3 5 lim = 0.5 2 2 n 1
Với cách bấm máy tương tự cho các ví dụ sau: 3 2 3 2 •
 2n  4n  3n  3
 2n  4n  3n  3 Ví dụ 4 : lim máy ghi 3 n  5n  7 3 n  5n  7 calc x ? nhập 15 10  Kq là – 2 3 2
 n  n  n  Vậy 2 4 3 3 lim  2  3 n  5n  7
Giáo viên thực hiện: Nguyễn Văn Phép Trang 5
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY X 1  X • 2  3 11 1
Ví dụ 5: máy ghi lim calc x=100 kq
3X 2  2 X 3  4 9 n 1   n   Vậy : 2 3 11 1 lim 
3n2  2n3  4 9 n X • 13.3  15 13  3  15 Ví dụ 6: lim máy ghi
calc X ? nhập 100  n n 3.2  4.5 X X 3  2  4 5 . 17 1 . 3 9755... 10 x đọc là 0 . n  Vậy 13.3 15 lim
 0 ( chú ý dấu nhân không ghi dấu chấm ) 3.2n  . 4 5n
C. Giới hạn vô cực : 3 3 •
 n  3n  5
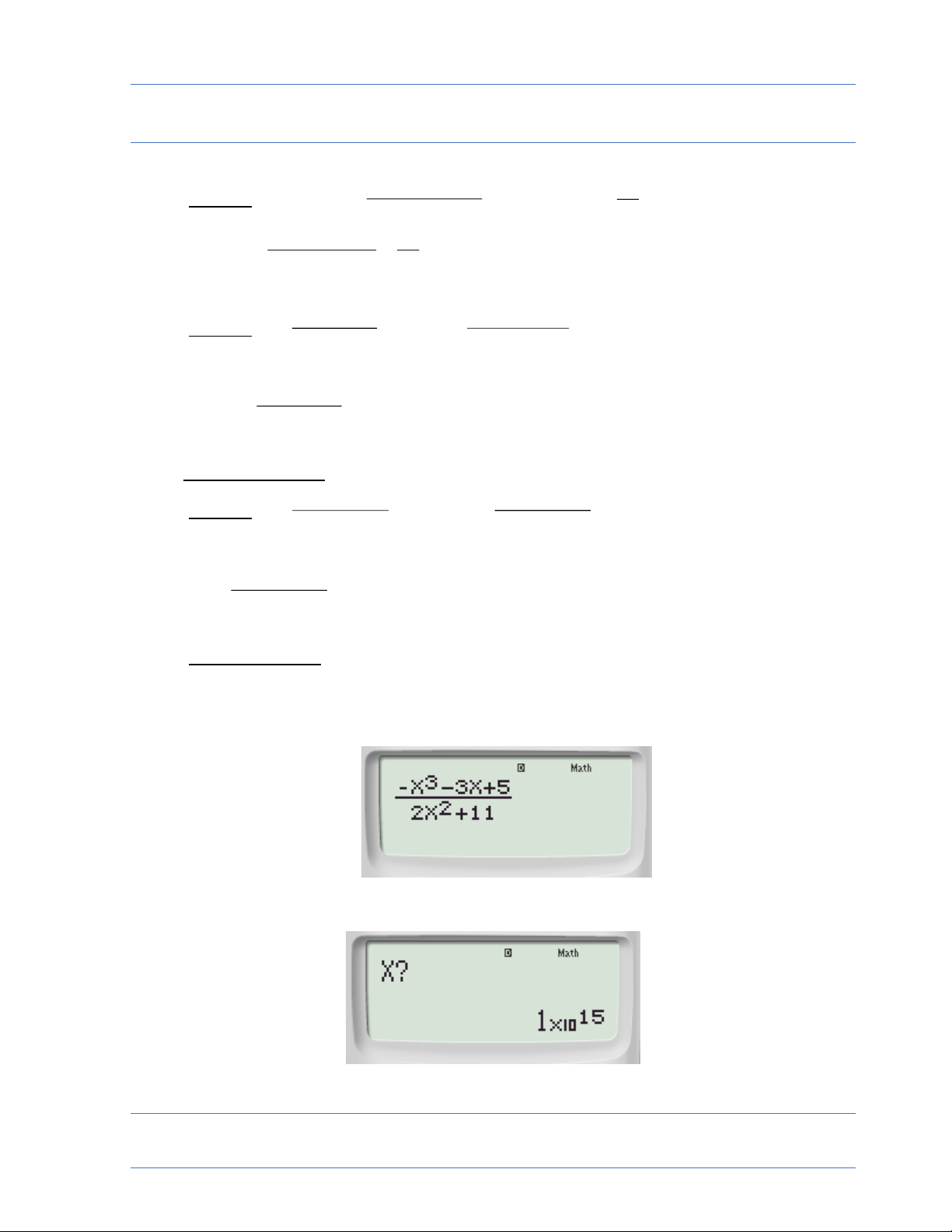
 n  3n  5 Ví dụ 1: lim máy ghi 2 2 n 11 2 2 n 11 calc x ? nhập 15 10  kq 14
 510 đọc là âm vô cực  3 n  3n  vậy 5 lim   2 2 n 11 Cách bấm máy:  Nhập vào máy tính: azQ)^3$p3Q)+5R2Q)d+11
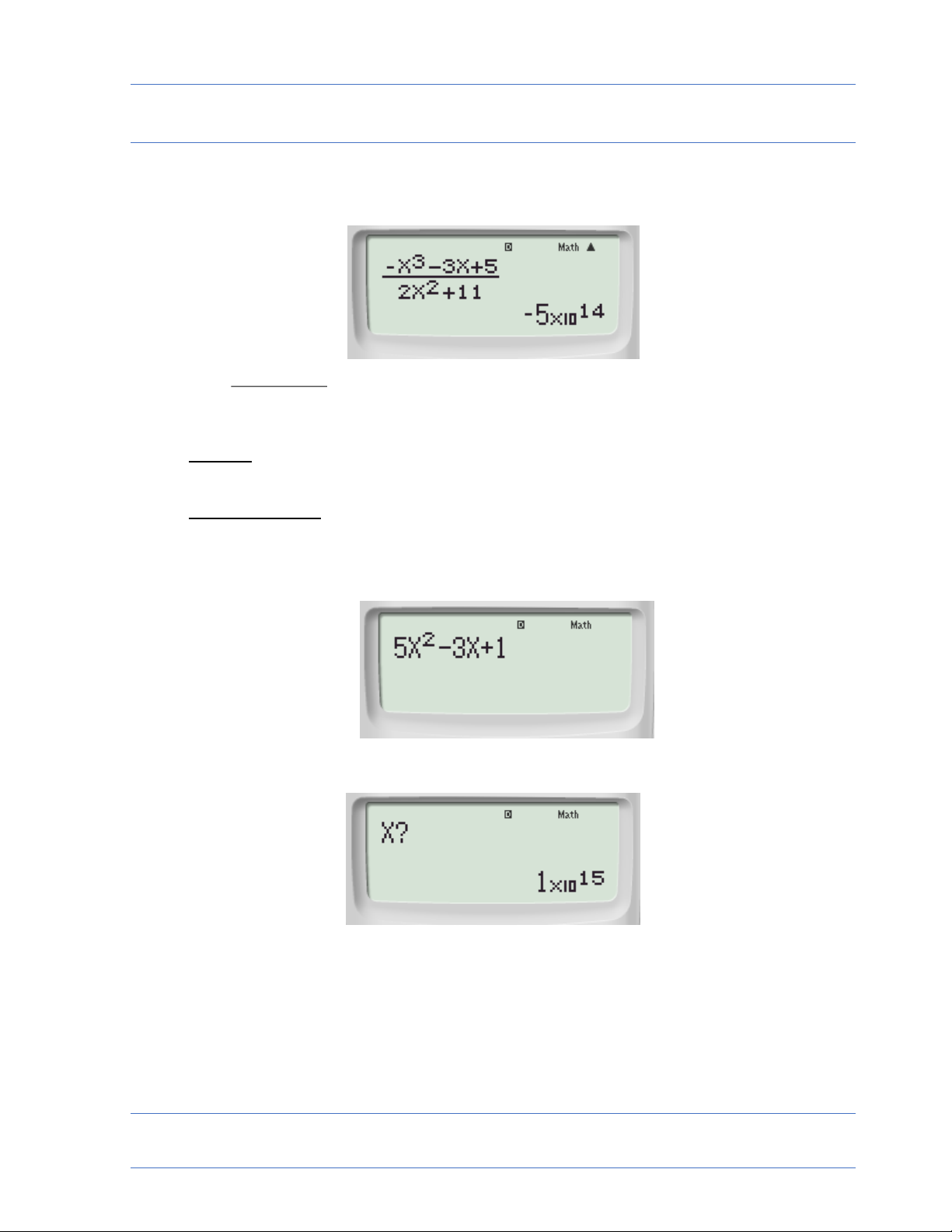
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác
ở dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)
Giáo viên thực hiện: Nguyễn Văn Phép Trang 6
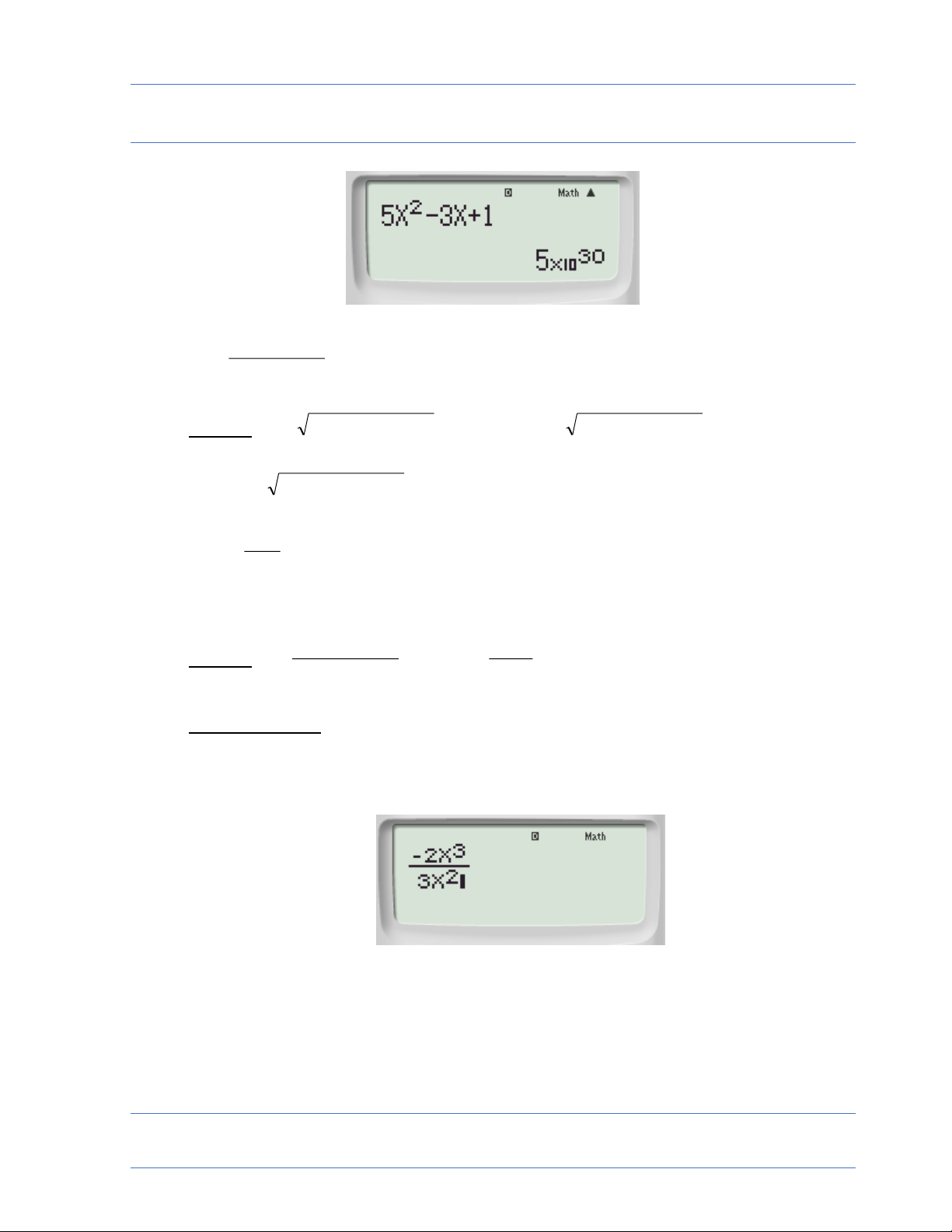
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  Ta nhập tiếp: 10^15=
Màn hình sẽ xuất hiện:  3 n  3n  vậy 5 lim   2 2 n 11
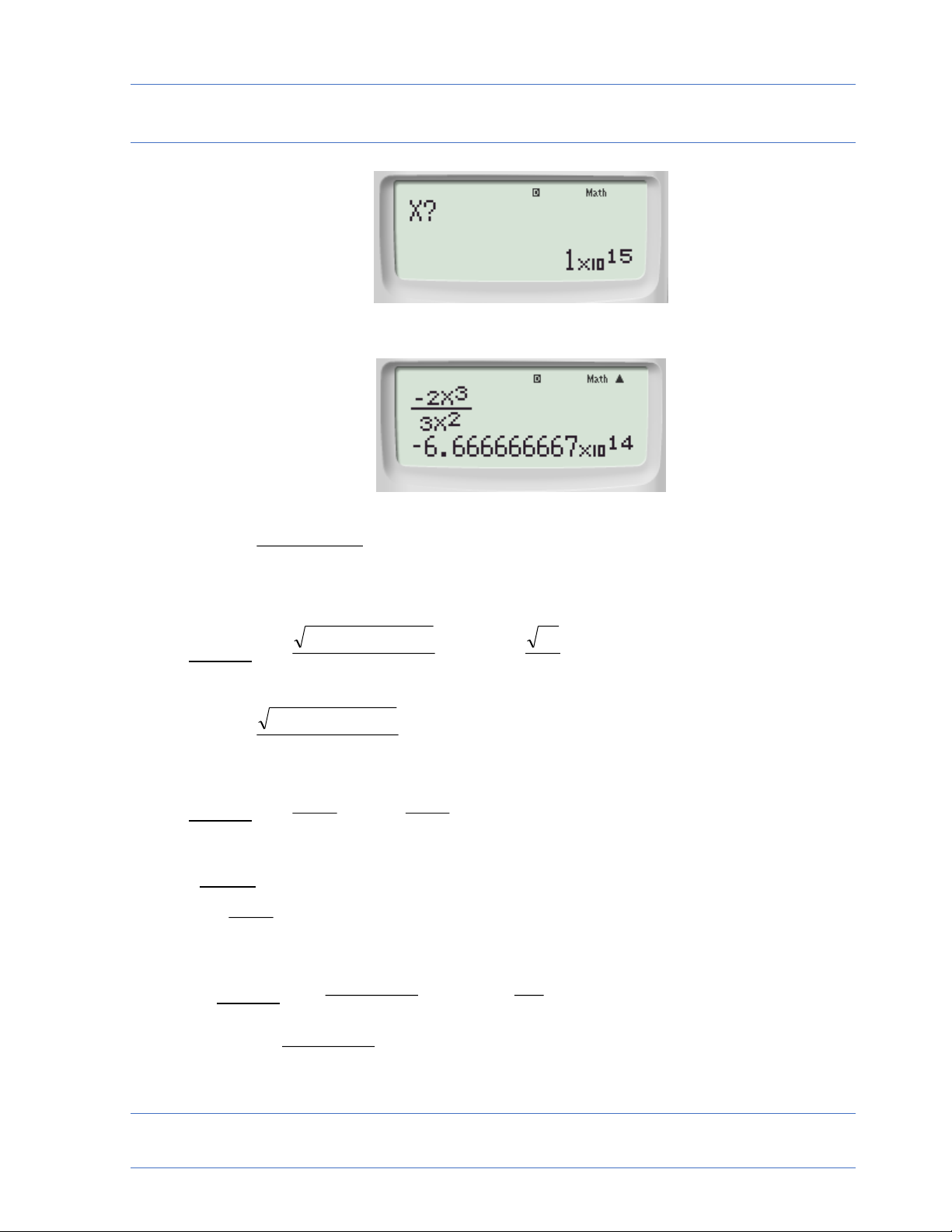
• Ví dụ 2 : lim5 2 n  3n   1 máy ghi : 5 2 n  3n   1 calc x ? nhập 15 10  kq là 30
5 10 (Đọc là dương vô cực ) Cách bấm máy:  Nhập vào máy tính: 5Q)dp3Q)+1
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số khác ở
dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)  Ta nhập tiếp: 10^15=
Màn hình sẽ xuất hiện:
Giáo viên thực hiện: Nguyễn Văn Phép Trang 7
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  3 n  3n  Vậy 5 lim   2 2 n 11 • Ví dụ 3: lim 3 4 n  5 2
n  n 1 máy ghi : 3 4 n  5 2 n  n 1 calc x ? nhập 15 10  kq : 30 7 . 1 3205.. 08 .
10 ( đọc là dương vô cực ) Vậy : lim 3 4 n  5 2
n  n 1  
(Nhập tương tự ví dụ 2) f n *Nếu
với f(n) ,g(n) là các đa thức theo n .Ta chú ý đến số hạng g n
chứa mũ cao nhất của n trong từng biểu thức f(n) ,g(n) 3 3 •
 2n  3n  2  2n Ví dụ 1: lim máy ghi calc x ? nhập 15 10  kq: 3 2 n  5 2 3n 14  6 .
6 6666667 10 (đọc là âm vô cực ) Cách bấm máy:
 Nhập vào máy tính: az2Q)^3R3Q)d
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con số
khác ở dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)
Giáo viên thực hiện: Nguyễn Văn Phép Trang 8
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  Ta nhập tiếp: 10^15=
Màn hình sẽ xuất hiện:  2 3 n  3n  Vậy 2 lim   3 2 n  5
Tương tự cho các ví dụ bên dưới 6 3 •
n  7n  5n  8 n6 Ví dụ 2: lim máy ghi calc x ? nhập 15 10  kq 30 110 n  12 n
( đọc là dương vô cực ) 6 n  7 3 n  5n  8 Vậy lim   n  12 n x • 3  1 3  1 Ví dụ 3: lim máy calc x ? 100  17 4065611 .. 10 x đọc là   . 2n  1 2 x  1
*CHÚ Ý : Gặp n a nhập n = 100 3n  Vậy 1 lim   2n  1 2 2 • n  4n  5 n Ví dụ 4 : lim máy ghi calc x ? nhập 15 10  kq :0 3 3 2 n  n  7 3 3n 2 n  n  vậy 4 5 lim  0 3 3 2 n  n  7
Giáo viên thực hiện: Nguyễn Văn Phép Trang 9
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY 4 4 • 2n  3n  2 2n 2 Ví dụ 5: lim máy ghi calc x ? nhập 15 10  kq: 2 2 n  n  3 2 2n 2
Nếu gặp dạng tổng- hiệu hai căn cần chú ý lượng liên hợp rút gọn trước khi áp dụng dạng trên . • n  1
Ví dụ 1: lim  n2  n 1  n ta có  n2  n 1  n  máy
n2  n  1  n n ghi calc x ? nhập 1 15 10  kq: n 2  n 2 Vậy lim  2
n  n   n 1 1  2 • 1 1 Ví dụ 2: lim ta có
 n  2  n 1  2 n
n  2  n  1
n  2  n  1 Mà lim n   Vậy : 1 lim  
n  2  n  1 • 1 1 Ví dụ 3: lim máy ghi calc x ? nhập 15 10 
3n  2  2n  1 n 3  2n kq: 0 vậy: 1 lim
 0 ( các hệ số trước n lệch nhau không
3n  2  2n  1
cần nhân lượng liên hợp. 2 2 •
n  1  n  1 n  n Ví dụ 4: lim máy ghi : calc x ? nhập 15 10 3n  2 n 3  kq: 1 3
Bài tập rèn luyện : Tìm các giới hạn sau: 2   2 3n  5  n 1. 4n n 1 lim (KQ :2) 2. lim (KQ: 0 ) 2 3  2n 2 1  2n
Giáo viên thực hiện: Nguyễn Văn Phép Trang 10
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY  1 2 2  3. lim n   (KQ:   ) 4. lim  2 2
n  n  n 1 (KQ: )  n  1 2 3  
2  3n n 1 2 3 5. 2n 3n 1 27 lim (KQ: -3) 6. lim (KQ: ) 3 2 n  n 5 1  4n 4 2
n  n  1  4 2 n  2 n n   7. 3 4 1 lim (KQ: -1 ) 8. lim (KQ: -1) n  3 n n 2.4  2 B. GIỚI HẠN HÀM SỐ
1.GIỚI HẠN HÀM SỐ TẠI MỘT ĐIỂM:
Lim 𝑓(𝑥) Nếu f x xác định tại x0 viết f x calc ? x0  f x 0  𝑥→𝑥0
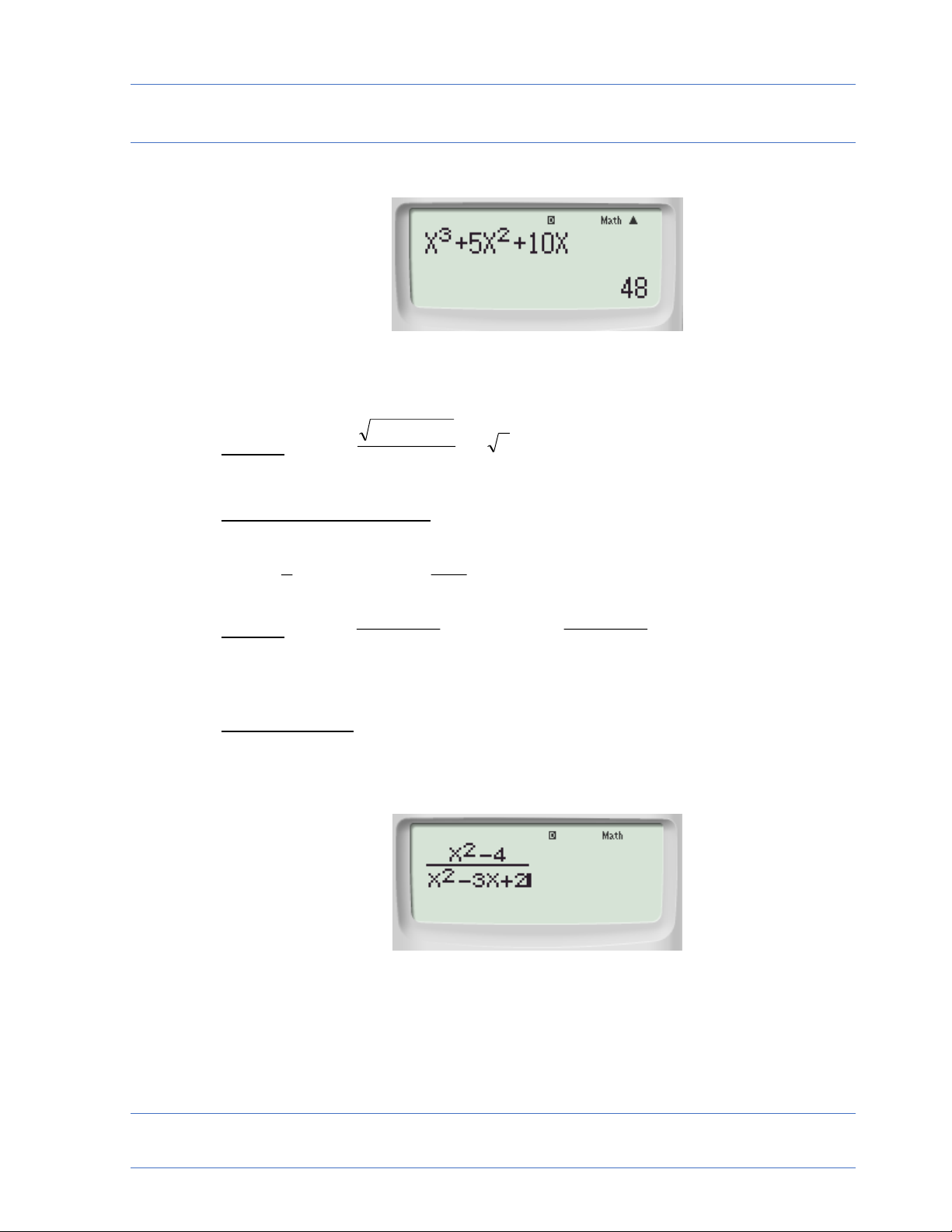
• Ví dụ 1: lim x3 5x2 10x máy viết : x3  5x2 10x calc X ? 2  𝑥→2 48 Cách bấm máy:
 Nhập vào máy tính: Q)^3$+5Q)d+10Q)
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con
số khác ở dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)  Ta nhập tiếp: 2=
Giáo viên thực hiện: Nguyễn Văn Phép Trang 11
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY
Màn hình sẽ xuất hiện: Vậy lim x  x   x x 2  3 5 2 10  48 Tương tự cho ví dụ 2 2 • x  5x  6 Ví dụ 2: lim   2  f x 1   1 x  2 2. CÁC DẠNG VÔ ĐỊNH: f x
2.1 Dạng 0 Khi tìm lim f x  g x   mà  và  0  0 0  0 0 x
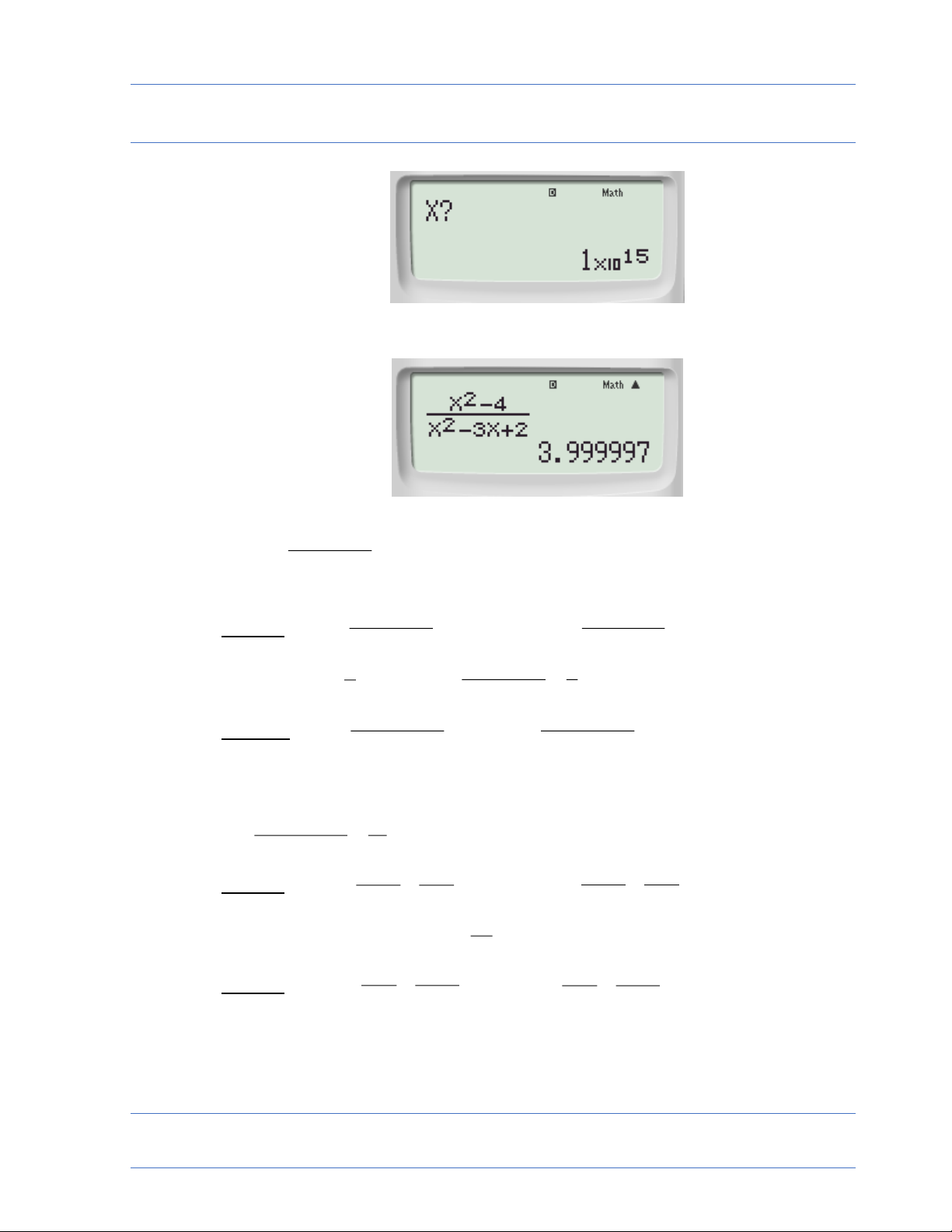
x0 gx 2 2 • x  4 x  4 Ví dụ 3 : lim máy ghi calc X ? nhập x2 2 x  3x  2 2 x  3x  2
2,000001 ( lớn hơn 2 một tí ti ) máy hiện 3,999997 làm tròn đọc là 4
hay nhập x= 1,999999999 ( nhỏ hơn 2 một tí ti )  4 Cách bấm máy:
 Nhập vào máy tính: aQdp4RQ)dp3Q)+2
Màn hình sẽ xuất hiện:
 Sau đó nhập: r, màn hình sẽ xuất hiện: (có thể sẽ xuất hiện con
số khác ở dòng hiển thị, không ảnh hưởng đến quá trình bấm máy)
Giáo viên thực hiện: Nguyễn Văn Phép Trang 12
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY
 Ta nhập tiếp: 2.000001=
Màn hình sẽ xuất hiện: 2 x  Vậy 4 lim  4 x2 2 x  3x  2
Tương tự cho các ví dụ tiếp theo 3 3 • x  3x  2 x  3x  2 Ví dụ 4: lim máy ghi calc X ? x 1  4 x  4x  3 4 x  4x  3 3 x  x 
Nhập 0,9999999  1 Vậy 3 2 1 lim  x 2 1 4 x  4x  3 2 4 2 4 2 • x  x  72 x  x  72 Ví dụ 5: lim máy ghi calc X ? nhập x3 2 x  2x  3 2 x  2x  3
3,0000001 kq :25,50000069 đọc là 25,5 hoặc nhập 2,9999999
kq : 25,49999993 đọc là 25,5 4 2 x  x  Vậy 72 51 lim  x3 2 x  2x  3 2 •  2 1   2 1  Ví dụ 6: lim máy ghi    calc X ? nhập x1     2 x 1 x 1  2 x 1 x 1  1,000000001  KQ : 1 2 •  1 3   1 3  Ví dụ 7 : lim máy ghi    calc X ? nhập x1    1 x 1 3 x  1 x  3 1 x 
1,000000001  -1 KQ: -1
Giáo viên thực hiện: Nguyễn Văn Phép Trang 13
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY 4 4 4 4 • x  a x  a Ví dụ 8: lim máy ghi calc xa x  a x  a
chọn a = 0 khi đó x  0 kq: 0
chọn a =1 khi đó x 1 kq :4= 3 4 1
chọn a = 2 khi đó x  2 kq:32= 3 4  2
chọn a = 3 khi đó x  3 kq :108 = 3 4  3 4 4  Vậy x a 3 lim  4a x a x  a
Nhận xét bài nầy thực hiện phép chia giải tự luận nhẹ hơn ! Bảng chia Hoc ne Hệ số của 1 0 0 0 4  a x a 1 a 2 a 3 a 0
x  a 3 2 2 3
x  ax  a x  a  3 2 2 3 lim  lim     xa
xa x ax a x a  3 4a x  a  f x 2.2 DẠNG:
Thường gặp khi x   nếu dạng không chứa căn bậc  g x
chẳn thì tính như giới hạn dãy Chỉ khác n thay bằng x, khi x   nhập 10 10 3 3 • 3x  2x  2 3x  2x  2  3 Ví dụ 1: lim máy ghi calc X ? 20 10 KQ: x  2 3 x  2 2 x  1  2 3 x  2 2 x  1 2 4 2 4 2 • x  3x  1 x  3x  1 Ví dụ 2: lim máy ghi: calc X ? 10 10 KQ:   x 3
 x  2x  2 3
 x  2x  2 4 2 4 2 • x  3x  1 x  3x  1 Ví dụ 3: lim máy ghi: calc X ? 10 10 KQ: x 3
 x  2x  2 3
 x  2x  2 1 20 10
  (đọc là trừ vô cực ) 2 2 •
x  3x  2x
x  3x  2x 1 Ví dụ 4 : lim máy ghi calc X ? 20 10 KQ : x 3x  1 3x  1 3
Giáo viên thực hiện: Nguyễn Văn Phép Trang 14
TÌM GIỚI HẠN BẰNG MÁY TÍNH CẦM TAY 2 •
4x  2x  1  2  x Ví dụ 5: lim X 
9x2  3x  2x 2     TH1: 4x 2x 1 2 x 1 lim CALC X ? 20 10 (trong căn) KQ: X 
9x2  3x  2x 5 2     TH2: 4x 2x 1 2 x lim CALC X ? 20 10 KQ: 3 X 
9x2  3x  2x • Ví dụ 6: lim ( 2
x  x  1  x) dạng    X  x  1 Máy ghi CALC X? 1 20 10 KQ
x 2  x  1  x 2 • Ví dụ 7: lim ( 2
x  x  1  x) Khi đó không phải dạng    . nên không X 
cần nhân lượng liên hợp Máy ghi : ( 2
x  x 1  x) CALC 20 10 KQ 20 2 10 đọc là   .
Giáo viên thực hiện: Nguyễn Văn Phép Trang 15