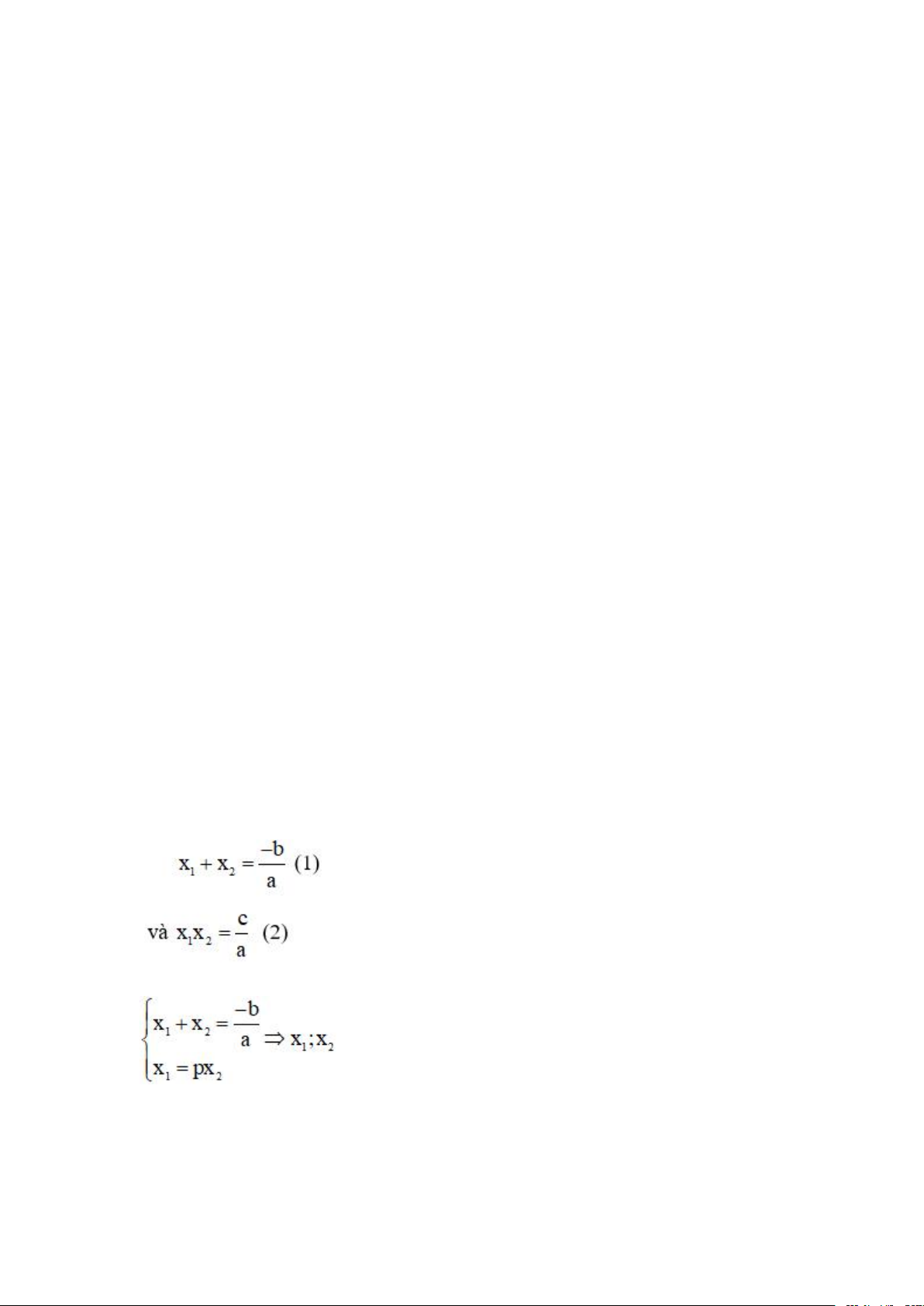




Preview text:
Tìm m để phương trình sau có nghiệm Toán lớp 9
1. Phương pháp giải dạng toán tìm tham số m để phương trình
có nghiệm thoả mãn điều kiện
Phương pháp giải bài toán phương trình bậc hai : ax2 + bx + c = 0 ( a khác
0 ) , tìm tham số m để phương trình có nghiệm theo đúng điều kiện .
Tìm m để phương trình có nghiệm thoả mãn điều kiện về dấu hoặc thoả
mãn đẳng thức , bất đẳng thức liên hệ giữa các nghiệm .
- Bước 1: Tìm điều kiện a khác 0 nếu cần và điều kiện để phương trình có nghiệm .
- Bước 2 : Áp dụng định lý Vi - ét sau đó tính tổng S và tích P của hai nghiệm .
- Bước 3 : Sử dụng hệ thức Vi - ét , kết hợp biến đổi đẳng thức , bất đẳng thức để tìm tham số .
- Bước 4 : Đối chiếu điều kiện và kết luận .
Tìm tham số m để phương trình có một nghiệm là x0 .
- Bước 1 : Tìm điều kiện để các phương trình có nghiệm
- Bước 2 : Tìm nghiệm chung và tìm tham số : Có thể giả sử x0 là nghiệm
chung , lập hệ phương trình hai ẩn ( x0 và tham số ) và giải hệ phương trình .
- Bước 3 : So sánh với điều kiện và kết luận .
Điều kiện để phương trình có hai nghiệm phân biệt sao cho x1 = p x2
( * ) ( với p là một số thực )
+ Bước 1: Tìm điều kiện để phương trình có hai nghiệm phân biệt
+ Bước 2 : Áp dụng định lý Vi - ét :
+ Bước 3 : Kết hợp ( 1 ) với ( * ) giải hệ phương trình :
+ Bước 4 : Thay x1 và x2 vào ( 2) => Tìm giá trị tham số
Tìm giá trị của thám số m để hai phương trình có ít nhất một nghiệm chung
- Bước 1 : tìm điều kiện để các phương trình có nghiệm .
- Bước 2 : Tìm nghiệm chung và tham số m : Có thể giả sử x0 là nghiệm
chung , lập hệ phương trình hai ẩn ( x0 và tham số m ) sau đó giải hệ phương trình .
- Bước 3 : So sánh với điều kiện và đưa ra kết luận
- Điều kiện để phương trình có hai nghiệm thoả mãn điều kiện I x1- x2 I =
k ( k thuộc R ) thì t làm lần lượt các bước sau :
+ Bình phương hhai vế của phương trình trên : ( x1 - x2 ) 2 = k 2 <=> ( x1 - x2 ) 2 - 4x1x2 = k2
+ Áp dụng định lý Vi - ét tính x1 + x2 và x1x2 thay vào biểu thức và đưa ra kết luận
- So sánh nghiệm của phương trình bậc hai với một số bất kỳ :
+ Tìm điều kiện để phương trình có nghiệm khi Ta có : .
Thay biểu thức Vi - ét vào hệ ( * ) để tìm m
+ Với bài toán : Tìm m để phương trình có hai nghiệm Ta có :
( * ) Thay biểu thức Vi - ét vào hệ ( * ) để tìm m
+ Với bài toán : Tìm m để phương trình có hai nghiệm x1 < a < x2
Ta có ( x1 - a ) ( x2 - a ) < 0 ( * ) Thay biểu thức Vi - ét vào ( * ) để tìm m
2. Những bài tập ôn luyện dạng toán tìm m để phương trình có nghiệm
Bài 1 : Cho phương trình x2 - ( 2m - 1 ) + m2 - 1 = 0 ( x là ẩn số )
a . Tìm điều kiện của m để phương trình đã có hai nghiệm phân biệt .
b . Tìm m để hai nghiệm x1 , x2 của phương trình đã cho thoả mãn ( x1 - x2 )2 = x1 - 3 x2 Giải a.
= ( 2m - 1) 2 - 4 ( m 2 - 1) = 4m 2 - 4m + 1 = 5 - 4m
Phương trình có hai nghiệm khi và chỉ khi m <= 5/4
Theo đề bài : ( x1 - x2 ) 2 = x1 - 3 x2
<=> ( x1 + x2 )2 - 4 ( m2 - 1 ) = x1 - 3 x2
<=> ( 2m - 1 ) 2 - 4 ( m 2 - 1 ) = x1 - 3 x2
<=> x1 - 3 x2 = 5 - 4m ( ** )
Từ ( * ) và ( ** ) ta có hệ phương trình như sau :
Bài 2 : Cho phương trình x2 - 10 mx + 9m = 0 ( m là tham số )
a . Giải phương trình đã cho với m = 1
b . Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân
biệt x1 , x2 thoả mãn điều kiện x1 - 9 x2 = 0 Lời giải :
a . Với m = 1 phương trình đã cho trở thành x2 - 10 x + 9 = 0
Ta có : a + b + c = 0 nên phương trình có hai nghiệm phân biệt x1 = 1 và x2 = 9 b .
= ( - 5 m )2 - 1.9 m = 25 m2 - 9m
Điều kiện phương trình đã cho có hai nghiệm phân biệt là > 0 khi và chỉ khi 25 x2 - 9m > 0
Theo hệ thức Vi - ét ta có : Từ ( * ) và giải hệ phương trình ta có :
Thay vào phương trình ( ** ) ta có : Với m = 0 ta có
= 25 m2 - 9m = 0 không thoả mãn điều kiện phương
trình có 2 nghiệm phân biệt . Với m = 1 ta có
= 25 m 2 - 9m = 16 > 0 thoả mãn điều kiện để
phương trình có 2 nghiệm phân biệt .
Kết luận : Vậy với m = 1 thì phương trình đã cho có hai nghiệm phân biệt x 1 ,
x2 thoả mãn điều kiện x1 = 9 x2
Bài 3 : Cho phương trình x2 - 2 ( m - 1) x + 2m - 5 = 0 ( trong đó m là tham số )
a . Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi m .
b. Tìm giá trị của m để phương trình có hai nghiệm x1 , x2 thoả mãn điều kiện : x1 < 1 < x2 Lời giải : a . Ta có :
= [ - 2 ( m - 1 ) 2 - 4 . 1 . (2m - 5 ) = 4m2 - 12 m + 22
= ( 2m )2 - 2.2.m . 3 + 9 + 13 = ( 2m - 3 ) 2 + 13 > 0 ( luôn đúng với mọi m )
b . theo hệ thức Vi - ét , ta có : Ta có x1 < 1 < x2 =>
=> ( x1 - 1 ) ( x2 - 1 ) < 0 => x1 x2 - ( x1 + x2 ) + 1 < 0 ( II )
Thay ( I ) vào ( II ) ta có ( 2m - 5 ) - ( 2m - 2 ) + 1 < 0.m - 2 < 0 ( đúng với mọi m )
Vậy mọi m thì phương trình trên có hai nghiệm x1 , x2 thoả mãn điều kiện
như đề bài yêu cầu x1 < 1 < x2
Bài 4 : Cho phương trình x2 + 2x - m2 - 1 = 0 ( m là tham số )
Tìm m để phương trình trên có hai nghiệm thoả mãn x1 = - 3. x2 Lời giải : Ta có :
= 12 - 1 ( - m2 - 1 ) = 1 + m2 + 1 = m2 + 2 > 0 ( Luôn đúng với mọi m )
Suy ra phương trình luôn có hai nghiệm phân biệt với mọi m Theo định lý Vi - ét ta có hệ phương trình sau :
Ta có : x1 + x2 = -2 ( do trên ) và x1 = - 3 . x2 nên ta có hệ phương trình sau :
Thay ( * ) vào biểu thức x1 . x2 = - m2 - 1 ta được : ( - 3 ) . 1 = - m2 - 1 <=>
m2 = 2 <=> m = cộng trừ căn bậc 2 của 2
Vậy m = +- V--2 là các giá trị cần được tìm.
Document Outline
- Tìm m để phương trình sau có nghiệm Toán lớp 9
- 1. Phương pháp giải dạng toán tìm tham số m để phư
- 2. Những bài tập ôn luyện dạng toán tìm m để phươn




