Tìm số hạng tổng quát của dãy số bằng phương pháp sai phân – Mai Xuân Việt

Tài liệu gồm 21 trang hướng dẫn tìm số hạng tổng quát của dãy số bằng phương pháp sai phân, tài liệu do tác giải Mai Xuân Việt biên soạn, nội dung gồm 6 phần:

106 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT)

Môn: Toán 11

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
TÌM SỐ HẠNG TỔNG QUÁT CỦA DÃY SỐ
BẰNG PHƢƠNG PHÁP SAI PHÂN
I-Phƣơng trình sai phân bậc nhất:
Dạng 1: Cho dãy số {x
n
} :
0
n+1
onst
ax 0
n
xc
bx

. Tìm số hạng tổng quát của dãy số?
Từ công thức truy hồi ta có :
2
1 2 0
. . .................... .
n
n n n
b b b
x x x x
a a a

Khi đó công thức tổng quát (CTTQ) của dãy số được xác định bởi :
0
.
n
n
b
xx
a




.
Thí dụ : Cho dãy số {x
n
} được xác định bởi :
0
1
5
3 0 ,
nn
x
x x n
.
Tìm số hạng tổng quát của dãy số.
Giải: Từ công thức truy hồi ta có :
2
1 2 0
3 3 ................. 3 5.3
nn
n n n n
x x x x hay x

.
Dạng 2: Cho dãy số {x
n
} :
0
n+1
ax ( )
nk
x
bx P n

, với
()
k
Pn
là đa thức bậc k của n.
Tìm số hạng tổng quát của dãy số ?
Giải: Xét phương trình đặc trưng :
0
b
ab
a

.
Đối với dạng này ta xét thêm một giá trị
gọi là nghiệm riêng của phương trình sai phân.
Khi đó số hạng tổng quát của dãy được xác định bởi :
*
.
n
nn
x c x

. Trong đó nghiệm
riêng
được xác định như sau :
Nếu a + b ≠ 0 thì nghiệm riêng
*
()
nk
x Q n
thay vào phương trình ta được:
. ( 1) . ( ) ( )
k k k
aQ n bQ n P n
. Đồng nhất hệ số ta tìm được
()
k
Qn
.
Nếu a + b = 0 thì nghiệm riêng
*
. ( )
nk
x nQ n
thay vào phương trình ta được:
( 1). ( 1) . ( ) ( )
k k k
a n Q n bnQ n P n
. Đồng nhất hệ số ta tìm được
. ( )
k
nQ n
.
Thí dụ 1: Cho dãy số {x
n
} :
0
2
1
7
2 3 4 5 , .
nn
x
x x n n n
.Tìm số hạng tổng quát x
n
.
Giải: Xét phương tình đặc trưng
2 0 2

.
Ta có : a + b = 1 – 2 = -1 ≠ 0 nên nghiệm riêng pt có dạng :
*2
n
x an bn c
. Thay
vào
pt, ta được :
2 2 2
( 1) ( 1) 2 2 2 3 4 5a n b n c an bn c n n
22
(2 ) 3 4 5an a b n a b c n n
.
Đồng nhất hệ số hai vế ta được :
*2
33
2 4 10 3 10 18
5 18
n
aa
a b b x n n
a b c c





.
CTTQ của số hạng trong dãy :
2
.2 3 10 18
n
n
x c n n
.
Từ
2
0
7 18 7 25. 25.2 3 10 18
n
n
x c c Suyra x n n
.
Thí dụ 2: Cho dãy số {x
n
} :
0
1
5
4 5 , .
nn
x
x x n n
. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
1 0 1

.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Ta có : a + b = 1 – 1 = 0 nên nghiệm riêng của pt có dạng
*2
()
n
x n an b an bn
.
vào pt,
ta được :
22
( 1) ( 1) 4 5a n b n an bn n
.
2 4 5an a b n
.
Đồng nhất hệ số hai vế ta được :
*2
2 4 2
23
53
n
aa
x n n
a b b




.
Số hạng tổng quát của dãy có dạng :
2
23
n
x c n n
.
Từ
2
0
5 5. 2 3 5.
n
x c Suy ra x n n
Dạng 3: Cho dãy số {x
n
} :
0
n+1
ax ( onst) , n .
n
x
bx d d c
Khi đó số hạng tổng quát của dãy số là :
0
0
1
. 0.
1
0.
n
n
n
n
b
d
a
b
x x neu a b
a
b
a
a
x x nd neu a b


















Thí dụ 1: Cho dãy số {x
n
} :
0
1
5
6 , .
nn
x
x x n
. Tìm CTTQ của x
n
.
Giải: Từ công thức truy hồi ta có :
1 2 3 0
6 2.6 3.6 ....... 6 6 5
n n n n n
x x x x x n hay x n
.
Thí dụ 2: Cho dãy số {x
n
} :
0
1
3
8 4 ,
nn
x
x x n
. Tìm CTT Q của x
n
.
Giải: Từ công thức truy hồi, ta có :
2
22
1 2 2 2 0
8 1 8 1
8 4 8 8 4 4 8 . 4 8 1 8 . 4. ........ 8 . 4.
8 1 8 1
n
n
n n n n n
x x x x x x


.
Suy ra
4 25 4
3.8 . 8 1 .8 .
7 7 7
n n n
n
x
Dạng 4: Cho dãy số {x
n
} :
0
1
.,
n
nn
x
ax bx d n
. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng :
0.
b
a b q
a

Nếu

thì nghiệm riêng của phương trình
*
.
n
n
xc
thay vào pt, ta được :
1*
. . . . .
nn
n n n
n
d d d
a c b c d c x do b qa
a b a b a q

.
Số hạng tổng quát của dãy :
*
11
. . .
n
nn
nn
d
x c q x c q
aq
Từ
0 1 1 0 0 0
. . .
( ) ( ) ( ) ( )
n n n
nn
n
d d d d d q
x c c x x x q x q
a q a q a q a q a q




Nếu

thì nghiệm riêng của phương trình
* n
n
x cn
thay vào pt, ta được :
1
( 1) ( )
( 1) ( 1)
n n n
d d d
ac n bcn d c do q
a n bn a n aqn aq

.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
1
*
nn
n
dnq dnq
Suyra x
aq a

.
Số hạng tổng quát của dãy :
1
*
11
..
n
nn
nn
dnq
x c q x c q
a
.
Từ
1
0 1 0
.
n
n
n
dnq
x c x x q
a
.
Vậy từ trên ta có :
0
1
.
.
.
nn
n
n
n
dq
neu q
aq
x x q
d
nq neu q
a

.
Thí dụ 1: Cho dãy số {x
n
} :
0
1
5
3 2.5 ,
n
nn
x
x x n
. Tìm CTTQ của x
n
.
Ta có :
3 ; 2 ; 5.
b
qd
a

Vì
q
nên ta có số hạng tổng quát của dãy sẽ là :
0
35
. . 5.3 2. 4.3 5 .
35
n n n n
n n n n
n
dq
x x q
aq


Thí dụ 2: Cho dãy {x
n
} :
0
1
2
3 5.3 ,
n
nn
x
x x n
. Tìm CTTQ của x
n
.
Ta có:
3 ; 3 ; 5.
b
qd
a

Vì
q
nên ta có số hạng tổng quát của dãy sẽ là :
1 1 1
0
. . 2.3 5 .3 (5 6).3
n n n n n
n
d
x x q nq n n
a
.
Dạng 5: Cho dãy số {x
n
} :
0
1 1 1 2 2
..... (1) ,
n n n
n n k k
x
ax bx d d d n
. Xác định
sô hạng tổng quát của dãy trên.
Gọi
*1
n
x
là nghiệm riêng của phương trình
1 1 1
n
nn
ax bx d

*2
n
x
là nghiệm riêng của phương trình
1 2 2
n
nn
ax bx d

...................................................................................
*k
n
x
là nghiệm riêng của phương trình
1
n
n n k k
ax bx d

.
Khi đó nghiệm riêng của phương trình (1) sẽ là
* *1 *2 *
....
k
n n n n
x x x x
.
Khi đó số hạng tổng quát
*
.
n
nn
b
x c x
a




.
Thí dụ: Cho dãy {x
n
} :
0
1
2
2 3.2 5.7 (*) , .
nn
nn
x
x x n
. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng :
2 0 2.

Do
1

nên nghiệm riêng
*1
1
.2
n
n
x d n
, thay vào phương trình, ta được :
1 *1 1
1 1 1
3
( 1).2 2 .2 3.2 3 .2
2
n n n n
n
d n d n d x n

.
Do
2

nên nghiệm riêng
*2
2
.7
n
n
xd
, thay vào phương trình, ta được :
1 *2
2 2 2
.7 2 .7 5.7 1 7
n n n n
n
d d d x
.
Số hạng tổng quát
*1 *2 1
.2 .2 3 .2 7
n n n n
n n n
x c x x c n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Từ
1
0
2 1 2 1. 2 3 .2 7
n n n
n
x c c Suyra x n
.
Dạng 6: Cho dãy số {x
n
} :
0
1
( ) ,
n
n n k
x
ax bx P n d n
. Tìm CTTQ của x
n
.
Ta gọi
*1
n
x
là nghiệm riêng của
1
()
n n k
ax bx P n

*2
n
x
là nghiệm riêng của
1
n
nn
ax bx d

.
Công thức tổng quát của dãy số được xác định là
*1 *2
.
n
n n n
x c x x
.
Từ giá trị của x
0
ta tìm được giá trị c.
Thí dụ: Cho dãy số {x
n
} :
0
1
3
5 3 2 2.3 ,
n
nn
x
x x n n
. Tìm CTTQ của x
n
.
Giải: Xét Phương trình đặc trưng :
5 0 5.

Gọi
*1
n
x
là nghiệm riêng của phương trình
*1
1
3 11
5 3 2
4 16
n n n
x x n x n
.
*2
n
x
là nghiệm riêng của phương trình
*2
1
5 2.3 3
nn
n n n
x x x
.
Số hạng tổng quát của dãy cho bởi:
*
3 11
. .5 3
4 16
n n n
nn
x c x c n
.
Từ
0
11 75 75 3 11
3 1 3 . .5 3 .
16 16 16 4 16
nn
n
x c c Suyra x n
II-Phƣơng trình sai phân bậc hai:
Dạng 1: Dạng thuần nhất và có phương trình đặc trưng bậc hai tồn tại nghiệm thực.
Cho dãy số {x
n
} :
01
21
;
0,
n n n
xx
ax bx cx n

. Tìm CTTQ của x
n
.
Xét phương trình đặc trưng
2
0 (1)a b c

.
Phương trình (1) có nghiệm
1 2 1 2
; ( )
thì số hạng tổng quát có dạng :
1 1 2 2
..
nn
n
x c c


. Từ x
0
; x
1
ta tìm được c
1
và c
2
.
Phương trình (1) có nghiệm
12

thì số hạng tổng quát có dạng :
12
( ).
n
n
x c nc

. Từ x
0
; x
1
ta tìm được c
1
và c
2.
Thí dụ 1: Cho dãy {x
n
} :
01
21
2; 5.
5 6 , .
n n n
xx
x x x n


. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
2
12
5 6 0 2 3.
Số hạng tổng quát của dãy có dạng
12
.2 .3
nn
n
x c c
.
Từ
0
1 2 1
1 2 2
1
2
21
. 2 3
2 3 5 1
5
nn
n
x
c c c
Suy ra x
c c c
x


.
Thí dụ 2: Cho dãy {x
n
} :
01
21
3; 10.
4 4 , .
n n n
xx
x x x n


. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
2
1,2
4 4 0 2.
Số hạng tổng quát của dãy có dạng
12
( ).2
n
n
x c nc
.
Từ
0
21
1 2 2
1
3
32
. (2 3).2
2( ) 10 3
10
n
n
x
cc
Suy ra x n
c c c
x



.
Dạng 2: Dạng thuần nhất và phương trình đặc trưng vô nghiệm thực.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Cho dãy số {x
n
} :
01
21
;
0,
n n n
xx
ax bx cx n

. Tìm CTTQ của x
n
.
Xét phương trình đặc trưng
2
0 (2)a b c

. Ta có phương trình (2) không tồn tại
nghiệm thực, khi đó số hạng tổng quát của dãy có dạng :
12
( os +c sin )
n
n
x r c c n n

.
Trong đó
22
B
; arctan
A
r A B
với
;
22
b
AB
aa
.
Từ hai giá trị x
0
và x
1
ta tìm được c
1
và c
2
.
Thí dụ: Cho dãy số {x
n
} :
01
21
1 ; 3 3 1
2 16 , .
n n n
xx
x x x n

. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
22
2 16 0 2 16 12 0co

.
Suy ra phương trình sai phân không có nghiệm thực.
Đặt
1 ; 3
22
b
AB
aa
và
22
B
2 ; arctan
A3
r A B
.
Khi đó số hạng tổng quát của x
n
có dạng :
12
n
2 os sin .
33
n
n
n
x c c c





Từ
1
0
1
12
2
1
1
1
1
n
. 2 os 3sin
3
2 3 3 1
3
33
3 3 1
22
n
n
c
x
c
n
Suyra x c
cc
c
x









.
Dạng 3: Cho dãy số {x
n
} :
01
21
;
,
n n n
xx
ax bx cx d n

. Tìm CTTQ của x
n
.
Gọi
là nghiệm riêng của phương trình. Khi đó nghiệm riêng
được xác định như sau:
*
*
*
0
0 ; 2 0
2
( 1) 0 ; 2 0.
2
n
n
n
d
x khi a b c
abc
dn
x khi a b c a b
ab
d
x n n khi a b c a b
a

.
Xét phương trình đặc trưng, xét nghiệm của phương trình đặc trưng như các trường hợp
trên. Kết hợp với nghiệm riêng ta có được công thức của x
n
.
Thí dụ 1: Cho dãy số {x
n
} :
01
21
4 ; 1
2 5 2 3 ,
n n n
xx
x x x n

. Tìm CTTQ của x
n
.
Xét phương trình đặc trưng :
2
12
1
2 5 2 0 2 .
2
Do a+b+c ≠ 0 nên nghiệm riêng của phương trình
*
3
3
2 5 2
n
d
x
abc
.
Số hạng tổng quát của dãy số :
12
1
.2 . 3
2
n
n
n
x c c
.
Từ
12
0
1
2
2
2
1
1
34
4
3
1
. 3.2 3
4
1
2
2 3 1
2
n
n
n
cc
x
c
Suyra x
c
c
x
c


.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Thí dụ 2: Cho dãy số {x
n
} :
01
21
89
5;
5
7 6 11,
n n n
xx
x x x n


. Tìm số hạng tổng quát x
n
.
Giải: Xét phương trình đặc trưng
2
12
7 6 0 1 6.
Do a+b+c=0 và 2a+b ≠ 0 nên nghiệm riêng
*
11 11
2 2 7 5
n
dn n
xn
ab

.
Số hạng tổng quát của dãy có dạng
12
11
.6 , .
5
n
n
x c c n n
Từ
0
12
1
2
12
1
5
5
2
11
. 2 3.6
11 89
89
3
5
6
55
5
n
n
x
cc
c
Suyra x n
c
cc
x



.
Thí dụ 3: Cho dãy {x
n
} :
01
21
3; 2
2 6 ,
n n n
xx
x x x n


. Xác định công thức tổng quát x
n
.
Giải: Xét phương trình đặc trưng
2
1,2
2 1 0 1.
Có a+b+c=0 và 2a+b=0 nên nghiệm riêng
*
( 1) 3 ( 1).
2
n
d
x n n n n
a
Số hạng tổng quát của dãy là :
12
3 ( 1) ,
n
x c nc n n n
.
Từ
0
21
2
1 2 2
1
3
31
. 3 4 3 , .
23
2
n
x
cc
Suy ra x n n n
c c c
x


Dạng 4: Cho dãy số {x
n
} :
01
21
;
,.
n
n n n
xx
ax bx cx dq n

. Xác định CTTQ của x
n
.
Gọi
là nghiệm riêng của phương trình sai phân trên. Khi đó nghiệm riêng này được xác
đinh như sau :
*
12
2
1
*
12
*2
12
.
.
2
( 1) . .
2
n
n
n
n
n
n
dq
x khi q q
aq bq c
ndq
x khi q q
aq b
d
x n n q khi q
a




.
Xét phương trình đặc trưng, lập công thức nghiệm và ta có được công thức x
n
.
Thí dụ 1: Cho dãy số {x
n
} :
01
21
2 ; 5
8 15 3.4 ,
n
n n n
xx
x x x n


. Lập công thức tính x
n.
Giải: Xét phương trình đặc trưng :
2
12
8 15 0 3 5.
Ta có
12
qq

nên nghiệm riêng của phương trình
*
2
3.4
3.4
16 32 15
nn
n
n
dq
x
aq bq c
.
Số hạng tổng quát của dãy là :
12
.3 .5 3.4 ,
n n n
n
x c c n
.
Từ
0
1 2 1
1 2 2
1
2
3 2 4
. 4.3 5 3.4 , .
3 5 12 5 1
5
n n n
n
x
c c c
Suy ra x n
c c c
x


Thí dụ 2: Cho dãy số {x
n
} :
01
21
8 ; 5.
11 28 6.7 , .
n
n n n
xx
x x x n


. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
2
12
11 28 0 4 7.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Ta có:
2
q
nên nghiệm riêng của phương trình
11
*1
6 .7
2 .7 .
2 2.1.7 11
nn
n
n
ndq n
xn
aq b


Số hạng tổng quát của dãy có dạng :
1
12
.4 .7 2 .7
n n n
n
x c c n
.
Từ
0 1 2
1
1
2
1 1 2
8
10
. 10.4 2.7 2 .7 , .
2
4 7 2 28
n n n
n
x c c
c
Suy ra x n n
c
x c c


Thí dụ 3: Cho dãy {x
n
} :
01
21
4 ; 5.
10 25 2.( 5) , .
n
n n n
xx
x x x n

. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
2
12
10 25 0 5
.
Ta có
12
q


nên nghiệm riêng của phương trình
* 2 2
( 1) . ( 1).( 5)
2
nn
n
d
x n n q n n
a

.
Số hạng tổng quát của dãy :
12
.( 5) ( 1).( 5) , .
nn
n
x c n c n n n
Từ
02
1
2
2
1 1 2
4
3
. ( 3 4).( 5) ( 1).( 5) ( 76 100).( 5) .
4
5( ) 5
n n n
n
xc
c
Suy ra x n n n n n n
c
x c c



Dạng 5: Cho dãy số {x
n
} được xác định bởi :
01
21
;
( ) , .
n n n k
xx
ax bx cx P n n

với
()
k
Pn
là đa thức bậc k theo n. Xác định số hạng tổng quát của dãy số.
Nghiệm riêng
cua phương trình đượ xác định như sau:
*
*
*2
( ) 0.
( ) 0 2 0.
( ) 0 2 0.
nk
nk
nk
x Q n khi a b c
x nQ n khi a b c a b
x n Q n khi a b c a b
Xác định công thức tổng quát theo trình tự các bước như đã trình bày ở các ví dụ trên.
Thí dụ : Cho dãy số {x
n
} :
01
21
31; 60.
7 10 8 12 14, .
n
n n n
xx
x x x n n n


. Tìm CTTQ của x
n.
Giải: Xét phương trình đặc trưng của dãy :
2
12
7 10 0 2 5.
Ta có : a+b+c ≠ 0 nên nghiệm riêng của phương trình
*2
n
x an bn c
. Thay vào công thức
truy hồi, tiến hành đồng nhất hệ số ta được :
*2
2 8 15
n
x n n
.
Số hạng tổng quát của dãy :
2
12
.2 .5 2 8 15.
nn
n
x c c n n
Từ
0 1 2
1
2
2
1 1 2
15 31
15
. 15.2 5 2 8 15, .
1
2 5 25 60
nn
n
x c c
c
Suy ra x n n n
c
x c c

Dạng 6: Cho dãy xác định bởi {x
n
} :
01
21
;
( ). , .
n
n n n k
xx
ax bx cx P n n

.Tìm CTTQ x
n.
Nghiệm riêng
của phương trình dạng này được xác định như sau :
*
12
*
12
*2
12
( ). .
. ( ). .
. ( ). .
n
nk
n
nk
n
nk
x Q n khi
x n Q n khi
x n Q n khi
Từ đây tìm được công thức tổng quát cảu x
n
.
Thí dụ: Cho dãy {x
n
} :
01
2
21
5; 18.
6 9 2(3 1).3 , .
n
n n n
xx
x x x n n


. Xác định công thức x
n
.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Giải: Xét phương trình đặc trưng
2
12
6 9 0 3.
Ta có
12

nên nghiệm riêng của pt
*2
.3
n
n
x n an b
. Thay
*
n
x
vào công thức truy hồi,
rút gọn và đồng nhất hệ số, ta được
* 3 2
2 .3
n
n
x n n
.
Số hạng tổng quát của dãy là
32
12
( ).3 ( 2 ).3 , .
nn
n
x c n c n n n
Từ
02
1
3 2 3 2
2
1 1 2
5
2
. (2 5).3 ( 2 ).3 2 2 5 .3
5
3( ) 3 18
n n n
n
xc
c
Suy ra x n n n n n n
c
x c c


.
Dạng 7: Cho dãy số được xác định bởi {x
n
} :
01
21
;.
. osn + sinn , n .
n n n
xx
ax bx cx c

. Xác định số hạng tổng quát của dãy trên.
Đối với phương trình dạng này, nghiệm riêng của nó có dạng :
*
osn +Bsinn
n
x Ac

.
Thay
vào công thức truy hồi để xác định được hai hệ số A và B.
Thí dụ: Cho dãy {x
n
} : được xác định bởi :
01
21
4 ; 4 2
n
3 2 3 3 2 . os sin , .
44
n n n
xx
n
x x x c n


. Tìm số hạng tổng quát của dãy.
Giải: Xét phương trình đặc trưng :
2
12
3 2 0 1 2.
Nghiệm riêng của phương trình có dạng :
*
n
os sin
44
n
n
x Ac B


. Thay vào công thức truy
hồi, ta được :
(n+2) ( 2) (n+1) ( 1) n
os sin 3 os sin 2 os sin
4 4 4 4 4 4
n n n
Ac B Ac B Ac B

n
3 3 2 . os sin
44
n
c


.
Phân tích vế trái và rút gọn ta được :
3 3 n 3 3 n
2 . os 2 .sin 3 3 2 os sin .
4 4 4 4
2 2 2 2
A B A B n n
B A c A B c
Đồng nhất hệ số, ta được :
*
33
2 3 3 2
1
n
22
os sin
3 3 1
44
21
22
n
AB
BA
A
n
xc
A B B
AA


.
Số hạng tổng quát của dãy :
12
n
.2 os sin .
44
n
n
n
x c c c

Từ
0 1 2
1
2
1 1 2
14
6
n
. 2 6 os sin , .
1
44
2 2 4 2
n
n
x c c
c
n
Suy ra x c n
c
x c c



Dạng 8: Cho dãy số dạng sau { x
n
} :
01
2 1 1 2
;
... (1), .
n n n n n nk
xx
ax bx cx d d d n

Trong đó
ni
d
là một trong các dạng sau : hắng số d,
.
n
d
,
()
k
Pn
,
. ( )
n
k
Pn
, ....
Khi đó ta gọi
*i
n
x
là nghiệm riêng của phương trình
21n n n ni
ax bx cx d

.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Nghiệm riêng của (1) được xác định là
**
1
k
i
nn
i
xx
. Sau đó ta thiết lập được công thức tổng
quát như các thí dụ đã cho.
III-Phƣơng trình sai phân bậc ba:
Loại 1: Phƣơng trình thuần nhất :
Dạng 1: Cho dãy {x
n
} :
0 1 2
3 2 1
;;
0.
n n n n
x x x
ax bx cx dx n
. Xác định số hạng tổng quát
x
n
của dãy số.
Xét phương trình đặc trưng
32
0a b c d
. Phương trình có 3 nghiệm phân biệt
1 2 3
; va
. Khi đó số hạng của dãy được xác định là :
1 1 2 2 3 3
. . .
n n n
n
x c c c
.
Từ các giá trị
0 1 2
;;x x x
ta xác định được các giá trị
1 2 3
;c c va c
.
Thí dụ: Cho dãy số {x
n
} :
0 1 2
3 2 1
1; 5 ; 8.
6 11 6 0 .
n n n n
x x x
x x x x n
. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng :
32
1 2 3
6 11 6 0 1; 2 ; 3.
Số hạng tổng quát của dãy có dạng :
1 2 3
.2 .3
nn
n
x c c c
.
Từ
1
0 1 2 3
1 1 2 3 2
2 1 2 3
3
11
1
2
11 5
2 3 5 9 . 9.2 .3 .
22
5
4 9 8
2
nn
n
c
x c c c
x c c c c Suy ra x n
x c c c
c




Dạng 2: : Cho dãy {x
n
} :
0 1 2
3 2 1
;;
0.
n n n n
x x x
ax bx cx dx n
. Xác định số hạng tổng
quát x
n
của dãy số.
Xét phương trình đặc trưng
32
0a b c d
có hai nghiệm phân biệt
1 2 3
va

.
Khi đó số hạng tổng quát của dãy số cho bởi :
1 1 2 3
..
nn
n
x c c n c

.
Từ các giá trị
0 1 2
;;x x x
ta xác định được các giá trị
1 2 3
;c c va c
.
Thí dụ: Cho dãy số {x
n
} :
0 1 2
3 2 1
5; 11 ; 16
11 32 28 0 , .
n n n n
x x x
x x x x n
. Tìm CTTQ của dãy.
Giải: Xét phương trình đặc trưng
32
1 2 3
11 32 28 0 7 2.
Số hạng tổng quát của dãy có dạng :
1 2 3
.7 .2
nn
n
x c c n c
Từ
1
0 1 3
1 1 2 3 2
2 1 2 3
3
6
35
5
13 6 13 181
7 2 2 11 . .7 .2 , .
14 35 14 35
49 4 4 16
181
35
nn
n
c
x c c
x c c c c Suy ra x n n
x c c c
c







Dạng 3: Cho dãy {x
n
} :
0 1 2
3 2 1
;;
0.
n n n n
x x x
ax bx cx dx n
. Xác định số hạng tổng quát
x
n
của dãy số.
Xét phương trình đặc trưng
32
0a b c d
có 1 nghiệm kép
1 2 3
. Khi đó
công thức nghiệm tổng quát có dạng :
2
1 2 3
.
n
n
x c n c n c
.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Từ các giá trị
0 1 2
;;x x x
ta xác định được các giá trị
1 2 3
;c c va c
.
Thí dụ: Cho dãy số {x
n
} :
0 1 2
3 2 1
3 ; 2 ; 8
3 3 0 , .
n n n n
x x x
x x x x n
. Xác định số hạng tổng
quát của dãy.
Giải: Xét phương trình đặc trưng :
32
1 2 3
3 3 1 0 1
.
Số hạng tổng quát của dãy có dạng :
2
1 2 3n
x c n c n c
.
Từ
1
03
2
1 1 2 3 2
2 1 2 3
3
7
2
3
9 7 9
2 . 3, .
2 2 2
4 2 8
3
n
c
xc
x c c c c Suy ra x n n n
x c c c
c




Dạng 4: Cho dãy {x
n
} :
0 1 2
3 2 1
;;
0.
n n n n
x x x
ax bx cx dx n
. Xác định số hạng tổng quát
x
n
của dãy số.
Xét phương trình đặc trưng
32
0a b c d
có 1 nghiệm thực
và hai nghiệm phức.
Khi đó số hạng tổng quát của phương trình có dạng :
1 2 3
. . osn +c .sin
n
n
x c c c n

.
Từ các giá trị
0 1 2
;;x x x
ta xác định được các giá trị
1 2 3
;c c va c
.
Thí dụ: Cho dãy số {x
n
} :
0 1 2
3 2 1
3; 4 3 ; 8 3.
5 22 48 0 , .
n n n n
x x x
x x x x n
. Tìm CTTQ của x
n
.
Giải: Xét phương trình đặc trưng
3 2 2
5 22 48 0 3 2 16 0
2
3
2 16 0 VN

. Phương trình sai phân bậc hai
2
2 16 0

không có nghiệm
thực nên theo thí dụ trong dạng 2 của phương trình sai phân bậc hai ta có số hạng tổng
quát là
'
23
n
. os sin
33
n
n
x c c c


. Vậy số hạng tổng quát
1 2 3
n
.3 . os .sin
33
n
n
n
x c c c c

.
Từ
0 1 2
1
3
2
1 1 2
3
3
2
21
3
1
3
n
3 4 3 2 . 3 2 os sin , .
2 2 3 3
2
3
9 8 3
22
n
n
x c c
c
c
c
n
x c c Suy ra x c n
c
c
c
xc







Loại 2: Phƣơng trình không thuần nhất.
Cho dãy số dạng {x
n
} :
0 1 2
3 2 1
;;
,.
n n n n n
x x x
ax bx cx dx d n
.
Trong đó
n
d
có thể là hăng số,
n
m
, đa thức bậc k theo n
()
k
Pn
, ....
Ta tiến hành tìm nghiệm riêng như dạng đối với phương trình bậc 2 đã trình bày ở trên.
IV-Phƣơng trình sai phân bậc cao.
Dạng 1: Phương trình thuần nhất :
0 1 1
...... 0
n k n k k n
a x a x a x
.
Xét phương trình đặc trưng :
1
01
.............. 0
kk
k
a a a

.
TH1: có k nghiệm thực phân biệt, khi đó số hạng tổng quát của dãy sẽ có dạng :
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
1 1 2 2 3 3
1
. . . ........... . .
k
n n n n n
n k k i i
i
x c c c c c
.
TH2: Có s nghiệm bằng nhau , (k – s) nghiệm khác nhau và khác với s nghiệm trên. Khi
đó số hạng tổng quát của dãy có dạng :
1
1
01
. . .
sk
p n n
n p i i
p i s
x c n c






.
TH3: Nếu phương trình đặc trưng có nghiệm phức :
os +isin
j
x A Bi r c

trong đó
22
r A B
;
B
arctan
A
và k – 2 nghiệm thực khác nhau thì số hạng tổng quát của dãy
số sẽ có dạng :
2
''
12
1
. . os +c .sin .
k
nn
n i i
i
x c r c c n n

Dạng 2: Phương trình không thuần nhất:
0 1 1
....... .
n k n k k n n
a x a x a x b
Ta xét thêm nghiệm riêng
tuỳ theo dạng của b
n
và các hệ số a
i
. Thiết lập công thức
tổng quát của x
n
từ các giả thiết của bài.
V-Một số dạng đặc biệt khác thƣờng gặp của dãy số trong các kì thi.
Dạng 1: Phương trình sai phân dạng " Hệ phương trình sai phân tuyến tính cấp một".
Cho dãy số {x
n
} , {y
n
} được xác định như sau :
1
1
n n n
n n n
x ax by
y cx dy


.
Tìm số hạng tổng quát x
n
và y
n
.
Đưa hệ về phương trình sai phân tuyến tính cập 2 của từng dãy {x
n
} và {y
n
} :
2 1 1 1 1 1 1
( ) ( ) ( ) ( )
n n n n n n n n n n n n
x ax by ax b cx dy ax bcx d x ax a d x bc ad x
2 1 1 1 1 1 1
( ) ( ) ( ) ( )
n n n n n n n n n n n n
y cx dy c ax by dy dy bcy a y dy a d y bc ad y
.
Đưa được hệ về dạng phương trình cơ bản, từ đây ta dễ dàng tìm được CTTQ của số hạng
từng dãy đã cho.
Thí dụ: Tìm CTTQ của dãy số {x
n
} và {y
n
} :
01
01
2; 2
.
1; 2
n n n
n n n
u u u v
n
v v u v

Giải: Ta có :
2 1 1
( ) ( ) 4 3
n n n n n
u a d u bc ad u u u
và
1
5u
.
Từ đây, ta có :
1
1
1
1 3 1 3
2.
22
n
n
n n n n
u v u u
Dạng 2: Phương trình sai phân dạng phân thức tuyến tính:
Tìm CTTQ của dãy số có công thức xác định như sau :
01
;.
n
n
n
ax b
x x n
cx d
Cách 1: Đặt
( 0).
k
kk
k
y
xz
z

Khi đó dãy được biến đổi thành :
1 2 1
1
1 2 1
1
.
( ) ( )
.
( ) ( )
.
n
n n n n n n
n n n n
n
n n n n n n
n n n
n
y
ab
y ay bz y a d y bc ad y
y z ay bz
n
y
z cy dz z a d z bc ad z
z cy dz
cd
z



Từ công thức tổng quát của {y
n
} và {z
n
} ta suy ra CTTQ của {x
n
} .
Cách 2: Đặt
nn
x u t
, thay vào công thức truy hồi của dãy ta có :
2
1
( ) ( )
(*).
nn
n
nn
au at b a ct x ct a d t b
ut
cu ct d cu ct d
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Ta chọn t sao cho
2
( ) 0.ct d a t b
Khi đó ta chuyển (*) về dạng :
1
11
.
nn
mn
uu

Từ đây ta tìm được
1
n
u
, suy ra
.
n
u
Thí dụ: Tìm CTTQ của dãy số {u
n
} :
1
1
1
2
9 24
2.
5 13
n
n
n
u
u
un
u

.
Cách 1: Đặt
n
n
n
x
u
y
, thay vào công thức truy hồi ta được :
1
1 2 1
1 1 1
1
1 2 1
11
1
9 24
9 24 4 3
9 24
.
5 13 4 3
5 13
5 13
n
n n n n n n
n n n n
n
n n n n n n
n n n
n
x
x x y x x x
x y x y
n
x
y x y y y y
y x y
y






Từ
12
42
2
23
uu
. Ta chọn
12
12
2 ; 42
1 ; 23
xx
yy

.
Từ đây ta tìm được :
1
1
1
1
22.3 24
22.3 24
. 2.
11.3 10
11.3 10
n
n
n
n
n
n
n
x
Suy ra u n
y


Cách 2: Đặt
nn
u x t
, thay vào công thức truy hồi ta được :
2
1
1
9 9 24 ( 9 5 ) 5 22 24
5 5 13 5 5 13
nn
nn
nn
x t t x t t
x t x
x t x t
Ta chọn t :
2
1
5 22 24 0 2 4.t t t x
11
1
11
11
1 3 1 11.3 10 4 22.3 24
5 2 .
5 3 4 11.3 10 11.3 10
nn
n
n n n n
nn
n n n n
x
x x u x
x x x x



Dạng 3: Hệ phương trình tuyến tính bậc 2.
Tìm CTTQ của dãy số (u
n
) và (v
n
) được xác định bởi :
22
1 1 1
1 1 1
.;
2 . ;
n n n
n n n
u u a v u
a
v u u v



1
1
11
11
22
22
1 1 1 1
11
22
11
1 1 1 1
22
22
. . ....... .
.
. 2 . .
. ....... .
1
2
1
2
n
n
nn
nn
n n n n
n n n
n n n
n n n n
n
n
u a v u a v u a v
u u a v
a v a u v
u av u a v u a v
u a a
v a a
a













.
Thí dụ: Xác định CTTQ của hai dãy số {u
n
} và {v
n
} thoả :
1
1
2
1
u
v
và
22
11
11
2
2.
2.
n n n
n n n
u u v
n
v u v




Giải:
Ta có:
2
22
11
11
2
11
11
22
2
2 2 2
22
n n n n
n n n
n n n
n n n n
u v u v
u u v
v u v
u v u v







Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
11
11
11
11
22
22
11
22
22
11
1
2 2 2 2
2 2 2 2
2
1
2 2 2 2
2 2 2 2
22
nn
nn
nn
nn
n
nn
nn
n
u
u v u v
u v u v
v












.
Dạng 4: Dạng phân thức bậc 2 trên bậc 1:
Tìm CTTQ của dãy {x
n
} :
1
2
1
1
2.
.
2
n
n
n
x
n
xa
xa
x


Đặt
n
n
n
u
x
v
, khi đó dãy trên được chuyên về hai dãy {u
n
} và {v
n
} như sau :
22
1 1 1
1 1 1
.;
2.
2 ; 1
n n n
n n n
u u a v u
n
v u v v




Khi đó
11
11
22
22
.
nn
nn
n
n
n
aa
u
xa
v
aa





Thí dụ: Xác định CTTQ của dãy số {x
n
} :
1
2
1
1
2
2
2.
2
n
n
n
x
x
xn
x
.
Giải: Xét hai dãy số {u
n
} và {v
n
} :
1
1
2
1
u
v
và
22
11
11
2
2.
2
n n n
n n n
u u v
n
v u v




Ta dễ dàng chứng minh được bằng quy nạp
n
n
n
u
x
v
.
Theo kết quả bài toán trên, ta có :
11
11
22
22
2 2 2 2
2. .
2 2 2 2
nn
nn
n
x


Dạng 5: Dạng có căn thức trong công thức truy hồi.
a) Với dãy số {u
n
} :
1
2
11
2.
n n n
u
u au bu c n

, với
2
1ab
ta xác định CTTQ như sau:
Từ dãy truy hồi
2 2 2
1 1 1 1
20
n n n n n n n
u au bu c u au u u c
Thay n bởi n – 1, ta được
22
2 2 1 1
2 0.
n n n n
u au u u c
Ta đây ta dễ thấy
và
2n
u
là nghiệm của phương trình bậc hai
22
11
20
nn
X au X u c

.
Theo định lý Vi-et, ta có
21
2
n n n
u u au


. Từ đây ta dễ dàng xác định CTTQ của x
n
.
b) Một cách biểu diễn khác : Cho dãy số {u
n
} :
1
1
2
1
2.
n
n
n
u
u
un
a cu b

, trong đó
2
0; 1 ; 1a a b
ta xác định CTTQ như sau :
Ta viết lại công thức tổng quát dưới dạng :
2
11
1
.
n n n
ab
c
u u u

Đặt
1
n
n
x
u
.
Ta có
2
11n n n
x ax bx c

đây là dãy mà ta đã xét ở trên.
Thí dụ: Cho dãy số {u
n
} :
1
11
1
5 24 8 2.
n n n
u
u u u n

Tìm
?
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Giải: Từ công thức truy hồi của dãy ta có :
2
2
11
5 24 8
n n n
u u u

22
11
10 8 0
n n n n
u u u u

(1) . Thay n bởi n – 1 ta được :
22
2 2 1 1
10 8 0
n n n n
u u u u
(2).
Từ (1) và (2)
2
,
nn
uu
là hai nghiệm của phương trình :
22
11
10 8 0
nn
t u t u

Áp dụng định lý Vi-et, ta có :
21
10 .
n n n
u u u


Ta dễ dàng tìm được
11
6 2 6 2
5 2 6 5 2 6 .
2 6 2 6
nn
n
u


Dạng 6: Công thức truy hồi bậc hai dạng phân thức.
Cho dãy số {u
n
} :
12
2
1
2
;
2.
n
n
n
uu
ua
un
u


. Tìm
?
Đối với dạng này thì từ công thức truy hồi u
3
, u
4
, u
5
. Ta giả sử
12n n n
u xu yu z

.
Lập hệ phương trình
3 2 1
4 3 2
5 4 3
u xu yu z
u xu yu z
u xu yu z
, , .x y z
Từ công thức truy hồi ta dễ dàng tìm được công thức tổng quát của u
n
.
Thí dụ: Tìm CTTQ của dãy số {u
n
} :
12
2
1
2
1
2
2.
n
n
n
uu
u
un
u

.
Giải: Ta có :
3 4 5
3; 11; 41.u u u
Ta giả sử
12
.
n n n
u xu yu z

Ta có hệ pt :
3 2 1
4 3 2 1 2
5 4 3
34
3 11 1 4
11 3 41 0
n n n
u xu yu z
x y z x
u xu yu z x y z y u u u
x y z z
u xu yu z



.
Ta dễ dạng tìm được
9 5 3 9 5 3
. 2 3 . 2 3 1.
66
nn
n
xn

VI-Sử dụng lƣợng giác để tìm công thức tổng quát của dãy số :
Dạng 1: Xác định công thức dãy số dạng {u
n
} :
1
2
1
2 1 2.
nn
u
u u n
ta làm như sau :
Nếu
1
1u
: ta đặt
1
osuc
. Khi đó ta có :
n-1
os2
n
uc
.
Nếu
1
1u
: ta đặt
1
11
2
ua
a




1
00a va au
. Khi đó
1
1
2 2 4 2
23
2 2 4
2
1 1 1 1 1 1 1 1
2 1 ........
2 2 2 2
n
n
n
u a a u a u a
a a a
a



.
Với cách xác định số a, ta có a là nghiệm (cùng dấu với u
1
) của phương trình
2
1
2 1 0a u a
. Do tích hai nghiệm la 1 nên nếu a là 1 nghiệm thì
1
a
sẽ là
nghiệm còn lại của phương trình. Khi đó công thức tổng quát có thể viết như
sau :
11
22
22
1 1 1 1
1
1 1 .
2
nn
n
u u u u u




Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Thí dụ 1: Cho dãy số {u
n
}:
1
2
1
1
2
2 1 2.
nn
u
u u n
. Xác định CTTQ của dãy {u
n
}.
Giải: Ta có
2
22
1 2 3
1 2 2 2
os 2 os 1 os 2 os 1 os
2 3 3 3 3 3
u c u c c u c c
Bằng quy nạp ta chứng minh được rằng
n-1
2
os 1.
3
n
u c n
.
Thí dụ 2: Cho dãy số {u
n
} :
1
2
1
3
2 1 2.
nn
u
u u n
. Xác định CTTQ của u
n
.
Giải: Gọi a là nghiệm lớn của phương trình :
2
11
3 6 1 0 3 2 2
2
a a a a
a



.
Ta có
2
1
11
6 1 0 3
2
a a u a
a



, khi đó
2
2
2
2
1 1 1
1.
2
u a a
aa



Giả sử
1
1
2
2
1
k
k
k
xa
a

thì
2
1
2
1
k
k
k
xa
a

.
Theo nguyên lý quy nạp, ta được
11
1
1
22
2
2
1
3 2 2 3 2 2
nn
n
n
n
xa
a

.
Thí dụ 3: Cho dãy số {x
n
} được xác định như sau :
2
11
5, 2 1
nn
x x x n
.
Tìm giá trị của
1
12
lim
.....
n
n
n
x
S
x x x

.
Giải: Chọn a là nghiệm lớn của phương trình
2
5 21
5 1 0 1.
2
x x a
Ta có
2
1
1
5 1 0 5a a x a
a
; khi đó
2
22
21
2
11
2 2 .x x a a
aa



Bằng quy nạp ta chứng minh được
1
1
2
2
1
1.
n
n
n
x a n
a
Chú ý rằng
11
11
2 2 2
2 2 2
1 1 1
k k k
k k k
a a a
a a a


,
ta có
2
1
2
2
1
2
12
12
22
11
1
1
1
1
..
11
1
.....
1
.....
n
n
n
n
nn
n
n
n
n
aa
ax
x
a
a
a
a
a
x x x a
a
a x x x
a
aa













Do đó
2
1
12
2
1
1
11
lim lim . 21.
1
......
1
n
n
n
nn
n
x
a
S a a
x x x a a
a
 



Dạng 2: Tìm CTTQ của dãy số {u
n
} :
1
3
11
4 3 2.
n n n
up
u u u n

, ta làm như sau :
Nếu
1p
, thì
0; : os =pc

. Khi đó bằng quy nạp ta chứng minh được :
n-1
os3
n
uc
.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Nếu
1p
thì ta đặt
11
11
0
2
u a au
a



. Bằng quy nạp ta chứng minh được
1
1
3
3
11
.
2
n
n
n
ua
a




hay
11
33
22
1 1 1 1
1
1 1 .
2
nn
n
u u u u u




Thí dụ 1: Xác định CTTQ của dãy {u
n
} :
1
3
1
2
2
4 3 , 2.
n n n
u
u u u n
.
Giải: Ta có
2
33
1 2 3
2 3 3 3 3
os 4 os 3 os os 4 os 3 os os
2 4 4 4 4 4 4 4
u c u c c c u c c c
.
Bằng quy nạp ta chứng minh được
n-1
3
os 1.
4
n
u c n
Thí dụ 2: Tìm CTTQ của dãy {x
n
} :
1
3
11
7
4 3 1.
n n n
x
x x x n

.
Giải: Gọi a là nghiệm lớn của phương trình
2
14 1 0 7 4 3x x a
.
Ta có
3
3
12
3
1 1 1 1 3 1 1 1
7
2 2 2 2
u a u a a a
a a a a
.
Bằng quy nạp ta dễ dàng chứng minh được
1
1
3
3
11
1.
2
n
n
n
u a n
a



Vậy công thức tổng quát của dãy là :
11
33
1
7 4 3 7 4 3 1.
2
nn
n
un




Dạng 3: Cho dãy {u
n
} :
1
3
11
4 3 , 2.
n n n
up
u u u n

. Để xác định công thức tổng quát của
nó ta có thể làm như sau :
Ta đặt
1
11
2
ua
a




. Khi đó bằng nạp ta chứng minh được :
11
1
1
33
3 2 2
1 1 1 1
3
1 1 1
1 1 .
22
nn
n
n
n
u a u u u u
a







Thí dụ : Xác định CTTQ của dãy {u
n
} :
1
32
1 1 1
3
6
24 12 6 15 6 2.
n n n n
u
u u u u n
Đặt
nn
u xv y
. Thay vào công thức truy hồi của dãy, biến đổi và rút gọn ta được :
3 3 2 2 2 2
1 1 1
32
24 12 6 6 3 24 8 6 5
24 12 6 15 6.
n n n n
xv y x v x y x v xy xy x v
y y y
Ta chọn y sao cho :
22
32
6 6 0
1
.
6
24 12 6 15 6
x y x
y
y y y y


Khi đó :
3 3 2 3
1 1 1 1
24 3 24 3
n n n n n n
xv x v xv v x v v
. Ta chọn
1
6
x
11
33
3
1 1 1
1
4 3 ; 2 2 5 2 5
2
nn
n n n n
v v v v v





Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
11
33
11
2 5 2 5 1.
2 6 6
nn
n
Suyra u n




Dạng 4: Xác định CTTQ của dãy {u
n
} :
1
2
1
2.
nn
u
u a bu n
với
1
2
a
ab
.
Khi đó ta đặt
2
2
12
os u os 1 2 os os2u ac a b ac a c ac
.
Bằng quy nạp ta ta chứng minh được
n-1
os 2 1.
n
u ac n
Thí dụ 1: Xác định CTTQ của {u
n
} :
1
2
1
3
2
2 2.
nn
u
u u n
.
Giải: Đặt
3
os , ; ,
42
c



khi đó :
2
12
2 os u 2(1 2 os ) 2 os2u c c c
.
Bằng quy nạp ta chứng minh được
n-1
2 os2 1.
n
u c n
Thí dụ 2: Tìm CTTQ của dãy số {x
n
} :
1
2
1
1
2
2 2 1
2.
2
n
n
x
u
xn

.
Giải: Ta có :
2
12
2 1 os
2 2 1 sin
6
1
6
sin sin
2 6 2 2 2.6
c
uu





Bằng quy nạp ta chứng minh được là :
1
sin 2.
2 .6
n
n
un
Thí dụ 3: Cho a, b là hai số dương không đổi thoả mãn a < b và hai dãy {a
n
} , {b
n
}
được xác định như sau :
1 1 1
11
1
;
2
; 2.
2
nn
n n n n
ab
a b ba
ab
a b a b n


. Tìm CTTQ của a
n
và b
n
.
Giải: Ta có
01
a
b

nên ta đặt
os
a
c
b
với
0;
2



.
Khi đó :
2
1
1 os
os +b
os
2 2 2
bc
bc
a bc

và
2
1
. os os
22
b b bc bc


2
2
11
2
2
os os
22
os . os
2 2 2 2
bc bc
ab
a bc c


và
2
2
os . os .
22
b bc c

Bằng quy nạp ta chứng minh được :
2
2
os os ..... os
2 2 2
n
n
a bc c c
và
2
2
os os ..... os
2 2 2
n
n
b bc c c
.
Dạng 5: Để tìm CTTQ của dãy {u
n
} :
1
1
1
2.
1
n
n
n
ua
ub
un
bu
Ta đặt
tana
và
tanb
, khi đó ta dễ dàng chứng minh được
tan ( 1)
n
un

.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Thí dụ 1 : Cho dãy {u
n
} :
1
1
1
3
21
2.
1 1 2
n
n
n
u
u
un
u


. Tính giá trị của
2011
u
.
Giải: Ta có
tan 2 1
8

và
1
3 tan
3
u

.
Khi đó,
2
tan tan
38
tan .
38
1 tan .tan
38
u






Bằng quy nạp ta chứng minh được :
tan ( 1) 2.
38
n
u n n




Suy ra
2011
5
tan 2010. tan 2 3.
3 8 3 4
u
Thí dụ 2: Tìm CTTQ của dãy số {u
n
} :
1
1
2
1
3
2.
11
n
n
n
u
u
un
u

Giải: Ta có :
2
11
1 1 1
1.
n n n
u u u

Đặt
1
n
n
x
u
, khi đó ta được dãy {x
n
} dược xác định như
sau :
1
1
3
x
và
2
11
1.
n n n
x x x

Vì
2
12
1 os
1
3
cot ot 1 ot cot
3 3 3 2.3
3
sin
3
c
x x c c
.
Bằng quy nạp ta chứng minh được :
11
cot tan 1,2,3...........
2 .3 2 .3
nn
nn
x u n


BÀI TẬP DÀNH CHO ĐỘC GIẢ TỰ LUYỆN
Bài 1: Xác định công thức tổng quát của các dãy số sau đây :
a) Cho
01
1; 3 2 0 0
nn
x x x n
b) Cho
01
1; 5 4 2 0.
n
nn
x x x n
c) Cho
2
01
2; 2 4 0.
nn
x x x n n n
d) Cho
01
5; 4 7 6 5 0.
nn
x x x n n
e) Cho
01
3; 13 0.
nn
x x x n
f) Cho
01
4; 3 2 23 0.
nn
x x x n
g) Cho
01
7; 3 2.3 0.
n
nn
x x x n
h) Cho
2
01
15; 2 2 0.
n
nn
x x x n
i) Cho
01
7
; 11 6 2.3 4 0.
5
nn
nn
x x x n
j) Cho
0 1 1 1 1
1; 4; 4 0 1.
n n n
x x x x x n
k) Cho
0 1 1 1
21
4; ; 0; 1.
34
n n n
x x x x x n

l) Cho
0 1 1 1
3; 3 4 3 ; 2 13 0 1
n n n
x x x x x n

.
m) Cho
0 1 1 1
5; 1; 6 3 14 1
n n n
x x x x x n

.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
n) Cho
0 1 1 1
4; 3; 2 3 6 1
n n n
x x x x x n

.
o) Cho
0 1 1 1
2; 4; 2 11 1.
n n n
x x x x x n

p) Cho
0 1 1 1
1; 5; 8 15 4.2 1.
n
n n n
x x x x n

q) Cho
0 1 1 1
1; 4; 3 4 3.4 1.
n
n n n
x x x x x n

r) Cho
0 1 1 1
4; 2; 6 9 5.3 ; 1.
n
n n n
x x x x x n

s) Cho
2
0 1 1 1
1; 3; 7 12 (2 3 1).2 1.
n
n n n
x x x x x n n n

t) Cho
0 1 1 1
2; 3; 7 10 (3 1).5 1.
n
n n n
x x x x x n n

u) Cho
2
0 1 1 1
1; 3; 8 16 (2 3).4 1.
n
n n n
x x x x x n n

v) Cho
0 1 1 1
1; 6 ; 3 2 3 os 2sin 1.
33
n n n
nn
x x x x x c n


w) Cho
0 2 1 1
1; 5 ; 2 7 5 2 5 1.
nn
n n n
x x x x x n

x) Cho
1
11
1
25
3; 2 ; 1.
53
n n n
n n n
x x y
x y n
y x y


y) Cho
11
27
2; ; 1.
43
n
n
n
x
x x n
x
Bài 2: Xác định Công thức tổng quát của các dãy số đặc biệt sau :
a) Cho
2
0 1 2
11
.
1
1; ;
2 2002 2001 2000
nn
n
n n n n
xx
x x x
x x x x


với n
0.
b) Cho
23
0 1 2 1
1; 2; . 0.
n n n
x x x x x n

c) Cho
11
2
1; 1
23
n
n
n
x
x x n
x

d) Cho
2
0 1 1
2; 6 33 ; 3 8 1 1
n n n
u u u u u n
e) Cho
1
1
1
3
3
23
2.
1 3 2
n
n
n
u
u
un
u


Bài 3: Cho dãy số {u
n
} thoả mãn như sau :
01
12
,.
1, 9
10. , 2.
n
n n n
un
uu
u u u n n



Chứng minh rằng
, 1.kk
a)
22
11
10 8
k n k k
u u u u

b)
1
54
kk
uu
và
2
3. 1 2
k
u
.
Bài 4: Cho dãy {x
n
} xác định như sau :
01
12
1; 0
2 2 2.
n n n
xx
x x x n


.
Xác định số tự nhiên n sao cho :
1
22685.
nn
xx

Bài 5: Cho day {x
n
} được xác định bởi :
01
11
1; 5
6 1.
n n n
xx
x x x n


.
Tìm
lim 2
n
n
x

( TH&TT T7/253)
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Bài 6: Xét dãy {a
n
} :
1
1
2
a
và
1
1
2
2
2
1
11
1.
2
n
n
a
an






Chứng minh rằng :
1 2 3 2005
...... 1,03a a a a
(TH&TT T10/335)
Bài 7: Cho dãy số {a
n
} :
2
01
2; 4 15 60 1.
n n n
a a a a n
Hãy xác định CTTQ của a
n
và
chứng minh rằng số
2
1
8
5
n
a
có thể biểu diễn thành tổng bình phương của 3 số nguyên
liên tiếp với
1.n
(TH&TT T6/262)
Bài 8: Cho dãy số
()pn
được xác định như sau :
(1) 1; ( ) (1) 2 (2) ....... ( 1) ( 1) 2.p p n p p n p n n
Xác định p(n) . (TH&TT T7/244).
Bài 9: Xét dãy {u
n
} :
1
32
1
2
3 2 9 9 3 2.
nn
u
u u n n n n
. Chứng minh rằng với mỗi số
nguyên tố p thì
1
1
2009
p
i
i
u
chia hết cho p (TH&TT T6/286).
Bài 10: Dãy số thực {x
n
} :
0
2
1
2 1 0.
nn
xa
x x n
.
Tìm tất cả giá trị của a để
00
n
xn
. (TH&TT T10/313)
Bài 11: Dãy số {x
n
} :
01
1
1;
2
xx
và
1
2
11
.
0.
2002 2001 2000 .
nn
n
n n n n
xx
xn
x x x x


Hãy tìm CTTQ của x
n
(TH&TT T8/298).
Bài 12: Cho dãy số {a
n
} được xác định như sau {a
n
} :
1
1
1
1
2
1.
21
n
n
n
a
a
an
na
Tính tổng
1 2 2010.
..........S a a a
Bài 13: Cho dãy số được xác định bởi :
12
1.2.3; 2.3.4; ......; ( 1)( 2).
n
a a a n n n
Đặt
12
.... .
nn
S a a a
Chứng minh rằng
41
n
S
là số chính phương .
( HSG Quốc Gia – 1991 Bảng B)
Bài 15: Cho hai dãy số {a
n
} và {b
n
} được xác định như sau :
00
1 1 1
2 ; 1
2
; 0.
nn
n n n n
nn
ab
ab
a b a b n
ab

.
Chứng minh rằng các dãy {a
n
} và {b
n
} có cùng giới hạn chung khi
n
.
Tìm giới hạn chung đó. ( HSG Quốc Gia – 1993 Bảng A ngày thứ 2)
Bài 16: Cho các số nguyên a, b. Xét dãy số nguyên {a
n
} được xác định như sau :
0 1 2
3 2 1
; ; 2 2
3 3 0.
n n n n
a a a b a b a
a a a a n
.
a) Tìm CTTQ của a
n
b) Tìm các số nguyen a, b để a
n
là số chính phương với
1998n
.
(HSG Quốc Gia – 1998 Bảng B).
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Bài 17: Cho dãy số (a
n
) :
0
1
3
3 6 18 1.
nn
a
a a n
. Tính
1
1
n
i
i
a
. ( Trung Quốc – 2004).
Bài 18: Cho dãy số (a
n
) :
0
2
11
1
7 45 36
1.
2
nn
n
a
aa
an


. Chứng minh rằng :
a)
n
a
là số nguyên dương với
0.n
b)
1
1
nn
aa
là số chính phương với
0.n
( Trung Quốc – 2005).
Bài 19: Cho dãy số (u
n
) :
12
12
1; 2
4 3.
n n n
uu
u u u n


. Chứng minh rằng
2
1
3
n
u
là số chính
phương ( Chọn đội tuyển Nghệ An – 2007 ).
Bài 20: Cho dãy số (b
n
) :
01
12
3
12;
2
. 3 2.
n n n
bb
b b b n


. Tính
2007
0
i
i
b
( Moldova 2007).
Bài 21: Cho dãy số {u
n
} được xác định như sau :
1
2
1
1
1; 0 1
11
2.
n
n
n
n
u u n
u
un
u

.
Chứng minh rằng
12
1
1
..... 1 1
42
n
n
S u u u



. (HSG Quảng Bình 2008 – 2009).
Bài 22: Cho đa thức
3
( ) 6 9P x x x
và
( ) ( (....( ( )))...)
n
P x P P P x
( n dấu ngoặc). Tìm số
nghiệm của P(x) và P
n
(x) ? ( Dự tuyển Olympic).
Bài 23: Cho dãy số (u
n
) được xác định như sau:
01
11
1
14 1.
n n n
uu
u u u n


.
Chúng minh rằng với
0n
thì
21
n
u
là một số chính phương.
( Chọn đội tuyển Romania 2002)
Trên đây là một phân nhỏ kiến thức về bài toán xác định công thức tổng quát của một dãy
số mà tôi đã lĩnh hội được và được xin trình bày cho các bạn tham khảo. Mong nhân được
những ý kiến đánh giá chân thật từ mọi người. Xin chân thành cảm ơn!
Name : Mai Xuân Việt
Address : Đội II – thôn Dƣơng Quang – Xã Đức Thắng – Huyện Mộ Đức – Tỉnh
Quảng Ngãi .
Email : xuanviet15@gmail.com
Tel : 01678336358 – 0938680277 – 0947572201
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

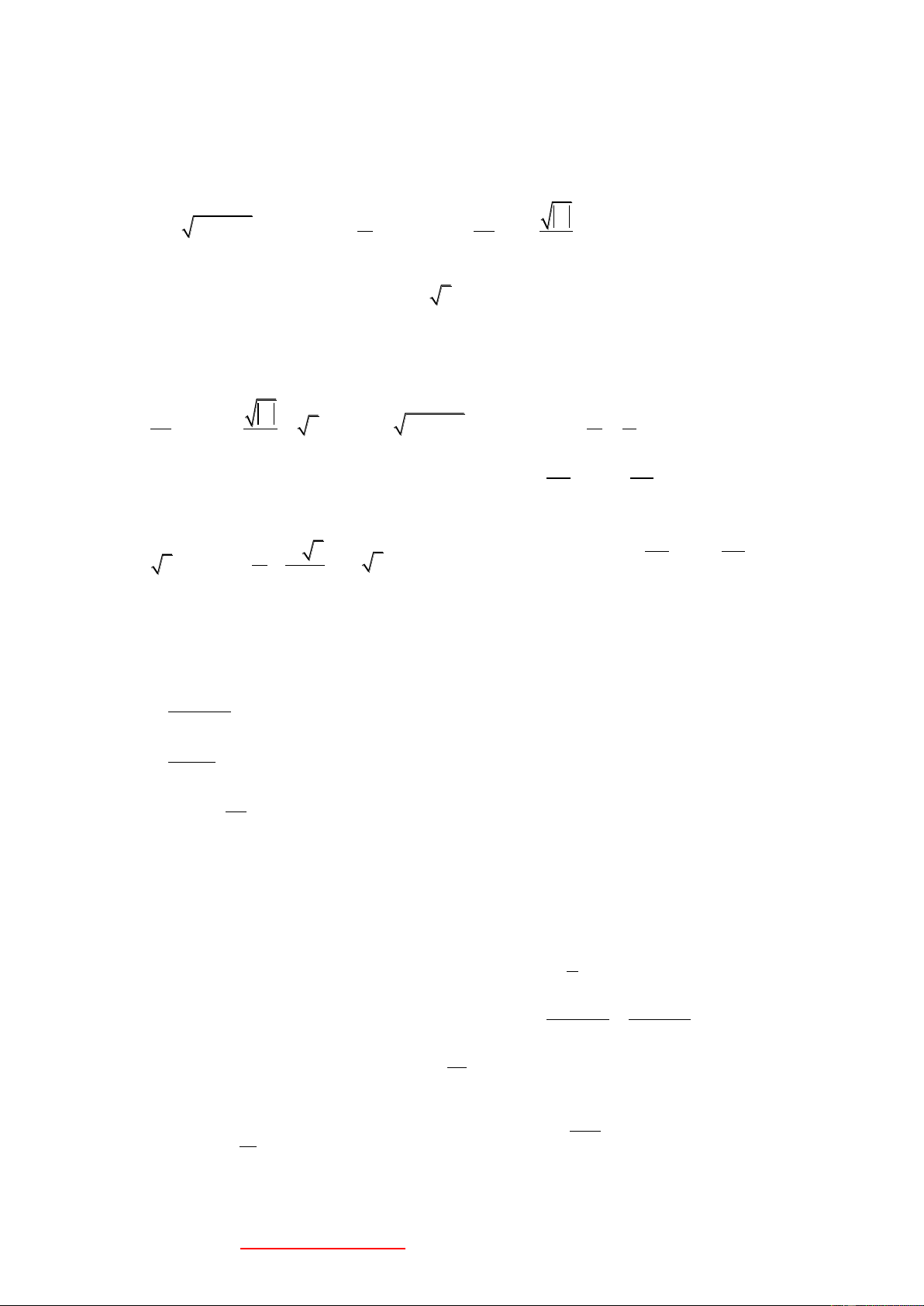
Preview text:

TÌM SỐ HẠNG TỔNG QUÁT CỦA DÃY SỐ
BẰNG PHƢƠNG PHÁP SAI PHÂN
I-Phƣơng trình sai phân bậc nhất:  
Dạng 1: Cho dãy số {x x o c nst n} : 0 
. Tìm số hạng tổng quát của dãy số? ax  bx  0  n+1 n 2 n
Từ công thức truy hồi ta có  b   b   b  : x   .x   .x
 ....................   .x n   n 1   n2   0  a   a   a nb
Khi đó công thức tổng quát (CTTQ) của dãy số được xác định bởi : x x .  . n 0    a     x 5
Thí dụ : Cho dãy số {x } được xác định bởi : 0 n  . x  3x  0 , n     n 1  n
Tìm số hạng tổng quát của dãy số.
Giải: Từ công thức truy hồi ta có : 2 x  3x  3 x
 .................  3n x hay x  5.3n . n n 1  n2 0 n  Dạng 2: x Cho dãy số {x
là đa thức bậc k của n. n} : 0  , với P (n) ax
bx P (n)  k n+1 n k
Tìm số hạng tổng quát của dãy số ? Giải: b
Xét phương trình đặc trưng : a  b  0     . a
Đối với dạng này ta xét thêm một giá trị *
x gọi là nghiệm riêng của phương trình sai phân. n
Khi đó số hạng tổng quát của dãy được xác định bởi : * x  . n
c   x . Trong đó nghiệm n n riêng *
x được xác định như sau : n
 Nếu a + b ≠ 0 thì nghiệm riêng *
x Q (n) thay vào phương trình ta được: n k .
a Q (n 1)  . b Q ( ) n P ( )
n . Đồng nhất hệ số ta tìm được Q (n) . k k k k
 Nếu a + b = 0 thì nghiệm riêng * x  .
n Q (n) thay vào phương trình ta được: n k
a(n 1).Q (n 1)  b . n Q ( ) n P ( )
n . Đồng nhất hệ số ta tìm được . n Q (n) . k k k kx  7
Thí dụ 1: Cho dãy số {x 
.Tìm số hạng tổng quát x n} : 0  2  n . x
 2x  3n  4n  5 , n   .   n 1  n
Giải: Xét phương tình đặc trưng   2  0    2 .
Ta có : a + b = 1 – 2 = -1 ≠ 0 nên nghiệm riêng pt có dạng : * 2
x an bn c . Thay * x vào n n pt, ta được : 2 2 2 a(n 1)  (
b n 1)  c  2an  2bn  2c  3n  4n  5 2 2
  an  (2a  )
b n a b c  3n  4n  5 .
Đồng nhất hệ số hai vế ta được : a  3 a  3    * 2
2a b  4  b   1  0  x  3
n 10n 18 . n  
a b c  5 c  1  8  
CTTQ của số hạng trong dãy : n 2 x  .
c 2  3n 10n 18 . n Từ n 2
x  7  c 18  7  c  25. Suy ra x  25.2  3n 10n 18 . 0 n   Thí dụ 2: x 5 Cho dãy số {x . Tìm CTTQ của x n} : 0  n. x
x  4n  5 , n   .   n 1  n
Giải: Xét phương trình đặc trưng  1 0   1.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Ta có : a + b = 1 – 1 = 0 nên nghiệm riêng của pt có dạng * 2 x  ( n an  )
b an bn . * x vào pt, n n ta được : 2 2 a(n 1)  (
b n 1)  an bn  4n  5.
 2an a b  4n  5.
Đồng nhất hệ số hai vế ta được : 2a  4 a  2 * 2   
x  2n  3n . a b  5 b   3 n
Số hạng tổng quát của dãy có dạng : 2
x c  2n  3n . n Từ 2
x  5  c  5. Suy ra x  2n  3n  5. 0 n  Dạng 3: x Cho dãy số {xn} : 0
ax bx d (d  o c nst) , n   .   n+1 n n   b     d   1    n     a b   
Khi đó số hạng tổng quát của dãy số là : x   .x
neu a b  0. n   0   a   b   a  1      a   
x x nd
neu a b  0.  n 0   Thí dụ 1: x 5 Cho dãy số {x . Tìm CTTQ của x n} : 0  n . xx  6 , n   .   n 1  n
Giải: Từ công thức truy hồi ta có : x x
 6  x  2.6  x  3.6  .......  x  6n hay x  6n  5. n n 1  n2 n 3  0 n   Thí dụ 2: x 3 Cho dãy số {xn} : 0  . Tìm CTT Q của xn . x 8x  4 , n     n 1  n
Giải: Từ công thức truy hồi, ta có : n   x  8x
 4  8 x    x    x    x  . n n 8 4 n  4 8 . 4 n 8  2 8 1 n 8 1 2 2 1 8 . 4. ........ 8 . 4. 1 2 2 n2 0 8 1 8 1 n 4 n 25 n 4 Suy ra x  3.8  .    n 8 1 .8 . 7 7 7 xDạng 4:  Cho dãy số {x . Tìm CTTQ của x n} : 0   n. ax
bx d. n  , n     n 1  n Giải: b
Xét phương trình đặc trưng : a  b  0      . q a
 Nếu    thì nghiệm riêng của phương trình * x  . n
c  thay vào pt, ta được : n n nd ddn 1 n n * . a . c   . b .
c   d.  c   x  
do b  qa . n a  b a  b
a   q   n
Số hạng tổng quát của dãy : d n *
x c .q x c . n q  . n 1 n 1
a   qn n n     Từ d d d d dq x c   c x   x x  . n q   x . n q  . 0 1 1 0 n  0  0 a(  q) a(  q)  a(  q)  a(  q) a   q
 Nếu    thì nghiệm riêng của phương trình * n x cn thay vào pt, ta được : nd d d n 1 ac(n 1) n n
  bcn  d  c    (do q   ) .
a(n 1)  bn
a(n 1)  aqn aq
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 n n 1 dnq dnq  * Suy ra x   . n aq a n 1 
Số hạng tổng quát của dãy : dnq n *
x c .q x c . n q  . n 1 n 1 a n 1  Từ dnq
x c x x . n q  . 0 1 n 0 a n nd q  . neu q    Vậy từ trên ta có :  a q 
x x . n q   . n 0 d n 1 .nq neu q   a    x 5 Thí dụ 1:  Cho dãy số {x . Tìm CTTQ của x n} : 0   n . x
 3x  2.5n , n     n 1  n b
Ta có :   q    3 ; d  2 ;   5. Vì q   nên ta có số hạng tổng quát của dãy sẽ là : a n n d q   n n 3n 5n
x x .q  .  5.3  2.
 4.3n  5 .n n 0 a q  3  5 x  2 
Thí dụ 2: Cho dãy {x . Tìm CTTQ của x n} : 0   n. x
 3x  5.3n , n     n 1  n b
Ta có:   q    3 ;   3 ; d  5. Vì q   nên ta có số hạng tổng quát của dãy sẽ là : a d n n 1  n n 1  n 1 x x .q .nq 2.3 5 . n 3 (5n 6).3        . n 0 ax
Dạng 5: Cho dãy số {x . Xác định n} : 0  n n
ax bx d   d  ..... nd  (1) , n     n 1  n 1 1 2 2 k k
sô hạng tổng quát của dãy trên. Gọi *1 x
là nghiệm riêng của phương trình n axbx d n n 1  n 1 1 *2
x là nghiệm riêng của phương trình n axbx d n n 1  n 2 2
................................................................................... *k
x là nghiệm riêng của phương trình n ax
bx d  . n n 1  n k k
Khi đó nghiệm riêng của phương trình (1) sẽ là * *1 *2 *
x x x  .... kx . n n n n
Khi đó số hạng tổng quát  b  * x  . n c   x    . n n    a  x  2 Thí dụ:  Cho dãy {x . Tìm CTTQ của x n} : 0   n. x
 2x  3.2n  5.7n (*) , n   .   n 1  n
Giải: Xét phương trình đặc trưng :   2  0    2.
 Do    nên nghiệm riêng *1
x d .2n n
, thay vào phương trình, ta được : 1 n 1 nn n 3 1 *1 n 1 d (n 1).2 2d . n 2 3.2 d x 3 . n 2         . 1 1 1 2 n
 Do    nên nghiệm riêng *2
x d .7n , thay vào phương trình, ta được : 2 n 2 n 1  n n *2 d .7
 2d .7  5.7  d 1 x  7n . 2 2 2 n Số hạng tổng quát n *1 *2 n n 1 x . c 2 x x . c 2 3 . n 2        7n n n n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 Từ n n 1 x 2 c 1 2 c 1. Suy ra x 2 3 . n 2           7n . 0 n   x Dạng 6:  Cho dãy số {x . Tìm CTTQ của x n} : 0   n. ax
bx P (n) nd , n     n 1  n k Ta gọi *1 x
là nghiệm riêng của ax bx P ( ) n n n 1  n k *2 x là nghiệm riêng của n ax
bx d . n n 1  n
Công thức tổng quát của dãy số được xác định là *1 *2 x  . n
c   x x . n n n
Từ giá trị của x0 ta tìm được giá trị c.    x 3 Thí dụ:  Cho dãy số {x . Tìm CTTQ của x n} : 0   n. x
 5x  3n  2  2.3n , n     n 1  n
Giải: Xét Phương trình đặc trưng :  5  0    5. Gọi 3 11 *1 x
là nghiệm riêng của phương trình *1 x
 5x  3n  2  x   n  . n n 1  n n 4 16 *2 x
là nghiệm riêng của phương trình n *2 x
5x  2.3  x  3n  . n n 1  n n
Số hạng tổng quát của dãy cho bởi: n n 3 11 * x  .
c   x  . c 5  n   3n . n n 4 16 Từ 11 75 75 n 3 11
x  3  c  1  3  c  . Suy ra x  .5  n   3 .n 0 16 16 n 16 4 16
II-Phƣơng trình sai phân bậc hai:
Dạng 1: Dạng thuần nhất và có phương trình đặc trưng bậc hai tồn tại nghiệm thực.  Cho dãy số {x x ; x . Tìm CTTQ của x n} : 0 1  n. ax
bx cx  0 , n     n2 n 1  n
Xét phương trình đặc trưng 2
a  b  c  0 (1) .
 Phương trình (1) có nghiệm  ; (   )thì số hạng tổng quát có dạng : 1 2 1 2
x c . n   c . n  . Từ x ta tìm được c n 1 1 2 2 0 ; x1 1 và c2.
 Phương trình (1) có nghiệm      thì số hạng tổng quát có dạng : 1 2
x  (c nc ). n  . Từ x ta tìm được c n 1 2 0 ; x1 1 và c2.    Thí dụ 1: x 2; x 5. Cho dãy {x . Tìm CTTQ của x n} : 0 1  n . x
 5x  6x , n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng 2
 5  6  0    2   3. 1 2
Số hạng tổng quát của dãy có dạng x c .2n c .3n . n 1 2        Từ x 2 c c 2 c 1 0 1 2 1     
. Suy ra x  2n  3n . x  5 2c  3c  5 c  1 n    1 1 2 2    Thí dụ 2: x 3; x 10. Cho dãy {x . Tìm CTTQ của x n} : 0 1  n . x
 4x  4x , n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng 2
  4  4  0    2. 1,2
Số hạng tổng quát của dãy có dạng x  (c nc ).2n . n 1 2       Từ x 3 c 3 c 2 0 2 1     
. Suy ra x  (2n  3).2n . x  10
2(c c )  10 c  3 n    1 1 2 2
Dạng 2: Dạng thuần nhất và phương trình đặc trưng vô nghiệm thực.
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201  Cho dãy số {x x ; x . Tìm CTTQ của x n} : 0 1  n . ax
bx cx  0 , n     n2 n 1  n
Xét phương trình đặc trưng 2
a  b  c  0 (2) . Ta có phương trình (2) không tồn tại
nghiệm thực, khi đó số hạng tổng quát của dãy có dạng : n
x r (c o
c sn+c sin n) . n 1 2 B b  Trong đó 2 2 r A B ;   arctan với A   ; B  . A 2a 2a Từ hai giá trị x ta tìm được c 0 và x1 1 và c2.       Thí dụ: x 1 ; x 3 3 1 Cho dãy số {x . Tìm CTTQ của x n} : 0 1   n . x
 2x 16x , n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng 2 2
  2 16  0 co   2 16  1  2  0.
Suy ra phương trình sai phân không có nghiệm thực.   Đặt b B A   1 ; B   3 và 2 2 r
A B  2 ;   arctan  . 2a 2a A 3
Khi đó số hạng tổng quát của x   n  n n   n có dạng : x 2 c o c s c sin . n  1 2   3 3  c 1 1 x 1        Từ 0 c 1  1 n n n     c c 3    . Suy ra x  2 o c s  3sin  . 1 2 nx  3 3 1 2       3 3 1 c  3     3 3  2 1 2 2     Dạng 3 x ; x : Cho dãy số {x . Tìm CTTQ của x n} : 0 1  n. ax
bx cx d , n     n2 n 1  n Gọi *
x là nghiệm riêng của phương trình. Khi đó nghiệm riêng *
x được xác định như sau: n nd * x
khi a b c  0
n a b cdn  * x
khi a b c  0 ; 2a b  0 . n  2a bd *
x n(n 1)
khi a b c  0 ; 2a b  0. n  2a
Xét phương trình đặc trưng, xét nghiệm của phương trình đặc trưng như các trường hợp
trên. Kết hợp với nghiệm riêng ta có được công thức của xn.     Thí dụ 1: x 4 ; x 1 Cho dãy số {x . Tìm CTTQ của x n} : 0 1  n. 2x
 5x  2x  3 , n     n2 n 1  n
Xét phương trình đặc trưng : 1 2
2  5  2  0    2    . 1 2 2
Do a+b+c ≠ 0 nên nghiệm riêng của phươ d 3 ng trình * x    3  . n
a b c 2  5  2
Số hạng tổng quát của dãy số : n 1
x c .2  c .  3. n 1 2 2n
c c  3  4  1 2       Từ x 4 c 3 0 1 n 1      . Suy ra x  3.2   3 c . n n2 2 x  1  2c   3 1 c  4    2 1 1 2  2
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201  89    Thí dụ 2: x 5; x Cho dãy số {x
. Tìm số hạng tổng quát x n} : 0 1  5 n.
x  7x  6x 11, n     n2 n 1  n
Giải: Xét phương trình đặc trưng 2
 7  6  0   1   6. 1 2
Do a+b+c=0 và 2a+b ≠ 0 nên nghiệm riêng dn 11n 11 * x     n . n 2a b 2  7 5
Số hạng tổng quát của dãy có dạng n 11
x c c .6  n , n   . n 1 2 5 x  5 c c  5 0 1 2     Từ c 2 1 n 11      . Suy ra x  2  3.6 89 11 89  n . n x c  6c   c  3    5 1 1 2 2  5  5 5    Thí dụ 3: x 3; x 2 Cho dãy {x
. Xác định công thức tổng quát x n} : 0 1  n. x
 2x x  6 , n     n2 n 1  n
Giải: Xét phương trình đặc trưng 2
  2 1 0   1. 1,2
Có a+b+c=0 và 2a+b=0 nên nghiệm riêng d *
x n(n 1)  3n(n 1). n 2a
Số hạng tổng quát của dãy là : x c nc  3 ( n n 1) , n   . n 1 2        Từ x 3 c 3 c 1 0 2 1 2      .
Suy ra x  3n  4n  3 , n   . x  2 c c  2 c  3 n    1 1 2 2   x ; x Dạng 4:  Cho dãy số {x . Xác định CTTQ của x n} : 0 1  n  n. ax
bx cx dq , n   .   n2 n 1  n Gọi *
x là nghiệm riêng của phương trình sai phân trên. Khi đó nghiệm riêng này được xác n ndq * x
khi q    q   .  n 2 1 2
aq bq cn 1   đinh như sau : ndq * x
khi q    q   . . n 1 2 2aq b   d * n2
x n(n 1) .q khi q     . n 1 2  2a
Xét phương trình đặc trưng, lập công thức nghiệm và ta có được công thức xn.
x  2 ; x  5 Thí dụ 1:  Cho dãy số {x . Lập công thức tính x n} : 0 1   n. x
8x 15x  3.4n , n     n2 n 1  n
Giải: Xét phương trình đặc trưng : 2
 8 15  0    3   5. 1 2 n dq 3.4n
Ta có q    q   nên nghiệm riêng của phương trình * x    3  .4n . 1 2 n 2
aq bq c 16  32 15
Số hạng tổng quát của dãy là : x c .3n c .5n 3.4n , n   . n 1 2         Từ x 2 c c 3 2 c 4 0 1 2 1     
. Suy ra x  4.3n  5n  3.4n, n   . x  5
3c  5c 12  5 c 1 n    1 1 2 2
x  8 ; x  5. Thí dụ 2:  Cho dãy số {x . Tìm CTTQ của x n} : 0 1   n . x
11x  28x  6.7n , n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng 2
 11  28  0    4   7. 1 2
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 n 1  n 1 ndq 6 . n 7 
Ta có: q   nên nghiệm riêng của phương trình * n 1 x 2 . n 7     . 2 n 2aq b 2.1.7 11
Số hạng tổng quát của dãy có dạng : n n n 1 x c .4 c .7 2 . n 7     . n 1 2       Từ x c c 8 c 10 0 1 2 1 n n n 1   
. Suy ra x  10.4  2.7  2 . n 7  , n   .
x  4c  7c  2  28 c  2 n    1 1 2 2      x 4 ; x 5. Thí dụ 3:  Cho dãy {x . Tìm CTTQ củ n} : 0 1  a x  n. x
10x  25x  2.( 5  )n , n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng 2
 10  25  0      5  . 1 2 d
Ta có q     nên nghiệm riêng của phương trình * n2 n2
x n(n 1) .q
n(n 1).( 5  ) . 1 2 n 2a
Số hạng tổng quát của dãy : x c n c   n n   n   n  .( 5)n ( 1).( 5)n , . 1 2  Từ x c  4 c   3  0 2 1 n n 2    . Suy ra x  ( 3  n  4).( 5  )  ( n n 1).( 5
 )  (n  76n 100).( 5  )n n    . x  5
 (c c )  5  c  4 n   1 1 2 2   x ; x
Dạng 5: Cho dãy số {x } được xác định bởi : 0 1 n  với P (n) ax
bx cx P (n) , n   .   k n2 n 1  n k
là đa thức bậc k theo n. Xác định số hạng tổng quát của dãy số. Nghiệm riêng *
x cua phương trình đượ xác định như sau: n *
x Q (n) khi a b c  0. n k  *
x nQ (n) khi a b c  0  2a b  0. n k  * 2
x n Q (n) khi a b c  0  2a b  0.  n k
Xác định công thức tổng quát theo trình tự các bước như đã trình bày ở các ví dụ trên.
x  31 ; x  60. Thí dụ :  Cho dãy số {x . Tìm CTTQ của x n} : 0 1   n. x
 7x 10x  8 n n 12n 14, n   .   n2 n 1  n
Giải: Xét phương trình đặc trưng của dãy : 2
  7 10  0    2   5. 1 2
Ta có : a+b+c ≠ 0 nên nghiệm riêng của phương trình * 2
x an bn c . Thay vào công thức n
truy hồi, tiến hành đồng nhất hệ số ta được : * 2
x  2n  8n 15. n
Số hạng tổng quát của dãy : n n 2
x c .2  c .5  2n  8n 15. n 1 2        Từ x c c 15 31 c 15 0 1 2 1 n n 2   
. Suy ra x  15.2  5  2n  8n 15, n   .
x  2c  5c  25  60 c  1 n   1 1 2 2 x ; xDạng 6:
Cho dãy xác định bởi {xn} : 0 1  .Tìm CTTQ x  n. ax
bx cx P (n). n  , n   .   n2 n 1  n k Nghiệm riêng *
x của phương trình dạng này được xác định như sau : n *
x Q (n). n
khi       . n k 1 2  * x  .
n Q (n). n
khi       . Từ đây tìm được công thức tổng quát cảu x n k 1 2 n.  * 2
x n .Q (n). n
khi      .  n k 1 2
x  5; x 18. Thí dụ  : Cho dãy {x . Xác định công thức x n} : 0 1  n2  n. x
 6x  9x  2(3n 1).3 , n   .   n2 n 1  n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Giải: Xét phương trình đặc trưng 2
  6  9  0      3. 1 2
Ta có      nên nghiệm riêng của pt * 2 x n an b . Thay *
x vào công thức truy hồi, n  .3n 1 2 n
rút gọn và đồng nhất hệ số, ta được * x   3 2
n  2n .3n . n
Số hạng tổng quát của dãy là n 3 2
x  (c n c ).3  (n  2n ).3n , n   . n 1 2      Từ x c 5 c 2 0 2 1 n 3 2   
. Suy ra x  (2n  5).3  (n  2n ).3n n n n  . n  3 2 2 2 5.3n
x  3(c c )  3  18 c  5   1 1 2 2
Dạng 7: Cho dãy số được xác định bởi {xn} : x ; x . 0 1 
. Xác định số hạng tổng quát của dãy trên. ax
bx cx  . o c sn+sinn , n   .   n2 n 1  n
Đối với phương trình dạng này, nghiệm riêng của nó có dạng : * x A o c sn+Bsinn . n Thay *
x vào công thức truy hồi để xác định được hai hệ số A và B. n
Thí dụ: Cho dãy {x } : được xác định bởi n : x  4  ; x  4   2 0 1  
. Tìm số hạng tổng quát của dãy. n n x
 3x  2x  3 3 2 . o c s  sin , n    . n2 n 1  n    4 4
Giải: Xét phương trình đặc trưng : 2
 3  2  0   1   2. 1 2  
Nghiệm riêng của phương trình có dạng : n n * x A o c s  Bsin . Thay vào công thức truy n 4 4 hồi, ta được :  (n+2) (n  2)   (n+1) (n 1)   n n  A o c s  Bsin  3 A o c s  Bsin  2 A o c s  Bsin         4 4   4 4   4 4     n n 3 3 2 . o c s  sin . 4 4
Phân tích vế trái và rút gọn ta được :  3A 3B  n  3A 3Bn      A c  A    B         n n B 2 . os 2 .sin 3 3 2 o c s  sin .  2 2  4  2 2  4 4 4  3A 3B B    2A  3 3 2     
Đồng nhất hệ số, ta được : 2 2 A 1 n n *     x  o c s  sin . 3A 3B  B 1 n 4 4 A    2A 1  2 2  
Số hạng tổng quát của dãy : n n n
x c c .2  o c s  sin . n 1 2 4 4
x c c 1  4        Từ 0 1 2 c 6 1 n n n   
. Suy ra x  2  6  o c s  sin , n    . n
x c  2c  2  4   2 c  1   4 4 2 1 1 2  Dạng 8: x ; x
Cho dãy số dạng sau { xn} : 0 1
ax bx cx d d ...d (1), n   .   n2 n 1  n 1 n n2 nk
Trong đó d là một trong các dạng sau : hắng số d, . n
d  , P (n) , n  .P ( ) n , .... ni k k Khi đó ta gọi *i x
là nghiệm riêng của phương trình ax bx cx d . n n2 n 1  n ni
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 k
Nghiệm riêng của (1) được xác định là * *i
x   x . Sau đó ta thiết lập được công thức tổng n n i 1 
quát như các thí dụ đã cho.
III-Phƣơng trình sai phân bậc ba:
Loại 1: Phƣơng trình thuần nhất :  Dạng 1: x ; x ; x Cho dãy {x
. Xác định số hạng tổng quát n} : 0 1 2
ax bx cx dx  0 n   .   n3 n2 n 1  n xn của dãy số.
Xét phương trình đặc trưng 3 2
a  b  c  d  0 . Phương trình có 3 nghiệm phân biệt
 ;  va . Khi đó số hạng của dãy được xác định là : x c . n   c . n   c . n  . 1 2 3 n 1 1 2 2 3 3
Từ các giá trị x ; x ; x ta xác định được các giá trị c ; c va c . 0 1 2 1 2 3     Thí dụ: x 1; x 5 ; x 8. Cho dãy số {x . Tìm CTTQ của x n} : 0 1 2  n . x
 6x 11x  6x  0 n   .   n3 n2 n 1  n
Giải: Xét phương trình đặc trưng : 3 2
 6 11  6  0   1 ;   2 ;   3. 1 2 3
Số hạng tổng quát của dãy có dạng : x c c .2n c .3n . n 1 2 3  11 c         1 x c c c 1 0 1 2 3 2   Từ 11 n 5
x c  2c  3c  5  c  9 . Suy ra x    9.2  .3n n    . 1 1 2 3 2 n 2 2  
x c  4c  9c  8 5  2 1 2 3 c   3  2  Dạng 2: x ; x ; x : Cho dãy {x
. Xác định số hạng tổng n} : 0 1 2
ax bx cx dx  0 n   .   n3 n2 n 1  n quát xn của dãy số.
Xét phương trình đặc trưng 3 2
a  b  c  d  0 có hai nghiệm phân biệt  va      . 1 2 3
Khi đó số hạng tổng quát của dãy số cho bởi : x c . n
  c n c . n  . n 1 1  2 3 
Từ các giá trị x ; x ; x ta xác định được các giá trị c ; c va c . 0 1 2 1 2 3     Thí dụ: x 5; x 11 ; x 16 Cho dãy số {x . Tìm CTTQ của dãy. n} : 0 1 2  x 11x 3
 2x  28x  0 , n   .   n3 n2 n 1  n
Giải: Xét phương trình đặc trưng 3 2
 11 32  28  0    7      2. 1 2 3
Số hạng tổng quát của dãy có dạng : x c .7n c n c .2n n 1  2 3   6 c    1 35
x c c  5  0 1 3 Từ   13 6   n 13 181
x  7c  2c  2c 11  c  . Suy ra x   .7  n  .2n , n    . 1 1 2 3 2   14 n 35   14 35 
x  49c  4c  4c  16  2 1 2 3  181 c   3  35  Dạng 3: x ; x ; x Cho dãy {x
. Xác định số hạng tổng quát n} : 0 1 2
ax bx cx dx  0 n   .   n3 n2 n 1  n xn của dãy số.
Xét phương trình đặc trưng 3 2
a  b  c  d  0 có 1 nghiệm kép        . Khi đó 1 2 3
công thức nghiệm tổng quát có dạng : x   2
c n c n c . n  . n 1 2 3 
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Từ các giá trị x ; x ; x ta xác định được các giá trị c ; c va c . 0 1 2 1 2 3     Thí dụ: x 3 ; x 2 ; x 8 Cho dãy số {x
. Xác định số hạng tổng n} : 0 1 2
x 3x 3x x  0 , n   .   n3 n2 n 1  n quát của dãy.
Giải: Xét phương trình đặc trưng : 3 2
 3 3 1 0       1. 1 2 3
Số hạng tổng quát của dãy có dạng : 2
x c n c n c . n 1 2 3  7 c   1 2 x c  3  0 3 Từ   9 7 9 2
x c c c  2
 c   . Suy ra x n n  3, n    . 1 1 2 3 2 2 n 2 2  
x  4c  2c c  8  2 1 2 3 c  3 3   Dạng 4: x ; x ; x Cho dãy {x
. Xác định số hạng tổng quát n} : 0 1 2
ax bx cx dx  0 n   .   n3 n2 n 1  n xn của dãy số.
Xét phương trình đặc trưng 3 2
a  b  c  d  0 có 1 nghiệm thực  và hai nghiệm phức.
Khi đó số hạng tổng quát của phương trình có dạng : x c . n   c . o
c sn+c .sin n . n 1 2 3
Từ các giá trị x ; x ; x ta xác định được các giá trị c ; c va c . 0 1 2 1 2 3         Thí dụ: x 3; x 4 3 ; x 8 3 . Cho dãy số {x . Tìm CTTQ của x n} : 0 1 2   n. x  5x
 22x  48x  0 , n   .   n3 n2 n 1  n
Giải: Xét phương trình đặc trưng 3 2            2 5 22 48 0 3   2 16  0   3   
. Phương trình sai phân bậc hai 2
  2 16  0 không có nghiệm 2   2 16  0  VN
thực nên theo thí dụ trong dạng 2 của phương trình sai phân bậc hai ta có số hạng tổng n n  nn n quát là ' x c . o c s  c sin
. Vậy số hạng tổng quát x c .3  c . o c s  c .sin . n 2 3 3 3 n 1 2 3 3 3 
x c c  3 0 1 2  c 1 1      Từ c c 3 n n n 2 3 x  3c  
 4  3  c  2 . Suy ra x  3  2 os c  sin , n    . 1 1 2   2 2 n    3 3  c  2  3  c c 3 2 3 x  9c    8  3 2 1  2 2
Loại 2: Phƣơng trình không thuần nhất.  Cho dãy số dạng {x x ; x ; x n} : 0 1 2  . axbx
cx dx d , n   .   n3 n2 n 1  n n
Trong đó d có thể là hăng số, n
m , đa thức bậc k theo n P (n) , .... n k
Ta tiến hành tìm nghiệm riêng như dạng đối với phương trình bậc 2 đã trình bày ở trên.
IV-Phƣơng trình sai phân bậc cao.
Dạng 1: Phương trình thuần nhất : a x a x
...... a x  0 . 0 nk 1 nk 1  k n
Xét phương trình đặc trưng : k k 1 a a   
.............. a  0 . 0 1 k
TH1: có k nghiệm thực phân biệt, khi đó số hạng tổng quát của dãy sẽ có dạng :
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 k
x c . n   c . n   c . n
 ........... c . n   c . n  . n 1 1 2 2 3 3 k k i i i 1 
TH2: Có s nghiệm bằng nhau , (k – s) nghiệm khác nhau và khác với s nghiệm trên. Khi s 1  k  
đó số hạng tổng quát của dãy có dạng : x  c . p n . n
   c . n  . n p 1  i ip0  is 1 
TH3: Nếu phương trình đặc trưng có nghiệm phức : x A Bi r  o
c s+isin trong đó j  B 2 2 r A B ;   arctan
và k – 2 nghiệm thực khác nhau thì số hạng tổng quát của dãy A k 2
số sẽ có dạng : x  c . n n   r c c nnn i i  ' ' . os +c .sin . 1 2  i 1 
Dạng 2: Phương trình không thuần nhất: a x a x
....... a x b . 0 nk 1 nk 1  k n n
Ta xét thêm nghiệm riêng *
x tuỳ theo dạng của b và các hệ số a . Thiết lập công thức n n i
tổng quát của xn từ các giả thiết của bài.
V-Một số dạng đặc biệt khác thƣờng gặp của dãy số trong các kì thi.
Dạng 1: Phương trình sai phân dạng " Hệ phương trình sai phân tuyến tính cấp một".    Cho dãy số {x
} được xác định như sau : x ax by n 1  n n n} , {yn  . ycx dyn 1 n n
Tìm số hạng tổng quát xn và yn.
Đưa hệ về phương trình sai phân tuyến tính cập 2 của từng dãy {xn} và {yn} : x
ax by ax  (
b cx dy )  ax
bcx d(x ax )  (a d)x  (bc ad)x n2 n 1  n 1  n 1  n n n 1  n n 1  n n 1  n y
cx dy c(ax by )  dy dy bcy a(y dy )  (a d)y  (bc ad)y . n2 n 1  n 1  n n n 1  n 1  n n 1  n n 1  n
Đưa được hệ về dạng phương trình cơ bản, từ đây ta dễ dàng tìm được CTTQ của số hạng từng dãy đã cho.     Thí dụ: u 2; u 2u v Tìm CTTQ của dãy số {x nn n    n} và {yn} : 0 1 n  . v  1; vu  2v  0 n 1  n n
Giải: Ta có : u  (a d)u  (bc ad)u  4u 3u và u  5. n2 n 1  n n 1  n 1 n 1  n 1  Từ đây, ta có : 1 3 1   3 u
v u  2u  . n n n 1  2 n 2
Dạng 2: Phương trình sai phân dạng phân thức tuyến tính:
Tìm CTTQ của dãy số có công thức xác định như sau : ax b x   ; n xn   . 0 n 1  cx d n y Cách 1: Đặt k x
(z  0). Khi đó dãy được biến đổi thành : k k zk y . n ab y z ay bz
y ay bzy
 (a d)y  (bc ad)yn 1  n n n2 n 1 1  n n n n n       n    . z y         n cy dz z cy dz z (a d )z (bc ad )z    n 1 n n n 1  n n n2 n 1 .  n c d zn
Từ công thức tổng quát của {y } ta suy ra CTTQ của {x n} và {zn n} .
Cách 2: Đặt x u t , thay vào công thức truy hồi của dãy ta có : n n 2
au at b
(a ct)x ct  (a d )t b n n u   t  (*). n 1 
cu ct d
cu ct d n n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 Ta chọn t sao cho 1 1 2
ct  (d a)t b  0. Khi đó ta chuyển (*) về dạng :  m  . n u u n n 1 
Từ đây ta tìm được 1 , suy ra u . u n n u   2 1 Thí dụ:  Tìm CTTQ của dãy số {u    n} : 9u 24 . n 1 u   n   2. n  5u 13  n 1  x Cách 1: Đặt n u
, thay vào công thức truy hồi ta được : n yn xn 1 9    24 x y 9  x  24yx  9  x  24yx  4x  3x    n 1  n n n2 n 1 1 1 1  n n n n n       n    . y x      n 1  5x 13y y 5x 13y y 4 y 3y    n n 1  n 1  n 1  n n n2 n 1 5 13  n yn 1      Từ 42 x 2 ; x 42
u  2  u   . Ta chọn 1 2  . 1 2 23
y  1 ; y  23  1 2 n 1  n 1     
Từ đây ta tìm được : x 22.3 24   n 22.3 24  . Suy ra u n   2. nn 1 n 1  y 11.3 1  0 11.3 1  0  n
Cách 2: Đặt u x t , thay vào công thức truy hồi ta được : n n 2 9
x  9t  24 ( 9
  5t)x  5t  22t  24 n n 1 x t   x   n 5x  5t 13 n 5x  5t 13 n n 1  Ta chọn t : 2
5t  22t  24  0  t  2   x  4. 1 n 1  n 1 x 1 3 1 11.3 10 4 2  2.3   24 n 1  x      5    x
u x  2  . n n n 1  n n n 1 5x  3 x x x 4 11.3 10 11.3  10 n 1  n n 1  n
Dạng 3: Hệ phương trình tuyến tính bậc 2. 2 2      Tìm CTTQ của dãy số (u
) được xác định bởi : u u . a v ; u n n 1  n 1  1  a    n) và (vn
v  2u .u ; v    n n 1  n 1  1 n  
u a.v ua v   u a v u
  u a vn n    . nnn n n 2 .......  . .  12 2 2 1 1 1 1 1 1    n
a.v  2 a.u .v   n nn
u av ua v   u a v n n   . nn 2 .......  .  1 2 1 1 1 1 1 1  . 1     u     a     an   n12   n12  2     1      v     a     a n    n12   n12  2 a  
Thí dụ: Xác định CTTQ của hai dãy số {u } thoả : n} và {vn u   2 2 2 u
  u  2v 1  và n n 1  n 1   n   2. v  1 
v  2u .v 1  n n 1  n 1  Giải:  
u  2v u  2    2 v u u v    1  1 n n   n n n n n 2 2 2 1 1 Ta có:   
 2v  2 2u v   n nn
u  2v uv n n   2 nn 2 1 1 1 1
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201             u v    1 n n n n u 2 2 2 2 2 u  2v  2  2  n   n n 1 1 2  2   12   12 1 1  2       .         u v u v   v     n n    n12   n12 1 n n 2 2 2 2 n  2 2  1 2 2 2 12 1 1   2 2  
Dạng 4: Dạng phân thức bậc 2 trên bậc 1: x   1 Tìm CTTQ của dãy {x  2     n} : x a n 2. n 1 x   a     n  . 2xn 1  Đặt un x
, khi đó dãy trên được chuyên về hai dãy {u } như sau : n n} và {vn vn n 1  n 1  2 2 2 2
  a   a uu   u  . a v ; u   n n 1  n 1  1  n   2. Khi đó n x   a n nn .  1 1 v  2u v ; v  1  2 2 v n n 1  n 1  1 n
  a   a x  2 1 Thí dụ:
Xác định CTTQ của dãy số {x 2 n} :  x  2 . n 1 x   n   2.  n 2xn 1    2 2    Giải: u 2 u u 2v Xét hai dãy số {u n n 1  n 1     n} và {vn} : 1  và n 2. v  1  v  2u v 1  n n 1  n 1 
Ta dễ dàng chứng minh được bằng quy nạp un x  . n vnnn 2  2  1 2  2 2 1 2
Theo kết quả bài toán trên, ta có : x  2. nnn 2  2  . 1 2  2 2 1 2
Dạng 5: Dạng có căn thức trong công thức truy hồi. u     1 a) Với dãy số {u
, với 2   ta xác định CTTQ như sau: n} :  a b 1 2 u
  au bu c n   2.  n n 1  n 1 
Từ dãy truy hồi  u au          2 2 2 bu c u 2au u u c 0 n n 1 n 1  n n n 1  n 1 
Thay n bởi n – 1, ta được 2 2 u
 2au u u c  0. n2 n2 n 1  n 1 
Ta đây ta dễ thấy u và u X  2au X uc  0 . n
n là nghiệm của phương trình bậc hai 2 2 2 n 1  n 1 
Theo định lý Vi-et, ta có u u  2au . Từ đây ta dễ dàng xác định CTTQ của x n n2 n 1  n. u    1 
b) Một cách biểu diễn khác : Cho dãy số {un} : u  , trong đó n 1 u   n   2. n  2 a cubn 1  2
 0; a 1 ; a b 1 ta xác định CTTQ như sau :
Ta viết lại công thức tổng quát dưới dạng : 1 a b   c  . Đặt 1 x  . 2 u u u n u n n 1  n 1  n Ta có 2 x ax
bx c đây là dãy mà ta đã xét ở trên. n n 1  n 1  u  1 Thí dụ:  Cho dãy số {un} : 1  Tìm u ? n u
  5u  24u 8 n   2.  n n 1  n 1 
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
Giải: Từ công thức truy hồi của dãy ta có : u 5u    2 2 24u 8 n n 1 n 1  2 2
u 10u u u 8  0 (1) . Thay n bởi n – 1 ta được : n n n 1  n 1  2 2 u
10u u u 8  0 (2). n2 n2 n 1  n 1 
Từ (1) và (2)  u ,u là hai nghiệm của phương trình : 2 2
t 10u t u 8  0 n2 n n 1  n 1 
Áp dụng định lý Vi-et, ta có : u u 10u . n n2 n 1  Ta dễ dàng tìm được     u     n  n 1  n 1 6 2 6 2 5 2 6 5 2 6 . 2 6 2 6
Dạng 6: Công thức truy hồi bậc hai dạng phân thức. u    ; u   1 2 Cho dãy số {u  2 n} :  ua . Tìm u ? n 1 u   n   2.  n n un2
Đối với dạng này thì từ công thức truy hồi u . Ta giả sử    3, u4, u5 u xu yu z . n n 1  n2 u
  xu yu z 3 2 1
Lập hệ phương trình u
  xu yu z  , x y, . z 4 3 2
u xu yu z  5 4 3
Từ công thức truy hồi ta dễ dàng tìm được công thức tổng quát của un. u   u 1 1 2 Thí dụ:  Tìm CTTQ của dãy số {u 2 n} :  u  2 . n 1 u   n   2.  n un2
Giải: Ta có : u  3; u 11; u  41.Ta giả sử u xu yu  . z 3 4 5 n n 1  n2 u
  xu yu z
x y z  3 x  4 3 2 1 Ta có hệ pt :    u
  xu yu z  3
x y z 11  y  1
  u  4u u . 4 3 2 n n 1  n2   
u xu yu z
11x  3y z  41 z  0    5 4 3 Ta dễ dạng tìm được 9  5 3  x     n   n  n 9 5 3 n . 2 3 .2 3  1. 6 6
VI-Sử dụng lƣợng giác để tìm công thức tổng quát của dãy số : u
Dạng 1: Xác định công thức dãy số dạng {un} : 1  ta làm như sau : 2 u  2u 1 n   2.  n n 1 
 Nếu u 1 : ta đặt u  os
c  . Khi đó ta có : n-1 u  o c s2  . 1 1 n  Nếu 1  1 
u  1 : ta đặt u a
a  0 va au  0 . Khi đó 1  1 1   2  a n 1 1  1  1  1  1  1  1   1  2 2 4 2 u a   2 1  a   u a   ........u a  . 2         2 2 3 n n 1 4  2 2  a  2  a  2  a  2  a
Với cách xác định số a, ta có a là nghiệm (cùng dấu với u ) của phương trình 1 2
a  2u a 1  0 . Do tích hai nghiệm la 1 nên nếu a là 1 nghiệm thì 1 sẽ là 1 a
nghiệm còn lại của phương trình. Khi đó công thức tổng quát có thể viết như n 1  n 1  2 2 1   sau : u u u   u u n  2 1  2 1 . 1 1 1 1   2  
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201  1   Thí dụ u 1: Cho dãy số {u
. Xác định CTTQ của dãy {u n}: 1  2 n}. 2 u
  2u 1 n   2.  n n 1  2      Giải: 1 2 2 2 Ta có 2 2 u   o c s  u  2 o c s 1  o c s  u  2 o c s 1  o c s 1 2 3 2 3 3 3 3 3 n-1
Bằng quy nạp ta chứng minh được rằng 2 u  o c s n  1.. n 3 u   3
Thí dụ 2: Cho dãy số {u . Xác định CTTQ của u n} : 1  2 n. u  2u 1 n   2.  n n 1 
Giải: Gọi a là nghiệm lớn của phương trình : 1  1  2 a
 3  a  6a 1  0  a  3 2 2   . 2  a  2 1  1  1  1  1 Ta có 2
a  6a 1  0  u a   3, khi đó 2 u a  1  a  . 1     2  a  2 2 2  a a k 1 k 1 Giả sử 1 2 x a  thì 2 xa  . k k 1   2 k 1 k a 2 a n 1  n 1 
Theo nguyên lý quy nạp, ta được n 1  2 2 1 2 x a      . n n 3 2 2 3 2 2 1 2     a
Thí dụ 3: Cho dãy số {x } được xác định như sau : 2      n x 5, x x 2 n 1. 1 n 1  n Tìm giá trị của xn 1 S  lim  .
n x x .....x 1 2 n Giải: 5  21
Chọn a là nghiệm lớn của phương trình 2
x  5x 1  0  a  1. 2 2 1  1  1 Ta có 2
a  5a 1  0  x a   5 ; khi đó 2 2
x x  2  a   2  a  . 1   a 2 1 2  a a
Bằng quy nạp ta chứng minh được n 1  1 2 x a     n n n 1. 1 2 a Chú ý rằng k 1  k 1  1   1 k   1  2 2 2 a      ,  a   a    k 1 k 1 2 2 2ka  a   a   1   1 n  1  2 1 a x a a         n 1 n 1 2 2n x   a   a  a   1  ta có n 1 a    . a  .   x x .....x  1 n  1 1 2  a  1 2 n a x x .....x a   n 1   1 2 n 2 2na a a 1 1 n Do đó 2 x  1  1 n 1  lim   lim a S . a   a   21.  
n x x ...... n x  1  a a 1 2 n 1 2n a u   p
Dạng 2: Tìm CTTQ của dãy số {u , ta làm như sau : n} : 1  3 u  4u  3u n   2.  n n 1  n 1 
 Nếu p 1, thì   0;  : o
c s =p . Khi đó bằng quy nạp ta chứng minh được : n-1 u  o c s3  . n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201  Nếu 1  1 
p  1thì ta đặt u a
au  0 . Bằng quy nạp ta chứng minh được 1    1  2  a n 1  n 1  3 3   n 1 1   1  1 3 u a  hay u u u   u u n  2 1  2 1 . 1 1 1 1  n    n . 1 3 2  a  2    2   Thí dụ u
1: Xác định CTTQ của dãy {un} : 1  2 .  3 u  4u  3u , n   2.  n n 1  n 2 2    3 3 3 3  Giải: Ta có 3 3 u   o c s  u  4 o c s  3 o c s  o c s  u  4 o c s  3 o c s  o c s . 1 2 3 2 4 4 4 4 4 4 4 n-1
Bằng quy nạp ta chứng minh được 3 u  o c s n  1. n 4 x  7
Thí dụ 2: Tìm CTTQ của dãy {xn} : 1  . 3 x  4x  3x n  1.  n n 1  n 1 
Giải: Gọi a là nghiệm lớn của phương trình 2
x 14x 1  0  a  7  4 3 . 3 1  1  1  1  3  1  1  1  Ta có 3 u a   7  u a   a   a  . 1   2       3 2  a  2  a  2  a  2  a
Bằng quy nạp ta dễ dàng chứng minh được n 1 1   1  3 u a      n nn 1. 1 3 2  an 1  n 1 
Vậy công thức tổng quát của dãy là :   u     n   n  3  3 1 7 4 3 7 4 3 1.  2   u   p
Dạng 3: Cho dãy {u
. Để xác định công thức tổng quát của n} : 1  3 u  4u  3u , n   2.  n n 1  n 1 
nó ta có thể làm như sau : 1  1  Ta đặt u a
. Khi đó bằng nạp ta chứng minh được : 1   2  a    1     n 1 1 n n 3 u a          u u u u n    n  2 1 1 3  2 1 . 1 1 1 1 3  13 1 1 2  a  2    3 u  Thí dụ
: Xác định CTTQ của dãy {un} : 1  6  3 2 u  24u
12 6u 15u  6 n   2.  n n 1  n 1  n 1 
Đặt u xv y . Thay vào công thức truy hồi của dãy, biến đổi và rút gọn ta được : n n 3 3
xv y  24x v 12 x y x vxy xy x v n n  2 2 6 6  2 3 n  2 24 8 6 5 1 1  n 1 3 2
 24y 12 6y 15y  6. 2 2   
Ta chọn y sao cho : 6x y 6x 0 1   y  . 3 2
24y 12 6y 15y  6  y 6 Khi đó : 3 3 2 3 xv  24x v
 3xv v  24x v  3v . Ta chọn 1 x n n 1  n 1  n n 1  n 1  6 1 nn  
v  4v  3v ; v  2  v     n nnn 2 5  1 2 5  1 3 3 3 1 1 1  2  
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201     Suy ra u      n   n   n1   n1 3 3 1 1 2 5 2 5 1.  2 6   6   u     
Dạng 4: Xác định CTTQ của dãy {un} : 1  với 1  a . 2
u a bu n   2.  n n 1  ab  2
Khi đó ta đặt u    a o
c s  u  a b a o
c s 2  a  2 1 2 o
c s   a o c s2 . 1 2 
Bằng quy nạp ta ta chứng minh được u  ac  n-1 os 2   n  1. n  3   Thí dụ u
1: Xác định CTTQ của {un} : 1  2 . 2 u   2 u n   2.  n n 1  Giải    : Đặt 3   o c s ,   ; ,   khi đó : 2 u  2  o
c s  u  2(1 2 o c s )  2  o c s2 . 4  2  1 2
Bằng quy nạp ta chứng minh được n-1 u  2  o c s2  n  1. n  1 x   1 2 Thí dụ
2: Tìm CTTQ của dãy số {xn} :  . 2  2  2 1 un 1  x n   2.  n  2     2 2  2 1 sin 2 1 o c s       Giải: 1 6 6 Ta có : u   sin  u    sin 1 2 2 6 2 2 2.6 
Bằng quy nạp ta chứng minh được là : u  sin n   2. n n 1 2  .6
Thí dụ 3: Cho a, b là hai số dương không đổi thoả mãn a < b và hai dãy {an} , {bn}  a b a  ; b ba  1 1 1
được xác định như sau :  2  . Tìm CTTQ của an và bn. abn 1  n 1 a   ; b a b n   2. n n n n 1   2  Giải: Ta có a a 0  1 nên ta đặt  os c  với     0;   . b b  2  o bc s +b b 1 o c s     Khi đó : 2 a    b os c và 2 b  . b b o c s  b o c s 1 2 2 2 1 2 2   2 b o c s  b o c s a b     1 1 2 2 2 a    b o c s . o c s và b b o c s . o c s . 2 2 2 2 2 2 2 2 2 2
Bằng quy nạp ta chứng minh được :       2 a b o c s o c s ..... o c s và 2 b b o c s o c s ..... o c s . n 2 2 2 2n n 2 2 2 2n u   a 1 Dạng
5: Để tìm CTTQ của dãy {u   n} : u b n 1 u   n   2. n  1 bun 1 
Ta đặt a  tan và b  tan  , khi đó ta dễ dàng chứng minh được u  tan  (n 1) . n
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 u   3 1  Thí dụ 1 : Cho dãy {u    . Tính giá trị của n} : u 2 1 u . u   n   2011 n   n 1   2. 1 1 2 un 1  Giải:   Ta có tan
 2 1 và u  3  tan . 8 1 3   tan  tan    Khi đó, 3 8  u   tan 
. Bằng quy nạp ta chứng minh được : 2      3 8  1 tan .tan 3 8           5  u  tan  (n 1) n   2. Suy ra u  tan  2010.  tan   2   3. n        3 8  2011  3 8   3 4  u   3 1 
Thí dụ 2: Tìm CTTQ của dãy số {un} :  un 1 u   n   2. n  2 1 1 un 1  Giải: 1 1 1 Ta có :   1 . Đặt 1 x
, khi đó ta được dãy {x } dược xác định như 2 n u u u n u n n 1  n 1  n 1 sau : x  và 2 x x  1 x . 1 n n 1  n 1  3  1 o c s 1     Vì 2 3 x   cot  x  o c t  1 o c t   cot . 1 2 3 3 3 3  2.3 sin 3  
Bằng quy nạp ta chứng minh được : x  cot  u  tan n  1,2,3...........  n n 1  n n 1 2 .3 2  .3
BÀI TẬP DÀNH CHO ĐỘC GIẢ TỰ LUYỆN
Bài 1: Xác định công thức tổng quát của các dãy số sau đây : a) Cho x 1; 3x  2x  0 n  0 0 n 1  n
b) Cho x 1; 5x  4x  2n n  0. 0 n 1  n c) Cho 2 x  2
 ; x x  2n n  4 n  0. 0 n 1  n d) Cho x  5; 4x
 7x  6n 5 n  0. 0 n 1  n e) Cho x  3  ; xx 13 n  0. 0 n 1  n f) Cho x  4; 3x  2x  23 n  0. 0 n 1  n g) Cho x  7; x 3x  2.3n n  0. 0 n 1  n h) Cho n2 x  15; 2xx  2 n  0. 0 n 1  n 7 i) Cho x  ; 11x
 6x  2.3n  4n n  0. 0 n 1  5 n
j) Cho x 1; x  4; x
 4x x  0 n  1. 0 1 n 1  n 1  n 1  2 1
k) Cho x  4; x  ; x
x x  0; n  1. 0 1 n 1  n n 1  3 4
l) Cho x  3; x  3 4 3 ; x
 2x 13x  0 n  1. 0 1 n 1  n n 1 
m) Cho x  5; x 1; x
 6x  3x 14 n  1. 0 1 n 1  n n 1 
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201
n) Cho x  4; x  3; x
 2x 3x  6 n  1. 0 1 n 1  n n 1 
o) Cho x  2; x  4; x
 2x x 11 n  1. 0 1 n 1  n n 1 
p) Cho x 1; x  5; x
8x 15  4.2n n  1. 0 1 n 1  n n 1 
q) Cho x 1; x  4; x
 3x  4x  3.4n n  1. 0 1 n 1  n n 1 
r) Cho x  4; x  2; x
 6x  9x  5.3n; n  1. 0 1 n 1  n n 1  s) Cho 2
x  1; x  3; x
 7x 12x  (2n  3n 1).2n n  1. 0 1 n 1  n n 1 
t) Cho x  2; x  3
 ; x  7x 10x  (3n 1).5n n  1. 0 1 n 1  n n 1  u) Cho 2
x  1; x  3; x
8x 16x  (2n  3).4n n  1. 0 1 n 1  n n 1  nn
v) Cho x  1; x  6 ; x
3x  2x  3 o c s  2sin n  1. 0 1 n 1  n n 1  3 3
w) Cho x 1 ; x  5 ; 2x
 7x  5x  2n  5n n  1. 0 2 n 1  n n 1 
x  2x  5y x) Cho n 1 
x  3; y  2 ; n nn  1. 1 1 y  5x  3yn 1 n n 2x  7 y) Cho x  2; n x  ; n  1. 1 n 1  4x  3 n
Bài 2: Xác định Công thức tổng quát của các dãy số đặc biệt sau : 1 x .x a) Cho n2 x  1; x  ; n x  với n  0. 0 1 n2 2 2002x
 2001x  2000x x n 1  n n 1  n b) Cho 2 3 x  1; x  2; xx .x n  0. 0 1 n2 n 1  n x c) Cho x  1; n xn  1 1 n 1  2 2  3  xn d) Cho 2 u  2; u  6  33 ; u
3u  8u 1 n  1 0 1 n 1  n n  3 u   1 3  e) Cho  u  2  3 u    n   n   n 1    2. 1 3 2 un 1  u    , n    . n
Bài 3: Cho dãy số {u } thoả mãn như sau :    n u 1, u 9 0 1
u 10.u u n    , n  2.  n n 1  n2 Chứng minh rằng k   , k 1. a) 2 2 u u 10u u  8  k n 1  k k 1 
b) 5u u 4 và 2 3.u 12 . k k 1  k
x 1; x  0
Bài 4: Cho dãy {x } xác định như sau : 0 1 n  . x  2xx  2 n   2.  n n 1  n2
Xác định số tự nhiên n sao cho : x x  22685. n 1  n
x 1; x  5
Bài 5: Cho day {x } được xác định bởi : 0 1 n  . x  6x x n  1.  n 1 n n 1  Tìm lim ( TH&TT T7/253)   x 2 nn
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201 1   1 1 an 1 2 2 1 2 Bài 6: Xét dãy {a    n} : a  và a n 1. 1    2 n 1 2    
Chứng minh rằng : a a a ...... a
1,03 (TH&TT T10/335) 1 2 3 2005
Bài 7: Cho dãy số {a       n} : 2 a 2; a 4a 15a 60
n 1. Hãy xác định CTTQ của a 0 n 1  n n n và
chứng minh rằng số 1 a 8 có thể biểu diễn thành tổng bình phương của 3 số nguyên 2  5 n liên tiếp với n
 1. (TH&TT T6/262)
Bài 8: Cho dãy số p(n
) được xác định như sau : p(1)  1; p( )
n p(1)  2 p(2) .......  (n 1) p(n 1) n
  2. Xác định p(n) . (TH&TT T7/244). u   2 Bài 9: Xét dãy {u
. Chứng minh rằng với mỗi số n} : 1  3 2 u  3u
 2n  9n  9n  3 n   2.  n n 1  p 1 
nguyên tố p thì 2009u chia hết cho p (TH&TT T6/286). i i 1  x a
Bài 10: Dãy số thực {xn} : 0  . 2 x  2x 1 n   0.  n 1 n
Tìm tất cả giá trị của a để x  0 n
  0 . (TH&TT T10/313) n 1 x .x Bài 11: Dãy số {x   nn    n} : x 1; x và 1 x n 0. 0 1  2 n 2 2002x
 2001x  2000x .x n 1  n n 1  n
Hãy tìm CTTQ của xn (TH&TT T8/298).  1 a   1  2
Bài 12: Cho dãy số {a } được xác định như sau {a n n} :  an 1 a   n  1. n  2na 1  n 1 
Tính tổng S a a .......... a 1 2 2010.
Bài 13: Cho dãy số được xác định bởi : a 1.2.3; a  2.3.4; ......; a  (
n n 1)(n  2). 1 2 n
Đặt S a a .... a . Chứng minh rằng 4S 1 là số chính phương . n 1 2 n n
( HSG Quốc Gia – 1991 Bảng B)
Bài 15: Cho hai dãy số {a
} được xác định như sau n} và {bn :
a  2 ; b 1 0 0   2a b . n n a  ; ba b n   0. n 1  n 1  n 1  na bn n
Chứng minh rằng các dãy {a
} có cùng giới hạn chung khi n} và {bn n   .
Tìm giới hạn chung đó. ( HSG Quốc Gia – 1993 Bảng A ngày thứ 2)
Bài 16: Cho các số nguyên a, b. Xét dãy số nguyên {a } được xác định như sau : n a  ; a a  ;
b a  2b a  2 0 1 2  . a  3a  3a a n   0.  n3 n2 n 1  n a) Tìm CTTQ của an
b) Tìm các số nguyen a, b để an là số chính phương với n  1998.
(HSG Quốc Gia – 1998 Bảng B).
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201a  3  n 1
Bài 17: Cho dãy số (a 0  n) :   . Tính
. ( Trung Quốc – 2004).  3 a
6 a 18 n  1.  a n n 1   i 1 ia 1 0 
Bài 18: Cho dãy số (a . Chứng minh rằng : n) : 2  7a  45a  36 n 1  n 1  a n  1. n  2
a) a là số nguyên dương với n   0. n
b) a a 1 là số chính phương với n   0.
( Trung Quốc – 2005). n 1  n u  1; u  2 2 u 1
Bài 19: Cho dãy số (u . Chứng minh rằng n n) : 1 2  là số chính u  4uu n   3.  3 n n 1  n2
phương ( Chọn đội tuyển Nghệ An – 2007 ).  3 b  12; b  2007
Bài 20: Cho dãy số (b  n) : 0 1  2 . Tính
b ( Moldova 2007).i i0 b bb . 3 n   2.  n n 1  n2 u
 1; u  0 n  1 1 n
Bài 21: Cho dãy số {u } được xác định như sau : 2 n  1 u 1 . n 1  u   n   2. n un 1  Chứng minh rằng   1 
S u u  .....  u  1 1
. (HSG Quảng Bình 2008 – 2009). 1 2 nn 1  4  2  
Bài 22: Cho đa thức 3
P(x)  x  6x  9 và P (x)  P(P(....(P(x)))...) ( n dấu ngoặc). Tìm số n
nghiệm của P(x) và P (x) ? ( Dự tuyển Olympic). n u   u 1
Bài 23: Cho dãy số (u ) được xác định như sau: 0 1 n  . u 14u u n  1.  n 1 n n 1 
Chúng minh rằng với n
  0 thì 2u 1 là một số chính phương. n
( Chọn đội tuyển Romania 2002)
Trên đây là một phân nhỏ kiến thức về bài toán xác định công thức tổng quát của một dãy
số mà tôi đã lĩnh hội được và được xin trình bày cho các bạn tham khảo. Mong nhân được
những ý kiến đánh giá chân thật từ mọi người. Xin chân thành cảm ơn! Name : Mai Xuân Việt
Address : Đội II – thôn Dƣơng Quang – Xã Đức Thắng – Huyện Mộ Đức – Tỉnh Quảng Ngãi .
Email : xuanviet15@gmail.com
Tel : 01678336358 – 0938680277 – 0947572201
Mai Xuân Việt – Email: xuanviet15@gmail.com – Tel : 01678336358 – 0938680277 – 0947572201