Tính chất đường phân giác của tam giác - Tài liệu tham khảo | Đại học Hoa Sen

Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress
TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC I.I LÝ L Ý THUYẾ H T UYẾ T 1. 1 Đị Đ nh n h lý l ý
- Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ
với hai cạnh kề với hai đoạn ấy.
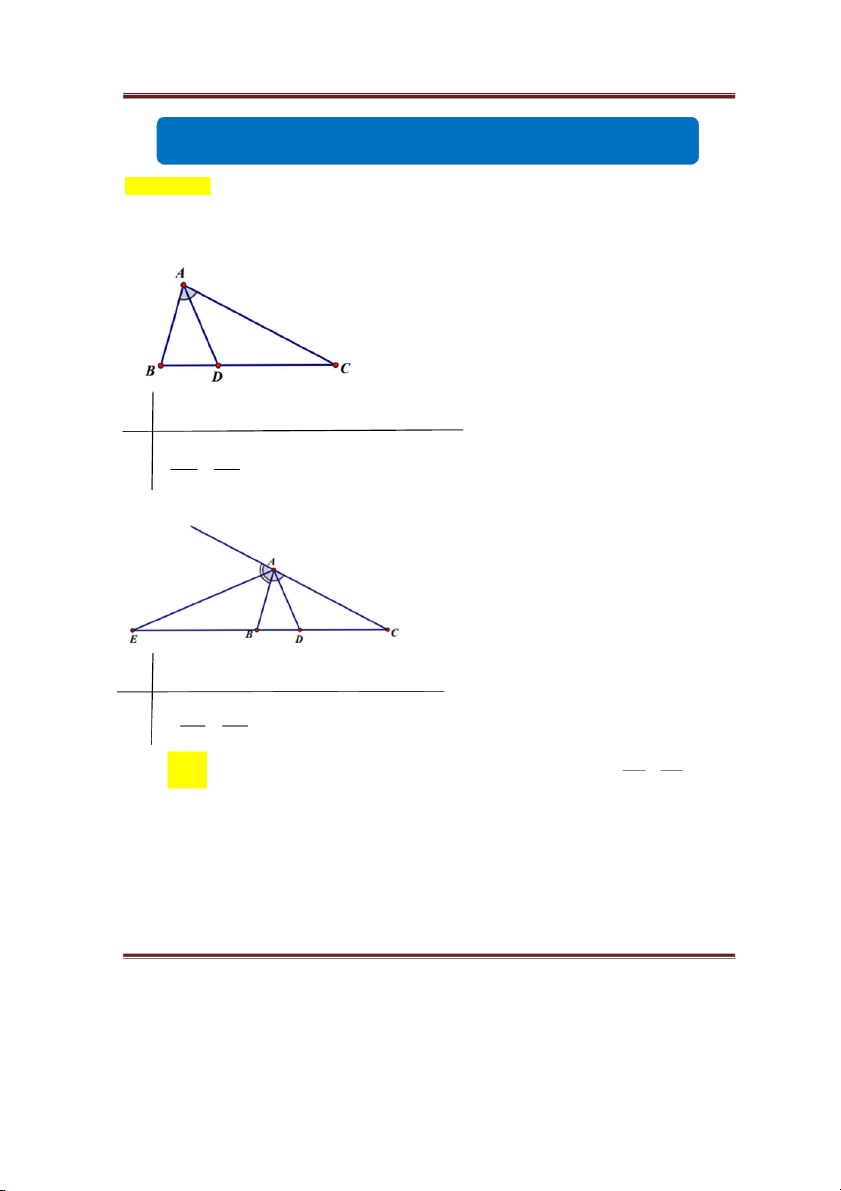
GT ABC có AD là phân giác của A (D BC) DB AB KL  DC AC 2. 2 Mở M ở rộn rộ g g GT G
T ABC có AE là phân giác ngoài đỉnh A EB AB KL K L  EC AC DB AB  Ch C ú h ú ý:
ý Trong tam giác ABC, nếu D là điểm thuộc cạnh BC và thoả mãn  thì AD DC AC
là đường phân giác trong của . A
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 1
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress II I .I BÀ B I À ITẬP Ậ P TR T ÊN Ê N LỚ L P Ớ Bà B i
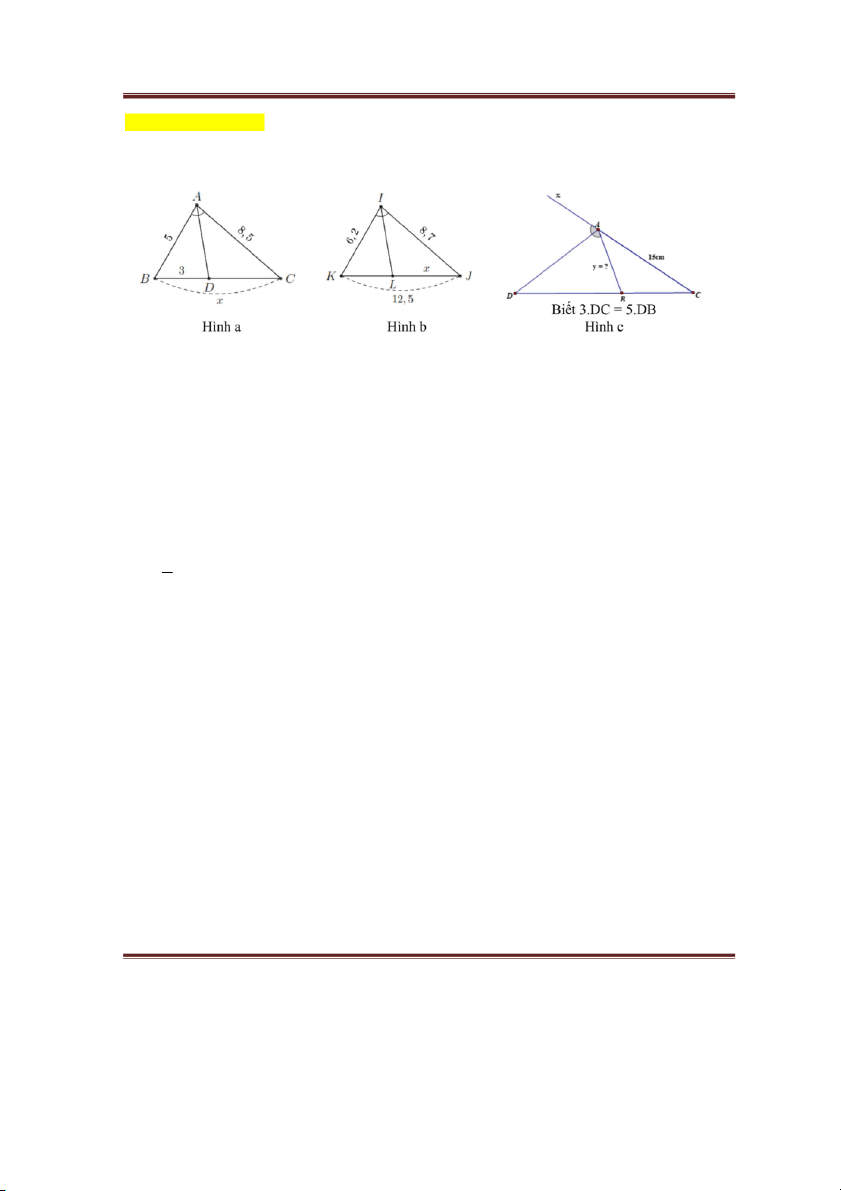
à i1. Tính x, y trong hình và làm tròn kết quả đến hàng phần mười Bà B i
à i2. Cho ABC có AB 12c , m AC  20c ,
m BC  28cm . Đường phân giác góc A cắt BC tại D.
Qua D kẻ DE / / AB(E  AC) . Tính độ dài các đoạn thẳng BD, DC và DE. Bà B i
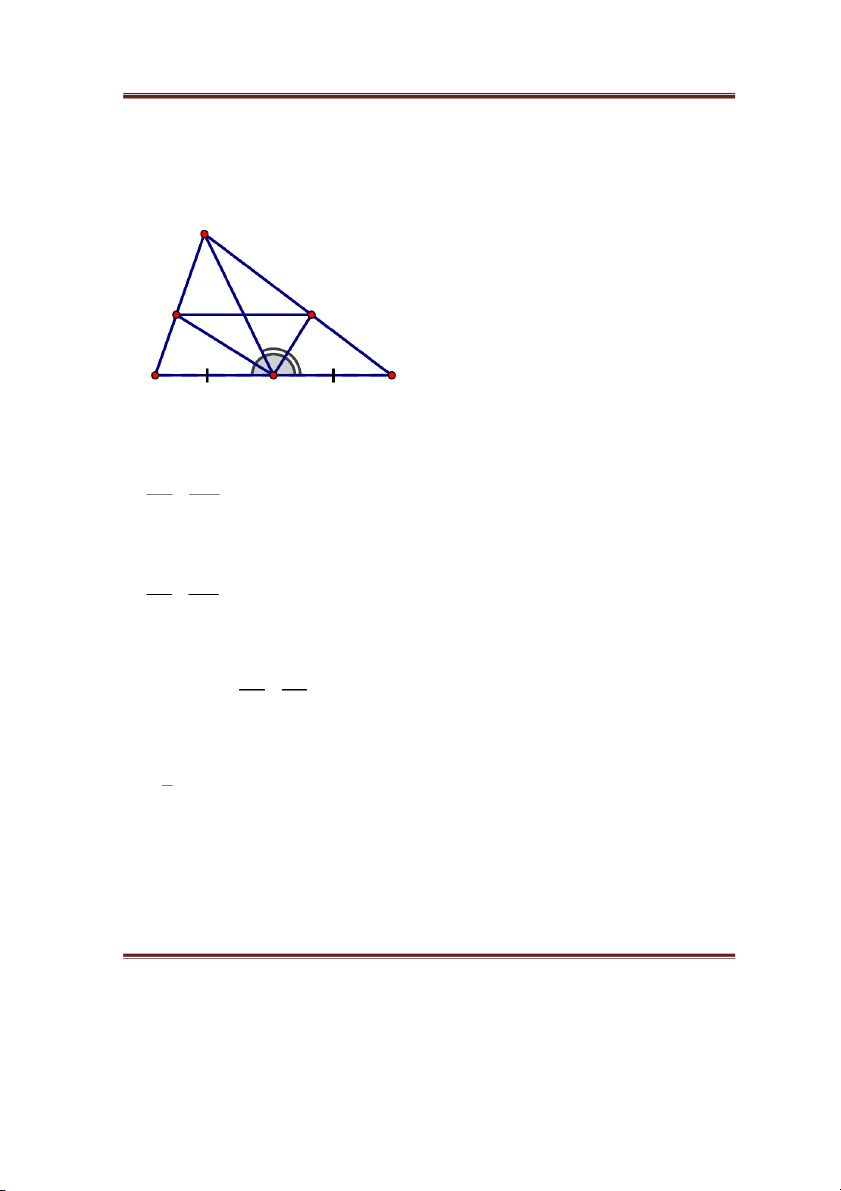
à i3. Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của 
AMB cắt cạnh AB ở D, tia phân giác của 
AMC cắt cạnh AC ở E. Chứng minh rằng DE//BC. Bà B i
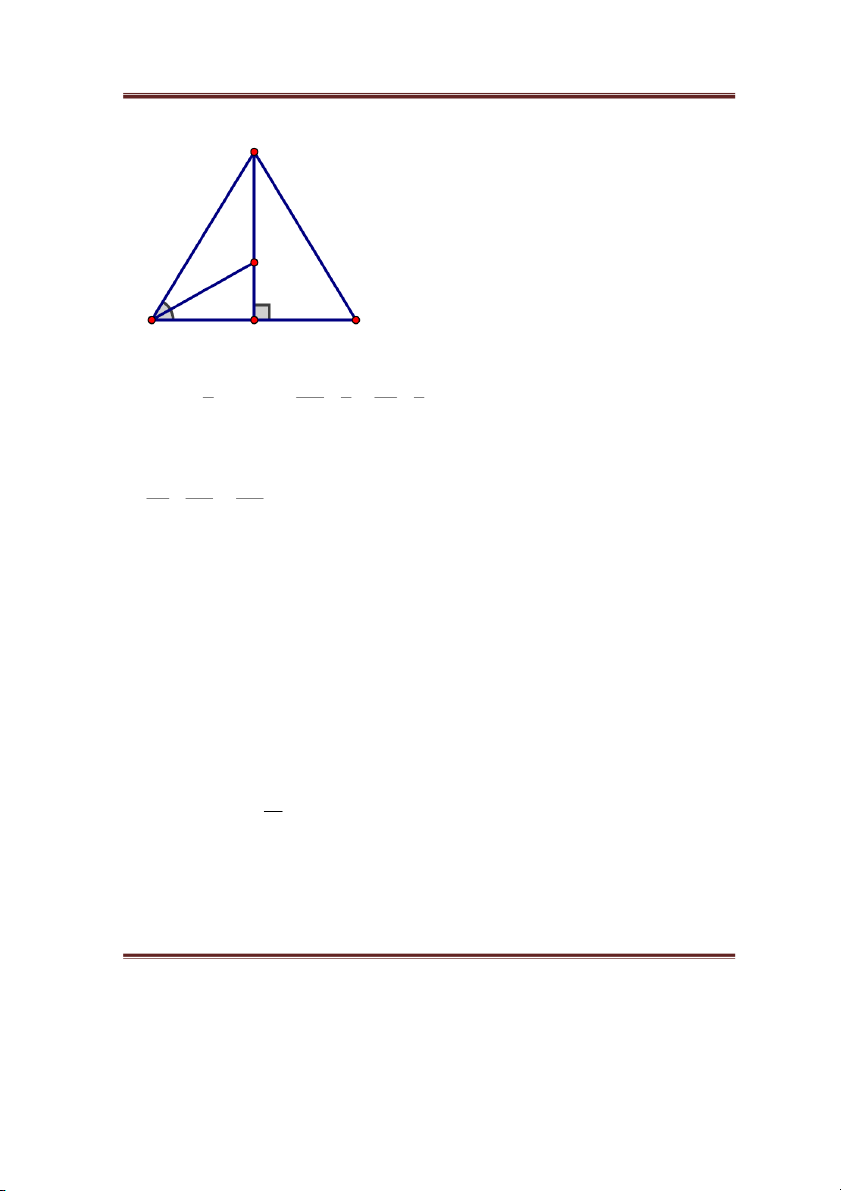
à i4. Cho ABC cân tại A có chu vi 60cm. Tia phân giác góc B cắt đường cao AH tại I. Biết 2 AI 
AH . Tính độ dài các cạnh của ABC . 3 Bà B i
à i5. Cho ABC vuông tại A, AB = 15cm, AC = 20cm, đường cao AH. Tia phân giác của  HAB
cắt HB tại D. Tia phân giác của 
HAC cắt HC tại E. Tính độ dài HD, HE. Bà B i
à i6. Cho ABC có AB = 5cm, AC = 6cm, BC = 7cm. Gọi G là trọng tâm ABC , O là giao điểm
của hai đường phân giác BD, AE.
a) Tính độ dài đoạn thẳng AD. b) Chứng minh OG // AC.
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 2
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress II I I I .I BÀ B I À TẬ T P Ậ P VỀ V NH N À H À Bà B i
à i1. Cho tam giác ABC có AB  7cm, AC  8cm, BC  6cm. Kẻ phân giác trong AD D BC .
Tính độ dài các đoạn thẳng DB , DC . Bà B i
à i2. Cho tam giác ABC vuông tại A. Kẻ phân giác trong AD D BC . Biết 45 DB  cm, 7 60 DC 
cm, tính độ dài các đoạn thẳng BC, AB và AC . 7 Bà B i
à i3. Cho tam giác ABC có phân giác trong AD D BC. Biết DB 15cm, DC  20cm,
AC  AB  10 cm, tính chu vi tam giác ABC. Bà B i
à i4. Cho hình vuông ABCD có độ dài cạnh là 6cm. Trên các cạnh AB, BC lần lượt hai điểm M , N sao cho 3
BM  BN. Đường chéo BD cắt MN tại I . Biết MN  5 cm. 4
a) Tính IM , IN, BM , BN.
b) Tính diện tích tam giác DMN. Bà B i
à i5. Cho tam giác ABC cân tại A có trung tuyến AD. Tia phân giác của 
ADB cắt AB tại M , tia phân giác của 
ADC cắt AC tại N.
a) Chứng minh MN // BC.
b) Gọi I là giao điểm của AD và MN . Chứng minh I là trung điểm của MN .
c) Tính độ dài cạnh MN , biết BC  24cm, AD  9cm. Bà B i
à i6. Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Tia phân giác của  BAD cắt DE AF
BD tại E và tia phân giác của 
CDA cắt AC tại F . Chứng minh  . EB FC
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 3
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress
NDBH - TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC I.I LÝ L Ý THUYẾ H T UYẾ T 1. 1 Đị Đ nh n h lý l ý
- Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ
với hai cạnh kề với hai đoạn ấy.
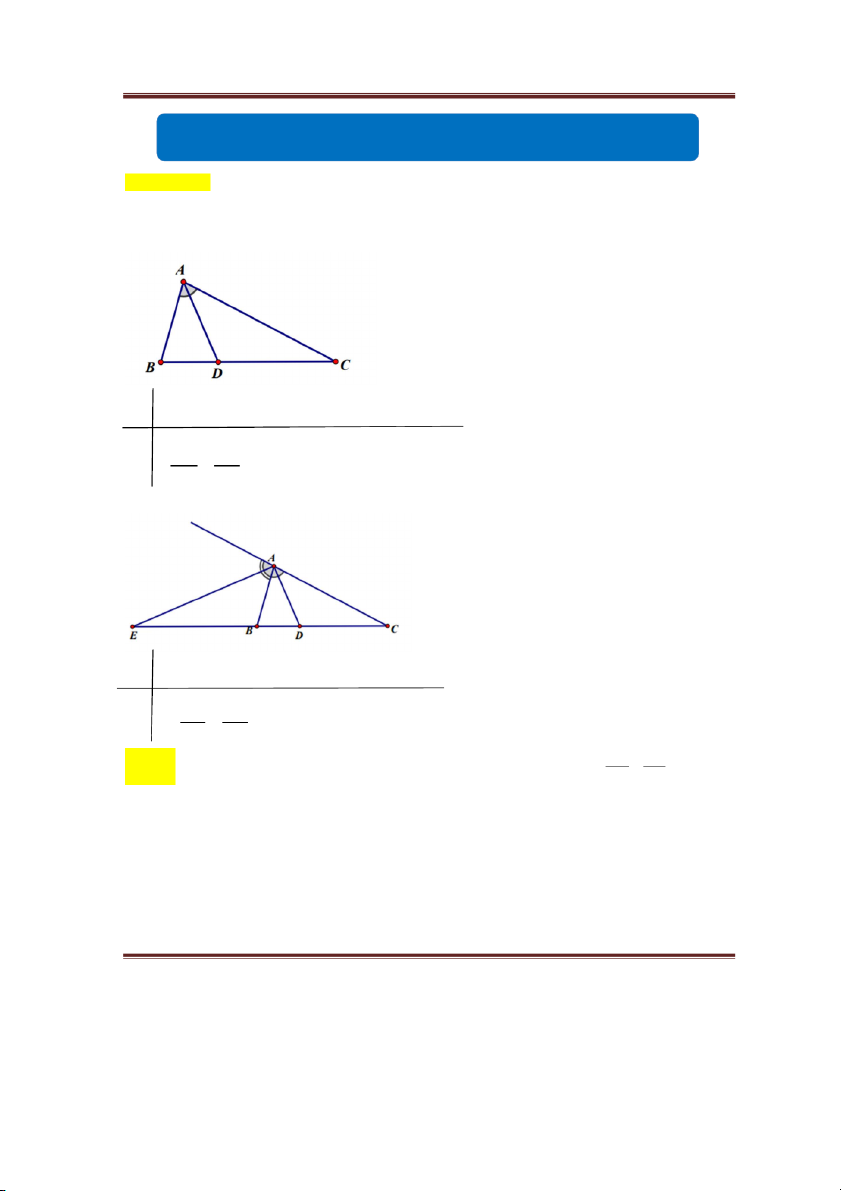
GT ABC có AD là phân giác của A (D BC) DB AB KL  DC AC 2. 2 Mở M ở rộn rộ g g GT G
T ABC có AE là phân giác ngoài đỉnh A EB AB KL K L  EC AC * * Chú h ú ý: ý Trong tam giác DB AB
ABC, nếu D là điểm thuộc cạnh BC và thoả mãn  thì AD là DC AC
đường phân giác trong của . A
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 4
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress II I .I BÀ B I À ITẬP Ậ P TR T ÊN Ê N LỚ L P Ớ Bà B i
à i1. Tính x, y trong hình và làm tròn kết quả đến hàng phần mười Lờ L i ờ igi g ả i i i
a) ABC có AD là phân giác của  BAC DB AB   (t/c pg của tam giác) DC AC 3 5 3.8,5 Hay   DC   5,1 DC 8,5 5
 BC  x  BD  DC  3  5,1  8,1.
b) IKJ có IL là phân giác của  KIJ KL IK   (t/c pg của tam giác) LJ IJ 12,5 x 6, 2 Hay 
 6,2x 8,7.(12,5 x) x 8,7
 6,2x  108,75  8,7x 14,9 x 108,75  x  7,3 DB 3 c) Ta có: 3DC = 5DB   DC 5
ABC có AD là phân giác ngoài góc A
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 5
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress DB AB y   3 hay 
 5 y  3.15  y  9cm DC AC 5 15 Bà B i
à i2. Cho  ABC có AB 12cm, AC  20cm, BC  28cm . Đường phân giác góc A cắt BC tại D.
Qua D kẻ DE / /AB(E  AC ) . Tính độ dài các đoạn thẳng BD, DC và DE. A E B D C
ABC có AD là tia phân giác của  BAC (gt) DB AB DB 12 3      DC AC DC 20 5 DB DC   3 5 DB DC DB  DC BC 28 7 Áp dụng t/c DTSBN ta có:      3 5 3 5 8 8 2  7
DB  .3  10,5cm  2   7
DC  .5 17,5cm  2
Xét  ABC có: DE//AB (gt) DE DC  
(hệ quả của đlý Thales) AB BC DE 17,5 Hay 
 DE  7,5cm 12 28
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 6
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress Bà B i
à i3. Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của 
AMB cắt cạnh AB ở D, tia phân giác của 
AMC cắt cạnh AC ở E. Chứng minh rằng DE//BC. A E D B M C
Xét  ABM có: DM là tia phân giác  AMB AD AM   (t/c phân giác. ) (1) DB BM
Xét  AMC có: ME là tia phân giác  AMC AE AM   (t/c phân giác…) (2) EC MC
Ta có: BM  MC (AM là trung tuyến) (3) AD AE Từ (1),(2),(3)  
 DE / /BC (định lý Thales đảo) DB EC Bà B i
à i4. Cho  ABC cân tại A có chu vi 60cm. Tia phân giác góc B cắt đường cao AH tại I. Biết 2
AI  AH . Tính độ dài các cạnh của  ABC . 3
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 7
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress A I B H C 2 AI 2 AI 2
Ta có: AI  AH (gt)      2 3 AH 3 IH 1
Xét  ABH có: BI là phân giác  ABH (gt) AI AB AB   
 2  AB  2BH IH BH BH
Xét  ABC cân tại A ta có AH là đường cao (gt)
 AH đồng thời là đường trung tuyến
 H là trung điểm của BC
 2BH  BC mà AB  2BH (cmt)  BC  AB
Lại có AB  AC(ABC cân tại A)
 AB  AC  BC ABC đều
Chu vi ABC  AB  AC  BC  60cm 60
 AB  AC  BC   20cm 3 Bà B i
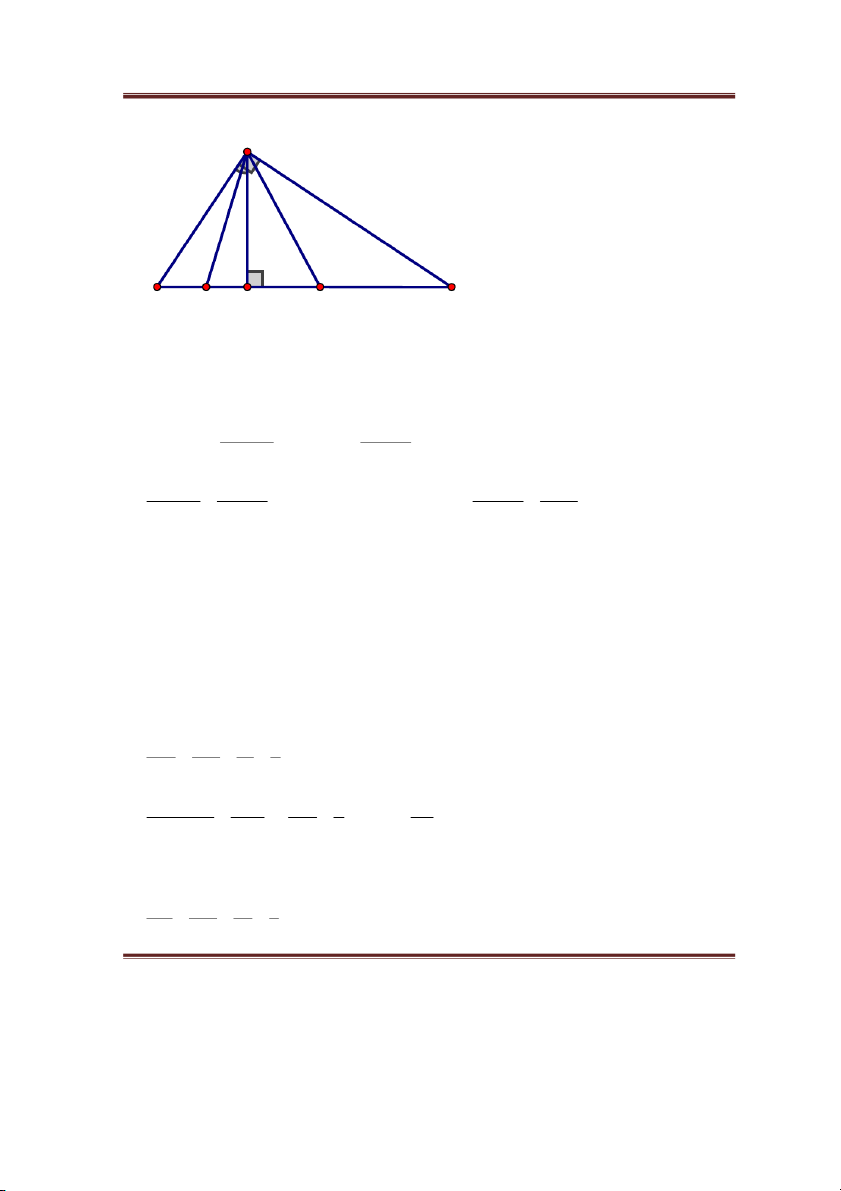
à i5. Cho  ABC vuông tại A, AB = 15cm, AC = 20cm, đường cao AH. Tia phân giác của  HAB
cắt HB tại D. Tia phân giác của 
HAC cắt HC tại E. Tính độ dài HD, HE.
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 8
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress A B D H E C
Xét  ABC vuông tại A có: 2 2 2
AB  AC  BC (định lý Pythagore) 2 2 2
15  20  BC  BC  25cm AH BC AB AC Ta có: . S  hay . S  ABC ABC 2 2 AH .BC AB.AC AB.AC 15.20  
 AH .BC  AB .AC  AH    12cm 2 2 BC 25
Xét  AHB vuông tại H có: 2 2 2
AH  BH  AB (định lý Pythagore) 2 2 2
12  BH 15  BH  9cm
Xét  AHC vuông tại H có: 2 2 2
AH  HC  AC (định lý Pythagore) 2 2 2
12  HC  20  HC 16cm
Xét  ABH có: AD là phân giác  BAH (gt) DH AH 12 4     (T/c phân giác…) BD AB 15 5 DH 4 DH 4 4.9      DH   4cm BD  DH 5  4 BH 9 9
Xét  AHC có AE là phân giác  CAH (gt) HE AH 12 3     (t/c phân giác….) EC AC 20 5
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 9
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress HE 3 3 HE 3 3    
  HE  .16  6cm EC  HE 5  3 8 HC 8 8 Bà B i
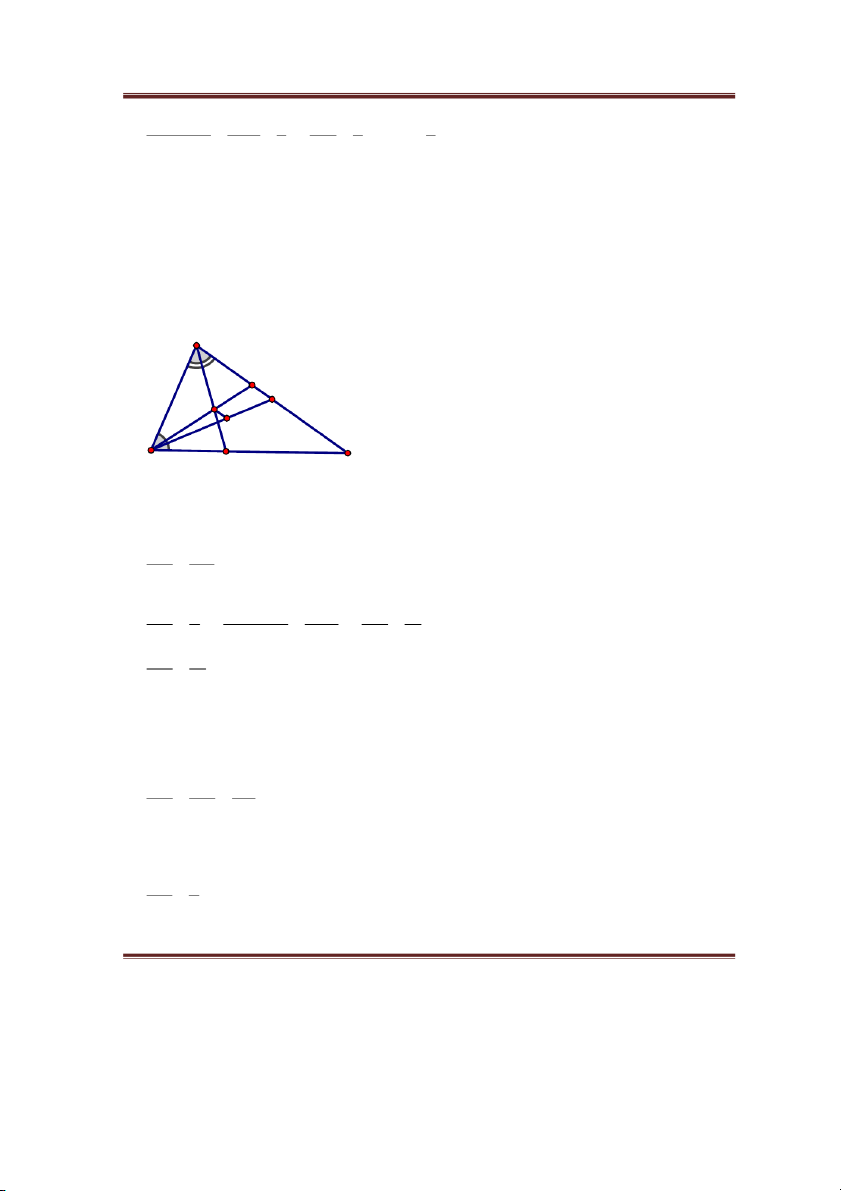
à i6. Cho  ABC có AB = 5cm, AC = 6cm, BC = 7cm. Gọi G là trọng tâm ABC , O là giao điểm
của hai đường phân giác BD, AE.
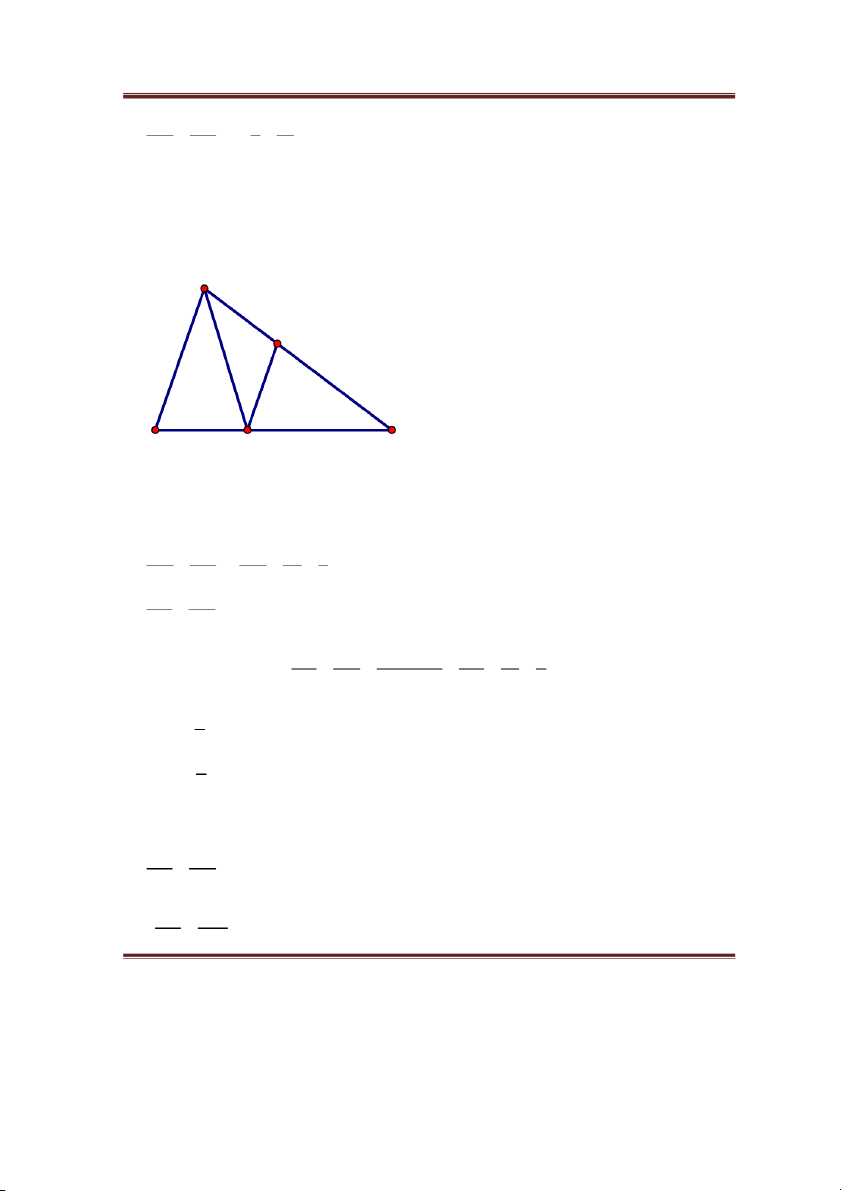
a) Tính độ dài đoạn thẳng AD. b) Chứng minh OG // AC. A D I O G B E C a) Xét A
 BC có: BD là phân giác  ABC (gt) AD AB   (t/c phân giác….) CD BC AD 5 AD 5 AD 5       CD 7 CD  AD 7  5 AC 12 AD 5    AD  2,5cm 6 12 b) Gọi BI là trung tuyến
Xét  ABD có: AO là phân giác (gt) BO AB 5   
 2 (t/c phân giác. .) (1) OD AD 2,5
Có BI là trung tuyến (cách vẽ), G là trọng tâm (gt) BG 2   (t/c trọng tâm) BI 3
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 10
Toán bồi dưỡng lớp 8 CLB Toán bồi dưỡng – MathExpress BG   2 (2) GI BO BG Từ (1),(2)  
 OG / /DI (định lý Thales đảo) OD GI
 OG / / AC(D AC, I  AC)
Giáo Viên: cô Nguyễn Ngọc Ánh – SĐT: 0339 148 928 Page 11