TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT THÀNH PHỐ HỒ CHÍ MINH
KHOA CƠ KHÍ ĐỘNG LỰC
TIỂU LUẬN MÔN THIẾT KẾ Ô TÔ Tên đề tài
TÍNH TOÁN KIỂM TRA NHÍP ĐẶT DỌC, DẠNG NHÍP
CÔNG XÔN THEO 3 CHẾ ĐỘ TẢI TRỌNG ĐẶC BIỆT SVTH: Nguyễn Đăng Quang MSSV: 20145201 Lớp: Thứ 4, tiết 11-12 GVHD: MSc. Đặng Quý
TP. HCM, ngày 27 tháng 11 năm 2023
ĐỀ BÀI (ĐỀ SỐ 3)
Hãy tính toán kiểm tra nhíp đặt dọc, dạng nhíp công xôn ở cầu sau 1 xe tải 2 cầu. Cầu
sau chủ động có tải trọng tĩnh tác dụng lên nó là G . Hình vẽ nhíp ở trang 151, giáo trình Ô 2
TÔ 2, Hình 7.20-b, hoặc ở trang 237, giáo trình Thiết kế ô tô, tác giả: MSc. Đặng Quý, Hình
9.19-b, cần vẽ thêm bánh xe để đặt lực Z . Hãy tính toán ứng suất xuất hiện ở nhíp theo 3 b
chế độ tải trọng đặc biệt sau đây:
1) Trường hợp 1: X = 0, Y = 0 (Y = 0), Z = Z = Z i i i imax b
2) Trường hợp 2: X = X , Y = 0, Z = Z i imax i b
3) Trường hợp 3: X = 0, Y = Y = m G φ , Z = Z i max 2 2 y i b MỤC LỤC
CHƯƠNG 1: CÁC LỰC TÁC DỤNG LÊN NHÍP ĐẶT DỌC KIỂU CÔNG XÔN STT Lực Định nghĩa Đơn vị 1 X
Phản lực tiếp tuyến tại bánh xe N i 2 Y
Phản lực ngang tại bánh xe N i 3 Z
Phản lực pháp tuyến tại bánh xe N i 4 Z
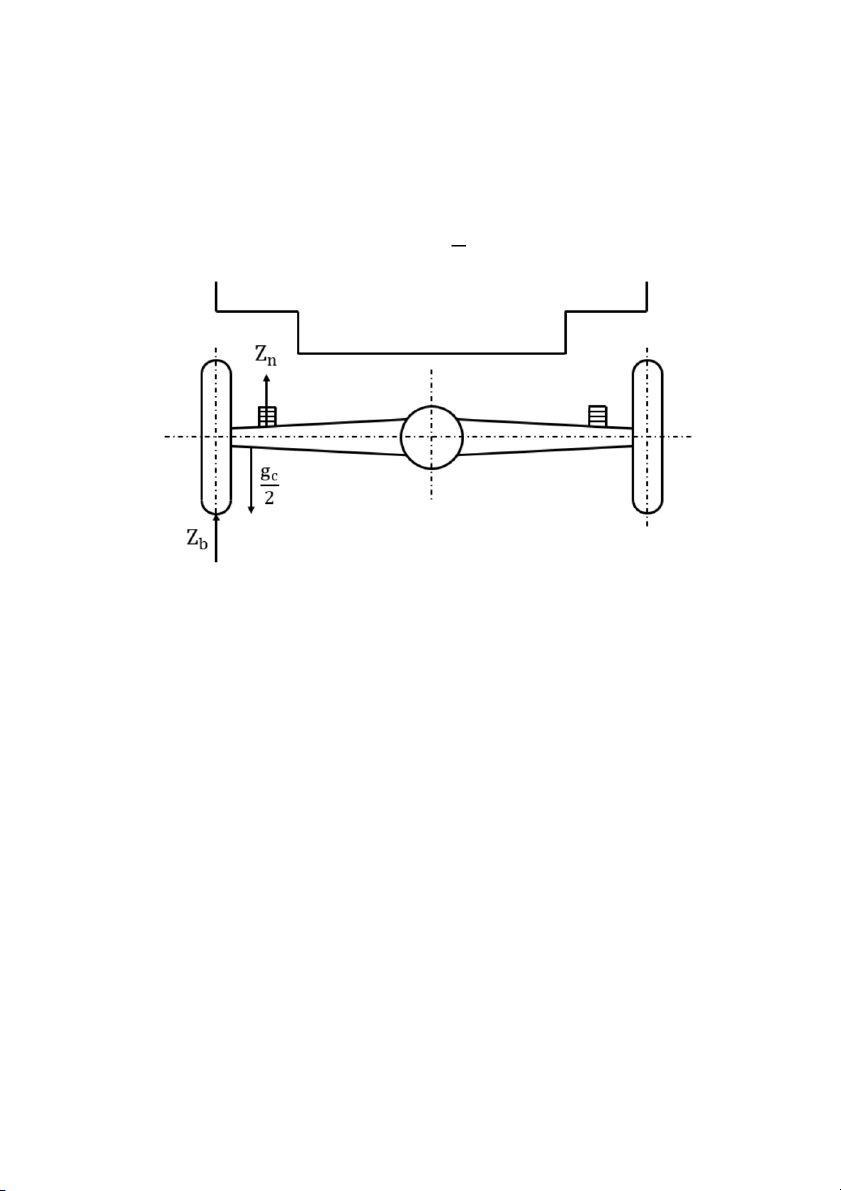
Phản lực từ mặt đường tác dụng lên nhíp N n 5 g
Trọng lượng phần không được treo N c 6 Z
Phản lực từ mặt đường tác dụng lên bánh xe N b 7 N , N
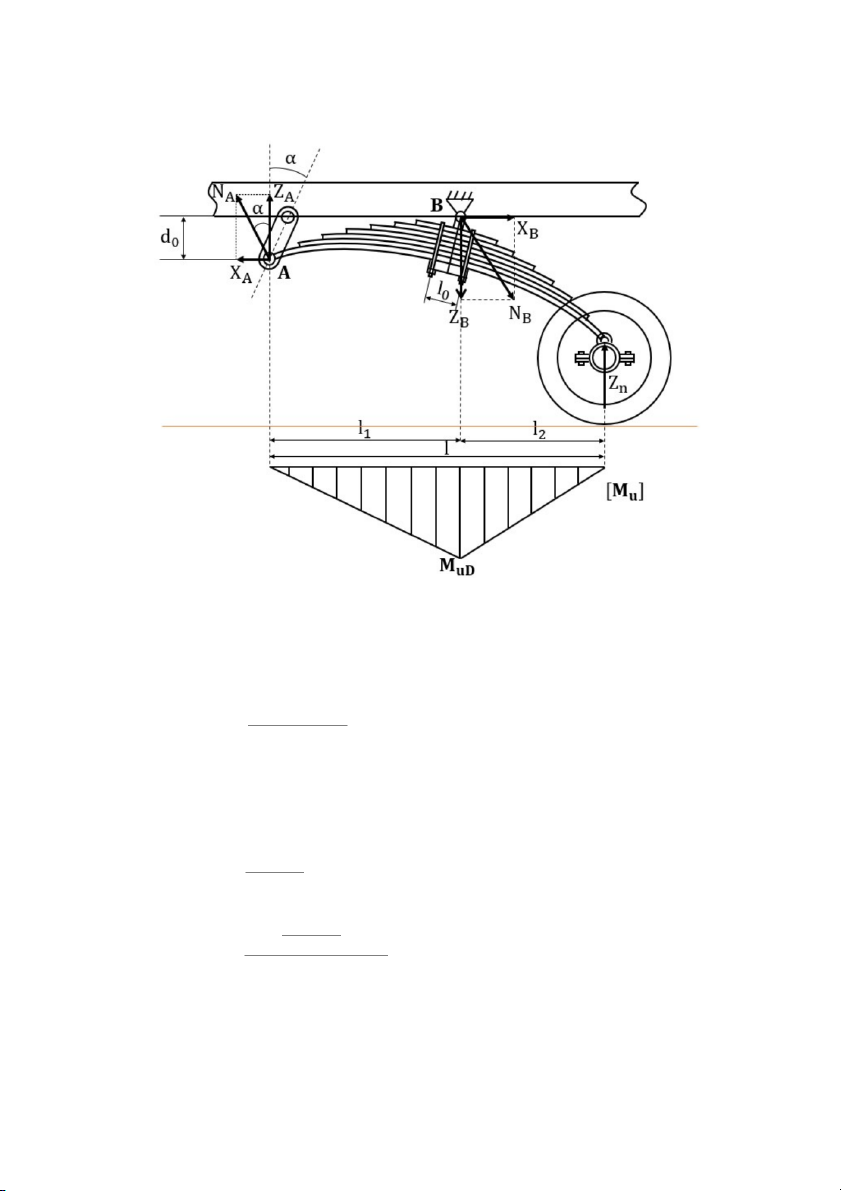
Phản lực tổng hợp tác dụng lên nhíp N A B
Các lực thành phần của N theo phương ngang và A 8 X , Z N A A thẳng đứng
Các lực thành phần của N theo phương ngang và B 9 X , Z N B B thẳng đứng 10 α Góc nghiêng của tai nhíp độ 11 l
Khoảng cách giữa các quang nhíp m 0
Hình chiếu của chiều dài nửa nhíp bên trái và bên 12 l , l m 1 2 phải lên phương ngang
Hình chiếu của chiều dài toàn bộ của quang nhíp lên 13 l m phương ngang 14 b Chiều rộng lá nhíp m 15 h
Chiều dày của lá nhíp thứ i m i 16 σ Ứng suất uốn N/ 2 u m 17 W
Moment chống uốn của mặt cắt ngang N.m ui 18 m .G
Trọng lượng tác dụng lên cầu sau xe MN 2 2 19 Y
Phản lực tổng hợp của lực ngang tác dụng lên xe kN 20 φ Hệ số bám ngang y 21 m
Hệ số tính đến sự thay đổi trọng lượng tác dụng lên i cầu 22 X Lực kéo N k 23 X Lực phanh N p
Phản lực của lực kéo hoặc lực phanh trong trường 24 X N
hợp kéo hoặc phanh tương ứng
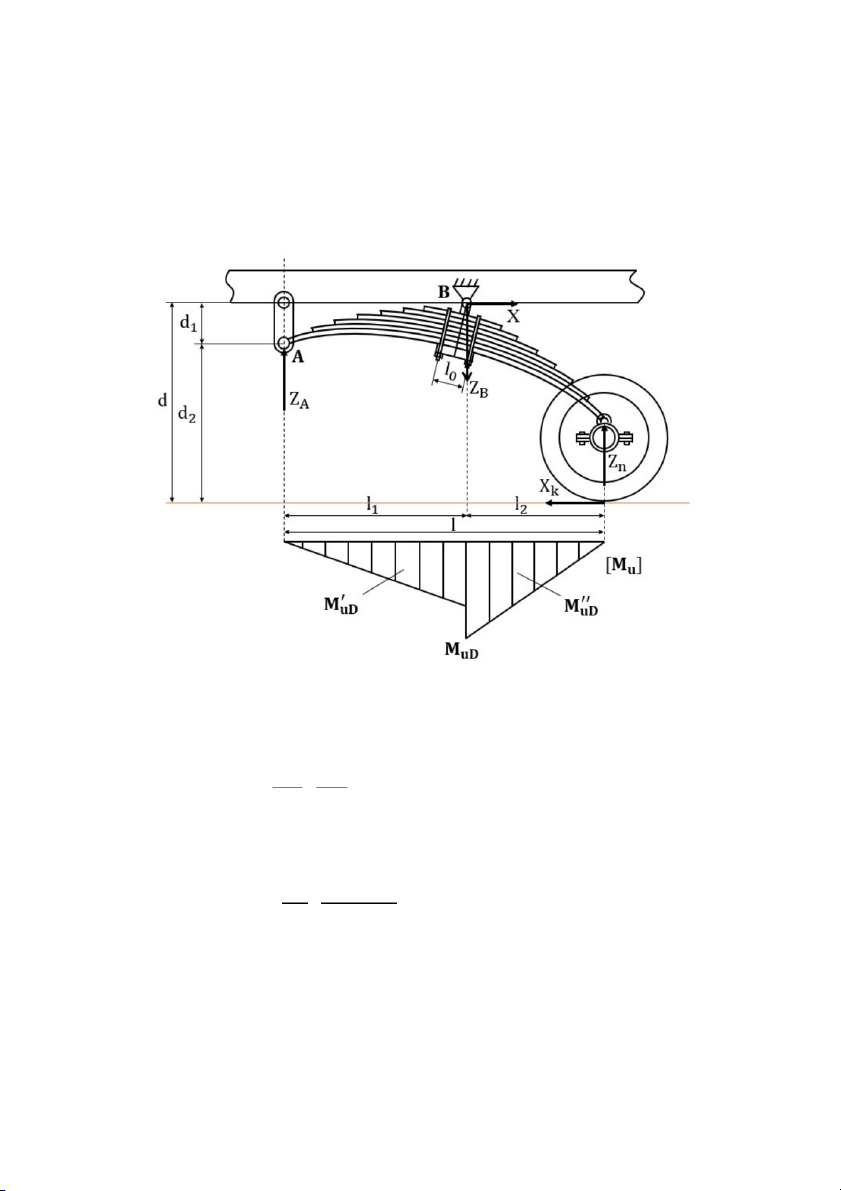
CHƯƠNG 2: TÍNH TOÁN NHÍP ĐẶT DỌC KIỂU CÔNG XÔN 2.1. Trường hợp 1
X = 0, Y = 0 (Y = 0), Z = Z = Z i i i imax b g
Z = Z - c n b 2  X = Z
A = X B = Z A .tgα ; Z n B −¿ Z A
 Phương trình cân bằng momen tại A:
X .d + Z .l −¿ Z .l = 0 B 0 B 1 n  Z .l .
A .tgα .d 0 + Z B 1 −¿ Z n l = 0
Z . l−Z . tgα . d n A 0 Z = B  (1) l1
 Phương trình cân bằng momen tại B:
X .d + Z .l . A 0 A
1 −¿ Z n l2 = 0  Z .l −¿ Z .
A .tgα .d 0 + Z A 1 n l2 = 0 Z .l 2 Z = n  (2) A tgα . d +l 0 1 Thay (2) vào (1) ta được: Z .l2 Z .l – n . tgα .d n tgα . d +l 0 ¿ 0 1 l1 ZB Z . l . tgα . d ¿ l n 2 0 Z . − n l
l (tgα . d +l ) 1 1 0 1
l . (l +tgα . d )−l . l ¿ 2 1 0 1 2 Z .[ l − ] n l
l (tgα . d +l ) 1 1 0 1 l l ¿ 2 2 Z .( l − + ) n l l tgα . d + l 1 1 0 1 l ¿ 2 Z .(1+ ) n tgα .d +l 0 1
Trong thực tế: góc α <10 ° tg 
α ≈ 0 suy ra ta được: Z . l l 2 2 l Z = n
; Z =Z . (1+ )=Z . A l B n l n l 1 1 1
 Momen uốn tại D: M =Z . l uD n 2 M
 Ứng suất uốn: σ = uD u n ∑ W
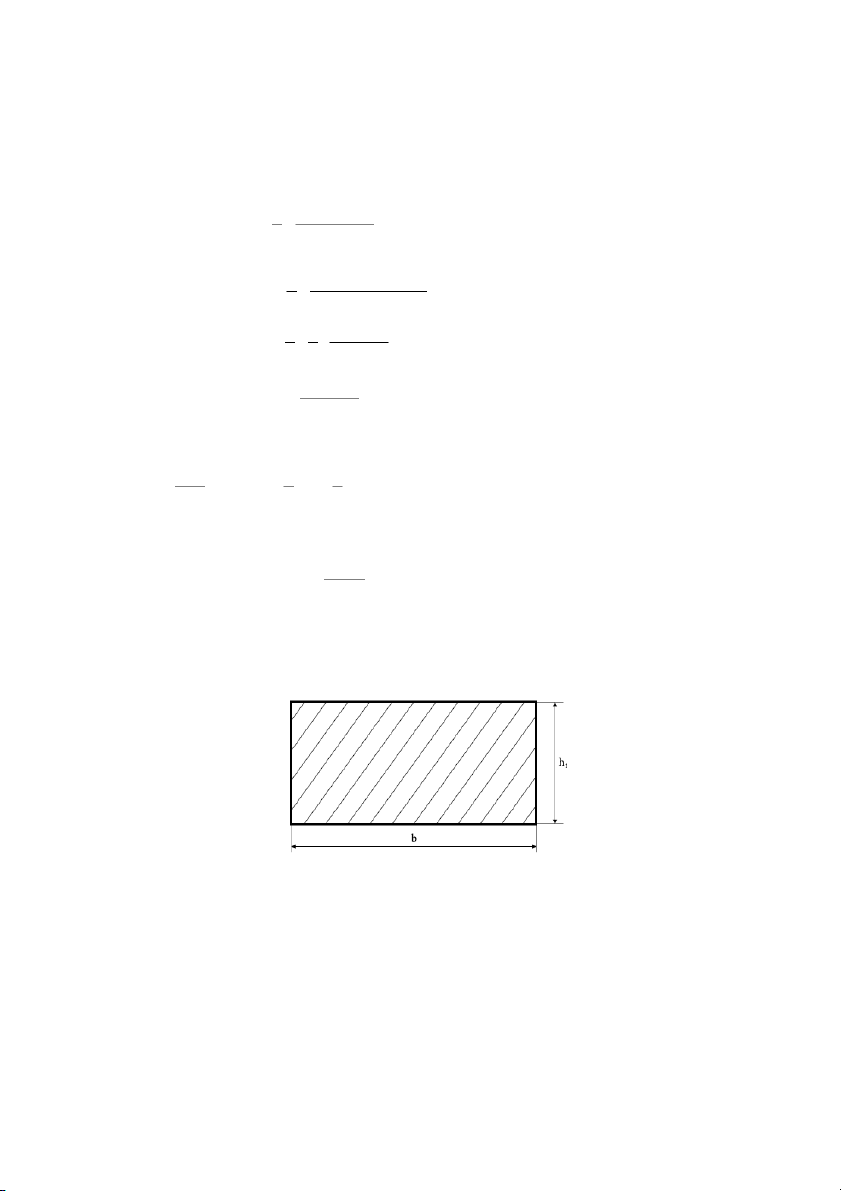
- Mặt cắt vuông góc của mỗi lá nhíp là hình chữ nhật có chiều rộng là b và chiều cao là h :i
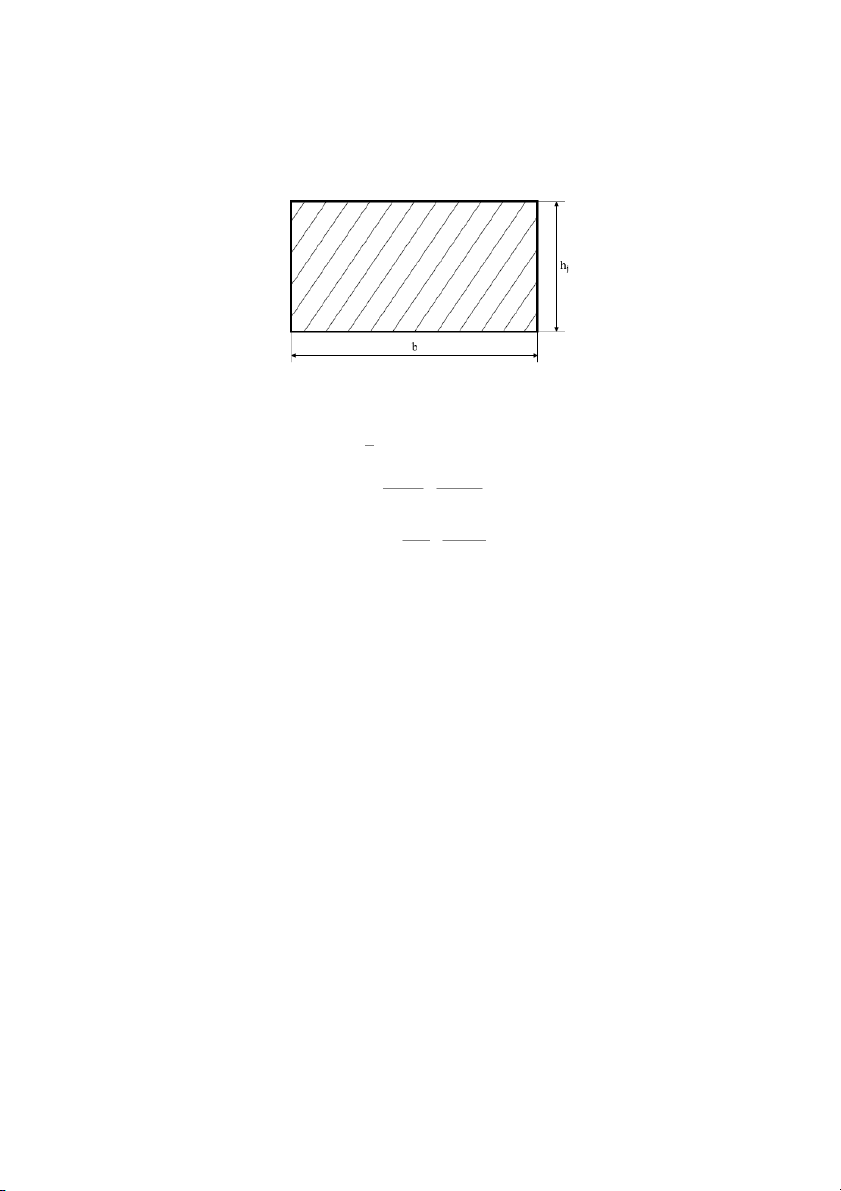
- Mặt cắt xiên theo phương của Z qua mỗi lá nhíp là hình chữ nhật có chiều rộng là b B
và chiều cao là h :j
Do trong thực tế, góc nghiêng của nhíp nhỏ hơn 10 ° nên có thể xem h ≈ h và tính toán j i theo h , khi đó: i 1 W = 2 b h ui 6 i M 6. Z . l Suy ra, ứng suất uốn: 2 σ = uD = n ≤[ σ ] u n n u ∑ 2 W b . ∑ h ui i X Z .tgα
Lá nhíp chính còn chịu kéo: σ = B = A ≤ [ σ ] k b . h b . h k c c
với b và h lần lượt là chiều rộng và chiều cao của lá nhíp chính. c
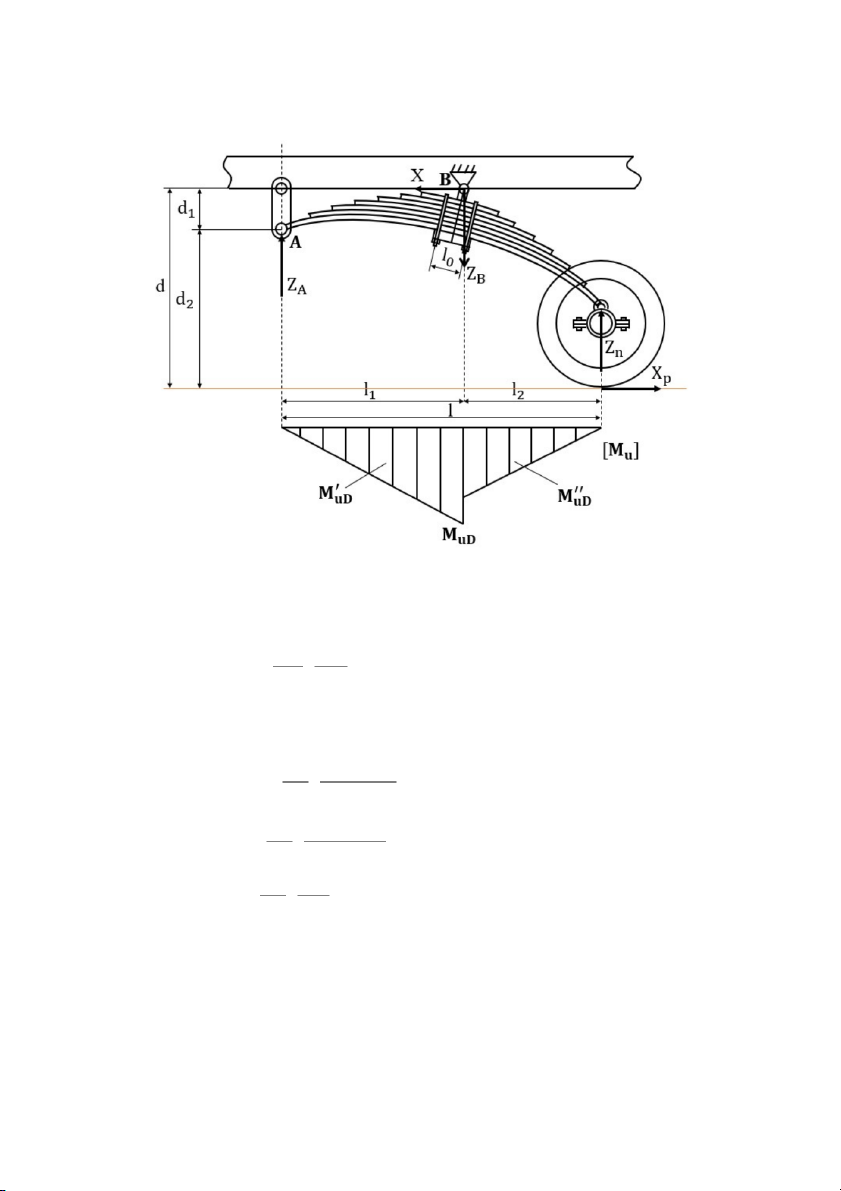
Tuy nhiên, trong thực tế góc nghiêng của nhíp nhỏ hơn 10 ° do đó σ rất nhỏ nên có thể k bỏ qua. 2.2. Trường hợp 2 X = X , Y = 0, Z = Z i imax i b
2.2.1. Khi truyền lực kéo cực đại
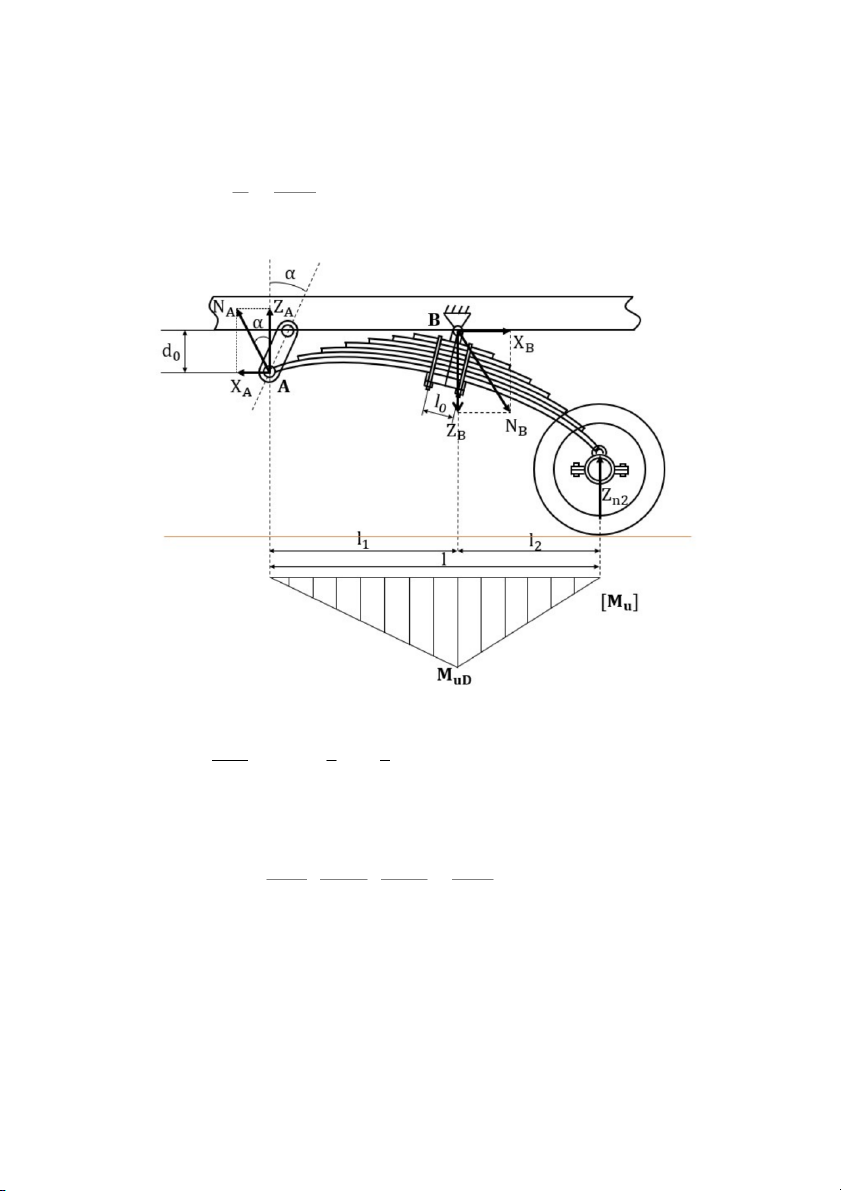
X ≠ 0 ; X =X =0 (do tai nhíp ở vị trí thẳng đứng k A B α =0 ° )  X =X = Z −Z k ; Z n B A
 Phương trình cân bằng momen tại B: Z .l − . l + X . d=0 1 Z A n 2 k Z . l X . d 2 Z = n − k
↓< Z ở trường hợp 1  A l l A 1 1
 Phương trình cân bằng momen tại A: Z .l −Z
+X . d + X . d =0 1 .l B n k 2 1 Z . l X . d + X . d  2 1 Z = n − k
↓<Z ở trường hợp 1 B l l B 1 1 Z .l X . d + . d 2 X ¿ n − k k 1 l l 1 1 Z .l X . d ¿ n − k l l 1 1
 Z và Z gây ra momen uốn ' và '' : A n M M uD uD
M ' =Z .l =Z .l − X .d < M '' =Z . l uD A 1 n 2 k uD n 2
 Gây ra ứng suất uốn chính: M' M ' ' σ ' = uD ; σ'' uD = uc n uc n ∑ W ∑W ui ui 1 W = b h2 Do ui nên: 6 i
(Z ¿¿ n .l −X 6. Z σ ' = 2 6. k . d); σ' = n . l2 ¿ uc n uc n b .∑ h2 b .∑ h2 i i
 Momen uốn phụ do X gây ra : M =X .d k up k M 6. X . d up k  Ứng suất uốn phụ: σ = = up n n ∑ 2 W b . ∑ h ui i
 Ứng suất uốn toàn toàn bộ: σ =σ +σ u uc up
+ Ứng suất uốn bên trái:
(Z ¿¿n . l − X .d ) 6. X . d 6. Z .l 2 k k n 2 σ ' = ' + = 6. + = ¿ u σ σ uc up n n n 2 2 2 b .∑ h b . ∑ h b .∑ h i i i
+ Ứng suất uốn bên phải: 6. Z . l 6. X . d
(Z ¿¿ n . l + X . d ) n 2 k 2 k σ ''= '' + = + =6. ¿ u σ σ uc up n n n 2 2 2
b .∑ h b .∑ h b .∑ h i i i
2.2.2. Khi phanh với lực phanh cực đại
X ≠ 0 ; X =X =0 (do tai nhíp ở vị trí thẳng đứng p A B α =0 ° )  X =X = Z −Z p ; Z n B A
 Phương trình cân bằng momen tại B: Z .l − . l −X =0 2 . d 1 Z A n p Z . l X .d 2 Z = n + p
↑> Z ở trường hợp1  A l l A 1 1
 Phương trình cân bằng momen tại A: Z .l −Z − X − X . d =0 1 .l .d B n p 2 1 Z . l X . d + X .d  2 1 Z = n + p
↑> Z ở trường hợp 1 B l l B 1 1  Z . l X . d + .d 2 X Z = n + p p 1 B l l 1 1 Z .l X . d ¿ n + p l l 1 1
 Z và Z gây ra momen uốn ' và '' : A n M M uD uD
M ' =Z .l =Z .l + X . d > M '' =Z . l uD A 1 n 2 p uD n 2
 Gây ra ứng suất uốn chính: M' M ' ' σ ' = uD ; σ'' uD = uc n uc n ∑ W ∑W ui ui 1 W = b h2 Do ui nên: 6 i
(Z ¿¿ n .l + X 6. Z σ ' = 2 6. p . d) ; σ' = n . l2 ¿ uc n uc n b . ∑ h 2 b . ∑ h2 i i
 Momen uốn phụ do X gây ra : M =X .d k up p M 6. X .d up p
 Ứng suất uốn phụ:: σ = = up n n ∑ 2 W b . ∑ h ui i
 Ứng suất uốn toàn toàn bộ: σ =σ +σ u uc up
+ Ứng suất uốn bên trái:
(Z ¿¿ n . l + X . d ) 6. X . d
(Z ¿¿n . l +2. X . d) 2 p p 2 p σ ' = ' + = 6. + =6. ¿¿ u σ σ uc up n n n b .∑ 2 2 2 h b .∑ h b . ∑ h i i i
+ Ứng suất uốn bên phải: 6. Z . l 6.
(Z ¿¿n . l + X . d ) n 2 X . d p 2 p σ ''= '' + = + =6. ¿ u σ σ uc up n n n 2 2 2
b .∑ h b .∑ h b .∑ h i i i 2.3. Trường hợp 3
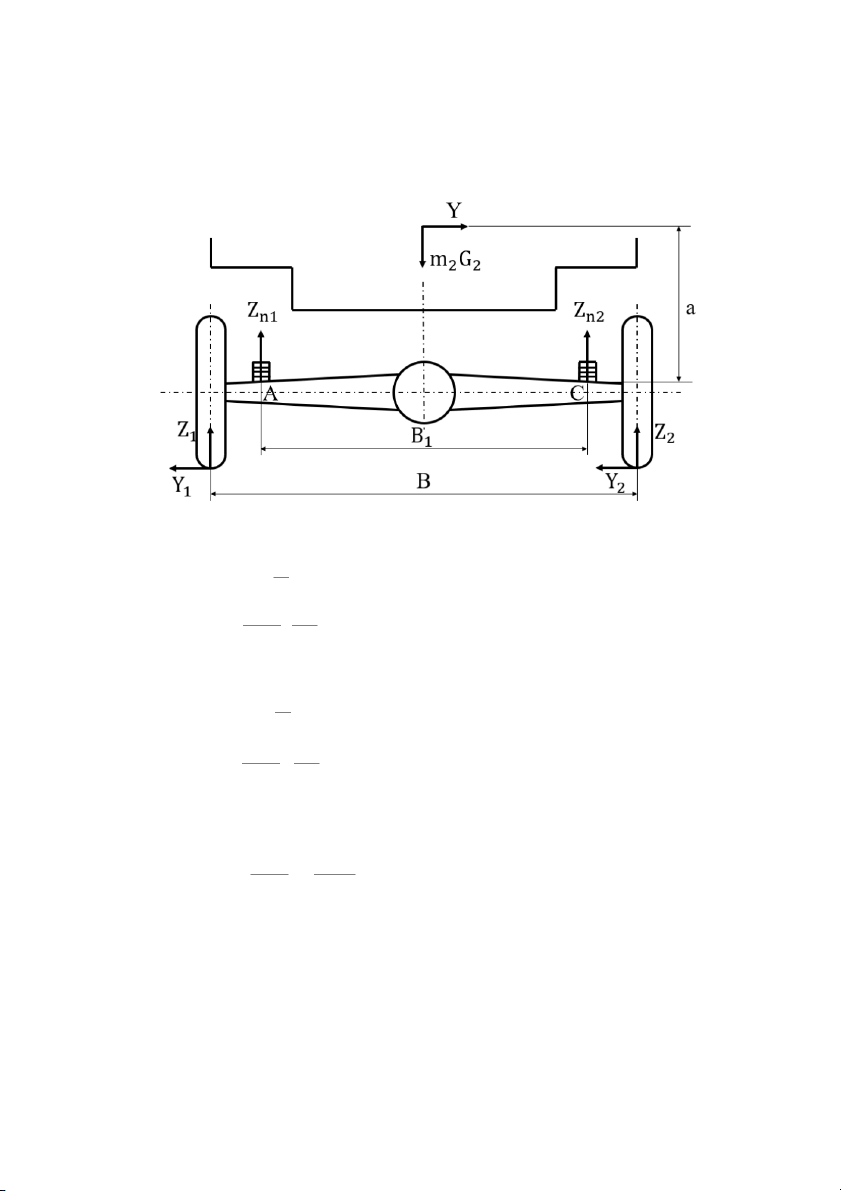
X = 0, Y = Y = m G φ , Z = Z i max 2 2 y i b
 Phương trình cân bằng momen tại A: B1 Y . a+m . −Z . B =0 2 . G2 2 n 2 1 m .G 2 2 Z = + Y . a  n2 2 B1
 Phương trình cân bằng momen tại C: B1 Y . a−m .G . +Z . B =0 2 2 2 n 1 1  m .G 2 2 Z = − Y . a n1 2 B1 
Z < Z  Tính toán theo Z n1 n 2 n2 Z =Z khi Y =Y =m φ 2 G n2 n 2 max max 2 y 2.  m .G φ . a 2 2 Z = (1+ y ) n2 2 B1 Khi Y =Y
Xe bắt đầu trượt ngang   m =1 max 2 G 2. φ . a  2 Z = (1+ y ) n1 2 B1
 Tính cho nhíp bên phải.
 Tính toán tương tự trường hợp 1, thay Z =Z ta được: n n 2 Z .l l 2 2 l Z = n2
; Z =Z (1+ )=Z . A l B n 2 l n 2 l 1 1 1
 Momen uốn tại D: M =Z .l uD n 2 2  Ứng suất uốn: M 6. Z .l 3. G . l 2. φ . a 2 2 2 σ = uD = n 2 =
(1+ y )≤[σ ] u n n n u ∑ B 2 2 1 W b . ∑ h b .∑ h ui i i