Luyện tập Toán 10 Bài 9 Kết nối tri thức Luyện tập 2
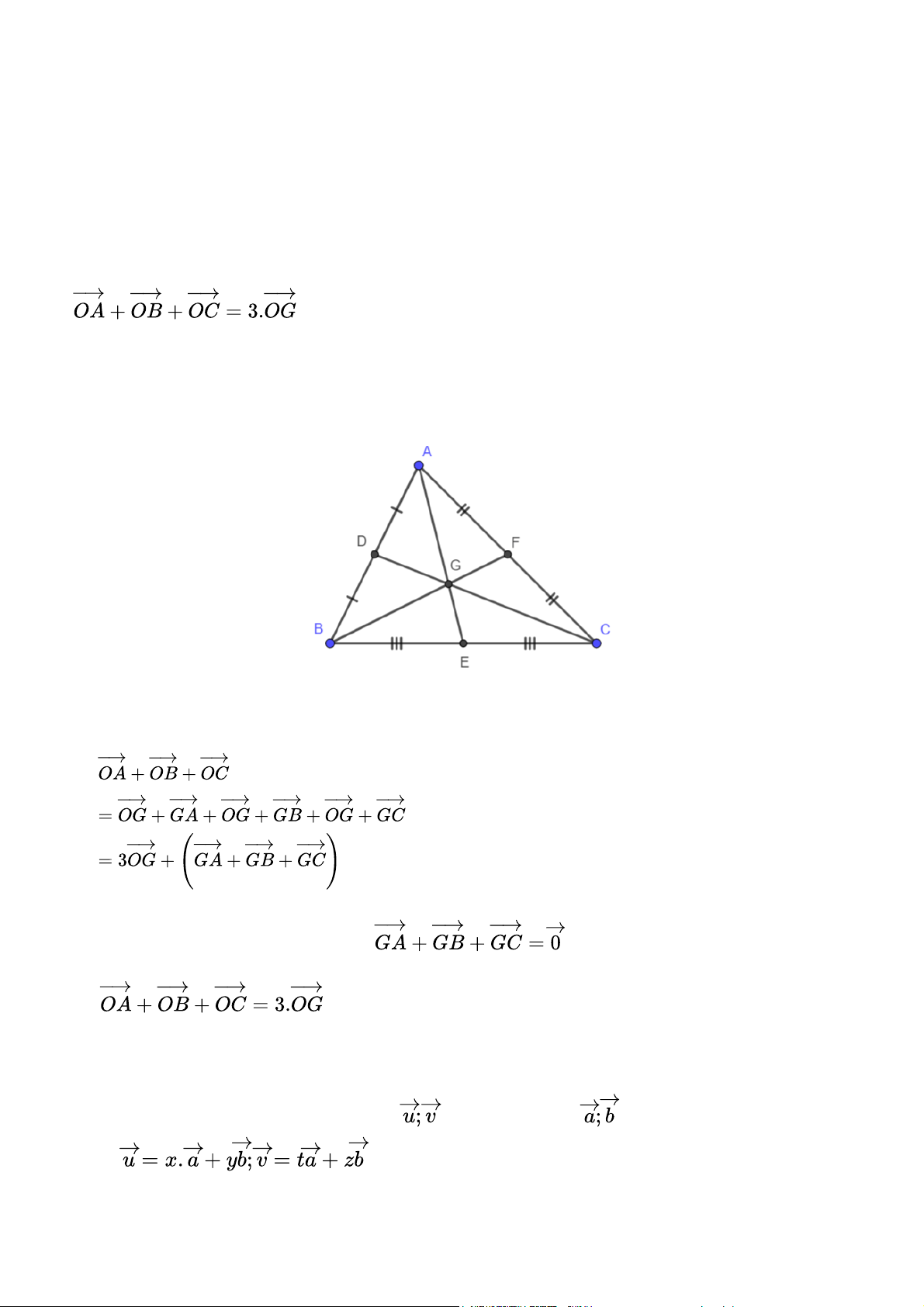
Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có: Gợi ý đáp án Hình vẽ minh họa: Ta có:
Do G là trọng tâm tam giác ABC => => Luyện tập 3
Trong hình 4.27, hãy biểu thị mỗi vecto theo hai vecto
, tức là tìm các số x, y, z, t để Gợi ý đáp án Hình vẽ minh họa:
Xét hình bình hành OABC ta có: Khi đó ta có: (Quy tắc hình bình hành)
Xét hình bình hành OMNP ta có: Khi đó ta có: Vậy
Giải Toán 10 trang 58, 59 Kết nối tri thức tập 1 Bài 4.11 trang 58
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị theo hai vecto và Gợi ý đáp án Học sinh tự vẽ hình
Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành. Do đó: Dễ thấy: Vậy Bài 4.12 trang 58
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh Gợi ý đáp án Ta có: Mặt khác: Tương tự ta cũng có: Vậy Bài 4.13 trang 58
Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho
b) Chứng minh rằng với mọi điểm O, ta có Gợi ý đáp án a) Ta có: Suy ra vectơ à
cùng phương, ngược chiều và KA = 2.KB
\Rightarrow K,A,Bthẳng hàng, K nằm giữa A và B thỏa mãn: KA = 2.KB Bài 4.14 trang 58 Cho tam giác ABC
a) Hãy xác định điểm M để
b) Chứng minh rằng với mọi điểm O, ta có Gợi ý đáp án a) Ta có:
Trên cạnh AB, AC lấy điểm D, E sao cho Khi đó
hay M là đỉnh thứ tư của hình bình hành AEMD. Bài 4.15 trang 59
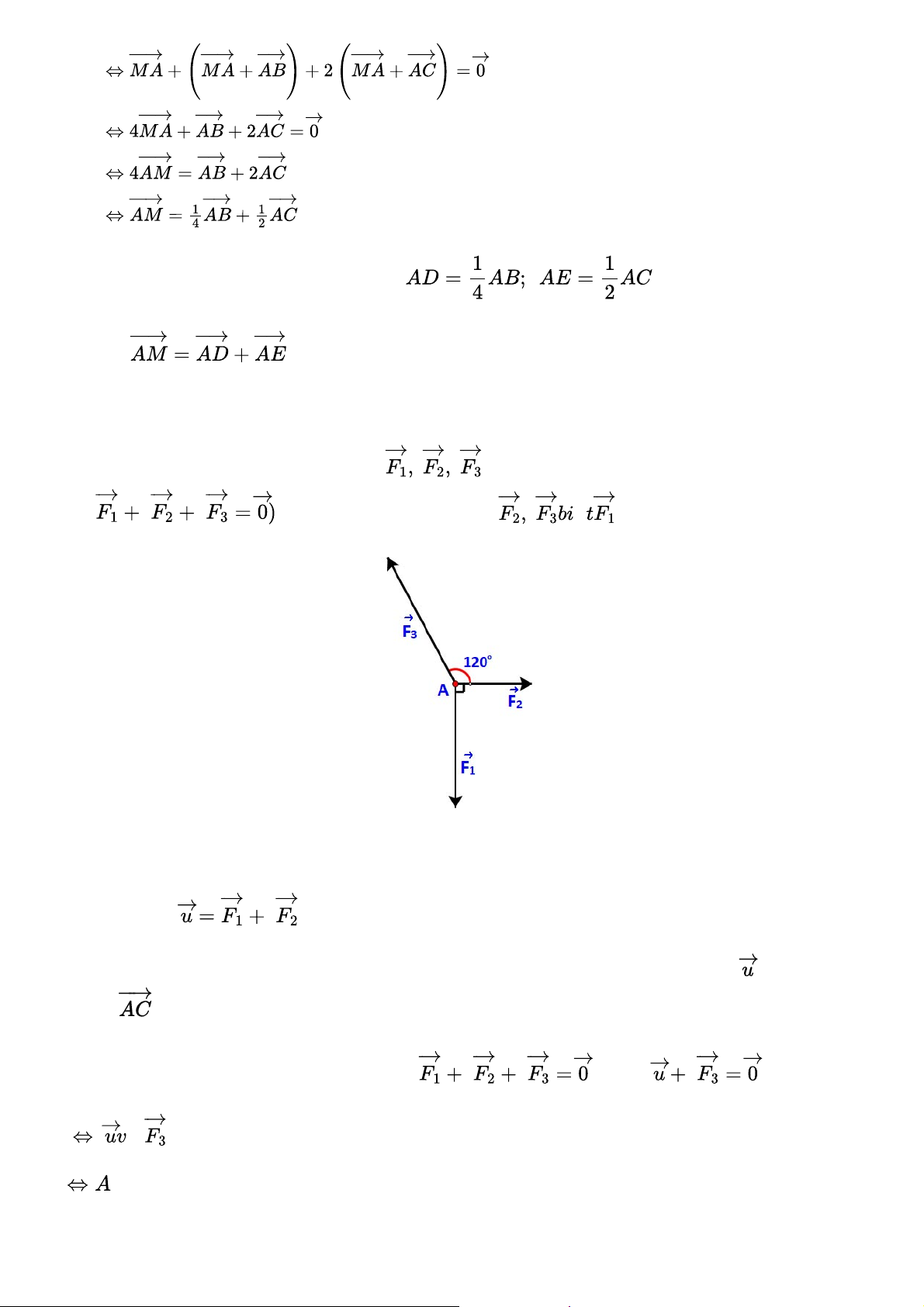
Chất điểm A chịu tác động của ba lực
như hình 4.30 và ở trạng thái cân bằng (tức là
. Tính độ lớn của các lực ế có độ lớn là 20N. Gợi ý đáp án Bước 1: Đặt
. Ta xác định các điểm như hình dưới.
Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto chính là vectơ
Vì chất điểm A ở trang thái cân bằng nên hay à là hai vecto đối nhau. là trung điểm của EC. Bước 2: Ta có: Do A, C, E thẳng hàng nên Vậy
Lý thuyết Tích của một vectơ với một số
1. Tích của vecto với một số
+) Tích của một vecto
với một số thực k là một vecto, kí kiệu là . +) Vecto có độ dài bằng và Cùng hướng với vecto nếu k > 0 Ngược hướng với vecto nếu k < 0 +) Quy ước: Nhận xét: Hai vecto và
cùng phương khi và chỉ khi tồn tại k để
2. Các tính chất của phép nhân vecto với 1 số +) Với hai vecto
và hai số thực k,t ta luôn có: +) Nhận xét: I là trung điểm của G là trọng tâm